(完整版)一次函数题型总结,推荐文档

合集下载

一次函数整体题型总结

一次函数整体题型总结一次函数（或直线函数）是形如f(x) = ax + b的函数形式，其中a 和b是常数，且a ≠ 0。

一次函数的特点是其图像是一条直线，并且其斜率为常数a。

以下是一次函数常见的题型总结：1. 求函数的表达式：已知一次函数的图像上的两个点(x1, y1)和(x2, y2)，求一次函数的表达式。

解题步骤：- 计算斜率a：a = (y2 - y1) / (x2 - x1)- 计算常数b：b = y1 - ax1- 得到一次函数的表达式：f(x) = ax + b2. 求函数的性质：已知一次函数的表达式f(x) = ax + b，求该函数的斜率和截距。

- 斜率：斜率a就是函数表达式中的a。

- 截距：截距b就是函数表达式中的b。

3. 求函数图像在x轴和y轴上的截距：已知一次函数的表达式f(x) = ax + b，求该函数图像与x轴和y轴的交点坐标。

- 求x轴截距：令f(x) = 0，解方程ax + b = 0，得x = -b / a，即x 轴截距为(-b / a, 0)。

- 求y轴截距：令x = 0，得到y = b，即y轴截距为(0, b)。

4. 求函数图像的斜率：已知一次函数的表达式f(x) = ax + b，求该函数图像在某个点(x1, y1)处的斜率。

- 斜率公式：斜率a就是函数表达式中的a。

5. 求函数图像的增减性：已知一次函数的表达式f(x) = ax + b，判断该函数在整个定义域上的增减性。

- 当a > 0时，函数递增；- 当a < 0时，函数递减。

6. 求函数图像与坐标轴的交点：已知一次函数的表达式f(x) = ax + b，求该函数与x轴和y轴的交点坐标。

- 求与x轴交点：令f(x) = 0，解方程ax + b = 0，得x = -b / a，即与x轴交点为(-b / a, 0)。

- 求与y轴交点：令x = 0，得到y = b，即与y轴交点为(0, b)。

一次函数经典题型+习题(精华,含答案)

一次函数题型一、点的坐标方法： x 轴上的点纵坐标为0，y 轴上的点横坐标为0；若两个点关于x 轴对称，则他们的横坐标相同，纵坐标互为相反数；若两个点关于y 轴对称，则它们的纵坐标相同，横坐标互为相反数；若两个点关于原点对称，则它们的横坐标互为相反数，纵坐标也互为相反数；1、若点A （m,n ）在第二象限，则点（|m|,-n ）在第____象限；2、若点P （2a-1,2-3b ）是第二象限的点，则a,b 的范围为______________________；3、已知A （4，b ），B （a,-2），若A ，B 关于x 轴对称，则a=_______,b=_________;若A,B 关于y 轴对称，则a=_______,b=__________;若若A ，B 关于原点对称，则a=_______,b=_________；4、若点M （1-x,1-y ）在第二象限，那么点N （1-x,y-1）关于原点的对称点在第______象限。

题型二、关于点的距离的问题方法：点到x 轴的距离用纵坐标的绝对值表示，点到y 轴的距离用横坐标的绝对值表示；若AB ∥x 轴，则(,0),(,0)A B A x B x 的距离为A B x x -；若AB ∥y 轴，则(0,),(0,)A B A y B y 的距离为A B y y -；点B （2，-2）到x 轴的距离是_________；到y 轴的距离是____________； 1、点C （0，-5）到x 轴的距离是_________；到y 轴的距离是____________；到原点的距离是____________；2、点D （a,b ）到x 轴的距离是_________；到y 轴的距离是____________；到原点的距离是____________； 3、已知点P （3,0），Q(-2,0),则PQ=__________,已知点110,,0,22M N ⎛⎫⎛⎫-⎪ ⎪⎝⎭⎝⎭,则MQ=________; ()()2,1,2,8E F --,则EF 两点之间的距离是__________;已知点G （2，-3）、H （3,4），则G 、H 两点之间的距离是_________；4、两点（3，-4）、（5，a ）间的距离是2，则a 的值为__________；5、已知点A （0,2）、B （-3，-2）、C （a,b ），若C 点在x 轴上，且∠ACB=90°，则C 点坐标为___________.题型三、一次函数与正比例函数的识别方法：若y=kx+b(k,b 是常数，k ≠0)，那么y 叫做x 的一次函数，特别的，当b=0时，一次函数就成为y=kx(k 是常数，k ≠0)，这时，y 叫做x 的正比例函数，当k=0时，一次函数就成为若y=b ，这时，y 叫做常函数。

初二一次函数题型汇总

一次函数题型汇总一、利用一次函数的概念求字母例1. 已知32-+=-a x y x y a 的函数解析式为关于，若函数是一次函数，则=a ，若函数是正比例函数，则=a 。

例2. 当k 为何值时，函数)0(84)3(1≠-++=+x x x k y k 是一次函数？二、求一次函数的解析式例3. 若一次函数的图象经过A （2，1），B （-1，-3），C （m ，3），则m = 。

例4. 已知一次函数b kx y += 的自变量的取值范围是63-≤≤x ，相应的函数的取值范围是25-≤≤y ，求一次函数的解析式。

例5. 已知直线b kx y +=经过点A （0，-6），且平行于直线x y 2-=.(1) 求直线b kx y +=对应的函数解析式；(2) 如果直线b kx y +=经过点P （m ，2），求m 的值。

例6. 已知2-y 与1+x 成正比例关系，且当62=-=y x 时，.(1) 写出y x 与之间的解析式；(2) 求当3-=x 时，y 的值；(3) 求当的值时，x y 4=。

例7. 已知成正比例与成正比例，与x z z y 1+，且当11==y x 时，；当时0=x ，3-=y ，求x y 与的函数解析式。

三、直线的平移例8.(1) 直线轴的交点坐标个单位长度后，与轴向下平移沿x y x y 622+=是多少？(2) 将直线12+=x y 向右平移3个单位长度，则这时直线对应的函数解析式为。

知识点扩展：将b kx y +=上下平移m 个单位长度，则）（m ±+=b kx y （b 上加下减）将b kx y +=左右平移n 个单位长度，则b n x k y +±=)( （x 左加右减）例9. 将直线12+=x y 先向上平移2个单位长度，再向左平移1个单位长度后，求平移后的函数解析式。

四、一次函数性质的运用例10. 已知一次函数)1()14(+-+=m x m y(1) 当m 为何值时，x y 随的增大而减小？(2) 当m 为何值时，函数图象与y 轴的交点在x 轴下方？(3) 当m 为何值时，函数图象经过第二、三、四象限？知识点补充：K 决定一次函数的增减性，b 决定一次函数与y 轴的交点位置。

一次函数常见题型归纳

一次函数主要常识：【1 】（一）数的概念：罕有题型一:断定一个表达式是否为函数,断定一个图像是否为函数图像1.下列解析式中,不是函数关系式的是（） A .y= x (x ≥0) B .y=－x (x ≥0) C . y=±x (x ≥0) D. y= －x (x ≤0)2.下列各曲线中不克不及暗示y 是x 的函数的是…………………………（）A ．B ．C ．D ．罕有题型二：函数自变量的取值规模1..函数y=x -2自变量x 的取值规模是_______2.下列函数中,自变量x 的取值规模是x ≥2的是（）A ．．C ．D ．3．函数y =x －2＋3－x 中自变量x 的取值规模是（）（A ）x ≥2 （B ）x ≤3 （C ）2≤x ≤3 （D ）x ≥3或x ≤2罕有题型三：函数在现实生涯中的图像表达李先生骑自行车上班,最初以某一速度匀速行进,•半途因为自行车产生故障,停下修车耽搁了几分钟,为了按时到校,李先生加速了速度,仍保持匀速行进,假如准时到校．在教室上,李先生请学生画出他行进的旅程y•（千米）与行进时光t （小时）的函数图象的示意图,同窗们画出的图象如图所示,你以为准确的是（）（二）正比例函数的界说及性质：罕有题型一：与正比例函数界说有关的字母题1.已知函数y=(m-1)x+m2-1是正比例函数,则m=_____________.2. 若函数y=（2m+1）x2+（1-2m）x（m为常数）是正比例函数,则m的值为（）A．m>12 B．m=12 C．m<12 D．m=-123.若函数2)1)2(--=k xky（是正比例函数,则k=罕有题型二：正比例函数性质的应用1.已知正比例函数y＝（m－1）25mx-的图象在第二.四象限,则m的值为_________,函数的解析式为__________2．P1(x1,y1),P2(x2,y2)是正比例函数图象上的两点,则下列断定准确的是( ) A．y1>y2B．y1<y2 C．当x1<x2时,y1>y2 D．当x1<x2时,y1<y2(三）一次函数的界说：罕有题型一：一次函数和正比例函数的接洽与差别2.下列函数关系式中,哪些是一次函数,哪些又是正比例函数？（1）y=-x-4 （2）256y x =+ （3）8y x =- (4) y=-8x3.下列说法不准确的是( )(A)一次函数不必定是正比例函数 (B)不是一次函数就必定不是正比例函数(C)正比例函数是特定的一次函数 (D)不是正比例函数就不是一次函数(四）一次函数的性质①平移：直线y ＝kx ＋b 可以看作由直线y ＝kx 平移_____个单位而得到,当b ＞0时,向_____平移,当b ＜0时,向_____平移.即k 值雷同时,直线必定平行.2.若把直线y=2x －3向上平移3个单位长度,得到直线( )A ．y=2x B.y=2x －6 C. y=5x －3 D.y=－x －33、若直线平行与直线125)3(+=+-=x y x m y ,则=m②增减性：当k ＞0时,y 随x 的增大而_____,这时函数的图象从左到右_____;当k ＜0时,y 随x 的增大而_____,这时函数的图象从左到右_____.1. 下列函数中,y 随x 的增大而减小的有（）A. 1个B. 2个C. 3个D. 4个 ③所经象限:xy )21(-=31x y +-=xy -=612+-=x y1.已知直线y=kx+b不经由第三象限则下列结论准确的是（）A．k＞0, b＞0;B．k＜0, b＞0;C．k＜0, b＜0; D．k＜0, b≥0;2.已知一次函数y=kx+b,y跟着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )(A) (B) （C）A． B． C． D．④图像与坐标轴的交点：直线），轴的交点坐标为（与bybkxy0+=3.一次函数y=kx+4的图象经由点（－3,－2）.（1）求这个函数表达式;（2）画出该函数的图象．（3）断定（－5,3）是否在此函数的图象上; (五）待定系数法求一次函数的表达式x O。

一次函数的知识点与题型总结.docx

在一个变化过程中只能取同一数值的量。

一次函数的章节的知识整理与题型总结第一节函数一、知识归纳1、变量：在一个变化过程屮可以取不同数值的量。

3、函数的概念：一般地，在某个变化过程中，冇两个变量x 和y,如呆给定一个x 值，相应地就确定了一个y 值，那么我们称y 是x 的函数，其中x 是自变量，y 是因变量。

*判断Y 是否为X 的函数，只要看X 取值确定的吋候，Y 是否有唯一确定的值与之对应4、定义域：一个函数的自变量允许取值的范围，叫做这个函数的定义域。

5、要使函数的解析式有意义（即确定函数定义域的方法）。

（1）函数的解析式是整式时，自变量可取全体实数；（2）函数的解析式是分式吋，自变量的取值应使分母壬0；（3）函数的解析式是二次根式时，自变量的取值应使被开方数N0。

（4）函数的解析式是三次根式时，自变量的取值应是一切实数。

（5）对于反映实际问题的函数关系，应使实际问题有意义。

6、函数的表示方法列表法：一口了然，使用起来方便，但列出的对应值是有限的，不易看出口变量与函数之间的对应规律。

解析式法：简单明了，能够准确地反映整个变化过程中自变量与函数Z 间的相依关系，但有些实际问题中的函数关系，不能用解析式表示。

图象法：形象直观，但只能近似地表达两个变量之间的函数关系。

7、函数的图像：一•般来说，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象.2、(2)1660 1400(3)3050例2•函数是研究A.常量Z间的对应关系的C.变量与常量之间对应关系的()B.常量与变量Z间的对应关系的D.变量之间的对应关系的8、描点法画函数图形的一般步骤第一步：列表(表中给出一些口变量的值及其对应的函数值)；第二步：描点(在直角坐标系中，以自变量的值为横坐标，相应的函数二、经典题型题型考点一求简单的函数关系式，识别自变量与因变量，给定自变量的值，相应地会求出函数的值。

(完整)一次函数知识点总结与常见题型,文档

一次函数知识点总结与常有题型根本看法1、变量：在一个变化过程中能够取不相同数值的量。

常量：在一个变化过程中只能取同一数值的量。

例题：在匀速运动公式s vt 中 , v 表示速度 , t 表示时间 , s 表示在时间 t 内所走的行程 ,那么变量是 ________,常量是 _______。

在圆的周长公式 C=2πr 中，变量是 ________，常量是 _________. 2、函数：一般的，在一个变化过程中，若是有两个变量 x 和 y ，而且关于 x 的每一个确定的值， y 都有唯一确定的值与其对应，那么我们就把 x 称为自变量，把 y 称为因变量， y 是 x 的函数。

* 判断 Y 可否为 X 的函数，只要看 X 取值确定的时候， Y 可否有唯一确定的值与之对应例题：以下函数〔1〕 y=πx (2)y=2x － 1(3) y=1(4)y= 1－ 3x (5) y=x 2－ 1 中，是一次函数的有〔〕x2〔A 〕4 个〔B 〕3 个〔C 〕2 个〔D 〕1 个3、定义域：一般的，一个函数的自变量赞同取值的范围，叫做这个函数的定义域。

4、确定函数定义域的方法：〔 1〕关系式为整式时，函数定义域为全体实数；〔 2〕关系式含有分式时，分式的分母不等于零；〔 3〕关系式含有二次根式时，被开放方数大于等于零；〔 4〕关系式中含有指数为零的式子时，底数不等于零；〔 5〕实责问题中，函数定义域还要和实质状况相吻合，使之有意义。

例题：以下函数中，自变量 x 的取值范围是 x ≥2的是〔〕 A ． y= 2 xB ．y=1 C ．y= 4 x2 D ． y= x 2 · x 2x 2函数 y x5 中自变量 x 的取值范围是 ___________. 函数 y1x 2，当1 x 1 时， y 的取值范围是〔〕25 y3 3 535 3 5A.2B.y2D.y2222225、函数的图像一般来说，关于一个函数，若是把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象． 6、函数解析式：用含有表示自变量的字母的代数式表示因变量的式子叫做解析式。

一次函数各类题型详解加练习

∴A的坐标为（0,2），B的坐标为（0，-3）
令 +2=-2 -3，解得 =
（提示：求两个函数之间的交点，令两个解析式相等即可得到交点横坐标）
将 = 带入y₁= +2
得：y₁= +2=
∴点C的坐标为（，）
（2）AB=2－（－3）=5（提示：AB与y轴重合，上y减下y求长度。）
（分析：以AB为底，点C到AB的距离为高，就可以求出△ABC的面积。）
求线段AB、CD的长度。
解：∵AB∥x轴
∴AB=6－(－3)= 9
（右x减左x，即可求得长度）
同理∵CD∥x轴
∴CD=5－2=3
③既不平行于x轴，也不平行于y轴：如：点A（x₁，y₁），点B（x₂，y₂），则使用求线段的通用公式AB=
例：点A的坐标为（3,3），点B的坐标为（-3，-5），
求线段AB的长度。
S△COP=
OC·OP= ×8×(2t-8)=8t－32（t≥4）
(上一问中刚求出)
－8t+32=2×16（0≤t＜4）
S△COP=2S△AOB，即或解，得：t=0或者t=8
8t－32=2×16（t≥4）
（4）思路：在△COP和△AOB中:∠COP=∠AOB=90°，OC =OA=8
还差一组条件就能证明两三角形全等了，因为整个题目并未有角度的信息，
解：AB中点的坐标为：（，）整理，得（，3）
∵直线AB的k₁=2，且k₁·k₂=－1
∴垂直于AB的直线的k₂=
设垂直平分线解析式为：y= +b，将（，3）代入解析式，
可得AB中垂线的解析式为y= +
把y=0代入解析式可得
点P的坐标为：（，0）
综上：符合要求的点P共有4个：

初中一次函数常见题型总结(附答案)

函数定义1、判断下列变化过程存在函数关系的是（）A. x, y是变量，y=±2&B.人的身高与年龄C.三角形的底边长与面积D.速度一定的汽车所行驶的路程与时间__ x . .2、已知函数y= -------- ,当x = a时,2x 1A.1B.—1C.33、下列各曲线中不能表示y是x的函数是（欢迎使用本资料，才版身体演、万事如意，阂彖欢乐。

■同学们僮鼾夬乐的成长。

早m为祖国的崇荣昌■奉献自己的力*正比例函数1、下列各函数中，y与x成正比例函数关系的是（其中k为常数）（）A、y=3x —2B、y=（k+1）xC、y=（|k|+1）xD、y= x 22、如果y=kx+b ,当时，y叫做x的正比例函数3、一次函数y=kx+k+1 ,当k=时，y叫做x正比例函数次函数的定义1、下列函数关系中，是一次函数的个数是（）基础义务教育资料欢迎使用本奏礼祝您身体僮射万事如意，■彖欢乐，■同学们1®鼾大乐的成长。

早m为祖国的崇荒昌■奉献自己的力,。

一次函数题型总结y = 1 ,则a的值为（）4、若函数 y= — x+m 与y=4x — 1的图象交于 .一-1 A. -1 B. 1 C.4 5.如图，表小一次函数 y = mx+n 与正比例函w是（）.AB. C.6、已知一次函数 y =（a -1）x+b 的图象如图A. a >1B. a <1C. a >y 轴上一点，则m 的值是（）D. 1I4数 y=mnx （m , n 是常数，且 mn w0）图像的* D.1所示，那么a 的取值范围是（）D, a<0V"/一 /O x2报效祖国 E图1①y= 一 ②y= 一 ③y=210—x ④y=x 2—2⑤ y=— +1x 3 3xA 、1B 、2C 、3D 、42、若函数y=（3 — m ）x m -9是正比例函数，则 m= 。

3、当m 、n 为何值时，函数 y=（5m — 3）x 2-n+（m+n ）（1）是一次函数（2）是正比例函数一次函数与坐标系1 .一次函数y= -2x+4的图象经过第象限，y 的值随x 的值增大而（增大或减少）图象与 x 轴交点坐标是，与 y 轴的交点坐标是 .2 .已知y+4与x 成正比例，且当 x=2时，y=1 ,则当x= — 3时，y=.3 .已知k>0, b >0,则直线y=kx+b 不经过第象限.7. 一次函数y=kx+ （k-3）的函数图象不可能是（）A B C D待定系数法求一次函数解析式1.已知直线经过点（1,2）和点（3,0）,求这条直线的解析式2.如图，一次函数y=kx+b的图象经过A、B两点，与x轴相交于（1）直线AC的函数解析式；（2）设点（a, -2）在这个函数图象上，求2、如图，两摞相同规格的饭碗整齐地叠放在桌面上，请根据图中给的数据信息，解答下列问题:（1）求整齐摆放在桌面上饭碗的高度y （cm）与饭碗数x （个）之间的一次函数解析（2）把这两摞饭碗整齐地摆成一摞时，这摞饭碗的高度是多少?r5cn4、东从A地出发以某一速度向B地走去，同时小明从B地出发以另一速度向A地而行,如图所示，图中的线段y i、y2分别表示小东、小明离B地的距离（千米）与所用时间（小*y（千米）时）的关系。

(完整word)《一次函数》知识点归纳和题型归类,推荐文档

2、点 D（a,b）到 x 轴的距离是_________；到 y 轴的距离是____________；题型三、一次函数与正比例函数的识别方法：若 y=kx+b(k,b 是常数，k≠0)，那么 y 叫做 x 的一次函数，特别的，当 b=0 时，一次函数就
成为 y=kx(k 是常数，k≠0)，这时，y 叫做 x 的正比例函数，当 k=0 时，一次函数就成为若 y=b，这时，y 叫做常函数。 ☆A 与 B 成正比例A=kB(k≠0)
1、当 k_____________时， y k 3x2 2x 3 是一次函数；
2、当 m_____________时， y m 3x2m1 4x 5 是一次函数；
3、当 m_____________时， y m 4x2m1 4x 5 是一次函数；
4、2y-3 与 3x+1 成正比例，且 x=2,y=12,则函数解析式为________________；
方法：点到 x 轴的距离用纵坐标的绝对值表示，点到 y 轴的距离用横坐标的绝对值表示；
若 AB∥x 轴，则 A(xA, 0), B(xB , 0) 的距离为 xA xB ；若 AB∥y 轴，则 A(0, yA ), B(0, yB ) 的距离为 yA yB ；
1、点 C（0，-5）到 x 轴的距离是_________；到 y 轴的距离是____________；到原点的距离是 ____________；
.
（2）在同一直角坐标系中画出这两个一次函数的
.
（3）这两条直线的
的坐标，就是这个二元一次方程组的解.
5．一次函数与一元一次不等式的关系
一次一次不等式 kxb>0(或 kxb<0)的解集，就是使一次函数
中 y>0(或 y<0)的

一次函数与几何综合(题型齐全)

一次函数与几何图形综合考点一、面积问题一次函数求面积的常用方法：（1）直接法（公式法）适用于规则图形，三角形中至少有一边与坐标轴重合或平行时，常用直接法求面积；（2）割补法（分割求和、补形作差）适用于不规则四边形，将四边形分割成两个三角形，分别计算两个三角形的面积再求和。

或者将四边形放在一个规则图形中（需要时做辅助线），此时四边形的面积可以看作一个规则图形面积减去补充的规则图形面积；（3）铅锤法（底相同，高运算）适用于三边均不与坐标轴平行的三角形（不规则三角形）；（4）平行线面积转化适用于存在平行线的情况下，利用平行线的性质，平行线间的距离处处相等做高；题型一：直接求图形面积1、正比例函数()110y k x k =≠与一次函数()220y k x b k =+≠的图象的交点坐标为()43A ，，一次函数的图象与y 轴的交点坐标为()03B -，．(1)求正比例函数和一次函数的解析式；(2)求AOB 的面积．2、如图，一次函数5y x =-+和1y kx =-的图象与x 轴分别交于A 、C 两点，与y 轴分别交于B 、D 两点，两个函数图象的交点为点E ，且E 点的横坐标为2．(1)求k 的值；(2)不解方程组，请直接写出方程组51x y kx y +=⎧⎨-=⎩的解；(3)求两函数图象与x 轴所围成的ACE △的面积．3、如图，直线443y x =-+与y 轴交于点A ，与直线4455y x =+交于点B ，且直线4455y x =+与x 轴交于点C ，求ABC 的面积．4、如图，在平面直角坐标系中，直线132x m l y =+：与直线2l 交于点()23A -，，直线2l 与x 轴交于点()40C ，，与y 轴交于点B ，将直线l 2向下平移8个单位长度得到直线3l ，3l 与y 轴交于点D ，与1l 交于点E ，连接AD ．(1)求直线2l 的解析式；(2)求△ADE V 的面积；5、如图，直线l 1：y ＝x +m 与y 轴交于点B ，与x 轴相交于点F ．直线l 2：y ＝kx ﹣9与x 轴交于点A ，与y 轴交于点C ，两条直线相交于点D ，连接AB ，且OA ：OC ：AB ＝1：3：．（1）求直线l 1、l 2的解析式；（2）过点C 作l 3∥l 1交x 轴于点E ，连接BE 、DE ．求△BDE 的面积．5、如图，一次函数()0y kx b k =+≠的图象与正比例函数2y x =-的图象交于点A ，与x 轴交于点C ，与y 轴交于点B ，5OB =，点A 的纵坐标为4．(1)求一次函数的解析式；(2)点D 和点B 关于x 轴对称，将直线2y x =-沿y 轴向上平移8个单位后分别交x 轴，y 轴于点,M N ，与直线()0y kx b k =+≠交于点E ，连接DE ，DC ，求ECD 的面积．题型二：已知面积求点的坐标1、如图，一次函数y kx b =+与反比例函数a y x=的图象在第一象限交于点()4,3A ，与y 轴的负半轴交于点B ，且OA OB =．(1)求一次函数y kx b =+与反比例函数a y x =的表达式；(2)已知点C 在x 轴上，且ABC 的面积是8，求此时点C 的坐标；2、如图，在平面直角坐标系中直线13:2l x m +与直线2l 交于点()2,3A -，直线2l 与x 轴交于点()4,0C ，与y 轴交于点B ，过BD 中点E 作直线3l y ⊥轴．(1)求直线2l 的解析式和m 的值；(2)点P 在直线1l 上，当6PBC S = 时，求点P 坐标；。

一次函数知识点总结与常见题型-一次函数知识点整理

一次函数知识点总结与常见题型-一次函数知识点整理基本概念1、变量：在一个变化过程中可以取不同数值的量。

常量：在一个变化过程中只能取同一数值的量。

例题：在匀速运动公式vt s =中,v 表示速度,t 表示时间,s 表示在时间t 内所走的路程,则变量是________,常量是_______。

在圆的周长公式C =2πr 中，变量是________，常量是_________.2、函数：一般的，在一个变化过程中，如果有两个变量x 和y ，并且对于x 的每一个确定的值，y 都有唯一确定的值与其对应，那么我们就把x 称为自变量，把y 称为因变量，y 是x 的函数。

*判断Y 是否为X 的函数，只要看X 取值确定的时候，Y 是否有唯一确定的值与之对应例题：下列函数（1）y =πx (2)y =2x －1 (3)y =1x (4)y =21－3x (5)y =x 2－1中，是一次函数的有（）（A ）4个（B ）3个（C ）2个（D ）1个3、定义域：一般的，一个函数的自变量允许取值的范围，叫做这个函数的定义域。

4、确定函数定义域的方法：（1）关系式为整式时，函数定义域为全体实数；（2）关系式含有分式时，分式的分母不等于零；（3）关系式含有二次根式时，被开放方数大于等于零；（4）关系式中含有指数为零的式子时，底数不等于零；（5）实际问题中，函数定义域还要和实际情况相符合，使之有意义。

例题：下列函数中，自变量x 的取值范围是x ≥2的是（）A ．yB ．yC ．yD ．y函数y =x 的取值范围是___________. 已知函数221+-=x y ，当11≤<-x 时，y 的取值范围是（）A .2325≤<-yB .2523<<yC .2523<≤yD .2523≤<y5、函数的图像6、函数解析式：78、函数的表示方法系，不能用解析式表示。

9、正比例函数及性质一般地，形如y =kx (k 是常数，注：正比例函数一般形式 y =当k >0时，直线y =kx 象限，从左向右下降，即随x (1) 解析式：y =kx （k 是常数，(2) 必过点：（0，0）、（1，(3) 走向：k >0(4) 增减性：k >0，y 随x (5) 倾斜度：|k |越大，越接近y 例题：(1).正比例函数(3y m =(2)若23y x b =+- A .0 B .23 .(3)函数y =(k －1)x ，y 随x A .0<k B .1>k (4)东方超市鲜鸡蛋每个0.4(5)平行四边形相邻的两边长为x、y，周长是30，则y与x的函数关系式是__________．10、一次函数及性质一般地，形如y=kx＋b(k,b是常数，k≠0)，那么y叫做x的一次函数.当b=0时，y=kx＋b即y=kx，所以说正比例函数是一种特殊的一次函数.注：一次函数一般形式y=kx+b (k不为零) ①k不为零②x指数为1 ③b取任意实数一次函数y=kx+b的图象是经过（0，b）和（－kb，0）两点的一条直线，我们称它为直线y=kx+b,它可以看作由直线y=kx平移|b|个单位长度得到.（当b>0时，向上平移；当b<0时，向下平移）（1）解析式：y=kx+b(k、b是常数，k≠0 （2）必过点：（0，b）和（－kb，0）（3）走向：k>0，图象经过第一、三象限；k<0，图象经过第二、四象限b>0，图象经过第一、二象限；b<0，图象经过第三、四象限⇔⎩⎨⎧>>bk直线经过第一、二、三象限⇔⎩⎨⎧<>bk直线经过第一、三、四象限⇔⎩⎨⎧><bk直线经过第一、二、四象限⇔⎩⎨⎧<<bk直线经过第二、三、四象限（4）增减性：k>0，y随x的增大而增大；k<0，y随x增大而减小.（5）倾斜度：|k| 越大，图象越接近于y轴；|k| 越小，图象越接近于x轴.（6）图像的平移：当b>0时，将直线y=kx的图象向上平移b个单位；（上加下减，左加右减）当b<0时，将直线y=kx的图象向下平移b个单位.例题：若关于x的函数1(1)my n x-=+是一次函数，则m= ，n..函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置正确的是（）将直线y＝3x向下平移5个单位，得到直线；将直线y＝－x－5向上平移5个单位，得到直线. 若直线axy+-=和直线bxy+=的交点坐标为(8,m),则=+ba____________.已知函数y＝3x+1，当自变量增加m时，相应的函数值增加（）Ａ．3m+1 Ｂ．3mＣ．m Ｄ．3m－111、一次函数y=kx＋b的图象的画法.根据几何知识：经过两点能画出一条直线，并且只能画出一条直线，即两点确定一条直线，所以画一次函数的图象时，只要先描出两点，再连成直线即可.一般情况下：是先选取它与两坐标轴的交点：与y轴的交点（0，b），与x轴的交点（kb-，0）.即横坐标或纵坐标为0的点.b>0 b<0 b=0k>0经过第一、二、三象限经过第一、三、四象限经过第一、三象限图象从左到右上升，y随x的增大而增大k<0经过第一、二、四象限经过第二、三、四象限经过第二、四象限图象从左到右下降，y随x的增大而减小☆k 、b 的符号对直线位置的影响☆图像过一、二、三象限图像过一、三、四象限图像过一、二、四象限图像过二、三、四象限（大大不过四）（大小不过二）（小大不过三）（小小不过一）思考：若m ＜0, n ＞0, 则一次函数y=mx+n 的图象不经过（）A .第一象限B . 第二象限C .第三象限D .第四象限 12、正比例函数与一次函数图象之间的关系一次函数y =kx ＋b 的图象是一条直线，它可以看作是由直线y =kx 平移|b |个单位长度而得到（当b >0时，向上平移；当b <0时，向下平移）.13、直线y =k 1x +b 1与y =k 2x +b 2的位置关系（1）两直线平行：k 1=k 2且b 1 ≠b 2 （2）两直线相交：k 1≠k 2 （3）两直线重合：k 1=k 2且b 1=b 2 （4）两直线垂直：k 1·k 2= –1 14、用待定系数法确定函数解析式的一般步骤：（1）根据已知条件写出含有待定系数的函数关系式；（2）将x 、y 的几对值或图象上的几个点的坐标代入上述函数关系式中得到以待定系数为未知数的方程；（3）解方程得出未知系数的值；（4）将求出的待定系数代回所求的函数关系式中得出所求函数的解析式. 15、一元一次方程与一次函数的关系任何一元一次方程到可以转化为ax +b =0（a ，b 为常数，a ≠0）的形式，所以解一元一次方程可以转化为：当某个一次函数的值为0时，求相应的自变量的值. 从图象上看，相当于已知直线y =ax +b 确定它与x 轴的交点的横坐标的值. 16、一次函数与一元一次不等式的关系任何一个一元一次不等式都可以转化为ax +b >0或ax +b <0（a ，b 为常数，a ≠0）的形式，所以解一元一次不等式可以看作：当一次函数值大（小）于0时，求自变量的取值范围. 17、一次函数与二元一次方程组（1）以二元一次方程ax +by =c 的解为坐标的点组成的图象与一次函数y =bcx b a +-的图象相同. （2）二元一次方程组⎩⎨⎧=+=+222111c y b x a c y b x a 的解可以看作是两个一次函数y =1111b c x b a +-和y =2222b cx b a +-的图象交点.18、一次函数的图像与两坐标轴所围成三角形的面积一次函数y =kx ＋b 的图象与两条坐标轴的交点：与y 轴的交点（0，b ），与x 轴的交点（kb-，0）. 直线（b ≠0）与两坐标轴围成的三角形面积为s =kb b k b 2212=⨯⨯常见题型一、考察一次函数定义 1、若函数()213m y m x=-+是y 关于x 的一次函数，则m 的值为；解析式为 .2、要使y =(m －2)x n －1+n 是关于x 的一次函数,n ,m 应满足 , . 二、考查图像性质1、已知一次函数y =（m －2）x +m －3的图像经过第一，第三，第四象限，则m 的取值范围是________．2、若一次函数y =（2－m ）x +m 的图像经过第一、•二、•四象限，•则m •的取值范围是______3、已知m 是整数，且一次函数(4)2y m x m =+++的图象不过第二象限，则m 为 .4、直线y kx b =+经过一、二、四象限，则直线y bx k =-的图象只能是图4中的（）5、直线0px qy r ++=(0)pq ≠如图5，则下列条件正确的是（）.,1A p q r == .,0B p q r == .,1C p q r =-= .,0D p q r =-=6、如果0ab >，0a c <，则直线a cy x b b=-+不通过（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限7、如图6，两直线1y kx b =+和2y bx k =+在同一坐标系内图象的位置可能是（）8、如果0ab >，0a c <，则直线a cy x b b=-+不通过（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限9、b 为时，直线2y x b =+与直线34y x =-的交点在x 轴上. 10、要得到y =－32x －4的图像，可把直线y =－32x （）．（A ）向左平移4个单位（B ）向右平移4个单位（C ）向上平移4个单位（D ）向下平移4个单位11、已知一次函数y =－kx +5，如果点P 1（x 1，y 1），P 2（x 2，y 2）都在函数的图像上，且当x 1<x 2时，有y 1<y 2成立，那么系数k 的取值范围是________．12、已知点（－4，y 1），（2，y 2）都在直线y =－ 12x +2上，则y 1 、y 2大小关系是( )（A ）y 1 >y 2 （B ）y 1 =y 2 （C ）y 1 <y 2 （D ）不能比较三、交点问题1、若直线y =3x －1与y =x －k 的交点在第四象限，则k 的取值范围是（）．（A ）k <13 （B ）13<k <1 （C ）k >1 （D ）k >1或k <132、若直线y x a =-+和直线y x b =+的交点坐标为(,8)m ，则a b += .3、一次函数y kx b =+的图象过点(,1)m 和(1,)m 两点，且1m >，则k = ，b 的取值范围是 .4、直线y kx b =+经过点(1,)A m -，(,1)B m (1)m >，则必有（）A . 0,0k b >> .0,0B k b >< .0,0C k b <> .0,0D k b <<5、如图所示，已知正比例函数xy 21-=和一次函数b x y +=，它们的图像都经过点P （a ，1），且一次函数图像与y 轴交于Q 点。

一次函数题型总结(含答案)

一次函数题型总结(含答案)一次函数题型总结(含答案)求一次函数解析式常见题型解析一次函数解析式的求法在初中数学内容中占有举足轻重的作用，如何把这一部分内容学得扎实有效呢，整理了一下材料，给大家提供一些题型及解题方法，期望对同学们有所帮助。

二.平移型两条直线l1：yk1xb1；l2：yk2xb2。

当k1k2，b1b2时，l1∥l2，解决问题时要抓住平行的直线k值相同这一特征。

例1.把直线y2x1向下平移2个单位得到的图像解析式为___________。

第一种情况：直接或间接已知函数是一次函数，采用待定系数法。

（已知是一次函数或已知解析式形式ykxb或已知函数图象是直线都是已知了一次函数）一、定义型一次函数的定义：形如ykxb，k、b为常数，且k≠0。

例1.已知函数ym3xm283是一次函数，求其解析式。

解析：由一次函数定义知m3，故一次函数的解析式为y3x3注意：利用定义求一次函数ykxb解析式时，要保证k≠0。

如本例中应保证m30。

例2.已知y-1与x＋1成正比例,且当x=1时,y=5.求y与x的函数关系式;解析：∵y-1与x＋1成正比例，∴可假设y-1=k（x＋1）又当x=1时,y=5，代入求出k=2，所以y-1=2（x＋1），变形为y=2x＋3注意：“两个量成正比例”和“两个量是正比例函数关系”是完全一致的，题目中已知y-1与x＋1成正比例就可以假设y-1=k（x＋1）。

解析：直线y2x1向下平移得到的直线与直线y2x1平行∴可设把直线y2x1向下平移2个单位得到的图像解析式为y2xb直线y2x1与y轴交点为（0，1）向下平移2个单位得到的点为（0，-1）∴可代入y2xb求出b=-1∴所求解析式为y2x1例2.已知直线ykxb与直线y2x平行，且与x轴交点横坐标为1，则直线的解析式为___________。

解析：直线ykxb与直线y2x平行，∴k2。

又直线ykxb与x轴交点横坐标为1，即过点（1,0）代入y2xb中可求出b2故直线的解析式为y2x2三.两点型从几何的角度来看，“两点确定一条直线”，所以两个点的坐标确定直线的解析式；从代数的角度来说，一次函数的解析式ykxb中含两个待定系数k和b，所以两个方程确定两个待定系数，因此想方设法找到两个点的坐标是解决问题的关键。

(完整版)一次函数经典题型+习题(精华,含答案)

一次函数知识点总结与常见题型-含答案

6、函数解析式：用含有表示自变量的字母的代数式表示因变量的式子叫做解析式。
7、描点法画函数图形的一般步骤
第一步：列表（表中给出一些自变量的值及其对应的函数值）；
第二步：描点（在直角坐标系中，以自变量的值为横坐标，相应的函数值为纵坐标，描出表格中数值对应的各点）；第三步：连线（按照横坐标由小到大的顺序把所描出的各点用平滑曲线连接起来）。
（2）二元一次方程组的解可以看作是两个一次函数y= 和y= 的图象交点.
18、一次函数的图像与两坐标轴所围成三角形的面积
一次函数y=kx＋b的图象与两条坐标轴的交点：与y轴的交点（0，b），与x轴的交点（，0）.
直线（b≠0）与两坐标轴围成的三角形面积为s=
常见题型
1、考察一次函数定义
1、若函数是y关于x的一次函数，则的值为；解析式为.
2、函数：一般的，在一个变化过程中，如果有两个变量x和y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就把x称为自变量，把y称为因变量，y是x的函数。
*判断Y是否为X的函数，只要看X取值确定的时候，Y是否有唯一确定的值与之对应
例题：下列函数（1）y=πx(2)y=2x－1 (3)y= (4)y= －3x(5)y=x2－1中，是一次函数的有（）
求（1）a的值；（2）k、b的值；（3）这两个函数图像与x轴所围成的三角形面积。
五、一次函数解析式的求法
（1）定义型例1.已知函数是一次函数，求其解析式。
（2）点斜型例2.已知一次函数的图像过点（2，－1），求这个函数的解析式。
（3）两点型例3.已知某个一次函数的图像与x轴、y轴的交点坐标分别是（－2，0）、（0，4），则这个函数的解析式为_____________。

一次函数题型总结(含答案)

二.平移型两条直线l1：yk1xb1；l2：yk2xb2。

当k1k2，b1b2时，l1∥l2，解决问题时要抓住平行的直线k值相同这一特征。

例1.把直线y2x1向下平移2个单位得到的图像解析式为___________。

第一种情况：直接或间接已知函数是一次函数，采用待定系数法。

（已知是一次函数或已知解析式形式ykxb或已知函数图象是直线都是已知了一次函数）一、定义型一次函数的定义：形如ykxb，k、b为常数，且k≠0。

例1.已知函数ym3xm283是一次函数，求其解析式。

解析：由一次函数定义知m3，故一次函数的解析式为y3x3注意：利用定义求一次函数ykxb解析式时，要保证k≠0。

如本例中应保证m30。

解析：直线ykxb与直线y2x平行，∴k2。

一次函数篇(解析版)--中考数学必考考点总结+题型专训

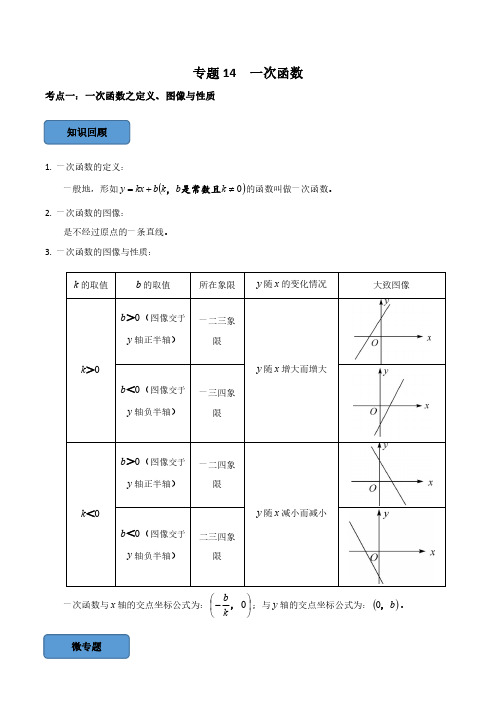
知识回顾微专题专题14一次函数考点一：一次函数之定义、图像与性质1.一次函数的定义：一般地，形如()0≠+=k b k b kx y 是常数且，的函数叫做一次函数。

2.一次函数的图像：是不经过原点的一条直线。

3.一次函数的图像与性质：一次函数与x 轴的交点坐标公式为：⎪⎭⎫ ⎝⎛-0 ，kb ；与y 轴的交点坐标公式为：()b ，0。

1．（2022•沈阳）在平面直角坐标系中，一次函数y＝﹣x+1的图象是（）A．B．C．D．【分析】依据一次函数y＝x+1的图象经过点（0，1）和（1，0），即可得到一次函数y＝﹣x+1的图象经过一、二、四象限．【解答】解：一次函数y＝﹣x+1中，令x＝0，则y＝1；令y＝0，则x＝1，∴一次函数y＝﹣x+1的图象经过点（0，1）和（1，0），∴一次函数y＝﹣x+1的图象经过一、二、四象限，故选：C．2．（2022•安徽）在同一平面直角坐标系中，一次函数y＝ax+a2与y＝a2x+a的图象可能是（）A．B．C．D．【分析】利用一次函数的性质进行判断．【解答】解：∵y＝ax+a2与y＝a2x+a，∴x＝1时，两函数的值都是a2+a，∴两直线的交点的横坐标为1，若a＞0，则一次函数y＝ax+a2与y＝a2x+a都是增函数，且都交y轴的正半轴，图象都经过第一、二、三象限；若a＜0，则一次函数y＝ax+a2经过第一、二、四象限，y＝a2x+a经过第一、三、四象限，且两直线的交点的横坐标为1；故选：D．3．（2022•辽宁）如图，在同一平面直角坐标系中，一次函数y＝k1x+b1与y＝k2x+b2的图象分别为直线l1和直线l2，下列结论正确的是（）A．k1•k2＜0B．k1+k2＜0C．b1﹣b2＜0D．b1•b2＜0【分析】根据一次函数y＝k1x+b1与y＝k2x+b2的图象位置，可得k1＞0，b1＞0，k2＞0，b2＜0，然后逐一判断即可解答．【解答】解：∵一次函数y＝k1x+b1的图象过一、二、三象限，∴k1＞0，b1＞0，∵一次函数y＝k2x+b2的图象过一、三、四象限，∴k2＞0，b2＜0，∴A、k1•k2＞0，故A不符合题意；B、k1+k2＞0，故B不符合题意；C、b1﹣b2＞0，故C不符合题意；D、b1•b2＜0，故D符合题意；故选：D．4．（2022•六盘水）如图是一次函数y＝kx+b的图象，下列说法正确的是（）A．y随x增大而增大B．图象经过第三象限C．当x≥0时，y≤b D．当x＜0时，y＜0【分析】根据一次函数的图象和性质进行判断即可．【解答】解：由图象得：图象过一、二、四象限，则k＜0，b＞0，当k＜0时，y随x的增大而减小，故A、B错误，由图象得：与y轴的交点为（0，b），所以当x≥0时，从图象看，y≤b，故C正确，符合题意；当x＜0时，y＞b＞0，故D错误．故选：C．5．（2022•兰州）若一次函数y＝2x+1的图象经过点（﹣3，y1），（4，y2），则y1与y2的大小关系是（）A．y1＜y2B．y1＞y2C．y1≤y2D．y1≥y2【分析】先根据一次函数的解析式判断出函数的增减性，再根据﹣3＜4即可得出结论．【解答】解：∵一次函数y＝2x+1中，k＝2＞0，∴y随着x的增大而增大．∵点（﹣3，y1）和（4，y2）是一次函数y＝2x+1图象上的两个点，﹣3＜4，∴y1＜y2．故选：A．6．（2022•凉山州）一次函数y＝3x+b（b≥0）的图象一定不经过（）A．第一象限B．第二象限C．第三象限D．第四象限【分析】根据一次函数的图象与系数的关系即可得出结论．【解答】解：∵函数y＝3x+b（b≥0）中，k＝3＞0，b≥0，∴当b＝0时，此函数的图象经过一、三象限，不经过第四象限；当b＞0时，此函数的图象经过一、二、三象限，不经过第四象限．则一定不经过第四象限．故选：D．7．（2022•济宁）已知直线y1＝x﹣1与y2＝kx+b相交于点（2，1）．请写出一个b值（写出一个即可），使x＞2时，y1＞y2．【分析】由题意可知，当b＞﹣1时满足题意，故b可以取0．【解答】解：直线y1＝x﹣1与y2＝kx+b相交于点（2，1）．∵x＞2时，y1＞y2．∴b＞﹣1，故b可以取0，故答案为：0（答案不唯一）．8．（2022•上海）已知直线y＝kx+b过第一象限且函数值随着x的增大而减小，请列举出来这样的一条直线：．【分析】根据一次函数的性质，写出符合条件的函数关系式即可．【解答】解：∵直线y＝kx+b过第一象限且函数值随着x的增大而减小，∴k＜0，b＞0，∴符合条件的函数关系式可以为：y＝﹣x+1（答案不唯一）．故答案为：y＝﹣x+1（答案不唯一）．9．（2022•无锡）请写出一个函数的表达式，使其图象分别与x轴的负半轴、y轴的正半轴相交：．【分析】设函数的解析式为y＝kx+b（k≠0），再根据一次函数的图象分别与x轴的负半轴、y轴的正半轴相交可知k＞0，b＞0，写出符合此条件的函数解析式即可．【解答】解：设一次函数的解析式为y＝kx+b（k≠0），∵一次函数的图象分别与x轴的负半轴、y轴的正半轴相交，∴k＞0，b＞0，∴符合条件的函数解析式可以为：y＝x+1（答案不唯一）．故答案为：y＝x+1（答案不唯一）．10．（2022•湘潭）请写出一个y随x增大而增大的一次函数表达式．【分析】根据y随着x的增大而增大时，比例系数k＞0即可确定一次函数的表达式．【解答】解：在y＝kx+b中，若k＞0，则y随x增大而增大，∴只需写出一个k＞0的一次函数表达式即可，比如：y＝x﹣2，故答案为：y＝x﹣2（答案不唯一）．11．（2022•宿迁）甲、乙两位同学各给出某函数的一个特征，甲：“函数值y随自变量x增大而减小”；乙：“函数图象经过点（0，2）”，请你写出一个同时满足这两个特征的函数，其表达式是．【分析】根据甲、乙两位同学给出的函数特征可判断出该函数为一次函数，再利用一次函数的性质，可得出k＜0，b＝2，取k＝﹣1即可得出结论．【解答】解：∵函数值y随自变量x增大而减小，且该函数图象经过点（0，2），∴该函数为一次函数．设一次函数的表达式为y＝kx+b（k≠0），则k＜0，b＝2．取k＝﹣1，此时一次函数的表达式为y＝﹣x+2．故答案为：y＝﹣x+2（答案不唯一）．12．（2022•甘肃）若一次函数y＝kx﹣2的函数值y随着自变量x值的增大而增大，则k＝（写出一个满足条件的值）．【分析】根据函数值y随着自变量x值的增大而增大得到k＞0，写出一个正数即可．【解答】解：∵函数值y随着自变量x值的增大而增大，∴k＞0，∴k＝2（答案不唯一）．故答案为：2（答案不唯一）．13．（2022•柳州）如图，直线y1＝x+3分别与x轴、y轴交于点A和点C，直线y2＝﹣x+3分别与x轴、y 轴交于点B和点C，点P（m，2）是△ABC内部（包括边上）的一点，则m的最大值与最小值之差为（）A．1B．2C．4D．6【分析】由于P的纵坐标为2P在直线y＝2上，要求符合题意的m值，则P点为直线y＝2与题目中两直线的交点，此时m存在最大值与最小值，故可求得．【解答】解：∵点P（m，2）是△ABC内部（包括边上）的一点，∴点P在直线y＝2上，如图所示，当P为直线y＝2与直线y2的交点时，m取最大值，当P为直线y＝2与直线y1的交点时，m取最小值，∵y2＝﹣x+3中令y＝2，则x＝1，y1＝x+3中令y＝2，则x＝﹣1，∴m 的最大值为1，m 的最小值为﹣1．则m 的最大值与最小值之差为：1﹣（﹣1）＝2．故选：B ．14．（2022•遵义）若一次函数y ＝（k +3）x ﹣1的函数值y 随x 的增大而减小，则k 值可能是（）A ．2B ．23C ．﹣21D ．﹣4【分析】根据一次项系数小于0时，一次函数的函数值y 随x 的增大而减小列出不等式求解即可．【解答】解：∵一次函数y ＝（k +3）x ﹣1的函数值y 随着x 的增大而减小，∴k +3＜0，解得k ＜﹣3．所以k 的值可以是﹣4，故选：D ．15．（2022•包头）在一次函数y ＝﹣5ax +b （a ≠0）中，y 的值随x 值的增大而增大，且ab ＞0，则点A （a ，b ）在（）A ．第四象限B ．第三象限C ．第二象限D ．第一象限【分析】根据一次函数的增减性，确定自变量x 的系数﹣5a 的符号，再根据ab ＞0，确定b 的符号，从而确定点A （a ，b ）所在的象限．【解答】解：∵在一次函数y ＝﹣5ax +b 中，y 随x 的增大而增大，∴﹣5a ＞0，∴a ＜0．∵ab ＞0，∴a ，b 同号，∴b ＜0．∴点A （a ，b ）在第三象限．故选：B ．16．（2022•眉山）一次函数y ＝（2m ﹣1）x +2的值随x 的增大而增大，则点P （﹣m ，m ）所在象限为（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【分析】根据一次函数的性质求出m 的范围，再根据每个象限点的坐标特征判断P 点所处的象限即可．【解答】解：∵一次函数y ＝（2m ﹣1）x +2的值随x 的增大而增大，∴2m ﹣1＞0，解得：m ＞，∴P （﹣m ，m ）在第二象限，故选：B ．17．（2022•天津）若一次函数y ＝x +b （b 是常数）的图象经过第一、二、三象限，则b 的值可以是（写出一个即可）．【分析】根据一次函数的图象可知b ＞0即可．【解答】解：∵一次函数y ＝x +b （b 是常数）的图象经过第一、二、三象限，∴b ＞0，可取b ＝1，故答案为：1．（答案不唯一，满足b ＞0即可）18．（2022•邵阳）在直角坐标系中，已知点A （23，m ），点B （27，n ）是直线y ＝kx +b （k ＜0）上的两点，则m ，n 的大小关系是（）A ．m ＜nB ．m ＞nC ．m ≥nD ．m ≤n【分析】根据k ＜0可知函数y 随着x 增大而减小，再根＞即可比较m 和n 的大小．【解答】解：点A （，m ），点B （，n ）是直线y ＝kx +b 上的两点，且k ＜0，∴一次函数y 随着x 增大而减小，∵＞，∴m ＜n ，故选：A ．19．（2022•株洲）在平面直角坐标系中，一次函数y ＝5x +1的图象与y 轴的交点的坐标为（）A ．（0，﹣1）B ．（﹣51，0）C ．（51，0）D ．（0，1）【分析】一次函数的图象与y 轴的交点的横坐标是0，当x ＝0时，y ＝1，从而得出答案．【解答】解：∵当x ＝0时，y ＝1，∴一次函数y ＝5x +1的图象与y 轴的交点的坐标为（0，1），故选：D ．20．（2022•绍兴）已知（x 1，y 1），（x 2，y 2），（x 3，y 3）为直线y ＝﹣2x +3上的三个点，且x 1＜x 2＜x 3，则以下判断正确的是（）A．若x1x2＞0，则y1y3＞0B．若x1x3＜0，则y1y2＞0C．若x2x3＞0，则y1y3＞0D．若x2x3＜0，则y1y2＞0【分析】根据一次函数的性质和各个选项中的条件，可以判断是否正确，从而可以解答本题．【解答】解：∵直线y＝﹣2x+3，∴y随x的增大而减小，当y＝0时，x＝1.5，∵（x1，y1），（x2，y2），（x3，y3）为直线y＝﹣2x+3上的三个点，且x1＜x2＜x3，∴若x1x2＞0，则x1，x2同号，但不能确定y1y3的正负，故选项A不符合题意；若x1x3＜0，则x1，x3异号，但不能确定y1y2的正负，故选项B不符合题意；若x2x3＞0，则x2，x3同号，但不能确定y1y3的正负，故选项C不符合题意；若x2x3＜0，则x2，x3异号，则x1，x2同时为负，故y1，y2同时为正，故y1y2＞0，故选项D符合题意；故选：D．21．（2022•盘锦）点A（x1，y1），B（x2，y2）在一次函数y＝（a﹣2）x+1的图象上，当x1＞x2时，y1＜y2，则a的取值范围是．【分析】根据一次函数的性质，建立不等式计算即可．【解答】解：∵当x1＞x2时，y1＜y2，∴a﹣2＜0，∴a＜2，故答案为：a＜2．22．（2022•永州）已知一次函数y＝x+1的图象经过点（m，2），则m＝．【分析】由一次函数y＝x+1的图象经过点（m，2），利用一次函数图象上点的坐标特征可得出2＝m+1，解之即可求出m的值．【解答】解：∵一次函数y＝x+1的图象经过点（m，2），∴2＝m+1，∴m＝1．故答案为：1．考点二：一次函数之几何变换与求函数解析式知识回顾1.一次函数的平移：微专题①若函数进行左右平移，则在函数的自变量上进行加减。

一次函数经典题型+习题(精华,含答案)

-
.
2、直线 y=kx+b 的图像经过 A〔3，4〕和点 B〔2，7〕，
3、一次函数的图像与 y=2x-5 平行且与 x 轴交于点〔-2,0〕求解析式。
题型六、平移
方法：直线 y=kx+b 与 y 轴交点为〔0，b〕，直线平移那么直线上的点〔0，b〕也
会同样的平移，平移不改变斜率 k，那么将平移后的点代入解析式求出 b 即可。
直线 y=kx+b 向左平移 2 向上平移 3 <=> y=k(x+2)+b+3;〔“左加右减，上加
下减〞〕。
1. 直线 y=5x-3 向左平移 2 个单位得到直线
。
2. 直线 y=-x-2 向右平移 2 个单位得到直线
3. 直线 y= 1 x 向右平移 2 个单位得到直线 2
4. 直线 y= 3 x 2 向左平移 2 个单位得到直线 2
3．在函数 y x 2 中，自变量 x 的取值范围是__________. x3
4．一次函数 y＝kx＋b 中，k、b 都是
，且 k ，自变量 x 的取值范围
是
，当 k ，b 时它是正比例函数．
5． y (m 3)xm28 是正比例函数，那么 m
．
6．函数 y (m 2)x 2n1 m n ，当 m=
4
A
3
2
1
0
1
2
3
4
B
6. 如图，点 A〔2，4〕，B〔-2，2〕，C〔4，0〕，求△ABC 的面积。
-
.
【一次函数习题】
一、填空题 1．函数 y 1 2x ，x＝__________时，y 的值时 0，x=______时，y 的值是 1；