5.1数组的类型定义
第05章数组和自定义类型

求元素和
通过循环将每个元素进行累加。
求数组中最小元素 假设第一个元素为最小,然后将 该数与其他元素逐一比较,若发现小于最小值,就用新 值替换最小值,同时记录下标值。 求最大值的方法与求最小值相似。
本章目录
5.2 数组的基本操作
5、交换元素
下标 初值 0 1 2 3 4 5 6 7 8 9
26 43 61 87 33 19 37 59 76 69
5.4 自定义数据类型及数组
数组能够存放性质相同的数据。但自定义数 据类型可以是不同数据类型的集合。
5.4 自定义数据类型及数组
一组不同类型变量的集合。相当于C语言中 的结构体;Pascal中的记录类型。
1.自定义类型的定义
Type 自定义类型名 元素名[(下标)] As 类型名 … [元素名[(下标)] As 类型名] End Type
可以多次使用ReDim来改 变数组的大小,也可以改变 数组的维数,但不允许改变 数组的数据类型
5.1.3 动态数组及声明
例5.2 编一个程序,显示有n个数的非波那契数序列
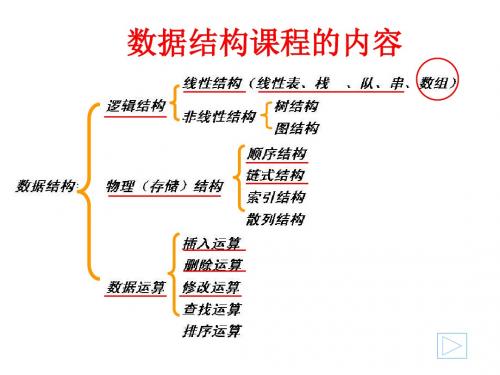
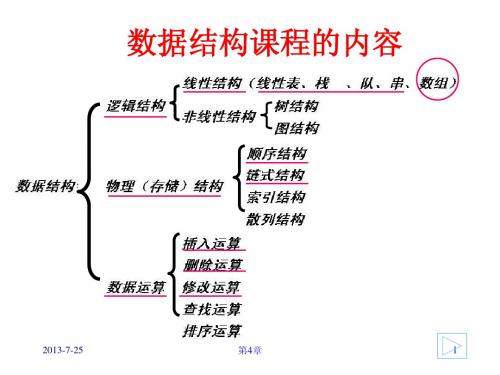
第五章 数组和自定义类型
5.1 数组
5.2 数组的基本操作 5.3 列表框和组合框控件 5.4 自定义类型及其数组 5.5 综合应用 5.6 数组中常见错误
(1)选择法排序 基本思想:每次在若干个无序Байду номын сангаас中找最小 (大)数,并放在相应的位置。 选择法演示
例5.5 对已知存放在数组中的6个数,用选择 法按递增顺序排序。
(2)冒泡法排序
冒泡法演示
本章目录
5.2 数组的基本操作
7、插入数据 数据插入演示
8、删除数据
数据删除演示
本章目录
数据结构 5数组和广义表A
1 Status Locate(Array A,va_list ap,int &off) 2{ 3 //若ap指示的各下标值合法,则求出该元素在A中,相对地
址off
4 off=0; 5 for(i=0;i<A.dim;++i) 6 { 7 ind=va_arg(ap,int); 8 if(ind<0||ind>A.bounds[i]) return OVERFLOW; 9 off+=A.constants[i] *ind; 10 } 11 return OK; 12 }
行数 总列数,即 第2维长度 元素个数
ij
补充:计算二维数组元素地址的通式
设一般的二维数组是A[c1..d1, c2..d2],这里c1,c2不一定是0。
单个元素 长度
二维数组列优先存储的通式为: LOC(aij)=LOC(ac1,c2)+[(j-c2)*(d1-c1+1)+i-c1)]*L
6
例1〖软考题〗:一个二维数组A[1..6, 0..7],每个数组元素
16
5.4
1、定义:
广义表的定义
广义表是线性表的推广,也称为列表(lists) 记为: LS = ( a1 , a2 , ……, an ) 广义表名 表头(Head) 表尾 (Tail) n是表长
在广义表中约定:
① 第一个元素是表头,而其余元素组成的表称为表尾; ② 用小写字母表示原子类型,用大写字母表示列表。
13
1 Status Value(Array A,ElemType &e,…){ 2 //A是n维数组,e为元素变量,随后是n个下标值,若各下
标不超界,则e赋值为所指定的A的元素值,即将指定元素值 读到e变量中。
C51的数据类型

C51的数据类型引言概述:C51是一种常用的单片机型号,它具有丰富的数据类型,这些数据类型在嵌入式系统中具有重要的作用。
本文将详细介绍C51的数据类型,包括基本数据类型、指针类型、数组类型、结构体类型以及枚举类型。
一、基本数据类型1.1 位类型(bit):C51提供了位类型,用于表示一个二进制位的数据。
位类型可以用于节省内存空间,特别适用于对一个变量的各个位进行操作的场景。
1.2 字符类型(char):C51的字符类型用于表示一个字符的数据,它占用一个字节的内存空间。
字符类型可以用于表示ASCII码字符,也可以用于表示整数。
1.3 整数类型(int):C51的整数类型用于表示整数数据。
根据不同的编译器和硬件平台,整数类型的长度可以不同,一般为2个字节或4个字节。
二、指针类型2.1 指针类型(*):C51的指针类型用于表示一个变量的地址。
通过指针类型,可以实现对变量的间接访问,提高程序的灵活性和效率。
2.2 空指针(NULL):C51提供了空指针常量NULL,用于表示一个无效的指针。
空指针在程序中常用于初始化指针变量或判断指针是否有效。
2.3 指针运算:C51支持指针的运算,包括指针的加法、减法和比较运算。
指针运算可以用于实现数组的访问和遍历。
三、数组类型3.1 一维数组:C51的一维数组用于存储相同类型的数据,可以通过下标访问数组元素。
一维数组在嵌入式系统中广泛应用,用于存储大量的数据。
3.2 多维数组:C51的多维数组是一种特殊的一维数组,它可以存储多维的数据。
多维数组可以用于表示矩阵、图像等复杂的数据结构。
3.3 字符串数组:C51的字符串数组是一种特殊的字符数组,用于存储字符串数据。
字符串数组在嵌入式系统中常用于存储文本信息。
四、结构体类型4.1 结构体定义:C51的结构体类型用于表示一组相关的数据,可以包含不同类型的成员变量。
通过结构体类型,可以方便地组织和操作复杂的数据结构。
4.2 结构体成员访问:C51使用点操作符(.)来访问结构体的成员变量。
C51的数据类型

C51的数据类型标题:C51的数据类型引言概述:C51是一种常用的单片机,对于程序员来说,了解C51的数据类型是非常重要的。
本文将详细介绍C51的数据类型,包括基本数据类型、派生数据类型、数组、结构体和枚举类型。
一、基本数据类型1.1 位类型(bit):C51中的位类型只能存储0或1,用于表示逻辑真假。
1.2 无符号整型(unsigned int):用于表示正整数,范围为0~65535。
1.3 有符号整型(int):用于表示带符号的整数,范围为-32768~32767。
二、派生数据类型2.1 字符型(char):用于表示一个字符,范围为-128~127。
2.2 浮点型(float):用于表示带有小数点的数值,精度较高。
2.3 双精度型(double):用于表示双精度浮点数,精度更高。
三、数组3.1 一维数组:用于存储相同类型的数据,通过下标访问数组元素。
3.2 多维数组:可以是二维、三维甚至更高维度的数组,用于存储复杂的数据结构。
3.3 数组名:数组名是数组的首地址,可以用来访问数组元素。
四、结构体4.1 结构体定义:用于存储不同类型的数据,通过成员名访问结构体成员。
4.2 结构体数组:可以定义结构体数组,每个元素都是一个结构体变量。
4.3 结构体指针:可以定义指向结构体的指针,方便对结构体成员进行操作。
五、枚举类型5.1 枚举定义:用于定义一组有序的常量,方便程序员使用。
5.2 枚举变量:可以定义枚举变量,取值为定义的枚举常量。
5.3 枚举类型转换:可以将枚举类型转换为整型,方便进行运算。
结论:通过本文的介绍,读者可以更加深入地了解C51的数据类型,包括基本数据类型、派生数据类型、数组、结构体和枚举类型。
掌握这些知识可以帮助程序员更好地编写C51程序,提高代码的质量和效率。
希望本文能对读者有所帮助。
Chapter05_数组和广义表_数据结构(C语言版)_严蔚敏_配套ppt课件

M
1 1 2 3 3 4
1 5 3 1 2 4
3 7 -1 -1 -2 2
N
1 1 2 3 4 5
1 3 3 2 4 1
3 -1 -2 -1 2 7
行列下 标调换
1 5 3 1 2 4
1 1 2 3 3 4
3 7 -1 -1 -2 2
按行下 标排序
法1:
按照矩阵M的列序进行转置,即按三元组A的 第二个字段值(列下标)由小到大的顺序进行转置。 为了找到M中每一列中所有的非零元素,需要对其 三元组表a.data从第一行起整个扫描一遍,由于 a.data是以M的行序为主序来存放每个非零元素 的,对于M中具有相同列下标的非零元来讲,先扫 描到的非零元的行下标一定小于后扫描到的非零元 的行下标,由此得到的恰是b.data应有的顺序。
• 压缩的含义
– 为多个值相同的元素只分配一个存贮空间; – 零元素不分配或少分配存贮空间。
• 特殊矩阵:元素值相同或零元素分布有 一定规律的矩阵。 • 稀疏矩阵:元素值相同或零元素分布没 有规律的矩阵。 • 特殊矩阵的压缩存贮实际是将二维数组 的数据元素压缩到一维数组上。
特殊矩阵的压缩存储
特殊矩阵: 非零元在矩阵中的分布有一定规则
常用的稀疏矩阵的存储方法
三元组表示法 顺序存储 行逻辑联接的顺序表 带辅助行向量的二元组表示法 伪地址表示法 带行指针向量的单链表示法 链接存储 散列存储 行列表示法(十字链表) 多链表示法(正交表)
顺序存储
1、三元组表示法 用一个线性表来表示稀疏矩阵,线性表的每个 结点对应稀疏矩阵的一个非零元素。其中包括三个 域,分别为该元素的行下标、列下标和值。结点间 的先后顺序按矩阵的行优先顺序排列(跳过零元 素),将线性表用顺序的方法存储在连续的存储区 里。
C51常用数据类型

C51常用数据类型引言:C51是一种广泛应用于嵌入式系统开发的微控制器,其数据类型对于程序的正确性和效率至关重要。
本文将介绍C51常用的数据类型,包括整型、浮点型、字符型、数组和结构体,并探讨它们的特点和适用场景。
正文内容:1. 整型数据类型1.1 无符号整型(unsigned int):用于表示非负整数,范围为0到2^16-1。
1.2 有符号整型(signed int):用于表示正负整数,范围为-2^15到2^15-1。
1.3 短整型(short int):用于表示较小范围的整数,范围为-2^7到2^7-1。
1.4 长整型(long int):用于表示较大范围的整数,范围为-2^31到2^31-1。
1.5 位域(bit):用于表示单个位的数据,可用于节省内存空间。
2. 浮点型数据类型2.1 单精度浮点数(float):用于表示小数,范围为3.4E-38到3.4E+38,精度为6位小数。
2.2 双精度浮点数(double):用于表示更大范围和更高精度的小数,范围为1.7E-308到1.7E+308,精度为15位小数。
3. 字符型数据类型3.1 字符(char):用于表示单个字符,范围为-128到127,可用于表示ASCII 码。
3.2 字符串(string):用于表示一串字符,以'\0'结尾,可用于存储文本数据。
4. 数组4.1 一维数组:用于存储一组具有相同数据类型的元素,可通过索引访问各个元素。
4.2 二维数组:用于存储表格数据,具有行和列的结构,可通过行列索引访问各个元素。
4.3 多维数组:用于存储更复杂的数据结构,可通过多个索引访问各个元素。
5. 结构体5.1 结构体(struct):用于自定义数据类型,可将不同类型的数据组合成一个整体。
5.2 结构体成员:用于定义结构体内部的各个数据成员,可以是各种数据类型。
5.3 结构体数组:用于存储多个结构体对象,可通过索引访问各个对象。
C51数据类型

C51数据类型引言概述:C51是一种广泛应用于嵌入式系统开辟的单片机编程语言,其中数据类型是程序设计中非常重要的组成部份。
正确理解和使用C51数据类型可以匡助程序员更高效地开辟嵌入式系统。
本文将详细介绍C51数据类型的相关知识。
一、基本数据类型1.1 位(bit):C51中最小的数据单位是位,用于表示二进制数据。
1.2 字节(byte):一个字节由8位组成,是C51中最基本的数据类型。
1.3 整型(int):C51中整型数据类型可以表示整数值,包括有符号和无符号整型。
二、浮点数据类型2.1 单精度浮点数(float):C51支持单精度浮点数,用于表示小数值。
2.2 双精度浮点数(double):C51也支持双精度浮点数,提供更高的精度。
2.3 浮点数据类型在嵌入式系统中通常用于处理需要高精度计算的场景。
三、数组数据类型3.1 一维数组:C51支持一维数组,可以存储相同类型的多个数据。
3.2 多维数组:除了一维数组,C51还支持多维数组,可以存储更复杂的数据结构。
3.3 数组数据类型在嵌入式系统中常用于存储传感器数据、采样数据等。
四、结构体数据类型4.1 结构体:C51支持结构体数据类型,可以将不同类型的数据组合在一起。
4.2 结构体成员:结构体可以包含多个成员变量,每一个成员变量可以是不同的数据类型。
4.3 结构体数据类型在嵌入式系统中常用于定义复杂的数据结构、数据包等。
五、枚举数据类型5.1 枚举:C51支持枚举数据类型,用于定义一组有限的命名常量。
5.2 枚举值:枚举类型中的每一个值都有一个对应的整数值。
5.3 枚举数据类型在嵌入式系统中常用于定义状态、标志位等。
结论:正确理解和使用C51数据类型对于嵌入式系统开辟至关重要。
程序员应该熟悉各种数据类型的特点和用法,合理选择适合的数据类型,以提高程序的效率和可靠性。
希翼本文对读者有所匡助,谢谢阅读。
数组的定义

二、数组的基本操作
1. 初始化 InitArray(A,n,bound1,…,boundn )
如果维数n和各维长度合法,则构造相应数组A,并 且返回1
2. 销毁
Destroyarray(A)
销毁已存在的数组A
3. 取值
Getarray(A,e,index1,…,indexn)
如果各下标不超界,则e被赋值为所指定的A的元素值, 并且返回1
5.3.1 特殊矩阵的压缩存储
一、对称矩阵 在一个n阶方阵A中,若元素满足下述性质: aij=aji ,0≦i,j≦n-1, 则称A为对称矩阵。 对称矩阵中的元素关于主对角线对称,故只要存储矩阵
中上三角或下三角中的元素,让每两个对称的元素共享一 个存储空间,这样,能节约近一半的存储空间。
不失一般性,我们按“行优先顺序”存储主对角线(包 括对角线)以下的元素。在这个下三角矩阵中,第i行恰 有i+1个元素,元素总数为:n(n+1)/2.
{
int p,q,col;
b->mu=a->nu; b->nu=a->mu; b->tu=a->tu;
if (b->tu)
{ q=0; for (col=0;col<a->nu;++col ) for (p=0;p<a->tu;++p )
//扫描A的所有列 //扫描所有非零元
if (a->data[p].j==col)
for(col=0;col<n;col++)
for(row=0;row<m;row++)
b[col][row]=a[row][col]; //其时间复杂度为0(nu×mu)
第5章演示

对称矩阵的压缩存储
(2)压缩存储: ③数组Sa中的元素与矩阵元素aij存在着一一对应的 关系。 假设数组元素Sa[k]中存放的是矩阵元素aij,则它们 之间的对应关系实质上就是下标值k和i、j之间的对应 关系。
对称矩阵的压缩存储的下标转换公式为:
i(i-1)/2+(j-1),当i>=j k= j(j-1)/2+(i-1),当i<j
稀疏矩阵
3、稀疏矩阵的存储结构 (2)算法:将矩阵M转置为矩阵T
M.data M.data[1] 1 2 12 M.data[2] 1 3 9 M.data[3] 3 M.data[4] 3 M.data[5] 4 M.data[6] 5 M.data[7] 6 M.data[8] 6 1 6 3 -3 14 24 T.data T.data[1] 1 3 -3 T.data[2] 1 6 15
稀疏矩阵的三元组表表示法节约了存储空间, 实现了压缩存储。
稀疏矩阵
注意:
稀疏矩阵 唯一 三元组表
不唯一
解决办法:在三元表的基础上,再引入总行数、 总列数和非零元素总个数即可。
稀疏矩阵
3、稀疏矩阵的存储结构 (1)三元组顺序表 以顺序存储结构表示的三元组表。 三元组类型定义: typedef struct { int i,j; elemtype e; }Triple;
5.4 广义表的定义
二、表示 (1)用关系定义表示; (2)用图表示。 说明: ①广义表是一个多层次结构; ②广义表之间可以共享; ③广义表可以递归定义; ④表头可以为原子或子表;表尾只能为子表; ⑤( )与( ( ) )不同。
5.4 广义表的定义 A =( ) B =(e) C =(a, (b,c,d)) D =(A, B, C) E =(a, E) F =(( ))
数组(Array)

//包含setw()
#include <stdlib.h>
typedef int DataType;
#include "SeqSynmeMatrix.h"
void main(void)
{ SeqSynmeMatrix matrixA(10), matrixB(10);
DataType a[] = {1,4,7,4,5,8,7,8,9};
a = (T**)new T[row]; //强制类型转换运算符
for( i = 0; i < m; i++)
a
{ a[i] = new T[n]; }
0
return a;
1
}
.
.
.
.
void main(void)
.
.
{ int **a;
m-1
a=Make2DArray<int>(3, 4);
0 1 …… n-1
a 0 a11
1 a12
… … 第1行 j-1 a1j
……
n-1 a1n
n a21
n+1 a22
… a2j
第2行
…
…
a2n …
ai1
ai2
k
… aij
第i行
…
ain
…
…
am1 am2
… amj
第m行
…
mn-1 amn
5.3 数组的应用——特殊矩阵的压缩存储
特殊矩阵:值相同的元素或零元素在矩阵中的分 布有一定规律。
Amn
ai1
a12 … a1 j … a1,n
a22 …
a2 j
C51常用数据类型

C51常用数据类型引言概述:C51是一种广泛应用于嵌入式系统开辟的单片机系列,其常用数据类型对于程序的编写和数据处理起着重要的作用。
本文将详细介绍C51常用的数据类型及其特点,包括基本数据类型、数组类型、结构体类型、指针类型和枚举类型。
正文内容:1. 基本数据类型1.1 位数据类型:C51提供了位数据类型bit,用于表示一个二进制位,可以进行逻辑运算和位操作。
1.2 字符数据类型:C51中的字符数据类型char用于表示一个字符,可以进行字符操作和ASCII码的转换。
1.3 整数数据类型:C51提供了不同长度的整数数据类型,如unsigned char、unsigned int和unsigned long,用于表示不同范围的整数。
2. 数组类型2.1 一维数组:C51支持一维数组,可以存储一组相同类型的数据,通过索引访问数组元素。
2.2 二维数组:C51还支持二维数组,可以存储表格型数据,通过两个索引访问数组元素。
2.3 多维数组:C51还支持多维数组,可以存储多维表格型数据,通过多个索引访问数组元素。
3. 结构体类型3.1 定义结构体:C51允许定义结构体类型,结构体可以包含多个不同类型的成员变量,用于表示复杂的数据结构。
3.2 访问结构体成员:通过结构体变量和成员运算符“.”,可以访问结构体的各个成员变量。
3.3 结构体作为函数参数:结构体可以作为函数的参数传递,方便地传递和处理复杂的数据结构。
4. 指针类型4.1 定义指针变量:C51支持指针类型,可以定义指向不同类型的指针变量。
4.2 指针的运算:指针可以进行运算,如指针的加减运算、指针与整数的运算等。
4.3 指针的应用:指针在C51中有广泛的应用,如动态内存分配、数组和字符串的处理等。
5. 枚举类型5.1 定义枚举类型:C51支持枚举类型,可以定义一组具有相同属性的常量。
5.2 枚举常量的使用:通过枚举类型定义的常量可以直观地表示某种状态或者选项。
数据结构第五章
5.3.1 特殊矩阵
是指非零元素或零元素的分布有一定规律的矩阵。
1、对称矩阵 在一个n阶方阵A中,若元素满足下述性质: aij = aji 0≦i,j≦n-1 则称A为对称矩阵。
对称矩阵中的元素关于主对角线对称,故只 要存储矩阵中上三角或下三角中的元素,这样, 能节约近一半的存储空间。
2013-7-25 第4章 18
5.3 矩阵的压缩存储
在科学与工程计算问题中,矩阵是一种常用 的数学对象,在高级语言编制程序时,常将 一个矩阵描述为一个二维数组。 当矩阵中的非零元素呈某种规律分布或者矩 阵中出现大量的零元素的情况下,会占用许 多单元去存储重复的非零元素或零元素,这 对高阶矩阵会造成极大的浪费。 为了节省存储空间,我们可以对这类矩阵进 行压缩存储:
5.2 数组的顺序表示和实现 由于计算机的内存结构是一维的, 因此用一维内存来表示多维数组,就必 须按某种次序将数组元素排成一列序列 ,然后将这个线性序列存放在存储器中 。 又由于对数组一般不做插入和删除 操作,也就是说,数组一旦建立,结构 中的元素个数和元素间的关系就不再发 生变化。因此,一般都是采用顺序存储 的方法来表示数组。
即为多个相同的非零元素只分配一个存储空间; 对零元素不分配空间。
课堂讨论: 1. 什么是压缩存储? 若多个数据元素的值都相同,则只分配一个元素值的 存储空间,且零元素不占存储空间。 2. 所有二维数组(矩阵)都能压缩吗? 未必,要看矩阵是否具备以上压缩条件。 3. 什么样的矩阵具备以上压缩条件? 一些特殊矩阵,如:对称矩阵,对角矩阵,三角矩阵, 稀疏矩阵等。 4. 什么叫稀疏矩阵? 矩阵中非零元素的个数较少(一般小于5%)
通常有两种顺序存储方式:
⑴行优先顺序——将数组元素按行排列,第i+1个行 向量紧接在第i个行向量后面。以二维数组为例,按 行优先顺序存储的线性序列为: a11,a12,…,a1n,a21,a22,…a2n,……,am1,am2,…,amn 在PASCAL、C语言中,数组就是按行优先顺序存 储的。 ⑵列优先顺序——将数组元素按列向量排列,第j+1 个列向量紧接在第j个列向量之后,A的m*n个元素按 列优先顺序存储的线性序列为: a11,a21,…,am1,a12,a22,…am2,……,an1,an2,…,anm 在FORTRAN语言中,数组就是按列优先顺序存储的。
教案5.1数值型数组(一)
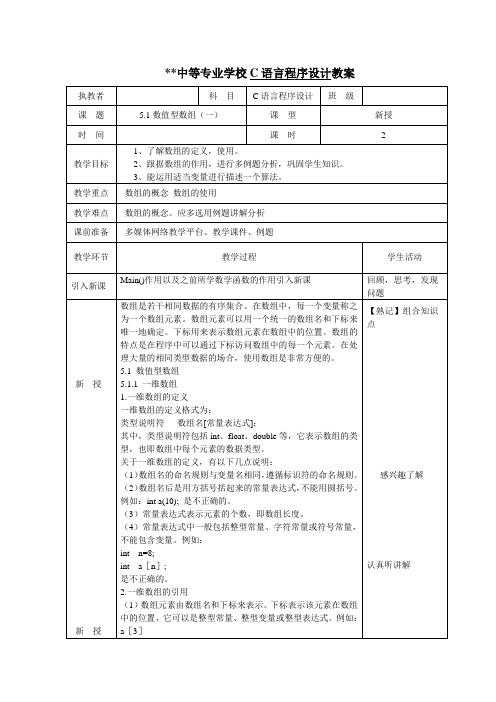
**中等专业学校C语言程序设计教案执教者科目C语言程序设计班级课题 5.1数值型数组(一)课型新授时间课时 2教学目标1、了解数组的定义,使用。
2、跟据数组的作用,进行多例题分析,巩固学生知识。
3、能运用适当变量进行描述一个算法。
教学重点数组的概念数组的使用教学难点数组的概念。
应多选用例题讲解分析课前准备多媒体网络教学平台、教学课件、例题教学环节教学过程学生活动引入新课Main()作用以及之前所学数学函数的作用引入新课回顾,思考,发现问题新授新授数组是若干相同数据的有序集合。
在数组中,每一个变量称之为一个数组元素。
数组元素可以用一个统一的数组名和下标来唯一地确定。
下标用来表示数组元素在数组中的位置。
数组的特点是在程序中可以通过下标访问数组中的每一个元素。
在处理大量的相同类型数据的场合,使用数组是非常方便的。
5.1 数值型数组5.1.1 一维数组1.一维数组的定义一维数组的定义格式为:类型说明符数组名[常量表达式];其中,类型说明符包括int、float、double等,它表示数组的类型,也即数组中每个元素的数据类型。
关于一维数组的定义,有以下几点说明:(1)数组名的命名规则与变量名相同,遵循标识符的命名规则。
(2)数组名后是用方括号括起来的常量表达式,不能用圆括号。
例如:int a(10); 是不正确的。
(3)常量表达式表示元素的个数,即数组长度。
(4)常量表达式中一般包括整型常量、字符常量或符号常量,不能包含变量。
例如:int n=8;int a[n];是不正确的。
2.一维数组的引用(1)数组元素由数组名和下标来表示。
下标表示该元素在数组中的位置,它可以是整型常量、整型变量或整型表达式。
例如:a[3]【熟记】组合知识点感兴趣了解认真听讲解a[3+2](2)C语言规定:数组元素下标从0开始,最大下标为数组长度减1。
例如:int a[5];数组a中有5个元素:a[0],a[1],a[2],a[3],a[4]。
vb第五章 数组

5.2 数组的基本操作
VB不允许对数组整体操作,例如: Dim A(2,3) As Integer A=2 不允许! 只能对数组元素进行操作,例如: A(1,1)=1 A(1,3)=2 A(2,2)=A(1,1)*2+A(1,3)
25
一、数组元素的赋值
1、用赋值语句给数组元素赋值 例如:A(1,1)=1 A(1,2)=5 2、通过循环语句给数组元素赋值 例如: For I=1 To 10 A(I)=Int(100*Rnd)+1 Next I 该循环语句产生10个100以内的随机整数,存 入数组A中。
22
For Each –Next举例(一维数组的使用) P90例
运行结果: Option base 1 14 21 28 35 42 49 Private Sub Form_Click() 56 63 Dim A(12) As Integer, V As Variant 70 77 84 91 Dim I%, Js% Js = 0 Js = 14 For Each V In A For I = 1 To 12 Js = Js + 1 A(I) = Js Print V; If Js Mod 6 = 0 Then Print Js = Js + 7 输出每行 Next V Next I 6个元素 Print End Sub
数组是具有相同数据类型的多个 值的集合,数组的所有元素按一定顺 序存储在连续的存储单元中。
14
一维数组的结构
逻辑结构 内存的存 放次序
StrA(0) StrA(1) StrA(2) StrA(3) StrA(4) StrA(5) StrA(6) StrA(7) StrA(8)
存储结构
零基础学单片机C语言程序设计 第5章 C51的数据结构

5.1 C51的数组
数组是把若干具有相同数据类型的变量按有序的形式组织 起来的集合。其中,数组中的每个变量称为数组元素。数 组属于聚合数据类型。一个数组可以包含多个数组元素, 这些数组元素可以是基本数据类型,也可以是聚合数据类 型。
在C51语言中,按照数组元素所属的基本数据类型,数组 可分为数值数组、字符数组、指针数组、结构数组等。其 中,指针数组将在指针部分再作介绍,结构数组将在结构 部分再作介绍。
1.指向一维数组的指针
2.指向二维数组的指针
3.指向一个由n个元素所组成的数组指针
4.指针和数组的关系
5.2.7 C51的指针数组
指针数组是同一数据类型的指针作为元素构成的数组。指 针数组中的每个数组元素都必须是指针变量。指针数组的 定义格式如下:
类型标识符 *数组名[常量表达式]; 其中,类型标识符是指针数组的类型,“[]”内的常量表
2.指针变量赋值
在C51语言中,变量的首地址是由编译系统自动分配,因此 用户不知道变量在内存中的具体地址。为了获得变量的地 址,C51语言中提供了地址运算符“&”,可以获取变量的 首地址。
&变量名
5.2.3 取址运算符和取值运算符
通过指针变量来访问其所指向的变量,需要首先定义该指
针变量。在程序中使用指针变量时,常有用到与指针变量
定义的一般形式为: 类型说明符 数组名 [常量表达式],……; 2.数组元素表示 数组元素,即数组中的变量,是组成数组的基本单元。在C51中,数组
元素是变量,其标识方法为数组名后跟一个下标。数组元素通常也称 为下标变量。数组元素表示的一般形式为:
数组名[下标]
5.1.2 一维数组
一维数组是指只有一个下标标号的数组。一维数组是一个 由若干同类型变量组成的集合,引用这些变量时可用同一 数组名。一维数组在存放时占用连续的存储单元,最低地 址对应于数组的第一个元素,最高地址对应于最后一个元 素。
C语言中的数组

int x[10]={1,2,3,4,5};
若只声明数组,而不为数组赋值,则数组中的元素值是不确定的 int x[10];
C语言数组的大小只能是常量,而不能使用变量
下面的代码是不合法的: int i=100; int a[i];
5.3.3 一维数组的引用
在C语言中,一维数组的引用其实就是对一维数组 元素的使用。一维数组的引用形式以及相关举例如 图5.8所示。
5.5.1 字符数组的声明和定义
概念 结束标志 存储形式
在C语言中,由若干字符组成的序列称为字符串 字符串一般以’\0’作为结束标志 字符串不能用一个变量存放,必须用字符数组来存放
5.5.1 字符数组的声明和定义
'h' ‘e’ ‘l’ ‘l’ ‘o’ \0
字符串的开端
字符串的结束
5.5.1 字符数组的声明和定义
一维数组是长度固定的数组,其存储空间是一片连 续的区域。本节将讲解一维数组的概念及其应用。
5.3.1 一维数组的声明和定义
声明数组是告诉编译器,数组名所使用的标识符。 数组的定义是令系统为该数组分配内存空间。在C 语言中,数组的声明和定义是同时进行的。
数据类型
数组名[长度];
长度是指一维数组 的存储变量的个数
5.2 数组的来源
前面章节中讲解的C语言的基本数据类型只能处理 一些简单的数据类型,如果遇到复杂的具有相同类 型的多个数据那么就很难解决。幸好,C语言提供 了数组来解决了这一个问题。
5.2 数组的来源
基本数据类型实现代码
#include <stdio.h> int mian() {
一维数组实现代码
可以对部分元素赋初值,而在每行的其他元素 的值为0或者为’\0’
《C语言程序设计》课件 第五章 数组

a(5948)
a[2](5964) a[1](5956) a[0](5948) 图 5-10
a[2][1] (5968) a[2][0] (5964) a[1][1] (5960) a[1][0] (5956) a[0][1] (5952) a[0][0](5948)
return 0;
}
5.1.4一维数组程序举例
3.用选择法对输入的n个学生的单科成绩进行 从小到大排序。
编程思路: 直接选择排序的过程是:首先在所有数据中找出值 最小(最大)的数据,把它与第1个数据交换,然后 在其余的数据中找出值最小(最大)的数据,与第2 个数据交换......依次类推,这样,n个数据经过n-1轮 交换后可得到有序结果。
printf("%3d ",a[i]); printf("\n"); return 0; }
5.1.3 一维数组的初始化 5.1.3 一维数组的初始化
数组初始化常见的格式:
1.用大括号括起来的常量表达式列表,常量表达式 之间用逗号进行分隔: int a[10]={1,2,3,4,5,6,7,8,9,10};
注意:
不要将a[i][j]写成a[i,j],否则编译系统会将逗号分隔 符作为逗号运算符处理,即将a[i,j]视为a[j]。
5.2.2二维数组元素的引用
可以将二维数组看成是特殊的一维数组。
例如,二维数组a[3][2]可以看成是长度为3的一维数组, 所含的3个数组元素分别为:a[0]、a[1]、a[2]
for(i=0;i<3;i++) for(j=0;j<5;j++)
数据结构第五章 数组和广义表

5.3.1
特殊矩阵
1、对称矩阵 在一个n阶方阵A中,若元素满足下述性质: aij = aji 1≤i,j≤n 则称A为对称矩阵。 a11 1 5 1 3 7 a21 a 22 5 0 8 0 0 a31 a32 a33 1 8 9 2 6 ……………….. 3 0 2 5 1 an 1 a n 2 a n 3 …a n n 7 0 6 1 3
第5章
数组和广义表
5.1 数组的定义
5.2 数组的顺序表示和实现
5.3 矩阵的压缩存储
5.3.1 特殊矩阵
5.3.2 稀疏矩阵
5.4 广义表的定义
5.1 数组的定义
数组-----线性表的扩展 A =(a0,a1,a2,…,an-1)
a00 a10 ┇ Am×n= ai0 ┇ am-1,0 a01 … a0j … a11 … a1j … ┇ ai2 … aij … ┇ am-1,2 … am-1,j … a0,n-1 a1,n-1 ai,n-1 am-1,n-1 α0 α1 ┇ Am×n= α i ┇ α m-1
Assign( &A, e, index1, ..., indexn) 赋值操作 初始条件:A是n维数组,e为元素变量,随后是n个下标值。 操作结果:若下标不超界,则将e的值赋给所指定的A的元 素,并返回OK。 对于数组来说一旦维数确定了,每个元素的下标确定了, 那么整个数组就确定了,这样的一个数组结构除了能改变 某元素的值,其他的不能再改变。
5.2 数组的顺序表示和实现
数组类型特点: 1) 只有引用型操作,没有加工型操作; 2) 数组是多维的结构,而存储空间是一个一维的结构。 有两种顺序映象的方式。
有两种顺序映像方法: 1)以行序为主序(行优先,先行后列):先存储行号较小 的元素,行号相同者先存储列号较小的元素;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Col = M.data[p].j; q = cpot[col];//转置后的位置 T.data[q].i = M.data[p].j; T.data[q].j = M.data[p].i; T.data[q].e = M.data[p].e; ++cpot[col]//第col列下一非零元的位置
一、三元组顺序表 二、行逻辑联接的顺序表 三、十字链表
24
一、三元组顺序表
#define MAXSIZE 12500 typedef struct { int i, j; //该非零元的行下标和列下标 ElemType e; // 该非零元的值 } Triple; // 三元组类型 typedef union { Triple data[MAXSIZE + 1]; int mu, nu, tu; } TSMatrix; // 稀疏矩阵类型
v 14 -5 -7 36 28
v 36 14 -7 28 -5
M
行列值互换
思路一
i 2 5 2 1 4 j 1 1 2 3 3 v 14 -5 -7 36 28
按行优先重排 三元组次序
T
30
思路二
按照M.data中三元组的次序进 行转置,并将转置后置入T中恰当的 位置。要找到这个恰当位置,必须 预先知道M中每一列的非零元在T中 的位置。
素存储位置的映象关系
LOC(j1, j2, ..., jn ) = LOC(0,0,...,0) + ∑ c j i i =1 i
n
其中 cn = L,ci-1 = bi ×ci , 1 < i n。
称为 n 维数组的映象函数。数组元素
的存储位置是其下标的线性函数
12
课堂练习
• 假设c语言中有二维数组A6×8,每个元素用 相邻的6个字节存储,存储器按字节编址。 已知A的起始存储位置为1000,计算: (1)数组A的体积(即存储量) (2)数组A的最后一个元素a57的第一个字 节的地址; (3)假设按行存储时,元素a14的第一个字 节的地址; (4)假设按列存储时,元素a47的第一个字 节的地址。
初始条件:A是n维数组,e为元素变量, 随后是n 个下标值。 操作结果:若下标不超界,则将e的值赋 给所指定的A的元素,并返回 OK。
9
5.2 数组的顺序表示和实现
类型特点: 1) 只有引用型操作,没有加工型操作; 2) 数组是多维的结构,而存储空间是 一个一维的结构。
有两种顺序映象的方式: 1)以行序为主序(低下标优先); 2)以列序为主序(高下标优先);
15
5.3 矩阵的压缩存储
何谓稀疏矩阵?
假设 m 行 n 列的矩阵含 t 个非零元素, 则称
mt n
为稀疏因子
通常认为 0.05 的矩阵为稀疏矩阵
16
怎样才能解决这些问题?
以常规方法,即以二维数组表示
高阶的稀疏矩阵时产生的问题: 1) 零值元素占了很大空间;
2) 计算中进行了很多和零值的运算, 遇乘法,白乘;遇除法,还需判别除数
ElemType value(RLSMatrix M, int r, int c) { p = M.rpos[r]; while (M.data[p].i==r &&M.data[p].j < c) p++; if (M.data[p].i==r && M.data[p].j==c) return M.data[p].e; else return 0; 时间复杂度为O(c) 接近于常数阶,具有一定随机存储特征 } // value
1 2 i n 1 i n 1 i n
3
二维数组的定义: 数据对象: D = {aij | 0≤i≤b1-1, 0 ≤j≤b2-1}
数据关系:
R = { ROW, COL }
ROW = {<ai,j,ai+1,j>| 0≤i≤b1-2, 0≤j≤b2-1}
COL = {<ai,j,ai,j+1>| 0≤i≤b1-1, 0≤ j≤b2-2}
32
Status FastTransposeSMatrix(TSMatrix M, TSMatrix &T){
T.mu = M.nu; T.nu = M.mu; T.tu = M.tu; if (T.tu) { for (col=1; col<=M.nu; ++col) num[col] = 0; for (t=1; t<=M.tu; ++t) ++num[M.data[t].j]; cpot[1] = 1; for (col=2; col<=M.nu; ++col) cpot[col] = cpot[col-1] + num[col-1]; for (p=1; p<=M.tu; ++p) { 转置矩阵元素 } } // if return OK; } // FastTransposeSMatrix 33
34
分析算法FastTransposeSMatrix的时 间复杂度:
for (col=1; col<=M.nu; ++col) … … for (t=1; t<=M.tu; ++t) … … for (col=2; col<=M.nu; ++col) … … for (p=1; p<=M.tu; ++p) … …
31
那么如何确定每一行的第一个非零 元在三元组中的位置?
1 1 2 3 3 2 15 5 -5 col 1 2 3 4 5 2 -7 Num[pos] 1 2 0 1 1 1 36 Cpot[col] 1 2 4 4 5 4 28 M的第col列的第一个非零元转置后在T的位置 cpot[1] = 1; for (col=2; col<=M.nu; ++col) cpot[col] = cpot[col-1] + num[col-1];
10
以“行序为主序”的存储映象
例如:
a0,0 a0,1 a0,2 a1,0 a1,1 a1,2
a0,0 a0,1 a0,2 a1,0 a1,1 a1,2
L
二维数组A中任一元素ai,j 的存储位置
LOC(i,j) = LOC(0,0) + (b2×i+j)×L
称为基地址或基址。
11
推广到一般情况,可得到 n 维数组数据元
22
三对角矩阵
将其3条对角线上的元素存于数组B[3n-2-1] 中,使得B[k] = A[i][j] ,A[i][j]与B[k] 的对应 关系如下(请推导):
k = f(i, j)= ? k=2i+j |i-j|<=1
k=1+ 3(i-1)+ (j-i+2) =2i+j
23
随机稀疏矩阵的压缩存储方法:
其时间复杂度为: O(mu×nu)
28
用“三元组”表示时如何实现? 1 1 2 3 3 2 14 5 -5 2 -7 1 36 4 28 M 1 2 2 4 5 3 36 1 14 2 -7 3 28 1 -5 T
29
i 1 1 2 3 3
i 1 2 2 4 5
j 2 5 2 1 4
j 3 1 2 3 1
37
为了便于随机存取任意一行 的非零元,则需知道每一行的第 一个非零元在三元组表的位置 (位序)。因此,可以将此指示 “行”信息的辅助数组固定在稀 疏矩阵的三元组表结构里面。
38
修改前述的稀疏矩阵的结构定义, 增加一个数据成员rpos, 其值在稀疏矩 阵的初始化函数中确定(目的是增加其 随机存储特性)。
M
0 0 36 14 7 0 0 0 0 0 0 28 5 0 0
T
27
用常规的二维数组表示时的算法
for (col=1; col<=nu; ++col)
for (row=1; row<=mu; ++row)
T[col][row] = M[row][col];
是否为零;
17
解决问题的原则:
1) 尽可能少存或不存零值元素;
2) 尽可能减少没有实际意义的运算;
3) 操作方便; 即: a.能尽可能快地找到与下标值(i,j) 对应的元素; b.能尽可能快地找到同一行或同 一列的非零值元;
18
有两类稀疏矩阵:
1) 特殊矩阵
非零元在矩阵中的分布有一定规则
例如: 三角矩阵
0<=(i,j)<n
②上三角矩阵中有A[i][j]与B[k] 的对应关 系如下:
k=i*(2*n-i+1)/2+j-i
0<=(i,j)<n
21
对称矩阵
满足性质:aij=aji 0<=(i, j)<=n 在存储时我们可以为每一对对称元素分 配一个存储空间,则可将n2个元素压缩 存储到n(n+1)/2个元的空间中。我们可以 参照下三角以行优先存储。 A[i][j]与B[k] 的对应关系如下: i*(i+1)/2+j 当i>=j ,0<=(i, j)<=n (下三角) k= j*(j+1)/2+i 当i<j, 0<=(i, j)<=n (上三角)
4
基本操作:
InitArray(&A, n, bound1, ..., boundn)
DestroyArray(&A)
Value(A, &e, index1, ..., indexn) Assign(&A, e, index1, ..., indexn)
