补充例题——等值电路、潮流计算
1.12 课程总结与例题分析—潮流计算

网络分类 1 开式网络(辐射网) 2 环形网络 (环式网络 和 两端供电网络) 电压质量指标: 电压降落、电压损耗、电压偏移、电压调整、 输电效率 运算负荷: 负荷功率、等值负荷功率、运算负荷 运算功率: 电源功率、等值电源功率、运算功率 循环功率 自然功率、经济功率(了解)
基本计算——辐射网
习题:
3-1,3-2**,3-3,3-4(第三问知原理即 可),3-6(若是额定功率的1/x时,该 如何简化计算该变压器损耗?),3-7 4-1,4-2,4-3,4-4,4-5,4-6,4-8
复杂电力系统示意图
动 力 系 统
电 电 力 网 系 统
课程内容结束! 谢谢 !
线路电压降落和功率损耗的计算; 电压降落的横分量和纵分量,及其表达式 (该表达式是否同时适用于相参数和线参 数?) 变压器电压降落和功率损耗的精确计算与 近似计算; 简单辐射网的潮流计算;
已知,末端电压、功率,求首端电压、功率 已知,首端电压、功率,求末端电压、功率 已知,首端电压、末端功率,求首端功率、末端 电压。(注意初始计算时末端电压的取值)
如何形成运算负荷和运算功率所表的简 化等值网络? 电压如何假设?变比如何假设?对地支 路损耗如何处理? 力矩法计算环形网络 确定功率分点
例题3
已知某环形网络如下图,其中各线路参数相同。 求网络中的初步功率分布,并找出功率分点。
100km
40km
20km 70km
70+j25(MVA)
80km
60+j10(MVA) 30+j6(MVA) 30+j10(MVA) 60km
70km
60+j11(MVA)
电力系统潮流计算

S 0 (GT jBT )U 2
注意单位! (4-29) (4-31)
双绕组变压器功率损耗计算
总的有功损耗:PT PTS P0 总的无功损耗:
QT QTS Q0
(一)电力网的功率损耗 ▪三绕组变压器的功率损耗计算
PT PTS1 PTS 2 PTS 3 P0 QT QTS1 QTS 2 QTS 3 Q0
开式电力网的潮流计算
解:
1)根据已知条件,进行各元件参数计算;
画出计算用等值电路:
已知量
待求量
2) 应用前述阻抗环节的功率、电压计算方法,由 末端往始端逐环节递推计算……
开式电力网的潮流计算
2)已知末端功率及始端电压,
求网络潮流分布
✓ 计算网络元件参数并作等值电路;
✓ 设全网为UN,从末端向始端逐段近似推算各元 件的功率损耗和功率分布;
➢ 给定网络始端(或末端)的功率及电压, 求潮流分布。(两种,但都属于已知为 同侧量)
➢ 给定网络末端功率及始端电压(或始端 功率及末端电压)求潮流分布。(两种, 但都属于已知为异侧量)
开式电力网的潮流计算 1)已知末端功率及电压,作潮流计算:
将电压和功率由末端向始端交替推进 ;
对于110KV及以下网络,可略去电压降落的 横分量,从而使计算简化;
电压的降落、损耗及偏移
输电系统其它相关技术经济指标: 电压损耗率% U1 U2 100 UN
始端电压偏移% U1 U N 100 UN
末端电压偏移% U 2 U N 100 UN
输电效率% P2 100 P1
二、开式电力网的潮流计算
简称”开式网”,可分为: ➢ 同一电压等级的开式网(无变压器) ➢ 多级电压开式网(含变压器)
1开式电力网潮流计算(答案)

1、开式电力网,由输电线路和降压变压器组成,降压变压器的额定电压为110/11kV ,归算到110kV 侧的等值电路如下图所示,末端负荷为20+j15MVA ,首端电压为113kV 。
其它参数如下:()Ω+=+5.205.8j jX R L L ;()S j B j 41082.22-⨯=; ()Ω+=+2.2022.1j jX R T T ;()MVA j S T 7.118.00+=∆∙。
试求潮流分布及各节点实际电压。
解:已知首端电压和末端功率,采用近似计算法。
先假设全网未知节点电压为额定电压,由于变压器参数归算至高压侧,故为110kV 。
潮流从末端推向首端,电压损耗及大小从首端推向末端。
(1)由末端负荷求功率分布变压器阻抗中的功率损耗).04.1j 06.0)2.20j 22.1(1101520)(22222323A MV jX R U Q P S T T N T (+=++=++=∙∆ 进入变压器绕组的功率:()MVA j j j S S S T 04.1606.2004.106.015203/2+=+++=+=∙∙∙∆进入变压器的功率: ()MVA j j j S S S T 74.1724.207.118.004.1606.200/22+=+++=+=∙∙∙∆线路首末端电容功率:()var 42.310*82.2*11024221M j j B jU Q N B -=-=-=- 线路环节末端功率: ()MVA j j j Q S S B 32.1424.2042.374.1724.2012//1+=-+=+=∙∙线路功率损耗:()MVA j j S L 06.144.0)5.205.8(11032.1424.20222+=++=∙∆∙//∙∙/∙3S L S ∆0T 2B j线路环节首端功率:()MVA j j j S S S L 38.1568.2006.144.032.1424.20//1/1+=+++=+=∙∙∙∆线路首端电容功率,因为线路首端电压已知,故()var 7.310*82.2*113242211M j j B jU Q B -=-=-=- 系统注入线路首端功率: ()MVA j j j Q S S B 96.1167.2042.338.1568.202/11+=-+=+=∙∙(2)由首端电压、首端功率求线路电压损耗,引起该损耗的功率为完全流过该支路的功率,即/1∙S()kV U X Q R P U LL L 35.41135.20*38.155.8*68.201/1/1=+=+=∆∙ ()kV U U U L 65.10835.411312=-=∆-=变压器电压降落为完全流过变压器绕组的功率即/2∙S 引起,故()kV U T 21.365.1082.20*04.1622.1*06.20=+=∆ 电压3U 为:()kV U U U T 44.10523=∆-=电压3U 归算到变压器低压侧:()kV k 544.10/44.105=。
电力线路的参数与等值电路以及潮流计算的简单介绍

规定最小直径
110KV—9.6mm 220KV—21.28mm 330KV—32.2mm 分裂导线 U2
103
S / km
电缆参数计算复杂,查手册
电力线路的参数与等值电路
二、电力线路的等值电路
一般线路的等值电路(正常运行时忽略g)
r1 jx1 r1 jx1 r1 jx1
两边同乘 e 3 j30 U U
U 1 U 2 U U 2 Z
e P Q 3 ( j30 2 j
)
2
U* 2
U 2 Z
3(P2 jQ2)
3e
j30
U* 2
U 2
Z
P2 jQ2 U* 2
**
U
U 1 U 2 Z
U U
20 2 100%
U20为线路末端空载电压
U2
三、功率损耗
线路、变压器存在阻抗和导纳,消耗P和Q 消耗能量,
产生热量,老化设备
1、线路中功率损耗的计算
S1 R+jX S 2
S L
1) 末端导纳中的损耗
QB 2
B 2
U2 2
U 1
1B 2
1B 2
U 2
2) 阻抗中的损耗
d
S RⅢ+ jX Ⅲ
Lc
S RⅡ + jXⅡ
Lb
RⅠ+ jXⅠ
a S La
11
c 11
b1 1
BⅢ 2
2 BⅢ
2 BⅡ 2 BⅡ
2 BⅠ 2 BⅠ
d
合并简化
S RⅢ+ jX Ⅲ Lc
电气

_电力系统潮流计算_大作业2015-7-4目录一、题目要求 (2)二解题步骤 (3)方法一:N-R法 (3)流程图 (3)源程序 (4)运行结果 (11)运算过程图示 (12)方法二P-Q解耦迭代法 (19)流程图 (19)三总结 (20)一、题目要求求解给定系统的潮流。
设发电机G1的端电压为1 p.u,发出的有功和无功可调;发电机G2的端电压为1 p.u.,按指定的有功P=0.5 p.u.发电,取ε=10^-4。
原始数据见表1和表2;系统等值电路见图1。
图1 系统等值电路表1 支路数据i j R X B/21 2 0.25 0.08 0.071 3 0.03 0.1 0.092 3 0.02 0.06 0.054 2 0 0.1905 1.05225 3 0 0.1905 1.0522表2 节点数据i U PG QG PD QD 类型1 待定0 0 0.8055 0.532 PQ2 待定0 0 0.18 0.12 PQ3 待定0 0 0 0 PQ4 1 0.5 待定0 0 PV5 1 待定待定0 0 Vθ二解题步骤解此题方法有两种其中有相同之处故此次报告着重阐述方法一,对于方法二步骤相同只是程序稍加改动在此不再冗述!方法一:N-R法流程图节点编号输入原始数据形成节点导纳矩阵设定初值,k=0计算失配功率△Pi,△QiMax{|△Pi,△Qi|}<εk=k+1 是否形成雅克比矩阵J解修正方程,得到U(k),Q(k)进行收敛后的有关计算输出结果牛顿—拉夫逊法潮流迭代框图源程序n=input('请输入节点数:n=');n1=input('请输入支路数:n1=');isb=input('请输入平衡节点号:isb=');pr=input('请输入误差精度:pr=');B1=input('请输入支路参数:B1=');B2=input('请输入节点参数:B2=');X=input('节点号和对地参数:X=');Y=zeros(n);Times=1; %置迭代次数为初始值%创建节点导纳矩阵for i=1:n1if B1(i,6)==0 %不含变压器的支路p=B1(i,1);q=B1(i,2);Y(p,q)=Y(p,q)-1/B1(i,3);Y(q,p)=Y(p,q);Y(p,p)=Y(p,p)+1/B1(i,3)+0.5*B1(i,4); Y(q,q)=Y(q,q)+1/B1(i,3)+0.5*B1(i,4); else %含有变压器的支路p=B1(i,1);q=B1(i,2);Y(p,q)=Y(p,q)-1/(B1(i,3)*B1(i,5));Y(q,p)=Y(p,q);Y(p,p)=Y(p,p)+1/B1(i,3);Y(q,q)=Y(q,q)+1/(B1(i,5)^2*B1(i,3)); endendYOrgS=zeros(2*n-2,1);DetaS=zeros(2*n-2,1); %将OrgS、DetaS初始化%创建OrgS,用于存储初始功率参数h=0;j=0;for i=1:n %对PQ节点的处理if i~=isb&B2(i,6)==2h=h+1;for j=1:nOrgS(2*h-1,1)=OrgS(2*h-1,1)+real(B2(i,3))*(real(Y(i,j))*r eal(B2(j,3))-imag(Y(i,j))*imag(B2(j,3)))+imag(B2(i,3))*(real(Y(i,j))* imag(B2(j,3))+imag(Y(i,j))*real(B2(j,3)));OrgS(2*h,1)=OrgS(2*h,1)+imag(B2(i,3))*(real(Y(i,j))*real( B2(j,3))-imag(Y(i,j))*imag(B2(j,3)))-real(B2(i,3))*(real(Y(i,j))*imag (B2(j,3))+imag(Y(i,j))*real(B2(j,3)));endendendfor i=1:n %对PV节点的处理,注意这时不可再将h初始化为0if i~=isb&B2(i,6)==3h=h+1;for j=1:nOrgS(2*h-1,1)=OrgS(2*h-1,1)+real(B2(i,3))*(real(Y(i,j))*r eal(B2(j,3))-imag(Y(i,j))*imag(B2(j,3)))+imag(B2(i,3))*(real(Y(i,j))* imag(B2(j,3))+imag(Y(i,j))*real(B2(j,3)));OrgS(2*h,1)=OrgS(2*h,1)+imag(B2(i,3))*(real(Y(i,j))*real( B2(j,3))-imag(Y(i,j))*imag(B2(j,3)))-real(B2(i,3))*(real(Y(i,j))*imag (B2(j,3))+imag(Y(i,j))*real(B2(j,3)));endendendOrgS%创建PVU 用于存储PV节点的初始电压PVU=zeros(n-h-1,1);t=0;for i=1:nif B2(i,6)==3t=t+1;PVU(t,1)=B2(i,3);endendPVU%创建DetaS,用于存储有功功率、无功功率和电压幅值的不平衡量h=0;for i=1:n %对PQ节点的处理if i~=isb&B2(i,6)==2h=h+1;DetaS(2*h-1,1)=real(B2(i,2))-OrgS(2*h-1,1);DetaS(2*h,1)=imag(B2(i,2))-OrgS(2*h,1);endendt=0;for i=1:n%对PV节点的处理,注意这时不可再将h初始化为0if i~=isb&B2(i,6)==3h=h+1;t=t+1;DetaS(2*h-1,1)=real(B2(i,2))-OrgS(2*h-1,1);DetaS(2*h,1)=real(PVU(t,1))^2+imag(PVU(t,1))^2-real(B2(i,3))^2-imag(B2(i,3))^2;endendDetaS%创建I,用于存储节点电流参数i=zeros(n-1,1);h=0;for i=1:nif i~=isbh=h+1;I(h,1)=(OrgS(2*h-1,1)-OrgS(2*h,1)*sqrt(-1))/conj(B2(i,3));endendI%创建Jacbi(雅可比矩阵)Jacbi=zeros(2*n-2);h=0;k=0;for i=1:n %对PQ节点的处理if B2(i,6)==2h=h+1;for j=1:nif j~=isbk=k+1;if i==j %对角元素的处理Jacbi(2*h-1,2*k-1)=-imag(Y(i,j))*real(B2(i,3))+real(Y(i,j))*imag(B2(i,3))+imag(I(h,1));Jacbi(2*h-1,2*k)=real(Y(i,j))*real(B2(i,3))+imag(Y(i,j))*imag(B2(i,3))+real(I(h,1));Jacbi(2*h,2*k-1)=-Jacbi(2*h-1,2*k)+2*real(I(h,1)); Jacbi(2*h,2*k)=Jacbi(2*h-1,2*k-1)-2*imag(I(h,1)); else %非对角元素的处理Jacbi(2*h-1,2*k-1)=-imag(Y(i,j))*real(B2(i,3))+real(Y(i,j))*imag(B2(i,3));Jacbi(2*h-1,2*k)=real(Y(i,j))*real(B2(i,3))+imag( Y(i,j))*imag(B2(i,3));Jacbi(2*h,2*k-1)=-Jacbi(2*h-1,2*k);Jacbi(2*h,2*k)=Jacbi(2*h-1,2*k-1);endif k==(n-1)%将用于内循环的指针置于初始值,以确保雅可比矩阵换行k=0;endendendendendk=0;for i=1:n %对PV节点的处理if B2(i,6)==3h=h+1;for j=1:nif j~=isbk=k+1;if i==j %对角元素的处理Jacbi(2*h-1,2*k-1)=-imag(Y(i,j))*real(B2(i,3))+re al(Y(i,j))*imag(B2(i,3))+imag(I(h,1));Jacbi(2*h-1,2*k)=real(Y(i,j))*real(B2(i,3))+imag( Y(i,j))*imag(B2(i,3))+real(I(h,1));Jacbi(2*h,2*k-1)=2*imag(B2(i,3));Jacbi(2*h,2*k)=2*real(B2(i,3));else %非对角元素的处理Jacbi(2*h-1,2*k-1)=-imag(Y(i,j))*real(B2(i,3))+re al(Y(i,j))*imag(B2(i,3));Jacbi(2*h-1,2*k)=real(Y(i,j))*real(B2(i,3))+imag( Y(i,j))*imag(B2(i,3));Jacbi(2*h,2*k-1)=0;Jacbi(2*h,2*k)=0;endif k==(n-1)%将用于内循环的指针置于初始值,以确保雅可比矩阵换行k=0;endendendendJacbi%求解修正方程,获取节点电压的不平衡量DetaU=zeros(2*n-2,1);DetaU=inv(Jacbi)*DetaS;DetaU%修正节点电压j=0;for i=1:n %对PQ节点处理if B2(i,6)==2j=j+1;B2(i,3)=B2(i,3)+DetaU(2*j,1)+DetaU(2*j-1,1)*sqrt(-1);endendfor i=1:n %对PV节点的处理if B2(i,6)==3j=j+1;B2(i,3)=B2(i,3)+DetaU(2*j,1)+DetaU(2*j-1,1)*sqrt(-1);endendB2%开始循环********************************************************************* *while abs(max(DetaU))>prOrgS=zeros(2*n-2,1);%初始功率参数在迭代过程中是不累加的,所以在这里必须将其初始化为零矩阵h=0;j=0;for i=1:nif i~=isb&B2(i,6)==2h=h+1;for j=1:nOrgS(2*h-1,1)=OrgS(2*h-1,1)+real(B2(i,3))*(real(Y(i,j))*r eal(B2(j,3))-imag(Y(i,j))*imag(B2(j,3)))+imag(B2(i,3))*(real(Y(i,j))* imag(B2(j,3))+imag(Y(i,j))*real(B2(j,3)));OrgS(2*h,1)=OrgS(2*h,1)+imag(B2(i,3))*(real(Y(i,j))*real( B2(j,3))-imag(Y(i,j))*imag(B2(j,3)))-real(B2(i,3))*(real(Y(i,j))*imag (B2(j,3))+imag(Y(i,j))*real(B2(j,3)));endendfor i=1:nif i~=isb&B2(i,6)==3h=h+1;for j=1:nOrgS(2*h-1,1)=OrgS(2*h-1,1)+real(B2(i,3))*(real(Y(i,j))*r eal(B2(j,3))-imag(Y(i,j))*imag(B2(j,3)))+imag(B2(i,3))*(real(Y(i,j))* imag(B2(j,3))+imag(Y(i,j))*real(B2(j,3)));OrgS(2*h,1)=OrgS(2*h,1)+imag(B2(i,3))*(real(Y(i,j))*real( B2(j,3))-imag(Y(i,j))*imag(B2(j,3)))-real(B2(i,3))*(real(Y(i,j))*imag (B2(j,3))+imag(Y(i,j))*real(B2(j,3)));endendendOrgS%创建DetaSh=0;for i=1:nif i~=isb&B2(i,6)==2h=h+1;DetaS(2*h-1,1)=real(B2(i,2))-OrgS(2*h-1,1);DetaS(2*h,1)=imag(B2(i,2))-OrgS(2*h,1);endendt=0;for i=1:nif i~=isb&B2(i,6)==3h=h+1;t=t+1;DetaS(2*h-1,1)=real(B2(i,2))-OrgS(2*h-1,1);DetaS(2*h,1)=real(PVU(t,1))^2+imag(PVU(t,1))^2-real(B2(i,3))^ 2-imag(B2(i,3))^2;endendDetaS%创建Ii=zeros(n-1,1);h=0;for i=1:nif i~=isbh=h+1;I(h,1)=(OrgS(2*h-1,1)-OrgS(2*h,1)*sqrt(-1))/conj(B2(i,3)); endendI%创建JacbiJacbi=zeros(2*n-2);h=0;k=0;for i=1:nif B2(i,6)==2h=h+1;for j=1:nif j~=isbk=k+1;if i==jJacbi(2*h-1,2*k-1)=-imag(Y(i,j))*real(B2(i,3))+real(Y(i,j))*imag(B2(i,3))+imag(I(h,1));Jacbi(2*h-1,2*k)=real(Y(i,j))*real(B2(i,3))+imag(Y(i,j))*imag(B2(i,3))+real(I(h,1));Jacbi(2*h,2*k-1)=-Jacbi(2*h-1,2*k)+2*real(I(h,1)); Jacbi(2*h,2*k)=Jacbi(2*h-1,2*k-1)-2*imag(I(h,1)); elseJacbi(2*h-1,2*k-1)=-imag(Y(i,j))*real(B2(i,3))+real(Y(i,j))*imag(B2(i,3));Jacbi(2*h-1,2*k)=real(Y(i,j))*real(B2(i,3))+imag(Y(i,j))*imag(B2(i,3));Jacbi(2*h,2*k-1)=-Jacbi(2*h-1,2*k);Jacbi(2*h,2*k)=Jacbi(2*h-1,2*k-1);endif k==(n-1)k=0;endendendendendk=0;for i=1:nif B2(i,6)==3h=h+1;for j=1:nif j~=isbk=k+1;if i==jJacbi(2*h-1,2*k-1)=-imag(Y(i,j))*real(B2(i,3))+real(Y(i,j))*imag(B2(i,3))+imag(I(h,1));Jacbi(2*h-1,2*k)=real(Y(i,j))*real(B2(i,3))+imag( Y(i,j))*imag(B2(i,3))+real(I(h,1));Jacbi(2*h,2*k-1)=2*imag(B2(i,3));Jacbi(2*h,2*k)=2*real(B2(i,3));elseJacbi(2*h-1,2*k-1)=-imag(Y(i,j))*real(B2(i,3))+re al(Y(i,j))*imag(B2(i,3));Jacbi(2*h-1,2*k)=real(Y(i,j))*real(B2(i,3))+imag( Y(i,j))*imag(B2(i,3));Jacbi(2*h,2*k-1)=0;Jacbi(2*h,2*k)=0;endif k==(n-1)k=0;endendendendendJacbiDetaU=zeros(2*n-2,1);DetaU=inv(Jacbi)*DetaS;DetaU%修正节点电压j=0;for i=1:nif B2(i,6)==2j=j+1;B2(i,3)=B2(i,3)+DetaU(2*j,1)+DetaU(2*j-1,1)*sqrt(-1);endendfor i=1:nif B2(i,6)==3j=j+1;B2(i,3)=B2(i,3)+DetaU(2*j,1)+DetaU(2*j-1,1)*sqrt(-1);endendB2Times=Times+1; %迭代次数加1endTimes运行结果在命令窗口中输入备注:此次电路参数按照例3-3输入执行后,经对照答案符合要求。
潮流计算 例题

例题:如图1所示的简单电力网中,已知变压器的参数为S N =31.5MV A ,0S S 031kW,190kW,%=10.5,%=0.7P P U I ∆=∆=;线路单位长度的参数为61110.21/km,0.416/km, 2.7410S/km r x b -=Ω=Ω=⨯。
如图所示的简单电力网中,当线路首端电压U A =120kV 时,试求:(1)线路和变压器的电压损耗;(2)变压器运行在额定变比时的低压侧电压及电压偏移。
说明:以上计算忽略电压降落的横分量。
图1解:如题画等值电路图如下:线路参数为:0.21408.40.4164016.64l l l l R rl X x l ==⨯=Ω==⨯=Ω变压器参数为Ω=⨯⨯⨯=⨯∆=317.210)105.31(110190103232322N N S T S U P R Ω=⨯⨯⨯⨯⨯=33.4010105.311001105.1010100%33232N N S T S U U X (1) 变压器的功率损耗和励磁功率为222T S 02N 2515()19031193.760.1937631.5S P P P kW MW S +∆=∆+∆=⨯+==222S 0N T N %%10.5(2515)0.731.5 3.0538var 10010010031.5100U S I S Q M S ⨯+⨯∆=+=+=⨯1点处线路的充电功率var 66308.01104074.22121222M lU b Q N l B =⨯⨯⨯==计算L S 2 为:MVAj j Q Q Q j P P S B T LD T LD L 39.1719.25)66308.00538.315(19376.025)(22+=-+++=-∆++∆+=线路阻抗中的功率损耗为:MW R U Q P P l L L l 65044.0104021.011017390251901032223222222=⨯⨯⨯+=⨯+=∆-- v a r 2885.11040416.011017390251901032223222222M X U Q P Q l L L l =⨯⨯⨯+=⨯+=∆-- 计算功率1S 为 M V Aj j Q Q j P P S l L l I 68.1884.25)2885.139.17(65044.019.25)(221+=+++=∆++∆+=线路电压损耗(忽略电压降落的横分量) 1125.848.418.6816.64 4.40120=l l l A PR Q X U kV U +⨯+⨯∆== 1点电压为:1120 4.40115.60-A l U U U kV =∆=-=计算功率TS 2 为 M V Aj j Q Q j P P S T LD T LD T 833.17163.25)833.215(163.025)(2+=+++='∆++'∆+= 变压器电压损耗 22125.163 2.3217.83340.33 6.73115.60=T T T T T P R Q X U kV U +⨯+⨯∆== (2) 变压器低压侧折算到高压侧的电压为21115.60 6.73108.87=-T U U U kV '∆=-= 变压器低压侧的实际电压 22108.8710.8910=U U kV k '== 电压偏移为2210.8910%100%8.9%10N N U U m U --=⨯==。
潮流计算实例计算

潮流计算实例计算潮流例题:根据给定的参数或⼯程具体要求(如图),收集和查阅资料;学习相关软件(软件⾃选:本设计选择Matlab进⾏设计)。
2.在给定的电⼒⽹络上画出等值电路图。
3.运⽤计算机进⾏潮流计算。
4.编写设计说明书。
⼀、设计原理1.⽜顿-拉夫逊原理⽜顿迭代法是取x0 之后,在这个基础上,找到⽐x0 更接近的⽅程的跟,⼀步⼀步迭代,从⽽找到更接近⽅程根的近似跟。
⽜顿迭代法是求⽅程根的重要⽅法之⼀,其最⼤优点是在⽅程f(x) = 0 的单根附近具有平⽅收敛,⽽且该法还可以⽤来求⽅程的重根、复根。
电⼒系统潮流计算,⼀般来说,各个母线所供负荷的功率是已知的,各个节点电压是未知的(平衡节点外)可以根据⽹络结构形成节点导纳矩阵,然后由节点导纳矩阵列写功率⽅程,由于功率⽅程⾥功率是已知的,电压的幅值和相⾓是未知的,这样潮流计算的问题就转化为求解⾮线性⽅程组的问题了。
为了便于⽤迭代法解⽅程组,需要将上述功率⽅程改写成功率平衡⽅程,并对功率平衡⽅程求偏导,得出对应的雅可⽐矩阵,给未知节点赋电压初值,⼀般为额定电压,将初值带⼊功率平衡⽅程,得到功率不平衡量,这样由功率不平衡量、雅可⽐矩阵、节点电压不平衡量(未知的)构成了误差⽅程,解误差⽅程,得到节点电压不平衡量,节点电压加上节点电压不平衡量构成新的节点电压初值,将新的初值带⼊原来的功率平衡⽅程,并重新形成雅可⽐矩阵,然后计算新的电压不平衡量,这样不断迭代,不断修正,⼀般迭代三到五次就能收敛。
⽜顿—拉夫逊迭代法的⼀般步骤:(1)形成各节点导纳矩阵Y。
(2)设个节点电压的初始值U和相⾓初始值e 还有迭代次数初值为0。
(3)计算各个节点的功率不平衡量。
(4)根据收敛条件判断是否满⾜,若不满⾜则向下进⾏。
(5)计算雅可⽐矩阵中的各元素。
(6)修正⽅程式个节点电压(7)利⽤新值⾃第(3)步开始进⼊下⼀次迭代,直⾄达到精度退出循环。
(8)计算平衡节点输出功率和各线路功率2.⽹络节点的优化1)静态地按最少出线⽀路数编号这种⽅法由称为静态优化法。
潮流计算

例3-1: 电力网络如图所示。
已知末端负荷MVA j S 25.1115~+=,末端电压36 kV ,计 算电网首端功率和电压。
20MVA 110/38.5 kVLGJ —120 80 km解: (1)选取 110kV 作为电压的基本级,计算网络参数,并画出等值电路。
(计算过程略)~~ 电力网络的等值电路~~~~(2)计算潮流分布根据画出的电力网络等值电路可见:已知末端功率MVA j S 25.1115~3+= ,将已知 末端电压36 kV 归算到电压基本级,则有 kV U 85.1025.38110363=⨯= 。
本网为辐射形电网,并且已知末端的功率和电压,求潮流分布,因此采用逐段推算法进行计算。
① 计算变压器阻抗上的功率损耗()()MVA j j jX R U Q P S T T ZT 11.216.05.6393.485.10225.1115~222232323+=+⨯+=++=∆ 则变压器阻抗始端功率MVA j j j S S S ZT 36.1316.1511.216.025.1115~~~33+=+++=∆+='② 计算变压器阻抗上的电压损耗kV U X Q R P U T 67.785.1025.6325.1193.415333=⨯+⨯=+=∆则变压器始端电压 kV U U U T 52.11067.785.10232=+=∆+= ③ 计算变压器导纳上的功率损耗()()MVA j j U jB G S T T YT 6.006.052.110105.4995.4~2622+=⨯⨯+=+=∆-④ 计算线路末端导纳上的功率损耗MVar j j U B j S Y 34.152.110101.12~24222-=⨯⨯-=-=∆-则线路阻抗末端的功率MOAj j j j S S S S Y YT 62.1222.1534.16.006.036.1316.15~~~~232+=-+++=∆+∆+'='⑤ 计算线路阻抗上的功率损耗()()MOA j j jX R U Q P S Z 056.1691.0336.2152.11062.1222.15~222222222+=+⨯+=+'+'=∆⑥ 计算线路阻抗上的电压损耗kV U X Q R P U 74.652.1103362.126.2122.15222=⨯+⨯='+'=∆则线路始端电压 kV U U U 26.11774.652.11021=+=∆+= ⑦ 计算线路始端导纳上的功率损耗MVar j j U B j S Y 51.126.117101.12~24211-=⨯⨯-=-=∆-则线路始端功率MVA j j j j S S S S Y Z 16.1291.1551.1056.1691.062.1222.15~~~~121+=-+++=∆+∆+'=例3-2: 如图10kV 三相配电线路。
例题-第四章 电力系统潮流的计算机计算

第4章复杂电力系统的潮流计算一、填空题1。
用计算机进行潮流计算时,按照给定量的不同,可将电力系统节点分为节点、节点、节点三大类,其中,节点数目最多,节点数目很少、可有可无,节点至少要有一个。
二、选择题1.若在两个节点i、j之间增加一条支路,则下列关于节点导纳矩阵的说法正确的是( )A。
阶数增加1B.节点i的自导纳不变C.节点i、j间的互导纳发生变化D。
节点j的自导纳不变2。
若从节点i引出一条对地支路,则下列关于节点导纳矩阵的说法正确的是( )A。
阶数增加1B.节点i的自导纳发生变化C.节点i和其余节点间的互导纳均发生变化D.节点导纳矩阵的所有元素均不变3。
若从两个节点i、j之间切除掉一条支路,则下列关于节点导纳矩阵的说法正确的是()A。
阶数减少1B。
节点i、j间的互导纳一定变为0C.节点i、j间的互导纳发生变化,但不一定变为0D。
节点i、j的自导纳均不变4。
若网络中增加一个节点k,且增加一条节点i与之相连的支路,则下列关于节点导纳矩阵的说法正确的是( )(1)阶数增加1(2)节点k的自导纳等于题干中所述支路的导纳(3)节点i的自导纳等于题干中所述支路的导纳(4)节点i、k间的互导纳等于题干中所述支路的导纳A。
(1)(2)B。
(2)(3)C。
(1)(4) D.(2)(4)三、简答题1. 什么是潮流计算?潮流计算的主要作用有哪些?潮流计算,电力学名词,指在给定电力系统网络拓扑、元件参数和发电、负荷参量条件下,计算有功功率、无功功率及电压在电力网中的分布。
潮流计算是电力系统非常重要的分析计算,用以研究系统规划和运行中提出的各种问题。
对规划中的电力系统,通过潮流计算可以检验所提出的电力系统规划方案能否满足各种运行方式的要求;对运行中的电力系统,通过潮流计算可以预知各种负荷变化和网络结构的改变会不会危及系统的安全,系统中所有母线的电压是否在允许的范围以内,系统中各种元件(线路、变压器等)是否会出现过负荷,以及可能出现过负荷时应事先采取哪些预防措施等。
例题——电力线路空载时的潮流计算最新实用版

解
(1)作该线路的等值电路如图2-22(b)所示。
1
UA
A
A
B
QF
S
' A
Z1
S
' B
UA
SB
B
SB
Y1
Y1
2
2
图2-22 [例2-7]的线路及等值电路 (a)线路图;(b)等值电路
(2)计算功率分布。 1)正常运行时
S
' B
SB
j
B 2
U
2 N
40
j30
j
1 (5.79104 ) 2202 2
UB 229.07(kV压,若以线路首端电压作参考相量,电压相量图如 图所示。
UA
U
o
U
UB
5
有一额定电压为220kV的输电线路如图2-22(a
)所示。线路末端接有负荷 SB 40 j30MVA 。已知线路首端 电压UA 224kV,线路参数如下:
R 16.9, X 83.1, B j5.79104S
试计算:(1)正常运行情况下,线路末端的电压;
(2)当线路末端的断路器QF跳开时,线路末端的电压。
83.119.18 224
16.9
)
2) QF跳开时 图2-22 [例2-7]的线路及等值电路
已知线路首端电压
,线路参数如下:
0.068516.9 13.6683.1 0.068583.1 (13.66) 16.9
U B 224 (
j
)
224
224
224 5.07 j1.05 229.07 j1.05(kV)
40 j16(MVA)
2
402 162
电力系统正常运行潮流计算
~
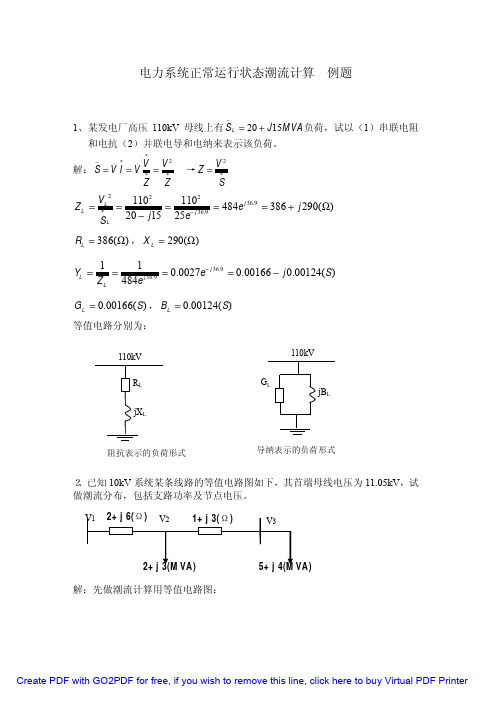
1、某发电厂高压 110kV 母线上有 S L = 20 + J15MVA 负荷,试以(1)串联电阻
和电抗(2)并联电导和电纳来表示该负荷。
*
~
解: S
.*
=V I
.
=V
V
*
=
V2
*
ZZ
→Z
=
V2
*
S
ZL
=
VL
*
2
SL
= 1102 20 − j15
=
1102 25e− j36.9
110kV
110kV
RL
GL
jBL
jXL
阻抗表示的负荷形式
导纳表示的负荷形式
2、已知 10kV 系统某条线路的等值电路图如下,其首端母线电压为 11.05kV,试 做潮流分布,包括支路功率及节点电压。
V1 2+ j 6(Ω) V2 1+ j 3(Ω)
V3
2+ j 3(MVA) 解= 386 +
j290(Ω )
RL = 386(Ω ) , X L = 290(Ω )
YL
=
1 ZL
=
1 484e j36.9
= 0.0027e− j36.9
= 0.00166 −
j0.00124(S )
GL = 0.00166(S ) , BL = 0.00124(S ) 等值电路分别为:
= 9.86 × 2 +15.59 ×6 11.05
= 10.249kV
Create PDF with GO2PDF for free, if you wish to remove this line, click here to buy Virtual PDF Printer
电力系统分析潮流计算例题

电力系统的潮流计算西安交通大学自动化学院 2012。
103.1 电网结构如图3-11所示,其额定电压为10KV 。
已知各节点的负荷功率及参数: MVAj S )2.03.0(2+=,MVAj S )3.05.0(3+=,MVA j S )15.02.0(4+=Ω+=)4.22.1(12j Z ,Ω+=)0.20.1(23j Z ,Ω+=)0.35.1(24j Z试求电压和功率分布.解:(1)先假设各节点电压均为额定电压,求线路始端功率。
0068.00034.0)21(103.05.0)(22223232232323j j jX R V Q P S N +=++=++=∆0019.00009.0)35.1(1015.02.0)(22224242242424j j jX R V Q P S N +=++=++=∆则: 3068.05034.023323j S S S +=∆+=1519.02009.024424j S S S +=∆+=6587.00043.122423'12j S S S S +=++=又0346.00173.0)4.22.1(106587.00043.1)(22212122'12'1212j j jX R V Q P S N +=++=++=∆故: 6933.00216.112'1212j S S S +=∆+=(2) 再用已知的线路始端电压kVV 5.101=及上述求得的线路始端功率12S ,求出线路各点电压.kVV X Q R P V 2752.05.104.26933.02.10216.1)(11212121212=⨯+⨯=+=∆ kV V V V 2248.101212=∆-≈kVV V V kV V X Q R P V 1508.100740.0)(242422424242424=∆-≈⇒=+=∆kVV V V kV V X Q R P V 1156.101092.0)(232322323232323=∆-≈⇒=+=∆(3)根据上述求得的线路各点电压,重新计算各线路的功率损耗和线路始端功率.0066.00033.0)21(12.103.05.022223j j S +=++=∆ 0018.00009.0)35.1(15.1015.02.022224j j S +=++=∆ 故 3066.05033.023323j S S S +=∆+=1518.02009.024424j S S S +=∆+=则 6584.00042.122423'12j S S S S +=++=又0331.00166.0)4.22.1(22.106584.00042.122212j j S +=++=∆ 从而可得线路始端功率 6915.00208.112j S +=这个结果与第(1)步所得计算结果之差小于0。
电力系统潮流的计算机计算(含答案).docx

第4章电力系统潮流的计算机计算一、填空题1.用计算机进行潮流计算吋,按照给定量的不同,可将电力系统节点分为节点、PV 节点、平衡节点三大类,其中,P0节点数目最多,PV节点数目很少、可有可无,平衡节点至少要有一个。
二、选择题1•若在两个节点i、j之间增加一条支路,则下列关于节点导纳矩阵的说法正确的是(C)A.阶数增加1B.节点i的自导纳不变C.节点i、j间的互导纳发生变化D.节点j的自导纳不变2•若从节点i引出一条对地支路,则下列关于节点导纳矩阵的说法正确的是(B)A.阶数增加1B.节点i的自导纳发生变化C.节点i和其余节点间的互导纳均发生变化D.节点导纳矩阵的所有元素均不变3.若从两个节点i、j之间切除掉一条支路,则下列关于节点导纳矩阵的说法正确的是(C)A.阶数减少1B.节点i、j间的互导纳一定变为0C.节点i、j间的互导纳发生变化,但不一定变为0D.节点i、j的自导纳均不变4.若网络中增加一个节点k,且增加一条节点i与之相连的支路,则下列关于节点导纳矩阵的说法正确的是(A)(1)阶数增加1(2)节点k的自导纳等于题干中所述支路的导纳(3)节点i的自导纳等于题干中所述支路的导纳(4)节点i、k间的互导纳等于题干中所述支路的导纳A. (1) (2) B. (2) (3) C. (1) (4) D. (2) (4)三、简答题1.节点导纳矩阵有些什么特点?其自导纳和互导纳元素各自的物理含义和计算方法分别是什么?2.潮流计算有哪些约束条件?四、综合题1..如图所示,四节点简单电力系统中各线路的阻抗标幺值已列于表中,而各线路対地导纳忽略。
支路电阻电抗1-20.050.151-30.100.302-30」50.452-40」00.303-40.050」5(a)求该系统中无虚线所示线路时的节点导纳矩阵;(b)如杲虚线支路被接入系统,那么,原节点导纳矩阵应作哪些修改?解:根据阻抗和导纳互为倒数的原理,求出各支路的导纳标幺值列入下表:支路电导电纳1-22・61-31・32-30.67■22-41■33-42■6(a) 根据网络接线图,计算出无虚线所示线路时的节点导纳矩阵中各元素,女口下:Y u=y i3=l-j3 Y22 = y23 + j24 = (0.67 - J2) + (1 - ;3) = 1.67 - j5Y33 = y l3 + 儿 3 + =d-J3) + (0.67 - J2) + (2 — J6) = 3.67 - jll 抵=J24 + J34 =d-J3) +(2-J6)=3-J9Yn =-Ji2= 0 Y l3 = r31= -J I3= -1+ J3Y]4 = 丫41 = _J14= °丫23 =丫32 = _『23= -0・67 + /2Y24 = Y42=-J24=-I+j3 r34 = r43 = -儿产-2+J6写出节点导纳矩阵如下(阶数为4X4):「1-庐0-1 + /3Y =0 1.67-J5-0.67 + J2-1 + J3 -1 + /3-0.67 + j2 3.67-jll-2 + /6 0一1 + /3一2 + /63-J9(b) 在系统中接入支路1・2后,节点1、2的自导纳和节点1、2间的互导纳会发生改变,原节点导纳矩阵中《、岭2、畑和孑22的值应作以下修改:^I=^U+J I2=(1-J3)+(2-J6)=3-J9Y22 =丫22 + 儿二(167 - J5) + (2-/6)二3.67 - J11丫;2 = y21=y i2-y12=0-(2-j6) = -2 + j6写出修改以后的节点导纳矩阵如下:_ 3-j9-2 + /6-1 + /301 Y =-2 + J6 3.67-jll-0.67 + /2-1+ J3 -1 + /3- 0.67 + jl 3.67-jll-2 + J6 0-1 + J3-2 + J63-j92.写出下图所示网络的节点导纳矩阵。
潮流计算

Sb SG STc S0c jQB 2 jQB3
1 b Tb 2 c Tc 3
A
d Td
SLDb
G
SG
SL D d
14
二、两级电压的开式电力网计算 计算方法一:包含理想变压器,计算时,经过理 想变压器功率保持不变,两侧电压之比等于实际 变比k。 T b d c L-1 L-2 SLD A
V1 arctg V1 V1
4
网络元件的功率损耗
功率损耗包括:电阻和等值电抗上的损耗 对地等值导纳上产生的损耗
V1S1 , I1 S ' I
jQB1
B j 2
R jX
S '', I S 2 , I 2 V2
jQB 2
B j 2
线路
VS1 , I1
线路
S0 (GT jBT )V 2
I0% S0 P0 jQ0 P0 j SN 100
开式网络的电压和功率分布计算
一、已知供电点电压和负荷点功率时的计算方法 已知末端的功率和电压:从末端开始依次计算出 电压降落和功率损耗。 已知电源点的电压和负荷的功率:采取近似的方 法通过叠代计算求得满足一定精度的结果
X2 k2 X2
T
A
A
B2 B2 / k 2 d c L-2 SLD
R'2+ j X'2 j B'2/2
16
R1+ jX1
j B1/2 j B1/2
b ΔS0
Z'T
c' j B'2/2
d'
SLD
二、两级电压的开式电力网计算 计算方法三:用π型等值电路代表变压器
电力线路的参数与等值电路以及潮流计算的简单介绍

U 2 Z
P Q j 2
2
U* 2
两边同乘 e3 j30 U U
U 1 U 2 U U 2 Z
e P Q 3 ( j30 2 j
)
2
U* 2
U 2 Z
3(P2 jQ2)
3e
j30
U* 2
U 2
Z
P2 jQ2 U* 2
**
U
U 1 U 2 Z
P2 jQ2 电压降落 U2
基本概念
二、电压降落、电压损耗、电压偏移
目的:对于一条线路(变压器)有负荷流过时,首末端电压不等,造
成电压 损耗,可以推导已知端的S和U时求另一端的S和U
u 1
I
u 2
R jX
S 2 P2 jQ2
1、已知U2及S2求U1
I
S 2 U 2
*
P Q j 2
2
U* 2
U 1 U 2 U U 2 Z I
电力线路的参数与等值电路
一.单位长度电力线路的参数
1、电阻 r1=ρ/ s
ρ电阻率
单位:Ω•mm2/km 铜:18.8 铝: 31.3
与温度有关
S 截面积 mm2
一般是查表 rt=r20(1+α(t-20))
钢线电阻:导磁集肤、磁滞效应交流电阻> 直流电阻,和电流有关查手册
电力线路的参数与等值电路
以U2为参考电压
U
(R
jX ) P2 jQ2 U2
I2
U 1 U U' U 2 U'
P2 R Q2 X j P2 X Q2 R U' j U'
U2
U2
纵分量 横分量
2、已知U1及S1求U2
补充例题——等值电路、潮流计算

补充例题3:如图,已知线路首端电压大小为121kV,试求 变压器低压侧的电压。
110kV,80km r1+jx1=0.14+j0.4Ω 15+j0MVA 15+j10MVA
变压器参数:SFL-20000/110,110/11kV,Δps=135kW, us(%)=10.5, Δp0=135kW,I0%=0.8。 思路:这是典型的已知首端电压和末端功率的情况,用 “前推回代法”求解。 解:等值电路图: ~
(30.132 j11.87) (0.97 j 2.77) 31.102 j14.64(MVA ) 以下过程为回推计算电压分布: 线路串联支路的电压降落纵分量、横分量分别为: P 31.102 11.2 14.64 32 1 RL Q1 X L U 1 6.75(kV) U1 121 P 31.102 32 14.64 11.2 1 X L Q1 RL U1 6.87(kV) U1 121
P 179.768 1.48 109.251 34.16 1 RT Q1 X T U 1 25.02(kV) ' U1 159.80 P 179.768 34.16 109.2511.48 1 X T Q1 RT U1 37.46(kV) ' U1 159.80
至此,已知道变压器串联支路始端功率和电压(归算前 的),为求得变压器串联支路末端电压(即所求的U A), 还需要知道变压器串联支路的阻抗RT和XT。 变压器串联支路阻抗归算到高压侧的值为:
2 pk U TN 1.46 2422 RT 1.48() 2 2 SN 240 2 uk % U TN 14 2422 XT 34.16() 100 S N 100 240
第三章 潮流计算习题

第三章 潮流计算习题1. 试写出牛顿-拉夫逊法潮流计算的基本步骤。
(华北电大)2. 牛顿-拉夫逊潮流计算总,极坐标形式的修正方程式可以写成如下形式: ⎥⎦⎤⎢⎣⎡ΔΔ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡ΔΔU U L K N H Q P /δ 说明为什么节点电压相位角的改变主要影响有功潮流,节点电压幅值的改变主要影响无功潮流?并写出PQ 分解法的修正方程式。
(华北电大)3. PQ 分解法潮流计算与牛顿-拉夫逊法潮流计算相比有何优缺点?这两种算法可得相同精度的结果吗?4. 电力系统潮流自然分布与经济分布,各与什么参数有关?5. P-Q 分解法潮流计算的原理和简化条件是什么?写出其修正方程式。
6. 试述电力网络潮流调整和控制的办法。
7. 对于存在R ≥X 的电力网络,是否可以采用P-Q 分解法进行潮流计算?为什么?8. 网络结构如图所示,各支路参数均为电抗标幺值,1-2支路理想变压器的变比是K *=1.1,试写出网络的导纳矩阵。
(数据精确到小数点后两位)(华北电大)9. 系统等值网络如图所示,节点类型:1是PV 节点;2、3、5为PQ 节点;4 是平衡节点。
各元件的标幺参数为电抗:X 12=0.4,X 23=0.5,X 34=0.2,X 24=0.4,X 45=0.2电拿:B 20=0.8,B 40=0.4求:(1)该网络的节点导纳矩阵。
(2)试写出采用直角坐标N-R 法进行潮流计算时的修正方程式结构。
(注:状态变量和运行变量用符号表示,雅可比矩阵中非零元素用“×”表示,零元素用“0” 表示。
)10. 已知两节点系统及标幺值参数如图所示,节点1 是平衡节点,给点电压为1.05pu ,支路阻抗为0.01+j0.03pu,节点2 的负荷为0.5+j0.1pu.求:(1)节点2 的功率方程;(2)牛顿-拉夫逊法直角坐标形式的修正方程式;(3)当给定初值()102=U 时,计算第一次迭代的电压()12U ?11. 5节点电力系统,节点1为PV 节点,节点5为平衡节点,其余为PQ 节点。
电力系统潮流计算问答题

潮流计算数学模型与数值方法1.什么是潮流计算?潮流计算的主要作用有哪些?潮流计算是根据给定的电网结构、参数和发电机、负荷等元件的运行条件,确定电力系统各部分稳态运行状态参数的计算.对于正在运行的电力系统,通过潮流计算可以判断电网母线电压、支路电流和功率是否越限,如果有越限,就应采取措施,调整运行方式。
对于正在规划的电力系统,通过潮流计算,可以为选择电网供电方案和电气设备提供依据。
潮流计算还可以为继电保护和自动装置定整计算、电力系统故障计算和稳定计算等提供原始数据。
2.潮流计算有哪些待求量、已知量?(已知量:1、电力系统网络结构、参数2、决定系统运行状态的边界条件待求量:系统稳态运行状态例如各母线上的电压(幅值及相角)、网络中的功率分布以及功率损耗等)通常给定的运行条件有系统中各电源和负荷点的功率、枢纽点电压、平衡点的电压和相位角。
待求的运行状态参量包括电网各母线节点的电压幅值和相角,以及各支路的功率分布、网络的功率损耗等。
3。
潮流计算节点分成哪几类?分类根据是什么?(分成三类:PQ节点、PV节点和平衡节点,分类依据是给定变量的不同)PU节点(电压控制母线)有功功率Pi 和电压幅值Ui为给定。
这种类型节点相当于发电机母线节点,或者相当于一个装有调相机或静止补偿器的变电所母线。
PQ节点注入有功功率Pi和无功功率Qi是给定的。
相当于实际电力系统中的一个负荷节点,或有功和无功功率给定的发电机母线.平衡节点用来平衡全电网的功率.平衡节点的电压幅值Ui和相角δi是给定的,通常以它的相角为参考点,即取其电压相角为零。
一个独立的电力网中只设一个平衡节点。
4. 教材牛顿—拉夫逊法及有功—无功分解法是基于何种电路方程?可否采用其它类型方程?基于节点电压方程,还可以采用回路电流方程和割集电压方程等。
但是后两者不常用。
5。
教材牛顿—拉夫逊法是基于节点阻抗方程、还是基于节点导纳方程进行迭代计算的?试阐述这两种方程的优点与缺点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P 179.768 1.48 109.251 34.16 1 RT Q1 X T U 1 25.02(kV) ' U1 159.80 P 179.768 34.16 109.2511.48 1 X T Q1 RT U1 37.46(kV) ' U1 159.80
评析: 1、本题为典型的已知末端功率和始端电压的类型, 用“前推回代法”求解。 2、已知条件未告诉线路单位长度的电纳,因此等 值电路图中没有线路的对地电容; 3、变压器的短路损耗、短路电压百分数既可以用 Δpk和uk%表示,也可以用本例中的ΔpS和uS(%) 来 表示; 4、求电压 U (相量)时,是以 U 1 为参考相量; 2 求电压 U 3 (相量)时,是以 U 2 为参考相量; 5、最后一步,需要将U3归算回低压侧,才是本题 所求。
(7.875+j43.1)Ω
-j25.652MVA
评析: 1、本题为双回线并列运行,与单回线相比阻抗减 半,导纳加倍; 2、本题主要考察用2.1节相关公式计算,而不是 查表; 3、本题中对地支路用充电功率表示,计算充电功 率时用的是网络额定电压(因实际电压未知), 故线路两端充电功率大小相等。
2 pS U TN 0.135 1102 RT 4.08() 2 2 SN 20 2 uS (%) U TN 10.5 1102 XT 63.53() 100 SN 100 20
变压器励磁支路功率损耗为:
I0 % S YT p0 jQ0 p0 j SN 100 0.8 0.022 j 20 0.022 j 0.16(MVA ) 100
U1
RL+jXL
U2
S3
RT+jXT
U3
S1
~
SL
~
~
S2
~
S YT
~
S ZT
~
S L 2 =15+j10MVA
~
S L1=15+j0MVA
注:参数均归算到高压侧
线路阻抗为: ZL=RL+jXL=(r1+jx1) l=(0.14+j0.4)×80=11.2+j32(Ω) 变压器归算到高压侧的阻抗参数为:
S 3 S L 2 S ZT (15 j10) (0.11 j1.71) 15.11 j11.71(MVA ) 线路串联支路末端功率为: ~ ~ ~ ~ S 2 S 3 S L1 S YT (15.11 j11.71) (15 j 0) (0.022 j 0.16) 30.132 j11.87(MVA )
则系统端电压(相量)为:
U A U 1 U1 jU1 159.80 25.02 j 37.46 134.78 j 37.46 139.89 15.53 (kV)
这说明系统端电压相量比机端电压滞后了15.53°。 如果仅关心系统端电压的大小,则可用带根号的公式计算:
补充例题3:如图,已知线路首端电压大小为121kV,试求 变压器低压侧的电压。
110kV,80km r1+jx1=0.14+j0.4Ω 15+j0MVA 15+j10MVA
变压器参数:SFL-20000/110,110/11kV,Δps=135kW, us(%)=10.5, Δp0=135kW,I0%=0.8。 思路:这是典型的已知首端电压和末端功率的情况,用 “前推回代法”求解。 解:等值电路图: ~
补充例题4:额定电压为10kV的两端供电网,干线AB的型 号为LJ-70,线间几何均距为 1m ,线路长度及功率分布如 U B 1050 (kV),求初步功率 图。电源电压 U A 105 1 (kV), 分布,并找出功率分点。 2.5km a 4km
U A (U 1 U1 ) 2 (U1 ) 2 (159.80 25.02) 2 37.462 139.89(kV)
'
评析: 1、本例中变压器串联支路电压降落的纵分量数值 小于横分量的数值,绝非巧合,可参见教材P44例 3.1; 2、等值电路中,发电机数学模型用空载电势 E q 和直轴同步电抗xd串联的模型表示,后面学习暂 态分析时会经常见到这种模型;xd%是发电机以 自身额定电压和额定容量为基准的电抗标幺值; 3、发电机发出的复功率为流入机端母线的功率。
解:先作出等值电路如下:
Eq
UA
~ ~
xd
SF
~
RT jX T
S1
~
ST
~
S2
SL
p0 jQ0
SC
~
注:图中各参数均归算至高压侧(机端电压归算后应是多少?)
解:由于发电机满载运行,故其发出有功PF=200MW,则发 电机发出的复功率(即流入机端母线的复功率)为:
S F PF jQF PF jPF tan 200 j 200 tan(arccos 0.85) 200 j123.95(MVA ) 则厂用电 ~ ~ S C 10% S F 20 12.395(MVA ) 而变压器励磁支路功率损耗为:
(30.132 j11.87) (0.97 j 2.77) 31.102 j14.64(MVA ) 以下过程为回推计算电压分布: 线路串联支路的电压降落纵分量、横分量分别为: P 31.102 11.2 14.64 32 1 RL Q1 X L U 1 6.75(kV) U1 121 P 31.102 32 14.64 11.2 1 X L Q1 RL U1 6.87(kV) U1 121
则变压器串联支路始端功率为: ~ ~
线路串联支路的功率损耗为: 2 2
SL
~
~
P2 Q2 ( RL jX L ) 2 UN 110
2
30.132 2 11.87 2
(11.2 j 32) 0.97 j 2.77(MVA )
则线路串联支路的始端功率为: ~ ~ S1 S 2 S L
S a (lab lbB ) S b lbB l Aa lab lbB (340 j 200) (4 3.5) (330 j160) 3.5 370.5 j 206(kVA ) 2.5 4 3.5 从电源点B往左流出的供载功率(复功率)为: S b (l Aa lab ) S a l Aa l Aa lab lbB (330 j160) (2.5 4) (340 j 200) 2.5 299.5 j154(kVA ) 2.5 4 3.5 两端电压相量差为: d U AB U A U B 10.5 1 10.5 0 0.0016 j 0.18(kV)
~
以下过程为前推计算功率分布: ~ 为计算变压器串联支路始端功率 S 3,必须先计算变压器串 联支路的功率损耗,其为:
S ZT
~
~ 2 PL22 QL 2 ( RT jX T ) 2 UN
152 10 2 110
2
(4.08 j 63.53) 0.11 j1.71(MVA )
补充例题2:某发电厂,发电机满载运行,机端电压为 10.4kV, 厂用电占发电机出厂的10%,求系统端电压 U A 。
200MW 10.4kV
UA
~
xd%=20 cosφ=0.85 厂用10% SFP-240000/220,242/15.75 ΔPk=1460kW, ΔP0=232kW I0%=0.96,uk%=14
以 U 1 为参考相量,则变压器高压侧母线电压为: U 2 U 1 U1 jU1 121 6.75 j 6.87
114.25 j 6.87 114.46 3.43 (kV) 变压器串联支路的电压降落纵分量、横分量分别为:
P3 RT Q3 X T 15.11 4.08 11.71 63.53 U 2 7.04(kV) U2 114.46 P3 X T Q3 RT 15.11 63.53 11.71 4.08 U2 7.97(kV) U2 114.46
I0 % p0 jQ0 p0 j SN 100 0.96 0.232 j 240 0.232 j 2.304(MVA ) 100
~
则变压器串联支路始端功率为: ~ ~ ~ S 1 S F S C (p0 jQ0 )
(200 j123.95) 90% (0.232 j 2.304) 179.768 j109.251(MVA )
340+j200kVA
330+j160kVA
提示:虽然两端电源电压幅值相等,但相位不同,因此会 在干线上产生循环功率。 解:先根据“力矩法”求供载功率,其与两端电源电压无 关。本例为特殊均一网(所有线路型号相同),因此应用 “力矩法”时线路长度就是“力臂”。
从电源点A往右流出的供载功率(复功率)为:
(说明:公式中UTN为变压器高压侧额定电压242kV,之所以 不用UN,是为了和网络额定电压相区分) 由题意知:机端电压为U 1 10.40 kV ,其归算到高压侧后 的值为: '
242 U 1 10.40 159.800 (kV) 15.75
则变压器串联支路上的电压降落纵分量、横分量分别为:
补充例题1:220kV双回线路并列运行,长度200km,线路型号 LGJ-400,水平排列,完全换位,线间距离8m,求线路等值参 数,并画出等值电路(导线直径d=27.68mm)。 解:取线路电阻率为31.5Ωmm2/km,又由题意知其横截面积为 S=400mm2,则其单位长度的电阻为 r1=ρ/S=31.5/400=0.0785(Ω/km) (如果查P175表II.4,为0.08 Ω/km) 则线路电阻为 R=r1×l/2=0.0785×200/2=7.875(Ω) (双回线并列运行,电阻减半) 导线的计算半径为r=d/2=13.84(mm) 几何均距Deq=1.26D=1.26×8000=10080(mm) 故单位长度的电抗为 x1=0.0157+0.1445lg(Deq/r) =0.0157+0.1445lg(10080/13.84)=0.431(Ω/km) 则双回线路的总电抗为 X=x1×l/2=0.431×200/2=43.1(Ω)
