人教版八年级数学上解题技巧专题:等腰三角形中辅助线的作法.docx
等腰三角形中做辅助线的七种常用方法典中典数学

等腰三角形中做辅助线的七种常用方法典中典数学等腰三角形中做辅助线的七种常用方法在数学中,等腰三角形是一种非常常见的三角形,其两边长度相等,而另外一边则为底边。
由于等腰三角形的对称性,中心轴线即底边中线,将等腰三角形分为两个对称的部分。
在解决等腰三角形问题时,我们可以运用七种常用的辅助线方法来简化解题过程。
下面将一步一步回答这个主题。
一、作中线中线是连接等腰三角形底边中点和对立角顶点的直线线段。
相比于直接解题,中线的作用是将等腰三角形分解成一个矩形和两个全等直角三角形。
我们可以利用三角形的性质和数学定理,来推导出等腰三角形的各种性质和解题方法。
例如,在求等腰三角形的面积时,利用中线将其分成两个全等直角三角形,再利用直角三角形面积公式求解。
二、作高线高线是从三角形一个顶点,垂直于另一条边所作的线段。
在等腰三角形中,高线不仅垂直于底边,而且还平分底边。
利用高线我们可以求出三角形的高和底边中分线段的长度。
例如,当已知等腰三角形的底边和顶角时,我们可以利用高线分割出一个全等直角三角形。
再根据勾股定理,直接求出等腰三角形的两边长度和面积。
三、作角平分线角平分线是从一个角的顶点,把角分成两个角度相等的线段。
在等腰三角形中,角平分线从顶点出发,与底边平行,平分底边长度,并将等腰三角形分成两个全等三角形。
例如,在已知等腰三角形两边长度和底边角度的情况下,我们可以画出角平分线并运用正弦定理求解。
四、作中垂线中垂线是连接等腰三角形底边中点和对立角的角平分线的垂线。
利用中垂线,我们可以将等腰三角形分解成一个底边中垂线分割的两个全等直角三角形。
例如,当已知等腰三角形的两边长度和底边长度时,可以利用中垂线将三角形分成两个全等直角三角形。
再根据直角三角形勾股定理求出等腰三角形的两边长度和面积。
五、作垂线垂线是从一个点到一条线段垂直的线段。
在等腰三角形中,垂线从顶点出发,垂直于底边,平分底边,并将等腰三角形分解成两个全等直角三角形。
八年级数学上册第12章三角形中常见辅助线的作法(人教版)

三角形中常见辅助线的作法
1、延长中线构造全等三角形
例1 如图1,已知△ABC中,AD是△ABC的中线,AB=8,AC=6,求AD 的取值范围.
提示:延长AD至A',使A'D=AD,连结BA'.根据“SAS”易证△A'BD≌△ACD,得AC=A'B.这样将AC转移到△A'BA中,根据三角形三边关系定理可解.
2、引平行线构造全等三角形
例2 如图2,已知△ABC中,AB=AC,D在AB上,E是AC延长线上一点,且BD=CE,DE与BC交于点F.
求证:DF=EF.
提示:此题辅助线作法较多,如:
①作DG∥AE交BC于G;
②作EH∥BA交BC的延长线于H;
再通过证三角形全等得DF=EF.
3、作连线构造等腰三角形
例3 如图3,已知RT△ACB中,∠C=90°,AC=BC,AD=AC,DE⊥AB,垂足为D,交BC于E.
求证:BD=DE=CE.
提示:连结DC,证△ECD是等腰三角形.
4、利用翻折,构造全等三角形.
例4 如图4,已知△ABC中,∠B=2∠C,AD平分∠BAC交BC于D.求证:AC=AB+BD.
提示:将△ADB沿AD翻折,使B点落在AC上点B'处,再证BD=B'D =B'C,易得△ADB≌△ADB',△B'DC是等腰三角形,于是结论可证.
5、作三角形的中位线
例5 如图5,已知四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,BA、CD的延长线交EF的延长线于点M、N.求证:∠BME=∠CNE.提示:连结AC并取中点O,再连结OE、OF.则OE∥AB,OF∥CD,故∠1=∠BME,∠2=∠CNE.且OE=OF,故∠1=∠2,可得证.。
八年级数学等腰三角形辅助线添加方法,赶快收藏!

八年级数学等腰三角形辅助线添加方法,赶快收藏!
成才路上
奥数国家级教练与四名特级
教师联手执教。
等腰三角形,是初中数学里的一个重点,和等腰三角形有关的考试题型,各种变式题也特别多。
方法一:做“三线合一”中的一线
三线合一,是等腰三角形里最重要的性质定理之一。
所谓三线,就是等腰三角形中,顶角的角平分线、底边的中线、底边的高线。
在等腰三角形中,如果做其中一线,必然三线合一。
方法二:做平行线法
在等腰三角形中,如果做一腰的平行线,马上得出两个角相等,从而得出全等三角形。
方法三:截长补短法
简单说,就是在某一条线段上截取一条线段,和已知线段相等,或者,延长某一线段,使之等于某已知线段。
此解题方法常用,需要大家多做多练,确实掌握截长补短法的解题技巧。
方法四:倍长中线法
如果题目中出现三角形的中线或者中点,我们可以将中线加倍,从而得到等腰三角形。
等腰三角形七种常见辅助线作法(方法梳理与题型分类讲解)(人教版)(教师版) 25学年八年级数学上册

专题13.14等腰三角形七种常见辅助线作法(方法梳理与题型分类讲解)第一部分【模型归纳与题型目录】题型目录【题型1】作等腰三角形底边上高线求值或证明 (1)【题型2】遇到中点作中线求值或证明 (6)【题型3】过一腰上的某一已知点作另一腰的平行线 (10)【题型4】过一腰上的某一已知点作底边的平行线 (14)【题型5】倍长中线构造等腰三角形 (20)【题型6】截长补短构造等腰三角形 (24)【题型7】延长相交构造或证明等腰三角形 (28)第二部分【题型展示与方法点拨】【题型1】作等腰三角形底边上高线求值或证明【例1】(2024·浙江·模拟预测)如图,ABC V 是等腰三角形,AB AC =.设BAC α∠=.(1)如图1,点D 在线段AB 上,若45ACD BAC ∠+∠=︒,求DCB ∠的度数(用含α的代数式表示).(2)如图2,已知AB AC BD ==.若180∠+∠=︒ABD BAC ,过点B 作BH AD ⊥于点H ,求证:12BH BC =.【答案】(1)452DCB ∠=+︒α(2)见解析【分析】本题主要考查了等腰三角形的判定和性质,角平分线的性质定理,(1)根据等腰三角形的性质可得B ACB ∠=∠,设ACD β∠=,DCB x ∠=,解出方程组,即可求解;(2)延长DB ,交AC 于点F ,过点A 作AE BC ⊥于点E .根据180∠+∠=︒ABD BAC ,可得ABF BAC α∠=∠=.再由等腰三角形的性质可得1122D DAB ABF α∠=∠=∠=,从而得到1122BAE BAF α∠=∠=,12BE BC =,进而得到DAB BAE ∠=∠,然后根据角平分线的性质定理,可得BH BE =,即可求证.解:(1)∵AB AC =,∴B ACB ∠=∠.设ACD β∠=,DCB x ∠=,则()452180x βαβα+=︒⎧⎨++=︒⎩解得:452x α=+︒,即452DCB ∠=+︒α;(2)如图,延长DB ,交AC 于点F ,过点A 作AE BC ⊥于点E .∵180∠+∠=︒ABD BAC ,180ABD ABF ∠+∠=︒.∴ABF BAC α∠=∠=.又∵AB BD =,∴1122D DAB ABF α∠=∠=∠=∵AB AC =,∴1122BAE BAF α∠=∠=,12BE BC =∴DAB BAE ∠=∠.又∵BH AD ⊥,BE AE ⊥,∴BH BE =,∴12BH BC =.【变式1】(24-25八年级上·全国·课后作业)如图,在ABC V 中,2AC AB =,AD 平分BAC ∠交BC 于点D ,E 是AD 上一点,且EA EC =.求证:EB AB ⊥.【分析】本题主要考查了等腰三角形的性质,角平分线的定义,全等三角形的判定和性质,正确作出辅助线,构建全等三角形是解题的关键.作EF AC ⊥于点F ,根据等腰三角形的性质得出12AF FC AC ==,再证明 ≌ABE AFE 即可得出结论.证明:如图,作EF AC ⊥于点F.EA EC = ,12AF FC AC ∴==.2AC AB = ,AF AB ∴=.AD 平分BAC ∠,BAD CAD ∴∠=∠.在BAE 和FAE 中,AB AF BAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩,()SAS ABE AFE ∴ ≌,90ABE AFE ∴∠=∠=︒,EB AB ∴⊥.【变式2】(22-23八年级上·江苏泰州·阶段练习)在ABC V 中,AB AC =,过点C 作射线CB ',使ACB ACB '∠=∠(点B '与点B 在直线AC 的异侧)点D 是射线CB '上一动点(不与点C 重合),点E 在线段BC 上,且90DAE ACD ∠+∠=︒.(1)如图1,当点E 与点C 重合时,AD 与CB '的位置关系是,若BC a =,则CD 的长为;(用含a 的式子表示)(2)如图2,当点E 与点C 不重合时,连接DE ,①若30DAE ∠=︒,求BAC ∠的度数;②用等式表示BAC ∠与DAE ∠直间的数量关系,并证明.【答案】(1)互相垂直;12a (2)①60︒;②2BAC DAE∠=∠【分析】(1)根据三角形内角和定理可得AD 与CB '的位置关系是互相垂直,过点A 作AM BC ⊥于点M ,根据等腰三角形性质得到1122CM BM BC ===,利用AAS 证明ACD ACM ≌ ,根据全等三角形性质即可得出12CD CM a ==;(2)当点E 与点C 不重合时,①求解60ACD ∠=︒,可得60ACB ACB '∠=∠=︒,由AB AC =,可得60ABC ACB ∠=∠=︒,可得60BAC ∠=︒;②过点A 作AM BC ⊥于点M 、AN CB '⊥于点N ,利用AAS 证明ACD ACM ≌ ,根据全等三角形性质即可得到2BAC DAE ∠=∠;解:(1)当点E 与点C 重合时,DAE DAC ∠=∠,∵90DAE ACD ∠+∠=︒,∴90DAC ACD ∠+∠=︒,∴90ADC ∠=︒,∴AD CB '⊥,即AD 与CB '的位置关系是互相垂直,若BC a =,过点A 作AM BC ⊥于点M ,如图:则90AMC ADC ∠∠=︒=,∵AB AC =,∴1122CM BM BC a ===,在ACD 与ACM △中,ADC AMC ACD ACM AC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AAS ACD ACM ≌,∴12CD CM a ==,即CD 的长为12a ,(2)解:①∵90DAE ACD ∠+∠=︒,30DAE ∠=︒,∴60ACD ∠=︒,∴60ACB ACB '∠=∠=︒,∵AB AC =,∴60ABC ACB ∠=∠=︒,∴60BAC ∠=︒;②当点E 与点C 不重合时,用等式表示BAC ∠与DAE ∠之间的数量关系是:2BAC DAE ∠=∠,证明如下:过点A 作AM BC ⊥于点M 、AN CB '⊥于点N,如图:则90AMC ANC ∠=∠=︒,∴90CAN ACB '∠+∠=︒,∵90DAE ACD ∠+∠=︒,即90DAE ACB '∠+∠=︒,∴DAE CAN ∠=∠,∵AB AC =,AM BC ⊥,∴22CA B C A A M B M ∠∠=∠=,在ACN △与ACM △中,ANC AMC ACN ACM AC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ACN ACM ≌,∴CAN CAM ∠=∠,∴222BAC CAM CAN DAE ∠=∠=∠=∠;【点拨】本题是三角形综合题,考查了等腰三角形的性质、全等三角形的判定与性质、三角形内角和定理、垂直定义等知识,熟练掌握等腰三角形的性质、全等三角形的判定与性质并作出合理的辅助线是解题的关键.【题型2】遇到中点作中线求值或证明【例3】(23-24七年级下·四川成都·阶段练习)在Rt ABC △中,AB AC =,45DEF ∠=︒且DEF ∠的顶点E 在边BC 上移动,在移动过程中,边DE ,EF 分别与AB ,AC 交于点M ,N ,(1)当BE CN =且M 与A 重合时,求证:ABE ECN△≌△(2)当E 为BC 中点时,连接MN ,求证:NC AM MN=+【分析】本题考查等腰三角形的性质、全等三角形的判定与性质、三角形外角的性质,(1)根据等腰直角三角形的性质可得==45ABE ECN ∠∠︒,利用三角形外角的性质与等量代换可得BAE CEN =∠∠,在根据全等三角形的判定即可证明;(2)连接AE ,在AC 上截取AM CG =,根据等腰直角三角形的性质可得AE EC =,===45MAE CAE ACE ∠∠∠︒,证得()AME CGE SAS ≌,可得=ME GE ,=MEA GEC ∠∠,利用等量代换可得==45MEN GEN ∠∠︒,证得()MEN GEN SAS ≌,可得MN GN =,即可得证.解:(1)证明:∵AB AC =,90BAC ∠=︒,∴==45ABE ECN ∠∠︒,∵==45AEC AEN CEN CEN ∠∠+∠︒+∠,又∵==45AEC ABE BAE BAE ∠∠+∠︒+∠,∴BAE CEN =∠∠,又∵BE CN =,∴()ABE ECN AAS ≌;(2)证明:连接AE ,在AC 上截取AM CG =,∵AB AC =,90BAC ∠=︒,E 为BC 中点,∴AE BC ⊥,AE EC =,∴===45MAE CAE ACE ∠∠∠︒,在AME △和CGE 中,AM CG MAE GCE AE CE =⎧⎪∠=∠⎨⎪=⎩,∴()AME CGE SAS ≌,∴=ME GE ,=MEA GEC ∠∠,∵90AEG GEC ∠+∠=︒,∴=90MEA AEG ∠+∠︒,即90MEG ∠=︒,∵45DEF ∠=︒,∴==45MEN GEN ∠∠︒,又∵NE NE =,=ME GE ,∴()MEN GEN SAS ≌,∴MN GN =,∵=CN CG GN +,∴=CN AM MN +.【变式1】(23-24八年级上·广东汕头·期中)如图,ABC V 中,AB AC =,D 是BC 的中点,E 、F 分别是AB 、AC 上的点,且AE AF =,求证:DE DF =.【分析】本题考查了等腰三角形的性质和全等三角形的判定和性质,属于基础题目,熟练掌握上述知识是解题的关键.连接AD ,根据等腰三角形的性质可得∠∠EAD FAD =,然后即可证明AED AFD ≌,进而可得结论.证明:连接AD ,AB AC = ,D 是BC 的中点,∴∠∠EAD FAD =,在AED △和AFD △中,AE AF EAD FAD AD AD =⎧⎪∠=∠⎨⎪=⎩,()AED AFD SAS ∴ ≌,DE DF ∴=.【变式2】(24-25八年级上·全国·课后作业)如图,在ABC 中,B C ∠∠=,过BC 的中点D 作DE AB ⊥,DF AC ⊥,垂足分别为点E ,F .(1)求证:DE DF =;(2)若40BDE ∠=︒,求BAC ∠的度数.【答案】(1)见解析;(2)80︒。
等腰三角形中作辅助线的四种常用方法课件
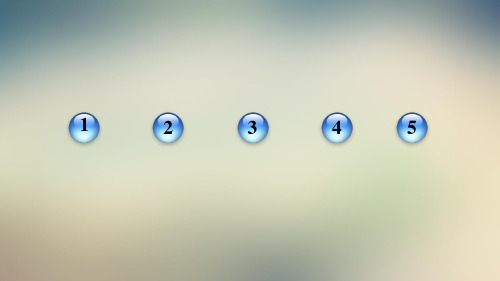
证明: 如图,延长BD至点E,使BE=AB, 连接CE,AE. ∵∠ABE=60°,BE=AB, ∴△ABE为等边三角形. ∴∠AEB=60°,AB=AE. 又∵∠ACD=60°,∴∠ACD=∠AEB.
∵AB=AC,AB=AE,∴AC=AE. ∴∠ACE=∠AEC.∴∠DCE=∠DEC. ∴DC=DE. ∴AB=BE=BD+DE=BD+CD, 即BD+DC=AB.
1
2
3
4
5
方法 1 作“三线”中的“一线”
1.如图,在△ABC中,AB=AC,D是BC的中点,过点 A作EF∥BC,且AE=AF.
求证:DE=DF.
证明:如图,连接AD. ∵AB=AC,BD=CD,∴AD⊥BC. ∵EF∥BC,∴AD⊥EF. ∴∠DAE=∠DAF=90°. ∵AE=AF,AD=AD, ∴△ADE≌△ADF(SAS).
(1)证明:如图,过点P作PF∥AC交BC于点F. ∵点P和点Q同时出发,且速度相同, ∴BP=CQ. ∵PF∥AQ, ∴∠PFB=∠ACB,∠DPF=∠CQD. 又∵AB=AC,∴∠B=∠ACB. ∴∠B=∠PFB.
返回
方法 3 截长补短法
3.如图,在△ABC中,AB=AC,D是△ABC外一 点,且∠ABD=60°,∠ACD=60°.
而CD=DE+EC,∴AB=EC. ∴AE=EC. ∴∠EAC=∠C. 设∠EAC=∠C=x,∵∠AEB为△AEC的外角, ∴∠AEB=∠EAC+∠C=2x. ∴∠B=2x,∠BAE=180°-2x-2x=180°-4x. ∵∠BAC=120°, ∴∠BAE+∠EAC=120°,
返回
即180°-4x+x=120°. 解得x=20°,则∠C=20°.
5.如图,CE,CB分别是△ABC,△ADC的中线,且 AB=AC.求证:CD=2CE.
等腰三角形中做辅助线的七种常用方法典中典数学

等腰三角形中做辅助线的七种常用方法典中典数学
等腰三角形中做辅助线的七种常用方法如下:
1.作腰的平行线:根据“平行线分线段成比例”定理,得出线段之间的关系,然后利用等腰三角形的性质可得出结论。
2.作底边上的高:利用“面积法”或“全等法”进行证明,利用等腰三角形的“三线合一”性质可得出线段之间的关系。
3.作腰的延长线:根据等腰三角形的性质,利用“三角形中位线”定理或“全等”得出线段之间的关系。
4.作底边的中线:根据“等腰三角形底边上的中线与顶角的平分线重合”的性质,利用“全等法”或“面积法”进行证明。
5.过顶点作底边的平行线:根据“平行线分线段成比例”定理和“等腰三角形底边上的中线与顶角的平分线重合”的性质,可得出线段之间的关系。
6.过一腰上的某一点作另一腰的平行线:根据“平行线分线段成比例”定理和等腰三角形的性质,可得出线段之间的关系。
7.作一角平分线:利用角平分线的性质,可得出线段和角度之间的关系,然后利用等腰三角形的性质可得出结论。
等腰三角形常见的辅助线的做法

等腰三角形常见的辅助线的做法
如何快速解决好等腰三角形问题,做到孰能生巧?今天总结了以下四种和等腰三角形题型有关的常见辅助线添加方法
方法一:做三线合一中的一线
三线合一,是等腰三角形里最重要的性质定理之一。
所谓三线,就是等腰三角形中,顶角的角平分线,底边的中线,底边的高线。
必然三线合一。
方法二:做平行线法
这个一般是做一腰的平行线,得出两个角相等,从而得出三角形全等
方法三:截长补短法,或者叫截长取短法
简单说,就是在某一条线段上截取一条线段,和已知线段相等。
或者,延长某一线段,使之等于某已知线段。
此解题方法常用,请大家细心钻研
方法四:加倍折半法,倍长中线法。
人教版八年级数学上册等腰三角形中作辅助线的八种常用方法

∵AB=AC,O 为 BC 的中点,∠BAC=90°, ∴AO⊥BC,∠B=∠C=45°, ∠OAM=12∠BAC=45°.
∵BM=AN,∴AB-BM=AC-AN,即 AM=CN. 在△OAM 和△OCN 中, O∠AO=AOMC=,∠C=45°, AM=CN, ∴△OAM≌△OCN(SAS).
∴OM=ON,∠AOM=∠CON.
又∵∠CON+∠AON=90°, ∴∠AOM+∠AON=90°, 即∠MON=90°. ∴△MON 是等腰直角三角形.
2.如图,在△ABC 中,AB=AC,BD⊥AC 于点 D. 求证∠BAC=2∠DBC.
证明:如图,过点 A 作 AE⊥BC 于点 E. ∵AB=AC,∴∠BAC=2∠CAE. 又∵BD⊥AC,∴∠CAE+∠C=∠DBC+∠C=90°. ∴∠CAE=∠DBC. ∴∠BAC=2∠DBC.
∴CF=CD. ∴CD=2CE.
6.如图,在等腰直角三角形 ABC 中,AB=AC,∠BAC=90°, BF 平分∠ABC,CD⊥BF 交 BF 的延长线于点 D.求证 BF=
2CD.
证明:如图,延长 BA,CD,交于点 E.
∵BF 平分∠ABC,CD⊥BD,BD=BD, ∴△BDC≌△BDE(ASA). ∴CD=ED,即 CE=2CD.
CD=DM+MC=DM+BM. ∵CD=DE,∴AB+(BM-DM)=DM+BM.
∴DM=12AB.
8.如图,在△ABC 中,AB=AC,D 是△ABC 外一点,且∠ABD =60°,∠ACD=60°.求证 BD+DC=AB.
证明:如图,延长 BD 至 E,使 BE=AB,连接 CE,AE. ∵∠ABE=60°,BE=AB, ∴△ABE 为等边三角形. ∴∠AEB=60°,AB=AE.
等腰三角形中辅助线的作法

在△ABC中,AD⊥BC,∠B=2∠C,求证:AB+BD=CD
A
B
D
E
C
在△ABC中,AD⊥BC,∠B=2∠C,求证:AB+BD=CD 证明:在DC上截取DE=DB ∵AD⊥BC ∴∠ADB=∠ADE ∴∠C=∠EAC
B
A
D
E
C
又∵∠AED=∠C+∠EAC
又∵AD=AD ∴△ADB≌△ADE(SAS) ∴AB=AE,∠ABD=∠AED ∵∠B=2∠C ∴∠AED=2∠C
图1BLeabharlann P 图2如图1,OA=2,OB=4,以A点为顶点,AB为腰在第三象限作等腰直角 △ABC. (1)点求C的坐标; 解:(1)如图1,过C作CM⊥x轴于M点, ∵∠MAC+∠OAB=90°, ∠OAB+∠OBA=90°,
C y
M
A O B x
则∠MAC=∠OBA,
又∠CMA=∠AOB=90°,AC=AB, ∴△MAC≌△OBA(AAS),
等腰三角形中辅助线的作法
一、已知等腰作垂线(或中线、角平分线)
如图,已知△ABC 中,AB=AC,CD⊥AD 于 D,CD= 在△ABC 外,求证:∠ACD=∠B. A
D B
1 BC,D 2
E
C
证明:过点 A 作 AE⊥BC 于点 E ∵AB=AC
1 ∴BE= BC 2 1 而 CD= BC 2 ∴BE=CD
求证:MN=BM+CN. A
M B D N C
∴AE=CE
∴AB+BD=AE+DE =CE+DE=CD.
练习:如图,在△ABC中,AB=AC,D是CB延长线上的一点, ∠ADB=60°,E是AD上一点,且有DE=DB.求证:AE=BE+BC.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学试卷
桑水出品
解题技巧专题:等腰三角形中辅助线的作法
——形成精准思维模式,快速解题◆类型一利用“三线合一”作辅助线
一、已知等腰作垂线(或中线、角平分线)
1.如图,在△ABC中,AB=AC,AE⊥BE于点E,
且BE=1
2
BC,若∠EAB=20°,则∠BAC=
__________.
2.如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,
F.
(1)求证:DE=DF;
(2)若∠A=90°,图中与DE相等的有哪些线段(不说明理由)?
3.如图,△ABC中,AC=2AB,AD 平分∠BAC交BC 于D,E是AD上一点,且EA=EC,求证:EB⊥AB.
二、构造等腰三角形
4.如图,△ABC的面积为1cm2,AP垂直∠ABC 的平分线BP于P,则△PBC的面积为 ( ) A.0.4cm2 B.0.5cm2
C.0.6cm2 D.0.7cm2
5.如图,已知△ABC是等腰直角三角形,∠A =90°,BD平分∠ABC交AC于点D,CE⊥BD.求证:BD=2CE.
◆类型二巧用等腰直角三角形构造全等
6.(2016·铜仁中考)如图,在△ABC中,AC =BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.
◆类型三等腰(边)三角形中截长补短或作平行线构造全等
7.如图,已知AB=AC,∠A =108°,BD平分∠ABC交AC于D,求证:BC=AB+CD.
8.如图,过等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于D.
(1)求证:PD=DQ;
(2)若△ABC的边长为1,求DE的长.
参考答案与解析
1.40°
2.(1)证明:如图,连接AD .∵AB =AC ,D 是BC 的中点,∴∠EAD =∠FAD .又∵DE ⊥AB ,DF ⊥AC ,∴DE =DF .
(2)解:若∠BAC =90°,图中与DE 相等的有线段DF ,AE ,AF ,BE ,CF .
3.证明:如图,作EF ⊥AC 于F .∵EA =EC ,∴
AF =FC =12
AC .∵AC =2AB ,∴AF =AB .∵AD 平分∠BAC ,∴∠BAD =∠CAD .又∵AE =AE ,∴△ABE ≌△AFE (SAS),∴∠ABE =∠AFE =90°.∴EB ⊥AB .
4.B
5.证明:如图,延长BA 和CE 交于点M .∵CE ⊥BD ,∴∠BEC =∠BEM =90°.∵BD 平分∠ABC ,∴∠MBE =∠CBE .又∵BE =BE ,∴△BME ≌△
BCE (ASA),∴EM =EC =12
MC .∵△ABC 是等腰直角三
角形,∴∠BAC =∠MAC =90°,BA =AC ,∴∠ABD +∠BDA =90°.∵∠BEC =90°,∴∠ACM +∠CDE =90°.∵∠BDA =∠EDC ,∴∠ABE =∠ACM .又∵AB =AC ,∴△ABD ≌△ACM (ASA),∴DB =MC ,∴BD =2CE .
6.证明:如图,连接CD .∵AC =BC ,D 是AB
的中点,∴CD 平分∠ACB ,CD ⊥AB ,∴∠CDB =90
°.∵∠ACB =90°,∴∠BCD =∠ACD =45°,∴∠B =180°-∠CDB -∠BCD =45°,∴∠ACD =∠B =∠BCD ,∴CD =BD .∵ED ⊥DF ,∴∠EDF =∠EDC +∠CDF =90°.又∵∠CDF +∠BDF =90°,∴∠EDC =∠BDF ,∴△ECD ≌△FBD (ASA),∴DE =DF .
7.证明:如图,在线段BC 上截取BE =BA ,连接DE .∵BD 平分∠ABC ,∴∠ABD =∠EBD .又∵BD =BD ,∴△ABD ≌△EBD (SAS),∴∠BED =∠A =108°,∴∠DEC =180°-∠DEB =72°.又∵AB =AC ,∠A
=108°,∴∠ACB =∠ABC =1
2×(180°-108°)=
36°,∴∠CDE =∠DEB -∠ACB =180°-36°=72°,∴∠CDE =∠DEC ,∴CD =CE ,∴BC =BE +EC =AB +CD .
8.(1)证明:如图,过P 作PF ∥BC 交AC 于点F ,∴∠AFP =∠ACB ,∠FPD =∠Q ,∠PFD =∠QCD .∵△ABC 为等边三角形,∴∠A =∠ACB =60°,∠AFP =60°,∴△APF 是等边三角形,∴AP =PF .∵AP =CQ ,∴PF =CQ ,∴△PFD ≌△QCD (ASA),∴PD =DQ .
(2)解:∵△APF 是等边三角形,PE ⊥AC ,∴AE =EF .∵△PFD ≌△QCD ,∴CD =DF ,∴DE =EF +DF =12AC .又∵AC =1,∴DE =12
.。
