大学物理习题答案03刚体运动学
第03章---刚体力学习题汇总

(A)匀角速转动; (B)匀角加速转动;
(D)
(C)角加速度越来越大的变加速运动;
(D)角加速度越来越小的变加速运动。
分析:当棒转到θ角位置时,棒所受 到的外力矩为:
θ
M 1 mgLcos 根据转动定律 M I ,有:
2
mg
1 mgL cos
可见角5
5. (a)(b)两图中的细棒和小球均相同,系统可绕o 轴在竖直面内自由转动系统从水平位置静止释放,转
(D)只有动量守恒
(C)
分析:
(A)错。非弹性碰撞,机械能不守恒。 (B)错。轴上有外力,动量不守恒。
(C)对。外力矩为零,角动量守恒。
2
2.一绕固定水平轴0匀速转动的转盘,沿图示的同一 水平直线从相反方向射入两颗质量相同、速率相等的 子弹并留在盘中,则子弹射入转盘后的角速度
(A)增大 (B)不变 分析:
边缘并粘在上面,则系统的角速度是
3v
。
分析:取如图的细长条面积:
4b
b
I r 2ds r 2adr
1 ab3 1 mb2
0
3
3
合外力矩为零,系统角动量守恒。
mvb (1 mb2 mb2 )
3
3v
4b
9
二、填空题
1.如图,半径为R,质量为M的飞轮,
可绕水平轴o在竖直面内自由转动(飞
R2
2 3
mgR
11
3.一飞轮的转动惯量为I,在t=0时角速度为 0 , 此后
飞轮经历制动过程。阻力矩M的大小与角速度的平方
成正比,比例系数K>0。当 0 / 3 时,飞轮的角加
速度 = k02 9I ,从开始制动到 0 / 3所经过
《大学物理》刚体力学练习题及答案解析

《大学物理》刚体力学练习题及答案解析一、选择题1.刚体对轴的转动惯量,与哪个因素无关 [ C ](A)刚体的质量(B)刚体质量的空间分布(C)刚体的转动速度(D)刚体转轴的位置2.有两个力作用在一个有固定轴的刚体上. [ B ](1)这两个力都平行于轴作用时,它们对轴的合力矩一定是零;(2)这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;(3)这两个力的合力为零时,它们对轴的合力矩也一定是零;(4)当这两个力对轴的合力矩为零时,它们的合力也一定是零.在上述说法中,(A)只有(1)是正确的;(B) (1)、(2) 正确, (3)、(4)错误;(C) (1)、(2)、(3)都正确, (4)错误;(D) (1)、(2)、(3)、(4)都正确.3.均匀细棒OA可绕通过其一端O而与棒垂直的水平固定光滑轴转动,今使棒从水平位置由静止开始自由下落,在棒摆动到竖立位置的过程中,下述说法哪一种是正确的[ A ](A) 角速度从小到大,角加速度从大到小;(B) 角速度从小到大,角加速度从小到大;(C) 角速度从大到小,角加速度从大到小;(D) 角速度从大到小,角加速度从小到大.4.如图所示,圆锥摆的小球在水平面内作匀速率圆周运动,小球和地球所组成的系统,下列哪些物理量守恒( C )(A)动量守恒,角动量守恒(B)动量和机械能守恒(C)角动量和机械能守恒(D)动量,角动量,机械能守恒5.一圆盘绕通过盘心且垂直于盘面的水平轴转动,轴间摩擦不计,如图射来两个质量相同,速度大小相同、方向相反并在一条直线上的子弹,它们同时射入圆盘并且留在盘内,在子弹射入后的瞬间,对于圆盘和子弹系统的角动量L以及圆盘的角速度ω则有( B )(A)L不变,ω增大(B)L不变,ω减小(C)L变大,ω不变(D)两者均不变6.一花样滑冰者,开始自转时,其动能为20021ωJ E =。
然后他将手臂收回,转动惯量减少为原来的1/3,此时他的角速度变为ω,动能变为E ,则下列关系正确的是( D ) (A )00,3E E ==ωω (B )003,31E E ==ωω (C )00,3E E ==ωω (D )003,3E E ==ωω1C 2.B ,3.A ,4.C ,5.B ,6.D二、填空1.当刚体受到的合外力的力矩为零时,刚体具有将保持静止的状态或_____________状态,把刚体的这一性质叫刚体___________。
大学物理练习册习题及答案4

习题及参考答案第3章 刚体力学参考答案思考题3-1刚体角动量守恒的充分而必要的条件是 (A )刚体不受外力矩的作用。
(B )刚体所受合外力矩为零。
(C)刚体所受的合外力和合外力矩均为零。
(D)刚体的转动惯量和角速度均保持不变。
答:(B )。
3-2如图所示,A 、B 为两个相同的绕着轻 绳的定滑轮。
A 滑轮挂一质量为M 的物体, B 滑轮受拉力F ,而且F =Mg 。
设A 、B 两 滑轮的角加速度分别为βA 和βB ,不计滑轮 轴的摩擦,则有(A )βA = βB (B )βA > βB(C )βA < βB (D )开始时βA = βB ,以后βA < βB 答:(C )。
3-3关于刚体对轴的转动惯量,下列说法中正确的是(A )只取决于刚体的质量,与质量的空间分布和轴的位置无关。
(B)取决于刚体的质量和质量的空间分布,与轴的位置无关。
(C )取决于刚体的质量、质量的空间分布和轴的位置。
(D)只取决于转轴的位置,与刚体的质量和质量的空间分布无 答:(C )。
3-4一水平圆盘可绕通过其中心的固定铅直轴转动,盘上站着一个人,初始时整个系统处于静止状态,当此人在盘上随意走动时,若忽略轴的摩擦,则此系统(A)动量守恒; (B)机械能守恒; (C)对转轴的角动量守恒;(D)动量、机械能和角动量都守恒; (E)动量、机械能和角动量都不守恒。
答:(C )。
3-5光滑的水平桌面上,有一长为2L 、质量为m 的匀质细杆,可绕过其中点o 且垂直于杆的竖直光滑固定轴自由转动,其转动惯量为213mL,起初杆静止,桌面上有两个质量均为m 的小球,各自在 垂直于杆的方向上,正对着杆的一端,以相同速率v 相向 运动,如图所示,当两小球同时与杆的两个端点发生完全非弹性碰撞后,就与杆粘在一起转动,则这一系统碰撞后的转动角速度应为AMF思考题3-2图v思考题3-5图(A)23L v (B)45L v (C)67L v (D)89L v (E)127L v答:(C )。
大物习题解答-大学物理习题答案(许瑞珍_贾谊明)-第3章 刚体力学

第三章 刚体力学3-1 一通风机的转动部分以初角速度ω0绕其轴转动,空气的阻力矩与角速度成正比,比例系数C 为一常量。
若转动部分对其轴的转动惯量为J ,问:(1)经过多少时间后其转动角速度减少为初角速度的一半?(2)在此时间内共转过多少转? 解:(1)由题可知:阻力矩ωC M -=,又因为转动定理 dtd JJ M ωβ== dtd JC ωω=-∴ dt JC d t ⎰⎰-=∴00ωωωω t JC-=0lnωω t JCe-=0ωω当021ωω=时,2ln CJt =。
(2)角位移⎰=tdt 0ωθ⎰-=2ln 00C J t JC dt eωCJ 021ω=,所以,此时间内转过的圈数为CJ n πωπθ420==。
3-2 质量面密度为σ的均匀矩形板,试证其对与板面垂直的,通过几何中心的轴线的转动惯量为)(1222b a ab J +σ=。
其中a ,b 为矩形板的长,宽。
证明一:如图,在板上取一质元dxdy dm σ=,对与板面垂直的、通过几何中心的轴线的转动惯量为 dm r dJ ⎰=2dxdy y x a a b b σ⎰⎰--+=222222)()(1222b a ab +=σ证明二:如图,在板上取一细棒bdx dm σ=,对通过细棒中心与棒垂直的转动轴的转动惯量为2121b dm ⋅,根据平行轴定理,对与板面垂直的、通过几何中心的轴线的转动惯量为22)2(121x adm b dm dJ -+⋅=dx x ab dx b 23)2(121-+=σσ 33121121ba a b dJ J σσ+==∴⎰)(1222b a ab +=σ3-3 如图3-28所示,一轻绳跨过两个质量为m 、半径为r 的均匀圆盘状定滑轮,绳的两端分别挂着质量为m 2和m 的重物,绳与滑轮间无相对滑动,滑轮轴光滑,求重物的加速度和各段绳中的张力。
解:受力分析如图ma T mg 222=- (1) ma mg T =-1 (2) βJ r T T =-)(2 (3) βJ r T T =-)(1 (4)βr a =,221mr J =(5) 联立求出g a 41=, mg T 811=,mg T 451=,mg T 232=3-4 如图3-29所示,一均匀细杆长为L ,质量为m ,平放在摩擦系数为μ的水平桌面上,设开始时杆以角速度0ω绕过细杆中心的竖直轴转动,试求:(1)作用于杆的摩擦力矩;(2)经过多长时间杆才会停止转动。
大学物理第三章刚体力学基础习题答案培训课件

1 )
t2
下次上课内容:
§5-1 简谐运动 §5-2 旋转矢量表示法 §5-3 单摆和复摆 §5-4 振动的能量
角动量定理
t2 Mdt
t1
J2
J1
角动量守恒 M 0, J 恒矢量
力的功
W
r F
drr
力矩的功 W Md
动 能 1 mv2
2
动能定理
W
1 2
mv22
1 2
mv12
转动动能 1 J 2
2
转动动能定理W
1 2
J22
1 2
J12
习 题 课 (三)
3-1 一轻绳绕在有水平轴的定滑轮上,绳下端挂一
的角加速度 =
。从开始制动到 =1/3 0所经过
的时间t = 。
M k2 J
k 2 k02
J 9J
k2 J d
dt
t k dt
0J
1 3
0
d
0
2
t 2J
k0
3-6 一长为L的轻质细杆,两端分别固定有质量为
m 和2m 的小球,此系统在铅直平面内可绕过中心点
O且与杆垂直的水平固定轴转动。开始时杆与水平成
方向上,正对着杆的一端以相同的速率v相向运动,
如图所示。当两小球同时与杆的两端发生完全非弹性
碰撞后,就与杆粘在一起转动,则这一系统碰撞后的
转动角速度为
m
(A) 2v
4v (B)
v
3L
✓(C)
6v 7L
5L (D) 8v
9L
(E) 12v v m
o
7L
2mvL 1 mL2 2mL2
3
6v
7L
大学物理第三章刚体力学基础习题答案

方向竖直向下
3-15 由角动量守恒得
mul J mvl 1 1 2 1 2 2 mu m v J 因弹性碰撞,系统机械能守恒: 2 2 2 1 1 2 2 又: J M 2l Ml 12 3 6mu M 3m u 联立可得: v M 3m l M 3m
2 2 2 1 mv l [m( l ) M l 2 ] 3 3 3
o
2 l 3
6mv (4m 3M ) l
v
m
A
3-9 电风扇在开启电源后,经过t1时间到达了额定 转速,此时相应的角速度为 0。当关闭电源后,经 过t2时间风扇停转。已知风扇转子的转动惯量为 J, 并假定摩擦力矩和电机的电磁力矩均为常量,试根据 已知量推算电机的电磁力矩。 解: 设电机的电磁力矩为M,摩擦力矩为Mf
1
0
t1
3-9 (1)
mg T ma
T mg sin 30 ma
g 2 a m/s 4
方向竖直向下
T2 N 2
mg
(2)
mg T1 ma
T2 mg sin 300 ma
T1r T2r J
a r
T1
1
mg
J k m r2
g 联立求解得: a 22 k
质点运动 m 质 量 力 F 刚体定轴转动 2 J r 转动惯量 m dm 力矩 M Fr sin
dp dL F m a F 第二定律 转动定律 M J M dt dt p mv 动 量 角动量 L J t t2 动量定理 t Fdt mv2 mv1 角动量定理 t Mdt J 2 J1 1 动量守恒 F 0, mv 恒矢量 角动量守恒 M 0, J 恒矢量 力矩的功 W Md 力 的 功 W F dr
大学物理第3章习题解答

第三章 刚体的定轴转动3-1掷铁饼运动员手持铁饼转动1.25圈后松手,此刻铁饼的速度值达到125-⋅=s m v 。
设转动时铁饼沿半径为R=1.0 m 的圆周运动并且均匀加速。
求: (1)铁饼离手时的角速度; (2)铁饼的角加速度;(3)铁饼在手中加速的时间(把铁饼视为质点)。
解:(1)铁饼离手时的角速度为(rad/s)250125===.//R v ω(2)铁饼的角加速度为)(rad/s 83925122252222..=⨯⨯==πθωα(3)铁饼在手中加速的时间为(s)628025251222..=⨯⨯==πωθt3-2一汽车发动机的转速在7.0s 内由2001min -⋅r 均匀地增加到3001min -⋅r 。
(1)求在这段时间内的初角速度和末角速度以及角加速度; (2)求这段时间内转过的角度和圈数;(3)发动机轴上装有一半径为r=0.2m 的飞轮,求它的边缘上一点在第7.0s 末的切向加速度、法向加速度和总加速度。
解:(1)初角速度为(rad/s)9206020020./=⨯=πω末角速度为(rad/s)3146030002=⨯=/πω角加速度为)(rad/s 9410792031420...=-=-=tωωα(2)转过的角度为)186(rad 1017172314920230圈=⨯=⨯+=+=..t ωωθ(3)切向加速度为)(m/s 388209412t ...=⨯==R a α法向加速度为)(m /s 10971203142422n ⨯=⨯==..R a ω总加速度为)(m/s 10971)10971(378242422n 2t ⨯=⨯+=+=...a a a总加速度与切向的夹角为9589378101.97arctan arctan 4t n '︒=⨯==.a a θ3-3 如图所示,在边长为a 的六边形顶点上分别固定有质量都是m 的6个小球(小球的直径a d <<)。
大学物理(上册)课后习题及答案

因此有: ,∴
⑵由 得: ,两边积分得:
∴
⑶质点停止运动时速度为零, ,即t→∞,
故有:
⑷ 时,其速度为: ,
即速度减至 的 .
2.13作用在质量为10 kg的物体上的力为 N,式中 的单位是s,⑴求4s后,这物体的动量和速度的变化,以及力给予物体的冲量。⑵为了使这力的冲量为200 N·s,该力应在这物体上作用多久,试就一原来静止的物体和一个具有初速度 m/s的物体,回答这两个问题。
将 ,及 代入上式,即得: 。
6.9沿绳子传播的平面简谐波的波动方程为 =0.05cos(10 ),式中 , 以米计, 以秒计。求:
⑴设 =100 N,问可使飞轮在多长时间内停止转动?在这段时间里飞轮转了几转?⑵如果在2s内飞轮转速减少一半,需加多大的力 ?
解:⑴先作闸杆和飞轮的受力分析图(如图(b))。图中 、 是正压力, 、 是摩擦力, 和 是杆在 点转轴处所受支承力, 是轮的重力, 是轮在 轴处所受支承力。
杆处于静止状态,所以对 点的合力矩应为零,设闸瓦厚度不计,则有:
解:因为
将以上初值条件代入上式,使两式同时成立之值即为该条件下的初位相。故有: ,
,
5.9一质量为 的物体作谐振动,振幅为 ,周期为 ,当 时位移为 。求:
⑴ 时,物体所在的位置及此时所受力的大小和方向;
⑵由起始位置运动到 处所需的最短时间;
⑶在 处物体的总能量。
解:由题已知 ,∴
又, 时,
故振动方程为:
⑴将 代入得:
方向指向坐标原点,即沿 轴负向。
⑵由题知, 时, ; 时,
∴
⑶由于谐振动中能量守恒,故在任一位置处或任一时刻的系统的总能量均为:
(完整版)大学物理课后习题答案详解

第一章质点运动学1、(习题1.1):一质点在xOy 平面内运动,运动函数为2x =2t,y =4t 8-。
(1)求质点的轨道方程;(2)求t =1 s t =2 s 和时质点的位置、速度和加速度。
解:(1)由x=2t 得,y=4t 2-8 可得: y=x 2-8 即轨道曲线 (2)质点的位置 : 22(48)r ti t j =+- 由d /d v r t =则速度: 28v i tj =+ 由d /d a v t =则加速度: 8a j =则当t=1s 时,有 24,28,8r i j v i j a j =-=+= 当t=2s 时,有 48,216,8ri j v i j a j =+=+=2、(习题1.2): 质点沿x 在轴正向运动,加速度kv a -=,k 为常数.设从原点出发时速度为0v ,求运动方程)(t x x =.解:kv dt dv-= ⎰⎰-=t vv kdt dv v 001 tk e v v -=0t k e v dtdx-=0 dt ev dx tk tx-⎰⎰=000)1(0t k e kv x --=3、一质点沿x 轴运动,其加速度为a = 4t (SI),已知t = 0时,质点位于x 0=10 m 处,初速度v 0 = 0.试求其位置和时间的关系式. 解: =a d v /d t 4=t d v 4=t d t ⎰⎰=vv 0d 4d tt t v 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰= x 2= t 3 /3+10 (SI)4、一质量为m 的小球在高度h 处以初速度0v 水平抛出,求:(1)小球的运动方程;(2)小球在落地之前的轨迹方程; (3)落地前瞬时小球的d d r t ,d d v t ,tv d d . 解:(1) t v x 0= 式(1)2gt 21h y -= 式(2) 201()(h -)2r t v t i gt j =+(2)联立式(1)、式(2)得 22v 2gx h y -=(3)0d -gt d rv i j t = 而落地所用时间 gh2t = 所以 0d -2gh d r v i j t =d d v g j t=- 2202y 2x )gt (v v v v -+=+= 2120212202)2(2])([gh v gh g gt v t g dt dv +=+=5、 已知质点位矢随时间变化的函数形式为22r t i tj =+,式中r 的单位为m ,t 的单位为s .求:(1)任一时刻的速度和加速度;(2)任一时刻的切向加速度和法向加速度。
大学物理习题答案03刚体运动学

⼤学物理习题答案03刚体运动学⼤学物理练习题三⼀、选择题1.⼀⼒学系统由两个质点组成,它们之间只有引⼒作⽤。
若两质点所受外⼒的⽮量和为零,则此系统(A) 动量、机械能以及对⼀轴的⾓动量都守恒。
(B) 动量、机械能守恒,但⾓动量是否守恒不能断定。
(C) 动量守恒,但机械能和⾓动量守恒与否不能断定。
(D) 动量和⾓动量守恒,但机械能是否守恒不能断定。
[ C ]解:系统=0合外F,内⼒是引⼒(保守内⼒)。
(1)021 F F,=0合外F ,动量守恒。
(2)2211r F r F A =合。
21F F,但21r r时0A 外,因此E不⼀定守恒。
(3)21F F,2211d F d F M =合。
两⼒对定点的⼒臂21d d 时,0 合外M,故L 不⼀定守恒。
2. 如图所⽰,有⼀个⼩物体,置于⼀个光滑的⽔平桌⾯上,有⼀绳其⼀端连结此物体,另⼀端穿过桌⾯中⼼的⼩孔,该物体原以⾓速度ω在距孔为R 的圆周上转动,今将绳从⼩孔往下拉。
则物体 (A) 动能不变,动量改变。
(B) 动量不变,动能改变。
(C) ⾓动量不变,动量不变。
(D) ⾓动量改变,动量改变。
(E)⾓动量不变,动能、动量都改变。
[ E ]解:合外⼒(拉⼒)对圆⼼的⼒矩为零,⾓动量O Rrmv L 守恒。
r 减⼩,v 增⼤。
因此p 、E k 均变化(m不变)。
3. 有两个半径相同,质量相等的细圆环A 和B 。
A 环的质量分布均匀,B 环的质量分布不均匀。
它们对通过环⼼并与环⾯垂直的轴的转动惯量分别为J A 和J B ,则(A)A J >B J (B) A J < B J(C) A J =B J (D) 不能确定A J 、B J 哪个⼤。
[ C ]解:2222mR dm R dm R dm r J, J 与m 的分布⽆关。
另问:如果是椭圆环,J 与质量分布有关吗?(是)4. 光滑的⽔平桌⾯上,有⼀长为2L 、质量为m 的匀质细杆,可绕过其中点且垂直于杆的竖直光滑固定轴O ⾃由转动,其转动惯量为31mL 2,起初杆静⽌。
大学物理课后习题答案详解

第一章质点运动学1、(习题:一质点在xOy 平面内运动,运动函数为2x =2t,y =4t 8-。
(1)求质点的轨道方程;(2)求t =1 s t =2 s 和时质点的位置、速度和加速度。
解:(1)由x=2t 得,y=4t 2-8 可得: y=x 2-8 即轨道曲线(2)质点的位置 : 22(48)r ti t j =+-r r r由d /d v r t =r r 则速度: 28v i tj =+r r r由d /d a v t =r r 则加速度: 8a j =r r则当t=1s 时,有 24,28,8r i j v i j a j =-=+=rr r rrrrr当t=2s 时,有 48,216,8r i j v i j a j =+=+=r r r r r rr r2、(习题): 质点沿x 在轴正向运动,加速度kv a -=,k 为常数.设从原点出发时速度为0v ,求运动方程)(t x x =.解:kv dtdv-= ⎰⎰-=t v v kdt dv v 001 t k e v v -=0t k e v dtdx-=0 dt e v dx t k tx-⎰⎰=000)1(0t k e kv x --=3、一质点沿x 轴运动,其加速度为a 4t (SI),已知t 0时,质点位于x 10 m处,初速度v0.试求其位置和时间的关系式.解: =a d v /d t 4=t d v 4=t d t ⎰⎰=vv 0d 4d tt t v 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰= x 2= t 3 /3+10 (SI)4、一质量为m 的小球在高度h 处以初速度0v 水平抛出,求:(1)小球的运动方程;(2)小球在落地之前的轨迹方程;(3)落地前瞬时小球的d d r t v ,d d v t v,tvd d .解:(1) t v x 0= 式(1)2gt 21h y -= 式(2) 201()(h -)2r t v t i gt j =+v v v(2)联立式(1)、式(2)得 22v 2gx h y -=(3)0d -gt d rv i j t=v v v 而落地所用时间 gh2t =所以0d d r v i j t =v vd d v g j t=-v v 2202y 2x )gt (v v v v -+=+=2120212202)2(2])([gh v gh g gt v t g dt dv +=+= 5、 已知质点位矢随时间变化的函数形式为22r t i tj =+v vv,式中r 的单位为m ,t 的单位为s .求:(1)任一时刻的速度和加速度;(2)任一时刻的切向加速度和法向加速度。
面向新世纪课程教材大学物理大作业答案——刚体力学作业
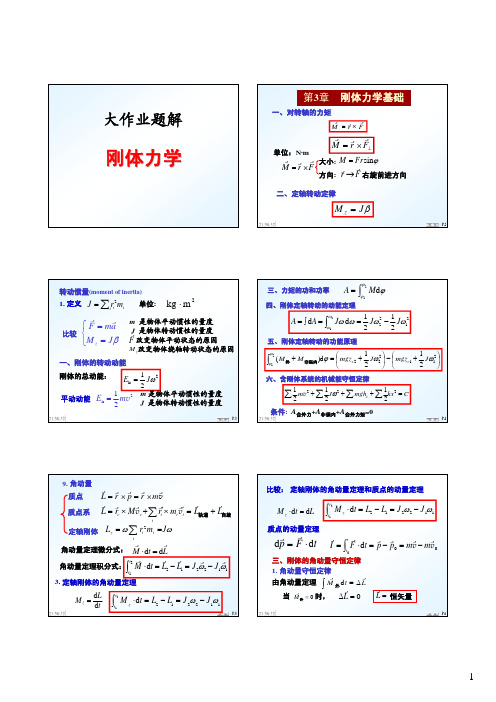
L2
−
L1
=
J 2ω2
−
J1ω1
质点的动量定理
dpr
=
r F
⋅
dt
∫ r
I
=
tr F ⋅ dt =
t0
pr − pr0 = mvr − mvr0
三、刚体的角动量守恒定律
1. 角动量守恒定律
∫ 由角动量定理
r M
当
r M外
=
0
时,
外
d
t r
ΔL
= =
Δ 0
r L
r L
=
恒矢量
P.6
1
区分两类冲击摆
(1)
大作业题解
刚体力学
第3章 刚体力学基础
一、对转轴的力矩
r M
=
rr
×
r F
单位:N·m
r M
=
rr
×
r F⊥
r M
=
rr
×
r F
大小: 方向:
M = Frsinϕ
rr
→
r F
右旋前进方向
二、定轴转动定律
M z = Jβ
P.2
转动惯量(moment of inertia)
∑ 1. 定义 J = iri2mi 单位: kg ⋅ m 2
l/4 O
[ A]
mg l = 1 Jω 2 J = 7 ml 2
22
48
⇒ ω = 4 3g 7l
P.11
9.如图所示,一人造卫星到地球中心C的最大距离和
最小距离分别为RA和RB。设人造卫星对应的角动量分
别为LA和LB,动能分别为EkA和EkB,则有
(A) LB > LA,EkB > EkA
大学物理课后习题及答案刚体

题:一汽车发动机曲轴的转速在s 12内由13min r 102.1-⋅⨯均匀的增加到13min r 107.2-⋅⨯。
(1)求曲轴转动的角加速度;(2)在此时间内,曲轴转了多少转题解:(1)由于角速度2n (n 为单位时间内的转数),根据角加速度的定义t d d ωα=,在匀变速转动中角加速度为()200s rad 1.132-⋅=-=-=tn n t πωωα (2)发动机曲轴转过的角度为()t n n t t t 0020221+=+=+=πωωαωθ在12 s 内曲轴转过的圈数为圈390220=+==t n n N πθ 题:某种电动机启动后转速随时间变化的关系为)1(0τωωt e --=,式中10s rad 0.9-⋅=ω,s 0.2=τ。
求:(1)s 0.6=t 时的转速;(2)角加速度随时间变化的规律;(3)启动后s 0.6内转过的圈数。
题解:(1)根据题意中转速随时间的变化关系,将t s 代入,即得100s 6.895.01--==⎪⎪⎭⎫ ⎝⎛-=ωωωτt e(2)角加速度随时间变化的规律为220s 5.4d d ---===tt e e t ττωωα (3)t = s 时转过的角度为rad 9.36d 1d 60060=⎪⎪⎭⎫ ⎝⎛-==⎰⎰-s t s t et τωωθ 则t = s 时电动机转过的圈数圈87.52==πθN 题:如图所示,一通风机的转动部分以初角速度0ω绕其轴转动,空气的阻力矩与角速度成正比,比例系数C 为一常量。
若转动部分对其轴的转动惯量为J ,问:(1)经过多少时间后其转动角速度减少为初角速度的一半(2)在此时间内共转过多少转题解:(1)通风机叶片所受的阻力矩为ωM C -=,由转动定律αM J =,可得叶片的角加速度为J C t ωωα-==d d (1)根据初始条件对式(1)积分,有⎰⎰-=ωωω00d d d t t J C t 由于C 和J 均为常量,得t J C e -=0ωω 当角速度由0021ωω→时,转动所需的时间为 2ln CJ t = (2)根据初始条件对式(2)积分,有⎰⎰-=t t J C t e 000d d ωθθ即CJ 20ωθ= 在时间t 内所转过的圈数为CJ N πωπθ420== 题:一燃气轮机在试车时,燃气作用在涡轮上的力矩为m N 1003.23⋅⨯,涡轮的转动惯量为2m kg 0.25⋅。
大学物理上册第3章习题解答

大学物理上册第3章习题解答第3章角动量定理和刚体的转动一、内容提要1、质点的角动量定理⑴质点对于某一定点的角动量和角动量定理:角动量L r mv =? 角动量定理 dL M dt=⑵质点对于z 轴的角动量和角动量定理:角动量z L r mv τ⊥=? 角动量定理 zz dL M dt=2、质点系的角动量定理刚体的转动惯量和定轴转动定理⑴质点系的角动量定理 i i iidM L dt =∑∑ ⑵刚体的转动惯量 2z iiiI r m =∑ 或2zI r dm =?⑶刚体的定轴转动定理 z z zd M I I dtωβ== 3、刚体的定轴转动动能定理⑴力矩的功z A M d θ=?⑵刚体的转动动能 212k z E I ω=⑶刚体的定轴转动动能定理 22211122z z z A M d I I θωω==-?4、角动量守恒定律⑴质点的角动量守恒定律:若0M =,则21L L = ⑵刚体的对轴角动量守恒定律:刚体对轴的角动量也可写为2z izizL r m I ωω=?=∑,若0iziM =∑,则0z z I I ωω=,即有0ωω=二、习题解答3.1 一发动机的转轴在7s 内由200/min r 匀速增加到3000/min r . 求:(1)这段时间内的初末角速度和角加速度. (2)这段时间内转过的角度和圈数. (3)轴上有一半径为2.0=r m 的飞轮, 求它边缘上一点在7s 末的切向加速度、法向加速度和总加速度.解:(1)初的角速度1200220.9/60rad s πω?=≈ 末的角速度230002314/60rad s πω?=≈角加速度231420.941.9/7rad s t ωβ?-==≈?(2)转过的角度为2211120.9741.97117622t t rad θωβ=+=?+??=117618622 3.14n r θπ===? (3)切向加速度241.90.28.38/a r m s τβ==?=法向加速度为:22423140.2 1.9710/n a r m s ω==?=?总的加速度为:421.9710/a m s ===?3.3 地球在1987年完成365次自转比1900年长14.1s. 求在1900年到1987年间, 地球自转的平均角加速度.解:平均角加速度为0003652365287T t T a t T ππωω??--+?==212373036523652 1.140.9610/8787(3.1510)t rad s T ππ-≈=-=-3.4一人手握哑铃站在转盘上, 两臂伸开时整个系统的转动惯量为22kgm . 推动后, 系统以15/min r 的转速转动. 当人的手臂收回时, 系统的转动惯量为20.8kgm . 求此时的转速.解:由刚体定轴转动的角动量守恒定律,1122I I ωω=121221537.5/min 0.8I r I ωω==?=3.5 质量为60kg , 半径为0.25m 的匀质圆盘, 绕其中心轴以900/min r 的转速转动. 现用一个闸杆和一个外力F 对盘进行制动(如图所示), 设闸与盘之间的摩擦系数为4.0. 求:(1)当100F N =, 圆盘可在多长时间内停止, 此时已经转了多少转?(2)如果在2s 内盘转速减少一半, F 需多大?图3-5 习题1.4图解:(1)设杆与轮间的正压力为N ,10.5l m =,20.75l m =,由杠杆平衡原理得121()F l l Nl +=121()F l l N l +=闸瓦与杆间的摩擦力为: 121()F l l f N l μμ+== 匀质圆盘对转轴的转动惯量为212I mR =,由定轴转动定律,M I β=,有 ()122112F l l R mR l μβ+-= 21212()40/3F l l rad s mRl μβ+=-=-停止转动所需的时间: 0900200607.06403t s πωβ--===- 转过的角度201532332.762t t rad rad θωβπ?=+=?≈532n θπ==圈(2)030ωπ=,在2s 内角速度减小一半,知0227.5/23.55/rad s rad s tωωβπ-=-=-=-()1222112F l l R mR l μβ+-= 112600.250.5(23.55)1772()20.4 1.25mRl F N l l βμ-=-=-≈+??3.6 发动机带动一个转动惯量为250kgm 的系统做定轴转动. 在0.5s 内由静止开始匀速增加到120/min r 的转速. 求发动机对系统施加的力矩.解:由题意,250I kgm =,00ω=,120/min 4/r rad s ωπ==系统角加速度为:20825.12/rad s t tωωωβπ-?====?? 由刚体定轴转动的转动定理,可知M I β=5025.121256M Nm =?=3.7一轻绳绕于半径为R 的圆盘边缘, 在绳端施以mg F =的拉力, 圆盘可绕水平固定光滑轴在竖直平面内转动. 圆盘质量为M , 并从静止开始转动. 求:(1)圆盘的角加速度及转动的角度和时间的关系. (2)如以质量为m 的物体挂在绳端, 圆盘的角加速度及转动的角度和时间的关系又如何?解:(1)由刚体转动定理可知:M I β= 上题可知: M FR mgR ==212I MR =代入上式得2mgMRβ=, 2212mg t t MRθβ==(2)对物体受力分析'mg F ma -= 'F R I β= a R β=,212I MR =由上式解得22mgMR mR β=+22122mg t t MR mRθβ==+3.8某冲床飞轮的转动惯量为32410kgm ?. 当转速为30/min r 时, 它的转动动能是多少?每冲一次, 其转速下降10/min r . 求每冲一次对外所做的功.解:由题意,转速为:()030/min /r rad s ωπ== 飞轮的转动动能为:232411410 1.9721022E I J ωπ===? 第一次对外做功为:22011122A I I ωω=- 1220/min 3r πω==()2422222301011111515410 3.14 1.0910*******A I I I I J ωωωωπ=-=-=?==?3.9半径为R , 质量为M 的水平圆盘可以绕中心轴无摩擦地转动. 在圆盘上有一人沿着与圆盘同心, 半径为R r <的圆周匀速行走, 行走速度相对于圆盘为v . 设起始时, 圆盘静止不动, 求圆盘的转动角速度.解:设圆盘的转动角速度为2ω,则人的角速度为12vrωω=-,圆盘的转动惯量为212MR ,人的转动惯量为2mr ,由角动量守恒定律, 222212v mr MR r ωω??-=即22222mrvmr MRω=+3.10 两滑冰运动员, 质量分别为60kg 和70kg , 他们的速率分别为7/m s 和6/m s , 在相距1.5m 的两平行线上相向滑行. 当两者最接近时, 互相拉手并开始绕质心做圆周运动. 运动中, 两者间距离保持m 5.1不变. 求该瞬时:(1)系统的总角动量. (2)系统的角速度.(3)两人拉手前后的总动能.解:⑴ 设1m 在原心,质心为c r70 1.50.87060c r m ?=≈+120.8, 1.50.810.7c r r m r m ===-=21112226070.870607630./J m v r m v r kg m s =+=??+??=⑵ 系统的转动惯量为: 222221122600.8700.772.7I m r m r kgm =+=?+?=6308.66/72.7J rad s I ω==≈ 222201122111160770627302222E m v m v J =+=??+??=221172.78.66272622E I J ω==??≈3.11半径为R 的光滑半球形碗, 固定在水平面上. 一均质棒斜靠在碗缘, 一端在碗内, 一端在碗外. 在碗内的长度为c , 求棒的全长.解:棒的受力如图所示本题属于刚体平衡问题,由于碗为光滑半球形,A 端的支持力沿半径方向,而碗缘B 点处的支持力方向不能确定,两个支持力和重力三者在竖直平面内。
《大学物理》刚体的转动练习题及答案

《大学物理》刚体的转动练习题及答案一、简答题:1、为什么刚体绕定轴转动的动能的改变只与外力矩有关,而与内力矩无关?答案:对刚体,由于刚体内各质点间相对位移始终为零,内力总是成对出现,每对内力大小相等,方向相反,在一直线上,故内力矩做功之和一定为零,故刚体绕定轴转动的动能的改变与内力矩无关。
2、简述刚体定轴转动的角动量守恒定律并给出其数学表达式?答案:刚体定轴转动时,若所受合外力矩为零或不受外力矩,则刚体的角动量保持不变。
3、下列物理量中,哪些量与原点的选择有关:(1) 速度,(2) 位矢,(3) 位移,(4) 角动量,(5) 动量 答案:与原点有关的物理量为:位矢,角动量。
4、质量、半径相同的两个圆盘,第一个质量分布均匀,第二个大部分质量分布在盘边缘,当它们以相同的角速度绕通过盘中心的轴转动时,哪个盘的转动动能大?为什么?答案:第二个盘的动能大。
因为由刚体转动动能221ωJ E k =知,在角速度一样时,转动惯量大的动能大;又因为2121mR J =,22mR J ≈,第二个转动惯量较大,所以转动动能较大。
5、在某一瞬时,刚体在一外力矩作用下,其角速度可以为零吗? 其角加速度可以为零吗?答案:由刚体转动定律αJ M =,知,在某一瞬时,刚体在一外力矩作用下,其角加速度不可以为零;由dtd ωα=,有⎰+=t dt 00αωω,可知其角速度此时可以为零。
6、写出刚体绕定轴转动的转动定律文字表达与数学表达式?答案:刚体绕定轴转动的转动定律:刚体绕定轴转动时,刚体的角加速度与它所受的合外力矩成正比,与刚体的转动惯量成反比。
表达式为:αJ M =。
7、简述刚体定轴转动时的特点有哪些, 常用哪些物理量来描述刚体的转动?答案:刚体定轴转动的特点:转轴相对参照系固定,刚体内所有点都具有相同的角位移、角速度、角加速度;质点在垂直转轴的平面内运动,且作圆周运动。
刚体的转动通常用转动惯量J 、力矩M 、角加速度α、角动量L 等来描述。
大学物理03章试题库刚体的定轴转动

《大学物理》试题库管理系统内容第三章 刚体的定轴转动1 题号:03001 第03章 题型:选择题 难易程度:较难试题: 某刚体绕定轴作匀变速转动,对刚体上距转轴为r 处的任一质元的法向加速度n a 和切向加速度τa 来说正确的是( ).A.n a 的大小变化,τa 的大小保持恒定B.n a 的大小保持恒定,τa 的大小变化C.n a 、τa 的大小均随时间变化D.n a 、τa 的大小均保持不变 答案: A2 题号:03002 第03章 题型:选择题 难易程度:适中试题: 有A 、B 两个半径相同、质量也相同的细环,其中A 环的质量分布均匀,而B 环的质量分布不均匀.若两环对过环心且与环面垂直轴的转动惯量分别为B A J J 和,则( ).A. B A J J =B. B A J J >C. B A J J <D. 无法确定B A J J 和的相对大小 答案: A3 题号:03003 第03章 题型:选择题 难易程度:适中试题: 一轻绳绕在具有水平转轴的定滑轮上,绳下端挂一物体,物体的质量为m ,此时滑轮的角加速度为β,若将物体取下,而用大小等于mg 、方向向下的力拉绳子,则滑轮的角加速度将( ).A.变大B.不变C.变小D.无法确定 答案: A试题: 一人张开双臂手握哑铃坐在转椅上,让转椅转动起来,若此后无外力矩作用,则当此人收回双臂时,人和转椅这一系统的( ).A.系统的角动量保持不变B.角动量加大C.转速和转动动能变化不清楚D.转速加大,转动动能不变 答案: A5 题号:03005 第03章 题型:选择题 难易程度:较难试题: 某力学系统由两个质点组成,它们之间仅有引力作用.若两质点所受外力的矢量和为零,则此力学系统( ).A.动量守恒,但机械能和角动量是否守恒不能确定B.动量和角动量守恒,但机械能是否守恒不能确定C.动量、机械能守恒,但角动量是否守恒不能确定D.动量、机械能以及对某一转轴的角动量一定守恒 答案: A6 题号:03006 第03章 题型:选择题 难易程度:较难试题: 如图所示,两个质量均为m 、半径均为R 的匀质圆盘形滑轮的两端,用轻绳分别系着质量为m 和2m 的小物块.若系统从静止释放,则释放后两滑轮之间绳内的张力为( ).A.mg 811 B.mg 23C.mg 21 D.mg答案: A试题: 某质点受的力为kx e F F -=0,若质点从静止开始运动(即,0=x 时0=v ),则该质点所能达到的最大动能为( ).A.k F 0 B. k eF0 C. k e kF 0 D. 0kF 答案: A8 题号:03008 第03章 题型:选择题 难易程度:适中试题: 如图所示,在水平光滑的圆盘上,有一质量为m 的质点,拴在一根穿过圆盘中心光滑小孔的轻绳上.开始时质点离中心的距离为r ,并以角速度转动.今以均匀速率向下拉绳,将质点拉至离中心2r 处时,拉力做的功为( ).A.2223ωmr B. 2225ωmr C.2227ωmr D. 2221ωmr 答案: A9 题号:03009 第03章 题型:选择题 难易程度:适中试题: 已知地球的质量为m ,太阳的质量为M ,地心与日心的距离为R ,引力常数为G ,则地球绕太阳作圆周运动的角动量为( ).A.GMR mB.R G MmC.R GMmD.RGMm 2 答案: A10 题号:03010 第03章 题型:选择题 难易程度:适中F ϖrm试题: 卫星绕地球做椭圆运动,地心为椭圆的一个焦点,在运动过程中,下列叙述中正确的是().A.角动量守恒B.动量守恒C.机械能不守恒D.动量和角动量都不守恒答案: A11 题号:03011 第03章题型:选择题难易程度:适中试题: 三个完全相同的轮子可绕一公共轴转动,角速度的大小都相同,但其中一轮的转动方向与另外两轮的转动方向相反.若使三个轮子靠近啮合在一起,则系统的动能与原来三个轮子的总动能相比为().A.减小到1/9B.减小到1/3C.增大9倍D.增大3倍答案: A12 题号:03012 第03章题型:选择题难易程度:较难试题: 下列说法中,错误的是().A.对于给定的刚体而言,他的质量和形状是一定的,则其转动惯量也是唯一确定的M=,其中M、J和β均是对同一转轴而言的B.刚体定轴转动的转动定律为βJC.刚体的转动动能等于刚体上各质元的动能之和D.刚体作定轴转动时,其上各点的角速度相同而线速度不同答案: A13 题号:03013 第03章题型:选择题难易程度:适中试题: 下列说法中,正确的是().A.作用在定轴转动刚体上的合力矩越大,刚体转动的角加速度越大B.作用在定轴转动刚体上的合力矩越大,刚体转动的角速度就越大C.作用在定轴转动刚体上的合力矩为零,刚体转动的角速度就为零D.作用在定轴转动刚体上的合力越大,刚体转动的角加速度就越大 答案: A14 题号:03014 第03章 题型:选择题 难易程度:难试题: 轮圈半径为R 、其质量M 均匀分布在轮缘上,长为R 、质量为m 的匀质辐条固定在轮心和轮缘间,辐条共有2N 根.今若将辐条数减少N 根,但保持轮对通过轮心、垂直于轮平面轴的转动惯量不变,则轮圈的质量应为( ).A.M m N +3 B.M m N +6 C.M m N +12 D. M m N +32 答案: A15 题号:03015 第03章 题型:选择题 难易程度:适中 试题: 如图一质量为m 的匀质杆长为l ,绕铅直轴O O '成θ角转动,其转动惯量为( ).A.θ22sin 31mlB.231mlC.θ22sin 41ml D.2121ml 答案: A16 题号:03016 第03章 题型:选择题 难易程度:适中 试题: 如图一质量为m 的匀质杆长为l ,绕铅直轴O O '成θ角转动,则匀质杆所受的合外力矩为( ).A.θsin 21mgl B.θcos 21mgl C.θsin mgl D.θcos mgl 答案: A17 题号:03017 第03章 题型:选择题 难易程度:适中 试题: 如图一质量为m 的匀质杆长为l ,绕铅直轴O O '成θ角转动,则匀质杆的角动量为( ).A.θω22sin 31mlB.ω231mlC.ω2121ml D.θω22sin 41ml 答案: A18 题号:03018 第03章 题型:选择题 难易程度:难 O O '成θ角转试题: 如图一质量为m 的匀质杆长为l ,绕铅直轴动,则匀质杆的角加速度为( ).A.θsin 23l g B.lg θsin 23C.l g θsin 32D.θsin 32l g 答案: A19 题号:03019 第03章 题型:选择题 难易程度:难试题: 如图所示,两根长度和质量分别相等的细杆分别绕着光滑的水平轴1O 和2O 转动,设他们自水平位置从静止释放时,角加速度分别为1β和2β,则二者角加速度之间的关系为( ).1Ol O32lA. 21ββ=B.21ββ>C. 21ββ<D.不能确定 答案: A20 题号:03020 第03章 题型:选择题 难易程度:难试题: 如图所示,光滑的水平桌面上有一长为2l 、质量为m 的匀质细杆,可绕通过中点O 、且与杆垂直的竖直轴自由转动,开始时细杆静止.现有一质量为m 的小球,沿桌面正对着杆的一端,以速度v ρ运动,并与杆的A 端碰撞后与杆粘在一起转动,则这一系统碰撞后的转动角速度为( ).A.lv43 B. l v 2C.l v 32 D. lv54 答案: A21 题号:03021 第03章 题型:填空题 难易程度:容易 试题: 刚体是一理想模型,他虽然有一定的形状和大小,但形状和大小永远保持 . 答案: 不变22 题号:03022 第03章 题型:填空题 难易程度:容易 试题: 刚体定轴转动的运动方程的表示式是 . 答案: )(t θθ=23 题号:03023 第03章 题型:填空题 难易程度:较难 试题: 把不涉及转动的原因,只研究如何描述刚体的定轴转动的问题称为 .Ol 2 mv ρmA答案: 刚体定轴转动运动学24 题号:03024 第03章 题型:填空题 难易程度:较难 试题: 把研究刚体定轴转动原因的问题称为 . 答案: 刚体定轴转动的动力学25 题号:03025 第03章 题型:填空题 难易程度:适中试题: 刚体的转动惯量取决于刚体的总质量、质量分布和 等三个因素. 答案: 转轴的位置26 题号:03026 第03章 题型:填空题 难易程度:较难试题: 一飞轮以1min rad 300-⋅的转速转动,转动惯量为2m kg 5⋅,现施加一恒定的制动力矩,使飞轮在2s 内停止转动,则该恒定制动力矩的大小为 . 答案: m N ⋅=5.78M27 题号:03027 第03章 题型:填空题 难易程度:适中 试题: 如图所示,质量为1m 和2m 的均匀细棒长度均为2l ,在两棒对接处嵌有一质量为m 的小球,对过A 的轴而言,若2222141127121ml l m l m J A ++=,则B J 为 . 答案:2222141127121ml l m l m ++ 28 题号:03028 第03章 题型:填空题 难易程度:较难试题: 质量为m 的匀质细杆,长为l ,以角速度ω绕过杆的端点且垂直于杆的水平轴转动,则杆的动量大小为 .答案:ωml 21A B29 题号:03029 第03章 题型:填空题 难易程度:适中试题: 质量为m 的匀质细杆,长为l ,以角速度ω绕过杆的端点且垂直于杆的水平轴转动,则杆绕转动轴的动能为 .答案:2261ωml 30 题号:03030 第03章 题型:填空题 难易程度:适中试题: 质量为m 的匀质细杆,长为l ,以角速度ω绕过杆的端点且垂直于杆的水平轴转动,则杆绕转动轴的角动量大小为 .答案: ω231ml31 题号:03031 第03章 题型:填空题 难易程度:适中试题: 若飞轮从静止开始作匀加速转动,在最初2min 转了3600转,则飞轮的角加速度为 . 答案: 2s rad -⋅=14.3β32 题号:03032 第03章 题型:填空题 难易程度:较难试题: 若飞轮从静止开始作匀加速转动,在最初1min 转了3600转,则飞轮在第50秒末的角速度为 . 答案: 1s rad -⋅=314ω33 题号:03033 第03章 题型:填空题 难易程度:适中 试题: 若某飞轮绕其中心轴转动的运动方程为t t t 4223+-=θ,其中θ的单位为rad ,t 的单位为s ,则飞轮在第2秒末的角加速度为 . 答案: 2s rad -⋅=12β34 题号:03034 第03章 题型:填空题 难易程度:较难试题: 若某飞轮绕其中心轴转动的运动方程为t t t 4223+-=θ,其中θ的单位为rad ,t 的单位为s ,则飞轮从s 2=t 到s 4=t 这段时间内的平均角加速度为 . 答案: 2s rad -⋅=12β35 题号:03035 第03章 题型:填空题 难易程度:较难试题: 若质量为m 、半径为R 的匀质薄圆盘绕过中心且与盘面垂直轴的转动惯量为221mR ,则质量为m 、半径为R 、高度为h 的匀质圆柱体绕过中心且与端面垂直轴的转动惯量为 .答案:221mR 36 题号:03036 第03章 题型:填空题 难易程度:适中试题: 一转动惯量为J 的刚体绕某固定轴转动,当他在外力矩M ρ的作用下,角速度从1ω变为2ω,则该刚体在此过程)(21t t →中所受的冲量矩⎰21t t dt M ρ等于 . 答案: 12ωωJ J -37 题号:03037 第03章 题型:填空题 难易程度:适中试题: 一转动惯量为J 的刚体绕某固定轴转动,当他在外力矩M ρ的作用下,角速度从1ω变为2ω,则该刚体在此过程)(21θθ→中力矩所做的功⎰21θθθMd 等于 .答案:21222121ωωJ J - 38 题号:03038 第03章 题型:填空题 难易程度:容易试题: 刚体角动量守恒的条件为 . 答案: 0=外M ρ39 题号:03039 第03章 题型:填空题 难易程度:较难试题: 一质量为m 的粒子,相对于坐标原点处于j y i x r ρρρ+=点,速度为j v i v v y x ρρρ+=,则该质点相对于坐标原点的角动量为 . 答案: k yv xv m L x y ρρ)(-=40 题号:03040 第03章 题型:填空题 难易程度:适中试题: 一飞轮的转动惯量为J ,0=t 时角速度为0ω,此后飞轮经历一制动过程,受到的阻力矩的大小与角速度成正比,即ωk M -=,式中k 为正的常量.当3ωω=时,飞轮的角加速度为 .答案: Jk 30ωβ-= 41 题号:03041 第03章 题型:计算题 难易程度:适中 试题: 一条缆索绕过一个定滑轮拉动升降机,如图所示.滑轮的半径为m 5.0=r ,如果升降机从静止开始以加速度2s m 4.0-⋅=a 匀加速上升,求:(1)滑轮的角加速度;(2)开始上升后t = 5s 末滑轮的角速度; (3)在这5秒内滑轮转过的圈数;(4)开始上升后s 1='t 末滑轮边缘上一点的加速度(假定缆索和滑轮之间不打滑).答案: 为了图示清晰,将滑轮放大为如图所示.a ρv ρ(1)由于升降机的加速度和滑轮边缘上的一点的切向加速度相等,所以滑轮的角加速度为2s rad 8.0-⋅===rar a τβ (2)由于00=ω,所以5秒末滑轮的角速度为1s rad 0.4-⋅==t βω(3)在这5秒内滑轮转过的角度为rad 10212==t βθ 所以在这5秒内滑轮转过的圈数为圈6.1210==πN(4)结合题意,由图可以看出2s m 4.0-⋅==a a τ2222s m 32.0-⋅===t r r a n βω由此可得滑轮边缘上一点在升降机开始上升后s 1='t 时的加速度为222s m 51.0-⋅=+='τa a a n这个加速度的方向与滑轮边缘的切线方向的夹角为117.384.032.0tan tan =⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛=--ταa a n 42 题号:03042 第03章 题型:计算题 难易程度:难 试题: 一绳跨过定滑轮,两端分别系有质量分别为m 和M 的物体,且m M >.滑轮可看作是质量均匀分布的圆盘,其质量为m ',半径为R有摩擦,滑轮转动时受到了摩擦阻力矩阻M 且与滑轮间无相对滑动.求物体的加速度及绳中的张力. 答案: 由于滑轮有质量,所以不得不考虑滑轮的转动惯性;在转动过程中滑轮还受到阻力矩的作用,在滑轮绕轴作加速转动时,它必须受到两侧绳子的拉力所产生的力矩,以便克服转动惯性与阻力矩的作用,因此滑轮两a ρ1a侧绳子中的拉力一定不相等.设两侧绳子中的拉力分别为1T 和2T ,则滑轮及两侧物体的受力如图所示,其中11T T '=,22T T '=(作用力与反作用力大小相等).因为m M >,所以左侧物体上升,右侧物体下降.设其加速度分别为1a 和2a ,据题意可知,绳子不可伸长,则21a a =,令它们为a .滑轮以顺时针转动,设其角加速度为β,则摩擦阻力矩阻M 的指向为逆时针方向,如图所示.对于上下作平动的两物体,可以视为质点,由牛顿第二运动定律得⎩⎨⎧=-=-Ma T Mg M mamg T m 21:对:对 (1) 滑轮作定轴转动,受到的外力矩分别为R T 2'和R T 1'及阻M (轴对滑轮的支持力N 通过了转轴,其力矩为零).若以顺时针方向转的力矩为正,逆时针转的方向为负,则由刚体定轴转动的转动定律得ββ⎪⎭⎫⎝⎛'==--21221R m J M R T R T 阻 (2)据题意可知,绳与滑轮间无相对滑动,所以滑轮边缘上一点的切向加速度和物体的加速度相等,即βτR a a == (3)联立(1)、(2)、(3)三个方程,得2)(m m M R M g m M a '++--=阻2)22()(1m m M R mM mg m M a g m T '++-'+=+=阻2)22()(2m m M R MM Mg m m a g M T '+++'+=-=阻43 题号:03043 第03章 题型:计算题 难易程度:适中试题: 求长为L ,质量为m 的均匀细棒AB 的转动惯量.(1)对于通过棒的一端与棒垂直的轴;(2)对于通过棒的中点与棒垂直的轴. 答案: (1)如图所示,以过A 端垂直于棒的o o '为轴,沿棒长方向为x 轴,原点在轴上,在棒上取一长度元dx ,则这一长度元的质量为dx Lmdm =,所以202231mL dx L m x dm x J L m =⎪⎭⎫ ⎝⎛==⎰⎰端点(2)同理,如图所示,以过中点垂直于棒的o o '为轴,沿棒长方向为x 轴,原点在轴上,在棒上取一长度元dx ,因此22222121mL dx L m x dm x J L L m=⎪⎭⎫ ⎝⎛==⎰⎰-中点 由此可见,对于同一均匀细棒,转轴的位置不同,棒的转动惯量不同. 44 题号:03044 第03章 题型:计算题 难易程度:容易试题: 试求质量为m 、半径为R 的匀质圆盘对垂直于平面且过中心轴的转动惯量. 答案: 已知条件如图所示.由于质量连续分布,所以220222mR dl R m R dm R J Rm=⎪⎭⎫ ⎝⎛==⎰⎰ππ 45 题号:03045 第03章 题型:计算题 难易程度:适中试题: 试求质量为m 、半径为R 的匀质圆环对垂直于平面且过中心轴的转动惯量.o AA dm答案: 已知条件如图所示.由于质量连续分布,设圆盘的厚度为l ,则圆盘的质量密度为lR m2πρ=.因圆盘可以看成是许多有厚度的圆环组成,所以()ρππρl R ldr r r dm r J R m 4022212=⋅⋅==⎰⎰代入圆盘的质量密度,得221mR J =46 题号:03046 第03章 题型:计算题 难易程度:较难试题: 如图所示,一质量为M 、半径为R 的匀质圆盘形滑轮,可绕一无摩擦的水平轴转动.圆盘上绕有质量可不计的绳子,绳子一端固定在滑轮上,另一端悬挂一质量为m 的物体,问物体由静止落下h 高度时,物体的速率为多少答案: 法一 用牛顿第二运动定律及转动定律求解.受力分析如图所示,对物体m 用牛顿第二运动定律得ma T mg =- (1)对匀质圆盘形滑轮用转动定律有βJ R T =' (2)物体下降的加速度的大小就是转动时滑轮边缘上切向加速度,所以βR a = (3)又由牛顿第三运动定律得T T '=(4)物体m 落下h 高度时的速率为lah v 2= (5)因为221MR J =,所以联立以上(1)、(2)、(3)、(4)和(5)式,可得物体m 落下h 高度时的速率为mM mghv 22+=(小于物体自由下落的速率gh 2).解法二 利用动能定理求解.如图所示,对于物体m 利用质点的动能定理有222121mv mv Th mgh -=- (6) 其中0v 和v 是物体的初速度和末速度.对于滑轮利用刚体定轴转动的转动定理有222121ωωθJ J TR -=∆ (7) 其中θ∆是在拉力矩TR 的作用下滑轮转过的角度,0ω和ω是滑轮的初角速度和末角速度.由于滑轮和绳子间无相对滑动,所以物体落下的距离应等于滑轮边缘上任意一点所经过的弧长,即θ∆=R h .又因为00=v ,00=ω,R v ω=,221MR J =,所以联立(6)和(7)式,可得物体m 落下h 高度时的速率为mM mghv 22+=.解法三 利用机械能守恒定律求解.若把滑轮、物体和地球看成一个系统,则在物体落下、滑轮转动的过程中,绳子的拉力T 对物体做负功(Th -),T '对滑轮做正功(Th )即内力做功的代数和为零,所以系统的机械能守恒.若把系统开始运动而还没有运动时的状态作为初始状态,系统在物体落下高度h 时的状态作为末状态,则0212121222=-+⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛mgh mv R v MR 所以物体m 落下h 高度时的速率为mM mghv 22+=.47 题号:03047 第03章 题型:计算题 难易程度:容易试题: 哈雷慧星绕太阳运行的轨道是一个椭圆,如图所示,它离太阳最近的距离是m 1075.810⨯=近日r ,此时速率为-14s m 1046.5⋅⨯=近日v ;它离太阳最远时的速率为-12s m 1008.9⋅⨯=远日v ,这时它离太阳的距离?远日=r答案: 彗星受太阳引力的作用,而引力通过了太阳,所以对太阳的力矩为零,故彗星在运行的过程中角动量守恒.于是有远日远日近日近日v r v r ρρρρ⨯=⨯因为远日远日近日近日,v r v r ρρρρ⊥⊥,所以有远日近日近日远日v v r r =代入数据,得m 1026.512⨯=远日r48 题号:03048 第03章 题型:计算题 难易程度:较难试题: 如图所示,一个长为l 、质量为M 的匀质杆可绕支点o 自由转动.一质量为m 、速率为v 的子弹以与水平方向成060角的方向射入杆内距支点为a 处,使杆的偏转角为030.问子弹的初速率为多少答案: 把子弹和匀质杆作为一个系统,由于该系统所受的外力有重力及轴对杆的约束力,在子弹射入杆的极短过程中,重力和约束力都通过了转轴o ,因此它们对转轴的力矩均为零,故该系统的角动量守恒.设ρ子弹射入杆后与杆一同前进的角速度为ω,则碰撞前的角动量等于碰撞后的角动量,即()ω⎪⎭⎫⎝⎛+=2203160cos ma Ml a v m子弹在射入杆后与杆一起摆动的过程中只有重力做功,所以由子弹、杆和地球组成的系统机械能守恒,因此有()()022230cos 1230cos 13121-⋅+-=⎪⎭⎫ ⎝⎛+l Mg mga ma Ml ω 联立上述这两个方程得子弹的初速率为()()22326322ma Ml ma Ml g mav ++-=49 题号:03049 第03章 题型:计算题 难易程度:较难试题: 如图所示,一根质量为M 、长为2 l 的均匀细棒,可以在竖直平面内绕通过其中心的光滑水平轴转动,开始时细棒静止于水平位置.今有一质量为m 的小球,以速度u ρ垂直向下落到了棒的端点,设小球与棒的碰撞为完全弹性碰撞.试求碰撞后小球的回跳速度v ρ及棒绕轴转动的角速度ω.答案: 以棒和小球组成的系统为研究对象,则该系统所受的外力有小球的重力、棒的重力和轴给予棒的支持力, 后两者的作用线都通过了转轴,对轴的力矩为零.由于碰撞时间极短,碰撞的冲力矩远大于小球所受的重力矩,所以小球对轴的力矩可忽略不计.分析可知所取系统的角动量守恒.由于碰撞前棒处于静止状态,所以碰撞前系统的角动量就是小球的角动量lmu . 由于碰撞后小球以速度v 回跳,其角动量为lmv ;棒获得的角速度为ω,棒的角动量为()ωω22312121Ml l M =⎥⎦⎤⎢⎣⎡.所以碰撞后系统的角动量为ω231Ml lmv +.由角动量守恒定律得omuω231Ml lmv lmu += (1) 注意:上式中u ,v 这两个速度是以其代数量来表示.以碰撞前小球运动的方向为正,即0>u ;碰撞后小球回跳,u 与v 的方向必然相反,应该有0<v .由题意知,碰撞是完全弹性碰撞,所以碰撞前后系统的动能守恒,即222231212121ω⎪⎭⎫⎝⎛+=Ml mv mu (2) 联立(1)和(2)式,可得小球的速度为u Mm Mm v +-=33棒的角速度为luM m m ⋅+=36ω讨论:由于碰撞后小球回跳,所以v 与u 的方向不同,而0>u ,则0<v .从结果可以看出,要保证0<v ,则必须保证m M 3>.否则,若M m 31≥,无论如何,碰撞后小球也不能回跳,杂耍运动员特别注意这一点.50 题号:03050 第03章 题型:计算题 难易程度:较难试题: 如图所示,一长为l 、质量为m 的匀质细棒竖直放置,其下端与一固定铰链o 相连结,并可绕其转动.由于此竖直放置的细棒处于非稳定平衡状态,当其受到微小扰动时,细棒将在重力的作用下由静止开始绕铰链o 转动.试计算细棒转到与竖直位置成θ角时的角加速度和角速度.答案: 法一 利用定轴转动的转动定律求解.分析受力如图所示,其中G ρ为细棒所受的重力、N ρ为铰链给细棒的约束力.由于约束力N ρ始终通过转轴,所以其作用力矩为零;铰链与细棒之间的摩擦力矩题中没有给定可认为不存在.又由于细棒为匀质细棒,所以重力G ρ的作用点在细棒中心.故由定轴转动的转动定律可得βθ⎪⎭⎫ ⎝⎛=231sin 21ml mgl 因此细棒转过θ角时的角加速度为θβsin 23lg=由角加速度的定义可得θθθωsin 23lgdt d d d =⋅ 整理可得θθωωd l g d ⎪⎭⎫⎝⎛=sin 23 由于0=t 时,0=θ,0=ω;而t t =时,θθ=,ωω=.所以上式两边取积分有θθωωθω⎰⎰⎪⎭⎫⎝⎛=0sin 23d l g d 因此细棒转过θ角时的角速度为()θωcos 13-=lg解法二 利用机械能守恒定律求解.以细棒和地球组成的系统为研究对象,由于细棒所受的重力为保守内力,铰链给细棒的约束力不做功,铰链与细棒之间的摩擦力题中没有给定可认为不存在,因此系统的机械能守恒.于是有()223121cos 12ωθ⎪⎭⎫ ⎝⎛=-⋅ml l mg 因此细棒转过θ角时的角速度为()θωcos 13-=lg此时的角加速度为θωβsin 23lgdt d ==解法三 利用定轴转动的动能定理求解.铰链的约束力对细棒不做功,摩擦力矩没有给定可以认为不存在,只有重力矩做功,所以对于细棒而言,合外力所做的功就是重力矩所做的功,即()θθθθθθcos 121sin 200-=⎪⎭⎫⎝⎛==⎰⎰mgl d l mg Md W由定轴转动的动能定理得()223121cos 121ωθ⎪⎭⎫ ⎝⎛=-ml mgl 因此细棒转过θ角时的角速度为()θωcos 13-=lg此时的角加速度为θωβsin 23lgdt d ==51 题号:03051 第03章 题型:计算题 难易程度:适中试题: 如图所示,在光滑的水平面上有一长为l 、质量为m 的匀质细棒以与棒长方向相互垂直的速度v ρ向前平动,平动中与一固定在桌面上的钉子o 相碰撞,碰撞后,细棒将绕点o 转动,试求其转动的角速度.答案: 由于细棒在光滑的水平面上运动,所以细棒与钉子o 碰撞的过程中遵守角动量守恒定律,则碰撞后碰撞前L L =对于转轴o 而言:⎪⎭⎫⎝⎛=4l mv L 碰撞前方向垂直于纸面向外;ωω⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-+==242l l m J J L o 中心轴碰撞后ωω2224874121ml l m ml =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+=方向垂直于纸面向外.所以有ω24874ml l mv =⎪⎭⎫⎝⎛ 故细棒碰撞后绕轴o 转动的角速度为lv712=ω 52 题号:03052 第03章 题型:计算题 难易程度:适中试题: 如图所示,在光滑的水平面上有一劲度系数为k 的轻质弹簧,它的一端固定,另一端系一质量为M 的滑块.最初滑块静止时,弹簧处于自然长度0l .现有一质量为m 的子弹以速度0v 沿水平方向并垂直于弹簧轴线射向滑块且留在其中,滑块在水平面内滑动.当滑块被拉伸到长度为l 时,求滑块速度的大小和方向.答案: 此题的物理过程有两个,第一个过程为子弹与滑块的碰撞过程.在该过程中子弹与滑块组成的系统所受的合外力为零,所以系统的动量守恒.于是有()V m M mv +=0第二个过程为滑块与子弹一起,以共同的速度V 在弹簧的约束下运动的过程.在该过程中弹簧的弹力不断增大,但始终通过转轴o ,它的力矩为零,所以角动量守恒;与此同时若以子弹、滑块、弹簧和地球组成的系统为研究对象,则该过程也满足机械能守恒定律.因此有()()θsin 0v m M l V m M +=+()()()2022212121l l k v m M V m M -++=+ 其中θ为滑块运动方向与弹簧轴线方向之间的夹角.联立以上三个方程可得滑块速度的大小和方向分别为()m M l l k m M mv v +--⎪⎪⎭⎫⎝⎛+=2020 ()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡+--⎪⎪⎭⎫ ⎝⎛++=--212020001sin m M l l k m M mv m M l l mv θ 53 题号:03053 第03章 题型:计算题 难易程度:适中试题: 一飞轮半径r = 1m ,以转速1min r 1500-⋅=n 转动,受制动均匀减速,经s 50=t 后静止.试求:(1)角加速度β和从制动开始到静止这段时间飞轮转过的转数N ;(2)制动开始后s 25=t 时飞轮的角速度ω;(3)在s 25=t 时飞轮边缘上一点的速度和加速度.答案: (1)角加速度20s rad 14.35060150014.325020-⋅-=⨯⨯-=-=-=ntπωωβ从制动开始到静止这段时间飞轮转过的转数62514.325014.3215060150014.322212220=⨯⨯⨯-⨯⨯⨯=+=∆=πβωπθtt N 圈(2)制动开始后s 25=t 时飞轮的角速度10s rad 5.782514.360150014.322-⋅=⨯-⨯⨯=+=+=t n t βπβωω (3)在s 25=t 时飞轮边缘上一点的速度和加速度分别为11s m 5.78s m )15.78()(--⋅=⋅⨯==τττωρρρρr v ()()τβωττρρρρρr n r a n a a n +=+=2()[]()232s m )14.31016.6(14.315.78-⋅-⨯=⨯-+⨯=ττρρρρn r n54 题号:03054 第03章 题型:计算题 难易程度:适中试题: 如图所示.细棒的长为l ,设转轴通过棒上离中心距离为d 的一点并与棒垂直.求棒对此轴的转动惯量o J '.试说明这一转动惯ol量o J '与棒对过棒中心并与此轴平行的转轴的转动惯量o J 之间的关系(此为平行轴定理).答案: 如图所示,以过o '点垂直于棒的直线为轴,沿棒长方向为x '轴,原点在o '点处,在棒上取一长度元x d ',则()⎰'='mo dm x J 2()⎰⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛''=d l d l x d lm x 22222121md ml +=所以o J '与o J 之间的关系为2md J J o o +='55 题号:03055 第03章 题型:计算题 难易程度:适中试题: 如图所示.两物体的质量分别为1m 和2m ,滑轮的转动惯量为J ,半径为r .若2m 与桌面的摩擦系数为μ,设绳子与滑轮间无相对滑动,试求系统的加速度a 的大小及绳子中张力1T 和2T 的大小.答案: 分析受力如题图所示.21m m 和设其加速度分别为1a 和2a ,则由牛顿运动定律得22221111⎩⎨⎧=-=-a m g m T a m T g m μ 滑轮作定轴转动,则由转动定律有βJ r T r T =-21由于绳子与滑轮间无相对滑动,所以r a a a β===21d ox 'x 1。
大学物理第3章刚体的定轴转动习题解答

习题3-1 一汽车发动机曲轴的转速在12s 内由每分钟1200转匀加速地增加到每分钟2700转,求:(1)角加速度;(2)在此时间内,曲轴转了多少转?解:(1))/(401s rad πω= )/(902s rad πω=)/(1.13)/(6251240902212s rad s rad t≈=-=∆-=πππωωβ匀变速转动(2))(78022122rad πβωωθ=-= )(3902圈==πθn 3-2 一飞轮的转动惯量为J ,在0=t 时角速度为0ω,此后飞轮经历制动过程。
阻力矩M 的大小与角速度ω的平方成正比,比例系数0>K 。
求:(1)当30ωω=时,飞轮的角加速度;(2)从开始制动到30ωω=所需要的时间。
解:(1)依题意 2ωβK J M -== )/(92202s rad JK J K ωωβ-=-= (2)由J K dt d 2ωωβ-== 得 ⎰⎰-=32000ωωωωK Jd dt t ωK Jt 2=3-3 如图所示, 发电机的轮A 由蒸汽机的轮B 通过皮带带动。
两轮半径A R =30cm ,=B R 75cm 。
当蒸汽机开动后,其角加速度π8.0=B βrad/s 2,设轮与皮带之间没有滑动。
求(1)经过多少秒后发电机的转速达到A n =600rev/min ?(2)蒸汽机停止工作后一分钟内发电机转速降到300rev/min ,求其角加速度。
解:(1)t A A βω= t B B βω=因为轮和皮带之间没有滑动,所以A 、B 两轮边缘的线速度相同,即B B A A R R ωω=又)/(20606002s rad A ππω=⨯=联立得)(10s R R t B B A A ==βω(2))/(10603002s rad A ππω=⨯=)/(62s rad t A A A πωωβ=-'= 3-4 一个半径为=R 1.0m 的圆盘,可以绕过其盘心且垂直于盘面的转轴转动。
大学物理第3章-刚体力学习题解答

第3章 刚体力学习题解答3.13 某发动机飞轮在时间间隔t 内的角位移为):,:(43s t rad ct bt at θθ-+=。
求t 时刻的角速度和角加速度。
解:23212643ct bt ct bt a dt d dtd -==-+==ωθβω3.14桑塔纳汽车时速为166km/h ,车轮滚动半径为0.26m ,发动机转速与驱动轮转速比为0.909, 问发动机转速为每分多少转?解:设车轮半径为R=0.26m ,发动机转速为n 1, 驱动轮转速为n 2, 汽车速度为v=166km/h 。
显然,汽车前进的速度就是驱动轮边缘的线速度,909.0/2212Rn Rn v ππ==,所以:min/1054.1/1024.93426.014.3210166909.02909.013rev h rev n R v ⨯=⨯===⨯⨯⨯⨯π3.15 如题3-15图所示,质量为m 的空心圆柱体,质量均匀分布,其内外半径为r 1和r 2,求对通过其中心轴的转动惯量。
解:设圆柱体长为h ,则半径为r ,厚为dr 的薄圆筒的质量dm 为:2..dm h r dr ρπ=对其轴线的转动惯量dI z 为232..z dI r dm h r dr ρπ==212222112..()2r z r I h r r dr m r r ρπ==-⎰ 3.17 如题3-17图所示,一半圆形细杆,半径为 ,质量为 ,求对过细杆二端轴的转动惯量。
解:如图所示,圆形细杆对过O 轴且垂直于圆形细杆所在平面的轴的转动惯量为mR 2,根据垂直轴定理z x y I I I =+和问题的对称性知:圆形细杆对过轴的转动惯量为12mR 2,由转动惯量的可加性可求得:半圆形细杆对过细杆二端轴的转动惯量为:214AA I mR '=3.18 在质量为M ,半径为R 的匀质圆盘上挖出半径为r 的两个圆孔,圆孔中心在半径R 的中点,求剩余部分对过大圆盘中心且与盘面垂直的轴线的转动惯量。
大学物理习题参考解答物理习题参考解答刚体基本运动_转动定律_动能定理

选择题_03图示单元四 刚体基本运动 转动动能 1一 选择题01. 一刚体以每分钟60转绕z 轴做匀速转动(ω沿转轴正方向)。
设某时刻刚体上点P 的位置矢量为345r i j k =++,单位210m -,以210/m s -为速度单位,则该时刻P 点的速度为: 【 B 】(A) 94.2125.6157.0v i j k =++;(B) 25.118.8v i j =-+;(C) 25.118.8v i j =--;(D) 31.4v k =。
02. 轮圈半径为R ,其质量M 均匀布在轮缘上,长为R ,质量为m 的均质辐条固定在轮心和轮缘间,辐条共有2N 根。
今若将辐条数减少N 根但保持轮对通过轮心,垂直于轮平面轴的转动惯量保持不变,则轮圈的质量为 【 D 】(A)12N m M +; (B) 6N m M +; (C) 23N m M +; (D) 3Nm M +。
03. 如图所示,一质量为m 的均质杆长为l ,绕铅直轴OO '成θ角转动,其转动惯量为 【 C 】(A)2112ml ;(B) 221sin 4ml θ;(C) 221sin 3ml θ; (D) 213ml 。
04. 关于刚体对轴的转动惯量,下列说法中正确的是 【 C 】 (A) 只取决于刚体的质量,与质量的空间分布和轴的位置无关; (B) 取决于刚体的质量和质量的空间分布,与轴的位置无关; (C) 取决于刚体的质量、质量的空间分布和轴的位置;(D) 只取决于转轴的位置,与刚体的质量和质量的空间分布无关。
05. 两个匀质圆盘A 和B 的密度分别为A ρ和B ρ,若A B ρρ>,但两圆盘的质量与厚度相同,如两盘对通过盘心垂直于盘面轴的转动惯量各为A J 和B J ,则 【 B 】(A) A B J J >; (B) B A J J >;(C) A B J J =; (D) A J 和B J 哪个大,不能确定。
大学物理 - 1-6章练习附答案

第一章 质点运动学1、已知一质点作直线运动,其加速度为 a =4+3t 2s m -⋅,开始运动时,x =5 m ,v =0,求该质点在t =10s 时的速度和位置。
解:∵ t tva 34d d +==分离变量,得 t t v d )34(d += 积分,得 12234c t t v ++= 由题知,0=t ,00=v ,∴01=c故 2234t t v += 又因为 2234d d t t t x v +==分离变量, t t t x d )234(d 2+=积分得 232212c t t x ++=由题知 0=t ,50=x ,∴52=c 故 521232++=t t x 所以s 10=t 时m70551021102s m 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v2、质点沿x 轴运动,其加速度和位置的关系为 a =2+62x ,a 的单位为2s m -⋅,x 的单位为 m 。
质点在x =0处,速度为101s m -⋅,试求质点在任何坐标处的速度值。
解: ∵ xv v t x x v t v a d d d d d d d d ===分离变量: 2d (26)d v v adx x x ==+ 两边积分得c x x v ++=322221 由题知,0=x 时,100=v ,∴50=c∴ 13s m 252-⋅++=x x v第二章 质点动力学1、质量为M 的大木块具有半径为R 的四分之一弧形槽,如图所示。
质量为m 的小立方体从曲面的顶端滑下,大木块放在光滑水平面上,二者都作无摩擦的运动,而且都从静止开始,求小木块脱离大木块时的速度。
解: m 从M 上下滑的过程中,机械能守恒,以m ,M ,地球为系统,以最低点为重力势能零点,则有222121MV mv mgR +=又下滑过程,动量守恒,以m 、M 为系统,则在m 脱离M 瞬间,水平方向有0=-MV mv联立以上两式,得2MgR v m M =+2、 哈雷彗星绕太阳运动的轨道是一个椭圆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学物理练习题三
一、选择题
1.一力学系统由两个质点组成,它们之间只有引力作用。
若两质点所受外力的矢量和为零,则此系统
(A) 动量、机械能以及对一轴的角动量都守恒。
(B) 动量、机械能守恒,但角动量是否守恒不能断定。
(C) 动量守恒,但机械能和角动量守恒与否不能断定。
(D) 动量和角动量守恒,但机械能是否守恒不能断定。
[ C ]
解:系统=0合外F ,内力是引力(保守内力)。
(1)021=+F F ,=0合外F ,动量守恒。
(2)2211r F r F A ∆⋅+∆⋅=合。
21F F -=, 但21r r ∆≠∆时0A ≠外,因此E不一定守恒。
(3)21F F -=,2211d F d F M ⋅-⋅=合。
两力对定点的力臂21d d ≠时,0≠合外M ,故L 不一定守恒。
2. 如图所示,有一个小物体,置于一个光滑的水平桌面上,有一绳其一端连结此物体,另一端穿过桌面中心的小孔,该物体原以角速度ω在距孔为R 的圆周上转动,今将绳从小孔往下拉。
则物体
(A) 动能不变,动量改变。
(B) 动量不变,动能改变。
(C) 角动量不变,动量不变。
(D) 角动量改变,动量改变。
(E)角动量不变,动能、动量都改变。
[ E ]
解: 合外力(拉力)对圆心的力矩为零,角动量 O R
rmv L =守恒。
r 减小,v 增大。
因此p 、E k 均变化(m 不变)。
3. 有两个半径相同,质量相等的细圆环A 和B 。
A 环的质量分布均匀,B 环的质量分布不均匀。
它们对通过环心并与环面垂直的轴的转动惯量分别为J A 和J B ,则
(A)A J >B J (B) A J < B J
(C) A J =B J (D) 不能确定A J 、B J 哪个大。
[ C ]
解:2222mR dm R dm R dm r J ⎰
⎰⎰====, J 与m 的分布无关。
另问:如果是椭圆环,J 与质量分布有关吗?(是)
4. 光滑的水平桌面上,有一长为2L 、质量为m 的匀质细杆,可绕过其中点且垂直于杆的竖直光滑固定轴O 自由转动,其转动惯量为31mL 2,起初杆静止。
桌面上有两个质量均为m 的小球,各自在垂直于杆的方向上,正对着杆的一端,以相同的速率v 相向运动,如图所示。
当两小球同时与杆的两个端点发生完全非弹性碰撞后与杆粘在一起转动,则这一系统碰撞后的转动角速度为
(A)L v 32. (B) L v 54 (C)L v 76 (D) L v 98 [ C ]
解:对两泥球与棒组成的系统,碰撞力为内力,0=合外M 。
对于转轴O 点,由角动量守恒有 ωω)(22mL J mv L mv L +=⋅+⋅,L v 76=ω
二、填空题
1. 绕定轴转动的飞轮均匀地减速,t=0时角速度ω0=5 rad/s ,t=20s 时角速度ω=0.8ω0,则飞轮的角加速度β= ,t=0到t=100s 时间内飞轮所转过的角度θ= 。
解:=
-=∆ω-ω=β2054t 02
s /rad 05.0-,
O v 俯视图
=⨯-⨯+⨯=β+ω=θ220100)201(211005t 21t rad 250
2.半径为30cm 的飞轮,从静止开始以0.502/s
rad 的匀角加速度转动,则飞轮边缘上一点在飞轮转 2400 时的切向加速度a t = ,法向加速度a n = 。
(提示:代入公式计算时,2400 要化为弧度) 解:3
4180240ππθ=⨯=, 2/05.0s rad =β, 34345.02022
02ππβθωω=⨯⨯+=+=,
=⨯=β=3.05.0R a t )s /m (15.02
,
=π=⨯π=ω=4.03.03
4R a 2n )s /m (26.12 3.一定滑轮质量为M 、半径为R ,对水平轴的转动惯量J=2
1MR 2。
在滑轮的边缘绕一细绳,绳的下端挂一物体。
绳的质量可以忽略且不能伸长,滑轮与轴承间无摩檫。
物体下落的加速度为a ,则绳中的张力T= 。
解:物体下落的加速度与轮边缘的切向加速度相等,R a β=,对于圆盘由转动定理有
a MR R a MR J TR 21212=⋅==β,=T
a M 2
1 4.决定刚体转动惯量的因素是 。
解:刚体的总质量,以及质量相对转轴的分布。
或者:总质量、质量分布、转轴。
5.质量为m 的质点以速度v 沿一直线运动,则它对直线外垂直距离为
d 的一点的角动量大小是 。
解:=
θ=sin rmv L mvd
6.有一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为J ,开始时转台以匀角速度0ω转动,此进有一质量为m 的人站在转台中心。
随后人沿半径向外跑去,当人到达转台边缘时,转台的角速度ω= 。
解:由角动量守恒有 ωωω)(2
0mR J J +=,20mR J J +=ωω
7.长为L 、质量为M 的匀质杆可绕通过杆一端O 的水平光滑固定轴转动,转动惯量为31ML 2,开始时杆竖直下垂,如图所示。
有一质量为m 的子弹以水平速度0v 射入杆上A 点,并嵌在
杆中,OA=2L/3,则子弹射入后瞬间杆的角速度
ω= 。
(标量式) 解:碰撞过程极短,杆可看作处于竖直位置(重力不产生力矩)。
由角动量守恒有
ω⎥⎦
⎤⎢⎣⎡+=⋅22031)32(32ML L m mv L ,=ωL )M 3m 4(mv 60+ (注)式右速度不能记作矢量。
8.一长为L 的轻质细杆,两端分别固定质量为m 和2m 的小球,此系统在竖直平面内可绕过中点O 且与杆垂直的水平光滑固定轴(O 轴)转动。
开始时杆与水平成600角,处于静止状态。
无初转速地释放以后,杆球这一刚体系统绕O 轴转动。
系统绕O 轴的转动惯量J= 。
释放后,当杆转到水平位置时,刚体受到的合外力矩M= ,角加速度β= 。
解:(1)=+=22)2)(2()2(L m L m J 243mL ;
(2)杆转到水平位置时=-=2L mg 2L mg 2M mgL 21;
(3)===4/32/2mL mgL J M βL g
32
0v A O 2L/3 m
三、计算题
1.质量为m ,长度为L 的匀质杆可绕通过其下端的水平光滑固定轴O 在竖直平面内转动,如图。
设它从竖直位置由静止倒下,求它倾倒到与水平面成θ角时的角速度ω和角加速度β。
(提示:对于质心,由机械能守恒定律求ω;由转动定理求β) 解:231mL J =,杆的质心高度改变量 )sin 1(2θ-=L h c , (1)由机械能守恒定律有 221ωJ h mg c =⋅
即22)31(21)sin 1(2ωθmL L mg =-⋅,
L
g )sin 1(3θω-= (2)由θcos 2L mg M ⋅=,βJ M =有
L g 2cos 3θβ=
2.质量为M 1=24 kg 的圆轮,可绕水平光滑固定轴转动,一轻绳缠绕于轮上,另一端通过质量为M 2=5 kg 的圆盘形定滑轮悬有m =10 kg 的物体。
设绳与定滑轮间无相对滑动,圆轮、定滑轮绕通过轮心且垂直于横截面的水平光滑轴的转动惯量分别为21121R M J =,2222
1r M J =。
求当重物由静止开始下降了h =0.5 m 时,(1) 物体的速度; (2) 绳中张力。
解: 对滑轮运用转动定理有
R
a J J R T 1111==β r
a J J r T r T 22212==-β h c
代入21121R M J =,22221r M J =
有 a M T 1121= ①
a M T T 2122
1=- ② 对于m: ma T mg =-2 ③
由①+②+③可得 4222
1=++=M M m mg a (2/s m )
(1) 因a 恒定,由ah v v 220
2=-可得
==ah v 2s m /2
(2) 由①式 ==a M T 1121)(48N 由③式 =-=)(2a g m T )(58N
*3.长为l 的匀质细杆,可绕过杆的一端O 点的水平光滑
固定轴转动,开始时静止于竖直位置。
紧挨O 点悬一单摆,轻质摆线的长度也是l ,摆球质量为m 。
若单摆从水平位置
由静止开始自由摆下,且摆球与细杆作完全弹性碰撞,碰撞
后摆球正好静止。
求:
(1) 细杆的质量。
(2) 细杆摆起的最大角度θ。
解:(1)棒的转动惯量3/2 M J =
碰撞过程角动量、动能守恒
ωJ mv = ①
222
121ωJ mv = ② 由①2/②得3/2
2Ml ml J ==,解得 m M 3=
(2)摆球减少的势能等于细杆增加的势能 )cos 1(23)cos 1(2θθ-=-= mg Mg mg 31cos =θ,31
cos ar =θ。
