钻头与钻削技术研究
钻削与钻头
二、麻花钻的几何角度 1．钻头角度的参考系 基面pr :主切削刃上任 意点的基面，即通过该 点，垂直于该点的切削 速度方向的平面。 切削平面ps : 主切削刃上 任意点的切削平面，是 包含该点的切削速度方 向，而又切于该点加工 表面的平面。 正交平面po、假定工作平 面pf和背平面pp
端平面pt：与钻头轴 线垂直的投影面。 中剖面pc：过钻头轴 线与两主切削刃平行 的平面。 柱剖面pz：过切削刃选定点作与钻头轴线平行的 直线，该直线绕钻头轴线旋转形成的圆柱面。
(7-10)
式中Mc——切削扭矩； vc——切削速度； d ——钻头直径。
影响钻削力的主要因素有： • 螺旋角ω： 螺旋角ω↑，则前角γo↑，并改善了排屑情况， 轴向力F与扭矩M都显著↓。但当螺旋角β>30。 时，其影响减小。
• 顶角2φ： 顶 角 2φ↑ ， 会 使 切 削 厚 度 hD↑ ， 切 削 宽 度↓，从而切 向 力 Fz↓ 及 切 削扭矩M，轴向 力F↑
2．进给量 普通钻头进给量可按以下经验公式估算： f = (0.01～0.02)d (7-11) 合理修磨的钻头可选用 f = 0.03d 3．钻削速度
第三节 钻头的修磨 一、标准高速钢麻花钻存在问题 (1)沿主切削刃各点前角值差别悬殊(由+30°～-30°)，横 刃上的前角竟达-54°～-60°，造成较大的轴向力和扭矩， 使切削条件恶化。 (2)棱边近似为圆柱面(有稍许倒锥)的一部分，副后角为零 度，摩擦严重。 (3)在主、副切削刃相交处，切削速度最大，散热条件最差， 因此磨损很快。 (4)两条主切削刃很长，切屑宽，各点切屑流出速度相差很 大，切屑呈宽螺卷状，排屑不畅，切削液难于注入切削区； (5)横刃较长，其前、后角与主切削刃后角不能分别控制
钻削加工钻头的磨制办法
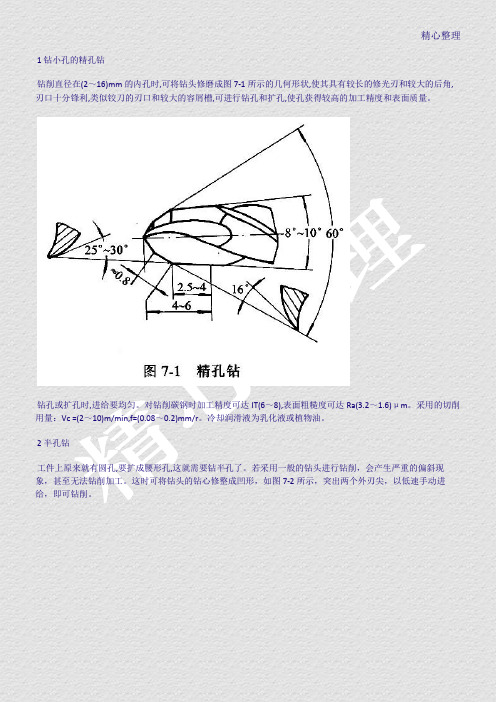
精心整理1 钻小孔的精孔钻钻削直径在(2～16)mm的内孔时,可将钻头修磨成图7-1所示的几何形状,使其具有较长的修光刃和较大的后角,刃口十分锋利,类似铰刀的刃口和较大的容屑槽,可进行钻孔和扩孔,使孔获得较高的加工精度和表面质量。
钻孔或扩孔时,进给要均匀。
对钻削碳钢时加工精度可达IT(6～8),表面粗糙度可达Ra(3.2～1.6)μm。
采用的切削用量：Vc =(2～10)m/min,f=(0.08～0.2)mm/r。
冷却润滑液为乳化液或植物油。
2 半孔钻工件上原来就有圆孔,要扩成腰形孔,这就需要钻半孔了。
若采用一般的钻头进行钻削，会产生严重的偏斜现象，甚至无法钻削加工。
这时可将钻头的钻心修整成凹形，如图7-2所示，突出两个外刃尖，以低速手动进给，即可钻削。
实际钻削时，还会遇到超过半孔和不超过半孔的情况，由于两者的切削分力情况不同，必须对半孔钻的几何参数作必要的修正，若条件可能的话，使用相应的钻套，就更好了。
3 平底孔钻平底又分平底解体4通孔和平底盲孔，如图7-5（b）、（c）所示。
这时，可把麻花钻磨成两刃平直且十分对称的切削刃，并把前角修磨成3°～8°，后角为2°～3°特别是后角不能大，大了以后不仅引起“扎刀”，而且孔底面呈波浪形，重则会造成钻头折断事故。
若钻削盲孔时，应把钻心磨成如图7-5(c)所示的凸形钻心，以便钻头定心，使钻削平稳。
4 薄板钻在(0.1～1.5)mm厚的薄钢板、马口铁皮、薄铝板、黄铜皮和紫铜皮上钻孔，不能用普通钻头，否则钻出的孔就会出现不圆、成多角形、孔口飞边、毛刺很大，甚至薄板扭曲变形，孔被撕破。
大的薄板很难固定在机床上，若用手握住薄板钻孔，当用普通麻花钻的钻尖刚钻透时，钻头失去定心的能力，工件发生抖动，刀刃突然多切，扎入薄板，切削力急增，易使钻头折断或手扶不住，造成事故。
图7-6所示的薄板钻，钻时钻尖先切人工件，起定心作用，两个风力的外尖迅速把中间切离，得到所要求的孔用它钻薄板的干净利落，安全可靠。
(完整版)钻削加工,钻头的磨制方法
1 钻小孔的精孔钻钻削直径在(2～16)mm的内孔时,可将钻头修磨成图7-1所示的几何形状,使其具有较长的修光刃和较大的后角,刃口十分锋利,类似铰刀的刃口和较大的容屑槽,可进行钻孔和扩孔,使孔获得较高的加工精度和表面质量。
钻孔或扩孔时,进给要均匀。
对钻削碳钢时加工精度可达IT(6～8),表面粗糙度可达Ra(3.2～1.6)μm。
采用的切削用量：Vc =(2～10)m/min,f=(0.08～0.2)mm/r。
冷却润滑液为乳化液或植物油。
2 半孔钻工件上原来就有圆孔,要扩成腰形孔,这就需要钻半孔了。
若采用一般的钻头进行钻削，会产生严重的偏斜现象，甚至无法钻削加工。
这时可将钻头的钻心修整成凹形，如图7-2所示，突出两个外刃尖，以低速手动进给，即可钻削。
实际钻削时，还会遇到超过半孔和不超过半孔的情况，由于两者的切削分力情况不同，必须对半孔钻的几何参数作必要的修正，若条件可能的话，使用相应的钻套，就更好了。
3 平底孔钻平底又分平底解体4通孔和平底盲孔，如图7-5（b）、（c）所示。
这时，可把麻花钻磨成两刃平直且十分对称的切削刃，并把前角修磨成3°～8°，后角为2°～3°特别是后角不能大，大了以后不仅引起“扎刀”，而且孔底面呈波浪形，重则会造成钻头折断事故。
若钻削盲孔时，应把钻心磨成如图7-5(c)所示的凸形钻心，以便钻头定心，使钻削平稳。
4 薄板钻在(0.1～1.5)mm厚的薄钢板、马口铁皮、薄铝板、黄铜皮和紫铜皮上钻孔，不能用普通钻头，否则钻出的孔就会出现不圆、成多角形、孔口飞边、毛刺很大，甚至薄板扭曲变形，孔被撕破。
大的薄板很难固定在机床上，若用手握住薄板钻孔，当用普通麻花钻的钻尖刚钻透时，钻头失去定心的能力，工件发生抖动，刀刃突然多切，扎入薄板，切削力急增，易使钻头折断或手扶不住，造成事故。
图7-6所示的薄板钻，钻时钻尖先切人工件，起定心作用，两个风力的外尖迅速把中间切离，得到所要求的孔用它钻薄板的干净利落，安全可靠。
1浅谈高速钢钻头钻削不锈1
浅谈高速钢钻头钻削不锈钢机械技术系数铣组不锈钢属切削性能较差材料，其硬度不高，但导热性较差，导热率大概只有碳素钢的1/3~1/4。
钻削时，除一部分切削热由切屑、冷却液及空气带走外，相当多的热量滞留工件中，传递并集中于钻头刃口处，因此该部位热量大、散热条件差、温度高，从而加大了切削刃的热负荷。
由于高速钢钻头的耐热性约为580℃左右，一旦超过此温度钻头刃口的耐磨性就会急剧下降。
另外，工件的发热和切削中的挤压使加工表面产生硬化层，加大了钻削难度。
不锈钢材料相比普通碳素钢材料具有塑性大、韧性好、切屑不易断裂等特点，因此不锈钢钻孔的参数及切削条件应进行适当调整，具体如下：1．线速度调整钻头线速度10m/min左右。
为此，各类不同直径钻头的转速应调整如下：Φ5钻头转速在600r/min左右；Φ10钻头300r/min左右；Φ20钻头150r/min左右；Φ30钻头100r/min左右。
钻削不锈钢材料时，其线速度为钻削普通碳素钢的1/2~1/3左右，此时其使用寿命较长。
而伴随线速度增大，其使用寿命就会缩短。
2．主切削刃角度修整主切削刃角度一般选取135°～150°左右。
当主切削刃与刃带螺旋角的展开角度成90°时，其排屑效果最佳。
当今市场上的钻头种类很多，包括适合各种不同材料、各种不同加工条件的新牌号刀具材料，其几何角度大小也有较大差异。
例如：加长钻刃带螺旋角度就小。
为此，主切削刃的夹角应根据刃带螺旋角的角度变化而变化。
而生产厂家由于技术专利等原因，对此类参数也多为保密。
3．横刃修整横刃部分主要是定心作用，它的切削过程是挤压切削。
不锈钢材料塑性大、韧性好，挤压产生热量使材料表面层变硬不利于切削。
因此，横刃应尽量修短。
4．后角、后刀面修整后角、后刀面应比钻削普通碳素钢角度略大，主切削刃锋利，使刀刃容易切入材料深层。
但后刀面角度也不应过大，否则会影响钻头的耐用度。
5．开分屑槽对于直径较大的钻头在主切削刃及后刀面上，开二、三条不对称的分屑槽有利于减轻主轴的负荷，使进给轻快，排屑畅通。
课题之钻头与孔加工
2、切削角度
要弄清其切削角度，先确定表示切削角度的辅助平面： 基面、切削平面、正交平面、端平面、中剖面、柱剖 面。
基面：麻花钻任一点的基面是通过该点，且
垂直于该点切削速度方向的平面，实际上就 是通过该点与钻心连线的径向平面。由于两 切削刃不通过钻心，所以主切削刃上各点的 基面也就不同。 切削平面：麻花钻主切削刃上任一点的切削 平面，是由该点的切削速度方向与该点切削 刃的切线所构成的平面。也就是该点与钻心 连线的垂线方向。 正交平面：是通过主切削刃上任一点并垂直 于基面和切削平面的平面。
4-5、修磨分屑槽
五、群钻
群钻是利用标准麻花钻头合理刃磨而成的高
生产率、高加工精度、适应性强、寿命长的 新型钻头。
群钻
铸铁群钻
钻头直径
尖高
圆弧半径
横刃长
分外刃长 L1/L2
总外刃长
外刃顶角
第二顶角
横刃斜角
外刃后角
圆弧后角
5~7
0.11
0.75
0.15
1.9
120
70
65
18
20
7~10
0.15
1.25
0.2
L1=L2
2.6
120
70
65
18
20
10~15
0.2
1.75
0.3
4
120
70
65
18
20
薄板群钻
钻头刃磨的三种境界：
二、衣带渐宽终不悔，为伊消） ——清朝、王国维
九、铰孔和铰刀
定义：用铰刀从孔壁上切除微量金属层，以提高其
尺寸精度和降低表面粗糙度值的方法。 特点：铰刀刀齿数量多，切削余量小，故切削阻力 小，导向性好，加工精度高，可达IT9~IT7级，表面 粗糙度可达Ra1.6 种类：1、整体圆柱铰刀（机用、手用）2、可调节 手用铰刀（铰削非标准孔、）3、锥铰刀包括1:50锥 铰刀（定位销孔）、1:30锥铰刀（套式刀具上的锥 孔）、莫氏锥铰刀（铰削0~6号莫氏锥孔，锥度近 似1:20）、1:10锥铰刀（铰削联轴器上的锥孔）4、 螺旋槽铰刀(铰削带键槽孔) 5、硬质合金机用铰刀
支罗钻头的磨法
支罗钻头的磨法全文共四篇示例，供读者参考第一篇示例：支罗钻头是一种常用的钻井工具，用于在地下岩层中钻取孔洞或者取样。
在使用过程中，支罗钻头往往会因为受到摩擦和冲击而磨损，严重影响其钻井效率和使用寿命。
正确的磨损处理对于延长支罗钻头的使用寿命至关重要。
下面介绍支罗钻头的磨法：1. 磨损分析：在进行磨损处理之前，首先需要对支罗钻头进行磨损分析。
通过观察支罗钻头的磨损程度，可以判断出哪些部位需要进行磨损处理，以及采取何种磨损方式。
2. 磨钝磨损：支罗钻头在使用过程中，由于长时间受到岩石的摩擦和冲击，会导致其切削刃变钝，影响钻头的钻进效率。
对于这种磨损情况，可以采取砂轮磨削的方式进行磨损处理。
首先需要选择适当的砂轮，然后将支罗钻头固定在磨床上，通过砂轮磨削使切削刃恢复锋利。
3. 表面磨损：支罗钻头在岩石中钻取孔洞时，会受到岩石表面的磨损，导致支罗钻头表面不光滑。
对于这种磨损情况，可以采取喷丸或者防磨涂层的方式进行磨损处理。
喷丸可以去除支罗钻头表面的氧化皮和污垢，恢复表面光滑度；而防磨涂层则可以在支罗钻头表面形成一层保护膜，减少表面磨损。
5. 耐磨层磨损：支罗钻头在使用过程中，由于长时间受到岩石的磨损会导致支罗钻头整体的耐磨层磨损严重，这种情况下需要采取特殊的磨损处理方式。
可以通过沉积焊接或者热喷涂等技术，将新的耐磨层覆盖在支罗钻头表面，提高支罗钻头的耐磨性能。
支罗钻头的磨损处理是确保其使用寿命和钻井效率的关键。
只有将支罗钻头的磨损情况及时分析，并采取合适的磨损处理方式，才能延长支罗钻头的使用寿命，提高钻井效率。
希望以上介绍的支罗钻头的磨法对您有所帮助。
第二篇示例：支罗钻头是一种常用的工具，用于在矿山、隧道等工地中进行钻孔工作。
钻头的磨法对于其性能和使用寿命都有着重要的影响，因此正确的磨法对于提高工作效率和降低成本都是非常重要的。
下面将介绍一种较为常用的支罗钻头的磨法，希望对大家在工作中有所帮助。
支罗钻头的磨法主要包括以下几个步骤：清洗钻头、夹紧钻头、调整磨削角度、进行粗磨和精磨、检查钻头磨削情况等。
钻削工艺与技巧
钻削工艺与技巧钻削是一种常见的金属加工工艺，广泛应用于机械制造、汽车制造、航空航天等行业。
正确的钻削工艺和技巧可以提高工作效率和产品质量。
本文将介绍钻削的一些基本工艺和技巧，供读者参考。
一、钻削的基本工艺1. 选择合适的刀具：钻削刀具的选择要根据被加工材料的硬度、切削性能和工艺要求来确定。
常用的钻头有普通刃钻头、中心钻头、深孔钻等，需根据实际情况选择合适的刀具。
2. 精确定位：在进行钻削之前，要使用中心钻或小直径钻头进行精确定位。
这样可以确保钻孔的准确度和垂直度。
3. 冷却润滑：钻削过程中产生剧烈的摩擦和热量，需要使用切削液进行冷却和润滑，以降低刀具磨损和工件变形的风险。
4. 控制切削速度：切削速度是决定钻削过程中切削效果和工作效率的重要参数。
具体的切削速度需根据被加工材料的硬度和切削刀具的材质来确定。
5. 控制进给量：进给量直接影响钻孔的形状和加工质量。
进给量过大容易引起刀具断裂，进给量过小则会降低加工效率。
需要根据被加工材料和刀具的特性来控制进给量。
二、钻削的技巧1. 正确操作钻削机床：在进行钻削操作之前，要熟悉钻削机床的使用方法和各项安全规范。
要保持机床的清洁和润滑，定期检查机床的磨损和故障，确保其正常工作。
2. 钻孔前预备工作：在进行钻孔之前，要清理工件表面的杂质和油污，以免影响钻削质量。
还要使用标尺等工具测量和标记钻孔位置，确保钻孔的准确度。
3. 斜刃钻削技巧：当被加工材料较硬或加工深孔时，可以采用斜刃钻削技巧，即在钻孔过程中适当移动刀具，使其形成较小的切削面积，降低切削阻力和温度。
4. 避免钻头卡孔：由于被加工材料的性质或操作不当，钻头可能会出现卡住的情况。
为了避免这种情况的发生，可以使用适当的切削液，减小进给量，合理选择钻头等方法。
5. 钻孔表面处理：在完成钻削后，要对钻孔进行一些表面处理。
可以使用酸洗、抛光等方法来去除钻削过程中产生的毛刺，提高钻孔的光洁度。
总结：钻削工艺是金属加工中常见的一项工艺，通过正确的钻削工艺和技巧，可以提高加工效率和产品质量。
实验10-钻头的修磨
车削切削温度的测定校外实验目的掌握钻头的角度掌握钻头的研磨方法实验设备与材料钻头砂轮机钻头研磨机实验原理概述钻头角度（详细）实验过程1、刃口要与砂轮面摆平。
磨钻头前，先要将钻头的主切削刃与砂轮面放置在一个水平面上，也就是说，保证刃口接触砂轮面时，整个刃都要磨到。
这是钻头与砂轮相对位置的第一步，位置摆好再慢慢往砂轮面上靠。
2、钻头轴线要与砂轮面斜出60°的角度。
这个角度就是钻头的锋角，此时的角度不对，将直接影响钻头顶角的大小及主切削刃的形状和横刃斜角。
这里是指钻头轴心线与砂轮表面之间的位置关系，取60°就行，这个角度一般比较能看得准。
这里要注意钻头刃磨前相对的水平位置和角度位置，二者要统筹兼顾，不要为了摆平刃口而忽略了摆好度角，或为了摆好角度而忽略了摆平刃口。
3、由刃口往后磨后面。
刃口接触砂轮后，要从主切削刃往后面磨，也就是从钻头的刃口先开始接触砂轮，而后沿着整个后刀面缓慢往下磨。
钻头切入时可轻轻接触砂轮，先进行较少量的刃磨，并注意观察火花的均匀性，及时调整手上压力大小，还要注意钻头的冷却，不能让其磨过火，造成刃口变色，而至刃口退火。
发现刃口温度高时，要及时将钻头冷却。
4、钻头的刃口要上下摆动，钻头尾部不能起翘。
这是一个标准的钻头磨削动作，主切削刃在砂轮上要上下摆动，也就是握钻头前部的手要均匀地将钻头在砂轮面上上下摆动。
而握柄部的手却不能摆动，还要防止后柄往上翘，即钻头的尾部不能高翘于砂轮水平中心线以上，否则会使刃口磨钝，无法切削。
这是最关键的一步，钻头磨得好与坏，与此有很大的关系。
在磨得差不多时，要从刃口开始，往后角再轻轻蹭一下，让刃后面更光洁一些。
5、保证刃尖对轴线，两边对称慢慢修。
一边刃口磨好后，再磨另一边刃口，必须保证刃口在钻头轴线的中间，两边刃口要对称。
有经验的师傅会对着亮光察看钻尖的对称性，慢慢进行修磨。
钻头切削刃的后角一般为10°-14°，后角大了，切削刃太薄，钻削时振动厉害，孔口呈三边或五边形，切屑呈针状；后角小了，钻削时轴向力很大，不易切入，切削力增加，温升大，钻头发热严重，甚至无法钻削。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
钻头与钻削技术研究人类认识和使用钻头的历史可以上溯到史前时代。
燧人氏“钻木取火”所使用的石钻，可以看作最原始的钻头。
现代工业加工中广泛使用的麻花钻（俗称钻头），是一种形状复杂的实工件孔加工刀具，诞生于一百多年前。
现在，全世界每年消耗的各类钻头数以亿计。
据统计，在美国的汽车制造业，机械加工中钻孔工序的比重约占50%；而在飞机制造业，钻孔工序所占的比重则更高。
尽管钻头的使用如此广泛，但众所周知，钻削加工也是最复杂的机械加工方法之一。
正因为如此，人们一直致力于钻头的改进和钻削过程的研究。
本文根据所能得到的英文文献资料，对两沟槽麻花钻的有关技术问题及钻削研究的历史、现状和发展趋势进行综述。
1．研究的主要领域和技术问题近几十年来，人们关于钻头和钻削的研究除了钻头制作材料的改进以外，主要集中在以下五个方面：①钻头数学模型和几何设计研究：包括螺旋沟槽、后刀面、主刃和横刃数学模型的建立，横向截形与钻尖结构参数的优化，切削角度（分布）的计算与控制，钻头结构的静态和动态特性分析，钻尖几何形状与切削和排屑性能关系的研究。
②钻头制造方法研究：包括钻头几何参数与后刀面刃磨参数之间关系的建立与优化，钻头制造精度和刃磨质量的评价与制造误差的测控，钻头螺旋沟槽加工工具截形的设计计算，钻头加工设备特别是数控磨床与加工软件的开发等。
③钻削过程与钻削质量研究：包括影响钻削过程的各种因素及出现的各种物理现象的分析、建模与监控（如钻削力、切削刃应力和温度分布的测量、建模和预报）；钻头磨损、破损机理与钻头寿命的研究；钻头的变形、偏斜、入钻时的打滑和钻尖摆动现象的研究；钻削工艺（如振动钻削、高速钻削、深孔钻削、钻削过程的稳定性等）与钻削质量（孔的位置精度、直线度、表面粗糙度、圆柱度、直径、孔口毛刺等）的研究。
④钻削机理与各种高性能钻头（如群钻、枪钻、干切削钻头、微孔、深孔钻头、长钻头、可转位钻头、合成材料加工用钻头、木工钻头、多螺旋槽钻头等）的研究。
⑤钻削过程模型验证和钻头性能评估过程的自动化，切削条件及钻头形状选用数据库和知识库的建立等。
目前，最具活力的研究领域是钻头数学模型、几何设计和制造方法（设备）的研究，钻削过程建模与钻削质量的研究等。
2．钻头数学模型与几何设计研究2.1 钻头的数学模型建立钻头的数学模型是对钻头进行几何设计、制造、切削性能分析和对钻削过程进行建模的基础。
第一个钻头数学模型由Galloway D F于1957年提出。
他推导了直线刃钻头前刀面的参数方程，给出了主刃前、后角和横刃斜角的定义、计算公式和测量方法，提出了“把钻头后刀面作为钻头在刃磨过程中与砂轮相互作用后形成的磨削锥的一部分”的观点。
20世纪70年代初期，Fujii S 等人对Galloway D F提出的模型进行了进一步研究，提出采用割平面法，将三维空间曲面后刀面化为二维平面曲线进行分析，并开发了一个麻花钻计算机辅助设计程序。
1972年，Armarego E J A和Rotenbery A发现：后刀面锥面刃磨法有4个独立的刃磨参数，而一般给出的钻尖几何参数只有3个，因此不能唯一确定钻尖后刀面形状和刃磨参数。
为此，他们提出用后刀面尾隙角作为补充几何参数，以获得刃磨参数的唯一解。
1979年，Tsai W D和Wu S M证明：锥面钻头、Racon钻头、螺旋钻头和Bickford钻头等的后刀面都可以用二次曲面来表示，并提出了表示钻头几何形状的综合数学模型，该模型可用于控制刃磨过程。
1983年，Radhakrishnan L等人提出了十字钻尖钻头后刀面的一个数学模型。
他们将后刀面分为第一后刀面和第二后刀面：对第一后刀面，以Tsai模型为基础，建立了一个改进的锥面模型；对第二后刀面，建立了一个平面模型。
Fugelso M A则提出了圆柱面钻尖的数学模型。
1985年，Fuh K H等人建立了一个用二次曲面表示的钻头后刀面数学模型，以便用计算机将其设计成椭球面、双曲面、锥面、圆柱面或它们的任意组合。
长期以来，人们一直将麻花钻的主刃设计为直线。
1990年，Fugelso M A发现，由于要求锥面麻花钻的主刃为直线，使靠近钻芯处的主刃后角变得过小，如果在刃磨之前，将钻头绕自身轴线旋转5°～10°，就可以解决这一问题，只是主刃将变得微微弯曲。
同年，Wang Y将主刃看作曲线，利用多项式插补方法建立了钻头螺旋前刀面的几何模型。
1991年，Lin C和Cao Z提出了一种适合于直线和曲线刃，采用锥面、柱面和平面后刀面的麻花钻综合数学模型。
1999年，Ren K C和Ni J提出用二项式表示任意形状的主刃曲线，钻头前刀面采用新的数学模型，并用向量分析方法，建立了二次曲面后刀面的刃磨参数与几何参数之间的关系。
2.2 钻头的结构优化由于广泛使用的锥面麻花钻的切削性能并不理想，人们一直致力于对其结构（参数）和刃磨方法进行改进，先后提出了200多种互不相同的钻头形状，以改善其切削性能。
其中，Shi H M 等人提出了通过改变主刃走向控制主刃前角分布的方法，并于1990年开发出使钻头主刃上各点前角均达到可能的最大值的曲线刃麻花钻。
1987年，Lee S J在考虑钻头偏斜的条件下，以消除钻削过程中钻尖的摆动现象为目标，提出了对钻头结构进行优化设计的方法。
1995年，Selvamhe S V和Sujatha C在研究麻花钻的变形时，用有限元方法对钻头几何形状进行了优化，得出的使钻头变形最小的结构参数优化值（钻头直径25mm）为：螺旋角39.776°，横刃斜角Ψ=54°～80°，锋角120°。
1997年，Chen W C提出了一种特殊截形的厚钻芯麻花钻，既具有足够的扭转刚度，又具有合理的主刃和横刃前角分布。
2005年，Paul A等人为确保优化钻头的可加工性，提出了一种基于刃磨参数的新钻尖模型，并用它对锥面钻尖、Racon钻尖和螺旋面钻尖进行了优化，以使其切削力达到最小2.3 螺旋沟槽截形和加工工具截形的计算1975年，Dibner L G提出了一种可以简化磨削螺旋沟槽砂轮截形计算、提高沟槽加工精度和完全排除砂轮直径变化影响的方法。
1990年，Ehmann K F提出了一个基于微分几何和运动学原理的求麻花钻螺旋沟槽加工工具截形的方法。
1998～2003年，Kang D C和Armarego E J A对螺旋沟槽加工的“正问题”和“反问题”（“由沟槽截形求工具截形”和“由工具截形求沟槽截形”）进行了研究，提出了直线刃麻花钻螺旋沟槽设计和制造的计算机辅助几何分析方法。
2.4 关于群钻与微型钻头的研究1982年，Shen J等人建立了群钻的第一个数学模型。
利用该模型，人们可以多次重复地磨制群钻。
1984年，Chen L和Wu S M对9种典型群钻进行了研究，改进了群钻的数学模型，为群钻的计算机辅助设计提供了可能。
1985年，Hsiao C 和Wu S M提出了用计算机对群钻进行辅助优化设计的具体方法。
1987年，Fuh K H 提出了一种利用综合二次曲面模型和有限元方法设计和分析群钻的方法。
Liang E J则提出了一个基于知识库技术的群钻刃磨CAD/CAM集成系统。
1991年，Liu T I采用一种两阶段策略设计和优化了一种加工机轴注油孔用群钻。
1994年，Huang H T等人推导了群钻切削刃的工作法后角和法前角的公式，提出了考虑内刃和圆弧刃之间过渡区的群钻精确几何模型。
2001年，Wang G C等人应用一种倾斜立体块方法，建立了群钻新的数学模型，解决了已有模型存在的横刃几何形状不确定的问题，保证了所设计群钻的可加工性。
1992年开始，Lin C、Kang S K、Ehmann K F和Chyan H C等人组成的研究小组对微型钻头进行了系统研究。
1992年，他们建立了平面微型钻尖的数学模型，提出了相应的刃磨方法。
1993年，他们又提出了螺旋面微型钻尖的数学模型和刃磨方法，并发现螺旋面微型钻尖在几何方面和切削性能方面均优于常用的平面微型钻尖。
1997年，他们指出：螺旋面微型钻尖与平面微型钻尖相比，具有两个方面的优点：①在同样的工作切削角度分布条件下，可以允许更大的进给量；②刃磨方法更简单，且不易受刃磨误差的影响。
2002年，他们制造出加工微孔用曲线刃形螺旋后刀面系列钻尖。
3．钻削力建模的研究3.1 钻削力建模的历史在过去的几十年中，人们报道了许多预报钻削力的方法，其中绝大部分是用于标准麻花钻的。
由于缺乏先进的计算机和测量设备，早期的研究主要集中在建立简单的经验性扭矩和轴向力模型上，模型参数就是钻头的几何参数（如钻头直径）和切削用量，建模方法是通过大量的切削实验，用统计方法拟合出钻削力的经验公式。
用分析方法建立的钻削力模型是随着人们对切削过程认识的深入而逐步出现的。
1955年，Oxford用显微照片记录下钻头主刃和横刃的切屑变形过程，并通过实验发现：钻削过程中，在钻尖上存在三个主要的切削区域，即主刃切削区、第二切削刃（横刃）切削区和钻芯附近的刻划区。
稍后，Shaw M C和Oxford C J Jr 证明了横刃在钻削加工中的重要性，因为它产生了50%～60%的轴向力。
1966年，Cook N H提出了一个用半分析法推导钻削力公式的方法。
Shaw M C（1962、1984年）在对切屑变形机理进行深入研究的基础上，提出了钻头主刃的切屑变形模型。
Williams A R（1974年）提出了一个基于单点刀具二维切削模型的钻头主刃切削力模型，并确定了钻头刻划区的直径。
Armarego E J A（1972年）应用斜角切削理论，提出了平面钻尖切削力预报模型。
Wiriyacosol S（1979年）等人根据切屑变形的薄剪切区（剪切平面）理论，将钻头主刃和横刃看作一系列与切削条件有关的单元斜角或直角切削刀具的组合，通过累加这些单元刀具的切削力来预报钻削力，即单元刀具线性综合法。
在剪切平面理论的基础上，Oxley C J Jr （1959、1962年）、Armarego E J A（1972、1979年）和Waston A R（1985年）分别建立了不同的钻削力模型；Stepenson D A（1988、1989年）提出了计算钻削力的数学方法。
3.2 钻削力建模的发展对于钻削力建模的研究是随着人们对各种新型钻头和钻削工艺的开发而不断深入的。
Wu S M等人在建立群钻切削力模型方面做了大量工作。
其中，Lee S W（1986年）和Fuh K H（1987年）以工作切削角度为准，对主切削刃使用斜角切削模型，对第二切削刃使用直角切削模型，建立了群钻的切削力模型；Huang H T（1992年）等人提出了一个用普通麻花钻的力学模型预报群钻轴向力和扭矩的方法。