西工大 电磁场 考研 期末 丁君
丁君版工程电磁场与电磁波答案 第八章 电磁波的辐射

6
例 3 电偶极子长10m ,电流振幅1A ,频率为1MHz ,求: 1)在垂直于偶极子轴方向上10m 及100km 处的E 、S 、Sav ;
2)该偶极子的辐射率Prav 。
解:依题意 f
= 106 Hz ,λ
=
c f
=
3 ×108 106
= 300m,
l
= 10m ,I 0
= 1A ,θ
= 90
第八章 电磁波的辐射 8.1 主要内容与重点 本章主要内容:电流元(基本电振子)和磁流元(基本磁振子)的辐射,天线基本参数、对称阵 子天线以及天线阵。 本章重点:电流元和磁流元远区辐射场及其特点;天线基本参数的定义及计算;对称阵子 远区辐射场及期特点,方向图的画法,二元阵乃至多元均匀线阵远区辐射场的推导,方向 图的画法以及利用镜像法分析接地导电平面附近的单元天线或天线阵。 8.2主要公式(基本公式) 8.2.1 滞后位
(8.27)
故半功率波瓣宽度为
θ 0.5
=
±π 4
2θ 0.5
=
π 2
。
(8.28) (8.29)
(3)天线效率:定义为
ηA =
Pr Pin
=
Pr Pr + Pd
=
Rr Rr + Rd
(8.30)
其中 Pr
=
1 2
I
2 m
Rr
,Pd
=
1 2
Im2 Rd 分别为天线的平均辐射功率和损耗功率,而Rd 为损耗电
在求解辐射问题时,一般都是根据已知的ρ 或 J ,由(8.4),(8.5)求出ϕ 和A ,再由(8.2)或
(8.3) 求解辐射点磁场。 8.2.2电偶极子的辐射 (1)偶极子天线的辐射场为
工程电磁场与电磁波 丁君版 答案第四章习题答案

工程电磁场与电磁波丁君版答案第四章习题答案第四章习题4-1解:选柱坐标系,在所求无源区内电位函数满足:02=?φφ只和r 相关0=???φ0=??z φ方程化为 0)(1=????rr r r φ21ln C r C +=φ为常数21,C C 由 006.0==φ时r 501.0-==φ时r得 88.27588.9721=-=C C88.275ln 88.97+-=r φr a rE ?188.97=-?=φ4—2:解:图一依据边界条件:?????====021R R R R U φφ0可得:???????--=-=00UR R R B U R R R R A 1211221 ∴()120212021R R U R R R R U R R ---=φ(2) ()R R a RR R U R R a R E ?1?212021?-=??-=-?=φφ (1) 如图一,依据题意可知:电位函数φ满足拉普拉斯方程。
接受球坐标系:2=?φ0=??θφ0=???φR 相关只于φ,方程化为: 0)(122=????R R R R φφ积分得:B RA +?=1φ(3) ()R R R aR R R U R E D ?12102001-?===εε内表 S S d D s Sρ=??内表S S D s ρ=内表∴)(12102R R R U R D s -==ερ内表4—3:解:选择直角坐标如图,由恒定电场的泊松方程可得:xy设两板间距离为d,代入边界条件?????====000U dz z φφ???????+=+==?ερερ22002021d d U d d U C C ∴)2()2(2002ερερφερερφd d U z E zdd U z +-=-?=++-=4—4:解:选择柱坐标系,依据恒定电磁场的拉普拉斯方程,(1) 02=?m φ,m φ只在?方向上有变化,所以:B A r m m+==???φ?φ:,01222积分得由 0=?时:0,0==B m 得φ∴?φA m = l m m a dld Hφφ-=-?=l d H d m?-=φ??-=?-=ππφ2020I l d H d m0,0,2=??=??-=?xy φφερφ方程可化为:,22ερφ-=??z2122:C z C z ++-=ερφ积分得B A I m m+=-==?φφπ?代入,2π2?=-A I π2I A -= ?πφ2Im -= (2) ??π?φφφa rI a d d r a dl d H m l m m21==-=-?=可见,利用拉普拉斯方程与安培环路定理求出来的结果一样。
西安交大西工大 考研备考期末复习 工程数学复变函数 级数

1
z
.
当 z 1时,lim zn 0,级数发散.
综上
z
n
收
敛,
n
且和
函
数
为 1
1
z
当 z 1时;
n0 发散 当 z 1时.
工程数学(二)
复变函数
例2.求下列幂级数的收敛半径
1)
n1
zn n3
(并讨论在收敛圆周上的情形)
2)
z 1n
(并讨论z 0,2时的情形)
n1 n
n1
n1
n1
工程数学(二)
实常数项级数审敛法
一.根据定义判断
1). aqn
n0
q 1时级数收敛
q
1时级数发散
复变函数
2).
1
发散
n1 n
二.正项级数审敛法
1.正项级数un收敛 部分和数列Sn有界。
n1
2.正项级数 un和 vn ,un vn n 1,2,
n1
n1
若 vn收敛,则un收敛;若un发散,则 vn发散。
复变幂级数的性质
复变函数
定理4 设 cnzn f (z) z R n0
(i) f (z)在 z R内解析.
(ii) f '(z) ( cnzn )' (cnzn )' ncnzn1 z R
n0
n0
n1
---幂级数的逐项求导运算
(iii)
f (z)dz
c
c
cnzndz
幂级 数的代换运 算在函数展 成幂级数中 很有用.
例3
把
z
1
b
表
成
形
如
西北工业大学《电磁场和电磁波》课后习题

或者 F , sin sin 六 解: 1)
cos sin 2 2
Sav
1 2 Em 100 2 m
w 2 10 7
Em 274.6 v
k1 w 0 0
15
E1 274.6 cos 2 10 7 t z a x v m 15 H1 0.728 cos 2 10 7 t z a y A m 15
2)
2 1 1 = 2 1 3
T
2 2 2 2 1 3 2 15
k2
j z ˆx E1 Em e jk1 z ax 91.5e 15 a
2 j z jk 2 z ˆx E2 TEm e a x 183e 15 a
R2 R3
2 2 2
2
v E1dr E2 dr
R1 R2
s 2 1 1 s 2 1 1 R1 R R R1 R R 3 0 2 0 3 1 2
C
Q 12 0 1 2 3 V R1 R2 R3
E E 1 E 2 j
I 0l e jkr 0 sin sin cos sin r 2
I 0l e jkr H j sin sin cos sin r 2
2) 方向性函数
F , sin sin cos sin 2
空间 P 点的电位:
( x, y , z )
其中:
q q q q , 4 0 r1 4 0 r2 4 0 r3 4 0 r4
r1 x 2 y 2 ( z d ) 2
西工大电磁场第4章静态场分析

——恒定磁场是有旋无散场
B H Jc
B A
A Jc
2 A ( A) A J c
2
洛仑兹规范 A 0
A J c ——矢量泊松方程
qm B dS
S
2 0
2m 0
(5)应用 • 电偶极子和磁偶极子辐射的对偶关系 • 波导中横电波(TE波)和横磁波(TM波)间的对偶关系
电磁场与电磁波
第4章 静态场分析
例1 已知无限长同轴电缆内、外半径分别为 R1 和 R 2 ,如图所 示,电缆中填充均匀介质,内外导体间的电位差为 U , 外导体接地。求其间各点的电位和电场强度。 解:采用圆柱坐标系
q+
E
E
P
E0
-
-
- - - - -
-
-
q -
最终问题: 确定镜像电荷电量 确定镜像电荷位置
电磁场与电磁波
第4章 静态场分析
镜像法的实质: ① 把实际上不均匀的媒质 处理为均匀媒质 ② 用简单分布的电荷或电 流代替实际边界上复杂 的电荷或电流分布 ③ 实际电荷或电流和镜像 电荷或电流共同产生的 场在待求区域满足泊松 方程或拉普拉斯方程 ④ 保持原边界处的边界条 件不变
S V
D E
E 0 D
E D E
无源区域 0
——静电场是有散(有源)无旋场,是保守场
()
——泊松方程
2
2 0 ——拉普拉斯方程
4 1
为何还要求解泊松方 程或拉普拉斯方程?
0
2
2009B-2西北工业大学《电磁场和电磁波》课后习题

(1 分) (2 分) (2 分)
ˆ Er = −10e jkz ax 1 jkz ˆ Hr = e ay 12π
(3)总场
ˆ E = 20sin kz sin ωtax H=
(4)电流
20
η
ˆ cos kz cos ωta y(4 分)ˆ J = n × Hz =0
=
20
η
ˆ cos(109 t )ax
π
(2 分) (2 分)
(2)方向性函数:
cos( cos θ ) π 2 F (θ , ϕ ) = cos( sin θ cos ϕ ) sin θ 4
π
(2 分)
1 d 2φ = −k x2 2 X ( x) dx
变量分离得:
1 d 2φ 2 = −k y 2 Y ( y ) dy
2 k x2 + k y = 0
由边界条件得方程的解为: nπ nπ (4 分) φ = Cn sh[ ( x + a )]sin( y ) n = 1, 2, b b ∞ nπ nπ φ ( x, y ) = ∑ Cn sh[ ( x + a )]sin( y ) 则: (1 分) b b n =1 ∞ 2anπ nπ 3π φ ( a, y ) = ∑ Cn sh sin( y ) = 10 sin( y) 由 b b b n =1 得:
三解(10 分)(1)该区域无源,电位函数满足拉普拉斯方程 :
∂ 2φ ∂ 2φ + =0 ∂x 2 ∂y 2
其边界条件为:
(1 分)
φ =0 φ =0 φ =0
0 ≤ x < ∞, y = 0
(1 分)
0 ≤ x < ∞, y = b x = − a, 0 < y < b 3π φ = 10sin( y ) x = a, 0 < y < b b
丁君版工程电磁场与电磁波答案 第二章 电磁学基本理论.

2π 0
dθ
1 0
ρS • r • 4πε0 r2 +1
1 dr r2 +1
∫ ∫ = 2π dθ 1 5r ×10-9 • r • 1 dr
0
0 4πε0 r2 +1 r2 +1
∫ = ρS 1
r2
dr
2ε0 0 (r2 +1) r2 +1
= ρS (ln(1+ 2ε 0
2
)
−
1 2
)az
=90π
a 2
⎞ ⎟⎠
r2( t ) =
d
2
+
⎛ ⎜⎝
a 2
⎞2 ⎟⎠
+
2
cos(
ωt
)⋅
d
⋅
⎛ ⎜⎝
a 2
⎞ ⎟⎠
∴
ψ
=
b 2π
μ0 I
ln
r2 (t) r1 (t )
(2) 求 εin
ε in
= − ∂ψ ∂t
= − bμ0I 2π
1 ( r2
dr2 (t) − 1 dt r1
dr1 (t ) ) dt
10z ⋅ dz (4 − z)2
az
∫ + 10−9
4πε 0
0 −2
−10 (4 −
zdz z)2
az
=
10−8 4πε 0
(− ln 2 +1− ln
2 3
−
1 )
3
⋅
az
=
5 ×10−9 2πε 0
(ln
3 4
+
2 3
)
⋅
az
=
西北工业大学《电磁场和电磁波》课后习题

y > 0, ε2 = 9 pF / m, µ2 = 4µ H / m, σ 2 = 0 。 在 区 域 I 内 , 一 极 化 方 向 为 aˆz ,
ω = 108 rad / s 的平面电磁波振幅为 500V/m,垂直投射到 y = 0 的边界面上,求:
v 1. 入射波 Ei ;
v 2. 反射系数 Γ 和反射波 Er ;
二、(15 分)球形电容器内外导体球之间填充介电常数为 3ε0 的介质,如图 1 所示。设内球上
面电荷密度为 ρs ,求:
1. 各区域的电位移矢量和电场强度; 2. 内外导体之间的电压; 3. 此电容器的电容。
三、(10 分)一点电荷 Q 位于两个半无限大接地导体平面形成的直角形区域内的 A 点(如图 2 所示),求区域内任一点 P 处的电位。
成 2004-2005 学年 第一学期
绩
开课学院 电子信息学院 课程 电磁场与电磁波 学时 考试日期 2004 年 12 月 16 日 考试时间 2 小时
54 开A
考试形式(闭 )( B )卷
考生班级
学号
姓名
[注: ε0
=
1 36π
×10−9
F
/
m
µ0 = 4π ×10−7 H / m ]
一、简答题(25 分)
教务处印制
第2页共2页
2. 命题教师和审题教师姓名应在试卷存档时填写。
教务处印制
第3页共2页
四、(10 分)一个金属槽如图 3 所示,侧面和底面的电位均为 0,顶盖与侧壁绝缘,其电位为
φ = sin(π x) ,求槽内电位分布。
教务处印制
第1页共2页
φ = sin(π x)
R1 R2
西北工业大学大学物理期末考试试卷(含答案)

西北工业大学大学物理期末考试试卷(含答案)一、大学物理期末选择题复习1.运动质点在某瞬时位于位矢r的端点处,对其速度的大小有四种意见,即(1)t r d d ; (2)dt r d ; (3)t s d d ; (4)22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x .下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确 (C) 只有(2)(3)正确 (D) 只有(3)(4)正确 答案D2.静电场中高斯面上各点的电场强度是由:( ) (A) 高斯面内的电荷决定的 (B) 高斯面外的电荷决定的 (C) 空间所有电荷决定的 (D) 高斯面内的电荷的代数和决定的 答案C3.在图(a)和(b)中各有一半径相同的圆形回路L 1 、L 2 ,圆周内有电流I 1 、I 2 ,其分布相同,且均在真空中,但在(b)图中L 2 回路外有电流I 3 ,P 1 、P 2 为两圆形回路上的对应点,则( )(A ) ⎰⎰⋅=⋅21L L d d l B l B ,21P P B B =(B ) ⎰⎰⋅≠⋅21L L d d l B l B ,21P P B B =(C ) ⎰⎰⋅=⋅21L L d d l B l B ,21P P B B ≠(D ) ⎰⎰⋅≠⋅21L L d d l B l B ,21P P B B ≠答案C4.一个半径为r 的半球面如图放在均匀磁场中,通过半球面的磁通量为( )(A )B r 2π2 (B ) B r 2π (C )αB r cos π22 (D ) αB r cos π2 答案D5. 一运动质点在某瞬间位于位矢(,)r x y 的端点处,对其速度的大小有四种意见,即 (1)dr dt ;(2)dr dt ;(3)ds dt ;(4)22()()dx dy dt dt+ 下列判断正确的是:(A )只有(1)(2)正确 (B )只有(2)正确 (C )只有(2)(3)正确 (D )只有(3)(4)正确 答案 D6.如图所示,湖中有一小船,有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动。
工程电磁场与电磁波丁君版课后习题全解

2 1 1 与 x 轴成 arcsin ax a y 方向相同, 5 5 5
1-4 证明:设矢量 r 的终点在 A.B.C 构成的平面上,则:
(r a ), (r b ), (r c ) 在此平面上 ,则必有不为 0 的实数 m, n, p 满足: m(r a ) n(r b ) p(r c ) 0
1 1 1 1 (1) ( ) ( R)3 2 ( x x' ) ax ( R) 3 2 ( y y ' ) a y ( R) 3 2 ( z z ' ) az R 2 2 2
( R)3 ( x x' ) ax ( R)3 ( y y ' ) ay ( R)3 ( z z ' ) az
-1-
Ax
即
Ay By Cy
Az
Az Bz 0 Cz
3 1 2 0 1 1
Bx Cx
Ax Ay By Cy
代入得 即得证
Bx Cx
Bz 1 3 4 1 3 4 0 4 2 6 0 0 0 Cz
1-3 解: (1) F合 F1 F2 F3 F4 代入数据得 F合 2ax a y (2) F合 4 1 5 (3) 合力方向与单位矢量
y
1 2 1 2
(a )dxdz+ y (A )y
S右
y
a 1 dxdz y
2
(A x )
S前
x
a dydz (A )x x
S后
x
( 1a )dydz x
2
又
(A z )
z
1 2
(A ) z
工程电磁场与电磁波答案(丁君)

工程电磁场与电磁波习题解答(试用本)主编:丁君第一章1-1 解: (1)z y x a a a B A vv v v v )125()93()32(3-++++-=+=z y x a a a v v v 712-+\B A vv 3+=194491441=++(2)266cos 26216cos cos cos -=Þ´-=××=×=×q q q qC BC BC B C B C v vv v v vv v vB r 方向的单位矢量为:26BB B b vv v v ==C r 在B s 方向的分矢量为:33cos (34)1313x y z C b B a a a q ·=-=-+-v v v v v v(3)191321cos cos cos -=×==×q q qBA BA B A B A v v v v vv v vπq Þ=- (4) z y x a a a C B vv v v v 553-+-=-C B vv -的单位矢量为:z y x z y x a a a C B a a a vv v vv v v v 595595593553-+-=--+-1-2证明:欲证明三矢量A 、B 、C 能构成一个三角形,则须证出三个线性无关的非零矢量位于同一平面上。
则有:0)(=´·C B A即 0=z y xz y xzy xC C C B B B A A A 代入得 000043111624431213=-=---=zyxz y xzy xC C C B B B A A A即得证1-3 解:(1)4321F F F F F +++=合代入数据得x y F 2a a =-v v合(2)514=+=合F (3)合力方向与单位矢量y x a a v v 5152-方向相同,与x 轴成-1-4 证明:设矢量r r的终点在A.B.C 构成的平面上,则:(),(),()r a r b r c ---v v v v v v在此平面上 ,则必有不为0的实数,,m n p 满足:()()()0m r a n r b p r c -+-+-=v v v v v v所以得:p n m cp b n a m r ++++=vv v v , p n m ,,为实数1-5 解:设A 点的坐标为),(11y x ,B 点坐标为),(22y x则a v=),(11y x ,b v =),(22y x 有题意得121211x x y y x x y y --=--Þ则过A ),(11y x ,B ),(22y x 点的方程为 ()111212y x x x x y y y +---=Þ1-6 解:欲使,A B v v 互相垂直,则有0A B ·=v v则有8220A B a ·=--=v v得 3=a1-7 解:矢量A v与坐标轴的夹角分别为:72cos 76cos 7343693cos ==-===++==A A A A AAz y x g b a 其中g b a ,,分别为矢量A v与三个坐标轴方向夹角。
西北工业大学级《力学》期末考试试卷(西北工业大学级《力学》期末考试标准答案及评分标准可在文

诚信保证
本人知晓我校考场规则和违纪处分条例的有关规定,保证遵守考场规则,诚实做人。
本人签字:
编号:
西北工业大学期末考试试题(卷)
2008~2009学年第一学期
开课学院理学院课程力学学时60
考试日期2009年1月12日考试时间2小时考试形式(闭)(A)卷
班级学号姓名
重要提示:
1.本试卷分为“单选题”、“填空题”和计算题三部分,总分为100分;2.在答题卡上答题,最后把试卷和答题卡一并交回;
3.答题卡分为两张,答题卡(1)为机读卡,答题卡(2)为书写卡;4.机读卡中数字用钢笔填写,涂点用2B铅笔填涂。
填空题答案栏每格填1位数字,小数点单独占1格,左对齐填写,按要求取位,4舍5入进位;5.题中所涉重力加速度g一律取9.8 m/s2计算;
6.草稿纸不再另发,将试题的背面作为草稿纸,
一、单选题(共30分,每小题3分,在答题卡(1)上完成)
1.对于惯性参考系,下列那项叙述是正确的?(a)在惯性参考系物体所受合力为零,则该物体保持静止或匀速运动的状态;(b)在任何惯性参考系所描述的物理现象都是相同的;(c)两不同惯性参考系间的相对运动,不一定是匀速运动。
A.abc皆正确;B.只有ab正确;
C.只有bc正确;D.只有ac正确。
西工大与西安交大期末复习考研备考大学物理题库 四、电磁学 13 电磁感应

答案:A
难度:易
选择题:如图所示,M、N为水平面内两根平行金属导轨,ab与cd为垂直于导轨并可在其上自由滑动的两根直裸导线.外磁场垂直水平面向上.当外力使ab向右平移时,cd( )
A、不动.B、转动.
C、向左移动.D、向右移动.
题目图片:
答案:D
难度:易
选择题:如图,长度为l的直导线ab在均匀磁场 中以速度 移动,直导线ab中的电动势为( )
C、铜环中感应电动势小,木环中感应电动势大.
D、两环中感应电动势相等.
答案:D
难度:易
选择题:一导体圆线圈在均匀磁场中运动,能使其中产生感应电流的一种情况是( )
A、线圈绕自身直径轴转动,轴与磁场方向平行.
B、线圈绕自身直径轴转动,轴与磁场方向垂直.
C、线圈平面垂直于磁场并沿垂直磁场方向平移.
D、线圈平面平行于磁场并沿垂直磁场方向平移.
题目图片:
答案:A
难度:易
选择题:在如图所示的装置中,当不太长的条形磁铁在闭合线圈内作振动时(忽略空气阻力),( )
A、振幅会逐渐加大.B、振幅会逐渐减小.
C、振幅不变.D、振幅先减小后增大.
题目图片:
答案:B
难度:易
选择题:一个圆形线环,它的一半放在一分布在方形区域的匀强磁场 中,另一半位于磁场之外,如图所示.磁场 的方向垂直指向纸内.欲使圆线环中产生逆时针方向的感应电流,应使( )
A、与线圈面积成正比,与时间无关.
B、与线圈面积成正比,与时间成正比.
C、与线圈面积成反比,与时间成正比.
D、与线圈面积成反比,与时间无关.
答案:A
难度:中
选择题:如图所示,一矩形线圈,以匀速自无场区平移进入均匀磁场区,又平移穿出.在(A)、(B)、(C)、(D)各I--t曲线中哪一种符合线圈中的电流随时间的变化关系(取逆时针指向为电流正方向,且不计线圈的自感)?( )
工程电磁场与电磁波_丁君版_答案第四章习题答案

第四章 习题4-1解:选柱坐标系,在所求无源区内电位函数满足: 2=∇φφ只和r 相关0=∂∂ϕφ0=∂∂zφ方程化为 0)(1=∂∂∂∂rrrr φ 21ln C r C +=φ 为常数21,C C由 006.0==φ时r 501.0-==φ时 r得 88.27588.9721=-=C C88.275ln 88.97+-=r φr a rE ˆ188.97=-∇=φ 4—2:解:图一根据边界条件:⎪⎩⎪⎨⎧====021R R R R U φφ0可得:⎪⎪⎩⎪⎪⎨⎧--=-=00U R R R B U R R R R A 1211221 ∴)120112021R R U R RR R U R R ---=φ(2) ()R R a R R R U R R a RE ˆ1ˆ212021⋅-=∂∂-=-∇=φφ (3) ()R R R aR R R U R ED ˆ12102001-⋅===εε内表 (1) 如图一,根据题意可知:电位函数φ满足拉普拉斯方程。
采用球坐标系:2=∇φ0=∂∂θφ0=∂∂ϕφR 相关 只于 φ,方程化为:0)(122=∂∂∂∂R RRR φφ积分得:B RA +⋅=1φSS d D s Sρ=⋅⎰内表SS D s ρ=内表 ∴)(12102R R R U R D s -==ερ内表4—3:解:选择直角坐标如图,由恒定电场的泊松方程可得:xy设两板间距离为d,代入边界条件⎪⎩⎪⎨⎧====00U dz z φφ⎪⎪⎩⎪⎪⎨⎧+=+==⇒ερερ22002012d d U d d U C C ∴)2()2(2002ερερφερερφddU z E zddU z +-=-∇=++-=4—4:解:选择柱坐标系,根据恒定电磁场的拉普拉斯方程,(1) 02=∇m φ,m φ只在ϕ方向上有变化,所以:BA rm m +==∂∂ϕφϕφ:,01222积分得由 0=ϕ时:0,0==B m 得φ ∴ϕφA m =lm m a dld H φφ-=-∇=l d H d m⋅-=φ⎰⎰-=⋅-=ππφ2020I l d H d mBA I m m+=-==ϕφφπϕ代入,20,0,2=∂∂=∂∂-=∇xyφφερφ方程可化为:,22ερφ-=∂∂z2122:C z C z ++-=ερφ积分得π2⋅=-A I π2I A -= ϕπφ2I m -=(2)ϕϕπϕφφφa rI a d d r a dl d H m l m m 21==-=-∇=可见,利用拉普拉斯方程与安培环路定理求出来的结果一样。
西工大与西安交大期末复习考研备考大学物理题库 八、跨章节综合题

八、跨篇章综合题一、选择题(共4题)选择题:假设一电梯室正在自由下落,电梯室天花板下悬一单摆(摆球质量为m ,摆长为l ).若使单摆摆球带正电荷,电梯室地板上均匀分布负电荷,那么摆球受到方向向下的恒定电场力F .则此单摆在该电梯室内作小角度摆动的周期为:( )A 、 Fmlπ2 .B 、 Flmπ2 . C 、 Fmlπ2 . D 、 mlFπ2 . 答案: C 难度:易选择题:图示为一固定的均匀带正电荷的圆环,通过环心O 并垂直于环面有一固定的绝缘体细棒,细棒上套着一个带负电的小球.假定起始时,小球在离O 较远的P 点,初速度为零,不计小球与细棒间摩擦,则小球将:( ) A 、 沿轴线向O 点运动,最后停止于O 点不动. B 、 沿轴线经O 点到达对称点P ′处停止不再运动. C 、 以O 点为平衡位置,沿轴线作振幅为A 的简谐振动.D 、 以O 点为平衡位置,沿轴线在PP ′两点的范围内作非简谐振动.答案: D 难度:易选择题:在水平均匀磁场中,一质量为m 的环形细导线自由悬挂在非弹性线上,沿着环流过的电流为I ,环相对铅直轴作微小的扭转振动的周期为T ,则磁场的磁感应强度的大小为 ( )A 、 22IT mπB 、24IT mπ C 、 23IT mD 、 232ITmπ答案: A 难度:中选择题:设氢原子的动能等于氢原子处于温度为T 的热平衡状态时的平均动能,氢原子的质量为m ,那么此氢原子的德布罗意波长为 ( )A 、 mkT h3=λ.B 、 mkT h5=λ.C 、 h mkT3=λ.D 、 hmkT5=λ.答案: A 难度:易二、填空题(共4题)填空题:在场强为E(方向垂直向上)的均匀电场中,有一个质量为m 、带有正电荷q 的小球,该球用长为L 的细线悬挂着.当小球作微小摆动时,其摆动周期T =_____________________ . 题目图片:答案:)/(2m qE g L-π3分难度:中填空题:一圆形平面载流线圈可绕过其直径的固定轴转动,将此装置放入均匀磁场中,并使磁场方向与固定轴垂直,若保持线圈中的电流不变,且初始时线圈平面法线与磁场方向有一夹角,那么此线圈将作______________________运动;若初始时刻线圈平面法线与磁场方向的夹角很小,则线圈的运动简化为________________.答案:机械振动2分;简谐振动 2分 难度:易填空题:已知中子的质量是m =1.67×10-27 kg ,当中子的动能等于温度为T = 300K的热平衡中子气体的平均动能时,其德布罗意波长为____________. (h =6.63×10-34 J ·s ,k =1.38×10-23 J ·K -1 )答案: 1.46 Å 3分 难度:易填空题:若用加热方法使处于基态的氢原子大量激发,那么最少要使氢原子气体的温度升高________________K .(假定氢原子在碰撞过程中可交出其热运动动能的一半) (玻尔兹曼常量k =1.38×10-23 J ·K -1,1 eV =1.60×10-19 J)答案: 15.8×104 3分 难度:中三、计算题(共19题)计算题:如图所示,一半径为R 的均匀带正电荷的细圆环,总电荷为Q .沿圆环轴线(取为x 轴,原点在环心O )放一根拉紧的光滑细线,线上套着一颗质量为m 、带负电荷-q 的小珠.今将小珠放在偏离环心O 很小距离b 处由静止释放,试分析小珠的运动情况并写出其运动方程.题目图片:答案:解:用场强叠加或电势梯度可求出圆环轴线上x 的场强为2/3220)(4x R QxE +π=ε 在x << R 处,场强近似为 304R QxE επ≈ 3分小珠在该处受到电场力为 kx R qQxF -=π-=304ε 式中k 为正值(304RqQk επ=),负号表示小珠受力方向与位移方向相反, 因而小珠作简谐振动. 2分 由牛顿第二定律,有 ma kx =-得到 0d d 222=+x txω 2分 其解为 )cos(φω+=t A x 由初始条件 x 0 = b 、v 0 = 0 可知A = b ,φ = 0 ∴ t mR qQb x 4cos30επ= 3分 难度:中计算题:半径为R 的均匀带电圆环上,总电荷为+Q .沿圆环轴线放一条拉紧的细线,线上套一颗质量为m 、电荷为-q 的小珠.当移动小珠使其偏离环心O 点很小距离时释放,若忽略小珠与细线间的摩檫,试证小珠将在细线上O 点附近作简谐振动,并求其振动频率. 题目图片:答案:解:把圆环轴线取作x 轴,环心O 点取作坐标原点.在离环心距离为x 处,带电圆环的场强为:])(4/[2/3220x R Qx E +π=ε 4分小珠受到的电场力为: ])(4/[2/3220x R qQx qE F +π-=-=ε 2分因x << R ,故 )4/(30R qQx F επ-≈kx -=式中 0)4/(30>π=R qQ k ε 2分 所以小珠的运动是以O 点为平衡位置的简谐振动.小珠的振动频率为:2/1033)]16/([2//m R qQ m k ενπ=π= 2分 难度:中计算题:如图所示,在场强为E 的均匀电场中,静止地放入一电矩为p、转动惯量为J 的电偶极子.若电矩p与场强E 之间的夹角θ很小,试分析电偶极子将作什么运动,并计算电偶极子从静止出发运动到p与E 方向一致时所经历的最短时间. 题目图片:pEθ答案:解:电偶极子在均匀电场中受力等于零,但受到一力偶矩 E p M⨯= 其大小为 θθpE pE M ≈=sin 3分 由转动定律可知, βθJ pE =- (β为角加速度)即 0d d 22=+θθJ pEt3分 可见,电偶极子将作角谐振动.其角频率为J pE /=ω 1分电偶极子从静止出发,转动到第一次使p与E 方向一致,需用四分之一周期的时间,即 pEJT t 24π==3分 难度:中计算题:一均匀带电球体,电荷体密度为ρ.在球体中开一直径通道,设此通道极细,不影响球体中的电荷及电场的原有分布.今将一电子放入此通道中除球心以外的任意处,试分析电子将作什么运动,并计算电子从通道口的一端从静止出发运动到另一端需经历多长时间.答案:解:按高斯定理求得球体内的电场强度分布为 03/ερr E = 如图选x 轴沿通道方向,原点在球心上,则通道内场强分布为 03/ερx E =电子在通道内任一位置受电场力为 )3/(0ερx e eE f -=-= 3分按牛顿第二定律,其动力学方程为 )3/(0ερx e -ma =即 03d d 022=+x me t x ερ可见电子将作简谐振动. 2分 电子从静止出发,由通道口一端运动到另一端需历时半个周期. )3/(0m e ερω=则 )/(3/2/0ρεωe m T t π=π== 3分 难度:中计算题:在两块水平大平行金属板之间建立起场强E竖直向上的均匀静电场,在此电场中用一长为l 的绳挂一个质量为m 、电荷为+q 的带电小球,求此小球作小幅度摆动的周期.答案:解:分析摆球受力如图:沿切向列牛顿方程 ma f mg e =+-θθsin sin 当θ很小时 l r /sin =θ 2分m f mg t r a e /sin )(/d d 22θ+-==)/()(ml r qE mg +-=)/()(ml r qE mg --=r 2ω-= 1分其中 )/()(2ml qE mg -=ω , qEmg mlT -π=π=22ω2分难度:中计算题:一质量为m 、电荷为-q 的粒子,在半径为R 、电荷为Q (>0)的均匀带电球体中沿径向运动.试证明粒子作简谐振动,并求其振动频率.证:由高斯定理求得球内场强为r R QE 304επ=粒子受力: r R qQqE F 304επ-=-= 由牛顿第二定律: ma F =∴ r R qQ 304επ-22d d t r m = , 22d d tr 0430=π+r mR qQ ε 3分 粒子沿径向作简谐振动, 其频率:3024mR qQ εωπ= , 304212mR qQεωνππ=π= 2分计算题:三个电荷均为q 的点电荷,分别放在边长为a 的正三角形的三个顶点上,如图所示.求:(1) 在三角形中心O 处放一个什么样的点电荷q ′可使这四个点电荷都达到受力平衡?(2) 设点电荷q ′的质量为m ,当它沿垂直于三角形平面的轴线作微小振动时的振动周期(重力可忽略不计). 题目图片:qq答案:解:(1) 在O 点放点电荷q ′,要使四个点电荷都受力平衡,必须考虑每一顶点上的点电荷q 受其余三个点电荷作用力的合力为零.顶点之一的点电荷受其余二个顶点的点电荷作用的合力f 为2022024330cos 42aq a q f εεπ=︒π⋅= 2分 而受到q ′的作用力f ′为204/b q q f επ'='204/3a q q επ'= (3/a b =) 2分 由 0='+f f 可得 3/q q -=' 1分 q ′为q 的异号电荷. (2) 当q ′垂直纸面作微小位移x 时,受一回复力F ,按牛顿第二定律222/122220d d )()(43txm x b x x b q q =+⋅+π'ε 4分考虑到 x << 3/a b =,得到 049d d 30222=π+x ma q t x ε 1分 令 m a q 30224/9εωπ=,得到振动周期am qa T 0342εωππ=π= 2分 难度:中计算题:如图所示,一细长小磁针,支在一轴尖O 上,在地磁场的作用下,平衡时指向南北方向;若使磁针偏离平衡位置一个小的角度后释放,它将绕平衡位置往复摆动.经实验测定,小磁针的摆动周期T = 2 s ,小磁针绕O 轴的转动惯量J = 8×10-8 kg ·m 2,地磁场的磁感应强度的水平分量B = 0.3×10-4 T .试求小磁针的等效磁矩. 题目图片:O SNB答案:解:设小磁针的等效磁矩为m p,则小磁针所受力矩为θθB p B p M m m -≈-=sin 1分式中θ为m p与B 间的夹角,负号表示该磁力矩为恢复力矩,由定轴转动定律22d d t J M θ= 1分θθJ B p tm -=22d d 1分 J B p m =2ω, Bp JT m π=2 1分解出 =π=)2(TB J p m 2.63×10-2 A ·m 2 1分 难度:中计算题:在水平匀强磁场中,质量m = 2g 的环形(半径为R )细导线,用一根细线悬挂起来,可以自由转动.当导线环流过强度I = 2A 的电流时,环相对于竖直轴作小幅度扭转振动,振动的周期T = 1.0s .求磁场的磁感应强度B . (细环以直径为轴转动时的转动惯量221mR J =)答案:解∶磁矩 2R I IS p m π== 受磁力矩 θθsin sin 2B R I B p M m π== 2分 按定轴转动定律 βJ M = 细环以直径为轴转动惯量 2/2mR J =2/2/22θβ mR mR M == 2分 把磁力矩代入转动定律 2/2θmR θsin 2B R I π-= 式中的负号是因为磁力矩总是转向θ 变小方向.小扭转时,θ < 5°, sin θ =θ即 θθmIB π-=2 3分 这是扭转振动微分方程,振动圆频率mIBπ=2ω,周期 IB m T π=2∴ =⨯⨯⨯π=π=-2320.1210222IT m B 6.28×10-3T 3分 难度:中计算题:如图所示,一个由10匝均匀细导线构成的正方形线圈,质量为5g ,被悬挂在一根轻细的棉线上,悬点在线框某边中点.线圈处在磁感应强度为B = 5×10-3 T 的均匀磁场中,磁场方向与线圈平面垂直.今在线圈中通以强度为I = 0.6 A 的电流,并使线圈作微小的扭转振动.求振动的周期T . 题目图片:IB×××××××××答案:解∶设线框边长l ,那么它的转动惯量为22261)2(4241212ml l m l m J =+⨯⨯= 2分通电后的磁矩为 2l NI p m =在磁场中受到的磁力矩为 θsin B p M m = 2分 作微小扭转时 θθ≈sin , θθB l NI B p M m 2== 1分由转动定律βJ M =可得, 6/22θθ ml B l NI -= 2分 负号是因为力矩是转向θ 变小的方向.上式表明,线圈是作扭转谐振动,振动圆频率可由下式得出 m NIB /62=ω周期 NIBmT 622π=π=ω2分= 1.05 s 1分 难度:中 计算题:在磁感强度为B的均匀磁场中,一质量为m ,半径为R ,载有电流i 的圆形平面线圈可绕垂直于磁场方向并过线圈直径的固定轴转动.设初始时刻线圈的磁矩沿磁场方向,使线圈转过一个很小的角度后,线圈可在磁场作用下摆动(忽略重力及轴处摩擦的影响),证明当线圈质量一定时, 线圈摆动的周期与线圈半径无关.答案:证: θsin iSB B p M m =⨯=2分由转动定律 θθsin iSB J -= 2分 当θ 很小时 θθiSB J + = 0 1分 式中 221mR J =, 2R S π= ∴ 02122=π+θθB R i mR 1分 02=π+θθm B i , mB i π=22ω 2分 iBm T π=π=22ω 2分 可见若m 一定线圈摆动的周期与线圈半径无关.难度:中计算题:一半径为R 的圆形线圈,通有强度为I 的电流,平面线圈处在均匀磁场B中,B的方向垂直纸面向里,如图.线圈可绕通过它的直径的轴OO '自由转动,线圈对该轴的转动惯量为J .试求线圈在其平衡位置附近做微小振动的周期. 题目图片:I RO O 'B答案:解∶B p M m⨯= θsin B p M m = 1分22d d sin tJ B p m θθ-= 2分在微小振动时θθ≈sin , I R p m 2π=,代入上式有∶0d d 222=π+θθJ BR I t∴ JB R I 2π=ω, IBJ R T π=22分 难度:中计算题:一面积为A 、总电阻为R 的导线环用一根扭转刚度为K 的弹性细丝(被扭转α角时,其弹性恢复扭力矩M K = K α )挂在均匀磁场B中,如图.线圈在yz 平面处于平衡,设线圈绕z 轴的转动惯量为I .现将环从图中位置转过一个小角度θ 后释放之,忽略线圈自感, 试用已知参数写出此线圈的转角与时间的方程. 题目图片:yzB答案:解:当线圈平面从图中位置转过小角度α时,穿过线圈的磁通量为:αΦsin BA =α变化时线圈中感应电动势为 tBA t d d cos d d ααΦ⋅==E 感应电流 ααcos d d tR BA R i ==E 3分磁矩 t R BA iA m d d cos 2αα⋅== 所受磁力矩 tR A B M m d d cos 222αα⋅= 3分 线圈还受到细丝弹性恢复力矩 M K = K α,两者均阻碍线圈运动.∴ 22222d d d d cos tI K t R A B αααα-=+⋅ 3分 ∵ θα≤ 0≈θ ∴ 1cos ≈α∴ 0d d d d 2222=+⋅+αααK t R A B t I其通解为: )sin cos (e 21rt A rt A t +=-βα其中 IRA B 222=β 2β-=I K r 利用初始条件: θα==0t0d d 0==t t α可得 θ=1A , 02=A rt t cos e βθα-= 3分 难度:难计算题:如图,由一绝热材料包围的圆管,横截面积为S ,一端封闭,另一端敞开,中部有一质量为m 的绝热塞子,塞子与管壁的摩擦可忽略,管内装有比热容比为γ的理想气体.设塞子在平衡位置时,气体体积为V ,压强为p ,现在把塞子稍向左移,然后放开,则塞子将振动.若管内气体所进行的过程可看作绝热过程,求塞子振动的周期. 题目图片:答案:解:沿管长方向取坐标x , 设平衡位置x = 0,塞子位移为x 时所受合力为F = d p ·S 1分 绝热过程 pV γ = C 1分 d p ·V γ + p γ V γ-1d V = 0 得 Sx V p V V p p )/(d )/(d γγ-=-=∴ F = d p ·S x S V p 2)/(γ-= 2分动力学方程: 22d d txm x S V p 2)/(γ-= 2分即 22d d tx 02=+mV xS p γ 此式为简谐振动的动力学方程式.圆频率为 2/12))/((mV S p γω= 2分∴ 振动周期 γωp mVS T π=π=22 2分难度:难计算题:氢原子气体在什么温度下的平均平动动能等于使氢原子从基态跃迁到第一激发态所需要的能量?(玻尔兹曼常量k =1.38×10-23 J ·K -1).答案:解:氢原子基态能量 6.131-=E eV 1分 第一激发态能量 4.32//21212-===E n E E eV 1分 假设温度为T ,则kT w )2/3(= 1分据题意12E E w -= 1分 =-=kE E T 3)(2127.88×104 K 1分 难度:计算题:设某气体的分子的平均平动动能与一波长为λ = 4000 Å的光子的能量相等,求该气体的温度.(普朗克常量h =6.63×10-34 J ·s ,玻尔兹曼常量k =1.38×10-23 J ·K -1)答案:解:光子的能量 λν/hc h E == 1分若 E kT w ==231分则 ===)3/(2)3/(2λk hc K E T 2.4×104 K 3分 难度:易计算题:设在碰撞中,原子可交出其动能的一半,如果要用加热的方式使基态氢原子大量激发,试估算氢原子气体的温度至少应为多少? (玻尔兹曼常量k =1.38×10-23 J ·K -1)答案:解:当加热到温度T 时,氢原子的平均动能 kT E 23=碰撞时可交出动能 212321⨯=kT E 2分 因此用加热的方式使之激发,则要求温度T 1满足1212321E E kT -≥ 式中, E 1=-13.6 eV , E 2= E 1 /22 =-3.4 eVk E E T /))(3/4(121-≥ 即 ≥1T 1.6×105 K 3分 难度:难计算题:波长为3500 Å的光子照射某种材料的表面,实验发现,从该表面发出的能量最大的光电子在B =1.5×10-5 T 的磁场中偏转而成的圆轨道半径R =18 cm ,求该材料的逸出功A 是多少电子伏特?(基本电荷e =1.60×10-19C ,电子质量m =9.11×10-31 kg ,普朗克常量h =6.63×10-34 J ·s ,1eV =1.60×10-19J )答案:解: 2)/(v v R m B e = ① 1分A m h +=221v ν ② 1分由① m eBR /)(=v 1分代入② meBR hc m h A 2)(2122-=-=λνv= 4.66×10-19J =2.91 eV 2分 难度:难计算题:一共轴系统的横截面如图所示,外面为石英圆筒,内壁敷上半透明的铝薄膜,内径r 2 =1 cm ,长为20 cm ,中间为一圆柱形钠棒,半径r 1 = 0.6 cm ,长亦为20 cm ,整个系统置于真空中.今用波长λ =3000 Å的单色光照射系统.忽略边缘效应,求平衡时钠棒所带的电荷.已知钠的红限波长为m λ=5400Å,铝的红限波长为mλ'=2960Å.(基本电荷e = 1.60×10-19 C ,普朗克常量 h = 6.63×10-34 J ·s ,真空电容率ε0=8.85×10-12 C 2·N -1·m -2) 题目图片:r 1 r 2钠棒半透明铝膜石英λ答案:解:铝不产生光电效应.钠在光照下,发射光电子,它们的最大初动能为m hc hc m λλ//212-=v ① 2分 这些光电子聚集在铝膜上,使钠棒和铝膜分别带上正、负电荷Q ,当它们间的电势差∆U 达到 e ∆U =221v m ② 2分时,系统达到平衡.由高斯定理,忽略边缘效应情况下,可求出钠棒与铝膜间电场)2/(0lr Q E επ= ③ 1分∆U 1ln 2d 12021r r l Qr E r r επ==⎰ ④ 2分 由式①、②、④得 e ∆U 120ln 2r r l Q eεπ=m hc hc m λλ//212-==v ∴ )11()/ln(2120mr r e lhc Q λλε-π=2分 = 4.01×10-11 C 1分 难度:难四、理论推导与证明题(共4题)理论推导与证明题:一电矩为l q p=的电偶极子,置于场强为E 的均匀电场中,如果将电偶极子的电矩方向偏离平衡位置一个微小角度后释放,则电偶极子将绕平衡位置作简谐振动(转动).已知电偶极子绕自身中心转动的转动惯量为I ,求证其振动频率为 IpEπ=21ν答案:证:当电矩p与场强E 夹角为θ 时,电偶极子受到一个力偶矩M 作用,其大小为 θθθpE pE qEl M ≈==sin sin 3分 此力偶矩是与θ 角反向的,是回复力矩,按转动定律得:22d d tI pE θθ=-即0d d 22=+θθI pEt 令 I pE /2=ω则 0d d 222=+θωθt5分 此即角谐振动的微分方程.其振动频率为IpE π=π=212ων 2分 答案图片:难度:易题目图片:答案:证∶ 沿径向单位长度有n 匝导线, )/(12R R N n -=故d r 宽度有电流 r nI I d d =它的磁矩 r R R NIr r nIr p m d d d 1222-π=π= 2分 总磁矩 ⎰⎰-π==21d d 212RR m m r r R R NI p P )(31313212R R R R NI --π= )(3212122R R R R NI ++π=2分 在磁场B 中受的磁力矩 θsin B P M m = 2分由转动定律 θβ J J M == 即 θ J θsin B P m-= 式中负号是因为力矩转向θ 变小的方向. 在小角度情况下 sin θ = θθθJB P m -= 2分 这是振动微分方程, 所以说线圈作扭转简谐振动.其振动圆频率为JBP m =ω 2分振动的振幅θ 0 和初相φ 0由初始条件决定.)cos(00φθθ+=t JBP m 2分难度:难理论推导与证明题:N 匝导线,密绕成内外示.通有电流I ,放在磁感强度为B的匀强的AA '轴的转动惯量为J .试证:当其偏动是一简谐振动. 写出关于θ 的振动方程.理论推导与证明题:如图所示,瓶内盛有一定质量的理想气体,一横截面为A 的玻璃管通过瓶塞插入瓶内,玻璃管内放有一不漏气又能上下无摩擦地滑动的活塞,质量为m ,设活塞在平衡位置时,瓶内气体的体积为V ,压强为p .现将活塞稍稍移动离开其平衡位置,然后放开,则活塞上下振动,试证明,活塞作简谐振动,且准弹性力为y V pA F )/(2γ-=, 式中 V p C C /=γ ,y 为位移(向下为正). (假设瓶内气体进行的过程为绝热过程)题目图片:答案:证:活塞离开平衡位置时,所受的回复力 A p F •∆-= 2分 由于瓶内气体是作绝热过程,故有 C pV =γ 2分 两边微分: 01=∆+∆-V V p p V γγγ ∴ ∆p = -γp ∆V /V= γpAy /V (y 为活塞位移,Ay V -=∆) 2分 故 F = -γpA 2y /V 2分 即回复力F 与位移y 大小成正比而反向, 故活塞作简谐振动. 2分难度:难证明题:已知原子中电子的轨道磁矩大小p m 和轨道角动量大小L 的关系为L m e p e m 2= 试证明该原子中电子的轨道角动量在外磁场B 中的进动角速度ω的大小为 em eB2=ω答案:证∶原子磁矩在外磁场中所受的力矩为θsin B p M m =θsin 2LB m ee= 2分 在力矩作用下,角动量将发生改变.根据角动量定理有ωθφθ⋅===sin d d sin d d L tL t L M 4分由以上两式有 em eB2=ω 2分难度:难五、错误改正题(共1题)错误改正题:如果室温下( t =27℃)中子的动能与同温度下理想气体分子的平均平动动能相同,则热中子的动能E K =?其德布罗意波长λ =?试指出下面解答错误之处,并给予改正.解: 3107.330031.82323⨯=⨯⨯==RT E K J由 λν/hc h E K ==可得 19104.5/-⨯==K E hc λ Å (中子质量m 0 =1.67×10-27 kg ,普朗克常量h =6.63×10-34 J ·s ,玻尔兹曼常量k =1.38×10-23 J ·K -1)答案:答:上述解题是错误的,因为RT E K 23≠ K E hc /≠λ 1分改正: 211021.623-⨯==kT E K J 2分146.0)2/(/2/10===m E h p h K λ nm 2分 难度:中六、回答问题(共1题)回答问题:如果中子的动能与同温度下理想气体分子的平均平动动能相同, 则T =104 K 的热中子通过直径为1 mm 的小孔或障碍物时,将表现出粒子性还是波动性?为什么?(中子质量m 0 =1.67×10-27 kg ,玻尔兹曼常量k =1.38×10-23 J ·K -1,普朗克常量h =6.63×10-34 J ·s)答案:答:将表现出粒子性. 2分因为热中子的动能为 ==kT E K 232.07×10-19 J其德布罗意波长 ==K E m h 02/λ 2.52×10-11 m <<1 mm 3分难度:中。
西工大与西安交大期末复习考研备考大学物理题库 三、静电学 9 真空中的静电场

B、均匀带电球体;
C、点电荷;
D、不均匀带电球面.
题目图片:
答案:C
难度:中
选择题:图中所示曲线表示某种球对称性静电场的场强大小E随径向距离r变化的关系,请指出该电场是由下列哪一种带电体产生的.()
A、半径为R的均匀带电球面;
B、半径为R的均匀带电球体;
C、点电荷;
D、外半径为R,内半径为R/2的均匀带电球壳体.
A、曲面S的电场强度通量不变,曲面上各点场强不变.
B、曲面S的电场强度通量变化,曲面上各点场强不变.
C、曲面S的电场强度通量变化,曲面上各点场强变化.
D、曲面S的电场强度通量不变,曲面上各点场强变化.
题目图片:
答案:D
难度:易
选择题:半径为R的均匀带电球面的静电场中各点的电场强度的大小E与距球心的距离r之间的关系曲线为:()
D、通过S面的电场强度通量为q/0,但S面上各点的场强不能直接由高斯
定理求出.
题目图片:
答案:D
难度:易
选择题:已知一高斯面所包围的体积内电荷代数和∑q=0,则可肯定:()
A、高斯面上各点场强均为零.
B、穿过高斯面上每一面元的电场强度通量均为零.
C、穿过整个高斯面的电场强度通量为零.
D、以上说法都不对.
D、以上说法都不正确.
答案:C
难度:中
选择题:电荷面密度均为+的两块“无限大”均匀带电的平行平板如图放置,其周围空间各点电场强度 随位置坐标x变化的关系曲线为:(设场强方向向右为正、
向左为负)()
题目图片:
答案:B
难度:中
选择题:如图所示,在坐标(a,0)处放置一点电荷+q,在坐标(-a,0)处放置另一点电荷-q.P点是x轴上的一点,坐标为(x,0).当x>>a时,该点场强的大小为:()
(完整word)西安电子科技大学电磁场期末试卷()
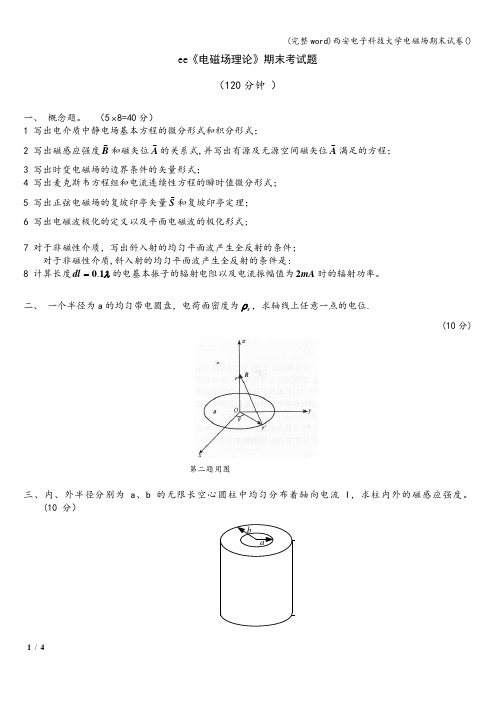
ee 《电磁场理论》期末考试题(120分钟 )一、 概念题。
(5⨯8=40分)1 写出电介质中静电场基本方程的微分形式和积分形式;2 写出磁感应强度B和磁矢位A 的关系式,并写出有源及无源空间磁矢位A 满足的方程; 3 写出时变电磁场的边界条件的矢量形式;4 写出麦克斯韦方程组和电流连续性方程的瞬时值微分形式;5 写出正弦电磁场的复坡印亭矢量S和复坡印亭定理;6 写出电磁波极化的定义以及平面电磁波的极化形式;7 对于非磁性介质,写出斜入射的均匀平面波产生全反射的条件; 对于非磁性介质,斜入射的均匀平面波产生全反射的条件是:8 计算长度λ10.=dl 的电基本振子的辐射电阻以及电流振幅值为mA 2时的辐射功率。
二、 一个半径为a 的均匀带电圆盘,电荷面密度为s ρ,求轴线上任意一点的电位.(10分)第二题用图三、内、外半径分别为a 、b 的无限长空心圆柱中均匀分布着轴向电流I ,求柱内外的磁感应强度。
(10 分)ab=l第三题用图四、一个截面如图所示的长槽,向y 方向无限延伸,两侧边的电位为零,槽内∞→y ,0=ϕ,底部电位为00U x =),(ϕ,求槽内电位。
(12分)=ϕ第四题用图五、从麦克斯韦方程组出发,推导各向同性、均匀、无耗介质中,无源区正弦电磁场的波动方程。
六.已知均匀平面电磁波的电场强度为)cos(ˆ)sin(ˆkz t E a kz t E aE y x i -+-=ωω00,将其作为入射波由空气向理想介质平面(0=z )垂直入射,坐标系如图(a )所示,介质的电磁参数为02029μμεε==,,计算:1、反射电磁波电场强度r E 和透射电磁波电场强度t E的复数值表达式;2、反射电磁波磁场强度r H 和透射电磁波磁场强度t H 的瞬时值表达式),(t z H r 和),(t z H t;3、判断入射电磁波、反射电磁波和透射电磁波是何种极化波;4、计算反射功率的时间平均值r av S , 和透射功率的时间平均值t av S ,;5、如果在理想介质分界面处加入厚度为d 的电磁介质如图(b )所示,试求交界面(0=z )无反射时,插入介质层的厚度d 以及相对介电常数r ε。
为什么要学习该课程及主要学习内容

电磁场与电磁波
教材:《电磁场与电磁波》丁君主
编 高等教育出版社出版
主讲教师:丁君教授
西北工业大学
绪论
第一讲:为什么要学习"电磁场与电磁波"课程 及 该课程的主要内容
第二讲:早期人类对电和磁的认识
第三讲:电和磁的关系
第四讲:电磁理论的建立
1.为什么要学习“电磁场与电磁波”呢?
电磁场绝对不是主观臆想的、虚无缥缈的东西
3.场的基=1本概念
(1)什么是场?
重力场、温度场、电磁场、……
a・从数学角度:场是给定区域内各点数值的集场中的物理量,T就是温度场
b・从物理角度:场是遍及一个被界定的或无限扩展的空间内的,能够
产生某种物理效应的特殊的物质,场是具有能量的。
2.该课程的主要内容
第一章:电磁学的数学基础——矢量运算 第二章:电磁学的理论基础——麦克斯韦方程组
第三章:微波炉的工作原理一 料的电磁特性及边界条件 第 章: 静态场分析 静态场的性质及其求解方法 第五章:场论与路论的关系——路量与场量之间的求解 第六章:隐身飞机是怎么隐身的?——平面电磁波的传播特性 第七章:电磁波是如何定向传输的? 一则波导和空腔谐振器 第八章:电磁波是怎么产生的?——电磁波的辐射原理
(2)场的分类 a. 按物理量的性质分为:
标量场:描述场的物理量是标量。 矢量场:描述场的物理量是矢量。
b. 按场量与时间的关系分为:
静态场:场量不随时间的变化而发生变化的场。 动态场:场量随时间的变化而变化的场。动态场也称为时变场。
小结: 1、 为什么要学习“电磁场与电磁波"这门课程 2、 介绍了该课程的主要内容 3、给出了场的基_b =—1本概念
比如银行业务、查阅资料、地图导航、淘宝购物等等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F dS V
S
V 0
Fu h 2 h 3 ( Fu h1 h3 ) ( Fu 3 h1 h 2 ) 1 2 h1 h 2 h3 u1 u2 u3 1
散度定理:
F dS
S
F dV
总复习
电场计算方法总结: (1)已知电荷分布用公式计算; 要求熟练掌握点电荷、线电荷的计算公式 (2)对称性的场用麦麦克斯韦积分方程计算;
D dS
S
V
V dV Q
H
(3)时变场用麦麦克斯韦微分方程计算; (4)用电位求电场;
E
D t
电磁场与电磁波
总复习
“电磁场与电磁波”总复习
一、基本概念
二、基本公式 三、基本方法
电磁场与电磁波
总复习
z
Az
第一章:矢量分析
1、矢量的定义
ˆ ˆ ˆ 矢量: A A x a x A y a y A z a z
A
模的计算:
单位矢量:a ˆ
2 2 2 | A | A x A y A z x Ay Ax A A ˆ ˆ ˆ a x a y z a z | A| | A| | A| | A|
B r 0H B 0 (H M )
电磁场与电磁波
总复习
第四章
一、基本概念
1、什么是静态场?静态场包括哪些场?有什么特点? 2、什么是对偶原理、唯一性原理、叠加原理? 3、镜像法的理论依据?实质(解题思路)? 4、分离变量法的原理是什么?
电磁场与电磁波
总复习
二、 静态场分析方法
x
q ( ll )
y r 1
P ( x, y , z )
h
0
h
q ( ll )
o
r2
x
电磁场与电磁波
总复习
q
电介质平面镜像
y
q l
1 2 1 2
y r 1
q
q q
2 1 1 2
q
l q
y
P ( x, y , z )
V
D
微分形式:
H JC
D t
E
B
S
S
B dS 0 V J C dS dV V t
t D V B 0 V JC t
电磁场与电磁波
(5)利用边界条件求电场; D1n D 2 n s (6)均匀平面波特点求电场;
j kz ˆ E Eme ax
E1 t E 2 t
(7)已知辐射源参数求辐射电场;
电磁场与电磁波
总复习
磁场计算方法总结: (1)已知电流分布用公式计算; 要求熟练掌握线电流、无限大面电流的计算公式。 (2)对称性的场用麦麦克斯韦积分方程计算;
dS
4、矢量磁位: B A 0 Id l A 4 l R
电磁场与电磁波
总复习
5、麦克斯韦方程组
积分形式:
H dl
l
l
S
S ( J C t ) d S B E dl dS S t D dS V dV
V
电磁场与电磁波
总复习
7、矢量场的旋度 定义:一矢量其大小等于某点最大环量密度,方向为该环 的法线方向,那么该矢量称为该点矢量场的旋度。 表达式: 计算:
F 1
ro t F lim
1 S
S 0
ˆ [an
ˆ h2 a u 2 u 2
l
F d l ]m ax
a d
q
q q Q (导体球的电荷)
b d
b a
2
ˆ h3 a u 3 u3
ˆ h1 a u1 h1 h 2 h 3 u 1 h1 F u
1
斯托克斯定理:
h 2 Fu
2
h3 Fu
3
( F ) d S
S
F dl
l
电磁场与电磁波
总复习
8、重要的场论公式
a. 两个零恒等式 b. 拉普拉斯算子
2
( ) 0
Ax Ay By Cy Az Bz Cz
3
A (B C ) Bx Cx
•体元: d V h1 h2 h3 d u1 d u 2 d u 3
5、标量场的梯度 定义: g ra d d a n ˆ 计算:
含义:
h3 u 3 ˆ au 3
dn
e.矢量三重积:
ˆ ˆ ˆ cos a x cos a y cos a z
Ax
o
Ay
y
方向角与方向余弦: , ,
Ax cos , |A| Ay cos , |A| Az cos |A|
电磁场与电磁波
总复习
2、矢量加减法: 加法:
( )
2
( F ) 0
h 2 h3 h1 h 3 h1 h 2 ( ) ( ) ( ) h1 h 2 h3 u 1 h1 u 1 u 2 h2 u 2 u 3 h3 u 3 1
静态场:E
b. 电位 点电荷的电位 q 4 π 0 R 无限长线电荷: l ln r 2π 0
时变场:E
A t
电磁场与电磁波
总复习
3、 磁场
a.
磁感应强度 B
的定义
qtv
无限大导流面:
B
B lim
ˆ Fm a v
ˆ 0 J S an 2
qt 0
b. 磁感应强度的计算 线电流:
0 B 4 ˆ Id l a R
l
无限长线电流:
0I ˆ B a 2r
R
2
面电流:
dI ˆ JS aI d l
0 B 4π
ˆ J S aR R
2
S
电磁场与电磁波
总复习
二、基本计算
1、三个物态方程:
2、边界条件:
导体: J E C
电介质:
D r 0 E D 0E P
D 1n D 2 n s E1 t E 2 t
磁介质:
B1 n B 2 n ˆ n (H1 H 2 ) J S
电磁场与电磁波
总复习
b. 角域镜像
c. 柱面镜像
y
r2
b
l
r1 l
c
x2
2 2
c
x1
2
a
x
x1 c a
x2 c b
2 2
2
x1 x 2 d
电磁场与电磁波
总复习
e. 导体球面镜像
a
d
q
a
q
a d
q
q
q
b a d
2
b d
不接地导体球镜像
a
q
q
q
q
q l q ' '
1
h
0
10
x
h
2
10
h
q 'l
o
r2
2
h
x
0
2
x
磁介质平面镜像
I I
I I
2 1 2 1
I
I I
1
2
d
1 1
d
H '
2 2
d
d
I'
H
d
H2
H1 H H '
A
b. 标量积(点积):
C
B
C A B
A B | A | | B | cos
B
ˆ ˆ ˆ A B ( Ax B x ) a x ( A y B y ) a y ( Az B z ) a z
A B Ax B x A y B y Az B z
B
(6)均匀平面波特点求磁场; H E m e j kz a ˆy
(7)已知辐射源参数求辐射磁场;
电磁场与电磁波
总复习
第三章
一、基本概念
1、什么是导体? 2、处在静电场中的导体会发生什么现象?有什么特点? 3、导体在恒定电场中会发生什么现象?有什么特点? 静电场和恒定电场有何不同? 4、什么是电介质的极化?极化后介质中的如何变化? 5、什么是磁介质的磁化?磁化后磁介质中的如何变化?
2 2
R sin
电磁场与电磁波
总复习
第二章
一、基本概念
1.什么是场?矢量场?标量场?静态场?时变场? 2.什么是电场?电场强度的定义?什么是电位?
3.什么是磁场?磁感应强度的定义?
4.麦克斯韦方程组的物理含义 5.什么是位移电流?位移电流的定义?
电磁场与电磁波
总复习
二、基本计算
1、 电场
A (B C ) B( A C ) C ( A B)
h1 u 1
