-基本初等函数的导数公式及四则运算
基本初等函数的导数公式及导数的运算法则
基本初等函数的导数公式及导数的运算法则（一）基本初等函数的导数公式表x y x y xy x y y x y cos )6(log )5(ln )4(1)3(5)2()1(125======、求下列函数的导数例 例处的切线方程。
在、求函数2cos 2π==x x y（二）导数的四则运算法则：（2）推论：[]''()()cf x cf x = （常数与函数的积的导数，等于常数乘函数的导数）例3、根据基本初等函数的导数公式和导数运算法则，求下列函数的导数．（1）323y x x =-+（2）y = （3）sin ln y x x x =⋅⋅；（4）4x x y =； （5）1ln 1ln x y x -=+． （6）2(251)x y x x e =-+⋅；三．课堂练习1、求下列函数的导数：)1()3( )sin ()2( cos )1(1)1(2322+=-=+-=x f y x b ax y xx x y ω 2、已知曲线C ：y ＝3 x 4－2 x 3－9 x 2＋4，求曲线C 上横坐标为1的点的切线方程；3、处的导数。
在求3332=++=x x x y 4、处的切线方程。
，在点求曲线)20(1P e y x += ______________________1216______________)42()04(4522处的切线方程为垂直，则过点的切线与直线上的点，若过点是曲线、的坐标为，则于处的切线恰好平行，若曲线上一点，、，上两点、曲线P x y P x y P P AB P B A x x y +-==-= 7、曲线3()2f x x x =+-在0P 点处的切线平行于直线41y x =-，则0P 点的坐标为 ．8、已知抛物线2y x bx c =++上的点（1，2）处的切线与直线2y x =-平行，求b ，c 的值。
基本初等函数的导数公式及导数的运算法则
上导乘下,下导乘上,差比下方
[ f ( x) g ( x)] f ( x) g ( x) f ( x) g ( x)
如果上式中f(x)=c,则公式变为：
[cg ( x)] cg ( x)
例2 根据基本初等函数的导数公式和导数
运算法则，求函数y=x3-2x+3的导数。
y (x 解：因为2x 3)
p(t ) p0 (1 5%)
t
解:根据基本初等函数导数公式表,有
(t ) 1.05t ln1.05 p
所以 p(10) 1.05 ln1.05 0.08(元 / 年)
10
因此,在第10个年头,这种商品的价格 约以0.08元/年的速度上涨.
导数的运算法则:(和差积商的导数)
导数的运算法则:(和差积商的导数)
[ f ( x) g ( x)]' f '( x) g '( x)
[ f ( x) g ( x)] f ( x) g ( x) f ( x) g ( x)
轮流求导之和
f ( x) f ( x) g ( x) f ( x) g ( x) ( g ( x) 0) g ( x) 2 g ( x)
是否有切线，如果有， 求出切线的方程.
试自己动手解答.
1 有,切y x 2
线的 方程 为
基本初等函数的导数公式
公式1.若f ( x) c, 则f '( x) 0; 公式2.若f ( x) x n , 则f '( x) nx n 1 ; 公式3.若f ( x) sin x, 则f '( x) cos x; 公式4.若f ( x) cos x, 则f '( x) sin x; 公式5.若f ( x) a x , 则f '( x) a x ln a ( a 0); 公式6.若f ( x) e x , 则f '( x) e x ; 1 公式7.若f ( x) log a x, 则f '( x) ( a 0, 且a 1); x ln a 1 公式8.若f ( x) ln x, 则f '( x) ; x
基本初等函数的导数公式及导数的运算法则
'
0.05eu 0.05e0.0 5x 1.
3函数y sinπx φ可以看作函数 y sinu和
u πx φ的复合函数 .
由复合函数求导法则有
' y'x yu u'x sinu' πx φ'
π cosu π cosπx φ.
我们无法用现有的方法 求函数 y lnx 2 的导数 . 下面, 我们先分析这个函数的 结构特点 . 若设 u x 2x 2 , 则y ln u.从而 y lnx 2 可以看成是由 y ln u 和u x 2x 2 经过 " 复 合" 得到的, 即y可以通过中间变量 u表示为自变量 x 的函数 . 如果把 y 与u的关系记作 y f u, u 和 x 的关系记作 u gx ,那么这个 " 复合 " 过程可表示为 y f u f gx lnx 2 . 我们遇到的许多函数都 可以看成是由两个函数 经过
思考 如何求函数y ln x 2 的导数呢?
" 复合" 得到的, 例如,函数y 2 x 3 由y u2和u 2 x 3" 复合" 而成,等等.
2
一般地 , 对于两个函数 y f u和u gx , 如果通过 变量 u, y可以表示成 x的函数 ,那么称这个函数为函 数y f u 和u g x 的 复 合 函 数 (composite fun ction),记作 y f gx . 复合函数 y f gx 的导数和函数 y f u,u gx 的 ' ' ' 导数间的关系为 y x yu ux .
基本初等函数的导数公式及导数的运算法则
讲解经济学中的温水煮青蛙现象。虽然每年只有8分钱，但在 不知不觉中物价已经让你承担不起。
例5 日常生活中的饮用水通常是经过净化的。随着水 纯净度的提高，所需净化费用不断增加。已知将1吨水 净化到纯净度x%时所需费用（单位：元）为
c(x) 5284 (80 x 100) 100 x
求净化到下列纯净度时，所需净化费用的瞬时变化率： （1）90％ （2）98％
解：净化费用的瞬时变化率就是净化费用函数的导数
c'(x)
( 5284 100 x
)'
5284'(100
x) 5284 (100 x)2Βιβλιοθήκη (100x)'
0 (100 x) 5284 (1) (100 x)2
5284 (100 x)2
例2 假设某国家在20年期间的平均通货膨胀率为5％，物价p(单位： 元)与时间t（单位：年）有如下函数关系
p(t) p0 (1 5%)t
其中p0为t = 0时的物价。假定某种商品的p0=1,那么在第10个年 头，这种商品的价格上涨的速度大约是多少（精确到）?
解：根据基本初等函数导数公式表，有
p'(t) 1.05t ln1.05 p'(10) 1.0510 ln1.05 0.08(元 / 年)
解：因为 y (x3 2x 3)
(x3 ) (2x) (3) 3x2 2
所以，函数y=x3-2x+3的导数是
y ' 3x2 2
既然导数可求，那可以求这个函数图像的切线吗？原来的旧方 法没用了吧！我们用几何画板画出此函数的图像。
2.已知函数y=xlnx (1)求这个函数的导数 (2)求这个函数在点x=1处的切线方程
导数的四则运算
dy 例12 y lnsin x , 求 . dx
解 dy lnsin x 1 sin x dx sin x
1 1 cos x sin x tan x
有限次四则运算的求导法则:
1 u v u v 2 uv uv uv
解
1
y x tan x x tan x tan x x
y | x 0 0
2
1 f x 5 2 5 x3 x x 2 f x 3 15x 2 1 x
f 1 16, f 1 12
(u v w)' u' v' w' .
(2) ( uv ) uv u v
证 设 f ( x ) u( x )v( x ) , 则有
u( x h)v( x h) u( x )v( x ) f ( x h) f ( x ) lim f ( x ) lim h 0 h 0 h h
v uv uv 3 u2 u
cu cu
u 1 2 u u
(c为常数）
u 0
4
若 y f u, u x , 则对于复合函数 y f x
dy dy du 有 y x yu u x 或 dx du dx
sin x cos x
解 (1)根据求导法则(1),得
(2)根据求导法则(2),得 y x 2 2 ln x sin x x 2 2 ln x sin x
2 2 x sin x x 2 2 ln x cos x x
公共基础课一导数的四则运算
y f x x f x x x
y
'
=
f x x f x lim x 0 x
机动
目录
上页
下页
返回
结束
二 求导步骤
例1 求函数 f x x 的导数. 解 求增量 算比值
y f x x f x x
2
公共基础课
1 f ' 3 , f ' . 2
解 求增量
2
y f x x f x
2
x x 1 x 1 x 2 xx
2
算比值 取极限 即
y 2 x x x
y f ' x lim lim x 2 x 2 x x 0 x x 0
y f x x f x x 1 x x x
公共基础课
f x x f x y lim lim 1 1 取极限 x 0 x 0 x 即 x 1
机动
目录
上页
下页
返回
结束
二 求导步骤
例2 求函数 f x x 1 的导数及
2
f ' x x 2 x
1 所以，f ' 3 6，f ' 1 2
机动
目录
上页
下页
返回
结束
三 解决问题
固定成本1000万元 ，生产x 辆轿车可 0.005 x 5 x 万元 变成本为
2
公共基础课
售价16万元/辆，能否决策 将月产量从1000辆增加到1001 辆？
导数的四则运算法则(教师版有答案)
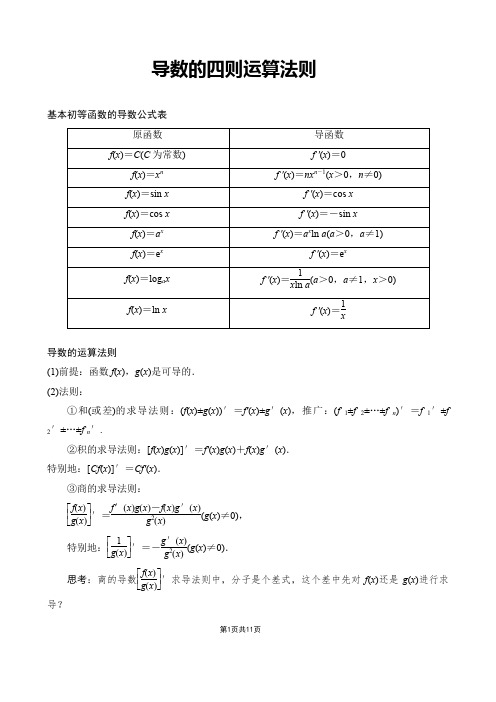
第1页共11页导数的四则运算法则基本初等函数的导数公式表导数的运算法则(1)前提：函数f (x )，g (x )是可导的． (2)法则：①和(或差)的求导法则：(f (x )±g (x ))′＝f′(x )±g ′(x )，推广：(f 1±f 2±…±f n )′＝f 1′±f2′±…±f n ′.②积的求导法则：[f (x )g (x )]′＝f′(x )g (x )＋f (x )g ′(x )． 特别地：[Cf (x )]′＝Cf′(x )．③商的求导法则：⎣⎢⎡⎦⎥⎤f (x )g (x )′＝f ′(x )g (x )－f (x )g ′(x )g 2(x )(g (x )≠0)，特别地：⎣⎢⎡⎦⎥⎤1g (x )′＝－g ′(x )g 2(x )(g (x )≠0)．思考：商的导数⎣⎢⎡⎦⎥⎤f (x )g (x )′求导法则中，分子是个差式，这个差中先对f (x )还是g (x )进行求导？第2页共11页[提示] 先对f (x )求导，即f′(x )g (x )，再对g (x )求导，即f (x )g ′(x )．1．下列结论不正确的是( ) A ．若y ＝3，则y ′＝0 B ．若f (x )＝3x ＋1，则f′(1)＝3 C ．若y ＝－x ＋x ，则y ′＝－12x＋1D ．若y ＝sin x ＋cos x ，则y ′＝cos x ＋sin xD [D 项，∵y ＝sin x ＋cos x ，∴y ′＝(sin x )′＋(cos x )′＝cos x －sin x ．] 2．设y ＝－2e x sin x ，则y ′等于( ) A ．－2e x cos x B ．－2e x sin x C ．2e x sin xD ．－2e x (sin x ＋cos x )D [y ′＝－2(e x sin x ＋e x cos x )＝－2e x (sin x ＋cos x )．] 3．已知函数f (x )＝ln xx ，则f′(1)＝________. 1 [∵f′(x )＝1x ×x －ln x x 2＝1－ln xx 2，∴f′(1)＝1.]用导数的求导法则求导数 【例1】 求下列函数的导数： (1)y ＝2x 2＋1x －3x 3； (2)y ＝x ＋3x 2＋3； (3)y ＝e x cos x ＋sin x ；(4)y ＝x 3＋lg x .[思路探究] 观察函数的特征，可先对函数式进行合理变形，然后利用导数公式及相应的四则运算法则求解．[解] (1)∵y ＝2x 2＋x －1－3·x －3， ∴y ′＝4x －x －2－3·(－3)x －4＝4x －1x 2＋9x 4. (2)y ′＝1·(x 2＋3)－2x (x ＋3)(x 2＋3)2＝－x 2－6x ＋3(x 2＋3)2.(3)y ′＝(e x cos x ＋sin x )′＝(e x cos x )′＋(sin x )′第3页共11页＝(e x )′cos x ＋e x (cos x )′＋cos x ＝e x cos x －e x sin x ＋cos x . (4)y ′＝3x 2＋1x ln 10.应用基本初等函数的导数公式和求导的四则运算法则可迅速解决一些简单函数的求导问题，要透彻理解函数求导法则的结构特点，准确熟记公式，还要注意挖掘知识的内在联系及其规律.对比较复杂的求导问题，可先进行恒等变形，再利用公式求导.提醒：当不易直接应用导数公式时，应先对函数进行化简，再求导.求下列函数的导数： (1)y ＝1x 2＋sin x 2cos x 2； (2)y ＝x ⎝ ⎛⎭⎪⎫x 2－32x －6＋2；(3)y ＝cos x ln x ；(4)y ＝xe x .[解] (1)y ′＝⎝ ⎛⎭⎪⎫1x 2＋sin x 2cos x 2′＝(x －2)′＋()12sin x ′ ＝－2x －3＋12cos x ＝－2x 3＋12cos x . (2)y ′＝⎝ ⎛⎭⎪⎫x 3－32x 2－6x ＋2′＝(x 3)′－⎝ ⎛⎭⎪⎫32x 2′－(6x )′＋(2)′＝3x 2－3x －6. (3)y ′＝(cos x ln x )′ ＝(cos x )′ln x ＋cos x (ln x )′ ＝－sin x ln x ＋cos xx .第4页共11页(4)y ′＝⎝ ⎛⎭⎪⎫x e x ′＝(x )′e x －x (e x)′(e x )2＝e x －x e x e 2x ＝1－xe x . 导数运算法则的应用 [探究问题]1．导数的和、差运算法则求导能拓展到多个函数吗？ [提示] [f 1(x )±f 2(x )±…±f n (x )]′＝f 1′(x )±f 2′(x )±…±f′n (x )． 2．导数的积、商运算法则有哪些相似的地方？区别是什么？[提示] 对于积与商的导数运算法则，应避免出现“积的导数就是导数的积，商的导数就是导数的商”这类想当然的错误，应特别注意积与商中符号的异同，积的导数法则中是“＋”，商的导数法则中分子上是“－”．【例2】 已知函数f (x )＝ln x －ax ＋1－ax －1(a ∈R )．当a ＝－1时，求曲线y ＝f (x )在点(2，f (2))处的切线方程．[思路探究] 先求导，再求切线斜率，根据点斜式得切线方程． [解] 因为当a ＝－1时，f (x )＝ln x ＋x ＋2x －1，x ∈(0，＋∞)． 所以f′(x )＝x 2＋x －2x 2，x ∈(0，＋∞)，因为f′(2)＝1，即曲线y ＝f (x )在点(2，f (2))处的切线斜率为1.又f (2)＝ln 2＋2， 所以曲线y ＝f (x )在点(2，f (2))处的切线方程为y －(ln 2＋2)＝x －2， 即x －y ＋ln 2＝0.1．(变换条件)本典例函数不变，条件变为“曲线y ＝f (x )在点(2，f (2))处的切线方程为x第5页共11页(1)此类问题往往涉及切点、切点处的导数、切线方程三个主要元素.其他的条件可以进行转化，从而转化为这三个要素间的关系.(2)准确求出已知函数式的导数、切线方程是解决此类问题的关键.1．思考辨析(1)若f (a )＝a 3＋2ax －x 2，则f′(a )＝3a 2＋2x . ( ) (2)⎣⎢⎡⎦⎥⎤C g (x )′＝－Cg ′(x )g 2(x ). ( ) (3)任何函数都可以应用导数的运算法则求导数． ( )[提示] (1)√ (2)√(3)× 应用导数的运算法则求导数的前提是f (x )，g (x )均为可导函数，即f′(x )，g ′(x )存在．2．对于函数f (x )＝e x x 2＋ln x －2kx ，若f′(1)＝1，则k 等于( ) A ．e2 B ．e3 C ．－e 2D ．－e 3A [∵f′(x )＝e x (x －2)x 3＋1x ＋2kx 2，第6页共11页∴f′(1)＝－e ＋1＋2k ＝1，解得k ＝e2，故选A.] 3．曲线y ＝sin x sin x ＋cos x －12在点M ⎝ ⎛⎭⎪⎫π4，0处的切线的斜率为( ) A ．－12 B ．12 C ．－22D ．22B [∵y ′＝cos x (sin x ＋cos x )－sin x (cos x －sin x )(sin x ＋cos x )2＝1(sin x ＋cos x )2，∴y ′|x ＝π4＝12，∴曲线在点M ⎝ ⎛⎭⎪⎫π4，0处的切线的斜率为12.] 4．已知a 为实数，f (x )＝(x 2－4)(x －a )，且f′(－1)＝0，则a ＝________.12[∵f (x )＝(x 2－4)(x －a )＝x 3－ax 2－4x ＋4a ，∴f′(x )＝3x 2－2ax －4. 又∵f′(－1)＝3＋2a －4＝0， ∴a ＝12.] 5．设函数f (x )＝13x 3－a2x 2＋bx ＋c ，其中a ＞0，曲线y ＝f (x )在点P (0，f (0))处的切线方程为y ＝1，确定b 、c 的值．[解] 由题意，得f (0)＝c ，f′(x )＝x 2－ax ＋b ，由切点P (0，f (0))既在曲线f (x )＝13x 3－a 2x 2＋bx ＋c 上又在切线y ＝1上，得⎩⎨⎧f ′(0)＝0，f (0)＝1，即⎩⎪⎨⎪⎧02－a ×0＋b ＝0，13×03－a 2×02＋b ×0＋c ＝1， 解得b ＝0，c ＝1.[基础达标练]第7页共11页1．已知函数f (x )＝sin x ＋ln x ，则f ′(1)的值为( ) A ．1－cos 1 B ．1＋cos 1 C ．cos 1－1D ．－1－cos 1B [∵f ′(x )＝cos x ＋1x ，∴f ′(1)＝cos 1＋1.]2．函数f (x )＝e x ＋x sin x －7x 在x ＝0处的导数等于( ) A ．－6 B ．6 C ．－4D ．－5A [∵f ′(x )＝e x ＋(sin x ＋x cos x )－7， ∴f ′(0)＝e 0＋(sin 0＋0)－7＝－6.]3．设曲线y ＝x ＋1x －1在点(3,2)处的切线与直线ax ＋y ＋1＝0垂直，则a 等于( )A ．2B ．12 C ．－12 D ．－2D [∵y ＝x ＋1x －1＝1＋2x －1， ∴y ′＝－2(x －1)2.∴y ′|x ＝3＝－12. ∴－a ＝2，即a ＝－2.]4．已知曲线y ＝x 3在点P 处的切线斜率为k ，则当k ＝3时的P 点坐标为( ) A ．(－2，－8) B ．(－1，－1)或(1,1) C ．(2,8) D.⎝ ⎛⎭⎪⎫－12，－18 B [∵y ′＝3x 2，k ＝3，∴3x 2＝3，∴x ＝±1. 故P 点坐标为(－1，－1)或(1,1)．] 5．已知点P 在曲线y ＝4e x＋1上，α为曲线在点P 处的切线的倾斜角，则α的取值范围是( )第8页共11页A ．⎣⎢⎡⎭⎪⎫0，π4B ．⎣⎢⎡⎭⎪⎫π4，π2C ．⎝ ⎛⎦⎥⎤π2，3π4D ．⎣⎢⎡⎭⎪⎫3π4，πD [y ′＝－4e x (e x ＋1)2＝－4e x e 2x ＋2e x ＋1，设t ＝e x∈(0，＋∞)，则y ′＝－4t t 2＋2t ＋1＝－4t ＋1t ＋2，∵t ＋1t ≥2，∴y ′∈[－1,0)，α∈⎣⎢⎡⎭⎪⎫3π4，π.] 6．已知f (x )＝13x 3＋3xf ′(0)，则f ′(1)＝________.1 [由于f ′(0)是一常数，∴f ′(x )＝x 2＋3f ′(0)，令x ＝0，则f ′(0)＝0，∴f ′(1)＝12＋3f ′(0)＝1.]7．若曲线y ＝x ln x 上点P 处的切线平行于直线2x －y ＋1＝0，则点P 的坐标是________． (e ，e) [设P (x 0，y 0)．∵y ＝x ln x ， ∴y ′＝ln x ＋x ·1x ＝1＋ln x .∴k ＝1＋ln x 0.又k ＝2，∴1＋ln x 0＝2，∴x 0＝e. ∴y 0＝eln e ＝e.∴点P 的坐标是(e ，e)．]8．若函数f (x )＝12x 2－ax ＋ln x 存在垂直于y 轴的切线，则实数a 的取值范围是________． [2，＋∞) [∵f (x )＝12x 2－ax ＋ln x ， ∴f ′(x )＝x －a ＋1x .∵f (x )存在垂直于y 轴的切线，∴f ′(x )存在零点， 即x ＋1x －a ＝0有解，∴a ＝x ＋1x ≥2.] 9．求下列函数的导数： (1)y ＝x ⎝ ⎛⎭⎪⎫x 2＋1x ＋1x 3；(2)y ＝(x ＋1)⎝ ⎛⎭⎪⎫1x －1；第9页共11页(3)y ＝sin 4x 4＋cos 4x4. [解] (1)∵y ＝x ⎝ ⎛⎭⎪⎫x 2＋1x ＋1x 3＝x 3＋1＋1x 2，∴y ′＝3x 2－2x 3.(2)∵y ＝(x ＋1)⎝ ⎛⎭⎪⎫1x －1＝－x 12＋x －12，∴y ′＝－12x －12－12x －32 ＝－12x ⎝ ⎛⎭⎪⎫1＋1x . (3)∵y ＝sin 4x 4＋cos 4x4＝⎝ ⎛⎭⎪⎫sin 2x 4＋cos 2x 42－2sin 2x 4cos 2x 4＝1－12sin 2x 2＝1－12·1－cos x 2＝34＋14cos x ，∴y ′＝－14sin x .10．已知函数f (x )＝ax 3＋bx 2＋cx 过点(1,5)，其导函数y ＝f ′(x )的图象如图所示，求f (x )的解析式．[解] ∵f ′(x )＝3ax 2＋2bx ＋c ， 又f ′(1)＝0，f ′(2)＝0，f (1)＝5，∴⎩⎨⎧3a ＋2b ＋c ＝0，12a ＋4b ＋c ＝0，a ＋b ＋c ＝5，解得a＝2，b ＝－9，c ＝12.第10页共11页∴f (x )的解析式是f (x )＝2x 3－9x 2＋12x .[能力提升练]1．设函数f (x )＝sin θ3x 3＋3cos θ2x 2＋tan θ，其中θ∈⎣⎢⎡⎦⎥⎤0，5π12，则导数f ′(1)的取值范围是( )A ．[－2,2]B ．[2，3]C ．[3，2]D ．[2，2]D [由已知，得f ′(x )＝sin θ·x 2＋3cos θ·x ，所以f ′(1)＝sin θ＋3cos θ＝2sin ⎝ ⎛⎭⎪⎫θ＋π3，又θ∈⎣⎢⎡⎦⎥⎤0，5π12，所以π3≤θ＋π3≤3π4，所以2≤2sin ⎝ ⎛⎭⎪⎫θ＋π3≤2，所以2≤f ′(1)≤2.]2．下列图象中，有一个是函数f (x )＝13x 3＋ax 2＋(a 2－1)x ＋1(a ∈R ，a ≠0)的导函数f ′(x )的图象，则f (－1)＝( )A ．13B ．－13C ．73D ．－13或53B [∵f ′(x )＝x 2＋2ax ＋(a 2－1)，∴导函数f ′(x )的图象开口向上．又a ≠0，∴f ′(x )不是偶函数，其图象不关于y 轴对称，∴f ′(x )的图象必为第三个图．由图象特征，知f ′(0)＝0，∴a 2－1＝0，且－a ＞0，∴a ＝－1，∴f (x )＝13x 3－x 2＋1，∴f (－1)＝－13－1＋1＝－13.]3．设a ∈R ，函数f (x )＝x 3＋ax 2＋(a －3)x 的导函数是f ′(x )，若f ′(x )是偶函数，则曲线y ＝f (x )在坐标原点处的切线方程为________．y＝－3x[∵f(x)＝x3＋ax2＋(a－3)x，∴f ′(x)＝3x2＋2ax＋a－3.又f ′(－x)＝f ′(x)，即3x2－2ax＋a－3＝3x2＋2ax＋a－3对任意x∈R都成立，∴a＝0，∴f ′(x)＝3x2－3，f ′(0)＝－3，∴曲线y＝f(x)在坐标原点处的切线方程为y＝－3x.]第11页共11页。
导数公式大全
复合函数的求导法则
定理2.2 若函数u u(x)在点x可导，函数y＝f (u)
在点u处可导，则复合函数y f (u(x))
在点x可导，且
dy dx
dy du
du dx
或记作：
dy dx
f
'(u) u '(x)
推论 设 y = f (u) ， u = (v) ， v =
(x) 均可导，则复合函数 y = f [ ( (x))] 也可
注：当两个二阶导数连续时，它们是相等的
即 f xy ( x, y) f yx (x, y)
例 3 设 z arctan xy,
试求函数的四个二阶偏导函数
2z 2z x2 y2
2z x y
2z y x
思考题一
求曲y 线2x x3 x
上与 轴平行的切线方程 .
思考题一解答
y 2 3x2 令 y 0 2 3x2 0
tan
x
(4) 把 tan x 当作中间变量， y ' (etan x ) ' etan x (tan x) ' sec2 xetan x
(5) 把 x 当作中间变量， y ' (2x ) ' 2x ln 2 (x) ' 2x ln 2
求导方法小结：
先将要求导的函数分解成基本初等函 数 , 或常数与基本初等函数的和、差、积、 商.
z y
2 y ln(x2
y2)
(x2
y2)
2y x2 y2
2 y[ln(x2 y2 ) 1]
二元函数的二阶偏导数
函数 z = f ( x , y ) 的两个偏导
数
z x
f x ( x, y),
基本初等函数的导数公式及导数的四则运算法则(一)_2022年学习资料
例用导数公式求下列函数的导数-1fx=x-2fx=-3fx=-sin x-4fx=Vx3-5fx=-cos -6fx=3x-7fx=21nx-8fx=1og3x-9fx=2e1-10fx=1gx-2fx=x2-6i到-7fx=l0g1x-朝-4f=2fx=1gx-湖
比比赛赛：-1y=fx=3-求在点M2,3处切线的方程-2y=fx=x,-求在点M2,2处切线的方程-3y fx=x2,-求在点M2,4处切线的方程-4yfx=-X-求在点M1,1/2处切线的方程
2.求函数y=的图象上点2，处的切线方程-X-3曲线y=x2的一条切线方程为6x-y-9=0,-求切点的坐 -4.求曲线y=3上过点1,3的切线方程.-陶
导数的运法则-1、和（差）的导数：[fx±g]=f'x±g'x-2、积的导数：[fx:gx]=f'·8x+ x8'x-推论：[cfx=c·f'-C为常数-f'x8x-fx8'x-8x≠0-[8x]
例题讲解-例题1：求下列函数的导数-1y=2x5-3x2+8-2y=x4+2xx3-2-3y=sinxco x-潮-4y=-2ex+1
练习：求下列函数的导数-1y=3x3-2x2+5-3y=x3x2-4-4y=2x-123x+2e-5y-1 2-2x+1-7y=2*Inx-6y=5*cosx-8y =tanx
作业-1、求下列函数的导数-1y=2x2+1-31nx-2-2y=e*.sinx-3y=-x+210gsx x2+3-x3-coS x-2.课本Ps5A组4,5,6,7
3.2,2基本初等函数的导数公式
基本初等函数的导数公式：-1、若fx=c,则f'x=0-常函数-2、-若∫x=x”,则f'x=nx”-一幂 数-3、若fx=sinx,则f'x=cosx-三角函数-4-若fx=cosx,则f'x=-sinx-5、若 x=a,则f'x=a.lna-指数函数-6、-若fx=e,则f'x=e-7、若fx=log。,则f'x=lna-对数函数-8、若fx=lnx,则f'x=二-X
基本初等函数的导数公式及导数的运算法则
(x 2) (x 1) 2x 3
sin x (sin x)'cos x sin x(cos x)'
(3) y' ( )' cos x
cos2 x
cos2 x sin cos2 x
2
x
1 cos2
x
sec2
x.
例2求下列函数的导数.
(1) y 2sin x cos x 2x2 1 (2) y cos2 x sin 2 x
【教育类精品资料】
基本初等函数的导数公式 及导数的运算法则
一、基本初等函数的导数公式:
C'0C为常 (数 xn)'n(x)n1(nQ)
(sin x) cos x (cxo)ssixn
(ax)' ax lna,(ex)' ex
(loga
x)'
1 ,(lnx)' xlna
1 x
二、导数的运算法则:(和差积商的导数)
[f(x ) g (x ) ]' f'(x ) g '(x )
函 数 和 （ 差 ） 的 导 数 等 于 它 们 导 数 的 和 （ 差 ） .
（可以推广到求有限个函数的和（差）的导数.）
(轮流求导之和)
[f(x)g(x)]'f'(x)g(x)f(x)g(x)' [gf((xx))]' f'(x)g([xg)(x)f]2(x)g(x)'(g(x)0)
(2 )y f(1 x 2) 2 x x f(1 x 2); 21 x 2 1 x 2
(3) y[f(sin2 x)f(cos2 x)]
高二数学(选修2-2人教B版)-导数公式表及导数的四则运算法则(1)
y' f (x)
y' ax ln a y' ex y' 1
x ln a y' 1
x
基本初等函数的导数公式表
y f (x)
y' f (x)
y sin x
y' cos x
y cos x
y' sin x
思考
如何求下面几个函数的导数？
① y x7 x6 3x5
思考 如何求函数 h(x) x x2 的导数？
h(x x) h(x) x x (x x)2 (x x2 ) x x x2 (x)2 2x x x x2
根据导数定义 1.求函数值增量
思考 如何求函数 h(x) x x2 的导数？
h(x x) h(x) x x (x x)2 (x x2 ) x x x2 (x)2 2x x x x2 x (x)2 2x x
② y x sin x ex x
③ y tan x
④ y (3x 1) sin 2x
思考
如何求下面几个函数的导数？
① y x7 x6 3x5
② y x sin x ex x
③ y tan x y sin x cos x
④ y (3x 1) sin 2x y sin 2x 2sin x cos x
思考 两个函数的积的导数、商的导数，与这两个函数的导数 又有什么关系呢？
举例 设 f (x) x ，g(x) x2 ，则 f '(x) 1 ，g '(x) 2x ， ( f (x) g(x))' (x x2 )' (x3)' 3x2
f '(x)g(x) f (x)g'(x) 1 x2 x 2x 3x2
基本初等函数的导数公式及导数的运算法则(侨中公开课)
f (x)
g(x)
f
(
x)
g
(x) f (
g ( x)2
x)
g
(
x)
(
g
(
x)
0)
上导乘下,下导乘上,差比下方
[例 2] 求下列函数的导数： (1)y＝15x5－43x3＋3x＋ 2； (2)y＝(3x5－4x3)(4x5＋3x3)；
(3)y＝33 x4＋4 x3.
公式一: C= 0 (C为常数)
公式二: (x ) x 1(是常数)
算一算：求下列函数的导数
(1) y=x4 ;
(2) y=x-5 ;
4x3
-5x-6
(3) y x ;
1
x
1 2
1 (4) y x2 ;
-2x-3
2
注意公式中,n的任意性.
公式三: (sin x) cos x
应用1: 求下列函数的导数 (1)y=x3+sinx
y' 3x2 cos x
(2)y=x4-x2-x+3.
y' 4x3 2x 1
(3) y x3 2x 3
1
(4) y x 4 log2 x
法则2:
f (x) g(x)' f '(x) g(x) f (x) g'(x)
（1）下列各式正确的是（ C ）
A.(sin )' cos(为常数）
B（. cos x)' sin x C.(sin x)' cos x D.( x5 )' 1 x6
5
（2）下列各式正确的是（ D ）
基本初等函数的导数公式及导数的运算法则
y'x表示y对x的导数
即 y对 x的导数 y对 u 等 的于 导u数 对 x的 与导数. 的
由此,y可 ln 3 得 x2对 x的导数 yln 等 u对 u的 于
导数 u3 与 x2对 x的导数 ,即 的乘积
y'xyu ' u'xln u'3x2' 1 u33x3 2.
1321,
所以,纯净度为 98%时,费用的瞬时变化率
是1321元/吨.
函数 fx 在某点处的导数的大小表示函数
在此点附近变化的快慢 .由上述 计算可知,
c' 98 25c' 90.它表示纯净度为98%左
右时净 化费用的变化率 ,大约是纯 净 度 为
90% 左右时净化费用变化率的 25 倍 .这说
当p0 5时,pt 5 1.05t.这时,求p关于t的导 数可以看成求函数ft 5与 gt 1.05t 乘积
的导数.下面的" 导数运算法则"可以帮助我们解 决两个函数加、减、乘、除的求导问题.
导数运算法则
1 . f x g x ' f 'x g 'x ;
2 . f x g x ' f ' x g x f x g ' x ;
3 . g fx x 'f'x g x g x f2 x g 'x g x 0 .
例2 根据基本初等函数的导数公式 和导数运算法则,求函数 y x3 2x 3的导数.
1 ;
x ln a
8.
若 fx ln x,则 f ' x
基本初等函数的导数公式及四则运算
导数是函数曲线在该点上的切线的斜率。
常见导函数的公式及图像
一次数
导数为常数，图像为直线。
二次函数
导数为一次函数，图像为抛物线。
正切函数
导数为幂函数，图像具有周期性。
指数函数
导数为自身，图像为逐渐增长的曲线。
对数函数的导数
对数函数的导数公式是1/x，其中x是对数函数的底数。对数函数的图像是单调 递增的。
反三角函数的导数
反三角函数的导数与对应的三角函数有关。例如，arcsin(x)的导数是1/√(1-x^2)，arccos(x)的导数是-1/√(1-x^2)。
初等函数导数的性质
初等函数的导数具有一些规律和性质，包括链式法则、求导法则和反函数求导法则。
四则运算简单例题及求导步骤
通过一些例题和求导步骤，了解如何对简单的四则运算进行求导。
函数复合法则及求导步骤
函数复合法则是求导一个函数由多个函数复合而成时使用的方法。通过一些 例题，了解如何使用函数复合法则求导。
反函数求导法则及求导步骤
反函数求导法则是求导一个函数的反函数时使用的方法。通过一些例题，了 解如何使用反函数求导法则求导。
基本初等函数的导数公式 及四则运算
了解基本初等函数的导数公式和四则运算是学习微积分的重要基础。本演示 将逐步介绍每个函数的导数公式，以及它们的几何和物理意义。
什么是导数及其定义
导数描述了函数在某一点上的变化率。简单来说，它是函数曲线的切线的斜率。定义为函数的极 限。
1 数学定义
导数是函数f(x)在某个点x处的极限lim(x→0)(f(x+h)-f(x))/h。
基本初等函数的导数公式及导数的运算法则-课件
题型三 求较复杂函数的导数 例3 求下列函数的导数：
(1)y＝2x2sin(2x＋5)； (2)y＝a3x·cos(2x＋1)． 【解】 (1)由于[sin(2x＋5)]′＝cos(2x＋5)·(2x＋5)′ ＝2cos(2x＋5)， ∴y′＝(2x2)′sin(2x＋5)＋2x2[sin(2x＋5)]′ ＝4xsin(2x＋5)＋4x2cos(2x＋5)．
所以 f(x0)＝g(x0)，f′(x0)＝g′(x0)，
12x20＋2x0＝3ln x0＋b. ∴
x0＋
2＝3 . x0
由
x0＋
2＝ 3 得， x0
x0＝
1，或
x0＝－ 3(舍去 )，
所以 b＝52.
(2)y＝f(x)(x＞ 0)， y＝ g(x)(x＞ 0)
在 且公f′共(x点)＝(xx0，＋y20a)处 ，的g′切(x线)＝相3x同a2，，
x .
(3)y′＝(ex)′ (x4－ 3x2－ 5x＋ 6)＋e x(x4－ 3x2－ 5x＋ 6)′
＝e x(x4－ 3x2－ 5x＋ 6)＋e x(4x3－ 6x－ 5)
＝e x(x4＋ 4x3－ 3x2－ 11x＋ 1)．
(4)y＝x－12sin x，
∴y′＝1－12cos x.
题型二 求复合函数的导数 例2 求下列函数的导数：
的图象的一个公共点，两函数的图象在点 P 处有相同的切
线，用 t 表示 a，b，c.
解：∵函数 f(x)，g(x)的图象都过点 P(t,0)， ∴f(t)＝0，即 t3＋at＝0. ∵ t≠ 0，∴ a＝－ t2. 又 g(t)＝0，即 bt2＋c＝0，∴c＝ab. 又∵ f(x)， g(x)在点(t,0)处有 相同的切线， ∴ f′(t)＝ g′ (t)． 而 f′(x)＝3x2＋a，g′(x)＝2bx， ∴ 3t2＋ a＝ 2bt. 将 a＝－t2 代入上式得 b＝t. ∴ c＝ ab＝－ t3.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例 1 求 f ( x ) x 2 x s i n x 在 x 0 时 的 导 数 .
3 2
例2
设 y = xlnx ， 求 y .
例3
解
设 y
x 1 , 求 y . 2 x 1
根据除法公式，有
2 2 x 1 ( x 1 )( x 1 ) ( x 1 ) ( x 1 ) y 2 2 2 x 1 ( x 1 )
常见函数的导数及四则运算
高二理科一二班卢
二、几种常见函数的导数
根据导数的定义可以得出一些常见函数的导数公式. 1) 函数y=f(x)=c的导数.
y 解 :y f( x ) C , y f( x x ) f( x ) CC , 0 , x y f ( x ) C l i m 0 . x 0 x
公式4:
(cos x ) sin x
公式5:对数函数的导数
1 ( 1 )( l o g x ) ( a 0 , a 1 ) . a x l n a 1 (2) (ln x) . x
公式6:指数函数的导数
x x
( 1 )() a a l n a ( a 0 , a 1 ) .
1 ( 2 ) 已知 y 2,求 f ( 3 ). x
3
1 2 f ( 3 ) 2 ( 3 ) 2 27 27
例3.求下列函数的导数
( 1 )y sin( x ) 2 ( 3 )y cos( 2 x )
( 2 )y sin 3
例4.求下列函数的导数
f( x )' f ( x ) g ( x ) f( x ) g ( x ) ) （3） ( 2 g ( x ) g( x )
特殊地 （c为常数） ( c f(x ) ) c f (x )
' '
'
'
g x 1 ' ( ) 2 g(x) g (x)
'
注意：1、前提条件导数存在； ２、和差导数可推广到任意有限个； ３、商的导数右侧分子中间“－”， 先 子导再母导。
(1 ) y x 2 x 3 1 2 (2 ) y 2 ; x x x (3 ) y ; 2 1 x ( 4 ) y ta n x ;
3 2
例4:求下列函数的导数:
2 3 答案: ( 1 )y x 2 ;
1 4 3; 2 x x 1 x2 (3) y ; 2 2 (1 x ) (2) y
例1：求下列函数的导数
( 1 )yx
5
( 2 )y x x x
例2: ( 1 ) 已知 y x , 求 f ( 2 ).
3
3 3 1 2 解： y ( x ) 3 x 3 x
2 f( 2 ) 3 ( 2 ) 12
2 2 1 3 解： y ( x ) 2 x 2 x
公式1: C = 0 (C为常数)
2)y f (x) x, y'1 3 ) y f ( x ) x , y ' 2x 1 1 4 ) y f (x) , y' 2 x x
2
公式2:
.) ( x) nx( n Q
n n 1
公式3:
(sin x ) cos x
e . ( 2 ) ( e)
x x
a 是两个不同 注意:关于ax和 x
的函数,例如:
(1 )( 3 ) 3 ln a
x
x
(2)(x ) 3 x
3
2
总结：我们今后可以直接使用的基本初等函数 的导数公式
公 式 1 .若 f ( x ) c , 则 f '( x ) 0; 公 式 2 .若 f ( x ) x n , 则 f '( x ) n x n 1 ; 公 式 3 .若 f ( x ) s in x , 则 f '( x ) c o s x ; 公 式 4 .若 f ( x ) c o s x , 则 f '( x ) s in x ; 公 式 5 .若 f ( x ) a x , 则 f '( x ) a x ln a ( a 0 ); 公 式 6 .若 f ( x ) e x , 则 f '( x ) e x ; 1 公 式 7 .若 f ( x ) lo g a x , 则 f '( x ) ( a 0 , 且 a 1); x ln a 1 公 式 8 .若 f ( x ) ln x , 则 f '( x ) ; x
( 1 ) y 4
x
( 2 ) y x l o g
3
(三)函数的和、差、积、商的求导法则 设f(x)、g(x)是可导的
f ( x ) g ( x )]' f ' ( x ) g ' ( x ); （1）x ) g ( x )) f ( x ) g ( x ) f ( x ) g ( x )
(5 ) y (2 x 3 ) 1 x ; 1 (6 ) y 4 ; x (7 ) y x x ;
2
1 (4) y ; 2 cos x 6 x3 x (5) y ; 2 1 x
(6) y
(7) y
4 ; 5 x
3 x; 2
练习： 求下列函数的导数： 5 3 2 2 (1)y＝x －3x －5x ＋6； (2)y＝(2x ＋3)(3x－2)； x－ 1 (3)y＝ ； (4)y＝x· tan x. x＋ 1
2 2 ( x 1 )[( x ) ( 1 ) ] [( x ) ( 1 ) ]( x 1 ) 2 2 ( x 1 )
2 2 ( x 1 ) 2 x ( x 1 ) 2 x x 1 2 2. 2 2 ( x 1 ) ( x 1 )