行星齿轮啮合频率计算

齿轮啮合频率计算

齿轮啮合频率计算齿轮啮合频率是齿轮系的重要指标之一，对于齿轮的设计和制造具有重要的意义。

它是两个齿轮啮合时产生的振动次数，直接影响齿轮的噪声、振动和寿命等。

齿轮啮合频率的计算公式为：啮合频率=齿轮齿数×转速/60，其中转速的单位是转/分。

例如，如果一对啮合齿轮上，一个齿轮的齿数为20，另一个齿轮的齿数为40，齿轮传动时转速为1200转/分，则其啮合频率为：f = 20×1200/60 + 40×1200/60 = 800 Hz。

对于定轴齿轮，单个行星轮与齿圈的啮合频率等于行星轮的转频乘以它的齿数，也等于齿圈的转频乘以齿圈的齿数。

而对于具有多个行星轮的行星齿轮箱，所有行星轮与齿圈的啮合频率需要乘以行星轮数量，这是因为单个行星轮啮合周期的相位通常彼此之间是变化的。

但如果所有行星轮啮合周期都同相位，那么啮合频率就不需要乘以行星轮数量。

以上信息仅供参考，如需了解更多关于齿轮啮合频率计算的信息，建议咨询专业的齿轮工程师或者查阅相关文献。

齿轮啮合频率和转速之间存在明显的区别，主要体现在以下两个方面：1.定义和表示方法：•转速，通常用于描述齿轮旋转一周所需的时间，一般用每分钟转数（rpm）来表示。

例如，主齿轮的转速可能为2200rpm，马达齿轮的转速可能为3600rpm。

•啮合频率，则是指齿轮啮合出现的频率，即齿轮齿顶之间相互接触的次数，通常用赫兹（Hz）来表示。

例如，主齿轮的啮合频率可能为36.67Hz，马达齿轮的啮合频率可能为60Hz。

2.所描述的物理现象：•转速主要描述的是齿轮的旋转速度，它反映了齿轮在单位时间内旋转的圈数。

•啮合频率则描述了齿轮齿顶之间的接触频率，它反映了齿轮在单位时间内啮合的次数。

啮合频率与齿轮的齿数、转速以及齿轮的啮合方式（如定轴齿轮、行星齿轮等）有关。

总的来说，转速和啮合频率都是描述齿轮工作状态的重要参数，但它们分别描述了不同的物理现象。

转速更注重描述齿轮的旋转速度，而啮合频率则更注重描述齿轮齿顶之间的接触次数和频率。

行星齿轮减速器的相关计算

行星齿轮减速器的相关计算行星齿轮减速器是一种常用的机械传动装置，其特点是结构紧凑、承载能力大、传动效率高。

在工程设计和机械计算中，对行星齿轮减速器的相关参数进行计算是必不可少的工作。

本文将详细介绍行星齿轮减速器的相关计算方法。

一、行星齿轮减速器的基本构造二、行星齿轮减速器的传动比计算传动比是指输入轴和输出轴的转速比，可以通过以下公式计算：i=(N_s+N_r)/N_s其中，i为传动比，N_s为太阳齿轮的齿数，N_r为行星齿轮的齿数。

行星齿轮减速器的传动比可以通过调整太阳齿轮和行星齿轮的齿数来实现。

三、行星齿轮减速器的传动效率计算η=(1-δ/100)*(1-ε/100)其中，η为传动效率，δ为齿间损失系数，ε为噪声损失系数。

行星齿轮减速器的传动效率受到齿轮的磨损和摩擦影响，一般情况下，传动效率在95%以上。

四、行星齿轮减速器的扭矩计算输入轴扭矩计算可以通过以下公式计算：T_in = P / (n * η)其中，T_in为输入轴扭矩，P为输出功率，n为输入轴转速，η为传动效率。

输出轴扭矩计算可以通过以下公式计算：T_out = i * T_in其中，T_out为输出轴扭矩，i为传动比，T_in为输入轴扭矩。

五、行星齿轮减速器的选择在实际工程中，选择合适的行星齿轮减速器需要考虑以下因素：1.承载能力：根据实际应用需求，选择承载能力适当的行星齿轮减速器。

2.传动比：根据需要的输出转速和输入转速，选择合适的行星齿轮减速器。

3.外形尺寸：根据实际安装空间，选择符合尺寸要求的行星齿轮减速器。

4.传动效率：选择传动效率高的行星齿轮减速器，以提高传动效率和节能效果。

5.稳定性：选择结构稳定、运行平稳的行星齿轮减速器，以减少振动和噪声。

六、行星齿轮减速器的基本计算流程1.确定输入功率、输入转速和输出转速。

2.根据输入功率和输入转速计算输入轴扭矩。

3.根据输入轴扭矩和传动比计算输出轴扭矩。

4.根据输出轴扭矩和输出转速计算输出功率。

风电机组齿轮箱振动特性分析

摘要齿轮箱作为风电机组中最重要的传动部件,负责将风轮叶片的低转速转换为发电机所需要的高转速，实现能量与扭矩的高效传输；振动是风电机组齿轮箱故障失效的主要原因，随着机组容量的增加, 长期处于恶劣条件下的齿轮箱，由于结构体积的增大和弹性增加，更易引发振动问题。

本文主要研究齿轮箱在变速变载下的振动特性，基于Romax软件建立齿轮箱的振动模型，分析齿轮箱各级齿轮的啮合频率和固有频率。

本文研究内容可为风电机组齿轮箱的优化设计、故障、预防和处理提供技术基础。

关键词: 齿轮箱,固有频率,啮合频率,共振,RomaxABSTRACTGear box is the most transmission Parts in the Wind turbine,it is responsible for the low-speed wind turbine blade into the high-speed generator required to achieve the efficient transmission of energy and torque.Vibration is the main reason of wind turbine gear box failure , along with the increase of unit capacity, long-term adverse conditions in the gear box, due to the increase of the structure and flexibility to increase volume, caused more vibration problems.This paper mainly research gear box's vibration characteristics in the speed change, established gearbox vibration model based on Romax software,analysis of gearbox gear mesh frequency and levels of natural frequency.The contents of this paper provide wind turbine gearbox optimized design, failure for technical basis for the prevention and treatment.Key words : Gear Box , Natural frequency , Meshing frequency, Resonance, Romax目录摘要 (I)ABSTRACT (II)第1章绪论 (1)1.1选题背景和意义 (1)1.2国内外研究现状 (2)1.3本文工作 (3)1.4本章小结 (3)第2章风电机组齿轮箱力学特点 (4)2.1 前言 (4)2.2 风电机组齿轮箱机械结构 (4)2.3 风电机组齿轮箱外部载荷 (5)2.4 风电机组齿轮箱内部激励 (6)2.5 齿轮箱振动机理 (6)2.6 机械振动系统 (8)2.7本章小结 (10)第3章基于romax的风电齿轮箱建模 (11)3.1世界各地对romax的应用 (11)3.2 Romax软件介绍 (11)3.3 Romax建模 (12)3.4本章小结 (17)第4章固有频率和啮合频率分析 (18)4.1传动比及啮合频率计算 (18)4.2固有频率和啮合频率分析比较 (21)4.3本章小结 (22)第5章结论和展望 (23)5.1结论 (23)5.2展望 (23)参考文献 (24)致谢 (25)第1章绪论1.1 选题背景和意义在人类越来越渴望清洁能源和环保能源的大时代背景下，风电作为一种新兴的清洁能源，受到全世界人类的广泛关注。

用杠杆法计算行星齿轮机构的啮合效率

用杠杆法计算行星齿轮机构的啮合效率李明圣【摘要】以5HP-24自动变速器行星齿轮机构传动为例,通过采用杠杆法计算行星轮系的啮合效率,杠杆法不但对求多排并联行星轮传动比比较简单,通过杠杆图建立转速图和受力图,可以方便判断各行星轮的啮合功率流向,是计算行星轮系传动啮合效率很有效的方法.【期刊名称】《装备制造技术》【年(卷),期】2012(000)008【总页数】3页(P45-47)【关键词】杠杆法;行星齿轮;啮合效率【作者】李明圣【作者单位】湛江师范学院物理科学与技术学院,广东湛江524048【正文语种】中文【中图分类】TH132.425传动比法，对求封闭式差动行星传动的啮合效率很方便，即只要求得传动比公式，便可以写出效率计算公式。

但公式中的指数x（等于+1或–l）通常需求偏导数才能确定，运算繁琐。

卢存光、段钦华在文献[1]对传动比法指数x的含义做了分析，给出了确定指数x的判断依据，使传动比法的应用更简单。

指数x由转化机构中啮合功率流向确定，啮合功率计算虽然不用求偏导数，功率流向计算过程还是比较繁琐。

本文提出一种新的确定啮合功率流向方法——杠杆法。

用此法不但可以快速求出多排并联行星轮传动比，通过转速图和受力图，可以方便判断各行星轮的啮合功率流向，容易确定指数x的取值，是计算行星轮系传动的啮合效率很有效方法。

1 杠杆法杠杆模拟法是将行星轮系中3个基本构件（太阳轮、齿圈和行星架）的角速度，模拟为一垂直杠杆上3个不同点对应的水平线速度，将轮系中3个基本构件受到的扭矩，模拟为杠杆上对应点受到的力。

杠杆模拟法的优点，是将一个旋转运动系统模拟为人们熟悉的直线运动系统，从而可以直观地对轮系各构件的受力情况进行分析。

如图1(a)所示，是单级单行星齿轮系的结构简图，图1(b)是单级单行星齿轮系的一垂直放置的模拟杠杆图。

杠杆图的3个构件点（a、b、H）分别代表单级行星齿轮系太阳论、齿圈和行星架。

图1 单级单行星齿轮系示意图具有2个自由度3个构件点的角速度，满足以下关系式：式中，κ为行星轮系的特性系数，κ=Zb/Za；ωa、ωb、ωH分别代表单级行星齿轮系太阳轮、齿圈和行星架的角速度，下同。

行星齿轮啮合频率的计算

假定内齿太阳轮齿数为77，外齿太阳轮齿数为44，行星轮共三个，齿数为33，内齿太阳轮固定不动，外齿太阳轮转速为12rps，则关于啮合频率的计算如下：
外齿太阳轮：44*12=528Hz；
内齿太阳轮：77*0=0Hz；
行星轮：44/33*12*33=528Hz。
ቤተ መጻሕፍቲ ባይዱ
同学你好，这个我了解一些。
对于你的第一个问题：行星齿轮的啮合频率计算公式形式上与定轴齿轮有区别，对于通常的固定内齿圈的行星轮系，其啮合频率计算公式为fm=zr*(nr+n0)/60，其中zr为任一参考齿轮齿数，nr为参考齿轮转速，n0为行星架转速，其中转速以rpm计。虽然其形式上与传统定轴齿轮的不同，但推导过程所遵循的运动规律是完全一致的。
第二种是内齿圈输入，行星架固定，太阳轴输出
第三种是前一级的内齿圈旋转，并连接本级的行星架旋转，前一级的太阳轴连接本级的内齿圈，本级太阳轴输出。
第一种算啮合频率的思想就是假设行星架不动，内齿圈输入，这样就可以想象成内齿圈输入，太阳轴输出，输入的转速就等于行星架的转速，太阳轴输入转速相当于“太阳轴实际转速-行星架的转速”，因为两者运动同向；啮合频率就是内齿圈齿数×行星架转频=太阳轴的绝对转频（太阳轴实际转速-行星架的转频）×太阳轴齿数。
啮合齿轮的啮合频率是相同的也就是说太阳轮、行星轮和外太阳轮的啮合频率肯定是一样的。根据动力输入齿的啮合频率可以推出其余齿轮啮合频率。若果非得要算的话可以这样：外太阳轮齿数为Zw,太阳轮齿数为Zt,行星轮转速为Nx(r/s),行星轮啮合频率为Fx=Nx(Zw+Zt)。
下面是我对此问题的理解，不知对否，请各位大虾指点。
啮合对的啮合频率应该相同，但问题是行星减速器中，行星轮和内齿圈和太阳轴齿轮同时啮合，此时是两个啮合对，但是有行星轮参与，啮合频率的计算似乎复杂一些。

行星传动比及啮合频率计算

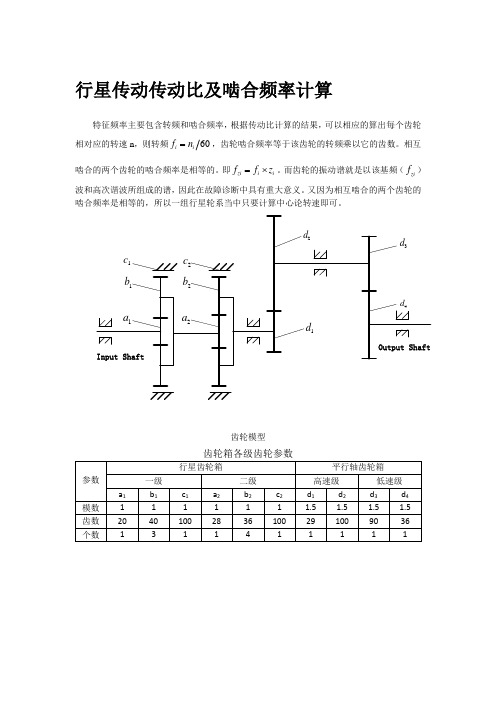
行星传动传动比及啮合频率计算特征频率主要包含转频和啮合频率，根据传动比计算的结果，可以相应的算出每个齿轮相对应的转速n ，则转频60i i f n =，齿轮啮合频率等于该齿轮的转频乘以它的齿数。

相互啮合的两个齿轮的啮合频率是相等的。

即zi i i f f z =⨯。

而齿轮的振动谱就是以该基频（zi f ）波和高次谐波所组成的谱，因此在故障诊断中具有重大意义。

又因为相互啮合的两个齿轮的啮合频率是相等的，所以一组行星轮系当中只要计算中心论转速即可。

1a 1b 1c 2a 2b 2c Input ShaftOutput Shaft2d 1d 3d 4d齿轮模型齿轮箱各级齿轮参数参数行星齿轮箱平行轴齿轮箱一级二级高速级低速级a 1b 1c 1 a 2 b 2 c 2d 1 d 2 d 3 d 4 模数 1 1 1 1 1 1 1.5 1.5 1.5 1.5 齿数 20 40 100 28 36 100 29 100 90 36 个数1311411111n –输入转速；Za1–第一级太阳轮齿数；Zb1 –第一级行星轮齿数；Zc1–第一级内齿圈齿数； Za2 –第二级太阳轮齿数；Zb2 –第二级行星轮齿数；Zc2 –第二级内齿圈齿数；（1）一级行星轮系：111111a H c c H a n n z n n z -=-- 其中，n n n a c ==11,0 ，则 )1//(11111+==a c a H b z z n n n =n 61（2）二级行星轮系：222222a H c c H a n n zn n z -=--其中，122,0H a c n n n ==，则)1//(22222+==a c a H b z z n n n =2327a n 行星轮系级: 传动比i =192/7 （3）平行轴：中间低速级：传动比i1= 小大n n =100/29高速级：传动比i2= 小大n n =2.5 平行轴传动比：i=8.6 总传动比：i=232齿轮箱振动特征频率 1. 啮合频率:1）转速同步频率 n f = n/60 式中，n 为轴转速（转/分）。

行星齿轮传动比计算公式

行星齿轮传动比计算公式
摘要：
一、行星齿轮传动简介
二、行星齿轮传动比计算公式
三、行星齿轮传动比计算公式的应用
正文：
行星齿轮传动是一种常见的机械传动方式，它具有体积小、重量轻、传动比稳定等优点，广泛应用于各种机械设备中。

在行星齿轮传动中，传动比的计算是非常重要的，下面我们来介绍行星齿轮传动比计算公式。

行星齿轮传动比计算公式如下：
传动比= (太阳轮齿数/ 行星轮齿数) × (行星轮转速/ 太阳轮转速)
其中，太阳轮齿数和行星轮齿数是指太阳轮和行星轮上的齿数，行星轮转速和太阳轮转速是指行星轮和太阳轮的转速。

这个公式可以帮助我们计算行星齿轮传动的传动比，从而更好地设计机械设备。

在实际应用中，行星齿轮传动的传动比计算公式是非常重要的，它可以帮助我们选择合适的齿轮参数，使机械设备能够正常运行。

除了计算传动比外，我们还可以利用行星齿轮传动比计算公式来分析行星齿轮传动的特点。

例如，我们可以通过计算不同齿轮参数下的传动比，来分析行星齿轮传动在传动比方面的优缺点。

这样，我们就可以更好地设计行星齿轮传动，使其在传动比方面更加优秀。

总之，行星齿轮传动比计算公式是行星齿轮传动设计中非常重要的一个公
式，它可以帮助我们计算行星齿轮传动的传动比，从而更好地设计机械设备。

行星齿轮计算

传动型式高变位1、太阳轮负变位，行星轮和内齿轮正变位。

即：-x A =x C =x Bx A 和x C 按手册图14-5-4及图14-5-5确定，也可按第一章的方法选择变位方式与变位系在渐开线行星齿轮传动中，合理采用变位齿轮可以获得如载能力，在保证所需传动比前提下得到合理的中心距、在保证装配及同心等条件下使齿数的选择具有较性。

变位齿轮有高变位和角变位，两者在渐开线行星齿轮传动中都有应用。

高变位主要用于消除根切和使轮的滑动比及弯曲强度大致相等。

角变位主要用于更灵活地选择齿数，拼凑中心距，改善啮合特性及提力。

由于高变位的应用在某些情况下受到限制，因此角变位在渐开线行星齿轮传动中应用更为广泛。

常用行星齿轮传动变位方式NGW 1、太阳轮正变位，行星轮和内齿轮负变位。

即：x A =-x C =-x Bx A 和x C 按手册图14-5-4及图14-5-5确定，也可按第1章的方法选择4<B AX i 4≥B AX i角变位1、不等角变位应用较广。

通常使啮合角在下列范围外啮合：α'AC =24º～26º30'(个别甚至达29º50'）内啮合：α'CB =17º30'～21º此法是在z A 和z B 不变，而将z C 减少1～2齿的情况下实现的。

这样可以显著提高外啮合的承载能力。

根据初选齿数，利用图14-5-4预计啮合角大小（初定啮合角于上述范围内）；然后计算出x ∑AC 、x ∑CB ，最后按图14-5-5或第一章的方法分配变位系数2、等角变位各齿轮齿数关系不变，即：z A +z C =z B -z C变位系数之间的关系为：x B =2x C +x A变位系数大小以齿轮不产生根切为准。

总变位系数不能过大，否则影响内齿轮弯曲强度。

通常取啮合角α'AC =α'CB =22º对于直齿轮传动，当z A <z C 时推荐取 x A =x C =0.53、当传动比时，推荐取α'AC =24º～25º，α'CB =20º，即外啮合为角变位，内啮合为高变位。

论述齿轮啮合频率产生的机理及齿轮故障诊断方法

一、论述齿轮啮合频率产生的机理及齿轮故障诊断方法一、齿轮啮合频率的机理由齿轮传动理论可知，渐开线齿廓齿轮在节点附近为单齿啮合，而在节线的两边为双齿啮合，啮合区的大小则由重叠系数ε决定。

因此，每对轮齿在啮合过程中承受的载荷是变化的，从而引起齿轮的振动，另外，一对轮齿在啮合过程中两齿面的相对滑动速度和摩擦力均在节点处改变方向，引起齿轮的振动.这两者形成了啮合频率fz 及其谐波Nfz ，其计算式为:60z nZf =式中 Z ——齿轮的齿数；n ——轴的转速，/min r 。

60z nZNf N =⋅式中N —自然数，1，2，3，……。

N=1称为基波，即啮合频率；N = 2，3，……时，称为二次，三次…谐波。

啮合频率fz 及其谐波Nfz 的频谱特点：①初始状态，啮合颇率的幅值最高，各次谐波的幅值依次减小(图1的实线部分)；②随着齿轮磨损的增加，渐开线齿廓逐渐受到破坏，使齿轮振动加剧，此时啮合频率及其各次谐波的幅值逐渐增大，而且各次谐波幅值的增加比啮合频率快得多(图中虚线所示)； ③磨损严重时，二次谐波幅值超过啮合频率幅值。

图1 啮合频率及其谐波图2 严重磨损时的啮合频率及其二次谐波由频谱图上啮合频率及其谐波幅值的增量可判断出齿轮的磨损程度。

啮合频率分析：（1）负载和啮合刚度的周期性变化负载和啮合刚度的变化可用两点来说明：一是随着啮合点位置的变化，参加啮合的单一齿轮的刚度发生了变化，二是参加啮合的齿数在变化。

如渐开线直齿轮，在节点附近是单齿啮合，在节线两侧某部位开始至齿顶、齿根区段为双齿啮合。

显然，在双齿啮合时，整个齿轮的载荷由两个齿分担，故此时齿轮的啮合刚度就较大；同理单齿啮合时，载荷由一个齿承担，此时齿轮的啮合刚度较小。

从一个轮齿开始进入啮合到下一个轮齿进入啮合，齿轮的负载和啮合刚度就变化一次，所以齿轮的负载和啮合刚度周期性变化的频率与齿轮旋转频率成整数倍关系。

（2）节线冲击的周期性变化齿轮在啮合过程中，轮齿表面既有相对滚动，又有相对滑动。

行星齿轮机构设计与计算

均衡。
•图(a)为行星轮装在弹性心轴上； •图(b)为行星轮装在非金属弹性衬套上； •图(c)为行星轮内孔与轴承外套的介轮之间留有较大间隙以形成厚油膜的所谓"油膜弹性浮动"结构。
2.行星轮系的均衡装置
3）采用杠杆联动的均衡装置这种均衡装置中装有偏心的行星轮轴和杠杆系统。当行星轮受力不均衡时，可通过杠杆系统的联锁动作自行调
整达到新的平衡位置。其优点是均衡效果较好，缺点是结构较复杂。
3.行星轮系传动比的计算
基本思路根据单排行星齿轮机构一般特性方程式
ntanq(1a)nj 0
将行星轮系转化成定轴轮系
行星架的角速度变成
HH
3.行星轮系传动比的计算
由于转化机构为一定轴轮系，因此其传动比大小为：
固定轴式自动变速器
辅助轴
1）D4和D3位的1档
1档离合器结合
2）D4和D3位的2档
1档离合器结合 2档离合器结合
3）D4和D3位的3档
1档离合器结合 3档离合器结合
4）D4位的4档
1档离合器结合 4档离合器结合
5）1位的1档
1档离合器结合 1档固定离合器结合
6）倒档
固定轴式自动变速器与行星齿轮自动变速器相比，有以下主要特点：
（1）固定轴式变速器采用普通外啮合齿轮，各相对齿轮都是固定啮合，但传递动力与否取决于相对应离合器是否啮合。
（2）固定轴式变速器多由三条平行轴构成，变速器的总长度较小，故一般都用在前轮驱动的轿车上。
（3）固定轴式变速器的操作组件只有多片式离合器和单向离合器，没有制动器；操作件的数目较少。
的数目与太阳轮、齿圈的齿数之间必须有一定的关系，否则便装配不起来。
•设需要k个行星轮均匀分布在太阳轮四周，则相邻两行星轮所夹

精密行星减速机的名词解释

精密行星减速机的名词解释齿啮合频率fz：齿啮合频率有时会带来技术装置的震动问题，如齿轮箱频率与技术装置的频率相同时。

输出端的震动频率可按公式fz=1.8?n2[min-1]计算得出。

如真有震动问题,要么改变技术装置的自身频率,要么选其它速比(=其它齿啮合频率)的齿轮箱。

定位精确度：在高速机械往复运动中做到精确定位的关键在于尽量减小通过运动产生的角偏差，定位精确度取决于两个值，一个是与加载有关的偏转角，涉及到回程间隙与扭转刚度，另一个是与运动控制有关偏转角，涉及到同步偏差问题。

转动惯量j[kgcm2]：则表示一个物体尽力维持自己旋转状态(或恒定或旋转)特性的一个值。

样本中的温如军指输出端的。

惯量比λ：是指负载惯量与传动系统惯量(电机加上齿轮箱)之间的比值。

这个比值决定了系统的可控性。

λ值越大，也就是各转动惯量差值越大，高动态的动作过程就越难精确控制，建议尽可能将入值控制在＜5。

齿轮箱可以将负载惯量降低1/i2。

改变刚度ct21[nm/arcmin]：由读取力矩和所产生的改变角之间的比率去定义。

ct21=△t/△ψ。

它表明须要用多小的力矩就可以把输入轴旋转一弧分。

改变刚度从阻滞曲线得出结论的。

在曲线图上只须要高度关注t2b的50%和100%这个范围，在这个范围内，曲线可以看作就是一条直线。

弧分[arcmin]：一度分为60弧分(=60arcmin=60′).如回程间隙标为1arcmin时,意思是说齿轮箱转一圈,输出端的角偏差为1/60°。

在实际应用中，这个角偏差与轴直径有关b=2?π?r?a°/360°。

就是说，输出端直径为500mm时，齿轮箱精度为jt=3′时，齿轮箱转一圈的偏差为b=0.4mm。

回程间隙jt[arcmin]：指齿轮箱输入轴与输出端的最小偏差角.测量时先将齿轮输出端的紧固居住,然后在输入端用力矩仪读取一定力矩(2%t2b),以消除齿轮箱内的磨擦力。

同步偏差：指在输出轴转一圈时所测得的输入转速与输出转速两值的偏差。

行星齿轮传动系统平移-扭转模型及计算

行星齿轮传动系统平移-扭转模型及计算张银龙;巫世晶;王晓笋;李思千【摘要】振动是行星齿轮传动系统的一个重要特性,它直接关系到传动的平稳性和系统的可靠性.为了避免系统运行时产生共振现象,研究动态特性,进行固有频率分析非常重要.文章首先根据系统的运动特性,通过受力分析,建立了行星齿轮传动系统的平移-扭转动力学模型,通过理论计算求解其模态和振型,分析了系统的振动情况.然后利用Pro/E建立了行星齿轮传动系统模型,在ABAQUS软件里面进行有限元仿真分析,利用Block Lanczos方法对系统进行模态分析,提取了系统的固有频率和振型图.结合有限元仿真结果与理论计算结果,分析了系统振动产生的主要部位,同时也为系统结构性能的改善和后期的优化设计提供了依据.【期刊名称】《机械设计与制造》【年(卷),期】2016(000)007【总页数】5页(P1-4,8)【关键词】行星齿轮;平移-扭转模型;模态分析;理论计算;仿真分析【作者】张银龙;巫世晶;王晓笋;李思千【作者单位】武汉大学动力与机械学院,湖北武汉430072;武汉大学动力与机械学院,湖北武汉430072;武汉大学动力与机械学院,湖北武汉430072;武汉大学动力与机械学院,湖北武汉430072【正文语种】中文【中图分类】TH16行星齿轮传动系统通常应用于大型工程设备之中，它工作平稳、结构紧凑、承载能力强，能够实现传动比的较大变化。

针对行星齿轮传动系统，国内外学者对其动静态特性进行了大量的研究[1-6]。

由于行星齿轮传动系统的结构特点，振动、噪声等因素对于系统的整体性能有着较大的影响[6-7]。

特别是当外部激励与行星齿轮传动系统中某个固有频率接近时，就会引起系统的共振，这将严重影响到整个系统的稳定性，甚至导致系统的损坏，从而造成安全事故，带来不可估量的损失。

因此，对行星轮传动系统进行模态分析，了解其固有特性，对于系统的设计和运行都具有重要的指导意义。

考虑到行星齿轮传动系统传动路线的多样性，针对内齿圈固定、太阳轮输入、行星架输出的传动方案进行了模态分析。

内齿行星传动的啮合力计算与啮合效率分析_吴斌

收稿日期:2006-09-26作者简介:吴斌(1971-),男,讲师。

文章编号:1671-7333(2006)04-0245-04内齿行星传动的啮合力计算与啮合效率分析吴斌,张锁怀(上海应用技术学院机械与自动化工程学院,上海 200235)摘要: 针对新型的三轴式内齿行星传动,分析了内齿平动的轮齿的啮合力和啮合效率,并以某种型号的三轴式内齿行星减速器为例进行了效率计算。

关键词: 内齿行星传动;啮合力;啮合效率中图分类号:TH 132 文献标识码:AThe Meshing -Force and Efficiency Analysis for theGear Transmission with Inner Planet GearW U Bin ,Z H AN G Suo -hai(School of Mechanical and Automati on Engineering,Shanghai Institute of Technology,Sh anghai 200235,China)Abstract :In view of a new -type three -shaft g ear transm ission w ith inner planet gear,the formulas formeshing-force and meshing -efficiency have been set up.And these formulas are used to compute some three -shaft gear transmission w ith inner planet gear.Key words :three -shaft g ear transmission w ith inner planet gear;meshing -force;meshing -efficiency内齿行星减速器根据输入轴、支承轴和输出轴之间不同的位置关系,有二种传统形式:对称型和偏置型。

精密行星减速机的名词解释

精密行星减速机的名词解释迟滞曲线：迟滞检测是为了得出齿轮箱的扭转刚度。

通过检测得到迟滞曲线。

检测时，先将齿轮箱输入端固定住，然后在输出端的两个旋转方向分别持续地加载到T2B最大加速力矩，继而逐步卸载，用仪器记录下力矩的仿差角，得到的曲线是一条闭合曲线，从中可以计算出齿轮箱的回程间隙(jt)和扭转刚度(Ct21) 。

齿啮合频率fz：齿啮合频率有时会带来技术装置的震动问题，如齿轮箱频率与技术装置的频率相同时。

输出端的震动频率可按公式fz=1.8•n2[min-1]计算得出。

如真有震动问题,要么改变技术装置的自身频率,要么选其它速比(=其它齿啮合频率)的齿轮箱。

定位精确度：在高速机械往复运动中做到精确定位的关键在于尽量减小通过运动产生的角偏差，定位精确度取决于两个值，一个是与加载有关的偏转角，涉及到回程间隙与扭转刚度，另一个是与运动控制有关偏转角，涉及到同步偏差问题。

转动惯量J[Kgcm2]：表示一个物体尽力保持自己转动状态(或静止或转动)特性的一个值。

样本中的值均指输入端。

惯量比λ：是指负载惯量与传动系统惯量(电机加上齿轮箱)之间的比值。

这个比值决定了系统的可控性。

λ值越大，也就是各转动惯量差值越大，高动态的动作过程就越难精确控制，建议尽可能将入值控制在＜5。

齿轮箱可以将负载惯量降低1/i2。

扭转刚度Ct21[Nm/Arcmin]：由加载力矩和所产生的扭转角之间的比率来定义。

Ct21=△T/△ψ。

它说明需要用多大的力矩才能把输出轴转动一弧分。

扭转刚度是从迟滞曲线得出的。

在曲线图上只需要关注T2B的50%和100%这个范围，在这个范围内，曲线可看成是一条直线。

弧分 [arcmin]：一度分为60弧分(=60 arcmin=60′).如回程间隙标为1 arcmin时,意思是说齿轮箱转一圈,输出端的角偏差为1/60°。

在实际应用中，这个角偏差与轴直径有关b=2•π•r•a°/360°。

中速磨减速机各阶齿轮啮合频率计算

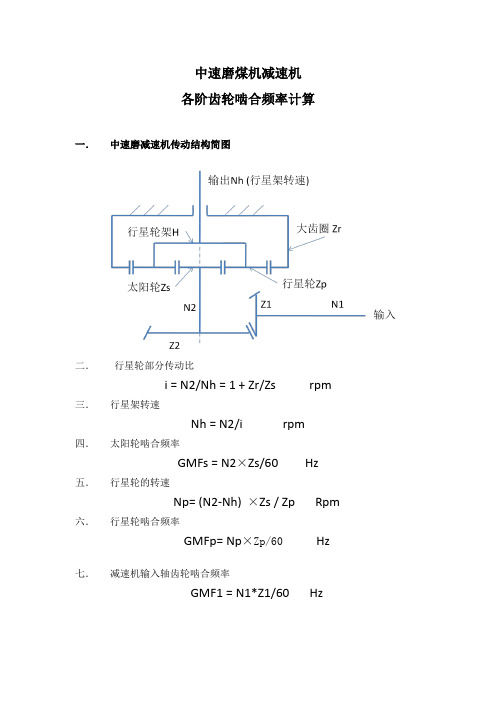
中速磨煤机减速机各阶齿轮啮合频率计算一．中速磨减速机传动结构简图二．行星轮部分传动比i = N2/Nh = 1 + Zr/Zs rpm 三．行星架转速Nh = N2/i rpm四．太阳轮啮合频率GMFs = N2×Zs/60 Hz 五．行星轮的转速Np= (N2-Nh)×Zs / Zp Rpm 六．行星轮啮合频率GMFp= Np×Zp/60Hz七．减速机输入轴齿轮啮合频率GMF1 = N1*Z1/60 Hz八．计算举例广西贵港电厂中速磨电机功率630Kw输入轴转速990 rpm减速机输入转速为990 Rpm输入伞齿轮齿数Z1=11大伞齿轮齿数Z2=54太阳轮齿数Zs=16行星轮齿数Zp=49大齿圈齿数Zr=116计算各阶啮合频率太阳轮转速Ns=990×11/54=201.67 Rpm太阳轮啮合频率GMFs=Ns×Zs/60=201.67×16/60= 53.78 Hz输入高速轴齿轮啮合频率GMF1=990×11/60 = 181.5 Hz行星减速机的传动比i = N2/Nh = 1 + Zr/Zs=1+116/16=8.25减速机输出转速Nh=N2/i=201.67/8.25=24.44 Rpm行星轮的转速Np= (N2-Nh)×Zs / Zp = (201.67-24.44)×16/49 = 57.87 rpm行星轮啮合频率GMFp=Np×Zp/60 =57.87×49/60 = 47.26 Hz2014.7.6 lsy。

论述齿轮啮合频率产生的机理及齿轮故障诊断方法

、论述齿轮啮合频率产生的机理及齿轮故障诊断方法一、齿轮啮合频率的机理由齿轮传动理论可知，渐开线齿廓齿轮在节点附近为单齿啮合，而在节线的两边为双齿啮合，啮合区的大小则由重叠系数&决定。

因此，每对轮齿在啮合过程中承受的载荷是变化的，从而引起齿轮的振动，另外，一对轮齿在啮合过程中两齿面的相对滑动速度和摩擦力均在节点处改变方向，引起齿轮的振动•这两者形成了啮合频率fz及其谐波Nfz，其计算式为nZ f z60式中Z 齿轮的齿数；n轴的转速，「/min 。

nZ60式中N —自然数，1 , 2 , 3 ,……。

N=1称为基波，即啮合频率；N = 2 , 3 ,……时，称为二次，三次…谐波。

啮合频率fz及其谐波Nfz的频谱特点:①初始状态，啮合颇率的幅值最高，各次谐波的幅值依次减小（图1的实线部分）;②随着齿轮磨损的增加，渐开线齿廓逐渐受到破坏，使齿轮振动加剧，此时啮合频率及其各次谐波的幅值逐渐增大，而且各次谐波幅值的增加比啮合频率快得多（图中虚线所示）;③磨损严重时，二次谐波幅值超过啮合频率幅值。

由频谱图上啮合频率及其谐波幅值的增量可判断出齿轮的磨损程度。

啮合频率分析：（1 ）负载和啮合刚度的周期性变化负载和啮合刚度的变化可用两点来说明：一是随着啮合点位置的变化，参加啮合的单一齿轮的刚度发生了变化，二是参加啮合的齿数在变化。

如渐开线直齿轮，在节点附近是单齿啮合，在节线两侧某部位开始至齿顶、齿根区段为双齿啮合。

显然，在双齿啮合时，整个齿轮的载荷由两个齿分担，故此时齿轮的啮合刚度就较大；同理单齿啮合时，载荷由一个齿承担，此时齿轮的啮合刚度较小。

从一个轮齿开始进入啮合到下一个轮齿进入啮合，齿轮的负载和啮合刚度就变化一次，所以齿轮的负载和啮合刚度周期性变化的频率与齿轮旋转频率成整数倍关系。

（2 ）节线冲击的周期性变化齿轮在啮合过程中，轮齿表面既有相对滚动，又有相对滑动。

主动轮带动从动轮旋转时，主动轮上的啮合点从齿根移向齿顶，啮合半径逐渐增大，速度渐次增高；而从动轮上的啮合点是由齿顶移向齿根，啮合半径逐渐减小，速度渐次降低。

ngw行星齿轮传动效率

ngw行星齿轮传动效率【最新版】目录一、行星齿轮传动概述二、行星齿轮传动的效率分析1.基本啮合效率2.升速与减速时的基本啮合效率差异3.行星齿轮减速机的传动效率三、行星齿轮减速机的优点与应用注意事项正文一、行星齿轮传动概述行星齿轮传动是一种常见的齿轮传动方式，因其结构紧凑、传动比稳定、承载能力大等特点而广泛应用于各种机械传动系统中。

在行星齿轮传动中，有一个或多个行星轮与一个太阳轮和一个或几个内齿轮啮合，实现动力传递和转速变换。

二、行星齿轮传动的效率分析1.基本啮合效率行星齿轮传动的基本啮合效率是计算其传动效率的基础。

根据齿轮的啮合原理，可以得出行星齿轮传动的基本啮合效率公式。

在实际应用中，行星齿轮传动的效率受到许多因素的影响，如齿轮材料、加工精度、负载等。

2.升速与减速时的基本啮合效率差异行星齿轮传动在升速和减速时的基本啮合效率是不相等的，升速时的基本啮合效率比减速时要高。

这与以往的观点不同，通过采用新的分析方法，可以得出这一结论。

3.行星齿轮减速机的传动效率行星齿轮减速机的传动效率通常较高，一般在 94% 到 98% 之间。

这是因为行星齿轮减速机采用了多级行星齿轮传动，相对于传统的单级齿轮传动，其传动效率更高。

此外，行星齿轮减速机的齿轮一般采用高强度合金钢材料制造，具有较高的硬度和强度，能够承受较大的负载，也有助于提高传动效率。

三、行星齿轮减速机的优点与应用注意事项行星齿轮减速机具有结构紧凑、传动比稳定、承载能力大等优点，在各种机械传动系统中得到了广泛应用。

然而，行星齿轮减速机的制造难度较高，成本也比较高，因此在应用时需要根据实际情况进行选择。

此外，在使用过程中要注意维护和保养，确保其正常工作和较长的使用寿命。

综上所述，行星齿轮传动具有较高的传动效率和优越的性能，为各种机械传动系统提供了可靠的动力传递。