用哈夫曼树实现图像压缩
数据压缩算法中的哈夫曼编码原理及应用

数据压缩算法中的哈夫曼编码原理及应用哈夫曼编码是一种常用的数据压缩算法,它的原理是通过对待压缩的数据进行频率统计,将频率较高的字符赋予较短的编码,频率较低的字符赋予较长的编码,从而实现对数据的高效压缩。
哈夫曼编码的应用广泛,包括文件压缩、通信传输、数据存储等方面。
哈夫曼编码的原理可以简单描述为以下几个步骤:1.频率统计:将待压缩的数据进行频率统计,统计每个字符出现的次数,得到字符频率表。
2.构建哈夫曼树:根据字符频率表,构建哈夫曼树。
哈夫曼树是一种特殊的二叉树,其中每个叶子节点对应着一个字符,其路径长度代表该字符的编码长度。
3.生成编码:从哈夫曼树的根节点开始,对每个叶子节点进行编码生成。
从根节点到叶子节点的路径上的边分为0和1,路径上的0表示向左走,1表示向右走,从而得到每个字符的哈夫曼编码。
4.压缩数据:将原始数据按照生成的哈夫曼编码进行压缩,将每个字符替换为对应的哈夫曼编码。
5.解压数据:根据压缩后的数据和哈夫曼树,进行解压还原。
从根节点开始,按照压缩数据的0和1进行路径遍历,当遇到叶子节点时,即可找到对应的字符。
哈夫曼编码的应用非常广泛,下面介绍几个常见的应用领域:1.文件压缩:哈夫曼编码在文件压缩中有着重要的应用。
通过统计文件中每个字符的出现频率,构建哈夫曼树,并生成对应的哈夫曼编码,将字符替换为哈夫曼编码后,可以大大减少文件的存储空间。
当文件中存在一些频率较高的字符时,哈夫曼编码的效果尤为显著。
2.图片压缩:在图片压缩中,哈夫曼编码通常用于无损压缩。
将图像中的像素点表示为字符,通过统计每个字符出现的频率,构建哈夫曼树,并生成对应的哈夫曼编码。
将像素点替换为哈夫曼编码后,图像的存储空间可以大大减小,同时保证了图像的质量不受损失。
3.音频压缩:在音频压缩中,哈夫曼编码常用于有损压缩,例如MP3格式的音频文件。
在有损压缩中,通过对音频数据进行量化和编码,可以减小文件的大小,从而方便传输和存储。
哈夫曼编码无损数据压缩的原理和实现

哈夫曼编码无损数据压缩的原理和实现无损数据压缩技术是计算机领域中的一项重要技术,而哈夫曼编码作为其中一种经典的压缩算法,被广泛应用于数据传输和存储中。
本文将介绍哈夫曼编码的原理和实现方法。
一、原理哈夫曼编码是一种变长编码(Variable Length Code)技术,它利用出现频率较高的字符使用较短的编码,而出现频率较低的字符使用较长的编码,从而达到数据压缩的目的。
其原理如下:1. 统计字符频率:首先,需要统计待编码的数据中每个字符出现的频率。
这可以通过扫描整个数据流来实现。
统计结果可以用于构建哈夫曼树。
2. 构建哈夫曼树:根据字符频率构建哈夫曼树,其中频率越高的字符位于树的顶部,频率越低的字符位于树的底部。
构建哈夫曼树的过程中,使用最小堆来选择两个最小频率的节点,将它们合并为一个新的节点,并更新频率。
3. 分配编码:通过沿着哈夫曼树的路径,从根节点到达叶子节点,将0或1分配给每个字符。
注意,由于哈夫曼树的性质,没有一个字符的编码是另一个字符编码的前缀,因此哈夫曼编码是一种无前缀编码(Prefix-Free Code)。
4. 压缩数据:根据哈夫曼编码表,将原始数据中的每个字符替换为对应的编码,从而得到压缩后的数据。
二、实现哈夫曼编码的实现通常包括以下几个步骤:1. 统计字符频率:读取待编码的数据流,统计每个字符的频率,并构建字符频率表。
2. 构建哈夫曼树:根据字符频率表构建哈夫曼树。
可以使用最小堆来选择两个最小频率的节点进行合并,直至构建出完整的哈夫曼树。
3. 生成哈夫曼编码表:通过遍历哈夫曼树的路径,生成每个字符对应的哈夫曼编码。
可以使用递归算法或迭代算法来实现。
4. 压缩数据:根据生成的哈夫曼编码表,将原始数据中的每个字符替换为对应的编码。
同时,需要记录编码后数据的长度和哈夫曼编码表,以便解码时使用。
5. 解压缩数据:根据哈夫曼编码表,将编码后的数据解码为原始数据。
在实际应用中,哈夫曼编码通常用于对文本文件、图像、音频等数据进行压缩。
哈夫曼树的实际应用

哈夫曼树的实际应用
哈夫曼树(Huffman Tree)是一种重要的数据结构,它在信息编码和压缩、数据传输和存储、图像处理等领域有广泛应用。
1. 数据压缩:哈夫曼树是一种无损压缩的方法,能够有效地减小数据的存储空间。
在进行数据压缩时,可以使用哈夫曼树构建字符编码表,将出现频率较高的字符用较短的编码表示,而出现频率较低的字符用较长的编码表示,从而减小数据的存储空间。
2. 文件压缩:在文件压缩领域,哈夫曼树被广泛应用于压缩算法中。
通过构建哈夫曼树,可以根据字符出现的频率来生成不同长度的编码,从而减小文件的大小。
常见的文件压缩格式如ZIP、GZIP等都使用了哈夫曼树。
3. 图像压缩:在图像处理中,哈夫曼树被用于图像压缩算法中。
通过将图像中的像素值映射为不同长度的编码,可以减小图像的存储空间,提高图像传输和存储的效率。
常见的图像压缩格式如JPEG、PNG等都使用了哈夫曼树。
4. 文件传输:在数据传输中,哈夫曼树被用于数据压缩和传输。
通过对数据进行压缩,可以减小数据的传输时间和带宽占用。
在传输过程中,接收方可以通过哈夫曼树解码接收到的数据。
5. 数据加密:在数据加密中,哈夫曼树可以用于生成密钥,从而实现数据的加密和解密。
通过将字符映射为不同长度的编码,可以实
现对数据的加密和解密操作。
哈夫曼树在信息编码和压缩、数据传输和存储、图像处理等领域有广泛应用,能够有效地减小数据的存储空间、提高数据传输效率、实现数据加密等功能。
哈夫曼编码 压缩

哈夫曼编码压缩标题:哈夫曼编码压缩:一个深度解析一、引言哈夫曼编码是一种用于数据压缩的算法,由戴维·A·哈夫曼在1952年提出。
这种编码方法通过创建一种特殊的二叉树(哈夫曼树)来实现数据压缩。
哈夫曼编码广泛应用于文本文件、音频文件、图像文件等的数据压缩。
二、哈夫曼树的构建哈夫曼树是一种特殊的二叉树,它的特点是左子节点小于父节点,右子节点大于父节点。
哈夫曼树的构建过程如下:1. 初始化:将所有字符及其出现频率作为叶子节点,构成一棵棵只有根节点和一个叶子节点的二叉树。
2. 合并:每次选取两个权值最小的节点,生成一个新的节点,新节点的权值是两个被选取节点权值之和,然后把这两个节点作为新节点的左右孩子。
这样就得到了一颗新的二叉树。
3. 重复第二步,直到只剩下一个节点,这棵树就是我们要找的哈夫曼树。
三、哈夫曼编码哈夫曼编码是指从哈夫曼树的根到每个叶子节点的路径上的0和1的序列。
具体做法是从根节点出发,向左走记为0,向右走记为1。
每个字符的哈夫曼编码就是从根节点到该字符所在叶子节点的路径上的0和1的序列。
四、哈夫曼编码的压缩与解压1. 压缩:对原始数据进行哈夫曼编码,得到压缩后的数据。
2. 解压:对压缩后的数据进行哈夫曼解码,还原出原始数据。
五、哈夫曼编码的优点与缺点优点:1. 数据压缩效率高:哈夫曼编码能够有效地减少数据存储空间,提高数据传输速度。
2. 简单易懂:哈夫曼编码的原理和实现都比较简单,易于理解和实现。
缺点:1. 对于稀疏数据,压缩效果不佳:哈夫曼编码依赖于字符的出现频率,如果字符出现频率相近,压缩效果会降低。
2. 需要额外的存储空间:为了恢复原始数据,需要保存哈夫曼树或者哈夫曼编码表,这会占用一定的存储空间。
六、总结哈夫曼编码是一种有效的数据压缩方法,它通过构建哈夫曼树来实现数据的压缩和解压。
虽然哈夫曼编码有一些缺点,但其高效性和简单性使其在实际应用中得到了广泛的应用。
在未来,随着数据量的不断增大,哈夫曼编码等数据压缩技术将会发挥更大的作用。
用Huffman编码实现图像压缩

用Huffman编码实现图像压缩摘要:当前,网络和多媒体技术日新月异,信息量急速膨胀。
针对这种情况,本文探讨了它的解决方法——数据压缩(主要是图像压缩)。
着重研究了无失真条件下的最佳编码方法——huffman编码,对其方法的优劣做了较为客观的评价。
关键词:图像压缩编码 huffman编码中图分类号:tp393.03 文献标识码:a 文章编号:1007-9416(2011)12-0238-021、前言随着科技的发展,现在各种各样的数据和信息正在急速膨胀,每天出现的新知识正以近乎指数的规律逐日上升。
如何方便快速地存储、处理和传输这些日益增加的信息,使之更好的为我们服务,已经成为多数行业共同的呼声。
特别是近几年来随着网络走进普通家庭,昔日老牛拉破车似的网速已让多数人所不能容忍。
因为数据在数据传输时,要占据很大的信道容量。
为此,人们想到了采用对图像新的表达方法以减小表示一幅图像所需数据量,这就是图像编码要解决的主要问题。
由于图像编码减少了数据量,因此人们也常称图像编码为图像压缩。
本文将着重研究huffman编码方法,并形成一个对huffman编码方法的较为完整的评价。
2、正文2.1 huffman编码huffman编码的主导思想是根据数据符号发生的概率进行编码。
在源数据中出现概率越高的符号,相应的码长越短;出现概率越小的符号,其码长越长,从而达到用尽可能少的码符号表示源数据。
huffman编码方法是接近压缩比上限的一种最佳的编码方法。
2.2 具体编码过程(1)将信源符号按出现概率由大到小排列。
(2)将2个最小概率相加,形成一新的概率集合,对应一新的信源,符号数减小一个,即具有q-1个符号数,称为缩减信源a。
(3)将缩减信源a中q-1个符号再按概率大小排列。
如符号间概率相等,则排列次序不论。
(4)如此继续,得到具有(q-2)、(q-3)、(q-4)、...个符号的缩减信源b、c、d等,直到只有2个符号为止。
哈夫曼树除哈夫曼编码之外的应用

哈夫曼树除哈夫曼编码之外的应用
除了用于哈夫曼编码外,哈夫曼树还有一些其他的应用,包括:
1. 数据压缩:哈夫曼树被广泛应用于数据压缩算法中,如在文件压缩中常用的Huffman压缩算法。
该算法利用哈夫曼树将
频率较高的字符编码为较短的比特序列,从而实现数据的有效压缩。
2. 图像压缩:哈夫曼树可以用于图像压缩算法中的灰度压缩。
通过统计每个灰度级出现的频率,构建哈夫曼树,并将灰度级映射成相应的哈夫曼编码,实现图像数据的压缩。
3. 加密算法:哈夫曼树可以用于加密算法中,比如基于哈夫曼树的可逆数据隐藏算法。
该算法利用哈夫曼树将目标数据隐藏到另一段数据中,通过哈夫曼编码实现隐藏过程,解密时再利用哈夫曼树将隐藏的数据提取出来。
4. 文件搜索:哈夫曼树可以应用于快速搜索文件数据的场景中。
通过构建文件的哈夫曼树,可以有效地进行关键字搜索,加快搜索速度。
5. 数据库索引:哈夫曼树可以用于数据库的索引结构中,如
B+树索引。
通过利用哈夫曼树的性质,将索引数据进行有序
排列,提高数据库的查询效率。
总之,哈夫曼树的应用非常广泛,不仅限于哈夫曼编码,还可
以应用于数据压缩、图像压缩、加密算法、文件搜索、数据库索引等领域。
哈夫曼树原理

哈夫曼树原理
哈夫曼树(Huffman Tree)是一种用于编码的树形结构,它采用了一种无损压缩的编码方式,通常用于图像和音频等大数据文件的压缩。
哈夫曼树的原理是,将文件中出现频率较高的字符编码为较短的二进制位,而频率较低的字符则使用较长的二进制位。
这样一来,文件中出现频率最高的字符,对应的编码就是一个比较短的二进制串,而出现次数最少的字符对应的编码则会比较长,从而可以实现文件的无损压缩。
哈夫曼树的构建过程是通过选择出现频率最低的两个字符进行合并,生成一个新的节点,并将它们的出现频率相加。
不断重复这个过程,直到所有的节点都被合并成一个根节点,构成了一棵哈夫曼树。
节点合并的过程可以通过最小堆等数据结构进行实现。
使用哈夫曼树进行压缩时,需要先构建这棵树,然后以根节点为起点,对整个树进行遍历,生成每个字符对应的编码。
将这些编码存储在哈夫曼编码表中,读取文件时,通过哈夫曼编码表将压缩后的二进制数据转换成原始字符。
哈夫曼树以其简单、高效的特点,被广泛应用于数据压缩、通信领域等。
图像的无损压缩程序设计 霍夫曼编码

成绩评定表课程设计任务书摘要哈夫曼编码(Huffman Coding)是一种编码方式,以哈夫曼树—即最优二叉树,带权路径长度最小的二叉树,经常应用于数据压缩。
在计算机信息处理中,“哈夫曼编码”是一种一致性编码法(又称"熵编码法"),用于数据的无损耗压缩。
这一术语是指使用一张特殊的编码表将源字符(例如某文件中的一个符号)进行编码。
这张编码表的特殊之处在于,它是根据每一个源字符出现的估算概率而建立起来的(出现概率高的字符使用较短的编码,反之出现概率低的则使用较长的编码,这便使编码之后的字符串的平均期望长度降低,从而达到无损压缩数据的目的)。
本课题通过MATLAB编写适当的函数,对一个随机信源进行哈夫曼编码,得出码字,平均码长和编码效率。
从而理解信源编码的基本思想与目的以及哈夫曼编码方法的基本过程与特点,并且提高综合运用所学理论知识独立分析和解决问题的能力。
关键字:哈夫曼;信源编码;MATLAB目录1设计目的及相关知识 (1)1.1设计目的 (1)1.2图像的霍夫曼编码概念 (1)1.3Matlab图像处理通用函数 (1)2课程设计分析 (3)2.1 图像的霍夫曼编码概述 (3)2.2 图像的霍夫曼编码举例 (4)3仿真 (6)4结果及分析 (9)5附录 (12)结束语 (15)参考文献 (16)1设计目的及相关知识1.1设计目的1)了解霍夫曼编码的原理。
2)理解图像的霍夫曼编码原理,了解其应用,掌握图像的霍夫曼编码的方法。
3)对图像编码程序设计进行较深入的认识,对知识牢固掌握。
4)掌握图像霍夫曼编码的整个过程及其中的注意事项。
5)了解图像无损压缩的目的及好处。
1.2图像的霍夫曼编码概念所谓霍夫曼编码的具体方法:先按出现的概率大小排队,把两个最小的概率相加,作为新的概率和剩余的概率重新排队,再把最小的两个概率相加,再重新排队,直到最后变成1。
每次相加时都将“0”和“1”赋与相加的两个概率,读出时由该符号开始一直走到最后的“1”,将路线上所遇到的“0”和“1”按最低位到最高位的顺序排好,就是该符号的霍夫曼编码1.3 Matlab图像处理通用函数colorbar 显示彩色条语法:colorbar \ colorbar('vert') \ colorbar('horiz') \ colorbar(h) \ h=colorbar(...) \ colorbar(...,'peer',axes_handle)getimage从坐标轴取得图像数据语法:A=getimage(h) \ [x,y,A]=getimage(h) \ [...,A,flag]=getimage(h) \ [...]=getimage imshow显示图像语法:imshow(I,n) \ imshow(I,[low high]) \ imshow(BW) \ imshow(X,map) \ imshow(RGB)\ imshow(...,display_option) \ imshow(x,y,A,...) \ imshow filename \h=imshow(...)montage 在矩形框中同时显示多幅图像语法:montage(I) \ montage(BW) \ montage(X,map) \ montage(RGB) \h=montage(...)immovie创建多帧索引图的电影动画语法:mov=immovie(X,map) \ mov=immovie(RGB)subimage在一副图中显示多个图像语法:subimage(X,map) \ subimage(I) \ subimage(BW) \ subimage(RGB) \ subimage(x,y,...) \ subimage(...)truesize调整图像显示尺寸语法:truesize(fig,[mrowsmcols]) \ truesize(fig)warp 将图像显示到纹理映射表面语法:warp(X,map) \ warp(I ,n) \ warp(z,...) warp(x,y,z,...) \ h=warp(...)zoom 缩放图像语法:zoom on \ zoom off \ zoom out \ zoom reset \ zoom \ zoom xon \ zoom yon\ zoom(factor) \ zoom(fig,option)2课程设计分析2.1 图像的霍夫曼编码概述赫夫曼(Huffman)编码是1952年提出的,是一种比较经典的信息无损熵编码,该编码依据变长最佳编码定理,应用Huffman算法而产生。
java实现哈弗曼树和哈夫曼树压缩

java实现哈弗曼树和哈夫曼树压缩本篇博⽂将介绍什么是哈夫曼树,并且如何在java语⾔中构建⼀棵哈夫曼树,怎么利⽤哈夫曼树实现对⽂件的压缩和解压。
⾸先,先来了解下什么哈夫曼树。
⼀、哈夫曼树哈夫曼树属于⼆叉树,即树的结点最多拥有2个孩⼦结点。
若该⼆叉树带权路径长度达到最⼩,称这样的⼆叉树为最优⼆叉树,也称为哈夫曼树(Huffman Tree)。
哈夫曼树是带权路径长度最短的树,权值较⼤的结点离根较近。
(⼀)树的相关概念1.路径和路径长度在⼀棵树中,从⼀个结点往下可以达到的孩⼦或孙⼦结点之间的通路,称为路径。
通路中分⽀的数⽬称为路径长度。
若规定根结点的层数为1,则从跟结点到第L层结点的路径长度为L-1。
2.结点的权和带权路径长度若将树中结点赋给⼀个有着某种含义的数值,则这个数值称为该结点的权。
结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
3.树的带权路径长度树的带权路径长度规定为所有叶⼦结点的带权路径长度之和,记为WPL。
(⼆)哈夫曼树的构造原理假设有n个权值,则构造出的哈夫曼树有n个叶⼦结点。
n个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为:(1) 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有⼀个结点);(2) 在森林中选出两个根结点的权值最⼩的树合并,作为⼀棵新树的左、右⼦树,且新树的根结点权值为其左、右⼦树根结点权值之和;(3)从森林中删除选取的两棵树,并将新树加⼊森林;(4)重复(2)、(3)步,直到森林中只剩⼀棵树为⽌,该树即为所求得的哈夫曼树。
(三)哈夫曼编码在数据通信中,需要将传送的⽂字转换成⼆进制的字符串,⽤0,1码的不同排列来表⽰字符。
例如,需传送的报⽂为“AFTER DATA EAR ARE ART AREA”,这⾥⽤到的字符集为“A,E,R,T,F,D”,各字母出现的次数为{8,4,5,3,1,1}。
现要求为这些字母设计编码。
图像编码中的哈夫曼编码技术解析(六)

图像编码中的哈夫曼编码技术解析在图像编码领域,哈夫曼编码技术无疑是一项非常重要的算法。
它通过将出现频率较高的符号赋予较短的二进制编码,从而实现对图像数据进行高效压缩和传输。
本文将对哈夫曼编码技术进行解析,探讨其原理、应用和优缺点。
一、哈夫曼编码的原理哈夫曼编码是一种变长编码方式,其核心思想是通过根据符号的出现频率构建一棵二叉树,并根据树中每个叶子节点相对于根节点的路径,为每个符号赋予一个唯一的二进制编码。
具体而言,哈夫曼编码的过程包括以下几个步骤:1. 统计符号出现频率:首先,需要对图像数据进行统计,计算每个符号(通常是灰度级)在图像中出现的频率。
2. 构建哈夫曼树:根据统计结果,将每个符号作为叶子节点,按照频率从低到高的顺序构建一棵二叉树。
构建的过程中,频率较小的符号离根节点较远,而频率较高的符号离根节点较近。
3. 为叶子节点赋予编码:从哈夫曼树的根节点开始,按照左、右子树的方向分别赋予编码0和1。
遍历树的路径直到叶子节点,并记录下路径上经过的0和1,即可得到每个符号的二进制编码。
通过以上步骤,我们可以得到一个针对当前图像数据的哈夫曼编码表,用于将图像数据进行压缩和传输。
二、哈夫曼编码的应用哈夫曼编码在图像编码中有着广泛的应用。
它可以用于图像压缩、图像传输和图像存储等方面。
1. 图像压缩:由于哈夫曼编码采用变长编码方式,将出现频率较高的符号用较短的二进制编码表示,从而实现对图像数据的高效压缩。
这样可以大大减小图像数据的存储空间,提高了图像传输的速度和效率。
2. 图像传输:在图像传输过程中,由于带宽限制和传输速度要求,需要将图像数据进行压缩。
哈夫曼编码可以对图像数据进行高效压缩,减小传输的数据量,从而提高传输的速度和质量。
3. 图像存储:在图像存储中,由于存储空间通常有限,需要对图像数据进行压缩。
哈夫曼编码可以对图像数据进行高效的压缩,将图像数据存储在较小的空间中。
三、哈夫曼编码的优缺点哈夫曼编码作为一种经典的压缩算法,虽然具有高效的压缩性能,但也存在一些不足之处。
哈夫曼树的实际应用

哈夫曼树的实际应用
哈夫曼树在实际中有许多应用,以下是一些例子:
1. 数据压缩:哈夫曼树常用于数据压缩算法,如哈夫曼编码。
哈夫曼编码是一种前缀编码,它可以将数据中的字符编码为二进制字符串,使得平均编码长度最短,从而达到数据压缩的效果。
2. 文件存储:在文件存储中,哈夫曼树可以用于数据存储和检索。
例如,可以使用哈夫曼树来存储文件索引,以便快速找到文件。
3. 图像处理:在图像处理中,哈夫曼树可以用于图像压缩和编码。
例如,可以使用哈夫曼树来编码图像中的像素值,从而减小图像文件的大小。
4. 通信网络:在通信网络中,哈夫曼树可以用于数据传输和调度。
例如,可以使用哈夫曼树来优化数据的传输路径和顺序,以提高网络传输的效率和可靠性。
5. 数据库优化:在数据库优化中,哈夫曼树可以用于索引和查询处理。
例如,可以使用哈夫曼树来构建索引,以便快速检索数据库中的数据。
总的来说,哈夫曼树在许多领域中都有广泛的应用,特别是在需要数据压缩、文件存储、图像处理、通信网络和数据库优化的领域中。
图像压缩中的哈夫曼编码算法研究

图像压缩中的哈夫曼编码算法研究图像压缩是一项重要的技术,在现代科技的发展中起到了非常重要的作用。
而哈夫曼编码算法作为一种流行的压缩算法被广泛应用于图像压缩中。
在图像压缩中,我们需要将图像的数据进行压缩,以达到减小数据量的目的。
而哈夫曼编码算法是一种有效的压缩算法,能够将数据进行非常高效的压缩。
它可以根据数据出现的概率来分配不同的编码,从而实现高效的数据压缩。
哈夫曼编码算法相对于其他压缩算法的优点在于它能够对数据进行无损压缩,即压缩后的数据能够完全还原成原始数据。
同时,哈夫曼编码算法还可以根据不同数据的出现频率来分配不同的编码,使得常用的数据可以使用较短的编码,从而实现更高效地压缩。
在哈夫曼编码算法中,我们首先需要对原始数据进行分析,以确定不同数据出现的概率。
然后,根据不同数据的概率分配不同的编码。
具体来说,我们可以将数据按照出现概率从小到大排序,然后按照哈夫曼编码的规则来分配不同的编码。
有了编码之后,我们就可以将原始数据用编码来代替,并且在编码的末尾加上一个标记,以便解码时能够正确还原数据。
解码时,我们需要读取数据,并根据编码进行还原。
需要注意的是,在哈夫曼编码算法中,我们需要尽量减小编码的长度,从而实现更高效地压缩。
在实际应用中,我们常常会对数据进行预处理,以便获得更高效的哈夫曼编码。
总的来说,哈夫曼编码算法是一种非常有效的压缩算法,能够在图像压缩中发挥非常重要的作用。
它能够根据数据的出现概率分配不同的编码,从而实现高效的数据压缩。
在实际应用中,我们需要根据数据的特点来选择不同的压缩算法,并对数据进行预处理,以获得更高效的哈夫曼编码。
jpeg格式中的哈夫曼编码

JPEG格式中的哈夫曼编码是一种有效的数据压缩方法,用于在JPEG文件中对图像数据进行编码。
哈夫曼编码是一种无损数据压缩算法,它通过创建一张哈夫曼树来对数据进行编码。
在JPEG格式中,哈夫曼编码被用于对图像的DC系数和AC系数进行压缩。
DC系数的哈夫曼编码由两部分组成:huffman编码的bitlen和additional bits。
DC系数的bitlen是能够表示DC系数y的最小bit数,通过一个定义可以获取。
而additional bits就是直接用二进制的编码表示DC系数值。
对于AC系数,哈夫曼编码的过程更为复杂。
首先,AC系数会被按照特定的顺序进行排序。
然后,根据排序后的AC系数,构建一个哈夫曼树。
哈夫曼树的构建过程是,将频率高的AC系数放在树的左边,频率低的AC系数放在树的右边。
在构建哈夫曼树的过程中,会计算每个节点到根节点的距离,并以此作为该节点的编码。
最后,使用这个哈夫曼树对AC系数进行编码。
对于每个AC系数,都会根据其在哈夫曼树中的位置,得到一个相应的二进制编码。
以上就是JPEG格式中的哈夫曼编码的基本过程。
通过哈夫曼编码,JPEG文件可以有效地压缩图像数据,减小文件大小,同时保持较高的图像质量。
基于哈夫曼编码的图像压缩技术研究

基于哈夫曼编码的图像压缩技术研究Owing to coded image of Hafuman, the compression technology studies 摘要哈夫曼编码是一种数据编码方式,以哈夫曼树——即最优二叉树,用带权路径长度最小的二叉树,对数据进行重编码,经常应用于数据压缩。
在计算机信息处理中,“哈夫曼编码”是一种一致性编码法(又称“熵编码法”),用于数据的无损压缩。
本文主要介绍了基于哈夫曼编码图像压缩技术的原理、算法、过程,并利用VB6.0作为编程开发工具,开发了一个对256色BMP图像进行压缩/解压缩的软件系统,验证了算法的合理性和可行性。
关键词哈夫曼编码;二叉树;熵;无损压缩1.前言哈夫曼编码是一种常用的压缩编码算法,采用变长码编码,属于无损压缩算法的一种,在无损压缩的编码范畴中,哈夫曼(Huffman)编码方法是一种较有效的编码方法,是哈夫曼在1952年根据香农在1948年和范若在1949年阐述的一种编码思想提出的一种不定长(变长)编码的方法,也称霍夫曼编码。
哈夫曼编码在图像压缩应用中具有非常重要的意义,哈夫曼编码是一种实用的无损压缩技术,经过多年的不断改进,已经形成了系统的理论和方法。
目前主要有两种类型的哈夫曼编码方式,即静态哈夫曼编码和动态哈夫曼编码。
图像压缩编码技术可以追溯到1948年提出的电视信号数字化,到今天已经有60多年的历史了。
在此期间出现了很多种图像压缩编码方法,本课题主要研究基于哈夫曼编码对图像进行无损压缩,基于哈夫曼编码的图像无损压缩过程通常分为两步,即去除相关和编码。
去除相关就是要去除图像数据的冗余部分,降低信源熵,这是对图像数据的压缩过程;编码就是对去除冗余后的图像数据重新用一种新的符号编码代替,这也是对图像数据的重编码进行存储的过程。
2.哈夫曼编码原理2.1.理论基础为了节省空间,在对数据进行编码时,可以对那些经常出现的数据指定较少的位数表示,而那些不常出现的数据指定较多的位数表示,从而降低冗余,这样从总的效果看就节省了存储空间。
哈夫曼树及哈夫曼编码的运用范围

哈夫曼树及哈夫曼编码的运用范围
哈夫曼树及哈夫曼编码是一种常用的数据压缩算法,广泛应用于数据传输和储存领域。
其运用范围主要包括以下几个方面:
1. 文件压缩:通过使用哈夫曼编码,可以将文件中的冗余信息压缩,减小文件的体积,从而提高文件传输的效率和节省存储空间。
2. 图像压缩:哈夫曼编码可以对图像进行数据压缩,删除冗余信息,减小图像的文件大小,提高图像传输速度和存储效率。
3. 音频压缩:哈夫曼编码常被用于音频数据的压缩,去除冗余数据,减小音频文件的大小,使其更易于传输和存储。
4. 视频压缩:哈夫曼编码也可以应用于视频数据的压缩,通过对视频中像素值的编码压缩,减小视频文件的体积,提高传输速度和存储效率。
5. 网络传输:在网络通信中,哈夫曼编码可以提高数据的传输效率,减小传输的数据量,提高网络的带宽利用率。
总之,哈夫曼树及哈夫曼编码在数据压缩和处理领域具有广泛的应用,可以减小文件、图像、音频和视频的体积,提高传输效率和存储效率。
图像压缩的几种常见算法介绍
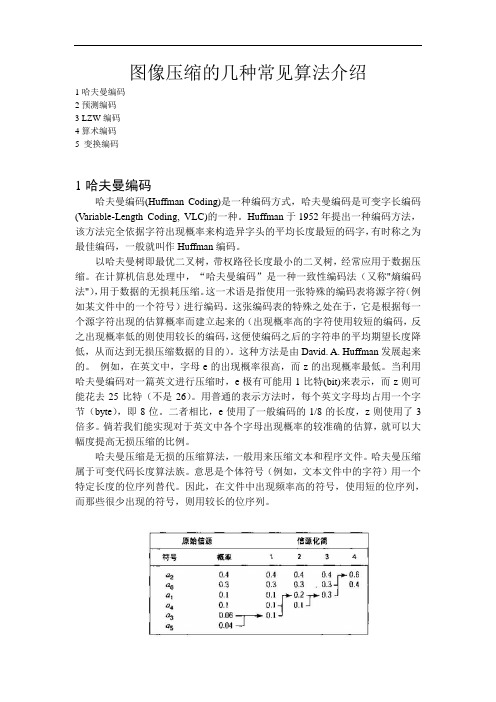
图像压缩的几种常见算法介绍1哈夫曼编码2预测编码3 LZW编码4算术编码5 变换编码1哈夫曼编码哈夫曼编码(Huffman Coding)是一种编码方式,哈夫曼编码是可变字长编码(Variable-Length Coding, VLC)的一种。
Huffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫作Huffman编码。
以哈夫曼树即最优二叉树,带权路径长度最小的二叉树,经常应用于数据压缩。
在计算机信息处理中,“哈夫曼编码”是一种一致性编码法(又称"熵编码法"),用于数据的无损耗压缩。
这一术语是指使用一张特殊的编码表将源字符(例如某文件中的一个符号)进行编码。
这张编码表的特殊之处在于,它是根据每一个源字符出现的估算概率而建立起来的(出现概率高的字符使用较短的编码,反之出现概率低的则使用较长的编码,这便使编码之后的字符串的平均期望长度降低,从而达到无损压缩数据的目的)。
这种方法是由David. A. Huffman发展起来的。
例如,在英文中,字母e的出现概率很高,而z的出现概率最低。
当利用哈夫曼编码对一篇英文进行压缩时,e极有可能用1比特(bit)来表示,而z则可能花去25比特(不是26)。
用普通的表示方法时,每个英文字母均占用一个字节(byte),即8位。
二者相比,e使用了一般编码的1/8的长度,z则使用了3倍多。
倘若我们能实现对于英文中各个字母出现概率的较准确的估算,就可以大幅度提高无损压缩的比例。
哈夫曼压缩是无损的压缩算法,一般用来压缩文本和程序文件。
哈夫曼压缩属于可变代码长度算法族。
意思是个体符号(例如,文本文件中的字符)用一个特定长度的位序列替代。
因此,在文件中出现频率高的符号,使用短的位序列,而那些很少出现的符号,则用较长的位序列。
图1 霍夫曼信源化简图2 霍夫曼编码分配过程2预测编码预测编码是根据离散信号之间存在着一定关联性的特点,利用前面一个或多个信号预测下一个信号,然后对实际值和预测值的差(预测误差)进行编码。
哈夫曼树算法用途

哈夫曼树算法用途哈夫曼树是一种常用的数据压缩算法,广泛应用于文件压缩、图像压缩、音频压缩等领域。
它可以根据数据的频率分布构建一颗最优的二叉树,从而实现数据的高效压缩和解压缩。
下面将从哈夫曼树的原理、构建方法和应用领域等方面进行详细阐述。
首先,我们来了解一下哈夫曼树的原理。
哈夫曼树是一颗带权路径长度最短的二叉树,其带权路径长度是指所有叶子结点的权值乘以其到根结点的路径长度之和。
对于一组给定的权值集合,构建哈夫曼树的过程是这样的:首先将权值按照从小到大的顺序排序,然后取权值最小的两个结点作为叶子结点,构建一个新的父节点,其权值为两个叶子结点的权值之和。
将这个新的父节点插入到原来的集合中,重复上述步骤直到只剩下一个根结点为止。
最终构建出的二叉树就是一颗哈夫曼树。
接下来,我们来介绍一下哈夫曼树的构建方法。
构建哈夫曼树的核心思想是贪心算法,即每次都选择权值最小的两个结点进行合并。
具体的构建步骤如下:1. 将待构建哈夫曼树的结点按照权值从小到大排序。
2. 创建一个空的哈夫曼树,将权值最小的两个结点作为叶子结点插入到树中,并创建一个新的父节点,其权值为这两个结点的权值之和。
3. 将这个新的父节点插入到原来的结点集合中,并将原来的两个结点从集合中删除。
4. 重复上述步骤,直到只剩下一个根结点为止,构建出的二叉树就是一颗哈夫曼树。
构建哈夫曼树的时间复杂度为O(nlogn),其中n为叶子结点的个数。
由于每次都需要排序,所以效率较低。
为了提高效率,可以使用最小堆这种数据结构来快速选择权值最小的结点。
哈夫曼树的应用领域非常广泛。
其中最为重要的应用之一就是数据压缩。
在计算机存储和传输过程中,数据通常需要经过压缩以减小存储空间和传输带宽。
哈夫曼树作为一种高效的数据压缩算法,可以根据数据的频率分布来构建一个最优的编码表,将频率高的字符用较短的编码表示,而将频率低的字符用较长的编码表示,从而实现数据的高效压缩。
在文件压缩中,哈夫曼树可以根据不同字符的出现频率来构建一个相对最优的编码表,然后将文件中的字符按照这个编码表进行替换。
哈夫曼编码在图像压缩中的应用与分析

Technology Application技术应用DCW189数字通信世界2021.010 引言在各个行业之间进行信息传输时,由于数据、图像的传输需要占据较大的信道容量,因此在数据、图像传输的过程中,会由于信道容量的大量被占用,导致网络卡顿。
为了解决这一问题,研究出了文件压缩、图像压缩等方式,在对数据和图像进行传输之前,首先对其进行压缩,使其传输过程中只需要占用比较小的内存,在接收信息后,再对文件和图像等进行解压。
本文所研究的重点是常用的图像压缩技术-哈夫曼编码,通过C++语言对编码算法进行实现,从而对图像压缩的相关技术进行研究,通过哈夫曼编码实现对图像的压缩和对比分析。
1 哈夫曼编码简介哈夫曼编码出现于19世纪60年代,是国际有效的二进制编码之一,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,被认为是接近于压缩比上限的最佳编码方法之一[1]。
哈夫曼编码是常用的编码方式,亦称为最佳编码、熵编码,适用于无损耗的数据压缩[2]。
在使用哈夫曼编码实现对图像的压缩过程中,首先实现的是对图像中所分解出来的数据进行扫描,计算出图像上各个像素所出现的概率,并根据各个数据出现概率的不同,指定哈夫曼编码中的惟一码字与各个不同概率的像素一一对应,并将所有码字组成哈夫曼码表,在图像加压的过程中,可以通过压缩时所组成的哈夫曼码表的对应关系,实现源图像数据的还原。
2 哈夫曼编码实现图像压缩2.1 哈夫曼编码实现图像压缩算法本文以C++为基础语言,结合哈夫曼编码的思想,使编码符号与被压缩的图像数据一一对应,利用二叉树的构造方法,不断置新新的根节点,使得最终的数据编码由两个子节点和一个根节点构成,算法如下:(1)定义哈夫曼树节点哈夫曼树主要由一个根节点和两个子节点,一共三个节点构成,因此本次哈夫曼树类型的构建一共定义4个整型成员,分别表示树根节点、左节点、右节点和数量。
(2)构建哈夫曼树按照哈夫曼树的构建步骤,按照出现概率的大小顺序对字符进行排序,将字符出现次数最少的两个节点构成哈夫曼树新的节点,使用循环,不断抽取排序中出现数量最少的节点,不断合并组成新节点,直到最后只剩下两组节点,构成最后的二叉树[3]。
无损图像压缩算法研究与实现

无损图像压缩算法研究与实现在现代社会中,图像已经成为人们不可或缺的一部分。
不论是人们拍摄的照片,还是网上浏览的图片,都需要占用储存空间。
因此,图像的压缩成为了必不可少的技术。
传统的图像压缩算法通常采用有损压缩,而无损压缩是一种相对较新的技术,它可以在不影响图像质量的前提下,达到压缩数据的目的。
本文主要介绍无损图像压缩算法的研究和实现。
一、无损压缩的实现原理1.差分编码法差分编码法是一种简单的无损压缩算法,它的原理就是将图像中每一个像素的值减去其邻域的像素值(比如它的左边或上边的像素)的值。
这样所得的差异值就可以很小,可以被用于压缩而没有过多的信息损失,这样就可以减少图像中每个像素所占用的位数,达到无损压缩的目的。
2.哈夫曼编码法哈夫曼编码法是一种更加普遍使用的无损压缩算法。
该算法的主要思想是将相似的像素值(在图像中相邻或者附近出现过的像素)编码为相似的编码,而不是使用每个值都有许多位的二进制编码。
这种编码方法可以将相似的像素编码在一起,减少信息的冗余。
同时,该算法中压缩率可以根据典型图像的特点进行调整,进一步提高压缩率。
二、无损压缩算法的实现1.差分编码法的实现差分编码法比较简单,只需要对每个像素进行单独的处理即可实现。
对于一张灰度图像,我们可以使用一个for循环来遍历每个像素,然后计算它的差异值,将其储存下来。
同时将图像的宽度,高度,比特率,以及诸如头文件等信息储存下来,用于还原时的图像储存。
2.哈夫曼编码法的实现哈夫曼编码法比较复杂,较为深入的了解需要一定的编程基础。
首先,我们需要用一个算法来生成每个像素值的哈夫曼编码,也就是用一串小于8位的二进制数字作为代表。
该算法需要建立一棵哈夫曼树,以树中的每个节点代表一个像素,节点之间的左右排布,就是相似度较高的像素,率先出现的祖先节点是最少出现、且概率最小的像素值,它所代表的二进制编码也就较短,这也是哈夫曼编码法的高压缩性能的原因。
建立好哈夫曼树后,需要将树的信息储存在压缩文件中,以便还原。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
char *_dictionary[MAX_CHARS]; //to store the encoding of each character
int _statistic[MAX_CHARS]; //To store the number of each character
在整个编码过程中,统计图像各灰度级出现的概率和编码这两步都很简单,关键的是Huffman树的构造。不但编码的时候需要用到这颗树,解码的时候也必须有这颗树才能完成解码工作,因此,Huffman树还得完整的传输到解码端。
Huffman树的构造可以按照下面图2的流程图来完成。首先对统计出来的概率从小到大进行排序,然后将最小的两个概率相加;到这儿的时候,先把已经加过的两个概率作为树的两个节点,并把他们从概率队列中删除;然后把相加所得的新概率加入到队列中,对这个新队列进行排序。如此反复,直到最后两个概率相加为1的时候停止。这样,Huffman树就建立起来了。
———用哈弗曼算法实现图像压缩
姓名:黄函
学号:2011221104210146
班级:11计科3班
算法设计课程论文
1.数字图像的冗余表现为以下几种形式:空间冗余、时间冗余、视 觉 冗余、信息熵冗余、结构冗余和知识冗余。
(1)空间冗余:图像内部相邻像素之间存在较强的相关性所造成的冗余。
(2)时间冗余:视频图像序列中的不同帧之间的相关性所造成的冗余。
压缩方法的质量经常使用峰值信噪比来衡量,峰值信噪比用来表示图象有损压缩带来的噪声。但是,观察者的主观判断也认为是一个重要的、或许是最重要的衡量标准。
4.以哈弗曼算法为实例了解图像压缩算法
Huffman码是一种变长码,其基本思想是:先统计图像(已经数字化)中各灰度出现的概率,出现概率较大的赋以较短的码字,而出现概率较小的则赋以较长的码字。我们可以用下面的框图来表示Huffman编码的过程:
质量渐进:又称层渐进,位流渐进更新重建的图像。
分辨率渐进:首先在低分辨率编码图像,然后编码与高分辨率之间的差别。
成分渐进:首先编码灰度数据,然后编码彩色数据。
感兴趣区域编码:图像某些部分的编码质量要高于其它部分,这种方法可以与可扩展编码组合在一起(首先编码这些部分,然后编码其它部分)。
元数据信息:压缩数据可以包含关于图像的信息用来分类、查询或者浏览图像。这些信息可以包括颜色、纹理统计信息、小预览图像以及作者和版权信息。
(3)软件压缩率至少达到30%
7.软件源代码:代码分为5个文件,compress.h , pg.h, compress.c , pg.c , main.c
compress.h
/*
* File: compress.h
* Purpose: To compress file using the Haffman algorithm
2.无损压缩很常见的例子是磁盘文件的压缩。有损压缩的实例是图像和声音的压缩。
3.图像压缩的目的就是在给定位速或者压缩比下实现最好的图像质量。但是,还有一些其它的图像压缩机制的重要特性:
可扩展编码 :又称渐进编码、嵌入式位流,通常表示操作位流和文件产生的质量下降(没有解压缩和再压缩)。尽管具有不同的特性,在无损编码中也有可扩展编码,它通常是使用粗糙到精细像素扫描的格式。尤其是在下载时预览图像(如浏览器中)或者提供不同的图像质量访问时(如在数据库中)可扩展编码非常有用,有几种不同类型的可扩展性:
(3)视觉冗余:是指人眼不能感知或不敏感的那部分图像信息。
(4)信息熵冗余:也称编码冗余,如果图像中平均每个像素使用的比特数大于该图像的信息熵,则图像中存在冗余,这种冗余称为信息熵冗余。
(5)结构冗余:是指图像中存在很强的纹理结构或自相似性。
(6)知识冗余:是指有些图像还包含与某些先验知识有关的信息。
#define BITS_PER_CHAR 8 //the number of bits in a char
#define MAX_CHARS 256 //the max number of chars
#define FILE_BUF_SIZE 8192 //the size of Buffer for FILE I/O
typedef struct FileCompressStruct FCS;
struct FileCompressStruct
{
HTN *_haffuman; //A pointer to the root of hafumman tree
unsigned int _charsCount; //To store the number ofபைடு நூலகம்chars
5.哈夫曼图像压缩算法性能评价
我们主要从三方面[ 2 ]来评价Huffman的性能:
(1)压缩比的大小;
(2)恢复效果的好坏,也就是能否尽可能的恢复原始数据;
(3)算法的简单易用性以及编、解码的速度。
6.我设计的哈弗曼树达到以下要求:
(1)软件设计支持灰度图像和彩色图像的压缩
(2)图像文件格式为bmp或者gif
* Author: puresky
* Date: 2011/05/01
*/
#ifndef _FILE_COMPRESSION_H
#define _FILE_COMPRESSION_H
//Haffuman Tree Node
typedef struct HaffumanTreeNode HTN;
struct HaffumanTreeNode
};
FCS *fcs_new();
void fcs_compress(FCS *fcs, const char *inFileName, const char *outFileName);
{
char _ch; //character
int _count; //frequency
struct HaffumanTreeNode *_left; //left child
struct HaffumanTreeNode *_right;//rigth child
};
//FileCompress Struct
