人工智能 谓词公式化为子句集
(完整版)人工智能习题解答
人工智能第1部分绪论1-1.什么是人工智能？试从学科和能力两方面加以说明。
答：从学科方面定义：人工智能是计算机科学中涉及研究、设计和应用智能机器的一个分支。
它的近期目标在于研究用机器来模拟和执行人脑的某些智力功能，并开发相关理论和技术从能力方面定义：人工智能是智能机器所执行的通常与人类智能有关的智能行为，如判断、推理、证明、识别、感知、理解、通信、设计、思考、规划、学习和问题求解等思维活动。
1-2.在人工智能的发展过程中，有哪些思想和思潮起了重要作用？答：1）数理逻辑和关于计算本质的新思想，提供了形式推理概念与即将发明的计算机之间的联系；2）1956年第一次人工智能研讨会召开，标志着人工智能学科的诞生；3）控制论思想把神经系统的工作原理与信息理论、控制理论、逻辑以及计算联系起来，影响了许多早期人工智能工作者，并成为他们的指导思想；4）计算机的发明与发展；5）专家系统与知识工程；6）机器学习、计算智能、人工神经网络和行为主义研究，推动人工智能研究的近一步发展。
1-3.为什么能够用机器（计算机）模仿人的智能？答：物理符号系统的假设：任何一个系统，如果它能够表现出智能，那么它就必定能执行输入符号、输出符号、存储符号、复制符号、建立符号结构、条件迁移6种功能。
反之，任何系统如果具有这6种功能，那么它就能够表现出智能（人类所具有的智能）。
物理符号系统的假设伴随有3个推论。
推论一：既然人具有智能，那么他（她）就一定是各物理符号系统；推论二：既然计算机是一个物理符号系统，它就一定能够表现出智能；推论三：既然人是一个物理符号系统，计算机也是一个物理符号系统，那么我们就能够用计算机来模拟人的活动。
1-4.人工智能的主要研究内容和应用领域是什么？其中，哪些是新的研究热点？答：研究和应用领域：问题求解（下棋程序），逻辑推理与定理证明（四色定理证明），自然语言理解，自动程序设计，专家系统，机器学习，神经网络，机器人学（星际探索机器人），模式识别（手写识别，汽车牌照识别，指纹识别），机器视觉（机器装配，卫星图像处理），智能控制，智能检索，智能调度与指挥（汽车运输高度，列车编组指挥），系统与语言工具。
简述谓词公式化为字句集的步骤
简述谓词公式化为字句集的步骤谓词公式化为字句集是一种将谓词逻辑表达式转化为一组命题的方法，它可以使得逻辑推理更加简洁和易于理解。
下面将介绍谓词公式化为字句集的步骤。
1. 定义谓词和变量：首先，需要明确谓词和变量的含义。
谓词是描述某个对象或者关系的函数，而变量则是谓词的参数。
例如，可以定义一个谓词“父亲”，它的变量可以是“x”和“y”。
2. 构建谓词公式：根据具体的问题，构建谓词公式。
谓词公式由谓词和变量组成，可以使用逻辑运算符（如∧、∨、¬等）连接多个谓词和变量。
例如，可以构建一个谓词公式“父亲(x,y)∧男性(x)”来表示“x是y的父亲，并且x是男性”。
3. 全称量化和存在量化：对于存在量化的变量，需要引入新的常量或者变量来替代。
例如，对于谓词公式“∃x 父亲(x,y)∧男性(x)”中的变量“x”，可以引入一个新的常量“a”来替代，得到谓词公式“父亲(a,y)∧男性(a)”。
4. 引入新的谓词和变量：根据具体的推理需求，可能需要引入新的谓词和变量来扩展谓词公式。
例如，可以引入一个新的谓词“祖父”，它的变量可以是“x”和“y”，并且定义为“∃z 父亲(x,z)∧父亲(z,y)”来表示“x是y的祖父”。
5. 消除存在量化：通过引入新的谓词和变量，将存在量化转化为全称量化。
例如，可以将谓词公式“∃x 父亲(x,y)”转化为“父亲(a,y)∨父亲(b,y)∨父亲(c,y)∨...”，其中“a”、“b”、“c”等是新引入的常量或者变量。
6. 拆解复合谓词：对于复合谓词，可以通过拆解成多个简单谓词来进行推理。
例如，可以将谓词公式“父亲(x,y)∧男性(x)”拆解为“父亲(x,y)”和“男性(x)”。
7. 去除冗余信息：在构建字句集时，可以去除一些冗余的谓词和变量。
例如，如果一个谓词没有被使用到，可以将其去除。
8. 构建字句集：根据上述步骤，将谓词公式转化为一组命题，即字句集。
字句集由多个字句组成，每个字句是一个命题。
人工智能练习题答案
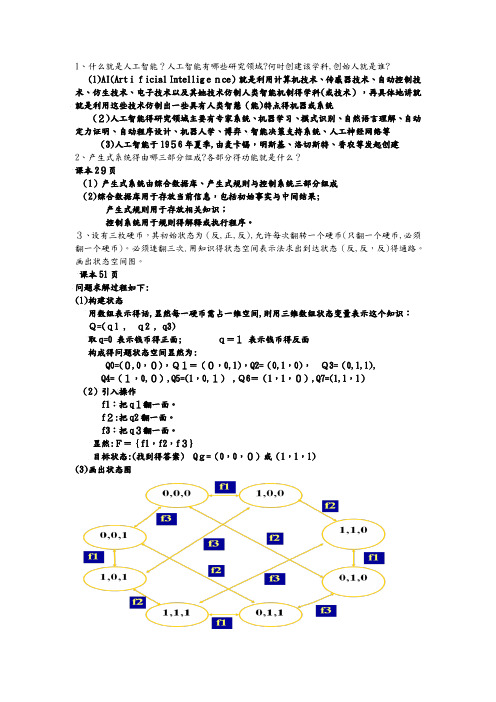
1、什么就是人工智能？人工智能有哪些研究领域?何时创建该学科,创始人就是谁?(1)AI(Artｉｆicial Intelligｅｎce）就是利用计算机技术、传感器技术、自动控制技术、仿生技术、电子技术以及其她技术仿制人类智能机制得学科(或技术），再具体地讲就就是利用这些技术仿制出一些具有人类智慧（能)特点得机器或系统(２)人工智能得研究领域主要有专家系统、机器学习、模式识别、自然语言理解、自动定力证明、自动程序设计、机器人学、博弈、智能决策支持系统、人工神经网络等（3)人工智能于19５6年夏季,由麦卡锡，明斯基、洛切斯特、香农等发起创建2、产生式系统得由哪三部分组成?各部分得功能就是什么？课本2９页（1）产生式系统由综合数据库、产生式规则与控制系统三部分组成（2)综合数据库用于存放当前信息，包括初始事实与中间结果;产生式规则用于存放相关知识；控制系统用于规则得解释或执行程序。
３、设有三枚硬币，其初始状态为（反,正,反),允许每次翻转一个硬币(只翻一个硬币,必须翻一个硬币)。
必须连翻三次.用知识得状态空间表示法求出到达状态（反,反，反)得通路。
画出状态空间图。
课本51页问题求解过程如下:(1)构建状态用数组表示得话,显然每一硬币需占一维空间,则用三维数组状态变量表示这个知识：Ｑ=(ｑ1 , ｑ2 , q3)取q=0 表示钱币得正面; ｑ＝１表示钱币得反面构成得问题状态空间显然为:Q0=(０,0，０)，Ｑ１＝（０，0,1)，Q2=（0,1，0)，Ｑ3=（0,1,1), Q4=（１，0,０）,Q5=(1，0,１） ,Ｑ6＝（1，1，０）,Q7=(1,1，1）（2）引入操作f1：把q１翻一面。
f２:把q2翻一面。
f3：把q３翻一面。
显然:Ｆ＝｛f1，f2，f３}目标状态:(找到得答案) Qｇ=（0，0，０）或（1，1，1)(3)画出状态图从状态图可知：从“反，正,反”（1,0,1）到“正，正，正”（0，０,0）没有解题路径;从“反，正,反"（1，０，1)到“反,反,反"（1，1,1）有几条解题路径f3 ｆ2 ｆ3，f1 f2 f1，…4、八数码问题：已知八数码得初始状态与目标状态如下：2 ８3 ＝〉 1 2 3１６ 4 8 47 5 7 ６ 5n),g(n)=d(n）,h(n）=ｐ(n）。
人工智能(第3版)王万森部分习题答案
第二章2.8设有如下语句，请用相应的谓词公式分别把他们表示出来：(1)有的人喜欢梅花，有的人喜欢菊花，有的人既喜欢梅花又喜欢菊花。
解：定义谓词P(x)：x是人L(x,y)：x喜欢y其中，y的个体域是{梅花，菊花}。
将知识用谓词表示为：(∃x )(P(x)→L(x, 梅花)∨L(x, 菊花)∨L(x, 梅花)∧L(x, 菊花))(2) 有人每天下午都去打篮球。
解：定义谓词P(x)：x是人B(x)：x打篮球A(y)：y是下午将知识用谓词表示为：(∃x )(∀y) (A(y)→B(x)∧P(x))(3)新型计算机速度又快，存储容量又大。
解：定义谓词NC(x)：x是新型计算机F(x)：x速度快B(x)：x容量大将知识用谓词表示为：(∀x) (NC(x)→F(x)∧B(x))(4) 不是每个计算机系的学生都喜欢在计算机上编程序。
解：定义谓词S(x)：x是计算机系学生L(x, pragramming)：x喜欢编程序U(x,computer)：x使用计算机将知识用谓词表示为：¬(∀x) (S(x)→L(x, pragramming)∧U(x,computer))(5)凡是喜欢编程序的人都喜欢计算机。
解：定义谓词P(x)：x是人L(x, y)：x喜欢y将知识用谓词表示为：(∀x) (P(x)∧L(x,pragramming)→L(x, computer))2.10用谓词表示法求解农夫、狼、山羊、白菜问题。
农夫、狼、山羊、白菜全部放在一条河的左岸，现在要把他们全部送到河的右岸去，农夫有一条船，过河时，除农夫外船上至多能载狼、山羊、白菜中的一种。
狼要吃山羊，山羊要吃白菜，除非农夫在那里。
似规划出一个确保全部安全过河的计划。
请写出所用谓词的定义，并给出每个谓词的功能及变量的个体域。
解：(1) 先定义描述状态的谓词要描述这个问题，需要能够说明农夫、狼、羊、白菜和船在什么位置，为简化问题表示，取消船在河中行驶的状态，只描述左岸和右岸的状态。
人工智能第4版部分课后答案
第２章附加题1.请写出用一阶谓词逻辑表示法表示知识的步骤。
步骤：（1）定义谓词及个体，确定每个谓词及个体的确切含义；（2）根据所要表达的事物或概念，为每个谓词中的变元赋予特定的值；（3）根据所要表达的知识的语义用适当的联接符号将各个谓词联接起来，形成谓词公式。
1.什么是子句？什么是子句集？请写出谓词公式子句集的步骤。
解：子句就是由一些文字组成的析取式。
由子句构成的集合称为子句集。
步骤：（1）消去谓词公式中的蕴涵和双条件符号，以~A∨B代替A→B，以(A∧B)∨(~A∧~B)替换A↔B。
（2）减少不定符号的辖域，使不定符号最多只作用到一个谓词上。
（3）重新命名变元名，使所有的变元的名字均不同，并且自由变元及约束变元亦不同。
（4）消去存在量词。
（5）把全称量词全部移到公式的左边，并使每个量词的辖域包括这个量词后面公式的整个部分。
（6）母式化为合取范式，建立起与其对应的子句集。
2-2用谓词表示法求解修道士和野人问题。
在河的北岸有三个修道士、三个野人和一条船，修道士们想用这条船将所有的人都运过河去，但要受到以下条件限制：(1) 修道士和野人都会划船，但船一次只能装运两个人。
(2) 在任何岸边，野人数不能超过修道士，否则修道士会被野人吃掉。
假定野人愿意服从任何一种过河安排，请规划出一种确保修道士安全的过河方案。
要求写出所用谓词的定义、功能及变量的个体域。
解：（1）定义谓词先定义修道士和野人人数关系的谓词：G(x,y,S)：在状态S下x大于yGE(x,y,S)：在状态S下x大于或等于y其中，x,y分别代表修道士人数和野人数，他们的个体域均为{0,1,2,3}。
再定义船所在岸的谓词和修道士不在该岸上的谓词：Boat(z,S)：状态S下船在z岸EZ(x,S)：状态S下x等于0，即修道士不在该岸上其中，z的个体域是{L,R}，L表示左岸，R表示右岸。
再定义安全性谓词：Safety(z,x,y,S)≡(G(x,0,S)∧GE(x,y,S))∨(EZ(x,S))其中，z,x,y的含义同上。
人工智能第3章参考答案
第3章确定性推理部分参考答案判断下列公式是否为可合一，若可合一，则求出其最一般合一。
(1) P(a, b), P(x, y)(2) P(f(x), b), P(y, z)(3) P(f(x), y), P(y, f(b))(4) P(f(y), y, x), P(x, f(a), f(b))(5) P(x, y), P(y, x)解：(1) 可合一，其最一般和一为：σ={a/x, b/y}。
(2) 可合一，其最一般和一为：σ={y/f(x), b/z}。
(3) 可合一，其最一般和一为：σ={ f(b)/y, b/x}。
(4) 不可合一。
(5) 可合一，其最一般和一为：σ={ y/x}。
把下列谓词公式化成子句集：(1)(∀x)(∀y)(P(x, y)∧Q(x, y))(2)(∀x)(∀y)(P(x, y)→Q(x, y))(3)(∀x)(∃y)(P(x, y)∨(Q(x, y)→R(x, y)))(4)(∀x) (∀y) (∃z)(P(x, y)→Q(x, y)∨R(x, z))解：(1) 由于(∀x)(∀y)(P(x, y)∧Q(x, y))已经是Skolem标准型，且P(x, y)∧Q(x, y)已经是合取范式，所以可直接消去全称量词、合取词，得{ P(x, y), Q(x, y)}再进行变元换名得子句集：S={ P(x, y), Q(u, v)}(2) 对谓词公式(∀x)(∀y)(P(x, y)→Q(x, y))，先消去连接词“→”得：(∀x)(∀y)(P(x, y)∨Q(x, y))此公式已为Skolem标准型。
再消去全称量词得子句集：S={P(x, y)∨Q(x, y)}(3) 对谓词公式(∀x)(∃y)(P(x, y)∨(Q(x, y)→R(x, y)))，先消去连接词“→”得：(∀x)(∃y)(P(x, y)∨(Q(x, y)∨R(x, y)))此公式已为前束范式。
再消去存在量词，即用Skolem函数f(x)替换y得：(∀x)(P(x, f(x))∨Q(x, f(x))∨R(x, f(x)))此公式已为Skolem标准型。
人工智能题解
习题六7.1，综合数据库定义5元组：（M, B, Box, On, H）其中：M：猴子的位置B：香蕉的位置Box：箱子的位置On=0：猴子在地板上On=1：猴子在箱子上H=0：猴子没有抓到香蕉H=1：猴子抓到了香蕉2，规则集r1: IF (x, y, z, 0, 0) THEN (w, y, z, 0, 0) 猴子从x处走到w处r2: IF (x, y, x, 0, 0) THEN (z, y, z, 0, 0) 如果猴子和箱子在一起，猴子将箱子推到z处r3: IF (x, y, x, 0, 0) THEN (x, y, x, 1, 0) 如果猴子和箱子在一起，猴子爬到箱子上r4: IF (x, y, x, 1, 0) THEN (x, y, x, 0, 0) 如果猴子在箱子上，猴子从箱子上下来r5: IF (x, x, x, 1, 0) THEN (x, x, x, 1, 1) 如果箱子在香蕉处，猴子在箱子上，猴子摘到香蕉其中x, y, z, w为变量3，初始状态（c, a, b, 0, 0）4，结束状态（x1, x2, x3, x4, 1）其中x1～x4为变量。
习题五1.求下列各谓词公式的子句集。
（1）y∀(P(x, y)∧Q(x, y))x∀解：对原式消全称量词，得：P(x, y)∧Q(x, y)变元改名，得：P(x, y)∧Q(u, v)所以原式的子句集S={ P(x, y)，Q(u, v)}(2) y∀(P(x, y)→Q(x, y))x∀解：消去→，得：y∀(⌝P(x, y)∨Q(x, y))x∀消全称量词，得：⌝P(x, y)∨Q(x, y)∴S= {⌝P(x, y)∨Q(x, y)}(3) y∀(P(x, y)∨(Q(x, y)→R(x, y)))x∃解：消蕴含词→，得：yx∃∀((P(x, y)∨(⌝Q(x, y)∨R(x, y))) 消存在量词，得：x∀(P(x, f(x))∨⌝Q(x, f(x))∨R(x, f(x))) 消全称量词，得：P(x, f(x))∨⌝Q(x, f(x))∨R(x, f(x))∴S= {P(x, f(x))∨⌝Q(x, f(x))∨R(x, f(x))}(4) y∀z∃(P(x, y)→Q(x, y)∨R(x, y))x∀解：消→，得：y∀z∃(⌝P(x, y)∨Q(x, y)∨R(x, y))x∀消∃，得：y∀(⌝P(x, f(x, y))∨Q(x, y)∨R(x, y))x∀消∀, 得：⌝P(x, f(x, y))∨Q(x, y)∨R(x, y)∴S= {⌝P(x, f(x, y))∨Q(x, y)∨R(x, y)}(5) w∃∀∃(P(x, y, z, u v, w)∧(Q(x, y, z, u, v, w)∨⌝R(x z, w)) ∀∃x∃yuvz解：消∃，得：v∀(P(a, b, z, f(z),v, g(z, v))∧(Q(a, b, z, f(z),v, g(z,z∀v))∨⌝R(a, z, g(z, v))消∀, 得：(P(a, b, z, f(z),v, g(z, v))∧(Q(a, b, z, f(z),v, g(z, v))∨⌝R(a, z, g(z, v))∴S= { P(a, b, z, f(z),v, g(z, v))，(Q(a, b, z, f(z),v, g(z, v))∨⌝R(a, z, g(z, v)) }2, 用归结原理证明R是P, (P∧Q)→R, (S∨U)→Q, U的逻辑结果。
人工智能确定性推理部分参考答案
⼈⼯智能确定性推理部分参考答案确定性推理部分参考答案1 判断下列公式是否为可合⼀，若可合⼀，则求出其最⼀般合⼀。
(1) P(a, b), P(x, y)(2) P(f(x), b), P(y, z)(3) P(f(x), y), P(y, f(b))(4) P(f(y), y, x), P(x, f(a), f(b))(5) P(x, y), P(y, x)解：(1) 可合⼀，其最⼀般和⼀为：σ={a/x, b/y}。
(2) 可合⼀，其最⼀般和⼀为：σ={y/f(x), b/z}。
(3) 可合⼀，其最⼀般和⼀为：σ={ f(b)/y, b/x}。
(4) 不可合⼀。
(5) 可合⼀，其最⼀般和⼀为：σ={ y/x}。
2 把下列谓词公式化成⼦句集：(1)(?x)(?y)(P(x, y)∧Q(x, y))(2)(?x)(?y)(P(x, y)→Q(x, y))(3)(?x)(?y)(P(x, y)∨(Q(x, y)→R(x, y)))(4)(?x) (?y) (?z)(P(x, y)→Q(x, y)∨R(x, z))解：(1) 由于(?x)(?y)(P(x, y)∧Q(x, y))已经是Skolem标准型，且P(x, y)∧Q(x, y)已经是合取范式，所以可直接消去全称量词、合取词，得{ P(x, y), Q(x, y)}再进⾏变元换名得⼦句集：S={ P(x, y), Q(u, v)}(2) 对谓词公式(?x)(?y)(P(x, y)→Q(x, y))，先消去连接词“→”得：(?x)(?y)(?P(x, y)∨Q(x, y))此公式已为Skolem标准型。
再消去全称量词得⼦句集：S={?P(x, y)∨Q(x, y)}(3) 对谓词公式(?x)(?y)(P(x, y)∨(Q(x, y)→R(x, y)))，先消去连接词“→”得：(?x)(?y)(P(x, y)∨(?Q(x, y)∨R(x, y)))此公式已为前束范式。