高三数学课件 指数函数与对数函数
合集下载
《指数函数》指数函数与对数函数PPT演示课件

过一个虚拟的人进行洗钱,当然,这一切只有他一个人知道。在监狱中,他因为冒死替狱友争取到了啤酒,从而赢得了狱友们的尊重
和友谊,从那些无所不能的狱友们弄到一把铁捶和一张明星的海报。一年又一年的监狱生活,带走了
对他来说,简直就是希望和救星,他找到监狱长,救他,说这是他可以翻案的机会,只要找到那名犯人,再加上他的学生做证,他就
讨论:
1
1
(1)如果 a<0,如 y=(-4)x,这时对于 x=4,x=2等,在实数范围内函数值
不存在;
(2)如果 a=0,
当 > 0 时, 恒等于 0,
当 ≤ 0 时, 无意义;
(3)如果a=1,y=1x=1,是个常数函数,没有研究的必要;
(4)如果0<a<1或a>1,即a>0且a≠1,x可以是任意实数.
指数函数与对数函数
4.2 指数函数
-1-
首页
课标阐释
思维脉络
1.理解指数函数的概念和意义,
能画出具体指数函数的图象.
2.初步掌握指数函数的性质,并
能解决与指数函数有关的定义
域、值域、定点问题.
3.逐步体会指数函数在实际问
题中的应用.
课前篇
自主预习
整部片子比较压抑,可能因为是讲述在监狱里发生的事情吧,但看完后心情却久久不能平静,那样的荡气回肠,那样的震憾人心!一
一
二
个年轻有为的银行家安迪,因为与妻子发生口角气跑了妻子,而当天妻子与她的情人双双被枪杀在床上,他成为最有杀人动机的嫌疑
犯,加上口吐莲花的律师,就这样,一个年轻有为的银行家被送了肖申克监狱。在监狱里发生了许多的事情,先是被老犯人们打赌,
第一晚谁会扛不住最先哭泣,最有权威的老犯人阿瑞看他白白净净,瘦瘦弱弱的样子,押了他两盒烟的赌注,第一次就让阿瑞输了赌
和友谊,从那些无所不能的狱友们弄到一把铁捶和一张明星的海报。一年又一年的监狱生活,带走了
对他来说,简直就是希望和救星,他找到监狱长,救他,说这是他可以翻案的机会,只要找到那名犯人,再加上他的学生做证,他就
讨论:
1
1
(1)如果 a<0,如 y=(-4)x,这时对于 x=4,x=2等,在实数范围内函数值
不存在;
(2)如果 a=0,
当 > 0 时, 恒等于 0,
当 ≤ 0 时, 无意义;
(3)如果a=1,y=1x=1,是个常数函数,没有研究的必要;
(4)如果0<a<1或a>1,即a>0且a≠1,x可以是任意实数.
指数函数与对数函数
4.2 指数函数
-1-
首页
课标阐释
思维脉络
1.理解指数函数的概念和意义,
能画出具体指数函数的图象.
2.初步掌握指数函数的性质,并
能解决与指数函数有关的定义
域、值域、定点问题.
3.逐步体会指数函数在实际问
题中的应用.
课前篇
自主预习
整部片子比较压抑,可能因为是讲述在监狱里发生的事情吧,但看完后心情却久久不能平静,那样的荡气回肠,那样的震憾人心!一
一
二
个年轻有为的银行家安迪,因为与妻子发生口角气跑了妻子,而当天妻子与她的情人双双被枪杀在床上,他成为最有杀人动机的嫌疑
犯,加上口吐莲花的律师,就这样,一个年轻有为的银行家被送了肖申克监狱。在监狱里发生了许多的事情,先是被老犯人们打赌,
第一晚谁会扛不住最先哭泣,最有权威的老犯人阿瑞看他白白净净,瘦瘦弱弱的样子,押了他两盒烟的赌注,第一次就让阿瑞输了赌
指数函数、幂函数、对数函数增长的比较(45张PPT)——高中数学必修第一册

一次函数y=kx(k>0),指数函数y=ax(a>1)和对数函数y=logbx(b>1)的增长有何差异?
一般地,无论k(k>0)、a(a>1)、b(b>1)如何取值,三种函数在区间(0,+∞)上都单调递增,但一次函数总是保持固定的增长速度;指数函数的增长速度都会越来越快,并且指数函数的函数值最终总会大于一次函数的函数值;对数函数的增长速度都会越来越慢,并且对数函数的函数值最终总会小于一次函数的函数值.
401
626
901
y2
2
32
1024
32768
1.05×106
3.36×107
1.07×109
y3
2
10
20
30
40
50
60
y4
2
4.322
5.322
5.907
6.322
6.644
6.907
【解析】(1)由于指数型函数的增长式为爆炸式增长,则当x越来越大时,函数y=的增长速度最快,故选A.
(2)从表格中可以看出,四个变量y1,y2,y3,y4均是从2开始变化,变量y1,y2,y3,y4都是越来越大,但是增长速度不同,其中变量y2的增长速度最快,可知变量y2关于x呈指数函数变化.
x
y=2x
y=2x
0
1
0
2
4
4
4
16
8
6
64
12
8
256
16
10
1024
20
12
4096
24
…
…
…
可以看到,当自变量x越来越大时,y=2x的图象就像与x轴垂直一样,2x的值快速增长;而函数y=2x的增长速度依然保持不变,与函数y=2x的增长速度相比几乎微不足道.
高中数学指数函数与对数函数课件PPT

2-9 指数函数与对数函数
1.掌握指数函数与对数函数的概念,图象和性 质.能利用指数函数和对数函数的性质解决某些简 单的实际问题。 2.理解指数函数y=ax(a>0且a≠1)与对数函数y=logax (a>0且a≠1)互为反函数,灵活运用指数函数、对数 函数的图象和性质,会用数形结合、分类讨论、函 数与方程(不等式)等数学思想方法解决一些综合 问题。
-3 x -2或 - 2 x 1. 函数定义域为(-3, -2)( -2, 1].
变式1.(1) 解:
求函数y loga [loga (loga x) ]的定义域(a 0且a 1). (loga x) 0 loga 1 loga log x 0 a x0
变式1.(2)
已知2
x2 x
1 x2 2 ( ) , 求函数y log 2 (3 x 6 x 4) 4
的值域. 解: 2x2 x 22( x2) , x2 x 2( x 2),
即x 2 3 x-4 0,
2
-4 x 1.
2
令u 3 x 6 x 4 3( x 1) 1 x [-4,1], u是减函数, 1 u 76. 又y log u是增函数, log2 1 log2 u log2 76.
考点梳理
1.指数函数与对数函数的概念: 指数函数: y=ax(a>0且a≠1) 对数函数: y=logax (a>0且a≠1)
2.指数、对数函数的图象与性质 根据图象写出函数的定义域、 值域、单调性、定点等性质.
y=ax的图象 0<a<1 a>1 y (0,1)
0
x
y=logax 的图象 3.指数函数与对数函数互为反函数. a>1 y 图象关于y=x对称,定义域、值域互换. 指数函数过点(0,1),(1,a),(-1,1/a)
1.掌握指数函数与对数函数的概念,图象和性 质.能利用指数函数和对数函数的性质解决某些简 单的实际问题。 2.理解指数函数y=ax(a>0且a≠1)与对数函数y=logax (a>0且a≠1)互为反函数,灵活运用指数函数、对数 函数的图象和性质,会用数形结合、分类讨论、函 数与方程(不等式)等数学思想方法解决一些综合 问题。
-3 x -2或 - 2 x 1. 函数定义域为(-3, -2)( -2, 1].
变式1.(1) 解:
求函数y loga [loga (loga x) ]的定义域(a 0且a 1). (loga x) 0 loga 1 loga log x 0 a x0
变式1.(2)
已知2
x2 x
1 x2 2 ( ) , 求函数y log 2 (3 x 6 x 4) 4
的值域. 解: 2x2 x 22( x2) , x2 x 2( x 2),
即x 2 3 x-4 0,
2
-4 x 1.
2
令u 3 x 6 x 4 3( x 1) 1 x [-4,1], u是减函数, 1 u 76. 又y log u是增函数, log2 1 log2 u log2 76.
考点梳理
1.指数函数与对数函数的概念: 指数函数: y=ax(a>0且a≠1) 对数函数: y=logax (a>0且a≠1)
2.指数、对数函数的图象与性质 根据图象写出函数的定义域、 值域、单调性、定点等性质.
y=ax的图象 0<a<1 a>1 y (0,1)
0
x
y=logax 的图象 3.指数函数与对数函数互为反函数. a>1 y 图象关于y=x对称,定义域、值域互换. 指数函数过点(0,1),(1,a),(-1,1/a)
《对数函数的概念》《对数函数的图象和性质》指数函数与对数函数PPT

-1
2
2
1
化简可得 ≤x2≤2.
2
再由 x>0 可得 2≤x≤
2
2
答案:(1)A (2)
, 2
2
2
2
2
1
,
2,故函数 f(x)的定义域为
2
,
2
2 .
课堂篇
探究学习
探究一
探究二
探究三
探究四
探究五
思想方法
随堂演练
反思感悟 定义域问题注意事项
(1)要遵循以前已学习过的求定义域的方法,如分式分母不为零,
偶次根式被开方式大于或等于零等.
a>1
0<a<1
图象
性
质
定义域
值域
过定点
单调性
奇偶性
(0,+∞)
R
(1,0),即当 x=1 时,y=0
在(0,+∞)
在(0,+∞)
上是增函数
上是减函数
非奇非偶函数
课前篇
自主预习
一
二
三
3.做一做
(1)若函数y=logax的图象如图所示,则a的值可能是 (
)
A.0.5 B.2
C.e D.π
(2)下列函数中,在区间(0,+∞)内
.
2 -2-8 = 0,
解析:(1)由题意可知 + 1 > 0, 解得 a=4.
+ 1 ≠ 1,
(2)设对数函数为f(x)=logax(a>0,且a≠1).
则由题意可得f(8)=-3,即loga8=-3,
所以
a-3=8,即
1
3
-
指数函数和对数函数ppt课件
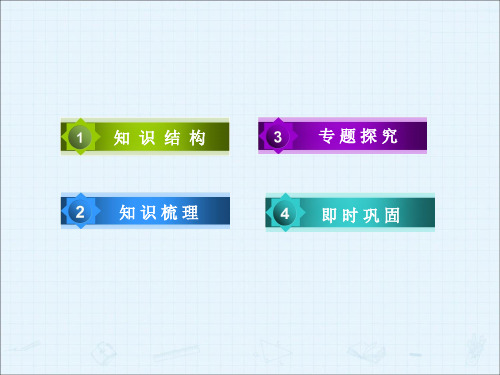
解法 2:a-b=ln22-ln33=3ln2-6 2ln3 =16(ln8-ln9)<0. ∴a<b.同理可得 c<a,∴c<a<b.故选 C.
[答案]C
4.考查函数的定义域 函数的定义域是历年高考中均考查的知识点,其难度 不大,属中低档题,但在求解时易漏掉部分约束条件造成错 解,因而也是易错题. [例 4] 函数 f(x)= 31x-2 x+lg(3x+1)的定义域是
[例 1] (1)化简
3 ÷(1-2
ba)×3 ab;
(2)求值:12lg3429-43lg 8+lg 245.
(2)解法一 12lg3429-43lg 8+lg 245 =lg472-lg4+lg7 5 =lg(472×14×7 5) =lg 10=12lg10=12.
解法二 原式=12(5lg2-2lg7)-43·32lg2+12(2lg7+lg5) =52lg2-lg7-2lg2+lg7+12lg5 =12lg2+12lg5 =12(lg2+lg5) =12lg10=12.
[例7]求不等式x-1<log6(x+3)的所有整数解. [解析]设y1=x-1,y2=log6(x+3),在同一坐标系中作
出它们的图像如图所示,两图像有两个交点,一交点的横坐标
显然在-3和-2之间,另一个交点设为P.
因为x=1时,log6(1+3)-(1-1)>0,x=2时, log6(2+3)-(2-1)<0,所以1<xP<2.
2.指数函数的概念与性质 (1)指数函数的定义
一般地,函数y=ax(a>0,且a≠1)叫作指数函数. (2)y=ax(a>0,a≠1)的图像
0<a<1
a>1
《对数》指数函数与对数函数PPT教学课件(第二课时对数的运算)

4.3 对 数
第二课时 对数的运算
第四章 指数函数与对数函数
考点
学习目标
核心素养
对数的运算 掌握对数的运算性质,能运用运算性 数学运算
性质 质进行对数的有关计算
了解换底公式,能用换底公式将一般
换底公式
数学运算
对数化为自然对数或常用对数
能灵活运用对数的基本性质、对数的 对数运算的
运算性质及换底公式解决对数运算 综合问题
栏目 导引
第四章 指数函数与对数函数
■名师点拨 对数的这三条运算性质,都要注意只有当式子中所有的对数都有意 义时,等式才成立.例如,log2[(-3)·(-5)]=log2(-3)+log2(-5) 是错误的. 2.换底公式
logcb logab=__l_o_g_ca_____ (a>0,且 a≠1;c>0,且 c≠1;b>0).
栏目 导引
第四章 指数函数与对数函数
2. 1 1+ 1 1=________. log149 log513 11
解析:log14119+log11513=llgg419+llgg513=- -22llgg23+- -llgg53=llgg23+llgg53=lg13= log310. 答案:log310
)
A.8
B.6
C.-8
D.-6
解析:选 C.log219·log3215·log514=log23-2·log35-2·log52-2= -8log23·log35·log52=-8.
栏目 导引
第四章 指数函数与对数函数
4.已知
a2=1861(a>0),则
log2a=________. 3
解析:由 a2=1861(a>0)得 a=49, 所以 log3249=log23232=2. 答案:2
第二课时 对数的运算
第四章 指数函数与对数函数
考点
学习目标
核心素养
对数的运算 掌握对数的运算性质,能运用运算性 数学运算
性质 质进行对数的有关计算
了解换底公式,能用换底公式将一般
换底公式
数学运算
对数化为自然对数或常用对数
能灵活运用对数的基本性质、对数的 对数运算的
运算性质及换底公式解决对数运算 综合问题
栏目 导引
第四章 指数函数与对数函数
■名师点拨 对数的这三条运算性质,都要注意只有当式子中所有的对数都有意 义时,等式才成立.例如,log2[(-3)·(-5)]=log2(-3)+log2(-5) 是错误的. 2.换底公式
logcb logab=__l_o_g_ca_____ (a>0,且 a≠1;c>0,且 c≠1;b>0).
栏目 导引
第四章 指数函数与对数函数
2. 1 1+ 1 1=________. log149 log513 11
解析:log14119+log11513=llgg419+llgg513=- -22llgg23+- -llgg53=llgg23+llgg53=lg13= log310. 答案:log310
)
A.8
B.6
C.-8
D.-6
解析:选 C.log219·log3215·log514=log23-2·log35-2·log52-2= -8log23·log35·log52=-8.
栏目 导引
第四章 指数函数与对数函数
4.已知
a2=1861(a>0),则
log2a=________. 3
解析:由 a2=1861(a>0)得 a=49, 所以 log3249=log23232=2. 答案:2
《指数》指数函数与对数函数PPT

1.(1)整数指数幂的运算性质有哪些?
提示:①am·an=am+n;②(am)n=am·n;
m-n
③ =a (m>n,a≠0);(4)(a·b)m=am·bm.
(2)零指数幂和负整数指数幂是如何规定的?
1
提示:规定:a0=1(a≠0);00 无意义,a-n=(a≠0).
课前篇
自主预习
在幂的运算中,对于形如 m0 的式子,要注意对底数 m 是否为零进
行讨论,因为只有在 m≠0 时,m 才有意义;而对于形如
0
们一般是先变形为
,再进行运算.
-
的式子,我
课堂篇
探究学习
探究一
解:(1)
探究二
2
3
125
27
探究三
探究四
2
3 -3
5
=
33
5-2
=
=
32
思想方法
随堂演练
9
= 25.
(1)a+a-1; (2)a2+a-2; (3)a2-a-2.
1
1
分析:解答本题可从整体上寻求各式与条件 2 + 2 = 5 的联
系,进而整体代入求值.
1
解:(1)将2
1
2
-
+ = 5的两边平方,
得a+a-1+2=5,即a+a-1=3.
(2)由a+a-1=3,两边平方,得a2+a-2+2=9,
数, =|a|=
-, < 0.
课前篇
自主预习
一
二
2.填空
三
四
提示:①am·an=am+n;②(am)n=am·n;
m-n
③ =a (m>n,a≠0);(4)(a·b)m=am·bm.
(2)零指数幂和负整数指数幂是如何规定的?
1
提示:规定:a0=1(a≠0);00 无意义,a-n=(a≠0).
课前篇
自主预习
在幂的运算中,对于形如 m0 的式子,要注意对底数 m 是否为零进
行讨论,因为只有在 m≠0 时,m 才有意义;而对于形如
0
们一般是先变形为
,再进行运算.
-
的式子,我
课堂篇
探究学习
探究一
解:(1)
探究二
2
3
125
27
探究三
探究四
2
3 -3
5
=
33
5-2
=
=
32
思想方法
随堂演练
9
= 25.
(1)a+a-1; (2)a2+a-2; (3)a2-a-2.
1
1
分析:解答本题可从整体上寻求各式与条件 2 + 2 = 5 的联
系,进而整体代入求值.
1
解:(1)将2
1
2
-
+ = 5的两边平方,
得a+a-1+2=5,即a+a-1=3.
(2)由a+a-1=3,两边平方,得a2+a-2+2=9,
数, =|a|=
-, < 0.
课前篇
自主预习
一
二
2.填空
三
四
第四章-指数函数与对数函数PPT课件

❖ 3、在ab=N中,N=__a_b _, a=_b_N__,b=?
-
43
在ab=N中,b叫以a为底N的对数.
2 3 8 中, 3叫以2为底8的对数, 记作3=log28.
3 2 9 中,
记作2=log39.
1
0
1 中,
2
0叫以1/2为底1的对数,记作0=log1/21.
5 -1 1 中, 5
(4)y
=
x-
3 2
.
解:(1)函数 y = x 3 的定义域为 R ;
-
16
4.3幂函数
二、幂函数应用
例1 写出下列函数的定义域:
(1)y = x 3 ;
1
(2)y = x 2 ;
(3)y = x -2 ;
(4)y
=
x-
3 2
.
解:(2)函数
y
=
x
1 2
,即
y
=
x
,
定义域为 [ 0,+∞);
-
17
的函数叫做指数函数,其中 x是自变量.
函数的定义域是 R .
-
27
变式练习: 请问同学们下面的式子是不是指数函 数?
y 32x
-
28
图象
y 2x
x -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
y 0.25 0.35 0.5 0. 71 1 1.41 2 2.83 4
y
y 2x
-
7
4.2 有理指数幂
❖ 2.有理指数幂的定义
❖ 正数的正分数指数幂的意义是:
❖ amn nam(a 0 ,m ,且 n N ) ❖ 正数的负分数指数幂:
❖
-
43
在ab=N中,b叫以a为底N的对数.
2 3 8 中, 3叫以2为底8的对数, 记作3=log28.
3 2 9 中,
记作2=log39.
1
0
1 中,
2
0叫以1/2为底1的对数,记作0=log1/21.
5 -1 1 中, 5
(4)y
=
x-
3 2
.
解:(1)函数 y = x 3 的定义域为 R ;
-
16
4.3幂函数
二、幂函数应用
例1 写出下列函数的定义域:
(1)y = x 3 ;
1
(2)y = x 2 ;
(3)y = x -2 ;
(4)y
=
x-
3 2
.
解:(2)函数
y
=
x
1 2
,即
y
=
x
,
定义域为 [ 0,+∞);
-
17
的函数叫做指数函数,其中 x是自变量.
函数的定义域是 R .
-
27
变式练习: 请问同学们下面的式子是不是指数函 数?
y 32x
-
28
图象
y 2x
x -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
y 0.25 0.35 0.5 0. 71 1 1.41 2 2.83 4
y
y 2x
-
7
4.2 有理指数幂
❖ 2.有理指数幂的定义
❖ 正数的正分数指数幂的意义是:
❖ amn nam(a 0 ,m ,且 n N ) ❖ 正数的负分数指数幂:
❖
《对数函数》指数函数与对数函数PPT教学课件(第2课时对数函数及其性质的应用)

解下列不等式:
(1)log1x>log1(4-x);
7
7
(2)logx12>1;
(3)loga(2x-5)>loga(x-1).
栏目 导引
【解】
(1)由题意可得4x->x0>,0, x<4-x,
解得 0<x<2.
所以原不等式的解集为(0,2).
(2)当 x>1 时,logx12>1=logxx,
解得 x<12,此时不等式无解.
栏目 导引
第四章 指数函数与对数函数
2.已知 a=30.5,b=log312,c=log32,则(
)
A.a>c>b
B.a>b>c
C.c>a>b
D.b>a>cog312<0,0<c=log32<1,所以
a>c>b.
栏目 导引
解对数不等式
第四章 指数函数与对数函数
栏目 导引
第四章 指数函数与对数函数
与对数函数有关的值域与最值问题 已知函数 f(x)=loga(1+x)+loga(3-x)(a>0,且 a≠1). (1)求函数 f(x)的定义域; (2)若函数 f(x)的最小值为-2,求实数 a 的值.
栏目 导引
【解】
第四章 指数函数与对数函数
(1)由题意得31-+xx>>00,,解得-1<x<3.
栏目 导引
第四章 指数函数与对数函数
(3)因为 0>log0.23>log0.24, 所以 1 < 1 ,
log0.23 log0.24 即 log30.2<log40.2. (4)因为函数 y=log3x 是增函数,且 π>3,所以 log3π>log33=1, 同理,1=logππ>logπ3,即 log3π>logπ3.
第三章指数函数和对数函数5.1对数函数的概念5.2对数函数的图象和性质ppt课件

反思与感悟 比较两个同底数的对数大小,首先要根据底数来判断对 数函数的增减性;然后比较真数大小,再利用对数函数的增减性判断 两对数值的大小.对于底数以字母形式出现的,需要对底数a进行讨论. 对 于 不 同 底 的 对 数 , 可 以 估 算 范 围 , 如 log22<log23<log24 , 即 1<log23<2,从而借助中间值比较大小.
学习目标
1.理解对数函数的概念. 2.掌握对数函数的性质. 3.了解对数函数在生产实际中的简单应用. 4.了解反函数的概念及它们的图像特点.
重、对数函数的概念
一般地,我们把
函数y=logax(a>0,a≠1) 叫 作 对 数 函 数 ,
性质 (4)当x>1时,y>0,
(4)当x>1时,y<0,
0<x<1时,y<0
0<x<1时,y>0
(5)是(0,+∞)上的增函数 (5)是(0,+∞)上的减函数
三、反函数的概念 一般地,像y=ax与y=logax(a>0,且a≠1)这样的两个函数互为反函数. (1)y=ax的定义域R,就是y=logax的值域,而y=ax的值域(0,+∞)就 是y=logax的定义域. (2) 互 为 反 函 数 的 两 个 函 数 y = ax(a > 0 , 且 a≠1) 与 y = logax(a > 0 , 且 a≠1)的图像关于直线y=x对称. (3)互为反函数的两个函数的单调性相同,但单调区间不一定相同.
跟踪训练 3 设 a=log3π,b=log2 3,c=log3 2,则
√A.a>b>c
B.a>c>b
C.b>a>c
D.b>c>a
解析 ∵a=log3π>1,b=12log23,
指数函数与对数函数的关系指数函数对数函数与幂函数PPT精品推荐课件
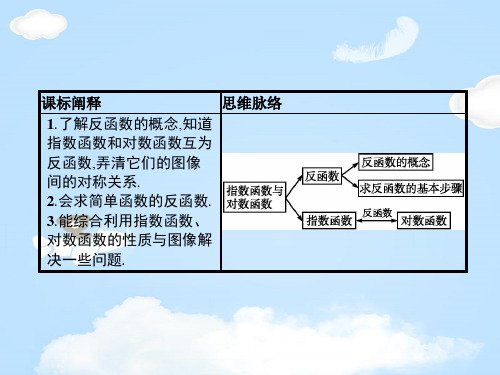
致性吗?
提示:当0<a<1时,上述两个函数均是其定义域上的减函数;当a>1
时,上述两个函数均是其定义域上的增函数.因此单调性具有一致
性,但变化速度有差异.
课前篇自主预习
一
二
3.填空.
(1)关系
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)互为反函数.
(2)图像特征
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)的图像关于
与f-1(x)互为反函数,对此不能对自变量x随意变化拓展.
课堂篇探究学习
探究一
探究二
探究三
思维辨析
当堂检测
正解:∵g(x)的图像过定点(1,2 018),
∴f(x+1)的图像过定点(2 018,1).
又∵f(x)的图像可以看作由f(x+1)的图像向右平移1个单位长度得
到的,∴f(x)过定点(2 019,1).
)
A.(0,0) B.(0,2) C.(1,1)
D.(2,0)
答案:B
解析:∵y=f(x)的图像过点(1,0),
∴其反函数y=f-1(x)的图像必过点(0,1),
即f-1(0)=1,∴y=f-1(x)+1的图像过点(0,2).
4.已知
1-3
4
f(x)= ,则 f-1 5
1+3
=
Hale Waihona Puke 答案:-21-3除D.故选B.
方法二:若0<a<1,则曲线y=ax下降且过点(0,1),而曲线y=loga(-x)
上升且过点(-1,0),所有选项均不符合这些条件.
提示:当0<a<1时,上述两个函数均是其定义域上的减函数;当a>1
时,上述两个函数均是其定义域上的增函数.因此单调性具有一致
性,但变化速度有差异.
课前篇自主预习
一
二
3.填空.
(1)关系
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)互为反函数.
(2)图像特征
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)的图像关于
与f-1(x)互为反函数,对此不能对自变量x随意变化拓展.
课堂篇探究学习
探究一
探究二
探究三
思维辨析
当堂检测
正解:∵g(x)的图像过定点(1,2 018),
∴f(x+1)的图像过定点(2 018,1).
又∵f(x)的图像可以看作由f(x+1)的图像向右平移1个单位长度得
到的,∴f(x)过定点(2 019,1).
)
A.(0,0) B.(0,2) C.(1,1)
D.(2,0)
答案:B
解析:∵y=f(x)的图像过点(1,0),
∴其反函数y=f-1(x)的图像必过点(0,1),
即f-1(0)=1,∴y=f-1(x)+1的图像过点(0,2).
4.已知
1-3
4
f(x)= ,则 f-1 5
1+3
=
Hale Waihona Puke 答案:-21-3除D.故选B.
方法二:若0<a<1,则曲线y=ax下降且过点(0,1),而曲线y=loga(-x)
上升且过点(-1,0),所有选项均不符合这些条件.
《指数与对数函数》课件

对数函数是一 种数学函数, 其定义域为所
有正实数。
对数函数的一 般形式为
y=loga(x), 其中a为底数,
x为真数。
对数函数的值 域为所有实数。
对数函数的图 像是一条向右 下方倾斜的曲 线,其斜率随 着x的增大而减
小。
对数函数的图像:一条曲线, 斜率为1/b,b为底数
指数函数的图像:一条直线, 斜率为1/b,b为底数
指数函数:定义域为全体实数, 值域为全体正实数
对数函数:定义域为正实数, 值域为全体实数
比较:指数函数的定义域更广, 对数函数的值域更广
应用:指数函数常用于描述增 长和衰减,对数函数常用于描 述对数运算和转换
指数函数: y=a^x, a>0,y随x 增大而增大
对数函数: y=loga(x), a>0,y随x 增大而减小
对数函数的性质:单调递增, 值域为R,定义域为(0, ∞)
对数函数的应用:在科学、工 程、经济等领域有广泛应用
科学计算:用于计算自然对数、 对数函数等
工程计算:用于计算电路、机 械、电子等领域的物理量
经济分析:用于计算经济增长 率、通货膨胀率等经济指标
生物学:用于计算种群数量、 基因频率等生物学指标
指数函数与对数函数的定义和性质
指数函数与对数函数的应用实例
添加标题
添加标题
添加标题
添加标题
指数函数与对数函数的图像和性质
指数函数与对数函数的综合应用技 巧
求指数函数y=2^x与对数函数y=log2(x)的交点坐标 求指数函数y=3^x与对数函数y=log3(x)的交点坐标 求指数函数y=4^x与对数函数y=log4(x)的交点坐标 求指数函数y=5^x与对数函数y=log5(x)的交点坐标
第11讲指数函数对数函数幂函数PPT课件

30
· 高中新课标总复习(第1轮)· 文科数学 · 湖南 · 人教版
立足教育 开创未来
题型三 幂函数及其简单应用
例3(1)设α∈{-1,1, 1 ,3},
则使函数y=xα的定义域为R且为2 奇函 数的所有α的值为 1,3 .
2
y=3u是增函数,
所以y 在[ 3
3-x2 3x2在(-∞,
3
2 ]上单调递增,
,+∞)上单调递减.
2
21
· 高中新课标总复习(第1轮)· 文科数学 · 湖南 · 人教版
立足教育 开创未来
点评 复合函数的值域可
采用换元法,结合中间变量的 范围求函数值域.
复合函数y=f(x)的单调性要 根据y=au,u=f(x)两函数在相应 区间上的单调性确定,遵循 “同增异减”的规律.
解析 由0<a<1知函数f(x)=logax为
减函数.故由logam<logan<0,得m>n>1.
6
· 高中新课标总复习(第1轮)· 文科数学 · 湖南 · 人教版
立足教育 开创未来
3.已知函数f(x)= 2x (x<4)
f(x-1) (x≥4), 则f(-2)= 1 ,f(5)= 8 .
4
解析
28
· 高中新课标总复习(第1轮)· 文科数学 · 湖南 · 人教版
立足教育 开创未来
变式 已知函数f(x)=log 1 (x2-2ax+3).
2
(1)若f(x)的定义域为R,求实数a的 取值范围;
(2)若函数f(x)在(-∞,1]上为增函数, 求实数a的取值范围.
解析(1)依题意,
x2-2ax+3>0对x∈R恒成立, 即Δ=(-2a)2-4×3<0,即a2<3, 解得a∈( - 3 , 3 ).
《对数的概念》指数函数与对数函数PPT优秀课件

思维脉络
公开课课件优质课课件PPT优秀课件PP T免费 下载《 对数的 概念》 指数函 数与对 数函数P PT
课前篇
自主预习
一
二
三
一、对数的概念
1.(1)某种细胞分裂时,由1个分裂成2个,2个分裂成4个,…依次类
推,那么1个这样的细胞分裂x次后,得到的细胞个数N是多少?
提示:N=2x.
(2)上述问题中,若已知分裂后得到的细胞的个数分别为8个,16个,
首页
课标阐释
1.理解对数的概念,掌握对数的
基本性质.
2.掌握指数式与对数式的互化,
能应用对数的定义和性质解方
程.
3.理解常用对数和自然对数的
定义形式以及在科学实践中的
应用.
4.了解对数的发展历史,了解数
学文化.
公开课课件优质课课件PPT优秀课件PP T免费 下载《 对数的 概念》 指数函 数与对 数函数P PT
(3)ln M=n用指数式如何表示?
提示:en=M.
2.填空
常用对数 以 10 为底数,记作 lg N
自然对数 以 e 为底数,记作 ln N,其中 e=2.718 28…
3.做一做
(1)lg 105=
答案:(1)5 (2)1
公开课课件优质课课件PPT优秀课件PP T免费 下载《 对数的 概念》 指数函 数与对 数函数P PT
(1)负数和零没有对数.
(2)loga1=0(a>0,a≠1).
(3)logaa=1(a>0,a≠1).
(4)对数恒等式log =N(a>0,且 a≠1,N>0).
公开课课件优质课课件PPT优秀课件PP T免费 下载《 对数的 概念》 指数函 数与对 数函数P PT
《对数与对数函数》指数函数、对数函数与幂函数PPT课件(对数函数的性质与图像)【品质课件PPT】

y= loga x PPT模板:/moban/
P P T背景:www.1ppt.c om /be ij ing/ P P T下载:www.1ppt.c om /xia za i/
资料下载:www.1ppt.c om /zilia o/
一般地,函数____________称为对数函数,其中 试卷下载:/shiti/
PPT教程: /powerpoint/
资料下载:www.1ppt.c om /zilia o/
个人简历:www.1ppt.c om /j ia nli/
试卷下载:www.1ppt.c om /shiti/
教案下载:www.1ppt.c om /j ia oa n/
手抄报:www.1ppt.c om /shouc ha oba o/
4.2 对数与对数函数 4.2.3 对数函数的性质与图像 第1课时 对数函数的性质与图像
第四章 指数函数、对数函数与幂函数
考点
学习目标
核心素养
理解对数函数的概念,会 对数函数的概念
判断对数函数
数学抽象
初步掌握对数函数的图
对数函数的图像
直观想象、数学运算
像与性质
对数函数的简单 能利用对数函数的性质
数学建模、数学运算
历史课件:www.1ppt.c om /ke j ia n/lishi/
问题导学
预习教材 P24-P27 的内容,思考以下问题: 1.对数函数的概念是什么?它的解析式具有什么特点? 2.对数函数的图像是什么,通过图像可观察到对数函数具有哪 些性质?
栏目 导引
第四章 指数函数、对数函数与幂函数
对数函数
历史课件:www.1ppt.c om /ke j ia n/lishi/
指数函数与对数函数PPT课件

16 4 2 4( 4 ) 2 3 27 ( ) ( ) ( ) 81 3 3 8
3 3
2. 用分数指数幂的形式表示下列各式:
1).
a2 a, a3 3 a2 , a a,
a a
5 2
a
3 4
11 3
3. 计算下列各式(式中字母都是正数)
2 3 1 2 1 2 1 3 1 6 5 6
练习
⑴ 比较大小: (2.5)
2 3<
, (2.5)
4 5
4 5
4 5
2.5
2 3
2.5 , 2.5 2.5
2 3
底数化为正数。 (2). 已知下列不等式,试比较m、n的大小
2 m 2 n ( ) ( ) 3 3
m<n
1.1m 1.1n
m<n
指数函数的应用
a>0时,向右平移a个单位; a<0时,向左平移|a|个单位.
2. y=f(x) →y=f(x)+b:上下平移
y=f(x)+b, b>0
y=f(x) y=f(x)+b, b<0
b>0时,向上平移b个单位; b<0时,向下平移|b|个单位.
对称变换 y=f(x) →y=f(-x): (关于y轴对称) y=f(x) →y= -f(x): (关于x轴对称) y=f(x) →y= -f(-x): (关于原点对称) y=f(-x)
a>1
6
0<a<1
6
图 象
1
5
5
4
4
3
3
2
2
1
1
1
-4
-2
3 3
2. 用分数指数幂的形式表示下列各式:
1).
a2 a, a3 3 a2 , a a,
a a
5 2
a
3 4
11 3
3. 计算下列各式(式中字母都是正数)
2 3 1 2 1 2 1 3 1 6 5 6
练习
⑴ 比较大小: (2.5)
2 3<
, (2.5)
4 5
4 5
4 5
2.5
2 3
2.5 , 2.5 2.5
2 3
底数化为正数。 (2). 已知下列不等式,试比较m、n的大小
2 m 2 n ( ) ( ) 3 3
m<n
1.1m 1.1n
m<n
指数函数的应用
a>0时,向右平移a个单位; a<0时,向左平移|a|个单位.
2. y=f(x) →y=f(x)+b:上下平移
y=f(x)+b, b>0
y=f(x) y=f(x)+b, b<0
b>0时,向上平移b个单位; b<0时,向下平移|b|个单位.
对称变换 y=f(x) →y=f(-x): (关于y轴对称) y=f(x) →y= -f(x): (关于x轴对称) y=f(x) →y= -f(-x): (关于原点对称) y=f(-x)
a>1
6
0<a<1
6
图 象
1
5
5
4
4
3
3
2
2
1
1
1
-4
-2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图象要看a 与1,大1撇来小1捺, 简洁明了单调性,指过(0,1)对(1,0)。
异底函数看一线,指看x=1,对看y=1, 平移对称注界线,常画图象好处多。
❖ 在区间[2,4]上是增函数?若存在,求出a的 取值范围。
1:已知m是非零常数,对x∈R成立f(x+m)= 1 f (x)
问f(x)是否是周期函数?
! f (x)
指对: 指对本源一家亲,恒等变换常使用; 两边乘方与对数,降级运算显神效。 运算比较相同底,正负确定明0、1; 换底公式帮对数,实在不行看图象。
变:设a>1实数x,y满足logax+logxa-logxy+3=0 (1)用logax表示logay (2)若y有最小值1/32,求此时a与x的值
例3、设函数f(x)=|lgx|,若0<a<b,且f(a)>f(b),
证明ab<1
例4、已知 2 x2 x ( 1 ) x2 ,求函数 y 2 x 2 x
❖ 变:已知log2x=log3y=log5z=-2,则
1
1
1
x 2、y 3、z 5 由小到大的排列顺序为__
1
1
1
y3 x2 z5
两边同乘方
7已知1<x<a,比较 log a 2 x logax2 、loga(logax)
的大小_____________
三、求函数的单调区间
1、函数y=log0.1(6+x-2x2)的单调递增区间
单调性 减函数 增函数 减函数 增函数
例1、若y=(a2-3a+3)ax是指数函数,则a=_____. 例2、已知函数y=ax在[0,1]上的最大值与最小值 之和为3,则a=_______
变:logax在[2,3]的最大值比最小值大1, 则a的值? 例3、函数y = 2-x+1(x>0)的反函数是( )一定二式
A(0,1/2) B(1/2,1) C(1,3/2) D(3/2,2)
▪ 5:若loga2/5<1,则实数a的取值范 围是_(0_,_2_/5_)_∪_(_1_,+_∞_).
分 类
log
a
2 5
log
a
a
讨
当0<a<1时,a<2/5,此时0<a<2/5;
论
当a>1时,a>2/5,此时a>1
❖ 变:已知loga(a2+1)<loga2a<0,则实数a的取值范
题题通:第12练 24页16
第14练 28页第16题
例2、已知函数f(x)=log3x+2,x∈[1,9],求函 数g(x)=[f(x)]2+f(x2)的最大值。
注意定义域
变、设不等式 2(log 1 x)2 9log 1 x 9 0 的
2
2
解集是M,求当x∈M时函数 的最大值与最小值。
f
(x)
是__[_1/_4,_2)__。
2、已知函数f(x)=log1/a(2-x)在其定义域上单 调递增,则函数g(x)=loga(1-x2)的单调递
减区间是_[0_,1_) _。
y=loga(2-ax) y=loga(ax2-x) 3、y=loga(2-ax)在[0,1]上是减函数,则a的取值
范围( ) A.(0,1) B.(1,2) C.(0,2) D.[2,+∞)
的值域。
4
例5、设
f
(log a
x)
a( x 2 x(a 2
1) 1)
.
⑴求f(x)的定义域;
⑵在y=f(x)的图象上是否存在两个不同的点,使过这 两点的直线与x轴平行?证明你的结论。
❖ 例6、已知函数
f (x) log
(x a)
2
的图象过原点.
❖ ⑴若 f (x 3), f ( 2 1), f (x 4)成等差数列,求x值
y lg( 2 1)
1 x
的图象关于( )
A.x轴成轴对称图形 B.y轴成轴对称图形
C.直线y=x成轴对称图形D.原点成中心对称图形
问y lg(1 x 2 ) 的奇偶性 | x 3 | 3
六、综合运用:
例1、已知三个不为1的正数a、b、c成等比数列, x>0。且x≠1。若logax,logbx,logcx成等差数列,求 证:logba•logbc=1。 例2:若lg(x-y)+lg(x+2y)=lg2+lgx+lgy, 求x/y的值。
A.0.76<log0.76<60.7 B.0.76<60.7<log0.76 C. log0.76<60.7<0.76 D. log0.76<0.76<60.7
3、f(x)在[0,2]是减函数,f(x-2)关于x=2对称, 比较f(-1),f(log0.51/4),f(lg0.5)的大小。
变:f(2x-1)是偶函数,f(2x)在(-∞,-1/2]是增函数 , 比较f(-1),f(log0.51/4),f(lg0.5)的大小。
⑴写出函数y=g(x)的解析式;
⑵若当x∈[a+2,a+3]时,恒有|f(x)-g(x)|≤1试确定a 的取值范围。
例10、已知定义域为R的奇函数,且满足 f(x+2)=-f(x),当x∈[0,1]时,f(x)=2x-1.
❖ 求f(log1/224)
❖ 例11、是否存在实数a,使得 f (x) loga(ax x)
A.y log 2 (x 1), x (1,2) B.y log 2 (x 1), x (1,2)
C.y log 2 (x 1), x (1,2] D.y log 2 (x 1), x (1,2]
❖ 例4、若a>1,0<b<1,且 alogb ( x3) 1
❖ 则x的取值范围是______。
(log 2
x 2
)(log
2
x) 8
可放在最值讲
五、函数的奇偶性
▪
1设a>0,
f (x)
ex a
a ex
是R上的偶函数,则
a=___________.
❖ 2、已知a>0且a≠1,
❖ 则f(x)是(A )
❖ A.奇函数 ❖ C.非奇非偶函数
f
(x)
1 1 ax
1 2
B.偶函数 D.奇偶性与a有关
3、函数
y=ax
?y=ax与y=a-x的图象关系______
?logax与log1/ax的图象关系____
▪ 例7、设函数f(x)=ax,g(x)=bx(a、b都是不等
于1的正数)的反函数分别为f-1(x),g-1(x),
若lga+lgb=0,则y=f-1(x),y=g-1(x)的图象
关于(B )
▪ A.直线y=x对称
围是( C )
❖ A.(0,1) B.(0,1/2) C.(1/2,1) D.(1,+∞)
▪ 6、设a、b、c都是正数,且3x=4y=6z,
▪ 则( B ) 两边同取对数、同乘方
▪ A.1/z=1/x+1/y
B.2/z=2/x+1/y
▪ C.1/z=2/x+2/y
D.2/z=1/x+2/y
变:比较3x、4y、6z的大小
四、求值域
❖ 1、当x∈[-1,1]时,函数f(x)=3x-2的值域 是( )
A.[-5/3,1] B.[-1,1] C.[1,5/3] D.[0,1]
❖ 2、已知函数y=4x-3·2x+3,当其值域为 [1,7]时,x的取值范围为( )
❖ A.[2,4]
B.(-∞,0]
❖ C.(0,1)∪[2,4) D.(-∞,0]U[1,2]
▪ 指数函数y=ax(a>0,a≠1)
▪ 当a>1时,a越大图象越接近y轴;
▪ 当0<a<1时,a越小图象越接近y轴。
第一象限
▪ 对数函数y=logax(a>0,a≠1)
图高底大 指 y对 x
▪ 当a>1时,a越大图象越接近x轴;
▪ 当0<a<1时,a越小图象越接近x轴。
异底函数看一线,指看x=1,对看y=1
B. x轴对称
▪ C. y轴对称
D.原点对称
一、函数的图象 ▪ 1(98高考)函数y=a|x|(a>1)的图象是( B )
y
y
y
y
1
1
1
0
x
0
x
A
B
0
x
0
x
C
D
▪ 3、设a>0且a≠1,并使得不等式ax>1的解集
是{x|x<0},则下面的图象可能成立的是( )C
y y=ax
y
y
y=|log ax| y=a|x|
4、用“<”或“>”填空:
1(
4
)
1 2
___<___(
9
1
)3;
5
10
无理化有理:
1、同乘方2、有理化
2log1.1 0.7 ___<___log1.2 0.7.
数形结合
5、函数f
(x)
ex ex
ex ex
的反函数f
1 (x),
k | f 1(0.8) | / | f 1(0.6) | 则k的范围
2010届高考数学复习 强化双基系列课件
09《指数函数与对数函数》
解析式 y=ax(a>0,a≠1)
定义域
R
y=logax(a>0,a≠1)
R+
值域 图象
R+
y 0<a<1
异底函数看一线,指看x=1,对看y=1, 平移对称注界线,常画图象好处多。
❖ 在区间[2,4]上是增函数?若存在,求出a的 取值范围。
1:已知m是非零常数,对x∈R成立f(x+m)= 1 f (x)
问f(x)是否是周期函数?
! f (x)
指对: 指对本源一家亲,恒等变换常使用; 两边乘方与对数,降级运算显神效。 运算比较相同底,正负确定明0、1; 换底公式帮对数,实在不行看图象。
变:设a>1实数x,y满足logax+logxa-logxy+3=0 (1)用logax表示logay (2)若y有最小值1/32,求此时a与x的值
例3、设函数f(x)=|lgx|,若0<a<b,且f(a)>f(b),
证明ab<1
例4、已知 2 x2 x ( 1 ) x2 ,求函数 y 2 x 2 x
❖ 变:已知log2x=log3y=log5z=-2,则
1
1
1
x 2、y 3、z 5 由小到大的排列顺序为__
1
1
1
y3 x2 z5
两边同乘方
7已知1<x<a,比较 log a 2 x logax2 、loga(logax)
的大小_____________
三、求函数的单调区间
1、函数y=log0.1(6+x-2x2)的单调递增区间
单调性 减函数 增函数 减函数 增函数
例1、若y=(a2-3a+3)ax是指数函数,则a=_____. 例2、已知函数y=ax在[0,1]上的最大值与最小值 之和为3,则a=_______
变:logax在[2,3]的最大值比最小值大1, 则a的值? 例3、函数y = 2-x+1(x>0)的反函数是( )一定二式
A(0,1/2) B(1/2,1) C(1,3/2) D(3/2,2)
▪ 5:若loga2/5<1,则实数a的取值范 围是_(0_,_2_/5_)_∪_(_1_,+_∞_).
分 类
log
a
2 5
log
a
a
讨
当0<a<1时,a<2/5,此时0<a<2/5;
论
当a>1时,a>2/5,此时a>1
❖ 变:已知loga(a2+1)<loga2a<0,则实数a的取值范
题题通:第12练 24页16
第14练 28页第16题
例2、已知函数f(x)=log3x+2,x∈[1,9],求函 数g(x)=[f(x)]2+f(x2)的最大值。
注意定义域
变、设不等式 2(log 1 x)2 9log 1 x 9 0 的
2
2
解集是M,求当x∈M时函数 的最大值与最小值。
f
(x)
是__[_1/_4,_2)__。
2、已知函数f(x)=log1/a(2-x)在其定义域上单 调递增,则函数g(x)=loga(1-x2)的单调递
减区间是_[0_,1_) _。
y=loga(2-ax) y=loga(ax2-x) 3、y=loga(2-ax)在[0,1]上是减函数,则a的取值
范围( ) A.(0,1) B.(1,2) C.(0,2) D.[2,+∞)
的值域。
4
例5、设
f
(log a
x)
a( x 2 x(a 2
1) 1)
.
⑴求f(x)的定义域;
⑵在y=f(x)的图象上是否存在两个不同的点,使过这 两点的直线与x轴平行?证明你的结论。
❖ 例6、已知函数
f (x) log
(x a)
2
的图象过原点.
❖ ⑴若 f (x 3), f ( 2 1), f (x 4)成等差数列,求x值
y lg( 2 1)
1 x
的图象关于( )
A.x轴成轴对称图形 B.y轴成轴对称图形
C.直线y=x成轴对称图形D.原点成中心对称图形
问y lg(1 x 2 ) 的奇偶性 | x 3 | 3
六、综合运用:
例1、已知三个不为1的正数a、b、c成等比数列, x>0。且x≠1。若logax,logbx,logcx成等差数列,求 证:logba•logbc=1。 例2:若lg(x-y)+lg(x+2y)=lg2+lgx+lgy, 求x/y的值。
A.0.76<log0.76<60.7 B.0.76<60.7<log0.76 C. log0.76<60.7<0.76 D. log0.76<0.76<60.7
3、f(x)在[0,2]是减函数,f(x-2)关于x=2对称, 比较f(-1),f(log0.51/4),f(lg0.5)的大小。
变:f(2x-1)是偶函数,f(2x)在(-∞,-1/2]是增函数 , 比较f(-1),f(log0.51/4),f(lg0.5)的大小。
⑴写出函数y=g(x)的解析式;
⑵若当x∈[a+2,a+3]时,恒有|f(x)-g(x)|≤1试确定a 的取值范围。
例10、已知定义域为R的奇函数,且满足 f(x+2)=-f(x),当x∈[0,1]时,f(x)=2x-1.
❖ 求f(log1/224)
❖ 例11、是否存在实数a,使得 f (x) loga(ax x)
A.y log 2 (x 1), x (1,2) B.y log 2 (x 1), x (1,2)
C.y log 2 (x 1), x (1,2] D.y log 2 (x 1), x (1,2]
❖ 例4、若a>1,0<b<1,且 alogb ( x3) 1
❖ 则x的取值范围是______。
(log 2
x 2
)(log
2
x) 8
可放在最值讲
五、函数的奇偶性
▪
1设a>0,
f (x)
ex a
a ex
是R上的偶函数,则
a=___________.
❖ 2、已知a>0且a≠1,
❖ 则f(x)是(A )
❖ A.奇函数 ❖ C.非奇非偶函数
f
(x)
1 1 ax
1 2
B.偶函数 D.奇偶性与a有关
3、函数
y=ax
?y=ax与y=a-x的图象关系______
?logax与log1/ax的图象关系____
▪ 例7、设函数f(x)=ax,g(x)=bx(a、b都是不等
于1的正数)的反函数分别为f-1(x),g-1(x),
若lga+lgb=0,则y=f-1(x),y=g-1(x)的图象
关于(B )
▪ A.直线y=x对称
围是( C )
❖ A.(0,1) B.(0,1/2) C.(1/2,1) D.(1,+∞)
▪ 6、设a、b、c都是正数,且3x=4y=6z,
▪ 则( B ) 两边同取对数、同乘方
▪ A.1/z=1/x+1/y
B.2/z=2/x+1/y
▪ C.1/z=2/x+2/y
D.2/z=1/x+2/y
变:比较3x、4y、6z的大小
四、求值域
❖ 1、当x∈[-1,1]时,函数f(x)=3x-2的值域 是( )
A.[-5/3,1] B.[-1,1] C.[1,5/3] D.[0,1]
❖ 2、已知函数y=4x-3·2x+3,当其值域为 [1,7]时,x的取值范围为( )
❖ A.[2,4]
B.(-∞,0]
❖ C.(0,1)∪[2,4) D.(-∞,0]U[1,2]
▪ 指数函数y=ax(a>0,a≠1)
▪ 当a>1时,a越大图象越接近y轴;
▪ 当0<a<1时,a越小图象越接近y轴。
第一象限
▪ 对数函数y=logax(a>0,a≠1)
图高底大 指 y对 x
▪ 当a>1时,a越大图象越接近x轴;
▪ 当0<a<1时,a越小图象越接近x轴。
异底函数看一线,指看x=1,对看y=1
B. x轴对称
▪ C. y轴对称
D.原点对称
一、函数的图象 ▪ 1(98高考)函数y=a|x|(a>1)的图象是( B )
y
y
y
y
1
1
1
0
x
0
x
A
B
0
x
0
x
C
D
▪ 3、设a>0且a≠1,并使得不等式ax>1的解集
是{x|x<0},则下面的图象可能成立的是( )C
y y=ax
y
y
y=|log ax| y=a|x|
4、用“<”或“>”填空:
1(
4
)
1 2
___<___(
9
1
)3;
5
10
无理化有理:
1、同乘方2、有理化
2log1.1 0.7 ___<___log1.2 0.7.
数形结合
5、函数f
(x)
ex ex
ex ex
的反函数f
1 (x),
k | f 1(0.8) | / | f 1(0.6) | 则k的范围
2010届高考数学复习 强化双基系列课件
09《指数函数与对数函数》
解析式 y=ax(a>0,a≠1)
定义域
R
y=logax(a>0,a≠1)
R+
值域 图象
R+
y 0<a<1
