北大光华管理学院金融经济学课件-课程大纲
lecture 4

1. 2. 3. We should care about an asset’s return and risk characteristics. Investors are risk-averse: For a given level of expected return, investors prefer less risk to more risk. There is an important difference between the risk of individual assets, versus portfolios of assets, all due to the impact of diversification. Thus, only the portion of an asset’s risk that is non-diversifiable (its market risk) matters to the investors because this is the risk they will be exposed to when they include the asset in a diversified portfolio. The impact of the asset’s diversifiable risk will be eliminated. Non-diversifiable risk is measured by the stock’s beta.
4.
5.
1
Learning Objectives
• Know how to calculate portfolio returns, betas, and required rates of return. • Be able to use the Capital Asset Pricing Model to assess whether an asset is correctly priced, overpriced or underpriced. • Be able to explain the effects of risk, risk aversion and inflation on required rates of return.
北大经济金融课件_本科生证券投资学讲义(光华)_证券投资学第10章

2012-8-20
证券投资学
期权定价的技巧被广泛的应用到许多金融领域
和非金融领域,包括各种衍生证券定价、公司 投资决策等。 学术领域内的巨大进步带来了实际领域的飞速 发展。期权定价的技巧对产生全球化的金融产 品和金融市场起着最基本的作用。 近年来,从事金融产品的创造及定价的行业蓬 勃发展,从而使得期权定价理论得到不断的改 进和拓展。
证券投资学
2012-8-20
p
K
2012-8-20 证券投资学 • 图2 看跌期权在到期日的收益
ST
注意,看跌期权在 T 时的价值是有界的,
而看涨期权在 T 时的价格是无界的。相 反,当写一份看涨期权时,可能的损失 是无界的。
ห้องสมุดไป่ตู้
2012-8-20
证券投资学
期权的写者的收益
– 看涨期权的写者在到期日的收益
既然期权的持有者获得的是权利而不需
要承担什么义务,他就必须花钱购买这 个权利,那么,公平的价格应该是多少? 这是证券投资学研究的重要内容。
2012-8-20
证券投资学
2 影响欧式期权价格的因素
本章的主要目的:如何确定以金融证券
为标的物的欧式期权的价格。 在整个一章中假设:如果无特殊说明, 标的物在到期日以前不支付红利。
• 如果在到期日之前的任何时间以及到期日都能执行,我们称这种 期权为美式期权。如果只能在到期日执行,称为欧式期权。 • 美式和欧式这两个名词曾代表了以股票为标的物的期权在美洲和 欧洲的结构形式。但是现在,它们已成为反映两种不同结构的期 权的标准名词,而不管期权是在哪儿发行的。
2012-8-20
证券投资学
金融工程北大光华金融工程研究生课程讲义

课程说明1.本课程为金融学专业硕士生的必修课程,系统地讲授课程说明1.授课方式:讲授课程说明1.评估方法课程说明1.授课教师:唐国正教学内容1.什么是金融工程?什么是金融工程?定义1.包括设计、开发和实施具有创新意义的金融工具和金什么是金融工程?创新1.创新的三个层次什么是金融工程?金融工程产品作为金融创新活动的结果,金融工程产品可能是教学内容1.什么是金融工程?金融创新的动机税法与监管的变化1.Merton Miller认为:金融创新的动机减少金融约束1.Silber认为金融创新的过程实质上是公司试图放松面金融创新的社会价值R. C. Merton认为金融创新可以从三个方面提升经济公司(RJR金融创新的社会价值零和对策?1.许多经济学家认为,从全社会的角度来看,以绕开监教学内容1.什么是金融工程?金融工程的创新标准1.一种金融工具或者金融策略成为一项金融创新的条件金融工程的创新标准1.如果用Van Horne的标准来衡量,那么一些过去被认金融工程的创新标准债权-股权互换的税收套利1.A公司:金融工程的创新标准债权-股权互换的税收套利1.这笔交易对A公司来说是有意义的教学内容1.什么是金融工程?推动金融工程发展的因素在综合了Miller、Silber与Van Horne的研究成果教学内容1.什么是金融工程?应用领域综述1.开展金融工程活动的主体应用领域融资1.在融资方面,一种类型的金融工程活动是:在各种约应用领域融资4.另一种类型的金融工程活动与公司并购有关,在并购应用领域投资与现金管理1.在投资方面,金融工程师开发出了各种各样的中长期应用领域管理发行人的风险1.在风险管理领域,金融工程发挥着重要作用应用领域管理投资者的风险1.挑战性q90年代市场上出现的与股票指数挂钩的债券应用领域风险管理管理投资者的风险与管理发行人的风险迥然不同应用领域套利1.开发交易策略来利用不同地点、不同时间、不同工具教学内容1.什么是金融工程?应用领域非金融类公司1.金融工程在公司层面有着非常重要的应用应用领域非金融类公司1.对公司来说,金融工程可以用来应用领域非金融类公司安然公司(Enron) 应用领域非金融类公司1.1993年,为了便于供应商与最终消费者管理价格风教学内容1.什么是金融工程?理论基础1.作为一门应用学科,金融工程的理论基础主要来自于基本工具1.金融工程的工具可以分成两部分,一部分是基本的金来,用以实现某一特定的目标其它理论、工具1.除了应用上述理论与工具以外,金融工程活动常常还。
金融学概论讲义(北大光华管理学院)lecture06

Principles of FinanceLecture 06Forward and Futures ContractsThe Nature of Derivatives∙ A derivative is an instrument whose value depends on the values of other more basic underlying variables∙Examples of derivatives-F orward-F utures-O ptions-S waps……Derivative Markets ∙Exchange Traded-Standard products-Trading floor or computer trading-Virtually no credit risk∙Over-the-Counter (OTC)-Non-standard products-Telephone market-Credit riskForward Contracts∙ A forward contract is an agreement made today to buy or sell an asset at a certain time in the future for a certain price (referred to as the forward price or the delivery price)∙The delivery price is usually chosen so that the initial value of the contract is zero; No money changes hands when contract is first negotiated and it is settled at maturity∙An OTC agreement between two parties and both parties are subject to credit risk∙Both parties have the obligation to honor the contractSettlement of Forward Contracts∙Physical: requires delivery of actual assets∙ Cash settled: requires only the exchange of the difference between the delivery price and the prevailing spot price at maturity∙Suppose that:Long 3-month Gold forwardDelivery price $300Spot price at t = 3 months: $320P/L from a Long Forward PositionS, TP/L from a Short Forward PositionSTFutures Contract∙Futures are standardized forward contracts.∙Whereas a forward contract is traded OTC a futures contract is traded on an exchange∙Specifications need to be defined:-The underlying asset-Delivery location-Maturity date and delivery time-Method of settlement∙Most contracts are closed out before maturityFeatures Promoting Liquidity ∙Standardized Contract-Maturity dates-Contract size-Price tick size, i.e. minimum price movement-The underlying asset (especially commodities) ∙Organized exchangesFeatures Reducing Credit Risk∙Daily settlement: Futures contracts are marked to market and settled at the end of every business day∙Margin account: To buy or sell a futures contract, the investor is required to post a specified margin to guarantee contract performance∙Clearinghouse: The clearinghouse does not take a position in any trade but interpose itself between two parties in every transactionMargin Accounts∙ A margin is cash or marketable securities deposited by an investor with his or her broker∙The balance in the margin account is adjusted to reflect daily settlement (profit or loss)∙Initial margin: The amount a trader must deposit into his/her trading account (i.e. margin account) when establishing a futures position∙When the balance in the margin account falls to, or below, a maintenance margin level, the trader receives a margin call and is requested to top up the account to the initial level. The extra funds deposited are known as a variation margin∙If the balance in the margin account exceeds the initial margin level, the trader is entitled to withdraw the excess funds in the accountExample of the Margin Account ∙An investor takes long position in $/£ futures∙Contract size: £62,500∙Initial margin: 1,485$∙Maintenance margin: 1,100$Date SettlementPrice OpeningBalance($)DailyP/L ($)ClosingBalance($)Margincall ($)Cumulative P/L ($)1.6500 1,48501/11 1.6508 1,485 50 1,535 50 02/11 1.6412 1,535 -600 935 550 -550 03/11 1.6384 1,485 -175 1,310 -725 04/11 1.6456 1,310 450 1,760 -275 05/11 1.6492 1,760 225 1,985 -50The Economic Function of Futures MarketsThe futures markets facilitate the re-allocation of exposure to commodity price risk among market participants.By providing a means to hedge the price risk associated with storing a commodity, futures contracts make it possible to separate the decision of whether to physically store a commodity from the decision to have financial exposure to price changes.The Economic Function of Futures MarketsThe existence of the futures market for wheat conveys information to all producers, distributors, and consumers; and this eliminates the necessity for market participants to gather and process information in order to forecast the future spot priceSuppose the commodity is wheat, and next year’s crop is expected to be much higher than average, then futures prices may be lower than the spot, (the spread may be negative,) nobody will store wheat.The Law of One Price and Arbitrage∙In a competitive market, if two assets are equivalent they will tend to have the same price∙The law of one price is enforced by a process called arbitrage∙Arbitrage is the purchasing of a set of assets, and immediate sale of another set of assets, in such a way as to earn a sure profit from price differences∙Arbitrage process brings two equivalent assets to the same price, this is known as market clearing.An Arbitrage Opportunity?∙Shares of General Motors (GM) are listed on both NYSE and LSE ∙The quoted price is £100 in London and $148 in New York∙The current exchange rate is $1.4500/£∙An arbitrage opportunity?Another Arbitrage Opportunity?∙There are two investment portfolios: portfolio A and portfolio B∙The payoffs at maturity are as follows:State 1 State 2Portfolio A $70 $100Portfolio B $70 $100∙The current quoted price of portfolio A is $80 and the current quoted price for portfolio B is $82∙An arbitrage opportunity?Framework for Forward/Future Pricing ∙Future price: price of the future∙Spot price: price of the underlying asset at present∙Future spot price: price of the underlying asset in the futureFramework for Forward/Future Pricing Suppose you have some spare cash, and you want to invest it in gold in a year’s time. There are 2 ways to do it:A.Buy gold at the spot price with your money, store it for a year(which means you incur some storage costs), sell it at the future spot price.B.Enter into a forward/future contract of gold, put your money in abank for a year, buy A at the forward/future price in the end of the year, sell it at the future spot price.Since the two strategies are equivalent, they must provide the same return so that there are no arbitrage opportunities.Framework for Forward/Future PricingDenote S as the spot price of gold, F as the forward/future price of gold, FS as the future spot price of gold, s as the storage cost of gold as a fraction of spot price, r as the risk-free interest rate:Return of A: FS S s S -- Return of B: FS FrS -+FS S FS Fs rS S---=+Therefore: (1)F r s S =++Framework for Forward/Future Pricing∙Forward price must be arbitrage-free∙Suppose that-The spot price of gold is US$300-The 1-year US$ interest rate is 8% per annum with annual compounding-Storage costs 2% of gold.-The forward-spot-price-parity relation implies that the one-year forward price is:+=++F⨯rs=S+08)30033002.0)1(.01(=∙Forward prices above $330 permit arbitrage-Suppose the forward price is $340-At time t = 0- Sell gold forward at $340- Borrow $300 at 8% pa- Purchase gold in the spot market at $300, store for a year (storage costs $6)-At time t = 1 year- Deliver gold and receive $340-Pay back loan with interest ($324)-Pay storage cost: ($6)- Make a profit of $10: 340-324-6=10∙Forward prices below $330 permit arbitrage-Suppose the forward price is $320-At time t = 0-Buy gold forward at $320-Sell short gold in the spot market at $300 (borrow gold and sell it immediately)-Deposit $300 at 8% pa-At time t = 1 year-Accept delivery of gold for $320: ($320)-Return the gold and receive storage cost: $6-Receive deposit with interest of $324-Make a profit of $10: 324+6-320=10Financial FuturesThe underlying asset of a financial future is a financial instrument, e.g. stock, bond, foreign currency, etc.Example: Share A has a spot price of $100 (S=100), the risk-free interest rate is 8% (r=0.08) with annual compounding, what’s the forward price?Forward-spot-price-parity for a share with no dividend with maturity of T years:T1(+=SrF)Financial FuturesThe investor has two equivalent investment strategies:1.buy one share A, hold it for a year, and sell it at the future spotprice of 1S. Cash flow in a year’s time: 1S2.buy a forward/future contract of share A at the price of F, make adeposit in a risk-free asset with future value of F, take the money out after a year, and buy the share at F, sell it in the market at the future spot price of 1S. Cash flow in a year’s time: 1SThe law of one price says that they should have the same price today since they produce the same amount of cash flow in a year’s time!Financial FuturesPrice of strategy 1: the spot price of share A: SPrice of strategy 2: the amount of cash invested into the risk-free asset so as to generate F in a year’s time: F/(1+r)Therefore: S=F/(1+r)Rearranging, we have:F+=S)1(rIf the futures contract matures in T years, it becomes:T=1(+rSF)Financial FuturesWhat if share A pays dividend of D in a year’s time?Again the investor has two equivalent strategies:Strategy 1: buy share A at the spot price S, hold it for one year, receive dividend of D, and sell the share at the future spot price of S. Cash flow in a year’s time: 1S+ D1Strategy 2: buy a forward/future contract at the price of F, make an investment in a risk-free asset with future value of F+D, take the money out after a year, buy the share at F, sell it in the market at the future spot price of 1S. Cash flow in a year’s time: 1S+DFinancial FuturesPrice of strategy 1: the spot price of share A: SPrice of strategy 2: the amount of cash invested into the risk-free assetso as to generate F+D in a year’s time (F+D)/(1+r)Applying the law of one price, we have: S=(F+D)/(1+r) Rearranging, we have the forward-spot-price-parity of a share with dividend payment:F=S(1+r)-DThe Forward Price is not a Forecast of Future Spot Price The forward price is obtained without risk from the current spot and risk free investmentThe spot value at a future date is obtained by investing in the security and accepting (market) risk, and this risk must be rewardedFX Forward RateDefine HC r and FC r as the effective interest rates at home andabroadFCHCr r S F ++=11where F and S are defined as the number of units of HC per unit of FC. For example, suppose £1=$1.6, then F =1.6 and $r r HC =, £r r FC = if you are buying a pound future; F =0.625 and £r r HC =, $r r FC = if you are buying a dollar future.The FX Forward RateSuppose an investor wants to buy a futures contract of pound sterling at F , i.e. he can buy pound at the price of £1=$F in a year’s time. The spot price of pound is S , i.e. £1=$S . So here pound is the foreign currency, dollar is the home currency. The risk-free interest rates are: $r r HC =, £r r FC =. What is the proper price of the future contract?The investor has two equivalent strategies: Stragegy 1:At t=0: Enter into a futures contract of pound with futures price of F . Cash flow: 0At t=1: Buy pound at F . Cash flow: FThe FX Forward RateStrategy 2:At t=0: Borrow )1/(£r S + of US dollars, change into £1/(1)r + of pounds, put it in a bank at the pound interest rate. Cash flow: 0At t=1, take the money out (in pound), pay back the dollar loan. Cashflow: $£11r Sr ++The FX Forward RateSince the two strategies both will give you one pound in a year’s time, the law of one price says that they have the same price, i.e. the amount of investment of these two strategies must be the same:$£11r F Sr +=+More generally:FCHCr r SF ++=11Pricing FX Forward Contract∙ Suppose that:Spot $/£: 1.4222One-year $ interest rate: %00.5 per annum with annual compounding One-year £ interest rate: %00.6 per annum with annual compounding∙ The six-month £ forward rate:415.10296.010247.014222.11111£$=++⨯=++=++=r r S r r S F FC HCAs a rule of thumb, if the foreign currency offers a higher interest rate, the future price of the foreign currency will be lower than the spot price.Corporate Applications: Hedging∙Receive FC payment at a future date ⇒ sells FC forward short∙Boeing has just sold 10 Boeing-747s to British Airways with total price of £200m payable in one year’s time∙Boeing can hedge this cash flow in £ by selling £ forward short∙If the one-year forward rate is $1.60/£, so Boeing will receive $320m no matter how exchange rate $/£ movesCorporate Applications: Hedging∙Make FC payment at a future date ⇒ buys FC forward (long)∙An US company imported some goods from Switzerland and is due to pay SFr100m in six months’ time∙The company can hedge its exposure to SFr by buying SFr forward. The six-month forward rate is SFr1.54/$, so the company is required to pay $64.94mThe Role of Expectations in Determining Exchange Rates Consider a world in which there are two countries, Domestic & Foreign, and conditions are such in each country that the yield curves are flat, with yields of 5% and 10% respectively.Further assume that the exchange rate is 1 todayThe 1-year forward is 1*1.05/1.10=0.9545The Role of Expectations in Determining Exchange Rates If the interest rate in Foreign is higher than in Domestic, one explanation may be that the rate of inflation is higher.Assume no taxes, and the interest rate difference is the result inflation being 5% and 10% respectively.Then the price dynamics of both countries will result in an exchange rate of 0.9545 next year, which is also the forward rate.The Role of Expectations in Determining Exchange Rates In real life, things are not so simple, but several mechanisms may be postulated that support the expectations hypothesis.International investor confidence, and their forecasts of inflation, place price pressure on both spot and forward exchange rates through the international bond market。
北大光华管理学院金融经济学课件百年回顾

到许多结果。
n
从此,金融经济学就开始以无套利假
设作为出发点。
PPT文档演模板
北大光华管理学院金融经济学课件百 年回顾
n 以无套利假设作为出发点的一大成就也就 是布莱克-肖尔斯期权定价理论。
n 所谓 (股票买入) 期权是指以某固定的执行 价格在一定的期限内买入某种股票的权利。 期权在它被执行时的价格很清楚,即:如果 股票的市价高于期权规定的执行价格,那么 期权的价格就是市价与执行价格之差;如果 股票的市价低于期权规定的执行价格,那么 期权是无用的,其价格为零。
北大光华管理学院金融经济学课件百 年回顾
1997 年诺贝尔经济奖获得者
•默顿 (R. Merton, 1944~) 《连续时间 金融学》
•肖尔斯 (M. Scholes, 1941~) 期 权定价公式
布莱克(F. Black, 1938~1995) 期权定价公式
1973 年布莱克-肖尔斯-默 顿期权定价理论问世
n 如果把各证券的投资比例看作变量,问题就归 结为怎样使证券组合的收益最大、风险最小的数 学规划。
PPT文档演模板
北大光华管理学院金融经济学课件百 年回顾
n
对每一固定收益都求出其最小风险,那么
在风险-收益平面上,就可画出一条曲线,它称
为组合前沿。
n
马科维茨理论的基本结论是:在证券允许
卖空的条件下,组合前沿是一条双曲线的一支;
在证券不允许卖空的条件下,组合前沿是若干段
双曲线段的拼接。
n
组合前沿的上半部称为有效前沿。对于有
效前沿上的证券组合来说,不存在收益和风险两
方面都优于它的证券组合。
PPT文档演模板
北大光华管理学院金融经济学课件百 年回顾
北京大学-光华管理学院-实证金融学EMF_MS_09_Lecture_5

• Shyam-Sunder and Myers(1999)说明,很多当前 的实证检验都缺乏区分这些理论的统计效力
税率
• 不同国家:公司面临的名义税率可能不同 • 公司实际有效税率=公司所得税 / 税前利润 • 由于存在执行过程中的各种税基调整(如税收优惠),使 得名义税率往往难以真实反映公司的所得税负担 • 针对名义税率,不同税制下税率之间也不具可比性
– 平均负债率 – 发展中国家之间差异与发达国家之间的差异 – 市值负债率与 帐面负债率度量差异
• 样本期间
– 不同期间-商业周期的影响
分析
• 10个发展中国家和G7国家债务比率的描述性统计 • 相对于发达国家,发展中国家之间的负债率和长期负债率 差别较大 • 发展中国家的长期债务较少
分析
• 样本的代表性
数据及变量选择
• 样本期间:1980-1991 • 资产负债率(负债率)
– 负债总额/(负债总额+净资产)
• 帐面长期负债率
– (负债总额-流动负债)/ (负债总额-流动负债+净资产)
• 市场长期负债率
– (负债总额-流动负债)/ (负债总额-流动负债+股票市值)
分析
• 10个发展中国家和G7国家债务比率的描述性统计 • 样本个数 • 各个指标的最大值、最小值 • 发展中国家和发达国家的比较
时期1
时期 T 时期 1
样本 2
时期 T 时期 1
样本 N
时期 T
线形模型
yit = β 0 + β1 x1it + β 2 x2it + ... + β k xkit + ε it
解释变量
ε it = λi + uit
残差分布
北京大学光华管理学院课程表
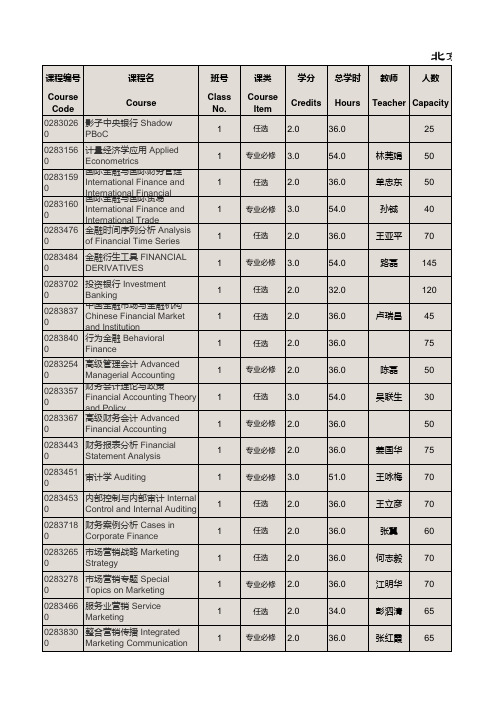
龚六堂 105
李辰旭 55
张翼
60
北京大学课程表
起止周 星期一 星期二 星期三 星期四 星期五 星期六 星期日 考试日期
Lecture Weeks
MON
TUE
WED
THU
FRI
SAT
SUN
Exam Date
1-16
8-9
7-14
2-4
2-4
12-16
5-7
5-7
1-16
10-12
1-12
2-4
1-16
中国社会与商业文化 Chinese Society and Business Culture
1
任选 2.0
32.0
李博柏 25
0283824 金融市场与金融机构
0
Financial Market
1
全校任选 2.0
36.0
卢瑞昌 70
0283825 人生规划与职业发展 Career
0
Develop Strategy
1
0283211 0
微观经济学 Microeconomics
1
0283222 0
民商法 Civil Business Law
1
0283250 0
中国经济改革与发展 China`s Economic Reforms and Developments
1
0283251 财务会计 Financial
0
Accounting
12 13 14 15 16 17
0283011 人力资源管理 Human
0
Resource Management
1
0283014 社会心理学 Social
光华管理学院培养方案选课计划课程大纲

选修:共9学分
课程号 02532590 06234840 02530140 课程名称 中华人民共和国经济史 信息经济学 计量经济学 周学时 2 4 3 学分 2 4 3 开课学期 一下 三上 三下 备注
注:大类平台选修课程若遇未开课情况,建议用本院开设的其他类型课程代替
3)学院课程:必修课:46学分(含大类平台课19学分)
注:未给定课号的课以实际开课时课号为准。
5)本科素质教育通选课:12学分 A.数学与自然科学类:和F类相加至少4学分 B.社会科学类:至少2学分 C.哲学与心理学类:至少2学分 D.历史学类:至少2学分 E.语言学、文学、艺术与美育类:至少2学分,其中至少一门是艺术与美育类课程 F. 社会可持续发展类:和A类相加至少4学分 6)学生选课要求 本院学生至少选修3门本院开设的英文课程,其中至少一门是本专业开设的课程 备注:此培养方案供同学们参考,具体执行以每学期课程表为准。
课程号 02830140 00131460 02833430 02834720 02831100 02832640 02834740 02832500 课程名称 社会心理学 线性代数 公司财务管理(中英文) 概率统计(中英文) 组织与管理 营销学 运作与信息管理 中国经济改革与发展 周学时 3 4 3 4 3 3 4 3 学分 3 4 3 4 3 3 4 3 开课学期 一下 一下 二上 二上 二上 二上 三上 三下 备注
2 2 3 2
2 1 4 2
二上 二上 二上 二上
03835064 04130004
大学英语(四) 体育(4)
0 2
2 1
二下 二下
注:政治课开课学期以每学期课表为准
2)大类平台课程:共28学分,其中非本院系课程不低于8学分 必修:19学分
北大经济金融本科生证券投资学讲义(光华)证券投资学第5章精品PPT课件

23.10.2020
证券投资学
– 假设1:在一期时间模型里,投资者以期望回报率 和标准差作为评价证券组合好坏的标准。
– 假设2:所有的投资者都是非满足的。 – 假设3:所有的投资者都是风险厌恶者。 – 假设4:每种证券都是无限可分的,即,投资者可
以购买到他想要的一份证券的任何一部分。
23ห้องสมุดไป่ตู้10.2020
证券投资学
• 这一特性称为分离定理: 我们不需要知 道投资者对风险和回报的偏好,就能够 确定其风险资产的最优组合。
• 分离定理成立的原因在于,有效集是线 性的。
23.10.2020
证券投资学
– 例子:考虑A、B、C三种证券,市场的无 风险利率为4%,我们证明了切点证券组合T 由A、B、C三种证券按0.12,0.19,0.69的 比例组成。如果假设1-10成立,则,第一个
风险利率借或者贷再投资到切点证券组合上。
23.10.2020
证券投资学
idea
• 所有的投资者为价格接受者:在给定的价格系 统下,决定自己对每种证券的需求。由于这种 需求为价格的函数,当我们把所有的个体需求 加总起来,得到市场的总需求时,总需求也为 价格的函数。价格的变动影响对证券的需求, 如果在某个价格系统下,每种证券的总需求正 好等于市场的总供给,证券市场就达到均衡, 这时的价格为均衡价格,回报率为均衡回报率。 这就是资本资产定价模型(Capital Asset Pricing Model,简称为CAPM)的思想。
23.10.2020
证券投资学
What if
• We will approach the CAPM by posing the question “what if”, where the “if” part refers to a simplified world. Positing an admittedly unrealistic world allows a relatively easy leap to “then” part. Once we accomplish this, we can add complexity to the hypothesized environment one step at a time and see how the conclusions must be amended. This process allows us to derive a reasonably realistic and comprehensible model.
金融经济学 教学大纲

金融经济学一、课程说明课程编号:160518Z10课程名称:金融经济学/Financal Economics课程类别:专业课程学时/学分:48/3先修课程:西方经济学适用专业:金融学教材、教学参考书:1.王江主编.金融经济学.北京:中国人民大学出版社.2006.6;2.宋逢明主编.金融经济学. 北京:高等教育出版社.2006年。
二、课程设置的目的意义金融经济学旨在用经济学的一般原理和方法来分析金融问题。
本课程是金融专业的主干课程,是金融学的微观经济学理论基础。
它着重从金融市场均衡来讨论金融资产的估值与定价,以及金融资产的风险管理。
因此是金融学其他重要领域如金融工程、投资学、公司财务、金融机构管理学等必不可缺的理论基础。
三、课程的基本要求知识:本课程要求学生掌握有关金融经济学的基本理论和知识,在了解金融经济学的基本概念和意义的基础上,以建立理性金融的行为基础和基本的均衡模型为基础,了解均衡模型框架下的金融资产的套利与定价;投资组合选择理论和基金分离定理以及资产定价模型——资本资产定价模型(CAPM)。
从而使学生完整地了解金融经济学基本定理,建立对整体金融理论的认识。
能力:从对金融经济学基本理论和知识的学习,提高对社会经济和金融发展规律的认识能力、分析能力和把握能力;从对均衡模型框架下金融资产的套利与定价以及投资组合选择理论和基金分离定理等相关知识的学习和掌握,建立和提高对金融领域投资选择、金融产品开发与定价等问题深层次成因探析和把握的能力。
素质:建立在金融经济学基本理论框架下运用金融经济学基本概念、一般原理分析金融问题的思维模式,具备理解和分析金融决策的基本素质,提高对实际金融问题进行自主判断和运用的专业素质。
四、教学内容、重点难点及教学设计五、实践教学内容和基本要求无六、考核方式及成绩评定。
光华管理学院本科生金融计量经济学讲义(1)

1.1 什么是金融计量经济学
当一家金融机构,面临某种制度(例如,引入独立董事制度、融资融券业务的推出,再 融资标准的变化,交易制度的引入或限制某种交易行为等)的引入时,需要考虑引入制度对 公司价值的提升作用或交易环境变化的影响进行相应决策。 假定你在一家投资银行工作, 你 可能需要研究几种不同的交易策略对所准备投资证券的收益影响。 假定你是有志作为一名学 术研究者,你需要验证市场上的各种变量之间的关系(例如长短期利率变化,汇率波动与净 出口贸易, 货币政策的变化对那些类别的资产价格会产生影响等) 来确定它们是否遵从相关 的金融理论和模型假设。 假若你是一个市场中的投资者, 你可能需要根据各种影响证券价值 变化的因素来选择投资的对象和买卖的时机。 要完成上述这些任务中的任意一项, 如果你希 望你的行为和决定是有一定科学依据的, 而不愿意象一个赌徒那样接受随机发生的结果, 你 就需要使用金融计量方法,对各种变量之间的关系通过统计方法进行分析和检验。为此,你 将要面对和使用大量的统计模型和计量方法。 金融计量经济学中将会大量使用统计模型和方法解决金融相关问题, 是不是金融计量就 等同于统计方法呢,尽管二者之间存在许多密不可分的联系,但答案仍然是否定的。为此金 融计量与统计之间的关系如何就是一个首先需要明确的问题。 金融学家最初所使用的方法大 多是基于模型的统计推断方法。然而,金融市场的发展日新月异,很对的金融问题已经没有 统计工具来帮助解决,因此,金融计量经济学是相对独立于数理统计而发展的。另一方面, 数理统计更多的是基于假设和可以重复实验, 而计量金融学主要集中在对不可重复试验数据
y f ( x1, x2 , x3 , x4 , x5 )
的特性只能从所获取的观测数据中去寻找。
(1.2)
模型中的干扰项 所具有的特征及其对结果的影响将是计量分析的重要内容。 而干扰项 为此, 接下来就要去收集相关的数据并通过计量方法进行验证。 因为没有通过验证的任 何理论,在经济金融领域只能算是一个假设或猜想,甚至是一个误认为。在后面的内容中再 详细讨论第二、 三两个步骤所涉及的相关内容。 在此, 我们要先来熟悉一下数据是什么样的, 常见都有那些数据类型?
金融经济学课程大纲

《金融经济学》课程大纲 4
《金融经济学》课程基本结构
中心问题: 中心问题:不确定的金融市场环境下对金融资产定价
一般经济均衡框架 有效市场理论 无套利假设 (正线性定价) 资产定价基本定理 线性定价法则 证券组合选择理论 资本资产定价模型 CAPM 套利定价理论 APT 期权定价理论 利率期限结构 (债券定价理论)
Cochrane, John H., Asset Pricing, Princeton University Press, Princeton, 2001, 2005.
《金融经济学》课程大纲 12
《金融经济学》参考书(续)
Bernstein, Peter L., Capital Ideas, The Improbable Origins of Modern Wall Street, Simon & Schster, New York, 1992 (中译本:《投资革命,源自象牙塔的华尔 街理论》,上海远东出版社,2001)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《金融经济学》参考书(续)
Cochrane, John H., Asset Pricing, Princeton University Press, Princeton, 2001. Bernstein, Peter L., Capital Ideas, The Improbable Origins of Modern Wall Street, Simon & Schster, New York, 1992 (中译本:《投资革命,源自 象牙塔的华尔街理论》,上海远东出版社, 2001)。
金融经济学 4
《金融经济学》教学大纲
不确定状况下的决策。von NeumannMorgenstern 效用函数。 CAPM 和 APT 的一般均衡理论模型。 有效市场理论。 Black-Scholes 期权定价理论。 债券的利率期限结构。 连续时间金融学。
金融经济学 5
《金融经济学》教学要求
金融经济学 2
《金融经济学》课程基本结构
中心问题:不确定的金融市场环境下对金融资产定价
一般经济均衡框架 有效市场理论
无套利假设 (正线性定价) 资产定价基本定理
线性定价法则 证券组合选择理论 资本资产定价模型 CAPM 套利定价理论 APT 期权定价理论 利率期限结构 (债券定价理论)
金融经济学
3
数学预备知识:多元微积分,线性代数, 初等概率论与数理统计。 相关课程:投资学,公司财务,金融工 程,金融计量经济学,高等金融经济学 专题。 考查方式:作业 (30%);完成论文一篇 (30%);期末考试 (40%)。
金融经济学 6
《金融经济学》参考书
1. Jarrow, R. A., V. Maksimovic & W. T. Ziemba (eds), Finance, Elsevier, Amsterdam, 1995, Chaps., 1, 2, 4, and 9. 2. Jarrow, R. A., Finance Theory, Prentice Hall, Englewood Cliffs, NJ, 1988. 3. Huang, Chi-fu & R. H. Litzenberger, Foundations for Financial Economics, Prentice Hall, Englewood Cliffs, NJ, 1988. (中 译本2003年出版) 4. Ingersoll, J. E. Jr., Theory of Financial Decision Making, Rowman & Littlefield Publishers, Maryland. 1987.
金融经济学
史树中
北京大学光华管理学院金融系 北京大学金融数学与金融工程研究中心 办公室:光华楼 416 电话: 62757074 e-mail: shisz@
金融经济学
1
《金融经济学》课程说明
本课程是金融学等专业的硕士必修课程。它讲授理 论金融经济学基础,并对以前出现在《投资学》、《公 司财务》等课程中来源于现代理论金融经济学中的各种 原理、方法纳入统一的理论框架中,使学生对它们有更 深刻的理解。现代金融经济学中最重要的是无套利假设 和一般经济均衡框架。所研究的中心问题是在不确定的 金融市场环境下对金融资产定价。中心结果是资产定价 基本定理。投资组合分析、资本资产定价模型 (CAPM)、 套利定价理论 (APT)、期权定价理论、市场有效性理论、 利率期限结构等都是这一框架中围绕这一中心结果的组 成部分。作为硕士课程,本课程力图在尽可能少的数学 要求下阐明基本经济思想。对数学要求较高的金融经济 学理论将在高级金融经济学专题中讲述。
金融经济学 8
《金融经济学》参考书(续)
LeRoy, S. F. and J. Werner, Principles of Financial Economics, Cambridge University Press, Cambridge, 2001.
金融经济学
9
《金融经济学》教学大纲
金融市场的不确定性。收益与风险。 金融经济学的理论与方法。 一般经济均衡与无套利假设。资产定价 基本定理与线性定价法则。 Modigliani-Miller 定理 (MMT)。 Markowitz 投资组合理论。资本资产定 价模型 (CAPM)。 套利定价理论 (APT)
