高一数学试卷及答案(人教版)
人教版高一上学期数学(必修二)《4.6函数的应用》同步测试题及答案

人教版高一上学期数学(必修二)《4.6函数的应用》同步测试题及答案1.某研究小组在一项实验中获得一组关于y,t的数据,将其整理得到如图所示的图形.下列函数中,最能近似刻画y与t之间关系的是()A.y=2tB.y=2t2C.y=t3D.y=log2t2.某种产品今年的产量是a,如果保持5%的年增长率,那么经过x年(x∈N*),该产品的产量y满足()A.y=a(1+5%x)B.y=a+5%C.y=a(1+5%)x-1D.y=a(1+5%)x3.中国茶文化博大精深.茶水的口感与茶叶类型和水的温度有关.经验表明,某种绿茶用85℃的水泡制,再等到茶水温度降至60℃时饮用,可以产生最佳口感.为分析泡制一杯最佳口感茶水所需的时间,某研究人员每隔1min测量一次茶水的温度,根据所得数据作出如图所示的散点图.观察散点图的分布情况,下列哪个函数模型可以近似地刻画茶水温度y随时间x变化的规律()A.y=mx2+n(m>0)B.y=mx+n(m>0)C.y=ma x+n(m>0,a>0,a≠1)D.y=m log a x+n(m>0,a>0,a≠1)4.大西洋鲑鱼每年都要逆流而上,洄游到产卵地产卵.科学家发现鲑鱼的游速v(单位:m/s)与鲑鱼的耗氧量的单位数P的关系为v=12log3P100,则鲑鱼静止时耗氧量的单位数为()A.1B.100C.200D.3005.国内首个百万千瓦级海上风电场—三峡阳江沙扒海上风电项目宣布实现全容量并网发电,为粤港澳大湾区建设提供清洁能源动力.风速预测是风电出力大小评估的重要工作,通常采用威布尔分布模型,有学者根据某地气象数据得到该地的威布尔分布模型:F(x)=1-e−(x2)k,其中k为形状参数,x为风速.已知风速为1m/s时,F≈0.221,则当风速为4m/s时,F约为(参考数据:ln0.779≈-0.25,e-4≈0.018)() A.0.920B.0.964C.0.975D.0.9826.(多选)某工厂生产一种溶液,按市场要求杂质含量不得超过0.1%,而这种溶液最初的杂质含量为2%,现进行过滤,已知每过滤一次杂质含量减少1,则使产品达到市场要求的过滤次数可以为(参考数据:lg2≈0.301,3lg3≈0.477)()A.6B.9C.8D.77.近来,国内多个城市纷纷加码布局“夜经济”,以满足不同层次的多元消费,并拉动就业、带动创业,进而提升区域经济发展活力.某夜市的一位工艺品售卖者,通过对每天销售情况的调查发现:该工艺品在过去的一个月内(以30天计),日销售量Q(x)(单位:件)与时间x(单位:天)的部分数据如表所示:x 10 15 20 25 30Q(x) 50 55 60 55 50给出以下四个函数模型:①Q(x)=ax+b;②Q(x)=a|x-m|+b;③Q(x)=a·b x;④Q(x)=a log b x.根据表中的数据,最适合用来描述日销售量Q(x)与时间x的变化关系的函数模型是.8.某种放射性元素的原子数N随时间t的变化规律是N=N0e-λt,其中N0,λ为正常数.由放射性元素的这种性质,可以制造高精度的时钟,用原子数表示时间t为.9.(10分)据观测统计,某湿地公园某种珍稀鸟类的现有个数约1000只,并以平均每年8%的速度增加.(1)求两年后这种珍稀鸟类的大约个数;(3分)(2)写出y(珍稀鸟类的个数)关于x(经过的年数)的函数关系式;(3分)(3)约经过多少年以后,这种鸟类的个数达到现有个数的3倍或以上?(结果为整数)(参考数据:lg2≈0.3010,lg 3≈0.4771)(4分)10.(12分)芦荟是一种经济价值很高的观赏、食用植物,不仅可美化居室、净化空气,又可美容保健,因此深受人们欢迎,在国内占有很大的市场.某人准备进军芦荟市场,栽培芦荟,为了了解行情,进行市场调研,从4月1日起,芦荟的种植成本Q(单位:元/10kg)与上市时间t(单位:天)的数据情况如表:t 50 110 250Q 150 108 150(1)根据表中数据,从下列函数中选取一个最能反映芦荟种植成本Q 与上市时间t 的变化关系的函数:Q =at +b ,Q =at 2+bt +c ,Q =a ·b t ,Q =a log b t ;(6分)(2)利用你选择的函数,求芦荟种植成本最低时的上市天数及最低种植成本.(6分)11.白细胞是一类无色、球形、有核的血细胞,正常成人白细胞计数为(4.0~10.0)×109/L ,可因每日不同时间和机体不同的功能状态而在一定范围内变化.若白细胞计数因为感染产生病理性持续升高,则需进一步探查原因,进行药物干预.研究人员在对某种药物的研究过程中发现,在特定实验环境下的某段时间内,可以用对数模型W (m )=-W 0ln(Km )描述白细胞计数W (m )(单位:109/L)与随用药量m (单位:mg)的变化规律,其中W 0为初始白细胞计数对应值,K 为参数.已知W 0=20,用药量m =50时,在规定时间后测得白细胞计数W =14,要使白细胞计数达到正常值,则需将用药量至少提高到(参考数据:e 15≈1.221)( ) A.58B.59 C.60D.6212.某食品的保鲜时间y (单位:小时)与储藏温度x (单位:℃)满足函数关系y =e kx +b (e 为自然对数的底数,k ,b 为常数).若该食品在0 ℃的保鲜时间是192 h ,在22 ℃的保鲜时间是48 h ,则该食品在33 ℃的保鲜时间是( ) A.16 hB.20 h C.24 hD.26 h13.某工厂生产过程中产生的废气必须经过过滤后才能排放,已知在过滤过程中,废气中的污染物含量p (单位:毫克/升)与过滤时间t (单位:小时)之间的关系为p (t )=p 0e -kt (e 为自然对数的底数,p 0为污染物的初始含量).过滤1小时后,检测发现污染物的含量减少了15,要使污染物的含量不超过初始值的110 000,至少还需过滤 小时(参考数据:lg 2≈0.301 0)( ) A.40B.38 C.44D.4214.光线通过一块玻璃,其强度要失掉原来的110,要使通过玻璃的光线强度为原来的12以下,至少需要这样的玻璃板的块数为 .(lg 2≈0.301 0,lg 3≈0.477 1)15.为了预防某种病毒,某商场需要通过喷洒药物对内部空间进行全面消毒.出于对顾客身体健康的考虑,相关部门规定空气中这种药物的浓度不超过0.25毫克/立方米时,顾客方可进入商场.已知从喷洒药物开始,商场内部的药物浓度y (毫克/立方米)与时间t (分钟)之间的函数关系为y ={0.1t,0≤t ≤10,(12)t10−a ,t >10,函数的图象如图所示.如果商场规定9:30顾客可以进入商场,那么开始喷洒药物的时间最迟是( )A.9:00B.8:40C.8:30D.8:0016.(12分)科学家发现某种特殊物质的温度y (单位:摄氏度)随时间x (单位:分钟)的变化规律满足关系式:y =m ·2x +21-x (0≤x ≤4,m >0).(1)若m =2,求经过多少分钟,该物质的温度为5摄氏度;(5分) (2)如果该物质温度总不低于2摄氏度,求m 的取值范围.(7分)参考答案1.D 2.D 3.C 4.B5.D [因为F (1)≈0.221 所以e−12k≈0.779,12k ≈-ln 0.779,2k ≈4,得k ≈2所以F (4)=1-e −2k≈1-e -4≈0.982.]6.BC [设经过n 次过滤,产品达到市场要求,则 2100×⎝⎛⎭⎫23n ≤11 000即⎝⎛⎭⎫23n ≤120,由n lg 23≤-lg 20即n (lg 2-lg 3)≤-(1+lg 2) 得n ≥1+lg 2lg 3-lg 2≈7.4.]7.② 8.t =-1λln NN 09.解 (1)依题意,得一年后这种鸟类的个数为 1 000+1 000×8%=1 080(只)两年后这种鸟类的个数为 1 080+1 080×8%≈1 166(只).(2)由题意可知珍稀鸟类的现有个数约1 000只,并以平均每年8%的速度增加 则所求的函数关系式为 y =1 000×1.08x ,x ∈N .(3)令1 000×1.08x ≥3×1 000,得1.08x ≥3,两边取常用对数得 lg 1.08x ≥lg 3,即x lg 1.08≥lg 3 因为lg 1.08>0,所以x ≥lg 3lg 1.08所以x ≥lg 3lg 108100=lg 3lg 108-2因为lg 108=lg(33×22)=3lg 3+2lg 2 所以x ≥lg 33lg 3+2lg 2-2≈0.477 13×0.477 1+2×0.301 0-2≈14.3故约经过15年以后,这种鸟类的个数达到现有个数的3倍或以上.10.解 (1)由所提供的数据可知,刻画芦荟种植成本Q 与上市时间t 的变化关系的函数不可能是常函数,若用函数Q =at +b ,Q =a ·b t ,Q =a log b t 中的任意一个来反映时都应有a ≠0,且上述三个函数均为单调函数,这与表格所提供的数据不符合,所以应选用二次函数Q =at 2+bt +c 进行描述,将表格所提供的三组数据分别代入函数Q =at 2+bt +c可得⎩⎨⎧150=2 500a +50b +c ,108=12 100a +110b +c ,150=62 500a +250b +c .解得a =1200,b =-32,c =4252.所以刻画芦荟种植成本Q 与上市时间t 的变化关系的函数为 Q =1200t 2-32t +4252.(2)由(1)可得,函数Q 为图象开口向上,对称轴为t =--322×1200=150的抛物线所以当t =150天时,芦荟种植成本最低为Q =1200×1502-32×150+4252=100(元/10 kg). 11.D [由已知W 0=20,m =50,W (50)=14,代入W (m )=-W 0ln(Km ) 则14=-20ln(50K ),解得K =e−71050则W (m )=-20ln (me −71050)因为用药量m =50时,在规定时间后测得白细胞计数W =14,白细胞计数值偏高 所以令W (m )=-20ln (me −71050)≤10 即ln (me−71050)≥-12解得m ≥50e 15≈50×1.221=61.05.所以要使白细胞计数达到正常值,则需将用药量至少提高到62.] 12.C [由题意可知,当x =0时,y =192;当x =22时,y =48 ∴⎩⎨⎧e b=192,e 22k +b =48,解得⎩⎪⎨⎪⎧e b=192,e 11k =12,则当x =33时 y =e 33k +b =(e 11k )3·e b =⎝⎛⎭⎫123×192=24.]13.D [根据题设,得45p 0=p 0e -k ∴e -k =45,所以p (t )=p 0⎝⎛⎭⎫45t ;由p (t )=p 0⎝⎛⎭⎫45t ≤110 000p 0,得⎝⎛⎭⎫45t ≤10-4,两边分别取以10为底的对数 并整理得t (1-3lg 2)≥4 ∴t ≥41-3lg 2≈41.2因此,至少还需过滤42小时.] 14.7解析 设至少需要x 块玻璃板由题意知⎝⎛⎭⎫1-110x <12即⎝⎛⎭⎫910x <12两边取对数lg ⎝⎛⎭⎫910x <lg 12即x ·(lg 9-lg 10)<-lg 2 即x ·(1-2lg 3)>lg 2 x >lg 21-2lg 3≈6.57 ∴x =7.15.A [根据函数的图象,可得函数的图象过点(10,1)代入函数的解析式,可得(12)1−a=1,解得a =1,所以y ={0.1t,0≤t ≤10,(12)t 10−1,t >10,令y ≤0.25,可得0.1t ≤0.25或(12)t10−1≤0.25解得0<t ≤2.5或t ≥30所以如果商场规定9:30顾客可以进入商场,那么开始喷洒药物的时间最迟是9:00.] 16.解 (1)由题意,得m =2 令y =2·2x +21-x =2·2x +22x =5解得x =1(负值舍去)因此,经过1分钟,该物质的温度为5摄氏度. (2)由题意得m ·2x +21-x ≥2对一切0≤x ≤4恒成立 则由m ·2x +21-x ≥2,得m ≥22x -222x 令t =2-x ,则116≤t ≤1且m ≥2t -2t 2构造函数f (t )=2t -2t 2 =-2⎝⎛⎭⎫t -122+12所以当t =12时,函数y =f (t )取得最大值12 则m ≥12.因此,实数m 的取值范围是⎣⎡⎭⎫12,+∞.。
人教版高一数学必修1必修4期末测试卷附答案

人教版高一数学必修1必修4期末测试卷附答案人教版高一数学必修1必修4期末测试卷姓名:__________ 班级:___________ 学号:____________ 分数:______________一、选择题(每题5分,共40分)1.集合A={x∈N*|-1<x<3}的子集的个数是(。
)。
A。
4.B。
8.C。
16.D。
322.函数f(x)=1/(1-x)+lg(1+x)的定义域是(。
)。
A。
(-∞,-1)。
B。
(1,+∞)。
C。
(-1,1)U(1,+∞)。
D。
(-∞,+∞)3.设a=log2,c=5-1/3,b=ln22,则(。
)。
A。
a<b<c。
B。
b<c<a。
C。
c<a<b。
D。
c<b<a4.函数y=-x^2+4x+5的单调增区间是(。
)。
A。
(-∞,2]。
B。
[-1,2]。
C。
[2,+∞)。
D。
[2,5]5.已知函数f(x)=x^2-2ax+3在区间(-2,2)上为增函数,则a的取值范围是(。
)。
A。
a≤2.B。
-2≤a≤2.C。
a≤-2.D。
a≥26.下列函数中,既是偶函数,又在区间(0,+∞)上单调递减的函数是(。
)。
A。
y=x-2.B。
y=x-1.C。
y=x^2.D。
y=x^37.若函数f(x)=x/(2x+1)(x-a)为奇函数,则a=(。
)。
A。
1/2.B。
2/3.C。
3/4.D。
1/88.已知α是第四象限角,XXX(π-α)=5/12,则sinα=(。
)。
A。
1/5.B。
-1/5.C。
5.D。
-59.若tanα=3,则sinαcosα=(。
)。
A。
3.B。
3/2.C。
3/4.D。
9/410.sin600°的值为(。
)。
A。
3/2.B。
-3/2.C。
-1/2.D。
1/211.已知cosα=3/5,π/4<α<π,则XXX(α+π/4)=(。
)。
A。
1.B。
-1.C。
5/8.D。
-5/812.在△ABC中,sin(A+B)=sin(A-B),则△ABC一定是(。
人教版高一数学必修1测试题(含答案)

数学必修1期末复习试题 本试卷包括选择题、填空题和解答题三部分,共4页,时量120分钟,满分150分 一、选择题选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、设集合{}{}{}1,2,3,4,5,1,2,3,2,5U A B ===,则()U A C B ⋂=( ) A 、{}2 B 、{}2,3 C 、{}3 D 、{}1,3 2、已知集合{}{}0,1,2,2,M N x x a a M ===∈,则集合 M N ⋂= ( ) A 、{}0 B 、{}0,1 C 、{}1,2 D 、{}0,2 3、函数()21log ,4y x x =+≥的值域是 ( ) A 、[)2,+∞ B 、()3,+∞ C 、[)3,+∞ D 、(),-∞+∞ 4、关于A 到B 的一一映射,下列叙述正确的是 ( ) ① 一一映射又叫一一对应 ② A 中不同元素的像不同 ③ B 中每个元素都有原像 ④ 像的集合就是集合B A 、①② B 、①②③ C 、②③④ D 、①②③④ 5、在221,2,,y y x y x x y x ===+= ( ) A 、1个 B 、2个 C 、3个 D 、4个 6、已知函数()223f x x x =-+,那么()1f x +的表达式是 ( ) A 、259x x -+ B 、223x x -- C 、259x x +- D 、22x + 7、若函数()x f x a x a =--有两零点,则a 的取值范围是 ( ) A 、()0,+∞ B 、()1,+∞ C 、()0,1 D 、∅ 8、若21025x =,则10x -等于 ( ) A 、15- B 、15 C 、150 D 、1625绝密★启用前9、若()2log 1log 20a a a a +<<,则a 的取值范围是 ( )A 、01a <<B 、112a <<C 、102a << D 、1a > 10、设 1.50.90.4814,8,2abc -⎛⎫=== ⎪⎝⎭,则,,a b c 的大小顺序为 ( )A 、a b c >>B 、a c b >>C 、b a c >>D 、c a b >>11、已知()()2212f x x a x =+-+在(],4-∞上单调递减,则a 的取值范围是 ( ) A 、3a ≤- B 、3a ≥- C 、3a =- D 、以上答案都不对12、若()lg f x x =,则()3f = ( )A 、lg 3B 、3C 、310D 、103二、填空题:本大题共4小题,每小题5分,共20分。
最新人教版高一下册数学期末考试含答案

2022年人教版高一下册期末考试数学试卷一、选择题1. 已知复数z =1−2i ,则z (z +2i )=( ) A.1−2i B.9+2i C.7−4i D.1+2i2. 将圆锥的高缩短到原来的12,底面半径扩大到原来的2倍,则圆锥的体积( ) A.缩小到原来的一半 B.缩小到原来的16 C.不变 D.扩大到原来的2倍3. 若一系列函数的解析式和值域相同,但其定义域不同,则称这些函数为“同族函数”,例如函数y =x 2,x ∈[1,2]与函数y =x 2,x ∈[−2,−1]即为“同族函数”.下面函数解析式中也能够被用来构造“同族函数”的是( ) A.y =sinx B.y =x 3 C.y =e x −e −xD.y =lnx4. 甲、乙、丙三人独立地去译一个密码,分别译出的概率为12,14,18,则密码能被译出的概率是( ) A.120 B.2132C.2164D.43645. 数据x 1,x 2,…,x 9的平均数为4,标准差为2,则数据3x 1+2,3x 2+2,…,3x 9+2的方差和平均数分别为( ) A.36,14 B.14,36 C.12,19 D.4,126. 设λ为实数,已知向量m →=(2,1−λ),n →=(2,1).若m →⊥n →,则向量m →−n →与n →的夹角的余弦值为( ) A.−√55B.−√1010C.−12D.√557. 若P (AB )=16,P(A)=13,P (B )=14,则事件A 与B 的关系是( ) A.互斥 B.相互独立C.互为对立D.无法判断8. 下图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象,则()A.函数y=f(x)的最小正周期为π2B.直线x=5π12是函数y=f(x)图象的一条对称轴C.点(−π6,0)是函数y=f(x)图象的一个对称中心D.函数y=f(x−π3)为奇函数9. 若定义在R上的奇函数f(x)在(0,+∞)上单调递减,且f(−π2)=0,则下列取值范围中的每个x都能使不等式f(x+π2)⋅cosx≥0成立的是()A.[−2π,−π]B.[−π,0]C.[0,π]D.{x|x=kπ2,k∈Z}10. 如图,在直三棱柱ABC−A1B1C1中,AC=BC,AB=AA1,D是A1B1的中点,点F 在BB1上,记B1F=λBF,若AB1⊥平面C1DF,则实数λ的值为()A.13B.12C.23D.111. 如图所示,在正方体ABCD −A 1B 1C 1D 1 中,点E ,F ,M ,N 分别为棱AB ,BC ,DD 1,D 1C 1上的中点,下列判断正确的是( )A.直线AD//平面MNEB.直线FC 1//平面MNEC.平面A 1BC//平面MNED.平面AB 1D 1//平面MNE12. 矩形ABCD 中,AB =√2,AD =1,M 是矩形ABCD 内(不含边框)的动点,|MA →|=1,则MC →⋅MD →的最小值为( ) A.−√6 B.−√6+1 C.−√6+2 D.3+√62二、填空题1.已知函数f (x )={sin (π4x),x ≤1,lnx,x >1,则f(f (e ))=________.2. 已知在△ABC 中,点D 满足BD →=34BC →,点E 在线段AD (不含端点A ,D )上移动,若AE →=λAB →+μAC →,则μλ=________.3.一组数据共有7个整数,m ,2,2,2,10,5,4,且2<m <10,若这组数据的平均数、中位数、众数中最大与最小数之和是该三数中间数字的两倍,则第三四分位数是________.4. 如图,在正三棱锥A −BCD 中,底面边长为√6,侧面均为等腰直角三角形,现该三棱锥的表面上有一动点O ,且OB =2,则动点O 在三棱锥表面所形成的轨迹曲线的长度为________.三、解答题1.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知√3bcosC =csinB . (1)求角C ;(2)若b =2,△ABC 的面积为2√3,求c .2.某药厂测试一种新药的疗效,随机选择1200名志愿者服用此药,结果如下:(1)若另一个人服用此药,请估计该病人病情恶化的概率;(2)现拟采用分层抽样的方法从服用此药的1200名志愿者中抽取6人组成样本,并从这抽出的6人中任意选取3人参加药品发布会,求抽取的3人病情都未恶化的概率.3. 已知向量a →=(sinx,1),b →=(1,sin (π3−x)),f (x )=a →⋅b →.(1)求函数f (x )的单调递增区间和最小正周期;(2)若当x ∈[0,π4]时,关于x 的不等式2f (x )−1≤m 有解,求实数m 的取值范围.4.如图,在四棱锥P −ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,AC ⊥CD ,∠ABC =60∘,PA =AB =BC ,E 是PC 的中点.(1)求二面角P −CD −A 的大小;(2)求证:AE ⊥PD .5.雪豹处于高原生态食物链的顶端,亦被人们称为“高海拔生态系统健康与否的气压计”.而由于非法捕猎等多种人为因素,雪豹的数量正急剧减少,现已成为濒危物种.在中国,雪豹的数量甚至少于大熊猫.某动物研究机构使用红外线触发相机拍摄雪豹的照片,已知红外线触发相机在它控制的区域内拍摄到雪豹的概率为0.2. (1)假定有5个红外线触发相机控制某个区域,求雪豹进入这个区域后未被拍摄到的概率;(2)要使雪豹一旦进入这个区域后有0.9以上的概率被拍摄到,需至少布置几个红外线触发相机(lg2≈0.301).6.如图,已知四棱锥P−ABCD,△ABD为等边三角形,直线PC,DC,BC两两垂直,且PC=CD=BC=2,M为线段PA上的一点.(1)若平面BDM⊥平面ABCD,求AM2;(2)若三棱锥P−MBD的体积为四棱锥P−ABCD体积的1,求点M到平面ABCD的距离.2参考答案与试题解析一、选择题1.【答案】B【解析】无2.【答案】D【解析】无3.【答案】A【解析】无4.【答案】D【解析】无5.【答案】A【解析】无6.【答案】A【解析】无7.【答案】B【解析】无8.【答案】C【解析】无9.【答案】B【解析】无10.【答案】D【解析】无11.【答案】D【解析】无12.【答案】C【解析】无二、填空题【答案】√22【解析】无【答案】3【解析】无【答案】5【解析】此题暂无解析【答案】3π2【解析】无三、解答题【答案】解:(1)由正弦定理可得√3sinBcosC=sinCsinB. 因为sinB≠0,所以√3cosC=sinC,所以tanC =√3.因为C ∈(0,π),所以C =π3.(2)由(1)得C =π3. 因为S △ABC =12absinC =√34ab =2√3,所以ab =8.因为b =2,所以a =4.由余弦定理得,c 2=a 2+b 2−2abcosC =16+4−8=12, 所以c =2√3. 【解析】 此题暂无解析 【答案】解:(1)由统计表可知在1200名志愿者中,服用药出现病情恶化的频率为2001200=16,所以估计另一个人服用此药病情恶化的概率为16.(2)采用分层抽样的方法,从病情好转的志愿者中抽4人,从疗效不明显及病情恶化的志愿者中各抽取1人组成6个人的样本.将6人中病情恶化的1人用符号A 代替,其余5人分别用1,2,3,4,5代替, 则从6人中任意抽取3人的基本事件表示如下: (A,1,2),(A,1,3),(A,1,4),(A,1,5),(A,2,3), (A,2,4),(A,2,5),(A,3,4),(A,3,5),(A,4,5), (2,3,4),(2,3,5),(2,4,5),(3,4,5),(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5),共20个基本事件. 其中没有抽到病情恶化的志愿者的基本事件为: (2,3,4),(2,3,5),(2,4,5),(3,4,5),(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5),共10个基本事件, 因此,抽取的3人中没有病情恶化的志愿者的概率为1020=12.【解析】 无 无 【答案】解:(1)因为f (x )=a →⋅b →=sinx +sin (π3−x)=12sinx +√32cosx =sin (x +π3),所以函数f (x )的最小正周期T =2π.因为函数y =sinx 的单调增区间为[−π2+2kπ,π2+2kπ],k ∈Z , 所以−π2+2kπ≤x +π3≤π2+2kπ,k ∈Z ,解得−5π6+2kπ≤x ≤π6+2kπ,k ∈Z ,所以函数f (x )的单调增区间为[−5π6+2kπ,π6+2kπ],k ∈Z .(2)不等式2f (x )−1≤m 有解,即m+12≥f (x )min .因为x ∈[0,π4],所以π3≤x +π3≤7π12.又sin 7π12=sin 5π12>sin π3,故当x +π3=π3,即x =0时,f (x )取得最小值,且最小值为f (0)=√32, 所以m ≥√3−1. 【解析】 此题暂无解析 【答案】(1)解:因为PA ⊥底面ABCD ,CD ⊂平面ABCD , 所以CD ⊥PA .因为CD ⊥AC,PA ∩AC =A , 所以CD ⊥平面PAC , 所以CD ⊥PC . 又AC ⊥CD ,故∠PCA 为二面角P −CD −A 的平面角. 又PA =AB =BC =AC ,故二面角P −CD −A 的大小为45∘. (2)证明:由于AE ⊂平面PAC , 所以AE ⊥CD .因为E 是PC 的中点,所以AE ⊥PC . 又PC ∩CD =C ,所以AE ⊥平面PCD . 又PD ⊂平面PCD ,所以AE ⊥PD . 【解析】 此题暂无解析 【答案】解:(1)雪豹被拍摄到的概率,即至少有1个红外线触发相机拍摄到雪豹的概率. 设雪豹被第k 个红外线触发相机拍摄到的事件为A k (k =1,2,3,4,5), 那么5个红外线触发相机都未拍摄到雪豹的事件为A 1⋅A 2⋅A 3⋅A 4⋅A 5. ∵ 事件A 1,A 2,A 3,A 4,A 5相互独立, ∴ 雪豹未被拍摄到的概率为 P(A 1⋅A 2⋅A 3⋅A 4⋅A 5)=P(A 1)⋅P(A 2)⋅P(A 3)⋅P(A 4)⋅P(A 5) =(1−0.2)5=(45)5,∴ 雪豹未被拍摄到的概率为(45)2.(2)设至少需要布置n 个红外线触发相机才能有0.9以上的概率拍摄到雪豹, 由(1)可知,雪豹被拍摄到的概率为1−(45)n.令1−(45)n≥0.9, ∴ (45)n≤110,两边取常用对数,得n ≥11−3lg2≈10.3.∵ n ∈N ∗, ∴ n =11,∴ 至少需要布置11个红外线触发相机才能有0.9以上的概率拍摄到雪豹. 【解析】 无 无 【答案】解:(1)连接AC 交BD 于点O .易知AC 为线段BD 的垂直平分线,且AC 为AP 在平面ABCD 上的投影, 所以MD =MB .连接MO ,则MO ⊥BD .又因为平面BDM ⊥平面ABCD ,平面BDM ∩平面ABCD =BD ,MO ⊂平面MBD , 所以MO ⊥平面ABCD .又因为AO ⊂平面ABCD ,所以MO ⊥AO .因为CO =√2,AO =√6,AP 2=AC 2+PC 2=12+4√3. 又因为AOAC =AM AP,即AM 2=18−6√3.(2)过点M 作平面ABCD 的垂线,垂足为O ′, V M−ABD =13×12×√6×2√2×MO ′=2√33⋅MO ′,V P−BCD =43,V P−ABCD =13×12×2√2×(√2+√6)×2=4(√3+1)3, 故V P−BCD +V M−ABDV P−ABCD=1−12,解得MO ′=1−√33, 故点M 到平面ABCD 的距离为1−√33. 【解析】 此题暂无解析。
新教材人教版高一数学上册单元测试题含答案全套

新教材人教版高一数学上册单元测试题含答案全套人教版高中数学必修第一册第一章测试题第Ⅰ卷一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合,,则等于( )A .B .C .D .【答案】B【解析】集合,,.2.是的( )条件 A .充分不必要 B .必要不充分 C .充要 D .既不充分也不必要 【答案】B【解析】由不能推得,反之由可推得, 所以是的必要不充分条件. 3.已知集合,,若,则实数的值为( )A .B .C .D .【答案】B【解析】∵集合,,且,∴,因此.4.下列命题中正确的是( )A .任何一个集合必有两个以上的子集B .空集是任何集合的子集C .空集没有子集D .空集是任何集合的真子集 【答案】B【解析】空集只有一个子集,故A 错;B 正确; 空集是本身的子集,故C 错;空集不能是空集的真子集,故D 错. 5.已知集合,则中元素的个数为( )A .B .C .D .【答案】A【解析】因为集合,{}1,2,3,4,5A ={}21,B y y x x A ==-∈A B {2,4}{1,3,5}{2,4,7,9}{1,2,3,4,5,7,9}{}1,2,3,4,5A ={}{}21,1,3,5,7,9B y y x x A ==-∈={}1,3,5A B =1x >4x >1x >4x >4x >1x >1x >4x >{1,3}A =-2{2,}B a ={1,2,3,9}A B =-a 1±3±1-3{1,3}A =-2{2,}B a ={1,2,3,9}AB =-29a =3a =±(){}22,3,,A x y xy x y =+≤∈∈Z Z A 9854(){}22,3,,A x y xy x y =+≤∈∈Z Z所以满足且,的点有,,,,,,,,共个.6.已知,则( )A .B .C .D .【答案】B 【解析】,故A 错,B 对,显然,所以C 不对,而,所以D 也不对,故本题选B .7.命题“存在实数,使”的否定是( ) A .对任意实数,都有 B .对任意实数,都有 C .不存在实数,使 D .存在实数, 【答案】B【解析】命题“存在实数,使”的否定是“对任意实数,都有”. 8.集合中的不能取的值的个数是( ) A .B .C .D .【答案】B【解析】由题意可知,且且, 故集合中的不能取的值的个数是个. 9.下列集合中,是空集的是( ) A . B .C .D .【答案】B【解析】对于A 选项,,不是空集, 对于B 选项,没有实数根,故为空集, 对于C 选项,显然不是空集,对于D 选项,集合为,故不是空集. 10.下列各组集合中表示同一集合的是( ) A ., B ., C ., D .,【答案】B223x y +≤x ∈Z y ∈Z (1,1)--(1,0)-(1,1)-(0,1)-(0,0)(0,1)(1,1)-(1,0)(1,1)9a ={A x x =≥a A ∉a A ∈{}a A ={}a a ∉>a A ∈{}a A ≠{}a a ∈x 1x >x 1x >x 1x ≤x 1x ≤x 1x ≤x 1x >x 1x ≤{}22,4,0x x --x 2345222040224x x x x x -≠-≠⇒≠-≠⎧⎪⎨⎪⎩-2x ≠-1x ≠-{}22,4,0x x --x 3{}0|2x x +={}210,x x x +=∈R {}1|x x <(){}22,,,x y yx x y =-∈R 2x =-210x +={(0,0)}{(3,2)}M ={3,2}N ={2,3}M ={3,2}N ={2,3}M ={2,3}N x y ==={(2,3)}M ={(5,4)}N =【解析】对于A ,,表示点集,,表示数集,故不是同一集合; 对于B ,,,根据集合的无序性,集合表示同一集合; 对于C ,集合的元素是数,集合的元素是等式;对于D ,,集合的元素是点,, 集合的元素是点,集合不表示同一集合.11.学校先举办了一次田径运动会,某班共有名同学参赛,又举办了一次球类运动会,这个班有名同学参赛,两次运动会都参赛的有人.两次运动会中,这个班总共的参赛人数为( ) A . B . C . D . 【答案】B【解析】因为参加田径运动会的有名同学,参加球类运动会的有名同学,两次运动会都参加的有人,所以两次运动会中,这个班总共的参赛人数为.12.已知集合,.若, 则实数的取值范围为( ) A . B .C .D .【答案】D【解析】, 当为空集时,;当不为空集时,,综上所述得.第Ⅱ卷二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.集合,则集合的子集的个数为 个. 【答案】【解析】由已知,集合的子集个数为.14.命题“”是命题“”的 (“充分不必要,必要不充分,充要,既不充分也不必要”)条件. 【答案】必要不充分【解析】的解为或,所以当“”成立时,则“”未必成立; 若“”,则“”成立,{(3,2)}M =M {3,2}N =N {2,3}M ={3,2}N =,M N M N {(2,3)}M =M (2,3){(5,4)}N =N (5,4),M N 8123201714238123812317+-={}|25A x x =-≤≤{}|121B x m x m =+≤≤-B A ⊆m 3m ≥23m ≤≤2m ≥3m ≤{}|121B x m x m =+≤≤-B 2112m m m -<+⇒<B 22152312m m m m ≥⎧⎪-≤⇒≤≤⎨⎪+≥-⎩3m ≤2{}1,A =A 4A 224=220x x --=1x =-220x x --=1x =-2x =220x x --=1x =-1x =-220x x --=故命题“”是命题“”的必要不充分条件.15.命题“,”的否定是 .【答案】,【解析】由全称量词命题的否定是存在量词命题可知,命题“,”的否定是“,”.16.设全集是实数集,,, 则图中阴影部分所表示的集合是 .【答案】【解析】由图可知,阴影部分为,∵,∴,∴.三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤) 17.(10分)已知集合,且,求的取值集合. 【答案】.【解析】∵,∴或,即或.当时,;当时,; 当时,不满足互异性, ∴的取值集合为{}1,3.18.(12分)已知集合,,若,求实数,的值.【答案】或.220x x --=1x =-x ∀∈R 23210x x -+>0x ∃∈R 2003210x x -+≤x ∀∈R 23210x x -+>0x ∃∈R 2003210x x -+≤U R {}22M x x x =<->或{}13N x x =<<{}12x x <≤Venn ()UN M {}22M x x x =<->或{}22UM x x -=≤≤(){}12UNM x x =<≤{}21,2,4M m m =++5M ∈m {}1,3{}251,2,4m m ∈++25m +=245m +=3m =1m =±3m ={}1,5,13M =1m ={}1,3,5M =1m =-{}1,1,5M =m {,,2}A a b =2{2,,2}B b a =A B =a b 01a b =⎧⎨=⎩1412a b ⎧=⎪⎪⎨⎪=⎪⎩【解析】由已知,得①,解得或, 当时,集合不满足互异性, 当时,集合,集合,符合题意;②,解得(舍)或,当时,集合,集合符合题意,综上所述,可得或.19.(12分)设集合,. (1)若,试判定集合与的关系; (2)若,求实数的取值集合.【答案】(1)是的真子集;(2). 【解析】(1),,∴是的真子集. (2)当时,满足,此时;当时,,集合,又,得或,解得或. 综上,实数的取值集合为.20.(12分)已知全集,集合,.求:A B =22a a b b =⎧⎨=⎩00a b =⎧⎨=⎩01a b =⎧⎨=⎩00a b =⎧⎨=⎩{0,0,2}A =01a b =⎧⎨=⎩{0,1,2}A ={2,1,0}B =22a b b a ⎧=⎨=⎩00a b =⎧⎨=⎩1412a b ⎧=⎪⎪⎨⎪=⎪⎩1412a b ⎧=⎪⎪⎨⎪=⎪⎩11{,,2}42A =11{2,,}42B =01a b =⎧⎨=⎩1412a b ⎧=⎪⎪⎨⎪=⎪⎩{}28150A x x x =-+=}10B =-=15a =A B B A ⊆a B A 110,,35⎧⎫⎨⎬⎩⎭{3,5}A ={5}B =B A B =∅B A ⊆0a =B ≠∅0a ≠1B a ⎧⎫=⎨⎬⎩⎭B A ⊆13a =15a=13a =15a 110,,35⎧⎫⎨⎬⎩⎭{}6U x x =∈<N {}1,2,3A ={}2,4B =(1),,;(2),;(3)设集合且,求的取值范围.【答案】(1)见解析;(2)见解析;(3). 【解析】(1),∵,,.(2),∴.(3)由(2)可知,∵,∴,解得.21.(12分)已知集合为全体实数集,,. (1)若,求;(2)若,求实数的取值范围. 【答案】(1);(2).【解析】(1)当时,,所以,所以.(2)①,即时,,此时满足.②当,即时,,由得,或, 所以.综上,实数的取值范围为.22.(12分)已知二次函数,非空集合.(1)当时,二次函数的最小值为,求实数的取值范围;(2)是否存在整数的值,使得“”是“二次函数的大值为”的充分条件, 如果存在,求出一个整数的值,如果不存在,请说明理由. 【答案】(1);(2)见解析.【解析】(1),当且仅当时,二次函数有最小值为,由已知时,二次函数的最小值为,则,所以. (2)二次函数,开口向上,对称轴为,作出二次函数图象如图所示,由“”是“二次函数的大值为”的充分条件, 即时,二次函数的最大值为,A B UA UB AB ()UA B {|21}C x a x a =-<≤-()UA CB ⊆a 3a ≥2A B ={0,1,2,3,4,5}U ={0,4,5}UA ={0,1,3,5}UB ={1,2,3,4}AB =(){0,5}UA B =(){0,5}UA B =()U A C B ⊆021521a a a a -<⎧⎪-≥⎨⎪->-⎩3a ≥U {}25M x x x =≤-≥或{}121N x a x a =+≤≤-3a =UMN N M ⊆a {}45Ux x x MN =<≥或{}24a a ≥或3a ={}45|N x x =≤≤{}45UN x x x =<>或{}45Ux x x MN =<≥或211a a -<+2a <N =∅N M ⊆211a a -≥+2a ≥N ≠∅N M ⊆15a +≥212a -≤-4a ≥a {}24a a a <≥或243y x x =-+{}|0A x x a =≤≤x A ∈1-a a x A ∈3a 2a ≥2243(2)1y x x x =-+=--2x =1-x A ∈1-2A ∈2a ≥2(2)1y x =--2x =x A ∈3x A ∈3,即为,令,解得或,由图像可知,当或时,二次函数的最大值不等于,不符合充分条件, 则,即可取的整数值为,,,,任意一个.第一册第二章测试题一元二次函数、方程和不等式注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
最新人教版高一数学必修1:测试题及答案
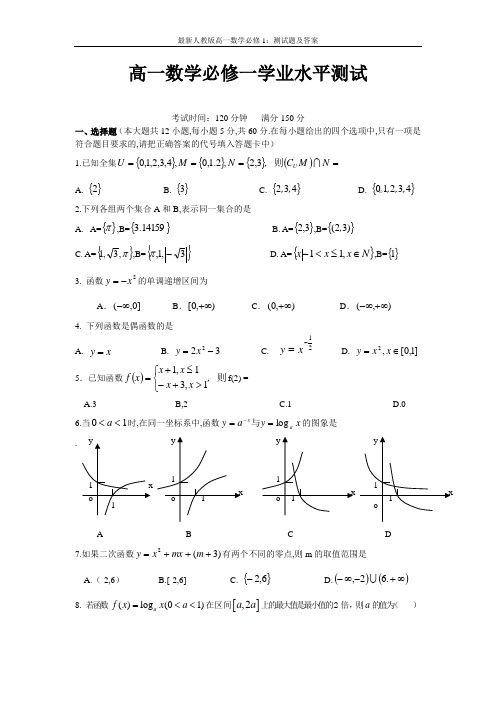
高一数学必修一学业水平测试考试时间:120分钟 满分150分一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填入答题卡中)1.已知全集{}{}{}()====N M C ,N M U U 则3,2,2.1,0,4,3,2,1,0 A. {}2 B. {}3 C. {}432,,D. {}43210,,,。
2.下列各组两个集合A 和B,表示同一集合的是A. A={}π,B={}14159.3 B. A={}3,2,B={})32(, C. A={}π,3,1,B={}3,1,-π D. A={}N x x x ∈≤<-,11,B={}1 3. 函数2x y -=的单调递增区间为A .]0,(-∞B .),0[+∞C .),0(+∞D .),(+∞-∞ 4. 下列函数是偶函数的是A. x y =B. 322-=x y C. 21-=xy D. ]1,0[,2∈=x x y5.已知函数()则,x x x x x f ⎩⎨⎧>+-≤+=1,31,1f(2) =A.3 B,2 C.1 D.06.当10<<a 时,在同一坐标系中,函数x y a y a xlog ==-与的图象是.A B C D 7.如果二次函数)3(2+++=m mx x y 有两个不同的零点,则m 的取值范围是A.(-2,6)B.[-2,6]C. {}6,2-D.()()∞+-∞-.62, 8. 若函数 ()log (01)a f x x a =<<在区间[],2a a 上的最大值是最小值的2倍,则a 的值为( )A、4 B、2 C 、14 D 、129.三个数3.0222,3.0log ,3.0===c b a 之间的大小关系是A b c a <<. B. c b a << C. c a b << D.a c b << 10. 已知奇函数()f x 在0x ≥时的图象如图所示,则不等式()0xf x <的解集为A.(1,2) B.(2,1)-- C.(2,1)(1,2)-- D.(1,1)-11.设()833-+=x x f x,用二分法求方程()2,10833∈=-+x x x在内近似解的过程中得()()(),025.1,05.1,01<><f f f 则方程的根落在区间A.(1,1.25)B.(1.25,1.5)C.(1.5,2)D.不能确定 12.计算机成本不断降低,若每隔三年计算机价格降低31,则现在价格为8100元的计算机9年后价格可降为A.2400元B.900元C.300元D.3600元二、填空题(每小题4分,共16分.)13.若幂函数y =()x f 的图象经过点(9,13), 则f(25)的值是_________- 14. 函数()()1log 143++--=x x xx f 的定义域是 15. 给出下列结论(1)2)2(44±=-(2)331log 12log 22-=21 (3) 函数y=2x-1, x ∈ [1,4]的反函数的定义域为[1,7 ](4)函数y=x12的值域为(0,+∞) 其中正确的命题序号为16. 定义运算()() ,.a ab a b b a b ≤⎧⎪*=⎨>⎪⎩ 则函数()12x f x =*的最大值为 .答 题 卡二、填空题:13. 14。
新教材人教版高一数学上册单元测试题含答案全套

新教材人教版高一数学上册单元测试题含答案全套人教版高中数学必修第一册第一章测试题第Ⅰ卷一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合,,则等于( )A .B .C .D .【答案】B【解析】集合,,.2.是的( )条件 A .充分不必要 B .必要不充分 C .充要 D .既不充分也不必要 【答案】B【解析】由不能推得,反之由可推得, 所以是的必要不充分条件. 3.已知集合,,若,则实数的值为( )A .B .C .D .【答案】B【解析】∵集合,,且,∴,因此.4.下列命题中正确的是( )A .任何一个集合必有两个以上的子集B .空集是任何集合的子集C .空集没有子集D .空集是任何集合的真子集 【答案】B【解析】空集只有一个子集,故A 错;B 正确; 空集是本身的子集,故C 错;空集不能是空集的真子集,故D 错. 5.已知集合,则中元素的个数为( )A .B .C .D .【答案】A【解析】因为集合,{}1,2,3,4,5A ={}21,B y y x x A ==-∈A B {2,4}{1,3,5}{2,4,7,9}{1,2,3,4,5,7,9}{}1,2,3,4,5A ={}{}21,1,3,5,7,9B y y x x A ==-∈={}1,3,5A B =1x >4x >1x >4x >4x >1x >1x >4x >{1,3}A =-2{2,}B a ={1,2,3,9}A B =-a 1±3±1-3{1,3}A =-2{2,}B a ={1,2,3,9}AB =-29a =3a =±(){}22,3,,A x y xy x y =+≤∈∈Z Z A 9854(){}22,3,,A x y xy x y =+≤∈∈Z Z所以满足且,的点有,,,,,,,,共个.6.已知,则( )A .B .C .D .【答案】B 【解析】,故A 错,B 对,显然,所以C 不对,而,所以D 也不对,故本题选B .7.命题“存在实数,使”的否定是( ) A .对任意实数,都有 B .对任意实数,都有 C .不存在实数,使 D .存在实数, 【答案】B【解析】命题“存在实数,使”的否定是“对任意实数,都有”. 8.集合中的不能取的值的个数是( ) A .B .C .D .【答案】B【解析】由题意可知,且且, 故集合中的不能取的值的个数是个. 9.下列集合中,是空集的是( ) A . B .C .D .【答案】B【解析】对于A 选项,,不是空集, 对于B 选项,没有实数根,故为空集, 对于C 选项,显然不是空集,对于D 选项,集合为,故不是空集. 10.下列各组集合中表示同一集合的是( ) A ., B ., C ., D .,【答案】B223x y +≤x ∈Z y ∈Z (1,1)--(1,0)-(1,1)-(0,1)-(0,0)(0,1)(1,1)-(1,0)(1,1)9a ={A x x =≥a A ∉a A ∈{}a A ={}a a ∉>a A ∈{}a A ≠{}a a ∈x 1x >x 1x >x 1x ≤x 1x ≤x 1x ≤x 1x >x 1x ≤{}22,4,0x x --x 2345222040224x x x x x -≠-≠⇒≠-≠⎧⎪⎨⎪⎩-2x ≠-1x ≠-{}22,4,0x x --x 3{}0|2x x +={}210,x x x +=∈R {}1|x x <(){}22,,,x y yx x y =-∈R 2x =-210x +={(0,0)}{(3,2)}M ={3,2}N ={2,3}M ={3,2}N ={2,3}M ={2,3}N x y ==={(2,3)}M ={(5,4)}N =【解析】对于A ,,表示点集,,表示数集,故不是同一集合; 对于B ,,,根据集合的无序性,集合表示同一集合; 对于C ,集合的元素是数,集合的元素是等式;对于D ,,集合的元素是点,, 集合的元素是点,集合不表示同一集合.11.学校先举办了一次田径运动会,某班共有名同学参赛,又举办了一次球类运动会,这个班有名同学参赛,两次运动会都参赛的有人.两次运动会中,这个班总共的参赛人数为( ) A . B . C . D . 【答案】B【解析】因为参加田径运动会的有名同学,参加球类运动会的有名同学,两次运动会都参加的有人,所以两次运动会中,这个班总共的参赛人数为.12.已知集合,.若, 则实数的取值范围为( ) A . B .C .D .【答案】D【解析】, 当为空集时,;当不为空集时,,综上所述得.第Ⅱ卷二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.集合,则集合的子集的个数为 个. 【答案】【解析】由已知,集合的子集个数为.14.命题“”是命题“”的 (“充分不必要,必要不充分,充要,既不充分也不必要”)条件. 【答案】必要不充分【解析】的解为或,所以当“”成立时,则“”未必成立; 若“”,则“”成立,{(3,2)}M =M {3,2}N =N {2,3}M ={3,2}N =,M N M N {(2,3)}M =M (2,3){(5,4)}N =N (5,4),M N 8123201714238123812317+-={}|25A x x =-≤≤{}|121B x m x m =+≤≤-B A ⊆m 3m ≥23m ≤≤2m ≥3m ≤{}|121B x m x m =+≤≤-B 2112m m m -<+⇒<B 22152312m m m m ≥⎧⎪-≤⇒≤≤⎨⎪+≥-⎩3m ≤2{}1,A =A 4A 224=220x x --=1x =-220x x --=1x =-2x =220x x --=1x =-1x =-220x x --=故命题“”是命题“”的必要不充分条件.15.命题“,”的否定是 .【答案】,【解析】由全称量词命题的否定是存在量词命题可知,命题“,”的否定是“,”.16.设全集是实数集,,, 则图中阴影部分所表示的集合是 .【答案】【解析】由图可知,阴影部分为,∵,∴,∴.三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤) 17.(10分)已知集合,且,求的取值集合. 【答案】.【解析】∵,∴或,即或.当时,;当时,; 当时,不满足互异性, ∴的取值集合为{}1,3.18.(12分)已知集合,,若,求实数,的值.【答案】或.220x x --=1x =-x ∀∈R 23210x x -+>0x ∃∈R 2003210x x -+≤x ∀∈R 23210x x -+>0x ∃∈R 2003210x x -+≤U R {}22M x x x =<->或{}13N x x =<<{}12x x <≤Venn ()UN M {}22M x x x =<->或{}22UM x x -=≤≤(){}12UNM x x =<≤{}21,2,4M m m =++5M ∈m {}1,3{}251,2,4m m ∈++25m +=245m +=3m =1m =±3m ={}1,5,13M =1m ={}1,3,5M =1m =-{}1,1,5M =m {,,2}A a b =2{2,,2}B b a =A B =a b 01a b =⎧⎨=⎩1412a b ⎧=⎪⎪⎨⎪=⎪⎩【解析】由已知,得①,解得或, 当时,集合不满足互异性, 当时,集合,集合,符合题意;②,解得(舍)或,当时,集合,集合符合题意,综上所述,可得或.19.(12分)设集合,. (1)若,试判定集合与的关系; (2)若,求实数的取值集合.【答案】(1)是的真子集;(2). 【解析】(1),,∴是的真子集. (2)当时,满足,此时;当时,,集合,又,得或,解得或. 综上,实数的取值集合为.20.(12分)已知全集,集合,.求:A B =22a a b b =⎧⎨=⎩00a b =⎧⎨=⎩01a b =⎧⎨=⎩00a b =⎧⎨=⎩{0,0,2}A =01a b =⎧⎨=⎩{0,1,2}A ={2,1,0}B =22a b b a ⎧=⎨=⎩00a b =⎧⎨=⎩1412a b ⎧=⎪⎪⎨⎪=⎪⎩1412a b ⎧=⎪⎪⎨⎪=⎪⎩11{,,2}42A =11{2,,}42B =01a b =⎧⎨=⎩1412a b ⎧=⎪⎪⎨⎪=⎪⎩{}28150A x x x =-+=}10B =-=15a =A B B A ⊆a B A 110,,35⎧⎫⎨⎬⎩⎭{3,5}A ={5}B =B A B =∅B A ⊆0a =B ≠∅0a ≠1B a ⎧⎫=⎨⎬⎩⎭B A ⊆13a =15a=13a =15a 110,,35⎧⎫⎨⎬⎩⎭{}6U x x =∈<N {}1,2,3A ={}2,4B =(1),,;(2),;(3)设集合且,求的取值范围.【答案】(1)见解析;(2)见解析;(3). 【解析】(1),∵,,.(2),∴.(3)由(2)可知,∵,∴,解得.21.(12分)已知集合为全体实数集,,. (1)若,求;(2)若,求实数的取值范围. 【答案】(1);(2).【解析】(1)当时,,所以,所以.(2)①,即时,,此时满足.②当,即时,,由得,或, 所以.综上,实数的取值范围为.22.(12分)已知二次函数,非空集合.(1)当时,二次函数的最小值为,求实数的取值范围;(2)是否存在整数的值,使得“”是“二次函数的大值为”的充分条件, 如果存在,求出一个整数的值,如果不存在,请说明理由. 【答案】(1);(2)见解析.【解析】(1),当且仅当时,二次函数有最小值为,由已知时,二次函数的最小值为,则,所以. (2)二次函数,开口向上,对称轴为,作出二次函数图象如图所示,由“”是“二次函数的大值为”的充分条件, 即时,二次函数的最大值为,A B UA UB AB ()UA B {|21}C x a x a =-<≤-()UA CB ⊆a 3a ≥2A B ={0,1,2,3,4,5}U ={0,4,5}UA ={0,1,3,5}UB ={1,2,3,4}AB =(){0,5}UA B =(){0,5}UA B =()U A C B ⊆021521a a a a -<⎧⎪-≥⎨⎪->-⎩3a ≥U {}25M x x x =≤-≥或{}121N x a x a =+≤≤-3a =UMN N M ⊆a {}45Ux x x MN =<≥或{}24a a ≥或3a ={}45|N x x =≤≤{}45UN x x x =<>或{}45Ux x x MN =<≥或211a a -<+2a <N =∅N M ⊆211a a -≥+2a ≥N ≠∅N M ⊆15a +≥212a -≤-4a ≥a {}24a a a <≥或243y x x =-+{}|0A x x a =≤≤x A ∈1-a a x A ∈3a 2a ≥2243(2)1y x x x =-+=--2x =1-x A ∈1-2A ∈2a ≥2(2)1y x =--2x =x A ∈3x A ∈3,即为,令,解得或,由图像可知,当或时,二次函数的最大值不等于,不符合充分条件, 则,即可取的整数值为,,,,任意一个.第一册第二章测试题一元二次函数、方程和不等式注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
人教版高一上期末数学试卷(有答案)

人教版高一上期末数学试卷(有答案) 无明显问题的段落:一、选择题:1.已知集合M={x∈R|x^2+2x=0},N={2},则M∩N={2}。
2.若一个扇形的弧长是3,半径是2,则该扇形的圆心角为3/4π。
3.设x∈R,向量a=(3,x),b=(-1,1),若a⊥b,则||a||=6.4.二次函数f(x)=ax^2+bx+1的最小值为f(1)=0,则a-b=-2.5.已知点O是平行四边形ABCD两条对角线的交点,给出下列向量组:①,②,③,④。
其中可作为该平面其他向量基底的是①④。
6.已知函数f(x)=|x-1|,则与y=f(x)相等的函数是g(x)=1-x。
7.已知a=log3 2,b=log3 4,c=log3 5,则c>b>a。
8.已知函数f(x)=x^2-4x+5,若g(x)=f(x)-m为奇函数,则实数m的值为2.9.某人欲购买标价为2700元的商品,他可以享受的实际折扣率约为75%。
10.将函数y=f(x)的图象上所有点向左平行移动1个单位长度,得到函数g(x)的图象,则g(x)图象的一条对称轴的方程是y=-1.11.函数y=f(x)的图象可能是D。
12.关于x的方程(a^2-1)x^2+2ax+a=0 (a>1且a≠-1)解的个数是2.二、填空题:13.函数f(x)=sin(x-π/2),则sinα=f(α+π/2),tan(π-α)=tanα。
14.已知角α为第四象限角,且tanα=-3/4,则cosα=4/5,sinα=-3/5.解得m=2c-1=2log3(5)-1。
故选:C.4.(3分)二次函数f(x)=ax2+bx+1的最小值为f(1)=0,则a-b=()A.-2 B.-1 C.1 D.3解:由题意可得f(1)=a+b+1=0,即a=-b-1,代入a-b中得a-b=-2b-1.所以选A。
5.(3分)设点O是平行四边形ABCD两条对角线的交点,给出下列向量组:①(3,1),②(1,1),③(1,-1),④(-2,-2)与(-1,2);其中可作为该平面其他向量基底的是()A.①② B.①③ C.①④ D.③④解:根据向量组共线或不共线的特性,可以排除②和④。
人教版高一数学必修一第一学期期末测试A卷(含答案和解析)

期末测试卷02(本卷满分150分,考试时间120分钟) 测试范围:必修第一册(人教A 版2019)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.1.设集合}034|{2<+-=x x x A ,}032|{>-=x x B ,则=B A ( )。
A 、)231(,B 、)31(, C 、)323(,D 、)1(∞+,【答案】C【解析】由题意得,}31|{<<=x x A ,}23|{>=x x B ,则)323(,=B A ,故选C 。
2.命题“全等三角形的面积一定都相等”的否定是( )。
A 、全等三角形的面积不一定都相等B 、不全等三角形的面积不一定都相等C 、存在两个不全等三角形的面积相等D 、存在两个全等三角形的面积不相等 【答案】D【解析】命题是省略量词的全称命题,故选D 。
3.已知0>a ,0>b ,且12=+b a ,则ba 11+的最小值为( )。
A 、223+ B 、243+ C 、263+ D 、283+ 【答案】A【解析】∵0>a ,0>b ,∴223221)11)(2(11+≥+++=++=+ab b a b a b a b a , 即最小值为223+,故选A 。
4.已知α为第三象限角,且α=-α2cos 22sin 2,则)42sin(π-α的值为( )。
A 、1027- B 、107- C 、107 D 、1027 【答案】D【解析】由已知得)1(cos 22sin 22-α=-α,则4tan 2=α,由α为第三象限角,得2tan =α,故552sin -=α,55cos -=α,∴1027)2cos 2(sin 22)42sin(=α-α=π-α,故选D 。
5.若函数)2lg()(2a x ax x f +-=的定义域为R ,则实数a 的取值范围为( )。
人教版高一数学必修四测试题(含详细答案)

高一数学试题(必修4)(特别适合按14523顺序的省份)必修4 第一章三角函数(1)一、选择题:1.已知A={第一象限角},B={锐角},C={小于90°的角},那么A、B、C关系是()A.B=A∩C B.B∪C=C C.AC D.A=B=C2 等于()A B C D3.已知的值为()A.-2 B.2 C.D.-4.下列函数中,最小正周期为π的偶函数是()A.y=sin2xB.y=cos C .sin2x+cos2x D. y=5 若角的终边上有一点,则的值是()A B C D6.要得到函数y=cos()的图象,只需将y=sin的图象()A.向左平移个单位 B.同右平移个单位C.向左平移个单位 D.向右平移个单位7.若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将整个图象沿x轴向左平移个单位,沿y轴向下平移1个单位,得到函数y=sinx的图象则y=f(x)是()A.y= B.y=C.y=D.8. 函数y=sin(2x+)的图像的一条对轴方程是()A.x=-B. x=- C .x=D.x=9.若,则下列结论中一定成立的是()A. B. C. D.10.函数的图象()A.关于原点对称 B.关于点(-,0)对称 C.关于y轴对称 D.关于直线x=对称11.函数是()A.上是增函数 B.上是减函数C.上是减函数D.上是减函数12.函数的定义域是()A.B.C. D.二、填空题:13. 函数的最小值是 .14 与终边相同的最小正角是_______________15. 已知则 .16 若集合,,则=_______________________________________三、解答题:17.已知,且.a)求sinx、cosx、tanx的值.b)求sin3x – cos3x的值.18 已知,(1)求的值(2)求的值19. 已知α是第三角限的角,化简20.已知曲线上最高点为(2,),由此最高点到相邻的最低点间曲线与x轴交于一点(6,0),求函数解析式,并求函数取最小值x的值及单调区间必修4 第一章三角函数(2)一、选择题:1.已知,则化简的结果为()A. B. C. D. 以上都不对2.若角的终边过点(-3,-2),则( )A.sin tan>0 B.cos tan>0C.sin cos>0 D.sin cot>03 已知,,那么的值是()A B C D4.函数的图象的一条对称轴方程是()A. B. C. D.5.已知,,则tan2x= ( ) A. B. C. D.6.已知,则的值为()A. B. 1 C. D. 2 7.函数的最小正周期为()A.1 B. C. D.8.函数的单调递增区间是()A. B.C. D.9.函数,的最大值为()A.1 B. 2 C. D.10.要得到的图象只需将y=3sin2x的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位 D.向右平移个单位11.已知sin(+α)=,则sin(-α)值为()A. B. — C. D. —12.若,则()A. B. C. D.二、填空题13.函数的定义域是14.的振幅为初相为15.求值:=_______________16.把函数先向右平移个单位,然后向下平移2个单位后所得的函数解析式为________________________________三、解答题17 已知是关于的方程的两个实根,且,求的值18.已知函数,求:(1)函数y的最大值,最小值及最小正周期;(2)函数y的单调递增区间19.已知是方程的两根,且,求的值20.如下图为函数图像的一部分(1)求此函数的周期及最大值和最小值(2)求与这个函数图像关于直线对称的函数解析式必修4 第三章三角恒等变换(1)一、选择题:1.的值为 ( )A 0BC D2.,,,是第三象限角,则()A B C D3.设则的值是( )A B C D4. 已知,则的值为()A B C D5.都是锐角,且,,则的值是()A B C D6. 且则cos2x的值是()A B C D7.在中,的取值域范围是 ( )A B C D8. 已知等腰三角形顶角的余弦值等于,则这个三角形底角的正弦值为()A B C D9.要得到函数的图像,只需将的图像()A、向右平移个单位B、向右平移个单位C、向左平移个单位D、向左平移个单位10. 函数的图像的一条对称轴方程是()A、 B、 C、 D、11.若是一个三角形的最小内角,则函数的值域是( )A B C D12.在中,,则等于 ( )A B C D二、填空题:13.若是方程的两根,且则等于14. .在中,已知tanA ,tanB是方程的两个实根,则15. 已知,则的值为16. 关于函数,下列命题:①若存在,有时,成立;②在区间上是单调递增;③函数的图像关于点成中心对称图像;④将函数的图像向左平移个单位后将与的图像重合.其中正确的命题序号(注:把你认为正确的序号都填上)三、解答题:17. 化简18. 求的值.19. 已知α为第二象限角,且sinα=求的值.20.已知函数,求(1)函数的最小值及此时的的集合。
人教版高一数学必修 测试题及答案全套

A. 9 2
B. 7 2
C. 5 2
D. 3 2
6.底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为 5 ,它的对角线的长
分别是 9 和15 ,则这个棱柱的侧面积是( )
A.130
B.140 C.150 D.160
二、填空题
1.一个棱柱至少有 _____个面,面数最少的一个棱锥有 ________个顶点,
人教版高一数学必修 2 测试题及答案全套
[基础训练 A 组]
一、选择题
1.有一个几何体的三视图如下图所示,这个几何体应是一个( )
A.棱台
B.棱锥
C.棱柱
D.都不对
主视图
左视图
2.棱长都是1的三棱锥的表面积为( )
A. 3
B. 2 3 பைடு நூலகம். 3 3
D. 4 3
俯视图
3.长方体的一个顶点上三条棱长分别是 3, 4, 5 ,且它的8 个顶点都在
同一球面上,则这个球的表面积是( )
A. 25 B. 50 C.125 D.都不对
4.正方体的内切球和外接球的半径之比为( )
A. 3 :1 B. 3 : 2 C. 2 : 3 D. 3 : 3
5.在△ABC 中, AB 2, BC 1.5, ABC 1200 ,若使绕直线 BC 旋转一周,
则所形成的几何体的体积是( )
顶点最少的一个棱台有 ________条侧棱。
1
PS:双击获取文档。Ctrl+A,Ctrl+C,然后粘贴到word即可。 未能直接提供word版,抱歉。
高一数学试题及答案上册人教版

高一数学试题及答案上册人教版一、选择题(每小题3分,共30分)1. 函数y=f(x)=2x+3的值域是()A. (-∞, +∞)B. [3, +∞)C. (-∞, 3]D. [2, +∞)2. 若直线l的方程为y=2x+b,且直线l与x轴交于点(1,0),则b的值为()A. -2B. 2C. -1D. 13. 已知集合A={x|x^2-5x+6=0},B={x|x^2-3x+2=0},则A∩B=()A. {1}B. {2}C. {1,2}D. 空集4. 若函数f(x)=x^3-3x在区间[-2,2]上单调递增,则f(1)的值为()A. -2B. -1C. 2D. 15. 已知等差数列{an}的首项a1=1,公差d=2,则其前n项和Sn的公式为()A. Sn=n^2B. Sn=n(n+1)C. Sn=n(n+1)/2D. Sn=n^2+n6. 函数y=f(x)=x^2-4x+4的图像关于直线x=()A. 0B. 2C. -2D. 47. 若复数z=1+i,则|z|=()A. 1B. √2C. 2D. √38. 已知向量a=(2,1),b=(1,-1),则向量a+b的坐标为()A. (3,0)B. (1,2)C. (3,-2)D. (1,0)9. 函数y=f(x)=x^3-3x+1的极值点个数为()A. 0B. 1C. 2D. 310. 已知双曲线C的方程为x^2/a^2-y^2/b^2=1(a>0,b>0),若双曲线C的渐近线方程为y=±(1/2)x,则a/b的值为()A. 2B. 1/2C. 1D. 4二、填空题(每小题4分,共20分)11. 函数y=f(x)=x^2-4x+m的顶点坐标为()。
12. 若直线l的倾斜角为45°,则直线l的斜率为()。
13. 已知等比数列{bn}的首项b1=2,公比q=1/2,则其前n项积Tn的公式为()。
14. 函数y=f(x)=x^3+3x^2-9x+5的单调递减区间为()。
人教版高一年级数学题及答案

人教版高一年级数学题及答案【导语】仰望天空时,什么都比你高,你会自卑;俯视大地时,什么都比你低,你会自负;只有放宽视野,把天空和大地尽收眼底,才能在苍穹沃土之间找到你真正的位置。
无需自卑,不要自负,坚持自信。
xx高一频道为你整理了《人教版高一年级数学题及答案》希望你对你的学习有所帮助!【一】第一卷(选择题共60分)一、选择题(本大题共12个小题,每题5分,共60分,在每题给出的四个选项中,只有一项为哪一项符号题目要求的。
)1.集合A={0,1,2,3,4,5},B={1,3,6,9},C={3,7,8},那么(A∩B)∪C等于()A.{0,1,2,6,8}B.{3,7,8}C.{1,3,7,8}D.{1,3,6,7,8}[答案]C[解析]A∩B={1,3},(A∩B)∪C={1,3,7,8},应选C.2.(09 陕西文)定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有f(x2)-f(x1)x2-x1 C.f(-2) [答案]A[解析]假设x2-x1>0,那么f(x2)-f(x1) ∴f(x)在[0,+∞)上是减函数, ∵3>2>1,∴f(3) 又f(x)是偶函数,∴f(-2)=f(2),∴f(3) 3.f(x),g(x)对应值如表.x01-1f(x)10-1x01-1g(x)-101那么f(g(1))的值为()A.-1B.0C.1D.不存在[答案]C[解析]∵g(1)=0,f(0)=1,∴f(g(1))=1.4.函数f(x+1)=3x+2,那么f(x)的解析式是()A.3x+2B.3x+1C.3x-1D.3x+4[答案]C[解析]设x+1=t,那么x=t-1,∴f(t)=3(t-1)+2=3t-1,∴f(x)=3x-1.5.f(x)=2x-1(x≥2)-x2+3x(x 又f(-x)=-f(x),∴f(x)为奇函数. 9.(08 天津文)函数f(x)=x+2,x≤0,-x+2,x>0,那么不等式f(x)≥x2的解集为()A.[-1,1]B.[-2,2]C.[-2,1]D.[-1,2][答案]A[解析]解法1:当x=2时,f(x)=0,f(x)≥x2不成立,排除B、D;当x=-2时,f(x)=0,也不满足f(x)≥x2,排除C,应选A.解法2:不等式化为x≤0x+2≥x2或x>0-x+2≥x2,解之得,-1≤x≤0或0 10.调查了某校高一一班的50名学生参加课外活动小组的情况,有32人参加了数学兴趣小组,有27人参加了英语兴趣小组,对于既参加数学兴趣小组,又参加英语兴趣小组的人数统计中,以下说法正确的选项是()A.最多32人B.最多13人C.最少27人D.最少9人[答案]D[解析]∵27+32-50=9,故两项兴趣小组都参加的至多有27人,至少有9人.11.设函数f(x)(x∈R)为奇函数,f(1)=12,f(x+2)=f(x)+f(2),那么f(5)=()A.0B.1C.52D.5[答案]C[解析]f(1)=f(-1+2)=f(-1)+f(2)=12,又f(-1)=-f(1)=-12,∴f(2)=1,∴f(5)=f(3)+f(2)=f(1)+2f(2)=52.12.f(x)=3-2|x|,g(x)=x2-2x,F(x)=g(x),假设f(x)≥g(x),f(x),假设f(x) A.值为3,最小值-1B.值为7-27,无最小值C.值为3,无最小值D.既无值,又无最小值[答案]B[解析]作出F(x)的图象,如图实线局部,知有值而无最小值,且值不是3,应选B.第二卷(非选择题共90分)二、填空题(本大题共4个小题,每题4分,共16分,把正确答案填在题中横线上)13.(2022 江苏,1)设集合A={-1,1,3},B={a+2,a2+4},A∩B={3},那么实数a=________.[答案]-1[解析]∵A∩B={3},∴3∈B,∵a2+4≥4,∴a+2=3,∴a=-1.14.函数y=f(n)满足f(n)=2(n=1)3f(n-1)(n≥2),那么f(3)=________. [答案]18[解析]由条件知,f(1)=2,f(2)=3f(1)=6,f(3)=3f(2)=18.15.函数f(x)=2-ax(a≠0)在区间[0,1]上是减函数,那么实数a的取值范围是________.[答案](0,2][解析]a0.由2-ax≥0得,x≤2a,∴f(x)在(-∞,2a]上是减函数,由条件2a≥1,∴0 16.国家规定个人稿费的纳税方法是:不超过800元的不纳税;超过800元而不超过4000元的按超过800元的14%纳税;超过4000元的按全部稿酬的11%纳税.某人出版了一本书,共纳税420元,那么这个人的稿费为________.[答案]3800元[解析]由于4000×11%=440>420,设稿费x元,x5},分别就以下条件求实数a的取值范围:(1)A∩B≠ ,(2)A∩B=A.[解析](1)因为A∩B≠ ,所以a5,即a2.(2)因为A∩B=A,所以A B,所以a>5或a+35或a0)∵f(0)=3,∴a=2,∴f(x)=2(x-1)2+1,即f(x)=2x2-4x+3.(2)由条件知2a 19.(此题总分值12分)图中给出了奇函数f(x)的局部图象,f(x)的定义域为[-5,5],试补全其图象,并比拟f(1)与f(3)的大小.[解析]奇函数的图象关于原点对称,可画出其图象如图.显见f(3)>f(1). 20.(此题总分值12分)一块形状为直角三角形的铁皮,直角边长分别为40cm 与60cm现将它剪成一个矩形,并以此三角形的直角为矩形的一个角,问怎样剪法,才能使剩下的残料最少?[解析]如图,剪出的矩形为CDEF,设CD=x,CF=y,那么AF=40-y.∵△AFE∽△ACB.∴AFAC=FEBC即∴40-y40=x60∴y=40-23x.剩下的残料面积为:S=12×60×40-x y=23x2-40x+1200=23(x-30)2+600∵0 ∴在边长60cm的直角边CB上截CD=30cm,在边长为40cm的直角边AC 上截CF=20cm时,能使所剩残料最少.21.(此题总分值12分)(1)假设a0,判断并证明f(x)=x+ax在(0,a]上的单调性.[解析](1)∵a =(x1+ax1)-(x2+ax2)=(x1-x2)+a(x2-x1)x1x2=(x1-x2)(1-ax1x2)>0,∴f(x1)>f(x2),∴f(x)在(0,a]上单调减.22.(此题总分值14分)设函数f(x)=|x-a|,g(x)=ax.(1)当a=2时,解关于x的不等式f(x) (2)记F(x)=f(x)-g(x),求函数F(x)在(0,a]上的最小值(a>0).[解析](1)|x-2|23.(2)F(x)=|x-a|-ax,∵0 ∴F(x)=-(a+1)x+a.∵-(a+1) A.3y C.log4x [答案]C[解析]∵0 ∴①由y=3u为增函数知3xlogy3,∴B错.③由y=log4u为增函数知log4x ④由y=14u为减函数知14x>14y,排除D. 6.方程|x|-ax-1=0仅有一个负根,那么a的取值范围是()A.a1D.a≥1[答案]D[解析]数形结合判断.7.a>0且a≠1,那么两函数f(x)=ax和g(x)=loga-1x的图象只可能是() [答案]C[解析]g(x)=loga-1x=-loga(-x),其图象只能在y轴左侧,排除A、B;由C、D知,g(x)为增函数,∴a>1,∴y=ax为增函数,排除D.∴选C.8.以下各函数中,哪一个与y=x为同一函数()A.y=x2xB.y=(x)2C.y=log33xD.y=2log2x[答案]C[解析]A∶y=x(x≠0),定义域不同;B∶y=x(x≥0),定义域不同;D∶y=x(x>0)定义域不同,应选C.9.(上海大学附中2022~2022高一期末)以下图为两幂函数y=xα和y=xβ的图像,其中α,β∈{-12,12,2,3},那么不可能的是()[答案]B[解析]图A是y=x2与y=x12;图C是y=x3与y=x-12;图D是y=x2与y=x-12,应选B.10.(2022 天津理,8)设函数f(x)=log2x,x>0,log12(-x),xf(-a),那么实数a的取值范围是()A.(-1,0)∪(0,1)B.(-∞,-1)∪(1,+∞)C.(-1,0)∪(1,+∞)D.(-∞,-1)∪(0,1)[答案]C[解析]解法1:由图象变换知函数f(x)图象如图,且f(-x)=-f(x),即f(x)为奇函数,∴f(a)>f(-a)化为f(a)>0,∴当x∈(-1,0)∪(1,+∞),f(a)>f(-a),应选C.解法2:当a>0时,由f(a)>f(-a)得,log2a>log12a,∴a>1;当af(-a)得,log12(-a)>log2(-a),∴-1 11.某市2022年新建住房100万平方米,其中有25万平方米经济适用房,有关部门方案以后每年新建住房面积比上一年增加5%,其中经济适用房每年增加10万平方米.按照此方案,当年建造的经济适用房面积首次超过该年新建住房面积一半的年份是(参考数据:1.052=1,1.053=1.16,1.054=1.22,1.055=1.28)()A.2022年B.2022年C.2022年D.2022年[答案]C[解析]设第x年新建住房面积为f(x)=100(1+5%)x,经济适用房面积为g(x)=25+10x,由2g(x)>f(x)得:2(25+10x)>100(1+5%)x,将条件代入验证知x =4,所以在2022年时满足题意.12.(2022 山东理,4)设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x +2x+b(b为常数),那么f(-1)=()A.3B.1C.-1D.-3[答案]D[解析]∵f(x)是奇函数,∴f(0)=0,即0=20+b,∴b=-1,故f(1)=2+2-1=3,∴f(-1)=-f(1)=-3.第二卷(非选择题共90分)二、填空题(本大题共4个小题,每题4分,共16分,把正确答案填在题中横线上)13.化简:(lg2)2+lg2lg5+lg5=________.[答案]1[解析](lg2)2+lg2lg5+lg5=lg2(lg2+lg5)+lg5=lg2+lg5=1.14.(09 重庆理)假设f(x)=12x-1+a是奇函数,那么a=________.[答案]12[解析]∵f(x)为奇函数,∴f(-1)=-f(1),即12-1-1+a=-12-1-a,∴a=12.15.集合A={x|x2-9x+14=0},B={x|ax+2=0}假设BA,那么实数a的取值集合为________.[答案]{0,-1,-27}[解析]A={2,7},当a=0时,B=满足BA;当a≠0时,B={-2a}由BA知,-2a=2或7,∴a=-1或-27综上可知a的取值集合为{0,-1,-27}.16.x23>x35,那么x的范围为________.[答案](-∞,0)∪(1,+∞)[解析]解法1:y=x23和y=x35定义域都是R,y=x23过一、二象限,y=x35过一、三象限,∴当x∈(-∞,0)时x23>x35恒成立x=0时,显然不成立.当x∈(0,+∞)时,x23>0,x35>0,∴=x115>1,∴x>1,即x>1时x23>x35∴x的取值范围为(-∞,0)∪(1,+∞).解法2:x0>x35成立;x>0时,将x看作指数函数的底数∵23>35且x23>x35,∴x>1.∴x的取值范围是(-∞,0)∪(1,+∞).[点评]变量与常量相互转化思想的应用.三、解答题(本大题共6个小题,共74分,解容许写出文字说明,证明过程或演算步骤)17.(此题总分值12分)用单调性定义证明函数f(x)=x-2x+1在(-1,+∞)上是增函数.[解析]证明:设x1>x2>-1,那么f(x1)-f(x2)=x1-2x1+1-x2-2x2+1=3(x1-x2)(x1+1)(x2+1)>0 ∴f(x1)>f(x2)∴f(x)在(-1,+∞)上是增函数.18.(此题总分值12分)全集R,集合A={x|x2+px+12=0},B={x|x2-5x +q=0},假设( RA)∩B={2},求p+q的值.[解析]∵( RA)∩B={2},∴2∈B,由B={x|x2-5x+q=0}有4-10+q=0,∴q=6,此时B={x|x2-5x+6}={2,3}假设 RA中有3,那么( RA)∩B={2,3}与( RA)∩B={2}矛盾,∵3∈R又3 ( RA),∴3∈A,由A={x|x2+px+12=0}有9+3p+12=0,∴p=-7.∴p+q=-1.19.(此题总分值12分)设f(x)=4x4x+2,假设0<a<1,试求:(1)f(a)+f(1-a)的值;(2)f(11001)+f(21001)+f(31001)+…+f(10001001)的值.[解析](1)f(a)+f(1-a)=4a4a+2+41-a41-a+2=4a4a+2+44+2×4a=4a+24a+2=1∴f(11001)+f(10001001)=f(21001)+f(9991001)=…=f(5001001)+f(5011001)=1.∴原式=500.20.(此题总分值12分)假设关于x的方程x2+2ax+2-a=0有两个不相等的实根,求分别满足以下条件的a的取值范围.(1)方程两根都小于1;(2)方程一根大于2,另一根小于2.[解析]设f(x)=x2+2ax+2-a(1)∵两根都小于1,∴Δ=4a2-4(2-a)>0-2a0,解得a>1.(2)∵方程一根大于2,一根小于2,∴f(2)11/ 11。
最新人教版高一数学上学期期末考试试题(附答案)

最新人教版高一数学上学期期末考试试题(附答案)最新人教版高一数学上学期期末考试试题(附答案)一、选择题(每题3分,共36分)1.已知集合$A=\{2,4,6\}$。
且当$a\in A$ 时,$6-a\in A$。
则 $a$ 为()A。
2 B。
4 C。
3 D。
12.$\sin(-1050)$ 的值为()A。
$\dfrac{3}{3}$ B。
$\dfrac{3}{2}$ C。
$0$ D。
$2$ 或$4$3.下列函数中,不满足 $f(2x)=2f(x)$ 的是()A。
$f(x)=|x|$ B。
$f(x)=x+1$ C。
$f(x)=-x$ D。
$f(x)=x-|x|$4.函数 $f(x)=|\cos x|$ 的最小正周期为()A。
$2\pi$ B。
$\pi$ C。
$3\pi$ D。
均不对5.函数 $y=2\sin x-2$ 的定义域为()A。
$[2k\pi,2k\pi+\dfrac{\pi}{4}]$,$k\in Z$ B。
$[2k\pi+\dfrac{\pi}{4},2k\pi+\dfrac{\pi}{2}]$,$k\in Z$C。
$[2k\pi+\dfrac{3\pi}{4},2k\pi+\pi]$,$k\in Z$ D。
$[2k\pi,2k\pi+3\pi]$,$k\in Z$6.函数 $f(x)=ax^2+bx+c$ 满足 $f(1)>0$,$f(2)<0$,则$f(x)$ 在 $(1,2)$ 上的零点()A。
至多有一个 B。
有1个或2个 C。
有且仅有一个 D。
一个也没有7.已知向量 $\bold{a}=(1,2,3)$,$|\bold{b}|=1$,且两向量夹 $120^\circ$,则 $|\bold{a}-\bold{b}|=$()A。
$\sqrt{3}$ B。
$3$ C。
$5$ D。
$7$8.将函数 $y=\sin(x+\phi)$,$(0<\phi<\pi)$ 的图像所有点的纵坐标不变,横坐标伸长到原来的2倍,再向左平移$\dfrac{1}{2}$ 个单位得到一个奇函数的图像,则$\phi=$()A。
高一数学试卷及答案(人教版)

高一数学试卷(人教版)一、填空题1.已知b a ==7log ,3log 32,用含b a ,的式子表示=14log 2 。
2. 方程)4lg(12lg lg +-=x x 的解集为 。
3. 设α是第四象限角,43tan -=α,则=α2sin ____________________. 4. 函数1sin 2y -=x 的定义域为__________。
5. 函数22cos sin 2y x x =+,x R ∈的最大值是 .6. 把ααcos 2sin 6+-化为)2,0(,0)(sin(πφφα∈>+A A 其中)的形式是 。
7. 函数f (x )=(31)|cos x |在[-π,π]上的单调减区间为__ _。
8. 函数2sin(2)3y x π=-+与y 轴距离最近的对称中心的坐标是____。
9.,且,则。
10.设函数f(x)是以2为周期的奇函数,且 ,若,则(4c o s 2)f α的值 .11.已知函数,求.12.设函数()⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-∈>+=2,2,0sin ππϕωϕωx y 的最小正周期为π,且其图像关于直线12x π=对称,则在下面四个结论中:(1)图像关于点⎪⎭⎫⎝⎛0,4π对称;(2) 图像关于点⎪⎭⎫⎝⎛0,3π对称;(3)在⎥⎦⎤⎢⎣⎡6,0π上是增函数;(4)在⎥⎦⎤⎢⎣⎡-0,6π上是增函数,那么所有正确结论的编号为____ 二、选择题13.已知正弦曲线y =A sin(ωx +φ),(A >0,ω>0)上一个最高点的坐标是(2,3),由这个最高点到相邻的最低点,曲线交x 轴于(6,0)点,则这条曲线的解析式是 ( )(A) y =3sin(8πx +4π)(B) y =3sin(8πx -2) (C) y =3sin(8πx +2)(D) y =3sin(8πx -4π)14.函数y=sin(2x+3π)的图象是由函数y=sin2x 的图像 ( ) (A) 向左平移3π单位 (B) 向左平移6π单位2. (C) 向左平移56π单位(D) 向右平移56π单位 15.在三角形△ABC 中, 36=a ,21=b ,60=A ,不解三角形判断三角形解的情况( ).(A) 一解 (B ) 两解 (C) 无解 (D) 以上都不对 16. 函数f (x )=cos2x +sin(2π+x )是 ( ). (A) 非奇非偶函数 (B) 仅有最小值的奇函数(C) 仅有最大值的偶函数(D) 既有最大值又有最小值的偶函数三、解答题17.(8分)设函数)1(),1(log )(2->+=x x x f (1)求其反函数)(1x f -;(2)解方程74)(1-=-x x f .18.(10分)已知2cos sin cos sin =+-xx xx .(1)求x tan 的值;(2)若x x cos ,sin 是方程02=+-n mx x 的两个根,求n m 22+的值. 19.(分)已知函数;(1).求f(x)的定义域;(2).写出函数()f x 的值域;(3).求函数()f x 的单调递减区间;20.(12分)设关于的方程在内有两相异解,;(1).求的取值范围; (2).求的值。
高一数学集合练习题及答案(人教版)-百度文库

高一数学集合练习题及答案(人教版)-百度文库一、单选题1.已知集合{}22A x x =-≥,集合{2,3,4,5}B =,那么集合A B =( ) A .[2,5] B .(3,5]C .{4,5}D .{2,3,4,5}2.已知集合(){}{}|20,|10M x x x N x x =-<=-<,则M N =( )A .(),2-∞B .(),1-∞C .()0,1D .()1,2 3.设全集U =R ,集合302x A x x ⎧⎫-=≤⎨⎬+⎩⎭,集合{}ln 1B x x =≥,则()U A B =() A .()e,3 B .[]e,3 C .[)2,e - D .()2,e - 4.已知集合{}2|4A x x =≤,{}2|log 1B x x =≥,则A B ⋃=( )A .[]22-,B .{}2C .[)2+∞,D .[)2+-∞,5.已知集合{|04,}P x x x Z =<<∈,且M P ⊆,则M 可以是( )A .{1,2}B .{2,4}C .{0,2}D .{3,4} 6.设集合{}1A x x =>,{}2B x x =≤,则A B =( )A .∅B .{}12x x <≤C .{}12x x x ≤>或D .R7.若集合{}220A x x x =--<,{}21B x x =<,则A B =( )A .AB .BC .()1,0-D .()0,2 8.集合{}220A x x x =--≤,{}10B x x =-<,则A B =( )A .{}1x x ≥B .{}11x x -≤<C .{}1x x <-D .{}21x x -≤<9.已知集合{}1,2,3A =,{}20B x x =-<,则A B =( )A .{}1B .{}1,2C .{}0,1,2D .{}1,2,310.已知集合{|A x y ==,集合{|1}B x x =<,则A B =( )A .[)1,1-B .(1,1)-C .(,1)-∞D .(0,1) 11.已知{}1,2,3,4,5,7,8U =,{}1,2,3,5,8A =,则U A 的子集个数为( ) A .2 B .3 C .4 D .512.已知全集{}1,2,3,4,5U =,{}2,3,4A =,{}3,5B =,则()U A B =( ) A .{}1 B .{}3 C .{}2,4 D .{}1,2,4,513.已知集合{}{}|2|21A x x B x x =≥-=-≤≤,,则下列关系正确的是( )A .AB = B .A B ⊆C .B A ⊆D .A B =∅ 14.已知集合{}31,A a a n n ==-∈Z ,{}31,B b b n n ==+∈Z ,全集U =Z ,则()U A B ⋂=( )A .AB .BC .∅D .Z 15.已知集合{|03}A x x =<<,集合2{|0log 1}B x x =<<,则A ∩B =( )A .{|13}x x <<B .{|12}x x <<C .{|23}x x <<D .{|02}x x << 二、填空题16.已知全集{1,2,3,4,5,6,7}U =,集合{}1,3,5,7A =,则U A ____________.17.若集合(){}21420A x a x x =-+-=有且仅有两个子集,则实数a 的值是____. 18.已知函数2()43f x x x =-+,()52g x mx m =+-,若对任意的[]11,4x ∈,总存在[]21,4x ∈,使12()()f x g x =成立,则实数m 的取值范围是 ________.19.将集合{220s t A t s =-≤<且,}s t Z ∈中所有的元素从小到大排列得到的数列记为{}n a ,则50a =___________(填数值).20.设函数()1ln12mx f x x+=-是定义在区间(),n n -上的奇函数(0m >,0n >),则实数n 取值范围为______. 21.已知集合{}1,0,1A =-,{}220B x x x =-=,则A B ⋃=______.22.若集合234|0A x x x ,{}|10B x ax =-=,且“x B ∈”是“x A ∈”的充分非必要条件,则实数a 组成的集合是______.23.给出下列关系:①1R 2;Q ;③3N ∈;④0Z ∈.其中正确的序号是______.24.已知全集{}1,2,3,4,5,6U =,集合{}{}1,2,2,3,4A B ==,则A B ⋃=___________25.若集合{}2A x x =<,101B x x ⎧⎫=>⎨⎬+⎩⎭,则A B =______. 三、解答题26.已知集合{}21,3,A a =,()(){}|120B x x x a =---=,是否存在实数a ,使得A B A ⋃=若存在,求出a 的值;若不存在,说明理由.27.已知函数()f x =A ,函数()g x 的定义域为集合B ,(1)当0a =时,求A B ;(2)设命题:p x A ∈,命题:q x B ∈,p q 是的充分不必要条件,求实数a 的取值范围.28.设集合{}()(){}2|20,|30,0A x x x B x x a x a a =--<=--<>,语句:p x A ∈,语句:q x B ∈.(1)当1a =时,求集合A 与集合B 的交集;(2)若p 是q 的必要不充分条件,求正实数a 的取值范围.29.已知集合{}4222x A x =<≤,{}122B x a x a =-<≤+(1)当0a =,求A B ;(2)若A B =∅,求a 的取值范围.30.(1)集合{a, b, c, d }的所有子集的个数是多少?(2)集合{a 1, a 2, …, an }的所有子集的个数是多少?【参考答案】一、单选题1.C【解析】【分析】解出不等式22x -≥,然后根据集合的交集运算可得答案.【详解】 因为{}{}224A x x x x =-≥=≥,{2,3,4,5}B =,所以{4,5}A B =,故选:C2.C【解析】【分析】分别求出集合M 和集合N ,然后取交集即可.【详解】集合(){}{}|20|02M x x x x x =-<=<<,{}|1N x x =<,则MN ={}()|010,1x x <<=, 故选:C3.D【解析】【分析】求出集合A 、B ,利用交集和补集的定义可求得集合()U A B ∩.【详解】 因为{}30232x A x x x x ⎧⎫-=≤=-<≤⎨⎬+⎩⎭,{}{}ln 1e B x x x x =≥=≥, 所以,{}e U B x x =<,因此,()()2,e U A B =-.故选:D.4.D【解析】【分析】先化简集合A 、B ,再去求A B【详解】{}{}2|4|22A x x x x =≤=-≤≤,{}{}2|log 1|2B x x x x =≥=≥ 则{}{}{}|22|2|2x x x B x A x x -≤≤⋃≥==≥-⋃故选:D5.A【解析】【分析】化简集合P ,根据集合的包含关系确定M .【详解】因为{|04,}={1,2,3}P x x x Z =<<∈,又M P ⊆,所以任取x M ∈,则{1,2,3}x ∈, 所以M 可能为{2,3},A 对,又 0M ∉,4M ∉,∴ M 不可能为{2,4},{0,2},{3,4},B ,C ,D 错,故选:A.6.B【解析】【分析】根据交集的定义计算可得;【详解】 解:因为{}1A x x =>,{}2B x x =≤, 所以{}12A B x x ⋂=<≤;故选:B7.B【解析】【分析】 由题知{}12A x x =-<<,{}11B x x =-<<,再求交集即可.【详解】解:解不等式220x x --<得12x -<<,故{}12A x x =-<<,解不等式21x <得11x -<<,故{}11B x x =-<<,所以A B ={}11x x B -<<=.故选:B8.B【解析】【分析】解不等式可求得集合,A B ,由交集定义可得结果.【详解】{}{}22012A x x x x x =--≤=-≤≤,{}{}101B x x x x =-<=<, {}11A B x x ∴⋂=-≤<.故选:B.9.A 【解析】【分析】 根据集合交集的概念及运算,即可求解.【详解】由题意,集合{}{}202B x x x x =-<=<,又由{}1,2,3A =,根据集合交集的概念及运算,可得{}1A B ⋂=.故选:A.10.A【解析】【分析】求出集合A ,根据集合的交集运算即可求得答案.【详解】由题意得:{|{|1}A x y x x ===≥-,故{|11}A B x x ⋂=-≤<,故选:A11.C【解析】【分析】求出补集,再由子集的定义求解.【详解】由已知{4,7}U A =,子集有4个. 故选:C . 12.D【解析】【分析】利用交集和补集的定义可求得结果.【详解】由已知可得{}3A B ⋂=,所以,(){}1,2,4,5U A B ⋂=. 故选:D.13.C【解析】【分析】由子集的定义即可求解.【详解】解:因为集合{}{}|2|21A x x B x x =≥-=-≤≤,,所以根据子集的定义可知B A ⊆,故选:C.14.A【解析】【分析】根据集合的描述判断集合,A B 的关系,进而判断,U A B 的包含关系,即可得答案.【详解】由题设,{...,4,1,2,5,8,...}A =--,{...,5,2,1,4,7,...}B =--,所以A B =∅,而{...,4,3,1,0,2,3,5,6,8,...}U B =---,则U A B ≠⊂, 所以()U A B A =.故选:A15.B【解析】【分析】化简集合B ,再求集合A,B 的交集即可.【详解】∵集合{|03}A x x =<<,集合2{|0lo {|}g 121}B x x x x =<<<<=,∴A B ={|12}x x <<.故选:B.二、填空题16.{}2,4,6【解析】【分析】由补集的定义即可求解.【详解】解:因为全集{1,2,3,4,5,6,7}U =,集合{}1,3,5,7A =,所以{}2,4,6U A =. 故答案为:{}2,4,617.±1【解析】【分析】分析出集合A 有1个元素,对a 讨论方程解的情况即可.【详解】因为集合(){}21420A x a x x =-+-=有且仅有两个子集, 所以集合A 有1个元素.当a =1时,{}1|4202A x x ⎧⎫=-==⎨⎬⎩⎭,符合题意; 当a ≠1时,要使集合A 只有一个元素,只需()()244120a ∆=--⨯-=,解得:1a =-;综上所述: 实数a 的值是1或-1.故答案为:±1.18.(,3][6,)-∞-⋃+∞【解析】【分析】根据对任意的[]11,4x ∈,总存在[]21,4x ∈,使得12()()f x g x =,可得两个函数值域的包含关系,进而根据关于m 的不等式组,解不等式组即可.【详解】因为()22()4321f x x x x =-+=--,所以函数()f x 的对称轴为2x =,对任意的[]11,4x ∈,记()[]1,3f x ∈-.记[]1,3A =-.由题意知,当0m =时不成立,当0m >时,()52g x mx m =+-在[]1,4上是增函数,所以[]()5,25g x m m ∈-+,记[]5,25B m m =-+由题意知,B A所以m m -≥-+≥⎧⎨⎩15253,解得6m ≥. 当0m <时,()52g x mx m =+-在[]1,4上是减函数,所以[]()25,5g x m m ∈+-,记[]25,5C m m =+-,由题意知,C A ⊇所以251{53m m +≤--≥,解得3m ≤-. 综上所述,实数m 的取值范围是(,3][6,)-∞-⋃+∞.故答案为: (,3][6,)-∞-⋃+∞【点睛】解决本题的关键是将问题转化为对任意的[]11,4x ∈,总存在[]21,4x ∈,使得12()()f x g x =, 可得两个函数值域的包含关系,进而分别求两个函数的值域.19.992【解析】【分析】列举数列的前几项,观察特征,可得出50a .【详解】由题意得10212032313012345622,22,22,22,22,22,,a a a a a a =-=-=-=-=-=-观察规律可得22s t -中,以2s 为被减数的项共有s 个,因为123945++++=,所以50a 是1022t -中的第5项,所以1055022992a =-=.故答案为:992.20.10,2⎛⎤⎥⎝⎦【解析】【分析】由奇函数的定义和对数的运算性质,解方程可得m ,再由对数的真数大于0解不等式,然后利用集合的包含关系即可求解.【详解】 解:因为函数1()ln 12mx f x x +=-是定义在区间(,)n n -上的奇函数(0,0)m n >>,所以()()f x f x -=-,即1112lnln ln 12121mx mx x x x mx -+-=-=+-+, 所以112121mx x x mx--=++,即222114m x x -=-, 所以24m =,解得2m =±,又0m >,所以2m =,此时,21()ln12x f x x +=-, 由21012x x +>-,解得1122x -<<, 所以()11,22,n n ⎛-⎫⊆- ⎪⎝⎭,又0n >, 所以实数n 取值范围为10,2⎛⎤ ⎥⎝⎦. 故答案为:10,2⎛⎤ ⎥⎝⎦. 21.{1,0,1,2}-【解析】【分析】根据给定条件求出集合B ,再利用并集的定义直接计算作答.【详解】解方程220x x -=得:0x =或2x =,则{}0,2B =,而{}1,0,1A =-,所以{1,0,1,2}A B =-.故答案为:{1,0,1,2}-22.10,1,4⎧⎫-⎨⎬⎩⎭【解析】【分析】解出集合A ,根据题意,集合B 为集合A 的真子集,进而求得答案.【详解】由题意,{}1,4A =-,因为“x B ∈”是“x A ∈”的充分非必要条件,所以集合B 为集合A 的真子集,若a =0,则B =∅,满足题意;若0a ≠,则1B a ⎧⎫=⎨⎬⎩⎭,所以111a a =-⇒=-或1144a a =⇒=. 故答案为:10,1,4⎧⎫-⎨⎬⎩⎭. 23.①③④【解析】【分析】根据数的分类直接判断.【详解】由题可得1R 2Q ,3N ∈,0Z ∈,故①③④正确. 故答案为:①③④.24.5,6##{}6,5【解析】【分析】先求出A B ,再进行补集运算及即可求解.【详解】因为集合{}{}1,2,2,3,4A B ==,所以{}1,2,3,4A B =, 因为{}1,2,3,4,5,6U =,所以{}5,6A B ⋃=, 故答案为:5,6.25.{}12x x -<<## ()1,2-【解析】【分析】求解绝对值不等式解得集合A ,求解分式不等式求得集合B ,再求交集即可.【详解】 因为{}2A x x =<{|22}x x =-<<,101B x x ⎧⎫=>⎨⎬+⎩⎭{}1x x =-, 故可得A B ={|12}x x -<<. 故答案为:{}12x x -<<.三、解答题26.存在,2【解析】【分析】先得到B A ⊆,分别讨论1a =-和1a ≠-两种情况即可.【详解】由A B A ⋃=,得B A ⊆,当21a +=,即1a =-时,{1}B =,此时21a =不合题意,故1a ≠- 当1a ≠-时,{}1,2B a =+,因为B A ⊆,所以2a A +∈ 所以23a +=或22a a +=,解得1a =或2a =, 当1a =时,21a =不合题意;当2a =时,{}1,3,4A =,{}1,4B =,符合题意, 综上所述,存在实数2a =,使得A B A ⋃=成立.27.(1)1{|03A B x x ⋂=-<≤或1}x =;(2)1a ≥或43a ≤-. 【解析】【分析】(1)求解分式不等式和一元二次不等式,解得集合,A B ,再求交集即可; (2)根据p q 是的充分不必要条件可知A 是B 的真子集,列不等式求a 的取值范围即可.(1)要使得()f x 有意义,则1031x x -≥+,得(1)(31)0310x x x -+≥⎧⎨+≠⎩,解得:113x ≤-<, 所以1|13A x x ⎧⎫=-<≤⎨⎬⎩⎭;当0a =时,()g x =()g x 有意义,则20x x -≥,解得:1x ≥或0x ≤, 所以{|1B x x =≥或0}x ≤, 故1{|03A B x x ⋂=-<≤或1}x =. (2)以为22(21)0x a x a a -+++≥,即[]()(1)0x a x a --+≥,解得:1x a ≥+或x a ≤, 所以{|1B x x a =≥+或}x a ≤,由题意可知A 是B 的真子集,所以1a ≥或113a +≤-(等号不同时成立), 得1a ≥或43a ≤-. 28.(1){|12}x x <<; (2)20,3⎛⎤ ⎥⎝⎦. 【解析】【分析】(1)解一元二次不等式求集合A 、B ,应用集合的交运算求交集即可.(2)根据必要不充分关系有B A ≠⊂,即可求a 的范围. (1)由题设,{|12}A x x =-<<,当1a =时{|13}B x x =<<,所以{|12}A B x x =<<;(2)由题设,{|3}B x a x a =<<,且{|12}A x x =-<<,若p 是q 的必要不充分条件,则B A ≠⊂,又a 为正实数,即320a a ≤⎧⎨>⎩,解得203a <≤, 故a 的取值范围为20,3⎛⎤ ⎥⎝⎦. 29.(1){12}A B xx ⋂=<≤∣(2)1,[5,)2⎛⎤-∞-⋃+∞ ⎥⎝⎦ 【解析】【分析】(1)首先求出集合,A B ,然后根据集合的交集运算可得答案; (2)分B =∅、B ≠∅两种情况讨论求解即可.(1)因为0a =,所以{12}B xx =-<≤∣ 因为{}4222{14}x A x x x =<≤=<≤∣, 所以{12}A B xx ⋂=<≤∣. (2)当B =∅,即122a a -≥+,3a ≤-时,符合题意当B ≠∅时可得12214a a a -<+⎧⎨-≥⎩或122221a a a -<+⎧⎨+≤⎩, 解得5a ≥或132a -<≤-. 综上,a 的取值范围为1,[5,)2⎛⎤-∞-⋃+∞ ⎥⎝⎦. 30.(1)16;(2)2n【解析】【分析】设集合A 为集合的子集,利用分步计数原理分析每个元素出现的情况,即得解【详解】(1)由题意,若A 为集合{a, b, c, d }的子集则集合A 中的元素只能从a, b, c, d 中选择,每个元素出现或者不出现有两种可能 故集合A 的不同情形有222216⨯⨯⨯=种情况故集合{a, b, c, d }的所有子集的个数是16(2)由题意,若A 为集合{a 1, a 2, …, an }的子集则集合A 中的元素只能从a 1, a 2, …, an 中选择,每个元素出现或者不出现有两种可能 故集合A 的不同情形有22...22n ⨯⨯⨯=种情况故集合{a 1, a 2, …, an }的所有子集的个数是2n。
人教版高一数学必修1测试题(含答案)

人教版数学必修I 测试题(含答案)一、选择题1、设集合{}{}{}1,2,3,4,5,1,2,3,2,5U A B ===,则()U AC B =( )A 、{}2B 、{}2,3C 、{}3D 、{}1,32、已知集合{}{}0,1,2,2,M N x x a a M ===∈,则集合 MN ( )A 、{}0B 、{}0,1C 、{}1,2D 、{}0,23、函数()21log ,4y x x =+≥的值域是 ( )A 、[)2,+∞B 、()3,+∞C 、[)3,+∞D 、(),-∞+∞4、关于A 到B 的一一映射,下列叙述正确的是 ( ) ① 一一映射又叫一一对应 ② A 中不同元素的像不同③ B 中每个元素都有原像 ④ 像的集合就是集合BA 、①②B 、①②③C 、②③④D 、①②③④5、在221,2,,y y x y x x y x===+= ( )A 、1个B 、2个C 、3个D 、4个 6、已知函数()213f x x x +=-+,那么()1f x -的表达式是 ( )A 、259x x -+B 、23x x --C 、259x x +-D 、21x x -+7、若方程0x a x a --=有两个解,则a 的取值范围是 ( )A 、()0,+∞B 、()1,+∞C 、()0,1D 、∅8、若21025x =,则10x -等于 ( )A 、15-B 、15C 、150D 、16259、若()2log 1log 20a a a a +<<,则a 的取值范围是 ( )A 、01a <<B 、112a << C 、102a << D 、1a > 10、设 1.50.90.4814,8,2a b c -⎛⎫=== ⎪⎝⎭,则,,a b c 的大小顺序为 ( )A 、a b c >>B 、a c b >>C 、b a c >>D 、c a b >>11、已知()()2212f x x a x =+-+在(],4-∞上单调递减,则a 的取值范围是 ( )A 、3a ≤-B 、3a ≥-C 、3a =-D 、以上答案都不对12、若()lg f x x =,则()3f = ( )A 、lg 3B 、3C 、310D 、103 二、填空题13、设{}{}12,0A x x B x x a =<<=-<,若A B Ø,则a 的取值范围是 ; 14、函数y =的定义域为 ; 15、若2x <,则3x -的值是 ; 16、100lg 20log 25+= 。
人教版高一数学必修四测试题(含详细答案)

高一数学试题(必修4)(特殊适合按14523依次的省份)必修4第一章三角函数(1)一、选择题:l已知A={第一象限角}'B={锐角}'C={小千90°的角},那么A、B、C关系是()A. B=Anc2.✓sin2120° 等千忒i A土——- B. B U C=CC. A宝D. A=B=C()五2B五2c1_2n i sin a —2cosa3已知=-5, 那么tana的值为3 sin a + 5 c os aA.—2B. 2C .23164. 下列函数中,最小正周期为兀的偶函数是A.y =sin 2xXB y =c s—2A , 4✓3B -4✓3C .s in 2x+c s 2x 5, 若角600°的终边上有一点(-4,a),则a的值是()23 D.16( )1-tan 2 xD. y =1 + tan2 x()c .土4✓3D✓3X冗X6. 要得到函数y=co s (—-—)的图象,只需将y=sin —的图象( )2 4 2冗冗A. 向左平移—个单位B 同右平移—个单位22冗冗C. 向左平移—个单位D. 向右平移—个单位4 47. 若函数y=f (x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将冗l整个图象沿x轴向左平移—个单位,沿y轴向下平移l个单位,得到函数y =-sin x 的图象22测y=f (x)是()l 兀A. y=—sin(2x+—) +12 2 l 兀C.y =—sin(2x+—) +1 2 4l 兀B.y =—sin(2x -—) +12 2 l 冗D. —sin(2x -—) +12 45兀8. 函数y=sin (2x+—-)的图像的一条对方程是2冗A.x=-— 冗B. x =-— 冗_8__ xc 19. 若sin0·cos0=—,则下列结论中肯定成立的是A .si n 0 = ✓22B. 五sin 0 = -—C. si n 0+cos0 = 1(三4(_ x D))冗10 函数y = 2si n (2x+—)的图象3冗A. 关千原点对称B.关千(——,0)对称c.6 冗11 函数y =s n (x+—)X E R 是2 兀冗A . [-—,—]上是增函数2 2C. [-冗OJ 上是减函数12函数y =✓2c o sx l的定义域是A . [2k三三}k EZ)C. [2k冗十f,2k冗+气}k EZ)D. si n 0—cos0=0()冗关千y 对称D .关千直线x =—对称6( )B. [O五上是减函数D. [-冗冗上是减函数()B. [2k 二,2k 兀三}k E Z ) 6 6D. [2k 兀一气,2k兀+气}k E Z ) 二、填空题:冗冗213. 函数y = cos (x -—) (x E [—,—兀)的最小值是8 6 314。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学试卷(人教版)
一、填空题
1.已知log23a, log 3 7 b ,用含 a, b 的式子表示log214。
2.方程lg x lg 12lg( x4) 的解集为。
3.设是第四象限角, tan 3
,则 sin 2____________________.4
4.函数y
2 sin x
1
的定义域为 __________。
5.函数y 2cos2x sin 2x ,x R的最大值是.
6.把 6 sin 2 cos 化为 A sin()(其中 A0,(0,2 ) )的形式是。
7.函数f( x)=(1)|cosx|在[-π,π]上的单调减区间为___。
3
8.函数y2sin(2 x) 与y轴距离最近的对称中心的坐标是____。
3
9.,且,则。
10.设函数f(x)是以2为周期的奇函数,且,若,则 f 4cos2( )的值.
11.已知函数,求
.
12.设函数y sin x0,,的最小正周期为,且其图像关于直线
22
x对称,则在下面四个结论中:(1)图像关于点,0 对称;(2)图像关于点,0 对1243
称;(3)在0,上是增函数;(4)在,0 上是增函数,那么所有正确结论的编号为____ 66
二、选择题
13. 已知正弦曲线=sin( ω
x +φ ) , (>0,ω >0) 上一个最高点的坐标是(2 , 3 ),由这个
y A A
最高点到相邻的最低点,曲线交x轴于 (6 , 0) 点,则这条曲线的解析式是()
(A)y= 3 sin(x+)(B) y= 3 sin(
8x-2)
84
(C)=3sin(x+2)(D)y=3sin(x-)
84
8
14.函数 y=sin(2x+
)的图象是由函数y=sin2x 的图像()
3
(A)向左平移3单位(B)向左平移6单位 2.
(C)
5单位(D)向右平移
5
单位向左平移66
15. 在三角形△ ABC中,a36, b21,A 60,不解三角形判断三角形解的情况().
(A)一解(B)两解
(C)无解(D)以上都不对
16. 函数f(x)=cos2x+sin(+x)是().
2
(A)非奇非偶函数(B)仅有最小值的奇函数
(C)仅有最大值的偶函数(D)既有最大值又有最小值的偶函数
三、解答题
17.( 8 分)设函数 f (x)log 2 ( x1), ( x 1)
(1)求其反函数
f 1
( ) ;x
(2)解方程 f 1 (x) 4x7 .
18.( 10 分)已知sin x
cos x 2 . sin x cos x
(1)求tanx的值;
(2)若sin x,cos x是方程x2mx n 0 的两个根,求m 22n 的值.
19.(分)已知函数;
(1).求f(x)的定义域;
(2).写出函数 f ( x) 的值域;
(3).求函数 f ( x)的单调递减区间;
20.(12 分)设关于的方程在内有两相异解,;
(1).求的取值范围;
(2).求的值。
21 .( 12 分)我们把平面直角坐标系中,函数y = f (x), x D 上的点P x, y ,满足
x N , y N 的点称为函数 y = f ( x) 的“正格点”.
⑴请你选取一个m 的值,使对函数 f (x) sin mx, x R 的图像上有正格点,并写出函数的
一个正格点坐标.
⑵若函数 f ( x) sin mx, x R ,m1,2 与函数g (x)lg x 的图像有正格点交点,求m 的值,并写出两个函数图像的所有交点个数.
⑶对于⑵中的 m 值,函数 f ( x)sin mx, x 0, 5
时,不等式9
log a x sin mx 恒成立,求实数 a 的取值范围.
高一期末数学试卷答案
1、1 ab
2、{2}
24
4 、2k,2k
5
3、(k Z )5、 2 1
2566
6、7、[-,0]及[,π] 8、(9、10、
22
11、12、 (2 )(4 )13、A14、 B15、 A16、 D
17.解:( 1) f 1 ( x)2x1,( x R) ;--------------------------------4分
(2)由已知2x1 4 x7(2x3)(2x2) 0
2x 3 0x log2 3-----------------------------------------------------4分18.解: (1) tanx3;-----------------------------------------4分(2)m sin x cos x,n sin x cos x ---------------------------------2分
m 22n 1 4 sin x cos x 1 2 sin 2x 1 2 2 tan x1---4分
1tan 2 x5
(另解:已知( sin x cos x)241sin 2x4sin 2 x 3 )
sin x cos x1sin 2x5
19.解 :(1)f(x)的定义域:
(2).函数f ( x)的值域:
(3).函数f ( x)的单调递减区间:
20.解: (1).由数形结合有:⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分(2). ∵,是方程的两根
∴ sinα + 3 cosα+a=0,且sinβ +cos β+a=0⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分
两式相减得:2sin()2sin() ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
33
∴
32k() , k
3
Z或
3
2k
3
, k Z⋯⋯⋯4分
∵
∴ α + β = or α + β
7
=
3
3
=
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分
21. 解:( 1)若取 m
时,
2
正格点坐标
1,1 5,1 , 9,1 等(答案不唯一)
(2)作出两个函数图像,
可知函数
f ( x) sin mx, x R ,与函数 g( x) l
g x 的图像有正格点交点只有一个点为 10,1 ,
2k
10m, m 4k 1 , k
Z
2 20
m 1,2
9 .
可得 m
20
5 个.
根据图像可知:两个函数图像的所有交点个数为
(3)由( 2)知 f ( x)
sin
9
x, x 0, 5
,
20
9
ⅰ)当 a
1 时,不等式 log a x sin mx 不能成立
5
2
5 2
ⅱ)当 0
a 1时,由图( 2)像可知
log a sin
a 1
9
42
9。
