【谷速软件】matlab源码-多径衰落与大尺度衰落
【谷速软件网】matlab有偿编程 B样条源码程序

function D = bspline_approx(k,t,x,M)% B-spline curve control point approximation with known knot vector.%% Input arguments:% k:% B-spline order (2 for linear, 3 for quadratic, etc.)% t:% knot vector% x:% B-spline values corresponding to which data points are observed% M:% d-by-m matrix of observed data points, possibly polluted with noise, % d is typically 2 for plane, 3 for space, or 3 or 4, respectively, if% weights are present%% Output arguments:% D:% d-by-n matrix of control points% Copyright 2010 Levente Hunyadivalidateattributes(k, {'numeric'}, {'positive','integer','scalar'}); validateattributes(t, {'numeric'}, {'real','vector'});validateattributes(x, {'numeric'}, {'real','vector'});validateattributes(M, {'numeric'}, {'real','2d'});B = bspline_basismatrix(k,t,x);Q = M * B;D = Q / (B'*B);function [y,x] = bspline_basis(j,n,t,x)% B-spline basis function value B(j,n) at x.%% Input arguments:% j:% interval index, 0 =< j < numel(t)-n% n:% B-spline order (2 for linear, 3 for quadratic, etc.)% t:% knot vector% x (optional):% value where the basis function is to be evaluated%% Output arguments:% y:% B-spline basis function value, nonzero for a knot span of n% Copyright 2010 Levente Hunyadivalidateattributes(j, {'numeric'}, {'nonnegative','integer','scalar'});validateattributes(n, {'numeric'}, {'positive','integer','scalar'});validateattributes(t, {'numeric'}, {'real','vector'});assert(all( t(2:end)-t(1:end-1) >= 0 ), ...'Knot vector values should be nondecreasing.');if nargin < 4x = linspace(t(n), t(end-n+1), 100); % allocate points uniformlyelsevalidateattributes(x, {'numeric'}, {'real','vector'});endassert(0 <= j && j < numel(t)-n, ...'Invalid interval index j = %d, expected 0 =< j < %d (0 =< j < numel(t)-n).', j, numel(t)-n); y = bspline_basis_recurrence(j,n,t,x);function y = bspline_basis_recurrence(j,n,t,x)y = zeros(size(x));if n > 1b = bspline_basis(j,n-1,t,x);dn = x - t(j+1);dd = t(j+n) - t(j+1);if dd ~= 0 % indeterminate forms 0/0 are deemed to be zeroy = y + b.*(dn./dd);endb = bspline_basis(j+1,n-1,t,x);dn = t(j+n+1) - x;dd = t(j+n+1) - t(j+1+1);if dd ~= 0y = y + b.*(dn./dd);endelsey(:) = t(j+1) <= x & x <= t(j+2);endfunction [B,x] = bspline_basismatrix(n,t,x)% B-spline basis function value matrix B(n) for x.%% Input arguments:% n:% B-spline order (2 for linear, 3 for quadratic, etc.)% t:% knot vector% x (optional):% an m-dimensional vector of values where the basis function is to be % evaluated%% Output arguments:% B:% a matrix of m rows and numel(t)-n columns% Copyright 2010 Levente Hunyadiif nargin > 2B = zeros(numel(x),numel(t)-n);for j = 0 : numel(t)-n-1B(:,j+1) = bspline_basis(j,n,t,x);endelse[b,x] = bspline_basis(0,n,t);B = zeros(numel(x),numel(t)-n);B(:,1) = b;for j = 1 : numel(t)-n-1B(:,j+1) = bspline_basis(j,n,t,x);endendfunction [C,U] = bspline_deboor(n,t,P,U)% Evaluate explicit B-spline at specified locations.%% Input arguments:% n:% B-spline order (2 for linear, 3 for quadratic, etc.)% t:% knot vector% P:% control points, typically 2-by-m, 3-by-m or 4-by-m (for weights)% u (optional):% values where the B-spline is to be evaluated, or a positive% integer to set the number of points to automatically allocate%% Output arguments:% C:% points of the B-spline curve% Copyright 2010 Levente Hunyadivalidateattributes(n, {'numeric'}, {'positive','integer','scalar'});d = n-1; % B-spline polynomial degree (1 for linear, 2 for quadratic, etc.) validateattributes(t, {'numeric'}, {'real','vector'});assert(all( t(2:end)-t(1:end-1) >= 0 ), 'bspline:deboor:InvalidArgumentValue', ...'Knot vector values should be nondecreasing.');validateattributes(P, {'numeric'}, {'real','2d'});nctrl = numel(t)-(d+1);assert(size(P,2) == nctrl, 'bspline:deboor:DimensionMismatch', ...'Invalid number of control points, %d given, %d required.', size(P,2), nctrl);if nargin < 4U = linspace(t(d+1), t(end-d), 10*size(P,2)); % allocate points uniformlyelseif isscalar(U) && U > 1validateattributes(U, {'numeric'}, {'positive','integer','scalar'});U = linspace(t(d+1), t(end-d), U); % allocate points uniformlyelsevalidateattributes(U, {'numeric'}, {'real','vector'});assert(all( U >= t(d+1) & U <= t(end-d) ), 'bspline:deboor:InvalidArgumentValue', ...'Value outside permitted knot vector value range.');endm = size(P,1); % dimension of control pointst = t(:).'; % knot sequenceU = U(:);S = sum(bsxfun(@eq, U, t), 2); % multiplicity of u in t (0 <= s <= d+1)I = bspline_deboor_interval(U,t);Pk = zeros(m,d+1,d+1);a = zeros(d+1,d+1);C = zeros(size(P,1), numel(U));for j = 1 : numel(U)u = U(j);s = S(j);ix = I(j);Pk(:) = 0;a(:) = 0;% identify d+1 relevant control pointsPk(:, (ix-d):(ix-s), 1) = P(:, (ix-d):(ix-s));h = d - s;if h > 0% de Boor recursion formulafor r = 1 : hq = ix-1;for i = (q-d+r) : (q-s);a(i+1,r+1) = (u-t(i+1)) / (t(i+d-r+1+1)-t(i+1));Pk(:,i+1,r+1) = (1-a(i+1,r+1)) * Pk(:,i,r) + a(i+1,r+1) * Pk(:,i+1,r);endendC(:,j) = Pk(:,ix-s,d-s+1); % extract value from triangular computation scheme elseif ix == numel(t) % last control point is a special caseC(:,j) = P(:,end);elseC(:,j) = P(:,ix-d);endendfunction ix = bspline_deboor_interval(u,t)% Index of knot in knot sequence not less than the value of u.% If knot has multiplicity greater than 1, the highest index is returned.i = bsxfun(@ge, u, t) & bsxfun(@lt, u, [t(2:end) 2*t(end)]); % indicator of knot interval in which u is[row,col] = find(i);[row,ind] = sort(row); %#ok<ASGLU> % restore original order of data pointsix = col(ind);function [dknots, dctrl] = bspline_deriv(order, knots, ctrl)% Knots and control points associated with the derivative of B-spline curve.%% Input arguments:% order:% B-spline order (2 for linear, 3 for quadratic, etc.)% knots:% knot vector% ctrl:% control points, typically 2-by-m, 3-by-m, or 4-by-m (for weights)%% Output arguments:% dctrl:% control points of the derivative of the input B-spline curve% dknots:% the new knot vector associated with the derivative B-spline curve% Copyright 2011 Joe Hays% Copyright 2010-2011 Levente Hunyadip = order - 1;tmp = size(ctrl);n = tmp(2)-1;dim = tmp(1);% derivative knotsdknots = knots(2:max(size(knots))-1);% derivative control pointsdctrl = zeros(dim,n);for i = 1 : ndctrl(:,i) = (p / (knots(i+p+1) - knots(i+1))) * (ctrl(:,i+1) - ctrl(:,i));endfunction D = bspline_estimate(k,t,M)% B-spline curve control point estimation without knowing parameter values. %% Input arguments:% k:% B-spline order (2 for linear, 3 for quadratic, etc.)% t:% knot vector% M:% d-by-m matrix of observed data points, possibly polluted with noise, % d is typically 2 for plane, 3 for space, or 3 or 4, respectively, if% weights are present%% Output arguments:% D:% d-by-n matrix of control points% Copyright 2010 Levente Hunyadix = linspace(t(k), t(end-k+1), size(M,2)); % allocate points uniformlyfor iter = 1 : 50D = bspline_approx(k,t,x,M);x = bspline_footpoint(k,t,D,M);if 0C = bspline_deboor(k,t,D);Y = bspline_deboor(k,t,D,x);hold on;plot(C(1,:), C(2,:), 'b');plot(M(1,:), M(2,:), 'kx');plot(Y(1,:), Y(2,:), 'rx');hold off;endendfunction [x,F] = bspline_footpoint(k,t,D,M)% B-spline foot point of a set of points.%% M:% d-by-m matrix of observed data points, possibly polluted with noise, % which are not necessarily lying on the B-spline curve%% Output arguments:% x:% parameter values for the B-spline foot points% F:% foot points on the B-spline curve% Copyright 2010 Levente Hunyadilb = t(k);ub = t(end-k+1);% simple algorithm, find close enough pointsu = linspace(lb, ub, 500);E = bspline_error(k,t,D,M,u);[v,ix] = min(E,[],2);x0 = u(ix);if 1 % refine foot crude point estimatesx = zeros(1,size(M,2));for i = 1 : size(M,2)x(i) = funminbnd(@(u) bspline_error(k,t,D,M(:,i),u), lb, ub, x0(i));endelsex = x0;endif nargin > 1F = bspline_deboor(k,t,D,x);endfunction E = bspline_error(k,t,D,M,x)% B-spline approximation error.%% Input arguments:% k:% B-spline order (2 for linear, 3 for quadratic, etc.)% t:% knot vector% D:% control points% M:% points whose error to compute% x:% parameter values w.r.t. which distance from m is minimized%% Output arguments:% E:% sum of squares approximation errorY = bspline_deboor(k,t,D,x);Y = reshape(Y, size(Y,1), 1, size(Y,2)); % extend data with a singleton dimensionM = reshape(M, size(M,1), size(M,2), 1);E = squeeze(sum(bsxfun(@minus, M, Y).^2, 1)); % calculate pairwise squared distance of points in M and YE = sqrt(E); % pairwise distance。
谷速软件MATLAB成品代码名称【项目0201】到【项目0300】

谷速软件MATLAB成品代码名称【项目0201】到【项目0300】【项目0201】基于matlab编程k均值算法输入二维的数据得到聚类源码程序【项目0202】基于matlab编程Lamb波传播组群速度及相速度求解源码程序【项目0203】基于MATLAB编程LASSO的TE过程质量变量预测研究【项目0204】基于matlab编程LDPC的Matlab便解码源码程序【项目0205】基于matlab编程ldpc的外信息转移表仿真程序源码【项目0206】基于matlab编程LMS算法的自适应线性预测源码程序【项目0207】基于matlab编程LMS算法在信道均衡器中的应用源码程序【项目0208】基于matlab编程LMS算法自适应滤波器仿真源码程序【项目0209】基于matlab编程LMS自适应滤波算法源码程序【项目0210】基于matlab编程LVQ神经网络的分类乳腺肿瘤诊断源码程序【项目0211】基于matlab编程L形区域几何多重网格算法源码程序【项目0212】基于matlab编程mimo-ofdm系统基于梳状导频的信道估计源码程序【项目0213】基于matlab编程MIMO系统递推最小二乘参数估计(本程序针对2入2出系统)源码程序【项目0214】基于matlab编程MK分析法之玉溪站气候变化分析源码程序【项目0215】基于matlab编程MMTD的EEG信号特征提取方法研究源码程序【项目0216】基于matlab编程MVTE算法的感知纹理维度分析源码程序【项目0217】基于matlab编程Narendra自适应控制律(不稳定对象)源码程序【项目0218】基于matlab编程Narendra自适应控制律源码程序【项目0219】基于matlab编程nlms信号滤波算法源码程序【项目0220】基于matlab编程NSGA-II算法源码程序【项目0221】基于matlab编程nuttall窗双谱线插值FFT算法实现电力谐波分析源码程序【项目0222】基于matlab编程oc 平面连续体结构拓扑优源码程序化【项目0223】基于matlab编程ofdm调制压缩感知中OMP算法源码程序【项目0224】基于matlab编程OMP算法实现对一维输入信号的重构BCS_MP源码程序【项目0225】基于matlab编程PCA神经网络在doa估计的经典算法源码程序【项目0226】基于matlab编程PCA算法轴承故障诊断程序源码【项目0227】基于matlab编程PID神经网络系统辨识源码程序【项目0228】基于matlab编程pso粒子群算法源码程序【项目0229】基于matlab编程PSO算法解决背包问题源码程序【项目0230】基于MATLAB编程PSO算法解决了6X6的车间调度算法源码【项目0231】基于matlab编程pso算法求函数最大值最小值源码程序【项目0232】基于matlab编程pso优化bp网络程序源码【项目0233】基于matlab编程pso优化pid仿真源码程序【项目0234】基于matlab编程RBF神经网络算法源码程序【项目0235】基于matlab编程RBF网络的动态设计源码程序【项目0236】基于matlab编程RBF网络的回归源码程序【项目0237】基于matlab编程RLS算法的自适应线性预测源码程序【项目0238】基于matlab编程RPEM聚类算法源码程序【项目0239】基于matlab编程RSSI和TOA定位算法仿真代码【项目0240】基于matlab编程SAR 成像多种算法仿真源码程序【项目0241】基于matlab编程SAR成像的wk算法源码程序【项目0242】基于matlab编程SAR成像的算法成像成像程序源码【项目0243】基于matlab编程SAR成像仿真三种算法源码程序【项目0244】基于matlab编程SAR成像算法之RD算法源码程序【项目0245】基于matlab编程SIMP和OC法的拓扑优化程序源码【项目0246】基于matlab编程SOM神经网络的数据分类源码程序【项目0247】基于matlab编程SSDA算法实现模板匹配源码程序【项目0248】基于matlab编程Stentiford细化算法源码程序【项目0249】基于matlab编程SVM的回归预测分析源码程序【项目0250】基于matlab编程SVM的手写字体识别源码程序【项目0251】基于matlab编程SVM的信息粒化时序回归预测源码程序【项目0252】基于matlab编程SVM回归机的图像数字水印算法研究源码程序【项目0253】基于matlab编程SVM线性回归分类源码程序【项目0254】基于matlab编程SVM支持向量机的时间序列预测、分类、自回归代码源码【项目0255】基于matlab编程TDD的LTE链路浮点仿真平台源码程序【项目0256】基于matlab编程TDOA定位算法源码程序【项目0257】基于matlab编程TLS系统仿真系统源码程序【项目0258】基于matlab编程wigner变换的应用程序源码【项目0259】基于matlab编程半监督学习的TE过程仿真源码程序【项目0260】基于matlab编程贝叶斯网络推理的建模诊断肺癌源码程序【项目0261】基于matlab编程边界随机微分方程拟合控制源码程序【项目0262】基于matlab编程蝙蝠算法( bat algorithm) 源码程序【项目0263】基于matlab编程蝙蝠算法解决离散的生产调度问题源码程序【项目0264】基于matlab编程泊松过程的模拟、检验及参数估计源码程序【项目0265】基于matlab编程布谷鸟算法求函数最优值源码程序【项目0266】基于matlab编程蔡氏电路范式源码程序【项目0267】基于matlab编程差分演化算法源码程序【项目0268】基于matlab编程常规遗传算法求解源码程序【项目0269】基于matlab编程潮流计算仿真case9.m源码程序【项目0270】基于matlab编程城市地区的路径损耗模型仿真源码程序【项目0271】基于matlab编程处理雷达信号系统仿真源码程序【项目0272】基于matlab编程带夹套连续搅拌反应器模型源码程序【项目0273】基于matlab编程递推极大似然参数估计(RML)源码程序【项目0274】基于matlab编程递推随机牛顿参数估计(RSNA)源码程序【项目0275】基于matlab编程递推最小二乘参数估计(RLS)源码程序【项目0276】基于matlab编程动态粒子群算法的动态环境寻优算法源码程序【项目0277】基于matlab编程多目标粒子群程序源码【项目0278】基于matlab编程多目标优化算法源码程序【项目0279】基于matlab编程多元线性回归源码程序【项目0280】基于matlab编程返回向前扫算法的径向分布系统源码程序【项目0281】基于matlab编程范围迁移算法源码程序【项目0282】基于matlab编程覆盖分布遗传算法和模拟退火算法源码程序【项目0283】基于matlab编程概率神经网络的手写体数字识别源码程序【项目0284】基于matlab编程广义最小方差控制(显式控制律)源码程序【项目0285】基于matlab编程广义最小方差自校正控制(间接算法)源码程序【项目0286】基于matlab编程广义最小方差自校正控制(直接算法)源码程序【项目0287】基于matlab编程含不同分布式电源的改进粒子群算法优化问题源码程序【项目0288】基于matlab编程和声搜索算法进行参数改进源码程序【项目0289】基于matlab编程灰色预测算法源码程序【项目0290】基于matlab编程绘制板材的lamb频散曲线源码程序【项目0291】基于matlab编程混合粒子群算法求解TSP问题源码【项目0292】基于matlab编程极点配置控制(PPC)(连续系统离散化)源码程序【项目0293】基于matlab编程计算固_液声子晶体的能带结构源码程序【项目0294】基于matlab编程聚类的RBF 网设计算法源码程序【项目0295】基于matlab编程卷积码编码、QPSK调制、AWGN信道、QPSK解调、Viterbi 译码源码程序【项目0296】基于matlab编程均匀采样S.T.的线性约束源码程序【项目0297】基于matlab编程卡尔曼滤波程序用于时间序列预测源码程序【项目0298】基于matlab编程卡尔曼滤波器源码程序【项目0299】基于matlab编程快速傅里叶变换和FFT的位反转源码程序【项目0300】基于matlab编程离散Hopfield神经网络的分类源码程序。
【谷速软件】matlab源码-多径衰落与大尺度衰落
1.大尺度衰落模型
假设信号频率为100MHZ,飞机的飞行速度为1000Km/h,飞机的距地面高度为8Km.每十秒观察一次。
纵坐标的单位为dB,横坐标为时间取对数。
改变飞机的速度为1500Km/h后,所得大尺度衰落曲线如图2.
2.瑞利衰落模型
多径衰落可以用瑞利衰落来近似,使用MATLAB可以绘制出瑞利衰落的曲线。
如图3
3.接收端的初步设计
大尺度衰落是不可避免的,而且它与飞行速度有关,与信号的频率关系不大;而多径效应会导致码间干扰(ISI),严重影响了接收信号的判决,在接收端应采用均衡措施。
假定传输信号的波形已知为方波,可以设计滤波器,来减小码间干扰。
ISIfilter的设计可以用MATLAB实现,图4
4.眼图
可以通过眼图的观察选择最佳的采样时间点。
眼图的观察效果如图5.。
matlab多径信道建模

matlab多径信道建模多径信道是无线通信中的一个重要概念,它是指信号在传播过程中经历多条不同路径的传播。
在无线通信中,信号从发送端到接收端的传播过程中,会经过多种路径,例如直射路径、反射路径、散射路径等。
这些路径的存在会导致信号的多普勒效应、时延扩展、频率选择性衰落等现象,对无线通信的性能产生重要影响。
因此,准确建模和仿真多径信道是无线通信系统设计中的重要任务之一。
为了对多径信道进行建模,我们可以使用matlab进行仿真。
在matlab中,可以使用复数矢量或矩阵来表示信号的传播路径和相位差。
我们可以根据具体的场景和信道模型,设置信号的多径路径数目、路径增益、时延和相位差等参数。
通过模拟这些参数,我们可以得到信号在多径信道中的传播效果。
在多径信道建模中,常用的信道模型包括瑞利衰落信道模型和莱斯衰落信道模型。
瑞利衰落信道模型适用于室内或城市环境中,其中信号经历多条散射路径导致多普勒效应,信道响应呈现高斯分布。
莱斯衰落信道模型适用于开阔区域或直射路径明显的环境中,其中信号有强烈的直射路径成分和少量散射路径成分,信道响应呈现瑞利分布。
在matlab中,我们可以使用内置的函数或自定义函数来生成瑞利衰落信道或莱斯衰落信道。
例如,可以使用rayleighchan函数来生成瑞利衰落信道对象,并设置信号的中心频率、采样率、路径增益和路径时延等参数。
通过调用该对象的函数,我们可以得到信号在多径信道中的时域响应、频域响应和自相关函数等信息。
除了瑞利衰落信道和莱斯衰落信道,还可以使用其他信道模型来建模多径信道。
例如,可以使用均匀线性阵列(ULA)模型来建模天线阵列接收到的多径信号。
在matlab中,可以使用phased.ULA函数来创建ULA对象,并设置天线间距、天线数目和信号到达角度等参数。
通过调用该对象的函数,我们可以得到不同角度下的信号功率谱密度、方向图和阵列响应等信息。
多径信道建模不仅可以用于无线通信系统的性能评估,还可以用于无线信号处理算法的设计和验证。
【谷速软件编程】matlab源码 汉诺塔游戏攻略 动画演示

hf=figure('name','汉诺塔游戏仿真'); %加标题axis([0,12,0,12]); %画坐标set(hf,'color','w'); %填充背景hold on; %保持图形axis('off'); %隐藏网络线rectangle('position',[0,0,12,0.5],'FaceColor',[0,1.0,0]); %画底版line([3;3],[0.5,8],'color','r','linestyle','-','linewidth', 1.5);line([6;6],[0.5,8],'color','r','linestyle','-','linewidth', 1.5);line([9;9],[0.5,8],'color','r','linestyle','-','linewidth', 1.5); %画出三条路线a=line([3;3],[0.5,1.0],'color','c','linestyle','-','linewid th',65); %画出一号长方体木块b=line([3;3],[1.0,1.5],'color','b','linestyle','-','linewid th',45);%画出二号长方体木块c=line([3;3],[1.5,2.0],'color','k','linestyle','-','linewid th',30); %画出三号长方体木块d=line([3;3],[2.0,2.5],'color','y','linestyle','-','linewid th',25);%画出四号长方体木块e=line([3;3],[2.5,3.0],'color','m','linestyle','-','linewidth',15);%画出五号长方体木块%设置五木板的运动%设置五号长方体木块的运动,竖直向上运动到第一条路线的最上方t1=2.5; dt=0.05;while t1<=8t1=t1+dt;set(e,'xdata',[3;3],'ydata',[t1;t1+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置五号长方体木块的运动,水平运动到第三条路线的最上方t2=3; dt=0.05;while t2<=9t2=t2+dt;set(e,'xdata',[t2;t2],'ydata',[t1;t1+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第三条路线的下方t3=8; dt=0.05;while t3>=0.5t3=t3-dt;set(e,'xdata',[9;9],'ydata',[t3;t3+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置四号长方体木块的运动,竖直向上运动到第一条路线的最上方t4=2.0; dt=0.05;while t4<=8t4=t4+dt;set(d,'xdata',[3;3],'ydata',[t4;t4+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,水平运动到第二条路线的最上方t5=3; dt=0.05;while t5<=6t5=t5+dt;set(d,'xdata',[t5;t5],'ydata',[t4;t4+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,竖直向下运动到第二条路线的最下方t6=8; dt=0.05;while t6>=0.5t6=t6-dt;set(d,'xdata',[6;6],'ydata',[t6;t6+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置五号长方体木块的运动,竖直向上运动到第三条路线的最上方t7=0.5; dt=0.05;while t7<=8t7=t7+dt;set(e,'xdata',[9;9],'ydata',[t7;t7+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,水平运动到第二条路线的最上方t8=9; dt=0.05;while t8>=6t8=t8-dt;set(e,'xdata',[t8;t8],'ydata',[t7;t7+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第二条路线的下方t9=8; dt=0.05;while t9>=1.0t9=t9-dt;set(e,'xdata',[6;6],'ydata',[t9;t9+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置三号长方体木块的运动,竖直向上运动到第一条路线的上方t10=1.5; dt=0.05;while t10<=8t10=t10+dt;set(c,'xdata',[3;3],'ydata',[t10;t10+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置三号长方体木块的运动,水平运动到第三条路线的上方t11=3; dt=0.05;while t11<=9t11=t11+dt;set(c,'xdata',[t11;t11],'ydata',[t10;t10+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置三号长方体木块的运动,竖直向下运动到第三条路线的下方t12=8; dt=0.05;while t12>=0.5t12=t12-dt;set(c,'xdata',[9;9],'ydata',[t12;t12+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向上运动到第二条路线的上方t13=1; dt=0.05;while t13<=8t13=t13+dt;set(e,'xdata',[6;6],'ydata',[t13;t13+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,水平运动到第一条路线的最上方t14=6; dt=0.05;while t14>=3t14=t14-dt;set(e,'xdata',[t14;t14],'ydata',[8;8+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第一条路线的下方t15=8; dt=0.05;while t15>=1.5t15=t15-dt;set(e,'xdata',[3;3],'ydata',[t15;t15+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,竖直向上运动到第二条路线的上方t16=0.5; dt=0.05;while t16<=8t16=t16+dt;set(d,'xdata',[6;6],'ydata',[t16;t16+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,水平运动到第三条路线的上方t17=6; dt=0.05;while t17<=9t17=t17+dt;set(d,'xdata',[t17;t17],'ydata',[8;8.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,竖直向下运动到第三条路线的下方t18=8;dt=0.05;while t18>=1t18=t18-dt;set(d,'xdata',[9;9],'ydata',[t18;t18+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向上运动到第一条路线的上方t19=1.0;dt=0.05;while t19<=8t19=t19+dt;set(e,'xdata',[3;3],'ydata',[t19;t19+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,水平运动到第三条路线的上方t20=3;dt=0.05;while t20<=9t20=t20+dt;set(e,'xdata',[t20;t20],'ydata',[8;8.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第三条路线的下方t21=8; dt=0.05;while t21>=1.5t21=t21-dt;set(e,'xdata',[9;9],'ydata',[t21;t21+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置二号长方体木块的运动,竖直向上运动到第一条路线的上方t22=1.0; dt=0.05;while t22<=8t22=t22+dt;set(b,'xdata',[3;3],'ydata',[t22;t22+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置二号长方体木块的运动,水平运动到第二条路线的上方t23=3; dt=0.05;while t23<=6t23=t23+dt;set(b,'xdata',[t23;t23],'ydata',[t22;t22+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置二号长方体木块的运动,竖直向下运动到第二条路线的最下方t24=8; dt=0.05;while t24>=0.5t24=t24-dt;set(b,'xdata',[6;6],'ydata',[t24;t24+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向上运动到第三条路线的上方t25=1.5; dt=0.05;while t25<=8t25=t25+dt;set(e,'xdata',[9;9],'ydata',[t25;t25+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,水平运动到第二条路线的上方t26=9; dt=0.05;while t26>=6t26=t26-dt;set(e,'xdata',[t26;t26],'ydata',[t25;t25+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第二条路线的下方t27=8; dt=0.05;while t27>=1.0t27=t27-dt;set(e,'xdata',[6;6],'ydata',[t27;t27+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,竖直向上运动到第三条路线的上方t28=1.5; dt=0.05;while t28<=8t28=t28+dt;set(d,'xdata',[9;9],'ydata',[t28;t28+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,水平运动到第一条路线的上方t29=9; dt=0.05;while t29>=3t29=t29-dt;set(d,'xdata',[t29;t29],'ydata',[t28;t28+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,竖直向下运动到第一条路线的下方t30=8; dt=0.05;while t30>=1.0t30=t30-dt;set(d,'xdata',[3;3],'ydata',[t30;t30+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向上运动到第二条路线的上方t31=1.0; dt=0.05;while t31<=8t31=t31+dt;set(e,'xdata',[6;6],'ydata',[t31;t31+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,水平运动到第一条路线的上方t32=6; dt=0.05;while t32>=3t32=t32-dt;set(e,'xdata',[t32;t32],'ydata',[t31;t31+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第一条路线的下方t33=8; dt=0.05;while t33>=1.5t33=t33-dt;set(e,'xdata',[3;3],'ydata',[t33;t33+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置三号长方体木块的运动,竖直向上运动到第三条路线的上方t34=0.5; dt=0.05;while t34<=8t34=t34+dt;set(c,'xdata',[9;9],'ydata',[t34;t34+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置三号长方体木块的运动,水平运动到第二条路线的上方t35=9; dt=0.05;while t35>=6t35=t35-dt;set(c,'xdata',[t35;t35],'ydata',[t34;t34+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置三号长方体木块的运动,竖直向下运动到第二条路线的下方t36=8; dt=0.05;while t36>=1.0t36=t36-dt;set(c,'xdata',[6;6],'ydata',[t36;t36+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向上运动到第三条路线的上方t37=1.5; dt=0.05;while t37<=8t37=t37+dt;set(e,'xdata',[3;3],'ydata',[t37;t37+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置五号长方体木块的运动,水平运动到第三条路线的最上方t38=3; dt=0.05;while t38<=9t38=t38+dt;set(e,'xdata',[t38;t38],'ydata',[t37;t37+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第三条路线的下方t39=8; dt=0.05;while t39>=0.5t39=t39-dt;set(e,'xdata',[9;9],'ydata',[t39;t39+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,竖直向上运动到第二条路线的上方t40=2.5; dt=0.05;while t40<=8t40=t40+dt;set(d,'xdata',[3;3],'ydata',[t40;t40+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置四号长方体木块的运动,水平运动到第二条路线的最上方t41=3; dt=0.05;while t41<=6t41=t41+dt;set(d,'xdata',[t41;t41],'ydata',[t40;t40+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,竖直向下运动到第二条路线的下方t42=8; dt=0.05;while t42>=1.5t42=t42-dt;set(d,'xdata',[6;6],'ydata',[t42;t42+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向上运动到第三条路线的上方t43=0.5; dt=0.05;while t43<=8t43=t43+dt;set(e,'xdata',[9;9],'ydata',[t43;t43+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置五号长方体木块的运动,水平运动到第二条路线的最上方t44=9; dt=0.05;while t44>=6t44=t44-dt;set(e,'xdata',[t44;t44],'ydata',[t43;t43+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第二条路线的下方t45=8; dt=0.05;while t45>=2.0t45=t45-dt;set(e,'xdata',[6;6],'ydata',[t45;t45+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置一号长方体木块的运动,竖直向上运动到第一条路线的上方t46=0.5; dt=0.05;while t46<=8t46=t46+dt;set(a,'xdata',[3;3],'ydata',[t46;t46+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置一号长方体木块的运动,水平运动到第三条路线的最上方t47=3; dt=0.05;while t47<=9t47=t47+dt;set(a,'xdata',[t47;t47],'ydata',[t46;t46+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置一号长方体木块的运动,竖直向下运动到第三条路线的最下方t48=8; dt=0.05;while t48>=0.5t48=t48-dt;set(a,'xdata',[9;9],'ydata',[t48;t48+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向上运动到第二条路线的上方t49=2.0; dt=0.05;while t49<=8t49=t49+dt;set(e,'xdata',[6;6],'ydata',[t49;t49+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置五号长方体木块的运动,水平运动到第一条路线的最上方t50=6; dt=0.05;while t50>=3t50=t50-dt;set(e,'xdata',[t50;t50],'ydata',[t49;t49+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第一条路线的最下方t51=8; dt=0.05;while t51>=0.5t51=t51-dt;set(e,'xdata',[3;3],'ydata',[t51;t51+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,竖直向上运动到第二条路线的上方t52=1.5; dt=0.05;while t52<=8t52=t52+dt;set(d,'xdata',[6;6],'ydata',[t52;t52+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置四号长方体木块的运动,水平运动到第三条路线的最上方t53=6; dt=0.05;while t53<=9t53=t53+dt;set(d,'xdata',[t53;t53],'ydata',[t52;t52+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,竖直向下运动到第三条路线的下方t54=8; dt=0.05;while t54>=1.0t54=t54-dt;set(d,'xdata',[9;9],'ydata',[t54;t54+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向上运动到第一条路线的上方t55=0.5; dt=0.05;while t55<=8t55=t55+dt;set(e,'xdata',[3;3],'ydata',[t55;t55+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置五号长方体木块的运动,水平运动到第三条路线的最上方t56=3; dt=0.05;while t56<=9t56=t56+dt;set(e,'xdata',[t56;t56],'ydata',[t55;t55+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第三条路线的下方t57=8; dt=0.05;while t57>=1.5t57=t57-dt;set(e,'xdata',[9;9],'ydata',[t57;t57+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置三号长方体木块的运动,竖直向上运动到第二条路线的最上方t58=1.0; dt=0.05;while t58<=8t58=t58+dt;set(c,'xdata',[6;6],'ydata',[t58;t58+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置三号长方体木块的运动,水平运动到第一条路线的最上方t59=6; dt=0.05;while t59>=3t59=t59-dt;set(c,'xdata',[t59;t59],'ydata',[t58;t58+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置三号长方体木块的运动,竖直向下运动到第一条路线的最下方t60=8; dt=0.05;while t60>=0.5t60=t60-dt;set(c,'xdata',[3;3],'ydata',[t60;t60+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向上运动到第三条路线的上方t61=1.5; dt=0.05;while t61<=8t61=t61+dt;set(e,'xdata',[9;9],'ydata',[t61;t61+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置五号长方体木块的运动,水平运动到第二条路线的最上方t62=9; dt=0.05;while t62>=6t62=t62-dt;set(e,'xdata',[t62;t62],'ydata',[t61;t61+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第二条路线的下方t63=8; dt=0.05;while t63>=1.0t63=t63-dt;set(e,'xdata',[6;6],'ydata',[t63;t63+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,竖直向上运动到第三条路线的最上方t64=1.0; dt=0.05;while t64<=8t64=t64+dt;set(d,'xdata',[9;9],'ydata',[t64;t64+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置四号长方体木块的运动,水平运动到第一条路线的最上方t65=9; dt=0.05;while t65>=3t65=t65-dt;set(d,'xdata',[t65;t65],'ydata',[t64;t64+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,竖直向下运动到第一条路线的下方t66=8; dt=0.05;while t66>=1.0t66=t66-dt;set(d,'xdata',[3;3],'ydata',[t66;t66+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向上运动到第二条路线的最上方t67=1.0; dt=0.05;while t67<=8t67=t67+dt;set(e,'xdata',[6;6],'ydata',[t67;t67+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置五号长方体木块的运动,水平运动到第一条路线的最上方t68=6; dt=0.05;while t68>=3t68=t68-dt;set(e,'xdata',[t68;t68],'ydata',[t67;t67+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第一条路线的下方t69=8; dt=0.05;while t69>=1.5t69=t69-dt;set(e,'xdata',[3;3],'ydata',[t69;t69+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置二号长方体木块的运动,竖直向上运动到第二条路线的上方t70=0.5; dt=0.05;while t70<=8t70=t70+dt;set(b,'xdata',[6;6],'ydata',[t70;t70+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置二号长方体木块的运动,水平运动到第三条路线的最上方t71=6; dt=0.05;while t71<=9t71=t71+dt;set(b,'xdata',[t71;t71],'ydata',[t70;t70+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置二号长方体木块的运动,竖直向下运动到第三条路线的最下方t72=8; dt=0.05;while t72>=1.0t72=t72-dt;set(b,'xdata',[9;9],'ydata',[t72;t72+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向上运动到第一条路线的最上方t73=1.5; dt=0.05;while t73<=8t73=t73+dt;set(e,'xdata',[3;3],'ydata',[t73;t73+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置五号长方体木块的运动,水平运动到第三条路线的最上方t74=3; dt=0.05;while t74<=9t74=t74+dt;set(e,'xdata',[t74;t74],'ydata',[t73;t73+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第三条路线的最下方t75=8; dt=0.05;while t75>=1.5t75=t75-dt;set(e,'xdata',[9;9],'ydata',[t75;t75+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置四号长方体木块的运动,竖直向上运动到第一条路线的最上方t76=1.0; dt=0.05;while t76<=8t76=t76+dt;set(d,'xdata',[3;3],'ydata',[t76;t76+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,水平运动到第二条路线的最上方t77=3; dt=0.05;while t77<=6t77=t77+dt;set(d,'xdata',[t77;t77],'ydata',[t76;t76+0.5]);drawnow; set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,竖直向下运动到第二条路线的最下方t78=8; dt=0.05;while t78>=0.5t78=t78-dt;set(d,'xdata',[6;6],'ydata',[t78;t78+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end%设置五号长方体木块的运动,竖直向上运动到第三条路线的最上方t79=2.0; dt=0.05;while t79<=8t79=t79+dt;set(e,'xdata',[9;9],'ydata',[t79;t79+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,水平运动到第二条路线的最上方t80=9; dt=0.05;while t80>=6t80=t80-dt;set(e,'xdata',[t80;t80],'ydata',[t79;t79+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第二条路线的下方t81=8; dt=0.05;while t81>=1.0t81=t81-dt;set(e,'xdata',[6;6],'ydata',[t81;t81+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置三号长方体木块的运动,竖直向上运动到第一条路线的上方t82=0.5; dt=0.05;while t82<=8t82=t82+dt;set(c,'xdata',[3;3],'ydata',[t82;t82+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置三号长方体木块的运动,水平运动到第三条路线的上方t83=3; dt=0.05;while t83<=9t83=t83+dt;set(c,'xdata',[t83;t83],'ydata',[t82;t82+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置三号长方体木块的运动,竖直向下运动到第三条路线的下方t84=8; dt=0.05;while t84>=1.5t84=t84-dt;set(c,'xdata',[9;9],'ydata',[t84;t84+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向上运动到第二条路线的上方t85=1; dt=0.05;while t85<=8t85=t85+dt;set(e,'xdata',[6;6],'ydata',[t85;t85+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,水平运动到第一条路线的最上方t86=6; dt=0.05;while t86>=3t86=t86-dt;set(e,'xdata',[t86;t86],'ydata',[8;8+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第一条路线的下方t87=8; dt=0.05;while t87>=0.5t87=t87-dt;set(e,'xdata',[3;3],'ydata',[t87;t87+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,竖直向上运动到第二条路线的上方t88=0.5; dt=0.05;while t88<=8t88=t88+dt;set(d,'xdata',[6;6],'ydata',[t88;t88+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,水平运动到第三条路线的上方t89=6; dt=0.05;while t89<=9t89=t89+dt;set(d,'xdata',[t89;t89],'ydata',[8;8.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置四号长方体木块的运动,竖直向下运动到第三条路线的下方t90=8;dt=0.05;while t90>=2.0t90=t90-dt;set(d,'xdata',[9;9],'ydata',[t90;t90+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向上运动到第一条路线的上方t91=0.5;dt=0.05;while t91<=8t91=t91+dt;set(e,'xdata',[3;3],'ydata',[t91;t91+0.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,水平运动到第三条路线的上方t92=3;dt=0.05;while t92<=9t92=t92+dt;set(e,'xdata',[t92;t92],'ydata',[8;8.5]);drawnow;set(gcf,'doublebuffer','on'); %消除震动end% 设置五号长方体木块的运动,竖直向下运动到第三条路线的下方t93=8; dt=0.05;while t93>=2.5t93=t93-dt;set(e,'xdata',[9;9],'ydata',[t93;t93+0.5]); drawnow;set(gcf,'doublebuffer','on'); %消除震动end。
【谷速软件】matlab源码-RS编码

RS编码RS(255,249) 码的生成多项式为G(x)= ,其中a为本原元,是本原多项式p(x)= 的根。
RS系统编码器可看作是一个多项式除法器,首先用乘以消息多项式m(x),即在信息码后附加(n-k)个“0”,将得到的结果m(x)除以g(x),得到余式,b(x)= 为所求的校验位,从而,可将码字多项式表示为c(x)= m(x)+b(x)。
RS译码由于RS 码是一种循环码,令码字多项式为c(x),错误多项式为e(x),则接收多项式可表示为r(x)= c(x)+ e(x)。
存在校验矩阵H,使c*=0,!,定义接收矢量的伴随式S= r* =()。
可得伴随式:j=1,2,3,…n可知伴随式完全由噪声E决定,充分反映了信道干扰的情况。
循环码编码循环码通常采用码多项式描述, 假设(7, 4)循环码的码字为(1001000), 就可用T(x)=1+x3 表示。
特别是用g(x)表示前k- 1 位皆为0 的码组, 称为生成多项式。
由循环码的性质可知, 循环码对生成矩阵可由码对生成多项式g(x) 及其循环移位构成, (7, 4)循环码生成多项式g(x)=1+x+x3(1011)或g(x)=1 +x2+x3(1101), 以选1011 为(7, 4)CRC 码的生成多项式, 用矩阵表示如下式2 - 1。
根据生成矩阵, 就可利用上面介绍的方法设计编码器了。
还可以利用循环码自身的循环性,更方便地实现编码器。
(7, 4)循环码为例, 若输入信息码元为u(x)=1+x3, 则: u(x)= =x+ 因此, 码多项式为:o(x)=r(x)+ u(x)=x+ 其中r(x)=x+x2 为信息码元置为高位后整除生成多项式的余式, 它正好对应于校验序列。
因此对应的输出码字为: c=(01 11001), 其中最右边的4 位是信息元。
循环码编码器的结构可用图1 所示的框图表示。
汉明码编码最简单的校验码是奇偶校验码,其基本思想是无论信息位有多少位,校验位只有一位。
【谷速软件】matlab源码-各种聚类算法的比较

聚类的目标是使同一类对象的相似度尽可能地小;不同类对象之间的相似度尽可能地大。
目前聚类的方法很多,根据基本思想的不同,大致可以将聚类算法分为五大类:层次聚类算法、分割聚类算法、基于约束的聚类算法、机器学习中的聚类算法和用于高维度的聚类算法。
摘自数据挖掘中的聚类分析研究综述这篇论文。
1、层次聚类算法1.1聚合聚类1.1.1相似度依据距离不同:Single-Link:最近距离、Complete-Link:最远距离、Average-Link:平均距离1.1.2最具代表性算法1)CURE算法特点:固定数目有代表性的点共同代表类优点:识别形状复杂,大小不一的聚类,过滤孤立点2)ROCK算法特点:对CURE算法的改进优点:同上,并适用于类别属性的数据3)CHAMELEON算法特点:利用了动态建模技术1.2分解聚类1.3优缺点优点:适用于任意形状和任意属性的数据集;灵活控制不同层次的聚类粒度,强聚类能力缺点:大大延长了算法的执行时间,不能回溯处理2、分割聚类算法2.1.1特点将密度足够大的相邻区域连接,能有效处理异常数据,主要用于对空间数据的聚类2.1.2典型算法1)DBSCAN:不断生长足够高密度的区域2)DENCLUE:根据数据点在属性空间中的密度进行聚类,密度和网格与处理的结合3)OPTICS、DBCLASD、CURD:均针对数据在空间中呈现的不同密度分不对DBSCAN作了改进2.2基于网格的聚类2.2.1特点利用属性空间的多维网格数据结构,将空间划分为有限数目的单元以构成网格结构;1)优点:处理时间与数据对象的数目无关,与数据的输入顺序无关,可以处理任意类型的数据2)缺点:处理时间与每维空间所划分的单元数相关,一定程度上降低了聚类的质量和准确性2.2.2典型算法1)STING:基于网格多分辨率,将空间划分为方形单元,对应不同分辨率2)STING+:改进STING,用于处理动态进化的空间数据3)CLIQUE:结合网格和密度聚类的思想,能处理大规模高维度数据4)WaveCluster:以信号处理思想为基础2.3.1特点转换为组合优化问题,并利用图论和相关启发式算法来解决,构造数据集的最小生成数,再逐步删除最长边1)优点:不需要进行相似度的计算2.3.2两个主要的应用形式1)基于超图的划分2)基于光谱的图划分2.4基于平方误差的迭代重分配聚类2.4.1思想逐步对聚类结果进行优化、不断将目标数据集向各个聚类中心进行重新分配以获最优解2.4.2具体算法1)概率聚类算法期望最大化、能够处理异构数据、能够处理具有复杂结构的记录、能够连续处理成批的数据、具有在线处理能力、产生的聚类结果易于解释2)最近邻聚类算法——共享最近邻算法SNN特点:结合基于密度方法和ROCK思想,保留K最近邻简化相似矩阵和个数不足:时间复杂度提高到了O(N^2)3)K-Medioids算法特点:用类中的某个点来代表该聚类优点:能处理任意类型的属性;对异常数据不敏感4)K-Means算法1》特点:聚类中心用各类别中所有数据的平均值表示2》原始K-Means算法的缺陷:结果好坏依赖于对初始聚类中心的选择、容易陷入局部最优解、对K值的选择没有准则可依循、对异常数据较为敏感、只能处理数值属性的数据、聚类结构可能不平衡3》K-Means的变体Bradley和Fayyad等:降低对中心的依赖,能适用于大规模数据集Dhillon等:调整迭代过程中重新计算中心方法,提高性能Zhang等:权值软分配调整迭代优化过程Sarafis:将遗传算法应用于目标函数构建中Berkh in等:应用扩展到了分布式聚类还有:采用图论的划分思想,平衡聚类结果,将原始算法中的目标函数对应于一个各向同性的高斯混合模型5)优缺点优点:应用最为广泛;收敛速度快;能扩展以用于大规模的数据集缺点:倾向于识别凸形分布、大小相近、密度相近的聚类;中心选择和噪声聚类对结果影响大3、基于约束的聚类算法3.1约束对个体对象的约束、对聚类参数的约束;均来自相关领域的经验知识3.2重要应用对存在障碍数据的二维空间按数据进行聚类,如COD(Clustering with Obstru cted Distance):用两点之间的障碍距离取代了一般的欧式距离3.3不足通常只能处理特定应用领域中的特定需求4、用于高维数据的聚类算法4.1困难来源因素1)无关属性的出现使数据失去了聚类的趋势2)区分界限变得模糊4.2解决方法1)对原始数据降维2)子空间聚类CACTUS:对原始空间在二维平面上的投影CLIQUE:结合基于密度和网格的聚类思想,借鉴Apriori算法3)联合聚类技术特点:对数据点和属性同时进行聚类文本:基于双向划分图及其最小分割的代数学方法4.3不足:不可避免地带来了原始数据信息的损失和聚类准确性的降低5、机器学习中的聚类算法5.1两个方法1)人工神经网络方法自组织映射:向量化方法,递增逐一处理;映射至二维平面,实现可视化基于投影自适应谐振理论的人工神经网络聚类2)基于进化理论的方法缺陷:依赖于一些经验参数的选取,并具有较高的计算复杂度模拟退火:微扰因子;遗传算法(选择、交叉、变异)5.2优缺点优点:利用相应的启发式算法获得较高质量的聚类结果缺点:计算复杂度较高,结果依赖于对某些经验参数的选择下面附上个人对聚类算法的选择及比较的理解:。
Matlab下多径衰落信道的仿真代码

%区别个条路径的均匀分布随机相位
theta=2*pi*rand(1,1)-pi;
for ii=1i*ii-pi+theta)/N;
N=40;
wm=2*pi*fd;
%每象限的入射波数目即振荡器数目
N0=N/4;
%信道函数的实部
Tc=zeros(1,length(t));
%信道函数的虚部
Ts=zeros(1,length(t));
%归一化功率系数
function [h]=rayleigh(fd,t)
%改进的jakes模型来产生单径的平坦型瑞利衰落信道
%输入变量说明:
% fd:信道的最大多普勒频移 单位Hz
% t :信号的抽样时间序列,抽样间隔单位s
% h为输出的瑞利信道函数,是一个时间函数复序列
%假设的入射波数目
衰落信道参数包括多径扩展和多普勒扩展。时不变的多径扩展相当于一个延时抽头滤波器,而多普勒扩展要注意多普勒功率谱密度,通常使用Jakes功率谱、高斯、均匀功率谱。
多径衰落信道由单径信道叠加而成,而单径信道中最重要的就是瑞利(Rayleigh)平坦衰落信道。
下面给出瑞利平坦衰落信道的改进Jakes模型的实现:
chan=rayleighchan(ts,fd);
y=filter(chan,x);%过信道
此内置函数可以直接生成一个频率选择多径衰落信道,每径为一个瑞利衰落过程。
chan=rayleighchan(ts,fd,tau,pdb);
%tau为每径相对时延向量
%pdb为每径相对增益
%对每个子载波而言在(-pi,pi)之间均匀分布的随机相位
MATLAB多径衰落对误码率影响的仿真与分析

MATLAB多径衰落对误码率影响的仿真与分析
刘芳
【期刊名称】《大陆桥视野》
【年(卷),期】2010(000)011
【摘要】本文利用MATLAB软件,对AWGN多径信道中QPSK系统进行了四种多径衰落(莱斯平坦衰落、莱斯频率选择性衰落、瑞利平坦衰落、瑞利频率选择性衰落)信道的BER性能的仿真和分析.
【总页数】2页(P149-150)
【作者】刘芳
【作者单位】乌鲁木齐铁路运输学校新疆乌鲁木齐 830000
【正文语种】中文
【相关文献】
1.MATLAB多径衰落对误码率影响的仿真与分析 [J], 刘芳
2.噪声调频干扰信号对直扩系统误码率影响的仿真分析 [J], 刘国芳;刘坤;李军杰;高慧敏
3.GMSK调制解调的MATLAB仿真与误码率分析 [J], 赵忠华;杨晓梅
4.基于MATLAB的雷电对智能组件影响的仿真分析及克服 [J], 芮新花; 赵珏斐; 张贝贝
5.基于MATLAB的雷电对智能组件影响的仿真分析及克服 [J], 芮新花; 赵珏斐; 张贝贝
因版权原因,仅展示原文概要,查看原文内容请购买。
【谷速软件】matlab源码-多径信道

时变、多径是无线信道的特点,相信很多人在看了很多书之后,对无线信道感觉还是一头雾水。
为什么多径导致频率选择性?为什么多普勒频移反映了信道的时变性?对这些问题感觉困惑的肯定大有人在。
下面我们就用一个简单的不能再简单的程序一一解开你的困惑。
首先,我们先说一下程序模拟的场景。
如图1所示。
图1 最简单的多径信道假设在一条笔直的高速公路上一端安装了一个固定的基站,在另一端有一面完全反射电磁波的墙面,基站距离反射墙的距离为d。
移动台距离基站初始距离为r0。
基站发射一个频率为f的正弦信号,表示为cos(2*pi*f*t)。
由于墙面的反射,移动台可以接收到2径信号,其中之一是从基站直接发射的信号,另一径是从反射墙反射过来的信号。
首先我们来看移动台静止的情况。
显然,从基站发出的直射信号到达移动台需要的时间为r0/c(c为光速),从反射墙反射过来的信号到达移动台所需要的时间为(d+d-r0)/c=(2d-r0)/c。
换句话说,在时刻t,移动台分别接收到了从时刻(t-r0/c)基站发出的直射信号和从时刻t-(2d-r0)/c基站发出的反射信号。
我们知道,信号在传播的过程中要衰减,自由空间中,电磁波功率随距离r按平方规律衰减,相应的电场强度(可以看成接收信号电压)随1/r规律衰减。
并且反射信号同直射信号的相位相反。
所以,时刻t移动台接收到的合成信号为:减号体现了反射信号与直射信号的相位相反。
在r0处的接收信号会有什么特点?让我们把它画出来。
下面是程序代码。
clear allf=1; %发射信号频率v=0; %移动台速度,静止情况为0c=3e8; %电磁波速度,光速r0=3; %移动台距离基站初始距离d=10; %基站距离反射墙的距离t1=0.1:0.0001:10; %时间E1=cos(2*pi*f*((1-v/c).*t1-r0/c))./(r0+v.*t1);E2=cos(2*pi*f*((1+v/c)*t1+(r0-2*d)/c))./(2*d-r0-v*t1); figureplot(t1,E1) %画出直射径的信号hold onplot(t1,-E2,'-g') %画出反射径的信号hold onplot(t1,E1-E2,'-r') %画出移动台总的接收信号。
matlab 多径衰落信道

matlab 多径衰落信道
摘要:
1.Matlab 多径衰落信道的概念
2.多径衰落信道的影响因素
3.Matlab 仿真多径信道瑞利衰落的方法
4.多径衰落信道在通信系统中的应用
5.总结
正文:
Matlab 多径衰落信道是一种在无线通信中常见的信道模型,它是由于信号在传播过程中经过多条路径,这些路径可能经历不同的时延、幅度衰落和相位变化,导致信号的叠加变得复杂。
这种信道模型对于信号传输的可靠性和稳定性有着重要的影响。
多径衰落信道的影响因素主要包括路径数、路径时延、路径幅度和路径相位等。
路径数越多,信号的衰落程度就越严重;路径时延和相位的变化会导致信号的波形发生畸变;路径幅度的变化则会影响信号的强度。
在实际应用中,多径衰落信道会对通信系统的性能产生负面影响,如增加误码率、降低信噪比等。
在Matlab 中,可以通过仿真多径信道瑞利衰落的方法来研究多径衰落信道的特性。
首先需要建立多径信道模型,然后设置模型的参数,如路径数、多普勒频移等。
在仿真过程中,可以观察信号的衰落情况,分析信号的波形和幅度变化,从而了解多径衰落信道的特性。
多径衰落信道在通信系统中有着广泛的应用,如扩频通信、无线通信等。
在扩频通信中,多径衰落信道会影响信号的传输效率和可靠性;在无线通信中,多径衰落信道会导致信号的强度衰减和波形畸变,从而影响通信质量。
因此,研究多径衰落信道的特性对于优化通信系统的性能具有重要意义。
总之,Matlab 多径衰落信道是一种重要的无线通信信道模型,它对于信号传输的可靠性和稳定性有着重要的影响。
matlab编程实现二分法牛顿法黄金分割法最速下降matlab程序代码

用二分法求解4224min ()f t t t t =--115[,.]t ∈内的极小值点,要求准 1.function [t d]=erfenfa(a,b)k=1; %记录循环次数while abs(a-b)>0.0005c=(a+b)/2;C(k)=c; %存储每次循环中点c 的值if ff(c)<0a=c;endif ff(c)==0t1=c;break ;endif ff(c)>0b=c;endk=k+1;endt=(a+b)/2; %最终符合要求的值d=f(t); %最优解Ckfunction y=f(t)y=t^4-2*t^2-4*t;function y=ff(t)y=4*t^3-4*t-4;运行结果>> [t d]=erfenfa(1,1.5)C =Columns 1 through 91.2500 1.3750 1.3125 1.3438 1.3281 1.3203 1.3242 1.32621.3252Column 101.3247k =11t =1.3250d =-5.72902.黄金分割法 f (x)=x3-2x+1 初始区间[0, 3],收敛精度0.5function [t,f]=huangjinfenge(a,b)m=1-(sqrt(5)-1)/2;t2=a+m*(b-a)f2=g(t2);t1=a+b-t2f1=g(t1);while abs(t1-t2)>0.5if f1<f2a=t2;t2=t1f2=f1;t1=a+b-t2f1=g(t1);elseb=t1;t1=t2f1=f2;t2=a+m*(b-a)f2=g(t2);endendt=(t1+t2)/2;f=g(t);function y=g(t)y=t^3-2*t+1;运行结果> [t,f]=huangjinfenge(0,3)t2 =1.1459t1 =1.8541t1 =1.1459t2 =0.7082t =0.9271f =-0.0574>>3. 用牛顿法求解291min ()sin f x x x =--初始迭代点为x 0=0.4,要求准确到小数 点后第5位小数function [t1,d]=Newton(t0)t=t0-ff(t0)/fff(t0);k=1;%记录迭代次数T(1)=t;%存储迭代点while abs(t-t0)>0.000005t0=t;t=t0-ff(t)/fff(t);k=k+1;T(k)=t;endt1=t0;d=f(t1);kTfunction y=f(x)y=9*x^2-sin(x)-1;function y=ff(x)y=18*x-cos(x);function y=fff(x)y=18+sin(x);运行结果>> [t1,d]=Newton(0.4)k =3T =0.0586 0.0555 0.0555t1 =0.0555d =-1.0277>>4. 最速下降法验证课本上的例题求解291min ()sin f x x x =--初始迭代点为x 0=0.4, 要求准确到小数点后第5位小数function [G,g,X,F]=zuisu(X0)F(1)=f(X0);%存储x 点处的值G(:,1)=h(X0); %存储梯度向量g(1)=norm(G(:,1));%存储梯度模长X(:,1)=X0; %存储x 值A=[2,0;0,8];for j=1:2X(:,j+1)=X(:,j)-(G(:,j)'*G(:,j))/(G(:,j)'*A*G(:,j))*G(:,j); F(j+1)=f(X(:,j+1));G(:,j+1)=h(X(:,j+1));g(j+1)=norm(G(:,j+1));endif (G(:,2)'*G(:,1)<1E-10& G(:,3)'*G(:,2)<1E-10)disp(['相邻两搜索方向是正交的'])endfunction y=f(X)y=X(1)^2+4*X(2)^2;function n=h(X)n=[2*X(1),8*X(2)]';运行结果>> [G,g,X,F]=zuisu(X0)相邻两搜索方向是正交的G =2.0000 1.4769 0.2215 8.0000 -0.3692 0.8862g =8.2462 1.5224 0.9134X =1.0000 0.7385 0.1108 1.0000 -0.0462 0.1108F =5.0000 0.5538 0.0613 >>。
MATLAB课件·第4章 通信系统的建模与仿真

B 这种典型的情况,带通采样定理所规定的采
样频率近似等于下界 2 B 。 对整个通信系统进行仿真开发时,选择对系统合适的采样频率是要做的一个基本决 定。除考虑上述信号带宽外,有许多因素影响所需的系统采样频率。具有反馈的系统、非 线性系统、多径信道等会导致更高的采样频率要求。对于无反馈的线性系统,必需的采样 频率可由可接受的混叠误差决定的,而这又有赖于发送滤波器成形脉冲的功率谱密度。成 形脉冲是假定时域有限的,因此不可能是带宽有限的,因而会产生在实际中不可能消除混 叠误差。为仿真选择合适的采样频率的一个策略就是在混叠误差和仿真时间之间达成一个 可以接受的折衷。目标是选择一个采样频率,使得混叠误差相对于仿真所考察的系统性能 的降低是可以忽略的。 有些要仿真的系统(如扩频通信系统)包含两个或多个不同信号带宽的子系统。扩频 通信系统同时包括窄带信号和宽带信号。如果使用单一的采样频率,那么这个采样频率必 须与宽带波形相适应,而用宽带信号所需的采样率对窄带信号进行采样,将导致仿真的时 间过大和效率降低。一般最有效的方法是对每个过程用它的奈奎斯特速率采样,对整个系 统而言采用多速率采样。系统中出现两个不同带宽时,可采用两个采样率:在窄带到宽带 的分界处提高采样频率(上采样),而在宽带到窄带的分界处降低采样频率(下采样)。 采样频率的提高是通过对在原始样点之间内插新的样点来完成;采样频率的降低是通过从 原样点每多个样点抽取一个来实现。 采样点的值在计算机中是用有限长的码字来量化,所以在仿真中都会出现量化误差。 计算机处理表示数字的方式可以分为定点和浮点两类。当用定点数表示时,字长每增加一 个比特,量化的信噪比增加 6dB 。在通用计算机上采用浮点数表示进行仿真操作时,由量 化导致的量化误差通常可以忽略不计。然而,这种噪声永远不会为零,在噪声累积的情况 过多时可能会严重地降低仿真结果的精度。 3. 信道编码器和译码器 信道编码器对数码流进行相应的处理,使系统具有一定的纠错能力和抗干扰能力。信 道编码的处理技术有差错控制码、交织编码器等。差错控制码有线性差错控制码(汉明 码、线性循环码等)、Reed-Solomon 码、卷积码、Turbo 码、LDPC 码等。信道译码器完 成信道编码的译码。交织编码技术可离散化并纠正信号衰落引起的突发性差错,改善信道
LTE-A网络的比例公平资源调度代码与使用说明

毕业设计成果使用说明书设计(论文)题目: LTE-A网络的比例公平资源调度设计和实现学生姓名:学号:专业:所在学院:指导教师:职称:一、架构图本次毕业设计主要模拟仿真了以下三类算法的资源调度过程,结构如下图所示:图1 算法仿真结构模块图二、MATLAB 仿真的系统及通信模型搭建本算法是基于MATLAB 进行的模拟仿真,首先需要下载并安装MATLAB 软件,建议版本:2014a 。
在安装程序完成后,即可双击本程序运行。
在MATLAB 的代码设计中包括如下几个部分:1、 参数设置图2 系统参数设置本段代码设置了单小区、单天线调度系统的各项参数:1) 调度次数number 、调度用户数user_number 、调度时隙数slot_number; 2) 基站覆盖半径covering_radius 、基站发射功率transmit_power;轮询算法最大载干比算法比例公平算法资源调度算法3)路径损耗公式中的参考距离distance、频率frequence、路径损耗指数pass_loss_exponent;4)计算噪声方差中的玻尔兹曼常数Boltzman_constant、温度temperature、带宽bandwidth;5)第一次调度的累积平均速率first_rate。
2、分配内存空间:图3 系统分配内存空间本段代码为单小区、单天线调度系统的各项参数分配相应的内存空间:1)用户半径user_radius、用户角度user_angel、x轴坐标x_coordinate、y轴坐标y_coordinate;2)路径损耗path_loss、衰落fading、转化后的功率power、脉冲响应impulse_response;3)信号功率signal_power、信噪比signal_noise_ratio、信道容量channal_capacity;4)累积平均速率cumulative_average_rate、累积速率cumulative_rate;5)最大载干比算法数据速率maximum_CI_data_rate;6)轮询算法数据速率round_robin_data_rate;7)比例公平算法数据速率proportional_fairness_data_rate;8)最大载干比算法总数据速率maximum_CI_total_data_rate、轮询算法总数据速率round_robin_total_data_rate、比例公平算法总数据速率proportional_fairness_total_data_rate。
最速下降法matlab代码

最速下降法matlab代码最速下降法(Steepest Descent Method)是一种优化算法,用于求解无约束最优化问题。
下面是一个使用MATLAB实现最速下降法的代码示例:```matlabfunction x = steepest_descent(f, grad_f, x0, tol, max_iter)% f: 目标函数% grad_f: 目标函数的梯度% x0: 初始点% tol: 迭代停止的容差% max_iter: 最大迭代次数x = x0; % 初始点iter = 0; % 迭代次数while norm(grad_f(x)) > tol && iter < max_iterp = -grad_f(x); % 计算搜索方向% 一维搜索,选择合适的步长alphaalpha = backtracking_line_search(f, grad_f, x, p);x = x + alpha * p; % 更新变量xiter = iter + 1;endendfunction alpha = backtracking_line_search(f, grad_f, x, p, alpha0, rho, c)% f: 目标函数% grad_f: 目标函数的梯度% x: 当前点% p: 搜索方向% alpha0: 初始步长% rho: 减小步长的比例因子% c: Armijo-Goldstein条件的常数因子if nargin < 6rho = 0.5; % 默认减小步长的比例因子endif nargin < 7c = 0.1; % 默认Armijo-Goldstein条件的常数因子endalpha = alpha0; % 初始步长while f(x + alpha * p) > f(x) + c * alpha * grad_f(x)' * palpha = rho * alpha; % 减小步长endend```在上述代码中,`steepest_descent`函数实现了最速下降法的主要逻辑。
matlab多径瑞利衰落信道

matlab多径瑞利衰落信道【原创实用版】目录1.多径瑞利衰落信道的概念和背景2.Matlab 在多径瑞利衰落信道仿真中的应用3.多径瑞利衰落信道仿真的重要性和挑战4.如何在 Matlab 中实现多径瑞利衰落信道的仿真5.总结与展望正文一、多径瑞利衰落信道的概念和背景多径瑞利衰落信道是一种无线通信信道模型,它描述了无线信号在传输过程中由于多径效应和瑞利衰落所引起的信号衰减和失真。
在城市密集区域、建筑物内部等环境中,无线信号会受到反射、折射、衍射等影响,导致信号强度的快速衰减和信道质量的恶化。
因此,研究多径瑞利衰落信道对于无线通信系统的设计和优化具有重要意义。
二、Matlab 在多径瑞利衰落信道仿真中的应用Matlab 是一种广泛应用于科学计算和工程设计的软件,其强大的数值计算和数据分析功能为多径瑞利衰落信道的仿真提供了便利。
在Matlab 中,可以通过编写自定义函数或使用现有的工具箱(如Communication Toolbox)来实现多径瑞利衰落信道的仿真。
三、多径瑞利衰落信道仿真的重要性和挑战多径瑞利衰落信道仿真对于无线通信系统的设计和优化具有重要意义,因为它可以帮助工程师了解系统在不同信道条件下的性能,从而指导系统参数的调整和优化。
然而,多径瑞利衰落信道仿真也面临着一些挑战,如信号模型的复杂性、参数设置的合理性、计算资源的需求等。
四、如何在 Matlab 中实现多径瑞利衰落信道的仿真在 Matlab 中实现多径瑞利衰落信道的仿真,可以采用如下步骤:1.创建信号模型:首先需要建立一个信号模型,描述信号在多径瑞利衰落信道中的传播过程。
这可以通过编写自定义函数或使用现有的工具箱来实现。
2.设置系统参数:在进行仿真之前,需要设置一些系统参数,如信号的调制方式、传输速率、信道带宽等。
这些参数的设置会影响到仿真结果的准确性和可靠性。
3.编写仿真代码:根据信号模型和系统参数,可以编写 Matlab 代码来实现多径瑞利衰落信道的仿真。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
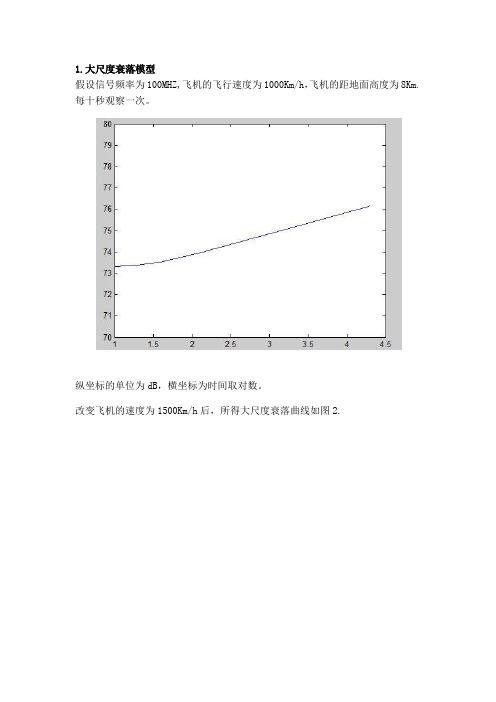
1.大尺度衰落模型
假设信号频率为100MHZ,飞机的飞行速度为1000Km/h,飞机的距地面高度为8Km.每十秒观察一次。
纵坐标的单位为dB,横坐标为时间取对数。
改变飞机的速度为1500Km/h后,所得大尺度衰落曲线如图2.
2.瑞利衰落模型
多径衰落可以用瑞利衰落来近似,使用MATLAB可以绘制出瑞利衰落的曲线。
如图3
3.接收端的初步设计
大尺度衰落是不可避免的,而且它与飞行速度有关,与信号的频率关系不大;而多径效应会导致码间干扰(ISI),严重影响了接收信号的判决,在接收端应采用均衡措施。
假定传输信号的波形已知为方波,可以设计滤波器,来减小码间干扰。
ISIfilter的设计可以用MATLAB实现,图4
4.眼图
可以通过眼图的观察选择最佳的采样时间点。
眼图的观察效果如图5.。
