EVIEWS序列相关检验2介绍
eviews时间序列一阶自相关检验命令

eviews时间序列一阶自相关检验命令在EViews中,我们可以使用AR(p)模型来进行时间序列的一阶自相关检验。
AR(p)模型表示自回归模型,其中p表示阶数。
一阶自相关检验是用来确定时间序列数据是否存在自相关性。
自相关是指序列中一个值与其在时间上前一时刻的值之间的相关性。
在时间序列分析中,我们希望序列的值是彼此相互独立的,因此自相关性可能会影响我们对序列的分析和预测。
在EViews中,可以通过以下步骤来进行一阶自相关检验:1.打开EViews软件并导入时间序列数据。
2.在EViews主菜单中选择“Quick/Estimate Equation”(快速估计方程)。
3.在“Equation Specification”(方程规范)对话框中,输入要估计的模型。
例如,如果要进行一阶自相关检验,则可以输入模型“y c ar(1)”。
- “y”表示被解释变量。
- “c”表示常数项。
- “ar(1)”表示自回归项,其中1表示阶数。
4.单击“OK”按钮以估计模型。
5.将结果显示为估计方程的系数,t统计量,R-squared(R平方值)等。
在估计方程后,EViews将为我们提供一阶自相关检验的结果。
重要的统计值包括Jarque-Bera(JB)统计量、ARCH LM检验、DW统计量等。
- Jarque-Bera(JB)统计量是用来检验数据是否服从正态分布。
如果JB统计量的p值小于0.05,则我们可以拒绝原假设,即数据不服从正态分布。
- ARCH LM检验旨在检验序列中是否存在异方差性。
如果ARCH LM 统计量的p值小于0.05,则我们可以拒绝原假设,即序列中存在异方差性。
- Durbin-Watson(DW)统计量是用来检验序列的自相关性。
DW统计量的值介于0和4之间,如果DW值接近于2,则表示序列不存在一阶自相关。
除了上述统计量之外,EViews还提供了其他有关模型估计的信息,包括系数的标准误差、置信区间、F统计量和R平方等。
Eviews 实验操作手册(部分)

Eviews实验操作记录(慢慢整理)相关系数检验:W AGE ED SEXW 1.000000 0.210152 0.495856 -0.260906AGE 0.210152 1.000000 -0.038637 0.144689ED 0.495856 -0.038637 1.000000 -0.084487SEX -0.260906 0.144689 -0.084487 1.000000①可以在命令窗口键入命令:cor x y z……,就会输出相关系数矩阵。
②假设你的样本数据序列:x1 x2从主菜单选择Quick/Group Statistics/Correlations之后会弹出个对话框,在对话框选择你的目标序列x1 x2说明:序列相关好像只有正相关、负相关、完全相关、完全不相关、强相关、弱相关等概念。
相关系数为1是完全正相关,-1是完全负相关,0是完全不相关。
个人感觉0.5左右的相关关系(趋势)就比较弱了。
eviews提供的相关计算是指序列之间的线性相关关系。
如果序列之间不存在线性相关,也有可能存在其他类型的相关关系,如对数相关、指数相关等等。
通常显著性是和建设检验关联的。
统计假设检验也称为显著性检验,即指样本统计量和假设的总体参数之间的显著性差异。
显著性是对差异的程度而言的,程度不同说明引起变动的原因也有不同:一类是条件差异,一类是随机差异。
显著性差异就是实际样本统计量的取值和假设的总体参数的差异超过了通常的偶然因素的作用范围,说明还有系统性的因素发生作用,因而就可以否定某种条件不起作用的假设。
假设检验时提出的假设称为原假设或无效假设,就是假定样本统计量与总体参数的差异都是由随机因素引起,不存在条件变动因素。
假设检验运用了小概率原理,事先确定的作为判断的界限,即允许的小概率的标准,称为显著性水平。
如果根据命题的原假设所计算出来的概率小于这个标准,就拒绝原假设;大于这个标准则接受原假设。
这样显著性水平把概率分布分为两个区间:拒绝区间,接受区间。
用EVIEWS处理时间序列分析

应用时间序列分析实验手册目录目录1第二章时间序列的预处理2一、平稳性检验2二、纯随机性检验9第三章平稳时间序列建模实验教程9一、模型识别9二、模型参数估计(如何判断拟合的模型以及结果写法)14三、模型的显著性检验17四、模型优化18第四章非平稳时间序列的确定性分析19一、趋势分析19二、季节效应分析34三、综合分析38第五章非平稳序列的随机分析44一、差分法提取确定性信息44二、ARIMA模型57三、季节模型61第二章时间序列的预处理一、平稳性检验时序图检验和自相关图检验(一)时序图检验根据平稳时间序列均值、方差为常数的性质,平稳序列的时序图应该显示出该序列始终在一个常数值附近随机波动,而且波动的X围有界、无明显趋势及周期特征例2.1检验1964年——1999年中国纱年产量序列的平稳性1.在Eviews软件中打开案例数据图1:打开外来数据图2:打开数据文件夹中案例数据文件夹中数据文件中序列的名称可以在打开的时候输入,或者在打开的数据中输入图3:打开过程中给序列命名图4:打开数据2.绘制时序图可以如下图所示选择序列然后点Quick选择Scatter或者XYline;绘制好后可以双击图片对其进行修饰,如颜色、线条、点等图1:绘制散点图图2:年份和产出的散点图10020030040050060019601970198019902000YEARO U T P U T图3:年份和产出的散点图(二)自相关图检验 例2.3导入数据,方式同上;在Quick 菜单下选择自相关图,对Qiwen 原列进行分析;可以看出自相关系数始终在零周围波动,判定该序列为平稳时间序列。
图1:序列的相关分析图2:输入序列名称图2:选择相关分析的对象图3:序列的相关分析结果:1.可以看出自相关系数始终在零周围波动,判定该序列为平稳时间序列2.看Q统计量的P值:该统计量的原假设为X的1期,2期……k期的自相关系数均等于0,备择假设为自相关系数中至少有一个不等于0,因此如图知,该P值都>5%的显著性水平,所以接受原假设,即序列是纯随机序列,即白噪声序列(因为序列值之间彼此之间没有任何关联,所以说过去的行为对将来的发展没有丝毫影响,因此为纯随机序列,即白噪声序列.)有的题目平稳性描述可以模仿书本33页最后一段.(三)平稳性检验还可以用:单位根检验:ADF,PP检验等;非参数检验:游程检验图1:序列的单位根检验表示不包含截距项图2:单位根检验的方法选择图3:ADF检验的结果:如图,单位根统计量ADF=-0.016384都大于EVIEWS给出的显著性水平1%-10%的ADF临界值,所以接受原假设,该序列是非平稳的。
计量经济学 —理论方法EVIEWS应用--第七章 序列相关性

在其他假设仍然成立的条件下,随机干扰项序列相关意味着
(7-2)
如果仅存在
E ( ) 0 , i 1 , 2 , . . . , n i i 1
(7-3)
则称为一阶序列相关或自相关(简写为AR(1)),这是常见的一种序列相关问题。
D .W .
不存在一阶自相关,构造如下统计量: t
t
( eˆ
t2
n
ˆt 1 ) 2 e
2 t
eˆ
t 1
n
杜宾—沃森证明该统计量的分布与出现在给定样本中的X值有复杂的关系,
其准确的抽样或概率分布很难得到;
因为D.W.值要从
eˆ t 中算出,而 eˆ t
又依赖于给定的X的值。
2 χ 因此D-W检验不同于t、F或 检验,它没有唯一的临界值可以导出拒绝或
用OLS法估计序列相关的模型得到的随机误差项的方差不仅是 有偏的,而且这一偏误也将传递到用OLS方法得到的参数估计 量的方差中来,从而使得建立在OLS参数估计量方差基础上的 变量显著性检验失去意义。
以一元回归模型为例,
Y X i 0 1 i i
2
ˆ) Var ( 1 2 xt
序列相关性及其产生原因序列相关性的影响序列相关性的检验序列相关的补救第一节序列相关性及其产生原因序列相关性的含义对于多元线性回归模型71在其他假设仍然成立的条件下随机干扰项序列相关意味着如果仅存在则称为一阶序列相关或自相关简写为ar1这是常见的一种序列相关问题
—理论· 方法· EViews应用
郭存芝 杜延军 李春吉 编著
二、回归检验法
, eˆ, 以 e ˆ t 为解释变量,以各种可能的相关变量,诸如 t1
eviews检验相关方法(2)

我用的是Eviews3.1注册版(因为其他的版本没注册都不稳定容易自己关闭程序),但大抵操作应该是相同的。
首先建立新的workfile,在命令窗口输入series,弹出新建的数列窗口,把要检验的数据存进去。
然后再数列窗口下点击view,找到unit root test就是单位根检验,弹出来的窗口的左上角是选择检验方式,一般保持默认的DF那一项就好了,Eviews里面的这个DF选项是把DF与ADF检验都包括在一起了。
右边的intercept啦intercept and trend啦是针对ADF 检验的不同模型,如果搞不清楚干脆就按默认吧。
左下角的level,1st differential,2st什么的是问你是针对原始数据、还是一阶差分、二阶差分来做检验,默认是level,就是原始数据。
都选好之后点击OK就好了。
输出的结果主要是看上面的表,第一个表左边给出一个值,右边给了三个值,分别是置信度99%,95%,90%的ADF检验临界值。
左边的值如果小于右边的某个值,说明该数据落在右边那个对应值的置信区间里。
比如左边给出-3,右边对应95%置信度的值是-1,-3<-1所以数据不存在单位根,是平稳的,这一检验的置信度是95%。
大概是这样吧,具体的ADF模型选择等等最好看一看相关书籍。
Eviews不难学的~~嘿嘿我也就是三天恶补大概看完的。
ADF检验的原假设是存在单位根,一般EVIEWS输出的是ADF检验的统计值,只要这个统计值是小于1%水平下的数字就可以极显著的拒绝原假设,认为数据平稳。
注意,ADF值一般是负的,也有正的,但是它只有小于1%水平下的才能认为是及其显著的拒绝原假设这样的话,如果你的变量是水平变量。
那么,你需要取对数,一般来说,取对数后的变量一般是平稳的,这样,你无需作协整;如果对数变量非平稳,再取一阶差分(绝大多数的水平变量取对数后再一阶差分是平稳的),你就可以作协整了了。
如果你的变量已是相对数,xt 与yt 并非I(1),那么,不能作协整,仅作一般的时间序列分析即可。
Eviews EG两步法2

模型建立—时间序列eviews协整检验EG两步法(Engle-Granger)1.首先,需要两列时间序列数据,将他们命名为future4,future5,存入eviews。
2.对两组数据取对数,得新的数据:P4=log(future4),P5=log(future5)。
可在eviews中点击Genr输入p4=log(future4)可自动产生对数数列。
为何取对数?:可以部分消除异方差的问题,另外,其差分可以表示发展速度的对数,也可以消除序列相关的问题.有时候要看经济意义!取对数也可减少数据的波动,在高频数据中尤是。
变量取对数是为了消除异方差,系数也是弹性系数,主要是为了消除金融时间序列的异方差现象,可以将可能的非线性关系转化为线性关系,减少变量的极端值、非正态分布以及异方差性(2012.4.10补充,针对上面提到的非线性关系转化为线性关系,做进一步的解释:经济序列通常做对数化处理,因为log有很多优良特性。
如取对数,很容易操作,正如上面所说,输入log(x)就可以产生原数列相应的对数数列。
还有一些关系式如log(a*b)=log(a)+log(b),log(a^2)=2*log(a),这种特性可以很容易的把函数之间的关系线性化。
加上log,常可以使得经济数列变得更容易处理。
)3.对两个时间序列分别做ADF检验。
1.eviews中选取时间序列P4,右键=》open。
在新的窗口中点击view=》unit root test。
2.ADF检验需要对3个模型依次检验,所以在unit root test窗口中先①选:level、trend and intercept。
然后确认=》得到第一行是所得t值,下面3行是临界值。
t=-2.0665>临界值,因此非平稳。
因此要继续检验②:level、intercept,假设还是非平稳。
继续检验③:level none。
假设还是非平稳,则做一阶差分,即将level换成1st difference,将之前①②③从新来过,一旦t<临界值就可以停止了。
Eviews实际案例:序列相关性
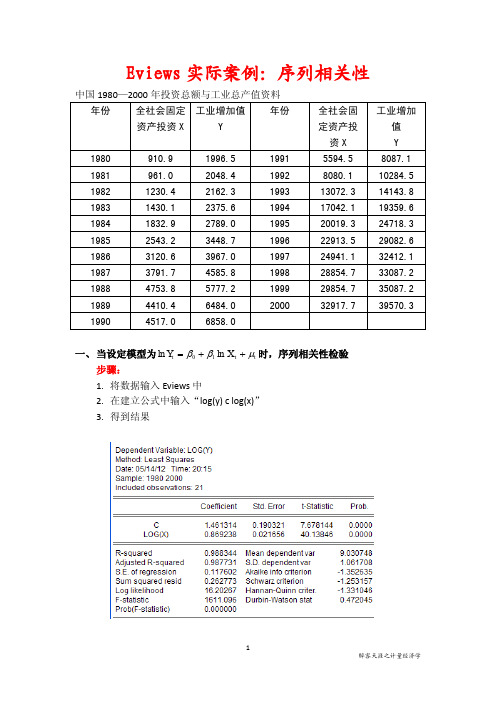
5
醉客天涯之计量经济学
(3.272) (23.671) D.W.=1.393 由于 D.W.=1.393,在 5%的显著性水平下,样本容量为 19 的 D.W.检验的临界值为上下限为
d L 1.18 , dU 1.40 ,检验值落在 (d L , dU ) 上,故不能确定是否存在一阶序列相关。
根据 LM 法进行检验。 在 eviews 输出结果窗口选择 “View\Residual Tests\Series Correlation LM Test”,在随后出现的对话框中填入滞后期数“1” ,得到:
二、 若按一阶自相关假设 计原模型 (一)杜宾两步法 第一步: 1. 估计模型为:
ln Yt p ln Yt 1 0 (1 p) 1 (ln X t p ln X t 1 )
t t 1 t ,试用杜宾两步法和广义最小二乘法估
或者
ln Yt p ln Yt 1 0 (1 p) 1 ln X t 1 p ln X t 1
检验统计量值为 1.248,查询 分布,
2
2 0.05
(1) 3.84 1 dU 2.59 ,检验值小于临界值,
因而不能拒绝原假设,认为模型不存在一阶序列相关。
ˆ 因此估计原模型为: ln Y t
0.4257 0.9017 ln X t 1 0.6278
ˆ 1.156 0.9017 ln X 即: ln Y t t
一、 当设定模型为 ln Yt 0 1 ln X t t 时,序列相关性检验 步骤: 1. 将数据输入 Eviews 中 2. 在建立公式中输入“log(y) c log(x)” 3. 得到结果
1
醉客天涯之计量经济学
eviews单位根检验解读

中有一种模型旳检验成果拒绝了零假设,就可以为时间序列是平稳旳。
13
分析数据旳平稳性软 件 操 作
在Pool对象,View/Unit Root Test,输入相应旳Pool序列名
填写序列 名
选择检验 措施
填写秩序
右边 全部 栏目 软件
自动 填写 无需 更改
填写模式,先做 序列图再选择
14
例10.4中I?旳水平变量旳全部措施旳单位根检验成果:
序图做出模式选择)。
秩序:水平(level)、一阶差分、二阶甚至高阶差分直至序列平稳为止。
备注:ADF检验是经过三个模型来完毕,首先从具有截距和趋势项旳模型开始,
再检验只含截距项旳模型,最终检验两者都不含旳模型。而且以为,只有三个模
型旳检验成果都不能拒绝原假设时,我们才以为时间序列是非平稳旳,而只要其
单位根检验
第一节 单序列单位根检验 第二节 面板数据单位根检验
1
第一节 单序列单位根检验
一 序列单位根检验在时间序列分析中旳地位 二 序列单位根检验软件有关操作
三 不同检验成果后续分析思绪
四 协整检验
2
一 序列单位根检验在时间序列分析中旳地位
时间序列总体分析思绪
时间序列
平稳性检验 原:不平稳
若是平稳序列
非平稳序列
单序列 多序列
考虑差分平稳
ARMA 多元回归分析 差分平稳I(d) 不平稳
单序列 多序列(同阶) 无规律分析终止
ARIMA
协整检验 原:不协整
协整 不协整
长久关系模型 分析终止
进一步考虑ECM(误差修正模型) 3
二 序列单位根检验软件有关操作
阐明 操作 成果
4
Eviews检验小结

各种检验总结1、偏度:①序列的分布是对称的,S值为0;②正的S值意味着序列分布有长的右拖尾;③负的S值意味着序列分布有长的左拖尾。
2、峰度:①如果K 值大于3,分布的凸起程度大于正态分布;②如果K值小于3,序列分布相对于正态分布是平坦的。
3、正态性检验:Q-Q图:看QQ图上的点是否近似地在一条直线附近, 是的话近似于正态分布。
Jarque-Bera 检验:①如果P值很小,则拒绝原假设,X不服从正态分布;②如果P值大于0.05(0.1)接受原假设, X 服从正态分布。
输入数据用鼠标单击“Quick”,出现下拉菜单,单击“Empty Group”,出现“Group”窗口。
在数据表的第一列中键入y的数据,并将该序列名取为y;在第二、第三列中分别键入x1 和x2的数据,并分别取名为x1和x2。
回归分析用鼠标单击“Quick”,出现下拉菜单,单击“Estimate Equation”,在弹出对话框中键入y c x1 x2;在“Estimation Settings”栏中选择“Least Squares”(最小二乘法);点击“OK”,屏幕显示回归分析结果如表3-16所示。
回归检验1、拟合优度检验:R2 =0.864267说明,回归方程即上述样本需求函数的解释能力为86.4%,即所有解释变量能对该被解释变量变动的86.4%作出解释。
回归方程的拟合优度较好。
2、回归模型的总体显著性检验:从全部因素的总体影响看,α表示显著性水平(一般取5%,也可取10%根据题目而定)假设在5%显著性水平上,若F检验的P值小于0.05,说明所有解释变量对被解释变量的共同影响显著。
3、单个回归系数的显著性检验:从单个因素的影响看,在5%显著性水平上,查看各个解释变量的T检验值若大于2,一般表示该解释变量对被解释变量有显著影响。
但是,最主要是看解释变量的P检验值,若P值小于0.05则表示该解释变量对被解释变量有显著影响。
异方差检验:(1)判断1.图示法——残差的图示检验通过resid 与x的散布图判断,图形成喇叭状。
eviews序列相关稳健标准误法

Eviews序列相关稳健标准误法序言Eviews是一种广泛使用的统计分析工具,具有强大的序列分析功能。
在进行序列分析时,我们经常要考虑序列的相关性及其稳健性。
本文将重点介绍Eviews中序列相关稳健标准误法的原理和应用。
一、序列相关性的概念及检验方法1.1 序列相关性的概念在时间序列分析中,序列相关性是指序列中各个观测值之间的相关关系。
如果序列中的观测值之间存在一定的相关性,那么我们就需要考虑相关性对模型估计和预测的影响。
1.2 序列相关性的检验方法在Eviews中,我们可以通过计算序列的自相关系数和偏自相关系数来检验序列相关性。
自相关系数是指序列与其自身滞后期的相关系数,而偏自相关系数则是通过排除中间滞后项的影响来计算序列间的相关系数。
二、序列相关稳健标准误法的原理2.1 序列相关稳健标准误法的概念在实际应用中,我们经常遇到序列中存在的异方差性和相关性问题。
传统的OLS估计方法在存在序列相关性和异方差性时会导致估计量的无偏性和有效性受到影响。
为了解决这一问题,引入了序列相关稳健标准误法。
2.2 序列相关稳健标准误法的原理序列相关稳健标准误法通过调整OLS估计量的标准误来适应序列相关性和异方差性的存在。
在Eviews中,我们可以通过设置相关稳健标准误来进行估计,以提高估计量的有效性和精确度。
三、Eviews中序列相关稳健标准误法的应用3.1 Eviews中设置序列相关稳健标准误的步骤在Eviews中,设置序列相关稳健标准误非常简单。
用户只需在进行估计时选择相关稳健标准误选项即可,Eviews会自动对估计量进行调整。
3.2 序列相关稳健标准误法的优势相比于传统的OLS估计方法,序列相关稳健标准误法能够更好地适应序列相关性和异方差性的存在,提高了估计量的精确度和有效性。
在实际应用中,我们更倾向于使用序列相关稳健标准误法来进行序列分析。
结论通过本文的介绍,我们了解了序列相关稳健标准误法在Eviews中的应用。
EVIEWS序列相关性检验及补救

EVIEWS序列相关性检验及补救⽬的:1、正确使⽤EVIEWS2、能根据计算结果进⾏序列相关性检验和补救。
3、数据为demo data3实例:国内⽣产总值和出⼝总额之间的关系分析(序列相关性检验及补救)根据某地区1978-1998年国内⽣产总值与出⼝总额的数据资料,其中X表⽰国内⽣产总值(⼈民币亿元),Y表⽰出⼝总额(⼈民币亿元)。
试建⽴⼀元线性回归函数。
设模型函数形式为:obs X Y19783624.100134.800019794038.200139.700019804517.800167.600019814860.300211.700019825301.800271.200019835957.400367.600019847206.700413.800019858989.100438.3000198610201.40580.5000198711954.50808.9000198814922.301082.100198916917.801470.000199018598.401766.700199121622.501956.000199226651.902985.800199334560.503827.100199446670.004676.300199557494.905284.800199666850.5010421.80199773142.7012451.80199878017.8015231.701、⽤OLS估计⽅法求模型的参数估计值点击NEW-WORKFILE,输⼊X,Y的数据。
点击QUICK-ESITMATE EQUATION,在对话框中输⼊Y C X,结果如下:2、⾃相关检验(1)图⽰法由上述OLS计算,可直接得到残差RESID,运⽤GENR命令⽣成序列E,则在QUICK菜单中选GRAPH,在图形对话框中输⼊:E E(-1),再点击SCATTER DIOGRAM。
得结果如下,从图中可以看出残差et呈线性⾃回归,表明随机误差ut存在⾃相关。
eviews各种检验

eviews各种检验(⼀)、ADF是单位根检验,第⼀列数据y做ADF检验,结果如下Null Hypothesis: Y has a unit rootExogenous: Constant, Linear Trend 外因的Lag Length: 0 (Automatic based on SIC, MAXLAG=10)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -3.820038 0.0213Test critical values: 1% level -4.0987415% level -3.47727510% level -3.166190在1%⽔平上拒绝原假设,序列y存在单位根,为不平稳序列。
但在5%、10%⽔平上均接受原假设,认为y平稳。
对y进⾏⼀阶差分,差分后进⾏ADF检验:Null Hypothesis: Y has a unit rootExogenous: NoneLag Length: 0 (Automatic based on SIC, MAXLAG=10)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -9.328245 0.0000Test critical values: 1% level -2.5999345% level -1.94574510% level -1.613633可见,在各⽔平上y都是平稳的。
因此,可以把原序列y看做⼀阶单整。
第⼆列xADF检验如下:Null Hypothesis: X has a unit rootExogenous: Constant, Linear TrendLag Length: 0 (Automatic based on SIC, MAXLAG=10)t-Statistic Prob.* Augmented Dickey-Fuller test statistic -3.216737 0.0898Test critical values: 1% level -4.0987415% level -3.47727510% level -3.166190在1%、5%⽔平上拒绝原假设,序列x存在单位根,为不平稳序列。
EVIEWS序列相关检验2介绍

EVIEWS序列相关检验2介绍
Eviews序列相关检验(Serial Correlation Test)使用EViews可
以快捷方便地进行序列相关检验。
该工具可以使用不同的统计检验来检验
序列数据中是否存在自相关性。
一、检验原理
序列相关检验,也称为自相关检验,用于检查序列数据中是否存在其
中一种自相关性。
假设序列数据由一个残差过程组成,其中残差经过自相
关过程。
自相关过程指的是延迟和移动残差之间的关系(即序列数据可能
存在其中一种趋势或周期性变化)。
序列相关检验的目的是检测残差序列
是否存在自相关性,以及其是否具有统计学意义。
二、序列相关检验方法
使用EViews可以实现以下几种序列相关检验方法:
1)Durbin-Watson法:该测试方法使用差分来计算系数,并计算残差。
如果系数的值落在特定的范围之内,则说明残差具有显著的自相关特性。
此外,Durbin-Watson法还可以用于检查残差是否具有趋势或移动性。
2)Dickey-Fuller测试:该测试法基于假设残差序列是一个时变趋
势的非周期性过程。
假如该假设成立,则可以拟合一个线性模型,用于描
述残差的趋势,然后通过相关指标来评估该模型的拟合程度。
3)Cum-Sum法:该测试法基于假设残差序列具有定常性质,即残差
中可能存在其中一种移动性。
eviews时间序列一阶自相关检验命令

eviews时间序列一阶自相关检验命令摘要:一、引言二、eviews 时间序列一阶自相关检验命令介绍1.语法结构2.参数说明三、eviews 时间序列一阶自相关检验命令实例1.数据准备2.命令执行3.结果解读四、结论正文:一、引言在时间序列分析中,自相关系数检验是评估时间序列数据之间关系的重要方法。
eviews 作为一款强大的时间序列分析软件,提供了丰富的自相关系数检验命令。
本文将详细介绍eviews 时间序列一阶自相关检验命令及其应用。
二、eviews 时间序列一阶自相关检验命令介绍1.语法结构eviews 时间序列一阶自相关检验命令为:ACF(depvar, type, lags, options)其中:- depvar:因变量(时间序列数据)- type:自相关系数类型,包括"ACF"(自相关系数)和"CCF"(偏自相关系数)- lags:滞后阶数- options:可选参数,如"plot"(绘制自相关系数图)2.参数说明在上述语法结构中,depvar 表示需要进行自相关检验的时间序列数据,type 表示需要计算的自相关系数类型,lags 表示需要计算的滞后阶数。
options 为可选参数,用于指定是否绘制自相关系数图等。
三、eviews 时间序列一阶自相关检验命令实例1.数据准备假设我们已经得到了一个时间序列数据集,包含以下变量:- 时间(time)- 因变量(y)2.命令执行我们可以通过以下命令计算时间序列一阶自相关系数:ACF(y, ACF, 1)该命令表示计算y 变量的一阶自相关系数(ACF),滞后阶数为1。
3.结果解读命令执行后,eviews 会显示计算得到的自相关系数结果。
对于一阶自相关系数,我们主要关注其p 值。
如果p 值小于显著性水平(通常为0.05),则说明因变量与自身存在显著的正相关或负相关关系;反之,则无法拒绝原假设,认为因变量与自身不存在显著的相关关系。
EVIEWS时间序列实验指导(上机操作说明)
在命令窗口中依次键入以下命令即可:
GENR LOGY=LOG(Y)
GENR LOGX=LOG(X)
GENR X1=X^2
GENR X2=1/X
GENR T=@TREND(84)
㈣选择若干变量构成数组,在数组中增加变量。
在工作文件窗口中单击所要选择的变量,按住Ctrl键不放,继续用鼠标选择要展示的变量,选择完以后,单击鼠标右键,在弹出的快捷菜单中点击Open/as Group,则会弹出数组窗口,其中变量从左至右按在工作文件窗口中选择变量的顺序来排列。
1
112
115
145
171
196
204
242
284
315
340
360
417
2
118
126
150
180
196
188
233
277
301
318
342
391
3
132
141
178
193
236
235
267
317
356
362
406
419
4
129
135
163
181
235
227
269
313
348
348
396
461
5
121
步骤:(1)打开该文件。
(2)观察序列usagdp的趋势图的特征,自相关图的特征。
(3)对该序列取一阶差分,生新的序列dgdp:Genr dgdp=d(usagdp)。观察其趋势图,自相关图。
(4)对该序列的自然对数取一阶差分,生成新的序列dlngdp:Genr dlngdp=dlog(gdp)。观察其趋势图,自相关图。
Eviews序列相关性实验报告

实验二序列相关性【实验目的】掌握序列相关性问题出现的来源、后果、检验及修正的原理,以及相关的Eviews 操作方法。
【实验内容】经济理论指出,商品进口主要由进口国的经济发展水平,以及商品进口价格指数与国内价格指数对比因素决定的。
由于无法取得价格指数数据,我们主要研究中国商品进口与国内生产总值的关系。
以1978-2001年中国商品进口额与国内生产总值数据为例,练习检查和克服模型的一、建立线性回归模型利用表中数据建立M关于GDP的散点图(SCAT GDP M)。
可以看到M与GDP呈现接近线性的正相关关系。
建立一个线性回归模型(LS M C GDP )。
即得到的回归式为:9461.02=R .=0.63 F=405二、 进行序列相关性检验1、 观察残差图做出残差项与时间以及与滞后一期的残差项的折线图,可以看出随机项存在正序列相关性。
2、 用.检验判断由回归结果输出.=。
若给定05.0=α,已知n=24,k=2,查.检验上下界表可得,45.1,27.1==U L d d 。
由于.=<=L d ,故存在正自相关。
3、 用LM 检验判断在估计窗口中选择Serial Correlation LM Test ,设定滞后期Lag=1,得到LM 检验结果。
由于P 值为,可以拒绝原假设,表明存在自相关。
4、 用回归检验法判断对初始估计结果得到的残差序列定义为E1,首先做一阶自回归(LS E1 E1(-1))。
采用LM 检验其自相关性,结果表明仍然存在自相关。
用残差项的二阶自回归形式重新建立模型(LS E1 E1(-1) E1(-2))。
再次用LM 检验,此时P 值达到,落在接受域,认为误差项不存在自相关。
可以得到残差的二阶回归式为:83.90..,66.02==e s R三、 克服自相关用广义最小二乘法估计回归参数。
根据残差二阶回归式的系数,对变量GDP 和M 作二阶广义差分,生成新变量序列:GENR GDGDP=*GDP(-1)+*GDP(-2)GENR GDM=*M(-1)+*M(-2)以GDGDP 、GDM 为样本再次回归(LS GDM C GDGDP ),得到结果输出为: LM 检验结果如下,已经很好地克服了自相关性。
EVIEWS序列相关检验2介绍

(3)布罗斯和戈弗雷证明在大洋本下,渐近有:
LM = (n − p)R2 ~ χ 2 ( p)
n为样本容量,R2为如下辅助回归的可决系数:
e%t = β0 + β1X1t + L + βk X kt + ρ1et−1 + ρ2et−2 + L + ρ pet− p + εt
−ρ 1 L 0
M MO M
0 0⎟
⎟ 0 0⎟
M
M
⎟ ⎟
⎜0
0 0 L − ρ 1 0⎟
⎜⎝ 0
0 0 L 0 − ρ 1⎟⎠
2、广义差分法
广义差分法是将原模型变换为满足OLS法的 差分模型,再进行OLS估计。
广义差分法
设线性回归模型 Yt = b0 + b1X t + μt 存在一阶
自相关性,μt = ρμt−1 + vt 其中 vt 为满足
⎪ ⎪
M
⎪⎩
X
* kt
=
X kt
−
ρ X k ,t−1
多元的广义差分变换
Y*
=
A + b1
X
* 1t
+ b2
X
* 2t
+ L+ bk
X
* kt
+ vt
多元广义差分模型
自相关为高阶
ut = ρ1ut−1 + ρ2ut−2 + L + ρ put− p + vt
一元线性回归模型的广义差分变换
⎧⎪ ⎨ ⎪⎩
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)构造统计量:
一阶自回归模型μi=ρμi‐1+εi
的参数估计。
n
∑ (e%t − e%t−1 )2
D.W . = t=2 n
∑ e%t2
t =1
展开D.W.统计量:
∑ ∑ ∑ n
e~t2 +
n
e~t
2 −1
−2
n
e~t e~t−1
D.W . = t=2
t=2
t=2
∑n e~t2
t =1
(*)
n
(多种函数形式进行试验)
• (3)对不同形式模型进行OLS参数估计,如果 检验的结果都不显著,则表明不相关
• 工作量大、繁琐
et = ρet−1 + vt
常用的函数 形式主要有
et
=
ρ
e2 t −1
+ vt
et = ρ1et−1 + ρ2et−2 + vt
et = ρ et−1 + vt
et = ρ / et−1 + vt
t=2
=ρ
n
n
∑ ∑ e%t2
e%
2 t−
1
t =1
t =1
∑n ~et ~et−1
D.W . ≈ 2(1 − t=2
) ≈ 2(1 − ρ )
∑n ~et2
t =1
(3)检验自相关性:
Q−1 ≤ ρ ≤ 1 ∴0 ≤ DW ≈ 2(1− ρ) ≤ 4
完全一阶正相关,即ρ=1,则 D.W.≈ 0 完全一阶负相关,即ρ= -1, 则 D.W.≈ 4 完全不相关, 即ρ=0,则 D.W.≈2
n
n
∑ ∑ ∑ 当n较大时, e%t2 e%t2−1 e%t2 大致相等,
t=2
t=2
t =1
则(*)
∑n e~t e~t−1
∑ 可简化
为:
D.W . ≈ 2(1 − t=2 n e~t2
) ≈ 2(1 − ρ )
t =1
n
∑ e%t e%t −1
t=2 n
≈
∑ e%t2
t =1
n
∑ e%t e%tρ=0 的假设,即认为存 在一阶自相关
z0.05/2 = 1.96
3、回归检验法
• 适用于任一随机变量序列相关的检验,并能提 供序列相关的具体形式及相关系数的估计值
• 三步: • (1)用OLS求模型样本估计式,用被解释变量
的观测值Yt,减去回归值 yˆt ,求出随机误
差项的估计值et (t=1,2…,n) • (2)建立et 与 ,et‐1、 et‐2的相互关系模型
不能确定
注意:是否取到等号
不 正能 相确 关定
0 dL dU
无
自
不
相 关
能 确负 定相
关
2 4‐dU 4‐dL 4
•DW的局限: •1阶;有两个无法判断的区域;不适用于联立 方程组模型中各单一方程随机误差项序列相关 的检验;不适用于含有滞后被解释变量的情况
例如:yt = b0 + b1xt + b2 yt−1 + μt
序列相关检验、处理及案例
内蒙古科技大学经济与管理学院 边璐 2011.11.10
内容安排
• 自相关性的检验 • 自相关性的解决方法 • 案例分析
自相关性的检验
• 1、图示法(上节课已说过) • 2、DW检验 • 3、回归检验法 • 4、高阶自相关性检验
2、杜宾-瓦森(Durbin-Watson)检验法 D‐W 检 验 是 杜 宾 ( J.Durbin ) 和 瓦 森 (G.S. Watson)于1951年提出的一种检验序列自相关 的方法。该方法的假定条件是: (1)解释变量X非随机; (2)随机误差项μi为一阶自回归形式:
μi = ρμi−1 + ε i
(3)回归模型中不应含有滞后因变量作为解释 变量,即不应出现下列形式:
Yi = β0 + β1 X1i + L + βk X ki + γ Yi−1 + μi
(4)回归含有截距项(5)统计数据比较完整
D.W. 检验基本原理及步骤
(1)提出假设,H0: ρ=0 ,即不存在(一阶)自相 关性; H1: ρ≠0 ,即存在(一阶)自相关性
• 只要知道DW统计量的概率分布,在给定 的显著性水平下,根据临界值的位置就 可以对原假设H0检验。
• 但DW统计量的分布很难确定,但德宾和 沃森在5%和1%的显著性水平下,导出了 临界值的下限dL和上限dU ,
• 编制了D—W检验的上、下限表
• 且这些上下限只与样本的容量n和解释变 量的个数k有关,而与解释变量X的取值 无关。
• 判断
• ①当 0≤D.W. ≤ dL,拒绝H0,即存在正 自相关(1阶),向0相关程度增强
• ②当 4-dL ≤ D.W. ≤ 4 ,拒绝H0,即存 在负自相关 ,向4相关程度增强
• ③当dU ≤ D.W. ≤ 4-dU,不能拒绝 H0 , 无自相关
• ④当dL < D.W. < dU 、 • ④ 当4-dU <D.W. < 4- dL
偏相关系数:Partial correlation-----PAC
AC PAC
• Correlograms and Q‐statistics • If you select View/Residual Tests/Correlogram‐Q‐
statistics on the equation toolbar, EViews will display the autocorrelation and partial autocorrelation functions of the residuals, together with the Ljung‐Box Q‐statistics for high‐ order serial correlation. If there is no serial correlation in the residuals, the autocorrelations and partial autocorrelations at all lags should be nearly zero, and all Q‐statistics should be insignificant with large p‐values.
4、高阶自相关性检验
• (1)偏相关系数检验 • (2)拉格朗日乘数
偏相关系数检验
在多个变量 Y , X1, X 2 ,L, X k 之间,如果只考虑 Y 与 Xi ,i = 1, 2,L, k 之间的相关关系,其他变量
固定不变,这种相关称为偏相关。
EVIEWS的实现: Equation 窗口,View—Residual Test— Correlogram—Q-statistics
改进
h = (1− DW ) 2
n 1− n ⋅ var(bˆ2 )
Durbin-h 统计量
h统计量近似服从标准正态分布,可利用 正态分布直接对一阶自相关性进行检验:
EVIEWS 的实现:
①建模:y c x y(-1)
②根据输出的DW统计值和 s(bˆ2 ) 计算h统
计量
标准差
z 方差链接
③查正态分布表 α /2 ,
