球面上的K 最近邻查询算法
1.简述k最近邻算法的原理、算法流程以及优缺点

1.简述k最近邻算法的原理、算法流程以及优缺点一、什么是K近邻算法k近邻算法又称knn算法、最近邻算法,是一种用于分类和回归的非参数统计方法。
在这两种情况下,输入包含特征空间中的k个最接近的训练样本,这个k可以由你自己进行设置。
在knn分类中,输出是一个分类族群。
一个对象的分类是由其邻居的“多数表决”确定的,k个最近邻居(k为正整数,通常较小),所谓的多数表决指的是,在k个最近邻中,取与输入的类别相同最多的类别,作为输入的输出类别。
简而言之,k近邻算法采用测量不同特征值之间的距离方法进行分类。
knn算法还可以运用在回归预测中,这里的运用主要是指分类。
二、k近邻算法的优缺点和运用范围优点:精度高、对异常值不敏感、无数据输入假定。
缺点:计算复杂度高、空间复杂度高。
适用范围:数值型和标称型、如手写数字的分类等。
三、k近邻算法的工作原理假定存在一个样本数据集合,并且样本集中的数据每个都存在标签,也就是说,我们知道每一个样本数据和标签的对应关系。
输入一个需要分类的标签,判断输入的数据属于那个标签,我们提取出输入数据的特征与样本集的特征进行比较,然后通过算法计算出与输入数据最相似的k个样本,取k个样本中,出现次数最多的标签,作为输入数据的标签。
四、k近邻算法的一般流程(1)收集数据:可以使用任何方法,可以去一些数据集的网站进行下载数据。
(2)准备数据:距离计算所需要的数值,最好是结构化的数据格式(3)分析数据:可以使用任何方法(4)训练算法:此步骤不适用于k近邻算法(5)测试算法:计算错误率(6)使用算法:首先需要输入样本数据和结构化的输出结构(统一数据格式),然后运行k近邻算法判定输入数据属于哪一种类别。
五、k近邻算法的实现前言:在使用python实现k近邻算法的时候,需要使用到Numpy科学计算包。
如果想要在python中使用它,可以按照anaconda,这里包含了需要python需要经常使用到的科学计算库,如何安装。
k-近邻算法梳理(从原理到示例)

k-近邻算法梳理(从原理到⽰例)https:///kun_csdn/article/details/88919091k-近邻算法是⼀个有监督的机器学习算法,k-近邻算法也被称为knn算法,可以解决分类问题。
也可以解决回归问题。
本⽂主要内容整理为如下:knn算法的原理、优缺点及参数k取值对算法性能的影响;使⽤knn算法处理分类问题的⽰例;使⽤knn算法解决回归问题的⽰例;使⽤knn算法进⾏糖尿病检测的⽰例;1 算法原理knn算法的核⼼思想是未标记样本的类别,由距离其最近的k个邻居投票来决定。
具体的,假设我们有⼀个已标记好的数据集。
此时有⼀个未标记的数据样本,我们的任务是预测出这个数据样本所属的类别。
knn的原理是,计算待标记样本和数据集中每个样本的距离,取距离最近的k个样本。
待标记的样本所属类别就由这k个距离最近的样本投票产⽣。
假设X_test为待标记的样本,X_train为已标记的数据集,算法原理的伪代码如下:遍历X_train中的所有样本,计算每个样本与X_test的距离,并把距离保存在Distance数组中。
对Distance数组进⾏排序,取距离最近的k个点,记为X_knn。
在X_knn中统计每个类别的个数,即class0在X_knn中有⼏个样本,class1在X_knn中有⼏个样本等。
待标记样本的类别,就是在X_knn中样本个数最多的那个类别。
1.1 算法优缺点优点:准确性⾼,对异常值和噪声有较⾼的容忍度。
缺点:计算量较⼤,对内存的需求也较⼤。
1.2 算法参数其算法参数是k,参数选择需要根据数据来决定。
k值越⼤,模型的偏差越⼤,对噪声数据越不敏感,当k值很⼤时,可能造成⽋拟合;k值越⼩,模型的⽅差就会越⼤,当k值太⼩,就会造成过拟合。
1.3 变种knn算法有⼀些变种,其中之⼀是可以增加邻居的权重。
默认情况下,在计算距离时,都是使⽤相同权重。
实际上,可以针对不同的邻居指定不同的距离权重,如距离越近权重越⾼。
K最近邻算法

K最近邻算法K最近邻(kNN,k-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的方法之一。
所谓K最近邻,就是k个最近的邻居的意思,说的是每个样本都可以用它最接近的k个邻居来代表。
kNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。
该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
kNN方法在类别决策时,只与极少量的相邻样本有关。
由于kNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,kNN方法较其他方法更为适合。
KNN算法的机器学习基础显示相似数据点通常如何彼此靠近存在的图像大多数情况下,相似的数据点彼此接近。
KNN算法就是基于这个假设以使算法有用。
KNN利用与我们童年时可能学过的一些数学相似的想法(有时称为距离、接近度或接近度),即计算图上点之间的距离。
例如,直线距离(也称为欧氏距离)是一个流行且熟悉的选择。
KNN通过查找查询和数据中所有示例之间的距离来工作,选择最接近查询的指定数字示例( K ),然后选择最常用的标签(在分类的情况下)或平均标签(在回归的情况下)。
在分类和回归的情况下,我们看到为我们的数据选择正确的K是通过尝试几个K并选择最有效的一个来完成的。
KNN算法的步骤1.加载数据2.将K初始化为你选择的邻居数量3.对于数据中的每个示例4.3.1 根据数据计算查询示例和当前示例之间的距离。
5.3.2 将示例的距离和索引添加到有序集合中6.按距离将距离和索引的有序集合从最小到最大(按升序)排序7.从已排序的集合中挑选前K个条目8.获取所选K个条目的标签9.如果回归,返回K个标签的平均值10.如果分类,返回K个标签的模式'为K选择正确的值为了选择适合你的数据的K,我们用不同的K值运行了几次KNN算法,并选择K来减少我们遇到的错误数量,同时保持算法在给定之前从未见过的数据时准确预测的能力。
基于自适应空间球的k最近邻域快速搜索算法

基于自适应空间球的k最近邻域快速搜索算法杨军;林岩龙;王小鹏;张瑞峰【摘要】To solve the problem of low efficiency and weak stability in searching k-nearest neighbor of large-scale scattered point cloud by using sphere space,a fast algorithm for finding k-nearest neighbor is presented. Point cloud data is divided into different sub-space by using partition strategy without considering k. The radius of the initial dynamic sphere is determined adaptively based on the approximate density of sampling points in a sub-space. The k-nearest candidate points are searched by the circumscribed cube of a dynamic sphere. When the number of k-nearest candidate points does not meet the requirement, or the search fails, the expanding extent is ensured by a circumsphere of the circumscribed cube. Experimental results show that the proposed method obtains not only a better performance and automation than the existing algorithms,but also a quite stability for the anticipated point number of the sub-space and sampling density.%利用空间球搜索大规模点云数据k邻域存在速率慢和稳定性差的问题,为此,提出一种新的k邻域快速搜索算法。
K近邻算法PPT课件

• 包含目标点的叶结点对应包含目标点的最小超矩形区域。以此叶 结点的实例点作为当前最近点。目标点的最近邻一定在以目标点 为中心并通过当前最近点的超球体内部。然后返回当前结点的父 结点,如果父结点的另一子结点的超矩形区域与超球体相交,那 么在相交的区域内寻找与目标点更近的实例点。如果存在这样的 点,将此点作为新的当前最近点。
➢ 问题:给这个绿色的圆分类? ➢ 如果K=3,绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝
色小正方形,少数从属于多数,基于统计的方法,判定绿色的这 个待分类点属于红色的三角形一类。 ➢ 如果K=5,绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色 正方形,还是少数从属于多数,基于统计的方法,判定绿色的这 个待分类点属于蓝色的正方形一类。
区域内没有实例时终止。在此过程中,将实例保存在相应的结点
上。
2020/7/23
9
K近邻法的实现:kd树
2020/7/23
10
K近邻法的实现:kd树
2020/7/23
11
K近邻法的实现:kd树
➢ 搜索kd树
• 利用kd树可以省去大部分数据点的搜索,从而减少搜索的计算量 。这里以最近邻为例,同样的方法可以应用到K近邻。
2020/7/23
5
K近邻的三个基本要素
2020/7/23
6
K近邻的三个基本要素
➢ K值的选择
• 如果选择较小的k值,就相当于用较小的邻域中的训练实例进行预 测, “学习”的近似误差会减小,只有与输入实例较近的训练实 例才会对预测结果起作用。但缺点是“学习”的估计误差会增大 ,预测结果会对近邻的实例点非常敏感。换句话说,k值的减小意 味着整体模型变得复杂,容易发生过拟合。
k近邻算法——精选推荐
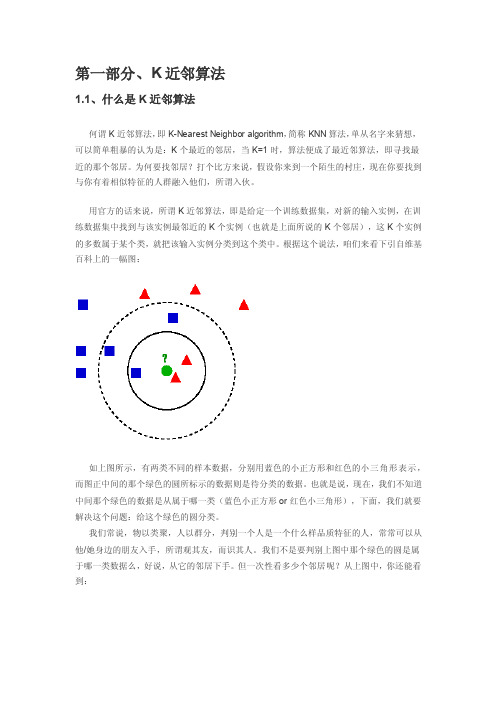
第一部分、K近邻算法1.1、什么是K近邻算法何谓K近邻算法,即K-Nearest Neighbor algorithm,简称KNN算法,单从名字来猜想,可以简单粗暴的认为是:K个最近的邻居,当K=1时,算法便成了最近邻算法,即寻找最近的那个邻居。
为何要找邻居?打个比方来说,假设你来到一个陌生的村庄,现在你要找到与你有着相似特征的人群融入他们,所谓入伙。
用官方的话来说,所谓K近邻算法,即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例(也就是上面所说的K个邻居),这K个实例的多数属于某个类,就把该输入实例分类到这个类中。
根据这个说法,咱们来看下引自维基百科上的一幅图:如上图所示,有两类不同的样本数据,分别用蓝色的小正方形和红色的小三角形表示,而图正中间的那个绿色的圆所标示的数据则是待分类的数据。
也就是说,现在,我们不知道中间那个绿色的数据是从属于哪一类(蓝色小正方形or红色小三角形),下面,我们就要解决这个问题:给这个绿色的圆分类。
我们常说,物以类聚,人以群分,判别一个人是一个什么样品质特征的人,常常可以从他/她身边的朋友入手,所谓观其友,而识其人。
我们不是要判别上图中那个绿色的圆是属于哪一类数据么,好说,从它的邻居下手。
但一次性看多少个邻居呢?从上图中,你还能看到:∙如果K=3,绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形,少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于红色的三角形一类。
∙如果K=5,绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形,还是少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于蓝色的正方形一类。
于此我们看到,当无法判定当前待分类点是从属于已知分类中的哪一类时,我们可以依据统计学的理论看它所处的位置特征,衡量它周围邻居的权重,而把它归为(或分配)到权重更大的那一类。
这就是K近邻算法的核心思想。
1.2、近邻的距离度量表示法上文第一节,我们看到,K近邻算法的核心在于找到实例点的邻居,这个时候,问题就接踵而至了,如何找到邻居,邻居的判定标准是什么,用什么来度量。
knn算法介绍与参数调优

KNN算法介绍与参数调优K近邻法(k-nearest neighbors,KNN)是一种很基本的机器学习方法了,在我们平常的生活中也会不自主的应用。
比如,我们判断一个人的人品,只需要观察他来往最密切的几个人的人品好坏就可以得出了。
这里就运用了KNN的思想。
KNN方法既可以做分类,也可以做回归,这点和决策树算法相同。
KNN做回归和分类的主要区别在于最后做预测时候的决策方式不同。
KNN做分类预测时,一般是选择多数表决法,即训练集里和预测的样本特征最近的K个样本,预测为里面有最多类别数的类别。
而KNN 做回归时,一般是选择平均法,即最近的K个样本的样本输出的平均值作为回归预测值。
由于两者区别不大,虽然本文主要是讲解KNN的分类方法,但思想对KNN的回归方法也适用。
由于scikit-learn里只使用了蛮力实现(brute-force),KD树实现(KDTree)和球树(BallTree)实现,本文只讨论这几种算法的实现原理。
1. KNN算法三要素KNN算法我们主要要考虑三个重要的要素,对于固定的训练集,只要这三点确定了,算法的预测方式也就决定了。
这三个最终的要素是k值的选取,距离度量的方式和分类决策规则。
对于分类决策规则,一般都是使用前面提到的多数表决法。
所以我们重点是关注与k值的选择和距离的度量方式。
对于k值的选择,没有一个固定的经验,一般根据样本的分布,选择一个较小的值,可以通过交叉验证选择一个合适的k值。
选择较小的k值,就相当于用较小的领域中的训练实例进行预测,训练误差会减小,只有与输入实例较近或相似的训练实例才会对预测结果起作用,与此同时带来的问题是泛化误差会增大,换句话说,K值的减小就意味着整体模型变得复杂,容易发生过拟合;选择较大的k值,就相当于用较大领域中的训练实例进行预测,其优点是可以减少泛化误差,但缺点是训练误差会增大。
这时候,与输入实例较远(不相似的)训练实例也会对预测器作用,使预测发生错误,且K值的增大就意味着整体的模型变得简单。
最近邻算法计算公式

最近邻算法计算公式最近邻算法(K-Nearest Neighbors algorithm,简称KNN算法)是一种常用的分类和回归算法。
该算法的基本思想是:在给定一个新的数据点时,根据其与已有的数据点之间的距离来判断其类别或预测其数值。
KNN算法的计算公式可以分为两个部分:距离计算和分类预测。
一、距离计算:KNN算法使用欧氏距离(Euclidean Distance)来计算数据点之间的距离。
欧氏距离是指在m维空间中两个点之间的直线距离。
假设有两个数据点p和q,p的坐标为(p1, p2, ..., pm),q的坐标为(q1, q2, ..., qm),则p和q之间的欧氏距离为:d(p, q) = sqrt((p1-q1)^2 + (p2-q2)^2 + ... + (pm-qm)^2)其中,sqrt表示求平方根。
二、分类预测:KNN算法通过比较距离,根据最近的K个邻居来进行分类预测。
假设有N个已知类别的数据点,其中k个属于类别A,另外K个属于类别B,要对一个新的数据点p进行分类预测,KNN算法的步骤如下:1.计算p与每个已知数据点之间的距离;2.根据距离的大小,将距离最近的K个邻居选取出来;3.统计K个邻居中每个类别的数量;4.根据数量的大小,将p分为数量最多的那个类别。
如果数量相同,可以通过随机选择或其他规则来决定。
其中,K是KNN算法的一个参数,表示选取最近的K个邻居进行分类预测。
K的选择通常是基于经验或交叉验证等方法来确定的。
较小的K值会使模型更加灵敏,但也更容易受到噪声的影响,较大的K值会使模型更加稳健,但也更容易混淆不同的类别。
总结起来,KNN算法的计算公式可以表示为:1.距离计算公式:d(p, q) = sqrt((p1-q1)^2 + (p2-q2)^2 + ... + (pm-qm)^2)2.分类预测步骤:1)计算p与每个已知数据点之间的距离;2)根据距离的大小,选取距离最近的K个邻居;3)统计K个邻居中每个类别的数量;4)将p分为数量最多的那个类别。
ball_tree算法原理

ball_tree算法原理
摘要:
1.介绍ball_tree 算法
2.ball_tree 算法的原理
3.ball_tree 算法在实际应用中的优势
4.总结
正文:
ball_tree 算法是一种用于查找最近邻数据的算法,它可以在大规模数据集中高效地找到与目标数据最近的k 个数据。
与kd 树类似,ball_tree 也是一种k 近邻搜索算法,但它的构建过程更加简单,且具有更好的性能。
ball_tree 算法的原理如下:
1.选择一个根节点,将数据集中的所有数据点作为该节点的子节点。
2.对于每个节点,根据其子节点的数据点分布,将其划分为k 个区域。
3.在每个区域内,选择一个代表点作为该节点的子节点。
4.递归地对每个子节点进行步骤2 和3,直到满足停止条件(如子节点数量小于设定值)。
ball_tree 算法在实际应用中的优势主要体现在以下几点:
1.构建速度快:ball_tree 算法的构建过程比kd 树更加简单,对于大规模数据集,其构建速度更快。
2.空间复杂度低:ball_tree 算法的空间复杂度为O(n),相比kd 树的空间复杂度O(nlogk),在数据集较大时,具有更好的性能。
3.适用于多种数据分布:ball_tree 算法不仅适用于线性分布的数据,还适用于高维数据和任意分布的数据。
总之,ball_tree 算法是一种高效、简单且适用于多种数据分布的最近邻搜索算法。
KNN(K近邻法)算法原理

KNN(K近邻法)算法原理⼀、K近邻概述k近邻法(k-nearest neighbor, kNN)是⼀种基本分类与回归⽅法(有监督学习的⼀种),KNN(k-nearest neighbor algorithm)算法的核⼼思想是如果⼀个样本在特征空间中的k(k⼀般不超过20)个最相邻的样本中的⼤多数属于某⼀个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。
简单地说,K-近邻算法采⽤测量不同特征值之间的距离⽅法进⾏分类。
通常,在分类任务中可使⽤“投票法”,即选择这k个实例中出现最多的标记类别作为预测结果;在回归任务中可使⽤“平均法”,即将这k个实例的实值输出标记的平均值作为预测结果;还可基于距离远近进⾏加权平均或加权投票,距离越近的实例权重越⼤。
k近邻法不具有显式的学习过程,事实上,它是懒惰学习(lazy learning)的著名代表,此类学习技术在训练阶段仅仅是把样本保存起来,训练时间开销为零,待收到测试样本后再进⾏处理K近邻算法的优缺点:优点:精度⾼、对异常值不敏感、⽆数据输⼊假定缺点:计算复杂度⾼、空间复杂度⾼适⽤数据范围:数值型和标称型⼆、K近邻法的三要素距离度量、k值的选择及分类决策规则是k近邻法的三个基本要素。
根据选择的距离度量(如曼哈顿距离或欧⽒距离),可计算测试实例与训练集中的每个实例点的距离,根据k值选择k个最近邻点,最后根据分类决策规则将测试实例分类。
根据欧⽒距离,选择k=4个离测试实例最近的训练实例(红圈处),再根据多数表决的分类决策规则,即这4个实例多数属于“-类”,可推断测试实例为“-类”。
k近邻法1968年由Cover和Hart提出1.距离度量特征空间中的两个实例点的距离是两个实例点相似程度的反映。
K近邻法的特征空间⼀般是n维实数向量空间Rn。
使⽤的距离是欧⽒距离,但也可以是其他距离,如更⼀般的Lp距离或Minkowski距离Minkowski距离(也叫闵⽒距离):当p=1时,得到绝对值距离,也称曼哈顿距离(Manhattan distance),在⼆维空间中可以看出,这种距离是计算两点之间的直⾓边距离,相当于城市中出租汽车沿城市街道拐直⾓前进⽽不能⾛两点连接间的最短距离,绝对值距离的特点是各特征参数以等权参与进来,所以也称等混合距离当p=2时,得到欧⼏⾥德距离(Euclidean distance),就是两点之间的直线距离(以下简称欧⽒距离)。
K-近邻算法

K-近邻算法⼀、概述k-近邻算法(k-Nearest Neighbour algorithm),⼜称为KNN算法,是数据挖掘技术中原理最简单的算法。
KNN 的⼯作原理:给定⼀个已知标签类别的训练数据集,输⼊没有标签的新数据后,在训练数据集中找到与新数据最邻近的k个实例,如果这k个实例的多数属于某个类别,那么新数据就属于这个类别。
可以简单理解为:由那些离X最近的k个点来投票决定X归为哪⼀类。
图1 图1中有红⾊三⾓和蓝⾊⽅块两种类别,我们现在需要判断绿⾊圆点属于哪种类别当k=3时,绿⾊圆点属于红⾊三⾓这种类别;当k=5时,绿⾊圆点属于蓝⾊⽅块这种类别。
举个简单的例⼦,可以⽤k-近邻算法分类⼀个电影是爱情⽚还是动作⽚。
(打⽃镜头和接吻镜头数量为虚构)电影名称打⽃镜头接吻镜头电影类型⽆问西东1101爱情⽚后来的我们589爱情⽚前任31297爱情⽚红海⾏动1085动作⽚唐⼈街探案1129动作⽚战狼21158动作⽚新电影2467?表1 每部电影的打⽃镜头数、接吻镜头数和电影分类表1就是我们已有的数据集合,也就是训练样本集。
这个数据集有两个特征——打⽃镜头数和接吻镜头数。
除此之外,我们也知道每部电影的所属类型,即分类标签。
粗略看来,接吻镜头多的就是爱情⽚,打⽃镜头多的就是动作⽚。
以我们多年的经验来看,这个分类还算合理。
如果现在给我⼀部新的电影,告诉我电影中的打⽃镜头和接吻镜头分别是多少,那么我可以根据你给出的信息进⾏判断,这部电影是属于爱情⽚还是动作⽚。
⽽k-近邻算法也可以像我们⼈⼀样做到这⼀点。
但是,这仅仅是两个特征,如果把特征扩⼤到N个呢?我们⼈类还能凭经验“⼀眼看出”电影的所属类别吗?想想就知道这是⼀个⾮常困难的事情,但算法可以,这就是算法的魅⼒所在。
我们已经知道k-近邻算法的⼯作原理,根据特征⽐较,然后提取样本集中特征最相似数据(最近邻)的分类标签。
那么如何进⾏⽐较呢?⽐如表1中新出的电影,我们该如何判断他所属的电影类别呢?如图2所⽰。
K最近邻方法

12
基于距离的分类方法
A
B
C
训练集(分3类)
9个未分类数据
将9个数据分类
13
基于距离的分类方法
输入: C1,C2,…Cm //样本有m个类 t //未知样本 输出 C //t 属于的类 基于距离的算法 Dist=∞ For i:=1 to m do if dis(Ci,t)<dist, then C= Ci dist=dis(Ci,t)
2
简单概念
3. K-近邻就是找出k个相似的实例来建立 目标函数逼近。这种方法为局部逼近。 复杂度低,不失为一个方法。
3
简单概念--相似
4. 相似实例:什么是相似? 对于距离的计算方法有许多。 样本为 X=(x1,x2,…xn)
明考斯基距离: d (i, j ) q (| x x |q | x x |q ... | x x |q )
25
贝叶斯公式 P(H | X) P(X | H)P(H) 给出了这些关系
P(X)
在给定的数据集情况下:
P(H):通过数据可以计算出来,一般为一常数。
P(X): 通过数据可以计算出来,一般为常数。
P(X|H):通过数据可以计算出来
P(H|X):由上述公式可计算出来。
26
朴素贝叶斯分类
1.
每个样本 X 由n维向量表示 X={ x1,x2,……xn }, 它代表n个属性A1, A2,…… An 一点取值, 如属性 是相互独立,我们称其为朴素贝叶斯,说明它的 属性间无关系,属性只与类有关。一个的属性取 值与其它属性取值无关。 C
K-NN算法例子2
5.d={(5,0)}, dt=sqr(5),N={(2,1),(2,3),(3,1), (5,0)}, d1=sqr(5),d2=sqr(5),d3=sqr(2),d4=sqr(5). 6.d={(5,-1)}, dt=sqr(10),N={(2,1),(2,3),(3,1), (5,0)}, d1=sqr(5),d2=sqr(5),d3=sqr(2),d4=sqr(5). 7.d={(6,1)}, dt=sqr(5),N={(2,3),(3,1), (5,0), (6,1)}, d1=sqr(5),d2=sqr(2),d3=sqr(5),d4=sqr(5).
k- 最近邻算法

k- 最近邻算法摘要:1.K-最近邻算法的定义和原理2.K-最近邻算法的计算方法3.K-最近邻算法的应用场景4.K-最近邻算法的优缺点正文:1.K-最近邻算法的定义和原理K-最近邻(K-Nearest Neighbors,简称KNN)算法是一种基于相似度度量的聚类分析方法。
该算法的基本思想是:在数据集中,每个数据点都与距离它最近的K 个数据点属于同一类别。
这里的K 是一个超参数,可以根据实际问题和数据情况进行调整。
KNN 算法的主要步骤包括数据预处理、计算距离、确定最近邻和进行分类等。
2.K-最近邻算法的计算方法计算K-最近邻算法的过程可以分为以下几个步骤:(1)数据预处理:将原始数据转换为适用于计算距离的格式,如数值型数据。
(2)计算距离:采用欧氏距离、曼哈顿距离等方法计算数据点之间的距离。
(3)确定最近邻:对每个数据点,找到距离最近的K 个数据点。
(4)进行分类:根据最近邻的数据点所属的类别,对目标数据点进行分类。
3.K-最近邻算法的应用场景K-最近邻算法广泛应用于数据挖掘、机器学习、模式识别等领域。
常见的应用场景包括:(1)分类:将数据点划分到不同的类别中。
(2)回归:根据特征值预测目标值。
(3)降维:通过将高维数据映射到低维空间,减少计算复杂度和噪声干扰。
4.K-最近邻算法的优缺点K-最近邻算法具有以下优缺点:优点:(1)简单易懂,易于实现。
(2)对数据规模和分布没有特殊要求。
(3)对噪声不敏感,具有较好的鲁棒性。
缺点:(1)计算复杂度高,尤其是大规模数据集。
(2)对离群点和噪声敏感。
k-近邻算法实例

k-近邻算法是一种基本分类与回归方法。
假设有一个由两类不同的样本数据组成的数据集,分别用蓝色的小正方形和红色的小三角形表示。
现在有一个绿色的圆点,需要确定它是属于哪一类。
如果K=3,即选择距离绿色圆点最近的3个点,其中有两个是红色的三角形,一个是蓝色的正方形,那么根据“少数服从多数”的原则,绿色圆点将被分类为红色的三角形一类。
如果K=5,即选择距离绿色圆点最近的5个点,其中有三个是蓝色的正方形,两个是红色的三角形,那么同样根据“少数服从多数”的原则,绿色圆点将被分类为蓝色的正方形一类。
以上就是k-近邻算法的一个基本实例。
在实际应用中,k值的选择、距离度量的方式以及分类决策规则等都会影响到算法的最终效果。
K最近邻算法(KNN)---sklearn+python实现方式

K最近邻算法(KNN)---sklearn+python实现⽅式k-近邻算法概述简单地说,k近邻算法采⽤测量不同特征值之间的距离⽅法进⾏分类。
k-近邻算法优点:精度⾼、对异常值不敏感、⽆数据输⼊假定。
缺点:计算复杂度⾼、空间复杂度⾼。
适⽤数据范围:数值型和标称型。
k-近邻算法(kNN),它的⼯作原理是:存在⼀个样本数据集合,也称作训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每⼀数据与所属分类的对应关系。
输⼊没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进⾏⽐较,然后算法提取样本集中特征最相似数据(最近邻)的分类标签。
⼀般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不⼤于20的整数。
最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
k近邻算法的⼀般流程收集数据:可以使⽤任何⽅法。
准备数据:距离计算所需要的数值,最好是结构化的数据格式。
分析数据:可以使⽤任何⽅法。
训练算法:此步骤不适⽤于k近邻算法。
测试算法:计算错误率。
使⽤算法:⾸先需要输⼊样本数据和结构化的输出结果,然后运⾏k近邻算法判定输⼊数据分别属于哪个分类,最后应⽤对计算出的分类执⾏后续的处理。
下⾯将经过编码来了解KNN算法:import numpy as npimport matplotlib.pyplot as pltfrom sklearn import datasetsplt.rcParams['font.sans-serif']=['SimHei'] #⽤来正常显⽰中⽂标签#准备数据集iris=datasets.load_iris()X=iris.dataprint('X:\n',X)Y=iris.targetprint('Y:\n',Y)#处理⼆分类问题,所以只针对Y=0,1的⾏,然后从这些⾏中取X的前两列x=X[Y<2,:2]print(x.shape)print('x:\n',x)y=Y[Y<2]print('y:\n',y)#target=0的点标红,target=1的点标蓝,点的横坐标为data的第⼀列,点的纵坐标为data的第⼆列plt.scatter(x[y==0,0],x[y==0,1],color='red')plt.scatter(x[y==1,0],x[y==1,1],color='green')plt.scatter(5.6,3.2,color='blue')x_1=np.array([5.6,3.2])plt.title('红⾊点标签为0,绿⾊点标签为1,待预测的点为蓝⾊')如图所⽰,我们要对图中蓝⾊的点进⾏预测,从⽽判断他属于哪⼀类,我们使⽤欧⽒距离公式,计算两个向量点之间的距离.计算完所有点之间的距离后,可以对数据按照从⼩到⼤的次序排序。
k近邻算法

2.2.1 归一化数值
公式:newValue=(oldValue-min)/(max-min)
2.3示例:手写识别系统
(1)收集数据:提供文本文件。
(2)准备数据:编写函数classify0(),将图像格式转换为分类器使用的list式。 (3)分析数据:在Python命令提示符中检查数据,确保它符合要求。 (4)训练算法:此步骤不适用于裕近邻算法。 (5)测试算法:编写函数使用提供的部分数据集作为测试样本,测试样本与非测 试样本的区别在于测试样本是已经完成分类的数据,如果预测分类与实际类别 不同,则标记为一个错误。 (6)使用算法:构建完整的应用程序,从图像中提取数字,并完成数字识别。美 国的邮件分拣系统就是一个实际运行的类似系统。
图2.1 使用打斗和接吻次数分类电影
4.电影分类的例子
图2.2 每部电影的打斗镜头数、接吻镜头数以及电影评 估类型
图2.3 已知电影与未知电影的距离
5.算法的三个基本要素:
1、K 值的选择会对算法的结果产生重大影响。K值较小意味着只有与输 入实例较近的训练实例才会对预测结果起作用,但容易发生过拟合;如果 K 值较大,优点是可以减少学习的估计误差,但缺点是学习的近似误差增大, 这时与输入实例较远的训练实例也会对预测起作用,是预测发生错误。在实 际应用中,K 值一般选择一个较小的数值。具体应用中k值的选择需要通过 大量的实验来选择。 2、该算法中的分类决策规则往往是多数表决,即由输入实例的 K 个最临
2.2 示例:使用k-近邻算法改进约会网站的配对效果
(1)收集数据:提供文本文件。 (2)准备数据:使用Python解析文本文件。 (3)分析数据:使用Matplotlib画二维扩散图。 (4)训练算法:此步骤不适用于k-近邻算法。 (5)测试算法:使用海伦提供的部分数据作为测试样本。 测试样本和非侧试样本的区别在于:侧试样本是已经完成分类的数据,如果 预测分类与实际类别不同,则标记为一个错误。 (6)使用算法:产生简单的命令行程序,然后海伦可以输入一些特征数据以判断对 方是否为自己喜欢的类型。
kNN算法:K最近邻(kNN,k-NearestNeighbor)分类算法

kNN算法:K最近邻(kNN,k-NearestNeighbor)分类算法⼀、KN N算法概述 邻近算法,或者说K最近邻(kNN,k-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的⽅法之⼀。
所谓K最近邻,就是k个最近的邻居的意思,说的是每个样本都可以⽤它最接近的k个邻居来代表。
Cover和Hart在1968年提出了最初的邻近算法。
KNN是⼀种分类(classification)算法,它输⼊基于实例的学习(instance-based learning),属于懒惰学习(lazy learning)即KNN没有显式的学习过程,也就是说没有训练阶段,数据集事先已有了分类和特征值,待收到新样本后直接进⾏处理。
与急切学习(eager learning)相对应。
KNN是通过测量不同特征值之间的距离进⾏分类。
思路是:如果⼀个样本在特征空间中的k个最邻近的样本中的⼤多数属于某⼀个类别,则该样本也划分为这个类别。
KNN算法中,所选择的邻居都是已经正确分类的对象。
该⽅法在定类决策上只依据最邻近的⼀个或者⼏个样本的类别来决定待分样本所属的类别。
提到KNN,⽹上最常见的就是下⾯这个图,可以帮助⼤家理解。
我们要确定绿点属于哪个颜⾊(红⾊或者蓝⾊),要做的就是选出距离⽬标点距离最近的k个点,看这k个点的⼤多数颜⾊是什么颜⾊。
当k取3的时候,我们可以看出距离最近的三个,分别是红⾊、红⾊、蓝⾊,因此得到⽬标点为红⾊。
算法的描述: 1)计算测试数据与各个训练数据之间的距离; 2)按照距离的递增关系进⾏排序; 3)选取距离最⼩的K个点; 4)确定前K个点所在类别的出现频率; 5)返回前K个点中出现频率最⾼的类别作为测试数据的预测分类⼆、关于K的取值 K:临近数,即在预测⽬标点时取⼏个临近的点来预测。
K值得选取⾮常重要,因为: 如果当K的取值过⼩时,⼀旦有噪声得成分存在们将会对预测产⽣⽐较⼤影响,例如取K值为1时,⼀旦最近的⼀个点是噪声,那么就会出现偏差,K值的减⼩就意味着整体模型变得复杂,容易发⽣过拟合; 如果K的值取的过⼤时,就相当于⽤较⼤邻域中的训练实例进⾏预测,学习的近似误差会增⼤。
球面上的K 最近邻查询算法

球面上的K 最近邻查询算法张丽平a ,李 松a ,郝晓红b(哈尔滨理工大学a. 计算机科学与技术学院;b. 计算中心,哈尔滨 150080)摘 要:针对球面上数据对象点集的特征和K 最近邻查询的需求,提出2种处理球面上K 最近邻查询的算法:基于查询轴的K 最近邻查询算法(PAM 方法)和基于查询圆面的K 最近邻查询算法(PCM 方法)。
对2种算法进行实验比较,结果表明,PAM 方法和PCM 方法都适合处理球面上的最近邻查询问题,PAM 方法在存储量和查询复杂度方面相对于PCM 方法具有一定优势,但PAM 方法的可扩展性远低于 PCM 方法,尤其不适合处理受限查询和带方向的查询。
关键词:最近邻;球面;查询轴;查询圆面;索引结构Algorithms for K-Nearest Neighbor Query on SphereZHANG Li-ping a , LI Song a , HAO Xiao-hong b(a. School of Computer Science and Technology; b. Computation Center, Harbin University of Science and Technology, Harbin 150080, China) 【Abstract 】According to the characteristics of the datasets on the sphere, the algorithm of the K -Nearest Neighbor query based on the query axis (PAM) and the algorithm of the K-Nearest Neighbor query based on the query circular planar(PCM) are presented. Theoretical research and experimental results show that both the two methods can handle the problem of the K -Nearest Neighbor query on the sphere, compared with the PCM, PAM has advantages on the memory capacitance and the query efficiency, but the expansibility of PAM is poor and PCM has high scalability. 【Key words 】nearest neighbor; sphere; query axis; query circular planar; index structure DOI: 10.3969/j.issn.1000-3428.2011.02.018计 算 机 工 程 Computer Engineering 第37卷 第2期 V ol.37 No.2 2011年1月January 2011·软件技术与数据库· 文章编号:1000—3428(2011)02—0052—02文献标识码:A中图分类号:TP3911 概述随着空间定位技术、地理信息系统和智能查询技术的发展, 对空间对象的近邻查询及其变种的研究成为空间数据库领域研究的热点和难点。
球面上的K最近邻查询算法

球面上的K最近邻查询算法张丽平;李松;郝晓红【期刊名称】《计算机工程》【年(卷),期】2011(037)002【摘要】According to the characteristics of the datasets on the sphere, the algorithm of the K-Nearest Neighbor query based on the query axis (PAM) and the algorithm of the K-Nearest Neighbor query based on the query circular planar(PCM) are presented.Theoretical research and experimental results show that both the two methods can handle the problem of the K-Nearest Neighbor query on the sphere, compared with the PCM, PAM has advantages on the memory capacitance and the query efficiency, but the expansibility of PAM is poor and PCM has high scalability.%针对球面上数据对象点集的特征和K最近邻查询的需求,提出2种处理球面上K最近邻查询的算法:基于查询轴的K最近邻查询算法(PAM方法)和基于查询圆面的K最近邻查询算法(PCM方法).对2种算法进行实验比较,结果表明,PAM方法和PCM方法都适合处理球面上的最近邻查询问题,PAM方法在存储量和查询复杂度方面相对于PCM方法具有一定优势,但PAM方法的可扩展性远低于PCM方法,尤其不适合处理受限查询和带方向的查询.【总页数】3页(P52-53,56)【作者】张丽平;李松;郝晓红【作者单位】哈尔滨理工大学计算机科学与技术学院,哈尔滨,150080;哈尔滨理工大学计算机科学与技术学院,哈尔滨,150080;哈尔滨理工大学计算中心,哈尔滨,150080【正文语种】中文【中图分类】TP391【相关文献】1.圆柱面和锥面上数据集的最近邻查询方法 [J], 张丽平;李松;郝晓红;王淼;蔡志涛2.球面上的最近邻查询方法研究 [J], 张丽平;李松;郝忠孝3.基于查询集空间分布的聚合最近邻查询算法 [J], 徐超;张东站;郑艳红;饶丽丽4.基于格网划分的道路最近邻查询算法 [J], 闫红松; George Almpanidis; 凡高娟5.基于4-叉树结构的路网数据最近邻查询算法 [J], 陈可心;陈业斌因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
球面上的K 最近邻查询算法张丽平a ,李 松a ,郝晓红b(哈尔滨理工大学a. 计算机科学与技术学院;b. 计算中心,哈尔滨 150080)摘 要:针对球面上数据对象点集的特征和K 最近邻查询的需求,提出2种处理球面上K 最近邻查询的算法:基于查询轴的K 最近邻查询算法(PAM 方法)和基于查询圆面的K 最近邻查询算法(PCM 方法)。
对2种算法进行实验比较,结果表明,PAM 方法和PCM 方法都适合处理球面上的最近邻查询问题,PAM 方法在存储量和查询复杂度方面相对于PCM 方法具有一定优势,但PAM 方法的可扩展性远低于 PCM 方法,尤其不适合处理受限查询和带方向的查询。
关键词:最近邻;球面;查询轴;查询圆面;索引结构Algorithms for K-Nearest Neighbor Query on SphereZHANG Li-ping a , LI Song a , HAO Xiao-hong b(a. School of Computer Science and Technology; b. Computation Center, Harbin University of Science and Technology, Harbin 150080, China) 【Abstract 】According to the characteristics of the datasets on the sphere, the algorithm of the K -Nearest Neighbor query based on the query axis (PAM) and the algorithm of the K-Nearest Neighbor query based on the query circular planar(PCM) are presented. Theoretical research and experimental results show that both the two methods can handle the problem of the K -Nearest Neighbor query on the sphere, compared with the PCM, PAM has advantages on the memory capacitance and the query efficiency, but the expansibility of PAM is poor and PCM has high scalability. 【Key words 】nearest neighbor; sphere; query axis; query circular planar; index structure DOI: 10.3969/j.issn.1000-3428.2011.02.018计 算 机 工 程 Computer Engineering 第37卷 第2期 V ol.37 No.2 2011年1月January 2011·软件技术与数据库· 文章编号:1000—3428(2011)02—0052—02文献标识码:A中图分类号:TP3911 概述随着空间定位技术、地理信息系统和智能查询技术的发展, 对空间对象的近邻查询及其变种的研究成为空间数据库领域研究的热点和难点。
近年来,国内外对空间对象的近邻关系查询问题进行了大量的工作,取得了一定的研究成 果[1-5],但其主要是对二维平面中的近邻查询问题进行分析,没有进一步给出球面上的数据对象集的最近邻查询的算法,研究成果在具体应用中具有一定的局限性。
本文着重对球面上数据对象点的K 最近邻查询算法进行研究。
2 球面上的K 最近邻查询算法根据球面上数据对象点的特征和K 最近邻查询的要求,本节给出基于查询轴的K 最近邻查询算法(PAM 方法)和基于查询圆面的K 最近邻查询算法(PCM 方法)。
2.1 基于查询轴的K 最近邻查询算法(PAM 方法)定义1 设P ={p 1, p 2,…, p n }(2≤n ≤∞)为球面S 2上的对象点集,X i 和X j 分别为点p i ∈S 和p j ∈S 的位置矢量,点p i 和p j 之间的最短距离定义为通过点p i 和p j 的大圆(其中心点即为球的中心)中较小弧段的长度。
这个距离用公式表达为:d (p i , p j )=arcos(T i j X X )≤π称此距离为点p i 和p j 之间的球面距离。
定义2 过查询点q 和球心o 的直线称之为q 的查询轴, q 的查询轴具有唯一性。
q 的查询轴与球面相交的另一点q ’称为q 的球面对称点。
以查询轴作为一维刻度轴,查询轴上的数据点到查询点q 的距离称为轴查询距离。
球面上的数据点在查询轴上的投影称之为轴投影点。
查询轴及查询圆面如图1所示,直线qq ’是查询轴,查询轴上的点o 3是球面上的点p 12的轴投影点。
由球的性质可知,判断球面上点集之间的弧的长短可以转化为判断欧式空间内的直线段的大小。
且球面上的数据对象点到查询点q 之间的球面距离大小关系在q 的查询轴上投影后保持不变。
若查询点q 的位置固定,球面上其他数据点在球面上移动,移动点到查询点q 的距离关系在查询轴上因数据点的移动而做相应变化,其变化情况与球面上的一致。
球面上数据点到q 的距离大小关系及其动态距离关系的变化在q 的查询轴上可得到较好的保持。
由此,可将查询点q 在球面数据集中的K 最近邻问题降维到q 的查询轴上进行处理,从而降低了查询的难度。
基于查询轴的方法主要适用于球面上的数据对象点是静态或动态、查询点q 的更新频率较低的情况。
图1 查询轴及查询圆面若球面S 2上数据集中的数据点是静态的,数据集的动态变化主要限于增加或删除数据点,此时可用二叉树或B 树来处理一维查询轴空间内的查询点q 的K 最近邻查询问题。
当球面数据集中增加点或删除点时,相应的树索引结构可进行局部的插入或删除更新。
具体算法如算法1所示。
基金项目:黑龙江省教育厅科学技术研究基金资助项目(11551084) 作者简介:张丽平(1976-),女,讲师、硕士,主研方向:数据结构,数据库理论;李 松,讲师、博士;郝晓红,高级实验师 收稿日期:2010-07-02 E-mail :zhanglptg@第37卷第2期张丽平,李松,郝晓红:球面上的K最近邻查询算法53算法1SPA_SNN()输入球面上的静态数据对象点集P,查询点q输出q的k个最近邻beginS[]←∅;if 没有构造q的查询轴 thenCon_PSA(q);//构造q的查询轴ProjA(P); //投影操作for pi∈P doS[]←D(pi,q);//计算各数据点到q的轴查询距离Construct(BST_TREE,S[]); //建立二叉排序树利用二叉排序树查询q的k个最近邻;end算法将数据集P中的数据对象点向查询轴上投影的时间复杂度为O(n),建立二叉排序树的时间复杂度为O(n log n),利用二叉排序树查询q的K最近邻的时间复杂度为O(k log n),故算法的总时间复杂度为O(n log n)。
若球面上查询点q是静态的,数据集中其他点在球面上是沿圆弧轨迹进行连续移动,则可在q的查询轴上分步进行查询q的k个最近邻。
具体的算法如算法2所示。
算法2DPA_SNN()输入球面上的动态态数据对象点集P,查询点q输出q的k个最近邻beginif 没有构造q的查询轴 thenCon_PSA(q);//构造q的查询轴ProjA(P);M←PO(P,d);//在限距d内找到所有投影对象集MS←NN(q,k,M);while 到下一时刻 dofor pi∈P doif 数据点pi离开限距范围或进入限距范围 then更新M;S←NN(q,k,M);for pj,pk∈S doif j<k and |pjq|>|pkq| thenS'←pj, pj←pk, pk←S'; //次序更新更新最近邻集S,endwhilereturn S;end2.2 基于查询圆面的K最近邻查询算法(PCM方法)上文提出的基于查询轴的K最近邻查询算法对具有受限最近邻查询和带有方向关系的最近邻查询无效。
为了弥补该方法的不足,本节给出基于查询圆面的K近邻查询算法。
定义3 如图1所示,过球心o和查询点q的查询轴垂直的平面与球面相交而成的圆面称为查询圆面。
查询圆面有2面,正对q的一面称为q的近查询圆面;背对q的一面称为q的远查询圆面。
定义4查询圆面将球面分成2个半球面,以查询点q为顶点的半球面称为近半球面,以q的球面对称点q’为顶点的半球面称为远半球面。
近半球面在查询圆面的投影即为近查询圆面,远半球面在查询圆面的投影即为远查询圆面。
定义5查询点q在近查询圆面上的投影q o和球心o重合,称为q的近查询投影点;q的球面对称点q’的投影q o’亦和球心o重合,称为q的远查询投影点。
由球的性质可知,近半球面上的数据点在q的近查询圆面上投影后,投影点到近查询投影点q o之间的球面距离大小关系和球面上的原始距离对应关系一致。
远半球面上的数据点在q的远查询圆面上投影后,投影点p i’到远查询投影点q o’之间的球面距离大小关系和球面上的原始点p i到q的原始距离大小对应关系相反。
基于查询圆面的K近邻查询算法如算法3所示。
算法3CPP_SNN()输入球面上的数据对象点集P,查询点q输出q的k个最近邻beginS←∅; S'←∅;S''←∅;if 没有构造q的远近查询圆面 thenCon_FNC(q); //构造q的远近查询圆面ProjP(P);ProjP(q);if 在查询圆面上没有构造查询树 thenCon_tree(NST_tree); //构建近查询树Con_tree(FST_tree); //构建远查询树if n'>k thenS←NNS(NST_tree,k);//用NST树查询q的k个最近邻return S;elseif n'<k thenS'←NNS(NST_tree,n');//用NST树查询q的n'个最近邻S''←NNS(FST_tree,(k-n''));//用FST树查询q的第n'+1到第k'个最近邻S←S'∪ S''; //将S'和S''的有序数据合并入S;end3 算法比较与实验分析本文2种方法的性能特征如表1所示。
