数学结构

合集下载

西师版小学数学知识结构

西师版小学数学内容框架教材一（上）主要内容安排表领域单元小节数一、10以内数的认识和加减法1—5的认识0的认识与比较数学文化（数的产生）代5以内数的加法5以内数的减法数6—10的认识6、7的加减法8、9的加减法10的加减法连加、连减、加减混合整理与复习三、11—20各数的认识认识11—20各数不进位加法和不退位减法整理与复习四、20以内的进位加法和退位减法9加几8加几7、6加几11减几12、13减几14、15减几16、17、18减几整理与复习空间二、分类、认识物体分类与数学文化（分类）图形认识物体统计五、统计统计与概率实践六、总复习单元整理与复习与总复习综合应用实践活动快乐的一天环保小卫士小小统计员教材一（下）主要内容安排表领单元小节域数一、100以内数的认识数数、数的组成写数、读数与数的顺序、大小比较代认识人民币整理与复习数四、100以内的加法和减法（一）整十数加、减整十数两位数加减两位数整理与复习六、100以内的加法和减法（二）进位加法退位减法整理与复习五、认识钟表认识钟表空二、位置与方向位置与方向间与图三、认识图形认识图形形统七、统计分类计与统计概率实八、总复习单元整理与复习践与总复习综合应实践活动赶场用参观滨江路春游教材二（上）主要内容安排表领单元小节域数一、表内乘法乘法的初步认识1，2的乘法口诀与3的乘法口诀4的乘法口诀代5的乘法口诀6，7的乘法口诀数8，9的乘法口诀整理与复习数学文化（乘号的来历）四、表内除法分一分除法的初步认识用乘法口诀求商倍的认识整理与复习数学文化（除号的来历）空二、角的初步认识角的初步认识间与用厘米作单位量长度图三、测量长度用米作单位量长度形五、方向与位置东、南、西、北数学文化（指南针）确定位置统六、统计统计计与概率实七、总复习践与各单元整理与复习综总复习合应实践活动小小测量员用庆祝元旦丰收教材二（下）主要内容安排表领单元小节域数一、万以内数的认识计数单位数数与写数、读数大小比较代较大数的估计整理与复习数二、克、千克、吨三、三位数的加减法整十、整百数加减加减法的估算三位数的加法三位数的减法探索规律聪明的高斯（数学文化）解决问题整理与复习五、时、分、秒认识钟表解决问题空四、测量长度（认识千米；知道毫米）间与计量的发展（数学文化）图六、认识图形长方形和正方形的认识锐角和钝角形平行四边形拼组图形七巧板（数学文化）统七、统计初步与不确定现象统计表计与条形统计图概不确定现象率实总复习践与综合应实践活动学习“当家”用学做“小买卖”参观养殖场教材三（上）主要内容安排表领单元小节域数一、两、三位数乘一位数整十、整百数乘一位数与两位数乘一位数三位数乘一位数代中间有0的数乘一位数解决问题数整理与复习四、两位数除以一位数两位数除以一位数两位数除以一位数的估算有余数的除法解决问题整理与复习五、年、月、日年、月、日24时计时法空二、方向与位置方向与位置四面八方（数学文化）间与三、旋转与平移旋转与平移图六、长方形、正方形的周长认识周长形统八、统计初步与不确定现象统计初步计与不确定现象概率实总复习践与综合应实践活动办数学小报用做一个家庭年历看看家乡新面貌教材三（下）主要内容安排表领单元小节域数一、两位数乘两位数的乘法两位数乘两位数的笔算与发现规律解决问题代整理与复习奇妙的乘法（数学文化）数三、三位数除以一位数的除法三位数除以一位数的口算三位数除以一位数的估算三位数除以一位数的笔算发现规律解决问题整理与复习五、小数的初步认识小数的初步认识一位小数的加减法空二、长方形和正方形的面积面积和面积单位间与图简单的换算形解决问题整理与复习）六、对称对称现象轴对称图形对称与建筑（数学文化）统四、统计初步与不确定现象数据整理计与平均数概不确定现象率实七、总复习践与综合应实践活动在实践活动基地用惊人的危害美化我们的小天地教材四年级（上）主要内容安排表领域单元小节数一、整数四则混合运算整数四则混合运算与二、多位数的认识多位数的读写代用万和亿作单位表示数整理与复习数进制（数学文化）三、整数加减法口算和估算用计算器计算加减法的关系加法运算律整理与复习五、整数乘法整数乘法解决问题整理与复习奇妙的乘法（数学文化）七、整数除法整数除法探索规律整理与复习空间四、角线段、直线和射线与角的度量图形六、相交与平行相交与平行八、统计）统计统计四、统计初步与不确定现象数据整理与平均数概率不确定现象实践总复习总复习与综合应用综合应用小小设计师节约一粒米小钱也能办大事教材四年级（下）主要内容安排表领单元小节域数一、整数四则混合运算整数四则混合运算括号的由来（数学文化与二、乘除法的关系和运算律乘除法的关系代乘法运算律及简便运算探索规律数解决问题整理与复习四、小数的意义和性质小数的意义小数的性质求一个小数的近似数小数与复名数整理与复习六、小数的加法和减法小数的加法和减法算筹与筹算（数学文化）空三、三角形认识三角形间与三角形的分类图探索规律形整理与复习五、平行四边形和梯形平行四边形梯形探索规律七、条形统计图条形统计图统八、可能性可能性计与概率实九、总复习践与综合应综合应用节约一滴水用三峡库区生态环境调查我们长高了教材五年级（上）主要内容安排表领单元小节域数一、小数乘法小数乘整数小数乘小数与积的近似值三、小数除法除数是整数的除法代除数是小数的除法商的近似值数循环小数五、小数四则混合运算小数四则混合运算解决问题七、用字母表示数用字母表示数空二、图形的旋转、平移与对称图形的平移间与图形的旋转图轴对称图形形四、确定位置确定位置六、多边形面积的计算平行四边形的面积三角形的面积梯形的面积不规则图形的面积解决问题九章算术（数学文化）统八、众数与中位数众数计与中位数概解决问题率实九、总复习践与综合应综合应用花边设计比赛用家庭用电调查我们的住房有多大教材五年级（下）主要内容安排表领单元小节域数一、倍数和因数倍数、因数与2、3、5的倍数的特征代合数、质数数二、分数分数的意义分数的基本性质约分通分分数与小数整理与复习四、分数加减法分数加减法五、方程等式方程解决问题整理与复习古老的方程（数学文化）空三、长方体、正方体长方体、正方体的认识间与长方体、正方体的表面积图体积与体积单位形解决问题整理与复习统六、折线统计图折线统计图计与概率实七、总复习各单元整理与复习践与总复习综合应综合应用设计长方体的包装方案用一年“吃掉”多少森林发豆芽教材六年级（上）主要内容安排表领单元小节域数一、分数乘法分数乘法与解决问题代三、分数除法分数除以整数数一个数除以分数按比例分配探索规律解决问题整理与复习五、分数混合运算分数混合运算解决问题六、负数负数空二、圆圆的认识间与圆的周长图形圆的面积解决问题整理与复习四、图形的变换和确定位置图形的放大或缩小设计图案比例尺物体位置的确定统七、设计简单方案设计简单方案计与概率实八、总复习各单元整理与复习践与总复习综合应综合应用研究故事中的数学问题用选择上学的路线教材六年级（下）主要内容安排表领单元小节域数一、百分数百分数的意义与代解决问题数整理与复习三、正比例和反比例比例正比例反比例整理与复习空二、圆柱和圆锥圆柱间与圆锥图整理与复习形古老的几何（数学文化）统四、统计扇形统计图计与综合统计活动概五、可能性可能性率实六、总复习数与代数践与综空间与图形合应统计与概率用实践与综合应用综合应用。

四年级上册数学教材结构图

四年级数学上册教材结构图（一）数与代数1．第一单元“理解更大的数”本单元是在第一学段学生理解万以内数的基础上，进一步理解亿以内的数在实际生活中的意义，掌握大数读写的方法，理解近似数及其作用。

本单元安排了四个情境活动：数一数（亿以内数的理解），人口普查（亿以内数的读写及比较大小），国土面积（大数的改写），森林面积（近似数的理解）。

通过本单元的学习，学生将经历收集日常生活中常见大数的过程，感受学习更大数的必要性，并能体验大数的实际意义；理解亿以内数的计数单位，理解各单位之间的关系，并会准确读、写；能比较亿以内数的大小；掌握万、亿为单位表示大数的方法；理解近似数，能求一个数的近似数，能对大数实行估计。

2．第三单元“乘法”本单元学习的内容主要有：三位数乘两位数，对一些较大的数实行估计，理解计算器以及使用计算器探索一些数学规律。

教材安排了六个情境活动：卫星运行时间（三位数乘两位数的乘法），体育场（较大数的估计方法），神奇的计算器（计算器的理解与使用），探索与发现（一）（有趣算式的探索），探索与发现（二）（乘法结合律的探索），探索与发现（三）（乘法分配律的探索）。

本单元又专题安排了“计算工具的演变”的阅读材料，以使学生理解计算工具的发展过程。

通过本单元的学习，学生将理解三位数乘两位数乘法的计算方法，并能准确计算，会使用所学知识解决一些实际问题；能对生活中具体事物的数量用不同的方法实行估计；掌握计算器的使用方法，会利用计算器探索一些数学规律。

3．第五单元“除法”本单元的学习是小学阶段整数运算的最后一个章节内容。

本单元学习的内容主要有：三位数除以整十数，三位数除以两位数，速度、时间与路程的数量关系，探索商的运算规律以及整数四则混合运算。

本单元安排了七个情境活动：买文具（除数是整十数的除法），路程、时间与速度（常见的数量关系），参观苗圃（一次试商的除数是两位数的除法），国家体育场（体会万、亿的实际意义），秋游（试商需要改商的除法），探索与发现（四）（探索商的变化规律），抗震救灾（三步的混合运算）。

数学课程的结构

数学课程的结构
数学课程的结构通常分为不同的级别、主题和概念。

下面是一般的数学课程结构示例：
1. 基础数学：这是数学课程的入门级别，主要涵盖基本数学概念和技巧。

它通常包括数字、整数、分数、小数、百分数、代数基础、几何基础和简单的方程和不等式。

2. 代数学：代数学是数学的重要分支，通常包括线性代数、多项式、函数、指数、对数和三角函数。

这个级别的课程通常会更深入地探索代数概念和技巧，包括解方程组、因式分解、图像和变换等。

3. 几何学：几何学研究形状、空间和位置关系。

几何课程通常会学习点、线、角、圆、多边形、体积等概念，以及相应的定理和证明。

高级几何课程还可能包括三角学和解析几何。

4. 概率和统计学：概率和统计学是数学的应用领域，用于研究随机事件和数据分析。

概率课程涵盖基本概率原理、组合、排列、期望值和方差等概念。

统计学课程则涉及数据收集与展示、概率分布、抽样、假设检验和回归分析等内容。

5. 分析学：分析学是数学的一个分支，主要研究函数、极限、连续性和微积分。

这个级别的课程涵盖微分学和积分学，包括导数、极值、曲线绘制、不定积分和定积分等概念和技巧。

以上只是数学课程结构的一般示例，实际的课程设置可能会有
所不同，具体内容和难度也会根据学校、年级和课程要求而有所差异。

数学结构主义

数学结构主义
数学结构主义是一种以数学结构为基础，把不同的概念和实体关联起来的哲学理论。

它的核心是把概念抽象化，把它们抽象化为数学结构，并将它们关联起来，它们之间可能具有对比或联系。

这是一种深方法论，因为它既试图通过专业练习来提取高层概念，也可以用抽象的思维实现高层概念的关联性。

数学结构主义基于许多学科，如数学、哲学、心理学等，可以用来解释和提炼实践以及理论。

它可以帮助我们更好地理解现实世界，从而获得更清晰的视角，并发现更有价值的信息。

它的实践有时与计算机科学、社会计算、非线性动力学等相关，它也可以用于数据科学、机器学习和人工智能等应用领域。

数学结构主义的实践是基于一系列的技巧，例如线框图（视图）、时空分析和可视化，它们用于识别、处理和分析信息和知识。

它还提出了许多有趣的概念，如增量学习、“蓝图”设计和“模型模块”设计。

这些技巧和概念都可以用来提高工作的效率和准确性，改进我们的决策能力和求知能力。

总之，数学结构主义是一种深方法论，基于许多学科，它既可以用于定义和检查概念，也可以分析实践和理论，可以提高我们的分析能力和求知能力。

它不仅关注概念，也关注实践；它不仅可以被应用于抽象理论研究，也可以用于实践应用；它不仅注重理论，也注重实践；它不仅是一种哲学理论，也是一种有用的工具。

高中数学重点知识结构总结

高中数学重点知识结构总结今天小编给大家带来高中数学的重点知识总结，去其糟粕，取其精华，为各位学子带来一针见血的复习大纲，希望能为大家节省时间做到每一分钟都没有浪费。

然后有更多的时间复习，努力吧，同学们!一、集合与简易逻辑1.集合的元素具有确定性、无序性和互异性.2.对集合，时，必须注意到“极端”情况：或 ;求集合的子集时是否注意到是任何集合的子集、是任何非空集合的真子集.3.对于含有个元素的有限集合，其子集、真子集、非空子集、非空真子集的个数依次为4.“交的补等于补的并，即”;“并的补等于补的交，即”.5.判断命题的真假关键是“抓住关联字词”;注意：“不‘或’即‘且’，不‘且’即‘或’”.6.“或命题”的真假特点是“一真即真，要假全假”;“且命题”的真假特点是“一假即假，要真全真”;“非命题”的真假特点是“一真一假”.7.四种命题中“‘逆’者‘交换’也”、“‘否’者‘否定’也”.原命题等价于逆否命题，但原命题与逆命题、否命题都不等价.反证法分为三步：假设、推矛、得果.注意：命题的否定是“命题的非命题，也就是‘条件不变，仅否定结论’所得命题”，但否命题是“既否定原命题的条件作为条件，又否定原命题的结论作为结论的所得命题” .8.充要条件二、函数1.指数式、对数式，2.(1)映射是“‘全部射出’加‘一箭一雕’”;映射中第一个集合中的元素必有像，但第二个集合中的元素不一定有原像( 中元素的像有且仅有下一个，但中元素的原像可能没有，也可任意个);函数是“非空数集上的映射”，其中“值域是映射中像集的子集”.(2)函数图像与轴垂线至多一个公共点，但与轴垂线的公共点可能没有，也可任意个.(3)函数图像一定是坐标系中的曲线，但坐标系中的曲线不一定能成为函数图像.3.单调性和奇偶性(1)奇函数在关于原点对称的区间上若有单调性，则其单调性完全相同.偶函数在关于原点对称的区间上若有单调性，则其单调性恰恰相反.注意：(1)确定函数的奇偶性，务必先判定函数定义域是否关于原点对称.确定函数奇偶性的常用方法有：定义法、图像法等等.对于偶函数而言有： .(2)若奇函数定义域中有0，则必有 .即的定义域时，是为奇函数的必要非充分条件.(3)确定函数的单调性或单调区间，在解答题中常用：定义法(取值、作差、鉴定)、导数法;在选择、填空题中还有：数形结合法(图像法)、特殊值法等等.(4)既奇又偶函数有无穷多个( ，定义域是关于原点对称的任意一个数集).(7)复合函数的单调性特点是：“同性得增，增必同性;异性得减，减必异性”.复合函数的奇偶性特点是：“内偶则偶，内奇同外”.复合函数要考虑定义域的变化。

整理苏教版小学数学教材结构体系

⑵了解数学与生活的广泛联系，能从不同角度发现实际问题中所包含的丰富的数学信息。能掌握和运用多种策略解决问题（包括列表、画图、枚举、逆推、替换、转化等），不指定具体使用何种策略解决问题，内容原则以课本例题要求为准。 ⑶应淡化类型，呈现形式要多样化，适当安排一些符合学生实际水平的开放性的问题，一般应用题不超过三步，分数、百分数应用题可为两到三步。 ⑷熟练运用百分数〔含百分率（利率、税率、折扣）〕知识解答常见的实际问题。 ⑸能够综合运用所学知识解决现实生活中实际问题，能够解答融生活性、现实性、实践性、操作性、探究性和活动性为一体的综合实践问题。
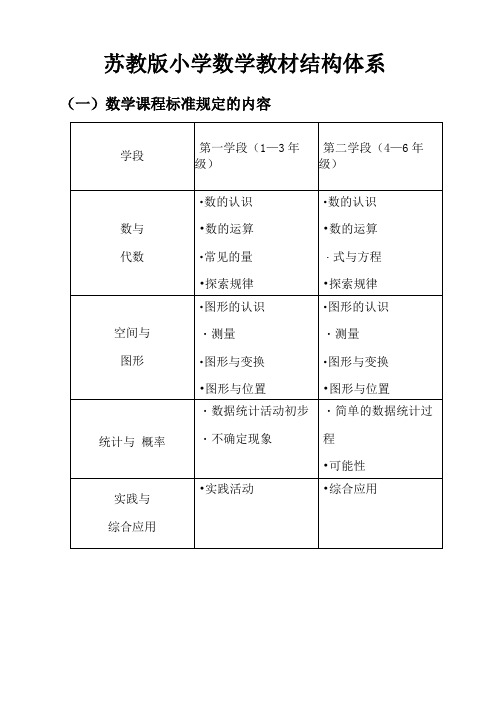
・不确定现象
・简单的数据统计过
程
•可能性
实践与
综合应用
•实践活动
•综合应用
（二）各册教学内容一年级
册
次
序
号
内容
页码
册次
序
号
内容
页码
▲
上
1
数一数
2
一下
1
减法
1
2
比一比
4
2
认识图形
16
3
分一分
7
3
认数
24
4认Βιβλιοθήκη 置9我们认识的数44
5
认数（一）
11
4
加法和减法
（一）
46
6
认物体
26
5
认识人民币
68
有趣的拼搭
（二）
86
奇妙的图形密铺
86
10
统计
105
9
解决问题的策略
88
了解周围的家庭
118
10
圆
93
11
整理与复习

(完整版)人教版初中数学知识结构

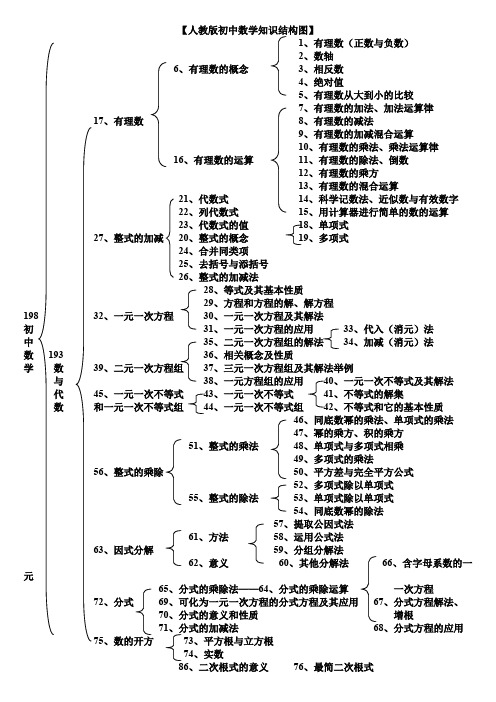
【人教版初中数学知识结构图】1、有理数（正数与负数）2、数轴6、有理数的概念3、相反数4、绝对值5、有理数从大到小的比较7、有理数的加法、加法运算律17、有理数8、有理数的减法9、有理数的加减混合运算10、有理数的乘法、乘法运算律16、有理数的运算11、有理数的除法、倒数12、有理数的乘方13、有理数的混合运算21、代数式14、科学记数法、近似数与有效数字22、列代数式15、用计算器进行简单的数的运算23、代数式的值18、单项式27、整式的加减20、整式的概念19、多项式24、合并同类项25、去括号与添括号26、整式的加减法28、等式及其基本性质29、方程和方程的解、解方程198 32、一元一次方程30、一元一次方程及其解法初31、一元一次方程的应用33、代入（消元）法中35、二元一次方程组的解法34、加减（消元）法数193 36、相关概念及性质学数39、二元一次方程组37、三元一次方程组及其解法举例与38、一元方程组的应用40、一元一次不等式及其解法代45、一元一次不等式43、一元一次不等式41、不等式的解集数和一元一次不等式组44、一元一次不等式组42、不等式和它的基本性质46、同底数幂的乘法、单项式的乘法47、幂的乘方、积的乘方51、整式的乘法48、单项式与多项式相乘49、多项式的乘法56、整式的乘除50、平方差与完全平方公式52、多项式除以单项式55、整式的除法53、单项式除以单项式54、同底数幂的除法57、提取公因式法61、方法58、运用公式法63、因式分解59、分组分解法62、意义60、其他分解法66、含字母系数的一元65、分式的乘除法——64、分式的乘除运算一次方程72、分式69、可化为一元一次方程的分式方程及其应用67、分式方程解法、70、分式的意义和性质增根71、分式的加减法68、分式方程的应用75、数的开方73、平方根与立方根74、实数86、二次根式的意义76、最简二次根式79、二次根式的乘除法77、二次根式的除法78、二次根式的乘法87、二次根式82、二次根式的加减法80、二次根式的加减法81、同类二次根式85、二次根式的混合运算83、二次根式的混合运算84、有理化因式88、直接开平方法89、配方法193 93、一元一次方程的解法90、公式法198 数98、一元二次方程的意义91、因式分解法初与100、二元二次方程组92、一元二次方式根的判别法中代102、一元二次方程99、*一元二次方程的根与系数的关系数数94、分式方程的解法学97、可化为一元二次方程95、*无理方程的意义、解法的分式方程和无理方程96、分式方程、无理方程的应用101、一元二次方程的应用103、一次函数与一元一次不等式106、一次函数104、一次函数图象的图象和性质105、正比例函数的图象和性质108、二次函数——107、二次函数的有关概念113、函数及其图象109、平面直角坐标系110、函数111、函数的图象112、反比例函数116、线段、角114、线段115、角117、相交线、对顶角、邻角、补角120、相交线118、垂线、点到直线的距离119、同位角、内错角、同旁内角126、相交、平行123、平行线121、平行线概念及性质122、平行线的判定124、空间直线、平面的位置关系125、命题、公理、定理127、三角形三边关系129、与三角有关的边128、三角形的相关概念及分类、134、全等三角形角平分、中线、高135、等腰三角形133、直角三角形——132、勾股定理131、与三角形有关的角、130、三角形的内角136、轴对称139、平行四边形的概念及其性质138、三角形137、基本作图140、平行四边形的判定144、平行四边形141、矩形的概念、性质和判定149、多边形142、菱形的概念、性质和判定151、四边形150、中心对称143、正方形的概念、性质和判定145、梯形的相关概念148、梯形146、等腰梯形的概念、性质和判定194 147、三角形、梯形的中位线空156、比例线段间158、相似图形157、相似多边形152、相似三角形的相关概念198 与155、相似三角形153、三角形相似的判定初图154、相似三角形的性质中形161、解直角三角形159、解直角三角形数163、解直角三角形160、解直角三角形的应用公式学162、锐角三角形164、圆的有关概念及对称性165、点和圆的位置关系166、过不在同一直线上三点的圆172、圆的有关性质167、三角形的外接圆168、垂径定理及其逆定理169、圆心角、弧、弦、弦心距185、圆170、圆周角定理171、圆内接四边形及其性质173、直线和圆的位置关系177、直线和圆的位置关系174、切线的判定和性质175、三角形的内切圆176、切线长定理179、正多边形和圆——178、正多边形的有关计算180、圆周长、弧长183、弧长和扇形面积181、圆、扇形、弓形的面积182、圆柱和圆锥的侧面展开图、侧面积184、圆和圆的位置关系186、几何体、几何图形187、平均数191、统计初步188、众数和中位数195、统计与概率189、级差、方差、标准差190、频数、频率、频率分布直方图192、概率初步———概率计算196、中考复习197、总复习初中数学1.2.7 3.4.5.7 6.7.78...⎧⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩⎪⎧⎪⎨⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎩⎩有理数整式（上）一元一次方程图形认识初步相交线与平行线年级平面直角坐标系三角形（下）二元一次方程组9不等式与不等式组10数据的收集与整理11.12.813.14.15.816.17.818.19.20.⎧⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎩⎨⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎩⎩全等三角形轴对称（上）实数一次函数整式的乘除与因式分解年级分式反比例函数（下）勾股定理四边形数据的分析21.22.923.24.25.926.27.928.29.⎧⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎨⎩⎪⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩⎩二次根式一元二次方程（上）旋转圆概率初步年级二次函数相似（下）锐角三角形投影与视图高中数学1.1.2.1 2.23..4.1. 1.3 2.4 2.3.1. 1.5 2.1-1 2.3.3.1.1-2 2.3.⎧⎧⎪⎪⎪⎨⎨⎪⎪⎩⎪⎩⎧⎧⎪⎨⎨⎩⎪⎩⎧⎧⎪⎪⎨⎨⎪⎪⎩⎩空间集合体集合与函数点，直线，平面之间的位置关系必修基本初等函数（1）必修直线与方程3函数的应用圆与方程算法初步三角函数必修统计必修平面向量概率解三角形常用逻辑语必修数列选修圆锥曲线与方程导数及其应用不等式统计案例选修推理证明数系的扩充 1.2-1 2.3.⎧⎧⎪⎪⎨⎨⎪⎪⎩⎩常用逻辑用语选修圆锥曲线与方程与复数的引入空间向量与立体几何。

(完整版)高中数学知识结构框图

高中数学知识结构框图
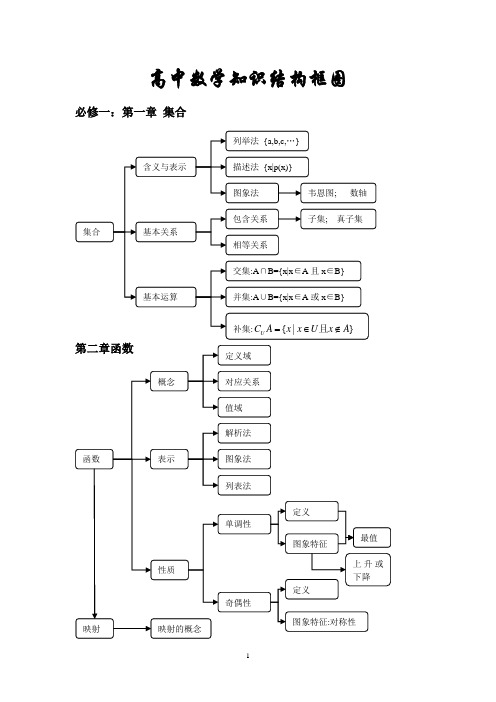
必修一：第一章集合
第三章基本初等函数(Ⅰ)
指数函数
对数数函数
定义域
值域
图象
性质
过定点
过定点
减函数
增函数
减函数
增函数
幂函数
奇函数
偶函数
第一象限性质
减函数
增函数
过定点
必修二：第一章立体几何初步
第二章平面解析几何初步
必修三：第一章算法初步
第二章统计
第三章概率
必修四：第一章基本初等函数（II）
函
数
性Байду номын сангаас
质
图象
定义域
值域
最值
当时，；当
时，．
当时，
；当
时，．
既无最大值也无最小值
周期性
奇偶性
奇函数
偶函数
奇函数
单调性
在
上是增函数；在
上是减函数．
在
上是增函数；在
上是减函数．
在
上是增函数．
对称性
对称中心
对称轴
对称中心
对称轴
对称中心
无对称轴
第二章平面向量
第三章三角恒等变换
必修五：第一章解三角形
第二章数列

小学数学知识结构归纳

小学数学知识结构归纳整数和小数整数部分：十进制计数法；一（个）、十、百、千、万……都叫做计数单位。

其中“一”是计数的基本单位。

10个1是10，10个10是100……每相邻两个计数单位之间的进率都是十。

这种计数方法叫做十进制计数法整数的读法：从高位一级一级读，读出级名（亿、万），每级末尾0都不读。

其他数位一个或连续几个0都只读一个“零”。

整数的写法：从高位一级一级写，哪一位一个单位也没有就写0。

四舍五入法：求近似数，看尾数最高位上的数是几，比5小就舍去，是5或大于5舍去尾数向前一位进1。

这种求近似数的方法就叫做四舍五入法。

整数大小的比较：位数多的数较大，数位相同最高位上数大的就大，最高位相同比看第二位较大就大，以此类推。

小数部分：把整数1平均分成10份、100份、1000份……这样的一份或几份是十分之几、百分之几、千分之几……这些分数可以用小数表示。

如1/10记作0.1,7/100记作0.07。

小数点右边第一位叫十分位，计数单位是十分之一（0.1）；第二位叫百分位，计数单位是百分之一（0.01）……小数部分最大的计数单位是十分之一，没有最小的计数单位。

小数部分有几个数位，就叫做几位小数。

如0.36是两位小数，3.066是三位小数小数的读法：整数部分整数读，小数点读点，小数部分顺序读。

小数的写法：小数点写在个位右下角。

小数的性质：小数末尾添0去0大小不变。

化简小数点位置移动引起大小变化：右移扩大左缩小，1十2百3千倍。

小数大小比较：整数部分大就大；整数相同看十分位大就大；以此类推。

分数和百分数■分数和百分数的意义1、分数的意义：把单位“1”平均分成若干份，表示这样的一份或者几份的数，叫做分数。

在分数里，表示把单位“1”平均分成多少份的数，叫做分数的分母；表示取了多少份的数，叫做分数的分子；其中的一份，叫做分数单位。

2、百分数的意义：表示一个数是另一个数的百分之几的数，叫做百分数。

也叫百分率或百分比。

小学数学知识结构图(知识树PPT)

ቤተ መጻሕፍቲ ባይዱ
工程问题
浓度问题
溶液=溶剂+溶质
浓度=溶质÷溶液×100%
解决问题----列方程解决问题
*弄清题意，找出要求的的未知数用X表示 *找出题中数量间的等量关系，列出方程 *解方程 *检验或验算，写出答案
列方程解决问题
一般步骤
找等量关系常用方法
关键语句常见的加、减、乘、除的数量关系常用的等量关系利用图形周长、面积、体积公式
分数问题类型
利息
*求a的几分之几（或百分之几）是多少 *一个数的几分之几（或百分之几）是a，求这个数 *求a是b的几分之几（或百分之几） *比a多（少）几分之几（或百分之几）的数是多少 *a比b多（少）几分之几（或百分之几），求b *求a比b多（少）几分之几（或百分之几）。
利息=本金×利率×时间
图形的认识
测量空间与图形图形与位置
图形与变换
基本图形
线：直线，射线，线段，平行线，垂线。（相交，垂直，平行）角：角的概念，角的分类平行四边形，长方形，正方形三角形梯形圆和圆环长方体，正方体圆柱
图形的认识
平面图形
立体图形
圆锥
球
基本图形
线角平行四边形，长方形，正方形的周长和面积三角形的周长和面积
一般不给出具体的的工作总量用单位1表示用分数表示工效工作效率工作时间工作总量工作总量工作效率工作时间工作总量工作时间工作效率数量关系浓度问题溶液溶剂溶质浓度溶质溶液100解决问题列方程解决问题列方程解决问题题弄清题意找出要求的的未知数用x表示找出题中数量间的等量关系列出方程解方程检验或验算写出答案找等量关系常用方法关键语句常见的加减乘除的数量关系常用的等量关系利用图形周长面积体积公式一般步骤典型应用题平均数问题归一问题归总问题和差问题差倍问题和倍问题倍比问题行程问题流水问题还原问题植树问题盈亏问题年龄问题鸡兔同笼问题解决问题行程问题行程问题一般行程问题火车过桥问题相遇问题追及问题路程速度时间速度路程时间时间路程速度路程桥长车长车速桥长车长通过时间通过时间桥长车长车速桥长车速通过时间车长车长车速通过时间桥长相遇路程速度和相遇时间相遇时间相遇路程速度和速度和相遇路程相遇时间速度差追及时间追及路程追及路程速度差追及时间追及路程追及时间速度差量与计量常见的量计量进率与换算度量衡名数与名数的改写常见的量量计量单位及进率率长度

2024年新高考数学试卷结构

2024年新高考数学试卷结构
2024年新高考数学试卷结构主要分为四大类题型，包括单选、多选、填空
和解答，总共有19道题。

其中，解答题的占比最高，共有5道题，总分数
高达77分，占总分值的51%。

具体来说，单选题为每题5分，共计15分；多选题每题6分，共计18分；填空题每题5分，共计20分；解答题则没
有具体的分值分布，因为解答题的分值会根据题目难度和解答步骤的不同而有所差异。

此外，新高考数学试卷结构中还提到了“难度”这一指标。

具体来说，新高考数学试卷的难度可能会达到竞赛一试的难度。

以上信息仅供参考，具体的高考数学试卷结构还需要以教育部门发布的官方信息为准。

高等数学知识结构框架

高等数学知识结构框架高等数学是大学数学的一门基础课程，它主要包括微积分和数学分析两个部分。

微积分主要研究函数、极限、导数、积分、微分方程等概念和方法；数学分析主要研究实数集、极限、连续性、一致连续性、可导性、不定积分、定积分、级数等概念和问题。

以下是高等数学中比较重要的知识结构框架及相关参考内容：一、函数与极限1. 函数的概念、基本初等函数以及函数的性质：韦达定理、复合函数、反函数等。

2. 极限的概念和性质：数列极限、函数极限、极限存在准则等。

3. 极限的计算方法：夹逼准则、单调有界数列的极限、洛必达法则等。

4. 无穷小量与无穷大量的定义与比较：无穷小量的阶、无穷大量的比较等。

二、导数与微分1. 导数的定义、性质和计算方法：导数的定义、导数的四则运算、高阶导数、隐函数与参数方程的导数等。

2. 函数的几何意义与微分中值定理：函数的单调性与极值点、罗尔中值定理、拉格朗日中值定理、柯西中值定理等。

3. 函数的图形与曲率：函数的图形、曲率、凹凸性与拐点。

三、不定积分与定积分1. 不定积分的定义与性质：原函数与不定积分的概念、基本积分表、换元积分法、分部积分法等。

2. 定积分的概念与性质：黎曼和与定积分的定义、定积分的性质、牛顿-莱布尼茨公式等。

3. 定积分的计算方法：变上限积分法、变量替换法、分段函数积分法等。

四、微分方程1. 常微分方程的基本概念与解法：一阶微分方程的基本概念、可分离变量方程、齐次方程、一阶线性非齐次方程等。

2. 高阶线性常微分方程的解法：二阶常系数齐次线性方程、二阶常系数非齐次线性方程、欧拉方程等。

五、级数1. 数列与级数：数列的极限、数列极限收敛性的准则、常数项级数、幂级数等。

2. 一致收敛性与函数级数：一致收敛性的概念、一致收敛级数的性质、Weierstrass判别法、Abel判别法、幂级数的收敛半径等。

以上是高等数学中较为重要的知识结构框架及相关参考内容，希望能为学习者提供一定的参考和指导。

数学中的代数结构

数学中的代数结构数学是一门富有创造性和严谨性的学科，它研究的范围广泛，包括了代数、几何、分析等多个分支。

而其中的代数结构则是数学中的一个重要概念，它涉及到数学对象之间的关系和运算规则。

本文将介绍数学中的代数结构及其应用。

一、代数结构的概念和基本性质代数结构是数学中研究对象之间关系的一种抽象模型。

代数结构通常由集合和集合上的运算构成。

常见的代数结构有群、环、域等等。

群是最基本的代数结构之一。

它由一个集合和一个二元运算组成，满足封闭性、结合律、单位元和逆元等性质。

群的例子包括整数加法群、对称群等。

环是在群的基础上扩展而来的。

它由一个集合和两个二元运算（加法和乘法）组成，满足封闭性、结合律、单位元、零元、交换律和分配律等性质。

整数环和多项式环都是环的例子。

域是代数结构中更为丰富和复杂的一个概念。

它由一个集合和两个二元运算（加法和乘法）组成，满足封闭性、结合律、单位元、零元、交换律、分配律以及存在乘法逆元等性质。

实数域和复数域是常见的域。

二、代数结构的应用代数结构在数学中的应用非常广泛，涉及到了许多领域。

下面将介绍几个与代数结构相关的应用示例。

1. 密码学密码学是研究如何保护信息安全的学科。

其中，代数结构在密码学中起到了重要作用。

例如，RSA加密算法就是基于数论和代数结构的。

它利用了大整数分解难题和模幂运算等数论性质，确保了信息的机密性和安全性。

2. 编码理论编码理论是研究如何有效地传输和存储信息的学科。

代数结构在编码理论中有着广泛的应用。

例如，线性码和循环码都是基于代数结构的。

线性码利用了有限域的性质，通过矩阵运算实现编码和解码；而循环码则利用了多项式环的特性，具有良好的纠错能力。

3. 图论图论是研究图及其性质的学科。

代数结构在图论中也有着重要的应用。

例如，邻接矩阵和邻接表等数据结构可以用来表示图，通过代数运算可以进行图的遍历、连通性判断等操作。

此外，图的同构性判断和染色问题等也与代数结构密切相关。

三、代数结构的拓展与发展代数结构作为数学的一个重要分支，不断地在发展和拓展。

初中数学知识结构图

初中数学知识结构图(总11页)
--本页仅作为文档封面，使用时请直接删除即可--
--内页可以根据需求调整合适字体及大小--
第一章有理数知识框架
第二章整式的加减知识框架
第三章一元一次方程知识框架
第四章图形的认识初步知识框架
第五章相交线与平行线知识框架
第六章平面直角坐标系知识框架
第七章三角形知识框架
第八章二元一次方程组知识结构图
第九章不等式与不等式组知识框架
第十章数据的收集、整理与描述知识框架
第十一章全等三角形知识框架
第十二章轴对称知识框架
第十三章实数知识框架：
有理数
实数
无理数
全面调查
抽样调查
收
集
数
据
描
述
数
据
整
理
数
据
分
析
数
据
得
出
结
论
第十四章一次函数知识框架
第十五章整式的乘除与分解因式知识框架
第十六章分式知识框架
第十七章反比例函数知识框架
整式乘法
整式除法
因式分解
乘法法则
第十八章勾股定理知识框架
第十九章四边形知识框架
第二十章数据的分析知识框架
第二十一章二次根式知识框架
第二十二章一元二次方程知识框架
第二十三章旋转知识框架
第二十四章圆知识框架
第二十五章概率
知识框架
第二十六章二次函数知识框架
第二十七章相似知识框架
第二十八章锐角三角函数知识框架
第二十九章投影与视图知识框架。

数学图形的结构知识点总结

数学图形的结构知识点总结1. 二维图形的结构：1.1 线段与射线的结构：线段是由两点之间的所有点组成的，而射线是一个起点和一个方向的无限延伸线段。

1.2 直线的结构：直线是由无数个点的集合组成的，这些点满足直线上的任意两个点之间的距离为常数。

1.3 多边形的结构：多边形是一个由直线段组成的封闭几何图形，其边界上的所有角都是直角。

1.4 正多边形的结构：正多边形是一个所有边和角相等的多边形。

1.5 圆的结构：圆是一个由平面上距离一个固定点的距离相等的所有点组成的图形。

2. 三维图形的结构：2.1 直线和射线的结构：在三维空间中，直线是由无穷个平行的点组成的，而射线是在一个端点的方向上无限延伸的直线段。

2.2 平面的结构：平面是一个无限延伸的二维图形，可以由三个非共线的点来唯一确定。

2.3 空间图形的结构：空间图形是一个由平面和直线组成的三维几何图形。

3. 图形的性质和特点：3.1 对称性：图形的对称性是指图形在某个轴或中心点上的镜像重合。

3.2 等边性：当一个图形的各边长度相等时，我们称之为等边图形。

3.3 等腰性：当一个图形的两条边长度相等时，我们称之为等腰图形。

3.4 直角性：当一个图形中的所有角都为直角时，我们称之为直角图形。

3.5 全等性：当一个图形的形状和大小都相同时，我们称之为全等图形。

4. 图形的相互关系：4.1 直线与平面的关系：直线可以在平面内或平面外相交，也可以平行于平面。

4.2 直线与直线的关系：两条直线可以相交、平行或重合。

4.3 点与直线的关系：一个点可以在直线上、在直线外或在直线上延伸成射线。

4.4 点与平面的关系：一个点可以在平面内、在平面外或在平面上。

4.5 线段与直线的关系：线段可以在直线上、在直线外或在直线上延伸成射线。

5. 图形的运动和变换：5.1 平移：平移是指图形在平面上沿着一定方向和距离移动的过程。

5.2 旋转：旋转是指图形以某个点为中心按一定角度转动的过程。

数学三大基本结构

数学三大基本结构
数学三大基本结构
数学是一门研究空间结构的科学，它具有以下三大基本结构： 1、运算结构：即数学中的运算，它是数学形式化的基础，通过它来表达和描述数学理论，把数学理论转化成数学表达式，它是数学的基本技能。

2、逻辑结构：即数学中的逻辑，它是数学理论的基础，它提供了推理的工具，它是数学的基本思维方法。

3、画面结构：即数学中的空间结构，它是数学解决问题的基础，是完整阐明数学问题的重要工具。

它是数学的基本技术手段。

以上三种基本结构是数学的基本构成部分，它们是数学的基本理论，数学的全部内容从这三种结构出发，构成了数学的全部知识体系与理论结构。

- 1 -。