博弈论第二章习题
博弈论测试2

博弈论测试题二1下表是两人博弈的战略式表述,其中是参与人2的战略空间。
(10分)U 和D 是参与人1的战略空间,L 和R当a,b,c,d,e,f,g,h 满足什么条件时,上述博弈存在:(1)上策均衡,(2)纯策略纳 什均衡。
2、用严格政策消去法求出下表中的纳什均衡。
(10分)3、、两个厂商生产一种完全同质的商品,该商品的市场需求函数为 Q = 100- P ,设厂商1和厂商2都没有固定成本。
若他们在相互知道对方 边际成本的情况下,同时作出产量决策是分别生产 20单位和30单位。
问这两个 厂商的边际成本各是多少?各自的利润是多少? ( 15分)4模型化下述划拳博弈:两个老朋友在一起划拳喝酒,每个人有四个策略:杆子, 老虎,鸡和虫子。
输赢规则是:杆子降老虎,老虎降鸡,鸡降虫子,虫子降杆子。
两个人同时出拳。
如果一个打败另一个,赢者的效用是 1,输者的效用是-1,否则效用为0。
( 10分) (1) 写出这个博弈的支付矩阵。
(2) 这个博弈有纯策略纳什均衡吗?计算出混合纳什均衡。
5、:三对夫妻的感情状态可以分别用下面三个得益矩阵对应的静态博弈来表示。
问:这三个博弈的纳什均衡分别是什么?这三对夫妻的感情状态究竟如何(写出 原因)?( 10分)矩阵1:矩阵2:矩阵3:6企业甲和企业乙都是彩电制造商,都可以选择生产低档产品或高档产品,每个企业在四种不同的情况下的利润如以下得益矩阵所示。
如果企业甲先于企业乙进行产品选择并投入生产,即企业乙在决定产品时已经知道企业甲的选择,而且这一点双方都清楚。
(10分)(1)用扩展型表示这一博弈。
(2)这一博弈的子博弈完美纳什均衡是什么?7、下面的博弈可以解释为两个寡头企业的价格竞争博弈,其中P是企业1的价格,q是企业2的价格。
企业1的利润函数是二i二(p-aq+c)2+q二2二(q-b)2+p求解(1)两个企业同时决策时的(纯战略)纳什均衡;(2)企业(1)先决策时的子博弈完美纳什均衡;(3)企业(2)先决策时的子博弈完美纳什均衡;本题(15分)8、案例分析(20分)2008年伊始,新加坡航空公司、新加坡淡马锡控股公司与中国国有企业中国东方航空公司轰轰烈烈”的股权交易(东新恋),被中国东方航空公司自己的股东否决了。
博弈论习题及解答

※第一章绪论§1.21. 什么是博弈论?博弈有哪些基本表示方法?各种表示法的基本要素是什么?(见教材)2. 分别用规范式和扩展式表示下面的博弈。
两个相互竞争的企业考虑同时推出一种相似的产品。
如果两家企业都推出这种产品,那么他们每家将获得利润400万元;如果只有一家企业推出新产品,那么它将获得利润700万元,没有推出新产品的企业亏损600万元;如果两家企业都不推出该产品,则每家企业获得200万元的利润。
企业B推出不推出企业A推出 (400,400) (700,-600) 不推出(-600,700) (-500,-500)3. 什么是特征函数? (见教材)4. 产生“囚犯困境”的原因是什么?你能否举出现实经济活动中囚徒困境的例子?原因:个体理性与集体理性的矛盾。
例子:厂商之间的价格战,广告竞争等。
※第二章完全信息的静态博弈和纳什均衡1. 什么是纳什均衡? (见教材)2. 剔除以下规范式博弈中的严格劣策略,再求出纯策略纳什均衡。
先剔除甲的严格劣策略3,再剔除乙的严格劣策略2,得如下矩阵博弈。
然后用划线法求出该矩阵博弈的纯策略Nash均衡。
乙甲1 31 2,0 4,22 3,4 2,33. 求出下面博弈的纳什均衡。
乙L R甲U 5,0 0,8 D 2,6 4,5由划线法易知,该矩阵博弈没有纯策略Nash均衡。
由表达式(2.3.13)~(2.3.16)可得如下不等式组Q=a+d-b-c=7,q=d-b=4,R=0+5-8-6=-9,r=-1将这些数据代入(2.3.19)和(2.3.22),可得混合策略Nash均衡((),()) 4. 用图解法求矩阵博弈的解。
解:设局中人1采用混合策略(x,1-x),其中x∈[0,1],于是有:,其中F(x)=min{x+3(1-x),-x+5(1-x),3x-3(1-x)}令z=x+3(1-x),z=-x+5(1-x),z=3x-3(1-x)作出三条直线,如下图,图中粗的折线,就是F(x)的图象由图可知,纳什均衡点与β1无关,所以原问题化为新的2*2矩阵博弈:由公式计算得:。
博弈论 第二章,课后习题(2)

q2=(a-q1-c2)/2
q2=(a+c1-2c2)/3
(2)当c1<c2<a,但2c2>a+c1时,此时q2<0.意味着厂商2不会生产, 厂商一成了垄断厂商不开发 100,0 0,0
开发
不开发
—10 ,—10 0, 100
第十题
U
6 7
D
1)很容易由划线法或箭头法得出,本博弈的两个纯策略纳什均衡为 (U,R),(D,L) 2) 本博弈还有一个混合策略纳什均衡,两博弈方各自以2/3,1/3的概率在各 自的两个策略 U/D 和 L/R 中随机选择。 3)本博弈没有帕累托上策均衡,各自偏好一个均衡策略 4)若根据风险上策均衡的思想分析,(U,L)是风险上策均衡
第九题
两寡头古诺模型,P(Q)=a-Q,边际成本分别为c1,c2.
(1)0<ci<a/2.纳什均衡产量。 解,两厂商的利润函数
π i=pqi-ciqi=(a-qi-qj)qi-ciqi
利润最大化,求反应函数 qi=(a-qj-ci)/2
具体写为: q1=(a-q2-c1)/2
直接求解得q1=(a-2c1+c2)/3
纯策略组合
箭头法
找混合策略组合:( 1 )设甲公司开发的概率为 pw(1), 不开发pw(2) 则 应有 -10Pw(1)+100Pw(2)=0
又 Pw(1)+Pw(2)=1 可算出混合策略均衡是两个公司 都以(10/11,1/11)的概率分布随机选择开发和不开发。 (二)开发补贴。
-10,10 0,120 100, 0 0 , 0
使不开发成为严格下策。
第十一题
(1)纯策略纳什均衡为(0.5,0.5)
博弈论课件习题_PPT课件

(3)
博T 弈 方 1M
L
2,0 3,4
博弈方2 R
4,2
2,3
(4)
这个2×2博弈有两个纯策略纳什均衡(M,L) 和(T,R)。
由于两个纯策略纳什均衡之间没有帕累托效率 意义上的优劣关系,双方利益有不一致性,因 此如果没有其他进一步的信息或者决策机制, 一次性静态博弈的结果不能肯定。由于双方在 该博弈中可能采取混合策略,因此实际上该博 弈的结果可能是4个纯策略组合中的任何一个。
L
M
R
博2 U 3,1
2,2
5,3
M 2,3 1,3
4,1
B 4,5 2,3
3,4
注:首先用严格下策反复消去法简化博弈,其次分析 选择列策略的博弈2的策略;最后求该博弈的混合策略 NE。
10、找出下列得益矩阵表示静态博弈的纳什么均 衡。
博方2
L
M
R
博2 U 4,3
5,1
6,2
M 2,1 8,4
U(s1)= s1 = 10 000- s2。因此s1 = 10 000- s2就是博
弈方1的反应函数。
(3)
博弈方2与博弈方1的利益函数和策略选 择是完全相似的,因此对博弈方1所选择 的任意金额s1,博弈方2的最优反应策略, 也就是反应函数是s2=10 000- s1。
本博弈有无穷多个纳什均衡,所有满足 该反应函数,也就是s1+s2=10 000的数 组( s1,s2)都是本博弈的纯策略纳什 均衡。
开发
甲 公 司 不开发
本国公司利益,有什
么好的方法?
乙公司
开发
不开发
-10,-10
100,0
0,100
0,0
博弈论各章节课后习题答案 (2)

1 π1 = (10 − 2q1 − 2q2 )q1 − 2 − 4q1
1 π2 = (10 − 2q1 − 2q2 )q2 − 2 − 4q2
求导得:
∂π1 ∂q1
= 10 − 4q1
−
2q 2
−
4
=
0
∂π2 ∂q 2
= 10 − 4q2
− 2q1 − 4 = 0
解得均衡时
q1=q2=1,则
p=8,利润为:π1=π2=
aijx*i y j 。由于 d 是
i =1 j=1
i =1 j=1
i =1 j=1
mn
mn
mn
∑∑ ∑∑ ∑∑ 常数,因此有
(aij + d)xi y j =
aijxi y j + d 。显然不等式
(aij + d)xi y*j ≤
i =1 j=1
i =1 j=1
i =1 j=1
mn
mn
∑ ∑ ∑ ∑ (aij + d)x*i y*j ≤
,要使(不开发,开发)成为该博弈的唯一纳什均衡点,只需
a>10。此时乙企
业的收益为 100+a。
11. 假设有一博弈 G=[N,S,P],其中 N={1,2},S1=[10,20],S2=[0,15], P1 (s) = 40s1 − 2s12 + 5s1s 2 ,
P2 (s)
= 50s 2
−
s
2 2
(aij + d)x*i y j 是成 立的 , 此即 为 XA2Y* ≤ X*A2Y* ≤ X*A2Y 。所以
i =1 j=1
i =1 j=1
(X*,Y*)是矩阵博弈 G2 的纳什均衡点,并且
博弈论习题2

《博弈论》习题一、选择题1. 博弈论中,局中人从一个博弈中得到的结果常被称为(B):A. 效用;B. 损益;C. 决策;D. 利润2. 下列关于策略的叙述哪个是错误的(C):A. 策略是局中人选择的一套行动计划;B. 参与博弈的每一个局中人都有若干个策略;C. 一个局中人在原博弈中的策略和在子博弈中的策略是相同的;D. 策略与行动是两个不同的概念,策略是行动的规则,而不是行动本身。
3. 囚徒困境说明(A):A. 双方都独立依照自己的利益行事,则双方不能得到最好的结果;B. 如果没有某种约束,局中人也可在(抵赖,抵赖)的基础上达到均衡;C. 双方都依照自己的利益行事,结果一方赢,一方输;D、每个局中人在做决策时,不需考虑对手的反应4. 一个博弈中,直接决定局中人损益的因素是(A):A. 策略组合;B. 策略;C. 信息;D. 行动。
5、策略式博弈,正确的说法是(B):A. 策略式博弈无法刻划动态博弈;B. 策略式博弈无法表明行动顺序;C. 策略式博弈更容易求解;D. 策略式博弈就是一个支付矩阵。
6. 下列有关策略和纳什均衡的叙述正确的有(ABCD):A. 纯策略是博弈方采取“要么做,要么不做”的策略形式;B. 混合策略是博弈方根据一组选定的概率,在两种或两种以上可能的行为中随机选择的策略;C. 有些博弈不存在纯策略纳什均衡,但存在混合策略的纳什均衡;D. 有些博弈既存在纯策略纳什均衡,也存在混合策略的纳什均衡。
7、古诺模型体现了寡头企业的( C )决策模型。
A 成本B 价格C 产量D 质量8、伯特兰德模型体现了寡头企业的什么决策模型。
BA 成本B 价格C 产量D 质量9、用囚徒困境来说明两个寡头企业的情况,说明了:(C)A、每个企业在做决策时,不需考虑竞争对手的反应B、一个企业制定的价格对其它企业没有影响C、企业为了避免最差的结果,将不能得到更好的结果D、一个企业制定的产量对其它企业的产量没有影响10、子博弈精炼纳什均衡(C ):A. 不是一个一般意义上的纳什均衡;B. 和纳什均衡没有什么关系;C. 要求某一策略组合在每一个子博弈上都构成一个纳什均衡;D. 要求某一策略组合在原博弈上都构成一个纳什均衡。
博弈论课后习题

第一章导论1、什么是博弈博弈论的主要研究内容是什么2、设定一个博弈模型必须确定哪几个方面3、举出烟草、餐饮、股市、房地产、广告、电视等行业的竞争中策略相互依存的例子。
4、“囚徒的困境”的内在根源是什么举出现实中囚徒的困境的具体例子。
5、博弈有哪些分类方法,有哪些主要的类型6、你正在考虑是否投资100万元开设一家饭店。
假设情况是这样的:你决定开,则的概率你讲收益300万元(包括投资),而的概率你将全部亏损;如果你不开,则你能保住本钱但也不会有利润,请你(a)用得益矩阵和扩展形式表示该博弈;(b)如果你是风险中性的,你会怎样选择(c)如果你是风险规避的,且期望得益的折扣系数为,你的策略选择是什么(d)如果你是风险偏好的,期望得益折算系数为,你的选择又是什么7、一逃犯从关押他的监狱中逃走,一看守奉命追捕。
如果逃犯逃跑有两条可选择的路线,看守只要追捕方向正确就一定能抓住逃犯。
逃犯逃脱可以少坐10年牢,但一旦被抓住则要加刑10年;看守抓住逃犯能得到1000元奖金。
请分别用得益矩阵和扩展形式表示该博弈,并作简单分析。
第二章完全信息静态博弈1、上策均衡、严格下策反复消去法和纳什均衡相互之间的关系是什么2、为什么说纳什均衡是博弈分析中最重要的概念3、找出现实经济或生活中可以用帕累托上策均衡、风险上策均衡分析的例子。
4、多重纳什均衡是否会影响纳什均衡的一致预测性质,对博弈分析有什么不利影响5、下面的得益矩阵表示两博弈方之间的一个静态博弈。
该博弈有没有纯策略纳什均衡博弈的结果是什么6、求出下图中得益矩阵所表示的博弈中的混合策略纳什均衡。
7、博弈方1和2就如何分10 000元进行讨价还价。
假设确定了以下规则:双方同时提出自己要求的数额S1和S2,0≤s1,s2≤10000,如果s1+s2≤10 000,则两博弈方的要求都得到满足,即分别得到s1和s2,但如果是s1+s2>10 000,则该笔钱就被没收。
问该博弈的纯策略纳什均衡是什么如果你是其中一个博弈方,你会要求什么数额,为什么8、设古诺模型中有n家厂商、qi 为厂商i的产量,Q=q1+…+qn 为市场总产量、P为市场出清价格,且已知P=P(Q)=a-Q(当Q<a时,否则P=0)。
博弈论第二章答案

nc + a a − c a−c a−c ⋅ −c⋅ = n +1 n +1 n +1 n +1
企业违背垄断产量时的各期利润:
n −1 (a − c ) − qi πi = a − qi − cqi 2n ∂π i (n − 1)(a − c) =a− − qi − q j − c = 0 ∂qi 2n n +1 (n + 1)a + (3n − 1)c (a − c), p = 4n 4n 2 (n + 1) 利润为 (a − c) 2 16n 2 ⇒ qi =
仅供参考! !
-4-
E-mail:beckham.23@
2
出) ,只要任何一方违背时,以后就转向阶段博弈的价格 pi = c 。 如一直使用垄断价格,则每个企业收益每期都一样为, π i = (a − c) / 8 如在t期某企业违背了战略, t+1期开始双方的收益相同都为0, 在t期它的最大收益为 ( a − c) / 4 (考虑此企业只是把价格边际上减少一点点,所有的利润都归它) ,如不违背则把以后无限期
一阶条件:
V ' ( I p − B) = kU 2' ( S + B) ,
反应函数满足:
−1 < dB* / dS = kU 2" /(−kU 2" − V " ) < 0 即,孩子储蓄减少,家
*
长给予更高的赠与。 接着最大化孩子的收益:给定反应函数 B ,来选 S:
MaxU1 ( I c − S ) + U 2 ( S + B* )
∂π i = a − ∑ qi − qi − c = 0 ∂qi a−c (i = 1,2,3 n) n +1
博弈论谢识予第四版第二章习题指南

博弈论谢识予第四版第二章习题指南下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!第一节博弈论基本概念。
1.1 博弈论的定义。
博弈论基础 习题2

博弈论基础 习题2【第四讲 完全信息动态博弈】1、 分别求下图所示的两个扩展式表述博弈的SPNE :2、 在历史上,卓文君与司马相如一见钟情,但是卓文君的父亲卓王孙却反对文君和相如在一起,于是有了以下版本的“文君当垆”博弈。
博弈由卓文君先行动,她有两个选择:与司马相如“私奔”(从而过着当垆卖酒的清贫生活)与“不私奔”。
如果选择不私奔,博弈结束,文君失去了如意郎君,其支付为1 ,而其父得到了他意愿的结果,其支付为1。
如果文君选择与司马相如私奔,那么在观察到文君的行动后轮到卓王孙行动,他有两个选择:“默许”与“断绝父女关系”。
如果默许,那么文君的支付为2,卓王孙的支付为0;如果选择了断绝关系,那么文君的支付为 1.5 ,卓王孙的支付为2 。
(1)画出这个动态博弈的博弈树;(2)将该博弈树用静态博弈的策略式支付矩阵表述出来,并利用划线法找出所有的纯策略纳什均衡;(3)那一(几)个均衡你认为是不合理的?为什么?找出这个动态博弈的SPNE3、 考虑如下的双寡头市场策略性投资模型:企业1和企业2目前的单位生产成本都是2c 。
企业1筹划引进一项新技术使单位生产成本降至1c ,但是该项技术需要的投资为f 。
第一阶段,企业1选择是否投资;第二阶段,企业2可以观察到企业1的投资决策,在企业1做出是否投资的决策之后,两个企业同时选择产量。
假定市场反需求函数为1214()p q q ,这里1q 、2q 分别是企业1、2选择的产量,p 是市场价格。
试问f 取什么值时,企业1将会投资引进新技术?【第五讲 多阶段博弈与重复博弈】1、 考虑第五讲课文中介绍的“囚徒困境-复仇”二阶段博弈。
请构建博弈双方的一个策略组合,使得第一阶段的行动选择(,)F m 能够作为一个SPNE 结果出现(贴现因子1 )。
2、 两个生产完全同质产品的厂商进行着价格博弈,若两个厂商都采用垄断价格(合作)则各自得到垄断利润的一半2m,一个厂商单独略微削价则可独得全部垄断利润m,恶性竞争(价格一直降到边际成本)则利润都为零。
博弈论 战略分析入门第二章课后题答案

Instructor’s Guide to Game Theory: A Nontechnical Introduction to theAnalysis of StrategyChapter 2. Games in Extensive and Normal Form1.Objectives and ConceptsThis chapter continues the discussion of the contrast between representation of games in extensive form and in normal form. A key concept here is that, as a matter of principle, any game can be represented in either form. The overall objective, then, is for the student to be able to take a game in one form and represent it in the other. But there are tricks to translating both ways, and these “tricks” are very important subsidiary objectives for this chapter:First, contingent strategies. For some games in extensive form, it is important that the strategies be expressed as contingent strategies. Failure to do this can lead to confusion, and this point is neglected in some texts. (I usually find it better not to offer horrible examples – since as certainly as I do, students give them back to me on quizzes, and explain that they were just doing what I said in class – and here it is right in their notes!) Contingency is itself an important concept, apart from its applications to Game Theory. It will be a new topic to many undergraduate students, and one that graduate students can use drill on. It leads on to a brief discussion of contingent planning. Applications of this concept are common in business but no less important in other fields related to decisions, such as military strategy, public policy, politics and law.Second, information sets. When decisions take place simultaneously, or one player is unaware of decisions already made by others, that player is in an informationset. In diagrams, this is represented by putting two or more branch points in the same oval. This is crucial in translating games like the Prisoner’s Dilemma into extensive form.Some of the games introduced in this chapter are important in themselves. In particular, the entry-retaliation game, in the first section, will recur in various forms again and again. Thus, clear understanding of this game should be another objective of the class.Accordingly, the key concepts areExtensive and normal form as alternative representations for any game.Contingent strategiesContingency planningInformation setsEntry and retaliation gamesCredibility of threatsmon Study ProblemsThe devil is in the details. It is pretty easy to memorize the definitions of contingent strategies but more difficult to apply them. It is probably enough, for this course, if the students are aware of the need for contingent strategies and don’t let it slip by – but (speaking for myself) I have to puzzle a lot over how to make the contingencies complete enough. Even in texts that do not neglect this concept, its application in practice is complicated and even simple examples can be demanding. (It belongs this close to the beginning of the book only because it is so basic for so many things that follow).Something similar seems to apply to information sets. Here, students seem usually to be able to recognize them when they see them (not without a certain number of false starts) but rarely take the initiative to use them when presented with new problems. Again, that level of mastery is generally sufficient for the course.Drawing both tables for normal form games and diagrams for games in extensive form can be challenging, but extensive form games are especially tricky for students who don’t happen to be up on drafting software. One of my students found an ingenious way to draw the diagrams in an Excel spreadsheet. It is shown in the answers to question 2.3.For Business StudentsHere, again, the business draw is pretty obvious, and leads off the chapter with a living–with-deregulation example.4.Class AgendaIn my undergraduate class, I show “A Beautiful Mind” the second week. This substitutes for one or more class hours – special arrangements are necessary as the movie runs nearly four hours. Discussion question: Does the Movie Nash give good advice in the bar? Answer – looks like not, since his proposals don’t correspond to a best response.However, these agendas do not assume that the movie has been shown.First hour:1)Quiz on earlier material2)Introductory presentation: Games in Normal and Extended Form•Assignments3)Discussion question: how can we make contingency plan for the emergence ofnew epidemics like SARS (which emerged in the spring of 2003)?Second Hour:1.Discussion of quiz and assignments2.Play a retaliation game in class. Handout follows:A Two-Part GameHere is a two-person game that is played in two stages. Each student will play each role. It works like this: player 1 chooses between two strategies: “aggressive” and “not aggressive.” If player 1 chooses “not aggressive,” then each player receives 3 GameBucks. If player 2 chooses “aggressive,” then player 2 must choose between “retaliate” and “accommodate.” If player 2 chooses “accommodate” then player 1 gets 5 GameBucks and player 2 gets 1 GameBuck. If player 2 chooses “retaliate,” then no-one gets any GameBucks.As player 1, you should fill in your name and your strategy choice below. The sheets will then be taken up and redistributed at random. You will receive a new sheet on which someone has already filled in the first stage choices. Fill in your name and your strategy choice or NA if your player 1 has chosen “not aggressive.”Player 1Student name ____________________________My strategy is (circle one)AggressiveNot aggressivePlayer 2Student name ____________________________My strategy is (circle one)RetaliateAccommodateNA3.Discussion: How could we represent this game in extended form? How aboutnormal form?Answers in handout on next page.Analysis of the Two-Part Agression-Retaliation Game120,05,13,3Player 2If player 1 is aggressive thenretaliate; if player 1 is not,then do nothing.If player 1 is aggressive thenaccommodate; if player 1 is not,then do nothing.aggressive0,05,1 Player1not3,33,35. Answers to Exercises and Discussion Questions1. Sibling Rivalry. Two sisters, Iris and Julia, are students at Nearby College, where all the classes are graded on the curve. Since they are the two best students and their class, each of the will top the curve unless they enroll in the same class. Iris and Julia each have to choose one more class this term, and each of them can choose between math and literature. They're both very good at math, but Iris is better at literature. Each wants to maximize her grade point average. The grade point averages are shown in the table below, which treats their friendly rivalry as a game in normal form.()Table E. 1. Grade Point Averages for Iris and JuliaIrismath litmath 3.7,3.8 4.0,4.0Julialit 3.8,4.0 3.7,4.0What are the strategies for this game? Express this game in extended form, assuming that the sisters make their decisions at the same time. Express this game in extended form, assuming that Iris makes her decision first, and Julia knows Iris's decision when she chooses her strategy.Suppose Iris doesn’t care what her own grade point average is, but she wants to maximize the difference between her grade point average and her sister's – just to show the little twerp up! (But Julia still wants to maximize her grade point average and is notconcerned about how her sister does.) Write the table for the game in normal form under this assumption, and redo the last three questions. What strategy will Iris choose if she chooses first?The strategies for Julia are to take Math or Lit, and the strategies for Iris are to take Math or Lit. Each sister will base her strategy on maximizing the absolute value of her GPA.Assuming the sisters make their decisions simultaneously, the extended form representation of the game is below:What will happen? Iris can assure herself of a 4.0 by choosing Lit, so probably that is what she will do. Anticipating that, Julia can get her 4.0 by choosing Math.This is the game in extended form assuming that Iris chooses first and Julia knows Iris’ DecisionWhat happens? Iris can now choose either strategy and be sure of her 4.0. If Iris chooses Math, Julia will choose Lit for 3.8 rather than 3.7. So we can no longer be sure that Iris will choose Lit.The New Game in Normal form is as followsIris MathLit Math3.7 , 0.14.0 , 0.0JuliaLit 3.8 , 0.2 3.7, 0.3Here is the game in extended form with simultaneous decisions:It is now pretty difficult to guess what will happen, since Iris will get the greater difference by competing directly with her sister and enrolling in whichever class her sister does, but Julia wants to do just the opposite – enroll in whatever class her sister does not. We will need some advanced analysis to figure out what will happen here!Here is the new game in extended form if Iris goes first:In this case we can do a little better. If Iris chooses Math then Julia will choose Lit – giving Iris a margin of 0.2. However, if Iris chooses Lit then Julia will choose Math, leaving Iris with 0.0. Therefore, Iris will choose Math and Julia will choose Lit.One thing we see from this example is that “little things mean a lot.” If some players are motivated by relative rather than absolute payoffs, it can make a difference; and if one player goes first rather than having both choose simultaneously, that, too, can make a difference.2. The Great Escape. A prisoner is trying to escape from jail. He can attempt to climb over the walls or dig a tunnel from the floor of his cell. The warden can prevent him from climbing by posting guards on the wall, and he can prevent the con from tunneling by staging regular inspections of the cells, but he has only enough guards to do one or the other, not both.What are the strategies and payoffs for this game? Express the payoffs in both non-numerical and numerical terms. Express this game in normal form. Express this game in extended form, assuming that the prisoner and the warden make their decisions at the same time. Express this game in extended form, assuming that the warden makes his decision first, and the prisoner knows the warden's decision when he chooses his strategy.There are two payoffs in the game depending on the player. For the prisoner, his payoff is freedom, or not getting caught by the guards while trying to escape. For the warden, his payoff is preventing the escape of the prisoner. The number “10” denotessuccess for the party, and “0” represents failure for the guards and a “-10” represents 10 more years in prison for the prisoner.If the prisoner were to attempt to climb the wall and the guards just happened to be protecting the wall, then the guards would be successful, receiving a “10” for their job well done and the prisoner receives 10 more years in jail for being caught trying to escape. However, if the prisoner were to dig a tunnel while the guards were protecting the wall, then the prisoner receives a “10” for success, or his freedom. The guards would receive a “0” for failing at their job.The strategies for the prisoner are dig or climb, while the strategies for the warden are to guard the walls or inspect the cells.Normal form:WardenProtect Wall Inspect Jail CellsClimb Wall-10,1010,0PrisonerDig Tunnel10,0-10,10Extended Form, Simultaneous decision:wall10,-10walltunnel0,10prisonerWardenwall0,10inspecttunnel10,-10Extended Form, Warden decides first:Wall10,-10wall prisonerTunnel0,10WardenWall0,10inspect prisonerTunnel10,-10Black WinsSince every move black can make leads to a move that can give red a win, red will win this game if both play their best strategies.4. It's good to be da Queen? Queen Elizabeth the First of England faced a difficult strategic problem. On the one hand, if she married, she would no longer have power since, under the customs of the time, her husband would assume all the power of a king. Elizabeth had seen how her father Henry treated several of his queens, with imprisonment or execution. On the other hand, if her nobles had known she would never marry and leave an heir to the throne, they would have seen rebellion as a lesser evil. That's why Liz kept her boyfriend Dudley on the string so long.Treat this problem as a game in which the players are Elizabeth and her nobles. What are their strategies? Express the game in both extensive and normal form. Are there any information sets?Queen Elizabeth’s objective is to retain her regal powers, while her nobles are interested in succeeding to the throne in the absence of what they considered a credible head of state. For the purposes of this game, a credible head of state is one that has regal powers and the potential to pass that credibility to an heir. Liz’s strategies are to marry or not marry and the nobles’ strategies are to rebel or not rebel.Payoffs are based on the following rationale: If Liz marries and the nobles rebel, their actions are completely unjustified and they lose their noble status in society. If she marries and they do not rebel, then everything happens as the world expects, causing no net change in the nobles’ status. However, by marrying, Liz loses her regal autonomy. Alternatively she might decide not to marry. If the nobles do not rebel, Liz keeps her autonomy and they keep their rank. If they do rebel, Liz loses her autonomy and the nobles all shift one position up the feudal ladder.The game is represented in both normal and extensive form below. An information set exists for Liz’s strategies because the nobles must decide to rebel or not without knowing whether Liz will ever marry or not.5. Nim strikes again. Translate the game of Nim (Chapter 1) from extensive to normal form.Nim in Normal FormAnnaTake one coin from top row Take onecoin from thesecond rowTake bothcoins fromsecond rowIf Anna takes one fromtop row, take one; ifAnna takes one from thesecond row, take onefrom the first row; ifAnna takes both coinsfrom the second row,take the remaining coinAnna wins Anna wins Barbara winsIf Anna takes one fromtop row, take one; ifAnna takes one from thesecond row, take onefrom the second row; ifAnna takes both coinsfrom the second row,take the remaining coinAnna wins Anna wins Barbara winsIf Anna takes one fromtop row, take two; ifAnna takes one from thesecond row, take one from the first row; if Anna takes both coins from the second row, take the remaining coin BarbarawinsAnna wins Barbara winsBarbaraIf Anna takes one fromtop row, take two; ifAnna takes one from thesecond row, take one from the second row; if Anna takes both coins from the second row, take the remaining coin BarbarawinsAnna wins Barbara winsNim in Normal Form with Numeric OutcomesAnnaTake one coin from toprowTake onecoin from thesecond rowTake bothcoins fromsecond rowIf Anna takes one from toprow, take one; if Anna takesone from the second row,take one from the first row;if Anna takes both coinsfrom the second row, takethe remaining coin-1,1-1,11,-1If Anna takes one from toprow, take one; if Anna takesone from the second row,take one from the secondrow; if Anna takes bothcoins from the second row,take the remaining coin-1,1-1,11,-1If Anna takes one from toprow, take two; if Anna takesone from the second row,take one from the first row; if Anna takes both coins from the second row, take the remaining coin 1,-1-1,11,-1BarbaraIf Anna takes one from toprow, take two; if Anna takesone from the second row,take one from the secondrow; if Anna takes bothcoins from the second row,take the remaining coin1,-1-1,11,-16. Quiz questionPlaced on the next page for convenience in copying and printing.Student name ____________________________Quiz – Game TheoryHere is a "tree diagram" of a game in extended form. The players are Joe (player J) and Irving (player I). Joe's strategies are "up " and "down," and Irving's strategies are "left" and "right."1)Write the payoff table to represent this game "in normal form."2)Explain what it means that Joe's decision's are shown in a single oval areaAnswer:Jleft rightup3,35,2Idown2,51,1The elongated oval is an information set, and it means that Joe does not know Irving’s decision when Joe makes his decision.2.21。
博弈论各章节课后习题答案 (1)
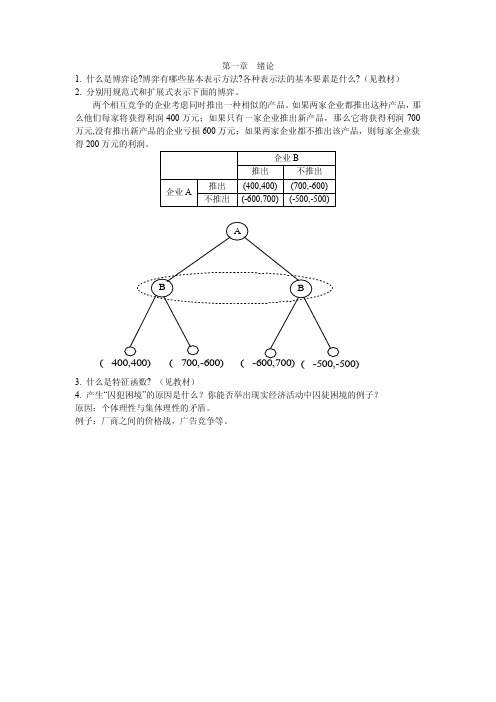
第一章绪论
1.什么是博弈论?博弈有哪些基本表示方法?各种表示法的基本要素是什么?(见教材)
2.分别用规范式和扩展式表示下面的博弈。
两个相互竞争的企业考虑同时推出一种相似的产品。
如果两家企业都推出这种产品,那么他们每家将获得利润400万元;如果只有一家企业推出新产品,那么它将获得利润700万元,没有推出新产品的企业亏损600万元;如果两家企业都不推出该产品,则每家企业获得200万元的利润。
3.什么是特征函数?(见教材)
4.产生“囚犯困境”的原因是什么?你能否举出现实经济活动中囚徒困境的例子?原因:个体理性与集体理性的矛盾。
例子:厂商之间的价格战,广告竞争等。
企业B
推出
不推出企业A 推出
(400,400)(700,-600)不推出(-600,700)(-500,-500)
(。
复旦大学博弈论第二章习题

问题1:设博弈方1和博弈方2就如何分10000元钱进行讨价还价。
假设确定了以下原则:双方提出自己要求的数额1s 和2s ,10000021≤≤s s ,。
如果,1000021≤+s s ,则两博弈方的要求都得到满足,即分得1s 和2s ;但如果1000021>+s s ,则该笔钱就被没收。
问该博弈的纯策略纳什均衡是什么?如果你是其中一个博弈方,你会选择什么数额,为什么?问题2:设古诺模型中有n 家厂商。
i q 为厂商i 的产量,n q q q Q +++= 21为市场总产量。
P 为市场出清价格,且已知Q a Q P P -==)((当a Q <时,否则0=P )。
假设厂商i 生产产量i q 的总成本为i i i i cq q C C ==)(,也就是说没有固定成本且各厂的边际成本都相同,为常数)(a c c <。
假设各厂同时选择产量,该模型的纳什均衡是什么?当趋向于无穷大时博弈分析是否仍然有效?问题3:两寡头古诺模型,Q a Q P P -==)(,但两个厂商的边际成本不同,分别为1c 和2c 。
如果2/0a c i <<,问纳什均衡产量各为多少?如果a c c <<21,但122c a c +>,则纳什均衡产量又为多少?问题4:如果双寡头垄断的市场需求函数是Q a Q P P -==)(,两个厂商都无固定成本边际成本为相同的常数c 。
如果两个厂商都只能要么生产垄断产量的一半,要么生产古诺产量。
证明:这是一个囚徒困境型的博弈。
问题5:两个厂商生产一种完全同质的商品,该商品的市场需求函数为P Q -=100,设厂商1和厂商2都没有固定成本。
若他们在相互知道对方边际成本的情况下,同时作出产量决策是分别生产20单位和30单位。
问这两个厂商的边际成本各是多少?各自的利润是多少?问题6:两个企业1、2各有一个工作空缺,企业i 的工资为i w ,并且121)2/1(w w w <<。
博弈论第二章习题

问题1:博弈方2就如何分10000元钱进行讨价还价。
假设确定了以下原则:双方提出自己要求的数额1s 和2s ,10000021≤≤s s ,。
如果设博弈方1和,1000021≤+s s ,则两博弈方的要求都得到满足,即分得1s 和2s ;但如果1000021>+s s ,则该笔钱就被没收。
问该博弈的纯策略纳什均衡是什么?如果你是其中一个博弈方,你会选择什么数额,为什么?解:112111210000()010000s s s u s s s ≤-⎧=⎨>-⎩,那么,1210000s s =-221222110000()010000s ss u s s s ≤-⎧=⎨>-⎩那么,2110000s s =-它们是同一条直线,1210000s s +=上的任意点12(,)s s ,都是本博弈的纯策略的Nash 均衡。
假如我是其中一个博弈方,我将选择15000s =元,因为(5000,5000)是比较公平和容易接受的。
它又是一个聚点均衡。
问题2:设古诺模型中有n 家厂商。
i q 为厂商i 的产量,n q q q Q +++= 21为市场总产量。
P 为市场出清价格,且已知Q a Q P P -==)((当a Q <时,否则0=P )。
假设厂商i 生产产量i q 的总成本为ii i i cq q C C ==)(,也就是说没有固定成本且各厂的边际成本都相同,为常数)(a c c <。
假设各厂同时选择产量,该模型的纳什均衡是什么?当趋向于无穷大时博弈分析是否仍然有效?解:1()ni i i j i j pq cq a c q q π==-=--∑,1,2,,i n =令20ii j j ii a c q q q π≠∂=---=∂∑,1,2,,i n =解得:***121na c q q q n -====+,2***121na c n πππ-⎛⎫==== ⎪+⎝⎭当n 趋向于无穷大时,这是一个完全竞争市场,上述博弈分析方法其实已经失效。
博弈论习题参考答案(2)

《博弈论》习题参考答案(第2次作业)一、选择题1.B2.C3.A4.A5.B6.ABCD7.C 8.B 9.C二、判断正误并说明理由1.F 上策均衡是比纳什均衡更严格的均衡概论2.T 上策均衡是比纳什均衡更严格的均衡概论3.T 博弈类型按局中人数多少分为单人博弈、双人博弈和多人博弈4.F 博弈双方偏好存在差异的条件下,一个博弈模型中可能存在2个纳什均衡,如性别战5.T 零和博弈指参与博弈各方在严格竞争下,一方收益等于另一方损失,博弈各方收益与损失之和恒为零,所以双方不存在合作可能性6.T 上策均衡是通过严格下策消去法(重复剔除下策)所得到的占优策略,只能有一个纳什均衡7.F 纳什均衡是上策的集合,指在给定的别人策略情况下,博弈方总是选择利益相对较大的策略,并不保证结果是最好的。
8.F 局中人总是以自己的利益最大化选择自己的策略,并不以对方收益的变化为目标9.T 纳什均衡是上策的集合,指在给定的别人策略情况下,没有人会改变自己的策略而减低自己的收益10.F 局中人总是以自己的利益最大化选择自己的策略,并不以对方收益的变化为目标11.F 局中人总是以自己的利益最大化选择自己的策略,并不以对方收益的变化为目标12.T 虽然斯塔格伯格模型各方利润总和小于古诺模型,但是领导者的利润比古诺模型时高三、计算与分析题1、 (1)画出A 、B 两企业的损益矩阵。
(2)求纯策略纳什均衡。
(做广告,做广告)2、画出两企业的损益矩阵求纳什均衡。
(1)画出A 、B 两企业的损益矩阵(2)求纳什均衡。
两个:(原价,原价),(涨价,涨价) 3、假定某博弈的报酬矩阵如下:甲乙 左 右 上 下(1)如果(上,左)是上策均衡,那么,a>?, b>?, g<?, f>? 答:a>e, b>d, f>h, g<c(2)如果(上,左)是纳什均衡,上述哪几个不等式必须满足? 答:a>e, b>d 4、答:(1)将这一市场用囚徒困境的博弈加以表示。
吉本斯《博弈论基础》课后习题答案

对 于 2 来 说 , 4(1− p*) = 2 p* + 3(1− p*) , 得 p* = 1/ 3 。
则 原 博 弈 的 混 合 战 略 纳 什 均 衡 为 : { (1/3, 2/3, 0), (2/3, 0, 1/3) }。 1.12 按 照 1.11 的 解 法 , 可 得 混 合 战 略 纳 什 均 衡 为 : { (2/3, 1/3), (3/4, 1/4) }。 过 程 略 。 1.13 此博弈有两个纯战略纳什均衡、一个混合战略纳什均衡。 纯 战 略 纳 什 均 衡 为 :( 向 企 业 1 申 请 , 向 企 业 2 申 请 );( 向 企 业 2 申 请 , 向 企 业 1 申 请 )。 混合战略纳什均衡为:
为:
qm/2
qc
qm/2
π1 , π1
π2 ,π3
qc
π3 ,π2
π4 ,π4
因 为 π1 < π3 , π 2 < π 4 , 所 以 每 一 方 都 有 一 个 严 格 劣 战 略 , 即 qm/2, 从 而 最 后 的 均 衡 为
博弈论课后习题

第一章导论1、什么是博弈?博弈论的主要研究内容是什么?2、设定一个博弈模型必须确定哪几个方面?3、举出烟草、餐饮、股市、房地产、广告、电视等行业的竞争中策略相互依存的例子。
4、“囚徒的困境”的内在根源是什么?举出现实中囚徒的困境的具体例子。
5、博弈有哪些分类方法,有哪些主要的类型?6、你正在考虑是否投资100万元开设一家饭店。
假设情况是这样的:你决定开,则0.35的概率你讲收益300万元(包括投资),而0.65的概率你将全部亏损;如果你不开,则你能保住本钱但也不会有利润,请你(a)用得益矩阵和扩展形式表示该博弈;(b)如果你是风险中性的,你会怎样选择?(c)如果你是风险规避的,且期望得益的折扣系数为0.9,你的策略选择是什么?(d)如果你是风险偏好的,期望得益折算系数为1.2,你的选择又是什么?7、一逃犯从关押他的监狱中逃走,一看守奉命追捕。
如果逃犯逃跑有两条可选择的路线,看守只要追捕方向正确就一定能抓住逃犯。
逃犯逃脱可以少坐10年牢,但一旦被抓住则要加刑10年;看守抓住逃犯能得到1000元奖金。
请分别用得益矩阵和扩展形式表示该博弈,并作简单分析。
第二章完全信息静态博弈1、上策均衡、严格下策反复消去法和纳什均衡相互之间的关系是什么?2、为什么说纳什均衡是博弈分析中最重要的概念?3、找出现实经济或生活中可以用帕累托上策均衡、风险上策均衡分析的例子。
4、多重纳什均衡是否会影响纳什均衡的一致预测性质,对博弈分析有什么不利影响?5、下面的得益矩阵表示两博弈方之间的一个静态博弈。
该博弈有没有纯策略纳什均衡?博弈的结果是什么?6、求出下图中得益矩阵所表示的博弈中的混合策略纳什均衡。
7、博弈方1和2就如何分10000元进行讨价还价。
假设确定了以下规则:双方同时提出自己要求的数额S1和S2,,如果s1+s2≤10000,则两博弈方的要求都得到满足,即分别得到s1和s2,但如果是s1+s2>10000,则该笔钱就被没收。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
问题1:博弈方2就如何分10000元钱进行讨价还价。
假设确定了以下原则:双方提出自己要求的数额1s 和2s ,10000021≤≤s s ,。
如果设博弈方1和,1000021≤+s s ,则两博弈方的要求都得到满足,即分得1s 和2s ;但如果1000021>+s s ,则该笔钱就被没收。
问该博弈的纯策略纳什均衡是什么?如果你是其中一个博弈方,你会选择什么数额,为什么?解:112111210000()010000s s s u s s s ≤-⎧=⎨>-⎩,那么,1210000s s =-221222110000()010000s ss u s s s ≤-⎧=⎨>-⎩那么,2110000s s =-它们是同一条直线,1210000s s +=上的任意点12(,)s s ,都是本博弈的纯策略的Nash 均衡。
假如我是其中一个博弈方,我将选择15000s =元,因为(5000,5000)是比较公平和容易接受的。
它又是一个聚点均衡。
问题2:设古诺模型中有n 家厂商。
i q 为厂商i 的产量,n q q q Q +++= 21为市场总产量。
P 为市场出清价格,且已知Q a Q P P -==)((当a Q <时,否则0=P )。
假设厂商i 生产产量i q 的总成本为ii i i cq q C C ==)(,也就是说没有固定成本且各厂的边际成本都相同,为常数)(a c c <。
假设各厂同时选择产量,该模型的纳什均衡是什么?当趋向于无穷大时博弈分析是否仍然有效?解:1()ni i i j i j pq cq a c q q π==-=--∑,1,2,,i n =令20ii j j ii a c q q q π≠∂=---=∂∑,1,2,,i n =解得:***121na c q q q n -====+,2***121na c n πππ-⎛⎫==== ⎪+⎝⎭当n 趋向于无穷大时,这是一个完全竞争市场,上述博弈分析方法其实已经失效。
问题3:两寡头古诺模型,Q a Q P P -==)(,但两个厂商的边际成本不同,分别为1c 和2c 。
如果2/0a c i <<,问纳什均衡产量各为多少?如果a c c <<21,但122c a c +>,则纳什均衡产量又为多少?解:双方的反应函数联立求解12112222q q a c q q a c +=-⎧⎨+=-⎩,解得:*112*2121(2)31(2)3q a c c q a c c ⎧=-+⎪⎪⎨⎪=+-⎪⎩当0/2i c a <<,就是这个博弈的Nash 均衡。
如果12c c a <<,但212c a c >+,当然可以推得*20q =。
那么厂商1就变成垄断商它的最佳产量当然是*12a c q -=,它的利润是:()2*14a c π-=。
问题4:如果双寡头垄断的市场需求函数是Q a Q P P -==)(,两个厂商都无固定成本边际成本为相同的常数c 。
如果两个厂商都只能要么生产垄断产量的一半,要么生产古诺产量。
证明:这是一个囚徒困境型的博弈。
解:古诺产量3a c -,垄断产量的一半4a c-,那么 ()iia c Q q π=--分别有四种情况:()29a c -,()28a c -,()2536a c -,()2548a c -问题5:两个厂商生产一种完全同质的商品,该商品的市场需求函数为P Q -=100,设厂商1和厂商2都没有固定成本。
若他们在相互知道对方边际成本的情况下,同时作出产量决策是分别生产20单位和30单位。
问这两个厂商的边际成本各是多少?各自的利润是多少?解:112111(100)q q q c q π=---,212222(100)q q q c q π=--- 令1112110020c q q q π∂=---=∂,2221210020c q q q π∂=---=∂ 代入**1220,30q q ==,所以:1230,20c c ==。
问题6:两个企业1、2各有一个工作空缺,企业i的工资为i w ,并且121)2/1(w w w <<。
设有两个工人同时决定申请这两个企业的工作,规定每个工人只能申请一份工作,如果一个企业的工作只有一个工人申请,该工人肯定能得到这份工作;但如果一个企业的工作同时有两个工人申请,则企业无偏向地随机选择一个工人,另一个工人则会因为错过向另一个企业申请的时机而失业(这时收益为0)。
该博弈的纳什均衡是什么?该博弈的结果有多少种可能性,各自的概率是多少?解:12122w w w w αβ-==+,2112211w w w w αβ--=-=+问题7:五户居民都可以在一个公共的池塘里放养鸭子。
每只鸭子的收益v 是鸭子总数N 的函数,并取决于N 是否超过某个临界值N ;如果N N <,收益N N v v -==50)(;如果N N ≥时,0)(≡N v 。
再假设每只鸭子的成本为2=c 元。
若所有居民同时决定养鸭的数量,问该博弈的纳什均衡是什么?问题7:i n 是第i 个农户养鸭子的数量,12345N n n n n n =++++,当N N <时,()2(50)2i i i i i u n v N n n N n =-=--,1,2,3,4,5i = 0,1,2,3,4,5iiu i n ∂==∂,那么 1234512345123451234512345248248248248248n n n n n n n n n n n n n n n n n n n nn n n n n ++++=⎧⎪++++=⎪⎪++++=⎨⎪++++=⎪++++=⎪⎩,那么*****123458n n n n n ===== (1)如果5840N >⨯=,则上述临界条件成立,五户居民每户养8只鸭子,就是该博弈的Nash均衡。
(2)如果40N≤,那么上述条件不成立,*****123455N n n n n n ⎡⎤=====⎢⎥⎣⎦解:有两个纯策略Nash 均衡。
(U ,R )和(D ,L ),但还有一个混合策略Nash 均衡。
,33⎛⎫ ⎪⎝⎭,,33⎛⎫⎪⎝⎭。
但效率不高,双方的期望收益都是143;不如(U ,L )的效率高,(U ,L )是Pearto 均衡。
应该设置一种机制,促使该Pearto 均衡实现。
问题9:三对夫妻的感情状态可以分别用下面三个得益矩阵对应的静态博弈来表示。
问:这三个博弈的纳什均衡分别是什么?这三对夫妻的感情状态究竟如何?9解:矩阵1有两个Nash 均衡(活着,活着),(死了,死了)和混合策略Nash 均衡,,2222⎛⎫⎛⎫↔⎪ ⎪⎝⎭⎝⎭。
两人的感情很好,同生死,共患难,极度恩爱,单独活着反而更加痛苦。
矩阵2有三个Nash 均衡,(活着,活着),(活着,死了),(死了,活着)。
说明两人感情恶化,生活很不幸福。
一方死了,另一方更好,但没有到相互不可容忍的地步。
这说明夫妻感情很不好,处于相当危险的状态。
矩阵3有两个Nash 均衡,(活着,死了),(死了,活着)。
达到你死我活、势不两立的程度。
这说明这对夫妻感情状态极度恶化,已经相互仇恨到了不共戴天的程度。
问题1:如果开金矿博弈中第三阶段乙选择打官司后的结果尚不能肯定,即下图中a 、b 数值不确定。
试讨论本博弈有哪几种可能的结果。
如果本博弈中的“威胁”和“承诺”是可信的,a 或b 应满足什么条件?①0a <,不借—不分—不打;②01a <<,且2b >,借—不分—打; ③1a >,且2b >,借—不分—打(,)a b ; ④0a >,且2b <,借—分—(2,2)问题2:三寡头市场需求函数Q P -=100,其中Q 是三个厂商的产量之和,并且已知三个厂商都有常数边际成本2而无固定成本。
如果厂商1和厂商2同时决定产量,厂商3根据厂商1和厂商2的产量决策,问它们各自的产量和利润是多少?1123111231(100)2(98)q q q q q q q q q π=----=--- 2123221232(100)2(98)q q q q q q q q q π=----=--- 3123331233(100)2(98)q q q q q q q q q π=----=--- 331230,(98)/2q q q q π∂=⇒=--∂代入,11212122(98)/2,(98)/2q q q q q q ππ=--=-- 12120,0q q ππ∂∂==∂∂,得***12398/3,49/3q q q ===***1234802/9,2401/9πππ===。
问题3:设两个博弈方之间的三阶段动态博弈如下图所示。
(1)若a 和b 分别等于100和150,该博弈的子博弈完美纳什均衡是什么?(2)T N L --是否可能成为该博弈的子博弈完美纳什均衡路径,为什么?(3)在什么情况下博弈方2会获得300单位或更高的得益?(a ,b )(0,4)(1)博弈方1在第一阶段选择R ,在第三阶段选择S ,博弈方2在第二阶段选择M 。
(2)不可能。
T N L --带来的利益50明显小于博弈方1在第一阶段R 的得益300;无论a和b 是什么数值,该路径都不能构成Nash 均衡,不能成为子博弈完美Nash 均衡。
(3)由于T N L --不是本博弈的子博弈完美Nash 均衡,因此博弈方2不可能通过该路径实现300单位的得益,唯一有可能实现300单位及以上的得益的路径为L N S --,要使该路径成为子博弈完美Nash 均衡而且博弈方2得到300单位及以上的得益必须300,300a b >≥。
问题4:企业甲和企业乙都是彩电制造商,都可以选择生产低档产品或高档产品,每个企业在四种不同的情况下的利润如以下得益矩阵所示。
如果企业甲先于企业乙进行产品选择并投入生产,即企业乙在决定产品时已经知道企业甲的选择,而且这一点双方都清楚。
(1)用扩展型表示这一博弈。
若甲选择低档,乙选择高档,那么甲得700元,乙得1000元, 所以:甲的策略为:选择生产高档产品;乙的策略是:若甲选择高档,乙选择低档;若甲选择低档,乙选择高档。
本博弈的子博弈Nash均衡是:甲选择生产高档彩电,乙选择生产低档彩电。
问题5:乙向甲索要1000元,并且威胁甲如果不给就与他同归于尽。
当然甲不一定相信乙的威胁。
请用扩展型表示该博弈,并找出纯策略纳什均衡和子博弈完美纳什均衡。
(a ,b )50,300两个纯策略Nash 均衡:(给,实施),(不给,不实施)实施的威胁不可信,甲在第一阶段选择不给,乙在第二阶段不实施(生命诚可贵);这是子博弈完美纳什均衡;另一个(给,实施)不可信。
