AStar算法解决野人渡河问题
A-star算法

A*算法
A* [1](A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法,也是许多其他问题的常用启发式算法。
注意——是最有效的直接搜索算法,之后涌现了很多预处理算法(如ALT,CH,HL等等),在线查询效率是A*算法的数千甚至上万倍。
公式表示为:f(n)=g(n)+h(n),
其中,f(n) 是从初始状态经由状态n到目标状态的代价估计,
g(n) 是在状态空间中从初始状态到状态n的实际代价,
h(n) 是从状态n到目标状态的最佳路径的估计代价。
(对于路径搜索问题,状态就是图中的节点,代价就是距离)
h(n)的选取
保证找到最短路径(最优解的)条件,关键在于估价函数f(n)的选取(或者说h(n)的选取)。
我们以d(n)表达状态n到目标状态的距离,那么h(n)的选取大致有如下三种情况:
1. 如果h(n)< d(n)到目标状态的实际距离,这种情况下,搜索的点数多,搜索
范围大,效率低。
但能得到最优解。
2. 如果h(n)=d(n),即距离估计h(n)等于最短距离,那么搜索将严格沿着最短路
径进行,此时的搜索效率是最高的。
3. 如果h(n)>d(n),搜索的点数少,搜索范围小,效率高,但不能保证得到最
优解。
[2]。
人工智能实验2传教士过河问题

人工智能实验报告班级:计研-12班学号:2012312120105 姓名:孔德星实验二知识表示方法1.实验目的(1)了解知识表示相关技术;(2)掌握问题规约法或者状态空间法的分析方法。
2.实验内容(2个实验内容可以选择1个实现)(1)梵塔问题实验。
熟悉和掌握问题规约法的原理、实质和规约过程;理解规约图的表示方法;(2)状态空间法实验。
从前有一条河,河的左岸有m个传教士、m个野人和一艘最多可乘n人的小船。
约定左岸,右岸和船上或者没有传教士,或者野人数量少于传教士,否则野人会把传教士吃掉。
搜索一条可使所有的野人和传教士安全渡到右岸的方案。
3.实验报告要求(1)简述实验原理及方法,并请给出程序设计流程图。
实验原理:假设开始时传教士、野人和船都在右岸,用数组(a,b,c)分别表示右岸传教士个数、右岸野人个数、船的位置,则可分为三种情况讨论:A、n>m/2。
此种情况下,先把所有的野人度过去,每次返回一个野人,当出现(m,0,0)情况时,返回m-n个野人(若m==n,返回1个野人)。
然后渡n个传教士,此时野人==传教士,然后返回一个野人和传教士,再开始最大限度的渡传教士,每次返回一个野人,最终直到a==b==c==0;B、n<=3&&n<=m/2 || n==1,显然此时无解;C、n>=4&&n<=m/2,此时只能每次传n/2个传教士和野人,每次返回一个野人和传教士,直到最终结果。
程序流程图:(2)源程序清单:本程序用C++语言编写。
#include"iostream"using namespace std;bool flag = false; //标记是否有解bool af = false; //标记a是否为0bool bf = false; //当b变为0后赋值为true;bool ef = false; //当a==b后赋值为truebool f = false; //判断n是否大于m/2int m;//传教士野人的个数int n;//船一次能装载的人数void mc(int a,int b,int c);int main(){cout<<"传教士与野人过河问题。
使用AStar算法实现自动寻路详解

使⽤AStar算法实现⾃动寻路详解@⽬录前些⽇⼦我有兄弟给我打电话,问我会不会⼈⼯智能,来实现⼀个机器⼈在仓库⾃动寻路的功能。
因为没有接触过这样的场景,但是⾃⼰⼜⽐较对此兴趣,所以就看了⼀些⾃动寻路的算法,⽐如:基于⼆叉树的深度优先遍历、D Star、A Star算法,其中我感觉A Star算法最好。
下⾯我给⼤家介绍⼀下,⾸次实现的语⾔是Java,但是Java不太直观,⼜不想使⽤Java的图形界⾯,所以就使⽤JS+HTML来实现的,⾸先展⽰⼀下效果图。
效果图如下:1、什么是A Start算法A*搜索算法是求出在⼀个⼆维平⾯中从起点到终点最低运算代价的算法,它可以算出A点到B点的最短距离,也就是最优路径。
常见的应有主要是在游戏中,⼈物的⾃动寻路;机器⼈探路;交通路线导航等。
2、A Star算法的原理和流程2.1 前提在讲述A Star算法之前,需要声明下列这些属性:(1)从起点开始扩散的节点;(2)最短距离计算公式:F = G + H;(3)欧⼏⾥得距离计算公式:p = $\sqrt (x_2 - x_1)^2+(y_2 - y_1)^2$(其实就是勾股定理);(4)OPENLIST 和 CLOSELIST;上⾯的属性和公式不懂没关系,下⾯我会对他们⼀⼀进⾏详细介绍。
⾮常简单!2.1.1 从起点开始扩散的节点我们在HTML页⾯上使⽤横和竖画出来的格⼦。
所谓扩散就是以起点为基点向上、下、左、右四个放向进⾏扩散,这些扩展的节点就是可以⾛的“路”。
如下图所⽰黄⾊的⽅格就是扩散的点:PS:A Star有四个⽅向和⼋个⽅向的扩散。
扩展四个⽅向的节点就是⽬前我们所说的;⼋个⽅向是还包含了,上左、上右、下左、下右四个⽅向的节点。
我们通篇使⽤的是四个⽅向的扩展。
2.1.2 最短距离计算公式:F = G + H如何在扩散的节点中找到最优也就是最短的⼀条路呢?就需要⽤到这个公式:F=G+H。
那么这个公式⾥⾯的属性都代表什么意识呢?下⾯我们就说明⼀下:(1)G:表⽰从起点到扩散的四个节点的距离,换句话说就是从起点到扩散的四个节点需要移动的格⼦。
人工智能:野人与修道士问题

野人与修道士问题(Missionaries-and-Cannibals Problem )[修道士与野人问题]:三个野人与三个传教士来到河边,打算乘一只船从右岸渡到左岸去,该船的最大负载能力为两个人。
在任何时候,如果野人人数超过传教士人数,那么野人就会把传教士吃掉。
用状态空间法表示修道士与野人问题并设计编写计算机程序求问题的解。
问题分析:从上图可知,修道士、野人和船一共有六种可能,M L 、C L 、B L 、M R 、C R 、B R 。
可以表示为q =(M ,C ,B ),其中m 表示修道士的数目(0、1、2、3)、c 表示野人的数目(0、1、2、3)、b 表示船在左岸(1)或右岸(0)。
1、定义状态的描述形式:(m ,c ,b )2、表示所有可能的状态,并确定初始状态集和目标状态集:s0(3,3,1) s8(1,3,1) s16(3,3,0) s24(1,3,0)s1(3,2,1) s9(1,2,1) s17(3,2,0) s25(1,2,0)s2(3,1,1) s10(1,1,1) s18(3,1,0) s26(1,1,0)s3(3,0,1) s11(1,0,1) s19(3,0,0) s27(1,0,0)s4(2,3,1) s12(0,3,1) s20(2,3,0) s28(0,3,0)s5(2,2,1) s13(0,2,1) s21(2,2,0) s29(0,2,0)s6(2,1,1) s14(0,1,1) s22(2,1,0) s30(0,1,0)s7(2,0,1) s15(0,0,1) s23(2,0,0) s31(0,0,0)初始状态:(3,3,1)目标状态:(0,0,0)3、定义算符:L ij :把i 个修道士,j 个野人从河的左岸送到右岸R ij :把i 个修道士,j 个野人从河的右岸送到左岸整个问题就抽象成了怎样从初始状态经中间的一系列状态达到目标状态。
问修道士M野 人C 左L 右R题状态的改变是通过划船渡河来引发的,所以合理的渡河操作就成了通常所说的算符,根据题目要求,可以得出以下5个算符(按照渡船方向的不同,也可以理解为10个算符):渡1野人、渡1牧师、渡1野人1牧师、渡2野人、渡2牧师即:L01或R01,L10或R10,L11或R11,L02或R02,L20或R204、状态空间图:5、设计编写计算机程序求问题的解:算法:在应用状态空间表示和搜索方法时,用(M,C,B)来表示状态描述,其中M和C分别表示在左岸的传教士与野人数。
人工智能过河问题算法深度优先算法&&A星算法

野人过河问题算法分析野人过河问题属于人工智能学科中的一个经典问题,问题描述如下:有三个牧师(也有的翻译为传教士)和三个野人过河,只有一条能装下两个人的船,在河的任何一方或者船上,如果野人的人数大于牧师的人数,那么牧师就会有危险. 你能不能找出一种安全的渡河方法呢?一、算法分析先来看看问题的初始状态和目标状态,假设和分为甲岸和乙岸:初始状态:甲岸,3野人,3牧师;乙岸,0野人,0牧师;船停在甲岸,船上有0个人;目标状态:甲岸,0野人,0牧师;乙岸,3野人,3牧师;船停在乙岸,船上有0个人;整个问题就抽象成了怎样从初始状态经中间的一系列状态达到目标状态。
问题状态的改变是通过划船渡河来引发的,所以合理的渡河操作就成了通常所说的算符,根据题目要求,可以得出以下5个算符(按照渡船方向的不同,也可以理解为10个算符):渡1野人、渡1牧师、渡1野人1牧师、渡2野人、渡2牧师算符知道以后,剩下的核心问题就是搜索方法了,本文采用深度优先搜索,通过一个FindNext(…)函数找出下一步可以进行的渡河操作中的最优操作,如果没有找到则返回其父节点,看看是否有其它兄弟节点可以扩展,然后用Process(…)函数递规调用FindNext(…),一级一级的向后扩展。
搜索中采用的一些规则如下:1、渡船优先规则:甲岸一次运走的人越多越好(即甲岸运多人优先),同时野人优先运走;乙岸一次运走的人越少越好(即乙岸运少人优先),同时牧师优先运走;2、不能重复上次渡船操作(通过链表中前一操作比较),避免进入死循环;3、任何时候河两边的野人和牧师数均分别大于等于0且小于等于3;4、由于只是找出最优解,所以当找到某一算符(当前最优先的)满足操作条件后,不再搜索其兄弟节点,而是直接载入链表。
5、若扩展某节点a的时候,没有找到合适的子节点,则从链表中返回节点a的父节点b,从上次已经选择了的算符之后的算符中找最优先的算符继续扩展b。
二、基本数据结构仔细阅读问题,可以发现有些基本东西我们必须把握,例如:每时刻河两岸野人牧师各自的数目、船的状态、整个问题状态。
A-STAR算法说明

序:搜索区域假设有人想从A点移动到一墙之隔的B点,如下图,绿色的是起点A,红色是终点B,蓝色方块是中间的墙。
[图1]你首先注意到,搜索区域被我们划分成了方形网格。
像这样,简化搜索区域,是寻路的第一步。
这一方法把搜索区域简化成了一个二维数组。
数组的每一个元素是网格的一个方块,方块被标记为可通过的和不可通过的。
路径被描述为从A到B我们经过的方块的集合。
一旦路径被找到,我们的人就从一个方格的中心走向另一个,直到到达目的地。
这些中点被称为“节点”。
当你阅读其他的寻路资料时,你将经常会看到人们讨论节点。
为什么不把他们描述为方格呢?因为有可能你的路径被分割成其他不是方格的结构。
他们完全可以是矩形,六角形,或者其他任意形状。
节点能够被放置在形状的任意位置-可以在中心,或者沿着边界,或其他什么地方。
我们使用这种系统,无论如何,因为它是最简单的。
开始搜索正如我们处理上图网格的方法,一旦搜索区域被转化为容易处理的节点,下一步就是去引导一次找到最短路径的搜索。
在A*寻路算法中,我们通过从点A开始,检查相邻方格的方式,向外扩展直到找到目标。
我们做如下操作开始搜索:1,从点A开始,并且把它作为待处理点存入一个“开启列表”。
开启列表就像一张购物清单。
尽管现在列表里只有一个元素,但以后就会多起来。
你的路径可能会通过它包含的方格,也可能不会。
基本上,这是一个待检查方格的列表。
2,寻找起点周围所有可到达或者可通过的方格,跳过有墙,水,或其他无法通过地形的方格。
也把他们加入开启列表。
为所有这些方格保存点A作为“父方格”。
当我们想描述路径的时候,父方格的资料是十分重要的。
后面会解释它的具体用途。
3,从开启列表中删除点A,把它加入到一个“关闭列表”,列表中保存所有不需要再次检查的方格。
在这一点,你应该形成如图的结构。
在图中,暗绿色方格是你起始方格的中心。
它被用浅蓝色描边,以表示它被加入到关闭列表中了。
所有的相邻格现在都在开启列表中,它们被用浅绿色描边。
astar算法 java模板

astar算法java模板astar算法java模板是一种用于解决寻路问题的常用算法,其基本思想是通过估算当前节点到终点的距离,并综合考虑已经走过的路径的代价,选择下一步路径中最有可能接近终点的节点。
本文将介绍astar算法的原理和步骤,并提供一份java模板代码。
一、astar算法原理astar算法是一种启发式搜索算法,通过估算当前节点到目标节点的最短路径长度,从而实现寻路的目标。
它在搜索过程中动态综合考虑已经走过的路径的代价和当前节点到目标节点的估算代价,并选择最有可能接近目标节点的路径进行搜索。
astar算法通过维护两个列表:open列表和closed列表。
open列表用于保存待扩展的节点,closed列表用于保存已经扩展过的节点。
在每一步中,从open列表中选择一个代价最小的节点,并将其加入到closed列表。
然后,对这个节点的邻居节点进行扩展,计算它们到目标节点的估算距离并加入open列表。
具体步骤如下:1. 初始化open列表和closed列表,将起始节点加入open列表。
2. 判断open列表是否为空,如果为空,则代表没有找到目标节点,寻路失败。
3. 从open列表中选择一个代价最小的节点,并将其从open列表移动到closed列表。
4. 判断当前节点是否为目标节点,如果是,则寻路成功,结束算法。
5. 否则,对当前节点的邻居节点进行扩展操作。
6. 对于每个邻居节点,计算它们到目标节点的估算距离,并更新它们的代价和父节点信息。
7. 将邻居节点加入open列表中。
8. 重复步骤3-7,直到找到目标节点或者open列表为空。
二、java模板代码下面是astar算法的java实现模板:javapublic class AStarAlgorithm {public static class Node {int x, y; 节点的坐标int f, g, h; f表示综合代价,g表示已走路径的代价,h表示到目标节点的估算代价Node parent; 父节点public Node(int x, int y) {this.x = x;this.y = y;}}public static List<Node> findPath(int[][] grid, Node start, Node end) {List<Node> openList = new ArrayList<>(); open列表List<Node> closedList = new ArrayList<>(); closed列表openList.add(start);while (!openList.isEmpty()) {Node currentNode = findLowestFScore(openList); 选择f值最小的节点openList.remove(currentNode);closedList.add(currentNode);if (currentNode == end) { 找到目标节点,寻路成功return reconstructPath(currentNode);}List<Node> neighbors = getNeighbors(grid, currentNode);for (Node neighbor : neighbors) {if (closedList.contains(neighbor)) {continue;}int tentativeGScore = currentNode.g + 1; 计算g 值if (!openList.contains(neighbor) tentativeGScore < neighbor.g) {neighbor.parent = currentNode;neighbor.g = tentativeGScore;neighbor.h = calculateHeuristic(neighbor, end);neighbor.f = neighbor.g + neighbor.h;if (!openList.contains(neighbor)) {openList.add(neighbor);}}}}return null; open列表为空,寻路失败}private static Node findLowestFScore(List<Node> openList) { Node lowestFScoreNode = openList.get(0);for (Node node : openList) {if (node.f < lowestFScoreNode.f) {lowestFScoreNode = node;}}return lowestFScoreNode;}private static List<Node> getNeighbors(int[][] grid, Node node) {List<Node> neighbors = new ArrayList<>();int[] dx = {-1, 0, 1, 0}; 上、右、下、左的顺序int[] dy = {0, 1, 0, -1};for (int i = 0; i < 4; i++) {int nx = node.x + dx[i];int ny = node.y + dy[i];if (isValidLocation(grid, nx, ny)) {neighbors.add(new Node(nx, ny));}}return neighbors;}private static boolean isValidLocation(int[][] grid, int x, int y) { int rows = grid.length;int cols = grid[0].length;return (x >= 0 && x < rows && y >= 0 && y < cols && grid[x][y] == 0);}private static int calculateHeuristic(Node node, Node end) { return Math.abs(node.x - end.x) + Math.abs(node.y - end.y);}private static List<Node> reconstructPath(Node currentNode) {List<Node> path = new ArrayList<>();path.add(currentNode);while (currentNode.parent != null) {path.add(currentNode.parent);currentNode = currentNode.parent;}Collections.reverse(path);return path;}public static void main(String[] args) {int[][] grid = {{0, 0, 1, 0, 0},{0, 0, 1, 0, 0},{0, 0, 0, 0, 0},{0, 0, 1, 0, 0},{0, 0, 1, 0, 0}};Node start = new Node(0, 0);Node end = new Node(4, 4);List<Node> path = findPath(grid, start, end);if (path != null) {for (Node node : path) {System.out.println("(" + node.x + ", " + node.y + ")");}} else {System.out.println("No path found.");}}}三、总结本文介绍了astar算法的原理和步骤,并提供了一份java模板代码。
传教士(牧师)与野人问题-模拟人工智能实验_CSDN博客_传教士与野人问题

传教士(牧师)与野人问题-模拟人工智能实验_结缘缘的博客-CSDN博客_传教士与野人问题题目有n个牧师和n个野人准备渡河但只有一条能容纳c个人的小船为了防止野人侵犯牧师要求无论在何处牧师的人数不得少于野人的人数(除非牧师人数为0) 且假定野人与牧师都会划船试设计一个算法确定他们能否渡过河去若能则给出小船来回次数最少的最佳方案。
实验步骤输入牧师人数(即野人人数) n 小船一次最多载人量c。
输出若问题无解则显示Failed 否则显示Successed输出所有可行方案并标注哪一组是最佳方案。
用三元组(X1, X2, X3)表示渡河过程中的状态。
并用箭头连接相邻状态以表示迁移过程初始状态- 中间状态- 目标状态。
例当输入n 2 c 2时输出221- 200- 211- 010- 021- 000 其中X1表示起始岸上的牧师人数X2表示起始岸上的野人人数X3表示小船现在位置(1表示起始岸0表示目的岸)。
要求写出算法的设计思想和源程序并有用户界面实现人机交互控制台或者窗口都可以进行输入和输出结果如Please input n: 2 Please input c: 2 Optimal Procedure: 221- 200- 211- 010- 021- 000Successed or Failed?: Successed实现代码#include stdio.h #include iostream #include stdlib.h using namespace std;struct State { int Lsavage; int Lgodfather; int Rsavage; int Rgodfather; int boat; //boat at left 0 ; boat at right struct State *States new State[150];struct routesave { int savage; int godfather;struct routesave* routesaves new routesave[150];int godfather, savage, boatnum;void init(State m) { cout 请输入野人和牧师的人数n 以及船的最大载量c endl; int n, c; cin n c; m.Rgodfather n; m.Rsavage n; godfather n, savage n; boatnum c; m.Lgodfather m.Lsavage 0; m.boat 1;void boaloading(int i, int s, int g) { //s个野人和g个传教士if (States[i].boat 0) { routesaves[i].savage s*-1; //左边到右边是负数个野人routesaves[i].godfather g * -1; //左边到右边负数个传教士States[i 1].LsavageStates[i].Lsavage - s; States[i 1].Lgodfather States[i].Lgodfather - g; States[i 1].Rsavage States[i].Rsavage s; States[i 1].Rgodfather States[i].Rgodfather g; States[i 1].boat 1; else{ routesaves[i].savage s; //右边到左边是正数个野人routesaves[i].godfather g; //右边到左边正数个传教士States[i 1].Rsavage States[i].Rsavage-s; States[i 1].RgodfatherStates[i].Rgodfather - g; States[i 1].Lsavage States[i].Lsavage s; States[i 1].Lgodfather States[i].Lgodfather g; States[i 1].boat0;bool checkState(State m) { if (m.Rgodfather 0 m.Rgodfather m.Rsavage) return false; if (m.Lgodfather 0 m.Lgodfatherm.Lsavage) return false; else return true;void showSolution(int i) { cout 问题解决解决路径为endl; for (int c 0; c i; c ) { if (routesaves[c].savage 0) cout 第c 1 步routesaves[c].savage 个野人和routesaves[c].godfather 个传教士乘船去左边endl; else cout 第c 1 步routesaves[c].savage * -1 个野人和routesaves[c].godfather * -1 个传教士乘船去有右边endl; void nextstep(int i) { int c; if (i 150) cout 试探路径过大无法计算; exit(0); for (c 0; c i; c ) /*if the current state is same to previous,retrospect*/ if (States[c].Lsavage States[i].Lsavage States[c].Lgodfather States[i].Lgodfather States[c].Rsavage States[i].Rsavage States[c].Rgodfather States[i].Rgodfather States[c].boat States[i].boat) goto a; if (States[i].Rsavage 0 States[i].Rgodfather 0 States[i].boat 0) { showSolution(i); exit(0); if (States[i].boat 1) { //船在右边for (int s 1; s boatnum s States[i].Rsavage; s ) {//g 0 int g 0; boaloading(i, s, g); if (checkState(States[i 1])) { nextstep(i 1); for (int g 1; g boatnum g States[i].Rgodfather; g ) { //g! 0 for (int s 0; s boatnum - g s States[i].Rsavage s g; s ) { boaloading(i, s, g); if(checkState(States[i 1])) { nextstep(i 1); if (States[i].boat 0) { //船在左边for (int s 1; s boatnum s States[i].Lsavage; s ) {//g 0int g 0; boaloading(i, s, g); if (checkState(States[i 1])) { nextstep(i 1); for (int g 1; g boatnum g States[i].Lgodfather; g ) { //g! 0 for (int s 0; s boatnum - g s States[i].Lsavage s g; s ) { boaloading(i, s, g); if (checkState(States[i 1])) { nextstep(i 1);a:return;void main() { init(States[0]); nextstep(0);实验结果展示。
《AStar算法详解》课件

谢谢观看
01
定义
优先队列是一种数据结构,允许根据特定优先级对元素进行排序和检索
。
02
作用
在A*算法中,优先队列用于存储待探索节点,并根据优先级顺序进行检
索。优先级通常基于节点到目标的实际距离和启发式函数的预估距离。
03
注意事项
优先队列的选择和实现方式对算法性能有较大影响,应选择高效的数据
结构和实现方式。
路径修复
《astar算法详解》ppt课件
目录
• A算法简介 • A算法的关键技术 • A算法的步骤和流程 • A算法的优缺点分析 • A算法的案例分析
01
A算法简介
A*算法的起源和背景
起源
A*算法最初由Anthony Stentz于 1944年提出,用于解决路径规划 问题。
背景
随着计算机技术的发展,A*算法 逐渐成为一种广泛应用于图形搜 索和路径规划领域的算法。
案例二:游戏AI路径规划
总结词
在游戏中,AI角色的行为需要合理规 划路径,以确保其能够高效地完成任 务或达到目标位置。A*算法为游戏开 发者提供了一种有效的路径规划工具 。
详细描述
在游戏AI路径规划中,A*算法可以帮助AI角 色找到从起点到终点的最佳路径。通过在游 戏地图上建立节点和边,A*算法能够考虑游 戏逻辑、障碍物和角色移动能力等因素,从 而生成符合游戏规则的合理路径。
05
A算法的案例分析
案例一:地图导航
总结词
地图导航是A*算法最常见的应用场景之一,通过使用A*算法,可以快速找到两 点之间的最短路径。
详细描述
在地图导航中,A*算法通常用于在道路网络中寻找两点之间的最短路径。通过 将地图中的道路和障碍物表示为图中的节点和边,A*算法能够综合考虑路径长 度和方向变化,从而找到最短且最直接的路径。
传教士和野人问题

传教士和野人问题(Missionaries and Cannibals)传教士和野人问题是一个经典的智力游戏问题。
在这个问题中,实际上隐含了这样一个条件:如果在河的某一岸只有野人,而没有传教士,也同样被认为是合法状态。
在具体书写某些条件时,为了简便,这一点有时并没有考虑,但我们默认这个条件是被考虑了的。
有N个传教士和N个野人来到河边准备渡河,河岸有一条船,每次至多可供k人乘渡。
问传教士为了安全起见,应如何规划摆渡方案,使得任何时刻,在河的两岸以及船上的野人数目总是不超过传教士的数目。
即求解传教士和野人从左岸全部摆渡到右岸的过程中,任何时刻满足M(传教士数)≥C (野人数)和M+C≤k的摆渡方案。
设N=3,k=2,则给定的问题可用图1.2表示,图中L和R表示左岸和右岸,B=1或0分别表示有船或无船。
约束条件是:两岸上M≥C,船上M+C≤2。
图1.2 M-C问题实例由于传教士和野人数是一个常数,所以知道了一岸的情况,另一岸的情况也就知道了。
因此为了简便起见,在描述问题时,只描述一岸--如左岸--的情况就可以了。
另外,该问题我们最关心的是在摆渡过程中,两岸状态的变化情况,因此船上的情况并不需要直接表达出来。
在一次摆渡过程中,船上究竟有几个传教士和野人,可以通过两个相连的状态简单得到。
这样表达更简练,突出了问题的重点。
(1)综合数据库:用三元组表示左岸的情况,即(,,),其中0≤,≤3,∈{0,1},其中表示在左岸的传教士人数,表示在左岸的野人数,=1表示船在左岸,=0表示船在右岸。
则此时问题描述可以简化为:(3,3,1)→(0,0,0)N=3的M-C问题,状态空间的总状态数为4×4×2=32,根据约束条件的要求,可以看出只有20个合法状态。
再进一步分析后,又发现有4个合法状态实际上是不可能达到的。
因此实际的问题空间仅由16个状态构成。
下表列出分析的结果:()(001)达不到(传教士()(000)均在右,船在左)(011)(021)(031)(101)不合法(右岸野人多)(111)(121)不合法(左岸野人多)(131)不合法(左岸野人多)(201)不合法(右岸野人多)(211)不合法(右岸野人多)(221)(231)不合法(左岸野人多)(301)达不到(311)(321)(331)(010)(020)(030)达不到(100)不合法(右岸野人多)(110)(120)不合法(左岸野人多)(130)不合法(左岸野人多)(200)不合法(右岸野人多)(210)不合法(右岸野人多)(230)不合法(右岸野人多)(300)(220)(310)(320)(330)达不到规则集可以划分为两组:一组是从左岸到右岸,称为p 操作,另一组是从右岸到左岸,称为q操作。
astar(a星)算法(精)

A*算法原理简介A*(A-Star)算法是一种静态路网中求解最短路最有A star算法在静态路网中的应用效的方法。
公式表示为: f(n)=g(n)+h(n),其中f(n) 是节点n从初始点到目标点的估价函数,g(n) 是在状态空间中从初始节点到n节点的实际代价,h(n)是从n到目标节点最佳路径的估计代价。
保证找到最短路径(最优解的)条件,关键在于估价函数h(n)的选取:估价值h(n)<= n到目标节点的距离实际值,这种情况下,搜索的点数多,搜索范围大,效率低。
但能得到最优解。
如果估价值>实际值, 搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。
估价值与实际值越接近估价函数取得就越好例如对于几何路网来说,可以取两节点间欧几理德距离(直线距离)做为估价值,即f=g(n)+sqrt((dx-nx)*(dx-nx)+(dy-ny)*(dy-ny));这样估价函数f在g值一定的情况下,会或多或少的受估价值h的制约,节点距目标点近,h值小,f值相对就小,能保证最短路的搜索向终点的方向进行。
明显优于Dijstra算法的毫无无方向的向四周搜索。
conditions of heuristicOptimistic (must be less than or equal to the real cost)As close to the real cost as possible详细内容主要搜索过程伪代码如下:创建两个表,OPEN表保存所有已生成而未考察的节点,CLOSED表中记录已访问过的节点。
算起点的估价值;将起点放入OPEN表;while(OPEN!=NULL){从OPEN表中取估价值f最小的节点n;if(n节点==目标节点){break;}for(当前节点n 的每个子节点X){算X的估价值;if(X in OPEN){if( X的估价值小于OPEN表的估价值 ){把n设置为X的父亲;更新OPEN表中的估价值; //取最小路径的估价值}}if(X inCLOSE) {if( X的估价值小于CLOSE表的估价值 ){把n设置为X的父亲;更新CLOSE表中的估价值;把X节点放入OPEN //取最小路径的估价值}}if(X not inboth){把n设置为X的父亲;求X的估价值;并将X插入OPEN表中; //还没有排序}}//end for将n节点插入CLOSE表中;按照估价值将OPEN表中的节点排序; //实际上是比较OPEN表内节点f的大小,从最小路径的节点向下进行。
navigation中的astar算法

navigation中的astar算法
A*算法是一种常用的图搜索算法,用于在图中找到两个节点之间的最短路径。
它通过综合考虑节点的实际代价和启发式估计值来选择下一个要搜索的节点。
在导航中,A*算法可以用于寻找从起点到终点的最短路径。
它将地图表示为一个图,节点表示地图上的位置,边表示位置之间的连接。
每个节点都有一个与其关联的代价,表示从起点到该节点的实际代价。
而启发式估计值则用于估计从当前节点到终点的估计代价。
A*算法的基本思想是按照启发式估计值优先的顺序来搜索节点,直到找到终点或者搜索完所有可能的节点。
具体步骤如下:
1. 创建一个优先级队列来存储待搜索的节点,初始时将起点加入队列。
2. 初始化每个节点的实际代价为无穷大,起点的实际代价为0。
3. 初始化每个节点的启发式估计值为从该节点到终点的估计距离。
4. 从队列中取出具有最小实际代价和启发式估计值的节点。
5. 如果取出的节点是终点,则搜索结束,找到了最短路径。
6. 否则,将该节点标记为已访问,并遍历其所有相邻的节点。
7. 对于每个相邻节点,计算从起点经过当前节点到该节点的实际代价,并更新其实际代价和启发式估计值。
8. 将更新后的相邻节点加入队列中,并继续下一次循环。
A*算法通过综合考虑实际代价和启发式估计值,能够有效地搜索到最短路径。
但是,启发式估计值的质量会直接影响算法的性能和结果,因此选择合适的启发式函数是使用A*算法的关键。
传教士和野人问题

状态空间法详解传教士和野人问题传教士和野人问题(The Missionaries and Cannibals Problem)在河的左岸有三个传教士、一条船和三个野人,传教士们想用这条船将所有的成员都运过河去,但是受到以下条件的限制:①教士和野人都会划船,但船一次最多只能装运两个;②②在任何岸边野人数目都不得超过传教士,否则传教士就会遭遇危险:被野人攻击甚至被吃掉。
此外,假定野人会服从任何一种过河安排,试规划出一个确保全部成员安全过河的计划。
(1)设定状态变量及确定值域。
为了建立这个问题的状态空间,设左岸传教士数为m,则m ={0,1,2,3};对应右岸的传教士数为3-m;左岸的野人数为c,则有c ={0,1,2,3};对应右岸野人数为3-c;左岸船数为b,故又有b={0,1},右岸的船数为1-b.(2)确定状态组,分别列出初始状态集和目标状态集。
问题的状态可以用一个三元数组来描述,以左岸的状态来标记,即Sk =(m,c,b),右岸的状态可以不必标出。
初始状态一个:S0 =(3,3,1),初始状态表示全部成员在河的左岸;目标状态也只一个:Sg =(0,0,0),表示全部成员从河左岸渡河完毕。
(3)定义并确定操作集。
仍然以河的左岸为基点来考虑,把船从左岸划向右岸定义为Pij操作。
其中,第一下标i表示船载的传教士数, 第二下标j表示船载的野人数;同理,从右岸将船划回左岸称之为Qij 操作,下标的定义同前。
则共有10种操作,操作集为F={P01,P10,P11,P02,P20,Q01,Q10,Q11,Q02,Q20}(4)估计全部的状态空间数,并尽可能列出全部的状态空间或予以描述之。
在这个问题世界中,S0 =(3,3,1)为初始状态,S31 = Sg =(0,0,0)为目标状态。
全部的可能状态共有32个,如表所示。
表1 传教士和野人问题的全部可能状态注意:按题目规定条件,应划去非法状态,从而加快搜索效率。
《AStar算法详解》课件

AStar算法的应用实践
AStar算法在游戏中的应用
在游戏中,AStar算法被广泛用于实现自动行走和角色 动画平滑移动。
AStar算法在路径规划中的应用
在寻找城市中特定地点的最短路径等问题上,AStar算 法能够帮助我们找到最佳解决方案。
未来,我们可以看到更多的AStar变体出现,以处理更复杂的场景,并开发更多用于自学 习和重用的模型。
3 应用前景和展望
随着机器人模型的批量生产和自主驾驶汽车的普及,AStar算法将有很大的应用前景。我 们可以期待AStar的进一步改进和高效应用。
AStar算法的改进
算法名称 加权AStar算法 IDAStar算法 迭代加深AStar算法 结合其他算法的AStar算法
改进方法 在计算代价时考虑一些额外的因素,例如地形难度, 以此来提高路径的准确性。 基于DFS算法,将AStar算法转化为迭代加深搜索。这 个算法可以有效地解决内存不足的问题。 类似于IDAStar,但是它每次迭代的深度都是动态的。
应用场景
AStar算法在许多领域都有广泛 的应用,例如:游戏制作、机 器人自主导航、自动驾驶等。 可以应用于任何需要进行路径 规划的领域。
算法思想
AStar算法采用启发式函数来评 估每个搜索状态的价值,其中 评估价值的启发式函数包括已 花费的代价和剩余的代价。它 在搜索过程中扩展代价最小的 节点,目标是找到代价最小的 路径。
AStar算法在自动驾驶中的应用
自动驾驶汽车需要一种高效的路线规划算法,以使它
AStar算法在其他领域的应用
除了游戏、自动驾驶和路径规划之外,AStar算法还在
Astar算法

若附加值=启发函数h,A* 搜索的点会变少。
另一种附加函数是当前点到起点和终点的向量 的叉积的模。这种附加函数在没有障碍物时很 好,不过在有障碍物时看上去比较奇怪(但仍 是对的)。
OPEN = priority queue containing START CLOSED = empty set while lowest rank in OPEN is not the GOAL: current = remove lowest rank item from OPEN add current to CLOSED for neighbors of current: cost = g(current) + movementcost(current, neighbor) if neighbor in OPEN and cost less than g(neighbor): remove neighbor from OPEN, because new path is better if neighbor in CLOSED and cost less than g(neighbor):(shouldn’t happen) remove neighbor from CLOSED if neighbor not in OPEN and neighbor not in CLOSED: set g(neighbor) to cost add neighbor to OPEN set priority queue rank to g(neighbor) + h(neighbor) set neighbor's parent to current
人工智能+野人传教士过河问题c程序+深度优先

open[top].m=M;
open[top].c=C;
open[top].s=S;
open[top].f=0;
open[top].pre=0;
inist();
find(pHead);
system("PAUSE");
{
flag=0;
break;
}
pTemp=pTemp->pre;
}
if(flag)
{
j++;
boatState[j].m = m;
boatState[j].c = c;
}
}
}
}
//*******************************************************************************
int goal(struct state * p) //判断当前状态是否目标状态
{
if(p->m==0&&p->c==0&&p->s==1) return 1;
else return 0;
}
//******************************************************************************
//初始状态:左岸,3野人,3牧师;
// 右岸,0野人,0牧师;
// 船停在左岸,船上有0个人
//目标状态:左岸,0野人,0牧师;
// 右岸,3野人,3牧师;
// 船停在右岸,船上有0个人;
AStar算法介绍
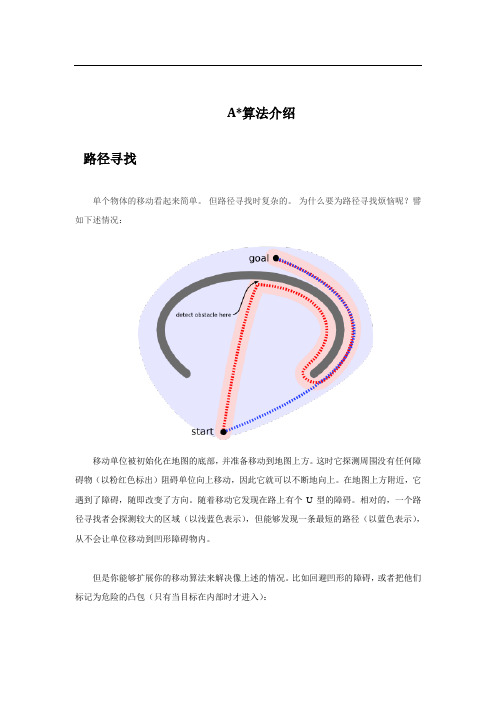
A*算法介绍路径寻找单个物体的移动看起来简单。
但路径寻找时复杂的。
为什么要为路径寻找烦恼呢?譬如下述情况:移动单位被初始化在地图的底部,并准备移动到地图上方。
这时它探测周围没有任何障碍物(以粉红色标出)阻碍单位向上移动,因此它就可以不断地向上。
在地图上方附近,它遇到了障碍,随即改变了方向。
随着移动它发现在路上有个U型的障碍。
相对的,一个路径寻找者会探测较大的区域(以浅蓝色表示),但能够发现一条最短的路径(以蓝色表示),从不会让单位移动到凹形障碍物内。
但是你能够扩展你的移动算法来解决像上述的情况。
比如回避凹形的障碍,或者把他们标记为危险的凸包(只有当目标在内部时才进入):路径寻找者让你向前看并做出计划,而不是等待直到最后发现了问题。
路径寻找者的制定计划和移动反应算法之间有一个权衡。
制定计划常常是缓慢的,但是能够得到更好的结果;而移动一般比较快,但可能会被阻塞。
如果游戏世界是不断变化的时候,那么在一开始制定计划只有较少的价值。
我建议同时使用他们:路径寻找应对大地图,缓慢变化的障碍和长路径;而移动应对当前区域,快速的变化和短路径。
算法在计算机科学教科书中,路径寻找算法在数学上的意义是一个用边连接起来的顶点集合。
砖块游戏地图能够被看做一个图,其中每个砖块为一个顶点,相邻的砖块之间由一条边连接:现在,我假定我们使用二维的网格。
后面,我们会讨论怎么建立其他类型的图来表示你的游戏世界。
来自AI或算法研究的大多数的路径寻找算法是为任意图设计的而不是基于网格的游戏。
我们想要找到一些有利于网格地图的算法。
有些我们认为是常识的事情,算法却不明白。
例如,关于方向,我们知道一般情况下,两个物体越远,那么从一个移动到另一个所花费的时间就越长;并且没有任何秘密的虫洞能让你到地图上从一个点传送的另一个点。
(嗯,我们假设没有;如果有,那么找到一条好的路径会变得很困难,应为你不知道从哪里看起。
)Dijkstra的算法和最佳优先搜索Dijkstra算法以对象的起始点作为访问图的开始节点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江南大学物联网工程学院实验报告
课程名称人工智能实验名称A*算法解决8数码问题实验日期2018.3.20
班级计科1501 姓名周启航学号1030415127
一、实验目的:
问题描述:设有3个传教士和3个野人来到河边,打算乘一只船从左岸渡到右岸去。
该船的负载能力为两人。
在任何时候,如果野人人数超过传教士人数,那么野人就会把传教士吃掉。
他们怎样才能用这条船安全地把所有人都渡河过去?试采用A*算法编一程序实现这一搜索过程。
二、算法描述:
1.状态描述
以河岸左边传教士的数目M,野人的数目C,船是否在B作为一个三元组作为一个状态即(M,C,B)。
2.启发函数设计
以现在的状态到目的状态所需的最少步数作为启发函数,即为h()=M+C-2*B。
3.规则的判断条件
岸边传教士不能少于野人个数,即M>=C,或者M=0,船在左岸时B=1。
4.算法流程图
5.核心代码
操作算子:
void Astar() {
while(!Q.empty()) Q.pop();
PathNode.clear();
memset(st, -1, sizeof(st));
PathNode.push_back(Node(M, C, B, 0, -1));
Q.push(AstarNode(0, PathNode[0]));
st[M][C][B] = 0;
int m, c, b, flag, id;
while(!Q.empty()) {
AstarNode as = Q.top(); Q.pop();
//printf("----%d %d %d %d %d----\n", as.f, as.g, as.node.m, as.node.c, as.node.b);
if(as.node.m == 0 && as.node.c == 0) {
printf("渡河方案如下:\n");
printf(" (M, C, B)\n");
printPath(as.node.id);
printf("可以安全渡河,来回最少需%d 次便可!\n", as.g);
Safe = true;
return;
}
if(as.node.b == 1) flag = -1;
else flag = 1;
b = 1 - as.node.b;
id = PathNode.size() - 1;
for(int i = 0; i < 5; ++i) {
m = as.node.m + flag * add[i][0];
c = as.node.c + flag * add[i][1];
if(OK(m, c, b)) {
++id;
st[m][c][b] = as.g + 1;
PathNode.push_back(Node(m, c, b, id, as.node.id));
Q.push(AstarNode(as.g + 1, PathNode[id]));
}
}
}
}
主函数:
int main(int argc, char *argv[]) {
int i=3;
M = C = i; B = 1; K = 2;
printf("M(修道士) = %d 人, C(野人) = %d 人, K(限乘) = %d 人, B(船) = %d条.\n", M, C, K, B);
Safe = false; Astar();
if(!Safe) {
printf("没有方案可以安全渡河!!!\n");
}
putchar(10);
return 0;
}
三、实验结果:
四、实验心得:
这次实验还是设计A*算法,整体的结构设计和上次没什么太大的出入,所以并没有什么困难的地方。
只要找准状态设计和启发函数就问题不大了。
教师评价优良中及
格不
及
格
教师
签名
日
期。
