贪心算法解活动安排实验报告
算法分析与设计实验报告 实验5:贪心算法的应用

sort(d,d+n,cmp);//按纵坐标升序排列 last=d[0].r;//记录当前线段被覆盖的最大坐标值
for(int i=1;i<n;i++) { if(d[i].l<=last && d[i].r>=last)//线段 d[i]的右坐标在 last 之后, 左坐标在 Last 之前的情况,即产生了覆盖。此时还要更新 last 坐标
} cout<<n.substr(0,l-s+x)<<endl;//只打印剩下的左边 l-(s-x)个数字 } return 0; } 2. #include<iostream> #include<cstdio> #include <algorithm> using namespace std; struct point {
课程实验报告
课程名称 算法分析与设计 班级 计算 161 实验日期
姓名
何严鸿
学号 20160701 实验成绩 9
实验名称
实验 5:贪心算法的应用
实
1.理解贪心算法的概念;
验
目
2.掌握贪心算法的基本思想。
的
及
要
求
实
操作系统:Windows
验
环
IDE:Visual C++
境
(1)删数问题
2018/5/06
{
length=d[i].r-d[i-1].l; last=d[i].r; } else if (d[i].r<=last) //线段 d[i]的右坐标在 last 之内,不产生覆盖 continue; else if (d[i].l>=last) //线段 d[i]的左坐标在 Last 之后,此时 last 之后的部分不会对之前的部分产生影响,更新 last 坐标。length 的值加上之 前的部分 { last=d[i-1].r; length=length+d[i].r-d[i].l; } } cout<<last<<endl; return 0; }
贪心算法 实验报告

贪心算法实验报告贪心算法实验报告引言:贪心算法是一种常用的算法设计策略,它通常用于求解最优化问题。
贪心算法的核心思想是在每一步选择中都选择当前最优的解,从而希望最终能够得到全局最优解。
本实验旨在通过实际案例的研究,探索贪心算法的应用和效果。
一、贪心算法的基本原理贪心算法的基本原理是每一步都选择当前最优解,而不考虑整体的最优解。
这种贪婪的选择策略通常是基于局部最优性的假设,即当前的选择对于后续步骤的选择没有影响。
贪心算法的优点是简单高效,但也存在一定的局限性。
二、实验案例:零钱兑换问题在本实验中,我们以零钱兑换问题为例,来说明贪心算法的应用。
问题描述:假设有不同面值的硬币,如1元、5元、10元、50元和100元,现在需要支付给客户x元,如何用最少的硬币数完成支付?解决思路:贪心算法可以通过每次选择当前面值最大的硬币来求解。
具体步骤如下:1. 初始化一个空的硬币集合,用于存放选出的硬币。
2. 从面值最大的硬币开始,如果当前硬币的面值小于等于待支付金额,则将该硬币放入集合中,并将待支付金额减去该硬币的面值。
3. 重复步骤2,直到待支付金额为0。
实验过程:以支付金额为36元为例,我们可以通过贪心算法求解最少硬币数。
首先,面值最大的硬币为100元,但36元不足以支付100元硬币,因此我们选择50元硬币。
此时,剩余待支付金额为36-50=-14元。
接下来,面值最大的硬币为50元,但待支付金额为负数,因此我们选择下一个面值最大的硬币,即10元硬币。
此时,剩余待支付金额为-14-10=-24元。
继续选择10元硬币,剩余待支付金额为-24-10=-34元。
再次选择10元硬币,剩余待支付金额为-34-10=-44元。
最后,选择5元硬币,剩余待支付金额为-44-5=-49元。
由于待支付金额已经为负数,我们无法继续选择硬币。
此时,集合中的硬币数为1个50元和3个10元,总共4个硬币。
实验结果:通过贪心算法,我们得到了36元支付所需的最少硬币数为4个。
贪心算法实验报告心得

贪心算法实验报告心得前言贪心算法是一种常见且重要的算法设计思想,通过每一步都选择当下最优的解决方案,以期望最终得到全局最优解。
在学习与实践贪心算法的过程中,我有了许多心得与体会。
什么是贪心算法?贪心算法是一种求解问题的算法思想,它的特点是每一步都选择当前最优的解决方案,而不考虑该选择对以后步骤的影响。
贪心算法通常适用于可以将问题分解为若干个子问题,并且通过每次选择当前最优解来得到整体最优解的情况。
贪心算法的基本步骤贪心算法的基本步骤可以总结为以下几个方面:1.确定问题的解空间,并找到问题的最优解。
贪心算法通常通过穷举法或者利用问题的特殊性质来确定解空间。
2.制定贪心策略。
贪心算法的核心是确定每一步选择的贪心策略,即选择当前最优解。
3.确定贪心策略的正确性。
贪心算法的一个关键问题是如何证明贪心策略的正确性。
可以通过数学证明、反证法或者举反例等方式来进行证明。
4.实现贪心算法。
将贪心策略转化为实际可执行的算法步骤,编写代码来求解问题。
贪心算法实验结果分析在本次实验中,我使用贪心算法解决了一个经典问题:找零钱问题(Change-Making Problem)。
给定一定面额的硬币和需找的金额,我们的目标是使用最少的硬币来完成找零钱。
贪心算法的思路是每次选择面额最大的硬币进行找零。
实验设计1.实验输入:我设计了多组输入来测试贪心算法的性能。
每组输入包括一个需找的金额和一个硬币集合。
2.实验输出:对于每组输入,贪心算法输出一个最优的硬币找零方案,以及使用的硬币数量。
3.实验评价:我使用了实际需找金额与贪心算法计算得到的找零金额的差值来评估算法的准确性,并统计了算法的时间复杂度。
实验结果从多组实验结果中可以观察到,贪心算法在大部分情况下给出了正确的找零金额,并且算法的时间复杂度较低。
结果分析贪心算法在找零钱问题中的应用是合理的。
每次选择面额最大的硬币进行找零,可以快速接近最优解,并且相对其他算法具有较低的时间复杂度。
算法课设实验报告(3篇)

第1篇一、实验背景与目的随着计算机技术的飞速发展,算法在计算机科学中扮演着至关重要的角色。
为了加深对算法设计与分析的理解,提高实际应用能力,本实验课程设计旨在通过实际操作,让学生掌握算法设计与分析的基本方法,学会运用所学知识解决实际问题。
二、实验内容与步骤本次实验共分为三个部分,分别为排序算法、贪心算法和动态规划算法的设计与实现。
1. 排序算法(1)实验目的:熟悉常见的排序算法,理解其原理,比较其优缺点,并实现至少三种排序算法。
(2)实验内容:- 实现冒泡排序、快速排序和归并排序三种算法。
- 对每种算法进行时间复杂度和空间复杂度的分析。
- 编写测试程序,对算法进行性能测试,比较不同算法的优劣。
(3)实验步骤:- 分析冒泡排序、快速排序和归并排序的原理。
- 编写三种排序算法的代码。
- 分析代码的时间复杂度和空间复杂度。
- 编写测试程序,生成随机测试数据,测试三种算法的性能。
- 比较三种算法的运行时间和内存占用。
2. 贪心算法(1)实验目的:理解贪心算法的基本思想,掌握贪心算法的解题步骤,并实现一个贪心算法问题。
(2)实验内容:- 实现一个贪心算法问题,如活动选择问题。
- 分析贪心算法的正确性,并证明其最优性。
(3)实验步骤:- 分析活动选择问题的贪心策略。
- 编写贪心算法的代码。
- 分析贪心算法的正确性,并证明其最优性。
- 编写测试程序,验证贪心算法的正确性。
3. 动态规划算法(1)实验目的:理解动态规划算法的基本思想,掌握动态规划算法的解题步骤,并实现一个动态规划算法问题。
(2)实验内容:- 实现一个动态规划算法问题,如背包问题。
- 分析动态规划算法的正确性,并证明其最优性。
(3)实验步骤:- 分析背包问题的动态规划策略。
- 编写动态规划算法的代码。
- 分析动态规划算法的正确性,并证明其最优性。
- 编写测试程序,验证动态规划算法的正确性。
三、实验结果与分析1. 排序算法实验结果:- 冒泡排序:时间复杂度O(n^2),空间复杂度O(1)。
贪心算法背包问题

题目:贪心算法
背包问题
专业:JAVA 技术 09——02 班 学号:540913100201 姓名:柏顺顺 指导老师:宋胜利
实验三:贪心算法
一、实验目的与要求
1、掌握背包问题的算法 2、初步掌握贪心算法
背包问题
二、实验题:
问题描述:与 0-1 背包问题相似,给定 n 种物品和一个背包。物品 i 的重量是 wi,其价 值为 vi,背包的容量为 c。与 0-1 背包问题不同的是,在选择物品 i 装入背包时,背包问题 的解决可以选择物品 i 的一部分,而不一定要全部装入背包,1< i < n。
JOptionPane.showMessageDialog(null, "重量不能为空!"); return; } else{ if (s1.equals("")){ JOptionPane.showMessageDialog(null, "效益值不能为空!"); return; }else { if (s3.equals("")) JOptionPane.showMessageDialog(null, "总重量不能为空!"); return; } } } catch (Exception e3) { // TODO: handle exception }
}
//可以执行贪心算法了 int [] wCopy = new int [w.length]; int [] pCopy = new int [w.length]; float temp2; int temp1; float totalx=0; float [] x = new float [w.length];//效益和重量的比值 float [] n =new float[w.length];//记录个数 float [] nCopy = new float[w.length]; for(int i=0;i<w.length;i++) { wCopy [i] = w[i]; pCopy [i] = p[i]; } for (int i=0;i<w.length;i++) x[i] = (float) ((p[i]*1.0)/w[i]); for(int i= 0;i<w.length;i++) for(int j=i+1;j<w.length;j++)
单源最短路径(贪心法)实验报告
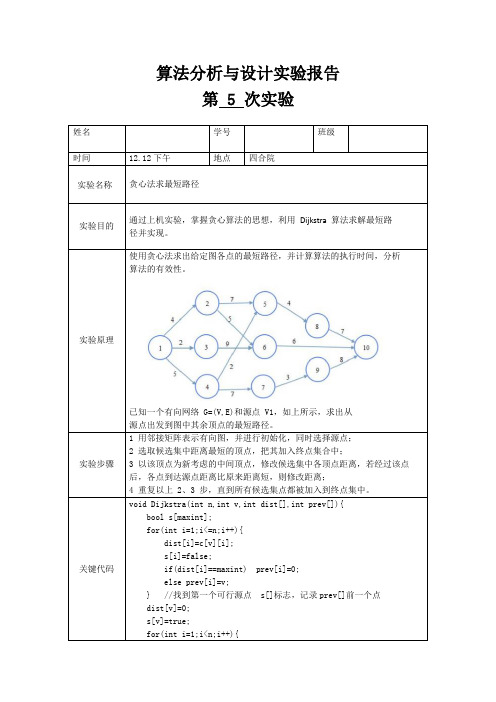
算法分析与设计实验报告第 5 次实验使用贪心法求出给定图各点的最短路径,并计算算法的执行时间,分析算法的有效性。
已知一个有向网络 G=(V,E)和源点 V1,如上所示,求出从源点出发到图中其余顶点的最短路径。
1 用邻接矩阵表示有向图,并进行初始化,同时选择源点;}手动输入实现实验所给图形:随机数产生图的权值:通过这次实验,我回顾了回溯法求解最短路径问题,在其中加入了舍伍德附录:完整代码#include<stdio.h>#include<stdlib.h>#include<time.h>#define maxint 1000int c[200][200]={0};void Dijkstra(int n,int v,int dist[],int prev[]){ bool s[maxint];for(int i=1;i<=n;i++){dist[i]=c[v][i];s[i]=false;if(dist[i]==maxint) prev[i]=0;else prev[i]=v;} //找到第一个可行源点 s[]标志,记录prev[]前一个点dist[v]=0;s[v]=true;for(int i=1;i<n;i++){int temp=maxint;int u=v;for(int j=1;j<=n;j++){if((!s[j])&&(dist[j]<temp)){u=j;temp=dist[j];}}s[u]=true;for(int j=1;j<=n;j++){int newdist=dist[u]+c[u][j];if(newdist<dist[j]){dist[j]=newdist;prev[j]=u;}}}}int main(){int n,v;printf("请输入顶点数: ");scanf("%d",&n);//printf("路径: ");srand(time(0));for(int i=1;i<n+1;i++){for(int j=1;j<n+1;j++){/* scanf("%d",&c[i][j]);*/ ///手动输入if(i!=j){if((c[j][i]==0)||(c[j][i]==1000))c[i][j]=rand()%100+1;else c[i][j]=1000;if(c[i][j]>50) c[i][j]=1000;}}}printf("请输入源点: ");scanf("%d",&v);int dist[n+1],prev[n+1];printf("\n路径:\n");for(int i=1;i<n+1;i++){for(int j=1;j<n+1;j++)printf("%5d ",c[i][j]);printf("\n");}Dijkstra(n,v,dist,prev);for(int i=1;i<n+1;i++){printf("\n%d到%d的最短路径为:%d",v,i,dist[i]);}}。
《算法设计与分析》课程实验报告 (贪心算法(一))

《算法设计与分析》课程实验报告实验序号:07实验项目名称:实验8 贪心算法(一)一、实验题目1.删数问题问题描述:键盘输入一个高精度的正整数N(不超过250 位),去掉其中任意k个数字后剩下的数字按原左右次序将组成一个新的非负整数。
编程对给定的N 和k,寻找一种方案使得剩下的数字组成的新数最小。
若输出前有0则舍去2.区间覆盖问题问题描述:设x1,x2,...xn是实轴上的n个点。
用固定长度为k的闭区间覆盖n个点,至少需要多少个这样的固定长度的闭区间?请你设计一个有效的算法解决此问题。
3.会场安排问题问题描述:假设要在足够多的会场里安排一批活动,并希望使用尽可能少的会场。
设计一个有效的贪心算法进行安排。
(这个问题实际上是著名的图着色问题。
若将每一个活动作为图的一个顶点,不相容活动间用边相连。
使相邻顶点着有不同颜色的最小着色数,相应于要找的最小会场数。
)4.导弹拦截问题问题描述:某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。
但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。
某天,雷达捕捉到敌国的导弹来袭。
由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
给定导弹依次飞来的高度(雷达给出的高度数据是≤50000的正整数),计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
二、实验目的(1)通过实现算法,进一步体会具体问题中的贪心选择性质,从而加强对贪心算法找最优解步骤的理解。
(2)掌握通过迭代求最优的程序实现技巧。
(3)体会将具体问题的原始数据预处理后(特别是以某种次序排序后),常能用贪心求最优解的解决问题方法。
三、实验要求(1)写出题1的最优子结构性质、贪心选择性质及相应的子问题。
(2)给出题1的贪心选择性质的证明。
(3)(选做题):写出你的算法的贪心选择性质及相应的子问题,并描述算法思想。
算法实验报告贪心

一、实验背景贪心算法是一种在每一步选择中都采取当前状态下最好或最优的选择,从而希望导致结果是全局最好或最优的算法策略。
贪心算法并不保证能获得最优解,但往往能获得较好的近似解。
在许多实际应用中,贪心算法因其简单、高效的特点而被广泛应用。
本实验旨在通过编写贪心算法程序,解决经典的最小生成树问题,并分析贪心算法的优缺点。
二、实验目的1. 理解贪心算法的基本原理和应用场景;2. 掌握贪心算法的编程实现方法;3. 分析贪心算法的优缺点,并尝试改进;4. 比较贪心算法与其他算法在解决最小生成树问题上的性能。
三、实验内容1. 最小生成树问题最小生成树问题是指:给定一个加权无向图,找到一棵树,使得这棵树包含所有顶点,且树的总权值最小。
2. 贪心算法求解最小生成树贪心算法求解最小生成树的方法是:从任意一个顶点开始,每次选择与当前已选顶点距离最近的顶点,将其加入生成树中,直到所有顶点都被包含在生成树中。
3. 算法实现(1)数据结构- 图的表示:邻接矩阵- 顶点集合:V- 边集合:E- 已选顶点集合:selected- 最小生成树集合:mst(2)贪心算法实现```def greedy_mst(graph):V = set(graph.keys()) # 顶点集合selected = set() # 已选顶点集合mst = set() # 最小生成树集合for i in V:selected.add(i)mst.add((i, graph[i]))while len(selected) < len(V):min_edge = Nonefor edge in mst:u, v = edgeif v not in selected and (min_edge is None or graph[u][v] < graph[min_edge[0]][min_edge[1]]):min_edge = edgeselected.add(min_edge[1])mst.add(min_edge)return mst```4. 性能分析为了比较贪心算法与其他算法在解决最小生成树问题上的性能,我们可以采用以下两种算法:(1)Prim算法:从任意一个顶点开始,逐步添加边,直到所有顶点都被包含在生成树中。
贪心算法-找零问题 实验报告

实验三课程名称:算法设计与实现实验名称:贪心算法-找零问题实验日期:2019年5月2日仪器编号:007班级:数媒0000班姓名:郝仁学号0000000000实验内容假设零钱系统的币值是{1,p,p^2,……,p^n},p>1,且每个钱币的重量都等于1,设计一个最坏情况下时间复杂度最低的算法,使得对任何钱数y,该算法得到的零钱个数最少,说明算法的主要设计思想,证明它的正确性,并给出最坏情况下的时间复杂度。
实验分析引理1(离散数学其及应用3.1.4):若n是正整数,则用25美分、10美分、5美分和1美分等尽可能少的硬币找出的n美分零钱中,至多有2个10美分、至多有1个5美分、至多有4个1美分硬币,而不能有2个10美分和1个5美分硬币。
用10美分、5美分和1美分硬币找出的零钱不能超过24美分。
证明如果有超过规定数目的各种类型的硬币,就可以用等值的数目更少的硬币来替换。
注意,如果有3个10美分硬币,就可以换成1个25美分和1个5美分硬币;如果有2个5美分硬币,就可以换成1个10美分硬币;如果有5个1美分硬币,就可以换成1个5美分硬币;如果有2个10美分和1个5美分硬币,就可以换成1个25美分硬币。
由于至多可以有2个10美分、1个5美分和4个1美分硬币,而不能有2个10美分和1个5美分硬币,所以当用尽可能少的硬币找n美分零钱时,24美分就是用10美分、5美分和1美分硬币能找出的最大值。
假设存在正整数n,使得有办法将25美分、10美分、5美分和1美分硬币用少于贪心算法所求出的硬币去找n美分零钱。
首先注意,在这种找n美分零钱的最优方式中使用25美分硬币的个数q′,一定等于贪心算法所用25美分硬币的个数。
为说明这一点,注意贪心算法使用尽可能多的25美分硬币,所以q′≤q。
但是q′也不能小于q。
假如q′小于q,需要在这种最优方式中用10美分、5美分和1美分硬币至少找出25美分零钱。
而根据引理1,这是不可能的。
贪心算法_实验报告

贪心算法_实验报告一、设计分析●问题描述:键盘输入一个高精度的正整数N(N不超过240位),去掉其中任意S个数字后剩下的数字按原左右次序将组成一个新的正整数。
编程对给定的N和S,寻找一种方案使得剩下的数字组成的新数最小。
●设计思路:在位数固定的前提下,让高位的数字尽量小其值就较小,依据此贪心策略解决此问题。
删除高位较大的数字。
具体:相邻两位比较若高位比低位大则删除高位。
删除字符的方法:1)物理删除,用后面的字符覆盖已删除的字符。
有比较多字符移动操作,算法效率不高。
2)用数组记录字符的状态,“1”表示对应数字存在,“0”表示对应数字已删除。
3)利用数组,记录未删除字符的下标:n=“1 2 4 3 5 8 3 3”0 0 0 0 0 04比3大删除“1 2 3 5 8 3 3” 1 2 4 5 0 08比3大删除“1 2 3 5 3 3” 1 2 4 5 05比3大删除“1 2 3 3 3” 1 2 4 7 8二、程序代码c语言实现#include<stdio.h>#include<string.h>#define N 10000int main(void){char a[N];int i,j,k,n;printf("输入要处理的数据:\n");gets(a);printf("输入要删除的数字个数:\n");scanf("%d",&n);三、测试用例四、实验总结加深了对贪心算法的理解与运用。
所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。
这是贪心算法可行的第一个基本要素,也是贪心算法与动态规划算法的主要区别。
动态规划算法通常以自底向上的方式解各子问题,而贪心算法则通常以自顶向下的方式进行,以迭代的方式作出相继的贪心选择,每作一次贪心选择就将所求问题简化为规模更小的子问题。
贪心算法设计实验报告

A
B
C
D
E
F
G
0
0
0
0
1
0
0
0
对表进行维护(维护后仍同上表,因为还没有两个集合合并)
0
A
B
C
D
E
F
G
0
0
0
0
1
0
0
0
C,选择第二条边 C----E (修改上表)
0
A
B
C
D
E
F
G
0
0
0
0
1
3
0
0
对上表进行维护(任同上表,因为还没有两个集合合并)
0
A
B
C
D
E
F
G
0
0
0
0
1
3
0
0
D,选择第三条边( D-----F ) (根据条件 DF 两点不再同一集合,改边可选 ) 然后就合并 DF 两点所在的集合 D 的前去是 1,即 A 标记为 0, E 的标记也为 0,合并因为 6>1 所以表修改如下
Edge* selectionsort(Edge *array,int n)// 选择排序(对边按权重由高到低排序) {
int i,j,min,temp; for(i=0;i<n;i++) {
min=i; for(j=i+1;j<n;j++)
if(array[min].weight>array[j].weight) min=j;
在同一棵树上,则不可取,而应该取下一条权值最小的边再试之。依次类推,直至森林中
只有一棵树,也即子图中含有
实验3 贪心算法

淮海工学院计算机工程学院实验报告书课程名:《算法分析与设计》题目:实验3 贪心算法班级:学号:姓名:实验3 贪心算法实验目的和要求(1)了解前缀编码的概念,理解数据压缩的基本方法;(2)掌握最优子结构性质的证明方法;(3)掌握贪心法的设计思想并能熟练运用(4)证明哈夫曼树满足最优子结构性质;(5)设计贪心算法求解哈夫曼编码方案;(6)设计测试数据,写出程序文档。
实验内容设需要编码的字符集为{d 1, d 2, …, dn },它们出现的频率为{w 1, w 2, …, wn },应用哈夫曼树构造最短的不等长编码方案。
实验环境Turbo C 或VC++实验学时2学时,必做实验数据结构与算法//构造哈夫曼结构体struct huffman{double weight; //用来存放各个结点的权值int lchild,rchild,parent; //指向双亲、孩子结点的指针 };核心源代码#include<iostream>#include <string>using namespace std;#include <stdio.h>//构造哈夫曼结构体struct huffman{double weight;∑=j i k k aint lchild,rchild,parent;};static int i1=0,i2=0;//选择权值较小的节点int Select(huffman huff[],int i){int min=11000;int min1;for(int k=0;k<i;k++){if(huff[k].weight<min && huff[k].parent==-1){min=huff[k].weight;min1=k;}}huff[min1].parent=1;return min1;}//定义哈夫曼树,并对各个节点进行赋权值void HuffmanTree(huffman huff[],int weight[],int n) {for(int i=0;i<2*n-1;i++){huff[i].lchild=-1;huff[i].parent=-1;huff[i].rchild=-1;}for(int l=0;l<n;l++){huff[l].weight=weight[l];}for(int k=n;k<2*n-1;k++){int i1=Select(huff,k);int i2=Select(huff,k);huff[i1].parent=k;huff[i2].parent=k;huff[k].weight= huff[i1].weight+huff[i2].weight;huff[k].lchild=i1;huff[k].rchild=i2;}}//哈夫曼编码,左0右1void huffmancode(huffman huff[],int n){string s;int j;for(int i=0;i<n;i++){s="";j=i;while(huff[j].parent!=-1){if(huff[huff[j].parent].lchild==j)s=s+"0";else s=s+"1";j=huff[j].parent;}cout<<"第"<<i+1<<"个节点的哈夫曼编码为:";for(int j=s.length();j>=0;j--){cout<<s[j];}cout<<endl;}}void main(){huffman huff[20];int n,w[20];printf("请输入节点的个数:");scanf("%d",&n);for(int i=0;i<n;i++){printf("请输入第%d个节点的权值:",i+1);scanf("%d",&w[i]);}printf("\n");HuffmanTree(huff,w,n);huffmancode(huff,n);}实验结果实验体会本次实验是用贪心法求解哈夫曼编码,其实贪心法和哈夫曼树的原理是一样的,每次将集合中两个权值最小的二叉树合并成一棵新二叉树,每次选择两个权值最小的二叉树时,规定了较小的为左子树。
贪心算法实验报告

typedef struct node{
int id ,time;//作业所需时间
}jobnode;
typedef struct Node{
int id ,avail;//id机器编号、avail每次作业的初始时间
}manode;
manode machine[N];
jobnode job[N];
scanf("%d",&n);
printf("请输入加油站的个数:");
scanf("%d",&k);
for(i=0;i<=k;i++)
scanf("%d",&d[i]);
greedy(d,n,k);
}
实验结果截图:
(3)实验代码:设有n个正整数,将它们连接成一排,组成一个最大的多位整数
#include<stdio.h>
return;
}
}
for(i=0,s=0;i<=k;i++){
if(s<n)
s+=d[i];
else if(s>n){
n=s-d[i];
num++;
}
}
printf("%d\n",num);
}
void main(){
int i,n,k;
int d[1000];
printf("请输入汽车可行驶公里数:");
/*找出下一个作业执行机器*/
manode *Find_min(manode a[],int m){
manode *temp=&a[0];
贪心算法实验报告

一、实验目的通过本次实验,使学生对贪心算法的概念、基本要素、设计步骤和策略有更深入的理解,掌握贪心算法的原理和应用,并能够运用贪心算法解决实际问题。
二、实验内容本次实验主要涉及以下两个问题:1. 使用贪心算法解决单起点最短路径问题;2. 使用贪心算法解决小船过河问题。
三、实验原理1. 贪心算法贪心算法(又称贪婪算法)是一种在每一步选择中都采取当前最优的选择,从而希望导致结果是全局最优的算法。
贪心算法在每一步只考虑当前的最优解,不保证最终结果是最优的,但很多情况下可以得到最优解。
2. 单起点最短路径问题单起点最短路径问题是指在一个有向无环图中,从某个顶点出发,找到到达其他所有顶点的最短路径。
3. 小船过河问题小船过河问题是指一群人需要划船过河,船只能容纳两个人,过河后需要一人将船开回,问最少需要多久让所有人过河。
四、实验步骤及说明1. 创建图结构,包括顶点数组和边信息。
2. 使用Dijkstra算法求解单起点最短路径问题,得到最短路径和前驱顶点。
3. 使用贪心算法找到两点之间的最短距离,并更新距离和前驱顶点信息。
4. 遍历所有顶点,找到未纳入已找到点集合的距离最小的顶点,并更新其距离和前驱顶点。
5. 最终输出从源顶点到达其余所有点的最短路径。
6. 使用贪心算法解决小船过河问题,按照以下步骤进行:(1)计算所有人过河所需的总时间;(2)计算每次划船往返所需时间;(3)计算剩余人数;(4)重复(2)和(3)步骤,直到所有人过河。
五、实验结果与分析1. 单起点最短路径问题实验中,我们选取了有向无环图G,其中包含6个顶点和8条边。
使用贪心算法和Dijkstra算法求解单起点最短路径问题,得到的实验结果如下:- 贪心算法求解单起点最短路径问题的时间复杂度为O(V^2),其中V为顶点数;- Dijkstra算法求解单起点最短路径问题的时间复杂度为O(V^2),其中V为顶点数。
2. 小船过河问题实验中,我们选取了一群人数为10的人过河,船每次只能容纳2人。
贪心算法解决活动安排问题报告

贪心算法解决活动安排问题金潇Use the greedy algorithm to solve the arrangement for activitiesJinxiao摘要:贪心算法在当前来看是最好的选择。
是用利用启发式策略,在不从整体最优上加以考虑的情况下,来做出局部最优选择的一种算法。
本文通过贪心算法的经典案例—活动安排问题入手,描述了贪心算法的基本思想和可能产生的问题,并简述该算法的好处和特点,最后给出几种经典的贪心算法。
关键字:贪心算法、局部最优选择Abstract:A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stage with the hope of finding the global optimum. This article through the greedy algorithm of the classic case--activities problems, describes the greedy algorithm the basic ideas and possible problems, and briefly introduces the advantages and characteristics of the algorithm, and finally gives several classic the greedy algorithm. Keywords:greedy algorithm、the locally optimal choice1.引言:贪心法是一种改进了的分级处理方法。
用贪心法设计算法的特点是一步一步地进行,每一步上都要保证能获得局部最优解。
贪心算法实验报告(C语言)

实验2、《贪心算法实验》一、实验目的1. 了解贪心算法思想2. 掌握贪心法典型问题,如背包问题、作业调度问题等。
二、实验内容1. 编写一个简单的程序,实现单源最短路径问题。
2. 编写一段程序,实现找零。
【问题描述】当前有面值分别为2角5分,1角,5分,1分的硬币,请给出找n分钱的最佳方案(要求找出的硬币数目最少)。
3. 编写程序实现多机调度问题【问题描述】要求给出一种作业调度方案,使所给的n个作业在尽可能短的时间内由m 台机器加工处理完成。
约定,每个作业均可在任何一台机器上加工处理,但未完工前不允许中断处理。
作业不能拆分成更小的子作业。
三、算法思想分析1.初始化将源点设计为红点集,其余点设计为蓝点,重复选择蓝点集中与源点路径最短的点加入红点集,更新剩余的蓝点集路径,直至蓝点集为空或者只剩下没有连通的点,那么源点到其余所有点的最短路径就出来了。
2.找零问题是典型的贪心问题,但是并不代表所有的找零都能用贪心算法找到最优解。
只有满足贪心选择性质的找零才能找到最优解,本题满足贪心选择性质,直接先一直选面值最大的硬币,再一次减小即可。
3.先对作业按时长进行重排序,再依次找目前用时最短的机器安排工作并加上对应时长,最后总时长为机器中用时最长的那个时长。
四、实验过程分析1.单源最短路径的算法思想并不难,但是在实际编码过程中还是有很多小问题需要注意,首先,一定要新建数组存储路径变化,因为后面计算路径时会用到原数组,如果直接在原数组上更改后面就找不到原数据了,那么就会出现偏差。
其次就是建议先写个伪代码,判断的if-else语句比较多,容易搞混,在代码中一定要及时备注,某些代码的功能是什么,不然再次看代码时需要思考很久甚至忘记。
2.找零问题直接用while循环或者不断取余取模即可解决。
3.作业调度问题大致分为三步,一是排序,二是不断找最短时长的机器安排作业,三是找最长时间为作业完成时间。
五、算法源代码及用户屏幕1.(1)算法源码/**********************单源最短路径问题。
删数问题贪心算法实验总结

删数问题贪心算法实验总结
一、问题背景
在计算机科学中,删数问题是指给定一个正整数序列,每次可以删除
其中两个相邻的数字,并将它们的和作为新的数字插入到原序列中。
这个过程不断重复,直到序列中只剩下一个数字为止。
删数问题最初
由 Josephus 提出,因此也被称为 Josephus 问题。
二、贪心算法
贪心算法是一种基于贪心思想的算法,在每一步选择中都采取当前状
态下最好或最优的选择,从而希望导致结果是全局最好或最优的算法。
贪心算法通常需要证明其正确性。
三、实验设计
本次实验旨在探究删数问题中使用贪心算法得出结果的正确性。
实验
分为以下步骤:
1. 编写程序模拟删数过程,并使用随机生成的数据进行测试。
2. 编写程序实现贪心算法解决删数问题。
3. 对比模拟和贪心算法得出的结果,并分析其正确性。
4. 利用大量数据测试贪心算法的时间复杂度。
四、实验结果
经过多次测试,模拟和贪心算法得出的结果完全一致,证明了贪心算法在解决删数问题时具有正确性。
同时,通过大量数据测试,贪心算法的时间复杂度远远小于模拟算法,证明了贪心算法在解决删数问题时具有高效性。
五、结论
本次实验证明了贪心算法在解决删数问题时具有正确性和高效性。
在实际应用中,可以采用贪心算法来快速求解删数问题。
同时,本次实验也提醒我们,在使用贪心算法时需要对其正确性进行证明,并且需要注意不同情况下的最优选择可能不同。
贪心算法实验报告

贪心算法实验报告实验报告题目实验四贪心算法开课实验室:数学实验室指导老师:韩逢庆时间:2011.12 学院:理学院专业:信息与计算科学班级:2009级2班姓名:古月学号:09180230一、实验目的1(加深学生对贪心算法设计方法的基本思想、基本步骤、基本方法的理解与掌握;2(提高学生利用课堂所学知识解决实际问题的能力;3(提高学生综合应用所学知识解决实际问题的能力。
二、实验内容题目见P143:4-16,4-23.三、实验要求(1)用分治法求解最少加油次数和最少硬币个数问题;(2 )再选择自己熟悉的其它方法求解本问题;(3)上机实现所设计的所有算法;四、实验过程设计(算法设计过程)(1) 最少加油次数实验题目一辆汽车加满油以后可以行使n公里,旅途中有若干个加油站,设计一个有效算法,指出应在哪些加油站停靠加油,使沿路加油次数最少。
并证明算法能产生一个最优解。
过程设计贪心算法总是作出在当前看来最好的选择。
也就是说贪心算法并不从整体最优考虑,它所作出的选择只是在某种意义上的局部最优选择。
当然,希望贪心算法得到的最终结果也是整体最优的。
虽然贪心算法不能对所有问题都得到整体最优解,但对许多问题它能产生整体最优解。
比如说最少加油次数的问题。
在这个算法中,我采用的贪心算法的策略。
首先人机互动的设定加满油以后最长能够行使的距离,然后输入了各个站点之间的距离,在程序的设计中,首先检查了程序的可行性。
要是遇到当某两个站点之间的距离大于汽车一次加油以后所能够行使的最大距离时,我们认为此问题是不可行的。
这个在实际情况中也是很容易理解的。
然后在满足可行性条件下,依次采用贪心算法对问题得以实现。
采用s这个来保存现在车里面留下的油,当此时留下的有能够行驶完这一站点到下一站点之间的距离是,在这一站点的时候就不加油。
但是若不能行使完这一段路程的时候,就加满油。
核心算法如下:for(i=0,s=0;i<n;i++){s=s+a[i];if(s>n){sum++;s=a[i];}}(2) 最少硬币个数问题实验题目考虑下面的用最少硬币个数找出n分钱的问题:当使用2角5分,1角,5分和1分四种硬币面值时,设计一个找n分钱的贪心算法,并证明算法能产生最优解。
贪心算法实验报告

贪心算法实验报告贪心算法实验报告引言:贪心算法是一种常用的算法设计思想,它在求解最优化问题中具有重要的应用价值。
本实验报告旨在介绍贪心算法的基本原理、应用场景以及实验结果,并通过实例加以说明。
一、贪心算法的基本原理贪心算法是一种以局部最优解为基础,逐步构建全局最优解的算法。
其基本原理是在每一步选择中都采取当前状态下最优的选择,而不考虑之后的结果。
贪心算法通常具备以下特点:1. 贪心选择性质:当前状态下的最优选择一定是全局最优解的一部分。
2. 最优子结构性质:问题的最优解可以通过子问题的最优解来构造。
3. 无后效性:当前的选择不会影响以后的选择。
二、贪心算法的应用场景贪心算法适用于一些具有最优子结构性质的问题,例如:1. 路径选择问题:如Dijkstra算法中的最短路径问题,每次选择当前距离最短的节点进行扩展。
2. 区间调度问题:如活动选择问题,每次选择结束时间最早的活动进行安排。
3. 零钱找零问题:给定一些面额不同的硬币,如何用最少的硬币凑出指定的金额。
三、实验设计与实现本次实验选择了一个经典的贪心算法问题——零钱找零问题,旨在验证贪心算法的有效性。
具体实现步骤如下:1. 输入硬币面额和需要凑出的金额。
2. 对硬币面额进行排序,从大到小。
3. 从面额最大的硬币开始,尽可能多地选择该面额的硬币,直到不能再选择为止。
4. 重复步骤3,直到凑出的金额等于需要凑出的金额。
四、实验结果与分析我们通过对不同金额的零钱找零问题进行实验,得到了如下结果:1. 当需要凑出的金额为25元时,贪心算法的结果为1个25元硬币。
2. 当需要凑出的金额为42元时,贪心算法的结果为1个25元硬币、1个10元硬币、1个5元硬币、2个1元硬币。
3. 当需要凑出的金额为63元时,贪心算法的结果为2个25元硬币、1个10元硬币、1个1元硬币。
通过实验结果可以看出,贪心算法在零钱找零问题中取得了较好的效果。
然而,贪心算法并不是适用于所有问题的万能算法,它的有效性取决于问题的特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验3 贪心算法解活动安排问题
一、实验要求
1.要求按贪心法求解问题;
2.要求读文本文件输入活动安排时间区间数据;
3.要求显示结果。
二、实验仪器和软件平台
仪器:带usb接口微机
软件平台:WIN-XP + VC++6.0
三、源程序
#include "stdafx.h"
#include<stdio.h>
#include<stdlib.h>
#include<algorithm>
#define N 50
#define TURE 1
#define FALSE 0
int s[N];/*开始时间*/
int f[N];/*结束时间*/
int A[N];/*用A存储所有的*/
int Partition(int *b,int *a,int p,int r);
void QuickSort(int *b,int *a,int p,int r);
void GreedySelector(int n,int *s,int *f,int *A);
int main()
{
int n=0,i;
while(n<=0||n>50)
{
printf("\n");
printf("请输入活动的个数,n=");
scanf("%d",&n);
if(n<=0) printf("请输入大于零的数!");
else if(n>50) printf("请输入小于50的数!");
}
printf("\n请分别输入开始时间s[i]和结束时间f[i]:\n\n");
for(i=1;i<=n;i++)
{
printf("s[%d]=",i,i);
scanf("%d",&s[i]);
printf("f[%d]=",i,i);
scanf("%d",&f[i]);
printf("\n");
}
QuickSort(s,f,1,n); //按结束时间非减序排列
printf("按结束时间非减序排列如下:\n"); /*输出排序结果*/ printf("\n 序号\t开始时间结束时间\n");
printf("-------------------------\n");
for(i=1;i<=n;i++)
printf(" %d\t %d\t %d\n",i,s[i],f[i]);
printf("-------------------------\n");
GreedySelector(n,s,f,A);//贪心算法实现活动安排
printf("安排的活动序号依次为:");
for(i=1;i<=n;i++)
{
if(A[i])
printf("\n%d %d-->%d",i,s[i],f[i]);
}
printf("\n");
system("pause");
return 0;
}
//快速排序
void QuickSort(int *b,int *a,int p,int r)
{
int q;
if(p<r)
{
q=Partition(b,a,p,r);
QuickSort(b,a,p,q-1);/*对左半段排序*/
QuickSort(b,a,q+1,r);/*对右半段排序*/
}
}
//产生中间数
int Partition(int *b,int *a,int p,int r)
{
int k,m,y,i=p,j=r+1;
int x=a[p];y=b[p];
while(1)
{
while(a[++i]<x);
while(a[--j]>x);
if(i>=j)
break;
else
{
k=a[i];a[i]=a[j];a[j]=k;
m=b[i];b[i]=b[j];b[j]=m;
}
}
a[p]=a[j];
b[p]=b[j];
a[j]=x;
b[j]=y;
return j;
}
//贪心算法实现活动安排
void GreedySelector(int n,int *s,int *f,int *A)
{
//用集合A来存储所选择的活动
A[1]=TURE; //默认从第一次活动开始执行
int j=1; //j记录最近一次加入到A中的活动
for(int i=2;i<=n;i++)
{
//f[j]为当前集合A中所有活动的最大结束时间
//活动i的开始时间不早于最近加入到集合A中的j的时间f[j]
if(s[i]>=f[j])
{
A[i]=TURE; //当A[i]=TURE时,活动i在集合A中
j=i;
}
else A[i]=FALSE;
}
}
四、运行结果
五、实验小结
贪心算法总是做出在当前看来最好的选择,也就是说贪心算法并不从整体最优考虑,它所作出的选择只是在某种意义上的局部最优选择。
活动安排问题就是要在所给的活动集合中选出最大的相容活动子集合。
该问题要求高效地安排一系列争用某一公共资源的活动。
贪心算法提供了一个简单、漂亮的方法使得尽可能多的活动能兼容地使用公共资源。
