利用矩阵理论详细推导MIMO信道容量
矩阵在mimo技术中的应用(一)
矩阵在mimo技术中的应用(一)矩阵在MIMO技术中的应用1. 空时编码技术•空时编码技术是MIMO系统中的一项关键技术，用于在多个天线之间编码和解码数据，实现高速无线通信。
•矩阵在空时编码技术中起到了重要作用，通过对发送信号进行线性变换，可以将多个天线之间的信号进行合理组合，从而实现信号的编码和解码。
2. 天线选择技术•在MIMO系统中，多个天线可以同时传输和接收信号，通过合理的天线选择技术可以提高系统的性能。
•矩阵在天线选择技术中用于计算天线选择的权重，通过最大化接收信号的信噪比来选择合适的天线组合。
3. 并行信道技术•MIMO技术利用了多个独立的并行信道进行数据传输，提高了系统的容量和性能。
•矩阵在并行信道技术中用于描述多个信道之间的关系，通过矩阵运算可以实现对独立信道之间的数据进行合理分配和处理。
4. 反馈技术•在MIMO系统中，反馈技术用于获取信道状态信息，以便发送端进行合适的天线选择和编码策略。
•矩阵在反馈技术中用于描述信道状态信息，通过采集信号样本，计算相关矩阵可以得到准确的信道状态信息。
5. 混合自适应调制技术•MIMO系统中的混合自适应调制技术结合了空时编码和调制技术，通过根据信道条件自适应地选择合适的调制方式和编码策略。
•矩阵在混合自适应调制技术中用于描述调制方式和编码策略的关系，通过调整矩阵参数可以实现不同调制方式和编码策略的切换和优化。
6. 信道估计技术•在MIMO系统中，准确的信道估计是实现高速无线传输的关键。
•矩阵在信道估计技术中用于描述信号传输过程中的信道损耗和信道变化情况，通过计算相关矩阵可以得到准确的信道估计结果。
7. 多用户检测技术•MIMO系统中的多用户检测技术用于解决多个用户同时传输数据时的干扰问题，并实现多用户间的并行通信。
•矩阵在多用户检测技术中用于描述用户之间的干扰关系，通过矩阵运算可以实现用户之间的分离和干扰消除。
以上是一些矩阵在MIMO技术中的应用示例，这些应用充分展示了矩阵在MIMO技术中的重要作用，为高速无线通信提供了强大的支持。
基于奇异值分解计算MIMO信道容量
基于奇异值分解计算MIMO 信道容量摘要 无线MIMO 技术是未来无线通信系统中实现高数据速率传输、改善传输质量、提高系统容量的重要途径，它被认为是现代通信技术中的重大突破之一，受到了广泛的研究与关注。
信道容量是信道的一个参数，反映了信道所能传输的最大信息量。
因此研究MIMO 的信道容量具有巨大的指导意义。
本文利用矩阵理论的相关知识，首先建立了MIMO 信道模型，利用信息论理论和奇异值分解的理论详细推导出MIMO 信道容量，并得出重要结论。
关键词： MIMO ；信道容量；奇异值分解一、 引言MIMO 系统是能够有效提高无线频谱利用率最重要的方案之一。
MIMO 系统使用多根发射天线、多根接收天线, 在系统容量、频谱效率、发射机和接收机的设计上都与传统的单发单收系统有很大差别。
然而，MIMO 无线系统大容量的实现和其它性能的提高极大地依赖于MIMO 无线信道的特性，MIMO 无线通信的难点也正在于信道的处理。
矩阵理论在通信，自动控制等工程领域里应用广泛，将矩阵理论与无线信道的研究是一个很好的切入点。
目前，MIMO 技术的信道容量和空时编码，空时复用等技术都离不开矩阵理论的应用。
二、 奇异值分解的概念下面介绍一下矩阵奇异值分解的理论。
首先，给出奇异值的概念。
设,m nH rA C A A ⨯∈的特征值为121n 0r r λλλλλ+≥≥≥>===……(2.1)则称1,2,...,)i i r σ==为矩阵A 的正奇异值。
进而，奇异值分解理论可以阐述为： 对任意矩阵m nrA C ⨯∈，12,,...,r σσσ是A 的r 个正奇异值，则存在m 阶酉矩阵U 及n 阶酉矩阵V ，使得D 0V 00A U ⎛⎫= ⎪⎝⎭(2.2)其中12D=diag ,,...,),r δδδ（而i δ满足||(1,2,...,)i i i r δσ==的复数。
三、 MIMO 信道模型的建立为了描述MIMO 信道，考虑考虑基站(BS)天线数R n ，移动台(MS)天线数为T n 的两个均匀线性天线阵列，假定天线为全向辐射天线。
2、MIMO信道容量推导
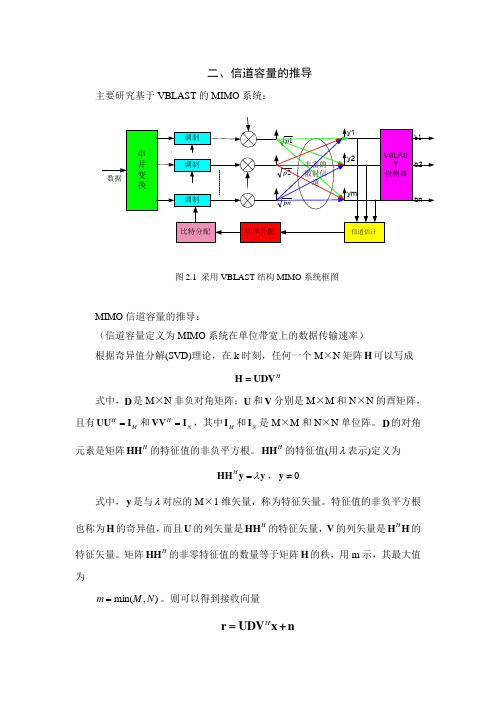
二、信道容量的推导主要研究基于VBLAST 的MIMO 系统：系统：串并变换调制调制调制VBLAST 检测器y1y2ym 比特分配功率分配b1bnb2信道估计丰富的散射信道2p 1p pn 数据图2.1 采用VBLAST 结构MIMO 系统框图系统框图MIMO 信道容量的推导：信道容量的推导：（信道容量定义为MIMO 系统在单位带宽上的数据传输速率）系统在单位带宽上的数据传输速率）根据奇异值分解(SVD)理论，在k 时刻，任何一个M ×N 矩阵H 可以写成可以写成HH =UDV 式中，D 是M ×N 非负对角矩阵；U 和V 分别是M ×M 和N ×N 的酉矩阵，且有H HM =UU I 和H N =VV I ，其中M I 和N I 是M ×M 和N ×N 单位阵。
D 的对角元素是矩阵H HH 的特征值的非负平方根。
H HH 的特征值(用l 表示)定义为定义为 H l =HH y y ，0¹y式中，y 是与l 对应的M ×1维矢量，称为特征矢量。
特征值的非负平方根也称为H 的奇异值，而且U 的列矢量是H HH 的特征矢量，V 的列矢量是HH H 的特征矢量。
矩阵H HH 的非零特征值的数量等于矩阵H 的秩，用m 示，其最大值为),min(N M m =。
则可以得到接收向量。
则可以得到接收向量 H =r UDV x +n引入几个变换H r'=U r ，H x'=V x ，H'n =U n ，这样等价的信道可以描述为：'''r =Dx +n 对于M ×N 矩阵H ，秩的最大值),min(N M m =，也就是说有m 个非零奇异值。
值。
将i l 代入上式，可以得到接收信号为：代入上式，可以得到接收信号为：'''i i i i r x n l =+(m i ,,2,1 =)''i i n r =(1,2,,i m m M =++ )可以看出等效的MIMO 信道是由m 去耦平行子信道组成的。
MIMO信道容量计算公式
MIMO信道容量计算公式
MIMO（Multiple-Input Multiple-Output）是一种通过同时使用多个发射天线和接收天线来增加无线通信系统容量的技术。
MIMO技术可以利用信道的冗余和多路径效应，提高信号的传输速率和可靠性。
1.SISO信道容量计算公式：
SISO信道容量的计算公式使用香农公式，用于计算传输速率。
香农公式如下：
C = B * log2(1 + SNR)
其中，C是信道容量，B是带宽，SNR是信噪比（Signal-to-Noise Ratio）。
SISO信道容量计算公式适用于只有一个天线的系统。
2.MIMO信道容量计算公式：
C = log2(det(I + H*SNR*H^H))
其中，C是信道容量，H是MIMO信道的传输矩阵，SNR是信噪比。
除了以上基本的MIMO信道容量计算公式，还有一些进一步考虑调制方式、信道状态信息等因素的改进公式，如ZF（Zero Forcing）和MMSE （Minimum Mean Square Error）等方法，用于提高MIMO系统的容量。
这些方法考虑了天线之间的干扰和多径效应，可以优化信号的传输和接收性能。
总结起来，MIMO信道容量的计算公式可以通过SISO信道容量公式和MIMO信道容量公式来表示，具体的计算方法需要综合考虑信道状况和系
统参数，并结合数值计算方法进行分析。
通过合理设计和优化，MIMO技术可以显著提高无线通信系统的容量和性能。
2、MIMO信道容量推导
二、信道容量的推导主要研究基于VBLAST 的MIMO 系统：图2.1 采用VBLAST 结构MIMO 系统框图MIMO 信道容量的推导：（信道容量定义为MIMO 系统在单位带宽上的数据传输速率）根据奇异值分解(SVD)理论，在k 时刻，任何一个M ×N 矩阵H 可以写成H H =UDV式中，D 是M ×N 非负对角矩阵；U 和V 分别是M ×M 和N ×N 的酉矩阵，且有H M =UU I 和H N =VV I ，其中M I 和N I 是M ×M 和N ×N 单位阵。
D 的对角元素是矩阵H HH 的特征值的非负平方根。
H HH 的特征值(用λ表示)定义为H λ=HH y y ，0≠y式中，y 是与λ对应的M ×1维矢量，称为特征矢量。
特征值的非负平方根也称为H 的奇异值，而且U 的列矢量是H HH 的特征矢量，V 的列矢量是H H H 的特征矢量。
矩阵H HH 的非零特征值的数量等于矩阵H 的秩，用m 示，其最大值为),min(N M m =。
则可以得到接收向量H =r UDV x +n引入几个变换H r'=U r ，H x'=V x ，H 'n =U n ，这样等价的信道可以描述为：'''r =Dx +n对于M ×N 矩阵H ，秩的最大值),min(N M m =，也就是说有m 个非零奇异值。
将i λ代入上式，可以得到接收信号为：'''i i i r n =+(m i ,,2,1 =)''i i n r =(1,2,,i m m M =++ )可以看出等效的MIMO 信道是由m 去耦平行子信道组成的。
为每个子信道分配矩阵H 的奇异值，相当于信道的幅度增益。
因此，信道功率增益等于矩阵H HH 的特征值。
因为子信道是去耦的，所以信道容量可以直接看做由多个SISO 信道容量直接相加。
mimo信道容量推导
mimo信道容量推导MIMO是多输入多输出技术的缩写，它可以显著提高通信系统的传输速率和可靠性。
MIMO系统中，多个天线同时工作来传输数据，这种技术可以提高信号的容量。
下面我们将推导MIMO信道容量的公式。
对于一个MIMO系统，假设有Nt个发送天线和Nr个接收天线。
我们可以通过矩阵来描述MIMO信道。
假设H是Nt×Nr的复矩阵，表示发送天线的信号被接收天线接收到时，信道的响应。
假设s是发送天线的信号，n是接收天线的噪声，则接收信号可以表示为：y = Hs + n为了使信号传输更稳定，我们可以使用梅斯纳矩阵（Hermitian matrix）来表示发送信号s。
因此，我们可以将s表示为：s = Uf其中，U是梅斯纳矩阵，f是发送天线的数据。
因此，我们可以将接收信号表示为：y = HUf + n我们可以对函数进行线性变换，将其变换为：y = WF + n其中，W = HU是一个线性变换矩阵。
我们可以对矩阵进行奇异值分解，将其分解为：W = UΣV*其中，U和V*是梅斯纳矩阵，Σ是一个对角线上有奇异值的矩阵。
因此，我们可以将接收信号表示为：y = UΣV*f + n我们可以将接收信号y表示为一个向量，f表示为另一个向量。
接着，我们可以计算信道的容量，即最大可能的数据传输速率。
根据香农公式，信道容量可以表示为：C = log2(det(I + SNR/NT H HH))其中，NT是发送天线的数量，SNR是信噪比，det表示矩阵的行列式。
因此，我们可以得出MIMO信道容量的公式。
总之，通过对MIMO系统中的信道进行线性变换和奇异值分解，我们可以推导出MIMO信道容量的公式，这个公式可以用来计算最大可能的数据传输速率。
MIMO信道的信道容量
Pi 1/ 0 1/ i 0 P
其中 0 为某个门限值。由此得到信道容量为
i 0 i 0 （1-6）
C B log 2 (
i: i 0
i ) 0
对于有一个发送天线和多个接收天线的单入多出系统，或者有多个发送天线 一个接收天线的多入单出系统，也可以定义出收发都有理想信道信息时的容量。 这些信道可以通过多天线获得分集增益和阵列增益，但没有复用增益。当发送端 和接收端都已知信道信息时， 其容量等于信号在发送端或接收端进行最大比合并 后得到的 SISO 信道的容量为
1 引言
信道容量的计算是研究噪声信道的主要关注点之一。信道容量的定义是以任 意小的差错率传输信息的最大速率，它建立了可靠通信的基本极限。因此，信道 容量广泛应用于衡量通信系统的性能。本文的主要目标是研究与 MIMO 无线信 道有关的信道容量。 MIMO 信道的香农容量是能够以任意小的差错率传输的最大数据率。中断容 量则定义为能使中断率不超过某个数值的最大数据率。 信道容量的大小和收发两 端是否已知信道增益矩阵或其分布有关。 下文先给出不同信道信息假设下静态信 道的容量，它是其后讨论的衰落信道容量的基础。
MIMO 信道的信道容量
摘要
由于 MIMO 可以在不需要增加带宽或总发送功率耗损（transmit power expenditure）的情况下大幅地增加系统的资料吞吐量（throughput）及传送距离， 使得此技术于近几年受到许多瞩目。MIMO 的核心概念为利用多根发射天线与 多根接收天线所提供之空间自由度来有效提升无线通信系统之频谱效率， 以提升 传输速率并改善通信品质。研究 MIMO 信道的容量是对 MIMO 进行深入分析的 基础，本文分析了 MIMO 信道的容量计算方法，分别介绍了在静态信道中的注 水法、平均功率分配法信道容量，以及衰落信道中遍历容量和中断容量。 关键词：MIMO，信道容量，注水法，平均功率分配，遍历容量，中断容量
MIMO信道的信道容量
x
x Vx
x
y Hx n
y
UH y y
y
图 2 发送预编码与接收成形 发送预编码和接收成形将 MIMO 信道变换成 RH 个并行的单入单出 SISO 信道， 其
。这一点可以从奇异值分解得到： ，输出为 y 输入为 x
Pi 1/ 0 1/ i 0 P
其中 0 为某个门限值。由此得到信道容量为
i 0 i 0 （1-6）
C B log 2 (
i: i 0
i ) 0
对于有一个发送天线和多个接收天线的单入多出系统，或者有多个发送天线 一个接收天线的多入单出系统，也可以定义出收发都有理想信道信息时的容量。 这些信道可以通过多天线获得分集增益和阵列增益，但没有复用增益。当发送端 和接收端都已知信道信息时， 其容量等于信号在发送端或接收端进行最大比合并 后得到的 SISO 信道的容量为
发送预编码将输入向量x经线性变换xvx后作为天线的输入接收成形将信道的输出y乘以发送预编码与接收成形发送预编码和接收成形将mimo信道变换成个并行的单入单出siso信道其输入为x输出为y
MIMO 信道的信道容量
摘要
由于 MIMO 可以在不需要增加带宽或总发送功率耗损（transmit power expenditure）的情况下大幅地增加系统的资料吞吐量（throughput）及传送距离， 使得此技术于近几年受到许多瞩目。MIMO 的核心概念为利用多根发射天线与 多根接收天线所提供之空间自由度来有效提升无线通信系统之频谱效率， 以提升 传输速率并改善通信品质。研究 MIMO 信道的容量是对 MIMO 进行深入分析的 基础，本文分析了 MIMO 信道的容量计算方法，分别介绍了在静态信道中的注 水法、平均功率分配法信道容量，以及衰落信道中遍历容量和中断容量。 关键词：MIMO，信道容量，注水法，平均功率分配，遍历容量，中断容量
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
利用矩阵理论详细推导MIMO 信道容量摘要 多输入多输出(MIMO)技术被认为是现代通信技术中的重大突破之一，以其能极大增加系统容量与改善无线链路质量的优点而受到了越来越多的重视与关注。
通信信道容量是信道进行无失真传输速率的上界，因此研究MIMO 的信道容量具有巨大的指导意义。
本文把矩阵理论知识与MIMO 技术信道容量中的应用紧密结合，首先建立了MIMO 信道模型，利用信息论理论和矩阵理论详细推导出MIMO 信道容量。
并得出重要结论。
关键词： MIMO ；信道容量；奇异值分解一、 引言MIMO Multiple Input-Multiple Output)是指在通信链路的发送端与接收端均使用多个天线元的传输系统,它能够将传统通信系统中存在的多径因素变成对用户通信性能有利的因素,从而成倍地提高业务传输速率。
矩阵理论在通信，自动控制等工程领域里应用广泛，而通信的难点在于信道的处理，因此，矩阵理论与无线信道的研究是一个很好的切入点。
目前，MIMO 技术的信道容量和空时编码，空时复用等技术都离不开矩阵理论的应用。
二、 利用矩阵理论详细推导MIMO 信道容量1) MIMO 信道介绍MIMO 是多输入多输出系统，当发送信号所占用的带宽足够小的时候，信道可以被认为是平坦的，这样，MIMO 系统的信道用一个R Tn n ⨯的复数矩阵H 描述，H 的子元素,j i h 表示从第(1,2,...)R j j n =根发射天线到第(1,2,...)T i i n =根接收天线之间的空间信道衰落系数[1]。
如下图所示：111212122212T T R T R R n n n n n n H h h h h h h h h h ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦(2.1)每个符号周期内，发送信号可以用一个1T n ⨯的列向量12[]T Ti n x x x x x =⋅⋅⋅⋅⋅⋅表示，其中i x表示在第i 个天线上发送的数据。
同时，用一个1R n ⨯的列向量12[]R Ti n y y y y y =⋅⋅⋅⋅⋅⋅表示，其中i y 表示在第i 个天线上发送的数据。
对于高斯信道,发射信号的最佳分布也是高斯分布[1]。
因此,x 的元素是零均值独立同分布的高斯变量。
发送信号的协方差可以表示为：{}H xx R E xx =(2.2)发送信号的功率可以表示为()xx P tr R =(2.3)接收信号和噪声可以分别用两个1R n ⨯的列向量y 和n 表示。
其中信道噪声是加性噪声，服从循环对称复高斯分布，并且与发射信号x 不相关，假设n 均值为0，功率为2σ。
噪声的协方差为：2R H nn n R E nn I σ⎡⎤==⎣⎦(2.4)通过这样一个线性模型，接收信号可以表示为y Hx n =+ (2.5)接收信号的协方差可表示为()()[]2[]RH yy HH H H H HH xx n R E yy E Hx n Hx n HE xx H E nn HE xn H E nx HR H I σ=⎡⎤=++⎣⎦⎡⎤⎡⎤⎡⎤=+++⎣⎦⎣⎦⎣⎦=+(2.6)因为x 与噪声n 不相关，所以[]0HE xn E nx ⎡⎤+=⎣⎦。
2) MIMO 信道容量一般公式推导下面根据信息论知识，我们对MIMO 信道容量做一般性推导。
在下面的推导过程中我们假设信道矩阵H 在接收端已经完全已知，但是它是随机的，因此我们可以得到瞬时信道容量为：[1]()()()max ,Xx C H I x y ƒ=(2.7)其中，(),I x y 是在已知信道H 的情况下输入x 与输出y 之间的互信息量，有：()()(),|I x y H y H y x =-(2.8)其中，()H y 是y 的信息熵（微分熵），定义：2()()log ()H y p y p y =-∑，其中()p y 是y 的概率（概率密度）。
()H y 是y 的差分嫡，(|)H y x 是给定x 条件下y 的差分嫡，由于发送信号与噪声之间是独立的，因此有(|)()H y x H n =[1]，所以上式可以重新写为：()()(),I x y H y H n =-(2.9)由于噪声概率密度函数确定，所以()H n 为定值，当信道为加性高斯信道时，信源x 服从高斯分布时此时接收信号y 也服从高斯分布，根据信息论理论，此时(,)I x y 取最大，即为信道容量。
此时y 和n 的信息熵分别为：[1]{}212()log det yy bit H y eR π⎡⎤⎣⎦= (2.10){}2212()log det R n bit H n e I πσ⎡⎤⎣⎦= (2.11)所以我们可以得到信道瞬时交互信息(,)I x y ，也即信息容量为：{}222222221()log det /det 21log det ()/det 21log det 2R R R R R yy n H xx n n n H xx n C H eR e I HR H e I I e I HR H I bit ππσπσπσσσ⎡⎤⎡⎤=⎣⎦⎣⎦⎧⎫⎡⎤⎪⎪⎡⎤=+⎨⎬⎢⎥⎣⎦⎪⎪⎣⎦⎩⎭⎧⎫⎡⎤⎪⎪=+⎨⎬⎢⎥⎪⎪⎣⎦⎩⎭(2.12)工程中一般定义信道容量为单位时间内的平均互信息，故定义MIMO 的信道容量：[2]()1C C H T=(2.13) 其中T 为一个符号周期，根据采样定理，(1/)2T B ≥，其中B 为信号带宽，取(1/)2T B =，代入（2.13）式，得：[2]22log det /R H xx n HR H C B I bit s σ⎧⎫⎡⎤⎪⎪=+⎨⎬⎢⎥⎪⎪⎣⎦⎩⎭(2.14)这即是MIMO 的信道容量一般公式。
3) 奇异值分解计算MIMO 信道容量对于MIMO 无线信道，信道是极其复杂的。
因此原始的信道矩阵也就显得复杂，不便于分析，而且一般矩阵不经过处理计算行列式很困难。
这就自然想到在信源端对发射信号做某种预处理，使得经过预处理的信号经过的信道变得简单易分析，而且具体实现也变得简单。
对于信道矩阵来说，对角矩阵是最简单的，所以自然就想到把信道矩阵分解，利用矩阵理论中的奇异值分解可以达到这种目的。
下面就矩阵的奇异值分解来计算MIMO 的信道容量。
由奇异值分解理论,任何一个R Tn n ⨯的矩阵H 可以写成：[3]H H UDV = (2.15)式中，D 是R T n n⨯的对角阵，其对角非零元素模值为H 的正奇异值，U 和V 分别为R Rn n ⨯和T Tn n ⨯的酉矩阵。
把公式（2.15）代入公式（2.5），得：H y UDV x n =+(2.16)公式（2.16）两边同时左乘酉矩阵H U ，利用H Rn U U I =，同时令Hy U y =，Hx V x =即对信源信号x 进行预编码，Hn U n =，得：[3]y Dx n =+ (2.17)根据矩阵理论，矩阵HHH 的特征值为非负数，非零特征值的个数等于矩阵H 的秩，用r 表示，对于R Tn n ⨯的矩阵H ，秩的最大值min(,)R T m n n =H （2.17）得：(1,2,...)i i i y n i r =+=(2.18)(1,...)i i R y n i r n ==+(2.19)式（2.19）显示，接收元素(1,...)i R y i r n =+并不依赖于发射信号，即信道增益为零。
另一方面,接收元素(1,2...,)i y i r =仅仅取决于发射元素i x ，因此,可以认为,通过式（2.18）和（2.19）得到的等效MIMO信道是由个去耦平行子信道组成的[4]。
其信道增益为矩阵H 的奇异值。
可以进一步推导出i y ，i x ，和i n 的协方差和迹：,,H H H yy xx nn y y xx nn R U R U R V R V R U R U ===(2.20)()(),()(),()()yy xx nn y y xx nn tr R tr R tr R tr R tr R tr R ===(2.21)对于接收端已知信道参数，发射端未知，发射端平均分配功率的MIMO 系统。
设发射端发射总功率为T P ，则每个天线发射功率为/T T P n ，此时{}H Txx T Tn P R E xx I n ==(2.22)根据式（2.20）得：H Txx x x T Tn P R V R V I n ==(2.23)然后把根据（2.15）算出H HH 后和（2.23）代入MIMO 信道一般公式（2.14）得：221log (1)/ri Ti TP C B bit s n λσ==+∑ (2.24)式（2.24）可以看出,MIMO 链路的信道容量很大程度上取决于H 的秩r 。
矩阵的秩越大，容量也越大。
所以，MIMO 正是利用无线信道的多径效应使相距超过半个波长的天线尽量不相关，从而使信道矩阵秩越大，进而在不增加带宽和发射功率的情况下增加系统容量。
[4]下面我们说明信道容量是如何与信道矩阵H 相关的。
令min(,)R T m n n =为矩阵H 的秩，定义：,,H R THR TH H n n Q HH n n ⎧>⎪=⎨<⎪⎩ (2.25)设(1,2,...)i i m λ=是Q 的特征值，则：1det()()mm i i I Q λλλ=-=-∏(2.26)用2T T n P σ-代替（2.26）中的λ，得：221det()(1)mi TT m i T T p P I Q n n λσσ=+=+∏ (2.27)把式(2.27)代入式（2.24）得平均功率分配的MIMO 信道容量：22log [det()]/T m T P C B I Q bit s n σ=+(2.28)当Tn 逐渐增大，使得1m TQ I n →，此时，可以得到信道容量的近似表达式：22log (1)/TP C Bm bit s σ=+(2.29)由此可以看出当发射天线数目很多时,信道容量随m 的增大而线性增大,也就是说可以在不增加带宽和发射功率的情况下成倍的提高信道容量。
参考文献：1 梁毓锋.MIMO无线通信系统的信道容量分析:[D].大连:大连海事大学，20082 Thomas M.Cover，Joy A.Thomas（著），阮吉寿，张华（译）.信息论基础[M].北京:机械工业出版社,20093 孙丹，张晓光.MIMO系统信道容量研究[J].现代电子技术,2006(19):4-64 刘冰.MIMO系统的信道容量分析[J].微计算机信息,2005,21(12-3):129-131。