数学建模之蚁群算法
蚁群算法内容简介

蚁群算法内容简介蚁群算法(ant colony optimization, ACO),又称蚂蚁算法,是一种用来在图中寻找优化路径的机率型算法群算法是由意大利学者Dorigo等人于20世纪90年代初期通过模拟自然界中蚂蚁集体寻经的行为而提出的一种基于种群的启发式随机搜索算法,蚁群算法具有并行性、鲁棒性、正反馈性等特点。
蚁群算法最早成功应用于解决著名的旅行商问题以及二次分配问题、车间任务调度问题、图的着色问题、网络路由等许多复杂的组合问题。
蚁群算法是一种模拟进化算法,初步的研究表明该算法具有许多优良的性质.针对PID控制器参数优化设计问题,将蚁群算法设计的结果与遗传算法设计的结果进行了比较,数值仿真结果表明,蚁群算法具有一种新的模拟进化优化方法的有效性和应用价值。
随着人们对效益的要求越来越高,人们发现组合优化的各种方法,但在一些复杂度比较高的问题上,一些传统的方法显示了他的限制,列如计算量上升太快,时间复杂度很高,这就需要一些新的方法来解决这些问题,从而有效地克服传统蚁群算法中容易陷入局部最优解和收敛速度慢的现象。
蚁群系统(Ant Colony System),这种算法是目前国内外启发式算法中的研究热点和前沿课题,被成功地运用于旅行商问题的求解,蚁群算法在求解复杂优化问题方面具有很大的优越性和广阔的前景。
但是,根据观察实验发现,蚁群中的多个蚂蚁的运动是随机的,在扩散范围较大时,在较短时间内很难找出一条较好的路径,在算法实现的过程中容易出现停滞现象和收敛速度慢现象。
在这种弊端的情况下,学者们提出了一种自适应蚁群算法,通过自适应地调整运行过程中的挥发因子来改变路径中信息素浓度,从而有效地克服传统蚁群算法中容易陷入局部最优解和收敛速度慢的现象。
下面是一些最常用的变异蚁群算法精英蚂蚁系统全局最优解决方案在每个迭代以及其他所有的蚂蚁的沉积信息素。
最大最小蚂蚁系统(MMAS)添加的最大和最小的信息素量[ τmax ,τmin ],只有全局最佳或迭代最好的巡逻沉积的信息素。
蚁群算法

蚁群算法目录1 蚁群算法基本思想 (1)1.1蚁群算法简介 (1)1.2蚁群行为分析 (1)1.3蚁群算法解决优化问题的基本思想 (2)1.4蚁群算法的特点 (2)2 蚁群算法解决TSP问题 (3)2.1关于TSP (3)2.2蚁群算法解决TSP问题基本原理 (3)2.3蚁群算法解决TSP问题基本步骤 (5)3 案例 (6)3.1问题描述 (6)3.2解题思路及步骤 (6)3.3MATLB程序实现 (7)3.1.1 清空环境 (7)3.2.2 导入数据 (7)3.3.3 计算城市间相互距离 (7)3.3.4 初始化参数 (7)3.3.5 迭代寻找最佳路径 (7)3.3.6 结果显示 (7)3.3.7 绘图 (7)1 蚁群算法基本思想1.1 蚁群算法简介蚁群算法(ant colony algrothrim ,ACA )是由意大利学者多里戈(Dorigo M )、马聂佐( Maniezzo V )等人于20世纪90初从生物进化的机制中受到启发,通过模拟自然界蚂蚁搜索路径的行为,提出来的一种新型的模拟进化算法。
该算法用蚁群在搜索食物源的过程中所体现出来的寻优能力来解决一些系统优化中的困难问题,其算法的基本思想是模仿蚂蚁依赖信息素,通过蚂蚁间正反馈的方法来引导每个蚂蚁的行动。
蚁群算法能够被用于解决大多数优化问题或者能够转化为优化求解的问题,现在其应用领域已扩展到多目标优化、数据分类、数据聚类、模式识别、电信QoS 管理、生物系统建模、流程规划、信号处理、机器人控制、决策支持以及仿真和系统辩识等方面。
蚁群算法是群智能理论研究领域的一种主要算法。
1.2 蚁群行为分析EABCDF d=3d=2 m=20 t=0AB C Dd=3d=2 m=10 m=10t=11.3 蚁群算法解决优化问题的基本思想用蚂蚁的行走路径表示待优化问题的可行解,整个蚂蚁群体的所有路径构成待优化问题的解空间。
路径较短的蚂蚁释放的信息量较多,随着时间的推进,较短路径上积累的信息浓度逐渐增高,选择该路径的蚂蚁个数愈来愈多。
蚁群算法及案例分析精选全文

群在选择下一条路径的时
候并不是完全盲目的,而是
按一定的算法规律有意识
地寻找最短路径
自然界蚁群不具有记忆的
能力,它们的选路凭借外
激素,或者道路的残留信
息来选择,更多地体现正
反馈的过程
人工蚁群和自然界蚁群的相似之处在于,两者优先选择的都
是含“外激素”浓度较大的路径; 两者的工作单元(蚂蚁)都
正反馈、较强的鲁棒性、全
局性、普遍性
局部搜索能力较弱,易出现
停滞和局部收敛、收敛速度
慢等问题
优良的分布式并行计算机制
长时间花费在解的构造上,
导致搜索时间过长
Hale Waihona Puke 易于与其他方法相结合算法最先基于离散问题,不
能直接解决连续优化问题
蚁群算法的
特点
蚁群算法的特点及应用领域
由于蚁群算法对图的对称性以
及目标函数无特殊要求,因此
L_ave=zeros(NC_max,1);
%各代路线的平均长度
while NC<=NC_max
%停止条件之一:达到最大迭代次数
% 第二步:将m只蚂蚁放到n个城市上
Randpos=[];
for i=1:(ceil(m/n))
Randpos=[Randpos,randperm(n)];
end
Tabu(:,1)=(Randpos(1,1:m))';
scatter(C(:,1),C(:,2));
L(i)=L(i)+D(R(1),R(n));
hold on
end
plot([C(R(1),1),C(R(N),1)],[C(R(1),2),C(R(N),2)])
蚁群算法的

蚁群算法的
蚁群算法是近几十年来智能计算领域中新兴的最重要的优化技
术之一,它被认为是能够模拟蚂蚁群体寻找最优解的算法,已经被广泛应用于工程中,包括机器的设计、航运系统的优化,和物流系统的规划等等代表众多应用。
蚁群算法是模拟蚂蚁群体搜索食物的行为,从而求解一个待求解的问题的优化技术,早在1995年的时候就已经被提出,在大规模问题下有很好的搜索性能。
蚁群算法通过模拟蚁群通过特定路径来搜索资源来求解优化问题,模拟理论上这是一个有效的优化算法,可以帮助系统找到最优解并获得最大回报。
蚁群算法的工作原理是通过模拟蚁群通过特定路径来搜索资源,每只蚂蚁经过一条路径时,就会根据路径的特性来选择继续前进的方向,而其他的蚂蚁也会根据当前的状态来决定自己前进的路径,从而形成一种合作的局部路径,一旦有蚂蚁发现有较好的路径就会被其他蚂蚁模仿,最终有效地把所有蚂蚁引导到最优解。
蚁群算法具有几个显著的优点,首先它所耗费的计算资源要比其他算法少得多,其次它的实施简单,能够快速的数据搜索,并且运行简单,容易理解,最后,它可以自我改进,也就是说,它能够实时地进行调整,以适应变化的环境。
虽然蚁群算法有许多优点,但它也有一些限制,首先,蚁群算法对全局最优解的搜索能力有限,其次,它容易陷入局部最优点,最后,它也存在一定的调参不利,对于参数的调整可能会导致算法效率的降
低。
总结而言,蚁群算法是一种有效的优化技术,使用它可以快速有效的搜索解决问题,在几乎所有的行业中都能取得较好的效果。
然而,它也需要注意参数的调整,以及全局最优解的搜索能力,才能发挥出最大的效力。
蚁群算法概述

蚁群算法概述一、蚁群算法蚁群算法(ant colony optimization, ACO),又称蚂蚁算法,是一种用来寻找最优解决方案的机率型技术。
它由Marco Dorigo于1992年在他的博士论文中引入,其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。
蚂蚁在路径上前进时会根据前边走过的蚂蚁所留下的分泌物选择其要走的路径。
其选择一条路径的概率与该路径上分泌物的强度成正比。
因此,由大量蚂蚁组成的群体的集体行为实际上构成一种学习信息的正反馈现象:某一条路径走过的蚂蚁越多,后面的蚂蚁选择该路径的可能性就越大。
蚂蚁的个体间通过这种信息的交流寻求通向食物的最短路径。
蚁群算法就是根据这一特点,通过模仿蚂蚁的行为,从而实现寻优。
这种算法有别于传统编程模式,其优势在于,避免了冗长的编程和筹划,程序本身是基于一定规则的随机运行来寻找最佳配置。
也就是说,当程序最开始找到目标的时候,路径几乎不可能是最优的,甚至可能是包含了无数错误的选择而极度冗长的。
但是,程序可以通过蚂蚁寻找食物的时候的信息素原理,不断地去修正原来的路线,使整个路线越来越短,也就是说,程序执行的时间越长,所获得的路径就越可能接近最优路径。
这看起来很类似与我们所见的由无数例子进行归纳概括形成最佳路径的过程。
实际上好似是程序的一个自我学习的过程。
3、人工蚂蚁和真实蚂蚁的异同ACO是一种基于群体的、用于求解复杂优化问题的通用搜索技术。
与真实蚂蚁通过外激素的留存/跟随行为进行间接通讯相似,ACO中一群简单的人工蚂蚁(主体)通过信息素(一种分布式的数字信息,与真实蚂蚁释放的外激素相对应)进行间接通讯,并利用该信息和与问题相关的启发式信息逐步构造问题的解。
人工蚂蚁具有双重特性:一方面,他们是真实蚂蚁的抽象,具有真实蚂蚁的特性,另一方面,他们还有一些在真实蚂蚁中找不到的特性,这些新的特性,使人工蚂蚁在解决实际优化问题时,具有更好地搜索较好解的能力。
人工蚂蚁与真实蚂蚁的相同点为:1.都是一群相互协作的个体。
蚁群算法——精选推荐

蚁群算法⼀、蚁群算法蚁群算法是在20世纪90年代由澳⼤利亚学者Marco Dorigo等⼈通过观察蚁群觅⾷的过程,发现众多蚂蚁在寻找⾷物的过程中,总能找到⼀条从蚂蚁巢⽳到⾷物源之间的最短路径。
随后他们在蚂蚁巢⽳到⾷物源之间设置了⼀个障碍,⼀段时间以后发现蚂蚁⼜重新⾛出了⼀条到⾷物源最短的路径。
通过对这种现象的不断研究,最后提出了蚁群算法。
蚁群算法在解决(即TSP问题)时,取得了⽐较理想的结果。
⼆、基本⼈⼯蚁群算法原理运⽤⼈⼯蚁群算法求解TSP问题时的基本原理是:将m个蚂蚁随机地放在多个城市,让这些蚂蚁从所在的城市出发,n步(⼀个蚂蚁从⼀个城市到另外⼀个城市为1步)之后返回到出发的城市。
如果m个蚂蚁所⾛出的m条路经对应的中最短者不是TSP问题的最短路程,则重复这⼀过程,直⾄寻找到满意的TSP问题的最短路径为⽌。
为了说明这⼀个算法下⾯⽤⼀个算法流程图来表⽰⼀下:三、蚁群算法中涉及到的参数及其符号::蚂蚁数量,约为城市数量的1.5倍。
如果蚂蚁数量过⼤,则每条路径上的信息素浓度趋于平均,正反馈作⽤减弱,从⽽导致收敛速度减慢;如果过⼩,则可能导致⼀些从未搜索过的路径信息素浓度减⼩为0,导致过早收敛,解的全局最优性降低:信息素因⼦,反映了蚂蚁运动过程中积累的信息量在指导蚁群搜索中的相对重要程度,取值范围通常在[1, 4]之间。
如果信息素因⼦值设置过⼤,则容易使随机搜索性减弱;其值过⼩容易过早陷⼊局部最优:启发函数因⼦,反映了启发式信息在指导蚁群搜索中的相对重要程度,取值范围在[3, 4.5]之间。
如果值设置过⼤,虽然收敛速度加快,但是易陷⼊局部最优;其值过⼩,蚁群易陷⼊纯粹的随机搜索,很难找到最优解:信息素挥发因⼦,反映了信息素的消失⽔平,相反的反映了信息素的保持⽔平,取值范围通常在[0.2, 0.5]之间。
当取值过⼤时,容易影响随机性和全局最优性;反之,收敛速度降低:信息素常数,表⽰蚂蚁遍历⼀次所有城市所释放的信息素总量。
04蚁群算法ACA

导言蚁群算法是20世纪90年代发展起来一种模仿蚂蚁群体行为的新的智能优化算法。
意大利学者Dorigo M等人提出一种模拟昆虫王国蚂蚁群体觅食行为方式的仿生优化算法——蚁群算法(Ant Colony Algorithm,ACA)。
该算法引入正反馈并行机制,具有较强的鲁棒性、优良的分布式计算机制、易于与其他方法结合等优点。
目前蚁群算法已经渗透到各个应用领域,从一维静态优化问题到多维动态优化问题,从离散问题到连续问题。
蚁群算法解决了许多复杂优化和经典NP-C问题,展现出优异的性能和广阔的发展前景。
基本蚁群算法的原理基本蚁群算法(Ant System,AS)是采用人工蚂蚁的行走路线来表示待求问题可行解得一种方法。
每只人工蚂蚁在解空间中独立的搜索可行解,当它们碰到一个还没有走过的路口时,就随机挑选一条路径前行,同时释放出与路径长度有关的信息素(pheromone) 。
路径越短信息素的浓度就越大。
当后继的人工蚂蚁再次碰到这个路口的时候,以相对较大的概率选择信息素较多的路径,并在“行走路径”上留下更多的信息素,影响后来的蚂蚁,形成正反馈机制。
随着算法的推进,代表最优解路线上的信息素逐渐增多,选择它的蚂蚁也逐渐增多,其他路径上的信息素却会随着时间的流逝而逐渐消减,最终整个蚂蚁在正反馈机制的作用下集中到代表最优解的路线上,也就找到了最优解。
在整个寻优过程中,单只蚂蚁的选择能力有限,但蚁群具有高度的自组织性,通过信息素交换路径信息,形成集体自催化行为,找到最优路径。
蚁群优化算法中,每个优化问题的解都是搜索空间的一只蚂蚁,蚂蚁都有一个由优化的目标函数决定的适应度函数值(与释放的信息素成正比) ,蚂蚁根据周围信息素的多少决定搜索方向,并在搜索过的路径上释放信息素以影响别的蚂蚁。
优缺点分析ACA 具有如下优点:(1)ACA 是一种正反馈算法,这是蚁群算法最显著的特点;(2)ACA 本质上一种分布式并行算法。
(3)ACA 具有较好的全局寻优特性。
蚁群算法——精选推荐
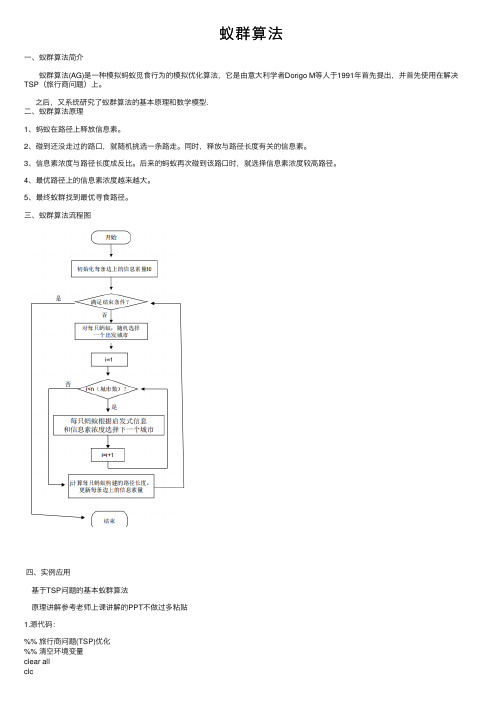
蚁群算法⼀、蚁群算法简介 蚁群算法(AG)是⼀种模拟蚂蚁觅⾷⾏为的模拟优化算法,它是由意⼤利学者Dorigo M等⼈于1991年⾸先提出,并⾸先使⽤在解决TSP(旅⾏商问题)上。
之后,⼜系统研究了蚁群算法的基本原理和数学模型.⼆、蚁群算法原理1、蚂蚁在路径上释放信息素。
2、碰到还没⾛过的路⼝,就随机挑选⼀条路⾛。
同时,释放与路径长度有关的信息素。
3、信息素浓度与路径长度成反⽐。
后来的蚂蚁再次碰到该路⼝时,就选择信息素浓度较⾼路径。
4、最优路径上的信息素浓度越来越⼤。
5、最终蚁群找到最优寻⾷路径。
三、蚁群算法流程图四、实例应⽤基于TSP问题的基本蚁群算法原理讲解参考⽼师上课讲解的PPT不做过多粘贴1.源代码:%% 旅⾏商问题(TSP)优化%% 清空环境变量clear allclc%% 导⼊数据citys = ceil(rand(50,2)*50000)%load newcitys.mat%% 计算城市间相互距离fprintf('Computing Distance Matrix... \n');n = size(citys,1);D = zeros(n,n);for i = 1:nfor j = 1:nif i ~= jD(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));elseD(i,j) = 1e-4;endendend%% 初始化参数fprintf('Initializing Parameters... \n');m = 50; % 蚂蚁数量alpha = 1; % 信息素重要程度因⼦beta = 5; % 启发函数重要程度因⼦rho = 0.05; % 信息素挥发因⼦Q = 1; % 常系数Eta = 1./D; % 启发函数Tau = ones(n,n); % 信息素矩阵Table = zeros(m,n); % 路径记录表iter = 1; % 迭代次数初值iter_max = 150; % 最⼤迭代次数Route_best = zeros(iter_max,n); % 各代最佳路径Length_best = zeros(iter_max,1); % 各代最佳路径的长度Length_ave = zeros(iter_max,1); % 各代路径的平均长度%% 迭代寻找最佳路径figure;while iter <= iter_maxfprintf('迭代第%d次\n',iter);% 随机产⽣各个蚂蚁的起点城市start = zeros(m,1);for i = 1:mtemp = randperm(n);start(i) = temp(1);endTable(:,1) = start;% 构建解空间citys_index = 1:n;% 逐个蚂蚁路径选择for i = 1:m% 逐个城市路径选择for j = 2:ntabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)allow_index = ~ismember(citys_index,tabu);allow = citys_index(allow_index); % 待访问的城市集合P = allow;% 计算城市间转移概率for k = 1:length(allow)P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta; endP = P/sum(P);% 轮盘赌法选择下⼀个访问城市Pc = cumsum(P);target_index = find(Pc >= rand);target = allow(target_index(1));Table(i,j) = target;endend% 计算各个蚂蚁的路径距离Length = zeros(m,1);for i = 1:mRoute = Table(i,:);for j = 1:(n - 1)Length(i) = Length(i) + D(Route(j),Route(j + 1));endLength(i) = Length(i) + D(Route(n),Route(1));end% 计算最短路径距离及平均距离if iter == 1[min_Length,min_index] = min(Length);Length_best(iter) = min_Length;Length_ave(iter) = mean(Length);Route_best(iter,:) = Table(min_index,:);else[min_Length,min_index] = min(Length);Length_best(iter) = min(Length_best(iter - 1),min_Length);Length_ave(iter) = mean(Length);if Length_best(iter) == min_LengthRoute_best(iter,:) = Table(min_index,:);elseRoute_best(iter,:) = Route_best((iter-1),:);endend% 更新信息素Delta_Tau = zeros(n,n);% 逐个蚂蚁计算for i = 1:m% 逐个城市计算for j = 1:(n - 1)Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i); endDelta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i); endTau = (1-rho) * Tau + Delta_Tau;% 迭代次数加1,清空路径记录表% figure;%最佳路径的迭代变化过程[Shortest_Length,index] = min(Length_best(1:iter));Shortest_Route = Route_best(index,:);plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');pause(0.3);iter = iter + 1;Table = zeros(m,n);% endend%% 结果显⽰[Shortest_Length,index] = min(Length_best);Shortest_Route = Route_best(index,:);disp(['最短距离:' num2str(Shortest_Length)]);disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);%% 绘图figure(1)plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');grid onfor i = 1:size(citys,1)text(citys(i,1),citys(i,2),[' ' num2str(i)]);endtext(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),' 起点');text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),' 终点');xlabel('城市位置横坐标')ylabel('城市位置纵坐标')title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])figure(2)plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')legend('最短距离','平均距离')xlabel('迭代次数')ylabel('距离')title('各代最短距离与平均距离对⽐')运⾏结果:利⽤函数citys = ceil(rand(50,2)*50000) 随机产⽣五⼗个城市坐标2.研究信息素重要程度因⼦alpha, 启发函数重要程度因⼦beta,信息素挥发因⼦rho对结果的影响为了保证变量唯⼀我重新设置五⼗个城市信息进⾏实验在原来设值运⾏结果:实验结果可知当迭代到120次趋于稳定2.1 alpha值对实验结果影响(1)当alpha=4时运⾏结果实验结果可知当迭代到48次左右趋于稳定(2)当alpha=8时运⾏结果:有图可知迭代40次左右趋于稳定,搜索性较⼩(3)当alpha= 0.5运⾏结果:有图可知迭代到140次左右趋于稳定(4)当alpha=0.2时运⾏结果:结果趋于110次左右稳定所以如果信息素因⼦值设置过⼤,则容易使随机搜索性减弱;其值过⼩容易过早陷⼊局部最优2.2 beta值对实验影响(1)当 beta=8时运⾏结果结果迭代75次左右趋于稳定(2)当 beta=1时运⾏结果:结果迭代130次左右趋于稳定所以beta如果值设置过⼤,虽然收敛速度加快,但是易陷⼊局部最优;其值过⼩,蚁群易陷⼊纯粹的随机搜索,很难找到最优解2.3 rho值对实验结果影响(1)当rho=3时运⾏结果:结果迭代75次左右趋于稳定(2)当rho=0.05运⾏结果:结果迭代125次左右趋于稳定所以如果rho取值过⼤时,容易影响随机性和全局最优性;反之,收敛速度降低总结:蚁群算法对于参数的敏感程度较⾼,参数设置的好,算法的结果也就好,参数设置的不好则运⾏结果也就不好,所以通常得到的只是局部最优解。
蚁群算法简述

2.蚁群算法的特征
下面是对蚁群算法的进行过程中采用的规则进行的一些说明. 范围
蚂蚁观察到的范围是一个方格世界,蚂蚁有一个参数为速度半径一般 是3,那么它能观察到的范围就是33个方格世界,并且能移动的距离也在这 个范围之内. 环境
蚂蚁所在的环境是一个虚拟的世界,其中有障碍物,有别的蚂蚁,还有 信息素,信息素有两种,一种是找到食物的蚂蚁洒下的食物信息素,一种是找 到窝的蚂蚁洒下的窝的信息素.每个蚂蚁都仅仅能感知它范围内的环境信 息.环境以一定的速率让信息素消失. 觅食规则
2.蚁群算法的特征
基本蚁群算法流程图详细
1. 在初始状态下,一群蚂蚁外出,此时没有信息素,那么各 自会随机的选择一条路径. 2. 在下一个状态,每只蚂蚁到达了不同的点,从初始点到这 些点之间留下了信息素,蚂蚁继续走,已经到达目标的蚂蚁 开始返回,与此同时,下一批蚂蚁出动,它们都会按照各条路 径上信息素的多少选择路线selection,更倾向于选择信息 素多的路径走当然也有随机性. 3. 又到了再下一个状态,刚刚没有蚂蚁经过的路线上的信 息素不同程度的挥发掉了evaporation,而刚刚经过了蚂蚁 的路线信息素增强reinforcement.然后又出动一批蚂蚁,重 复第2个步骤. 每个状态到下一个状态的变化称为一次迭代,在迭代多次 过后,就会有某一条路径上的信息素明显多于其它路径,这 通常就是一条最优路径.
人工蚁群算法
基于以上蚁群寻找食物时的最优路径选择问题,可 以构造人工蚁群,来解决最优化问题,如TSP问题.
人工蚁群中把具有简单功能的工作单元看作蚂蚁. 二者的相似之处在于都是优先选择信息素浓度大的路 径.较短路径的信息素浓度高,所以能够最终被所有蚂 蚁选择,也就是最终的优化结果.
两者的区别在于人工蚁群有一定的记忆能力,能够 记忆已经访问过的节点.同时,人工蚁群再选择下一条 路径的时候是按一定算法规律有意识地寻找最短路径, 而不是盲目的.例如在TSP问题中,可以预先知道当前 城市到下一个目的地的距离.
蚁群算法简介

蚁群算法简介蚁群算法是一种优化技术,受到自然界中蚂蚁寻找食物的行为的启发。
这种算法模拟了蚂蚁的信息共享和移动模式,用于解决复杂的组合优化问题,如旅行商问题(TSP)、车辆路径问题(VRP)等。
一、蚁群算法的基本原理在自然界中,蚂蚁寻找食物的行为非常有趣。
它们会在路径上留下信息素,后续的蚂蚁会根据信息素的强度选择路径,倾向于选择信息素浓度高的路径。
这样,一段时间后,大多数蚂蚁都会选择最短或最佳的路径。
这就是蚁群算法的基本原理。
二、蚁群算法的主要步骤1.初始化:首先,为每条边分配一个初始的信息素浓度。
通常,所有边的初始信息素浓度都是相等的。
2.路径选择:在每一步,每个蚂蚁都会根据当前位置和周围信息素浓度选择下一步的移动方向。
选择概率与信息素浓度成正比,与距离成反比。
这意味着蚂蚁更倾向于选择信息素浓度高且距离短的路径。
3.释放信息素:当蚂蚁完成一次完整的路径后,它会在其经过的边上留下信息素。
信息素的浓度与解决问题的质量成正比,即如果蚂蚁找到了一条更好的路径,那么这条路径上的信息素浓度会增加。
4.更新:经过一段时间后,信息素会随时间的推移而挥发,这使得那些不再被认为是最优的路径上的信息素浓度逐渐减少。
同时,每条边上的信息素浓度也会随着时间的推移而均匀增加,这使得那些从未被探索过的路径也有被选择的可能性。
5.终止条件:算法会在找到满足条件的最优解或达到预设的最大迭代次数后终止。
三、蚁群算法的优势和局限性蚁群算法的优势在于其对于组合优化问题的良好性能和其自然启发式的搜索过程。
这种算法能够有效地找到全局最优解,并且在搜索过程中能够避免陷入局部最优解。
此外,蚁群算法具有较强的鲁棒性,对于问题的规模和复杂性具有较强的适应性。
然而,蚁群算法也存在一些局限性。
首先,算法的性能高度依赖于参数的设置,如信息素的挥发速度、蚂蚁的数量、迭代次数等。
其次,对于一些复杂的问题,可能需要很长的计算时间才能找到最优解。
此外,蚁群算法可能无法处理大规模的问题,因为这可能导致计算时间和空间的复杂性增加。
蚁群算法

蚁群算法
目录
1 2 3
4
蚁群算法概述 蚁群算法分析 蚁群算法应用 实例仿真
蚁群算法概述——概念
20世纪50年代中期创立了仿生学,人们从生物进化的机 理中受到启发。提出了许多用以解决复杂优化问题的新 方法,如进化规划、进化策略、遗传算法等,这些算法 成功地解决了一些实际问题。 蚁群算法(ant colony optimization, ACO )又称为 蚂蚁算法, 是对自然界蚂蚁的寻径方式进行模似而得 出的一种仿生算法。
蚁群算法概述——发展历史
• 1998年,Dorigo发起了第一次蚁群算法的专题会议 • 1998年,Stützle提出初步的并行实现 • 1999年,Bonabeau, Dorigo和Theraulaz的出版了一本书,主要 关于人工蚂蚁 • 2000年,未来计算机系统杂志上发表了蚂蚁算法特刊 • 2000年,调度的最早期的应用程序,调度了序列和约束的满意 度 • 2000年,Gutjahr提供了一个蚁群算法收敛的第一个证据 • 2001年,COA算法首次被使用(Eurobios和AntOptima) • 2001年,IREDA和他的同事们发表了第一个多对象算法 • 2002年,调度设计的首次应用,贝叶斯网络 • 2002年,比安奇和她的同事提出了随机问题的最早算法 • 2004年,Zlochin和Dorigo表明,有些算法等价于随机梯度下降 ,交叉熵和估计分布算法 • 2005年,首次在蛋白质折叠问题上的应用。
蚁群算法概述——蚂蚁觅食过程
• 蚂蚁搜寻食物的具体过程。在蚁群寻找食物时,它们总能找到一条从 食物到巢穴之间的最优路径。在最开始觅食时如下图1,蚂蚁随机选 择一条路径开始觅食;但随着时间的改变,所有的蚂蚁都会选择较短 的路线,如下图2所示。
第22讲 蚁群算法

To Matlab exp12_3_2.m
综上,某条路径上走过的蚂蚁越多,则后来者选择该路径的概率越大,所以我们可以 认为蚁群在毫无提示的前提条件下,正确地选择了最短路径,达到了最快觅食的目的,并 且可以在周围环境变化的情况下,依靠信息素的变化迅速调整并找到新的最短路径。
二、蚁群算法数学模型
下面以旅行商问题(TSP)为例来更深入地介绍蚁群算法,并建立其数学模 型。并假设: (1) 蚂蚁根据与城市间距离和路径上信息素含量有关的某一概率函数选择 下一个需要访问的城市; (2)每只蚂蚁在完成一次周游(指蚂蚁走完所有的城市)以前,不允许转 到已访问的城市; (3)蚂蚁在完成一次周游时,在每一条走过的边上释放信息素; (4)蚂蚁留在边上的信息素会随着时间地推移不断挥发。
n
ij (t 1) (1 ) ij (t ) ij
k ij ij k 1
(3-2、3)
k 其中,信息素增量 ij 可以有三种不同的计算方式,分别为
1)蚁密系统
Q 若蚂蚁k在本次周游中经过路径lij k ij 否则 0
Q 为正常数。
(3-4)
2)蚁量系统
Q / dij k ij 0
3)蚁周系统
若蚂蚁k在本次周游中经过路径lij 否则
(3-5)
Q / Lk k ij 0
若蚂蚁k在本次周游中经过路径lij 否则
(3-6)
Lk 为第 k 只蚂蚁在本次周游中所走的路径长度。
以上三种计算方式可根据不同的情况进行选取,它们之间的对比如下表所示: 方 式 最 优 解 收敛速度 算法效率 蚁密系统 局部最优 慢 较低 蚁量系统 局部最优 较快 较高 蚁周系统 全局最优 快 高
一、蚁群算法基本思想
蚁群算法的讲解

路径的蚂蚁多,所以信息素的积累速度比较长路径快。因此,当后续蚂蚁在路口时
,就能感知先前蚂蚁留下的信息,并倾向于选择一条较短的路径前行。这种正反馈
机制使得越来越多的蚂蚁在巢穴与食物之间的最短路径上行进。由于其他路径上的
信息素会随着时间蒸发,最终所有的蚂蚁都在最优路径上行进。
TSP作为应用实例提出的。
TSP 问题(Traveling Salesman Problem,旅行商问题)
是数学领域中著名问题之一。
问题概述:假设有一个旅行商人要拜访n个城市,他必须
选择所要走的路径,路径的限制是每个城市只能拜访一次,
而且最后要回到原来出发的城市。路径的选择目标是要求得
的路径路程为所有路径之中的最小值。TSP问题是一个NP问
整数,表示算法已经收敛,不再需要继续;
4. 目标值控制规则,给定优化问题(目标最小化)的一
个下界和一个误差值,当算法得到的目标值同下界之
差小于给定的误差值时,算法终止。
71
例 1 旅行商问题(TSP 问题)假设有一个旅行商人
要拜访全国 31 个省会城市,他需要选择所要走的路
径,路径的限制是每个城市只能拜访一次,而且最
后要回到原来出发的城市。路径的选择要求是:所
选路径的路程为所有路径之中的最小值。全国 31 个
省会城市的坐标为 [1304 2312; 3639 1315; 4177
2244; 3712 1399; 3488 1535; 3326 1556; 3238
1229; 4196 1004; 4312 790; 4386 570; 3007 1970;
致、有形的结构。经过“演化”,有些死亡,有些静止,有些
蚁群算法

Food
1
1
D
B
Obstacle
1
A
1
Nest
2 C
2
图1.1 蚁群系统示意图
2. 蚁群算法基本原理
蚁群算法是一种随机搜索算法,与其他模型进化算法一样, 通过候选解组成的群体的进化过程来寻求最优解,该过程包括两 个阶段:适应阶段和协助阶段。
⑴在适应阶段,各候选解根据积累的信息不断调整自身结构; ⑵在协助阶段,候选解之间通过信息交流,以期望产生性能更 好的解。
城市,tabuk (k 1, 2, , m) 用以记录蚂蚁 k 当前所走过的城市,集合tabuk 随着进
化过程作动态调整。ij 表示边弧 (i, j) 的能见度,用某种启发式算法算出,一般
取ij 1 dij , dij 表示城市 i 与城市 j 之间的距离。 表示轨迹的相对重要性,
表示能见度的相对重要性。
Obstacle
C
在 t=5 时刻,两组蚂蚁在 D 点相遇,
此时,DB 上的信息素数量与 DC 上的相
1
A
2
同,因为各有 10 只蚂蚁选择了相应的道
1
路,从而有 5 只返回的蚂蚁将选择 BD 而
另外 5 只将选择 CD;
Nest
图1.1 蚁群系统示意图
2. 蚁群算法基本原理
在 t=8 时刻,前 5 只蚂蚁将返回巢穴, 而 AC、DC、BD 上各有 5 只蚂蚁;
Food
1
1
D
B
Obstacle
1
A
1
Nest
2 C
2
图1.1 蚁群系统示意图
2. 蚁群算法基本原理
在 t=0 时刻,20 只蚂蚁从巢穴出发移
蚁群算法

蚁群算法蚁群算法(ant colony optimization, ACO),又称蚂蚁算法,是一种用来在图中寻找优化路径的机率型技术。
它由Marco Dorigo于1992年在他的博士论文中引入,其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。
蚁群算法是一种模拟进化算法,初步的研究表明该算法具有许多优良的性质.针对PID控制器参数优化设计问题,将蚁群算法设计的结果与遗传算法设计的结果进行了比较,数值仿真结果表明,蚁群算法具有一种新的模拟进化优化方法的有效性和应用价值.蚁群算法是一种求解组合最优化问题的新型通用启发式方法,该方法具有正反馈、分布式计算和富于建设性的贪婪启发式搜索的特点。
通过建立适当的数学模型,基于故障过电流的配电网故障定位变为一种非线性全局寻优问题。
由柳洪平创建。
预期的结果:各个蚂蚁在没有事先告诉他们食物在什么地方的前提下开始寻找食物。
当一只找到食物以后,它会向环境释放一种信息素,吸引其他的蚂蚁过来,这样越来越多的蚂蚁会找到食物!有些蚂蚁并没有象其它蚂蚁一样总重复同样的路,他们会另辟蹊径,如果令开辟的道路比原来的其他道路更短,那么,渐渐,更多的蚂蚁被吸引到这条较短的路上来。
最后,经过一段时间运行,可能会出现一条最短的路径被大多数蚂蚁重复着。
原理:为什么小小的蚂蚁能够找到食物?他们具有智能么?设想,如果我们要为蚂蚁设计一个人工智能的程序,那么这个程序要多么复杂呢?首先,你要让蚂蚁能够避开障碍物,就必须根据适当的地形给它编进指令让他们能够巧妙的避开障碍物,其次,要让蚂蚁找到食物,就需要让他们遍历空间上的所有点;再次,如果要让蚂蚁找到最短的路径,那么需要计算所有可能的路径并且比较它们的大小,而且更重要的是,你要小心翼翼的编程,因为程序的错误也许会让你前功尽弃。
这是多么不可思议的程序!太复杂了,恐怕没人能够完成这样繁琐冗余的程序。
然而,事实并没有你想得那么复杂,上面这个程序每个蚂蚁的核心程序编码不过100多行!为什么这么简单的程序会让蚂蚁干这样复杂的事情?答案是:简单规则的涌现。
23个基本测试函数 蚁群算法

23个基本测试函数蚁群算法蚁群算法是一种模拟蚂蚁行为的启发式算法,它通过模拟蚁群寻找食物的行为,来解决各种优化问题。
蚁群算法的核心思想是通过信息交流和反馈机制来寻找问题的最优解。
本文将介绍蚁群算法的基本原理,并以23个基本测试函数为例,展示蚁群算法在解决优化问题中的应用。
1. 算法简介蚁群算法最早由意大利学者Dorigo在1992年提出,其灵感来自于观察蚂蚁在寻找食物时的行为。
蚁群算法将问题抽象成一个图论模型,其中蚂蚁代表解空间中的候选解,信息素则代表蚂蚁之间的信息交流。
蚂蚁根据信息素的浓度和距离选择路径,并在路径上释放信息素,从而影响其他蚂蚁的选择。
通过多次迭代,蚂蚁群体逐渐收敛于最优解。
2. 蚁群算法的基本步骤蚁群算法主要包括初始化、路径选择、信息素更新和收敛判断等步骤。
2.1 初始化在蚁群算法中,需要初始化蚂蚁的位置和信息素的浓度。
蚂蚁的初始位置可以随机选择或者根据问题的特点进行设置。
信息素的初始浓度通常设置为一个较小的常数。
2.2 路径选择在路径选择阶段,蚂蚁根据信息素的浓度和距离选择路径。
通常情况下,信息素浓度较高的路径会有更多的蚂蚁选择,但也存在一定的随机性,以保证算法能够全局搜索。
2.3 信息素更新在信息素更新阶段,蚂蚁根据问题的优化目标更新路径上的信息素。
通常情况下,蚂蚁在路径上释放的信息素与路径的优化程度成正比。
信息素的更新规则可以根据具体问题进行设计。
2.4 收敛判断在每轮迭代之后,需要判断算法是否收敛。
通常情况下,可以通过设定一个停止准则来判断算法是否继续迭代。
常用的停止准则包括迭代次数、目标函数值的变化幅度等。
3. 蚁群算法在优化问题中的应用蚁群算法在解决各种优化问题中具有广泛的应用。
下面以23个基本测试函数为例,展示蚁群算法在不同问题中的应用。
3.1 球面函数球面函数是一个简单的优化问题,目标是找到一个全局最小值。
蚁群算法通过信息素的交流和反馈机制,可以在搜索空间中快速找到最优解。
蚁群算法求解函数最小值

蚁群算法求解函数最小值蚁群算法是一种群体智能算法,它模拟蚂蚁在寻找食物时留下信息、跟随信息和更新信息的行为。
其主要思想是让一群智能体(蚂蚁)在问题空间中随机游走,通过留下信息来指导其他蚂蚁的搜索,最终找到问题的最优解。
本文将介绍如何使用蚁群算法求解函数最小值问题。
1. 问题描述我们要求解函数f(x)的最小值,其中x是一个d维向量,f(x) = ∑(x_i^2),i=1,2,...,d。
因为所有维度上的值都是正的,所以函数的最小值为0。
但在搜索过程中,优化器需要在向量空间中寻找最小值。
2. 蚁群算法基本思想3. 蚁群算法具体实现1)初始化初始化迭代次数、蚁群大小、信息素浓度以及每只蚂蚁的位置和速度。
对于每个蚂蚁的初始位置和速度,可以使用随机值来生成。
同时,需要记录当前所有蚂蚁中最优的位置和最优的适应度值。
2)信息素选取蚂蚁在搜索过程中留下信息,用于指导其他蚂蚁的行动。
信息素的选择需要权衡两个因素,即蚂蚁个体的局部搜索策略和群体策略。
在局部策略方面,蚂蚁会在已经访问的路径上留下信息素,吸引其他蚂蚁走向已经访问过的区域。
在群体策略方面,信息素可以加速全局搜索,吸引更多的蚂蚁在全局范围内搜索。
3)更新信息素蚂蚁在搜索过程中留下信息,导致当前路径上信息素的浓度增加。
信息素的浓度会随着时间的推移而逐渐降低。
信息素的更新根据当前路径的质量,决定增加或者减少信息素的浓度。
4)更新速度和位置根据留下的信息素和当前位置,更新蚂蚁的速度和位置。
5)计算适应度根据当前位置计算适应度。
这里的适应度即函数的值。
6)更新最优值如果当前的适应度比已记录的最优适应度更优,则更新记录的最优适应度值和位置。
7)终止条件循环运行以上步骤,直到达到指定的迭代次数或满足特定的终止条件。
4. 代码实现示例以Python语言为例,下面给出了求解函数最小值的蚁群算法实现示例:```pythonimport numpy as npclass Ant(object):def __init__(self, dim, max_pos, min_pos):self.dim = dimself.max_pos = max_posself.min_pos = min_posself.pos = np.random.uniform(min_pos, max_pos, size=dim)self.velocity = np.random.uniform(min_pos, max_pos, size=dim)self.pbest = self.posself.pbest_fitness = float('inf')self.fitness = float('inf')def evaluate(self, f):self.fitness = f(self.pos)if self.fitness < self.pbest_fitness:self.pbest = self.posself.pbest_fitness = self.fitnessdef update_velocity(self, other_ant_pos, w, c1, c2, max_velocity):r1 = np.random.rand(self.dim)r2 = np.random.rand(self.dim)self.velocity = w * self.velocity + c1 * r1 * (self.pbest - self.pos) + c2 * r2 * (other_ant_pos - self.pos)self.velocity = np.clip(self.velocity, -max_velocity, max_velocity)def update_pos(self):self.pos = self.pos + self.velocityself.pos = np.clip(self.pos, self.min_pos, self.max_pos)class ACO(object):def __init__(self, f, dim=2, max_iter=100, n_ant=10, max_velocity=1, w=0.5, c1=1, c2=1, max_pos=10, min_pos=-10):self.f = fself.dim = dimself.max_iter = max_iterself.n_ant = n_antself.max_velocity = max_velocityself.w = wself.c1 = c1self.c2 = c2self.max_pos = max_posself.min_pos = min_posself.global_best_fitness = float('inf')self.global_best_pos = np.zeros(dim)self.ants = [Ant(dim, max_pos, min_pos) for i in range(n_ant)]self.init_random_ant()def init_random_ant(self):for ant in self.ants:ant.evaluate(self.f)if ant.fitness < self.global_best_fitness:self.global_best_fitness = ant.fitnessself.global_best_pos = ant.posdef search(self):for i in range(self.max_iter):for ant in self.ants:for other_ant in self.ants:if ant != other_ant:ant.update_velocity(other_ant.pos, self.w, self.c1, self.c2, self.max_velocity)ant.update_pos()ant.evaluate(self.f)if ant.fitness < self.global_best_fitness:self.global_best_fitness = ant.fitnessself.global_best_pos = ant.posdef run(self):self.search()print("best fitness: {:.6f}, best position:{}".format(self.global_best_fitness, self.global_best_pos))def f(x):return np.sum(x**2)aco = ACO(f)aco.run()```在这个实现中,我们用Ant表示每个蚂蚁,包含了位置、速度、适应度等信息。
蚁群算法简述

4.蚁群算法的模型类型
下面是一些最常用的变异蚁群算法 1.精英蚂蚁系统 全局最优解决方案在每个迭代以及其他所有的蚂蚁的沉积信息素。 2.最大最小蚂蚁系统( MMAS) 添加的最大和最小的信息素量[ τmax , τmin ],只有全局最佳或迭代最好的 巡逻沉积的信息素。所有的边缘都被初始化为τmax并且当接近停滞时重新初始化 为τmax。 3.蚁群系统 蚁群系统已被提出。 4.基于排序的蚂蚁系统( ASrank ) 所有解决方案都根据其长度排名。然后为每个解决方案衡量信息素的沉积量, 最短路径相比较长路径的解沉积了更多的信息素。 5.连续正交蚁群(COAC) COAC的信息素沉积机制能使蚂蚁协作而有效地寻解。 利用正交设计方法, 在可行域的蚂蚁可以使用增大的全局搜索能力和精度,快速、高效地探索他们选 择的区域。 正交设计方法和自适应半径调整方法也可推广到其他优化算法中,在 解决实际问题施展更大的威力。
4.蚁群算法的模型类型
根据信息素更新策略的不同, M. Dorigo 曾提出3 种不同的基本蚁群算法模型,其差别在于Δτkij (t)求法的 不同,即: Ant - Cycle 模型 Ant - Quantity 模型 Ant - Density 模型 其中Ant - antity 模型和Ant - Density 模型利用的 是局部信息; 而Ant- Cycle 模型利用的是整体信息, 在 求解TSP 时性能较好, 因此通常采用Ant - Cycle 模型 作为蚁群算法的基本模型。
4.蚁群算法的模型类型
Ant-Cycle模型
式中,Q表示信息素强度,它在一定程度上影 响算法的收敛速度;Lk表示第k只蚂蚁在本次 循环中所走路径的总长度。
蚁群算法

§2.3蚁群算法§2.3.1 蚁群算法的思想蚁群算法是受生物界中蚂蚁觅食行为启发而来。
生物界中的蚂蚁有能力在没有任何可见提示下找出从蚁穴到食物源的最短路径,并且能够随环境的变化而变化去搜索新路径,产生新选择,其机理在于蚂蚁在其走过的路径上释放一种信息素,信息素承载着路况信息,蚂蚁在行进过程中能够感知这种信息素的存在和其强度,并指导自己的行进方向,使蚂蚁倾向于向信息素强度高的方向爬行。
这无疑非常适合动态航迹规划问题。
蚁群算法最重要的特点就是创造性地使用了启发信息,即通过引入信息素播撒机制[14],将之前搜索到的最优解用于指导后续的搜索。
在蚁群算法的众多改进算法中,对信息素播撒机制的改进是研究者最为关注的一点。
蚁群算法与其他搜索算法相结合,来改进蚁群算法是一条重要途径。
§2.3.2 蚁群算法模型一只蚂蚁的智力是很有限的,但很多蚂蚁之间通过一些信息激素进行协同作用,实现蚂蚁之间的信息交流,其效果往往令人惊讶。
下面将简单的介绍一下蚂蚁群是怎样通过信息素进行协同作用的,并如何最终找到从蚁穴到食物的最短路径。
在图2.6中,A为出发点(即蚁穴),B为食物源,从图上可见蚂蚁要获得食物有两条路可走,我们可以很容易的比较出路径A-C-B较路径A-D-B长,然而蚂蚁是不知道这一点的。
现在假设有两只蚂蚁1和2,在蚂蚁1和2向食物移动的方向上有两条路径可以选择,在初始条件下,两条路径上的信息素量都为零,因此两只蚂蚁选择两条路径的概率均为0.5,在这里,假设蚂蚁1选择了路径A-C-B,蚂蚁2选择了路径A-D-B,在此强调两只蚂蚁的行走速度是一样的。
很明显,选择短路径的蚂蚁2将先到达B点,当蚂蚁2要返回时,要选择信息素气味重的路径,由于此时蚂蚁1还在路上,故蚂蚁2选择了原路返回,当蚂蚁2到达A点时,假设的蚂蚁3出发,根据蚂蚁会选择信息素气味较重的路径这一原理,蚂蚁3选择路径A-D-B,因为此路径已经有两次蚂蚁通过的经历,如此由大量的蚂蚁组成的群体便表现出一种信息正反馈现象,即随着路径A-D-B上通过蚂蚁数量的增加,后来的蚂蚁选择此路径的概率就越大,而这正是两点之间的最短路径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6
1.3 蚁群优化算法研究背景
与大多数基于梯度的应用优化算法不同,群智能依 靠的是概率搜索算法。虽然概率搜索算法通常要采用 较多的评价函数,但是与梯度方法及传统的演化算法 相比,其优点还是显著的 ,主要表现在以下几个方 面: 1 无集中控制约束,不会因个别个体的故障影响整 个问题的求解,确保了系统具备更强的鲁棒性 2 以非直接的信息交流方式确保了系统的扩展性 3 并行分布式算法模型,可充分利用多处理器 4 对问题定义的连续性无特殊要求 5 算法实现简单
8
1.4 蚁群优化算法研究现状
90年代Dorigo最早提出了蚁群优化算法---蚂蚁系统 (Ant System, AS)并将其应用于解决计算机算法学中经 典的旅行商问题(TSP)。 从蚂蚁系统开始,基本的蚁群算法得到了不断的发展和 完善,并在TSP以及许多实际优化问题求解中进一步得到了 验证。这些AS改进版本的一个共同点就是增强了蚂蚁搜索 过程中对最优解的探索能力,它们之间的差异仅在于搜索控 制策略方面。而且,取得了最佳结果的ACO是通过引入局部 搜索算法实现的,这实际上是一些结合了标准局域搜索算法 的混合型概率搜索算法,有利于提高蚁群各级系统在优化问 题中的求解质量。
7
1.3 蚁群优化算法研究背景
群智能方法易于实现,算法中仅涉及各种基本的 数学操作,其数据处理过程对CPU和内存的要求也 不高。而且,这种方法只需目标函数的输出值,而 无需其梯度信息。已完成的群智能理论和应用方法 研究证明群智能方法是一种能够有效解决大多数全 局优化问题的新方法。更为重要是,群智能潜在的 并行性和分布式特点为处理大量的以数据库形式存 在的数据提供了技术保证。无论是从理论研究还是 应用研究的角度分析,群智能理论及其应用研究都 是具有重要学术意义和现实价值的。
12
1.5 蚁群优化算法应用现状
ACO还在许多经典组合优化问题中获得了成功的应用, 如二次规划问题(QAP)、机器人路径规划、作业流程规划、 图着色(Graph Coloring)等问题。 经过多年的发展,ACO已成为能够有效解决实际二次规 划问题的几种重要算法之一。AS在作业流程计划(Jobshop Scheduling)问题中的应用实例已经出现,这说明了 AS在此领域的应用潜力。利用MAX-MIN AS解决PAQ也取 得了比较理想的效果,并通过实验中的计算数据证明采用该 方法处理PAQ比较早的SA算法更好,且与禁忌搜索算法性 能相当。利用ACO实现对生产流程和特料管理的综合优化, 并通过与遗传、模拟退火和禁忌搜索算法的比较证明了 ACO的工程应用价值。
9
1.4蚁群优化算法研究现状
M.Dorigo 最初提出的AS(Ant-System)有三种版本: Ant-density(蚁密)、Ant-quantity(蚁量)和Ant-cycle(蚁 周)。 在Ant-density和Ant-quantity中蚂蚁在两个位置节点间每 移动一次后即更新信息素,而在Ant-cycle中当所有的蚂蚁都 完成了自己的行程后才对信息素进行更新,而且每个蚂蚁所 释放的信息素被表达为反映相应行程质量的函数。通过与其 它各种通用的启发式算法相比,在不大于75城市的TSP中, 这三种基本算法的求解能力还是比较理想的,但是当问题规 模扩展时,AS的解题能力大幅度下降。 对此,后面的研究者提出了多种不同的改进蚁群算法。
10
1.5 蚁群优化算法应用现状
随着群智能理论和应用算法研究的不断发展,研究者 已尝试着将其用于各种工程优化问题,并取得了意想不到 的收获。多种研究表明,群智能在离散求解空间和连续求 解空间中均表现出良好的搜索效果,并在组合优化问题中 表现突出。 蚁群优化算法并不是旅行商问题的最佳解决方法,但是 它却为解决组合优化问题提供了新思路,并很快被应用到 其它组合优化问题中。比较典型的应用研究包括:网络路 由优化、数据挖掘以及一些经典的组合优化问题。
5
1.3 蚁群优化算法研究背景
群智能理论研究领域有两种主要的算法:蚁群 算法(Ant Colony Optimization, ACO)和微粒群(或 称为粒子群)算法(Particle Swarm Optimization, PSO)。 前者是对蚂蚁群落食物采集过程的模拟,已成 功应用于许多离散优化问题。微粒群算法也是起源 于对简单社会系统的模拟,最初是模拟鸟群觅食的 过程,但后来发现它是一种很好的优化工具。
蚁群算法
国防科技大学理学院数学系 成礼智 2011年夏季学期数学建模竞赛讲座
1
1. 2. 3. 4. 5. 6.
蚁群优化算法概述 蚁群优化算法概念 算法模型和收敛性分析 算法实现的技术问题 应用 参考资料
2
1 蚁群优化算法概述 1.1 起源 1.2 应用领域 1.3 研究背景 1.4 研究现状 1.5 应用现状
3
1.1 蚁群优化算法起源
20世纪90年代意大利学者M.Dorigo, V.Maniezzo,A.Colorni等从生物进化的机制中 受到启发,通过模拟自然界蚂蚁搜索路径的行为, 提出来一种新型的模拟进化算法—— 蚁群算法,是 群智能理论研究领域的一种主要算法。用该方法求 解TSP问题、分配问题、job-shop调度问题,取得了 较好的试验结果.虽然研究时间不长,但是现在的 研究显示出,蚁群算法在求解复杂优化问题(特别 是离散优化问题)方面有一定优势,表明它是一种 有发展前景的算法.
4
1.2 蚁群优化算法应用领域
蚁群算法是一种群智能方法,能够被用于解 决大多数优化问题或者能够转化为优化求解的 问题。现在其应用领域已扩展到多目标优化、 数据分类、数据聚类、模式识别、电信管理、 生物系统建模、流程规划、信号处理、机器人 控制、决策支持以及仿真和系统辩识等方面, 群智能理论和方法为解决这类应用问题提供了 新的途径。
11
1.5 蚁群优化算法应用现状
蚁群算法在电信路由优化中已取得了一定的应用成果。 HP公司和英国电信公司在90年代中后期都开展了这方面的研 究,设计了蚁群路由算法(Ant Colony Routing, ACR)。 每只蚂蚁就像蚁群优化算法中一样,根据它在网络上的经 验与性能,动态更新路由表项。如果一只蚂蚁因为经过了网 络中堵塞的路由而导致了比较大的延迟,那么就对该表项做 较大的增强。同时根据信息素挥发机制实现系统的信息更 新,从而抛弃过期的路由信息。这样,在当前最优路由出现 拥堵现象时,ACR算法就能迅速的搜寻另一条可替代的最优 路径,从而提高网络的均衡性、负荷量和利用率。目前这方 面的应用研究仍在升温,因为通信网络的分布式信息结构、 非稳定随机动态特性以及网络状态的异步演化与ACO的算法 本质和特性非常相似。
