大学物理精讲精练答案解析
高考物理总复习章节精练精析(第3章)(带答案与解析)解答解析、考点详解.doc

高考物理总复习章节精练精析(第3章)(带答案与解析)的正确答案、解答解析、考点详解姓名:_____________ 年级:____________ 学号:______________题型选择题填空题解答题判断题计算题附加题总分得分1.【题文】(2011年金华一中检测)关于惯性,下列说法正确的是( )A.静止的火车启动时速度变化缓慢,是因为火车静止时惯性大B.战斗机投入战斗时,必须抛掉副油箱,是要减少惯性,保证其运动的灵活性C.在绕地球运转的宇宙飞船内的物体处于失重状态,因而不存在惯性D.乒乓球可以快速抽杀,是因为乒乓球惯性大的缘故【答案】选B.【解析】物体的质量是物体惯性大小的量度,物体的惯性是物体的固有属性,只与质量有关,与物体的运动状态无关,抛掉副油箱可以减小质量,故选B.2.【题文】吊在大厅天花板上的吊扇的总重力为G,静止时固定杆对吊环的拉力大小为F,当接通电源,让扇叶转动起来后,吊杆对吊环的拉力大小为F′,则有( )A.F=G,F′=FB.F=G,F′FC.F=G,F′GD.F′=G,F′F【答案】C【解析】略3.【题文】如图所示,物块P与木板Q叠放在水平地面上,木板Q对物块P的支持力的反作用力是( )A.物块P受到的重力B.地面对木板Q的弹力C.物块P对木板Q的压力D.地球对木板Q的吸引力【答案】选C.【解析】两个物体之间的作用力和反作用力总是大小相等,方向相反,作用在同一条直线上,所以Q对P 的支持力的反作用力是P对Q的压力.评卷人得分4.【题文】(思维创新题)如图所示,一只盛水的容器固定在一个小车上,在容器中分别悬挂和拴着一只铁球和一只乒乓球.容器中的水和铁球、乒乓球都处于静止状态.当容器随小车突然向右运动时,两球的运动状况是(以小车为参考系)( )A.铁球向左,乒乓球向右B.铁球向右,乒乓球向左C.铁球和乒乓球都向左D.铁球和乒乓球都向右【答案】A【解析】因为小车突然向右运动时,由于惯性,铁球和乒乓球都有向左运动趋势,但由于与同体积的“水球”相比铁球的质量大,惯性大,铁球的运动状态难改变,即速度变化慢,而同体积的水球的运动状态容易改变,即速度变化快,而且水和车一起加速运动,所以小车加速运动时,铁球相对于小车向左运动,同理由于与同体积的“水球”相比乒乓球的质量小,惯性小,乒乓球向右运动.故选A.5.【题文】(2011年山东潍坊模拟) 质量为60 kg的人站在水平地面上,用定滑轮装置将质量为m=40 kg 的重物送入井中.当重物以2 m/s2的加速度加速下落时,忽略绳子和定滑轮的质量及定滑轮的摩擦,则人对地面的压力大小为(g取10 m/s2)( )A.200 NB.280 NC.320 ND.920 N【答案】选B.【解析】根据牛顿第二定律有mg-F=ma,得绳子的拉力大小等于F=320 N,然后再对人进行受力分析,由物体的平衡知识得m0g=F+FN,得FN=280 N,根据牛顿第三定律可知人对地面的压力为280 N.B正确.6.【题文】如图所示为杂技“顶竿”表演,一人站在地上,肩上扛一质量为M的竖直竹竿,当竿上一质量为m的人以加速度a加速下滑时,竿对“底人”的压力大小为( )A.(M+m)gB.(M+m)g-maC.(M+m)g+maD.(M-m)g【答案】选B.【解析】对竿上的人分析:受重力mg,摩擦力Ff,有mg-Ff=ma.竿对人有摩擦力,人对竿也有反作用力——摩擦力,且大小相等,方向相反.对竿分析:受重力Mg,摩擦力Ff,方向向下,支持力FN,Mg+Ff=FN,又因为竿对“底人”的压力和“底人”对竿的支持力是一对作用力与反作用力,由牛顿第三定律,得FN=(M+m)g-ma.7.【题文】(2011年慈溪中学月考)就一些实际生活中的现象,某同学试图从惯性角度加以解释,其中正确的是( )A.采用了大功率的发动机后,某些赛车的速度甚至能超过某些老式螺旋桨飞机的速度.这表明,可以通过科学进步使小质量的物体获得大惯性B.射出枪膛的子弹在运动相当长一段距离后连一件棉衣也穿不透,这表明它的惯性小了C.货运列车运行到不同的车站时,经常要摘下或加挂一些车厢,这会改变它的惯性D.摩托车转弯时,车手一方面要控制适当的速度,另一方面要将身体稍微向里倾斜,通过调控人和车的惯性达到急转弯的目的【答案】选C.【解析】A、采用了大功率的发动机后,一级方程式赛车的速度甚至能超过某些老式螺旋桨飞机的速度,不是由于使小质量的物体获得大惯性,是由于功率增大的缘故.故A错误.B、射出枪膛的子弹在运动一段距离后连一件棉衣也穿不透,是由于速度减小了,不是由于惯性减小,子弹的惯性没有变化.故B错误.C、货车运行到不同的车站时,经常要摘下或加挂一些车厢,质量改变了,会改变它的惯性.故C正确.D、摩托车转弯时,车手一方面要控制适当的速度,另一方面要将身体稍微向里倾斜,改变向心力,防止侧滑,而人和车的惯性并没有改变.故D错误.故选C8.【题文】(2010年高考广东卷)下列关于力的说法正确的是( )A.作用力和反作用力作用在同一物体上B.太阳系中的行星均受到太阳的引力作用C.运行的人造地球卫星所受引力的方向不变D.伽利略的理想实验说明了力不是维持物体运动的原因【答案】选BD.【解析】作用力和反作用力作用在两个不同的物体上,A错误;太阳系中的所有行星都要受到太阳的引力,且引力方向沿着两个星球的连线指向太阳,B正确,C错误;伽利略理想实验说明力不是维持物体运动的原因,D正确.9.【题文】(2011年台州模拟)“嫦娥二号”的成功发射,一方面表明中国航天事业已走在了世界的前列,另一方面“嫦娥二号”的发射也带动了高科技的发展.目前计算机的科技含量已相当高,且应用于各个领域或各个方面.如图是利用计算机记录的“嫦娥二号”发射时,火箭和地面的作用力和反作用力变化图线,根据图线可以得出的结论是( )A.作用力大时,反作用力小B.作用力和反作用力的方向总是相反的C.作用力和反作用力是作用在同一个物体上的D.牛顿第三定律在物体处于非平衡状态时不再适用【答案】选B.【解析】作用力与反作用力总是大小相等,方向相反,分别作用在两个物体上的,A、C错,B对.牛顿第三定律反映的规律与运动状态无关,D错.10.【题文】 2008年9月25日地处西北戈壁荒滩的酒泉卫星发射中心,“长征”号火箭第109次发射,将“神舟”七号载人航天飞船发射到太空,并成功完成了中国宇航员第一次太空行走.下面关于飞船与火箭起飞的情形,叙述正确的是( )A.火箭尾部向下喷气,喷出的气体反过来对火箭产生一个反作用力,从而让火箭获得了向上的推力B.火箭尾部喷出的气体对空气产生一个作用力,空气的反作用力使火箭获得飞行的动力C.火箭飞出大气层后,由于没有空气,火箭虽然向下喷气,但也无法获得前进的动力D.飞船进入运行轨道之后,与地球之间仍然存在一对作用力与反作用力【答案】选AD.【解析】火箭升空时,其尾部向下喷气,火箭箭体与被喷出的气体是一对相互作用的物体,火箭向下喷气时,喷出的气体同时对火箭产生向上的反作用力,即为火箭上升的推力,此动力并不是由周围的空气对火箭的反作用力提供的,因而与是否飞出大气层,是否在空气中飞行无关,因而B、C选项错误,A项正确;当飞船进入轨道后,飞船与地球之间依然存在着相互吸引力,即地球吸引飞船,飞船也吸引地球,这是一对作用力和反作用力,故D项正确.11.【题文】 (2009年高考安徽卷)在2008年北京残奥会开幕式上,运动员手拉绳索向上攀登,最终点燃了主火炬,体现了残疾运动员坚韧不拔的意志和自强不息的精神.为了探求上升过程中运动员与绳索和吊椅间的作用,可将过程简化.一根不可伸缩的轻绳跨过轻质的定滑轮,一端挂一吊椅,另一端被坐在吊椅上的运动员拉住,如图所示.设运动员质量为65 kg,吊椅的质量为15 kg,不计定滑轮与绳子间的摩擦,重力加速度取g=10 m/s2,当运动员与吊椅一起以a=1 m/s2的加速度上升时,试求:(1)运动员竖直向下拉绳的力;(2)运动员对吊椅的压力.【答案】(1)440 N (2)275 N【解析】(1)设运动员和吊椅的质量分别为M和m,绳拉运动员的力为F.以运动员和吊椅整体为研究对象,受到重力的大小为(M+m)g,向上的拉力为2F,根据牛顿第二定律2F-(M+m)g=(M+m)aF=440 N根据牛顿第三定律,运动员拉绳的力大小为440 N,方向竖直向下.(2)以运动员为研究对象,运动员受到三个力的作用,重力大小Mg,绳的拉力F,吊椅对运动员的支持力FN.根据牛顿第二定律F+FN-Mg=MaFN=275 N根据牛顿第三定律,运动员对吊椅压力大小为275 N,方向竖直向下.12.【题文】如图所示,一辆卡车后面用轻绳拖着质量为m的物体A,A与地面的摩擦不计.(1)当卡车以a1=g的加速度运动时,绳的拉力为mg,则A 对地面的压力为多大?(2)当卡车的加速度a2=g时,绳的拉力为多大?【答案】(1)mg (2)mg【解析】(1)卡车和A的加速度一致.由图知绳的拉力的分力使A产生了加速度,故有:mgcosα=m·g解得cosα=,sinα=.设地面对A的支持力为FN,则有FN=mg-mg·sinα=mg由牛顿第三定律得:A对地面的压力为mg.(2)设地面对A弹力为零时,物体的临界加速度为a0,则a0=g·cotθ=g,故当a2=ga0时,物体已飘起.此时物体所受合力为mg,则由三角形知识可知,拉力F2==mg. 13.【题文】如图所示,车内绳AB与绳BC拴住一小球,BC水平,车由原来的静止状态变为向右加速直线运动,小球仍处于图中所示的位置,则( )A.AB绳、BC绳拉力都变大B.AB绳拉力变大,BC绳拉力变小C.AB绳拉力变大,BC绳拉力不变D.AB绳拉力不变,BC绳拉力变大【答案】选D.【解析】如图,车加速时,球的位置不变,则AB绳拉力沿竖直方向的分力仍为FT1cosθ,且等于重力G,即FT1=,故FT1不变.向右的加速度只能是由BC绳上增加的拉力提供,故FT2增加,所以D 正确.14.【题文】(2011年嘉兴模拟)一物块以某一初速度沿粗糙的斜面向上沿直线滑行,到达最高点后自行向下滑动,不计空气阻力,设物块与斜面间的动摩擦因数处处相同,下列图象能正确表示物块在这一过程中的速率与时间关系的是( )【答案】C【解析】由于整个过程当中摩擦力始终对物体做负功,故物体的机械能持续减小,所以物体回到出发点的速率小于开始运动时的初速度,故D错误.由于物体上升和下降过程中通过的路程相同,而上升时的平均速度大于下降时的平均速度,故物体上升的时间小于物体下降的时间.故AB错误,而C正确.故选C.15.【题文】(2011年北京西城区抽样测试)如图所示,倾角为θ的传送带沿逆时针方向以加速度a加速转动时,小物体A与传送带相对静止,重力加速度为g.则( )A.只有agsinθ,A才受沿传送带向上的静摩擦力作用B.只有agsinθ,A才受沿传送带向上的静摩擦力作用C.只有a=gsinθ,A才受沿传送带向上的静摩擦力作用D.无论a为多大,A都受沿传送带向上的静摩擦力作用【答案】选B.【解析】A与传送带相对静止,倾角为θ的传送带沿逆时针方向以加速度a加速转动时,A有沿斜面向下的加速度a,对A受力分析可知只有agsinθ,A才受沿传送带向上的静摩擦力作用,B正确.16.【题文】如图所示,在光滑的水平面上,质量分别为m1和m2的木块A和B之间用轻弹簧相连,在拉力F作用下,以加速度a做匀加速直线运动,某时刻突然撤去拉力F,此瞬时A和B的加速度为a1和a2,则( )A.a1=a2=0B.a1=a,a2=0C.a1=a,a2= aD.a1=a,a2=- a【答案】选D.【解析】首先研究整体,求出拉力F的大小F=(m1+m2)a.突然撤去F,以A为研究对象,由于弹簧在短时间内弹力不会发生突变,所以A物体受力不变,其加速度a1=a.以B为研究对象,在没有撤去F时有:F -F′=m2a,而F=(m1+m2)a,所以F′=m1a.撤去F则有:-F′=m2a2,所以a2=-a.D项正确.17.【题文】(2011年杭州模拟)如图所示,质量为m的小球用水平轻弹簧系住,并用倾角为30°的光滑木板AB托住,小球恰好处于静止状态.当木板AB突然向下撤离的瞬间,小球的加速度大小为( )A.0B.gC.gD.g【答案】选B.【解析】撤离木板时,小球所受重力和弹簧弹力没变,二者合力的大小等于撤离木板前木板对小球的支持力FN,由于FN==mg,所以撤离木板后,小球加速度大小为:a==g.B项正确.18.【题文】如图所示,放在光滑面上的木块受到两个水平力F1与F2的作用而静止不动,现保持F1大小和方向不变,F2方向不变,使F2随时间均匀减小到零,再均匀增加到原来的大小,在这个过程中,能正确描述木块运动情况的图象是( )【答案】A【解析】如图所示,放在光滑面上的木块受到两个水平力F1与F2的作用而静止不动,现保持F1大小和方向不变,F2方向不变,使F2随时间均匀减小到零,再均匀增加到原来的大小,在这个过程中,能正确描述木块运动情况的图象是A。
大学物理2精讲精练答案

第十一章静电场例题答案:11-1 (B ) 11-2(B )11-3(B )11-4.;从O 点指向()30220824R qdd R R qd εεπ≈-ππ缺口中心点11-5.;;沿矢径OP0/ελd ()2204dR d-πελ11-6(D)11-7.向右 ;向右2εσ023εσ11-8(1),r <R;(2)o2r 4r k E ε=,r >R 。
204r r 4RkE ε=[解](1)作与球体同心、而半径r <R 的球面S 1。
球体内电荷密度ρ随r 变化,因此,球面S 1内包含的电荷。
根据高斯定理和已知的电荷体密度ρ(r ),()dr r r 4Q ro21⎰ρπ=可求得球体内任意点的场强。
即,得:()⎰⎰ρπε=⋅=Φr2s o r dr r r 41s d E 1 ,r <R 。
o2r 4r k E ε=(2)作与球体同心、半径r >R 的球面S 2,因R 外电荷为零,故S 2内的电荷Q 2=Q 1,根据高斯定理得:Φ==4πr 2E r =,∴()⎰⎰ρπε=⋅R 02s 0r dr r r 41s d E 2⎰πεR3dr kr 41,r >R 。
204r r 4R kE ε=11-9(D) 11-10(C) 11-11.单位正电荷在d 0L⋅=⎰A E l 静电场中沿任意闭合路径绕行一周,电场力作功等于零有势(或保守力)11-12. 45 V —15 V 11-13. -2000V 11-14. (B) 11-15.,0,,。
20R4QπεR 4Q 0πε20r 4Qπε11-16()()a b b c R R R R /ln /ln 21=λλ[解]:设B 上带正电荷,内表面上电荷线密度为λ1,外表面上电荷线密度为λ2,而A 、C 上相应地感应等量负电荷,如图所示.则A 、B 间场强分布为 E 1=λ1 / 2πε0r ,方向由B 指向A B 、C 间场强分布为 E 2=λ2 / 2πε0r ,方向由B 指向CB 、A 间电势差11100ln 22E r d d a ab bR R b BA R R aR r r R λλεε=⋅=-=ππ⎰⎰UB 、C 间电势差22200ln 22E r d d ccb b R Rc BC R R bR r U r R λλεε=⋅=-=ππ⎰⎰因U BA =U BC ,得到()()a b b c R R R R /ln /ln 21=λλ练习详解:11-1.(1)E 0=0;(2)E 0=0;(3)=k ;(4)0E 2aq 4i= k 0E 2aq 2i[解](1)如图(a )所示,各点电荷在点o 处产生的场强两两对应相消,所以,点o 处场强E 0=0(2)取图中(b )所示坐标。
高考物理复习精讲+精练题组含答案精华(原创)

第一章 质点的直线运动第一节 加速度及运动图像一、加速度(描述物体速度变化快慢的物理量). 1、定义:单位时间内速度的变化量. 2、表达式:tva ∆∆=⇒t a v ∆⋅=∆(求速度变化量) 例1.关于加速度,下列说法中正确的是( C ) A.速度变化越大,加速度一定越大。
B.速度变化所用时间越短,加速度一定越大。
C.速度变化越快,加速度一定越大。
D.速度为零,加速度一定为零。
3、用t v -图像理解加速度. 4、匀变速直线运动(1)定义:沿着一条直线,加速度不变的运动. (2)分类:①加速度方向与初速度方向相同,则为匀加速直线运动.②加速度方向与初速度方向相反,则为匀减速直线运动.(3)特点:①加速度大小,方向都不变. ②相同时间内速度变化量相同(t a v ∆⋅=∆) ③t v -图像为一条倾斜的直线. 5、对加速度理解的误区.(1)物体具有加速度,一定做加速运动.(2)物体的速度方向改变,加速度方向一定改变. (3)物体的速度为零,加速度也为零. (4)物体的加速度为零,初速度也为零. (5)物体速度大,加速度也大. (6)物体加速度大,速度也大.例2.下列说法中正确的是( ABC )A.加速度越大,单位时间内质点速度的变化量越大。
B.某一时刻的速度为零,加速度有可能不为零。
C.速度变化越来越快,加速度有可能越来越小。
D.速度的变化量相同,加速度越大,则所用时间越短。
例3.根据给出的速度和加速度的正负,对下列运动性质的判断正确的是( BCD )A.00<v ,0>a ,物体先做加速运动后做减速运动。
B.00<v ,0<a ,物体做加速运动。
C.00>v ,0<a ,物体先做减速运动,后做加速运动D.00>v ,0=a ,物体做匀速直线运动。
例4.下述运动中可能出现的是(ABC )A.物体的加速度增加,速度反而减小。
B.物体的速度为零时,加速度却不为零。
大学物理试题讲解及答案

大学物理试题讲解及答案一、选择题1. 光的波长为λ,频率为f,光速为c,下列关系式正确的是()。
A. λf = cB. λf = 2cC. λf = c/2D. λf = c^2答案:A2. 一个物体在水平面上做匀加速直线运动,已知加速度a=2m/s²,初速度v₀=3m/s,那么2秒后的速度v₂为()。
A. 7m/sB. 9m/sC. 11m/sD. 13m/s答案:B二、填空题3. 根据牛顿第二定律,物体的加速度a与作用力F和物体质量m的关系是a=______。
答案:F/m4. 一个物体从静止开始下落,忽略空气阻力,其下落过程中的加速度为______。
答案:g(重力加速度)三、计算题5. 一个质量为m的物体,从高度h处自由下落,求物体落地时的速度v。
解:由能量守恒定律可知,物体的势能转化为动能,即:mgh = 1/2 * mv²解得:v = √(2gh)答案:v = √(2gh)6. 一列火车以速度v₀进入一个隧道,隧道长度为L,火车长度为l,求火车完全通过隧道所需的时间t。
解:火车完全通过隧道时,其尾部刚好离开隧道口,此时火车行驶的距离为L+l。
由速度公式v = s/t,得:t = (L+l)/v₀答案:t = (L+l)/v₀四、简答题7. 简述牛顿第三定律的内容。
答案:牛顿第三定律指出,对于两个相互作用的物体,它们之间的作用力和反作用力大小相等、方向相反。
8. 什么是电磁感应现象?答案:电磁感应现象是指当导体在磁场中运动,或者磁场发生变化时,导体中会产生感应电动势的现象。
五、论述题9. 论述相对论中时间膨胀的概念。
答案:时间膨胀是相对论中的一个重要概念,指的是当一个物体以接近光速的速度运动时,相对于静止观察者的时间会变慢。
这种现象表明,时间并不是绝对的,而是相对的,取决于观察者的运动状态。
10. 试述量子力学与经典力学的主要区别。
答案:量子力学与经典力学的主要区别在于它们描述的物理现象的尺度不同。
大学物理试题讲解及答案

大学物理试题讲解及答案一、选择题(每题2分,共20分)1. 光在真空中的传播速度是()。
A. 3×10^5 km/sB. 3×10^8 m/sC. 3×10^9 km/sD. 3×10^11 m/s答案:B2. 根据牛顿第二定律,力和加速度的方向()。
A. 总是相同B. 总是相反C. 有时相同,有时相反D. 无关答案:A3. 一个物体的质量为2kg,受到的力为10N,那么它的加速度是()。
A. 5 m/s^2B. 10 m/s^2C. 20 m/s^2D. 无法确定答案:A4. 一个点电荷在电场中从静止开始运动,其电势能将()。
A. 增加B. 减少C. 保持不变D. 先增加后减少答案:B5. 根据热力学第一定律,一个系统在绝热过程中()。
A. 内能增加B. 内能减少C. 内能不变D. 无法确定答案:D6. 光的折射定律表明,入射角和折射角的关系是()。
A. 入射角大,折射角小B. 入射角小,折射角大C. 入射角和折射角成正比D. 入射角和折射角成反比答案:C7. 一个物体在自由下落过程中,其动能和重力势能的关系是()。
A. 动能增加,重力势能减少B. 动能减少,重力势能增加C. 动能和重力势能之和保持不变D. 动能和重力势能之和增加答案:C8. 根据麦克斯韦方程组,电磁波的传播速度是()。
A. 光速的一半B. 光速C. 超过光速D. 低于光速答案:B9. 在理想气体定律中,气体的压强与体积成()。
A. 正比B. 反比C. 无关D. 先正比后反比答案:B10. 根据欧姆定律,电阻两端的电压与通过电阻的电流之间的关系是()。
A. 正比B. 反比C. 无关D. 先正比后反比答案:A二、填空题(每题2分,共20分)1. 牛顿第三定律指出,作用力和反作用力大小相等、方向相反、作用在_________上。
答案:不同物体2. 在国际单位制中,力的单位是_________。
大学物理学(清华C5版)分章配套精品题目及答案(第三章)

第三章 动量和角动量【例题精讲】例3-1 一颗子弹在枪筒里前进时所受的合力大小为 t F 31044005⨯-= (SI) 子弹从枪口射出时的速率为 300 m/s .假设子弹离开枪口时合力刚好为零,则子弹在枪筒中所受力的冲量I = ;子弹的质量m = 。
0.6 N·s 2 g例3-2一质量为1 kg 的物体,置于水平地面上,物体与地面之间的静摩擦系数μ 0=0.20,滑动摩擦系数μ=0.16,现对物体施一水平拉力F =t+0.96(SI),则2秒末物体的速度大小v = 。
2秒末物体的加速度大小a = 。
0.89 m/s 1.39 m/s 2例3-3 质量分别为m A 和m B (m A >m B )、速度分别为A v ϖ和B v ϖ(v A > v B )的两质点A 和B ,受到相同的冲量作用,则 (A) A 的动量增量的绝对值比B 的小。
(B) A 的动量增量的绝对值比B 的大。
(C) A 、B 的动量增量相等。
(D) A 、B 的速度增量相等。
[ C ]例3-4 一人用恒力F ϖ推地上的木箱,经历时间∆ t 未能推动木箱,此推力的冲量等于多少?木箱既然受了力F ϖ 的冲量,为什么它的动量没有改变?【答】推力的冲量为t F ∆ϖ。
动量定理中的冲量为合外力的冲量,此时木箱除受力F ϖ外还受地面的静摩擦力等其它外力,木箱未动说明此时木箱的合外力为零,故合外力的冲量也为零,根据动量定理,木箱动量不发生变化。
例3-5 如图,用传送带A 输送煤粉,料斗口在A 上方高h =0.5 m 处,煤粉自料斗口自由落在A 上.设料斗口连续卸煤的流量为q m =40 kg/s ,A 以v=2.0 m/s 的水平速度匀速向右移动.求装煤的过程中,煤粉对A 的作用力的大小和方向。
(不计相对传送带静止的煤粉质重)【解】 煤粉自料斗口下落,接触传送带前具有竖直向下的速度gh 20=v 设煤粉与A 相互作用的∆t 时间内,落于传送带上的煤粉质量为 t q m m ∆=∆ 设A 对煤粉的平均作用力为f ϖ,由动量定理写分量式:0-∆=∆v m t f x )(00v m t f y ∆--=∆ 将 t q m m ∆=∆代入得 v m x q f =, 0v m y q f = ∴ 14922=+=y x f f f Nf ϖ与x 轴正向夹角为α = arctg (f x / f y ) = 57.4° 由牛顿第三定律煤粉对A 的作用力f ′= f = 149 N ,方向与图(b)中f ϖ相反。
大学物理精讲精练解答

第十四章 稳恒磁场例题答案:例14-1例14-2 (C).例14-3 μ0i ; 沿轴线方向朝右 例14-4 (D) 例14-5 (D)例14-6 B=1.8×10-4 T ;α =225°,α为 B 与x 轴正向的夹角【解】 取d l 段,其中电流为π=π=π21=θθd 2d 2d d I R IR R l I I 在P 点 θμθμμd d 222d d 2000RII R R I B π=π⋅π=π= 选坐标如图R I B x 20d sin d π-=θθμ, RI B y20d c o s d π-=θθμ ⎰ππ-=2/020d sin θθμR I B x R I 20π-=μ⎰ππ-=2/020d cos θθμRIB y R I20π-=μ =+=2/122)(y x B B B =πRI 202μ 1.8×10-4 T方向 1/tg ==x y B B α,225=α,为 B 与x 轴正向的夹角。
例14-7 (1) a ._ 0 __ b . 2πB R c . 2πcos α-B R ;(2) Φm =2πcos θB R ;(3)d =⎰SB S 0 。
例 14-8 -μ0I 1 ; μ0(I 1+I 2) ; 0. 例14-9 (D) 例14-10 (C) 例14-11 (B ) 例14-12 0222()μ=πbIB R -a例题14-6答案图【解】 导体内的电流密度 )a π(b IJ 22-=由于电流和磁场分布的对称性,磁感线是以轴为中心的一些同心圆,去半径为r 的一条磁感线为环路,有安培环路定理:d I μ⋅=∑⎰B l有 )(2222022ab a r I )a πr J(πμr B 20--=-=⋅μπ ra b π2a r I μB 22220)()(--=∴例14-13 0312()ln 22πμ=I F I -I ;若 12I I >,则F 的方向向下;若12I I <,则F 的方向向上【解】 载流导线MN 上任一点处的磁感强度大小为: )(210x r I B +π=μ)2(220x r I -π-μMN 上电流元I 3d x 所受磁力: x B I F d d 3=)(2[103x r I I +π=μx x r I d ])2(210-π-μ010230d 2π()2π(2)⎡⎤⎢⎥⎣⎦⎰r μI μI F =I -x r +x r -x 0310[d 2πr μ=-+⎰I I x r x 2d ]2r-⎰I x r x]2ln 2ln[22130r rI r r I I +π=μ ]2ln 2ln [22130I I I -π=μ 2ln )(22130I I I -π=μ若 12I I >,则F 的方向向下, 12I I <,则F 的方向向上。
高考物理总复习章节精练精析(第5章)(带答案与解析)解答解析、考点详解.doc

高考物理总复习章节精练精析(第5章)(带答案与解析)的正确答案、解答解析、考点详解姓名:_____________ 年级:____________ 学号:______________题型选择题填空题解答题判断题计算题附加题总分得分1.【题文】长为L的轻质细绳悬挂一个质量为m的小球,其下方有一个倾角为θ的光滑斜面体,放在水平面上,开始时小球与斜面刚刚接触且细绳恰好竖直,如图所示,现在用水平推力F缓慢向左推动斜面体,直至细绳与斜面体平行,则下列说法中正确的是( )A.由于小球受到斜面的弹力始终与斜面垂直,故对小球不做功B.细绳对小球的拉力始终与小球运动方向垂直,故对小球不做功C.小球受到的合外力对小球做功为零,故小球在该过程中机械能守恒D.若水平面光滑,则推力做功为mgL(1-cosθ)【答案】B.【解析】小球受到斜面的弹力沿竖直方向有分量,故对小球做正功,A错误;细绳拉力方向始终和小球运动方向垂直,故对小球不做功,B正确;合外力对小球做功等于小球动能的改变量,虽然合外力做功为零,但小球重力势能增加,机械能不守恒,C错误;若水平面光滑,则推力做功为mgL(1-sinθ),D错误.2.【题文】2010年11月24日,在广州亚运会男子110米栏决赛中,刘翔以13.09秒的优异成绩获得冠军并打破之前创造的赛会纪录.刘翔在比赛中,主要有起跑加速、途中匀速跨栏和加速冲刺三个阶段,他的脚与地面间不会发生相对滑动,以下说法正确的是( )A.加速阶段地面对人的摩擦力做正功B.匀速阶段地面对人的摩擦力做负功C.由于人的脚与地面间不发生相对滑动,所以不论加速还是匀速,地面对人的摩擦力始终不对人做功D.无论加速还是匀速阶段,地面对人的摩擦力始终做负功【答案】C.【解析】由于人的脚与地面间不发生相对滑动,地面对人产生摩擦力的瞬间,力的作用点位移为零,所以地面对人的摩擦力不做功,选项C正确.3.【题文】(2011年广东六校联合体联考)如图所示,滑雪者由静止开始沿斜坡从A点自由滑下,然后在水平面上前进至B点停下.已知斜坡、水平面与滑雪板之间的动摩擦因数都为μ,滑雪者(包括滑雪板)的质量为m.A、B两点间的水平距离为L.在滑雪者经过AB段运动的过程中,克服摩擦力做的功( )评卷人得分A.大于μmgL B.等于μmgLC.小于μmgL D.以上三种情况都有可能【答案】B.【解析】设斜面的倾角为θ,则对滑雪者从A到B的运动过程中摩擦力做的功为:WFf=μmgACcosθ+μmgCB①,由图可知ACcosθ+CB=L②,由①②两式联立可得:WFf=μmgL,故B正确.4.【题文】(2011年湖北黄冈模拟)如图所示,质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,B自由下落,最后到达同一水平面,则( )A.重力对两物体做的功相同B.重力的平均功率相同C.到达底端时重力的瞬时功率PA=PBD.到达底端时两物体的动能相同,速度相同【答案】A.【解析】由于两个物体质量相同、下落高度相同,所以重力对两物体做的功相同,A选项正确.由于下落的时间不同,所以重力的平均功率不相同,B选项错误.根据机械能守恒可知,两物体到达底端时动能相同,即速度大小相同、方向不同,D选项错误.由瞬时功率的计算式可得PA=mgvsinθ(θ为斜面倾角),PB=mgv,因此,到达底端时重力的瞬时功率PAPB,C选项错误.5.【题文】(2011年浙江部分重点中学联考)汽车发动机的额定功率为P1,它在水平路面上行驶时受到的阻力Ff大小恒定,汽车在水平路面上由静止开始做直线运动,最大车速为v.汽车发动机的输出功率随时间变化的图象如图所示.则( )A.汽车开始时做匀加速运动,t1时刻速度达到v,然后做匀速直线运动B.汽车开始时做匀加速直线运动,t1时刻后做加速度逐渐减小的直线运动,速度达到v后做匀速直线运动C.汽车开始时牵引力逐渐增大,t1时刻牵引力与阻力大小相等D.汽车开始时牵引力恒定,t1时刻牵引力与阻力大小相等【答案】B.【解析】开始时,汽车的功率与时间成正比,即:P=Fv=Fat,所以汽车牵引力恒定,汽车加速度恒定,汽车做匀加速直线运动;在t1时刻达到最大功率,此时,牵引力仍大于阻力,但随着速度的增大,汽车牵引力减小,汽车加速度逐渐减小至零后做匀速直线运动,B正确.6.【题文】一起重机的钢绳由静止开始匀加速提起质量为m的重物,当重物的速度为v1时,起重机的有用功率达到最大值P,以后起重机保持该功率不变,继续提升重物,直到以最大速度v2匀速上升为止,物体上升的高度为h,则整个过程中,下列说法不正确的是( )A.钢绳的最大拉力为B.钢绳的最大拉力为C.重物的最大速度v2=D.重物匀加速运动的加速度为-g【答案】A.【解析】由F-mg=ma和P=Fv可知,重物匀加速上升过程中钢绳拉力大于重力且不变,达到最大功率P 后,随v增加,钢绳拉力F变小,当F=mg时重物达到最大速度v2,故v2=,最大拉力F=mg+ma=,A 错误,B、C正确.由-mg=ma得:a=-g,D正确.7.【题文】(2011年宁波模拟)提高物体(例如汽车)运动速率的有效途径是增大发动机的功率和减小阻力因数(设阻力与物体运动速率的平方成正比,即Ff=kv2,k是阻力因数).当发动机的额定功率为P0时,物体运动的最大速率为vm,如果要使物体运动的速率增大到2vm,则下列办法可行的是( )A.阻力因数不变,使发动机额定功率增大到2P0B.发动机额定功率不变,使阻力因数减小到C.阻力因数不变,使发动机额定功率增大到8P0D.发动机额定功率不变,使阻力因数减小到【答案】CD.【解析】速度达到最大时,=kv即P=kv.由此可知,若vm增大到2vm时,当k不变,功率P变为原来的8倍,当功率不变,阻力因数变为原来的.8.【题文】(2009年高考宁夏卷)水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ(0μ1).现对木箱施加一拉力F,使木箱做匀速直线运动.设F的方向与水平面夹角为θ,如图,在θ从0逐渐增大到90°的过程中,木箱的速度保持不变,则( )A.F先减小后增大B.F一直增大C.F的功率减小D.F的功率不变【答案】AC.【解析】木箱在F作用下向右匀速运动的过程中,受4个力作用而平衡.即Fcosθ=μ(mg-Fsinθ),解得:F=,F有极值,所以A正确B错误;F的功率P=Fvcosθ=,所以C正确D错误.9.【题文】汽车在水平路面上从静止开始做匀加速直线运动,t1末关闭发动机,做匀减速直线运动,t2末静止,其v-t图象如图所示,图中αβ,若汽车牵引力做功为W,平均功率为P;汽车加速和减速过程中克服摩擦力做功分别为W1和W2,平均功率分别为P1和P2,则( )A.W=W1+W2B.W1W2C.P=P1D.P1=P2【答案】ABD.【解析】整个过程动能变化量为零,所以合力的功为零,A项正确.摩擦力大小相等,第一段位移大,所以B项正确.第一段是加速的,牵引力大于摩擦力,所以PP1,C项错.加速阶段和减速阶段平均速度相等,所以摩擦力的平均功率相等,D项正确.10.【题文】(2011年北京四中检测)如图甲所示,物体受到水平推力F的作用在粗糙水平面上做直线运动.通过力传感器和速度传感器监测到推力F、物体速度v随时间t变化的规律如图乙所示.取g=10 m/s2.则( )A.物体的质量m=1.0 kgB.物体与水平面间的动摩擦因数μ=0.20C.第2秒内物体克服摩擦力做的功W=2.0 JD.前2秒内推力F做功的平均功率=1.5 W【答案】CD.【解析】物体在第3秒内做匀速运动,则有F3=μmg=2 N,第2秒内物体做加速运动,有F2-μmg=ma,其中加速度为a==2 m/s2,解得m=0.5 kg,μ=0.4.第2秒内的位移为1 m,克服摩擦力做功为W=μmgs=2.0 J.前2秒内拉力做功为3 J,则平均功率为1.5 W.11.【题文】(2011年慈溪中学模拟)一辆汽车质量为1×103 kg,最大功率为2×104 W,在水平路面上由静止开始做直线运动,最大速度为v2,运动中汽车所受阻力恒定.发动机的最大牵引力为3×103 N,其行驶过程中牵引力F与车速的倒数的关系如图所示.试求:(1)根据图线ABC判断汽车做什么运动?(2)v2的大小;(3)整个运动过程中的最大加速度;(4)匀加速运动过程的最大速度是多大?当汽车的速度为10 m/s时发动机的功率为多大?【答案】(1)见解析(2)20 m/s (3)2 m/s2 (4)6.67 m/s 2×104 W【解析】(1)题图中图线AB段牵引力F不变,阻力Ff不变,汽车做匀加速直线运动,图线BC的斜率表示汽车的功率P,P不变,则汽车做加速度减小的加速运动,直至达到最大速度v2,此后汽车做匀速直线运动.(2)当汽车的速度为v2时,牵引力为F1=1×103 N,v2==m/s=20 m/s.(3)汽车做匀加速直线运动时的加速度最大阻力Ff==N=1000 Na==m/s2=2 m/s2.(4)与B点对应的速度为v1=m/s≈6.67 m/s.当汽车的速度为10 m/s时处于图线BC段,故此时的功率最大,为Pm=2×104 W.12.【题文】(2009年高考四川卷)图为修建高层建筑常用的塔式起重机.在起重机将质量m=5×104 kg的重物竖直吊起的过程中,重物由静止开始向上做匀加速直线运动,加速度a=0.2 m/s2,当起重机输出功率达到其允许的最大值时,保持该功率直到重物做vm=1.02 m/s的匀速运动.取g=10 m/s2,不计额外功.求:(1)起重机允许输出的最大功率.(2)重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率.【答案】(1)5.1×105 W(2)5 s 2.04×105 W【解析】(1)当起重机的功率达到允许最大值,且重物达到最大速度vm时,拉力和重力相等,即F=mg.根据P=FvPm=mgvm=5×104×10×1.02 W=5.1×105 W.(2)根据牛顿第二定律F-mg=ma又Pm=Fvv=at解得:t=5 s.当t′=2 s时v′=at′P′=Fv′解得P′=2.04×105 W.13.【题文】如图所示,质量为m的物体静止于倾角为α的斜面体上,现对斜面体施加一水平向左的推力F,使物体随斜面体一起沿水平面向左匀速移动x,则在此匀速运动过程中斜面体对物体所做的功为( )A.FxB.mgxcosαsinαC.mgxsinαD.0【答案】D.【解析】由于物体做匀速运动,其处于平衡状态.物体动能和势能在运动过程中都不发生变化,故根据动能定理知合外力对物体做功为零 .而重力做功为零,所以斜面体对物体做功为零,故应选D.14.【题文】(2011年诸暨中学检测)光滑斜面上有一小球自高为h的A处由静止开始滚下,抵达光滑的水平面上的B点时速度大小为v0,光滑水平面上每隔相等的距离设置了一个与小球运动方向垂直的活动阻挡条,如图所示,小球越过n条活动阻挡条后停下来.若让小球从h高处以初速度v0滚下,则小球能越过活动阻挡条的条数为(设小球每次越过活动阻挡条时克服阻力做的功相同)( )A.nB.2nC.3nD.4n【答案】B【解析】略15.【题文】(2009年高考广东卷)物体在合外力作用下做直线运动的vt图象如图所示.下列表述正确的是( )A.在0~1 s内,合外力做正功B.在0~2 s内,合外力总是做负功C.在1 s~2 s内,合外力不做功D.在0~3 s内,合外力总是做正功【答案】A.【解析】由动能定理可知,合外力做的功等于动能的增量,0~1 s内,速度增加,合外力做正功,A正确.1 s~2 s内动能减小,合外力做负功,0~3 s内,动能增量为零,合外力不做功,而0~2 s内,动能增大,合外力做正功,故B、C、D均错.16.【题文】(2011年安徽如皋模拟)如图所示,斜面AB和水平面BC是从同一板材上截下的两段,在B处用小圆弧连接.将小铁块(可视为质点)从A处由静止释放后,它沿斜面向下滑行,进入平面,最终静止于P 处.若从该板材上再截下一段,搁置在A、P之间,构成一个新的斜面,再将铁块放回A处,并轻推一下使之沿新斜面向下滑动.关于此情况下铁块运动情况的描述,正确的是( )A.铁块一定能够到达P点B.铁块的初速度必须足够大才能到达P点C.铁块能否到达P点与铁块质量有关D.以上说法均不对【答案】A.【解析】设AB=x1,BP=x2,AP=x3,动摩擦因数为μ,由动能定理得:mgx1sinα-μmgcosαx1-μmgx2=0,可得:mgx1sinα=μmg(x1cosα+x2),设沿AP滑到P的速度为vP,由动能定理得:mgx1sinα-μmgcosβ·x3=mv,因x1cosα+x2=x3cosβ,故得:vP=0,即铁块恰好沿AP滑到P点,故A正确.17.【题文】如图所示,一个小环沿竖直放置的光滑圆环轨道做圆周运动.小环从最高点A(初速度为零)滑到最低点B的过程中,小环线速度大小的平方v2随下落高度h的变化图象可能是图中的( )【答案】B.【解析】考虑环下降过程中受到的各个力的做功情况,重力做正功,圆环对小环的支持力始终与小环运动方向垂直,不做功,由动能定理ΔEk=mv2=mgh,v2与h的关系为线性关系,又因h=0时,v也为零.所以图象过原点,只有B符合条件,选B.18.【题文】2010年在加拿大城市温哥华举办的冬奥会上,瑞典女队又一次获得冰壶比赛世界冠军.运动员以一定的初速度将冰壶沿水平面抛出,由于摩擦阻力的作用,其动能随位移变化图线如图所示,已知冰壶质量为19 kg,g取10 m/s2,则以下说法正确的是( )A.μ=0.05B.μ=0.02C.滑行时间t=5 sD.滑行时间t=10 s【答案】D.【解析】对冰壶由动能定理得:-μmgx=0-mv,得:μ===0.01,A、B错误.冰壶运动时:a=μg=0.1 m/s2由运动学公式x=at2得:t=10 s,D正确.19.【题文】(2011年杭州学军中学检测)人通过滑轮将质量为m的物体,沿粗糙的斜面由静止开始匀加速地由底端拉上斜面,物体上升的高度为h,到达斜面顶端的速度为v,如图所示.则在此过程中( )A.物体所受的合外力做功为mgh+mv2B.物体所受的合外力做功为mv2C.人对物体做的功为mghD.人对物体做的功大于mgh【答案】BD【解析】.物体沿斜面做匀加速运动,根据动能定理:W合=WF-WFf-mgh=mv2,其中WFf为物体克服摩擦力做的功.人对物体做的功即是人对物体的拉力做的功,所以W人=WF=WFf+mgh+mv2,A、C错误,B、D 正确.20.【题文】(2011年江苏无锡质量调研)如图所示,质量为M、长度为l的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动.物块和小车之间的摩擦力为Ff.物块滑到小车最右端时,小车运动的距离为s.在这个过程中,下列说法正确的是( )A.物块到达小车最右端时具有的动能为F(l+s)B.物块到达小车最右端时,小车具有的动能为FfsC.物块克服摩擦力所做的功为Ff(l+s)D.物块和小车增加的机械能为Ffs【答案】BC.【解析】合外力做功引起物体动能的变化,物块到达小车最右端时具有的动能对应这个过程中物块所受合外力做的功,做的功为(F-Ff)(l+s),所以A错误;物块和小车增加的机械能为动力和阻力对系统做功之和,即F(l+s)-Ffl,所以D错误.21.【题文】某物体沿直线运动的v-t关系如图所示,已知在第1 s内合外力对物体做的功为W,则( )A.从第1 s末到第3 s末合外力做功为4WB.从第3 s末到第5 s末合外力做功为-2WC.从第5 s末到第7 s末合外力做功为WD.从第3 s末到第4 s末合外力做功为-0.75W【答案】CD.【解析】由题图知:第1 s末、第3 s末、第7 s末速度大小关系:v1=v3=v7,由题知W=mv-0,则由动能定理得第1 s末到第3 s末合外力做功W1=mv-mv=0,故A错.第3 s末到第5 s末合外力做功W2=mv-mv=0-mv=-W,故B错.第5 s末到第7 s末合外力做功W3=mv-0=mv=W,故C正确.第3 s末到第4 s末合外力做功W4=mv-mv=m(v1)2-mv=-0.75W,故D对.22.【题文】(2011年湖北黄冈检测)在新疆旅游时,最刺激的莫过于滑沙运动.某人坐在滑沙板上从沙坡斜面的顶端由静止沿直线下滑到斜面底端时,速度为2v0,设人下滑时所受阻力恒定不变,沙坡长度为L,斜面倾角为α,人的质量为m,滑沙板质量不计,重力加速度为g.则( )A.若人在斜面顶端被其他人推了一把,沿斜面以v0的初速度下滑,则人到达斜面底端时的速度大小为3v0 B.若人在斜面顶端被其他人推了一把,沿斜面以v0的初速度下滑,则人到达斜面底端时的速度大小为v0C.人沿沙坡下滑时所受阻力Ff=mgsinα-2mv/LD.人在下滑过程中重力功率的最大值为2mgv0【答案】BC.【解析】对人进行受力分析如图所示,根据匀变速直线运动的规律有:(2v0)2-0=2aL,v-v=2aL,可解得:v1=v0,所以A错误,B正确;根据动能定理有:mgLsinα-FfL=m(2v0)2,可解得Ff=mgsinα-2mv/L,C正确;重力功率的最大值为Pm=2mg v0sinα,D错误.23.【题文】(2011年宁波效实中学抽样测试)如图甲所示,在倾角为30°的足够长光滑斜面AB前,有一粗糙水平面OA,OA长为4 m.有一质量为m的滑块,从O处由静止开始受一水平向右的力F作用.F按图乙所示的规律变化.滑块与OA间的动摩擦因数μ=0.25,g取10 m/s2,试求:(1)滑块到A处的速度大小;(2)不计滑块在A处的速率变化,滑块冲上斜面AB的长度是多少?【答案】(1)5m/s (2)5 m【解析】(1)由题图乙知,在前2 m内,F1=2mg,做正功;在第3 m内,F2=-0.5mg,做负功;在第4 m内,F3=0.滑动摩擦力Ff=-μmg=-0.25mg,始终做负功.对OA过程由动能定理列式得F1x1+F2x2+Ff·x=mv-0.即2mg×2-0.5mg×1-0.25mg×4=mv,解得vA=5m/s.(2)冲上斜面的过程,由动能定理得-mg·L·sin30°=0-mv,所以冲上斜面AB的长度L=5 m.24.【题文】如图所示为“S”形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成的,固定在竖直平面内,轨道弯曲部分是由两个半径相等的半圆连接而成的,圆半径比细管内径大得多,轨道底端与水平地面相切,弹射装置将一个小球(可视为质点)从a点水平射向b点并进入轨道,经过轨道后从p点水平抛出,已知小球与地面ab段间的动摩擦因数μ=0.2,不计其他机械能损失,ab段长L=1.25 m,圆的半径R=0.1 m,小球质量m=0.01 kg,轨道质量为M=0.15 kg,g=10 m/s2,求:(1)若v0=5 m/s,小球从p点抛出后的水平射程;(2)若v0=5 m/s,小球经过轨道的最高点时,管道对小球作用力的大小和方向;(3)设小球进入轨道之前,轨道对地面的压力大小等于轨道自身的重力,当v0至少为多大时,轨道对地面的压力为零.【答案】(1)0.4m(2)1.1 N,方向竖直向下(3)5 m/s【解析】(1)设小球运动到p点时的速度大小为v,对小球由a点运动到p点的过程,应用动能定理得:-μmgL-4Rmg=mv2-mv①小球从p点抛出后做平抛运动,设运动时间为t,水平射程为x,则4R=gt2②x=v t③联立①②③代入数据解得x=0.4m.(2)设在轨道最高点时管道对小球的作用力大小为F,取竖直向下为正方向,有:F+mg=m④联立①④代入数据解得F=1.1 N,方向竖直向下.(3)分析可知,要使小球以最小速度v0运动,且轨道对地面的压力为零,则小球的位置应该在“S”形轨道的中间位置,则有:F′+mg=m,F′=Mg-μmgL-2mgR=mv-mv解得:v0=5 m/s.25.【题文】(2011年瑞安中学检测)在一次课外趣味游戏中,有四位同学分别将四个质量不同的光滑小球沿竖直放置的内壁光滑的半球形碗的碗口内侧同时由静止释放,碗口水平,如图所示.他们分别记下了这四个小球下滑速率为v时的位置,则这些位置应该在同一个( )A.球面B.抛物面C.水平面D.椭圆面【答案】C.【解析】因半球形碗的内壁光滑,所以小球下滑过程中机械能守恒,取小球速率为v时所在的平面为零势能面,则根据机械能守恒定律得mgh=mv2,因为速率v相等,所以高度相等,与小球的质量无关,即这些位置应该在同一个水平面上,C正确.26.【题文】(2011年东北地区名校联考)如图所示,一物体以速度v0冲向光滑斜面AB,并能沿斜面升高h,下列说法正确的是( )A.若把斜面从C点锯断,由机械能守恒定律知,物体冲出C点后仍能升高hB.若把斜面弯成如图所示的半圆弧形,物体仍能沿AB′升高hC.若把斜面从C点锯断或弯成如图所示的半圆弧形,物体都不能升高h,因为物体的机械能不守恒D.若把斜面从C点锯断或弯成如图所示的半圆弧形,物体都不能升高h,但物体的机械能仍守恒【答案】D.【解析】若把斜面从C点锯断,物体到达最高点时水平速度不为零,由机械能守恒定律知,物体冲出C点后不能升高h;若把斜面弯成如题图所示的半圆弧形,物体在升高h之前已经脱离轨道.物体在这两种情况下机械能均守恒.27.【题文】(2011年河南安阳质检)ABCD是一段竖直平面内的光滑轨道,AB段与水平面成α角,CD段与水平面成β角,其中BC段水平,且其长度大于L.现有两小球P、Q,质量分别是2m、m,用一长为L的轻质直杆连接,将P、Q由静止从高H处释放,在轨道转折处用光滑小圆弧连接,不考虑两小球在轨道转折处的能量损失.则小球P滑上CD轨道的最大高度h为( )A.h=HB.h=H+C.h=H+LsinβD.h=H+【答案】B【解析】P、Q整体上升的过程中,机械能守恒,以地面为重力势能的零势面,根据机械能守恒定律有:mgH +2mg(H+Lsinα)=2mgh+mg(h+Lsinβ),解方程得:h=H+.28.【题文】(2011年衢州一中检测)如图所示,一质量为m的滑块以初速度v0从固定于地面的斜面底端A 开始冲上斜面,到达某一高度后返回A,斜面与滑块之间有摩擦.下列各项分别表示它在斜面上运动的速度v、加速度a、势能Ep和机械能E随时间的变化图象,可能正确的是( )【答案】C【解析】由牛顿第二定律可知,滑块上升阶段有:mgsinθ+Ff=ma1,下滑阶段有:mgsinθ-Ff=ma2,因此a1a2,B选项错误;且v0和v0时,速度图象的斜率不同,故A选项错误;由于摩擦力始终做负功,机械能一直减小,故选项D错误;重力势能先增大后减小,且上升阶段加速度大,势能变化快,下滑阶段加速度小,势能变化慢,故选项C正确.29.【题文】如图所示,在两个质量分别为m和2m的小球a和b之间,用一根长为L的轻杆连接(杆的质量可不计),而小球可绕穿过轻杆中心O的水平轴无摩擦转动,现让轻杆处于水平位置,然后无初速度释放,重球b向下,轻球a向上,产生转动,在杆转至竖直的过程中( )A.b球的重力势能减小,动能增加B.a球的重力势能增加,动能减小C.a球和b球的总机械能守恒D.a球和b球的总机械能不守恒【答案】AC【解析】考点:机械能守恒定律。
高考物理总复习章节精练精析第13章(带答案与解析)解答解析、考点详解.doc

高考物理总复习章节精练精析第13章(带答案与解析)的正确答案、解答解析、考点详解姓名:_____________ 年级:____________ 学号:______________1.【题文】关于物质的波粒二象性,下列说法中不正确的是( ) A .不仅光子具有波粒二象性,一切运动的微粒都具有波粒二象性B .运动的微观粒子与光子一样,当它们通过一个小孔时,都没有特定的运动轨道C .波动性和粒子性,在宏观现象中是矛盾的、对立的,但在微观高速运动的现象中是统一的D .实物粒子的运动有特定的轨道,所以实物不具有波粒二象性【答案】D【解析】实物粒子与光子都具有波粒二象性,A 、B 、C 正确.2.【题文】(2009年高考辽宁、宁夏理综卷)关于光电效应,下列说法正确的是( )A .极限频率越大的金属材料逸出功越大B .只要光照射的时间足够长,任何金属都能产生光电效应C .从金属表面出来的光电子的最大初动能越大,这种金属的逸出功越小D .入射光的光强一定时,频率越高,单位时间内逸出的光电子数就越多【答案】A.【解析】由hν0=W 知A 正确;入射光频率低于极限频率,光照时间不论有多长,都不能发生光电效应,B 错;由Ekm =hν-W 知,最大初动能的大小既与入射光频率有关,也与逸出功有关,C 错;单位时间内逸出的光电子数只与光强有关,与光频率无关,D 错.3.【题文】(2009年高考广东卷)硅光电池是利用光电效应原理制成的器件.下列表述正确的是()A .硅光电池是把光能转变为电能的一种装置B .硅光电池中吸收了能量的电子都能逸出C .逸出的光电子的最大初动能与入射光的频率无关D .任意频率的光照射到硅光电池上都能产生光电效应【答案】:A【解析】略4.【题文】(2010年高考四川卷)用波长为2.0×10-7 m 的紫外线照射钨的表面,释放出来的光电子中最大的动能是4.7×10-19 J .由此可知,钨的极限频率是(普朗克常量h =6.63×10-34 J·s,光速c =3.0×108 m/s ,结果取两位有效数字)( )A .5.5×1034 HzB .7.9×1014 HzC .9.8×1014 HzD .1.2×1015 Hz【答案】B.【解析】该题考查光电效应方程,由mv2=h-W0和W0=hν0可得ν0=7.9×1014 Hz,B选项正确.5.【题文】在单缝衍射实验中,中央亮纹的光强占整个从单缝射入的光强的95%以上,假设现在只让一个光子通过单缝,那么该光子( )A.一定落在中央亮纹处B.一定落在亮纹处C.可能落在暗纹处D.落在中央亮纹处的可能性最大【答案】:CD【解析】略6.【题文】(2011年东阳中学高三月考)用频率为ν1的单色光照射某种金属表面,发生了光电效应现象.现改为频率为ν2的另一单色光照射该金属表面,下面说法正确的是( )A.如果ν2>ν1,能够发生光电效应B.如果ν2<ν1,不能够发生光电效应C.如果ν2>ν1,逸出光电子的最大初动能增大D.如果ν2>ν1,逸出光电子的最大初动能不受影响【答案】AC.【解析】对一定的金属,入射光的频率必须大于或等于某一频率ν时才会产生光电效应,频率ν称为截止频率,如果入射光的频率低于截止频率ν,则不论光强多大,照射时间多长,都不会产生光电效应,不同的金属有不同的截止频率.所以当ν2>ν1时能够发生光电效应,ν2<ν1时不一定能够发生光电效应,A正确,B错误;又光电子的初动能随着入射光频率的增加而线性增加,所以当ν2>ν1时逸出光电子的初动能增大,C正确,D错误.7.【题文】图是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象.由图象可知( )A.该金属的逸出功等于EB.该金属的逸出功等于hν0C.入射光的频率为2ν0时,产生的光电子的最大初动能为ED.入射光的频率为ν0/2时,产生的光电子的最大初动能为E/2【答案】:ABC【解析】略8.【题文】(2010年高考浙江卷)在光电效应实验中,飞飞同学用同一光电管在不同实验条件下得到了三条光电流与电压之间的关系曲线(甲光、乙光、丙光),如图所示.则可判断出( )A.甲光的频率大于乙光的频率B.乙光的波长大于丙光的波长C.乙光对应的截止频率大于丙光的截止频率D.甲光对应的光电子最大初动能大于丙光的光电子最大初动能【答案】B.【解析】由于是同一光电管,因而不论对哪种光,极限频率和金属的逸出功相同,对于甲、乙两种光,反向截止电压相同,因而频率相同,A项错误;丙光对应的反向截止电压较大,因而丙光的频率较高,波长较短,对应的光电子的最大初动能较大,故C、D均错,只有B项正确.9.【题文】紫光的波长为4000 A,金属钠的逸出功为3.5×10-19 J,求:(1)每个紫光光子的能量为多少?(2)若用该紫光照射金属钠时,产生的光电子的最大初动能是多少?【答案】:(1)5.0×10-19 J (2)1.5×10-19 J【解析】(1)因E=hν,而ν=,所以E==J=5.0×10-19 J.(2)由爱因斯坦的光电效应方程得:hν=W+Ekmax,所以Ekmax=hν-W=5.0×10-19 J-3.5×10-19 J=1.5×10-19 J.10.【题文】(2011年温州八校联考)普朗克常量h=6.63×10-34 J·s,铝的逸出功W0=6.72×10-19 J,现用波长λ=200 nm的光照射铝的表面(结果保留三位有效数字).(1)求光电子的最大初动能;(2)若射出的一个具有最大初动能的光电子正对一个原来静止的电子运动,求在此运动过程中两电子电势能增加的最大值(电子所受的重力不计).【答案】:(1)3.23×10-19 J(2)1.62×10-19 J【解析】(1)Ek=hν-W0ν=c/λ∴Ek=3.23×10-19 J.(2)增加的电势能来自系统损失的动能,当两电子的速度相等时电势能最大,由动量守恒定律得mv0=2mv损失的动能:ΔEk=mv-(2m)v2=1.62×10-19 J所以,电势能增加的最大值为1.62×10-19 J.11.【题文】(2011年广东广州模拟)仔细观察氢原子的光谱,发现它只有几条分离的不连续的亮线,其原因是( )A.氢原子只有几个能级B.氢原子只能发出平行光C.氢原子有时发光,有时不发光D.氢原子辐射的光子的能量是不连续的,所以对应的光的频率也是不连续的【答案】D.【解析】光谱中的亮线对应不同频率的光,“分离不连续亮线”对应着不同频率的光,B、C错.氢原子在不同的能级之间跃迁时,辐射不同能量的光子,并且满足E=hν.能量不同,相应光子频率不同,体现在光谱上是一些不连续的亮线,A错误D正确.12.【题文】许多物质在紫外线照射下能发出荧光,紫外线照射时,这些物质的原子先后发生两次跃迁,其能量变化分别为ΔE1和ΔE2,则下列说法正确的是( )A.两次跃迁均向高能级跃迁,且ΔE1>ΔE2B.两次跃迁均向低能级跃迁,且ΔE1<ΔE2C.先向高能级跃迁,再向低能级跃迁,且ΔE1>ΔE2D.先向低能级跃迁,再向高能级跃迁,且ΔE1<ΔE2【答案】C.【解析】第一次跃迁是吸收紫外线光子,第二次跃迁是放出可见光光子.由于hν1>hν2,故ΔE1>ΔE2,C项正确.13.【题文】(2009年高考全国卷Ⅰ)氦氖激光器能产生三种波长的激光,其中两种波长分别为λ1=0.6328 μm,λ2=3.39 μm.已知波长为λ1的激光是氖原子在能级间隔为ΔE1=1.96 eV的两个能级之间跃迁产生的.用ΔE2表示产生波长为λ2的激光所对应的跃迁的能级间隔,则ΔE2的近似值为( )A.10.50 eVB.0.98 eVC.0.53 eVD.0.36 eV【答案】D.【解析】由跃迁公式得ΔE1=,ΔE2=,联立可得ΔE2=·ΔE1=0.36 eV,选项D对.。
大学物理第五版课后答案解析(上)完整版

⼤学物理第五版课后答案解析(上)完整版1-1 。
分析与解 (1) 质点在t ⾄(t +Δt )时间内沿曲线从P 点运动到P ′点,各量关系如图所⽰, 其中路程Δs =PP ′, 位移⼤⼩|Δr |=PP ′,⽽Δr =|r |-|r |表⽰质点位⽮⼤⼩的变化量,三个量的物理含义不同,在曲线运动中⼤⼩也不相等(注:在直线运动中有相等的可能).但当Δt →0 时,点P ′⽆限趋近P 点,则有|d r |=d s ,但却不等于d r .故选(B).(2) 由于|Δr |≠Δs ,故tst ΔΔΔΔ≠r ,即|v |≠v .但由于|d r |=d s ,故tst d d d d =r ,即|v |=v .由此可见,应选(C). 1-2。
分析与解trd d 表⽰质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率.通常⽤符号v r 表⽰,这是速度⽮量在位⽮⽅向上的⼀个分量;td d r 表⽰速度⽮量;在⾃然坐标系中速度⼤⼩可⽤公式t s d d =v 计算,在直⾓坐标系中则可由公式22d d d d ??+? =t y t x v 求解.故选(D).1-3 。
分析与解td d v表⽰切向加速度a t,它表⽰速度⼤⼩随时间的变化率,是加速度⽮量沿速度⽅向的⼀个分量,起改变速度⼤⼩的作⽤;t r d d 在极坐标系中表⽰径向速率v r (如题1 -2 所述);ts d d 在⾃然坐标系中表⽰质点的速率v ;⽽td d v表⽰加速度的⼤⼩⽽不是切向加速度a t.因此只有(3) 式表达是正确的.故选(D). 1-4 。
分析与解加速度的切向分量a t起改变速度⼤⼩的作⽤,⽽法向分量a n 起改变速度⽅向的作⽤.质点作圆周运动时,由于速度⽅向不断改变,相应法向加速度的⽅向也在不断改变,因⽽法向加速度是⼀定改变的.⾄于a t是否改变,则要视质点的速率情况⽽定.质点作匀速率圆周运动时, a t恒为零;质点作匀变速率圆周运动时, a t为⼀不为零的恒量,当a t改变时,质点则作⼀般的变速率圆周运动.由此可见,应选(B).1-5 。
《大学物理讲义》 习题答案

dr i dt
v0 v0 r 2 h 2
-
r
1 2 r h2 2
3 2
2rv0 i
2 2 2 v0 r h
- r
1 2
2
h2
r 2 i
2 2 2 2 r h -r v0 i 2 2 3 ( r h )
船的加速度矢量为
d dx d a i v0 [r r 2 h 2 dt dt dt
-
1 2
]i
4
《大学物理讲义》习题解答
dr v0 r 2 h 2 dt
-
1 2
-r
1 2
1 2 r h2 2
3 2
2r
3 2
3i 54 j i 2 j 2i 52 j i 26 jm / s
2 2
t 1s
1 ~ 3s 内的平均加速度为 v t 3 s v a 3 1
i 54 j i 6 j 24 jm / s
x2 x3 x2 2 1 1m
a
t 2s O
1
习题 1-1 解答图
t 0 5 x/m
前 3s 内它的路程
S x1 x2 4 1 5m
前 3s 内它的位移
x x1 x2 4 1 3m
1-2 有一质点沿 x 轴作直线运动,t 时刻的坐标为
dr v i 6t 2 j m / s dt
大学物理习题答案解析第三章

第三章动量守恒定律和能量守恒定律3 -1对质点组有以下几种说法:(1) 质点组总动量的改变与内力无关;(2) 质点组总动能的改变与内力无关;(3) 质点组机械能的改变与保守内力无关.下列对上述说法判断正确的是()(A) 只有(1)是正确的(B) (1)、(2)是正确的(C) (1)、(3)是正确的(D) (2)、(3)是正确的分析与解在质点组中内力总是成对出现的,它们是作用力与反作用力.由于一对内力的冲量恒为零,故内力不会改变质点组的总动量.但由于相互有作用力的两个质点的位移大小以及位移与力的夹角一般不同,故一对内力所作功之和不一定为零,应作具体分析,如一对弹性内力的功的代数和一般为零,一对摩擦内力的功代数和一般不为零,对于保守内力来说,所作功能使质点组动能与势能相互转换,因此保守内力即使有可能改变质点组的动能,但也不可能改变质点组的机械能.综上所述(1)(3)说法是正确的.故选(C).3 -2有两个倾角不同、高度相同、质量一样的斜面放在光滑的水平面上,斜面是光滑的,有两个一样的物块分别从这两个斜面的顶点由静止开始滑下,则()(A) 物块到达斜面底端时的动量相等(B) 物块到达斜面底端时动能相等(C) 物块和斜面(以及地球)组成的系统,机械能不守恒(D) 物块和斜面组成的系统水平方向上动量守恒分析与解对题述系统来说,由题意知并无外力和非保守内力作功,故系统机械能守恒.物体在下滑过程中,一方面通过重力作功将势能转化为动能,另一方面通过物体与斜面之间的弹性内力作功将一部分能量转化为斜面的动能,其大小取决其中一个内力所作功.由于斜面倾角不同,故物体沿不同倾角斜面滑至底端时动能大小不等.动量自然也就不等(动量方向也不同).故(A)(B)(C)三种说法均不正确.至于说法(D)正确,是因为该系统动量虽不守恒(下滑前系统动量为零,下滑后物体与斜面动量的矢量和不可能为零.由此可知,此时向上的地面支持力并不等于物体与斜面向下的重力),但在水平方向上并无外力,故系统在水平方向上分动量守恒.3 -3对功的概念有以下几种说法:(1) 保守力作正功时,系统内相应的势能增加;(2) 质点运动经一闭合路径,保守力对质点作的功为零;(3) 作用力和反作用力大小相等、方向相反,所以两者所作功的代数和必为零.下列上述说法中判断正确的是()(A) (1)、(2)是正确的(B) (2)、(3)是正确的(C) 只有(2)是正确的(D) 只有(3)是正确的分析与解保守力作正功时,系统内相应势能应该减少.由于保守力作功与路径无关,而只与始末位置有关,如质点环绕一周过程中,保守力在一段过程中作正功,在另一段过程中必然作负功,两者之和必为零.至于一对作用力与反作用力分别作用于两个质点所作功之和未必为零(详见习题3 -2 分析),由此可见只有说法(2)正确,故选(C).3 -4如图所示,质量分别为m1和m2的物体A和B,置于光滑桌面上,A和B之间连有一轻弹簧.另有质量为m1和m2的物体C和D分别置于物体A与B 之上,且物体A和C、B和D之间的摩擦因数均不为零.首先用外力沿水平方向相向推压A和B,使弹簧被压缩,然后撤掉外力,则在A和B弹开的过程中,对A、B、C、D 以及弹簧组成的系统,有()(A) 动量守恒,机械能守恒 (B) 动量不守恒,机械能守恒(C) 动量不守恒,机械能不守恒 (D) 动量守恒,机械能不一定守恒分析与解 由题意知,作用在题述系统上的合外力为零,故系统动量守恒,但机械能未必守恒,这取决于在A 、B 弹开过程中C 与A 或D 与B 之间有无相对滑动,如有则必然会因摩擦内力作功,而使一部分机械能转化为热能,故选(D).3 -5 如图所示,子弹射入放在水平光滑地面上静止的木块后而穿出.以地面为参考系,下列说法中正确的说法是( )(A) 子弹减少的动能转变为木块的动能(B) 子弹-木块系统的机械能守恒(C) 子弹动能的减少等于子弹克服木块阻力所作的功(D) 子弹克服木块阻力所作的功等于这一过程中产生的热分析与解 子弹-木块系统在子弹射入过程中,作用于系统的合外力为零,故系统动量守恒,但机械能并不守恒.这是因为子弹与木块作用的一对内力所作功的代数和不为零(这是因为子弹对地位移大于木块对地位移所致),子弹动能的减少等于子弹克服阻力所作功,子弹减少的动能中,一部分通过其反作用力对木块作正功而转移为木块的动能,另一部分则转化为热能(大小就等于这一对内力所作功的代数和).综上所述,只有说法(C)的表述是完全正确的.3 -6 一架以3.0 ×102 m·s-1 的速率水平飞行的飞机,与一只身长为0.20 m 、质量为0.50 kg 的飞鸟相碰.设碰撞后飞鸟的尸体与飞机具有同样的速度,而原来飞鸟对于地面的速率甚小,可以忽略不计.试估计飞鸟对飞机的冲击力(碰撞时间可用飞鸟身长被飞机速率相除来估算).根据本题的计算结果,你对于高速运动的物体(如飞机、汽车)与通常情况下不足以引起危害的物体(如飞鸟、小石子)相碰后会产生什么后果的问题有些什么体会?分析 由于鸟与飞机之间的作用是一短暂时间内急剧变化的变力,直接应用牛顿定律解决受力问题是不可能的.如果考虑力的时间累积效果,运用动量定理来分析,就可避免作用过程中的细节情况.在求鸟对飞机的冲力(常指在短暂时间内的平均力)时,由于飞机的状态(指动量)变化不知道,使计算也难以进行;这时,可将问题转化为讨论鸟的状态变化来分析其受力情况,并根据鸟与飞机作用的相互性(作用与反作用),问题就很简单了.解 以飞鸟为研究对象,取飞机运动方向为x 轴正向.由动量定理得式中F ′为飞机对鸟的平均冲力,而身长为20cm 的飞鸟与飞机碰撞时间约为Δt =l /v ,以此代入上式可得0Δ-='v m t F鸟对飞机的平均冲力为式中负号表示飞机受到的冲力与其飞行方向相反.从计算结果可知,2.25 ×105 N 的冲力大致相当于一个22 t 的物体所受的重力,可见,此冲力是相当大的.若飞鸟与发动机叶片相碰,足以使发动机损坏,造成飞行事故.3 -7 质量为m 的物体,由水平面上点O 以初速为v 0 抛出,v 0与水平面成仰角α.若不计空气阻力,求:(1) 物体从发射点O 到最高点的过程中,重力的冲量;(2) 物体从发射点到落回至同一水平面的过程中,重力的冲量.分析 重力是恒力,因此,求其在一段时间内的冲量时,只需求出时间间隔即可.由抛体运动规律可知,物体到达最高点的时间,物体从出发到落回至同一水平面所需的时间是到达最高点时间的两倍.这样,按冲量的定义即可求得结果.另一种解的方法是根据过程的始、末动量,由动量定理求出.解1 物体从出发到达最高点所需的时间为则物体落回地面的时间为 于是,在相应的过程中重力的冲量分别为 解2 根据动量定理,物体由发射点O 运动到点A 、B 的过程中,重力的冲量分别为3 -8 F x =30+4t (式中F x 的单位为N,t 的单位为s)的合外力作用在质量m =10 kg 的物体上,试求:(1) 在开始2s 内此力的冲量;(2) 若冲量I =300 N·s,此力作用的时间;(3) 若物体的初速度v 1 N 1055.252⨯=='lm F v N 1055.25⨯-='-=FF gαt sin Δ01v =gαt sin Δ01v =gαt t sin Δ2Δ012v ==j j F I αm t mg t t sin Δd 011Δ1v -=-==⎰j j F I αm t mg t t sin 2Δd 022Δ2v -=-==⎰j j j I αm y m mv Ay sin 001v v -=-=j j j I αm y m mv By sin 2002v v -=-==10 m·s -1 ,方向与Fx 相同,在t =6.86s 时,此物体的速度v 2 .分析 本题可由冲量的定义式,求变力的冲量,继而根据动量定理求物体的速度v 2.解 (1) 由分析知(2) 由I =300 =30t +2t 2 ,解此方程可得t =6.86 s(另一解不合题意已舍去)(3) 由动量定理,有I =m v 2- m v 1由(2)可知t =6.86 s 时I =300 N·s ,将I 、m 及v 1代入可得3 -9 高空作业时系安全带是非常必要的.假如一质量为51.0 kg 的人,在操作时不慎从高空竖直跌落下来,由于安全带的保护,最终使他被悬挂起来.已知此时人离原处的距离为2.0 m ,安全带弹性缓冲作用时间为0.50 s .求安全带对人的平均冲力.分析 从人受力的情况来看,可分两个阶段:在开始下落的过程中,只受重力作用,人体可看成是作自由落体运动;在安全带保护的缓冲过程中,则人体同时受重力和安全带冲力的作用,其合力是一变力,且作用时间很短.为求安全带的冲力,可以从缓冲时间内,人体运动状态(动量)的改变来分析,即运用动量定理来讨论.事实上,动量定理也可应用于整个过程.但是,这时必须分清重力和安全带冲力作用的时间是不同的;而在过程的初态和末态,人体的速度均为零.这样,运用动量定理仍可得到相同的结果.解1 以人为研究对象,按分析中的两个阶段进行讨论.在自由落体运动过程中,人跌落至2 m 处时的速度为(1)在缓冲过程中,人受重力和安全带冲力的作用,根据动量定理,有(2)由式(1)、(2)可得安全带对人的平均冲力大小为解2 从整个过程来讨论.根据动量定理有3 -10 质量为m 的小球,在合外力F =-kx 作用下运动,已知x =A cos ωt ,其中k 、ω、A 均为正常量,求在t =0 到 时间内小球动量的增量. 分析 由冲量定义求得力F 的冲量后,根据动量原理,即为动量增量,注意用式积分前,应先将式中x 用x =A cos ωt 代之,方能积分.解 力F 的冲量为 ⎰=21d t t t F I ()s N 68230d 43020220⋅=+=+=⎰t t t t I 112s m 40-⋅=+=mm I v v gh 21=v ()12Δv v m m t -=+P F ()N 1014.1Δ2ΔΔ3⨯=+=+=tgh mg t m Δmg F v N 1014.1/2Δ3⨯=+=mg g h tmg F ωt 2π=⎰21d t t t F即 3 -11 如图所示,在水平地面上,有一横截面S =0.20 m 2 的直角弯管,管中有流速为v =3.0 m·s-1 的水通过,求弯管所受力的大小和方向.分析 对于弯曲部分AB 段内的水而言,由于流速一定,在时间Δt 内,从其一端流入的水量等于从另一端流出的水量.因此,对这部分水来说,在时间Δt 内动量的增量也就是流入与流出水的动量的增量Δp =Δm (v B -v A );此动量的变化是管壁在Δt 时间内对其作用冲量I 的结果.依据动量定理可求得该段水受到管壁的冲力F ;由牛顿第三定律,自然就得到水流对管壁的作用力F′=-F .解 在Δt 时间内,从管一端流入(或流出) 水的质量为Δm =ρυS Δt ,弯曲部分AB 的水的动量的增量则为Δp =Δm (v B -v A ) =ρυS Δt (v B -v A )依据动量定理I =Δp ,得到管壁对这部分水的平均冲力从而可得水流对管壁作用力的大小为作用力的方向则沿直角平分线指向弯管外侧.3 -12 一作斜抛运动的物体,在最高点炸裂为质量相等的两块,最高点距离地面为19.6 m .爆炸1.00 s 后,第一块落到爆炸点正下方的地面上,此处距抛出点的水平距离为1.00×102 m .问第二块落在距抛出点多远的地面上.(设空气的阻力不计)分析 根据抛体运动规律,物体在最高点处的位置坐标和速度是易求的.因此,若能求出第二块碎ωkA t t ωkA t kx t F I ωt t t t -=-=-==⎰⎰⎰2/π02121d cos d d ()ωkA m -=vΔ()A B t S ρtv v v -==ΔΔI F N 105.2232⨯-=-=-='v S ρFF片抛出的速度,按抛体运动的规律就可求得落地的位置.为此,分析物体在最高点处爆炸的过程,由于爆炸力属内力,且远大于重力,因此,重力的冲量可忽略,物体爆炸过程中应满足动量守恒.由于炸裂后第一块碎片抛出的速度可由落体运动求出,由动量守恒定律可得炸裂后第二块碎片抛出的速度,进一步求出落地位置.解 取如图示坐标,根据抛体运动的规律,爆炸前,物体在最高点A 的速度的水平分量为(1) 物体爆炸后,第一块碎片竖直落下的运动方程为 当该碎片落地时,有y 1 =0,t =t 1 ,则由上式得爆炸后第一块碎片抛出的速度(2) 又根据动量守恒定律,在最高点处有 (3) (4) 联立解式(1)、(2)、(3) 和(4),可得爆炸后第二块碎片抛出时的速度分量分别为爆炸后,第二块碎片作斜抛运动,其运动方程为(5)(6) 落地时,y 2 =0,由式(5)、(6)可解得第二块碎片落地点的水平位置x 2 =500 m3 -13 A 、B 两船在平静的湖面上平行逆向航行,当两船擦肩相遇时,两船各自向对方平稳地传递50 kg 的重物,结果是A 船停了下来,而B 船以3.4 m·s -1的速度继续向前驶去.A 、B 两船原有质量分别为0.5×103 kg 和1.0 ×103 kg,求在传递重物前两船的速度.(忽略水对船的阻力)分析 由于两船横向传递的速度可略去不计,则对搬出重物后的船A 与从船B 搬入的重物所组成的系统Ⅰ来讲,在水平方向上无外力作用,因此,它们相互作用的过程中应满足动量守恒;同样,对搬出重物后的船B 与从船A 搬入的重物所组成的系统Ⅱ亦是这样.由此,分别列出系统Ⅰ、Ⅱ的动量守hg x t x x 21010==v 21121gt t h y --=v 12121t gt h -=v x x m m 2021v v =y m m 2121210v v +-=1102s m 100222-⋅===hg x x x v v 112112s m 7.1421-⋅=-==t gt h y v v 2212t v x x x +=2222221gt t h y y -+=v恒方程即可解出结果.解 设A 、B 两船原有的速度分别以v A 、v B 表示,传递重物后船的速度分别以v A ′ 、v B ′ 表示,被搬运重物的质量以m 表示.分别对上述系统Ⅰ、Ⅱ应用动量守恒定律,则有(1)(2)由题意知v A ′ =0, v B ′ =3.4 m·s -1 代入数据后,可解得也可以选择不同的系统,例如,把A 、B 两船(包括传递的物体在内)视为系统,同样能满足动量守恒,也可列出相对应的方程求解.3 -14 质量为m′ 的人手里拿着一个质量为m 的物体,此人用与水平面成α角的速率v 0 向前跳去.当他达到最高点时,他将物体以相对于人为u 的水平速率向后抛出.问:由于人抛出物体,他跳跃的距离增加了多少? (假设人可视为质点)分析 人跳跃距离的增加是由于他在最高点处向后抛出物体所致.在抛物的过程中,人与物之间相互作用力的冲量,使他们各自的动量发生了变化.如果把人与物视为一系统,因水平方向不受外力作用,故外力的冲量为零,系统在该方向上动量守恒.但在应用动量守恒定律时,必须注意系统是相对地面(惯性系)而言的,因此,在处理人与物的速度时,要根据相对运动的关系来确定.至于,人因跳跃而增加的距离,可根据人在水平方向速率的增量Δv 来计算.解 取如图所示坐标.把人与物视为一系统,当人跳跃到最高点处,在向左抛物的过程中,满足动量守恒,故有式中v 为人抛物后相对地面的水平速率, v -u 为抛出物对地面的水平速率.得人的水平速率的增量为 而人从最高点到地面的运动时间为 ()A A B A A m m m m v v v '=+-()''=+-B B A B B m m m m v v v ()()12s m 40.0-⋅-=---'-=m m m m m m m A B B B A v v ()()()12s m 6.3-⋅=---'-=m m m m m m m m B A B B A B vv ()()u m m αm m -+'='+v v v cos 0u mm m α'++=cos 00v v u m m m α'+=-=cos Δ0v v v所以,人跳跃后增加的距离 *3 -15 一质量均匀柔软的绳竖直的悬挂着,绳的下端刚好触到水平桌面上.如果把绳的上端放开,绳将落在桌面上.试证明:在绳下落过程中的任意时刻,作用于桌面上的压力等于已落到桌面上绳的重量的三倍.分析 由于桌面所受的压力难以直接求出,因此,可转化为求其反作用力,即桌面给绳的托力.但是,应注意此托力除了支持已落在桌面上的绳外,还有对d t 时间内下落绳的冲力,此力必须运用动量定理来求.解 取如图所示坐标,开始时绳的上端位于原点,Oy 轴的正向竖直向下.绳的总长为l ,以t 时刻,已落到桌面上长为y 、质量为m′的绳为研究对象.这段绳受重力P 、桌面的托力F N 和下落绳子对它的冲力F (如图中所示)的作用.由力的平衡条件有(1) 为求冲力F ,可取d t 时间内落至桌面的线元d y 为研究对象.线元的质量,它受到重力d P 和冲力F 的反作用力F ′的作用,由于F ′>>d P ,故由动量定理得 (2) 而 (3)由上述三式可得任意时刻桌面受到的压力大小为 gαt sin 0v =()gm m αm t x '+==sin ΔΔ0vv 0N =-+F F yg l m y lm m d d =y lm t F d 0d v -='F F '-=g m yg lm l m yg l m F F '==+=-='332N N v*3 -16 设在地球表面附近,一初质量为5.00 ×105 kg 的火箭,从尾部喷出气体的速率为2.00 ×103 m·s -1 .(1) 试问:每秒需喷出多少气体,才能使火箭最初向上的加速度大小为4.90 m·s -2 .(2) 若火箭的质量比为6.00,求该火箭的最后速率.分析 这是一个系统内质量转移的问题.为了讨论火箭的运动规律,仍需建立其在重力场中的动力学方程.为此,以t 时刻质量为m 的火箭为研究对象,它在t →t +Δt 的时间内,将分离成火箭主体(包括尚剩的燃料)和排出的燃料两部分.根据它们的总动量的增量Σd P i 和系统所受的外力———重力(阻力不计),由动量定理可得到-mg =u d m′/d t +m d v /d t (推导从略,见教材),即火箭主体的动力学方程.由于在d t 时间内排出燃料的质量d m ′很小,式中m 也就可以视为此刻火箭主体的质量, 而燃料的排出率d m ′/d t 也就是火箭质量的变化率-d m /d t .这样,上述方程也可写成.在特定加速度a 0 的条件下,根据初始时刻火箭的质量m 0 ,就可求出燃料的排出率d m /d t .在火箭的质量比( 即t 时刻火箭的质量m 与火箭的初始质量m 0之比) 已知的条件下,可算出火箭所经历的时间,则火箭运动的速率可通过对其动力学方程积分后解得.解 (1) 以火箭发射处为原点,竖直向上为正方向.该火箭在重力场中的动力学方程为 (1) 因火箭的初始质量为m 0 =5.00 ×105 kg, 要使火箭获得最初的加速度a 0 =4.90 m·s -2,则燃气的排出率为(2) 为求火箭的最后速率,可将式(1)改写成分离变量后积分,有 火箭速率随时间的变化规律为 (2) 因火箭的质量比为6.00,故经历时间t 后,其质量为 得 (3) 将式(3)代入式(2),依据初始条件,可得火箭的最后速率 ma mg tm u=-d d ma mg tm u =-d d ()1300s kg 1068.3d d -⋅⨯=+=ua g m t m tm mg t m ud d d d v =-⎰⎰⎰-=t mm t g m m u 0d d d 00v v v gt m m u --=00lnv v m t t m m m 61d d 0=-=tm m t d /d 650=13000s m 1047.2d /d 65ln ln -⋅⨯=-=-='tm m m m u gt m m u v3 -17 质量为m 的质点在外力F 的作用下沿Ox 轴运动,已知t =0 时质点位于原点,且初始速度为零.设外力F 随距离线性地减小,且x =0 时,F =F 0 ;当x =L 时,F =0.试求质点从x =0 处运动到x =L 处的过程中力F 对质点所作功和质点在x =L 处的速率.分析 由题意知质点是在变力作用下运动,因此要先找到力F 与位置x 的关系,由题给条件知.则该力作的功可用式 计算,然后由动能定理求质点速率. 解 由分析知, 则在x =0 到x =L 过程中作功, 由动能定理有 得x =L 处的质点速率为 此处也可用牛顿定律求质点速率,即 分离变量后,两边积分也可得同样结果.3 -18 如图所示,一绳索跨过无摩擦的滑轮,系在质量为1.00 kg 的物体上,起初物体静止在无摩擦的水平平面上.若用5.00 N 的恒力作用在绳索的另一端,使物体向右作加速运动,当系在物体上的绳索从与水平面成30°角变为37°角时,力对物体所作的功为多少? 已知滑轮与水平面之间的距离d =1.00 m .分析 该题中虽施以“恒力”,但是,作用在物体上的力的方向在不断变化.需按功的矢量定义式来求解.解 取图示坐标,绳索拉力对物体所作的功为3 -19 一物体在介质中按规律x =ct 3 作直线运动,c 为一常量.设介质对物体的阻力正比于速度的平方.试求物体由x 0 =0 运动到x =l 时,阻力所作的功.(已知阻力系数为k )分析 本题是一维变力作功问题,仍需按功的定义式来求解.关键在于寻找力函数F =F (x ).根据运动学关系,可将已知力与速度的函数关系F (v ) =k v 2 变换到F (t ),进一步按x =ct 3 的x LF F F 00-=⎰L x F 0d x L F F F 00-=2d 0000L F x x L F F W L =⎪⎭⎫ ⎝⎛-=⎰0212-=v m W mL F 0=v xm t m x L F F d d d d 00v v v ==-⎰⋅=s F d W J 69.1d d cos d 2122=+-==⋅=⎰⎰⎰x x d Fx x θF W x x x F ⎰⋅=x F d W关系把F (t )转换为F (x ),这样,就可按功的定义式求解.解 由运动学方程x =ct 3 ,可得物体的速度按题意及上述关系,物体所受阻力的大小为则阻力的功为3 -20 一人从10.0 m 深的井中提水,起始桶中装有10.0 kg 的水,由于水桶漏水,每升高1.00 m 要漏去0.20 kg 的水.水桶被匀速地从井中提到井口,求所作的功.分析 由于水桶在匀速上提过程中,拉力必须始终与水桶重力相平衡.水桶重力因漏水而随提升高度而变,因此,拉力作功实为变力作功.由于拉力作功也就是克服重力的功,因此,只要能写出重力随高度变化的关系,拉力作功即可题3 -20 图求出.解 水桶在匀速上提过程中,a =0,拉力与水桶重力平衡,有F +P =0在图示所取坐标下,水桶重力随位置的变化关系为P =mg -αgy其中α=0.2 kg/m,人对水桶的拉力的功为3 -21 一质量为0.20 kg 的球,系在长为2.00 m 的细绳上,细绳的另一端系在天花板上.把小球移至使细绳与竖直方向成30°角的位置,然后从静止放开.求:(1) 在绳索从30°角到0°角的过程中,重力和张力所作的功;(2) 物体在最低位置时的动能和速率;(3) 在最低位置时的张力.23d d ct tx ==v 3/43/242299x kc t kc k F ===v ⎰⋅=x F W d 3/73/23/403/20727d 9d 180cos d l kc x x kc x W l o l -=-==⋅=⎰⎰⎰xF ()J 882d d 1000=-=⋅=⎰⎰y agy mg W l y F分析 (1) 在计算功时,首先应明确是什么力作功.小球摆动过程中同时受到重力和张力作用.重力是保守力,根据小球下落的距离,它的功很易求得;至于张力虽是一变力,但是,它的方向始终与小球运动方向垂直,根据功的矢量式,即能得出结果来.(2) 在计算功的基础上,由动能定理直接能求出动能和速率.(3) 在求最低点的张力时,可根据小球作圆周运动时的向心加速度由重力和张力提供来确定.解 (1) 如图所示,重力对小球所作的功只与始末位置有关,即在小球摆动过程中,张力F T 的方向总是与运动方向垂直,所以,张力的功(2) 根据动能定理,小球摆动过程中,其动能的增量是由于重力对它作功的结果.初始时动能为零,因而,在最低位置时的动能为小球在最低位置的速率为(3) 当小球在最低位置时,由牛顿定律可得3 -22 一质量为m 的质点,系在细绳的一端,绳的另一端固定在平面上.此质点在粗糙水平面上作半径为r 的圆周运动.设质点的最初速率是v 0 .当它运动一周时,其速率为v 0 /2.求:(1) 摩擦力作的功;(2) 动摩擦因数;(3) 在静止以前质点运动了多少圈?分析 质点在运动过程中速度的减缓,意味着其动能减少;而减少的这部分动能则消耗在运动中⎰⋅=s d F W ()J 53.0cos 1Δ=-==θmgl h P W P s F d T T ⋅=⎰W J 53.0k k ==E E 1P K s m 30.222-⋅===mW m E v lm P F 2T v =-N 49.22T =+=lm mg F v克服摩擦力作功上.由此,可依据动能定理列式解之.解 (1) 摩擦力作功为(1) (2) 由于摩擦力是一恒力,且F f =μmg ,故有(2)由式(1)、(2)可得动摩擦因数为(3) 由于一周中损失的动能为,则在静止前可运行的圈数为 圈 3 -23 如图(a)所示,A 和B 两块板用一轻弹簧连接起来,它们的质量分别为m 1 和m 2 .问在A 板上需加多大的压力,方可在力停止作用后,恰能使A 在跳起来时B 稍被提起.(设弹簧的劲度系数为k )分析 运用守恒定律求解是解决力学问题最简捷的途径之一.因为它与过程的细节无关,也常常与特定力的细节无关.“守恒”则意味着在条件满足的前提下,过程中任何时刻守恒量不变.在具体应用时,必须恰当地选取研究对象(系统),注意守恒定律成立的条件.该题可用机械能守恒定律来解决.选取两块板、弹簧和地球为系统,该系统在外界所施压力撤除后(取作状态1),直到B 板刚被提起(取作状态2),在这一过程中,系统不受外力作用,而内力中又只有保守力(重力和弹力)作功,支持力不作功,因此,满足机械能守恒的条件.只需取状态1 和状态2,运用机械能守恒定律列出方程,并结合这两状态下受力的平衡,便可将所需压力求出.解 选取如图(b)所示坐标,取原点O 处为重力势能和弹性势能零点.作各状态下物体的受力图.对A 板而言,当施以外力F 时,根据受力平衡有F 1 =P 1 +F (1)当外力撤除后,按分析中所选的系统,由机械能守恒定律可得式中y 1 、y 2 为M 、N 两点对原点O 的位移.因为F 1 =ky 1 ,F 2 =ky 2 及P 1 =m 1g ,上式可写为F 1 -F 2 =2P 1 (2)由式(1)、(2)可得20202k 0k 832121v v v m m m E E W -=-=-=mg μr πs F W 2180cos o f -==rgπμ16320v =2083v m 34k0==W En 2221212121mgy ky mgy ky +=-F=P1+F2(3) 当A板跳到N点时,B板刚被提起,此时弹性力F′2=P2 ,且F2=F′2.由式(3)可得F=P1+P2=(m1+m2 )g应注意,势能的零点位置是可以任意选取的.为计算方便起见,通常取弹簧原长时的弹性势能为零点,也同时为重力势能的零点.3 -24如图(a)所示,有一自动卸货矿车,满载时的质量为m′,从与水平成倾角α=30.0°斜面上的点A 由静止下滑.设斜面对车的阻力为车重的0.25 倍,矿车下滑距离l时,与缓冲弹簧一道沿斜面运动.当矿车使弹簧产生最大压缩形变时,矿车自动卸货,然后矿车借助弹簧的弹性力作用,使之返回原位置A 再装货.试问要完成这一过程,空载时与满载时车的质量之比应为多大?分析矿车在下滑和返回的全过程中受到重力、弹力、阻力和支持力作用.若取矿车、地球和弹簧为系统,支持力不作功,重力、弹力为保守力,而阻力为非保守力.矿车在下滑和上行两过程中,存在非保守力作功,系统不满足机械能守恒的条件,因此,可应用功能原理去求解.在确定重力势能、弹性势能时,应注意势能零点的选取,常常选取弹簧原长时的位置为重力势能、弹性势能共同的零点,这样做对解题比较方便.解取沿斜面向上为x轴正方向.弹簧被压缩到最大形变时弹簧上端为坐标原点O.矿车在下滑和上行的全过程中,按题意,摩擦力所作的功为Wf=(0.25mg+0.25m′g)(l+x) (1) 式中m′和m分别为矿车满载和空载时的质量,x为弹簧最大被压缩量.根据功能原理,在矿车运动的全过程中,摩擦力所作的功应等于系统机械能增量的负值,故有Wf=-ΔE=-(ΔE P+ΔEk)由于矿车返回原位时速度为零,故ΔEk=0;而ΔE P=(m -m′) g(l+x) sinα,故有Wf=-(m-m′) g(l+x) sinα (2) 由式(1)、(2)可解得。
大学物理课后答案详解

大学物理课后答案详解第一章:力学1.1 牛顿定律的三种形式第一种形式:惯性定律牛顿的第一定律,也被称为惯性定律。
它的表述为:一个物体如果没有外力作用,将保持静止或匀速直线运动的状态。
这意味着在没有外力作用时,物体的加速度为零,速度保持不变。
这个定律的重要性在于它说明了运动的惯性特性。
举个例子,当我们在车上紧急刹车时,我们的身体会有向前的惯性,因为车突然减速,而我们的身体仍保持原来的运动状态。
第二种形式:动量定律牛顿的第二定律,也被称为动量定律。
它的表述为:一个物体的加速度正比于作用在它上面的合外力,反比于物体的质量。
通过数学表达式可以得到 F = ma,其中 F表示物体所受合外力的大小,m表示物体的质量,a表示加速度。
这个定律说明了力是一种导致物体加速度变化的物理量。
第三种形式:作用与反作用定律牛顿的第三定律,也被称为作用与反作用定律。
它的表述为:如果物体A对物体B施加了一个力,那么物体B对物体A也会施加一个大小相等、方向相反的力。
这一个定律解释了为什么当我们敲击桌子时,手感到疼痛,因为我们的手会受到桌子的反作用力。
同样地,当我们踢足球时,脚球会受到我们脚的力的影响而向前踢出。
1.2 动力学动力学是力学的一个重要分支,它研究的是物体在受力作用下的运动规律。
其中最常见的运动学参数有位移、速度和加速度。
1.2.1 位移位移是一个矢量量,它表示物体从初始位置到最终位置的改变。
位移的大小等于物体在运动过程中实际移动的距离。
位移的方向由初始位置和最终位置的连线所决定。
1.2.2 速度速度是一个矢量量,它表示物体单位时间内移动的位移。
速度的大小等于单位时间内移动的位移,而速度的方向由位移的方向和时间的方向所决定。
1.2.3 加速度加速度是一个矢量量,它表示单位时间内速度的变化量。
加速度的大小等于单位时间内速度的改变量,而加速度的方向由速度的方向和时间的方向所决定。
1.3 弹力和重力1.3.1 弹力弹力是一种垂直于两个物体接触面的力,它是由于两个物体之间的接触而产生的。
大学物理学(清华C5版)分章配套精品题目及答案(第一章)
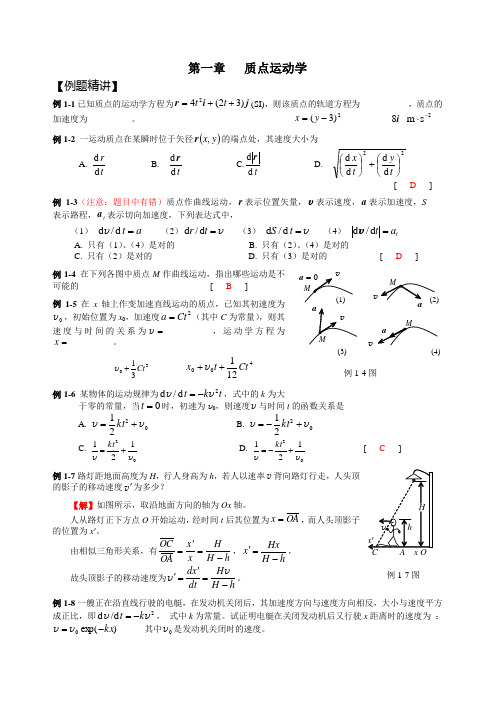
第一章 质点运动学【例题精讲】例1-1已知质点的运动学方程为j i r )32(42++=t t (SI),则该质点的轨道方程为___________,质点的加速度为__________。
2)3(-=y x 2s m 8-⋅ i例1-2 一运动质点在某瞬时位于矢径()y x ,r 的端点处,其速度大小为A.tr d d B.td d r C.td d r D.22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x [ D ] 例1-3(注意:题目中有错)质点作曲线运动,r 表示位置矢量,v 表示速度,a 表示加速度,S表示路程,t a 表示切向加速度,下列表达式中,(1) a t = d /d v (2)v =t r d /d (3) v =t S d /d (4) t a t =d /d v A. 只有(1)、(4)是对的 B. 只有(2)、(4)是对的C. 只有(2)是对的D. 只有(3)是对的 [ D ] 例1-4 在下列各图中质点M 作曲线运动,指出哪些运动是不可能的 [ B ] 例1-5在x 轴上作变加速直线运动的质点,已知其初速度为0v ,初始位置为x 0,加速度2Ct a =(其中C 为常量),则其速度与时间的关系为=v __________,运动学方程为=x __________。
3031Ct +v 400121Ct t x ++v例1-6 某物体的运动规律为t k t 2d /d v v -=,式中的k 为大于零的常量,当0=t 时,初速为v 0,则速度v 与时间t 的函数关系是A. 0221v v +=kt B. 0221v v +-=ktC. 02121v v +=kt D. 02121v v+-=kt [ C ]例1-7路灯距地面高度为H ,行人身高为h ,若人以速率v 背向路灯行走,人头顶的影子的移动速度v '为多少?【解】如图所示,取沿地面方向的轴为Ox 轴。
物理精讲精练答案

v
dv dt
2分
t = 0, v = 0.
1分
∫ (mg − kv - F)/m = ∫ d t
0 0
dv
t
v = ( mg − F )(1 − e )/k 2分 2、解:(1)以 A、B、绳为研究对象 F-mg-mA g-mB g=(m + mA + mB ) a F − ( m + m A + mB )g F a= ∴ = −g m + m A + mB m + m A + mB (2)以绳下段 x 长和物体 A 为研究对象 T(x)-(mA + m x / L )g =(mA + m x / L ) a ∴ T(x) = (mA+m x /L ) (g + a ) F (mA + mx / L) = = (96 + 24 x) N m + m A + mB
由于只有保守力做功,系统机械能守恒,即:
2分 2分
x
EK 0 +
1 2 1 1 kx0 + mg ( x − x 0 ) sin α = mv 2 + kx 2 2 2 2
2分
5
在平衡位置有: mgsinα =kx0 ∴ x0 = mg sin α k 代入上式整理得:
2分 2分
1 1 (mg sin α ) 2 mv 2 = E K 0 + mgx sin α − kx 2 − 2 2 2k
4、解:根据牛顿第二定律
k dv dv d x dv =m =m ⋅ = mv 2 dt d x dt dx x v A/ 4 k dx ∴ v d v = −k , ∫v dv = − ∫ dx 2 2 mx 0 A mx 1 2 k 4 1 3 v = ( − )= k 2 m A A mA ∴ v = 6k /(mA) K K 5、解:球 A 只受法向力 N 和重力 mg ,根据牛顿第二定律 2 法向: N − mg cosθ = mv / R ① 切向: mg sin θ = mat ② f =−
全新高考物理总复习专题精讲精练汇编(共55页 附答案)

全新高考物理总复习专题精讲精练汇编(共55页附答案)目录专题一:直线运动解题思路与方法专题二:处理平衡问题的几种方法专题三:应用牛顿第二定律的常用方法专题四:曲线运动问题的解法专题五:求解变力做功的方法专题六:机械能守恒在模型中的应用专题七:电学量的判断技巧专题八:电阻的测量方法专题九:测电源电动势和内阻的方法专题十:确定带电粒子在磁场中运动轨迹的方法专题十一:“杆+导轨”模型问题专题十二:交变电流的综合应用专题一:直线运动解题思路与方法解析 设初速度方向为正方向,根据匀变速直线运动规律v =v 0+at ,有-16=10-2t ,所以经过t =13 s 物体的速度大小为16 m/s.由x =v 0t +12at 2可知这段时间内的位移为x =(10×13-12×2×132)m =-39 m ,物体的运动分为两个阶段,第一阶段速度从10 m/s 减到0,此阶段位移大小为x 1=02-v 202a =02-102-2×2m =25 m ,第二阶段速度从0反向加速到16 m/s ,位移大小为x 2=v ′2-02-2a =162-022×2m =64 m ,则总路程为L=x 1+x 2=25 m +64 m =89 m. 答案 13 s 25 m 89 m5.极值法有些问题用一般的分析方法求解难度较大,甚至中学阶段暂时无法求出,我们可以把研究过程推向极端情况来加以分析,往往能很快得出结论.例5两个光滑斜面,高度和斜面的总长度相等,如图所示,两个相同的小球,同时由两个斜面顶端由静止开始释放,不计拐角处能量损失,则两球谁先到达底端?解析甲斜面上的小球滑到斜面底端的时间很容易求出.设斜面高度为h ,长度为L ,斜面的倾角为θ.则由L =12g 21sin θ、sin θ=h L ,解得t 1=2L2gh.乙斜面上的小球滑到斜面底端的时间很难直接计算.可将乙斜面作极端处理:先让小球竖直向下运动,然后再水平运动,易解得这种运动过程中小球运动的时间为t 2= 2h g+L -h 2gh =L +h2gh<t 1,所以,乙斜面上的小球先到达斜面底端. 答案 乙斜面上的小球先到达斜面底端6.图象法利用图象法可直观地反映物理规律,分析物理问题.图象法是物理研究中常用的一种重要方法.运动学中常用的图象为v -t 图象.在理解图象物理意义的基础上,用图象法分析解决有关问题(如往返运动、定性分析等)会显示出独特的优越性,解题既直观又方便.需要注意的是在v -t 图象中,图线和坐标轴围成的“面积”应该理解成物体在该段时间内发生的位移.例6汽车从甲地由静止出发,沿平直公路驶向乙地.汽车先以加速度a 1做匀加速直线运动,然后做匀速运动,最后以大小为a 2的加速度做匀减速直线运动,到乙地恰好停止.已知甲、乙两地的距离为x ,求汽车从甲地到乙地的最短时间t 和运行过程中的最大速度v m .解析 由题意作出汽车做匀速运动时间长短不同的v -t 图象,如图所示.不同的图线与横轴所围成的“面积”都等于甲、乙两地的距离x .由图象可知汽车做匀速运动的时间越长,从甲地到乙地所用的时间就越长,所以当汽车先做匀加速直线运动,后做匀减速直线运动,中间无匀速运动时,行驶的时间最短.设汽车做匀加速直线运动的时间为t 1,则匀减速直线运动的时间为(t -t 1).则有v m =a 1t 1=a 2(t -t 1),解得t 1=a 2t a 1+a 2,则v m =a 1a 2ta 1+a 2, 由图象中三角形面积的物理意义有x =12v m t =a 1a 2t 2a 1+a 2,解得t = 2xa 1+a 2a 1a 2,故v m =2xa 1a 2a 1+a 2.答案 t = 2x a 1+a 2a 1a 2 v m =2xa 1a 2a 1+a 27.相对运动法以系统中的一个物体为参考系研究另一个物体运动情况的方法.例7物体A 、B 从同一地点,同时沿同一方向运动,A 以10 m/s 的速度做匀速直线运动,B 以2 m/s 2的加速度从静止开始做匀加速直线运动,求A 、B 相遇前两物体间的最大距离.解析 因为本题求解的是A 、B 间的相对距离,所以可以利用相对运动法求解.选B 为参考系,从计时开始到A 、B 相遇前两物体间出现最大距离的过程中,A 相对于B 的初速度、末速度和加速度分别为:v 0=10 m/s ,v =0,a =-2 m/s 2, 根据v 2-v 20=2a Δx max ,有Δx max =v 2-v 202a,解得Δx max =25 m. 答案 25 m8.逆向思维法对于物体做匀减速直线运动的问题,可以当作逆向的匀加速直线运动处理.这样更符合思维习惯,容易理解.例8一物体以某一初速度在粗糙水平面上做匀减速直线运动,最后停下来,若此物体在最初5 s 内和最后5 s 经过的路程之比为11:5.则此物体一共运动了多长时间?解析 若依据匀变速直线运动规律列式,将会出现总时间t 比前后两个5 s 的和10 s 是大还是小的问题:若t >10 s ,可将时间分为前5 s 和后5 s 与中间的时间t 2,经复杂运算得t 2=-2 s ,再得出t =8 s 的结论.若用逆向的初速度为零的匀加速直线运动处理,将会简便得多.视为反向的初速度为零的匀加速直线运动,则最后5 s 内通过的路程为x 2=12a ×52=12.5a ,最初5 s 内通过的路程为x 1=12at 2-12a (t -5)2=12a (10t -25),由题中已知的条件:x 1:x 2=11:5,得(10t -25) :25=11:5, 解得物体运动的总时间t =8 s. 答案 8 s9.比值法对初速度为零的匀加速直线运动,利用匀变速直线运动的基本公式可推出以下几个结论: (1)连续相等时间末的瞬时速度之比为:v 1:v 2:v 3:…:v n =1:2:3:…:n(2)t 、2t 、3t 、…、nt 内的位移之比为:x 1t :x 2t :x 3t :…:x nt =12:22:32:…:n 2(3)连续相等时间内的位移之比为:x 1:x 2:x 3:…:x n =1:3:5:…: (2n -1)(4)连续相等位移所用的时间之比为:t 1:t 2:t 3:…:t n =1: (2-1) : (3-2):…: (n -n -1)在处理初速度为零的匀加速直线运动时,首先考虑用以上的几个比值关系求解,可以省去很多繁琐的推导及运算.例9一个物体从塔顶做自由落体运动,在到达地面前最后1 s 内发生的位移是总位移的7/16,求塔高.(取g =10 m/s 2)解析 由初速度为零的匀加速直线运动规律推论知,第1 s 内、第2 s 内、第3 s 内、第4 s 内的位移之比为1:3:5:7,第4 s 运动的位移与总位移的比值为7/16,故物体下落的总时间t 总=4 s ,塔高h =12gt 2总=80 m.答案 80专题二:处理平衡问题的几种方法1.合成、分解法利用力的合成与分解能解决三力平衡的问题,具体求解时有两种思路:一是将某力沿另两个力的反方向进行分解,将三力转化为四力,构成两对平衡力.二是某二力进行合成,将三力转化为二力,构成一对平衡力.例1如图甲所示,质量为m 的重球,由细绳悬挂放在斜面上,斜面光滑,倾角θ=30°,细绳与竖直方向夹角也为30°,求细绳受到的拉力及斜面受到的压力.解析 对重球受力分析,如图乙所示,重球在斜面对球的支持力N 、细绳的拉力T 、重力mg 的作用下处于平衡状态,由平衡条件可得,支持力N 与拉力T 的合力与重力mg 构成平衡力,由几何关系可得N =T =mg2cos θ=3mg /3,由牛顿第三定律可得,重球对斜面的压力为N ′=3mg /3,方向垂直于斜面向下.细绳受到的拉力为T′=3mg/3,方向沿绳斜向下.2.相似三角形法“相似三角形”的主要性质是对应边成比例,对应角相等.在物理中,一般当涉及矢量运算,又构建了三角形时,若矢量三角形与图中的某几何三角形为相似三角形,则可用相似三角形法解题.例2如图甲所示,两球A、B用劲度系数为k1的轻弹簧相连,球B用长为l的细绳悬于O点,球A固定在O点正下方,且OA之间的距离恰为l,系统平衡时绳子所受的拉力为F1.现把A、B间的弹簧换成劲度系数为k2的轻弹簧,仍使系统平衡,此时绳子所受的拉力为F2,则F1与F2的大小之间的关系为( )A.F1>F2B.F1=F2C.F1<F2D.无法确定解析如图乙所示,分析B球的受力情况,B球受到重力、弹簧的弹力和绳的拉力,△OAB 与△BDE相似,由于OA=OB,则绳的拉力等于B球的重力,所以F1=F2=mg.答案 B3.图解法此方法适用于一个物体受到三个力(或可等效为三个力)而平衡的问题,特别是物体的动态平衡问题或平衡中的临界、极值问题.例3如图甲所示,光滑的小球静止在斜面和竖直放置的木板之间,已知球重为G,斜面的倾角为θ,现使木板沿逆时针方向绕O点缓慢移动,问小球对斜面和挡板的压力怎样变化?解析小球的受力如图乙所示,小球受重力、斜面的支持力和挡板的支持力,在这三个力的作用下处于平衡状态,这三个力可构成力的三角形.挡板绕O点缓慢移动,可视为动态平衡.因挡板对小球的支持力F N2的方向与水平方向之间的夹角由90°缓慢减小,重力的大小和方向都不变,斜面对小球的支持力F N1的方向也不变,由矢量三角形知,F N1必将变小,F N2将先变小后变大.4.正交分解法将各力分解到x轴和y轴上,运用两坐标轴上的合力等于零(∑F x=0,∑F y=0)的条件解题,多用于三个以上共点力作用下的物体的平衡问题.值得注意的是,x、y方向选择的原则:(1)在平衡状态下,少分解力或将容易分解的力分解.(2)在非平衡状态下,通常沿加速度方向和垂直加速度方向进行分解.(3)尽量不要分解未知力.例4如图所示,斜劈A静止放置在水平地面上.质量为m的物体B在外力F1和F2的共同作用下沿斜劈表面向下运动.当F1方向水平向右,F2方向沿斜劈的表面向下时斜劈受到地面的摩擦力方向向左.则下列说法中正确的是( )A.若同时撤去F1和F2,物体B的加速度方向一定沿斜面向下B.若只撤去F1,在物体B仍向下运动的过程中,A所受地面摩擦力方向可能向右C.若只撤去F2,在物体B仍向下运动的过程中,A所受地面摩擦力方向可能向右D.若只撤去F2,在物体B仍向下运动的过程中,A所受地面摩擦力不变解析对物体B和斜劈A分别受力分析如图(a)、(b)所示,由于水平方向受力平衡,且斜劈受到地面的摩擦力方向向左,对斜劈分析有N B sinθ>f′B cosθ,f′B=f B=μN B,即μ<tanθ,所以当同时撤去外力F1、F2时,mg sinθ>μmg cosθ,物体B的加速度方向一定沿斜面向下,A正确;若只撤去F1,N″B=mg cosθ,f″B=μmg cosθ<mg sinθ,则N″B sinθ>f″B cosθ,A所受地面摩擦力方向仍向左,B错;若只撤去F2,A所受地面摩擦力方向向左不变,C错D对.答案AD规律总结(1)物体或系统受四个或四个以上作用力时,一般采用正交分解法求解.(2)当物体或系统受力发生变化,在比较变化前、后的受力或运动情况时,要分清不变力和变化力,抓住变化力或者变化力的某方向上的分量进行比较,可以简化运算过程;如上题中,要求讨论斜劈A所受地面摩擦力的变化,只要抓住斜劈A所受变化力中的水平分力进行比较,就能较快地得出结论.(3)要善于转换研究对象.选择研究对象时优先整体也是相对的,当整体法有困难时一定记得要选择恰当的隔离体作研究对象.5.正弦定理法三力平衡时,三力的合力为0,三个力可构成一封闭三角形,若由题设条件寻找到角度关系,则可用正弦定理列式求解.例5一盏电灯重力为G,悬于天花板上A点,在电线O处系一细线OB,使电线OA与竖直方向的夹角为β=30°,如图甲所示.现保持β角不变,缓慢调整OB方向至OB线上拉力最小为止,此时OB与水平方向的夹角α等于多少?最小拉力是多少?解析对电灯受力分析如图乙所示,据三力平衡特点可知:OA、OB 对O点的作用力T A、T B的合力T与G等大反向,即T=G①在△OT B T中,∠TOT B=90°-α,又∠OTT B=∠TOA=β,故∠OT B T=180°-(90°-α)-β=90°+α-β,由正弦定理得T B sin β=T+α-β②联立解得T B =G sin βα-β,因β不变,故当α=β=30°时,T B 最小,且T B =G sin β=G /26.整体法和隔离法选择研究对象是解决物理问题的首要环节.若一个系统中涉及两个或者两个以上物体的平衡问题,在选取研究对象时,要灵活运用整体法和隔离法.对于多物体问题,如果不求物体间的相互作用力,我们优先采用整体法,这样涉及的研究对象少,未知量少,方程少,求解简便;很多情况下,通常采用整体法和隔离法相结合的方法.例6如图所示,顶端装有定滑轮的斜面体放在粗糙水平面上,A 、B 两物体通过细绳相连,并处于静止状态(不计绳的质量和绳与滑轮间的摩擦).现用水平向右的力F 作用于物体B 上,将物体B 缓慢拉高一定的距离,此过程中斜面体与物体A 仍然保持静止.在此过程中( ) A .水平力F 一定变小B .斜面体所受地面的支持力一定变大C .物体A 所受斜面体的摩擦力一定变大D .地面对斜面体的摩擦力一定变大解析 隔离物体B 为研究对象,分析其受力情况如图所示.则有F =mg tan θ,T =mgcos θ,在物体B 缓慢拉高的过程中,θ增大,则水平力F 随之变大,对A 、B 两物体与斜面体这个整体而言,由于斜面体与物体A 仍然保持静止,则地面对斜面体的摩擦力一定变大,但是因为整体竖直方向并没有其他力,故斜面体所受地面的支持力不变;在这个过程中尽管绳子张力变大,但是由于物体A 所受斜面体的摩擦力开始并不知道其方向,故物体A 所受斜面体的摩擦力的情况无法确定,所以答案为D.7.平衡问题中极值的求法极值是指研究平衡问题中某物理量变化时出现的最大值或最小值.中学物理的极值问题可分为简单极值问题和条件极值问题,区分的依据是是否受附加条件制约.若受附加条件制约,则为条件极值.例7如图所示,物体放在水平面上,与水平面间的动摩擦因数为μ,现施一与水平面成α角且斜向下的力F推物体,问:α至少为多大时,F无论多大均不能推动物体(设最大静摩擦力等于滑动摩擦力)?解析设物体的质量为m,静摩擦力为F,现取注意到题中“无论F多大……”,可设想:当F→∞时,必有右边分式的分母→0.专题三:应用牛顿第二定律的常用方法1.应用牛顿第二定律的常用方法——合成法、分解法(一)合成法合成法需要首先确定研究对象,画出受力分析图,将各个力按照力的平行四边形定则在加速度方向上合成,直接求出合力,再根据牛顿第二定律列式求解,此方法被称为合成法,具有直观简便的特点.(二)分解法分解法需确定研究对象,画出受力分析图,根据力的实际作用效果,将某一个力分解成两个分力,然后根据牛顿第二定律列式求解,此方法被称为分解法.分解法是应用牛顿第二定律解题的常用方法,但此法要求对力的作用效果有着清楚的认识,要按照力的实际效果进行分解.例1如图所示,沿水平方向做匀变速直线运动的车厢中,悬挂小球的悬线偏离竖直方向37°角,球和车厢相对静止,球的质量为m =1 kg.(g =10 m/s 2,sin37°=0.6,cos37°=0.8)求:(1)车厢运动的加速度并说明车厢的运动情况; (2)悬线对球的拉力.解析 球和车厢相对静止,它们的运动情况相同,由于对球的受力情况知道的较多,故应以球为研究对象.通过对小球受力分析,可以确定小球的加速度,即车厢的加速度不确定,但车厢的运动情况还与初速度方向有关,因此车厢的运动性质具有不确定性.深入细致的审题是防止漏解和错解的基础.(1)解法一:合成法以球为研究对象,受力如图甲所示.球受两个力作用,重力mg 和线的拉力F T ,由球随车一起沿水平方向做匀变速直线运动,故其加速度沿水平方向,合外力沿水平方向.做出mg 和F T 合成的平行四边形如图甲所示,由数学知识得球所受的合力为F 合=mg tan37°. 由牛顿第二定律F 合=ma 得球的加速度为a =F 合m=g tan37°=7.5 m/s 2,方向水平向右.故车厢可能向右做匀加速直线运动,也可能向左做匀减速直线运动.解法二:分解法以球为研究对象,画出受力图,如图乙所示.绳的拉力在竖直方向和水平方向上分别产生两个效果,一是其竖直分力F 1和小球的重力平衡,二是其水平分力F 2使小球产生向右的加速度,故F T cos37°=mg ,F T sin37°=ma ,解得a =g tan37°=7.5 m/s 2,故车厢可能向右做匀加速直线运动,也可能向左做匀减速直线运动.(2)由受力图可得,线对球的拉力大小为F T =mgcos37°=12.5 N.答案 (1)见解析 (2)12.5 N2.正交分解法正交分解法需确定研究对象,画出受力分析图,建立直角坐标系,将相关作用力投影到相互垂直的两个坐标轴上,然后在两个坐标轴上分别求合力,再根据牛顿第二定律列式求解,此方法被称为正交分解法.直角坐标系的选取,原则上是任意的,但坐标系建立的不合适,会给解题带来很大的麻烦,如何快速准确地建立坐标系,要依据题目的具体情境而定,正交分解的最终目的是为了合成.当物体受到两个以上的力作用而产生加速度时,通常采用正交分解法解题.为减少矢量的分解,建立坐标系时,确定x 轴的正方向常有以下两种选择.(1)分解力而不分解加速度分解力而不分解加速度,通常以加速度a 的方向为x 轴的正方向,建立直角坐标系,将物体所受的各个力分解在x 轴和y 轴上,分别求得x 轴和y 轴上的合力F x 和F y .根据力的独立作用原理,各个方向上的力分别产生各自的加速度,得F x =ma ,F y =0.例2如图所示,小车在水平面上以加速度a 向左做匀加速直线运动,车厢内用OA 、OB 两根细绳系住一个质量为m 的物体,OA 与竖直方向的夹角为θ,OB 是水平的.求OA 、OB 两绳的拉力F T 1和F T 2的大小.解析 m 的受力情况及直角坐标系的建立如图所示(这样建立只需分解一个力),注意到a y =0,则有F T 1sin θ-F T 2=ma , F T 1cos θ-mg =0,解得F T 1=mgcos θ,F T 2=mg tan θ-ma .答案F T1=mgcosθF T2=mg tanθ-ma(2)分解加速度而不分解力物体受几个互相垂直的力的作用,应用牛顿运动定律求解时,若分解的力太多,则比较繁琐,所以在建立直角坐标系时,可根据物体的受力情况,使尽可能多的力位于两坐标轴上而分解加速度a,得a x和a y,根据牛顿第二定律得F x=ma x,F y=ma y,再求解.这种方法一般是以某个力的方向为x轴正方向时,其他的力都落在或大多数落在两个坐标轴上而不需要再分解的情况下应用.例3如图所示,倾角为θ的光滑斜面固定在水平地面上,质量为m的物块A叠放在物体B 上,物体B的上表面水平.当A随B一起沿斜面下滑时,A、B保持相对静止.求B对A的支持力和摩擦力.解析当A随B一起沿斜面下滑时,物体A受到竖直向下的重力mg、B对A竖直向上的支持力F N和水平向左的摩擦力F f的作用而随B一起做加速运动.设B的质量为M,以A、B为整体,根据牛顿第二定律有(m+M)g sinθ=(m+M)a,得a=g sinθ.将加速度沿水平方向和竖直方向进行分解,如图所示.则a x=a cosθ=g sinθcosθ,a y=a sinθ=g sin2θ,所以F f=ma x=mg sinθcosθ,由mg-F N=ma y=mg sin2θ,得F N=mg cos2θ.答案mg sinθcosθmg cos2θ3.整体法和分隔法如果系统是由几个物体组成,它们有相同的加速度,在求它们之间的作用力时,往往是先用整体法求它们的共同加速度,再用分隔法求它们之间的作用力.例4如图所示,质量为2m 的物体A 与水平地面间的摩擦可忽略不计,质量为m 的物体B 与地面间的动摩擦因数为μ,在水平推力F 的作用下,A 、B 做匀加速直线运动,则A 对B 的作用力为多大?解析 以A 、B 整体为研究对象进行受力分析,受重力G 、支持力F N 、水平向右的推力F 、水平向左的摩擦力F f (F f =μmg ).设加速度为a ,根据牛顿第二定律得F -F f =3ma .以B 为研究对象进行受力分析,受重力G B 、支持力F N B 、A 对B 水平向右的作用力F AB 、水平向左的摩擦力F fB (F fB =μmg ).根据牛顿第二定律得F AB -F fB =ma . 联立以上各式得F AB =F +2μmg3.答案 F +2μmg34.极限分析法在处理临界问题时,一般用极限法,特别是当某些题目的条件比较隐蔽、物理过程又比较复杂时.例5如图所示,质量为M 的木板上放着一质量为m 的木块,木块与木板间的动摩擦因数为μ1,木板与水平地面间的动摩擦因数为μ2.若要将木板从木块下抽出,则加在木板上的力F 至少为多大?解析 木板与木块通过摩擦力联系,只要当两者发生相对滑动时,才有可能将木板从木块下抽出.此时对应的临界状态是:木板与木块间的摩擦力必定是最大静摩擦力F f m (F f m =μ1mg ),且木块运动的加速度必定是两者共同运动时的最大加速度a m.以木块为研究对象,根据牛顿第二定律得F f m=ma m.①a m也就是系统在此临界状态下的加速度,设此时作用在木板上的力为F0,取木板、木块整体为研究对象,则有F0-μ2(M+m)g=(M+m)a m.②联立①、②式得F0=(M+m)(μ1+μ2)g.当F>F0时,必能将木板抽出,即F>(M+m)(μ1+μ2)g 时,能将木板从木块下抽出.答案F>(M+m)(μ1+μ2)g5.假设法假设法是解物理问题的一种重要方法.用假设法解题,一般依题意从某一假设入手,然后用物理规律得出结果,再进行适当的讨论,从而得出正确答案.例6如图所示,火车车厢中有一个倾角为30°的斜面,当火车以10 m/s2的加速度沿水平方向向左运动时,斜面上质量为m的物体A保持与车厢相对静止,求物体所受到的静摩擦力.(取g =10 m/s2)解析物体受三个力作用:重力mg、支持力F N和静摩擦力F f,因静摩擦力的方向难以确定,且静摩擦力的方向一定与斜面平行,所以假设静摩擦力的方向沿斜面向上.根据牛顿第二定律,在水平方向上有F N sin30°-F f cos30°=ma.①在竖直方向上有F N cos30°+F f sin30°=mg.②由①、②式得F f=-5(3-1)m,负号说明摩擦力F f的方向与假设的方向相反,即沿斜面向下.答案-5(3-1)m6.传送带类问题的分析方法例7如图所示,传送带与地面倾角θ=37°,从A到B长度为16 m,传送带以10 m/s的速率逆时针转动.在传送带上端A处无初速度地放一个质量为0.5 kg的物体,它与传送带之间的动摩擦因数为0.5.求物体从A 运动到B 所需要时间是多少?(sin37°=0.6,cos37°=0.8,g =10 m/s 2)分析传送带逆时针转动,在物体加速到速度等于传送带速度之前,物体受到沿斜面方向向下的摩擦力,这一动力学条件是在审题过程中容易发现的,当物体的速度达到传送带速度之后,物体受到的摩擦力会发生怎样的变化呢?这是审题过程中要注意研究的问题.解析 物体放在传送带上后,开始的阶段,由于传送带的速度大于物体的速度,物体所受的摩擦力沿传送带向下,受力如图甲所示,物体由静止加速,由牛顿第二定律得mg sin θ+μmg cos θ=ma 1解得a 1=10 m/s 2物体加速至与传送带相同的速度需要的时间为t 1=v a 1=1010s =1 s物体加速到与传送带相同的速度经过的位移为s =12a 1t 21=5 m由于μ<tan θ(μ=0.5,tan θ=0.75),物体在重力作用下将继续加速运动,当物体速度大于传送带的速度时,物体受到沿传送带向上的摩擦力,受力如 图乙所示由牛顿第二定律得mg sin θ-μmg cos θ=ma 2 解得a 2=2 m/s 2设后一阶段物体滑至底端所用的时间为t 2, 由L -s =vt 2+12a 2t 22解得t 2=1 s(t 2=-11 s 舍去)所以,物体从A 运动到B 所用时间t =t 1+t 2=2 s. 答案 2 s规律总结传送带类问题的求解思路和技巧解决传送带类问题的关键是找准临界情况,即物体与传送带速度相等时,此时物体受到的摩擦力会发生突变,有时是摩擦力的大小发生突变(传送带水平放置),有时是摩擦力的方向发生突变(传送带倾斜放置,如例7),然后正确运用运动学知识即可顺利求解.专题四:曲线运动问题的解法1.分解法应用平行四边形定则(或三角形定则),将矢量进行分解(如合速度分解为分速度)的方法. 例1 如图所示,一辆汽车沿水平地面匀速行驶,通过跨过定滑轮的轻绳将一物体A 竖直向上提起,在此过程中,物体A 的运动情况是( )A .加速上升,且加速度不断增大B .加速上升,且加速度不断减小C .减速上升,且加速度不断减小D .匀速上升解析 物体A 的速率即为左段绳子上移的速率,而左段绳子上移的速率与右段绳子在沿绳方向的分速率是相等的.右段绳子实际上同时参与两个运动:沿绳方向拉长及绕定滑轮逆时针转动.将右段绳子与汽车相连的端点的运动速度v 沿绳子方向和沿与绳子垂直的方向分解,如图所示,则沿绳方向的速率即为物体A 的速率v A =v 1=v sin θ,随着汽车的运动,θ增大,v A 增大,故物体A 应加速上升.θ角在0°~90°范围内增大,由正弦曲线形状可知v A 的变化率减小,故。
大学物理学(清华C5版)分章配套精品题目及答案(第四章)

第四章 功和能【例题精讲】例4-1 一个质点同时在几个力作用下的位移为:k j i r 654+-=∆ (SI),其中一个力为恒力k j i F 953+--= (SI),则此力在该位移过程中所作的功为A. -67 JB. 17 JC. 67 JD. 91 J [ C ] 例4-2 质量为m 的汽车,在水平面上沿x 轴正方向运动,初始位置x 0=0,从静止开始加速,在其发动机的功率P 维持不变、且不计阻力的条件下,证明:在时刻t 其速度表达式为:m Pt /2=v 。
【证明】 由P =Fv 及F =ma ,P =mav 代入 t a d d v =P =tm d d v v 由此得 P d t =mv d v ,两边积分, 则有⎰⎰=ttm t P 0d d v v∴ 221v m Pt = ∴ m Pt /2=v例4-3 质量m =1 kg 的物体,在坐标原点处从静止出发在水平面内沿x 轴运动,其所受合力方向与运动方向相同,合力大小为F =3+2x (SI),那么,物体在开始运动的3 m 内,合力所作的功W = ;且x =3 m 时,其速率v = 。
18 J 6 m/s例4-4 一质量为m 的质点在Oxy 平面上运动,其位置矢量为j i r t b t a ωωsin cos +=(SI)式中a 、b 、是正值常量,且a >b 。
(1) 求质点在A 点(a ,0)时和B 点(0,b )时的动能;(2 )求质点所受的合外力F 以及当质点从A 点运动到B 点的过程中F 的分力x F 作的功。
解: (1) 位矢j i r t b t a ωωsin cos += (SI)t a x ωcos = t b y ωsin =t a t xx ωωsin d d -==v ,t b ty ωωcos d dy -==v在A 点(a ,0) ,1cos =t ω,0sin =t ω E KA =2222212121ωmb m m y x =+v v在B 点(0,b ) ,0cos =t ω,1sin =t ω E KB =2222212121ωma m m y x =+v v(2) j i F y x ma ma +==j i t mb t ma ωωωωsin cos 22--由A →B ⎰⎰-==2d cos d aax x x t a m x F W ωω=⎰=-022221d ama x x m ωω 例4-5 已知地球的半径为R ,质量为M ,现有一质量为m 的物体,在离地面高度为2R 处。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例15-3矫顽力较小,磁滞损耗小;适宜于制造变压器、电磁铁和电机中的铁心
例15-4铁磁质;顺磁质;抗磁质
例15-5矫顽力小;容易退磁
练习题答案:
15-1(A)
15-2(D)
15-3(B)
15-4(C)
15-5答:不能。因为它并不是真正在磁介质表面流动的传导电流,而是由分子电流叠加而成,只是在产生磁场这一点上与传导电流相似。
例16-20(A)
练习题答案:
16-1 2×10-1A= 0.987 A
解:n=1000(匝/m)
=2×10-1sin 100t(SI)
2×10-1A=0.987 A
16-2
方向:当d(t) /dt>0时,i与选定的正方向相反.
当d(t) /dt<0时,i与选定的正方向相同.
解:取半径为r,宽度为dr 的带电圆环,产生的电流 ,
在圆形导体外,与导体中心轴线相距r处的磁感强度大小为
因而,穿过导体外画斜线部分平面的磁通2为
穿过整个矩形平面的磁通量
14-11 的方向垂直x轴及图面向里
解:由磁场的磁感应强度叠加,知 ,
方向垂直x轴及图面向里
14-12答:安培环路定理只适用于闭合电流,有限长载流直导线不闭合,故环路定律不适用.
14-13
在圆心处产生的磁场磁感应强度 ,
整个圆环在圆心处产生的 ,
则小导体环里通过的磁通量 ,
导体环中的感应电流 。
方向:当d(t) /dt>0时,i与选定的正方向相反.
当d(t) /dt<0时,i与选定的正方向相同.
16-3 ;线圈中的感应电流是顺时针方向.
解:(1) 载流为I的无限长直导线在与其相距为r处产生的磁感强度为:
(2)m= ;
(3) 0。
例 14-80I1;0(I1+I2); 0.
例14-9(D)
例14-10(C)
例14-11(B)
例14-12
【解】 导体内的电流密度
由于电流和磁场分布的对称性,磁感线是以轴为中心的一些同心圆,去半径为r的一条磁感线为环路,有安培环路定理:
有
例14-13 ;
若 ,则 的方向向下;若 ,则 的方向向上
解:(1) 取半径r的闭合回路,逆时针为正方向,由安培环路定理:
;
(2) 取半径r的闭合回路,逆时针为正方向,由安培环路定理:
;
(2) 取半径r的闭合回路,逆时针为正方向,由安培环路定理:
14-10
解:在圆柱体内部与导体中心轴线相距为r处的磁感强度的大小,由安培环路定
律可得:
因而,穿过导体内画斜线部分平面的磁通1为
例16-8(D)
例16-9(D)
例16-10 =3.68mV;方向:沿adcb绕向.
【解】大小:
=3.68mV
方向:沿adcb绕向。
例16-11(A)
例16-12(C)
例16-13(D)
例16-140.400H
例16-15(D)
例16-16(C)
例16-17(D)
例16-18(C)
例16-19(C)
∴
,
∴ ,
在无限大平面上沿z轴方向上取长dl,沿x轴方向取宽da,则其面积为
dS= dlda,面元所受的安培力为:
单位面积所受的力
例14-17(D)
例14-18(A)
例14-19(1)Mm=9.40×10-4N·m;
(2)= 15°
【解】 (1) ,方向垂直于线圈平面。
= 9.40×10-4N·m
(2) 设线圈绕AD边转动,并且线圈稳定时,线圈平面与竖直平面夹角为 ,则磁场对线圈的力矩为
【解】 载流导线MN上任一点处的磁感强度大小为:
MN上电流元I3dx所受磁力:
若 ,则 的方向向下, ,则 的方向向上。
例14-14(A)
例14-15
【解】如图示位置,线圈所受安培力的合力为
方向向右,从x=a到x=2a磁场所作的功为
例14-16(1) , ;
(2) ;
(3)
【解】设i为载流平面的面电流密度, 为无限大载流平面产生的磁场, 为均匀磁场的磁感强度,作安培环路abcda,由安培环路定理得:
重力矩:
于是
例14-200.80×10-13 (N)
例14-21(B)
例14-22(C)
例14-23(D)
练习题答案:
14-1
解:通电圆环中心处磁感应强度 ,
由题意, ,所以有 ,即
14-2
解:电流在O点产生的磁场相当于CA+AD一段导线上电流产生的磁场,
∴
14-3(1) , (2)0
14-4
解: ,方向垂直纸面向里;
解:(1)运动带电质点在O点产生的磁场的磁感应强度B的大小:
,带入数值,得 ;
(2)带电质点产生的磁矩大小 , ,
所以 ,带入数值,得 7.20×10-7A·m2
14-16
解:运动电荷在磁场中运动的轨迹半径 ,
入射点和出射点之间距离为 。
第十五章磁介质
例题答案:
例15-1I/ (2r);I/ (2r)
t1→t2时间内通过的电荷为
∴ T
例16-4(1) (2)
【解】
(1)
(2)
例16-5(D)
例16-6(B)
例16-7 ; 方向:ACBA(即顺时针)
【解】建立坐标系,长直导线为y轴,BC边为x轴,原点在长直导线上,则斜边的方程为 ,式中r是t时刻B点与长直导线的距离。
三角形中磁通量
当r=d时,
方向:ACBA(即顺时针)
证明:长直导线内任意一点磁场的磁感应强度 ,
对应该点处的磁场能量密度 ,
单位长度导线所储存的磁能为:
第十七章 电磁波
例题答案:
例17-1(C)
例17-2垂直;横:相同;同时
例17-3
练习题答案:
17-1证明略
17-2
17-3能流密度矢量,其大小表示单位时间内流过与能量传输方向垂直的单位横截面积的能量,其方向为能量的传输方向;
第十四章稳恒磁场
例题答案:
例14-1
例14-2(C).
例14-30i;沿轴线方向朝右
例14-4(D)
例14-5(D)
例14-6B=1.8×10-4T;=225°,为 与x轴正向的夹角
【解】 取dl段,其中电流为
在P点
选坐标如图
,
1.8×10-4T
方向 , ,为 与x轴正向的夹角。
例14-7(1) a._0__b. c. ;
,方向垂直纸面向外;
,
所以
Hale Waihona Puke 14-5解:取宽为 的长直导线,其上通有电流 ,在P点处产生磁感应强度为
,
则
14-6R=2r
解:在圆盘上取宽度为 的圆环,其上带电量 ,
电流 , ,
, ,
,所以R=2r
14-7×10-3T
解:长直螺线管内部磁感应强度:
14-8 ; 0 ;
14-9(1) ;
(2) ;
(3) 0
D端电势高
16-7 ;当 >0时,电动势沿顺时针方向.
解:取回路正向顺时针,则
当 >0时,电动势沿顺时针方向.
16-8证明
证:取长直导线之一的轴线上一点作坐标原点,设电流为I,则在两长直导线的平面上两线之间的区域中B的分布为
穿过单位长的一对导线所围面积(如图中阴影所示)的磁通为
16-9
解:
∴ A
16-10
解:d= , , ,
所有电流元受力方向相同,积分可得电流I2受磁力大小
F= = = ,
则有Fy=Fcos= ,FX=Fsin=F = 。
14-14 ;在图面中向上
解:根据线圈在磁场中受到的磁力矩:
,线圈磁矩为 ,则带电圆环旋转时产生电流 , ,
所以磁力矩大小 ,方向在图面中竖直向上。
14-15(1)6.67×10-7T(2)7.20×10-7A·m2
∴
的方向沿着杆指向上端.
16-5
解: 间的动生电动势:
b点电势高于O点.
间的动生电动势:
a点电势高于O点.
∴
16-6 ; D端电势高
解:以C点为坐标原点,沿CD方向建立x轴正方向,取距离C点x位置处,长度为dx的杆,两导线在该位置处产生的磁场的磁感应强度:
,方向垂直纸面向外,
产生的感应电动势: ,
CD杆上产生的感应电动势:
以顺时针绕向为线圈回路的正方向,与线圈相距较远的导线在线圈中产生的磁通量为:
与线圈相距较近的导线对线圈的磁通量为:
总磁通量
感应电动势为:
由 >0和回路正方向为顺时针,所以的绕向为顺时针方向,线圈中的感应电流
亦是顺时针方向.
16-4 ; 的方向沿着杆指向上端
解:在距O点为l处的dl线元中的动生电动势为
第十六章变化的电磁场
例题答案:
例16-1(A)
例16-2(C)
例16-3 T
【解】设在时间t1→t2中线圈法线从平行于磁场的位置转到垂直于磁场的位置,则在t1时刻线圈中的总磁通为 (S为线圈的面积),在t2时刻线圈的总磁通为零,于是在t1→t2时间内总磁通变化为
令t时刻线圈中的感应电动势为 ,则电流计中通过的感应电流为
