多边形膨胀算法
凸多边形的面积

凸多边形的面积
凸多边形的面积是一个重要的数学问题,也是实际应用中常见的计算
题目。
在几何学中,凸多边形是指所有内角都小于180度的多边形。
相比于一般的多边形,凸多边形的面积计算相对简单,有多种方法可
以用来求解。
1. 分割法:
将凸多边形分割成若干三角形,然后分别计算每个三角形的面积,最
后将这些三角形的面积加起来,就可以得到凸多边形的面积。
这种方
法比较直观,可以用来解决一些简单的问题,但对于复杂的凸多边形
不太适用。
2. 矩阵法:
将凸多边形的顶点坐标按顺序排列成一个矩阵,再对这个矩阵做数学
运算,就能得到凸多边形的面积。
这种方法比起分割法更加普适,可
以用来解决复杂的凸多边形面积问题。
不过需要进行一些繁琐的计算。
3. 海龙公式:
海龙公式是求解任意三角形面积的公式,也可以用来计算凸多边形的面积。
首先我们需要将凸多边形分割成若干个三角形,然后对每个三角形分别运用海龙公式求解面积,最后将这些三角形的面积加起来就是凸多边形的面积了。
4. 叉积法:
叉积法是一种基于向量的方法,对于二维空间中的凸多边形,可以运用叉积法求解它的面积。
假设凸多边形的顶点依次为a1,a2,a3,…,an,那么我们可以选择其中一个顶点作为起点,分别计算这个顶点与相邻顶点所形成的向量的叉积,然后将这些叉积结果相加,最后将和的绝对值除以2,就是凸多边形的面积了。
综上所述,凸多边形的面积可以采用多种方法求解,选择哪种方法主要取决于凸多边形的形状复杂程度以及计算要求的准确度。
在实际应用中,我们可以根据具体情况选用适当的计算方法,以便更好地解决凸多边形的面积问题。
凸包面积和周长的计算

凸包面积和周长的计算凸包是在平面上给定的一组点中构成的最小凸多边形。
凸包的面积和周长是计算凸包重要的指标,可以用来分析数据分布的紧密程度和形状特征。
本文将介绍凸包的定义和生成算法,并详细说明如何计算凸包的面积和周长。
一、凸包的定义凸包是指在平面上给定的一组点中,由这些点构成的最小凸多边形。
凸多边形的特点是:任意两点之间的线段都在多边形内部。
凸包是凸多边形中的最小面积的凸多边形,即是在所有凸多边形中,面积最小的凸多边形。
二、凸包的生成算法1. Jarvis算法(也叫作包裹算法或者旋转卡壳算法):该算法基于以下思想:从一组点中找到一个起始点,将其作为凸包的一个顶点。
然后,从这个点开始,寻找下一个能保证凸包深度最大的点,并将其加入凸包。
不断重复这个过程,直到回到起始点为止。
该算法的时间复杂度为O(nh),其中n是点的个数,h是凸包的顶点数。
2.快速凸包算法:该算法基于Graham扫描算法改进而来。
首先选择一个y坐标最小的点,将其他点按照与这个点的连线的极角进行排序。
然后依次处理排序后的点,对每个点进行判断,如果点在逆时针方向上,则加入凸包,否则舍弃。
最后得到凸包。
该算法的时间复杂度为O(nlogn),是一种高效的凸包生成算法。
三、凸包面积的计算凸包的面积可以用以下公式进行计算:S = (x1y2 + x2y3 + ... + xn-1yn + xny1 - x2y1 - x3y2 - ... - xnyn-1 - x1yn) / 2其中,(x1, y1), (x2, y2), ..., (xn, yn)是凸包的顶点的坐标。
计算凸包的面积可以通过以上公式进行求解,公式中的坐标是有顺序的,要按照逆时针或者顺时针的方向依次输入。
四、凸包周长的计算凸包的周长可以通过计算凸包顶点之间的距离之和来得到。
对于凸包的n个顶点,可以依次计算相邻顶点之间的距离,并将其累加得到凸包的周长。
保证计算的正确性需要注意以下几点:1.凸包的顶点要按照逆时针或者顺时针的方向依次输入,以保证计算出的面积和周长的结果正确。
解多边形面积计算难题的方法与技巧

解多边形面积计算难题的方法与技巧多边形面积计算是几何学中的一个基本问题,但对于复杂的多边形,求解其面积可能会变得困难。
本文将介绍一些解决多边形面积计算难题的方法与技巧。
一、分割法分割法是一种常用的解决多边形面积计算难题的方法。
通过将复杂的多边形分割成简单的几何形状,如三角形、矩形等,再分别计算各个简单形状的面积,最后将它们加起来得到多边形的总面积。
例如,对于一个不规则的五边形,我们可以将其分割成三个三角形和一个矩形,然后分别计算每个三角形和矩形的面积,最后将它们相加得到五边形的面积。
二、向量法向量法是另一种解决多边形面积计算难题的方法。
通过将多边形的顶点表示为向量,然后利用向量的叉积运算来求解面积。
具体步骤如下:首先,将多边形的顶点按照顺时针或逆时针的顺序连接起来,形成一个封闭的多边形;然后,将多边形的顶点分别表示为向量;接下来,计算相邻两个向量的叉积,并将其结果累加;最后,将累加的结果除以2,即得到多边形的面积。
三、三角剖分法三角剖分法是一种将多边形分割成若干个三角形,并计算每个三角形的面积,最后将它们相加得到多边形面积的方法。
三角剖分法的步骤如下:首先,选择一个多边形内部的点作为顶点,然后将多边形分割成若干个三角形,使得每个三角形的一个顶点为选择的点;接下来,计算每个三角形的面积,并将它们相加,即得到多边形的面积。
四、格林公式格林公式是一种通过计算多边形边界上的积分来求解多边形面积的方法。
格林公式的表达式为:A = 1/2 * ∑(x[i] * y[i+1] - x[i+1] * y[i])其中,A表示多边形的面积,x[i]和y[i]分别表示多边形边界上的第i个点的横坐标和纵坐标。
通过计算多边形边界上各个点的坐标,然后代入格林公式的表达式中,即可求解多边形的面积。
五、数值积分法数值积分法是一种通过数值计算来求解多边形面积的方法。
该方法将多边形分割成若干个小面积的矩形或三角形,然后利用数值积分的方法对每个小面积进行计算,最后将它们相加得到多边形的面积。
腐蚀膨胀算法详细解释
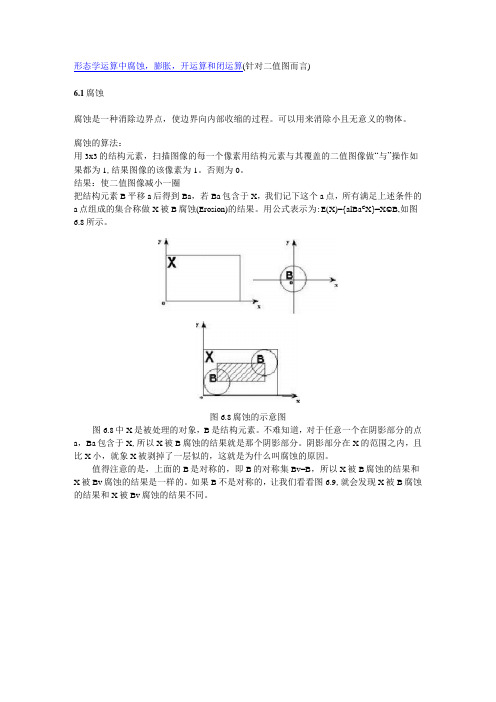
形态学运算中腐蚀,膨胀,开运算和闭运算(针对二值图而言)6.1腐蚀腐蚀是一种消除边界点,使边界向内部收缩的过程。
可以用来消除小且无意义的物体。
腐蚀的算法:用3x3的结构元素,扫描图像的每一个像素用结构元素与其覆盖的二值图像做“与”操作如果都为1,结果图像的该像素为1。
否则为0。
结果:使二值图像减小一圈把结构元素B平移a后得到Ba,若Ba包含于X,我们记下这个a点,所有满足上述条件的a点组成的集合称做X被B腐蚀(Erosion)的结果。
用公式表示为:E(X)={alBa C X}=X©B,如图6.8所示。
图6.8腐蚀的示意图图6.8中X是被处理的对象,B是结构元素。
不难知道,对于任意一个在阴影部分的点a,Ba包含于X,所以X被B腐蚀的结果就是那个阴影部分。
阴影部分在X的范围之内,且比X小,就象X被剥掉了一层似的,这就是为什么叫腐蚀的原因。
值得注意的是,上面的B是对称的,即B的对称集Bv=B,所以X被B腐蚀的结果和X被Bv腐蚀的结果是一样的。
如果B不是对称的,让我们看看图6.9,就会发现X被B腐蚀的结果和X被Bv腐蚀的结果不同。
y图6.9结构元素非对称时,腐蚀的结果不同图6.8和图6.9都是示意图,让我们来看看实际上是怎样进行腐蚀运算的。
在图6.10中,左边是被处理的图象X (二值图象,我们针对的是黑点),中间是结构元素B ,那个标有origin 的点是中心点,即当前处理元素的位置,我们在介绍模板操作时也有过类似的概念。
腐蚀的方法是,拿B 的中心点和X 上的点一个一个地对比,如果B 上的所有点都在X 的范围内,则该点保留,否则将该点去掉;右边是腐蚀后的结果。
可以看出,它仍在原来X 的范围内,且比X 包含的点要少,就象X 被腐蚀掉了一层。
o Q Q Q o & QO Qo Q o O oooo o o o o o 0- 0 O 0 o o •• • ■ Oo o oo o o 0 o o o o o 0 0 o o o ••o o o oo o o o ■ ■ o o 0 0 o o o ••o 0 0 oo o o 0 ■ • ♦ o QQ Q ■0 0 & o Q Q Q 0 0 * * 0 0 0 O 0 0 • ♦ ♦■ 0 Q Q ◎ 00o o ■ •0 0 o O ■ ■ ■ ■ *« O Q Qo o■ ■ ■ ■ Q Q c- O■ * ■ o GO O O O o o •o o ■ •• ■ o o o o O oO ■ ■ ■o 0o O O o O ♦<Q 0■••■ o a o o O o O o o 0 0 o 0oO o oooo\>o0 00o o o o 0 0 0'originFEX e 6图6.10腐蚀运算 图6.11为原图,图6.12为腐蚀后的结果图,能够很明显地看出腐蚀的效果。
多边形化算法

多边形化算法
多边形化算法是指将给定的点集或线段组合成封闭的多边形的过程。
这个问题在计算几何学、计算机图形学和地理信息系统等领域中经常遇到。
以下是一些常见的多边形化算法:
1. 凸包算法:凸包算法是最常用的多边形化算法之一。
它的目标是找到包含所有点的最小凸多边形。
常见的凸包算法有Graham扫描算法、Jarvis步进算法和快速凸包算法。
2. 三角剖分算法:三角剖分算法将给定的点集或线段划分为一组互不相交的三角形,从而形成多边形。
常见的三角剖分算法有Delaunay三角剖分算法和Ear Clipping算法。
3. 最小生成树算法:最小生成树算法可以用于生成一个连接给定点集的最小权重树形结构,在某些情况下可以用来构建多边形。
Prim算法和Kruskal算法是两种常用的最小生成树算法。
4. Alpha形算法:Alpha形算法是一种基于给定参数Alpha 的多边形化算法。
它通过连接在给定距离内的点来构建多边形,从而生成不规则的凸多边形。
5. Voronoi图算法:Voronoi图算法将给定的点集划分为一组区域,其中每个区域都由距离最近的点支配。
这些区域可以被视为多边形的一部分。
这些算法在实际应用中根据具体需求和数据特征的不同,选择合适的算法进行多边形化处理。
需要根据具体情况评估算法的效率、精确性和适用性。
三维泰森多边形算法 -回复

三维泰森多边形算法-回复什么是三维泰森多边形算法?三维泰森多边形算法是一种用于计算三维空间中一组点集的最小外包凸壳的算法。
泰森多边形是一个多边形,它将一组点集分割成一组不相交的三角形,使得这些三角形的外接圆包围了所有点集。
三维泰森多边形算法通过计算这些外接圆的半径和中心点,确定最小外包凸壳的形状。
三维泰森多边形算法的基本原理是使用一个递归的分而治之方法。
它通过将点集分为两个较小的子集,并分别计算它们的最小外包凸壳,然后将子集合并为一个更大的外包凸壳。
通过不断重复这个过程,最终得到整个点集的最小外包凸壳。
该算法的步骤如下:1. 输入一组三维空间中的点集P。
2. 如果P中的点数小于等于3个,则返回这些点作为最小外包凸壳的顶点。
3. 找到点集P中的一个点pivot,它的选择可能影响算法的性能。
一种常用的选择方法是选择z值最小的点。
4. 根据pivot将点集P分成两个子集P1和P2。
将P1中所有点的z值小于等于pivot的点放入P1,将其他点放入P2。
5. 递归地计算子集P1和P2的最小外包凸壳。
6. 合并子集P1和P2的最小外包凸壳,得到整个点集P的最小外包凸壳。
7. 返回最小外包凸壳作为算法的输出。
为了计算子集的最小外包凸壳,可以使用相同的算法步骤。
递归实现的关键在于确定pivot点和将点集分割为两个子集。
三维泰森多边形算法的时间复杂度为O(n log n),其中n是点集P的大小。
这是因为每次递归都将点集分割为两个子集,每个子集的大小约为原点集的一半。
因此,算法的递归深度为O(log n)。
在每一层递归中,需要计算子集的最小外包凸壳,这需要O(n)的时间。
因此,总的时间复杂度为O(n log n)。
三维泰森多边形算法在计算机图形学、地理信息系统和计算几何等领域中有广泛的应用。
它可以用于计算三维物体的几何结构,并支持一些常见的操作,如点位置检测、线段相交以及点对之间的最近距离计算。
总结起来,三维泰森多边形算法是一种用于计算三维空间中一组点集的最小外包凸壳的算法。
七年级上《4.5多边形和圆的初步认识》课时练习含答案解析

北师大版数学七年级上册第四章4.5多边形和圆的初步认识同步练习一、选择题1.过多边形的一个顶点的所有对角线把多边形分成8个三角形,这个多边形的边数是()A.8B.9C.10D.11答案:C解析:解答:设多边形有n条边,则n-2=8,解得n=10.故这个多边形的边数是10.故选:C.分析:经过n边形的一个顶点的所有对角线把多边形分成(n-2)个三角形,根据此关系式求边数.2.从一个多边形的任何一个顶点出发都只有5条对角线,则它的边数是()A.6B.7C.8D.9答案:C解析:解答:设这个多边形是n边形.依题意,得n-3=5,解得n=8.故这个多边形的边数是8.故选C.分析:根据多边形的对角线的定义可知,从n边形的一个顶点出发,可以引(n-3)条对角线,由此可得到答案.3.过多边形某个顶点的所有对角线,将这个多边形分成7个三角形,这个多边形是()A.八边形B.九边形C.十边形D.十一边形答案:B解析:解答:设多边形有n条边,则n-2=7,解得:n=9.所以这个多边形的边数是9,故选:B.分析:经过n边形的一个顶点的所有对角线把多边形分成(n-2)个三角形,根据此关系式求边数.4.七边形的对角线共有()A.10条B.15条C.21条D.14条答案:D解析:解答:七边形的对角线总共有:()773142⨯-=条.故选D.分析:可根据多边形的对角线与边的关系求解.5.连接多边形的一个顶点与其他顶点的线段把这个多边形分成了6个三角形,则原多边形是()边形.A.五B.六C.七D.八答案:D解析:解答:设原多边形是n 边形, 则n -2=6, 解得n =8. 故选:D .分析:根据n 边形从一个顶点出发可把多边形分成(n -2)个三角形进行计算. 6.一个多边形有五条对角线,则这个多边形的边数为( ) A .8 B .7 C .6 D .5 答案:D解析:解答:设多边形的边数为n ,则()352n n -=,整理得23100n n --=, 解得15n =,22n =-(舍去). 所以这个多边形的边数是5. 故选:D .分析:根据n 边形的对角线公式()32n n -进行计算即可得解.7.已知过一个多边形的某一个顶点共可作条对角线,则这个多边形的边数是( ) A . B . C . D . 答案:D解析:解答:∵多边形从一个顶点出发可引出条对角线, 设多边形为n 边形,则 n -3=, 解得n =. 故选:D .分析:根据从多边形的一个顶点可以作对角线的条数公式(n-3)求出边数即可得解.8.若从一多边形的一个顶点出发,最多可引10条对角线,则它是()A.十三边形B.十二边形C.十一边形D.十边形答案:A解析:解答:设这个多边形是n边形.依题意,得n-3=10,∴n=13.故这个多边形是13边形.故选:A.分析:根据多边形的对角线的定义可知,从n边形的一个顶点出发,可以引(n-3)条对角线,由此可得到答案.9.高中要好的五个学生,相互约定在毕业后的一周,每两人通话一次.则在毕业后的一周,这五位同学一共通讯()次.A.8B.10C.14D.12答案:B解析:解答:5×(5-1)÷2=5×4÷2=20÷2=10(次).故选:B.分析:5个人每两个人通话一次,则每个人都要和其他4个人分别通话,则每人通话的次数为:5-1=4次,则所有的人通话的次数为:5×4=20次,由于通话是在两个人之间进行的,所以共通话20÷2=10次.10.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿1ADA 、1A E 2A 、2A F 3A 、3A GB 路线爬行,乙虫沿AC 1B 路线爬行,则下列结论正确的是( )A .甲先到B 点 B .乙先到B 点C .甲、乙同时到BD .无法确定 答案:C解析:解答:12π(A 1A +1A 2A +2A 3A +3A B )12π×AB ,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等, 因此两个同时到B 点. 故选C .分析:甲虫走的路线应该是4段半圆的弧长,那么应该是12π(A 1A +1A 2A +2A 3A +3A B )=12π×AB ,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等,因此两个同时到B 点.11.下列说法,正确的是( ) A .弦是直径 B .弧是半圆 C .半圆是弧D .过圆心的线段是直径 答案:C解析:解答:A.弦是连接圆上任意两点的线段,只有经过圆心的弦才是直径,不是所有的弦都是直径.故本选项错误;B.弧是圆上任意两点间的部分,只有直径的两个端点把圆分成的两条弧是半圆,不是所有的弧都是半圆.故本选项错误;C.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.所以半圆是弧是正确的.D.过圆心的弦才是直径,不是所有过圆心的线段都是直径,故本选项错误.故选:C.分析:根据弦,弧,半圆和直径的概念进行判断.弦是连接圆上任意两点的线段.弧是圆上任意两点间的部分.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.直径是过圆心的弦.12.有下列四个说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.其中错误说法的个数是()A.1B.2C.3D.4答案:B解析:解答:①圆确定的条件是确定圆心与半径,是假命题,故此说法错误;②直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;③弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;④半圆是弧,但弧不一定是半圆,圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆,是真命题,故此说法正确.其中错误说法的是①③两个.故选:B.分析:根据弦的定义、弧的定义、以及确定圆的条件即可解决.13.下列说法中,结论错误的是()A.直径相等的两个圆是等圆B.长度相等的两条弧是等弧C.圆中最长的弦是直径D.一条弦把圆分成两条弧,这两条弧可能是等弧答案:B解析:解答:A.直径相等的两个圆是等圆,正确,不符合题意;B.长度相等的两条弧圆周角不一定相等,它们不一定是等弧,原题的说法是错误的,符合题意;C.圆中最长的弦是直径,正确,不符合题意;D.一条直径把圆分成两条弧,这两条弧是等弧,正确,不符合题意, 故选:B .分析:利用圆的有关定义进行判断后利用排除法即可得到正确的答案;14.有两个圆,⊙1O 的半径等于地球的半径,⊙2O 的半径等于一个篮球的半径,现将两个圆都向外膨胀(相当于作同心圆),使周长都增加1米,则半径伸长的较多的圆是( ) A .⊙1O B .⊙2OC .两圆的半径伸长是相同的D .无法确定 答案:C解析:解答:设⊙1O 的半径等于R ,膨胀后的半径等于R ′;⊙2O 的半径等于r ,膨胀后的半径等于r ′,其中R >r .由题意得,2πR +1=2πR ′,2πr +1=2πr ′,解得R ′=R +12π,R ′=R +12π; 所以R ′-R =12π,R ′-R =12π,所以,两圆的半径伸长是相同的. 故选C .分析:由L =2πR 计算出半径的伸长量,然后比较大小. 15.下列语句中,不正确的个数是( )①直径是弦;②弧是半圆;③长度相等的弧是等弧;④经过圆内一定点可以作无数条直径. A .1个 B .2个 C .3个 D .4个答案:C解析:解答:①根据直径的概念,知直径是特殊的弦,故正确;②根据弧的概念,知半圆是弧,但弧不一定是半圆,故错误;③根据等弧的概念:在同圆或等圆中,能够互相重合的弧是等弧.长度相等的两条弧不一定能够重合,故错误;④如果该定点和圆心不重合,根据两点确定一条直线,则只能作一条直径,故错误.故选C.分析:根据弦、弧、等弧的定义即可求解.二、填空题16.若点M取在多边形的一条边上(不是顶点),再将点M与n边形个顶点连结起来,将此多边形分割成9个三角形,则n边形是_____边形.答案:十解析:解答:多边形一条边上的一点M(不是顶点)出发,连接各个顶点得到9个三角形,则这个多边形的边数为9+1=10.故答案为:十.分析:可根据多边形的一点(不是顶点)出发,连接各个顶点得到的三角形个数与多边形的边数的关系求解.17.从多边形的一个顶点出发引对角线,可以把这个多边形分割成7个三角形,则该多边形为_____边形.答案:九解析:解答:由题意可知,n-2=7,解得n=9.则这个多边形的边数为9,多边形为九边形.故答案为:九.分析:从一个n边形的某个顶点出发,可以引(n-3)条对角线,把n边形分为(n-2)的三角形.18.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是_____.答案:8解析:解答:设多边形有n条边,则n-2=6,解得n=8.故答案为:8.分析:根据从一个n边形的某个顶点出发,可以引(n-3)条对角线,把n边形分为(n-2)的三角形作答.19.如图,MN为⊙O的弦,∠M=50°,则∠MON等于_____.答案:80°解析:解答:∵OM=ON,∴∠N=∠M=50°,∴∠MON=180°-∠M-∠N=80°,故答案为80°.分析:利用等腰三角形的性质可得∠N的度数,根据三角形的内角和定理可得所求角的度数.20.如图,以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E,连结OD、OE,若∠A =65°,则∠DOE=_____.答案:50°解析:解答:如图,连接BE.∵BC为⊙O的直径,∴∠CEB=∠AEB=90°,∵∠A=65°,∴∠ABE=25°,∴∠DOE=2∠ABE=50°,(圆周角定理)故答案为:50°.分析:如图,连接BE.由圆周角定理和三角形内角和定理求得∠ABE=25°,再由“同弧所对的圆周角是所对的圆心角的一半”进行答题.三、解答题21.(1)六边形从一个顶点可引出几条对角线?共有几条对角线?答案:3|9解答:(1)六边形从一个顶点可引出对角线:6-3=3(条),共有对角线:() 66392⨯-=(条);(2)n边形从一个顶点可以引出几条对角线?共有几条对角线?答案:(n-3)|()32 n n-解答:n边形从一个顶点可以引出(n-3)条对角线,共有()32n n-条对角线.解析:分析:根据n边形从一个顶点可引出(n-3)条对角线,及n边形一共()32n n-条对角线可求解(1)与(2).22.在凸多边形中,四边形的对角线有两条,五边形的对角线有5条,经过观察、探索、归纳,你认为凸九边形的对角线为多少?简单扼要地写出你的思考过程.答案:27条.解答:27条.通过四边形和五边形的对角线图形可知,过n边形的1个顶点可以作(n-3)条对角线,故过n个顶点可作n(n-3)条对角线,而这些对角线重复一遍,故n边形的对角线为()32n n-条,所以凸九边形的对角线为()993272⨯-=.解析:分析:作出四边形与五边形的对角线,然后观察从一个顶点作出的对角线的条数,从而确定规律并求出n边形的对角线的条数公式,再令n=9进行计算即可得解.23.画出下面多边形的全部对角线.答案:解答:如图所示:解析:分析:此图为5边形,有()55352⨯-=条对角线,依次画出即可.24.实践探究:有一个周长62.8米的圆形草坪,准备为它安装自动旋转喷灌装置进行喷灌,现有射程为20米、15米、10米的三种装置,你认为应选哪种比较合适?安装在什么地方?答案:选射程为10米的喷灌装置,安装在圆形草坪的中心处.解答:设圆形草坪的半径为R,则由题意知,2πR=62.8,解得:R≈10m.所以选射程为10米的喷灌装置,安装在圆形草坪的中心处.解析:分析:具体应选哪一种装置,取决于圆形草坪的半径,周长为62.8米的圆的半径约是10米.25.(1)经过凸n边形(n>3)其中一个顶点的对角线有_______条;答案:(n-3).解答:n边形过每一个顶点的对角线有(n-3)条;故答案为:(n-3).(2)一个凸边形共有20条对角线,它是几边形;答案:八解答:根据()32n n-=20,解得:n=8或n=-5(舍去),∴它是八边形.(3)是否存在有18条对角线的凸多边形?如果存在,它是几边形?如果不存在,说明得出结论的道理.答案:不存在,理由:()3n n-=18,解得:3317n±=,∵n不为正整数,∴不存在.解析:分析:(1)根据n边形从一个顶点出发可引出(n-3)条对角线即可求解;(2)根据任意凸n边形的对角线有()32n n-条,即可解答;(3)不存在,根据()32n n-=18,解得:3317n±,n不为正整数所以不存在.。
多边形轮廓缩小算法

多边形轮廓缩小算法
多边形轮廓缩小算法(Polygon Shrinking Algorithm)是一种用于减小多边形轮廓的算法,可以用于图像处理、计算机图形学等领域。
该算法的主要思想是在保持多边形形状不变的前提下,减小多边形的大小。
常见的多边形轮廓缩小算法有以下几种:
1. 边缘向内收缩法(Edge Inward Shrinking):该算法将多边
形的每条边向内收缩一定距离,然后根据新的边界点重新构造多边形。
具体实现时可以通过计算每条边的法向量,然后将法向量向内平移一定距离得到新的边界点。
2. 平移折线法(Translation Polygon Algorithm):该算法将多
边形的每个顶点向多边形内部平移一定距离,并根据新的顶点重新构造多边形。
具体实现时可以通过计算每个顶点的法向量,然后将法向量乘以缩小系数得到平移向量,再将原始顶点平移得到新的顶点。
3. 多边形边界法(Polygon Boundary Algorithm):该算法将多边形的边界点按一定规则重新排列,从而减小多边形的大小。
具体实现时可以将边界点按顺时针或逆时针方向重排,并根据新的边界点重新构造多边形。
以上算法在实际应用中可根据具体需求选择使用。
在实现过程中,可能需要考虑多边形的凸凹性、重叠部分的处理以及边界点的重新构造等问题。
膨胀、腐蚀、开、闭运算,你这么解释,小学生都看得懂了

膨胀、腐蚀、开、闭运算,你这么解释,小学生都看得懂了膨胀、腐蚀、开、闭运算,你这么解释,小学生都看得懂了!看过我前面一些章节内容的小伙伴肯定已经不止一次遇到过这几个词了。
对图像的形态学处理也避不开这几个。
但是想要准确理解他们的意思似乎不是那么简单。
首先,这四个运算都是用一个结构元对需要处理的region进行相应的形态学变换后得到想要的处理后的region。
就像你要对一个数做减法,你需要给他一个减数,这样'被减数-减数=差',才能求出差。
膨胀:就是把region变大,变大的方式就是用一个结构元的中心点在原来的region轮廓上游走一遍,所走过的区域加上原来的region 区域就是膨胀后的区域,如下图(图 3-14-1),如果我原来的region 是左边的大矩形,结构元是右边的cell。
图 3- 14 -1那么结构元的中心点就是圆心了,让cell在大矩形的轮廓上游走一圈,就是下图(图3-14-2)这样了:图 3-14-2游走途径的像素点再加上regionSource原来覆盖的区域一起,就是膨胀后的区域了。
其实就是这个矩形各个方向再往外扩大这个小圆的半径,拐角部分的直角变成了圆角,如下图(图3-14-3)。
(像极了原本90斤的女朋友后来变成了120斤,体积大了一圈,棱角变圆了,真是一个悲伤的故事~~)。
图3-14-3膨胀弄懂了,腐蚀也就不难了。
腐蚀:就是把region变小。
变小的方式就是用一个结构元的中心点在原来的region内部游走一遍,(注意这里不是轮廓了)。
当中心点到某个位置,整个结构元都在region内部的时候,所有符合这个条件的点,合在一起就是新的腐蚀后的区域了。
还是用原来的regionSource和cell,腐蚀的话就是下图(图 3-14-4)这样:图 3-14-4外面红色矩形是原来的regionSource,圆形就是结构元cell,为了满足所有的点都在regionSource内部,这个cell最边缘的位置也就是图中的位置了,那么cell的圆心所在位置就是腐蚀后的region,那么整个regionSource内所有符合这些条件的点就是图中绿色矩形了。
数字图像处理填空题复习

1 图像按照人眼的视觉特性可以分为可见图像和不可见图像。
Page 12 图像按照所含波段数可以分为单波段图像和多波段图像及超波段图像。
Page 13 图像按照空间坐标的连续性可分为模拟图像和数字图像。
Page 14 不可见的图像包括不可见光成像和不可见量按数学模型生成的图像。
Page 15 数字图像是一种空间坐标和灰度均不连续的,用离散数字表示的图像。
Page 16 数字图像处理可分为狭义图像处理、图像分析和图像理解三个层次。
Page 27 狭义图像处理是对输入图像进行某种变换得到输出图像,是一种图像到图像的处理过程,如图像增强等。
Page 28 模拟图像指空间坐标和亮度都是连续变化的图像。
Page 19数字图像处理即用计算机对图像进行处理。
Page 21 视网膜的表面分布有大量的光敏细胞,按照形状可以分为两类:锥状细胞和杆状细胞。
P112 人眼分辨率和被观察对象的相对对比度有关,当相对对比度小时,会导致人眼分辨率下降。
P123 在RGB彩色空间的原点上,若三个基色均没有亮度,则原点为黑色。
P144 图像中最大亮度和最小亮度的比值称为图像对比度。
P125 图像中最大亮度与最小亮度之差和最小亮度的比值称为相对对比度。
P126 物体的颜色是人的视觉器官感受光后在大脑的一种反映。
P137 一幅图像可以看成是空间上各点光强度的集合,若只考虑光的能量而不考虑光波长,则称为亮度图像。
P158 在彩色图像中,每个像素的颜色含有R,G和B三个分量。
P189 当两种或两种以上有色光同时照射到消色物体上时,物体呈现加色法效应。
P1410 BMP图像文件包括文件信息头,位图信息和位图数据三部分。
P3411 Windows在生成位图文件时,按照从左到右,从下到上的顺序记录位图的各个像素值。
P3612 描述数字图像的基本单元是像素。
P1613 图像噪声按其对图像的影响可分为加性噪声模型和乘性噪声模型两大类。
P4114 椒盐噪声的幅值基本相同,而噪声出现的位置是随机的。
形态学中的腐蚀与膨胀

数学形态学运算——腐蚀、膨胀、开运算、闭运算腐蚀简单说:就是以结构B的原点为基点沿着将要被腐蚀的图像A中的所有点移动,如果此时结构B中的所有点(包括原点)被A包含,那么被B原点沿着的A中的该点就保留,否则,该点就被抛弃。
可以看出,执行完该腐蚀指令后,A中突出部分,以及外围至少减少了结构B的一半(假设B的原点为B的中心)。
膨胀简单说:就是以结构B的原点为基点沿着将要被膨胀前的图像A中的所有点移动,如果此时结构B中至少有一个点(包括原点)被A包含,那么被沿着的A中的该点及周围就被B扩充,扩充范围为B的整个区域。
可以看出,膨胀后,原A沿着边缘外围被扩充了B的一半(假设B的原点为B的中心)。
数学形态学操作可以分为二值形态学和灰度形态学,灰度形态学由二值形态学扩展而来。
数学形态学有2个基本的运算,即腐蚀和膨胀,而腐蚀和膨胀通过结合又形成了开运算和闭运算。
开运算就是先腐蚀再膨胀,闭运算就是先膨胀再腐蚀。
腐蚀粗略的说,腐蚀可以使目标区域范围“变小”,其实质造成图像的边界收缩,可以用来消除小且无意义的目标物。
式子表达为:该式子表示用结构B腐蚀A,需要注意的是B中需要定义一个原点,【而B的移动的过程与卷积核移动的过程一致,同卷积核与图像有重叠之后再计算一样】当B的原点平移到图像A的像元(x,y)时,如果B在(x,y)处,完全被包含在图像A重叠的区域,(也就是B中为1的元素位置上对应的A图像值全部也为1)则将输出图像对应的像元(x,y)赋值为1,否则赋值为0。
我们看一个演示图。
B依顺序在A上移动(和卷积核在图像上移动一样,然后在B的覆盖域上进行形态学运算),当其覆盖A的区域为[1,1;1,1]或者[1,0;1,1]时,(也就是B中‘1’是覆盖区域的子集)对应输出图像的位置才会为1。
膨胀粗略地说,膨胀会使目标区域范围“变大”,将于目标区域接触的背景点合并到该目标物中,使目标边界向外部扩张。
作用就是可以用来填补目标区域中某些空洞以及消除包含在目标区域中的小颗粒噪声。
空间缓冲区生成算法的概述与比较

空间缓冲区生成算法的概述与比较摘要:空间分析是空间信息系统的核心和关键功能之一,也是评价一个空间信息系统功能强弱的重要指标。
缓冲区分析是空间信息系统中的空间分析基本功能之一,是众多空间分析方法的基础。
缓冲区分析是指为了识别某地理实体或空间物体对其周围的邻近性或影响度而在其周围建立的一定宽度的带状区。
本文对空间对象的缓冲区分析算法作了说明,讨论了分别利用图形学方法和图像处理的形态学方法建立地理信息系统中空间对象的缓冲区算法,并且就两种算法的异同做出了分析。
在矢量算法中,各类地理要素根据其空间形态特征分为点、线、面三类,分别以计算机屏幕数据的点、线、面图形对象表示,进行缓冲区分析。
在栅格算法中,地理空间被划分为规则的小单元(像元),空间位置由像元的行、列号表示。
以膨胀法原理为基础,进行缓冲区分析。
关键词:地理信息系统;空间分析;缓冲区分析;矢量法;栅格法;膨胀法引言地理信息系统( Geographic Information System简称GIS) 是一项以计算机为基础的新兴技术,围绕着这项技术的研究、开发和应用形成了一门交叉性、边缘性的学科。
它具有空间数据的输入、存储、管理、分析和输出等功能,地理信息系统的主要目的是为了分析空间数据,以提供空间决策支持信息,因此,空间分析是地理信息系统的主要功能,是核心,是灵魂。
空间分析是利用计算机对数字地图进行分析,从而获取和传输空间信息[1]。
由于空间分析对空间信息(特别是隐含信息)所具有的提取和传输功能,它已经成为地理信息系统区别于一般信息系统的功能特征,也成为评价一个地理信息系统功能的主要指标之一。
缓冲区分析是地理信息系统最重要和最基本的空间操作功能之一。
缓冲区分析是根据点、线、面实体基础,自动建立其周围一定宽度范围内的缓冲区多边形实体,从而实现空间数据在其领域得以扩展的信息分析方法。
例如,公共设施(商场、邮局、银行、医院等)的服务半径,大型水库建设引起的搬迁,都是一个邻近度的问题。
多边形的偏移填充算法

多边形的偏移填充算法多边形偏移(polygon offset)算法可能我们印象不深,不过用过autoCAD的同学也印象autoCAD 上面也还是有这个功能的。
我们可以用autoCAD上的“正多边形”功能画一个多边形,然后用修改工具中“偏移”按钮,对多边形进行偏移,见图1,从外面的一个大的5边形按照边偏移至里面小的5边形,其中相应边偏移的距离定义为offset值。
图1 AutoCAD中的多边形偏移效果图当然,这只是简单的情况,复杂的情况可能是有多个多边形,其中1个outer多边形,多个inner 多边形,然后offset的时候应该是outer多边形向内offset,inner多边形向外offset。
当一个多边形(特别是凹多边形)初步offset时,可能会发生自交;然后多边形之间也可能会发生相交。
大概思路:这里就需要首先将自交的多边形分裂出来,并选择正确的多边形;然后将选择出来的多边形进行求交计算,再一次将有相交的多边形合并分裂出来,并且选择正确的多边形,这个时候得到的全部多边形就是一次offset出来的结果。
1、为了保证outer多边形能向内offset,inner多边形能向外offset,这里需要保证outer多边形是逆时针方向旋转的,inner多边形是顺时针方向旋转的。
1.1 这里就稍稍讲下多边形的顺逆判断。
在多边形是简单多边形的前提下,其实还是挺简单的,只要找出多边形左下角的一个顶点,然后判断与这个顶点相连的两条边的叉积是否大于0就行了;如果多边形不是简单多边形,比如有自相交,有顶点夹角为0的情况等等,这个时候多边形就不应该有顺逆这种属性吧2、对单个多边形,根据角平分线初步偏移得到角点对于一个角点,可以设这个顶点为curPoint,相连的前一个点为prePoint,下一个点为nexPoint,于是可以得到两个向量a = prePoint – curPoint,b=nexPoint – curPoint。
多边形收缩算法

多边形收缩算法多边形收缩算法,简单来说就是把一个多边形按照一定的规则给变小喽。
你想啊,就像把一个大大的图形慢慢往中心缩。
比如说,咱们有一个很不规则的多边形,可能边边弯弯绕绕的,这个算法就像一个魔法,让这个多边形的每条边都往里面挪一挪。
那这个算法是怎么做到的呢?这里面可大有学问。
一种常见的做法是从多边形的顶点入手。
我们可以想象每个顶点就像一个小钉子,固定着多边形的形状。
当要收缩的时候呢,就把这些小钉子往中心拽一拽。
不过这拽也不是随便拽的哦。
要是拽得太猛或者太随意,那多边形可就变形得不成样子啦。
比如说一个五边形,它的五个顶点都有自己的位置。
我们要计算每个顶点到多边形中心的距离,这个中心可不是随随便便找个点就行的。
可能要通过一些数学方法,像把所有顶点的坐标加起来再除以顶点的个数之类的方法来找到这个中心。
然后呢,根据这个距离和一定的比例,把顶点往中心移动一点点。
在这个过程中,还有很多细节要考虑呢。
就像走钢丝一样,要小心翼翼。
比如说,如果多边形有凹进去的部分,那在收缩的时候就更要注意啦。
不能让这个凹进去的部分变得更奇怪或者消失不见。
这就需要更复杂的计算啦。
我们可能要分别判断每个顶点的情况,看看它周围的边是怎么连接的,再决定这个顶点到底要往中心移动多少。
而且呀,这个算法在很多地方都有用处。
在游戏开发里,你知道吧,很多游戏里的地图或者角色的形状可能就是多边形。
要是想让这个地图或者角色变小一点,就可以用到多边形收缩算法啦。
还有在图形处理软件里,如果要对一个多边形的图案进行缩放或者变形,这个算法也能派上大用场呢。
另外呢,多边形收缩算法也不是只有一种实现方式。
不同的人可能根据不同的需求想出不同的办法。
有的可能更注重速度,希望这个算法能快速地把多边形收缩起来。
那他们可能会采用一些比较简单直接的计算方法,虽然可能不是那么精确,但是速度快呀。
而有的呢,就像那些完美主义者,他们想要让收缩后的多边形看起来特别的整齐、美观,那就会采用更复杂、更精确的计算方式,可能要考虑更多的因素,像多边形的角度啊,边的长度比例啊之类的。
多边形外扩一定的距离算法

多边形外扩一定的距离算法
多边形外扩一定的距离可以采用以下算法:
1. 首先对多边形进行三角剖分,得到多个三角形。
2. 对每个三角形进行处理,将每个顶点沿法向外移动一定距离。
移动的距离可以根据需要进行调整。
3. 对每个三角形处理后生成新的三角形,将它们组合起来形成新的多边形。
4. 对新的多边形进行合并操作,去除重复顶点和线段,生成最终的外扩多边形。
需要注意的是,外扩距离过大可能会导致两个多边形之间产生重叠,因此需要进行适当的调整。
同时,该算法对于非凸多边形的处理可能会存在一定的问题,需要考虑相关算法的改进。
ue4 多边形外扩一定的距离算法

ue4 多边形外扩一定的距离算法UE4(Unreal Engine 4)是一款流行的游戏引擎,它提供了强大的功能和工具,用于创建高质量的三维游戏和虚拟现实体验。
在UE4中,多边形外扩算法是一个常见的需求,特别是在游戏开发中需要对角色或物体进行碰撞检测时。
本文将一步一步介绍UE4中多边形外扩算法的实现方法。
第一步:了解多边形外扩算法的概念多边形外扩算法是将给定的多边形区域沿法向量方向外扩一定的距离,从而得到一个外扩后的多边形区域。
在游戏开发中,外扩后的多边形通常用于碰撞检测或边界检测,以确保角色或物体与其他对象之间的交互正确进行。
第二步:理解法向量的概念在计算几何中,法向量是垂直于给定平面的向量。
在多边形外扩算法中,我们需要计算每个多边形边的法向量,以便确定外扩方向。
第三步:获取多边形的边在UE4中,我们可以使用边数组来表示一个多边形的边。
每个边由两个点构成,我们可以通过遍历多边形的边数组来获取每个边的起点和终点。
第四步:计算法向量对于每个边,我们需要计算它的法向量。
假设有一个边由点A和点B构成,我们可以通过以下公式计算法向量:N = (B.y - A.y, A.x - B.x)其中N是法向量,(B.y - A.y)是终点B的y坐标减去起点A的y坐标,(A.x - B.x)是起点A的x坐标减去终点B的x坐标。
第五步:归一化法向量为了使法向量的长度为1,我们需要对其进行归一化。
在UE4中,可以使用Normalize函数来实现法向量的归一化。
第六步:外扩点的计算对于每个边,我们可以计算外扩点的位置。
假设有一个边由点A和点B构成,外扩距离为d,我们可以通过以下公式计算外扩点的位置:P = A + N * d其中P是外扩点的位置,A是边的起点,N是归一化后的法向量,d是外扩距离。
第七步:创建外扩后的多边形在计算了每个外扩点的位置后,我们可以使用这些点来创建外扩后的多边形。
在UE4中,可以使用AddVertex函数来添加新的顶点,使用AddEdge函数来添加新的边,从而创建外扩后的多边形。
costmap footprint 膨胀系数 -回复

costmap footprint 膨胀系数-回复问题并解释相关概念。
首先,我们需要了解什么是代价地图(costmap)。
代价地图是一个在机器人导航中广泛使用的概念,它提供了一个用于规划路径的环境模型。
代价地图结合了传感器数据和环境约束,为机器人提供了一个表示可行路径和障碍物的二维或三维网格。
代价地图中的每个单元格都有一个代价值,用来表示该单元格距离威胁等级的远近。
通常,代价值越低的单元格表示越安全的区域,而代价值越高的单元格则表示越危险的区域。
这些代价值可以根据实际情况进行设置,以便对不同类型的障碍物或路径约束进行编码。
膨胀系数是指在代价地图中对机器人的占据区域进行膨胀的一个系数。
膨胀是指将机器人的占据区域进行扩展,以考虑机器人的实际尺寸和动态特性。
通常情况下,机器人的占据区域用一个多边形来表示,而膨胀系数则用来控制多边形的扩展程度。
膨胀系数可以从两个方面影响代价地图的生成与路径规划。
首先,膨胀系数可以影响代价地图中障碍物的表示。
当膨胀系数越大时,机器人被认为占据了更大的空间,因此障碍物在代价地图中的表示也会更大。
这样可以避免机器人与障碍物之间的碰撞,提供更安全的路径。
其次,膨胀系数还可以影响路径规划算法对路径的选择。
路径规划算法在寻找可行路径时会考虑代价地图中每个单元格的代价值。
膨胀系数越大,机器人被认为占据了更大的空间,因此路径规划算法往往会选择相对开阔的路径,以确保机器人能够通过。
相反,当膨胀系数较小时,路径规划算法可能会选择更接近障碍物的路径,以尽可能缩短路径长度。
在实际应用中,确定膨胀系数的大小是一个关键问题。
膨胀系数过小可能导致机器人与障碍物发生碰撞,路径规划失败;而膨胀系数过大则可能导致机器人规避这些障碍物,绕行较远的路径,导致路径冗余。
因此,我们需要根据实际应用场景和机器人的尺寸来选择合适的膨胀系数。
在代价地图中,膨胀系数可以通过多种方法来设置。
一种常见的方法是基于机器人的尺寸进行设置。
js多边形膨胀算法

js多边形膨胀算法在计算机图形学中,多边形膨胀(Polygon Inflation)是指在一个给定的多边形的基础上,生成一个新的多边形,该新多边形的每个边都比原始多边形的对应边更远。
多边形膨胀的算法可以采用一种称为“膨胀 Dilation)”的形态学操作。
以下是一个简单的JavaScript 示例,使用图形学库`paper.js` 来实现多边形膨胀的效果。
在实际应用中,你可能需要根据具体情况选择适当的库或算法。
首先,确保你已经安装了`paper.js`,可以通过以下命令进行安装:npm install paper然后,使用以下代码进行多边形膨胀:const paper = require('paper');// 创建一个Paper.js项目paper.setup();// 原始多边形的顶点坐标const originalPolygonPoints = [new paper.Point(100, 100),new paper.Point(200, 100),new paper.Point(200, 200),new paper.Point(150, 250),new paper.Point(100, 200)];// 创建原始多边形const originalPolygon = new paper.Path(originalPolygonPoints); originalPolygon.strokeColor = 'black';// 定义膨胀的距离const inflationDistance = 10;// 进行多边形膨胀const inflatedPolygon = originalPolygon.clone();inflatedPolygon.flatten(inflationDistance);// 绘制膨胀后的多边形inflatedPolygon.strokeColor = 'red';// 将绘制结果渲染到HTML页面中paper.view.draw();这个示例使用`paper.js` 库来创建一个原始多边形,然后通过`flatten` 方法对原始多边形进行膨胀。
costmap footprint 膨胀系数 -回复

costmap footprint 膨胀系数-回复“costmap footprint 膨胀系数”是机器人导航和避障中的重要概念。
在这篇文章中,我们将一步一步解释costmap、footprint和膨胀系数的概念,并讨论它们如何相互关联以及如何影响机器人的导航能力。
首先,我们来了解什么是costmap。
在机器人导航中,costmap用于表示机器人周围环境的“代价”。
代价可以理解为一种度量,用于评估机器人在特定位置行走的难易程度。
在2D导航中,costmap通常是一个二维的矩阵,将机器人周围的环境划分为网格。
每个网格都有一个代价值,表示在该位置行走的难易程度,例如自由空间的网格代价较低,障碍物的网格代价较高。
接下来,我们来了解什么是footprint。
Footprint表示机器人本身的形状,通常是一个多边形,用于表示机器人的轮廓。
在进行导航规划时,机器人的轮廓需要与环境的costmap进行比较,以确定机器人是否能够通过某个位置。
如果机器人的某个轮廓点与高代价的网格相交,那么机器人将被认为不能通过该位置。
在机器人导航中,为了考虑到机器人本身的大小,需要对costmap进行膨胀处理。
膨胀就是将costmap中每个网格的代价向四周扩展,以考虑机器人的轮廓。
膨胀系数是控制膨胀程度的参数,它决定了轮廓点与高代价网格之间的最小距离。
膨胀系数越大,机器人与障碍物的最小间隔就越大,导航算法将会选择更安全的路径。
膨胀系数越小,机器人与障碍物的最小间隔就越小,导航算法会更接近障碍物,可能产生碰撞的风险。
在实际应用中,选择合适的costmap膨胀系数是非常重要的。
如果膨胀系数过大,机器人将会过度躲避障碍物,可能导致冗余的路径规划和偏离目标的行为。
如果膨胀系数过小,机器人可能会碰撞到障碍物或无法规划出避障路径,从而导致导航失败。
因此,合理选择膨胀系数可以最大限度地平衡机器人的安全性和导航效率。
在确定costmap膨胀系数时,需要考虑机器人的尺寸、形状以及移动速度等因素。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多边形膨胀算法
多边形膨胀算法是计算机图形学中常用的一种算法,用于将多边形进行膨胀操作,即向外扩展多边形的边界。
本文将介绍多边形膨胀算法的原理和实现方法。
一、多边形膨胀算法的原理
多边形膨胀算法的原理是通过对多边形的每条边进行一系列的操作,使得多边形的边界向外扩展一定的距离。
具体而言,可以通过以下步骤来实现多边形的膨胀操作:
1. 确定膨胀的距离:首先需要确定多边形膨胀的距离,即多边形边界向外扩展的距离。
这个距离可以是固定的值,也可以根据具体需求进行动态调整。
2. 计算边界点的法向量:对于每条多边形的边,需要计算该边的法向量。
法向量的计算可以通过求取边的单位法向量,并乘以膨胀距离来实现。
3. 计算膨胀后的边界点:通过将每个顶点沿着其法向量方向移动膨胀距离的长度,可以得到膨胀后的边界点。
4. 连接膨胀后的边界点:将膨胀后的边界点按顺序连接起来,形成膨胀后的多边形。
多边形膨胀算法可以使用多种方式来实现,下面介绍其中两种常用
的实现方法。
1. 顶点法:
顶点法是一种简单而直观的实现方法,它通过对多边形的每个顶点进行处理来实现膨胀操作。
具体步骤如下:
(1)遍历多边形的每个顶点,计算该顶点的法向量。
(2)将每个顶点沿着其法向量方向移动膨胀距离的长度。
(3)连接膨胀后的顶点,形成膨胀后的多边形。
2. 边法:
边法是一种更加高效的实现方法,它通过对多边形的每条边进行处理来实现膨胀操作。
具体步骤如下:
(1)遍历多边形的每条边,计算该边的法向量。
(2)将每个顶点沿着其法向量方向移动膨胀距离的长度,得到膨胀后的边界点。
(3)连接膨胀后的边界点,形成膨胀后的多边形。
三、多边形膨胀算法的应用
多边形膨胀算法在计算机图形学中有着广泛的应用,下面介绍其中两个常见的应用场景。
1. 地图缓冲区生成:
在地图绘制中,常常需要生成地物的缓冲区,以提高地物的可视性。
多边形膨胀算法可以用来生成地物的缓冲区,将地物进行膨胀操作,形成地物的扩展区域。
2. 碰撞检测:
在游戏开发中,碰撞检测是一个重要的技术问题。
多边形膨胀算法可以用来对游戏中的物体进行碰撞检测,通过对物体进行膨胀操作,将物体的边界扩展,从而实现更加准确的碰撞检测。
四、总结
多边形膨胀算法是一种常用的计算机图形学算法,可以实现对多边形的边界进行膨胀操作。
通过对多边形的顶点或边进行处理,可以得到膨胀后的多边形。
多边形膨胀算法在地图缓冲区生成和碰撞检测等应用场景中具有重要的作用。
通过深入理解多边形膨胀算法的原理和实现方法,可以更好地应用于实际的计算机图形学问题中。
