Proe 三角函数公式大全及参数详细说明
三角函数公式大全

三角函数公式大全三角函数是数学中非常重要的概念,它们在几何、三角学、物理学等领域都有着广泛的应用。
在学习三角函数的过程中,掌握三角函数的基本公式是非常重要的。
本文将为大家详细介绍三角函数的公式大全,帮助大家更好地理解和掌握三角函数的知识。
1. 正弦函数的公式。
正弦函数是最基本的三角函数之一,其公式为,sinθ = 对边/斜边。
其中,θ为角度,对边为与角度θ相对的直角三角形的斜边,斜边为直角三角形的斜边。
正弦函数的图像是一条连续的曲线,其周期为2π,在0到2π之间有一个完整的周期。
2. 余弦函数的公式。
余弦函数也是常见的三角函数,其公式为,cosθ = 邻边/斜边。
其中,θ为角度,邻边为与角度θ相邻的直角三角形的斜边,斜边为直角三角形的斜边。
余弦函数的图像也是一条连续的曲线,其周期也为2π,与正弦函数的图像相似。
3. 正切函数的公式。
正切函数是另外一个常见的三角函数,其公式为,tanθ = 对边/邻边。
其中,θ为角度,对边为与角度θ相对的直角三角形的斜边,邻边为与角度θ相邻的直角三角形的斜边。
正切函数的图像在一些特定的角度上会出现无穷大的情况,因此在使用时需要注意。
4. 余切函数的公式。
余切函数是正切函数的倒数,其公式为,cotθ= 邻边/对边。
其中,θ为角度,邻边为与角度θ相邻的直角三角形的斜边,对边为与角度θ相对的直角三角形的斜边。
余切函数的图像也会在一些特定的角度上出现无穷大的情况。
5. 正割函数的公式。
正割函数是余弦函数的倒数,其公式为,secθ= 斜边/邻边。
其中,θ为角度,邻边为与角度θ相邻的直角三角形的斜边,斜边为直角三角形的斜边。
正割函数的图像是一条连续的曲线,其周期也为2π。
6. 余割函数的公式。
余割函数是正弦函数的倒数,其公式为,cscθ= 斜边/对边。
其中,θ为角度,对边为与角度θ相对的直角三角形的斜边,斜边为直角三角形的斜边。
余割函数的图像也是一条连续的曲线,其周期也为2π。
(完整word版)三角函数公式和图像大全,推荐文档

初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质反三角函数的图形反三角函数的性质三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=AA cos 1cos 1-+ tan(2A )=A A sin cos 1-=AA cos 1sin + 和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosacos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosatgA=tanA =aacos sin万能公式sina=2)2(tan 12tan2aa + cosa=22)2(tan 1)2(tan 1aa+- tana=2)2(tan 12tan2aa -a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=a b ] a•sin(a)-b•cos(a) =)b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2其他非重点三角函数 csc(a) =asin 1 sec(a) =a cos 1 双曲函数 sinh(a)=2e -e -aa cosh(a)=2e e -aa + tg h(a)=)cosh()sinh(a a 公式一设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)= sinαcos (2kπ+α)= cosαtan (2kπ+α)= tanαcot (2kπ+α)= cotα设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三任意角α与-α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tanαcot(2π-α)= -cotα2π±α及23π±α与α的三角函数值之间的关系: sin (2π+α)= cosα cos (2π+α)= -sinα tan (2π+α)= -cotα cot (2π+α)= -tanα sin (2π-α)= cosα cos (2π-α)= sinα tan (2π-α)= cotα cot (2π-α)= tanα sin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotα cot (23π+α)= -tanα sin (23π-α)= -cosα cos (23π-α)= -sinα tan (23π-α)= cotα cot (23π-α)= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h。
(完整版)三角函数公式大全

三角函数公式一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=, 正弦函数:r y=αsin 余弦函数:r x =αcos 正切函数:x y =αtan余切函数:y x =αcot 正割函数:xr=αsec余割函数:yr=αcsc二、同角三角函数的基本关系式六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”倒数关系:1csc sin =⋅x x ,1sec cos =⋅x x ,1cot tan =⋅x x 。
商数关系:x x x cos sin tan =,xxx sin cos cot =。
平方关系:1cos sin 22=+x x ,x x 22sec tan 1=+,x x 22csc cot 1=+。
积的关系:sinx=tanx·cosx cosx=sinx·cotx tanx=sinx·secxcotx=cosx·cscx secx=tanx·cscx cscx=secx·cotx三、诱导公式公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα cos(2kπ+α)=cosαtan(2kπ+α)=tanα cot(2kπ+α)=cotα (其中k∈Z) 公式二:设α为任意角,π+α的三角函数的值与α的三角函数值之间的关系: sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系: sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα 公式五:απ-2与α的三角函数值之间的关系:sin(απ-2)=cosα cos(απ-2)=sinα tan(απ-2)=cotα cot(απ-2)=tanα公式六:απ+2与α的三角函数值之间的关系:sin(απ+2)=cosα cos(απ+2)=-sinαtan(απ+2)=-cotα cot(απ+2)=-tanα公式七:απ-23与α的三角函数值之间的关系:sin(απ-23)=-cosα cos(απ-23)=-sinαtan(απ-23)=cotα cot(απ-23)=tanα公式八:απ+23与α的三角函数值之间的关系:sin(απ+23)=-cosα cos(απ+23)=sinαtan(απ+23)=-cotα cot(απ+23)=-tanα公式九:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系: sin(2π-α)=-sinα cos(2π-α)=cosα tan(2π-α)=-tanα cot(2π-α)=-cotα⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值,前面加上一个把α看成..锐角时原函数值的符号。
proe关系式详解

在ProE关系式中我们可以使用系统函数,ProE对数学函数有强大的支持能力,通过这些函数我们可以来进行一些特定的运算得到所期望的值,这里就对一些比较常用的系统函数进行一个概括总结。
1、数学函数在ProE中,我们可以使用灵活的数学函数,常用的函数列表如下:sin()、cos()、tan()函数:这三个都是数学上的三角函数,分别使用角度的度数值来求得角度对应的正弦、余弦和正切值,比如:A=sin(30),A=0.5B=cos(30),B=0.866C=tan(30),C=0.577asin()、acos()、atan()函数:这三个是上面三个三角函数的反函数,通过给定的实数值求得对应的角度值,如:A=asin(0.5),A=30B=acos(0.5),B=60C=atan(0.5),C=26.6log():求得10为底的对数值,如:A=log(1),A=0A=log(10),A=1A=log(5),A=0.6989ln():求得以自然数e为底的对数值,e是自然数,值是2.718...,如:A=ln(1),A=0A=ln(5),A=1.609exp():求得以自然数e为底的开方数,如:A=exp(2),A=e^2=7.387abs():求得给定参数的绝对值,如:A=abs(-1.6),A=1.6B=abs(3.5),B=3.5max()、min():求得给定的两个参数之中的最大最小值,如:A=max(3.8,2.5),A=3.8B=min(3.8,2.5),B=2.5mod():求第一个参数除以第二个参数得到的余数,如:A=mod(20,6),A=2B=mod(20.7,6.1),B=2.4sqrt():开平方,如:A=sqrt(100),A=10;B=sqrt(2),B=1.414pow():指数函数,如A=pow(10,2),A=100B=pow(100,0.5),B=10ceil():不小于其值的最小整数floor():不超过其值的最大整数ceil(10.2)值为11floor(10.2)=10也可以使用指定小数部分位数的ceil和floor函数,如:ceil(10.255,2)=10.26floor(10.255,1)=10.2floor(10.255,2)=10.252、字符串函数:string_length():字符串长度求值用法:String_length(Parameter name or string),括弧内参数名或字符串,字符串要用" "括起,空格亦算一个字符。
三角函数公式表(全)

三角函数公式表同角三角函数的基本关系式倒数关系: 商的关系:平方关系:tanα·cotα=1sinα·cscα=1 sinα/cosα=tanαsin2α+cos2α=11+tan2α=sec2α(六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”)诱导公式(口诀:奇变偶不变,符号看象限。
)sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(π/2+α)=cosαsin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotαsin(π+α)=-sinαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanαsin(3π/2+α)=-cosαsin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotαsin(2kπ+α)=sinαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα(其中k∈Z)两角和与差的三角函数公式万能公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtanα+tanβtan(α+β)=———----———1-tanα·tanβtanα-tanβtan(α-β)=—————-------—1+tanα·tanβ2tan(α/2) sinα=——————1+tan2(α/2)1-tan2(α/2) cosα=——————1+tan2(α/2)2tan(α/2) tanα=——————1-tan2(α/2)半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=—————1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=——————1-3tan2α三角函数的和差化积公式三角函数的积化和差公式Sinα+sinβ=2sin[(α+β)/2]·cos[(α-β)/2] sinα-sinβ=2cos[(α+β)/2]·sin[(α-β)/2] cos α+cos β=2cos[(α+β)/2]·cos[(α-β)/2] cosα-cosβ=-2sin[(α+β)/2]·sin[(α-β)/2]1sinα·cosβ=-[sin(α+β)+sin(α-β)]21cosα·sinβ=-[sin(α+β)-sin(α-β)]21cosα·cosβ=-[cos(α+β)+cos(α-β)]21sinα·sinβ=— -[cos(α+β)-cos(α-β)]2化asinα±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)THANKS致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求欢迎您的下载,资料仅供参考。
三角函数公式表大全

三角函数公式表大全以下是常用的三角函数公式表:1. 正弦函数(Sine Function):- 正弦函数的定义:sinθ = 对边/斜边- 余弦函数与正弦函数的关系:cosθ = 邻边/斜边- 正弦函数的倒数:cosecθ = 1/sinθ- 余弦函数的倒数:secθ = 1/cosθ- 正弦函数的平方:sin^2θ + cos^2θ = 1- 正弦函数的和差公式:sin(α ± β) = sinαcosβ ± cosαsinβ- 正弦函数的倍角公式:sin2θ = 2sinθcosθ2. 余弦函数(Cosine Function):- 余弦函数的定义:cosθ = 邻边/斜边- 正弦函数与余弦函数的关系:sinθ = 对边/斜边- 余弦函数的倒数:secθ = 1/cosθ- 正弦函数的倒数:cosecθ = 1/sinθ- 余弦函数的平方:cos^2θ + sin^2θ = 1- 余弦函数的和差公式:cos(α ± β) = cosαcosβ ∓sinαsinβ- 余弦函数的倍角公式:cos2θ = cos^2θ - sin^2θ3. 正切函数(Tangent Function):- 正切函数的定义:tanθ = 对边/邻边= sinθ/cosθ- 正切函数的倒数:cotθ = 1/tanθ = cosθ/sinθ- 正切函数与正弦、余弦的关系:tanθ = sinθ/cosθ = (对边/斜边) / (邻边/斜边) = 对边/邻边- 正切函数的和差公式:tan(α ± β) = (tanα ± tanβ) / (1 ∓tanαtanβ)4. 反三角函数:- 反正弦函数(Arcsine Function):sin⁻¹(x) = θ,其中-π/2 ≤ θ ≤ π/2- 反余弦函数(Arccosine Function):cos⁻¹(x) = θ,其中0 ≤ θ ≤ π- 反正切函数(Arctangent Function):tan⁻¹(x) = θ,其中-π/2 < θ < π/2这些是常用的三角函数公式,可以根据具体的问题和需要,灵活运用这些公式进行计算和推导。
proe曲线方程大集合_含三角函数公式大全
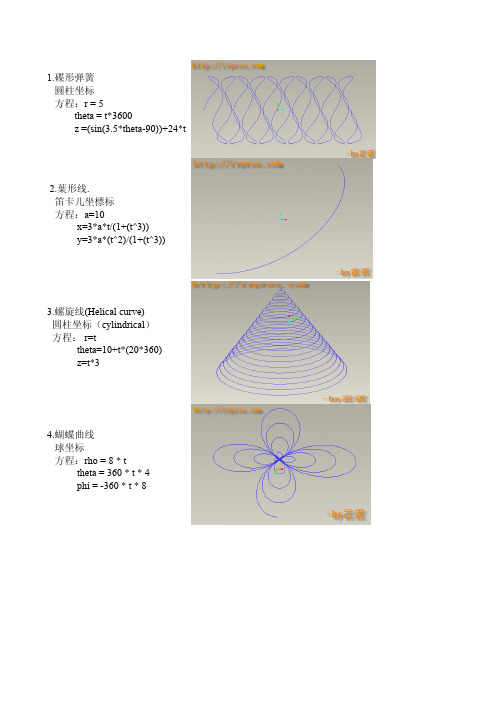
61.正弦周弹簧 笛卡尔: ang1=t*360 ang2=t*360*20 x=ang1*2*pi/360 y=sin(ang1)*5+cos(ang2) z=sin(ang2)
62.环形螺旋线 笛卡尔: x= (50+10*sin(t*360*15))*cos(t *360) y=(50+10*sin(t*360*15))*sin( t*360) z=10*cos(t*360*5)
36.一峰三驻点曲线 x = 3*t-1.5 y=(x^2-1)^3+1
37.八字曲线 x = 2 * cos ( t *(2*180)) y = 2 * sin ( t *(5*360)) z = 0
38.螺旋曲线 r=t*(10*180)+1 theta=10+t*(20*180) z=t
39.圆 x = cos ( t *(5*180)) y = sin ( t *(5*180)) z = 0
43.8字形曲线 柱坐标 theta = t*360 r=10+(8*sin(theta))^2
44.椭圆曲线 笛卡尔坐标系 a = 10 b = 20 theta = t*360 x = a*cos(theta) y = b*sin(theta)
45.梅花曲线 柱坐标 theta = t*360 r=10+(3*sin(theta*2.5))^2
52 簪形线 球坐标 方程: rho=200*t theta=900*t phi=t*90*10
53.螺旋上升曲线 r=t^10 theta=t^3*360*6*3+t^3*360*3* 3 z=t^3*(t+1)
54.蘑菇曲线 rho=t^3+t*(t+1) theta=t*360 phi=t^2*360*20*20
三角函数公式大全表格数学最全公式整理

三角函数公式大全表格数学最全公式整理三角函数公式看似很多、很复杂,但只要掌握了三角函数的本质及内部规律,就会发现三角函数各个公式之间有强大的联系。
三角函数公式大全表格一、倍角公式1、Sin2A=2SinA*CosA2、Cos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-13、tan2A=(2tanA)/(1-tanA^2)(注:SinA^2 是sinA的平方 sin2(A))二、降幂公式1、sin^2(α)=(1-cos(2α))/2=versin(2α)/22、2cos^2(α)=(1+cos(2α))/2=covers(2α)/23、tan^2(α)=(1-cos(2α))/(1+cos(2α))三、推导公式1、1tanα+cotα=2/sin2α2、tanα-cotα=-2cot2α3、1+cos2α=2cos^2α4、、4-cos2α=2sin^2α5、1+sinα=(sinα/2+cosα/2)^2=2sina(1-sin2a)+(1-2sin2a)sina四、两角和差1、1cos(α+β)=cosα·cosβ-sinα·sinβ2、cos(α-β)=cosα·cosβ+sinα·sinβ3、sin(α±β)=sinα·cosβ±cosα·sinβ4、4tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)5、tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)五、和差化积1、sinθ+sinφ =2 sin[(θ+φ)/2] cos[(θ-φ)/2]2、sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]3、cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]4、cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]5、tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)六、积化和差1、sinαsinβ = [cos(α-β)-cos(α+β)] /22、sinαcosβ = [sin(α+β)+sin(α-β)]/23、cosαsinβ = [sin(α+β)-sin(α-β)]/2七、诱导公式1、(-α) = -sinα、cos(-α) = cosα2、tan (—a)=-tanα、sin(π/2-α) = cosα、cos(π/2-α) = sinα、sin(π/2+α) = cosα3、3cos(π/2+α) = -sinα4、(π-α) = sinα、cos(π-α) = -cosα5、5tanA= sinA/cosA、tan(π/2+α)=-cotα、tan(π/2-α)=cotα6、tan(π-α)=-tanα、tan(π+α)=tanα八、锐角三角函数公式1、sin α=∠α的对边 / 斜边2、α=∠α的邻边 / 斜边3、tan α=∠α的对边/ ∠α的邻边4、cot α=∠α的邻边/ ∠α的对边高中数学最全公式1.几何与常用逻辑用语2.复数3.平面向量4.算法、推理与证明5.不等式、线性规划6.排列组合与二项式定理7.函数、基本初等函数的图像与性质8.函数与方程,函数模型及其应用9.导数及其应用10.三角函数的图形与性质11.三角恒等变化与解三角形12.等差数列、等比数列13.数列求和及数列的简单应用14.空间几何体15.空间点、直线、平面位置关系16.空间向量与立体几何17.直线与圆的方程18.圆锥曲线的定义、方程与性质19.圆锥曲线的热点问题20.概率21.离散型随机变量及其分布22.统计与统计案例23.函数与方程思想,数学结合思想24.分类与整合思想,化归与转化思想25.坐标系与参数方程26.不等式选讲。
Creo常用函数.doc

Creo(PROE)中关系式的理解一)关系式中可以用下列数学函数式表达:1)、正弦sin( )2)、余弦cos( )3)、正切tan( )4)、反正弦asin( )5)、反余弦acos( )6)、反正切atan( )7)、双曲线正弦sinh( )8)、双曲线余弦cosh( )9)、双曲线正切tanh( )以上九种三角函数式所使用的单位均为“度”。
10)、平方根sqrt( )11)、以10为底的对数log( )12)、自然对数ln( )13)、e的幂exp( )14)、绝对值abs( )15)、不小于其值的最小整数(上限值)ceil( )16)、不超过其值的最大整数(下限值)floor( )可以给函数ceil和floor加一个可选的自变量,用它指定要圆整的小数位数。
带有圆整参数的这些函数的语法是:ceil(parameter_name或number, number_of_dec_places)floor (parameter_name 或number, number_of_dec_places)其中的parameter_name或number意为参数名称或者一个带小数位的精确数值后面跟随着的number_of_dec_places意为十进位的小数位数,是可选值:A)可以被表示为一个数或一个使用者自定义参数。
如果该参数值是一个实数,则被截尾成为一个整数。
B)它的最大值是8。
如果超过8,则不会舍入要舍入的数(第一个自变量),并使用其初值。
C)如果不指定它,则功能同前期版本一样。
使用不指定小数部分位数的ceil和floor函数,其举例如下:ceil (10.2) 值为11floor (10.2) 值为10使用指定小数部分位数的ceil和floor函数,其举例如下:ceil (10.255, 2) 等于10.26ceil (10.255, 0) 等于11 [ 与ceil (10.255)相同]ceil(10.25531415926,7)等于10.2553142ceil(10.25531415926,8)等于10.25531416floor (10.255, 2) 等于10.25floor (10.255, 0) 等于10.Floor(10.2531415926,7)等于10.2553141Floor(10.2531415926,8)等于10.25531415举例一:以上函数式通常用的四种表达式如下图:以上两种曲线是在proe中的曲线—从方程—指定坐标系(选系统中固有的坐标系)—选笛卡儿坐标,就会出现公式界面,再输入如上公式。
三角函数公式大全整理都有哪些

三角函数公式大全整理都有哪些三角函数公式大全整理都有哪些三角函数与幂函数、指数函数、对数函数等一样,属于基本初等函数。
三角函数是以角的弧度数为自变量的函数,常见的三角函数包括正弦函数、余弦函数、正切函数,以下是小编整理的三角函数的知识点,大家可以参考。
1三角函数公式大全整理公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα2三角函数怎样算度数一、sin度数公式1、sin30=1/22、sin45=根号2/23、sin60=根号3/2二、cos度数公式1、cos30=根号3/22、cos45=根号2/23、cos60=1/2三、tan度数公式1、tan30=根号3/32、tan45=13、tan60=根号3知识拓展:sin0=sin0°=0cos0=cos0°=1tan0=tan0°=0sin15=0.650; sin15°=0.259cos15=-0.759;cos15°=0.966 tan15=-0.855;tan15°=0.268 sin30°=1/2。
proe函数公式

proe函数公式名称:正弦曲线建立环境:Pro/E软件、笛卡尔坐标系x=50*ty=10*sin(t*360)z=0名称:螺旋线(Helical curve) 建立环境:PRO/E;圆柱坐标(cylindrical)r=ttheta=10+t*(20*360)z=t*3蝴蝶曲线球坐标 PRO/E方程:rho = 8 * ttheta = 360 * t * 4phi = -360 * t * 8Rhodonea 曲线采用笛卡尔坐标系theta=t*360*4x=25+(10-6)*cos(theta)+10*cos((10/6-1)*theta) y=25+(10-6)*sin(theta)-6*sin((10/6-1)*theta) *********************************圆内螺旋线采用柱座标系theta=t*360r=10+10*sin(6*theta)z=2*sin(6*theta)渐开线的方程r=1ang=360*tx0=s*cos(ang)y0=s*sin(ang)x=x0+s*sin(ang)y=y0-s*cos(ang)z=0对数曲线z=0x = 10*ty = log(10*t+0.0001)球面螺旋线(采用球坐标系)rho=4theta=t*180phi=t*360*20名称:双弧外摆线卡迪尔坐标方程: l=2.5b=2.5x=3*b*cos(t*360)+l*cos(3*t*360) Y=3*b*sin(t*360)+l*sin(3*t*360)名称:星行线卡迪尔坐标方程:a=5x=a*(cos(t*360))^3y=a*(sin(t*360))^3名稱:心脏线建立環境:pro/e,圓柱坐標a=10r=a*(1+cos(theta))theta=t*360名稱:葉形線建立環境:笛卡儿坐標a=10x=3*a*t/(1+(t^3))y=3*a*(t^2)/(1+(t^3))笛卡儿坐标下的螺旋线x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t一抛物线笛卡儿坐标x =(4 * t)y =(3 * t) + (5 * t ^2)z =0名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24*t方程: 阿基米德螺旋线x = (a +f sin (t))cos(t)/ay = (a -2f +f sin (t))sin(t)/bpro/e关系式、函数的相关说明资料?关系中使用的函数数学函数下列运算符可用于关系(包括等式和条件语句)中。
三角函数公式表(全)

三角函数公式表同角三角函数的基本关系式倒数关系: 商的关系:平方关系:tanα ·cotα=1 sinα ·cscα=1 sinα/cosα=tanαsin2α+cos2α=11+tan2α=sec2α(六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”)诱导公式(口诀:奇变偶不变,符号看象限。
)sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotαsin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotαsin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα(其中k∈Z)两角和与差的三角函数公式万能公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=co sαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtanα+tanβtan(α+β)=———----———1-tanα ·tanβtanα-tanβtan(α-β)=—————-------—1+tanα ·tanβ2tan(α/2)sinα=——————1+tan2(α/2)1-tan2(α/2) cosα=——————1+tan2(α/2)2tan(α/2)tanα=——————1-tan2(α/2)半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=—————1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=——————1-3tan2α三角函数的和差化积公式三角函数的积化和差公式Sinα+sinβ=2sin[(α+β)/2]·cos[(α-β)/2] sinα-sinβ=2cos[(α+β)/2]·sin[(α-β)/2] cos α+cosβ=2cos[(α+β)/2]·cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]·sin[(α-β)/2 ] 1sinα ·cosβ=-[sin(α+β)+sin(α-β)]21cosα ·sinβ=-[sin(α+β)-sin(α-β)]21cosα ·cosβ=-[cos(α+β)+cos(α-β)]21sinα ·sinβ=— -[cos(α+β)-cos(α-β)]2化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)。
三角函数公式表及其图表

三角函数公式表及其图表三角函数常用公式:(^表示乘方,例如^2表示平方)正弦函数sinθ=y/r余弦函数cosθ=x/r正切函数tanθ=y/x余切函数cotθ=x/y正割函数secθ=r/x余割函数cscθ=r/y以及两个不常用,已趋于被淘汰的函数:正矢函数versinθ =1-cosθ余矢函数vercosθ =1-sinθ同角三角函数间的基本关系式:·平方关系:sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)·积的关系:sinα=tanα*cosαcosα=cotα*sinαtanα=sinα*secαcotα=cosα*cscαsecα=tanα*cscαcscα=secα*cotα·倒数关系:tanα·cotα=1sinα·cscα=1cosα·secα=1直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,三角函数恒等变形公式·两角和与差的三角函数:cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·辅助角公式:Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)·倍角公式:sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]·三倍角公式:sin(3α)=3sinα-4sin^3(α)cos(3α)=4cos^3(α)-3cosα·半角公式:sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=vercos(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))·万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]两角和公式sin(a+b)=sinacosb+cosasinbsin(a-b)=sinacosb-sinbcosacos(a+b)=cosacosb-sinasinbcos(a-b)=cosacosb+sinasinbtan(a+b)=(tana+tanb)/(1-tanatanb)tan(a-b)=(tana-tanb)/(1+tanatanb)cot(a+b)=(cotacotb-1)/(cotb+cota)cot(a-b)=(cotacotb+1)/(cotb-cota)倍角公式tan2a=2tana/[1-(tana)^2]cos2a=(cosa)^2-(sina)^2=2(cosa)^2 -1=1-2(sina)^2sin2a=2sina*cosa半角公式sin(a/2)=√((1-cosa)/2) sin(a/2)=-√((1-cosa)/2)cos(a/2)=√((1+cosa)/2) cos(a/2)=-√((1+cosa)/2)tan(a/2)=√((1-cosa)/((1+cosa)) tan(a/2)=-√((1-cosa)/((1+cosa)) cot(a/2)=√((1+cosa)/((1-cosa)) cot(a/2)=-√((1+cosa)/((1-cosa)) tan(a/2)=(1-cosa)/sina=sina/(1+cosa)和差化积2sinacosb=sin(a+b)+sin(a-b)2cosasinb=sin(a+b)-sin(a-b) )2cosacosb=cos(a+b)-sin(a-b)-2sinasinb=cos(a+b)-cos(a-b)sina+sinb=2sin((a+b)/2)cos((a-b)/2cosa+cosb=2cos((a+b)/2)sin((a-b)/2)tana+tanb=sin(a+b)/cosacosb积化和差公式sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)sin(pi/2-a)=cos(a)cos(pi/2-a)=sin(a)sin(pi/2+a)=cos(a)cos(pi/2+a)=-sin(a)sin(pi-a)=sin(a)cos(pi-a)=-cos(a)sin(pi+a)=-sin(a)cos(pi+a)=-cos(a)tga=tana=sina/cosa万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2))cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))其它公式a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c) [其中,tan(c)=b/a] a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c) [其中,tan(c)=a/b] 1+sin(a)=(sin(a/2)+cos(a/2))^21-sin(a)=(sin(a/2)-cos(a/2))^2其他非重点三角函数csc(a)=1/sin(a)sec(a)=1/cos(a)双曲函数sinh(a)=(e^a-e^(-a))/2cosh(a)=(e^a+e^(-a))/2tgh(a)=sinh(a)/cosh(a)。
Proe中的常用函数关系

Proe中的部分函数关系一、函数关系sin 正弦Cos 余弦tan 正切asin 反正弦acos 反余弦atan 反正切sinh 双曲线余弦cosh 双曲线正弦tanh 双曲线正切spar 平方根exp e的幂方根abs 绝对值log 以10为底的对数ln 自然对数ceil 不小于其值的最小整数floor 不超过其值的最大整数二、齿轮公式alpha=20m=2z=30c=0.25ha=1db=m*z*cos(alpha)r=(db/2)/cos(t*50)theta=(180/pi)*tan(t*50)-t*50z=0三、蜗杆的公式da=8为蜗杆外径m=0.8 为模数angle=20压力角L=30长度q直径系数d分度圆直径f齿根圆直径n实数其中之间的关系q=da/m-2 d=q*m df=(q-2.4)*m n=ceil(2*l/(pi*m)) 在可变剖面扫描的时候运用公式sd4=trajpar*360*n在扫描切口的时候绘制此图形,其中红色的高的计算公式是sd5=pi*m/2五、方向盘的公式sd4=sd6*(1-(sin(trajpar*360*36)+1)/8)其中sd4是sd6的(3/4或者7/8),sin(trajpar*360*36的意思是转过360度且有36个振幅似的六、凸轮的公式sd5=evalgraph("cam2",trajpar*360)r=150theta=t*360z=9*sin(10*t*360) 在方向按sin(10*t*360)的函数关系,9为高的9倍10为10个振幅似的七、锥齿轮公式m=4模数z =50齿轮齿数z-am=40与之啮合的齿轮齿数angle=20压力角b=30齿厚long分度圆锥角d分度圆直径da齿顶圆直径df齿根圆直径db基圆直径关系:long=atan(z/z-am) d=m*z da=d+2*m*cos(long)df=d-2.4*m*cos(long) db=d*cos(angle)螺纹从M6到M16的画法:螺距M6为1,M16为2,中间M7-M15都以0.25为等差数列(eg:M7=1.25)!!M20-M24以0.5递增(M20为2.5)八、螺纹收尾直齿轮渐开线公式r=db/2theta=t*45x=r*cos(theta)+r*sin(theta)*theta*pi/180y=r*sin(theta)-r*cos(theta)*theta*pi/180z=0涡轮公式GAMMMA=ATAN(Z1/Q)BETA=GAMMAALPHA_T=ATAN(TAN(ALPHA)/COS(BETA))S=pi*Z1*MD0=M*Q/2D1=M*(Q+Z2+2*X2)/2D7=360/(4*Z2)-180*TAN(ALPHA_T)/pi+ALPHA_TD8=M*Z2D9=D8+2*MD10=D8*COS(ALPHA_T) D11=D8-2.4*mD20=2*D1D19=M*Q/2D29=BETAD34=D8+2*(1+X2)*MIF Z1<=1D33=D34+2*MENDIFIF Z1>1IF Z1<=3D33=D34+1.5*MENDIFENDIFIF Z1>3D33=D34+MENDIFD32=BD35=M*(Q-2)/2汽车的方向盘公式sd25=sd4*(1-(sin(trajpar*360*36)+1)/8) (其中,25为竖直高度,4为上半圆的半径)齿轮公式alpha=20m=2z=30c=0.25ha=1db=m*z*cos(alpha)r=(db/2)/cos(t*50)theta=(180/pi)*tan(t*50)-t*50z=0阿基米德螺线公式theta=t*360*5(360为一圈的角度,5为5圈)r=2.5+4*t*5(2.5为起始半径,4为螺距,5为5圈)z=0(阿基米德螺线卷线器proe造型-icefai-新浪播客)PROE曲线公式名称:正弦曲线建立环境:Pro/E软件、笛卡尔坐标系x=50*ty=10*sin(t*360)z=0/Article/UploadFiles/200409/20040918204445198.jpg 名称:正弦曲线建立环境:Pro/E软件、笛卡尔坐标系x=50*ty=10*sin(t*360)z=0名称:螺旋线(Helical curve)建立环境:PRO/E;圆柱坐标(cylindrical)r=ttheta=10+t*(20*360)z=t*3/Article/UploadFiles/200409/20040918204446214.jpg 蝴蝶曲线球坐标PRO/E方程:rho = 8 * ttheta = 360 * t * 4phi = -360 * t * 8/Article/UploadFiles/200409/20040918204446240.jpg Rhodonea 曲线采用笛卡尔坐标系theta=t*360*4x=25+(10-6)*cos(theta)+10*cos((10/6-1)*theta)y=25+(10-6)*sin(theta)-6*sin((10/6-1)*theta)*********************************圆内螺旋线采用柱座标系theta=t*360r=10+10*sin(6*theta)z=2*sin(6*theta)/Article/UploadFiles/200409/20040918204446171.jpg 渐开线的方程r=1ang=360*ts=2*pi*r*tx0=s*cos(ang)y0=s*sin(ang)x=x0+s*sin(ang)y=y0-s*cos(ang)z=0/Article/UploadFiles/200409/20040918204447490.jpg 对数曲线z=0x = 10*ty = log(10*t+0.0001)/Article/UploadFiles/200409/20040918204447584.jpg 球面螺旋线(采用球坐标系)rho=4theta=t*180phi=t*360*20/Article/UploadFiles/200409/20040918204447175.jpg 名称:双弧外摆线卡迪尔坐标方程:l=2.5b=2.5x=3*b*cos(t*360)+l*cos(3*t*360)Y=3*b*sin(t*360)+l*sin(3*t*360)/Article/UploadFiles/200409/20040918204447186.jpg 名称:星行线卡迪尔坐标方程:a=5x=a*(cos(t*360))^3y=a*(sin(t*360))^3/Article/UploadFiles/200409/20040918204447139.jpg 名稱:心臟線建立環境:pro/e,圓柱坐標a=10r=a*(1+cos(theta))theta=t*360/Article/UploadFiles/200409/20040918204447387.jpg 名稱:葉形線建立環境:笛卡儿坐標a=10x=3*a*t/(1+(t^3))y=3*a*(t^2)/(1+(t^3))/Article/UploadFiles/200409/20040918204448710.jpg 笛卡儿坐标下的螺旋线x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t/Article/UploadFiles/200409/20040918204448724.gif 一抛物线笛卡儿坐标x =(4 * t)y =(3 * t) + (5 * t ^2)z =0/Article/UploadFiles/200409/20040918204448549.jpg 名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24。
proe关系式大全

proe关系式大全 cos 余弦 tan 正切 sin 正弦 sqrt 平方根 asin 反正弦 acos 反余弦 atan 反正切sinh 双曲线正弦 cosh 双曲线余弦 tanh 双曲线正切注释所有三角函数都使用单位度。
log 以10为底的对数 ln 自然对数 exp e的幂 abs 绝对值 ceil 不小于其值的最小整数 floor 不超过其值的最大整数可以给函数ceil和floor加一个可选的自变量用它指定要圆整的小数位数。
带有圆整参数的这些函数的语法是ceilparameter_name或number number_of_dec_places floor parameter_name 或number number_of_dec_places 其中number_of_dec_places是可选值 1、可以被表示为一个数或一个使用者自定义参数。
如果该参数值是一个实数则被截尾成为一个整数。
2、它的最大值是8。
如果超过8则不会舍入要舍入的数第一个自变量并使用其初值。
3、如果不指定它则功能同前期版本一样。
使用不指定小数部分位数的ceil和floor函数其举例如下 ceil 10.2 值为11 floor 10.2 值为 11 使用指定小数部分位数的ceil 和floor函数其举例如下 ceil 10.255 2 等于10.26 ceil 10.255 0 等于11 与ceil 10.255相同 floor 10.255 1 等于10.2 floor 10.255 2 等于10.26 曲线表计算曲线表计算使使用者能用曲线表特征通过关系来驱动尺寸。
尺寸可以是草绘器、零件或组件尺寸。
格式如下 evalgraphgraph_name x 其中graph_name 是曲线表的名称x是沿曲线表x-轴的值返回y值。
对于混合特征可以指定轨线参数trajpar作为该函数的第二个自变量。
注释曲线表特征通常是用于计算x-轴上所定义范围内x值对应的y值。
三角函数公式大全

三角函数公式大全一、基本定义及性质1. 正弦函数(sin):sin A = 对边 / 斜边cos A = 临边 / 斜边tan A = 对边 / 临边余切函数(cot):cot A = 临边 / 对边2.零度三角函数:sin 0° = 0, cos 0° = 1, tan 0° = 0, cot 0° = ∞3.π/6弧度三角函数:sin (π/6) = 1/2, cos (π/6) = √3/2, tan (π/6) = 1/√3, cot (π/6) = √34.π/4弧度三角函数:sin (π/4) = √2/2, cos (π/4) = √2/2, tan (π/4) = 1, cot (π/4) = 15.π/3弧度三角函数:sin (π/3) = √3/2, cos (π/3) = 1/2, tan (π/3) = √3, cot (π/3) = 1/√36.相反角关系:sin (-A) = -sin A, cos (-A) = cos A, tan (-A) = -tan A, cot (-A) = -cot A7.90°三角函数:sin 90° = 1, cos 90° = 0, tan 90° = ∞, cot 90° = 08.π/2弧度三角函数:sin (π/2) = 1, cos (π/2) = 0, tan (π/2) = ∞, cot (π/2) = 09.倒数关系:sin (π - A) = sin A, cos (π - A) = -cos A, tan (π - A) = -tan A, cot (π - A) = -cot A10.余角关系:sin (π/2 - A) = cos A, cos (π/2 - A) = sin A, tan (π/2 -A) = cot A, cot (π/2 - A) = tan A二、和差与倍角公式1.和差公式:sin (A ± B) = sin A cos B ± cos A sin Bcos (A ± B) = cos A cos B ∓ sin A sin Btan (A ± B) = (tan A ± tan B) / (1 ∓ tan A tan B)2.二倍角公式:sin 2A = 2 sin A cos Acos 2A = cos^2 A - sin^2 A = 2 cos^2 A - 1 = 1 - 2 sin^2 A tan 2A = (2 tan A) / (1 - tan^2 A)三、万能角公式(三角函数的倒数、减角公式、二倍角公式的推广形式)1.正弦函数倒数公式:csc A = 1 / sin A2.余弦函数倒数公式:sec A = 1 / cos A3.正切函数倒数公式:cot A = 1 / tan A4.减角公式:sin (A - B) = sin A cos B - cos A sin Bcos (A - B) = cos A cos B + sin A sin Btan (A - B) = (tan A - tan B) / (1 + tan A tan B)5.二倍角公式推广形式:sin 2A = 2 sin A cos Acos 2A = cos^2 A - sin^2 A = 2 cos^2 A - 1 = 1 - 2 sin^2 A tan 2A = (2 tan A) / (1 - tan^2 A)四、积和差公式1.积公式:sin A sin B = (1/2)[cos(A-B) - cos(A+B)]cos A cos B = (1/2)[cos(A-B) + cos(A+B)]sin A cos B = (1/2)[sin(A-B) + sin(A+B)]2.差公式:sin A - sin B = 2 cos[(A+B)/2] sin[(A-B)/2]cos A - cos B = -2 sin[(A+B)/2] sin[(A-B)/2]sin A + sin B = 2 sin[(A+B)/2] cos[(A-B)/2]cos A + cos B = 2 cos[(A+B)/2] cos[(A-B)/2]五、其他重要性质1. 正弦函数的周期:2π,即sin (x + 2π) = sin x余弦函数的周期:2π,即cos (x + 2π) = cos x2.正弦函数的奇偶性:sin (-x) = -sin x,即 sin 函数是奇函数sin (π + x) = -sin x,即 sin 函数是周期为2π的周期函数3.余弦函数的奇偶性:cos (-x) = cos x,即 cos 函数是偶函数cos (π + x) = -cos x,即 cos 函数是周期为2π的周期函数4.正弦函数和余弦函数的间接关系:sin^2 x + cos^2 x = 1。
proe关系式详解

一)关系式中可以用下列数学函数式表达:1)、正弦sin( )2)、余弦cos( )3)、正切tan( )4)、反正弦asin( )5)、反余弦acos( )6)、反正切atan( )7)、双曲线正弦sinh( )8)、双曲线余弦cosh( )9)、双曲线正切tanh( )以上九种三角函数式所使用的单位均为“度”。
10)、平方根sqrt( )11)、以10为底的对数log( )12)、自然对数ln( )13)、e的幂exp( )14)、绝对值abs( )15)、不小于其值的最小整数(上限值)ceil( )16)、不超过其值的最大整数(下限值)floor( )可以给函数ceil和floor加一个可选的自变量,用它指定要圆整的小数位数。
带有圆整参数的这些函数的语法是:ceil(parameter_name或number, number_of_dec_places)floor (parameter_name 或number, number_of_dec_places)其中的parameter_name或number意为参数名称或者一个带小数位的精确数值后面跟随着的number_of_dec_places意为十进位的小数位数,是可选值:A)可以被表示为一个数或一个使用者自定义参数。
如果该参数值是一个实数,则被截尾成为一个整数。
B)它的最大值是8。
如果超过8,则不会舍入要舍入的数(第一个自变量),并使用其初值。
C)如果不指定它,则功能同前期版本一样。
使用不指定小数部分位数的ceil和floor函数,其举例如下:ceil (10.2) 值为11floor (10.2) 值为10使用指定小数部分位数的ceil和floor函数,其举例如下:ceil (10.255, 2) 等于10.26ceil (10.255, 0) 等于11 [ 与ceil (10.255)相同]ceil(10.25531415926,7)等于10.2553142ceil(10.25531415926,8)等于10.25531416floor (10.255, 2) 等于10.25floor (10.255, 0) 等于10.Floor(10.2531415926,7)等于10.2553141Floor(10.2531415926,8)等于10.25531415二)关系式中还可以用下列曲线表计算式表达:曲线表计算使用者能用曲线表特征,通过关系来驱动尺寸。
完整版)完整三角函数公式表

完整版)完整三角函数公式表三角函数公式表同角三角函数的基本关系式三角函数是数学中的重要概念,它们在数学和物理学中都有广泛的应用。
同角三角函数的基本关系式包括倒数关系、商的关系和平方关系。
其中,倒数关系式如下:tan\alpha\cdot\cot\alpha=1$$sin\alpha\cdot\csc\alpha=1$$cos\alpha\cdot\sec\alpha=1$$商的关系式如下:frac{\sin\alpha}{\cos\alpha}=\tan\alpha=\frac{\sec\alpha}{\csc\alpha}$$frac{\cos\alpha}{\sin\alpha}=\cot\alpha=\frac{\csc\alpha}{\sec\alpha}$$平方关系式如下:sin^2\alpha+\cos^2\alpha=1$$2^2+ \tan^2\alpha=\sec^2\alpha$$1+\cot^2\alpha=\csc^2\alpha$$这些关系式可以用六边形记忆法和记忆方法来记忆。
其中,六边形记忆法是指图形结构“上弦中切下割,左正右余中间1”,而记忆方法是指对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
诱导公式诱导公式是指通过已知的三角函数值来推导其他角度的三角函数值的公式。
它们可以用口诀“奇变偶不变,符号看象限”来记忆。
具体来说,诱导公式包括三角函数的奇偶性和象限问题。
奇偶性公式如下:sin(-\alpha)=-\sin\alpha$$cos(-\alpha)=\cos\alpha$$tan(-\alpha)=-\tan\alpha$$cot(-\alpha)=-\cot\alpha$$象限问题公式如下:sin\left(\frac{3\pi}{2}-\alpha\right)=-\cos\alpha$$ cos\left(\frac{3\pi}{2}-\alpha\right)=-\sin\alpha$$ sin(2\pi-\alpha)=-\sin\alpha$$cos(2\pi-\alpha)=\cos\alpha$$tan\left(\frac{3\pi}{2}-\alpha\right)=\cot\alpha$$ tan(2\pi-\alpha)=-\tan\alpha$$cot\left(\frac{3\pi}{2}-\alpha\right)=\tan\alpha$$ cot(2\pi-\alpha)=-\cot\alpha$$另外,还有两个特殊的角度:sin\left(\frac{\pi}{2}-\alpha\right)=\cos\alpha$$cos\left(\frac{\pi}{2}-\alpha\right)=\sin\alpha$$ tan\left(\frac{\pi}{2}-\alpha\right)=\cot\alpha$$ cot\left(\frac{\pi}{2}-\alpha\right)=\tan\alpha$$ sin\left(\frac{\pi}{2}+\alpha\right)=\cos\alpha$$ cos\left(\frac{\pi}{2}+\alpha\right)=-\sin\alpha$$ tan\left(\frac{\pi}{2}+\alpha\right)=-\cot\alpha$$ cot\left(\frac{\pi}{2}+\alpha\right)=-\tan\alpha$$ sin(\pi-\alpha)=\sin\alpha$$cos(\pi-\alpha)=-\cos\alpha$$tan(\pi-\alpha)=-\tan\alpha$$cot(\pi-\alpha)=-\cot\alpha$$sin(\pi+\alpha)=-\sin\alpha$$cos(\pi+\alpha)=-\cos\alpha$$tan(\pi+\alpha)=\tan\alpha$$cot(\pi+\alpha)=\cot\alpha$$两角和与差的三角函数公式最后,还有两角和与差的三角函数公式。
ProE系统函数
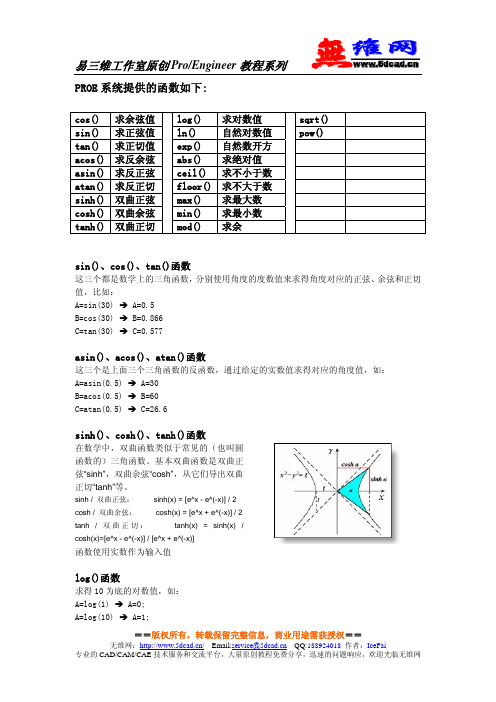
PROE 系统提供的函数如下:cos() 求余弦值 log() 求对数值 sqrt() sin() 求正弦值 ln() 自然对数值 pow()tan() 求正切值 exp() 自然数开方 acos() 求反余弦 abs() 求绝对值 asin() 求反正弦 ceil() 求不小于数 atan() 求反正切 floor()求不大于数 sinh() 双曲正弦 max() 求最大数 cosh() 双曲余弦 min() 求最小数 tanh() 双曲正切 mod() 求余sin()、cos()、tan()函数这三个都是数学上的三角函数,分别使用角度的度数值来求得角度对应的正弦、余弦和正切值,比如:A=sin(30) Î A=0.5 B=cos(30) Î B=0.866 C=tan(30) Î C=0.577asin()、acos()、atan()函数这三个是上面三个三角函数的反函数,通过给定的实数值求得对应的角度值,如: A=asin(0.5) Î A=30 B=acos(0.5) Î B=60 C=atan(0.5) Î C=26.6sinh()、cosh()、tanh()函数在数学中,双曲函数类似于常见的(也叫圆函数的)三角函数。
基本双曲函数是双曲正弦“sinh”,双曲余弦“cosh”,从它们导出双曲正切“tanh”等。
sinh / 双曲正弦: sinh(x) = [e^x - e^(-x)] / 2 cosh / 双曲余弦: cosh(x) = [e^x + e^(-x)] / 2tanh / 双曲正切: tanh(x) = sinh(x) / cosh(x)=[e^x - e^(-x)] / [e^x + e^(-x)]函数使用实数作为输入值log()函数求得10为底的对数值,如: A=log(1) Î A=0; A=log(10) Î A=1;==版权所有,转载保留完整信息,商业用途需获授权==A=log(5) Î A=0.6989...;ln()函数求得以自然数e为底的对数值,e是自然数,值是2.718...;如:A=ln(1) Î A=0;A=ln(5) Î A=1.609...;exp()函数求得以自然数e为底的开方数,如:A=exp(2) Î A=e^2=7.387...;abs()函数求得给定参数的绝对值,如A=abs(-1.6) Î A=1.6B=abs(3.5) Î B=3.5max()、min()函数求得给定的两个参数之中的最大最小值,如A=max(3.8,2.5) Î A=3.8B=min(3.8,2.5) Î B=2.5mod()函数求第一个参数除以第二个参数得到的余数,如:A=mod(20,6) Î A=2B=mod(20.7,6.1) Î B=2.4sqrt()函数pow()函数ceil和floor均可有一个附加参数,用它可指定舍去的小数位.ceil(parameter_name or number, number_of_dec_places). floor(parameter_name or number, number_of_dec_places). | |参数名或数值. 要保留的小数位(可省略) number_of_ded_places:它的取值的不同可有不同的结果.i)可以为数值亦可为参数,若为实数则取整.ii)若number_of_dec_place>8,则不作任何处理,用原值若number_of_dec_place≦8,则舍去其后的小数位,则进位 例如:==版权所有,转载保留完整信息,商业用途需获授权==Ceil(10.2)-->11 比10.2大的最小整数为11.floor(-10.2)-->-11 比-10.2小的最大整数为-11.floor(10.2)-->10 比10.2小的最大整数为10.Ceil(10.255,2)-->10.26. 比10.255大的最小符合数. Ceil(10.255,0)-->11floor(10.255,1)-->10.2Len1=ceil(20.5) ==>Len1=21Len2=floor(-11.3) ==>Len2=-12Len=Len1+Len2 ==>Len=9o string_length( )用法:String_length(Parameter name or string).参数名或字符串例:strlen1=string_length("material") 则 strlen1=8若material="steel",strlen2=string_length(material),则strlen2=5,字符串要用" "括起,空格亦算一个字符.o rel_model_name( )用法:rel_model_name( ) 注意括号内为空的,返回目前模型名称.例:当前模型为-part1,则partName=rel_model_name( )==>partName="part1"如在装配图中,则需加上进程号(session Id),例如partName=rel_model_name:2( )o rel_model_type( ) 返回目前模型类型用法: rel_model_type( )例:如当前模型为装配图parttype=rel_model_type( ) ==>parttype="ASSEMBLY".若为一零件图则 ==>parttype="PART".o exists( ) 测试项目存在与否用法:exists(Item) Item可以是参数或尺寸.例:If exists(d5) 检查零件内是否有d5尺寸.==版权所有,转载保留完整信息,商业用途需获授权==If exists("material") 检查零件内是否有material参数.o itos( ) 将整数换成字符串用法: Itos(integer) 整数,若为实数则舍去小数点.例:S1=Itos(123)==>s1="123"S2=itos(123.57)==>s2="123"intl=123.5 s3=itos(intl)==>s3="123"o search( ) 查找字符串,返回位置值用法:search(string,substring).string:原字符串substring:要找的字符串.查到则返回位置,否则返回0,第一个字符位置值为1,依此类推.例 :Parstr=abcdef.则Where=search(parstr,"bcd"")==>Where=2.Where=search(parstr,"bed")==>where=0(没查到).o extract( ) 提取字符串用法:extract(string,position,length)| | |原字符串 提取位 提取字符数position:大于0而小于字符串长度.length: position+length-1 不能大于字符串长度.例:new=extraecl("abcded",2,3)==>new="bcd".其含义是: 从"abcdef"串的第2个字符(b)开始取出3个字符.下例演示在PROE关系由标准文件名(bxxx-2xxx-xxx)分离出项目号,零件号及零件名:FileName=rel_modle_name() /* 获得文件名=>FileNameStrLen=string_length(FileName) /* 计算文件名长度=>StrLenProject_No=extract(FileName,1,4) /* 提取第1~4个字符=>Project_No Part_No=extract(FileName,6,4) /* 提取第6~9个字符=>Part_NoPart_Name=extract(FileName,11,StrLen-10) /*提取第10以后的字符=>Part_Nameo evalgraph()计算函数用法:evalgraph(graph_name,x_value),其中graph_name是指控制图表(graph)的名字,要用==版权所有,转载保留完整信息,商业用途需获授权==双引号括起,x_value是graph中的横坐标值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不超過其值的最大整數 可以給函數 ceil 和 floor 加一個可選的自變量,用它指 定要圓整的小數位數。 帶有圓整參數的這些函數的語法是:
下列運算符可用於關係(包括等式和條件語句)中。 關係中也可以包括下列數學函數: cos () 余弦 tan () 正切 sin () 正弦 sqrt () 平方根 asin () 反正弦 acos () 反余弦 atan () 反正切 sinh () 雙曲線正弦 cosh () 雙曲線余弦 tanh () 雙曲線正切 注釋:所有三角函數都使用單位度。 log() 以 10 為底的對數 ln() 自然對數 exp() e 的冪 abs() 絕對值 ceil() 不小於其值的最小整數 floor() ceil(parameter_name number_of_dec_places) floor (parameter_name number_of_dec_places) 或 number,
19. 抛物线 笛卡儿坐标 方程:x =(4 * t) y =(3 * t) + (5 * t ^2) z =0
20.螺旋线 圓柱坐标 方程:r = 5 theta = t*1800 z =(cos(theta90))+24*t
21.三叶线 圆柱坐标 方程:a=1 theta=t*380 b=sin(theta) r=a*cos(theta)*(4*b*b-1)
15.费马曲线(有点像螺纹线) 数学方程:r*r = a*a*theta 圓柱坐标 方程1: theta=360*t*5 a=4 r=a*sqrt(theta*180/pi) 方程2: theta=360*t*5 a=4 r=-a*sqrt(theta*180/pi) 由于Pro/e只能做连续的 曲线,所以只能分两次做
或
number,
其中 number_of_dec_places 是可選值: ·可以被表示為一個數或一個使用者自定義參數。如果 該參數值是一個實數,則被截尾成為一個整數。 ·它的最大值是 8。如果超過 8,則不會舍入要舍入的 數(第一個自變量) ,並使用其初值。 ·如果不指定它,則功能同前期版本一樣。 使用不指定小數部分位數的 ceil 和 floor 函數,其舉例 如下: ceil (10.2) 值為 11 floor (10.2) 值為 11 使用指定小數部分位數的 ceil 和 floor 函數,其舉例如 下: ceil (10.255, 2) 等於 10.26 ceil (10.255, 0) 等於 11 [ 與 ceil (10.255)相同 ] floor (10.255, 1) 等於 10.2 floor (10.255, 2) 等於 10.26 曲線表計算 曲線表計算使使用者能用曲線表特征,通過關係來驅 動尺寸。尺寸可以是草繪器、零件或組件尺寸。格式 如下: evalgraph("graph_name", x) ,其中 graph_name 是曲線表的名稱,x 是沿曲線表 x-軸的值,返回 y 值。 對於混合特征,可以指定軌線參數 trajpar 作為該函數 的第二個自變量。 注釋:曲線表特征通常是用於計算 x-軸上所定義範圍 內 x 值對應的 y 值。當超出範圍時,y 值是通過外推的 方法來計算的。對於小於初始值的 x 值,系統通過從 初始點延長切線的方法計算外推值。同樣,對於大於 終點值的 x 值,系統通過將切線從終點往外延伸計算 外推值。
6.螺旋线. 笛卡儿坐标 方程:x = 4 * cos ( t *(5*360)) y = 4 * sin ( t *(5*360)) z = 10*t
7.对数曲线 笛卡尔坐标系 方程:z=0 x = 10*t y = log(10*t+0.0001)
8.球面螺旋线 采用球坐标系 方程:rho=4 theta=t*180 phi=t*360*20
9.双弧外摆线 卡迪尔坐标 方程: l=2.5 b=2.5 x=3*b*cos(t*360)+l*cos(3*t*360) Y=3*b*sin(t*360)+l*sin(3*t*360)
10.星行线 卡迪尔坐标 方程:a=5 x=a*(cos(t*360))^3 y=a*(sin(t*360))^3
16.Talbot 曲线 卡笛尔坐标 方程:theta=t*360 a=1.1 b=0.666 c=sin(theta) f=1 x = (a*a+f*f*c*c)*cos(theta)/a y = (a*a2*f+f*f*c*c)*sin(theta)/b
18.Rhodonea 曲线 采用笛卡尔坐标系 方程:theta=t*360*4 x=25+(106)*cos(theta)+10*cos((10/61)*theta) y=25+(106)*sin(theta)-6*sin((10/61)*theta)
4.蝴蝶曲线 球坐标 方程:rho = 8 * t theta = 360 * t * 4 phi = -360 * t * 8
5.渐开线 采用笛卡尔坐标系 方程:r=1 ang=360*t s=2*pi*r*t x0=s*cos(ang) y0=s*sin(ang) x=x0+s*sin(ang) y=y0-s*cos(ang) z=0
增加關係 復合曲線軌道函數 可以把關係增加到: 在關係中可以使用復合曲線的軌道參數 trajpar_of_pnt。 下列函數返回一個 0.0 和 1.0 之間的值: trajpar_of_pnt("trajname", "pointname") 其中 trajname 是復合曲線名, pointname 是基準點名。 軌線是一個沿復合曲線的參數,在它上面垂直於曲線 切線的平面通過基準點。因此,基準點不必位於曲線 上;在曲線上距基準點最近的點上計算該參數值。 如果復合曲線被用作多軌道掃瞄的骨架,則 trajpar_of_pnt 與 trajpar 或 1.0 - trajpar 一致(取決 於為混合特征選擇的起點) 。 關於關係 關係(也被稱為參數關係)是使用者自定義的符號尺 寸和參數之間的等式。關係捕獲特征之間、參數之間 或組件元件之間的設計關係,因此,允許使用者來控 制對模型修改的影響作用。 關係是捕獲設計知識和意圖的一種方式。和參數一 樣,它們用於驅動模型 - 改變關係也就改變了模型。 關係可用於控制模型修改的影響作用、定義零件和組 件中的尺寸值、為設計條件擔當約束(例如,指定與 零件的邊相關的孔的位置) 。 它們用在設計過程中來描述模型或組件的不同部分之 間的關係。關係可以是簡單值(例如,d1=4)或復雜 的條件分支語句。 關係類型 注釋: 有兩種類型的關係: ·等式 - 使等式左邊的一個參數等於右邊的表達式 。 這 種關係用於給尺寸和參數賦值。例如: 簡單的賦值:d1 = 4.75 復雜的賦值:d5 = d2*(SQRT(d7/3.0+d4)) ·比較 - 比較左邊的表達式和右邊的表達式 。 這種關係 通常用於作為一個約束或用於邏輯分支的條件語句 中。例如: 作為約束:(d1 + d2) > (d3 + 2.5) 在條件語句中;IF (d1 + 2.5) >= d7 ─如果組件試圖給已經由零件或子組件關係驅動的尺 寸變量指派值時,出現兩個錯誤資訊。刪除關係之一 並重新生成。 ─修改模型的單位可使關係無效,因為它們沒有隨該模 型縮放。有關修改單位的詳細資訊,請參閱“關於公制 和非公制度量單位”幫助主題。 關係中使用參數符號 ─如果試圖將截面之外的關係指派給已經由截面關係 驅動的參數,則系統再生模型時給出錯誤資訊。試圖 將關係指派給已經由截面之外關係驅動的參數時也同 樣。刪除關係之一並重新生成。 ·特征(在零件或組件模式下) 。 ·零件(在零件或組件模式下) 。 ·組件(在組件模式下) 。 當第一次選擇關係功能表時,預設為查看或改變當前 模型(例如,零件模式下的一個零件)中的關係。 要獲得對關係的訪問,從“部件”或“組件”功能表中選擇 “關係 ”,然后從“ 模型關係”功能表中選擇下列命令之 一: ·組件關係 - 使用組件中的關係。如果組件包含一個或 多個子組件,“組件關係”功能表出現並帶有下列命令: ─當前 - 缺省時是頂層組件。 ─名稱 - 鍵入組件名。 ·骨架關係 - 使用組件中骨架模型的關係 (只對組件適 用) 。 ·零件關係 - 使用零件中的關係。 ·特征關係 - 使用特征特有的關係。如果特征有一個截 面,那麼使用者就可選擇:獲得對截面(草繪器)中 截面(草繪器)中關係的訪問,或者獲得對作為一個 整體的特征中的關係的訪問。 ·陣列關係 - 使用陣列所特有的關係。 ·特征的截面 (在草繪模式中,如果最初通過選擇“草繪 器”>“關係”>“增加”來創建截面) 。
11.心脏线 圓柱坐标 方程:a=10 r=a*(1+cos(theta)) theta=t*360
12.圆内螺旋线 采用柱座标系 方程:theta=t*360 r=10+10*sin(6*theta) z=2*sin(6*theta)
13.正弦曲线 笛卡尔坐标系 方程:x=50*t y=10*sin(t*360) z=0
在關係中使用四種類型的參數符號: ·尺寸符號 - 支持下列尺寸符號類型: ─d# - 零件或組件模式下的尺寸。 ─d#:# - 組件模式下的尺寸。組件或元件的進程標識 添加為后綴。 ─rd# - 零件或頂層組件中的參考尺寸。 ─rd#:# - 組件模式中的參考尺寸 (組件或元件的進程 標識添加為后綴) 。 ─rsd# - 草繪器中(截面)的參考尺寸。 ─kd# - 在草繪(截面)中的已知尺寸(在父零件或組 件中) 。 ·公差 - 這些是與公差格式相關連的參數 。 當尺寸由數 字的轉向符號的時侯出項這些符號。 ─tpm# - 加減對稱格式中的公差;#是尺寸數。 ─tp# - 加減格式中的正公差;#是尺寸數。 ─tm# - 加減格式中的負公差;#是尺寸數。 ·實例數 - 這些是整數參數,是陣列方向上的實例個 數。 ─p# - 其中#是實例的個數。 注釋:如果將實例數改變為一個非整數值, Pro/ENGINEER 將截去其小數部分。例如,2.90 將變 為 2。 ·使用者參數 - 這些可以是由增加參數或關係所定義 的參數。 例如: Volume = d0*d1*d2 Vendor = "Stockton Corp." 注釋: ─使用者參數名必須以字母開頭 (如果它們要用於關係 的話) 。 ─不能使用 d#、kd#、rd#、tm#、tp#、或 tpm#作 為使用者參數名,因為它們是由尺寸保留使用的。 ─使用者參數名不能包含非字母數字字符,諸如!、@、 #、$。 下列參數是由系統保留使用的: G(引力常數) 缺省值 = 9.8 米/秒 2 (C1、C2、C3 和 C4 是缺省值,分別等於 1.0、2.0、 3.0 和 4.0。) 可以使用 “關係”功能表中的“增加” 命令改變這些系統 參數的值。這些改變的值應用於當前工作區的所有模 型。 PI(幾何常數) 值 = 3.14159 (不能改變該值。)
