第7章MATLAB工程计算
学会使用Matlab进行科学与工程计算

学会使用Matlab进行科学与工程计算第一章:Matlab简介Matlab是一种强大的数值计算和数据可视化工具,广泛应用于科学与工程领域。
本章将介绍Matlab的基本特点和功能,以及如何安装和启动Matlab。
1.1 Matlab的基本特点Matlab是一种基于矩阵运算的高级编程语言,具有以下特点:- 可以处理多维数组和矩阵- 支持矩阵运算、数值计算和数据分析- 提供各种工具箱,如信号处理、图像处理和控制系统等- 具有友好的用户界面和丰富的帮助文档1.2 安装和启动Matlab可以从MathWorks官网上下载Matlab的安装程序,并按照提示进行安装。
安装完成后,可以通过双击桌面上的Matlab图标来启动Matlab。
第二章:Matlab基础本章将介绍Matlab的基础知识,包括变量和数据类型、运算符和控制流程等,以便读者快速上手Matlab编程。
2.1 变量和数据类型在Matlab中,可以使用赋值语句创建变量,并指定其数据类型。
常见的数据类型有数值类型、字符类型、逻辑类型等。
2.2 运算符Matlab支持各种数学运算符和逻辑运算符,用于执行数值计算和条件判断。
2.3 控制流程Matlab提供了多种控制流程语句,如条件语句和循环语句,用于实现程序的控制和流程调节。
第三章:数据处理与可视化本章将介绍Matlab中数据处理和可视化的基本方法,包括数据导入和导出、数据处理和数据可视化。
3.1 数据导入和导出可以使用Matlab内置的函数或者工具箱中的函数来导入和导出数据,常见的数据格式包括文本文件、Excel文件和图像文件等。
3.2 数据处理Matlab提供了丰富的数据处理函数,用于对数据进行加工、计算和分析,如统计分析、滤波和图像处理等。
3.3 数据可视化Matlab拥有强大的图形绘制功能,可以生成各种静态图和动态图,如散点图、折线图和柱状图等,以便更好地展示数据和分析结果。
第四章:数值计算本章将介绍Matlab中常用的数值计算方法和技巧,包括数值积分、方程求解和优化等。
MATLAB7.0使用详解-第7章 数据可视化

7.2.1 调用plot函数绘制二维图形
二维绘图函数中最基本的是plot函数,其余函数都是围绕 其发展扩充形成的。本小节首先介绍如何调用plot函数来 绘制图形。 MATLAB中调用plot函数的方式有3种,具体格式、功能及举 例如下。 1.plot(X,'s') 如X为实数向量时,MATLAB以X中元素的下标为横坐标,元 素值为纵坐标绘制连续曲线。如下绘制实数向量的图形。 2.plot(X,Y,'s') 如X和Y为同维向量,MATLAB以X为横坐标、以Y为纵坐标绘 制图形。 3.plot(X1,Y1,'s',X2,Y2,'s',X3,Y3,'s',…) 此种方式与第2种类似,不同的只是同时在图形窗口中绘制 多条互不影响的连续曲线。
7.2.4 设置坐标轴范围
在绘制某些图形的时候,用户对坐标轴的范围和刻度要求常常比 较严格,虽然MATLAB拥有便捷智能的函数和内部自适应设置,但 是显示的图形往往仍达不到用户所要求的效果。所以,MATLAB提 供给用户一系列坐标轴操作控制指令,使用户可以根据自己的具 体需要和爱好,有针对性地调整和设置坐标轴的某些参数。下面 首先列出MATLAB中常用的坐标轴操作函数。
7.3.2 使用mesh函数绘制三Байду номын сангаас网格图
用户在绘制三维图形时,常需要绘制曲线网格图,MATLAB提供了专门绘制 曲线网格图的函数mesh,此函数可以绘制出完整的曲面,其常用的调用格 式及功能如下。 mesh(Z):分别以矩阵Z的列、行下标作为x、y轴的自变量,进行绘图。 绘制一个随机5阶矩阵的曲线网格图,代码如下。 >> x=rand(5); >> mesh(x) 随即生成图形,如图所示。 mesh(X,Y,Z): 最常用的一般调用格式。 mesh(X,Y,Z,C):完整的调用格式,其中‘C’作用为指定图形的着色, ‘C’没有指定,系统默认C=Z。
matlab的教学课程设计

matlab 的教学课程设计一、课程目标知识目标:1. 掌握MATLAB的基础知识,包括数据类型、矩阵运算、程序流程控制等;2. 学会使用MATLAB进行数据可视化、图像处理、数值计算等操作;3. 了解MATLAB在工程领域的应用,并能结合所学专业进行简单的数据分析。
技能目标:1. 能够熟练运用MATLAB编写程序,解决实际问题;2. 学会使用MATLAB进行数据导入、导出,以及与Excel、Word等软件的数据交互;3. 培养学生运用MATLAB进行科学计算和工程问题求解的能力。
情感态度价值观目标:1. 培养学生对MATLAB编程的兴趣和热情,激发学生主动探索精神;2. 培养学生严谨的科学态度,提高学生的团队协作能力;3. 引导学生认识到MATLAB在现代工程技术中的重要性,树立正确的价值观。
课程性质:本课程为实践性较强的课程,旨在培养学生的编程能力和实际应用能力。
学生特点:学生具备一定的数学基础和编程兴趣,但对MATLAB编程可能较为陌生。
教学要求:结合学生特点和课程性质,注重理论与实践相结合,以案例教学为主,培养学生的实际操作能力。
在教学过程中,关注学生的个体差异,鼓励学生提问、讨论,提高学生的参与度和积极性。
通过课程学习,使学生能够独立完成MATLAB程序编写,解决实际问题。
二、教学内容1. MATLAB基础知识:数据类型、矩阵运算、程序流程控制等;教材章节:第一章 MATLAB概述,第二章 MATLAB基础知识。
2. 数据可视化与图像处理:绘图函数、图像处理基本操作等;教材章节:第三章 数据可视化,第四章 图像处理。
3. 数值计算:线性方程组求解、数值积分、插值等;教材章节:第五章 数值计算。
4. MATLAB在实际工程中的应用:结合所学专业,进行数据分析与处理;教材章节:第六章 MATLAB在工程中的应用。
5. MATLAB与其他软件的数据交互:数据导入、导出,与Excel、Word等软件的数据交互;教材章节:第七章 MATLAB与其他软件的数据交互。
MATLAB工程计算和仿真案例分析

MATLAB工程计算和仿真案例分析第一章:MATLAB的基础知识与编程技巧在工程计算和仿真领域中,MATLAB是一种广泛使用的软件工具。
本章将介绍MATLAB的基础知识和编程技巧,为后续的案例分析打下基础。
1.1 MATLAB的安装和配置在使用MATLAB之前,首先需要将其正确地安装在计算机上,并根据需要进行相关的配置。
本节将介绍如何下载、安装和配置MATLAB软件。
1.2 MATLAB的基本语法和命令MATLAB具有简洁而强大的编程语法和丰富的函数库,能够快速实现各种工程计算和仿真任务。
本节将介绍MATLAB的基本语法和常用命令,比如变量的定义与赋值、数学运算、矩阵操作等。
1.3 MATLAB的脚本文件和函数文件在实际应用中,通常需要编写包含多行MATLAB命令的脚本文件或函数文件。
本节将介绍如何编写和调用这些文件,以便更好地组织和管理代码。
第二章:MATLAB在工程计算中的应用本章将以几个具体的案例来演示MATLAB在工程计算中的应用。
从结构分析、信号处理到优化设计,MATLAB都可以提供强大的功能和灵活性。
2.1 结构分析案例结构分析是工程领域中重要的一部分,用于评估和优化工程结构的性能。
本节将介绍如何使用MATLAB进行结构分析,比如求解静力学和动力学问题,计算应力和变形等。
2.2 信号处理案例信号处理在许多应用领域中都扮演着重要角色,比如通信、音频处理等。
本节将介绍如何使用MATLAB进行信号处理,包括滤波、频谱分析、傅里叶变换等。
2.3 优化设计案例在工程设计中,优化是一个关键的任务,旨在寻找最优的设计方案。
本节将介绍如何使用MATLAB进行优化设计,包括单目标和多目标优化问题的求解,约束条件的处理等。
第三章:MATLAB在工程仿真中的应用本章将以几个具体的案例来演示MATLAB在工程仿真中的应用。
从系统仿真、控制系统设计到电路仿真,MATLAB具有丰富的工具箱和函数,为仿真提供了强大的支持。
数学建模案例分析--MATLAB在电气工程中的应用

Current directory
Launch pad
M-File
Figure
Model
GUI 2019/5/8
16
标题栏 发射台
菜单栏
常用工具栏
工作区间
命令 窗口
历史命令 当前目录
2019/5/8
17
2019/5/8
18
MATLAB命令窗口
MATLAB语句形式 >>变量=表达式;
当A是标量时: x b A
当A是非奇异矩阵时: x A1b
当A是行数大于列数的满秩阵时,
称超定方程组或矛盾方程组: x ( AT A)1 AT b
当A的列数大于行数时,有无数解。
MATLAB只用一条指令: x=A\b。
2019/5/8
3
MATLAB简介
例:绘制二元函数曲面:
z
y
பைடு நூலகம்
1 x2 y2
2019/5/8
26
1.4 MATLAB常用命令
1.5 MATLAB两种工作方式
【matlab-7】Matlab与线性代数(一)

【matlab-7】Matlab与线性代数(⼀)⼀、线性代数基本⽅程组基本⽅程组:矩阵表⽰:解决问题的视⾓:1、解联⽴⽅程的视⾓ (⾏阶梯变换 & 矩阵运算)着重研究解x,即研究线性⽅程组的解法。
中学⾥的解⽅程和MATLAB的矩阵除法就是这样。
要点:矩阵的每⼀⾏代表⼀个⽅程,m⾏代表m个线性联⽴⽅程。
n列代表n个变量。
如果m是独⽴⽅程数,根据m<n、m=n、m>n确定⽅程是 ‘⽋定’、‘适定’ 还是 ‘超定’。
对这三种情况都会求解了,研究就完成了。
必须剔除⾮独⽴⽅程。
⾏阶梯形式、⾏列式和秩的概念很⼤程度上为此⽬的⽽建⽴。
2、向量空间中向量的合成的视⾓ (⽤向量空间解⽅程组)把A各列看成n个m维基本向量,线性⽅程组看成基向量的线性合成:要点:解x是这些基向量的系数。
它可能是常数(适定⽅程),也可能成为其中的⼀个⼦空间(⽋定⽅程) 。
要建⽴其⼏何概念,并会求解或解空间。
3、线性变换或映射的视⾓ (线性变换及其特征)把b看成变量y,着重研究把Rn空间的x变换为Rm空间y 的效果,就是研究线性变换系数矩阵A的特征对变换的影响。
要点:就是要找到适当的变换,使研究问题的物理意义最为明晰。
特征值问题就是⼀例。
⼆、线性代数建模与应⽤概述介绍⼀些⼤的系统⼯程中使⽤线性代数的情况,使读者知道为什么线性代数在近⼏⼗年来变得如此的重要。
Leontief教授把美国的经济⽤500个变量的500个线性⽅程来描述,在1949年利⽤当时的计算机解出了42×42的简化模型,使他于1973年获得诺贝尔经济奖,从⽽⼤⼤推动了线性代数的发展。
把飞⾏器的外形分成若⼲⼤的部件,每个部件沿着其表⾯⼜⽤三维的细⽹格划分出许多⽴⽅体,这些⽴⽅体包括了机⾝表⾯以及此表⾯内外的空⽓。
对每个⽴⽅体列写出空⽓动⼒学⽅程,其中包括了与它相邻的⽴⽅体的共同边界变量,这些⽅程通常都已经简化为线性⽅程。
对⼀个飞⾏器,⼩⽴⽅体的数⽬可以多达400,000个,⽽要解的联⽴⽅程可能多达2,000,000个。
《Matlab教案》课件

《MATLAB教案》PPT课件第一章:MATLAB概述1.1 MATLAB简介介绍MATLAB的历史和发展解释MATLAB的含义(Matrix Laboratory)强调MATLAB在工程和科学计算中的应用1.2 MATLAB界面介绍MATLAB的工作空间解释MATLAB的菜单栏和工具栏演示如何创建、打开和关闭MATLAB文件1.3 MATLAB的基本操作介绍MATLAB的数据类型演示如何进行矩阵运算解释MATLAB中的向量和矩阵运算规则第二章:MATLAB编程基础2.1 MATLAB脚本编程解释MATLAB脚本文件的结构演示如何编写和运行MATLAB脚本强调注释和代码的可读性2.2 MATLAB函数编程介绍MATLAB函数的定义和结构演示如何创建和使用MATLAB函数强调函数的重用性和模块化编程2.3 MATLAB编程技巧介绍变量和函数的命名规则演示如何进行错误处理和调试强调代码的优化和性能提升第三章:MATLAB数值计算3.1 MATLAB数值解算介绍MATLAB中的数值解算工具演示如何解线性方程组和不等式解释MATLAB中的符号解算和数值解算的区别3.2 MATLAB数值分析介绍MATLAB中的数值分析工具演示如何进行插值、拟合和数值积分解释MATLAB中的误差估计和数值稳定性3.3 MATLAB优化工具箱介绍MATLAB优化工具箱的功能演示如何使用优化工具箱进行无约束和约束优化问题解释MATLAB中的优化算法和参数设置第四章:MATLAB绘图和可视化4.1 MATLAB绘图基础介绍MATLAB中的绘图命令和函数演示如何绘制二维和三维图形解释MATLAB中的图形属性设置和自定义4.2 MATLAB数据可视化介绍MATLAB中的数据可视化工具演示如何绘制统计图表和散点图解释MATLAB中的数据过滤和转换4.3 MATLAB动画和交互式图形介绍MATLAB中的动画和交互式图形功能演示如何创建动画和交互式图形解释MATLAB中的图形交互和数据探索第五章:MATLAB应用案例5.1 MATLAB在信号处理中的应用介绍MATLAB在信号处理中的基本概念演示如何使用MATLAB进行信号处理操作解释MATLAB在信号处理中的优势和应用场景5.2 MATLAB在控制系统中的应用介绍MATLAB在控制系统中的基本概念演示如何使用MATLAB进行控制系统分析和设计解释MATLAB在控制系统中的优势和应用场景5.3 MATLAB在图像处理中的应用介绍MATLAB在图像处理中的基本概念演示如何使用MATLAB进行图像处理操作解释MATLAB在图像处理中的优势和应用场景《MATLAB教案》PPT课件第六章:MATLAB Simulink基础6.1 Simulink简介介绍Simulink作为MATLAB的一个集成组件解释Simulink的作用:模型化、仿真和分析动态系统强调Simulink在系统级设计和多领域仿真中的优势6.2 Simulink界面介绍Simulink库浏览器和模型窗口演示如何创建、编辑和运行Simulink模型解释Simulink中的块和连接的概念6.3 Simulink仿真介绍Simulink仿真的基本过程演示如何设置仿真参数和启动仿真解释Simulink仿真结果的查看和分析第七章:MATLAB Simulink高级应用7.1 Simulink设计模式介绍Simulink的设计模式,包括连续、离散、混合和事件驱动模式演示如何根据系统特性选择合适的设计模式解释不同设计模式对系统性能的影响7.2 Simulink子系统介绍Simulink子系统的概念和用途演示如何创建和管理Simulink子系统解释子系统在模块化和层次化设计中的作用7.3 Simulink Real-Time Workshop介绍Simulink Real-Time Workshop的功能演示如何使用Real-Time Workshop进行代码解释代码对于硬件在环仿真和嵌入式系统开发的重要性第八章:MATLAB Simulink库和工具箱8.1 Simulink库介绍Simulink库的结构和分类演示如何访问和使用Simulink库中的块解释Simulink库对于模型构建和功能复用的意义8.2 Simulink工具箱介绍Simulink工具箱的概念和功能演示如何安装和使用Simulink工具箱解释Simulink工具箱在特定领域仿真和分析中的作用8.3 自定义Simulink库介绍如何创建和维护自定义Simulink库演示如何将自定义块添加到库中解释自定义库对于个人和组织级模型共享的重要性第九章:MATLAB Simulink案例分析9.1 Simulink在控制系统中的应用介绍控制系统模型在Simulink中的构建演示如何使用Simulink进行控制系统设计和分析解释Simulink在控制系统教育和研究中的应用9.2 Simulink在信号处理中的应用介绍信号处理模型在Simulink中的构建演示如何使用Simulink进行信号处理仿真解释Simulink在信号处理领域中的优势和实际应用9.3 Simulink在图像处理中的应用介绍图像处理模型在Simulink中的构建演示如何使用Simulink进行图像处理仿真解释Simulink在图像处理领域中的优势和实际应用第十章:MATLAB Simulink项目实践10.1 Simulink项目实践流程介绍从需求分析到模型验证的Simulink项目实践流程演示如何使用Simulink进行项目规划和实施解释Simulink在项目管理和协作中的作用10.2 Simulink与MATLAB的交互介绍Simulink与MATLAB之间的数据交互方式演示如何在Simulink中使用MATLAB函数和脚本解释混合仿真模式对于复杂系统仿真的优势10.3 Simulink项目案例分析具体的Simulink项目案例演示如何解决实际工程问题解释Simulink在工程教育和项目开发中的应用价值《MATLAB教案》PPT课件第十一章:MATLAB App Designer入门11.1 App Designer简介介绍App Designer作为MATLAB中的应用程序开发环境解释App Designer的作用:快速创建跨平台的MATLAB应用程序强调App Designer在简化MATLAB代码部署和用户交互中的优势11.2 App Designer界面介绍App Designer的用户界面和工作流程演示如何创建新应用和编辑应用界面解释App Designer中的组件和布局的概念11.3 App Designer编程介绍App Designer中的MATLAB编程模式演示如何使用App Designer中的MATLAB代码块解释App Designer中事件处理和应用程序生命周期管理的重要性第十二章:MATLAB App Designer高级功能12.1 App Designer用户界面设计介绍App Designer中用户界面的定制方法演示如何使用样式、颜色和主题来美化应用界面解释用户界面设计对于提升用户体验的重要性12.2 App Designer数据模型介绍App Designer中的数据模型和模型视图概念演示如何创建、使用和绑定数据模型和视图解释数据模型在应用程序中的作用和重要性12.3 App Designer部署和分发介绍App Designer应用程序的部署和分发流程演示如何打包和发布应用程序解释如何为不同平台安装和运行App Designer应用程序第十三章:MATLAB App Designer案例研究13.1 图形用户界面(GUI)应用程序设计介绍使用App Designer设计的GUI应用程序案例演示如何创建交互式GUI应用程序来简化MATLAB脚本解释GUI应用程序在数据输入和结果显示中的作用13.2 数据分析和可视化应用程序设计介绍使用App Designer进行数据分析和可视化的案例演示如何创建应用程序来处理和显示大型数据集解释App Designer在数据分析和决策支持中的优势13.3 机器学习和深度学习应用程序设计介绍使用App Designer实现机器学习和深度学习模型的案例演示如何将MATLAB中的机器学习和深度学习算法集成到应用程序中解释App Designer在机器学习和深度学习应用部署中的作用第十四章:MATLAB App Designer实战项目14.1 App Designer项目规划和管理介绍App Designer项目的规划和管理方法演示如何组织和维护大型应用程序项目解释项目管理和版本控制对于团队协作的重要性14.2 App Designer与MATLAB的集成介绍App Designer与MATLAB之间的数据和功能集成演示如何在App Designer中调用MATLAB函数和脚本解释集成MATLAB强大计算和分析能力的重要性14.3 App Designer项目案例实现分析具体的App Designer项目案例实现过程演示如何解决实际工程项目中的问题解释App Designer在工程项目实践中的应用价值第十五章:MATLAB App Designer的未来趋势15.1 App Designer的新功能和技术介绍App Designer的最新功能和技术发展演示如何利用新功能和技术提升应用程序的性能和用户体验强调持续学习和适应新技术的重要性15.2 App Designer在跨平台开发中的应用介绍App Designer在跨平台应用程序开发中的优势演示如何创建适用于不同操作系统的应用程序解释跨平台开发对于扩大应用程序市场的重要性15.3 App Designer的未来趋势和展望讨论App Designer在未来的发展趋势和潜在应用领域激发学生对于应用程序开发和创新的兴趣强调持续探索和创造新应用的重要性重点和难点解析本文档为您提供了一份详尽的《MATLAB教案》PPT课件,内容涵盖了MATLAB 的基本概念、编程基础、数值计算、绘图和可视化、应用案例、Simulink的基础知识、高级应用、库和工具箱的使用、案例分析以及项目实践、App Designer 的基础知识、高级功能、案例研究、实战项目和未来趋势等方面的内容。
matlab程序算例

matlab程序算例Matlab程序算例Matlab是一种广泛应用于科学和工程领域的高级计算机编程语言及环境。
它的简洁、高效和强大的功能使得许多人选择使用Matlab来解决复杂的数学和工程问题。
在本文中,我将以一个具体的Matlab程序算例为例,详细说明每一步是如何完成的。
那么我们首先来看一下这个具体的Matlab程序算例。
假设我们希望计算并绘制一个二维正弦函数,代码如下:matlab设置步长,定义x轴的范围dx = 0.1;x = 0:dx:10;计算对应的y值y = sin(x);绘制图像plot(x, y);在这个例子中,我们通过定义一个步长`dx`和一个x轴的范围`x`来生成一系列的x值。
然后,我们使用`sin()`函数计算对应的y值,并将结果保存在`y`中。
最后,我们使用`plot()`函数绘制x和y的图像。
现在,让我们一步一步来回答这个程序算例中的问题。
第一步:设置步长和定义x轴的范围。
matlabdx = 0.1;x = 0:dx:10;这里我们设置步长`dx`为0.1,表示x轴上两个相邻点之间的间距为0.1。
然后,我们使用冒号运算符`:`创建一个从0到10的向量`x`,其中每个元素之间的间隔为`dx`。
也就是说,`x`中的元素为0, 0.1, 0.2, …, 9.9, 10。
第二步:计算对应的y值。
matlaby = sin(x);这里,我们使用`sin()`函数计算每个x值对应的正弦值,并将结果保存在`y`中。
例如,如果x的第一个元素为0,则使用`sin(0)`计算得到y的第一个元素的值。
第三步:绘制图像。
matlabplot(x, y);最后,我们使用`plot()`函数将x和y的值绘制成图像。
这样就可以观察到x和y之间的关系。
在这个例子中,由于x的范围是从0到10,并且y是对应的正弦值,因此我们将得到一个周期为2π的正弦函数的图像。
以上就是这个Matlab程序算例的每一步的解释。
Matlab与工程计算 第七章 数值积分、微分

Xiamen University
Matlab and Engineering Calculation
dx=diff(f([x,3.01]))/0.01; %直接对f(x)求数值导数 gx=g(x); %求函数f的导函数g在假设点的导数
plot(x,dpx,x,dx,'.',x,gx, 'r-'); %作图
Xiamen University
Matlab and Engineering Calculation
f ' ( x) =
f ( x + h) − f ( x ) h
Xiamen University
Matlab and Engineering Calculation
例6-6 生成以向量V=[1,2,3,4,5,6]为基础的范得蒙矩阵,按列 进行差分运算。 命令如下: V=vander(1:6) DV=diff(V) %计算V的一阶差分
7.1.2 数值积分的实现方法(Quadrature)
1.自适应辛普生法 基于变步长辛普生法,MATLAB给出了quad函数来 求定积分。该函数的调用格式为: [I,n]=quad(fun,a,b,tol,trace) fun是被积函数名、句柄或内联函数对象; a和b分别是定积分的下限和上限; tol用来控制积分精度,缺省时取tol=10-6; trace控制是否展现积分过程,若取非0则展现积分过 程,取0则不展现,缺省时取trace=0 I即定积分值,n为被积函数的调用次数。
第7章分形维数应用与MATLAB实现

第7章分形维数应用与MATLAB实现分形维数是描述分形结构复杂性的一个重要指标,通过分形维数可以对分形物体的几何特征进行度量。
分形维数的应用十分广泛,可以应用于自然科学、工程技术、生物医学等多个领域。
在自然科学中,分形维数被广泛应用于地理地貌、气象学、流体力学等领域。
例如,在地理地貌中,通过计算地形的分形维数可以揭示地形的形态特征,如地表的复杂程度、地面的起伏程度等。
在气象学中,通过计算云雾的分形维数可以揭示云雾的形态特征,如云雾的密度、结构等。
在流体力学中,通过计算流体流动的分形维数可以揭示流体流动的特征,如流体流动的无规则性、混沌性等。
在工程技术中,分形维数被广泛应用于图像处理、信号处理、网络优化等领域。
例如,在图像处理中,通过计算图像的分形维数可以对图像进行压缩、去噪等操作,提高图像的质量和处理效率。
在信号处理中,通过计算信号的分形维数可以对信号进行分析和识别,提取出信号的特征信息。
在网络优化中,通过计算网络的分形维数可以对网络结构进行优化,提高网络的传输和通信效率。
在生物医学中,分形维数被广泛应用于医学图像处理、疾病诊断、脑信号分析等领域。
例如,在医学图像处理中,通过计算病理图像的分形维数可以对病灶的形态特征进行量化,帮助医生进行病症的诊断和分析。
在疾病诊断中,通过计算生物信号(如心电图、脑电图等)的分形维数可以对疾病的发展和变化进行监测和分析,提供辅助诊断的依据。
MATLAB作为一种专门用于科学计算和数据可视化的工具,可以很方便地实现分形维数的计算和分析。
MATLAB提供了丰富的数学工具箱和图形工具箱,可以实现各种分形维数的算法和可视化方法。
通过调用相关函数和工具,用户可以快速、准确地计算和分析分形维数,并可视化展示分形结构的特征。
总之,分形维数在科学研究和工程应用中具有重要的作用。
通过应用分形维数,可以深入了解和揭示物体的几何特征和复杂性,为科学研究、工程技术和生物医学提供有效的分析工具和方法。
如何通过MATLAB进行复杂计算

如何通过MATLAB进行复杂计算MATLAB是一个强大的科学计算软件,可用于许多不同的领域,包括工程、自然科学、数学和金融等。
由于其简单易用的界面和广泛的支持,MATLAB已成为许多工程师、科学家和学生的首选软件。
在本文中,将介绍如何使用MATLAB进行复杂计算。
1.了解MATLAB的基础知识在开始使用MATLAB之前,了解MATLAB的基本知识非常重要。
MATLAB可以用于数值计算和符号计算。
数值计算可以用于执行数学和科学计算,符号计算可以用于求解代数方程和微积分问题。
了解所需要的计算类型将有助于确定如何使用MATLAB。
2.使用MATLAB计算向量和矩阵MATLAB是为矩阵运算而设计的,因此可以轻松地执行向量和矩阵计算。
使用MATLAB进行向量或矩阵运算非常简单。
要创建向量,请在MATLAB命令窗口中输入要使用的向量,并按回车键。
例如,要创建长度为5的向量[1,2,3,4,5],只需在命令窗口中输入“[1,2,3,4,5]”并按回车键即可。
要创建矩阵,请在命令窗口中输入矩阵并按回车键。
矩阵的行数和列数用分号分隔。
例如,要创建一个3×3的矩阵,其中第一行为[1,2,3],第二行为[4,5,6],第三行为[7,8,9],请输入“[1,2,3; 4,5,6; 7,8,9]”并按回车键。
3.使用MATLAB执行基本操作MATLAB可以用于执行许多基本操作,例如加、减、乘、除等等。
要使用MATLAB执行这些基本操作,请输入相应的运算符并按回车键。
例如,要计算2 + 3,输入“2 + 3”并按回车键。
要计算2×3,输入“2 * 3”并按回车键。
4.使用MATLAB计算函数MATLAB内置了许多函数,可以轻松地执行各种计算。
要使用MATLAB内置函数,请输入函数名称及其参数,并按回车键。
例如,要计算sin(π/2),输入“sin(pi/2)”并按回车键。
您还可以使用MATLAB绘图函数来可视化计算结果。
matlab及工程运用全

Command Window操作要旨
1.指令窗的显示方式 :默认的输入显示方式、运算
结果的显示、显示方式的永久设置。
2.指令中的标点符号: 3.常用控制指令 4.常用键盘控制
指令窗的显示方式
指令中的 标点符号
常用控制指令
常用键盘控制
帮助系统及其使用
常用帮助指令
help 列出所有函数分组名(Topic Name) help TopicName 列出指定名称函数组中的所有函数 help FunName 给出指定名称函数的使用方法 helpwin 列出所有函数分组名(Topic Name) helpwin TopicName列出指定名称函数组中的所有函数 helpwin FunName 给出指定名称函数的使用方法 doc ToolboxName 列出指定名称工具包中的所有函数名 doc FunName 给出指定名称函数的使用方法
逻辑操作
常用的逻辑运算符:&(与)、|(或)、~(非)和 xor(异或)。在逻辑运算中,非0元素表示true,0元 素表示false。 标量可以与任何维数数组进行逻辑运算。 当逻辑运算中没有标量时,参与运算的数组必须维数 相同。
在MATLAB表达式中同时出现多种运算符时,优先 级按:
设标量a和数组B =[bij]mXn进行算术运算的结果是cij=a#bij 函数f(.)的数组运算规则是指‚该函数对数组的逐个元素 起作用‛(表2.2常用数组运算函数)
MATLAB计算方法与实现
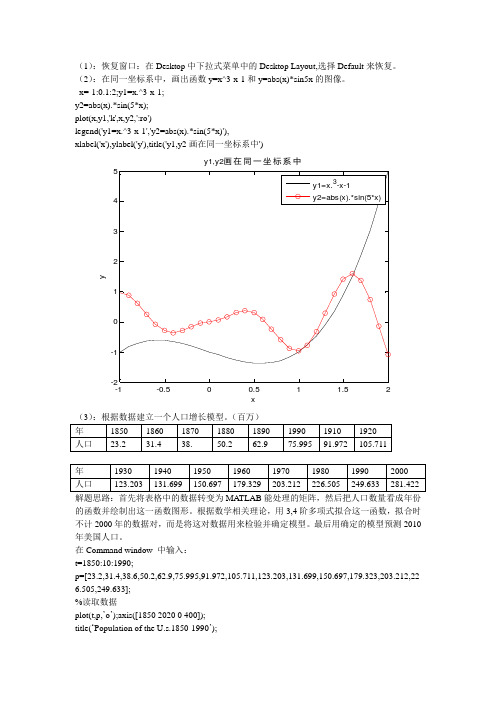
(1):恢复窗口:在Desktop 中下拉式菜单中的Desktop Layout,选择Default 来恢复。
(2):在同一坐标系中,画出函数y=x^3-x-1和y=abs(x)*sin5x 的图像。
x=-1:0.1:2;y1=x.^3-x-1; y2=abs(x).*sin(5*x); plot(x,y1,'k',x,y2,':ro')legend('y1=x.^3-x-1','y2=abs(x).*sin(5*x)'),xlabel('x'),ylabel('y'),title('y1,y2画在同一坐标系中')-1-0.500.51 1.52xyy1,y2画在同一坐标系中(3):根据数据建立一个人口增长模型。
(百万)的函数并绘制出这一函数图形。
根据数学相关理论,用3,4阶多项式拟合这一函数,拟合时不计2000年的数据对,而是将这对数据用来检验并确定模型。
最后用确定的模型预测2010年美国人口。
在Command window 中输入: t=1850:10:1990;p=[23.2,31.4,38.6,50.2,62.9,75.995,91.972,105.711,123.203,131.699,150.697,179.323,203.212,226.505,249.633]; %读取数据plot(t,p,’o ’);axis([1850 2020 0 400]); title(‘Population of the U.s.1850-1990’);ylabel(‘Millions ’);%绘制出数据的函数图形并加以修饰f1=polyfit(t,p,3);f2=polyfit(t,p,4);%对数据做3,4阶多项式拟合,结果分别为f1和f2 v=[polyval(f1,2000),polyval(f2,2000)];%计算当t=2000时多项式f1,f2的值 abs(v-251.422) %计算两个模型与2000年人口数的绝对误差。
第7章 MATLAB数值微分与积分

在科学实验和工程应用中,函数关系表达式往往是 不知道的,只有实验测定的一组样本点和样本值, 这时,人们就无法使用quad等函数计算其定积分。 在MATLAB中,对由表格形式定义的函数关系的求 定积分问题用梯形积分函数trapz,其调用格式为:
I=trapz(X,Y)
其中,向量X、Y定义函数关系Y = f(X)。X、Y是两 个等长的向量:X = (x1,x2,…,xn),Y = (y1, y2,…,yn),并且x1<x2<…<xn,积分区间是[x1, xn]。
用不同的方法求函数f(x)的数值导数,并在同一个 坐标系中做出f‘(x)的图像。
f=@(x) sqrt(x.^3+2*x.^2-x+12)+(x+5).^(1/6)+5*x+2;
g=@(x) (3*x.^2+4*x-1)./sqrt(x.^3+2*x.^2-x+12)/2+1/6./(x+5).^(5/6)+5;
第7章 MATLAB数值微分与积分
5.累计梯形积分 在MATLAB中,提供了对数据积分逐步累计的函数 cumtrapz。该函数调用格式如下。 Z=cumtrapz(Y) Z=cumtrapz(X,Y) 对于向量Y,Z是一个与Y等长的向量;对于矩阵Y,Z 是一个与Y相同大小的矩阵,累计计算Y每列的积分。 函数其他参数的含义和用法与trapz函数的相同。例如:
f
(a)
f
(b)]
基本辛普森公式:
S2
ba[ 6
f
(a) 4
f
(a b) 2
f
(b)]
复合梯形公式:
s3
h[ f 2
MATLAB在工程计算中的几则技巧

国各个 行 业 的科 研 和工作 进 程 。
2 M A A 的使 用 技 巧 TL B
2 1向量 化 .
更接 近我们 通 常 进 行计 算 时 的思 维 方式 , 有 编 具
使程 序运 行更 快 的方法 之 一是将 构 造程序 的 算 法进 行 向量 化 。 在 其 他 程 序语 言 可 能使 用 fr o 循 环 或 d 环 的地 方 , TL 可 以使 用 向 量 o循 MA A B 或矩 阵操 作 。对 于 下 面的程 序
多 的程 序相 当有 用 。例如 对 于使 用搜 索算 法求 最
短树 、 最短路径 、 旅行商等 问题时 , 每增加一个点 , 循环 次数 成指 数 增 长 , 用矩 阵 为一 个 基 本 单 位 来
Ab ta t sr c :Ab ta tTh ril to u e o kl f ATL i sdi r . src : ea t ei rd c s mes iso c n s l M B whc i u e p o h s n
ic ac lt n . e h p tc n a ta t t e e e r h r n C i a t a t n in t AT. e t lua i c o W o e i a tr c h rr s a c e s i h n o p y a t t o M o e o
X=0. 1 O ; f rk= 1 1 0 o :0 1
程简单直观, 用户界面友善, 开放性强 , 易于扩充 等优点 。因此其 自面世 以来 , 国际上很快得到 在
了推广 利用 , IE 被 E E称 为 国际 公 认 最 优 秀 的 科 技 应 用 软 件 。1近 年 来 , 国 很 多 高 校 开 设 了 l J 我 MA TL 方 面 的课 程 , 很多 学生 已经 开始 用该 软 件 完成 毕 业 设 计 。通 过 对 该 科 学 计 算 软件 的使 用 , 大 地 提 高 了科研 人 员 的工 作 效 率 , 以 更 极 可 快 、 准确地完 成 计算 方案 的设计 , 以在 必要 的 更 可 时候 用 图形 图像表 示计 算结 果和 描述运 行 机制 。 我们在 多 年 对 M TL 的 使 用 过 程 中 , A B A 遇 到不少 的科 研人 员 常常 由于一 些数 据不 能处 理或 者 一些 问题 不 能求解 而致 使他们 的研 究进 程相 当 缓 慢 , 实 际 他 们 的 问题 只 需 要 使 用 M T A 而 A L B 进行 简 单 的编 程 就 能实 现 。 于是 , 们 整 理 了一 我 些 M TL B使 用 的 技 巧 与 大 家 分 享 , 望 能 够 A A 希
Matlab-GUI学习指南

第七章 GUIDE入门
提示:
第3页,共92页。
第七章 GUIDE入门
图7-1 MATLAB图形用户界面示例
第4页,共92页。
第七章 GUIDE入门
通过如图7-1所示的界面,用户可以不必过多了解内部细节就可 以使用MATLAB的强大数据可视化和计算的功能了。例如,单击用 户界面右边的按钮,可以在图形窗体的绘图区域绘制各种图形,同 时在文本显示区域显示具体命令行代码,如图7-2所示。
HandleVisibility = on
HitTest = on
Interruptible = on Parent = [101.001] Selected = off
SelectionHighlight = on Tag = Type = line UIContextMenu = []
UserData = [] Visible = on
005 % 修改坐标线的色彩 006 set(0,'DefaultAxesXColor',[0.5 0 0]);
007 set(0,'DefaultAxesYColor',[0.5 0 0]); 008 % 修改文本的色彩
第24页,共92页。
第七章 GUIDE入门 009set(0,'DefaultTextColor',[0 0.5 0]);
除了能够直接设置具体图形对象的属性以外,MATLAB还允许用户 对图形对象的默认属性进行修改。所谓图形对象的默认属性,就是那些 MATLAB图形对象所固有的预定义的“出厂设置”,例如在默认的条件 下图形窗体的背景色为深灰色,而坐标轴的背景色为白色等,在没有指定 特殊的属性值之前,MATLAB就使用这些默认的图形对象属性来显示图 形对象。
《Matlab程序设计》课程教学大纲

Matlab程序设计Matlab Program Design一、课程基本情况课程类别:专业任选课课程学分:2学分课程总学时:32学时,其中讲课:24学时,实验(含上机):8学时课程性质:选修开课学期:第4学期先修课程:计算机基础,高等数学,线形代数适用专业:电子科学与技术教材:MATLAB程序设计教程,中国水利水电出版社,刘卫国,2010,第2版开课单位:电子与信息工程学院电子科学与技术系二、课程性质、教学目标和任务MATLAB程序设计是电子与电气信息类相关专业的专业任选课程之一。
MATLAB是由MathWorks 公司1985 年推出的一种面向科学与工程的计算软件,它具有极强的数值计算、图形文字处理、数据分析、动态仿真、信号处理等功能,涉及了数值分析、自动控制、信号处理、图像处理等十几个领域的计算和图形显示,功能强大。
因此,将MATLAB引入教学,强化应用能力培养,学生在学习专业基础课程时,增加工程应用背景,在打好专业基础的同时,提高学生的应用、创新意识。
通过本课程的学习,使学生学习和掌握如何利用MATLAB对所学理论、原理和方法进行计算机仿真,通过仿真,加深对所学知识的理解和掌握,解决学习相关课程中遇到的抽象问题,为后续专业课程的学习奠定基础。
通过工程软件在电气类专业基础课程的应用,提高学生动手能力、分析问题与解决问题的能力,到达对学生的工程意识培养的目的。
三、教学内容和要求第1章MATLAB系统环境(2学时)(1 )了解MATLAB的影响及其开展历史和MATLAB 7.0的主要功能;(2)理解MATLAB 7.0的运行环境与安装过程,熟悉菜单栏、工具栏的使用;( 3)掌握命令窗口、历史记录窗口、当前目录窗口的使用方法;重点:命令窗口、历史记录窗口、当前目录窗口的使用方法;难点:MATLAB 7.0的辅助局部和MATLAB的数学函数库。
第2章MATLAB数据及其运算(2学时)(1 )了解元胞数组、结构与结构数组;( 2)理解一、二维数组的创立方法;( 3)掌握数值表示、变量表达式、矩阵的表示、字符串矩阵的算术运算、数组运算;重点:矩阵线性运算;创立数组、数组的算术运算;难点:数组运算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、建立主程序文件
选择File—>New->M-file,即进入M文 件编辑器。
输入程序,完成后,在当前目录下保存 文件名。
在命令窗口,输入文件名,即执行程序。
主程序格式特征
以%开始为注释 全局变量定义:
Global 变量名1 变量名2 人机交互语句:
x= input(‘n=’) % 将值付给x,屏幕显 示’n=‘
符号变量
在使用符号运算工具箱之前,需要把一 些变量声明为“符号变量”,以区别于 常规的数值变量。
例如声明a,b,c,d 为符号变量:
syms a b c d
一、因式分解
Factor函数 Syms x s=x^9-1 Factor(s)
二、求极限值
极限可以用limit函数求得 Limit(f,x,a) 求符号表达式f当x->a时的极限 Limit(f,a) 对系统默认变量且该变量x->a时的
二、常量
I或j pi eps
realmin
realmax Inf NaN
虚数单位
圆周率 = 3.1415…
计算机浮点数识别精度 eps/2=1.11*10^(-16) 最 小 正 实 数 realmin^1.051= 4.9407*10^(-324) 最大正实数 1.7977*10^308
无穷大
x1 3x2 13x3 6
A*x1-b %验证最小二乘解
显示:
1.0e-014 *
-0.0888
-0.0888
-0.1332
0
说明x1不是方程Ax=b的精确解。
第六节 数值分析
Matlab提供符号运算,可进行多种数值 分析,包括因式分解、求极限值、求微 分、求导数等
求解方程组
2x1-x2+3x3=3 4x1+2x2+5x3=4 2x1 +2x3=6
A=[2 -1 3;4 2 5; 2 0 2]; b=[3 4 6]’; X=A\b 结果: 7.6667 -1.6667 -4.6667
例
2 x1 x2 5x3 x4 8
x1 3x2 6 x4 9
0.54e0.75x2 3,75 y2 1.5 y
x y 1
p(x, y)
0.7575ex26 y2
1 x y 1
0.5457e0.75x2 3.75 y2 1.5 y
x y 1
第5节 线性方程式的求解
a11x11 a21x1
... am1xm1
不定值
三、变量
变量命名规则 必须以字母为开头 可以由字母、数字和下划线混合组成,
区分大小写 字符长度不大于31个
变量数据类型
MatLab有五种基本数据类型, 数值数组(double array) 字符串(char array) 符号对象(Symbolic object) 单元数组(Cell array) 结构(Structure)
第7章 MATLAB工程计算
本章内容
第四节 M文件及其语言基础 第五节 MATLAB线性方程组求解 第六节 数值分析
第一节 MATLAB概述
MATLAB是“矩阵实验室”(MATrix LABoratory)的缩写。
最初是Cleve More博士用FORTRAN语言开发 的矩阵分析软件, 80年代初, Moler和John Little用C改写,不久他们成立MathWorks公司, 84年推向市场,2000年推出了MATLAB 6.0版 本。
MATLAB是应用最广泛的工程计算软件,发 达国家理工类学生必须掌握的数学分析工具。
第四节 M文件及其语言基础
在命令窗口下,键入一行命令后,系统 立即执行。这种方法程序可读性差且难 以存储。对于复杂的问题,应编成程序 文件。
由MatLab语句构成的文件称作M文件, 它将m作为文件的扩展名,可以用任何 文件编辑器进行调试。
log10 log2 log round fix gcd lcm
七、程序控制语句
For 循环 基本格式为:
for 循环变量=起始值:步长:终止值 循环体
end
While 循环 While 逻辑表达式 循环体
end
求从1+2+3+…+100之和 sum=0; i=1; while i<=100 sum=sum+I; i=i+1; End sum
求超定方程组
A=[2 -1 3;3 1 -5;4 -1 1;1 3 -13]
b=[3 0 3 -6]’
x1=A\b
x1 = 1.0000 2.0000 1.0000
%左除解方程
X2=pinv(A)*b %广义逆求解
2x1 x2 3x3 3
3x1 x2 5F=[(1:6).^3] diff(F)
二、一维数值积分
Quad: 采用simpson法计算积分。 调用格式:
q=quad(‘fun’,a,b,tol,trace,p1,p2,…) fun:被积函数, a,b:上限 下限 tol: 误差,缺省 0.0001 Trace:画图 p1,p2:传递参数
一 、恰定方程组
恰定方程组由n个未知数的n个方程构成,方程有唯一 的一组解。其形式:
Ax=b 其中,A是方阵,b是一个列向量。 在线性代数中,最常用的方程解法有: 利用crammer公式求解 利用矩阵求逆法求解 利用gaussian消去法 利用lu法求解 在MATLAB中,直接采用表达式:x=A\b’
条件转移语句
if 逻辑表达式 执行语句1 else 执行语句2 end
多重条件分支
Switch 语句 switch Case 值1 语句1 Case 值2 语句2 Otherwise 语句3 end
例题
编写一个M文件,画出分段函数所表示的曲 面
极限
例如
求下式中默认变量->2时的极限
lim
x 2
x2 x4 4
Syms x Limit((x-2)/(x^2-4),2)
三、计算数值向量的数值差分
差分可以用diff()函数求出 语法:Y=diff(F,n,dim) F是向量;n是差分阶数;dim是指沿着
数组的哪一维进行差分
求数值积分
function y=funq(x) y=x^3+x^2+2 q=quad(‘funq’,-1,1,1e-4,1)
a12 x12 a22 x22
... am2 xm2
... a1n x1n ... a2n xn ... ... ... amnxmn
b1 b2 ... ... bm
第5节 线性方程式的求解
MATLAB采用除法运算符“/”和“\”求解 X=A\b’ 表示求矩阵方程AX=B的解 X=A/b’ 表示求矩阵方程XA=B的解
对方程X=A\B,要求矩阵A和B有相同的行数, X和B有相同的列数,它的行数等于矩阵A的 列数。
方程X=B/A同理
如果矩阵A不是方阵,其维数是m×n,则有: m=n 恰定方程,寻求精确解 m>n 超定方程,寻求最小二乘解 m<n 不定方程,寻求基本解,其中至多有m
个非零元素。
针对不同的情况,matlab采用不同的算法。
四、关系与逻辑运算
<
小于
<=
小于等于
>
大于
>=
大于等于
==
等于
~=
不等于
&
与
|
或
~
非
五、矩阵运算符
转置 加与减 数乘矩阵 矩阵乘方 数与矩阵加减 矩阵除法
A’ A+B 与 A-B k*A 或 A*k A^k k+A 与 k-A 左除 A\B, 右除 B/A
六、数学函数
sin cos tan cot asin exp sqrt
2 x2 x3 2 x4 5
x1 4 x2 7 x3 6 x4 0
二、超定方程组
对于方程组Ax=b,A为n×m矩阵,如果A列满 秩,且n>m,则方程没有精确解,此时方程组 称为超定方程组。
线性超定方程经常遇到的问题是数据的曲线拟 合。对于超定方程组,在MatLab中,利用左除 命令x=A\b,来寻求它的最小二乘解,还可以用 广义逆来求,即x=pinv(A),所得到的解不一定 满足Ax=b,x只是最小二乘意义上的解。
