三角形中位线和直角三角形斜边上的中线练习题
专题14 直角三角形斜边上的中线-2020-2021学年八年级数学下册常考题专练(人教版)(解析版)

专题14直角三角形斜边上的中线★知识归纳●直角三角形斜边上的中线的性质直角三角形斜边上的中线等于斜边的一半.要点梳理:(1)直角三角形斜边上的中线的性质是矩形性质的推论.性质的前提是直角三角形,对一般三角形不可使用.(2)学过的直角三角形主要性质有:①直角三角形两锐角互余;②直角三角形两直角边的平方和等于斜边的平方;③直角三角形中30°所对的直角边等于斜边的一半.(3)性质可以用来解决有关线段倍分的问题.★实操夯实一.选择题(共16小题)1.如图,在三角形ABC中,AB=AC,BC=6,三角形DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF=()A.B.C.D.7【解答】解:∵AF⊥BC,BE⊥AC,D是AB的中点,∴DE=DF=AB,∵AB=AC,AF⊥BC,∴点F是BC的中点,∴BF=FC=3,∵BE⊥AC,∴EF=BC=3,∴△DEF的周长=DE+DF+EF=AB+3=7,∴AB=4,由勾股定理知AF==,故选:B.2.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为()A.3B.3.5C.4D.4.5【解答】解:∵∠ACB=90°,∠ABC=60°,∴∠A=30°,∵BD平分∠ABC,∴∠CBD=∠DBA=30°,∴BD=AD,∵AD=6,∴BD=6,∵P点是BD的中点,∴CP=BD=3.故选:A.3.如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离()A.不变B.变小C.变大D.无法判断【解答】解:不变.连接OP,在Rt△AOB中,OP是斜边AB上的中线,那么OP=AB,由于木棍的长度不变,所以不管木棍如何滑动,OP都是一个定值.故选:A.4.如图,∠ABC=∠ADC=Rt∠,E是AC的中点,则()A.∠1>∠2B.∠1=∠2C.∠1<∠2D.∠1与∠2大小关系不能确定【解答】解:∵∠ABC=∠ADC=90°,E是AC的中点,∴DE=AC,BE=AC,∴DE=BE,∴∠1=∠2.故选:B.5.如图,在△ABC中,∠ACB=90°,AC=8,BC=6,点D为斜边AB上的中点,则CD为()A.10B.3C.5D.4【解答】解:在Rt△ABC中,AC=8,BC=6,∴AB===10,∵点D为斜边AB上的中点,∴CD=AB=×10=5,故选:C.6.已知直角三角形斜边上的中线长为3,则斜边长为()A.3B.6C.9D.12【解答】解:∵直角三角形斜边上的中线长为3,∴斜边长是6.故选:B.7.直角三角形的斜边长为6cm,则斜边上的中线长为()A.2cm B.2.5cm C.3cm D.4cm【解答】解:直角三角形的斜边长为6cm,则斜边上的中线长为3cm,故选:C.8.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=10,则CD=()A.2B.3C.4D.6【解答】解:在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=10,∴AE=CE=10,∵AD=2,∴DE=8,∵CD为AB边上的高,在Rt△CDE中,CD===6,故选:D.9.在Rt△ABC中,∠ACB=90°,AB=6cm,D为AB的中点,则CD等于()A.2cm B.2.5cm C.3cm D.4cm【解答】解:∵∠ACB=90°,D为AB的中点,∴CD=AB=×6=3cm.故选:C.10.如图,在△ABC中,∠BAC=90°,点D在BC延长线上,且AD=BC,若∠D=40°,则∠B=()A.10°B.20°C.30°D.40°【解答】解:取BC的中点E,连接AE,∵∠BAC=90°,点E是BC的中点,∴AE=BC=BE,∴∠B=∠EAB,∵AD=BC,∴AE=AD,∴∠AED=∠D=40°,∴∠B=20°,故选:B.11.如图,△ABC中,AB=AC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则DE的长为()A.10B.6C.8D.5【解答】解:∵AB=AC=10,AD平分∠BAC,∴AD⊥BC,∵E为AC的中点,∴DE=AC=×10=5,故选:D.12.如图在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=3,BC=8,则△EFM的周长是()A.21B.15C.13D.11【解答】解:∵CF⊥AB,BE⊥AC,M为BC的中点,∴EM=FM=BC=×8=4,∴△EFM的周长=8+8+3=11.故选:D.13.如图,边长为2的等边三角形ABC,点A,B分别在y轴和x轴正半轴滑动,则原点O到C的最长距离()A.B.C.D.【解答】解:取AB的中点D,连接OD,CD,在△OCD中,OC<OD+CD,只有当O,D,C三点在一条线上时,OC=OD+CD,此时OC最大,如图所示,OC⊥AB,∵△AOB为等腰直角三角形,AB=2,∴OD=AB=1,在Rt△BCD中,BC=2,BD=1,根据勾股定理得:CD==,∴OC=+1.故选:D.14.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是()A.2.5B.C.D.2【解答】解:如图,连接AC、CF,∵正方形ABCD和正方形CEFG中,BC=1,CE=3,∴AC=,CF=3,∠ACD=∠GCF=45°,∴∠ACF=90°,由勾股定理得,AF===2,∵H是AF的中点,∴CH=AF=×2=.故选:B.15.如图,△ABC中,∠A+∠B=90°,AD=DB,CD=3,则AB的长度为()A.3B.4C.5D.6【解答】解:∵△ABC中,∠A+∠B=90°,∴∠ACB=90°.∵AD=DB,∴CD是该直角三角形斜边AB上的中线,∴AB=2CD=6.故选:D.16.如图,在△ABC中,AB=AC=3,BC=4,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的周长是()A.3B.4C.5D.6【解答】解:∵在△ABC中,AB=AC=3,AE平分∠BAC,∴BE=CE=BC=2,又∵D是AB中点,∴BD=AB=,∴DE是△ABC的中位线,∴DE=AC=,∴△BDE的周长为BD+DE+BE=++2=5.故选:C.二.填空题(共7小题)17.如图,BE、CF分别是△ABC的高,M为BC的中点,EF=4,BC=10,则△EFM的周长是14.【解答】解:∵BE、CF分别是△ABC的高,M为BC的中点,BC=8,∴在Rt△BCE中,EM=BC=5,在Rt△BCF中,FM=BC=5,又∵EF=4,∴△EFM的周长=EM+FM+EF=5+5+4=14.故答案是:14.18.如图,已知△ABC中,AB=AC,AD平分∠BAC,E是AC的中点,若AB=6,则DE的长为3.【解答】解:∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴∠ADC=90°,∵点E为AC的中点,∴DE=AC=3.故答案为:3.19.如图所示,在△ABC中,∠C=2∠B,点D是BC上一点,AD=5,且AD⊥AB,点E是BD上的点,AE=BD,AC=6.5,则AB的长度为12.【解答】解:∵Rt△ABD中,AE=BD,∴AE=BE=DE;∴∠B=∠BAE,即∠AED=2∠B;∵∠C=2∠B,∴∠AEC=∠C,即AE=AC=6.5;∴BD=2AE=13;由勾股定理,得:AB==12.20.如图,△AEF是直角三角形,∠AEF=90°,B为AE上一点,BG⊥AE于点B,GF∥BE,且AD=BD=BF,∠BFG=60°,则∠AFG的度数是20°.【解答】解:∵四边形BEFG是长方形,∴FG∥BE,∴∠FBE=∠BFG=60°,∵AD=BD=BF,∴∠A=∠ABD,∠BDF=∠BFD,∵∠BDF=∠DFB=∠A+∠ABD=2∠A,∴∠EBF=∠A+∠AFB=3∠A=60°,∴∠A=20°,∵FG∥BE,∴∠AFG=∠A=20°,故答案为:20°.21.如图,在△ABC中,∠BAC=90°,点D是BC的中点,点E、F分别是AB、AC上的动点,∠EDF=90°,M、N分别是EF、AC的中点,连接AM、MN,若AC=6,AB=5,则AM﹣MN的最大值为.【解答】解:如图,连接DM,DN,由图可以得到M的轨迹是一条线段(AD的垂直平分线的一部分),M在AN上的时候最大(此时AM最大,MN最小),当M在AN上时,设AM=x,则MN=3﹣x,DM=AM=x,DN=AB=,在直角三角形DMN中,根据勾股定理,得DM2=DN2+MN2,∴x2=(3﹣x)2+2.52,解得x=,∴3﹣x=,此时AM﹣MN=﹣=.∴AM﹣MN的最大值为.故答案为:.22.如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=CD,过点B 作BE∥DC交AF的延长线于点E,则BE的长为6.【解答】解:∵Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,∴CD=AB=4.5.∵CF=CD,∴DF=CD=×4.5=3.∵BE∥DC,∴DF是△ABE的中位线,∴BE=2DF=6.故答案为6.23.如图,在Rt△ABC中,∠ACB=90°,将边BC沿斜边上的中线CD折叠到CB′,若∠B=50°,则∠ACB′=10°.【解答】解:∵∠ACB=90°,∠B=50°,∴∠A=40°,∵∠ACB=90°,CD是斜边上的中线,∴CD=BD,CD=AD,∴∠BCD=∠B=50°,∠DCA=∠A=40°,由翻折变换的性质可知,∠B′CD=∠BCD=50°,∴∠ACB′=∠B′CD﹣∠DCA=10°,故答案为:10°.三.解答题(共4小题)24.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.(1)求证:CG=EG.(2)已知BC=13,CD=5,连接ED,求△EDC的面积.【解答】(1)证明:连接DE,在Rt△ADB中,点E是AB的中点,∴DE=AB=AE,∵CD=AE,∴DE=DC,又DG⊥CE,∴CG=EG.(2)解:作EF⊥BC于F,∵BC=13,CD=5,∴BD=13﹣5=8,∵DE=BE,EF⊥BC,∴DF=BF=4,∴EF===3,∴△EDC的面积=×CD×EF=×5×3=7.5.25.如图:BE、CF是锐角△ABC的两条高,M、N分别是BC、EF的中点,若EF=6,BC=24.(1)证明∠ABE=∠ACF;(2)判断EF与MN的位置关系,并证明你的结论;(3)求MN的长.【解答】解:(1)∵BE、CF是锐角△ABC的两条高,∴∠ABE+∠A=90°,∠ACF+∠A=90°,∴∠ABE=∠ACF;(2)MN垂直平分EF.证明:如图,连接EM、FM,∵BE、CF是锐角△ABC的两条高,M是BC的中点,∴EM=FM=BC,∵N是EF的中点,∴MN垂直平分EF;(3)∵EF=6,BC=24,∴EM=BC=×24=12,EN=EF=×6=3,由勾股定理得,MN===3.26.拓展:如图四边形ABCD中,∠ABC=∠ADC=90°,E是AC中点,EF平分∠BED交BD于点F.(1)猜想EF与BD具有怎样的关系?(2)试证明你的猜想.【解答】解:(1)EF垂直平分BD,(2)∵∠ABC=∠ADC=90°,E是AC中点,∴BE=AE=EC,ED=AE=EC,∴BE=DE,∵EF平分∠BED交BD于点F,∴EF⊥BD,BF=FD,即EF垂直平分BD.27.如图,在Rt△ABC中,∠ACB=90°,M是斜边AB的中点,AM=AN,∠N+∠CAN=180°.求证:MN=AC.【解答】证明:∵∠ACB=90°,M是斜边AB的中点,∴CM=AM,∴∠MCA=∠MAC,∵AM=AN,∴∠AMN=∠ANM,∵∠N+∠CAN=180°,∴AC∥MN,∴∠AMN=∠MAC,∴∠AMC=∠NAM,∴AN∥MC,又AC∥MN,∴四边形ACMN是平行四边形,∴MN=AC.。
湘教版数学八年级下册_《三角形的中位线》提高训练

《三角形的中位线》提高训练一、选择题1.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=16,E为AC中点,DE∥BC,D为AB上的点,则DE的长度为()A.2B.4C.6D.82.如图,△ABC中,BE平分∠ABC,AE⊥BE于点E,M为AB的中点,连接ME 并延长交AC于点N.若AB=6,BC=12,则线段EN的长为()A.2B.3C.4D.53.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=25°,则∠EPF的度数是()A.100°B.120°C.130°D.150°4.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、FD 得△DEF,如果△ABC的周长是24cm,那么△DEF的周长是()A.6cm B.12cm C.18cm D.48cm5.如图,△ABC中,D、E分别是AB、AC边的中点,延长DE至F,使EF=DF,若BC=8,则DF的长为()A.6B.8C.4D.二、填空题6.如图,△ABC中,AB=7cm,BC=6cm,AC=5cm,D,E,F分别是AB,BC,AC 的中点,则四边形ADEF的周长等于cm.7.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=7,则EF的长为.8.如图,已知等边三角形ABC边长为1,△ABC的三条中位线组成△A1B1C1,△A1B1C1的三条中位线组成△A2B2C2,依此进行下去得到△A5B5C5的周长为.9.如图,已知△ABC中,∠ABC的角平分线BE交AC于点E,DE∥BC,如果点D是边AB的中点,AB=8,那么DE的长是.10.如图所示,在△ABC中,AB=AC,D,E分别是AB,AC的中点,G,H为BC 上的点连接DH,EG.若AB=5cm,BC=6cm,GH=3cm,则图中阴影部分的面积为.三、解答题11.在△ABC中,AB=AC=6,点D为BC的中点,点E为AC的中点,连接DE,求DE的长.12.如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.(1)求证:EF垂直平分AD.(2)若四边形AEDF的周长为24,AB=15,求AC的长;13.如图、在△ABC中,AB=AC,M,N分别为AC,BC的中点,以AC为斜边在△ABC的外侧作Rt△ACD,且∠CAD=30°,连接MN,DM,DN.(1)求证:△DMN是等腰三角形;(2)若AC平分∠BAD,AB=6,求DN的长.14.如图,△ABC中,过点A分别作∠ABC,∠ACB的外角的平分线的垂线AD,AE.D,E为垂足,求证:(1)ED∥BC;(2)ED=(AB+AC+BC).15.(1)如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG.求证:FG=(AB+BC+AC).[提示:分别延长AF、AG与直线BC相交](2)如图2,若BD、CE分别是△ABC的内角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG.线段FG与△ABC的三边又有怎样的数量关系?写出你的猜想,并给予证明.《三角形的中位线》提高训练参考答案与试题解析一、选择题1.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=16,E为AC中点,DE∥BC,D为AB上的点,则DE的长度为()A.2B.4C.6D.8【分析】先根据直角三角形的性质求出BC的长,再由三角形中位线定理即可得出结论.【解答】解:∵在Rt△ABC中,∠C=90°,∠A=30°,AB=16,∴BC=AB=8.∵D为AB的中点,E为AC的中点,∴DE是△ABC的中位线,∴DE=BC=4.故选:B.【点评】本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.2.如图,△ABC中,BE平分∠ABC,AE⊥BE于点E,M为AB的中点,连接ME 并延长交AC于点N.若AB=6,BC=12,则线段EN的长为()A.2B.3C.4D.5【分析】延长AE交BC于H,根据等腰三角形的判定和性质得到AE=EH,BH=AB,求出HC,根据三角形中位线定理计算.【解答】解:延长AE交BC于H,∵BE平分∠ABC,AE⊥BE,∴AE=EH,BH=AB=6,∴HC=BC﹣BH=6,∵AE=EH,AN=NC,∴EN=HC=3,故选:B.【点评】本题考查的是三角形中位线定理、等腰三角形的判定和性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.3.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=25°,则∠EPF的度数是()A.100°B.120°C.130°D.150°【分析】根据三角形中位线定理得到PE=AD,PF=BC,根据等腰三角形的性质、三角形内角和定理计算即可.【解答】解:∵P是对角线BD的中点,E,F分别是AB,CD的中点,∴PE=AD,PF=BC,∵AD=BC,∴PE=PF,∴∠PFE=∠PEF=25°,∴∠EPF=130°,故选:C.【点评】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.4.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、FD 得△DEF,如果△ABC的周长是24cm,那么△DEF的周长是()A.6cm B.12cm C.18cm D.48cm【分析】利用三角形的中位线定理可以得到:DE=AC,EF=AB,DF=BC,则△DEF的周长是△ABC的周长的一半,据此即可求解.【解答】解:∵D、E分别是△ABC的边AB、BC的中点,∴DE=AC,同理,EF=AB,DF=BC,=DE+EF+DF=AC+BC+AB=(AC+BC+AC)=×24=12cm.∴C△DEF故选:B.【点评】本题考查了三角形的中位线定理,正确根据三角形中位线定理证得:△DEF的周长是△ABC的周长的一半是关键.5.如图,△ABC中,D、E分别是AB、AC边的中点,延长DE至F,使EF=DF,若BC=8,则DF的长为()A.6B.8C.4D.【分析】根据三角形中位线定理求出DE,根据题意计算即可.【解答】解:∵D、E分别是AB、AC边的中点,∴DE=BC=4,∵EF=DF,∴EF=2,∴DF=6,故选:A.【点评】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.二、填空题6.如图,△ABC中,AB=7cm,BC=6cm,AC=5cm,D,E,F分别是AB,BC,AC 的中点,则四边形ADEF的周长等于12cm.【分析】根据三角形中位线定理得到DE∥AC,DE=AC,EF∥AB,EF=AB,得到四边形ADEF是平行四边形,计算即可.【解答】解:∵D,E分别是AB,BC的中点,∴DE∥AC,DE=AC=2.5cm,同理,EF∥AB,EF=AB=3.5cm,∴四边形ADEF是平行四边形,∴四边形ADEF的周长=2×(2.5+3.5)=12(cm),故答案为:12.【点评】本题考查的是三角形中位线定理、平行四边形的判定和性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.7.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=7,则EF的长为1.【分析】根据三角形中位线定理得到DE=BC=3.5,根据直角三角形的性质得到DF=AB=2.5,计算即可.【解答】解:∵DE是△ABC的中位线,∴DE=BC=3.5,DE∥BC,∵∠AFB=90°,D为AB的中点,∴DF=AB=2.5,∴EF=DE﹣DF=1,故答案为:1.【点评】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半和在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.8.如图,已知等边三角形ABC边长为1,△ABC的三条中位线组成△A1B1C1,△A1B1C1的三条中位线组成△A2B2C2,依此进行下去得到△A5B5C5的周长为.【分析】根据三角形的中位线平行于第三边并且等于第三边的一半求出A1B1=AC,B1C1=AB,A1C1=BC,从而得到△A1B1C1是△ABC周长的一半,依此类推,下一个三角形是上一个三角形的周长的一半,根据此规律求解即可.【解答】解:∵△ABC的三条中位线组成△A1B1C1,∴A1B1=AC,B1C1=AB,A1C1=BC,∴△A1B1C1的周长=△ABC的周长=×3=,依此类推,△A2B2C2的周长=△A1B1C1的周长=×=,故答案为:.【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半的性质,求出后一个三角形的周长等于前一个三角形的周长的一半是解题的关键.9.如图,已知△ABC中,∠ABC的角平分线BE交AC于点E,DE∥BC,如果点D是边AB的中点,AB=8,那么DE的长是4.【分析】根据三角形的中位线定理即可求出答案.【解答】解:连接BE,∵BE平分∠ABC,∴∠ABE=∠CBE,∵DE∥BC,∴∠DEB=∠ABE,∴∠ABE=∠DEB,∴BD=DE,∵D是AB的中点,∴AB=BD,∴DE=AB=4,故答案为:4【点评】本题考查三角形的综合问题,涉及角平分线的性质,平行线的性质等性质,需要学生灵活运用所学知识.10.如图所示,在△ABC中,AB=AC,D,E分别是AB,AC的中点,G,H为BC 上的点连接DH,EG.若AB=5cm,BC=6cm,GH=3cm,则图中阴影部分的面积为6cm2.【分析】连接DE,作AF⊥BC于F,根据三角形中位线定理求出DE,根据勾股定理求出AF,根据相似三角形的判定定理和性质定理计算即可.【解答】解:连接DE,作AF⊥BC于F,∵D,E分别是AB,AC的中点,∴DE=BC=3,DE∥BC,∵AB=AC,AF⊥BC,∴BF=BC=3,在Rt△ABF中,AF==4,∴△ABC的面积=×6×4=12,∵DE∥BC,∴△ADE∽△ABC,∴△ADE的面积=12×=3,∴四边形DBCE的面积=12﹣3=9,△DOE的面积+△HOG的面积=×3×2=3,∴图中阴影部分的面积=9﹣3=6(cm2),故答案为:6cm2.【点评】本题考查的是三角形中位线定理、相似三角形的判定和性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.三、解答题11.在△ABC中,AB=AC=6,点D为BC的中点,点E为AC的中点,连接DE,求DE的长.【分析】利用三角形中位线定理可以直接求得DE的长度.【解答】解:∵点D为BC的中点,点E为AC的中点,∴DE是△ABC的中位线,∴DE=AB.又AB=AC=6,∴DE=3.【点评】本题考查了三角形的中位线的性质:三角形的中位线平行于第三边,且等于第三边的一半.12.如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.(1)求证:EF垂直平分AD.(2)若四边形AEDF的周长为24,AB=15,求AC的长;【分析】(1)根据直角三角形的性质得到DE=AE,DF=AF,根据线段垂直平分线的判定定理证明;(2)根据直角三角形的性质得到DE=AE=AB=,DF=AF=AC,根据四边形的周长公式计算.【解答】(1)证明:∵AD是高,∴∠ADB=∠ADC=90°,又E、F分别是AB、AC的中点,∴DE=AB=AE,DF=AC=AF,∴EF垂直平分AD;(2)解:由(1)得,DE=AE=AB=,DF=AF=AC,∵四边形AEDF的周长为24,∴AE+ED+DF+FA=24,∴DF+FA=24﹣15=9,∴AC=9.【点评】本题考查的是线段垂直平分线的判定,直角三角形的性质,掌握直角三角形中,斜边上的中线等于斜边的一半是解题的关键.13.如图、在△ABC中,AB=AC,M,N分别为AC,BC的中点,以AC为斜边在△ABC的外侧作Rt△ACD,且∠CAD=30°,连接MN,DM,DN.(1)求证:△DMN是等腰三角形;(2)若AC平分∠BAD,AB=6,求DN的长.【分析】(1)依据三角形的中位线定理可得到MN=AB,由直角三角形斜边上中线的性质可得到DM=AM=AC,然后结合已知条件可得到DM=MN;(2)由AM=DM可得到∠CAD=∠ADM=30°,从而可得到∠DMC=60°,然后再证明∠CMN=30°,从而可得到∠DMN=90°,最后,依据勾股定理求解即可.【解答】解:(1)∵在△ABC中,M、N分别是AC、BC的中点,∴MN∥AB,MN=AB,AM=MC=AC.∵∠ADC=90°,DM为斜边上的中线,∴MD=AC.∵AC=AB,∴MN=DM.∴△DMN是等腰三角形.(2)∵∠CAD=30°,AC平分∠BAD,∴∠BAC=∠CAD=30°.∵MN∥AB,∴∠NMC=∠BAC=30°.由(1)DM=AM,∴∠DMC=60°.∴∠DMN=∠DMC+∠NMC=30°+60°=90°.在Rt△ABC中,DN2=DM2+MN2,DM=MN=AB=3,∴DN=3.【点评】本题主要考查的是三角形的中位线定理、勾股定理、等腰三角形的判断,熟练掌握相关知识是解题的关键.14.如图,△ABC中,过点A分别作∠ABC,∠ACB的外角的平分线的垂线AD,AE.D,E为垂足,求证:(1)ED∥BC;(2)ED=(AB+AC+BC).【分析】(1)分别延长AD、AE与直线BC交于点F、G,根据AD⊥BD,得到∠ADB=∠FDB=90°,再根据BD=BD,∠ABD=∠FBD,证得△ABD≌△FBD,进而得到AD=FD、AE=EG,证得DE∥BC.(2)根据上题证得的△ABD≌△FBD,AB=BF,同理AC=CG,证得GF=FB+BC+GC=AB+BC+AC,从而证得结论.【解答】证明:(1)分别延长AD、AE与直线BC交于点F、G,∵AD⊥BD,∴∠ADB=∠FDB=90°,∵BD=BD,∠ABD=∠FBD,∴△ABD≌△FBD∴AD=FD,同理可得AE=EG,∴DE∥BC;(2)由(1)知△ABD≌△FBD,∴AB=BF,同理AC=CG,∵DE=FG∴GF=FB+BC+GC=AB+BC+AC,∴DE=(AB+BC+AC)【点评】本题考查了三角形的中位线定理及三角形的有关知识,解题的关键是正确的利用中位线定理得到中位线与第三边的位置或数量关系.15.(1)如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG.求证:FG=(AB+BC+AC).[提示:分别延长AF、AG与直线BC相交](2)如图2,若BD、CE分别是△ABC的内角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG.线段FG与△ABC的三边又有怎样的数量关系?写出你的猜想,并给予证明.【分析】(1)利用全等三角形的判定定理ASA证得△ABF≌△MBF,然后由全等三角形的对应边相等进一步推出MB=AB,AF=MF,同理CN=AC,AG=NG,由此可以证明FG为△AMN的中位线,然后利用中位线定理求得FG=(AB+BC+AC);(2)延长AF、AG,与直线BC相交于M、N,与(1)类似可以证出答案.【解答】解:(1)如图1,∵AF⊥BD,∠ABF=∠MBF,∴∠BAF=∠BMF,在△ABF和△MBF中,,∴△ABF≌△MBF(ASA),∴MB=AB,∴AF=MF,同理:CN=AC,AG=NG,∴FG是△AMN的中位线,∴FG=MN,=(MB+BC+CN),=(AB+BC+AC).(2)猜想:FG=(AB+AC﹣BC),证明:如图2,延长AG、AF,与直线BC相交于M、N,∵由(1)中证明过程类似证△ABF≌△NBF,∴NB=AB,AF=NF,同理CM=AC,AG=MG,∴FG=MN,∴MN=2FG,∴BC=BN+CM﹣MN=AB+AC﹣2FG,∴FG=(AB+AC﹣BC).【点评】本题主要考查了三角形的中位线定理,三角形的内角和定理,等腰三角形的性质和判定等知识点,解此题的关键是作辅助线转化成三角形的中位线.。
2022-2023学年初二数学第二学期培优专题14 三角形斜边中线与中位线

2022-2023学年初二数学第二学期培优专题14 三角形斜边中线与中位线结合【例题讲解】(1)如图1,已知△ABC中,F是BC上一点,AB=BF,BE⊥AF,垂足是E,D是AC的中点,请说明FC和DE有怎样的关系?(请写出详细的推理过程)(2)如图2,在△ABC中,M、D分别是边AB、AC的中点,E是线段MD上的一点.连接AE、BE,∠AEB =90°,且AB=8,BC=14,则DE的长是______.解:(1)12DE FC DE FC=∥,,理由如下:∵AB=BF,BE⊥AF,∴AE=EF,即点E是AF的中点,又∵D是AC的中点,∴DE是△ACF的中位线,∴12DE FC DE FC=∥,;(2)∵M、D分别是AB、AC的中点,∴MD是△ABC的中位线,∴172MD BC==,∵∠AEB=90°,AB=8,M是AB的中点,∴142ME AB==,∴DE=MD-ME=3.【综合演练】1.如图,在Rt△ABC中,∠ABC=90°,BF是AC边上的中线,DE是△ABC的中位线,若DE=10,则BF的长为()A .10B .5C .8D .62.如图,在ABC 中,BF 平分ABC ∠,AF BF ⊥于点F ,D 为AB 的中点,连接DF 延长交AC 于点.E 若10AB =,=16BC ,则线段EF 的长为( )A .2B .3C .4D .53.如图,在RtΔABC 中,∠ACB =90,AC =6、BC =4,点F 为射线CB 上一动点,过点C 作CM ⊥AF 于M 交AB 于E , D 是AB 的中点,则DM 长度的最小值是( )A .3B .2C .1D .6-24.如图,在正方形ABCD 中,对角线AC 与BD 相交于点O ,E 为BC 上一点,CE =5,F 为DE 的中点.若△CEF 的周长为18,则OF 的长为( )A .3B .4C .52D .72第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题(共0分)5.已知,如图,在△ABC 中,D 、E 、F 分别是各边的中点,AH 是高,已知AB =6cm ,AC =8cm ,7cm 3CH BH -=,则△DHE 的周长为________cm .6.如图,在Rt ABC 中,90ACB ∠=︒,30A ∠=︒,D ,E ,F 分别为AB ,AC ,AD 的中点,若6BC =,则EF 的长度为 _____.7.如图,菱形ABCD 中,DE AB ⊥,垂足为E ,点F 、G 分别为边AD 、DC 的中点,5,8EF FG ==,则ABCD S =菱形___________.8.如图,在ABC 和ABD △中,90ACB ADB ∠=∠=︒,E 、F 、G 分别为AB 、AC 、BC 的中点,若1DE =,则FG =_________.9.如图,在正方形ABCD 中,F 在AB 上,E 在BC 的延长线上,AF =CE ,连接DF 、DE 、EF ,EF 交对角线BD 于点N ,M 为EF 的中点,连接MC ,下列结论:①△DEF 为等腰直角三角形;②∠FDB =∠FEC ;③直线MC 是BD 的垂直平分线;④若BF =2,则MC =2;其中正确结论的有_______.10.如图,ABC ∆中,90ACB ∠=,D 为AC 边上的中点,E 为AB 边上一点,4AB BE =,连接CE DE 、,延长DE 交CB 延长线于F ,若3BF =,10AB =,则CE =________.11.如图,在Rt ABC 中,90,8,6ACB AC BC ∠=︒==,点P 是平面内一个动点,且4AP =,Q 为BP 的中点,在P 点运动过程中,设线段CQ 的长度为m ,则m 的取值范围是_______.三、解答题(共0分)12.如图,在四边形ABCD 中,∠ABC =90°,AC=AD ,M ,N 分别是AC ,CD 的中点,连接BM ,MN ,BN .(1)求证:BM=MN;(2)若∠BAD=60°,AC平分∠BAD,AC=2.①求∠BMN的度数;②求BN的长.13.如图,D、E、F分别是△ABC三边中点,AH⊥BC于H.求证:(1)∠BDF=∠BAC;(2)DF=EH.14.在平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AB,点E、F分别是OA、BC的中点,连接BE、EF.BC;(1)求证:EF=12(2)在上述条件下,若AC=BD,G是BD上一点,且BG:GD=3:1,连接EG、FG,试判断四边形EBFG的形状,并证明你的结论.15.如图,在平面直角坐标系中,A(0,4),B(4,0),C(6,2),连接AB,BC,平移BC至AD(点B 与点A对应,点C与点D对应),连接CD.(1)①直接写出点D的坐标为.②判断四边形ABCD的形状,并证明你的结论;(2)如图1,点E为AB边上一点,连接DE,DF平分∠EDC交BC于F,连接EF,若∠DFE=45°,求BE 的长;(3)如图2,N为BC边的中点,若∠AMC=90°,连接MN,请直接写出MN的取值范围.16.已知,在△ABC中,以△ABC的两边BC,AC为斜边向外测作Rt△BCD和Rt△ACE,使∠CAE=∠CBD,取△ABC边AB的中点M,连接ME,MD.特例感知:(1)如图1,若AC=BC,∠ACB=60°,∠CAE=∠CBD=45°,取AC,BC的中点F,G,连接MF,MG,EF,DG,则ME与MD的数量关系为______,∠EMD=______;(2)如图2,若∠ACB=90°,∠CAE=∠CBD=60°,取AC,BC的中点F,G,连接MF,MG,EF,DG,请猜想ME与MD的数量关系以及∠EMD的度数,并给出证明;类比探究:(3)如图3,当△ABC是任意三角形,∠CAE=∠CBD=α时,连接DE,请猜想△DEM的形状以及∠EMD 与α的数量关系,并说明理由.中,D为BC中点,BE、CF与射线AE分别相交于点E、F(射线AE不经过点D).17.在ABC(2)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND.求证:AM=AN(3)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND.求证:∠EMD=∠FND.18.(1)如图1,已知△ABC中,F是BC上一点,AB=BF,BE⊥AF,垂足是E,D是AC的中点,请说明FC和DE有怎样的关系?(请写出详细的推理过程)(2)如图2,在△ABC中,M、D分别是边AB、AC的中点,E是线段MD上的一点.连接AE、BE,∠AEB =90°,且AB=8,BC=14,则DE的长是______.答案与解析【例题讲解】(1)如图1,已知△ABC中,F是BC上一点,AB=BF,BE⊥AF,垂足是E,D是AC的中点,请说明FC和DE有怎样的关系?(请写出详细的推理过程)(2)如图2,在△ABC中,M、D分别是边AB、AC的中点,E是线段MD上的一点.连接AE、BE,∠AEB =90°,且AB=8,BC=14,则DE的长是______.解:(1)12DE FC DE FC=∥,,理由如下:∵AB=BF,BE⊥AF,∴AE=EF,即点E是AF的中点,又∵D是AC的中点,∴DE是△ACF的中位线,∴12DE FC DE FC=∥,;(2)∵M、D分别是AB、AC的中点,∴MD是△ABC的中位线,∴172MD BC==,∵∠AEB=90°,AB=8,M是AB的中点,∴142ME AB==,∴DE=MD-ME=3.【综合演练】1.如图,在Rt△ABC中,∠ABC=90°,BF是AC边上的中线,DE是△ABC的中位线,若DE=10,则BF的长为()A.10 B.5 C.8 D.6【分析】根据三角形中位线定理求出AC ,根据直角三角形的斜边上的中线等于斜边的一半计算,得到答案.【解答】解:∵DE 是△ABC 的中位线,若DE =10,∴AC =2DE =20,在Rt △ABC 中,∠ABC =90°,BF 是AC 边上的中线,∴BF =12AC =10,故选:A . 【点评】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.2.如图,在ABC 中,BF 平分ABC ∠,AF BF ⊥于点F ,D 为AB 的中点,连接DF 延长交AC 于点.E 若10AB =,=16BC ,则线段EF 的长为( )A .2B .3C .4D .5 【答案】B【分析】先求出152DF AB AD BD ====,然后证明DE BC ∥,根据平行线分线段成比例可得=AE EC ,再根据三角形中位线定理求出DE 即可.【解答】解:AF BF ⊥,90AFB ∴∠=︒,10AB =,D 为AB 中点,152DF AB AD BD ∴====, ABF BFD ∠∠∴=,又BF 平分ABC ∠,ABF CBF ∠∠∴=,CBF DFB ∠∠∴=,∴DE BC ∥,∴=AD AE DB EC,182DE BC ∴==, 853EF DE DF ∴=-=-=,故选:B .【点评】本题考查了直角三角形斜边中线的性质,等腰三角形的判定和性质,平行线的判定,平行线分线段成比例定理以及三角形中位线定理等知识,证明DE BC ∥是解答本题的关键.3.如图,在RtΔABC 中,∠ACB =90,AC =6、BC =4,点F 为射线CB 上一动点,过点C 作CM ⊥AF 于M 交AB 于E , D 是AB 的中点,则DM 长度的最小值是( )A .3B .2C .1D .6-2【答案】C【分析】取AC 的中点T ,连接DT ,MT .利用三角形的中位线定理求出DT ,利用直角三角形的中线的性质求出MT ,再根据DM MT DT ≥-,可得结论.【解答】解:如图,取AC 的中点T ,连接DT ,MT .∵AD DB =,AT TC =,∴122DT BC ==. ∵CE AF ⊥,∴90AMC ∠=︒,∴132TM AC ==, ∴点M 的运动轨迹是以T 为圆心,TM 为半径的圆,∴321DM TM DT ≥-=-=,∴DM 的最小值为1,故选:C .【点评】本题考查点与圆的位置关系,三角形中位线定理,直角三角形斜边中线的性质等知识,解题的关键是学会添加常用辅助线,构造三角形中位线,直角三角形斜边中线解决问题.4.如图,在正方形ABCD 中,对角线AC 与BD 相交于点O ,E 为BC 上一点,CE =5,F 为DE 的中点.若△CEF 的周长为18,则OF 的长为( )A .3B .4C .52D .72 【答案】D【分析】先根据直角三角形的性质求出DE 的长,再由勾股定理得出CD 的长,进而可得出BE 的长,由三角形中位线定理即可得出结论.【解答】∵CE=5,△CEF 的周长为18,∴CF+EF=18-5=13.∵F 为DE 的中点,∴DF=EF .∵∠BCD=90°,∴CF=12DE ,∴EF=CF=12DE=6.5,∴DE=2EF=13,∴CD=2212DE CE -=,∵四边形ABCD是正方形,∴BC=CD=12,O为BD的中点,∴OF是△BDE的中位线,∴OF=12(BC-CE)=12(12-5)=3.5,故选D.【点评】本题考查的是正方形的性质,涉及到直角三角形的性质、三角形中位线定理等知识,难度适中.使用勾股定理是解决这个问题的关键.5.已知,如图,在△ABC中,D、E、F分别是各边的中点,AH是高,已知AB=6cm,AC=8cm,7 cm 3CH BH-=,则△DHE的周长为________cm.【答案】496##186【分析】根据直角三角形斜边上的中线的性质求出DH,根据三角形中位线定理求出DE,根据三角形的周长公式计算,得到答案.【解答】解:∵AH是△ABC的高,∴∠AHB=90°,∵点D是AB的中点,∴DH=12AB=12×6=3cm,∵D、E分别是BA、BC的中点,∴DE是△ABC的中位线,∴DE=12AC=12×8=4cm,∵BE=EC,CH-BH=73 cm,∴HE=76 cm,∴△DHE的周长=DH+DE+HE=496cm,故答案为:496.【点评】本题考查的是三角形中位线定理、直角三角形斜边上的中线的性质,掌握三角形中位线等于第三边的一半是解题的关键.6.如图,在Rt ABC 中,90ACB ∠=︒,30A ∠=︒,D ,E ,F 分别为AB ,AC ,AD 的中点,若6BC =,则EF 的长度为 _____.【答案】3【分析】根据含30°的直角三角形的性质求出CD ,根据直角三角形的性质求出CD ,根据三角形中位线定理计算,得到答案.【解答】解:∵∠ACB =90°,∠A =30°,∴AB =2BC =12.∵∠ACB =90°,D 为AB 的中点,∴CD =12AB =6,∵E ,F 分别为AC ,AD 的中点,∴EF 为△ACD 的中位线,∴EF =12CD =3.故答案为:3.【点评】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.7.如图,菱形ABCD 中,DE AB ⊥,垂足为E ,点F 、G 分别为边AD 、DC 的中点,5,8EF FG ==,则ABCD S =菱形___________.【答案】96【分析】连接,AC BD ,交于点O ,先根据直角三角形斜边上的中线等于斜边的一半可得10AD =,再根据三角形的中位线定理可得16AC =,然后根据菱形的性质和勾股定理可得12BD =,最后利用菱形的面积公式即可得.【解答】解:如图,连接,AC BD ,交于点O ,,5DE AB EF ⊥=,且点F 为边AD 的中点,210AD EF ∴==,点,F G 分别为边,AD DC 的中点,8FG =,216AC FG ∴==,四边形ABCD 是菱形,1,8,22AC BD OA AC BD OD ∴⊥===, 226OD AD OA ∴=-=,12BD ∴=,1116129622ABCD S AC BD ∴=⋅=⨯⨯=菱形, 故答案为:96.【点评】本题考查了直角三角形斜边上的中线等于斜边的一半、三角形的中位线定理、勾股定理、菱形的性质,熟练掌握菱形的性质是解题关键.8.如图,在ABC 和ABD △中,90ACB ADB ∠=∠=︒,E 、F 、G 分别为AB 、AC 、BC 的中点,若1DE =,则FG =_________. 【答案】1【分析】由直角三角形斜边中线的性质得出AB =2DE ,再由三角形中位线的性质可得FG 的长;【解答】解:∵Rt △ABC 中,点E 是AB 的中点,DE =1,∴AB =2DE =2,∵点F 、G 分别是AC 、BC 中点,∴112FG AB ==,故答案为:1【点评】本题考查了直角三角形的性质及三角形中位线的性质等知识;熟练掌握中位线定理是解题的关键. 9.如图,在正方形ABCD 中,F 在AB 上,E 在BC 的延长线上,AF =CE ,连接DF 、DE 、EF ,EF 交对角线BD 于点N ,M 为EF 的中点,连接MC ,下列结论:①△DEF 为等腰直角三角形;②∠FDB =∠FEC ;③直线MC 是BD 的垂直平分线;④若BF =2,则MC =2;其中正确结论的有_______.【答案】①②③④【分析】先根据SAS 定理证出ADF CDE ≅,再根据全等三角形的性质可得,DF DE ADF CDE =∠=∠,然后根据等腰直角三角形的判定即可判断①;先根据等腰直角三角形的性质可得45DEF DFE ∠=∠=︒,再根据对顶角相等可得DNF BNE ∠=∠,然后根据三角形的内角和定理即可得判断②;连接BM DM ,,先根据直角三角形斜边上的中线等于斜边的一半可得12BM DM EF ==,再根据线段垂直平分线的判定即可判断③;取BE 的中点O ,连接MO ,先根据三角形中位线定理可得11,2MO BF MO BF ==∥,再根据等腰三角形的三线合一可得1452BCM BCD ∠=∠=︒,然后在Rt MOC 中,利用勾股定理即可得.【解答】解:四边形ABCD 是正方形,,90,45AB AD CD BC A ABC BCD ADC CBD ∴===∠=∠=∠=∠=︒∠=︒,在ADF △和CDE 中,90AD CD A DCE AF CE =⎧⎪∠=∠=︒⎨⎪=⎩,()SAS ADF CDE ∴≅,,DF DE ADF CDE ∴=∠=∠,90EDF CDE CDF ADF CDF ADC ∴∠=∠+∠=∠+∠=∠=︒,DEF ∴为等腰直角三角形,结论①正确;45DEF DFE ∴∠=∠=︒,又45,CBD DNF BNE ∠=︒∠=∠,180180DNF CBD BN E E DF ∴︒-∠=︒-∠-∠∠-,即FDB FEC ∠=∠,结论②正确;如图,连接BM DM ,,M 为Rt DEF △和Rt BEF △斜边EF 上的中点,12BM DM EF ∴==, 又BC CD =,∴直线MC 是BD 的垂直平分线,结论③正确;如图,取BE 的中点O ,连接MO ,1121,22MO BF MO BF ∴==⨯=∥,90MOC ABC ∴∠=∠=︒,直线MC 是BD 的垂直平分线,BC CD =,1452BCM BCD ∴∠=∠=︒(等腰三角形的三线合一), Rt COM ∴是等腰直角三角形,且1OC MO ==,222MC MO OC ∴=+=,结论④正确;综上,正确结论的有①②③④,故答案为:①②③④.【点评】本题考查了正方形的性质、三角形全等的判定与性质、等腰直角三角形的判定与性质、勾股定理、线段垂直平分线的判定、三角形中位线定理等知识点,熟练掌握各判定与性质是解题关键.10.如图,ABC ∆中,90ACB ∠=,D 为AC 边上的中点,E 为AB 边上一点,4AB BE =,连接CE DE 、,延长DE 交CB 延长线于F ,若3BF =,10AB =,则CE =________.【答案】972【分析】取AB 的中点G ,连接DG ,则AB =2BG ,可得BE =EG ,再利用三角形中位线定理得BC =2DG ,DG BF ∥,利用ASA 证明△GDE ≌△BFE ,得DG =BF =3,DE =EF ,从而解决问题.【解答】解:取AB 的中点G ,连接DG ,则AB =2BG ,∵AB =4BE ,∴BE =EG ,∵D 为AC 边上的中点,G 为AB 的中点,∴DG 为△ABC 的中位线,∴BC =2DG ,DG BF ∥, ∴∠GDE =∠F ,在△GDE 和△BFE 中,GDE F DEG FEB GE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△GDE ≌△BFE (ASA ),∴DG =BF =3,DE =EF ,∴BC =6,∴CF =9,由勾股定理得,AC =8,∴CD =4,在Rt △CDF 中,由勾股定理得,DF =22224997CD CF +=+=,∵∠ACB =90°,EF =DE ,∴CE =12DF =972, 故答案为:972. 【点评】本题主要考查了勾股定理,三角形中位线定理,全等三角形的判定与性质,直角三角形斜边上中线的性质等知识,证明点E 是DF 的中点是解题的关键.11.如图,在Rt ABC 中,90,8,6ACB AC BC ∠=︒==,点P 是平面内一个动点,且4AP =,Q 为BP 的中点,在P 点运动过程中,设线段CQ 的长度为m ,则m 的取值范围是_______.【答案】3m 7≤≤【分析】取AB 的中点M ,连接QM 、CM ,得到QM 是△APB 的中位线,CM 是Rt ABC 斜边上的中线,求得QM 、CM 的长,在△QMC 中利用三角形三边关系得到CQ 的范围即可.【解答】取AB 的中点M ,连接QM 、CM ,∴QM 是△APB 的中位线,CM 是Rt ABC 斜边上的中线,∴122QM AP ==,12CM AB =, 在Rt ABC 中,90,8,6ACB AC BC ∠=︒==,∴226810AB =+=,∴CM =5,∵点P 是平面内一个动点,∴点Q 是动点,且点Q 以点M 为圆心,QM 长为半径的圆上运动,∴C 、Q 、M 可以三点共线,∴CM -MQ ≤CQ ≤CM +MQ ,∴3m 7≤≤,故答案为:3m 7≤≤.【点评】本题考查勾股定理、直角三角形斜边中线的性质,中位线定理、三角形三边关系等知识,分析点Q 的运动是解题的关键.12.如图,在四边形ABCD 中,∠ABC =90°,AC=AD ,M ,N 分别是AC ,CD 的中点,连接BM ,MN ,BN .(1)求证:BM=MN ;(2)若∠BAD =60°,AC 平分∠BAD ,AC =2.①求∠BMN 的度数;②求BN 的长.题的关键是灵活应用三角形的中位线平行于第三边,并且等于第三边的一半.13.如图,D、E、F分别是△ABC三边中点,AH⊥BC于H.求证:(1)∠BDF=∠BAC;(2)DF=EH.【答案】(1)见解析;(2)见解析.【分析】(1)根据三角形中位线定理得到DF//AC,根据平行线的性质证明结论;AC,等量代换证明结论.(2)根据直角三角形的性质得到EH=12【解答】(1)∵D、F分别是△ABC两边中点,∴DF是△ABC的中位线,AC,∴DF//AC,DF=12∴∠BDF=∠BAC;(2)∵AH⊥BC于H,E是AC的中点,AC,∴EH=12由(1)得,DF=12 AC,∴DF=EH.【点评】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.14.在平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AB,点E、F分别是OA、BC的中点,连接BE、EF.BC;(1)求证:EF=12(2)在上述条件下,若AC=BD,G是BD上一点,且BG:GD=3:1,连接EG、FG,试判断四边形EBFG的形状,并证明你的结论.∴EBFG是平行四边形,连接CG,∵G是OD的中点,而CO=12AC=12BD=AB=CD,∴CG⊥OD,而F是BC的中点,∴GF=12BC=BF,∴平行四边形EBFG是菱形.【点评】本题考查了平行四边形的性质和判定,矩形性质,菱形性质,三角形的中位线,直角三角形斜边上中线性质,等腰三角形的性质等知识点,主要考查学生综合运用定理进行推理的能力,注意:直角三角形斜边上中线等于斜边的一半.15.如图,在平面直角坐标系中,A(0,4),B(4,0),C(6,2),连接AB,BC,平移BC至AD(点B 与点A对应,点C与点D对应),连接CD.(1)①直接写出点D的坐标为.②判断四边形ABCD的形状,并证明你的结论;(2)如图1,点E为AB边上一点,连接DE,DF平分∠EDC交BC于F,连接EF,若∠DFE=45°,求BE 的长;(3)如图2,N为BC边的中点,若∠AMC=90°,连接MN,请直接写出MN的取值范围.段CD上取一点G,使DG=DE,∵∠FDE=∠FDG,DF=DF,∴△DFE≌△DFG(SAS),∴∠DFE=∠DFG=45°,EF=GF,∴∠EFG=90°,∵∠EFB+∠GFC=90°,∠GFC+∠FGC=90°,∴∠EFB=∠FGC,∵∠EBF=∠FCG=90°,EF=GF,∴△EBF≌△FCG(AAS),∴EB=FC,BF=CG,设EB=FC=x,则22BF CG BC x x==-=-,∴222222(42)(22)DE AE AD x DG=+=-+=,∵222()(4222)DG CD GC x=-=-+,∴222 (4222)(42)(22)x x-+=-+,解得:423x,即423BE=;(3)解:如图,连接AC,取AC的中点H,连接MH,NH,∵点A(0,4),B(4,0),D(2,6),∴42,210AB AC==,∵H为AC的中点,N为BC边的中点,∴1122,1022NH AB HM AC====,∵HM-NH≤MN≤HM+NH,∴MN的取值范围为10222210MN-≤≤+.【点评】本题是四边形综合题,主要考查了平行四边形和矩形的性质、三角形全等、勾股定理的运用,直角三角形的性质,三角形中位线定理等,综合性强,难度较大,熟练掌握相关知识点是解题的关键.16.已知,在△ABC中,以△ABC的两边BC,AC为斜边向外测作Rt△BCD和Rt△ACE,使∠CAE=∠CBD,取△ABC 边AB 的中点M ,连接ME ,MD .特例感知:(1)如图1,若AC =BC ,∠ACB =60°,∠CAE =∠CBD =45°,取AC ,BC 的中点F ,G ,连接MF ,MG ,EF ,DG ,则ME 与MD 的数量关系为______,∠EMD =______;(2)如图2,若∠ACB =90°,∠CAE =∠CBD =60°,取AC ,BC 的中点F ,G ,连接MF ,MG ,EF ,DG ,请猜想ME 与MD 的数量关系以及∠EMD 的度数,并给出证明;类比探究:(3)如图3,当△ABC 是任意三角形,∠CAE =∠CBD =α时,连接DE ,请猜想△DEM 的形状以及∠EMD 与α的数量关系,并说明理由. 【答案】(1)ME=MD ,∠EMD=90°;(2)ME=MD ,∠EMD=120°;(3)△DEM 是等腰三角形,∠EMD=2α.【分析】(1)如图1,证明△EAM ≌△DBM ,可得EM=DM ,先根据三角形的中位线得:11FM AC MG BC 22===,由直角三角形斜边中线等于斜边一半可得12EF AC =,得EF=FM ,且顶角∠EFM=150°,得∠FEM=∠FME=15°,同理∠DMG=15°,相加可得结论;(2)如图2,证明△MEF ≌△DMG ,可得EM=DM ,∠EMF=∠MDG=15°,相加可得∠EMD=120°;(3)如图,作辅助线,取AC ,BC 的中点F ,G ,连接MF ,MG ,EF ,DG ,同理可证出EF=MG ,DG=FM ,∠3=2∠2,∠4=2∠1,证明△MEF ≌△DMG .则EM=DM ,∠EMF=∠MDG .表示∠EMD=∠MDG+∠DMG+∠ACB ,代入可得结论.【解答】解:(1)ME=MD ,∠EMD=90°;理由是:如图1,∵AC=BC ,∠ACB=60°,∴△ABC 是等边三角形,∴∠CAB=∠CBA=60°,在 Rt △BCD 和Rt △ACE 中,∠CAE=∠CBD=45°,∴AC=2AE,BC=2BD,∴AE=BD,∵M是AB的中点,∴AM=BM,∵∠EAM=45°+60°=105°,∠DBM=45°+60°=105°,∴∠EAM=∠DBM,∴△EAM≌△DBM,∴EM=DM,∵F、G分别是AC、BC的中点,∴FM=MG=12AC=CF=CG,∴四边形CFMG是菱形,∴∠FMG=∠BCA=60°,Rt△ACE中,∵F是斜边AC的中点,∴EF=12AC=FM,∵∠EFM=90°+60°=150°,∴∠FEM=∠FME=15°,同理∠DMG=15°,∴∠EMD=60°+15°+15°=90°,故答案为EM=DM,90°;(2)ME=MD,∠EMD=120°;证明:∵F,G,M是△ABC的三边AC,BC,AB的中点,∴FM=12BC=CG,FM∥BC,MG=12AC=CF,MG∥AC.∴四边形CFMG是平行四边形,∴∠AFM=∠FMG=∠ACB=∠MGD=90°.∵∠AEC=∠BDC=90°,F,G是AC,BC的中点,∴EF=AF=FC=12AC,CG=BG=DG=12BC.∴∠2=∠CEF,∠1=∠CDG,EF=MG,DG=FM.∴∠3=∠2+∠CEF=2∠2,∠4=∠1+∠CDG=2∠1.∵∠2+∠EAC=90°,∠1+∠CBD=90°,∠CAE=∠CBD=60°,∴∠1=∠2=30°.∴∠3=∠4=60°.∴∠EFM=∠3+∠AFM=150°,∠DGM=∠4+∠CGM=150°∴∠EFM=∠DGM.又∵EF=MG,FM=DG,∴△MEF≌△DMG.∴EM=DM,∠EMF=∠MDG=15°.∴∠EMD=90°+2×15°=90°30°=120°;(3)△DEM是等腰三角形,∠EMD=2α.证明:取AC,BC的中点F,G,连接MF,MG,EF,DG,同(2)证法相同,可证出EF=MG,DG=FM,∠3=2∠2,∠4=2∠1.∵∠2+∠EAC=90°,∠1+∠CBD=90°,∠CAE=∠CBD=α,∴∠1=∠2=90°-α.∴∠3=∠4=2(90°-α).∴∠EFM=∠3+∠AFM=∠3+∠ACB,∠DGM=∠4+∠BGM=∠4+∠ACB.∴∠EFM=∠DGM.又∵EF=MG,FM=DG,∴△MEF≌△DMG.∴EM=DM,∠EMF=∠MDG.∴△DEM是等腰三角形;∵∠EMD=∠FME+∠FMG+∠DMG,由(2)知∠FMG=∠ACB,∴∠EMD=∠MDG+∠DMG+∠ACB.∵∠MDG+∠DMG=180°-∠DGM=180°-(∠4+∠ACB )=180°-2(90°-α)-∠ACB=2α-∠ACB.∴∠EMD=2α-∠ACB+∠ACB=2α.【点评】本题是三角形的综合题,考查了三角形全等的性质和判定、三角形中位线定理、直角三角形斜边中线的性质、平行四边形的性质、等边三角形的性质等知识,并运用了类比的思想依次解决问题.∆中,D为BC中点,BE、CF与射线AE分别相交于点E、F(射线AE不经过点D).17.在ABC(1)如图①,当BE∥CF时,连接ED并延长交CF于点H. 求证:四边形BECH是平行四形;(2)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND.求证:AM=AN(3)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND.求证:∠EMD=∠FND.【答案】(1)证明见解析(2)证明见解析(3)证明见解析【分析】(1)根据两直线平行内错角相等求得∠DBE=∠DCH,然后依据ASA求得BDE≅CDH得出ED=HD,最后根据有一组对边平行且相等的四边形是平行四边形求得.(2)连接FD、ED,延长ED交CF于点H,根据直角三角形斜边的中线定理和三角形的中位线定理求得ME=DN,MD=NF,从而证得AM=AN;(3)在(2)的条件下根据SSS 即可证明MED ≅NDF ,最后根据全等三角形的对应角相等求得∠EMD =∠FND . (1)如图①,∵D 为BC 的中点,∴BD =CD ,∵BE ∥CF ,∴∠DBE =∠DCH ,在BDE 与CDH 中,DBE DCH BD CD BDE CDH ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴BDE ≅CDH (AAS ),∴ED =HD ,∴四边形BECH 是平行四边形;(2)如图②连接FD 、ED ,延长ED 交CF 于点H ,∵BE ⊥AE ,CF ⊥AE ,)可知BDE≅CDHRt EHFRt AEBRt ACF在MED与NDF∴MED≅NDF。
三角形中位线定理专练

三角形中位线定理专练1.如图,在△ ABC中,D是AB上一点,且AD=AC,AE⊥ CD,垂足是E,F 是CB的中点.求证:BD=2EF.2.如图所示,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点.求证:△ EFG是等腰三角形.3.在△ ABC中,中线BE、CF交于点O,M、N分别是BO、CO中点,则四边形MNEF是什么特殊四边形?并说明理由.4.如图,BE,CF是△ ABC的角平分线,AN⊥ BE于N,AM⊥ CF于M,求证:MN∥ BC.5.如图,BM、CN分别平分△ABC的外角∠ ABD、∠ ACE,过A分别作BM、CN的垂线,垂足分别为M、N,交CB、BC的延长线于D、E,连结MN.求证:MN=(AB+BC+AC)6.如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.(1)求证:四边形ADEF是平行四边形;(2)求证:∠ DHF=∠ DEF.7.如图,在四边形ABCD中,对角线AC、BD交于点O,E、F分别是AB、CD 的中点,且AC=BD.求证:OM=ON.8.如图,M是△ ABC的边BC的中点,AN平分∠ BAC,BN⊥ AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3(1)求证:BN=DN;(2)求△ ABC的周长.三角形中位线定理专练参考答案与试题解析一.解答题(共8小题)1.(2014?山东模拟)如图,在△ABC中,D是AB上一点,且AD=AC,AE⊥CD,垂足是E,F是CB的中点.求证:BD=2EF.【考点】三角形中位线定理.菁优网版权所有【专题】常规题型.【分析】根据三角形的中位线定理,在三角形中准确应用,并且求证E为CD 的中点,再求证EF为△BCD的中位线.【解答】证明:在△ACD中,因为AD=AC 且AE⊥CD,所以根据等腰三角形中底边的垂线与底边的交点即中点,可以证明:E为CD的中点,又因为F是CB的中点,所以,EF∥BD,且EF为△BCD的中位线,因此EF=BD,即BD=2EF.【点评】此题主要是中位线定理在三角形中的应用,考查在三角形中位线为对应边长的的定理.2.(2015春?天津校级期中)如图所示,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点.求证:△EFG是等腰三角形.【考点】三角形中位线定理;等腰三角形的判定.菁优网版权所有【专题】证明题.【分析】由于E,F,G分别是AB,CD,AC的中点,利用中位线定理,GF=AD,GE=BC,又因为AD=BC,所以GF=GE.【解答】证明:∵E,F,G分别是AB,CD,AC的中点.∴GF=AD,GE=BC.又∵AD=BC,∴GF=GE,即△EFG是等腰三角形.【点评】本题通过给出的中点,利用中位线定理,证得边相等,从而证明等腰三角形,是一道基础题.3.(2015秋?青岛校级月考)在△ABC中,中线BE、CF交于点O,M、N分别是BO、CO中点,则四边形MNEF是什么特殊四边形?并说明理由.【考点】三角形中位线定理;平行四边形的判定.菁优网版权所有【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC,MN∥BC且MN=BC,从而得到EF∥MN且EF=MN,再根据一组对边平行且相等的四边形是平行四边形判断.【解答】解:四边形MNEF是平行四边形.理由如下:∵BE、CF是中线,∴E、F分别是AC、AB的中点,∴EF是△ABC的中位线,∴EF∥BC且EF=BC,∵M、N分别是BO、CO中点,∴MN是△OBC的中位线,∴MN∥BC且MN=BC,∴EF∥MN且EF=MN,∴四边形MNEF是平行四边形.【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定,熟记定理并准确识图是解题的关键.4.(2015春?泗洪县校级期中)如图,BE,CF是△ABC的角平分线,AN⊥BE 于N,AM⊥CF于M,求证:MN∥BC.【考点】三角形中位线定理;等腰三角形的判定与性质.菁优网版权所有【专题】证明题.【分析】延长AN、AM分别交BC于点D、G,根据BE为∠ABC的角平分线,BE⊥AG可知∠BAN=∠BGN故△ABG为等腰三角形,所以BN也为等腰三角形的中线,即AM=GN.同理AM=DM,根据三角形中位线定理即可得出结论.【解答】证明:延长AN、AM分别交BC于点D、G.∵BE为∠ABC的角平分线,BE⊥AG,∴∠BAG=∠BGA,∴△ABG为等腰三角形,∴BN也为等腰三角形的中线,即AN=GN.同理AM=DM,∴MN为△ADG的中位线,∴MN∥BC.【点评】本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.5.(2015春?富顺县校级月考)如图,BM、CN分别平分△ABC的外角∠ABD、∠ACE,过A分别作BM、CN的垂线,垂足分别为M、N,交CB、BC的延长线于D、E,连结MN.求证:MN=(AB+BC+AC)【考点】三角形中位线定理;等腰三角形的判定与性质.菁优网版权所有【专题】证明题.【分析】首先通过△ABM≌△DBM,得到AB=DB,AM=DM,同理:AN=EN,AC=CE,再根据三角形的中位线定理即可得到结果.【解答】证明:∵AM⊥BM,∴∠AMB=∠DMB=90°,∵BM平分∠ABD,∴∠ABM=∠DBM,在△ABM与△DBM中,,∴△ABM≌△DBM(asa),∴AB=DB,AM=DM,同理:AN=EN,AC=CE,∴MN=DE=(DB+BC+CE)=(AB+BC+AC).【点评】本题考查了三角形的中位线定理,全等三角形的判定与性质,证明三角形全等是解题的关键.6.(2014?宿迁)如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.(1)求证:四边形ADEF是平行四边形;(2)求证:∠DHF=∠DEF.【考点】三角形中位线定理;直角三角形斜边上的中线;平行四边形的判定.菁优网版权所有【专题】证明题;几何综合题.【分析】(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥AB,DE∥AC,再根据平行四边形的定义证明即可;(2)根据平行四边形的对角相等可得∠DEF=∠BAC,根据直角三角形斜边上的中线等于斜边的一半可得DH=AD,FH=AF,再根据等边对等角可得∠DAH=∠DHA,∠FAH=∠FHA,然后求出∠DHF=∠BAC,等量代换即可得到∠DHF=∠DEF.【解答】证明:(1)∵点D,E,F分别是AB,BC,CA的中点,∴DE、EF都是△ABC的中位线,∴EF∥AB,DE∥AC,∴四边形ADEF是平行四边形;(2)∵四边形ADEF是平行四边形,∴∠DEF=∠BA C,∵D,F分别是AB,CA的中点,AH是边BC上的高,∴DH=AD,FH=AF,∴∠DAH=∠DHA,∠FAH=∠FHA,∵∠DAH+∠FAH=∠BAC,∠DHA+∠FHA=∠DHF,∴∠DHF=∠BAC,∴∠DHF=∠DEF.【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰三角形的性质,直角三角形斜边上的中线等于斜边的一半的性质,平行四边形的判定与性质,熟记各性质并准确识图是解题的关键.7.(2014?丹阳市校级模拟)如图,在四边形ABCD中,对角线AC、BD交于点O,E、F分别是AB、CD的中点,且AC=BD.求证:OM=ON.【考点】三角形中位线定理;平行线的性质;等腰三角形的判定与性质.菁优网版权所有【专题】证明题.【分析】取AD的中点G,连接EG,FG,构造三角形的中位线,根据三角形的中位线定理进行证明即可.【解答】证明:取AD的中点G,连接EG,FG,∵G、F分别为AD、CD的中点,∴GF是△ACD的中位线,∴GF=AC,同理可得,GE=BD,∵AC=BD,∴GF=GE=AC=BD.∴∠GFN=∠GEM,又∵EG∥OM,FG∥ON,∴∠OMN=∠GEM=∠GFN=∠ONM,∴OM=ON.【点评】本题考查了三角形的中位线性质定理,解题的关键是构造三角形的中位线.运用三角形的中位线的数量关系和位置关系进行分析证明.8.(2013?永州)如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN 于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3(1)求证:BN=DN;(2)求△ABC的周长.【考点】三角形中位线定理;等腰三角形的判定与性质.菁优网版权所有【分析】(1)证明△ABN≌△ADN,即可得出结论;(2)先判断MN是△BDC的中位线,从而得出CD,由(1)可得AD=AB=10,从而计算周长即可.【解答】(1)证明:在△ABN和△ADN中,∵,∴△ABN≌△ADN(ASA),∴BN=DN.(2)解:∵△ABN≌△ADN,∴AD=AB=10,又∵点M是BC中点,∴MN是△BDC的中位线,∴CD=2MN=6,故△ABC的周长=AB+BC+CD+AD=10+15+6+10=41.【点评】本题考查了三角形的中位线定理及等腰三角形的判定,注意培养自己的敏感性,一般出现高、角平分线重合的情况,都需要找到等腰三角形.。
2020中考数学 三角形的中位线 综合练习(含答案)

2020中考数学 三角形的中位线 综合练习(含答案)一、单选题(共有9道小题)1.如图,在△ABC 中,点D 、E 分别是AB 、AC 的中点,∠A=50°,∠ADE=60°,则∠C 的度数为( )A .50° B.60° C.70° D.80°2.如图,△ABC 中,AB=AC=10,BC=8,AD 平分∠BAC 交BC 于点D ,点E 为AC 的中点,连接DE ,则△CDE 的周长为( )A .20B . 12C .14D . 133.如图,为测量池塘岸边A 、B 两点的距离,小明在池塘的一侧选取一点O ,测得OA 、OB 的中点分别是点D 、E ,且DE =14米,则A 、B 间的距离是( )A .18 米B .24米C .28米D . 30米4.如图,△ABC 中,AB=AC=10,BC=8,AD 平分∠BAC 交BC 于点D ,点E 为AC 的中点,连接DE ,则△CDE 的周长为( )A .20B . 12C .14D . 135.如图,已知在Rt△ABC 中,∠ABC=90°,点D 是BC 边的中点,分别以B,C 为圆心,大于线段BC 长度一半的长为半径画弧,两弧在直线BC 上方的交点为P ,直线PD 交AC 于点E,连结BE.则下列结论中,一定正确的是( )①ED ⊥BC ②∠A=∠EBA ③EB 平分∠AED ④12ED AB =A.①②③B.①②④C.①③④D.②③④ED B CAE DA C BEDAB OE D A C B E DBCAP6.如图,在四边形ABCD 中,E 、F 分别是AB ,AD 的中点,若EF=2,BC=5,CD=3,则tanC 等于( )A.34B.43C.35D.457.如图,已知在△ABC 中,∠BAC >90°,点D 为BC 的中点,点E 在AC 上,将△CDE 沿DE 折叠,使得点C 恰好落在BA 的延长线上的点F 处,连结AD ,则下列结论不一定正确的是( ) A .AE =EFB .AB =2DEC .△ADF 和△ADE 的面积相等D .△ADE 和△FDE 的面积相等8.如果三角形的两边长分别是方程28150x x -+=的两个根,那么连接这个三角形三边的中点,得到的三角形的周长可能是( )A .5.5B .5C .4.5D .4 9.如果三角形的两边分别为3和5,那么连结这个三角形三边中点所得的三角形的周长可能是( )A .5.5B .5C .4.5D .4 二、填空题(共有7道小题)10.在Y ABCD 中,点O 是对角线AC 、BD 的交点,点E 是边CD 的中点,且AB=6,BC=10,则OE=______________.11.如图,顺次连结四边形 ABCD 四边的中点 E 、F 、G 、H ,则四边形 EFGH 的形状一定是 .EF BC ADBF CADE FHEG B C D A12.如图,在△ABC 中,∠ACB=90°,M 、N 分别是AB 、AC 的中点,延长BC 至点D ,使13CD BD =,连接DM 、DN 、MN ,若AB=6,则DN 。
专题12 三角形中位线定理-2020-2021学年八年级数学下册常考题专练(人教版)(解析版)

专题12三角形中位线定理★知识归纳●三角形的中位线1.连接三角形两边中点的线段叫做三角形的中位线.2.定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.要点梳理:(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系.(2)三角形的三条中位线把原三角形分成可重合的4个小三角形.因而每个小三角形的周长为原三角形周长的12,每个小三角形的面积为原三角形面积的14.(3)三角形的中位线不同于三角形的中线.★实操夯实一.选择题(共18小题)1.如图,在△ABC中,AB=3,BC=6,AC=4,点D,E分别是边AB,CB的中点,那么DE的长为()A.1.5B.2C.3D.4【解答】解:∵点D,E分别是边AB,CB的中点,∴DE=AC=2,故选:B.2.如图,△ABC中,D是AB的中点,E在AC上,且∠AED=90°+∠C,则BC+2AE等于()A.AB B.AC C.AB D.AC【解答】解:如图,过点B作BF∥DE交AC于点F.则∠BFC=∠DEF.又∵点D是AB的中点,∴EF=AE.∵∠DEF=∠BFC=180°﹣∠AED=180°﹣(90°+∠C)=90°﹣∠C,∴∠FBC=∠BFC,∴BC=FC,∴BC+2AE=AC.故选:B.3.如图,在△ABC中,E,F分别为AC,BC中点,若AB=6,BC=7,AC=8,则EF=()A.3B.3.5C.4D.4.5【解答】解:∵E,F分别为AC,BC中点,∴EF是△ABC的中位线,∴EF=AB=×6=3,故选:A.4.如图,平地上A、B两点被池塘隔开,测量员在岸边选一点C,并分别找到AC和BC的中点M、N,测量得MN =8米,则A、B两点间的距离为()A.4米B.24米C.16米D.48米【解答】解:∵点M、N分别为AC和BC的中点,∴MN是△ABC的中位线,∴AB=2MN=16(米),故选:C.5.如图,EF是△ABC的中位线,BD平分∠ABC交EP于D,BE=3,DF=1,则BC的长为()A.2B.4C.6D.8【解答】解:∵BD平分∠ABC,∴∠ABD=∠CBD,∵EF是△ABC的中位线,∴EF∥BC,BC=2EF,∴∠EDB=∠CBD,∴∠ABD=∠EDB,∴ED=EB=3,∴EF=ED+DF=4,∴BC=2EF=8,故选:D.6.一个三角形的三条中位线的长为6、7、8,则此三角形的周长为()A.10.5B.21C.42D.63【解答】解:∵三角形的三条中位线的长为6、7、8,∴三角形的三边长分别为12、14、16,∴此三角形的周长=12+14+16=42,故选:C.7.如图,在四边形ABCD中,点P是边CD上的动点,点Q是边BC上的定点,连接AP,PQ,E,F分别是AP,PQ的中点,连接EF.点P在由C到D运动过程中,线段EF的长度()A.保持不变B.逐渐变小C.先变大,再变小D.逐渐变大【解答】解:连接AQ,∵点Q是边BC上的定点,∴AQ的大小不变,∵E,F分别是AP,PQ的中点,∴EF=AQ,∴线段EF的长度保持不变,故选:A.8.如图,△ABC中,D,E分别是BC,AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是()A.3B.4C.5D.6【解答】解:∵D,E分别是BC,AC的中点,∴DE∥AB,∴∠BFD=∠ABF,∵BF平分∠ABC,∴∠DBF=∠ABF,∴∠BFD=∠DBF,∴DF=DB=BC=3,故选:A.9.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是()A.2B.3C.4D.5【解答】解:∵点D,E分别是边AB,AC的中点,∴DE是△ABC的中位线,∵BC=14,∴DE=BC=7,∵∠AFB=90°,AB=8,∴DF=AB=4,∴EF=DE﹣DF=7﹣4=3,故选:B.10.△ABC中,点D,E分别是△ABC的边AB,AC的中点,连接DE.若∠C=68°,则∠AED=()A.22°B.68°C.96°D.112°【解答】解:∵点D、E分别是△ABC的边AB、AC的中点,∴DE∥BC,∴∠AED=∠C,∵∠C=68°,∴∠AED=∠C=68°.故选:B.11.如图,△ABC中,D、E分别是AB、AC边的中点,延长DE至F,使EF=DF,若BC=8,则DF的长为()A.6B.8C.4D.【解答】解:∵D、E分别是AB、AC边的中点,∴DE=BC=4,∵EF=DF,∴EF=2,∴DF=6,故选:A.12.如图,在直角三角形ABC中,∠C=90°,点E、F分别为AC和AB的中点,AF=5,AE=4,则BC=()A.3B.6C.8D.10【解答】解:∵点E、F分别为AC和AB的中点,∴EF∥BC,BC=2EF,∴∠AEF=∠C=90°,∴EF===3,∴BC=6,故选:B.13.如图,△ABC的周长为32,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为()A.3B.4C.5D.6【解答】解:∵BQ平分∠ABC,BQ⊥AE,∴∠ABQ=∠EBQ,∵∠ABQ+∠BAQ=90°,∠EBQ+∠BEQ=90°,∴∠BAQ=∠BEQ,∴AB=BE,同理:CA=CD,∴点Q是AE中点,点P是AD中点(三线合一),∴PQ是△ADE的中位线,∵BE+CD=AB+AC=32﹣BC=32﹣12=20,∴DE=BE+CD﹣BC=8,∴PQ=DE=4.故选:B.14.如图,四边形ABCD中,AC⊥BC,AD∥BC,BC=3,AC=4,AD=6.M是BD的中点,则CM的长为()A.B.2C.D.3【解答】解:延长BC到E使BE=AD,则四边形ABED是平行四边形,∵BC=3,AD=6,∴C是BE的中点,∵M是BD的中点,∴CM=DE=AB,∵AC⊥BC,∴AB===5,∴CM=,故选:C.15.如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD=20°,∠BDC=70°,则∠NMP的度数为()A.50°B.25°C.15°D.20°【解答】解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,∴PN,PM分别是△CDB与△DAB的中位线,∴PM=AB,PN=DC,PM∥AB,PN∥DC,∵AB=CD,∴PM=PN,∴△PMN是等腰三角形,∵PM∥AB,PN∥DC,∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,∴∠MPN=∠MPD+∠NPD=20°+(180﹣70)°=130°,∴∠PMN==25°.故选:B.16.如图,已知CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB,给出下列结论:①AE=2AC;②CE =2CD;③∠ACD=∠BCE;④CB平分∠DCE,则以上结论正确的是()A.①②④B.①③④C.①②③D.①②③④【解答】解:①∵CB是三角形ACE的中线,∴AE=2AB,又AB=AC,∴AE=2AC.故此选项正确;②取CE的中点F,连接BF.∵AB=BE,CF=EF,∴BF∥AC,BF=AC.∴∠CBF=∠ACB.∵AC=AB,∴∠ACB=∠ABC.∴∠CBF=∠DBC.又∵CD是三角形ABC的中线,∴AC=AB=2BD.∴BD=BF.又∵BC=BC,∴△BCD≌△BCF,∴CF=CD.∴CE=2CD.故此选项正确.③若要∠ACD=∠BCE,则需∠ACB=∠DCE,又∠ACB=∠ABC=∠BCE+∠E=∠DCE,则需∠E=∠BCD.根据②中的全等,得∠BCD=∠BCE,则需∠E=∠BCE,则需BC=BE,显然不成立,故此选项错误;④根据②中的全等,知此选项正确.故选:A.17.如图,已知△ABC中,AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G,下列结论:①AD⊥BC;②AE∥BC;③AE=AG;④AD2+AE2=4AG2.其中正确结论的个数是()A.1B.2C.3D.4【解答】解:连接EC,∵AB=AC,AD是∠BAC的平分线,∴AD⊥BC,故①正确;∵AB=AC,∴∠B=∠ACB,∵AE平分∠F AC,∴∠F AC=2∠F AE,∵∠F AC=∠B+∠ACB,∴∠F AE=∠B,∴AE∥BC,故②正确;∵AE∥BC,DE∥AB,∴四边形ABDE是平行四边形,∴AE=BD,∵AB=AC,AD⊥BC,∴CD=BD,∴AE=CD,∵AE∥BC,∠ADC=90°,∴四边形ADCE是矩形,∴AC=DE,AG=CG,DG=EG,∴DG=AG=CG=EG,在Rt△AED中,AD2+AE2=DE2=AC2=(2AG)2=4AG2,故④正确;∵AE=BD=BC,AG=AC,∴AG=AE错误(已知没有条件AC=BC),故③错误;即正确的个数是3个,故选:C.18.如图,△ABC中,AB>AC,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,则①EF∥AB;②∠BCG=(∠ACB﹣∠ABC);③EF=(AB﹣AC);④(AB﹣AC)<AE<(AB+AC).其中正确的是()A.①②③④B.①②C.②③④D.①③④【解答】解:∵AD平分∠BAC,∴∠GAF=∠CAF,∵CG⊥AD,∴∠AFG=∠AFC=90°,在△AFG和△AFC中∴△AFG≌△AFC(ASA),∴GF=CF,∵AE为△ABC的中线,∴BE=CE,∴EF∥AB,故①正确;∵△AFG≌△AFC,∴∠AGC=∠ACG,∠AGF=∠ACF,∵∠AGC=∠B+∠BCG,∴∠ACG=∠B+∠BCG,∴∠BCG=∠ACB﹣∠ACG=∠ACB﹣(∠B+∠BCG),∴2∠BCG=∠ACB﹣∠B,∴∠BCG=(∠ACB﹣∠B),故②正确;∵△AFG≌△AFC,∴AC=AG,∴BG=AB﹣AG=AB﹣AC,∵F、E分别是CG、BC的中点,∴EF=BG,∴EF=(AB﹣AC),故③正确;∵∠AFG=90°,∴∠EAF<90°,∵∠AFE=∠AFG+∠EFG>90°,∴∠AFE>∠EAF,∴AE>EF,∵EF=(AB﹣AC),∴(AB﹣AC)<AE,延长AE到M,使AE=EM,连接BM,∵在△ACE和△MBE中∴△ACE≌△MBE(SAS),∴AC=MB,在△ABM中,AM<AB+MB=AB+AC,∵AE=EM,∴2AE<AB+AC,∴AE<(AB+AC),即(AB﹣AC)<AE<(AB+AC),故④正确;故选:A.二.填空题(共6小题)19.如图,在△ABC中,点D,E,F分别是边AB,BC,CA上的中点,且AB=10cm,AC=16cm,则四边形ADEF 的周长等于26cm.【解答】解:∵点D,E,F分别是边AB,BC,CA上的中点,∴DE,EF都是△ABC的中位线,∴DE=AC=8cm,DE∥AC,EF=AB=5cm,EF∥AB,∴四边形ADEF是平行四边形,∴四边形ADEF的周长=2(DE+EF)=2×13=26(cm).故答案为:26.20.如图,△ABC的面积为4,分别取AC,BC两边的中点A1,B1,记△A1B1C的面积为S1;再分别取A1C,B1C 的中点A2,B2,记△A2B2C的面积为S2,再分别取A2C,B2C的中点A3,B3,记△A3B3C的面积为S3;则S3的值等于.【解答】解:∵点A1,B1是AC,BC两边的中点,∴A1B1是△ABC的中位线,∴A1B1=AB,A1B1∥AB,∴△CA1B1∽△CAB,∴=()2=,∵△ABC的面积为4,∴S1=1,同理可得,S3=,故答案为:.21.如图,四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=35°,则∠PFE的度数是35°.【解答】解:∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,∴FP,PE分别是△CDB与△DAB的中位线,∴PF=BC,PE=AD,∵AD=BC,∴PF=PE,故△EPF是等腰三角形.∵∠PEF=35°,∴∠PEF=∠PFE=35°,故答案为:35°.22.如图,已知在Rt△ABC中,∠ACB=90°,点D是AC延长线上的一点,AD=24,点E是BC上一点,BE=10,连接DE,M、N分别是AB、DE的中点,则MN=13.【解答】解:连接BD,取BD的中点F,连接MF、NF,如图所示:∵M、N、F分别是AB、DE、BD的中点,∴NF、MF分别是△BDE、△ABD的中位线,∴NF∥BE,MF∥AD,NF=BE=5,MF=AD=12,∵∠ACB=90°,∴AD⊥BC,∵MF∥AD,∴MF⊥BC,∵NF∥BE,∴NF⊥MF,在Rt△MNF中,由勾股定理得:MN===13;故答案为:13.23.如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到100个小三角形,则需要操作的次数是33.【解答】解:∵第一次操作后,三角形共有4个;第二次操作后,三角形共有4+3=7个;第三次操作后,三角形共有4+3+3=10个;…∴第n次操作后,三角形共有4+3(n﹣1)=3n+1个;当3n+1=100时,解得:n=33,故答案为:33.24.如图,在△ABC中,BF平分∠ABC,AG⊥BF,垂足为点D,交BC于点G,E为AC的中点,连接DE,DE =2.5cm,AB=4cm,则BC的长为9cm.【解答】解:∵BF平分∠ABC,AG⊥BF,∴△ABG是等腰三角形,∴AB=GB=4cm,∵BF平分∠ABC,∴AD=DG,∵E为AC的中点,∴DE是△AGB的中位线,∴DE=CG,∴CG=2DE=5cm,∴BC=BG+CG=4+5=9cm,故答案为:9三.解答题(共6小题)25.如图,在△ABC中,BC>AC,点D在BC上,且DC=AC.(1)利用直尺与圆规先作∠ACB的平分线,交AD于F点,再作线段AB的垂直平分线,交AB于点E,最后连接EF.(2)若线段BD的长为6,求线段EF的长.【解答】解:(1)所作图形如下:(2)∵CF平分∠ACB∴∠ACF=∠BCF又∵DC=AC∴CF是△ACD的中线∴点F是AD的中点∵点E是AB的垂直平分线与AB的交点∴点E是AB的中点∴EF是△ABD中位线∴EF=BD=326.在△ABC中,E是AC边上一点,线段BE垂直∠BAC的平分线于D点,点M为BC边的中点,连接DM.(1)求证:DM=CE;(2)若AD=6,BD=8,DM=2,求AC的长.【解答】(1)证明:在△ADB和△ADE中,,∴△ADB≌△ADE(ASA)∴AE=AB,BD=DE,∵BD=DE,BM=MC,∴DM=CE;(2)解:在Rt△ADB中,AB==10,∴AE=10,由(1)得,CE=2DM=4,∴AC=CE+AE=14.27.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.(1)求证:DE=CF;(2)求EF的长.【解答】解:(1)∵D、E分别为AB、AC的中点,∴DE∥BC,DE=BC,∵EF∥CD∴四边形DEFC是平行四边形,∴DE=CF.(2)∵四边形DEFC是平行四边形,∴DC=EF,∵D为AB的中点,等边△ABC的边长是2,∴AD=BD=1,CD⊥AB,BC=2,∴DC=EF=.28.如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.【解答】证明:如图,连接BD,作BD的中点M,连接EM、FM.∵点E是AD的中点,∴在△ABD中,EM∥AB,EM=AB,∴∠MEF=∠P同理可证:FM∥CD,FM=CD.∴∠MFQ=∠CQF,又∵AB=CD,∴EM=FM,∴∠MEF=∠MFE,∴∠P=∠CQF..29.△ABC的中线BD、CE相交于O,F,G分别是BO、CO的中点,求证:EF∥DG,且EF=DG.【解答】证明:连接DE,FG,∵BD、CE是△ABC的中线,∴D,E是AB,AC边中点,∴DE∥BC,DE=BC,同理:FG∥BC,FG=BC,∴DE∥FG,DE=FG,∴四边形DEFG是平行四边形,∴EF∥DG,EF=DG.30.如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,求证:AF=CF.【解答】证明:如图,过D作DG∥AC,则∠EAF=∠EDG,∵AD是△ABC的中线,∴D为BC中点,∴G为BF中点,∴DG=CF,∵E为AD中点,∴AE=DE,在△AEF和△DEG中,,∴△AEF≌△DEG(ASA),∴DG=AF,∴AF=CF.。
三角形的中位线基础题30道解答题

9.5 三角形的中位线基础题汇编(3)BCBC=3DE=6中点重合)EF=EF=CE=,求BCD=EM=(9.5 三角形的中位线基础题汇编(3)参考答案与试题解析一.解答题(共30小题)1.如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.四边形EGFH是平行四边形吗?请证明你的结论.2.请写出“如图,在△ABC中,若DE是△ABC的中位线,则DE=BC”的逆命题.判断逆命题的真假,并说明你的理由?BC3.在四边形ABCD中,BD、AC相交于点O,AC=BD,E、F分别是AB、CD的中点,连接EF,分别交AC、BD 于点M、N.判断△MON的形状,并说明理由.EG=4.如图,在△ABC中,AD⊥BC于点D,E、F、G分别是BC、AC、AB的中点,若AB=BC=3DE=6,求四边形DEFG的周长.BC=3DE=6BC=3DE=6EF=×BC=×,AB=×=GF+DG+DE+EF=+3+2+3=.5.如图,在△ABC中(AB≠AC),M为BC的中点,AD平分∠BAC交BC于D,BE⊥AD于E,CF⊥AD于F,求证:ME=MF.MF=ME=GBME=6.△ABC中,D为BC中点,E为AD中点,直线BE交AC于F,求证:AC=3AF.7.如图,已知△XYZ中,MY=NZ,A、B分别是YN、MZ的中点,延长AB、BA分别交XZ、XY于点D、C,求证:XC=XD.BE=NZ BE=MY8.如图,AB为⊙O的一条弦,CD为直径(C不与A、B及中点重合),作CE⊥AB于E,DF⊥AB于F,问CE﹣DF的值是否变化?为什么?9.△ABC中,D为CB的延长线上一点,BE是∠ABD的角平分线,AE⊥BE,F是AC的中点,试说明:EF∥BC,且EF=(AB+BC).EF=10.如图,在四边形ABCD中,E、F分别是AD、BC的中点,连接FE并延长,分别交CD的延长线于点M、N,∠BME=∠CNE,求证:AB=CD.GE=GF=CDAB GF=CD11.已知,如图,AB=AC=BE,CD为△ABC中AB边上的中线,求证:CE=2CD.12.如图,在△ABC中,∠ACB=90°,点D在AB上,AC=AD,DE⊥CD交BC于点E,AF平分∠BAC交BC于F点.(1)求证:AF∥DE;(2)当AC=6,AB=10时,求BE的长.==,,BE=13.在四边形ABCD中,AB∥CD,E、F是AD、BC中点.求证:EF=(AB+CD),EF∥CD.EF=DM=14.如图,已知△ABC中,点D是BA上一点,BD=AC,E,F分别是BC,DA的中点,EF和CA的延长线相交于点G.求证:AG=AF.15.如图,AD是△ABC的中线,E,F,G分别是AB,AD,DC的中点,求证:EG与DF互相平分.ACED=16.已知:如图,点B是AD的中点,点E是AB的中点,AB=AC 求证:CE=CD.ACBE=CDCE=17.在△ABC中,AD⊥BC于D点,BE为中线,且∠CBE=30°.求证:AD=BE.EF=EF=EF=18.如图,在△ABC中,D、E、F分别是AB、BC、AC的中点,AB=6,AC=8,DF=5,求AE的长.BC=519.已知如图,△ABC中,AD为BC的中线,E为AD的中点,延长CE交AB于点F,求的值.(用多种方法解答);或过BF=DM==20.在△ABC中,D是AB的中点,DC⊥AC且tan∠BCD=,求tanA的值.BCD=,设,即BCD==ABBE=CE=AC.21.已知在△ABC中,M是BC的中点,AN平分∠BAC,AN⊥BN,求证:MN∥AC.22.已知:如图,在△ABC中,AB>AC,AD平分∠BAC,BE垂直AD延长线于E,M是BC中点.求证:EM=(AB﹣AC).CF=CF23.如图,在△ABC中,若∠B=2∠C,AD⊥BC,E为BC边中点,求证:AB=2DE.24.如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.求证:∠PMN=∠PNM.PM=PN=ADBC PN=AD25.如图,△ABC中,BM平分∠ABC,AM⊥BM,垂足M点,点N为AC的中点,AB=10,BC=6,求MN长度.MN=26.已知:△ABC,用刻度尺量出△ABC的各边的长度,并取各边的中点,画出△ABC的三条中线,你发现了什么?27.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为E,F是BC中点,探究BD与EF的关系.并说明理由.EF=28.如图,平行四边形ABCD的对角线AC,BD相交于点O,AE=EB.求证:OE∥BC.29.△ABC中,AD是∠BAC的平分线,G是BC的中点,过G作直线FG平行于AD,分别交AB和CA的延长线于点E和点F,求证:BE=CF=(AB+AC).BF=CE=30.如图,在△ABC中,AD=DE=EF=FB,AG=GH=HI=IC,已知BC=8,则DG+EH+FI的长是多少?BCBC BCDG+EH+FI=BC+BC=。
2021年九年级数学中考一轮复习专题突破训练:三角形的中位线(附答案)

2021年九年级数学中考一轮复习专题突破训练:三角形的中位线(附答案)1.如图,△ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为()A.B.1C.D.72.如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为P A,PB的中点,对下列各值:①线段MN的长;②△P AB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.其中会随点P的移动而变化的是()A.②③B.②⑤C.①③④D.④⑤3.如图,四边形ABCD中,∠A=90°,AB=,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为()A.3B.4C.4.5D.54.如图,在矩形ABCD中,P、R分别是BC和DC上的点,E、F分别是AP和RP的中点,当点P在BC上从点B向点C移动,而点R不动时,下列结论正确的是()A.线段EF的长逐渐增长B.线段EF的长逐渐减小C.线段EF的长始终不变D.线段EF的长与点P的位置有关5.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为()A.B.2C.D.36.如图,△ABC的面积是12,点D、E、F、G分别是BC、AD、BE、CE的中点,则△AFG 的面积是()A.4.5B.5C.5.5D.67.如图,△ABC中,已知AB=8,∠C=90°,∠A=30°,DE是中位线,则DE的长为()A.4B.3C.D.28.如图,在△ABC中,BD、CE是角平分线,AM⊥BD于点M,AN⊥CE于点N.△ABC 的周长为30,BC=12.则MN的长是()A.15B.9C.6D.39.如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD =20°,∠BDC=70°,则∠NMP的度数为()A.50°B.25°C.15°D.20°10.如图,在△ABC中,延长BC至D,使得CD=BC,过AC中点E作EF∥CD(点F 位于点E右侧),且EF=2CD,连接DF.若AB=8,则DF的长为()A.3B.4C.2D.311.如图,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F,则下列结论正确的是()A.EF=CF B.EF=DE C.CF<BD D.EF>DE12.如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是()A.10B.8C.6D.513.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是()A.7B.9C.10D.1114.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=10,BC =15,MN=3,则AC的长是()A.12B.14C.16D.1815.如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC 的周长是()A.6B.12C.18D.2416.如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE 并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为.17.如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD 上,P为AE的中点,连接PG,则PG的长为.18.如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若CD=5,则EF的长为.19.如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB,连接CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是.20.如图,∠ACB=90°,D为AB中点,连接DC并延长到点E,使CE=CD,过点B 作BF∥DE交AE的延长线于点F.若BF=10,则AB的长为.21.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=8,则EF的长为.22.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为.23.如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长.24.在四边形ABCD中,对角线AC⊥BD且AC=6、BD=8,E、F分别是边AB、CD的中点,则EF=.25.如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=BD,连接DM、DN、MN.若AB=6,则DN=.26.如图,在四边形ABDC中,E、F、G、H分别为AB、BC、CD、DA的中点,并且E、F、G、H四点不共线.当AC=6,BD=8时,四边形EFGH的周长是.27.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,点M为边AC的中点,点N 为边BC上任意一点,若点C关于直线MN的对称点C′恰好落在△ABC的中位线上,则CN的长为.28.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD =BC,∠FPE=100°,则∠PFE的度数是.29.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF =BC,连接CD和EF.(1)求证:DE=CF;(2)求EF的长.30.如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.(1)求证:四边形ADEF是平行四边形;(2)求证:∠DHF=∠DEF.31.如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.(1)求证:BM=MN;(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.32.如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=10,AC=6,求DF的长.33.如图,在四边形ABCD中,AC⊥BD,BD=12,AC=16,E,F分别为AB,CD的中点,求EF的长.34.在△ABC中,E是AC边上一点,线段BE垂直∠BAC的平分线于D点,点M为BC边的中点,连接DM.(1)求证:DM=CE;(2)若AD=6,BD=8,DM=2,求AC的长.35.如图,在四边形ABCD中,AB=DC,E、F分别是AD、BC的中点,G、H分别是对角线BD、AC的中点.(1)求证:四边形EGFH是菱形;(2)若AB=,则当∠ABC+∠DCB=90°时,求四边形EGFH的面积.36.如图,E、F、G、H分别为四边形ABCD四边之中点.(1)求证:四边形EFGH为平行四边形;(2)当AC、BD满足时,四边形EFGH为菱形.当AC、BD满足时,四边形EFGH为矩形.当AC、BD满足时,四边形EFGH为正方形.37.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC﹣AB);(2)如图2,写出线段AB、AC、EF的数量关系,并证明你的结论.38.已知:△ABC中,AB=10.(1)如图①,若点D、E分别是AC、BC边的中点,求DE的长;(2)如图②,若点A1,A2把AC边三等分,过A1,A2作AB边的平行线,分别交BC 边于点B1,B2,求A1B1+A2B2的值;(3)如图③,若点A1,A2,…,A10把AC边十一等分,过各点作AB边的平行线,分别交BC边于点B1,B2,…B10.根据你所发现的规律,直接写出A1B1+A2B2+…+A10B10的结果.参考答案1.解:∵AD是△ABC角平分线,CG⊥AD于F,∴△AGC是等腰三角形,∴AG=AC=3,GF=CF,∵AB=4,AC=3,∴BG=1,∵AE是△ABC中线,∴BE=CE,∴EF为△CBG的中位线,∴EF=BG=,故选:A.2.解:∵点A,B为定点,点M,N分别为P A,PB的中点,∴MN是△P AB的中位线,∴MN=AB,即线段MN的长度不变,故①错误;P A、PB的长度随点P的移动而变化,所以,△P AB的周长会随点P的移动而变化,故②正确;∵MN的长度不变,点P到MN的距离等于l与AB的距离的一半,∴△PMN的面积不变,故③错误;直线MN,AB之间的距离不随点P的移动而变化,故④错误;∠APB的大小点P的移动而变化,故⑤正确.综上所述,会随点P的移动而变化的是②⑤.故选:B.3.解:如图,连结DN,∵DE=EM,FN=FM,∴EF=DN,当点N与点B重合时,DN的值最大即EF最大,在Rt△ABD中,∵∠A=90°,AD=3,AB=3,∴BD===6,∴EF的最大值=BD=3.故选A.4.解:连接AR,∵矩形ABCD固定不变,R在CD的位置不变,∴AD和DR不变,∵由勾股定理得:AR=,∴AR的长不变,∵E、F分别为AP、RP的中点,∴EF=AR,即线段EF的长始终不变,故选:C.5.解:∵BN平分∠ABC,BN⊥AE,∴∠NBA=∠NBE,∠BNA=∠BNE,在△BNA和△BNE中,∴△BNA≌△BNE,∴BA=BE,∴△BAE是等腰三角形,同理△CAD是等腰三角形,∴点N是AE中点,点M是AD中点(三线合一),∴MN是△ADE的中位线,∵BE+CD=AB+AC=19﹣BC=19﹣7=12,∴DE=BE+CD﹣BC=5,∴MN=DE=.故选:C.6.解:∵点D,E,F,G分别是BC,AD,BE,CE的中点,∴AD是△ABC的中线,BE是△ABD的中线,CE是△ACD的中线,AF是△ABE的中线,AG是△ACE的中线,∴△AEF的面积=×△ABE的面积=×△ABD的面积=×△ABC的面积=,同理可得△AEG的面积=,△BCE的面积=×△ABC的面积=6,又∵FG是△BCE的中位线,∴△EFG的面积=×△BCE的面积=,∴△AFG的面积是×3=,故选:A.7.解:∵∠C=90°,∠A=30°,∴BC=AB=4,又∵DE是中位线,∴DE=BC=2.故选:D.8.证明:∵△ABC的周长为30,BC=12.∴AB+AC=30﹣BC=18.延长AN、AM分别交BC于点F、G.如图所示:∵BM为∠ABC的角平分线,∴∠CBM=∠ABM,∵BM⊥AG,∴∠ABM+∠BAM=90°,∠G+∠CBM=90°,∴∠BAM=∠AGB,∴AB=BG,∴AN=GN,同理AC=CF,AM=MF,∴MN为△AFG的中位线,GF=BG+CF﹣BC,∴MN=(AB+AC﹣BC)=(18﹣12)=3.故选:D.9.解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,∴PN,PM分别是△CDB与△DAB的中位线,∴PM=AB,PN=DC,PM∥AB,PN∥DC,∵AB=CD,∴PM=PN,∴△PMN是等腰三角形,∵PM∥AB,PN∥DC,∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,∴∠MPN=∠MPD+∠NPD=20°+(180﹣70)°=130°,∴∠PMN==25°.故选:B.10.解:取BC的中点G,连接EG,∵E是AC的中点,∴EG是△ABC的中位线,∴EG=AB==4,设CD=x,则EF=BC=2x,∴BG=CG=x,∴EF=2x=DG,∵EF∥CD,∴四边形EGDF是平行四边形,∴DF=EG=4,故选:B.11.解:∵DE是△ABC的中位线,∴E为AC中点,∴AE=EC,∵CF∥BD,∴∠ADE=∠F,在△ADE和△CFE中,∵,∴△ADE≌△CFE(AAS),∴DE=FE.故选:B.12.解:平行四边形ADCE的对角线的交点是AC的中点O,当OD⊥BC时,OD最小,即DE最小.∵OD⊥BC,BC⊥AB,∴OD∥AB,又∵OC=OA,∴CD=DB,∴OD是△ABC的中位线,∴OD=AB=3,∴DE=2OD=6.故选:C.13.解:∵BD⊥DC,BD=4,CD=3,由勾股定理得:BC==5,∵E、F、G、H分别是AB、AC、CD、BD的中点,∴HG=BC=EF,EH=FG=AD,∵AD=6,∴EF=HG=2.5,EH=GF=3,∴四边形EFGH的周长是EF+FG+HG+EH=2×(2.5+3)=11.故选:D.14.解:延长线段BN交AC于E.∵AN平分∠BAC,∴∠BAN=∠EAN,在△ABN与△AEN中,∵,∴△ABN≌△AEN(ASA),∴AE=AB=10,BN=NE,又∵M是△ABC的边BC的中点,∴CE=2MN=2×3=6,∴AC=AE+CE=10+6=16.故选:C.15.解:∵D、E分别是AB、AC的中点,∴AD=AB,AE=AC,DE=BC,∴△ABC的周长=AB+AC+BC=2AD+2AE+2DE=2(AD+AE+DE)=2×6=12.故选:B.16.解:当△A′EF为直角三角形时,存在两种情况:①当∠A'EF=90°时,如图1,∵△A′BC与△ABC关于BC所在直线对称,∴A'C=AC=4,∠ACB=∠A'CB,∵点D,E分别为AC,BC的中点,∴D、E是△ABC的中位线,∴DE∥AB,∴∠CDE=∠MAN=90°,∴∠CDE=∠A'EF,∴AC∥A'E,∴∠ACB=∠A'EC,∴∠A'CB=∠A'EC,∴A'C=A'E=4,Rt△A'CB中,∵E是斜边BC的中点,∴BC=2A'E=8,由勾股定理得:AB2=BC2﹣AC2,∴AB==4;②当∠A'FE=90°时,如图2,∵∠ADF=∠A=∠DFB=90°,∴∠ABF=90°,∵△A′BC与△ABC关于BC所在直线对称,∴∠ABC=∠CBA'=45°,∴△ABC是等腰直角三角形,∴AB=AC=4;综上所述,AB的长为4或4;故答案为:4或4;17.解:方法1、延长GE交AB于点O,作PH⊥OE于点H.则PH∥AB.∵P是AE的中点,∴PH是△AOE的中位线,∴PH=OA=(3﹣1)=1.∵直角△AOE中,∠OAE=45°,∴△AOE是等腰直角三角形,即OA=OE=2,同理△PHE中,HE=PH=1.∴HG=HE+EG=1+1=2.∴在Rt△PHG中,PG===.故答案是:.方法2、如图1,延长DA,GP相交于H,∵四边形ABCD和四边形EFCG是正方形,∴EG∥BC∥AD,∴∠H=∠PGE,∠HAP=∠GEP,∵点P是AE的中点,∴AP=EP,∴△AHP≌△EGP,∴AH=EG=1,PG=PH=HG,∴DH=AD+AH=4,DG=CD﹣CG=2,根据勾股定理得,HG==2,∴PG=,故答案为.18.解:∵△ABC是直角三角形,CD是斜边的中线,∴CD=AB,又∵EF是△ABC的中位线,∴AB=2CD=2×5=10cm,∴EF=×10=5cm.故答案为:5.19.解:如图,分别延长AC、BD交于点H,过G作MN∥AB,分别交AH于M,BH于N,∵△APC和△BPD是等边三角形,∴∠A=∠B=60°,∴△AHB是等边三角形,∵∠A=∠DPB=60°,∴AH∥PD,∵∠B=∠CP A=60°,∴BH∥PC,∴四边形CPDH为平行四边形,∴CD与HP互相平分.∵G为CD的中点,∴G正好为PH中点,∵△ABH是等边三角形,∴在P的运动过程中,G始终为PH的中点,所以G的运行轨迹为△HAB的中位线MN.∴MN=AB=5,即G的移动路径长为5.故答案为:5.20.解:∵点D是AB的中点,BF∥DE,∴DE是△ABF的中位线.∵BF=10,∴DE=BF=5.∵CE=CD,∴CD=5,解得CD=4.∵△ABC是直角三角形,∴AB=2CD=8.故答案为:8.21.解:∵DE为△ABC的中位线,∠AFB=90°,∴DE=BC,DF=AB,∵AB=6,BC=8,∴DE=×8=4,DF=×6=3,∴EF=DE﹣DF=4﹣3=1.故答案为:1.22.解:∵DE为△ABC的中位线,∴AD=BD,∵∠AFB=90°,∴DF=AB=2.5,∵DE为△ABC的中位线,∴DE=BC=4,∴EF=DE﹣DF=1.5,故答案为:1.5.23.解:∵△ABC的周长是26,BC=10,∴AB+AC=26﹣10=16,∵∠ABC的平分线垂直于AE,∴在△ABQ和△EBQ中,,∴△ABQ≌△EBQ,∴AQ=EQ,AB=BE,同理,AP=DP,AC=CD,∴DE=BE+CD﹣BC=AB+AC﹣BC=16﹣10=6,∵AQ=DP,AP=DP,∴PQ是△ADE的中位线,∴PQ=DE=3.故答案是:3.24.解:如图,取BC的中点G,连接EG、FG,∵E、F分别是边AB、CD的中点,∴EG∥AC且EG=AC=×6=3,FG∥BD且FG=BD=×8=4,∵AC⊥BD,∴EG⊥FG,∴EF===5.故答案为:5.25.解:连接CM,∵M、N分别是AB、AC的中点,∴NM=CB,MN∥BC,又CD=BD,∴MN=CD,又MN∥BC,∴四边形DCMN是平行四边形,∴DN=CM,∵∠ACB=90°,M是AB的中点,∴CM=AB=3,∴DN=3,故答案为:3.26.解:∵F,G分别为BC,CD的中点,∴FG=BD=4,FG∥BD,∵E,H分别为AB,DA的中点,∴EH=BD=4,EH∥BD,∴FG∥EH,FG=EH,∴四边形EFGH为平行四边形,∴EF=GH=AC=3,∴四边形EFGH的周长=3+3+4+4=14,故答案为:1427.解:取BC、AB的中点H、G,连接MH、HG、MG.如图1中,当点C′落在MH上时,设NC=NC′=x,由题意可知:MC=MC′=2,MH=,HC′=,HN=﹣x,在Rt△HNC′中,∵HN2=HC′2+NC′2,∴(﹣x)2=x2+()2,解得x=.如图2中,当点C′落在GH上时,设NC=NC′=x,在Rt△GMC′中,MG=CH=,MC=MC′=2,∴GC′=,∵△HNC′∽△GC′M,∴=,∴=,∴x=.如图3中,当点C′落在直线GM上时,易证四边形MCNC′是正方形,可得CN=CM=2.此时点C′在中位线GM的延长线上,不符合题意舍弃.综上所述,满足条件的线段CN的长为或.故答案为为或.28.解:∵P是对角线BD的中点,E是AB的中点,∴EP=AD,同理,FP=BC,∵AD=BC,∴PE=PF,∵∠FPE=100°,∴∠PFE=40°,故答案为:40°.29.(1)证明:∵D、E分别为AB、AC的中点,∴DE为△ABC的中位线,∴DE BC,∵延长BC至点F,使CF=BC,∴DE=FC;(2)解:∵DE FC,∴四边形DEFC是平行四边形,∴DC=EF,∵D为AB的中点,等边△ABC的边长是2,∴AD=BD=1,CD⊥AB,BC=2,∴DC=EF=.30.证明:(1)∵点D,E,F分别是AB,BC,CA的中点,∴DE、EF都是△ABC的中位线,∴EF∥AB,DE∥AC,∴四边形ADEF是平行四边形;(2)∵四边形ADEF是平行四边形,∴∠DEF=∠BAC,∵D,F分别是AB,CA的中点,AH是边BC上的高,∴DH=AD,FH=AF,∴∠DAH=∠DHA,∠F AH=∠FHA,∵∠DAH+∠F AH=∠BAC,∠DHA+∠FHA=∠DHF,∴∠DHF=∠DEF.31.(1)证明:在△CAD中,∵M、N分别是AC、CD的中点,∴MN∥AD,MN=AD,在RT△ABC中,∵M是AC中点,∴BM=AC,∵AC=AD,∴MN=BM.(2)解:∵∠BAD=60°,AC平分∠BAD,∴∠BAC=∠DAC=30°,由(1)可知,BM=AC=AM=MC,∴∠BMC=∠BAM+∠ABM=2∠BAM=60°,∵MN∥AD,∴∠NMC=∠DAC=30°,∴∠BMN=∠BMC+∠NMC=90°,∴BN2=BM2+MN2,由(1)可知MN=BM=AC=1,∴BN=32.解:延长CF交AB于点G,∵AE平分∠BAC,∴AF垂直平分CG,∴AC=AG,GF=CF,又∵点D是BC中点,∴DF是△CBG的中位线,∴DF=BG=(AB﹣AG)=(AB﹣AC)=2.33.解:如图,取BC边的中点G,连接EG、FG.∵E,F分别为AB,CD的中点,∴EG是△ABC的中位线,FG是△BCD的中位线,∴EG AC,FG BD.又BD=12,AC=16,AC⊥BD,∴EG=8,FG=6,EG⊥FG,∴在直角△EGF中,由用勾股定理,得EF===10,即EF的长度是10.34.(1)证明:在△ADB和△ADE中,,∴△ADB≌△ADE(ASA)∴AE=AB,BD=DE,∵BD=DE,BM=MC,∴DM=CE;(2)解:在Rt△ADB中,AB==10,∴AE=10,由(1)得,CE=2DM=4,∴AC=CE+AE=14.35.(1)证明:∵在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是对角线BD、AC的中点,∴EG∥AB,EG=AB,HF∥AB,HF=AB,∴EG∥HE,EG=HE,∴四边形EGFH是平行四边形.又EH=CD,AB=CD,∴EG=EH,∴平行四边形EGFH是菱形;(2)解:∵四边形ABCD中,G、F、H分别是BD、BC、AC的中点,∴GF∥DC,HF∥AB.∴∠GFB=∠DCB,∠HFC=∠ABC.∴∠HFC+∠GFB=∠ABC+∠DCB=90°.∴∠GFH=90°.∴菱形EGFH是正方形.∵AB=,∴EG=AB=.∴正方形EGFH的面积=()2=.36.(1)证明:如图,连接BD,∵E、F、G、H分别为四边形ABCD四边之中点,∴EH是△ABD的中位线,FG是△BCD的中位线,∴EH∥BD且EH=BD,FG∥BD且FG=BD,∴EH∥FG且EH=FG,∴四边形EFGH为平行四边形;(2)解:连接AC,同理可得EF∥AC且EF=AC,所以,AC=BD时,四边形EFGH为菱形;AC⊥BD时,四边形EFGH为矩形;AC=BD且AC⊥BD时,四边形EFGH为正方形.故答案为:AC=BD;AC⊥BD;AC=BD且AC⊥BD.37.(1)证明:如图1中,∵AE⊥BD,∴∠AED=∠AEB=90°,∴∠BAE+∠ABE=90°,∠DAE+∠ADE=90°,∵∠BAE=∠DAE,∴∠ABE=∠ADE,∴AB=AD,∵AE⊥BD,∴BE=DE,∵BF=FC,∴EF=DC==(AC﹣AB).(2)结论:EF=(AB﹣AC),理由:如图2中,延长AC交BE的延长线于P.∵AE⊥BP,∴∠AEP=∠AEB=90°,∴∠BAE+∠ABE=90°,∠P AE+∠APE=90°,∵∠BAE=∠P AE,∴∠ABE=∠APE,∴AB=AP,∵AE⊥BD,∴BE=PE,∵BF=FC,∴EF=PC=(AP﹣AC)=(AB﹣AC).38.解:(1)∵D、E分别是AC、BD的中点,且AB=10,∴DE=AB=5;(2)设A1B1=x,则A2B2=2x.∵A1、A2是AC的三等分点,且A1B1∥A2B2∥AB,∴A2B2是梯形A1ABB1的中位线,即:x+10=4x,得x=,∴A1B1+A2B2=10;(3)同理可得:A1B1+A2B2+…+A10B10=。
八年级数学三角形中位线培优专题训练

八年级数学三角形中位线培优专题训练一、内容提要1. 三角形中位线平行于第三边,并且等于第三边的一半。
梯形中位线平行于两底,并且等于两底和的一半。
2. 中位线性质定理的结论,兼有位置和大小关系,可以用它判定平行,计算线段的长度,确定线段的和、差、倍关系。
3. 运用中位线性质的关键是从出现的线段中点,找到三角形或梯形,包括作出辅助线。
4. 中位线性质定理,常与它的逆定理结合起来用。
它的逆定理就是平行线截比例线段定理及推论,①一组平行线在一直线上截得相等线段,在其他直线上截得的线段也相等 ②经过三角形一边中点而平行于另一边的直线,必平分第三边 ③经过梯形一腰中点而平行于两底的直线,必平分另一腰 5. 有关线段中点的其他定理还有: ①直角三角形斜边中线等于斜边的一半②等腰三角形底边中线和底上的高,顶角平分线互相重合 ③对角线互相平分的四边形是平行四边形 ④线段中垂线上的点到线段两端的距离相等 因此如何发挥中点作用必须全面考虑。
二、例题例1. 已知:△ABC 中,分别以AB 、AC 为斜边作等腰直角三角形ABM 和CAN ,P 是BC 的中点。
求证:PM =PN证明:作ME ⊥AB ,NF ⊥AC ,垂足E ,F ∵△ABM 、△CAN 是等腰直角三角形∴AE =EB=ME ,AF =FC =NF ,根据三角形中位线性质 PE =21AC =NF ,PF =21AB =MEPE ∥AC ,PF ∥AB∴∠PEB =∠BAC =∠PFC 即∠PEM =∠PFN∴△PEM ≌△PFN ∴PM =PN例2.已知△ABC 中,AB =10,AC =7,AD 是角平分线,CM ⊥AD 于M ,且N 是BC 的中点。
求MN 的长。
分析:N 是BC 的中点,若M 是另一边中点, 则可运用中位线的性质求MN 的长, 根据轴称性质作出△AMC 的全等三角形即可。
辅助线是:延长CM 交AB 于E (证明略 例3.如图已知:△ABC 中,AD 是角平分线,BE =CF ,M 、N 分别是BC 和EF 的中点 求证:MN ∥AD 证明一:连结EC ,取EC 的中点P ,连结PM 、PNP NMP ∥AB ,MP =21AB ,NP ∥AC ,NP =21AC ∵BE =CF ,∴MP =NP∴∠3=∠4=2MPN-180∠∠MPN +∠BAC =180(两边分平行的两个角相等或互补)∴∠1=∠2=2MPN-180∠ , ∠2=∠3∴NP ∥AC ∴MN ∥AD证明二:连结并延长EM 到G ,使MG =ME 连结CG ,FG则MN ∥FG ,△MCG ≌△MBE ∴CG =BE =CF ∠B =∠BCG∴AB ∥CG ,∠BAC +∠FCG =180∠CAD =21(180-∠FCG ) ∠CFG =21(180-∠FCG )=∠CAD ∴ MN ∥AD 例4. 已知:△ABC 中,AB =AC ,AD 是高,CE 是角平分线,EF ⊥BC 于F ,GE ⊥CE交CB 的延长线于G 求证:FD =41CG 证明要点是:延长GE 交AC 于H , 可证E 是GH 的中点过点E 作EM ∥GC 交HC 于M ,则M 是HC 的中点,EM ∥GC ,EM =21GC由矩形EFDO 可得FD =EO =21EM =41GC三、练习1. 如图11,M 、P 分别为△ABC 的AB 、AC 上 的点,且AM=BM ,AP=2CP ,BP 与CM 相交于N ,已知PN=1,则PB 的长为 ( ) A. 2 B. 3 C .4 D. 52. 如图12,△ABC 中,∠B =2∠C ,AD ⊥BC 于D ,M 为BC 的中点,AB=10,则MD 的长为 ( )A. 10B. 8 C .6 D. 53. 如图13,△ABC 是等边三角形,D 、E 、F 分别是AB 、BC 、AC 的中点,P 为不同于B 、E 、C 的BC 上的任意一点,△DPH 为等边三角形.连接FH ,则EP 与FH 的大小关系是 ( ) A. E P>FH B. EP=FH C. EP<FH D.不确定4. 如图14,在△ABC 中,AD 平分∠BAC ,BD ⊥AD ,DE ∥AC ,交AB 于E ,若AB=5,则DE 的长为 .C5. 如图15,△ABC中,AB=4,AC=7,M为BC的中点,AD平分∠BAC,过M作MF∥AD,交AC于F,则FC的长等于.6. 如图25,P为△ABC内一点,∠P AC=∠PBC,PM⊥AC于M,PN⊥BC于N.D是AB的中点.求证:DM=DN7. 如图16,在△ABC中,D、E是AB、AC上的点,且BD=CE,M、N分别是BE、CD的中点,直线MN分别交AB、AC于P、Q.求证:AP=AQ8. 如图17,BE、CF是△ABC的角平分线,AN⊥BE于N,AM⊥CF于M.求证:MN∥BC.9. 如图18,在△ABC中,AD平分∠BAC,AD=AB,CM⊥AD于M.求证:AB+AC=2AM10.如图19,四边形ABCD中,G、H分别是AD、BC的中点,AB=CD.BA、CD的延长线交HG的延长线于E、F.求证:∠BEH=∠CFH.1. 如图20,在△ABC中,∠ABC=2∠C,AD平分∠BAC,过BC的中点M作ME⊥AD,交BA的延长线于E,交AD的延长线于F.求证:12BE BD.2. 如图21,在△ABC中,AB<AC,P为AC上的点,CP=AB,K为AP的中点,M为BC的中点,MK的延长线交BA的长线于N.求证:AN=AK.3. 如图22,分别以△ABC的边AC、BC为腰,A、B为直角顶点,作等腰直角△ACE和等腰直角△BCD,M为ED的中点.求证:AM⊥BM.4. 如图23,点O是四边形ABCD内一点,∠AOB=∠COD=1200,AO=BO,CO=DO,E、F、G分别为AB、CD、BC的中点.求证:△EFG为等边三角形.5. 如图24,△ABC中,M是AB的中点,P是AC的中点,D是MB的中点,N是CD的中点,Q是MN的中点,直线PQ交MB于K.求证:K是DB的中点.6. 如图25,P为△ABC内一点,∠P AC=∠PBC,PM⊥AC于M,PN⊥BC于N.D是AB的中点.求证:DM=DN图21 图22 图23 图24 图257. 如图26,AP是△ABC的角平分线,D、E分别是AB、AC上的点,且BD=CE.又G、H分别为BC、DE的中点.求证:HG∥AP.8. 如图27,已知△ABD和△ACE都是直角三角形,且∠ABD=∠ACE=900,如图(a),连接DE,设M为DE的中点.(1)求证:MB=MC;(2)设∠BAD=∠CAE,固定△ABD,让Rt△ACE绕顶点A在平面内旋转到图(b)的位置,试问MB=MC是否成立?并证明其结论.9. 已知△ABC面积为S,作直线l∥BC,交AB于D,交AC于E,若△BED的积为K.求证:S≥4K.10.如图28,在△ABC中,AB=AC,D是BC边上的一点,E是线段AD上的一点.且∠BED=2∠CED=∠BAC.求证:BD=2CD.图26 图27。
讲义九 三角形的中位线及直角三角形的性质

讲义九 三角形的中位线及直角三角形的性质一、填空1. 已知△ABC 中,AB =10,AC =6.(1)BC 边上的中线AD 的取值范围为 .(2)若BC 边上的中线AD =4,则△ABC 的面积为 .2. (1)如图,△ABC 中,AB =AC =13,BC =10,D 是AB 的中点,过D 作DE ⊥AC 于E ,则DE = .(2)如图,△ABC 中,AB =AC =13,BC =10,DE 为△ABC 的中位线,G 、H 两点在BC 上,且GH =5,则图中的阴影部分的面积为 .2题(1) 2题(2) 3题3. 如图,在△ABC 中,∠ACB =90,∠A =60,AC =a ,作斜边AB 边中线CD ,得到第一个三角形ACD ;DE ⊥BC 于点E ,作Rt △BDE 斜边DB 上的中线EF ,得到第二个三角形DEF ,依次作下去……,则第n 个三角形的面积为 .二、解答题1. 如图,AF 与BE 互相平分,交点为M ,EC 与DF 互相平分,交点为N ,求证:四边形ABCD 为平行四边形.EDC B AHDECBAF NMEDCBAC BE AFAECBD2. 如图,△ABC 中,AD 平分∠BAC ,AD ⊥BD 于D ,过点D 作DE ∥AB 交AC 于点E ,若BD =3,AD=4,求DE 的长.3. 如图,△ABC 中,D 为CB 延长线上一点,BE 平分∠ABD ,AE ⊥BE 于E ,F 是AC 的中点,试说明:EF ∥BC 且EF =12(AB+AC ).4. 如图,四边形ABCD 的对角线AC 、BD 相交于点F ,M 、N 分别为AB 、CD 的中点,直线MN 分别交BD ,AC 于点P 、Q ,且∠FPQ =∠FQP ,若BD =10,求AC 的长.FED CB A NMQ P E D CBACBMO E DA5. 如图,D 、E 分别是△ABC 的边AB 、AC 上的点,BD =CE ,M 、N 分别为BE 、CD 的中点,直线MN 分别交AB 、AC 于点P 、Q. 求证:AP =AQ.6. 如图,在四边形ABCD 中,AD ∥BC ,E 、F 分别是对角线AC 、BD 的中点.求证:EF =12(BC -AD ).7. 如图,在□ABCD 中,BD =2AD ,AC 、BD 交于点O ,E 为OA 中点,M 为DC 中点,试探究EM 与DC 的数量关系,并说明理由.FEBCOAD8. 如图,矩形ABCD 中,AC 、BD 交于点O ,E 是CB 延长线上一点,CF ⊥AE 于F ,求证:DF ⊥BF.9. 如图,AD 为△ABC 的高,∠B =2∠C ,M 为BC 的中点.求证:DM =12AB.。
中位线经典习题及答案

2014年4月王强的初中数学组卷2014年4月王强的初中数学组卷一.选择题(共10小题)1.(2013•铜仁地区)已知△ABC的各边长度分别为3cm,4cm,5cm,则连结各边中点的三角形的周长为()A.2cm B.7cm C.5cm D.6cm2.(2013•怀化)如图,为测量池塘边A、B两点的距离,小明在池塘的一侧选取一点O,测得OA、OB的中点分别是点D、E,且DE=14米,则A、B间的距离是()A.18米B.24米C.28米D.30米3.(2012•泰安)如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是()A.4B.3C.2D.14.(2013•淄博)如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB 的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为()A.B.C.3D.45.(1997•海南)用反证法证明命题:“如图,如果AB∥CD,AB∥EF,那么CD∥EF”,证明的第一个步骤是()A.假定CD∥EF B.假定CD不平行于EFC.已知AB∥EF D.假定AB不平行于EF6.用反证法证明命题“在Rt△ABC中,若∠A=90°,则∠B≤45°或∠C≤45°“时,应先假设()A.∠B>45°,∠C≤45°B.∠B≤45°,∠C>45°C.∠B>45°,∠C>45°D.∠B≤45°,∠C≤45°7.用反证法证明“若a⊥c,b⊥c,则a∥b”,第一步应假设()A.a∥b B.a与b垂直C.a与b不一定平行D.a与b相交8.能证明命题“x是实数,则(x﹣3)2>0”是假命题的反例是()A.x=4 B.x=3 C.x=2 D.x=159.下列说法正确的是()A.等腰三角形的角平分线、中线、高线互相重合B.面积相等的两个三角形一定全等C.用反证法证明命题“三角形中至少有一个角不大于60°”的第一步是“假设三角形中三个角都大于60°”D.反比例函数y=中函数值y随自变量x的增大一定而减小10.下列命题宜用反证法证明的是()A.等腰三角形两腰上的高相等B.有一个外角是1200的等腰三角形是等边三角形C.两条直线都与第三条直线平行,则这两条直线互相平行D.全等三角形的面积相等二.填空题(共4小题)11.(2013•烟台)如图,▱ABCD的周长为36,对角线AC,BD相交于点O.点E是CD的中点,BD=12,则△DOE 的周长为_________.12.(2013•乌鲁木齐)如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为_________.13.(2012•枣庄)如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为_________.14.(2011•柳州)如图,要测量的A、C两点被池塘隔开,李师傅在AC外任选一点B,连接BA和BC,分别取BA和BC的中点E、F,量得E、F两点间的距离等于23米,则A、C两点间的距离_________米.三.解答题(共16小题)15.(2013•永州)如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3(1)求证:BN=DN;(2)求△ABC的周长.16.(2012•湘西州)如图,在Rt△ABC中,∠C=90°,∠B=60°,AB=8cm,E、F分别为边AC、AB的中点.(1)求∠A的度数;(2)求EF的长.17.(2005•乌鲁木齐)如图所示,在△ABC中,∠ACB=90°,点D,E分别为AC,AB的中点,点F在BC的延长线上,且∠CDF=∠A.求证:四边形DECF为平行四边形.18.(2004•苏州)已知:如图,正△ABC的边长为a,D为AC边上的一个动点,延长AB至E,使BE=CD,连接DE,交BC于点P.(1)求证:DP=PE;(2)若D为AC的中点,求BP的长.19.(2013•镇江)如图,AB∥CD,AB=CD,点E、F在BC上,且BE=CF.(1)求证:△ABE≌△DCF;(2)试证明:以A、F、D、E为顶点的四边形是平行四边形.20.(2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.求证:四边形BECF是平行四边形.21.(2013•鞍山)如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.求证:(1)△AFD≌△CEB;(2)四边形ABCD是平行四边形.22.(2011•天水)已知,如图E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE,四边形ABCD是平行四边形吗?请说明理由.23.(2010•东莞)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.(1)试说明AC=EF;(2)求证:四边形ADFE是平行四边形.24.(2006•镇江)已知:如图,在四边形ABCD中,AC与BD相交于点O,AB∥CD,AO=CO.求证:四边形ABCD是平行四边形.25.(2006•湛江)如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点,试判断四边形EFGH 的形状,并证明你的结论.26.证明:在一个三角形中,至少有一个内角小于或等于60度.27.请用反证法证明:如果两个整数的积是偶数,那么这两个整数中至少有一个是偶数.28.判断下列命题是真命题还是假命题,若是假命题,请举出一个反例说明.(1)有一个角是60°的等腰三角形是等边三角形.(2)有两个角是锐角的三角形是锐角三角形.29.(2013•南充)如图,在平行四边形ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于E,交CD 于F.求证:OE=OF.30.(2013•茂名)如图,在▱ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.(1)求证:△ADE≌△BFE;(2)若DF平分∠ADC,连接CE.试判断CE和DF的位置关系,并说明理由.2014年4月王强的初中数学组卷参考答案与试题解析一.选择题(共10小题)1.(2013•铜仁地区)已知△ABC的各边长度分别为3cm,4cm,5cm,则连结各边中点的三角形的周长为()A.2cm B.7cm C.5cm D.6cm考点:三角形中位线定理.分析:由中点和中位线定义可得新三角形的各边长为原三角形各边长的一半,即可求其周长.解答:解:如图,D,E,F分别是△ABC的三边的中点,则DE=AC,DF=BC,EF=AB,∴△DEF的周长=DE+DF+EF=(AC+BC+AB)=6cm,故选D.点评:解决本题的关键是利用中点定义和中位线定理得到新三角形各边长与原三角形各边长的数量关系.2.(2013•怀化)如图,为测量池塘边A、B两点的距离,小明在池塘的一侧选取一点O,测得OA、OB的中点分别是点D、E,且DE=14米,则A、B间的距离是()A.18米B.24米C.28米D.30米考点:三角形中位线定理.分析:根据D、E是OA、OB的中点,即DE是△OAB的中位线,根据三角形的中位线定理:三角形的中位线平行于第三边且等于第三边的一半,即可求解.解答:解:∵D、E是OA、OB的中点,即CD是△OAB的中位线,∴DE=AB,∴AB=2CD=2×14=28m.故选C.点评:本题考查了三角形的中位线定理应用,正确理解定理是解题的关键.3.(2012•泰安)如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是()A.4B.3C.2D.1考点:三角形中位线定理;全等三角形的判定与性质.专题:压轴题.分析:连接DE并延长交AB于H,由已知条件可判定△DCE≌△HAE,利用全等三角形的性质可得DE=HE,进而得到EF是三角形DHB的中位线,利用中位线性质定理即可求出EF的长.解答:解:连接DE并延长交AB于H,∵CD∥AB,∴∠C=∠A,∠CDE=∠AHE,∵E是AC中点,∴AE=CE,∴△DCE≌△HAE(AAS),∴DE=HE,DC=AH,∵F是BD中点,∴EF是△DHB的中位线,∴EF=BH,∴BH=AB﹣AH=AB﹣DC=2,∴EF=1.故选D.点评:本题考查了全等三角形的判定和性质、三角形的中位线的判定和性质,解题的关键是连接DE和AB相交构造全等三角形,题目设计新颖.4.(2013•淄博)如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB 的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为()A.B.C.3D.4考点:三角形中位线定理;等腰三角形的判定与性质.专题:压轴题.分析:首先判断△BAE、△CAD是等腰三角形,从而得出BA=BE,CA=CD,由△ABC的周长为26,及BC=10,可得DE=6,利用中位线定理可求出PQ.解答:解:∵BQ平分∠ABC,BQ⊥AE,∴△BAE是等腰三角形,同理△CAD是等腰三角形,∴点Q是AE中点,点P是AD中点(三线合一),∴PQ是△ADE的中位线,∵BE+CD=AB+AC=26﹣BC=26﹣10=16,∴DE=BE+CD﹣BC=6,∴PQ=DE=3.故选C.点评:本题考查了三角形的中位线定理,解答本题的关键是判断出△BAE、△CAD是等腰三角形,利用等腰三角形的性质确定PQ是△ADE的中位线.5.(1997•海南)用反证法证明命题:“如图,如果AB∥CD,AB∥EF,那么CD∥EF”,证明的第一个步骤是()A.假定CD∥EF B.假定CD不平行于EFC.已知AB∥EF D.假定AB不平行于EF考点:反证法.分析:根据要证CD∥EF,直接假设CD不平行于EF即可得出.解答:解:∵用反证法证明命题:如果AB∥CD,AB∥EF,那么CD∥EF.∴证明的第一步应是:从结论反面出发,假设CD不平行于EF.故选:B.点评:此题主要考查了反证法的第一步,根据题意得出命题结论的反例是解决问题的关键.6.用反证法证明命题“在Rt△ABC中,若∠A=90°,则∠B≤45°或∠C≤45°“时,应先假设()A.∠B>45°,∠C≤45°B.∠B≤45°,∠C>45°C.∠B>45°,∠C>45°D.∠B≤45°,∠C≤45°考点:反证法.分析:用反证法证明命题的真假,应先按符合题设的条件,假设题设成立,再判断得出的结论是否成立即可.解答:解:用反证法证明命题“在Rt△ABC中,若∠A=90°,则∠B≤45°或∠C≤45°”时,应先假设∠B>45°,∠C>45°.故选:C.点评:此题主要考查了反证法,注意逆命题的与原命题的关系是解题关键.7.用反证法证明“若a⊥c,b⊥c,则a∥b”,第一步应假设()A.a∥b B.a与b垂直C.a与b不一定平行D.a与b相交考点:反证法.分析:根据反证法的步骤,直接得出即可.解答:解:∵用反证法证明“若a⊥c,b⊥c,则a∥b”,∴第一步应假设:若a⊥c,b⊥c,则a、b相交.故选:D.点评:此题主要考查了反证法,解此题关键要懂得反证法的意义及步骤.反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.8.能证明命题“x是实数,则(x﹣3)2>0”是假命题的反例是()A.x=4 B.x=3 C.x=2 D.x=15考点:反证法.分析:根据x=3时,(x﹣3)2=0,得出能证明命题“x是实数,则(x﹣3)2>0”是假命题的反例是:x=3.解答:解:∵x=3时,(x﹣3)2=0,∴能证明命题“x是实数,则(x﹣3)2>0”是假命题的反例是:x=3.故选:B.点评:本题主要考查了命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题是假命题只要找到一个反例即可.9.下列说法正确的是()A.等腰三角形的角平分线、中线、高线互相重合B.面积相等的两个三角形一定全等C.用反证法证明命题“三角形中至少有一个角不大于60°”的第一步是“假设三角形中三个角都大于60°”D.反比例函数y=中函数值y随自变量x的增大一定而减小考点:反证法;反比例函数的性质;全等三角形的判定;等腰三角形的性质.分析:分别根据等腰三角形的性质以及全等三角形的判定与性质和反证法的证明第一步以及反比例函数的增减性得出即可.解答:解:A、等腰三角形的顶角平分线和底边上的中线、高线互相重合,故此选项错误;B、面积相等的两个三角形不一定全等,故此选项错误;C、用反证法证明命题“三角形中至少有一个角不大于60°”的第一步是“假设三角形中三个角都大于60°”,此选项正确;D、反比例函数y=中,每个象限内,函数值y随自变量x的增大一定而减小,故此选项错误;故选:C.点评:此题主要考查了反证法、反比例函数性质、等腰三角形的性质等知识,正确把握相关性质是解题关键.10.下列命题宜用反证法证明的是()A.等腰三角形两腰上的高相等B.有一个外角是1200的等腰三角形是等边三角形C.两条直线都与第三条直线平行,则这两条直线互相平行D.全等三角形的面积相等考点:反证法.分析:利用直接证明的方法不易证明的结论,可以考虑利用反证法证明,据此即可判断.解答:解:A、利用三角形的面积公式比较容易证明,故选项错误;B、利用等边三角形的判定定理即可直接证明,故选项错误;C、正确;D、根据全等的定义可以直接证明,故选项错误.故选C.点评:本题结合角的比较考查反证法,解此题关键要懂得反证法应用的条件,直接证明的方法不易证明的结论,可以考虑利用反证法证明.二.填空题(共4小题)11.(2013•烟台)如图,▱ABCD的周长为36,对角线AC,BD相交于点O.点E是CD的中点,BD=12,则△DOE 的周长为15.考点:三角形中位线定理;平行四边形的性质.分析:根据平行四边形的对边相等和对角线互相平分可得,OB=OD,又因为E点是CD的中点,可得OE是△BCD 的中位线,可得OE=BC,所以易求△DOE的周长.解答:解:∵▱ABCD的周长为36,∴2(BC+CD)=36,则BC+CD=18.∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,∴OD=OB=BD=6.又∵点E是CD的中点,∴OE是△BCD的中位线,DE=CD,∴OE=BC,∴△DOE的周长=OD+OE+DE=BD+(BC+CD)=6+9=15,即△DOE的周长为15.故答案是:15.点评:本题考查了三角形中位线定理、平行四边形的性质.解题时,利用了“平行四边形对角线互相平分”、“平行四边形的对边相等”的性质.12.(2013•乌鲁木齐)如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为.考点:三角形中位线定理;等腰三角形的判定与性质.专题:压轴题.分析:延长CF交AB于点G,证明△AFG≌△AFC,从而可得△ACG是等腰三角形,GF=FC,点F是CG中点,判断出DF是△CBG的中位线,继而可得出答案.解答:解:延长CF交AB于点G,∵AE平分∠BAC,∴∠GAF=∠CAF,∵AF垂直CG,∴∠AFG=∠AFC,在△AFG和△AFC中,∵,∴△AFG≌△AFC(ASA),∴AC=AG,GF=CF,又∵点D是BC中点,∴DF是△CBG的中位线,∴DF=BG=(AB﹣AG)=(AB﹣AC)=.故答案为:.点评:本题考查了三角形的中位线定理,解答本题的关键是作出辅助线,同学们要注意培养自己的敏感性,一般出现即是角平分线又是高的情况,我们就需要寻找等腰三角形.13.(2012•枣庄)如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为.考点:三角形中位线定理;直角三角形斜边上的中线.专题:压轴题.分析:利用直角三角形斜边上的中线等于斜边的一半,可求出DF的长,再利用三角形的中位线平行于第三边,并且等于第三边的一半,可求出DE的长,进而求出EF的长解答:解:∵∠AFB=90°,D为AB的中点,∴DF=AB=2.5,∵DE为△ABC的中位线,∴DE=BC=4,∴EF=DE﹣DF=1.5,故答案为1.5.点评:本题考查了直角三角形斜边上的中线性质:在直角三角形中,斜边上的中线等于斜边的一半和三角形的中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半.14.(2011•柳州)如图,要测量的A、C两点被池塘隔开,李师傅在AC外任选一点B,连接BA和BC,分别取BA和BC的中点E、F,量得E、F两点间的距离等于23米,则A、C两点间的距离46米.考点:三角形中位线定理.专题:计算题;压轴题.分析:根据E、F分别是线段AB、BC中点,利用三角形中位线定理,即可求出AC的长.解答:解:∵E、F分别是线段AB、BC中点,∴FE是三角形ABC的中位线,∴FE=AC,∴AC=2FE=23×2=46米.故答案为46.点评:此题考查学生对三角形中位线定理的理解和掌握,要求学生熟练掌握三角形中位线定理,为进一步学习奠定基础.三.解答题(共16小题)15.(2013•永州)如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3(1)求证:BN=DN;(2)求△ABC的周长.考点:三角形中位线定理;等腰三角形的判定与性质.分析:(1)证明△ABN≌△ADN,即可得出结论;(2)先判断MN是△BDC的中位线,从而得出CD,由(1)可得AD=AB=10,从而计算周长即可.解答:(1)证明:在△ABN和△ADN中,∵,∴△ABN≌△ADN,∴BN=DN.(2)解:∵△ABN≌△ADN,∴AD=AB=10,DN=NB,又∵点M是BC中点,∴MN是△BDC的中位线,∴CD=2MN=6,故△ABC的周长=AB+BC+CD+AD=10+15+6+10=41.点评:本题考查了三角形的中位线定理及等腰三角形的判定,注意培养自己的敏感性,一般出现高、角平分线重合的情况,都需要找到等腰三角形.16.(2012•湘西州)如图,在Rt△ABC中,∠C=90°,∠B=60°,AB=8cm,E、F分别为边AC、AB的中点.(1)求∠A的度数;(2)求EF的长.考点:三角形中位线定理;含30度角的直角三角形.分析:(1)由“直角三角形的两个锐角互余”的性质来求∠A的度数;(2)由“30度角所对的直角边等于斜边的一半”求得AB=2BC,则BC=4cm.然后根据三角形中位线定理求得EF=BC.解答:解:(1)如图,∵在Rt△ABC中,∠C=90°,∠B=60°,∴∠A=90°﹣∠B=30°,即∠A的度数是30°;(2)∵由(1)知,∠A=30°.∴在Rt△ABC中,∠C=90°,∠A=30°,AB=8cm,∴BC=AB=4cm.又E、F分别为边AC、AB的中点,∴EF是△ABC的中位线,∴EF=BC=2cm.点评:本题考查了三角形中位线定理、含30度角的直角三角形.在直角三角形中,30°角所对的直角边等于斜边的一半.17.(2005•乌鲁木齐)如图所示,在△ABC中,∠ACB=90°,点D,E分别为AC,AB的中点,点F在BC的延长线上,且∠CDF=∠A.求证:四边形DECF为平行四边形.考点:平行四边形的判定;三角形中位线定理.专题:证明题.分析:根据DE是三角形的中位线得到DE∥BC,根据CE是直角三角形斜边上的中线得到CE=AE,得∠A=∠ACE∵∠CDF=∠A∴∠CDF=∠ACE∴DF∥CE.再根据:两组对边分别平行的四边形是平行四边形而得证.解答:证明:∵D,E分别为AC,AB的中点,∴DE为△ACB的中位线.∴DE∥BC.∵CE为Rt△ACB的斜边上的中线,∴CE=AB=AE.∴∠A=∠ACE.又∵∠CDF=∠A,∴∠CDF=∠ACE.∴DF∥CE.又∵DE∥BC,∴四边形DECF为平行四边形.点评:本题利用了:①三角形中位线的性质.②直角三角形的斜边上的中线等于斜边的一半.③等边对等角.④平行四边形的性质和判定.⑤内错角相等,两直线平行.18.(2004•苏州)已知:如图,正△ABC的边长为a,D为AC边上的一个动点,延长AB至E,使BE=CD,连接DE,交BC于点P.(1)求证:DP=PE;(2)若D为AC的中点,求BP的长.考点:等边三角形的性质;全等三角形的判定与性质;三角形中位线定理.专题:计算题;证明题.分析:(1)过点D作DF∥AB,构造三角形全等,可证得△CDF为等边三角形,得到DF=BE,可由AAS证得△DFP≌△EBP⇒DP=EP;(2)若D为AC的中点,则DF是△ABC的中位线,有BF=BC=a,点P是BF的中点,得到BP=BF=a.解答:(1)证明:过点D作DF∥AB,交BC于F.∵△ABC为正三角形,∴∠CDF=∠A=60°.∴△CDF为正三角形.∴DF=CD.又BE=CD,∴BE=DF.又DF∥AB,∴∠PEB=∠PDF.∵在△DFP和△EBP中,∵,∴△DFP≌△EBP(AAS).∴DP=PE.(2)解:由(1)得△DFP≌△EBP,可得FP=BP.∵D为AC中点,DF∥AB,∴BF=BC=a.∴BP=BF=a.点评:本题利用了等边三角形的判定和性质,全等三角形的判定和性质求解.19.(2013•镇江)如图,AB∥CD,AB=CD,点E、F在BC上,且BE=CF.(1)求证:△ABE≌△DCF;(2)试证明:以A、F、D、E为顶点的四边形是平行四边形.考点:平行四边形的判定;全等三角形的判定与性质.专题:证明题.分析:(1)由全等三角形的判定定理SAS证得△ABE≌△DCF;(2)利用(1)中的全等三角形的对应角相等证得∠AEB=∠DFC,则∠AEF=∠DFE,所以根据平行线的判定可以证得AE∥DF.由全等三角形的对应边相等证得AE=DF,则易证得结论.解答:证明:(1)如图,∵AB∥CD,∴∠B=∠C.∵在△ABE与△DCF中,,∴△ABE≌△DCF(SAS);(2)如图,连接AF、DE.由(1)知,△ABE≌△DCF,∴AE=DF,∠AEB=∠DFC,∴∠AEF=∠DFE,∴AE∥DF,∴以A、F、D、E为顶点的四边形是平行四边形.点评:本题考查了平行四边形的判定、全等三角形的判定与性质.在证明(2)题时,利用了“一组对边平行且相等的四边形是平行四边形”的判定定理.20.(2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.求证:四边形BECF是平行四边形.考点:平行四边形的判定;全等三角形的判定与性质.专题:证明题.分析:通过全等三角形(△AEB≌△DFC)的对应边相等证得BE=CF,由“在同一平面内,同垂直于同一条直线的两条直线相互平行”证得BE∥CF.则四边形BECF是平行四边形.解答:证明:∵BE⊥AD,CF⊥AD,∴∠AEB=∠DFC=90°,∵AB∥CD,∴∠A=∠D,在△AEB与△DFC中,,∴△AEB≌△DFC(ASA),∴BE=CF.∵BE⊥AD,CF⊥AD,∴BE∥CF.∴四边形BECF是平行四边形.点评:本题考查了平行四边形的判定、全等三角形的判定与性质.一组对边平行且相等的四边形是平行四边形.21.(2013•鞍山)如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.求证:(1)△AFD≌△CEB;(2)四边形ABCD是平行四边形.考点:平行四边形的判定;全等三角形的判定.专题:证明题;压轴题.分析:(1)利用两边和它们的夹角对应相等的两三角形全等(SAS),这一判定定理容易证明△AFD≌△CEB.(2)由△AFD≌△CEB,容易证明AD=BC且AD∥BC,可根据一组对边平行且相等的四边形是平行四边形.解答:证明:(1)∵DF∥BE,∴∠DFE=∠BEF.又∵AF=CE,DF=BE,∴△AFD≌△CEB(SAS).(2)由(1)知△AFD≌△CEB,∴∠DAC=∠BCA,AD=BC,∴AD∥BC.∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形).点评:此题主要考查了全等三角形的判定和平行四边形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.平行四边形的判定,一组对边平行且相等的四边形是平行四边形.22.(2011•天水)已知,如图E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE,四边形ABCD是平行四边形吗?请说明理由.考点:平行四边形的判定;全等三角形的判定与性质.专题:压轴题.分析:首先根据条件证明△AFD≌△CEB,可得到AD=CB,∠DAF=∠BCE,可证出AD∥CB,根据一条对边平行且相等的四边形是平行四边形可证出结论.解答:解:结论:四边形ABCD是平行四边形,证明:∵DF∥BE,∴∠AFD=∠CEB,又∵AF=CE DF=BE,∴△AFD≌△CEB(SAS),∴AD=CB,∠DAF=∠BCE,∴AD∥CB,∴四边形ABCD是平行四边形.点评:此题主要考查了平行四边形的判定,以及三角形全等的判定与性质,解题的关键是根据条件证出△AFD≌△CEB.23.(2010•东莞)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.(1)试说明AC=EF;(2)求证:四边形ADFE是平行四边形.考点:平行四边形的判定;全等三角形的判定与性质;等边三角形的性质.专题:证明题;压轴题.分析:(1)首先Rt△ABC中,由∠BAC=30°可以得到AB=2BC,又因为△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,然后即可证明△AFE≌△BCA,再根据全等三角形的性质即可证明AC=EF;(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形.解答:证明:(1)∵Rt△ABC中,∠BAC=30°,∴AB=2BC,又∵△ABE是等边三角形,EF⊥AB,∴AB=2AF∴AF=CB,在Rt△AFE和Rt△BCA中,,∴△AFE≌△BCA(HL),∴AC=EF;(2)由(1)知道AC=EF,而△ACD是等边三角形,∴∠DAC=60°∴EF=AC=AD,且AD⊥AB,而EF⊥AB,∴EF∥AD,∴四边形ADFE是平行四边形.点评:此题是首先利用等边三角形的性质证明全等三角形,然后利用全等三角形的性质和等边三角形的性质证明平行四边形.24.(2006•镇江)已知:如图,在四边形ABCD中,AC与BD相交于点O,AB∥CD,AO=CO.求证:四边形ABCD是平行四边形.考点:平行四边形的判定;全等三角形的判定与性质.专题:证明题.分析:要证四边形ABCD是平行四边形,根据平行四边形的判定,和已知条件,只需证AB=CD,继而需求证△ABO≌△CDO,由已知条件很快确定ASA,即证.解答:证明:∵AB∥CD,∴∠ABO=∠CDO.∵AO=CO,∠AOB=∠COD,∴△ABO≌△CDO.∴AB=CD,又∵AB∥CD∴四边形ABCD是平行四边形.点评:平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.25.(2006•湛江)如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点,试判断四边形EFGH 的形状,并证明你的结论.考点:平行四边形的判定;三角形中位线定理.专题:压轴题;探究型.分析:四边形EFGH是平行四边形,连接AC,根据中位线定理,可证得EF∥AC,且EF=AC.GH∥AC,且GH=AC,∴EF GH.∴四边形EFGH是平行四边形.解答:解:四边形EFGH是平行四边形证明:连接AC,如图.∵E,F分别是AB,BC的中点,∴EF是△ABC的中位线,∴EF∥AC,且EF=AC.同理:GH∥AC,且GH=AC,∴EF GH.∴四边形EFGH是平行四边形.点评:此题主要考查平行四边形的判定,综合运用了中位线定理,作辅助线是关键.26.证明:在一个三角形中,至少有一个内角小于或等于60度.考点:反证法.专题:证明题.分析:当条件较少,无法直接证明时,可用反证法证明;先假设结论不成立,然后得到与定理矛盾,从而证得原结论成立.解答:证明:假设在一个三角形中没有一个角小于或等于60°,即都大于60°;那么,这个三角形的三个内角之和就会大于180°;这与定理“三角形的三个内角之和等于180°”相矛盾,原命题正确.点评:本题结合三角形内角和定理考查反证法,解此题关键要懂得反证法的意义及步骤.反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.27.请用反证法证明:如果两个整数的积是偶数,那么这两个整数中至少有一个是偶数.考点:反证法.分析:首先假设这两个整数都是奇数,其中一个奇数为2n+1,另一个奇数为2p+1,利用多项式乘以多项式得出(2n+1)(2p+1)=2(2np+n+p)+l,进而得出矛盾,则原命题正确.解答:证明:假设这两个整数都是奇数,其中一个奇数为2n+1,另一个奇数为2p+1,(n、p为整数),则(2n+1)(2p+1)=2(2np+n+p)+l,∵无论n、p取何值,2(2np+n+p)+1都是奇数,这与已知中两个奇数的乘积为偶数相矛盾,所以假设不成立,∴这两个整数中至少一个是偶数.点评:此题主要考查了反证法的证明以及多项式乘以多项式以及数的奇偶性,熟练掌握反证法证明步骤是解题关键.28.判断下列命题是真命题还是假命题,若是假命题,请举出一个反例说明.(1)有一个角是60°的等腰三角形是等边三角形.(2)有两个角是锐角的三角形是锐角三角形.考点:反证法.分析:(1)真命题,不管底角还是顶角为60°,都可推出等腰三角形的每个角都为60°(2)假命题,举一个反例即可.解答:解:(1)真命题,(2)假命题.假设原命题为真命题,那么在△ABC中,∠A=20°,∠B=30°,∠C=130°,则△ABC就应该是锐角三角形;而实际上△ABC就应该是钝角三角形,所以假设错误,所以原命题为假命题.点评:本题考查了命题的判断,可反证法来证明.29.(2013•南充)如图,在平行四边形ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于E,交CD 于F.求证:OE=OF.考点:平行四边形的性质;全等三角形的判定与性质.专题:证明题;压轴题.分析:由四边形ABCD是平行四边形,可得OA=OC,AB∥CD,又由∠AOE=∠COF,易证得△OAE≌△OCF,则可得OE=OF.解答:证明:∵四边形ABCD是平行四边形,∴OA=OC,AB∥CD,∴∠OAE=∠OCF,∵在△OAE和△OCF中,,∴△OAE≌△OCF(ASA),∴OE=OF.点评:此题考查了平行四边形的性质以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.30.(2013•茂名)如图,在▱ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.(1)求证:△ADE≌△BFE;(2)若DF平分∠ADC,连接CE.试判断CE和DF的位置关系,并说明理由.。
直角三角形中线专练

直角三角形中线专练一.解答题(共30小题)1.如图,M 是△ABC 的边BC 的中点,AN 平分∠BAC ,BN ⊥AN 于点N ,延长BN交AC 于点D ,已知AB=10,AC=16.(1)求证:BN=DN ;(2)求MN 的长.2.如图,在△ABC 中,AE 平分∠BAC ,BE ⊥AE 于点E ,点F 是BC 的中点.(1)如图1,BE 的延长线与AC 边相交于点D ,求证:EF=12(AC ﹣AB ); (2)如图2,请直接写出线段AB 、AC 、EF 的数量关系.3.如图,在△ABC 中,BD 、CE 是高,G 、F 分别是BC 、DE 的中点,连接GF 、EG 、DG .求证:(1)EG=DG ;(2)GF ⊥DE .4.已知:如图,在△ABC 中,∠BAC=90°,M 是斜边BC 的中点,BN ⊥AM ,垂足为点N ,且BN 的延长线交AC 于点D .(1)求证:△ABC∽△ADB;(2)如果BC=20,BD=15,求AB的长度.5.已知:△ABD和△ACE都是直角三角形,且∠ABD=∠ACE=90°.如图甲,连接DE,设M为DE的中点.(1)说明:MB=MC;(2)设∠BAD=∠CAE,固定△ABD,让Rt△ACE绕顶点A在平面内旋转到图乙的位置,试问:MB=MC是否还能成立?并证明其结论.6.探究问题1已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为.拓展问题2已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.推广问题3如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.7.如图,在△ABC中,点D在边AC上,DB=BC,E是CD的中点,F是AB的中点,求证:EF=12 AB.8.已知:如图,∠ACB=∠ADB=90°,点E、F分别是线段AB、CD的中点.求证:EF⊥CD.9.如图,△ABC中,∠ACB=90°,D为AB的中点,连接CD,过点B作CD的平行线EF,求证:BC平分∠ABF.10.如图,已知AC⊥BC,AD⊥BD,E为AB的中点,(1)如图1,求证:△ECD是等腰三角形;(2)如图2,CD与AB交点为F,若AD=BD,EF=3,DE=4,求CD的长.11.如图,△ABC中,BE⊥AC,CF⊥AB,垂足分别为E、F,M为BC的中点.(1)求证:ME=MF;(2)若∠A=50°,求∠FME的度数.12.如图,在△ABC中,∠C=90°,∠ABD=2∠EBC,AD∥BC,求证:DE=2AB.13.已知:如图,BD、CE是△ABC的高,M为BC的中点.试判断点B、C、D、E是否在以点M为圆心的同一圆上?并说明理由.14.如图,在△ABC中,AD是高,CE是中线,DC=BE,DG⊥CE于点G.求证:(1)G是CE的中点;(2)∠B=2∠BCE.15.如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,G,H分别是AC,BD的中点.如果∠BEC=80°,求∠GHE的度数为?16.如图,△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.(1)求证:MN⊥DE;(2)连结DM,ME,求证:∠DME=180°﹣2∠A;(3)若将锐角△ABC变为钝角△ABC,如图,上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需证明;若结论不成立,直接写出正确的结论.17.在Rt△ABC中,∠ACB=90°,D,E分别为AB,BC的中点,点F在AC的延长线上,CF=12 AC.(1)DC=EF吗?说明理由;(2)若AC=6,AB=10,求四边形DCFE的面积.18.如图,∠ACB=∠ADB=90°,M、N分别为AB、CD的中点.求证:MN⊥CD.19.已知:如图,四边形ABCD中,∠ABC=90°,∠ADC=90°,点E为AC中点,点F为BD中点.求证:EF⊥BD.20.如图,在Rt△ABC中,∠ABC=90°,点D是AC的中点,作∠ADB的角平分线DE交AB于点E,(1)求证:DE∥BC;(2)若AE=3,AD=5,点P为线段BC上的一动点,当BP为何值时,△DEP为等腰三角形.请求出所有BP的值.21.抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)点P为抛物线对称轴上一点.①当PA+PC最小时,求点P的坐标;②当△PAC是直角三角形时,求点P的坐标.22.已知:如图,∠BAC=∠BDC=90°,点E在BC上,点F在AD上,BE=EC,AF=FD.求证:EF⊥AD.23.如图1,点P是∠AOB的内部任意一点,PM⊥OA,PN⊥OB,垂足分别是M、N,D是OP的中点.求证:∠MDN=2∠MON.小尧同学思路如下:因为PM⊥OA,垂足是M,D是OP的中点.由“直角三角形斜边上的中线等于斜边的一半”,得到MD=OD,…课后,小尧同学发现上题中,当“点P是∠AOB的外部任意一点”结论也成立,请你证明其正确.如图2,P是∠AOB的外部任意一点,PM⊥OA,PN⊥OB,垂足分别是M、N,D 是OP的中点.求证:∠MDN=2∠MON.24.如图,BD、CE是△ABC的高,G、F分别是BC、DE的中点.求证:FG⊥DE.25.已知,如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.(1)求证:MN⊥BD;(2)在边AD上能否找到一点P,使得PB=PD?请说明理由.26.如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,且CD=12 AB,DE⊥CF于E.求证:CE=EF.27.如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=6,CD=AC=8,M、N分别是对角线BD、AC的中点.(1)求证:MN⊥AC.(2)求MN的长.28.如图所示,四边形ABCD中,∠BAD=∠BCD=90°,E,F分别是BD,AC的中点.(1)求证:AE=CE;(2)判断EF与AC的位置关系,并说明理由.29.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.(1)若EF=3,BC=8,求△EFM的周长;(2)若∠ABC=50°,∠ACB=60°,求∠EMF的度数.30.在四边形ABCD中,∠ACB=∠ADB=90°,M、N分别是对角线AB、CD的中点,连接MN,MN与CD有怎样的特殊位置关系?证明你的结论.直角三角形中线专练参考答案与试题解析一.解答题(共30小题)1.如图,M 是△ABC 的边BC 的中点,AN 平分∠BAC ,BN ⊥AN 于点N ,延长BN交AC 于点D ,已知AB=10,AC=16.(1)求证:BN=DN ;(2)求MN 的长.【分析】(1)证明△ABN ≌△ADN ,即可得出结论;(2)先判断MN 是△BDC 的中位线,从而得出MN .【解答】证明:(1)∵AN 平分∠BAC∴∠1=∠2,∵BN ⊥AN∴∠ANB=∠AND ,在△ABN 和△ADN 中,{∠1=∠2AN =AN ∠ANB =∠AND,∴△ABN ≌△ADN (ASA )∴BN=DN ;(2)∵△ABN ≌△ADN∴AD=AB=10,DN=NB ,∴CD=AC ﹣AD=16﹣10=6,又∵点M 是BC 中点,∴MN 是△BDC 的中位线,∴MN=12CD=3. 【点评】本题考查了三角形的中位线定理,关键是根据全等三角形的判定证明△ABN ≌△ADN .2.如图,在△ABC 中,AE 平分∠BAC ,BE ⊥AE 于点E ,点F 是BC 的中点.(1)如图1,BE 的延长线与AC 边相交于点D ,求证:EF=12(AC ﹣AB ); (2)如图2,请直接写出线段AB 、AC 、EF 的数量关系.【分析】(1)先证明AB=AD ,根据等腰三角形的三线合一,推出BE=ED ,根据三角形的中位线定理即可解决问题.(2)结论:EF=12(AB ﹣AC ),先证明AB=AP ,根据等腰三角形的三线合一,推出BE=ED ,根据三角形的中位线定理即可解决问题.【解答】(1)证明:如图1中,∵AE ⊥BD ,∴∠AED=∠AEB=90°,∴∠BAE +∠ABE=90°,∠DAE +∠ADE=90°,∵∠BAE=∠DAE ,∴∠ABE=∠ADE ,∴AB=AD ,∵AE ⊥BD ,∴BE=DE ,∵BF=FC ,∴EF=12DC=12(AC −AD)=12(AC ﹣AB ). (2)结论:EF=12(AB ﹣AC ), 理由:如图2中,延长AC 交BE 的延长线于P .∵AE⊥BP,∴∠AEP=∠AEB=90°,∴∠BAE+∠ABE=90°,∠PAE+∠APE=90°,∵∠BAE=∠PAE,∴∠ABE=∠ADE,∴AB=AP,∵AE⊥BD,∴BE=PE,∵BF=FC,∴EF=12PC=12(AP﹣AC)=12(AB﹣AC).【点评】本题考查三角形的中位线定理、等腰三角形的判定和性质等知识,解题的关键是熟练应用所学知识解决问题,属于中考常考题型.3.如图,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,连接GF、EG、DG.求证:(1)EG=DG;(2)GF⊥DE.【分析】(1)利用直角三角形斜边上的中线等于斜边的一半进行证明;(2)由(1)知DG=EG=12BC,再根据等腰三角形三线合一的证明即可.【解答】证明:(1)∵BD、CE是高,点G是BC的中点,∴GE=12BC,GD=12BC,∴GE=GD;(2)证明:如图,连接EG 并延长至H 使EG=GH ,∵点G 是BC 中点,∴BG=CG=12BC , ∴四边形BHCE 是平行四边形,∵∠BEC=90°,∴平行四边形BHCE 是矩形,∴EH=BC ,∴EG=12BC , 连接DG ,同理,DG=12BC ∴GE=GD=12BC , ∴△GED 是等腰三角形,∵F 是DE 的中点,∴GF ⊥DE .【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质并作出辅助线构造出等腰三角形是解题的关键.4.已知:如图,在△ABC 中,∠BAC=90°,M 是斜边BC 的中点,BN ⊥AM ,垂足为点N ,且BN 的延长线交AC 于点D .(1)求证:△ABC ∽△ADB ;(2)如果BC=20,BD=15,求AB 的长度.【分析】(1)根据直角三角形的性质和相似三角形的判定证明即可;(2)根据相似三角形的性质解答即可.【解答】证明:(1)∵M是斜边BC的中点,∴AM=CM,∴∠MAC=∠C,∵∠MAC+∠BAN=90°,∠ABD+∠BAN=90°,∴∠MAC=ABD,∴∠C=∠ABD,∵∠BAC=∠DAB=90°,∴△ABC∽△ADB;(2)∵△ABC∽△ADB,∴ACAB =BCBD=2015=43,设AC=4x,AB=3x,可得:(4x)2+(3x)2=202,解得:x=±4(负值舍去),∴AB=3x=12.【点评】此题考查相似三角形的判定和性质,关键是根据直角三角形的性质和相似三角形的判定和性质解答.5.已知:△ABD和△ACE都是直角三角形,且∠ABD=∠ACE=90°.如图甲,连接DE,设M为DE的中点.(1)说明:MB=MC;(2)设∠BAD=∠CAE,固定△ABD,让Rt△ACE绕顶点A在平面内旋转到图乙的位置,试问:MB=MC是否还能成立?并证明其结论.【分析】(1)在AD 上取点P ,MP ∥CE ∥BD ,再根据平行线分线段成比例定理可得P 是BC 的中点,再由线段垂直平分线上的点到线段两端的距离相等即可求解;(2)取AD 、AE 的中点F 、G ,连接BF 、MF 、MG 、CG ,由M 是BE 的中点可知,线段MG 、MF 都是△ADE 的中位线,根据三角形的中位线定理及平行四边形的判定定理可判断MFAG 是平行四边形,可用AD .AE 表示出MG .MF 的长,再由直角三角形的性质可求出BF 的长,再根据∠BAD=∠CAE 通过等量代换可得∠BFM=∠MGC ,可求出△BFM ≌△MGC ,由三角形全等即可得出答案.【解答】证明:(1)作点M 作MP ⊥AB 于点P ,∵∠ABD=∠ACE=90°.∴MP ∥CE ∥BD .∵M 为DE 的中点,∴CP=BP ,∴MP 是BC 的中垂线,∴△BCM 是等腰三角形,∴MB=MC ;(2)MB=MC 成立.取AD 、AE 的中点F 、G ,连接BF 、MF 、MG 、CG 显然线段MG 、MF 都是△ADE的中位线,∴四边形MFAG 是平行四边形,MG=12AD ,MF=12AE , ∴∠MFA=∠AGM ,又∵∠DBA=∠ACE=90°,∴Rt△斜边中线BF=12AD=MG,CG=12AE=MF,∵∠DAB=∠CAE,∴∠BDA=∠CEA,∴∠BFA=2∠BDA=2∠CEA=∠CGA,∴∠BFM=∠BFA﹣∠MFA=∠CGA﹣∠AGM=∠MGC,∴△BFM≌△MGC,∴MB=MC.【点评】此题比较复杂,(1)主要是利用线段垂直平分线的性质;在解(2)时要作出辅助线,构造出平行其性质求解四边形及直角三角形的中线是解答此题的关键.6.探究问题1已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为1.拓展问题2已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC 的内部,且∠MAC=∠MBC ,过点M 分别作ME ⊥BC ,MF ⊥AC ,垂足分别为点E ,F ,连接DE ,DF .求证:DE=DF .推广问题3如图3,若将上面问题2中的条件“CB=CA”变为“CB ≠CA”,其他条件不变,试探究DE 与DF 之间的数量关系,并证明你的结论.【分析】(1)利用直角三角形的性质“直角三角形斜边中线等于斜边的一半”得到DE=DF ;(2)利用等腰三角形的性质和判定得出结论,从而判定△MEB ≌△MFA (AAS ),得到DE=DF .(3)利用三角形的中位线和直角三角形的性质根据SAS 证明△DHE ≌△FGD 可得.【解答】解:(1)∵AE ⊥BC ,BF ⊥AC∴△AEB 和△AFB 都是直角三角形∵D 是AB 的中点∴DE 和DF 分别为Rt △AEB 和Rt △AFB 的斜边中线∴DE=12AB ,DF=12AB (直角三角形斜边中线等于斜边的一半) ∴DE=DF∵DE=kDF∴k=1;(2)∵CB=CA∴∠CBA=∠CAB∵∠MAC=∠MBE∴∠CBA ﹣∠MBC=∠CAB ﹣∠MAC即∠ABM=∠BAM∴AM=BM∵ME ⊥BC ,MF ⊥AC∴∠MEB=∠MFA=90又∵∠MBE=∠MAF∴△MEB ≌△MFA (AAS )∴BE=AF∵D 是AB 的中点,即BD=AD又∵∠DBE=∠DAF∴△DBE ≌△DAF (SAS )∴DE=DF ;(3)DE=DF如图1,作AM 的中点G ,BM 的中点H ,∵点 D 是 边 AB 的 中点∴DG ∥BM ,DG=12BM 同理可得:DH ∥AM ,DH=12AM ∵ME ⊥BC 于E ,H 是BM 的中点∴在Rt △BEM 中,HE=12BM=BH ∴∠HBE=∠HEB∠MHE=∠HBE +∠HEB=2∠MBC又∵DG=12BM ,HE=12BM ∴DG=HE同理可得:DH=FG,∠MGF=2∠MAC ∵DG∥BM,DH∥GM∴四边形DHMG是平行四边形∴∠DGM=∠DHM∵∠MGF=2∠MAC,∠MHE=2∠MBC 又∵∠MBC=∠MAC∴∠MGF=∠MHE∴∠DGM+∠MGF=∠DHM+∠MHE∴∠DGF=∠DHE在△DHE与△FGD中{DG=HE∠DGF=∠DHEDH=FG,∴△DHE≌△FGD(SAS),∴DE=DF.【点评】本题主要考查三角形全等的判定和性质;在证明三角形全等时,用到的知识点比较多,用到直角三角形的性质、三角形的中位线、平行四边形的性质和判定.7.如图,在△ABC中,点D在边AC上,DB=BC,E是CD的中点,F是AB的中点,求证:EF=12 AB.【分析】连接BE,根据等腰三角形三线合一的性质可得BE⊥AC,再根据直角三角形斜边上的中线等于斜边的一半证明.【解答】证明:如图,连接BE,∵在△BCD 中,DB=BC ,E 是CD 的中点,∴BE ⊥CD ,∵F 是AB 的中点,∴在Rt △ABE 中,EF 是斜边AB 上的中线,∴EF =12AB【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质并作辅助线构造出直角三角形是解题的关键.8.已知:如图,∠ACB=∠ADB=90°,点E 、F 分别是线段AB 、CD 的中点.求证:EF ⊥CD .【分析】根据直角三角形斜边上的中线是斜边的一半可以求得DE=CE ,再根据等腰三角形的性质可以得到EF ⊥CD ,从而可以证明结论成立.【解答】证明:连接DE 、CE ,∵△ABC 中,∠ACB=90°,E 是AB 中点,∴CE=12AB , 同理可得,DE=12AB , ∴DE=CE .∵△CDE 中,F 是CD 中点,∴EF ⊥CD .【点评】本题考查直角三角形斜边上的中线、等腰三角形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.9.如图,△ABC中,∠ACB=90°,D为AB的中点,连接CD,过点B作CD的平行线EF,求证:BC平分∠ABF.【分析】根据直角三角形的性质得到CD=BD,根据等边对等角得到∠ABC=∠DCB,根据平行线的性质证明即可.【解答】证明:∵∠ACB=90°,D为AB的中点,∴CD=12AB=BD,∴∠ABC=∠DCB,∵DC∥EF,∴∠CBF=∠DCB,∴∠CBF=∠ABC.∴BC平分∠ABF.【点评】本题考查的是直角三角形的性质、平行线的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.10.如图,已知AC⊥BC,AD⊥BD,E为AB的中点,(1)如图1,求证:△ECD是等腰三角形;(2)如图2,CD与AB交点为F,若AD=BD,EF=3,DE=4,求CD的长.【分析】(1)根据直角三角形的性质得到CE=12AB ,DE=12AB ,得到CE=DE ,证明结论;(2)过点E 作EH ⊥CD ,根据三角形的面积公式求出EH ,根据勾股定理求出DH ,根据等腰三角形的性质计算即可.【解答】(1)证明:∵AC ⊥BC ,AD ⊥BD ,∴∠ACB=90°,∠ADB=90°,又∵E 为AB 的中点,∴CE=12AB ,DE=12AB ∴CE=DE ,即△ECD 是等腰三角形;(2)∵AD=BD ,E 为AB 的中点,∴DE ⊥AB ,已知DE=4,EF=3,∴DF=5,过点E 作EH ⊥CD ,∵∠FED=90°,EH ⊥DF ,∴EH=EF⋅ED DF =125, ∴DH=√DE 2−EH 2=165, ∵△ECD 是等腰三角形,∴CD=2DH=325.【点评】本题考查的是直角三角形的性质、等腰三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.11.如图,△ABC 中,BE ⊥AC ,CF ⊥AB ,垂足分别为E 、F ,M 为BC 的中点.(1)求证:ME=MF ;(2)若∠A=50°,求∠FME 的度数.【分析】(1)根据直角三角形斜边上的中线等于斜边的一半得到ME=12BC ,MF=12BC ,得到答案;(2)根据四点共圆的判定得到B 、C 、E 、F 四点共圆,根据圆周角定理得到答案.【解答】(1)证明:∵BE ⊥AC ,CF ⊥AB ,M 为BC 的中点,∴ME=12BC ,MF=12BC , ∴ME=MF ;(2)解:∵CF ⊥AB ,∠A=50°,∴∠ACF=40°,∵BE ⊥AC ,CF ⊥AB ,∴B 、C 、E 、F 四点共圆,∴∠FME=2∠ACF=80°.【点评】本题考查的是直角三角形的性质和四点共圆的知识,掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.12.如图,在△ABC中,∠C=90°,∠ABD=2∠EBC,AD∥BC,求证:DE=2AB.【分析】取ED的中点O,连接AO,结合已知,可知∠EBC=∠D,OD=AO=OE,∠AOE=2∠D,即可推出∠ABD=∠AOB,所以DE=2AB=2OA.【解答】证明:取ED的中点O,连接AO,∵∠CAD=90°,∴OD=AO=OE,∴∠AOE=2∠D,∵AD∥BC,∴∠EBC=∠D,∴∠AOE=2∠EBC,∵∠ABD=2∠EBC,∴∠ABD=∠AOB,∴AB=OA,∴DE=2AB=2OA.【点评】本题主要考查平行线的性质、直角三角形斜边上的中线的性质、等腰三角形的判定和性质,解题的关键在于作出斜边DE上的中线,求证OA=AB即可.13.已知:如图,BD、CE是△ABC的高,M为BC的中点.试判断点B、C、D、E是否在以点M为圆心的同一圆上?并说明理由.【分析】分别连接ME 、MF ,根据直角三角形中,斜边上的中线等于斜边的一半可得到ME=MD=MC=MB ,可证得结论.【解答】证明:连接ME 、MD ,∵BD 、CE 分别是△ABC 的高,M 为BC 的中点,∴ME=MD=MC=MB=12BC , ∴点B 、C 、D 、E 在以点M 为圆心的同一圆上.【点评】本题主要考查直角三角形的性质,根据直角三角形中斜边上的中线等于斜边的一半得到ME=MF=MC=MB 是解题的关键.14.如图,在△ABC 中,AD 是高,CE 是中线,DC=BE ,DG ⊥CE 于点G .求证:(1)G 是CE 的中点;(2)∠B=2∠BCE .【分析】(1)连接DE ,根据直角三角形的性质得到DC=DE ,根据等腰三角形的三线合一证明;(2)根据等腰三角形的性质得到∠B=∠EDB ,根据三角形的外角的性质证明.【解答】证明:(1)连接DE ,∵CE 是△ABC 的中线,∴DE 是△ABD 的中线,∵AD 是高,∴∠ADB=90°,又DE 是△ABD 的中线,∴DE=12AB=BE , ∵DC=BE ,∴DC=DE ,又DG ⊥CE ,∴G 是CE 的中点;(2)∵DE=BE ,∴∠B=∠EDB ,∵DE=DC ,∴∠DEC=∠DCE ,∴∠EDB=2∠BCE ,∴∠B=2∠BCE .【点评】本题考查的是直角三角形的性质,等腰三角形的性质,掌握直角三角形中,斜边上的中线等于斜边的一半,等腰三角形的三线合一是解题的关键.15.如图,在四边形ABCD 中,∠BCD=∠BAD=90°,AC ,BD 相交于点E ,G ,H 分别是AC ,BD 的中点.如果∠BEC=80°,求∠GHE 的度数为?【分析】连接AH 、CH ,利用直角三角形的性质可证得AH=CH ,利用等腰三角形的性质可求得GH ⊥AC ,则可求得∠GHE 的度数.【解答】解:如图,连接AH 、CH ,∵∠BAD=∠BCD=90°,H 为BD 的中点,∴AH=CH=12BD , ∵G 为AC 的中点,∴GH ⊥AC ,即∠HGE=90°,∵∠BEC=80°,∴∠GEH=80°,∴∠GHE=10°.【点评】本题主要考查直角三角形的性质及等腰三角形的判定和性质,利用直角三角形的性质求得AH=CH 是解题的关键.16.如图,△ABC 中,CD 、BE 分别是AB 、AC 边上的高,M 、N 分别是线段BC 、DE 的中点.(1)求证:MN ⊥DE ;(2)连结DM ,ME ,求证:∠DME=180°﹣2∠A ;(3)若将锐角△ABC 变为钝角△ABC ,如图,上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需证明;若结论不成立,直接写出正确的结论.【分析】(1)连接DM 、ME ,根据直角三角形斜边上的中线等于斜边的一半可得DM=12BC ,ME=12BC ,从而得到DM=ME ,再根据等腰三角形三线合一的性质证明;(2)根据三角形的内角和定理可得∠ABC +∠ACB=180°﹣∠A ,再根据等腰三角形两底角相等表示出∠BMD +∠CME ,然后根据平角等于180°表示出∠DME ,整理即可得解;(3)根据三角形的内角和定理可得∠ABC +∠ACB=180°﹣∠A ,再根据等腰三角形两底角相等和三角形的一个外角等于与它不相邻的两个内角的和表示出∠BME +∠CME ,然后根据平角等于180°表示出∠DME ,整理即可得解.【解答】证明:(1)如图,连接DM ,ME ,∵CD 、BE 分别是AB 、AC 边上的高,M 是BC 的中点,∴DM=12BC ,ME=12BC , ∴DM=ME又∵N 为DE 中点,∴MN ⊥DE ;(2)∵DM=ME=BM=MC ,∴∠BMD +∠CME=(180°﹣2∠ABC )+(180°﹣2∠ACB ),=360°﹣2(∠ABC +∠ACB ),=360°﹣2(180°﹣∠A ),=2∠A ,∴∠DME=180°﹣2∠A ;(3)结论(1)成立,结论(2)不成立,理由如下:在△ABC 中,∠ABC +∠ACB=180°﹣∠A ,∵DM=ME=BM=MC ,∴∠BME +∠CMD=2∠ACB +2∠ABC ,=2(180°﹣∠A ),=360°﹣2∠A ,∴∠DME=180°﹣(360°﹣2∠A ),=2∠A ﹣180°.【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形两底角相等的性质,三角形的内角和定理,整体思想的利用是解题的关键.17.在Rt△ABC中,∠ACB=90°,D,E分别为AB,BC的中点,点F在AC的延长线上,CF=12 AC.(1)DC=EF吗?说明理由;(2)若AC=6,AB=10,求四边形DCFE的面积.【分析】(1)根据直角三角形斜边上的中线等于斜边的一半可得CD=BD,再根据等边对等角可得∠B=∠DCE,然后求出∠FEC=∠DCE,根据等腰三角形三线合一的性质可得∠CED=90°,然后求出∠CED=∠ECF=90°,再利用“角边角”证明△CDE和△ECF全等,根据全等三角形对应边相等证明即可.(2)由三角形的中位线定理得到DE的长度,再由平行四边形的面积公式求得.【解答】解:(1)证明:∵∠ACB=90°,点D是AB的中点,∴CD=BD,∴∠B=∠DCE,∵∠FEC=∠B,∴∠FEC=∠DCE,∵点E是BC的中点,∴∠CED=90°,∴∠CED=∠ECF=90°,在△CDE和△ECF中,{∠CED =∠ECF =90°CE =EC ∠FEC =∠DCE∴△CDE ≌△ECF (ASA ),∴CF=DE ;(2)在Rt △ABC 中,∠ACB=90°,∴BC=√AB 2−AC 2=8,∵点D 、E 分别是AB 、BC 的中点,∴DE=12AC=3,CE=12, ∴S 四边形DCFE =3×4=12.【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形的性质,全等三角形的判定与性质,熟记各性质并确定出全等三角形是解题的关键.18.如图,∠ACB=∠ADB=90°,M 、N 分别为AB 、CD 的中点.求证:MN ⊥CD .【分析】连接CM 、DM ,根据直角三角形斜边上的中线等于斜边的一半可得CM=DM=12AB ,再根据等腰三角形三线合一的性质证明即可. 【解答】证明:如图,连接CM 、DM ,∵∠ACB=∠ADB=90°,M 为AB 的中点,∴CM=12AB ,DM=12AB , ∴CM=DM=12AB , ∵N 为CD 的中点,∴MN ⊥CD .【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质并作辅助线构造出等腰三角形是解题的关键.19.已知:如图,四边形ABCD 中,∠ABC=90°,∠ADC=90°,点E 为AC 中点,点F 为BD 中点.求证:EF ⊥BD .【分析】连接BE 、DE ,根据直角三角形斜边上的中线等于斜边的一半可得BE=DE=12AC ,再根据等腰三角形三线合一的性质证明. 【解答】证明:如图,连接BE 、DE ,∵∠ABC=90°,∠ADC=90°,点E 是AC 的中点,∴BE=DE=12AC , ∵点F 是BD 的中点,∴EF ⊥BD .【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质并作出辅助线是解题的关键.20.如图,在Rt △ABC 中,∠ABC=90°,点D 是AC 的中点,作∠ADB 的角平分线DE 交AB 于点E ,(1)求证:DE ∥BC ;(2)若AE=3,AD=5,点P 为线段BC 上的一动点,当BP 为何值时,△DEP 为等腰三角形.请求出所有BP 的值.【分析】(1)根据直角三角形斜边上的中线等于斜边的一半可得BD=AD=12AC ,再根据等腰三角形三线合一的性质可得DE ⊥AB ,再根据垂直于同一直线的两直线平行证明;(2)利用勾股定理列式求出DE 的长,根据等腰三角形三线合一的性质求出BE=AE ,然后分DE=EP 、DP=EP 、DE=DP 三种情况讨论求解.【解答】(1)证明:∵∠ABC=90°,点D 是AC 的中点,∴BD=AD=12AC , ∵DE 是∠ADB 的角平分线,∴DE ⊥AB ,又∵∠ABC=90°,∴DE ∥BC ;(2)解:∵AE=3,AD=5,DE ⊥AB ,∴DE=√AD 2−AE 2=4,∵DE ⊥AB ,AD=BD ,∴BE=AE=3,①DE=EP 时,BP=√42−32=√7,②DP=EP 时,BP=12DE=12×4=2, ③DE=DP 时,过点D 作DF ⊥BC 于F ,则DF=BE=3,由勾股定理得,FP=√42−32=√7,点P 在F 下边时,BP=4﹣√7,点P 在F 上边时,BP=4+√7,综上所述,BP 的值为√7,2,4﹣√7,4+√7.【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形的判定与性质,平行线的判定,难点在于(2)要分情况讨论.21.抛物线y=﹣x 2+bx +c 经过点A (﹣1,0)和C (0,3).(1)求抛物线的解析式;(2)点P 为抛物线对称轴上一点.①当PA +PC 最小时,求点P 的坐标;②当△PAC 是直角三角形时,求点P 的坐标.【分析】(1)利用待定系数法即可解决.(2)求出直线BC 与对称轴的交点就是点P .(3)分三种情形讨论:①当∠ACP 1=90°时,求出直线P 1C 为y=﹣13x +3即可.②当∠CAP 2=90°,求出直线AP 2为y=﹣13x ﹣13即可.③当∠AP 3C=90°时,作CE ⊥对称轴于E ,设P (1,k ),由△P 3CE ∽△AP 3F 得到CE P 3F =EP 3AF,即可解决问题. 【解答】解:(1)把点A (﹣1,0)和C (0,3),代入y=﹣x 2+bx +c 得{−b +c =0c =3, 解得{b =2c =3. 故抛物线解析式为y=﹣x 2+2x +3.(2)①设直线BC 为y=kx +b ,直线BC 与对称轴的交点就是点P .∵抛物线对称轴x=1,点B 坐标(3,0),则{3k +b =0b =3解得{k =−1b =3, ∴直线BC 为y=﹣x +3,与对称轴的交点为(1,2),∴点P 坐标(1,2).②当∠ACP 1=90°时,∵直线AC 解析式为y=3x +3,∴直线P 1C 为y=﹣13x +3, ∴点P 1(1,83). 当∠CAP 2=90°,直线AP 2为y=﹣13x ﹣13, ∴点P 2(1,﹣23). 当∠AP 3C=90°时,作CE ⊥对称轴于E ,设P (1,k )由△P 3CE ∽△AP 3F 得到CE P 3F =EP 3AF, ∴1k =3−k 2, ∴k=1或2,∴点P 坐标(1,1)或(1,2).综上所述点P 坐标(1,1)或(1,2)或(1,83)或(1,﹣23).【点评】本题考查二次函数性质、最小值问题、直角三角形,相似三角形的判定和性质等知识,解题的关键是学会待定系数法确定函数解析式,学会分类讨论思想,利用一次函数解决问题,属于中考常考题型.22.已知:如图,∠BAC=∠BDC=90°,点E 在BC 上,点F 在AD 上,BE=EC ,AF=FD .求证:EF ⊥AD .【分析】连接AE ,DE ,由直角三角形斜边的中线是斜边的一半易得AE=DE=12BC ,由全等三角形的判定定理可得△AEF ≌△DEF ,由全等三角形的性质定理可得∠AFE=∠DFE=90°,即得出结论.【解答】解:连接AE ,DE ,∵∠BAC=∠BDC=90°,BE=EC ,∴AE=12BC ,DE=12BC , ∴AE=DE ,在△AEF 与△DEF 中,{AE =DE EF =EF AF =FD,∴△AEF ≌△DEF (SSS ),∴∠AFE=∠DFE=90°,即EF ⊥AD .【点评】本题主要考查了直角三角形斜边上的中线和全等三角形的判定及性质,作出适当的辅助线是解答此题的关键.23.如图1,点P是∠AOB的内部任意一点,PM⊥OA,PN⊥OB,垂足分别是M、N,D是OP的中点.求证:∠MDN=2∠MON.小尧同学思路如下:因为PM⊥OA,垂足是M,D是OP的中点.由“直角三角形斜边上的中线等于斜边的一半”,得到MD=OD,…课后,小尧同学发现上题中,当“点P是∠AOB的外部任意一点”结论也成立,请你证明其正确.如图2,P是∠AOB的外部任意一点,PM⊥OA,PN⊥OB,垂足分别是M、N,D 是OP的中点.求证:∠MDN=2∠MON.【分析】根据直角三角形的性质得到MD=OD,得到∠DOM=∠DMO,根据三角形的外角性质得到∠PDM=2∠AOP,结合图形解答.【解答】证明:如图1,∵PM⊥OA,D是OP的中点,∴MD=OD,∴∠DOM=∠DMO,∴∠PDM=2∠AOP,同理,∠PDN=2∠BOP,∴∠MDN=∠PDM +∠PDN=2(∠AOP +∠BOP )=2∠MON ,如图2,由1得,∠PDM=2∠AOP ,∠PDN=2∠BOP ,∴∠MDN=∠PDN ﹣∠PDM=2(∠BOP +∠AOP )=2∠MON .【点评】本题考查的是直角三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.24.如图,BD 、CE 是△ABC 的高,G 、F 分别是BC 、DE 的中点.求证:FG ⊥DE .【分析】根据直角三角形斜边上的中线等于斜边的一半证得DG=EG ,然后利用三线合一定理即可求得.【解答】证明:∵BD 是△ABC 的高,即∠BDC=90°,又∵G 是BC 的中点,∴DG=12BC , 同理,EG=12BC , ∴DG=EG ,∵F 是DE 的中点,∴FG ⊥DE .【点评】本题考查了直角三角形的性质:直角三角形斜边上的中线等于斜边的一半,以及三线合一定理,正确作出辅助线是关键.25.已知,如图,∠ABC=∠ADC=90°,M 、N 分别是AC 、BD 的中点.(1)求证:MN ⊥BD ;(2)在边AD 上能否找到一点P ,使得PB=PD ?请说明理由.【分析】(1)连接BM、CM,根据在直角三角形中,斜边上的中线等于斜边的一半得到BM=12AC,DM=12AC,根据等腰三角形的三线合一得到答案;(2)根据线段垂直平分线的性质作图即可.【解答】解:(1)连接BM、CM,∵∠ABC=∠ADC=90°,M是AC的中点,∴BM=12AC,DM=12AC,∴BM=DM,又N为BD的中点,∴MN⊥BD;(2)作线段BD的垂直平分线交AD于P,根据线段垂直平分线上的点与线段两个端点的距离相等可知,PB=PD.【点评】本题考查的是直角三角形的性质和等腰三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半、等腰三角形的三线合一是解题的关键.26.如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,且CD=12 AB,DE⊥CF于E.求证:CE=EF.【分析】连接DF ,根据直角三角形的性质得到DF=12AB ,根据题意得到DF=DC ,根据等腰三角形的三线合一证明结论.【解答】证明:连接DF ,∵AD 是边BC 上的高,CF 是边AB 上的中线,∴∠ADB=90°,AF=FB ,∴DF=12AB ,又CD=12AB , ∴DF=DC ,又DE ⊥CF ,∴CE=EF .【点评】本题考查的是直角三角形的性质和等腰三角形的性质,掌握直角三角形斜边上的中线等于斜边的一半、等腰三角形的三线合一是解题的关键.27.如图,在四边形ABCD 中,∠BAD=∠BCD=90°,BC=6,CD=AC=8,M 、N 分别是对角线BD 、AC 的中点.(1)求证:MN ⊥AC .(2)求MN 的长.【分析】(1)连接AM 、CM ,根据直角三角形斜边上的中线等于斜边的一半可得AM=CM=BM=DM=12BD ,再根据等腰三角形三线合一的性质证明; (2)利用勾股定理类似求出BD ,再求出AM 、AN ,再利用勾股定理列式计算即可得解.【解答】(1)证明:如图,连接AM 、CM ,∵∠BAD=∠BCD=90°,M 是BD 的中点,∴AM=CM=BM=DM=12BD , ∵N 是AC 的中点,∴MN ⊥AC ;(2)解:∵∠BCD=90°,BC=6,CD=8,∴BD=√BC 2+CD 2=√62+82=10,∴AM=12×10=5, ∵AC=8,N 是AC 的中点,∴AN=12×8=4, ∴MN=√AM 2−AN 2=3.【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,勾股定理,熟记性质与定理并作辅助线构造出等腰三角形是解题的关键.28.如图所示,四边形ABCD 中,∠BAD=∠BCD=90°,E ,F 分别是BD ,AC 的中点.(1)求证:AE=CE ;(2)判断EF 与AC 的位置关系,并说明理由.【分析】(1)根据直角三角形斜边上的中线等于斜边的一半可得AE=12BD ,CE=12BD ,。
专题13 斜边上的中线问题(解析版)-2021年中考数学二轮复习经典问题专题训练

专题13 斜边上的中线问题【规律总结】直角三角形中遇到斜边上的中点,常联想“斜边上的中线等于斜边的一半”【典例分析】例1.(2021·上海九年级专题练习)一副三角板如图摆放,点F 是45角三角板ABC 的斜边的中点,4AC .当30角三角DEF 的直角顶点绕着点F 旋转时,直角边DF EF ,分别与,AC BC 相交于点.M N ,则CMFN 的面积为____________.【答案】4【分析】连结CF ,证明CFM BFN =,根据12BFC ACB CMFN S SS ==四边形即可求解. 【详解】解:连结CF ,如图,点F 是45角三角板ABC 的斜边的中点,CF BF CF ∴=,平分,,45ACB CF AB B ∠⊥∠=︒,45,2345ACF ∴∠=︒∠+∠=︒1290∠+∠=︒,13∴∠=∠,在CFM △和BFN 中,13MCF B CF BF∠=∠⎧⎪=⎨⎪∠=∠⎩()CFM BFN ASA ∴=,CFM BFNS S ∴=,111444222BFC ACB CMFN S SS ∴===⨯⨯⨯=四边形. 【点睛】 此题考查的知识点有等腰直角三角形,全等三角形的判定与性质等知识点,综合性强,难度较大,是一道难题.例2.(2020·湖北恩施土家族苗族自治州·九年级期中)如图,在等腰直角三角形ABC 中,90C ∠=︒,AC a =,点E 为边AC 上任意一点,点D 为AB 的中点,过点D 作DF DE ⊥交BC 于点F .求证:CE CF +为定值.【答案】证明见解析【分析】连接CD ,证明△CDE△△BDF ,得CE=BF ,进一步证明CE+CF=BC=AC a =,从而得到结论.【详解】 证明:连接CD ,如图,△△ABC 是等腰直角三角形,且D 为AB 的中点,△CD△AB ,CD 平分△ACB ,AD=BD=CD△△DCA=△DCB=△DBC=45°又DE△DF△△EDC+△FDC=90°而△FDC+△FDB=90°△△EDC=△FDB在△CDE 和△BDF 中,DCE DBF CD CDEDC BDF ∠=∠⎧⎪=⎨⎪∠=∠⎩△△CDE△△BDF△CE=BF△BC=AC=a△CE+CF=BE+CF=BC=AC=a ,故:CE CF +为定值.【点睛】此题主要考查了全等三角形的判定与性质以及等腰直角三角形的性质,证明CE=BF 是解答此题的关键.【真题演练】一、填空题1.(2020·哈尔滨市萧红中学八年级月考)如图,在ABC 中,∠B=60°,CD 为AB 边上的高,E 为AC 边的中点,点 F 在BC 边上,∠EDF=60°,若 BF=3,CF=5,则AC 边的长为 .【答案】【分析】如图(见解析),先根据直角三角形的性质、勾股定理得出,4D B F D ==,再根据等边三角形的判定与性质得出4,60DH BDH =∠=︒,然后根据三角形的中位线定理、平行线的性质得出60EHD BDH ∠=∠=︒,从而可得EHD B ∠=∠,BDF HDE ∠=∠,最后根据三角形全等的判定定理与性质得出DE DF ==据此根据直角三角形斜边上的中线等于斜边的一半即可得.【详解】如图,过点D 作DG BC ⊥于点G3,5BF CF ==8BC BF CF ∴=+=在Rt BCD 中,60B ∠=︒,9030BCD B ∠=︒-∠=︒142BD BC ∴== 在Rt BDG 中,60B ∠=︒,9030BDG B ∠=︒-∠=︒12,2BG BD DG ∴====1GF BF BG ∴=-=,DF =取BC 的中点H ,连接DH 、EH142DH BH BC BD ∴==== BDH ∴是等边三角形60BDH ∴∠=︒点E 是AC 边的中点∴EH 是ABC 的中位线//EH AB ∴60EHD BDH ∴∠=∠=︒60EHD B ∴∠=∠=︒又60BDF FDH BDH ∠+∠=∠=︒,60HDE FDH EDF ∠+∠=∠=︒BDF HDE ∴∠=∠在HDE 和BDF 中,EHD B DH DBHDE BDF ∠=∠⎧⎪=⎨⎪∠=∠⎩()HDE BDF ASA ∴≅DE DF ∴==则在Rt ACD △中,12DE AC =,即2AC DE ==故答案为:【点睛】本题考查了直角三角形的性质、等边三角形的判定与性质、三角形全等的判定定理与性质、三角形的中位线定理等知识点,通过作辅助线,构造等边三角形和全等三角形是解题关键.二、解答题2.(2020·庆云县第二中学八年级期中)已知:在ABC 中,AC=BC ,∠ACB=90°,点D 是AB 的中点,点E 是AB 边上一点.(1)直线BF 垂直于CE 于点F ,交CD 于点G (如图1),求证:AE=CG ;(2)直线AH 垂直于CE ,垂足为H ,交CD 的延长线于点M (如图2),求证:BCE CAM ≌.【答案】(1)证明见解析;(2)证明见解析.【分析】(1)运用等腰直角三角形性质,三线合一,可以得到△AEC 和△CGB 一组对应边、一组对应角相等,AC BC =,CAE BCG ∠=∠;然后利用同角的余角相等,证得ACE CBG ∠=∠;两角及其夹边对应相等()ASA 则两三角形全等.(2)运用等腰直角三角形性质,三线合一,可以得到△BCE 和△CAM 一组对应边、一组对应角相等,AC BC =,ACM CBE ∠=∠;然后利用同角的余角相等,证得BEC CMA ∠=∠;两角及其中一角的对边对应相等()AAS 则两三角形全等.【详解】(1)证明:△点D 是AB 中点,AC=BC ,△ACB=90°,△CD△AB ,△ACD=△BCD=45°,△△CAD=△CBD=45°,△△CAE=△BCG ,又△BF△CE ,△△CBG+△BCF=90°,又△△ACE+△BCF=90°,△△ACE=△CBG ,在△AEC 和△CGB 中,CAE BCG AC BCACE CBG ∠=∠⎧⎪=⎨⎪∠=∠⎩△△AEC△△CGB (ASA ),△AE=CG ,(2)证明:△CH△HM ,CD△ED ,△△CMA+△MCH=90°,△BEC+△MCH=90°,△△CMA=△BEC ,又△△ACM=△CBE=45°,在△BCE 和△CAM 中,BEC CMA ACM CBE BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩△△BCE△△CAM (AAS ).【点睛】本题考查全等三角形判定定理,从题中找到对应边、角的信息,灵活运用三角形判定定理是解题关键.3.(2020·张家港市梁丰初级中学八年级期中)已知,∠ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,若E是线段CA上任意一点,DF∠DE,交直线BC于F点.G为EF的中点,连接CG并延长交直线AB于点H.(1)试说明:①AE=CF;②CG=GD;(2)若AE=6,CH=10,求边AC的长.【答案】(1)理由见详解;(2)AC=14【分析】(1)①由题意易得AD=DC=DB,△A=△B=45°,CD△AB,进而可证△ADE△△CDF,然后根据全等三角形的性质可得;②由直角三角形斜边中线定理可得11,22CG EF DG EF==,进而问题得证;(2)由(1)可得AE=CF=6,由题意易得12DG CH=,则有EF=CH=10,然后根据勾股定理可求解.【详解】解:(1)①AE=CF,理由如下:△AC=BC,△ACB=90°,CD为边AB上的中线,△AD=DC=DB,△A=△B=45°,CD△AB,△△A=△BCD=45°,△DF△DE,△△EDC+△CDF=90°,又△△ADE+△EDC=90°,△△ADE=△CDF,△△ADE△△CDF(ASA),△AE=CF,②CG=GD,理由如下:△△ACB=90°,△EDF=90°,EG=GF,△11,22CG EF DG EF==,△CG=GD;(2)由(1)得:AE=CF=6,CG=GD,12DG EF=,△△GCD=△GDC,△△GCD+△CHD=90°,△GDC+△GDH=90°,△△CHD=△GDH,△GH=GD,△12DG CH=,△CH=10,△CH=EF=10,在Rt△CEF 中,222+=CF CE EF ,即222610CE +=,解得:CE=8,△AC=AE+CE=14.【点睛】本题主要考查等腰三角形的性质与判定、勾股定理及直角三角形斜边中线定理,熟练掌握等腰三角形的性质与判定、勾股定理及直角三角形斜边中线定理是解题的关键.4.(2019·陇东学院附属中学八年级期末)如图在Rt ABC △中,AB AC =,90BAC ∠=︒,O 为BC 的中点.(1)写出点O 到ABC 的三个顶点A 、B 、C 的距离的大小关系.(2)如果点M 、N 分别在线段AB 、AC 上移动,移动中保持AN BM =,请判断OMN 的形状,并证明你的结论.(3)当点M 、N 分别在AB 、AC 上运动时,四边形AMON 的面积是否发生变化?说明理由.【答案】(1)OA OB OC ==;(2)OMN 是等腰直角三角形,证明见解析;(3)四边形AMON 的面积不变,理由见解析【分析】(1)连接OA ,由O 为BC 的中点可得OC OB =,由直角三角形斜边上的中线的性质可得12OA BC =,即可得OA OB OC ==. (2)由(1)不难证明45CAO B ∠=∠=︒,结合已知条件进而证明OAN △OBM ,即可得OM ON =,NOA MOB ∠=∠,即90NOM AOB ∠=∠=︒,所以OMN 是等腰直角三角形.(3)由(2)可得OAN S =OBM S ,进而将四边形AMON 的面积转化为AOB 的面积,AOB 的面积保持不变,故四边形AMON 的面积保持不变.【详解】(1)连接OA ,Rt ABC △中,O 为BC 的中点,∴12OA BC =,OC OB =, ∴122OA OB OB =⨯⨯=, ∴OA OB OC ==.(2)OMN 是等腰直角三角形,证明如下:AB AC =,O 为BC 的中点,∴AO BC ⊥,∴90AOB ∠=︒,OA OB OC ==,∴45CAO B ∠=∠=︒,在OAN 与OBM 中,OA OB CAO B AN BM =⎧⎪∠=∠⎨⎪=⎩,∴OAN △OBM ,∴OM ON =,NOA MOB ∠=∠,∴90NOM AOB ∠=∠=︒,∴OMN 是等腰直角三角形.(3)四边形AMON 的面积保持不变,理由如下:由(2)可得: OAN S =OBM S , ∴OAN AOM OBM AOM AOB AMON S S S S S S =+=+=四边形. AOB 的面积保持不变∴四边形AMON 的面积保持不变.【点睛】本题主要考查直接三角形斜边上中线的性质以及全等三角形的判定与性质,掌握全等三角形的判定与性质定理并灵活运用是解题关键.5.(2020·乌兰察布市·内蒙古凉城县宏远中学八年级月考)已知:三角形ABC 中,∠A =90°,AB =AC ,D 为BC 边的中点,(1)如图①,E ,F 分别是AB ,AC 上的点,且BE =AF ,求证:∠DEF 为等腰直角三角形.(2)如图②,若E ,F 分别为AB ,CA 延长线上的点,仍有BE =AF ,其他条件不变,那么,∠DEF 是否仍为等腰直角三角形?证明你的结论.【答案】(1)见解析;(2)△DEF为等腰直角三角,证明见解析【分析】(1)先连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有△CAD=△BAD=45°,AD=BD=CD,而△B=△C=45°,所以△B=△DAF,再加上BE=AF,AD=BD,可证出:△BED△△AFD,从而得出DE=DF,△BDE=△ADF,从而得出△EDF=90°,即△DEF是等腰直角三角形;(2)还是证明:△BED△△AFD,主要证△DAF=△DBE(△DBE=180°-45°=135°,△DAF=90°+45°=135°),再结合两组对边对应相等,所以两个三角形全等.【详解】(1)证明:连接AD,△AB=AC,△BAC=90°,D为BC的中点,△AD△BC,BD=AD.△△B=△DAC=45° 又BE=AF,△△BDE△△ADF(SAS).△ED=FD,△BDE=△ADF.△△EDF=△EDA+△ADF=△EDA+△BDE=△BDA=90°.△△DEF为等腰直角三角形.(2)△DEF为等腰直角三角形.证明:若E,F分别是AB,CA延长线上的点,如图所示:连接AD,△AB=AC,△△ABC为等腰三角形,△△BAC=90°,D为BC的中点,△AD=BD,AD△BC(三线合一),△△DAC=△ABD=45°.△△DAF=△DBE=135°.又AF=BE,△△DAF△△DBE(SAS).△FD=ED,△FDA=△EDB.△△EDF=△EDB+△FDB=△FDA+△FDB=△ADB=90°.△△DEF仍为等腰直角三角形.【点睛】本题利用了等腰直角三角形底边上的中线平分顶角,并且等于底边的一半,还利用了全等三角形的判定和性质,及等腰直角三角形的判定.6.(2019·全国九年级专题练习)如图所示,E,F分别是正方形ABCD的边AD,CD上AB=,连DH.求线段DH长度的最小的两个动点,且AE DF=,BE交AF于点H,2值.【答案】DH1【解析】【分析】根据正方形性质可得AB=DA ,△BAD=△ADF=90°,又根据AE=DF ,利用SAS 可证得△ABE△△DAF ,于是△ABE=△DAF ;由于△DAF+△BAH=△ABE+△BAH=90°,从而△AHB=90°,取AB 的中点O ,连接OH 、OD ,则OH=12AB=1,在Rt△AOD 中,根据勾股定理计算出OD 的值;根据三角形的三边关系,可得OH+DH >OD ,于是当O 、D 、H 三点共线时,DH 的长度最小为OD -OH ,据此解答.【详解】解:△四边形ABCD 是正方形,△AB=DA ,△BAD=△ADF=90°,又△AE=DF ,△△ABE△△DAF ,△△ABE=△DAF.△△DAF+△BAH=△ABE+△BAH=90°,△△AHB=90°,取AB 的中点O ,连OH 、OD ,△112OH AB ==,OD ==OHD ∆中有DH OD OH >-,即1DH >.故O、H、D三点共线时DH最小,△DH1.【点睛】本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边的中线等于斜边的一半,勾股定理及三角形三条边的关系,确定出点H的位置是解答本题的关键.。
三角形的中位线基础题30道填空题附详细答案

9.5 三角形的中位线基础题汇编(2)AB9.5 三角形的中位线基础题汇编(2)参考答案与试题解析一.填空题(共30小题)1.(2014•鞍山)如图,H是△ABC的边BC的中点,AG平分∠BAC,点D是AC上一点,且AG⊥BD于点G.已知AB=12,BC=15,GH=5,则△ABC的周长为49.2.(2014•海门市模拟)如图,在△ABC中,∠ACB=52°,点D,E分别是AB,AC的中点.若点F在线段DE上,且∠AFC=90°,则∠FAE的度数为64°.EF=EFC=3.(2014•昆明模拟)如图,A,B两点被池塘隔开,在A,B外选一点C,连接AC和BC,并分别找出AC和BC 的中点M,N,如果测得MM=20m,那么A,B两点间的距离是40m.MN=4.(2014•秦淮区一模)如图,在△ABC中,AB=AC=13,DE是△ABC的中位线,F是DE的中点.已知B(﹣1,0),C(9,0),则点F的坐标为(4,6).=5.(2014•兴化市二模)如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C=70°.6.(2013•漳州)如图,△ABC中,D,E分别为AB,AC的中点,∠B=70°,则∠ADE=70度.7.(2013•澄海区模拟)如图,平地上A、B两点被池塘隔开,测量员在岸边选一点C,并分别找到AC和BC的中点M、N,经量得MN=24米,则AB=48米.MN=8.(2013•滨湖区二模)如图,在Rt△ABC中,∠ACB=90°,D、E分别是AC、AB的中点,DE=3,CE=5,则AC= 8.AC==89.(2013•丰南区二模)如图,DE是△ABC的中位线,△ADE的面积=2,则四边形BCED的面积=6.利用三角形中位线定理以及相似三角形的判定与性质得出,进而求出即可.DE BC,=10.(2012•盐城)如图,在△ABC中,D、E分别是边AB、AC的中点,∠B=50°.先将△ADE沿DE折叠,点A 落在三角形所在平面内的点为A1,则∠BDA1的度数为80°.11.(2012•阜新)如图,△ABC的周长是32,以它的三边中点为顶点组成第2个三角形,再以第2个三角形的三边中点为顶点组成的第3个三角形,…,则第n个三角形的周长为26﹣n.×=32×,××=32)(12.(2012•德阳)如图,点D、E分别是△ABC的边AB、AC的中点,连接DE,若DE=5,则BC=10.BC13.(2012•大东区二模)如图,D、E分别是△ABC的边AB、AC的中点,若DE的长是3,则BC的长是6.14.(2012•义乌市模拟)如图,DE是△ABC的中位线,DE=2cm,则BC=4cm.×15.(2011•沙坪坝区模拟)如图,DE是△ABC的中位线,△ABC的周长为8,则△ADE的周长是4.AD=AB AE=BCBCAB AC(16.(2011•路南区一模)在△ABC中,D、E分别是边AB、AC的中点,若BC=3,则DE的长是.AB,故答案为:17.(2009•来宾)已知AB、CD分别是梯形ABCD的上、下底,且AB=8,CD=12,EF是梯形的中位线,则EF= 10.((18.(2008•房山区一模)如图,在△ABC中,D、E分别是AB、AC边的中点,AB=4,AC=6,DE=2.4,则△ABC 的周长是14.8.19.(2008•安溪县校级质检)梯形的上底、下底长分别是3cm、7cm,则它的中位线长为5cm.(20.(2007•静安区二模)在⊙O中,AB是直径,弦AC的弦心距为3,那么BC的长为6.OF= 21.(2005•遵义)如图,在梯形ABCD中,AD∥BC,中位线EF=5cm,高AH=4cm,则S梯形ABCD=20cm2.22.如图,△ABC中,AB=AC,D是AB边的中点,E是AB延长线上一点,且BE=AB,则CD:CE=1:2.ABCE=23.在△ABC中,∠BAC的角平分线AN⊥BN,M是BC的中点,已知AB=10,AC=22,则MN=6.中,MN=EC=((24.如图,M、P分别为△ABC的边AB、AC上的点,且AM=BM,AP=2CP,BP与CM相交于N.已知PN=1,则PB的长为4.25.如图,四边形ABCD的对角线AC、BD相交于点O,E、F、G分别是AB、OC、OD的中点,OA=AD,OB=BC,CD=AB,则∠FEG的角度是120°.GE=FE=CD=CD=ABABFEH==26.如图,△ABC中,D、F在AB上,且AD=BF,DE∥BC交AC于E,FG∥BC交AC于G.求证:DE+FG=BC.MN=MN=MN=MN=27.(2011•南充自主招生)如图△ABC中,AC>AB,AB=4,AC=x,AD平分∠BAC,BD⊥AD于D,点E是BC 的中点,DE=y,则y关于x的函数关系式为y=x﹣2.CF=(xx28.(2011•鼓楼区校级自主招生)如图,△ABC的三边长分别为3、5、6,BD与CE都是△ABC的外角平分线,M、N是直线BC上两点,且AM⊥BD于D,AN⊥CE于E,则DE的长等于7.29.(2014•安阳校级模拟)如图,DE是△ABC的中位线,DE=2cm,AB+AC=12cm,则梯形DBCE的周长为12 cm.AB CE=ACBD+CE+DE+BC=(×30.(2011•常州校级模拟)如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是3,△EDC与△ABC的面积之比为.BD=的面积之比为:.21 / 21。
初二数学三角形中位线练习题(含答案)

初二数学三角形中位线练习题一.选择题(共5小题)1.如图,为了测量池塘边A、B两地之间的距离,在线段AB的同侧取一点C,连结CA并延长至点D,连结CB并延长至点E,使得A、B分别是CD、CE的中点,若18DE m=,则线段AB的长度是()A.9m B.12m C.8m D.10m2.已知三角形的周长是16,它的三条中位线围成的三角形的周长是()A.16B.12C.8D.43.如图,在四边形ABCD中,点P是边CD上的动点,点Q是边BC上的定点,连接AP,PQ,E,F分别是AP,PQ的中点,连接EF.点P在由C到D运动过程中,线段EF的长度() A.保持不变B.逐渐变小C.先变大,再变小D.逐渐变大4.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD BC=,∠的度数是()∠=︒,则EFPEPF136A.68︒B.34︒C.22︒D.44︒5.如图,D是ABC⊥,E、F、G、H分别是边AB、BD、CD、AC的中点.若∆内一点,BD CDCD=,则四边形EFGH的周长是()BD=,6AD=,810A.24B.20C.12D.10第3题图第4题图第5题图二.填空题(共5小题)6.某直角三角形的两条边长分别是10和24,则连接两条直角边中点的线段的长是.7.如图,在Rt ABCABC∠=︒,点D、E、F分别是AB、AC,∆中,90BE=,则DF=.BC边上的中点,连结BE,DF,已知58.如图,在四边形ABCD中,220∠+∠=︒,E、F分别是AC、ADC BCDBD 的中点,P 是AB 边上的中点,则EPF ∠= ︒.9.如图,在四边形ABCD 中,//AB CD ,E ,F 分别是AC ,BD 的中点,已知12AB =,6CD =,则EF = .10.如图,在ABC ∆中,8AB =,6AC =,AM 平分BAC ∠,CM AM ⊥于点M ,N 为BC 的中点,连结MN ,则MN 的长为 .第8题图 第9题图 第10题图三.解答题(共3小题)11.如图所示,在ABC ∆中,点D 在BC 上且CD CA =,CF 平分ACB ∠,AE EB =,求证:12EF BD =.12.如图:D 、E 是ABC ∆边AB ,AC 的中点,O 是ABC ∆内一动点,F 、G 是OB ,OC 的中点.判断四边形DEGF 的形状,并证明.13.已知:如图,在四边形ABCD 中,对角线AC 、BD 相交于O ,且AC BD =,E 、F 分别是AB 、CD 的中点,E 、F 分别交BD 、AC 于点G 、H .求证:OG OH =.答案与解析一.选择题(共5小题)1.如图,为了测量池塘边A 、B 两地之间的距离,在线段AB 的同侧取一点C ,连结CA 并延长至点D ,连结CB 并延长至点E ,使得A 、B 分别是CD 、CE 的中点,若18DE m =,则线段AB 的长度是( )A .9mB .12mC .8mD .10m【分析】根据三角形的中位线定理解答即可. 【解答】解:A 、B 分别是CD 、CE 的中点, ∴AB 是△CDE 的中位线,192AB DE m ∴==, 故选:A .2.已知三角形的周长是16,它的三条中位线围成的三角形的周长是( ) A .16 B .12 C .8 D .4【分析】由中位线定义可得新三角形的各边长为原三角形各边长的一半,即可得出其周长等于原三角形周长的一半.【解答】解:三角形的周长是16,∴它的三条中位线围成的三角形的周长是11682⨯=. 故选:C .3.如图,在四边形ABCD 中,点P 是边CD 上的动点,点Q 是边BC 上的定点,连接AP ,PQ ,E ,F 分别是AP ,PQ 的中点,连接EF .点P 在由C 到D 运动过程中,线段EF 的长度( )A .保持不变B .逐渐变小C .先变大,再变小D .逐渐变大 【分析】连接AQ ,根据三角形中位线定理解答即可. 【解答】解:如图所示,连接AQ , 点Q 是边BC 上的定点, AQ ∴的大小不变,E ,F 分别是AP ,PQ 的中点, ∴EF 是△APQ 的中位线, 12EF AQ ∴=, ∴线段EF 的长度保持不变,故选:A .4.如图,在四边形ABCD 中,P 是对角线BD 的中点,E 、F 分别是AB 、CD 的中点,AD BC =,136EPF ∠=︒,则EFP ∠的度数是( )A .68︒B .34︒C .22︒D .44︒【分析】根据三角形中位线定理得到12PE AD =,12PF BC =,根据等腰三角形的性质、三角形内角和定理计算即可.【解答】解:P 是BD 的中点,E 是AB 的中点, ∴EP 是△BCD 的中位线, 12PE AD ∴=, 同理,12PF BC =, AD BC =, PE PF ∴=,1(180)222EFP EPF ∴∠=⨯︒-∠=︒,故选:C . 5.如图,D 是ABC ∆内一点,BD CD ⊥,E 、F 、G 、H 分别是边AB 、BD 、CD 、AC 的中点.若10AD =,8BD =,6CD =,则四边形EFGH 的周长是( )A .24B .20C .12D .10【分析】利用勾股定理列式求出BC 的长,再根据三角形的中位线平行于第三边并且等于第三边的一半求出12EH FG BC ==,12EF GH AD ==,然后代入数据进行计算即可得解. 【解答】解:BD CD ⊥,8BD =,6CD =,22228610BC BD CD ∴=+=+,E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点,12EH FG BC ∴==,12EF GH AD ==,∴四边形EFGH 的周长EH GH FG EF AD BC =+++=+, 又10AD =,∴四边形EFGH 的周长101020=+=, 故选:B .二.填空题(共5小题)6.某直角三角形的两条边长分别是10和24,则连接两条直角边中点的线段的长是 13或12 . 【分析】根据勾股定理求出AB ,根据三角形中位线定理计算,得到答案. 【解答】解:分两种情况讨论:①当24是直角边时,由勾股定理得,斜边2222241026AB AC BC =+=+=,M 、N 分别为CA 、CB 的中点, ∴MN 是△ABC 的中位线,1132MN AB ∴==,②当24是斜边时,1122MN AB ==,故答案为:13或12.7.如图,在Rt ABC ∆中,90ABC ∠=︒,点D 、E 、F 分别是AB 、AC ,BC 边上的中点,连结BE ,DF ,已知5BE =,则DF = 5 .【分析】已知BE 是Rt ABC ∆斜边AC 的中线,那么12BE AC =;DF 是ABC ∆的中位线,则12DF AC =,则5DF BE ==. 【解答】解:ABC ∆是直角三角形,BE 是斜边的中线, 12BE AC ∴=, 又DF 是ABC ∆的中位线,12DF AC ∴=, 5DF BE ∴==. 故答案为5.8.如图,在四边形ABCD 中,220ADC BCD ∠+∠=︒,E 、F 分别是AC 、BD 的中点,P 是AB 边上的中点,则EPF ∠= 40 ︒.【分析】依据四边形内角和即可得到140BAD ABC ∠+∠=︒,再根据三角形中位线定理即可得到BPF BAD ∠=∠,APE ABC ∠=∠,进而得出140APE BPF ∠+∠=︒,即可得到EPF ∠的度数. 【解答】解:四边形ABCD 中,220ADC BCD ∠+∠=︒, 360220140BAD ABC ∴∠+∠=︒-︒=︒,E 、F 分别是AC 、BD 的中点,P 是AB 边上的中点, PE ∴是ABC ∆的中位线,PF 是ABD ∆的中位线, //PE BC ∴,//PF AD ,BPF BAD ∴∠=∠,APE ABC ∠=∠,140APE BPF BAD ABC ∴∠+∠=∠+∠=︒, 18014040EPF ∴∠=︒-︒=︒,故答案为:40.9.如图,在四边形ABCD 中,//AB CD ,E ,F 分别是AC ,BD 的中点,已知12AB =,6CD =,则EF = 3 .【分析】连接CF 并延长交AB 于G ,证明FDC FBG ∆≅∆,根据全等三角形的性质得到6BG DC ==,CF FG =,求出AG ,根据三角形中位线定理计算,得到答案. 【解答】解:连接CF 并延长交AB 于G , //AB CD ,FDC FBG ∴∠=∠, 在FDC ∆和FBG ∆中, FDC FBG FD FBDFC BFG ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()FDC FBG ASA ∴∆≅∆ 6BG DC ∴==,CF FG =, 1266AG AB BG ∴=-=-=, CE EA =,CF FG =, ∴EF 是△ACG 的中位线, 132EF AG ∴==, 故答案为:3. 10.如图,在ABC ∆中,8AB =,6AC =,AM 平分BAC ∠,CM AM ⊥于点M ,N 为BC 的中点,连结MN ,则MN 的长为 1 .【分析】延长CM 交AB 于H ,证明AMH AMC ∆≅∆,根据全等三角形的性质得到6AH AC ==,CM MH =,根据三角形中位线定理解答. 【解答】解:延长CM 交AB 于H , 在AMH ∆和AMC ∆中, 90MAH MAC AM AMAMH AMC ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ()AMH AMC ASA ∴∆≅∆6AH AC ∴==,CM MH =, 2BH AB AH ∴=-=, CM MH =,CN BN =, ∴MN 是△BCH 的中位线, 112MN BH ∴==, 故答案为:1. 三.解答题(共3小题)11.如图所示,在ABC ∆中,点D 在BC 上且CD CA =,CF 平分ACB ∠,AE EB =,求证:12EF BD =.【分析】首先根据等腰三角形的性质可得F 是AD 中点,再根据三角形的中位线定理可得12EF BD =.【解答】证明:CD CA =,CF 平分ACB ∠, F ∴是AD 中点, AE EB =, E ∴是AB 中点,EF ∴是ABD ∆的中位线, 12EF BD ∴=. 12.如图:D 、E 是ABC ∆边AB ,AC 的中点,O 是ABC ∆内一动点,F 、G 是OB ,OC 的中点.判断四边形DEGF 的形状,并证明.【分析】根据三角形中位线定理得到12DE BC =,//DE BC ,12FGT BC =,//FG BC ,得到DE FG =,//DE FG ,根据平行四边形的判定定理证明结论. 【解答】解:四边形DEGF 是平行四边形, 理由:D 、E 是ABC ∆边AB ,AC 的中点, ∴DE 是△ABC 的中位线,12DE BC ∴=,//DE BC , F 、G 是OB ,OC 的中点, ∴FG 是△BCO 的中位线,12FG BC ∴=,//FG BC ,DE FG ∴=,//DE FG∴四边形DEGF 是平行四边形.13.已知:如图,在四边形ABCD中,对角线AC、BD相交于O,且AC BD=,E、F分别是AB、CD的中点,E、F分别交BD、AC于点G、H.求证:OG OH=.【分析】取BC边的中点M,连接EM,FM,则根据三角形的中位线定理,即可证得EMF∆是等腰三角形,根据等边对等角,即可证得MEF MFE∠=∠,然后根据平行线的性质证得OGH OHG∠=∠,根据等角对等边即可证得.【解答】解:取BC边的中点M,连接EM,FM,M、F分别是BC、CD的中点,∴MF是△BCD的中位线,//MF BD ∴,12MF BD=,同理://ME AC,12ME AC=,AC BD=ME MF∴=MEF MFE∴∠=∠,//MF BD,MFE OGH∴∠=∠,同理,MEF OHG∠=∠,OGH OHG∴∠=∠OG OH∴=.。
三角形的中位线(专项练习)-2020-2021学年八年级数学下册基础知识专项讲练(华东师大版)
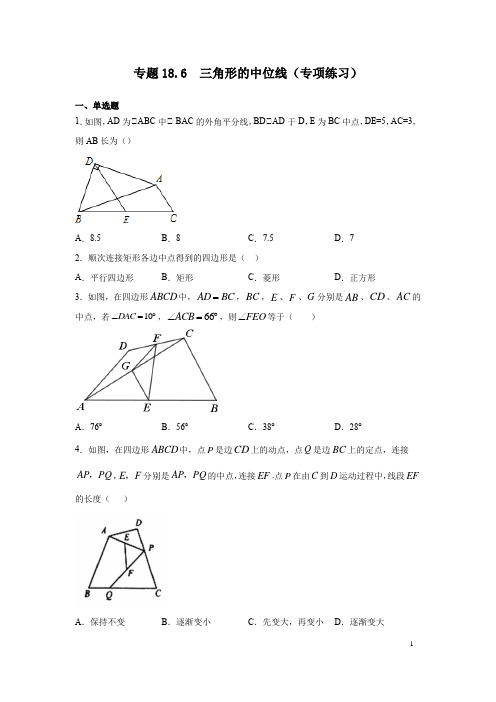
专题18.6 三角形的中位线(专项练习)一、单选题1.如图,AD 为△ABC 中△ BAC 的外角平分线,BD△AD 于D ,E 为BC 中点,DE=5,AC=3,则AB 长为()A .8.5B .8C .7.5D .72.顺次连接矩形各边中点得到的四边形是( )A .平行四边形B .矩形C .菱形D .正方形 3.如图,在四边形ABCD 中,AD BC =,BC ,E 、F 、G 分别是AB 、CD 、AC 的中点,若10DAC ∠=︒,66ACB ∠=︒,则FEO ∠等于( )A .76°B .56°C .38°D .28° 4.如图,在四边形ABCD 中,点P 是边CD 上的动点,点Q 是边BC 上的定点,连接AP PQ ,,EF ,分别是AP PQ ,的中点,连接EF .点P 在由C 到D 运动过程中,线段EF 的长度( )A .保持不变B .逐渐变小C .先变大,再变小D .逐渐变大5.ABC 中,D 、E 分别为AB 、AC 边的中点,若BC=8cm ,则DE 为( ) A .16cm B .8cm C .4cm D .2cm6.在Rt ABC △中,90,13,5ACB AB AC ︒∠===,点D 是AB 上一动点,作//DE AC ,且2DE =,连结,BE CD P Q ,,分别是BE DC 、的中点连结PQ ,则PQ 长为( )A B .C .6 D .6.57.如图,已知△ABC 中,点M 是BC 边上的中点,AN 平分△BAC ,BN△AN 于点N ,若AB =8,MN =2,则AC 的长为( )A .12B .11C .10D .98.如图,将三角形纸片ABC 沿过,AB AC 边中点D 、E 的线段DE 折叠,点A 落在BC 边上的点F 处,下列结论中,一定正确的个数是( )△BDF 是等腰三角形 △12DE BC = △四边形ADFE 是菱形 △2BDF FEC A ∠+∠=∠A .1B .2C .3D .4二、填空题9.如图,在Rt ABC 中,90ACB ∠=︒,30A ∠=︒,点D ,E 分别是AB 和AC 边的中点,若4CD =,则DE =__________.10.如图,,,D E F 分别是ABC ∆各边的中点,AH 是高,,5AB AC ED ≠=,判断AD ________AH (大小),FHC ∆是___________(类别),四边形AEDF 是______________________(类别)11.如图,在Rt △ABC 中,△ACB =90°,点D 、E 、F 分别为AB 、AC 、AD 的中点,若AB =12,则EF 的长为__________.12.如图,CD 是ABC ∆的中线,点E 、F 分别是AC 、DC 的中点,3BD =,则EF =_________.13.如图,在ABC中,AB=AC,AM BC⊥,延长AC到点D,连接BD,取BD的中点N,连接MN.若AB=3,AD=5,则MN=_______________.14.如图,在△ABC中,D是AC边的中点,且BD△AC,ED△BC,ED交AB于点E,若AC=4,BC=6,则△ADE的周长为______.15.如图,△ABC的中位线DE=6cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为_____cm2.16.如图,在ABC中,△ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=13BD,连接DM、DN、MN.若AB=4,则DN=_____.17.如图,在ABC∆中,D、E分别为BC、AC的中点,且ABC的面积为16,则ADE 的面积是______.18.如图,面积为16的菱形ABCD 中,点O 为对角线的交点,点E 是边BC 的中点,过点E 作EF BD ⊥ 于点F ,EG AC ⊥于点G ,则四边形EFOG 的面积为__.19.如图,在菱形ABCD 中,45B ∠=︒,BC =E ,F 分别是边CD ,BC 上的动点,连接AE ,EF ,G ,H 分别为AE ,EF 的中点,连接GH ,则GH 的最小值为________.20.如图,有一块形状为Rt △ABC 的斜板余料,△A =90°,AB =6cm ,AC =8cm ,要把它加工成一个形状为□DEFG 的工件,使GF 在边BC 上,D 、E 两点分别在边AB 、AC 上,若点D 是边AB 的中点,则DEFG 的面积为_________2cm .21.如图,在平行四边形纸片ABCD 中,2cm AB =,将纸片沿对角线AC 对折至CF ,交AD 边于点E ,此时BCF △恰为等边三角形,则图中折叠重合部分的面积是________.22.如图,在ABC 中,点D E 、分别在边AB 、 AC 上,//DE BC ,将ADE 沿直线DE 翻折后与 FDE 重合,DF 、EF 分别与边BC 交于点M 、N ,如果 8DE =,23AD AB =,那么MN 的长是 _____ .23.如图,△ABC 是边长为1的等边三角形,取BC 边中点E ,作ED △AB ,EF △AC ,得到四边形EDAF ,它的周长记作C 1;取BE 中点E 1,作E 1D 1△FB ,E 1F 1△EF ,得到四边形E 1D 1FF 1,它的周长记作C 2.照此规律作下去,则C 2020=__.24.如图,在Rt ABC △中,90A ︒∠=,2AB =,点D 是BC 边的中点,点E 在AC 边上,若45DEC ︒∠=,那么DE 的长是__________.三、解答题25.在正方形ABCD 中,点E 是边CD 的中点,点P 是边AD 上一点(与点A 、D 不重合),射线PE 与BC 的延长线交于点Q .(1)如图,求证:PE QE =;(2)如图,连接PB ,PB PQ =,过点E 作//EF BC 交PB 于点F ,连接AF ,在不添加任何辅助线的情况下,请直接写出与线段AF 相等的所有线段.26.如图,在ABC 中,AB AC =,E ,F 分别是BC ,AC 的中点,连接EF ,以AC 为斜边作直角三角形ADC ,连接DE 、DF .(1)求证:FE FD =.(2)若24CAD CAB ∠=∠=︒,求EDF ∠的度数.27.如图,在△ABC 中,点D ,E 分别是BC ,AC 的中点,延长BA 至点F ,使得AF =12AB ,连接DE ,AD ,EF ,DF .(1)求证:四边形ADEF 是平行四边形;(2)若AB =6,AC =8,BC =10,求EF 的长.28.如图,等边ABC ∆中,D ,E 分别是AB ,AC 的中点,延长BC 到点F ,使12CF BC =,连结DE ,CD ,EF .(1)求证:四边形DCFE 是平行四边形;(2)若等边ABC ∆的边长为6,求EF 的长.29.如图,在ABC 中,D E 、分别是AB AC 、的中点,延长DE 到点,F 使得,EF BE =连接CF .若EC 平分BEF ∠.(1)求证:四边形BCFE 是菱形;(2)若8,120AC BCF =∠=︒,求菱形BCFE 的面积.参考答案1.D【分析】延长BD、CA交于点F,易证△ADF≌△ADB(ASA),则BD=DF,AB=AF,得到点D为BF中点,即DE为△BCF的中位线,再根据已知线段的长度,即可顺利求得AB的长.【详解】解:如图,分别延长BD、AC交于点F,△AD为△ABC中△BAC的外角平分线,△△FAD=△BAD,△BD△AD,△△FDA=△BDA=90°,在△BDA和△FDA中,FAD BAD AD ADFDA BDA ∠=∠⎧⎪=⎨⎪∠=∠⎩,△△BDA≌△FDA(ASA),△AB=AF,BD=FD,即D为BF的中点,△E为BC中点,△DE为△BCF的中位线,△DE=5,AC=3,△CF=2DE=2⨯5=10,△AF=CF-AC=10-3=7.△AB=AF=7.故选D.【点拨】本题考查三角形的综合,涉及的知识点有全等三角形的判定,中位线定理等,难度一般,是中考的常考知识点,正确作出辅助线并证明全等是顺利解题的关键.2.C【分析】根据三角形的中位线定理,得新四边形各边都等于原四边形的对角线的一半,进而可得连接对角线相等的四边形各边中点得到的四边形是菱形.【详解】解:如图,矩形ABCD 中,,AC BD ∴=,,,E F G H 分别为四边的中点,1//,,2EF BD EF BD ∴=1//,,2GH BD GH BD = 1,2FG AC = //,,EF GH EF GH ∴=∴ 四边形ABCD 是平行四边形, 11,,,22AC BD EF BD FG AC === ,EF FG ∴=∴ 四边形EFGH 是菱形.故选C .【点拨】本题主要考查了矩形的性质、菱形的判定,以及三角形中位线定理,关键是掌握三角形的中位线定理及菱形的判定.3.D 【分析】利用EG 、FG 分别是ABC ∆和ADC ∆两个三角形的中位线,求出EG FG =,从而得出FGC ∠和EGC ∠,再根据EG FG =,利用三角形内角和定理即可求出FEG ∠的度数.【详解】解:△E 、F 、G 分别是AB 、CD 、AC 的中点, △EG 、FG 分别是ABC ∆和ADC ∆两个三角形的中位线, △//EG BC ,//FG AD ,且22AD BCEG FG ===, △10FGC DAC ∠=∠=︒,180114EGC ACB ∠=︒-∠=︒, △124EGF FGC EGC ∠=∠+∠=︒, 又△EG FG =, △()()111801801242822FEG EGF ∠=-∠=-︒=︒︒︒. 故本题答案为:D . 【点拨】本题考查了三角形内角和定理,等腰三角形的判定与性质,三角形中位线定理.解决本题的关键是正确理解题意,熟练掌握三角形中位线定理,通过等腰三角形的性质找到相等的角. 4.A 【分析】连接AQ ,则可知EF 为△PAQ 的中位线,可知EF =12AQ ,可知EF 不变. 【详解】 如图,连接AQ ,△E 、F 分别为PA 、PQ 的中点, △EF 为△PAQ 的中位线, △EF =12AQ , △Q 为定点,△AQ 的长不变, △EF 的长不变, 故选:A .【点拨】本题主要考查三角形中位线定理,掌握三角形中位线平行第三边且等于第三边的一半是解题的关键. 5.C 【分析】先画出图形,再根据三角形的中位线定理即可得. 【详解】由题意,画出图形如下:点D 、E 分别为AB 、AC 边的中点,DE ∴是ABC 的中位线, 1184()22DE BC cm ∴==⨯=, 故选:C . 【点拨】本题考查了三角形的中位线定理,熟记三角形的中位线定理是解题关键. 6.A 【分析】由勾股定理得出,取BD 中点F ,连接PF 、QF ,证出PF 是△BDE的中位线,FQ是△BCD的中位线,由三角形中位线定理得出PF△ED,PF=12DE=1,FQ△BC,FQ=12BC=6,证出PF△FQ,再由勾股定理求出PQ即可.【详解】解:△△ACB=90°,AB=13,AC=5,,取BD中点F,连接PF、QF,如图所示:△P、Q分别是BE、DC的中点,△PF是△BDE的中位线,FQ是△BCD的中位线,△PF△ED,PF=12DE=1,FQ△BC,FQ=12BC=6,△DE△AC,AC△BC,△PF△FQ,==故选:A.【点拨】本题考查了三角形中位线定理、勾股定理、平行线的性质;熟练掌握勾股定理,由三角形中位线定理得出PF△ED,FQ△BC是解题的关键.7.A【分析】延长BN交AC于D,证明△ANB△△AND,根据全等三角形的性质、三角形中位线定理计算即可.【详解】解:延长BN交AC于D,在△ANB 和△AND 中,90NAB NAD AN ANANB AND ∠∠⎧⎪⎨⎪∠∠︒⎩====, △△ANB△△AND , △AD=AB=8,BN=ND , △M 是△ABC 的边BC 的中点, △DC=2MN=4, △AC=AD+CD=12, 故选:A . 【点拨】本题考查的是三角形中位线定理,三角形的中位线平行于第三边,并且等于第三边的一半. 8.C 【分析】根据菱形的判定和等腰三角形的判定,采用排除法,逐条分析判断. 【详解】 解:△△DE △BC ,△△ADE =△B ,△EDF =△BFD , 又△△ADE △△FDE ,△△ADE =△EDF ,AD =FD ,AE =CE , △△B =△BFD ,△△BDF 是等腰三角形,故△正确; 同理可证,△CEF 是等腰三角形, △BD =FD =AD ,CE =FE =AE , △DE 是△ABC 的中位线,△DE =12BC ,故△正确; △△B =△BFD ,△C =△CFE ,又△△A +△B +△C =180°,△B +△BFD +△BDF =180°,△C +△CFE +△CEF =180°, △△BDF +△FEC =2△A ,故△正确.而无法证明四边形ADFE 是菱形,故△错误. 所以一定正确的结论个数有3个, 故选:C . 【点拨】本题考查了菱形的判定,中位线定理,等腰三角形的判定和性质,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:△定义;△四边相等;△对角线互相垂直平分.具体选择哪种方法需要根据已知条件来确定. 9.2 【分析】由直角三角形斜边上的中线等于斜边的一半可得出28AB CD ==,又因为30A ∠=︒,所以4BC =,由三角形的中位线定理可得出122DE BC ==. 【详解】解:△CD 是Rt ABC 中斜边上的中线,4CD = △28AB CD ==△90ACB ∠=︒,30A ∠=︒ △4BC =△点D ,E 分别是AB 和AC 边的中点 △122DE BC == 故答案为:2. 【点拨】本题考查的知识点是三角形的中位线定理,由直角三角形斜边上的中线等于斜边的一半可得出28AB CD ==,是解此题的关键. 10.> 等腰三角形 平行四边形 【分析】(1)连接AD 可知,在Rt ADH 中,AH 为直角边,AD 为斜边,可得AH 与AD 大小关系;(2)在Rt AHC 中,11,22HF AC FC AC ==,可得HF FC =,可得FHC 为等腰三角形;(3)根据中位线的性质,可得//,//DE AF AE DF ,可得AEDF 的形状 【详解】(1)连接AD ,在Rt ADH 中,AH 为直角边,AD 为斜边,得AD AH >; 故答案为:>(2)在Rt ADC 中,F 为AC 中点 △11,22HF AC FC AC ==, △HF FC =,△FHC 为等腰三角形; 故答案为:等腰三角形(3)△,,D E F 分别是ABC ∆各边的中点 △//,//DE AF AE DF△四边形AEDF 为平行四边形 故答案为:平行四边形 【点拨】本题考查了直角三角形的边角关系,以及中点的应用,熟知中点的作用是解题的关键. 11.3 【分析】根据直角三角形的性质求出CD ,根据三角形中位线定理计算即可. 【详解】在Rt△ABC中,△ACB=90°,D为AB的中点,△CD12=AB=6△E,F分别为AC,AD的中点,△EF12=CD=3.故答案为:3【点拨】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.12.1.5【分析】先由中线知BD=AD,求出AD,再利用三角形中位线是性质即可解答.【详解】解:△CD是ABC的中线,3BD=△AD=BD= 3△点E、F分别是AC、DC的中点,△EF是ACD的中位线,△EF=12AD=1.5,故答案为:1.5.【点拨】本题考查了三角形的中线和中位线,熟练掌握三角形中位线的性质是解答的关键.13.1【分析】由题意易得BM=MC,则有MN△CD,12MN CD=,进而可求解.【详解】解:AB=AC,AM BC⊥,∴BM=MC,BN=ND,∴MN△CD,12MN CD=,AB=3,AD=5,∴CD=2,∴MN=1;故答案为1.【点拨】本题主要考查等腰三角形的性质及三角形中位线,熟练掌握等腰三角形的性质及三角形中位线是解题的关键.14.8【分析】根据线段垂直平分线的性质得到AB=BC=6,根据三角形中位线定理求出DE,根据直角三角形的性质求出AE,根据三角形的周长公式计算,得到答案.【详解】△D是AC边的中点,BD△AC,△BD是线段AC的垂直平分线,AD12=AC=2,△AB=BC=6,△D是AC边的中点,ED△BC,△点E是AB的中点,DE12=BC=3,在Rt△ADB中,点E是AB的中点,△DE12=AB=3,△△ADE的周长=AE+DE+AD=8,故答案为:8.【点拨】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.15.48【分析】根据对称轴垂直平分对应点连线,可得AF即是△ABC的高,再由中位线的性质求出BC,继而可得△ABC的面积.【详解】解:连接AF,△DE是△ABC的中位线,△DE△BC,BC=2DE=12cm;由折叠的性质可得:AF△DE,△AF△BC,△S△ABC=12BC×AF=12×12×8=48cm2.故答案为:48.【点拨】本题考查了翻折变换的性质及三角形的中位线定理,解答本题的关键是得出AF是△ABC的高.16.2【分析】连接CM,根据直角三角形的性质求出CM,根据三角形中位线定理得到MN=12BC,MN//BC,证明四边形NDCM是平行四边形,根据平行四边形的性质解答.【详解】解:连接CM,△△ACB=90°,M是AB的中点,△CM=12AB=2,△M、N分别是AB、AC的中点,△MN=12BC,MN//BC,△CD=13 BD,△CD=12 BC,△MN=CD,又MN//BC,△四边形NDCM是平行四边形,△DN=CM=2,故答案为:2.【点拨】本题考查直角三角形斜边的中线定理、三角形中位线定理、平行四边形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.17.4【分析】先根据D点是BC的中点,E点是AC的中点,得出S△ADE=14×S△ABC,即可得出答案.【详解】△D点是BC的中点,△S△ABD=S△ADC=12S△ABC,△E点是AC的中点,△S△ADE=S△DCE=12S△ADC=14×S△ABC△S△ABC=16,△S△ADE=4,故答案为:4.【点拨】本题考查了三角形中线的性质,得出S△ADE=14×S△ABC是解题关键.18.2【分析】由菱形的性质得出OA=OC,OB=OD,AC△BD,面积=12AC×BD,证出四边形EFOG是矩形,EF//OC,EG//OB,得出EF、EG都是△OBC的中位线,则EF=12OC=14AC,EG =12OB =14BD ,由矩形面积即可得出答案. 【详解】解:△四边形ABCD 是菱形,△OA =OC ,OB =OD ,AC△BD ,面积=12AC×BD=16, △AC×BD=32△EF△BD 于F ,EG△AC 于G ,△四边形EFOG 是矩形,EF//OC ,EG//OB ,△点E 是线段BC 的中点,△EF 、EG 都是△OBC 的中位线,△EF =12OC =14AC ,EG =12OB =14BD , △矩形EFOG 的面积=EF×EG =14AC×14BD =116×32=2; 故答案为:2.【点拨】本题考查了菱形的性质、矩形的判定与性质、三角形中位线定理等知识;熟练掌握菱形的性质和矩形的性质是解题的关键.19.2【分析】连结AF ,利用中位线的性质GH=12AF ,要使GH 最小,只要AF 最小,由点F 在BC ,当AF△BC 时,AF 最小,利用菱形性质求出AB =45B ∠=︒确定△ABF 为等腰直角三角形,得出AF=BF ,由勾股定理得:22222AB BF AF AF =+=求出AF 即可.【详解】连结AF ,△G ,H 分别为AE ,EF 的中点,△GH△AF ,且GH=12AF , 要使GH 最小,只要AF 最小,由点F 在BC ,当AF△BC 时,AF 最小,在菱形ABCD 中,BC = △AB =在Rt△ABF 中,45B ∠=︒,△△ABF 为等腰直角三角形,△AF=BF ,由勾股定理得:22222AB BF AF AF =+=,△(22=2AF ,△AFGH 最小=12【点拨】本题考查动点图形中的中位线,菱形的性质,等腰直角三角形的性质,勾股定理应用问题,掌握中位线的性质,菱形性质,等腰直角三角形的性质, 点F 在BC 上,AF 最短,点A 到BC 直线的距离最短时由点A 向直线BC 作垂线,垂线段AF 为最短是解题关键. 20.12【分析】作AH BC ⊥交BC 于H 点,交DE 于I 点,根据90,6,8A AB cm AC cm 可得BC 10cm =,根据D 是边AB 的中点可知DE 是ABC 的中位线,得12AIIH AH ,利用三角形面积1122ABC S AC AB BC AH ,可得245AH =,11225IH AH ,则根据DEFG S DE IH ,计算可得结果.【详解】如图示,作AH BC ⊥交BC 于H 点,交DE 于I 点,△90,6,8A AB cm AC cm△BC 10cm =△D 是边AB 的中点,//DE BC ,△DE 是ABC 的中位线,5DE cm = △12AIIH AH , 又△1122ABCS AC AB BC AH , 即有6810AH , △245AH =, △1124122255IHAH , △2125125DEFG S DE IHcm , 故答案为:12.【点拨】本题考查了三角形中位线的应用,勾股定理,三角形的面积和平行四边形的面积,熟悉相关性质定理是解题的关键.中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.212cm【分析】BCF △为等边三角形,点A 为BF 的中点,可得90BAC ∠=︒,求得12ACD S AC CD =,再证明出点E 为AD 的中点,得到12ACE ACD S S =,可求出面积. 【详解】解:ABC 折叠至ACF 处,∴AB=AF=2cm ,BC=BF=CF=4cm ,BCF △为等边三角形,AC BF ∴⊥,90BAC ∠=︒, 又四边形ABCD 为平行四边形,∴//AB CD ,90ACD ∴∠=︒,AC ==,CD=AB=2cm ,12ACD S AC CD ∴==212⨯=2cm , 点A 为BF 的中点,//AE BC ,∴AE 为BCF △的中位线,1122AE BC AD ∴==, ∴点E 为AD 的中点, 12ACE ACD S S ∴==12⨯2cm 为折叠重合部分的面积,2cm .【点拨】本题考查了折叠问题以及等边三角形和平行四边形的综合问题,还涉及勾股定理,需要有一定的推理论证能力,熟练掌握等边三角形和平行四边形的性质是解题的关键.22.4【分析】设3AB a =,从而可得2,a AD a BD ==,先根据平行线的性质可得,ADE B EDM BMD ∠=∠∠=∠,再根据翻折的性质可得,2ADE EDM DF AD a ∠=∠==,从而可得B BMD ∠=∠,然后根据等腰三角形的判定可得DM BD a ==,从而可得FM a =,最后根据三角形的中位线定理即可得.【详解】设3AB a =,则2,BD D a A a A AB D =-==,//DE BC ,,ADE B EDM BMD ∠=∠∠=∠∴,由翻折的性质得:,2ADE EDM DF AD a ∠=∠==,B BMD ∴∠=∠,DM BD a ∴==,FM DF DM a DM ∴=-==,即点M 是DF 的中点,又//DE BC ,MN ∴是FDE 的中位线,118422MN DE ∴==⨯=, 故答案为:4.【点拨】本题考查了翻折的性质、等腰三角形的判定、三角形的中位线定理等知识点,熟练掌握翻折的性质是解题关键.23.201812【分析】先计算出C 1、C 2的长,进而得到规律,最后求出C 2020的长即可.【详解】解:△E 是BC 的中点,ED △AB ,△DE 是△ABC 的中位线,△DE =12AB =12,AD =12AC =12, △EF △AC ,△四边形EDAF 是菱形,△C 1=4×12, 同理C 2=4×12×12=4×212, …C n =4×12n , △20202020201811422C =⨯=. 故答案为:201812.【点拨】本题考查了中位线的性质,菱形的判定与性质,根据题意得到规律是解题关键.24【分析】过D作DF△AC于F,得到AB△DF,求得AF=CF,根据三角形中位线定理得到DF=12 AB=1,根据等腰直角三角形的性质即可得到结论.【详解】解:过D作DF△AC于F,△△DFC=△A=90°,△AB△DF,△点D是BC边的中点,△BD=DC,△AF=CF,△DF=12AB=1,△△DEC=45°,△△DEF是等腰直角三角形,△DE DF,【点拨】本题考查了三角形的中位线定理,平行线的判定和性质,等腰直角三角形的性质,正确的作出辅助线构造等腰直角三角形是解题的关键.25.(1)见解析;(2)BF、PF、PE、QE.【分析】(1)根据正方形的性质及对顶角相等利用ASA即可证明PDE QCE≌,再利用全等三角形的性质即可得证;(2)根据三角形中位线的判定及性质定理、直角三角形斜边上的中线即可得出答案.【详解】(1)证明:如图,△四边形ABCD 是正方形△90D ECQ ∠=∠=︒,△E 是CD 的中点△DE CE =,又△DEP CEQ ∠=∠△()PDE QCE ASA ≌△△△PE QE =(2)如图,BF 、PF 、PE 、QE,//PB PQ EF BC =,PE QE =∴EF 为PBQ △的中位线PF FB PE EQ ∴===,四边形ABCD 为正方形,90BAP ∴∠=︒,∴AF 为BAP Rt △斜边的中线12AF BP BF PF ∴=== ∴与线段AF 相等的所有线段为:BF 、PF 、PE 、QE .【点拨】本题考查了正方形的性质、三角形中位线的判定及性质定理、直角三角形斜边上的中线、全等三角形的判定及性质,熟练掌握性质定理是解题的关键.26.(1)见解析;(2)54︒【分析】(1)根据三角形中位线定理推出12FE AB =,根据直角三角形斜边上的中线等于斜边的一半推出12FD AC =,即可证明FE FD =; (2)根据三角形中位线定理推出24EFC BAC ∠=∠=︒,根据直角三角形斜边上的中线的性质结合三角形的外角性质推出48DFC ∠=︒,利用(1)的结论结合三角形内角和定理即可求得EDF ∠的度数.【详解】(1)△E ,F 分别是BC ,AC 的中点, △12FE AB =, △F 是AC 的中点,90ADC ∠=︒, △12FD AC =, △AB AC =,△FE FD =;(2)△E ,F 分别是BC ,AC 的中点,△//FE AB ,△24EFC BAC ∠=∠=︒,△F 是AC 的中点,90ADC ∠=︒,△FD AF =,△24ADF CAD ︒∠=∠=,△48DFC ∠=︒,△72EFD ∠=︒,△FE FD=,△18072542FED EDF︒-︒∠=∠==︒.【点拨】本题考查了三角形中位线定理,直角三角形斜边上的中线等于斜边一半,平行线的性质,三角形的外角性质等,灵活运用有关定理来分析、判断、推理或解答是解题的关键.27.(1)见解析;(2)EF=5.【分析】(1)利用三角形的中位线的性质与等量代换得出DE=AF,DE△AF,从而得出结论.(2)先利用(1)中的结论得出EF=AD,再利用勾股定理的逆定理,求出△ABC是直角三角形,再利用直角三角形斜边上的中线等于斜边的一半求出。
八年级数学三角形中位线,直角三角形斜边上的中线

三角形中位线、直角三角形斜边上的中线练习题1.如图,为了测量池塘边A、B两地之间的距离,在线段AB的同侧取一点C,连结CA并延长至点D,连结CB并延长至点E,使得A、B分别是CD、CE的中点,若DE=18m,则线段AB的长度是()A.9m B.12m C.8m D.10m2.如图,在△ABC中,点D是BC的中点,点E是AC 的中点,若DE=3,则AB等于()A.4 B.5 C.5.5 D.63.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠EPF=136°,则∠EFP的度数是()A.68°B.34°C.22°D.44°4.如图,在△ABC中,D是AC边的中点,且BD⊥AC,ED∥BC,ED交AB于点E,若AC=4,BC=6,则△ADE的周长为()A.6 B.8 C.10 D.125.如图,在△ABC中,AB=AC,D、E、F分别是边AB、AC、BC的中点,若CE=2,则四边形ADFE的周长为()A.2 B.4 C.6 D.86.△ABC的周长是24cm,则它的三条中位线所围成的三角形的周长是()(自己画图)A.6 cm B.18cm C.12cm D.24cm7.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°,则∠PFE的度数是()A.9°B.18°C.27°D.36°8.如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=4,F为CE的中点,连接DF,则AF的长等于()A.2 B.3 C .D.2第1页(共4页)9.如图,Rt△AMC中,∠C=90°,∠AMC=30°,N,B分别是MC,AC的中点,CN=2cm,则AM的长度为()A.4cm B.8cm C.9cm D.6cm10.如图是一块等腰三角形空地ABC,已知点D,E分别是边AB,AC的中点,量得AC=10米,AB=BC=6米,若用篱笆围成四边形BCED来放养小鸡,则需要篱笆的长是()A.22米B.17米C.14米D.11米11.如图,a∥b,点A在直线a上,点B,C在直线b 上,AC⊥b,如果AB=5cm,BC=3cm,那么平行线a,b之间的距离为()A.5cm B.4cm C.3cm D.不能确定12.如图,AD,CE是△ABC的高,过点A作AF∥BC,则下列线段的长可表示图中两条平行线之间的距离的是()A.AB B.AD C.CE D.AC13.如图,直线a∥b,点A、B分别在直线a、b上,∠1=45°,若点C在直线b上,∠BAC=105°,且直线a和b的距离为3,则线段AC的长度为()A .B .C.3 D.614.到x轴的距离等于2的点组成的图形是()A.过点(0,2)且与x轴平行的直线B.过点(2,0)且与y轴平行的直线C.过点(0,﹣2)且与x轴平行的直线D.分别过(0,2)和(0,﹣2)且与x轴平行的两条直线(自己画图)16.如图,a∥b,下列线段中是a,b之间的距离的是()A.AB B.AE C.EF D.BC第2页(共4页)17.如图,在△ABC中,∠ACB=90°,点D是AB的中点,CD=3,且∠A=30°,则△ABC的周长为()A.6 B.9+3C.6+3D.318.如图,在△ABC中,AB=AC,AD为BC边上的高,点E为AC的中点,连接DE.若△ABC的周长为20,则△CDE的周长为()A.10 B.12 C.14 D.1619.如图,一根竹竿AB,斜靠在竖直的墙上,P是AB 中点,A′B′表示竹竿AB端沿墙上、下滑动过程中的某个位置,则在竹竿AB滑动过程中OP()A.下滑时,OP增大B.上升时,OP减小C.无论怎样滑动,OP不变D.只要滑动,OP就变化20.如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是边BC的中点,ED=3,AD=4,则DC的长是()A.1 B .C.2 D .21.到直角三角形的三个顶点距离相等的点()A.是该三角形三个内角平分线的交点B.是斜边上的中点C.在直角三角形的外部D.在直角三角形的内部22.如果一个直角三角形的两边分别是6,8,那么斜边上的中线长为()(自己画图)A.4 B.5 C.3或5 D.4或523.如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为()A .B .C .D .第3页(共4页)24.如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离()A.不变B.变小C.变大D.无法判断25.如图,公路AC,BC互相垂直,公路AB的中点M 与点C被湿地隔开,若测得BM的长为12km,则M,C两点间的距离为()A.5km B.6km C.9km D.12km26.如图,△ABC中,D为AB的中点,BE⊥AC,垂足为E.若DE=4,AE=6,则BE的长度是()A.10 B .C.8 D .27.在△ABC中,∠B=90°,D是AC的中点,若∠A =20°,则∠BDC的度数为()(自己画图)A.20°B.30°C.40°D.50°第4页(共4页)。
三角形的中位线中考题汇编

4. 三角形的中位线一、 选择题1. (2017·宜昌)如图,要测量被池塘隔开的A ,B 两点的距离.可以在AB 外选一点C ,连接AC ,BC ,并分别找出它们的中点D ,E ,连接ED.现测得AC =30 m ,BC =40 m ,DE =24 m ,则AB 的长为( )A. 50 mB. 48 mC. 45 mD. 35 m第1题 第2题2. (2017·毕节)如图,在Rt △ABC 中,∠ACB =90°,斜边AB =9,D 为AB 的中点,F 为CD 上一点,且CF =13CD ,过点B 作BE ∥DC 交AF 的延长线于点E ,则BE 的长为( )A. 6B. 4C. 7D. 123. (2017·西宁)如图,O 是矩形ABCD 的对角线AC 的中点,OM ∥AB 交AD 于点M.若OM =3,BC =10,则OB 的长为( )A. 5B. 4C.342D. 34 第3题第4题4. (2017·遵义)如图,△ABC 的面积是12,点D ,E ,F ,G 分别是BC ,AD ,BE ,CE 的中点,则△AFG 的面积是( )A. 4.5B. 5C. 5.5D. 65. (2017·株洲)如图,点E ,F ,G ,H 分别为四边形ABCD 的边AB ,BC ,CD ,DA 的中点,则关于四边形EFGH ,下列说法正确的为( )A. 一定不是平行四边形B. 一定不是中心对称图形C. 可能是轴对称图形D. 当AC =BD 时,它是矩形第5题 第6题6. (2017·江西)如图,在任意四边形ABCD 中,E ,F ,G ,H 分别是边AB ,BC ,CD ,DA 上的点,对于四边形EFGH 的形状,某班的学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )A. 当E ,F ,G ,H 是各边的中点,且AC =BD 时,四边形EFGH 为菱形B. 当E ,F ,G ,H 是各边的中点,且AC ⊥BD 时,四边形EFGH 为矩形C. 当E ,F ,G ,H 不是各边的中点时,四边形EFGH 可以为平行四边形D. 当E ,F ,G ,H 不是各边的中点时,四边形EFGH 不可能为菱形7. (导学号11744102)(2017·营口)如图,在△ABC 中,AB =AC ,E ,F 分别是BC ,AC 的中点,以AC 为斜边作 Rt △ADC ,若∠CAD =∠CAB =45°,则下列结论不正确的是( )第7题A. ∠ECD =112.5°B. DE 平分∠FDCC. ∠DEC =30°D. AB =2CD 二、 填空题8. (1) (2017·南通)如图①,DE 是△ABC 的中位线,BC =8,则DE =________;(2) (2017·徐州)在△ABC 中,D ,E 分别是AB ,AC 的中点,DE =7,则BC =________;(3) (2017·河北)如图②,A ,B 两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C ,连接CA ,CB ,分别延长到点M ,N ,使AM =AC ,BN =BC ,测得MN =200 m ,则A ,B 间的距离为________m.第8题9. (2017·淮安)如图,在Rt △ABC 中,∠ACB =90°,D ,E 分别是AB ,AC 的中点,F 是AD 的中点.若AB =8,则EF =________.第9题第10题10. (2017·宿迁)如图,在△ABC 中,∠ACB =90°,D ,E ,F 分别是AB ,BC ,CA 的中点.若CD =2,则线段EF 的长是________.11. (2017·宁夏)如图,在△ABC 中,AB =6,D 是AB的中点,过点D 作DE ∥BC ,交AC 于点E ,点M 在DE 上,且ME =13DM.当AM ⊥BM 时,BC 的长为________.第11题第12题12. (2017·怀化)如图,在▱ABCD 中,对角线AC ,BD 相交于点O ,E 是AB 的中点,OE =5 cm ,则AD 的长是________cm.13. (2017·天津)如图,正方形ABCD 和正方形EFCG 的边长分别为3和1,点F ,G 分别在边BC ,CD 上,P 为AE 的中点,连接PG ,则PG 的长为________.第13题第14题14. (2017·广安)如图,在Rt △ABC 中,∠C =90°,BC =6,AC =8,D ,E 分别为AC ,AB 的中点,连接DE ,则△ADE 的面积是________.15. (2017·绥化)如图,顺次连接腰长为2的等腰直角三角形各边的中点得到第1个小三角形,再顺次连接所得的小三角形各边的中点得到第2个小三角形,如此操作下去,则第n 个小三角形的面积为________.第15题三、 解答题16. (2017·贵阳)如图,在△ABC 中,∠ACB =90°,D ,E 分别是边BC ,AB 的中点,连接DE 并延长至点F ,使EF =2DE ,连接CE ,AF.(1) 求证:AF =CE ;(2) 当∠B =30°时,试判断四边形ACEF 的形状并说明理由.第16题17. (导学号11744103)(2017·南通)如图,在矩形ABCD 中,E 是AD 上一点,PQ 垂直平分BE ,分别交AD ,BE ,BC 于点P ,O ,Q ,连接BP ,EQ.(1) 求证:四边形BPEQ 是菱形;(2) 若AB =6,F 为AB 的中点,OF +OB =9,求PQ 的长.第17题18. (2017·呼和浩特)如图,在等腰三角形ABC 中,BD ,CE 分别是两腰上的中线.(1) 求证:BD =CE ;(2) 设BD 与CE 相交于点O ,M ,N 分别为线段BO 和CO 的中点,当△ABC 的重心到顶点A 的距离与底边长相等时,判断四边形DEMN 的形状,并说明理由.第18题4. 三角形的中位线一、 1. B 2. A 3. D 4. A 5. C 6. D 7. C 二、 8. (1) 4 (2) 14 (3) 100 9. 2 10. 2 11. 8 12. 10 13. 5 14. 6 15.122n -1三、 16. (1) ∵ D ,E 分别是边BC ,AB 的中点,∴ DE ∥AC ,DE =12 AC.又∵ EF =2DE ,即DE =12EF ,∴ EF =AC.∴ 四边形ACEF 是平行四边形.∴ AF =CE (2) 当∠B =30°时,四边形ACEF 是菱形 理由:∵ ∠ACB =90°,∠B =30°,∴ ∠BAC =60°,AC =12AB =AE.∴ △AEC 是等边三角形.∴AC =CE.又∵ 四边形ACEF 是平行四边形,∴ 四边形ACEF 是菱形.17. (1) ∵ PQ 垂直平分BE ,∴ QB =QE ,OB =OE.∵ 四边形ABCD 是矩形,∴ AD ∥BC.∴ ∠QBO =∠PEO.在△BOQ 与△EOP 中,⎩⎪⎨⎪⎧∠QBO =∠PEO ,OB =OE ,∠BOQ =∠EOP ,∴ △BOQ ≌△EOP.∴ PE =QB.又∵ AD ∥BC ,即PE ∥QB ,∴ 四边形BPEQ 是平行四边形.∵ QB =QE ,∴ 平行四边形BPEQ 是菱形(2) ∵ △BOQ ≌△EOP ,∴ OB =OE.∴ BE =2OB.∵ F 为AB 的中点,∴ BF =FA.∴ OF 为△BAE 的中位线.∴ AE =2OF.∵ OF +OB =9,∴ AE +BE =2OF +2OB =18.设AE =x ,则BE =18-x.∵ 四边形ABCD 是矩形,∴ ∠BAE =90°.∴ 在Rt △ABE 中,62+x 2=(18-x)2,解得x =8.∴ AE =8,BE =18-x =10.∴ OB =12BE =5.设PE =y ,则AP =8-y.∵ 四边形BPEQ 是菱形,∴ BP =PE =y ,PQ =2PO.在Rt △ABP 中,由62+(8-y)2=y 2,得y =254,即BP =254.∴ 在Rt △BOP中,PO =BP 2-OB 2=154.∴ PQ =15218. (1) 由题意,得AB =AC.∵ BD ,CE 分别是两腰上的中线,∴ AD =12AC ,AE =12AB.∴ AD =AE.在△ABD 和△ACE中,⎩⎪⎨⎪⎧AB =AC ,∠A =∠A ,AD =AE ,∴ △ABD ≌△ACE.∴ BD =CE(2) 四边形DEMN 是正方形 理由:如图,∵ E ,D 分别是AB ,AC 的中点,∴ ED 是△ABC 的中位线.∴ ED ∥BC ,ED =12BC.∵ M ,N 分别为线段BO 和CO 中点,∴ BM =OM ,CN =ON ,MN 是△OBC 的中位线.∴ MN ∥BC ,MN =12BC.∴ ED∥MN ,ED =MN.∴ 四边形DEMN 是平行四边形.∴ OD =OM ,OE =ON.∴ OD =OM =BM ,OE =ON =CN.由(1)知BD =CE ,∴ DM =EN.∴ ▱DEMN 是矩形.∵ BD ,CE 分别是AC ,AB 上的中线,∴ 点O 是△ABC 的重心.连接OA ,则OA =BC.∵ 在△AOC 中,N ,D 分别是OC ,AC 的中点,∴ DN 是△AOC 的中位线.∴ DN =12OA.∴ MN =DN.∴ 矩形DEMN 是正方形.第18题。
专题 直角三角形斜边上的中线的运用(原卷版)

八年级下册数学《第十八章 平行四边形》专题 直角三角形斜边上的中线的运用【例题1】(2022春•镇江期末)如图,在Rt △ABC 中,∠ACB =90°,点D ,E ,F 分别为AB ,AC ,BC 的中点.若CD =5,则EF 的长为 .【变式1-1】如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,E是AC的中点.若DE=3,则AB的长为 .【变式1-2】(2022秋•海口期末)如图,在△ABC中,AD平分∠BAC,BD⊥AD于点D,过点D作DE ∥AC,交AB于点E,若AB=6,则DE的长为( )A.2.5B.3C.3.5D.4【变式1-3】如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=5,则CD=( )A.2B.3C.4D.【变式1-4】如图,在△ABC中,D是BC上一点,AB=AD,E、F分别是AC、BD的中点,EF=2,则AC的长是( )A .3B .4C .5D .6【变式1-5】(2022秋•工业园区校级期中)如图∠ADB =∠ACB =90°,E 、F 分别是AB 、CD 的中点,若AB =26,CD =24,则△DEF 的周长为( )A .12B .30C .27D .32【变式1-6】(2022春•南岗区校级期中)如图,△ABC 中,∠ACB =90°,D 是AB 的中点,过点D 作AB 的垂线,交BC 于E ,连接CD ,AE ,CD =4,AE =5,则AC =( )A .3B .245C .5D .247【变式1-7】(2021•饶平县校级模拟)如图,在三角形ABC 中,AB =AC ,BC =6,三角形DEF 的周长是7,AF ⊥BC 于F ,BE ⊥AC 于E ,且点D 是AB 的中点,则AF =( )A B C D .7【变式1-8】如图,在△ABC 中,CF ⊥AB 于F ,BE ⊥AC 于E ,M 为BC 的中点,EF =7,BC =10,则△EFM 的周长是( )A .17B .21C .24D .27【例题2】(2022秋•莲湖区期中)如图所示,在Rt △ABC 中,∠ACB =90°,∠A =62°,CD ⊥AB ,垂足为D ,点E 是BC 的中点,连接ED ,则∠EDB 的度数是 .【变式2-1】如图,在Rt △ABC 中,∠BAC =90°,AD 是BC 边上的中线,ED ⊥BC 于D ,交BA 延长线于点E ,若∠E =35°,则∠BDA 的度数是.【变式2-2】(2022秋•仓山区校级期末)如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD,若∠BAD=52°,则∠EBD= °.【变式2-3】(2022•碑林区校级模拟)如图,△ABC中,CD⊥AB,垂足为D,E为BC边的中点,AB=4,AC=2,DE=ACD=( )A.15°B.30°C.22.5°D.45°【变式2-4】(2021秋•潍坊期末)如图,四边形ABCD中,∠ADC=∠ABC=90°,E为对角线AC的中点,∠DAC=30°,∠CAB=40°,连结BE,DE,BD,则∠BDE= 度.【变式2-5】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,∠ECD是 度.【变式2-6】(2021秋•温州期中)如图,在△ABC中,∠ACB=90°,∠CAB=30°.以AB长为一边作△ABD,且AD=BD,∠ADB=90°,取AB中点E,连DE、CE、CD.则∠EDC= °.【变式2-7】如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,点G,H分别是AC,BD的中点,若∠BEC=80°,那么∠GHE等于( )A.5°B.10°C.20°D.30°【变式2-8】(2022秋•市中区校级月考)如图,已知△ABC中,∠ACB=90°,O为AB的中点,点E 在BC上,且CE=AC,∠BAE=15°,求∠COE的度数.【例题3】如图,在四边形ABCD 中,∠ABC =∠ADC =90°,M 、N 分别是AC 、BD 的中点,试说明:(1)MD =MB ;(2)MN ⊥BD .【变式3-1】(2022春•零陵区校级期中)如图,△ABC 中,BE 平分∠ABC ,BE ⊥AF 于F ,D 为AB 中点,请说明DF ∥BC 的理由.【变式3-2】(2021秋•虹口区校级期末)如图,已知△ABC 的高BD 、CE 相交于点O ,M 、N 分别是BC 、AO 的中点,求证:MN 垂直平分DE.【变式3-3】如图,△ABC中,AD是边BC上的高,CF是边AB上的中线,DC=BF,点E是CF的中点.(1)求证:DE⊥CF;(2)求证:∠B=2∠BCF.【变式3-4】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD中点,过A作AF∥BC交BE的延长线于点F,连接CF.(1)求证:AD=AF;(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.【变式3-5】在Rt△ABC中,∠ABC=90°,BD为∠ABC的角平分线,F为AC的中点,AE∥BC交BD 的延长线于点E,其中∠FBC=2∠FBD.(1)求∠EDC的度数.(2)求证:BF=AE.【变式3-6】已知,如图,在Rt△ABC中,∠C=90°,点E在AC上,AB=12DE,AD∥BC.求证:∠CBA=3∠CBE.【变式3-7】如图,已知四边形ABCD中,∠ABC=∠ADC=90°,点E是AC中点,点F是BD中点.(1)求证:EF⊥BD;(2)过点D作DH⊥AC于H点,如果BD平分∠HDE,求证:BA=BC.【变式3-8】(2021•安顺模拟)如图,在△ABC中,点D在AB上,且CD=CB,E为BD的中点,F为AC的中点,连接EF交CD于点M,连接AM.(1)求证:EF=12 AC;(2)若EF⊥AC,求证:AM+DM=CB.【变式3-9】(2022秋•宿城区期中)如图,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.(1)求证:MN⊥DE.(2)连接DM,ME,猜想∠A与∠DME之间的关系,并证明你的猜想.(3)当∠BAC变为钝角时,如图②,上述(1)(2)中的结论是否都成立?若成立,直接回答,不需证明;若不成立,请说明理由.且AF⊥CF,若AC=3,BC=6,则DF的长为( )A.1.5B.1C.0.5D.2【变式4-1】(2022春•南岗区校级期中)如图,在△ABC中,D,E分别是AB,AC的中点,连接ED,F 是ED延长线上一点,连接AF、CF,若∠AFC=90°,DF=1,AC=6,则BC的长度为( )A.2B.3C.4D.5【变式4-2】(2022•金乡县三模)如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E、F分别是AB、AC边的中点,若AB=8,AC=6,则△DEF的周长为 .【变式4-3】如图,△ABC的周长为16,G、H分别为AB、AC的中点,分别以AB、AC为斜边向外作Rt △ADB和Rt△AEC,连接DG、GH、EH,则DG+GH+EH的值为( )A.6B.7C.8D.9【变式4-4】(2022春•大足区期末)如图,在Rt△ABC中∠ACB=90°,∠A=30°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=12BC,若EF=2,则DE的长为( )A.2B.1C D+1【变式4-5】(2021春•赣榆区期中)如图,在△ABC中,E、F分别是AB、AC的中点,延长EF交△ABC 的外角∠ACD的平分线于点G.AG与CG有怎样的位置关系?证明你的结论.【变式4-6】(2022春•海淀区校级期中)如图,在△ABC中,点D,点E分别是边AC,AB的中点,点F在线段DE上,AF=5,BF=12,AB=13,BC=19,求DF的长度.【变式4-7】(2022春•徐州期中)已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.(1)求证:DH=EF;(2)求证:∠DHF=∠DEF.【变式4-8】(2021春•罗湖区校级期末)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.(1)求证:BM=MN;(2)若∠BAD=60°,AC平分∠BAD,AC=2,写出求BN长的思路.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形中位线和直角三角形斜边上的中线练习题
一.选择题
1.如图,在Rt△ABC中,∠ACB=90°,CD、CM分别是斜边上的高和中线,那么下列结论中错误的是()
4.如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=4,AO=3,则四边形DEFG 的周长为()
6.如图,在矩形ABCD中,P、R分别是BC和DC上的点,E、F分别是AP和RP的中点,当点P在BC上从点B 向点C移动,而点R不动时,下列结论正确的是()
7.如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为()
的度数是()
9.直角三角形两条直角边长分别是6和8,则连接两条直角边中点的线段长是()
11.如图,平行四边形ABCD的周长为16cm,AC与BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为()
D
形EFCD的周长是()
15.在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可能是()
19.如图,平行四边形ABCD的对角线AC、BD相交于点O,下列结论正确的是()
那么四边形BCFE的周长为()
21.如图平行四边形ABCD中,AE⊥BC,AF⊥CD,∠EAF=45°,且,则平行四边形ABCD的周长是()
2
时,MN∥BC;③BN=2AN;④AN:AB=AM:AC,一定正确的有()
面积是()
26
24.在矩形ABCG中,点D是AG的中点,点E是AB上一点,且BE=BC,DE⊥DC,CE交BD于F,下列结论:
①BD平分∠CDE;②2AB+EF=4AD;③(﹣1)CD=DE;④CF:AE=(+1):1.
其中正确的是()
25.如图,在矩形ABCD中,AB=2BC,E为CD上一点,且AE=AB,M为AE的中点.下列结论:①DM=DA;②EB 平分∠AEC;③S△ABE=S△ADE;④=8﹣4.正确的个数是()
二.解答题
26.如图,在△ABC中,∠A、∠B、∠C的度数之比为1:2:3,AB边上的中线DC=4,求△ABC的面积.
27.已知在△ABC中,∠C=90°,D为AB上的中点,连接C、D,求证:AD=CD=BD.
28.如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE
(1)若AC=10,BD=8,求△BDE的周长;
(2)判断△BDE的形状,并说明理由.
29.已知∠ABC=∠ACD=90°,M、N分别是AC、BD的中点.若AC=10,BD=8,求MN的长.
30.已知:如图,BD、CE是△ABC的两条高,M是BC的中点.求证:ME=MD.
参考答案
一.选择题
1.D 2.A 3.B 4.B 5.B 6.C 7.C 8.D 9.D 10.D 11.C 12.B 13.C 14.A 15.D 16.C 17.B 18.C 19.A 20.C 21.D 22.C 23.D 24.C 25.C。
