内插法计算公式
内插法计算公式

内插法计算公式内插法计算公式1、X1、Y1为《建设工程监理与相关服务收费标准》附表二中计费额的区段值;Y1、Y2为对应于X1、X2的收费基价;X为某区段间的插入值道;Y为对应于X由插入法计算而得的收费基价。
2、计费额小于500万元的,以计费额乘以3.3%的收费专率计算收费基价;3、计费额大于1,000,000万元的,以计费额乘以1.039%的收费率计算收费基价。
【例】若计算得计费额为600万元,计算其收费基价属。
根据《建设工程监理与相关服务收费标准》附表二:施工监理服务收费基价表,计费额处于区段值500万元(收费基价为16.5万元)与1000万元(收费基价为30.1万元)之间,则对应于600万元计费额的收费基价:内插法(Interpolation Method)什么是内插法在通过找到满足租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值等于租赁资产的公平价值的折现率,即租赁利率的方法中,内插法是在逐步法的基础上,找到两个接近准确答案的利率值,利用函数的连续性原理,通过假设关于租赁利率的租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值与租赁资产的公平价值之差的函数为线性函数,求得在函数值为零时的折现率,就是租赁利率。
内插法原理数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
内插法的具体方法求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
以每期租金先付为例,函数如下:A表示租赁开始日租赁资产的公平价值;R表示每期租金数额;S表示租赁资产估计残值;n表示租期;r表示折现率。
内插法计算公式

附件:
收费基价直线内插法计算公式
)
(1121
21X X X X Y Y Y Y -⨯--+
=
说明:
1、X 1、Y 1为《建设工程监理与相关服务收费标准》附表二中计费额的区段值;Y 1、Y 2为对应于X 1、X 2的收费基价;X 为某区段间的插入值;Y 为对应于X 由插入法计算而得的收费基价。
2、计费额小于500万元的,以计费额乘以3.3%的收费率计算收费基价;
3、计费额大于1,000,000万元的,以计费额乘以1.039%的收费率计算收费基价。
【例】若计算得计费额为600万元,计算其收费基价。
根据《建设工程监理与相关服务收费标准》附表二:施工监理服务收费基价表,计费额处于区段值500万元(收费基价为16.5万元)与1000万元(收费基价为30.1万元)之间,则对应于600万元计费额的收费基价:
万元)
(22.19)500600(500
10005
.161.305.16=-⨯--+=Y
Y (收费基价) Y 2 Y Y 1
12 X (计费额)
附表二
施工监理服务收费基价表
注:计费额大于1000000万元的,以计费额乘以1.039%的收费率计算收费基价。
其他未包含的其收费由双方协商议定。
线性内插法计算公式

线性内插法计算公式
线性内插是假设在二个已知数据中的变化为线性关系,因此可由已知二点的坐标(a, b)去计算通过这二点的斜线。
其中a 函数值。
举个例子,已知x=1时y=3,x=3时y=9,那么x=2时用线性插值得到y就是3和9的算术平均数6。
写成公式就是:Y=Y1+(Y2-Y1)×(X-X1)/(X2-X1)
通俗地讲,线性内插法就是利用相似三角形的原理,来计算内插点的数据。
线性内插法
内插法又称插值法。
根据未知函数f(x)在某区间内若干点的函数值,作出在该若干点的函数值与f (x)值相等的特定函数来近似原函数f(x),进而可用此特定函数算出该区间内其他各点的原函数f(x)的近似值,这种方法,称为内插法。
按特定函数的性质分,有线性内插、非线性内插等;按引数(自变量)个数分,有单内插、双内插和三内插等。
线性内插法的基本计算过程是根据一组已知的未知函数自变量的值和它相对应的函数值,利用等比关系去求一种求未知函数其他值的近似计算方法,是一种求位置函数逼近数值的求解方法。
内插法计算公式
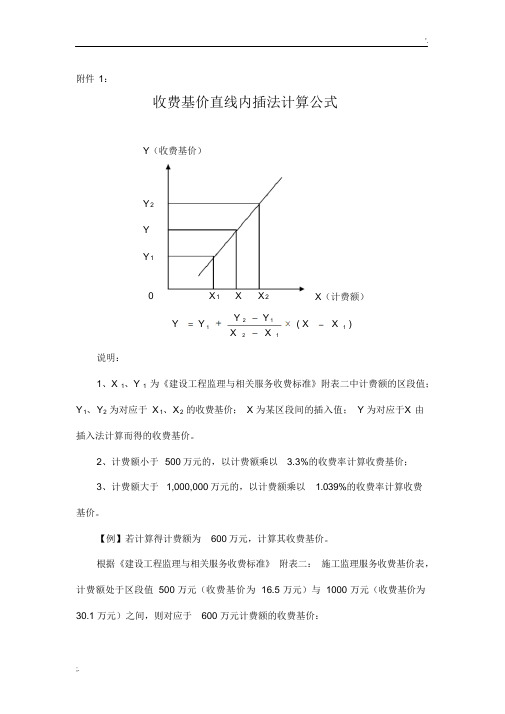
说明:
1、X 1、Y 1 为《建设工程监理与相关服务收费标准》附表二中计费额的区段值;
Y 1、Y 2 为对应于 X 1、X 2 的收费基价; X 为某区段间的插入值; Y 为对应于X 由插入法计算而得的收费基价。
2、计费额小于 500 万元的,以计费额乘以 3.3%的收费率计算收费基价;
3、计费额大于 1,000,000 万元的,以计费额乘以 1.039%的收费率计算收费
基价。
【例】若计算得计费额为 600 万元,计算其收费基价。
根据《建设工程监理与相关服务收费标准》 附表二: 施工监理服务收费基价表,计费额处于区段值 500 万元(收费基价为 16.5 万元)与 1000 万元(收费基价为 30.1 万元)之间,则对应于 600 万元计费额的收费基价:
附件 1:
收费基价直线内插法计算公式
Y (收费基价)
Y 2
Y
Y 1
X 1 X X 2 X (计费额) Y
Y Y 2 Y 1 1 X ( X X ) 1 2 X 1
30.1 16.5 1000 (600 500) 19.22(万元)
500
Y 16.5。
内插法计算公式
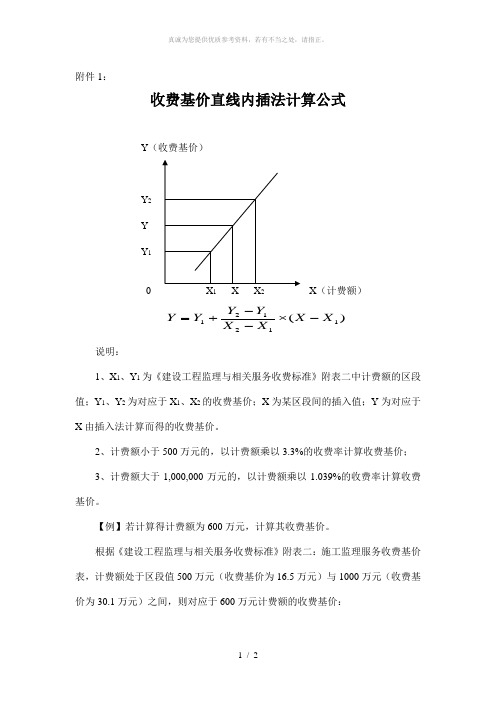
附件1:
收费基价直线内插法计算公式
)(112121X X X X Y Y Y Y -⨯--+
=
说明: 1、X 1、Y 1为《建设工程监理与相关服务收费标准》附表二中计费额的区段值;Y 1、Y 2为对应于X 1、X 2的收费基价;X 为某区段间的插入值;Y 为对应于X 由插入法计算而得的收费基价。
2、计费额小于500万元的,以计费额乘以3.3%的收费率计算收费基价;
3、计费额大于1,000,000万元的,以计费额乘以1.039%的收费率计算收费基价。
【例】若计算得计费额为600万元,计算其收费基价。
根据《建设工程监理与相关服务收费标准》附表二:施工监理服务收费基价表,计费额处于区段值500万元(收费基价为16.5万元)与1000万元(收费基价为30.1万元)之间,则对应于600万元计费额的收费基价:
Y (收费基价) Y 2 Y Y 1 0
12 X (计费额)
万元)(22.19)500600(500
10005.161.305.16=-⨯--+=Y。
内插法的计算公式

内插法(Interpolation Method)什么是内插法在通过找到满足租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值等于租赁资产的公平价值的折现率,即租赁利率的方法中,内插法是在逐步法的基础上,找到两个接近准确答案的利率值,利用函数的连续性原理,通过假设关于租赁利率的租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值与租赁资产的公平价值之差的函数为线性函数,求得在函数值为零时的折现率,就是租赁利率。
内插法原理数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
内插法的具体方法求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
以每期租金先付为例,函数如下:A表示租赁开始日租赁资产的公平价值;R表示每期租金数额;S表示租赁资产估计残值;n表示租期;r表示折现率。
通过简单的试错,找出二个满足上函数的点(a1,b1)(a2,b2),然后,利用对函数线性的假设,通过以下比例式求出租赁利率:内插法应用举例内插法在财务管理中应用很广泛,如在货币时间价值的计算中,求利率i,求年限n;在债券估价中,求债券的到期收益率;在项目投资决策指标中,求内含报酬率。
中级和CPA教材中都没有给出内插法的原理,很多同学都不太理解是怎么一回事。
下面我们结合实例来讲讲内插法在财务管理中的应用。
一、在内含报酬率中的计算内插法在内含报酬率的计算中应用较多。
内含报酬率是使投资项目的净现值等于零时的折现率,通过内含报酬率的计算,可以判断该项目是否可行,如果计算出来的内含报酬率高于必要报酬率,则方案可行;如果计算出来的内含报酬率小于必要报酬率,则方案不可行。
内插法计算公式-内插法公式

内插法计算公式-内插法公式内插法计算公式内插法公式在数学和统计学中,内插法是一种非常有用的工具,用于在已知数据点之间估计未知值。
内插法公式的应用广泛,涉及到金融、工程、科学等多个领域。
接下来,让我们深入了解一下内插法计算公式。
内插法的基本思想是假设在两个已知数据点之间存在线性关系。
也就是说,如果我们知道两个点的坐标(x1, y1)和(x2, y2),那么对于位于 x1 和 x2 之间的某个 x 值,我们可以通过线性关系来估计对应的 y 值。
内插法公式可以表示为:y = y1 +((x x1) (y2 y1))/(x2 x1)在这个公式中,x 是我们要估计 y 值的那个点的横坐标,y 是我们要估计的纵坐标。
x1 和 y1 是已知的第一个数据点的坐标,x2 和 y2 是已知的第二个数据点的坐标。
为了更好地理解这个公式,让我们通过一个具体的例子来进行说明。
假设我们有以下两个数据点:(2, 5) 和(4, 9),现在我们想要估计 x= 3 时的 y 值。
首先,我们确定 x1 = 2,y1 = 5,x2 = 4,y2 = 9。
然后,将这些值代入内插法公式:y = 5 +((3 2) (9 5))/(4 2)y = 5 +(1 4) / 2y = 5 + 2y = 7所以,当 x = 3 时,估计的 y 值为 7。
内插法不仅可以用于两个数据点之间的线性估计,还可以扩展到多个数据点的情况。
例如,在某些情况下,我们可能有一系列的数据点(x1, y1),(x2, y2),(x3, y3)等等。
如果这些数据点呈现出一定的规律,比如近似的线性关系,我们可以使用分段内插法来进行估计。
分段内插法就是将数据区间分成若干个小段,在每个小段内使用两个相邻的数据点进行内插计算。
这样可以提高估计的准确性,特别是当数据的变化趋势不是完全线性的时候。
内插法在金融领域有着重要的应用。
比如,在计算债券的收益率、股票的估值等方面,常常需要根据已知的市场数据进行内插估计。
热电偶内插法计算公式

热电偶内插法计算公式
热电偶内插法是一种通过测量热电偶被插入物体中的温度来测量物体表面温度的方法。
它使用一对热电偶,一个安装在物体表面,另一个安装在物体内部。
热电偶内插法可以用来测量蒸汽、热水、液体等物体的表面温度。
热电偶内插法的计算公式是:T表面=T内部+[(R1/(R1+R2))*(T表面-T内部)],其中T表面是物体表面的温度,T内部是物体内部的温度,R1是热电偶1的电阻,R2是热电偶2的电阻。
热电偶内插法有许多优点,首先,它可以实现精确的温度测量,因为它可以准确测量物体表面和内部的温度。
其次,它可以有效地测量热水、蒸汽等较高温度的物体表面温度,因为它可以将温度测量范围扩展到超出一般温度范围的温度。
最后,它可以用于各种材料,因为可以使用各种热电偶,根据不同的物质而变化。
热电偶内插法是一种非常有用的技术,可以准确测量物体表面的温度,也可以用于不同的材料。
然而,它也有一些缺点,例如,它需要插入到物体内部,安装起来可能会比较麻烦,而且安装不当可能会影响测量结果。
此外,由于它需要使用两个热电偶,因此成本也会比较高。
总之,热电偶内插法是一种有效的温度测量方法,可以准确测量各
种物体表面的温度,但它也有一些缺点,需要注意。
财务管理内插法计算公式

财务管理内插法计算公式财务管理是企业管理的重要组成部分,它涉及到企业的资金运作、投资决策、财务分析等方面。
在财务管理中,计算是一个必不可少的环节,而内插法是一种常用的计算方法。
本文将介绍内插法的基本概念、计算公式及其应用。
一、内插法的概念内插法(Interpolation)是指在已知的数据点之间通过某种方法推算出一个或多个新的数据点的过程。
内插法常用于寻找两个已知数据点之间的中间值。
内插法可以用于计算金融和财务中的各种指标,如收益率、成本、折现率等。
二、内插法的计算公式内插法的计算公式有很多种,下面介绍两种常用的方法。
1. 线性内插法线性内插法是指在两个已知数据点之间,通过一条直线来推算出中间值。
假设已知两个数据点(x1,y1)和(x2,y2),需要推算出中间点(x,y),则可以使用以下公式:y = y1 + (x - x1) * (y2 - y1) / (x2 - x1)其中,x为要求的中间点的横坐标。
2. 折现率内插法折现率内插法是指在两个已知的折现率之间,通过一条直线来推算出中间的折现率。
假设已知两个折现率(p1,f1)和(p2,f2),需要推算出中间折现率(p,f),则可以使用以下公式:f = f1 + (p - p1) * (f2 - f1) / (p2 - p1)其中,p为要求的中间折现率。
三、内插法的应用内插法在财务管理中有广泛的应用。
下面列举一些常见的应用场景。
1. 计算成本在企业管理中,成本是一个重要的指标。
在计算成本时,有时会遇到需要推算出两个已知成本之间的中间值的情况。
此时可以使用内插法来计算。
2. 计算收益率收益率是一个重要的投资指标,用于评估投资的回报率。
在计算收益率时,有时需要通过已知的两个收益率来推算出中间的收益率,此时也可以使用内插法。
3. 计算折现率折现率是用于计算未来现金流的现值的重要指标。
在计算折现率时,有时需要通过已知的两个折现率来推算出中间的折现率,此时也可以使用内插法。
内插法的计算公式

内插法的计算公式内插法(Interpolation)是数值分析中常用的一种数值逼近方法,它通过已知数据点的函数值来估计在其它位置上的函数值。
在给定已知点的坐标和函数值的情况下,内插法用一个多项式来逼近这些已知点,并且认为这个多项式逼近函数在这些点上的函数值与实际函数值相等。
以下是几种常见的内插方法及其计算公式:1. 线性插值(Linear Interpolation)线性插值方法是用一条直线来逼近已知点,以估计其他位置上的函数值。
设已知点为(x₀,y₀)和(x₁,y₁),要估计在介于这两点之间的位置(x,y)的函数值,线性插值公式如下:y=y₀+(y₁-y₀)*(x-x₀)/(x₁-x₀)2. 拉格朗日插值(Lagrange Interpolation)拉格朗日插值方法使用拉格朗日多项式来逼近已知点,并以此估计其他位置上的函数值。
给定已知的n个点和函数值(x₀,y₀),(x₁,y₁),...,(xₙ,yₙ),拉格朗日插值公式如下:L(x) = Σ(yₙ * ℒₙ(x)), j=0 to n其中,ℒₙ(x) = Π((x - xₙ) / (xₙ - xₙ)), k ≠ j, k=0 to n 在这个公式中,ℒₙ(x)称为拉格朗日插值基函数,L(x)为拉格朗日插值多项式。
3. 牛顿插值(Newton Interpolation)牛顿插值方法使用牛顿插值多项式来逼近已知点,并以此估计其他位置上的函数值。
给定已知的n个点和函数值(x₀,y₀),(x₁,y₁),...,(xₙ,yₙ),牛顿插值公式如下:N(x) = y₀ + Σ(δₙ₋₁ * ℒₙ(x)), k=1 to n其中,ℒₙ(x)=Π(x-xₙ₋₁),δ₂=(y₁-y₀)/(x₁-x₀),δ₃=(δ₂-δ₁)/(x₂-x₀),...,δₙ=(δₙ₋₁-δₙ₋₂)/(xₙ-xₙ₋₂)以上是几种常见的内插方法及其计算公式。
根据需要,可以选择适用的方法进行内插计算。
内插法的计算公式

内插法的计算公式内插法是一种常用的数值计算方法,用于在已知数据点之间估计未知数据点的值。
内插法通过构造合理的插值函数,在插值区间内进行计算。
本文将介绍两种常见的内插法,分别是线性插值和拉格朗日多项式插值。
一、线性插值线性插值是一种简单且直观的内插法,适用于数据点较少的情况。
它基于线性函数的特性进行计算,公式如下:设已知数据点为 (x0, y0) 和 (x1, y1),要估计在 x0 和 x1 之间的某个点 x 的值 y,则线性插值公式为:y = y0 + (x - x0) * (y1 - y0) / (x1 - x0) (1)其中,y0 和 y1 分别是已知数据点 x0 和 x1 对应的函数值。
使用线性插值时需要注意两点:首先,x 的取值范围必须在 x0 和 x1 之间;其次,线性插值的准确性受到数据点的分布和函数曲线变化的影响。
二、拉格朗日多项式插值拉格朗日多项式插值是一种更为精确的内插方法,适用于数据点较多且分布不规则的情况。
它利用多个数据点构造一个多项式函数,并根据插值点的位置进行计算。
拉格朗日多项式插值的计算公式如下:假设已知的 n+1 个数据点为 (x0, y0),(x1, y1),...,(xn, yn),要估计在 x0 至 xn 之间某个点 x 的值 y,则拉格朗日插值多项式的计算公式为:y = L0(x)*y0 + L1(x)*y1 + ... + Ln(x)*yn (2)其中,Ln(x) 是拉格朗日基函数,由以下公式给出:Ln(x) = Π(j=0;j≠i)ⁿ (x - xj) / (xi - xj) (3)公式(3)中,i 表示基函数 Ln(x) 对应的数据点的索引。
拉格朗日多项式插值具有较高的精度和稳定性,但当数据点数量较大时,计算量会增加,同时插值函数的高次项可能引发数值计算的误差。
综上所述,线性插值和拉格朗日多项式插值是常见的两种内插法,可用于估计已知数据点之间的未知数据点的值。
内插法计算公式

内插法计算公式内插法计算公式1、X1、Y1为《建设工程监理与相关服务收费标准》附表二中计费额的区段值;Y1、Y2为对应于X1、X2的收费基价;X为某区段间的插入值道;Y为对应于X由插入法计算而得的收费基价。
2、计费额小于500万元的,以计费额乘以3.3%的收费专率计算收费基价;3、计费额大于1,000,000万元的,以计费额乘以1.039%的收费率计算收费基价。
【例】若计算得计费额为600万元,计算其收费基价属。
根据《建设工程监理与相关服务收费标准》附表二:施工监理服务收费基价表,计费额处于区段值500万元(收费基价为16.5万元)与1000万元(收费基价为30.1万元)之间,则对应于600万元计费额的收费基价:内插法(Interpolation Method)什么是内插法在通过找到满足租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值等于租赁资产的公平价值的折现率,即租赁利率的方法中,内插法是在逐步法的基础上,找到两个接近准确答案的利率值,利用函数的连续性原理,通过假设关于租赁利率的租赁交易各个期间所支付的最低租金支付额及租赁期满时租赁资产估计残值的折现值与租赁资产的公平价值之差的函数为线性函数,求得在函数值为零时的折现率,就是租赁利率。
内插法原理数学内插法即“直线插入法”。
其原理是,若A(i1,b1),B(i2,b2)为两点,则点P(i,b)在上述两点确定的直线上。
而工程上常用的为i在i1,i2之间,从而P在点A、B之间,故称“直线内插法”。
数学内插法说明点P反映的变量遵循直线AB反映的线性关系。
上述公式易得。
A、B、P三点共线,则(b-b1)/(i-i1)=(b2-b1)/(i2-i1)=直线斜率,变换即得所求。
内插法的具体方法求得满足以下函数的两个点,假设函数为线性函数,通过简单的比例式求出租赁利率。
以每期租金先付为例,函数如下:A表示租赁开始日租赁资产的公平价值;R表示每期租金数额;S表示租赁资产估计残值;n表示租期;r表示折现率。
最新内插法的定义及计算公式

最新内插法的定义及计算公式1.线性插值:线性插值是最简单和最常用的内插方法之一、它基于线性函数的性质,假设两个相邻数据点之间的关系是线性的。
设已知数据点为(x1,y1)和(x2,y2),要估算的未知数据点为(x,y)。
线性插值公式如下:y=y1+(x-x1)*(y2-y1)/(x2-x1)2.多项式插值:多项式插值是通过一个多项式函数来逼近已知数据点的曲线形状。
该方法假设未知数据点之间的关系可以用多项式函数来表示。
设已知数据点为(x1, y1),(x2, y2),...,(xn, yn),要估算的未知数据点为(x, y),多项式插值公式如下:y = P(x) = a0 + a1 * (x - x1) + a2 * (x - x1) * (x - x2)+ ... + an * (x - x1) * (x - x2) * ... * (x - xn-1)其中,a0, a1, a2, ..., an为多项式的系数,可以通过求解线性方程组来确定。
3.样条插值:样条插值使用分段多项式来逼近已知数据点的曲线形状。
该方法假设未知数据点之间的关系可以用不同的多项式函数段来表示。
设已知数据点为(x1, y1),(x2, y2),...,(xn, yn),要估算的未知数据点为(x, y),样条插值公式如下:y = S(x) = Si(x) = ai + bi * (x - xi) + ci * (x - xi)^2 + di * (x - xi)^3其中,Si(x)表示第i段多项式,ai, bi, ci, di为每个多项式的系数,可以通过求解线性方程组来确定。
不同的样条插值方法具有不同的限制条件,如自然边界条件、固定边界条件等,这些限制条件有助于确保插值结果的平滑和连续性。
以上是最新内插法的几种常见形式,它们在实际应用中具有广泛的适用性。
根据具体问题的特点和数据的性质,选择合适的内插方法能够提高估算的准确性和可靠性。
内插法计算公式

内插法计算公式-CAL-FENGHAI.-(YICAI)-Company One1
附件1:
收费基价直线内插法计算公式
)(112121X X X X Y Y Y Y -⨯--+
=
说明: 1、X 1、Y 1为《建设工程监理与相关服务收费标准》附表二中计费额的区段值;Y 1、Y 2为对应于X 1、X 2的收费基价;X 为某区段间的插入值;Y 为对应于X 由插入法计算而得的收费基价。
2、计费额小于500万元的,以计费额乘以%的收费率计算收费基价;
3、计费额大于1,000,000万元的,以计费额乘以%的收费率计算收费基价。
【例】若计算得计费额为600万元,计算其收费基价。
根据《建设工程监理与相关服务收费标准》附表二:施工监理服务收费基价表,计费额处于区段值500万元(收费基价为万元)与1000万元(收费基价为万元)之间,则对应于600万元计费额的收费基价:
Y (收费基价) Y 2 Y Y 1
12
万元)(22.19)500600(500
10005.161.305.16=-⨯--+=Y。
内插法计算公式

内插法计算公式内插法是一种常用的数值计算方法,用于估算两个已知数据之间的未知数据。
在工程预算中,内插法可以用来估算工程项目的成本、工期等相关指标。
下面详细介绍内插法的计算公式及其应用。
内插法的计算公式如下:线性内插公式:y=y1+(x-x1)*(y2-y1)/(x2-x1)其中,(x1,y1)和(x2,y2)是已知的两个数据点,x是要估算的未知数据点,y是所估算的值。
内插法在工程预算中的应用:1.成本估算:内插法可以用于估算工程项目的成本。
例如,已知两个类似项目的成本分别为100万元和150万元,而要估算一个中间规模的项目的成本。
根据已知数据,假设项目规模的增长与成本呈线性关系,可以使用内插法计算出中间规模下的成本估算。
2.工期估算:内插法也可以用于估算工程项目的工期。
例如,已知两个类似项目的工期分别为10个月和15个月,而要估算一个中间规模的项目的工期。
根据已知数据,假设项目规模的增长与工期呈线性关系,可以使用内插法计算出中间规模下的工期估算。
3.资源分配:内插法还可以用于工程项目中的资源分配。
例如,已知两个类似项目在不同工期下的资源需求量,而要估算一个中间工期的资源需求量。
根据已知数据,假设工期与资源需求量呈线性关系,可以使用内插法计算出中间工期下的资源需求量估算。
需要注意的是,内插法的准确度和可靠性受到已知数据质量的影响。
如果已知数据存在误差或不准确,估算结果可能会产生偏差。
因此,在应用内插法进行工程预算时,需要尽量确保已知数据的准确性,并进行合理的数据分析和处理。
综上所述,内插法是一种常用的数值计算方法,在工程预算中可以用于估算成本、工期等相关指标。
通过内插法,可以在已知数据的基础上,合理地估算未知的数据,为工程项目的规划和决策提供有力的支持。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
内插法计算公式
说明:已知道一个数字的上下限,以及其对应的取值时,当我们要求的取值的数值位于这个区
间时,即可根据本内插法公式计算对应取值。
下列公式中,X1为已知数值的下限,对应的值为Y1;X2为已知数值的上线,对应的值为Y2;我们所求的值Y,为对应的已知数值X的取值。
则可采用下列公式计算;
例:如右图的某工程设计收费,当我们要计算投资X为8750万元时的收费基价时,则找到8750万元计费额的下限X1为8000,此时对应的取值Y1为249.6;再找到8750万元计费额的上限X2为10000,此时对应的Y2为304.8,则可计算当X为8750时,对应的取值Y=270.3,如下公式所示:基本原理为两点间直线公式,则可求得,Y=(X-X1)*(Y2-Y1)/(X2-X1)+Y1。
现已编好公式,可
直接用下表进行批量化计算:
X1Y1X2Y2X Y
8000249.610000304.88750270.30
50020.9100038.878030.92。
