数据结构多项式实验报告
(2023)数据结构利用链表计算一元多项式课程设计实验报告(一)

(2023)数据结构利用链表计算一元多项式课程设计实验报告(一)2023数据结构课程设计实验报告——利用链表计算一元多项式实验背景和目的在本课程设计实验中,我们旨在通过使用链表数据结构,实现对一元多项式的计算功能。
通过本次实验,我们将深入学习和掌握链表的基础知识和应用技能,掌握实现链表操作的代码实现方式,提高编程实践能力和解决问题的能力。
思路和方法首先,我们需要定义链表节点数据结构,包含多项式中的系数和指数两个数据成员。
然后,我们需要实现一元多项式的相加、相减、求导、求值等基本操作。
其中,相加和相减操作需要利用链表遍历的方式,比较两个多项式中的指数,进行对应系数的加减,并将结果存储到新的链表中。
求导操作只需要遍历链表,将每一项的指数减一,系数乘以指数值,再将其插入到新的链表中即可。
求值操作仅需要遍历链表,根据指数和系数计算多项式值即可。
在具体实现过程中,我们需要注意边界条件的判断和处理,如何处理空链表、单项式情况等。
还需要精细设计代码逻辑,避免重复遍历链表,浪费时间和空间资源。
结果分析和展示经过数次测试和调试,我们最终实现了一元多项式的链表计算功能。
我们在终端输入多项式的系数和指数,再根据指令进行相应的操作。
结果能够准确输出,并且经过大量数据测试,程序运行稳定,没有出现崩溃和错误的情况。
总结和反思通过本次实验,我们进一步深入学习了链表数据结构的应用方法和相关算法。
我们学会了如何通过遍历链表实现复杂计算操作,如一元多项式的求导、求值等。
在实现过程中,我们对代码结构和逻辑设计进行反复思考和优化,提高了自己的编程能力和解决问题的能力。
同时,我们也需要进一步加强数据结构的学习,提升自己的算法水平,为后续的专业学习和职业发展打下坚实的基础。
可能的改进和优化方案虽然我们已经实现了一元多项式链表计算功能,但是我们也发现了以下几点可以改进和优化的方案:•异常处理:在用户输入有误或者数据不规范的情况下,程序可能会出现崩溃或者不符合预期的结果。
数据结构实习报告——一元稀疏多项式运算器的设计

数据结构实习报告——一元稀疏多项式运算器的设计一、引言在计算机科学领域中,数据结构是研究数据组织、存储和管理的关键概念之一。
在本次实习中,我设计并实现了一个一元稀疏多项式运算器,旨在使用适当的数据结构和算法来高效地进行多项式的加法、减法和乘法运算。
本报告将详细介绍该运算器的设计思路、算法实现以及性能评估。
二、设计思路1. 多项式的表示在设计多项式运算器时,首先需要确定多项式的表示方法。
为了高效地处理稀疏多项式,我选择使用链表作为基本数据结构。
每个节点包含多项式的系数和指数,并通过指针连接在一起形成链表。
这种表示方法可以有效地处理稀疏多项式,减少了不必要的空间浪费。
2. 多项式的输入和输出为了方便用户输入和输出多项式,我设计了简单的交互界面。
用户可以通过命令行输入多项式的系数和指数,并选择进行的运算操作。
运算结果将直接在命令行中输出。
三、算法实现1. 多项式的加法多项式的加法是指将两个多项式相加得到一个新的多项式。
为了实现这个功能,我设计了一个算法如下:- 创建两个空的链表,分别表示两个多项式。
- 逐个读取用户输入的系数和指数,并将其插入到相应的链表中。
- 对两个链表进行遍历,根据指数的大小关系进行合并操作。
- 将合并后的结果链表输出。
2. 多项式的减法多项式的减法是指将一个多项式减去另一个多项式得到一个新的多项式。
为了实现这个功能,我设计了一个算法如下:- 创建两个空的链表,分别表示两个多项式。
- 逐个读取用户输入的系数和指数,并将其插入到相应的链表中。
- 对第二个链表中的每个节点的系数取相反数。
- 对两个链表进行遍历,根据指数的大小关系进行合并操作。
- 将合并后的结果链表输出。
3. 多项式的乘法多项式的乘法是指将两个多项式相乘得到一个新的多项式。
为了实现这个功能,我设计了一个算法如下:- 创建一个空的链表,表示乘法结果。
- 逐个读取用户输入的系数和指数,并将其插入到链表中。
- 对第一个链表中的每个节点,与第二个链表中的每个节点进行乘法运算,并将结果插入到结果链表中。
数据结构之多项式相乘编程实验报告
实验报告:多项式相乘题目:输入两个多项式,求出相乘的结果。
分析:分别相乘,同指数相加,放在一个链表中。
测试:附:源码#include <iostream.h>#include <process.h>#define Max 9999struct Node{int a;int b;Node *next;};void create(Node *&h) //创建一个多项式链表{int d1,d2;cout<<"输入多项式,两个一组,第一个系数,第二个指数,0 0结束"<<endl;Node *p;h=p=new Node;if(p==NULL)1/ 4{cout <<"ERROR"<<endl;exit(0);}h->a=-1;cin>>d1>>d2;while(d1!=0){p->next=new Node;if(p->next==NULL){cout <<"ERROR"<<endl;exit(0);}p=p->next;p->a=d1;p->b=d2;cin>>d1>>d2;}p->next=0;}int cmp(int a,int b){if(a>b)return 1;if(a==b)return 0;if(a<b)return -1;}void main (void){Node *h1,*h2,*h3;Node *q1,*q2,*q3,*q4,*n1,*n2;create(h1);create(h2);q1=h1->next;q2=h2->next;h3=new Node;h3->a=-1;q3=new Node;h3->next=q3;q4=q3;while(q1!=NULL){q3->a=(q2->a)*(q1->a);q3->b=(q2->b)+(q1->b);q3=new Node;q4->next=q3;q4=q3;q1=q1->next;}q3->b=Max;q1=h1->next;q3=h3->next;q4=h3;q2=q2->next;while(q2!=NULL){while(q1!=NULL){while(q1->b+q2->b>q3->b){if(q3->next!=NULL){q4=q3;q3=q3->next;}}switch(cmp((q1->b+q2->b),q3->b)){case -1:n1=new Node;n1->a=(q1->a)*(q2->a);n1->b=q1->b+q2->b;q4->next=n1;n1->next=q3;q4=n1;break;case 0:q3->a=(q1->a)*(q2->a+q3->a);break;case 1:n2=new Node;n2->a=(q1->a)*(q2->a);3/ 4n2->b=q1->b+q2->b;q3->next=n2;q4=q3;q3=n2;}q1=q1->next;}q1=h1->next;q3=h3->next;q4=h3;q2=q2->next;}while(q3->b!=Max){cout<<q3->a<<' '<<q3->b<<endl;q3=q3->next;}}。
数据结构实验报告-一元多项式

数据结构实验报告-一元多项式
实验目的
1.使用C语言编写一元多项式运算的程序
2.理解和掌握链表的基本概念和操作
3.熟悉链表在实际问题中的应用
实验内容
1.设计一元多项式数据结构,支持多项式的输入、输出、加、减、乘、求导等计算。
2.使用链表来实现多项式数据结构。
3.编写测试程序,测试多项式数据结构的正确性和效率。
实验步骤
1.设计一元多项式数据结构,包括多项式中的每一项所包含的系数和指数,以及链表节点结构体定义。
typedef struct node
{
float coef; // 系数
int expn; // 指数
struct node *next; // 指向下一个节点的指针
} Node, *pNode;
2.按照上述定义的结构体,实现多项式的输入函数。
3.利用链表实现多项式的加法函数。
6.编写测试程序,测试多项式数据结构的正确性和效率。
实验结果
1.输入第一个多项式为 3x^3+2x^2+3 第二个多项式为 2x^3+x^2+4x+1
2.经过程序的处理,两个多项式的加法结果为 5.00x^3+
3.00x^2+
4.00x+4.00
两个多项式的乘法结果为
6.00x^6+10.00x^5+5.00x^4+10.00x^3+14.00x^2+19.00x+3.00
第一个多项式求导结果为 9.00x^2+4.00x
1.链表可以有效地实现多项式数据结构的存储和操作,具有较好的效率和灵活性。
2.通过本次实验,能够更加深入地理解数据结构中链表的应用,有助于提高编程能力和实际问题解决能力。
数据结构线性表多项式加减实验报告

数据结构实验报告实验名称:实验一——线性表日期:2013年10月28日1.实验要求实验目的1、熟悉C++语言的基本编程方法,掌握集成编译环境的调试方法2、学习指针、模板类、异常处理的使用3、掌握线性表的操作的实现方法4、学习使用线性表解决实际问题的能力实验内容利用线性表实现一个一元多项式Polynomialf(x) = a0 + a1x + a2x2 + a3x3+ … + a n x nPolynomial的结点结构如下:struct term{float coef; //系数int expn; //指数};要求:1、能够实现一元多项式的输入和输出2、能够进行一元多项式相加3、能够进行一元多项式相减4、能够计算一元多项式在x处的值5、能够计算一元多项式的导数(选作)6、能够进行一元多项式相乘(选作)7、编写测试main()函数测试线性表的正确性2. 程序分析考虑到数据结构的实现,因为多项式是线性结构因此选择线性表,而本次实验中涉及到多项式的加减,要进行节点的添加或者删除,用顺序表显然不能满足要求,而且由于不知道多项式的项数,很容易造成空间的浪费,当两个多项式指数相差很远时,操作要移动很多项,步骤很麻烦繁琐。
综上,我选择了单链表,每个节点有三个部分,分别储存系数、指数、和指针,这样在计算加减或者指数不等时,只需要简单的摘连加链即可,而且不会造成空间的太多浪费。
每次利用尾插法将结点插入基准多项式。
2.1 存储结构本次实验采取的多项式加减算法是将一个多项式作为基准,把另一个多项式加到基准多项式中去,求和后的多项式仍然存储在第一个线性表中,因此用单链表的数据结构更为方便。
单链表存储结构在本次实验中,因为形式的特殊性,每个节点如下图表示:空链表 非空链表其中每个结点前两个分别储存float 型系数coef 和int 型指数expn ,第三个作为指针指向下一个节点(不是最后一个结点时,否则为NUll )2.2 关键算法分析1、输入多项式自然语言描述:1) 指定多项式的项数n2) 建立一个叫term 的struct 结构类型,用来储存指定多项式的系数和指数的数据。
数据结构多项式实验报告

数据结构实验报告--Week05姓名:覃兆坤学号:10389355一、实验目的用线性表实现多项式的相关操作,加强对线性表的理解和练习,熟练对线性表的操作。
二、实验题目一个d阶多项式有如下形式:c d x d+c d−1x d−1+c d−2x d−2…+c0其中,c d≠0,指数都是非负数。
每一个c i x i是多项式中的一项。
设计一个C++的模板类Polynomial<T>,T给出系数的类型,要求能够实现多项式的表示和运算。
Polynomial类应该包括私有变量degree,和其他需要的变量。
对多项式的表示要求用线性表的形式,例如(c0,c1,c2,…,c d)表示系数表。
并设计以下成员函数和操作:(a) Polynomial(),创建零阶多项式,即构造函数(b) Degree(),返回多项式的阶数degree(c) Input(),输入多项式,指数升序依次输入每一项的指数和系数。
例如输入: 0 c0 1 c1 2 c2…d c d。
重载>>完成输入。
(d) Output(),输出多项式,和输入的格式相同。
重载<<完成输出。
(e) Add(b),和b多项式相加,并返回结果多项式。
重载+。
(f) Subtract(b),和b多项式相减返回结果多项式。
重载-。
(g) Multiply(b),和b多项式相乘返回结果多项式。
重载*。
(h) Value(x),返回x代入多项式的值。
重载( ),例如对于多项式对象P, P(x)能够返回代入x的多项式值。
三、实验设计设计方法:本次实现采用链表的结构,实现建立多项式,对多项式进行相加相减相乘求值的操作。
一共写了2个文件Polynomial.h和test.cpp文件。
其中前者实现多项式的相关功能,后者为人机交互式测试其功能。
1:Polynomial.h:共有2个类:Node为一个节点其中index; modulus; next 分别为指数,系数和指向下一个节点的指针。
数据结构多项式求和实验报告

1.实验题目设计一种用单链表存储多项式的结构(每个结点存储一项的系数和指数,类型都为int),并编写一个产生多项式链表的函数和一个实现两个多项式相加的函数。
2 .实验内容顺序存储结构的实现。
先输入多项式最高项数,然后按照(系数,指数)的格式输入顺序表类型定义如下:typedef struct term{int coef;int expn;struct term *next;}term,*Polynomial;3.实验要求(1)利用C语言完成算法设计和程序设计。
(2)上机调试通过实验程序。
(3)输入数据,检验程序运行结果。
(4)给出具体的算法分析,包括时间复杂度和空间复杂度。
(5)撰写实验报告。
4.实验步骤与源程序⑴实验步骤首先分析实验内容,要实现多项式求和,必须创建两个函数,然后先建立一个多项式a和多项式b,接着输入每个多项式的系数和指数,再实现多项式a和b的求和将求出的多项式放在多项式a中,最后输出求出的多项式的结果。
⑵源代码#include<stdio.h>#include<stdlib.h>#include<string.h>#include<time.h>#include<malloc.h>/*定义存储结构,用单链表存储多项式,链表中每个结点存储多项式中的一项。
*/typedef struct term{int coef;//定义多项式系数为coefint expn;//定义多项式指数为expnstruct term *next;}term,*Polynomial;void Create_Polynomial(Polynomial *P,int n){ /*建立多项式*/int i;term *t1,*t2;(*P)=(term *)malloc(sizeof(term));(*P)->coef=0;(*P)->expn=0;(*P)->next=NULL;t1=(*P);for(i=0;i<=n;i++){ /*输入每一项的系数和指数*/ t2=(term *)malloc(sizeof(term));scanf("%d,%d",&(t2->coef),&(t2->expn));t1->next=t2;t1=t1->next;}t2->next=NULL;}void Add_Polynomial(Polynomial *a,Polynomial *b){ /*多项式a和多项式b求和,结果存放在a中。
云南大学软件学院数据结构实验二实验报告——多项式计算器

云南大学软件学院数据结构实验报告2010秋季学期(本实验项目方案受“教育部人才培养模式创新实验区(X3108005)”项目资助)学号:姓名:专业:指导老师:实验难度A□B□ C □承担任务(难度为C时填写)指导教师评分(签名)【实验题目】实验2. 线性表及其应用【问题描述】用C或C++语言设计并实现一个一元稀疏多项式的简单计算器。
【基本要求】一元稀疏多项式简单计算器的基本功能是:1、输入并建立多项式2、输出多项式,序列按指数降序排列3、多项式A(x)和B(x)相加,并建立多项式A(x)+B(x)4、多项式A(x)和B(x)相减,并建立多项式A(x)-B(x)5、给定 x 的值,计算多项式6、多项式A(x)和B(x)相乘,建立多项式A(x)*B(x) (* 选做,作为难度B的操作)【CDIO项目要求】1、有完整的CDIO四个阶段描述2、有友好美观的操作界面3、有软件使用说明或帮助文档4、项目成员分工明确,团结协作【实现提示】一、【实验构思(Conceive)】(10%)本实验通过C语言实现了多项式加法、减法、乘法、多项式求导、多项式积分的功能。
利用了冒泡排序的算法作为排序的核心算法。
运用了高等数学中多项式的求导积分的知识。
二、【实验设计(Design)】(15%)本程序定义了抽象数据结构listnode,用于存储多项式的系数和指数并存储指向下一个listnode的指针来构成链表。
本程序包含如下*个函数:Main函数:调用input函数—>调用bubble_sort函数—>调用operplus函数—>调用oper_minus函数—>调用oper_mul函数—>调用oper_dy函数—>调用oper_jifen 函数。
Oper_plus函数:将两个链表的相应项系数相加,指数不同项不操作,存入新链表,再调用排序算法,使之为降序排列。
Oper_minus函数:将两个链表的相应项系数相减,指数不同项不操作,存入新链表,再调用排序算法,使之为降序排列。
数据结构一元多项式报告
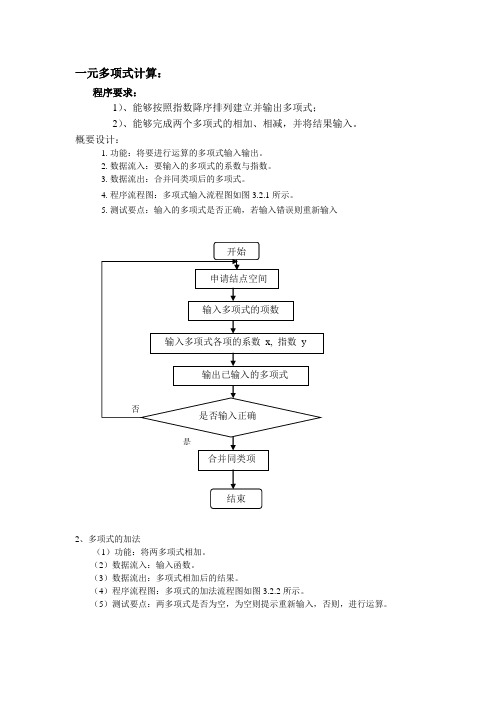
一元多项式计算:程序要求:1)、能够按照指数降序排列建立并输出多项式;2)、能够完成两个多项式的相加、相减,并将结果输入。
概要设计:1.功能:将要进行运算的多项式输入输出。
2.数据流入:要输入的多项式的系数与指数。
3.数据流出:合并同类项后的多项式。
4.程序流程图:多项式输入流程图如图3.2.1所示。
5.测试要点:输入的多项式是否正确,若输入错误则重新输入2、多项式的加法(1)功能:将两多项式相加。
(2)数据流入:输入函数。
(3)数据流出:多项式相加后的结果。
(4)程序流程图:多项式的加法流程图如图3.2.2所示。
(5)测试要点:两多项式是否为空,为空则提示重新输入,否则,进行运算。
3、多项式的减法(1)功能:将两多项式相减。
(2)数据流入:调用输入函数。
(3)数据流出:多项式相减后的结果。
(4)程序流程图:多项式的减法流程图如图3.2.3所示。
(5)测试要点:两多项式是否为空,为空则提示重新输入,否则,进行运算。
详细代码:#include<iostream>#include<conio.h>#include<stdlib.h>using namespace std; struct Node{float coef;//结点类型int exp;};typedef Node polynomial;struct LNode{polynomial data;//链表类型LNode *next;};typedef LNode* Link;void CreateLink(Link &L,int n);void PrintList(Link L);void PolyAdd(Link &pc,Link pa,Link pb);void PolySubstract(Link &pc,Link pa,Link pb); void CopyLink(Link &pc,Link pa);void PolyMultiply(Link &pc,Link pa,Link pb);int JudgeIfExpSame(Link pa,Link e);void DestroyLink(Link &L);int CompareIfNum(int i);void DestroyLink(Link &L){Link p;p=L->next;while(p){L->next=p->next;delete p;p=L->next;}delete L;L=NULL;}//创建含有n个链表类型结点的项,即创建一个n项多项式void CreateLink(Link &L,int n){if(L!=NULL){DestroyLink(L);}Link p,newp;L=new LNode;L->next=NULL;(L->data).exp=-1;//创建头结点p=L;for(int i=1;i<=n;i++){newp=new LNode;cout<<"请输入第"<<i<<"项的系数和指数:"<<endl;cout<<"系数:";cin>>(newp->data).coef;cout<<"指数:";cin>>(newp->data).exp;if(newp->data.exp<0){cout<<"您输入有误,指数不允许为负值!"<<endl;delete newp;i--;continue;}newp->next=NULL;p=L;if(newp->data.coef==0){cout<<"系数为零,重新输入!"<<endl;delete newp;i--;continue;}while((p->next!=NULL)&&((p->next->data).exp<(newp->data).exp)){p=p->next; //p指向指数最小的那一个}if(!JudgeIfExpSame( L, newp)){newp->next=p->next;p->next=newp;}else{cout<<"输入的该项指数与多项式中已存在的某项相同,请重新创建一个正确的多项式"<<endl;delete newp;DestroyLink(L);CreateLink(L,n); //创建多项式没有成功,递归调用重新创建break;}}}/*判断指数是否与多项式中已存在的某项相同*/int JudgeIfExpSame(Link L,Link e){Link p;p=L->next;while(p!=NULL&&(e->data.exp!=p->data.exp))p=p->next;if(p==NULL)return 0;else return 1;}/*输出链表*/void PrintList(Link L){Link p;if(L==NULL||L->next==NULL)cout<<"该一元多项式为空!"<<endl;else{p=L->next;//项的系数大于的种情况if((p->data).coef>0){if((p->data).exp==0)cout<<(p->data).coef;else if((p->data).coef==1&&(p->data).exp==1)cout<<"x";else if((p->data).coef==1&&(p->data).exp!=1)cout<<"x^"<<(p->data).exp;else if((p->data).exp==1&&(p->data).coef!=1)cout<<(p->data).coef<<"x";else cout<<(p->data).coef<<"x^"<<(p->data).exp; }//项的系数小于的种情况if((p->data).coef<0){if((p->data).exp==0)cout<<(p->data).coef;else if(p->data.coef==-1&&p->data.exp==1)cout<<"-x";else if(p->data.coef==-1&&p->data.exp!=1)cout<<"-x^"<<p->data.exp;else if(p->data.exp==1)cout<<p->data.coef<<"x";else cout<<(p->data).coef<<"x^"<<(p->data).exp; }p=p->next;while(p!=NULL){if((p->data).coef>0){if((p->data).exp==0)cout<<"+"<<(p->data).coef;else if((p->data).exp==1&&(p->data).coef!=1)cout<<"+"<<(p->data).coef<<"x";else if((p->data).exp==1&&(p->data).coef==1)cout<<"+"<<"x";else if((p->data).coef==1&&(p->data).exp!=1)cout<<"+"<<"x^"<<(p->data).exp;else cout<<"+"<<(p->data).coef<<"x^"<<(p->data).exp; }if((p->data).coef<0){if((p->data).exp==0)cout<<(p->data).coef;else if(p->data.coef==-1&&p->data.exp==1)cout<<"-x";else if(p->data.coef==-1&&p->data.exp!=1)cout<<"-x^"<<p->data.exp;else if(p->data.exp==1)cout<<p->data.coef<<"x";else cout<<(p->data).coef<<"x^"<<(p->data).exp;}p=p->next;}}cout<<endl;}/*把一个链表的内容复制给另一个链表*/void CopyLink(Link &pc,Link pa){Link p,q,r;pc=new LNode;pc->next=NULL;r=pc;p=pa;while(p->next!=NULL){q=new LNode;q->data.coef=p->next->data.coef;q->data.exp=p->next->data.exp;r->next=q;q->next=NULL;r=q;p=p->next;}}/*将两个一元多项式相加*/void PolyAdd(Link &pc,Link pa,Link pb){Link p1,p2,p,pd;CopyLink(p1,pa);CopyLink(p2,pb);pc=new LNode;pc->next=NULL;p=pc;p1=p1->next;p2=p2->next;while(p1!=NULL&&p2!=NULL){if(p1->data.exp<p2->data.exp){p->next=p1;p=p->next;p1=p1->next;}else if(p1->data.exp>p2->data.exp){p->next=p2;p=p->next;p2=p2->next;}else{p1->data.coef=p1->data.coef+p2->data.coef;if(p1->data.coef!=0){p->next=p1;p=p->next;p1=p1->next;p2=p2->next;}else{pd=p1;p1=p1->next;p2=p2->next;delete pd;}}}if(p1!=NULL){p->next=p1;}if(p2!=NULL){p->next=p2;}}/*将两个多项式相减*/void PolySubstract(Link &pc,Link pa,Link pb) {Link p,pt;CopyLink(pt,pb);p=pt;while(p!=NULL){(p->data).coef=(-(p->data).coef);p=p->next;}PolyAdd(pc,pa,pt);DestroyLink(pt);}//清屏函数void Clear(){system("pause");system("cls");}/*将两个一元多项式相乘*/void PolyMultiply(Link &pc,Link pa,Link pb) {Link p1,p2,p,pd,newp,t;pc=new LNode;pc->next=NULL;p1=pa->next;p2=pb->next;while(p1!=NULL){pd=new LNode;pd->next=NULL;p=new LNode;p->next=NULL;t=p;while(p2){newp=new LNode;newp->next=NULL;newp->data.coef=p1->data.coef*p2->data.coef;newp->data.exp=p1->data.exp+p2->data.exp;t->next=newp;t=t->next;p2=p2->next;}PolyAdd(pd,pc,p);CopyLink(pc,pd);p1=p1->next;p2=pb->next;DestroyLink(p);DestroyLink(pd);}}//菜单函数void Menu(){cout<<""<<endl;cout<<endl;cout<<"\t=========================一元多项式的简单运算========================="<<endl;cout<<"\t\t\t\t\t\t\t\t "<<endl;cout<<"\t\t\t [1] 创建要运算的两个一元多项式\t\t "<<endl; cout<<"\t\t\t [2] 将两个一元多项式相加\t\t\t "<<endl; cout<<"\t\t\t [3] 将两个一元多项式相减\t\t\t "<<endl; cout<<"\t\t\t [4] 将两个一元多项式相乘\t\t\t "<<endl; cout<<"\t\t\t [5] 显示两个一元多项式\t\t\t "<<endl;cout<<"\t\t\t [6] 销毁所创建的二个多项式\t\t "<<endl; cout<<"\t\t\t [7] 退出\t\t\t\t\t "<<endl;cout<<"\t\t\t\t\t\t\t\t "<<endl;cout<<"\t=========================一元多项式的简单运算========================="<<endl;cout<<endl;cout<<"\t\t 请选择:";}//判断输入的整数是不是为到的数字int CompareIfNum(int i){if(i>0&&i<8)return 0;else return 1;}void main(){{system("color b");//system("pause");system("color a");//system("pause");}int n;Link L,La=NULL,Lb=NULL;//La,Lb分别为创建的两个多项式int choose;while(1){Menu(); //调用菜单函数cin>>choose;switch(choose){case 1:cout<<"请输入你要运算的第一个一元多项式的项数:"<<endl; cin>>n;if(CompareIfNum(n)==1){cout<<"您的输入有误,请重新输入……"<<endl;Clear();break;}CreateLink(La,n);cout<<"请输入你要运算的第二个一元多项式的项数:"<<endl; cin>>n;if(CompareIfNum(n)==1){cout<<"您的输入有误,请重新输入……"<<endl;Clear();break;}CreateLink(Lb,n);Clear();break;case 2:if(La==NULL||Lb==NULL){cout<<"您的多项式创建有误,请重新选择……"<<endl; Clear();break;}PolyAdd(L,La,Lb);cout<<""<<endl;cout<<"待相加的两个一元多项式为:"<<endl;cout<<""<<endl;cout<<"A的多项式为:";PrintList(La);cout<<""<<endl;cout<<"B的多项式为:";PrintList(Lb);cout<<""<<endl;cout<<"相加后的结果为:";PrintList(L);cout<<""<<endl;Clear();DestroyLink(L);break;case 3:if(La==NULL||Lb==NULL){cout<<"您的多项式创建有误,请重新选择……"<<endl; Clear();break;}PolySubstract(L,La,Lb);cout<<"相减的两个一元多项式为:"<<endl;cout<<""<<endl;cout<<"A的多项式为:";PrintList(La);cout<<""<<endl;cout<<"B的多项式为:";PrintList(Lb);cout<<""<<endl;cout<<"相减后的结果为:";PrintList(L);cout<<""<<endl;Clear();DestroyLink(L);break;case 4:if(La==NULL||Lb==NULL){cout<<"您的多项式创建有误,请重新选择……"<<endl; Clear();break;}PolyMultiply(L,La,Lb);cout<<"相乘的两个一元多项式为:"<<endl;cout<<""<<endl;cout<<"A的多项式为:";PrintList(La);cout<<""<<endl;cout<<"B的多项式为:";PrintList(Lb);cout<<""<<endl;cout<<"相乘后的结果为:";PrintList(L);DestroyLink(L);cout<<""<<endl;Clear();break;case 5:if(La==NULL||Lb==NULL){cout<<"您的多项式创建有误,请重新选择……"<<endl; Clear();break;}cout<<"一元多项式A为:"<<endl;PrintList(La);cout<<""<<endl;cout<<"一元多项式B为:"<<endl;PrintList(Lb);cout<<""<<endl;Clear();break;case 6:if(La&&Lb){DestroyLink(La);DestroyLink(Lb);cout<<"多项式销毁成功!"<<endl;Clear();}else{cout<<"多项式不存在,请重新选择^^^"<<endl;Clear();}break;case 7:exit(0); //exit(0)强制终止程序,返回状态码表示正常结束default:cout<<"您的输入有误,请重新选择操作……"<<endl;Clear();break;}}}。
数据结构《一元多项式》

一元多项式相加问题实验报告本实验的目的是进一步熟练掌握应用链表处理实际问题的能力。
一、问题描述通过键盘输入两个形如Po+P₁X¹+P₂X²+…+PX的多项式,经过程序运算后在屏幕上输出它们的相加和。
二、数据结构设计分析任意一元多项式的描述方法可知,一个一元多项式的每一个子项都由“系数-指数”两部份组成,因此可将其抽象为包含系数coef、指数 exp、指针域next 构成的链式线性表。
对多项式中系数为0的子项可以不记录它的指数值,将两个多项式分别存放在两个线性表中,然后经过相加后将所得多项式存放在一个新的线性表中,但是不用再开辟新的存储空间,只依靠结点的挪移来构成新的线性表,期间可以将某些不需要的空间回收。
基于这样的分析,可以采用不带头结点的单链表来表示一个一元多项式。
具体数据类型定义为:struct nodefloat coef;//系数域int exp; //指数域struct node *next;};三、功能函数设计1、输入并建立多项式的功能模块具体函数为node *in f un()此函数的处理较为全面,要求用户按照指数递增的顺序和一定的输入格式输入各个系数不为0的子项,输入一个子项建立一个相关结点,当遇到输入结束标志时住手输入。
关键步骤具体如下:(1)控制用户按照指数递增的顺序输入r=a;while(r!=q->next)if(y<=r->exp)cout<<"请按照指数递增顺序输入,请重新输入";cin>>x>>y;break;r=r->next;从头开始遍历,若遇到目前输入的指数不是最大时,就跳出循环,让用户重新输入。
(2)当输入的系数为零时,不为其分配存储空间存储while(x==0){cin>>x>>y;continue;}即若系数为0,再也不进行动态分配并新建结点,而是重新提取用户输入的下一个子项的系数和指数,利用continue 进入下一次循环。
数据结构实验报告1
按格式输出多项式。
in_order();
无
待排序的多项式链表头指针:head
链表头指针:newhead
利用新建链表将多项式按升序排列。
combine();
无
待合并同类项的链表头指针:head
链表头指针:head
合并同类项。.
addexp();
待计算的两多项式链表头指针:head1,head2.
链表头指针:head
见附页
相加:***The expression is:+3x^2+14x^3-4x^5-6x^9
***Total number of item is :4
相减:***The expression is:+1x^2+4x^3-2x^5+6x^9
***Total number of item is :4
程序代码
实验报告(一)
设计者
日期
测试者
编程语言
C
功能描述
一元稀疏多项式计算器
(1)输入并建立多项式;
(2)输出多项式,输出形式为整数序列:n,c1,e1,c2,e2,……cn,en,其中n是多项式的项数,ci和ei分别是第i项的系数和指数,序列按指数降序排列;
(3)多项式a和b相加,建立多项式a+b;
(4)多项式a和b相减,建立多项式a-b;
将两个多项式合并。
subexp();
无
待反转每项符号的多项式链表头指针:head
链表头指针:head
反转多项式每项符号。
数据说明
1、 多项式结点结构体:struct node
{
char sign; /*系数符号*/
int coef; /*系数绝对值*/*
数据结构多项式相加实验报告doc

数据结构多项式相加实验报告篇一:数据结构实验多项式加法数据结构实验报告实验名称:多项式加减法学号:1XX10419姓名:林强实验日期:XX.5.05一、实验目的通过实现多项式的加减法,对链表有更深入的了解二、实验具体内容1、实验题目1:(1)题目设计一个一元稀疏多项式简单的加减法计算器实现要求:一元稀疏多项式简单计算器的基本功能是:(1)输入并建立多项式:A(x)?7?3x?9x8?5x17;B(x)?8x?22x7?9x8(2)输出多项式(3)多项式A和B相加,建立多项式C=A+B,并输出相加的结果多项式C(4)选作:多项式A和B相减,建立多项式C=A-B,并输出相加的结果多项式D(2)分析1:本程序的任务是实现两个多项式的加法其中多项式的系数为浮点型,指数为整数,输出的结果也为系数和指数。
(1)输入的形式和输入值的范围:输入多项式的系数a和未知数X的指数b,当a和b都为零时,输入结束。
输入值的范围:a为实数,b为整数。
(2)输出形式:输出多项式的系数和多项式未知数X 的指数即(a,b)形式。
(3)程序所能达到的功能,实现两个多项式的加法,并输出最后的结果2:整个程序运行期间实行动态创建节点,一边输入数据,一边创建节点当将全部数据输入到单链表中后再调用多项式加法这个函数,并一边实现多项式的相加,一边释放节点,有效防止了在程序反复运行过程中可能出现系统空间不够分配的现象(3)实验代码typedef int Status;#define OVERFLOW -1#define null 0typedef struct Lnode{float coef; //存储项系数int expn;//存储项指数struct Lnode *next;}Lnode,*LinkList;typedef LinkList polynomial;Status InitList_L(LinkList &L) {//初始化头节点L=(LinkList)malloc(sizeof(Lnode));if(!L)return(-1);L->next=null;return 1;}void AddPolyn(polynomial pa, polynomial pb){ //实现两个多项式相加的算法float x;polynomial qa;polynomial qb;polynomial s;polynomial u;qa=pa->next; qb=pb->next; s=pa;while(qa&&qb){if(qa->expnexpn){s=qa;qa=qa->next;}else if(qa->expn==qb->expn){x=qa->coef+qb->coef;if(x!=0){qa->coef=x;s=qa;qa=qa->next;u=qb;qb=qb->next;free(u);}else{s->next=qa->next;free(qa);qa=s->next;u=qb;qb=qb->next;free(u);}}else if(qa->expn>qb->expn){ u=qb->next;s->next=qb;s=qb;qb->next=qa;qb=u;}}if(qb)qa->next=qb;free(pb);}void main(){float a;int b;polynomial L1;polynomial L2; LinkList q;LinkList p;LinkList m;LinkList n;InitList_L(L1);q=L1;InitList_L(L2);p=L2;cout 请输入数据:" for(;;){ cin>>a;cin>>b;if(a==0&&b==0) break;m=new Lnode;m->coef=a;m->expn=b;q->next=m;q=m;q->next=null;}//循环输入第一个多项式的系数与指数for(;;){cin>>a;cin>>b;if(a==0&&b==0)break;n=new Lnode;n->coef=a;n->expn=b;p->next=n;p=n;p->next=null;}//循环输入第二个多项式的系数与指数AddPolyn(L1,L2);//调用多项式相加的算法while((L1->next)!=null){coutnext->coefnext->expn L1=L1->next;}//输出计算结果}三、实验小结通过编写多项加法这个程序,我将自己所学到的创建链表,初始化链表和多项式加法算法都应用了一次,这使我们不仅仅只是理论化的学习书本上的知识,而是将学习到的理论知识应用到实际的操作中来增强我们的实际操作能力,这使我增加了实际操作经验,也使我通过实际操作来认识到自己在程序编写上的不足从而增强了我的实际编写程序的能力。
数据结构一元多项式求和实验报告

xx大学xxx学院算法与数据结构试验报告设计名称:算法与数据结构设计题目:链表的应用学生学号:xx专业班级:xx学生姓名:xx学生成绩:指导教师(职称):课题工作时间:2012年4月10日说明:实验课程类别:课程内实验实验课程性质:必修适用专业、年级:2010级计算机工程、计算机网络开课院、系:计算机科学与工程学院计算机工程教研室学时:18编写依据:《算法与数据结构》实验教学大纲修订时间:2012年2月《算法与数据结构》课程实验指导书(以下简称:指导书)是针对计算机学院所开设的对应课程的上机实验而编写的教学文件,供学生上机实验时使用。
上机的工作环境要求:Windows 2000或以上操作系统、VC++ 6.0或者其它高级程序设计语言。
学生应按指导教师的要求独立完成实验,并按要求撰写实验报告。
每一个实验,编程上机调试并且提交电子文档实验报告,以学号姓名作为文件名上传。
报告内容至少包含如下内容:1、学生基本情况:专业班级、学号、姓名2、实验题目、实验内容3、设计分析4、源程序代码5、测试用例(尽量覆盖所有分支)6、实验总结一.实验内容与学时分配一、试验课题链表的应用二、试验内容一元多项式求和。
把任意给定的两个一元多项式P(x),Q(x)输入计算机,计算它们的和并输出计算结果。
三、试验分析系数指数一元多项式链表的结点结构四、源程序代码#include<stdio.h> #include<stdlib.h> /*链表数据类型定义*/ typedef struct LNode {int x,z;struct LNode *next; }LinkList;void OutLinkList(LinkList *L); /*输出函数*/void PutLinkList(LinkList *&L,int n); /*输入函数*/LinkList *AddLinkList(LinkList *a,LinkList *b); /*求和函数*/ void OutXLinkList(LinkList *L); void OutZLinkList(LinkList *L); void main() {int n,m;LinkList *a,*b,*c;printf("\t\t\t本程序可以完成两个一元多项式的加法运算。
数据结构实系数一元多项式运算实验报告

实系数一元多项式问题实验报告2010级计算机科学与技术(非师范)鲁静2011年10月14日星期五1、需求分析实现实系数一元多项式的创建,打印以及两个一元多项式的加、减、乘运算。
(1)程序所能达到的功能:a.实现一元多项式的输入;b.实现一元多项式的输出;c.计算两个一元多项式的和并输出结果;d.计算两个一元多项式的差并输出结果;e.计算两个一元多项式的积并输出结果;(2)输入的形式和输入值的范围:输入要求:分行输入,每行输入一项,先输入多项式的指数,再输入多项式的系数,以0 0为结束标志,结束一个多项式的输入。
输入形式:2 3-1 23 01 20 0-2 1-3 3-1 -10 0输入值的范围:系数为int型,指数为float型。
(3)输出的形式:要求:第一行输出多项式1;第二行输出多项式2;第三行输出多项式1与多项式2相加的结果多项式;第四行输出多项式1与多项式2相减的结果多项式;第五行输出多项式1与多项式2相乘的结果多项式注:多项式的每一项形如:2.0x^3,注意指数应保留一位小数;多项式按照升幂次序排列;系数为1的非零次项应略去系数,系数为0的项不能出现在结果中;指数为0的项应只输出系数;多项式的第一项系数符号为正时,不要输出“+”,其他项要输出“+”,“-”符号。
输出形式:3.0+2.0x^3-x^-1-2.0x-3.0x^3-x^-1+3.0-2.0x-x^3x^-1+3.0+2.0x+5.0x^3-3.0x^-1-6.0x-2.0x^2-9.0x^3-4.0x^4-6.0x^62、概要设计抽象数据类型一元多项式的定义如下:ADT Polynomial{数据对象:D={ai | ai∈TermSet,i=1,2,…,m,m≥0TermSet 中的每个元素包含一个表示系数的实数和表示指数的整数}数据关系:R1={< ai-1,ai>| ai-1, ai∈D,且ai-1中的指数值<ai中的指数值,i=2,…,n}基本操作:sort(Polyn & h); //对多项式进行排序print(Polyn h); //输出多项式delZeroCoef(Polyn & h); //判断系数为零的情况merge(Polyn & h); //合并指数相同的项createList(); //创建多项式addPoly(Polyn h1,Polyn h2); //多项式相加subPoly(Polyn h1,Polyn h2); //多项式相减multPoly(Polyn h1,Polyn h2); //多项式相乘} ADT Polynomial多项式的抽象数据类型的定义:typedef struct Polynomial //结点类型{float coef; //系数int exp; //指数struct Polynomial * next;}PolyNode,*Polyn;主程序的流程图:3、详细设计伪码算法:主函数:int main(){Polyn h1=createList();//创建多项式1Polyn h2=createList();//创建多项式2print(h1); //输出多项式1print(h2); //输出多项式2addPoly(h1,h2); //实现多项式1和2的相加,并输出 subPoly(h1,h2); //实现多项式1和2的相减,并输出 multPoly(h1,h2); //实现多项式1和2的相乘,并输出 return 0;}分支函数:void sort(Polyn & h); //排序void print(Polyn h); //输出多项式void delZeroCoef(Polyn & h);//判断处理系数为0的情况void merge(Polyn & h); //合并多项式Polyn createList(); //创建多项式void addPoly(Polyn h1,Polyn h2);//两个多项式相加并输出 void subPoly(Polyn h1,Polyn h2);//两个多项式相减并输出void multPoly(Polyn h1,Polyn h2);//两个多项式相乘并输出函数的调用关系:4、调试分析a.调试过程中遇到的问题是如何解决的以及对设计与实现的回顾讨论和分析:在输入诸如“0,3”,“2,0”时,程序无法正常运行或总是出错.解决:对指数或系数为0的情况应单独讨论。
数据结构实验报告完成多项式的运算

简单介绍:本次作业力在学会链表表示线性表的插入、删除、查找等基本操作设计与实现,学习利用链表提供的接口去求解实际问题,同时熟悉链表的的存储方法。
再基于线性链表的基础设计完成多项式的相加运算程序。
一、实验目的和要求完成多项式的相加、相乘运算。
(1)掌握线性表的插入、删除、查找等基本操作设计与实现(2)学习利用线性表提供的接口去求解实际问题(3)熟悉线性表的的存储方法二、实验内容和原理1.实验内容设计一个一元多项式的简单计算程序,其基本功能有:(1)输入并建立多项式;(2)输出多项式;(3)多项式的相加运算。
利用单链表实现。
2.实验原理使用单链表实现一元多项式的存储,并实现两个一元多项式的加法运算。
三、实验环境硬件:(1)学生用微机(2)多媒体教室或远程教学(3)局域网环境软件:(1)Windows XP中文操作系统(2)VC6.0四、算法描述及实验步骤1、描述:加法:输入建立一元多项式,进行简单加法运算,输出结果;通过建立单链表A和B分别存放多项式的a和b的各项系数及指数;并且利用A使得不产生新的节点而在A中存放数据运算结果;该过程通过定义指针变量p和q使它们分别指向两个多项式的第一个节点,之后依次比较它们所指向的项的指数,即一种情况指数相等时系数相加且和不为零,修改当前p所指项的系数(和),同时删除q所指项,若和为零则同时删除p和q各自所指;情况二,p当前项指数大于q当前项,将q所指插入p所指之前作为结果项之一;情况三,p当前项指数小于q当前项,p所指作为多项式和的一项,移动p指向下一项,进行比较,在移动p,q至其中以个链空,把另一个链余下节点插在p所指之后;乘法:定义指针p,q指向所操作节点,通过A链表的每一项与B链表各项相乘,指数相加,系数相乘,将值赋给新节点各自域,构成一新的链表,最后返回头结点。
可这样有一个问题,即新生成的链表,即最终结果混乱,没有对数据进行过滤,相同指数项应在执行加法运算,所以可以这样实现,通过A链表的每一项与B链表各项相乘的新生成节点单独构成一链表,并将第一个链表加入另一新链表,循环此操作将后生成的链表加之先前的链表,即可实现排序问题。
多项式运算实训报告

多项式运算实训报告信息工程学院数据结构实训报告题目:多项式基本运算学号:14090323姓名:卫哲君班级:强化3班目录一、目的概述。
3二、实验(设计)仪器设备和材料清单。
3三、项目分析和设计。
3四、项目关键代码。
4五、项目调试和运行。
10六、实训设计的心得体会。
12数据结构实训设计报告一、目的概述我这次实训的项目主要是多项式基本运算系统,多项式基本运算系统主要实现的是多项式的相加相减相乘和赋值计算。
这次实训的项目主要通过C语言来实现程序的运行,主要通过C语言中的函数调用和链表来做程序,还要用到许多小的知识点,例如:用冒泡法实现排序;scanf、printf语句;while()语句实现循环;if……el se语句实现选择……等等。
二、实验(设计)仪器设备和材料清单1.硬:PC机2.软:turboc2.0,visulac++6.0三、项目分析和设计这个项目的程序可分为几个板块来做,每个板块有每个板块的作用,通过不同程序的不同作用相互调用即可实现整个程序的运行,这个项目程序主要可以分为以下几个板块:1、定义头文:运用#include,#include头文2、定义链表:运用typedefstructNODE{多项式项数和系数和指数信息……}变量名表列;3、对调用函数进行声明:根据所写程序对有些函数进行声明,例如:intInitpolyn(polynomialP);在程序中实现的是构造一个多项式链表P。
4、主函数:Voidmain()为主函数,在主函数中通过while语句和switch……case语句或者printf语句进行选择和函数调用。
Voidmain(){while()……{switch()……}}5、菜单函数:主要用printf语句输出菜单函数,并且还通过主函数调用菜单函数实现对多项式操作的选择。
6、输入多项式的信息:定义函数为intorderinsertpolyn(polynomialP,Nodee)Nodee为链表指针,在此函数中,通过指针的移动实现多项式信息的输入。
数据结构 多项式 实验报告

数据结构实验报告实验名称:实验一——多项式的实现学生姓名:班级:班内序号:学号:日期:2011年10月29日1.实验要求实验目的:1.熟悉C++语言的基本编程方法,掌握集成编译环境的调试方法2.学习指针、模板类、异常处理的使用3.掌握线性表的操作的实现方法4.学习使用线性表解决实际问题的能力实验内容:利用线性表实现一个一元多项式Polynomialf(x) = a0 + a1x + a2x2 + a3x3+ … + a n x n要求:1.能够实现一元多项式的输入和输出2.能够进行一元多项式相加3.能够进行一元多项式相减4.能够计算一元多项式在x处的值5.能够计算一元多项式的导数(选作)6.能够进行一元多项式相乘(选作)7.编写测试main()函数测试线性表的正确性2. 程序分析由于多项式是线性结构,故选择线性表来实现,在这个程序中我采用的是单链表结构,每个结点代表一个项,多项式的每一项可以用其系数和指数唯一的表示。
如果采用顺序存储,那么对于结点的插入和删除的操作会比较麻烦,而且顺序表的结点个数固定,对于可能发生的情况无法很好的处理,而采用链表就会简单许多,还能自由控制链表的长度。
两个多项式要进行多次的计算,为了保护原始的数据,方便进行以后的计算,故选择把结果存储在一个新建的链表里。
本程序完成的主要功能:1.输入和输出:需要输入的信息有多项式的项数,用来向系统动态申请内存;多项式各项的系数和指数,用来构造每个结点,形成链表。
输出即是将多项式的内容向屏幕输出。
2.多项式相加与相减:多项式的加减要指数相同即是同类项才能实现,所以在运算时要注意判断指数出现的各种不同的情况,分别写出计算方法。
将每项运算得到的结果都插入到新的链表中,形成结果多项式。
3.多项式的求导运算:多项式的求导根据数学知识,就是将每项的系数乘以指数,将指数减1即可,将每项得到的结果插入到结果多项式的链表中。
4.多项式在某点的值:由用户输入x的值,然后求出每项的值相加即可。
数据结构实验-多项式的相加减

集美大学数据结构课程实验报告课程名称:数据结构班级:网络0911实验成绩:指导教师:姓名:实验项目名称:多项式的相加减学号上机实践日期:实验项目编号:组号:上机实践时间:学时一、目的(本次实验所涉及并要求掌握的知识点)学习和掌握如何运用链表来实现一元稀疏多项式的相加减。
多项式的输入和输出的应注意的要点,规定输出的多项式的顺序。
二、实验内容与设计思想(设计思路、主要数据结构、主要代码结构、)实验内容:一元稀疏多项式的相加减设计思路:建立数据结构存放常数和系数以及指向下一个节点的指数,用链表存放各个节点,通过对常数和系数的的运算,实现多项式的相加减主要数据结构:结构体,链表主要代码结构:struct Polyn;void addPolyn(Polyn * a,Polyn * b,int add);void display( );void tip()’Polyn * CreatPolyn(int m);三、实验使用环境(本次实验所使用的平台和相关软件)Dev-C++、windows XP四、实验步骤和调试过程(实验步骤、测试数据设计、测试结果分析)需说明出,加入必要的截图说明。
#include<iostream>#include<vector>using namespace std;struct Polyn{float coef;int expn;Polyn *next;};//构建结构体vector <Polyn *> ve;void addPolyn(Polyn * a,Polyn * b,int add);void display(Polyn *n);//打印void tip();//屏幕显示Polyn * CreatPolyn(int m); //建立多项式int main(){tip();system("pause");}void tip(){Polyn *first, *second,*s;int m;for( int i=1;i;){cout<<" 多项式运算.\n";cout<<"======================="<<"\n"; cout<<" 1------ 构造多项式.\n";cout<<" 2------ 多项式相加.\n";cout<<" 3------ 多项式相减.\n";cout<<" 0------ 结束.\n";cout<<"======================="<<"\n"; cout<<" 请输入您的选择.\n";cin>>i;switch(i){case 1:cout<<"请输入多项式的项数.\n";cin>>m;s=CreatPolyn(m);display(s);ve.push_back(s);break;case 2:first=ve.back();ve.pop_back();second=ve.back();addPolyn(first,second,0);break;case 3:first=ve.back();ve.pop_back();second=ve.back();addPolyn( first,second,1);break;case 0:cout<<" 再见"<<"\n";break;};}}Polyn* CreatPolyn(int m){Polyn* px=new Polyn[m];cout<<" 输入系数.\n";for(int i=0;i<m;i++)cin>>px[i].coef;cout<<"输入与系数相对应的指数.\n";for(int i=0;i<m;i++){cin>>px[i].expn;if(i!=m-1)px[i].next=&px[i+1];elsepx[i].next=NULL;}return px;}void display(Polyn *n){int q=0;Polyn * r;r=n;for(;r;r=r->next){if(r->coef)q++;if(r==n){if(r->coef!=0)cout<<r->coef<<"X"<<"^"<<r->expn;}else{if( r->coef>0)cout<<"+"<<r->coef<<"X"<<"^"<<r->expn;if(r->coef<0)cout<<r->coef<<"X"<<"^"<<r->expn;}}cout<<"\n";if(q==0)cout<<"0"<<"\n";}void addPolyn(Polyn * a,Polyn * b,int add)//两个多项式的加减{float c;int a1=1,b1=1,s,e;Polyn *ha,*hb,*p,*r;ha=a;hb=b;p=ha;r=hb;for(int i=0;ha[i].next;++i)a1++;for(int i=0;hb[i].next;++i)b1++;ha[a1-1].next=hb;for(int j=0;j<b1;j++){for(int i=0;i<a1;i++){if(a[i].expn-b[j].expn==0){if(add)ha[i].coef=ha[i].coef-hb[j].coef;elseha[i].coef=ha[i].coef+hb[j].coef;if(hb!=&hb[j])hb[j-1].next=hb[j].next;else{hb=hb[j].next;ha[a1-1].next=hb;}i=a1;}}}for(;p;p=p->next){for( Polyn * t=p->next;t;t=t->next)if( p->expn>t->expn){e=p->expn;p->expn=t->expn;t->expn=e;c=p->coef;p->coef=t->coef;t->coef=c;}}display(ha);}五、实验小结(实验中遇到的问题及解决过程、实验体会和收获)至少两点1.刚开始实现多项式的相加减运算时,申请一个新的空间来存放结果,结果指针乱了,后来改成了现在的程序。
数据结构多项式相加实验报告

试验一多项式相加一. 实验内容:多项式相加二.实验目的和要求:利用双向链表实现通讯录的建立、删除、检索和列表,并可保存至文件,可重新装入。
用链式存储结构实现一元多项式的相加运算。
三.算法思想描述:1. 以单链表为存储结构插入多项式: 多项式输入:多项式按幂从高到低,以“系数,幂”的格式输入,并以“0,0”结束。
printf("Please input coef:");scanf("%d",&i);printf("Please input exp: ");scanf("%d",&j);while(i!=0){q=(pnode)malloc(sizeof(struct node));q->coef=i;q->exp=j;p->link=q;p=q;printf("Please input coef:");scanf("%d",&i);printf("Please input exp: ");scanf("%d",&j);}p->link=NULL;2. 多项式相加单链表合并:由两个多项式对应的单链表头节点开始,依次扫描各节点。
(1)若两表的节点均非空:比较二者的幂,按幂大者先入表。
如果幂相等,则系数相加再入表。
具体由以下代码实现:while(p!=NULL && q!=NULL){if(p->exp==q->exp){x=p->coef+q->coef;if(x!=0){s=(pnode)malloc(sizeof(struct node));s->coef=x;s->exp=p->exp;r->link=s;r=s;}p=p->link;q=q->link;}else if(p->exp<q->exp){s=(pnode)malloc(sizeof(struct node));s->coef=q->coef;s->exp=q->exp;r->link=s;r=s;q=q->link;}else{s=(pnode)malloc(sizeof(struct node));s->coef=p->coef;s->exp=p->exp;r->link=s;r=s;p=p->link;}(2). 若有一链表已空,则将非空链表插入新表:while(p!=NULL){s=(pnode)malloc(sizeof(struct node));s->coef=p->coef;s->exp=p->exp;r->link=s;r=s;p=p->link;}while(q!=NULL){s=(pnode)malloc(sizeof(struct node));s->coef=q->coef;s->exp=q->exp;r->link=s;r=s;q=q->link;}3. 输出合并后的链表:while(head->link!=NULL){head=head->link;printf(" %d*x^%d",head->coef,head->exp);}4. 主函数调用,完成多项式相加。
多项式运用实验报告

《数据结构》实验报告实验题目:多项式运用班级:学号:姓名:完成日期:1.需求分析实现实系数一元多项式的创建,打印以及两个一元多项式的加、乘运算。
(1)输入形式和输入值的范围输入要求:分行输入,每行输入一项,先输入多项式的系数,再输入多项式的指数,以0 0为结束标志,结束一个多项式的输入。
输入形式:2.0 31.2 23.4 03.2 20.1 02.5 13.2 31.9 10.4 0输入值的范围:系数为float型,指数为int型。
(2)输出的形式:3.0x^0+2.0x^3-x^-1-2.0x-3.0x^3-x^-1+3.0x^0-2.0x^1-x^3x^-1+3.0x^0+2.0x^1+5.0x^3-3.0x^-1-6.0x^1-2.0x^2-9.0x^3-4.0x^4-6.0x^6(3)程序所能达到的功能:a、根据所输入的多项式每个项的系数和指数,创建两个多项式单链表,结点按升幂排序。
b、按升幂顺序分别输出所创建的两个多项式。
c、求两个多项式的积求并输出积多项式。
d、两个多项式和并输出和多项式。
e、销毁上述4个多项式。
(4)测试数据:第一组数据:输入:2 43 21 52 30 02 36 53 67 44 80 0输出:3.0x^2+2.0x^3+2.0x^4+1.0x^57.0x^3+7.0x^4+6.0x^5+3.0x^6+4.0x^83.0x^2+9.0x^3+9.0x^4+7.0x^5+3.0x^6+4.0x^821.0x^5+35.0x^6+46.0x^7+42.0x^8+25.0x^9+24.0x^10+11.0x^11+8.0x^1 2+4.0x^13第二组数据:输入:4 60 43 35 24 10 02 03 53 64 70 0输出:4.0x^1+5.0x^2+3.0x^3+4.0x^62.0x^0+3.0x^5+3.0x^6+4.0x^72.0x^0+4.0x^1+5.0x^2+3.0x^3+3.0x^5+7.0x^6+4.0x^78.0x^1+10.0x^2+6.0x^3+20.0x^6+27.0x^7+40.0x^8+29.0x^9+12.0x^10+1 2.0x^11+12.0x^12+16.0x^13Press any key to continue第三组数据:输入:-2 12 -33 09 57 -40 0-6 55 -6-3 49 00 0输出:7.0x^-4+2.0x^-3+3.0x^0-2.0x^1+9.0x^55.0x^-6+9.0x^0-3.0x^4-6.0x^55.0x^-6+7.0x^-4+2.0x^-3+12.0x^0-2.0x^1-3.0x^4+3.0x^535.0x^-10+10.0x^-9+15.0x^-6-10.0x^-5+63.0x^-4+18.0x^-3+45.0x^-1+6.0x^0-66.0x^1-12.0x^2-9.0x^4+69.0x^5+12.0x^6-27.0x^9-54.0x^102.概要设计(1)抽象数据类型一元多项式的定义如下:ADT Polynomial{数据对象:D={ai | ai∈TermSet,i=1,2,…,m,m≥0TermSet 中的每个元素包含一个表示系数的实数和表示指数的整数}数据关系:R1={< ai-1,ai>| ai-1, ai∈D,且ai-1中的指数值<ai中的指数值,i=2,…,n}基本操作:CreatPolyn(); //创建多项式,m为项数DestroyPolyn (Polynode &List); //销毁多项式PrintPolyn (Polynode &List); //输出多项式AddPolyn (Polynode &La,Polynode &Lb); //两个多项式相加MultipyPolyn(Polynode &La,Polynode &Lb); //两个多项式相乘} ADT Polynomial(2)主程序的流程图:开始输入两个多项式h1,h2判断h1,h2系数是否为0(3)各模块之间的调用关系如下:主程序模块单向循环列表模块3.详细设计1、1)结点类型typedef struct Pnode {float coef; //系数 int exp; //指数struct Pnode *next; //指向下一结点的指针 }Polynode;2) 基本操作函数如下:Polynode* CreatPolyn() //构造一个空的多项式并按升序排列 {Polynode *List; Polynode *p,*q,*s; int e,i=1; float c;List=(Polynode *)malloc(sizeof(Polynode)); //申请一个新结点List->next=NULL;p=List; //指向头结点 printf("请输入多项式第%d 项的系数和指数(以输入0 0结束): ",i); scanf("%f %d",&c,&e);while(c!=0) // 当系数不等于零时 {调用print()函数,输出,合并过并排好序的h1,h2调用addPoly(h1,h2),合并并输出调用multPoly(h1,h2)合并并输出结 束s=(Polynode*)malloc(sizeof(Polynode)); //申请一个新结点s->coef=c; //赋值s->exp=e;p=List; //p指向头结点q=p->next; //q为p的下一个结点while(q!=NULL&&q->exp<e) //进行循环直到q为空且q的指数大于e时{p=q;q=p->next;}s->next=q; //此时p->exp<s->exp<q->expp->next=s;i++;printf("请输入多项式第%d项的系数和指数(以输入0 0结束):",i);scanf("%f %d",&c,&e);}return(List);}void DestroyPolyn (Polynode &List) //销毁多项式{Polynode *p;Polynode *q;p=List; //p指向头结点q=p->next; //q为p的下一个结点while(q!=NULL) //当q不为空时,释放p,并将p指向下一个结点{free(p);p=q;q=p->next;}free(p); //释放最后一个结点List=NULL; //释放头结点}void PrintPolyn (Polynode &List) //输出多项式{Polynode *p=List->next;while(p!=NULL){printf("%.1fX^%d",p->coef,p->exp);if(p->next&&(p->next->coef)>0) printf("+"); //当后一项不为空且值大于零时输出加号p=p->next;}}Polynode * AddPolyn (Polynode &La,Polynode &Lb) //两个多项式相加{float sum;Polynode *newnode,*Lc;Polynode *p=La->next,*q=Lb->next,*r;Lc=(Polynode *)malloc(sizeof(Polynode)); //建立Lc r=Lc; //r指向Lc while(p!=NULL&&q!=NULL) //当p,q不为空{newnode=(Polynode *)malloc(sizeof(Polynode)); //申请新结点r->next=newnode; //r的下个结点为newnodeif(p->exp<q->exp) //La此时的指数小于Lb的指数{r->next->coef=p->coef; //将La的值赋给Lcr->next->exp=p->exp;r=r->next;p=p->next;}else if(p->exp>q->exp) //Lb此时的指数小于La的指数{r->next->coef=q->coef; //将Lb的值赋给Lcr->next->exp=q->exp;r=r->next;q=q->next;}else //La,Lb指数相等{ sum=(p->coef)+(q->coef); //将p,q的系数相加if(sum!=0) //和不等于0时{p->coef=sum;r->next->coef=p->coef; //和赋给Lcr->next->exp=p->exp; //取La的指数赋给Lcr=r->next;p=p->next;q=q->next;}else //和等于零时{ p=p->next; //跳过,La,Lb直接到下一个结点q=q->next;}}if(p!=NULL) r->next=p; //La未完else r->next=q; //Lb未完}return Lc;}Polynode* MultipyPolyn(Polynode &La,Polynode &Lb) //两个多项式相乘{Polynode *Lc,*newnode,*s;Polynode *p=La->next,*q=Lb->next;Lc=(Polynode *)malloc(sizeof(Polynode)); //建立Lcs=Lc; //s指向Lcwhile(p!=NULL) //La未完{while(q!=NULL) //Lb未完{newnode=(Polynode *)malloc(sizeof(Polynode)); //申请新结点s->next=newnode; //s的下个结点为newnodes=s->next; //s指向下个结点s->coef=(p->coef)*(q->coef); //将La,Lb系数相乘的积赋给新结点的系数s->exp=(p->exp)+(q->exp); //将La,Lb指数相加的和赋给新结点的指数q=q->next;}p=p->next; //p指向下一个结点q=Lb->next; //q从Lb的头结点开始新一轮乘法}s->next=NULL; //Lc的尾指针设为空return Lc;}(3)主函数:int main(){Polynode *La,*Lb,*Lc,*Ld;printf("请输入第一个多项式:\n");La=CreatPolyn( );printf("请输入第二个多项式:\n");Lb=CreatPolyn( );printf("按照升序排列:\n");printf("第一个多项式:\n");PrintPolyn(La);printf("\n");printf("第二个多项式:\n");PrintPolyn(Lb);printf("\n");Lc=MultipyPolyn(La,Lb);printf("积多项式:\n");PrintPolyn(Lc);printf("\n");Ld=AddPolyn(La,Lb);printf("和多项式:\n");PrintPolyn(Ld);printf("\n");DestroyPolyn(La);DestroyPolyn(Lb);DestroyPolyn(Lc);DestroyPolyn(Ld);return 0;}2、各模块流程图1)主程序模块:Main输入第一个多项式La输入第二个多项式Lb按升序排列输出第一个多项式La按升序排列输出第一个多项式Lb输出积多项式输出和多项式销毁四个多项式end2)单向循环列表模块CreatPolyn申请链表的头结点输入多项式第i项的系数和指数c,ewhile(c!=0)?noyes申请一个新结点将c,e赋值给新结点用p指向头结点,q指向p的下一个结点申请一个新结点While(q!=NULL&&q->exp<e)?Yes no遍历链表将s插入p和q之间i++;输入多项式第i项的系数和指数c,eEndDestroyPolyn用p指向头结点,q指向p的下一个结点while(q!=NULL)?yes No释放p,并将p指向下一个结点释放最后一个结点释放头结点EndPrintPolyn用p指向头结点的下一个结点while(p!=NULL)?yes No输出p的系数和指数当后一项不为空且值大于零时输出加号EndAddPolyn建立头结点用r指向头结点while(p!=NULL&&q!=NULL)?no yes申请新结点newnode用r指向newnodeLa指数小于Lb La,Lb指数相等Lb指数小于La La的值赋给Lc 将p,q的系数相加Lb的值赋给Lc和不等于0 和等于零和赋给Lc的系数跳过取La的指数赋给Lc的指数La,Lb直接到下一个结点p,q,r取下个结点La未完Lb未完Lc接La剩余值Lc接La剩余值EndMultipyPolyn建立头结点用s指向头结点while(p!=NULL)?Yes nowhile(q!=NULL)yes no申请新结点用s指向s的下个结点newnode将La ,Lb 系数相乘的积赋给新结点的系数,指数相加的和赋给新结点的指数q=q->next;p 指向下一个结点q 从Lb 的头结点开始新一轮乘法Lc 的尾指针设为空End3、函数的调用关系图4.调试分析内容包括:a .回顾讨论和分析1、在输出多项式时,没有考虑到数的正负,导致出现了+-2.0x^2类似的有歧义的表达。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据结构实验报告--Week05
姓名:覃兆坤学号:10389355
一、实验目的
用线性表实现多项式的相关操作,加强对线性表的理解和练习,熟练对线性表的操作。
二、实验题目
一个d阶多项式有如下形式:c d x d+c d−1x d−1+c d−2x d−2…+c0
其中,c d≠0,指数都是非负数。
每一个c i x i是多项式中的一项。
设计一个C++的模板类Polynomial<T>,T给出系数的类型,要求能够实现多项式的表示和运算。
Polynomial类应该包括私有变量degree,和其他需要的变量。
对多项式的表示要求用线性表的形式,例如(c0,c1,c2,…,c d)表示系数表。
并设计以下成员函数和操作:
(a) Polynomial(),创建零阶多项式,即构造函数
(b) Degree(),返回多项式的阶数degree
(c) Input(),输入多项式,指数升序依次输入每一项的指数和系数。
例如输入: 0 c0 1 c1 2 c2…d c d。
重载>>完成输入。
(d) Output(),输出多项式,和输入的格式相同。
重载<<完成输出。
(e) Add(b),和b多项式相加,并返回结果多项式。
重载+。
(f) Subtract(b),和b多项式相减返回结果多项式。
重载-。
(g) Multiply(b),和b多项式相乘返回结果多项式。
重载*。
(h) Value(x),返回x代入多项式的值。
重载( ),例如对于多项式对象P, P(x)能够返回代入x的多项式值。
三、实验设计
设计方法:
本次实现采用链表的结构,实现建立多项式,对多项式进行相加相减相乘求值的操作。
一共写了2个文件Polynomial.h和test.cpp文件。
其中前者实现多项式的相关功能,后者为人机交互式测试其功能。
1:Polynomial.h:共有2个类:
Node为一个节点其中index; modulus; next 分别为指数,系数和
指向下一个节点的指针。
Polynomial为一个多项式,私有成员有degree为多项式阶数,
head为表头指针。
公有函数:
friend ostream& operator << <T> (ostream& out,const Polynomial<T>& b);
friend istream& operator >> <T> (istream& in, Polynomial<T>& b);
Polynomial();
~Polynomial();
int Degree();
void Merger_of_similar_items();
void delete_first_zero();
Polynomial(const Polynomial& a);
Polynomial<T>& Input();
Polynomial<T>& Output();
Polynomial<T> Add( Polynomial<T>& b);
Polynomial<T> Subtract(Polynomial<T>& b);
Polynomial<T> Multiply(Polynomial<T>& b);
T Value(T &x);
Polynomial<T> operator +(Polynomial<T>& b);
Polynomial<T> operator -(Polynomial<T>& b);
Polynomial<T> operator *(Polynomial<T>& b);
T operator ()(T& b);
其中,void Merger_of_similar_items();void delete_first_zero();分别为对多项式合并同类项的操作和对多项式最高项系数为0 进行处理的函数。
其他函数的意义在此不一一解释。
2:test.cpp测试函数
while(1){
cout << "***************Polynomial**************" << endl;
cout << "1:Add 2:Subtract" << endl;
cout << "3:Multiply 4:P(x) " << endl;
cout << "0:exit " << endl;
cout << "***************************************" << endl;
实现对加法,减法,乘法,求值的操作的检验。
设计思想:
加法实现:创建一个新的链表,用于存放相加的结果。
用ptr和ptr1分别指向2个链表,指针遍历所有节点,如果2个指针指向的位置指数相同,就创建一个新的节点链在新表的后面,系数为2个相加,如果不相等,则创造2个节点,把各自表中的节点的信息复制到新表中,最后,调用合并同类型操作。
因此,本程序能够实现中间少项的操作。
减法实现:与加法类似,相应的位置改为减。
乘法实现:类似冒泡排序的方法,用一个链表的每一个元素分别与另一个链表的每一个元素相乘,结果存放在新的链表之中。
最后再调用合并同类项的函数。
输入输出申明为友元函数,必须同时申明2个类的友元函数,不能程序无法运行。
在申明之中,还要中意<T>的运用。
四、实验结果
加法的操作演示
正常减法操作演示
当相减结果最高位为0,应该去掉此项,演示如上
乘法操作演示
求值操作的演示
输入错误,提示重新输入
正常退出
五、实验心得
本次实验相比前一个实验容易一些,原因可能是对链表更加熟练了一些。
但是实验中还是出现了一些错误。
比如,作多项式相加时,对应系数相加,只考虑到了两个链表相同位置的系数相加存到新的链表,而没考虑到相同位置存的项未必是相同系数的,这是思维上漏洞,造成时间上的浪费。
乘法操作相对比较困难,合并同类项的函数的创建能够很好的分模块的解决为题,使难题迎刃而解。
在操作符重载上有一些问题就是输入输出函数申明为友元函数,必须同时申明2个类的友元函数,不能程序无法运行。
在申明之中,还要中意<T>的运用。
