吸收塔的物料衡算与操作线方程一
合集下载
气体吸收计算一
第五节 气体吸收计算在有害气体治理的吸收操作中，都是将混合气体中少量的可溶部份吸收下来，这些溶质即便全数吸收，进出塔的气体和液体的流量也改变很小，因此塔内的气体和液体的流量都可视为常数，那个特点使吸收的有关计算大为简化。
由于气体吸收多采纳塔器，因此，气体吸收计算要紧讲述吸收塔的计算。
一、吸收塔的物料衡算与操作线方程（一）物料衡算一个处于稳固操作状态下的逆流接触吸收塔。
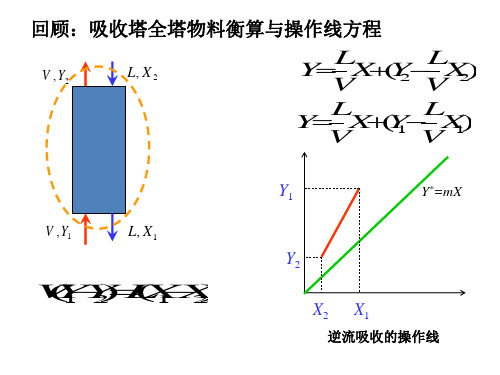
V 、L 、Y 、X 别离代表进出塔的气液流量（kmol/）和浓度（摩尔比），规定塔底为1端（浓端），塔顶为2端（稀端）。
对单位时刻内进、出塔的物料A 的量作衡算，可写出下式：一样情形下，进塔气体的组成与流量是吸收任务规定了的，若是吸收剂的组成与流量已经确信，那么V 、Y 1、L 及X 2皆为已知数，又依照吸收任务所规定的A 的吸收率，能够得知气体出塔时应有的浓度Y 2：式中 A ϕ—A 的吸生效率。
由此，通过全塔物料衡算式：(2-47) 能够求得塔底吸收液排出的浓度X 1。
于是，在填料层底部与顶部两个端面上的液、气组成X 1、Y 1及X 2、Y 2均成为已知数。
（二）吸收塔的操作线方程与操作线在逆流操作的吸收塔内，气体自下而上，其浓度由Y 1慢慢变到Y 2；液体浓()()21211221X X L Y Y V LX VY LX VY -=-+=+或()A Y Y ϕ-=112()()2121X X L Y Y V -=-度自上而下慢慢由X 2变到X 1；设图中截面m-n 处气、液浓度别离为Y 与X ，现对m-n 截面与塔底端作A 的物料衡算：或 (2-48) 对m-n 截面与塔顶端作A 的物料衡算，又得：式（2-48）与（2-48a ）是等效的，因由式（2—47）可知：式（2-48）与式（2-48a ）皆可称作逆流吸收塔的操作线方程，它说明塔内任一截面上气相浓度Y 与液相浓度X 之间成直线关系，直线的斜率为 (称为液气比)，且此直线通过B （X 1，Y 1）及T （X 2，Y 2）两点。
化工原理吸收塔的计算
填料层高度＝传质单元高度×传质单元数
（1）传质单元数（以NOG为例）
•定义：N OG
N OG
Y1
dY Y Y
*
Y2
气相总传质单元数
气相组成变化 平均传质推动力
Y1
dY Y Y
*
Y1 Y2 (Y Y ) m
*
Y2
• 传质单元数的意义： 反映了取得一定吸收效果的难易程度。
第四节
吸收塔的计算
吸收塔的计算内容：
• 设计型：流向、流程、吸收剂用量、吸收剂
浓度、塔高、塔径。
• 操作型：核算、操作条件与吸收结果的关系。
• 计算依据：物料恒算、相平衡、吸收速率方程。
一、物料衡算与操作线方程
虚框范围内，对溶质作物料衡算：
LX GY2 LX 2 GY L G Y Y Y2 X X2 L G X (Y2 L G
* mG Y1 Y2 mG ln 1 * mG L Y2 Y2 L 1 L
S
mG L
—解吸因数（脱吸因数）
影响NOG的因素：
L、G、m、X2、Y1、Y2
(1) L、G、m
L , G , m m不变, L G 推动力Ym N OG m 平衡线斜率 远离操作线 推动力Ym N OG L mG N OG
当所要求的(Y1-Y2)为一定值时，平均吸收推动力(YY*)m越大，NOG就越小，所需的填料层高度就越小。
（2）传质单元高度
•定义： H OG
G K ya
气相总传质单元高度，m。
•传质单元高度的意义:
完成一个传质单元分离效果所需的填料层高度，
（1）传质单元数（以NOG为例）
•定义：N OG
N OG
Y1
dY Y Y
*
Y2
气相总传质单元数
气相组成变化 平均传质推动力
Y1
dY Y Y
*
Y1 Y2 (Y Y ) m
*
Y2
• 传质单元数的意义： 反映了取得一定吸收效果的难易程度。
第四节
吸收塔的计算
吸收塔的计算内容：
• 设计型：流向、流程、吸收剂用量、吸收剂
浓度、塔高、塔径。
• 操作型：核算、操作条件与吸收结果的关系。
• 计算依据：物料恒算、相平衡、吸收速率方程。
一、物料衡算与操作线方程
虚框范围内，对溶质作物料衡算：
LX GY2 LX 2 GY L G Y Y Y2 X X2 L G X (Y2 L G
* mG Y1 Y2 mG ln 1 * mG L Y2 Y2 L 1 L
S
mG L
—解吸因数（脱吸因数）
影响NOG的因素：
L、G、m、X2、Y1、Y2
(1) L、G、m
L , G , m m不变, L G 推动力Ym N OG m 平衡线斜率 远离操作线 推动力Ym N OG L mG N OG
当所要求的(Y1-Y2)为一定值时，平均吸收推动力(YY*)m越大，NOG就越小，所需的填料层高度就越小。
（2）传质单元高度
•定义： H OG
G K ya
气相总传质单元高度，m。
•传质单元高度的意义:
完成一个传质单元分离效果所需的填料层高度，
化工原理第7章气体吸收
再看积分号内
y1
y2
dy ： 分子、分母具有相同的单位。 y ye
∴ 积分值为一个无因次量，把它认为相当于气相总传质
单元高度HOG的一个倍数，称它为 “气相总传质单元 数”
用“NOG”表示 即： NOG=
y1
y2
dy y ye
则，总传质总元高度H=单元高度×倍数（单元数）
H=HOGNOG
则
Kya dy dh y ye G
Kxa dx dh xe x L
稳定操作时：L、G、a、A为常数 稀溶液： K x 、K y
y1
也视为常数
∴可对上式进行在全塔范围内积分：
Kya H dy dh y2 y ye G 0 x1 Kxa H dx x2 xe x L 0 dh
取最小吸收剂用量Lmin的1.1～2倍。 L L 即 ≈（1.1～2）（ ）min G G 即 L =（1.1~2）Lmin
Lmin的求取： （1）平衡线如上图所示，则只要从T点连接y=y1 与平衡线的交点B*点即TB*，则TB*线所对应的斜率
L/G即为最小吸收剂用量下的斜率（ L ）min G y y 而( L )min= tgα= y1 y2 Lmin G 1 2 x1e x2 x1e x2 G
K x a ——液相总体积吸收系数，kmol/(m3.s)
二、传质单元高度与传质单元数
G y1 dy 分析式： Z K y a y2 y ye
其中：
G ∴ K ya
G K ya
单位为m，即高度的单位。
称为单元高度，全称“气相总传质单元
高度”。以“HOG”表示 G 即： HOG= K ya
吸收液（即出塔吸收液）中浓度加大（x1加大），则吸
吸收塔物料衡算与操作线关系
物料衡算
二、操作线方程
Y
L V
X
Y1
L V
X
1YBiblioteka L VXY2
L V
X2
当 L/V 一定，操作线方程在 Y-X 图上均呈直线， 称为吸收操作线。
Y1
斜率： L 过两点：( X1,Y1), ( X 2 ,Y2 )
V
T
L Y1 Y2 ---液气比 V X1 X2
Y2 X2
B X1
物料衡算
下标“1”代表塔内填料层下底截面， 下标“2”代表填料层上顶截面。 V —— 惰性气体B的摩尔流量kmol/s； L —— 吸收剂S的摩尔流量kmol/s； Y —— 溶质A在气相中的摩尔比浓度； X —— 溶质A在液相中的摩尔比浓度。
L, X1
物料衡算
一、 全塔物料衡算（逆流流动）
L, X2
若 GA 为吸收塔的传质负荷，即气体通过填料塔时，单位时间内 溶质被吸收剂吸收的量 kmol/s，则
V, Y
L, X V, Y1
L, X1
逆流操作线方程
若取填料层任一截面与塔的塔底端面之间的填料层为物料衡 算的范围，则所得溶质 A 的物料衡算式为
VY LX1 VY1 LX
Y
L V
X
Y1
L V
X
1
同理，若在任一截面与塔顶端面间作溶质A的物料衡算，有
Y
L V
X
Y2
L V
X2
上两式均称为吸收操作线方程，代表逆流操作时塔内任一截面上 的气、液两相组成 Y 和 X 之间的关系。
吸收技术 ---物料衡算
物料衡算
一、 全塔物料衡算（逆流流动）
目的：计算给定吸收任务下所需的吸收剂用量 L 或吸收剂出口浓度 X1。
吸收塔的物料衡算与操作线方程1
气体摩尔流量的比，即处理含单位千摩尔惰性气的原 料气所用的纯吸收剂耗用量大小。液气比对吸收设备 尺寸和操作费用有直接的影响。
吸收塔的最小液气比
当吸收剂用量增大，即操作线的斜率L V 增大，则 操作线向远离平衡线方向偏移，如图8-6中AC线所示， 此时操作线与平衡线间的距离增大，即各截面上吸收 推动力（Y Y ）增大。若在单位时间内吸收同样数量 的溶质时，设备尺寸可以减小，设备费用降低；但是 ，吸收剂消耗量增加，出塔液体中溶质含量降低，吸 收剂再生所需的设备费和操作费均增大。
最小液气比可用图解或计算法求出：
（1）图解法 一般情况下，平衡线如图所示的曲线
，则由图读出与 Y1 相平衡的的数值后，用下式计算最
小液气比：
L V
m in
Y1 Y2 X1 X 2
如果平衡线为图8-6（b）所示的曲线，则应过点作
平衡曲线的切线，由图读出点的横坐标
X
1
的数值，代
Y
L V
X
(Y2
L V
X2)
——逆流吸收塔操作线方程 表明 ：塔内任一截面的气相浓度Y与液相浓度X之间成直线
关系，直线的斜率为L/V。
二、吸收剂用量的确定
1．吸收剂的单位耗用量
由逆流吸收塔的物料衡算可知
L Y1 Y2 V X1 X2
（8-23）
在 V 、Y1 、Y2 、X 2 已知的情况下，吸收塔操作线的一个端点
若减少吸收剂用量， L V 减小，操作线向平衡线 靠近，传质推动力（ Y Y ）必然减小，所需吸收设备 尺寸增大，设备费用增大。当吸收剂用量减小到使操 作线的一个端点与平衡线相交，如图8-6中AD线所示， 在交点处相遇的气液两相组成已相互平衡，此时传质 过程的推动力为零，因而达到此平衡所需的传质面积 为无限大（塔为无限高）。这种极限情况下的吸收剂 用量称为最小吸收剂用量，用Lmin 表示，相应的液气比 称为最小液气比，用 (L V )min 表示。显然，对于一定的 吸收任务，吸收剂的用量存在着一个最低极限，若实 际液气比小于最小液气比时，便不能达到设计规定的 分离要求。
吸收塔的最小液气比
当吸收剂用量增大，即操作线的斜率L V 增大，则 操作线向远离平衡线方向偏移，如图8-6中AC线所示， 此时操作线与平衡线间的距离增大，即各截面上吸收 推动力（Y Y ）增大。若在单位时间内吸收同样数量 的溶质时，设备尺寸可以减小，设备费用降低；但是 ，吸收剂消耗量增加，出塔液体中溶质含量降低，吸 收剂再生所需的设备费和操作费均增大。
最小液气比可用图解或计算法求出：
（1）图解法 一般情况下，平衡线如图所示的曲线
，则由图读出与 Y1 相平衡的的数值后，用下式计算最
小液气比：
L V
m in
Y1 Y2 X1 X 2
如果平衡线为图8-6（b）所示的曲线，则应过点作
平衡曲线的切线，由图读出点的横坐标
X
1
的数值，代
Y
L V
X
(Y2
L V
X2)
——逆流吸收塔操作线方程 表明 ：塔内任一截面的气相浓度Y与液相浓度X之间成直线
关系，直线的斜率为L/V。
二、吸收剂用量的确定
1．吸收剂的单位耗用量
由逆流吸收塔的物料衡算可知
L Y1 Y2 V X1 X2
（8-23）
在 V 、Y1 、Y2 、X 2 已知的情况下，吸收塔操作线的一个端点
若减少吸收剂用量， L V 减小，操作线向平衡线 靠近，传质推动力（ Y Y ）必然减小，所需吸收设备 尺寸增大，设备费用增大。当吸收剂用量减小到使操 作线的一个端点与平衡线相交，如图8-6中AD线所示， 在交点处相遇的气液两相组成已相互平衡，此时传质 过程的推动力为零，因而达到此平衡所需的传质面积 为无限大（塔为无限高）。这种极限情况下的吸收剂 用量称为最小吸收剂用量，用Lmin 表示，相应的液气比 称为最小液气比，用 (L V )min 表示。显然，对于一定的 吸收任务，吸收剂的用量存在着一个最低极限，若实 际液气比小于最小液气比时，便不能达到设计规定的 分离要求。
吸收塔的计算
m，一般取Hb=1.2～1.5m；
Hb
n——填料层分层数
2020/10/22
【填料塔高度的近似计算】
【说明】由于液体再分布器、喷淋装置、支承装置、捕沫器等的结构不同时其高 度不同，当一时无法准确确定时，也可采用下式近似计算塔高：
H=1.2Z+Hd+Hb
Hd——塔顶空间高(不包括封头部分)，m； Hb——塔底空间高(不包括封头部分)，m。
∵
G 1000 273 （1－0.09）＝37.85(mol / s)
22.4 293
故吸收用水量为： L＝35.5G＝35.5×37.85＝1343(mol/s)＝1.343(kmol/s)
2020/10/22
三、吸收塔填料层高度的计算
1、填料塔的高度
【说明】填料塔的高度 主要决定于填料层高度。
（2） HOG愈小，吸收设备的传质阻力愈小，传质效能愈高，完成一定分离任务所 需填料层高度愈小。
2020/10/22
【体积传质系数（ KY a ）——参数归并法】
（1）有效比表面积（a）与填料的类型、形状、尺寸、填充情况有关，还随流体 物性、流动状况而变化，其数值不易直接测定； （2）通常将a与传质系数（KY）的乘积合并为一个物理量KY a （ 单位kmol/m3·s）， 称为体积传质系数，通过实验测定其数值； （3）在低浓度吸收的情况下，体积传质系数在全塔范围内为常数，或可取平均值。
2020/10/22
【解】已知 y1＝0.09 η＝95％＝0.95
∴
Y1
y1 1 y1
0.09 1 0.09
0.099
Y2＝(1－η)Y1＝(1－0.95)×0.099＝0.00495 据 Y*＝31.13X 知： m＝31.13
吸收塔的计算
最小液气比的求法
图解法 •正常的平衡线
(L V
)min
Y1 Y2 X1* X 2
Lmin
V
Y1 Y2
X
* 1
X
2
•平衡线为上凸形时
(L V
)
min
Y1 Y2
X
1
X
2
Lmin
V
Y1 Y2
X
1
X
2
计算法
适用条件：平衡线符合亨利定律，可用 Y * mX 表示
(L V
) m in
Y1 Y2
1、填料层高度的基本计算式
对组分A作物料衡算 单位时间内由气相转入液相的 A的物质量为：
dGA VdY LdX
dGA NAdA N A (adZ)
微元填料层内的吸收速率方程式为：
N A KY (Y Y * )及N A K X ( X * X )
dGA KY (Y Y * )adz dGA K X ( X * X )adz
试写出用膜系数及相应的推动力表示的填料层高度的计算式。
Z HG NG
HG
V k y a
—气膜传质单元高度，m
NG
Y1
Y2
Y
dY Yi
—气膜传质单元数
Z HL NL
HL
L k x a
—液膜传质单元高度，m
NL
X1
X2
dX Xi X
—液膜传质单元数
2）传质单元高度的物理意义
NOG
Y1
Y2
Lmin
V (Y1 Y2 )
Y1 m
X
2
34.5(0.0133 0.000133) 0.0133 0
0.757
化工原理吸收解析
X2 0
Lmin
G(Y1 Y2 )
Y1 m
X
2
3.125 0.096 0
869kmol / h
26.7
2020/10/31
L 1.65Lmin 1.65869 1434kmol / h
2）出塔吸收液浓度：
G(Y1 Y2 ) L(X1 X2 )
X1
X2
G(Y1 Y2 L
)
0
3.125 1434
X2 0
m 0.757
Lmin
G(Y1 Y2 )
Y1 m
X
2
34.5(0.0133 0.000133) 0.0133 0 0.757
25.8kmol/ h
L 2Lmin 2 25.8 51.6kmol/ h
2020/10/31
三、填料层高度的计算
1、填料层高度的基本计算式
对组分A作物料衡算 单位时间内由气相转入液相的 A的物质量为：
dY Y
*
Z
dZ
0
G Y1 dY Y2 KY a Y Y *
LdX KX (X * X )adZ
dZ L dX KX a X * X
Z
dZ
X1
L
dX
0
X2 K X a X * X
2020/10/31
低浓度气体吸收时填料层的基本关系式为
Z G
KY a
Y1 dY Y2 Y Y *
GdY LdX
NAdA NA(adZ )
2020/10/31
微元填料层内的吸收速率方程式为：
N A KY (Y Y * )及N A K X ( X * X )
dG KY (Y Y *)adZ dG KX (X * X )adZ
化工原理 吸收(或解析)塔计算
NOG仅与气体的进出口浓度、相平衡关系有关，与塔的结构、 操作条件(G、L)无关，反映分离任务的难易程度。
(2)传质单元高度
H
＝
OG
K
G y a
kmol 单位： m2 • s m
kmol m3 • s
HOG与操作条件G、L、物系的性质、填料几何特性有关，是吸收 设备性能高低的反映。其值由实验确定，一般为0.15~1.5米。
y4
•B
y3
E3
yN1
y2
y1 A
E1
E2
x0 x1
x2
x3
解析法求理论板数
x0
y1
平衡线方程：y=mx
y1
操作线方程：y=y1+L/G(x-x0)
由第一板下的截面到塔顶作物料衡算：
y2
y1
L G
x1
x0
y1 mx1
y2
y1
L G
y1 m
x0
(1
A) y1
Amx0
1
2
x1 y2
x2 y3
xN 2 y N 1
N 11 A A1
N－1
N xN 1 y N
yN 1
xN
y2
x2
吸收
y1
x1
y1
解吸
y2
六、塔板数
• 板式塔与填料塔的区别在于组成沿塔高是阶跃 式而不是连续变化的。
x0
y1
1
x1 y2
2
x2 y3
xN 2 y N 1
N－1
yN
N xN 1
xN
理论板：气液两相在塔板上充分接触， 传质、传热达平衡。
相平衡关系：yn f (xn )
化工原理下2-4吸收计算
KYa 气相 总体积吸收系数(Kmol.m-3.s-1) Kxa 液相 总体积吸收系数
2、传质单元高度与传质单元数
Z V Y1 dY
KYa Y2 YY*
K Y V a Ω (k m o l/m (k 2 s m )(o m l/2s/)m 3)(m 2) m
令HOG＝KYVa，[m]
处理量V 一定
L ～ L/V
～ 动力
消耗
操作 费用
～ ～ 推动
力
填料层 高度
设备 费用
根据生产实践经验，取
VL1.1~2.0VLmin 适宜液气比
L1.1~2.0Lm in 适宜溶剂用量
6
2.3.3 塔径的计算
工业上的吸收塔通常为圆柱形，故吸收塔的直 径可根据圆形管道内的流量公式计算，即
π 4
D
2u
15
（3）传质单元高度的影响因素
H
＝
OG
K
V Y a
与 V/ Ω、KYa（反映传质阻力、填料性能、润 湿情况等）有关
对每种填料而言，传质单元高度变化不大，查有 关资料或经验公式计算
（4）传质单元数的影响因素
反应吸收过程的难易程度：
N ＝Y1 OG Y2
dY Y Y*
• 任务所要求的气体浓度变化（Z
Z V Y1 dY
KYa Y2 YY*
同 理 ： Z L X1 KXaX2
dX X*X
Y+dY
截
X+dX
面
积
Ω
V,Y1
L,X1
Z V Y1 dY
KYa Y2 YY*
Z L X1 dX
KXa X2 X*X
a 有效比表面： • 被流动的液体膜层覆盖的填料表面。 • 与填料形状、尺寸填充情况有关；流体流 动情况有关 • 难测定
吸收塔的计算
最小液气比的计算 1. 平衡曲线一般情况
L V
min
Y1 Y2
X
* 1
X2
X*1——与Y1相平衡的液相组成。
返回
平衡关系符合亨利定律时：
L V
2. 平衡曲线为凸形曲线情况
min
Y1 Y2
Y1 m
X2
Y1
L V
min
Y1 Y2 X1,max X 2
Y2
Y1 C
Y2
D
Y3
A
X1 X2
B
X3 返回
5.5.2 吸收剂用量的确定
E
Y1
B
B1
Y
P
A Y2
O X2 X1
X
X*1
返回
一、最小液气比 最小液气比定义：针对一定的分离任务，操作条 件和吸收物系一定，塔内某截面吸收推动力为零， 达到分离程度所需塔高无穷大时的液气比。
L V min
返回
（4）吸收操作线在平衡线的上方，解吸操作线在平 衡线OE下方。
（5）平衡线与操作线共同决定吸收推动力。操作线 离平衡线愈远吸收的推动力愈大；
Y
B Y* f (X)
Y
K.
Y* A
X
X* X
返回
2. 并流吸收
VY+LX=VY2+ LX2
L
L
Y
V
X
(Y2
V
X2)
逆流与并流的比较：
况增加还是减少？塔底吸收液组成变为多少？
已知101.3kPa，20℃条件下SO2在水中的平衡数据与 Y1相平衡的液相组成=0.0032
一,吸收塔的物料衡算和操作线方程
第三节 吸收过程的计算一、吸收塔的物料衡算和操作线方程设：稳定流动V —惰性气体的摩尔流量。
kmol/hL —吸收剂的摩尔流量。
kmol/hY 1、X 1—塔底气液组成；Y 2、X 2—塔顶气液组成；1.全塔物料衡算（逆流）气相：Y 1 ↘Y 2 ；吸收质减少量：V （Y 1 -Y 2）。
液相：X 2↗X 1； 吸收质增加量：L （X 1- X 2）。
G A —单位时间内气相向液相转移的吸收质的量kmolA/h ；出塔液组成： 2211)(X Y Y LV X +-= 吸收过程中常以吸收率φ作为分离指标，既气相中被吸收的溶质占气相中原有溶质的百分数。
1211211)(Y Y Y VY Y Y V VY G A -=-==φ 练习题：一填料吸收塔，用来从空气和丙酮蒸气组成的混合气中吸收丙酮，用水作吸收剂。
已知混合气中丙酮蒸气的体积分数为6%，所处理的混合气中空气量为1400m 3/h,操作温度293K ，操作压强101.3kp ，要求丙酮的吸收率达到98%，若吸收剂用量为154kol/h ，求：出塔液的浓度。
（X A ）2．操作线方程与操作线在 m —n 截面与塔底截面之间作组分A 的衡算气相：Y 1 ↘Y ；吸收质减少量：V （Y 1 -Y ）。
液相：X ↗X 1； 吸收质增加量：L （X 1- X ）。
AG X X L Y Y V =-=-)()(2121)1(12φ-=Y Y即： ——吸收操作线方程（逆流） 在m —n 截面与塔顶截面之间作组分A 的衡算得： 操作线意义：塔内任一截面处的气相浓度Y 与液相浓度X 之间的变化关系。
操作线为过B （X 1、Y 1）点，斜率为L/V 的一条直线。
又：XX Y Y X X Y Y V L --=--=112121 操作线过塔底B （X 1、Y 1）及塔顶A （X 2、Y 2）点，斜率为L/V 。
塔底B （X 1、Y 1）→浓端；塔顶A （X 2、Y 2）→稀端L/V ——液气比。
吸收剂用量的确定
第六章 吸收
第四节 吸收塔的计算
一、吸收塔的物料衡算与操作线方程
1、物料衡算
目的 ： 确定各物流之间的量的关系 以及设备中任意位置两物料
组成之间的关系。
对单位时间内进出吸收塔的A的物
质量作衡算
VY1 LX 2 VY2 LX 1
V (Y1 Y2 ) L( X1 X 2 )
L L Y1 X 1 Y2 X 2 V V
随堂习题
4、清水吸收焦炉气中的氯化氢，已知混合气体中 氯化氢的比摩尔分率0.015kmolHCl/kmol载体，载 体流量200kmol/h，氯化氢的吸收率为90%，吸收剂 用量为最小流量的2倍，操作条件下平衡关系Y* =1.2X，求吸收剂的用量。
随堂习题
5、在常压逆流填料吸收塔中，用清水吸收焦炉气中氨，焦 炉气处理量为100Kmol/h，进塔气体组成5%（摩尔分率）。 氨的回收率为90%。水的用量为最小用量的2倍。操作条件 下平衡关系为Y* =1.5X（X ,Y 为摩尔比）。求水的用量及 出塔溶液浓度。
Lmin
Y1 Y2 V Y1 X2 m
例：空气与氨的混合气体，总压为101.33kPa，其中氨的分 压为 1333Pa，用 20 ℃的水吸收混合气中的氨，要求氨的回 收率为99%，每小时的处理量为1000kg空气。物系的平衡关 系列于本例附表中，若吸收剂用量取最小用量的2倍，试
求每小时送入塔内的水量。
Y2 (1 0.99)Y1 0.01 0.0133 0.000133
X2 0
Lmin
m 0.757
V (Y1 Y2 ) 34.5(0.0133 0.000133) 0.0133 Y1 0 X2 0.757 m
第四节 吸收塔的计算
一、吸收塔的物料衡算与操作线方程
1、物料衡算
目的 ： 确定各物流之间的量的关系 以及设备中任意位置两物料
组成之间的关系。
对单位时间内进出吸收塔的A的物
质量作衡算
VY1 LX 2 VY2 LX 1
V (Y1 Y2 ) L( X1 X 2 )
L L Y1 X 1 Y2 X 2 V V
随堂习题
4、清水吸收焦炉气中的氯化氢，已知混合气体中 氯化氢的比摩尔分率0.015kmolHCl/kmol载体，载 体流量200kmol/h，氯化氢的吸收率为90%，吸收剂 用量为最小流量的2倍，操作条件下平衡关系Y* =1.2X，求吸收剂的用量。
随堂习题
5、在常压逆流填料吸收塔中，用清水吸收焦炉气中氨，焦 炉气处理量为100Kmol/h，进塔气体组成5%（摩尔分率）。 氨的回收率为90%。水的用量为最小用量的2倍。操作条件 下平衡关系为Y* =1.5X（X ,Y 为摩尔比）。求水的用量及 出塔溶液浓度。
Lmin
Y1 Y2 V Y1 X2 m
例：空气与氨的混合气体，总压为101.33kPa，其中氨的分 压为 1333Pa，用 20 ℃的水吸收混合气中的氨，要求氨的回 收率为99%，每小时的处理量为1000kg空气。物系的平衡关 系列于本例附表中，若吸收剂用量取最小用量的2倍，试
求每小时送入塔内的水量。
Y2 (1 0.99)Y1 0.01 0.0133 0.000133
X2 0
Lmin
m 0.757
V (Y1 Y2 ) 34.5(0.0133 0.000133) 0.0133 Y1 0 X2 0.757 m
物料衡算和操作线方程
5－2 物料衡算和操作线方程
一、全塔物料衡算 F=D+W FxF DxD WxW
D
Dx D FxF
100%
W
W (1 xD ) 100% F(1 xF )
二、精馏段操作线方程
总物料衡算 V=L+D
①
易挥发组分衡算 Vyn+1=Lxn+DxD ②
①代入② 令 R L
D
回流比
三、q 线方程（进料方程）
Vy=Lx+DxD ① V'y=L'x－WxW ②
进料板连接着精馏段与提 馏段，因此组成相同，下 标省略！
① － ②：
1.0
（V'－V）y=(L'－L)x－(DxD+WxW)
q=1 q>1
a
0<q<1
（q－1)F y=q F x－F xF
y q x xF q 1 q 1 ——q线方程
L
D
yn1 L D xn L D xD
yn1
R R
1
xn
R
1
1
xD
精馏段操作线方程
V, y1
L, xD 1 2
3
n
L, xn
n+1 V, yn+1
D, xD
精馏段操作线方程式表示在一定条件下，精馏段内任意一块
板（第n板）下降的液相组成xn与其相邻的下一块板（第n+1
板）上升的气相组成yn+1
IL≈IL'
代入②式并 与①联立
V,IV
L,IL
V’, IV’ L’, IL’
（V－V'） IV =F IF－(L'－L) IL
一、全塔物料衡算 F=D+W FxF DxD WxW
D
Dx D FxF
100%
W
W (1 xD ) 100% F(1 xF )
二、精馏段操作线方程
总物料衡算 V=L+D
①
易挥发组分衡算 Vyn+1=Lxn+DxD ②
①代入② 令 R L
D
回流比
三、q 线方程（进料方程）
Vy=Lx+DxD ① V'y=L'x－WxW ②
进料板连接着精馏段与提 馏段，因此组成相同，下 标省略！
① － ②：
1.0
（V'－V）y=(L'－L)x－(DxD+WxW)
q=1 q>1
a
0<q<1
（q－1)F y=q F x－F xF
y q x xF q 1 q 1 ——q线方程
L
D
yn1 L D xn L D xD
yn1
R R
1
xn
R
1
1
xD
精馏段操作线方程
V, y1
L, xD 1 2
3
n
L, xn
n+1 V, yn+1
D, xD
精馏段操作线方程式表示在一定条件下，精馏段内任意一块
板（第n板）下降的液相组成xn与其相邻的下一块板（第n+1
板）上升的气相组成yn+1
IL≈IL'
代入②式并 与①联立
V,IV
L,IL
V’, IV’ L’, IL’
（V－V'） IV =F IF－(L'－L) IL
化工原理第五章(吸收塔的计算)
2020/4/3
【解】已知 y1＝0.09 η＝95％＝0.95
∴
Y1
y1 1 y1
0.09 1 0.09
0.099
Y2＝(1－η)Y1＝(1－0.95)×0.099＝0.00495
据 Y*＝31.13X 知： m＝31.13
据
L (G )min
Y1 Y2 Y1 / m X 2
∴
L
0.099 0.00495
2020/4/3
2、填料层高度的基本计算式 【计算依据】 （1）物料衡算式； （2）传质速率方程式。 【操作特点】在填料塔内任一截面上的吸收的推动 力（Y－Y*）均沿塔高连续变化，所以不同截面上 的传质速率各不相同。 【处理方法】不能对全塔进行计算，只可首先对一 微分段计算，得到微分式，然后得到积分式运用于 全塔。
质的摩尔比。
物料衡算示意图
逆流吸收操作线推导示意图
2020/4/3
【假设】溶剂不挥发，惰性气体不溶于溶剂（即操作
过程中L、G为常数）。以单位时间为基准，在全塔
范围内，对溶质A作物料衡算得： G, Y2
L, X2
GY1 LX2 GY2 LX1
（进入量＝引出量）
或 G(Y1 Y2 ) L(X1 X2 )
2020/4/3
Y Y1 Y Y2 Y*
0
2020/4/3
NA KY (Y Y *) NA KX ( X * X )
Y=f(X)
吸收推动力 X*－X
吸收推动力 Y－Y*
X2
X
X1
X*
X
吸收推动力
二、吸收剂用量与最小液气比
1、最小液气比 【定义】对于一定的分离任务、操作条件和吸收物 系，当塔内某截面吸收推动力为零时（气液两相平 衡Y－Y*＝0），达到分离要求所需塔高为无穷大时 的液气比称为最小液气比，以（L/G）min表示。
【解】已知 y1＝0.09 η＝95％＝0.95
∴
Y1
y1 1 y1
0.09 1 0.09
0.099
Y2＝(1－η)Y1＝(1－0.95)×0.099＝0.00495
据 Y*＝31.13X 知： m＝31.13
据
L (G )min
Y1 Y2 Y1 / m X 2
∴
L
0.099 0.00495
2020/4/3
2、填料层高度的基本计算式 【计算依据】 （1）物料衡算式； （2）传质速率方程式。 【操作特点】在填料塔内任一截面上的吸收的推动 力（Y－Y*）均沿塔高连续变化，所以不同截面上 的传质速率各不相同。 【处理方法】不能对全塔进行计算，只可首先对一 微分段计算，得到微分式，然后得到积分式运用于 全塔。
质的摩尔比。
物料衡算示意图
逆流吸收操作线推导示意图
2020/4/3
【假设】溶剂不挥发，惰性气体不溶于溶剂（即操作
过程中L、G为常数）。以单位时间为基准，在全塔
范围内，对溶质A作物料衡算得： G, Y2
L, X2
GY1 LX2 GY2 LX1
（进入量＝引出量）
或 G(Y1 Y2 ) L(X1 X2 )
2020/4/3
Y Y1 Y Y2 Y*
0
2020/4/3
NA KY (Y Y *) NA KX ( X * X )
Y=f(X)
吸收推动力 X*－X
吸收推动力 Y－Y*
X2
X
X1
X*
X
吸收推动力
二、吸收剂用量与最小液气比
1、最小液气比 【定义】对于一定的分离任务、操作条件和吸收物 系，当塔内某截面吸收推动力为零时（气液两相平 衡Y－Y*＝0），达到分离要求所需塔高为无穷大时 的液气比称为最小液气比，以（L/G）min表示。
3物料衡算 吸收剂 化工原理
§2.4.4 低浓气体吸收时填料层高度
一．填料层高度的一般计算式
单位时间内:
Y2 Y X X2
气相中溶质 A 的减少量 = 液相中溶质 A 的增加量 = 从气相到液相的传质量
Z
dh
填料层所具有的有效传 质面积 引入 a 填料体积
X+dX Y+dY
VdY LdX
N AdA N A (adh)
Y1
V X Y Y2 X 2 L
S Y Y2 Y2
V Y mX b m Y Y2 mX 2 b L
mV 脱吸因数，无因次 S L
L A 吸收因数，无因次 mV
Y
N OG
*
S Y Y2 Y2
S
或:
若平衡关系可用亨利定律来表示 :
• 如果平衡曲线呈现如下图
二、适宜的液气比
在吸收任务一定的情况下，吸收剂用量越小， 溶剂的消耗、输送及回收等操作费用减少，但吸 收过程的推动力减小，所需的填料层高度及塔高 增大，设备费用增加。 可见，吸收剂用量的大小，应从设备费用与操 作费用两方面综合考虑，选择适宜的液气比，使 两种费用之和最小。根据生产实践经验，一般情 况下取吸收剂用量为最小用量的1.1～2.0倍是比较 适宜的，即：
§2.4 吸收塔的计算
§2.4.1吸收塔的物料衡算与操作线方程 一、物料衡算
V (Y1 Y2 ) L( X1 X 2 )
图中 V——单位时间通过吸收塔的惰性气体量， kmol(B)/s； L——单位时间通过吸收塔的溶剂量， kmol(S)/s； Y1、Y2——进塔、出塔气体中溶质组分 的摩尔比，kmol(A)/kmol(B) ； X1、X2——出塔、进塔液体中溶质组分 的摩尔比，kmol(A)/kmol(S)。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
吸收剂
y yi
yi N xi
xi x
气 (a)吸 收 塔
N （ b)浓 度 分 布
由膜模型传质理论，气相传质速率可表示为
N A kG ( pG pi ) kG P ( pG pi ) P P
令 得
k y kG P
N A k y ( y yi )
同理，由膜模型理论，液相传质速率式为
pA* ExA
若溶质在液相中的浓度用物质的量浓度ｃ表示，则亨 利定律可表示成：
p A* cA H
若溶质在液相和气相中的浓度分别用摩尔分率 x 与 y 表 示，则亨利定律可表示成
y* mx
• 8.3 吸收过程模型及传质速率方程
8.3.1双膜模型在吸收中的应用 气体吸收是把气相中的溶质传到液相的过程，即相际 间的传质。它由气相与界面的对流传质、界面上溶质组 分的溶解、界面与液相的对流传质三个步骤串联而成。
二、吸收过程分类 按照吸收过程是否伴有化学反应将吸收区分为化学 吸收和物理吸收两大类。 在气体吸收中，若混合气体中只有一个组分在吸收 剂中有一定的溶解度，其余的组分的溶解度可以忽略， 这样的吸收过程称为单组分吸收。如果有两个或更多的 组分能溶解于吸收剂中，这一过程称为多组分吸收。 在吸收过程中，当气体溶解于液体中时，通常有溶 解热产生，若进行伴有放热的化学吸收时，还要放出反 应热，因此随着吸收过程的进行液相温度要逐渐增高， 这样的吸收称为非等温吸收。但若热效应很小，或被吸 收的组分浓度很低，且吸收剂的用量较大，则温度的变 化不显著，此时吸收过程可认为是等温吸收。
i * i *
或
( y yi ) / m x* xi
不同的推动力所对应的不同传质系数和速率方程。
表8—1 传质速率方程的各种形式 浓度组成表示法 摩尔分率 物质得量浓度或分压
N A k y ( y yi )
传质速率方程
N A kG ( pG pi )
k x (ci cL ) kG ( pG pL* ) k L (cG* cL )
N A k L (ci cL ) k LC ( ci cL ) C C
令 得
k x kLC
N A kx ( xi x)
8.3.2传质速率方程 一、传质速率方程
y a 斜率 E A
如图所示，吸收塔一截面气 y P y x 液两相主体浓度在 y B 上可用一点a表示。此点一般 0 不在平衡线上。如双膜模型 x x x 图 8－ 4 主 体 浓 度 与 截 面 浓 度 示 意 图 假设成立，表示界面上两相 组成关系的点Ｐ必位于平衡 线上。若在Ｐ点附近两项组成x，y所涉及的范围内，平衡 县可近似看成斜率为m的直线（若服从亨利定律，则ｍ为 相平衡常数）则 m( xi x) yi y*
cA* f ( pA )
当然，也可以选择液相的浓度 c 作自变量，这时，在 * 一定温度下的气相平衡分压 p A 和 cA 的函数：
A
pA* f (cA )
气液平衡关系一般通过实验方法对具体物系进行测定。
8.2.2亨利定律 亨利定律是稀溶液重要的经验定律，在低压（通常 指总压小于0.5MPa）和一定温度下，气液相达到平衡状 态时，其数学表达式如下：
Kx C KL
K y P KG
k x ( xi x) k y ( y y* ) k x ( x* x )
Ky 1 1 m k y kx
1 H 1 kG k L
k x C kL
其中
cG* HpG , cL HpL*
1 1 1 kG Hk L
k y P kG
第八章
8.1 概述
气体吸收
8.2 吸收过程相平衡基础 8.3 吸收过程模型及传质速率方程 8.4 吸收（或脱吸）塔计算 8.5 其他类型吸收
一、气体吸收在化工中的应用 吸收是将气体混合物与适当的液体接触，利用个组 分在液体中溶解度的差异而使气体中不同组分分离的操 作。混合气体中，能够溶解于液体中的组分称为吸收质 或溶质；不能溶解的组分称为惰性气体；吸收操作所用 的溶剂称为吸收剂；溶有溶质的溶液称为吸收液或简称 溶液；派出的气体称为吸收尾气。 吸收操作是气体混合物的主要分离方法，化工生产 中它有以下几种具体的应用： １．化工产品 ２．分离气体混合物 ３．从气体中回收有用组分 ４．气体净化(原料气的净化和尾气、废气的净化) ５．生化工程
KL
总传质系数
KL
K y m Kx K G HK L
Kx
1 1 1 k y m kx
二、界面浓度的求取 当ｍ随浓度变化时，用分传质速率方程式计算更加方 便，界面浓度 xi 与 yi 存在关系有： （1）有双膜模型理论，yi 与 xi 在平衡线上。如果平衡线以
y f ( x) 表示，则 yi f ( xi ) 。
F c 2 3 2 2 3
即在温度、总压和气、液组成共四个变量中，有三个是 自变量，另一个是它们的函数。
在一定的操作温度和压力下，溶质在液相中的溶解 度由其相中的组成决定。在总压不很高的情况下，可以 认为气体在液体中的溶解度只取决于该气体的分压 pA ， cA*与 pA 得函数关系可写成 而与总压无关。于是，
三、工业吸收过程 工业的吸收过程常在吸收塔中进行。生产中除少部分直 接获得液体产品的吸收操作外，一般的吸收过程都要求 对吸收后的溶剂进行再生，即在另一称之为解析他的设 备中进行于吸收相反的操作－解吸。因此，一个完整地 吸收分离过程一般包括吸收和解吸两部分。
8.2 吸收过程相平衡基础
8.2.1气液相平衡关系 气体混合物与溶剂 S相接触时，将发生溶质气体向 液相的转移，使得溶液中溶质（A）的浓度增加。充分 接触后的气液两相，液相中溶质达到饱和，此时瞬间内 进入液相的溶质分子数与从液相逸出的溶质分子数恰好 相抵，在宏观上过程就像停止一样，这种状态称为相际 动平衡，简称相平衡或平衡。 对于单组分物理吸收，组分数 c=3 （溶质 A 、惰性 气体B、溶剂S），相数（气、液），自由度数F应为
y yi
yi N xi
xi x
气 (a)吸 收 塔
N （ b)浓 度 分 布
由膜模型传质理论，气相传质速率可表示为
N A kG ( pG pi ) kG P ( pG pi ) P P
令 得
k y kG P
N A k y ( y yi )
同理，由膜模型理论，液相传质速率式为
pA* ExA
若溶质在液相中的浓度用物质的量浓度ｃ表示，则亨 利定律可表示成：
p A* cA H
若溶质在液相和气相中的浓度分别用摩尔分率 x 与 y 表 示，则亨利定律可表示成
y* mx
• 8.3 吸收过程模型及传质速率方程
8.3.1双膜模型在吸收中的应用 气体吸收是把气相中的溶质传到液相的过程，即相际 间的传质。它由气相与界面的对流传质、界面上溶质组 分的溶解、界面与液相的对流传质三个步骤串联而成。
二、吸收过程分类 按照吸收过程是否伴有化学反应将吸收区分为化学 吸收和物理吸收两大类。 在气体吸收中，若混合气体中只有一个组分在吸收 剂中有一定的溶解度，其余的组分的溶解度可以忽略， 这样的吸收过程称为单组分吸收。如果有两个或更多的 组分能溶解于吸收剂中，这一过程称为多组分吸收。 在吸收过程中，当气体溶解于液体中时，通常有溶 解热产生，若进行伴有放热的化学吸收时，还要放出反 应热，因此随着吸收过程的进行液相温度要逐渐增高， 这样的吸收称为非等温吸收。但若热效应很小，或被吸 收的组分浓度很低，且吸收剂的用量较大，则温度的变 化不显著，此时吸收过程可认为是等温吸收。
i * i *
或
( y yi ) / m x* xi
不同的推动力所对应的不同传质系数和速率方程。
表8—1 传质速率方程的各种形式 浓度组成表示法 摩尔分率 物质得量浓度或分压
N A k y ( y yi )
传质速率方程
N A kG ( pG pi )
k x (ci cL ) kG ( pG pL* ) k L (cG* cL )
N A k L (ci cL ) k LC ( ci cL ) C C
令 得
k x kLC
N A kx ( xi x)
8.3.2传质速率方程 一、传质速率方程
y a 斜率 E A
如图所示，吸收塔一截面气 y P y x 液两相主体浓度在 y B 上可用一点a表示。此点一般 0 不在平衡线上。如双膜模型 x x x 图 8－ 4 主 体 浓 度 与 截 面 浓 度 示 意 图 假设成立，表示界面上两相 组成关系的点Ｐ必位于平衡 线上。若在Ｐ点附近两项组成x，y所涉及的范围内，平衡 县可近似看成斜率为m的直线（若服从亨利定律，则ｍ为 相平衡常数）则 m( xi x) yi y*
cA* f ( pA )
当然，也可以选择液相的浓度 c 作自变量，这时，在 * 一定温度下的气相平衡分压 p A 和 cA 的函数：
A
pA* f (cA )
气液平衡关系一般通过实验方法对具体物系进行测定。
8.2.2亨利定律 亨利定律是稀溶液重要的经验定律，在低压（通常 指总压小于0.5MPa）和一定温度下，气液相达到平衡状 态时，其数学表达式如下：
Kx C KL
K y P KG
k x ( xi x) k y ( y y* ) k x ( x* x )
Ky 1 1 m k y kx
1 H 1 kG k L
k x C kL
其中
cG* HpG , cL HpL*
1 1 1 kG Hk L
k y P kG
第八章
8.1 概述
气体吸收
8.2 吸收过程相平衡基础 8.3 吸收过程模型及传质速率方程 8.4 吸收（或脱吸）塔计算 8.5 其他类型吸收
一、气体吸收在化工中的应用 吸收是将气体混合物与适当的液体接触，利用个组 分在液体中溶解度的差异而使气体中不同组分分离的操 作。混合气体中，能够溶解于液体中的组分称为吸收质 或溶质；不能溶解的组分称为惰性气体；吸收操作所用 的溶剂称为吸收剂；溶有溶质的溶液称为吸收液或简称 溶液；派出的气体称为吸收尾气。 吸收操作是气体混合物的主要分离方法，化工生产 中它有以下几种具体的应用： １．化工产品 ２．分离气体混合物 ３．从气体中回收有用组分 ４．气体净化(原料气的净化和尾气、废气的净化) ５．生化工程
KL
总传质系数
KL
K y m Kx K G HK L
Kx
1 1 1 k y m kx
二、界面浓度的求取 当ｍ随浓度变化时，用分传质速率方程式计算更加方 便，界面浓度 xi 与 yi 存在关系有： （1）有双膜模型理论，yi 与 xi 在平衡线上。如果平衡线以
y f ( x) 表示，则 yi f ( xi ) 。
F c 2 3 2 2 3
即在温度、总压和气、液组成共四个变量中，有三个是 自变量，另一个是它们的函数。
在一定的操作温度和压力下，溶质在液相中的溶解 度由其相中的组成决定。在总压不很高的情况下，可以 认为气体在液体中的溶解度只取决于该气体的分压 pA ， cA*与 pA 得函数关系可写成 而与总压无关。于是，
三、工业吸收过程 工业的吸收过程常在吸收塔中进行。生产中除少部分直 接获得液体产品的吸收操作外，一般的吸收过程都要求 对吸收后的溶剂进行再生，即在另一称之为解析他的设 备中进行于吸收相反的操作－解吸。因此，一个完整地 吸收分离过程一般包括吸收和解吸两部分。
8.2 吸收过程相平衡基础
8.2.1气液相平衡关系 气体混合物与溶剂 S相接触时，将发生溶质气体向 液相的转移，使得溶液中溶质（A）的浓度增加。充分 接触后的气液两相，液相中溶质达到饱和，此时瞬间内 进入液相的溶质分子数与从液相逸出的溶质分子数恰好 相抵，在宏观上过程就像停止一样，这种状态称为相际 动平衡，简称相平衡或平衡。 对于单组分物理吸收，组分数 c=3 （溶质 A 、惰性 气体B、溶剂S），相数（气、液），自由度数F应为