经济计量学第五章异方差与自相关问题PPT课件
计量经济学庞皓课件(第五章 异方差性)

绘制出
ei2
对
X
的散点图
i
◆如果 ui 不随 Xi 而变化,则表明不存在异方差;
◆如果 ui 随 Xi 而变化,则表明存在异方差。
19
二、Goldfeld-Quanadt检验
作用:检验递增性(或递减性)异方差。
基本思想:将样本分为两部分,然后分别对两个样 本进行回归,并计算两个子样的残差平方和所构成 的比,以此为统计量来判断是否存在异方差。
E(Yi ) 1 2 X 2i 3X3i ... k X ki (5.2)
的分散程度,因此同方差性指的是所有观测值的
分散程度相同。
6
异方差性的含义
设模型为
Yi 1 2 X2i 3 X3i ... k X ki ui i 1, 2,..., n
如果对于模型中随机误差项 ui 有:
即认为存在异方差性。
38
第四节 异方差性的补救措施
主要方法:
●模型变换法 ●加权最小二乘法 ●模型的对数变换
39
一、模型变换法
以一元线性回归模型为例:
Yi 1 2 X i ui
经检验 ui 存在异方差,且
var(ui )
2 i
2
f
(Xi)
其中 σ 2是常数,f (Xi ) 是 X i的某种函数。
40
变换模型时,用 f (Xi) 除以模型的两端得:
Yi = f(Xi )
β1 f(X i
)
+
β2
Xi + f(Xi )
ui f(Xi )
记 Yi* 则有:
Yi f (Xi)
;
X
* i
Xi f (Xi)
; 1*
Yi*
计量经济学第五章

Variables-Likelihood Ratio • 出现对话框时,写入删除变量名--OK • 对比删除前后的AIC与SC信息值,信息
值小的结论是应采纳的。
9
用Eviews的误设定检验3
• 第一,估计出简单(单纯)方程 • 第二,在命令窗口上写入genr v_hat=resid 或者 Procs/Generate Series中 v_hat=resid 发现 v_hat • 第三,估计出新的回归方程
无约束模型(U)
有约束模型(K) (general to simple)
计算统计量F
F=(RSSK-RSSu)/J RSSu/(n-k-1)
~F(J, n-k)
J 为表示约束条件数, K 为表示自变量数 或者 应估计的参数数, n 为表示样本数(obs)
4
2. LM检验(Lagrange Multiplier
多重共线性多出现在横截面资料上。
16
三、异方差性的检验及对策
Var(ℇi)≠Var(ℇj) (i≠j)时, ℇi中存在异方差性(Herteroskedasticity)。 即随机项中包含着对因变量的影响因素。 异方差性多发生在横截面资料上。
17
异方差性的检验
1.图示检验法 如模型为Yi=0+1X1i+2X2i+…+ℇi 时,
7
用Eviews的误设定检验1
• 首先估计出简单(单纯)方程 • View/Coefficient Tests/Omitted
Variables-Likelihood Ratio • 出现对话框时,写入新变量名 OK • 检验结果出现在上端,如果P值很小时, 拒
庞浩 计量经济学5第五章 异方差性

同方差
递增型异方差
递减型异方差
复杂型异方差
18
2.借助X-e2散点图进行判断 观察散点的纵坐标是否随解释变量Xi的变化而 变化。
~2 e2e i ei e2 ~2
X 同方差 递增异方差
X
e2
~2 e i
~2 e 2 e i
X 递减异方差 复杂型异方差
X
19
二、戈德菲尔德—夸特 (Goldfeld-Quanadt)检验
3
说明1
矩阵表示: Y X u 随机扰动项向量 其方差—协 u1 u 方差矩阵不 2 u 再是: un n1 而是:
2 2 Var Cov ( ui ) 2 nn
ei X i v i
ei
1 vi Xi
ei X i v i 1 ei vi Xi
③利用上述回归的R2、t统计量、F统计量等判断,R2 好、t统计量和F统计量显著,即可判定存在异方差。 28
说明: 1.也可以用 e i 与可能产生异方差的多个解释变 量进行回归模拟; 2.戈里瑟检验的优点在于不仅检验了异方差是否 存在,同时也给出了异方差存在时的具体表现 形式,为克服异方差提供了方便。 3.试验模型选得不好,也可能导致检验不出是否 存在异方差性。
12 2 2 Var Cov ( ui ) 2 n nn
4
说明2
随机扰动项 ui具有异方差性,可理解释为被解释变量 的条件分散程度随解释变量的变化而变化,如下图所 示:var( ui ) i2 2 f ( X i)(i 1,2,, n)
10
第二节 异方差性的后果
第五讲 异方差和自相关ppt课件

42
Cochrane-Orcutt(1949) 估计(舍弃第一期观察 值)
prais D.rs LD.r20,corc
prais D.rs LD.r20,rho(dw) corc Prais-Winsten(1954) 估计(对第一期观察值进行 处理 sqrt(1-rho^2)*y1)
prais D.rs LD.r20
estat hettest,rhs (使用方程右边的解释变量,而
不是yˆ )
最初的BP 检验假设扰动项服从正态分布,有一定局
限性。Koenker(1981)将此假定放松为iid,在
实际中较多采用,其命令为:
estat hettest, iid
estat hettest, rhs iid
整理版课件
16
系数完全相同,但标准差和t值不同。
整理版课件
40
可行广义最小二乘法(FGLS):广义差分法:
CO-PW方法Cochrane-Orcutt(1949) 估计 (舍弃第一期观察值)
Prais-Winsten(1954) 估计(对第一期观察值 进行处理 sqrt(1-rho^2)*y1)
整理版课件
41
整理版课件
1
n
E
121n nn1n2va1 r)( co1 v ,(n) 2 0
2I
con v,(1) varn)( 0 2
整理版课件
2
此时可得:
Var()2(X'X)1
在存在异方差的情况下:
V a r ()2 (X 'X ) 1 X ' X (X 'X ) 1
estat hettest,normal
整理版课件
计量经济学自相关性课件

t (b)
et 1
如图(b)所示,扰动项的估计值呈锯齿状,随时间 逐次改变符号,表明存在负相关。
二、D-W检验
(一) 假定条件
1、假定变量X是非随机的; 2、随机误差项为一阶自回归形式,即
ut ut 1 t (且误差项 t 满足古典假定 );
3、无滞后的内生变量作为解释变量; 4、截距项不为零; 5、无缺损数据
ts
注:自相关多出现在时间序列数据中。
二、自相关性产生的原因
1、经济变量惯性的作用 由于经济发展存在一定的趋势(自相关性主要产生于时间序列),形成惯性,所 以许多经济变量前后期总是相互关联的,即期的变量受以前各期的影响。这样,
在建立回归模型时,随机扰动项将会序列相关。
例如:当年的投资规模与前一年、甚至前几年的投资有关; 当期家庭消费水平在很大程度受上期消费水平的制约; 企业第 t 期的产量与第 t-1、t-2、--- 期密切相关。 2、滞后效应
Yt 0 1 X 1t 2 X 2t 3Yt 1 t Yt 0 1 X 1t 2 X 2t t
则随机干扰项很可能有自相关。
3、随机偶然因素的干扰
战争、自然灾害等偶然(随机)因素的干扰造成的影响,常常要延续若干时期,反 映在模型中就是干扰项有序列相关。
将残差对时间描点。
如图(a)所示,扰动项的估计值呈循环形,并不频繁地改变符号, 而是相继若干个正的以后跟着几个负的。表明存在正自相关。
et
. . . . . . . . . . .
et
.
. . .. . . . . .. .
.
. .
.
.
. . .
t
et 1
计量经济学课件-异方差

PPT文档演模板
2020/12/8
计量经济学课件-异方差
PPT文档演模课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
PPT文档演模板
计量经济学课件-异方差
3rew
演讲完毕,谢谢听讲!
再见,see you again
PPT文档演模板
2020/12/8
计量经济学课件-异方差
计量经济学课件:第五章-异方差性汇总
第五章异方差性本章教学要求:根据类型,异方差性是违背古典假定情况下线性回归模型建立的另一问题。
通过本章的学习应达到,掌握异方差的基本概念包括经济学解释,异方差的出现对模型的不良影响,诊断异方差的方法和修正异方差的方法。
经过学习能够处理模型中出现的异方差问题。
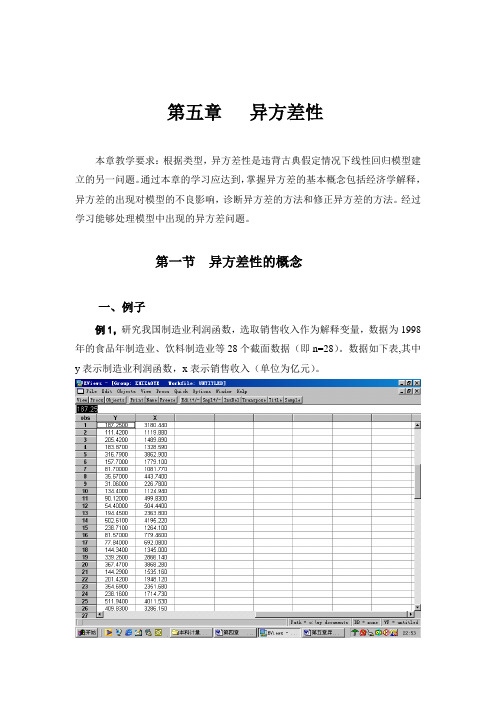
第一节异方差性的概念一、例子例1,研究我国制造业利润函数,选取销售收入作为解释变量,数据为1998年的食品年制造业、饮料制造业等28个截面数据(即n=28)。
数据如下表,其中y表示制造业利润函数,x表示销售收入(单位为亿元)。
Y对X的散点图为从散点图可以看出,在线性的基础上,有的点分散幅度较小,有的点分散幅度较大。
因此,这种分散幅度的大小不一致,可以认为是由于销售收入的影响,使得制造业利润偏离均值的程度发生了变化,而这种偏离均值的程度大小不同是一种什么现象?如何定义?如果非线性,则属于哪类非线性,从图形所反映的特征看并不明显。
下面给出制造业利润对销售收入的回归估计。
模型的书写格式为2ˆ12.03350.1044(0.6165)(12.3666)0.8547,..84191.34,152.9322213.4639,146.4905Y YX R S E FY s =+=====通过变量的散点图、参数估计、残差图,可以看到模型中(随机误差)很有可能存在一种系统性的表现。
例2,改革开放以来,各地区的医疗机构都有了较快发展,不仅政府建立了一批医疗机构,还建立了不少民营医疗机构。
各地医疗机构的发展状况,除了其他因素外主要决定于对医疗服务的需求量,而医疗服务需求与人口数量有关。
为了给制定医疗机构的规划提供依据,分析比较医疗机构与人口数量的关系,建立卫生医疗机构数与人口数的回归模型。
根据四川省2000年21个地市州医疗机构数与人口数资料对模型估计的结果如下:i iX Y 3735.50548.563ˆ+-= (291.5778) (0.644284) t =(-1.931062) (8.340265)785456.02=R 774146.02=R 56003.69=F式中Y 表示卫生医疗机构数(个),X 表示人口数量(万人)。
异方差、自相关、多重共线性比较(计量经济学)

基本思想:
由OLS法得到残差e,取e的绝对值,然后将此绝对值对某个解释变量X回归,根部回归模型的显著性和拟合优度来判断是否存在异方差。
操作步骤:
1.根据样本数据建立回归模型,并求残差序列e.
2.用残差绝对值对X进行回归,由于|e|与X的真实函数形式并不知道,可用各种函数形式去试验,从中选择最佳形式。
2.quick/equation estimation输入“e2 c e2(-1) e2(-2) e2(-3) e2(-4) e2(-5) e2(-6)”
3.view/residual diagnostics/heteroskedasticity tests,选择arch。
2.Quick/graph,在series list对话框中输入“e(-1) e”,选择scatter’,得到e(-1)与e的散点图。
方法二:1.用OLS估计Resid→e。
2.Quick/graph,在series list对话框中输入“e”,得到e随时间t的变化图示。
操作思想
操作步骤
适用性
软件操作
实际检验中可逐次向更高阶检验,并结合辅助回归中滞后项参数的显著性去帮助判断自相关的阶数。
ห้องสมุดไป่ตู้DW检验
操作思想:
DW与ρ的关系:DW≈2(1-ρ)
ρ的取值范围0≤DW≤4.
根据样
本容量n和解释变量的数目k'(不包括常数项),查DW分布表,可得临界值dl和du,
DW取值范围
自相关状态
[0,dl]
正自相关
(dl,du]
5.判断。给定显著性水平α,查F分布表,得临界值。 > ,拒绝 ,反之不拒绝 。
适用性:
该方法得到的F分布是近似的,而且只是对异方差是否存在进行判断,在多个解释变量的情况下,对判断是哪一个变量引起异方差还存在局限。此检验方法也可将样本分为多个组,从中任选两个组进行检验。
计量经济学第五章 异方差

X 20000
5.3异方差的侦查
利用残差图——绘制残差平方与X散点图
(一般把异方差看成是由于解释变量的变化而引起的)
5.1异方差的概念
三、异方差产生的原因 模型设定误差:省略了重要的解释变量
例:真实模型 Yi 1 2 X 2i 3 X 3i i 采用模型 Yi 1 2 X 2i i
如果X3随着X2的不同而对Y产生不同的影响,则 该影响体现在扰动项中。
测量误差: 一方面,测量误差常常在一定时间内逐渐增加,如X 越大,测量误差就会趋于增大 另一方面,测量误差随时间变化趋于减少,如抽样技 术的改进使得测量误差减少。
)
2 i
5.1异方差的概念
6 Y
4
300 Y
200
2
100
0 0
X
0
X
10
20
30
0
5000
10000
15000
20000
250
Y
二、常见的异方差类型: 200
递增型异方差:
150
100
递减型异方差:
50
条件异方差(略):
0 0
X
10
20
30
时间序列数据和截面数据中都有可能存在异方差。
经济时间序列中的异方差常为递增型异方差。
ˆ 2 ei2 (Yi ˆX i )2 (( ˆ) X i i )2
n 1
n 1
n 1
5.2异方差的后果
E (vaˆr(ˆ ))
E(
ˆ 2
X
2 i
)
E(
(( ˆ)X
(n 1)
计量经济学ppt课件 自相关

原因4-蛛网现象
许多农产品的供给呈现为 蛛网现象,供给对价格的 反应要滞后一段时间,因 为供给需要经过一定的时
间才能实现。如果时期 t
的价格 Pt 低于上一期的 价格 Pt-1 ,农民就会减少 时期 t 1的生产量。如
此则形成蛛网现象,此时 的供给模型为:
蛛网现象是微观经济学中的 一个概念。它表示某种商品 的供给量受前一期价格影响 而表现出来的某种规律性, 即呈蛛网状收敛或发散于供 需的均衡点。
18
第二节 自相关的后果
➢OLS估计虽然是线性无偏的,但不再是有 效的估计。 ➢OLS估计的标准误差估计不再准确(通常 是低估) ➢参数显著性 t 检验失效(通常是高估) ➢模型预测精度下降
19
第三节 自相关的检验
本节基本内容:
图示检验法 DW检验法 序列相关的LM检验
20
一、图示检验法
需要人为设定滞后期长度,一般从s=1开始, 多试几次,比如直到s=10左右。如果检验结 果均不显著,则可以认为不存在自相关性。
3399
第四节 自相关的补救
本节基本内容:
●相关系数已知时:广义差分法 ●计算相关系数:科克伦-奥克特迭代法 ●其他方法简介
40
一、广义差分法
对于自相关的结构已知的情形可采用广义差分法解决。
而建立模型时,模型设定为: Yt = 1 + 2 X 2t + ut
则 X3t 对 Yt 的影响便归入随机误差项 ut 中,由于 在不同观测点上是相关的,这就造成了 ut 在不同 观测点是相关的,呈现出系统模式,此时 ut 是自
相关的。
13
模型形式设定偏误也会导致自相关现象。如将成本 曲线设定为线性成本曲线,则必定会导致自相关。 由设定偏误产生的自相关是一种虚假自相关,可通 过改变模型设定予以消除。
计量经济学 第五章 异方差 ppt课件

H0:ut不存在异方差, H1:ut存在异方差。
10
5.4 异方差检验
(2) White检验
④在同方差假设条件下,统计量
TR 2 2(5)
其中T表示样本容量,R2是辅助回归式的OLS估计的可决系数。 自由度5表示辅助回归式中解释变量项数(注意,不计算常数 项)。T R 2属于LM统计量。 ⑤判别规则是
2
1
0
-1
1
0 20 40 60 80 100 120 140 160 180 200
-2
-3 0
T
50
100
150
200
散点图
残差图
7
5.4 异方差检验
(1) Goldfeld-Quandt 检验
H0: ut 具有同方差, H1: ut 具有递增型异方差。
①把原样本分成两个子样本。具体方法是把成对(组)的观 测值按解释变量顺序排列,略去m个处于中心位置的观测值 (通常T 30时,取m T / 4,余下的T- m个观测值自然分成 容量相等,(T- m) / 2,的两个子样本。)
主对角线上的部分或全部元素都不为零,误差项就是自相关的。
异方差通常有三种表现形式,(1)递增型,(2)递减型,(3)条件自回
归型。 7
Байду номын сангаас
6
Y 6
4
DJ P Y
5
2
4
0
3
-2
2
-4
1
-6
0 20 40 60 80 100 120 140 160 180 200
-8
计量经济学 自相关PPT课件

et 2 ≈
et
2 1
≈
et 2
t2
t2
t 1
T
T
2
et
2 1
2
et et1
T
et et1
所以 DW 可以近似表示为, DW≈ t2
t2
T
et
2 1
= 2 (1 - t2
) = 2 (1 - ˆ )
T
et
2 1
t2
t2
第6页/共23页
6.3 自相关检验
DW= 2 (1 - ˆ )
的取值范围是 [-1, 1],所以DW统计量的取值范围是 [0, 4]。
H0: = 0 (ut 不存在自相关)。H1: 0 (ut 存在一阶自相关) 用残差值 et 计算统计量 DW。
DW =
T
(et et1 ) 2
t2
=
T
et 2
t 1
T
T
T
et 2
et
2 1
2
et et1
t2
t2
t2
T
et 2
t 1
(第2版167页) (第3版142页)
T
T
T
因为在样本容量充分大条件下有
(第2版177页) (第3版151页)
1. 用 DW 统计量的值计算。
ˆ = 1 -(DW / 2)
2. 直接拟合估计。
第12页/共23页
6.6 案例分析
(第2版177页) (第3版152页)
例6.1 天津市城镇居民人均消费与人均可支配收入的关系。
天津市城镇居民人均消费性支出(CONSUM),人均可支配收入(INCOME)关
LM(BG)自相关检验辅助回归式估计结果是
异方差

第一节 异方差的概念
例:以某一行业的企业为样本建立企业生产函数模 型 Yi=Ai1 Ki2 Li3ei 被解释变量:产出量Y 解释变量:资本K、劳动L、技术A, 那么:每个企业所处的外部环境对产出量的影响被 包含在随机误差项中。 每个企业所处的外部环境对产出量的影响程度不同 ,造成了随机误差项的异方差性。 这时,随机误差项的方差并不随某一个解释变量观 测值的变化而呈规律性变化,呈现复杂型。
第三节 异方差性的检验
三、戈里瑟(Gleiser)检验 1969年戈里瑟提出的,它不但可以检验异方差是 否存在,而且可以近似探测随机误差项的方差是 怎样随解释变量的变化而变化的。 基本思想:由OLS法得到残差 e i ,取 e i 的绝对 值 ,然后将 对某个 X i回归,根据回归模 ei ei 型的显著性和拟合优度来判断是否存在异方差。
二、异方差性的后果
ˆ
2
e
2 i
n2
ˆ s(1 )
ˆ ki
2
2
ˆ2
(Xi X )
2
但是,在异方差的情况下
ˆ* s( i ) ˆ ki i
2 2
ˆ i ki
2 2
ˆ ki
2
2
i ki ki
2
2
=
ˆ s(i )
i Байду номын сангаасi
第三节 异方差性的检验
计量经济学异方差精品PPT资料

• 一般经验,对于采用截面数据作样本的 计量经济学问题,由于不同样本点上解
释变量以外的其他因素的差异较大,所 以往往存在异方差。
二、异方差性的后果 Consequences of Using OLS in the
Presence of Heteroskedasticity
V ar(i)E(i2)e ~ i2 最 好 在 大 样 本 条 件 下 (使 2用 .4 .7)
即 用 e ~ i2来 表 示 随 机 误 差 项 的 方 差 。
从而可进一步考察其与X的相关性及其具体的形式。
( 2 1 ) X - e ~ i 2 的 散 点 图 进 行 判 断
看是否形成一斜率为零的直线
问题在于如何获得随机误差项 (从总体带来的)的方差
• 问题在于如何获得随机误差项 (从总体带 WLS估计的Eviews软件的实现
以案例1为例:由于不知ei与Xi之间具体的函数关系。
i
来的)的方差 从而可进一步考察其与X的相关性及其具体的形式。
White1980年提出。 假设6:随机项满足正态分布
一般的处理方法:
2 任 意 选 择 c 个 中 间 观 测 值 略 去 . 经 验 表 明 , 略 去 数 目 c 的 大 小 , 大 约 相 当 于
样 本 观 测 值 个 数 的 1 .剩 下 的 n c 个 观 测 值 平 均 分 成 两 组 , 每 组 观 测 值 的 个 数 为 n c.
4
2
(3)对每个子样本分别进行OLS,并分别计算各自的残差平方和。
E
X
X
1
X
X
X
X
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
co ~ ) v2 ( (X 1 X ) 1
(c)伪协方差矩阵
2(XX)1
§5.2 异方差问题
(一)异方差概念
vaU ri)(Ei2 U i2
2 i
(i1,2, ,n)不全相同
vaYir)(vaU ri)(
异方差概念理解
(二)异方差的检测
U i Y i (0 1 X 1 i k X k )i
{ai ,bi}
i1,,n
并由此产生等级变量 a 与 b 。a与 b 的线性相关系数,称为 q
与 z的等级相关系数 。
rs
(ai a)b(i b) (ai a)2 (bi b)2
rs
16(ai bi)2
n(n2 1)
§5.2 异方差问题
等级相关检验
(a) 完成模型的OLS估计,获取残差数据 e i ;
f (X j1)
f (X j1)
X12
Xk2
f (X j2)
f (X j2)
X1n f (X jn)
f
Xkn (X jn)
Y~ Y f (X j)
X~i
Xi f (X j)
X~0
1 f (X j)
i1,,k
Y ~ 0 X ~ 0 1 X ~ 1 k X ~ k U ~
§5.3 异方差模型的估计
§5.3 异方差模型的估计
(三)异方差模型的广义最小平方估计
Y1 Y2 Yn
1 1 1
X 11 X 12
X 1n
X k1 X k2
X kn
f f f
Y1
(X j1) Y2
(X j2) Yn
(X jn)
1
f (X j1) 1
f (X j2) 1
f (X jn)
X11
Xk1
4
的观测值序号为准,进行相应的删与留,形成A、B两个子样本;
(b)两个子样本分别进行OLS估计,获取两个残差平方和:
e
2 i
A
e
2 i
B
(c)构造统计量 Fei2 ei2或
A
B
Fei2 ei2;
B
A
(d)根据显著性水平,以及双自由度 nc (k 1) ,查取 F 分布临 2
界值 F 。若经比较 F F ,则接受模型存在单调形式的异方差,否
Actual
Fitted
§5.3 异方差模型的估计
例5.1 异方差性的等级相关检验
rs 0.5594
T2.8632
t 2.101 2
等级相关检验表明模型存在递增形式的异方差。
例5.1 异方差性的 F检验
按照销售收入水平的排序,从中心删去第9-12号样本点,形成
两个子样本A与B:
ei2 1.451
则拒绝异方差。
§5.3 异方差模型的估计
(一)广义最小平方估计对于异方差模型的意义
1
1
d12
1 d
2 n
(Y ~X ~~)(Y ~X ~~)(YX ~) 1(YX ~) d 1 i2ei2
对于与具有较小方差相应的残差,给以较大的权数,使其在确定回
归函数时,起较为重要的作用。或者说使回归函数主要参照那些对应
e i Y i (ˆ 0 ˆ 1 X 1 i ˆ k X k)i
1. 图示法 ( X ji ,Yi )
(X ji ,ei )
§5.2 异方差问题
2. 等级相关检验 : 等级相关系数
设变量 q 与 z有 n组观测值,
{qi , zi }
i1,,n
按照某种性能,同方向分别指定各观测值的等级:
第五章 异方差与自相关问题
除了本章讨论所涉及的同方差性与不自相关性以外, 关于线性回归模型的其它假定在本章中都成立。 ——广义最小平方估计; ——异方差模型及其估计; ——自相关模型及其估计; ——异方差模型、自相关模型的预测。
§5.1 广义最小平方法
同方差且不自相关 coU v)(2I
异方差或自相关 covU()2 正定
t ,则判定 2
模型存在单调形式的异方差,否则拒绝异方差。
§5.2 异方差问题
3. F 检验
(a)选择可能与异方差有关的解释变量 X j 。将 X j的样本观测值由小到
大进行排列,然后从这一排列的中心删去约 n c 的观测值,并使剩余的
两个子列具有相同数目(
c n
2
)的观测值。再对模型中的其余变量,以
较小方差的样本点而被决定。
§5.3 异方差模型的估计
(二)参数 d i
的估计
P
1 d1
1
d
n
散点图( X ji , ei )e f(Xj)V
几种常见的可供参考的函数形式:
e 0 X j
取 d 为函数 f ( X j ) 中的可变部分 : X j
X
1 j
Xj
YXU PPI
Y~X~U ~ (~)
——(~)模型满足关于线性回归模型的全部基本假定,(~)模型
的普通最小平方估计将给出系数 的线性无偏最小方差估计。
~ (X 1X ) 1X 1 Y
§5.1 广义最小平方法
三个所谓协方差矩阵
(a)OLS估计 ˆ 的协方差矩阵
co ˆ) v2 ( ( X X ) 1 X X (X X ) 1
FA
ei2 37.169
B
ei2
F B 25.616
ei2
A
检验表明模型存在递增形式的异方差。
§5.3 异方差模型的估计
例5.1 的广义最小平方估计
试探性考虑异方差的 e X 形式, 1 。经过若干次试验最
后选取
e f(X)X1.7
4
3
ABSE
2
1
0
0
50
100
150
200
X
§5.3 异方差模型的估计
(b) 选择可能与异方差有关的解释变量rs ( j),计算变量 X j 与变 量 e 的等级相关系数 X j ;
(c) 计算统计量
Tj
rs ( j) n 2 1 rs2 ( j)
;
(d)T j 近似服从自由度为n2 的 t分布。根据显著性水平
t 及自由度 n2,查取
分布临界值 t 2
。如果
Tj
(四)异方差模型示例5.1
设 Y 表示商场利润总额,X表示商场销售收入。北京市20家最大
的百货商店的销售资料 ,商场按照销售收入规模从大到小排序。
Y ˆ0.51 60.06X 68
15
残差图提示递增
10
形式的异方差。
4
5
2
0
0
-2
-4 2
4 6 8 10 12 14 16 18 20
Residual
施实变换
Y ~YX 1.7
X ~1X0.7
X ~0X1.7
(~)模型的OLS估计结果: Y ~ ˆ0.63 X ~070.07 X ~12
(-2.087) (6.636) DW1.980 F14.747
0.008
0.006
0.004 0.002 0.000
0.004 0.002 0.000
