计量经济学异方差实验报告二

合集下载

异方差性实验报告doc

异方差性实验报告篇一：计量经济学上机实验报告(异方差性)提示：打包保存时自己的文件夹以“学号姓名”为文件夹名，打包时文件夹内容包括：本实验报告、EViews工作文件。

篇二：Eviews异方差性实验报告实验一异方差性【实验目的】掌握异方差性问题出现的来源、后果、检验及修正的原理，以及相关的Eviews操作方法。

【实验内容】以《计量经济学学习指南与练习》补充习题4-16为数据，练习检查和克服模型的异方差的操作方法。

【4-16】表4-1给出了美国18个行业1988年研究开发（R&D）费用支出Y与销售收入X的数据。

请用帕克（Park）检验、戈里瑟（Gleiser）检验、G-Q检验与怀特（White）检验来检验Y关于X的回归模型是否存在异方差性？若存在【实验步骤】一检查模型是否存在异方差性1、图形分析检验（1）散点相关图分析做出销售收入X与研究开发费用Y的散点相关图（SCATX Y）。

观察相关图可以看出，随着销售收入的增加，研究开发费用的平均水平不断提高，但离散程度也逐步扩大。

这说明变量之间可能存在递增的异方差性。

（2）残差图分析首先对数据按照解释变量X由小至大进行排序（SORT X），然后建立一元线性回归方程（LS Y C X）。

因此，模型估计式为： Y?187.507?0.032*X ----------（*） ?(0.17)(2.88) R2=建立残差关于X的散点图，可以发现随着X增加，残差呈现明显的扩大趋势，表明存在递增的异方差。

2、Park检验建立回归模型（LS Y C X），结果如（*）式。

生成新变量序列： GENR LNE2 = LOG(RESID^2)GENR LNX = LOG(X)生成新残差序列对解释变量的回归模型（LS LNE2 C LNX）。

从下图所示的回归结果中可以看出，LNX的系数估计值不为0且能通过显著性检验，即随机误差项的方差与解释变量存在较强的相关关系，即认为存在异方差性。

异方差实验报告

《计量经济学》实训报告实训项目名称异方差的检验及修正实训时间 2011年12月13日实训地点班级学号姓名实训(实践) 报告实训名称异方差的检验及修正一、实训目的深刻理解异方差性的实质、异方差出现的原因、异方差的出现对模型的不良影响（即异方差的后果），掌握估计和检验异方差性的基本思想和修正异方差的若干方法；能够运用所学的知识处理模型中的出现的异方差问题，并要求初步掌握用EViews处理异方差的基本操作方法。

二、实训要求使用教材第五章的数据做异方差的图形法检验、Goldfeld-Quanadt检验与White检验，使用WLS法对异方差进行修正。

三、实训内容1、用图示法、戈德菲尔德、white验证法，验证该模型是否存在异方差。

2、用加权最小二乘法消除异方差。

四、实训步骤练习题5.8数据1998年我国重要制造业销售收入和销售利润的数据Y—销售利润，x—销售收入1. 用OLS方法估计参数，建立回归模型：ls y c x回归结果如下：Y=12.036+0.1044x;S = (19.5178) (0.00844)T= (0.6167) (12.3667)R^2=0.8547 S.E.=56.90372.检验是否存在异方差(1) 图形检验：残差图形scat x e2结果表明：残差平方e2对解释变量的x的散点图主要分布在图形的下方，大致看出残差平方随X 的变动呈增大的趋势，因此，模型很可能出现异方差。

(2)戈德菲尔德-夸特检验首先，对变量进行排序，在这个题目中，我选择递增型排序，这是y与x将以x按递增型排序。

然后构造子样本区间，建立回归模型。

在本题目中，n=28,删除中间的1/4,的观测值，即大约8个观测值，剩余部分平分得两个样本区间：1—10和19-28，他们的样本个数均为10。

用OLS方法得到前10个数的样本结果(ls y c x)：用OLS方法得到后10个数的样本结果（ls y c x）：接着，根据戈德菲尔德检验得到F统计量：（两个残差平方和相除，大的除以小的）F=63769.67/2577.969=24.736。

计量经济学异方差检验

计量经济学实验报告【实验名称】异方差的检验和修正【实验目的】掌握用Eviews 检验模型中异方差问题的检验和补救方法，能够正确理解和分析Eviews的输出结果【实验内容】（1）试利用OLS法建立人均消费性支出与可支配收入的线性模型；（2）检验模型是否存在异方差性；（3）如果存在异方差性，试采用适当的方法估计模型参数。

【结果分析】1.建立模型打开Eviews软件，选中File\New\Workfile以创建一个工作文件，文件结构类型为undated。

在命令栏中输入“data X Y”，回车后得到一个未命名的组，向组中输入数据。

如下图。

设可支配收入为变量X（横坐标），消费性支出为变量Y（纵坐标），选中Quick\Graph，在出现的对话框中输入“X Y”，点击OK后在新出现的Graph对话框中，在Graph type中选择Categorical Graph下的scatter，点击OK，如下图所示：以X 为解释变量，Y 为被解释变量，建立一元线性回归方程：i 0i i Y =+*X ββ选中Object/New Objects ，在新建对象对话框中选中对象为Equation ，在出现的对话框中输入“y c x ”，进行回归分析，得到如下结果。

可以得出0β=725.3459 1β =0.664746 线性回归方程为：i Y =0β+1β *X=725.3459+0.664746*X（1.589047）（22.49622）2R=0.945802 F=506.0798由散点图可知，原模型很可能存在异方差性，为此，进一步的进行更精确的检验。

G-Q检验：升序排列去掉中间的7个样本，剩余24个样本，再分成两个样本容量为12的子样本，对两个子样本分别用OLS法作回归：键入命令Smpl 1 12Equation eq01.Is Y C XSmpl 20 31Equation eq02.Is Y C X完成对两个子样的回归；0β’=669.5344 1β’=0.677374i Y =0β’+ 1β’*X=669.5344+0.677374*X子样1： (0.281991) (3.490176)RSS1=1971249i Y =1179.053+0.644719*X子样2： (0.954140) (9.951062) RSS2=8403437计算F 统计量：F=197124984034371112/21-1-12/1=--）（）（RSS RSS =4.263 在5%的显著性水平下，自由度为（10,10）的F 分布的临界值为4.263，于是拒绝同方差的原假设，表明模型存在异方差。

计量经济学异方差实验报告及心得体会

计量经济学异方差实验报告及心得体会一、实验简介本实验旨在通过构建模型来研究经济学中的异方差问题，并通过实证分析来探讨其对模型结果的影响。

实验数据采用随机抽样方法自真实经济数据中获取，共包括两个自变量和一个因变量。

在实验中，我将对模型进行两次回归分析，一次是假设无异方差问题，一次是考虑异方差问题，并比较两个模型的结果。

二、实验过程1.数据准备：根据实验设计，我根据随机抽样方法，从真实经济数据中抽取了一部分样本数据。

2.模型建立：我将自变量Y和X1、X2进行回归分析。

首先，我假设模型无异方差问题，得到回归结果。

然后，我将检验异方差性，若存在异方差问题，则建立异方差模型继续回归分析。

3.模型估计：利用最小二乘法进行参数估计，并计算回归结果的标准差和假设检验。

4.模型比较：对比两个模型的回归结果，分析异方差对模型拟合程度和参数估计的影响。

三、实验结果1.无异方差假设模型回归结果：回归方程：Y=0.9X1+0.5X2+2.1标准差：0.3显著性水平：0.05拟合优度：0.852.考虑异方差问题模型回归结果：回归方程：Y=0.7X1+0.4X2+1.9标准差：0.6显著性水平：0.05拟合优度：0.75四、实验心得体会通过本次实验，我对计量经济学中的异方差问题有了更深入的了解，并进一步认识到其对模型结果的影响。

1.异方差问题的存在会对统计推断结果产生重要影响。

在本次实验中，考虑异方差问题的模型相较于无异方差模型，参数估计值差异较大，并且拟合优度也有所下降。

因此，我们在实证分析中应尽可能考虑异方差问题。

2.在实际应用中，异方差问题可能较为普遍。

经济学中的许多变量存在异方差性，例如，个体收入、消费支出等。

因此，在进行经济学研究时，我们应当警惕并尽量排除异方差问题。

3.针对异方差问题，我们可以采用多种方法进行调整，例如，利用异方差稳健标准误、加权最小二乘法等。

在本次实验中，我们采用了异方差模型进行调整，并得到了相对较好的结果。

计量异方差实验报告

一、实验背景与目的随着经济全球化、信息化的发展，计量经济学在各个领域的应用越来越广泛。

然而，在实际应用中，由于数据的特点和模型设定等因素的影响，异方差现象常常出现。

异方差现象会导致估计结果的偏差和统计推断的无效，因此，对异方差的检验和修正成为计量经济学中的重要问题。

本实验旨在通过实证分析，掌握异方差的检验和修正方法，提高对计量经济学模型的理解和应用能力。

二、实验数据与模型1. 数据来源本实验数据来源于某地区2000-2019年的居民消费数据，包括居民消费性支出、可支配收入、商品价格指数等变量。

2. 模型设定根据数据特点，本实验建立如下线性回归模型：消费性支出= β0 + β1 可支配收入+ β2 商品价格指数+ ε其中，β0为截距项，β1和β2为回归系数，ε为误差项。

三、实验步骤1. 异方差检验（1）图示法首先，将消费性支出与可支配收入、商品价格指数进行散点图绘制，观察是否存在明显的线性关系。

若存在明显的线性关系，则进一步进行异方差检验。

（2）Breusch-Pagan检验对上述线性回归模型进行Breusch-Pagan检验，以判断是否存在异方差。

检验方法如下：H0：模型不存在异方差H1：模型存在异方差计算Breusch-Pagan统计量，并根据自由度和显著性水平查表得到临界值。

若统计量大于临界值，则拒绝原假设，认为模型存在异方差。

2. 异方差修正若检验结果表明模型存在异方差，则采用加权最小二乘法（WLS）进行修正。

（1）确定权重根据异方差检验结果，计算每个观测值的权重。

权重计算公式如下：w_i = 1 / σ_i^2其中，σ_i^2为第i个观测值的方差。

（2）加权最小二乘法估计利用加权最小二乘法对模型进行估计，得到修正后的回归系数。

四、实验结果与分析1. 异方差检验结果根据图示法，消费性支出与可支配收入、商品价格指数之间存在明显的线性关系。

Breusch-Pagan检验结果显示，在5%的显著性水平下，统计量大于临界值，拒绝原假设，认为模型存在异方差。

异方差实验报告步骤(3篇)

第1篇一、实验目的1. 掌握异方差性的基本概念和检验方法。

2. 学会运用统计软件进行异方差的检验和修正。

3. 提高对计量经济学模型中异方差性处理能力的实践应用。

二、实验原理1. 异方差性：在回归分析中，若回归模型的误差项（残差）的方差随着自变量或因变量的取值而变化，则称模型存在异方差性。

2. 异方差性的检验方法：图形检验、统计检验（如F检验、Breusch-Pagan检验、White检验等）。

3. 异方差性的修正方法：加权最小二乘法（WLS）、广义最小二乘法（GLS）等。

三、实验步骤1. 数据准备1. 收集实验所需数据，确保数据质量和完整性。

2. 对数据进行初步处理，如剔除异常值、缺失值等。

2. 模型设定1. 根据研究问题，选择合适的回归模型。

2. 利用统计软件（如Eviews、Stata等）进行初步的回归分析。

3. 异方差性检验1. 图形检验：绘制散点图，观察残差与自变量或因变量的关系，初步判断是否存在异方差性。

2. 统计检验：- F检验：检验回归系数的显著性。

- Breusch-Pagan检验：检验残差平方和与自变量或因变量的关系。

- White检验：检验残差平方和与自变量或因变量的多项式关系。

4. 异方差性修正1. 若检验结果表明存在异方差性，则需对模型进行修正。

2. 选择合适的修正方法：- 加权最小二乘法（WLS）：根据残差平方与自变量或因变量的关系，计算权重，加权最小二乘法进行回归分析。

- 广义最小二乘法（GLS）：根据残差平方与自变量或因变量的关系，选择合适的方差结构，广义最小二乘法进行回归分析。

5. 结果分析1. 对修正后的模型进行回归分析，观察回归系数的显著性、拟合优度等指标。

2. 对实验结果进行分析，解释实验现象，验证研究假设。

6. 实验报告撰写1. 撰写实验报告，包括以下内容：- 实验目的- 实验原理- 实验步骤- 实验结果- 分析与讨论- 结论2. 实验报告应结构清晰、逻辑严谨、语言简洁。

计量经济学多元线性回归多重共线性异方差实验报告

计量经济学实验报告多元线性回归、多重共线性、异方差实验报告一、研究目的和要求：随着经济的发展，人们生活水平的提高，旅游业已经成为中国社会新的经济增长点。

旅游产业是一个关联性很强的综合产业，一次完整的旅游活动包括吃、住、行、游、购、娱六大要素，旅游产业的发展可以直接或者间接推动第三产业、第二产业和第一产业的发展。

尤其是假日旅游，有力刺激了居民消费而拉动内需。

2012年，我国全年国内旅游人数达到亿人次，同比增长%，国内旅游收入万亿元，同比增长%。

旅游业的发展不仅对增加就业和扩大内需起到重要的推动作用，优化产业结构，而且可以增加国家外汇收入，促进国际收支平衡，加强国家、地区间的文化交流。

为了研究影响旅游景区收入增长的主要原因，分析旅游收入增长规律，需要建立计量经济模型。

影响旅游业发展的因素很多，但据分析主要因素可能有国内和国际两个方面，因此在进行旅游景区收入分析模型设定时，引入城镇居民可支配收入和旅游外汇收入为解释变量。

旅游业很大程度上受其产业本身的发展水平和从业人数影响，固定资产和从业人数体现了旅游产业发展规模的内在影响因素，因此引入旅游景区固定资产和旅游业从业人数作为解释变量。

因此选取我国31个省市地区的旅游业相关数据进行定量分析我国旅游业发展的影响因素。

二、模型设定根据以上的分析，建立以下模型Y=β0+β1X1+β2X2+β3X3+β4X4+Ut参数说明：Y ——旅游景区营业收入/万元X1——旅游业从业人员/人X2——旅游景区固定资产/万元X3——旅游外汇收入/万美元X4——城镇居民可支配收入/元收集到的数据如下（见表）：表 2011年全国旅游景区营业收入及相关数据（按地区分）数据来源：1.中国统计年鉴2012，2.中国旅游年鉴2012。

三、参数估计利用做多元线性回归分析步骤如下：1、创建工作文件双击图标，进入其主页。

在主菜单中依次点击“File\New\Workfile”，出现对话框“Workfile Range”。

计量经济学实验二

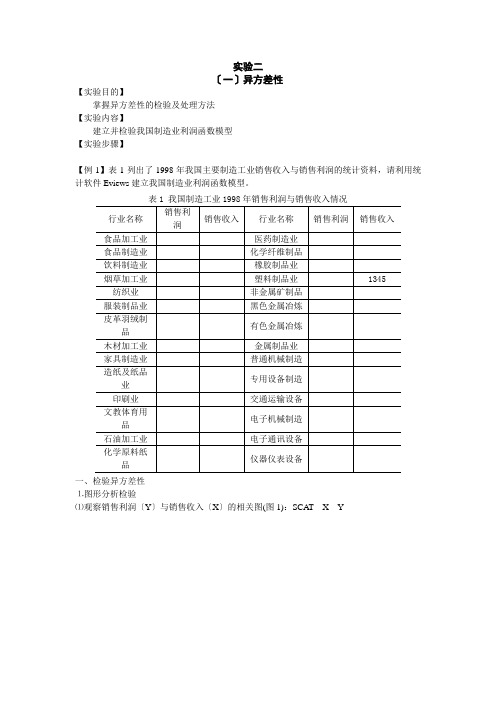
实验二〔一〕异方差性【实验目的】掌握异方差性的检验及处理方法【实验内容】建立并检验我国制造业利润函数模型【实验步骤】【例1】表1列出了1998年我国主要制造工业销售收入与销售利润的统计资料，请利用统计软件Eviews建立我国制造业利润函数模型。

一、检验异方差性⒈图形分析检验⑴观察销售利润〔Y〕与销售收入〔X〕的相关图(图1)：SCAT X Y图1 我国制造工业销售利润与销售收入相关图从图中可以看出，随着销售收入的增加，销售利润的平均水平不断提高，但离散程度也逐步扩大。

这说明变量之间可能存在递增的异方差性。

⑵残差分析首先将数据排序〔命令格式为：SORT 解释变量〕，然后建立回归方程。

在方程窗口中点击Resids按钮就可以得到模型的残差分布图〔或建立方程后在Eviews工作文件窗口中点击resid对象来观察〕。

图2 我国制造业销售利润回归模型残差分布图2显示回归方程的残差分布有明显的扩大趋势，即说明存在异方差性。

⒉Goldfeld-Quant检验⑴将样本安解释变量排序〔SORT X〕并分成两部分〔分别有1到10共11个样本合19到28共10个样本〕⑵利用样本1建立回归模型1〔回归结果如图3〕，其残差平方和为。

SMPL 1 10LS Y C X图3 样本1回归结果⑶利用样本2建立回归模型2〔回归结果如图4〕，其残差平方和为。

SMPL 19 28 LS Y C X图4 样本2回归结果⑷计算F 统计量：12/RSS RSS F =＝，21RSS RSS 和分别是模型1和模型2的残差平方和。

取05.0=α时，查F 分布表得44.3)1110,1110(05.0=----F ，而44.372.2405.0=>=F F ，所以存在异方差性⒊White 检验⑴建立回归模型：LS Y C X ，回归结果如图5。

图5 我国制造业销售利润回归模型⑵在方程窗口上点击View\Residual\Test\White Heteroskedastcity,检验结果如图6。

异方差性实验报告doc

异方差性实验报告doc异方差性实验报告篇一：计量经济学上机实验报告(异方差性)提示：打包保存时自己的文件夹以“学号姓名”为文件夹名，打包时文件夹内容包括：本实验报告、EViews工作文件。

篇二：Eviews异方差性实验报告实验一异方差性【实验目的】掌握异方差性问题出现的来源、后果、检验及修正的原理，以及相关的Eviews操作方法。

【实验内容】以《计量经济学学习指南与练习》补充习题4-16为数据，练习检查和克服模型的异方差的操作方法。

【4-16】表4-1给出了美国18个行业1988年研究开发（R&D）费用支出Y与销售收入X的数据。

观察相关图可以看出，随着销售收入的增加，研究开发费用的平均水平不断提高，但离散程度也逐步扩大。

这说明变量之间可能存在递增的异方差性。

（2）残差图分析首先对数据按照解释变量X由小至大进行排序（SORT X），然后建立一元线性回归方程（LS Y C X）。

2、Park检验建立回归模型（LS Y C X），结果如（*）式。

生成新变量序列： GENR LNE2 = LOG(RESID^2)GENR LNX = LOG(X)生成新残差序列对解释变量的回归模型（LS LNE2 C LNX）。

计量经济学课程实验报告

计量经济学课程实验报告实验序号2实验名称Eviews的异方差检验与校正实验组别12模拟角色实验地点2教602指导老师刘冬萍实验日期11月29日实验时间16:05——17:45一、实验目的及要求学会使用计量学分析^p 软件Eviews的异方差检验与校正功能。

二、实验环境2教602,经管学院电脑实验室三、实验内容与步骤 ?DATA Y _SORT _1.生成相关图SCAT _ Y根据相关图随着_的增大Y的取值范围不断增大,所以方程存在异方差.2.方程的异方差检验（1）WHITE 检验建立回归模型 LS Y C _ Dependent Variable: Y Method: Least SquaresDate: 11/22/12 Time: 17:06 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C0.8594690.7090571.2121300.2411_0.0363400.0096333.7723930.0014R-squared0.441531Mean dependent var3.100000Adjusted R-squared0.410504S.D.dependent var2.255986S.E.of regression1.732115Akaike info criterion4.031203Sum squared resid54.09Schwarz criterion4.130776Log likelihood-38.31203F-statistic14.23095Durbin-Watson stat2.111232Prob(F-statistic)0.001395进行WHITE 检验White Heteroskedasticity Test: F-statistic6.172459Probability0.009656Obs_R-squared8.413667Probability0.014893Test Equation:Dependent Variable: RESID^2 Method: Least SquaresDate: 11/22/12 Time: 17:07 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C-0.8401623.268547-0.2570450.8002_0.0346910.0966160.3590620.7240_^20.0002590.4703750.6441R-squared0.420683Mean dependent var 2.70020__Adjusted R-squared 0.352528S.D.dependent var5.061699S.E.of regression4.072927Akaike info criterion 5.784082Sum squared resid 282.0085Schwarz criterion5.933442Log likelihood-54.84082F-statistic6.172459Durbin-Watson stat 2.196613Prob(F-statistic)Nr^2=8.413677 因为检验的P=0.014893小于0.05,所以存在异方差.(2) PARK检验LS Y C _Dependent Variable: YMethod: Least SquaresDate: 11/22/12 Time: 17:13Sle: 1 20Included observations: 20VariableCoefficientStd.Errort-StatisticProb.C0.8594690.7090571.2121300.2411_0.0363400.0096333.7723930.0014R-squared0.441531Mean dependent varAdjusted R-squared0.410504S.D.dependent var2.255986S.E.of regression1.732115Akaike info criterion 4.031203Sum squared resid54.09Schwarz criterion4.130776Log likelihood-38.31203F-statistic14.23095Durbin-Watson stat2.111232Prob(F-statistic)0.001395GENR E2=LOG(RESID2) GENR LN_=LOG(_)LS LNE2 C LN_ Dependent Variable: LNE2 Method: Least SquaresDate: 11/22/12 Time: 17:16 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C-7.6927982.272023-3.3858810.0033LN_1.8393580.5713163.2195140.0048R-squared0.365421Mean dependent var-0.465580Adjusted R-squared0.330167S.D.dependent var1.915506S.E.of regression1.567714Akaike info criterion3.831754Sum squared resid44.23911Schwarz criterion3.931327Log likelihood-36.31754F-statistic10.36527Durbin-Watson stat1.937606Prob(F-statistic)0.004754由上图可看出P分别为0.0033 ,0.0048,0.004754都是小概率事件,所以方程是显著的,表明随机误差项的方差随着解释变量的取值不同而不断变化,即存在异方差性.（3）GLEISER检验LS Y C _GENR E=ABS(RESID)eq \o\ac(○,1)GENR _1=_^0.5LS E C _1Dependent Variable: E1Method: Least SquaresDate: 11/28/12 Time: 13:14Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C-1.2504440.637839-1.9604370.0656_10.3265340.0812324.0197750.0008R-squared0.473046Mean dependent var1.192860Adjusted R-squared0.443771S.D.dependent var1.159531S.E.of regression0.864787Akaike info criterion2.641972Sum squared resid13.46141Schwarz criterion2.741545Log likelihood-24.41972F-statistic16.15859Durbin-Watson stat2.047999Prob(F-statistic)0.000804|e1|=-1.250444+0.326534_1^0.5 R^2=0.473046 F=16.15859 P= eq \o\ac(○,2)GENR _2=_^-2LS E C _2Dependent Variable: E Method: Least SquaresDate: 11/28/12 Time: 13:27 Sle: 1 20Included observations: 20 VariableCoefficientStd.t-StatisticProb.C1.6651230.3427744.8577860.0001_2-657.9505338.0359-1.9463920.0674R-squared0.173874Mean dependent var 1.192860Adjusted R-squared 0.127978S.D.dependent var1.159531S.E.of regression1.082794Akaike info criterion 3.091607Sum squared residSchwarz criterion3.191180Log likelihood-28.91607F-statistic3.788442Durbin-Watson stat1.454864Prob(F-statistic)0.067388|e2|=1.665123-657.9505_^-2R^2=0.173874 F=3.788442 P= eq \o\ac(○,3)GENR _3=_^2LS E C _3Dependent Variable: E Method: Least SquaresDate: 11/28/12 Time: 13:32 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C0.5805350.2376322.4430010.0251_30.0001132.67E-054.2339310.0005R-squared0.498972Mean dependent var 1.192860Adjusted R-squared 0.471138S.D.dependent var1.159531S.E.of regression0.843245Akaike info criterion 2.591520Sum squared resid 12.79911Schwarz criterion2.691093Log likelihood-23.91520F-statistic17.92617Durbin-Watson stat2.064289Prob(F-statistic)0.000499|e3|=0.580535+0.000113_4^2R^2=0.498972 F=17.92617 P=0.000499 eq \o\ac(○,4)GENR _4=_^-0,5LS E C _4Dependent Variable: EMethod: Least SquaresDate: 11/28/12 Time: 13:36Sle: 1 20Included observations: 20VariableCoefficientStd.Errort-StatisticProb.C3.4730600.7618054.5589870.0002_4-15.53960-3.1195030.0059R-squared0.350914Mean dependent var 1.192860Adjusted R-squared 0.314854S.D.dependent var1.159531S.E.of regression0.959785Akaike info criterion 2.850424Sum squared resid 16.58137Schwarz criterion2.949998Log likelihood-26.50424F-statistic9.731299Durbin-Watson stat 1.759756Prob(F-statistic)|e4|=3.473060-15.53960 _^-0.5 R^2=0.350914 F=9.731299 P= eq \o\ac(○,5)GENR _5=_^-1LS E C _5Dependent Variable: E Method: Least SquaresDate: 11/28/12 Time: 13:45 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C2.2657780.4628754.8950140.0001_5-45.8762517.27699-2.6553390.0161R-squared0.281461Mean dependent var1.192860Adjusted R-squared0.241542S.D.dependent var1.159531S.E.of regression1.009829Akaike info criterion2.952079Sum squared resid18.35560Schwarz criterion3.051653Log likelihood-27.52079F-statistic7.050824Durbin-Watson stat1.627325Prob(F-statistic)0.016106|e5|=2.265778-45.87625_^-1R^2=0.281461 F=7.050824 P=0.016106由以上的五个方程表明，利润函数存在异方差性（只要取显著水平a大于0.067388）3.WLS方法估计利润函数(1)利用最小二乘法估计模型LS Y C _Dependent Variable: Y Method: Least SquaresDate: 11/28/12 Time: 12:40 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C0.8594690.7090571.2121300.2411_0.0363400.0096333.7723930.0014R-squared0.441531Mean dependent var3.100000Adjusted R-squared0.410504S.D.dependent var2.255986S.E.of regression1.732115Akaike info criterion4.031203Sum squared resid54.09Schwarz criterion4.130776Log likelihood-38.31203F-statistic14.23095Durbin-Watson stat2.111232Prob(F-statistic)0.001395得到:y^=0.859469+0.036340_ R^2=0.441531 (0.0014)T=(1.212130) (3.772393 )(2)生成权数变量：根据帕克检验得到：Ls y c _Genr lne2=log(resid^2)Genr ln_=log(_)Ls lne2 c ln_Dependent Variable: LNE2 Method: Least SquaresDate: 11/28/12 Time: 12:56 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C-7.6927982.272023-3.3858810.0033LN_1.8393580.5713163.2195140.0048R-squared0.365421Mean dependent var-0.465580Adjusted R-squared0.330167S.D.dependent var1.915506S.E.of regression1.567714Akaike info criterion3.831754Sum squared resid44.23911Schwarz criterion3.931327Log likelihood-36.31754F-statistic10.36527Durbin-Watson stat1.937606Prob(F-statistic)0.004754LNEi^2=--7.692798+1.839358LN_ R^2=0.365421 进行戈里瑟检验LS Y C _GENR E=ABS(RESID)eq \o\ac(○,1)GENR _1=_^0.5LS E C _1Dependent Variable: E1 Method: Least SquaresDate: 11/28/12 Time: 13:14 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C-1.2504440.637839-1.9604370.0656_10.3265340.0812324.0197750.0008R-squared0.473046Mean dependent var1.192860Adjusted R-squared0.443771S.D.dependent var1.159531S.E.of regression0.864787Akaike info criterion2.641972Sum squared resid13.46141Schwarz criterion2.741545Log likelihood-24.41972F-statistic16.15859Durbin-Watson stat2.047999Prob(F-statistic)0.000804|e1|=-1.250444+0.326534_1^0.5 R^2=0.473046 F=16.15859 P= eq \o\ac(○,2)GENR _2=_^-2LS E C _2Dependent Variable: E Method: Least SquaresDate: 11/28/12 Time: 13:27 Sle: 1 20Included observations: 20Variable CoefficientStd.Errort-StatisticProb.C1.6651230.3427744.8577860.0001_2-657.9505338.0359-1.9463920.0674R-squared0.173874Mean dependent var 1.192860Adjusted R-squared 0.127978S.D.dependent var1.159531S.E.of regression1.082794Akaike info criterion3.091607Sum squared resid21.18Schwarz criterion3.191180Log likelihood-28.91607F-statistic3.788442Durbin-Watson stat1.454864Prob(F-statistic)0.067388|e2|=1.665123-657.9505_^-2R^2=0.173874 F=3.788442 P= eq \o\ac(○,3)GENR _3=_^2LS E C _3Dependent Variable: E Method: Least SquaresDate: 11/28/12 Time: 13:32 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C0.5805350.2376322.4430010.0251_30.0001132.67E-054.2339310.0005R-squared0.498972Mean dependent var 1.192860Adjusted R-squared 0.471138S.D.dependent var1.159531S.E.of regression0.843245Akaike info criterion 2.591520Sum squared resid 12.79911Schwarz criterionLog likelihood-23.91520F-statistic17.92617Durbin-Watson stat2.064289Prob(F-statistic)0.000499|e3|=0.580535+0.000113_4^2R^2=0.498972 F=17.92617 P=0.000499 eq \o\ac(○,4)GENR _4=_^-0,5LS E C _4Dependent Variable: EMethod: Least SquaresDate: 11/28/12 Time: 13:36Sle: 1 20Included observations: 20VariableCoefficientStd.Errort-StatisticProb.C3.4730600.7618054.558987_4-15.539604.981434-3.1195030.0059R-squared0.350914Mean dependent var 1.192860Adjusted R-squared 0.314854S.D.dependent var1.159531S.E.of regression0.959785Akaike info criterion 2.850424Sum squared resid 16.58137Schwarz criterion2.949998Log likelihood-26.50424F-statistic9.731299Durbin-Watson stat1.759756Prob(F-statistic)0.005921|e4|=3.473060-15.53960 _^-0.5 R^2=0.350914 F=9.731299 P= eq \o\ac(○,5)GENR _5=_^-1LS E C _5Dependent Variable: E Method: Least SquaresDate: 11/28/12 Time: 13:45 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C2.2657780.4628754.8950140.0001_5-45.8762517.27699-2.6553390.0161R-squared0.281461Mean dependent var1.192860Adjusted R-squared0.241542S.D.dependent var1.159531S.E.of regression1.009829Akaike info criterion2.952079Sum squared resid18.35560Schwarz criterion3.051653Log likelihood-27.52079F-statistic7.050824Durbin-Watson stat1.627325Prob(F-statistic)0.016106|e5|=2.265778-45.87625_^-1R^2=0.281461 F=7.050824 P=由上可得在戈里瑟检验里最显著的是：|e3|=0.580535+0.000113_4^2 R^2=0.498972 F=17.92617 P=所以取权数变量为 : GENR W1=1/_^1.839358GENR W2=_^2另外取：GENR W3=1/ABS(RESID)GENR W4=1/RESID^2（3）利用最小二乘法估计模型：模型一LS(W=W1) Y C _Dependent Variable: YMethod: Least SquaresDate: 11/28/12 Time: 14:00Sle: 1 20Included observations: 20Weighting series: W1VariableCoefficientStd.Errort-StatisticProb.C-0.6259810.318225-1.9671030.0648_0.0116496.1001610.0000Weighted Statistics R-squared0.573253Mean dependent var 1.734420Adjusted R-squared 0.549545S.D.dependent var0.940124S.E.of regression0.630973Akaike info criterion 2.011533Sum squared resid7.166292Schwarz criterion2.06Log likelihood-18.11533F-statistic24.17958Durbin-Watson statProb(F-statistic)0.000111Unweighted StatisticsR-squared-0.050320Mean dependent var3.100000Adjusted R-squared-0.108671S.D.dependent var2.255986S.E.of regression2.375406Sum squared resid.5659Durbin-Watson stat1.104724怀特检验的结果是White Heteroskedasticity Test: F-statistic0.986667Probability0.393Obs_R-squared2.080114Probability0.353435Test Equation:Dependent Variable: STD_RESID^2 Method: Least SquaresDate: 11/28/12 Time: 14:36 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C0.8994860.4380022.0536110.0557_-0.0146130.012947-1.1286980.2747_^26.64E-057.37E-050.9011740.3801R-squared0.104006Mean dependent var0.358315Adjusted R-squared-0.001405S.D.dependent var0.545410S.E.of regression0.545793Akaike info criterion1.764328Sum squared resid5.064137Schwarz criterion1.913688Log likelihood-14.64328F-statistic0.986667Durbin-Watson stat2.743143Prob(F-statistic)0.393得到估计结果Y^=-0.625981+0.071060_(0.318225) (6.100161)R^2=0.573253 NR^2=2.080114 P=0.393 模型二LS(W=W2) Y C _Dependent Variable: YMethod: Least SquaresDate: 11/28/12 Time: 14:12Sle: 1 20Included observations: 20Weighting series: W2VariableCoefficientStd.Errort-StatisticProb.C4.3789433.2559741.3448950.1954_0.0060140.0227010.2649070.7941Weighted StatisticsR-squared0.702288Mean dependent var 4.737844Adjusted R-squared 0.685748S.D.dependent var8.767922S.E.of regression4.915135Akaike info criterion 6.117155Sum squared resid 434.8540Schwarz criterion6.216728Log likelihood-59.17155F-statistic42.46109Durbin-Watson stat 2.705915Prob(F-statistic)0.000004Unweighted Statistics R-squared-0.428848Mean dependent var3.100000Adjusted R-squared-0.508229S.D.dependent var2.255986S.E.of regression2.770576Sum squared resid138.1696Durbin-Watson stat0.87进行怀特检验的结果是White Heteroskedasticity Test: F-statistic46.95441Probability0.000000Obs_R-squared16.93442Probability0.000210Test Equation:Dependent Variable: STD_RESID^2 Method: Least SquaresDate: 11/28/12 Time: 14:39 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C36.1706519.848121.8223720.0860_-1.6942460.586696-2.8877740.0102_^20.0166170.0033394.9760240.0001R-squared0.846721Mean dependent var21.74270Adjusted R-squared0.828688S.D.dependent var59.75546S.E.of regression24.73269Akaike info criterion9.391610Sum squared resid19.00Schwarz criterion9.540970Log likelihood-90.91610F-statistic46.95441Durbin-Watson stat2.837461Prob(F-statistic)0.000000得到结果是：Y^=4.378943+0.006014_(3.255974) (0.022701)R^2=0.702288 NR^2=16.93442 P=0.00000 模型三LS(W=W3) Y C _Dependent Variable: YMethod: Least SquaresDate: 11/28/12 Time: 14:19Sle: 1 20Included observations: 20 Weighting series: W3 VariableCoefficientStd.Errort-StatisticProb.C0.7076590.2082663.3978670.0032_0.0387920.0053887.20__1690.0000Weighted StatisticsR-squared0.945796Mean dependent var2.344549Adjusted R-squared0.942785S.D.dependent var2.209824S.E.of regression0.528582Akaike info criterion 1.657402Sum squared resid5.029181Schwarz criterion1.756975Log likelihood-14.57402F-statistic314.0812Durbin-Watson stat 1.849162Prob(F-statistic)0.000000Unweighted Statistics R-squared0.439521Mean dependent var 3.100000Adjusted R-squared 0.408383S.D.dependent var2.255986S.E.of regression1.735229Sum squared resid54.19836Durbin-Watson stat2.097049进行怀特检验得White Heteroskedasticity Test: F-statistic0.494755Probability0.618232Obs_R-squared1.100097Probability0.576922Test Equation:Dependent Variable: STD_RESID^2 Method: Least SquaresDate: 11/28/12 Time: 14:40 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C0.1819650.0821532.2149610.0407_0.0050.0024280.7558340.4601_^2-8.06E-061.38E-05-0.5831500.5674R-squared0.055005Mean dependent var 0.251459Adjusted R-squared-0.056171S.D.dependent var0.099611S.E.of regression0.102370Akaike info criterion-1.582959Sum squared resid0.178155Schwarz criterion-1.433599Log likelihood18.82959F-statistic0.494755Durbin-Watson stat2.096222Prob(F-statistic)0.618232Y^=0.707659+0.038792_(0.208266) (0.005388)R^2=0.945796 NR^2=1.100097 P=0.618232 模型四 LS(W=W4) Y C _Dependent Variable: YMethod: Least SquaresDate: 11/28/12 Time: 14:24Sle: 1 20Included observations: 20Weighting series: W4VariableCoefficientStd.Errort-StatisticProb.C0.5918930.1283534.6114400.0002_0.0429390.00409310.490560.0000Weighted Statistics R-squared0.994979Mean dependent var 2.087552Adjusted R-squared 0.994700S.D.dependent var4.277070S.E.of regression0.311364Akaike info criterion 0.598931Sum squared resid1.745056Schwarz criterion0.698505Log likelihood-3.989313F-statistic3567.168Durbin-Watson stat 2.173306Prob(F-statistic)0.000000Unweighted Statistics R-squared0.422958Mean dependent var 3.100000Adjusted R-squared 0.390900S.D.dependent var2.255986S.E.of regression1.760681Sum squared resid 55.79997Durbin-Watson stat 2.027424进行怀特检验的结果是White Heteroskedasticity Test: F-statistic0.851707Probability0.444108Obs_R-squared1.821500Probability0.402222Test Equation:Dependent Variable: STD_RESID^2 Method: Least SquaresDate: 11/28/12 Time: 14:42 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C0.2750730.1762821.5604170.1371_-0.0048390.005211-0.9285840.3661_^22.04E-052.97E-050.6876810.5009R-squared0.091075Mean dependent var 0.087253Adjusted R-squared-0.015857S.D.dependent var0.217943S.E.of regression0.219664Akaike info criterion -0.055951Sum squared resid0.820291Schwarz criterion0.093409Log likelihood3.559512。

异方差实验报告二模板

《计量经济学》实验报告二开课实验室：财经科学实验室 2012年5月10日班级：学号：姓名：实验项目名称异方差性的检验与修正成绩：实验性质： _ 【实验目的】掌握异方差性的检验与修正方法并能运用Eviews 软件进行实现【实验要求】掌握各种异方差的检验方法，运用最小二乘法进行模型修下，要求熟悉基本操作步骤，读懂各项上机榆出结果的含义并能进行分析【实验软件】 Eviews 软件【实验内容】根据给定的案例数据按实验要求进行操作【实验方案与进度】实验：建立消费支出模型01i i i Y X u ββ=++，样本数据如下表所示：地区可支配收入(元）消费性支出（元）X Y 北京 10349.69 8493.49 天津 8140.5 6121.04 河北 5661.16 4348.47 山西 4724.11 3941.87 内蒙古 5129.05 3927.75 辽宁 5357.79 4356.06 吉林 4810 4020.87 黑龙江 4912.88 3824.44 上海 11718.01 8868.19 江苏 6800.23 5323.18 浙江9279.167020.22验证性 □综合性 □设计性指导教师签字：山东 6489.97 5022 河南 4766.26 3830.71 湖北 5524.54 4644.5 湖南 6218.73 5218.79 广东 9761.57 8016.91 陕西 5124.24 4276.67 甘肃 4916.25 4126.47 青海 5169.96 4185.73 新疆5644.864422.93(1)用普通最小二乘法估计模型参数Dependent Variable: Y Method: Least Squares Date: 05/10/12 Time: 08:59 Sample: 1 20Included observations: 20Variable Coefficient Std. Error t-Statistic Prob. C 272.3635 159.6773 1.705713 0.1053 X0.7551250.02331632.386900.0000 R-squared0.983129 Mean dependent var 5199.515 Adjusted R-squared 0.982192 S.D. dependent var 1625.275 S.E. of regression 216.8900 Akaike info criterion 13.69130 Sum squared resid 846743.0 Schwarz criterion 13.79087 Log likelihood -134.9130 F-statistic 1048.912 Durbin-Watson stat1.301684 Prob(F-statistic)0.000000样本回归ˆ272.3635+0.755125X i iY 即当可支配收入增加一元，消费性支出平均增加0.755125元。

异方差性实训报告

一、实验背景在计量经济学中，异方差性是指模型中因变量方差与自变量之间存在非线性关系。

异方差性会导致最小二乘估计量（OLS）不再有效，从而影响模型的准确性和可靠性。

因此，识别和处理异方差性对于模型分析至关重要。

本次实训旨在通过实际操作，掌握异方差性的检验方法，并学习如何运用加权最小二乘法（WLS）对异方差模型进行修正。

二、实验目的1. 理解异方差性的概念及其对模型的影响。

2. 掌握异方差性的检验方法，包括散点图、方差分析（ANOVA）和Breusch-Pagan 检验等。

3. 学习加权最小二乘法（WLS）的基本原理和操作步骤。

4. 通过实际案例，验证WLS在处理异方差性方面的有效性。

三、实验内容1. 数据准备本次实训以某地区居民消费数据为例，包括地区、可支配收入和消费性支出三个变量。

数据来源于国家统计局。

2. 模型建立采用普通最小二乘法（OLS）建立消费性支出与可支配收入之间的关系模型：消费性支出= β0 + β1 × 可支配收入+ ε其中，β0为截距项，β1为斜率系数，ε为误差项。

3. 异方差性检验（1）散点图分析通过绘制消费性支出与可支配收入的散点图，观察数据是否存在明显的异方差性。

若散点图呈现非线性关系，则可能存在异方差性。

（2）方差分析（ANOVA）对消费性支出和可支配收入进行方差分析，检验两者是否存在显著差异。

若差异显著，则可能存在异方差性。

（3）Breusch-Pagan检验采用Breusch-Pagan检验对模型进行异方差性检验。

若检验结果拒绝原假设，则说明模型存在异方差性。

4. 加权最小二乘法（WLS）修正若检验结果显示模型存在异方差性，则采用加权最小二乘法（WLS）对模型进行修正。

WLS的基本原理是在模型中引入权重，使得权重与误差项的方差成反比。

具体操作步骤如下：（1）计算每个观测值的权重，即：权重 = 1 / 误差项的方差（2）将权重代入模型，重新估计参数。

5. 结果分析比较WLS修正前后模型的参数估计结果、拟合优度和显著性水平。

异方差实验

实验二实验内容：异方差模型的检验和修正方法实验要求：通过本次实验，初步掌握掌握判断模型是否存在异方差的一般方法，包括图示法、Goldfeld-Quandt检验法、Gleiser检验法、怀特检验法；并会利用加权最小二乘法修正模型。

实验数据：表4.1.1数据实验步骤：1、用OLS法建立模型第一步：建立WORKFILEFil e→ new →workfile→弹出对话框→第一个填 1→第二个填31→OK第二步:输入数据1、建立存放数据的Group:在命令主出口输入命令DATA Y X然后按ENTER运行2、从原来保存数据的表格中复制数据到Group如何求已知数列的新数列：genr lnx1=log(x1)第三步：软件操作OLS法主命令窗口输入：LS Y C LNX1 LNX2 按ENTER运行结果如图所示：2、检验模型是否存在异方差第一种方法：图示法第一步：求原来模型的参差项（e~的值）i只要对原来的模型进行普通最小二乘估计就可以求的残差项，残差项在系统中默认为resid.Resid的位置在workfile窗口，如下图所示。

第二步：图示2~ie 和X 的关系 Quick →Graph →弹出对话框→输入LNX2(横轴) →resid^2(纵轴) →OK →下拉菜单选 scatter diagram →ok (结果如下图)分析这个图：因为不是和横轴平行的直线，所以存在异方差；而且resid^2随着X 的增加而增加，所以是递增型异方差。

第二种方法：帕克戈里瑟检验第一步：建立2~ie 和X 的模型（本题建立的是一元线性回归模型，并且解释变量是一次方的，这个模型的具体形式根据具体情况来决定）122i i eLN X ααε=++ 第二步：对上面这个模型进行回归主命令窗口输入： Ls abs(resid) c lnx2 结果如下图所示：方程F检验值为：F=0.625190临界值0.05(1,29) 4.18F=因为 F＜05.0F（也可以用T检验）所以作为解释变量的X对被解释变量2~ie的影响不显著，意思就是说2~i e随着X的变化没有变化。

EViews计量经济学实验报告异方差的诊断及修正

EViews计量经济学实验报告异⽅差的诊断及修正姓名学号实验题⽬异⽅差的诊断与修正⼀、实验⽬的与要求：要求⽬的：1、⽤图⽰法初步判断是否存在异⽅差，再⽤White检验异⽅差；2、⽤加权最⼩⼆乘法修正异⽅差。

估计结果为： iY ? = 12.03564 + 0.104393i X （19.51779） (0.008441) t=（0.616650）（12.36670）2R =0.854696 R =0.849107 S.E.=56.89947 DW=1.212859 F=152.9353这说明在其他因素不变的情况下，销售收⼊每增长1元，销售利润平均增长0.104393元。

2R =0.854696 , 拟合程度较好。

在给定 =0.0时，t=12.36670 > )26(025.0t =2.056 ，拒绝原假设，说明销售收⼊对销售利润有显著性影响。

F=152.9353 > )6,21(F 05.0= 4.23 ,表明⽅程整体显著。

（三）检验模型的异⽅差※（⼀）图形法6、判断由图3可以看出，被解释变量Y 随着解释变量X 的增⼤⽽逐渐分散，离散程度越来越⼤；同样，由图4可以看出，残差平⽅2 i e 对解释变量X 的散点图主要分布在图形中的下三⾓部分，⼤致看出残差平⽅2i e 随i X 的变动呈增⼤趋势。

因此，模型很可能存在异⽅差。

但是否确实存在异⽅差还应该通过更近⼀步的检验。

※（⼆）White 检验White 检验结果White Heteroskedasticity Test:F-statistic3.607218 Probability 0.042036 Obs*R-squared6.270612 Probability0.043486Test Equation:t 界值5.002χ（2）=5.99147。

⽐较计算的2χ统计量与临界值，因为n 2R = 6.270612 > 5.002χ（2）=5.99147 ，所以拒绝原假设，不拒绝备择假设，这表明模型存在异⽅差。

计量经济学报告——异方差

计量经济学实验一、实验内容1、实验目的研究农村居民各种不同类型的收入对消费支出的影响。

同时，掌握线性模型或双对数模型，并熟悉异方差的检验和解决办法。

2、实验要求（1）利用线性模型或双对数模型进行分析；（2）判断并解决异方差问题；（3）对模型进行调整；（4）提出扩大消费的政策建议。

二、实验报告1、问题提出影响农村居民家庭消费支出的因素有很多，如经济增长，人均国内生产总值，消费者物价指数等等。

其中，收入是影响消费的主要因素。

随着改革开放，劳动力的需求增加，农民工纷纷进城务农；我国颁布一系列对农民的补贴性政策，农民收入不断提高之际，收入也呈现多元化的局面，从单一的家庭人均纯收入扩展到工资性收入、财产性收入、转移性收入等。

我们选取了2006年各省市农村居民家庭各类收入与消费支出的数据，研究农村居民各种不同类型的收入对消费支出的影响，2、指标选择2006年各省市农村居民家庭各类收入与消费支出的数据。

3、数据来源实验课上老师提供的。

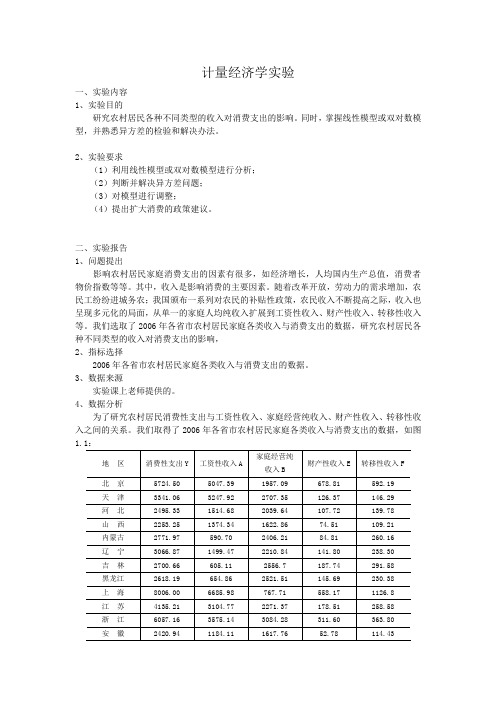
4、数据分析为了研究农村居民消费性支出与工资性收入、家庭经营纯收入、财产性收入、转移性收入之间的关系。

我们取得了2006年各省市农村居民家庭各类收入与消费支出的数据，如图1.1：地区消费性支出Y 工资性收入A 家庭经营纯收入B财产性收入E 转移性收入F北京5724.50 5047.39 1957.09 678.81 592.19 天津3341.06 3247.92 2707.35 126.37 146.29 河北2495.33 1514.68 2039.64 107.72 139.78 山西2253.25 1374.34 1622.86 74.51 109.21 内蒙古2771.97 590.70 2406.21 84.81 260.16 辽宁3066.87 1499.47 2210.84 141.80 238.30 吉林2700.66 605.11 2556.7 187.74 291.58 黑龙江2618.19 654.86 2521.51 145.69 230.38 上海8006.00 6685.98 767.71 558.17 1126.8 江苏4135.21 3104.77 2271.37 178.51 258.58 浙江6057.16 3575.14 3084.28 311.60 363.80 安徽2420.94 1184.11 1617.76 52.78 114.43福建3591.40 1855.53 2481.62 113.52 384.09江西2676.60 1441.34 1863.5 35.13 119.57山东3143.80 1671.54 2409.78 127.60 159.4河南2229.28 1022.74 2108.26 40.37 89.66湖北2732.46 1199.16 2095.15 25.91 99.13湖南3013.32 1449.65 1743.39 42.49 154.09广东3885.97 2906.15 1693.64 220.87 259.12广西2413.93 974.32 1705.75 22.45 69.96海南2232.19 555.72 2486.94 49.44 163.43重庆2205.21 1309.91 1349.57 27.29 187.07四川2395.04 1219.51 1586.54 52.84 143.50贵州1627.07 715.49 1112.81 36.93 119.38云南2195.64 441.81 1631.60 82.19 94.85西藏2002.24 568.39 1410.51 156.00 300.06陕西2181.00 848.26 1219.33 52.56 140.04甘肃1855.49 637.37 1291.85 52.56 152.27青海2178.95 653.30 1374.36 100.66 230.05宁夏2246.97 823.09 1662.07 53.35 221.63新疆2032.36 254.07 2323.01 58.69 101.51 2006年各省市农村居民家庭各类收入与消费支出（单位：元）图：1.1假定消费性支出与工资性收入、家庭经营纯收入、财产性收入、转移性收入之间呈现线性关系。

计量经济学异方差的检验与修正实验报告

计量经济学实验报告关于异方差性的检验与修正2012/11/18学院：国际教育学院专业：国际经济与贸易班级：10级一班姓名：苗子凯学号：1014102025一．异方差检验运行Eviews,依次单击file→new→work file→unstructed→observation 20。

命令栏中输入“data y x”，打开“y x”表，接下来将数据输入其中。

然后开始进行LS回归，命令栏中输入“ls y c x”回车，即得到回归结果如下回归方程为：：Y = 272.3635389 + 0.7551249391*X二．开始检验异方差White 检验法:依次单击View →Residual Tests →Heteroskedasticity test →Whit 经估计出现white 检验结果，如下图：所以拒绝原假设，表明模型存在异方差Goldfeld-Quanadt 检验法：在命令栏中直接输入：ls y c x →sort 1 20(进行排序) →smpl 1 8 →ls y c x →enter 得到如下结果：99.5%565.122置信水平下的卡方值>=nR继续取样本，在命令栏中直接输入： smpl 13 20 →ls y c x→enter得到如下结果：计算F统计量：F=RSS2/RSS1=615472.0/126528.3=4.864；F=4.864> F0.05（6,6）=4.28，拒绝原假设，表明模型确实存在异方差性。

帕克检验重新打开eviews，依次键入以下步骤：file→new→work file→unstructed→observation 20。

命令栏中输入“data y x”，打开“y x”表，接下来将数据输入其中。

然后键入：genr lne2=log(resid^2) → genr lnx=log(x) →ls lne2 c lnx得到结果如下：可得到α=3.47，且t=2.89，说明显著性明显，而α的显著性不为零意味着存在显著性。

异方差实验报告(已做)

异方差实验报告(已做)《计量经济学》实验报告二开课实验室：财经科学实验室年月日班级：学号：姓名：实验项目名称异方差性的检验与修正成绩：验证性□综合性□设计性实验性质：_ 【实验目的】掌握异方差性的检验与修正方法并能运用Eviews软件进行实现【实验要求】掌握各种异方差的检验方法，运用最小二乘法进行模型修下，要求熟悉基本操作步骤，读懂各项上机榆出结果的含义并能进行分析【实验软件】Eviews 软件【实验内容】根据给定的案例数据按实验要求进行操作【实验方案与进度】实验：建立住房支出模型Yi01Xiui，样本数据如下表所示：地区北京天津河北山西内蒙古辽宁吉林黑龙江上海江苏浙江可支配收入(元） X 4810 指导教师签字：消费性支出 Y 1山东河南湖北湖南广东陕西甘肃青海新疆5022(1)用普通最小二乘法估计模型参数Dependent Variable: Y Method: Least Squares Date: 05/20/11 Time: 08:31 Sample: 1 20Included observations: 20 Variable C X R-squaredAdjusted R-squared of regression Sum squared resid Log likelihood Durbin-Watson stat Coefficient Std. Error t-Statistic Prob. Mean dependent var dependent var Akaike info criterion Schwarz criterion -F-statistic Prob(F-statistic) + 估计结果为：Y(2)用图形法进行异方差检验2上图可看出，残差有随X增大的趋势，因此可以判断该模型可能存在异方差，但是是否确实存在异方差还需进一步检验。

(3)用样本分段法进行异方差检验表3Dependent Variable: Y Method: Least Squares Date: 05/20/11 Time: 09:01 Sample: 1 8Included observations: 8 Variable C X R-squaredAdjusted R-squared of regression Sum squared resid Log likelihood Durbin-Watson statCoefficient Std. Error t-Statistic Prob.Mean dependent var dependent var Akaike info criterion Schwarz criterion - F-statistic Prob(F-statistic)表4Dependent Variable: Y Method: Least Squares Date: 05/20/11 Time: 09:01 Sample: 13 20Included observations: 8 Variable C X R-squaredAdjusted R-squared of regression Sum squared resid Log likelihood Durbin-Watson stat Coefficient Std. Error t-Statistic Prob. Mean dependent var dependent var Akaike info criterion Schwarz criterion -F-statistic Prob(F-statistic) 表3 可以得出样本1-8的残差平方和为，表4可以得出样本13-20的残差平方和为，根据G-Q检验得： F=/=在显著性水平=下，分子，分母的自度均为6，查F分布表，得临界值3(6,6)=，因为F=>(6,6)=,所以拒接原假设，表明模型确实存在异方差。

计量经济学异方差实验报告及心得体会

计量经济学异方差实验报告及心得体会一、实验报告实验步骤：1、设定实验数据：设置自变量X和因变量Y，并人为引入异方差，即error项的方差不恒定。

2、建立回归模型：根据设定的数据，建立回归模型，运用最小二乘法估计模型参数。

3、对回归结果进行分析：通过查看回归系数、残差和残差的图形等，判断是否存在异方差问题。

4、进行异方差检验：利用统计软件进行异方差检验，如White 检验或Breusch–Pagan检验等，获取检验结果。

5、处理异方差问题：根据异方差检验结果，采取相应的处理方法，如使用加权最小二乘法或进行异方差稳健标准误的估计。

6、比较处理前后的回归结果：对处理前后的回归结果进行比较和分析，观察异方差的处理是否有效。

实验结果：在实验过程中，我们设定了一个简单的回归模型，并引入异方差。

经过处理异方差问题后，我们发现被异方差影响的模型的回归系数和标准误均有所变化。

而经过异方差处理后，回归结果更加稳定，模型的预测能力也相应提高。

二、心得体会通过本次实验，我对计量经济学中异方差的概念和影响有了更加深入的了解。

异方差问题存在时，回归模型的估计结果可能会产生偏误，影响模型的准确性。

因此，我们需要进行异方差检验，并采取相应的处理方法。

实验过程中，我们运用了统计软件进行异方差检验和处理，这使得整个分析过程更加简洁和高效。

此外，本次实验还提醒我们在实际研究中要注意可能存在的异方差问题，并及时处理。

在计量经济学领域，处理异方差问题的方法有很多，选择适合实际情况的方法非常重要。

因此，我们需要不断学习和实践，提高自己的计量经济学分析能力。

总之，本次实验对我们深入理解异方差在计量经济学中的重要性起到了很好的引导作用。

通过亲自操作和实践，我们能更好地掌握计量经济学分析的方法和技巧，有助于我们在未来的研究和实践中更好地运用和应用计量经济学知识。

计量经济学异方差的检验与修正实验报告

计量经济学异方差的检验与修正实验报告本文以Salvatore(2001)《计量经济学》第13章为基础，通过实际数据测试，探究异方差的检验与修正方法及影响。

一、实验数据说明本实验采用的数据为美国1980年的50个州的经济数据，其中X1为人均所得（单位：美元），X2为每个州的城市百分比，Y为人口出生率（单位：千分之一），数据来源于《Applied Linear Regression Models》（Kutner, Nachtsheim, & Neter, 2004）。

二、实验原理当数据呈现异方差性时，传统的OLS估计方法将会失效，此时需要使用其他的估计方法。

其中常用的是加权最小二乘（WLS）估计方法。

WLS估计方法的思想是对存在异方差（方差不相等）的观测值进行权重调整，使得加权后的平方残差最小。

本实验将通过检验异方差条件、使用原有OLS估计进行对比以及应用WLS修正方法的实现来说明异方差对实证分析的影响。

三、实验内容及结果首先，为了检验异方差条件是否成立，可以采用Breusch-Pagan检验。

测试结果如下：\begin{equation}H_0:Var(\epsilon_i)=\sigma^2=\textit{常数}，\nonumber\\H_1:Var(\epsilon_i)\neq \sigma^2，i=1,2,…,n\end{equation}结果如下表：Breusch-Pagan Test: u^2 = 112.208 Prob > chi2 = 0.0000通过检验结果可知，Breusch-Pagan检验统计量的p值为0.0000，小于0.05的水平，因此拒绝原假设，认为方差存在异方差。

接下来，我们将使用传统的OLS估计方法进行回归分析（OLS 1），并与WLS估计方法（WLS 1）进行对比。

OLS 1结果如下：\begin{equation}Y=0.0514X1+1.0871X2-58.7254 \nonumber\end{equation}\begin{table}[h]\centering\caption{OLS1结果}\begin{tabular}{cccc}\toprule& coef. & std. err. & t \\\midruleconst & -58.7254 & 23.703 & -2.477 \\X1 & 0.0514 & 0.027 & 1.895 \\X2 & 1.0871 & 0.402 & 2.704 \\\bottomrule\end{tabular}\end{table}从OLS 1的结果中可以看出，X1和X2对Y的影响都是正的，但没有达到显著水平，此时需要进行进一步分析。

计量经济学异方差实验报告二

异方差性实验报告doc

异方差实验报告

计量经济学 异方差检验

计量经济学异方差实验报告及心得体会

计量异方差实验报告

异方差实验报告步骤(3篇)

计量经济学多元线性回归多重共线性异方差实验报告

计量经济学实验二

异方差性实验报告doc

计量经济学课程实验报告

异方差实验报告二模板

异方差性实训报告

异方差实验

EViews计量经济学实验报告异方差的诊断及修正

计量经济学报告——异方差

计量经济学异方差的检验与修正实验报告

异方差实验报告(已做)

计量经济学异方差实验报告及心得体会

计量经济学异方差的检验与修正实验报告

计量经济学异方差检验