高考中档大题规范练(二)
高考数学中档大题规范练中档大题1.docx

中档大题规范练中档大题1 三角函数1.设向量a =(3sin x ,sin x ),b =(cos x ,sin x ),x ∈⎣⎢⎡⎦⎥⎤0,π2.(1)若|a |=|b |,求x 的值;(2)设函数f (x )=a ·b ,求f (x )的值域.2.已知0<α<π2,π2<β<π且tan α2=12,sin(α+β)=513.(1)分别求cos α与cos β的值; (2)求tanα-β2的值.3.(2015·无锡模拟)已知函数f (x )=4cos x sin ⎝⎛⎭⎪⎫x +π6+a 的最大值为2.(1)求实数a 的值及f (x )的最小正周期; (2)在坐标纸上作出f (x )在[0,π]上的图象.4.(2015·苏州二模)已知函数f (x )=cos ⎝ ⎛⎭⎪⎫π3+x ·cos ⎝ ⎛⎭⎪⎫π3-x ,g (x )=12sin 2x -14.(1)求函数f (x )的最小正周期;(2)求函数h (x )=f (x )-g (x )的最大值,并求使h (x )取得最大值的x 的集合. 5.(2015·盐城二模)如图所示,经过村庄A 有两条夹角为60°的公路AB ,AC ,根据规划拟在两条公路之间的区域内建一工厂P ,分别在两条公路边上建两个仓库M ,N (异于村庄A ),要求PM =PN =MN =2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远)?6.设f (x )=sin x +sin ⎝ ⎛⎭⎪⎫x +π6-cos ⎝⎛⎭⎪⎫x +4π3,x ∈[0,2π].(1)求函数f (x )的最小正周期和单调区间;(2)在锐角△ABC 中,若f (A )=2,a =2,b =6,求∠C 及边c .答案精析中档大题规范练中档大题1 三角函数1.解 (1)由于|a |=(3sin x )2+(sin x )2=2|sin x |, |b |=(cos x )2+(sin x )2=1, 而|a |=|b |,则有2|sin x |=1,又x ∈⎣⎢⎡⎦⎥⎤0,π2,则有sin x =12,所以x =π6.(2)由于f (x )=a ·b =3sin x cos x +sin 2x =32sin 2x -12cos 2x +12=sin ⎝⎛⎭⎪⎫2x -π6+12,又x ∈⎣⎢⎡⎦⎥⎤0,π2,则有2x -π6∈⎣⎢⎡⎦⎥⎤-π6,5π6, 所以当2x -π6=π2,即x =π3时,sin ⎝ ⎛⎭⎪⎫2x -π6取得最大值1,此时f (x )取得最大值32;当2x -π6=-π6,即x =0时,sin ⎝⎛⎭⎪⎫2x -π6取得最小值-12,此时f (x )取得最小值0. 故f (x )的值域为⎣⎢⎡⎦⎥⎤0,32.2.解 (1)cos α=cos 2α2-sin2α2=cos 2α2-sin2α2cos 2α2+sin 2α2=1-tan2α21+tan 2α2=35,∵0<α<π2,∴sin α=45.∵α+β∈⎝⎛⎭⎪⎫π2,3π2,sin(α+β)=513,∴cos(α+β)=-1213.∴cos β=cos[(α+β)-α]=cos(α+β)cos α+sin(α+β)sin α =⎝ ⎛⎭⎪⎫-1213·35+513·45=-1665.(2)∵2cos2β2-1=cos β=-1665且β2∈⎝ ⎛⎭⎪⎫π4,π2, ∴cos β2=7130,∴sin β2=9130.∴tan β2=97.∴tan α-β2=tan α2-tan β21+tan α2tanβ2=-1123.3.解 (1)f (x )=4cos x ⎝ ⎛⎭⎪⎫sin x cos π6+cos x sin π6+a=3sin 2x +cos 2x +1+a =2sin ⎝⎛⎭⎪⎫2x +π6+a +1,最大值为3+a =2,∴a =-1.T =2π2=π.(2)列表如下:画图如下:4.解 (1)f (x )=cos ⎝ ⎛⎭⎪⎫π3+x cos ⎝ ⎛⎭⎪⎫π3-x=⎝ ⎛⎭⎪⎫12cos x -32sin x ⎝ ⎛⎭⎪⎫12cos x +32sin x=14cos 2x -34sin 2x =1+cos 2x 8-3-3cos 2x 8=12cos 2x -14,∴f (x )的最小正周期为2π2=π.(2)h (x )=f (x )-g (x )=12cos 2x -12sin 2x=22cos ⎝⎛⎭⎪⎫2x +π4,当2x +π4=2k π (k ∈Z )时,h (x )取得最大值22.h (x )取得最大值时,对应的x 的集合为{x |x =k π-π8,k ∈Z }.5.解 设∠AMN =θ,在△AMN 中,MN sin 60°=AMsin (120°-θ).因为MN =2,所以AM =433sin(120°-θ).在△AMP 中,cos ∠AMP =cos(60°+θ).AP 2=AM 2+MP 2-2AM ·MP ·cos ∠AMP=163sin 2(120°-θ)+4-2×2×433sin(120°-θ)cos(60°+θ) =163sin 2(θ+60°)-1633sin(θ+60°)cos(θ+60°)+4=83[1-cos(2θ+120°)]-833sin(2θ+120°)+4 =-83[3sin(2θ+120°)+cos(2θ+120°)]+203=203-163sin(2θ+150°),θ∈(0°,120°). 当且仅当2θ+150°=270°,即θ=60°时,AP 2取得最大值12,即AP 取得最大值2 3. 所以设计∠AMN =60°时,工厂产生的噪声对居民影响最小.6.解 (1)因为f (x )=sin x +sin x cos π6+cos x sin π6-⎝ ⎛⎭⎪⎫cos x cos 4π3-sin x sin 4π3=sin x +32sin x +12cos x +12cos x -32sin x =sin x +cos x =2sin ⎝⎛⎭⎪⎫x +π4,所以f (x )的最小正周期T =2π. 由x ∈[0,2π],可知x +π4∈⎣⎢⎡⎦⎥⎤π4,9π4.当x +π4∈⎣⎢⎡⎭⎪⎫π4,π2,即x ∈⎣⎢⎡⎭⎪⎫0,π4时,f (x )为单调递增函数;当x +π4∈⎣⎢⎡⎭⎪⎫π2,3π2,即x ∈⎣⎢⎡⎭⎪⎫π4,5π4时,f (x )为单调递减函数; 当x +π4∈⎣⎢⎡⎦⎥⎤3π2,9π4,即x ∈⎣⎢⎡⎦⎥⎤5π4,2π时,f (x )为单调递增函数. 所以f (x )的单调递增区间为⎣⎢⎡⎭⎪⎫0,π4,⎣⎢⎡⎦⎥⎤5π4,2π,函数f (x )的单调递减区间为⎣⎢⎡⎭⎪⎫π4,5π4. (2)由f (A )=2sin ⎝⎛⎭⎪⎫A +π4=2,得sin ⎝⎛⎭⎪⎫A +π4=1,故A +π4=π2,得A =π4.由正弦定理知b sin B =a sin A ,即6sin B =2sinπ4,得sin B =32,又B ∈⎝⎛⎭⎪⎫0,π2,因此B =π3,所以C =π-(A +B )=π-⎝ ⎛⎭⎪⎫π4+π3=5π12.由正弦定理知,c sin C =a sin A =222=22,得c =22sin 5π12=22·6+24=3+1.。
2019年高考数学(文科)中档大题规范练(三角函数)(含答案)

高考数学精品复习资料2019.5中档大题规范练中档大题规范练——三角函数1.已知函数f (x )=(sin x -cos x )sin 2x sin x. (1)求f (x )的定义域及最小正周期;(2)求f (x )的单调递增区间.解 (1)由sin x ≠0得x ≠k π(k ∈Z ),故f (x )的定义域为{x ∈R |x ≠k π,k ∈Z }.因为f (x )=(sin x -cos x )sin 2x sin x=2cos x (sin x -cos x )=sin 2x -2cos 2x=sin 2x -(1+cos 2x ) =2sin ⎝⎛⎭⎫2x -π4-1, 所以f (x )的最小正周期T =2π2=π. (2)函数y =sin x 的单调递增区间为⎣⎡⎦⎤2k π-π2,2k π+π2(k ∈Z ). 由2k π-π2≤2x -π4≤2k π+π2,x ≠k π(k ∈Z ), 得k π-π8≤x ≤k π+3π8,x ≠k π(k ∈Z ).所以f (x )的单调递增区间为⎣⎡⎭⎫k π-π8,k π和⎝⎛⎦⎤k π,k π+3π8(k ∈Z ). 2.已知△ABC 的三个内角A ,B ,C 成等差数列,角B 所对的边b =3,且函数f (x )=23sin 2x +2sin x cos x -3在x =A 处取得最大值.(1)求f (x )的值域及周期;(2)求△ABC 的面积.解 (1)因为A ,B ,C 成等差数列,所以2B =A +C ,又A +B +C =π,所以B =π3,即A +C =2π3. 因为f (x )=23sin 2x +2sin x cos x - 3 =3(2sin 2x -1)+sin 2x =sin 2x -3cos 2x=2sin ⎝⎛⎭⎫2x -π3, 所以T =2π2=π. 又因为sin ⎝⎛⎭⎫2x -π3∈[-1,1], 所以f (x )的值域为[-2,2].(2)因为f (x )在x =A 处取得最大值,所以sin ⎝⎛⎭⎫2A -π3=1. 因为0<A <23π,所以-π3<2A -π3<π, 故当2A -π3=π2时,f (x )取到最大值, 所以A =512π,所以C =π4. 由正弦定理,知3sin π3=c sin π4⇒c = 2. 又因为sin A =sin ⎝⎛⎭⎫π4+π6=2+64, 所以S △ABC =12bc sin A =3+34. 3.已知函数f (x )=3sin 2x +2cos 2x +a .(1)求函数f (x )的最小正周期以及单调递增区间;(2)当x ∈[0,π4]时,函数f (x )有最大值4,求实数a 的值. 解 f (x )=3sin 2x +2cos 2x +a=cos 2x +3sin 2x +1+a=2sin(2x +π6)+a +1. (1)函数f (x )的最小正周期为2π2=π,由2k π-π2≤2x +π6≤2k π+π2,k ∈Z , 解得k π-π3≤x ≤k π+π6,k ∈Z . 故函数f (x )的单调递增区间为[k π-π3,k π+π6](k ∈Z ). (2)∵x ∈[0,π4],∴2x +π6∈[π6,2π3], 从而sin(2x +π6)∈[12,1]. ∴f (x )=2sin(2x +π6)+a +1∈[a +2,a +3], ∵f (x )有最大值4,∴a +3=4,故a =1.4.设向量a =(3sin x ,sin x ),b =(cos x ,sin x ),x ∈[0,π2]. (1)若|a |=|b |,求x 的值;(2)设函数f (x )=a ·b ,求f (x )的最大值.解 (1)由|a |2=(3sin x )2+(sin x )2=4sin 2x ,|b |2=(cos x )2+(sin x )2=1,由|a |=|b |,得4sin 2x =1.又x ∈[0,π2],从而sin x =12, 所以x =π6. (2)f (x )=a ·b =3sin x ·cos x +sin 2x =32sin 2x -12cos 2x +12=sin(2x -π6)+12. 当x =π3∈[0,π2]时,sin(2x -π6)取最大值1, 所以f (x )的最大值为32. 5.已知函数f (x )=4cos ωx ·sin(ωx -π6)+1(ω>0)的最小正周期是π. (1)求f (x )的单调递增区间;(2)求f (x )在[π8,3π8]上的最大值和最小值. 解 (1)f (x )=4cos ωx ·sin(ωx -π6)+1 =23sin ωx cos ωx -2cos 2ωx +1=3sin 2ωx -cos 2ωx =2sin(2ωx -π6). 最小正周期是2π2ω=π,所以,ω=1, 从而f (x )=2sin(2x -π6). 令-π2+2k π≤2x -π6≤π2+2k π,k ∈Z . 解得-π6+k π≤x ≤π3+k π,k ∈Z . 所以函数f (x )的单调递增区间为[-π6+k π,π3+k π](k ∈Z ). (2)当x ∈[π8,3π8]时,2x -π6∈[π12,7π12], f (x )=2sin(2x -π6)∈[6-22,2], 所以f (x )在[π8,3π8]上的最大值和最小值分别为2,6-22. 6.在斜度一定的山坡上的一点A 测得山顶上一建筑物顶端对于山坡的斜度为15°,如图所示,向山顶前进100 m 后,又从B 点测得斜度为45°,设建筑物的高为50 m .求此山对于地平面的斜度θ的余弦值.解 在△ABC 中,∠BAC =15°,∠CBA =180°-45°=135°,AB =100 m , 所以∠ACB =30°. 由正弦定理,得100sin 30°=BC sin 15°,即BC =100sin 15°sin 30°. 在△BCD 中,因为CD =50,BC =100sin 15°sin 30°,∠CBD =45°,∠CDB =90°+θ, 由正弦定理,得50sin 45°=100sin 15°sin 30°sin (90°+θ), 解得cos θ=3-1.因此,山对地面的斜度的余弦值为3-1.。
高高考数学中档大题规范练(数列).docx

高中数学学习材料马鸣风萧萧*整理制作中档大题规范练——数列1.已知公差大于零的等差数列{a n }的前n 项和S n ,且满足:a 2a 4=64,a 1+a 5=18.(1)若1<i <21,a 1,a i ,a 21是某等比数列的连续三项,求i 的值.(2)设b n =n (2n +1)S n,是否存在一个最小的常数m 使得b 1+b 2+…+b n <m 对于任意的正整数n 均成立,若存在,求出常数m ;若不存在,请说明理由.解 (1)数列{a n }为等差数列,因为a 1+a 5=a 2+a 4=18,又a 2a 4=65,所以a 2,a 4是方程x 2-18x +65=0的两个根,又公差d >0,所以a 2<a 4,所以a 2=5,a 4=13.所以⎩⎪⎨⎪⎧a 1+d =5,a 1+3d =13,① 所以a 1=1,d =4.所以a n =4n -3.由1<i <21,a 1,a i ,a 21是某等比数列的连续三项,所以a 1a 21=a 2i ,即1×81=(4i -3)2,解得i =3.(2)由(1)知,S n =n ×1+n (n -1)2×4=2n 2-n , 所以b n =1(2n -1)(2n +1)=12(12n -1-12n +1),② 所以b 1+b 2+…+b n=12(1-13+13-15+…+12n -1-12n +1)=n 2n +1, 因为n 2n +1=12-12(2n +1)<12,③ 所以存在m =12使b 1+b 2+…+b n <m 对于任意的正整数n 均成立.2.设S n 为数列{a n }的前n 项和,已知a 1≠0,2a n -a 1=S 1·S n ,n ∈N *.(1)求a 1,a 2,并求数列{a n }的通项公式;(2)求数列{na n }的前n 项和.解 (1)令n =1,得2a 1-a 1=a 21,即a 1=a 21.因为a 1≠0,所以a 1=1.令n =2,得2a 2-1=S 2=1+a 2,解得a 2=2.当n ≥2时,由2a n -1=S n,2a n -1-1=S n -1,两式相减得2a n -2a n -1=a n ,即a n =2a n -1.于是数列{a n }是首项为1,公比为2的等比数列.因此,a n =2n -1. 所以数列{a n }的通项公式为a n =2n -1. (2)由(1)知,na n =n ·2n -1. 记数列{n ·2n -1}的前n 项和为B n ,于是 B n =1+2×2+3×22+…+n ×2n -1.① 2B n =1×2+2×22+3×23+…+n ×2n .②①-②,得-B n =1+2+22+…+2n -1-n ·2n =2n -1-n ·2n . 从而B n =1+(n -1)·2n .即数列{na n }的前n 项和为1+(n -1)·2n .3.设数列{a n }的前n 项和为S n ,满足2S n =a n +1-2n +1+1,n ∈N *,且a 1=1,设数列{b n }满足b n =a n +2n .(1)求证数列{b n }为等比数列,并求出数列{a n }的通项公式;(2)若数列c n =6n -3b n,T n 是数列{c n }的前n 项和,证明:T n <3. (1)解 当n ≥2时,由⎩⎪⎨⎪⎧2S n =a n +1-2n +1+1,2S n -1=a n -2n +1 ⇒2a n =a n +1-a n -2n⇒a n +1=3a n +2n ,从而b n +1=a n +1+2n +1=3(a n +2n )=3b n , 故{b n }是以3为首项,3为公比的等比数列,b n =a n +2n =3×3n -1=3n , a n =3n -2n (n ≥2),因为a 1=1也满足,于是a n =3n -2n .(2)证明 c n =6n -3b n =2n -13n -1,则T n =130+331+532+…+2n -33n -2+2n -13n -1,① 13T n =131+332+533+…+2n -33n -1+2n -13n ,② ①-②,得23T n =130+231+232+…+23n -1-2n -13n =1+23·1-13n -11-13-2n -13n =2-13n -1-2n -13n =2-2(n +1)3n, 故T n =3-n +13n -1<3. 4.已知单调递增数列{a n }的前n 项和为S n ,满足S n =12(a 2n +n ). (1)求数列{a n }的通项公式;(2)设c n =⎩⎪⎨⎪⎧1a 2n +1-1,n 为奇数,3×2a n -1+1,n 为偶数,求数列{c n }的前n 项和T n . 解 (1)n =1时,a 1=12(a 21+1),得a 1=1, 由S n =12(a 2n +n ),① 则当n ≥2时,S n -1=12(a 2n -1+n -1),② ①-②得a n =S n -S n -1=12(a 2n -a 2n -1+1), 化简得(a n -1)2-a 2n -1=0, a n -a n -1=1或a n +a n -1=1(n ≥2),又{a n }是单调递增数列,故a n -a n -1=1,所以{a n }是首项为1,公差为1的等差数列,故a n =n .(2)c n =⎩⎪⎨⎪⎧1a 2n +1-1,n 为奇数,3×2a n -1+1,n 为偶数,当n 为偶数时,T n =(c 1+c 3+…+c n -1)+(c 2+c 4+…+c n )=(122-1+142-1+…+1n 2-1)+3×(21+23+…+2n -1)+n 2 =11×3+13×5+…+1(n -1)×(n +1)+3×2(1-4n 2)1-4+n 2 =12×(11-13+13-15+…+1n -1-1n +1)+2×(4n 2-1)+n 2 =2n +1+n 2-2n -42(n +1). 当n 为奇数时,T n =(c 1+c 3+…+c n )+(c 2+c 4+…+c n -1)=[122-1+142-1+…+1(n +1)2-1]+3×(21+23+…+2n -2)+n -12 =12×(11-13+13-15+…+1n -1n +2)+2×(4n -12-1)+n -12=2n+n 2-2n -92(n +2). 所以T n =⎩⎪⎨⎪⎧ 2n +n 2-2n -92(n +2)(n 为奇数),2n +1+n 2-2n -42(n +1)(n 为偶数).5.已知函数f (x )=2x +33x ,数列{a n }满足a 1=1,a n +1=f (1a n),n ∈N *. (1)求数列{a n }的通项公式;(2)令b n =1a n -1a n(n ≥2),b 1=3,S n =b 1+b 2+…+b n ,若S n <m -2 0142对一切n ∈N *恒成立,求最小正整数m .解 (1)∵a n +1=f (1a n )=2a n +33a n=2+3a n 3=a n +23, ∴{a n }是以1为首项,23为公差的等差数列. ∴a n =1+(n -1)×23=23n +13. (2)当n ≥2时,b n =1a n -1a n =1(23n -13)(23n +13) =1(2n -1)(2n +1)9=92(12n -1-12n +1),又b 1=3=92(1-13), ∴S n =b 1+b 2+…+b n =92(1-13+13-15+…+12n -1-12n +1)=92(1-12n +1)=9n 2n +1, ∵S n <m -2 0142对一切n ∈N *恒成立, 即9n 2n +1<m -2 0142对一切n ∈N *恒成立, 又9n 2n +1<92,∴m -2 0142≥92, 即m ≥2 023.∴最小正整数m 为2 023.6.某工厂为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中的维护费用会逐年增加,第一年的维护费用是4万元,从第二年到第七年,每年的维护费用均比上年增加2万元,从第八年开始,每年的维护费用比上年增加25%.(1)设第n 年该生产线的维护费用为a n ,求a n 的表达式;(2)若该生产线前n 年每年的平均维护费用大于12万元时,需要更新生产线.求该生产线前n 年每年的平均维护费用,并判断第几年年初需要更新该生产线?解 (1)由题意知,当n ≤7时,数列{a n }是首项为4,公差为2的等差数列,所以a n =4+(n -1)×2=2n +2.当n ≥8时,数列{a n }从a 7开始构成首项为a 7=2×7+2=16,公比为1+25%=54的等比数列, 则此时a n =16×⎝⎛⎭⎫54n -7,所以a n =⎩⎪⎨⎪⎧2n +2,n ≤7,16×⎝⎛⎭⎫54n -7,n ≥8.(2)设S n 为数列{a n }的前n 项和,当1≤n ≤7时,S n =4n +n (n -1)2×2=n 2+3n , 当n ≥8时,由S 7=72+3×7=70,则S n =70+16×54×1-⎝⎛⎭⎫54n -71-54=80×⎝⎛⎭⎫54n -7-10, ∴该生产线前n 年每年的平均维护费用为S n n =⎩⎨⎧ n +3,1≤n ≤7,80×⎝⎛⎭⎫54n -7-10n,n ≥8. 当1≤n ≤7时,⎩⎨⎧⎭⎬⎫S n n 为递增数列,当n ≥8时,∵S n +1n +1-S n n =80×⎝⎛⎭⎫54n -6-10n +1-80×⎝⎛⎭⎫54n -7-10n =80×⎝⎛⎭⎫54n -7·⎝⎛⎭⎫n 4-1+10n (n +1)>0, ∴S n +1n +1>S n n. ∴⎩⎨⎧⎭⎬⎫S n n 也为递增数列.又∵S 77=10<12,S 88=80×54-108=11.25<12, S 99=80×⎝⎛⎭⎫542-109≈12.78>12, 则第9年年初需更新生产线.。
高考数学中档大题规范练(2)——数列.docx

专题分层训练(二十九) 中档大题规范练(2)——数列1.(2015·江西省八校联考)已知f (x )=2sin π2x ,集合M ={x ||f (x )|=2,x >0},把M 中的元素从小到大依次排成一列,得到数列{a n },n ∈N *.(1)求数列{a n }的通项公式;(2)记b n =1a 2n +1,设数列{b n }的前n 项和为T n ,求证:T n <14. 解 (1)∵|f (x )|=2,∴π2x =k π+π2,k ∈Z ,x =2k +1,k ∈Z . 又∵x >0,∴a n =2n -1(n ∈N *).(2)∵b n =1a 2n +1=1(2n +1)2=14n 2+4n +1<14n 2+4n =14⎝ ⎛⎭⎪⎫1n -1n +1, ∴T n =b 1+b 2+…+b n <14(1-12+12-13+…+1n -1n +1)=14-14(n +1)<14,∴T n <14得证.2.(2015·石家庄市第一次模拟)设数列{a n }的前n 项和为S n ,a 1=1,a n+1=λS n +1(n ∈N *,λ≠-1),且a 1、2a 2、a 3+3为等差数列{b n }的前三项. (1)求数列{a n },{b n }的通项公式;(2)求数列{a n b n }的前n 项和.解 (1)解法一:∵a n +1=λS n +1(n ∈N *), ∴a n =λS n -1+1(n ≥2), ∴a n +1-a n =λa n ,即a n +1=(λ+1)a n (n ≥2),λ+1≠0, 又a 1=1,a 2=λS 1+1=λ+1,∴数列{a n }是以1为首项,公比为λ+1的等比数列, ∴a 3=(λ+1)2,∴4(λ+1)=1+(λ+1)2+3, 整理得λ2-2λ+1=0,解得λ=1, ∴a n =2n -1,b n =1+3(n -1)=3n -2. 解法二:∵a 1=1,a n +1=λS n +1(n ∈N *), ∴a 2=λS 1+1=λ+1,a 3=λS 2+1=λ(1+λ+1)+1=λ2+2λ+1, ∴4(λ+1)=1+λ2+2λ+1+3, 整理得λ2-2λ+1=0,解得λ=1, ∴a n +1=S n +1(n ∈N *), ∴a n =S n -1+1(n ≥2),∴a n +1-a n =a n (n ≥2),即a n +1=2a n (n ≥2), 又a 1=1,a 2=2,∴数列{a n }是以1为首项,公比为2的等比数列, ∴a n =2n -1,b n =1+3(n -1)=3n -2. (2)由(1)知,a n b n =(3n -2)×2n -1, 设T n 为数列{a n b n }的前n 项和,∴T n =1×1+4×21+7×22+…+(3n -2)×2n -1,①∴2T n =1×21+4×22+7×23+…+(3n -5)×2n -1+(3n -2)×2n .② ①-②得,-T n =1×1+3×21+3×22+…+3×2n -1-(3n -2)×2n =1+3×2×(1-2n -1)1-2-(3n -2)×2n ,整理得:T n =(3n -5)×2n +5.3.已知单调递增数列{a n }的前n 项和为S n ,满足S n =12(a 2n +n ). (1)求数列{a n }的通项公式; (2)设c n =⎩⎪⎨⎪⎧1a 2n+1-1,n 为奇数,3×2an -1+1,n 为偶数,求数列{c n }的前n 项和T n .解 (1)n =1时,a 1=12(a 21+1),得a 1=1, 当n ≥2时,S n -1=12(a 2n -1+n -1), 得a n =S n -S n -1=12(a 2n -a 2n -1+1),化简得(a n -1)2-a 2n -1=0,a n -a n -1=1或a n +a n -1=1(n ≥2), 又{a n }是单调递增数列,故a n -a n -1=1, 所以{a n }是首项为1,公差为1的等差数列, 故a n =n .(2)c n =⎩⎪⎨⎪⎧1a 2n +1-1,n 为奇数,3×2an -1+1,n 为偶数,当n 为偶数时,T n =(c 1+c 3+…+c n -1)+(c 2+c 4+…+c n )=⎝ ⎛⎭⎪⎫122-1+142-1+…+1n 2-1+3×(21+23+…+2n -1)+n2 =11×3+13×5+…+1(n -1)×(n +1)+3×2(1-4n 2)1-4+n 2 =12×(11-13+13-15+…+1n -1-1n +1)+2×(4n 2-1)+n 2=2n +1+n 2-2n -42(n +1).当n 为奇数时,T n =(c 1+c 3+…+c n )+(c 2+c 4+…+c n -1)=⎣⎢⎡⎦⎥⎤122-1+142-1+…+1(n +1)2-1+3×(21+23+…+2n -2)+n -12 =12×⎝ ⎛⎭⎪⎫11-13+13-15+…+1n -1n +2+2×(4n -12-1)+n -12=2n+n 2-2n -92(n +2).所以T n=⎩⎪⎨⎪⎧2n +n 2-2n -92(n +2),n 为奇数,2n +1+n 2-2n -42(n +1),n 为偶数.4.已知函数f (x )=2x +33x ,数列{a n }满足a 1=1,a n +1=f ⎝ ⎛⎭⎪⎫1a n ,n ∈N *.(1)求数列{a n }的通项公式; (2)令b n =1a n -1a n(n ≥2),b 1=3,S n =b 1+b 2+…+b n ,若S n <m -2 0142对一切n ∈N *成立,求最小正整数m .解 (1)∵a n +1=f ⎝ ⎛⎭⎪⎫1a n =2a n +33a n =2+3a n 3=a n +23, ∴{a n }是以1为首项,23为公差的等差数列. ∴a n =1+(n -1)×23=23n +13. (2)当n ≥2时,b n =1a n -1a n =1⎝ ⎛⎭⎪⎫23n -13⎝ ⎛⎭⎪⎫23n +13=1(2n -1)(2n +1)9=92⎝ ⎛⎭⎪⎫12n -1-12n +1,又b 1=3=92(1-13), ∴S n =b 1+b 2+…+b n=92⎝ ⎛⎭⎪⎫1-13+13-15+…+12n -1-12n +1 =92⎝ ⎛⎭⎪⎫1-12n +1 =9n 2n +1, ∵S n <m -2 0142对一切n ∈N *成立, 即9n 2n +1<m -2 0142对一切n ∈N *成立, 又9n 2n +1<92,∴m -2 0142≥92, 即m ≥2 023.∴最小正整数m 为2 023.5.设数列{a n }的前n 项和为S n ,如果S nS 2n为常数,则称数列{a n }为“幸福数列”.(1)等差数列{b n }的首项为1,公差不为零,若{b n }为“幸福数列”,求{b n }的通项公式;(2)数列{c n }的各项都是正数,前n 项和为S n ,若c 31+c 32+c 33+…+c 3n =S 2n 对任意n ∈N *都成立,试推断数列{c n }是否为“幸福数列”?并说明理由.解 (1)设等差数列{b n }的公差为d (d ≠0), S nS 2n =k ,因为b 1=1,则n +12n (n -1)d =k ⎣⎢⎡⎦⎥⎤2n +12·2n (2n -1)d , 即2+(n -1)d =4k +2k (2n -1)d . 整理得,(4k -1)dn +(2k -1)(2-d )=0,因为对任意正整数n 上式恒成立,则⎩⎪⎨⎪⎧d (4k -1)=0(2k -1)(2-d )=0,解得⎩⎨⎧d =2k =14.故数列{b n }的通项公式是b n =2n -1.(2)由已知,当n =1时,c 31=S 21=c 21.因为c 1>0,所以c 1=1.当n ≥2时,c 31+c 32+c 33+…+c 3n =S 2n , c 31+c 32+c 33+…+c 3n -1=S 2n -1.两式相减,得c 3n =S 2n -S 2n -1=(S n -S n -1)(S n +S n -1)=c n ·(S n +S n -1). 因为c n >0,所以c 2n =S n +S n -1=2S n -c n .显然c 1=1适合上式,所以当n ≥2时,c 2n -1=2S n -1-c n -1. 于是c 2n -c 2n -1=2(S n -S n -1)-c n +c n -1=2c n -c n +c n -1=c n +c n -1.因为c n +c n -1>0,则c n -c n -1=1,所以数列{c n }是首项为1,公差为1的等差数列. 所以S n S 2n =n (n +1)2n (2n +1)=n +14n +2不为常数,故数列{c n }不是“幸福数列”.。
高考中档大题规范练(二).docx

高考中档大题规范练(二)数 列1.已知函数f (x )=7x +5x +1,数列{a n }满足:2a n +1-2a n +a n +1a n =0且a n ≠0.数列{b n }中,b 1=f (0)且b n =f (a n -1).(1)求证:数列⎩⎨⎧⎭⎬⎫1a n 是等差数列; (2)求数列{|b n |}的前n 项和T n .2.已知等差数列{a n }是递增数列,且满足a 4·a 7=15,a 3+a 8=8.(1)求数列{a n }的通项公式;(2)令b n =19a n -1a n(n ≥2),b 1=13,求数列{b n }的前n 项和S n .3.(2015·天津)已知数列{a n }满足a n +2=qa n (q 为实数,且q ≠1),n ∈N *,a 1=1,a 2=2,且a 2+a 3,a 3+a 4,a 4+a 5成等差数列.(1)求q 的值和{a n }的通项公式;(2)设b n =log 2a 2n a 2n -1,n ∈N *,求数列{b n }的前n 项和.4.已知数列{a n }的前n 项和S n =a n +n 2-1,数列{b n }满足3n b n +1=(n +1)a n +1-na n ,且b 1=3.(1)求a n ,b n ;(2)设T n 为数列{b n }的前n 项和,求T n ,并求满足T n <7时n 的最大值.5.(2015·广东)数列{a n }满足:a 1+2a 2+…+na n =4-n +22n -1,n ∈N *. (1)求a 3的值;(2)求数列{a n }前n 项和T n ;(3)令b 1=a 1,b n =T n -1n+⎝⎛⎭⎫1+12+13+…+1n a n (n ≥2),证明:数列{b n }的前n 项和S n 满足S n <2+2ln n .答案精析高考中档大题规范练(二)数 列1.(1)证明 由2a n +1-2a n +a n +1a n =0得1a n +1-1a n =12, 所以数列⎩⎨⎧⎭⎬⎫1a n 是等差数列.(2)解 因为b 1=f (0)=5,所以7a 1-1+5a 1-1+1=5, 7a 1-2=5a 1,所以a 1=1,1a n =1+(n -1)×12,所以a n =2n +1. b n =7a n -2a n=7-(n +1)=6-n . 当n ≤6时,T n =n 2(5+6-n )=n 11-n 2; 当n ≥7时,T n =15+n -62(1+n -6) =n 2-11n +602. 所以,T n =⎩⎨⎧ n 11-n 2,n ≤6,n 2-11n +602,n ≥7.2.解 (1)根据题意a 3+a 8=8=a 4+a 7,a 4·a 7=15,所以a 4,a 7是方程x 2-8x +15=0的两根,且a 4<a 7,解得a 4=3,a 7=5.设数列{a n }的公差为d ,由a 7=a 4+(7-4)·d ,得d =23. 故等差数列{a n }的通项公式为a n =a 4+(n -4)·d =3+(n -4)·23=2n +13. (2)当n ≥2时,b n =19a n -1a n =19·2n -13·2n +13=12n -12n +1 =12(12n -1-12n +1), 又b 1=13=12(1-13), 所以S n =b 1+b 2+…+b n =12(1-13+13-15+…+12n -1-12n +1) =12(1-12n +1)=n 2n +1. 即数列{b n }的前n 项和S n =n 2n +1. 3.解 (1)由已知,有(a 3+a 4)-(a 2+a 3)=(a 4+a 5)-(a 3+a 4),即a 4-a 2=a 5-a 3,所以a 2(q -1)=a 3(q -1),又因为q ≠1,故a 3=a 2=2,由a 3=a 1q ,得q =2.由递推公式得当n =2k -1(k ∈N *)时,a n =a 2k -1=2k -1=2n -12; 当n =2k (k ∈N *)时,a n =a 2k =2k =2n 2. 所以,{a n }的通项公式为a n=⎩⎪⎨⎪⎧ 2n -12,n 为奇数,22n ,n 为偶数.(2)由(1)得b n =log 2a 2n a 2n -1=n 2n -1. 设{b n }的前n 项和为S n ,则S n =1×120+2×121+3×122+…+(n -1)×12n -2+n ×12n -1,12S n =1×121+2×122+3×123+…+(n -1)×12n -1+n ×12n . 上述两式相减得:12S n =1+12+122+…+12n -1-n 2n =1-12n 1-12-n 2n =2-22n -n 2n , 整理得,S n =4-n +22n -1,n ∈N *. 所以,数列{b n }的前n 项和为4-n +22n -1,n ∈N *. 4.解 (1)n ≥2时,S n =a n +n 2-1,S n -1=a n -1+(n -1)2-1,两式相减,得a n =a n -a n -1+2n -1,∴a n -1=2n -1.∴a n =2n +1,∴3n b n +1=(n +1)(2n +3)-n (2n +1)=4n +3,∴b n +1=4n +33n , ∴当n ≥2时,b n =4n -13n -1,又b 1=3适合上式, ∴b n =4n -13n -1. (2)由(1)知,b n =4n -13n -1, ∴T n =31+73+1132+…+4n -53n -2+4n -13n -1,① 13T n =33+732+1133+…+4n -53n -1+4n -13n ,② ①-②,得23T n =3+43+432+…+43n -1-4n -13n =3+4·131-13n -11-13-4n -13n =5-4n +53n . ∴T n =152-4n +52·3n -1. T n -T n +1=4n +1+52·3n -4n +52·3n -1=-4n +33n<0. ∴T n <T n +1,即{T n }为递增数列.又T 3=599<7,T 4=649>7, ∴T n <7时,n 的最大值为3.5.(1)解 a 1=1,a 1+2a 2=2,a 2=12,a 1+2a 2+3a 3=4-54,a 3=14. (2)解 n ≥2时,a 1+2a 2+…+(n -1)·a n -1=4-n +12n -2, 与原式相减,得na n =n 2n -1,a n =12n -1,n =1也符合,T n =1-12n 1-12=2-12n -1. (3)证明 n ≥2时,b n =T n -1n+⎝⎛⎭⎫1+12+13+…+1n a n =a 1+a 2+…+a n -1n+ ⎝⎛⎭⎫1+12+13+…+1n a n ,故S n =∑i =1n b i =a 1+a 12+⎝⎛⎭⎫1+12a 2+a 1+a 23+⎝⎛⎭⎫1+12+13a 3+…+a 1+a 2+…+a n -1n+⎝⎛⎭⎫1+12+…+1n a n =⎝ ⎛⎭⎪⎪⎫∑i =1n 1i a 1+⎝ ⎛⎭⎪⎪⎫∑i =1n 1i a 2+⎝ ⎛⎭⎪⎪⎫∑i =1n 1i a 3+…+⎝ ⎛⎭⎪⎪⎫∑i =1n 1i a n =⎝ ⎛⎭⎪⎪⎫∑i =1n 1i T n = ⎝⎛⎭⎫1+12+…+1n ⎝⎛⎭⎫2-12n -1 <2⎝⎛⎭⎫1+12+…+1n , 只需证明2⎝⎛⎭⎫1+12+…+1n <2+2ln n ,n ∈N *. 对于任意自然数k ∈N ,令x =-1k +1∈ (-1,0)时,ln ⎝⎛⎭⎫-1k +1+1+1k +1<0,即1k +1<ln(k +1)-ln k . ∴k =1时,12<ln 2-ln 1,k =2时,13<ln 3-ln 2. …k =n -1时,1n<ln n -ln(n -1). ∴1+12+13+ (1)<1+(ln 2-ln 1)+(ln 3-ln 2)+…+[ln n -ln(n -1)], 即1+12+13+…+1n <1+ln n ,∴n ≥2时,2⎝⎛⎭⎫1+12+13+ (1)<2+2ln n ,综上n ∈N *时,S n <2+2ln n .。
高考理科数学中档大题保分专练15套(经典珍藏解析版)

(Ⅱ)若选取的是 12 月 1 日与 12 月 5 日的两组数据,请根据 12 月 2 日至 12 月 4 日的数据,
求 y 关于 x 的线性回归方程 y bx a ;
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过 2 颗,则认为
得到的线性回归方程是可靠的,试问(Ⅱ)中所得的线性回归方程是否可靠?
i 1
xi2
112
132
122
434
2
, 3x
432 ,由公式求
得
第 2 页 共 57 页
中档大题保分专练 15 套
3
b
xi yi
i 1
977 972 5 ,a y bx 3
3
xi 2
2
3x
434 432
2
i 1
.
x 2 cos
4.
(广西名校第一次摸底)已知曲线
M
的参数方程为
12 月 2 日
12 月 3 日
12 月 4 日
12 月 5 日
温差 x (℃) 10
11
13
12
8
发芽数 y(颗) 23
25
30
26
16
该农科所确定的研究方案是:先从这 5 组数据中选取 2 组,用剩下的 3 组数据求线性回归方
程,再对被选取的 2 组数据进行检验.
(Ⅰ)求选取的 2 组数据恰好是不相邻的 2 天数据的概率;
,
∴曲线 N 的普通方程为 3x y 16 0 .……………………………………5 分
(Ⅱ)圆 M 的圆心 M 0 ,2 ,半径 r 2.
2 16
d
7
点 M 到直线 N 的距离为
高考数学(理)考前三个月考前抢分必做 中档大题规范练2 Word版含解析

中档大题规范练2 立体几何与空间向量1.如图,在四棱锥P —ABCD 中,侧面P AD ⊥底面ABCD ,侧棱P A =PD =2,P A ⊥PD ,底面ABCD 为直角梯形,其中BC ∥AD ,AB ⊥AD ,AB =BC =1,O 为AD 的中点.(1)求证:PO ⊥平面ABCD ;(2)求B 点到平面PCD 的距离;(3)线段PD 上是否存在一点Q ,使得二面角Q —AC —D 的余弦值为63?若存在,求出PQ QD 的值;若不存在,请说明理由.(1)证明 因为P A =PD =2,O 为AD 的中点,所以PO ⊥AD ,因为侧面P AD ⊥底面ABCD ,所以PO ⊥平面ABCD .(2)解 以O 为原点,OC ,OD ,OP 分别为x 轴,y 轴,z 轴,建立空间直角坐标系O -xyz ,则B (1,-1,0),C (1,0,0),D (0,1,0),P (0,0,1).PB →=(1,-1,-1),设平面PDC 的法向量为u =(x ,y ,z ),CP →=(-1,0,1),PD →=(0,1,-1).则⎩⎪⎨⎪⎧ u ·CP →=-x +z =0,u ·PD →=y -z =0,取z =1,得u =(1,1,1), B 点到平面PDC 的距离d =|BP →·u ||u |=33. (3)解 假设存在,则设PQ →=λPD → (0<λ<1),因为PD →=(0,1,-1),所以Q (0,λ,1-λ),设平面CAQ 的法向量为m =(a ,b ,c ),则⎩⎪⎨⎪⎧ m ·AC →=0,m ·AQ →=0,即⎩⎪⎨⎪⎧a +b =0,(λ+1)b +(1-λ)c =0, 所以取m =(1-λ,λ-1,λ+1),平面CAD 的法向量n =(0,0,1),因为二面角Q —AC —D 的余弦值为63, 所以|m·n||m||n |=63, 所以3λ2-10λ+3=0, 所以λ=13或λ=3(舍去),所以PQ QD =12. 2.如图,在长方体ABCD —A 1B 1C 1D 1中,AA 1=AB =2AD =2,E 为AB 的中点,F 为D 1E 上的一点,D 1F =2FE .(1)证明:平面DFC ⊥平面D 1EC ;(2)求二面角A —DF —C 的大小.(1)证明 以D 为原点,分别以DA 、DC 、DD 1所在直线为x 轴、y 轴、z 轴建立如图所示空间直角坐标系,则A (1,0,0),B (1,2,0),C (0,2,0),D 1(0,0,2).∵E 为AB 的中点,∴E 点坐标为(1,1,0),∵D 1F =2FE ,∴D 1F →=23D 1E →=23(1,1,-2) =(23,23,-43), DF →=DD 1→+D 1F →=(0,0,2)+(23,23,-43) =(23,23,23). 设n =(x ,y ,z )是平面DFC 的法向量,则⎩⎪⎨⎪⎧ n ·DF →=0,n ·DC →=0,∴⎩⎪⎨⎪⎧23x +23y +23z =0,2y =0,取x =1得平面FDC 的一个法向量n =(1,0,-1).设p =(x ,y ,z )是平面ED 1C 的法向量,则⎩⎪⎨⎪⎧ p ·D 1F →=0,p ·D 1C →=0,∴⎩⎪⎨⎪⎧ 23x +23y -43z =0,2y -2z =0,取y =1得平面D 1EC 的一个法向量p =(1,1,1).∵n·p =(1,0,-1)·(1,1,1)=0,∴平面DFC ⊥平面D 1EC .(2)解 设q =(x ,y ,z )是平面ADF 的法向量,则q ·DF →=0,q ·DA →=0.∴⎩⎪⎨⎪⎧23x +23y +23z =0,x =0,取y =1得平面ADF 的一个法向量q =(0,1,-1),设二面角A —DF —C 的平面角为θ,由题中条件可知θ∈(π2,π), 则cos θ=-|n·q |n|·|q ||=-0+0+12×2=-12, ∴二面角A —DF —C 的大小为120°.3.如图所示,在直三棱柱A 1B 1C 1—ABC 中,AB ⊥AC ,AB =AC =2,A 1A =4,点D 是BC 的中点.(1)求异面直线A 1B 与C 1D 所成角的余弦值;(2)求平面ADC 1与平面ABA 1所成二面角的正弦值.解 (1)以A 为坐标原点,建立如图所示的空间直角坐标系A -xyz ,则A (0,0,0),B (2,0,0),C (0,2,0),D (1,1,0),A 1(0,0,4),C 1(0,2,4),所以A 1B →=(2,0,-4),C 1D →=(1,-1,-4).因为cos 〈A 1B →,C 1D →〉=A 1B →·C 1D →|A 1B →||C 1D →|=1820×18=31010,所以异面直线A 1B 与C 1D 所成角的余弦值为31010. (2)设平面ADC 1的法向量为n 1=(x ,y ,z ),因为AD →=(1,1,0),AC 1→=(0,2,4),所以n 1·AD →=0,n 1·AC 1→=0,即x +y =0且y +2z =0,取z =1,得x =2,y =-2,所以n 1=(2,-2,1)是平面ADC 1的一个法向量.取平面AA 1B 的一个法向量为n 2=(0,1,0),设平面ADC 1与平面ABA 1所成二面角的大小为θ.由|cos θ|=⎪⎪⎪⎪n 1·n 2|n 1||n 2|=29×1=23, 得sin θ=53. 因此,平面ADC 1与平面ABA 1所成二面角的正弦值为53. 4.如图,在四棱锥P —ABCD 中,平面P AD ⊥底面ABCD ,其中底面ABCD 为等腰梯形,AD ∥BC ,P A =AB =BC =CD =2,PD =23,P A ⊥PD ,Q 为PD 的中点.(1)证明:CQ ∥平面P AB ;(2)求二面角D —AQ —C 的余弦值.(1)证明 如图所示,取P A 的中点N ,连结QN ,BN .在△P AD 中,PN =NA ,PQ =QD ,所以QN ∥AD ,且QN =12AD . 在△APD 中,P A =2,PD =23,P A ⊥PD ,所以AD =P A 2+PD 2=22+(23)2=4,而BC =2,所以BC =12AD . 又BC ∥AD ,所以QN ∥BC ,且QN =BC ,故四边形BCQN 为平行四边形,所以BN ∥CQ .又CQ ⊄平面P AB ,BN ⊂平面P AB ,所以CQ ∥平面P AB .(2)解 如图,在平面P AD 内,过点P 作PO ⊥AD 于点O ,连结OB .因为平面P AD ⊥平面ABCD ,平面P AD ∩平面ABCD =AD ,所以PO ⊥平面ABCD .又PO ⊥AD ,AP ⊥PD ,所以PO =AP ×PD AD =2×234=3, 故AO =AP 2-PO 2=22-(3)2=1.在等腰梯形ABCD 中,取AD 的中点M ,连结BM ,又BC =2,AD =4,AD ∥BC ,所以DM =BC =2,DM ∥BC ,故四边形BCDM 为平行四边形.所以BM =CD =AB =2.在△ABM 中,AB =AM =BM =2,AO =OM =1,所以BO ⊥AD .又平面P AD ⊥平面ABCD ,平面P AD ∩平面ABCD =AD ,所以BO ⊥平面P AD .如图,以O 为坐标原点,分别以OB ,OD ,OP 所在直线为x 轴,y轴,z 轴建立空间直角坐标系,则O (0,0,0),D (0,3,0),A (0,-1,0),B (3,0,0),P (0,0,3),C (3,2,0),则AC →=(3,3,0).因为Q 为DP 的中点,故Q ⎝⎛⎭⎫0,32,32, 所以AQ →=⎝⎛⎭⎫0,52,32. 设平面AQC 的法向量为m =(x ,y ,z ),则⎩⎪⎨⎪⎧ m ⊥AC →,m ⊥AQ →,可得⎩⎨⎧ m ·AC →=3x +3y =0,m ·AQ →=52y +32z =0,令y =-3,则x =3,z =5.故平面AQC 的一个法向量为m =(3,-3,5).因为BO ⊥平面P AD ,所以OB →=(3,0,0)是平面ADQ 的一个法向量.故cos 〈OB →,m 〉=OB →·m |OB →|·|m |=333·32+(-3)2+52=337=33737. 从而可知二面角D —AQ —C 的余弦值为33737. 5.在四棱锥P —ABCD 中,侧面PCD ⊥底面ABCD ,PD ⊥CD ,底面ABCD 是直角梯形,AB ∥CD ,∠ADC =90°,AB =AD =PD =1,CD =2.(1)求证:BC ⊥平面PBD ;(2)在线段PC 上是否存在一点Q ,使得二面角Q —BD —P 为45°?若存在,求PQ PC 的值;若不存在,请说明理由. (1)证明 平面PCD ⊥底面ABCD ,PD ⊥CD ,所以PD ⊥平面ABCD ,所以PD ⊥AD .如图,以D 为原点建立空间直角坐标系D -xyz ,则A (1,0,0),B (1,1,0),C (0,2,0),P (0,0,1),DB →=(1,1,0),BC →=(-1,1,0),所以BC →·DB →=0,BC ⊥DB ,又由PD ⊥平面ABCD ,可得PD ⊥BC ,因为PD ∩BD =D ,所以BC ⊥平面PBD .(2)解 平面PBD 的法向量为BC →=(-1,1,0),PC →=(0,2,-1),设PQ →=λPC →,λ∈(0,1),所以Q (0,2λ,1-λ),设平面QBD 的法向量为n =(a ,b ,c ),DB →=(1,1,0),DQ →=(0,2λ,1-λ),由n ·DB →=0,n ·DQ →=0,得⎩⎪⎨⎪⎧a +b =0,2λb +(1-λ)c =0, 令b =1,所以n =(-1,1,2λλ-1), 所以cos 45°=|n ·BC →||n ||BC →|=22 2+(2λλ-1)2=22, 注意到λ∈(0,1),得λ=2-1,所以在线段PC 上存在一点Q ,使得二面角Q —BD —P 为45°,此时PQ PC=2-1.。
高考数学中档大题规范练中档大题3.docx

扩大我国中等收入阶层比重的对策研究作者:牟粼琳王刚来源:《群文天地》2011年第02期扩大中等收入阶层比重是我国现代化发展的必然趋势,其研究对加快我国现代化进程具有深刻意义。
本文对我国收入分配的现状进行分析,找出现阶段贫富差距扩大的根本原因,针对多元原因,提出培养和扩大中等收入阶层比重的对策,以期为我国解决贫富差距的问题,实现共同富裕做出贡献。
一、我国中等收入阶层现状分析目前中国经济社会发展的总体水平不是很高,导致中等收入者的比重相对过低。
根据中科院的测算标准,家庭财产在15万元至30万元之间可以算作是“中产”。
目前中国城市居民中有49%的家庭符合这一标准,但考虑到中国农村大多数家庭收入偏低的现实,最终可以推测出,目前我国的中等收入阶层人数只占全国人口的19%左右,这个比例很低。
而我国2002年全年城镇居民人均可支配收入为7500元,农民人均纯收入仅为2470元,我们的中收系数较高是建立在总体收入水平不高和高收入人群过于集中的基础之上的,这导致拥有有效需求能力和稳定心态的中等收入者的比重在这一经济发展阶段相对较低。
从纵向比较来看,中等收入者比重的增幅小于高收入者,1986至1999年,10%的最高收入户的收入就增长了8倍,远远高于中低收入层的增长,而且这种趋势还没有明显缓和的迹象,这使中等收入者比重趋于降低。
二、扩大中等收入阶层比重的积极作用1、扩大中等收入者比重有助于刺激消费,拉动经济增长。
我国现阶段消费差距很大:低收入人群收入太低,消费不足;而高收入阶层虽然拥有巨额财富,应有尽有,但他们要么不消费,导致资金闲置,要么过度消费,导致浪费资源,这种消费很不持续。
而我国中等收入阶层,他们消费意识和消费能力很强,为了过上更好的生活,他们积极工作,努力拼搏。
如果我国中等阶层人数占绝大多数,这意味将有一个庞大的消费市场,这有利于缓解和消除“需求不足”的市场经济问题;同时,中等收入阶层可以理性消费,可持续消费,对其它阶层有很好的示范作用,可以促进整个国家的经济持续、有序的发展。
广东省佛山市三水区2012高考数学 中低档题型专题训练(2)理

2012广东省理科数学大题(中低档题型)专题训练(二)1.已知向量a )3cos 3,3(cos ),3cos ,3(sin x x b x x ==b )3cos 3,3(cos ),3cos ,3(sin xx b x x a ==,函数()f x a b = a ·b ,(Ⅰ)求函数)(x f 的单调递增区间;(Ⅱ)如果△ABC的三边a 、b 、c 满足acb =2,且边b 所对的角为x ,试求x 的范围及函数)(x f 的值域.解:122()()sin cos cos sin cos )33332331222sin cos sin()23232332x x x x x xf x a b x x x π=⋅=+=+=++=++ Ⅰ3分令2233222πππππ+≤+≤-k x k ,解得,)(,43453Z k k x k ∈+≤≤-ππππ.故函数)(x f 的单调递增区间为)(],43,453[Z k k k ∈+-ππππ. 6分 22222221(),cos .2222a cb ac ac ac ac b ac x ac ac ac +-+--===≥= Ⅱ 8分953323,301cos 21ππππ≤+<∴≤<<≤∴x x x ,, 2sinsin()1333x ππ∴<+≤, 10分 23123)332sin(3+≤++<∴πx 即)(x f 的值域为]231,3(+. 综上所述,)(],3,0(x f x π∈的值域为]231,3(+. 12分 2.四个大小相同的小球分别标有数字1、1、2、2,把它们放在一个盒子里,从中任意摸出两个小球,它们所标有的数字分别为x 、y ,记y x +=ξ; (Ⅰ)求随机变量ξ的分布列和数学期望;(Ⅱ)设“函数1)(2--=x x x f ξ在区间)3,2(上有且只有一个零点”为事件A ,求事件A 发生的概率.解:(Ⅰ)由题意可知随机变量ξ的可能取值为2,3,4,从盒子中摸出两个小球的基本事件总数为624=C , 2分当2=ξ时,摸出小球所标的数字为1,1,61)2(==ξP , 当4=ξ时,摸出小球所标的数字为2,2,61)4(==ξP ,可知,当3=ξ时,3261611)3(=--==ξP ; 5分 得ξ的分布列为:12343636E ξ=⨯+⨯+⨯=; 7分(Ⅱ)由“函数1)(2--=x x x f ξ在区间)3,2(上有且只有一个零点”可知0)3()2(<f f ,即0)38)(23(<--ξξ,解得3823<<ξ, 又ξ的可能取值为2,3,4,故2=ξ,∴事件A 发生的概率为61。
高考数学(文科)中档大题规范练(三角函数)(含答案)

中档大题规范练中档大题规范练——三角函数1.已知函数f (x )=(sin x -cos x )sin 2x sin x. (1)求f (x )的定义域及最小正周期;(2)求f (x )的单调递增区间.解 (1)由sin x ≠0得x ≠k π(k ∈Z ),故f (x )的定义域为{x ∈R |x ≠k π,k ∈Z }.因为f (x )=(sin x -cos x )sin 2x sin x=2cos x (sin x -cos x )=sin 2x -2cos 2x=sin 2x -(1+cos 2x ) =2sin ⎝⎛⎭⎫2x -π4-1, 所以f (x )的最小正周期T =2π2=π. (2)函数y =sin x 的单调递增区间为⎣⎡⎦⎤2k π-π2,2k π+π2(k ∈Z ). 由2k π-π2≤2x -π4≤2k π+π2,x ≠k π(k ∈Z ), 得k π-π8≤x ≤k π+3π8,x ≠k π(k ∈Z ).所以f (x )的单调递增区间为⎣⎡⎭⎫k π-π8,k π和⎝⎛⎦⎤k π,k π+3π8(k ∈Z ). 2.已知△ABC 的三个内角A ,B ,C 成等差数列,角B 所对的边b =3,且函数f (x )=23sin 2x +2sin x cos x -3在x =A 处取得最大值.(1)求f (x )的值域及周期;(2)求△ABC 的面积.解 (1)因为A ,B ,C 成等差数列,所以2B =A +C ,又A +B +C =π,所以B =π3,即A +C =2π3. 因为f (x )=23sin 2x +2sin x cos x - 3 =3(2sin 2x -1)+sin 2x =sin 2x -3cos 2x=2sin ⎝⎛⎭⎫2x -π3, 所以T =2π2=π. 又因为sin ⎝⎛⎭⎫2x -π3∈[-1,1], 所以f (x )的值域为[-2,2].(2)因为f (x )在x =A 处取得最大值,所以sin ⎝⎛⎭⎫2A -π3=1. 因为0<A <23π,所以-π3<2A -π3<π, 故当2A -π3=π2时,f (x )取到最大值, 所以A =512π,所以C =π4. 由正弦定理,知3sin π3=c sin π4⇒c = 2. 又因为sin A =sin ⎝⎛⎭⎫π4+π6=2+64, 所以S △ABC =12bc sin A =3+34. 3.已知函数f (x )=3sin 2x +2cos 2x +a .(1)求函数f (x )的最小正周期以及单调递增区间;(2)当x ∈[0,π4]时,函数f (x )有最大值4,求实数a 的值. 解 f (x )=3sin 2x +2cos 2x +a=cos 2x +3sin 2x +1+a=2sin(2x +π6)+a +1. (1)函数f (x )的最小正周期为2π2=π, 由2k π-π2≤2x +π6≤2k π+π2,k ∈Z , 解得k π-π3≤x ≤k π+π6,k ∈Z .故函数f (x )的单调递增区间为[k π-π3,k π+π6](k ∈Z ). (2)∵x ∈[0,π4],∴2x +π6∈[π6,2π3], 从而sin(2x +π6)∈[12,1]. ∴f (x )=2sin(2x +π6)+a +1∈[a +2,a +3], ∵f (x )有最大值4,∴a +3=4,故a =1.4.设向量a =(3sin x ,sin x ),b =(cos x ,sin x ),x ∈[0,π2]. (1)若|a |=|b |,求x 的值;(2)设函数f (x )=a ·b ,求f (x )的最大值.解 (1)由|a |2=(3sin x )2+(sin x )2=4sin 2x ,|b |2=(cos x )2+(sin x )2=1,由|a |=|b |,得4sin 2x =1.又x ∈[0,π2],从而sin x =12, 所以x =π6. (2)f (x )=a ·b =3sin x ·cos x +sin 2x =32sin 2x -12cos 2x +12=sin(2x -π6)+12. 当x =π3∈[0,π2]时,sin(2x -π6)取最大值1, 所以f (x )的最大值为32. 5.已知函数f (x )=4cos ωx ·sin(ωx -π6)+1(ω>0)的最小正周期是π. (1)求f (x )的单调递增区间;(2)求f (x )在[π8,3π8]上的最大值和最小值. 解 (1)f (x )=4cos ωx ·sin(ωx -π6)+1 =23sin ωx cos ωx -2cos 2ωx +1=3sin 2ωx -cos 2ωx =2sin(2ωx -π6). 最小正周期是2π2ω=π,所以,ω=1,从而f (x )=2sin(2x -π6). 令-π2+2k π≤2x -π6≤π2+2k π,k ∈Z . 解得-π6+k π≤x ≤π3+k π,k ∈Z . 所以函数f (x )的单调递增区间为[-π6+k π,π3+k π](k ∈Z ). (2)当x ∈[π8,3π8]时,2x -π6∈[π12,7π12], f (x )=2sin(2x -π6)∈[6-22,2], 所以f (x )在[π8,3π8]上的最大值和最小值分别为2,6-22. 6.在斜度一定的山坡上的一点A 测得山顶上一建筑物顶端对于山坡的斜度为15°,如图所示,向山顶前进100 m 后,又从B 点测得斜度为45°,设建筑物的高为50 m .求此山对于地平面的斜度θ的余弦值.解 在△ABC 中,∠BAC =15°,∠CBA =180°-45°=135°,AB =100 m , 所以∠ACB =30°. 由正弦定理,得100sin 30°=BC sin 15°,即BC =100sin 15°sin 30°. 在△BCD 中,因为CD =50,BC =100sin 15°sin 30°,∠CBD =45°,∠CDB =90°+θ, 由正弦定理,得50sin 45°=100sin 15°sin 30°sin (90°+θ), 解得cos θ=3-1.因此,山对地面的斜度的余弦值为3-1.。
高考数学二轮复习 中档大题满分练(二)三角函数与解三角形(B组)-人教版高三全册数学试题

中档大题满分练2.三角函数与解三角形(B组)
中档大题集训练,练就慧眼和规X,筑牢高考满分根基!
1.已知△ABC中,角A,B,C所对的边分别是a,b,c,且asinA+csinC-bsinB
=asinC.
(1)求角B的大小.
(2)设向量m=(cosA,cos2A),n=(12,-5),边长a=4,当m·n取最大值时,求b的长. 【解析】(1)由题意,asinA+csinC-bsinB=asinC,
所以a2+c2-b2=ac,
所以cos B===,B∈(0,π),所以B=.
(2)因为m·n=12cos A-5cos 2A
=-10+,
所以当cos A=时,m·n取最大值,
此时,sin A=.
由正弦定理得,b=a·= .
2.如图,在平面四边形ABCD中,∠ABC=π,AB⊥AD,AB=1.
(1)若AC=,求△ABC的面积.
(2)若∠ADC=,CD=4,求sin∠CAD.
【解析】(1)在△ABC中,由余弦定理得,
AC2=AB2+BC2-2AB·BC·cos∠ABC,
即5=1+BC2+BC,解得BC=或-2(舍去),
所以△ABC的面积S△ABC=AB·BC·sin∠ABC=×1××=.
(2)设∠CAD=θ,在△ACD中,由正弦定理得,=,即=, 所以AC=.
在△ABC中,∠BAC=-θ,∠BCA=θ-,
则=,即=,
即4=sin θ,
整理得sin θ=2cos θ.
又因为sin2θ+cos2θ=1,
解得sin θ=,即sin∠CAD=.。
2020年新课标高考数学二轮复习-中档解答题规范练(6套)

2020年新课标高考数学二轮复习-中档解答题规范练(6套)目录2020年新课标高考数学二轮复习-中档解答题规范练(6套) (1)1、三角函数与解三角形 (2)2、数列 (8)3、立体几何 (14)4、概率与统计 (24)5、坐标系与参数方程 (35)6、不等式选讲 (41)1、三角函数与解三角形1.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且b =3,cos A sin B +(c -sin A )·cos(A +C )=0. (1)求角B 的大小;(2)若△ABC 的面积为32,求sin A +sin C 的值. 解 (1)由cos A sin B +(c -sin A )cos(A +C )=0, 得cos A sin B -(c -sin A )cos B =0,即sin(A +B )=c cos B ,sin C =c cos B ,sin Cc =cos B , 因为sin C c =sin B b , 所以sin B 3=cos B ,即tan B =3,又0<B <π,所以B =π3. (2)由S =12ac sin B =32,得ac =2,由b =3及余弦定理得(3)2=a 2+c 2-2ac cos B =a 2+c 2-ac =(a +c )2-3ac , 所以a +c =3,所以sin A +sin C =sin B b (a +c )=32.2.已知函数f (x )=12sin 2ωx cos φ+cos 2ωx sin φ+12cos ⎝ ⎛⎭⎪⎫π2+φ(0<φ<π),其图象上相邻两条对称轴之间的距离为π,且过点⎝ ⎛⎭⎪⎫π6,12.(1)求ω和φ的值;(2)求函数y =f (2x ),x ∈⎣⎢⎡⎦⎥⎤0,π2的值域.解 (1)f (x )=12sin 2ωx cos φ+1+cos 2ωx 2sin φ-12sin φ =12(sin 2ωx cos φ+cos 2ωx sin φ)=12sin(2ωx +φ). 由题意可知,T =2π=2π|2ω|,则ω=±12,当ω=12,把点⎝ ⎛⎭⎪⎫π6,12代入f (x )=12sin(2ωx +φ)中,可得φ=π3+2k π,k ∈Z ,而0<φ<π,解得φ=π3.当ω=-12,把点⎝ ⎛⎭⎪⎫π6,12代入f (x )=12sin(2ωx +φ)中,可得φ=2π3+2k π,k ∈Z ,而0<φ<π,解得φ=2π3.(2)由题可知,当ω=12,f (2x )=12sin ⎝ ⎛⎭⎪⎫2x +π3,0≤x ≤π2,∴π3≤2x +π3≤4π3,则函数f (2x )的值域为⎣⎢⎡⎦⎥⎤-34,12.当ω=-12时,f (2x )=12sin ⎝ ⎛⎭⎪⎫-2x +2π3=12sin ⎝ ⎛⎭⎪⎫2x +π3,∵0≤x ≤π2,∴π3≤2x +π3≤4π3,则函数f (2x )的值域为⎣⎢⎡⎦⎥⎤-34,12.综上,函数f (2x )的值域为⎣⎢⎡⎦⎥⎤-34,12.3.已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且满足a =1,sin (2A +B )sin A =2(1-cos C ). (1)求b 的值;(2)若△ABC 的面积为32,求c 的值. 解 (1)∵sin(2A +B )=2sin A (1-cos C ), ∴sin[(A +B )+A ]=2sin A -2sin A cos C ,sin(A +B )cos A +cos(A +B )sin A =2sin A +2sin A cos(A +B ), sin(A +B )cos A -cos(A +B )sin A =2sin A , ∴sin B =2sin A ,由正弦定理得b =2a ,又a =1, ∴b =2.(2)∵S △ABC =12ab sin C =12×1×2sin C =32, ∴sin C =32,cos C =±12,当cos C =12时,cos C =a 2+b 2-c 22ab =1+4-c 24=12,∴c =3;当cos C =-12时,cos C =a 2+b 2-c 22ab =1+4-c 24=-12,∴c =7. 故c =3或c =7.4.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,角A ,B ,C 的度数成等差数列,b =13.(1)若3sin C =4sin A ,求c 的值; (2)求a +c 的最大值.解 (1)由角A ,B ,C 的度数成等差数列,得2B =A +C . 又A +B +C =π,所以B =π3. 由正弦定理,得3c =4a ,即a =3c4. 由余弦定理,得b 2=a 2+c 2-2ac cos B , 即13=⎝ ⎛⎭⎪⎫3c 42+c 2-2×3c 4×c ×12,解得c =4.(2)由正弦定理,得asin A=csin C=bsin B=1332=2133,所以a=2133sin A,c=2133sin C.所以a+c=2133(sin A+sin C)=2133[sin A+sin(A+B)]=2133⎣⎢⎡⎦⎥⎤sin A+sin⎝⎛⎭⎪⎫A+π3=2133⎝⎛⎭⎪⎫32sin A+32cos A=213sin⎝⎛⎭⎪⎫A+π6.由0<A<2π3,得π6<A+π6<5π6.所以当A+π6=π2,即A=π3时,(a+c)max=213.5.在△ABC中,角A,B,C的对边分别为a,b,c,已知向量m=()cos A,cos B,n=()a,2c-b,且m∥n.(1)求角A的大小;(2)若a=4,求△ABC面积的最大值.解(1)∵m∥n,∴a cos B-()2c-b cos A=0,由正弦定理得sin A cos B-()2sin C-sin B cos A=0,∴sin A cos B+sin B cos A=2sin C cos A,∴sin(A+B)=2sin C cos A,由A+B+C=π,得sin C=2sin C cos A由于0<C<π,因此sin C>0,∴cos A=12,由于0<A<π,∴A=π3.(2)由余弦定理得a2=b2+c2-2bc cos A,∴16=b 2+c 2-bc ≥2bc -bc =bc ,∴bc ≤16,当且仅当b =c =4时,等号成立, ∴△ABC 面积S =12bc sin A ≤43, ∴△ABC 面积的最大值为4 3.6.已知函数f (x )=A sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,|φ|<π2的部分图象如图所示.(1)求函数f (x )的解析式;(2)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若(2a -c )cos B =b cos C ,求f ⎝ ⎛⎭⎪⎫A 2的取值范围. 解 (1)由图象知A =1,T =4⎝ ⎛⎭⎪⎫5π12-π6=π,ω=2,将点⎝ ⎛⎭⎪⎫π6,1代入解析式得sin ⎝ ⎛⎭⎪⎫π3+φ=1,因为|φ|<π2,所以φ=π6, 所以f (x )=sin ⎝ ⎛⎭⎪⎫2x +π6. (2)由(2a -c )cos B =b cos C 及正弦定理, 得(2sin A -sin C )cos B =sin B cos C . 所以2sin A cos B =sin(B +C ), cos B =12,B =π3,A +C =2π3,f ⎝ ⎛⎭⎪⎫A 2=sin ⎝ ⎛⎭⎪⎫A +π6,0<A <2π3,π6<A +π6<5π6,所以sin ⎝ ⎛⎭⎪⎫A +π6∈⎝ ⎛⎦⎥⎤12,1,所以f ⎝ ⎛⎭⎪⎫A 2的取值范围是⎝ ⎛⎦⎥⎤12,1.2、数列1.已知S n =na 1+(n -1)a 2+…+2a n -1+a n ,n ∈N *. (1)若{a n }是等差数列,且S 1=5,S 2=18,求a n ; (2)若{a n }是等比数列,且S 1=3,S 2=15,求S n .解 (1)设{a n }的公差为d ,则S 1=a 1=5,S 2=2a 1+a 2=10+a 2=18, 所以a 2=8,d =a 2-a 1=3,a n =5+3(n -1)=3n +2.(2)设{a n }的公比为q ,则S 1=a 1=3,S 2=2a 1+a 2=6+a 2=15, 所以a 2=9,q =a 2a 1=3,a n =3×3n -1=3n ,所以S n =n ×3+(n -1)×32+…+2×3n -1+3n , ① 3S n =n ×32+(n -1)×33+…+2×3n +3n +1,②②-①,得2S n =-3n +(32+33+…+3n )+3n +1=-3n +32(1-3n -1)1-3+3n +1=-3n -92+3n +12+3n +1=3n +2-6n -92,所以S n =3n +2-6n -94.2.已知等差数列{a n }的前n 项和为S n ,且a 3=5,S 3=9. (1)求数列{a n }的通项公式;(2)设等比数列{b n }的前n 项和为T n ,若q >0且b 3=a 5,T 3=13,求T n ; (3)设c n =1a n a n +1,求数列{c n }的前n 项和S n .解(1)⎩⎨⎧a 3=a 1+2d =5,S 3=3a 1+3×22d =9,解得⎩⎪⎨⎪⎧a 1=1,d =2,所以a n =a 1+(n -1)d =2n -1.(2)由题意可知,b 3=a 5=9,T 3=13,所以公比q =3, 从而b 1=1,所以T n =b 1(1-q n )1-q =1×(1-3n )1-3=12(3n-1).(3)由(1)知,a n =2n -1.所以c n =1a n a n +1=1(2n -1)(2n +1)=12⎝⎛⎭⎪⎫12n -1-12n +1, 所以S n =c 1+c 2+…+c n=12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1-13+⎝ ⎛⎭⎪⎫13-15+…+⎝ ⎛⎭⎪⎫12n -1-12n +1=12⎝ ⎛⎭⎪⎫1-12n +1=n 2n +1.3.设数列{a n }的前n 项之积为T n ,且log 2T n =n (n -1)2,n ∈N *. (1)求数列{a n }的通项公式;(2)设b n =λa n -1(n ∈N *),数列{b n }的前n 项之和为S n .若对任意的n ∈N *,总有S n+1>S n ,求实数λ的取值范围.解 (1)由log 2T n =n (n -1)2,n ∈N *,得T n =(1)22n n -,所以T n -1=(1)(2)22n n --(n ∈N *,n ≥2),所以a n =T nT n -1=(1)(1)(1)(2)222(1)(2)2222n n n n n n n n -------==2n -1,n ∈N *,n ≥2.又a 1=T 1=20=1,所以a n =2n -1,n ∈N *. (2)由b n =λa n -1=λ2n -1-1,得S n =λ·1-2n1-2-n =()2n-1λ-n ,所以S n +1>S n ⇔()2n +1-1λ-()n +1>()2n -1λ-n ⇔2nλ>1⇔λ>12n ,因为对任意的n ∈N *,12n ≤12, 故所求的λ的取值范围是⎝ ⎛⎭⎪⎫12,+∞.4.已知数列{a n }的前n 项和为S n ,向量a =(S n ,n ),b =(9n -7,2),且a 与b 共线.(1)求数列{}a n 的通项公式;(2)对任意m ∈N *,将数列{a n }中落入区间(9m ,92m )内的项的个数记为b m ,求数列{b m }的前m 项和T m .解 (1)a 与b 共线,S n =n (9n -7)2=92n 2-72n ,a 1=1,a n =S n -S n -1=9n -8,n ≥2,所以a n =9n -8,n ∈N *. (2)对m ∈N *,若9m <a n <92m , 则9m +8<9n <92m +8. 因此9m -1+1≤n ≤92m -1. 故得b m =92m -1-9m -1. 于是T m =b 1+b 2+…+b m=(9+93+…+92m -1)-(1+9+…+9m -1) =9(1-81m )1-81-1-9m 1-9=9×92m +1-10×9m80.5.已知数列{a n }的通项公式为a n =n ·3n3n-1(n ≥1,n ∈N *).(1)求a 1,a 2,a 3的值;(2)求证:对任意的自然数n ∈N *,不等式a 1·a 2·…·a n <2·n !成立. (1)解 将n =1,2,3代入可得a 1=32,a 2=94,a 3=8126. (2)证明 由a n =n ·3n3n-1=n1-13n(n ≥1,n ∈N *)可得 a 1·a 2·…·a n =n !⎝ ⎛⎭⎪⎫1-13⎝ ⎛⎭⎪⎫1-132…⎝ ⎛⎭⎪⎫1-13n ,因此欲证明不等式a 1·a 2·…·a n <2·n !成立,只需要证明对任意非零自然数n ,不等式⎝ ⎛⎭⎪⎫1-13⎝ ⎛⎭⎪⎫1-132…⎝ ⎛⎭⎪⎫1-13n >12恒成立即可,显然左端每个因式都为正数,因为1-⎝ ⎛⎭⎪⎫13+132+…+13n =1-13⎝ ⎛⎭⎪⎫1-13n 1-13=1-12⎝ ⎛⎭⎪⎫1-13n >1-12=12.故只需证明对每个非零自然数,不等式⎝ ⎛⎭⎪⎫1-13⎝ ⎛⎭⎪⎫1-132…⎝ ⎛⎭⎪⎫1-13n ≥1-⎝ ⎛⎭⎪⎫13+132+…+13n 恒成立即可.(*)下面用数学归纳法证明该不等式成立: ①显然当n =1时,不等式(*)恒成立;②假设当n =k (k ≥1,k ∈N *)时不等式(*)也成立,即不等式 ⎝ ⎛⎭⎪⎫1-13⎝ ⎛⎭⎪⎫1-132…⎝ ⎛⎭⎪⎫1-13k ≥1-⎝ ⎛⎭⎪⎫13+132+…+13k 成立. 那么当n =k +1时,⎝ ⎛⎭⎪⎫1-13⎝ ⎛⎭⎪⎫1-132…⎝ ⎛⎭⎪⎫1-13k ⎝ ⎛⎭⎪⎫1-13k +1≥⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫13+132+…+13k ⎣⎢⎡⎦⎥⎤1-13k +1,即⎝ ⎛⎭⎪⎫1-13⎝ ⎛⎭⎪⎫1-132…⎝ ⎛⎭⎪⎫1-13k +1≥1-⎝ ⎛⎭⎪⎫13+132+…+13k -13k +1+13k +1⎝ ⎛⎭⎪⎫13+132+…+13k ,注意到13k +1⎝⎛⎭⎪⎫13+132+…+13k >0,所以⎝ ⎛⎭⎪⎫1-13⎝ ⎛⎭⎪⎫1-132…⎝ ⎛⎭⎪⎫1-13k +1≥1-⎝ ⎛⎭⎪⎫13+132+…+13k +13k +1,这说明当n =k +1时,不等式(*)也成立.因此由数学归纳法可知,不等式(*)对任意非零自然数都成立,即 ⎝ ⎛⎭⎪⎫1-13⎝ ⎛⎭⎪⎫1-132…⎝ ⎛⎭⎪⎫1-13n ≥1-⎝ ⎛⎭⎪⎫13+132+…+13n >12恒成立, 故不等式a 1·a 2·…·a n <2·n !对任意非零自然数都成立.6.(2017·北京)设{a n }和{b n }是两个等差数列,记c n =max{b 1-a 1n ,b 2-a 2n ,…,b n -a n n }(n =1,2,3,…),其中max{x 1,x 2,…,x s }表示x 1,x 2,…,x s 这s 个数中最大的数.(1)若a n =n ,b n =2n -1,求c 1,c 2,c 3的值,并证明{c n }是等差数列;(2)证明:或者对任意正数M ,存在正整数m ,当n ≥m 时,c nn >M ;或者存在正整数m ,使得c m ,c m +1,c m +2,…是等差数列. (1)解 c 1=b 1-a 1=1-1=0,c 2=max{b 1-2a 1,b 2-2a 2}=max{1-2×1,3-2×2}=-1,c 3=max{b 1-3a 1,b 2-3a 2,b 3-3a 3}=max{1-3×1,3-3×2,5-3×3}=-2. 当n ≥3时,(b k +1-na k +1)-(b k -na k )=(b k +1-b k )-n (a k +1-a k )=2-n <0, 所以b k -na k 在k ∈N *时单调递减.所以c n =max{b 1-a 1n ,b 2-a 2n ,…,b n -a n n }=b 1-a 1n =1-n . 所以对任意n ≥1,c n =1-n ,于是c n +1-c n =-1, 所以{c n }是等差数列.(2)证明 设数列{a n }和{b n }的公差分别为d 1,d 2,则b k -na k =b 1+(k -1)d 2-[a 1+(k -1)d 1]n =b 1-a 1n +(d 2-nd 1)(k -1). 所以c n =⎩⎪⎨⎪⎧b 1-a 1n +(n -1)(d 2-nd 1),d 2>nd 1,b 1-a 1n ,d 2≤nd 1.①当d 1>0时,取正整数m >d 2d 1,则当n ≥m 时,nd 1>d 2,因此,c n =b 1-a 1n ,此时,c m ,c m +1,c m +2,…是等差数列. ②当d 1=0时,对任意n ≥1,n ∈N *,c n =b 1-a 1n +(n -1)max{d 2,0}=b 1-a 1+(n -1)(max{d 2,0}-a 1). 此时,c 1,c 2,c 3,…,c n ,…是等差数列. ③当d 1<0时,当n >d 2d 1时,有nd 1<d 2,所以c n n =b 1-a 1n +(n -1)(d 2-nd 1)n =n (-d 1)+d 1-a 1+d 2+b 1-d 2n≥n (-d 1)+d 1-a 1+d 2-|b 1-d 2|. 对任意正数M ,取正整数m >max ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫M +|b 1-d 2|+a 1-d 1-d 2-d 1,d 2d 1, 故当n ≥m 时,c nn >M .3、立体几何1.(2017·全国Ⅲ)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(1)证明:平面ACD⊥平面ABC;(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D-AE-C的余弦值.(1)证明由题设可得△ABD≌△CBD.从而AD=CD,又△ACD为直角三角形,所以∠ADC=90°,取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO,又因为△ABC是正三角形,故BO⊥AC,所以∠DOB为二面角D-AC-B的平面角,在Rt△AOB中,BO2+OA2=AB2,又AB=BD,所以BO2+DO2=BO2+AO2=AB2=BD2,故∠DOB=90°,所以平面ADC⊥平面ABC.(2)解由题设及(1)知,OA,OB,OD两两垂直,以O为坐标原点,OA →为x 轴正方向,OB →为y 轴正方向,OD →为z 轴正方向,|OA →|为单位长度,建立如图所示的空间直角坐标系Oxyz ,则O (0,0,0),A ()1,0,0,D ()0,0,1,B ()0,3,0,C (-1,0,0), 由题意知,四面体ABCE 的体积为四面体ABCD 的体积的12,从而E 到平面ABC 的距离为D 到平面ABC 的距离的12,即E 为DB 的中点,得E ⎝ ⎛⎭⎪⎫0,32,12,故AE →=⎝⎛⎭⎪⎫-1,32,12,AD →=()-1,0,1,OA→=()1,0,0. 设平面AED 的法向量为n 1=(x 1,y 1,z 1),平面AEC 的法向量为n 2=(x 2,y 2,z 2), 则⎩⎪⎨⎪⎧ AE →·n 1=0,AD →·n 1=0,解得n 1=⎝ ⎛⎭⎪⎫1,33,1,⎩⎪⎨⎪⎧AE →·n 2=0,OA →·n 2=0,解得n 2=(0,-1,3),设二面角D -AE -C 为θ,易知θ为锐角, 则cos θ=|n 1·n 2||n 1||n 2|=77.2.在如图所示的直三棱柱ABC -A 1B 1C 1中,D ,E 分别是BC ,A 1B 1的中点. (1)求证:DE ∥平面ACC 1A 1;(2)若AB ⊥BC ,AB =BC ,∠ACB 1=60°,求直线BC 与平面AB 1C 所成角的正切值.(1)证明取AB中点F,连接DF,EF.在△ABC中,因为D,F分别为BC,AB的中点,所以DF∥AC,又DF⊄平面ACC1A1,AC⊂平面ACC1A1,所以DF∥平面ACC1A1. 在矩形ABB1A1中,因为E,F分别为A1B1,AB的中点,所以EF∥AA1,又EF⊄平面ACC1A1,AA1⊂平面ACC1A1,所以EF∥平面ACC1A1.因为DF∩EF=F,所以平面DEF∥平面ACC1A1.因为DE⊂平面DEF,故DE∥平面ACC1A1.(2)解因为三棱柱ABC-A1B1C1为直三棱柱,所以BC⊥BB1,又AB⊥BC,AB∩BB1=B,所以BC⊥平面ABB1A1.因为AB=BC,BB1=BB1,所以△ABB1≌△CBB1,AB1=CB1,又∠ACB1=60°,所以△AB1C为正三角形,所以AB1=AB2+BB21=AC=2AB,所以BB1=AB.取AB1的中点O,连接BO,CO,所以AB1⊥BO,AB1⊥CO,所以AB1⊥平面BCO,所以平面AB1C⊥平面BCO,点B在平面AB1C上的射影在CO上,所以∠BCO即为直线BC与平面AB1C所成的角.在Rt △BCO 中,BO =22AB =22BC , 所以tan ∠BCO =BO BC =22.3.如图,在矩形ABCD 中,AB =1,AD =a ,P A ⊥平面ABCD ,且P A =1,E ,F 分别为AD ,P A 的中点,在BC 上有且只有一个点Q ,使得PQ ⊥QD .(1)求证:平面BEF ∥平面PDQ ; (2)求二面角E -BF -Q 的余弦值.(1)证明 方法一 (向量法)以A 点为原点,分别以AB →,AD →,AP →的方向为x 轴,y轴,z 轴的正方向,建立空间直角坐标系Axyz ,则A (0,0,0),B (1,0,0),D (0,a ,0),P (0,0,1), 设Q (1,x ,0),则PQ→=(1,x ,-1),QD →=(-1,a -x ,0),若PQ ⊥QD ,则PQ →·QD →=-1+x (a -x )=0,即x 2-ax +1=0,Δ=a 2-4=0, ∴a =2,x =1.∴Q ()1,1,0,QD→=()-1,1,0, 又E 是AD 的中点,∴E ()0,1,0,BE→=()-1,1,0,∴QD →=BE →, ∴BE ∥DQ ,又BE ⊄平面PDQ ,DQ ⊂平面PDQ , ∴BE ∥平面PDQ , 又F 是P A 的中点, ∴EF ∥PD ,∵EF ⊄平面PDQ ,PD ⊂平面PDQ , ∴EF ∥平面PDQ ,∵BE ∩EF =E ,BE ,EF ⊂平面BEF , ∴平面BEF ∥平面PDQ .方法二 (几何法)题意转化为矩形ABCD 中AQ 垂直于QD 的点Q 只有一个,则以AD 为直径的圆与线段BC 相切,易得BC =2,Q 是线段BC 的中点,由BE ∥QD ,EF ∥DP ,易得两平面平行.(2)解 设平面BFQ 的一个法向量m =()x ,y ,z , 则m ·BF →=m ·BQ→=0, 由(1)知,BF →=⎝ ⎛⎭⎪⎫-1,0,12,BQ →=()0,1,0, ∴-x +12z =y =0,取z =2,得m =()1,0,2,同样求得平面BEF 的一个法向量n =()1,1,2,cos 〈m ,n 〉=m ·n ||m ||n =306, ∵二面角E -BF -Q 为锐角, ∴二面角E -BF -Q 的余弦值为306.4.在四棱锥P-ABCD中,底面ABCD是正方形,侧面P AD⊥底面ABCD,且P A=PD=22AD,E,F分别为PC,BD的中点.(1)求证:EF∥平面P AD;(2)在线段AB上是否存在点G,使得二面角C-PD-G的余弦值为33,若存在,请求出点G的位置;若不存在,请说明理由.(1)证明连接AC,由正方形性质可知,AC与BD相交于点F,所以在△P AC中,EF∥P A,又P A⊂平面P AD,EF⊄平面P AD,所以EF∥平面P AD.(2)解取AD的中点O,连接OP,OF,因为P A=PD,所以PO⊥AD,又因为侧面P AD⊥底面ABCD,交线为AD,所以PO⊥平面ABCD,以O为原点,分别以射线OA,OF和OP为x轴,y轴和z轴建立空间直角坐标系Oxyz,不妨设AD =2,则P ()0,0,1,D ()-1,0,0,C ()-1,2,0,假设在AB 上存在点G ()1,a ,0,0<a <2,则PC→=()-1,2,-1,PD →=()-1,0,-1,DG →=()2,a ,0. 因为侧面P AD ⊥底面ABCD ,交线为AD ,且底面是正方形, 所以CD ⊥平面P AD ,则CD ⊥P A , 由P A 2+PD 2=AD 2,得PD ⊥P A , 又PD ∩CD =D ,PD ,CD ⊂平面PDC ,所以P A ⊥平面PDC ,即平面PDC 的一个法向量为P A →=(1,0,-1). 设平面PDG 的法向量为n =(x ,y ,z ), 由⎩⎪⎨⎪⎧PD →·n =0,DG →·n =0,即⎩⎪⎨⎪⎧-x -z =0,2x +ay =0,亦即⎩⎨⎧z =-x ,y =-2xa ,可取n =(a ,-2,-a ). 所以|cos 〈P A →,n 〉|=|P A →·n ||P A →||n |=2a 2×4+2a2=33, 解得a =1或a =-1(舍去).所以线段AB 上存在点G ,且G 为AB 的中点,使得二面角C -PD -G 的余弦值为33.5.已知三棱锥A -BCD 中,△ABC 是等腰直角三角形,且AC ⊥BC ,BC =2,AD ⊥平面BCD ,AD =1.(1)求证:平面ABC ⊥平面ACD ;(2)若E 为AB 的中点,求二面角A -CE -D 的余弦值.(1)证明 因为AD ⊥平面BCD ,BC ⊂平面BCD ,所以AD ⊥BC , 又因为AC ⊥BC ,AC ∩AD =A ,AD ,AC ⊂平面ACD , 所以BC ⊥平面ACD ,又BC ⊂平面ABC , 所以平面ABC ⊥平面ACD .(2)解 由已知可得CD =3,如图所示建立空间直角坐标系,由已知C (0,0,0),B (0,2,0),A (3,0,1),D (3,0,0),E ⎝ ⎛⎭⎪⎫32,1,12,则CE →=⎝ ⎛⎭⎪⎫32,1,12,CA →=(3,0,1),CD→=(3,0,0), 设平面ACE 的法向量n =(x 1,y 1,z 1), 则⎩⎪⎨⎪⎧n ·CA →=0,n ·CE →=0,⎩⎨⎧3x 1+z 1=0,32x 1+y 1+12z 1=0,令x 1=1,得n =(1,0,-3),设平面CED 的法向量m =(x 2,y 2,z 2), 则⎩⎪⎨⎪⎧m ·CD →=0,m ·CE →=0,⎩⎨⎧3x 2=0,32x 2+y 2+12z 2=0,令y 2=1,得m =(0,1,-2),二面角A -CE -D 的余弦值cos 〈m ,n 〉=|n ·m ||n ||m |=2325=155.6.如图,在梯形ABCD 中,AB ∥CD ,AD =DC =CB =1,∠ABC =60°,四边形ACFE 为矩形,平面ACFE ⊥平面ABCD ,CF =1.(1)求证:BC ⊥平面ACFE ;(2)点M 在线段EF 上运动,设平面MAB 与平面FCB 所成二面角为θ()θ≤90°,试求cos θ的取值范围. (1)证明 在梯形ABCD 中,因为AB ∥CD ,AD =DC =CB =1,∠ABC =60°,所以AB =2, 所以AC 2=AB 2+BC 2-2AB ·BC ·cos 60°=3, 所以AB 2=AC 2+BC 2,所以BC ⊥AC .因为平面ACFE ⊥平面ABCD ,平面ACFE ∩平面ABCD =AC , BC ⊂平面ABCD ,所以BC ⊥平面ACFE .(2)解 建立以直线CA ,CB ,CF 为x 轴,y 轴,z 轴的空间直角坐标系如图所示,令FM =λ(0≤λ≤3),则C (0,0,0),A (3,0,0),B (0,1,0),M (λ,0,1), 所以AB→=(-3,1,0),BM →=(λ,-1,1), 设n 1=(x ,y ,z )为平面MAB 的一个法向量, 由⎩⎪⎨⎪⎧n 1·AB →=0,n 1·BM →=0,得⎩⎪⎨⎪⎧-3x +y =0,λx -y +z =0,取x =1,所以n 1=(1,3,3-λ), 因为n 2=(1,0,0)是平面FCB 的一个法向量. 所以cos θ=|n 1·n 2||n 1||n 2|=11+3+(3-λ)2×1=1(λ-3)2+4.因为0≤λ≤3,所以当λ=0时,cos θ有最小值77, 当λ=3时,cos θ有最大值12.所以cos θ∈⎣⎢⎡⎦⎥⎤77,12.4、概率与统计1.某学校甲、乙两个班各派10名同学参加英语口语比赛,并记录他们的成绩,得到如图所示的茎叶图.现拟定在各班中分数超过本班平均分的同学为“口语王”.(1)记甲班“口语王”人数为m ,乙班“口语王”人数为n ,比较m ,n 的大小; (2)随机从“口语王”中选取2人,记X 为来自甲班“口语王”的人数,求X 的分布列和期望.解 (1)因为x 甲=60+72+75+77+80+80+84+88+91+9310=80,所以m =4,x 乙=61+64+70+72+73+85+86+88+94+9710=79,所以n =5,所以m <n .(2)X 取0,1,2,所以P (X =0)=C 04C 25C 29=518,P (X =1)=C 14C 15C 29=59,P (X =2)=C 24C 05C 29=16,所以X 的分布列为所以E (X )=0×518+1×59+2×16=89.2.为了解我校2017级本部和大学城校区的学生是否愿意参加自主招生培训的情况,对全年级2 000名高三学生进行了问卷调查,统计结果如下表:(1)若从愿意参加自主招生培训的同学中按分层抽样的方法抽取15人,则大学城校区应抽取几人;(2)现对愿意参加自主招生的同学组织摸底考试,考试共有5道题,每题20分,对于这5道题,考生“如花姐”完全会答的有3题,不完全会的有2道,不完全会的每道题她得分S的概率满足:P(S=6k)=4-k6,k=1,2,3,假设解答各题之间没有影响,①对于一道不完全会的题,求“如花姐”得分的期望E(S);②试求“如花姐”在本次摸底考试中总得分的期望.解(1)大学城校区应抽取15×80220+80=4(人).(2)①由题知:对一道不完全会的题,“如花姐”得分的分布列为P(S=6k)=4-k 6,k=1,2,3,即所以对于一道不完全会的题,“如花姐”得分的期望为E (S )=6×12+12×13+18×16=10.②记ξ为“如花姐”做2道不完全会的题的得分总和, 则ξ=12,18,24,30,36, P (ξ=12)=12×12=14; P (ξ=18)=12×13×2=13; P (ξ=24)=12×16×2+13×13=518; P (ξ=30)=13×16×2=19; P (ξ=36)=16×16=136;E (ξ)=12×14+18×13+24×518+30×19+36×136=20. 所以“如花姐”最后得分的期望为20×3+E (ξ)=80.3.某中学拟在高一下学期开设游泳选修课,为了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为35.(1)请将上述列联表补充完整:并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;(2)针对问卷调查的100名学生,学校决定从喜欢游泳的人中按分层抽样的方法随机抽取6人成立游泳科普知识宣传组,并在这6人中任选2人作为宣传组的组长,设这两人中男生人数为X ,求X 的分布列和期望. 下面的临界值表仅供参考:参考公式:K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ),其中n =a +b +c +d .解 (1)因为从100人中随机抽取1人抽到喜欢游泳的学生的概率为35, 所以喜欢游泳的学生人数为100×35=60.其中女生有20人,则男生有40人,列联表补充如下:因为K 2=100(40×30-20×10)260×40×50×50≈16.67>10.828.所以有99.9%的把握认为喜欢游泳与性别有关.(2)喜欢游泳的共60人,按分层抽样抽取6人,则每个个体被抽到的概率均为110, 从而需抽取男生4人,女生2人. 故X 的所有可能取值为0,1,2.P(X=0)=C22C26=115,P(X=1)=C14C12C26=815,P(X=2)=C24C26=615=25,所以X 的分布列为E (X )=0×115+1×815+2×25=43.4.(2017·全国Ⅰ)为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N (μ,σ2).(1)假设生产状态正常,记X 表示一天内抽取的16个零件中其尺寸在(μ-3σ,μ+3σ)之外的零件数,求P (X ≥1)及X 的期望;(2)一天内抽检零件中,如果出现了尺寸在(μ-3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.(ⅰ)试说明上述监控生产过程方法的合理性; (ⅱ)下面是检验员在一天内抽取的16个零件的尺寸: 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95 经计算得x -=116∑i =116x i =9.97,s =116∑i =116(x i -x -)2=116(∑i =116x 2i -16x -2)≈0.212,其中x i 为抽取的第i 个零件的尺寸,i =1,2, (16)用样本平均数x -作为μ的估计值μ^,用样本标准差s 作为σ的估计值σ^,利用估计值判断是否需对当天的生产过程进行检查?剔除(μ^-3σ^,μ^+3σ^)之外的数据,用剩下的数据估计μ和σ(精确到0.01).附:若随机变量Z 服从正态分布N (μ,σ2),则P (μ-3σ<Z <μ+3σ)=0.997 4,0.997 416≈0.959 2,0.008≈0.09.解 (1)抽取的一个零件的尺寸在(μ-3σ,μ+3σ)之内的概率为0.997 4,从而零件的尺寸在(μ-3σ,μ+3σ)之外的概率为0.002 6,故X ~B (16,0.002 6). 因此P (X ≥1)=1-P (X =0)=1-0.997 416≈0.040 8. X 的期望E (X )=16×0.002 6=0.041 6.(2)(ⅰ)如果生产状态正常,一个零件尺寸在(μ-3σ,μ+3σ)之外的概率只有0.002 6,一天内抽取的16个零件中,出现尺寸在(μ-3σ,μ+3σ)之外的零件的概率只有0.040 8,发生的概率很小,因此一旦发生这种情况,就有理由认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查,可见上述监控生产过程的方法是合理的.(ⅱ)由x =9.97,s ≈0.212,得μ的估计值μ^=9.97,σ的估计值σ^=0.212,由样本数据可以看出有一个零件的尺寸在(μ^-3σ^,μ^+3σ^)之外,因此需对当天的生产过程进行检查.剔除(μ^-3σ^,μ^+3σ^)之外的数据9.22,剩下数据的平均数为115×(16×9.97-9.22)=10.02.因此μ的估计值为10.02.i =116x 2i =16×0.2122+16×9.972≈1 591.134.剔除(μ^-3σ^,μ^+3σ^)之外的数据9.22,剩下数据的样本方差为115×(1 591.134-9.222-15×10.022)≈0.008,因此σ的估计值为0.008≈0.09.5.(2017·重庆市调研)为了研究家用轿车在高速公路上的车速情况,交通部门随机对50名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在30名男性驾驶员中,平均车速超过100 km/h的有20人,不超过100 km/h 的有10人.在20名女性驾驶员中,平均车速超过100 km/h的有5人,不超过100 km/h的有15人.(1)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过100 km/h的人与性别有关;(2)以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随机抽取3辆,记这3辆车中驾驶员为女性且车速不超过100 km/h的车辆数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列和期望.参考公式:K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d),其中n=a+b+c+d. 参考数据:解 (1)∵K 2=50(20×15-10×5)230×20×25×25=253≈8.333>7.879,∴有99.5%的把握认为平均车速超过100 km/h 与性别有关.(2)根据样本估计总体的理想,从高速公路上行驶的大量家用轿车中随机抽取1辆,驾驶员为女性且车速不超过100 km/h 的车辆的概率为1550=310. ∴ξ的可能取值为0,1,2,3,且ξ~B ⎝ ⎛⎭⎪⎫3,310,∴P (ξ=0)=C 03⎝ ⎛⎭⎪⎫3100⎝ ⎛⎭⎪⎫7103=3431 000,P (ξ=1)=C 13⎝ ⎛⎭⎪⎫3101⎝ ⎛⎭⎪⎫7102=4411 000,P (ξ=2)=C 23⎝⎛⎭⎪⎫3102⎝ ⎛⎭⎪⎫7101=1891 000, P (ξ=3)=C 33⎝ ⎛⎭⎪⎫3103⎝ ⎛⎭⎪⎫7100=271 000, ∴ξ的分布列为E(ξ)=0×3431 000+1×4411 000+2×1891 000+3×271 000=910=0.9或E(ξ)=np=3×310=0.9.6.(2017届湖南株州模拟)某市对某环城快速车道进行限速,为了调查该道路车速情况,于某个时段随机对100辆车的速度进行取样,测量的车速制成如下条形图:经计算:样本的平均值μ=85,标准差σ=2.2,以频率值作为概率的估计值.已知车速过慢与过快都被认为是需矫正速度,现规定车速小于μ-3σ或车速大于μ+2σ是需矫正速度.(1)从该快速车道上所有车辆中任取1个,求该车辆是需矫正速度的概率;(2)从样本中任取2个车辆,求这2个车辆均是需矫正速度的概率;(3)从该快速车道上所有车辆中任取2个,记其中是需矫正速度的个数为ξ,求ξ的分布列和期望.解(1)记事件A为“从该快速车道上所有车辆中任取1个,该车辆是需矫正速度”.因为μ-3σ=78.4,μ+2σ=89.4,由样本条形图可知,所求的概率为P(A)=P(x<μ-3σ)+P(x>μ+2σ)=P(x<78.4)+P(x>89.4)=1100+4100=120.(2)记事件B为“从样本中任取2个车辆,这2个车辆均是需矫正速度”.由题设可知,样本容量为100,又需矫正速度个数为5,故所求概率为P(B)=C25C2100=1495.(3)需矫正速度的个数ξ服从二项分布,即ξ~B ⎝ ⎛⎭⎪⎫2,120,所以P ()ξ=0=C 02⎝ ⎛⎭⎪⎫1200⎝ ⎛⎭⎪⎫19202=361400, P ()ξ=1=C 12⎝ ⎛⎭⎪⎫1201⎝ ⎛⎭⎪⎫19201=19200, P ()ξ=2=C 22⎝ ⎛⎭⎪⎫1202⎝ ⎛⎭⎪⎫19200=1400,因此ξ的分布列为由ξ~B ⎝ ⎛⎭⎪⎫2,120知,期望E (ξ)=2×120=110.5、坐标系与参数方程1.在平面直角坐标系中xOy 中,已知直线l 的参数方程为⎩⎨⎧x =-8+t ,y =t2(t 为参数),曲线C 的参数方程为⎩⎪⎨⎪⎧x =2s 2,y =22s(s 为参数).设P 为曲线C 上的动点,求点P 到直线l 的距离的最小值.解 直线l 的普通方程为x -2y +8=0, 因为点P 在曲线C 上,设P (2s 2,22s ), 从而点P 到直线的距离d =|2s 2-42s +8|5=|2(s -2)2+4|5,当s =2时,d min =455.因此当点P 的坐标为(4,4)时,曲线C 上的点P 到直线l 的距离取到最小值455. 2.在直角坐标系xOy 中,直线l 的参数方程为⎩⎪⎨⎪⎧x =1+t cos α,y =2+t sin α(t 为参数),在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,圆C 的方程为ρ=6sin θ. (1)求圆C 的直角坐标方程;(2)设圆C 与直线l 交于点A ,B .若点P 的坐标为(1,2),求||P A +||PB 的最小值. 解 (1)由ρ=6sin θ,得ρ2=6ρsin θ, 化为直角坐标方程为x 2+y 2=6y ,即x 2+(y -3)2=9.(2)将l 的参数方程代入圆C 的直角坐标方程, 得t 2+2(cos α-sin α)t -7=0, 由Δ=(2cos α-2sin α)2+4×7>0, 故可设t 1,t 2是上述方程的两根, 所以⎩⎪⎨⎪⎧t 1+t 2=-2()cos α-sin α,t 1·t 2=-7,又直线l 过点()1,2, 故结合t 的几何意义得||P A +||PB =⎪⎪⎪⎪t 1||+t 2||=t 1-t 2=()t 1+t 22-4t 1t 2=4()cos α-sin α2+28=32-4sin 2α≥32-4=27,所以||P A +||PB 的最小值为27.3.在直角坐标系xOy 中,已知点P ()0,3,曲线C 的参数方程为⎩⎪⎨⎪⎧x =2cos φ,y =2sin φ(φ为参数).以原点为极点, x 轴正半轴为极轴建立极坐标系,直线l 的极坐标方程为ρ=32cos ⎝ ⎛⎭⎪⎫θ-π6.(1)判断点P 与直线l 的位置关系并说明理由; (2)设直线l 与曲线C 的两个交点分别为A , B ,求1||P A +1||PB 的值. 解 (1)点P 在直线上,理由如下: 直线l :ρ=32cos ⎝ ⎛⎭⎪⎫θ-π6,即2ρcos ⎝ ⎛⎭⎪⎫θ-π6=3,即3ρcos θ+ρsin θ=3,所以直线的直角坐标方程为3x +y =3,易知点P 在直线上. (2)由题意,可得直线l 的参数方程为⎩⎪⎨⎪⎧x =-12t ,y =3+32t ,(t 为参数),曲线C 的普通方程为x 22+y 24=1,将直线l 的参数方程代入曲线C 的普通方程, 得2⎝ ⎛⎭⎪⎫-12t 2+⎝ ⎛⎭⎪⎫3+32t 2=4,∴5t 2+12t -4=0,两根为t 1, t 2, ∴t 1+t 2=-125,t 1t 2=-45<0, 故t 1与t 2异号, ∴||P A +||PB =||t 1-t 2=()t 1+t 22-4t 1t 2=4145,∴||P A ||PB =|t 1||t 2|=-t 1t 2=45,∴1||P A +1||PB =||P A +||PB ||P A ||PB =14. 4.在直角坐标系xOy 中,曲线C 1的参数方程为⎩⎪⎨⎪⎧x =2+2cos φ,y =2sin φ(φ为参数).以原点O 为极点, x 轴正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ=4sin θ.(1)求曲线C 1的普通方程和C 2的直角坐标方程;(2)已知曲线C 3的极坐标方程为θ=α(0<α<π,ρ∈R ),点A 是曲线C 3与C 1的交点,点B 是曲线C 3与C 2的交点,且A , B 均异于原点O ,且||AB =42,求α的值.解 (1)由⎩⎪⎨⎪⎧x =2+2cos φ,y =2sin φ消去参数φ可得C 1的普通方程为(x -2)2+y 2=4.∵ρ=4sin θ, ∴ρ2=4ρsin θ, 由⎩⎪⎨⎪⎧x =ρcos θ,y =ρsin θ,得曲线C 2的直角坐标方程为x 2+(y -2)2=4. (2)由(1)得曲线C 1:(x -2)2+y 2=4, 其极坐标方程为ρ=4cos θ, 由题意设A (ρ1,α), B (ρ2,α), 则||AB =||ρ1-ρ2=4||sin α-cos α =42⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α-π4=42, ∴ sin ⎝ ⎛⎭⎪⎫α-π4=±1,∴ α-π4=π2+k π(k ∈Z ), 又 0<α<π, ∴ α=3π4.5.已知曲线C 1:⎩⎪⎨⎪⎧x =1+cos θ,y =sin θ(θ为参数), C 2:⎩⎪⎨⎪⎧x =-32t ,y =233+t 2(t 为参数).(1)曲线C 1,C 2的交点为A ,B ,求||AB ;(2)以原点O 为极点, x 轴正半轴为极轴,建立极坐标系,过极点的直线l 1与曲线C 1交于O , C 两点,与直线ρsin θ=2交于点D ,求||OC ||OD 的最大值.解 (1)方法一 曲线C 1:(x -1)2+y 2=1,将C 2的参数方程代入,得⎝ ⎛⎭⎪⎫-32t -12+⎝ ⎛⎭⎪⎫233+t 22=1,化简得,t 2+533t +43=0, 所以||AB =||t 1-t 2=()t 1+t 22-4t 1t 2=3.方法二 曲线C 2的直角坐标方程为y =-33x +233, 过点()2,0, C 1过点()2,0,不妨令A ()2,0, 则∠OBA =90°, ∠OAB =30°, 所以||AB =2×32= 3.(2)C 1的极坐标方程为ρ=2cos θ, 令l 1的极角为α,则||OD =ρ1=2sin α,||OC =ρ2=2cos α,||OC ||OD =sin αcos α=12sin 2α≤12, 当α=π4时取得最大值12.6.已知α∈[)0,π,在直角坐标系xOy 中,直线l 1的参数方程为⎩⎪⎨⎪⎧x =t cos α,y =t sin α(t为参数);在以坐标原点O 为极点,x 轴的正半轴为极轴的极坐标系中,直线l 2的极坐标方程是ρcos ()θ-α=2sin ⎝ ⎛⎭⎪⎫α+π6.(1)求证:l 1⊥l 2;(2)设点A 的极坐标为⎝ ⎛⎭⎪⎫2,π3, P 为直线l 1, l 2的交点,求||OP ·||AP 的最大值. (1)证明 易知直线l 1的普通方程为x sin α-y cos α=0. 又ρcos ()θ-α=2sin ⎝ ⎛⎭⎪⎫α+π6可变形为 ρcos θcos α+ρsin θsin α =2sin ⎝ ⎛⎭⎪⎫α+π6,即直线l 2的直角坐标方程为 x cos α+y sin α-2sin ⎝ ⎛⎭⎪⎫α+π6=0. 因为sin α·cos α+()-cos αsin α=0, 根据两直线垂直的条件可知, l 1⊥l 2. (2)解 当ρ=2, θ=π3时,ρcos ()θ-α=2cos ⎝ ⎛⎭⎪⎫π3-α=2sin ⎝ ⎛⎭⎪⎫α+π6,所以点A ⎝ ⎛⎭⎪⎫2,π3在直线ρcos ()θ-α=2sin ⎝ ⎛⎭⎪⎫α+π6上.设点P 到直线OA 的距离为d ,由l 1⊥l 2可知, d 的最大值为||OA 2=1. 于是||OP ·||AP =d ·||OA =2d ≤2, 所以||OP ·||AP 的最大值为2.6、不等式选讲1.(2017·全国Ⅰ)已知函数f (x )=-x 2+ax +4,g (x )=|x +1|+|x -1|.(1)当a =1时,求不等式f (x )≥g (x )的解集;(2)若不等式f (x )≥g (x )的解集包含[-1,1],求a 的取值范围.解 (1)当a =1时,不等式f (x )≥g (x )等价于x 2-x +|x +1|+|x -1|-4≤0.① 当x <-1时,①式化为x 2-3x -4≤0,无解;当-1≤x ≤1时,①式化为x 2-x -2≤0,从而-1≤x ≤1;当x >1时,①式化为x 2+x -4≤0,得1<x ≤-1+172.所以f (x )≥g (x )的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ -1≤x ≤-1+172.(2)当x ∈[-1,1]时,g (x )=2,所以f (x )≥g (x )的解集包含[-1,1]等价于当x ∈[-1,1]时,f (x )≥2.又f (x )在[-1,1]上的最小值必为f (-1)与f (1)之一,所以f (-1)≥2且f (1)≥2,得-1≤a ≤1.所以a 的取值范围为[-1,1].2.已知函数f (x )=⎪⎪⎪⎪2x -a ||+x -1, a ∈R .(1)若不等式f (x )≥2-||x -1恒成立,求实数a 的取值范围;(2)当a =1时,直线y =m 与函数f (x )的图象围成三角形,求m 的取值范围. 解 (1)因为f (x )≥2-||x -1恒成立,即⎪⎪⎪⎪⎪⎪x -a 2+|x -1|≥1恒成立, 所以⎝ ⎛⎭⎪⎫⎪⎪⎪⎪⎪⎪x -a 2+|x -1|min ≥1成立, 由⎪⎪⎪⎪⎪⎪x -a 2+|x -1|≥⎪⎪⎪⎪⎪⎪x -a 2-x +1=⎪⎪⎪⎪⎪⎪a 2-1, 得⎪⎪⎪⎪⎪⎪a 2-1≥1, 解得a ≤0或a ≥4,所以a 的取值范围为(-∞,0]∪[4,+∞). (2)当a =1时, f (x )=⎪⎪⎪⎪2x -1||+x -1=⎩⎪⎨⎪⎧ 2-3x ,x ≤12,x ,12<x <1,3x -2,x ≥1,作出f (x )的图象,如图所示.由图象可知,当12<m ≤1时,直线y =m 与函数f (x )的图象围成三角形,故所求m 的取值范围为⎝ ⎛⎦⎥⎤12,1. 3.设函数f (x )=⎪⎪⎪⎪x +2||-x -1.(1)求不等式f (x )>1的解集;(2)若关于x 的不等式f (x )+4≥||1-2m 有解,求实数m 的取值范围.解 (1)函数f (x )可化为f (x )=⎩⎪⎨⎪⎧ -3,x ≤-2,2x +1,-2<x <1,3,x ≥1,当x ≤-2时, f (x )=-3<0,不合题意;当-2<x <1时, f (x )=2x +1>1⇒x >0,即0<x <1;当x ≥1时, f (x )=3>1,即x ≥1.综上,不等式f (x )>1的解集为(0,+∞).(2)关于x 的不等式f (x )+4≥||1-2m 有解等价于()f (x )+4max ≥||1-2m , 由(1)可知,f (x )max =3,(也可由||f (x )=⎪⎪⎪⎪⎪⎪⎪⎪x +2||-x -1||≤()x +2-(x -1)=3,得f (x )max =3),即||1-2m ≤7,解得-3≤m ≤4.4.已知f (x )=||x +a , g (x )=||x +3-x ,记关于x 的不等式f (x )<g (x )的解集为M .(1)若a -3∈M ,求实数a 的取值范围;(2)若[]-1,1⊆M ,求实数a 的取值范围.解 (1)依题意有||2a -3<||a -()a -3,若a ≥32,则2a -3<3,∴32≤a <3,若0≤a <32,则3-2a <3,∴0<a <32,若a ≤0,则3-2a <-a -()a -3,无解.综上所述, a 的取值范围为()0,3.(2)由题意可知,当x ∈[]-1,1时,f (x )<g (x )恒成立,∴||x +a <3恒成立,即-3-x <a <3-x ,当x ∈[]-1,1时,-2<a <2.5.已知函数f (x )=2||x +a +⎪⎪⎪⎪⎪⎪x -1a ()a ≠0. (1)当a =1时,解不等式f (x )<4;(2)求函数g (x )=f (x )+f (-x )的最小值.解 (1)∵ a =1,∴原不等式为2⎪⎪⎪⎪x +1||+x -1<4,∴⎩⎪⎨⎪⎧ x <-1,-2x -2-x +1<4或⎩⎪⎨⎪⎧-1≤x ≤1,2x +2-x +1<4或⎩⎪⎨⎪⎧ x >1,2x +2+x -1<4,∴-53<x <-1或-1≤x <1或∅,∴原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪⎪⎪⎪-53<x <1. (2)由题意得g (x )=f (x )+f (-x )=2⎝⎛⎭⎫||x +a +||x -a +⎝ ⎛⎭⎪⎫⎪⎪⎪⎪⎪⎪x +1a +⎪⎪⎪⎪⎪⎪x -1a ≥2||2a +2||a =4||a +2||a ≥42, 当且仅当2||a =1||a ,即a =±22,且-22≤x ≤22时,g (x )取最小值4 2.6.已知f (x )=||x -a +||2x +1(1)若a =1,解不等式f (x )≤3;(2)f (x )≤2a +x 在[)a ,+∞上有解,求a 的取值范围. 解 (1)⎩⎨⎧ x <-12,1-x -1-2x ≤3或⎩⎨⎧ -12≤x ≤1,1-x +2x +1≤3或⎩⎪⎨⎪⎧ x >1,x -1+2x +1≤3,-1≤x <-12或-12≤x ≤1或∅,所以原不等式解集为{x |-1≤x ≤1}.(2)因为x ∈[)a ,+∞,所以f (x )=||x -a +⎪⎪⎪⎪2x +1||=x -a +2x +1≤2a +x ,推出||2x +1≤3a 有解,所以a ≥0,所以不等式化为2x +1≤3a 有解, 即2a +1≤3a ⇒a ≥1.所以a 的取值范围为[1,+∞).。
2015届高考数学(文科,通用)二轮复习突破练 高考中档大题规范练(二) Word版含答案

高考中档大题规范练(二)——数 列(推荐时间:60分钟)1.已知{a n }为等差数列,且a 2=-1,a 5=8. (1)求数列{|a n |}的前n 项和; (2)求数列{2n ·a n }的前n 项和.解 (1)设等差数列{a n }的公差为d ,因为a 2=-1,a 5=8,所以⎩⎪⎨⎪⎧a 1+d =-1,a 1+4d =8,解得a 1=-4,d =3,所以a n =-4+3(n -1)=3n -7,因此|a n |=|3n -7|=⎩⎪⎨⎪⎧-3n +7,n =1,2,3n -7,n ≥3记数列{|a n |}的前n 项和为S n , 当n =1时,S 1=|a 1|=4, 当n =2时,S 2=|a 1|+|a 2|=5,当n ≥3时,S n =S 2+|a 3|+|a 4|+…+|a n |=5+(3×3-7)+(3×4-7)+…+(3n -7) =5+(n -2)[2+3n -7]2=32n 2-112n +10.又当n =2时满足此式,综上,S n =⎩⎪⎨⎪⎧4,n =1,32n 2-112n +10,n ≥2.(2)记数列{2n ·a n }的前n 项和为T n , 则T n =2a 1+22a 2+23a 3+…+2n a n , 2T n =22a 1+23a 2+24a 3+…+2n a n -1+2n +1a n ,所以-T n =2a 1+d (22+23+…+2n )-2n +1a n .由(1)知,a 1=-4,d =3,a n =3n -7, 所以-T n =-8+3×4(1-2n -1)1-2-(3n -7)×2n +1=-20-(3n -10)×2n +1,故T n =20+(3n -10)×2n +1.2.已知函数f (x )=14x +2(x ∈R ).(1)证明:f (x )+f (1-x )=12;(2)若数列{a n }的通项公式为a n =f (nm )(m ∈N *,n =1,2,…,m ),求数列{a n }的前m 项和S m ;(3)设数列{b n }满足b 1=13,b n +1=b 2n +b n ,T n =1b 1+1+1b 2+1+…+1b n +1,若(2)中的S m 满足对不小于2的任意正整数m ,S m <T n 恒成立,试求m 的最大值. (1)证明 因为f (x )=14x +2,所以f (1-x )=141-x +2=4x 4+2·4x =4x2(4x +2).所以f (x )+f (1-x )=14x +2+4x2(4x +2)=2+4x 2(4x +2)=12. (2)解 由(1),知f (x )+f (1-x )=12,所以f (k m )+f (1-k m )=12(1≤k ≤m -1)(k ∈N *),即f (k m )+f (m -k m )=12.由题设知,a n =f (n m ),所以a k +a m -k =12,a m =f (m m )=f (1)=16.又S m =a 1+a 2+…+a m -1+a m ,① S m =a m -1+a m -2+…+a 1+a m ,②由①+②,得2S m =(m -1)×12+2a m =m 2-16,即S m =m 4-112(m ∈N *).(3)解 由b 1=13,b n +1=b 2n +b n =b n (b n +1), 显然对任意n ∈N *,b n >0, 则1b n +1=1b n (b n +1)=1b n -1b n +1, 即1b n +1=1b n -1b n +1, 所以T n =(1b 1-1b 2)+(1b 2-1b 3)+…+(1b n -1b n +1)=1b 1-1b n +1=3-1b n +1. 因为b n +1-b n =b 2n >0,所以b n +1>b n ,即数列{b n }是单调递增数列. 所以T n 关于n 递增,所以当n ∈N *时,T n ≥T 1.因为b 1=13,b 2=(13)2+13=49,所以T n ≥T 1=3-1b 2=34.由题意,知S m <34,即m 4-112<34,解得m <103,所以m 的最大值为3.3.设数列{a n }的前n 项和为S n ,满足2S n =a n +1-2n +1+1,n ∈N *,且a 1=1,设数列{b n }满足b n =a n +2n .(1)求证数列{b n }为等比数列,并求出数列{a n }的通项公式; (2)若数列c n =6n -3b n,T n 是数列{c n }的前n 项和,证明T n <3.(1)解 当n ≥2时,由⎩⎪⎨⎪⎧2S n =a n +1-2n +1+12S n -1=a n -2n+1⇒2a n =a n +1-a n -2n ,所以a n +1=3a n +2n , 从而b n +1=a n +1+2n +1=3(a n +2n )=3b n ,故{b n }是以3为首项,3为公比的等比数列, b n =a n +2n =3×3n -1=3n ,a n =3n -2n (n ≥2),因为a 1=1也满足,于是a n =3n -2n . (2)证明 c n =6n -3b n =2n -13n -1,则T n =130+331+532+…+2n -33n -2+2n -13n -1,①13T n =131+332+533+…+2n -33n -1+2n -13n ,② ①-②得,23T n =130+231+232+…+23n -1-2n -13n =1+23·1-13n -11-13-2n -13n =2-13n -1-2n -13n =2-2(n +1)3n, 故T n =3-n +13n -1<3.4.已知单调递增数列{a n }的前n 项和为S n ,满足S n =12(a 2n +n ).(1)求数列{a n }的通项公式;(2)设c n =⎩⎪⎨⎪⎧1a 2n +1-1,n 为奇数,3×2a n -1+1,n 为偶数,求数列{c n }的前n 项和T n .解 (1)n =1时,a 1=12(a 21+1),得a 1=1,当n ≥2时,S n -1=12(a 2n -1+n -1),得a n =S n -S n -1=12(a 2n -a 2n -1+1), 化简得(a n -1)2-a 2n -1=0,a n -a n -1=1或a n +a n -1=1(n ≥2), 又{a n }是单调递增数列,故a n -a n -1=1,所以{a n }是首项为1,公差为1的等差数列,故a n =n . (2)c n =⎩⎪⎨⎪⎧1a 2n +1-1,n 为奇数,3×21n a -+1,n 为偶数,当n 为偶数时,T n =(c 1+c 3+…+c n -1)+(c 2+c 4+…+c n ) =(122-1+142-1+…+1n 2-1)+3×(21+23+…+2n -1)+n 2=11×3+13×5+…+1(n -1)×(n +1)+3×2(1-42n)1-4+n 2=12×(11-13+13-15+…+1n -1-1n +1)+2×(42n-1)+n 2=2n +1+n 2-2n -42(n +1). 当n 为奇数时,T n =(c 1+c 3+…+c n )+(c 2+c 4+…+c n -1) =[122-1+142-1+…+1(n +1)2-1]+3×(21+23+…+2n -2)+n -12 =12×(11-13+13-15+…+1n -1n +2)+2×(412n --1)+n -12=2n +n 2-2n -92(n +2).所以T n=⎩⎪⎨⎪⎧2n+n 2-2n -92(n +2),n 为奇数,2n +1+n 2-2n -42(n +1),n 为偶数.5.已知函数f (x )=2x +33x ,数列{a n }满足a 1=1,a n +1=f (1a n ),n ∈N *.(1)求数列{a n }的通项公式;(2)令b n =1a n -1a n (n ≥2),b 1=3,S n =b 1+b 2+…+b n ,若S n <m -2 0142对一切n ∈N *成立,求最小正整数m .解 (1)∵a n +1=f (1a n )=2a n +33a n =2+3a n 3=a n +23,∴{a n }是以1为首项,23为公差的等差数列.∴a n =1+(n -1)×23=23n +13.(2)当n ≥2时,b n =1a n -1a n =1(23n -13)(23n +13) =1(2n -1)(2n +1)9=92(12n -1-12n +1),又b 1=3=92(1-13),∴S n =b 1+b 2+…+b n =92(1-13+13-15+…+12n -1-12n +1)=92(1-12n +1)=9n2n +1,∵S n <m -2 0142对一切n ∈N *成立,即9n 2n +1<m -2 0142对一切n ∈N *成立,又9n 2n +1<92,∴m -2 0142≥92,即m ≥2 023.∴最小正整数m 为2 023.6.某工厂为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中的维护费用会逐年增加,第一年的维护费用是4万元,从第二年到第七年,每年的维护费用均比上年增加2万元,从第八年开始,每年的维护费用比上年增加25%. (1)设第n 年该生产线的维护费用为a n ,求a n 的表达式;(2)若该生产线前n 年每年的平均维护费用大于12万元时,需要更新生产线.求该生产线前n 年每年的平均维护费用,并判断第几年年初需要更新该生产线?解 (1)由题意知,当n ≤7时,数列{a n }是首项为4,公差为2的等差数列, ∴a n =4+(n -1)×2=2n +2.当n ≥8时, 数列{a n }从a 7开始构成首项为a 7=2×7+2=16, 公比为1+25%=54的等比数列,则此时a n =16×⎝⎛⎭⎫54n -7,∴a n =⎩⎪⎨⎪⎧2n +2,n ≤7,16×⎝⎛⎭⎫54n -7,n ≥8.(2)设S n 为数列{a n }的前n 项和,当1≤n ≤7时,S n =4n +n (n -1)2×2=n 2+3n ,当n ≥8时,由S 7=70,则S n =70+16×54×1-⎝⎛⎭⎫54n -71-54=80×⎝⎛⎭⎫54n -7-10, ∴该生产线前n 年每年的平均维护费用为 S nn =⎩⎨⎧n +3,1≤n ≤7,80×⎝⎛⎭⎫54n -7-10n,n ≥8.当1≤n ≤7时,⎩⎨⎧⎭⎬⎫S n n 为递增数列,当n ≥8时,∵S n +1n +1-S nn =80×⎝⎛⎭⎫54n -6-10n +1-80×⎝⎛⎭⎫54n -7-10n=80×⎝⎛⎭⎫54n -7·⎝⎛⎭⎫n 4-1+10n (n +1)>0,∴S n +1n +1>S n n.∴⎩⎨⎧⎭⎬⎫S n n 也为递增数列. 又∵S 77=10<12,S 88=80×54-108=11.25<12,S 99=80×⎝⎛⎭⎫542-109≈12.78>12, ∴第9年年初需要更新生产线.。
甘肃省武威市铁路中学2014届高三数学(文)专题训练:中档大题保分练(二)Word版含答案

(推荐时间:50分钟)1. 已知函数f (x )=32sin 2x -12(cos 2x -sin 2x )-1,x ∈R ,将函数f (x )向左平移π6个单位后得到函数g (x ),设△ABC 三个内角A ,B ,C 的对边分别为a ,b ,c . (1)若c =7,f (C )=0,sin B =3sin A ,求a 和b 的值;(2)若g (B )=0且m =(cos A ,cos B ),n =(1,sin A -cos A tan B ),求m ·n 的取值范围. 解 (1)f (x )=32sin 2x -12x -1=sin ⎝⎛⎭⎫2x -π6-1 g (x )=sin ⎣⎡⎦⎤2⎝⎛⎭⎫x +π6-π6-1=sin ⎝⎛⎭⎫2x +π6-1 由f (C )=0,∴sin ⎝⎛2C -π6=1.∵0<C <π,∴-π6<2C -π6<116π,∴2C -π6=π2,∴C =π3.由sin B =3sin A ,∴b =3a .由余弦定理得(7)2=a 2+b 2-2ab cos π3.∴7=a 2+9a 2-3a 2,∴a =1,b =3. (2)由g (B )=0得sin ⎝⎛⎭⎫2B +π6=1,∵0<B <π,∴π6<2B +π6<136π,∴2B +π6=π2,∴B =π6.∴m ·n =cos A +cos B (sin A -cos A tan B ) =cos A +sin A cos B -cos A sin B =32sin A +12cos A =sin ⎝⎛⎭⎫A +π6. ∵A +C =5π6,∴0<A <5π6, ∴π6<A +π6<π,∴0<sin ⎝⎛⎭⎫A +π6≤1. ∴m ·n 的取值范围是(0,1].2. 某园林局对1 000株树木的生长情况进行调查,其中杉树600株,槐树400株.现用分层抽样方法从这1 000株树木中随机抽取100株,杉树与槐树的树干周长(单位:cm)的抽查结果如下表:(2)如果杉树的树干周长超过60 cm 就可以砍伐,请估计该片园林可以砍伐的杉树有多少株?(3)树干周长在30 cm 到40 cm 之间的4株槐树有1株患虫害,现要对这4株树逐一进行排查直至找出患虫害的树木为止.求排查的树木恰好为2株的概率. 解 (1)按分层抽样方法随机抽取100株,可得槐树为40株,杉树为60株, ∴x =60-6-19-21=14,y =40-4-20-6=10. 估计槐树树干周长的众数为45 cm. (2)1460600=140, 估计该片园林可以砍伐的杉树有140株.(3)设4株树为B 1,B 2,B 3,D ,设D 为有虫害的那株,基本事件为(D ),(B 1,D ),(B 2,D ),(B 3,D ),(B 1,B 2,D ),(B 1,B 3,D ),(B 2,B 1,D ),(B 2,B 3,D ),(B 3,B 1,D ),(B 3,B 2,D ),(B 1,B 2,B 3),(B 1,B 3,B 2),(B 2,B 1,B 3),(B 2,B 3,B 1),(B 3,B 1,B 2),(B 3,B 2,B 1)共16种,设事件A :排查的树木恰好为2株,事件A 包含(B 1,D ),(B 2,D ),(B 3,D )3种, ∴P (A )=316.3. 如图,在四棱锥S -ABCD 中,AB ⊥AD ,AB ∥CD ,CD =3AB =3,平面SAD ⊥平面ABCD ,E 是线段AD 上一点,AE =ED =3,SE ⊥AD .(1)证明:平面SBE ⊥平面SEC ; (2)若SE =1,求三棱锥E -SBC 的高.(1)证明 ∵平面SAD ⊥平面ABCD ,平面SAD ∩平面ABCD =AD ,SE ⊂平面SAD , SE ⊥AD , ∴SE ⊥平面ABCD .∵BE ⊂平面ABCD ,∴SE ⊥BE .∵AB ⊥AD ,AB ∥CD ,CD =3AB =3,AE =ED =3, ∴∠AEB =30°,∠CED =60°. ∴∠BEC =90°,即BE ⊥CE .结合SE ∩CE =E ,得BE ⊥平面SEC . ∵BE ⊂平面SBE ,∴平面SBE ⊥平面SEC .(2)解 如图,作EF ⊥BC 于F ,连接SF . 由BC ⊥SE ,SE 和EF 相交, 得BC ⊥平面SEF . 由BC 在平面SBC 内, 得平面SEF ⊥平面SBC . 过E 作EG ⊥SF 于点G , 则EG ⊥平面SBC ,即线段EG 的长即为三棱锥E -SBC 的高. 由SE =1,BE =2,CE =23得BC =4,EF =3, 所以SF =2.在Rt △SEF 中,EG =SE ·EF SF =32,所以三棱锥E -SBC 的高为32. 4. 已知n ∈N *,数列{d n }满足d n =3+(-1)n2,数列{a n }满足a n =d 1+d 2+d 3+…+d 2n ;又知数列{b n }中,b 1=2,且对任意正整数m ,n ,b m n =b nm .(1)求数列{a n }和数列{b n }的通项公式;(2)将数列{b n }中的第a 1项,第a 2项,第a 3项,……,第a n 项,……删去后,剩余的项按从小到大的顺序排成新数列{c n },求数列{c n }的前2 013项和. 解 方法一 (1)∵d n =3+(-1)n 2,∴a n =d 1+d 2+d 3+…+d 2n . =3×2n2=3n . 又由题知:令m =1,则b 2=b 21=22,b 3=b 31=23,…,b n =b n 1=2n. 若b n =2n ,则b m n =2nm ,b n m =2mn , ∴b m n =b n m 恒成立.若b n ≠2n ,当m =1,b m n =b nm 不成立, ∴b n =2n .(2)由题知将数列{b n }中的第3项、第6项、第9项……删去后构成的新数列{c n }中的奇数列与偶数列仍成等比数列,首项分别是b 1=1,b 2=4,公比均是8, T 2 013=(c 1+c 3+c 5+…+c 2 013)+(c 2+c 4+c 6+…+c 2 012)=2×(1-81 007)1-8+4×(1-81 006)1-8=20×81 006-67.方法二 (1)a n =d 1+d 2+…+d 2n =32×2n =3n .由b m n =b nm 及b 1=2>0知b n >0,对b m n =b nm 两边取对数得,m lg b n =n lg b m , 令m =1,得lg b n =n lg b 1=n lg 2=lg 2n , ∴b n =2n.(2)T 2 013=c 1+c 2+…+c 2 013=b 1+b 2+b 4+b 5+b 7+b 8+…+b 3 018+b 3 019 =(b 1+b 2+…+b 3 019)-(b 3+b 6+…+b 3 018) =2(1-23 019)1-2-8(1-81 006)1-23=20×81 006-67.。
高考数学中档大题规范练2

中档大题规范练2 立体几何与空间向量1.如图,在四棱锥P —ABCD 中,侧面PAD ⊥底面ABCD ,侧棱P A =PD =2,P A ⊥PD ,底面ABCD 为直角梯形,其中BC ∥AD ,AB ⊥AD ,AB =BC =1,O 为AD 的中点.(1)求证:PO ⊥平面ABCD ; (2)求B 点到平面PCD 的距离;(3)线段PD 上是否存在一点Q ,使得二面角Q —AC —D 的余弦值为63?若存在,求出PQQD的值;若不存在,请说明理由 (1)证明 因为P A =PD =2,O 为AD 的中点, 所以PO ⊥AD ,因为侧面P AD ⊥底面ABCD , 所以PO ⊥平面ABCD .(2)解 以O 为原点,OC ,OD ,OP 分别为x 轴,y 轴,z 轴,建立空间直角坐标系Oxyz ,则B (1,-1,0),C (1,0,0),D (0,1,0),P (0,0,1).PB→=(1,-1,-1),设平面PDC 的法向量为u =(x ,y ,z ),CP →=(-1,0,1),PD→=(0,1,-1).则⎩⎪⎨⎪⎧u ·CP ,→=-x +z =0,u ·PD ,→=y -z =0,取z =1,得u =(1,1,1),B 点到平面PDC 的距离 d =|BP ,→·u ||u |=33.(3)解 假设存在,则设PQ→=λPD → (0<λ<1), 因为PD→=(0,1,-1),所以Q (0,λ,1-λ), 设平面CAQ 的法向量为m =(a ,b ,c ),则⎩⎪⎨⎪⎧m ·AC ,→=0,m ·AQ ,→=0,即⎩⎨⎧a +b =0,(λ+1)b +(1-λ)c =0, 所以取m =(1-λ,λ-1,λ+1), 平面CAD 的法向量n =(0,0,1), 因为二面角Q —AC —D 的余弦值为63,所以|m·n||m||n |=63, 所以3λ2-10λ+3=0,所以λ=13或λ=3(舍去),所以PQ QD =122.如图,在长方体ABCD —A 1B 1C 1D 1中,AA 1=AB =2AD =2,E 为AB 的中点,F 为D 1E 上的一点,D 1F =2FE .(1)证明:平面DFC ⊥平面D 1EC ; (2)求二面角A —DF —C 的大小.(1)证明 以D 为原点,分别以DA 、DC 、DD 1所在直线为x 轴、y 轴、z轴建立如图所示空间直角坐标系,则A (1,0,0),B (1,2,0),C (0,2,0),D 1(0,0,2). ∵E 为AB 的中点, ∴E 点坐标为(1,1,0), ∵D 1F =2FE ,∴D 1F →=23D 1E →=23 (1,1,-2)=(23,23,-43), DF →=DD 1→+D 1F →=(0,0,2)+(23,23,-43)=(23,23,23). 设n =(x ,y ,z )是平面DFC 的法向量,则⎩⎪⎨⎪⎧n ·DF →=0,n ·DC →=0,∴⎩⎨⎧23x +23y +23z =0,2y =0,取x =1得平面FDC 的一个法向量n =(1,0,-1). 设p =(x ,y ,z )是平面ED 1C 的法向量,则⎩⎪⎨⎪⎧p ·D 1F →=0,p ·D 1C →=0,∴⎩⎨⎧23x +23y -43z =0,2y -2z =0,取y =1得平面D 1EC 的一个法向量p =(1,1,1). ∵n·p =(1,0,-1)·(1,1,1)=0, ∴平面DFC ⊥平面D 1EC .(2)解 设q =(x ,y ,z )是平面ADF 的法向量, 则q ·DF→=0,q ·DA →=0. ∴⎩⎨⎧23x +23y +23z =0,x =0,取y =1得平面ADF 的一个法向量q =(0,1,-1), 设二面角A —DF —C 的平面角为θ, 由题中条件可知θ∈(π2,π),则cos θ=-|n·q|n|·|q ||=-0+0+12×2=-12,∴二面角A —DF —C 的大小为120°.3.如图所示,在直三棱柱A 1B 1C 1—ABC 中,AB ⊥AC ,AB =AC =2,A 1A =4,点D 是BC 的中点.(1)求异面直线A 1B 与C 1D 所成角的余弦值; (2)求平面ADC 1与平面ABA 1所成二面角的正弦值.解 (1)以A 为坐标原点,建立如图所示的空间直角坐标系Axyz ,则A (0,0,0),B (2,0,0),C (0,2,0),D (1,1,0),A 1(0,0,4),C 1(0,2,4),所以A 1B →=(2,0,-4),C 1D →=(1,-1,-4).因为cos 〈A 1B →,C 1D →〉=A 1B ,→·C 1D →|A 1B →||C 1D →|=1820×18=31010,所以异面直线A 1B 与C 1D 所成角的余弦值为31010.(2)设平面ADC 1的法向量为n 1=(x ,y ,z ),因为AD →=(1,1,0),AC 1→=(0,2,4), 所以n 1·AD →=0,n 1·AC 1→=0, 即x +y =0且y +2z =0, 取z =1,得x =2,y =-2,所以n 1=(2,-2,1)是平面ADC 1的一个法向量. 取平面AA 1B 的一个法向量为n 2=(0,1,0), 设平面ADC 1与平面ABA 1所成二面角的大小为θ.由|cos θ|=⎪⎪⎪⎪⎪⎪n 1·n 2|n 1||n 2|=29×1=23, 得sin θ=53. 因此,平面ADC 1与平面ABA 1所成二面角的正弦值为53.4.如图,在四棱锥P —ABCD 中,平面P AD ⊥底面ABCD ,其中底面ABCD 为等腰梯形,AD ∥BC ,P A =AB =BC =CD =2,PD =23,P A ⊥PD ,Q 为PD 的中点.(1)证明:CQ ∥平面P AB ; (2)求二面角D —AQ —C 的余弦值.(1)证明 如图所示,取P A 的中点N ,连接QN ,BN .在△P AD 中,PN =NA ,PQ =QD , 所以QN ∥AD ,且QN =12AD .在△APD中,P A=2,PD=23,P A⊥PD,所以AD=P A2+PD2=22+(23)2=4,而BC=2,所以BC=12AD.又BC∥AD,所以QN∥BC,且QN=BC,故四边形BCQN为平行四边形,所以BN∥CQ.又CQ⊄平面P AB,BN⊂平面P AB,所以CQ∥平面P AB.(2)解如图,在平面P AD内,过点P作PO⊥AD于点O,连接OB.因为平面P AD⊥平面ABCD,平面P AD∩平面ABCD=AD,所以PO⊥平面ABCD.又PO⊥AD,AP⊥PD,所以PO=AP×PDAD=2×234=3,故AO=AP2-PO2=22-(3)2=1.在等腰梯形ABCD中,取AD的中点M,连接BM,又BC=2,AD=4,AD∥BC,所以DM=BC=2,DM∥BC,故四边形BCDM为平行四边形.所以BM=CD=AB=2.在△ABM中,AB=AM=BM=2,AO=OM=1,所以BO⊥AD.又平面P AD⊥平面ABCD,平面P AD∩平面ABCD=AD,所以BO⊥平面P AD.如图,以O为坐标原点,分别以OB,OD,OP所在直线为x轴,y轴,z 轴建立空间直角坐标系,则O(0,0,0),D(0,3,0),A(0,-1,0),B(3,0,0),P(0,0,3),C(3,2,0),则AC→=(3,3,0).因为Q 为DP 的中点,故Q ⎝⎛⎭⎪⎫0,32,32,所以AQ→=⎝⎛⎭⎪⎫0,52,32. 设平面AQC 的法向量为m =(x ,y ,z ),则⎩⎪⎨⎪⎧m ⊥AC→,m ⊥AQ →,可得⎩⎪⎨⎪⎧m ·AC →=3x +3y =0,m ·AQ →=52y +32z =0,令y =-3,则x =3,z =5.故平面AQC 的一个法向量为m =(3,-3,5). 因为BO ⊥平面P AD ,所以OB→=(3,0,0)是平面ADQ 的一个法向量. 故cos 〈OB →,m 〉=OB →·m |OB →|·|m |=333·32+(-3)2+52=337=33737. 从而可知二面角D —AQ —C 的余弦值为33737.5.在四棱锥P —ABCD 中,侧面PCD ⊥底面ABCD ,PD ⊥CD ,底面ABCD 是直角梯形,AB ∥CD ,∠ADC =90°,AB =AD =PD =1,CD =2.(1)求证:BC ⊥平面PBD ;(2)在线段PC 上是否存在一点Q ,使得二面角Q —BD —P 为45°?若存在,求PQPC的值;若不存在,请说明理由. (1)证明 平面PCD ⊥底面ABCD ,PD ⊥CD , 所以PD ⊥平面ABCD ,所以PD ⊥AD . 如图,以D 为原点建立空间直角坐标系Dxyz ,则A (1,0,0),B (1,1,0),C (0,2,0),P (0,0,1), DB→=(1,1,0),BC →=(-1,1,0), 所以BC→·DB →=0,BC ⊥DB , 又由PD ⊥平面ABCD ,可得PD ⊥BC , 因为PD ∩BD =D , 所以BC ⊥平面PBD .(2)解 平面PBD 的法向量为BC→=(-1,1,0), PC→=(0,2,-1),设PQ →=λPC →,λ∈(0,1), 所以Q (0,2λ,1-λ),设平面QBD 的法向量为n =(a ,b ,c ), DB→=(1,1,0),DQ →=(0,2λ,1-λ), 由n ·DB→=0,n ·DQ →=0, 得⎩⎨⎧a +b =0,2λb +(1-λ)c =0,令b =1,所以n =(-1,1,2λλ-1), 所以cos 45°=|n ·BC→||n ||BC →|=222+(2λλ-1)2=22, 注意到λ∈(0,1),得λ=2-1,所以在线段PC 上存在一点Q ,使得二面角Q —BD —P 为45°,此时PQPC=2-1.。
高三数学高考大题专项训练全套(15个专项)(典型例题)(含答案)

⾼三数学⾼考⼤题专项训练全套(15个专项)(典型例题)(含答案)1、函数与导数(1)2、三⾓函数与解三⾓形3、函数与导数(2)4、⽴体⼏何5、数列(1)6、应⽤题7、解析⼏何8、数列(2)9、矩阵与变换10、坐标系与参数⽅程11、空间向量与⽴体⼏何12、曲线与⽅程、抛物线13、计数原理与⼆项式分布14、随机变量及其概率分布15、数学归纳法⾼考压轴⼤题突破练 (⼀)函数与导数(1)1.已知函数f (x )=a e xx+x .(1)若函数f (x )的图象在(1,f (1))处的切线经过点(0,-1),求a 的值;(2)是否存在负整数a ,使函数f (x )的极⼤值为正值?若存在,求出所有负整数a 的值;若不存在,请说明理由.解 (1)∵f ′(x )=a e x (x -1)+x 2x 2,∴f ′(1)=1,f (1)=a e +1.∴函数f (x )在(1,f (1))处的切线⽅程为 y -(a e +1)=x -1,⼜直线过点(0,-1),∴-1-(a e +1)=-1,解得a =-1e.(2)若a <0,f ′(x )=a e x (x -1)+x 2x 2,当x ∈(-∞,0)时,f ′(x )>0恒成⽴,函数在(-∞,0)上⽆极值;当x ∈(0,1)时,f ′(x )>0恒成⽴,函数在(0,1)上⽆极值.⽅法⼀当x ∈(1,+∞)时,若f (x )在x 0处取得符合条件的极⼤值f (x 0),则x 0>1,f (x 0)>0,f ′(x 0)=0,则00000200201,e 0,e (1)0,x x x a x x a x x x ?> +> -+ = ?①②③由③得0e x a =-x 20x 0-1,代⼊②得-x 0x 0-1+x 0>0,结合①可解得x 0>2,再由f (x 0)=0e x a x +x 0>0,得a >-020e x x ,设h (x )=-x 2e x ,则h ′(x )=x (x -2)e x ,当x >2时,h ′(x )>0,即h (x )是增函数,∴a >h (x 0)>h (2)=-4e2.⼜a <0,故当极⼤值为正数时,a ∈-4e 2,0,从⽽不存在负整数a 满⾜条件.⽅法⼆当x ∈(1,+∞)时,令H (x )=a e x (x -1)+x 2,则H ′(x )=(a e x +2)x ,∵x ∈(1,+∞),∴e x ∈(e ,+∞),∵a 为负整数,∴a ≤-1,∴a e x ≤a e ≤-e ,∴a e x +2<0,∴H ′(x )<0,∴H (x )在(1,+∞)上单调递减.⼜H (1)=1>0,H (2)=a e 2+4≤-e 2+4<0,∴?x 0∈(1,2),使得H (x 0)=0,且当10,即f ′(x )>0;当x >x 0时,H (x )<0,即f ′(x )<0.∴f (x )在x 0处取得极⼤值f (x 0)=0e x a x +x 0.(*)⼜H (x 0)=0e x a (x 0-1)+x 20=0,∴00e x a x =-x 0x 0-1,代⼊(*)得f (x 0)=-x 0x 0-1+x 0=x 0(x 0-2)x 0-1<0,∴不存在负整数a 满⾜条件.2.已知f (x )=ax 3-3x 2+1(a >0),定义h (x )=max{f (x ),g (x )}=f (x ),f (x )≥g (x ),g (x ),f (x )(1)求函数f (x )的极值;(2)若g (x )=xf ′(x ),且?x ∈[1,2]使h (x )=f (x ),求实数a 的取值范围.解 (1)∵函数f (x )=ax 3-3x 2+1,∴f ′(x )=3ax 2-6x =3x (ax -2),令f ′(x )=0,得x 1=0或x 2=2a ,∵a >0,∴x 1当x 变化时,f ′(x ),f (x )的变化情况如下表:∴f (x )的极⼤值为f (0)=1,极⼩值为f 2a =8a 2-12a 2+1=1-4a 2. (2)g (x )=xf ′(x )=3ax 3-6x 2,∵?x ∈[1,2],使h (x )=f (x ),∴f (x )≥g (x )在[1,2]上有解,即ax 3-3x 2+1≥3ax 3-6x 2在[1,2]上有解,即不等式2a ≤1x 3+3x在[1,2]上有解,设y =1x 3+3x =3x 2+1x3(x ∈[1,2]),∵y ′=-3x 2-3x 4<0对x ∈[1,2]恒成⽴,∴y =1x 3+3x 在[1,2]上单调递减,∴当x =1时,y =1x 3+3x 的最⼤值为4,∴2a ≤4,即a ≤2.⾼考中档⼤题规范练 (⼀)三⾓函数与解三⾓形1.(2017·江苏宿迁中学质检)已知函数f (x )=sin 2x +23sin x cos x +sin x +π4sin x -π4,x ∈R . (1)求f (x )的最⼩正周期和值域;(2)若x =x 00≤x 0≤π2为f (x )的⼀个零点,求sin 2x 0的值.解 (1)易得f (x )=sin 2x +3sin 2x +12(sin 2x -cos 2x )=1-cos 2x 2+3sin 2x -12cos 2x =3sin 2x -cos 2x +12=2sin 2x -π6+12,所以f (x )的最⼩正周期为π,值域为-32,52. (2)由f (x 0)=2sin 2x 0-π6+12=0,得 sin 2x 0-π6=-14<0,⼜由0≤x 0≤π2,得-π6≤2x 0-π6≤5π6,所以-π6≤2x 0-π6<0,故cos 2x 0-π6=154,此时sin 2x 0=sin 2x 0-π6+π6 =sin 2x 0-π6cos π6+cos 2x 0-π6sin π6 =-14×32+154×12=15-38.2.(2017·江苏南通四模)已知向量m =sin x 2,1,n =1,3cos x2,函数f (x )=m ·n . (1)求函数f (x )的最⼩正周期;(2)若f α-2π3=23,求f 2α+π3的值.解 (1)f (x )=m ·n =sin x 2+3cos x2=212sin x 2+32cos x2=2sin x 2cos π3+cos x 2sin π3 =2sin x 2+π3,所以函数f (x )的最⼩正周期为T =2π12=4π.(2)由f α-2π3=23,得2sin α2=23,即sin α2=13. 所以f 2α+π3=2sin α+π2=2cos α=2?1-2sin 2α2=149. 3.(2017·江苏南师⼤考前模拟)已知△ABC 为锐⾓三⾓形,向量m =cos A +π3,sin A +π3,n =(cos B ,sin B ),并且m ⊥n . (1)求A -B ;(2)若cos B =35,AC =8,求BC 的长.解 (1)因为m ⊥n ,所以m ·n =cos A +π3cos B +sinA +π3sin B=cosA +π3-B =0. 因为0所以A +π3-B =π2,即A -B =π6.(2)因为cos B =35,B ∈0,π2,所以sin B =45,所以sin A =sin B +π6=sin B cos π6+cos B sin π6 =45×32+35×12=43+310,由正弦定理可得BC =sin A sin B×AC =43+3.4.(2017·江苏镇江三模)在△ABC 中,⾓A ,B ,C 的对边分别为a ,b ,c ,且(a -c )(sin A +sin C )=(b -3c )sin B . (1)求⾓A ;(2)若f (x )=cos 2(x +A )-sin 2(x -A ),求f (x )的单调递增区间.解 (1)由(a -c )(sin A +sin C )=(b -3c )sin B 及正弦定理,得(a -c )(a +c )=(b -3c )b ,即a 2=b 2+c 2-3bc . 由余弦定理,得cos A =32,因为06.(2)f (x )=cos 2(x +A )-sin 2(x -A ) =cos 2x +π6-sin 2x -π6 =1+cos 2x +π32-1-cos ?2x -π32=12cos 2x ,令π+2k π≤2x ≤2π+2k π,k ∈Z ,得π2+k π≤x ≤π+k π,k ∈Z . 则f (x )的单调增区间为π2+k π,π+k π,k ∈Z .(⼆)函数与导数(2)1.设函数f (x )=2(a +1)x (a ∈R ),g (x )=ln x +bx (b ∈R ),直线y =x +1是曲线y =f (x )的⼀条切线. (1)求a 的值;(2)若函数y =f (x )-g (x )有两个极值点x 1,x 2. ①试求b 的取值范围;②证明:g (x 1)+g (x 2)f (x 1)+f (x 2)≤1e 2+12.解 (1)设直线y =x +1与函数y =f (x )的图象相切于点(x 0,y 0),则y 0=x 0+1,y 0=2(a +1)x 0,a +1x 0=1,解得a =0. (2)记h (x )=f (x )-g (x ),则h (x )=2x -ln x -bx .①函数y =f (x )-g (x )有两个极值点的必要条件是h ′(x )有两个正零点. h ′(x )=1x -1x-b =-bx +x -1x ,令h ′(x )=0,得bx -x +1=0(x >0).令x =t ,则t >0.问题转化为bt 2-t +1=0有两个不等的正实根t 1,t 2,等价于Δ=1-4b >0,t 1t 2=1b >0,t 1+t 2=1b>0,解得04.当04时,设h ′(x )=0的两正根为x 1,x 2,且x 1则h ′(x )=-bx +x -1x =-b (x -x 1)(x -x 2)x =-b (x -x 1)(x -x 2)x (x +x 1)(x +x 2).当x ∈(0,x 1)时,h ′(x )<0;当x ∈(x 1,x 2)时,h ′(x )>0;当x ∈(x 2,+∞)时,h ′(x )<0.所以x 1,x 2是h (x )=f (x )-g (x )的极值点,∴b 的取值范围是0,14. ②由①知x 1x 2=x 1+x 2=1 b.可得g (x 1)+g (x 2)=-2ln b +1b -2,f (x 1)+f (x 2)=2b ,所以g (x 1)+g (x 2)f (x 1)+f (x 2)=12-b ln b -b .记k (b )=12-b ln b -b 0令k ′(b )=0,得b =1e 2∈0,14,且当b ∈0,1e 2时,k ′(b )>0,k (b )单调递增;当b ∈1e 2,14时,k ′(b )<0,k (b )单调递减,且当b =1e 2时,k (b )取最⼤值1e 2+12,所以g (x 1)+g (x 2)f (x 1)+f (x 2)≤1e 2+12.2.设函数f (x )=2ax +bx+c ln x .(1)当b =0,c =1时,讨论函数f (x )的单调区间;(2)若函数f (x )在x =1处的切线为y =3x +3a -6且函数f (x )有两个极值点x 1,x 2,x 1解 (1)f (x )=2ax +bx+c ln x ,x >0,f ′(x )=2a -b x 2+c x =2ax 2+cx -bx 2.当b =0,c =1时,f ′(x )=2ax +1x. 当a ≥0时,由x >0,得f ′(x )=2ax +1x >0恒成⽴,所以函数f (x )在(0,+∞)上单调递增.当a <0时,令f ′(x )=2ax +1x >0,解得x <-12a ;令f ′(x )=2ax +1x <0,解得x >-12a,所以,函数f (x )在0,-12a 上单调递增,在-12a ,+∞上单调递减.综上所述,①当a ≥0时,函数f (x )在(0,+∞)上单调递增;②当a <0时,函数f (x )在? 0,-12a上单调递增,在-12a ,+∞上单调递减. (2)①函数f (x )在x =1处的切线为y =3x +3a -6,所以f (1)=2a +b =3a -3,f ′(1)=2a +c -b =3,所以b =a -3,c =-a ,f ′(x )=2a -b x 2+c x =2ax 2-ax +3-ax 2,函数f (x )有两个极值点x 1,x 2,x 1则⽅程2ax 2-ax +3-a =0有两个⼤于0的解,Δ=(-a )2-8a (3-a )>0,a 2a >0,3-a2a >0,解得83所以a 的取值范围是83,3. ②2ax 22-ax 2+3-a =0, x 2=a +9a 2-24a 4a =141+9-24a ,由832x 22-x 2-1.f (x 2)=2ax 2+a -3x 2-a ln x 2=a 2x 2+1x 2-ln x 2-3x 2 =-32x 2+1x 2-ln x 22x 22-x 2-1-3x 2. 设φ(t )=-32t +1t -ln t2t 2-t -1-3t,t ∈14,12,φ′(t )=-32-1t 2-1t (2t 2-t -1)-2t +1t -ln t (4t -1)(2t 2-t -1)2+3t2 =-31t 2(2t 2-t -1)2+32t +1t -ln t (4t -1)(2t 2-t -1)2+3t 2=32t +1t -ln t (4t -1)(2t 2-t -1)2. 当t ∈14,12时,2t +1t-ln t >0,4t -1>0,φ′(t )>0,所以φ(t )在14,12上单调递增,φ(t )∈163ln 2,3+3ln 2,所以f (x 2)的取值范围是163ln 2,3+3ln 2. (⼆)⽴体⼏何1.(2017·江苏扬州调研)如图,在四棱锥P -ABCD 中,底⾯ABCD 为梯形,CD ∥AB ,AB =2CD ,AC 交BD 于O ,锐⾓△P AD 所在平⾯⊥底⾯ABCD ,P A ⊥BD ,点Q 在侧棱PC 上,且PQ =2QC .求证:(1)P A ∥平⾯QBD ; (2)BD ⊥AD .证明 (1)如图,连结OQ ,因为AB ∥CD ,AB =2CD ,所以AO =2OC . ⼜PQ =2QC ,所以P A ∥OQ . ⼜OQ ?平⾯QBD ,P A ?平⾯QBD ,所以P A ∥平⾯QBD .(2)在平⾯P AD 内过P 作PH ⊥AD 于点H ,因为侧⾯P AD ⊥底⾯ABCD ,平⾯P AD ∩平⾯ABCD =AD ,PH ?平⾯P AD ,所以PH ⊥平⾯ABCD .⼜BD ?平⾯ABCD ,所以PH ⊥BD .⼜P A ⊥BD ,P A ∩PH =P ,所以BD ⊥平⾯P AD . ⼜AD ?平⾯P AD ,所以BD ⊥AD .2.如图,在四棱锥P -ABCD 中,底⾯ABCD 是正⽅形,AC 与BD 交于点O ,PC ⊥底⾯ABCD ,E 为PB 上⼀点,G 为PO 的中点.(1)若PD∥平⾯ACE,求证:E为PB的中点;(2)若AB=2PC,求证:CG⊥平⾯PBD.证明(1)连结OE,由四边形ABCD是正⽅形知,O为BD的中点,因为PD∥平⾯ACE,PD?平⾯PBD,平⾯PBD∩平⾯ACE=OE,所以PD∥OE. 因为O为BD的中点,所以E为PB的中点.(2)在四棱锥P-ABCD中,AB=2PC,因为四边形ABCD是正⽅形,所以OC=22AB,所以PC=OC.因为G为PO的中点,所以CG⊥PO.⼜因为PC⊥底⾯ABCD,BD?底⾯ABCD,所以PC⊥BD.⽽四边形ABCD是正⽅形,所以AC⊥BD,因为AC,PC?平⾯P AC,AC∩PC=C,所以BD⊥平⾯P AC,因为CG?平⾯P AC,所以BD⊥CG.因为PO,BD?平⾯PBD,PO∩BD=O,所以CG⊥平⾯PBD.3.(2017·江苏怀仁中学模拟)如图,在四棱锥E-ABCD中,△ABD为正三⾓形,EB=ED,CB=CD.(1)求证:EC⊥BD;(2)若AB⊥BC,M,N分别为线段AE,AB的中点,求证:平⾯DMN∥平⾯BCE.证明(1)取BD的中点O,连结EO,CO.∵CD=CB,EB=ED,∴CO⊥BD,EO⊥BD.⼜CO∩EO=O,CO,EO?平⾯EOC,∴BD⊥平⾯EOC.⼜EC?平⾯EOC,∴BD⊥EC.(2)∵N是AB的中点,△ABD为正三⾓形,∴DN⊥AB,∵BC⊥AB,∴DN∥BC.⼜BC?平⾯BCE,DN?平⾯BCE,∴DN∥平⾯BCE.∵M为AE的中点,N为AB的中点,∴MN∥BE,⼜MN?平⾯BCE,BE?平⾯BCE,∴MN∥平⾯BCE.∵MN∩DN=N,∴平⾯DMN∥平⾯BCE.4.(2017·江苏楚⽔中学质检)如图,在三棱锥P-ABC中,点E,F分别是棱PC,AC的中点.(1)求证:P A∥平⾯BEF;(2)若平⾯P AB⊥平⾯ABC,PB⊥BC,求证:BC⊥P A.证明(1)在△P AC中,E,F分别是棱PC,AC的中点,所以P A∥EF.⼜P A?平⾯BEF,EF?平⾯BEF,所以P A∥平⾯BEF.(2)在平⾯P AB内过点P作PD⊥AB,垂⾜为D.因为平⾯P AB ⊥平⾯ABC ,平⾯P AB ∩平⾯ABC =AB ,PD ?平⾯P AB ,所以PD ⊥平⾯ABC ,因为BC ?平⾯ABC ,所以PD ⊥BC ,⼜PB ⊥BC ,PD ∩PB =P ,PD ?平⾯P AB ,PB ?平⾯P AB ,所以BC ⊥平⾯P AB ,⼜P A ?平⾯P AB ,所以BC ⊥P A .(三)数列(1)1.已知数列{a n }的前n 项和为S n ,且S n +a n =4,n ∈N *. (1)求数列{a n }的通项公式;(2)已知c n =2n +3(n ∈N *),记d n =c n +log C a n (C >0且C ≠1),是否存在这样的常数C ,使得数列{d n }是常数列,若存在,求出C 的值;若不存在,请说明理由.(3)若数列{b n },对于任意的正整数n ,均有b 1a n +b 2a n -1+b 3a n -2+…+b n a 1=12n -n +22成⽴,求证:数列{b n }是等差数列. (1)解 a 1=4-a 1,所以a 1=2,由S n +a n =4,得当n ≥2时,S n -1+a n -1=4,两式相减,得2a n =a n -1,所以a n a n -1=12,数列{a n }是以2为⾸项,公⽐为12的等⽐数列,所以a n =22-n (n ∈N *).(2)解由于数列{d n }是常数列, d n =c n +log C a n =2n +3+(2-n )log C 2 =2n +3+2log C 2-n log C 2=(2-log C 2)n +3+2log C 2为常数,则2-log C 2=0,解得C =2,此时d n =7.(3)证明 b 1a n +b 2a n -1+b 3a n -2+…+b n a 1 =12n -n +22,①当n =1时,b 1a 1=12-32=-1,其中a 1=2,所以b 1=-12.当n ≥2时,b 1a n -1+b 2a n -2+b 3a n -3+…+b n -1a 1=12n -1-n +12,②②式两边同时乘以12,得b 1a n +b 2a n -1+b 3a n -2+…+b n -1a 2=12n -n +14,③由①-③,得b n a 1=-n -34,所以b n =-n 8-38(n ∈N *,n ≥2),且b n +1-b n =-18,⼜b 1=-12=-18-38,所以数列{b n }是以-12为⾸项,公差为-18的等差数列.2.在数列{a n }中,已知a 1=13,a n +1=13a n -23n +1,n ∈N *,设S n 为{a n }的前n 项和.(1)求证:数列{3n a n }是等差数列; (2)求S n ;(3)是否存在正整数p ,q ,r (p ""(1)证明因为a n +1=13a n -23n +1,所以3n +1a n +1-3n a n =-2.⼜因为a 1=13,所以31·a 1=1,所以{3n a n }是⾸项为1,公差为-2的等差数列. (2)解由(1)知3n a n =1+(n -1)·(-2)=3-2n ,所以a n =(3-2n )13n ,所以S n =1·131+(-1)·132+(-3)·133+…+(3-2n )·13n ,所以13S n =1·132+(-1)·133+…+(5-2n )·13n +(3-2n )·13n +1,两式相减,得23S n =13-2132+133+…+13n -(3-2n )·13n +1=13-219×1-13n -11-13+(2n -3)·13n +1=2n ·13n +1,所以S n =n3n .(3)解假设存在正整数p ,q ,r (p ""3q =p 3p +r 3r. 当n ≥2时,a n =(3-2n )13n<0,所以数列{S n }单调递减.⼜p ""①当q ≥3时,p 3p ≥q -13q -1≥2q 3q ,⼜r 3r >0,所以p 3p +r 3r >2q3q ,等式不成⽴.②当q =2时,p =1,所以49=13+r 3r ,所以r 3r =19,所以r =3({S n }单调递减,解惟⼀确定).综上可知,p ,q ,r 的值为1,2,3.(三)应⽤题1.已知某⾷品⼚需要定期购买⾷品配料,该⼚每天需要⾷品配料200千克,配料的价格为1.8元/千克,每次购买配料需⽀付运费236元.每次购买来的配料还需⽀付保管费⽤,其标准如下:7天以内(含7天),⽆论重量多少,均按10元/天⽀付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克⽀付.(1)当9天购买⼀次配料时,求该⼚⽤于配料的保管费⽤P 是多少元?(2)设该⼚x 天购买⼀次配料,求该⼚在这x 天中⽤于配料的总费⽤y (元)关于x 的函数关系式,并求该⼚多少天购买⼀次配料才能使平均每天⽀付的费⽤最少?解 (1)当9天购买⼀次时,该⼚⽤于配料的保管费⽤ P =70+0.03×200×(1+2)=88(元).。
中档大题规范练2(数列)

2.数 列1.(2017·湖北部分重点中学联考)已知数列{a n }的前n 项和为S n ,且a 1=2,a 2=8,a 3=24,{a n +1-2a n }为等比数列,n ∈N *.(1)求证:⎩⎨⎧⎭⎬⎫a n 2n 是等差数列;(2)求证:S n ≥2.证明 (1)∵a 2-2a 1=4,a 3-2a 2=8, ∴a n +1-2a n =4×2n -1, ∴a n +12n +1-a n2n =1, ∴⎩⎨⎧⎭⎬⎫a n 2n 是以1为首项,1为公差的等差数列. (2)由(1)可得a n2n =1+(n -1)×1=n ,∴a n =n ×2n ,∴S n =1×2+2×22+3×23+…+n ×2n , ① 2S n =1×22+2×23+3×24+…+n ×2n +1,②由①-②得-S n =(1-n )×2n +1-2, ∴S n =(n -1)×2n +1+2. ∵n ∈N *,∴S n ≥2.2.(2017届黑龙江虎林一中月考)已知等差数列{a n }的前n 项和为S n ,且a 3=5,S 3=9. (1)求数列{a n }的通项公式;(2)设等比数列{b n }的前n 项和为T n ,若q >0且b 3=a 5,T 3=13,求T n ; (3)设c n =1a n a n +1,求数列{c n }的前n 项和S n .解 (1)⎩⎪⎨⎪⎧a 3=a 1+2d =5,S 3=3a 1+3×22d =9,解得⎩⎪⎨⎪⎧a 1=1,d =2,所以a n =a 1+(n -1)d =2n -1.(2)由题意可知,b 3=a 5=9,T 3=13,所以公比q =3,从而b 1=1, 所以T n =b 1(1-q n )1-q =1×(1-3n )1-3=12(3n-1).(3)由(1)知,a n =2n -1.所以c n =1a n a n +1=1(2n -1)(2n +1)=12⎝ ⎛⎭⎪⎫12n -1-12n +1, 所以S n =c 1+c 2+…+c n=12⎣⎢⎡⎦⎥⎤⎝⎛⎭⎫1-13+⎝⎛⎭⎫13-15+…+⎝ ⎛⎭⎪⎫12n -1-12n +1 =12⎝ ⎛⎭⎪⎫1-12n +1=n 2n +1. 3.(2017·广东七校联考)设数列{a n }的前n 项之积为T n ,且log 2T n =n (n -1)2,n ∈N *.(1)求数列{a n }的通项公式;(2)设b n =λa n -1(n ∈N *),数列{b n }的前n 项之和为S n .若对任意的n ∈N *,总有S n +1>S n ,求实数λ的取值范围.解 (1)由log 2T n =n (n -1)2,n ∈N *,得T n =(1)22n n -,所以T n -1=(1)(2)22n n --(n ∈N *,n ≥2),所以a n =T nT n -1=(1)2(1)(2)222n n n n ---=(1)(1)(2)222n n n n ----=2n -1,n ∈N *,n ≥2.又a 1=T 1=20=1, 所以a n =2n -1,n ∈N *. (2)由b n =λa n -1=λ2n -1-1, 得S n =λ·1-2n1-2-n =()2n-1λ-n ,所以S n +1>S n ⇔()2n +1-1λ-()n +1>()2n-1λ-n ⇔2n λ>1⇔λ>12n ,因为对任意的n ∈N *,12n ≤12,故所求的λ的取值范围是⎝⎛⎭⎫12,+∞. 4.(2017·湖北黄冈质检)已知数列{a n }的前n 项和为S n ,向量a =(S n ,n ),b =(9n -7,2),且a 与b 共线.(1)求数列{}a n 的通项公式;(2)对任意m ∈N *,将数列{a n }中落入区间(9m ,92m )内的项的个数记为b m ,求数列{b m }的前m项和T m .解 (1)a 与b 共线,S n =n (9n -7)2=92n 2-72n ,a 1=1,a n =S n -S n -1=9n -8,n ≥2, 所以a n =9n -8,n ∈N *. (2)对m ∈N *,若9m <a n <92m , 则9m +8<9n <92m +8. 因此9m -1+1≤n ≤92m -1. 故得b m =92m -1-9m -1. 于是T m =b 1+b 2+…+b m=(9+93+…+92m -1)-(1+9+…+9m -1) =9(1-81m )1-81-1-9m 1-9=9×92m +1-10×9m80.5.(2017·河北衡水中学调研)设S n 为各项不相等的等差数列{a n }的前n 项和,已知a 3a 5=3a 7,S 3=9.(1)求数列{}a n 的通项公式;(2)设T n 为数列⎩⎨⎧⎭⎬⎫1a n a n +1的前n 项和,求T na n +1的最大值.解 (1)设{a n }的公差为d ,则由题意知,⎩⎨⎧()a 1+2d ()a 1+4d =3()a 1+6d ,3a 1+3×22d =9,解得⎩⎪⎨⎪⎧ d =0,a 1=3(舍去)或⎩⎪⎨⎪⎧d =1,a 1=2,∴a n =2+()n -1×1=n +1. (2)∵1a n a n +1=1()n +1()n +2=1n +1-1n +2, ∴T n =1a 1a 2+1a 2a 3+…+1a n a n +1=⎝⎛⎭⎫12-13+⎝⎛⎭⎫13-14+…+⎝ ⎛⎭⎪⎫1n +1-1n +2 =12-1n +2=n 2()n +2, ∴T na n +1=n 2()n +22=n 2()n 2+4n +4=12⎝⎛⎭⎫n +4+4n ≤12⎝⎛⎭⎫4+2n ·4n =116, 当且仅当n =4n ,即n =2时“=”成立,即当n =2时,T n a n +1取得最大值116.6.(2017·广西柳州模拟)已知数列{a n }中,a 1=1,a 4=7,且a n +1=a n +λn . (1)求λ的值及数列{}a n 的通项公式;(2)设b n =1a n +1-1,数列{}b n 的前n 项和为T n ,证明:T n <2.(1)解 ∵a 1=1,a n +1=a n +λn , ∴a 2=1+λ,a 3=1+3λ,a 4=1+6λ, 由a 4=1+6λ=7,∴λ=1, 于是a n +1=a n +n ,∴a 1=1,a 2=a 1+1,a 3=a 2+2,a 4=a 3+3,…, a n =a n -1+(n -1),n ≥2,以上各式累加得a n =1+1+2+3+4+…+(n -1)=1+(n -1)(1+n -1)2=n 2-n +22,n ≥2,又a 1=1=12-1+22,∴a n =n 2-n +22,n ∈N *.(2)证明 b n =1a n +1-1=2n (n +1)=2⎝⎛⎭⎪⎫1n -1n +1,∴T n =b 1+b 2+b 3+…+b n=2⎝⎛⎭⎫1-12+2⎝⎛⎭⎫12-13+2⎝⎛⎭⎫13-14+…+2⎝ ⎛⎭⎪⎫1n -1n +1=2⎝ ⎛⎭⎪⎫1-1n +1, ∴T n <2.。
高考中档大题规范练(二)
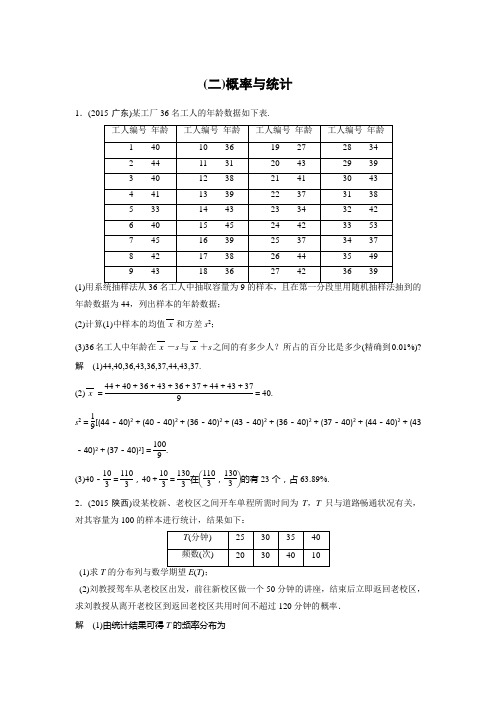
(二)概率与统计1.(2015·广东)某工厂36名工人的年龄数据如下表.(1)年龄数据为44,列出样本的年龄数据; (2)计算(1)中样本的均值x 和方差s 2;(3)36名工人中年龄在x -s 与x +s 之间的有多少人?所占的百分比是多少(精确到0.01%)? 解 (1)44,40,36,43,36,37,44,43,37.(2)x =44+40+36+43+36+37+44+43+379=40.s 2=19[(44-40)2+(40-40)2+(36-40)2+(43-40)2+(36-40)2+(37-40)2+(44-40)2+(43-40)2+(37-40)2]=1009.(3)40-103=1103,40+103=1303在⎝⎛⎭⎫1103,1303的有23个,占63.89%. 2.(2015·陕西)设某校新、老校区之间开车单程所需时间为T ,T 只与道路畅通状况有关,对其容量为100的样本进行统计,结果如下:(1)求T (2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率. 解 (1)由统计结果可得T 的频率分布为以频率估计概率得T 的分布列为从而E (T )=25×0.2+30×0.3+35×0.4+40×0.1 =32(分钟).(2)设T 1,T 2分别表示往,返所需时间,T 1,T 2的取值相互独立,且与T 的分布列相同, 设事件A 表示“刘教授共用时间不超过120分钟”,由于讲座时间为50分钟,所以事件A 对应于“刘教授在路途中的时间不超过70分钟”.方法一 P (A )=P (T 1+T 2≤70)=P (T 1=25,T 2≤45)+P (T 1=30,T 2≤40)+P (T 1=35,T 2≤35)+P (T 1=40,T 2≤30)=0.2×1+0.3×1+0.4×0.9+0.1×0.5=0.91.方法二 P (A )=P (T 1+T 2>70)=P (T 1=35,T 2=40)+P (T 1=40,T 2=35)+P (T 1=40,T 2=40)=0.4×0.1+0.1×0.4+0.1×0.1=0.09, 故P (A )=1-P (A )=0.91.3.某项竞赛分为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是34,12,14,且各阶段通过与否相互独立.(1)求该选手在复赛阶段被淘汰的概率;(2)设该选手在竞赛中回答问题的个数为ξ,求ξ的分布列与均值.解 (1)记“该选手通过初赛”为事件A ,“该选手通过复赛”为事件B ,“该选手通过决赛”为事件C ,则P (A )=34,P (B )=12,P (C )=14.那么该选手在复赛阶段被淘汰的概率 P =P (A B )=P (A )P (B )=34×(1-12)=38.(2)ξ可能取值为1,2,3.P (ξ=1)=1-34=14,P (ξ=2)=34×(1-12)=38,P (ξ=3)=34×12=38.故ξ的分布列为ξ的均值为E (ξ)=1×14+2×38+3×38=178.4.袋中装有若干个质地均匀、大小一致的红球和白球,白球数量是红球数量的两倍.每次从袋中摸出一个球然后放回,若累计3次摸到红球则停止摸球,否则继续摸球直到第5次摸球后结束.(1)求摸球3次就停止的事件发生的概率;(2)记摸到红球的次数为ξ,求随机变量ξ的分布列及其均值.解 (1)由题意,知从袋中任意摸出一个球,摸到红球的概率为13,摸到白球的概率为23.摸球3次就停止,说明前三次都摸到了红球,则摸球3次就停止的事件发生的概率为P =(13)3=127.(2)依题意,随机变量ξ的所有可能取值为0,1,2,3,则 P (ξ=0)=C 05·(1-13)5=32243, P (ξ=1)=C 15·13·(1-13)4=80243, P (ξ=2)=C 25·(13)2·(1-13)3=80243, P (ξ=3)=C 33·(13)3+C 23·(13)2·(1-13)·13+C 24·(13)2·(1-13)2·13=1781. 随机变量ξ的分布列为随机变量ξ的均值为E (ξ)=32243×0+80243×1+80243×2+1781×3=13181. 5.某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品称出它们的重量作为样本(单位:克),重量的分组区间为(490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图所示.(1)根据频率分布直方图,求重量超过505克的产品数量;(2)在上述抽取的40件产品中任取2件,设Y 为重量超过505克的产品数量,求Y 的分布列; (3)从该流水线上任取5件产品,求恰有2件产品的重量超过505克的概率.解 (1)根据频率分布直方图可知,重量超过505克的产品数量为[(0.01+0.05)×5]×40=12(件).(2)Y 的可能取值为0,1,2. P (Y =0)=C 228C 240=63130,P (Y =1)=C 128C 112C 240=56130,P (Y =2)=C 212C 240=11130.Y 的分布列为(3)利用样本估计总体,该流水线上产品重量超过505克的概率为0.3. 令ξ为任取的5件产品中重量超过505克的产品数量, 则ξ~B (5,0.3),故所求概率为P (ξ=2)=C 25(0.3)2·(0.7)3=0.3 087.。
高考数学中档大题规范练中档大题2

高中数学学习材料金戈铁骑整理制作中档大题2概率与统计1.某校为了了解学生孝敬父母的情况(选项,A:为父母洗一次脚;B:帮父母做一次家务;C:给父母买一件礼物;D:其他).在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):学生孝敬父母情况统计表选项频数频率A m 0.15B 60pC n 0.4D 480.2学生孝敬父母情况条形统计图根据以上信息解答下列问题:(1)这次被调查的学生有多少人?(2)求表中m、n、p的值,并补全条形统计图.(3)该校有1 600名学生,估计该校全体学生中选择B选项的有多少人?2.为使学生更好地了解中华民族伟大复兴的历史知识,某校组织了一次以“我的梦,中国梦”为主题的知识竞赛,每班选25名同学参加比赛,成绩分为A ,B ,C ,D 四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图:请根据以上提供的信息解答下列问题: (1)把一班竞赛成绩统计图补充完整. (2)写出下表中a ,b ,c 的值:平均数(分)中位数(分)众数(分) 一班 a b 90 二班87.680c(3)请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析; ①从平均数和中位数方面来比较一班和二班的成绩; ②从平均数和众数方面来比较一班和二班的成绩;③从B 级以上(包括B 级)的人数方面来比较一班和二班的成绩.3.甲、乙两人各射击一次,击中目标的概率分别是23和34.假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响. (1)求甲射击4次,至少有1次未击中目标的概率;(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;(3)假设某人连续2次未击中目标,则中止其射击,则乙恰好射击5次后被中止射击的概率是多少?4.小昆和小明相约玩一种“造数”游戏,游戏规划如下:同时抛掷一枚均匀的硬币和一枚均匀的骰子,硬币的正、反面分别表示“新数”的符号(约定硬币正面向上记为“+”号,反面向上记为“-”号),与骰子投出面朝上的数字组合成一个“新数”;如抛掷结果为硬币反面向上,骰子面朝上的数字是“4”,记为“-4”.(1)利用树状图或列表的方法(只选其中一种)表示出游戏可能出现的所有结果;(2)写出组合成的所有“新数”;(3)若约定投掷一次的结果所组合的“新数”是3的倍数,则小昆获胜;若是4或5的倍数,则小明获胜.你觉得他们的约定公平吗?为什么?5.2014年12月初,南京查获了一批问题牛肉,滁州市食药监局经民众举报获知某地6个储存牛肉的冷库有1个冷库牛肉被病毒感染,需要通过对库存牛肉抽样化验病毒DNA来确定感染牛肉,以免民众食用有损身体健康.下面是两种化验方案:方案甲:逐个化验样品,直到能确定感染冷库为止.方案乙:将样品分为两组,每组3个,并将它们混合在一起化验,若存在病毒DNA,则表明感染牛肉在这3个样品当中,然后逐个化验,直到确定感染冷库为止;若结果不含病毒DNA,则在另外一组样品中逐个进行化验.(1)求依据方案乙所需化验恰好为2次的概率;(2)首次化验化验费10元,第二次化验化验费8元,第三次及其以后每次化验费都是6元,列出方案甲所需化验费用的概率分布,并估计用方案甲平均需要化验费多少元?(3)试比较两种方案,估计哪种方案有利于尽快查找到感染冷库.6.某次知识竞赛中,从6道备选题中一次性随机抽取3道,并独立完成所抽取的3道题.甲选手能正确完成其中4道题;乙选手能正确完成每道题的概率都为23,且每道题正确完成与否互不影响.规定至少正确答对其中2道题目便可过关. (1)求甲选手能晋级的概率;(2)记所抽取的3道题中,甲选手答对的题目数为ξ,写出ξ的概率分布,并求E (ξ); (3)记乙选手能答对的题目数为η,求η的概率分布与V (η).7.我国的高铁技术发展迅速,铁道部门计划在A ,B 两城之间开通高速列车,假设在试运行期间,每天8:00-9:00,9:00-10:00两个时间段内各发一趟由A 城开往B 城的列车(两车发车情况互不影响),A 城发车时间及其概率如表所示:发车 时间 8:10 8:30 8:50 9:10 9:30 9:50 概率161312161312若甲、乙两位旅客打算从A 城到B 城,假设他们到达A 城火车站候车的时间分别是周六8:00和周日8:20(只考虑候车时间,不考虑其他因素). (1)求甲、乙二人候车时间相等的概率;(2)设乙候车所需时间为随机变量ξ,求ξ的概率分布和均值E (ξ).答案精析中档大题2 概率与统计1.解 (1)∵48÷0.2=240, ∴这次被调查的学生有240人.(2)m =240×0.15=36,n =240×0.4=96, p =60÷240=0.25. 补全条形统计图如图.(3)∵1 600×0.25=400.∴估计该校全体学生中选择B 选项的有400人. 2.解 (1)25-6-12-5=2(人).(2)a =87.6,b =90,c =100.(3)①一班和二班平均数相等,一班的中位数大于二班的中位数,故一班的成绩好于二班. ②一班和二班平均数相等,一班的众数小于二班的众数,故二班的成绩好于一班; ③B 级以上(包括B 级)一班18人,二班12人,故一班的成绩好于二班. 3.解 (1)甲至少有一次未击中目标的概率为 P 1=P 1(1)+P 1(2)+P 1(3)+P 1(4) =1-P 1(0)=1-(23)4(13)0=6581.(2)甲射击4次恰击中2次的概率为P 2=C24(23)2(13)2=827,乙射击4次恰击中3次的概率为 P 3=C34(34)3×14=2764,由乘法公式,所求概率 P =P 2·P 3=827×2764=18.(3)乙恰好5次停止射击,则最后两次未击中,前三次都击中或第一与第二次恰有一次击中,第三次必击中,故所求概率为 P =(34)3(14)2+C12(34)2(14)3=451 024.4.解 (1)根据题意画树状图如下:(2)组合成的新数为1,2,3,4,5,6,-1,-2,-3,-4,-5,-6.(3)所有的组合成的新数中是3的倍数的有3,6,-3,-6这四个,因此P (3的倍数)=412=13,是4或5的倍数的有4,5,-4,-5这四个,因此P (4或5的倍数)=412=13,由于两者的概率相同,所以他们的约定公平.5.解 (1)方案乙所需化验次数恰好为2次的事件有两种情况:第一种,先化验一组,结果不含病毒DNA ,再从另一组中任取一个样品进行化验,则恰含有病毒的概率为C 35C 36×1C 13=16.第二种,先化验一组,结果含有病毒DNA ,再从中逐个化验,恰第1个样品含有病毒的概率为C 25C 36×1C 13=16. 所以依据方案乙所需化验恰好为2次的概率为 16+16=13. (2)设方案甲化验的次数为ξ,则ξ可能的取值为1,2,3,4,5,对应的化验费用为η元,则P (ξ=1)=P (η=10)=16,P (ξ=2)=P (η=18)=56×15=16,P (ξ=3)=P (η=24)=56×45×14=16,P (ξ=4)=P (η=30)=56×45×34×13=16,P (ξ=5)=P (η=36)=56×45×34×23=13.则其化验费用η的概率分布为η 10 18 24 30 36 P1616161613所以E (η)=10×16+18×16+24×16+30×16+36×13=773(元).所以方案甲平均需要化验费773元. (3)由(2)知方案甲平均化验次数为E (ξ)=1×16+2×16+3×16+4×16+5×13=103.设方案乙化验的次数为δ,则δ可能的取值为2,3, 所以P (δ=2)=13,P (δ=3)=1-P (δ=2)=23,所以E (δ)=2×13+3×23=83.则E (ξ)>E (δ),所以方案乙化验次数的期望值较小,可以尽快查找到感染冷库.6.解 (1)记甲选手能晋级为事件A ,则基本事件总数n =C 36=20, 事件A 包含的基本事件m =C 34+C 24C 12=16,所以P (A )=m n =45.(2)ξ的所有可能取值为1,2,3.P (ξ=1)=C 14C 22C 36=15,P (ξ=2)=C 24C 12C 36=35,P (ξ=3)=C 34C 36=15.则ξ的概率分布为ξ 1 2 3 P153515所以E (ξ)=1×15+2×35+3×15=2.(3)依题意知,η服从B ⎝⎛⎭⎫3,23.P (η=k )=C k 3⎝⎛⎭⎫23k ⎝⎛⎭⎫1-233-k ,k =0,1,2,3.即P (η=0)=C 03⎝⎛⎭⎫230⎝⎛⎭⎫133=127, P (η=1)=C 13·⎝⎛⎭⎫231⎝⎛⎭⎫132=29, P (η=2)=C 23⎝⎛⎭⎫232⎝⎛⎭⎫131=49,P (η=3)=C 33⎝⎛⎭⎫233⎝⎛⎭⎫130=827. 则η的概率分布为η 0 1 2 3 P1272949827所以V (η)=3×23×13=23.7.解 (1)甲到达火车站的时间为周六8:00,所以甲的候车时间有三种情况,如表所示.发车时间 8:10 8:30 8:50 候车时间(分)103050乙到达火车站的时间为周日8:20,所以乙的候车时间有五种情况,如表所示.发车时间 8:30 8:50 9:10 9:30 9:50 候车时间 (分)1030507090根据表格可知:甲、乙二人候车时间均为10分钟的概率为:16×13=118;甲、乙二人候车时间圴为30分钟的概率为:13×12=16;甲、乙二人候车时间均为50分钟的概率为:12×16×16=172.所以甲、乙二人候车时间相等的概率为: 118+16+172=1772. (2)乙候车所需时间为随机变量ξ=10,30,50,70,90. P (ξ=10)=13;P (ξ=30)=12;P (ξ=50)=16×16=136;P (ξ=70)=16×13=118;P (ξ=90)=16×12=112.所以ξ的概率分布为:ξ 10 30 50 70 90 P1312136118112均值E (ξ)=10×13+30×12+50×136+70×118+90×112=2809.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考中档大题规范练
(二)数 列
1.已知函数f (x )=7x +5x +1
,数列{a n }满足:2a n +1-2a n +a n +1a n =0且a n ≠0.数列{b n }中,b 1=f (0)且b n =f (a n -1).
(1)求证:数列⎩⎨⎧⎭
⎬⎫1a n 是等差数列; (2)求数列{|b n |}的前n 项和T n .
2.已知等差数列{a n }是递增数列,且满足a 4·a 7=15,a 3+a 8=8.
(1)求数列{a n }的通项公式;
(2)令b n =19a n -1a n (n ≥2),b 1=13
,求数列{b n }的前n 项和S n .
3.(2015·天津)已知数列{a n }满足a n +2=qa n (q 为实数,且q ≠1),n ∈N *,a 1=1,a 2=2,且a 2+a 3,a 3+a 4,a 4+a 5成等差数列.
(1)求q 的值和{a n }的通项公式;
(2)设b n =log 2a 2n a 2n -1
,n ∈N *,求数列{b n }的前n 项和.
4.已知数列{a n }的前n 项和S n =a n +n 2-1,数列{b n }满足3n b n +1=(n +1)a n +1-na n ,且b 1=3.
(1)求a n ,b n ;
(2)设T n 为数列{b n }的前n 项和,求T n ,并求满足T n <7时n 的最大值.
5.(2015·广东)数列{a n }满足:a 1+2a 2+…+na n =4-
n +22n -1,n ∈N *
. (1)求a 3的值;
(2)求数列{a n }前n 项和T n ;
(3)令b 1=a 1,b n =
T n -1n +⎝ ⎛⎭⎪⎫1+12+13+…+1n a n (n ≥2),证明:数列{b n }的前n 项和S n 满足S n <2+2ln n .
答案精析
高考中档大题规范练
(二)数 列
1.(1)证明 由2a n +1-2a n +a n +1a n =0 得1a n +1-1a n =12
, 所以数列⎩⎨⎧⎭⎬⎫1a n 是等差数列.
(2)解 因为b 1=f (0)=5,
所以7a 1-1+5a 1-1+1
=5, 7a 1-2=5a 1,所以a 1=1,
1
a n =1+(n -1)×12,所以a n =2n +1.
b n =7a n -2a n
=7-(n +1)=6-n . 当n ≤6时,T n =n 2
(5+6-n )=n 11-n 2; 当n ≥7时,T n =15+
n -62(1+n -6) =n 2-11n +60
2.
所以,T n =⎩⎪⎨⎪⎧ n 11-n 2,n ≤6,
n 2-11n +602,n ≥7.
2.解 (1)根据题意a 3+a 8=8=a 4+a 7,a 4·a 7=15,
所以a 4,a 7是方程x 2
-8x +15=0的两根,且a 4<a 7,
解得a 4=3,a 7=5.
设数列{a n }的公差为d ,
由a 7=a 4+(7-4)·d ,得d =23
. 故等差数列{a n }的通项公式为
a n =a 4+(n -4)·d =3+(n -4)·23 =2n +13. (2)当n ≥2时,
b n =19a n -1a n =19·2n -13·2n +13=12n -12n +1 =12(12n -1-12n +1
), 又b 1=13=12(1-13
), 所以S n =b 1+b 2+…+b n =12(1-13+13-15+…+12n -1-12n +1
) =12(1-12n +1)=n 2n +1
. 即数列{b n }的前n 项和S n =
n 2n +1
. 3.解 (1)由已知,
有(a 3+a 4)-(a 2+a 3)=(a 4+a 5)-(a 3+a 4),
即a 4-a 2=a 5-a 3,
所以a 2(q -1)=a 3(q -1),又因为q ≠1,
故a 3=a 2=2,由a 3=a 1q ,得q =2.
由递推公式得
当n =2k -1(k ∈N *)时, a n =a 2k -1=2k -1=2n -12
; 当n =2k (k ∈N *)时,a n =a 2k =2k =2n
2
. 所以,{a n }的通项公式为a n =⎩⎪⎨⎪⎧ 2n -12,n 为奇数,
22n ,n 为偶数.
(2)由(1)得b n =log 2a 2n a 2n -1=n 2n -1
. 设{b n }的前n 项和为S n ,
则S n =1×120+2×121+3×122+…+(n -1)×12n -2+n ×12
n -1,
12S n =1×121+2×122+3×123+…+(n -1)×12n -1+n ×12n . 上述两式相减得:
12S n =1+12+122+…+12n -1-n 2n =1-12n 1-12
-n 2n =2-22n -n 2n , 整理得,S n =4-n +2
2n -1,n ∈N *
. 所以,数列{b n }的前n 项和为4-
n +22n -1,n ∈N *. 4.解 (1)n ≥2时,S n =a n +n 2-1,S n -1=a n -1+(n -1)2-1,
两式相减,得a n =a n -a n -1+2n -1,
∴a n -1=2n -1.
∴a n =2n +1,
∴3n
b n +1=(n +1)(2n +3)-n (2n +1)=4n +3,
∴b n +1=4n +33
n , ∴当n ≥2时,b n =4n -13
n -1,又b 1=3适合上式, ∴b n =4n -13
n -1. (2)由(1)知,b n =4n -13
n -1, ∴T n =31+73+1132+…+4n -53n -2+4n -13
n -1,① 13T n =33+732+1133+…+4n -53n -1+4n -13
n ,② ①-②,得23T n =3+43+432+…+43n -1-4n -13
n =3+4·131-13n -11-13
-4n -13n =5-4n +53
n . ∴T n =152-4n +52·3n -1. T n -T n +1=4n +1+5
2·3n -4n +5
2·3
n -1
=-4n +33n <0. ∴T n <T n +1,即{T n }为递增数列.
又T 3=599<7,T 4=649
>7, ∴T n <7时,n 的最大值为3.
5.(1)解 a 1=1,a 1+2a 2=2,a 2=12,a 1+2a 2+3a 3=4-54,a 3=14
. (2)解 n ≥2时,a 1+2a 2+…+(n -1)·a n -1=4-n +1
2n -2,
与原式相减,得na n =n 2n -1,a n =12
n -1,n =1也符合, T n =1-12n 1-12
=2-12n -1. (3)证明 n ≥2时,
b n =T n -1n +⎝ ⎛⎭⎪⎫1+12+13
+…+1n a n =a 1+a 2+…+a n -1n
+ ⎝ ⎛⎭⎪⎫1+12+13+…+1n a n ,故S n =∑i =1
n b i =a 1+a 12+⎝ ⎛⎭⎪⎫1+12a 2+a 1+a 23+⎝ ⎛⎭⎪⎫1+12+13a 3+…+a 1+a 2+…+a n -1n +⎝ ⎛⎭⎪⎫1+12+…+1n a n =⎝ ⎛⎭⎪⎪⎫∑i =1n 1i a 1+⎝ ⎛⎭⎪⎪⎫∑i =1n 1i a 2+⎝ ⎛⎭⎪⎪⎫∑i =1n 1i a 3+…+⎝ ⎛⎭⎪⎪⎫∑i =1n 1i a n =⎝ ⎛⎭
⎪⎪⎫∑i =1n 1i T n = ⎝ ⎛⎭⎪⎫1+12+…+1n ⎝ ⎛⎭
⎪⎫2-12n -1 <2⎝ ⎛⎭⎪⎫1+12
+…+1n , 只需证明2⎝ ⎛⎭⎪⎫1+12
+…+1n <2+2ln n ,n ∈N *. 对于任意自然数k ∈N ,令x =-
1k +1∈ (-1,0)时,ln ⎝ ⎛⎭⎪⎫-
1k +1+1+1k +1<0, 即1k +1
<ln(k +1)-ln k .
∴k =1时,12
<ln2-ln1, k =2时,13
<ln3-ln2.
… k =n -1时,1n
<ln n -ln(n -1). ∴1+12+13+ (1)
<1+(ln2-ln1)+(ln3-ln2)+...+[ln n -ln(n -1)], 即1+12+13+ (1)
<1+ln n , ∴n ≥2时,2⎝ ⎛⎭⎪⎫1+12+13
+…+1n <2+2ln n ,
综上n ∈N *时,S n <2+2ln n .。
