一次回归正交设计例子
第七章 回归正交试验设计

个因素之间的函数关系。
因素水平编码表
自然变量xj 规范变量zj 1 -1 0 △j x1 700 300 500 200 x2 2400 1800 2100 300 x3 10 8 9 1
7.1.2一次回归方程的建立
设总的试验次数为N,其中原正交表所规定的二水平试验次数为 mc,零水平试验次数为m0,即有: N 建立回归方程
m
mc m0
ˆ a b j x j bkj xk x j,k 1,2,, m 1( j k ) y
j 1 k j
其系数的计算公式如下:
将被剔除变量的偏回归平方和、自由度并入到剩余平方和与自由度中,
然后再进行相关的方差分析计算。具体例子见书P126~129例8-1。
7.1 一次回归正交试验设计及结果分析
14
用石墨炉原子吸收分光光度计法测定食品中的铅,为提高吸光度,
对x1(灰化温度/℃)、x2(原子化温度/℃)和x3(灯电流/mA)三个
F0.05(1,6)=5.99 F0.01(1,6)=13.74
可见因素z2对指标影响高度显著,所建的回归方程高度显著:
y 0.50475 0.03375z2
7.1 一次回归正交试验设计及结果分析
N 1 SST Lyy ( yi y ) 2 yi2 ( yi ) 2 N i 1 i 1 i 1 N N
7.1 一次回归正交试验设计及结果分析
10
②一次项zj偏回归平方和
SS j m b ,j= 1 , 2, ,m
回归正交试验设计

-1
-1
1
1
1
1/3
1/3
5
1
0
0
1
0
1/3
-2/3
6
-1
0
0
1
0
1/3
-2/3
7
0
1
0
0
1
-2/3
1/3
8
0
-1
0
0
1
-2/3
1/3
9
0
0
0
0
0
-2/3
-2/3
二元二次回归正交组合设计编码表
因素水平编码
01
试验因素的水平被编为-γ,-1,0,1,γ
02
变化间距:Δj=上水平-零水平=零水平-下水平
第8章 回归正交试验设计
Orthogonal Regression Design
演讲人姓名
正交设计:优方案只能限制在已定的水平上,而不是一定试验范围内的最优方案 回归正交设计(orthogonal regression design) : 可以在因素的试验范围内选择适当的试验点 用较少的试验建立回归方程 能解决试验优化问题 不适合非数量性因素
8.1 一次回归正交试验设计及结果分析
建立试验指标(y)与m个试验因素x1,x2,…,xm之间的一次回归方程 例:m=3时,一次回归方程: y=a+b1x1+b2x2+b3x3+b12x1x2+b13x1x3+b23x2x3 其中x1,x2,x3表示3个因素;x1x2,x1x3,x2x3表示交互作用 若不考虑交互作用,为三元一次线形回归方程: y=a+b1x1+b2x2+b3x3
二次项偏回归平方和:
一次项偏回归平方和:
回归正交试验设计

回归正交试验设计一、概述(1)回归分析与正交试验设计的主要优缺点回归分析的主要优点是可以由试验数据求出经验公式,用于描述自变量与因变量之间的函数关系。
它的主要缺点是毫不关心试验数据如何取得,这样,不仅盲目地增加了试验次数,而且试验数据还往往不能提供充分的信息。
因此,有些工作者将经典的回归分析方法描述成:“这是撒大网,捉小鱼,有时还捉不到鱼”。
所以说,回归分析只是被动地处理试验数据,并且回归系数之间存在相关关系,若从回归方程中剔除某个不显著因素时,需重新计算回归系数,耗费大量的时间。
正交试验设计的主要优点是科学地安排试验过程,用最少的试验次数获得最全面的试验信息,并对试验结果进行科学分析(如方差分析),从而得到最佳试验条件,但是它的主要缺点是试验结果无法用一个经验公式来表达,从而不便于考察试验条件改变后,试验指标将作如何变化。
(2)回归正交试验设计回归正交试验设计,实际上就是将线性回归分析与正交试验设计两者有机地结合起来而发展出的一种试验设计方法,它利用正交试验设计法的“正交性”特点,有计划、有目的、科学合理地在正交表上安排试验,并将试验结果用一个明确的函数表达式即回归方程来表示,从而达到既减少试验次数、又能迅速地建立经验公式的目的。
根据回归模型的次数,回归正交试验设计又分为一次回归试验设计和二次回归试验设计。
二、一次回归正交试验设计(一)一次回归正交试验设计的概念一次回归设计研究的是一个因素z (或多个因素z 1,z 2,……)与试验指标y 之间的线性关系。
当只研究一个因素时,其线性回归模型:y =β0+β1z +e (1)其回归方程为:z y ∧∧∧+=10ββ (2)式中∧0β、∧1β称为回归系数,e 是随机误差,是一组相互独立、且服从正态分布N(0,σ2)的随机变量。
可以证明,∧0β、∧1β和∧y 是β0、β1和y 的无偏估计,即E(∧0β)=β0,E(∧1β)=β1,E(∧y )=y一次回归正交试验设计是通过编码公式x =f(z) −− 即变量变换,将式(2)变为:x b b y 10+=∧(3)且使试验方案具有正交性,即使得编码因素X的各水平之和为零:∑==mi ix1(4)式中m 是因素x 的水平数。
回归正交试验设计45页PPT

21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
6、法律的基础有两个,而且只有两个……公平和实用。——伯克 7、有两种和平的暴力,那就是法律和礼节。——歌德
8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
正交回归设计(2)

2.检验一次方程的合适性 为了了解是否存在因子间的交互作用,是否有因子的高次效 应,在中心点进行了m=5次试验,结果为: 40.3,40.5,40.7,40.2,40.6 5 其平均值为 y 0 40.46 ,偏差平方和为 S0 ( y0i y0 ) 2 0.172 , i 1 其自由度=4。 采用方法1中的检验统计量t作检验。 ˆ 0 40.425, y 0 40.46 , 现在 y
1u 表示为行向 其中 ,1u 表示元素均为1的u维列向量, 量, I u 表示u阶单位阵,J uv 表示u行v列的矩阵,其元素均为 1, h mc 2 2 ,G是p阶对称方阵,其对角元均为 f mc 2 4 , 非对角元均为mc,即 f mc mc m c f mc G m m f c c
0
S e ( y 0i y 0 ) 2,f e m0 1
i 1
m0
S Lf S E S e,f Lf f E f e
可对二次回归模型的合适性进行检验。
例8.4.1 为提高钻头的寿命,在数控机床上进行试验,考察 钻头的寿命与钻头轴向振动频率F及振幅A的关系。在试验中, F与A的变动范围分别为:[125 Hz,375Hz]与[1.5,5.5],采用 二次回归正交组合设计,并在中心点重复进行三次试验。
(2)用二水平正交表L4(23)安排试验,试验方案与结果如下:
(3)建立一次回归方程:
所得一次回归方程为:
ˆ 40.425 0.775 x1 0.325 x2 y
链接31
对回归方程与回归系数作显著性检验的方差分析表如下:
若取 0.05 ,那么 F0.95 (2,1) 200 ,所以方程在显著性水 平0.05上是显著的,又 F0.95 (1,1) 161 ,则两个系数也是显著 的。
正交试验设计例题解析

正交试验设计例题解析例题一:正交试验设计(10分)(1)。
如果试验变量是因变量x和自变量y,应如何设计对比试验?(5分)(2)。
用图解法作一次因素设计的正交试验,试写出其图解并分析因素X和因素Y的作用效果。
(5分)(3)。
某高校食堂每天提供三种早点,每周选择三天进行消费者满意度调查。
试设计其满意度指标为:非常不满意0分、很不满意1分、不满意2分。
(5分)(4)。
已知药物A和B治疗血压降低有显著的效果。
如果让学生选择药物A或B进行治疗,那么哪种治疗更合理?(5分)(3)。
题干是要设计三个指标来衡量药物A与B哪一[gPARAGRAPH3]更好,这就是我们通常所说的指标体系。
(设计要求:写出该设计的指标体系,要考虑指标的因素和指标之间的关系,能够清楚地表达设计思想)(4)。
从表面上看, B组的两种治疗方案都能使血压下降,但相对于A组而言,由于两组治疗后所得的效果差异太大,最终会引起学生对治疗方案的怀疑,导致治疗无效。
(设计思想:没有真实的实验设计中,有时我们往往是凭借主观臆断在做一件事情,最终结果只能是人云亦云,毫无自己的判断,还很有可能在执行过程中遇到麻烦,甚至是无法解决的问题。
这就需要通过实验设计来验证,同时根据原始数据回归到最开始的假设上,通过控制和处理影响实验结果的不确定因素,增加实验的可靠性。
)(5)。
设计步骤为:设计出三个指标,建立三个指标体系;XY组设计为治疗组, X组设计为对照组,对照组不变,治疗组治疗后服用预防高血压药物;D组也就是检验组不变。
其它各组的操作过程完全相同。
(步骤写清楚就可以了)(6)。
(6)。
设计类型:因素设计,分析原因时可以采用图解法。
(注意不是单纯的因素设计)(7)。
给出不同分布区间上的同一正态随机数。
(题目不给出)例题二:正交试验设计(20分)总结:从例题一中可以看出,设计者首先要确定一个研究对象,即研究样本;然后设计多个具有代表性的变量,以使变量之间的关系能从多个角度进行考察,避免变量不足或重复的问题;接着设计正交试验方案(具体包括变量的水平及顺序、对照的情况、因素等);最后进行统计学检验,以得出最佳的试验设计方案。
一次回归正交设计、二次回归正交设计、二次回归旋转设计说明

一次回归正交设计、二次回归正交设计、二次回归旋转设计说
明
一次回归正交设计是一种广泛应用于实验设计中的设计方式,该设计最基本的特点是每一个自变量只考虑一次。
这种设计方法可以通过排列组合的方式得到各种不同的设计方案,使得实验者可以通过设计来达到用最少的实验次数获取尽可能多的信息的目的。
一次回归正交设计在实验设计中被广泛使用,尤其在化学制药、工业生产等领域得到了广泛运用。
二次回归正交设计是一种基于一次回归正交设计的设计方式,这种设计方式可以进一步增加实验信息的获取。
在二次回归正交设计中,依然按照一次正交设计的方式来设计实验,但是在每个单独的自变量上,提高对其的测量次数,使得对这些自变量的测量更加准确。
同时,在某些需要深入探究的因素上,可以通过将这些因素的实验次数进一步提高,来获取相关信息。
二次回归旋转设计是一种在二次回归正交设计的基础上发展而来的设计方式。
在二次回归旋转设计中,实验者可以通过旋转矩阵来达到实验变量间的协方差为0的目的。
这样可以在保证基本信息获取的同时,增加获取高阶信息的可能性。
旋转设计特别适合于需要同时考虑多个变量的实验设计,可以使各个变量之间更加独立,减少不必要的干扰。
总的来说,在实验设计领域中,三种设计方法各自有着各自的优势。
对于需要更精准的信息获取的实验,应该选择更高阶的设计方法,在更基础的实验中则可以选择更为简单的设计方法。
另外,在选择设计方法的过程中,还应该根据实验具体情况灵活选择,使得实验设计更加科学合理。
一次回归正交设计、二次回归正交设计、二次回归旋转设计
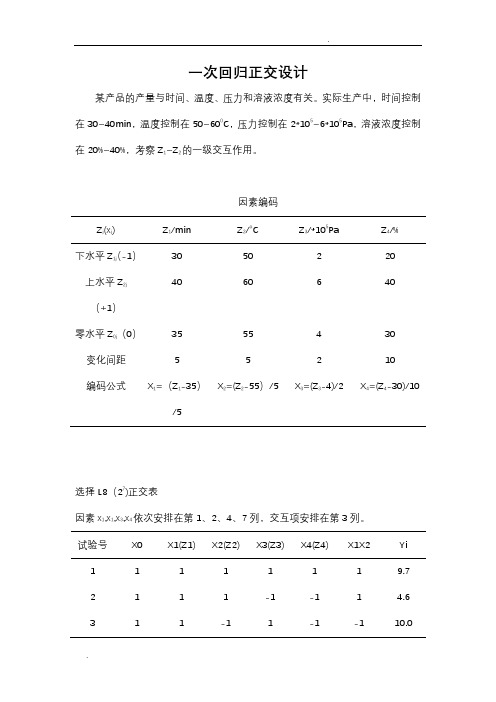
一次回归正交设计
某产品的产量与时间、温度、压力和溶液浓度有关。实际生产中,时间控制 在 30~40min,温度控制在 50~600C,压力控制在 2*105~6*105Pa,溶液浓度控制 在 20%~40%,考察 Z1~Z2 的一级交互作用。
因素编码
Zj(xj)
Z1/min
Z2/oC
Z3/*105Pa
Z4/%
下水平 Z(1j -1)
30
50
2
20
上水平 Z2j
40
60
6
40
(+1)
零水平 Z0j(0)
35
55
4
30
变化间距
5
5
2
10
编码公式 X1=(Z1-35) X2=(Z2-55)/5 X3=(Z3-4)/2 X4=(Z4-30)/10
/5
选择 L8(27)正交表
因素 x1,x1,x3,x4 依次安排在第 1、2、4、7 列,交互项安排在第 3 列。
试验号 X0 X1(Z1) X2(Z2) X3(Z3) X4(Z4) X1X2
Yi
1
1
1
1
1
1
1
9.7
2
1
1
1
-1
-1
1
4.6
3
1
1
-1
1
-1
-1
10.0
.
.
4
1
1
-1
-1
1
-1
11.0
5
1
-1
1
1
-1
-1
9.0
6
1
-1
1
-1
1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次回归正交设计
某冶炼厂排出的废水中含有大量的镉、鉮、铅等有害元素,对环境造成严重污染。
考察的试验因素为温度(x1)、碱与硫酸亚铁之比(x2)以及硫酸亚铁用量(x3)对指标除镉效率(y)的影响。
不考虑交互作用。
已知x l=60~80℃,x2=8~12,x3=1~3ml。
(1)因素水平编码及试验方案的确定
表1 因素水平编码表
编码z j温度(x1)
碱与硫酸亚铁之比
(x2)硫酸亚铁用量
(x3)
-1 60 8 1
0 70 10 2
1 80 1
2 3
△j 10 2 1
由于不考虑交互作用,所以建立一个三元线性方程。
因素水平编码如表1所示。
选正交表L8(27)安排试验,将三个因素分别安排在回归正交表的第1、2、4列,试验方案及试验结果见表2,表中的第9、
10、11号试验为零水平试验。
表2 试验方案及试验结果
试验
号z1 z2 z3 温度(x1)
碱与硫酸亚
铁之比(x2)
硫酸亚铁用
量(x3)
除镉效率
y/%
1 1 1 1 80 1
2
3 8.0
2 1 1 -1 80 12 1 7. 3
3 1 -1 1 80 8 3 6. 9
4 l -1 -l 80 8 l 6.4
5 -1 1 1 60 12 3 6.9
6 -1 1 -1 60 12 1 6.5
7 -1 -1 l 60 8 3 6.0
8 -1 -1 -1 60 8 1 5.1
9 0 0 0 70 10 2 6.6
10 0 0 0 70 10 2 6.5
11 0 0 0 70 10 2 6.6
⑵回归方程的建立
表3试验结果及计算表
提取率y
y2 z1y z2y z3y 试验号z1 z2 z3
/%
1 1 1 1 8.0 64.00 8.0 8.0 8.0
2 1 1 -1 7.
3 53.29 7.3 7.3 -7.3
3 l -1 1 6.9 47.61 6.9 -6.9 6.9
4 1 -1 -1 6.4 40.96 6.4 -6.4 -6.4
5-1 1 1 6.9 47.61 -6.9 6.9 6.9
6 -1 1 -1 6.5 42.25 -6.5 6.5 -6.5
7 -1 -1 1 6.0 36.00 -6.0 -6.0 6.0
8 -1 -1 -1 5.1 26.01 -5.1 -5.1 -5.1
9 0 0 0 6.6 43.56 0.0 0.0 0.0 10 0 0 0 6.5 42.25 0.0 0.0 0.0 11 0 0 0 6.6 43.56 0.0 0.0 0.0 ∑
72.8
487.1
4.1
4.3
2.5
由表3计算
1172.16.618211
n i i a y y n =====∑
11
1 4.1
0.51258
n
i
i
i c
z
y b m ==
==∑
21
2 4.30.53758
n
i
i
i c
z
y b m ==
==∑
31
3 2.50.31258
n
i
i
i c
z
y b m ==
==∑
回归方程为
1236.61820.51250.53750.3125y z z z =+++
由该回归方程偏回归系数绝对值的大小,可以得到各因素的主次顺序为:x 2>x 1>x 3,即液固比>乙醇浓度>回流次数。
又由于各偏回归系数都为正,所以这些影响因素取上水平时,试验指标最好。
(3)回归方程显著性检验
2
221
1172.8487.1 5.29611n
n
T i
i i i SS y y n ==⎛⎫
=-=-= ⎪⎝⎭∑∑
221180.5125 2.101c SS m b ==⨯=
2
22280.5375 2.311c SS m b ==⨯=
223380.31250.781c SS m b ==⨯=
1231213 2.101 2.3110.781 5.193
R SS SS SS SS SS SS =++++=++=
5.296 5.1930.e T R
S S S S S S =-=-=
方差分析结果见表4。
表4 方差分析表
差异源 SS df MS F 显著性 z 1 2.101 1 2.101 142.9 ﹡﹡ z 2 2.311 1 2.311 157.2 ﹡﹡ z 3 0.781 1 0.781 53.1 ﹡﹡ 回归 5.193 3 1.731 117.8 ﹡﹡ 残差 0.103 7 0.0147 总和
5.296
n -1=10
注:F 0.01(1,7)=12.25,F 0.01(3,7) =8.45
可见,三个因素对试验指标都有非常显著的影响,所建立的回归方程也非常显著。
(4)失拟性检验
本试验中,零水平试验次数m 0=3,可以进行失拟性检验,有关计算如下。
()
02
2
2
10001
1101m m m e i i i i i i SS y y
y y m ===⎛⎫=-=- ⎪⎝⎭
∑∑∑
()()2143.5642.2543.56 6.6 6.5 6.63
=++-
++ 0.00667=
10.1030.006670.0963e
Lf e SS SS SS =-=-=
101312e df m =-=-=
1725Lf e e df df df =-=-=
0.111
0.0963/5 5.775(5,2)9.290.00667/2
Lf Lf Lf e e SS df F F SS df =
==<= 检验结果表明,失拟不显著,回归模型与实际情况拟合得很好。
(5)回归方程的回代
根据编码公式:
1170
10
x z -=,22102x z -=,33
3221x z x -==- 代人上述回归方程得:
()12370106.61820.51250.53750.31252102x x y x --⎛⎫⎛⎫
=+++- ⎪ ⎪⎝⎭⎝⎭
整理后得到:
1230.28180.051250.268750.3125y x x x =-+++。
