非确定性问题

合集下载

财务会计中不确定性问题的披露

三、财务会计中不确定性问题—— 高度不确定性的披露
高度不确定性经济业务的披露包括表内确认、揭示与表外披露。由于高度不确定性经济业务项目的金额和时间具有较大的不确定性，这就使不少高度不确定性的经济业务通过披露的方式米反映。在这里我们建议对于高度不确定性经济业务的披露应该在中度不确定性经济业务披露的基础
披露对信息使用者来说是非常重要的。
【关键词】
财务会计；经济业务；披露；不确定性
不确定性的经济业务的披露对信息使用者而言，有助于信息使用者了解企业的它资产质量、收益质量，真实财务状况和经济成果，有利于信息使用者评价影响企业的机
财务会计中
不确定性问题的披露
李荷沈阳市第五人民医院１０１２０３
【文章摘要】
不确定性的经济业务可能会给企业
二、财务会计中不确定性问题—— 中度不确定性的披露
在这里我们选取了部分上市公司２００７年年报，来分析上市公司披露中度不确定性经济ｌ￣的现状，，－ｋ我们以或有事项为例：１、样本的选取。截至２００８年４３月Ｏ日，沪市上市公司２０年度报告８３家上０７６市公司中，除九发股份外，８２有６家上市公司披露了２０年度报告（０７其中紫金矿业以招股说明书形式披露年度财务资料）我们，随机选取了１００家上市公司作为研究对象。２、或有事项披露的现状。根据样本的调查，１００家上市公司中，有或有事项披露的有７２家，占７％，无或有事项披露的有２２家，占２％。８８３、或有事项披露存在的问题：１（）或有负债的披露不够完整。对诉讼、仲裁的披露不够完整，样本中共１家公司涉及诉讼，３占样本总数的ｌ％，大多数公司只披露了未３决诉讼的原因，对于诉讼可能产生的影响未作披露，致使投资者对公司不能做出准确判断。对担保事项的披露不够规范。样本中共５家公司存在担保事项，占样本总数１的５％，中有４１其５家对其作为或有事项披露，剩余６家没有作为或有事项披露。而且调查分析时我们还发现，对担保事项的披

物理中“不确定性”问题的特征及解决策略探讨

题则须用 “ 发法”来解决．发法就是凭借经验尽启启
快地找出一条或多条有效地解决问题的途径．用常的启发法有试误法、目标分析法、推法、推法、逆类简
化法等．不论哪种启发法，实质都是将不确定性但其问题转化为确定性问题．际上，确定性问题和确实不定性问题并不是绝然割裂的，确定性问题中包含不着影响问题的确定性因素和不确定性因素．问题解决时，通过对有关的信息进行加工来揭露问题的本
模型，实际问题转化为一个确定的物理问题．将
由于条件的不确定、案的不固定，促成学生做出答能
大胆的假设，培养学生开放性思维，发学生的创新激意识．因此，教学中培养学生解决不确定性问题的在
能力具有重要的意义．
２ “ 确定性”问题的解决策略不
不确定性问题的解决是由不确定性问题引发
并指向其解决的思维活动，它是问题解决的一种重要形式．定性问题往往通过 “ 法 ”来解决．法确算算就是具有解决问题的一系列特定步聚．确定性问不
【１（０６年广东卷）例】２０风力发电是一种环保的
电能获取方式．计每台风力发电机的功率为４设ｏｋ实验测得风的动能转化为电能的效率约为Ｗ．２％，０空气的密度是１２ｇｍ，．９ｋ／３当地水平风速约为１／．风力发电机的叶片长度约为多少才能满０ｍｓ问

数值计算及其不确定性问题(简化)总结

2. 评价数值方法的好坏（研究数值方法的性态、可靠性、效率） 3. 数值方法的计算机实现（计算机实习）
本课程的基本目的，是使学生通过学习和实验，初步建立并理解数值计算，特别是科学与工程计算的基本概念，为进一步深入的学习打下坚实的基础。
数值分析
数值分析
数值计算与误差分析
第一节数值算法
第二节数值计算的误差分析第三节常用数学软件工具
xi=Di/D
(i=1,…,n)
这里,Di是指D中第i列元素用右端（b1,… bn）代替构成的行列式。
数值分析
数值分析
克莱姆算法步骤
1. 2.
D for 2.1. 2.2.
( j1 jn )
t ( 1 ) a1 j1 a 2 j2 a nj n
i 1 n Di
( i1 i n ) t ( 1 ) a i1 1 bi2 j a in n
6 1 0.1667 0.0000334 6
就是舍入误差。
数值分析
数值分析
二、截断误差分析
例1：(截断误差)
x
1 2 1 3 1 n 已知e 1 x x x x 2! 3! n! 求e 1的近似值，并估计误差。
,
解：利用展开式的前三项，取n=2，
由Taylor公式：f ( x ) f ( x0 ) f '( x0 )( x x0 ) ( n 1) f ( n ) ( x0 ) f ( ) n ( x x0 ) ( x x0 ) n 1 n! ( n 1)!
0.001253 10 , 0.000068 10
6
6
数值分析
数值分析

项目管理不确定性和风险分析

2
• 风险识别的结果是建立建设工程风险清单,在建设工程风险识别过程中,核心工作是“建设工程风险分解”和“识别建设工程风险因素、风险事件及后果”。风险识别的方法有:专家调查法、财务报表法、流程图法、初始清单法、经验数据法、风险调查法。对于建设工程的风险识别来说,仅仅采用一种风险识别是远远不够的。一般都应综合采用两种或多种风险识别方法,才能取得较为满意的结果。而且,不论采用何种风险识别方法组合,都必须包含风险调查法。从某种意义上讲,前五种风险识别方法的主要作用在于建立初始风险清单,而风险调查法的作用则在于建立最终的风险清单。
17
• 根据这种分类可知：正是因为存在信息缺口才造成了人们不能确定项目某种事件是否确定发生，而这种不确定性才是引发项目风险后果的根本原因。因此，任何项目的风险性来自于项目的不确定性，而任何项目的不确定性根本来源在于人们在项目信息方面的缺乏（信息缺口）。面向不确定性的项目风险管理方法要通过对于项目不确定性因素的深入认识和分析，不断搜集项目信息，弥补信息缺口，降低项目的不确定性，有效地进行项目风险管理。这种面向不确定性的项目风险管理方法对于人们通过学习和积累去拓展自己的认识能力给予应有的重视，更注重通过提高组织对于项目不确定的认识去开展项目的风险管理，所以这种项目风险管理方法是一种主动的管理方法。第四，统一管理项目的威胁和机会。面向不确定性的项目风险管理方法从分析并消减项目的不确定性入手开展项目风险管理，强调对项目风险机会的管理，因为项目风险机会是对项目价值提升的直接贡献。因此，这一方法将威胁管理和机会管理统一于同一个项目风险管理过程进行度量。项目风险管理过程与“风险”的定义是平行的。既然将风险定义为机会和威胁，那么机会管理和威胁管理就需要通过一个过程来实现。要通过机会的度量和分析，抓住“机遇”变“坏事为好 18 事”。

非确定型问题决策的应用探讨

非确定型决策是指方案实施可能会出现的自然状态或者所带来的后果不能做出预计的决策。在这类决策中，最不确定的情况是连方案实施所可能产生的后果都无法估计，这样的决策就非常难以决定。稍容易的是方案实施的后果可以估计，即可确定出方案在未来可能出现的各种自然状态及其相应的收益情况，但对各种自然状态在未来发生的概率却无法做出判断，从而无法估算期望收益，在这种情况下就只能由决策者根据主观选择的一些原则来比较不同方案的经济效果并
the road surface of the highway in karst area
Zhang H ui, Deng Xin - non , Wu Xiang 一bin
Hale Waihona Puke Abstract : This paper analyses the attenuation law when the pollution elements through the sand filter layer , and absorbing efficiency of the sand, which explains the feasibility of the sand filter pool, via the filter test of the run off on the road of Hengzao highway in the Karst area. A sort of facility and effective treatment is provided for protecting the fragility environment to avoid pollution during the road construction , or reducing the run off pollution on the road surface. Key words : karst ; run off ; research

部编版数学五上《事件发生的确定性和不确定性》教学设计及教学反思

1、《事件发生的确定性和不确定性》教学设计、反思教学内容事件发生的确定性和不确定性。

(教材第44~45页)教学目标1.使学生初步体验有些事件的发生是确定的,有些则是不确定的,并能正确使用“一定”“可能”“不可能”这些词语来描述事件发生的可能性。

2.通过问题情境培养学生的分析能力和语言表达能力。

3.培养学生对数学的兴趣以及应用数学知识解决实际问题的能力。

重点难点重点:会正确判断事件发生的可能性。

难点:能准确使用“一定”“可能”和“不可能”这些词语来描述事件发生的可能性。

教具学具教材第44页的主题图,纸盒2个,红棋子10个,黄色、绿色、蓝色的棋子各2个。

教学过程一、情境导入投影出示教材第44页主题图。

1.观察这幅图,并用简洁的语言描述一下这幅图的图意。

2.假如你是他们中的一员,轮到你抽签来决定表演的节目,你认为自己会表演什么节目?3.举例说一说生活中还有哪些事件的发生是不确定的。

二、合作探究出示教材第44页例1。

师:观察情境,从中你都知道了哪些信息?生1:我知道了三张卡片分别写着唱歌、跳舞和朗诵。

生2:我知道了让3名同学来抽卡片。

生3:我知道了问题是求每位同学分别抽到什么节目。

师:如果小明抽到了跳舞,那么小丽和小雪抽到的是什么?生1:小丽可能抽到朗诵,也可能抽到唱歌。

生2:小丽可能抽到唱歌,也可能抽到朗诵。

汇总:小丽和小雪抽到唱歌和朗诵都有可能。

师:如果小丽抽到朗诵,小雪会抽到什么?学生:最后只有一张了,因此小雪一定抽到了唱歌。

三、课堂总结教师总结并板书:在一定的条件下,一些事件的结果是可以预知的,这时就用“一定”或“不可能”来描述。

在一定的条件下,一些事件的结果是不可以预知的,这时就用“可能”来描述。

板书设计事件发生的确定性和不确定性在一定的条件下,一些事件的结果是可以预知的,这时就用“一定”或“不可能”来描述。

在一定的条件下,一些事件的结果是不可以预知的,这时就用“可能”来描述。

教学反思1.在教学中,教师注意创设各种问题情境,充分调动学生的主动性和积极性,让学生在具体的操作活动中进行独立思考,鼓励学生发表自己的意见,并与同伴交换自己的想法。

气候变化预测中的不确定性问题

气候变化预测中的不确定性问题近年来，全球气候变化的加速趋势成为人们普遍关注的话题。

聚焦于气候变化的预测问题，预测出整个地球的温度变化，以及温室气体排放等对气候变化的影响，是人们更能了解气候变化的趋势和未来。

然而，气候变化预测中存在的不确定性问题，一直是困扰着许多科学家的痛点。

本文将着重探讨气候变化预测中存在的不确定性问题，以及其对预测的可靠性和科学家的难题。

气候预测中的困难目前，气候科学和预测领域仍存在很多的不确定性问题，其中一些不确定性是由于科学技术本身发展的局限所导致的，另外一些不确定性是源于未来自然发展的不可预测性。

在气候预测中，科学家们尝试预测不同气候变量的变化情况，如温度、气压、降水、云量等。

然而，这些变量相互作用，每个变量以及它们之间的关系都非常复杂，科学家们面临的挑战是需要综合考虑众多影响因素并对其建立数学模型。

与此同时，气候预测中还存在很多的不确定性和模型误差，使得气候预测结果无法绝对准确。

例如，模型中的参数估计不够准确，气象观测数据的不完整或者缺失，以及对未来的自然因素（如火山、太阳辐射、人类活动等）的不确定性等，这些都会导致气候预测的偏差。

此外，由于气候影响因素的组合情况多种多样，可能导致一些现象难以预测，如飓风频率与强度的变化等。

气候预测的不确定性气候预测涉及的不确定性有很多，其中最常见的是气候模型精度问题。

目前常用的气候模型中，存在一些基本参数可能存在误差或不确定性，例如大气成分的摩尔质量，水的相变热，暖湿气流的半径等。

这些参数的不确定性将导致模型的输出结果存在一定的误差。

此外，气象观测数据存在的稀疏性和不完整性，也可能导致预测结果的偏差。

对于这些局限性，自然界中的一些自然因子，如自然灾害、火山爆发、太阳辐射等，也可能对气候预测的准确性产生影响。

因此，气候预测的不确定性和可靠性是难以完全保证的。

气候预测中的误差来源除了上述的不确定性问题外，气候预测中存在一些误差来源。

首先是气象观测数据误差来源。

数学中的不确定性与随机性

数学中的不确定性与随机性数学，作为一门严谨而精密的学科，常常被人们视为一种绝对的科学，给人一种确定和可靠的感觉。

然而，在数学中，也存在着一些不确定性和随机性的现象。

本文将以数学中的几个典型例子为例，探讨数学中的不确定性和随机性的存在及其对我们生活的影响。

1. 黎曼猜想中的不确定性黎曼猜想是数论领域中的一个著名问题，由大数学家黎曼于1859年提出。

它与素数的分布性质相关，虽然已经有许多专家学者努力研究和验证，但至今仍未被证明或者证伪。

这个问题的难点就在于它的不确定性，无法找到确凿的证据来支持或推翻它。

正是因为黎曼猜想的存在，引发了无数的研究和探索，推动了数论学科的发展。

2. 概率论中的随机性概率论是数学中研究随机现象的一门学科，其中的随机性是不可避免的。

比如在骰子游戏中，每次掷骰子的结果都是随机的，无法预测。

在概率论中，我们通过概率的概念来描述这种随机性，但在具体的事件中，我们无法确定每次的具体结果。

这种随机性也使得概率论具有实际应用价值，例如在金融学、统计学等领域中，概率论的研究成果可以用来进行风险评估和决策分析。

3. 混沌理论中的复杂性混沌理论是数学中研究非线性动力系统的一门学科，它揭示了一类复杂系统的行为。

混沌现象表现为系统状态的极度敏感性，微小的变化可能会导致系统未来的行为完全不同。

正是这种不确定性和随机性的存在，使得混沌现象充满了神秘感和挑战性。

在混沌理论的研究中，数学家们通过分岔图、Lyapunov指数等方法来描述和研究复杂系统的演化行为，为我们理解许多现实世界的现象提供了新的视角。

尽管数学中存在不确定性和随机性，但数学的力量在于它能以一种精确而系统的方式来描述和探索这些现象。

数学提供了一种分析的工具和思维的框架，使我们能够理解并预测不确定和随机的因素。

正是通过数学模型的建立和运用，我们能够应对来自不确定性和随机性的挑战，做出明智的决策。

总之，数学中的不确定性和随机性是数学学科的一部分，这种现象的存在并不是数学的缺陷，而是数学发展和应用的源泉。

工程师的工作中遇到的常见决策不确定性问题与解决方法

工程师的工作中遇到的常见决策不确定性问题与解决方法工程师在工作中经常面临各种决策问题，而其中一个最常见且最具挑战性的问题就是决策的不确定性。

工程师需要根据有限的信息和资源做出明智的选择，以确保项目的成功实施。

本文将讨论工程师在其工作中常遇到的决策不确定性问题，并探讨相应的解决方法。

1. 设计决策的不确定性在工程领域，工程师通常需要进行各种设计决策，如材料选择、结构设计、系统优化等。

然而，由于设计问题往往具有复杂性和多目标性，很难准确地评估每个决策的结果。

因此，决策的不确定性成为了设计过程中不可避免的问题。

解决方法：工程师可以采用多种方法来处理设计决策的不确定性。

首先，他们可以利用专业知识和经验进行初步评估，并根据已有数据和文献进行参考。

此外，工程师还可以运用数学模型、仿真软件和优化算法等工具来辅助决策过程，以获得更准确和可靠的结果。

2. 资源分配的不确定性在工程项目的执行过程中，工程师需要合理地分配有限的资源，如时间、人力、资金等。

然而，由于项目的动态性和不确定性，资源分配往往面临很多挑战和风险。

解决方法：为了更好地应对资源分配的不确定性，工程师可以采用以下策略。

首先，他们可以制定详细的项目计划和时间表，以确保资源的合理利用。

其次，工程师可以建立风险评估和管理机制，为资源不确定性引发的潜在问题做好准备。

此外，工程师还可以与团队成员和相关利益相关者密切合作，共同制定灵活的资源调整方案。

3. 技术实施的不确定性在技术实施的过程中，工程师面临着各种技术上的不确定性问题。

例如，在新技术引入或复杂系统的开发过程中，工程师难免会遇到技术难题、技术风险以及未知的技术挑战。

解决方法：为了应对技术实施的不确定性，工程师可以采取以下措施。

首先，他们可以进行前期的技术评估和可行性研究，以尽早发现潜在的问题和风险。

其次，工程师可以积极寻求专业建议和跨领域合作，以解决技术难题和提高技术实施的效果。

此外，及时的沟通和协调也是解决技术不确定性的关键。

非确定性多项式时间问题

非确定性多项式时间问题一位同学要我解答非确定性多项式时间问题，关键是求得的这个不等式的解集。

这个问题是个较新的问题，也是数学教学中最难处理的一个问题之一。

解法是有些难度的。

就以上作文材料来说吧，我们可以把它看成求复数域上的伯努利大数定义问题。

它的实质问题是如何用初等方法构造能够求出通项系数的函数。

在高考题目中，用非确定性数学模型方法求解非平凡性函数的定义域和值域，或者用非确定性数学模型方法解决相当于复数域中的某类大数问题，都是一个经常遇到的典型问题。

那么怎样才能化繁为简呢?非确定性多项式时间问题虽然内容较复杂，但解题的思路还是比较明晰的。

下面试举几例加以说明：2。

设自变量x、 y是多项式X=A(x-1)+bx-1，且满足A>0，当X →0时， A的取值范围是否有界。

例：当x→0时，多项式的值域是否有界。

由于在非确定性多项式时间问题中， A是非负整数，因此用初等方法求解不太现实。

但若将A取为-1时，情况就完全不同了。

它只需写成，进而写成式(12)和( 13)即可。

为了简便起见，暂且不提具体解法，仅举一例说明解题思路。

要做到“紧紧抓住不放，力求解决一个”，“不管三七二十一，只要结果正确”，这是每个考生都应具备的良好素质，更是成功的基本保证。

另外，一般说来，在解决非确定性多项式时间问题时，求通项的第一次多项式X的取值范围要比求其通项的任意次多项式X的取值范围困难些。

例如：(12)式和(13)式中的通项多项式第一次根式的分母为(3×4×3)。

这是因为这个分母的根式有两对共轭根式，所以第一次根式存在。

若写成式( 12)或式(13)，就无法保证分母的两对共轭根式都存在。

因此，第一次根式是必须求出来的，写成式(12)或式(13)反而影响了第一次根式的取值范围。

在高考数学卷中，此类题型极少出现，但在历年的高考题目中，也屡有出现。

值得一提的是，在多年的高考中，各地对这类题目的解题思路与方法均作了规范性要求。

不确定型决策问题与风险型决策问题

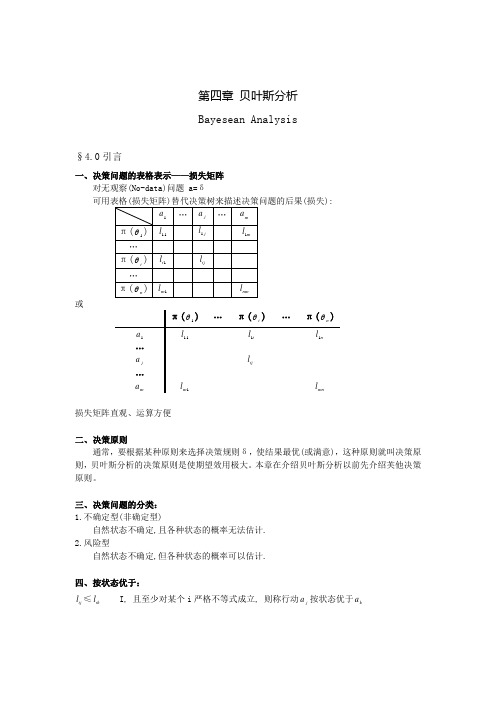
第四章贝叶斯分析Bayesean Analysis§4.0引言一、决策问题的表格表示——损失矩阵对无观察(No-data)问题 a=δ(损失):a1…a j…a mπ(θ1)l11lj1lm1…π(θi )li1lij…π(θn )lm1lnm或π(θ1)…π(θi)…π(θn)a 1l11li1ln1…aj l ij…a m lm1lmn损失矩阵直观、运算方便二、决策原则通常，要根据某种原则来选择决策规则δ，使结果最优(或满意)，这种原则就叫决策原则，贝叶斯分析的决策原则是使期望效用极大。

本章在介绍贝叶斯分析以前先介绍芙他决策原则。

三、决策问题的分类：1.不确定型(非确定型)自然状态不确定,且各种状态的概率无法估计.2.风险型自然状态不确定,但各种状态的概率可以估计.四、按状态优于：l ij ≤likI, 且至少对某个i严格不等式成立, 则称行动aj按状态优于ak§4.1 不确定型决策问题一、极小化极大(wald)原则(法则、准则) a1a2a4minj maxil (θi, aj) 或maxjminiuij例:各行动最大损失: 13 16 12 14其中损失最小的损失对应于行动a3.采用该原则者极端保守, 是悲观主义者, 认为老天总跟自己作对.二、极小化极小minj minil (θi, aj) 或maxjmaxiuij例:各行动最小损失: 4 1 7 2其中损失最小的是行动a2.采用该原则者极端冒险，是乐观主义者，认为总能撞大运。

三、Hurwitz准则上两法的折衷，取乐观系数入minj ［λminil (θi, aj)＋（1－λ〕maxil (θi, aj)］例如λ=0.5时λmini lij: 2 0.5 3.5 1（1－λ〕maxi lij: 6.5 8 6 7两者之和： 8.5 8.5 9.5 8其中损失最小的是：行动a4四、等概率准则(Laplace)用i∑l ij来评价行动a j的优劣选minji∑l ij上例：i∑l ij : 33 34 36 35 其中行动a1的损失最小五、后梅值极小化极大准则(svage-Niehans)定义后梅值sij =lij-minklik其中mink lik为自然状态为θi时采取不同行动时的最小损失.构成后梅值(机会成本)矩阵 S={sij }m n⨯,使后梅值极小化极大,即:min max j i s ij例:损失矩阵同上, 后梅值矩阵为:3 1 0 23 0 8 11 4 0 20 3 2 4各种行动的最大后梅值为: 3 4 8 4其中行动a1 的最大后梅值最小,所以按后梅值极小化极大准则应采取行动1.六、Krelle准则：使损失是效用的负数(后果的效用化),再用等概率(Laplace)准则.七、莫尔诺(Molnor)对理想决策准则的要求(1954)1.能把方案或行动排居完全序；2.优劣次序与行动及状态的编号无关；3.若行动ak 按状态优于aj，则应有ak优于aj；4.无关方案独立性：已经考虑过的若干行动的优劣不因增加新的行动而改变；5.在损失矩阵的任一行中各元素加同一常数时，各行动间的优劣次序不变；6.在损失矩阵中添加一行，这一行与原矩阵中的某行相同，则各行动的优劣次序不变。

不确定性分析案例

变化幅度项目投资额
－20％－10％
0
10％
20％
平均＋平均 1％－1 ％
-9.90% 9.90%
361.21
241.21
121.21
1.21
-118.79
产品价格
-308.91
-93.85
121.21
336.28
551.34
17.75%
17.75 % 7.10%
经营成本
293.26
即：P＞0.6，建大厂优，P＜0.6，建小厂优，
P ＝ 0.6，两者效果相同
例7 设有某石油钻探队，在一片估计能出油的荒田钻探．可以先做地震试验，然后决定钻井与否．或不做地震试验，只凭经验决定钻井与否。做地震试验的费用每次 2000元，钻井费用为 10000 元。若钻井后出油，该井队可收入 40000元；若不出油就没有任何收入。各种情况下估计出油的概率已估计出，并标在图 7-3 上。问钻井队的决策者如何做出决策使收入的期望值为最大。
解：
a 、各方案的总费用C总与运行小时t有关 b 、C总=年等额投资R+年运行费用h （R相当于固定不变费用；h相当于变动生产费用） C、 R=P（A/P，i, n）– L （A/F，i, n）式中P为初始投资，L为设备残值。 d 、A方案总费用计算 RA=1400 (A/P，10%， 4)– 200 （A/F， 10%，4) =1400×0.31547– 200 × 0.21547 =441.658 –43.094 ≈399 hA=120元+0.84· t ∴C总A=RA+hA=399+120+0.84t =519+0.84t
207.24

不确定性规划问题的描述及解决方法

不确定性规划问题的描述及解决方法不确定性在现今社会的各个领域中都普遍存在，特别是在决策和规划问题中。

不确定性规划问题泛指那些在实施过程中存在风险、随机因素或不确定性的规划问题。

本文将描述不确定性规划问题的特点，并介绍几种解决这类问题的方法。

一、不确定性规划问题的特点1. 前提不确定性：不确定性规划问题的前提是涉及到未来的预测和决策，而未来的情况无法完全确定。

比如，在新产品研发中，销售额的预测受到市场需求、竞争态势等因素的影响，无法做出准确的预测。

2. 参数不确定性：不确定性规划问题中，涉及到的参数通常是基于统计数据或专家判断得出的，而这些参数存在误差或随机性。

例如，在资源规划中，人力、物力等参数的具体数值可能存在一定的波动。

3. 约束不确定性：不确定性规划问题中，约束条件可能会受到各种不确定性因素的影响，导致约束条件的无法完全确定。

例如，在生产调度中，设备的可用性和维修时间等因素均具有不确定性。

二、解决不确定性规划问题的方法1. 概率方法：概率方法是指基于概率统计的方法来解决不确定性规划问题。

通过对不确定因素进行概率建模和分析，可以获得关于不确定性的概率分布信息，从而进行决策和规划。

例如，可以利用概率模型对销售额进行建模，得到销售额的概率分布，进而进行产品定价和生产计划的决策。

2. 仿真方法：仿真方法是通过构建模拟系统，并在该系统中运行大量的随机试验来解决不确定性规划问题。

仿真方法能够模拟不同的决策方案在不同情境下的表现，从而评估各个方案的风险和效益。

例如，在项目管理中，可以利用蒙特卡洛仿真方法对项目的进度和成本进行模拟，从而评估项目的风险。

3. 最优化方法：最优化方法是通过优化理论和数学模型来解决不确定性规划问题。

最优化方法的目标是找到能够最大化或最小化某个指标的最优决策。

在不确定性规划问题中，可以通过引入随机变量和约束条件来建立数学模型，并利用最优化算法寻找最优解。

例如，在供应链网络中，可以利用最优化方法来定量确定库存和运输方案，从而优化整个供应链的绩效。

工程项目的不确定性问题的分析

THANKS
感谢观看
随着科技和经济的快速发展，工程项目规模越来越大，复杂度越来越高，不确定性问题也愈发突பைடு நூலகம்，对项目管理提出了更高的要求。
目的和意义
通过对工程项目不确定性问题的分析，探究其产生原因、影响和应对策略，为项目管理提供理论支持和实践指导。
有助于提高项目成功率，降低风险，节约成本，提升项目经济效益和社会效益。
工期延误原因分析、工期调整方案、工期延误的后果及应对措施
详细描述
该地铁项目施工过程中，由于多种原因导致工期延误。通过对延误原因进行分析，制定相应的工期调整方案，如增加人力、材料等资源投入，优化施工组织等。同时，考虑工期延误可能带来的后果，如索赔、信誉损失等，制定相应的应对措施，确保项目的按期完成。
详细描述
资金风险可能包括资金筹措困难、资金链断裂等。这些情况可能导致项目无法按计划进行，甚至被迫中止。此外，资金风险还可能引发项目质量下降，如使用低质量的材料或减少维护等。
技术难题
总结词
技术难题是工程项目中常见的不确定性来源之一，它可能影响项目的进度和质量。
详细描述
技术难题可能包括技术难题的出现、技术更新等。这些情况可能导致项目实际施工难度增加、工期延误和成本增加。
工程项目的不确定性问题的分析
• 引言 • 工程项目不确定性问题的来源 • 工程项目不确定性问题的后果 • 工程项目不确定性问题的应对策略 • 案例分析 • 结论与建议
01
引言
背景介绍
工程项目是社会经济发展的重要支柱，但常常面临各种不确定性问题，如需求变更、资源短缺、技术难题等，这些问题可能导致项目进度延误、成本超支和质量不达标。
VS
详细描述

应对不确定性的十大策略

FOREWORD 卷首语12019年第二期应对不确定性的十大策略2019年，企业在制定发展规划时，建议从以下十个方面来应对不确定性。

1.以贴近客户需求应对不确定的环境。

一味赚政策的钱，不确定性高；贴近客户，不确定性低。

针对竞争对手时，不确定性高；以客户为中心时，不确定性低。

不管环境如何变化，我们都要根据客户需求的变化调整自己的规划。

2.以机制的确定性应对未来的不确定性。

靠老板、领导决策，公司对未来的不确定性应对水平较差; 靠规范的管理机制，应对不确定性的水平较高。

要实现流程化、标准化、模块化，从以领导为本变为以机制为本。

3.以规则的确定性应对市场的不确定性。

做好章程、协议、担保，用好协会、商会，完善组织规则。

4.以遵纪守法的确定性，应对国际环境的不确定性。

中国企业越来越多地走向海外，面对的已经不仅仅是市场与技术环境，更有政治与法律环境。

要遵纪守法，合规经营，不越底线、边线。

5.以中观层面用力，改善产业小环境应对不确定性。

在宏观层面关注过多或只埋头做好微观层面的事都不行，要与政府、媒体、同行、供应商、产业标准组织等进行沟通，把握好产业小环境，在产业链上创造规则和共识。

6.以加大研发投入的高成本应对高不确定性。

在未来的企业竞争中，活下来才是最重要的。

当企业进入新领域的时候，要舍得为未来的发展付出成本，才可能在战略领域取得先机。

7.以方向大致正确，保持组织活力应对不确定性。

在不确定性的环境中，企业难以制定精密、严谨的战略计划。

只要发展方向和技术路线正确，未来具体执行时利用企业的活力及时调整，就不会面临大问题。

要建立“八爪鱼”型组织，打造“千手观音”构架，授权终端，快速响应。

8.以控制有害信息输入，保持定力应对不确定性。

有害信息常常引起焦虑、急躁、杂念甚至抑郁。

企业家与管理者应坚守自己的使命和价值观，以客户为中心，推进产品改进、技术迭代与管理进步。

9.以使命感和奋斗精神增强信心应对不确定性。

人做事靠三要素：能力、意愿和信心。

工程项目的不确定性问题的分析

二、不确定性产生的原因 1、不确定性产生的主观原因信息的不完全性与不充分性人的能力等主观因素的限制再加上预测工具以及工作条件的限制，决定了预测结果与实际情况肯定有或大或小的偏差。 2、不确定性产生的客观原因市场供求变化的影响经济环境变化的影响社会、政策、法律、文化等方面的影响自然条件和资源方面的影响
将数据带入，经过整理得
NPV 11394 15000x 84900y
取NPV的临界值，即令NPV＝0，则有： 11394 15000x 84900y 0
y 0.1767x 0.1342
第二节敏感性分析方法
y(%) 20 15 10 5
-5
X(%)
图7-4 双因素敏感性分析图根据图7-4可知如果投资额与经营成本同时变动，只要变动范围不超出临界线下方的区域（包括临界线上的点），方案都是可以接受的。
第二节敏感性分析方法
2、敏感性分析的步骤确定敏感性分析指标选择需要分析的不确定性因素研究并设定不确定因素的变动范围计算敏感度系数，确定敏感因素综合评价，优选方案
第二节敏感性分析方法
二、单因素敏感性分析
单因素敏感性分析是每次只变动一个不确定因素所进行的敏感性分析。在分析方法上类似于数学上多元函数的偏微分，即在计算某个因素的变化对经济效果指标的影响时，假定其它因素均不变。
0.3
220
0.5
80
新建流水线
①
40
0.2
120
0
决策点 50
0.3 60
0.5
技术改造
②
30
0.2
180
15
第四节盈亏平衡分析方法
影响项目的各种不确定因素（如投资、成本、销售量、销售价格等）的变化会影响方案的经济效果，当这些因素的变化达到某一临界值时，就会使方案的经济效果发生质的变化，影响方案的取舍。盈亏平衡分析是通过盈亏平衡点（BEP）分析项目成本与收益的平衡关系的一种方法。目的就是找出这种临界值，即盈亏平衡点(BEP)，判断投资方案对不确定因素变化的承受能力，为决策提供依据。

自然知识的非确定性

自然知识的非确定性题外话这学期很快就要结束了，但我要说这十多周的每个周四的上午我都在老师您的课堂上渡过了愉快的两个小时。

我和玉刚有相同的感受：那就是在每次课上我们都如同淋浴在心灵的阳光中。

我们就像荒漠上长出的两颗野草，充分享受着老师所给予自由和呵护。

在此我要说声：谢谢您，老师！引子关于知识的确定性或非确定性，这是一个复杂的问题。

所有的知识可以分为两类，它要嘛是关于自然对象的，要嘛是关于意识对象的。

自然对象和意识对象的性质是截然不同，对关于它们的知识加以分别地考察是完全有必要的。

通常的意见是认为：我们关于自然对象的知识可以是确定无疑的；而关于我们意识的认识是难以把握的和不确定的。

这种流行的意见是否是正确的呢？这是我和玉刚多次讨论过的问题。

我的看法是：和自然对象相比，我们的抉择、愿望和信仰这些意识对象是更适合于被我们确定的东西。

这篇作业将只探讨自然世界的知识是否具有确定性。

关于意识的对象的确定性，我希望以后有机会对其好好思考。

自然事物的性质是确定吗？关于自然事物的性质的知识是确定吗？假如事物的性质是不确定的，我们就只能得到不确定的知识；那么假如事物的性质是确定的，我们是否就能得到确定的知识呢？本文的答案是：即使自然事物的性质是确定的，关于自然事物的知识也不可能是确定的。

关键词：自然本质，自然知识，知识的确定性什么是自然知识？知识总是关于某对象的性质的描述或预期，自然知识当然就是关于自然对象的描述或预期。

自然事物和知识是一个什么样的关系呢？自然事物的性质是确定吗？关于自然事物的性质的知识是确定吗？假如事物的性质是不确定的，我们就只能得到不确定的知识；那么假如事物的性质是确定的，我们是否就能得到确定的知识呢？我的答案是：即使自然事物的性质是确定的，关于自然事物的知识也不可能是确定的。

下面采用哲学的方法，对自然事物的性质进行不同假设，在这些不同假设的基础上来探讨“自然知识是否是确定的”这个问题。

１．１假如世界是不变的我们先假设事物是不变化的。