高中数学新教材选择性必修第一册第一章《1.4空间向量的应用》全部课件
合集下载
空间向量的应用(第一课时课件)高二数学(人教A版2019选择性必修第一册)
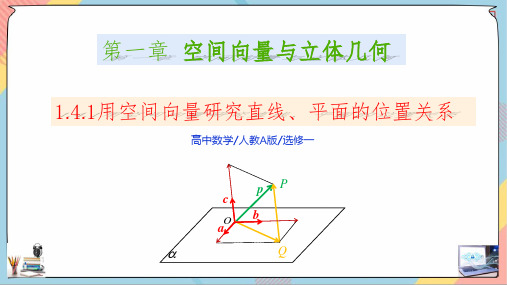
方
法
面面垂直转化为两个平面的法向量垂直.
本题中平面BFQ(D)的法向量可以观察得出.
z
y
x
3.如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,
问
核
心
素
养
题
解
z
建立空间直角坐标系如图.由题意知各点坐标如下:
A(0,- 3,0),B(1,0,0),A1(0,- 3,4),B1(1,0,2),C1(0, 3,1).
B’F=2FD’,试在棱AD上确定一点P,使得平面GEC’F∥平
面MNP.
如图建系.不妨设AB=6,则M(0,3,0),N(0,0,3),
E(3,6,0),G(4,4,0), F(2,2,6); 设P(t,0,0).
分 则 =(t,-3,0), =(0,-3,3), =(1,-2,0),
=(1,0,0), ’=(0,-1,2).设面EFC’有一法
析 向量n1=(x,y,z);由n1∙ =0 及n1∙ ’ = 0
得:x=0, 2y+z=0; 取y=1,得n1=(0,1,-2);同理可
求得面GHB’A’一个法向量为n2=(0,2,1), 由
n1∙n2=0 知n1⊥n2. 所以平面C’EF⊥平面A’GHB’.
空间平面的法向量
课堂小结
二、本节课提升的核心素养:
逻辑推理
数学运算
数据分析
数学建模
课堂小结
三、本节课训练的数学思想方法:
待定系数
转化与化归
方程思想
坐标思想
+
数
学
运
算
求证:AB1⊥平面A1B1C1
以AC中点为坐标原点O,OB为x轴、OC为y轴正方向
法
面面垂直转化为两个平面的法向量垂直.
本题中平面BFQ(D)的法向量可以观察得出.
z
y
x
3.如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,
问
核
心
素
养
题
解
z
建立空间直角坐标系如图.由题意知各点坐标如下:
A(0,- 3,0),B(1,0,0),A1(0,- 3,4),B1(1,0,2),C1(0, 3,1).
B’F=2FD’,试在棱AD上确定一点P,使得平面GEC’F∥平
面MNP.
如图建系.不妨设AB=6,则M(0,3,0),N(0,0,3),
E(3,6,0),G(4,4,0), F(2,2,6); 设P(t,0,0).
分 则 =(t,-3,0), =(0,-3,3), =(1,-2,0),
=(1,0,0), ’=(0,-1,2).设面EFC’有一法
析 向量n1=(x,y,z);由n1∙ =0 及n1∙ ’ = 0
得:x=0, 2y+z=0; 取y=1,得n1=(0,1,-2);同理可
求得面GHB’A’一个法向量为n2=(0,2,1), 由
n1∙n2=0 知n1⊥n2. 所以平面C’EF⊥平面A’GHB’.
空间平面的法向量
课堂小结
二、本节课提升的核心素养:
逻辑推理
数学运算
数据分析
数学建模
课堂小结
三、本节课训练的数学思想方法:
待定系数
转化与化归
方程思想
坐标思想
+
数
学
运
算
求证:AB1⊥平面A1B1C1
以AC中点为坐标原点O,OB为x轴、OC为y轴正方向
1.4.1 用空间向量研究直线、平面的位置关系(PPT)-
第一阶段 课前自学质疑
情境导学 感知新课
情境导学 由直线的方向向量和平面的法向量可以确定直线和平面的位置 关系.因此,可用向量方法解决线面垂直关系的判断及证明.若直线 的方向向量与平面的法向量平行,则该直线与平面有什么关系?若两 平面的法向量垂直,则两平面垂直吗?学习了本节课的知识之后,你 就能很快地解决这个问题.
1,1,2 B. 3 3
2,1,1 C. 3 3
1,2,1 D. 3 3
【例 2】 已知平面 α 经过三点 A(1,2,3),B(2,0,-1),C(3, -2,0),求平面 α 的一个法向量.
例 1 A 解析: 因为 A-21,0,21,B21,2,27,所以A→B=(1, 2,3)为直线 l 的一个方向向量,故所有与A→B共线的向量都可以是直 线 l 的方向向量,故选 A.
(2)取 PA 的中点 M,连接 DM, 则 M12,-1, 23. 因为D→M=32,0, 23,P→B=(1,0,- 3), 所以D→M·P→B=32×1+0×0+ 23×(- 3)=0, 所以D→M⊥P→B,即 DM⊥PB.
解:设正方体 ABCD A1B1C1D1 的棱长为 2,则 D(0,0,0),
B(2,2,0),A(2,0,0),C(0,2,0),E(1,0,2). (1)连接 AC,因为 AC⊥平面 BDD1B1, 所以A→C=(-2,2,0)为平面 BDD1B1 的一个法向量. (2)D→B=(2,2,0),D→E=(1,0,2).
1.求直线的方向向量的方法:在直线上随意取两个点,则这两 个点确定的向量就是直线的方向向量,而且与该向量共线的非零向量 也是直线的方向向量.
2.求法向量的步骤:
在正方体 ABCD A1B1C1D1 中,E,F 分别为棱 A1D1,A1B1 的
1.4空间向量的应用课件-高二上学期数学人教A版(2019)选择性必修第一册

中点.求证:MN⊥AB,MN⊥CD.
课本P43:“习题1.4”:T8.
如图,四面体ABCD的每条棱长都等于a,M,N分别是AB,CD的中点.求证:
MN⊥AB,MN⊥CD.
→ →
→
→
→
→
1 →
解:以{ , ,
}为基底,
= (
+
−
),
2
→
→
→
→ →
→ →
=
−
,故
如图,在直三棱柱ABC-A₁B₁C₁中,AB⊥AC,AB=AC=1,
AA₁=2.以A为原点,建立如图所示空间直角坐标系.
(1)求平面BCC₁B₁的法向量;(2)求平面A₁BC的法向量.
→
(2)A₁(0,0,2),B(1,0,0),C(0,1,0),A₁B=(1,0,-2),
→
→
=(-1,1,0).设平面A₁BC的法向量为 =(x,y,z),则
(1)求证:A₁C⊥平面EFGHKL;
(2)求DB₁与平面EFGHKL所成角的余弦值.
→
→
→
解:(1)以{ , ,₁}为单位正交基底,
→
→
→
→
→ 1 → 1 →
得₁ =−
+
− ₁, =
− ₁,
2 2
→ →
→ →
于是 ₁ ∙
=0,同理 ₁ ∙
=0.所以A₁C⊥KL,
BC
→ →
=
,
∙ A₁B = 0,
− 2 = 0,
1
所以
所以
→ →
= .
− + = 0.
课本P43:“习题1.4”:T8.
如图,四面体ABCD的每条棱长都等于a,M,N分别是AB,CD的中点.求证:
MN⊥AB,MN⊥CD.
→ →
→
→
→
→
1 →
解:以{ , ,
}为基底,
= (
+
−
),
2
→
→
→
→ →
→ →
=
−
,故
如图,在直三棱柱ABC-A₁B₁C₁中,AB⊥AC,AB=AC=1,
AA₁=2.以A为原点,建立如图所示空间直角坐标系.
(1)求平面BCC₁B₁的法向量;(2)求平面A₁BC的法向量.
→
(2)A₁(0,0,2),B(1,0,0),C(0,1,0),A₁B=(1,0,-2),
→
→
=(-1,1,0).设平面A₁BC的法向量为 =(x,y,z),则
(1)求证:A₁C⊥平面EFGHKL;
(2)求DB₁与平面EFGHKL所成角的余弦值.
→
→
→
解:(1)以{ , ,₁}为单位正交基底,
→
→
→
→
→ 1 → 1 →
得₁ =−
+
− ₁, =
− ₁,
2 2
→ →
→ →
于是 ₁ ∙
=0,同理 ₁ ∙
=0.所以A₁C⊥KL,
BC
→ →
=
,
∙ A₁B = 0,
− 2 = 0,
1
所以
所以
→ →
= .
− + = 0.
高中数学新教材选择性必修第一册第一章《1.4空间向量的应用》全部课件

返回
当堂训练
1 2345
1.若A(-1,0,1),B(1,4,7)在直线l上,则直线l的一个方向向量为( A )
A.(1,2,3)
B.(1,3,2)
C.(2,1,3)
D.(3,2,1)
解析 因为―AB→=(2,4,6),
所以与―A→B 共线的非零向量都可以作为直线 l 的方向向量.
解析答案
1 2345
l∥m⇔_a_∥__b_⇔a=kb (k∈R) l∥α⇔a⊥μ⇔_a_·_μ__=0
α∥β⇔μ∥v⇔_μ_=__k_v_(_k_∈__R_)_ l⊥m⇔a⊥b⇔_a_·_b_=__0_
l⊥α⇔a∥μ⇔_a_=__k_μ_(_k∈__R__) α⊥β⇔μ⊥v⇔_μ_·_v_=__0__
答案
知识点二 利用空间向量处理平行问题 思考 (1)设v1=(a1,b1,c1),v2=(a2,b2,c2)分别是直线l1,l2的方向向 量.若直线l1∥l2,则向量v1,v2应满足什么关系. 答案 由直线方向向量的定义知若直线l1∥l2,则直线l1,l2的方向向量共 线,即l1∥l2⇔v1∥v2⇔v1=λv2(λ∈R).
∴a=-2b,∴a∥b,∴l1∥l2. ②∵a=(5,0,2),b=(0,1,0),∴a·b=0,∴a⊥b,
∴l1⊥l2.
解析答案
(2)设 μ,v 分别是不同的平面 α,β 的法向量,根据下列条件判断 α,β 的
位置关系:
①μ=(-1,1,-2),v=(3,2,-12);
②μ=(3,0,0),v=(-2,0,0);
解析答案
1 2345
3.若μ=(2,-3,1)是平面α的一个法向量,则下列向量中能作为平面α的法
向量的是( D )
A.(0,-3,1)
当堂训练
1 2345
1.若A(-1,0,1),B(1,4,7)在直线l上,则直线l的一个方向向量为( A )
A.(1,2,3)
B.(1,3,2)
C.(2,1,3)
D.(3,2,1)
解析 因为―AB→=(2,4,6),
所以与―A→B 共线的非零向量都可以作为直线 l 的方向向量.
解析答案
1 2345
l∥m⇔_a_∥__b_⇔a=kb (k∈R) l∥α⇔a⊥μ⇔_a_·_μ__=0
α∥β⇔μ∥v⇔_μ_=__k_v_(_k_∈__R_)_ l⊥m⇔a⊥b⇔_a_·_b_=__0_
l⊥α⇔a∥μ⇔_a_=__k_μ_(_k∈__R__) α⊥β⇔μ⊥v⇔_μ_·_v_=__0__
答案
知识点二 利用空间向量处理平行问题 思考 (1)设v1=(a1,b1,c1),v2=(a2,b2,c2)分别是直线l1,l2的方向向 量.若直线l1∥l2,则向量v1,v2应满足什么关系. 答案 由直线方向向量的定义知若直线l1∥l2,则直线l1,l2的方向向量共 线,即l1∥l2⇔v1∥v2⇔v1=λv2(λ∈R).
∴a=-2b,∴a∥b,∴l1∥l2. ②∵a=(5,0,2),b=(0,1,0),∴a·b=0,∴a⊥b,
∴l1⊥l2.
解析答案
(2)设 μ,v 分别是不同的平面 α,β 的法向量,根据下列条件判断 α,β 的
位置关系:
①μ=(-1,1,-2),v=(3,2,-12);
②μ=(3,0,0),v=(-2,0,0);
解析答案
1 2345
3.若μ=(2,-3,1)是平面α的一个法向量,则下列向量中能作为平面α的法
向量的是( D )
A.(0,-3,1)
1.4.1 用空间向量研究直线、平面的位置关系(PPT)

平面 α 的法向量的是( )
A.(0,-3,1)
B.(2,0,1)
C.(-2,-3,1)
D.(-2,3,-1)
D 解析:与向量 n 共线的非零向量都可以作为平面 α 的法向
量.故选 D.
3.已知平面 α 内的两个向量 a=(2,3,1),b=(5,6,4),则平
面 α 的一个法向量为( )
A.(1,-1,1)
预习验收 衔接课堂
1.若 A(-1,0,1),B(1,4,7)在直线 l 上,则直线 l 的一个方
向向量为( )
A.(1,2,3)
B.(1,3,2)
C.(2,1,3)
D.(3,2,1)
A 解析:A→B=(2,4,6),而与A→B共线的非零向量都可以作为
直线 l 的方向向量,故选 A.
2.若 n=(2,-3,1)是平面 α 的一个法向量,则下列可以作为
【例 3】 如图,在三棱锥 P ABC 中,PA⊥ 底面 ABC,∠BAC=90°,点 D,E,N 分别为棱 PA,PC,BC 的中点,M 是线段 AD 的中点,PA =AC=4,AB=2.
求证:MN∥平面 BDE.
证明: 如图,以 A 为原点,AB,AC,AP 所在直线为 x 轴、y 轴、z 轴,建立空间直角坐标系,依题意可得 A(0,0,0),B(2,0, 0),C(0,4,0),P(0,0,4),D(0,0,2),E(0,2,2),M(0,0, 1),N(1,2,0).
定位置 定点
点 A 和向量 a 可以确定直线 l 的__位__置____ 可以具体表示出 l 上的任意__一__点____
取定空间中的任意一点 O,可以得到点 P 在直线 l 上的充要条件
是存在实数 t,使O→P=__O_→_A_+__t_O→_B___.
人教A版高中数学选择性必修第一册第1章1-4-1第2课时空间中直线、平面的平行课件

反思领悟 向量法证明直线平行的两种思路
类型2 直线和平面平行 【例2】 如图所示,在空间图形P-ABCD中,PC⊥平面ABCD,PC =2,在四边形ABCD中,CD∥AB,∠ABC=∠BCD=90°,AB= 4 , CD = 1 , 点 M 在 PB 上 , 且 PB = 4PM , ∠PBC = 30° , 求 证 : CM∥平面PAD.
B.l⊥α
√C.l⊂α或l∥α
D.l与α斜交
C [因为a=(1,0,2),n=(-2,1,1),所以a·n=1×(-2)+0×1
+2×1=0,所以l⊂α或l∥α.故选C.]
1234
3.设平面α的法向量为(1,2,-2),平面β的法向量为(-2,-4,
k),若α∥β,则k=( )
A.2
B.-4
√C.4
D.-2
1234
4.若平面α外的一条直线l的一个方向向量是n=(-1,2,-3),平 面 α 的 一 个 法 向 量 为 m = (4 , - 1 , - 2) , 则 l 与 α 的 位 置 关 系 是 ___平__行___. 平行 [n·m=(-1,2,-3)·(4,-1,-2)=0, 所以n⊥m.又l⊄α,所以直线l与平面α平行,即l∥α.]
面面平行 设n1,n2分别是平面α,β的法向量,则α∥β⇔ n1∥n2⇔∃λ∈R,使得n1=λn2
思考 若已知平面外一直线的方向向量和平面的法向量,则这两向量 满足哪些条件可说明直线与平面平行? 提示:可探究直线的方向向量与平面的法向量是否垂直,进而确定 线面是否平行.
提醒 用向量方法证明线线平行时,必须说明两直线不重合;证明线 面平行时,必须说明直线不在平面内;证明面面平行时,必须说明 两个平面不重合.
因为DD1⊂平面AA1D1D,CC1⊄平面AA1D1D, 所以CC1∥平面AA1D1D. 因为DA⊂平面AA1D1D,CF⊄平面AA1D1D, 所以CF∥平面AA1D1D. 又CF∩CC1=C,CF⊂平面FCC1, CC1⊂平面FCC1, 所以平面AA1D1D∥平面FCC1.
高中数学选择性必修一课件:1.4.1 空间中点、直线和平面的向量表示,空间中直线、平面的平行

D.(-2,3,-6)
素养点睛:考查数学抽象、直观想象的
核心素养.
|自学导引|
|课堂互动|
|素养达成|
课后提能训练
【答案】(1)7102 (2)A
【解析】(1)∵b=(-1,3)是直线 l2 的一个法向量,∴c=(3,1)是直线
l2 的一个方向向量.∴cos〈a,c〉=|aa|·|cc|=
7 5×
与平面α共面的所有向量,是正确的.
(2)当a,b共线时,n就不是平面α的一个法向量.
|自学导引|
|课堂互动|
|素养达成|
课后提能训练
2.已知向量 a=(1,2,5),b=(3,x,y),分别是直线 l1,l2 的方向向
量,若 l1∥l2,则
()
A.x=6,y=15
B.x=3,y=15
C.x=38,y=130 【答案】A
得向量A→D=(x,-3,z-5),向量B→C=(-1,3,0). 因为直线 AD∥BC,所以有向量A→D∥B→C,即有A→D=λB→C, 从而 x=-λ,-3=3λ,z-5=0,得 x=1,z=5.
故点 D 的坐标为(1,0,5).
|自学导引|
|课堂互动|
|素养达成|
课后提能训练
【例题迁移 1】 (变换条件)将本例条件“AD 交坐标平面 Ozx 于点
|自学导引|
|课堂互动|
|素养达成|
课后提能训练
用向量表示平面的位置
1.通过平面 α 上的一个定点 O 和两个向量 a 和 b 来确定 条件 平面 α 内两条___相__交___直线的方向向量 a,b 和交点 O 形式 对于平面 α 上任意一点 P,存在有序实数对(x,y)使得O→P=
_x_a_+__y_b__
高中数学 第一章 空间向量与立体空间向量研究距离、夹角问题课件 新人教A版选择性必修第一册

,1 2
,1 2
,故
PB
DE 0 1 1 0 . 22
所以 PB DE .
由已知 EF PB,且 EF DE E ,所以 PB 平面 EFD.
25
(3)解:已知 PB EF ,由(2)可知 PB DF ,故 EFD 是平面 CPB 与平面
PBD 的夹角. 设点 F 的坐标为 (x ,y ,z) ,则 PF (x ,y ,z 1) .
2
2
设向量 CN 与 MA 的夹角为 ,
则直线 AM 和 CN 夹角的余弦值等于| cos | .
13
步骤二:进行向量运算
CN MA 1 (CA CD) (CA 1 CB)
2
2
1
2
CA
1
CA
CB 1 CD
CA 1 CD
CB
2
4
2
4
11111. 2848 2
又 △ABC 和△ACD 均为等边三角形,所以| MA | | CN | 3 . 2
则 n2 n2
PQ PR
0 0
,所以
2x y
y
2z
z 0
0
,所以
x y
3z 2 2z
.
取 n2
(3,4 ,2) ,则 cos n1 ,n2
n1 n1
n2 (0 ,0 ,1)
n2
1
(3,4 ,2) 2 29 .
29Biblioteka 29步骤三:回到图形问题
设平面
PQR
与平面
A1B1C1 的夹角为
,则 cos
设
m
(x,
y,
z)
是平面
A1BE
的法向量,则
2025版新教材高中数学第1章空间向量及其线性运算课件新人教A版选择性必修第一册

②若空间向量a,b满足|a|=|b|,则a=±b; ③在正方体 ABCD-A1B1C1D1 中,必有A→C=A→1C1;
④若空间向量m,n,p满足m=n,n=p,则m=p; ⑤在三棱柱 ABC-A1B1C1 中,模与A→A1的模相等的向量一共有 4 个.
其中不正确的命题的个数是( C )
A.1
B.2
(2)方法一(转化为加法运算) (A→B-C→D)-(A→C-B→D)=A→B-C→D-A→C+B→D =A→B+D→C+C→A+B→D =A→B+B→D+D→C+C→A=0. 方法二(转化为减法运算) (A→B-C→D)-(A→C-B→D) =(A→B-A→C)+(B→D-C→D) =C→B+B→C=0.
提示:(1)三条直线不一定在同一平面内. (2)当M→A与M→B共线,M→P与M→A不共线时,x,y 不存在. (3)由 2a-b=2·a+(-1)·b 得 2a-b 与 a,b 共面.
关键能力•攻重难
题型探究
题型一
空间向量及相关概念的理解
1.给出下列命题: ①两个空间向量相等,则它们起点相同,终点也相同;
C.3
D.4
[解析] 当两向量的起点相同,终点也相同时,这两个向量必相等; 但当两个向量相等时,它们的起点和终点均不一定相同,故①错;模相
等的两个向量不一定为相等向量或相反向量,故②错;根据正方体 ABCD -A1B1C1D1 中,向量A→C与A→1C1的方向相同,模也相等,必有A→C=A→1C1, 故③正确;命题④显然正确;在三棱柱 ABC-A1B1C1 中,与A→A1的模一定 相等的向量是A→1A,B→B1,B→1B,C→C1,C→1C,一共有 5 个.故⑤错.
[规律方法] 证明空间三点共线的三种思路 对于空间三点 P、A、B 可通过证明下列结论来证明三点共线. (1)存在实数 λ,使P→A=λP→B成立. (2)对空间任一点 O,有O→P=O→A+tA→B(t∈R). (3)对空间任一点 O,有O→P=xO→A+yO→B(x+y=1).
新教材人教A版高中数学选择性必修第一册1.4空间向量的应用 教学课件

22,1,
所以A→M=-
22,-
22,1.
所以N→E=A→M,且 A∉NE,所以 NE∥AM.
又因为 NE⊂平面 BDE,AM⊄平面 BDE,
所以 AM∥平面 BDE.
题型四
利用向量方法证明面面平行
典例 4 如图所示,在正方体ABCD- A1B1C1D1中,O为底面ABCD的中心,P是 DD1的中点,设Q是CC1上的点,问:当点Q 在什么位置时,平面D1BQ∥平面PAO?
设平面 A1B1CD 的法向量 n2=(x2,y2,z2), 由A→1B1=(1,0,0),A→1D=(0,1,-1),
而 n2⊥A→1B1,n2⊥A→1D,所以xy22= -0z2,=0,
x2=0, 令 z2=1,则y2=1,
z2=1,
∴n2=(0,1,1).
题型二
利用向量方法证明线线平行
典例 2 在长方体ABCD-A1B1C1D1中,AB=4,AD=3, AA1=2,点P,Q,R,S分别是AA1,D1C1,AB,CC1的中 点.求证:PQ∥RS.
方法 1:因为O→P=-12,-12,12,B→D1=(-1,-1,1),所以O→P∥B→D1, 于是 OP∥BD1.
A→P=-1,0,12,B→Q=(-1,0,m),当 m=21时,A→P=B→Q,即 AP∥ BQ,有平面 PAO∥平面 D1BQ,即当点 Q 为 CC1 的中点时,平面 D1BQ ∥平面 PAO.
[分析] 建立空间直角坐标系,设出点Q的坐标,然后可根据面面平 行的判定定理转化为向量共线问题或者利用两个平面的法向量共线进行 证明.
[解析] 如图所示,分别以DA,DC,DD1所在直线为x,y,z 轴,建立空间直角坐标系,在CC1上任取一点Q,连接BQ, D1Q.
新教材人教A版高中数学选择性必修第一册 1.4空间向量的应用 精品教学课件

程可以为A→P=tA→B. [提示] (1)× (2)√ (3)√ (4)√
()
2.已知向量 a=(2,3,5),b=(3,x,y)分别是直线 l1,l2 的方向 向量,若 l1∥l2 则( )
A.x=92,y=15
B.x=3,y=125
C.x=3,y=15
D.x=92,y=125
D [由 l1∥l2,得 a∥b,即32=3x=5y. 解得 x=92,y=125,故选 D.]
即M→N可用A→1B与D→B线性表示,故M→N与A→1B,D→B是共面向量,故 MN∥平面 A1BD.
1.本例中条件不变,试证明平面 A1BD∥平面 CB1D1. [证明] 由例题解析知,C(0,1,0),D1(0,0,1),B1(1,1,1), 则C→D1=(0,-1,1),D→1B1=(1,1,0), 设平面 CB1D1 的法向量为 m=(x1,y1,z1),
平行 c1),u2=(a2,b2,c2),则 l1∥l2⇔_u_1_∥__u_2_⇔ _(a_1_,__b_1,__c_1_)=__λ_(_a_2,__b_2_,_c_2_) __
线面 设 l 的方向向量为 u=(a1,b1,c1),α 的法向量为 n=(a2,
平行 b2,c2),则 l∥α⇔__u_·n__=_0__⇔__a_1a_2_+__b_1b_2_+__c1_c_2=__0__
1.空间中点、直线和平面的向量表示 在空间中,取一定点 O 作为基点,那么空间中任意一
点 P 的位 点 P 可以用向量_O→_P_表示,我们把向量_O→_P_称为点 P 的
置向量 位置向量.
a 是直线 l 的方向向量,在直线 l 上取A→B=a,取定空间 空间直线
中的任意一点 O,可以得到点 P 在直线 l 上的充要条件 的向量表
数学人教A版选择性必修第一册1.4空间向量的应用

量的定义可知,如果两条直线平行,那么它们的方向向量一
定平行;反过来,如果两条直线的方向向量平行,那么这两
条直线也平行.所以 l1∥l2⇔u1∥u2⇔ ∃λ∈R,使得 u1 =λu2.
l1
u1
l2
u2
二、知识讲解
2.空间中直线、平面的平行
u
n
类似地,如图,设 u 是直线 l 的方向向量,n 是
平面 α的法向量,l⊄α则 l∥α⇔u⊥n⇔u ·n=0.
?思 考
如何用向量表示空间中的一个点?
如图,在空间中,我们取一定点 O 作为基点,
那么空间中任意一点 P 就可以用向量 来表示.我
们把向量 称为点 P 的位置向量.
P
p
O
二、知识讲解
1.空间中点、直线和平面的向量表示
?思 考
我们知道,空间中给定一个点 A 和一个方向就能唯一确定一条直线 l.如
如图,设 n1,n2 分别是平面 α,β的法向量,则
α
α∥β⇔n1∥n2⇔ ∃λ∈R,使得 n1 =λn2.
n2
β
α
n1
l
二、知识讲解
2.空间中直线、平面的平行
例2
证明“平面与平面平行的判定定理”:若一个平面内
的两条相交直线与另一个平面平行,则这两个平面平行.
已知:如图 α⊂β,b⊂β,a∩b=P,a∥α, b∥α.
·
)2.
A
?思 考
类比点到直线的距离的求法,如何求两条平行直线之间的距离?
P
Q l
二、知识讲解
4.用空间向量研究距离问题
l
P
我们再来看平面 α外一点 P 到平面 α的距离问题.
如图,已知平面 α的法向量为 n,A 是平面 α内的定点,
定平行;反过来,如果两条直线的方向向量平行,那么这两
条直线也平行.所以 l1∥l2⇔u1∥u2⇔ ∃λ∈R,使得 u1 =λu2.
l1
u1
l2
u2
二、知识讲解
2.空间中直线、平面的平行
u
n
类似地,如图,设 u 是直线 l 的方向向量,n 是
平面 α的法向量,l⊄α则 l∥α⇔u⊥n⇔u ·n=0.
?思 考
如何用向量表示空间中的一个点?
如图,在空间中,我们取一定点 O 作为基点,
那么空间中任意一点 P 就可以用向量 来表示.我
们把向量 称为点 P 的位置向量.
P
p
O
二、知识讲解
1.空间中点、直线和平面的向量表示
?思 考
我们知道,空间中给定一个点 A 和一个方向就能唯一确定一条直线 l.如
如图,设 n1,n2 分别是平面 α,β的法向量,则
α
α∥β⇔n1∥n2⇔ ∃λ∈R,使得 n1 =λn2.
n2
β
α
n1
l
二、知识讲解
2.空间中直线、平面的平行
例2
证明“平面与平面平行的判定定理”:若一个平面内
的两条相交直线与另一个平面平行,则这两个平面平行.
已知:如图 α⊂β,b⊂β,a∩b=P,a∥α, b∥α.
·
)2.
A
?思 考
类比点到直线的距离的求法,如何求两条平行直线之间的距离?
P
Q l
二、知识讲解
4.用空间向量研究距离问题
l
P
我们再来看平面 α外一点 P 到平面 α的距离问题.
如图,已知平面 α的法向量为 n,A 是平面 α内的定点,
人教A版高中数学选择性必修第一册1.4.2空间向量的应用课件

∵M为BC中点,
∴M14, 43,0. ∴―M→N=-14, 43,14,―A→B 1=(1,0,1),
∴―M→N·―A→ B 1=-14+0+14=0. ∴―M→N⊥―A→ B 1,∴AB1⊥MN.
反思与感悟
证明两直线垂直的基本步骤:建立空间直角坐标系―→ 写出点的坐标―→ 求直线的方向向量―→证明向量垂直―→得到两直线垂直.
梳理 设直线l的方向向量a=(a1,b1,c1),平面α的法向量μ=(a2,b2,c2), 则l⊥α⇔a∥μ⇔_a_=__k_μ_(_k_∈__R_)_.
知识点三 向量法判断面面垂直 思考 平面α,β的法向量分别为μ1=(x1,y1,z1),μ2=(x2,y2,z2),用向 量坐标法表示两平面α,β垂直的关系式是什么? 答案 x1x2+y1y2+z1z2=0.
23a,
23a,0,D(0,
3a,0),E
43a,
43a,a2,
F(0, 23a,a2),
故―A→ B =(0,0,-a),―BC→=
23a,
23a,0.
设平面ABC的法向量为n1=(x1,y1,z1),
则nn11··― ―BACB→ →= =00, ,
即-x1+azy1=1=00,,
取 x1=1, ∴n1=(1,-1,0)为平面 ABC 的一个法向量. 设n2=(x2,y2,z2)为平面BEF的一个法向量, 同理可得 n2=(1,1,- 3). ∵n1·n2=(1,-1,0)·(1,1,- 3)=0, ∴平面 BEF⊥平面 ABC.
梳理 若平面α的法向量为μ=(a1,b1,c1),平面β的法向量为ν=(a2,b2, c2),则α⊥β⇔μ⊥ν⇔μ·ν=0⇔_a_1_a_2+__b_1_b_2_+__c1_c_2_=__0_.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答案
(2)若已知平面外一直线的方向向量和平面的法向量,则这两向量满足哪些 条件可说明直线与平面平行? 答案 可探究直线的方向向量与平面的法向量是否垂直,进而确定线面 是否平行. (3)用向量法处理空间中两平面平行的关键是什么? 答案 关键是找到两个平面的法向量,利用法向量平行来说明两平面平行.
答案
l∥m⇔_a_∥__b_⇔a=kb (k∈R) l∥α⇔a⊥μ⇔_a_·_μ__=0
α∥β⇔μ∥v⇔_μ_=__k_v_(_k_∈__R_)_ l⊥m⇔a⊥b⇔_a_·_b_=__0_
l⊥α⇔a∥μ⇔_a_=__k_μ_(_k∈__R__) α⊥β⇔μ⊥v⇔_μ_·_v_=__0__
答案
知识点二 利用空间向量处理平行问题 思考 (1)设v1=(a1,b1,c1),v2=(a2,b2,c2)分别是直线l1,l2的方向向 量.若直线l1∥l2,则向量v1,v2应满足什么关系. 答案 由直线方向向量的定义知若直线l1∥l2,则直线l1,l2的方向向量共 线,即l1∥l2⇔v1∥v2⇔v1=λv2(λ∈R).
直线的方 向向量
能平移到直线上的_非__零__向量, 叫做直线的一个方向向量
平面的 法向量
直线l⊥α,取直线l的_方__向__向__ _量__n__,叫做平面α的法向量
答案
(2)空间中平行关系的向量表示 设直线l,m的方向向量分别为a,b,平面α,β的法向量分别为μ,v,则
线线平行 线面平行 面面平行 线线垂直 线面垂直 面面垂直
4.若直线 l∥α,且 l 的方向向量为(2,m,1),平面 α 的法向量为1,12,2,
则 m 为( C )
A.-4
B.-6
C.-8
D.8
解析 ∵l∥α,平面 α 的法向量为1,12,2, ∴(2,m,1)·1,12,2=0.
∴2+12m+2=0.∴m=-8.
解析答案
1 2345
5.在正方体ABCD-A1B1C1D1中,平面ACD1的一个法向量为________. 解析 不妨设正方体的棱长为1,建立空间直角坐标系,
(5)证明线面平行的方法 ①设n是平面α的一个法向量,v是直线l的方向向量,则v⊥n且l上至少有 一点A∉α,则l∥α. ②根据线面平行的判定定理:“如果平面外直线与平面内的一条直线平 行,那么这条直线和这个平面平行”,要证明一条直线和一个平面平行, 也可以在平面内找一个向量与已知直线的方向向量是共线向量. ③根据共面向量定理可知,如果一个向量和两个不共线的向量是共面向 量,那么这个向量与这两个不共线向量确定的平面必定平行,因此要证 明平面外一条直线和一个平面平行,只要证明这条直线的方向向量能够 用平面内两个不共线向量线性表示即可.
∴P(0,0,1),C(1,1,0),D(0,2,0), 设 E(0,y,z),则―P→E =(0,y,z-1),―PD→=(0,2,-1),
∵―PE→∥―PD→,
∴y(-1)-2(z-1)=0,
①
∵―AD→=(0,2,0)是平面 PAB 的法向量,
又―C→E =(-1,y-1,z),CE∥平面 PAB, ∴―C→E ⊥―AD→,∴(-1,y-1,z)·(0,2,0)=0. ∴y=1,代入①得 z=1,CE∥平面PAB.
②μ=(2,-3,0),a=(8,-12,0).
解 ①∵μ=(2,2,-1),a=(-6,8,4),
∴μ·a=-12+16-4=0,
∴μ⊥a,∴l⊂α或l∥α.
②∵μ=(2,-3,0),a=(8,-12,0).
∴μ=14a,∴μ∥a,∴l⊥α.
反思与感悟
解析答案
跟踪训练1 根据下列条件,判断相应的线、面位置关系: (1)直线l1与l2的方向向量分别是a=(2,3,-1),b=(-6,-9,3); 解 ∵a=(2,3,-1),b=(-6,-9,3) ∴a=-13b,∴a∥b,∴l1∥l2.
2.已知直线l1的方向向量a=(2,-3,5),直线l2的方向向量b=(-4,x,y),
若两直线l1∥l2,则x,y的值分别是( A )
A.6和-10
B.-6和10
C.-6和-10
D.6和10
解析 由两直线l1∥l2,得两向量a,b平行, 即-24=-x3=5y,所以 x,y 的值分别是 6 和-10.
即nn11··――DAE→→A = =22xy11= +0z1,=0,
得xz11==-0,2y1,
令 z1=2,则 y1=-1,所以 n1=(0,-1,2). 因为―FC→1·n1=-2+2=0,所以―FC→1⊥n1.
又因为 FC1⊄平面 ADE,所以 FC1∥平面 ADE.
(证2)明平面因AD为E∥C―1→平B1=面(B21,C0,10F).,
所以xx= =yz,, 不妨取 x=1,a=(1,1,1).(注:答案不唯一,只要与所给答
案共线都对)
规律与方法
(1)空间中一条直线的方向向量有无数个. (2)方向向量在判断线线、线面位置关系时起到重要的作用. (3)线段中点的向量表达式:对于―AP→=t―A→B ,当 t=12时,我们就得到线段中 点的向量表达式.设点 M 是线段 AB 的中点,则O―M→=12(―O→A +―O→B ),这就是 线段 AB 中点的向量表达式. (4)利用待定系数法求平面的法向量,求出向量的横、纵、竖坐标是具有某 种关系的,而不是具体的值,可设定某个坐标为常数,再表示其他坐标.
返回
当堂训练
1 2345
1.若A(-1,0,1),B(1,4,7)在直线l上,则直线l的一个方向向量为( A )
A.(1,2,3)
B.(1,3,2)
C.(2,1,3)
D.(3,2,1)
解析 因为―AB→=(2,4,6),
所以与―A→B 共线的非零向量都可以作为直线 l 的方向向量.
解析答案
1 2345
解析答案
证明 建立如图所示空间直角坐标系Dxyz,
则有D(0,0,0),A(2,0,0),C(0,2,0),C1(0,2,2),E(2,2,1),F(0,0,1),B1(2,2,2), 所以―FC→1=(0,2,1),―D→A =(2,0,0),―AE→=(0,2,1). 设 n1=(x1,y1,z1)是平面 ADE 的法向量,则 n1⊥―D→A ,n1⊥―AE→,
(3)平面:①空间中平面 α 的位置可以由 α 内两个不共线向量确定.对于平面 α 上的任一点 P,a,b 是平面 α 内两个不共线向量,则存在有序实数对(x, y),使得―O→P =xa+yb. ②空间中平面 α 的位置还可以用垂直于平面的直线的方向向量表示.
梳理 (1)直线的方向向量和平面的法向量
题型探究
类型一 利用方向向量和法向量判定线面的位置关系
例1 (1)设a,b分别是不重合的直线l1,l2的方向向量,根据下列条件判断l1, l2的位置关系: ①a=(4,6,-2),b=(-2,-3,1);
②a=(5,0,2),b=(0,1,0);
解 ①∵a=(4,6,-2),b=(-2,-3,1),
解析答案
(2)直线l1与l2的方向向量分别是a=(-2,1,4),b=(6,3,3); 解 ∵a=(-2,1,4),b=(6,3,3), ∴a·b≠0且a≠kb(k∈R), ∴a,b既不共线也不垂直, 即l1与l2相交或异面,但不垂直.
解析答案
(3)平面α与β的法向量分别是μ=(2,-3,4),v=(4,-2,1); 解 ∵μ=(2,-3,4),v=(4,-2,1), ∴μ·v≠0且μ≠kv(k∈R), ∴μ与v既不共线也不垂直,即α和β相交但不垂直.
则各点坐标为:A(1,0,0),C(0,1,0),D1(0,0,1), 设则平a·面―AAC→C=D01的, a一·―A个D→1法=向0.量a=(x,y,z),
因为―AC→=(-1,1,0),―AD→1=(-1,0,1),
所以
-1·x+1·y+0·z=0,
-1·x+0·y+1·z=0,
所以xx--zy==00,,
∴a=-2b,∴a∥b,∴l1∥l2. ②∵a=(5,0,2),b=(0,1,0),∴a·b=0,∴a⊥b,
∴l1⊥l2.
解析答案
(2)设 μ,v 分别是不同的平面 α,β 的法向量,根据下列条件判断 α,β 的
位置关系:
①μ=(-1,1,-2),v=(3,2,-12);
②μ=(3,0,0),v=(-2,0,0);
解 ①∵μ=(-1,1,-2),v=3,2,-12, ∴μ·v=-3+2+1=0,
∴μ⊥v,∴α⊥β. ②∵μ=(3,0,0),v=(-2,0,0),∴μ=-32v,∴μ∥v,∴α∥β.
解析答案
(3)设μ是平面α的法向量,a是直线l的方向向量,根据下列条件判断平面α
与l的位置关系:
①μ=(2,2,-1),a=(-6,8,4);
答案 (1)点:在空间中,我们取一定点 O 作为基点,那么空间中任意一点 P 的位置就可以用向量―O→P 来表示.我们把向量―O→P 称为点 P 的位置向量.
(2)直线:①直线的方向向量:和这条直线平行或共线的非零向量. ②对于直线 l 上的任一点 P,存在实数 t,使得―A→ P =t―A→ B ,此方程称为直线 的向量参数方程.
解析答案
1 2345
3.若μ=(2,-3,1)是平面α的一个法向量,则下列向量中能作为平面α的法
向量的是( D )
A.(0,-3,1)
B.(2,0,1)
C.(-2,-3,1)
D.(-2,3,-1)
解析 能作为平面α的法向量的向量与μ=(2,-3,1)共线,(-2,3,-1)=-μ.
解析答案
1 2345
反思与感悟
解析答案
跟踪训练3 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面成的
角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=
(2)若已知平面外一直线的方向向量和平面的法向量,则这两向量满足哪些 条件可说明直线与平面平行? 答案 可探究直线的方向向量与平面的法向量是否垂直,进而确定线面 是否平行. (3)用向量法处理空间中两平面平行的关键是什么? 答案 关键是找到两个平面的法向量,利用法向量平行来说明两平面平行.
答案
l∥m⇔_a_∥__b_⇔a=kb (k∈R) l∥α⇔a⊥μ⇔_a_·_μ__=0
α∥β⇔μ∥v⇔_μ_=__k_v_(_k_∈__R_)_ l⊥m⇔a⊥b⇔_a_·_b_=__0_
l⊥α⇔a∥μ⇔_a_=__k_μ_(_k∈__R__) α⊥β⇔μ⊥v⇔_μ_·_v_=__0__
答案
知识点二 利用空间向量处理平行问题 思考 (1)设v1=(a1,b1,c1),v2=(a2,b2,c2)分别是直线l1,l2的方向向 量.若直线l1∥l2,则向量v1,v2应满足什么关系. 答案 由直线方向向量的定义知若直线l1∥l2,则直线l1,l2的方向向量共 线,即l1∥l2⇔v1∥v2⇔v1=λv2(λ∈R).
直线的方 向向量
能平移到直线上的_非__零__向量, 叫做直线的一个方向向量
平面的 法向量
直线l⊥α,取直线l的_方__向__向__ _量__n__,叫做平面α的法向量
答案
(2)空间中平行关系的向量表示 设直线l,m的方向向量分别为a,b,平面α,β的法向量分别为μ,v,则
线线平行 线面平行 面面平行 线线垂直 线面垂直 面面垂直
4.若直线 l∥α,且 l 的方向向量为(2,m,1),平面 α 的法向量为1,12,2,
则 m 为( C )
A.-4
B.-6
C.-8
D.8
解析 ∵l∥α,平面 α 的法向量为1,12,2, ∴(2,m,1)·1,12,2=0.
∴2+12m+2=0.∴m=-8.
解析答案
1 2345
5.在正方体ABCD-A1B1C1D1中,平面ACD1的一个法向量为________. 解析 不妨设正方体的棱长为1,建立空间直角坐标系,
(5)证明线面平行的方法 ①设n是平面α的一个法向量,v是直线l的方向向量,则v⊥n且l上至少有 一点A∉α,则l∥α. ②根据线面平行的判定定理:“如果平面外直线与平面内的一条直线平 行,那么这条直线和这个平面平行”,要证明一条直线和一个平面平行, 也可以在平面内找一个向量与已知直线的方向向量是共线向量. ③根据共面向量定理可知,如果一个向量和两个不共线的向量是共面向 量,那么这个向量与这两个不共线向量确定的平面必定平行,因此要证 明平面外一条直线和一个平面平行,只要证明这条直线的方向向量能够 用平面内两个不共线向量线性表示即可.
∴P(0,0,1),C(1,1,0),D(0,2,0), 设 E(0,y,z),则―P→E =(0,y,z-1),―PD→=(0,2,-1),
∵―PE→∥―PD→,
∴y(-1)-2(z-1)=0,
①
∵―AD→=(0,2,0)是平面 PAB 的法向量,
又―C→E =(-1,y-1,z),CE∥平面 PAB, ∴―C→E ⊥―AD→,∴(-1,y-1,z)·(0,2,0)=0. ∴y=1,代入①得 z=1,CE∥平面PAB.
②μ=(2,-3,0),a=(8,-12,0).
解 ①∵μ=(2,2,-1),a=(-6,8,4),
∴μ·a=-12+16-4=0,
∴μ⊥a,∴l⊂α或l∥α.
②∵μ=(2,-3,0),a=(8,-12,0).
∴μ=14a,∴μ∥a,∴l⊥α.
反思与感悟
解析答案
跟踪训练1 根据下列条件,判断相应的线、面位置关系: (1)直线l1与l2的方向向量分别是a=(2,3,-1),b=(-6,-9,3); 解 ∵a=(2,3,-1),b=(-6,-9,3) ∴a=-13b,∴a∥b,∴l1∥l2.
2.已知直线l1的方向向量a=(2,-3,5),直线l2的方向向量b=(-4,x,y),
若两直线l1∥l2,则x,y的值分别是( A )
A.6和-10
B.-6和10
C.-6和-10
D.6和10
解析 由两直线l1∥l2,得两向量a,b平行, 即-24=-x3=5y,所以 x,y 的值分别是 6 和-10.
即nn11··――DAE→→A = =22xy11= +0z1,=0,
得xz11==-0,2y1,
令 z1=2,则 y1=-1,所以 n1=(0,-1,2). 因为―FC→1·n1=-2+2=0,所以―FC→1⊥n1.
又因为 FC1⊄平面 ADE,所以 FC1∥平面 ADE.
(证2)明平面因AD为E∥C―1→平B1=面(B21,C0,10F).,
所以xx= =yz,, 不妨取 x=1,a=(1,1,1).(注:答案不唯一,只要与所给答
案共线都对)
规律与方法
(1)空间中一条直线的方向向量有无数个. (2)方向向量在判断线线、线面位置关系时起到重要的作用. (3)线段中点的向量表达式:对于―AP→=t―A→B ,当 t=12时,我们就得到线段中 点的向量表达式.设点 M 是线段 AB 的中点,则O―M→=12(―O→A +―O→B ),这就是 线段 AB 中点的向量表达式. (4)利用待定系数法求平面的法向量,求出向量的横、纵、竖坐标是具有某 种关系的,而不是具体的值,可设定某个坐标为常数,再表示其他坐标.
返回
当堂训练
1 2345
1.若A(-1,0,1),B(1,4,7)在直线l上,则直线l的一个方向向量为( A )
A.(1,2,3)
B.(1,3,2)
C.(2,1,3)
D.(3,2,1)
解析 因为―AB→=(2,4,6),
所以与―A→B 共线的非零向量都可以作为直线 l 的方向向量.
解析答案
1 2345
解析答案
证明 建立如图所示空间直角坐标系Dxyz,
则有D(0,0,0),A(2,0,0),C(0,2,0),C1(0,2,2),E(2,2,1),F(0,0,1),B1(2,2,2), 所以―FC→1=(0,2,1),―D→A =(2,0,0),―AE→=(0,2,1). 设 n1=(x1,y1,z1)是平面 ADE 的法向量,则 n1⊥―D→A ,n1⊥―AE→,
(3)平面:①空间中平面 α 的位置可以由 α 内两个不共线向量确定.对于平面 α 上的任一点 P,a,b 是平面 α 内两个不共线向量,则存在有序实数对(x, y),使得―O→P =xa+yb. ②空间中平面 α 的位置还可以用垂直于平面的直线的方向向量表示.
梳理 (1)直线的方向向量和平面的法向量
题型探究
类型一 利用方向向量和法向量判定线面的位置关系
例1 (1)设a,b分别是不重合的直线l1,l2的方向向量,根据下列条件判断l1, l2的位置关系: ①a=(4,6,-2),b=(-2,-3,1);
②a=(5,0,2),b=(0,1,0);
解 ①∵a=(4,6,-2),b=(-2,-3,1),
解析答案
(2)直线l1与l2的方向向量分别是a=(-2,1,4),b=(6,3,3); 解 ∵a=(-2,1,4),b=(6,3,3), ∴a·b≠0且a≠kb(k∈R), ∴a,b既不共线也不垂直, 即l1与l2相交或异面,但不垂直.
解析答案
(3)平面α与β的法向量分别是μ=(2,-3,4),v=(4,-2,1); 解 ∵μ=(2,-3,4),v=(4,-2,1), ∴μ·v≠0且μ≠kv(k∈R), ∴μ与v既不共线也不垂直,即α和β相交但不垂直.
则各点坐标为:A(1,0,0),C(0,1,0),D1(0,0,1), 设则平a·面―AAC→C=D01的, a一·―A个D→1法=向0.量a=(x,y,z),
因为―AC→=(-1,1,0),―AD→1=(-1,0,1),
所以
-1·x+1·y+0·z=0,
-1·x+0·y+1·z=0,
所以xx--zy==00,,
∴a=-2b,∴a∥b,∴l1∥l2. ②∵a=(5,0,2),b=(0,1,0),∴a·b=0,∴a⊥b,
∴l1⊥l2.
解析答案
(2)设 μ,v 分别是不同的平面 α,β 的法向量,根据下列条件判断 α,β 的
位置关系:
①μ=(-1,1,-2),v=(3,2,-12);
②μ=(3,0,0),v=(-2,0,0);
解 ①∵μ=(-1,1,-2),v=3,2,-12, ∴μ·v=-3+2+1=0,
∴μ⊥v,∴α⊥β. ②∵μ=(3,0,0),v=(-2,0,0),∴μ=-32v,∴μ∥v,∴α∥β.
解析答案
(3)设μ是平面α的法向量,a是直线l的方向向量,根据下列条件判断平面α
与l的位置关系:
①μ=(2,2,-1),a=(-6,8,4);
答案 (1)点:在空间中,我们取一定点 O 作为基点,那么空间中任意一点 P 的位置就可以用向量―O→P 来表示.我们把向量―O→P 称为点 P 的位置向量.
(2)直线:①直线的方向向量:和这条直线平行或共线的非零向量. ②对于直线 l 上的任一点 P,存在实数 t,使得―A→ P =t―A→ B ,此方程称为直线 的向量参数方程.
解析答案
1 2345
3.若μ=(2,-3,1)是平面α的一个法向量,则下列向量中能作为平面α的法
向量的是( D )
A.(0,-3,1)
B.(2,0,1)
C.(-2,-3,1)
D.(-2,3,-1)
解析 能作为平面α的法向量的向量与μ=(2,-3,1)共线,(-2,3,-1)=-μ.
解析答案
1 2345
反思与感悟
解析答案
跟踪训练3 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面成的
角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=
