机械工程控制基础期末试卷+答案2
机械工程控制基础考试题及答案

填空题每空1分,共20分1. 线性控制系统最重要的特性是可以应用___叠加__原理,而非线性控制系统则不能;2.反馈控制系统是根据输入量和__反馈量__的偏差进行调节的控制系统;3.在单位斜坡输入信号作用下,0型系统的稳态误差e ss =∞___; 4.当且仅当闭环控制系统特征方程的所有根的实部都是__负数__时,系统是稳定的;5.方框图中环节的基本连接方式有串联连接、并联连接和__反馈 _连接;6.线性定常系统的传递函数,是在_ 初始条件为零___时,系统输出信号的拉氏变换与输入信号的拉氏变换的比; 7.函数te -at的拉氏变换为2)(1a s +;8.线性定常系统在正弦信号输入时,稳态输出与输入的相位移随频率而变化的函数关系称为__相频特性__;9.积分环节的对数幅频特性曲线是一条直线,直线的斜率为__-20__dB /dec;10.二阶系统的阻尼比ξ为 _ 0_ 时,响应曲线为等幅振荡; 11.在单位斜坡输入信号作用下,Ⅱ型系统的稳态误差e ss =__0__; 12.0型系统对数幅频特性低频段渐近线的斜率为___0___dB/dec,高度为20lgKp;13.单位斜坡函数t 的拉氏变换为21s ;14. 根据系统输入量变化的规律,控制系统可分为__恒值__控制系统、___随动___ 控制系统和程序控制系统;15. 对于一个自动控制系统的性能要求可以概括为三个方面:稳定性、__快速性__和准确性;16. 系统的传递函数完全由系统的结构和参数决定,与__输入量、扰动量__的形式无关;17. 决定二阶系统动态性能的两个重要参数是阻尼系数ξ和_无阻尼自然振荡频率w n ;18. 设系统的频率特性Gj ω=R ω+jI ω,则幅频特性|Gj ω|=)()(22w I w R +;19. 分析稳态误差时,将系统分为0型系统、I 型系统、II 型系统…,这是按开环传递函数的__积分__环节数来分类的; 20. 线性系统稳定的充分必要条件是它的特征方程式的所有根均在复平面的___左___部分;21.ω从0变化到+∞时,惯性环节的频率特性极坐标图在____第四____象限,形状为___半___圆;22. 用频域法分析控制系统时,最常用的典型输入信号是_正弦函数_;23.二阶衰减振荡系统的阻尼比ξ的范围为10<<ξ; 24.Gs=1+Ts K的环节称为___惯性__环节;25.系统输出量的实际值与_输出量的希望值__之间的偏差称为误差;26.线性控制系统其输出量与输入量间的关系可以用___线性微分__方程来描述;27. 稳定性 、 快速性 和准确性是对自动控制系统性能的基本要求;28.二阶系统的典型传递函数是2222nn nw s w s w ++ξ;29.设系统的频率特性为)(jI )j (R )j (G ω+ω=ω,则)(R ω称为 实频特性 ;30. 根据控制系统元件的特性,控制系统可分为__线性__ 控制系统、 非线性_控制系统;31. 对于一个自动控制系统的性能要求可以概括为三个方面:稳定性、快速性和_准确性__;32.二阶振荡环节的谐振频率ωr 与阻尼系数ξ的关系为ωr =ωn122-ξ;33.根据自动控制系统是否设有反馈环节来分类,控制系统可分为__开环_控制系统、_闭环__控制系统;34.用频率法研究控制系统时,采用的图示法分为极坐标图示法和__对数坐标_图示法;35.二阶系统的阻尼系数ξ=时,为最佳阻尼系数;这时系统的平稳性与快速性都较理想;1. 传递函数的定义是对于线性定常系统,在初始条件为零的条件下,系统输出量的拉氏变换与输入量的拉氏变换之比;2. 瞬态响应是系统受到外加作用激励后,从初始状态到最终或稳定状态的响应过程;3. 判别系统稳定性的出发点是系统特征方程的根必须为负实根或负实部的复数根,即系统的特征根必须全部在复平面的左半平面是系统稳定的充要条件;4. I 型系统G s Ks s ()()=+2在单位阶跃输入下,稳态误差为 0 ,在单位加速度输入下,稳态误差为 ∞ ;5. 频率响应是系统对正弦输入稳态响应,频率特性包括幅频和相频两种特性;6. 如果系统受扰动后偏离了原工作状态,扰动消失后,系统能自动恢复到原来的工作状态,这样的系统是渐进稳定的系统;7. 传递函数的组成与输入、输出信号无关,仅仅决定于系统本身的结构和参数,并且只适于零初始条件下的线性定常系统;8. 系统的稳态误差与输入信号的形式及系统的结构和参数或系统的开环传递函数有关;9. 如果在系统中只有离散信号而没有连续信号,则称此系统为离散数字控制系统,其输入、输出关系常用差分方程来描述; 10. 反馈控制系统开环对数幅频特性三频段的划分是以ωc 截止频率附近的区段为中频段,该段着重反映系统阶跃响应的稳定性和快速性;而低频段主要表明系统的稳态性能;11. 对于一个自动控制系统的性能要求可以概括为三个方面:稳定性、快速 性和精确或准确性; 单项选择题:1.当系统的输入和输出已知时,求系统结构与参数的问题,称为 A.最优控制 B.系统辩识 C.系统校正 D.自适应控制2.反馈控制系统是指系统中有A.反馈回路B.惯性环节C.积分环节 调节器3. =1s a+,a 为常数;A. Le -atB. Le atC. Le-t -aD. Le-t+at 2e 2t= A. 123()s - B. 1a s a ()+C.223()s + D. 23s5.若Fs=421s +,则Lim f t t →0()= A. 4 B. 2 C. 0 D. ∞ 6.已知ft=e at,a 为实数,则L f t dt t()0⎰=A. as a- B. 1a s a ()+ C.1s s a ()- D. 1a s a ()-t=3202t t ≥<⎧⎨⎩,则Lft=A. 3sB. 12s e s -C. 32s e s -D. 32se s 8.某系统的微分方程为52000 () ()()()x t x t x t x t i +⋅=,它是A.线性系统B.线性定常系统C.非线性系统D.非线性时变系统 9.某环节的传递函数为Gs=e-2s,它是A.比例环节B.延时环节C.惯性环节D.微分环节 10.图示系统的传递函数为A. 11RCs + B. RCs RCs +1C. RCs+1D. RCs RCs+1 11.二阶系统的传递函数为Gs=341002s s ++,其无阻尼固有频率ωn 是A. 10B. 5C.D. 25 12.一阶系统K Ts 1+的单位脉冲响应曲线在t=0处的斜率为 A. K T B. KT C. -K T2D. K T 213.某系统的传递函数Gs=KT s +1,则其单位阶跃响应函数为A. 1T e Kt T -/B. K Te t T -/ C. K1-e -t/TD. 1-e-Kt/T14.图示系统称为 型系统;A. 0B. ⅠC. ⅡD. Ⅲ15.延时环节Gs=e-τs的相频特性∠Gjω等于A. τωB. –τωC.90°D.180°16.对数幅频特性的渐近线如图所示,它对应的传递函数Gs为A. 1+TsB. 11+TsD. 1+Ts2C. 1Ts17.图示对应的环节为A. TsB. 11+TsC. 1+TsD. 1Ts18.设系统的特征方程为Ds=s3+14s2+40s+40τ=0,则此系统稳定的τ值范围为A. τ>0B. 0<τ<14C. τ>14D. τ<019.典型二阶振荡环节的峰值时间与 有关;A.增益B.误差带C.增益和阻尼比D.阻尼比和无阻尼固有频率20.若系统的Bode 图在ω=5处出现转折如图所示,这说明系统中有环节; A. 5s+1 B. 5s+12C. +1D.10212(.)s +21.某系统的传递函数为Gs=()()()()s s s s +-+-72413,其零、极点是 A.零点s=-,s=3;极点s=-7,s=2 B.零点s=7,s=-2;极点s=,s=3C.零点s=-7,s=2;极点s=-1,s=3D.零点s=-7,s=2;极点s=-,s=3 22.一系统的开环传递函数为32235()()()s s s s +++,则系统的开环增益和型次依次为A. 0.4,ⅠB. ,ⅡC. 3,ⅠD. 3,Ⅱ23.已知系统的传递函数Gs=K Te sts 1+-,其幅频特性|Gj ω|应为A. K T e 1+-ωτB. KT e 1+-ωτωC.K T e 2221+-ωτω D.K T 122+ω24.二阶系统的阻尼比ζ,等于A.系统的粘性阻尼系数B.临界阻尼系数与系统粘性阻尼系数之比C.系统粘性阻尼系数与临界阻尼系数之比D.系统粘性阻尼系数的倒数25.设ωc 为幅值穿越交界频率,φωc 为开环频率特性幅值为1时的相位角,则相位裕度为A. 180°-φωcB. φωcC. 180°+φωcD. 90°+φωc 26.单位反馈控制系统的开环传递函数为Gs=45s s ()+,则系统在rt=2t 输入作用下,其稳态误差为A. 104B. 54C. 45D. 0 27.二阶系统的传递函数为Gs=1222s s n n++ζωω,在0<ζ<22时,其无阻尼固有频率ωn 与谐振频率ωr 的关系为A. ωn <ωrB. ωn =ωrC. ωn >ωrD. 两者无关28.串联相位滞后校正通常用于A.提高系统的快速性B.提高系统的稳态精度C.减少系统的阻尼D.减少系统的固有频率29.下列串联校正装置的传递函数中,能在频率ωc =4处提供最大相位超前角的是A. 411s s ++B. s s ++141C. 01106251..s s ++ D. 06251011..s s ++30.从某系统的Bode 图上,已知其剪切频率ωc ≈40,则下列串联校正装置的传递函数中能在基本保持原系统稳定性及频带宽的前提下,通过适当调整增益使稳态误差减至最小的是A. 000410041..s s ++B. 04141.s s ++C. 41101s s ++ D. 41041s s ++. 单项选择题每小题1分,共30分二、填空题每小题2分,共10分1.系统的稳态误差与系统开环传递函数的增益、_______和_______有关;2.一个单位反馈系统的前向传递函数为K s s s3254++,则该闭环系统的特征方程为_______开环增益为_______;3.二阶系统在阶跃信号作用下,其调整时间t s 与阻尼比、_______和_______有关;4.极坐标图Nyquist 图与对数坐标图Bode 图之间对应关系为:极坐标图上的单位圆对应于Bode 图上的_______;极坐标图上的负实轴对应于Bode 图上的_______;5.系统传递函数只与_______有关,与______无关; 填空题每小题2分,共10分1.型次 输入信号+5s 2+4s+K=0,K 43.误差带 无阻尼固有频率分贝线 -180°线5.本身参数和结构 输入1. 线性系统和非线性系统的根本区别在于CA .线性系统有外加输入,非线性系统无外加输入;B .线性系统无外加输入,非线性系统有外加输入;C .线性系统满足迭加原理,非线性系统不满足迭加原理;D .线性系统不满足迭加原理,非线性系统满足迭加原理;2.令线性定常系统传递函数的分母多项式为零,则可得到系统的 BA .代数方程B .特征方程C .差分方程D .状态方程3. 时域分析法研究自动控制系统时最常用的典型输入信号是DA .脉冲函数B .斜坡函数C .抛物线函数D .阶跃函数 4.设控制系统的开环传递函数为Gs=)2s )(1s (s 10++,该系统为BA .0型系统B .I 型系统C .II 型系统D .III 型系统5.二阶振荡环节的相频特性)(ωθ,当∞→ω时,其相位移)(∞θ为 BA .-270°B .-180°C .-90°D .0°6. 根据输入量变化的规律分类,控制系统可分为 AA.恒值控制系统、随动控制系统和程序控制系统B.反馈控制系统、前馈控制系统前馈—反馈复合控制系统C.最优控制系统和模糊控制系统D.连续控制系统和离散控制系统7.采用负反馈连接时,如前向通道的传递函数为Gs,反馈通道的传递函数为Hs,则其等效传递函数为 CA .)s (G 1)s (G + B .)s (H )s (G 11+C .)s (H )s (G 1)s (G +D .)s (H )s (G 1)s (G -8. 一阶系统Gs=1+Ts K 的时间常数T 越大,则系统的输出响应达到稳态值的时间AA .越长B .越短C .不变D .不定9.拉氏变换将时间函数变换成DA .正弦函数B .单位阶跃函数C .单位脉冲函数D .复变函数10.线性定常系统的传递函数,是在零初始条件下DA .系统输出信号与输入信号之比B .系统输入信号与输出信号之比C .系统输入信号的拉氏变换与输出信号的拉氏变换之比D .系统输出信号的拉氏变换与输入信号的拉氏变换之比 11.若某系统的传递函数为Gs=1Ts K+,则其频率特性的实部R ω是A A .22T 1Kω+ B .-22T1Kω+C .T1K ω+D .-T1K ω+12. 微分环节的频率特性相位移θω= AA. 90°B. -90°C. 0°D. -180°13. 积分环节的频率特性相位移θω= BA. 90°B. -90°C. 0°D. -180°14.传递函数反映了系统的动态性能,它与下列哪项因素有关 CA.输入信号B.初始条件C.系统的结构参数D.输入信号和初始条件15. 系统特征方程式的所有根均在根平面的左半部分是系统稳定的 CA.充分条件B.必要条件C.充分必要条件D.以上都不是16. 有一线性系统,其输入分别为u 1t 和u 2t 时,输出分别为y 1t 和y 2t;当输入为a 1u 1t+a 2u 2t 时a 1,a 2为常数,输出应为 BA. a 1y 1t+y 2tB. a 1y 1t+a 2y 2tC. a 1y 1t-a 2y 2tD. y 1t+a 2y 2t17. I 型系统开环对数幅频渐近特性的低频段斜率为 BA. -40dB/decB. -20dB/decC. 0dB/decD. +20dB/dec 18. 设系统的传递函数为Gs=255252++s s ,则系统的阻尼比为CA.25B. 5C. 21D. 119.正弦函数sintω的拉氏变换是BA.ω+s 1B.22s ω+ωC.22s s ω+ D.22s 1ω+20.二阶系统当0<ζ<1时,如果增加ζ,则输出响应的最大超调量%σ将 BA.增加B.减小C.不变D.不定 21.主导极点的特点是DA.距离实轴很远B.距离实轴很近C.距离虚轴很远D.距离虚轴很近 22.余弦函数costω的拉氏变换是CA.ω+s 1B.22s ω+ωC.22s s ω+ D.22s 1ω+23.设积分环节的传递函数为Gs=s1,则其频率特性幅值M ω=CA.ωKB.2K ω C.ω1 D.21ω24. 比例环节的频率特性相位移θω= C° ° ° °25. 奈奎斯特稳定性判据是利用系统的 C 来判据闭环系统稳定性的一个判别准则;A.开环幅值频率特性B.开环相角频率特性C.开环幅相频率特性D.闭环幅相频率特性 26. 系统的传递函数CA.与输入信号有关B.与输出信号有关C.完全由系统的结构和参数决定D.既由系统的结构和参数决定,也与输入信号有关 27. 一阶系统的阶跃响应,DA.当时间常数T 较大时有振荡B.当时间常数T 较小时有振荡C.有振荡D.无振荡28. 二阶振荡环节的对数频率特性相位移θω在 D 之间;°和90° °和-90° °和180° °和-180° 29. 某二阶系统阻尼比为,则系统阶跃响应为 CA. 发散振荡B. 单调衰减C. 衰减振荡D. 等幅振荡 二.设有一个系统如图1所示,k 1=1000N/m, k 2=2000N/m, D=10N/m/s,当系统受到输入信号t t x i sin 5)(= 的作用时,试求系统的稳态输出)(t x o ;15分 解:()()()1015.001.021211+=++=s sk k Ds k k Ds k s X s X i o 然后通过频率特性求出 ()() 14.89sin 025.0+=t t x o三.一个未知传递函数的被控系统,构成单位反馈闭环;经过测试,得知闭环系统的单位阶跃响应如图2所示;10分问:1 系统的开环低频增益K 是多少 5分2 如果用主导极点的概念用低阶系统近似该系统,试写出其近似闭环传递函数;5分 解:100718K K =+,07K =2 ()()8025.07+=s s X s X i o四.已知开环最小相位系统的对数幅频特性如图3所示;10分 1. 写出开环传递函数Gs 的表达式;5分 2. 概略绘制系统的Nyquist 图;5分 1.)100s )(01.0s (s 100)1100s )(101.0s (s K)s (G ++=++=2.五.已知系统结构如图4所示, 试求:15分 1. 绘制系统的信号流图;5分 2. 求传递函数)()(s X s X i o 及)()(s N s X o ;10分六.系统如图5所示,)(1)(t t r =为单位阶跃函数,试求:10分 1. 系统的阻尼比ξ和无阻尼自然频率ωn ;5分2. 动态性能指标:超调量M p 和调节时间%)5(=∆s t ;5分1.)2s (s )2S (S 4n 2nξω+ω=+ 2.%5.16%100eM 21p =⨯=ξ-ξπ-七.如图6所示系统,试确定使系统稳定且在单位斜坡输入下e ss ≤225.时,K的数值;10分由劳斯判据:第一列系数大于零,则系统稳定得54K 0<< 又有:K9e ss =≤可得:K ≥4 ∴ 4≤K <54八.已知单位反馈系统的闭环传递函数32)(+=Φs s ,试求系统的相位裕量γ;10分解:系统的开环传递函数为1s 2)s (W 1)s (W )s (G +=-=112|)j (G |2cc =+ω=ω,解得3c =ω三、设系统的闭环传递函数为Gcs=ωξωωnn ns s 2222++,试求最大超调量σ%=%、峰值时间tp=秒时的闭环传递函数的参数ξ和ωn 的值;解:∵%100%21⨯=--ξξπσe=%∴ξ= ∵t p =πωξn 12-=∴ωn =πξt p 13140210622-=-=...s四、设一系统的闭环传递函数为G c s=ωξωωnn nss 2222++,试求最大超调量σ%=5%、调整时间t s =2秒△=时的闭环传递函数的参数ξ和ωn的值;解:∵%100%21⨯=--ξξπσe =5%∴ξ= ∵t s =ξωn 3=2∴ωn = rad/s五、设单位负反馈系统的开环传递函数为 )6(25)(+=s s s G k 求1系统的阻尼比ζ和无阻尼自然频率ωn ;2系统的峰值时间t p 、超调量σ%、 调整时间t S △=;解:系统闭环传递函数2562525)6(25)6(251)6(25)(2++=++=+++=s s s s s s s s s G B 与标准形式对比,可知 62=n w ξ ,252=n w故 5=n w , 6.0=ξ 又 46.015122=-⨯=-=ξnd w w六、某系统如下图所示,试求其无阻尼自然频率ωn ,阻尼比ζ,超调量σ%,峰值时间p t ,调整时间s t △=;解: 对于上图所示系统,首先应求出其传递函数,化成标准形式,然后可用公式求出各项特征量及瞬态响应指标;与标准形式对比,可知 08.02=n w ξ ,04.02=n w 七、已知单位负反馈系统的开环传递函数如下: 求:1 试确定系统的型次v 和开环增益K ; 2试求输入为t t r 31)(+=时,系统的稳态误差; 解:1将传递函数化成标准形式 可见,v =1,这是一个I 型系统 开环增益K =50;2讨论输入信号,t t r 31)(+=,即A =1,B =3 根据表3—4,误差06.006.00503111=+=+∞+=++=V p ss K B K A e 八、 已知单位负反馈系统的开环传递函数如下: 求:1 试确定系统的型次v 和开环增益K ; 2试求输入为2425)(t t t r ++=时,系统的稳态误差; 解:1将传递函数化成标准形式可见,v =2,这是一个II 型系统 开环增益K =100; 2讨论输入信号,2425)(t t t r ++=,即A =5,B =2, C=4根据表3—4,误差04.004.00010042151=++=+∞+∞+=+++=a V p ssK C K B K A e 九、 已知单位负反馈系统的开环传递函数如下: 求:1 试确定系统的型次v 和开环增益K ; 2试求输入为2252)(t t t r ++=时,系统的稳态误差; 解:1该传递函数已经为标准形式 可见,v =0,这是一个0型系统 开环增益K =20;2讨论输入信号,2252)(t t t r ++=,即A =2,B =5,C=2 根据表3—4,误差∞=∞+∞+=+++=+++=212020520121Ka C K B K A e V p ss十、设系统特征方程为s 4+2s 3+3s 2+4s+5=0试用劳斯-赫尔维茨稳定判据判别该系统的稳定性;解:用劳斯-赫尔维茨稳定判据判别,a 4=1,a 3=2,a 2=3,a 1=4,a 0=5均大于零,且有所以,此系统是不稳定的; 十一、设系统特征方程为试用劳斯-赫尔维茨稳定判据判别该系统的稳定性;解:用劳斯-赫尔维茨稳定判据判别,a 4=1,a 3=6,a 2=12,a 1=10,a 0=3均大于零,且有 所以,此系统是稳定的; 十二、设系统特征方程为试用劳斯-赫尔维茨稳定判据判别该系统的稳定性;解:用劳斯-赫尔维茨稳定判据判别,a 4=1,a 3=5,a 2=2,a 1=4,a 0=3均大于零, 且有所以,此系统是不稳定的; 十三、设系统特征方程为试用劳斯-赫尔维茨稳定判据判别该系统的稳定性;解:1用劳斯-赫尔维茨稳定判据判别,a 3=2,a 2=4,a 1=6,a 0=1均大于零,且有所以,此系统是稳定的;十四、设系统开环传递函数如下,试绘制系统的对数幅频特性曲线;解:该系统开环增益K =30;有一个积分环节,即v =1;低频渐近线通过1,20lg30这点,斜率为-20dB/dec ;有一个惯性环节,对应转折频率为5002.011==w ,斜率增加-20dB/dec;系统对数幅频特性曲线如下所示;20lg30十五、设系统开环传递函数如下,试绘制系统的对数幅频特性曲线;解:该系统开环增益K =100;有一个积分环节,即v =1;低频渐近线通过1,20lg100这点,即通过1,40这点斜率为-20dB/dec ; 有两个惯性环节,对应转折频率为101.011==w ,10001.012==w ,斜率分别增加-20dB/dec系统对数幅频特性曲线如下所示;十六、设系统开环传递函数如下,试绘制系统的对数幅频特性曲线;解:该系统开环增益K =1;无积分、微分环节,即v =0,低频渐近线通过1,20lg1这点,即通过1,0这点斜率为0dB/dec ;有一个一阶微分环节,对应转折频率为101.011==w ,斜率增加20dB/dec;系统对数幅频特性曲线如下所示;dec十七、如下图所示,将方框图化简,并求出其传递函数;解:十八、如下图所示,将方框图化简,并求出其传递函数; 解:十九、如下图所示,将方框图化简,并求出其传递函数;L /dB20 dB / dec 10rad/s一一H 1G 1 G 2H 2 RSCS一 一H 1/G 2 G 1 G 2H 2RS CS一 H 1/G 2 G 1 RS CS G 2 1+ G 2H 2 一H 1/G 2RSCS G 1G 2 1+ G 2H 2 RSCSG 1G 2 1+ G 2H 2+G 1H 1解:三、简答题共16分1.4分已知系统的传递函数为2432s s ++,求系统的脉冲响应表达式;2.4分已知单位反馈系统的开环传递函数为K s s ()71+,试问该系统为几型系统系统的单位阶跃响应稳态值为多少3.4分已知二阶欠阻尼系统的单位阶跃响应如下,如果将阻尼比ζ增大但不超过1,请用文字和图形定性说明其单位阶跃响应的变化;4.4分已知各系统的零点o 、极点x 分布分别如图所示,请问各个系统是否有非主导极点,若有请在图上标出; 四、计算题本大题共6小题,共44分一 一 G 1G 3H 1 RSCSG 2H 1一 H 1 G 3 RSCSG 1G 2 1+ G 2H 1RSCSG 1G 2G 31+ G 2H 1+ G 1G 2H 1一一G 1G 3RSCSG 2H 11.7分用极坐标表示系统14212s s ++的频率特性要求在ω→∞、ω=0、ω=ωn 等点准确表示,其余定性画出;2.7分求如下系统Rs 对Cs 的传递函数,并在图上标出反馈通道、顺馈通道;3.6分已知系统的调节器为问是否可以称其为PID 调节器,请说明理由;4.8分求如图所示机械网络的传递函数,其中X 为输入位移,Y 为输出位移;5.10分已知单位反馈闭环系统的开环传递函数为40110011s s s (.)(.)++,请绘出频率特性对数坐标图Bode 图,并据图评价系统的稳定性、动态性能和静态性能要说明理由;6.6分请写出超前校正装置的传递函数,如果将它用于串联校正,可以改善系统什么性能 三、简答题共16分1.24311132s s s s ++=++-+ gt=e -t -e -3t ,t ≥0 2.Ⅰ型;稳态值等于13.上升时间变大;超调量减少;调节时间减小大体上;4.无非主导极点;非主导极点;非主导极点四、计算题共44分1.ω→∞点ω=0点ωn=点曲线大体对2.C sR s G G GG Gf() ()() =++13.6分G0s=T3+T4+T3T4s+1/sG 0s 由比例部分T 3+T 4、微分部分T 3T 4s 及积分部分1/s 相加而成 4.8分B ( )xy Ky --=0 Gs=Ts Ts +1,T=B/k 5.开环传递函数在复半平面无极点,据图相位裕度为正,幅值裕度分贝数为正,根据乃奎斯特判据,系统稳定;系统为Ⅰ型,具有良好的静态性能;相位裕度约为60度,具有良好的动态性能;s=K Ts Tsαα++≥111,可增加相位裕度,调整频带宽度;设系统的特征方程为DS =S 5+3S 4+4S 3+12S 2-5S-15 试用Routh 表判别系统的稳定性,并说明该系统具有正实部特征根的个数; 解:根据特征方程的系数,列Routh 表如下:S 5 1 4-5 0S 4 3 12 -15 0 S 3由第二行各元素得辅助方程2p=4,p=2FS= 3S 4+12S 2-15=0 取FS 对S 的导数,则得新方程12S3+24S=0得如下的Routh表S5 1 4 -5 0S4 3 12 -15 0S312 24 0 0S2 6 -15 0S154 0S0-15 符号改变一次,系统不稳定该系统具有正实部特征根个数为1;。
机械工程控制基础考试题及答案

机械工程控制基础考试题及答案机械工程控制基础是机械工程专业中非常重要的一个方面,掌握该领域的基本知识对机械工程师的工作至关重要。
在进行机械工程控制基础考试时,掌握学科基础知识与技巧应是首要准备,同样重要的还有解题能力。
因此,我们在此提供几道机械工程控制基础考试题及答案供大家参考。
1. 下列哪些控制系统是模糊控制系统?A. 摆线刀切削力控制系统B. 滤波器控制系统C. 股票市场交易系统D. 空调控制系统正确答案:A、C、D。
模糊控制系统是一种以模糊逻辑为基础,实现对复杂非线性系统的控制的一种方法。
股票市场交易系统属于复杂非线性系统,可以用模糊控制系统进行控制。
2. 控制系统的传递函数为:G(s) = 1 / [(s + 1)(s + 3)],求其单位阶跃响应。
正确答案:G(s)的单位阶跃响应为:Y(s) = [1 / (s + 1)] - [1 / (s + 3)],通过部分分式分解得到Y(t) = 1/2 - 1/2e^(-2t)。
因此,该系统的单位阶跃响应为Y(t) = 1/2 - 1/2e^(-2t)。
3. 下列哪个量不是PID控制器中的一个参数?A. 比例系数B. 积分时间C. 微分时间D. 控制信号正确答案:D。
PID控制器包括比例控制、积分控制和微分控制三个部分,分别由比例系数、积分时间和微分时间控制。
4. 一个反馈控制系统的开环传递函数为:G(s) = 1 / (s -1),闭环传递函数为:H(s) = G(s) / (1 + G(s)), 求该控制系统的稳态误差。
正确答案:该控制系统的稳态误差为0。
5. 已知一个控制系统稳定,其零极点分布情况如下:零点为s= -1, -2;极点为s = -3, -4,判断该系统稳定类型。
正确答案:由于该控制系统的极点均位于左半平面,因此该控制系统稳定。
6. 下列哪种控制模式比例带宽越大,相对带宽越小?A. 位置控制模式B. 速度控制模式C. 加速度控制模式D. 跟踪控制模式正确答案:B。
(完整版)机械控制工程基础复习题及参考答案

机械控制工程基础一、单项选择题:1. 某二阶系统阻尼比为0,则系统阶跃响应为 [ ]A. 发散振荡B. 单调衰减C. 衰减振荡D. 等幅振荡2. 一阶系统G(s)=1+Ts K的时间常数T 越小,则系统的输出响应达到稳态值的时间[ ]A .越长B .越短C .不变D .不定 3. 传递函数反映了系统的动态性能,它与下列哪项因素有关? [ ]A.输入信号B.初始条件C.系统的结构参数D.输入信号和初始条件4.惯性环节的相频特性)(ωθ,当∞→ω时,其相位移)(∞θ为 [ ]A .-270°B .-180°C .-90°D .0° 5.设积分环节的传递函数为G(s)=s1,则其频率特性幅值M(ω)= [ ] A.ωKB. 2K ωC. ω1D. 21ω6. 有一线性系统,其输入分别为u 1(t)和u 2(t)时,输出分别为y 1(t)和y 2(t)。
当输入为a 1u 1(t)+a 2u 2(t)时(a 1,a 2为常数),输出应为 [ ]A. a 1y 1(t)+y 2(t)B. a 1y 1(t)+a 2y 2(t)C. a 1y 1(t)-a 2y 2(t)D. y 1(t)+a 2y 2(t)7.拉氏变换将时间函数变换成 [ ]A .正弦函数B .单位阶跃函数C .单位脉冲函数D .复变函数8.二阶系统当0<ζ<1时,如果减小ζ,则输出响应的最大超调量%σ将 [ ]A.增加B.减小C.不变D.不定9.线性定常系统的传递函数,是在零初始条件下 [ ]A .系统输出信号与输入信号之比B .系统输入信号与输出信号之比C .系统输入信号的拉氏变换与输出信号的拉氏变换之比D .系统输出信号的拉氏变换与输入信号的拉氏变换之比10.余弦函数cos t ω的拉氏变换是 [ ]A.ω+s 1B.22s ω+ω C.22s s ω+ D. 22s 1ω+ 11. 微分环节的频率特性相位移θ(ω)= [ ]A. 90°B. -90°C. 0°D. -180°12. II 型系统开环对数幅频渐近特性的低频段斜率为 [ ]A. -40(dB/dec)B. -20(dB/dec)C. 0(dB/dec)D. +20(dB/dec) 13.令线性定常系统传递函数的分母多项式为零,则可得到系统的 [ ]A .代数方程B .特征方程C .差分方程D .状态方程14. 主导极点的特点是 [ ]A.距离实轴很远B.距离实轴很近C.距离虚轴很远D.距离虚轴很近15.采用负反馈连接时,如前向通道的传递函数为G(s),反馈通道的传递函数为H(s),则其等效传递函数为 [ ]A .)s (G 1)s (G + B .)s (H )s (G 11+C .)s (H )s (G 1)s (G + D .)s (H )s (G 1)s (G -二、填空题:1.线性定常系统在正弦信号输入时,稳态输出与输入的相位移随频率而变化的函数关系称为__ __。
机械工程控制基础 自动控制原理 期末考试题目 带答案

第一章1. 闭环控制系统中的反馈作用()A.依输入信号的大小而存在B.不一定存在C.必然存在D.一定不存在闭环系统一定存在反馈作用。
闭环的作用是(进行偏差控制)负反馈是将输出量引回输入端,与输入信号比较,比较的结果称为偏差。
系统的输出信号对控制作用的影响(闭环有)关于反馈的说法正确的是( D )A.反馈实质上就是信号的并联B.反馈就是输入信号与反馈信号相加C.反馈都是人为加入的D.反馈是输出以不同的方式对系统作用对于系统的抗干扰能力()A.开环强 B. 闭环强 C. 都强 D. 都不强关于闭环控制的不正确说法是()A.输入与输出信号只有顺向传递,没有反向联系B.输入与输出信号既有顺向传递,又有反向联系C.闭环控制精度高,抗干扰性好D.闭环控制引入反馈,参数选择不当不易稳定2.控制系统是由控制器和被控对象组成。
控制系统所要操纵的对象称为被控对象。
3.作为系统开环不振荡。
开环控制系统的控制信号取决于()A.系统的实际输出。
B.系统的实际输出与理想输出之差C.输入与输出之差D.输入4.如果系统的被控量随着输入量的变化而变化,则称为随动系统5.负反馈控制原理是将输出信号引回输入端,与输入信号比较,利用所得的偏差信号进行控制,使偏差减小或消除。
6. 某系统的微分方程为.3()()()()o o o ix t x t x t x t-+=,则它是非线性系统。
系统的动态方程为...2()()()()x t x t x t y t++=,则该系统为非线性系统。
7.以下几个微分方程表示的系统中,属于线性定常系统的是...222 o o o i x x x x ++=某系统的微分方程为...33()2()()()o o o ix t x t x t x t-+=,则它是(D )A.线性定常系统B.线性系统C .非线性时变系统D .非线性系统系统的动态方程为'''()4()3()()x t x t x t y t ++=,则该系统为 线性 系统。
2机械控制工程基础第二章答案
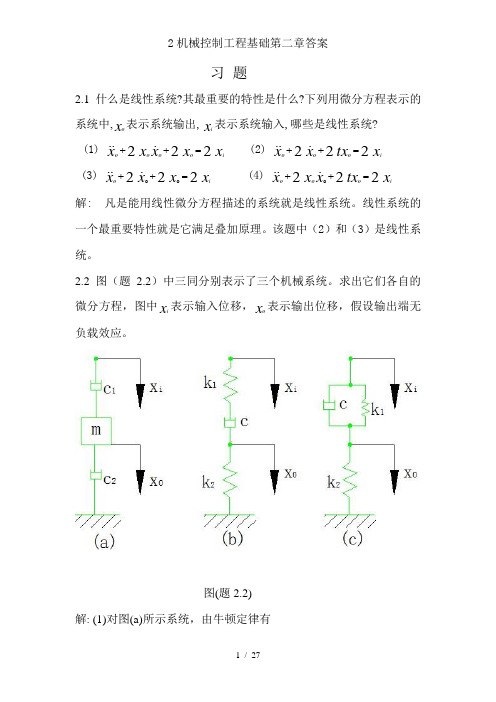
习 题2.1 什么是线性系统?其最重要的特性是什么?下列用微分方程表示的系统中,x o 表示系统输出,x i 表示系统输入,哪些是线性系统? (1) x x x x x ioooo 222=++ (2) x tx x xiooo222=++ (3) x x x xio 222oo=++ (4) x tx x x xiooo222o=++ 解: 凡是能用线性微分方程描述的系统就是线性系统。
线性系统的一个最重要特性就是它满足叠加原理。
该题中(2)和(3)是线性系统。
2.2 图(题2.2)中三同分别表示了三个机械系统。
求出它们各自的微分方程,图中x i 表示输入位移,x o 表示输出位移,假设输出端无负载效应。
图(题2.2) 解: (1)对图(a)所示系统,由牛顿定律有xm x c x x c ioo2o1)(=-- 即x c x c c xm i121oo )(=++ (2)对图(b)所示系统,引入一中间变量x,并由牛顿定律有)1()()(1x xc k x x oi-=- )2()(2x k x xc oo=-消除中间变量有x ck x k k xk k c io121o21)(=-- (3)对图(c)所示系统,由牛顿定律有 x k x x k x xc ooioi21)()(=-+-即x k x c x k k xc iioo121)(+=++ 2.3求出图(题2.3)所示电系统的微分方程。
图(题2.3)解:(1)对图(a)所示系统,设i 1为流过R 1的电流,i 为总电流,则有⎰+=idt Ci R u o122i R u u o i 11=-dti i Cu u oi)(111⎰-=-消除中间变量,并化简有u R C u CC R R uR C u R C u C C R R u R C iiiooo12211221222121211)()1(1+++=-+++(2)对图(b)所示系统,设i 为电流,则有⎰++=idtC i R u u oi111⎰+=i R idt Cu o221 消除中间变量,并化简有u Cu R u C C u R R iioo2221211)11()(+=+++2.4 求图(题2.4)所示机械系统的微分方程。
2机械控制工程基础第二章答案

习 题2.1 什么是线性系统其最重要的特性是什么下列用微分方程表示的系统中,x o 表示系统输出,x i 表示系统输入,哪些是线性系统 (1) x x x x x ioooo 222=++&&& (2) x tx x xiooo222=++&&& (3) x x x x io222oo=++&&& (4) x tx x x xiooo222o=++&&& 解: 凡是能用线性微分方程描述的系统就是线性系统。
线性系统的一个最重要特性就是它满足叠加原理。
该题中(2)和(3)是线性系统。
2.2 图(题2.2)中三同分别表示了三个机械系统。
求出它们各自的微分方程,图中x i 表示输入位移,x o 表示输出位移,假设输出端无负载效应。
图(题2.2) 解: (1)对图(a)所示系统,由牛顿定律有 即xc x c c x m i&&&&121oo )(=++ (2)对图(b)所示系统,引入一中间变量x,并由牛顿定律有 消除中间变量有(3)对图(c)所示系统,由牛顿定律有 即x k x c x k k x c iioo121)(+=++&&2.3求出图(题2.3)所示电系统的微分方程。
图(题2.3)解:(1)对图(a)所示系统,设i 1为流过R 1的电流,i 为总电流,则有 消除中间变量,并化简有u R C u CC R R u R C u R C u C C R R u R C iiiooo12211221222121211)()1(1+++=-+++&&&&&&&(2)对图(b)所示系统,设i 为电流,则有 消除中间变量,并化简有2.4 求图(题2.4)所示机械系统的微分方程。
图中M 为输入转矩,C m 为圆周阻尼,J 为转动惯量。
2机械控制工程基础第二章答案
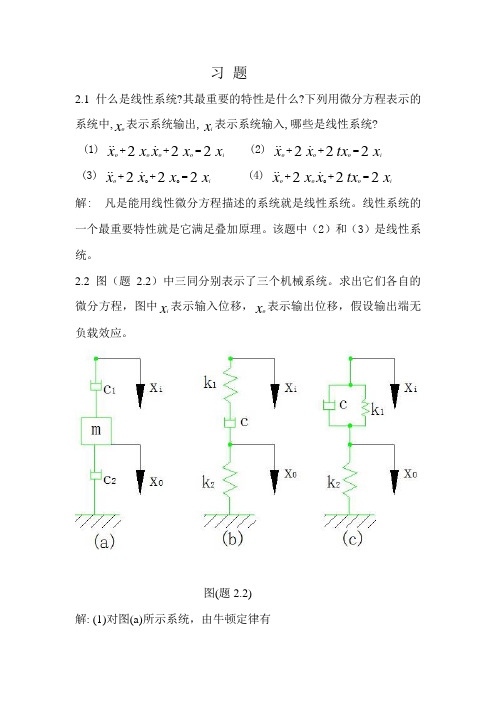
习 题2.1 什么是线性系统?其最重要的特性是什么?下列用微分方程表示的系统中,x o 表示系统输出,x i 表示系统输入,哪些是线性系统? (1) x x x x x ioooo 222=++ (2) x tx x xiooo222=++ (3) x x x xio 222oo=++ (4) x tx x x xiooo222o=++ 解: 凡是能用线性微分方程描述的系统就是线性系统。
线性系统的一个最重要特性就是它满足叠加原理。
该题中(2)和(3)是线性系统。
2.2 图(题2.2)中三同分别表示了三个机械系统。
求出它们各自的微分方程,图中x i 表示输入位移,x o 表示输出位移,假设输出端无负载效应。
图(题2.2) 解: (1)对图(a)所示系统,由牛顿定律有xm x c x x c ioo2o1)(=-- 即x c x c c xm i121oo )(=++ (2)对图(b)所示系统,引入一中间变量x,并由牛顿定律有)1()()(1x xc k x x oi-=- )2()(2x k x xc oo=-消除中间变量有x ck x k k xk k c io121o21)(=-- (3)对图(c)所示系统,由牛顿定律有 x k x x k x xc ooioi21)()(=-+-即x k x c x k k xc iioo121)(+=++ 2.3求出图(题2.3)所示电系统的微分方程。
图(题2.3)解:(1)对图(a)所示系统,设i 1为流过R 1的电流,i 为总电流,则有⎰+=idt Ci R u o122i R u u o i 11=-dti i Cu u oi)(111⎰-=-消除中间变量,并化简有u R C u CC R R uR C u R C u C C R R u R C iiiooo12211221222121211)()1(1+++=-+++(2)对图(b)所示系统,设i 为电流,则有⎰++=idtC i R u u oi111⎰+=i R idt Cu o221 消除中间变量,并化简有u Cu R u C C u R R iioo2221211)11()(+=+++2.4 求图(题2.4)所示机械系统的微分方程。
机械工程控制基础期末试卷+答案 ()

一. 填空题(每小题2.5分,共25分)1. 对控制系统的基本要求一般可以归纳为稳定性、 和 。
2. 按系统有无反馈,通常可将控制系统分为 和 。
3. 在控制工程基础课程中描述系统的数学模型有 、 等。
4. 反映出稳态响应偏离系统希望值的程度,它用来衡量系统 的程度。
5. 一阶系统11Ts 的单位阶跃响应的表达是 。
6. 有系统的性能指标按照其类型分为时域性能指标和 。
7. 频率响应是线性定常系统对 输入的稳态响应。
8. 稳态误差不仅取决于系统自身的结构参数,而且与 的类型有关。
9. 脉冲信号可以用来反映系统的 。
10. 阶跃信号的拉氏变换是 。
二. 图1为利用加热器控制炉温的反馈系统(10分)炉温控制系统图1 炉温控制结构图试求系统的输出量、输入量、被控对象和系统各部分的组成,且画出原理方框图,说明其工作原理。
三、如图2为电路。
求输入电压i u 与输出电压0u 之间的微分方程, 并求该电路的传递函数(10分)图2Ru 0u iL Cu 0u i (a)(b)(c)四、求拉氏变换与反变换(10分)1.求[0.5]t te-(5分)2.求13[] (1)(2)ss s-++(5分)五、化简图3所示的框图,并求出闭环传递函数(10分)图3六、图4示机械系统由质量m 、阻尼系数C 、弹簧刚度K 和外力)(t f 组成的机械动力系统。
图4(a)中)(t x o 是输出位移。
当外力)(t f 施加3牛顿阶跃力后(恒速信号),记录仪上记录质量m 物体的时间响应曲线如图4(b )所示。
试求: 1)该系统的微分方程数学模型和传递函数;(5分) 2)该系统的自由频率n ω、阻尼比ξ;(2分)3)该系统的弹簧刚度质量m 、阻尼系数C 、弹簧刚度k ;(3分) 4)时间响应性能指标:上升时间s t 、调整时间r t 、稳态误差ss e (5分)。
1.0x 0图4(a) 机械系统 图4(b )响应曲线图4七、已知某系统是单位负反馈系统,其开环传递函数1510+=s G k ,则该系统在单位脉冲、单位阶跃和单位恒速信号(斜坡信号)作用下的稳态误差ss e 分别是多少?(10分)八、设有如图5所示的反馈控制系统,试求根据劳斯判据确定传递函数k 值的取值范围(10分)。
完整版机械工程控制期末考试试题和标准答案及评分标准模板

X i (s )J agX °(s)《机械工程控制基础》试题(A 卷)(考试时间:120分钟)、单项选择题(共10分,每小题2分)1.控制系统中,下列元件通常属于反馈元件的是 A.电压放大器;B .热电偶;C.液压马达; D •电动机;A.比例环节;B.惯性环节;C.积分环节;D. —阶微分环节; 3.二阶系统的时域性能指标上升时间 t r 、峰值时间t p 、调整时间t s 、最大超调量M p 和振荡次数N ,反应系统稳定性的是 ____________ 。
A. t r 、M p ; B. t p 、t s ; C. t r 、N ; D . M p 、N ;A. 1 ;B. 2;C. 3;D. 4 ;5. PID 校正是针对 ____________ 进行比例、积分和微分运算后形成的控制规律。
A.输入信号X j (t) ;B.输出信号x 0(t) ;C.误差信号e(t) ;D.偏差信号 (t);二、填空题(共20分,每空2分)6.1954年,我国科学家 _______________ 发表了《工程控制论》,奠定了控制工程的理论基础。
7. 对于受干扰的闭环系统,如果系统只受输入X't)作用时的输出是x 01(t),系统只受干扰n(t)作用时的输出是x °2(t),则系统同时受X i (t)和n(t)作用时的输出 X 0 (t) ______________ 。
8. 如图所示的信号流图, 前向通道的传递函数为 ___________ ,反馈通道有 _________ 条,系统 的传递函数为 __________ 。
2.某系统的传递函数是 G(s)(s 20.5),其中没有(s 1)(S s 1)环节。
4.某放大器的传递函数G(s)(Ts 1)1rad / s ,相频为 45,贝U T 的值为s(2s1)入时的稳态误差分别为 _________ 、__________ 。
期末复习题 机械控制工程考试试题与答案.doc

复习题参考答案一、单项选择题1. 开环系统与闭环系统最本质的区别是( A )A.开环系统的输出对系统无控制作用,闭环系统的输出对系统有控制作用B.开环系统的输入对系统无控制作用,闭环系统的输入对系统有控制作用C.开环系统不一定有反馈回路,闭环系统有反馈回路D.开环系统不一定有反馈回路,闭环系统也不一定有反馈回路 2. 若f t t t (),,=⎧⎨⎩⎪00515≤<≥,则L f t [()]=( B )A.e ss - B.e s s-5C.1sD.15s e s3. 已知f t t ().,=+051其L f t [()]=( C )A.s s +052. B.052.s C.1212s s + D.12s4. 若f t te t()=-2,则L f t [()]=( B )A.12s +B.122()s + C.12s -D.122()s - 5. 线性系统与非线性系统的根本区别在于( C )A.线性系统微分方程的系数为常数,而非线性系统微分方程的系数为时变函数B.线性系统只有一个外加输入,而非线性系统有多个外加输入C.线性系统满足迭加原理,非线性系统不满足迭加原理D.线性系统在实际系统中普遍存在,而非线性系统在实际中存在较少 6. 系统方框图如图示,则该系统的开环传递函数为( B )A.1051s + B.2051s s +C.10251s s ()+D.2s7. 二阶系统的极点分别为s s 12054=-=-.,,系统增益为5,则其传递函数为( D ) A.2054(.)()s s --B.2054(.)()s s ++C.5054(.)()s s ++ D.10054(.)()s s ++ 8. 某系统的传递函数为2s 5)s (G +=,则该系统的单位脉冲响应函数为( A ) A.52et-B.5t()R s ()C s 1051s +2sC.52e tD.5t9. 二阶欠阻尼系统的上升时间t r 定义为( C ) A.单位阶跃响应达到稳态值所需的时间B.单位阶跃响应从稳态值的10%上升到90%所需的时间C.单位阶跃响应从零第一次上升到稳态值时所需的时间D.单位阶跃响应达到其稳态值的50%所需的时间10. 系统类型λ、开环增益K 对系统稳态误差的影响为( A ) A.系统型次λ越高,开环增益K 越大,系统稳态误差越小 B.系统型次λ越低,开环增益K 越大,系统稳态误差越小 C.系统型次λ越高,开环增益K 越小,系统稳态误差越小 D.系统型次λ越低,开环增益K 越小,系统稳态误差越小 11. 一系统的传递函数为G s KTs ()=+1,则该系统时间响应的快速性( C ) A.与K 有关 B.与K 和T 有关C.与T 有关D.与输入信号大小有关12. 一闭环系统的开环传递函数为G s s s s s ()()()()=+++83232,则该系统为( C )A.0型系统,开环增益为8B.I 型系统,开环增益为8C.I 型系统,开环增益为4D.0型系统,开环增益为413. 瞬态响应的性能指标是根据哪一种输入信号作用下的瞬态响应定义的( B ) A.单位脉冲函数 B.单位阶跃函数 C.单位正弦函数 D.单位斜坡函数 14.二阶系统的传递函数为G s Ks s ()=++2212,当K 增大时,其( C ) A.无阻尼自然频率ωn 增大,阻尼比ζ增大 B.无阻尼自然频率ωn 增大,阻尼比ζ减小C.无阻尼自然频率ωn 减小,阻尼比ζ减小D.无阻尼自然频率ωn 减小,阻尼比ζ增大15. 所谓最小相位系统是指( B )A.系统传递函数的极点均在S 平面左半平面B.系统开环传递函数的所有零点和极点均在S 平面左半平面C.系统闭环传递函数的所有零点和极点均在S 平面右半平面D.系统开环传递函数的所有零点和极点均在S 平面右半平面 16. 一系统的传递函数为G s s ()=+102,则其截止频率ωb 为( A ) A. 2rad s / B.0.5rad s / C.5rad s / D.10rad s /17. 一系统的传递函数为G s Ks Ts ()()=+1,则其相位角ϕω()可表达为( B )A.--tg T 1ωB.-︒--901tg T ωC.901︒--tg T ω D.tg T -1ω18. 一系统的传递函数为G s s ()=+22,当输入r t t ()sin =22时,则其稳态输出的幅值为( A ) A.2B.22/C.2D.419. 一单位反馈系统的开环传递函数为G s Ks s s ()()()=++12,当K 增大时,对系统性能能的影响是( A ) A.稳定性降低 B.频宽降低 C.阶跃输入误差增大 D.阶跃输入误差减小 20. 一单位反馈系统的开环Bode 图已知,其幅频特性在低频段是一条斜率为-20dB dec/的渐近直线,且延长线与0dB 线的交点频率为ωc =5,则当输入为r t t ().=05时,其稳态误差为( A ) A.0.1 B.0.2 C.0 D.0.5 21. 利用乃奎斯特稳定性判据判断系统的稳定性时,Z P N =-中的Z 表示意义为( D ) A.开环传递函数零点在S 左半平面的个数 B.开环传递函数零点在S 右半平面的个数 C.闭环传递函数零点在S 右半平面的个数 D.闭环特征方程的根在S 右半平面的个数22. 关于劳斯—胡尔维茨稳定性判据和乃奎斯特稳定性判据,以下叙述中正确的是( B )A.劳斯—胡尔维茨判据属代数判据,是用来判断开环系统稳定性的B.乃奎斯特判据属几何判据,是用来判断闭环系统稳定性的C.乃奎斯特判据是用来判断开环系统稳定性的D.以上叙述均不正确23.以下频域性能指标中根据开环系统来定义的是( D ) A.截止频率ωb B.谐振频率ωr 与谐振峰值M r C.频带宽度 D.相位裕量γ与幅值裕量kg 24. 一单位反馈系统的开环传递函数为G s Ks s K ()()=+,则该系统稳定的K 值范围为( A )A.K >0B.K >1C.0<K <10D. K >-1 25. 对于开环频率特性曲线与闭环系统性能之间的关系,以下叙述中不正确的有( A ) A.开环频率特性的低频段表征了闭环系统的稳定性 B.中频段表征了闭环系统的动态特性 C.高频段表征了闭环系统的抗干扰能力D.低频段的增益应充分大,以保证稳态误差的要求26. 以下性能指标中不能反映系统响应速度的指标为( D ) A.上升时间t r B.调整时间t s C.幅值穿越频率ωcD.相位穿越频率ωg27. 当系统采用串联校正时,校正环节为G s s s c ()=++121,则该校正环节对系统性能的影响是( D )A.增大开环幅值穿越频率ωcB.增大稳态误差C.减小稳态误差D.稳态误差不变,响应速度降低 28. 串联校正环节G s As Bs c ()=++11,关于A 与B 之间关系的正确描述为( A ) A.若G c (s)为超前校正环节,则A >B >0B.若G c (s)为滞后校正环节,则A >B >0C.若G c (s)为超前—滞后校正环节,则A ≠BD.若G c (s)为PID 校正环节,则A=0,B >0 29.适合应用传递函数描述的系统是:( A )A 、单输入,单输出的线性定常系统;B 、单输入,单输出的线性时变系统;C 、单输入,单输出的定常系统;D 、非线性系统。
2机械控制工程基础第二章答案

习 题什么是线性系统其最重要的特性是什么下列用微分方程表示的系统中,x o 表示系统输出,x i 表示系统输入,哪些是线性系统 (1) x x x x x ioooo 222=++&&& (2) x tx x xiooo222=++&&& (3) x x x x io222oo=++&&& (4) x tx x x xiooo222o=++&&& 解: 凡是能用线性微分方程描述的系统就是线性系统。
线性系统的一个最重要特性就是它满足叠加原理。
该题中(2)和(3)是线性系统。
图(题)中三同分别表示了三个机械系统。
求出它们各自的微分方程,图中x i 表示输入位移,x o 表示输出位移,假设输出端无负载效应。
图(题 解: (1)对图(a)所示系统,由牛顿定律有 即xc x c c x m i&&&&121oo )(=++ (2)对图(b)所示系统,引入一中间变量x,并由牛顿定律有 消除中间变量有(3)对图(c)所示系统,由牛顿定律有 即x k x c x k k x c iioo121)(+=++&&求出图(题所示电系统的微分方程。
图(题)解:(1)对图(a)所示系统,设i 1为流过R 1的电流,i 为总电流,则有 消除中间变量,并化简有u R C u CC R R u R C u R C u C C R R u R C iiiooo12211221222121211)()1(1+++=-+++&&&&&&&(2)对图(b)所示系统,设i 为电流,则有 消除中间变量,并化简有求图(题所示机械系统的微分方程。
图中M 为输入转矩,C m 为圆周阻尼,J 为转动惯量。
解:设系统输入为M (即),输出θ(即),分别对圆盘和质块进行动力学分析,列写动力学方程如下:消除中间变量x,即可得到系统动力学方程KM M c Mm C R c k KJ c C km R cJ mC mJ mmm++=++-++++&&&&&&&&&θθθθ)(22)()()4( 输出y(t)与输入x(t)的关系为y(t)= 2x(t)+x 3(t)。
机械工程控制基础题库2

第二章1. 在转速、电流双闭环调速系统中,速度调节器通常采用[ B ]调节器。
a.比例 b.比例积分c.比例微分 d.比例积分微分2. 在直流电动机的电枢回路中,以电流为输出,电压为输入,两者之间的传递函数是[ A ]A.比例环节 B.积分环节C.惯性环节 D.微分环节3. 在转速、电流双闭环调速系统中,速度调节器通常采用[ B ]调节器。
A.比例 B.比例积分C.比例微分 D.比例积分微分4. 振荡环节的传递函数为( a )。
A. ωn /(S2+2ξωn S+1) (0<ξ<1) ;B. ωn /(S2+2ξωn S+1) (ξ=1);5.函数b + ce-at(t≥0)的拉氏变换是( c )。
A、bS + c/(S+1) ;B、 bS – c/(S+a) ;C、 b/S + c/(S+a) ;D、 b/S + c/(S-a)6.某机械平移系统如图所示,则其传递函数的极点数P 为( )。
A. 3 ; B. 4 ; C.5 ; D. 67. cos2t 的拉普拉斯变换式是 〔 〕 A. S 1B.442+SC.42+S SD. 21S8. 已知 f(t)=0.5t+1,其L[f(t)]=( ): A .S+0.5S 2 B. 0.5S 2 C.S S1212+ D. S 21 9.下列函数既可用初值定理求其初值又可用终值定理求其终值的为:( )。
A. 5/(S 2+25);B.5/(S 2+16);C. 1/(S-2);D.1/(S+2)10.函数b + ce -at (t ≥0)的拉氏变换是( )。
A 、 bS + c/(S+1) ;B 、bS – c/(S+a) ;C 、b/S + c/(S+a) ;D 、b/S + c/(S-a)11.振荡环节的传递函数为( )。
A.ωn /(S 2+2ξωn S+1) (0<ξ<1) ;B.ωn /(S 2+2ξωn S+1)(ξ=1);C. T 2/(T 2S 2+2ξTS+1) (0<ξ<1) ;D.1/[S (TS+1)]12.下列函数既可用初值定理求其初值又可用终值定理求其终值的为:( )。
2机械控制工程基础第二章答案解析
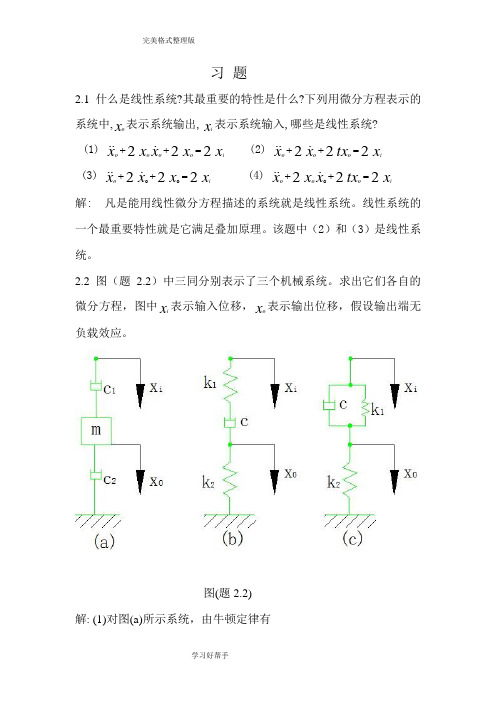
习 题2.1 什么是线性系统?其最重要的特性是什么?下列用微分方程表示的系统中,x o 表示系统输出,x i 表示系统输入,哪些是线性系统? (1) x x x x x ioooo 222=++ (2) x tx x xiooo222=++ (3) x x x xio 222oo=++ (4) x tx x x xiooo222o=++ 解: 凡是能用线性微分方程描述的系统就是线性系统。
线性系统的一个最重要特性就是它满足叠加原理。
该题中(2)和(3)是线性系统。
2.2 图(题2.2)中三同分别表示了三个机械系统。
求出它们各自的微分方程,图中x i 表示输入位移,x o 表示输出位移,假设输出端无负载效应。
图(题2.2) 解: (1)对图(a)所示系统,由牛顿定律有xm x c x x c ioo2o1)(=-- 即x c x c c xm i121oo )(=++ (2)对图(b)所示系统,引入一中间变量x,并由牛顿定律有)1()()(1x xc k x x oi-=- )2()(2x k x xc oo=-消除中间变量有x ck x k k xk k c io121o21)(=-- (3)对图(c)所示系统,由牛顿定律有 x k x x k x xc ooioi21)()(=-+-即x k x c x k k xc iioo121)(+=++ 2.3求出图(题2.3)所示电系统的微分方程。
图(题2.3)解:(1)对图(a)所示系统,设i 1为流过R 1的电流,i 为总电流,则有⎰+=idt Ci R u o122i R u u o i 11=-dti i Cu u oi)(111⎰-=-消除中间变量,并化简有u R C u CC R R uR C u R C u C C R R u R C iiiooo12211221222121211)()1(1+++=-+++(2)对图(b)所示系统,设i 为电流,则有⎰++=idtC i R u u oi111⎰+=i R idt Cu o221 消除中间变量,并化简有u Cu R u C C u R R iioo2221211)11()(+=+++2.4 求图(题2.4)所示机械系统的微分方程。
机械工程控制基础考试题及答案

填空题( 每空 1 分,共20 分)1.线性控制系统最重要的特色是能够应用___叠加__原理,而非线性控制系统则不能够。
2.反响控制系统是依照输入量和 __反响量 __的误差进行调治的控制系统。
3.在单位斜坡输入信号作用下,0 型系统的稳态误差e ss= ___。
4.当且仅当闭环控制系统特色方程的全部根的实部都是__负数__时,系统是牢固的。
5.方框图中环节的基本连接方式有串通连接、并联连接和__反响_连接。
6.线性定常系统的传达函数,是在_ 初始条件为零 ___时,系统输出信号的拉氏变换与输入信号的拉氏变换的比。
7.函数 te -at的拉氏变换为1。
( s a)28.线性定常系统在正弦信号输入时,稳态输出与输入的相位移随频率而变化的函数关系称为__相频特色 __。
9.积分环节的对数幅频特色曲线是一条直线,直线的斜率为__ -20__dB/ dec。
10.二阶系统的阻尼比ξ为_ 0_时,响应曲线为等幅振荡。
11.在单位斜坡输入信号作用下,Ⅱ型系统的稳态误差e ss=__0__。
12.0型系统对数幅频特色低频段渐近线的斜率为___0___dB/dec ,高度为 20lgKp 。
13.单位斜坡函数 t 的拉氏变换为 1 。
s214.依照系统输入量变化的规律,控制系统可分为 __恒值 __控制系统、 ___随动 ___ 控制系统和程序控制系统。
15.对于一个自动控制系统的性能要求能够概括为三个方面:稳定性、 __快速性 __和正确性。
16.系统的传达函数完好由系统的结构和参数决定,与__输入量、扰动量 __的形式没关。
17.决定二阶系统动向性能的两个重要参数是阻尼系数ξ和_无阻尼自然振荡频率w n 。
18.设系统的频率特色G(j ω )=R( ω )+jI( ω ), 则幅频特色|G(jω )|=R2 (w)I 2 (w) 。
19.解析稳态误差时,将系统分为 0 型系统、I 型系统、II 型系统,这是按开环传达函数的 __积分 __环节数来分类的。
(完整版)机械工程控制基础期末试卷+答案2

一. 填空题 (每小题 2.5 分,共 25 分)1. 对控制系统的基本要求一般可以归纳为稳定性、 和 。
2. 按系统有无反馈,通常可将控制系统分为 和 。
3. 在控制工程基础课程中描述系统的数学模型有 、 等。
4.反映出稳态响应偏离系统希望值的程度,它用来衡量系统 的程度5. 一阶系统 1的单位阶跃响应的表达是 。
Ts 16. 有系统的性能指标按照其类型分为时域性能指标和 。
7. 频率响应是线性定常系统对 输入的稳态响应。
8. 稳态误差不仅取决于系统自身的结构参数,而且与 的类型有关。
9. 脉冲信号可以用来反映系统的 。
10. 阶跃信号的拉氏变换是 。
图 1 为利用加热器控制炉温的反馈系炉统温(控制系10统分)图1 炉温控制结构图 试求系统的输出量、输入量、被控对象和系统各部分的组成,且画出原理方框图,说明 其工作原理。
三、如图 2 为电路。
求输入电压 u i 与输出电压 u 0之间的微分方程, 并求该电路的传递函数 ( 10 分)ui R u 0ui C Ru(a )(图b )2uiLCu(c )+热电偶 - +-U功放率大自偶调 压器电U g给定毫伏信号 U e电压 放加热器220Vf 减-速器可逆 电机四、求拉氏变换与反变换(10 分) 1.求l [0.5 te t](5 分)1 2.求l 1[ 3s(s 1)(s 2) ](5 分)五、化简图 3 所示的框图,并求出闭环传递函数(10 分)机械工程控制基础期末试卷X O(S) 图3机械工程控制基础期末试卷六、图 4 示机械系统由质量 m、阻尼系数 C、弹簧刚度 K 和外力f (t)组成的机械动力系统。
图 4(a)中x o(t)是输出位移。
当外力f (t)施加 3 牛顿阶跃力后(恒速信号),记录仪上记录质量 m 物体的时间响应曲线如图 4( b )所示。
试求:1)该系统的微分方程数学模型和传递函数;(5 分)2)该系统的自由频率n、阻尼比;(2 分)3)该系统的弹簧刚度质量 m、阻尼系数 C、弹簧刚度 k;(3 分)4)时间响应性能指标:上升时间t s 、调整时间t r 、稳态误差e ss(5 分)。
2机械控制工程基础第二章答案

习 题2.1 什么是线性系统其最重要的特性是什么下列用微分方程表示的系统中,x o 表示系统输出,x i 表示系统输入,哪些是线性系统 (1) x x x x x ioooo 222=++ (2) x tx x xiooo222=++ (3) x x x xio 222oo=++ (4) x tx x x xiooo222o=++ 解: 凡是能用线性微分方程描述的系统就是线性系统。
线性系统的一个最重要特性就是它满足叠加原理。
该题中(2)和(3)是线性系统。
2.2 图(题2.2)中三同分别表示了三个机械系统。
求出它们各自的微分方程,图中x i 表示输入位移,x o 表示输出位移,假设输出端无负载效应。
图(题2.2) 解: (1)对图(a)所示系统,由牛顿定律有 即x c x c c xm i121oo )(=++ (2)对图(b)所示系统,引入一中间变量x,并由牛顿定律有 消除中间变量有(3)对图(c)所示系统,由牛顿定律有 即x k x c x k k xc iioo121)(+=++ 2.3求出图(题2.3)所示电系统的微分方程。
图(题2.3)解:(1)对图(a)所示系统,设i 1为流过R 1的电流,i 为总电流,则有 消除中间变量,并化简有u R C u CC R R u R C uR C u C C R R u R C iiiooo12211221222121211)()1(1+++=-+++(2)对图(b)所示系统,设i 为电流,则有 消除中间变量,并化简有2.4 求图(题2.4)所示机械系统的微分方程。
图中M 为输入转矩,C m 为圆周阻尼,J 为转动惯量。
解:设系统输入为M (即),输出θ(即),分别对圆盘和质块进行动力学分析,列写动力学方程如下:消除中间变量x,即可得到系统动力学方程KM M c Mm C R c k KJ c C km R cJ mC mJ mmm++=++-++++ θθθθ)(22)()()4(2.5 输出y(t)与输入x(t)的关系为y(t)= 2x(t)+0.5x 3(t)。
机械工程控制基础》试卷及其答案

机械工程控制基础》试卷及其答案-CAL-FENGHAI.-(YICAI)-Company One120120701兰州机械控制工程基础课程考试试卷课程名称: 机械控制工程基础1;试卷编号:C 卷;考试时间:120分钟;考试形式:闭卷 试卷得分表题 号 一 二 三 四 五 六 总 分 应得分 实得分一、填空( 每小题4分,共20分)得分评卷人 复查人1、某系统传递函数为21s ,在输入t t r 3sin 2)( 作用下,输出稳态分量的幅值为 。
2、谐波输入下,系统的 响应称为频率响应。
3、已知某系统开环传递函数的零点都在左半S 平面,其开环频率特性曲线如图1.5所示,则该系统位于右半S 平面的极点数有 个。
4、控制系统的基本要求主要有: ,, 。
5、Nyquist 图上以原点为圆心的单位圆对应于Bode 图上的 线。
二、选择题( 每小题3分,共30分 )1、关于反馈的说法,正确的是( )A .反馈实质上就是信号的并联B .反馈都是人为加入的C .正反馈就是输入信号与反馈相加D .反馈就是输出以不同方式作用于系统2、关于系统模型的说法,正确的是( )A .每个系统只有一种数据模型B .动态模型在一定条件下可简化为静态模型C .动态模型比静态模型好D .静态模型比动态模型好3、某环节的传递函数为s1,则该环节为( ) 学院专业班级 年级姓名 学号装订线(答题不得超过此线)A. 惯性环节B. 积分环节C .微分环节D .比例环节4、系统的传递函数( )A .与外界无关B .反映了系统、输出、输入三者之间的关系C .完全反映了系统的动态特性 D. 与系统的初始状态有关5、二阶欠阻尼系统的上升时间为( )A .阶跃响应曲线第一次达到稳定值的98%的时间B .阶跃响应曲线达到稳定值的时间C .阶跃响应曲线第一次达到稳定值的时间D .阶跃响应曲线达到稳定值的98%的时间6、关于线性系统时间响应,说法正确的是( )A .时间响应就是系统输出的稳态值B .由单位阶跃响应和单位脉冲响应组成C .由强迫响应和自由响应组成D .与系统初始状态无关7、系统的单位脉冲响应函数为t et w 2.03)(-=,则系统的传递函数为( ) A .2.03)(+=S s G B. 32.0)(+=S s G C .2.06.0)(+=S s G D .36.0)(+=S s G 8、以下系统中,属于最小相位系统的是( )A .s s G 01.011)(-=B .s s G 01.011)(+=C .101.01)(-=s s G D .)1.01(1)(s s s G -= 9、一个线性系统稳定与否取决于( )A .系统的结构和参数B .系统的输入C .系统的干扰D .系统的初始状态10、一个系统稳定的充要条件是( )A .系统的全部极点都在[S]平面的右半平面内B .系统的全部极点都在[S]平面的上半平面内C .系统的全部极点都在[S]平面的左半平面内D .系统的全部极点都在[S]平面的下半平面内 三、系统结构图如下图所示,求)()(s R s Y (15分)四、系统在静止平衡状态下,加入输入信号t t r +=1)(,测得响应为9.09.0)(10+-=-t e t t C试求系统的传递函数。
期末复习题 机械控制工程考试试题与答案.doc

复习题参考答案一、单项选择题1. 开环系统与闭环系统最本质的区别是( A )A.开环系统的输出对系统无控制作用,闭环系统的输出对系统有控制作用B.开环系统的输入对系统无控制作用,闭环系统的输入对系统有控制作用C.开环系统不一定有反馈回路,闭环系统有反馈回路D.开环系统不一定有反馈回路,闭环系统也不一定有反馈回路 2. 若f t t t (),,=⎧⎨⎩⎪00515≤<≥,则L f t [()]=( B )A.e ss - B.e s s-5C.1sD.15s e s3. 已知f t t ().,=+051其L f t [()]=( C )A.s s +052. B.052.s C.1212s s + D.12s4. 若f t te t()=-2,则L f t [()]=( B )A.12s +B.122()s + C.12s -D.122()s - 5. 线性系统与非线性系统的根本区别在于( C )A.线性系统微分方程的系数为常数,而非线性系统微分方程的系数为时变函数B.线性系统只有一个外加输入,而非线性系统有多个外加输入C.线性系统满足迭加原理,非线性系统不满足迭加原理D.线性系统在实际系统中普遍存在,而非线性系统在实际中存在较少 6. 系统方框图如图示,则该系统的开环传递函数为( B )A.1051s + B.2051s s +C.10251s s ()+D.2s7. 二阶系统的极点分别为s s 12054=-=-.,,系统增益为5,则其传递函数为( D ) A.2054(.)()s s --B.2054(.)()s s ++C.5054(.)()s s ++ D.10054(.)()s s ++ 8. 某系统的传递函数为2s 5)s (G +=,则该系统的单位脉冲响应函数为( A ) A.52et-B.5t()R s ()C s 1051s +2sC.52e tD.5t9. 二阶欠阻尼系统的上升时间t r 定义为( C ) A.单位阶跃响应达到稳态值所需的时间B.单位阶跃响应从稳态值的10%上升到90%所需的时间C.单位阶跃响应从零第一次上升到稳态值时所需的时间D.单位阶跃响应达到其稳态值的50%所需的时间10. 系统类型λ、开环增益K 对系统稳态误差的影响为( A ) A.系统型次λ越高,开环增益K 越大,系统稳态误差越小 B.系统型次λ越低,开环增益K 越大,系统稳态误差越小 C.系统型次λ越高,开环增益K 越小,系统稳态误差越小 D.系统型次λ越低,开环增益K 越小,系统稳态误差越小 11. 一系统的传递函数为G s KTs ()=+1,则该系统时间响应的快速性( C ) A.与K 有关 B.与K 和T 有关C.与T 有关D.与输入信号大小有关12. 一闭环系统的开环传递函数为G s s s s s ()()()()=+++83232,则该系统为( C )A.0型系统,开环增益为8B.I 型系统,开环增益为8C.I 型系统,开环增益为4D.0型系统,开环增益为413. 瞬态响应的性能指标是根据哪一种输入信号作用下的瞬态响应定义的( B ) A.单位脉冲函数 B.单位阶跃函数 C.单位正弦函数 D.单位斜坡函数 14.二阶系统的传递函数为G s Ks s ()=++2212,当K 增大时,其( C ) A.无阻尼自然频率ωn 增大,阻尼比ζ增大 B.无阻尼自然频率ωn 增大,阻尼比ζ减小C.无阻尼自然频率ωn 减小,阻尼比ζ减小D.无阻尼自然频率ωn 减小,阻尼比ζ增大15. 所谓最小相位系统是指( B )A.系统传递函数的极点均在S 平面左半平面B.系统开环传递函数的所有零点和极点均在S 平面左半平面C.系统闭环传递函数的所有零点和极点均在S 平面右半平面D.系统开环传递函数的所有零点和极点均在S 平面右半平面 16. 一系统的传递函数为G s s ()=+102,则其截止频率ωb 为( A ) A. 2rad s / B.0.5rad s / C.5rad s / D.10rad s /17. 一系统的传递函数为G s Ks Ts ()()=+1,则其相位角ϕω()可表达为( B )A.--tg T 1ωB.-︒--901tg T ωC.901︒--tg T ω D.tg T -1ω18. 一系统的传递函数为G s s ()=+22,当输入r t t ()sin =22时,则其稳态输出的幅值为( A ) A.2B.22/C.2D.419. 一单位反馈系统的开环传递函数为G s Ks s s ()()()=++12,当K 增大时,对系统性能能的影响是( A ) A.稳定性降低 B.频宽降低 C.阶跃输入误差增大 D.阶跃输入误差减小 20. 一单位反馈系统的开环Bode 图已知,其幅频特性在低频段是一条斜率为-20dB dec/的渐近直线,且延长线与0dB 线的交点频率为ωc =5,则当输入为r t t ().=05时,其稳态误差为( A ) A.0.1 B.0.2 C.0 D.0.5 21. 利用乃奎斯特稳定性判据判断系统的稳定性时,Z P N =-中的Z 表示意义为( D ) A.开环传递函数零点在S 左半平面的个数 B.开环传递函数零点在S 右半平面的个数 C.闭环传递函数零点在S 右半平面的个数 D.闭环特征方程的根在S 右半平面的个数22. 关于劳斯—胡尔维茨稳定性判据和乃奎斯特稳定性判据,以下叙述中正确的是( B )A.劳斯—胡尔维茨判据属代数判据,是用来判断开环系统稳定性的B.乃奎斯特判据属几何判据,是用来判断闭环系统稳定性的C.乃奎斯特判据是用来判断开环系统稳定性的D.以上叙述均不正确23.以下频域性能指标中根据开环系统来定义的是( D ) A.截止频率ωb B.谐振频率ωr 与谐振峰值M r C.频带宽度 D.相位裕量γ与幅值裕量kg 24. 一单位反馈系统的开环传递函数为G s Ks s K ()()=+,则该系统稳定的K 值范围为( A )A.K >0B.K >1C.0<K <10D. K >-1 25. 对于开环频率特性曲线与闭环系统性能之间的关系,以下叙述中不正确的有( A ) A.开环频率特性的低频段表征了闭环系统的稳定性 B.中频段表征了闭环系统的动态特性 C.高频段表征了闭环系统的抗干扰能力D.低频段的增益应充分大,以保证稳态误差的要求26. 以下性能指标中不能反映系统响应速度的指标为( D ) A.上升时间t r B.调整时间t s C.幅值穿越频率ωcD.相位穿越频率ωg27. 当系统采用串联校正时,校正环节为G s s s c ()=++121,则该校正环节对系统性能的影响是( D )A.增大开环幅值穿越频率ωcB.增大稳态误差C.减小稳态误差D.稳态误差不变,响应速度降低 28. 串联校正环节G s As Bs c ()=++11,关于A 与B 之间关系的正确描述为( A ) A.若G c (s)为超前校正环节,则A >B >0B.若G c (s)为滞后校正环节,则A >B >0C.若G c (s)为超前—滞后校正环节,则A ≠BD.若G c (s)为PID 校正环节,则A=0,B >0 29.适合应用传递函数描述的系统是:( A )A 、单输入,单输出的线性定常系统;B 、单输入,单输出的线性时变系统;C 、单输入,单输出的定常系统;D 、非线性系统。
