人教版数学八年级下册压轴题含答案
初二下学期压轴题练习- 勾股定理的应用(含答案)

专题04勾股定理的应用一.选择题1.(2021秋•朝阳区期末)如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm.若这支铅笔长为18cm,则这只铅笔在笔筒外面部分长度不可能的是()A.3cm B.5cm C.6cm D.8cm2.(2020秋•碑林区校级期末)有长为5cm,13cm的两根木条,现想找一根木条和这两根木条首尾顺次相连组成直角三角形,则下列木条长度适合的是()A.10cm B.12cm C.18cm D.20cm3.(2021秋•兴平市期中)国庆假期间,妍妍与同学去玩寻宝游戏,按照藏宝图,她从门口A处出发先往东走9km,又往北走3km,遇到障碍后又往西走7km,再向北走2km,再往东走了4km,发现走错了之后又往北走1km,最后再往西走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是()A.3km B.10km C.6km D.km4.(2021秋•赣榆区期中)在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何?它的意思是:一根竹子原高一丈(10尺),中部一处折断,竹梢触地面处离竹根3尺,试问折断处离地面()尺.A.4B.3.6C.4.5D.4.555.(2020秋•长沙期末)如图,有一个绳索拉直的木马秋千,绳索AB的长度为5米,若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,则此时木马上升的高度为()A.1米B.米C.2米D.4米6.(2021秋•高新区校级月考)如图,一棵大树在离地面6m,10m两处折成三段,中间一段AB恰好与地面平行,大树顶部落在离大树底部12m处,则大树折断前的高度是()A.14m B.16m C.18m D.20m7.(2021秋•高州市校级月考)国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是()A.20km B.14km C.11km D.10km8.(2021春•爱辉区期末)如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要()A.4米B.5米C.6米D.7米9.(2020秋•新城区校级月考)如图,八年级一班的同学准备测量校园人工湖的深度,他们把一根竹竿AB 竖直插到水底,此时竹竿AB离岸边点C处的距离CD=0.8米.竹竿高出水面的部分AD长0.2米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则人工湖的深度BD为()A.1.5米B.1.7米C.1.8米D.0.6米二.填空题10.(2020春•鹿城区期中)图1是小红在“淘宝•双11”活动中所购买的一张多挡位可调节靠椅,挡位调节示意图如图2所示.已知两支脚AB=AC,O为AC上固定连接点,靠背OD=10分米.挡位为Ⅰ挡时,OD∥AB,挡位为Ⅱ挡时,OD′⊥AC,过点O作OG∥BC,则∠DOG+∠D′OG=°当靠椅由Ⅰ挡调节为Ⅱ挡时,靠背顶端D向后靠至D′,此时点D移动的水平距离是2分米,即ED′=2分米.DH⊥OG 于点H,则D到直线OG的距离为分米.11.(2020秋•仪征市期末)如图,某斜拉桥的主梁AD垂直于桥面MN于点D,主梁上两根拉索AB、AC 长分别为13米、20米,主梁AD的高度为12米,则固定点B、C之间的距离为米.12.(2020秋•苏州期末)“东方之门”座落于美丽的金鸡湖畔,高度约为301.8米,是苏州的地标建筑,被评为“中国最高的空中苏式园林”.现以现代大道所在的直线为x轴,星海街所在的直线为y轴,建立如图所示的平面直角坐标系(1个单位长度表示的实际距离为100米),东方之门的坐标为A(6,﹣4),小明所在位置的坐标为B(﹣2,2),则小明与东方之门的实际距离为米.13.(2021春•越秀区校级期中)如图,公路MN和公路PQ在点P处交汇,公路PQ上点A处有学校,点A到公路MN的距离为80m.现有一卡车在公路MN上以5m/s的速度沿PN方向行驶,卡车行驶时周围100m以内都会受到噪音的影响,请你算出该学校受影响的时间为秒.14.(2014秋•招远市期中)小明家有一块如图所示的地,其中阴影部分是两个正方形,其他的是两个直角三角形和一个正方形,大直角三角形的斜边和一条直角边的长分别为34米,30米,小明家打算在阴影部分的土地上种花生,则种花生的面积为米2.15.(2021秋•茂名期中)如图所示,校园内有两棵树相距8m,一棵树高13m,另一棵树高7m,一只小鸟从一棵树顶端飞到另一棵树的顶端,小鸟至少要飞米.16.(2021•盂县一模)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是寸.17.(2020秋•石景山区期末)我国古代的数学名著《九章算术》中有这样一道题目“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?”译文为“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵索沿地面退行,在离木柱根部8尺处时,绳索用尽.问绳索长是多少?”示意图如图所示,设绳索AC的长为x尺,木柱AB的长用含x的代数式表示为尺,根据题意,可列方程为.三.解答题18.(2021秋•紫金县期末)如图,一个直径为12cm(即BC=12cm)的圆柱形杯子,在杯子底面的正中间点E处竖直放一根筷子,筷子露出杯子外2cm(即FG=2cm),当筷子GE倒向杯壁时(筷子底端不动),筷子顶端正好触到杯D,求筷子GE的长度.19.(2021秋•济宁期末)一架云梯长25m,如图那样斜靠在一面墙上,云梯顶端离地面24m.(1)这架云梯的底端距墙角有多远?(2)如果云梯的顶端下滑了4m,那么它的底部在水平方向滑动了多少m?20.(2021秋•长春期末)如图,长方形ABCD为一个花园,其中AB=15米,BC=8米,在花园内修一条长13米的笔直小路EF,小路出口一端E选在AD边上距D点3米处,另一端出口F应选在AB边上距B点几米处?21.(2021秋•铁西区期中)甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6千米/小时的速度向正东行走.1小时后乙出发,他以5千米/小时的速度向正北行走.上午10:00,甲、乙二人相距多远?22.(2020秋•重庆期末)如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,在A处有一所中学,AP=120米,此时有一辆消防车在公路MN上沿PN方向以每秒5米的速度行驶,假设消防车行驶时周围100米以内有噪音影响.(1)学校是否会受到影响?请说明理由.(2)如果受到影响,则影响时间是多长?23.(2021秋•淮阴区期中)为整治城市街道的汽车超速现象,交警大队在某街道旁进行了流动测速.如图,一辆小汽车在某城市街道上直行,某一时刻刚好行驶到离车速检测仪A处60m的C处,过了4s后,小汽车到达离车速检测仪A处100m的B处.(1)求BC的长;(2)已知该段城市街道的限速为70km/h,这辆小汽车超速了吗?请通过计算说明.24.(2021春•饶平县校级期中)如图,某校科技创新兴趣小组用他们设计的机器人,在平坦的操场上进行走展示.输入指令后,机器人从出发点A先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米到达终止点B.求终止点B与原出发点A的距离AB.25.(2021春•吉林期末)如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16nmile,“海天”号每小时航行12nmile.它们离开港口一个半小时后分别位于点Q,R处,且相距30nmile.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?26.(2021秋•重庆期末)如图是俱乐部新打造的一款儿童游戏项目,工作人员告诉小敏,该项目AB段和BC段均由不锈钢管材打造,总长度为26米,长方形ADCG和长方形DEFC均为木质平台的横截面,点G在AB上,点C在GF上,点D在AE上,经过现场测量得知:CD=1米,AD=15米.(1)小敏猜想立柱AB段的长为10米,请判断小敏的猜想是否正确?如果正确,请写出理由,如果错误,请求出立柱AB段的正确长度;(2)为加强游戏安全性,俱乐部打算再焊接一段钢索BF,经测量DE=3米,请你求出要焊接的钢索BF的长.(结果不必化简成最简二次根式)专题04勾股定理的应用一.选择题1.(2021秋•朝阳区期末)如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm.若这支铅笔长为18cm,则这只铅笔在笔筒外面部分长度不可能的是()A.3cm B.5cm C.6cm D.8cm【思路引导】首先根据题意画出图形,利用勾股定理计算出AC的长度.然后求其差.【完整解答】解:根据题意可得图形:AB=12cm,BC=9cm,在Rt△ABC中:AC===15(cm),所以18﹣15=3(cm),18﹣12=6(cm).则这只铅笔在笔筒外面部分长度在3cm~6cm之间.观察选项,只有选项D符合题意.故选:D.【考察注意点】此题主要考查了勾股定理的应用,正确得出笔筒内铅笔的最短长度是解决问题的关键.2.(2020秋•碑林区校级期末)有长为5cm,13cm的两根木条,现想找一根木条和这两根木条首尾顺次相连组成直角三角形,则下列木条长度适合的是()A.10cm B.12cm C.18cm D.20cm【思路引导】根据勾股定理即可得到结论.【完整解答】解:∵52+132=()2,132﹣52=122,∴木条长度适合的是12cm,故选:B.【考察注意点】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.3.(2021秋•兴平市期中)国庆假期间,妍妍与同学去玩寻宝游戏,按照藏宝图,她从门口A处出发先往东走9km,又往北走3km,遇到障碍后又往西走7km,再向北走2km,再往东走了4km,发现走错了之后又往北走1km,最后再往西走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是()A.3km B.10km C.6km D.km【思路引导】根据题意先求A、B两地的水平距离和竖直距离,运用勾股定理求AB的长.【完整解答】解:过点B作BC⊥AC,垂足为C.观察图形可知AC=9﹣7+4﹣1=5(km),BC=3+2+1=6(km),在Rt△ACB中,AB=(km).答:门口A到藏宝点B的直线距离是km,故选:D.【考察注意点】本题考查了矩形的性质以及勾股定理的应用,解题的关键是结合图形,读懂题意,根据题意找到需要的数量关系,运用勾股定理求线段的长度.4.(2021秋•赣榆区期中)在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何?它的意思是:一根竹子原高一丈(10尺),中部一处折断,竹梢触地面处离竹根3尺,试问折断处离地面()尺.A.4B.3.6C.4.5D.4.55【思路引导】画出图形,设折断处离地面x尺,则AB=(10﹣x)尺,由勾股定理得出方程,解方程即可.【完整解答】解:如图,由题意得:∠ACB=90°,BC=3尺,AC+AB=10尺,设折断处离地面x尺,则AB=(10﹣x)尺,在Rt△ABC中,由勾股定理得:x2+32=(10﹣x)2,解得:x=4.55,即折断处离地面4.55尺.故选:D.【考察注意点】此题主要考查了勾股定理的应用,正确应用勾股定理得出方程是解题的关键.5.(2020秋•长沙期末)如图,有一个绳索拉直的木马秋千,绳索AB的长度为5米,若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,则此时木马上升的高度为()A.1米B.米C.2米D.4米【思路引导】作CF⊥AB,根据勾股定理求得AF的长,可得BF的长度.【完整解答】解:过点C作CF⊥AB于点F,根据题意得:AB=AC=5,CF=DE=3,由勾股定理可得AF2+CF2=AC2,∴AF=,∴BF=AB﹣AF=5﹣4=1,∴此时木马上升的高度为1米,故选:A.【考察注意点】本题主要考查勾股定理的应用,添加辅助线构建直角三角形是解题的关键.6.(2021秋•高新区校级月考)如图,一棵大树在离地面6m,10m两处折成三段,中间一段AB恰好与地面平行,大树顶部落在离大树底部12m处,则大树折断前的高度是()A.14m B.16m C.18m D.20m【思路引导】作BO⊥DC于点O,首先由题意得:AD=BO=6m,AB=OD=4m,然后根据DC=6米,得到OC=8米,最后利用勾股定理得BC的长度即可.【完整解答】解:如图,作BO⊥DC于点O,由题意得:AD=BO=6m,AB=OD=4m,∵DC=12m,∴OC=8m,∴由勾股定理得:BC=(m),∴大树的高度为10+10=20(m),故选:D.【考察注意点】本题考查了勾股定理的应用,正确的构造直角三角形是解答本题的关键.7.(2021秋•高州市校级月考)国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是()A.20km B.14km C.11km D.10km【思路引导】根据题意先求A、B两地的水平距离和竖直距离,运用勾股定理求AB的长.【完整解答】解:过点B作BC⊥AC,垂足为C.观察图形可知AC=AF﹣MF+MC=8﹣3+1=6(km),BC=2+5=7(km),在Rt△ACB中,AB===10(km).答:登陆点到宝藏埋藏点的直线距离是10km,故选:D.【考察注意点】本题考查了矩形的性质以及勾股定理的应用,解题的关键是结合图形,读懂题意,根据题意找到需要的数量关系,运用勾股定理求线段的长度.8.(2021春•爱辉区期末)如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要()A.4米B.5米C.6米D.7米【思路引导】先求出AC的长,利用平移的知识可得出地毯的长度.【完整解答】解:在Rt△ABC中,AC==4米,故可得地毯长度=AC+BC=7米,故选:D.【考察注意点】此题考查了勾股定理的应用及平移的知识,属于基础题,利用勾股定理求出AC的长度是解答本题的关键.9.(2020秋•新城区校级月考)如图,八年级一班的同学准备测量校园人工湖的深度,他们把一根竹竿AB 竖直插到水底,此时竹竿AB离岸边点C处的距离CD=0.8米.竹竿高出水面的部分AD长0.2米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则人工湖的深度BD为()A.1.5米B.1.7米C.1.8米D.0.6米【思路引导】设BD的长度为xm,则AB=BC=(x+0.2)m,根据勾股定理构建方程即可解决问题.【完整解答】解:设BD的长度为xm,则AB=BC=(x+0.2)m,在Rt△CDB中,0.82+x2=(x+0.2)2,解得x=1.5.故选:A.【考察注意点】本题考查勾股定理的应用,解题的关键是理解题意,学会利用参数构建方程解决问题.二.填空题10.(2020春•鹿城区期中)图1是小红在“淘宝•双11”活动中所购买的一张多挡位可调节靠椅,挡位调节示意图如图2所示.已知两支脚AB=AC,O为AC上固定连接点,靠背OD=10分米.挡位为Ⅰ挡时,OD∥AB,挡位为Ⅱ挡时,OD′⊥AC,过点O作OG∥BC,则∠DOG+∠D′OG=°当靠椅由Ⅰ挡调节为Ⅱ挡时,靠背顶端D向后靠至D′,此时点D移动的水平距离是2分米,即ED′=2分米.DH⊥OG 于点H,则D到直线OG的距离为分米.【思路引导】先利用平行线的性质与等腰三角形的性质证明∠DOG=∠COG,再利用等量代换计算出∠DOG+∠D′OG=∠COD′=90°;先构造Rt△OMD′,再利用全等的性质以及勾股定理计算DH的长即可.【完整解答】解:设AB与OH交于点N,作D′M⊥OG于M,∵OD∥AB,OG∥BC,∴∠DOG=∠ANO,∠ANO=∠ABC,∠ACB=∠COG,∵AB=AC,∴∠ABC=∠ACB,∴∠DOG=∠ABC=∠ACB=∠COG,∵OD′⊥AC,∴∠COD′=90°,∴∠DOG+∠D′OG=∠COD′=∠COG+∠D′OG=∠COD′=90°;∵DH⊥OG,D′M⊥OG,∴∠OHD=∠OMD′=90°,在Rt△OHD中∠DOG+∠ODH=90°,又∠DOG+∠D′OG=90°,∴∠ODH=∠D′OG,∵当靠椅由Ⅰ挡调节为Ⅱ挡时,靠背顶端D向后靠至D′,即OD旋转到OD′,在△ODH和△D′OM中∴,∵△ODH≌△D′OM,∴DH=OM,又∵HM=ED′=2,∴DH=OM=OH+HM=OH+2,设OH=x,则DH=x+2,在Rt△OHD中,OD=10,由勾股定理得:OH2+DH2=OD2,即x2+(x+2)2=102,解得:x1=6,x2=﹣8(舍去),∴点D到直线OG的距离为DH=x+2=8.故答案为:90,8.【考察注意点】本题考查了全等三角形的性质和判定,勾股定理,等腰三角形的性质,解题的关键是构造全等三角形.11.(2020秋•仪征市期末)如图,某斜拉桥的主梁AD垂直于桥面MN于点D,主梁上两根拉索AB、AC 长分别为13米、20米,主梁AD的高度为12米,则固定点B、C之间的距离为21米.【思路引导】根据勾股定理即可得到结论.【完整解答】解:∵AD⊥BC,∴∠ADB=∠ADC=90°,∵AB、AC长分别为13米、20米,AD的高度为12米,∴BD=(米),DC=(米)∴BC=BD+DC=5+16=21(米),故答案为:21.【考察注意点】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.12.(2020秋•苏州期末)“东方之门”座落于美丽的金鸡湖畔,高度约为301.8米,是苏州的地标建筑,被评为“中国最高的空中苏式园林”.现以现代大道所在的直线为x轴,星海街所在的直线为y轴,建立如图所示的平面直角坐标系(1个单位长度表示的实际距离为100米),东方之门的坐标为A(6,﹣4),小明所在位置的坐标为B(﹣2,2),则小明与东方之门的实际距离为1000米.【思路引导】根据两点之间的距离和勾股定理解答即可.【完整解答】解:小明与东方之门的实际距离=,10×100=1000(米),故答案为:1000.【考察注意点】此题考查勾股定理的应用,关键是根据两点之间的距离和勾股定理解答.13.(2021春•越秀区校级期中)如图,公路MN和公路PQ在点P处交汇,公路PQ上点A处有学校,点A到公路MN的距离为80m.现有一卡车在公路MN上以5m/s的速度沿PN方向行驶,卡车行驶时周围100m以内都会受到噪音的影响,请你算出该学校受影响的时间为24秒.【思路引导】设卡车开到C处刚好开始受到影响,行驶到D处时结束,在Rt△ACB中求出CB,继而得出CD,再由卡车的速度可得出所需时间.【完整解答】解:设卡车开到C处刚好开始受到影响,行驶到D处时结束了噪声的影响.则有CA=DA=100m,在Rt△ABC中,CB==60(m),∴CD=2CB=120(m),则该校受影响的时间为:120÷5=24(s).答:该学校受影响的时间为24秒,故答案为:24.【考察注意点】本题考查了勾股定理的应用,解答本题的关键是熟练掌握勾股定理的表达式,画出示意图,另外要求掌握时间=路程÷速度.14.(2014秋•招远市期中)小明家有一块如图所示的地,其中阴影部分是两个正方形,其他的是两个直角三角形和一个正方形,大直角三角形的斜边和一条直角边的长分别为34米,30米,小明家打算在阴影部分的土地上种花生,则种花生的面积为256米2.【思路引导】两个阴影正方形的面积和等于直角三角形另一未知边的平方.利用勾股定理即可求出.【完整解答】解:两个阴影正方形的面积和为342﹣302=256(米2).故种花生的面积为256米2.故答案为:256.【考察注意点】本题考查了直角三角形中勾股定理的运用,考查了正方形面积的计算,本题中根据勾股定理求阴影部分的边长是解题的关键.15.(2021秋•茂名期中)如图所示,校园内有两棵树相距8m,一棵树高13m,另一棵树高7m,一只小鸟从一棵树顶端飞到另一棵树的顶端,小鸟至少要飞10米.【思路引导】根据“两点之间线段最短”可知:小鸟沿着两棵树的顶端进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出.【完整解答】解:两棵树高度相差为AE=13﹣7=6m,之间的距离为BD=CE=8m,即直角三角形的两直角边,故斜边长AC==10m,即小鸟至少要飞10m.故答案为:10.【考察注意点】本题考查勾股定理的应用,主要是将小鸟的飞行路线转化为求直角三角形的斜边,利用勾股定理解答即可.16.(2021•盂县一模)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是101寸.【思路引导】取AB的中点O,过D作DE⊥AB于E,根据勾股定理解答即可得到结论.【完整解答】解:取AB的中点O,过D作DE⊥AB于E,如图2所示:由题意得:OA=OB=AD=BC,设OA=OB=AD=BC=r寸,则AB=2r(寸),DE=10寸,OE=CD=1寸,∴AE=(r﹣1)寸,在Rt△ADE中,AE2+DE2=AD2,即(r﹣1)2+102=r2,解得:r=50.5,∴2r=101(寸),∴AB=101寸,故答案为:101.【考察注意点】本题考查了勾股定理的应用,弄懂题意,构建直角三角形是解题的关键.17.(2020秋•石景山区期末)我国古代的数学名著《九章算术》中有这样一道题目“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?”译文为“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵索沿地面退行,在离木柱根部8尺处时,绳索用尽.问绳索长是多少?”示意图如图所示,设绳索AC的长为x尺,木柱AB的长用含x的代数式表示为x﹣3尺,根据题意,可列方程为x2﹣(x﹣3)2=82.【思路引导】设绳索长为x尺,根据勾股定理列出方程解答即可.【完整解答】解:设绳索长为x尺,根据题意得:x2﹣(x﹣3)2=82,故答案为:x﹣3;x2﹣(x﹣3)2=82.【考察注意点】本题考查了勾股定理的应用,找准等量关系,正确列出一元二次方程是解题的关键.三.解答题18.(2021秋•紫金县期末)如图,一个直径为12cm(即BC=12cm)的圆柱形杯子,在杯子底面的正中间点E处竖直放一根筷子,筷子露出杯子外2cm(即FG=2cm),当筷子GE倒向杯壁时(筷子底端不动),筷子顶端正好触到杯D,求筷子GE的长度.【思路引导】根据题意可得DE=GE,EF=GE﹣2,在Rt△DFE中,根据勾股定理列出方程,解方程即可求解.【完整解答】解:设筷子GE的长度是xcm,那么杯子的高度是(x﹣2)cm,∵杯子的直径为12cm,∴杯子半径为6cm,∴(x﹣2)2+62=x2,即x2﹣4x+4+36=x2,解得:x=10,答:筷子GE的长度是10cm.【考察注意点】本题考查勾股定理的应用,解题的关键是理解题意,学会利用参数构建方程解决问题.19.(2021秋•济宁期末)一架云梯长25m,如图那样斜靠在一面墙上,云梯顶端离地面24m.(1)这架云梯的底端距墙角有多远?(2)如果云梯的顶端下滑了4m,那么它的底部在水平方向滑动了多少m?【思路引导】(1)在RtADE中,利用勾股定理即可求出DE的长;(2)首先求出A′E的长,利用勾股定理可求出D′E的长,进而得到DD′=ED′﹣ED的值.【完整解答】解:(1)在Rt△ADE中,由勾股定理得AE2+DE2=AD2,即DE2+242=252,∴DE==7(m),答:这架云梯的底端距墙角有7m远;(2)∵云梯的顶端A下滑了4m至点A′,∴A′E=AE﹣AA′=24﹣4=20(m),在Rt△A′ED′中,由勾股定理得A′E2+D′E2=A′D′2,即202+D′E2=252,∴D′E==15(m),∴DD′=ED′﹣ED=15﹣7=8(m),答:梯子的底端在水平方向也滑动了8m.【考察注意点】本题考查了勾股定理在实际生活中的应用,本题中根据梯子长不会变的等量关系求解是解题的关键.20.(2021秋•长春期末)如图,长方形ABCD为一个花园,其中AB=15米,BC=8米,在花园内修一条长13米的笔直小路EF,小路出口一端E选在AD边上距D点3米处,另一端出口F应选在AB边上距B点几米处?【思路引导】根据勾股定理直接求出AF的长,即可得出FB即可得出答案.【完整解答】解:由题意知EF=13米,EA=5米.在Rt△EAF中,由勾股定理,得AF2=EF2﹣EA2,即AF2=132﹣52=144,则AF=12(取正值).所以FB=15﹣12=3(米),即另一端出口F应选在AB边上距B点3米处.【考察注意点】此题主要考查了勾股定理的应用,正确的记忆勾股定理确定好斜边与直角边是解决问题的关键.21.(2021秋•铁西区期中)甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6千米/小时的速度向正东行走.1小时后乙出发,他以5千米/小时的速度向正北行走.上午10:00,甲、乙二人相距多远?【思路引导】要求甲、乙两人的距离,就要确定甲、乙两人在平面的位置关系,由于甲往东、乙往北,所以甲所走的路线与乙所走的路线互相垂直,然后求出甲、乙走的路程,利用勾股定理,即可求得甲、乙两人的距离.【完整解答】解:如图,甲从上午8:00到上午10:00一共走了2小时,走了12千米,即OA=12.乙从上午9:00到上午10:00一共走了1小时,走了5千米,即OB=5.在Rt△OAB中,AB2=122十52=169,∴AB=13,因此,上午10:00时,甲、乙两人相距13千米.∵15>13,∴甲、乙两人还能保持联系.答:上午10:00甲、乙两人相距13千米,两人还能保持联系.【考察注意点】本题勾股定理的应用,方位角等知识,学会用转化的思想思考问题,属于中考常考题型.22.(2020秋•重庆期末)如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,在A处有一所中学,AP=120米,此时有一辆消防车在公路MN上沿PN方向以每秒5米的速度行驶,假设消防车行驶时周围100米以内有噪音影响.(1)学校是否会受到影响?请说明理由.(2)如果受到影响,则影响时间是多长?【思路引导】(1)作AB⊥MN于B,根据含30度的直角三角形三边的关系得到AB=PA=60m,由于这个距离小于100m,所以可判断拖拉机在公路MN上沿PN方向行驶时,学校受到噪音影响;(2)以点A为圆心,100m为半径作⊙A交MN于C、D,根据垂径定理得到BC=BD,再根据勾股定理计算出BC=80m,则CD=2BC=160m,根据速度公式计算出拖拉机在线段CD上行驶所需要的时间.【完整解答】解:(1)学校受到噪音影响.理由如下:作AB⊥MN于B,如图1,∵PA=120m,∠QPN=30°,∴AB=PA=60m,而60m<100m,∴消防车在公路MN上沿PN方向行驶时,学校受到噪音影响;(2)以点A为圆心,100m为半径作⊙A交MN于C、D,如图,∵AB⊥CD,∴CB=BD,在Rt△ABC中,AC=100m,AB=60m,CB==80m,∴CD=2BC=160m,∵消防车的速度5m/s,∴消防车在线段CD上行驶所需要的时间=160÷5=32(秒),∴学校受影响的时间为32秒.【考察注意点】本题考查了勾股定理的应用,直线与圆的位置关系:设⊙O的半径为r,圆心O到直线。
中学数学八年级下册 期末压轴题(含答案)

八年级下册期末压轴题一.填空题(共1小题)1.(2018春•西城区期末)在查阅勾股定理证明方法的过程中,小红看到一种利用“等积变形﹣﹣同底等高的两个平行四边形的面积相等”证明勾股定理的方法,并尝试按自己的理解将这种方法介绍给同学.(1)根据信息将以下小红的证明思路补充完整:①如图1,在△ABC中,∠ACB=90°,四边形ADEC,四边形BCFG,四边形ABPQ都是正方形.延长QA交DE于点M,过点C作CN∥AM交DE的延长线于点N,可得四边形AMNC的形状是;②在图1中利用“等积变形”可得S正方形ADEC=;③如图2,将图1中的四边形AMNC沿直线MQ向下平移MA的长度,得到四边形A′M′N′C′,即四边形QACC′;④设CC′交AB于点T,延长CC′交QP于点H,在图2中再次利用“等积变形”可得S四边形QACC'=,则有S正方形ADEC=;⑤同理可证S正方形BCFG=S四边形HTBP,因此得到S正方形ADEC+S正方形BCFG=S正方形ABPQ,进而证明了勾股定理.(2)小芳阅读完小红的证明思路后,对其中的第③步提出了疑问,请将以下小红对小芳的说明补充完整:图1中△≌△,则有=AB=AQ,由于平行四边形的对边相等,从而四边形AMNC沿直线MQ向下平移MA的长度,得到四边形QACC′.二.解答题(共42小题)2.(2020春•海淀区校级期末)已知△ABC中,∠BAC=90°,AB=AC,点M为BC的中点,点P为AB边上一动点,点N为线段BM上一动点,以点P为旋转中心,将△BPN逆时针旋转90°得到△DPE,且点B的对应点为D,点N的对应点为E.(1)当点N与点M重合,且点P不是AB的中点时.①依据题意补全图1;②证明:以A,M,E,D为顶点的四边形是矩形.(2)连接EM,若AB=4,写出一个BN的值,使得EM=EA成立,并证明.3.(2020春•海淀区校级期末)∠MON=45°,点P在射线OM上,点A,B在射线ON上(点B与点O在点A的两侧),且AB=1,以点P为旋转中心,将线段AB逆时针旋转90°,得到线段CD(点C与点A对应,点D与点B对应).(1)如图,若OA=1,OP=,依题意补全图形;(2)若OP=,当线段AB在射线ON上运动时,线段CD与射线OM有公共点,求OA的取值范围.(要写过程)4.(2019•都江堰市模拟)定义:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根为x1,x2(x1<x2),分别以x1,x2为横坐标和纵坐标得到点M(x1,x2),则称点M为该一元二次方程的衍生点.(1)若方程为x2﹣2x=0,写出该方程的衍生点M的坐标.(2)若关于x的一元二次方程x2﹣(2m+1)x+2m=0(m<0)的衍生点为M,过点M 向x轴和y轴作垂线,两条垂线与坐标轴恰好围成一个正方形,求m的值.(3)是否存在b,c,使得不论k(k≠0)为何值,关于x的方程x2+bx+c=0的衍生点M 始终在直线y=kx﹣2(k﹣2)的图象上,若有请直接写出b,c的值,若没有说明理由.5.(2020春•海淀区校级期末)如图,在正方形ABCD中,AB=6,M是CD边上一动点(不与D点重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB到点F,使得BF=DM,连接EF,AF.(1)当DM=2时,依题意补全图1;(2)在(1)的条件下,求线段EF的长;(3)当点M在CD边上运动时,能使△AEF为等腰三角形,请直接写出此时DM与AD 的数量关系.6.(2019春•朝阳区期末)对于平面直角坐标系xOy中的图形M和点P(点P在M内部或M上),给出如下定义:如果图形M上存在点Q,使得0≤PQ≤2,那么称点P为图形M 的和谐点.已知点A(﹣4,3),B(﹣4,﹣3),C(4,﹣3),D(4,3).(1)在点P₁(﹣2,1),P2(﹣1,0),P3(3,3)中,矩形ABCD的和谐点是;(2)如果直线y=上存在矩形ABCD的和谐点P,直接写出点P的横坐标t的取值范围;(3)如果直线y=上存在矩形ABCD的和谐点E,F,使得线段EF上的所有点(含端点)都是矩形ABCD的和谐点,且EF,直接写出b的取值范围.7.(2017春•昌平区期末)(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.①如果AD=4,BD=9,那么CD=;②如果以CD的长为边长作一个正方形,其面积为S1,以BD,AD的长为邻边长作一个矩形,其面积为S2,则S1S2(填“>”、“=”或“<”).(2)基于上述思考,小泽进行了如下探究:①如图2,点C在线段AB上,正方形FGBC,ACDE和EDMN,其面积比为1:4:4,连接AF,AM,求证AF⊥AM;②如图3,点C在线段AB上,点D是线段CF的黄金分割点,正方形ACDE和矩形CBGF的面积相等,连接AF交ED于点M,连接BF交ED延长线于点N,当CF=a时,直接写出线段MN的长为.8.(2018春•浉河区期末)如图1,点A(a,b)在平面直角坐标系xOy中,点A到坐标轴的垂线段AB,AC与坐标轴围成矩形OBAC,当这个矩形的一组邻边长的和与积相等时,点A称作“垂点”,矩形称作“垂点矩形”.(1)在点P(1,2),Q(2,﹣2),N(,﹣1)中,是“垂点”的点为;(2)点M(﹣4,m)是第三象限的“垂点”,直接写出m的值;(3)如果“垂点矩形”的面积是,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标;(4)如图2,平面直角坐标系的原点O是正方形DEFG的对角线的交点,当正方形DEFG 的边上存在“垂点”时,GE的最小值为.9.(2018春•丰台区期末)如图,菱形ABCD中,∠BAD=60°,过点D作DE⊥AD交对角线AC于点E,连接BE,取BE的中点F,连接DF.(1)请你根据题意补全图形;(2)请用等式表示线段DF、AE、BC之间的数量关系,并证明.10.(2018春•丰台区期末)在平面直角坐标系xOy中,M为直线l:x=a上一点,N是直线l外一点,且直线MN与x轴不平行,若MN为某个矩形的对角线,且该矩形的边均与某条坐标轴垂直,则称该矩形为直线l的“伴随矩形”.如图为直线l的“伴随矩形”的示意图.(1)已知点A在直线l:x=2上,点B的坐标为(3,﹣2)①若点A的纵坐标为0,则以AB为对角线的直线l的“伴随矩形”的面积是;②若以AB为对角线的直线l的“伴随矩形”是正方形,求直线AB的表达;(2)点P在直线l:x=m上,且点P的纵坐标为4,若在以点(2,1),(﹣2,1),(﹣2,﹣1),(2,﹣1)为顶点的四边形上存在一点Q,使得以PQ为对角线的直线l的“伴随矩形”为正方形,直接写出m的取值范围.11.(2019春•海淀区期末)如图,在平面直角坐标系xOy中,直线y=kx+7与直线y=x﹣2交于点A(3,m)(1)求k,m的值;(2)已知点P(n,n),过点P作垂直于y轴的直线与直线y=x﹣2交于点M,过点P 作垂直于x轴的直线与直线y=kx+7交于点N(P与N不重合).若PN≤2PM,结合图象,求n的取值范围.12.(2019春•海淀区期末)在Rt△ABC中,∠BAC=90°,点O是△ABC所在平面内一点,连接OA,延长OA到点E,使得AE=OA,连按OC,过点B作BD与OC平行,并使∠DBC=∠OCB,且BD=OC,连按DE.(1)如图一,当点O在Rt△ABC内部时,①按题意补全图形;②猜想DE与BC的数量关系,并证明.(2)若AB=AC(如图二),且∠OCB=30°,∠OBC=15°,求∠AED的大小.13.(2017春•西城区期末)如图所示,在平面直角坐标系xOy中,B,C两点的坐标分别为B(4,0),C(4,4),CD⊥y轴于点D,直线l经过点D.(1)直接写出点D的坐标;(2)作CE⊥直线l于点E,将直线CE绕点C逆时针旋转45°,交直线l于点F,连接BF.①依题意补全图形;②通过观察、测量,同学们得到了关于直线BF与直线l的位置关系的猜想,请写出你的猜想;③通过思考、讨论,同学们形成了证明该猜想的几种思路:思路1:作CM⊥CF,交直线l于点M,可证△CBF≌△CDM,进而可以得出∠CFB=45°,从而证明结论.思路2:作BN⊥CE,交直线CE于点N,可证△BCN≌△CDE,进而证明四边形BFEN 为矩形,从而证明结论.…请你参考上面的思路完成证明过程.(一种方法即可)解:(1)点D的坐标为,(2)①补全图形,②直线BF与直线l的位置关系是,③证明:14.(2017春•西城区期末)如图,在由边长都为1个单位长度的小正方形组成的6×6正方形网格中,点A,B,P都在格点上请画出以AB为边的格点四边形(四个顶点都在格点的四边形),要求同时满足以下条件:条件1:点P到四边形的两个顶点的距离相等;条件2:点P在四边形的内部或其边上;条件3:四边形至少一组对边平行.(1)在图①中画出符合条件的一个▱ABCD,使点P在所画四边形的内部;(2)在图②中画出符合条件的一个四边形ABCD,使点P在所画四边形的边上;(3)在图③中画出符合条件的一个四边形ABCD,使∠D=90°,且∠A≠90°.15.(2017春•西城区期末)如图,在平面直角坐标系xOy中,动点A(a,0)在x轴的正半轴上,定点B(m,n)在第一象限内(m<2≤a),在△OAB外作正方形ABCD和正方形OBEF,连接FD,点M为线段FD的中点,作BB1⊥x轴于点B1,作FF1⊥x轴于点F1.(1)填空:由≌△,及B(m,n)可得点F的坐标为,同理可得点D的坐标为;(说明:点F,点D的坐标用含m,n,a的式子表示)(2)直接利用(1)的结论解决下列问题:①当点A在x轴的正半轴上指定范围内运动时,点M总落在一个函数图象上,求该函数的解析式(不必写出自变量x的取值范围);②当点A在x轴的正半轴上运动且满足2≤a≤8时,求点M所经过的路径的长.16.(2019春•西城区期末)四边形ABCD是正方形,AC是对角线,E是平面内一点,且CE<BC,过点C作FC⊥CE,且CF=CE.连接AE、AF,M是AF的中点,作射线DM 交AE于点N.(1)如图1,若点E,F分别在BC,CD边上.求证:①∠BAE=∠DAF;②DN⊥AE;(2)如图2,若点E在四边形ABCD内,点F在直线BC的上方,求∠EAC与∠ADN 的和的度数.17.(2019春•西城区期末)如图1,在菱形ABCD中,对角线AC,BD相交于点O,AC=4cm,BD=2cm,E,F分别是AB,BC的中点,点P是对角线AC上的一个动点,设AP =xcm,PE=y1cm,PF=y2cm.小明根据学习函数的经验,分别对这两种函数随自变量的变化而变化的情况进行了探究,下面是小明探究过程,请补充完整:(1)画函数y1的图象①按表中自变量的值进行取点、画图、测量,得到了y1与x的几组对应值:x/cm00.51 1.52 2.53 3.54y1/cm 1.120.50.71 1.12 1.58 2.06 2.55 3.04②在图2所给坐标系中描出补全后的表中的各对应值为坐标的点,画出函数y1的图象;(2)画函数y2的图象,在同一坐标系中,画出函数y2的图象;(3)根据画出的函数y1的图象、函数y2的图象,解决问题①函数y1的最小值是;②函数y1的图象与函数y2的图象的交点表示的含义是;③若PE=PC,AP的长约为cm18.(2019春•西城区期末)平面直角坐标系xOy中,对于点M和图形W,若图形W上存在一点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称点M与图形W是“中心轴对称”.对于图形W1和图形W2,若图形W1和图形W2分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形W1和图形W2是“中心轴对称”的.特别地,对于点M和点N,若存在一条经过原点的直线l,使得点M与点N关于直线l对称,则称点M和点N是“中心轴对称”的.(1)如图1,在正方形ABCD中,点A(1,0),点C(2,1),①下列四个点P1(0,1),P2(2,2),P3(﹣,0),P4(﹣,﹣)中,与点A是“中心轴对称”的是;②点E在射线OB上,若点E与正方形ABCD是“中心轴对称”的,求点E的横坐标x E的取值范围;(2)四边形GHJK的四个顶点的坐标分别为G(﹣2,2),H(2,2),J(2,﹣2),K (﹣2,﹣2),一次函数y=x+b图象与x轴交于点M,与y轴交于点N,若线段MN 与四边形GHJK是“中心轴对称”的,直接写出b的取值范围.19.(2019春•大兴区期末)有这样一个问题:探究函数y=+1的图象与性质.小东根据学习函数的经验,对函数y=+1的图象与性质进行了探究.下面是小东的探究过程,请补充完整:(1)函数y=+1的自变量x的取值范围是;(2)如表是y与x的几组对应值.x…﹣3﹣2﹣112345…y…393m…求m的值;(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(4)结合函数的图象,写出该函数的一条性质:.20.(2019春•大兴区期末)如图1,四边形ABCD是平行四边形,A,B是直线l上的两点,点B关于AD的对称点为M,连接CM交AD于F点.(1)若∠ABC=90°,如图1,①依题意补全图形;②判断MF与FC的数量关系是;(2)如图2,当∠ABC=135°时,AM,CD的延长线相交于点E,取ME的中点H,连结HF.用等式表示线段CE与AF的数量关系,并证明.21.(2019春•大兴区期末)在平面直角坐标系xOy中,记y与x的函数y=a(x﹣m)2+n (m≠0,n≠0)的图象为图形G,已知图形G与y轴交于点A,当x=m时,函数y=a (x﹣m)2+n有最小(或最大)值n,点B的坐标为(m,n),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线.(1)如图1,若函数y=(x﹣2)2+1的图象记为图形G,求图形G的伴随直线的表达式;(2)如图2,若图形G的伴随直线的表达式是y=x﹣3,且伴随四边形的面积为12,求y与x的函数y=a(x﹣m)2+n(m>0,n<0)的表达式;(3)如图3,若图形G的伴随直线是y=﹣2x+4,且伴随四边形ABCD是矩形,求点B 的坐标.22.(2019春•石景山区期末)正方形ABCD中,点P是直线AC上的一个动点,连接BP,将线段BP绕点B顺时针旋转90°得到线段BE,连接CE.(1)如图1,若点P在线段AC上,①直接写出∠ACE的度数为°;②求证:P A2+PC2=2PB2;(2)如图2,若点P在CA的延长线上,P A=1,PB=,①依题意补全图2;②直接写出线段AC的长度为.23.(2020春•浦东新区期末)在平面直角坐标系xOy中,若P,Q为某个矩形不相邻的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.图1为点P,Q的“相关矩形”的示意图.已知点A的坐标为(1,2).(1)如图2,点B的坐标为(b,0).①若b=﹣2,则点A,B的“相关矩形”的面积是;②若点A,B的“相关矩形”的面积是8,则b的值为.(2)如图3,点C在直线y=﹣1上,若点A,C的“相关矩形”是正方形,求直线AC 的表达式;(3)如图4,等边△DEF的边DE在x轴上,顶点F在y轴的正半轴上,点D的坐标为(1,0).点M的坐标为(m,2),若在△DEF的边上存在一点N,使得点M,N的“相关矩形”为正方形,请直接写出m的取值范围.24.(2016春•无锡期末)已知:如图1,在平面直角坐标中,A(12,0),B(6,6),点C 为线段AB的中点,点D与原点O关于点C对称.(1)利用直尺和圆规在图1中作出点D的位置(保留作图痕迹),判断四边形OBDA的形状,并说明理由;(2)在图1中,动点E从点O出发,以每秒1个单位的速度沿线段OA运动,到达点A 时停止;同时,动点F从点O出发,以每秒a个单位的速度沿OB→BD→DA运动,到达点A时停止.设运动的时间为t(秒).①当t=4时,直线EF恰好平分四边形OBDA的面积,求a的值;②当t=5时,CE=CF,请直接写出a的值.25.(2019春•东城区期末)有这样一个问题:探究函数y=﹣3的图象与性质.小亮根据学习函数的经验,对y=﹣3的图象与性质进行了探究下面是小亮的探究过程,请补充完整:(1)函数y=3中自变量x的取值范围是(2)下表是y与x的几组对应值.x…﹣3﹣2﹣102345…y…﹣﹣﹣4﹣5﹣7m﹣1﹣2﹣﹣…求m的值;(1)在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;(2)根据画出的函数图象,发现下列特征:该函数的图象与直线x=1越来越靠近而永不相交,该函数的图象还与直线越来越靠近而永不相交.26.(2019春•东城区期末)在正方形ABCD中,点E是射线AC上一点,点F是正方形ABCD 外角平分线CM上一点,且CF=AE,连接BE,EF.(1)如图1,当E是线段AC的中点时,直接写出BE与EF的数量关系;(2)当点E不是线段AC的中点,其它条件不变时,请你在图2中补全图形,判断(1)中的结论是否成立,并证明你的结论;(3)当点B,E,F在一条直线上时,求∠CBE的度数.(直接写出结果即可)27.(2019春•东城区期末)对于平面直角坐标系xOy中的点P和正方形给出如下定义:若正方形的对角线交于点O,四条边分别和坐标轴平行,我们称该正方形为原点正方形.当原点正方形上存在点Q,满足PQ≤1时,称点P为原点正方形的友好点.(1)当原点正方形边长为4时,①在点P1(0,0),P2(﹣1,1),P3(3,2)中,原点正方形的友好点是;②点P在直线y=x的图象上,若点P为原点正方形的友好点,求点P横坐标的取值范围;(2)一次函数y=﹣x+2的图象分别与x轴,y轴交于点A,B,若线段AB上存在原点正方形的友好点,直接写出原点正方形边长a的取值范围.28.(2019春•昌平区期末)如图,△ABC中,AB=BC=5cm,AC=6cm,点P从顶点B出发,沿B→C→A以每秒1cm的速度匀速运动到A点,设运动时间为x秒,BP长度为ycm.某学习小组对函数y随自变量x的变化而变化的规律进行了探究.下面是他们的探究过程,请补充完整:(1)通过取点,画图,测量,得到了x(秒)与y(cm)的几组对应值:x01234567891011y0.0 1.0 2.0 3.0 4.0 4.5 4.14 4.5 5.0要求:补全表格中相关数值(保留一位小数);(2)在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当x约为时,BP=CP.29.(2019春•昌平区期末)在矩形ABCD中,AB=3,AD=2,点E是射线DA上一点,连接EB,以点E为圆心EB长为半径画弧,交射线CB于点F,作射线FE与CD延长线交于点G.(1)如图1,若DE=5,则∠DEG=°;(2)若∠BEF=60°,请在图2中补全图形,并求EG的长;(3)若以E,F,B,D为顶点的四边形是平行四边形,此时EG的长为.30.(2019春•昌平区期末)在平面直角坐标系中,过一点分别作x轴,y轴的垂线,如果由这点、原点及两个垂足为顶点的矩形的周长与面积相等,那么称这个点是平面直角坐标系中的“巧点”.例如,图1中过点P(4,4)分別作x轴,y轴的垂线,垂足为A,B,矩形OAPB的周长为16,面积也为16,周长与面积相等,所以点P是巧点.请根据以上材料回答下列问题:(1)已知点C(1,3),D(﹣4,﹣4),E(5,﹣),其中是平面直角坐标系中的巧点的是;(2)已知巧点M(m,10)(m>0)在双曲线y=(k为常数)上,求m,k的值;(3)已知点N为巧点,且在直线y=x+3上,求所有满足条件的N点坐标.31.(2019春•延庆区期末)已知:在正方形ABCD中,点H在对角线BD上运动(不与B,D重合)连接AH,过H点作HP⊥AH于H交直线CD于点P,作HQ⊥BD于H交直线CD于点Q.(1)当点H在对角线BD上运动到图1位置时,则CQ与PD的数量关系是.(2)当H点运动到图2所示位置时①依据题意补全图形.②上述结论还成立吗?若成立,请证明.若不成立,请说明理由.(3)若正方形边长为,∠PHD=30°,直接写出PC长.32.(2019春•延庆区期末)对于一次函数y=kx+b(k≠0),我们称函数y[m]=为它的m分函数(其中m为常数).例如,y=3x+2的4分函数为:当x≤4时,y[4]=3x+2;当x>4时,y[4]=﹣3x﹣2.(1)如果y=x+1的﹣1分函数为y[﹣1],①当x=4时,y[﹣1];当y[﹣1]=﹣3时,x=.②求双曲线y=与y[﹣1]的图象的交点坐标;(2)如果y=﹣x+2的0分函数为y[0],正比例函数y=kx(k≠0)与y=﹣x+2的0分函数y[0]的图象无交点时,直接写出k的取值范围.33.(2017春•西城区校级期末)如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.34.(2017春•西城区校级期末)某学习小组有a个男生,b个女生,其中a和b同时满足以下三个条件:①男生人数不少于女生人数;②a,b是一元二次方程mx2﹣(3m+8)x+24=0的两个实数根;③男生和女生的总人数不超过10人.请根据以上信息,回答下面两个问题:(1)求整数m的值?(2)若T=ma+b,求T的所有可能的值?35.(2017春•西城区校级期末)设p,q都是实数,且p<q.我们规定:如果变量x的取值范围为p≤x≤q,则把实数L=q﹣p叫做变量x的取值宽度.如果反比例函数y=在p ≤x≤q的函数值y的取值宽度与自变量x的取值宽度相等,则称此函数在p≤x≤q上具有“等宽性”.例如:函数y=的函数值y的取值范围为≤y≤2,故而函数y=具有“等宽性”.(1)下列函数哪些函数具有“等宽性”:(填序号)①y=(1≤x≤2);②y=﹣(﹣2≤x≤﹣1);③y=﹣(1≤x≤6);④y=﹣(﹣4≤x≤﹣1);(2)已知函数y=﹣在a≤x≤﹣1上具有“等宽性”,求a的值;(3)已知直线y=kx+b与函数y=﹣交于A(x1,y1)、B(x2,y2)两点,且函数y=﹣在x1≤x≤x2上具有“等宽性”,则k=.36.(2018春•海淀区期末)在正方形ABCD中,连接BD,P为射线CB上的一个动点(与点C不重合),连接AP,AP的垂直平分线交线段BD于点E,连接AE,PE.提出问题:当点P运动时,∠APE的度数,DE与CP的数量关系是否发生改变?探究问题:(1)首先考察点P的两个特殊位置:①当点P与点B重合时,如图1﹣1所示,∠APE=°,用等式表示线段DE与CP之间的数量关系:;②当BP=BC时,如图1﹣2所示,①中的结论是否发生变化?直接写出你的结论:;(填“变化”或“不变化”)(2)然后考察点P的一般位置:依题意补全图2﹣1,2﹣2,通过观察、测量,发现:(1)中①的结论在一般情况下(填“成立”或“不成立”)(3)证明猜想:若(1)中①的结论在一般情况下成立,请从图2﹣1和图2﹣2中任选一个进行证明;若不成立,请说明理由.37.(2018春•海淀区期末)在平面直角坐标系xOy中,A(O,2),B(4,2),C(4,0).P 为矩形ABCO内(不包括边界)一点,过点P分别作x轴和y轴的平行线,这两条平行线分矩形ABCO为四个小矩形,若这四个小矩形中有一个矩形的周长等于OA,则称P 为矩形ABCO的矩宽点.例如:下图中的为矩形ABCO的一个矩宽点.(1)在点D(,),E(2,1),F(,)中,矩形ABCO的矩宽点是;(2)若G(m,)为矩形ABCO的矩宽点,求m的值;(3)若一次函数y=k(x﹣2)﹣1(k≠0)的图象上存在矩形ABCO的矩宽点,则k的取值范围是.38.(2019春•曲阜市期末)如图,在菱形ABCD中,CE⊥AB交AB延长线于点E,点F为点B关于CE的对称点,连接CF,分别延长DC,CF至点G,H,使FH=CG,连接AG,DH交于点P.(1)依题意补全图1;(2)猜想AG和DH的数量关系并证明;(3)若∠DAB=70°,是否存在点G,使得△ADP为等边三角形?若存在,求出CG的长;若不存在,说明理由.39.(2018春•朝阳区期末)在平面直角坐标系xOy中,对于与坐标轴不平行的直线l和点P,给出如下定义:过点P作x轴,y轴的垂线,分别交直线l于点M,N,若PM+PN≤4,则称P为直线l的近距点,特别地,直线上l所有的点都是直线l的近距点.已知点A(﹣,0),B(0,2),C(﹣2,2).(1)当直线l的表达式为y=x时,①在点A,B,C中,直线l的近距点是;②若以OA为边的矩形OAEF上所有的点都是直线l的近距点,求点E的纵坐标n的取值范围;(2)当直线l的表达式为y=kx时,若点C是直线l的近距点,直接写出k的取值范围.40.(2018春•昌平区期末)如图,将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3).动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动秒时,动点P从点A出发以相同的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).(1)OP=,OQ=;(用含t的代数式表示)(2)当t=1时,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处.①求点D的坐标;②如果直线y=kx+b与直线AD平行,那么当直线y=kx+b与四边形P ABD有交点时,求b的取值范围.41.(2018春•昌平区期末)在四边形ABCD中,E、F分别是边BC、CD的中点,连接AE,AF.(1)如图1,若四边形ABCD的面积为5,则四边形AECF的面积为;(2)如图2,延长AE至G,使EG=AE,延长AF至H,使FH=AF,连接BG、GH、HD、DB.求证:四边形BGHD是平行四边形;(3)如图3,对角线AC、BD相交于点M,AE与BD交于点P,AF与BD交于点N.直接写出BP、PM、MN、ND的数量关系.42.(2018春•西城区期末)在矩形ABCD中,BE平分∠ABC交CD边于点E.点F在BC 边上,且FE⊥AE.(1)如图1,①∠BEC=°;②在图1已有的三角形中,找到一对全等的三角形,并证明你的结论;(2)如图2,FH∥CD交AD于点H,交BE于点M.NH∥BE,NB∥HE,连接NE.若AB=4,AH=2,求NE的长.43.(2018春•西城区期末)在△ABC中,M是BC边的中点.(1)如图1,BD,CE分别是△ABC的两条高,连接MD,ME,则MD与ME的数量关系是;若∠A=70°,则∠DME=°;(2)如图2,点D,E在∠BAC的外部,△ABD和△ACE分别是以AB,AC为斜边的直角三角形,且∠BAD=∠CAE=30°,连接MD,ME.①判断(1)中MD与ME的数量关系是否仍然成立,并证明你的结论;②求∠DME的度数;(3)如图3,点D,E在∠BAC的内部,△ABD和△ACE分别是以AB,AC为斜边的直角三角形,且∠BAD=∠CAE=α,连接MD,ME.直接写出∠DME的度数(用含α的式子表示).八年级下册期末压轴题参考答案与试题解析一.填空题(共1小题)1.(2018春•西城区期末)在查阅勾股定理证明方法的过程中,小红看到一种利用“等积变形﹣﹣同底等高的两个平行四边形的面积相等”证明勾股定理的方法,并尝试按自己的理解将这种方法介绍给同学.(1)根据信息将以下小红的证明思路补充完整:①如图1,在△ABC中,∠ACB=90°,四边形ADEC,四边形BCFG,四边形ABPQ都是正方形.延长QA交DE于点M,过点C作CN∥AM交DE的延长线于点N,可得四边形AMNC的形状是平行四边形;②在图1中利用“等积变形”可得S正方形ADEC=S四边形AMNC;③如图2,将图1中的四边形AMNC沿直线MQ向下平移MA的长度,得到四边形A′M′N′C′,即四边形QACC′;④设CC′交AB于点T,延长CC′交QP于点H,在图2中再次利用“等积变形”可得S四边形QACC'=S四边形QATH,则有S正方形ADEC=S四边形QATH;⑤同理可证S正方形BCFG=S四边形HTBP,因此得到S正方形ADEC+S正方形BCFG=S正方形ABPQ,进而证明了勾股定理.(2)小芳阅读完小红的证明思路后,对其中的第③步提出了疑问,请将以下小红对小芳的说明补充完整:图1中△ADM≌△ABC,则有AM=AB=AQ,由于平行四边形的对边相等,从而四边形AMNC沿直线MQ向下平移MA的长度,得到四边形QACC′.【分析】根据平行四边形的性质、正方形的性质、全等三角形的判定和性质、等高模型即可解决问题;【解答】解:(1)∵四边形ACED是正方形,∴AC∥MN,∵AM∥CN,∴四边形AMNC是平行四边形,∴S正方形ADEC=S平行四边形AMNC,∵AD=AC,∠D=∠ACB,∠DAC=∠MAB,∴∠DAM=∠CAB,∴△ADM≌△ACB,∴AM=AB=AQ,∴图1中的四边形AMNC沿直线MQ向下平移MA的长度,得到四边形A′M′N′C′,即四边形QACC′,∴S四边形QACC′=S四边形QATH,则有S正方形ADEC=S四边形QATH,∴同理可证S正方形BCFG=S四边形HTBP,因此得到S正方形ADEC+S正方形BCFG=S正方形ABPQ;故答案为平行四边形,S四边形AMNC,S四边形QATH,S四边形QATH;(2)由(1)可知:△ADM≌△ACB,∴AM=AB=AQ,故答案为ADM,ACB,AM;【点评】本题考查平行四边形的性质、正方形的性质、全等三角形的判定和性质、等高模型等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,属于中考创新题目.二.解答题(共42小题)2.(2020春•海淀区校级期末)已知△ABC中,∠BAC=90°,AB=AC,点M为BC的中点,点P为AB边上一动点,点N为线段BM上一动点,以点P为旋转中心,将△BPN 逆时针旋转90°得到△DPE,且点B的对应点为D,点N的对应点为E.(1)当点N与点M重合,且点P不是AB的中点时.①依据题意补全图1;②证明:以A,M,E,D为顶点的四边形是矩形.(2)连接EM,若AB=4,写出一个BN的值,使得EM=EA成立,并证。
专题16.1 二次根式的化简求值(压轴题专项讲练)(解析版)-八年级数学下册

专题16.1二次根式的化简求值整体思想:指把研究对象的某一部分(或全部)看成一个整体,通过观察与分析,找出整体与局部的联系,从而在客观上寻求解决问题的新途径。
整体是与局部对应的,按常规不容易求某一个(或多个)未知量时,可打破常规,根据题目的结构特征,把一组数或一个代数式看作一个整体,从而使问题得到解决。
一、二次根式的定义形如(≥0)的式子叫做二次根式,叫做二次根号,叫做被开方数.二、二次根式有意义的条件1.二次根式中的被开方数是非负数;2.二次根式具有非负性:≥0.三、判断二次根式有意义的条件1.如果一个式子中含有多个二次根式,那么它们有意义的条件是:各个二次根式中的被开方数都必须是非负数;2.如果所给式子中含有分母,则除了保证被开方数为非负数外,还必须保证分母不为零.四、二次根式的性质性质1:2=(≥0),即一个非负数的算术平方根的平方等于它本身;性质2:2==(≥0)−(<0),即一个任意实数平方的算术平方根等于它本身的绝对值.五、同类二次根式把几个二次根式化为最简二次根式以后,如果被开方数相同,那么这几个二次根式叫做同类二次根式.①同类二次根式类似于整式中的同类项;②几个同类二次根式在没有化简之前,被开方数完全可以互不相同;③判断两个二次根式是否是同类二次根式,首先要把它们化为最简二次根式,然后再看被开方数是否相同.六、二次根式的加减法则二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变.七、二次根式的乘除法则①二次根式的乘法法则:∙=∙o≥0,≥0);②积的算术平方根:∙=∙o≥0,≥0);≥0,>0);=≥0,>0).八、最简二次根式我们把满足①被开方数不含分母;②被开方数中不含能开得尽方的因数或因式.这两个条件的二次根式,叫做最简二次根式.九、分母有理化1.分母有理化是指把分母中的根号化去:分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式;2.两个含二次根式的代数式相乘时,它们的积不含二次根式,这样的两个代数式成互为有理化因式.一个二次根式的有理化因式不止一个.【典例1】阅读下列材料,然后回答问题.====3−1以上这种化简的步骤叫做分母有理化.②学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算,比如我们熟悉的下面这个题:已知a+b=2,ab=-3,求2+2.我们可以把a+b和ab看成是一个整体,令x=a+b,y=ab,则2+2=(+p2−2B=2−2=4+6=10.这样,我们不用求出a,b,就可以得到最后的结果.(1(2)m是正整数,a b22+1823B+22=2019.求m.(3)已知15+2−26−2=1,求15+2+26−2的值.(1)由题目所给出的规律进行计算即可;(2)先求出+=2(2+1),B=1再由22+1823B+22=2019进行变形再求值即可;(3)先得到15+2⋅26−2=20,然后可得(15+2+26−2)2=(15+2−26−2)2+415+2⋅26−2=81,最后由15+2≥0,26−2≥0,求出结果.解:(1)原式=2+++⋯+2=3−1+5−3+7−5+⋯+2019−20172=(2)∵a b∴+==2(2+1),B=1,∵22+1823B+22=2019,∴2(2+2)+1823=2019,∴2+2=98,∴4(2+1)2=100,∴2=±5−1,∵m是正整数,∴m=2.(3)由15+2−26−2=1得出(15+2−26−2)2=1,∴15+2⋅26−2=20,∵(15+2+26−2)2=(15+2−26−2)2+415+2⋅26−2=81,又∵15+2≥0,26−2≥0,∴15+2+26−2=9.1.(2023下·浙江·八年级阶段练习)已知=2−3,=2+3,则代数式2+2B+2+−−4的值为()A B.34C.3−1D【思路点拨】根据已知,得到+=2−3+2+3=22,−=2−3−2−3=−23,整体思想带入求值即可.【解题过程】解:∵=2−3,=2+3,∴+=2−3+2+3=22,−=2−3−2−3=−23,∴2+2B+2+−−4=+2+−−4=222−23−4=8−23−4=4−23=32−23+1=3−12=3−1.故选C.2.(2022下·广西钦州·八年级统考阶段练习)已知+1=7(0<<1),则−)【思路点拨】,故<,将−由0<<1,得0<<1【解题过程】解:∵0<<1,∴0<<1,∴<2=−2+1,+1=7(0<<1),∵(−∴(−∴=-5或−=5,∵<0,∴∴故选B.3.(2023·浙江宁波·校考一模)若2+2=1,则2−4+4+B−3+−3的值为()A.0B.1C.2D.3【思路点拨】先根据2+2=1得出−1≤≤1,−1≤≤1,根据2−4+4+B−3+−3要有意义,得出+ 1−3≥0,根据−3<0得出+1≤0,从而得出J−1,将J−1代入即可求出式子的值.【解题过程】解:∵2+2=1,∴−1≤≤1,−1≤≤1,∵2−4+4+B−3+−3要有意义,∴B−3+−3≥0,整理得:+1−3≥0,∵−3<0,∴+1≤0,∴J−1,∴2−4+4+B−3+−3=−22++1−3=−1−22+−1+1−3=3+0=3,故D正确.故选:D.4.(2023上·四川达州·八年级校考期中)已知xx6﹣22019x5﹣x4+x3﹣22020x2+2x﹣2020的值为()A.0B.1C.2019D.2020【思路点拨】对已知进行变形,再代入所求式子,反复代入即可.【解题过程】解:∵=2020−=2020+2019,∴6−220195−4+3−220202+2−2020,=5−22019−4+2−22020+2−2020,=52020+2019−22019−4+22020+2019−22020+2−2020,=52020−2019−4+22019−2020+2−2020,=42020−2019−1+22019−2020+2−2020,=2020+20192019−2020+2−2020=−+2−2020,=−2020,=2019,故选:C.5.(2023·安徽·校联考模拟预测)设a为3+5−3−5的小数部分,b为6+33−6−33的小数部分,则2b−1的值为()A.6+2−1B.6−2+1C.6−2−1 D.6+2+1【思路点拨】首先分别化简所给的两个二次根式,分别求出a、b对应的小数部分,然后化简、运算、求值,即可解决问题.【解题过程】解:3+5−3−5-=5+15-1=2∴a的小数部分为2-1,6+336−33−=3+33-3=6∴b的小数部分为6-2,∴2b−1=6+2-2-1=6-2+1,故选:B.6.(2022上·湖南益阳·八年级统考期末)设1=1+112+122,2=1+122+132,3=1+132+142,……,=1+ 12+1(r1)2.其中n为正整数,则1+2+3+⋅⋅⋅+2021的值是()A.202020192020B.202020202021C.202120202021D.202120212022【思路点拨】根据题意,先求出=1+1or1),然后把代数式进行化简,再进行计算,即可得到答案.【解题过程】解:∵n为正整数,∴=2+r1or1)=1+1or1);∴1+2+3+⋯+2021=(1+11×2)+(1+12×3)+(1+13×4)+…+(1+12021×2022)=2021+1﹣12+12−13+13−14+⋯+12021−12022=2021+1﹣12022=202120212022.故选:D.7.(2023上·上海金山·八年级校考期中)如果=5−2,则1=.【思路点拨】本题考查了二次根式的化简求值,熟练掌握二次根式的性质、完全平方公式是解题关键.先根据二次根式的分母有理化可得1,从而可得1−>0,再利用完全平方公式化简二次根式,代入计算即可得.【解题过程】解:∵=5−2,∴1=5−2=5−2=5+2,∴1−55−2∴1=1+=1+−=5+2+4=5+6.故答案为:5+6.8.(2022上·湖南长沙·七年级校联考阶段练习)已知==42−3B+42=.【思路点拨】先把和的值分母有理化得到==−=−12,B=1,再利用完全平方公式变形原式得到4(−p2+5B,然后利用整体代入的方法计算.【解题过程】解:∵==∴====∴−=−12,B=1,∴原式=4(−p2+5B=4×(−12)2+5×1=6.故答案为6.9.(2022下·浙江杭州·八年级校考期中)已知=2的值等于.【思路点拨】通过完全平方公式求出+1=2,把待求式的被开方数都用+1的代数式表示,然后再进行计算.【解题过程】=2,解:∵+∴=4,∴+1+2=4∴+12===10.(2023下·广东深圳·九年级深圳中学校考自主招生)已知x,y为正整数,+−7−7+ 7B=7,求+=.【思路点拨】将等式进行因式分解,得到++7B−7=0,求得B=7,即可求解.【解题过程】解:∵+−7−7+7B=7,∴+−7−7+7B−7=0,∴B+−7++7B−7=0,∴+B−7+7B−7=0,∴++7B−7=0,∵++7>0,∴B−7=0,∴B=7,又x,y为正整数,则s=1,7或7,1,从而+=8,故答案为:8.11.(2023下·黑龙江绥化·八年级校考阶段练习)设=3−2,则6+35+113+2+1=.【思路点拨】利用+22=2+4+4和=3−2,推得2+4+1=0,借助该式将多项式进行降幂化简,即可求解.【解题过程】解:∵=3−2,∴+22=3−2+22=3,又∵+22=2+4+4,即2+4+4=3,整理得2+4+1=0,6+35+113+2+1=42+4+1+35+113+2+1−45−4=−5−4+113+2+1=−32+4+1−4+113+2+1+44+3=34+123+2+1=322+4+1+2+1−32=−32+2+1=−32+4+1+2+1+12+3=14+4,将=3−2代入原式可得14×3−2+4=143−24.故答案为:143−24.12.(2022下·湖北武汉·九年级统考自主招生)已知=则代数式23−32−7+2022的值为.【思路点拨】将已知条件=2−3=−1,再将所求代数式变形为23−62+32−7+2022,由此即可求解.【解题过程】解:已知=∴2=3+5,即2−3=5,等式两边同时平方得,2−32=52,整理得,42−12+9=5,即42−12=−4,∴2−3=−1,∵23−32−7+2022=2o2−3p+32−7+20022把2−3=−1代入得,=2×−1+32−7+2022=32−2−7+2022=32−9+2022=3(2−3p+2022把2−3=−1代入得,=3×−1+2022=2019,故答案为:2019.13.(2022上·上海闵行·=3,=13.【思路点拨】首先对第一个式子的分子利用平方差公式分解,第二个式子利用完全平方公式分解,然后约分,合并同类二次根式即可化简,然后代入数值计算即可.【解题过程】解:原式=K=+++=2+2当=3,=13时,原式=23+=23+=14.(2023·北京·九年级专题练习)已知==,求2+2的值.【思路点拨】首先把x和y进行分母有理化,然后将其化简后的结果代入计算即可.【解题过程】解:∵==5−26,===5+26,∴原式=(5+2(5−26)=2620626206=26)(49206)6)(49206)6)(492026)(49206)=245−1006−986+240+245+1006+986+240=970.15.(2023下·山东威海·九年级校考期中)已知+=−8,B=12,求+【思路点拨】根据题意可判断a和b都是负数,然后二次根式的乘、除法公式和合并同类二次根式法则化简并求值即可.【解题过程】解:∵+=−8,B=12,∴a和b均为负数,2+2−2B=40=B+B=2B2B=2+2B=−−==2=−4012=−401212=−40×2312=−203316.(2023上·上海杨浦·七年级校考阶段练习)已知−2B−15=0【思路点拨】讨论:当>0,>0,利用因式分解的方法得到−5+3=0,解得=25,当I0,<0,则−−+5−−−3−=0,解得=9,然后把=25,=9化简求解.【解题过程】解:∵−2B−15=0要有意义,即B≥0,∴>0且>0或I0且<0,当>0且>0时,∵−2B−15=−5+3=0,∴−5=0或+3=0(舍去),解得:=25,把=25=25r5r225K10r=2;当I0且<0时,∵−2B−15=−−+5−−−3−=0,∴−r5−=0(舍去)或−−3−=0,解得:=9,把=9==9K3r29r6r=12.17.(2023上·四川成都·八年级成都市三原外国语学校校考阶段练习)已知==(2【思路点拨】(1)先将x、y进行分母有理化,再代入式子计算可得;(2)先将式子化简再代入x、y进行计算即可.【解题过程】(1)∵=10−3=10+3,=10−3,=∴+=210,−=6,∴2+2B+2=(+p2=(210)2=40.(2)∵=10+3,=10−3,∴1∴o−2)=−2o−2)−+1o+1)=1−1=1010=10−3−10−3=−6.18.(2023上·河北衡水·八年级校联考阶段练习)已知=2−3,=2+3.(1)求+和B的值;(2)求2+2−3B的值;(3)若的小数部分是,的整数部分是,求B−B的值.【思路点拨】本题考查了二次根式的混合运算、利用完全平方公式进行计算、无理数的估算,熟练掌握以上知识点并灵活运用是解此题的关键.(1)代入=2−3,=2+3即可求出+和B的值;(2)将原式变形为+2−5B,代入数值进行计算即可;(3)先估算出1<3<2,从而得出=2−3,=3,再代入进行计算即可得出答案.【解题过程】(1)解:∵=2−3,=2+3,∴+=2−3+2+3=4,B=2−32+3=4−3=1;(2)解:由(1)得:+=4,B=1,∴2+2−3B=+2−5B=42−5×1=11(3)解:∵1<3<4,∴1<3<4,即1<3<2,∴−2<−3<−1,∴0<2−3<1,∵的小数部分是,∴=2−3,∵3<2+3<4,的整数部分是,∴=3,∴B−B=2−32−3−32+3=4−43+3−6−33=1−73.19.(2023下·广东江门·八年级统考期中)有这样一类题目:将±2化简,如果你能找到两个数m、n,使2+2=且B =,±2将变成2+2±2B ,即变成(±p 2,从而使±2得以化简.(1)例如,∵5+26=3+2+26=(3)2+(2)2+22×3=(3+2)2,∴5+26=(3+2)2=______,请完成填空.(2)仿照上面的例子,请化简4−23;(3)利用上面的方法,设=6+42,=3−5,求A +B 的值.【思路点拨】(1)根据二次根式的性质:2==o >0)0(=0)−o <0),即可得出相应结果.(2)根据(1)中“5+26=3+2+26=(3)2+(2)2+22×3=(3+2)2”,将代数式转化为完全平方公式的结构形式,再根据二次根式的性质化简求值,即可得出结果.(3)根据题意,首先把A 式和B 式分别转化为完全平方公式的结构形式,再根据二次根式的性质把A 式和B 式的结果分别算出,最后把A 式和B 式再代入A +B 中,求出A +B 的值.【解题过程】(1)∵5+26=2+3+26=22+32+2×2×3=2+32∴5+26=(3+2)2=3+2故答案为:3+2(2)∵4−23=3+1−23=32+1−23=3−12∴4−23=(3−1)2=3−1.(3)∵=6+42=4+2+42=42+22+2×4×2=(2+2)2∴=6+42=2+2∵=3−5=∴=3−5====∴把A 式和B 式的值代入A +B 中,得:+=2+2=2+2220.(2023下·广西钦州·八年级校考阶段练习)我们将+、−称为一对“对偶式”,因为+−=(p2−(p2=−,所以构造“和−====3+22.像这中的“”样,通过分子,分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化根据以上材料,理解并运用材料提供的方法,解答以下问题:“>”、“<”或“=”填空);(1(2)已知==,求K2rB2的值;+…+(3【思路点拨】(1)先分母有理化,然后根据作差法,比较大小即可求解;(2)先求得−s B的值,然后代入即可求解;(3)将每一项分母有理化,然后就根据二次根式的加减进行计算即可求解.【解题过程】(17−2=7−2===∵7>6,2>3−137−6+2−3>0,>故答案为:>.(2)∵==5+45+4=9+45,==5+2=5−45+4=9−45,∴+=9+45+9−45=18,−=9+45+−9+45=85,B=9+45945−80=1,∴K 2rB2+⋯+(3=3)2(53−35)35)(5−3979799⋯+2(99979799)(99979799)(9997−97=1−33+33−55+55−77+⋯+9797−9999=1−9999=1−。
人教版数学八年级下册压轴题含答案

1、如图11,已知正比例函数和反比例函数的图像都经过点M (-2,1-),且P (1-,-2)为双曲线上的一点,Q 为坐标平面上一动点,PA 垂直于x 轴,QB 垂直于y 轴,垂足分别是A 、B .(1)写出正比例函数和反比例函数的关系式;(2)当点Q 在直线MO 上运动时,直线MO 上是否存在这样的点Q ,使得△OBQ 与△OAP 面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图12,当点Q 在第一象限中的双曲线上运动时,作以OP 、OQ 为邻边的平行四边形OPCQ ,求平行四边形OPCQ 周长的最小值.M (2-2x2,于是211112224OBQ S OB BQ m m m △=?创=, 而1(1)(2)12OAP S △=-?=, 所以有,2114m =,解得2m =± 所以点Q 的坐标为1(21)Q ,和2(21)Q ,-- (3)因为四边形OPCQ 是平行四边形,所以OP =CQ ,OQ =PC ,而点P (1-,2-)是定点,所以OP 的长也是定长,所以要求平行四边形OPCQ 周长的最小值就只需求OQ 的最小值.因为点Q 在第一象限中双曲线上,所以可设点Q 的坐标为2()Q n n,, 由勾股定理可得222242()4OQ n n n n=+=-+, 所以当22()0n n -=即20n n-=时,2OQ 有最小值4, 又因为OQ 为正值,所以OQ 与2OQ 同时取得最小值, 所以OQ 有最小值2.由勾股定理得OP OPCQ 周长的最小值是图2()2)4OP OQ +==.2.已知:如图,正比例函数y =ax 的图象与反比例函数xky的图象交于点A (3,2). (1)试确定上述正比例函数和反比例函数的表达式;(2)根据图象回答,在第一象限内,当x 取何值时,反比例函数的值大于正比例函数的值; (3)M (m ,n )是反比例函数图象上的一动点,其中0<m <3,过点M 作直线MB ∥x 轴,交y 轴于点B ;过点A 作直线AC ∥y 轴交y 轴于点C ,交直线MB 于点D .当四边形OADM 的面积为6时,请判断线段BM 与DM 的大小关系,并说明理由. 解答:解:(1)将A (3,2)分别代入y=,y=ax 中,得:2=,3a=2 ∴k=6,a=(2分)∴反比例函数的表达式为:y=(3分) 正比例函数的表达式为y=x (4分)(2)观察图象,得在第一象限内,当0<x <3时,反比例函数的值大于正比例函数的值.(6分)(3)BM=DM (7分)理由:∵MN ∥x 轴,AC ∥y 轴, ∴四边形OCDB 是平行四边形, ∵x 轴⊥y 轴,∴?OCDB 是矩形.∵S △OMB =S △OAC =×|k|=3,又S 四边形OADM =6, ∴S 矩形OBDC =S 四边形OADM +S △OMB +S △OAC =3+3+6=12, 即OC?OB=12 ∵OC=3∴OB=4(8分) 即n=4 ∴m=∴MB=,MD=3﹣= ∴MB=MD (9分).3.如图,直线y=x+b (b ≠0)交坐标轴于A 、B 两点,交双曲线y=x2于点D ,过D 作两坐标轴的垂线DC 、DE ,连接OD . (1)求证:AD 平分∠CDE ; (2)对任意的实数b (b ≠0),求证BE ·OE 为定值;(3)是否存在直线AB ,使得四边形OBCD 为平行四边形?若存在,求出直线的解析式;若不存在,请说明理由.4.如图(1),直线122y x =-+交x 轴、y 轴于A 、B 两点,C 为直线AB 上第二象限内一点,且S △AOC =8,双曲线ky x=经过点C(1)求k 的值(2)如图(2),过点C 作CM ⊥y 轴于M,反向延长CM 于H ,使CM=CH ,过 H 作HN ⊥x 轴于N ,交双曲线y=xk于D ,求四边形OCHD 的面积 (3)如图(3),点G 和点A 关于y 轴对称,P 为第二象限内双曲线上一个动点, 过P 作PQ ⊥x 轴于Q ,分别交线段BG 于E,交射线BC 于F ,试判断线段 QE+QF 是否为定值,若为定值,证明并求出定值;若不是定值,请说明 理由。
新人教版八年级下数学第十七章勾股定理提高练习与常考难题和培优题压轴题(含解析)-

新人教版八年级下第十七章勾股定理提高练习与常考难题和培优题压轴题(含解析)一.选择题(共8小题)1.直角三角形两直角边长度为5,12,则斜边上的高()A.6 B.8 C.D.2.下列说法中正确的是()A.已知a,b,c是三角形的三边,则a2+b2=c2B.在直角三角形中两边和的平方等于第三边的平方C.在Rt△ABC中,∠C=90°,所以a2+b2=c2D.在Rt△ABC中,∠B=90°,所以a2+b2=c23.如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于()A.195cm B.200cm C.205cm D.210cm4.如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是()A.10尺B.11尺C.12尺D.13尺5.如图所示,在数轴上点A所表示的数为a,则a的值为()A.﹣1﹣B.1﹣C.﹣D.﹣1+6.一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了()A.1.5米B.0.9米C.0.8米D.0.5米7.在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为()A.2 B.2.6 C.3 D.48.如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为()A.13 B.19 C.25 D.169二.填空题(共5小题)9.将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是.10.如图,一场暴雨过后,垂直于地面的一棵树在距地面1米的点C处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为米.11.已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC的面积等于.12.观察下列勾股数第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1第四组:9=2×4+1,40=2×4×(4+1),41=2×4×(4+1)+1…观察以上各组勾股数组成特点,第7组勾股数是(只填数,不填等式)13.观察下列一组数:列举:3、4、5,猜想:32=4+5;列举:5、12、13,猜想:52=12+13;列举:7、24、25,猜想:72=24+25;…列举:13、b、c,猜想:132=b+c;请你分析上述数据的规律,结合相关知识求得b=,c=.三.解答题(共27小题)14.a,b,c为三角形ABC的三边,且满足a2+b2+c2+338=10a+24b+26c,试判别这个三角形的形状.15.如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.试求:(1)∠BAD的度数;(2)四边形ABCD的面积.16.如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,的三角形,请你帮助小华作出来.17.如图所示,在一次夏令营活动中,小明坐车从营地A点出发,沿北偏东60°方向走了100km到达B点,然后再沿北偏西30°方向走了100km到达目的地C点,求出A、C两点之间的距离.18.如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.(1)台风中心在移动过程中,与气象台A的最短距离是多少?(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长?19.如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC 边上的动点,点P从点A开始沿A⇒B方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t 秒.(1)出发2秒后,求PQ的长;(2)从出发几秒钟后,△PQB能形成等腰三角形?(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.20.在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.(1)△ABC的面积为:.(2)若△DEF三边的长分别为、、,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积为.(3)如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.(4)如图4,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13m2、25m2、36m2,则六边形花坛ABCDEF的面积是m2.21.(1)在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.如图1,某同学在解答这道题时,先建立一个每个小正方形的边长都是1的网格,再在网格中画出边长符合要求的格点三角形ABC(即△ABC三个顶点都在小正方形的顶点处),这样不需要求△ABC的高,而借用网格就能就算出它的面积.请你将△ABC的面积直接填写在横线上.思维拓展:(2)已知△ABC三边的长分别为a(a>0),求这个三角形的面积.我们把上述求△ABC面积的方法叫做构图法.如图2,网格中每个小正方形的边长都是a,请在网格中画出相应的△ABC,并求出它的面积.类比创新:(3)若△ABC三边的长分别为(m>0,n >0,且m≠n),求出这个三角形的面积.如图3,网格中每个小长方形长、宽都是m,n,请在网格中画出相应的△ABC,用网格计算这个三角形的面积.22.有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m的一棵大树上,大树高14m,且巢离树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,那它至少需要多少时间才能赶回巢中?23.(拓展创新)在教材中,我们通过数格子的方法发现了直角三角形的三边关系,利用完全相同的四个直角三角形采用拼图的方式验证了勾股定理的正确性.问题1:以直角三角形的三边为边向形外作等边三角形,探究S′+S″与S的关系(如图1).问题2:以直角三角形的三边为斜边向形外作等腰直角三角形,探究S′+S″与S 的关系(如图2).问题3:以直角三角形的三边为直径向形外作半圆,探究S′+S″与S的关系(如图3).24.如图,在平面坐标系中,点A、点B分别在x轴、y轴的正半轴上,且OA=OB,另有两点C(a,b)和D(b,﹣a)(a、b均大于0);(1)连接OD、CD,求证:∠ODC=45°;(2)连接CO、CB、CA,若CB=1,C0=2,CA=3,求∠OCB的度数;(3)若a=b,在线段OA上有一点E,且AE=3,CE=5,AC=7,求△OCA的面积.25.11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题“小溪边长着两棵棕榈树,恰好隔岸相望.一棵树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻飞去抓鱼,并且同时到达目标.问这条鱼出现的地方离开比较高的棕榈树的树根有多远?26.(1)先化简,再求值:x(x﹣2)﹣(x+1)(x﹣1),其中x=10.(2)已知,求代数式(x+1)2﹣4(x+1)+4的值.(3)如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,请在给定的网格中按要求画图:①从点A出发在图中画一条线段AB,使得AB=;②画出一个以(1)中的AB为斜边的等腰直角三角形,使三角形的三个顶点都在格点上,并根据所画图形求出等腰直角三角形的腰长.27.[问题情境]勾股定理是一条古老的数学定理,它有很多种证明方法.我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数学关系”(勾股定理)带到其它星球,作为地球人与其他星球“人”进行第一次“谈话”的语言;[定理表述]请你根据图1中的直角三角形叙述勾股定理;[尝试证明]以图1中的直角三角形为基础,将两个直角边长为a,b,斜边长为c 的三角形按如图所示的方式放置,连接两个之间三角形的另外一对锐角的顶点(如图2),请你利用图2,验证勾股定理;[知识扩展]利用图2中的直角梯形,我们可以证明<,其证明步骤如下:∵BC=a+b,AD=又∵在直角梯形ABCD中,有BCAD(填大小关系),即∴.28.观察、思考与验证(1)如图1是一个重要公式的几何解释,请你写出这个公式;(2)如图2所示,∠B=∠D=90°,且B,C,D在同一直线上.试说明:∠ACE=90°;(3)伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(发表在1876年4月1日的《新英格兰教育日志》上),请你写出验证过程.29.超速行驶容易引发交通事故.如图,某观测点设在到公路l的距离为100米的点P处,一辆汽车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,是判断此车是否超过了每小时80千米的限制速度?(参考数据:=1.41,=1.73)30.中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C 处截住了渔船.(1)请用直尺和圆规作出C处的位置;(2)求我国海监船行驶的航程BC的长.31.在一次“构造勾股数”的探究性学习中,老师给出了下表:m 2 3 3 4…n1123…a22+1232+1232+2242+32…b4 6 1224 …c22﹣1232﹣1232﹣2242﹣32…其中m、n为正整数,且m>n.(1)观察表格,当m=2,n=1时,此时对应的a、b、c的值能否为直角三角形三边的长?说明你的理由.(2)探究a,b,c与m、n之间的关系并用含m、n的代数式表示:a=,b=,c=.(3)以a,b,c为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.32.如图1,在4×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒1个单位,点Q的运动速度为每秒0.5个单位,当点P运动到点C时,两个点都停止运动,设运动时间为t(0<t<8).(1)请在4×8的网格纸图2中画出t为6秒时的线段PQ.并求其长度;(2)当t为多少时.△PQB是以BP为底的等腰三角形.33.阅读下面的情景对话,然后解答问题:(1)理解:①根据“奇异三角形”的定义,请你判断:“等边三角形一定是奇异三角形”吗?(填是或不是)②若某三角形的三边长分别为1、、2,则该三角形(是或不是)奇异三角形.(2)探究:若Rt△ABC是奇异三角形,且其两边长分别为2、2,则第三边的长为,且这个直角三角形的三边之比为(从小到大排列,不得含有分母).(3)设问:请提出一个和奇异三角形有关的问题.(不用解答)34.观察下列各式,你有什么发现?32=4+5,52=12+13,72=24+25,92=40+41,…用你的发现解决下列问题:(1)填空:112=+ ;(2)请用含字母n(n为正整数)的关系式表示出你发现的规律:;(3)结合勾股定理有关知识,说明你的结论的正确性.35.小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完?36.如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.37.如图,四边形ABCD的三边(AB、BC、CD)和BD的长度都为5厘米,动点P从A出发(A→B→D)到D,速度为2厘米/秒,动点Q从点D出发(D→C→B→A)到A,速度为2.8厘米/秒.5秒后P、Q相距3厘米,试确定5秒时△APQ的形状.38.一艘轮船以20海里/时的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区域,当轮船到A处时测得台风中心移到位于点A正南方的B 处,且AB=100海里.若这艘轮船自A处按原速度继续航行,在途中是否会遇到台风?若会,则求出轮船最初遇到台风的时间;若不会,请说明理由.39.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地°送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(AC=1尺),将它往前推进两步(EB=10尺),此时踏板升高离地五尺(BD=5尺),求秋千绳索(OA或OB)的长度.40.如图,∠AOB=90°,OA=45cm,OB=15cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?1.已知直角三角形两边的长为3和4,则此三角形的周长为()A.12 B.7+C.12或7+D.以上都不对2.图中字母所代表的正方形的面积为144的选项为()A.B.C.D.3.如图,数轴上的点A所表示的数为x,则x的值为()A.B.﹣C.2 D.﹣24.如图,带阴影的正方形面积是.5.如图,在Rt△ABC中,∠BCA=90°,点D是BC上一点,AD=BD,若AB=8,BD=5,则CD=.6.正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,(1)在图①中,画一个面积为10的正方形;(2)在图②、图③中,分别画两个不全等的直角三角形,使它们的三边长都是无理数.初二数学勾股定理提高练习与常考难题和培优题压轴题(含解析)参考答案与试题解析一.选择题(共8小题)1.(2016秋•吴江区期中)直角三角形两直角边长度为5,12,则斜边上的高()A.6 B.8 C.D.【分析】首先根据勾股定理,得:斜边==13.再根据直角三角形的面积公式,求出斜边上的高.【解答】解:由题意得,斜边为=13.所以斜边上的高=12×5÷13=.故选D.【点评】运用了勾股定理.注意:直角三角形斜边上的高等于两条直角边的乘积除以斜边.2.(2016春•抚顺县期中)下列说法中正确的是()A.已知a,b,c是三角形的三边,则a2+b2=c2B.在直角三角形中两边和的平方等于第三边的平方C.在Rt△ABC中,∠C=90°,所以a2+b2=c2D.在Rt△ABC中,∠B=90°,所以a2+b2=c2【分析】在直角三角形中只有斜边的平方等于其他两边的平方的和,且斜边对角为直角,根据此就可以直接判断A、B、C、D选项.【解答】解:在直角三角形中只有斜边的平方等于其他两边的平方的和,且斜边对角为直角.A、不确定c是斜边,故本命题错误,即A选项错误;B、不确定第三边是否是斜边,故本命题错误,即B选项错误;C、∠C=90°,所以其对边为斜边,故本命题正确,即C选项正确;D、∠B=90°,所以斜边为b,所以a2+c2=b2,故本命题错误,即D选项错误;故选C.【点评】本题考查了勾股定理的正确运用,只有斜边的平方才等于其他两边的平方和.3.(2016春•临沭县期中)如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于()A.195cm B.200cm C.205cm D.210cm【分析】作出直角三角形后分别求得直角三角形的两直角边的长后即可利用勾股定理求得斜边AB的长.【解答】解:如图,由题意得:AC=15×5=75cm,BC=30×6=180cm,故AB===195cm.故选A.【点评】本题考查了勾股定理的应用,解题的关键是从实际问题中抽象出直角三角形,难度不大.4.(2015春•青山区期中)如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是()A.10尺B.11尺C.12尺D.13尺【分析】找到题中的直角三角形,设水深为x尺,根据勾股定理解答.【解答】解:设水深为x尺,则芦苇长为(x+1)尺,根据勾股定理得:x2+()2=(x+1)2,解得:x=12,芦苇的长度=x+1=12+1=13(尺),故选D.【点评】本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.5.(2016春•南陵县期中)如图所示,在数轴上点A所表示的数为a,则a的值为()A.﹣1﹣B.1﹣C.﹣D.﹣1+【分析】点A在以O为圆心,OB长为半径的圆上,所以在直角△BOC中,根据勾股定理求得圆O的半径OA=OB=,然后由实数与数轴的关系可以求得a的值.【解答】解:如图,点A在以O为圆心,OB长为半径的圆上.∵在直角△BOC中,OC=2,BC=1,则根据勾股定理知OB===,∴OA=OB=,∴a=﹣1﹣.故选A.【点评】本题考查了勾股定理、实数与数轴.找出OA=OB是解题的关键.6.(2015春•蓟县期中)一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了()A.1.5米B.0.9米C.0.8米D.0.5米【分析】先根据梯子的顶端下滑了0.4米求出A′C的长,再根据勾股定理求出B′C 的长,进而可得出结论.【解答】解:(1)∵在Rt△ABC中,AB=2.5m,BC=0.7m,∴AC===2.4(m).∵梯子的顶端下滑了0.4米,∴A′C=2m,∵在Rt△A′B′C中,A′B′=2.5m,A′C=2m,∴B′C==1.5m,∴BB′=B′C﹣BC=1.5﹣0.7=0.8m.故选C.【点评】此题主要考查了勾股定理的应用,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.7.(2015春•罗田县期中)在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为()A.2 B.2.6 C.3 D.4【分析】根据勾股定理求出AB的长即可解答.【解答】解:在Rt△ABC中,根据勾股定理,AB==13,又∵AC=12,BC=5,AM=AC,BN=BC,∴AM=12,BN=5,∴MN=AM+BN﹣AB=12+5﹣13=4.故选D.【点评】本题综合考查了勾股定理的应用,找到关系MN=AM+BN﹣AB是关键.8.(2016春•重庆校级期中)如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为()A.13 B.19 C.25 D.169【分析】根据勾股定理,知两条直角边的平方等于斜边的平方,此题中斜边的平方即为大正方形的面积13,2ab即四个直角三角形的面积和,从而不难求得(a+b)2的值.【解答】解:(a+b)2=a2+b2+2ab=大正方形的面积+四个直角三角形的面积和=13+(13﹣1)=25.故选C.【点评】考查了勾股定理的证明,注意完全平方公式的展开:(a+b)2=a2+b2+2ab,还要注意图形的面积和a,b之间的关系.二.填空题(共5小题)9.(2016春•固始县期中)将一根24cm的筷子,置于底面直径为15cm,高8cm 的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是7cm≤h≤16cm.【分析】如图,当筷子的底端在A点时,筷子露在杯子外面的长度最短;当筷子的底端在D点时,筷子露在杯子外面的长度最长.然后分别利用已知条件根据勾股定理即可求出h的取值范围.【解答】解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,∴h=24﹣8=16cm;当筷子的底端在A点时,筷子露在杯子外面的长度最短,在Rt△ABD中,AD=15,BD=8,∴AB==17,∴此时h=24﹣17=7cm,所以h的取值范围是7cm≤h≤16cm.故答案为:7cm≤h≤16cm.【点评】本题考查了勾股定理的应用,求出h的值最大值与最小值是解题关键.10.(2015春•汕头校级期中)如图,一场暴雨过后,垂直于地面的一棵树在距地面1米的点C处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为(1+)米.【分析】根据题意利用勾股定理得出BC的长,进而得出答案.【解答】解:由题意得:在直角△ABC中,AC2+AB2=BC2,则12+22=BC2,∴BC=,∴则树高为:(1+)m.故答案为:(1+).【点评】此题主要考查了勾股定理的应用,熟练利用勾股定理得出BC的长是解题关键.11.(2016春•高安市期中)已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC的面积等于24cm2.【分析】利用勾股定理列出关系式,再利用完全平方公式变形,将a+b与c的值代入求出ab的值,即可确定出直角三角形的面积.【解答】解:∵Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,∴由勾股定理得:a2+b2=c2,即(a+b)2﹣2ab=c2=100,∴196﹣2ab=100,即ab=48,则Rt△ABC的面积为ab=24(cm2).故答案为:24cm2.【点评】此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.12.(2016春•嘉祥县期中)观察下列勾股数第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1第四组:9=2×4+1,40=2×4×(4+1),41=2×4×(4+1)+1…观察以上各组勾股数组成特点,第7组勾股数是15,112,113(只填数,不填等式)【分析】通过观察,得出规律:这类勾股数分别为2n+1,2n(n+1),2n(n+1)+1,由此可写出第7组勾股数.【解答】解:∵第1组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1,第2组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1,第3组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1,第4组:9=2×4+1,40=2×4×(4+1)41=2×4×(4+1)+1,∴第7组勾股数是2×7+1=15,2×7×(7+1)=112,2×7×(7+1)+1=113,即15,112,113.故答案为:15,112,113.【点评】此题考查的知识点是勾股数,属于规律性题目,关键是通过观察找出规律求解.13.(2009春•武昌区期中)观察下列一组数:列举:3、4、5,猜想:32=4+5;列举:5、12、13,猜想:52=12+13;列举:7、24、25,猜想:72=24+25;…列举:13、b、c,猜想:132=b+c;请你分析上述数据的规律,结合相关知识求得b=84,c=85.【分析】认真观察三个数之间的关系:首先发现每一组的三个数为勾股数,第一个数为从3开始连续的奇数,第二、三个数为连续的自然数;进一步发现第一个数的平方是第二、三个数的和;最后得出第n组数为(2n+1),(),(),由此规律解决问题.【解答】解:在32=4+5中,4=,5=;在52=12+13中,12=,13=;…则在13、b、c中,b==84,c==85.【点评】认真观察各式的特点,总结规律是解题的关键.三.解答题(共27小题)14.(2016春•黄冈期中)a,b,c为三角形ABC的三边,且满足a2+b2+c2+338=10a+24b+26c,试判别这个三角形的形状.【分析】现对已知的式子变形,出现三个非负数的平方和等于0的形式,求出a、b、c,再验证两小边的平方和是否等于最长边的平方即可.【解答】解:由a2+b2+c2+338=10a+24b+26c,得:(a2﹣10a+25)+(b2﹣24b+144)+(c2﹣26c+169)=0,即:(a﹣5)2+(b﹣12)2+(c﹣13)2=0,由非负数的性质可得:,解得,∵52+122=169=132,即a2+b2=c2,∴∠C=90°,即三角形ABC为直角三角形.【点评】本题考查勾股定理的逆定理的应用、完全平方公式、非负数的性质.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.15.(2016秋•永登县期中)如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.试求:(1)∠BAD的度数;(2)四边形ABCD的面积.【分析】连接AC,则在直角△ABC中,已知AB,BC可以求AC,根据AC,AD,CD的长可以判定△ACD为直角三角形,(1)根据∠BAD=∠CAD+∠BAC,可以求解;(2)根据四边形ABCD的面积为△ABC和△ACD的面积之和可以解题.【解答】解:(1)连接AC,∵AB⊥CB于B,∴∠B=90°,在△ABC中,∵∠B=90°,∴AB2+BC2=AC2,又∵AB=CB=,∴AC=2,∠BAC=∠BCA=45°,∵CD=,DA=1,∴CD2=5,DA2=1,AC2=4.∴AC2+DA2=CD2,由勾股定理的逆定理得:∠DAC=90°,∴∠BAD=∠BAC+∠DAC=45°+90°=135°;(2)∵∠DAC=90°,AB ⊥CB 于B ,∴S △ABC =,S △DAC =,∵AB=CB=,DA=1,AC=2, ∴S △ABC =1,S △DAC =1而S 四边形ABCD =S △ABC +S △DAC ,∴S 四边形ABCD =2.【点评】本题考查了勾股定理在直角三角形中的运用,考查了根据勾股定理逆定理判定直角三角形,考查了直角三角形面积的计算,本题中求证△ACD 是直角三角形是解题的关键.16.(2016春•邹城市校级期中)如图,小华准备在边长为1的正方形网格中,作一个三边长分别为4,5,的三角形,请你帮助小华作出来.【分析】直接利用网格结合勾股定理求出答案.【解答】解:如图所示:△ABC 即为所求.【点评】此题主要考查了勾股定理,正确借助网格求出是解题关键.17.(2015春•平南县期中)如图所示,在一次夏令营活动中,小明坐车从营地A 点出发,沿北偏东60°方向走了100km到达B点,然后再沿北偏西30°方向走了100km到达目的地C点,求出A、C两点之间的距离.【分析】根据所走的方向可判断出△ABC是直角三角形,根据勾股定理可求出解.【解答】解:∵AD∥BE∴∠ABE=∠DAB=60°∵∠CBE=30°∴∠ABC=180°﹣∠ABE﹣∠CBE=180°﹣60°﹣30°=90°,在Rt△ABC中,∴==200,∴A、C两点之间的距离为200km.【点评】本题考查勾股定理的应用,先确定是直角三角形后,根据各边长,用勾股定理可求出AC的长,且求出∠DAC的度数,进而可求出点C在点A的什么方向上.18.(2015秋•新泰市期中)如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.(1)台风中心在移动过程中,与气象台A的最短距离是多少?(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长?【分析】(1)过A作AE⊥BD于E,线段AE的长即为台风中心与气象台A的最短距离,由含30°角的直角三角形的性质即可得出结果;(2)根据题意得出线段CD就是气象台A受到台风影响的路程,求出CD的长,即可得出结果.【解答】解:(1)过A作AE⊥BD于E,如图1所示:∵台风中心在BD上移动,∴AE的长即为气象台距离台风中心的最短距离,在Rt△ABE中,∠ABE=90°﹣60°=30°,∴AE=AB=160,即台风中心在移动过程中,与气象台A的最短距离是160km.(2)∵台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响,∴线段CD就是气象台A受到台风影响的路程,连接AC,如图2所示:在Rt△ACE中,AC=200km,AE=160km,∴CE==120km,∵AC=AD,AE⊥CD,∴CE=ED=120km,∴CD=240km.∴台风影响气象台的时间会持续240÷20=12(小时).【点评】本题考查了勾股定理在实际生活中的应用、垂径定理、含30°角的直角三角形的性质等知识;熟练掌握垂径定理和勾股定理,求出CD是解决问题(2)的关键.19.(2015春•阳东县期中)如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿A⇒B方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.(1)出发2秒后,求PQ的长;(2)从出发几秒钟后,△PQB能形成等腰三角形?(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.。
初二数学:平行四边形知识点总结及压轴题练习(附答案解析)

A C BD 初二平行四边形所有知识点总结和常考题知识点:1、平行四边形定义:有两组对边分别平行的四边形叫做平行四边形。
2、平行四边形的性质:⑴平行四边形的对边相等;⑵平行四边形的对角相等:⑶平行四边形的对角线互相平分。
3平行四边形的判定:⑴.两组对边分别相等的四边形是平行四边形; ⑵对角线互相平分的四边形是平行四边形;⑶两组对角分别相等的四边形是平行四边形; ⑷一组对边平行且相等的四边形是平行四边形。
4、矩形的定义:有一个角是直角的平行四边形。
5、矩形的性质:⑴矩形的四个角都是直角;⑵矩形的对角线相等。
6、矩形判定定理:⑴ 有三个角是直角的四边形是矩形;⑵对角线相等的平行四边形是矩形。
7、中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半。
直角三角形斜边上的中线等于斜边的一半。
(连接三角形两边中点的线段叫做三角形的中位线。
)8、菱形的定义 :有一组邻边相等的平行四边形。
9、菱形的性质:⑴菱形的四条边都相等;⑵菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
S 菱形=1/2×ab (a 、b 为两条对角线长)10、菱形的判定定理:⑴四条边相等的四边形是菱形。
⑵对角线互相垂直的平行四边形是菱形。
11、正方形定义:一个角是直角的菱形或邻边相等的矩形。
12正方形判定定理:⑴ 邻边相等的矩形是正方形。
⑵有一个角是直角的菱形是正方形。
(矩形+菱形=正方形)常考题:一.选择题(共14小题)1.矩形具有而菱形不具有的性质是( )A .两组对边分别平行B .对角线相等C .对角线互相平分D .两组对角分别相等2.平行四边形ABCD 中,AC 、BD 是两条对角线,如果添加一个条件,即可推出平行四边形ABCD 是矩形,那么这个条件是( )A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD3.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()A.当AB=BC时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD时,它是正方形4.顺次连接任意四边形四边中点所得的四边形一定是()A.平行四边形B.矩形C.菱形D.正方形5.在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是()A.(3,7) B.(5,3) C.(7,3) D.(8,2)6.如图,▱ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是()A.8 B.9 C.10 D.117.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12 B.24 C.12D.168.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于()A.50°B.60°C.70°D.80°9.如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为()A.4 B.6 C.8 D.1010.如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为()A.14 B.15 C.16 D.1711.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为()A.2 B.4 C.4 D.812.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为()A.16 B.17 C.18 D.1913.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF ⊥AB,垂足为F,则EF的长为()A.1 B.C.4﹣2D.3﹣414.如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为()A.45°B.55°C.60°D.75°二.填空题(共13小题)15.已知菱形的两对角线长分别为6cm和8cm,则菱形的面积为cm2.16.如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD的周长等于.17.如图,▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO 的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=厘米.18.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD 和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为.19.如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D在y轴上,则点C的坐标是.20.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于度.21.如图,▱ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是.22.如图所示,菱形ABCD的边长为4,且AE⊥BC于E,AF⊥CD于F,∠B=60°,则菱形的面积为.23.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是.24.如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C (0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为.25.如图,已知△ABC的三个顶点的坐标分别为A(﹣2,0),B(﹣1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D的坐标.26.如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为.27.如图,四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为.三.解答题(共13小题)28.如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.求证:四边形BECF是平行四边形.29.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,(1)求证:四边形ADCE为矩形;(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.30.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.(1)试说明AC=EF;(2)求证:四边形ADFE是平行四边形.31.如图,矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.求证:BE=CF.32.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)线段BD与CD有什么数量关系,并说明理由;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.33.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.(1)求证:四边形BCFE是菱形;(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.34.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?35.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.36.如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证:(1)△AEH≌△CGF;(2)四边形EFGH是菱形.37.如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E.(1)求证:△ABD≌△EBD;(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.38.如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.(1)求证:△BCP≌△DCP;(2)求证:∠DPE=∠ABC;(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE=度.39.在数学活动课中,小辉将边长为和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.40.数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线CF于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.初二平行四边形所有知识点总结和常考题提高难题压轴题练习(含答案解析)参考答案与试题解析一.选择题(共14小题)1.(2013•宜宾)矩形具有而菱形不具有的性质是()A.两组对边分别平行B.对角线相等C.对角线互相平分 D.两组对角分别相等【分析】根据矩形与菱形的性质对各选项分析判断后利用排除法求解.【解答】解:A、矩形与菱形的两组对边都分别平行,故本选项错误;B、矩形的对角线相等,菱形的对角线不相等,故本选项正确;C、矩形与菱形的对角线都互相平分,故本选项错误;D、矩形与菱形的两组对角都分别相等,故本选项错误.故选B.【点评】本题考查了矩形的性质,菱形的性质,熟记两图形的性质是解题的关键.2.(2014•河池)平行四边形ABCD中,AC、BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是()A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD【分析】根据对角线相等的平行四边形是矩形判断.【解答】解:A、是邻边相等,可得到平行四边形ABCD是菱形,故不正确;B、是对角线相等,可推出平行四边形ABCD是矩形,故正确;C、是对角线互相垂直,可得到平行四边形ABCD是菱形,故不正确;D、无法判断.故选B.【点评】本题主要考查的是矩形的判定定理.但需要注意的是本题的知识点是关于各个图形的性质以及判定.3.(2008•扬州)如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()A.当AB=BC时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD时,它是正方形【分析】根据邻边相等的平行四边形是菱形;根据所给条件可以证出邻边相等;根据有一个角是直角的平行四边形是矩形;根据对角线相等的平行四边形是矩形.【解答】解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB=BC时,它是菱形,故A选项正确;B、∵四边形ABCD是平行四边形,∴BO=OD,∵AC⊥BD,∴AB2=BO2+AO2,AD2=DO2+AO2,∴AB=AD,∴四边形ABCD是菱形,故B选项正确;C、有一个角是直角的平行四边形是矩形,故C选项正确;D、根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形,不是正方形,故D选项错误;综上所述,符合题意是D选项;故选:D.【点评】此题主要考查学生对正方形的判定、平行四边形的性质、菱形的判定和矩形的判定的理解和掌握,此题涉及到的知识点较多,学生答题时容易出错.4.(2011•张家界)顺次连接任意四边形四边中点所得的四边形一定是()A.平行四边形B.矩形C.菱形D.正方形【分析】顺次连接任意四边形四边中点所得的四边形,一组对边平行并且等于原来四边形某一对角线的一半,说明新四边形的对边平行且相等.所以是平行四边形.【解答】解:连接BD,已知任意四边形ABCD,E、F、G、H分别是各边中点.∵在△ABD中,E、H是AB、AD中点,∴EH∥BD,EH=BD.∵在△BCD中,G、F是DC、BC中点,∴GF∥BD,GF=BD,∴EH=GF,EH∥GF,∴四边形EFGH为平行四边形.故选:A.【点评】本题三角形的中位线的性质考查了平行四边形的判定:三角形的中位线平行于第三边,且等于第三边的一半.5.(2006•南京)在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是()A.(3,7) B.(5,3) C.(7,3) D.(8,2)【分析】因为D点坐标为(2,3),由平行四边形的性质,可知C点的纵坐标一定是3,又由D点相对于A点横坐标移动了2,故可得C点横坐标为2+5=7,即顶点C的坐标(7,3).【解答】解:已知A,B,D三点的坐标分别是(0,0),(5,0),(2,3),∵AB在x轴上,∴点C与点D的纵坐标相等,都为3,又∵D点相对于A点横坐标移动了2﹣0=2,∴C点横坐标为2+5=7,∴即顶点C的坐标(7,3).故选:C.【点评】本题主要是对平行四边形的性质与点的坐标的表示及平行线的性质和互为余(补)角的等知识的直接考查.同时考查了数形结合思想,题目的条件既有数又有形,解决问题的方法也要既依托数也依托形,体现了数形的紧密结合,但本题对学生能力的要求并不高.6.(2014•河南)如图,▱ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是()A.8 B.9 C.10 D.11【分析】利用平行四边形的性质和勾股定理易求BO的长,进而可求出BD的长.【解答】解:∵▱ABCD的对角线AC与BD相交于点O,∴BO=DO,AO=CO,∵AB⊥AC,AB=4,AC=6,∴BO==5,∴BD=2BO=10,故选:C.【点评】本题考查了平行四边形的性质以及勾股定理的运用,是中考常见题型,比较简单.7.(2013•南充)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12 B.24 C.12D.16【分析】在矩形ABCD中根据AD∥BC得出∠DEF=∠EFB=60°,由于把矩形ABCD 沿EF翻折点B恰好落在AD边的B′处,所以∠EFB=∠DEF=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,AB=A′B′,在△EFB′中可知∠DEF=∠EFB=∠EB′F=60°故△EFB′是等边三角形,由此可得出∠A′B′E=90°﹣60°=30°,根据直角三角形的性质得出A′B′=AB=2,然后根据矩形的面积公式列式计算即可得解.【解答】解:在矩形ABCD中,∵AD∥BC,∴∠DEF=∠EFB=60°,∵把矩形ABCD沿EF翻折点B恰好落在AD边的B′处,∴∠DEF=∠EFB=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,AB=A′B′,在△EFB′中,∵∠DEF=∠EFB=∠EB′F=60°∴△EFB′是等边三角形,Rt△A′EB′中,∵∠A′B′E=90°﹣60°=30°,∴B′E=2A′E,而A′E=2,∴B′E=4,∴A′B′=2,即AB=2,∵AE=2,DE=6,∴AD=AE+DE=2+6=8,∴矩形ABCD的面积=AB•AD=2×8=16.故选D.【点评】本题考查了矩形的性质,翻折变换的性质,两直线平行,同旁内角互补,两直线平行,内错角相等的性质,解直角三角形,作辅助线构造直角三角形并熟记性质是解题的关键.8.(2013•扬州)如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于()A.50°B.60°C.70°D.80°【分析】连接BF,根据菱形的对角线平分一组对角求出∠BAC,∠BCF=∠DCF,四条边都相等可得BC=DC,再根据菱形的邻角互补求出∠ABC,然后根据线段垂直平分线上的点到线段两端点的距离相等可得AF=BF,根据等边对等角求出∠ABF=∠BAC,从而求出∠CBF,再利用“边角边”证明△BCF和△DCF全等,根据全等三角形对应角相等可得∠CDF=∠CBF.【解答】解:如图,连接BF,在菱形ABCD中,∠BAC=∠BAD=×80°=40°,∠BCF=∠DCF,BC=DC,∠ABC=180°﹣∠BAD=180°﹣80°=100°,∵EF是线段AB的垂直平分线,∴AF=BF,∠ABF=∠BAC=40°,∴∠CBF=∠ABC﹣∠ABF=100°﹣40°=60°,∵在△BCF和△DCF中,,∴△BCF≌△DCF(SAS),∴∠CDF=∠CBF=60°.故选:B.【点评】本题考查了菱形的性质,全等三角形的判定与性质,线段垂直平分线上的点到线段两端点的距离相等的性质,综合性强,但难度不大,熟记各性质是解题的关键.9.(2015•河南)如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC 于点E.若BF=6,AB=5,则AE的长为()A.4 B.6 C.8 D.10【分析】由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.【解答】解:连结EF,AE与BF交于点O,如图,∵AB=AF,AO平分∠BAD,∴AO⊥BF,BO=FO=BF=3,∵四边形ABCD为平行四边形,∴AF∥BE,∴∠1=∠3,∴∠2=∠3,∴AB=EB,而BO⊥AE,∴AO=OE,在Rt△AOB中,AO===4,∴AE=2AO=8.故选C.【点评】本题考查了平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.也考查了等腰三角形的判定与性质和基本作图.10.(2013•凉山州)如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为()A.14 B.15 C.16 D.17【分析】根据菱形得出AB=BC,得出等边三角形ABC,求出AC,长,根据正方形的性质得出AF=EF=EC=AC=4,求出即可.【解答】解:∵四边形ABCD是菱形,∴AB=BC,∵∠B=60°,∴△ABC是等边三角形,∴AC=AB=4,∴正方形ACEF的周长是AC+CE+EF+AF=4×4=16,故选C.【点评】本题考查了菱形性质,正方形性质,等边三角形的性质和判定的应用,关键是求出AC的长.11.(2013•泰安)如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC 的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为()A.2 B.4 C.4 D.8【分析】由AE为角平分线,得到一对角相等,再由ABCD为平行四边形,得到AD与BE平行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到AD=DF,由F为DC中点,AB=CD,求出AD与DF的长,得出三角形ADF 为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD 与DG的长,利用勾股定理求出AG的长,进而求出AF的长,再由三角形ADF 与三角形ECF全等,得出AF=EF,即可求出AE的长.【解答】解:∵AE为∠DAB的平分线,∴∠DAE=∠BAE,∵DC∥AB,∴∠BAE=∠DFA,∴∠DAE=∠DFA,∴AD=FD,又F为DC的中点,∴DF=CF,∴AD=DF=DC=AB=2,在Rt△ADG中,根据勾股定理得:AG=,则AF=2AG=2,∵平行四边形ABCD,∴AD∥BC,∴∠DAF=∠E,∠ADF=∠ECF,在△ADF和△ECF中,,∴△ADF≌△ECF(AAS),∴AF=EF,则AE=2AF=4.故选:B【点评】此题考查了平行四边形的性质,全等三角形的判定与性质,勾股定理,等腰三角形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.12.(2013•菏泽)如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为()A.16 B.17 C.18 D.19【分析】由图可得,S1的边长为3,由AC=BC,BC=CE=CD,可得AC=2CD,CD=2,EC=;然后,分别算出S1、S2的面积,即可解答.【解答】解:如图,设正方形S2的边长为x,根据等腰直角三角形的性质知,AC=x,x=CD,∴AC=2CD,CD==2,∴EC2=22+22,即EC=;∴S2的面积为EC2==8;∵S1的边长为3,S1的面积为3×3=9,∴S1+S2=8+9=17.故选:B.【点评】本题考查了正方形的性质和等腰直角三角形的性质,考查了学生的读图能力.13.(2013•连云港)如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为()A.1 B.C.4﹣2D.3﹣4【分析】根据正方形的对角线平分一组对角可得∠ABD=∠ADB=45°,再求出∠DAE 的度数,根据三角形的内角和定理求∠AED,从而得到∠DAE=∠AED,再根据等角对等边的性质得到AD=DE,然后求出正方形的对角线BD,再求出BE,最后根据等腰直角三角形的直角边等于斜边的倍计算即可得解.【解答】解:在正方形ABCD中,∠ABD=∠ADB=45°,∵∠BAE=22.5°,∴∠DAE=90°﹣∠BAE=90°﹣22.5°=67.5°,在△ADE中,∠AED=180°﹣45°﹣67.5°=67.5°,∴∠DAE=∠AED,∴AD=DE=4,∵正方形的边长为4,∴BD=4,∴BE=BD﹣DE=4﹣4,∵EF⊥AB,∠ABD=45°,∴△BEF是等腰直角三角形,∴EF=BE=×(4﹣4)=4﹣2.故选:C.【点评】本题考查了正方形的性质,主要利用了正方形的对角线平分一组对角,等角对等边的性质,正方形的对角线与边长的关系,等腰直角三角形的判定与性质,根据角的度数的相等求出相等的角,再求出DE=AD是解题的关键,也是本题的难点.14.(2014•福州)如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE 相交于点F,则∠BFC为()A.45°B.55°C.60°D.75°【分析】根据正方形的性质及全等三角形的性质求出∠ABE=15°,∠BAC=45°,再求∠BFC.【解答】解:∵四边形ABCD是正方形,∴AB=AD,又∵△ADE是等边三角形,∴AE=AD=DE,∠DAE=60°,∴AB=AE,∴∠ABE=∠AEB,∠BAE=90°+60°=150°,∴∠ABE=(180°﹣150°)÷2=15°,又∵∠BAC=45°,∴∠BFC=45°+15°=60°.故选:C.【点评】本题主要是考查正方形的性质和等边三角形的性质,本题的关键是求出∠ABE=15°.二.填空题(共13小题)15.(2008•恩施州)已知菱形的两对角线长分别为6cm和8cm,则菱形的面积为24cm2.【分析】根据菱形的面积等于两对角线乘积的一半求得其面积即可.【解答】解:由已知得,菱形的面积等于两对角线乘积的一半即:6×8÷2=24cm2.故答案为:24.【点评】此题主要考查菱形的面积等于两条对角线的积的一半.16.(2015•梅州)如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD 的周长等于20.【分析】根据四边形ABCD为平行四边形可得AE∥BC,根据平行线的性质和角平分线的性质可得出∠ABE=∠AEB,继而可得AB=AE,然后根据已知可求得结果.【解答】解:∵四边形ABCD为平行四边形,∴AE∥BC,AD=BC,AB=CD,∴∠AEB=∠EBC,∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ABE=∠AEB,∴AB=AE,∴AE+DE=AD=BC=6,∴AE+2=6,∴AE=4,∴AB=CD=4,∴▱ABCD的周长=4+4+6+6=20,故答案为:20.【点评】本题考查了平行四边形的性质,解答本题的关键是根据平行线的性质和角平分线的性质得出∠ABE=∠AEB.17.(2013•厦门)如图,▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=3厘米.【分析】根据AC+BD=24厘米,可得出出OA+OB=12cm,继而求出AB,判断EF 是△OAB的中位线即可得出EF的长度.【解答】解:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,又∵AC+BD=24厘米,∴OA+OB=12cm,∵△OAB的周长是18厘米,∴AB=6cm,∵点E,F分别是线段AO,BO的中点,∴EF是△OAB的中位线,∴EF=AB=3cm.故答案为:3.【点评】本题考查了三角形的中位线定理,解答本题需要用到:平行四边形的对角线互相平分,三角形中位线的判定定理及性质.18.(2007•临夏州)如图,矩形ABCD的对角线AC和BD相交于点O,过点O 的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为3.【分析】根据矩形是中心对称图形寻找思路:△AOE≌△COF,图中阴影部分的面积就是△BCD的面积.【解答】解:∵四边形ABCD是矩形,∴OA=OC,∠AEO=∠CFO;又∵∠AOE=∠COF,在△AOE和△COF中,,∴△AOE≌△COF,∴S△AOE =S△COF,∴图中阴影部分的面积就是△BCD的面积.S△BCD=BC×CD=×2×3=3.故答案为:3.【点评】此题主要考查了矩形的性质以及全等三角形的判定和性质,能够根据三角形全等,从而将阴影部分的面积转化为矩形面积的一半,是解决问题的关键.19.(2014•宿迁)如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B 的坐标分别为(﹣3,0),(2,0),点D在y轴上,则点C的坐标是(5,4).【分析】利用菱形的性质以及勾股定理得出DO的长,进而求出C点坐标.【解答】解:∵菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D 在y轴上,∴AB=5,∴DO=4,∴点C的坐标是:(5,4).故答案为:(5,4).【点评】此题主要考查了菱形的性质以及坐标与图形的性质,得出DO的长是解题关键.20.(2015•黄冈)如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于65度.【分析】根据正方形的性质得出∠BAE=∠DAE,再利用SAS证明△ABE与△ADE 全等,再利用三角形的内角和解答即可.【解答】解:∵正方形ABCD,∴AB=AD,∠BAE=∠DAE,在△ABE与△ADE中,,∴△ABE≌△ADE(SAS),∴∠AEB=∠AED,∠ABE=∠ADE,∵∠CBF=20°,∴∠ABE=70°,∴∠AED=∠AEB=180°﹣45°﹣70°=65°,故答案为:65【点评】此题考查正方形的性质,关键是根据正方形的性质得出∠BAE=∠DAE,再利用全等三角形的判定和性质解答.21.(2013•十堰)如图,▱ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是1.【分析】根据平行四边形性质推出AB=CD,AB∥CD,得出平行四边形ABDE,推出DE=DC=AB,根据直角三角形性质求出CE长,即可求出AB的长.【解答】解:∵四边形ABCD是平行四边形,∴AB∥DC,AB=CD,∵AE∥BD,∴四边形ABDE是平行四边形,∴AB=DE=CD,即D为CE中点,∵EF⊥BC,∴∠EFC=90°,∵AB∥CD,∴∠DCF=∠ABC=60°,∴∠CEF=30°,∵EF=,∴CE==2,∴AB=1,故答案为:1.【点评】本题考查了平行四边形的性质和判定,平行线性质,勾股定理,直角三角形斜边上中线性质,含30度角的直角三角形性质等知识点的应用,此题综合性比较强,是一道比较好的题目.22.(2013•黔西南州)如图所示,菱形ABCD的边长为4,且AE⊥BC于E,AF ⊥CD于F,∠B=60°,则菱形的面积为.【分析】根据已知条件解直角三角形ABE可求出AE的长,再由菱形的面积等于底×高计算即可.【解答】解:∵菱形ABCD的边长为4,∴AB=BC=4,∵AE⊥BC于E,∠B=60°,∴sinB==,∴AE=2,∴菱形的面积=4×2=8,故答案为8.【点评】本题考查了菱形的性质:四边相等以及特殊角的三角函数值和菱形面积公式的运用.23.(2013•鞍山)如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是11.【分析】利用勾股定理列式求出BC的长,再根据三角形的中位线平行于第三边并且等于第三边的一半求出EH=FG=AD,EF=GH=BC,然后代入数据进行计算即可得解.【解答】解:∵BD⊥CD,BD=4,CD=3,∴BC===5,∵E、F、G、H分别是AB、AC、CD、BD的中点,∴EH=FG=AD,EF=GH=BC,∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC,又∵AD=6,∴四边形EFGH的周长=6+5=11.故答案为:11.【点评】本题考查了三角形的中位线定理,勾股定理的应用,熟记三角形的中位线平行于第三边并且等于第三边的一半是解题的关键.24.(2015•攀枝花)如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为(2.5,4),或(3,4),或(2,4),或(8,4).【分析】由矩形的性质得出∠OCB=90°,OC=4,BC=OA=10,求出OD=AD=5,分情况讨论:①当PO=PD时;②当OP=OD时;③当DP=DO时;根据线段垂直平分线的性质或勾股定理即可求出点P的坐标.【解答】解:∵四边形OABC是矩形,∴∠OCB=90°,OC=4,BC=OA=10,∵D为OA的中点,∴OD=AD=5,①当PO=PD时,点P在OD得垂直平分线上,∴点P的坐标为:(2.5,4);②当OP=OD时,如图1所示:则OP=OD=5,PC==3,∴点P的坐标为:(3,4);③当DP=DO时,作PE⊥OA于E,则∠PED=90°,DE==3;分两种情况:当E在D的左侧时,如图2所示:OE=5﹣3=2,∴点P的坐标为:(2,4);当E在D的右侧时,如图3所示:OE=5+3=8,∴点P的坐标为:(8,4);综上所述:点P的坐标为:(2.5,4),或(3,4),或(2,4),或(8,4);故答案为:(2.5,4),或(3,4),或(2,4),或(8,4).【点评】本题考查了矩形的性质、坐标与图形性质、等腰三角形的判定、勾股定理;本题有一定难度,需要进行分类讨论才能得出结果.25.(2013•阜新)如图,已知△ABC的三个顶点的坐标分别为A(﹣2,0),B(﹣1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D 的坐标(3,2),(﹣5,2),(1,﹣2).【分析】首先根据题意画出图形,分别以BC,AB,AC为对角线作平行四边形,即可求得答案.【解答】解:如图:以A,B,C为顶点的平行四边形的第四个顶点D的坐标分别为:(3,2),(﹣5,2),(1,﹣2).故答案为:(3,2),(﹣5,2),(1,﹣2).【点评】此题考查了平行四边形的性质.注意坐标与图形的关系.26.(2014•丹东)如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为.【分析】延长AB至M,使BM=AE,连接FM,证出△DAE≌EMF,得到△BMF 是等边三角形,再利用菱形的边长为4求出时间t的值.。
人教版八年级下册数学 第19章 一次函数 综合(压轴题)示范

人教版八年级下册数学第19章 一次函数 综合(压轴题)示范1.如图,直线l 1的解析式为y =12x+1,且l 1与x 轴交于点D ,直线l 2经过定点A 、B ,直线l 1与l 2交于点C .(1)求直线的解析式; (2)求△ADC 的面积;(3)在x 轴上是否存在一点E ,使△BCE 的周长最短?若存在,请求出点E 的坐标;若不存在,说明理由.【分析】(1)利用待定系数法即可直接求得l 2的函数解析式;(2)首先解两条之间的解析式组成的方程组求得C 的坐标,然后利用三角形的面积公式即可求解; (3)求得C 关于y 轴的对称点,然后求得经过这个点和B 点的直线解析式,直线与x 轴的交点就是E . 【解析】(1)设l 2的解析式是y =kx+b ,根据题意得:{4k +b =0−k +b =5,解得{k =−1b =4,则函数的解析式是:y =﹣x+4;(2)在y =12x+1中令y =0,即y =12x+1=0,解得:x =﹣2,则D 的坐标是(﹣2,0). 解方程组{y =−x +4y =12x +1,解得{x =2y =2,则C 的坐标是(2,2).则S △ADC =12×AD ×y C =12×6×2=6;(3)存在,理由:设C (2,2)关于y 轴的对称点C ′(2,﹣2),连接BC ′交x 轴于点E ,则点E 为所求点, △BCE 的周长=BC+BE+CE =BC+BE+C ′E =BC+BC ′为最小,设经过(2,﹣2)和B 的函数解析式是y =mx+n ,则{2m +n =−2−m +m =5,解得:{m =−73n =83, 则直线的解析式是y =−73x +83,令y =0,则y =−73x +83=0,解得:x =87.则E 的坐标是(87,0).【小结】本题考查了待定系数法求一次函数的解析式,以及对称的性质,正确确定E 的位置是本题的关键. 2、矩形ABCD 在如图所示的平面直角坐标系中,点A 的坐标为(0,3),BC =2AB ,直线经过点B ,交AD 边于点P 1,此时直线l 的函数表达式是y =2x +1. (1)求BC ,AP 1的长;(2)沿y 轴负方向平移直线l ,分别交AD ,BC 边于点P ,E . ①当四边形BEPP 1是菱形时,求平移的距离;②设AP =m ,当直线l 把矩形ABCD 分成两部分的面积之比为3:5时,求m 的值.解:(1)∵直线y =2x +1经过y 轴上的B 点,∴B (0,1),又∵A 的坐 标为(0,3);∴AB=2;BC=2AB=4;P 1(1,3);AP 1=1;(2)①当四边形BEPP 1是菱形时,BP 1=BE=5;∴E (5,1);设平移之后的直线解析式为:y =2x +b ,将点E 代入;b=1-25; 与y 轴的交点B ’(0,1-25),∴沿y 轴负方向平移距离为25;②∵AP=m ;AP 1=1;PP 1=BE=m-1;而S 梯形ABEP =83S 矩形ABCD 或S 梯形ABEP =85S 矩形ABCD ; ∴53m 1-m 221或)(=+⨯;m=2或3. 3、如图,一次函数y 1=54x+n 与x 轴交于点B ,一次函数y 2=−34x+m 与y 轴交于点C ,且它们的图象都经过点D (1,−74).(1)则点B 的坐标为 ,点C 的坐标为 ;(2)在x 轴上有一点P (t ,0),且t >125,如果△BDP 和△CDP 的面积相等,求t 的值;(3)在(2)的条件下,在y 轴的右侧,以CP 为腰作等腰直角△CPM ,直接写出满足条件的点M 的坐标.【分析】(1)根据待定系数法,可得函数解析式,分别令y =0和x =0,可得B 、C 点坐标; (2)根据面积的和差,可得关于t 的方程,根据解方程,可得答案;(3)分情况讨论,注意是在y 轴的右侧,有三个符合条件的点M ,作辅助线,构建三角形全等,根据全等三角形的判定与性质,可得M 的坐标.【解析】(1)将D (1,−74)代入y =54x+n ,解得n =﹣3,即y =54x ﹣3,当y =0时,54x ﹣3=0.解得x =125,即B 点坐标为(125,0); 将(1,−74)代入y =−34x+m ,解得m =﹣1,即y =−34x ﹣1,当x =0时,y =﹣1.即C 坐标为(0,﹣1); (2)如图1,S △BDP =12(t −125)×|−74|=78t −2110,当y =0时,−34x ﹣1=0,解得x =−43,即E 点坐标为(−43,0), S △CDP =S △DPE ﹣S △CPE =12(t +43)×74−12×(t +43)×|﹣1|=38t +12,由△BDP 和△CDP 的面积相等,得:78t −2110=38t +12,解得t =5.2;(3)以CP 为腰作等腰直角△CPM ,有以下两种情况: ①如图2,当以点C 为直角顶点,CP 为腰时,点M 1在y 轴的左侧,不符合题意,过M 2作M 2A ⊥y 轴于A , ∵∠PCM 2=∠PCO+∠ACM 2=∠PCO+∠OPC =90°,∴∠ACM 2=∠OPC ,∵∠POC =∠CAM 2,PC =CM 2,∴△POC ≌△CAM 2(AAS ),∴PO =AC =5.2,OC =AM 2=1, ∴M 2(1,﹣6.2);②如图3,当以点P 为直角顶点,CP 为腰时,过M 4作M 4E ⊥x 轴于E ,同理得△COP ≌△PEM 4,∴OC =EP =1,OP =M 4E =5.2,∴M 4(6.2,﹣5.2), 同理得M 3(4.2,5.2);综上所述,满足条件的点M 的坐标为(1,﹣6.2)或(6.2,﹣5.2)或(4.2,5.2).【小结】本题考查了一次函数综合题,利用待定系数法求函数解析式;利用面积的和差得出关于t 的方程是解题关键;利用全等三角形的判定与性质得出对应边相等是解题关键.4、如图,已知直线y =2x+2与y 轴、x 轴分别交于A 、B 两点,点C 的坐标为(﹣3,1). (1)直接写出点A 的坐标 ,点B 的坐标 . (2)求证△ABC 是等腰直角三角形.(3)若直线AC 交x 轴于点M ,点P (−52,k )是线段BC 上一点,在线段BM 上是否存在一点N ,使直线PN 平分△BCM 的面积?若存在,请求出点N 的坐标;若不存在,请说明理由.【分析】(1)利用待定系数法解决问题即可.(2)作CD ⊥x 轴于点D ,证明△CDB ≌△BOA (SAS )即可解决问题. (3)求出点P 的坐标,利用面积法求出BN 的长即可解决问题.【解答】(1)对于直线y =2x+2,令x =0,得到y =2,令y =0,得到x =﹣1,∴A (0,2),B (﹣1,0). (2)证明:作CD ⊥x 轴于点D ,由题意可得CD =1,OD =3,OB =1,OA =2,∴CD =OB =1,BD =OA =2, ∵∠CDB =∠AOB =90˚,∴△CDB ≌△BOA (SAS ),∴BC =BA ,∠CBD =∠BAO ,∵∠ABO+∠BAO =90˚,∴∠ABO+∠CBD =90˚,即∠ABC =90˚,∴△ABC 是等腰直角三角形. (3)∵P (−52,k )在直线BC :y =−12x −12上,∴P (−52,34),∵直线AC :y =13x +2交x 轴于M ,∴M (﹣6,0),∵S △BCM =12×5×1=52,假设存在点N ,使直线PN 平分△BCM 的面积,则S △BPN =12⋅BN ⋅34=12×52,∴BN =103,∴ON =BN+OB =103+1=133,∴N(−133,0).【小结】本题考查属于一次函数综合题,考查了一次函数的性质,等腰直角三角形的判定,三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.5、如图1,在平面直角坐标系xOy 中,直线y =kx+8分别交x 轴,y 轴于A 、B 两点,已知A 点坐标(6,0),点C 在直线AB 上,横坐标为3,点D 是x 轴正半轴上的一个动点,连结CD ,以CD 为直角边在右侧构造一个等腰Rt △CDE ,且∠CDE =90°.(1)求直线AB 的解析式以及C 点坐标;(2)设点D 的横坐标为m ,试用含m 的代数式表示点E 的坐标;(3)如图2,连结OC ,OE ,请直接写出使得△OCE 周长最小时,点E 的坐标. 【分析】(1)把A (6,0)代入y =kx+8中,得6k+8=0,解得:k =−43,即可求解; (2)证明△CDF ≌△DEG (AAS ),则CF =DG =4,DF =EG =3﹣m ,OG =4+m ,则E (4+m ,m ﹣3); (3)过点O 作直线l 的对称点O ′,连接CO ′交直线l 于点E ′,则点E ′为所求点,即可求解. 【解析】(1)把A (6,0)代入y =kx+8中,得6k+8=0,解得:k =−43,∴y =−43x +8,把x =3代入,得y =4,∴C (3,4); (2)作CF ⊥x 轴于点F ,EG ⊥x 轴于点G ,∵△CDE 是等腰直角三角形,∴CD =DE ,∠CDE =90°, ∴∠CDF =90°﹣∠EDG =∠DEG ,且∠CFD =∠DGE =90°,∴△CDF ≌△DEG (AAS )∴CF =DG =4,DF =EG =3﹣m ,∴OG =4+m ,∴E (4+m ,m ﹣3); (3)点E (4+m ,m ﹣3),则点E 在直线l :y =x ﹣7上,设:直线l 交y 轴于点H (0,﹣7),过点O 作直线l 的对称点O ′, ∵直线l 的倾斜角为45°,则HO ′∥x 轴,则点O ′(7,﹣7), 连接CO ′交直线l 于点E ′,则点E ′为所求点,OC 是常数,△OCE 周长=OC+CE+OE =OC+OE ′+CE ′=OC+CE ′+O ′E ′=OC+CO ′为最小,由点C 、O ′的坐标得,直线CO ′的表达式为:y =−114x +494联立{y =x −7y =−114x +494,解得:{x =7715y =−2815,故:E(7715,−2815). 【小结】本题考查的是一次函数综合运用,涉及到一次函数的性质、等腰直角三角形的性质、点的对称性等,综合性很强,难度较大.6.如图①,直线y =x +1交x 轴于点A ,交y 轴于点C ,OB =30A ,M 在直线AC 上,AC =CM . (1)求直线BM 的解析式;(2)如图①,点N 在MB 的延长线上,BN =AC ,连CN 交x 轴于点P ,求点P 的坐标;(3)如图②,连接OM ,在直线BM 上是否存在点K ,使得∠MOK =45°,若存在,求点K 的坐标,若不存在,说明理由.解:(1)利用A(-1,0);C (0,1);AC=AM;∴M (1,2);B (3,0);∴BM :y =-x +3.(2)过C 作CS ∥MN 交x 轴与S 点,可证△PCS ≌△PNB ,可证P 为BS 的中点,可证OA=OS=1; 则BS=2;则P (2,0)。
人教版八年级数学下册经典压轴题考点及例题解析

人教版八年级数学下册经典压轴题考点及例题解析例题1古希腊数学家把数 1 , 3 , 6 , 10 ,15 , 21 ,...... 叫做三角形数,它有一定的规律性。
若把第一个三角形数记为 a1 ,第二个三角形数记为 a2 ,......,第 n 个三角形数记为 an ,则 an + a(n+1) = ?答案:(n + 1)^2 。
例题2在平面直角坐标系中,对于平面内任意一点 P(a , b)若规定以下三种变换:① f(a , b)= (-a , b),如 f(2 , 5)= (-2 , 5);② g(a , b) = (b , a), 如 g(2 , 5)= (5 , 2);③ h(a , b)= (-a , -b),如 h(2 , 5)= (-2 , -5)。
根据以上变换,那么 f(h(5 , -3))等于多少?答案:(5,3)。
例题3如图,已知等腰直角△ABC 的直角边长为 1 ,以 Rt△ABC 的斜边 AC 为直角边,画第二个等腰 Rt△ACD ,在以 Rt△ACD 的斜边 AD 为直角边,画第三个等腰 Rt△ADE , ... ,依次类推到第五个等腰 Rt△AFG ,则由这五个等腰直角三角形所构成的图形的面积是多少?答案:31/2 。
例题4如图所示,直线 OP 经过点 P(4,4√3),过 x 轴上的点 1、3、5、7、9、11 ......分别作 x 轴的垂线,与直线 OP 相交得到一组梯形,其阴影部分梯形的面积从左至右依次记为 S1 , S2 , S3 , ... , Sn , 则 Sn 关于 n 的函数关系式是?答案:Sn = 4√3 (2n - 1)。
例题5现将 1、√2、√3、√6 四个数按下列方式排列。
若规定(m , n)表示第 m 排从左到右第 n 个数,则(5 , 4)与(15 , 7)表示的两数之积是多少?答案:2√3 。
例题6现将一块直角三角形的花圃进行改造,已知两直角边长分别为 6 m 、8 m 。
八年级下册数学期末压轴题(含答案)

八年级数学下册期末压轴题练习(含答案)一、填空题:1.如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ 的最小值为 .2.如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6,则另一直角边BC的长为.3.如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AE PQ的周长取最小值时,四边形AEPQ 的面积是.4.如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A.点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.现给出以下四个命题(1)∠APB=∠BPH;(2)当点P在边AD上移动时,△PDH的周长不发生变化; (3)∠PBH=450 ; (4)BP=BH.其中正确的命题是.5.如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是.二、综合题:6. (1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.(3)运用(1)(2)解答中所积累的经验和知识,完成下题:如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD的面积.7.如图,已知等腰Rt△ABC和△CDE,AC=BC,CD=CE,连接BE、AD,P为BD中点,M为AB中点、N为DE中点,连接PM、PN、MN.(1)试判断△PMN的形状,并证明你的结论;(2)若CD=5,AC=12,求△PMN的周长.8.已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转.(1)①当E点旋转到DA的延长线上时(如图1),△ABE与△ADG的面积关系是:.②当E点旋转到CB的延长线上时(如图2),△ABE与△ADG的面积关系是:(2)当正方形AEFG旋转任意一个角度时(如图3),(1)中的结论是否仍然成立?若成立请证明,若不成立请说明理由.(3)已知△ABC,AB=5cm,BC=3cm,分别以AB、BC、CA为边向外作正方形(如图4),则图中阴影部分的面积和的最大值是 cm2.9.一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为,周长为;(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为,周长为;(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.10.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.参考答案1.答案为:3.3.答案为:4.5.2.答案为:7;解法一:如图1所示,过O作OF⊥BC,过A作AM⊥OF,∵四边形ABDE为正方形,∴∠AOB=90°,OA=OB,∴∠AOM+∠BOF=90°,又∠AMO=90°,∴∠AOM+∠OAM=90°,∴∠BOF=∠OAM,在△AOM和△BOF 中,,∴△AOM≌△BOF(AAS),∴AM=OF,OM=FB,又∠ACB=∠AMF=∠CFM=90°,∴四边形ACFM为矩形,∴AM=CF,AC=MF=5,∴OF=CF,∴△OCF为等腰直角三角形,∵OC=6,∴根据勾股定理得:CF2+OF2=OC2,解得:CF=OF=6,∴FB=OM=OF﹣FM=6﹣5=1,则BC=CF+BF=6+1=7.故答案为:7.解法二:如图2所示,过点O作OM⊥CA,交CA的延长线于点M;过点O作ON⊥BC于点N.易证△OMA≌△ONB,∴OM=ON,MA=NB.∴O点在∠ACB的平分线上,∴△OCM为等腰直角三角形.∵OC=6,∴CM=ON=6.∴MA=CM﹣AC=6﹣5=1,∴BC=CN+NB=6+1=7.故答案为:7.4.答案为:(1)(2)(3).5.答案为:2;解:作D 关于AE 的对称点D′,再过D′作D′P′⊥AD于P′,∵DD′⊥AE,∴∠AFD=∠AFD′,∵AF=AF,∠DAE=∠CAE,∴△DAF≌△D′AF,∴D′是D关于AE的对称点,AD′=AD=4,∴D′P′即为DQ+PQ的最小值,∵四边形ABCD是正方形,∴∠DAD′=45°,∴AP′=P′D′,∴在Rt△AP′D′中,P′D′2+AP′2=AD′2,AD′2=16,∵AP′=P′D',2P′D′2=AD′2,即2P′D′2=16,∴P′D′=2,即DQ+PQ的最小值为2,6. (1)证明:∵四边形ABCD是正方形,∴BC=CD,∠B=∠CDF=90°,∵∠ADC=90°,∴∠FDC=90°.∴∠B=∠FDC,∵BE=DF,∴△CBE≌△CDF(SAS).∴CE=CF.(2)证明:如图2,延长AD至F,使DF=BE,连接CF.由(1)知△CBE≌△CDF,∴∠BCE=∠DCF.∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∠GCE=45°,∴∠GCF=∠GCE=45°.∵CE=CF,GC=GC,∴△ECG≌△FCG.∴GE=GF,∴GE=GF=DF+GD=BE+GD.(3)解:如图3,过C作CG⊥AD,交AD延长线于G.在直角梯形ABCD中,∵AD∥BC,∴∠A=∠B=90°,又∵∠CGA=90°,AB=BC,∴四边形ABCG为正方形.∴AG=BC.…∵∠DCE=45°,根据(1)(2)可知,ED=BE+DG.…∴10=4+DG,即DG=6.设AB=x,则AE=x﹣4,AD=x﹣6,在Rt△AED中,∵DE2=AD2+AE2,即102=(x﹣6)2+(x﹣4)2.解这个方程,得:x=12或x=﹣2(舍去).…∴AB=12.∴S梯形ABCD=0.5(AD+BC)•AB=0.5×(6+12)×12=108.即梯形ABCD的面积为108.…7.解:(1)①∵正方形ABCD和正方形AEFG有公顶点A,将正方形AEFG绕点A旋转,E 点旋转到DA的延长线上,∴AE=AG,AB=AD,∠EAB=∠GAD,∴△ABE≌△ADG(SAS),∴△ABE的面积=△ADG的面积;②作GH⊥DA交DA的延长线于H,如图2,∴∠AHG=90°,∵E点旋转到CB的延长线上,∴∠ABE=90°,∠HAB=90°,∴∠GAH=∠EAB,在△AHG和△AEB中,∴△AHG≌△AEB,∴GH=BE,∵△ABE的面积=0.5EB•AB,△ADG的面积=0.5GH•AD,∴△ABE的面积=△ADG的面积;(2)结论仍然成立.理由如下:作GH⊥DA交DA的延长线于H,EP⊥BA交BA的延长线于P,如图3,∵∠PAD=90°,∠EAG=90°,∴∠PAE=∠GAH,在△AHG和△AEP中,∴△AHG≌△AEP(AAS),∴GH=BP,∵△ABP的面积=0.5EP•AB,△ADG的面积=0.5GH•AD,∴△ABP的面积=△ADG的面积;(3)∵AB=5cm,BC=3cm,∴AC==4cm,∴△ABC的面积=0.5×3×4=6(cm2);根据(2)中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=18cm2.故答案为相等;相等;18.8.解:(1)∵AM=MC=AC=a,则∴重叠部分的面积是△ACB的面积的一半为0.25a2,周长为(1+)a.(2)∵重叠部分是正方形∴边长为0.5a,面积为0.25a2,周长为2a.(3)猜想:重叠部分的面积为0.25a2.理由如下:过点M分别作AC、BC的垂线MH、MG,垂足为H、G 设MN与AC的交点为E,MK与BC的交点为F∵M是△ABC斜边AB的中点,AC=BC=a∴MH=MG=0.5a又∵∠HME+∠HMF=∠GMF+∠HMF,∴∠HME=∠GMF,∴Rt△MHE≌Rt△MGF∴阴影部分的面积等于正方形CGMH的面积∵正方形CGMH的面积是MG•MH=0.5a×0.5a =0.25a2,∴阴影部分的面积是0.25a2.9.(1)证明:∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°,∵∠EAF=45°,∴∠GAE=45°,在△AGE与△AFE中,,∴△AGE≌△AFE(SAS);(2)证明:设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.则△ADF≌△ABG,DF=BG.由(1)知△AEG≌△AEF,∴EG=EF.∵∠CEF=45°,∴△BME、△DNF、△CEF均为等腰直角三角形,∴CE=CF,BE=BM,NF=DF,∴a﹣BE=a﹣DF,∴BE=DF,∴BE=BM=DF=BG,∴∠BMG=45°,∴∠GME=45°+45°=90°,∴EG2=ME2+MG2,∵EG=EF,MG=BM=DF=NF,∴EF2=ME2+NF2;(3)解:EF2=2BE2+2DF2.如图所示,延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由(1)知△AEH≌△AEF,则由勾股定理有(GH+BE)2+BG2=EH2,即(GH+BE)2+(BM﹣GM)2=EH2又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,即2(DF2+BE2)=EF2。
八年级数学下期末压轴题练习含答案

2018年八年级数学下册期末压轴题练习(含答案)一、填空题:1.如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为 .2.如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6,则另一直角边BC的长为.3.如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AE PQ的周长取最小值时,四边形AEPQ的面积是.4.如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A.点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.现给出以下四个命题(1)∠APB=∠BPH;(2)当点P在边AD上移动时,△PDH的周长不发生变化;(3)∠PBH=450 ; (4)BP=BH.其中正确的命题是.5.如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是.二、综合题:6. (1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.(3)运用(1)(2)解答中所积累的经验和知识,完成下题:如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD的面积.7.如图,已知等腰Rt△ABC和△CDE,AC=BC,CD=CE,连接BE、AD,P为BD中点,M为AB中点、N 为DE中点,连接PM、PN、MN.(1)试判断△PMN的形状,并证明你的结论;(2)若CD=5,AC=12,求△PMN的周长.8.已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转.(1)①当E点旋转到DA的延长线上时(如图1),△ABE与△ADG的面积关系是:.②当E点旋转到CB的延长线上时(如图2),△ABE与△ADG的面积关系是:(2)当正方形AEFG旋转任意一个角度时(如图3),(1)中的结论是否仍然成立?若成立请证明,若不成立请说明理由.(3)已知△ABC,AB=5cm,BC=3cm,分别以AB、BC、CA为边向外作正方形(如图4),则图中阴影部分的面积和的最大值是 cm2.9.一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为,周长为;(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为,周长为;(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.10.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.参考答案1.答案为:3.2.答案为:7;解法一:如图1所示,过O作OF⊥BC,过A作AM⊥OF,∵四边形ABDE为正方形,∴∠AOB=90°,OA=OB,∴∠AOM+∠BOF=90°,又∠AMO=90°,∴∠AOM+∠OAM=90°,∴∠BOF=∠OAM,在△AOM和△BOF中,,∴△AOM≌△BOF(AAS),∴AM=OF,OM=FB,又∠ACB=∠AMF=∠CFM=90°,∴四边形ACFM为矩形,∴AM=CF,AC=MF=5,∴OF=CF,∴△OCF为等腰直角三角形,∵OC=6,∴根据勾股定理得:CF2+OF2=OC2,解得:CF=OF=6,∴FB=OM=OF﹣FM=6﹣5=1,则BC=CF+BF=6+1=7.故答案为:7.解法二:如图2所示,过点O作OM⊥CA,交CA的延长线于点M;过点O作ON⊥BC于点N.易证△OMA≌△ONB,∴OM=ON,MA=NB.∴O点在∠ACB的平分线上,∴△OCM为等腰直角三角形.∵OC=6,∴CM=ON=6.∴MA=CM﹣AC=6﹣5=1,∴BC=CN+NB=6+1=7.故答案为:7.3.答案为:4.5.4.答案为:(1)(2)(3).5.答案为:2;解:作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,∵DD′⊥AE,∴∠AFD=∠AFD′,∵AF=AF,∠DAE=∠CAE,∴△DAF≌△D′AF,∴D′是D关于AE的对称点,AD′=AD=4,∴D′P′即为DQ+PQ的最小值,∵四边形ABCD是正方形,∴∠DAD′=45°,∴AP′=P′D′,∴在Rt△AP′D′中,P′D′2+AP′2=AD′2,AD′2=16,∵AP′=P′D',2P′D′2=AD′2,即2P′D′2=16,∴P′D′=2,即DQ+PQ的最小值为2,6. (1)证明:∵四边形ABCD是正方形,∴BC=CD,∠B=∠CDF=90°,∵∠ADC=90°,∴∠FDC=90°.∴∠B=∠FDC,∵BE=DF,∴△CBE≌△CDF(SAS).∴CE=CF.(2)证明:如图2,延长AD至F,使DF=BE,连接CF.由(1)知△CBE≌△CDF,∴∠BCE=∠DCF.∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∠GCE=45°,∴∠GCF=∠GCE=45°.∵CE=CF,GC=GC,∴△ECG≌△FCG.∴GE=GF,∴GE=GF=DF+GD=BE+GD.(3)解:如图3,过C作CG⊥AD,交AD延长线于G.在直角梯形ABCD中,∵AD∥BC,∴∠A=∠B=90°,又∵∠CGA=90°,AB=BC,∴四边形ABCG为正方形.∴AG=BC.…∵∠DCE=45°,根据(1)(2)可知,ED=BE+DG.…∴10=4+DG,即DG=6.设AB=x,则AE=x﹣4,AD=x﹣6,在Rt△AED中,∵DE2=AD2+AE2,即102=(x﹣6)2+(x﹣4)2.解这个方程,得:x=12或x=﹣2(舍去).…∴AB=12.∴S梯形ABCD=0.5(AD+BC)•AB=0.5×(6+12)×12=108.即梯形ABCD的面积为108.…7.解:(1)①∵正方形ABCD和正方形AEFG有公顶点A,将正方形AEFG绕点A旋转,E点旋转到DA的延长线上,∴AE=AG,AB=AD,∠EAB=∠GAD,∴△ABE≌△ADG(SAS),∴△ABE的面积=△ADG的面积;②作GH⊥DA交DA的延长线于H,如图2,∴∠AHG=90°,∵E点旋转到CB的延长线上,∴∠ABE=90°,∠HAB=90°,∴∠GAH=∠EAB,在△AHG和△AEB中,∴△AHG≌△AEB,∴GH=BE,∵△ABE的面积=0.5EB•AB,△ADG的面积=0.5GH•AD,∴△ABE的面积=△ADG的面积;(2)结论仍然成立.理由如下:作GH⊥DA交DA的延长线于H,EP⊥BA交BA的延长线于P,如图3,∵∠PAD=90°,∠EAG=90°,∴∠PAE=∠GAH,在△AHG和△AEP中,∴△AHG≌△AEP(AAS),∴GH=BP,∵△ABP的面积=0.5EP•AB,△ADG的面积=0.5GH•AD,∴△ABP的面积=△ADG的面积;(3)∵AB=5cm,BC=3cm,∴AC==4cm,∴△ABC的面积=0.5×3×4=6(cm2);根据(2)中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=18cm2.故答案为相等;相等;18.8.解:(1)∵AM=MC=AC=a,则∴重叠部分的面积是△ACB的面积的一半为0.25a2,周长为(1+)a.(2)∵重叠部分是正方形∴边长为0.5a,面积为0.25a2,周长为2a.(3)猜想:重叠部分的面积为0.25a2.理由如下:过点M分别作AC、BC的垂线MH、MG,垂足为H、G设MN与AC的交点为E,MK与BC的交点为F∵M是△ABC斜边AB的中点,AC=BC=a∴MH=MG=0.5a又∵∠HME+∠HMF=∠GMF+∠HMF,∴∠HME=∠GMF,∴Rt△MHE≌Rt△MGF∴阴影部分的面积等于正方形CGMH的面积∵正方形CGMH的面积是MG•MH=0.5a×0.5a =0.25a2,∴阴影部分的面积是0.25a2.9.(1)证明:∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°,∵∠EAF=45°,∴∠GAE=45°,在△AGE与△AFE中,,∴△AGE≌△AFE(SAS);(2)证明:设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.则△ADF≌△ABG,DF=BG.由(1)知△AEG≌△AEF,∴EG=EF.∵∠CEF=45°,∴△BME、△DNF、△CEF均为等腰直角三角形,∴CE=CF,BE=BM,NF=DF,∴a﹣BE=a﹣DF,∴BE=DF,∴BE=BM=DF=BG,∴∠BMG=45°,∴∠GME=45°+45°=90°,∴EG2=ME2+MG2,∵EG=EF,MG=BM=DF=NF,∴EF2=ME2+NF2;(3)解:EF2=2BE2+2DF2.如图所示,延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由(1)知△AEH≌△AEF,则由勾股定理有(GH+BE)2+BG2=EH2,即(GH+BE)2+(BM﹣GM)2=EH2又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,即2(DF2+BE2)=EF2。
八年级下册数学压轴题(含答案)

八年级下册数学压轴题(含答案)四边形AOBC的对角线互相平分,且相等,故为菱形;又因为OC经过翻折后落在AB上,且AC与x轴垂直,故OC垂直于AB,故AO=OC=OB=BC,故AOBC是一个菱形;3)设点P的坐标为(x,y),则BPC为直角三角形,且BP=PC,又因为BP在y轴下方,故y<0,且BP与BC垂直,故BP的斜率为-2;设BP的解析式为y=-2x+b,且B点坐标为(0,-5),则有b=-5;又因为BP=PC,故PC的解析式为y=2x+b,且C点坐标为(a,0),代入得a=5;又因为XXX在BC下方,故y<0,代入得y=-2x-5;代入BP的解析式得x=5/3,代入得y=-25/3;故存在点P(5/3,-25/3),使△BCP为等腰直角三角形。
题目:在平面直角坐标系中,已知点A(0,0),B(5,0),C(0,5√2),D从A出发沿AC方向以1m/s的速度向C匀速运动,同时点E从B出发沿BA方向以√2m/s的速度向A匀速运动。
当其中一个点到达终点时,另一个点也随之停止运动。
设点D,E运动的时间是t(0<t≤10)秒。
过点E作EF⊥BC于点F,连接DE,DF。
1)求BE和CD的长度。
2)试说明,无论t为何值,四边形ADEF都是平行四边形。
3)当t为何值时,△DEF为直角三角形?请说明理由。
解法:1)由题意可知,BE=√2t,CD=t,故BE=√2t,CD=t。
2)如图所示,由题意可得,∠C=90°,∠A=45°,故∠B=45°。
又因为EF⊥BC,所以∠EFB=90°,∠FEB=45°,所以BE=EF。
又因为AE=√2t,DE=CD,所以DE=√2t。
因此,四边形ADEF的对角线相等,且相互平分,所以ADEF是平行四边形。
3)如图所示,当EF⊥BC时,由勾股定理可知,DE²=DF²+EF²,即(√2t)²=(t+BE)²+(5√2-BF)²。
2020-2021学年人教版数学八年级下册期末压轴题专项复习卷(含答案)

2021年人教版数学八年级下册期末《压轴题专项》复习卷1.如图,点A的坐标是(-2,0),点B的坐标是(6,0),点C在第一象限内且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD,垂足为E,交OC于点F.(1)求直线BD的函数表达式;(2)求线段OF的长;(3)连接BF,OE,试判断线段BF和OE的数量关系,并说明理由.2.阅读下面材料:我们知道一次函数y=kx+b(k≠0,k、b是常数)的图象是一条直线,到高中学习时,直线通常写成Ax+By+C=0(A≠0,A、B、C是常数)的形式,点P(x0,y0)到直线Ax+By+C=0的距离可用公式d=计算.例如:求点P(3,4)到直线y=﹣2x+5的距离.根据以上材料解答下列问题:(1)求点Q(﹣2,2)到直线3x﹣y+7=0的距离;(2)如图,直线y=﹣x沿y轴向上平移2个单位得到另一条直线,求这两条平行直线之间的距离.3.已知正方形ABCD,AB=8,点E、F分别从点A、D同时出发,以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动,设运动时间为t.(1)求证:OE=OF.(2)在点E、F的运动过程中,连结AF.设线段AE、OE、OF、AF所形成的图形面积为S.探究:①S的大小是否会随着运动时间为t的变化而变化?若会变化,试求出S与t的函数关系式;若不会变化,请说明理由.②连结EF,当运动时间为t为何值时,△OEF的面积恰好等于的S.4.如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数的图象交点为C(m,4).求:(1)一次函数y=kx+b的解析式;(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,则点D的坐标为;(3)在x轴上求一点P使△POC为等腰三角形,请求出所有符合条件的点P的坐标.5.将正方形ABCD放在如图所示的直角坐标系中,A点的坐标为(4,0),N点的坐标为(3,0),MN平行于y轴,E是BC的中点,现将纸片折叠,使点C落在MN上,折痕为直线EF.(1)求点G的坐标;(2)求直线EF的解析式;(3)设点P为直线EF上一点,是否存在这样的点P,使以P, F, G的三角形是等腰三角形?若存在,直接写出P点的坐标;若不存在,请说明理由.6.如图,已知直线y=kx+1经过点A(3,-2)、点B(a,2),交y轴于点M.(1)求a的值及AM的长(2)在x轴的负半轴上确定点P,使得△AMP成等腰三角形,请你直接写出点P的坐标.(3)将直线AB绕点A逆时针旋转45°得到直线AC,点D(-3,b)在AC上,连接BD,设BE是△ABD 的高,过点E的射线EF将△ABD的面积分成2:3两部分,交△ABD的另一边于点F,求点F的坐标.7.阅读理解:运用“同一图形的面积相等”可以证明一些含有线段的等式成立,这种解决问题的方法我们称之为面积法.如图1,在等腰△ABC中,AB=AC,AC边上的高为h,点M为底边BC 上的任意一点,点M到腰AB、AC的距离分别为h1、h2,连接AM,利用S△ABC=S△ABM+S△ACM,可以得出结论:h=h1+h2.类比探究:在图1中,当点M在BC的延长线上时,猜想h、h1、h2之间的数量关系并证明你的结论.拓展应用:如图2,在平面直角坐标系中,有两条直线l1:y=0.75x+3,l2:y=﹣3x+3,若l2上一点M到l1的距离是1,试运用“阅读理解”和“类比探究”中获得的结论,求出点M 的坐标.8.如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x ﹣2与x轴、y轴分别交于点E、F.(1)求:①点D的坐标;②经过点D,且与直线FC平行的直线的函数表达式;(2)直线y=x﹣2上是否存在点P,使得△PDC为等腰直角三角形?若存在,求出点P 的坐标;若不存在,请说明理由.(3)在平面直角坐标系内确定点M,使得以点M、D、C、E为顶点的四边形是平行四边形,请直接写出点M的坐标.9.如图,在平面直角坐标系中,△AOB的顶点O为坐标原点,点A的坐标为(4,0),点B的坐标为(0,1),点C为边AB的中点,正方形OBDE的顶点E在x轴的正半轴上,连接CO,CD,CE.(1)线段OC的长为;(2)求证:△CBD≌△COE;(3)将正方形OBDE沿x轴正方向平移得到正方形O1B1D1E1,其中点O,B,D,E的对应点分别为点O1,B1,D1,E1,连接CD,CE,设点E的坐标为(a,0),其中a≠2,△CD1E1的面积为S.①当1<a<2时,请直接写出S与a之间的函数表达式;②在平移过程中,当S=时,请直接写出a的值.10.如图,直线y=2x+m(m>0)与x轴交于点A(-2,0)直线y=-x+n(n>0)与x轴、y轴分别交于B、C 两点,并与直线y=2x+m(m>0)相交于点D,若AB=4.(1)求点D的坐标;(2)求出四边形AOCD的面积;(3)若E为x轴上一点,且△ACE为等腰三角形,直接写出点E的坐标.11.如图,直线l:交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.(1)点A坐标是, BC= .(2)当点P在什么位置时,△APQ≌△CBP,说明理由。
解答题压轴题训练(四)(解析版)-2020-2021学年八年级数学下学期期中考试压轴题专练(人教版)

2021年八下期中考试金牌解答题压轴题训练(四)(时间:60分钟总分:100)班级姓名得分一、解答题1.观察下列等式:1 ========回答下列问题:(1(2;(3….【答案】(1(2(3)1【分析】(1)根据题目的运算,先将分式通分,然后化简计算,即可得答案;(2)根据题目的运算,先将分式通分,然后化简计算,即可得答案;(32121121n nn n,化简求值即可.【详解】(1257575222757552775=(222121212121n n n n n2222212121n n n n22212121n n n n22221n n2121n n(3)由(22121121n n n n53757573=15375757331537573717573175531【点睛】本题考查了利用平方差公式对二次根式进行有理化,熟悉相关运算法则是解题的关键. 2.(1)如图1,平面直角坐标系中A(0,a ),B(a ,0)(a >0).C 为线段AB 的中点,CD⊥x 轴于D ,若⊥AOB 的面积为2,则⊥CDB 的面积为 .(2)如图2,⊥AOB 为等腰直角三角形,O 为直角顶点,点E 为线段OB 上一点,且OB =3OE , C 与E 关于原点对称,线段AB 交x 轴于点D ,连CD ,若CD⊥AE ,试求ADDB的值.(3)如图3,点C 、E 在x 轴上,B 在y 轴上,OB =OC ,⊥BDE 是以B 为直角顶点的等腰直角三角形,直线CB 、ED 交于点A ,CD 交y 轴于点F ,试探究:CO EOBF-是否为定值?如果是定值,请求出该定值;如果不是,请求出其取值范围.【答案】(1)12;(2)2AD DB =;(3)是定值,2CO EO BF-=. 【分析】(1)根据等腰直角三角形的性质和勾股定理可得12DC BD a ==,分别表示∴AOB 和∴CDB 的面积,根据∴AOB 的面积为2即可得出结论;(2)连接AC ,作DM∴BC ,与BC 交于M ,证明∴ACO∴∴DCM 可得OE=CO=DM=MB ,设它们为m ,从而可得OB=3m ,借助勾股定理和线段的和差分别表示AD 和BD ,即可得出它们的比值;(3)作DN∴OB ,交y 轴与N ,证∴ACO∴∴DCM 和∴COF∴∴DNF 全等,借助全等三角形的性质和线段的和差可得2F C E B O O -=,由此可得结论. 【详解】解:(1)∴A(0,a ),B(a ,0),∴AO=OB=a ,∴ABO=45°,, ∴C 为线段AB 的中点,∴122BC AB ==, ∴CD∴x 轴,∴∴CDB=90°,∴DCB=90°-∴ABO=45°, ∴DC=BD ,∴222DC DB BC +=,∴12DC BD a ==, ∴∴AOB 的面积为2,即2122a =, ∴2111111222422CDB S a a a ∆=⋅⋅=⋅=, 故答案为:12; (2)如下图连接AC , ∴C 与E 关于原点对称, ∴CO=OE ,∴∴AOB 为等腰直角三角形, ∴∴OAB=∴B=45°,AO∴CB , ∴∴EAO+∴AEC=90°,AC=AE , ∴∴CAO=∴EAO , ∴AE∴CD ,∴∴BCD+∴AEC=90°, ∴∴CAO=∴EAO=∴BCD ,∴∴ADC=∴BCD+∴B ,∴CAB=∴CAO+∴OAB, ∴∴ADC=∴CAB , ∴AC=CD ,作DM∴BC ,与BC 交于M ,∴∴DMC=90°,∴∴MDB=∴B=45°,∴DM=MB,在∴ACO和∴DCM中,∴DMC AOCCAO BCDAC CD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴∴ACO∴∴DCM(AAS),∴OE=CO=DM=MB,∴OB=3OE,设OE=CO=DM=MB=m,∴OB=3OE,∴OA=OB=3m,∴,BD AB====,∴AD=,∴2ADDB==;(3)是定值,作DN∴OB,交y轴与N,∴∴DNB=∴BOE=∴BOC=90°, ∴∴DBN+∴NBD=90°, ∴∴BDE 为等腰直角三角形, ∴∴DBN+∴OBE=90°,BD=BE , ∴∴NBD=∴OBE , 在∴NBD 和∴OEB 中∴90NBD OBE DNB BOE BD BE ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩, ∴∴NBD∴∴OEB (AAS ), ∴ND=OB=OC ,NB=OE , 在∴COF 和∴DNF 中∴90CFO NFD DNB BOC CO ND ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴∴COF∴∴DNF (AAS ), ∴NF=OF ,∴OE BN NF BF OF BF ==-=-,OC OB OF BF ==+, ∴()2F CO E OF BF O O F BF B +-=--=,∴2CO EOBF-=.【点睛】本题考查等腰直角三角形的性质和判定,勾股定理,坐标与图形,全等三角形的性质和判定等.能正确作出辅助线,构造全等三角形建立线段之间的联系是解题关键. 3.在平面直角坐标系中点A 、B 的坐标分别为()0,A a ,(),0Bb .(1)如图1,若点C 、B 关于y 轴对称,126CAB ∠=︒,请直接写出ABC ∠的度数ABC ∠=___________;(2)如图2,点D 的坐标为()1,2D c a b c ⎛⎫< ⎪⎝⎭,ADO ABO ∠=∠,试用字母b 、c 表示线段AB 的长;(3)如图3,点D 的坐标为()(),0D a a b <,且EA ED EB EF ===,点F 的坐标分别为(),F m m ,试用字母a 、b 、m 表示线段AB 的长. 【答案】(1)27°;(2)AB=2c -b ;(3)2AB m a b =-- 【分析】(1)由点C 、B 关于y 轴对称可得AB=AC ,再根据等腰三角形的性质和三角形的内角和定理求解即可;(2)作辅助线如图,易得DE 是∴AOG 的中位线,可得AD=DG ,根据直角三角形的性质可得AD=OD=DG ,然后根据等腰三角形的性质、三角形的内角和以及等量代换可得∴BAD=∴BGD ,从而可得AB=BG ,进一步即可求出答案;(3)连接OE ,作EG∴DB 于G ,EH∴x 轴于H ,如图,易证O 、E 、F 三点共线,设E (n ,n ),根据两点间的距离公式可得)EF m n =-,由等腰三角形的性质可推出2a bn +=,然后在Rt∴BEG 中,由勾股定理结合上述结论即可得出结论. 【详解】解:(1)∴点C 、B 关于y 轴对称, ∴AB=AC , ∴126CAB ∠=︒, ∴ABC ∠=1801801262722CAB ︒-∠︒-︒==︒;故答案为:27°;(2)延长AD 交x 轴于点G ,作DE∴y 轴于E ,DF∴x 轴于F ,如图, ∴()1,2D c a b c ⎛⎫< ⎪⎝⎭,∴OE=DF=12a ,DE∴OG ,∴OA=a , ∴AE=OE=12a , ∴DE 是∴AOG 的中位线, ∴AD=DG , ∴AD=OD=DG , ∴∴DOG=∴DGO ,∴∴ADO=∴ABO ,∴AHD=∴OHB , ∴∴DAB=∴DOG , ∴∴BAD=∴BGD , ∴AB=BG ,∴DO=DG ,DF∴x 轴, ∴OG=2OF=2c ,又∴OG=OB+BG=b+AB=2c , ∴AB=2c -b ;(3)连接OE ,作EG∴DB 于G ,EH∴x 轴于H ,如图,∴EA=ED ,OA=OD=a ,OE=OE , ∴∴AOE∴∴DOE , ∴∴AOE=∴DOE=45°, ∴OE 平分∴AOD , ∴(),F m m ,∴F 在∴AOD 的平分线上, ∴O 、E 、F 三点共线,设E (n ,n ),则)EF m n ==-,∴ED=EB ,EG∴DB ,∴DG=BG ,即n -a=b -n ,可得2a bn +=, 在Rt∴BEG 中,由勾股定理得()222222222222a b a b a b BE BG EG n b n +-+⎛⎫⎛⎫=+=+-=+= ⎪ ⎪⎝⎭⎝⎭, ∴222AB a b =+,∴()222222AB BE EF m n ===-,∴()222442a b AB m n m +⎛⎫=-=- ⎪⎝⎭,∴2AB m a b =--. 【点睛】本题以平面直角坐标系为载体,主要考查了轴对称的性质、等腰三角形的判定和性质、三角形的中位线定理、全等三角形的判定和性质、直角三角形的性质、勾股定理以及整式的乘法运算等知识,综合性强、具有相当的难度,正确添加辅助线、熟练掌握上述知识、灵活应用数形结合的思想是解题的关键.4.阅读下述材料:我们在学习二次根式时,熟悉的分母有理化以及应用.其实,有一个类似的方法叫做“分子有理化”:与分母有理化类似,分母和分子都乘以分子的有理化因式,从而消掉分子中的根式比如:==分子有理化可以用来比较某些二次根式的大小,也可以用来处理一些二次根式的最值问题.例如:==><再例如:求y=的最大值.做法如下:解:由20,20x x+≥-≥可知2x≥,而y==当2x=2,所以的最大值是2.解决下述问题:(1)比较4和(2)求y=【答案】(1)4<;(2)y的最大值为21.【分析】(1)利用分子有理化得到4=然后比较4和的大小即可得到4与(2)利用二次根式有意义的条件得到01x ,而y 利用当0x =时,有最大值11得到所以y 的最大值;利用当1x =时,10得到y 的最小值.【详解】解:(1)4==,=,而>4>4∴>4∴<(2)由10x -,10x +,0x 得01x ,y =+∴当0x =11,所以y 的最大值为2;当1x =有最大值,1,0,所以y 1.【点睛】 本题考查了非常重要的一种数学思想:类比思想.解决本题关键是要读懂例题,然后根据例题提供的知识点和方法解决问题.同时要注意所解决的问题在方法上类似,但在细节上有所区别.5.已知:在⊥ABC 中,CA =CB ,⊥ACB =90º,D 为⊥ABC 外一点,且满足⊥ADB =90°. (1)如图1,若2AC =,AD =1,求DB 的长.(2)如图1,求证:DA DB +=.(3)如图2所示,过C 作CE ⊥AD 于E ,BD =2,AD =6,求CE 的长.【答案】(1)DB=(2)见解析;(3)2【分析】(1)在Rt∴ABC中,根据勾股定理,得AB=2,在Rt∴ABD中,根据勾股定理,得DB=;(2)过C点作CF∴CD,构造手拉手模型,运用等腰直角三角形的性质可得证;(3)过C点作CF∴CD,构造手拉手模型,运用三角形全等可得证.【详解】(1)解:在Rt∴ABC中,∴CA CB==∴2AB=,∴在Rt∴ABD中,DB==(2)证明:如图,过C点作CF∴CD交DB的延长线于点F.∴∴ACB=∴DCF=90°,∴∴ACD=∴BCF,∴∴CAD+∴CBD=360°-(∴ACB+∴ADB)=180°,∴CBF+∴CBD=180°,∴∴CAD=∴CBF,又∴CA=CB,∴∴CAD∴∴CBF(ASA),∴CD=CF,AD=BF,∴DF=,∴DF=DB+BF=DB+DA,∴DA DB+=.(3)解:如图,过C点作CF∴CD交AD与F点,∴∴ACB=∴DCF=90°,即∴ACF+∴BCF=∴BCD+∴BCF=90°,∴∴ACF=∴BCD,∴∴AFC=∴FCD+∴CDA=90°+∴CDA,∴CDB=∴CDA+∴ADB=90°+∴CDA,∴∴AFC=∴CDB,又∴CA=CB,∴∴CAF∴∴CBD(AAS),∴CF=CD,AF=BD,∴∴CDF是等腰直角三角形,又∴CE∴AD,∴E为DF中点,∴AD=6,AF=BD=2,∴FD=AD-AF=4,∴122CE DF==.【点睛】本题考查了勾股定理,等腰直角三角形的性质,等腰三角形的性质,三角形的全等,手拉手模型的构造,熟练构造手拉手模型是解题的关键.6.如图,平面直角坐标系xOy中,矩形OABC如图放置,点B(4,3),E,F分别为OA,BC边上的中点,动点P从点E出发以每秒2个单位速度沿EO方向向点O运动,同时,动点Q从点F出发以每秒1个单位速度沿FB方向向点B运动.当一个点到达终点时,另一个点随之停止.连接EF、PQ,且EF与PQ相交于点M,连接AM.(1)求线段AM的长度;(2)过点A作AH⊥PQ,垂足为点H,连接CH,求线段CH长度的最小值.【答案】(1)【分析】(1)证明∴FMQ∴∴EMP,且相似比为1=2=FM FQME PE,由EF=3求出FM=1,ME=2,再在Rt∴MEA中,由勾股定理即可求出AM的长度;(2)连接AM,取MA中点I,只要C、H、I,此时会形成∴ICH,根据三角形两边之差小于第三边可知,CH>IC-IH,当且仅当C、H、I三点共线时,有CH=IC-IH,此时CH有最小值,由此即可求解.【详解】解:(1)∴BC∥OA,∴∴FQM=∴EPM,且∴FMQ=∴EMP,∴∴FQM∴∴EPM,设运动时间为t,则FQ=t,PE=2t∴1=2=FM FQME PE,又FE=3,∴FM=1,ME=2,又E为OA的中点,∴EA=OE=2,∴在Rt∴MEA中,===MA故答案为:(2)如下图所示,连接AM,取AM中点I,当且仅当C、H、I三点共线时,有CH=IC-IH,此时CH有最小值,否则构成∴ICH,三角形两边之差小于第三边CH,过I点作IN∴BC于N,连接IH,∴FM ∥IN ∥AB ,且I 是AM 的中点,∴IN 是梯形MFBA 的中位线,∴IN=11()(13)222+=+=MF AB ,112==FN FB ,在Rt∴CIN 中,由勾股定理:CI又I 为直角∴AHM 斜边AM 上的中点,∴111222=====IH IM MA∴当C 、H 、I 三点共线时,CH 有最大值为=-=CH CI IH【点睛】本题考查了矩形的性质,勾股定理,梯形中位线,直角三角形斜边上的中线等于斜边的一半,三角形两边之差小于第三边等知识点,具有一定的综合性,熟练掌握各性质是解决本题的关键.7.阅读下列材料,然后回答问题.⊥一样的式子,其实我们还可以将其进一步化简:===1)2=1以上这种化简的步骤叫做分母有理化.⊥学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算,比如我们熟悉的下面这个题:已知 a +b =2,ab = -3 ,求 a 2 + b 2 .我们可以把a +b 和ab 看成是一个整体,令 x =a +b , y = ab ,则 a 2 + b 2 = (a + b)2 - 2ab = x 2- 2y = 4+ 6=10.这样,我们不用求出a ,b ,就可以得到最后的结果.(1+...(2)已知 m 是正整数, a,b 2a 2+ 1823ab + 2b 2 = 2019 .求 m .(31=【答案】(1)12-;(2)2;(3)9 【分析】(1)先将式子的每一项进行分母有理化,再计算即可;(2)先求出,a b ab +的值,再用换元法计算求解即可;(31=的值,再对【详解】解:(1)原式12019+2222=+++12019122+++==(2)∴a ,b∴2(21),1a b m ab +==+= ∴2a 2+ 1823ab + 2b 2 = 2019∴222()18232019a b ++=∴2298a b +=∴24(21)100m +=∴251m =±-∴m 是正整数∴m=2.(31=得出21=20=∴2281=+=0≥≥9=.【点睛】本题考查的知识点是分母有理化以及利用换元思想求解,解此题的关键是读懂题意.理解分母有理化的方法以及利用换元方法解题的方法.8.已知ABC 中,60BAC ∠=︒,以AB 和BC 为边向外作等边ABD △和等边BCE .(1)连接AE 、CD ,如图1,求证:AE CD =;(2)若N 为CD 中点,连接AN ,如图2,求证:2CE AN =;(3)若AB BC ⊥,延长AB 交DE 于M ,DB =3,则BM = .(直接写出结果)【答案】(1)见解析;(2)见解析;(3)2. 【分析】(1)由等边ABD △和等边BCE .AB=DB ,BC=BE ,可推得∴ABE=∴DBC ,可证(SAS)ABE DBC △≌△由性质AE CD =即可;(2)延长AN 使NF AN =,连接FC ,由N 为CD 中点,可得CN=DN ,可证(SAS)ADN FCN △≌△,可得CF AD AB ==,NCF NDA ∠=∠,可求∴DAC=120°,可推出60ACF ∠=︒,可证(SAS)ABC CFA ≌,由性质得2CE BC AF AN ===即可;(3)过E 作EG∴BE ,交AM 延长线于G 由AB BC ⊥,60BAC ∠=︒,DB =∴EBM =30°,求得∴G==60°=∴CAB ,可证∴CAB∴∴BGE (AAS )由性质得GE=AB=DB =,利用30°角的直角边与斜边关系得,再证∴AD∴∴GME (AAS ),得AM=GM 可求得BG=即可.【详解】(1)证明:∴等边ABD △和等边BCE .AB=DB ,BC=BE ,∴ABD=∴CBE=60°,∴∴ABD+∴ABC=∴CBE+∴ABC ,∴∴ABE=∴DBC ,(SAS)ABE DBC △≌△,AE CD ∴=;(2)延长AN 使NF AN =,连接FC ,∴N 为CD 中点,∴CN=DN ,又∴AND=∴FNC ,(SAS)ADN FCN △≌△,CF AD AB ∴==,NCF NDA ∠=∠,∴60BAC ∠=︒,∴DAB=60°,∴∴DAC=120°,∴60ACF ACD NCF ACD ADN ∠=∠+∠=∠+∠=︒,BAC ACF ∴∠=∠,∴AC=CA ,(SAS)ABC CFA ≌,2CE BC AF AN ∴===;(3)过E 作EG∴BE ,交AM 延长线于G ,∴AB BC ⊥,60BAC ∠=︒,DB =,,由勾股定理得:=∴∴EBM=180°-∴ABC -∴CBE=30°,∴∴G=180°-∴GBE -∴BEG=60°=∴CAB ,∴BC=EB ,∴∴CAB∴∴BGE (AAS ),∴GE=AB=DB =,∴∴DAM=60°=∴G ,又∴∴AMD=∴GME ,∴∴AD∴∴GME (AAS ),∴AM=GM ,∴GM=AB+BM ,,,∴2BM =.故答案为:2.【点睛】本题考查等边三角形的性质,三角形全等判定与性质,直角三角形的性质,勾股定理,线段中点,线段和差,掌握等边三角形的性质,三角形全等判定与性质,直角三角形的性质,勾股定理应用,线段中点,线段和差计算是解题关键.9.定义:我们把对角线互相垂直的四边形叫做和美四边形,对角线交点称为和美四边形中心.(1)写出一种你学过的和美四边形________;(2)顺次连接和美四边形四边中点所得四边形是________A .矩形B .菱形C .正方形D .无法确定(3)如图1,点O 是和美四边形ABCD 的中心,E F G H 、、、分别是边AB BC CD DA 、、、的中点,连接OE OF OG OH 、、、,记四边形AEOH BEOF CGOF DHOG 、、、的面积为1234S S S S 、、、,用等式表示1234S S S S 、、、的数量关系(无需说明理由)(4)如图2,四边形ABCD 是和美四边形,若3,2,4AB BC CD ===,求AD 的长.【答案】(1)正方形;(2)A;(3)S1+S3=S2+S4;(4【分析】(1)根据正方形的对角线互相垂直解答;(2)根据矩形的判定定理解答;(3)根据三角形的中线把三角形分为面积相等的两部分解答;(4)根据和美四边形的定义、勾股定理计算即可.【详解】解:(1)正方形是学过的和美四边形,故答案为:正方形;(2)顺次连接和美四边形四边中点所得四边形是矩形,故选:A.(3)由和美四边形的定义可知,AC∴BD,则∴AOB=∴BOC=∴COD=∴DOA=90°,又E、F、G、H分别是边AB、BC、CD、DA的中点,∴∴AOE的面积=∴BOE的面积,∴BOF的面积=∴COF的面积,∴COG的面积=∴DOG的面积,∴DOH的面积=∴AOH的面积,∴S1+S3=∴AOE的面积+∴COF的面积+∴COG的面积+∴AOH的面积=S2+S4;(4)如图2,连接AC、BD交于点O,则AC∴BD,∴在Rt∴AOB中,AO2=AB2-BO2,Rt∴DOC中,DO2=DC2-CO2,AB=3,BC=2,CD=4,∴可得AD2=AO2+DO2=AB2-BO2+DC2-CO2=AB2+DC2-BC2=32+42-22=21,即可得AD.【点睛】本题考查的是和美四边形的定义、矩形的判定、勾股定理的应用,正确理解和美四边形的定义、掌握矩形的判定定理是解题的关键.。
人教版八年级下册数学期末动点问题压轴题训练

人教版八年级下册数学期末动点问题压轴题训练1.如图,在Rt△ABC 中,△ACB =90°,AB =10,AC =6,动点P 从点B 出发,以每秒2个单位长的速度,沿射线BC 运动,设运动时间为t 秒,请解答以下问题:(1)BC 边的长为________;(2)当△ABP 为直角三角形时,求t 的值,写出求解过程; (3)当△ABP 为等腰三角形时,直接写出t 的值.2.综合与实践,如图,E 、F 是等腰Rt ABC △的斜边BC 上的两动点,45EAF ∠=︒,CD BC ⊥且CD BE =.(1)求证:△ABE △△ACD ;(2)深入探究:猜想EF 、BE 、CF 之间的关系,并说明理由.3.如图1,在△ABC 中,AB =AC ,△BAC =90°,D 为AC 边上一动点,且不与点A 点C重合,连接BD 并延长,在BD 延长线上取一点E ,使AE =AB =AC ,连接CE .(1)若△AED =20°,则△CAE =______°,△AEC =______°.(2)若△AED =α,小明说△BEC 一定是45°,你认为正确吗?请说明理由.(3)如图2,过点A 作AF △BE 于点F ,AF 的延长线与EC 的廷长线交于点H ,求证:EH 2+CH 2=2AB 2.4.如图,在正方形ABCD 中,E 为BC 边上一动点(不与点B ,重合),延长AE 到点F ,连接BF ,使得45AFB ∠=︒.G 为DC 边一点,且DG BE =,连接DF .点F 关于直线AB 的对称点为P ,连接AP ,BP .(1)依据题意补全图形,证明:DAG BAP ∠=∠;(2)延长PB 交AG 的延长线于点Q ,则APQ ∆的形状是 ; (3)用等式表示线段BP ,AB 与DF 的数量关系,并证明.5.已知:在ABC ∆中,6AB =,5AC =,ABC ∆的面积为9.点P 为边AB 上动点,过点B 作//BD AC ,交CP 的延长线于点D .ACP ∠的平分线交AB 于点E .时,求PA的长;(1)如图1,当CD AB(2)如图2,当点E为AB的中点时,请猜想并证明:线段AC、CD、DB的数量关系.6.在菱形ABCD中,△B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP△AB交直线CD于点P,连接NM、NP,设运动时间为t秒.(1)当t=2时,△NMP=________度;(2)求t为何值时,以A、M、C、P为顶点的四边形是平行四边形;(3)当△NPC为直角三角形时,求此时t的值.7.已知:在平面直角坐标系中,四边形ABCD是长方形,△A=△B=△C=△D=90°,AB∥CD,AB=CD=8,AD=BC=6,D点与原点重合.(1)直接写出点B的坐标.(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发,以每秒4个单位长度的速度沿射线CD方向匀速运动,若P、Q两点同时出发,设运动时间为t秒,当t为何值时,PQ∥y轴?(3)在Q的运动过程中,当Q运动到什么位置时,使△ADQ的面积为9?求出此时Q 点的坐标.8.已知:在矩形ABCD中,AB=6,BC=3,BD的垂直平分线EF分别交AB,CD于点E,F,垂足为O.(1)如图1,连接DE,BF.△求证:四边形DEBF为菱形;△直接写出AE的长.(2)如图2,动点P,Q分别从D,B两点同时出发,沿DEA和BCF各边匀速运动一周,即点P自D→E→A→D停止,点Q自B→C→F→B停止,在运动过程中,若点P,Q的运动路程分别为x,y(xy≠0),已知A,C,P,Q四点为顶点的四边形是平行四边形,请直接写出x与y满足的数量关系式.9.如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A—B—C—D—A返回到点A停止,点P的运动时间为t秒.(1)当t=3秒时,BP=cm;(2)当t 为何值时,连结CP ,DP ,△CDP 为等腰三角形;(3)Q 为AD 边上的点,且DQ =5,当t 为何值时,以长方形的两个顶点及点P 为顶点的三角形与△DCQ 全等.10.已知正方形ABCD ,点F 是射线DC 上一动点(不与C 、D 重合),连接AF 并延长交直线BC 于点E ,交BD 于H ,连接CH ,过点C 作CG △HC 交AE 于点G . (1)若点F 在边CD 上,如图1. △证明:△DAH =△DCH ; △猜想GFC 的形状并说明理由.(2)取DF 中点M ,连结MG .若MG =5,正方形边长为8,求BE 的长.11.如图,在ABCD 中,点O 是边AD 的中点,连接BO 并延长,交CD 的延长线于点E ,连接BD 、AE .(1)求证:四边形AEDB 是平行四边形;(2)请在图1中用一把无刻度的直尺画出AB 边的中点F (保留画图痕迹,无需证明过程);(3)若90BDC ∠=︒,4DC =,5BC =,动点P 从点E 出发,以每秒1个单位的速度沿EC CB BA --向终点A 运动,设点P 运动的时间为()0t t >秒.△若点Q 为直线AB 上的一点,当P 运动时间t 为何值时,以B 、C 、P 、Q 构成的四边形BCPQ 可以是菱形?△在点P 运动过程中,直接写出点P 到四边形AECB 相邻两边距离相等时t 的值.12.已知四边形OABC 是边长为4的正方形,分别以OA 、OC 所在的直线为x 轴、y 轴,建立如图1所示的平面直角坐标系,直线l 经过A 、C 两点.(1)写出点A 、点C 坐标并求直线l 的函数表达式;(2)若P 是直线l 上的一点,当△OP A 的面积是5时,请求出点P 的坐标;(3)如图2,点D (3,-1),E 是直线l 上的一个动点,求出使|BE -DE |取得最大值时点E 的坐标和最大值(不需要证明).13.如图,在平面直角坐标系中,O 为坐标原点.ABC 的边BC 在x 轴上,A 、C 两点的坐标分别为()0,A m 、(),0C n ,()10,0B -,且()260n -=,点P 为x 轴上任意一点.(1)求A 、C 两点的坐标;(2)连接PA ,当POA 的面积等于AOB 面积的14时,求PB 的长度;(3)点M 为直线AC 上的动点,当APM △是以AP 为直角边的等腰三角形时,请直接写出点M 的坐标.14.如图,直线24y x =-+与x 轴交于点A ,与y 轴交于点B ,点C 的坐标是()0,1-,P 为直线AB 上的动点,连接PO ,PC ,AC .(1)求A ,B 两点的坐标. (2)求证:ABC 为直角三角形.(3)当PBC 与POA 面积相等时,求点P 的坐标.15.已知:如图,一次函数334y x =-的图像分别与x 轴、y 轴相交于点A 、B ,且与经过x 轴负半轴上的点C 的一次函数y =kx +b 的图像相交于点D ,直线CD 与y 轴相交于点E ,E 与B 关于x 轴对称,OA =3OC .(1)直线CD 的函数表达式为______;点D 的坐标______;(直接写出结果) (2)点P 为线段DE 上的一个动点,连接BP .△若直线BP 将△ACD 的面积分为79∶两部分,试求点P 的坐标;△点P 是否存在某个位置,将△BPD 沿着直线BP 翻折,使得点D 恰好落在直线AB 上方的坐标轴上?若存在,求点P的坐标;若不存在,请说明理由.16.如图,在平面直角坐标系中,过点B(﹣6,0)的直线AB与直线OA相交于点A(﹣4,2),动点N沿路线O→A→C运动.(1)求直线AB的解析式;(2)求OAC的面积;(3)当ONC的面积是OAC面积的1时,求出这时点N的坐标.217.如图1,在平面直角坐标系中,点A,B的坐标分别为(4,0),(0,4),P为线段AB上的一点.(1)如图1,若S△AOP=6,求点P的坐标.(2)如图2,若P为AB的中点,点M,N分别是OA,OB边上的动点,点M从顶点A 出发向点O运动,点N从顶点O同时出发向点B运动,且它们的速度都为1单位长度/秒,在点M,N运动的过程中,探究线段PM,PN之间的关系并证明.(3)如图3,若P为线段AB上异于A,B的任意一点,过点B作BD△OP,分别交OP、OA于F,D两点,E为OA上一点,且△PEA=△BDO,探究线段OD与AE的关系并说明理由.18.如图,在平面直角坐标系中,一次函数12y x m =-+的图象1l 分别与x ,y 轴交于A ,B 两点,正比例函数的图象2l 与1l 交于点()2,4C .(1)求m 的值及2l 的解析式;(2)若点M 是直线12y x m =-+上的一个动点,连接OM ,当AOM 的面积是BOC 面积的2倍时,请求出符合条件的点M 的坐标;(3)一次函数2y kx =+的图象为3l ,且1l ,2l ,3l 不能围成三角形,直接写出k 的值.19.如图1,在平面直角坐标系xOy 中,点O 为坐标原点,直线AB :32y kx =+与直线AC :2y x b =-+交于点A ,两直线与x 轴分别交于点()3,0B -和点()2,0C .(1)求直线AB 和AC 的函数表达式;(2)点P为y轴上一动点,当PA PC最小时,求点P的坐标;(3)点M为直线AC上一动点,当△ABM是等腰直角三角形时,请直接写出点M的坐标.20.如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(﹣3,0),点B (0,﹣4),点C(2,﹣1)是直线BC上一点.(1)求直线AB和直线BC的函数表达式;(2)点D是y轴上的一个动点,连接CD,当△BCD是以BC为腰的等腰三角形时,请直接写出点D的纵坐标为;(3)点E是直线AB上的一个动点,在x轴上找一个点F,连接CE,EF,CF,当△CEF 是以CE为底边的等腰直角三角形时,请直接写出△CEF的面积为.参考答案:1.(1)8(2)t =4或t =254(3)t =5或t =8或t =2582. (2)222EF BE CF =+,3.(1)50,65(2)正确,4. (2)等腰直角三角形(3)2222BP DF AB +=,5.(1)PA 的长为4(2)AC=CD +DB ;6.(1)30;(2)1;(3)t = 83 或t =103时,△PNC 是直角三角形. 7.(1)(8,6);(2)87;(3)Q 点的坐标(3,0)或(-3,0). 8.(1)△94;(2)x +y =9 9.(1)2;(2)1或3或9;(3)2.5或4.5或7.5或9.510.(1)△见解析;△GFC 是等腰三角形,理由见解析;(2)BE 的长为14或2. 11.(1)见解析;(2)见解析;(3)△3或398;△0或3或8或13或14或17 12.(1)A (4,0)和C (0,4),y =﹣x +4 (2)P 1(32,52)、P 2(132,5-2)(3)(6,-2)13.(1)点A 的坐标是()0,8,点C 的坐标是()6,0 (2)152或252(3)点M 的坐标是88,3⎛⎫- ⎪⎝⎭或568,3⎛⎫- ⎪⎝⎭或488,77⎛⎫- ⎪⎝⎭或()48,56- 14.(1)()2,0A ,()0,4B (3)820,99P ⎛⎫ ⎪⎝⎭或()8,20P -15.(1)934y x =+,(-4,-6) (2)△P 点坐标为5334⎛⎫-- ⎪⎝⎭,或918⎛⎫- ⎪⎝⎭,;△存在,P 点坐标为2421,1111⎛⎫-- ⎪⎝⎭或833⎛⎫-- ⎪⎝⎭, 16.(1)6y x =+(2)12(3)N 1(﹣2,1)或N 2(﹣2,4) 17.(1)(1,3)(2)PM =PN ,PM △PN ,(3)OD =AE ,18.(1)5m =,2l 的解析式为2y x =(2)()6,2M 或()142-,(3)12k =-或2或1 19.(1)1322y x =+,24y x =-+ (2)40,3P ⎛⎫ ⎪⎝⎭(3)()1,6M -或()3,2-20.(1)443AB y x =--;342BC y x =-;(2)(0,4-+或(0,4-或(0,2) (3)30598或5772。
八年级下册数学期末压轴题专辑(含解析-Word版)
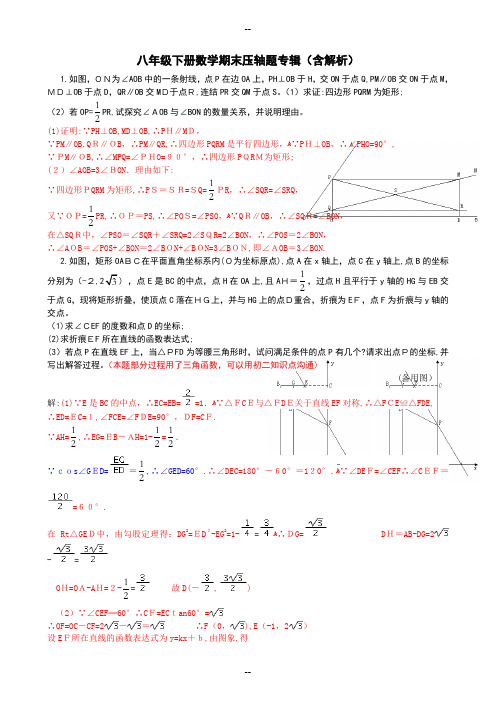
--八年级下册数学期末压轴题专辑(含解析)1.如图,ON为∠AOB 中的一条射线,点 P 在边 OA 上,PH⊥OB 于 H,交 ON 于点 Q,PM∥OB 交 ON 于点 M, MD⊥OB 于点 D,QR∥OB 交 MD于点R,连结 PR 交 QM 于点 S。
(1)求证:四边形 PQRM 为矩形;(2)若 OP= 1 PR,试探究∠AOB 与∠BON 的数量关系,并说明理由。
2(1)证明:∵PH⊥OB,MD⊥OB,∴PH∥MD, ∵PM∥OB,QR∥OB,∴PM∥QR,∴四边形 PQRM 是平行四边形,∵ﻫPH⊥OB,∴∠PHO=90°, ∵PM∥OB,∴∠MPQ=∠PHO=90°,∴四边形 PQRM为矩形; (2)∠AOB=3∠BON.理由如下:∵四边形PQRM 为矩形,∴PS=SR=SQ= 1 PR,∴∠SQR=∠SRQ, 2又∵OP= 1 PR,∴OP=PS,∴∠POS=∠PSO,∵ﻫQR∥OB,∴∠SQR=∠BON, 2在△SQR中,∠PSO=∠SQR+∠SRQ=2∠SQR=2∠BON,∴∠POS=2∠BON, ∴∠AOB=∠POS+∠BON=2∠BON+∠BON=3∠BON,即∠AOB=3∠BON.2.如图,矩形 OABC在平面直角坐标系内(O为坐标原点),点 A 在 x 轴上,点 C 在 y 轴上,点 B 的坐标分别为(-2,2 3 ) ,点 E 是 BC 的中点,点 H 在 OA 上,且 AH= 1 ,过点 H 且平行于 y 轴的 HG 与 EB 交 2于点 G,现将矩形折叠,使顶点 C 落在HG上,并与 HG 上的点D重合,折痕为 EF,点 F 为折痕与 y 轴的 交点。
(1)求∠CEF 的度数和点 D 的坐标; (2)求折痕EF 所在直线的函数表达式; (3)若点 P 在直线 EF 上,当△PFD 为等腰三角形时,试问满足条件的点 P 有几个?请求出点P的坐标,并 写出解答过程。
八年级数学下册期末动点问题及压轴题带答案

1.(12分)已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.(1)求证:BD∥AC;(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.2.(12分)如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm.一动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB 边向点B以3cm/s的速度运动.P,Q分别从点A和点C同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t s,则(1)t为何值时,四边形PQCD为平行四边形?(2)t为何值时,四边形PQCD为等腰梯形?(3)AB边的长是否存在一数值,使四边形PQCD为菱形.如果存在,请求出AB 边的长,如果不存在,请说出理由.3.(本题10分)已知:在正方形ABCD 中,AB =6,P 为边CD 上一点,过P 点作PE ⊥BD 于点E ,连接BP(1) O 为BP 的中点,连接CO 并延长交BD 于点F① 如图1,连接OE ,求证:OE ⊥OC② 如图2,若53=EF BF ,求DP 的长 (2) CP EP 22+=___________4.(本题12分)如图1,直线333+-=x y 分别与y 轴、x 轴交于点A 、点B ,点C 的坐标为(-3,0),D 为直线AB 上一动点,连接CD 交y 轴于点E(1) 点B 的坐标为__________,不等式0333>+-x 的解集为___________(2) 若S △COE =S △ADE ,求点D 的坐标(3) 如图2,以CD 为边作菱形CDFG ,且∠CDF =60°.当点D 运动时,点G 在一条定直线上运动,请求出这条定直线的解析式.5.(11分)如图1,在平面直角坐标系中,点O 是坐标原点,四边形ABCO 是菱形,点A 的坐标为(﹣3,4),点C 在x 轴的正半轴上,直线AC 交y 轴于点M ,AB 边交y 轴于点H ,连接BM .(1)菱形ABCO的边长是 ;(2)求直线AC 的解析式;(3)动点P 从点A 出发,沿折线ABC 方向以2个单位/秒的速度向终点C 匀速运动,设△PMB 的面积为S (S≠0),点P 的运动时间为t 秒.①求S 与t 之间的函数关系式;②在点P 运动过程中,当S =3,请直接写出t 的值.6.(11分)如图,在直角梯形ABCD 中,AD ∥BC ,∠B=90°,且AD=12cm ,AB=8cm ,DC=10cm ,若动点P 从A 点出发,以每秒2cm 的速度沿线段AD 向点D 运动;动点Q 从C 点出发以每秒3cm 的速度沿CB 向B 点运动,当P 点到达D 点时,动点P 、Q 同时停止运动,设点P 、Q 同时出发,并运动了t 秒,回答下列问题:(1)BC= cm ;(2)当t 为多少时,四边形PQCD 成为平行四边形?(3)当t 为多少时,四边形PQCD 为等腰梯形?(4)是否存在t ,使得△DQC 是等腰三角形?若存在,请求出t 的值;若不存在,说明理由.7、如图①,已知正方形ABCD的边长为1,点P是AD边上的一个动点,点A关于直线BP的对称点是点Q,连接PQ、D Q、CQ、BQ,设AP=x.(1)BQ+DQ的最小值是_______,此时x的值是_______;(2)如图②,若PQ的延长线交CD边于点E,并且∠CQD=90°.①求证:点E是CD的中点;②求x的值.(3)若点P是射线AD上的一个动点,请直接写出当△CDQ为等腰三角形时x 的值.8、如图1,平面直角坐标系中,直线AB:y=﹣x+b交x轴于点A(8,0),交y轴正半轴于点B.(1)求点B的坐标;(2)如图2,直线AC交y轴负半轴于点C,AB=BC,P为线段AB上一点,过点P 作y轴的平行线交直线AC于点Q,设点P的横坐标为t,线段PQ的长为d,求d与t之间的函数关系式;(3)在(2)的条件下,M为CA延长线上一点,且AM=CQ,在直线AC上方的直线AB上是否存在点N,使△QMN是以QM为斜边的等腰直角三角形?若存在,请求出点N的坐标及PN的长度;若不存在,请说明理由.1.【解答】解:(1)∵A(0,4),B(0,2),∴OA=4,OB=2,点B为线段OA的中点,又点D为OC的中点,即BD为△AOC的中位线,∴BD∥AC;(2)如图1,作BF⊥AC于点F,取AB的中点G,则G(0,3),∵BD∥AC,BD与AC的距离等于1,∴BF=1,∵在Rt△ABF中,∠AFB=90°,AB=2,点G为AB的中点,∴FG=BG=AB=1,∴△BFG是等边三角形,∠ABF=60°.∴∠BAC=30°,设OC=x,则AC=2x,根据勾股定理得:OA==x,∵OA=4,∴x=∵点C在x轴的正半轴上,∴点C的坐标为(,0);(3)如图2,当四边形ABDE为平行四边形时,AB∥DE,∴DE⊥OC,∵点D为OC的中点,∴OE=EC,∵OE⊥AC,∴∠OCA=45°,∴OC=OA=4,∵点C在x轴的正半轴上,∴点C的坐标为(4,0),设直线AC的解析式为y=kx+b(k≠0).将A(0,4),C(4,0)代入AC的解析式得:解得:∴直线AC的解析式为y=﹣x+4.2.【解答】解:(1)由运动知,AP=t,CQ=3t,∴DP=AD﹣AP=24﹣t,∵四边形PQCD为平行四边形,∴DP=CQ,∴24﹣t=3t,∴t=6;(2)如图2,过点D作DE⊥BC于E,过点P作PF⊥BC于F,∴四边形EFPD是矩形,∴DE=PF,[来源:Z|xx|]∵四边形PQCD是等腰梯形,∴∠PQC=∠DCQ,∵∠PFQ=∠DEC=90°,∴△PFQ≌△DEC,∴FQ=CE,∴BE=AD=24,∴CE=BC﹣BE=2,∵四边形PQCD为等腰梯形,∴CQ=DP+2CE,由运动知,AP=t,CQ=3t,∴DP=AD﹣AP=24﹣t,∴24﹣t+2×2=3t,∴t=7,(3)AB边的长是8时,四边形PQCD为菱形,理由:由(1)知,t=6时,四边形PQCD是平行四边形,∴DP=24﹣6=18,∵平行四边形PQCD是菱形,∴CD=DP=18,如图2,过点D作DE⊥BC于E,∴四边形ABED是矩形,∴AB=DE,在Rt△CDE中,CE=2,CD=18,∴DE==8.3.证明:(1) ① ∵∠PEB =∠PCB =90°,O 为BP 的中点∴OE =OB =OP =OC∴∠POE =2∠DBP ,∠POC =2∠CBP∴∠COE =∠POE +∠POC =2(∠DBP +∠CBP )=90°∴OE ⊥OC② 连接OE 、CE∵△COE 为等腰直角三角形∴∠ECF =45°在等腰Rt △BCD 中,BF 2+DE 2=EF 2设BF =3x ,EF =5x ,则DE =4x∴3x +4x +5x =26,解得x =22 ∴DP =2DE =424=x(2) ∵62==-+=+CD C DP CP EP ∴2322=+CP EP4.解:(1) (3,0)、x <3(2) ∵S △COE =S △ADE∴S △AOB =S △CBD 即33321621⨯⨯=⨯⨯D y ,y D =233 当y =233时,23233333==+-x x ,∴D (23323,) (3) 连接CF∵∠CDF =60°∴△CDF 为等边三角形连接AC∵AB =AC =BC =6∴△ABC 为等边三角形∴△CAF ≌△CBD (SAS )∴∠CAF =∠ACB =60°∴AF ∥x 轴设D (m ,333+-m )过点D 作DH ⊥x 轴于H∴BH =3-m ,DB =6-2m =AF∴F (2m -6,33)由平移可知:G (m -9,m 3-) 令⎪⎩⎪⎨⎧-=-=m y m x 39∴点G 在直线393--=x y 上6.解:根据题意得:PA=2t ,CQ=3t ,则PD=AD-PA=12-2t .(1)如图,过D 点作DE ⊥BC 于E ,则四边形ABED 为长方形,DE=AB=8cm ,AD=BE=12cm ,在直角△CDE 中,∵∠CED=90°,DC=10cm ,DE=8cm ,∴22DC DE -,∴BC=BE+EC=18cm .…………………………………………………………………2分(直接写出最后结果18cm 即可)(2)∵AD ∥BC ,即PD ∥CQ ,∴当PD=CQ 时,四边形PQCD 为平行四边形,即12-2t=3t ,解得t=125秒, 故当t=125秒时四边形PQCD 为平行四边形;………………………………………4分(3)如图,过D 点作DE ⊥BC 于E ,则四边形ABED 为长方形,DE=AB=8cm ,AD=BE=12cm ,当PQ=CD 时,四边形PQCD 为等腰梯形.过点P 作PF ⊥BC 于点F ,过点D 作DE ⊥BC 于点E ,则四边形PDEF 是长方形,EF=PD=12-2t ,PF=DE .在Rt △PQF 和Rt △CDE 中,PQ CD PF DE ==⎧⎨⎩, ∴Rt △PQF ≌Rt △CDE (HL ),∴QF=CE ,∴QC-PD=QC-EF=QF+EC=2CE ,即3t-(12-2t )=12,解得:t=245, 即当t=245时,四边形PQCD 为等腰梯形;……………………………………………8分(4)△DQC 是等腰三角形时,分三种情况讨论:①当QC=DC 时,即3t=10,∴t=103;②当DQ=DC时,36 2t=∴t=4;③当QD=QC时,3t×65 10=∴t=259.故存在t,使得△DQC是等腰三角形,此时t的值为103秒或4秒或259秒.………11分③在Rt△DMQ中,DQ2=DM2+QM2222 (3)8(38) t t=+-36t=100t=25 97.解:(1);-1;(2)①证明:在正方形ABCD中,AB=BC,∠A=∠BCD=90°∵Q点为A点关于BP的对称点∴AB=QB,∠A=∠PQB=90°∴QB=BC,∠BQE=∠BCE∴∠BQC=∠BCQ∴∠EQC=∠EQB-∠CQB=∠ECB-∠QCB=∠ECQ∴EQ=EC在Rt△ABC中∵∠QDE=90°-∠QCE,∠DQE=90°-∠EQC∴∠QDE=∠DQE∴EQ+ED∴CE=EQ=ED即E是CD的中点②(3)或或8.解:(1)∵y=﹣x+b交x轴于点A(8,0),∴0=﹣×8+b,b=6,∴直线AB解析式为y=﹣x+6,令x=0,y=6,B(0,6);(2)∵A(8,0),B(0,6),∴OA=8,OB=6,∵∠AOB=90°,∴AB=10=BC,∴OC=4,∴点C(0,﹣4),设直线AC解析式为y=kx+b’,∴,∴∴直线AC解析式为y=x﹣4,∵P在直线y=﹣x+6上,∴可设点P(t,﹣t+6),∵PQ∥y轴,且点Q在y=x﹣4 上,∴Q(t, t﹣4),∴d=(﹣t+6)﹣(t ﹣4)=﹣t+10;(3)过点M作MG⊥PQ于G,∴∠QGM=90°=∠COA,∵PQ∥y轴,∴∠OCA=∠GQM,∵CQ=AM,∴AC=QM,在△OAC与△GMQ中,,∴△OAC≌△GMQ,∴QG=OC=4,GM=OA=8,过点N作NH⊥PQ于H,过点M作MR⊥NH于点R,∴∠MGH=∠RHG=∠MRH=90°,∴四边形GHRM是矩形,∴HR=GM=8,可设GH=RM=k,∵△MNQ是等腰直角三角形,∴∠QMN=90°,NQ=NM,∴∠HNQ+∠HQN=90°,∴∠HNQ+∠RNM=90°,∴∠RNM=∠HQN,∴△HNQ≌△RMN,∴HN=RM=k,NR=QH=4+k,∵HR=HN+NR,∴k+4+k=8,∴k=2,∴GH=NH=RM=2,∴HQ=6,∵Q(t,t﹣4),∴N(t+2,t﹣4+6)即 N(t+2,t+2)∵N在直线AB:y=﹣x+6上,∴t+2=﹣(t+2)+6,∴t=2,∴P(2,),N(4,3),∴PH=,NH=2,∴PN==.。
勾股定理 期末压轴题训练(含答案) 2022—2023学年人教版数学八年级下册
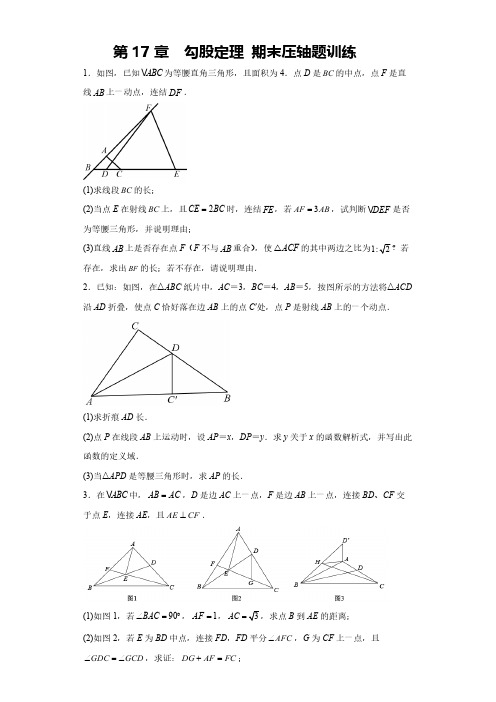
1.如图,已知 VABC 为等腰直角三角形,且面积为 4.点 D 是 BC 的中点,点 F 是直 线 AB 上一动点,连结 DF .
(1)求线段 BC 的长; (2)当点 E 在射线 BC 上,且 CE 2BC 时,连结 FE ,若 AF 3AB ,试判断 VDEF 是否 为等腰三角形,并说明理由; (3)直线 AB 上是否存在点 F(F 不与 AB 重合),使△ACF 的其中两边之比为1: 2 ?若 存在,求出 BF 的长;若不存在,请说明理由. 2.已知:如图,在△ABC 纸片中,AC=3,BC=4,AB=5,按图所示的方法将△ACD 沿 AD 折叠,使点 C 恰好落在边 AB 上的点 C′处,点 P 是射线 AB 上的一个动点.
(1)如图 1,若 BAC 90 , AF 1, AC 3 ,求点 B 到 AE 的距离; (2)如图 2,若 E 为 BD 中点,连接 FD,FD 平分 AFC ,G 为 CF 上一点,且 GDC GCD ,求证: DG AF FC ;
(3)如图 3,若 BAC 120 , BC 12 ,将△ABD 沿着 AB 翻折得△ABD ,点 H 为 BD 的中点,连接 HA、HC,当△HAC 周长最小时,请直接写出 AD 的值.
(1)如图 1,△ABC 与△ADE 互为“底余等腰三角形”. ①若连接 BD,CE,判断△ABD 与△ACE 是否互为“底余等腰三角形”:_______ (填 “是”或“否”) ;
②当∠BAC=90°时,若△ADE 的“余高”AH= 5 ,则 DE=_______;
③当 0°<∠BAC<180°时,判断 DE 与 AH 之间的数量关系,并证明; (2)如图 2,在四边形 ABCD 中,∠ABC=60°,DA⊥BA,DC⊥BC,且 DA=DC. ①画出△OAB 与△OCD,使它们互为“底余等腰三角形”; ②若△OCD 的“余高”长为 a,则点 A 到 BC 的距离为_______(用含 a 的式子表示). 7.已知:△ABC 是等腰直角三角形,动点 P 在斜边 AB 所在的直线上,以 PC 为直角 边作等腰直角三角形 PCQ,其中∠PCQ=90°,探究并解决以下问题: (1)如图 1,若点 P 在线段 AB 上,且 AC=4,PA= 2 ,则①线段 PB= ,PC= .② 猜想: PA2, PB2, PQ2 三者之间的数量关系为 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版数学八年级下册
压轴题含答案
Document number【980KGB-6898YT-769T8CB-246UT-18GG08】
1、如图11,已知正比例函数和反比例函数的图像都经过点M (-2,1),且
P (1,-2)为双曲线上的一点,Q 为坐标平面上一动点,PA 垂直于x 轴,Q B
垂
直
于
y 轴,垂足分别是A 、B .
(1)写出正比例函数和反比例函数的关系式;
(2)当点Q 在直线MO 上运动时,直线MO 上是否存在这样的点Q ,使得△OBQ 与△OAP 面积相等如果存在,请求出点的坐标,如果不存在,请说明理由; (3)如图12,当点Q 在第一象限中的双曲线上运动时,作以OP 、OQ 为邻边的平行四边形OPCQ ,求平行四边形OPCQ 周长的最小值.
解:(1)设正比例函数解析式为y kx =,将点M (2-,1-)坐标代入得
1
2
k
,所以正比例函数解析式为12y x 同样可得,反比例函数解析式为2y x
(2)当点Q 在直线DO 上运动时,
设点Q 的坐标为1
()2
Q m m ,,
于是2
111
12224
OBQ S OB BQ m m
m △, 而1
(1)(2)12OAP S △,
所以有,21
14
m ,解得2m =±
所以点Q 的坐标为1(21)Q ,
和2(21)Q , (3)因为四边形OPCQ 是平行四边形,所以OP =CQ ,OQ =PC ,
而点P (1-,2-)是定点,所以OP 的长也是定长,所以要求平行四边形OPCQ 周长的最小值就只需求OQ 的最小值.
因为点Q 在第一象限中双曲线上,所以可设点Q 的坐标为2
()Q n n
,,
图
由勾股定理可得2222
42()4OQ n n
n n
,
所以当22()0n
n
即20n n
时,2OQ 有最小值4,
又因为OQ 为正值,所以OQ 与2OQ 同时取得最小值, 所以OQ 有最小值2.
由勾股定理得OP =5,所以平行四边形OPCQ 周长的最小值是
2()
2(5
2)
25
4OP
OQ .
2.已知:如图,正比例函数y =ax 的图象与反比例函数x
k
y
的图象交于点A (3,2).
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x 取何值时,反比例函数的值大于正比
例函数的值;
(3)M (m ,n )是反比例函数图象上的一动点,其中0<m <3,过点M 作直线MB
∥x 轴,交y 轴于点B ;过点A 作直线AC ∥y 轴交y 轴于点C ,交直线MB 于点D .当四边形OADM 的面积为6时,请判断线段BM 与DM 的大小关系,并说明理由.
解答:解:(1)将A (3,2)分别代入y=,y=ax 中,得:2=,3a=2 ∴k=6,a=(2分)
∴反比例函数的表达式为:y=(3分) 正比例函数的表达式为y=x (4分)
(2)观察图象,得在第一象限内,当0<x <3时,反比例函数的值大于正比例函数的值.(6分)
(3)BM=DM(7分)
理由:∵MN∥x轴,AC∥y轴,
∴四边形OCDB是平行四边形,
∵x轴⊥y轴,
∴?OCDB是矩形.
∵S△OMB=S△OAC =×|k|=3,又S四边形OADM=6,
∴S矩形OBDC=S四边形OADM+S
△OMB
+S△OAC=3+3+6=12,
即OC?OB=12
∵OC=3
∴OB=4(8分)
即n=4
∴m=
∴MB=,MD=3﹣=
∴MB=MD(9分).
3.如图,直线y=x+b(b≠0)交坐标轴于A、B两点,交双曲线y=
x
2于点D,过D
作两坐标轴的垂线DC、DE,连接OD.
(1)求证:AD平分∠CDE;
(2)对任意的实数b(b≠0),求证BE·OE为定值;
(3)是否存在直线AB,使得四边形OBCD为平行四边形若存在,求出直线的解析式;
若不存在,请说明理由.
A B C
E O
D
x y
4.如图(1),直线1
22
y x =-
+交x 轴、y 轴于A 、B 两点,C 为直线AB 上第二象限内一点,且S △AOC =8,双曲线k
y x
=经过点C
(1)求k 的值
(2)如图(2),过点C 作CM ⊥y 轴于M,反向延长CM 于H ,使CM=CH ,过
H 作HN ⊥x 轴于N ,交双曲线y=x
k
于D ,求四边形OCHD 的面积
(3)如图(3),点G 和点A 关于y 轴对称,P 为第二象限内双曲线上一个动点,
过P 作PQ ⊥x 轴于Q ,分别交线段BG 于E,交射线BC 于F ,试判断线段 QE+QF 是否为定值,若为定值,证明并求出定值;若不是定值,请说明
理由
x
y
O
C
A
B M H
D N
图(2)
图
y
O
C A
B G P
F
E
Q
x
y
O
C
A
B 图(1)。
