线代19答案 线性代数试题库
2019年春线性代数补充习题与参考答案

线性代数补充习题第一章 行列式一、填空题1.220a b a b =,则b a ,满足的条件是________ .2.若0010413≠xx x,则x 满足的条件是________ .3.排列3712456的逆序数为________ . 4.排列123(n 1)n -L 的逆序数为________ .5.行列式=0001000000000c b a ________ .6.行列式=-00001002001000ΛΛΛΛΛΛΛΛΛnn ________ . 7.设行列式12230503--a中,余子式632=M ,则=a ________ . 二、选择题1.下列行列式中值为0的是( ).(A )行列式中有两行对应元素之和为0 (B )行列式中对角线上元素全为0(C )行列式中有两行含有相同的公因子 (D )行列式中有一行与另一列对应元素成比例2.在函数xx x xxx f 21112)(---=中,3x 的系数是( ).(A )1 (B )-2 (C )3 (D )43.设121=b b ,则=++22121121111b a a a b a a a ( ).(A )-2 (B )-1 (C )1 (D )24.设1333231232221131211=a a a a a a a a a ,则111112132121222331313233423423423a a a a a a a a a a a a --=-( ). (A )-12 (B )12 (C )-24 (D )245.设0333231232221131211≠=a a a a a a a a a D ,ij A 是D 元素ij a 的代数余子式(3,2,1,=j i ),若0333223113≠++j j j A a A a A a ,则( ).(A )1=j (B )2=j (C )3=j (D )1=j 或3=j 6.下列选项是偶排列的是( )(A )12435 (B )54321 (C )32514 (D )542317.设001000102001000a =-,则a =( ) (A )12-(B )12(C )1 (D )-1 8.如果线性方程组12312312313231x x x x x x x x x λλ+-=⎧⎪-+=⎨⎪-+=⎩有唯一解,则λ必须满足( )(A )1λ≠ (B )15λ≠-(C )15λ≠ (D )1λ≠- 三、判断题1.交换行列式的两行(列),行列式的值不变.( )2.n 阶行列式中,若有n n -2个以上元素为0,则行列式的值为0.( )3.333333222222111111d c c b b a d c c b b a d c c b b a +++++++++333222111c b a c b a c b a =333222111d c b d c b d c b +.( )4.元素ij a 的代数余子式ij A 与ij a 所在有行、列有关,而与ij a 的值无关.( )5.10100001111010001100111001111100010111100010001d c b a dc b a +++=.( )6.n 阶行列式中,某行元素全为0,则行列式的值为0.( )第一章 行列式1、a b =2、0≠x 且2≠x3、74、05、abc6、!)1(2)1(n n n -- 7、3-二、选择题1、A2、B3、C4、A5、C6、B7、A8、B三、判断题1、×2、√3、×4、√5、√6、√第二章 矩阵一、填空题1.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=100010501,10001001B x A ,且B A =,则=x ________ . 2.设⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=23,1102b a B A ,若BA AB =,则b a ,为 .3.设⎥⎦⎤⎢⎣⎡=101a A ,则=nA . 4.设()⎥⎦⎤⎢⎣⎡=+-=2011,522A x x x f ,则()=A f . 5.设⎥⎦⎤⎢⎣⎡=5221A ,则A 的伴随矩阵=*A . 6.设)0(≠-⎥⎦⎤⎢⎣⎡=cb ad d c b a A ,则A -1= . 7.若⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n a a a A O21(n i a i ,,2,1,0Λ=≠),则=-1A .8.设3=A ,且A 为二阶方阵,则=A 3 .9.已知⎥⎦⎤⎢⎣⎡=012301A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=100021B ,则=AB .10.21121214X ⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦,则=X .1.=⎥⎦⎤⎢⎣⎡++++c b b a z y y x ( ). (A )⎥⎦⎤⎢⎣⎡+++⎥⎦⎤⎢⎣⎡++c b b z y y c b a z y x (B )⎥⎦⎤⎢⎣⎡+++⎥⎦⎤⎢⎣⎡++c b z y b a y x (C )⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡c b z y b a y x (D )⎥⎦⎤⎢⎣⎡+++⎥⎦⎤⎢⎣⎡++c b a z y x b b a y y x2.设C B A ,,均为n 阶方阵,且E ABC =,则必有( ). (A )E CBA = (B )E BCA = (C )E BAC = (D )E ACB =3.已知矩阵 )(,n m B A m n n m ≠⨯⨯,则下列运算结果不为n 阶方阵的是( ). (A )BA (B )AB (C )TBA )( (D )T T B A 4.若A 是( ),则必有A A T-=.(A )可逆矩阵 (B )三角矩阵 (C )初等矩阵 (D )反对称矩阵 5.设B A ,均为n 阶方阵,则下列运算正确的是( ).(A )()kk kB A AB = (B )A A -=-(C )()()B A B A B A +-=-22 (D )若A 可逆,0≠k ,则()111---=A k kA6.矩阵A 经初等行变换化为行阶梯形矩阵后( ).(A ) 秩变大 (B )秩变小 (C )秩不变 (D )化为单位方阵 7.设A 是3阶可逆矩阵,λ为实数,如果A A 8=λ,则( ). (A )2=λ (B )2-=λ (C )1=λ (D )8=λ 8.设A 是n 阶方阵,k 为非零实数,则=-kA ( ).(A )()A k nn1- (A )A k n(C )A k - (D )A k9.设B A ,均为n 阶矩阵,则必有( ).(A )B A B A +=+ (B )BA AB = (C )BA AB = (D )()111---+=+B A B A三、判断题1.设B A ,都是n m ⨯矩阵,则A B B A +=+.( ) 2.两个n 阶可逆矩阵之和一定是可逆矩阵.( )3.如果A 与B 可交换,且A 可逆,则1-A 与B 可交换.( ) 4.n 阶方阵A 可逆的充分必要条件是0=A .( )5.设C B A ,,都是n 阶方阵,且0≠A ,若AC AB =,则C B =.( ) 6.设B A ,都是n 阶方阵,若0=AB ,则0=B .( ) 7.若A 与B 为n 阶方阵,则BA AB =.( )8.设A 与B 为n 阶方阵,且A 为对称矩阵,则AB B T 也是对称矩阵.( ) 9.设A 与B 为n 阶方阵,则B A AB =.( )10.若A 和B 皆为n 阶方阵,则必有B A B A +=+.( )第二章 矩阵一、填空题1、52、0,11==b a3、⎥⎦⎤⎢⎣⎡101na 4、⎥⎦⎤⎢⎣⎡5014 5、⎥⎦⎤⎢⎣⎡--1225 6、⎥⎦⎤⎢⎣⎡---a c b d bc ad 17、⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡---11211n a a a O8、27 9、6- 10、1012⎡⎤⎢⎥-⎣⎦二、选择题1、C2、B3、B4、D5、D6、C7、A8、A9、C三、判断题1、√2、×3、√4、×5、√6、×7、×8、√9、√ 10、×第三章 向量组的线性相关性一、填空题1.设()()TT2,3,1,1,1,221-=-=αα,若()T5,,13λα=可由21,αα线性表示 ,则=λ .2.设()()()1231,2,3,5,4,1ααα===,则12,αα的线性相关性为线性 .3.设()()()1231,2,3,2,2,1,3,4,3ααα===,则123,,ααα的线性相关性为线性 .4.若向量组321,,ααα线性无关,则321321211,2,αααβααβαβ++=+==的线性关系为 . 5.若向量组()()()TTTt t 1,0,0,0,2,1,0,1,12321+==+=ααα的秩为2,则=t .6.若向量组()()()TTTk k k 0,1,,2,2,,7,1,6321==+=ααα的秩为3,则≠k .二、选择题1.向量组n ααα,,,21Λ线性无关的充要条件是( ). (A) n ααα,,,21Λ均不为零向量(B) n ααα,,,21Λ中任意两个向量的对应分量不成比例 (C) n ααα,,,21Λ中有一个部分向量线性无关(D) n ααα,,,21Λ中任意一个向量都不能由其余1-n 个向量线性表示 2.设向量组321,,ααα线性无关,则与321,,ααα等价的向量组为( ). (A) 3221,αααα++ (B) 2121214,3,,αααααα-+ (C) 31312121,,,αααααααα-+-+ (D) 3221,αααα-+ 3.设向量组γβα,,线性无关,δβα,,线性相关,则( ). (A) α必可由δγβ,,线性表示 (B) β必不可由δγα,,线性表示 (C)δ必可由γβα,,线性表示 (D) δ必不可由γβα,,线性表示4.设向量组12,s αααL 的秩等于3,则( ).(A) 12,s αααL 任意3个向量都线性无关 (B) 12,s αααL 中没有零向量(C) 12,s αααL 任意4个向量都线性相关 (D) 12,s αααL 任意2个向量都线性无关5. 向量组123(,1,1),(1,,1),(1,1,)T T Ta a a ααα==-=-线性相关,则=a ( )(A) 12-或 (B)13-或 (C) 10或 (D)32或三、判断题1.设向量组r ααα,,,21Λ与s βββ,,,21Λ都线性相关,且可以互相线性表示,则必有s r =.( ) 2.n 维向量组)1(,,,21>s s αααΛ线性相关的充要条件是其中有一个向量可由其余向量线性表示.( ) 3.设n 维向量组r ααα,,,21Λ中每一个向量均可由s βββ,,,21Λ线性表示,且s r >,则r ααα,,,21Λ必线性相关.( )4.设n ααα,,,21Λ为n 个m 维向量,且m n >,则该向量组必定线性相关.( ) 5.设321,,ααα是线性无关向量组,则向量组32121105,3,2ααααα+-也线性无关.( )6.设向量组r ααα,,,21Λ与s βββ,,,21Λ等价,则r ααα,,,21Λ的任一极大无关组与s βββ,,,21Λ的任一极大无关组可互相线性表示.( )第三章 向量组的线性相关性一、填空题1、-82、线性相关3、线性无关4、线性无关5、16、23-和4 二、选择题1、D2、C3、C4、C5、A三、判断题1、×2、√3、√4、√5、√6、√第四章 线性方程组一、填空题1.n 元齐次线性方程组0=Ax 的系数矩阵A 的秩为r ,则0=Ax 仅有零解的充分必要条件是 .2.n 元非齐次线性方程组Ax b =,其增广矩阵记为A% 则方程组有唯一解的充要条件为 . 3.n 元非齐次线性方程组Ax b =,其增广矩阵记为A% 则方程组有无穷多解的充要条件为 . 4.若方程组⎪⎩⎪⎨⎧=++=++=++23213213211k kx x x k x kx x x x kx 无解,则=k .5.设方程组⎪⎩⎪⎨⎧-=+-=++-=++4224321321321kx x x x kx x kx x x 有唯一解,则≠k .6.齐次线性方程组()⎪⎩⎪⎨⎧=-+=+++=++02023202321321321x ax x x a x x x x x 只有零解,则≠a .7.齐次线性方程组⎪⎩⎪⎨⎧=+-=+-=+-020743032321321321ax x x x x x x x x 有非零解,则=a .二、选择题1.设A 为n m ⨯矩阵,则齐次线性方程组0=Ax 仅有零解的充分必要条件是系数矩阵A 的秩为r ( ). (A) m r < (B) n r < (C) m r = (D) n r =2.设n 元齐次线性方程组0=Ax ,若n r A R <=)(,则该方程组的基础解系( ).(A )唯一存在 (B )共有r n -个 (C )含有r n -个解向量 (D )含有无穷多个解向量3.已知321,,ααα是线性方程组0=Ax 的一个基础解系,则必有( ). (A )321,,ααα线性相关 (B )321,,ααα线性无关(C )133221,,αααααα+++线性相关 (D )133221,,αααααα+++不是0=Ax 基础解系 4.方程组⎩⎨⎧=+--=-++032054354325431x x x x x x x x 的一组基础解系是由( )个解向量组成的.(A )2 (B )1 (C )3 (D )05. n 元非齐次线性方程组Ax b =,其增广矩阵记为A % 则方程组无解的充要条件为( ). (A )()(A)r Ar >% (B )()(A)r A r =% (C )()(A)r A r <% (D )()(A)r A r ≠% 6.设s ααα,,,21Λ是n 元齐次线性方程组0=Ax 的基础解系,则( ). (A )s ααα,,,21Λ线性相关 (B )0=Ax 的任意1+s 个解向量线性相关 (C )n A R s =-)( (D )0=Ax 的任意1-s 个解向量线性相关 7.若321,,ααα是齐次线性方程组0=Ax 的一个基础解系,则( ).(A )133221,,αααααα+++也是0=Ax 的一个基础解系 (B )基础解系具有唯一性 (C )133221,,αααααα+++不一定是0=Ax 的基础解系 (D )以上说法都不对 8.设A 为n m ⨯矩阵,非齐次线性方程组b Ax =的导出组为0=Ax ,若n m <,则( ). (A )b Ax =必有无穷多解 (B )b Ax =必有唯一解 (C )0=Ax 必有非零解 (D )0=Ax 必有唯一解三、判断题1.设21,ξξ为齐次线性方程组0=Ax 的解,1η为非齐次线性方程组b Ax =的解,则22111ξξηk k ++为b Ax =的通解(21,k k 为任意实数).( )2.设21,ξξ为齐次线性方程组0=Ax 的解,21,ηη为非齐次线性方程组b Ax =的解,则()()2121ηηξξ-++为0=Ax 的解.( ) 3.含有n 个方程的n 元齐次线性方程组0=Ax ,仅有零解的充要条件是0A =.( ) 4.含有n 个方程的n 元齐次线性方程组0=Ax ,有非零解的充要条件是0A ≠.( )5.若方程组⎪⎩⎪⎨⎧=++=++=++000321321321kx x x x kx x x x kx 有非零解,则k 应满足的条件是0=k 或1=k .( )6.若方程组⎪⎩⎪⎨⎧=+=++=++03 02032321321x kx x x x x kx x 只有零解,则k 应满足的条件是53=k .( )第四章 线性方程组一、填空题1、r n =2、(A)r(A)n r ==% 3、(A)r(A)n r =<% 4、2- 5、1-和2- 6、1-和3 二、选择题1、D2、C3、B4、C5、D6、B7、A8、C三、判断题1、√2、√3、×4、×5、×6、×第五章 矩阵的特征值一、填空题1.设()()TT0,1,2,1,0,121==αα,则内积[]=21,αα .2.设()Tk 2,1,2=α为单位向量,则=k .3.设321,,ξξξ是矩阵A 的属于不同特征根321,,λλλ的特征向量,则321,,ξξξ是线性 . 4.设A 的特征值为1,2-,3,则A 2的特征值为 .5.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=014020112A ,则A 的特征值为 . 6.若0λ为A 的一个特征值,则矩阵多项式()A f 有一个特征值为 . 7.已知三阶矩阵A 的三个特征值为1, -1,2,则()2E A -的特征值为 .8.设0≠λ为方阵A 的一个特征值,则()13-A 有一个特征值为 .9.设A 为n 阶方阵,方程组0=Ax 有非零解,则A 必有一个特征值为 . 10.n 阶矩阵A 可对角化的充分必要条件是A 有 个线性无关的特征向量.11.0是矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=a A 01020101的特征值,则=a .二、选择题1.下列结论中不正确的是( ).(A )若n 维向量α与β正交,则对任意实数l k ,,αk 与βl 也正交; (B )若n 维向量β与21,αα都正交,则β与21,αα的任意线性组合也正交; (C )若n 维向量α与β正交,则βα,中至少有一个是零向量; (D )若n 维向量α与任意n 维向量都正交,则α是零向量. 2.设A 是正交矩阵,则下列结论不正确的是( ).(A )1-A 是正交矩阵 (B )T A 是正交矩阵 (C )1±=A (m 是正整数) (D )kA (1≠k )是正交矩阵 3.下列说法正确的是( ).(A )因为特征向量都是非零向量,所以它对应的特征值非零; (B )一个特征值可对应多个特征向量; (C )一个特征向量可以属于多个特征值; (D )n 阶矩阵有n 个不同的特征值.4.设n 阶可逆矩阵A 有一特征值为λ,则A *的特征值之一是( ). (A )nA 1-λ (B )A 1-λ(C )A λ (D )nA λ5.设n 阶可逆矩阵A 有一特征值为λ,则1*--A A 的特征值之一是( ).(A )11---λλA (B )11--+λλA (C )λλ+-A 1 (D )λλ--A 16.n 阶方阵A 有n 个不同的特征值是A 与对角阵相似的( ).(A )充分而非必要条件 (B )充要条件 (C )必要而非充分条件 (D )无关的条件7.设n λλλ,,,21Λ是n 阶对称矩阵A 的特征值,{}n diag λλλ,,,21Λ=Λ,则( )不成立. (A )A 与()()Λ=r A r (B )kA 与kΛ相似 (C )Λ=A (D )Λ≠A8.下列矩阵中与矩阵⎥⎦⎤⎢⎣⎡=Λ2011相似的是( ). (A )⎥⎦⎤⎢⎣⎡--2001 (B )⎥⎦⎤⎢⎣⎡2211 (C )⎥⎦⎤⎢⎣⎡2001 (D )⎥⎦⎤⎢⎣⎡10119.矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=Λ10000002,210100002y B ,若B A ,相似,则=y ( ). (A) 1 (B) 2 (C) 1- (D) 2-10.对于实矩阵A ,以下结论正确的是( ).(A )一定有n 个不同的特征值 (B )存在可逆矩阵B ,使AB B 1-为对角矩阵(C )它的特征值一定是实数 (D )属于不同特征值的特征向量一定线性无关三、判断题1.线性无关向量组一定可以化为等价的正交向量组.( )2.正交向量组必线性无关.( )3.若n 阶方阵A 与B 相似,则A 与B 必有相同的特征值和特征向量.( )4.设21,ξξ分别是实对称方阵A 对应于两个不同特征值21,λλ的特征向量,则内积[]0,21=ξξ.( )5.n 阶矩阵A 可逆的充要条件是A 的任一特征值不等于0.( )6.n 阶矩阵A 可与对角阵相似的充分必要条件是A 有n 个相异的特征值.( )7.n 阶矩阵A 可与对角阵相似的充分必要条件是A 有n 个线性无关的特征向量.( )8.n 阶方矩阵A 一定可与对角阵相似.( )9.特征多项式相同的矩阵一定相似.( ).第五章 矩阵对角化一、填空题1、22、31± 3、无关 4、2,4-,6 5、1-,2,2 6、)(0λf 7、0,1,4 6,11 8、131-λ 9、0 10.n 11. 1二、选择题1、C2、D3、B4、B5、A6、A7、D8、C9、A三、判断题1、√2、√3、×4、√5、√6、×7、√8、√9、×期考大题题型及分值计算题(一)(本大题共2小题,每小题4分,共8分.请写出计算过程、步骤.) 1.计算行列式201325143.2.121110212,231123341A B ⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭计算23A B +计算题(二)(本大题共5小题,每题8分,共40分.请写出计算过程、步骤.)1.计算行列式0111101111011110.2.求111011101A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦的逆矩阵.3.求向量组()()()()12341,0,3,1,1,3,0,1,2,1,7,2,4,2,14,4T T T Tαααα==--==的秩与它的一个极大无关组,并将其余向量用此极大无关组线性表示.4.解方程组:1231231234441624x x x x x x x x x ++=⎧⎪-++=⎨⎪-+=-⎩5.求⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111020011A 的特征值证明题(6分)设321,,ααα线性无关,3211αααβ--=,3212αααβ-+-=,3213αααβ+--=,证明:321,,βββ线性无关.。
2018-2019学年线性代数试题及答案.ppt

线性无关。
3、设4阶方阵A满足条件 3E 2A 0, AAT 2E, A 0 求A的伴随矩阵 A 的一个特征值。
五、解矩阵方程(满分7分)
2 设矩阵 A 3
2 6
1 3
三、计算行列式(每小题5分,共10 分)
410 5 1、 D 3 1 1 2
2 0 6 4 2 5 3 2
218
1 a1 1
2、Dn 1 1
1 1 a2
1 1
1 1 1 a3 1
其中 ai 0 (i 1,2, , n)
1
1
1
n1 n (1 i1 ai ) i1 ai
一、填空题(每小题2分,共14分)
1、设A是3阶矩阵,且 A ,1A 是A的伴随矩阵,则:
2
(3A)1 2A
16 27
2、设四元非齐次线性方程组 Ax b 的系数矩阵A的秩为3,且
1 (1,2,3,4)T ,2 (2,3,4,5)T 是该方程组的两个解,则
方程组 Ax b 的通解为: (1,2,3,4)T k(1,1,1,1)T , k R
则 A B 32
2 0 0
2 0 0
6、已知矩阵 A 0 0 1 与 B 0 y 0 相似,
0 1 x
0 0 1
则x 0
y 1
7、已知实二次型
f (x1, x2 , x3 ) a(x12 x22 x32 ) 4x1x2 4x1x3 4x2 x3
0
可知
3 2
是A的一个特征值。
201819线性代数II1B试题答案

1,2 ,3 必须线性无关,该向量组的最大线性无关组是1,2 ,3 . 3. A 的特征值为 2, 0.5, 2 ,三阶矩阵 3E 2 A 特征值为 1, 2,7 ,| 3E 2A | 14 0 ,矩
阵 3E 2A 可逆
4.不一定正确。阶数相等就正确,阶数不相等就不正确
若 A, B 都是 n 可逆矩阵,则 A ~ E, B ~ E , A ~ B, 存在可逆矩阵 P,Q ,使得 PAQ B
4 1 3
4 1 3
5 2 1
5 2 1
M31 1 0 1 8, M41 1 0 1 6
4 1 3
3 13
M11 M21 M31 M41 6 解法 2 M11 M21 M31 M41 A11 A21 A31 A41
1
1 5 2 1 1 5 2 1
1 1
0
1 1
1
1 21 0 1 1 0 1 6
;2.
B ;3.3 ;4.
6 ;5.
1.5
k1
3
k2
1
0.5 2 2
;6.
1 2
y22
4 y32
.
解 1. | ,1,2 ,3 | a,| ,1,2 ,3 | b,
| 2 ,1,2 ,3 | 2 | ,1,2 ,3 | 2(| ,1,2 ,3 | | ,1,2 ,3 |) 2(b a)
1 3 1 3 1 3 13
1
5.
4 1 3 0 (课本 128 页 6 题) n
1 0 0 3 , R( A)
11 1 , Ax
3 0 的基础解系中只有两个解向量.因为
1
3 = (1
2 )
(2
3 )
=
线性代数习题库及答案

线性代数习题库一、选择题(每题约3分)1.的值为则的秩若矩阵a A r a a A ,2)(2101210211=⎪⎪⎪⎭⎫ ⎝⎛---=( )11-(D)1-(C)1-0(B)0(A)或者或2.=-=*,1||A A A 则,且为正交矩阵设( ) A -(D)•••••••••••••A•••••••••(C)A -(B)••••••••••••••••••••A (A)T T3.设βα,是n 维列向量,0≠βαT,n 阶方阵T E A αβ+=,3≥n ,则在A 的n 个特征值中,必然( )(A) 有n 个特征值等于1 (B) 有1-n 个特征值等于1 (C) 有1个特征值等于1 (D) 没有1个特征值等于14.则阶方阵,且秩相等,既为设,)()(,B r A r n B A =( )B)(A)(B),r(A (D)r(A)2B),r(A (C)r(A)2B)(A (B)0B)r(A (A)r r r +≤==+=- 5.b Ax n A r A n m ==⨯则非齐次线性方程组的秩设矩阵,)(( ) )(A 一定无解 )(B 可能有解 )(C 一定有唯一解 )(D 一定有无穷多解6、设n 阶行列式D =n ija ,ji A 是D 中元素ji a 的代数余子式,则下列各式中正确的是( )(A)1=∑=ni ij ijA a;(B)1=∑=nj ij ijA a;(C)DA anj ij ij=∑=1;(D)DA ani i i =∑=1217. n 阶实对称矩阵A 和B 相似的充分必要条件是( )(A) A 与B 都有n 个线性无关的特征向量; (B) )()(B r A r =;(C) A 和B 的主对角线上的元素的和相等;(D) A 与B 的n 个特征值都相等 8. 设1α,2α,3α,4α是齐次线性方程组0=Ax 的一个基础解系,则下列向量组中不再是0=Ax 的基础解系的为( ) (A) 1α,1α+2α,1α+2α+3α,1α+2α+3α+4α;(B) 1α+2α,2α+3α,3α+4α,4α-1α; (C) 1α+2α,2α-3α,3α+4α,4α+1α; (D) 1α+2α,2α+3α,3α+4α,4α+1α9. 设方程组⎪⎩⎪⎨⎧=++=--=++222513321321321x x x b x x x x x x 有无穷多组解,则必有( )(A) b =1 (B) b =-1 (C) b =2 (D) b =-2 10. 设向量组[Ⅰ]是向量组[Ⅱ]的线性无关的部分向量组,则( )(A) 向量组[Ⅰ]是[Ⅱ]的极大线性无关组 (B) 向量组[Ⅰ]与[Ⅱ]的秩相等(C) 当[Ⅰ]中向量均可由[Ⅱ]线性表出时,向量组[Ⅰ],[Ⅱ]等价 (D) 当[Ⅱ]中向量均可由[Ⅰ]线性表出时,向量组[Ⅰ],[Ⅱ]等价 11.设矩阵ji j i j i j i b a b B a A 2)(,)(4444-===⨯⨯且,,则行列式=||B ( )(A) ||24A -; (B) ||24A ; (C) ||24A --; (D)||24A - 12.设三阶矩阵⎪⎪⎪⎭⎫⎝⎛=a b b b a b b b a A ,已知伴随矩阵*A 的秩为1,则必有( ) (A) 02≠+≠b a b a 且; (B) 02=+≠b a b a 且; (C) 02≠+b a b a 或=; (D) 02=+=b a b a 或13.设α是n 维非零实列向量,矩阵TE A αα+=,3≥n ,则( )(A) A 至少有n -1个特征值为1; (B) A 恰有1-n 个特征值为1; (C) A 只有1个特征值为1; (D) A 没有1个特征值为114.则,且,阶方阵为设)()(,B r A r n B A =( )(A) 0)(=-B A r ; (B) )(2)(A r B A r =+;(C) )(2)(A r B A r =,; (D) )()()(B r A r B A r +≤, 15.已知解向量组4321,,,αααα是齐次线性方程组0=Ax 的基础解系,以下解向量组中,也是0=Ax 的基础解系的是( ))(A 14433221αααααααα+,+,+,+; )(B 14433221αααααααα-,-,-,-; )(C 14433221αααααααα-,+,+,+;)(D 14433221αααααααα-,-,+,+16、向量组321,,ααα线性无关的充要条件为( ) A 、321,,ααα均不是零向量B 、321,,ααα中任意两个向量的分量不成比例 C 、321,,ααα中任意一个向量均不能由其余两个向量线性表出D 、321,,ααα中一部分向量线性无关17、设A 为n 阶矩阵|A|=0,则( )A 、 A 中有两行(列)的元素对应成比例B 、 A 中任意一行(列)向量是其余各行(列)的线性组合C 、 A 中至少有一行元素全为0D 、 A 中必有一行(列)向量是其余各行(列)的线性组合 18、若321,,ααα21,ββ都为四维向量且四阶行列式m =1321,,,βααα,n =2321,,,βααα,则四阶行列式=+)(,,,21321ββααα( )A 、n m -B 、)(n m +-C 、n m +D 、m n - 19、设A 为n 阶方矩阵,且|A|=a ≠0,而A *为A 的伴随矩阵,则|A *|=( )A 、aB 、1-n aC 、a 1D 、na20、A 为m ×n 矩阵,C 为n 阶可逆矩阵,r(A)=r,矩阵B=AC 的秩为r 1,则( ) A 、1r r > B 、2r r < C 、r 与r 1关系依赖与矩阵C D 、1r r =21、已知3阶矩阵A 的特征值为1、-1、2,则矩阵3A 2+2I 的特征值为( ) A 、1、-1、2 B 、5、1、14 C 、1、1、2 D 、1、1、12 22、设Q P ,均为n 阶初等阵,下列结论错误的是( )。
2019考研线性代数基础讲义(含答案)

2019考研线性代数基础讲义参考答案目录第一章行列式 (1)考试内容 (1)考试要求 (1)§1.行列式的定义 (1)§2.行列式的性质 (2)§3.行列式的展开式定理 (3)§4、常见行列式计算 (6)第二章矩阵 (8)考试内容 (8)考试要求 (8)§1.矩阵及其运算 (8)§2.逆矩阵 (12)§3.初等变换与初等矩阵 (15)§4.矩阵的秩 (17)§5.分块矩阵 (19)第三章向量 (23)考试内容 (23)考试要求 (23)§1.n维向量的概念及其运算 (23)§2.向量组的线性相关性 (24)§3.向量组的秩和极大无关组 (27)§4.向量的内积与施密特正交化 (30)第四章线性方程组 (32)考试内容 (32)考试要求 (32)§1.线性方程组有解的判定 (32)§2.向量组的线性相关性与方程组的关系 (39)第五章矩阵的特征值与特征向量 (42)考试内容 (42)考试要求 (42)§1.特征值与特征向量 (42)§2.矩阵的相似对角化 (45)§3.实对称矩阵的相似对角化 (48)第六章二次型 (51)考试内容 (51)考试要求 (51)§1.二次型的概念 (51)§2.二次型的标准型与规范型 (53)§3.正定二次型 (57)附录向量空间(数一) (58)。
线性代数试题及答案解析

线性代数试题及答案解析一、选择题(每题4分,共40分)1. 矩阵A和矩阵B相乘,得到的结果矩阵的行列数为()。
A. A的行数乘以B的列数B. A的行数乘以B的行数C. A的列数乘以B的列数D. A的列数乘以B的行数答案:D解析:矩阵乘法中,结果矩阵的行数等于第一个矩阵的行数,列数等于第二个矩阵的列数。
2. 向量α和向量β线性相关,则下列说法正确的是()。
A. α和β可以是零向量B. α和β可以是任意向量C. α和β中至少有一个是零向量D. α和β中至少有一个是另一个的倍数答案:D解析:线性相关意味着存在不全为零的系数,使得这些系数乘以对应的向量和为零向量,因此至少有一个向量是另一个向量的倍数。
3. 对于n阶方阵A,下列说法不正确的是()。
A. A的行列式可以是0B. A的行列式可以是负数C. A的行列式可以是正数D. A的行列式一定是正数答案:D解析:方阵的行列式可以是正数、负数或0,因此选项D不正确。
4. 矩阵A和矩阵B相等,当且仅当()。
A. A和B的对应元素相等B. A和B的行数相等C. A和B的列数相等D. A和B的行数和列数都相等答案:A解析:两个矩阵相等,必须满足它们具有相同的行数和列数,并且对应元素相等。
5. 向量组α1,α2,…,αn线性无关的充分必要条件是()。
A. 由这些向量构成的矩阵的行列式不为0B. 这些向量不能构成齐次方程组的非零解C. 这些向量不能构成齐次方程组的非平凡解D. 这些向量可以构成齐次方程组的平凡解答案:C解析:向量组线性无关意味着它们不能构成齐次方程组的非平凡解,即唯一的解是零向量。
6. 矩阵A可逆的充分必要条件是()。
A. A的行列式不为0B. A的行列式为1C. A的行列式为-1D. A的行列式为任何非零数答案:A解析:矩阵可逆当且仅当其行列式不为0。
7. 矩阵A的特征值是()。
A. 矩阵A的行数B. 矩阵A的列数C. 矩阵A的对角线元素D. 满足|A-λI|=0的λ值答案:D解析:矩阵的特征值是满足特征方程|A-λI|=0的λ值。
4月全国线性代数自考试题及答案解析

全国2019年4月高等教育自学考试线性代数试题课题代码:02198试卷说明:A T 表示矩阵A 的转置矩阵,A *表示矩阵A 的伴随矩阵,E 是单位矩阵,|A |表示方阵A 的行列式。
第一部分 选择题 (共20分)一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.对任意n 阶方阵A 、B 总有( )A.AB =BAB.|AB |=|BA |C.(AB )T =A T B TD.(AB )2=A 2B 22.在下列矩阵中,可逆的是( )A.⎪⎪⎪⎭⎫ ⎝⎛100010000B.⎪⎪⎪⎭⎫ ⎝⎛100022011C.⎪⎪⎪⎭⎫ ⎝⎛121110011D.⎪⎪⎪⎭⎫ ⎝⎛101111001 3.设A 是3阶方阵,且|A |=-2,则|A -1|等于( )A.-2B.21-C.21 D.2 4.设A 是n m ⨯矩阵,则齐次线性方程组Ax =0仅有零解的充分必要条件是( )A.A 的行向量组线性无关B.A 的行向量组线性相关C.A 的列向量组线性无关D.A 的列向量组线性无关5.设有m 维向量组(I):n 21,,,ααα⋅⋅⋅,则( )A.当m <n 时,(I)一定线性相关B.当m>n 时,(I)一定线性相关C.当m <n 时,(I)一定线性无关D.当m >n 时,(I)一定线性相关6.已知1β、2β是非齐次线性方程组Ax =b 的两个不同的解,1α、2α是其导出组Ax =0的一个基础解系,k 1、k 2为任意常数,则方程组Ax=b 的通解可表成( ) A.2)(2121211ββββα-+++k k B.2)(2121211ββββα++++k k C.2212211ββαα-++k kD.2212211ββαα+++k k 7.设n 阶可逆矩阵A 有一个特征值为2,对应的特征向量为x ,则下列等式中不正确...的是( )A.Ax =2xB.A -1x =21x C.A -1x =2x D. A 2x =4x 8.设矩阵A =⎪⎪⎪⎭⎫ ⎝⎛+λ132121111的秩为2,则λ=( )A.2B.1C.0D.-19.二次型322123222132110643),,(x x x x x x x x x x f ++-+=的矩阵是( ) A.⎪⎪⎪⎭⎫ ⎝⎛-405033531B.⎪⎪⎪⎭⎫ ⎝⎛-4001030061C.⎪⎪⎪⎭⎫ ⎝⎛-450533031D.⎪⎪⎪⎭⎫ ⎝⎛-41001036061 10.二次型2323223213212)()(),,(x x x x x x x x x f +++--=是( )A.正定的B.半正定的C.负定的D.不定的第二部分 非选择题 (共80分)二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案。
线性代数考试题及答案

线性代数考试题及答案**线性代数考试题及答案**一、单项选择题(每题3分,共30分)1. 矩阵A的行列式为0,则矩阵A()A. 可逆B. 不可逆C. 可交换D. 不可交换答案:B2. 若矩阵A和B均为n阶方阵,且AB=0,则()A. A=0或B=0B. A和B至少有一个为0C. A和B都为0D. A和B可能都不为0答案:D3. 向量组α1,α2,…,αs线性无关,则()A. s ≤ nB. s > nC. s ≥ nD. s < n答案:A4. 矩阵A的特征值是()A. 矩阵A的行最简形式B. 矩阵A的列最简形式C. 矩阵A的对角线元素D. 满足|A-λE|=0的λ值答案:D5. 矩阵A和B相等的充要条件是()A. A和B的对应元素相等B. A和B的行向量组相同C. A和B的列向量组相同D. A和B的秩相等答案:A6. 若矩阵A可逆,则下列说法正确的是()A. |A|≠0B. A的秩为nC. A的行列式为1D. A的转置矩阵可逆答案:AA. r(A+B) = r(A) + r(B)B. r(AB) ≤ min{r(A), r(B)}C. r(A) = r(A^T)D. r(A) = r(A^-1)答案:C8. 向量组α1,α2,…,αn线性相关,则()A. 存在不全为0的k个向量,使得k个向量线性组合等于0B. 存在不全为0的n个向量,使得n个向量线性组合等于0C. 存在不全为0的n+1个向量,使得n+1个向量线性组合等于0D. 存在不全为0的m个向量,使得m个向量线性组合等于0,其中1≤m≤n答案:DA. r(A+B) = r(A) + r(B)B. r(AB) ≤ min{r(A), r(B)}C. r(A) = r(A^T)D. r(A) = r(A^-1)答案:B10. 若矩阵A和B均为n阶方阵,且AB=0,则()A. A=0或B=0B. A和B至少有一个为0C. A和B都为0D. A和B可能都不为0答案:D二、填空题(每题4分,共20分)1. 若矩阵A的行列式|A|=2,则矩阵A的伴随矩阵的行列式|adj(A)|= _ 。
线性代数练习题及答案10套

1 0 1 14.设矩阵 A= 0 2 0 ,矩阵 B A E ,则矩阵 B 的秩 r(B)= __2__. 0 0 1 0 0 1 B A E = 0 1 0 ,r(B)=2. 0 0 0
15.向量空间 V={x=(x1,x2,0)|x1,x2 为实数}的维数为__2__. 16.设向量 (1,2,3) , (3,2,1) ,则向量 , 的内积 ( , ) =__10__. 17.设 A 是 4×3 矩阵,若齐次线性方程组 Ax=0 只有零解,则矩阵 A 的秩 r(A)= __3__. 18 . 已 知 某 个 3 元 非 齐 次 线 性 方 程 组 Ax=b 的 增 广 矩 阵 A 经 初 等 行 变 换 化 为 :
三、计算题(本大题共 6 小题,每小题 9 分,共 54 分)
Ibugua
交大打造不挂女神的领跑者
123 23 3 21.计算 3 阶行列式 249 49 9 . 367 67 7 123 23 3 100 20 3 解: 249 49 9 200 40 9 0 . 367 67 7 300 60 7
线代练习题及答案(一)
一、单项选择题(本大题共 10 小题,每小题 2 分,共 20 分)
1.设 A 为 3 阶方阵,且 | A | 2 ,则 | 2 A 1 | ( D A.-4 B.-1 C. 1 ) D.4
| 2 A 1 | 2 3 | A | 1 8
1 4. 2
)
1 2 3 1 2 2. 设矩阵 A= (1, 2) , B= C= 则下列矩阵运算中有意义的是 ( B 4 5 6 , 3 4 ,
行成比例值为零.
a1b2 a 2 b2 a 3 b2
全国高等教育自学考试线性代数(经管类)(04184)2019年4月历年真题及答案

2019年4月高等教育自学考试全国统一命题考试线性代数(经管类) 试卷(课程代码04184)注意事项:1.本试卷分为两部分,第一部分为选择题,第二部分为非选择题2.应考者必须按试题顺序在答题卡(纸)指定位置上作答,答在试卷上无效3.涂写部分,画图部分必须使用2B铅笔,书写部分必须使用黑色字迹签字表说明:在本卷中,表示矩阵么的转置矩阵,A*表示矩阵A的伴随矩阵,E是单位矩阵,|A|表示方阵A的行列式,r(A)表示矩阵A的秩。
第一部分选择题一、单项选择题:本大题共5小题,每小题2分,共10分。
在每小题列出的备选项中只有一个是符合题目要求的,请将其选出。
1.行列式,则A.-2B.-1C.1D.22.设A为2阶矩阵,将A的第1行与第2行互换得到矩阵B,再将B的第2行加到第1行得到矩阵C,则满足PA=C 的可逆矩阵P=3.设向量可由向量组线性表出,则数a,b满足关系式A.a-b=4B.a-b=0C.a+b=4D. a+b=04.设齐次线性方程组有非零解,则数k=A.-2B.-1C.1D.25.设3阶实对称矩阵A的秩为2,则A的特征值λ=0的重数为A.0B.1C.2D.3第二部分非选择题二、填空题:本大题共10小题,每小题2分,共20分。
6.设某3阶行列式第2行元素分别为1,-2,3,对应的余子式为3,2,-2,则该行列式的值为7.已知行列式8.9.设n阶矩阵A满足10.设向量组的秩为2,则数a=11.与向量正交的单位向量12.设4元非齐次线性方程组Ax=b的增广矩阵经初等行变换化为若该线性方程组有惟一解,,则数a的取值应满足13.设A为n阶矩阵,若非齐次线性方程组Ax=b有无穷多解,则14.设A为n阶矩阵,且满足则A必有一个特征值为15.二次型的矩阵A=三、计算题:本大题共7小题,每小题9分,共63分16.计算4阶行列式17.设向量18.设矩阵A,B满足关系式X=XA+B,其中,求矩阵X19.求矩阵的秩和列向量组的一个极大无关组,并将其余列向量由该极大无关组线性表出20.设线性方程组确定数a,b为何值时,方程组有无穷多解,并求出其通解(要求用其一个特解和导出组的基础解系表示)21.设矩阵判定A是否可对角化,若可以,求可逆矩阵P和对角矩阵A,22.求正交换x=Qy,将二次型化为标准形四、证明题:本题7分23.已知向量β可由向量组线性表出,证明:如果表示法惟一,则线性无关24.25.。
2019-2020学年线性代数期末考试题(含答案)

线性代数2019-2020学年第二学期期末考试试卷一、填空题(本大题共5个小题,每小题3分,共15分。
)1. 行列式11111111---x 的展开式中x 的系数是_________;2. 已知3阶矩阵A 的特征值为0,1,2,则=+-E A A 752__________;3. 向量组)0,0,1(),1,1,1(),1,1,0(),1,0,0(4321====αααα的秩为______;4. 设⎪⎪⎪⎭⎫ ⎝⎛-=12032211t A ,若3阶非零方阵B 满足0=AB ,则=t ;5. 设3阶可逆方阵A 有特征值2,则方阵12)(-A 有一个特征值为_________。
二、单项选择题(从下列各题四个备选答案中选出一个正确答案,并将其代号写在答题纸相应位置处。
答案错选或未选者,该题不得分。
每小题3分,共15分。
) 1. A 是n 阶方阵,*A 是其伴随矩阵,则下列结论错误的是【 】A .若A 是可逆矩阵,则*A 也是可逆矩阵;B .若A 不是可逆矩阵,则*A 也不是可逆矩阵;C .若0||*≠A ,则A 是可逆矩阵;D .AE AA =||*。
2. 设⎪⎪⎪⎭⎫ ⎝⎛=333222111c b a c b a c b a A ,若⎪⎪⎪⎭⎫ ⎝⎛=333222111b c a b c a b c a AP ,则P =【 】 A . ⎪⎪⎪⎭⎫ ⎝⎛010100001; B . ⎪⎪⎪⎭⎫ ⎝⎛010001100;C . ⎪⎪⎪⎭⎫ ⎝⎛001010100;D . ⎪⎪⎪⎭⎫ ⎝⎛010100000.3. n m >是n 维向量组m ααα,,,21 线性相关的【 】.A 充分条件 .B 必要条件.C 充分必要条件 .D 必要而不充分条件4.设321,,ααα是0=Ax 的基础解系,则该方程组的基础解系还可以表示为【 】A .321,,ααα的一个等价向量组;B. 321,,ααα的一个等秩向量组;C. 321221,,αααααα+++;D . 133221,,αααααα---.5. s ααα,,,21 是齐次线性方程组0=AX (A 为n m ⨯矩阵)的基础解系,则=)(A R 【 】A .sB .s n -C .s m -D .s n m -+三、计算题(要求在答题纸相应位置上写出详细计算步骤及结果。
(完整版)线性代数习题集带答案

第一部分 专项同步练习第一章 行列式一、单项选择题1.下列排列是5阶偶排列的是 ( ).(A) 24315 (B) 14325 (C) 41523 (D)243512.如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是( ). (A)k (B)k n - (C)k n -2! (D)k n n --2)1(3. n 阶行列式的展开式中含1211a a 的项共有( )项.(A) 0 (B)2-n (C) )!2(-n (D) )!1(-n4.=0001001001001000( ).(A) 0 (B)1- (C) 1 (D) 25.=0001100000100100( ).(A) 0 (B)1- (C) 1 (D) 26.在函数1323211112)(x x xxx f ----=中3x 项的系数是( ).(A) 0 (B)1- (C) 1 (D) 27. 若21333231232221131211==a a a a a a a a a D ,则=---=323133312221232112111311122222 2a a a a a a a a a a a a D ( ). (A) 4 (B) 4- (C) 2 (D) 2- 8.若a a a a a =22211211,则=21112212ka a ka a ( ).(A)ka (B)ka - (C)a k 2 (D)a k 2-9. 已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为x ,1,5,2-, 则=x ( ).(A) 0 (B)3- (C) 3 (D) 210. 若5734111113263478----=D ,则D 中第一行元的代数余子式的和为( ). (A)1- (B)2- (C)3- (D)011. 若2235001011110403--=D ,则D 中第四行元的余子式的和为( ). (A)1- (B)2- (C)3- (D)012. k 等于下列选项中哪个值时,齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x kx x kx x kx x x 有非零解.( )(A)1- (B)2- (C)3- (D)0二、填空题1. n 2阶排列)12(13)2(24-n n 的逆序数是.2.在六阶行列式中项261365415432a a a a a a 所带的符号是.3.四阶行列式中包含4322a a 且带正号的项是.4.若一个n 阶行列式中至少有12+-n n 个元素等于0, 则这个行列式的值等于.5. 行列式=100111010100111.6.行列式=-000100002000010n n .7.行列式=--001)1(2211)1(111n n n n a a a a a a .8.如果M a a a a a a a a a D ==333231232221131211,则=---=323233312222232112121311133333 3a a a a a a a a a a a a D .9.已知某5阶行列式的值为5,将其第一行与第5行交换并转置,再用2乘所有元素,则所得的新行列式的值为.10.行列式=--+---+---1111111111111111x x x x .11.n 阶行列式=+++λλλ111111111.12.已知三阶行列式中第二列元素依次为1,2,3, 其对应的余子式依次为3,2,1,则该行列式的值为.13.设行列式5678123487654321=D ,j A 4)4,3,2,1(=j 为D 中第四行元的代数余子式,则=+++44434241234A A A A .14.已知db c a cc a b b a b c a cb a D =, D 中第四列元的代数余子式的和为.15.设行列式62211765144334321-==D ,j A 4为)4,3,2,1(4=j a j 的代数余子式,则=+4241A A ,=+4443A A .16.已知行列式nn D001030102112531-=,D 中第一行元的代数余子式的和为.17.齐次线性方程组⎪⎩⎪⎨⎧=+-=+=++0020232121321x x x kx x x x kx 仅有零解的充要条件是.18.若齐次线性方程组⎪⎩⎪⎨⎧=+--=+=++0230520232132321kx x x x x x x x 有非零解,则k =.三、计算题1.cb a db a dc a dc bd c b a d c ba d cb a++++++++33332222; 2.yxyx x y x y y x y x +++;3.解方程0011011101110=x x xx ; 4.111111321321221221221----n n n n a a a a x a a a a x a a a a xa a a a x ;5. na a a a 111111111111210(n j a j ,,1,0,1 =≠); 6. bn b b----)1(1111211111311117. n a b b b a a b b a a a b 321222111111111; 8.xa a a a x a a a a x a a a a x n nn 321212121;9.2212221212121111nn n nnx x x x x x x x x x x x x x x +++; 10. 21000120000021001210001211.aa a a a a aa a D ---------=110001100011000110001.四、证明题1.设1=abcd ,证明:011111111111122222222=++++dddd c c c c b b b b a a a a .2.3332221112333332222211111)1(c b a c b a c b a x c b x a x b a c b x a x b a c b x a xb a -=++++++.3.))()()()()()((111144442222d c b a c d b d b c a d a c a b d c b a d c b adc b a +++------=.4.∏∑≤<≤=----=nj i i jni innn nn nn n nna aa a a a a a a a a a a a a 1121222212222121)(111.5.设c b a ,,两两不等,证明0111333=c b a c ba 的充要条件是0=++cb a .参考答案一.单项选择题A D A C C D ABCD B B 二.填空题1.n ;2.”“-;3.43312214a a a a ;4.0;5.0;6.!)1(1n n --;7.1)1(212)1()1(n n n n n a a a ---; 8.M 3-; 9.160-; 10.4x ; 11.1)(-+n n λλ; 12.2-;13.0; 14.0; 15.9,12-; 16.)11(!1∑=-nk k n ; 17.3,2-≠k ; 18.7=k三.计算题1.))()()()()()((c d b d b c a d a c a b d c b a ------+++-; 2. )(233y x +-; 3. 1,0,2-=x ; 4.∏-=-11)(n k kax5.)111()1(00∑∏==-+-nk k nk k a a ; 6. ))2(()1)(2(b n b b ---+- ;7. ∏=--nk k kna b1)()1(; 8. ∏∑==-+nk k nk k a x a x 11)()(;9. ∑=+nk k x 11; 10. 1+n ;11. )1)(1(42a a a ++-. 四. 证明题 (略)第二章 矩阵一、单项选择题1. A 、B 为n 阶方阵,则下列各式中成立的是( )。
2019年线性代数A(A卷)解答

浙江理工大学2019年学年第二学期《线性代数A 》期末考试试题(A 卷)参考答案与评分标准一.单项选择题(每小题3分,共3⨯8分=24分)1.A 2.D 3.C 4.C 5.B 6.A 7.B 8.C二.填空题(每小题3分,共3⨯7分=21分)1.⎪⎪⎭⎫⎝⎛-808715 2.0=x 3.23=λ 4.2 5.4 6.2-=a 7.6三.计算题(前4题各6分,第5题10分,第6题11分,满分45分)1.解:14,3,21111111*********r r i i x x x xD -==+--+=00001111xxxx x x x -----+ ………3分000000111xxx x--=4x -= ………6分2.解: B X AX =+2,B X E A =+)2(, ……………………1分⎪⎪⎪⎭⎫ ⎝⎛----=+225221************),2(B E A ………………3分⎪⎪⎪⎭⎫ ⎝⎛→205100010010205001. 所以⎪⎪⎪⎭⎫ ⎝⎛=205010205X . ……6分 3.解:由题设知,A 有两个特征值,2,521==λλ ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=21,3221ξξ是分别对应于特征值5,2的特征向量,即22112,5ξA ξξA ξ==, …………2分又215ξξξ+-=, …………3分所以 21215)5(ξA ξA ξξA ξA nnnn+-=+-=⎪⎪⎭⎫⎝⎛⋅+⋅-⋅+⋅-=⋅+-=+12125532552255n n n n nnξξ. …………6分4.解:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----=1110523130110321),,,(4321αααα …………1分⎪⎪⎪⎪⎪⎭⎫⎝⎛→0000000011100321⎪⎪⎪⎪⎪⎭⎫⎝⎛-→0000000011102101 …………4分由此可见2),,,(4321=ααααR ,21,αα就是一个所求的极大线性无关组,且.2,214213αααααα+-=+= …………6分5.解:对增广矩阵作初等行变换,⎪⎪⎪⎭⎫⎝⎛---+-----=213112111121)(2λλλλb A,⎪⎪⎪⎭⎫⎝⎛-+-+---→32200211012122λλλλλλλr…………4分 (1) 当022≠-+λλ,即1≠λ且2-≠λ时,),(3)(b A A R R ==,有惟一解; (2) 当2-=λ时,3),(,2)(==b A A R R ,方程组无解; …………7分 (3) 当1=λ时,32),()(<==b A A R R ,方程组有无穷多个解,通解为⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛101025321k x x x ,k 为任意常数. …………10分6.解:二次型的矩阵为⎪⎪⎪⎭⎫ ⎝⎛--=a 11122122A , …………2分(1) 因为正交变换UY X =可将f 化为标准形2322212by y y f ++-=,所以矩阵A 的特征值为b ,2,1-, …………4分由,02,0=-=+E A E A 得1=a ,由b tr ++-=21)(A ,得4-=b ; …………6分(2) 当1=a 时,对应特征值1-,解方程组0)(=+X E A ,可得()T 3131311,,-=η,对应特征值2,解方程组0)2(=-X E A ,可得()T 6261612,,=η,对应特征值4-,解方程组0)4(=+X E A ,可得()T0,,21213-=η,…….. 9分因此,所求的正交矩阵为⎪⎪⎪⎪⎭⎫ ⎝⎛--=06231216131216131U . …………….11分四、证明题(每小题5分,满分10分)1.证:设t ξξξ,,,21Λ是方程组0=AX 的基础解系,因为0=AB ,所以B 的每一个列向量都是0=AX 的解,…………….2分因而,B 的列向量组能由t ξξξ,,,21Λ线性表示,因此)()(A B R n t R -=≤,即n R R ≤+)()(B A . …………….5分2.证:设n λλλ,,,21Λ是A 的特征值,因为A 是正定矩阵,所以0>∀i λ,…2分 而t E +A 的特征值为n t t t λλλ+++,,,21Λ,有t t i >+∀λ,因此n n t t t t t >+++=+)())((21λλλΛA E . …………….5分。
2019-2020学年线性代数期末考试题(含答案)

线性代数19-20第一学期期末考试试卷一、填空题(本大题共5个小题,每小题3分,共15分)不写解答过程。
1. 设4阶矩阵234234(,,,),(,,,)A B αγγγβγγγ==,其中234,,,,αβγγγ均为4维列向量,且已知4,1,A B ==则行列式A B +=_________;2. 设01000010,00011000A ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭则1_____A -=; 3. 设(),()ij p p ij p q A a B b ⨯⨯==且(),R B p =如果0,AB =则()____;R A = 4. 设3阶方阵A 的特征值为1,2(二重),I 是3阶单位矩阵,*A 是A 的伴随矩阵, 1A -是A 的可逆矩阵,则矩阵*12A A I -++的特征值为_________; 5. 如果向量组12:,,,t A βββ可由向量组12:,,,s B ααα线性表示,且,t s >则向量组12:,,,t A βββ线性_________。
二、单项选择题(从下列各题四个备选答案中选出一个正确答案,并将其代号写在答题纸相应位置处。
答案错选或未选者,该题不得分。
每小题3分,共15分。
) 1. 设三阶矩阵A 的特征值为1,2,3,I 是3阶单位矩阵,则=--I A 261【 】A . -2B . -1C . 1D . 0 2. 设向量组m ααα,,,21 的秩为r,则【 】A .向量组中任意r-1个向量均线性无关.B .向量组中任意r 个向量均线性无关.C .向量组中任意r+1个向量均线性相关.D .向量组中向量的个数必大于r.3.若齐次方程组0AX =有非零解,则非齐次线性方程组AX B =【 】A .必有无穷多组解B .必有唯一解C .必定没有解D .C B A ,,,都不对 4. 设B A ,均为n 阶方阵,下列命题中正确的是【 】A .00=⇔=A AB 或0B =B .00AB A ≠⇔≠且0B ≠C .00=⇒=A AB 或0B =D .00≠⇒≠A AB 或0B ≠5. 设B A ,都是三阶实对称矩阵,且特征值都是1,1,1,则【 】A .A 与B 的特征多项式相同,但A 与B 不相似 B .A 与B 的特征多项式不一定相同,A 与B 不相似C .A 与B 的特征多项式相同,A 与B 相似D .A 与B 的特征多项式相同,但不能确定A 与B 是否相似 三、计算题(本大题共2小题,每小题5分,共10分)请写出解答过程。
线性代数19-20试题及答案(南京农业大学)
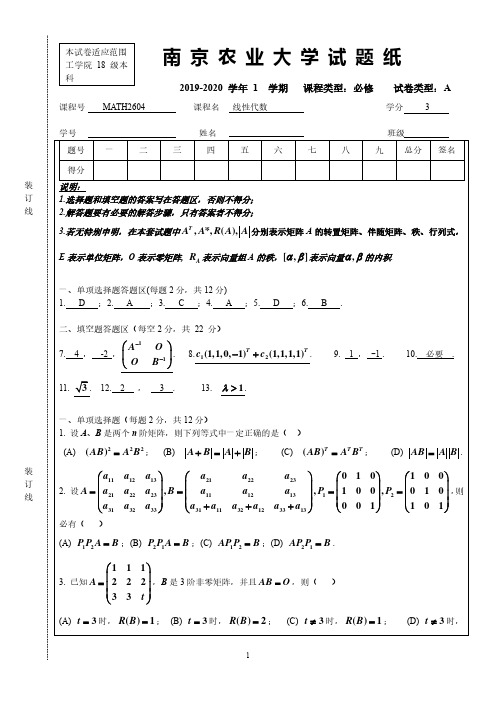
A + A−1
=
n i =1
(i
+
1 i
)
0 ,即
A
+
A−1 是可逆的.(2
分)
教研室主任 毛敏芳
出卷人 唐中良
5
二、填空题答题区(每空 2 分,共 22 分)
7.
4,
-2
,
A−1
O
O
B
−1
.
8. c1(1,1, 0, −1)T + c2 (1,1,1,1)T .
11. 3 . 12. 2 , 3 .
13. 1 .
9. 1 , -1 .
10. 必要 .
一、单项选择题(每题 2 分,共 12 分) 1. 设 A、B 是两个 n 阶矩阵,则下列等式中一定正确的是( )
−1 1 0 1 1
解:原方程等价于 ( A + E )X = B (2 分),
2 −1 1 1 0 1 0 0 0 −1
0 −1
又因为 ( A + E, B) = −2
1
0
0
1
r
→
0
1
0
0
−1 (6 分)所以 X = 0
−1 (2 分)
−1 1 1 1 1 0 0 1 1 1
1 1
2 −1 1 方法二:原方程等价于 ( A + E )X = B (2 分),又因为 A + E = −2 1 0 = −1 0 (2 分)
102
1 0 0 −1
又因为
[1
,
2
,
3
,
]
r
→
0
1
0
−2 ,所以 在基1 ,2 ,3 下的坐标为 (−1, −2, 2)T .(2 分)
《线性代数》习题集(含答案)

《线性代数》习题集(含答案)第一章【1】填空题 (1) 二阶行列式2a ab bb=___________。
(2) 二阶行列式cos sin sin cos αααα-=___________。
(3) 二阶行列式2a bi b aa bi+-=___________。
(4) 三阶行列式xy zzx y yzx =___________。
(5) 三阶行列式a bc c a b c a bbc a+++=___________。
答案:1.ab(a-b);2.1;3.()2a b -;4.3333x y z xyz ++-;5.4abc 。
【2】选择题(1)若行列式12513225x-=0,则x=()。
A -3;B -2;C 2;D 3。
(2)若行列式1111011x x x=,则x=()。
A -1, B 0, C 1, D 2,(3)三阶行列式231503201298523-=()。
A -70;B -63;C 70;D 82。
(4)行列式00000000a ba b b a ba=()。
A 44a b -;B ()222a b-;C 44b a -;D 44a b 。
(5)n 阶行列式0100002000100n n -=()。
A 0;B n !;C (-1)·n !;D ()11!n n +-•。
答案:1.D ;2.C ;3.A ;4.B ;5.D 。
【3】证明33()by az bz ax bx ay x y z bx ay by az bz ax a b zx y bz ax bx ay by azyzx++++++=++++ 答案:提示利用行列式性质将左边行列式“拆项”成八个三阶行列式之和,即得结果。
【4】计算下列9级排列的逆序数,从而确定他们的奇偶性: (1)134782695;(2)217986354;(3)987654321。
答案:(1)τ(134782695)=10,此排列为偶排列。
2019年自考历年线性代数考试试题及答案解析精选

自考历年线性代数考试试题及答案解析精选第一部分选择题(共28分)一、 单项选择题[本大题共14小题,每小题2分,共28分]在每小题列出的四个选项中只有一个是符合题目要求的,请将其代码填在题后的括号内.错选或未选均无分.1、设行列式=m, =n,则行列式等于[] A 、m+n B 、-(m+n) C 、n -m D 、m -n2、设矩阵A=,则A -1等于[]A 、B 、C 、D 、3、设矩阵A=,A *是A 的伴随矩阵,则A *中位于[1,2]的元素是[] A 、–6 B 、6 C 、2 D 、–24、设A 是方阵,如有矩阵关系式AB=AC,则必有[] A 、A=0 B 、BC 时A=0 C 、A0时B=C D 、|A|0时B=C5、已知3×4矩阵A 的行向量组线性无关,则秩[A T ]等于[] A 、1 B 、2 C 、3 D 、46、设两个向量组α1,α2,…,αs 和β1,β2,…,βs 均线性相关,则[]A 、有不全为0的数λ1,λ2,…,λs 使λ1α1+λ2α2+…+λs αs =0和λ1β1+λ2β2+…λs βs =0B 、有不全为0的数λ1,λ2,…,λs 使λ1[α1+β1]+λ2[α2+β2]+…+λs [αs +βs ]=0C 、有不全为0的数λ1,λ2,…,λs 使λ1[α1-β1]+λ2[α2-β2]+…+λs [αs -βs ]=0D 、有不全为0的数λ1,λ2,…,λs 和不全为0的数μ1,μ2,…,μs 使λ1α1+λ2α2+…+λs αs =0和μ1β1+μ2β2+…+μs βs =0 7、设矩阵A 的秩为r,则A 中[]A 、全部r -1阶子式都不为0B 、全部r -1阶子式全为0C 、至少有一个r 阶子式不等于0D 、全部r 阶子式都不为08、设Ax=b 是一非齐次线性方程组,η1,η2是其任意2个解,则下面结论错误的是[]A 、η1+η2是Ax=0的一个解B 、η1+η2是Ax=b 的一个解C 、η1-η2是Ax=0的一个解D 、2η1-η2是Ax=b 的一个解 9、设n 阶方阵A 不可逆,则必有[]A 、秩(A)<nB 、秩(A)=n -1C 、A=0D 、方程组Ax=0只有零解 10、设A 是一个n(≥3)阶方阵,下面陈述中正确的是[]A 、如存在数λ和向量α使A α=λα,则α是A 的属于特点值λ的特点向量B 、如存在数λ和非零向量α,使(λE -A)α=0,则λ是A 的特点值C 、A 的2个不同的特点值能够有同一个特点向量D 、如λ1,λ2,λ3是A 的3个互不相同的特点值,α1,α2,α3依次是A 的属于λ1,λ2,λ3的特点向量,则α1,α2,α3有可能线性相关11、设λ0是矩阵A 的特点方程的3重根,A 的属于λ0的线性无关的特点向量的个数为k,则必有[]A 、k ≤3B 、k<3C 、k=3D 、k>3 12、设A 是正交矩阵,则下面结论错误的是[] A 、|A|2必为1 B 、|A|必为1C 、A -1=A TD 、A 的行[列]向量组是正交单位向量组 13、设A 是实对称矩阵,C 是实可逆矩阵,B=C T AC 、则[] A 、A 和B 相似 B 、A 和B 不等价C 、A 和B 有相同的特点值D 、A 和B 合同14、下面矩阵中是正定矩阵的为[] A 、 B 、 C 、 D 、 第二部分非选择题[共72分]二、填空题[本大题共10小题,每小题2分,共20分]不写解答过程,将正确的答案写在每小题的空格内.错填或不填均无分. 15、 、16、设A=,B=、则A+2B= 、17、设A=(a ij )3×3,|A|=2,A ij 表示|A|中元素a ij 的代数余子式[i,j=1,2,3],则(a 11A 21+a 12A 22+a 13A 23)2+(a 21A 21+a 22A 22+a 23A 23)2+(a 31A 21+a 32A 22+a 33A 23)2= 、18、设向量[2,-3,5]和向量[-4,6,a]线性相关,则a= 、19、设A 是3×4矩阵,其秩为3,若η1,η2为非齐次线性方程组Ax=b 的2个不同的解,则它的通解为 、20、设A 是m ×n 矩阵,A 的秩为r(<n),则齐次线性方程组Ax=0的一个基础解系中含有解的个数为 、21、设向量α、β的长度依次为2和3,则向量α+β和α-β的内积[α+β,α-β]= 、22、设3阶矩阵A 的行列式|A|=8,已知A 有2个特点值-1和4,则另一特点值为 、23、设矩阵A=,已知α=是它的一个特点向量,则α所对应的特点值为 、 24、设实二次型f(x 1,x 2,x 3,x 4,x 5)的秩为4,正惯性指数为3,则其规范形为 、三、计算题[本大题共7小题,每小题6分,共42分] 25、设A=,B=、求[1]AB T ;[2]|4A|、 26、试计算行列式、27、设矩阵A=,求矩阵B 使其满足矩阵方程AB=A+2B 、 28、给定向量组α1=,α2=,α3=,α4=、试判断α4是否为α1,α2,α3的线性组合;若是,则求出组合系数. 29、设矩阵A=、 求:[1]秩[A];[2]A 的列向量组的一个最大线性无关组.30、设矩阵A=的全部特点值为1,1和-8、求正交矩阵T 和对角矩阵D,使T -1AT=D 、 31、试用配方法化下面二次型为标准形 f(x 1,x 2,x 3)=,并写出所用的满秩线性变换.四、证明题[本大题共2小题,每小题5分,共10分]32、设方阵A 满足A 3=0,试证明E -A 可逆,且[E -A]-1=E+A+A 2、33、设η0是非齐次线性方程组Ax=b 的一个特解,ξ1,ξ2是其导出组Ax=0的一个基础解系、试证明[1]η1=η0+ξ1,η2=η0+ξ2均是Ax=b 的解; [2]η0,η1,η2线性无关. 答案:一、单项选择题[本大题共14小题,每小题2分,共28分]1、D2、B3、B4、D5、C6、D7、C8、A9、A 10、B 11、A 12、B 13、D 14、C 二、填空题[本大题共10空,每空2分,共20分] 15、6 16、 17、4 18、–1019、η1+c(η2-η1)[或η2+c(η2-η1)],c 为任意常数 20、n -r 21、–5 22、–2 23、1 24、三、计算题[本大题共7小题,每小题6分,共42分] 25、解[1]AB T = =、[2]|4A|=43|A|=64|A|,而|A|=、所以|4A|=64·[-2]=-128 26、解= =27、解AB=A+2B 即[A -2E]B=A,而 [A -2E]-1=所以B=(A -2E)-1A==28、解一所以α4=2α1+α2+α3,组合系数为[2,1,1]、 解二考虑α4=x 1α1+x 2α2+x 3α3, 即方程组有唯一解[2,1,1]T ,组合系数为[2,1,1]、29、解对矩阵A施行初等行变换A=B、[1]秩[B]=3,所以秩[A]=秩[B]=3、[2]由于A和B的列向量组有相同的线性关系,而B是阶梯形,B的第1、2、4列是B的列向量组的一个最大线性无关组,故A的第1、2、4列是A的列向量组的一个最大线性无关组.[A的第1、2、5列或1、3、4列,或1、3、5列也是]30、解A的属于特点值λ=1的2个线性无关的特点向量为ξ1=[2,-1,0]T,ξ2=[2,0,1]T、经正交标准化,得η1=,η2=、λ=-8的一个特点向量为ξ3=,经单位化得η3=所求正交矩阵为T=、对角矩阵D=[也可取T=、]31、解f(x1,x2,x3)=[x1+2x2-2x3]2-2x22+4x2x3-7x32=[x1+2x2-2x3]2-2[x2-x3]2-5x32、设,即,因其系数矩阵C=可逆,故此线性变换满秩.经此变换即得f(x1,x2,x3)的标准形y 12-2y22-5y32、四、证明题[本大题共2小题,每小题5分,共10分]32、证由于[E-A][E+A+A2]=E-A3=E,所以E-A可逆,且[E-A]-1=E+A+A2、33、证由假设Aη0=b,Aξ1=0,Aξ2=0、[1]Aη1=A[η+ξ1]=Aη+Aξ1=b,同理Aη2=b,所以η1,η2是Ax=b的2个解.[2]考虑l0η+l1η1+l2η2=0,即[l0+l1+l2]η+l1ξ1+l2ξ2=0、则l0+l1+l2=0,否则η将是Ax=0的解,矛盾.所以l 1ξ1+l2ξ2=0、又由假设,ξ1,ξ2线性无关,所以l1=0,l2=0,从而l=0、所以η0,η1,η2线性无关.线性代数期末考试题一、填空题[将正确答案填在题中横线上.每小题2分,共10分]1、若,则__________.2、若齐次线性方程组只有零解,则应满足 .3、已知矩阵,满足,则和分别是阶矩阵.4、矩阵的行向量组线性 .5、阶方阵满足,则 .二、判断正误[正确的在括号内填”√”,错误的在括号内填”×”.每小题2分,共10分]1、若行列式中每个元素都大于零,则.[]2、零向量一定能够表示成任意一组向量的线性组合.[]3、向量组中,假如和对应的分量成比例,则向量组线性相关.[]4、,则.[]5、若为可逆矩阵的特点值,则的特点值为.<>三、单项选择题(每小题仅有一个正确答案,将正确答案题号填入括号内.每小题2分,共10分)1、设为阶矩阵,且,则[].①②③④42、维向量组[3≤s≤n]线性无关的充要条件是[].①中任意两个向量都线性无关②中存在一个向量不能用其它向量线性表示③中任一个向量都不能用其它向量线性表示④中不含零向量3、下面命题中正确的是<>.①任意个维向量线性相关②任意个维向量线性无关③任意个维向量线性相关④任意个维向量线性无关4、设,均为n阶方阵,下面结论正确的是<>.①若,均可逆,则可逆②若,均可逆,则可逆③若可逆,则可逆④若可逆,则,均可逆5、若是线性方程组的基础解系,则是的[]①解向量②基础解系③通解④A的行向量四、计算题(每小题9分,共63分)1、计算行列式.解·2、设,且求.解、,3、设且矩阵满足关系式求.4、问取何值时,下面向量组线性相关?.5、为何值时,线性方程组有唯一解,无解和有无穷多解?当方程组有无穷多解时求其通解.①当且时,方程组有唯一解;②当时方程组无解③当时,有无穷多组解,通解为6、设求此向量组的秩和一个极大无关组,并将其它向量用该极大无关组线性表示.7、设,求的特点值及对应的特点向量.五、证明题(7分)若是阶方阵,且证明.其中为单位矩阵.×××大学线性代数期末考试题答案一、填空题1、52、3、4、相关5、二、判断正误1、×2、√3、√4、√5、×三、单项选择题1、③2、③3、③4、②5、①四、计算题1、2、,3、4、当或时,向量组线性相关.5、①当且时,方程组有唯一解;②当时方程组无解③当时,有无穷多组解,通解为6、则,其中构成极大无关组,7、特点值,对于λ1=1,,特点向量为五、证明题∴,∵【线性代数】复习提纲第一部分:基本要求[计算方面]四阶行列式的计算;N阶特殊行列式的计算[如有行和、列和相等];矩阵的运算[包含加、减、数乘、乘法、转置、逆等的混合运算];求矩阵的秩、逆[两种方法];解矩阵方程;含参数的线性方程组解的情况的讨论;齐次、非齐次线性方程组的求解[包含唯一、无穷多解];讨论一个向量能否用和向量组线性表示;讨论或证明向量组的相关性;求向量组的极大无关组,并将多余向量用极大无关组线性表示;将无关组正交化、单位化;求方阵的特点值和特点向量;讨论方阵能否对角化,如能,要能写出相似变换的矩阵及对角阵;通过正交相似变换[正交矩阵]将对称矩阵对角化;写出二次型的矩阵,并将二次型标准化,写出变换矩阵;判定二次型或对称矩阵的正定性.第二部分:基本知识一、行列式1、行列式的定义用n^2个元素aij组成的记号称为n阶行列式.[1]它表示全部可能的取自不同行不同列的n个元素乘积的代数和;[2]展开式共有n!项,其中符号正负各半;2、行列式的计算一阶|α|=α行列式,二、三阶行列式有对角线法则;N阶[n>=3]行列式的计算:降阶法定理:n阶行列式的值等于它的任意一行[列]的各元素和其对应的代数余子式乘积的和.方法:选取比较简单的一行[列],保保留一个非零元素,其它元素化为0,利用定理展开降阶.特殊情况上、下三角形行列式、对角形行列式的值等于主对角线上元素的乘积;[2]行列式值为0的几种情况:Ⅰ行列式某行[列]元素全为0;Ⅱ行列式某行[列]的对应元素相同;Ⅲ行列式某行[列]的元素对应成比例;Ⅳ奇数阶的反对称行列式.二、矩阵1、矩阵的基本概念[表示符号、一些特殊矩阵――如单位矩阵、对角、对称矩阵等];2、矩阵的运算[1]加减、数乘、乘法运算的条件、结果;[2]关于乘法的几个结论:①矩阵乘法通常不满足交换律[若AB=BA,称A、B是可交换矩阵];②矩阵乘法通常不满足消去律、零因式不存在;③若A、B为同阶方阵,则|AB|=|A|*|B|;④|kA|=k^n|A|3、矩阵的秩[1]定义非零子式的最大阶数称为矩阵的秩;[2]秩的求法通常不用定义求,而用下面结论:矩阵的初等变换不改变矩阵的秩;阶梯形矩阵的秩等于非零行的个数[每行的第一个非零元所在列,从此元开始往下全为0的矩阵称为行阶梯阵].求秩:利用初等变换将矩阵化为阶梯阵得秩.4、逆矩阵[1]定义:A、B为n阶方阵,若AB=BA=I,称A可逆,B是A的逆矩阵[满足半边也成立];[2]性质: (AB)^-1=(B^-1)*(A^-1),(A')^-1=(A^-1)';(AB的逆矩阵,您懂的)[注意顺序][3]可逆的条件:①|A|≠0;②r(A)=n;③A->I;[4]逆的求解伴随矩阵法A^-1=(1/|A|)A*;(A*A的伴随矩阵~)②初等变换法[A:I]->(施行初等变换)[I:A^-1]5、用逆矩阵求解矩阵方程:AX=B,则X=[A^-1]B;XB=A,则X=B(A^-1);AXB=C,则X=(A^-1)C(B^-1)三、线性方程组1、线性方程组解的判定定理:(1)r(A,b)≠r(A)无解;(2)r(A,b)=r(A)=n有唯一解;(3)r(A,b)=r(A)<n有无穷多组解;特别地:对齐次线性方程组AX=0(1)r(A)=n只有零解;(2)r(A)<n有非零解;再特别,若为方阵,(1)|A|≠0只有零解(2)|A|=0有非零解2、齐次线性方程组[1]解的情况:r(A)=n,[或系数行列式D≠0]只有零解;r(A)<n,[或系数行列式D=0]有无穷多组非零解.[2]解的结构:X=c1α1+c2α2+…+Cn-rαn-r.[3]求解的方法和步骤:①将增广矩阵通过行初等变换化为最简阶梯阵;②写出对应同解方程组;③移项,利用自由未知数表示全部未知数;④表示出基础解系;⑤写出通解.3、非齐次线性方程组[1]解的情况:利用判定定理.[2]解的结构: X=u+c1α1+c2α2+…+Cn-rαn-r.[3]无穷多组解的求解方法和步骤: 和齐次线性方程组相同.[4]唯一解的解法:有克莱姆法则、逆矩阵法、消元法[初等变换法].四、向量组1、N维向量的定义注:向量实际上就是特殊的矩阵[行矩阵和列矩阵].2、向量的运算:[1]加减、数乘运算[和矩阵运算相同];[2]向量内积α'β=a1b1+a2b2+…+anbn;[3]向量长度|α|=√α'α=√(a1^2+a2^2+…+an^2)(√根号)[4]向量单位化(1/|α|)α;5]向量组的正交化[施密特方法]设α1,α2,…,αn线性无关,则β1=α1,β2=α2-[α2’β1/β1’β]*β1,β3=α3-[α3’β1/β1’β1]*β1-[α3’β2/β2’β2]*β2,……….3、线性组合[1]定义若β=k1α1+k2α2+…+knαn,则称β是向量组α1,α2,…,αn的一个线性组合,或称β能够用向量组α1,α2,…,αn的一个线性表示.[2]判别方法将向量组合成矩阵,记A=(α1,α2,…,αn),B=(α1,α2,…,αn,β)若r(A)=r(B),则β能够用向量组α1,α2,…,αn的一个线性表示;若r(A)≠r(B),则β不能够用向量组α1,α2,…,αn的一个线性表示.[3]求线性表示表达式的方法:将矩阵B施行行初等变换化为最简阶梯阵,则最后一列元素就是表示的系数.4、向量组的线性相关性[1]线性相关和线性无关的定义设k1α1+k2α2+…+knαn=0 若k1,k2,…,kn不全为0,称线性相关;若k1,k2,…,kn全为0,称线性无关.[2]判别方法:①r(α1,α2,…,αn)<n,线性相关;r(α1,α2,…,αn)=n,线性无关.②若有n个n维向量,可用行列式判别: n阶行列式aij=0,线性相关[≠0无关](行列式太不好打了)5、极大无关组和向量组的秩[1]定义极大无关组所含向量个数称为向量组的秩[2]求法设A=(α1,α2,…,αn),将A化为阶梯阵,则A的秩即为向量组的秩,而每行的第一个非零元所在列的向量就构成了极大无关组.五、矩阵的特点值和特点向量1、定义对方阵A,若存在非零向量X和数λ使AX=λX,则称λ是矩阵A的特点值,向量X称为矩阵A的对应于特点值λ的特点向量.2、特点值和特点向量的求解: 求出特点方程|λI-A|=0的根即为特点值,将特点值λ代入对应齐次线性方程组(λI-A)X=0中求出方程组的全部非零解即为特点向量.3、重要结论:[1]A可逆的充要条件是A的特点值不等于0;[2]A和A的转置矩阵A'有相同的特点值;[3]不同特点值对应的特点向量线性无关.六、矩阵的相似1、定义对同阶方阵A、B,若存在可逆矩阵P,使P^-1AP=B,则称A和B相似.2、求A和对角矩阵∧相似的方法和步骤[求P和∧]:求出全部特点值;求出全部特点向量;若所得线性无关特点向量个数和矩阵阶数相同,则A可对角化[否则不能对角化],将这n个线性无关特点向量组成矩阵即为相似变换的矩阵P,依次将对应特点值构成对角阵即为∧.3、求通过正交变换Q和实对称矩阵A相似的对角阵:方法和步骤和通常矩阵相同,只是第三歩要将所得特点向量正交化且单位化.七、二次型1、定义n元二次多项式f(x1,x2,…,xn)=∑aijxixj称为二次型,若aij=0(i≠j),则称为二交型的标准型.i,j=12、二次型标准化: 配方法和正交变换法.正交变换法步骤和上面对角化完全相同,这是由于对正交矩阵Q,Q^-1=Q',即正交变换既是相似变换又是合同变换.3、二次型或对称矩阵的正定性:[1]定义[略];[2]正定的充要条件:①A为正定的充要条件是A的全部特点值都大于0;②A为正定的充要条件是A的全部顺序主子式都大于0高等教育自学考试试题部分说明:本卷中,A T表示矩阵A的转置,αT表示向量α的转置,E表示单位矩阵,|A|表示方阵A的行列式,A-1表示方阵A的逆矩阵,r[A]表示矩阵A的秩、一、单项选择题[本大题共10小题,每小题2分,共30分]在每小题列出的四个备选项中只有一个是符合题目要求的,请将代码填写在题后的括号内.错选、多选或未选均无分.1、设行列式[]A、B、1C、2D、2、设A,B,C为同阶可逆方阵,则[ABC]-1=[]A、A-1B-1C-1B、C-1B-1A-1C、C-1A-1B-1D、A-1C-1B-13、设α1,α2,α3,α4是4维列向量,矩阵A=[α1,α2,α3,α4]、假如|A|=2,则|-2A|=[]A 、-32B 、-4C 、4D 、32 4、设α1,α2,α3,α4是三维实向量,则[]A 、α1,α2,α3,α4一定线性无关B 、α1一定可由α2,α3,α4线性表出C 、α1,α2,α3,α4一定线性相关D 、α1,α2,α3一定线性无关 5、向量组α1=[1,0,0],α2=[1,1,0],α3=[1,1,1]的秩为[] A 、1 B 、2 C 、3 D 、46、设A 是4×6矩阵,r[A]=2,则齐次线性方程组Ax=0的基础解系中所含向量的个数是[]A 、1B 、2C 、3D 、47、设A 是m ×n 矩阵,已知Ax=0只有零解,则以下结论正确的是[] A 、m ≥n B 、Ax=b[其中b 是m 维实向量]必有唯一解 C 、r[A]=m D 、Ax=0存在基础解系 8、设矩阵A=,则以下向量中是A 的特点向量的是[] A 、[1,1,1]T B 、[1,1,3]T C 、[1,1,0]T D 、[1,0,-3]T9、设矩阵A=的三个特点值分别为λ1,λ2,λ3,则λ1+λ2+λ3=[] A 、4 B 、5 C 、6 D 、7 10、三元二次型f[x 1,x 2,x 3]=的矩阵为[] A 、 B 、 C 、 D 、二、填空题[本大题共10小题,每小题2分,共20分] 请在每小题的空格中填上正确答案.错填、不填均无分. 11、行列式=_________、 12、设A=,则A -1=_________、13、设方阵A 满足A 3-2A+E=0,则[A 2-2E]-1=_________、14、实数向量空间V={[x 1,x 2,x 3]|x 1+x 2+x 3=0}的维数是_________、15、设α1,α2是非齐次线性方程组Ax=b 的解、则A[5α2-4α1]=_________、 16、设A 是m ×n 实矩阵,若r[A T A]=5,则r[A]=_________、 17、设线性方程组有无穷多个解,则a=_________、18、设n 阶矩阵A 有一个特点值3,则|-3E+A|=_________、19、设向量α=[1,2,-2],β=[2,a,3],且α和β正交,则a=_________、 20、二次型的秩为_________、三、计算题[本大题共6小题,每小题9分,共54分] 21、计算4阶行列式D=、22、设A=,判断A 是否可逆,若可逆,求其逆矩阵A -1、 23、设向量α=[3,2],求[αT α]101、24、设向量组α1=[1,2,3,6],α2=[1,-1,2,4],α3=[-1,1,-2,-8],α4=[1,2,3,2]、 [1]求该向量组的一个极大线性无关组;[2]将其它向量表示为该极大线性无关组的线性组合、 线性代数试题 课程代码:04184一、单项选择题[本大题共20小题,每小题1分,共20分]在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内.错选、多选或未选均无分.1、已知2阶行列式=m, =n,则=[]A、m-nB、n-mC、m+nD、-[m+n]2、设A,B,C均为n阶方阵,AB=BA,AC=CA,则ABC=[]A、ACBB、CABC、CBAD、BCA3、设A为3阶方阵,B为4阶方阵,且行列式|A|=1,|B|=-2,则行列式||B|A|之值为[]A、-8B、-2C、2D、84、已知A=,B=,P=,Q=,则B=[]A、PAB、APC、QAD、AQ5、已知A是一个3×4矩阵,下面命题中正确的是[]A、若矩阵A中全部3阶子式都为0,则秩[A]=2B、若A中存在2阶子式不为0,则秩[A]=2C、若秩[A]=2,则A中全部3阶子式都为0D、若秩[A]=2,则A中全部2阶子式都不为06、下面命题中错误..的是[]A、只含有一个零向量的向量组线性相关B、由3个2维向量组成的向量组线性相关C、由一个非零向量组成的向量组线性相关D、两个成比例的向量组成的向量组线性相关7、已知向量组α1,α2,α3线性无关,α1,α2,α3,β线性相关,则[]A、α1必能由α2,α3,β线性表出B、α2必能由α1,α3,β线性表出C、α3必能由α1,α2,β线性表出D、β必能由α1,α2,α3线性表出8、设A为m×n矩阵,m≠n,则齐次线性方程组Ax=0只有零解的充分必要条件是A 的秩[]A、小于mB、等于mC、小于nD、等于n9、设A为可逆矩阵,则和A必有相同特点值的矩阵为[]A、A TB、A2C、A-1D、A*10、二次型f[x1,x2,x3]=的正惯性指数为[]A、0B、1C、2D、3二、填空题[本大题共10小题,每小题2分,共20分]请在每小题的空格中填上正确答案.错填、不填均无分.11、行列式的值为_________________________、12、设矩阵A=,B=,则A T B=____________________________、13、设4维向量[3,-1,0,2]T,β=[3,1,-1,4]T,若向量γ满足2γ=3β,则γ=__________、14、设A为n阶可逆矩阵,且|A|=,则|A-1|=___________________________、15、设A为n阶矩阵,B为n阶非零矩阵,若B的每一个列向量都是齐次线性方程组Ax=0的解,则|A|=__________________、16、齐次线性方程组的基础解系所含解向量的个数为________________、17、设n阶可逆矩阵A的一个特点值是-3,则矩阵必有一个特点值为_____________、18、设矩阵A=的特点值为4,1,-2,则数x=________________________、19、已知A=是正交矩阵,则a+b=_______________________________.20、二次型f[x1,x2,x3]=-4x1x2+2x1x3+6x2x3的矩阵是_______________________________.三、计算题[本大题共6小题,每小题9分,共54分] 21、计算行列式D=的值.22、已知矩阵B=[2,1,3],C=[1,2,3],求[1]A=B T C ;[2]A 2.23、设向量组求向量组的秩及一个极大线性无关组,并用该极大线性无关组表示向量组中的其它向量.24、已知矩阵A=,B=、[1]求A -1;[2]解矩阵方程AX=B.25、问a 为何值时,线性方程组有惟一解?有无穷多解?并在有解时求出其解[在有无穷多解时,要求用一个特解和导出组的基础解系表示全部解].26、设矩阵A=的三个特点值分别为1,2,5,求正的常数a 的值及可逆矩阵P,使P -1AP=.四、证明题[本题6分]27、设A,B,A+B 均为n 阶正交矩阵,证明[A+B]-1=A -1+B -1. 全国2016年7月高等教育自学考试试卷说明:在本卷中,A T 表示矩阵A 的转置矩阵;A *表示A 的伴随矩阵;R(A)表示矩阵A 的秩;|A|表示A 的行列式;E 表示单位矩阵.1、设3阶方阵A=[α1,α2,α3],其中αi (i=1,2,3)为A 的列向量, 若|B|=|[α1+2α2,α2,α3]|=6,则|A|=[]A 、-12 B 、-6C 、6 D 、122、计算行列式[]A 、-180 B 、-120C 、120 D 、1803、设A=,则|2A *|=[]A 、-8 B 、-4C 、4 D 、8 4、设α1,α2,α3,α4都是3维向量,则必有A 、α1,α2,α3,α4线性无关B 、α1,α2,α3,α4线性相关C 、α1可由α2,α3,α4线性表示D 、α1不可由α2,α3,α4线性表示5、若A 为6阶方阵,齐次线性方程组Ax=0的基础解系中解向量的个数为2,则R(A)=[]A 、2 B3C 、4 D 、56、设A 、B 为同阶矩阵,且R(A)=R(B),则[]A 、A 和B 相似 B 、|A|=|B|C 、A 和B 等价 D 、A 和B 合同7、设A 为3阶方阵,其特点值分别为2,l,0则|A+2E|=[]A 、0 B 、2C 、3 D 、24 8、若A 、B 相似,则下面说法错误..的是[]A 、A 和B 等价 B 、A 和 B 合同C 、|A|=|B|D 、A 和B 有相同特点9、若向量α=(1,-2,1)和β=(2,3,t)正交,则t=[]A 、-2 B 、0C 、2 D 、4 10、设3阶实对称矩阵A 的特点值分别为2,l,0,则[]A 、A 正定 B 、A 半正定C 、A 负定 D 、A 半负定二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案.错填、不填均无分.1l 、设A=,B=,则AB=________、12、设A 为3阶方阵,且|A|=3,则|3A -l |=________、 13、三元方程x 1+x 2+x 3=0的结构解是________、14、设α=(-1,2,2),则和α反方向的单位向量是______、15、设A 为5阶方阵,且R(A)=3,则线性空间W={x|Ax=0}的维数是______、 16、设A 为3阶方阵,特点值分别为-2,,l,则|5A -1|=_______、17、若A 、B 为同阶方阵,且Bx=0只有零解,若R(A)=3,则R(AB)=________、 18、二次型f(x 1,x 2,x 3)= -2x 1x 2+-x 2x 3所对应的矩阵是________、19、设3元非齐次线性方程组Ax=b 有解α1=,α2=,且R(A)=2,则Ax=b 的通解是________、20、设α=,则A=ααT 的非零特点值是_____、三、计算题(本大题共6小题,每小题9分,共54分) 21、计算5阶行列式D=22、设矩阵X 满足方程X=求X 、 23、求非齐次线性方程组 的结构解、24、求向量组α1=[1,2,3,4],α2=[0,-1,2,3],α3=[2,3,8,11], α4=[2,3,6,8]的秩、25、已知A=的一个特点向量=[1,1,-1]T ,求a,b 及所对应的特点值,并写出对应于这个特点值的全部特点向量、26、用正交变换化二次型f(x 1,x 2,x 3)=为标准形,并写出所用的正交变换、 四、证明题[本大题共1小题,6分]27、设α1,α2,α3是齐次线性方程组Ax=0的一个基础解系、证明α1,α1+α2,α2+α3也是Ax=0的基础解系、全国2016年10月高等教育自学考试 线性代数(经管类)试题 课程代码:04184说明:在本卷中,A T 表示矩阵A 的转置矩阵,A *表示矩阵A 的伴随矩阵,E 是单位矩阵,|A|表示方阵A 的行列式,r(A)表示矩A 的秩、一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内.错选、多选或未选均无分. 1、设A 为3阶矩阵,|A|=1,则|-2A T |=<> A 、-8B 、-2C 、2 D 、8 2、设矩阵A=,B=(1,1),则AB=<> A 、0B 、(1,-1)C 、 D 、3、设A 为n 阶对称矩阵,B 为n 阶反对称矩阵,则下面矩阵中为反对称矩阵的是<> A 、AB-BAB 、AB+BAC 、ABD 、BA4、设矩阵A 的伴随矩阵A *=,则A -1=<> A 、 B 、 C 、 D 、5、下面矩阵中不是..初等矩阵的是<> A 、 B 、 C 、 D 、6、设A,B 均为n 阶可逆矩阵,则必有<>A 、A+B 可逆B 、AB 可逆C 、A-B 可逆D 、AB+BA 可逆 7、设向量组α1=(1,2),α2=(0,2),β=(4,2),则<> A 、α1,α2,β线性无关B 、β不能由α1,α2线性表示C 、β可由α1,α2线性表示,但表示法不惟一D 、β可由α1,α2线性表示,且表示法惟一8、设A 为3阶实对称矩阵,A 的全部特点值为0,1,1,则齐次线性方程组(E-A)x=0的基础解系所含解向量的个数为<>A 、0B 、1C 、2D 、3 9、设齐次线性方程组有非零解,则为<> A 、-1B 、0C 、1 D 、210、设二次型f(x)=x TAx 正定,则下面结论中正确的是<>A 、对任意n 维列向量x,x T Ax 都大于零B 、f 的标准形的系数都大于或等于零C 、A 的特点值都大于零D 、A 的全部子式都大于零 二、填空题(本大题共10小题,每小题2分,共20分) 请在每小题的空格中填上正确答案.错填、不填均无分.11、行列式的值为_________、12、已知A=,则|A|中第一行第二列元素的代数余子式为_________、13、设矩阵A=,P=,则AP3=_________、14、设A,B都是3阶矩阵,且|A|=2,B=-2E,则|A-1B|=_________、15、已知向量组α1,=(1,2,3),α2=(3,-1,2),α3=(2,3,k)线性相关,则数k=_________、16、已知Ax=b为4元线性方程组,r(A)=3,α1,α2,α3为该方程组的3个解,且则该线性方程组的通解是_________、17、已知P是3阶正交矩,向量_________、18、设2是矩阵A的一个特点值,则矩阵3A必有一个特点值为_________、19、和矩阵A=相似的对角矩阵为_________、20、设矩阵A=,若二次型f=x T Ax正定,则实数k的取值范围是_________、三、计算题(本大题共6小题,每小题9分,共54分)21、求行列式D=22、设矩阵A=求满足矩阵方程XA-B=2E的矩阵X、23、若向量组的秩为2,求k的值、24、设矩阵(1)求A-1;(2)求解线性方程组Ax=b,并将b用A的列向量组线性表出、25、已知3阶矩阵A的特点值为-1,1,2,设B=A2+2A-E,求(1)矩阵A的行列式及A的秩、(2)矩阵B的特点值及和B相似的对角矩阵、26、求二次型f(x1,x2,x3)=-4x1x2+2x1x3+2x2x3经可逆线性变换所得的标准形、四、证明题(本题6分)27、设n阶矩阵A满足A2=E,证明A的特点值只能是、。
线性代数复习题带参考答案

线性代数复习题带参考答案线性代数考试练习题带答案说明:本卷中,A -1表示方阵A 的逆矩阵,r (A )表示矩阵A 的秩,(βα,)表示向量α与β的内积,E 表示单位矩阵,|A |表示方阵A 的行列式.一、单项选择题(本大题共10小题,每小题2分,共20分)1.设行列式333231232221131211a a a a a a a a a =4,则行列式333231232221131211333222a a a a a a a a a =() A.12 B.24 C.36D.482.设矩阵A ,B ,C ,X 为同阶方阵,且A ,B 可逆,AXB =C ,则矩阵X =() A.A -1CB -1B.CA -1B -1C.B -1A -1CD.CB -1A -13.已知A 2+A -E =0,则矩阵A -1=() A.A -E B.-A -E C.A +ED.-A +E4.设54321,,,,ααααα是四维向量,则()A.54321,,,,ααααα一定线性无关B.54321,,,,ααααα一定线性相关C.5α一定可以由4321,,,αααα线性表示D.1α一定可以由5432,,,αααα线性表出5.设A 是n 阶方阵,若对任意的n 维向量x 均满足Ax =0,则() A.A =0 B.A =E C.r (A )=nD.0<="" )6.设A 为n 阶方阵,r (A )B.Ax =0的基础解系含r (A )个解向量C.Ax =0的基础解系含n -r (A )个解向量D.Ax =0没有解7.设21,ηη是非齐次线性方程组Ax =b 的两个不同的解,则()A.21ηη+是Ax =b 的解B.21ηη-是Ax =b 的解C.2123ηη-是Ax =b 的解D.2132ηη-是Ax =b 的解8.设1λ,2λ,3λ为矩阵A =??200540093的三个特征值,则321λλλ=() A.20 B.24 C.28D.309.设P 为正交矩阵,向量βα,的内积为(βα,)=2,则(βαP P ,)=() A.21B.1C.23 D.210.二次型f (x 1,x 2,x 3)=323121232221222x x x x x x x x x +++++的秩为() A.1 B.2C.3D.4二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案。
考研数学一(线性代数)模拟试卷19(题后含答案及解析)

考研数学一(线性代数)模拟试卷19(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.设A、B、A+B、A—1+B—1均为n阶可逆方阵,则(A—1+B—1)—1=( ) A.A—1+B—1B.A+BC.A(A+B)—1BD.(A+B)—1正确答案:C解析:由(A—1+B—1)[A(A+B)—1B]=(E+B—1A)CA+B)—1B=B—1(B+A)(A+B)—1B=B—1B=E,或A(A+B)—1B=[B—1(A+B)A—1]—1=(B—1AA —1+B—1BA—1)—1=(B—1+A—1)—1=(A—1+B—1)—1即知只有(C)正确.知识模块:线性代数2.设n维行向量α=(),矩阵A=I—αTα,β=I+2αα,其中I为n阶单位矩阵,则AB( )A.0.B.一I.C.1.D.I+αTα.正确答案:C解析:AB=(I—αTα)(I+2αTα)=I+2αTα一αTα—2αTααTα一I+αT α一2αT(ααT)α,而ααT=,故得AB=I.知识模块:线性代数3.设三阶矩阵A=,若A的伴随矩阵的秩等于1,则必有( )A.a=b或a+2b=0.B.a=b或a+2b≠0.C.a≠b且a+2b=0.D.a≠b且a+2b≠0.正确答案:C解析:由r(A*)=1,知A*至少有一个元素Aij=(一1)ijMij≠0,其中Mij为A 的(i,j)元素的余子式——即A的一个2阶子式,故r(A)≥2,又由0=|A*|=|A|*,知|A|=0,故得,r(A)=2.由0=|A |=(a+2b)(a一b) 2得a=b或a+2b=0,若a=b,则显然有r(A)≤1,与r(A)=2矛盾,故a≠b且a+2b=0.知识模块:线性代数4.设矩阵B=,已知矩阵A相似于B,则秩(A一2E)与秩(A—E)之和等于( )A.2.B.3.C.4.D.5.正确答案:C解析:由条件知存在可逆矩阵P,使P—1AP=B.故有P—1(A一2E)P=P—1AP一2E=B一2E=.知识模块:线性代数5.设其中A可逆,则B—1等于( )A.A—1P1P2B.P1A—1P2C.P1P2A—1D.P2A—1P1正确答案:C解析:利用初等变换与初等矩阵的关系,可得B=AP2P1,故B—1=P1—1P2—1A—1=P2P2A—1.知识模块:线性代数6.设矩阵A=(aij)3×3满足A*=AT,其中A*为A的伴随矩阵,AT为A 的转置矩阵.若a11,a12,a13为三个相等的正数,则a11为( ) A.B.3C.D.正确答案:A解析:由比较A*=AT对应元素知a=Aij(i,j=1,2,3),其中Aij为|A|中aij的代数余子式,利用行列式按行展开法则得|A|==3a112>0.又由A*=AT 两端取行列式得|A|2=|A|,→|A|=1,故得3a112=1,→a11=.知识模块:线性代数填空题7.设α为3维单位列向量,E为3阶单位矩阵,则矩阵E一ααT的秩为________.正确答案:2.解析:若取单位向量α=(1,0,0)T,则矩阵E一ααT=的秩为2,本题作为填空题,要求一般成立的结果,自然应对个例成立,所以矩阵E—ααT的秩为2.知识模块:线性代数8.设A=(aij)是3阶非零矩阵,|A|为A的行列式,Aij为aij的代数余子式.若aij+Aij=0(i,j=1,2,3),则|A|=________.正确答案:一1.解析:由A≠0,不妨设aij≠0,由已知的Aij=—aij(i,j=1,2,3),得及A=一(A*)T,其中A*为A的伴随矩阵.以下有两种方法:用AT右乘A=一(A*)T 的两端,得AAT=一(A*)AT=一(AAT)T=一(|A|I)T,其中I为3阶单位矩阵,上式两端取行列式,得|A|T=(—1)3|A|3,或|A|2(1+|A|)=0,因|A|≠0,所以|A|=一1.知识模块:线性代数9.设则秩(AB)=______.正确答案:2解析:秩(AB)=秩(A)=2.知识模块:线性代数10.设B≠0满足BA=0,则t=______.正确答案:t=一3.解析:BA=O且B≠0时,必有|A|=0.知识模块:线性代数11.设矩阵B满足A2一AB=2B+4E,则B=______.正确答案:解析:B=(A+2E)—1(A2一4E)=(A+2E)—1(A+2E)(A一2E)=A一2E= 知识模块:线性代数12.设n(n≥3)阶方阵的秩为n—1,则a=______.正确答案:解析:=n一1→|A|=[1+(n一1)a](1—a)n—1≠0→a=或a=1,而当a=1时,有r(A)=1;而当a=时,有r(A)=n一1.知识模块:线性代数13.设的伴随矩阵为A*,且A*BA=2BA一8E,则矩阵B=________.正确答案:解析:B=8(2E—A*)—1A—1=8[A(2E—A*)]—1=8(2A—AA*)—1=8(2A—|A|E)—1=8(2A+2E)—1=4(A+E)—1=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
苏州大学《线性代数》课程(第十九卷)答案 共3页
院系 专业
一、选择题:(15%)
(1)a (2) a (3) b (4) d (5) b
二、填空题:(15%)
(1) 53 (2) 0 (3) ⎪⎪⎪⎪⎭
⎫ ⎝⎛---121113A A A (4) 0或 -1 (5) 6,3,2 三、(8%)解:))((bc ad fg eh D --= (根据行列式的定义计算)
四、(10%)解:
()⎪⎪⎪⎭⎫ ⎝⎛----→→121101*********Λb A ⎪⎪⎪⎭
⎫ ⎝⎛---→000001211043301 (4%)
基础解系:()T 0,
1,1,31-=ξ,()T 1,0,2,32-=ξ, (3%) 特解;()T 0,0,1,40-=μ (2%) 全部解:322110ξξμk k X ++= (21,k k 为任意常数) (1%)
五、(12%)解:()⎪⎪⎪⎭
⎫ ⎝⎛--→→=02001010111321a a a A Λβααα
(1) 当2,0≠≠a a 时,向量组321,,ααα线性无关; (3%)
(2) 当2,0≠≠a a 时, β可由向量组321,,ααα唯一地线性表示; (2%)
(3) 当0=a 时,2),,(321=αααr ,3),,,(321=βαααr ,β不能由向量组321,,ααα线
性表示; (3%)
(4) 当2=a 时,==2),,(321αααr ),,,(321βαααr ,β可由向量组321,,ααα线性表示,且表达式为;k k k ( 2
1321αααβ++-=为任意常数) (4%)
六(12%)解:因为3阶矩阵A 是实对称矩阵,所以可以对角化,且属于不同的特征值的特 征向量两两正交,设()T x x x 3213,,=ξ,得⎩⎨⎧=+=+0
03121x x x x
得对应于-2的一个特征向量()T
1,1,13-=ξ (5%) 即存在可逆矩阵P ,使得Λ=-AP P 1
⎪⎪⎪⎭⎫ ⎝⎛-=110101111P ,⎪⎪⎪⎭
⎫ ⎝⎛-=Λ200020002,1-Λ=P P A (2%)
⎪⎪⎪⎭
⎫ ⎝⎛---=-111211121311P (3%) ⎪⎪⎪⎭
⎫ ⎝⎛--=12221222132A (2%) 七、(18%)解:(1)2)1)(10(2
22254
245
--=-----=-λλλλλλA I (2%) 特征值:101=λ,13,2=λ (2%) 对于101=λ,特征向量为()T
1,2,21-=ξ, 11ξk ( 01≠k )为对于101=λ的所有特征向量 (3%) 对于13,2=λ,特征向量为 (),2,0,12T =ξ()T
0,1,13=ξ +22ξk 33ξk ( 2k 、3k 不全为0)为对应于13,2=λ的所有特征向量 (3%)
(2) 将2ξ、3ξ正交化: 22ξβ=,
T T T ⎪⎭⎫ ⎝⎛-=-=52,1,5
42222333ββββξξβ (3%) 将321,,ββξ单位化:(),1,2,2311T -=η (),2,0,15
12T =η (),2,5,4451
3T
-=η (3%)
正交矩阵()321ηηη=Q ,使得Λ=-AQ Q 1=⎪⎪⎪⎭
⎫ ⎝⎛1110 (2%)
八、(10%)证明题:n B r AB r E r n ≤≤==)()()(,即n B r =)(。
