最小二乘法Matlab自编函数实现及示例.docx
用matlab中最小二乘法编程求解

个人收集整理-ZQ
解:拟合两组数据、,已知,只需确定多项式系数、、.根据最小二乘原则,使所求问题成为三元一次函数()地极小点问题.
由多元函数取极值地必要条件知比为
,,
地解,即满足
将三元一次线性方程组带入,其程序如下:
>> [,...资料个人收集整理,勿做商业用途
];资料个人收集整理,勿做商业用途
[,...资料个人收集整理,勿做商业用途
,...资料个人收集整理,勿做商业用途
];
>> (*.^)(*.^)(*.^)(*.^)(*.^)(*.*)(*.^.*)(*.^.*)资料个人收集整理,勿做商业用途
>> []('***','***','*** ','');资料个人收集整理,勿做商业用途
>> ()()()
1 / 1。
最小二乘法MATLAB程序及结果

最小二乘一次完成算法的MATLAB仿真针对辨识模型,有z(k)-+a1*z(k-1)+a2*z(k-2)=b1*u(k-1)+b2*u(k-2)+v(k)模型结构,对其进行最小二乘一次完成算法的MATLAB仿真,对比真值与估计值。
更改a1、a2、b1、b2参数,观察结果。
仿真对象:z(k)-1.5*z(k-1)+0.7z(k-2)=u(k-1)+0.5*u(k-2)+v(k)程序如下:u=[-1,1,-1,1,1,1,1,-1,-1,-1,1,-1,-1,1,1];%输入信号为一个周期的M序列z=zeros(1,16);for k=3:16z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2);%以理想输出值作为观测值endsubplot(3,1,1)stem(u)subplot(3,1,2)i=1:1:16;plot(i,z)subplot(3,1,3)stem(z),grid onu,z %显示输入信号与输出观测信号L=14;HL=[-z(2) -z(1) u(2) u(1);-z(3) -z(2) u(3) u(2);-z(4) -z(3) u(4) u(3);-z(5) -z(4) u(5) u(4);-z(6) -z(5) u(6) u(5);-z(7) -z(6) u(7) u(6);-z(8) -z(7) u(8) u(7);-z(9) -z(8) u(9) u(8);-z(10) -z(9) u(10) u(9);-z(11) -z(10) u(11) u(10);-z(12) -z(11) u(12) u(11);-z(13) -z(12) u(13)u(12);-z(14) -z(13) u(14) u(13);-z(15) -z(14) u(15) u(14)] %给样本矩阵HL赋值ZL=[z(3);z(4);z(5);z(6);z(7);z(8);z(9);z(10);z(11);z(12);z(13);z(14);z(15);z(16)] %给样本矩阵ZL 赋值c1=HL'*HL;c2=inv(c1);c3=HL'*ZL;c=c2*c3a1=c(1),a2=c(2),b1=c(3),b2=c(4)程序运行结果如下:u =-1 1 -1 1 1 1 1 -1 -1 -1 1 -1 -1 1 1z =Columns 1 through 90 0 0.5000 0.2500 0.5250 2.1125 4.3012 6.4731 6.1988Columns 10 through 163.2670 -0.9386 -3.1949 -4.6352 -6.2165 -5.5800 -2.5185HL =0 0 1.0000 -1.0000-0.5000 0 -1.0000 1.0000-0.2500 -0.5000 1.0000 -1.0000-0.5250 -0.2500 1.0000 1.0000 -2.1125 -0.5250 1.0000 1.0000 -4.3012 -2.1125 1.0000 1.0000 -6.4731 -4.3012 -1.0000 1.0000-6.1988 -6.4731 -1.0000 -1.0000-3.2670 -6.1988 -1.0000 -1.00000.9386 -3.2670 1.0000 -1.00003.1949 0.9386 -1.0000 1.00004.6352 3.1949 -1.0000 -1.00006.2165 4.6352 1.0000 -1.00005.58006.2165 1.0000 1.0000 ZL =0.50000.25000.52502.11254.30126.47316.19883.2670-0.9386-3.1949-4.6352-6.2165-5.5800-2.5185c =-1.50000.70001.00000.5000a1 =-1.5000a2 =0.7000b1 =1.0000b2 =0.5000程序运行曲线:图.1 最小二乘一次完成算法仿真实例输入信号与输出观测值分析:从仿真结果知,由于所用的输出观测值没有任何噪声成分,所以辨识结果也无任何误差。
matlab最小二乘法求微分方程系数

matlab最小二乘法求微分方程系数在Matlab中,可以使用最小二乘法来求解微分方程的系数。
最小二乘法是一种统计方法,用于寻找一组参数,使得这组参数与数据之间的误差平方和最小化。
下面是使用Matlab实现最小二乘法求解微分方程系数的步骤:1. 首先,定义微分方程的形式,如y'(t) = a * y(t) + b *u(t),其中y'(t)表示y关于t的导数,a和b是待求解的系数,u(t)是输入函数。
2. 生成输入数据u(t)和对应的输出数据y(t)。
将输入数据和输出数据存储在向量中。
3. 创建误差函数,该函数计算模型预测值与实际输出值之间的误差。
根据微分方程的形式,计算预测值y_pred(t) = a * y(t-Δt) + b * u(t-Δt),其中Δt是时间步长。
4. 使用Matlab的非线性最小二乘函数(如lsqnonlin)来求解最小二乘问题。
将误差函数作为目标函数,并给定初始猜测的参数值,通过迭代优化参数值以最小化误差函数。
5. 获取最优参数值。
下面是使用Matlab实现最小二乘法求解微分方程系数的示例代码:```matlab% 定义微分方程形式 y'(t) = a * y(t) + b * u(t)% 生成输入数据 u(t) 和输出数据 y(t)% 将输入数据和输出数据存储在向量 u 和 y 中% 创建误差函数function error = diff_eqn_coefficients(x, u, y, dt)a = x(1);b = x(2);y_pred = a * y(1:end-1) + b * u(1:end-1);error = y(2:end) - y_pred;end% 给定初始猜测的参数值x0 = [1, 1];% 使用 lsqnonlin 求解最小二乘问题coefficients = lsqnonlin(@(x) diff_eqn_coefficients(x, u, y, dt), x0);% 获取最优参数值a = coefficients(1);b = coefficients(2);```在实际应用中,需根据具体的微分方程形式和数据进行适当的修改和调整。
matlab function编程最小二乘法

matlab function编程最小二乘法在MATLAB中,使用最小二乘法拟合数据通常涉及到使用函数进行编程。
以下是一个简单的MATLAB函数,用于实现最小二乘法拟合直线的例子:function [coefficients, fittedData] = leastSquaresFit(x, y, degree)% x: 输入数据的 x 值% y: 输入数据的 y 值% degree: 拟合多项式的次数% 创建 Vandermonde 矩阵A = zeros(length(x), degree + 1);for i = 1:degree + 1A(:, i) = x.^(degree + 1 - i);end% 使用最小二乘法计算系数coefficients = (A' * A)\(A' * y);% 生成拟合曲线的数据fittedData = polyval(coefficients, x);% 绘制原始数据和拟合曲线figure;plot(x, y, 'o', x, fittedData, '-');legend('原始数据', '拟合曲线');xlabel('X轴');ylabel('Y轴');title('最小二乘法拟合');end你可以通过调用这个函数并提供你的数据和拟合多项式的次数来进行最小二乘法拟合。
例如:x = [1, 2, 3, 4, 5];y = [2.1, 2.8, 3.4, 3.7, 4.2];degree = 1;[coefficients, fittedData] = leastSquaresFit(x, y, degree);disp('拟合系数:');disp(coefficients);这是一个简单的线性拟合的例子。
你可以根据需要修改该函数,以适应高次多项式的情况。
matlab 最小二乘法 多个自变量

matlab 最小二乘法多个自变量多个自变量的最小二乘法在MATLAB中的应用最小二乘法(Least Squares Method)是一种常见的数据拟合方法,在MATLAB中具有广泛的应用。
它可以用于多个自变量的情况,即多元线性回归问题。
本文将介绍如何使用MATLAB进行多个自变量的最小二乘法拟合,并给出一个实际案例进行说明。
我们需要明确什么是多元线性回归问题。
在统计学中,回归分析是研究两个或多个变量之间关系的一种方法。
多元线性回归是回归分析中的一种常见形式,其模型可以表示为:Y = β0+ β1*X1 + β2*X2 + ... + βn*Xn + ε其中,Y是因变量,X1、X2、...、Xn是自变量,β0、β1、β2、...、βn是回归系数,ε是误差项。
我们的目标是通过拟合数据,估计回归系数的值。
在MATLAB中,可以使用“polyfit”函数来进行多元线性回归拟合。
该函数的基本用法如下:p = polyfit(X, Y, n)其中,X是自变量的矩阵,Y是因变量的向量,n是多项式的次数。
函数的返回值p是一个向量,包含了拟合多项式的系数。
使用polyval函数可以通过这些系数来计算拟合的值。
下面我们通过一个实际案例来演示多个自变量的最小二乘法拟合在MATLAB中的应用。
假设我们有一组数据,包含两个自变量X1和X2,和一个因变量Y。
我们的目标是通过这些数据来拟合一个多元线性回归模型。
我们需要准备数据。
我们可以使用rand函数生成一组随机数据作为示例数据,代码如下:X1 = rand(100,1);X2 = rand(100,1);Y = 2*X1 + 3*X2 + randn(100,1);接下来,我们可以使用polyfit函数进行拟合,代码如下:p = polyfit([X1, X2], Y, 1);这里我们将X1和X2合并成一个矩阵作为自变量。
函数的第三个参数1表示拟合一个一次多项式。
拟合完成后,我们可以使用polyval函数来计算拟合的值,代码如下:Y_fit = polyval(p, [X1, X2]);现在,我们已经得到了拟合的值Y_fit。
多元最小二乘法matlab

多元最小二乘法matlab
以下是使用MATLAB实现多元最小二乘法的示例代码:
假设我们有以下数据:
X1=[1,2,3,4,5]';。
X2=[2,3,4,5,6]';。
Y=[8,10,12,14,16]';。
我们的目标是拟合一个线性模型Y=b1*X1+b2*X2+e,其中b1和b2是系数,e是误差项。
首先,我们需要将数据构建成矩阵形式:
X=[X1X2];。
A = [ones(length(X1), 1) X];。
然后,可以使用MATLAB内置函数(\)来计算多元最小二乘解:
b=A\Y;。
在这里,MATLAB计算AX≈Yb,其中AX是我们的设计矩阵,Y是响应变量,b是我们的参数估计值。
最后,我们可以使用参数估计值来预测新数据:
X_new = [6,7,8]';。
Y_new = [ones(length(X_new), 1) X_new] * b;。
这将返回一个新的响应变量向量Y_new,其中包含新数据的预测值。
有关更多详细信息,可以阅读MATLAB文档中关于多元最小二乘法的章节。
(完整word版)最小二乘法拟合圆公式推导及matlab实现

2009-01-17 |最小二乘法(least squares analysis) 是一种数学优化技术,它通过最小化误差的平方和找到一组数据的最佳函数匹配。
最小二乘法是用最简的方法求得一些绝对不可知的真值,而令误差平方之和为最小。
小二乘法通常用于曲线拟合(least squares fitti ng) 。
这里有拟合圆曲线的公式推导过程和vc实现。
最小二乘法拟會圆曲线;= (x- +R2 = +- 2By4-B2令a=-2J4b = -2Bc = J^ +矿-0可得圆曲线方程的另一个册式Ix2 -\-y3十切十u = 0只要求出参数就可以求得圆心半径的参教;d)样本集(禺<并e (123…N)中点到圆心的距离为a:打=(禺・4)2+(E傢点(耳乙)到圆边嫌的距离的平方与和半径平方的差为:@=£2_衣=(圣.4)2+(込.8)2_氏2=血2+込2+込+&乙+卍令Q(a,b,c)为Q的平方和:Q(aM = Z^2=工【(*/ + §2 + 込+b 齐+C)]2求参数a f b,c使得Q(a,g的值最小值。
解・PTT •平方差Qgg大于0,因此函数存在大于或等于0的极小值,极大值为无穷大.F(a,M)对a,吐求偏导,令偏导等于0,得到极值点,比较所有极值点的函数值即可得到最小值.绘仏"疋)=工2窗 +里+込+埒+c)Xjda —=0 迤(a,bQ =匸2阳+貯+込+坷+训=0範仏上疋)=工2(禺2+乙2+込 +空+° = 0 d解这个方程组。
(2)(3)(4)di(诵先消去c(2) W ⑷*工扎得:Ng 代'+Y-+aX +bY + c)X -工莎‘ +严 +aX +bY+c)x^X = 0 N^(X 2 +Y : +bY)X -^(X : +Y : +aX +bY)x^X =0("工禺2_工兀工兀)a + (“Y*占一工禺工齐仏(*+ + M 工*必2 -工牡丁 +去2)工禺=0(3) *N_⑷*工£得:N 工(X’ + y' + oZ +bY+c)Y-^(X 2 +Y- +aX +bY + c)x^Y =Q 吧(/+护 +aX +bY)Y +Y : +aX +dK)xVy =o (N'X 必一工禺工齐归+ (“丫呼一工§工齐)3 +“Y+N 工厅一 g af +严)三齐=o C =〔NgQ -gX 二X)D = (N 工尤F -工龙三卩)E-N^X 、+N^XY -工疔+丫‘)工XG = (NM 旷-三丫工丫)H =NW X'Y 七NT H -工 2’ +K-)YK可解得:|G? + Db + 5 = 0Da+Gb + H = 0HD-EG a = r CG-D 、v HC- ED o =D' _GC 工(疔+齐2)+幺工兀+c ―― ---------------------------------------------- N得A 、B 、R 的估计拟合值:R= - Ja‘ +2?' -牡 2(6)matlab 实现:function [R,A,B]=circ(x,y,N)x1 = 0;x2 = 0;x3 = 0;y1 = 0;y2 = 0;y3 = 0;x1y1 = 0;x1y2 = 0;x2y1 = 0;for i = 1 : Nx1 = x1 + x(i);x2 = x2 + x(i)*x(i);x3 = x3 + x(i)*x(i)*x(i);y1 = y1 + y(i);y2 = y2 + y(i)*y(i);y3 = y3 + y(i)*y(i)*y(i); x1y1 = x1y1 + x(i)*y(i); x1y2 = x1y2 +x(i)*y(i)*y(i); x2y1 = x2y1 + x(i)*x(i)*y(i); endC = N * x2 - x1 * x1;D = N * x1y1 - x1 * y1;E = N * x3 + N * x1y2 - (x2 + y2) * x1;G = N * y2 - y1 * y1;H = N * x2y1 + N * y3 - (x2 + y2) * y1;a = (H * D - E * G)/(C * G - D * D);b = (H * C - E * D)/(D * D - G * C);c = -(a * x1 + b * y1 + x2 + y2)/N;A = a/(-2); %x 坐标B = b/(-2); %y 坐标R = sqrt(a * a + b * b - 4 * c)/2;void CViewActionImageTool::LeastSquaresFitting(){if (m_nNum<3){ return; } int i=0;double X1=0;double Y1=0;double X2=0;double Y2=0;double X3=0;double Y3=0;double X1Y1=0;double X1Y2=0;double X2Y1=0;for (i=0;i<m_nNum;i++){X1 = X1 + m_points[i].x;Y1 = Y1 + m_points[i].y;X2 = X2 + m_points[i].x*m_points[i].x;Y2 = Y2 + m_points[i].y*m_points[i].y;X3 = X3 + m_points[i].x*m_points[i].x*m_points[i].x;Y3 = Y3 + m_points[i].y*m_points[i].y*m_points[i].y;X1Y1 = X1Y1 + m_points[i].x*m_points[i].y;X1Y2 = X1Y2 + m_points[i].x*m_points[i].y*m_points[i].y;X2Y1 = X2Y1 + m_points[i].x*m_points[i].x*m_points[i].y; } double C,D,E,G ,H,N;double a,b,c;N = m_nNum;C = N*X2 - X1*X1;D = N*X1Y1 - X1*Y1;E = N*X3 + N*X1Y2 - (X2+Y2)*X1;G = N*Y2 - Y1*Y1;H = N*X2Y1 + N*Y3 - (X2+Y2)*Y1;a = (H*D-E*G)/(C*G-D*D);b = (H*C-E*D)/(D*D-G*C);c = -(a*X1 + b*Y1 + X2 + Y2)/N;double A,B,R;A = a/(-2);B = b/(-2);R = sqrt(a*a+b*b-4*c)/2; m_fCenterX = A; m_fCenterY = B;m_fRadius = R; return;}。
matlab最小二乘法实现三参数拟合

matlab最小二乘法实现三参数拟合
在MATLAB中,你可以使用`polyfit`函数来实现三参数的最小二乘拟合。
以下是一个示例,其中我们试图拟合一个三次多项式:
```matlab
% 创建一些示例数据
x = linspace(-10,10,100);
y = 3x.^3 + 2x.^2 + x + randn(size(x));
% 使用polyfit进行三参数拟合
p = polyfit(x, y, 3);
% 绘制原始数据和拟合曲线
plot(x, y, 'o');
hold on;
plot(x, polyval(p, x), '-');
hold off;
```
在这个例子中,`polyfit(x, y, 3)`函数试图找到一个三次多项式,该多项式能最小化所有`(xi, yi)`的平方和。
返回的`p`是一个包含三个系数的向量,这些系数对应于多项式的最高次项,即`p(1)x^3 + p(2)x^2 + p(3)x + p(4)`。
在这个例子中,我们没有提供第四个系数,所以它默认为0。
请注意,由于MATLAB中的`polyfit`函数默认使用最小二乘法进行拟合,因此我们不需要做任何额外的最小二乘法计算。
最小二乘法MATLAB程序及结果

最小二乘递推算法的MATLAB仿真针对辨识模型,有z(k)-+a1*z(k-1)+a2*z(k-2)=b1*u(k-1)+b2*u(k-2)+v(k)模型结构,对其进行最小二乘递推算法的MATLAB仿真,对比真值与估计值。
更改a1、a2、b1、b2参数,观察结果。
仿真对象:z(k)-1.5*z(k-1)+0.7*z(k-2)=u(k-1)+0.5*u(k-2)+v(k)程序如下:L=15;y1=1;y2=1;y3=1;y4=0; %四个移位寄存器的初始值for i=1:L; %移位循环x1=xor(y3,y4);x2=y1;x3=y2;x4=y3;y(i)=y4; %取出作为输出信号,即M序列if y(i)>0.5,u(i)=-0.03; %输入信号else u(i)=0.03;endy1=x1;y2=x2;y3=x3;y4=x4;endfigure(1);stem(u),grid onz(2)=0;z(1)=0;for k=3:15;z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2); %输出采样信号endc0=[0.001 0.001 0.001 0.001]'; %直接给出被识别参数的初始值p0=10^6*eye(4,4); %直接给出初始状态P0E=0.000000005;c=[c0,zeros(4,14)];e=zeros(4,15);for k=3:15; %开始求kh1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]';x=h1'*p0*h1+1;x1=inv(x);k1=p0*h1*x1; %开始求k的值d1=z(k)-h1'*c0;c1=c0+k1*d1;e1=c1-c0;e2=e1./c0; %求参数的相对变化e(:,k)=e2;c0=c1;c(:,k)=c1;p1=p0-k1*k1'*[h1'*p0*h1+1]; %求出P(k)的值p0=p1;if e2<=E break;endendc,e %显示被辨识参数及其误差情况a1=c(1,:);a2=c(2,:);b1=c(3,:);b2=c(4,:);ea1=e(1,:);ea2=e(2,:);eb1=e(3,:);eb2=e(4,:);figure(2);i=1:15;plot(i,a1,'r',i,a2,':',i,b1,'g',i,b2,':')title('Parameter Identification with Recursive Least Squares Method')figure(3);i=1:15;plot(i,ea1,'r',i,ea2,'g',i,eb1,'b',i,eb2,'r:')title('Identification Precision')程序运行结果:p0 =1000000 0 0 00 1000000 0 00 0 1000000 00 0 0 1000000c =Columns 1 through 90.0010 0 0.0010 -0.4984 -1.2325 -1.4951 -1.4962 -1.4991 -1.49980.0001 0 0.0001 0.0001 -0.2358 0.6912 0.6941 0.6990 0.69980.0010 0 0.2509 1.2497 1.0665 1.0017 1.0020 1.0002 0.99990.0010 0 -0.2489 0.7500 0.5668 0.5020 0.5016 0.5008 0.5002Columns 10 through 15-1.4999 -1.5000 -1.5000 -1.5000 -1.4999 -1.49990.6999 0.7000 0.7000 0.7000 0.7000 0.70000.9998 0.9999 0.9999 0.9999 0.9999 0.99990.5002 0.5000 0.5000 0.5000 0.5000 0.5000e =1.0e+003 *Columns 1 through 90 0 0 -0.4994 0.0015 0.0002 0.0000 0.0000 0.00000 0 0 0 -2.3592 -0.0039 0.0000 0.0000 0.00000 0 0.2499 0.0040 -0.0001 -0.0001 0.0000 -0.0000 -0.00000 0 -0.2499 -0.0040 -0.0002 -0.0001 -0.0000 -0.0000 -0.0000Columns 10 through 150.0000 0.0000 0.0000 -0.0000 -0.0000 0.00000.0000 0.0000 -0.0000 0.0000 0.0000 0.0000-0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000-0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000程序运行曲线:图1.输入信号图2.a1,a2,b1,b2辨识仿真结果图3. a1,a2,b1,b2各次辨识结果收敛情况分析:由运行结果可看出,输出观测值没有任何噪声成分时,辨识结果最大相对误差达到3位数。
matlab两组数最小二乘法拟合

matlab两组数最小二乘法拟合最小二乘法是一种常用的数据拟合方法,在MATLAB中可以很方便地实现。
假设我们有两组数据,X和Y,我们希望找到一个线性表达式y=ax+b,使得拟合的结果最接近实际数据。
首先,我们需要使用polyfit函数进行拟合。
这个函数可以根据指定的阶数,对两组数据进行最小二乘拟合,并返回拟合系数。
例如,如果我们希望进行一次拟合(即线性拟合),可以使用以下命令:```p = polyfit(X, Y, 1);```这个命令会返回一个长度为2的数组p,其中p(1)表示拟合直线的斜率a,p(2)表示拟合直线的截距b。
接下来,我们可以使用polyval函数根据拟合系数p来计算拟合的结果。
例如,如果我们有一个新的输入x,希望得到对应的拟合结果y,可以使用以下命令:```y = polyval(p, x);```这个命令会返回一个与x长度相同的数组y,其中每个元素表示对应x的拟合结果。
最后,我们可以使用plot函数将实际数据和拟合结果进行可视化比较。
例如,假设我们有一个绘图窗口fig,可以使用以下命令绘制实际数据点和拟合直线:```figure(fig);plot(X, Y, 'o'); % 绘制实际数据点hold on;plot(x, y); % 绘制拟合直线```这个命令会在同一个图形窗口中绘制实际数据点和拟合直线。
通过以上步骤,我们就可以在MATLAB中实现两组数据的最小二乘法拟合了。
需要注意的是,拟合结果的准确性取决于数据本身的分布以及拟合模型的选择。
最小二乘法原理及其MATLAB实现

最小二乘法原理及其MATLAB实现一、本文概述最小二乘法是一种广泛应用于数学、统计学、工程学、物理学等众多领域的数学优化技术。
其核心原理在于通过最小化误差的平方和来寻找最佳函数匹配,从而实现对数据的最佳逼近。
本文将对最小二乘法的原理进行详细阐述,并通过MATLAB编程实现,帮助读者深入理解并掌握这一强大的数据分析工具。
文章将首先介绍最小二乘法的基本原理,包括其历史背景、基本概念以及数学模型的构建。
然后,通过实例分析,展示如何应用最小二乘法进行线性回归模型的拟合,以及如何处理过拟合和欠拟合等问题。
接着,文章将详细介绍如何在MATLAB中实现最小二乘法,包括数据准备、模型构建、参数估计以及结果可视化等步骤。
文章还将对最小二乘法的优缺点进行讨论,并探讨其在不同领域的应用前景。
通过本文的学习,读者将能够全面理解最小二乘法的原理和应用,掌握其在MATLAB中的实现方法,为实际工作中的数据处理和分析提供有力支持。
二、最小二乘法原理最小二乘法(Least Squares Method)是一种数学优化技术,它通过最小化误差的平方和寻找数据的最佳函数匹配。
这种方法起源于19世纪的统计学,由数学家阿德里安-马里·勒让德(Adrien-Marie Legendre)和卡尔·弗里德里希·高斯(Carl Friedrich Gauss)分别独立发展。
建立模型:我们需要建立一个描述数据关系的数学模型。
这通常是一个线性方程,如 y = ax + b,其中 a和b是待求解的参数。
误差计算:对于给定的数据集,我们可以将每个数据点代入模型中进行计算,得到预测值。
预测值与真实值之间的差异就是误差。
平方误差和:为了衡量模型的拟合程度,我们需要计算所有误差的平方和。
这是因为平方误差和能够更好地反映误差的大小,尤其是在误差较大时。
最小化平方误差和:最小二乘法的核心思想是找到一组参数,使得平方误差和达到最小。
这通常通过求导和令导数等于零来实现,从而找到使平方误差和最小的参数值。
最小二乘法 matlab

最小二乘法(附MATLAB代码)今天我主要是从如何使用MATLAB实现最小二乘法,首先给出今天重点使用的两个函数。
比如我想拟合下面这组数据x=[9,13,15,17,18.6,20,23,29,31.7,35];y=[-8,-6.45,-5.1,-4,-3,-1.95,-1.5,-0.4,0.2,-0.75];我先用matlab将这组离散点画出来,plot(x,y,'o')嗯,大概这个样子,这时我们想使用一次函数拟合上述曲线,可使用以下代码clearclcx=[9,13,15,17,18.6,20,23,29,31.7,35];y=[-8,-6.45,-5.1,-4,-3,-1.95,-1.5,-0.4,0.2,-0.75];coeff icient=polyfit(x,y,1); %用一次函数拟合曲线,想用几次函数拟合,就把n设成那个数y1=polyval(coefficient,x);%plot(x,y,'-',x,y1,'o'),这个地方原来'-'和'o'写反了,现已更正,可以得到正确的图形。
plot(x,y,'o',x,y1,'-')得到的结果是coefficient=[0.2989,-9.4107]所以得到的一次函数为y=0.2989*x-9.4107同理如果用二次函数拟合该曲线,得到的各项系数为coefficient=[-0.0157 1.0037 -16.2817]所以得到的二次函数为y=-0.0157*x^2+1.0037*x-16.2817其他阶数依此类推。
但是使用polyfit(x,y,n)函数有一个注意事项:举个例子,比如说我们想用9阶多项式拟合上述曲线时,我们发现拟合的曲线是正常的,得到的各项系数也是正常的但是当我们用10阶多项式拟合曲线时,此时各项系数如下,得到的曲线如下很明显出现了问题,所以使用polyfit(x,y,n)函数时要严格遵守上述事项。
最小二乘法曲线拟合的Matlab程序

方便大家使用的最小二乘法曲线拟合的Matlab程序非常方便用户使用,直接按提示操作即可;这里我演示一个例子:(红色部分为用户输入部分,其余为程序运行的结果,结果图为Untitled.fig,Untitled2.fig) 请以向量的形式输入x,y.x=[1,2,3,4]y=[3,4,5,6]通过下面的交互式图形,你可以事先估计一下你要拟合的多项式的阶数,方便下面的计算.polytool()是交互式函数,在图形上方[Degree]框中输入阶数,右击左下角的[Export]输出图形回车打开polytool交互式界面回车继续进行拟合输入多项式拟合的阶数m = 4Warning: Polynomial is not unique; degree >= number of data points. > In polyfit at 72In zxecf at 64输出多项式的各项系数a = 0.0200000000000001a = -0.2000000000000008a = 0.7000000000000022a = 0.0000000000000000a = 2.4799999999999973输出多项式的有关信息 SR: [4x5 double]df: 0normr: 2.3915e-015Warning: Zero degrees of freedom implies infinite error bounds.> In polyval at 104In polyconf at 92In zxecf at 69观测数据拟合数据x y yh1.0000 3.0000 3.00002.0000 4.0000 4.00003 5 54.0000 6.0000 6.0000剩余平方和 Q = 0.000000标准误差 Sigma = 0.000000相关指数 RR = 1.000000请输入你所需要拟合的数据点,若没有请按回车键结束程序.输入插值点x0 = 3输出插值点拟合函数值 y0 = 5.0000>>结果:untitled.figuntitled2.fig一些matlab优化算法代码的分享代码的目录如下:欢迎讨论1.约束优化问题:minRosen(Rosen梯度法求解约束多维函数的极值)(算法还有bug) minPF(外点罚函数法解线性等式约束)minGeneralPF(外点罚函数法解一般等式约束)minNF(内点罚函数法)minMixFun(混合罚函数法)minJSMixFun(混合罚函数加速法)minFactor(乘子法)minconPS(坐标轮换法)(算法还有bug)minconSimpSearch(复合形法)2.非线性最小二乘优化问题minMGN(修正G-N法)3.线性规划:CmpSimpleMthd(完整单纯形法)4.整数规划(含0-1规划)DividePlane(割平面法)ZeroOneprog(枚举法)5.二次规划QuadLagR(拉格朗日法)ActivedeSet(起作用集法)6.辅助函数(在一些函数中会调用)minNT(牛顿法求多元函数的极值)Funval(求目标函数的值)minMNT(修正的牛顿法求多元函数极值)minHJ(黄金分割法求一维函数的极值)7.高级优化算法1)粒子群优化算法(求解无约束优化问题)1>PSO(基本粒子群算法)2>YSPSO(待压缩因子的粒子群算法)3>LinWPSO(线性递减权重粒子群优化算法)4>SAPSO(自适应权重粒子群优化算法)5>RandWSPO(随机权重粒子群优化算法)6>LnCPSO(同步变化的学习因子)7>AsyLnCPSO(异步变化的学习因子)(算法还有bug)8>SecPSO(用二阶粒子群优化算法求解无约束优化问题)9>SecVibratPSO(用二阶振荡粒子群优化算法求解五约束优化问题)10>CLSPSO(用混沌群粒子优化算法求解无约束优化问题)11>SelPSO(基于选择的粒子群优化算法)12>BreedPSO(基于交叉遗传的粒子群优化算法)13>SimuAPSO(基于模拟退火的粒子群优化算法)2)遗传算法1>myGA(基本遗传算法解决一维约束规划问题)2>SBOGA(顺序选择遗传算法求解一维无约束优化问题)3>NormFitGA(动态线性标定适应值的遗传算法求解一维无约束优化问题)4>GMGA(大变异遗传算法求解一维无约束优化问题)5>AdapGA(自适应遗传算法求解一维无约束优化问题)6>DblGEGA(双切点遗传算法求解一维无约束优化问题)7>MMAdapGA(多变异位自适应遗传算法求解一维无约束优化问题)自己编写的马尔科夫链程序A 代表一组数据序列一维数组本程序的操作对象也是如此t=length(A); % 计算序列“A”的总状态数B=unique(A); % 序列“A”的独立状态数顺序,“E”E=sort(B,'ascend');a=0;b=0;c=0;d=0;for j=1:1:ttLocalization=find(A==E(j)); % 序列“A”中找到其独立状态“E”的位置for i=1:1:length(Localization)if Localization(i)+1>tbreak; % 范围限定elseif A(Localization(i)+1)== E(1)a=a+1;elseif A(Localization(i)+1)== E(2)b=b+1;elseif A(Localization(i)+1)== E(3)c=c+1;% 依此类推,取决于独立状态“E”的个数elsed=d+1;endendT(j,1:tt)=[a,b,c,d]; % “T”为占位矩阵endTT=T;for u=2:1:ttTT(u,:)= T(u,:)- T(u-1,:);endTT; % 至此,得到转移频数矩阵Y=sum(TT,2);for uu=1:1:ttTR(uu,:)= TT(uu,:)./Y(uu,1);endTR % 最终得到马尔科夫转移频率/概率矩阵% 观测序列马尔科夫性质的检验:N=numel(TT);uuu=1;Col=sum(TT,2); % 对列求和Row=sum(TT,1); % 对行求和Total=sum(Row); % 频数总和for i=1:1:ttfor j=1:1:ttxx(uuu,1)=sum((TT(i,j)-(Row(i)*Col(j))./Total).^2./( (Row(i)*Col(j)). /Total));uuu=uuu+1; % 计算统计量x2endendxx=sum(xx)。
matlab和C语言实现最小二乘法

matlab和C语⾔实现最⼩⼆乘法Matlab代码:N = 8;x = [12345678 ];y = [6784102120137155172190];subplot(2,1,1);plot(x,y,'*');% 图形的⼀些设置xlabel('时间(秒)');ylabel('位移(⽶)');title('原始数据离散点')grid onsubplot(2,1,2);p = polyfit(x,y,1); %得出P就是线性拟合的系数% 0:0.01:9x1 = 0:1:N; %起始为0,终点为N,步长1y1 = polyval(p,x1);plot(x,y,'*',x1,y1,'r')xlabel('时间(秒)');ylabel('位移(⽶)');title('红线为最⼩⼆乘法拟合')grid onsumxyji =sum(x.*y); %向量内积sumx = sum(x);sumy = sum(y);sumxx = sum(x.*x);k = (N*sumxyji - sumx*sumy)/(N*sumxx-sumx*sumx)b = (sumy-k*sumx)/N效果:⾃⼰C语⾔实现:公式:#include <stdio.h>#include <stdlib.h>//函数功能:进⾏最⼩⼆乘曲线拟合(拟合y=a0+a1*x),计算出对应的系数a//参数说明:// n: 给定数据点的个数// x[]: 存放给定n个数据点的X坐标// y[]: 存放给定n个数据点的Y坐标// k,b: 拟合多项式的系数,表⽰多项式的k,bvoid polyfit(int n,double x[],double y[],double &k,double &b){int i,j;double sumxymultiply = 0.0;double sumx = 0.0;double sumy = 0.0;double sumxx = 0.0;for (i=0;i<n;i++){sumx += x[i];sumy += y[i];sumxymultiply += (x[i]*y[i]);sumxx += (x[i]*x[i]);}k = (n*sumxymultiply - sumx*sumy)/(n*sumxx - sumx*sumx);b = (sumy-k*sumx)/n;}void printArr(double *arr,int n){for(int i=0;i<n;++i)printf("%lf ",arr[i]);printf("\n");}int main(){const int N = 8;double x[N] = {1,2,3, 4,5,6,7,8};double y[N] = {67,84,102,120,137,155,172,190}; double k,b;polyfit(N,x,y,k,b);printf("%lf %lf\n",k,b);return0;}。
matlab三角函数最小二乘法拟合

matlab三角函数最小二乘法拟合在MATLAB 中,您可以使用内置的polyfit 和polyval 函数来实现使用最小二乘法对数据进行拟合的任务。
下面是一个简单的例子,演示如何使用这些函数来拟合一个简单的三角函数。
假设您有一些数据,这些数据是三角函数的输出,您想要找到这个函数的参数。
三角函数的一般形式是y = a * sin(b * x + c),其中a、b 和c 是您需要找到的参数。
首先,您需要创建一些模拟数据。
然后,您可以使用polyfit 函数来找到最佳拟合参数。
最后,您可以使用polyval 函数来验证拟合结果。
下面是一个示例代码:matlab复制代码:% 创建模拟数据x = linspace(0, 2*pi, 100); % x 数据a = 1;b = 1;c = 0; % 假设的参数y = a * sin(b * x + c) + 0.1*randn(size(x)); % y 数据,加入一些噪声% 使用最小二乘法拟合数据p = polyfit(x, y, 2); % 2 表示我们要拟合一个二次多项式,这对应于我们的三角函数形式% 验证拟合结果y_fit = polyval(p, x); % 使用拟合参数计算y 值% 绘制原始数据和拟合曲线plot(x, y, 'bo'); % 原始数据hold on;plot(x, y_fit, 'r-'); % 拟合曲线legend('原始数据', '拟合曲线');在这个例子中,polyfit 函数的第三个参数表示我们要拟合的多项式的次数。
对于三角函数,这应该是2,因为我们正在拟合一个二次多项式,其形式为y = a * sin(b * x + c)。
最小二乘法--计算方法
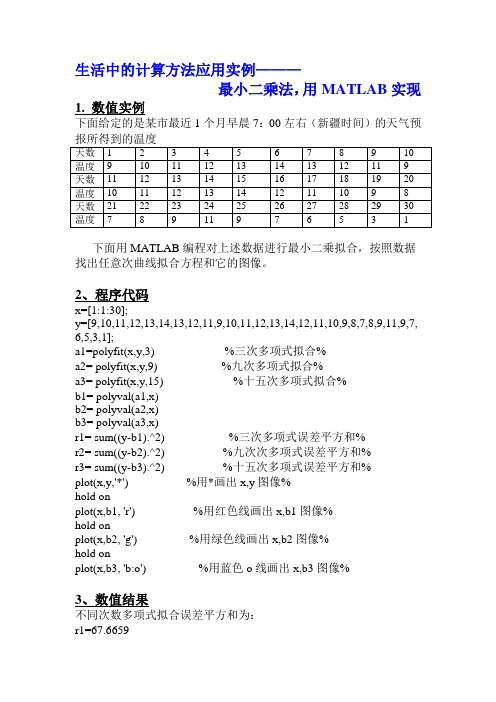
生活中的计算方法应用实例———最小二乘法,用MATLAB实现1. 数值实例下面给定的是某市最近1个月早晨7:00左右(新疆时间)的天气预报所得到的温度天数 1 2 3 4 5 6 7 8 9 10 温度9 10 11 12 13 14 13 12 11 9 天数11 12 13 14 15 16 17 18 19 20 温度10 11 12 13 14 12 11 10 9 8 天数21 22 23 24 25 26 27 28 29 30 温度7 8 9 11 9 7 6 5 3 1下面用MATLAB编程对上述数据进行最小二乘拟合,按照数据找出任意次曲线拟合方程和它的图像。
2、程序代码x=[1:1:30];y=[9,10,11,12,13,14,13,12,11,9,10,11,12,13,14,12,11,10,9,8,7,8,9,11,9,7, 6,5,3,1];a1=polyfit(x,y,3) %三次多项式拟合%a2= polyfit(x,y,9) %九次多项式拟合%a3= polyfit(x,y,15) %十五次多项式拟合%b1= polyval(a1,x)b2= polyval(a2,x)b3= polyval(a3,x)r1= sum((y-b1).^2) %三次多项式误差平方和%r2= sum((y-b2).^2) %九次次多项式误差平方和%r3= sum((y-b3).^2) %十五次多项式误差平方和%plot(x,y,'*') %用*画出x,y图像%hold onplot(x,b1, 'r') %用红色线画出x,b1图像%hold onplot(x,b2, 'g') %用绿色线画出x,b2图像%hold onplot(x,b3, 'b:o') %用蓝色o线画出x,b3图像%3、数值结果不同次数多项式拟合误差平方和为:r1=67.6659r2=20.1060r3=3.7952r1、r2、r3分别表示三次、九次、十五次多项式误差平方和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
、最小二乘拟合原理
x= xl x2 ... xn
y= yl y2 ... yn
求m 次拟合 «力*
y 卅…I ZA ;
A T A = ZX 茁 X x i - X x i +1 ,- «
«
«
[函Oi …备F =⑷矿丄• A T y 所以m 次拟合曲线为y = a 0 +勿・怎+吐■审+•・・・ +如■牙皿 二、 Matlab 实现程序
function p=funLSM (x, y, m) %x z y 为序列长度相等的数据向量,m 为拟合多项式次数
format short;
A=zeros(m+l,m+l);
for i=0:m
for j=0:m
A(i + 1, j + 1)=sum(x.A (i+j));
end
b(i+1)=sum(x.A i.*y);
end
a=A\b 1;
p=fliplr (a');
三、 作业
题1:给出如下数据,使用最小二乘法球一次和二次拟合多项式(取小数点后3位) X 1.36 1.49 1.73 1.81 1.95 2.16 2.28 2.48
Y 14.094 15.069 16.844 17.378 18.435 19.949 20.963 22.495 解:
» x=[1.36 1.49 1.73 1. 81 1. 95 2. 16 2. 28 2. 48]:
» y=[14.094 15.069 16.844 17. 378 18.435 19.949 20.963 22.495]; >> p=funLSM(x, y? 1)
P =
7.4639 3.9161
>> p=funLSM(x, y? 2)
P =
0.3004 6.3145 4.9763
一次拟合曲线为:
y = 7.464x+ 3.91S
二次拟合曲线为:
y = +6.315^4-4.976
一次拟合仿真图
二次拟合仿真图例5-8 给定函数y二f(x)的实例数据表题
2:
1 2 3 4 6 7 8
yt 2 3 6 7 5 3 2
试用最小二乘法求二次拟合多项式。
解:
» x=[l 2 3 4 6 7 8];
» y=[2 3 6 7 5 3 2];
>> p=funLSM(Xj y y 2)
P =
-0.3864 3.4318 -1.3182
所以
y = —0.3864%' + 3.4318X' —1.3152。
