第八章-组合变形及连接部分的计算-习题选解
第八章-组合变形和连接件习题.doc
(即图示虚线处的截面),最合理的是图( )。
一、填空和选择1 .试分析图示杆件各段杆的变形类型。
(a ) AB, BC, CD(b ) AB, BC, CD o 2 .偏心压缩实际上为 和 的组合变形。
3. 铸铁构件受力如图,危险点为图中。
题4图4. 图示三种受压杆件,分别写出1,2,3号杆中最大压应力(绝对值),"max,2 — ------------ ,"max,3 — ------------------5. 图示等直圆折杆,杆直径d,杆在x, z 方向长度均为L,折杆危险截面上危险点的应力状态为;并写出危险点应力状态的b =, 7 =。
7圆轴同时受到转矩T 、弯曲力偶M 和轴力F 的作用,下列强度条件中()是正确的。
(a) (b)题3图6图示铸铁制压力机立柱的截面中d 和匕则拉杆的剪切面积是 挤压面积是50 kN9. 图示连接板中,最危险的销钉为 10, 图示连接件中,2t<6时,销钉的名义剪切应力为 名义挤压应力为二、图示悬臂梁由25b 工字钢制成,受图示荷载作用。
已知g=3kN/m, F=7kN, /=3m, [o]=170MPa,试校核其强度。
三、图示传动轴 P1=4.5KN, P2=4KN, P3=13.5KN, P4=5.2KN, Df=100mm, d=50mm,许用应(D)8.已知图示拉杆尺寸D, 题9图300 500 200力[cr] = 300MPa 。
试求:(1)画轴的受力简图;(2)做内力图(弯矩图和扭矩图, 并且内力图需与受力位置相对应);(3)分别按第三、第四强度理论校核轴的强度。
四、图示圆轴直径 d=20mm,已知 ml=0.1KN.m, m2=0.2KN.m, m3=0.3KN.m, P=10KN,试求 轴内危险截面的主应力和最大剪应力,若材料许用应力[b] = 170MPa,按第三、第四 强度理论校核该轴的强度。
(要求画单元体)五、托架如图,已知AB 为矩形截血梁,宽度b=20mm, h=40mm,杆cd 为圆管,外径D=30mm,Z?内径d=24mm,材料的[a] = 1 60MPa,按强度要求计算该结构的许用载荷[q].(注, 杆cd 不考虑稳定性问题,只考虑强度问题),0.6m q六、图示圆截面杆受力P 和力偶m 的联合作用,今测得A 点轴向应变£o =4x10^, B 点与母线成45°方向应变句5 =3.75x101。
第八章组合变形及连接部分的计算-资料

z
tg Iy tg
Iz
M
y
(2) 对于圆形、正方形等截面 Iy=Iz ,所以有 = 。
z
tg Iy tg
Iz
M
y
梁发生平面弯曲,正应力可用合成弯矩 M 按正应力计算公式计算
z
tg Iy tg
Iz
M
y
梁的挠曲线一般仍是一条空间曲线,故梁的扰曲线方程仍应分别 按两垂直面内的弯曲来计算,不能直接用合成弯矩进行计算。
四、 强度分析
中性轴
作平行于中性轴的两直线分别与
D1 z
o
横截面周边相切于 D1 、D2两点
,D1 、D2 两点分别为横截面上
最大拉应力点和最大压应力点。
D2
y
D1
D1
oz
D2
y
中性轴
z o
D2
y
中性轴
对于矩形、工字形等有两个相互垂直的对称轴的截面梁横截面的
最大正应力发生在截面的棱角处。 可根据梁的变形情况,直接确定截面上最大拉,压应力点的
x
P1
m
x
y
m
z x
My
m
y
P1 在 m—m 面内产生的弯矩为 My = P1 x (使梁在 XZ 平面内弯曲,y 为中性轴)
P2 a
m
z
x
P1
m
x
y
m
MZ z x
My
m
y
P2 在 m—m 面内产生的弯矩为 MZ = P2 (x-a) (使梁在 XY 平面内弯曲,z 为中性轴)
二 、 梁横截面上的应力分析 (任意点 C(y, z) 的正应力)
材料力学(I)第八章 组合变形及连接部分的计算

同,故可将同一截面上的弯矩Mz和My按矢量相加。 例如,B截面上的弯矩
sb
12
M max Fl 。 W 4W
材 料 力 学 Ⅰ 电 子 教 案
第八章 组合变形及连接部分的计算
在FN 和Mmax共同作用下,危险 截面上正应力沿高度的变化随sb和st
ห้องสมุดไป่ตู้
的值的相对大小可能有图d ,e ,f 三种
情况。危险截面上的最大正应力是拉 应力:
s t ,max
Ft Fl A 4W
可见此杆产生弯一压组合变形。现按大刚度杆来计算应力。
15
材 料 力 学 Ⅰ 电 子 教 案
第八章 组合变形及连接部分的计算
2. AC杆危险截面m-m上的最大拉应力st,max和最大压应力
sc,max分别在下边缘f点处和上边缘g点处(图b):
s t ,max
F M FN M max 或 s c ,max N max A W A W
强度条件为
26
s r 3 [s ] 或
s r 4 [s ]
材 料 力 学 Ⅰ 电 子 教 案
第八章 组合变形及连接部分的计算
究竟按哪个强度理论计算相当应力,在不同设计规范中并不
一致。注意到发生扭-弯变形的圆截面杆,其危险截面上危 险点处:
M W
s
T T Wp 2W
2 2
为便于工程应用,将上式代入式(a),(b)可得:
(a)
3. 根据钢管的横截面尺寸算得:
π 2 [ D ( D 2d ) 2 ] 4 40.8 10 4 m 2 π I [ D 4 ( D 2d ) 4 ] 64 868108 m 4 I W 124 10 6 m3 D/2 A
第八章_组合变形与连接件的实用计算

y
z
10
A bh 50106 m2
Wy
1 6
b2h
1 6
52
10 10 9
4.17 10 8 m3
Wz
1 6
bh2
1 6
510 2
10 9
8.33 10 8 m3
5
危险点在切槽截 max
FN A
My Wy
Mz Wz
面的左上角。
1000 5105
x
max
My Wy
Mz Wz
F1
6 F1 2L 6 F2L
hb2
bh2
L
L
y
1、内力分析 2、应力分析 3、强度计算
max
9.979MPa
max
9.979MPa
§8-3 拉伸(或压缩)与弯曲
Ⅰ.横向力与轴向力共同作用
一、受力特点
作用在杆件上的外力既有轴向拉( 压 )力,
还有横向力
F1
F1 产生弯曲变形 F2
F2
F2 产生拉伸变形
二、变形特点 杆件将发生拉伸 (压缩 ) 与弯曲组合变形
三、内力分析 横截面上内力
1、拉(压) :轴力 FN
2、弯曲
弯矩 MZ 剪力 FS
MZ z
0
x
FN
y
因为引起的剪应力较小,故一般不考虑。
四、应力分析
横截面上任意一点 ( z, y) 处的
正应力计算公式为
1 、拉伸正应力
' FN
A
2、弯曲正应力
'' Mz y
第8章组合变形及连接部分的计算(答案)

第8章组合变形及连接部分的计算(答案)8.1梁的截⾯为2100100mm ?的正⽅形,若kN P30=。
试作轴⼒解:求得约束反⼒24Ax F KN =,9Ay F KN =,9B F KN =为压弯组合变形,弯矩图、轴⼒图如右图所⽰可知危险截⾯为C 截⾯最⼤拉应⼒maxmax 67.5ZM MPa W σ== 最⼤压应⼒max max69.9N Z M FMPa W Aσ=+=8.2若轴向受压正⽅形截⾯短柱的中间开⼀切槽,其⾯积为原来⾯积的⼀半,问最⼤压应⼒增⼤⼏倍?解:如图,挖槽后为压弯组合变形挖槽前最⼤压应⼒挖槽后最⼤压应⼒22222286/)2/(4/2/a P a a Pa a P W M A N c =+=+=σ8//82212==a P a P c c σσ211a P A N c ==σ8.3外悬式起重机,由矩形梁AB (2=bh尺⼨。
解:吊车位于梁中部的时候最危险,受⼒如图解得BC F P =,2Ax F P =,2Ay P F =梁为压弯组合变形,危险截⾯为梁中N F =压),4PL M =(上压下拉)[]max4NZ F PL W A σσ=+≤,代⼊()226Z b b W =,A bh =,由2h b = 解得125b mm =, 250h mm =8.4图⽰为⼀⽪带轮轴(1T 、2T 与3T 相互垂直)。
已知1T 和2T 均为kN 5.1,1、2轮的直径均为mm 300,3轮的直径为mm 450,轴的直径为mm 60。
若M P a 80][=σ,试按第三强度理论校核该轴。
解:由已知条件解得32T KN = 内⼒图如右:最⼤弯矩所在截⾯可能为:1C M KN m ==?1.2D M KN m =?故危险截⾯为D 截⾯32T KN =由第三强度理论[]360r MPa σσ==故安全38.5铁道路标圆信号板装在外径mm D 60=的空⼼圆柱上,若信号板上所受的最⼤风载2/2m kN p =,MPa 60][=σ,试按第三强度理论选择空⼼柱的厚度。
第八章组合变形习题集

8-2 人字架及承受的荷载如图所示。
试求m-m 截面上的最大正应力和A 点的正应力。
m解:(1)外力分析,判变形。
由对称性可知,A 、C 两处的约束反力为P/2 ,主动力、约束反力均在在纵向对称面内,简支折将发生压弯组合变形。
引起弯曲的分力沿y 轴,中性轴z 过形心与对称轴y 轴垂直。
截面关于y 轴对称,形心及惯性矩1122123122328444A A 20010050200100(100100)125A +A 200100+200100200100200100(12550)12100200100200(300125100)123.0810 3.0810C z zzy y y I I I -+⨯⨯+⨯⨯+===⨯⨯⨯=+=+⨯⨯-⨯++⨯⨯--=⨯=⨯mmmm m(2)内力分析,判危险面:沿距B 端300毫米的m-m 横截面将人字架切开,取由左边部分为研究对象,受力如图所示。
梁上各横截面上轴力为常数:,m-m 250(1.80.3sin )(1.80.3202.5(k 22250cos =100(k )22y N P M P F ϕϕ=⨯-=⨯-=⋅=⨯=N m)N(3)应力分析,判危险点,如右所示图①m-m 截面上边缘既有比下边缘较大的弯曲压应力,还有轴力应力的压应力,故该面上边缘是出现最大压应力。
m mmax33410010202.510(0.30.125)(Pa) 2.5115.06MPa 117.56MPa 2(0.20.1) 3.0810N zF M y A I σ---=+⋅-⨯⨯=-⨯-=--=-⨯⨯⨯上② A 点是压缩区的点,故m m33410010202.510(0.30.1250.1)(Pa) 2.549.31MPa 51.83MPa 2(0.20.1) 3.0810N a a zF M y A I σ--=+⋅-⨯⨯=-⨯--=--=-⨯⨯⨯注意:最大拉应力出现在下边缘m mmax33410010202.5100.125(Pa) 2.582.18MPa 79.68MPa2(0.20.1) 3.0810N zF M y A I σ---=+⋅-⨯⨯=+⨯=-+=⨯⨯⨯下8-3 图示起重机的最大起吊重量为W=35kN ,横梁AC 由两根NO.18槽钢组成。
武汉理工大学材料力学课件8 组合变形及连接部分的计算--JK

若横截面周边具有棱角,则无需确定中性轴的位置,直 接根据梁的变形情况,确定最大拉应力和最大压应力点 的位置。 D D
1 1
z
z D2 y 中性轴
D2
y
中性轴
强度条件:
()若 [ t ] [ c ] [ ], 则 1 (2)若 [ t ] [ c ], 则
t ,max [ t ] ,
z
c ,max
FN M max [ c ] A Wz
(1)若F 的作用点在杆的一对称轴上, F M 则强度条件为: [ t ] t , max A Wz 其中 M Fe
c ,max
F M [ c ] A Wz
23
(2) 若F 的作用点不在杆的任一对称轴上
FN My A Iz
z
c ,max
(2)若 t ] [ c ] [ ] , [
则
FN M max [ c ] A Wz
max Max { t ,max , c ,max } [ ]
20
[例8-3-1] 最大吊重为 P=20kN的简易吊车,如图所 示,AB为工字A3钢梁,许用应力[σ]=100MPa,试选 T YA 择工字梁型号。 Ty XA D
另外, 和 的正负号可由My和 Mz引起的变形是拉 8 还是压直接判断。
sin cos 则,F引起的应力为: M ( I z I y) y z
二、中性轴的位置 令(y0,z0)是中性轴上任一点,则有: 显然,中性轴是一条通过坐标原点的直线, 设其与z轴的夹角为α,则有:
A Tx
C
B F
A
30° 2m
C
1m
组合变形习题讲解[1]
![组合变形习题讲解[1]](https://img.taocdn.com/s3/m/db62dabd1a37f111f1855b16.png)
第八章 组合变形习题讲解【习题5-29】解:矩形截面木榫头在力F 作用下可能发生挤压、剪切、横截面强度破坏,因此应分别满足这三方面的强度条件。
(1)挤压强度校核挤压面:BC 面,挤压面积:0.25b s A a=;挤压力:50b sF F k N==于是有,35010[]0.25b s b sb s b sF A a σσ⨯==≤⨯ 则20a m m≥(2)剪切强度校核剪切面:BE 和CD 面,剪切面积:0.25sA l=;剪切力:50sF F k N==于是有,35010[]0.25s ssF A l στ⨯==≤⨯则 200l m m ≥ (3)横截面强度校核1-1截面(如图(a )所示):由于只有轴力150N k N=,所以按照轴向拉压强度条件进行强度校核。
即:31115010[](2)0.25t N A a c σσ⨯==≤+⨯则 233.3a c m m+≥。
2-2截面:截面上存在轴力250N k N=,弯矩0.5()M F a c =+,所以应按照组合变形(偏心拉伸)来考虑。
根据2-2截面上的内力分量可知:危险点位于该截面的下边缘,应力为:题 5-29 图(a )题 5-29 图(b )233222250100.55010()[]10.250.256t N M a c A Wccσσ⨯⨯⨯⨯+=+=+≤⨯⨯⨯则146.9c m m≥【习题5-32】解:(1)外力分析以ABC 横梁为研究对象,受力图如图所示(a )。
列静力平衡方程()00.1120A B D x B D y M F F F F =⨯+⨯-⨯=∑其中,B D xB D yF F =。
则27.272B D xB D y F F k N==绘制ABC 横梁的受力简图如图(b )所示。
其中0.1 2.7272B D x M F k N m=⨯=⋅(2)内力分析根据横梁上作用的载荷可知,AE 段发生弯曲与拉伸的组合变形,EC 段发生平面弯曲变形。
08组合变形及连接件的计算

2 2
M2 T2 W
强度条件: r 3
M 2 T2 W
§8-4 扭转与弯曲
σ
M W
T Wt
W
d3
32
, Wt
2
d3
16
τ
主应力
1
2 2 2
C1
F
B
T
M
C1 C2
τ
σ C2
τ
σ
§8-4 扭转与弯曲
C1
τ
σ
τ
2
σ
M W
W
d3
32
3
, Wt
T Wt d3
16
2
主应力
1
2 2 2
2 0
2 2 2
第三强度理论相当应力:
r3 1 3 2 4 2
强度条件: r 4
M 2 0.75T 2 W
§8-4 扭转与弯曲
圆截面杆弯扭组合变形时的相当应力:
M T r3 W
2 2
r4
M 0.75T W
2 2
Fa t F M F 2 4 2 a c A W a a 2 2 6
8F a2 4F 2 a
m M=Fa/4 F
m
F a a/2 a/2
§8-3 拉伸(压缩)与弯曲
铸铁压力机框架,立柱横截面尺寸如图所示,材料的许 用拉应力[t]=30MPa,许用压应力[c]=120MPa。试按 立柱的强度计算许可载荷F。解:(1)计算横截面的形 心、面积、惯性矩
《材料力学》第8章-组合变形及连接部分的计算-习题解教学教材
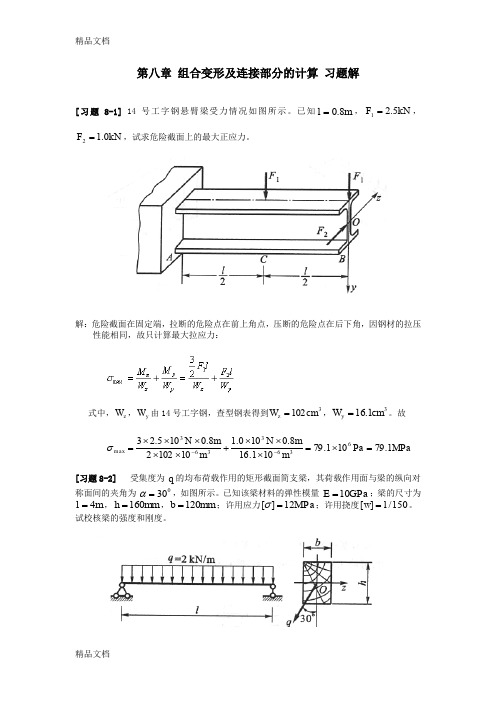
第八章 组合变形及连接部分的计算 习题解[习题8-1] 14号工字钢悬臂梁受力情况如图所示。
已知m l 8.0=,kN F 5.21=,kN F 0.12=,试求危险截面上的最大正应力。
解:危险截面在固定端,拉断的危险点在前上角点,压断的危险点在后下角,因钢材的拉压性能相同,故只计算最大拉应力:式中,z W ,y W 由14号工字钢,查型钢表得到3102cm W z =,31.16cm W y =。
故MPa Pa mm N m m N 1.79101.79101.168.0100.11010228.0105.236363363max=⨯=⨯⨯⨯+⨯⨯⨯⨯⨯=--σ [习题8-2] 受集度为 q 的均布荷载作用的矩形截面简支梁,其荷载作用面与梁的纵向对称面间的夹角为 030=α,如图所示。
已知该梁材料的弹性模量 GPa E 10=;梁的尺寸为m l 4=,mm h 160=,mm b 120=;许用应力MPa 12][=σ;许用挠度150/][l w =。
试校核梁的强度和刚度。
解:(1)强度校核)/(732.1866.0230cos 0m kN q q y =⨯== (正y 方向↓))/(15.0230sin 0m kN q q z =⨯== (负z 方向←))(464.34732.1818122m kN l q M y zmaz ⋅=⨯⨯== 出现在跨中截面)(241818122m kN l q M z ymaz ⋅=⨯⨯== 出现在跨中截面)(5120001601206161322mm bh W z =⨯⨯==)(3840001201606161322mm hb W y =⨯⨯==最大拉应力出现在左下角点上:yy z z W M W M maxmax max +=σ MPa mmmm N mm mm N 974.1138400010251200010464.33636max=⋅⨯+⋅⨯=σ因为 MPa 974.11max =σ,MPa 12][=σ,即:][max σσ<所以 满足正应力强度条件,即不会拉断或压断,亦即强度上是安全的。
材料力学第八章组合变形及连接部分的计算

二、叠加原理
构件在小变形和服从胡克定律的条件下,力 的独立性原理是成立的。即所有载荷作用下的内 力、应力、应变等是各个单独载荷作用下的值的 叠加。
解决组合变形的基本方法是将其分解为几种基 本变形;分别考虑各个基本变形时构件的内力、应 力、应变等;最后进行叠加。
§8–1 两相互垂直平面内的弯曲
的强度计算许可载荷F。
解:(1)计算横截面的形心、
面积、惯性矩
F 350
F 350
A 15000mm2
F
M
z0 75mm
FN
y1 z0 y z1
z1 125 mm I y 5.31107 mm4 (2)立柱横截面的内力
50
FN F
150
M F350 75103
50
对圆形、正方形截面
Iy Iz
一般生产车间所用的吊车大梁,两端由钢轨支撑,可以简化为简支 梁,如图示.图中l=4m。大梁由32a热轧普通工字钢制成,许用应力 [σ]=160MPa。起吊的重物重量F=80kN,且作用在梁的中点, 作用线与y轴之间的夹角α=5°,试校核吊车大梁的强度是否安全。
F2
M y F1 2L
z
Mz F2 L
x
max
My Mz Wy Wz
F1
6 F1 2L 6 F2L
L
L
y
b2h
bh2
t,max 9.979MPa
c,max 9.979MPa
§8.3 拉伸或压缩与弯曲的组合
一、横向力与ቤተ መጻሕፍቲ ባይዱ向力共同作用
=+
10-3
t ,max
=
c,max
材料力学第八章组合变形

0.456qa2 0.383qa2
弯矩图 (z轴为中性轴)
A DC 0.444qa2 0.321qa2
B My图 z轴往下
在xoz主轴平面内的 弯矩图(y轴为中性轴)
0.266qa2
0.642qa2
材料力学
中南大学土木工程学院
26
横截面在xoz、 xoy平面的弯曲截面系数,可查表得
W z 2 3 7 1 0 6 m 3 W y 3 1 .5 1 0 6 m 3
解:图中所有外荷载虽在同一平 面但并不位于梁的形心主惯性平 面内,所以是斜弯曲。将均布荷 载q向形心主惯性轴分解为
qy=qcos ,qz=qsin
在檩条跨中处弯矩最大,其值为
M z m a x 1 8 q y l2 1 8 q l2 c o s M y m a x 1 8 q z l2 1 8 q l2 s in
40.810.88 16066m348.280.35106m317.80MPa[]160MPa
材料力学
中南大学土木工程学院
30
可见选25a工字钢不能满足强度条件,于是再改选大一号的25b工字钢。 由附录查得查得25b工字钢的Wz=422.72cm3,Wy=52.423 cm3,自重 q1=0.41KN/m。所以,强度条件为
12
键 连 接
M
材料力学
中南大学土木工程学院
13
木榫接头
F
材料力学
m
m
c
n
n
l
l
中南大学土木工程学院
F
14
榫齿 连接
材料力学
中南大学土木工程学院
15
§8.2 相互垂直平面内的弯曲-斜弯曲
结构力学 第八章
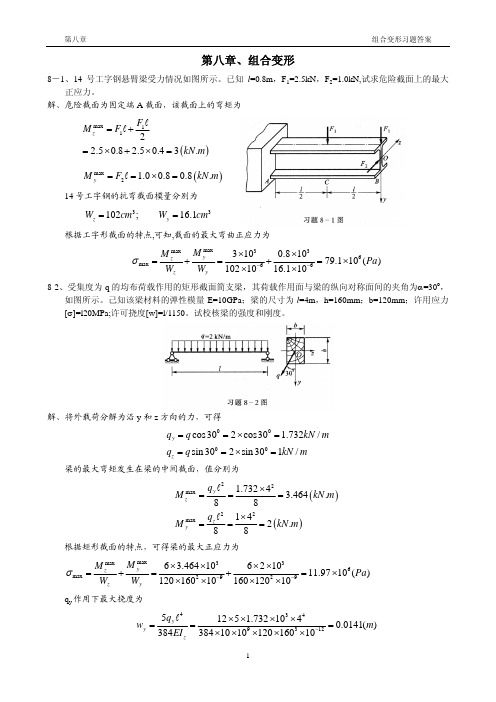
根据工字形截面的特点,可知,截面的最大弯曲正应力为
σ max
8-2、受集度为 q 的均布荷载作用的矩形截面简支梁,其荷载作用面与梁的纵向对称面间的夹角为α=30o, 如图所示。己知该梁材料的弹性模量 E=10GPa;梁的尺寸为 l=4m,h=160mm;b=120mm;许用应力 [σ]=l20MPa;许可挠度[w]=l/1150。试校核梁的强度和刚度。
max My = F2 l = 1.0 × 0.8 = 0.8 ( kN .m )
14 号工字钢的抗弯截面模量分别为
Wz = 102cm3 ;
Wy = 16.1cm3
max 3 × 103 0.8 ×103 M zmax M y = + = + = 79.1× 106 ( Pa ) −6 −6 102 × 10 16.1×10 Wz Wy
8-10、受拉构件形状如图,己知截面尺寸为 40mm×5mm,承受轴向拉力 F=l2kN。现拉杆开有切口,如不 计应力集中影响,当材料的[σ]=100MPa 时,试确定切口的最大许可深度,并绘出切口截面的应力变 化图。
38MPa
100 MPa A-A 截面应力分布图
解、由于切口的存在,在切口截面载荷为偏心力,切口截面上的轴力和弯矩分别为
3 3 2⎤ ⎡1 ⎤ ⎡1 I zC = ⎢ ( 4a )( 2a ) + ( 4a )( 2a ) a 2 ⎥ + ⎢ a ( 4a ) + ( 4a )( a )( 2a ) ⎥ = 32a 4 ⎣12 ⎦ ⎣12 ⎦ 1 1 3 I yC = ( 2a )( 4a ) + ( 4a ) a 3 = 11a 4 12 12
2
, FN = qx x = qx sin α
第8章 组合变形及连接部分的计算(10)

zMz
Fy
My
目录
22
横截面上应力分析:
x
z Mz 1
FN
MZ
My
Fy 2 My
压
F A
Mz
Mz y Iz
My
Myz Iy
全 压 区 任 c 意 F A一 M Izzy 点 M Iy yz
cmaxF AW Mzz W Myy
弯曲全 t F A 拉 M Iz 区 zyM Iy yz
tmaxF AW Mzz W Myy
σ
σ或 σ
σ
强度条件: max[]
目录
33
§8-4 扭转与弯曲
绞车的鼓轮轴
目录
34
扭转与弯曲
传动轴
目录
35
扭转与弯曲 FP
目录
36
扭转与弯曲组合变形问题的分析过程
1、分析外力、内力及应力
l
Fa
F
S
a
Fa
T
(+)
Fl
M (-)
F
S平面
y
1
zT
x
2 Mz
1
τ T Wp
σ Mz Wz
2
τ T Wp
r4W 1 M 20.7T 5 2[]
只适用塑性材料的圆截面杆纯弯扭组合变形
式中W 为抗弯截面系数,M、T 为轴危险面的
弯矩和扭矩
W d 3
32
WD3 14 32
41
例题
圆杆直径为d = 0.1m,T = 7kN·m, P = 50kN,
[]=100MPa,按第三强度理论校核强度。
解:拉扭组合,危险点应力状态如图
F
F
F
材料力学第8章 组合变形

b.未通过轴线或形心主惯性轴,向其分解
注意:荷载分解、简化的前提是不改变研究段的内力。
(2)内力分析方法
用截面法计算任意截面的内力,通过内力确定变形的组成
z
Fsz My
Ty
Fsy
M z FN
FN
T
x M z , Fsy M y , Fsz
轴向拉、压 扭转 x,y面内的平面弯曲 x,z面内的平面弯曲
§8-2 两相互垂直平面内的弯曲
F sin
F cos F
(2)求B点的应力
MB FN
WA
12.32103 25103
0.1 0.22
0.1 0.2
6
B
17.23 MPa
(3)求B点30º斜截面上的正应力
300 cos2 30 17.23 cos2 30 12.99 MPa
(4)求B点的主应力
1 0 2 0 3 17.23 MPa
z
面梁,其横截面都有两个相互垂直的对称 轴,且截面的周边具有棱角,故横截面上
Mz
的最大正应力发生在截面的棱角处。于是
,可根据梁的变形情况,直接确定截面上
My
最大拉、压应力点的位置,而无需定出其
y
中性轴。
因危险点为单向应力状态(忽略弯曲切应力的影响), 故,强度条件为:
max
M y max Wy
F sin
12.32kN m
F cos F
例: 如图示一矩形截面折杆,已知F=50kN,尺寸如图所示, α=30°。(1)求B点横截面上的应力;(2)求B点α=30°截
面上的正应力;(3)求B点的主应力σ1、 σ2、 σ3。
FN
B
MB 100mm
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习 题[8-1] 14号工字钢悬臂梁受力情况如图所示。
已知m l 8.0=,kN F 5.21=,kN F 0.12=,试求危险截面上的最大正应力。
解:危险截面在固定端,拉断的危险点在前上角点,压断的危险点在后下角,因钢材的拉压性能相同,故只计算最大拉应力:yz yyz zW l F W lF lF W M W M 211max 2++⋅=+=σ式中,z W ,y W 由14号工字钢,查型钢表得到3102cm W z =,31.16cm W y =。
故MPa Pa mm N m m N 1.79101.79101.168.0100.11010228.0105.236363363max=⨯=⨯⨯⨯+⨯⨯⨯⨯⨯=--σ [8-2] 矩形截面木檩条的跨度m l 4=,荷载及截面尺寸如图所示,木材为杉木,弯曲许用正应力MPa 12][=σ,GPa E 9=,许可挠度200/][l w =。
试校核檩条的强度和刚度。
图习题⋅-28解:(1)受力分析)/(431.13426cos 6.1cos '0m kN q q y ===α )/(716.03426sin 6.1sin '0m kN q q z ===α(2)内力分析)(432.14716.0818122max ,m kN l q M z y ⋅=⨯⨯===)(864.24432.1818122max ,m kN l q M y z ⋅=⨯⨯===(3)应力分析最大的拉应力出现在跨中截面的右上角点,最大压应力出现在左下角点。
zz yy W M W M max ,max ,max +=+σ式中,32232266*********mm hb W y ≈⨯== 32246933361601106mm bh W z ≈⨯== MPa mm mm N mm mm N 54.1046933310864.232266710432.13636max=⋅⨯+⋅⨯=+σ(4)强度分析因为MPa 54.10max =+σ,MPa 12][=σ,即][max σσ<+,所以杉木的强度足够。
(5)变形分析最大挠度出现在跨中,查表得:z y cy EI l q w 38454=,yz cz EI l q w 38454=式中,)(177466671211016012433mm hb I y ≈⨯== 433375466671216011012mm bh I z ≈⨯== mm mm mm N mm mm N EI l q w z y cy 12.1437546667/1093844000/431.153845423444≈⨯⨯⨯⨯⨯==mm mm mm N mm mm N EI l q w y z cz .94.1417746667/1093844000/716.053845423444≈⨯⨯⨯⨯⨯==)(56.2094.1412.142222mm w w w cz cy c ≈+=+=(6)刚度分析因为)(56.20max mm w w c ==,)(202004000200][mm l w ===,即][max w w >,所以,从理论上讲,变形过大,不符合刚度要求。
但是,因为%5%8.2202056.20][][max <=-=-w w w ,所以从工程的角度来说,误差在允许的范围,所以可以认为刚度符合要求,不需重新设计杉木的截面尺寸。
[8-5] 砖砌烟囱高m h 30=,底截面m m -的外径m d 31=,内径m d 22=,自重kN P 20001=,受m kN q /1=的风力作用。
试求:(1)烟囱底截面上的最大压应力;(2)若烟囱的基础埋深m h 40=,基础及填土自重按kN P 10001=计算,土壤的许用压应力MPa 3.0][=σ,圆形基础的直径D 应为多大?注:计算风力时,可略去烟囱直径的变化,把它看作是等截面的。
解:烟囱底截面上的最大压应力:==土壤上的最大压应力 :即即解得:m[8-6] 一弓形夹紧器如图所示。
弓形架的长度mm l 1501=,偏心距mm e 60=,截面为矩形mm mm h b 2010⨯=⨯,弹性模量GPa E 2001=。
螺杆的长度mm l 1002=,直径mm d 82=,弹性模量GPa E 2202=。
工件的长度mm l 403=,直径mm d 103=,弹性模量GPa E 1803=。
当螺杆与工件接触后,再将螺杆旋进mm 0.1以村紧工件。
试求弓形架内的最大正应力,以及弓形架两端A 、B 间的相对位移AB δ。
图习题⋅-68AB弓形架F螺杆工件受力分析图解:(1)求弓形架内的最大正应力这是一次超静定问题。
变形协调方程为: δδδδ=++32AB ...... (a) 物理方程为2222A E l F l ⋅=∆3333A E l F l ⋅=∆; e I E l Fe A E Fl I E Fe yy AB⋅++⨯=1111113)(23δ。
......(b) 其中AB δ可用叠加法求解。
其求解过程如图所示。
A B弓形架BAB3yI E Fe 133++=e I E l Fe y⋅11)(在弯矩作用下A 、B 两点的相对位移,可由简支梁CD (支座反力为0)查表求得:y y y D C MAB I E Fel e I E l Fe e I E l Fe e e C1311111,263=⋅⋅+⋅=⋅+⋅=θθδ (↓↑) y y y D D MAB I E Fel e I E l Fe e I E l Fe e e D1311111,263=⋅⋅+⋅=⋅+⋅=θθδ (↓↑) e EI Fle EI Fl e EI Fl y y y M AB M AB M AB DC⋅=⋅+⋅=∆+∆=111,,,22δ(↓↑) (b)代入(a)得:δ=++⋅++⨯3332221111113)(23A E Fl A E Fl e I E l Fe A E Fl I E Fe y yδ=++++F A E l A E l I E l e A E l I E e y y )32(33322211211113δ13331222112113)32(E F A E l E A E l E I l e A l I e y y =++++ δ13331222112113)3332(E F A E l E A E l E I l e A l I e y y =++++ δ13331222112311)332(E F A E l E A E l E I l e e A l y =++++ δ1333122211211]3)32([E F A l E E A l E E I l e e A l y =⋅+⋅+++33312221121113)32(A l E E A l E E I l e e A l E F y ⋅+⋅+++=δ式中,)(103220101211214433mm bh I y ⨯=⨯⨯==22224422223514.340180200414.310022020010323)1503602(602001501/10200mm mmmm mm mm mm mm mm mm mmmm N F ⨯⋅+⨯⋅+⨯⨯⨯+⨯+⨯⨯=N 1894=弓形架内的最大正应力是拉应力,出现在横截面的左边缘。
yyt W M A F +=max ,σ )61(62max ,h e bh F bh Fe bh F t +=+=σ )206061(201018942mm mmmm N ⨯+⨯=MPa 93.179= MPa 180≈e I E l Fe A E Fl I E Fe y y AB ⋅++⨯=1111113)(23δ y y ABI E l Fe A E Fl I E Fe 112111133332++=δ 1111123332A E Fl I E l Fe Fe y AB ++=δ1111123)32(A E Fl I E l e Fe y AB++=δ 223442322200/1020015018941032/102003)1503602(601894mm mm N mm N mmmm N mm mm N AB⨯⨯⨯+⨯⨯⨯⨯⨯+⨯⨯⨯=δmm 9787.0≈ mm 98.0≈DA CBF AyF AzF ByF BzF P P15.0F5.0zxyP15.0DAC B图⋅T P15.0P12.0P06.0C BA DyM zM O[8-14] 一手摇绞车如图所示。
已知轴的直径mm d 25=,材料为Q235钢,其许用应力MPa 80][=σ。
试用第四强度理论求绞车的最大起吊重量P 。
解:轴是弯扭组合变形构件。
把外力向轴平移后得如图所示的受力图。
支座反力P F F Bz Az 5.0==P F 15.05.0=P F 3.0=在xoy 平面内,0=∑B M 06.01=⨯-⨯Ay F F 06.03.0=⨯-Ay F P P F Ay 5.0= 0=∑y F 0=-+Ay By F F FP F P F F F Ay By 2.03.05.0=-=-=轴的扭矩图与弯矩图如图所示。
从内力图可知,C 截面是危险截面。
由第四强度理论可得:][32/75.0)(75.03322222224σπτσσ≤++=+=+=d T M M W T M z y r 63222108032/025.014.3)15.0(75.0)06.0()15.0(⨯≤⨯⨯++P P P63222108032/025.014.3)15.0(75.0)06.0()15.0(⨯≤⨯⨯++P P P661080105332.12073.0⨯=⨯-P )(59.0)(684.591kN N P ≈=⊗•F FmmD 60=mma 5=55BC D αRzTz y55[8-17] 边长mm a 5=的正方形截面的弹簧垫圈,外圈的直径mm D 60=。
在开口处承受一对铅垂力F 作用,如图所示。
垫圈材料的许用应力MPa 300][=σ,试按第三强度理论,计算垫圈的许可荷载。
解:垫圈任一横截面上的内力有:αsin PR M = (下侧受力) )cos 1(α--=PR T)(5.27)5060(41)(41)22(212mm d D d D d R =+=+=-+=当0180=α时,0=M ,PR T 2-=0=σ,2max hbTατ=。
由15/5/==b h 查表得:208.0=α。
于是1953max105208.0105.272P --⨯⨯⨯⨯=τ (下边缘中点处的切应力) ][)105208.055(4042631223στσσ≤⨯⨯⨯+=+=P r6611030010125208.0552⨯≤⨯⨯⨯P30025104.0111≤⨯P)(91.701125104.03001N P =⨯⨯≤当090=α时,PR M =,PR T -=26292321032.11055105.2766P P bh M W M z ⨯=⨯⨯⨯⨯===--σ (下边缘的正应力) 262953max10058.1105208.0105.27P P ⨯≈⨯⨯⨯=--τ (下边缘中点处的切应力) ][)10058.1(4)1032.1(4226226223στσσ≤⨯⨯+⨯=+=P P r622622610300)10058.1(4)1032.1(⨯≤⨯⨯+⨯P P6261030010692.1⨯≤⨯P 6261030010692.1⨯≤⨯P)(3.1772N P ≤从上以计算可知,垫圈的许可荷载由0180=α截面的内力条件决定,)(91.70][N P =[8-18] 直径mm d 20=的折杆,A 、D 两端固定支承,并使折杆ABCD 保持水平(B 、C 为直角),在BC 中点E 处承受铅垂荷载F ,如图所示。
