高一数学数列专项测试及答案
高一必修数列测试题及答案详解高一数学

高一必修数列测试题及答案详解高一数学一、填空题1. 若\[a_n = 2n - 1\],则数列\[\{a_n\}\]的前5项分别为\[1, 3, 5, 7, 9\]。
2. 若\[b_n = 3^n\],则数列\[\{b_n\}\]的前4项分别为\[3, 9, 27, 81\]。
3. 若\[c_n = \frac{n(n+1)}{2}\],则数列\[\{c_n\}\]的前6项分别为\[1, 3, 6, 10, 15, 21\]。
二、选择题1. 以下是等差数列的是(B)。
A. 1, 2, 4, 7, 11B. 2, 4, 8, 16, 32C. 1, 3, 6, 10, 15D. 3, 8, 15, 24, 352. 若\[a_1=2\],\[a_2=5\],则\[a_3=8\),\[a_4=11\),则\(a_n\)的通项公式是(C)。
A. \(a_n=2n+1\)B. \(a_n=3n-1\)C. \(a_n=3n-1\)D. \(a_n=2n+4\)3. 若对于等差数列\(\{a_n\}\)有\(\frac{{a_5 - a_2}}{7}=3\),则\(d=\)(A)。
A. 1B. 2C. 3D. 4三、解答题1. 求等差数列\(\{a_n\}\)的前5项之和,已知\(a_1=1\),\(a_3=7\)。
(解答略)2. 若等差数列\(\{a_n\}\)的首项为-3,公差为4,求该数列的第n项和。
\({S_n}=\)(解答略)3. 若等差数列\(\{a_n\}\)的首项为2,公差为3,已知\(\frac{{a_m+a_n}}{2}=13\),求\(m\)与\(n\)的值。
(解答略)四、解题思路详解1. 填空题1解析:根据数列通项公式\[a_n = 2n - 1\],带入\[n=1,2,3,4,5\],即可得到\[a_n\]的前5项。
2. 填空题2解析:根据数列通项公式\[b_n=3^n\],带入\[n=1,2,3,4\],即可得到\[b_n\]的前4项。
高一数学数列练习题含答案

一、选择题:1、等差数列9}{,7,3,}{51第则数列中n n a a a a ==项等于( C ) A 、9 B 、10 C 、11 D 、122、等比数列{}n a 中, ,243,952==a a 则{}n a 的第4项为( A ) A 、81 B 、243 C 、27 D 、1923、已知一等差数列的前三项依次为34,22,++x x x ,那么22是此数列的第( D )项 A 、2 B 、4 C 、6 D 、84、已知等差数列{a n }中,a 7+a 9=16,a 4=1,则a 12的值是( A )A 、15B 、30C 、31D 、645、设等差数列{}n a 的前n 项和为n S ,若39S =,636S =,则789a a a ++=( B )A 、63B 、45C 、36D 、276、已知m 和2n 的等差中项是4,2m 和n 的等差中项是5,则m 和n 的等差中项是( B )A 、2B 、3C 、6D 、97、在等差数列{}n a 中,若4681012120a a a a a ++++=,则10122a a -的值为( C ) A 、20 B 、22 C 、24 D 、288、已知等差数列{a n }满足56a a +=28,则其前10项之和为 ( A )A 、140B 、280C 、168D 、569、等差数列{a n }共有2n+1项,其中奇数项之和为4,偶数项之和为3,则n 的值是( A )A 、3B 、5C 、7D 、910、在数列{a n }中,对任意n ∈N *,都有a n +1-2a n =0(a n ≠0),则2a 1+a 22a 3+a 4等于( D )A 、1B 、12C 、13D 、1411、在各项均为正数的等比数列{a n }中,若a 5a 6=9,则log 3a 1+log 3a 2+…+log 3a 10等于( B )A 、12B 、10C 、8D 、2+log 35 12、设数列{n a }的通项公式是1002+=n na n ,则{n a }中最大项是( B )A.9aB.10aC.9a 和10aD.8a 和9a 二、填空题:13、数列{n a }是等差数列,47a =,则7s =_________4914、已知数列{n a }的前n 项和210n S n n =-+,则其通项n a =211n -+;当n = 5 时n S 最大,且最大值为 2515、已知数列{a n }满足a 1=1,a n +1=a n 1+a n ,则a 5=_______1516、已知数列{}n a 满足123n n a a -=+且11a =,则数列{}n a 的通项公式为__________123n n a +=-三、解答题:17、设{}n a 为等差数列,{}n b 为等比数列,,,,134234211a b b b a a b a ==+==分别求出{}n a 及{}n b 的前10项的和1010T S 及.解:设等差数列{}n a 的公差为,d 等比数列{}n b 的公比为q . d q q b d a d a 42,,31,122342+=∴=+=+= ①又,,21,,2333342b a d a q b q b =+=== d q 214+=∴ ② 则由①,②得242q q =-.22,21,02±==∴≠q q q 将212=q 代入①,得855,8310-=∴-=S d当22=q 时,)22(323110+=T , 当22-=q 时,)22(323110-=T 18、等差数列{a n }的各项均为正数,a 1=3,前n 项和为S n ,{b n }为等比数列,b 1=1,且b 2S 2=64,b 3S 3=960.(1)求a n 与b n ;(2)证明:1S 1+1S 2+…+1S n <34.解 (1)设{a n }的公差为d ,{b n }的公比为q ,则d >0,q ≠0,a n =3+(n -1)d ,b n =q n -1,依题意有⎩⎪⎨⎪⎧b 2S 2=6+d q =64,b 3S 3=9+3d q 2=960.解得⎩⎪⎨⎪⎧d =2,q =8,或⎩⎪⎨⎪⎧d =-65,q =403,(舍去).故a n =2n +1,b n =8n -1.(2)证明:由(1)知S n =3+2n +12×n =n (n +2),1S n =1nn +2=12⎝ ⎛⎭⎪⎫1n -1n +2, ∴1S 1+1S 2+…+1S n =11×3+12×4+13×5+…+1n n +2=12⎝ ⎛⎭⎪⎫1-13+12-14+13-15+…+1n -1n +2=12⎝ ⎛⎭⎪⎫1+12-1n +1-1n +2=34-2n +32n +1n +2∵2n +32n +1n +2>0∴1S 1+1S 2+…+1S n <34. 19、已知数列{a n }的前n 项和为S n ,且S n =2n 2+n ,n ∈N *,数列{b n }满足a n =4log 2b n +3,n ∈N *. (1)求a n ,b n ;(2)求数列{a n ·b n }的前n 项和T n .解 (1)由S n =2n 2+n ,得当n =1时,a 1=S 1=3; 当n ≥2时,a n =S n -S n -1=4n -1.∴a n =4n -1(n ∈N *). 由a n =4log 2b n +3=4n -1,得b n =2n -1(n ∈N *).(2)由(1)知a n ·b n =(4n -1)·2n -1,n ∈N *,∴T n =3+7×2+11×22+…+(4n -1)×2n -1,2T n =3×2+7×22+…+(4n -5)×2n -1+(4n -1)×2n.∴2T n -T n =(4n -1)×2n-[3+4(2+22+…+2n -1]=(4n -5)2n+5.故T n =(4n -5)2n+5.20、已知数列{a n }满足a 1=1,a n -2a n -1-2n -1=0(n ∈N *,n ≥2).(1)求证:数列{a n2n }是等差数列;(2)若数列{a n }的前n 项和为S n ,求S n . 解 (1)∵a n -2a n -1-2n -1=0,∴a n 2n -a n -12n -1=12,∴{a n 2n }是以12为首项,12为公差的等差数列. (2)由(1),得a n 2n =12+(n -1)×12,∴a n =n ·2n -1,∴S n =1·20+2·21+3·22+…+n ·2n -1①则2S n =1·21+2·22+3·23+…+n ·2n②①-②,得-S n =1+21+22+…+2n -1-n ·2n=1·1-2n1-2-n ·2n =2n -1-n ·2n,∴S n =(n -1)·2n +1.21、设数列{}n a 的前项n 和为n S ,若对于任意的正整数n 都有n a S n n 32-=. (1)设3n n b a =+,求证:数列{}n b 是等比数列,并求出{}n a 的通项公式。
高一数学数列练习题及答案

高一数学数列练习题及答案一、选择题1. 设数列 {an} 为等差数列,已知 a1 = 3,d = 2,求 a4 的值。
A. 4B. 5C. 6D. 72. 若数列 {bn} 的前 n 项和为 Sn = 2n^2 + 3n,求 b1 的值。
A. 3B. 4C. 5D. 63. 已知数列 {cn} 为等差数列,前 n 项和为 Sn = 3n^2 + n,求通项c3 的值。
A. 4B. 5C. 6D. 74. 数列 {dn} 的通项公式为 an = 2n^3,求第 5 项的值。
A. 200B. 250C. 300D. 3505. 若数列 {en} 的前 n 项和为 Sn = n(5n + 1),求 e1 的值。
A. 0B. 1C. 2D. 3二、填空题1. 设数列 {an} 的前 n 项和为 Sn = 3n^2 + 4n,其中 a1 = 2,则 a2 的值为 ________。
2. 已知等差数列 {bn} 的前 n 项和为 Sn = n^2 + 3n,其中 b2 = 7,则b1 的值为 ________。
3. 若数列 {cn} 的通项公式为 cn = 2n^2 + n,则第 4 项的值为________。
4. 设数列 {dn} 的前 n 项和为 Sn = 4n + 5n^2,则 d1 的值为________。
5. 已知数列 {en} 的前 n 项和为 Sn = 2n(3n + 1),其中 e3 = 28,则e1 的值为 ________。
三、解答题1. 设等差数列 {an} 前 n 项和为 Sn,已知 a1 = 3,an = 7,求 n 的值及 Sn 的表达式。
2. 设等差数列 {bn} 前 n 项和为 Sn,已知 b1 = 1,d = 5,求 n 的值及 Sn 的表达式。
3. 已知等差数列 {cn} 的通项公式为 cn = an - 2n,前 n 项和为 Sn = 3n^2 + 2n,求 a1 的值。
高一数学数列试题答案及解析

高一数学数列试题答案及解析1.(本小题满分12分)已知数列{an }满足 a1=1,an+1=.,写出它的前5项,并归纳出数列的一个通项公式(不要求证明)【答案】解:∵a1=1,an+1=,∴a2==, a3==, a4==, a5==.∴它的前5项依次是1,,,,…………………….8分故它的一个通项公式为an=. (12)【解析】略2.设数列的首项,则【答案】【解析】略3.在等差数列中,公差,这三项构成等比数列,则公比【答案】2【解析】略4.数列满足,若,则数列的第2010项的值为()A.B.C.D.【答案】A【解析】本题考查数列通项的求法因为所以;由所以;由所以;由所以;依此可得即数列的周期为,所以所以故正确答案为5.数列满足,若,则数列的第2010项的值为()A.B.C.D.【答案】A【解析】本题考查数列通项的求法因为所以;由所以;由所以;由所以;依此可得即数列的周期为,所以所以故正确答案为6.定义:称为个正数的“均倒数”,若数列{}的前项的“均倒数”为,则数列{}的通项公式为()A.B.C.D.【答案】C【解析】有定义知:,所以,所以等价于,当时,,当时,,当时,,成立,所以.【考点】已知求7.已知数列{an }(n Î N)中,a1=1,an+1=,则an=()A.2n-1B.2n +1C.D.【答案】C【解析】两边取倒数得到:,整理为:,所以是以为首项,为公差的等差数列,所以,那么.【考点】1.递推公式求通项公式;2.等差数列.8.若,是等比数列中的项,且不等式的解集是,则的值是()A.B.C.D.【答案】C【解析】由不等式的解集可知【考点】1.二次方程根与系数的关系;2.韦达定理9.(14分)已知数列的前n项和为,且,(1)求数列的通项公式;(2)令,且数列的前n项和为,求;(3)若数列满足条件:,又,是否存在实数,使得数列为等差数列?【答案】(1)(2)(3)【解析】(1)中考察的主要是由数列的前n项和求数列通项的问题,求解时主要借助于公式解决,分别求完后要验证看时候能将结果合并到一起;(2)首先将通项整理为的形式,然后采用裂项相消法求和;(3)首项将代入整理出数列的递推公式,由第一项求得第二三两项,找到数列的前三项,前三项成等差得到参数的值,然后验证求得的值满足数列所有项均构成等差数列试题解析:(14分)(1)n=1时,n当n=1时所以(2),(3),即,假设存在这样的实数,满足条件,又,成等差数列,即,解得,此时:,数列是一个等差数列,所以【考点】1.数列求通项公式;2.裂项相消求和;3.等差数列的判定10.(本小题满分14分)已知数列满足且,且,设,数列满足.(1)求证是等比数列并求出数列的通项公式;(2)求数列的前项和;(3)对于任意恒成立,求实数的取值范围.【答案】(1)(2)(3)【解析】(1)本题考察的是等比数列的证明,一般采用定义法或者等比中项法,本题中根据题目所给条件得到,即可证明是等比数列.然后求出新数列的通项公式,从而求出数列的通项公式.(2)本题考察的是求数列的前项和,根据(1)求出的数列的通项公式,求出,继而求出的通项公式,然后通过错位相减法求出的前项和.(3)本题考察的是不等式恒成立问题,根据的单调性,求出的最大值,然后由含参一元二次不等式恒成立,然后根据一元二次不等式在定区间恒成立,从而求出参数的取值范围.试题解析:(1)因为∴,∴是等比数列,其中首项是,公比为∴,(2)由(1)知,,两式相减得(3)…10分∴当时,当∴当或时,取最大值是只须即对于任意恒成立即【考点】(1)等比数列的通项公式(2)求数列的前项和(3)不等式恒成立问题11.等比数列{}中,,是方程的两根,则等于()A.8B.-8C.±8D.以上都不对【答案】C【解析】根据韦达定理,,又根据等比数列的定义,,所以.【考点】1.等比数列的性质;2.韦达定理.12.设数列的前n项和,则的值为()A.15B.16C.49D.64【答案】A【解析】.故A正确.【考点】求数列中的项.13.设为等比数列的前项和,,则()A.11B.5C.D.【答案】D【解析】..故D正确.【考点】等比数列的前项和公式.14.(10分)以数列的任意相邻两项为坐标的点()都在一次函数的图象上,数列满足.(1)求证:数列是等比数列;(2)设数列,的前项和分别为,且,求的值.【答案】(1)见答案;(2)【解析】(1)由且得=-=(2+k)-(2+k)=2(-)=2.又由,故数列是以为首项的等比数列由(1)=()·=-从而求出=()·-k.又因为所以即∴.又∴可得试题解析:解:(1)点都在一次函数y=2x+k图像上,则有=-=(2+k)-(2+k)=2(-)=2.∴=2故是以为首项,2为公比的等比数列. 4分(2)∵=()·=-=()·-k∴,又即∴即∴∴又∴∴k=8 10分【考点】等比数列数列通向公式及前n项和的综合问题.15.已知成等差数列,且成等比数列,则的值为()A.—B.C.或—D.【答案】B【解析】设等差数列公差为,等比数列公比为q,则根据题意有,,所以;【考点】等差、等比数列的通项公式;16.设等比数列的前n项和为,若=3则 = ()A.2B.C.D.3【答案】B【解析】试题分析: 由等比数列前项和性质:成等比得:成等比,根据等比中项性质得:,又,将其带入上式得,因为等比数列项不为0,则化简得.【考点】1.等比数列前项和的性质;2.等比数列项不为0.17.在等比数列()中,若,,则该数列的前10项和为()A.B.C.D.【答案】B【解析】设等比数列公比为,由题意可得:,所以该数列的前10项和为:,故选择B【考点】等比数列求和18.已知是等差数列,,公差,为其前项和,若成等比数列,则【答案】64【解析】由数列为等差数列,且成等比数列,所以,则,所以,因为,所以,根据等差数列前n项和公式,。
高一数学数列试题答案及解析

高一数学数列试题答案及解析1.数列1,,,…,,….是()A.递增数列B.递减数列C.常数列D.摆动数列【答案】【解析】显然该数列从第二项起,各项的分母是偶数且越来越大,所以数列的各项越来越小.【考点】数列增减性的判断.2.设数列满足:,,则()A.B.C.D.【答案】A【解析】由题可得:,对n分别取正整数后进进迭加,可得,又,当n=19时有,所以.【考点】迭加法求数列的通项公式.3.正项数列的前项和满足:(1)求数列的通项公式;(2)令,求数列的前项和.【答案】(1) ,(2)【解析】(1) 先化简关系式:,,再利用与关系,得时.最后验证,得到数列的通项. (2)因为数列通项是“等比乘等差”型,需用错位相减法求解前项和.运用错位相减法求和时需注意三点:一是相减时注意项的符号,二是求和时注意项的个数,三是最后结果需除以由相减得:所以.试题解析:(1)解:由,得.由于是正项数列,所以.于是时,.综上,数列的通项.(2),由相减得:所以【考点】由求,错位相减法求和4.(本小题满分12分)已知数列{an }满足 a1=1,an+1=.,写出它的前5项,并归纳出数列的一个通项公式(不要求证明)【答案】解:∵a1=1,an+1=,∴a2==, a3==, a4==, a5==.∴它的前5项依次是1,,,,…………………….8分故它的一个通项公式为an=. (12)【解析】略5.在等差数列中,已知,=4,则公差d等于()A.1 B. C.- 2 D 3【答案】C【解析】,所以.6.数列为等差数列,为正整数,其前项和为,数列为等比数列,且,数列是公比为64的等比数列,.(1)求;(2)求证.【答案】(1)(2)见解析【解析】(1)设的公差为,的公比为,则为正整数,,.依题意有①由知为正有理数,故为的因子之一,解①得,故.(2),∴.7.设,且则()A.B.C.D.【答案】C【解析】,,所以数列是等比数列,,首项,所以【考点】1.复合函数;2.等比数列.8.已知数列(Ⅰ)计算(Ⅱ)令是等比数列;(Ⅲ)设、分别为数列、的前,使得数列为等差数列?若存在,试求出的值;若不存在,请说明理由.【答案】(Ⅰ)(Ⅱ)详见解析(Ⅲ)【解析】(Ⅰ)将点代入直线可得到数列的递推公式,由首项可逐个求出的值;(Ⅱ)首先将数列的通项公式整理化简,找到相邻的两项,证明数列是等比数列主要需要证明相邻两项的比值是常数,常数即公比,需要说明数列首项不为零;(Ⅲ)首先由已知整理出两数列通项公式和前n项和,代入中化简,由定义数列是等差数列需满足相邻两项的差值为常数,因此找到数列的相邻项相减,使其为常数时寻求此时的取值试题解析:(Ⅰ)由题意,同理(Ⅱ)因为所以又,所以数列是以为首项,为公比的等比数列.(Ⅲ)由(2)得,又所以由题意,记则故当【考点】1.数列的通项公式递推公式;2.等差等比数列的判定;3.数列求和9.已知数列满足,(),则().A.0B.C.D.-【答案】D【解析】所以a的周期为3,.【考点】数列性质的应用10.等比数列的前项的和,且,,则.【答案】【解析】根据等比数列前项和的性质,,,,是等比数列,所以,,那么,所以.【考点】等比数列前项和的性质11.(本小题满分13分)已知数列的前项和,,等差数列中(1)求数列、的通项公式;(2)是否存在正整数,使得若存在,求出的最小值,若不存在,请说明理由.【答案】(1);;(2)存在,.【解析】(1)数列是等差数列,所以待定系数求首项和公差,求数列的通项公式的方法是已知求,当时,,然后两式相减,得到递推,再求的值,最后再写出通项;(2)第一步,先求的通项公式,是等差数列乘以等比数列,所以求和,采用错位相减法求和,,然后再解关于的不等式,求出整数.试题解析:(1)当时,,相减得:又数列是以1为首项,3为公比的等比数列,.又(2)令①②①-②得:…9分即,当,,当。
高中数列试题训练及答案

高中数列试题训练及答案一、选择题1. 已知数列{a_n}满足a_1=1,a_{n+1}=2a_n+1,求a_5的值。
A. 31B. 63C. 127D. 2552. 若数列{b_n}是等差数列,且b_1=3,b_3=7,求b_5的值。
A. 11B. 13C. 15D. 173. 对于等比数列{c_n},若c_1=2,c_3=8,求c_5的值。
A. 32B. 64C. 128D. 2564. 若数列{d_n}满足d_1=2,d_{n+1}=3d_n-2,求d_4的值。
A. 20B. 26C. 34D. 42二、填空题5. 已知数列{e_n}是等差数列,且e_1=1,e_3=5,求e_5的值。
6. 对于等比数列{f_n},若f_1=4,f_4=64,求f_7的值。
7. 若数列{g_n}满足g_1=1,g_{n+1}=4g_n+3,求g_4的值。
8. 已知数列{h_n}是等差数列,且h_1=-1,h_5=9,求h_9的值。
三、解答题9. 已知数列{a_n}满足a_1=2,a_{n+1}=3a_n-2,求a_10的值。
10. 对于等比数列{b_n},若b_1=6,b_3=24,求b_6的值。
答案:一、选择题1. C解析:根据递推公式a_{n+1}=2a_n+1,我们可以计算出a_2=2a_1+1=3,a_3=2a_2+1=7,a_4=2a_3+1=15,a_5=2a_4+1=31。
所以a_5的值为31。
2. C解析:根据等差数列的性质,我们可以得出公差d=b_3-b_1=7-3=4,因此b_5=b_3+2d=7+2*4=15。
3. C解析:根据等比数列的性质,我们可以得出公比q=c_3/c_1=8/2=4,因此c_5=c_3*q^2=8*4^2=128。
4. C解析:根据递推公式d_{n+1}=3d_n-2,我们可以计算出d_2=3d_1-2=4,d_3=3d_2-2=10,d_4=3d_3-2=28。
高一数列专项典型练习题及解析答案
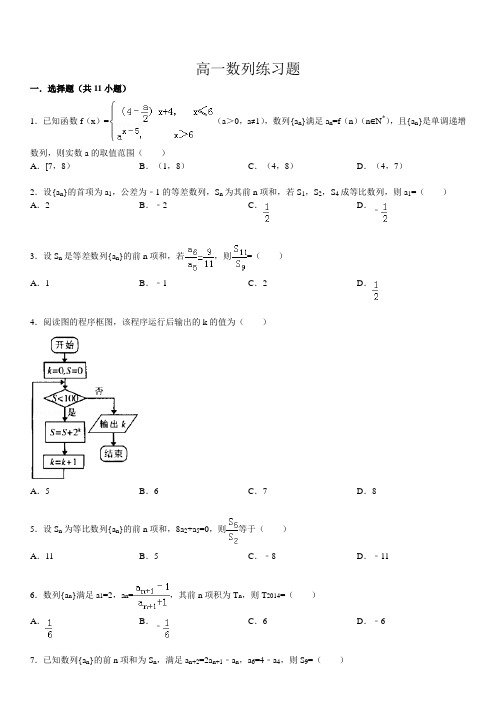
高一数列练习题一.选择题(共11小题)1.已知函数f(x)=(a>0,a≠1),数列{a n}满足a n=f(n)(n∈N*),且{a n}是单调递增数列,则实数a的取值范围()A.[7,8)B.(1,8)C.(4,8)D.(4,7)2.设{a n}的首项为a1,公差为﹣1的等差数列,S n为其前n项和,若S1,S2,S4成等比数列,则a1=()A.2B.﹣2 C.D.﹣3.设S n是等差数列{a n}的前n项和,若,则=()A.1B.﹣1 C.2D.4.阅读图的程序框图,该程序运行后输出的k的值为()A.5B.6C.7D.85.设S n为等比数列{a n}的前n项和,8a2+a5=0,则等于()A.11 B.5C.﹣8 D.﹣116.数列{a n}满足a1=2,a n=,其前n项积为T n,则T2014=()C.6D.﹣6A.B.﹣A.9B.12 C.14 D.188.已知S n为等差数列{a n}的前n项和,S7=28,S11=66,则S9的值为()A.47 B.45 C.38 D.549.在等比数列{a n}中,,则a3=()A.±9 B.9C.±3 D.310.阅读右边的程序框图,运行相应的程序,则输出s的值为()A.8B.18 C.26 D.8011.在等差数列{a n}中,4(a3+a4+a5)+3(a6+a8+a14+a16)=36,那么该数列的前14项和为()A.20 B.21 C.42 D.84二.填空题(共7小题)12.)设{a n}是首项为a1,公差为﹣1的等差数列,S n为其前n项和,若S1,S2,S4成等比数列,则a1的值为_________.13.某公司推出了下表所示的QQ在线等级制度,设等级为n级需要的天数为a n(n∈N*),等级等级图标需要天数等级等级图标需要天数1 5 7 772 12 8 963 21 12 1924 32 16 3205 45 32 11526 60 48 2496则等级为50级需要的天数a50=_________.14.数列{a n}为等比数列,a2+a3=1,a3+a4=﹣2,则a5+a6+a7=_________.15.已知数列{a n}中,a n+1=2a n,a3=8,则数列{log2a n}的前n项和等于_________.17.记等差数列{a n}的前n项和为S n,已知a2+a4=6,S4=10.则a10=_________.18.设S n是等比数列{a n}的前n项和,S3,S9,S6成等差数列,且a2+a5=2a m,则m=_________.三.解答题(共12小题)19.设{a n}是等差数列,{b n}是各项都为正数的等比数列,且a1=b1=1,a3+b5=21,a5+b3=13(Ⅰ)求{a n}、{b n}的通项公式;(Ⅱ)求数列的前n项和S n.20.已知数列{a n}的前n项和S n=﹣a n﹣+2(n∈N*),数列{b n}满足b n=2n a n.(1)求证数列{b n}是等差数列,并求数列{a n}的通项公式;(2)设数列{a n}的前n项和为T n,证明:n∈N*且n≥3时,T n>;(3)设数列{c n}满足a n(c n﹣3n)=(﹣1)n﹣1λn(λ为非零常数,n∈N*),问是否存在整数λ,使得对任意n∈N*,都有c n+1>c n.21.在等差数列{a n}中,a1=3,其前n项和为S n,等比数列{b n}的各项均为正数,b1=1,公比为q,且b2+S2=12,.(Ⅰ)求a n与b n;(Ⅱ)设c n=a n•b n,求数列{c n}的前n项和T n.22.(2009•河西区二模)已知等差数列{a n}满足a3+a4=9,a2+a6=10;又数列{b n}满足nb1+(n﹣1)b2+…+2b n﹣1+b n=S n,其中S n是首项为1,公比为的等比数列的前n项和.(1)求a n的表达式;(2)若c n=﹣a n b n,试问数列{c n}中是否存在整数k,使得对任意的正整数n都有c n≤c k成立?并证明你的结论.23.已知等比数列{a n}中,a1=,公比q=.(Ⅰ)S n为{a n}的前n项和,证明:S n=(Ⅱ)设b n=log3a1+log3a2+…+log3a n,求数列{b n}的通项公式.24.已知等差数列{a n}的前n项和为s n=pm2﹣2n+q(p,q∈R),n∈N*(I)求q的值;(Ⅱ)若a3=8,数列{b n}}满足a n=4log2b n,求数列{b n}的前n项和.25.已知数列{a n}(n∈N*)是等比数列,且a n>0,a1=3,a3=27.(1)求数列{a n}的通项公式a n和前项和S n;(2)设b n=2log3a n+1,求数列{b n}的前项和T n.26.已知等差数列{a n} 的前n项和为S n,a2=9,S5=65.(I)求{a n} 的通项公式:(II)令,求数列{b n}的前n项和T n.27.已知等比数列{a n}满足a2=2,且2a3+a4=a5,a n>0.(1)求数列{a n}的通项公式;(2)设b n=(﹣1)n3a n+2n+1,数列{b n}的前项和为T n,求T n.28.已知等比数列{a n}的公比为q,前n项的和为S n,且S3,S9,S6成等差数列.(1)求q3的值;(2)求证:a2,a8,a5成等差数列.29.已知S n是等比数列{a n}的前n项和,,.(I)求a n;(II)若,求数列{b n}的前n项和T n.30.已知{a n}是等差数列,其前n项和为S n,已知a2=8,S10=185.(1)求数列{a n}的通项公式;高一数列专项典型练习题参考答案与试题解析一.选择题(共11小题)1.解答:解:∵{a n}是单调递增数列,∴,解得7≤a<8.故选:A.点评:本题考查了分段函数的意义、一次函数和指数函数的单调性,属于中档题.2.解答:解:∵{a n}是首项为a1,公差为﹣1的等差数列,S n为其前n项和,∴S1=a1,S2=2a1﹣1,S4=4a1﹣6,由S1,S2,S4成等比数列,得:,即,解得:.故选:D.点评:本题考查等差数列的前n项和公式,考查了等比数列的性质,是基础的计算题.3.解答:解:由题意可得====1故选A点评:本题考查等差数列的求和公式,涉及等差数列的性质,属基础题.4.解答:解:程序在运行过程中各变量的值如下表示:循环前:k=0,s=0,每次循环s,k的值及是否循环分别如下第一圈:S=2°<100,k=1;是第二圈:S=2°+21<100,k=2;是第三圈:S=2°+21+22<100,k=3;是第四圈:S=2°+21+22+23<100,k=4;是第五圈:S=2°+21+22+23+24<100,k=5;是第六圈:S=2°+21+22+23+24+25<100,k=6:是故选C点评:本小题主要考查循环结构、等比数列等基础知识.根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,5.解答:解:设等比数列{a n}的公比为q,(q≠0)由题意可得8a2+a5=8a1q+a1q4=0,解得q=﹣2,故====﹣11 故选D点评:本题考查等比数列的性质,涉及等比数列的求和公式,属中档题.6.解答:解:∵a n=,∴a n+1=,∵a1=2,∴a2=﹣3,a3=﹣,a4=,a5=2,…,∴数列{a n}是周期为4的周期数列,且a1a2a3a4=1,∵2014=4×503+2,∴T2014=﹣6.故选:D.点评:本题考查数列递推式,考查学生分析解决问题的能力,确定数列{a n}是周期为4的周期数列,且a1a2a3a4=1是关键.7.解答:解:∵a n+2=2a n+1﹣a n,∴2a n+1=a n+a n+2∴数列{a n}是等差数列.又a6=4﹣a4,∴a4+a6=4,由等差数列的性质知:2a5=a4+a6=4,得a5=2.∴S9=9a5=9×2=18.故选:D.点评:本题考查数列递推式,考查了等差关系得确定,考查了等差数列的性质及前n项和,是中档题.8.解答:解:设公差为d,由S7=28,S11=66得,,即,解得,所以S9=9×1=45.9.解答:解:设等比数列{a n}的公比为q,则∵,∴=27,=3 两式相除,可得∴a3=±3故选C.点评:本题考查等比数列的定义,考查学生的计算能力,属于基础题.10.解答:解:∵数列{a n}为等差数列,∴a3+a5=2a4,a8+a14=a6+a16=2a11,又4(a3+a4+a5)+3(a6+a8+a14+a16)=36,∴12a4+12a11=36,即a4+a11=3,∵a1+a14=a4+a11=3,则该数列的前14项和S14==21.故选B点评:此题考查了等差数列的性质,以及等差数列的求和公式,熟练掌握性质及公式是解本题的关键.二.填空题(共7小题)12.解答:解:由题意可得,a n=a1+(n﹣1)(﹣1)=a1+1﹣n,S n==,再根据若S1,S2,S4成等比数列,可得=S1•S4,即=a1•(4a1﹣6),解得a1=﹣,故答案为:﹣.点评:本题主要考查等差数列的前n项和公式,等比数列的定义和性质,属于中档题.13.解答:解:由表格可知:a n=5+7+…+(2n+3)==n(n+4),∴a50=50×54=2700.故答案为:2700.点评:本题考查了等差数列的通项公式与前n项和公式、归纳推理等基础知识与基本技能方法,属于基础题.14.解答:解:由a2+a3=1,a3+a4=﹣2,两式作商得q=﹣2.代入a2+a3=1,得a1(q+q2)=1.解得a1=.456点评:本题考查对数计算与等比数列性质的运用,属于基本计算题15.解答:解:∵数列{a n}中,a n+1=2a n,∴=2,∴{a n}是公比为2的等比数列,∵a3=8,∴,解得a1=2,∴,∴log2a n=n,∴数列{log2a n}的前n项和:S n=1+2+3+…+n=.故答案为:.点评:本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意对数函数的性质的灵活运用.16.解答:解:∵数列{a n}的前n项和为S n,并满足a n+2=2a n+1﹣a n,∴数列{a n}是等差数列,∵a6=4﹣a4,∴a6+a4=4,∴=.故答案为:18.点评:本题考查数列的前9项和的求法,解题时要认真审题,注意等差数列的性质的合理运用.17.解答:解:等差数列{a n}的前n项和为S n,∵a2+a4=6,S4=10,设公差为d,∴,解得a1=1,d=1,∴a10=1+9=10.故答案为:10.点评:本题考查等差数列中第10项的求法,是基础题,解题时要认真审题,要熟练掌握等差数列的性质.18.解答:解:∵S n是等比数列{a n}的前n项和,且S3,S9,S6成等差数列,∴2S9=S3+S6,即=+,整理得:2(1﹣q9)=1﹣q3+1﹣q6,即1+q3=2q6,又a2+a5=a1q+a1q4=a1q(1+q3)=2a1q7,2a m=2a1q m﹣1,且a2+a5=2a m,∴2a1q7=2a1q m﹣1,即m﹣1=7,则m=8.故答案为:8点评:此题考查了等差数列的性质,等比数列的通项公式及求和公式,熟练掌握性质及公式是解本题的关键.19.解答:解:(Ⅰ)设{a n}的公差为d,{b n}的公比为q,则依题意有q>0且解得d=2,q=2.所以a n=1+(n﹣1)d=2n﹣1,b n=q n﹣1=2n﹣1.(Ⅱ).,①,②②﹣①得,===.点评:本题主要考查等差数列的通项公式和用错位相减法求和.20.分析:(1)由已知条件推导出2n a n=2n﹣1a n﹣1+1.由此能证明{数列b n}是首项和公差均为1的等差数列.从而求出a n=.(2)由(1)知=(n+1)•()n,利用错位相减法能求出T n=3﹣.再用数学归纳法能证明n∈N*且n≥3时,T n>.(3)由a n(c n﹣3n)=(﹣1)n﹣1λn可求得c n,对任意n∈N+,都有c n+1>c n即c n+1﹣c n>0恒成立,整理可得(﹣1)n﹣1•λ<()n﹣1,分n为奇数、偶数两种情况讨论,分离出参数λ后转化为函数最值即可解决.解答:(1)证明:在S n=﹣a n﹣+2(n∈N*)中,令n=1,得S1=﹣a1﹣1+2=a1,解得a1=,当n≥2时,S n﹣1=﹣a n﹣1﹣()n﹣2+2,∴a n=S n﹣S n﹣1=﹣a n+a n﹣1+()n﹣1,∴2a n=a n﹣1+()n﹣1,即2n a n=2n﹣1a n﹣1+1.∵b n=2n a n,∴b n=b n﹣1+1,即当n≥2时,b n﹣b n﹣1=1,又b1=2a1=1,∴{数列b n}是首项和公差均为1的等差数列.于是b n=1+(n﹣1)•1=n=2n a n,∴a n=.(2)证明:∵,∴=(n+1)•()n,∴T n=2×+3×()2+…+(n+1)×()n,①23n+1①﹣②,得:=1+=1+﹣(n+1)•()n+1=,∴T n=3﹣.∴T n﹣=3﹣=,∴确定T n与的大小关系等价于比较2n与2n+1的大小.下面用数学归纳法证明n∈N*且n≥3时,T n>.①当n=3时,23>2×3+1,成立②假设当n=k(k≥3)时,2k>2k+1成立,则当n=k+1时,2k+1=2•2k>2(2k+1)=4k+2=2(k+1)+1+(2k﹣1)>2(k+1)+1,∴当n=k+1时,也成立.于是,当n≥3,n∈N*时,2n>2n+1成立∴n∈N*且n≥3时,T n>.(3)由,得=3n+(﹣1)n﹣1•λ•2n,∴c n+1﹣c n=[3n+1+(﹣1)n•λ•2n+1]﹣[3n+(﹣1)n﹣1•λ•2n]=2•3n﹣3λ(﹣1)n﹣1•2n>0,∴,①当n=2k﹣1,k=1,2,3,…时,①式即为λ<,②依题意,②式对k=1,2,3…都成立,∴λ<1,当n=2k,k=1,2,3,…时,①式即为③,依题意,③式对k=1,2,3…都成立,∴,∴,又λ≠0,∴存在整数λ=﹣1,使得对任意n∈N*有c n+1>c n.点评:本题考查数列递推式、等差数列的通项公式、数列求和等知识,考查恒成立问题,考查转化思想,错位相减法对数列求和是高考考查的重点内容,要熟练掌握.21.分析:(1)根据b2+S2=12,{b n}的公比,建立方程组,即可求出a n与b n;(2)由a n=3n,bn=3n﹣1,知c n=a n•b n=n•3n,由此利用错位相减法能求出数列{c n}的前n项和T n.解答:解:(1)∵在等差数列{a n}中,a1=3,其前n项和为S n,等比数列{b n}的各项均为正数,b1=1,公比为q,且b2+S2=12,.∴b2=b1q=q,,(3分)解方程组得,q=3或q=﹣4(舍去),a2=6(5分)∴a n=3+3(n﹣1)=3n,b n=3n﹣1.(7分)(2)∵a n=3n,b n=3n﹣1,∴c n=a n•b n=n•3n,∴数列{c n}的前n项和T n=1×3+2×32+3×33+…+n×3n,∴3T n=1×32+2×33+3×34+…+n×3n+1,∴﹣2T n=3+32+33+…+3n﹣n×3n+1=﹣n×3n+1=﹣n×3n+1,∴T n=×3n+1﹣.点评:本题考查数列的通项公式和前n项和公式的求法,解题时要认真审题,注意等差数列、等比数列的性质和错位相减法的合理运用.(1)利用等差数列的通项公式即可得出;22.分析:(2)利用等比数列的通项公式、、分类讨论的思想方法即可得出.解答:解:(1)设等差数列{a n}的公差为d,∵a3+a4=9,a2+a6=10,∴,解得,∴a n=2+1×(n﹣1)=n+1.(2)∵S n是首项为1,公比为的等比数列的前n项和,∴nb1+(n﹣1)b2+…+2b n﹣1+b n=,①(n﹣1)b1+(n﹣2)b2+…+2b n﹣2+b n﹣1=…+,②①﹣②得b1+b2+…+b n=,即.当n=1时,b1=T n=1,当n≥2时,b n=T n﹣T n﹣1==.∴..于是c n=﹣a n b n.设存在正整数k,使得对∀n∈N*,都有c n≤c k恒成立.当n=1时,,即c2>c1.当n≥2时,==.∴当n<7时,c n+1>c n;当n=7时,c8=c7;当n>7时,c n+1<c n.∴存在正整数k=7或8,使得对∀n∈N*,都有c n≤c k恒成立.点评:熟练掌握等差数列的图象公式、分类讨论的思想方法、等比数列的通项公式、、分类讨论的思想方法是解题的关键.23.分(I)根据数列{a n}是等比数列,a1=,公比q=,求出通项公式a n和前n项和S n,然后经过运算即可证明.析:(II)根据数列{a n}的通项公式和对数函数运算性质求出数列{b n}的通项公式.解答:证明:(I)∵数列{a n}为等比数列,a1=,q=∴a n=×=,S n=又∵==S n∴S n=(II)∵a n=∴b n=log3a1+log3a2+…+log3a n=﹣log33+(﹣2log33)+…﹣nlog33=﹣(1+2+…+n)=﹣∴数列{b n}的通项公式为:b n=﹣点评:本题主要考查等比数列的通项公式、前n项和以及对数函数的运算性质.24.解答:解:(I)当n=1时,a1=s1=p﹣2+q当n≥2时,a n=s n﹣s n﹣1=pn2﹣2n+q﹣p(n﹣1)2+2(n﹣1)﹣q=2pn﹣p﹣2 由{an}是等差数列,得p﹣2+q=2p﹣p﹣2,解得q=0.(Ⅱ)由a3=8,a3=6p﹣p﹣2,于是6p﹣p﹣2=8,解得p=2所以a n=4n﹣4又a n=4log2b n,得b n=2n﹣1,故{b n}是以1为首项,2为公比的等比数列.所以数列{b n}的前n项和Tn=.点评:本题考查了数列的前n项和与通项间的关系及等比数列的求和问题,在解题中需注意前n项和与通项间的关系是个分段函数的关系,但最后要验证n=1是否满足n≥2时的情况,属于基础题.25.解答:解:(1)设公比为q,则a3=a1•q2,∴27=3q2,即q2=9∵a n>0,∴(2)由(1)可知b n=2log33n+1=2n+1,∴b1=3,又b n+1﹣b n=2(n+1)+1﹣(2n+1)=2,故数列{b n}是以3为首项,2为公差的等差数列,∴.点评:本题考查了等差数列和等比数列的前n项和,此题比较容易,只要认真作答就可以保障正确,属于基础题.26.解答:解:(I)(2分)解得:(4分),所以a n=4n+1(6分)(II)由(I)知(7分)因为,(8分)所以{b n} 是首项为b1=32,公比q=16的等比数列(9分),所以.(12分)点评:在数列的基本量的求解中要求考生熟练掌握基本公式,具备一定的计算能力,本题属于基础试题.27.分析:(Ⅰ)设等比数列{a n}的首项为a1,公比为q,则,解方程可求a1,q结合等比数列的通项公式即可求解(Ⅱ)由b n=(﹣1)n3a n+2n+1=﹣3•(﹣2)n﹣1+2n+1,利用分组求和,结合等比与等差数列的求和公式即可求解解答:(本小题满分12分)解:(Ⅰ)设等比数列{a n}的首项为a1,公比为q,则…(2分)整理得q2﹣q﹣2=0,即q=﹣1或q=2,∵a n>0,∴q=2.代入可得a1=1∴.…(6分)(Ⅱ)∵b n=(﹣1)n3a n+2n+1=﹣3•(﹣2)n﹣1+2n+1,…(9分)∴T n=﹣3[1﹣2+4﹣8+…+(﹣2)n﹣1]+(3+5+…+2n+1)=﹣3×=(﹣2)n+n2++2n﹣1.…(12分)点评:本题主要考查了等比数列的通项公式及求和公式的应用,分组求和方法的应用,属于数列知识的简单综合28.分析:(1)由S3,S9,S6成等差数列,得S3+S6=2S9,然后考虑当q=1时关系式不成立,所以当q不等于1时,利用等比数列的前n项和的公式化简此等式,根据q不等于1,利用换元法即可求出q3的值;(2)由q3的值分别表示出a8和a5,然后分别求出a8﹣a2和a5﹣a8的值,得到两者的值相等即可得证.解答:解:(1)由S3,S9,S6成等差数列,得S3+S6=2S9,若q=1,则S3+S6=9a1,2S9=18a1,由a1≠0得S3+S6≠2S9,与题意不符,所以q≠1.由S3+S6=2S9,得.整理,得q3+q6=2q9,由q≠0,1,设t=q3,则2t2﹣t﹣1=0,解得t=1(舍去)或t=﹣,所以;(2)由(1)知:,则a8﹣a2=a5﹣a8,所以a2,a8,a5成等差数列.点评:此题考查学生灵活运用等差数列的性质化简求值,灵活运用等比数列的前n项和的公式化简求值,是一道中档题.29分析:(I)由题意可得,公比q≠1,则①②,相除可得公比q,求得首项和公比,即可求出通项公式.(II)首先根据(1)求出数列{b n}的通项公式,然后利用分组法求出前n项和.解答:解:(I)若q=1,则S6=2S3,这与已知矛盾,所以q≠1,(1分)则①②(3分)②式除以①式,得,所以,代入①得a1=2,所以.(7分)(II)因为,(9分)所以T n=(2﹣1+20+21++2n﹣2)+(1+2+3++n)=(12分)==.(14分)点评:本题考查等比数列的前n项和公式和通项公式,(2)问中数列{b n}是等差数列和等比数列和的形式,采取分组法求解.属于中档题.30.分析:(1)由题意等差数列{a n}中a2=8,S10=185,利用通项公式及前n项和公式建立首项与公差的方程求出即可得到数列{a n}的通项公式a n;(2)把(1)中求出的a n的通项公式代入a n=log2b n中,确定出b n的通项公式,利用等于常数得到数列{b n}是等比数列,求出等比数列的首项和公比,根据首项和公比写出等比数列的前n项和即可.解答:解:(1)解得:d=3,a1=5,∴a n=3n+2(2)b n=∴===23=8(n=1,2,3,…)∴{bn}是公比为8的等比数列∵b1==32∴T n==(8n﹣1).点评:本题考查了等差数列的通项公式、数列求和以及灵活运用等比数列的前n项和公式化简求值,是一道中档题.。
高一数学数列试题及答案

高一数学数列试题及答案一、选择题1. 已知数列{a_n}是等差数列,且a_1=1,a_4=7,那么a_7的值为()。
A. 13B. 14C. 15D. 162. 等比数列{b_n}中,b_1=2,b_3=8,则b_5的值为()。
A. 16B. 32C. 64D. 1283. 数列{c_n}的前n项和为S_n,若S_5=15,S_10=35,则S_15的值为()。
A. 55B. 50C. 60D. 654. 数列{d_n}满足d_1=1,d_{n+1}=2d_n+1,求d_3的值为()。
A. 5B. 7C. 9D. 11二、填空题5. 已知等差数列{a_n}的前n项和为S_n,若S_3=9,S_6=21,则a_4+a_5+a_6的值为______。
6. 等比数列{b_n}中,b_1b_2b_3=8,b_2=2,则b_4的值为______。
7. 数列{c_n}满足c_1=2,c_{n+1}=c_n+n,求c_5的值为______。
三、解答题8. 已知数列{a_n}是等差数列,且a_1=2,a_3+a_5=22,求a_7的值。
9. 等比数列{b_n}中,b_1=3,b_2b_3=45,求b_5的值。
10. 数列{c_n}满足c_1=1,c_{n+1}=2c_n+1,求c_4的值。
答案:一、选择题1. C解析:已知等差数列{a_n},a_1=1,a_4=7,设公差为d,则有a_4=a_1+3d,即7=1+3d,解得d=2。
因此,a_7=a_1+6d=1+6×2=13。
2. C解析:已知等比数列{b_n},b_1=2,b_3=8,设公比为q,则有b_3=b_1q^2,即8=2q^2,解得q=2或q=-2。
由于等比数列的公比不能为负数,所以q=2。
因此,b_5=b_1q^4=2×2^4=64。
3. C解析:已知数列{c_n}的前n项和为S_n,S_5=15,S_10=35。
由于S_5,S_10-S_5,S_15-S_10构成等差数列,所以有2(S_10-S_5)=S_5+(S_15-S_10),即2×(35-15)=15+(S_15-35),解得S_15=60。
高一数列测试题及答案

高一数列测试题及答案一、选择题(每题5分,共30分)1. 数列1, 1/2, 1/3, 1/4, ...的前n项和为S_n,那么S_5等于()A. 2B. 3C. 4D. 52. 已知数列{a_n}是等差数列,且a_1=2,公差d=3,则a_5等于()A. 14B. 15C. 16D. 173. 等比数列{b_n}的前n项和为S_n,若S_3=7,b_1=1,公比q=2,则b_3等于()A. 4B. 8C. 16D. 324. 数列{c_n}满足c_1=1,c_{n+1}=2c_n+1,那么c_3等于()A. 5B. 7C. 9D. 115. 已知数列{d_n}的通项公式为d_n=3n-2,那么d_5等于()A. 13B. 14C. 15D. 166. 数列{e_n}满足e_1=2,e_{n+1}=e_n+2n,那么e_4等于()A. 16B. 18C. 20D. 22二、填空题(每题5分,共20分)7. 等差数列{f_n}的前n项和为S_n,若a_5=10,a_1=2,则公差d等于______。
8. 等比数列{g_n}中,若g_3=8,g_1=2,则公比q等于______。
9. 数列{h_n}满足h_1=3,h_{n+1}=3h_n-2,那么h_4等于______。
10. 数列{i_n}的通项公式为i_n=2^n,那么i_5等于______。
三、解答题(每题10分,共50分)11. 已知数列{j_n}是等差数列,且j_1=5,j_3=11,求数列的通项公式。
12. 等比数列{k_n}中,若k_1=3,k_2k_4=324,求公比q。
13. 数列{l_n}满足l_1=1,l_{n+1}=2l_n+n,求l_5。
14. 数列{m_n}的通项公式为m_n=n^2-n+1,求m_1到m_5的和。
15. 数列{n_n}满足n_1=1,n_{n+1}=n_n+n,求n_4。
答案:一、选择题1. B2. C3. C4. D5. C6. A二、填空题7. 28. 29. 1710. 32三、解答题11. 通项公式为j_n=2n+3。
最全的高中数学数列练习题_附答案与解析

交,∴ f( k) = f( k- 1) + ( k- 1) .
由 f( 3) = 2,
f( 4) = f( 3) + 3= 2+ 3= 5,
f( 5) = f( 4) + 4= 2+ 3+ 4= 9, ……
第 6页 共 8页
∴ S13= 13( a1+a13 ) = 13( a4+a10 ) = 13 4 = 26.
2
2
2
15.- 49.
解析:∵ d= a6- a5=- 5,
∴ a4+ a5+…+ a10
= 7( a4+a10 ) 2
= 7( a5-d+a5+5d) 2
= 7( a5+ 2d)
=- 49.
16. 5, 1 ( n+1)( n- 2) . 2
4. C
解析:
解法 1:设 a1= 1 , a2= 1 + d, a3= 1 + 2d, a4= 1 + 3d,而方程 x2- 2x+ m= 0 中两根之和为 2, x2
4
4
4
4
-2x+ n= 0 中两根之和也为 2,
∴ a1+ a2+ a3+ a4=1+ 6d= 4,
∴ d= 1 , a1= 1 , a4= 7 是一个方程的两个根, a1= 3 , a3= 5 是另一个方程的两个根.
∴ d=- 1, q2= 2,
∴ a2 a1 = d = 1 .
b2
q2
2
10. C
解析:∵ { an} 为等差数列,∴ an2 =an -1+ an+1,∴ an2 = 2an,
又 an≠ 0,∴ an= 2, { an} 为常数数列,
而 an= S2n 1 ,即 2n- 1= 38 = 19,
高一数列试题及答案

高一数列试题及答案一、选择题1. 已知数列{a_n}是等差数列,且a_1+a_3=10,a_2+a_4=12,则a_5的值为()。
A. 14B. 16C. 18D. 20答案:A解析:设等差数列的公差为d,则a_3=a_1+2d,a_4=a_2+2d。
根据题意,有a_1+a_1+2d=10,a_2+a_2+2d=12。
解得a_1=4,d=2。
因此,a_5=a_1+4d=4+4×2=14。
2. 已知数列{a_n}是等比数列,且a_1a_3=8,a_2=4,则a_4的值为()。
A. 16B. 32C. 64D. 128答案:C解析:设等比数列的公比为q,则a_3=a_1q^2,a_2=a_1q。
根据题意,有a_1a_1q^2=8,a_1q=4。
解得a_1=2,q=2。
因此,a_4=a_1q^3=2×2^3=16。
3. 已知数列{a_n}满足a_1=1,a_{n+1}=2a_n+1,求a_5的值为()。
A. 21B. 33C. 65D. 129答案:C解析:根据递推关系,可得a_2=2a_1+1=3,a_3=2a_2+1=7,a_4=2a_3+1=15,a_5=2a_4+1=31。
因此,a_5=65。
二、填空题4. 已知数列{a_n}是等差数列,且a_1=3,公差d=2,则a_10的值为______。
答案:23解析:根据等差数列的通项公式,a_n=a_1+(n-1)d,代入n=10,得a_10=3+(10-1)×2=23。
5. 已知数列{a_n}是等比数列,且a_1=2,公比q=3,则a_5的值为______。
答案:486解析:根据等比数列的通项公式,a_n=a_1q^(n-1),代入n=5,得a_5=2×3^(5-1)=486。
三、解答题6. 已知数列{a_n}满足a_1=1,a_{n+1}=3a_n+2,求a_5的值。
答案:121解析:根据递推关系,可得a_2=3a_1+2=5,a_3=3a_2+2=17,a_4=3a_3+2=53,a_5=3a_4+2=161。
高中数学数列经典题型专题训练试题(含答案)

高中数学数列经典题型专题训练试题学校:___________姓名:___________班级:___________考号:___________说明:1、本试卷包括第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分100分。
考试时间120分钟。
2、考生请将第Ⅰ卷选择题的正确选项填在答题框内,第Ⅱ卷直接答在试卷上。
考试结束后,只收第Ⅱ卷第Ⅰ卷(选择题)一.单选题(共15小题,每题2分,共30分)1.数列{a n},已知对任意正整数n,a1+a2+a3+…+a n=2n-1,则a12+a22+a32+…+a n2等于()A.(2n-1)2B.C.D.4n-12.若{a n}为等比数列a5•a11=3,a3+a13=4,则=()A.3B.C.3或D.-3或-3.已知各项均为正数的等比数列{a n},a1a2a3=5,a7a8a9=10,则a4a5a6=()A.B.7C.6D.4.等差数列{a n}中,a1=1,a3=4,则公差d等于()A.1B.2C.D.5.数列的前n项和为S n,a n=,则S n≥0的最小正整数n的值为()6.若数列{a n}的前n项和S n=2n2-2n,则数列{a n}是()A.公差为4的等差数列B.公差为2的等差数列C.公比为4的等比数列D.公比为2的等比数列7.已知数列{a n}的前n项和S n=2n-1,则此数列奇数项的前n项和为()A.B.C.D.8.在等比数列{a n} 中,a1=4,公比为q,前n项和为S n,若数列{S n+2}也是等比数列,则q 等于()A.2B.-2C.3D.-39.在数列{a n}中,a1=2,a2=2,a n+2-a n=1+(-1)n,n∈N*,则S60的值为()A.990B.1000C.1100D.9910.若数列{a n}是公差为2的等差数列,则数列是()A.公比为4的等比数列B.公比为2的等比数列C.公比为的等比数列D.公比为的等比数列11.在数列{a n}中,a1=0,a n=4a n-1+3,则此数列的第5项是()A.252B.255C.215D.52212.数列{a n}、{b n}满足a n•b n=1,a n=n2+3n+2,则{b n}的前10项之和等于()A.B.C.D.13.等比数列{a n}中,a1+a2=8,a3-a1=16,则a3等于()14.已知在等比数列{a n}中,S n为其前n项和,且a4=2S3+3,a5=2S4+3,则此数列的公比q为()A.2B.C.3D.15.数列{a n}的通项,则数列{a n}中的最大项是()A.第9项B.第8项和第9项C.第10项D.第9项和第10项二.填空题(共10小题,每题2分,共20分)16.已知等差数列{a n},有a1+a2+a3=8,a4+a5+a6=-4,则a13+a14+a15=______.17.在等差数列{a n}中,a3+a5+a7+a9+a11=20,则a1+a13=______.18.数列{a n}的通项公式为a n=2n+2n-1,则数列a n的前n项和为______.19.数列{a n}中,a1=1,a n+1=2a n+1,则通项a n=______.20.数列{a n}是公差不为0的等差数列,且a2+a6=a8,则=______.21.已知数列{a n},a n+1=2a n+1,且a1=1,则a10=______.22.设正项等比数列{an}的公比为q,且,则公比q=______.23.已知数列{a n}满足a1=3,a n+1=2a n+1,则数列{a n}的通项公式a n=______.24.数列{a n}为等差数列,已知a3+2a8+a9=20,则a7______.25.设数列{a n}为正项等比数列,且a n+2=a n+1+a n,则其公比q=______.第Ⅱ卷(非选择题)三.简答题(共5小题,50分)26.(10分)已知等差数列{a n},前n项和为S n=n2+Bn,a7=14.(1)求B、a n;(2)设c n=n•,求T n=c1+c2+…+c n.27.(8分)已知等差数列{a n}满足:a5=11,a2+a6=18(Ⅰ)求数列{a n}的通项公式;(Ⅱ)若b n=a n+3n,求数列{b n}的前n项和S n.28.(7分)已知数列{a n}是公差不为0的等差数列,a1=2,且a2,a3,a4+1成等比数列.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=,求数列{b n}的前n项和S n.29.(12分)已知数列{a n}满足.(1)求a2,a3,a4的值;(2)求证:数列{a n-2}是等比数列;(3)求a n,并求{a n}前n项和S n.30.(12分)在数列{a n}中,a1=16,数列{b n}是公差为-1的等差数列,且b n=log2a n(Ⅰ)求数列{a n}和{b n}的通项公式;(Ⅱ)在数列{b n}中,若存在正整数p,q使b p=q,b q=p(p>q),求p,q得值;(Ⅲ)若记c n=a n•b n,求数列{c n}的前n项的和S n.参考答案一.单选题(共__小题)1.数列{a n},已知对任意正整数n,a1+a2+a3+…+a n=2n-1,则a12+a22+a32+…+a n2等于()A.(2n-1)2B.C.D.4n-1答案:C解析:解:∵a1+a2+a3+…+a n=2n-1…①∴a1+a2+a3+…+a n-1=2n-1-1…②,①-②得a n=2n-1,∴a n2=22n-2,∴数列{a n2}是以1为首项,4为公比的等比数列,∴a12+a22+a32+…+a n2==,故选C.2.若{a n}为等比数列a5•a11=3,a3+a13=4,则=()A.3B.C.3或D.-3或-答案:C解析:解:∵{a n}为等比数列a5•a11=3,∴a3•a13=3①∵a3+a13=4②由①②得a3=3,a13=1或a3=1,a13=3∴q10=或3,∴=或3,故选C.3.已知各项均为正数的等比数列{a n},a1a2a3=5,a7a8a9=10,则a4a5a6=()A.B.7C.6D.答案:A解析:解:a1a2a3=5⇒a23=5;a7a8a9=10⇒a83=10,a52=a2a8,∴,∴,故选A.4.等差数列{a n}中,a1=1,a3=4,则公差d等于()A.1B.2C.D.答案:D解析:解:∵数列{a n}是等差数列,a1=1,a3=4,∴a3=a1+2d,即4=1+2d,解得d=.故选:D.5.数列的前n项和为S n,a n=,则S n≥0的最小正整数n的值为()A.12B.13C.14D.15答案:A解析:解:令a n=<0,解得n≤6,当n>7时,a n>0,且a6+a7=a5+a8=a4+a9=a3+a10=a2+a11=a1+a12=0,所以S12=0,S13>0,即使S n≥0的最小正整数n=12.故选A.6.若数列{a n}的前n项和S n=2n2-2n,则数列{a n}是()A.公差为4的等差数列B.公差为2的等差数列C.公比为4的等比数列D.公比为2的等比数列答案:A解析:解:∵S n=2n2-2n,则S n-S n-1=a n=2n2-2n-[2(n-1)2-2(n-1)]=4n-4故数列{a n}是公差为4的等差数列故选A.7.已知数列{a n}的前n项和S n=2n-1,则此数列奇数项的前n项和为()A.B.C.D.答案:C解析:解:当n=1时,a1=S1=21-1=1,当n≥2时,a n=Sn-Sn-1=2n-1-(2n-1-1)=2•2n-1-2n-1=2n-1,对n=1也适合∴a n=2n-1,∴数列{a n}是等比数列,此数列奇数项也构成等比数列,且首项为1,公比为4.∴此数列奇数项的前n项和为==故选C8.在等比数列{a n} 中,a1=4,公比为q,前n项和为S n,若数列{S n+2}也是等比数列,则q 等于()A.2B.-2C.3D.-3答案:C解析:解:由题意可得q≠1由数列{S n+2}也是等比数列可得s1+2,s2+2,s3+2成等比数列则(s2+2)2=(S1+2)(S3+2)代入等比数列的前n项和公式整理可得(6+4q)2=24(1+q+q2)+12解可得q=3故选C.9.在数列{a n}中,a1=2,a2=2,a n+2-a n=1+(-1)n,n∈N*,则S60的值为()A.990B.1000C.1100D.99答案:A解析:解:当n为奇数时,a n+2-a n=1+(-1)n=0,可得a1=a3=…=a59=2.当n为偶数时,a n+2-a n=1+(-1)n=2,∴数列{a2n}为等差数列,首项为2,公差为2,∴a2+a4+…+a60=30×2+=930.∴S60=(a1+a3+…+a59)+(a2+a4+…+a60)=30×2+930=990.故选:A.10.若数列{a n}是公差为2的等差数列,则数列是()A.公比为4的等比数列B.公比为2的等比数列C.公比为的等比数列D.公比为的等比数列答案:A解析:解:∵数列{a n}是公差为2的等差数列∴a n=a1+2(n-1)∴∴数列是公比为4的等比数列故选A11.在数列{a n}中,a1=0,a n=4a n-1+3,则此数列的第5项是()A.252B.255C.215D.522答案:B解析:解:由a n=4a n-1+3可得a n+1=4a n-1+4=4(a n-1+1),故可得=4,由题意可得a1+1=1即数列{a n+1}为首项为1,公比为4的等比数列,故可得a5+1=44=256,故a5=255故选B12.数列{a n}、{b n}满足a n•b n=1,a n=n2+3n+2,则{b n}的前10项之和等于()A.B.C.D.答案:B解析:解:∵a n•b n=1∴b n==∴s10==(-)+=-=故选项为B.13.等比数列{a n}中,a1+a2=8,a3-a1=16,则a3等于()A.20B.18C.10D.8答案:B解析:解:设等比数列{a n}的公比为q,∵a1+a2=8,a3-a1=16,∴,解得,∴=2×32=18.故选:B.14.已知在等比数列{a n}中,S n为其前n项和,且a4=2S3+3,a5=2S4+3,则此数列的公比q为()A.2B.C.3D.答案:C解析:解:∵a4=2S3+3,a5=2S4+3,即2S4=a5-3,2S3=a4-3∴2S4-2S3=a5-3-(a4-3)=a5-a4=2a4,即3a4=a5∴3a4=a4q解得q=3,故选C15.数列{a n}的通项,则数列{a n}中的最大项是()A.第9项B.第8项和第9项C.第10项D.第9项和第10项答案:D解析:解:由题意得=,∵n是正整数,∴=当且仅当时取等号,此时,∵当n=9时,=19;当n=9时,=19,则当n=9或10时,取到最小值是19,而取到最大值.故选D.二.填空题(共__小题)16.已知等差数列{a n},有a1+a2+a3=8,a4+a5+a6=-4,则a13+a14+a15=______.答案:-40解析:解:设等差数列{a n}的公差为d,∵a1+a2+a3=8,a4+a5+a6=-4,∵a4+a5+a6=(a1+3d)+(a2+3d)+(a3+3d)=a1+a2+a3+9d,∴-4=8+9d,解得d=-,∴a13+a14+a15=a1+a2+a3+36d=8-×36=-40,故答案为:-4017.在等差数列{a n}中,a3+a5+a7+a9+a11=20,则a1+a13=______.答案:8解析:解:由等差数列的性质可得a3+a5+a7+a9+a11=(a3+a11)+a7+(a5+a9)=2a7+a7+2a7=5a7=20∴a7=4∴a1+a13=2a7=8故答案为:818.(2015秋•岳阳校级月考)数列{a n}的通项公式为a n=2n+2n-1,则数列a n的前n项和为______.答案:2n+n2-1解析:解:数列a n的前n项和S n=(2+22+23+…+2n)+[1+3+5+…+(2n-1)]=+=2n-1+n2.故答案为:2n-1+n2.19.数列{a n}中,a1=1,a n+1=2a n+1,则通项a n=______.答案:2n-1解析:解:由题可得,a n+1+1=2(a n+1),则=2,又a1=1,则a1+1=2,所以数列{a n+1}是以2为首项、公比的等比数列,所以a n+1=2•2n-1=2n,则a n=2n-1.故答案为:2n-1.20.数列{a n}是公差不为0的等差数列,且a2+a6=a8,则=______.答案:3解析:解:设等差数列{a n}的首项为a1,公差为d,由a2+a6=a8,得a1+d+a1+5d=a1+7d,即a1=d,所以==.故答案为3.21.已知数列{a n},a n+1=2a n+1,且a1=1,则a10=______.答案:1023解析:解:由题意,两边同加1得:a n+1+1=2(a n+1),∵a1+1=2∴{a n+1}是以2为首项,以2为等比数列∴a n+1=2•2n-1=2n∴a n=2n-1∴a10=1024-1=1023.故答案为:1023.22.设正项等比数列{an}的公比为q,且,则公比q=______.答案:解析:解:由题意知得∴6q2-q-1=0∴q=或q=-(与正项等比数列矛盾,舍去).故答案为:23.已知数列{a n}满足a1=3,a n+1=2a n+1,则数列{a n}的通项公式a n=______.答案:2n+1-1解析:解:由题意知a n+1=2a n+1,则a n+1+1=2a n+1+1=2(a n+1)∴=2,且a1+1=4,∴数列{a n+1}是以4为首项,以2为公比的等比数列.则有a n+1=4×2n-1=2n+1,∴a n=2n+1-1.24.数列{a n}为等差数列,已知a3+2a8+a9=20,则a7______.答案:=5解析:解:等差数列{a n}中,∵a3+2a8+a9=20,∴(a1+2d)+2(a1+7d)+(a1+8d)=4a1+24d=4(a1+6d)=4a7=20,∴a7=5.故答案为:5.25.设数列{a n}为正项等比数列,且a n+2=a n+1+a n,则其公比q=______.答案:解析:解:由题设条件知a1+a1q=a1q2,∵a1>0,∴q2-q-1=0解得,∵数列{a n}为正项等比数列,∴.故答案:.三.简答题(共__小题)26.已知等差数列{a n},前n项和为S n=n2+Bn,a7=14.(1)求B、a n;(2)设c n=n•,求T n=c1+c2+…+c n.答案:解:(1)∵a7=14.即a7=S7-S6=72+7B-62-6B=14.解得B=1,当n=1时,a1=S1=2;当n≥2时,a n=S n-S n-1=n2+n-(n-1)2-(n-1)=2n.n=1时也适合∴a n=2n(2)由(1)c n=n•=n•4n,T n=c1+c2+…+c n.=1•41+2•42+3•43+…n•4n①4T n=1•42+2•43+3•44+…(n-1)•4n+n•4n+1,②①-②得-3T n=41+42+43+…4n-n•4n+1=-n•4n+1=•4n+1∴T n=•4n+1解析:解:(1)∵a7=14.即a7=S7-S6=72+7B-62-6B=14.解得B=1,当n=1时,a1=S1=2;当n≥2时,a n=S n-S n-1=n2+n-(n-1)2-(n-1)=2n.n=1时也适合∴a n=2n(2)由(1)c n=n•=n•4n,T n=c1+c2+…+c n.=1•41+2•42+3•43+…n•4n①4T n=1•42+2•43+3•44+…(n-1)•4n+n•4n+1,②①-②得-3T n=41+42+43+…4n-n•4n+1=-n•4n+1=•4n+1∴T n=•4n+127.已知等差数列{a n}满足:a5=11,a2+a6=18(Ⅰ)求数列{a n}的通项公式;(Ⅱ)若b n=a n+3n,求数列{b n}的前n项和S n.答案:解:(Ⅰ)设等差数列{a n}的公差为d,∵a5=11,a2+a6=18,∴,解得a1=3,d=2.∴a1=2n+1.(Ⅱ)由(I)可得:b n=2n+1+3n.∴S n=[3+5+…+(2n+1)]+(3+32+…+3n)=+=n2+2n+-.解析:解:(Ⅰ)设等差数列{a n}的公差为d,∵a5=11,a2+a6=18,∴,解得a1=3,d=2.∴a1=2n+1.(Ⅱ)由(I)可得:b n=2n+1+3n.∴S n=[3+5+…+(2n+1)]+(3+32+…+3n)=+=n2+2n+-.28.已知数列{a n}是公差不为0的等差数列,a1=2,且a2,a3,a4+1成等比数列.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=,求数列{b n}的前n项和S n.答案:解:(Ⅰ)设数列{a n}的公差为d,由a1=2和a2,a3,a4+1成等比数列,得(2+2d)2-(2+d)(3+3d),解得d=2,或d=-1,当d=-1时,a3=0,与a2,a3,a4+1成等比数列矛盾,舍去.∴d=2,∴a n=a1+(n-1)d=2+2(n-1)=2n.即数列{a n}的通项公式a n=2n;(Ⅱ)由a n=2n,得b n==,∴S n=b1+b2+b3+…+b n==.解析:解:(Ⅰ)设数列{a n}的公差为d,由a1=2和a2,a3,a4+1成等比数列,得(2+2d)2-(2+d)(3+3d),解得d=2,或d=-1,当d=-1时,a3=0,与a2,a3,a4+1成等比数列矛盾,舍去.∴d=2,∴a n=a1+(n-1)d=2+2(n-1)=2n.即数列{a n}的通项公式a n=2n;(Ⅱ)由a n=2n,得b n==,∴S n=b1+b2+b3+…+b n==.29.已知数列{a n}满足.(1)求a2,a3,a4的值;(2)求证:数列{a n-2}是等比数列;(3)求a n,并求{a n}前n项和S n.答案:解:(1)∵数列{a n}满足,∴.…(3分)(2)∵,又a1-2=-1,∴数列{a n-2}是以-1为首项,为公比的等比数列.…(7分)(注:文字叙述不全扣1分)(3)由(2)得,…(9分)∴.…(12分)解析:解:(1)∵数列{a n}满足,∴.…(3分)(2)∵,又a1-2=-1,∴数列{a n-2}是以-1为首项,为公比的等比数列.…(7分)(注:文字叙述不全扣1分)(3)由(2)得,…(9分)∴.…(12分)30.在数列{a n}中,a1=16,数列{b n}是公差为-1的等差数列,且b n=log2a n(Ⅰ)求数列{a n}和{b n}的通项公式;(Ⅱ)在数列{b n}中,若存在正整数p,q使b p=q,b q=p(p>q),求p,q得值;(Ⅲ)若记c n=a n•b n,求数列{c n}的前n项的和S n.答案:解:(Ⅰ)数列{a n}中,a1=16,数列{b n}是公差为-1的等差数列,且b n=log2a n;∴b n+1=log2a n+1,∴b n+1-b n=log2a n+1-log2a n=log2=-1;∴=,∴{a n}是等比数列,通项公式为a n=16×=;∴{b n}的通项公式b n=log2a n=log2=5-n;(Ⅱ)数列{b n}中,∵b n=5-n,假设存在正整数p,q使b p=q,b q=p(p>q),则,解得,或;(Ⅲ)∵a n=,b n=5-n,∴c n=a n•b n=(5-n)×;∴{c n}的前n项和S n=4×+3×+2×+…+[5-(n-1)]×+(5-n)×①,∴s n=4×+3×+2×+…+[5-(n-1)]×+(5-n)×②;①-②得:s n=4×----…--(5-n)×=64--(5-n)×=48+(n-3)×;∴s n=96+(n-3)×.解析:解:(Ⅰ)数列{a n}中,a1=16,数列{b n}是公差为-1的等差数列,且b n=log2a n;∴b n+1=log2a n+1,∴b n+1-b n=log2a n+1-log2a n=log2=-1;∴=,∴{a n}是等比数列,通项公式为a n=16×=;∴{b n}的通项公式b n=log2a n=log2=5-n;(Ⅱ)数列{b n}中,∵b n=5-n,假设存在正整数p,q使b p=q,b q=p(p>q),则,解得,或;(Ⅲ)∵a n=,b n=5-n,∴c n=a n•b n=(5-n)×;∴{c n}的前n项和S n=4×+3×+2×+…+[5-(n-1)]×+(5-n)×①,∴s n=4×+3×+2×+…+[5-(n-1)]×+(5-n)×②;①-②得:s n=4×----…--(5-n)×=64--(5-n)×=48+(n-3)×;∴s n=96+(n-3)×.。
数列多选题专项训练测试试题及答案

一、数列多选题1.已知数列0,2,0,2,0,2,,则前六项适合的通项公式为( ) A .1(1)n n a =+- B .2cos 2n n a π= C .(1)2sin 2n n a π+= D .1cos(1)(1)(2)n a n n n π=--+-- 答案:AC【分析】对四个选项中的数列通项公式分别取前六项,看是否满足题意,得出答案.【详解】对于选项A ,取前六项得:,满足条件;对于选项B ,取前六项得:,不满足条件;对于选项C ,取前六项得:,解析:AC【分析】对四个选项中的数列通项公式分别取前六项,看是否满足题意,得出答案.【详解】对于选项A ,1(1)n n a =+-取前六项得:0,2,0,2,0,2,满足条件;对于选项B ,2cos2n n a π=取前六项得:0,2,0,2,0,2--,不满足条件; 对于选项C ,(1)2sin 2n n a π+=取前六项得:0,2,0,2,0,2,满足条件; 对于选项D ,1cos(1)(1)(2)n a n n n π=--+--取前六项得:0,2,2,8,12,22,不满足条件;故选:AC2.黄金螺旋线又名等角螺线,是自然界最美的鬼斧神工.在一个黄金矩形(宽长比约等于0.618)里先以宽为边长做正方形,然后在剩下小的矩形里以其宽为边长做正方形,如此循环下去,再在每个正方形里画出一段四分之一圆弧,最后顺次连接,就可得到一条“黄金螺旋线”.达·芬奇的《蒙娜丽莎》,希腊雅典卫城的帕特农神庙等都符合这个曲线.现将每一段黄金螺旋线与其所在的正方形所围成的扇形半径设为a n (n ∈N *),数列{a n }满足a 1=a 2=1,a n =a n -1+a n -2 (n ≥3).再将扇形面积设为b n (n ∈N *),则( )A .4(b 2020-b 2019)=πa 2018·a 2021B .a 1+a 2+a 3+…+a 2019=a 2021-1C .a 12+a 22+a 32…+(a 2020)2=2a 2019·a 2021D .a 2019·a 2021-(a 2020)2+a 2018·a 2020-(a 2019)2=0 答案:ABD【分析】对于A ,由题意得bn=an2,然后化简4(b2020-b2019)可得结果;对于B ,利用累加法求解即可;对于C ,数列{an}满足a1=a2=1,an =an -1+an -2 (n≥3解析:ABD【分析】对于A ,由题意得b n =4πa n 2,然后化简4(b 2020-b 2019)可得结果;对于B ,利用累加法求解即可;对于C ,数列{a n }满足a 1=a 2=1,a n =a n -1+a n -2 (n ≥3),即a n -1=a n -2-a n ,两边同乘a n -1 ,可得a n -12=a n -1 a n -2-a n -1 a n ,然后累加求解;对于D ,由题意a n -1=a n -a n -2,则a 2019·a 2021-(a 2020)2+a 2018·a 2020-(a 2019)2,化简可得结果 【详解】由题意得b n =4πa n 2,则4(b 2020-b 2019)=4(4πa 20202-4πa 20192)=π(a 2020+a 2019)(a 2020-a 2019)=πa 2018·a 2021,则选项A 正确; 又数列{a n }满足a 1=a 2=1,a n =a n -1+a n -2 (n ≥3),所以a n -2=a n -a n -1(n ≥3),a 1+a 2+a 3+…+a 2019=(a 3-a 2)+(a 4-a 3)+(a 5-a 4)+…+(a 2021-a 2020)=a 2021-a 2=a 2021-1,则选项B 正确;数列{a n }满足a 1=a 2=1,a n =a n -1+a n -2 (n ≥3),即a n -1=a n -2-a n ,两边同乘a n -1 ,可得a n -12=a n -1 a n -2-a n -1 a n ,则a 12+a 22+a 32…+(a 2020)2=a 12+(a 2a 1-a 2a 3)+(a 3a 2-a 3a 4)+…+(a 2020a 2019-a 2020a 2021)=a 12-a 2020a 2021=1-a 2020a 2021,则选项C 错误;由题意a n -1=a n -a n -2,则a 2019·a 2021-(a 2020)2+a 2018·a 2020-(a 2019)2=a 2019·(a 2021-a 2019)+a 2020·(a 2018-a 2020)=a 2019·a 2020+a 2020·(-a 2019)=0,则选项D 正确;故选:ABD.【点睛】此题考查数列的递推式的应用,考查累加法的应用,考查计算能力,属于中档题3.已知数列{}n a 的前4项为2,0,2,0,则该数列的通项公式可能为( )A .0,2,n n a n ⎧=⎨⎩为奇数为偶数 B .1(1)1n n a -=-+ C .2sin2n n a π= D .cos(1)1n a n π=-+ 答案:BD【分析】根据选项求出数列的前项,逐一判断即可.【详解】解:因为数列的前4项为2,0,2,0,选项A :不符合题设;选项B :,符合题设;选项C :,不符合题设;选项D :,符合题设解析:BD【分析】根据选项求出数列的前4项,逐一判断即可.【详解】解:因为数列{}n a 的前4项为2,0,2,0,选项A :不符合题设;选项B :01(1)12,a =-+=12(1)10,a =-+= 23(1)12,a =-+=34(1)10a =-+=,符合题设;选项C :,12sin 2,2a π==22sin 0,a π==332sin 22a π==-不符合题设; 选项D :1cos 012,a =+=2cos 10,a π=+=3cos 212,a π=+=4cos310a π=+=,符合题设.故选:BD.【点睛】本题考查数列的通项公式的问题,考查了基本运算求解能力,属于基础题.4.在等差数列{}n a 中,公差0d ≠,前n 项和为n S ,则( )A .4619a a a a >B .130S >,140S <,则78a a >C .若915S S =,则n S 中的最大值是12SD .若2n S n n a =-+,则0a =答案:AD【分析】对于,作差后利用等差数列的通项公式运算可得答案;对于,根据等差数列的前项和公式得到和, 进而可得,由此可知,故不正确; 对于,由得到,,然后分类讨论的符号可得答案;对于,由求出及解析:AD【分析】对于A ,作差后利用等差数列的通项公式运算可得答案;对于B ,根据等差数列的前n 项和公式得到70a >和780a a +<, 进而可得80a <,由此可知78||||a a <,故B 不正确;对于C ,由915S S =得到,12130a a +=,然后分类讨论d 的符号可得答案;对于D ,由n S 求出n a 及1a ,根据数列{}n a 为等差数列可求得0a =.【详解】对于A ,因为46191111(3)(5)(8)a a a a a d a d a a d -=++-+215d =,且0d ≠,所以24619150a a a a d -=>,所以4619a a a a >,故A 正确;对于B ,因为130S >,140S <,所以77713()1302a a a +=>,即70a >,787814()7()02a a a a +=+<,即780a a +<,因为70a >,所以80a <,所以7878||||0a a a a -=+<,即78||||a a <,故B 不正确;对于C ,因为915S S =,所以101114150a a a a ++++=,所以12133()0a a +=,即12130a a +=,当0d >时,等差数列{}n a 递增,则12130,0a a <>,所以n S 中的最小值是12S ,无最大值;当0d <时,等差数列{}n a 递减,则12130,0a a ><,所以n S 中的最大值是12S ,无最小值,故C 不正确;对于D ,若2n S n n a =-+,则11a S a ==,2n ≥时,221(1)(1)n n n a S S n n a n n a -=-=-+--+--22n =-,因为数列{}n a 为等差数列,所以12120a a =⨯-==,故D 正确.故选:AD【点睛】关键点点睛:熟练掌握等差数列的通项公式、前n 项和公式是解题关键.5.已知数列{}2n na n +是首项为1,公差为d 的等差数列,则下列判断正确的是( )A .a 1=3B .若d =1,则a n =n 2+2nC .a 2可能为6D .a 1,a 2,a 3可能成等差数列 答案:ACD【分析】利用等差数列的性质和通项公式,逐个选项进行判断即可求解【详解】因为,,所以a1=3,an =[1+(n-1)d](n+2n).若d =1,则an =n(n+2n);若d =0,则a2=解析:ACD【分析】利用等差数列的性质和通项公式,逐个选项进行判断即可求解【详解】 因为1112a =+,1(1)2nn a n d n =+-+,所以a 1=3,a n =[1+(n -1)d ](n +2n ).若d =1,则a n =n (n +2n );若d =0,则a 2=6.因为a 2=6+6d ,a 3=11+22d ,所以若a 1,a 2,a 3成等差数列,则a 1+a 3=a 2,即14+22d =12+12d ,解得15d =-. 故选ACD6.等差数列{}n a 中,n S 为其前n 项和,151115,a S S ==,则以下正确的是( )A .1d =-B .413a a =C .n S 的最大值为8SD .使得0n S >的最大整数15n = 答案:BCD【分析】设等差数列的公差为,由等差数列的通项公式及前n 项和公式可得,再逐项判断即可得解.【详解】设等差数列的公差为,由题意,,所以,故A 错误;所以,所以,故B 正确;因为,所以当解析:BCD【分析】设等差数列{}n a 的公差为d ,由等差数列的通项公式及前n 项和公式可得1215d a =-⎧⎨=⎩,再逐项判断即可得解.【详解】设等差数列{}n a 的公差为d , 由题意,1115411105112215a d a d a ⨯⨯⎧+=+⎪⎨⎪=⎩,所以1215d a =-⎧⎨=⎩,故A 错误; 所以1131439,129a a d a d a =+==+=-,所以413a a =,故B 正确;因为()()2211168642n n n a n d n n n S -=+=-+=--+, 所以当且仅当8n =时,n S 取最大值,故C 正确; 要使()28640n S n =--+>,则16n <且n N +∈,所以使得0n S >的最大整数15n =,故D 正确.故选:BCD.7.(多选题)在数列{}n a 中,若221n n a a p --=,(2n ≥,*n N ∈,p 为常数),则称{}n a 为“等方差数列”.下列对“等方差数列”的判断正确的是( )A .若{}n a 是等差数列,则{}2n a 是等方差数列 B .(){}1n-是等方差数列 C .若{}n a 是等方差数列,则{}kn a (*k N ∈,k 为常数)也是等方差数列D .若{}n a 既是等方差数列,又是等差数列,则该数列为常数列答案:BCD【分析】根据定义以及举特殊数列来判断各选项中结论的正误.【详解】对于A 选项,取,则不是常数,则不是等方差数列,A 选项中的结论错误; 对于B 选项,为常数,则是等方差数列,B 选项中的结论正解析:BCD【分析】根据定义以及举特殊数列来判断各选项中结论的正误.【详解】对于A 选项,取n a n =,则()()()422444221111n n a a n n n n n n +⎡⎤⎡⎤-=+-=+-⋅++⎣⎦⎣⎦()()221221n n n =+++不是常数,则{}2n a 不是等方差数列,A 选项中的结论错误;对于B 选项,()()22111110n n +⎡⎤⎡⎤---=-=⎣⎦⎣⎦为常数,则(){}1n -是等方差数列,B 选项中的结论正确;对于C 选项,若{}n a 是等方差数列,则存在常数p R ∈,使得221n n a a p +-=,则数列{}2n a 为等差数列,所以()221kn k n a a kp +-=,则数列{}kn a (*k N ∈,k 为常数)也是等方差数列,C 选项中的结论正确;对于D 选项,若数列{}n a 为等差数列,设其公差为d ,则存在m R ∈,使得n a dn m =+,则()()()()2221112222n n n n n n a a a a a a d dn m d d n m d d +++-=-+=++=++, 由于数列{}n a 也为等方差数列,所以,存在实数p ,使得221n n a a p +-=,则()222d n m d d p ++=对任意的n *∈N 恒成立,则()2202d m d d p ⎧=⎪⎨+=⎪⎩,得0p d ==, 此时,数列{}n a 为常数列,D 选项正确.故选BCD.【点睛】本题考查数列中的新定义,解题时要充分利用题中的定义进行判断,也可以结合特殊数列来判断命题不成立,考查逻辑推理能力,属于中等题.8.设等差数列{}n a 的前n 项和为n S ,若39S =,47a =,则( )A .2n S n =B .223n S n n =-C .21n a n =-D .35n a n =-答案:AC【分析】利用等差数列的前项和公式、通项公式列出方程组,求出,,由此能求出与.【详解】等差数列的前项和为.,,,解得,,.故选:AC .【点睛】本题考查等差数列的通项公式求和公解析:AC【分析】利用等差数列{}n a 的前n 项和公式、通项公式列出方程组,求出11a =,2d =,由此能求出n a 与n S .【详解】等差数列{}n a 的前n 项和为n S .39S =,47a =, ∴31413239237S a d a a d ⨯⎧=+=⎪⎨⎪=+=⎩, 解得11a =,2d =,1(1)221n a n n ∴+-⨯=-=.()21212n n n S n +-== 故选:AC .【点睛】本题考查等差数列的通项公式求和公式的应用,考查等差数列的性质等基础知识,考查运算求解能力,是基础题.9.下面是关于公差0d >的等差数列{}n a 的四个命题,其中的真命题为( ). A .数列{}n a 是递增数列B .数列{}n na 是递增数列C .数列{}n a n是递增数列 D .数列{}3n a nd +是递增数列答案:AD【分析】根据等差数列的性质,对四个选项逐一判断,即可得正确选项.【详解】, ,所以是递增数列,故①正确,,当时,数列不是递增数列,故②不正确,,当时,不是递增数列,故③不正确,,因解析:AD【分析】根据等差数列的性质,对四个选项逐一判断,即可得正确选项.【详解】0d >,10n n a a d +-=> ,所以{}n a 是递增数列,故①正确,()()2111n na n a n d dn a d n =+-=+-⎡⎤⎣⎦,当12d a n d-<时,数列{}n na 不是递增数列,故②不正确,1n a a d d n n -=+,当10a d -<时,{}n a n不是递增数列,故③不正确, 134n a nd nd a d +=+-,因为0d >,所以{}3n a nd +是递增数列,故④正确, 故选:AD【点睛】本题主要考查了等差数列的性质,属于基础题.10.设公差不为0的等差数列{}n a 的前n 项和为n S ,若1718S S =,则下列各式的值为0的是( )A .17aB .35SC .1719a a -D .1916S S - 答案:BD【分析】由得,利用可知不正确;;根据可知 正确;根据可知不正确;根据可知正确.【详解】因为,所以,所以,因为公差,所以,故不正确;,故正确;,故不正确;,故正确.故选:BD.解析:BD【分析】由1718S S =得180a =,利用17180a a d d =-=-≠可知A 不正确;;根据351835S a =可知 B 正确;根据171920a a d -=-≠可知C 不正确;根据19161830S S a -==可知D 正确.【详解】因为1718S S =,所以18170S S -=,所以180a =,因为公差0d ≠,所以17180a a d d =-=-≠,故A 不正确;135********()35235022a a a S a +⨯====,故B 正确; 171920a a d -=-≠,故C 不正确;19161718191830S S a a a a -=++==,故D 正确.故选:BD.【点睛】本题考查了等差数列的求和公式,考查了等差数列的下标性质,属于基础题.。
高一数学数列练习题含答案(可编辑修改word版)

n高一 级 数 学 数 列 练 习 题一、选择题:1、等差数列{a n }中, a 1 = 3, a 5 = 7, 则数列{a n }第9 项等于( C )A 、9B 、10C 、11D 、122、等比数列{a n }中, a 2 = 9, a 5 = 243, 则{a n }的第 4 项为( A )A 、81B 、243C 、27D 、1923、已知一等差数列的前三项依次为 x ,2x + 2,4x + 3 ,那么 22 是此数列的第( D )项A 、 2B 、 4C 、6D 、8 4、已知等差数列{a n }中,a 7+a 9=16,a 4=1,则 a 12 的值是( A )A 、15B 、30C 、31D 、645、设等差数列{a n }的前 n 项和为 S n ,若 S 3 = 9 , S 6 = 36 ,则 a 7 + a 8 + a 9 = ( B )A 、63B 、45C 、36D 、276、已知 m 和 2n 的等差中项是 4,2m 和 n 的等差中项是 5,则 m 和 n 的等差中项是( B )A 、2B 、3C 、6D 、97、在等差数列{a n } 中,若 a 4 + a 6 + a 8 + a 10 + a 12 = 120 ,则 2a 10 - a 12 的值为( C )A 、20B 、22C 、24D 、288、已知等差数列{a n }满足 a 5 + a 6 =28,则其前 10 项之和为 ( A)A 、140B 、280C 、168D 、569、等差数列{a n }共有 2n+1 项,其中奇数项之和为 4,偶数项之和为 3,则 n 的值是( A )A 、3B 、5C 、7D 、92a 1+a 210、在数列{a n}中,对任意 n ∈N *,都有 an +1-2a n =0(a n ≠0),则 3+ 4等于( D )1 A 、1B 、21 C 、31 D 、42a a11、在各项均为正数的等比数列{a n }中,若 a 5a 6=9,则 log 3a 1+log 3a 2+…+log 3a 10 等于( B )A 、12B 、10C 、8D 、2+log 3512、设数列{ a n }的通项公式是 a n = n 2 + 100,则{ a n }中最大项是( B )A. a 9二、填空题:B. a 10C. a 9 和 a 10D. a 8 和 a 913、数列{ a n }是等差数列, a 4 = 7 ,则 s 7 =4914、已知数列{ a n }的前 n 项和 S n = -n 2 +10n ,则其通项 a n = -2n +11;当 n = 5时 S n 最大,且最大值为2532 2n 1 n 2 a n115、已知数列{a n }满足 a 1=1,a n +1= ,则 a 5=1+a n16、已知数列{a }满足 a = 2a+ 3 且 a = 1,则数列{a }的通项公式为a = 2n +1 - 3nnn -11nn三、解答题:17、设{a n }为等差数列, {b n }为等比数列, a 1 = b 1 = 1, a 2 + a 4 = b 3 , b 2 b 4 = a 3 , 分别求出{a n }及{b n }的前 10 项 的和 S 10 及T 10 .解:设等差数列{a n }的公差为 d , 等比数列{b n }的公比为 q .a 2 = 1 + d , a 4 = 1 + 3d ,b 3 = q 2 , ∴ q 2 = 2 + 4d①又 b 2 = q , b 4 = q 3 , a 3 = 1 + 2d , a 3 = b 2 , ∴ q 4 = 1 + 2d ②则由①,②得 2q 4 = q 2 -将 q 2 = 1代入①,得 d = - 3, ∴ S= - 55当 q =2 82时, T =31(2 + 1082 ) ,210 32 当 q = -2 时, T = 31 (2 - 2 ) 210 32 18、等差数列{a n }的各项均为正数,a 1=3,前 n 项和为 S n ,{b n }为等比数列,b 1=1,且 b 2S 2=64,b 3S 3=960.(1)求 a n 与 b n ;1 1 1 3(2) 证 明 : + +…+ < .S 1 S 2S n 4 解 (1)设{a n }的公差为 d ,{b n }的公比为 q ,则 d >0,q ≠0,a n =3+(n -1)d ,b n =q n -1,依题意有 Error!解得Error!或Error!(舍去). 故 a n =2n +1,b n =8n -1.3+2n +1(2)证明:由(1)知 S n = 2×n =n (n +2),1 1 1 1 1 = = ( - ), S n n ?n +2? 2 n n +2 1 1 1 1 1 1 1 ∴ 1+ 2+…+ n = + + +…+ S S S 1 × 3 2 × 4 3 × 5 1 1 1 1 1 1 1 1 n ?n +2? = (1- + - + - +…+ - )2 3 2 4 3 5 1 1 1 1n n +2 = (1+ - + - +)3 2n +3 = -4 2?n +1??n +2?2n +3 ∵ >0 2?n +1??n +2?1 1 1 3 ∴ 1+ 2+…+ n < . S S S 419、已知数列{a n }的前 n 项和为 S n ,且 S n =2n 2+n ,n ∈N *,数列{b n }满足 a n =4log 2b n +3,n ∈N *. (1)求 a n ,b n ;(2)求数列{a n ·b n }的前 n 项和 T n .解 (1)由 S n =2n 2+n ,得当 n =1 时,a 1=S 1=3; 当 n ≥2 时,a n =S n -S n -1=4n -1.∴a n =4n -1(n ∈N *). 由 a n =4log 2b n +3=4n -1,得 b n =2n -1(n ∈N *). (2)由(1)知 a n ·b n =(4n -1)·2n -1,n ∈N *, ∴T n =3+7×2+11×22+…+(4n -1)×2n -1, 2T n =3×2+7×22+…+(4n -5)×2n -1+(4n -1)×2n .∴2T n -T n =(4n -1)×2n -[3+4(2+22+…+2n -1]=(4n -5)2n +5. 故 T n =(4n -5)2n +5.20、已知数列{a n }满足 a 1=1,a n -2a n -1-2n -1=0(n ∈N *,n ≥2).a n(1) 求证:数列{2n }是等差数列;(2) 若数列{a n }的前 n 项和为 S n ,求 S n .a n a n -1 1 解 (1)∵a n -2a n -1-2n -1=0,∴ -= , 2n 2n -1 2a n 1 1∴{2n }是以 为首项, 为公差的等差数列. 2 2 a n 1 1 (2)由(1),得 = +(n -1)× ,2n 2 2 ∴a n =n ·2n -1,∴S n =1·20+2·21+3·22+…+n ·2n -1① 则 2S n =1·21+2·22+3·23+…+n ·2n ② ①-②,得1·?1-2n ? -S n =1+21+22+…+2n -1-n ·2n = -n ·2n =2n -1-n ·2n ,1-2 ∴S n =(n -1)·2n +1.21、设数列{a n }的前项 n 和为 S n ,若对于任意的正整数 n 都有 S n = 2a n - 3n .(1) 设b n = a n + 3 ,求证:数列{b n } 是等比数列,并求出{a n }的通项公式。
高一数学《数列》测试题答案

《数列》练习题答案班级 学号 姓名 一、选择题(本大题共8小题,每小题5分,共40分)1.已知a b c d ,,,成等比数列,且曲线223y x x =-+的顶点是()b c ,,则ad 等于(B ) A.3B.2C.1D.2-2.设等差数列{}n a 的前n 项和为n S ,若39S =,636S =,则789a a a ++=( B ) A .63B .45C .36D .273.等差数列{a n }中,a 1+a 2+…+a 50=200,a 51+a 52+…+a 100=2700,则a 1等于( C ) A .-1221B .-21.5C .-20.5D .-204.各项均为正数的等比数列{}n a 的前n 项和为S n ,若S 10=2,S 30=14,则S 40等于( B ) A. 80 B . 30 C. 26 D. 165.设等差数列{}n a 的公差d 不为0,19a d =.若k a 是1a 与2k a 的等比中项,则k =(B ) A.2B.4C.6D.86.等差数列{n a }中,2511=a ,从第10项开始大于1,则d 的取值范围是( D ) A .(+∞,758) B .(758,∞-) C .[253,758) D .(253,758]7.设S n 是等差数列{a n }的前n 项和,若S 3S 6=13,则S 6S 12=( A )A. 310 B . 13 C. 18 D. 198.已知数列{}n a 是等比数列,若,a a a a 41813229=+则数列{}n a 的前30项的积=30T (B )A.154B.152 C.1521⎪⎭⎫ ⎝⎛ D.153二.填空题(本大题共4小题,每小题5分,共20分)9.设{n a }为公比q>1的等比数列,若2004a 和2005a 是方程03842=+-x x 的两根,则=+20072006a a __18________.10.已知等差数列{}n a 的前n 项和为n S ,若1221S =,则25811a a a a +++=7.11.等比数列{}n a 的前n 项和为n S ,已知1S ,22S ,33S 成等差数列,则{}n a 的公比为 13.12.在7和56之间插入a 、b ,使7、a 、b 、56成等比数列,若插入c 、d ,使7、c 、d 、56成等差数列,则a +b +c +d =___105__________三.解答题(本大题共4小题,每小题10分,共40分)13.设{}n a 是公比大于1的等比数列,n S 为数列{}n a 的前n 项和.已知37S =,且123334a a a ++,,构成等差数列. (1)求数列{}n a 的通项公式. (2)令31ln 12n n b a n +==,,,,求数列{}n b 的前n 项和T .解:(1)由已知得1231327:(3)(4)3.2a a a a a a ++=⎧⎪⎨+++=⎪⎩,解得22a =.设数列{}n a 的公比为q ,由22a =,可得1322a a q q==,. 又37S =,可知2227q q ++=,即22520q q -+=,解得12122q q ==,. 由题意得12q q >∴=,.11a ∴=.故数列{}n a 的通项为12n n a -=.(2)由于31ln 12n n b a n +==,,,, 由(1)得3312n n a += 3ln 23ln 2nn b n ∴==又13ln 2n n n b b +-={}n b ∴是等差数列.12n n T b b b ∴=+++故3(1)ln 22n n n T +=. 14.等差数列{}n a 的前n项和为1319n S a S ==+, (Ⅰ)求数列{}n a 的通项n a 与前n 项和n S ; (Ⅱ)设()nn S b n n*=∈N ,求证:数列{}n b 中任意不同的三项都不可能成为等比数列. 解:(Ⅰ)由已知得111339a a d ⎧=⎪⎨+=+⎪⎩,2d ∴=,故21(n n a n S n n =-=.(Ⅱ)由(Ⅰ)得n n Sb n n==假设数列{}n b 中存在三项p q r b b b ,,(p q r ,,互不相等)成等比数列,则2q p r b b b =.2((q p r +=.2()(20q pr q p r ∴-+--=p q r *∈N ,,,2020q pr q p r ⎧-=∴⎨--=⎩,, 22()02p r pr p r p r +⎛⎫∴=-=∴= ⎪⎝⎭,,.与p r ≠矛盾.所以数列{}n b 中任意不同的三项都不可能成等比数列.15.已知数列{}n a ,{}n b 满足12a =,11b =,且11113114413144n n n n n n a a b b a b ----⎧=++⎪⎪⎨⎪=++⎪⎩(2n ≥)(I )令n n n c a b =+,求数列{}n c 的通项公式; (II )求数列{}n a 的通项公式及前n 项和公式n S .15.(I)解:由题设得11()2(2)n n n n a b a b n --+=++≥,即12n n c c -=+(2n ≥)易知{}n c 是首项为113a b +=,公差为2的等差数列,通项公式为21n c n =+. (II )解:由题设得111()(2)2n n n n a b a b n ---=-≥,令n n n d a b =-,则 11(2)2n n d d n -=≥.易知{}n d 是首项为111a b -=,公比为12的等比数列,通项公式为112n n d -=. 由12112n n n n n a b n a b -+=+⎧⎪⎨-=⎪⎩,解得 1122n n a n =++,求和得21122n n n S n =-+++. 16.已知数列{}n a 和{}n b 满足:11a =,22a =,0n a >,n b =*n ∈N ),且{}n b 是以q 为公比的等比数列. (I )证明:22n n a a q +=;(II )若2122n n n c a a -=+,证明数列{}n c 是等比数列; (III )求和:1234212111111n na a a a a a -++++++. 16.解法1:(I )证:由1nn b q b +=nq ==,∴ 22()n n a a q n +=∈N*. (II )证:22n n a q q -=,22221231n n n a a q a q ---∴===,222222n n n a a q a q --===,22222222212121222(2)5n n n n n n n c a a a q a q a a q q -----∴=+=+=+=.{}n c ∴是首项为5,以2q 为公比的等比数列.(III )由(II )得2221111n n q a a --=,222211n n q a a-=,于是 1221321242111111111n n n a a a a a a a a a -⎛⎫⎛⎫+++=+++++++⎪ ⎪⎝⎭⎝⎭24222422121111111111n n a q q q a q qq --⎛⎫⎛⎫=+++++++++ ⎪ ⎪⎝⎭⎝⎭2122311112n q qq -⎛⎫=++++⎪⎝⎭. 当1q =时,2422122111311112n n a a a q qq -⎛⎫+++=++++ ⎪⎝⎭32n =. 当1q ≠时,2422122111311112n n a a a q qq -⎛⎫+++=++++ ⎪⎝⎭223121n q q --⎛⎫-= ⎪-⎝⎭2222312(1)n n q q q -⎡⎤-=⎢⎥-⎣⎦.故21222223121111 1.(1)nn n n q q a a a q q q -⎧=⎪⎪+++=⎨⎡⎤3-⎪≠⎢⎥⎪2-⎣⎦⎩, ,, 解法2:(I )同解法1(I ).(II )证:222*1212221221221222()22n n n n nn n n n nc a a q a q a q n c a a a a +++---++===∈++N ,又11225c a a =+=,{}n c ∴是首项为5,以2q 为公比的等比数列.(III )由(II )的类似方法得222221212()3n n n n a a a a qq ---+=+=, 34212121221234212111n nn n na a a a a a a a a a a a a a a --++++++=+++,2222212442123322k k k k k k k a a q qa a q --+---+==,12k n =,,,.2221221113(1)2n k q q a a a --+∴+++=+++.17.(选做题) 在数列{}n a 中,12a =,1431n n a a n +=-+,n ∈*N . (Ⅰ)证明数列{}n a n -是等比数列; (Ⅱ)求数列{}n a 的前n 项和n S ; (Ⅲ)证明不等式14n n S S +≤,对任意n ∈*N 皆成立. 17.(Ⅰ)证明:由题设1431n n a a n +=-+,得1(1)4()n n a n a n +-+=-,n ∈*N .又111a -=,所以数列{}n a n -是首项为1,且公比为4的等比数列.(Ⅱ)解:由(Ⅰ)可知14n n a n --=,于是数列{}n a 的通项公式为14n n a n -=+.所以数列{}n a 的前n 项和41(1)32n n n n S -+=+.(Ⅲ)证明:对任意的n ∈*N ,1141(1)(2)41(1)443232n n n n n n n n S S ++⎛⎫-++-+-=+-+ ⎪⎝⎭21(34)02n n =-+-≤.所以不等式14n n S S +≤,对任意n ∈*N 皆成立.。
高一数学《必修五》数列测试题-(含答案)

高一数学《必修五》数列测试题一、选择题1、等差数列—3,1,5,…的第15项的值是( B ) A .40 B .53 C .63 D .762、设n S 为等比数列{}n a 的前项和,已知3432S a =-,2332S a =-,则公比q =( B ) A .3 B .4C .5D .63、已知,231,231-=+=b a 则b a ,的等差中项为( A )A .3B .2C .31 D .214、已知等差数列}{n a 的前n 项和为S n ,若854,18S a a 则-=等于( D ) A .18 B .36 C .54 D .725、设4321,,,a a a a 成等比数列,其公比为2,则432122a a a a ++的值为( A )A .41 B .21 C .81 D .16、在数列{}n a 中,12a =, 11ln(1)n n a a n+=++,则n a = ( A )A .2ln n +B .2(1)ln n n +-C .2ln n n +D .1ln n n ++ 7、等差数列{a n }中,10a <,n S 为第n 项,且316S S =,则nS取最大值时,n 的值( C )A .9B .10C .9或10D .10或11 8、设n S 为等差数列{}n a 的前项和,若36324S S ==,,则9a =( A ) A . 15 B . 45 C .192 D . 279、某种细菌在培养过程中,每20分钟分裂一次(一个分裂为两个),经过3小时,这种细菌由1个可繁殖成 ( B )A .511个B .512个C .1023个D .1024个10、等比数列{}n a 中,===+q a a a a 则,8,63232( C ) A .2B .21 C .2或21D .-2或21-11、已知{}n a 是等比数列,a n >0,且a 4a 6+2a 5a 7+a 6a 8=36,则a 5+a 7等于 ( A ) A .6 B .12 C .18 D .2412、已知8079--=n n a n ,(+∈N n ),则在数列{n a }的前50项中最小项和最大项分别是( C )A .501,a aB .81,a aC . 98,a aD .509,a a二、填空题13、两个等差数列{}{},,n n b a ,327......2121++=++++++n n b b b a a a n n 则55b a=___________.14、数列{}n a 的前n项的和13++=n S nn ,则此数列的通项公式a n =_ .15、数列{}n a 中,11,111+==-n n a a a ,则=4a .16、设n S 是等差数列{}n a 的前n 项和,且8765S S S S >=< ,则下列结论一定正确的有 . ①0<d ; ②07=a ; ③59S S >; ④01<a ; ⑤6S 和7S 均为n S 的最大值.三、解答题17、已知等比数列{}n b 与数列{}n a 满足*,3N n b n an ∈=(1)求证:{}n a 是等差数列; (2) 若2021138,101b b b a a Λ求=+ 解析:(1){}n b Θ是等比数列,依题意可设{}n b 的公比为)0(>q q2(1≥=∴-n q b b n n ) )2(331≥=∴-n q n na a )2(31≥=∴--n q n n a a )2(log 31≥=-∴-n q a a n n 为一常数。
数列综合测试题及答案

高一数学数列综合测试题1.{a n }是首项a 1=1,公差为d =3的等差数列,如果a n =2 005,则序号n 等于( ). A .667B .668C .669D .6702.在各项都为正数的等比数列{a n }中,首项a 1=3,前三项和为21,则a 3+a 4+a 5=( ). A .33B .72C .84D .1893.如果a 1,a 2,…,a 8为各项都大于零的等差数列,公差d ≠0,则( ). A .a 1a 8>a 4a 5B .a 1a 8<a 4a 5C .a 1+a 8<a 4+a 5D .a 1a 8=a 4a 54.已知方程(x 2-2x +m )(x 2-2x +n )=0的四个根组成一个首项为41的等差数列,则|m -n |等于( ).A .1B .43C .21D . 835.等比数列{a n }中,a 2=9,a 5=243,则{a n }的前4项和为( ). A .81 B .120 C .168 D .1926.若数列{a n }是等差数列,首项a 1>0,a 2 003+a 2 004>0,a 2 003·a 2 004<0,则使前n 项和S n >0成立的最大自然数n 是( ). A .4005B .4006C .4007D .40087.已知等差数列{a n }的公差为2,若a 1,a 3,a 4成等比数列, 则a 2=( ). A .-4B .-6C .-8D . -108.设S n 是等差数列{a n }的前n 项和,若35a a =95,则59S S =( ). A .1B .-1C .2D .219.已知数列-1,a 1,a 2,-4成等差数列,-1,b 1,b 2,b 3,-4成等比数列,则212b a a -的值是( ). A .21B .-21C .-21或21D .4110.在等差数列{a n }中,a n ≠0,a n -1-2n a +a n +1=0(n ≥2),若S 2n -1=38,则n =( ). A .38B .20C .10D .9二、填空题 11.设f (x )=221+x ,利用课本中推导等差数列前n 项和公式的方法,可求得f (-5)+f (-4)+…+f (0)+…+f (5)+f (6)的值为 . 12.已知等比数列{a n }中,(1)若a 3·a 4·a 5=8,则a 2·a 3·a 4·a 5·a 6= .(2)若a 1+a 2=324,a 3+a 4=36,则a 5+a 6= . (3)若S 4=2,S 8=6,则a 17+a 18+a 19+a 20= . 13.在38和227之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为 . 14.在等差数列{a n }中,3(a 3+a 5)+2(a 7+a 10+a 13)=24,则此数列前13项之和为 . 15.在等差数列{a n }中,a 5=3,a 6=-2,则a 4+a 5+…+a 10= .16.设平面内有n 条直线(n ≥3),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用f (n )表示这n条直线交点的个数,则f (4)= ;当n >4时,f (n )= . 三、解答题17.(1)已知数列{a n }的前n 项和S n =3n 2-2n ,求证数列{a n }成等差数列.(2)已知a1,b1,c1成等差数列,求证a cb +,b ac +,cba +也成等差数列. 18.设{a n }是公比为 q 的等比数列,且a 1,a 3,a 2成等差数列. (1)求q 的值;(2)设{b n }是以2为首项,q 为公差的等差数列,其前n 项和为S n ,当n ≥2时,比较S n 与b n 的大小,并说明理由.19.数列{a n }的前n 项和记为S n ,已知a 1=1,a n +1=nn 2+S n (n =1,2,3…). 求证:数列{nS n}是等比数列. 20.已知数列{a n }是首项为a 且公比不等于1的等比数列,S n 为其前n 项和,a 1,2a 7,3a 4成等差数列,求证:12S 3,S 6,S 12-S 6成等比数列.高一数学数列综合测试题参考答案一、选择题 1.C解析:由题设,代入通项公式a n =a 1+(n -1)d ,即2 005=1+3(n -1),∴n =699. 2.C解析:本题考查等比数列的相关概念,及其有关计算能力. 设等比数列{a n }的公比为q (q >0),由题意得a 1+a 2+a 3=21, 即a 1(1+q +q 2)=21,又a 1=3,∴1+q +q 2=7. 解得q =2或q =-3(不合题意,舍去), ∴a 3+a 4+a 5=a 1q 2(1+q +q 2)=3×22×7=84. 3.B .解析:由a 1+a 8=a 4+a 5,∴排除C . 又a 1·a 8=a 1(a 1+7d )=a 12+7a 1d ,∴a 4·a 5=(a 1+3d )(a 1+4d )=a 12+7a 1d +12d 2>a 1·a 8. 4.C 解析:解法1:设a 1=41,a 2=41+d ,a 3=41+2d ,a 4=41+3d ,而方程x 2-2x +m =0中两根之和为2,x 2-2x +n =0中两根之和也为2,∴a 1+a 2+a 3+a 4=1+6d =4,∴d =21,a 1=41,a 4=47是一个方程的两个根,a 1=43,a 3=45是另一个方程的两个根. ∴167,1615分别为m 或n , ∴|m -n |=21,故选C .解法2:设方程的四个根为x 1,x 2,x 3,x 4,且x 1+x 2=x 3+x 4=2,x 1·x 2=m ,x 3·x 4=n .由等差数列的性质:若+s =p +q ,则a +a s =a p +a q ,若设x 1为第一项,x 2必为第四项,则x 2=47,于是可得等差数列为41,43,45,47,∴m =167,n =1615, ∴|m -n |=21. 5.B解析:∵a 2=9,a 5=243,25a a =q 3=9243=27, ∴q =3,a 1q =9,a 1=3,∴S 4=3-13-35=2240=120.6.B 解析:解法1:由a 2 003+a 2 004>0,a 2 003·a 2 004<0,知a 2 003和a 2 004两项中有一正数一负数,又a 1>0,则公差为负数,否则各项总为正数,故a 2 003>a 2 004,即a 2 003>0,a 2 004<0.∴S 4 006=2+006400641)(a a =2+006400420032)(a a >0,∴S 4 007=20074·(a 1+a 4 007)=20074·2a 2 004<0, 故4 006为S n >0的最大自然数. 选B .解法2:由a 1>0,a 2 003+a 2 004>0,a 2 003·a 2 004<0,同解法1的分析得a 2 003>0,a 2 004<0,∴S 2 003为S n 中的最大值.∵S n 是关于n 的二次函数,如草图所示, ∴2 003到对称轴的距离比2 004到对称轴的距离小,∴20074在对称轴的右侧. 根据已知条件及图象的对称性可得4 006在图象中右侧零点B 的左侧,4007,4 008都在其右侧,S n >0的最大自然数是4 006.7.B解析:∵{a n }是等差数列,∴a 3=a 1+4,a 4=a 1+6, 又由a 1,a 3,a 4成等比数列,∴(a 1+4)2=a 1(a 1+6),解得a 1=-8, ∴a 2=-8+2=-6. 8.A解析:∵59S S =2)(52)(95191a a a a ++=3559a a ⋅⋅=59·95=1,∴选A .9.A解析:设d 和q 分别为公差和公比,则-4=-1+3d 且-4=(-1)q 4, ∴d =-1,q 2=2, ∴212b a a -=2q d -=21. 10.C解析:∵{a n }为等差数列,∴2n a =a n -1+a n +1,∴2n a =2a n , 又a n ≠0,∴a n =2,{a n }为常数数列, 而a n =1212--n S n ,即2n -1=238=19,∴n =10. 二、填空题 11.23. 解析:∵f (x )=221+x, ∴f (1-x )=2211+-x =xx2222⋅+=x x22221+, (第6题)∴f (x )+f (1-x )=x 221++xx22221+⋅=x x 222211+⋅+=x x 22)22(21++=22. 设S =f (-5)+f (-4)+…+f (0)+…+f (5)+f (6), 则S =f (6)+f (5)+…+f (0)+…+f (-4)+f (-5),∴2S =[f (6)+f (-5)]+[f (5)+f (-4)]+…+[f (-5)+f (6)]=62, ∴S =f (-5)+f (-4)+…+f (0)+…+f (5)+f (6)=32. 12.(1)32;(2)4;(3)32. 解析:(1)由a 3·a 5=24a ,得a 4=2, ∴a 2·a 3·a 4·a 5·a 6=54a =32.(2)9136)(324222121=⇒⎩⎨⎧=+=+q q a a a a , ∴a 5+a 6=(a 1+a 2)q 4=4. (3)2=+=+++=2=+++=4444821843214q qS S a a a S a a a a S ⇒⎪⎩⎪⎨⎧⋅⋅⋅,∴a 17+a 18+a 19+a 20=S 4q 16=32. 13.216.解析:本题考查等比数列的性质及计算,由插入三个数后成等比数列,因而中间数必与38,227同号,由等比中项的中间数为22738⋅=6,∴插入的三个数之积为38×227×6=216. 14.26.解析:∵a 3+a 5=2a 4,a 7+a 13=2a 10, ∴6(a 4+a 10)=24,a 4+a 10=4, ∴S 13=2+13131)(a a =2+13104)(a a =2413⨯=26. 15.-49.解析:∵d =a 6-a 5=-5, ∴a 4+a 5+…+a 10=2+7104)(a a =25++-755)(d a d a=7(a 5+2d ) =-49.16.5,21(n +1)(n -2).解析:同一平面内两条直线若不平行则一定相交,故每增加一条直线一定与前面已有的每条直线都相交,∴f (k )=f (k -1)+(k -1).由f (3)=2,f (4)=f (3)+3=2+3=5, f (5)=f (4)+4=2+3+4=9, ……f (n )=f (n -1)+(n -1),相加得f (n )=2+3+4+…+(n -1)=21(n +1)(n -2). 三、解答题17.分析:判定给定数列是否为等差数列关键看是否满足从第2项开始每项与其前一项差为常数. 证明:(1)n =1时,a 1=S 1=3-2=1,当n ≥2时,a n =S n -S n -1=3n 2-2n -[3(n -1)2-2(n -1)]=6n -5,n =1时,亦满足,∴a n =6n -5(n ∈N*).首项a 1=1,a n -a n -1=6n -5-[6(n -1)-5]=6(常数)(n ∈N*), ∴数列{a n }成等差数列且a 1=1,公差为6. (2)∵a1,b1,c1成等差数列, ∴b2=a1+c 1化简得2ac =b (a +c ).a cb ++c b a +=ac ab a c bc +++22=ac c a c a b 22+++)(=ac c a 2+)(=2++2)()(c a b c a =2·b ca +,∴a cb +,b ac +,cba +也成等差数列. 18.解:(1)由题设2a 3=a 1+a 2,即2a 1q 2=a 1+a 1q , ∵a 1≠0,∴2q 2-q -1=0, ∴q =1或-21.(2)若q =1,则S n =2n +21-)(n n =23+2n n .当n ≥2时,S n -b n =S n -1=22+1-))((n n >0,故S n >b n .若q =-21,则S n =2n +21-)(n n (-21)=49+-2n n .当n ≥2时,S n -b n =S n -1=4-11-)0)((n n ,故对于n ∈N +,当2≤n ≤9时,S n >b n ;当n =10时,S n =b n ;当n ≥11时,S n <b n .19.证明:∵a n +1=S n +1-S n ,a n +1=nn 2+S n , ∴(n +2)S n =n (S n +1-S n ),整理得nS n +1=2(n +1) S n , 所以1+1+n S n =nSn 2. 故{nS n}是以2为公比的等比数列. 20.证明:由a 1,2a 7,3a 4成等差数列,得4a 7=a 1+3a 4,即4 a 1q 6=a 1+3a 1q 3, 变形得(4q 3+1)(q 3-1)=0, ∴q 3=-41或q 3=1(舍).由3612S S =qq a qq a ----1)1(121)1(3161=1213q +=161; 6612S S S -=612S S -1=qq a q q a ----1)1(1)1(61121-1=1+q 6-1=161; 得3612S S =6612S S S -.∴12S 3,S 6,S 12-S 6成等比数列.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学数列专项测试及答案
一、选择题
1.(2005.全国2)如果a 1,a 2,…,a g 是各项都大于零的等差数列,公差d ≠0,则( ) A .a 1a 8>a 4a 5
B .a 1a 8<a 4a 5
C .a 1+a 8>a 4+a 5
D .a 1a 8=a 4a 5
2.(2005.福建)已知等差数列{a n }中,a 7+a 9=16,a 4=1,则a 12的值是( ) A .15 B .30
C .31
D .64
3.(2005.江苏)在各项都为正数的等比数列{a n }中,a 1=3,前三项和为21,则a 3+a 4
+a 5=( )
A .33
B .72
C .84
D .189
4.(2001京、内、皖)据市场调查结果,预测某种家用商品从年初开始的n 个月内累积的需求量S n (万件)近似地满足S n =
n
90
(21n -n 2-5),(n =1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是( )
A .5、6月
B .6、7月
C .7、8月
D .8、9月
5.若数列{a n }前8项值各异,且a n +8=a n 对任意n ∈N +
都成立,则下列数列中可取遍{a n }前8项值的数列为( )
A .{a 2k +1}
B .{a 3k +1}
C .{a 4k +1}
D .{a 6k +1}
6.设f(n)=1n +1+1n +2+…+12n ,(n ∈N +),则f(n +1)-f(n)等于( )
A .1
2n +1
B .12n +2
C .12n +1+12n +2
D .
12n +1-12n +2
7.数列{a n }的通项公式a n =3n 2-28n ,则数列各项中最小项是( ) A .第4项 B .第5项
C .第6项
D .第7项
8.已知m 和2n 的等差中项为4,2m 和n 的等差中项为5,则m 和n 的等差中项为( ) A .2 B .3
C .6
D .9
9.{a n }为等差数列,且a 2
4+2a 4a 7+a 6a 8=2004,则a 5a 6等于( ) A .501 B .±501
C .2004
D .±2004
10.等差数列共有2n +1项,所有奇数项之和为132,所有偶数项之和为120,则n =( ) A .9 B .10
C .11
D .12
11.某工厂生产总值月平均增长率为P ,则年平均增长率为( ) A .P B .12P
C .(1+P)12
D .(1+P)12-1
12.已知公差不为0的等差数列的第k 、n 、p 项构成等比数列的连续三项,则等比数列的公比为( )
A .n -p k -n
B .p -n p -k
C .n -k n -p
D .k -p n -p
二、填空题
13.(2005.天津)数列{a n }中,a 1=1,a 2=2,且a n +2-a n =1+(-1)n ,(n ∈N +
),则S 100
=___.
14.(2005.湖北)设等比数列{a n }的公比为q ,前n 项和为S n ,若S n +1,S n ,S n +2成等差
数列,则q 值为_____.
15.等差数列{a n },{b n }前n 项和分别为S n 与T n ,若S n T n =2n 3n +1,则a n
b n =_____.
16.已知{a n }是正项等比数列,公比q =2,且a 1a 2…a 30=230,则a 3a 6a 9…a 30=___. 三、解答题
17.(1)已知S n =2n 2-3n ,求a n ;
(2)已知S n =5n -3,求a n .
18.(2005.全国2)
已知等差数列{a n },a n >0,lga 1、lga 2、lga 4成等差,又b n =1
a 2n .
(1)证明:{b n }为等比数列.
(2)若无穷等比数列{b n }各项和S =1
3,求数列{a n }的首项a 1及公差d .
19.数列{a n }的前n 项和记为S n ,已知a 1=1,a n +1=n +2
n S n
,(n =1, 2, 3……).证明: (1)数列{S n
n }是等比数列;
(2)S n +1=4a n .
20.(2005.全国1)
设等比数列{a n }的公比为q ,前n 项和S n >0,(n =1,2…). (1)求q 的取值范围;
(2)设b n =a n +2-3
2a n +1,记{b n }的前n 项和为T n ,试比较S n 与T n 的大小.
21.已知数列{a n }的前n 项和S n =-32n 2+205
2n ,求数列{|a n |}的前n 项和T n .
22.设数列{a n }的前n 项和S n =2a n -4,数列{b n }满足b n +1=a n +2b n ,且b 1=2. (1)求通项a n ;(2)求{b n }的前n 项和T n .
22.(2000.全国理)
(1)已知数列{c n },其中c n =2n +3n ,且数列{c n +1-pc n }为等比数列,求常数p ;
(2)设{a n }、{b n }是公比不相等的两个等比数列,c n =a n +b n ,证明数列{c n }不是等比数列.
数列专练答案
一.选择题
1.B 2.A 3.C 4.C 5.B 6.D 7.B 8.B 9.A 10.B 11.D 12.A 二.填空题
13.2600 14.-2 15.2131
n n -- 16.20
2 三.解答题
17.(1)45n a n =- (2)1
2(1)
45(2)n n n a n -=⎧
=⎨
≥⎩ 18.(1) 设{}n a 公差为d,依题得1112,2n n
n a d a na a a =∴==
1121221
22
n n n n n n a b b a +++∴=== 故{}n b 为等比数列
(2)111121
211
1,12312
a b s a a =
===- 所以13a d == 19.(1) 11122
21n n n n n n n s s n n a s s s s n n n n
+++++=
⇒-=⇒=+
故{
}n
s n
是以2为公比的等比数列 (2)由(1)得
114(2)11
n n s s
n n n +-=≥+- 1
14(1)
4(2)1
n n n s s n a n n -+∴=+=≥- 又213,3a s ==,故2124s a a =+= 故对任意正整数n>1,都有14n n s a +=
20.(1)10,0,1n s a q >∴>=时10,1n s na q =>≠时,1(1)
01n n a q s q
-=
>- 由10110n q q q -<⎧>⎨-<⎩得,由1010n
q q ->⎧≠⎨->⎩
得-1q 1且q 0 综上述:(1,0)(0,)q ∈-+∞
(2)由2132n n n b a a ++=-
23()2n n b a q q ∴=- 23
()2n n T q q s ∴=- 231
(1)()(2)22n n n n T s s q q s q q ∴-=--=+-
故当1
12
q -<<-或q>2时,n n T s >
当1
22
q -<<≠且q 0时,n n T s
当1
22
q =-或q=时,n n T s =
21.1101,2a n =≥时,1
3104n n n a s s
n -=-=-+
令034,35,0n n a n n a ≥⇒≤∴≥< (1)当2320534,22
n n n T S n n ≤==-+ (2)当
21343534320535,()()2350222
n n n n T a a a a S S n n ≥=++-++=-=
-+ 故223205(34)22
32053502(35)22
n n n n T n n n ⎧
-+≤⎪⎪=⎨⎪-+≥⎪⎩
22.(1)14,2a n =≥时,1
11222n n n n n n n a S S
a a a a ---=-=-∴=
故1
2n n a +=
(2)1
11122
122n n n
n n n n
b b b b ++++-=⇒
-= 1
(1)1222
n n n n b b n n b n ∴
=+-=∴= 123
1222322n n T n ∴=+++
+ 234121222322n n T n +=+++
+
相减得:1
(1)22n n T n +=-+。
