中考数学一轮复习之四边形
2024成都中考数学第一轮专题复习之第五章 第一节 平行四边形与多边形 知识精练(含答案)

2024成都中考数学第一轮专题复习之第五章第一节平行四边形与多边形知识精练基础题1.(2023衡阳)如图,在四边形ABCD中,已知AD∥B C.添加下列条件不能..判定四边形ABCD 是平行四边形的是()第1题图A.AD=BCB.AB∥DCC.AB=DCD.∠A=∠C2.(2023兰州)如图①是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中,如图②是八角形空窗的示意图,它的一个外角∠1=()图①图②第2题图A.45°B.60°C.110°D.135°3.若平行四边形中两个内角的度数比为1∶4,则其中较小的内角是()A.36°B.40°C.45°D.48°4.如图,在▱ABCD中,对角线AC与BD相交于点O,已知△CDO的周长为15,AC=7,BD=11,则CD的长为()A.5B.6C.8D.9第4题图5.(2023自贡)第29届自贡国际恐龙灯会“辉煌新时代”主题灯组上有一幅不完整的正多边形图案,小华量得图中一边与对角线的夹角∠ACB=15°,算出这个正多边形的边数是()第5题图A.9B.10C.11D.126.如图,在平行四边形ABCD中,AD=2AB,点E为BC中点,连接AE,ED,则下列结论错误的是()A.AE=CEB.AE平分∠BADS▱ABCDC.AE⊥EDD.S△AED=12第6题图7.(2022乐山)如图,在平行四边形ABCD中,过点D作DE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F.若AB=6,AC=8,DE=4,则BF的长为()第7题图D.2A.4B.3C.528.(2023扬州)如果一个多边形每一个外角都是60°,那么这个多边形的边数为________.9.(2023株洲)如图所示,在平行四边形ABCD中,AB=5,AD=3,∠DAB的平分线AE交线段CD于点E,则EC=________.第9题图10.(2023兰州)如图,在▱ABCD中,BD=CD,AE⊥BD于点E,若∠C=70°,则∠BAE=________°.第10题图11.(2023凉山州)如图,▱ABCO的顶点O,A,C的坐标分别是(0,0),(3,0),(1,2),则顶点B的坐标是________.第11题图12.(2023枣庄改编)如图,一束太阳光线平行照射在放置于地面的正六边形上,若∠1=44°,则∠2的度数为________.第12题图13.如图,在△ABC中,中线AF与中位线DE交于点O,连接DF,EF.(1)求证:四边形ADFE是平行四边形;(2)若AB=8,AC=6,AF=5,求BC的长及四边形ADFE的面积.第13题图14.(2023株洲)如图所示,在△ABC中,点D,E分别为AB,AC的中点,点H在线段CE 上,连接BH,点G,F分别为BH,CH的中点.(1)求证:四边形DEFG为平行四边形;(2)若DG⊥BH,BD=3,EF=2,求线段BG的长度.第14题图拔高题15.(2023山西改编)蜂巢结构精巧,其巢房横截面的形状均为正六边形,如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点P,Q,M均为正六边形的顶点.若点P,Q的坐标分别为(-23,3),(0,-3),则点M的坐标为________.第15题图16.(2022毕节)如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,点P为BC边上任意一点,连接P A,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ长度的最小值为________.第16题图参考答案与解析1.C2.A【解析】∵正八边形的外角和为360°,∴每一个外角为360°÷8=45°.3.A 【解析】如解图,∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠B =∠D ,∠B +∠C =180°.∵平行四边形中两内角度数比为1∶4,∴∠B ∶∠C =1∶4,∴∠C =4∠B ,∴∠B +4∠B =180°,解得∠B =36°.第3题解图4.B 【解析】∵四边形ABCD 是平行四边形,∴OB =OD ,OA =OC .∵AC =7,BD =11,∴OC +OD =12AC +12BD =12(AC +BD )=9.又∵△CDO 的周长为15,∴CD =15-(OD +OC )=6.5.D 【解析】由题意得,AB =BC ,∠ACB =15°,∴∠BAC =15°,∴这个正多边形的一个外角为∠ACB +∠BAC =30°,∴这个正多边形的边数为360°30°=12.6.A 【解析】由题意可知,AD =BC ,∵E 为BC 的中点,AD =2AB ,∴AB =BE ,∴∠BAE =∠BEA .∵AD ∥BC ,∴∠DAE =∠BEA ,∴∠BAE =∠DAE ,即AE 平分∠BAD ,故B 正确;∵AB =BE =CE =CD ,∴∠CED =∠CDE ,∵AD ∥BC ,∴∠ADE =∠CED ,∴∠ADE =∠CDE ,∴DE 平分∠ADC ,∵AB ∥DC ,∴∠BAD +∠CDA =180°,∴∠EAD +∠EDA=90°,∴AE ⊥ED ,故C 正确;∵△ADE 与平行四边形ABCD 同底等高,∴S △AED =12S ▱ABCD ,故D 正确;不能推出AE =CE ,∴错误的是A.7.B 【解析】在平行四边形ABCD 中,S △ABC =12S 平行四边形ABCD ,∵DE ⊥AB ,BF ⊥AC ,∴12AC ·BF =12AB ·DE ,∵AB =6,AC =8,DE =4,∴8BF =6×4,解得BF =3.8.6【解析】∵多边形的外角和是360°,多边形的每一个外角是60°,∴多边形的边数为360°÷60°=6.9.2【解析】∵四边形ABCD 是平行四边形,∴AD ∥BC ,DC =AB .∴∠DEA =∠EAB .∵∠DAB 的平分线AE 交DC 于点E ,∴∠EAB =∠DAE ,∴∠DEA =∠DAE ,∴AD=DE .∵AD =3,AB =5,∴EC =DC -DE =AB -AD =5-3=2.10.50【解析】在△DBC 中,∵BD =CD ,∠C =70°,∴∠DBC =∠C =70°.又∵在▱ABCD 中,AD ∥BC ,∴∠ADB =∠DBC =70°,∠BAD =∠C =70°.又∵AE ⊥BD ,∴∠DAE =90°-∠ADB =90°-70°=20°,∴∠BAE =∠BAD -∠DAE =50°.11.(4,2)【解析】∵▱ABCO 中,O (0,0),A (3,0),∴BC =OA =3,∵BC ∥AO ,∴点B 的纵坐标与点C 的纵坐标相等,∵C (1,2),∴B (4,2).12.16°【解析】如解图,∵正六边形的一个外角的度数为360°6=60°,∴正六边形的一个内角的度数为180°-60°=120°,即∠FAB =120°,∵一束太阳光线平行照射在放置于地面的正六边形上,∠1=44°,∴∠3=∠1=44°,∵AB ∥ED ,∴∠AGF =∠3=44°,∴∠2=180°-∠FAB -∠AGF =16°.第12题解图13.(1)证明:∵DE 是△ABC 的中位线,∴点D 是AB 的中点,点E 是AC 的中点.∵AF 是△ABC 的中线,∴点F 是BC 的中点,∴DF 和EF 是△ABC 的中位线,∴EF ∥AB ,DF ∥AC ,∴四边形ADFE 是平行四边形;(2)∵点D 是AB 的中点,点E 是AC 的中点,∴AD =BD =12AB =4,AE =CE =12AC =3.∵四边形ADFE 是平行四边形,∴EF =AD =4.∵AF =5,∴AE 2+EF 2=AF 2,∴△AEF 是直角三角形,∴EF⊥AC,∴EF是AC的垂直平分线,∴AF=CF=5.∵BF=CF,∴BC=2CF=10.∵EF⊥AC,∴S四边形ADFE=EF·AE=12.14.(1)证明:∵点D,E分别为AB,AC的中点,∴DE∥BC,DE=12 BC.∵点G,F分别为BH,CH的中点.∴GF∥BC,GF=12 BC,∴GF∥DE,GF=DE.∴四边形DEFG为平行四边形;(2)解:∵四边形DEFG为平行四边形,∴DG=EF=2.∵DG⊥BH,∴∠DGB=90°.∵BD=3,∴BG=BD2-DG2=32-22=5.15.(33,-2)【解析】由题意可得,P(-23,3),Q(0,-3),如解图,正六边形的顶点在坐标轴上,∴2∠CDO=120°,即∠CDO=60°.过点P作x轴,y轴的垂线分别交坐标轴于点A,B,设点C为正六边形落在x轴上的顶点,∴点C为AO的中点,又∵x P=-23,∴AC=OC=3.∵OC=3,∠CDO=60°,∴OD=1.又∵OB=|y P|=3,∴OD=1,BD=2,即正六边形的边长为2.由解图可得|y M|=BD,|x M|=3OC,且点M位于第四象限,∴M(33,-2).第15题解图16.125【解析】∵∠BAC =90°,AB =3,BC =5,∴AC =BC 2-AB 2=52-32=4.∵四边形APCQ 是平行四边形,∴PO =QO ,CO =AO =2,∵PQ 最短也就是PO 最短,∴过点O 作BC 的垂线OP ′,∵∠ACB =∠P ′CO ,∠CP ′O =∠CAB =90°,∴△CAB ∽△CP ′O ,∴CO BC =OP ′AB ,∴25=OP ′3,∴OP ′=65,∴PQ 的最小值为2OP ′=125.第16题解图。
中考数学一轮复习专题突破练习—四边形

中考数学一轮复习专题突破练习—四边形一、单选题1.(2022·上海嘉定·九年级)下列命题:①等腰梯形的两个底角相等;①两个底角相等的梯形是等腰梯形;①等腰梯形的对角线等;①对角线相等的梯形是等腰梯形,其中真命题的个数是()A.0B.2C.3D.4【答案】D【分析】根据等腰梯形的性质对①①进行判断;根据等腰梯形的判定方法对①①进行判断.【详解】解:等腰梯形的两个底角相等,所以①为真命题;两个底角相等的梯形是等腰梯形,所以①为真命题;等腰梯形的对角线相等,所以①为真命题;对角线相等的梯形是等腰梯形,所以①为真命题.故选:D.2.(2022·临沂第九中学九年级月考)如图,在□ABCD中,对角线BD①AD,AB=10,AD=6,O为BD的中点,E为边AB上一点,直线EO交CD于点F,连接DE、BF,下列结论不成立的是()A.四边形DEBF为平行四边形B.若AE=3.6,则四边形DEBF为矩形C.若AE=5,则四边形DEBF为菱形D.若AE=4.8,则四边形DEBF为正方形 【答案】D 【分析】根据平行四边形的判定方法,矩形的判定方法,菱形的判定方法,正方形的判定方法解答即可. 【详解】解:①O 为BD 的中点, ①OB =OD ,①四边形ABCD 为平行四边形, ①DC //AB ,①①CDO =①EBO ,①DFO =①OEB , ①①FDO ①①EBO (AAS ), ①OE =OF ,①四边形DEBF 为平行四边形, 故A 选项不符合题意, 若AE =3.6,AD =6, ①3.6365AE AD ==, 又①63105ADAB ==, ①AE ADAD AB=, ①①DAE =①BAD , ①①DAE ①①BAD ,①①AED=①ADB=90°.①四边形DEBF为矩形.故B选项不符合题意,①AB=10,AE=5,①BE=5,又①①ADB=90°,①DE=1AB=5,2①DE=BE,①四边形DEBF为菱形.故C选项不符合题意,①AE=3.6时,四边形DEBF为矩形,AE=5时,四边形DEBF为菱形,①AE=4.8时,四边形DEBF不可能是正方形.故选项D符合题意.故选:D.3.(2022·重庆字水中学九年级)下列命题是假命题的是()A.有一组邻边相等的矩形是正方形B.对角线相等的平行四边形是矩形C.对角线互相平分的四边形是平行四边形D.对角线互相垂直的四边形是菱形【答案】D【分析】根据正方形、矩形、平行四边形、菱形的判定定理逐一判断即可.【详解】A:是真命题,是正方形的判定定理;B:是真命题,是矩形的判定定理;C:是真命题,是平行四边形的判定定理;D:不正确,是假命题,对角线互相垂直平分的平行四边形是菱形;故选:D.4.(2022·沙坪坝·重庆八中九年级月考)如图,正方形ABCD和正方形CEFG中,点D在CG上,2AD=,423DG=,H是AF的中点,那么CH的长是()A.3B.583C.15D.974【答案】B【分析】连接AC、CF,根据正方形性质求出AC、CF,①ACD=①GCF=45°,再求出①ACF=90°,然后利用勾股定理列式求出AF,再根据直角三角形斜边中线的性质解答即可.【详解】如图,连接AC、CF,①正方形ABCD 和正方形CEFG ,2AD =,423DG =, ①①ACD =①GCF =45°,723CG =, ①()222222AC AD ==⨯=,2271422233CF CG ⎛⎫==⨯=⎪⎝⎭,①ACF =90°, ①在Rt ACF 中,222214258233AF AC CF ⎛⎫=+=+= ⎪⎝⎭, ①H 是AF 的中点, ①11258582233CH AF ==⨯=.故选:B .5.(2022·广东九年级期末)如图,将矩形ABCD 绕点B 顺时针旋转90°至矩形EBGF 的位置,连接AC 、EG ,取AC 、EG 的中点M 、N ,连接MN ,若AB =8,BC =6,则MN =( )A .8B .6C .5D .52【答案】D 【分析】连接BD ,BF ,DF ,由矩形的性质可以得到MN 是①BDF 的中位线,即12MN DF =,由旋转的性质可以得到BF =BD ,①DBF =90°,利用勾股定理求出DF 的长即可得到答案.【详解】解:如图所示,连接BD ,BF ,DF ,①四边形ABCD 和四边形BGFE 都是矩形,M ,N 分别是AC 和EG 的中点, ①M 和N 分别也是BD 和BF 的中点, ①MN 是①BDF 的中位线, ①12MN DF =①AB =8,BC =6,①ABC =90°, ①2210BD AC AB BC ==+=,①将矩形ABCD 绕点B 顺时针旋转90°至矩形EBGF 的位置, ①BF =BD =10,①DBF =90°, ①22102DF BD BF =+=, ①1522MN DF ==, 故选D .6.(2022·深圳市宝安中学(集团)九年级)下列判断正确的是( ). A .对角线相等的四边形是矩形B .将一个矩形风景画的四周镶上宽度相等的金边后得到的新矩形与原矩形相似C .如果两个相似多边形的面积比为16①9,那么这两个相似多边形的周长比可能是4①3D.若点C是AB的黄金分割点,且6cmAB=,则BC的长为()3cm【答案】C【分析】A.利用矩形的判定定理对角线相等的平行四边形可判断;B.一个矩形风景画的四周镶上宽度相等的金边后得到的新矩形与原矩形相似应满足长与宽相等时可以,而矩形的长与宽一般不等;C.利用相似图形的性质即可;D.利用黄金分割法可求出BC有两个值即可.【详解】解:A、对角线相等的平行四边形是矩形,故此选项错误;B、将一个矩形风景画的四周镶上宽度相等的金边后得到的新矩形与原矩形不一定相似,故此选项错误;C、如果两个相似多边形的面积比为16:9,则两个相似多边形的相似比为4:3,那么这两个相似多边形的周长比等于相似比是4:3,故此选项正确;D、若点C是AB的黄金分割点,且AB=6cm,则BC的长为()3cm或(-,故此选项错误;9cm故选C.7.(2022·山东济宁学院附属中学)如图,矩形纸片ABCD,6cmBC=,AB=,8cmE为边D上一点,将BCE沿BE所在的直线折叠,点C恰好落在AD边上的点F 处,过点F作FM BE⊥,垂足为点M,取AF的中点N,连接MN,则MN=()cm.A .5B .6C .245D .27【答案】A 【分析】连接AC ,MC ,可求得M 为CF 的中点,根据中位线的性质可得12MN AC =,勾股定理求得AC 即可. 【详解】解:连接AC ,MC由折叠的性质可得CF EB ⊥,CE EF = 又①FM BE ⊥①点M 在线段FC 上,90EMF EMC ∠=∠=︒ 又①ME ME = ①()EMF EMC HL △≌△ ①FM MC = 又①AF 的中点N①MN 为ACF 的中位线 ①12MN AC =在Rt ACB 中,2210cm AC AB BC =+= ①5cm MN = 故选A8.(2022·全国九年级专题练习)如图,在平行四边形ABCD 中,AD =2AB ,作CE ①AB 于点E ,点F 是AD 的中点,连接CF ,EF .关于下列四个结论:①①BCF =①DCF ;①①FEC =①FCE ;①①AEF =①CFD ;①S ①CEF =S ①BCE ,则所有正确结论的序号是( )A .①①①①B .①①①C .①①①D .①①【答案】B 【分析】由平行四边形的性质结合等腰三角形的判定与性质可得①DFC =①BCF ,①DFC =①DCF ,可证明①;取EC 的中点G ,连接FG ,则FG 为梯形AECD 的中位线,再证明 FG ①CE ,可证明①;根据平行线的性质可得①AEC =①DCE =90°,进而可证明①;而无法证明①. 【详解】解:①四边形ABCD 为平行四边形, ①AB ①CD ,AD ①BC ,AB =CD , ①①DFC =①BCF ,①点F是AD的中点,①AD=2DF,①AD=2AB,①AD=2CD,①DF=CD,①①DFC=①DCF,①①BCF=①DCF,故①正确;取EC的中点G,连接FG,则FG为梯形AECD的中位线,①FG①AB,①CE①AB,①FG①CE,①EF=CF,①①FEC=①FCE,故①正确;①CE①AB,AB①CD,①CE①CD,①①AEC=①DCE=90°,即①AEF+①FEC=①DCF+①FCE=90°,①①AEF=①DCF,①①DCF=①CFD,①①AEF=①CFD,故①正确;①1•2CEFS CE BE =()()()11111112222222••••2BCESCE FG CE AE CD CE AE AB CE AE BE ==+=+=+ 而2AE BE +不一定等于2BE ①CEF S △不一定等于BCES ,故①错误;故选:B .9.(2022·全国九年级专题练习)如图,在梯形ABCD 中,AD ①BC ,EF 是梯形ABCD 的中位线,若①BEF 的面积为4cm 2,则梯形ABCD 的面积为( )A .8cm 2B .12cm 2C .16cm 2D .20cm 2【答案】C 【分析】如图,过A 作AN①BC 于N ,交EF 于M ,根据梯形的中位线性质得出AD+BC =2EF ,AM =MN ,由此再根据已知三角形的面积得出EF×AM =8,由此进一步根据梯形面积公式变形求解即可. 【详解】如图,过A 作AN①BC 于N ,交EF 于M , ①EF 是梯形ABCD 的中位线,①AD+BC =2EF ,EF①AD①BC , ①AM①EF ,AM =MN , ①①BEF 的面积为4cm 2, ①12EF×AM =4, ①EF×AM =8,①梯形ABCD 的面积为12(AD+BC)×AN =12×2EF×2AM =2EF×AM =16cm 2, 故选:C .10.(2022·珠海市文园中学九年级)如图,在边长为2的正方形ABCD 中,,E F 分别为,BC CD 的中点,连接AE BF ,交于点G ,将BCF ∆沿BF 对折,得到BPF ∆,延长FP 交BA 延长线于点Q .下列结论①QB QF =; ①AE BF ⊥;①4BGE ECFG S S ∆=四边形; ①4sin 5BQP ∠=,正确的有( )A .4B .3C .2D .1【答案】A 【分析】①①BCF 沿BF 对折,得到①BPF ,利用角的关系求出QF =QB ;①首先证明①ABE ①①BCF ,再利用角的关系求得①BGE =90°,即可得到AE ①BF ; ①利用QF =QB ,解出BP ,QB ,根据正弦的定义即可求解;①可证①BGE 与①BCF 相似,进一步得到相似比,再根据相似三角形的性质即可求解. 【详解】解:①根据题意得,FP =FC ,①PFB =①BFC ,①FPB =90°①CD ①AB , ①①CFB =①ABF , ①①ABF =①PFB , ①QF =QB ,故正确;①①E ,F 分别是正方形ABCD 边BC ,CD 的中点, ①CF =BE ,在①ABE 和①BCF 中,AB BC ABE BCF BE CF =⎧⎪∠=∠⎨⎪=⎩, ①①ABE ①①BCF (SAS ), ①①BAE =①CBF , 又①①BAE +①BEA =90°, ①①CBF +①BEA =90°, ①①BGE =90°,①AE ①BF ,故正确; ①由①知,QF =QB , 令PF =k (k >0),则PB =2k 在Rt ①BPQ 中,设QB =x , ①x 2=(x ﹣k )2+4k 2, ①x =52k,①sin①BQP =45BPQB ,故正确; ①①①BGE =①BCF ,①GBE =①CBF , ①①BGE ①①BCF ,①BE =12BC ,BF BC ,①BE :BF =1①①BGE 的面积:①BCF 的面积=1:5, ①S 四边形ECFG =4S ①BGE ,故正确. 综上所述,共有4个结论正确. 故选A . 二、填空题11.(2022·上海崇明·九年级)如果一个等腰梯形的周长为50厘米,一条腰长为12厘米,那么这个梯形的中位线长为_____厘米. 【答案】13 【分析】根据梯形的周长公式列式进行计算即可得到两底的和,再根据梯形的中位线等于两底和的一半求出中位线的长即可.【详解】①等腰梯形的周长为50厘米,一条腰长为12厘米,①两底的和为5012226-⨯=(厘米),①这个梯形的中位线长为126132⨯=(厘米),故答案为:13.12.(2022·浙江九年级月考)如图,已知ABCD的对角线4cmBD=,将ABCD绕其对称中心O旋转180︒,则点D所转过的路径长为______cm.【答案】2π【分析】点D所转过的路径是一段圆心角为180°,半径为OD的弧,根据平行四边形的性质可得OD=12BD,根据弧长公式计算即可得答案.【详解】①四边形ABCD是平行四边形,4cmBD=,①OD=12BD=2cm,①将ABCD绕其对称中心O旋转180︒,①点D所转过的路径是一段圆心角为180°,半径为OD的弧,①点D所转过的路径长=122ODπ⨯⋅=2π,故答案为:2π13.(2022·哈尔滨市虹桥初级中学校九年级开学考试)如图,矩形ABCD 的对角线AC 、BD 相交于点O ,过点O 作OE ①BC ,垂足为点E ,过点A 作AF ①OB ,垂足为点F ,若BC =2AF ,OD =6,则BE 的长为____.【答案】33【分析】证明ABF BOE △≌△,进而证明ABO 是等边三角形,结合矩形的性质以及全等三角形的性质,勾股定理,进而即可求得BE . 【详解】四边形ABCD 是矩形6AO BO OD OC ∴====,90ABC ∠=︒90ABF OBE ∴∠+∠=︒ AF OB ⊥,90ABF BAF ∴∠+∠=︒,90AFB ∠=︒BAF OBE ∴∠=∠OE ①BC ,OB OC =12BE EC BC ∴==,90BEO ∠=︒ BC =2AF ,12AF BC BE ∴==∴ABF BOE △≌△AB BO ∴=,BE AF = OB OA =ABO ∴是等边三角形AF BO ⊥1302BAF BAO ∴∠=∠=︒12BF AB ∴=2232AF AB BF AB ∴=-= 6AB OA == 33∴=AF 33BE AF ∴==.故答案为:33.14.(2022·广东)如图,在梯形ABCD 中,AB ①CD ,BD ①AD ,BC =CD ,①A =60°,CD =2,则下底AB 的长等于__.【答案】4 【分析】由已知可得梯形为等腰梯形,从而可得AD =2,再根据含30°角直角三角形的性质可以得到AB 的值 . 【详解】解:①①A =60°,BD ①AD ,①①ABD=30°,又①AB①CD,①①CDB=①ABD=30°,①BC=CD,①①CBD=①CDB=30°,①①ABC=60°=①A,①AD=BC=CD=2,①AB=2AD=4.故答案为:4.15.(2022·哈尔滨市虹桥初级中学校九年级开学考试)已知矩形ABCD中,BE 平分①ABC交矩形的一条边于点E,若BD=10,①EBD=15°,则AB=___.【答案】5或53【分析】画出符合条件的两种情况,根据矩形性质求出①A=①ABC=①BCD=90°,①ABE =①CBE=45°,求出①DBC的度数,求出CD即可得出结论.【详解】解:有两种情况:①BE与边AD相交时,如图1,①四边形ABCD 是矩形,①①A =①ABC =①BCD =90°,AB =CD , ①BE 平分①ABC , ①①CBE =12①ABC =45°, ①①EBD =15°,①①DBC =①CBE −①DBE =30°, ①CD =12BD =12×8=5, ①AB=5;①BE 与边CD 相交时,如图2,①四边形ABCD 是矩形, ①①A =∠ABC =①C =90°, ①BE 平分①ABC , ①①ABD =12①ABC =45°, ①①EBD =15°,①①ABD =①CBE -①DBE =30°, ①152AD BD ==, ①2253AB BD AD =-=故答案为:5或53.三、解答题16.(2022·福建省同安第一中学九年级)如图,已知四边形ABCD是矩形,(1)尺规作图,求作正方形BECF,使得顶点E在矩形ABCD内;(2)连接DE,若AB=6,AD=8,求DE的长.【答案】(1)见解析;(2)25【分析】(1)要使得正方形BECF的顶点E在矩形ABCD内,则应考虑以BC为对角线,因为①B=①C=90°,要构成正方形则E点应为①B和①C的角平分线的交点,所以可先作①B与①C的角平分线,然后再根据正方形的对称性作图即可;(2)连接FE交BC于G点,并延长FE交AD于H点,根据矩形和正方形的性质分别求出DH和HE的长度,从而利用勾股定理求解即可.【详解】解:(1)如图所示,先作①B和①C的角平分线,交于E点,则此时①BEC为等腰直角三角形,然后分别以B,C两点为圆心,BE,CE为半径作圆弧在BC下方交于F点,①此时四边形BECF即为所求正方形;(2)如图所示,连接FE交BC于G点,并延长FE交AD于H点,①四边形ABCD为矩形,①①ADC=①BCD=90°,CD=AB=6,AD=BC=8,由(1)可知四边形BECF为正方形,BC=4,EG①BC,①EG=GC=12①①ADC=①BCD=①EGC=90°,即四边形CDHG为矩形,①DH=CG=4,GH=CD=6,①DHE=90°,①HE=GH-GE=2,在Rt①HDE中,根据勾股定理得:DE=22+=25.DH HE17.(2022·西安市铁一中学九年级开学考试)如图,在ABC中,AB AC=,D是边BC延长线上的一点,连接AD,过点A、D分别作//DE AB,AE、DEAE BD、//交于点E ,连接CE .求证:AD CE =. 【答案】见解析 【详解】证明:①AB =AC , ①①B =①ACB , ①//AE BD 、//DE AB ,①四边形AEDB 是平行四边形, ①DE =AB ,①EDB +①B =180°, ①DE =AC ,①①ACB +①ACD =180°, ①①ACD =①EDC , 在①ADC 与①EDC 中AC DE ACD EDC CD DC =⎧⎪∠=∠⎨⎪=⎩, ①①ADC ①①EDC (SAS ), ①AD =CE .18.(2022·宜兴市实验中学九年级)如图所示,ABCD 的对角线AC 的垂直平分线与边AD ,BC 分别相交于点E ,F .求证:四边形AFCE 是菱形.【答案】见解析 【分析】根据题意先证明()ASA AOE COF ≌△△,即可证明四边形AFCE 为平行四边形,根据EF AC ⊥可得结果. 【详解】证明:①四边形ABCD 是平行四边形 ①//AE FC ,AO CO =, ①EAC FCA ∠=∠,①EF 是AC 的垂直平分线, ①EF AC ⊥,在AOE △与COF 中,EAO FCO AO COAOE COF ∠=∠⎧⎪=⎨⎪∠=∠⎩①()ASA AOE COF ≌△△, ①EO FO =,①四边形AFCE 为平行四边形, 又①EF AC ⊥, ①四边形AFCE 为菱形.19.(2022·长沙市雅礼实验中学九年级月考)如图所示,正方形ABCD 的边长是4,点E 是边BC 上的一个动点且90AEF ∠=︒,EF 交DC 于点G ,交正方形外角平分线CF 于点F ,点M 是AB 的中点,连按EM . (1)求证:BAE FEC ∠=∠;(2)若E 为BC 的中点,求证:AE EF =;(3)点E 在何位置吋线段DG 最短,并求出此时DG 的值.【答案】(1)见解析;(2)见解析;(3)E 为BC 中点时,DG =3 【分析】(1)由正方形性质可得90AEB BAE ∠+∠=︒,由90AEF ∠=︒得90AEB CEF ∠+∠=︒,由同角的余角相等即可求证结论;(2)由正方形的性质求证()AME ECF ASA ≌△△,继而即可求证结论; (3)易知ABE GEC ∽△△,设设BE x =,4CE x =-,利用已知边表示出关于DG 的二次函数关系,继而求得DG 的值. 【详解】解:(1)四边形ABCD 是正方形 ①90B ∠=︒,90AEB BAE ∠+∠=︒, ①90AEF ∠=︒,①90AEB CEF ∠+∠=︒, ①BAE CEF ∠=∠, (2)如图①四边形ABCD 是正方形,①AB BC =,90B BCD DCG ∠=∠=∠=︒, ①点E 是边BC 的中点, ①AM EC BE ==,①45BME BEM ∠=∠=︒,①135AME ∠=︒, ①CF 平分DCG ∠,①45DCF FCG ∠=∠=︒, ①180135ECF FCG ∠=︒-∠=︒,①AME ECF ∠=∠, ①90AEF ∠=︒,①90AEB CEF ∠+∠=︒, 又90AEB MAE ∠+∠=︒,①MAE CEF ∠=∠, ①()AME ECF ASA ≌△△,①AE EF =;(3)设BE x =,4CE x =-,由(1)知BAE GEC ∠=∠,又90B ECG ∠=∠=︒ ①ABE GEC ∽△△,①AB BE EC GC =,①44xx GC=- ①()144GC x x =-①()()2211144423444DG x x x x x =--=-+=-+当2x =即E 为BC 中点时,DG 的最小值为3.20.(2022·福建厦门双十中学思明分校九年级期末)如图,已知四边形ABCD是平行四边形.(1)请用直尺和圆规在AB上取一点E,使得EA=ED;(2)在(1)的条件下,连接CE,若①A=60°,AB=6,AD=4,求线段CE的长.【答案】(1)作图见解析;(2)27.【分析】(1)作线段AD的垂直平分线交AB于E即可;(2)过点E作EH①CD于H,求出E H,CH,即可解决问题.【详解】解:(1)如图,线段DE即为所求作,(2)过点E作EH①CD于H,①①A=60°,EA=ED,①①ADE是等边三角形,①①AED=60°,AE=AD=DE=4,①四边形ABCD是平行四边形,①AB①CD,①①CDE=①AED=60°,①①DHE=①CHE=90°,①①DEH=30°,①DH=1DE=2,2由勾股定理得EH=22-=,4223①AB=CD=6,①CH=CD-DH=4,①EC=()2222+=+=.CH EH4232721.(2022·长沙市开福区青竹湖湘一外国语学校九年级开学考试)如图,E为长方形ABCD的边AB上一点,将长方形沿CE折叠,使点B恰好落在ED上的点F处.(1)求证:AE=DF;(2)若BE=1,BC=3,求CD的长.【答案】(1)见解析;(2)5【分析】(1)根据矩形的性质和折叠性质证得①AED=①CDF,AD=CF,①A=①CFD=90°,进而证明①ADE①①FCD即可;(2)设CD x==,利用勾股定=,则1=-,根据全等三角形性质得到ED CD xAE x理列出x的方程,解之即可解答.【详解】解:(1)①四边形ABCD是长方形,①AD=BC,AB=CD,①A=①B=90°,AB①CD,①①AED=①CDF,由折叠可知:AD=BC=CF,①B=①CFE=90°,①①A=①CFD=90°,①①ADE①①FCD(AAS),①AE=DF;(2)设CD x=,则1=-,AE x由折叠得:AD=CF=BC=3,①①ADE①①FCD,①ED CD x==,Rt①AED中,222+=,AE AD ED①222-+=,(x1)3x解得:5x=,即CD=5.22.(2022·上海九年级专题练习)如图,在梯形ABCD中,AD BC∥,AC DB⊥,∠=︒,DBCAC=,305(1)求对角线BD 的长度; (2)求梯形ABCD 的面积. 【答案】(1)3;(2253. 【分析】(1)如图,过A 作AE DB 交CB 延长线于E ,①AC①DB ,AE①DB ,①AC①AE ,①AEC=①DBC=30°,即①EAC 为直角三角形,四边形AEBD 为平行四边形,根据勾股定理求解;(2)记梯形ABCD 的面积为S ,过A 作AF①BC 于F ,则①AFE 为直角三角形,求出梯形的高AF ,根据梯形面积公式即可求解. 【详解】解;(l )如图,过A 作AE DB 交CB 延长线于E , ①AC DB ⊥,AE DB .①AC AE ⊥,30AEC DBC ∠=∠=︒, ①90EAC ∠=︒,即EAC ∆为直角三角形, ①210EC AC ==,①222210553AE EC AC =--= ①AD BC ∥且AE DB . ①四边形AEBD 为平行四边形.①53DB AE ==;(2)记梯形ABCD 的面积为S ,过A 作AF BC ⊥于F ,则AFE ∆为直角三角形. ①30AEF ∠=︒ ①15322AF AE ==,即梯形ABCD 的高532AF =, ①四边形AEBD 为平行四边形, ①AD EB =.1()2S AD BC AF =+⨯1153253102222EC AF =⨯=⨯⨯=.23.(2020·浙江)已知:如图,四边形ABCD 中,AD ①BC ,对角线BD 平分①ABC ,且BD ①DC ,E 为BC 中点,AB =DE . (1)求证:四边形ABED 是菱形;(2)若①C =60°,CD =4,求四边形ABCD 的面积.【答案】(1)详见解析;(2)3【解析】 【分析】(1)由直角三角形斜边上的中线等于斜边的一半推出BE =ED =EC ,再由边关系推出角相等进而推出平行,由双平行推出平行四边形,加上邻边相等的平行四边形是菱形,可以推出结论.(2)作DF①BC于F,利用30的直角三角形,求出DF的长度,再由梯形的面积公式即可求出.【详解】证明:(1)①BD①DC,E为BC中点,①BE=ED=EC,①①DBE=①BDE;又AD①BC,①①ADB=①DBE,①①ADB=①BDE,①AB=AD,①①ABD=①ADB①①BDE=①ABD①DE①AB又①AD①BC,即AD①BE,①四边形ABCD为平行四边形又AB=AD,①平行四边形ABCD为菱形.(2)由(1)得,BE=EC=AD=DE,①①C=60°,①①DEC 为等边三角形.作DF①BC 于F ,则DF DC , BC =2BE =2AD =8, ①S梯形ABCD =12 (AD+BC )×DF =12×(4+8)=。
中考一轮复习数学几何专题:四边形压轴训练(二)

2022年中考一轮复习数学几何专题:四边形压轴训练(二)1.【实验操作】如图1是一张矩形纸片,点E在边AB上,把△BCE沿着直线CE对折,点B恰好落在对角线AC上的点F处.【性质探究】如图2,连接DF,若点E,F,D在同一直线上.(1)请写出图中与边DC相等的线段并说明理由.(2)若AE=2,求EF的长.【迁移应用】(3)如图3,延长EF交边AD于点G,若DG:AG=n,且AE=2,求BE的长(请用含n的代数式来表示).2.(1)问题提出如图①,△ACB和△DCE均为等边三角形,点A,D,E在同一条直线上,连接BE,线段AD,BE之间的数量关系为,∠AEB的度数为;(2)问题探究如图②,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E 在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由;(3)问题解决如图③,在正方形ABCD中,CD=2,若点P满足PD=2,且∠BPD=90°,请直接写出点A到BP的距离.3.定义:在四边形ABCD中,如果∠ABC+∠ADC=90°,那么我们把这样的四边形称为余对角四边形.【问题探索】问题:如图1,已知AC、BD是余对角四边形ABCD的对角线,AC=BC,∠ACB=60°.求证:AD2+DC2=BD2.探索:小明同学通过观察、分析、思考,对上述问题形成了如下想法:因为AC=BC,∠ACB=60°,所以△ABC是等边三角形,将△CBD绕点C顺时针方向旋转60°,得△CAE,连接DE.……请参考小明同学的想法,完成该问题的解答过程.【问题推广】已知AC、BD是余对角四边形ABCD的对角线,AC=k⋅BC,tan∠ACB=.(1)如图2,当k=1时,类比前面问题的解决,探究DA、DB、DC三者之间关系,并说明理由.(2)如图3,当AD=,BD=,DC=5时,则k的值为;【灵活运用】如图4,已知AC、BD是余对角四边形ABCD的对角线,AC=2,BC=,∠ACB=90°,∠ADB=30°,AD=.4.在平面直角坐标系xOy中,A(0,2),B(﹣2,0),连接AB,点C是线段OA上一点,以OC为边作正方形OCDE,如图1.(1)问题发现图1中,线段BE与AC的数量关系是,位置关系是.(2)问题探究如图2,将正方形OCDE绕点O顺时针旋转α(0°<α<360°),连接AC,BE,则(1)中的结论是否仍然成立?请说明理由.(3)拓展应用若OC=1,将正方形OCDE绕点O旋转,当B,E,C三点共线时,请直接写出线段AC 的长.5.如图,四边形ABCD中,AD∥BC,∠A=∠D=90°,点E是AD的中点,连接BE,将△ABE沿BE折叠后得到△GBE,且点G在四边形ABCD内部,延长BG交DC于点F,连接EF.(1)求证:△EGF≌△EDF;(2)求证:BG=CD;(3)若点F是CD的中点,BC=8,求CD的长.6.(1)证明推断:如图(1),在正方形ABCD中,点E,Q分别在边BC,AB上,DQ ⊥AE于点O,点G,F分别在边CD,AB上,GF⊥AE.求证:AE=FG;(2)类比探究:如图(2),在矩形ABCD中,=k(k为常数).将矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形FEPG,EP交CD于点H,连接AE交GF于点O.试探究GF与AE之间的数量关系,并说明理由;(3)拓展应用:在(2)的条件下,连接CP,当时k=,若tan∠CGP=,GF=2,求CP的长.7.如图1,点E为正方形ABCD内一点,∠AEB=90°,现将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBE′(点A的对应点为点C),延长AE交CE′于点F.(1)如图1,求证:四边形BEFE′是正方形;(2)连接DE,①如图2,若DA=DE,求证:F为CE′的中点;②如图3,若AB=15,CF=3,试求DE的长.8.在平面直角坐标系中,有正方形OBCD和正方形OEFG,E(2,0),B(0,2).(Ⅰ)如图①,求BE的长;(Ⅱ)将正方形OBCD绕点O逆时针旋转,得正方形OB′C′D′.①如图②,当点B′恰好落在线段D'G上时,求B'E的长;②将正方形OB'C'D'绕点O继续逆时针旋转,线段D'G与线段B'E的交点为H,求△GHE与△B'HD'面积之和的最大值,并求出此时点H的坐标(直接写出结果).9.已知,如图①将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,然后把纸片展平;再如图②,将图①中的矩形纸片ABCD沿过点E的直线折叠,点C恰好落在AD上的C'处,点B落在B'处,得到折痕EF,B'C'交AB于点M,C'F交DE于点N,再把纸片展平.(Ⅰ)如图①,填空:若AD=3,则ED的长为;(Ⅱ)如图②,连接EC',△MC′E是否一定是等腰三角形?若是,请给出证明;若不是,请说明理由;(Ⅲ)如图②,若AC'=2cm,DC′=4cm,求DN:EN的值.(直接写出结果即可)10.探究:如图1和图2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.(1)①如图1,若∠B、∠ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,直接写出线段BE、DF和EF之间的数量关系;②如图2,若∠B、∠D都不是直角,但满足∠B+∠D=180°,线段BE、DF和EF之间的结论是否仍然成立,若成立,请写出证明过程,若不成立,请说明理由.(2)拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=2.点D、E均在边BC 边上,且∠DAE=45°,若BD=1,请直接写出DE的长.11.如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,顶点C在y轴上,OA=8,OC=4,点P为对角线AC上一动点,过点P作PQ⊥PB,PQ交x轴于点Q.(1)tan∠ACB=;(2)在点P从点C运动到点A的过程中,的值是否发生变化?如果变化,请求出其变化范围;如果不变,请求出其值;(3)若将△QAB沿直线BQ折叠后,点A与点P重合,求PC的长.12.如图1,在矩形纸片ABCD中,AB=6,AD=10,折叠纸片使B点落在边AD上的点E 处,折痕为PQ.过点E作EF∥AB交PQ于F,连接BF.(1)求证:四边形PBFE为菱形;(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动.①当点Q与点C重合时(如图2),求菱形PBFE的边长;②若限定P、Q分别在边BA、BC上移动,菱形PBFE的面积有最值吗?若有,请写出,若没有,填“无”.最大值为;最小值为.13.如图,点E是正方形ABCD的边BA延长线上一点,连接DE,过点A作AH∥DE交CD于点H,交BC延长线于点F,点M、N分别是DE、AH的中点,连接AM、DN.(1)求证:四边形AMDN是菱形;(2)若S菱形MADN:S正方形ABCD=1:3,求CF:AB的值.14.矩形ABCD中,AB=CD=3cm,AD=BC=4cm,AC是对角线,动点P从点A出发沿AC方向向点C匀速运动,速度为1cm/s,动点Q从点C出发沿CD方向向点D匀速运动,速度为2cm/s.过点P作BC的垂线段PH,运动过程中始终保持PH与BC互相垂直,连接HQ交AC于点O.若点P和点Q同时出发,设运动时间为t(s)(0<t<1.5),解答下列问题.(1)求当t为何值时,四边形PHCQ为矩形;(2)是否存在一个时刻,使HQ与AC互相垂直?如果存在,请求出t值;如果不存在,请说明理由;(3)是否存在一个时刻,使矩形ABCD的面积是四边形PHCQ面积的,如果存在,请求出t值;如果不存在,请说明理由;(4)如果△COQ是等腰三角形,请直接写出所有符合题意的时刻:.15.问题情景:如图1,我们把对角线互相垂直的四边形叫做“垂美四边形”,按照此定义,我们学过的平行四边形中的菱形、正方形等都是“垂美四边形”,“筝形”也是“垂美四边形”.概念理解:(1)如图2,已知等腰梯形ABCD是“垂美四边形”,AB=6,CD=8,求AD的长.性质探究:(2)如图3,已知四边形ABCD是“垂美四边形”,试探究其两组对边AB,CD与BC,AD之间的数量关系,并写出证明过程.问题解决:(3)如图4,分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG与正方形ABDE,连接CE,BG,GE,CE与BG交于点O,已知AC=3,AB=5,求△OGE 的中线OH的长.。
最新中考数学第一轮复习—四边形
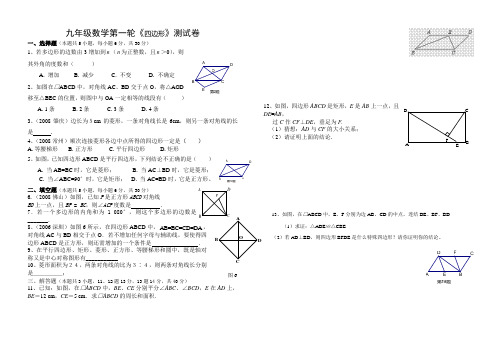
BC D A P A B CDO九年级数学第一轮《四边形》测试卷一、选择题(本题共5小题,每小题6分,共30分)1、若多边形的边数由3增加到n (n 为正整数,且n >0),则其外角的度数和( ) A. 增加 B. 减少 C. 不变 D. 不确定2、如图在□ABCD 中,对角线AC 、BD 交于点O ,将△AOD 移至△BEC 的位置,则图中与OA 一定相等的线段有( )A. 1条B. 2条C. 3条D. 4条3、(2008肇庆)边长为5cm 的菱形,一条对角线长是6cm ,则另一条对角线的长是 .4、(2008常州)顺次连接菱形各边中点所得的四边形一定是( ) A .等腰梯形 B .正方形 C .平行四边形 D .矩形5、如图,已知四边形ABCD 是平行四边形,下列结论不正确的是( )A. 当AB=BC 时,它是菱形;B. 当AC ⊥BD 时,它是菱形;C. 当∠ABC=90°时,它是矩形;D. 当AC=BD 时,它是正方形。
二、填空题(本题共5小题,每小题6分,共30分)6.(2008佛山)如图,已知P 是正方形ABCD 对角线BD 上一点,且BP = BC ,则∠ACP 度数是 .7.若一个多边形的内角和为 1 080°,则这个多边形的边数是_______. 8、(2006深圳)如图6所示,在四边形ABCD 中,AB=BC=CD=DA ,对角线AC 与BD 相交于点O .若不增加任何字母与辅助线,要使得四边形ABCD 是正方形,则还需增加的一个条件是 .9、在平行四边形、矩形、菱形、正方形、等腰梯形和圆中,既是轴对称又是中心对称图形有___________10、菱形面积为24,两条对角线的比为3∶4,则两条对角线长分别是_____; 三、解答题(本题共3小题,11、12题13分,13题14分,共40分)11、已知:如图,在□ABCD 中,BE 、CE 分别平分∠ABC 、∠BCD ,E 在AD 上, BE =12 cm ,CE =5 cm .求□ABCD 的周长和面积.12、如图,四边形ABCD 是矩形,E 是AB 上一点,且DE =AB ,过C 作CF ⊥DE ,垂足为F .(1)猜想:AD 与CF 的大小关系; (2)请证明上面的结论.13、如图,在□ABCD 中,E 、F 分别为边AB 、CD 的中点,连结DE 、BF 、BD (1)求证:△ADE ≌△CBE(2)若AD ⊥BD ,则四边形BFDE 是什么特殊四边形?请你证明你的结论。
中考数学一轮复习平行四边形知识点及练习题含答案

中考数学一轮复习平行四边形知识点及练习题含答案一、选择题1.如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE,分别交AC、AD于点F、G,连接OG,则下列结论:①OG=12AB;②图中与△EGD 全等的三角形共有5个;③以点A、B、D、E为项点的四边形是菱形;④ S四边形ODGF= S△ABF.其中正确的结论是()A.①③B.①③④C.①②③D.②②④2.如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤22PD=EC.其中有正确有()个.A.2 B.3 C.4 D.53.如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( ).A5B21C.212+D.512+4.如图,正方形ABCD中,AB=12,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC ;③AG ∥CF ;④S △FGC =28.8. 其中正确结论的个数是( )A .4B .3C .2D .15.如图,在ABC ,90C ∠=︒,8AC =,6BC =,点P 为斜边AB 上一动点,过点P 作PE AC ⊥于点E ,PF BC ⊥于点F ,连结EF ,则线段EF 的最小值为( )A .1.2B .2.4C .2.5D .4.86.如图,点E 在正方形ABCD 外,连接AE BE DE ,,,过点A 作AE 的垂线交DE 于F ,若210AE AF BF ===,,则下列结论不正确的是( )A .AFD AEB ∆≅∆B .点B 到直线AE 的距离为2C .EB ED ⊥ D .16AFD AFB S S ∆∆+=+7.如图所示,在四边形ABCD 中,AD BC =,E 、F 分别是AB 、CD 的中点,AD 、BC 的延长线分别与EF 的延长线交于点H 、G ,则( )A .AHE BGE ∠>∠B .AHE BGE ∠=∠C .AHE BGE ∠<∠D .AHE ∠与BGE ∠的大小关系不确定8.线段AB上有一动点C(不与A,B重合),分别以AC,BC为边向上作等边△ACM和等边△BCN,点D是MN的中点,连结AD,BD,在点C的运动过程中,有下列结论:①△ABD可能为直角三角形;②△ABD可能为等腰三角形;③△CMN可能为等边三角形;④若AB=6,则AD+BD的最小值为37. 其中正确的是()A.②③B.①②③④C.①③④D.②③④9.如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连结EF,则线段EF的长的最小值是( )A.2.5 B.2.4 C.2.2 D.210.如图,矩形ABCD和矩形CEFG,AB=1,BC=CG=2,CE=4,点P在边GF上,点Q 在边CE上,且PF=CQ,连结AC和PQ,M,N分别是AC,PQ的中点,则MN的长为()A.3 B.6 C.372D.17二、填空题11.在平行四边形ABCD 中, BC边上的高为4 ,AB=5 ,25AC ,则平行四边形ABCD 的周长等于______________ .12.如图,某景区湖中有一段“九曲桥”连接湖岸A,B两点,“九曲桥”的每一段与AC平行或BD平行,若AB=100m,∠A=∠B=60°,则此“九曲桥”的总长度为_____.13.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,3AB =,2AC =,则BD 的长为_______________.14.如图,四边形ABCD ,四边形EBFG ,四边形HMPN 均是正方形,点E 、F 、P 、N 分别在边AB 、BC 、CD 、AD 上,点H 、G 、M 在AC 上,阴影部分的面积依次记为1S ,2S ,则12:S S 等于__________.15.如图,以Rt ABC 的斜边AB 为一边,在AB 的右侧作正方形ABED ,正方形对角线交于点O ,连接CO ,如果AC=4,CO=62,那么BC=______.16.如图,在正方形ABCD 中,点,E F 将对角线AC 三等分,且6AC =.点P 在正方形的边上,则满足5PE PF +=的点P 的个数是________个.17.如图,在矩形ABCD 中,AB =2,AD =3,E 为BC 边上一动点,作EF ⊥AE ,且EF =AE .连接DF ,AF .当DF ⊥EF 时,△ADF 的面积为_____.18.如图,▱ABCD 中,∠DAB =30°,AB =6,BC =2,P 为边CD 上的一动点,则2PB+ PD 的最小值等于______.19.如图,有一张长方形纸片ABCD ,4AB =,3AD =.先将长方形纸片ABCD 折叠,使边AD 落在边AB 上,点D 落在点E 处,折痕为AF ;再将AEF ∆沿EF 翻折,AF 与BC 相交于点G ,则FG 的长为___________.20.如图,在四边形ABCD 中, //,5,18,AD BC AD BC E ==是BC 的中点.点P 以每秒1个单位长度的速度从点A 出发,沿AD 向点D 运动;点Q 同时以每秒3个单位长度的速度从点C 出发,沿CB 向点B 运动.点P 停止运动时,点Q 也随之停止运动,当运动时间为t 秒时,以点,,,P Q E D 为顶点的四边形是平行四边形,则t 的值等于_______.三、解答题21.如图,在Rt ABC 中,∠B =90°,AC =60cm ,∠A =60°,点D 从点C 出发沿CA 方向以4cm/s 的速度向点A 匀速运动.同时点E 从点A 出发沿AB 方向以2cm/秒的速度向点B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D 、E 运动的时间是ts (0<t≤15).过点D 作DF ⊥BC 于点F ,连接DE ,EF .(1)求证:AE =DF ;(2)四边形AEFD 能够成为菱形吗?如果能,求出相应的t 值,如果不能,说明理由; (3)当t 为何值时,DEF 为直角三角形?请说明理由.22.如图1,在正方形ABCD 中,点M 、N 分别在边BC 、CD 上,AM 、AN 分别交BD 于点P 、Q ,连接CQ 、MQ .且CQ MQ =.(1)求证:QAB QMC ∠=∠(2)求证:90AQM ∠=︒(3)如图2,连接MN ,当2BM =,3CN =,求AMN 的面积图1 图223.如图,点A 、F 、C 、D 在同一直线上,点B 和点E 分别在直线AD 的两侧,且AB =DE ,∠A =∠D ,AF =DC .(1)求证:四边形BCEF 是平行四边形;(2)若∠DEF =90°,DE =8,EF =6,当AF 为 时,四边形BCEF 是菱形.24.已知:如图,在△ABC 中,D 是BC 边上的一点,E 是AD 的中点,过点A 作BC 的平行线交于BE 的延长线于点F ,且AF=DC ,连接CF .(1)求证:D 是BC 的中点;(2)如果AB=AC ,试判断四边形ADCF 的形状,并证明你的结论.25.如图,在矩形ABCD 中,∠BAD 的平分线交BC 于点E ,AE =AD ,作DF ⊥AE 于点F . (1)求证:AB =AF ;(2)连BF 并延长交DE 于G .①EG =DG ;②若EG =1,求矩形ABCD 的面积.26.如图,在平面直角坐标系中,已知▱OABC 的顶点A (10,0)、C (2,4),点D 是OA 的中点,点P 在BC 上由点B 向点C 运动.(1)求点B 的坐标;(2)若点P 运动速度为每秒2个单位长度,点P 运动的时间为t 秒,当四边形PCDA 是平行四边形时,求t 的值;(3)当△ODP 是等腰三角形时,直接写出点P 的坐标.27.(解决问题)如图1,在ABC ∆中,10AB AC ==,CG AB ⊥于点G .点P 是BC 边上任意一点,过点P 作PE AB ⊥,PF AC ⊥,垂足分别为点E ,点F .(1)若3PE =,5PF =,则ABP ∆的面积是______,CG =______.(2)猜想线段PE ,PF ,CG 的数量关系,并说明理由.(3)(变式探究)如图2,在ABC ∆中,若10AB AC BC ===,点P 是ABC ∆内任意一点,且PE BC ⊥,PF AC ⊥,PG AB ⊥,垂足分别为点E ,点F ,点G ,求PE PF PG ++的值.(4)(拓展延伸)如图3,将长方形ABCD 沿EF 折叠,使点D 落在点B 上,点C 落在点C '处,点P 为折痕EF 上的任意一点,过点P 作PG BE ⊥,PH BC ⊥,垂足分别为点G ,点H .若8AD =,3CF =,直接写出PG PH +的值.28.已知正方形ABCD 与正方形(点C 、E 、F 、G 按顺时针排列),是的中点,连接,.(1)如图1,点E 在上,点在的延长线上,求证:DM =ME ,DM ⊥.ME简析: 由是的中点,AD ∥EF ,不妨延长EM 交AD 于点N ,从而构造出一对全等的三角形,即 ≌ .由全等三角形性质,易证△DNE 是 三角形,进而得出结论.(2)如图2, 在DC 的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.(3)当AB=5,CE=3时,正方形的顶点C 、E 、F 、G 按顺时针排列.若点E 在直线CD 上,则DM= ;若点E 在直线BC 上,则DM= .29.如图,四边形ABCD 为正方形.在边AD 上取一点E ,连接BE ,使60AEB ∠=︒.(1)利用尺规作图(保留作图痕迹):分别以点B 、C 为圆心,BC 长为半径作弧交正方形内部于点T ,连接BT 并延长交边AD 于点E ,则60AEB ∠=︒;(2)在前面的条件下,取BE 中点M ,过点M 的直线分别交边AB 、CD 于点P 、Q . ①当PQ BE ⊥时,求证:2BP AP =;②当PQ BE =时,延长BE ,CD 交于N 点,猜想NQ 与MQ 的数量关系,并说明理由.30.点E 在正方形ABCD 的边BC 上,点F 在AE 上,连接FB ,FD ,∠ABF=∠AFB . (1)如图1,求证:∠AFD=∠ADF ;(2)如图2,过点F 作垂线交AB 于G ,交DC 的延长线于H ,求证:DH=2 AG ; (3)在(2)的条件下,若EF=2,CH=3,求EC 的长.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【解析】【分析】由AAS 证明△ABG ≌△DEG ,得出AG=DG ,证出OG 是△ACD 的中位线,得出OG=12 CD=12AB ,①正确;先证明四边形ABDE 是平行四边形,证出△ABD 、△BCD 是等边三角形,得出AB=BD=AD ,因此OD=AG ,得出四边形ABDE 是菱形,③正确;由菱形的性质得得出△ABG ≌△BDG ≌△DEG ,由SAS 证明△ABG ≌△DCO ,得出△ABO ≌△BCO ≌△CDO ≌△AOD ≌△ABG ≌△BDG ≌△DEG ,得出②不正确;证出OG 是△ABD 的中位线,得出OG//AB ,OG=12AB ,得出△GOD ∽△ABD ,△ABF ∽△OGF ,由相似三角形的性质和面积关系得出S 四边形ODGF =S △ABF ;④不正确;即可得出结果.【详解】解:四边形ABCD 是菱形,,//,,,,AB BC CD DA AB CD OA OC OB OD AC BDBAG EDG ABO BCO CDO AOD CD DEAB DE∴=====⊥∴∠=∠∆≅∆≅∆=∴=在△ABG 和△DEG 中,BAG EDG AGB DGE AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABG ≌△DEG (AAS ),∴.AG=DG ,∴OG 是△ACD 的中位线,∴OG=12CD=12AB ,①正确; ∵AB//CE ,AB=DE ,∴四边形ABDE 是平行四边形,∴∠BCD=∠BAD=60°,∴△ABD 、△BCD 是等边三角形,∴AB=BD=AD ,∠ODC=60°,∴OD=AG ,四边形ABDE 是菱形,③正确;∴AD ⊥BE ,由菱形的性质得:△ABG ≌△BDG ≌△DEG ,在△ABG 和△DCO 中,60OD AG ODC BAG AB DC ︒=⎧⎪∠=∠=⎨⎪=⎩∴△ABG ≌△DCO∴△ABO ≌△BCO ≌△CDO ≌△AOD ≌△ABG ≌△BDG ≌△DEG ,则②不正确。
特殊平行四边形-中考数学第一轮总复习课件(全国通用)

中考数学第一轮总复习典例精讲考点聚集查漏补缺拓展提升第五单元 四边形专题5.2 特殊平行四边形知识点矩 形01菱 形02正 方 形03中点四边形04拓展训练05【例1-1】如图,在□ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF.求证:四边形ABFC是矩形.A EFD CB利用对角线相等的平行四边形是矩形证明方法一:利用△ABE≌△FCE证平行四边形;证法二:利用△ABE∽△FCE证平行四边形考点聚焦一个角为直角对角线相等平行四边形平行四边形直角证明四边形ABCD 是矩形的方法(三种)①先证明四边形ABCD为___________,再证明□ABCD的任意_____________;②先证明四边形ABCD为___________,再证明□ABCD的____________;【例1-2】如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( ) A.1 B.1.5 C.2 D.4AHGECBD F C 考点聚焦对边平行且相等四角都是直角对角线互相平分且相等矩形的性质(1)边:________________;(2)角:________________;(3)对角线:______________________.1.已知□ABCD,下列条件中,不能判定这个平行四边形为矩形的是( ) A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC2.如图,矩形ABCD的对角线AC=10,P,Q分别为AO,AD的中点,则PQ=_____.3.如图,矩形ABCD中,AB=3,BC=4,则图中四个小矩形的周长之和为____.4.如图,矩形OCDE,矩形OFGH,矩形OMNP各有一边在半⊙O的直径AB上,D,G,N都在半⊙O上,比较EC,HF,MP的大小_________.B 2.514EC=HF=EP5.如图,在矩形ABCD中,AB=8,AD=4,E为CD边上一点,CE=5,点P从B点出发,以每秒1个单位的速度沿着BA边向终点A运动,设点P运动的时间为t秒,则当t=_______时,△PAE是以PE为腰的等腰三角形.6.如图,将矩形ABCD绕点B顺时针旋转,得到矩形EBFG,且点E落在CD上,过点C作FG的垂线,垂足为H,若FH=HG,则BC:AB的值为_______.7.如图,在Rt△ABC中,∠BAC=90º,BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小最为_____.M2.4知识点矩 形01菱 形02正 方 形03中点四边形04拓展训练05【例2-1】如图,在等腰△ABC中,AD平分顶角∠BAC,交底边BC于点H,点E在AD上,BE=BD,求证:四边形BDCE是菱形.考点聚焦证明四边形ABCD 是菱形的方法(三种)①先证明四边形ABCD为___________,再证明□ABCD的任意_____________;②先证明四边形ABCD为___________,再证明□ABCD的________________平行四边形一组邻边相等平行四边形对角线互相垂直四边相等AH E DCB利用“三线合一”得出AD 垂直平分BC,从而得出四边相等。
中考数学一轮复习《四边形》综合复习练习题(含答案)

中考数学一轮复习《四边形》综合复习练习题(含答案)一、单选题1.一个多边形的内角和为900°,则这个多边形是( )A .七边形B .八边形C .九边形D .十边形 2.如图,将三角形纸片剪掉一角得四边形,设△ABC 与四边形BCDE 的外角和的度数分别为α,β,则正确的是( )A .0αβ-=B .0αβ-<C .0αβ->D .无法比较α与β的大小3.如图,把一个长方形纸片沿EF 折叠后,点D 、C 分别落在D ′、C ′的位置,若∠EFB =65°,则∠AED ′等于( )A .50°B .55°C .60°D .65°4.若一个正多边形的一个外角是60°,则这个正多边形的边数是( )A .10B .9C .8D .65.如图,四边形ABCD 是平行四边形,下列结论中正确的是( )A .当ABCD 是矩形时,90BAC ∠=︒B .当ABCD 是菱形时,AB BC ⊥ C .当ABCD 是正方形时,AC BD = D .当ABCD 是菱形时,AB AC =6.如图,在正方形ABCD 中,AE 平分BAC ∠交BC 于点E ,点F 是边AB 上一点,连接DF ,若BE AF =,则CDF ∠的度数为( )A .45︒B .60︒C .67.5︒D .775︒.7.如图,要拧开一个边长为()=6mm a a 的正六边形,扳手张开的开口b 至少为( )A .43mmB .63mmC . 42mmD . 12mm8.如图,菱形ABCD 中,∠BAD = 60°,AB = 6,点E ,F 分别在边AB ,AD 上,将△AEF 沿EF 翻折得到△GEF ,若点G 恰好为CD 边的中点,则AE 的长为( )A .34B .214C 3154D .39.以下说法不正确的是( )A .平行四边形是抽对称图形B .矩形对角线相等C .正方形对角线互相垂直平分D .菱形四条边相等10.陈师傅应客户要求加工4个长为4cm 、宽为3cm 的矩形零件.在交付客户之前,陈师傅需要对4个零件进行检测.根据零件的检测结果,图中有可能不合格的零件是( )A.B.C.D.11.如图,AB是半圆O的直径,以弦AC为折痕折叠AC后,恰好经过点O,则AOC∠等于()A.120°B.125°C.130°D.145°12.如图,在平面直角坐标系中,矩形ABCD的对角线AC经过坐标原点O,矩形的边分别平行于坐标轴,点B在函数kyx=(k≠0,x>0)的图像上,点D的坐标为(﹣3,1),则k的值为()A.53B.3-C.3D.53-二、填空题13.如果一个多边形的每一个外角都是60︒,那么这个多边形的边数是_______.14.如图,在矩形ABCD中,E是AD边上一点,且2AE DE=,BD与CE相交于点F,若DEF 的面积是3,则BCF △的面积是______.15.如果正多边形的一个外角是45︒,则这个正多边形的内角和是________︒.16.巧板是我国古代劳动人民的一项发明,被誉为“东方魔板”,它由五块等腰直角三角形、一块正方形和一块平行四边形组成.如图是利用七巧板拼成的正方形,随机向该图形内抛一枚小针,则针尖落在阴影部分的概率为 _____.17.如图,四边形ABCD 是菱形,42BD =,26AD =,点E 是CD 边上的一动点,过点E 作EF ⊥OC 于点F ,EG ⊥OD 于点G ,连接FG ,则FG 的最小值为_________.18.如图,矩形ABCD 的对角线AC 、BD 相交于点O ,过点O 作OE AC ⊥交AD 于点E ,若4AB =,8BC =,则DE 的长为______.19.已知ABC 中,65A ∠=︒,将B C ∠∠、按照如图所示折叠,若35ADB '∠=︒,则123∠+∠+∠=_____︒.CE ,F 20.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,5为DE的中点.若CEF△的周长为18,则OF的长为______.三、解答题21.如图,一组正多边形,观察每个正多边形中a的变化情况,解答下列问题.(1)将表格补充完整.正多边形的边数 3 4 5 6α的度数(2)观察上面表格中α的变化规律,角α与边数n的关系为.(3)根据规律,当α=18°时,多边形边数n=.22.如图,在ABCD中,AC=BC,M、N分别是AB和CD的中点.(1)求证:四边形AMCN是矩形;(2)若∠B=60°,BC=8,求ABCD的面积.23.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD 的中点,延长AE至G,使EG=AE,连接CG.(1)求证:△ABE≌△CDF;(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.24.如图,矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连接CG.(1)求证:四边形CEFG是菱形;(2)若AB=6,AD=10,求四边形CEFG的面积.25.如图,点E为矩形ABCD外一点,AE = DE.求证:△ABE≌△DCE26.如图,已知四边形ABCD为正方形,AB=2,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;(2)探究:①CE与CG有怎样的位置关系?请说明理由.②CE+CG的值为.27.某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:【现察与猜想】(1)如图1,在正方形ABCD中,点E,F分别是AB,AD上的两点,连接DE,CF,DE⊥CF,则DECF的值为______.(2)如图2,在矩形ABCD中,AD=7,CD=4,点E是AD上的一点,连接CE,BD,且CE⊥BD,则CEBD的值______.【类比探究】(3)如图3,在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,连接DE,过点C作DE 的垂线交ED的延长线于点G,交AD的延长线于点F,求证:DE•AB=CF•AD.28.在矩形ABCD中,AB=6,AD=4,点M为AB边上一个动点,连接DM,过点M作MN⊥DM,且MN=32DM,连接DN.(1)如图1,连接BD与BN,BD交MN于点E.①求证:△ABD∽△MND;②求证:∠CBN=∠DNM.(2)如图2,当AM=4BM时,求证:A,C,N三点在同一条直线上.参考答案1.A2.A3.A4.D5.C6.C7.B8.B9.A10.C11.A12.B13.614.2715.108016.381718.319.265︒20.7221.(1)正多边形每个内角的度数为180(2)n n -. 1803,603n α===; 904,452n α===; 正五边形的内角180(52)1085-=,1801085,362n α-===; 正五边形的内角180(62)1206-=,1801206,302n α-===.(2)观察(1)中结论,1803,603n == 1804,454n == 1805,365n == 1806,306n == 总结规律,则有180n α=. (3)借助(2)中公式,有180n α=,即18018n= 解得10n =.22.(1)证明:∵四边形ABCD 是平行四边形, ∴AB ∥CD ,AB =CD ,∵M 、N 分别是AB 和CD 的中点, ∴AM =BM ,AM ∥CN ,AM =CN , ∴四边形AMCN 是平行四边形,又∵AC =BC ,AM =BM ,∴CM ⊥AB ,∴∠CMA =90°,∴四边形AMCN 是矩形;(2)解:∵∠B =60°,BC =8,∠BMC =90°, ∴∠BCM =30°,∴Rt △BCM 中,BM =12BC =4,CM∵AC =BC ,CM ⊥AB ,∴AB =2BM =8,∴ABCD 的面积为AB ×CM23.(1)证明:∵四边形ABCD 是平行四边形, ∴AB =CD ,AB ∥CD ,OB =OD ,OA =OC , ∴∠ABE =∠CDF ,∵点E ,F 分别为OB ,OD 的中点, ∴BE =12OB ,DF =12OD ,∴BE =DF ,在△ABE 和△CDF 中,AB CD ABE CDF BE DF ⎧⎪∠∠⎨⎪⎩===,∴△ABE ≌△CDF (SAS ) .(2)当AB =12AC 时,四边形EGCF 是矩形;理由如下: 当AB =12AC 时,∵AC =2OA ,AC =2AB ,∴AB =OA ,∵E 是OB 的中点,∴AG⊥OB,∴∠OEG=90°,同理:CF⊥OD,∴AG∥CF,∴EG∥CF,由(1)得:△ABE≌△CDF,∴AE=CF,∵EG=AE,∴EG=CF,∴四边形EGCF是平行四边形,∵∠OEG=90°,∴四边形EGCF是矩形.24.(1)证明:由题意可得,△BCE≌△BFE,∴∠BEC=∠BEF,FE=CE,∵FG∥CE,∴∠FGE=∠CEB,∴∠FGE=∠FEG,∴FG=FE,∴FG=EC,∴四边形CEFG是平行四边形,又∵CE=FE,∴四边形CEFG是菱形;(2)解:∵矩形ABCD 中,AB =6,AD =10,BC =BF ,∴∠BAF =90°,AD =BC =BF =10,∴AF =8,∴DF =2,设EF =x ,则CE =x ,DE =6-x ,∵∠FDE =90°,∴22+(6-x )2=x 2,解得,x =103, ∴CE =103, ∴四边形CEFG 的面积是:CE •DF =103×2=203. 25.解:四边形ABCD 是矩形,AB DC ∴=,90BAD CDA ∠=∠=︒,AE DE =,EAD EDA ∴∠=∠,EAB BAD EAD CDA EDA EDC ∴∠=∠+∠=∠+=∠, 在ABE ∆和DCE ∆中,AE DE EAB EDC AB DC =⎧⎪∠=∠⎨⎪=⎩()ABE DCE SAS ∴∆∆≌.26.(1)如图,作EM ⊥BC 于M ,EN ⊥CD 于N ,又∠BCD =90°,∴∠MEN =90°,∵点E 是正方形ABCD 对角线上的点,∴EM =EN ,∵∠DEF =90°,∴∠DEN =∠MEF =90°﹣∠FEN ,∵∠DNE =∠FME =90°,在△DEN 和△FEM 中,DNE FME EN EMDEN FEM ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△DEN ≌△FEM (ASA ),∴EF =DE ,∵四边形DEFG 是矩形,∴矩形DEFG 是正方形;(2)①CE ⊥CG ,理由如下:∵正方形DEFG 和正方形ABCD ,∴DE =DG ,AD =DC ,∵∠CDG +∠CDE =∠ADE +∠CDE =90°,∴∠CDG =∠ADE ,在△ADE 和△CDG 中,AD CD ADE CDG DE DG =⎧⎪∠=∠⎨⎪=⎩,∴△ADE ≌△CDG (SAS ),∴∠DAE =∠DCG ,∵∠ACD +∠CAD +∠ADC =180°,∠ADC =90°,∴∠ACG =∠ACD +∠DCG =∠ACD +∠CAD =90°, ∴CE ⊥CG ;②由①知,△ADE ≌△CDG ,∴AE =CG ,∴CE +CG =CE +AE =ACAB=2,故答案为:2.27.(1)解:设DE与CF的交点为G,∵四边形ABCD是正方形,∴∠A=∠FDC=90°,AD=CD,∵DE⊥CF,∴∠DGF=90°,∴∠ADE+∠CFD=90°,∠ADE+∠AED=90°,∴∠CFD=∠AED,在△AED与△DFC中,A FDCCFD AEDAD CD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AED≌△DFC(AAS),∴DE=CF,∴DECF=1,故答案为:1;(2)解:如图,设DB与CE交于点G,∵四边形ABCD是矩形,∴∠A=∠EDC=90°,∵CE⊥BD,∴∠DGC=90°,∴∠CDG +∠ECD =90°,∠ADB +∠CDG =90°,∴∠ECD =∠ADB ,∵∠CDE =∠A ,∴△DEC ∽△ABD , ∴47CE DC BD AD ==, 故答案为:47; (3)证明:如图,过点C 作CH ⊥AF 交AF 的延长线于点H ,∵CG ⊥EG ,∴∠G =∠H =∠A =∠B =90°,∴四边形ABCH 为矩形,∴AB =CH ,∠FCH +∠CFH =∠DFG +∠FDG =90°,∴∠FCH =∠FDG =∠ADE ,∠A =∠H =90°,∴△AED ∽△HFC ,∴DE AD CF CH =, ∴DE AD CF AB=, ∴DE •AB =CF •AD .28.(1)①证明:∵四边形ABCD 是矩形,DM ⊥MN ∴∠A =∠DMN =90°∵AB =6,AD =4,MN =32DM ∴23AD DM AB MN == ∴△ABD ∽△MND .②证明:∵四边形ABCD 是矩形,DM ⊥MN ∴∠ABC =∠DMN =90°∴∠ABD +∠CBD =90°由①得△ABD ∽△MND∴∠ABD =∠DNM又∵∠MEB =∠DEN∴△MBE ∽△DNE ∴ME BE DE NE = ∴ME DE BE NE= 又∠MED =∠BEN∴△DME ∽△NBE∴∠NBE =∠DME =90°∴∠CBN +∠CBD =90°又∠ABD +∠CBD =90°,∠ABD =∠DNM ∴∠CBN =∠DNM .(2) 如图②,过点N 作NF ⊥AB 于点F ,连接AC ,AN ∴∠NF A =90°∵四边形ABCD 是矩形,AD =4,AB =6 ∴∠A =∠ABC =90°,BC =AD =4∴23BC AB =,∠ADM +∠AMD =90° ∵AM =4BM ,AB =6∴42455AM AB ==又DM ⊥MN∴∠AMD +∠FMN =90° ∴∠ADM =∠FMN∴△ADM ∽△FMN ∴AD AM DM MF FN MN== 又MN =32DM ∴24425=3DM MF FN MN == ∴MF =6,FN =365∴AF =AM +MF =2454655+= ∴23NF AF = ∴NF BC AF AB = ∵∠ABC =∠AFN =90° ∴△ABC ∽△AFN∴∠BAC =∠F AN∴A ,C ,N 三点在同一条直线.。
备考2023年中考数学一轮复习-图形的性质_四边形_平行四边形的性质-填空题专训及答案

备考2023年中考数学一轮复习-图形的性质_四边形_平行四边形的性质-填空题专训及答案平行四边形的性质填空题专训1、(2021泰州.中考模拟) 如图,平行四边形ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则的最小值等于________.2、(2017襄城.中考模拟) 如图,在平面直角坐标系中,▱ABCD的顶点B,C在x轴上,A,D两点分别在反比例函数y=﹣(x<0)与y= (x>0)的图象上,则▱ABCD的面积为________.3、(2017于洪.中考模拟) 在平行四边形ABCD中,连接AC,按以下步骤作图,分别以A、C为圆心,以大于AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F.若AB=6,BC=4,则△ADE的周长为________.4、(2017松北.中考模拟) 如图,▱ABCD中,E是AB的中点,AB=10,AC=9,DE=12,则△CDE的面积S=________.5、(2017徐汇.中考模拟) 如图,在平行四边形ABCD中,AE⊥CD,垂足为E,AF⊥BC,垂足为F,AD=4,BF=3,∠EAF=60°,设= ,如果向量=k (k≠0),那么k的值是________.6、(2017青浦.中考模拟) 如图,在平行四边形ABCD中,点E在边AD上,联结CE 并延长,交对角线BD于点F,交BA的延长线于点G,如果DE=2AE,那么CF:EF:EG=________.7、(2017徐州.中考模拟) 如图,已知▱ABCD的顶点A、C分别在直线x=2和x=5上,O是坐标原点,则对角线OB长的最小值为________.8、(2017玄武.中考模拟) 如图,在▱ABCD中,E、F分别是AD、CD的中点,EF与BD相交于点M,若△DEM的面积为1,则▱ABCD的面积为________.9、(2017昌乐.中考模拟) 如图,在▱ABCD中,DB=DC,∠C的度数比∠ABD的度数大54°,AE⊥BD于点E,则∠DAE的度数等于________.10、(2017曹.中考模拟) 如图,▱ABCD的对角线AC,BD相交于点O,点E是CD的中点,△ABD的周长为16cm,则△DOE的周长是________ cm.11、(2016东营.中考真卷) 如图,在Rt△ABC中,∠B=90°,AB=4,BC>AB,点D 在BC上,以AC为对角线的平行四边形ADCE中,DE的最小值是________.12、(2017郑州.中考模拟) 如图,在平行四边形ABCD中,连接AC,按一下步骤作图,分别以点A,点C为圆心,以大于AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F,若AB=5,BC=3,则△ADE的周长为________.13、(2017焦作.中考模拟) 如图,在▱ABCD中,DB=DC,∠C=58°,AE⊥BD于E,则∠DAE=________度.14、(2016黄陂.中考模拟) 在▱ABCD中,已知∠A=25°,将△BDA沿BD翻折至△BDA′,连接CA′,∠DA′C=55°,则∠ABD=________.15、(2019海珠.中考模拟) 在直角坐标系内,设A(0,0),B(4,0),C(t+4,4),D(t,4)(t为实数),记N为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则N的值可能为________.16、(2014崇左.中考真卷) 如图,A(4,0),B(3,3),以AO,AB为边作平行四边形OABC,则经过C点的反比例函数的解析式为________.17、(2017宁夏回族自治区.中考真卷) 如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点A'处.若∠1=∠2=50°,则∠A'为________.18、(2019高港.中考模拟) 如图,四边形ABCD是平行四边形,其中边AD是⊙O的直径,BC与⊙O相切于点B,若⊙O的周长是12π,则四边形ABCD的面积为________.19、(2020金华.中考真卷) 如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是________°.20、(2020贵港.中考模拟) 如图,已知反比例函数y= (x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A'(4,b)与点B'均在反比例函数的图象上,点B在直线y=x上,四边形AA'B'B是平行四边形,则B点的坐标为.平行四边形的性质填空题答案1.答案:2.答案:3.答案:4.答案:5.答案:6.答案:7.答案:8.答案:9.答案:10.答案:11.答案:12.答案:13.答案:14.答案:15.答案:16.答案:17.答案:18.答案:19.答案:20.答案:。
中考数学一轮复习平行四边形(讲义及答案)含答案

中考数学一轮复习平行四边形(讲义及答案)含答案一、解答题1.如图, 平行四边形ABCD 中,3AB cm =,5BC cm =,60B ∠=, G 是CD 的中点,E 是边AD 上的动点,EG 的延长线与BC 的延长线交于点F ,连接CE ,DF . (1) 求证:四边形CEDF 是平行四边形;(2) ①当AE 的长为多少时, 四边形CEDF 是矩形;②当AE = cm 时, 四边形CEDF 是菱形, (直接写出答案, 不需要说明理由).2.已知:如图,在△ABC 中,D 是BC 边上的一点,E 是AD 的中点,过点A 作BC 的平行线交于BE 的延长线于点F ,且AF=DC ,连接CF .(1)求证:D 是BC 的中点;(2)如果AB=AC ,试判断四边形ADCF 的形状,并证明你的结论.3.如图所示,四边形ABCD 是正方形, M 是AB 延长线上一点.直角三角尺的一条直角边经过点D ,且直角顶点E 在AB 边上滑动(点E 不与点A B 、重合),另一直角边与CBM ∠的平分线BF 相交于点F .(1)求证: ADE FEM ∠=∠;(2)如图(1),当点E 在AB 边的中点位置时,猜想DE 与EF 的数量关系,并证明你的猜想;(3)如图(2),当点E 在AB 边(除两端点)上的任意位置时,猜想此时DE 与EF 有怎样的数量关系,并证明你的猜想.4.我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.(发现与证明..)ABCD 中,AB BC ≠,将ABC ∆沿AC 翻折至'AB C ∆,连结'B D . 结论1:'AB C ∆与ABCD 重叠部分的图形是等腰三角形;结论2:'B D AC .试证明以上结论.(应用与探究)在ABCD 中,已知2BC =,45B ∠=,将ABC ∆沿AC 翻折至'AB C ∆,连结'B D .若以A 、C 、D 、'B 为顶点的四边形是正方形,求AC 的长.(要求画出图形)5.直线1234,,,,l l l l 是同一平面内的一组平行线.(1)如图1.正方形ABCD 的4个顶点都在这些平行线上,若四条直线中相邻两条之间的距离都是1,其中点A ,点C 分别在直线1l 和4l 上,求正方形的面积;(2)如图2,正方形ABCD 的4个顶点分别在四条平行线上,若四条直线中相邻两条之间的距离依次为123h h h ,,.①求证:13h h =;②设正方形ABCD 的面积为S ,求证222211 2 2 S h h h h =++.6.(解决问题)如图1,在ABC ∆中,10AB AC ==,CG AB ⊥于点G .点P 是BC 边上任意一点,过点P 作PE AB ⊥,PF AC ⊥,垂足分别为点E ,点F .(1)若3PE =,5PF =,则ABP ∆的面积是______,CG =______.(2)猜想线段PE ,PF ,CG 的数量关系,并说明理由.(3)(变式探究)如图2,在ABC ∆中,若10AB AC BC ===,点P 是ABC ∆内任意一点,且PE BC ⊥,PF AC ⊥,PG AB ⊥,垂足分别为点E ,点F ,点G ,求PE PF PG ++的值.(4)(拓展延伸)如图3,将长方形ABCD 沿EF 折叠,使点D 落在点B 上,点C 落在点C '处,点P 为折痕EF 上的任意一点,过点P 作PG BE ⊥,PH BC ⊥,垂足分别为点G ,点H .若8AD =,3CF =,直接写出PG PH +的值.7.如图,ABC ADC ∆≅∆,90,ABC ADC AB BC ︒∠=∠==,点F 在边AB 上,点E 在边AD 的延长线上,且,DE BF BG CF =⊥,垂足为H ,BH 的延长线交AC 于点G .(1)若10AB =,求四边形AECF 的面积;(2)若CG CB =,求证:2BG FH CE +=.8.在正方形AMFN 中,以AM 为BC 边上的高作等边三角形ABC ,将AB 绕点A 逆时针旋转90°至点D ,D 点恰好落在NF 上,连接BD ,AC 与BD 交于点E ,连接CD ,(1)如图1,求证:△AMC ≌△AND ;(2)如图1,若3,求AE 的长;(3)如图2,将△CDF 绕点D 顺时针旋转α(090α<<),点C,F 的对应点分别为1C 、1F ,连接1AF 、1BC ,点G 是1BC 的中点,连接AG ,试探索1AG AF 是否为定值,若是定值,则求出该值;若不是,请说明理由.9.如图,已知正方形ABCD与正方形CEFG如图放置,连接AG,AE.(1)求证:AG AE=(2)过点F作FP AE⊥于P,交AB、AD于M、N,交AE、AG于P、Q,交BC于H,.求证:NH=FM10.在四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF,GH分别交边AB、CD,AD、BC于点E、F、G、H.(1)观察发现:如图①,若四边形ABCD是正方形,且EF⊥GH,易知S△BOE=S△AOG,又因为S△AOB=14S四边形ABCD,所以S四边形AEOG=S正方形ABCD;(2)类比探究:如图②,若四边形ABCD是矩形,且S四边形AEOG=14S矩形ABCD,若AB=a,AD=b,BE=m,求AG的长(用含a、b、m的代数式表示);(3)拓展迁移:如图③,若四边形ABCD是平行四边形,且S四边形AEOG=14S▱ABCD,若AB=3,AD=5,BE=1,则AG=.【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)证明见解析;(2)①当AE=3.5时,平行四边形CEDF 是矩形;②2【分析】(1)证明△FCG ≌△EDG (ASA ),得到FG=EG 即可得到结论;(2)①当AE=3.5时,平行四边形CEDF 是矩形.过A 作AM ⊥BC 于M ,求出BM=1.5,根据平行四边形的性质得到∠CDA=∠B=60°,DC=AB=3,BC=AD=5,求出DE=1.5=BM ,证明△MBA ≌△EDC(SAS),得到∠CED=∠AMB=90°,推出四边形CEDF 是矩形;②根据四边形CEDFCEDF 是菱形,得到CD ⊥EF ,DG=CG=1212CD=1.5,求出∠DEG=30°,得到DE=2DG=3,即可求出AE=AD-DE=5-3=2.【详解】(1)证明:∵ 四边形ABCD 是平行四边形,∴ CF ∥ED ,∴ ∠FCG =∠EDG ,∵ G 是CD 的中点,∴ CG =DG ,在△FCG 和△EDG 中,FCG EDG CG DG CGF DGE ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴ △FCG ≌△EDG (ASA ),∴ FG =EG ,∵ CG =DG ,∴ 四边形CEDF 是平行四边形;(2)解:①当AE=3.5时,平行四边形CEDF 是矩形,理由是:过A 作AM ⊥BC 于M ,∵∠B=60°,∴∠BAM=30°,∵AB=3,∴BM=1.5,∵四边形ABCD 是平行四边形,∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5,∵AE=3.5,∴DE=1.5=BM ,在△MBA 和△EDC 中,BM DE B CDE AB CD =⎧⎪∠=∠⎨⎪=⎩,∴△MBA ≌△EDC(SAS),∴∠CED=∠AMB=90°,∵四边形CEDF 是平行四边形,∴四边形CEDF 是矩形;②∵四边形CEDFCEDF 是菱形,∴CD ⊥EF ,DG=CG=1212CD=1.5,∵∠CDE=∠B=60∘∠B=60∘,∴∠DEG=30°,∴DE=2DG=3,∴AE=AD-DE=5-3=2,故答案为:2.【点睛】此题考查了平行四边形的性质,矩形的判定定理,菱形的性质定理,直角三角形30度角所对的直角边等于斜边的一半,三角形全等的判定及性质定理,熟练掌握各定理并运用解答问题是解题的关键.2.(1)见详解;(2)四边形ADCF 是矩形;证明见详解.【分析】(1)可证△AFE ≌△DBE ,得出AF=BD ,进而根据AF=DC ,得出D 是BC 中点的结论; (2)若AB=AC ,则△ABC 是等腰三角形,根据等腰三角形三线合一的性质知AD ⊥BC ;而AF 与DC 平行且相等,故四边形ADCF 是平行四边形,又AD ⊥BC ,则四边形ADCF 是矩形.【详解】(1)证明:∵E 是AD 的中点,∴AE=DE .∵AF ∥BC ,∴∠FAE=∠BDE ,∠AFE=∠DBE .在△AFE 和△DBE 中,FAE BDE AFE DBE AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△AFE ≌△DBE (AAS ).∴AF=BD .∵AF=DC ,∴BD=DC .即:D 是BC 的中点.(2)解:四边形ADCF 是矩形;证明:∵AF=DC ,AF ∥DC ,∴四边形ADCF 是平行四边形.∵AB=AC ,BD=DC ,∴AD ⊥BC 即∠ADC=90°.∴平行四边形ADCF 是矩形.【点睛】此题主要考查了全等三角形的判定和性质,等腰三角形的性质,平行四边形、矩形的判定等知识综合运用.解题的关键是熟练掌握矩形的判定方法,以及全等三角形的判定和性质进行证明.3.(1)详见解析;(2)DE EF =,理由详见解析;(3)DE EF =,理由详见解析【分析】(1)根据90,90AED FEB ADE AED ∠+∠=︒∠+∠=︒,等量代换即可证明;(2)DE=EF ,连接NE ,在DA 边上截取DN=EB ,证出△DNE ≌△EBF 即可得出答案;(3)在DA 边上截取DN EB =,连接NE ,证出()DNE EBF ASA ≌即可得出答案.【详解】(1)证明:∵90DAB DEF ∠=∠=︒,∴90,90AED FEB ADE AED ∠+∠=︒∠+∠=︒,∴ADE FEM ∠=∠;(2) ;DE EF =理由如下:如图,取AD 的中点N ,连接NE ,∵四边形ABCD 为正方形,∴AD AB = ,∵,N E 分别为,AD AB 中点 ∴11,22AN DN AD AE EB AB ====, ∴,DN BE AN AE == 又∵90A ∠=︒∴45ANE ∠=︒∴180135DNE ANE ∠=︒-∠=︒,又∵90CBM ∠=︒,BF 平分CBM ∠∴45,135CBF EBF ∠=︒∠=︒.∴DNE EBF ∠=∠在DNE △和EBF △中ADE FEB DN EBDNE EBF ∠=∠⎧⎪=⎨⎪∠=∠⎩()DNE EBF ASA ≌,∴DE EF =(3) DE EF =.理由如下:如图,在DA 边上截取DN EB =,连接NE ,∵四边形ABCD 是正方形, DN EB =,∴AN AE =,∴AEN △为等腰直角三角形,∵45ANE ∠=︒∴18045135DNE ∠=︒-︒=︒,∵BF 平分CBM ∠, AN AE =,∴9045135EBF ∠=︒+︒=︒,∴DNE EBF ∠=∠,在DNE △和EBF △中ADE FEB DN EBDNE EBF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()DNE EBF ASA ≌,∴DE EF =.【点睛】此题主要考查了正方形的性质以及全等三角形的判定与性质等知识,解决本题的关键就是求证△DNE ≌△EBF .4.【发现与证明..】结论1:见解析,结论2:见解析;【应用与探究】AC 2或2. 【分析】【发现与证明..】由平行四边形的性质得出∠EAC=∠ACB ,由翻折的性质得出∠ACB=∠ACB ′,证出∠EAC=∠ACB ′,得出AE=CE ;得出DE=B ′E ,证出∠CB′D=∠B′DA=12(180°-∠B′ED),由∠AEC=∠B′ED,得出∠ACB′=∠CB′D,即可得出B′D∥AC;【应用与探究】:分两种情况:①由正方形的性质得出∠CAB′=90°,得出∠BAC=90°,再由三角函数即可求出AC;②由正方形的性质和已知条件得出AC=BC=2.【详解】【发现与证明..】:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠EAC=∠ACB,∵△ABC≌△AB′C,∴∠ACB=∠ACB′,BC=B′C,∴∠EAC=∠ACB′,∴AE=CE,即△ACE是等腰三角形;∴DE=B′E,∴∠CB′D=∠B′DA=12(180°−∠B′ED),∵∠AEC=∠B′ED,∴∠ACB′=∠CB′D,∴B′D∥AC;【应用与探究】:分两种情况:①如图1所示:∵四边形ACDB′是正方形,∴∠CAB′=90°,∴∠BAC=90°,∵∠B=45°,∴AC=222BC ;②如图2所示:AC=BC=2;综上所述:AC2或2.【点睛】本题考查平行四边形的性质, 正方形的性质, 翻折变换(折叠问题).【发现与证明..】对于结论1,要证明三角形是等腰三角形,只需要证明它的两条边相等,而在同一个三角形内要证明两条线段相等只需要证明它们所对应的角相等(即用等角对等边证明).结论2:要证明两条线段平行,本题用到了内错角相等,两直线平行.所以解决【发现与证明..】的关键是根据已知条件找到对应角之间的关系. 【应用与探究】折叠时,因为正方形的四个角都是直角,所以对应线段之间存在共线情况,所以分BA 和AB’共线和BC 和B’C 两种情况讨论,能根据题意画出两种情况对应的图形,是解题关键.5.(1)9或5;(2)①见解析,②见解析【分析】(1)分两种情况:①如图1-1,得出正方形ABCD 的边长为3,求出正方形ABCD 的面积为9;②如图1-2,过点B 作EF ⊥l 1于E ,交l 4于F ,则EF ⊥l 4,证明△ABE ≌△BCF (AAS ),得出AE=BF=2由勾股定理求出AB=225AE BE +=,即可得出答案;(2)①过点B 作EF ⊥l 1于E ,交l 4于F ,作DM ⊥l 4于M ,证明△ABE ≌△BCF (AAS ),得出AE=BF ,同理△CDM ≌△BCF (AAS ),得出△ABE ≌△CDM (AAS ),得出BE=DM 即可; ②由①得出AE=BF=h 2+h 3=h 2+h 1,得出正方形ABCD 的面积S=AB 2=AE 2+BE 2,即可得到答案.【详解】解:(1)①如图,当点B D ,分别在14,l l 上时,面积为:339⨯=;②如图,当点B D ,分别在23,l l 上时,过点B 作EF ⊥l 1于E ,交l 4于F ,则EF ⊥l 4,∵四边形ABCD 是正方形,∴AB=BC ,∠ABC=90°,∴∠ABE+∠CBF=180°-90°=90°,∵∠CBF+∠BCF=90°,∴∠ABE=∠BCF ,在△ABE 和△BCF 中90ABE BCF AEB BFC AB BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,∴△ABE ≌△BCF (AAS ),∴AE=BF=2,∴AB=2222215AE BE +=+=,∴正方形ABCD 的面积=AB 2=5;综上所述,正方形ABCD 的面积为9或5;(2)①证明:过点B 作EF ⊥l 1于E ,交l 4于F ,作DM ⊥l 4于M ,如图所示:则EF ⊥l 4,∵四边形ABCD 是正方形,∴AB=BC ,∠ABC=90°,∴∠ABE+∠CBF=180°-90°=90°,∵∠CBF+∠BCF=90°,∴∠ABE=∠BCF ,在△ABE 和△BCF 中,90ABE BCF AEB BFC AB BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,∴△ABE ≌△BCF (AAS ),∴AE=BF ,同理△CDM ≌△BCF (AAS ),∴△ABE ≌△CDM (AAS ),∴BE=DM ,即h 1=h 3.②解:由①得:AE=BF=h 2+h 3=h 2+h 1,∵正方形ABCD 的面积:S=AB 2=AE 2+BE 2,∴S=(h 2+h 1)2+h 12=2h 12+2h 1h 2+h 22.【点睛】本题考查了正方形的性质、全等三角形的判定和性质、勾股定理等知识;熟练掌握正方形的性质,证明三角形全等是解题的关键.6.(1)15,8;(2)PE PF CG +=,见解析;(3)534)4【分析】解决问题(1)只需运用面积法:ABC ABP ACP S S S ∆∆∆=+,即可解决问题;(2)解法同(1);(3)连接PA 、PB 、PC ,作AM BC ⊥于M ,由等边三角形的性质得出152BM BC ==,由勾股定理得出2253AM AB BM =-=,得出ABC ∆的面积12532BC AM =⨯=,由ABC ∆的面积BCP =∆的面积ACP +∆的面积APB +∆的面积1111()2532222BC PE AC PF AB PG AB PE PF PG =⨯+⨯+⨯=++=,即可得出答案; (4)过点E 作EQ BC ⊥,垂足为Q ,易证BE BF =,过点E 作EQ BF ⊥,垂足为Q ,由解决问题(1)可得PG PH EQ +=,易证EQ DC =,BF DF =,只需求出BF 即可.【详解】解:(1)∵PE AB ⊥,10AB =,3PE =,∴ABP ∆的面积111031522AB PE =⨯=⨯⨯=, ∵PE AB ⊥,PF AC ⊥,CG AB ⊥,且ABC ABP ACP S S S ∆∆∆=+,∴AB CG AB PE AC PF ⋅=⋅+⋅,∵AB AC =,∴358CG PE PF =+=+=.故答案为:15,8.(2)∵PE AB ⊥,PF AC ⊥,CG AB ⊥,且ABC ABP ACP S S S ∆∆∆=+,∴AB CG AB PE AC PF ⋅=⋅+⋅,∵AB AC =,∴CG PE PF =+.(3)连接PA 、PB 、PC ,作AM BC ⊥于M ,如图2所示:∵10AB AC BC ===,∴ABC ∆是等边三角形,∵AM BC ⊥,∴152BM BC ==, ∴222210553AM AB BM =-=-=,∴ABC ∆的面积11105325322BC AM =⨯=⨯⨯=, ∵PE BC ⊥,PF AC ⊥,PG AB ⊥,∴ABC ∆的面积BCP =∆的面积ACP +∆的面积APB +∆的面积111222BC PE AC PF AB PG =⨯+⨯+⨯1()2AB PE PF PG =++ 253=,∴22535310PE PF PG ⨯++==. (4)过点E 作EQ BC ⊥,垂足为Q ,如图3所示:∵四边形ABCD 是矩形,∴AD BC =,90C ADC ∠=∠=︒,∵8AD =,3CF =,∴5BF BC CF AD CF =-=-=,由折叠可得:5DF BF ==,BEF DEF ∠=∠,∵90C ∠=︒,∴2222534DC DF FC =-=-=,∵EQ BC ⊥,90C ADC ∠=∠=︒,∴90EQC C ADC ∠=︒=∠=∠,∴四边形EQCD 是矩形,∴4EQ DC ==,∵//AD BC ,∴DEF EFB ∠=∠,∵BEF DEF ∠=∠,∴BEF EFB ∠=∠,∴BE BF =,由解决问题(1)可得:PG PH EQ +=,∴4PG PH +=,即PG PH +的值为4.【点睛】本题是四边形综合题目,考查了矩形的性质与判定、等腰三角形的性质与判定、平行线的性质与判定、等边三角形的性质、勾股定理等知识,考查了用面积法证明几何问题,考查了运用已有的经验解决问题的能力,体现了自主探究与合作交流的新理念,是充分体现新课程理念难得的好题.7.(1)100;(2)见解析.【分析】(1)先证明四边形ABCD 是正方形,再根据已知条件证明△BCF ≌△DCE ,即可得到四边形AECF 的面积=正方形ABCD 的面积;(2) 延长BG 交AD 于点M ,作AN ⊥MN ,连接FG ,先证明四边形BCEM 是平行四边形,得到BM=CE ,证明△BCF ≌△GCF ,得到BF=GF ,∠FGC=∠FBC=90︒,由AN ⊥MN ,得GM=2MN ,根据∠BAC=45︒,BC ∥AD 得到AM=BF ,再证△BFH ≌△AMN,得到GM=2FH , 由此得到结论.【详解】(1)∵9,0ABC AB BC ︒∠==,∴△ABC 是等腰直角三角形,∵ABC ADC ∆≅∆,∴AB=AD=BC=DC ,∴四边形ABCD 是菱形,∵90ABC ADC ︒∠=∠=,∴四边形ABCD 是正方形,∴∠BCD=90ABC ADC ︒∠=∠=,∴∠CDE=90ABC ADC ︒∠=∠=,∵BF=DE,BC=DC ,∴△BCF ≌△DCE ,∴四边形AECF 的面积=S 正方形ABCD =AB 2=102=100.(2)延长BG 交AD 于点M ,作AN ⊥MN ,连接FG,∵△BCF ≌△DCE ,∴∠BCF=∠DCE ,∴∠FCE=∠BCD=90︒,∵BG ⊥CF ,∴∠FHM=∠FCE=90︒,∴BM ∥CE,∵BC ∥AD,∴四边形BCEM 是平行四边形,∴BM=CE.∵CG CB =,BG ⊥CF ,∴∠BCH=∠GCH,∠CBM=∠CGB,∴△BCF ≌△GCF,∴BF=GF,∠FGC=∠FBC=90︒,∵∠BAC=45︒,∴∠AFG=∠BAC=45︒,∴FG=AG,∵BC ∥AD,∴∠CBM=∠AMB,∴∠AGM=∠CGB=∠CBM=∠AMB,∴AM=AG,∵AN ⊥MN ,∴GM=2MN,∵∠BAD=∠ANM=90︒,∴∠ABM+∠AMN=∠MAN+∠AMN=90︒,∴∠ABM=∠MAN,∵AM=AG=FG=BF,∠BHF=∠ANM=90︒,∴△BFH ≌△AMN,∴FH=MN,∴GM=2FH,∵BG+GM=CE,∴2BG FH CE +=.【点睛】此题是四边形的综合题,考查正方形的判定及性质,全等三角形的判定及性质,等腰三角形的性质,平行四边形的性质,解题中注意综合思想的方法积累.8.(1)见解析;(2)AE =33)(3)122AG AF =,理由见解析. 【分析】(1)运用四边形AMFN 是正方形得到判断△AMC,△AND 是Rt △,进一步说明△ABC 是等边三角形,在结合旋转的性质,即可证明.(2)过E 作EG ⊥AB 于G,在BC 找一点H ,连接DH,使BH=HD ,设AG =x ,则AE=2x 3x ,得到△GBE 是等腰直角三角形和∠DHF=30°,再结合直角三角形的性质,判定Rt △AMC ≌Rt △AND ,最后通过计算求得AE 的长;(3)延长F 1G 到M,延长BA 交11F C 的延长线于N,使得1GM FG =,可得GMB ∆≌11GFC ∆,从而得到111BM FC DF == 1BMG GFN ∠=,可知BM ∥1F N , 再根据题意证明ABM ∆≌1ADF ∆,进一步说明1AMF ∆是等腰直角三角形,然后再使用勾股定理求解即可.【详解】(1)证明:∵四边形AMFN 是正方形,∴AM=AN ∠AMC=∠N=90°∴△AMC,△AND 是Rt △∵△ABC 是等边三角形∴AB=AC∵旋转后AB=AD∴AC=AD∴Rt △AMC ≌Rt △AND(HL)(2)过E 作EG ⊥AB 于G,在BC 找一点H ,连接DH,使BH=HD ,设AG =x则AE=2x 3x易得△GBE 是等腰直角三角形∴BG=EG 3x∴AB=BC=31)x易得∠DHF=30°∴HD=2DF=3,HF=3∴BF=BH+HF=233∵Rt △AMC ≌Rt △AND(HL)∴易得3∴BC=BF-CF=233333=+∴(31)33x =∴3x =∴AE =223x=(3)12AG AF =; 理由:如图2中,延长F 1G 到M,延长BA 交11F C 的延长线于N,使得1GM FG =,则GMB ∆≌11GFC ∆,∴111BM FC DF == 1BMG GFN ∠=, ∴BM ∥1F N ,∴MBA N ∠=∠∵0190NAO OF D ∠=∠= 1AON DOF ∠=∠∴1N ADF ∠=∠∴1ABM ADF ∠=∠,∵AB AD = ∴ABM ∆≌1ADF ∆(SAS )∴1AM AF = 1MAB DAF ∠=∠∴0190MAF BAD ∠=∠=∴1AMF ∆是等腰直角三角形∴1AG MF ⊥ 1AG GF =∴12AF∴122AG AF = 【点睛】本题考查正方形的性质、三角形全等、以及勾股定理等知识点,综合性强,难度较大,但解答的关键是正确做出辅助线.9.(1)证明见解析;(2)证明见解析.【分析】(1)根据正方形的性质证得BG=DE ,利用SAS 可证明ABG ≌ADE ,再利用全等的性质即可得到结论;(2)过M 作MK ⊥BC 于K ,延长EF 交AB 于T ,根据ASA 可证明MHK △≌AED ,得到AE=MH ,再利用AAS 证明TNF △≌DAE △,得到NF=AE ,从而证得MH=NF ,即可得到结论.【详解】证明:(1)∵四边形ABCD 与四边形CEFG 均为正方形,∴AB=AD=BC=CD ,CG=CE ,∠ABG=∠ADE=90°,∴BC -GC=CD -EC ,即BG=DE ,∴ABG ≌ADE ,∴AG=AE ;(2)过M 作MK ⊥BC 于K ,则四边形MKCD 为矩形,∴∠MKH=∠ADE=90°,MK=CD ,∠AMK=90°,∴MK=AD ,∠AMP+∠HMK=90°,又∵FP AE ,∴∠EAD+∠AMP=90°,∴∠HMK=∠EAD ,∴MHK △≌AED ,∴MH=AE ,延长EF 交AB 于T ,则四边形TBGF 为矩形,∴FT=BG ,∠FTN=∠ADE=90°,∵ABG ≌ADE ,∴DE=BG ,∴FT=DE ,∵FP ⊥AE ,∠DAB=90°,∴∠N+∠NAP=∠DAE+∠NAP=90°,∴∠N=∠DAE ,∴TNF △≌DAE △,∴FN=AE ,∴FN=MH ,∴FN-FH=MH-FH,∴NH=FM.【点睛】本题考查了正方形的性质,矩形的判定与性质,及全等三角形的判定与性质,熟练掌握各性质、判定定理是解题的关键.10.(1)14;(2)mbAGa;(3)53【分析】(1)如图①,根据正方形的性质和全等三角形的性质即可得到结论;(2)如图②,过O作ON⊥AD于N,OM⊥AB于M,根据图形的面积得到14mb=14AG•a,于是得到结论;(3)如图③,同理:过O作QM⊥AB,PN⊥AD,先根据平行四边形面积可得OM和ON 的比,同理可得S△BOE=S△AOG,根据面积公式可计算AG的长.【详解】解:(1)如图①,∵四边形ABCD是正方形,∴OA=OC,∠OAG=∠EBO=45°,∠AOB=90°,∵EF⊥GH,∴∠EOG=90°,∴∠BOE=∠AOG(SAS),∴△BOE≌△AOG,∴S△BOE=S△AOG,又∵S△AOB=14S四边形ABCD,∴S四边形AEOG=14S正方形ABCD,故答案为:14.(2)解:如图②,过O作OM⊥AB于M,ON⊥AD于N,∴S△AOB=S△AOD=14S矩形ABCD,∵S四边形AEOG=14S矩形ABCD,∴S△AOB=S四边形AEOG,∴S△BOE=S△AOG,∵S△BOE=12BE•OM=14mb,S△AOG=12AG•ON=14AG•a,∴mb=AG•a,∴AG=mba;(3)如图③,过O作OM⊥AB于M,ON⊥AD于N,∵S△AOB=S△AOD=14S▱ABCD,S四边形AEOG=14S▱ABCD,∴S△AOB=S四边形AEOG,∴S△BOE=S△AOG,∵S△BOE=12BE•OM=12OM,S△AOG=12AG•ON,∴OM=AG•ON,∵S▱ABCD=3×2OM=5×2 ON,∴53 OMON,∴AG=53;【点睛】本题是四边形综合题,考查了正方形、矩形、平行四边形的性质及三角形、四边形的面积问题,认真阅读材料,理解并证明S△BOE=S△AOG是解决问题的关键.。
中考数学一轮复习 四边形与平行四边形

FH PACBED考数学复习二十——四边形与平行四边形一、中考要求:1.探索并了解多边形的内角和与外角和公式,了解正多边形的概念;掌握多边形的内角和定理与外角和定理;了解n 边形的对角线的条数公式。
2.通过探索平面图形的镶嵌,知道任意一个三角形、四边形或正六边形可以镶嵌平面,并能运用这几种图形进行简单的镶嵌设计。
3.掌握平行四边形的定义、性质和判定方法(从边、角、对角线三个方面);知道平行四边形是中心对称图形,具备不稳定性,4.会用平行四边形的性质与判定解决简单的问题。
二、知识要点:1.一般地,由n 条不在同一直线上的线段 连结组成的平面图形称为n 边形,又称为多边形。
2.如果多边形的各边都 ,各内角也都 ,则称这个多边形为正多边形。
3.连结多边形不相邻的两个顶点的线段叫做多边形的 。
4.n 边形的内角和为 。
正n 边形的一个内角是 。
5.任意多边形的外角和为 。
正n 边形的一个外角是 。
6.从n 边形的一个顶点可引 条对角线,n 边形一共有 条对角线。
7.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个 角时,这几个多边形就能拼成一个平面图形。
两种图形的平面镶嵌:正三角形可以与边长相等的 镶嵌。
8.平行四边形的定义两组对边分别 的四边形叫做平行四边形。
9.平行四边形的性质(1)边: (2)角: (3)对角线: (4)对称性:10.两条平行线间的距离: 11.平行四边形的识别从边考虑⎪⎩⎪⎨⎧ ⎪⎭⎪⎬⎫ 是平行四边形。
从角考虑: (4)两组对角 的四边形是平行四边形。
说说此判定的证明方法:从对角线考虑(5)对角线 的四边形是平行四边形。
三、典例剖析:例1.如图,已知在□ABCD 中,E 、F 是对角线BD 上的两点,BE =DF ,点G 、H 分别在BA 和DC 的延长线上,且AG =CH ,连接GE 、EH 、HF 、FG . 求证:四边形GEHF 是平行四边形.例2.如图,在平行四边形ABCD 中,E 、F 分别是边AD 、BC 的中点,AC 分别交BE 、DF 于点M 、N . 给出下列 结论:①△ABM ≌△CDN ;②AM =31AC ;③DN =2NF ; ④S △AMB =21S △ABC .其中正确的结论是 (只填序号).例3.已知四边形ABCD 的对角线AC 与BD 交于点O ,给出下列四个论断 ① OA =OC ② AB =CD ③ ∠BAD =∠DCB ④ AD ∥BC请你从中选择两个论断作为条件,以“四边形ABCD 为平行四边形”作为结论,完成下列各题: ①构造一个真命题...: ; ②构造一个假命题...: , 举反例加以说明 . 例4.如图,在△ABC 中,AB =AC =5,BC =6,动点P 从点A 出发沿AB 向点B 移动,(点P 与点A 、B 不重合),作PD //BC 交AC 于点D ,在DC 上取点E ,以DE 、DP 为邻边作平行四边形PFED ,使点F 到PD 的距离16FH PD =,连接BF ,设AP x =(1)△ABC 的面积等于NMFEDBA(1)两组对边 的四边形 (2)两组对边 的四边形 (3)一组对边 且 的四边形(2)设△PBF 的面积为y ,求y 与x 的函数关系,并求y 的最大值;(3)当BP =BF 时,求x 的值随堂演练:1.图中是一个五角星图案,中间部分的五边形ABCDE 是一个正五边形, 则图中∠ABC 的度数是 .2.如果只用一种正多边形进行镶嵌,那么在下列的正多边形中, 不能镶嵌成一个平面的是( ).A .正三角形B .正方形C .正五边形D .正六边形 3.一个多边形内角和是,则这个多边形是( ) A .六边形B .七边形C .八边形D .九边形4.在平行四边形ABCD 中,点1A ,2A ,3A ,4A 和1C ,2C ,3C ,4C 分别是AB 和CD 的五等分点,点1B ,2B 和1D ,2D 分别是BC 和DA 的三等分点,已知四边形4242A B C D 的面积为1,则平行四边形ABCD 的面积为( ) A .2B .35C .53D .155.边长为的正六边形的面积等于( ) A .B .C .D .6.如图,在周长为20cm 的□ABCD 中,AB ≠AD ,AC 、BD 相交于点O ,OE ⊥BD 交AD 于E ,则△ABE 的周长为7.下列四种边长均为a 的正多边形中,能与边长为a 的正三角形作平面镶嵌的正多边形有1080a 243a 2a 2233a 233a A BCDEABCDOED D 1D 2 AA 1 A 2 A 3 A 4B 1B 2 CC 2 13 4 B()①正方形②正五边形③正六边形④正八边形A.4种B.3种C.2种D.1种8.如图,在□ABCD中,对角线AC、BD相交于点O,若AC=14,BD=8,AB=10,则△OAB的周长为.9.如图,在平行四边形ABCD中,DB=DC、65=∠A,CE⊥BD于E,则=∠BCE.10. 如图是对称中心为点的正八边形.如果用一个含角的直角三角板的角,借助点(使角的顶点落在点处)把这个正八边形的面积等分.那么的所有可能的值有()A.2个B.3个C.4个D.5个11. 问题背景(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:四边形DBFE的面积S=,△EFC的面积1S=,△ADE的面积2S=.探究发现(2)在(1)中,若BF a=,FC b=,DE与BC间的距离为h.请证明2124S S S=.拓展迁移(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用..(2.)中的结论....求△ABC的面积.O45O O nnB CD GFE图2AB CDFE图1A36214.四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图l,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点.(1)如图2,画出菱形ABCD的一个准等距点.(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法).(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形AB CD的准等距点.图1中考数学复习作业二十1.如图下面对图形的判断正确的是( )A .非对称图形B .既是轴对称图形,又是中心对称图形C .是轴对称图形,非中心对称图形D .是中心对称图形,非轴对称图形 2.如图所示,顺次连接矩形ABCD 各边中点,得到菱形EFGH , 这个由矩形和菱形所组成的图形( ) A .是轴对称图形但不是中心对称图形 B .是中心对称图形但不是轴对称图形C .既是轴对称图形又是中心对称图形D .没有对称性3.只用下列正多边形地砖中的一种,能够铺满地面的是( ) A .正十边形 B .正八边形 C .正六边形 D .正五边形4.A 、B 、C 、D 在同一平面内,从①AB ∥CD ;②AB =CD ;③BC ∥AD ;④BC =AD 这四个条件中任选两个,能使四边形ABCD 是平行四边形的选法有 ( )A .3种B .4种C .5种D .6种5.平行四边形ABCD 中,AB =3,BC =5,∠B 的平分线把长边分成两条线段之比是( )A .3:2B .3:1C .4:2D .4:16.如果平行四边形的一条边长是4,一条对角线长是10,那么它的另一条对角线的长m 的取值范围是( )A .6<m <14B .1<m <9C .3<m <7D .2<m <18 7.三角形纸片ABC 中,∠A =65°,∠B =75°,将纸片的一角折叠,使 点C 落在ABC 内(如图),若∠1=20°,则∠2的度数为。
人教版初中数学中考复习一轮复习-多边形和平行四边形(知识点+中考真题)

(1) 平行四边形的对边平行且相等. (2) 平行四边形的邻角互补,对角相.等.
推论:夹在两条平行线间的 平行线段 相等. (3) 平行四边形的对角线互相平分 .
(4)若一直线过平行四边形两对角线的交点, 则: 则二等这分条此直平线行被四一边组形对的边面截积下的线段以对角线的交点为中点,并且这两条直.线
是 中心 对称图形.②正n边形有 n 条对称轴 .
3.平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全 覆盖 ,叫做用多边形
覆盖平面(或平面镶嵌).平面镶嵌的条件:当围绕一点拼在一起的几个多边形的内
角和为 360° 时,可以平面镶嵌.
知识点梳理——平行四边形
1.平行四边形的概念: 两组对边分别平行的四边形叫做平行.四边形
【解答】证明:∵DE=DC,∴∠DEC=∠C. ∵∠B=∠C, ∴∠B=∠DEC, ∴ AB∥BE, ∵AD∥BC, ∴四边形ABED是平行四边形. ∴AD=BE.
14.(10分)(2021•怀化)已知:如图,四边形ABCD为平行四边形,点E、 A、C、F在同一直线上,AE=CF. 求证:(1)△ADE≌△CBF;
C ∠D=58°,则∠AEC的大小是( )
A.61° B.109° C.119° D.122°
典型例题
7.(2021•恩施州)如图,在▱ABCD中,AB=13,AD=5,
AC⊥BC,则▱ABCD的面积为( B )
A.30 B.60
C.65 D.
典型例题
8.(2021·安顺、贵阳) 如图,在▱ABCD中,∠ABC的平分线交AD于点E,
形的边数是
.
2.(2020•陕西12/25)如图,在正五边形ABCDE中,DM是边CD的延长线,连接BD ,则∠BDM的度数是 .
2022年人教版中考数学一轮复习:四边形综合 专项练习题2(Word版,含答案)

2022年人教版中考数学一轮复习:四边形综合专项练习题2
1.如图,已知四边形ABCD是平行四边形,从①AB=AD,②AC=BD,③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形,则其选择是(限填序号).
2.如图1,平行四边形纸片ABCD的面积为120,AD=15.今沿两对角线将四边形ABCD剪成甲、乙.丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成一个对称图形戊,如图2所示.则图形戊的两条对角线长度之和为.
3.如图,菱形ABCD的两条对角线AC,BD交于点O,BE⊥AD于点E,若AC=8,BD=6,则BE的长为.
4.如图,在▱ABCD中,∠A=70°,DB=DC,CE⊥BD于E,则∠BCE=.
5.如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE
交于点H,若CG=1,则S
=.
四边形BCDG
6.如图,正方形瓷砖图案是四个全等且顶角为45°的等腰三角形.已知该瓷砖的面积是1m2,则中间小正方形的面积为m2.
7.如图所示,在Rt△ABC外作等边△ADE,点E在AB边上,AC=5,∠ABC=30°,AD=3.将△ADE沿AB方向平移,得到△A′D′E′,连接BD′.给出下列结论:①AB=10;②四边形ADD′A′为平行四边形;③AB平分∠D′BC;④当平移的距离为4时,BD′=3.其中正确的是(填上所有正确结论的序号).
8.如图,菱形ABCD的对角线AC,BD相交于点O,P为AB边上一动点(不与点A,B重合),PE⊥OA于点E,PF⊥OB于点F,若AB=4,∠BAD=60°,则EF的最小值为.。
2024年中考第一轮复习特殊平行四边形2

3.[2019·上海]如图25-7,在正方形ABCD中,E是边AD的中点.将△ABE沿直线BE
翻折,点A落在点F处,连结DF,那么∠EDF的正切值是
图25-7
.
[答案]2
1
[解析] 如图所示,由折叠可得 AE=FE,∠AEB=∠FEB= ∠AEF,
■ 知识梳理
1.定义:顺次连结四边形各边中点所得的四边形称为中点四边形.
2.任意四边形的中点四边形是① 平行四边形 .
对角线相等的四边形的中点四边形是② 菱形
.
对角线垂直的四边形的中点四边形是③ 矩形
.
对角线互相垂直且相等的四边形的中点四边形是④ 正方形 .
考向一
中点四边形
例1 如图25-4,D,E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB,AC的中点
1
2
∵AC=BD=8,AE=CF=2,∴OD=4,OE=OF= (8-2-2)=2.
由勾股定理,得 DE= 2 + 2 = 42 + 22 =2 5,
∴四边形 BEDF 的周长=4DE=4×2 5=8 5.
■ 知识梳理
图25-2
考点二
中点四边形
4.顺次连结任意四边形各边的中点,所得的四边形一定是
,O是△ABC所在平面上的动点,连结OA,OB,OC,点G,F分别是OB,OC的中点,顺
次连结点D,G,F,E.
(1)当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
解:(1)证明:∵D,E 分别是 AB,AC 的中点,
1
∴DE∥BC,且 DE=2BC.
1
同理,GF∥BC,且 GF=2BC,
2020年中考数学一轮复习精选题 四边形(含答案)

2020年中考数学一轮复习精选题四边形一、选择题1.若一个正多边形的一个外角是45°,则这个正多边形的边数是()A.7 B.8 C.9 D.102.一个多边形的内角和比它的外角和的3倍少1800,这个多边形的边数是()A.5条B.6条C.7条D.8条3.如图,▱ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO周长是( )A.10B.14C.20D.224.如图,在四边形ABCD中,∠DAC=∠ACB,要使四边形ABCD成为平行四边形,则应增加的条件不能是( )A.AD=BCB.OA=OCC.AB=CDD.∠ABC+∠BCD=180°5.矩形具有而平行四边形不一定具有的性质是()A.对角相等B.对边相等C.对角线相等D.对角线互相平分6.如图,矩形ABCD中,E在AD上,EF⊥EC,EF=EC,DE=2,矩形周长为16,则AE长是( )A.3B.4C.5D.77.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )A.当AB=BC时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD时,它是正方形8.如图,菱形ABCD周长为20,对角线AC、BD相交于点O,E是CD的中点,则OE的长是( )A.2.5 B.3 C.4 D.59.如图,在菱形ABCD中,AB=5,对角线AC=6.若过点A作AE⊥BC,垂足为E,则AE的长为( )A.4B.2.4C.4.8D.510.如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,则∠E=()A.90°B.45°C.30°D.22.5°11.如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B′处,AB′与y轴交于点D,则点D的坐标为()A.(0,-)B.(0,-)C.(0,-)D.(0,-)12.如图,正方形ABCD的对角线AC与BD相交于O点,在BD上截取BE=BC,连接CE,点P是CE上任意一点,PM⊥BD于M,PN⊥BC于N,若正方形ABCD的边长为1,则PM+PN=()A.1B.C. D.1+二、填空题13.如图,点O是正五边形ABCDE的中心,则∠BAO的度数为.14.如图,平行四边形ABCD的周长为40,△BOC的周长比△AOB的周长多10,则AB为.15.如图所示,在菱形ABCD中,AE垂直平分BC,垂足为E,AB=4 cm.那么,菱形ABCD的面积是________,对角线BD的长是________.16.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF= cm.17.在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= .(结果保留根号)18.如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连结DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系式是.三、解答题19.如图,已知在▱ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.(1)求证:△AEM≌△CFN;(2)求证:四边形BMDN是平行四边形.20.如图在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.(1)证明:四边形ACDE是平行四边形;(2)若AC=8,BD=6,求△ADE的周长.21.如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥DG,交BG于点H.连接HF,AF,其中AF交EC于点M.(1)求证:△AHF为等腰直角三角形.(2)若AB=3,EC=5,求EM的长.22.如图,正方形ABCD的对角线交于点O,点E,F分别在AB,BC上(AE<BE),且∠EOF=90°,OE,DA 的延长线交于点M,OF,AB的延长线交于点N,连接MN.(1)求证:OM=ON;(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.23.如图,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点,AD=BC.求证:四边形EFGH是菱形.24.如图,四边形ABCD是平行四边形,以AB为直径的圆O经过点D,E是⊙O上一点,且∠AED=45°.(1)判断CD与⊙O的位置关系,并说明理由;(2)若⊙O半径为6cm,AE=10cm,求∠ADE的正弦值.参考答案1.B2.C3.B.4.C5.C.6.A7.D8.答案为:A.9.C10.D11.B12.C13.答案为:54°.14.答案为:5.16.答案为:2.5.17.答案为:.18.答案为:y=12x-1.19.证明:(1)四边形ABCD是平行四边形,∴∠DAB=∠BCD,∴∠EAM=∠FCN,又∵AD∥BC,∴∠E=∠F.∵在△AEM与△CFN中,,∴△AEM≌△CFN(ASA);(2)∵四边形ABCD是平行四边形,∴AB CD,又由(1)得AM=CN,∴BM DN,∴四边形BMDN是平行四边形.20.解:(1)证明:∵四边形ABCD是菱形,∴AB∥CD,AC⊥BD,∴AE∥CD,∠AOB=90°,又∵DE⊥BD,即∠EDB=90°,∴∠AOB=∠EDB.∴DE∥AC.∴四边形ACDE是平行四边形.(2)∵四边形ABCD是菱形,AC=8,BD=6,∴AO=4,DO=3,∴AD=CD=5.又∵四边形ACDE是平行四边形,∴AE=CD=5,DE=AC=8.∴△ADE的周长为AD+AE+DE=5+5+8=18.21.证明:(1)∵四边形ABCD,四边形ECGF都是正方形∴DA∥BC,AD=CD,FG=CG,∠B=∠CGF=90°∵AD∥BC,AH∥DG∴四边形AHGD是平行四边形∴AH=DG,AD=HG=CD∵CD=HG,∠ECG=∠CGF=90°,FG=CG∴△DCG≌△HGF(SAS)∴DG=HF,∠HFG=∠HGD∴AH=HF,∵∠HGD+∠DGF=90°∴∠HFG+∠DGF=90°∴DG⊥HF,且AH∥DG∴AH⊥HF,且AH=HF∴△AHF为等腰直角三角形.(2)∵AB=3,EC=5,∴AD=CD=3,DE=2,EF=5∵AD∥EF∴=,且DE=2∴EM=22.解:(1)证明:正方形ABCD中,AC=BD,OA=0.5AC,OB=OD=0.5BD,所以OA=OB=OD,因为AC⊥BD,所以∠AOB=∠AOD=90°,所以∠OAD=∠OBA=45°,所以∠OAM=∠OBN,又因为∠EOF=90°,所以∠AOM=∠BON,所以△AOM≌△BON,所以OM=ON.(2)如图,过点O作OP⊥AB于P,所以∠OPA=90°,∠OPA=∠MAE,因为E为OM中点,所以OE=ME,又因为∠AEM=∠PEO,所以△AEM≌△PEO,所以AE=EP,因为OA=OB,OP⊥AB,所以AP=BP=0.5AB=2,所以EP=1.Rt△OPB中,∠OBP=45°,所以OP=PB=2,Rt△OEP中,OE=错误!未找到引用源。
专题28 四边形综合-中考数学一轮复习精讲+热考题型(解析版)

专题28 四边形综合【知识要点】四边形之间的从属关系特殊四边形的性质与判定:【考查题型】考查题型一四边形综合典例1.(浙江温州市·中考真题)如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR分别交边DE,BH于点P,Q.若QH=2PE,PQ=15,则CR 的长为()A.14B.15C.D.【答案】A【提示】连接EC,CH,设AB交CR于点J,先证得△ECP∽△HCQ,可得12PC CE EPCQ CH HQ===,进而可求得CQ=10,AC:BC=1:2,由此可设AC=a,则BC=2a,利用AC∥BQ,CQ∥AB,可证得四边形ABQC为平行四边形,由此可得AB=CQ=10,再根据勾股定理求得AC=BC=求得4CJ=,进而可求得CR的长.【详解】解:如图,连接EC,CH,设AB交CR于点J,∵四边形ACDE,四边形BCIH都是正方形,∴∠ACE=∠BCH=45°,∵∠ACB=90°,∠BCI=90°,∴∠ACE+∠ACB+∠BCH=180°,∠ACB+∠BCI=180°,∴点E 、C 、H 在同一直线上,点A 、C 、I 在同一直线上, ∵DE ∥AI ∥BH , ∴∠CEP =∠CHQ , ∵∠ECP =∠QCH , ∴△ECP ∽△HCQ , ∴12PC CE EP CQ CH HQ ===, ∵PQ =15, ∴PC =5,CQ =10, ∵EC :CH =1:2, ∴AC :BC =1:2, 设AC =a ,则BC =2a , ∵PQ ⊥CR ,CR ⊥AB , ∴CQ ∥AB ,∵AC ∥BQ ,CQ ∥AB , ∴四边形ABQC 为平行四边形, ∴AB =CQ =10, ∵222AC BC AB +=, ∴25100a =,∴a =∴AC =BC = ∵1122AC BC AB CJ ⋅⋅=⋅⋅,∴4CJ =, ∵JR =AF =AB =10, ∴CR =CJ +JR =14, 故选:A .变式1-1.(江苏无锡市·中考真题)如图,在四边形ABCD 中()AB CD >,90ABC BCD ∠=∠=︒,3AB =,BC =,把Rt ABC ∆沿着AC 翻折得到Rt AEC ∆,若tan 2AED ∠=,则线段DE 的长度为( )A .3B .3C .2D .5【答案】B【提示】根据已知,易求得AC =CD 交AE 于F ,可得2AF CF ==,则=1EF ,再过点D作DG EF ⊥,设DG =,则2GE x =,ED =,12FG x =-,在t R FGD 中,根据GD =,代入数值,即可求解.【详解】解:如图∵ 90B ∠=︒,BC =,3AB =,∴30BAC ∠=︒,∴AC =∵90DCB ∠=︒, ∴//AB CD ,∴30DCA ∠=︒,延长CD 交AE 于F , ∴ 2AF CF ==,则=1EF ,=60EFD ∠︒ ,过点D 作DG EF ⊥,设DG =,则2GE x =,ED =,∴12FG x =-,∴在t R FGD GD =)12x -, 解得:1=3x ,∴3ED =. 故选B .变式1-2.(浙江中考真题)四边形具有不稳定性,对于四条边长确定的四边形.当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD 的内角,正方形ABCD 变为菱形ABC ′D ′.若∠D ′AB =30°,则菱形ABC ′D ′的面积与正方形ABCD 的面积之比是( )A .1B .12C .2D 【答案】B 【提示】如图,连接DD ',延长C 'D '交AD 于E ,由菱形ABC 'D ',可得AB ∥C 'D ',进一步说明∠ED 'D=30°,得到菱形AE=12AD;又由正方形ABCD,得到AB=AD,即菱形的高为AB 的一半,然后分别求出菱形ABC 'D '和正方形ABCD 的面积,最后求比即可. 【详解】解:如图:延长C 'D '交AD 于E ∵菱形ABC 'D ' ∴AB ∥C 'D '∵∠D 'AB=30°∴∠A D 'E=∠D 'AB=30° ∴AE=12AD 又∵正方形ABCD∴AB=AD,即菱形的高为AB 的一半∴菱形ABC ′D ′的面积为212AB ,正方形ABCD 的面积为AB 2. ∴菱形ABC ′D ′的面积与正方形ABCD 的面积之比是12. 故答案为B .变式1-3.(四川眉山市·中考真题)如图,在菱形ABCD 中,已知4AB =,60ABC ∠=,60EAF ∠=,点E 在CB 的延长线上,点F 在DC 的延长线上,有下列结论:①BE CF =;②EAB CEF ∠=∠;③ABEEFC ∆∆;④若15BAE∠=,则点F 到BC 的距离为2-.则其中正确结论的个数是( )A .1个B .2个C .3个D .4个【答案】B 【提示】①只要证明BAE CAF ∆≅∆即可判断;②根据等边三角形的性质以及三角形外角的性质即可判断;③根据相似三角形的判定方法即可判断;④求得点F 到BC 的距离即可判断.综上即可得答案. 【详解】∵四边形ABCD 是菱形,∴AB BC =,ACB ACD ∠=∠, ∵∠ABC=60°,∴ABC ∆是等边三角形, ∴∠ACD=∠ACB=60°,AB=AC , ∴∠ABE=∠ACF=120°, ∵60BAC EAF ∠=∠=,∴∠BAE+∠BAF=∠CAF+∠BAF=60°, ∴BAE CAF ∠=∠, ∴ABE ACF ∠=∠,在BAE ∆和CAF ∆中,BAE CAF AB AC ABE ACF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()BAE CAF SAS ∆≅∆,∴AE AF =,BE CF =.故①正确; ∵60EAF ∠=, ∴AEF ∆是等边三角形, ∴60AEF ∠=,∵60AEB CEF AEB EAB ∠+∠=∠+∠=, ∴EAB CEF ∠=∠,故②正确; ∵60ACD ACB ∠=∠=, ∴60ECF ∠=, ∵60AEB ∠<,∴ABE ∆和EFC ∆不会相似,故③不正确;过点A 作AG BC ⊥于点G ,过点F 作FH EC ⊥于点H , ∵15EAB ∠=,60ABC ∠=, ∴45AEB ∠=,∵在Rt AGB ∆中,60ABC ∠=,4AB =,∴2BG =,AG =∵在Rt AEG ∆中,45AEG EAG ∠=∠=,∴AG GE ==∴2EB EG BG =-=, ∵AEB AFC ∆≅∆,∴120ABE ACF ∠=∠=,2EB CF ==, ∴60FCE ∠=,∴在Rt CHF ∆中,30CFH ∠=,2CF =,∴112CH CF ==.∴)13FH ===∴点F 到BC 的距离为3,故④不正确. 综上,正确结论有①②,共2个, 故选B .变式1-4.(四川攀枝花市·九年级一模)如图,正方形ABCD 中,E 为CD 的中点,AE 的垂直平分线分别交AD ,BC 及AB 的延长线于点F ,G ,H ,连接HE ,HC ,OD ,连接CO 并延长交AD 于点M .则下列结论中: ①FG=2AO ;②OD ∥HE ;③BH AMEC MD=;④2OE 2=AH•DE ;⑤GO+BH=HC 正确结论的个数有( )A .2B .3C .4D .5【答案】B 【提示】建立以B 点位坐标原点的平面直角坐标系,分别求出相应直线的解析式和点的坐标,求出各线段的距离,可得出结论. 【详解】 解:如图,建立以B 点为坐标原点的平面直角坐标系,设正方形边长为2,可分别得各点坐标, A(0,2),B(0,0),C(2,0),D(2,2), E 为CD 的中点,可得E 点坐标(2,1),可得AE 的直线方程,122y x =-+,由OF 为直线AE 的中垂线可得O 点为02213(,)(1,)222++=,设直线OF 的斜率为K ,得1()12k ⨯-=-,可得k=2,同时经过点O(31,2),可得OF 的直线方程:122y x =-,可得OF 与x 轴、y 轴的交点坐标G(14,0),H(0,12-),及F(54,2),同理可得:直线CO 的方程为:332y x =-+,可得M 点坐标(23,2),=,AO=1122AE =, 故FG=2AO ,故①正确;②:由O 点坐标3(1,)2,D 点坐标(2,2),可得OD 的方程:112y x =+, 由H 点坐标(0,12-),E 点坐标(2,1),可得HE 方程:3142y x =-,由两方程的斜率不相等,可得OD 不平行于HE ,故②错误;③由A(0,2),M (23,2),H(0,12-),E (2,1), 可得:BH=12,EC=1,AM=23,MD=24233-=,故BH AM EC MD ==12, 故③正确;④:由O 点坐标3(1,)2,E (2,1),H(0,12-),D(2,2), 可得:222315(12)(1)1244OE =-+-=+=,AH=15222+=,DE=1,∴有2OE 2=AH•DE ,故④正确; ⑤:由G(14,0),O 点坐标3(1,)2,H(0,12-),C(2,0),可得:GO ==,BH=12=可得:GO≠BH+HC, 故正确的有①③④, 故选B.变式1-5.(广东九年级三模)如图,在一张矩形纸片ABCD 中,4AB =,8BC =,点E ,F 分别在AD , BC 上,将纸片ABCD 沿直线EF 折叠,点C 落在AD 上的一点H 处,点D 落在点G 处,有以下四个结论:①四边形CFHE 是菱形;②EC 平分DCH ∠;③线段BF 的取值范围为34BF ≤≤;④当点H 与点A重合时,EF =以上结论中,你认为正确的有( )个.A .1B .2C .3D .4【答案】C【提示】①先判断出四边形CFHE是平行四边形,再根据翻折的性质可得CF=FH,然后根据邻边相等的平行四边形是菱形证明,判断出①正确;②根据菱形的对角线平分一组对角线可得∠BCH=∠ECH,然后求出只有∠DCE=30°时EC平分∠DCH,判断出②错误;③点H与点A重合时,设BF=x,表示出AF=FC=8-x,利用勾股定理列出方程求解得到BF的最小值,点G与点D重合时,CF=CD,求出最大值BF=4,然后写出BF的取值范围,判断出③正确;④过点F作FM⊥AD于M,求出ME,再利用勾股定理列式求解得到EF,判断出④正确.【详解】解:①∵FH与CG,EH与CF都是矩形ABCD的对边AD、BC的一部分,∴FH∥CG,EH∥CF,∴四边形CFHE是平行四边形,由翻折的性质得,CF=FH,∴四边形CFHE是菱形,(故①正确);②∴∠BCH=∠ECH,∴只有∠DCE=30°时EC平分∠DCH,(故②错误);③点H与点A重合时,此时BF最小,设BF=x,则AF=FC=8-x,在Rt△ABF中,AB2+BF2=AF2,即42+x2=(8-x)2,解得x=3,点G与点D重合时,此时BF最大,CF=CD=4,∴BF=4,∴线段BF的取值范围为3≤BF≤4,(故③正确);过点F作FM⊥AD于M,则ME=(8-3)-3=2,由勾股定理得,EF=(故④正确);综上所述,结论正确的有①③④共3个,故选C.考查题型二连接四边形中点得到新四边形,探索其性质典例2.(黑龙江双鸭山市模拟)若顺次连接四边形ABCD各边的中点所得四边形是菱形.则四边形ABCD一定是( )A.菱形B.对角线互相垂直的四边形C.矩形D.对角线相等的四边形【答案】D【提示】根据三角形的中位线定理得到EH∥FG,EF=FG,EF=12BD,要是四边形为菱形,得出EF=EH,即可得到答案.【详解】解:∵E,F,G,H分别是边AD,DC,CB,AB的中点,∴EH=12AC,EH∥AC,FG=12AC,FG∥AC,EF=12BD,∴EH∥FG,EF=FG,∴四边形EFGH是平行四边形,假设AC=BD,∵EH=12AC,EF=12BD,则EF=EH,∴平行四边形EFGH是菱形,即只有具备AC=BD即可推出四边形是菱形,故选D .变式2-1.(河北模拟)如图,AC ,BD 是四边形ABCD 的对角线,点E ,F 分别是AD ,BC 的中点,点M ,N 分别是AC ,BD 的中点,连接EM ,MF ,FN ,NE ,要使四边形EMFN 为正方形,则需添加的条件是( )A .AB CD =,AB CD ⊥ B .AB CD =,AD BC = C .AB CD =,AC BD ⊥ D .AB CD =,//AD BC【答案】A 【提示】证出EN 、NF 、FM 、ME 分别是ABD ∆、BCD ∆、ABC ∆、ACD ∆的中位线,得出////EN AB FM ,////ME CD NF ,12EN AB FM ==,12ME CD NF ==,证出四边形EMFN 为平行四边形,当AB CD =时,EN FM ME NF ===,得出平行四边形ABCD 是菱形;当AB CD ⊥时,EN ME ⊥,即90MEN ∠=︒,即可得出菱形EMFN 是正方形.【详解】点E ,F 分别是AD ,BC 的中点,点M ,N 分别是AC ,BD 的中点,EN ∴、NF 、FM 、ME 分别是ABD ∆、BCD ∆、ABC ∆、ACD ∆的中位线,////EN AB FM ∴,////ME CD NF ,12EN AB FM ==,12ME CD NF ==, ∴四边形EMFN 为平行四边形,当AB CD =时,EN FM ME NF ===,∴平行四边形ABCD 是菱形;当AB CD ⊥时,EN ME ⊥,即90MEN ∠=︒,∴菱形EMFN 是正方形;故选:A .变式2-2.(四川成都市一模)顺次连结一个平行四边形的各边中点所得四边形的形状是( )A.平行四边形B.矩形C.菱形D.正方形【答案】A【详解】试题提示:连接平行四边形的一条对角线,根据中位线定理,可得新四边形的一组对边平行且等于对角线的一半,即一组对边平行且相等.则新四边形是平行四边形.解:顺次连接平行四边形ABCD各边中点所得四边形必定是:平行四边形,理由如下:(如图)根据中位线定理可得:GF=12BD且GF∥BD,EH=12BD且EH∥BD,∴EH=FG,EH∥FG,∴四边形EFGH是平行四边形.故选A.变式2-3.(河北保定市模拟)如图,在任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是()A.当E,F,G,H是各边中点,且AC BD=时,四边形EFGH为菱形B.当E,F,G,H是各边中点,且AC BD⊥时,四边形EFGH为矩形C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形【答案】D【提示】当E,F,G,H是四边形ABCD各边中点时,连接AC、BD,如图,根据三角形的中位线定理可得四边形EFGH是平行四边形,然后根据菱形的定义和矩形的定义即可对A、B两项进行判断;画出符合题意的平行四边形EFGH,但满足E,F,G,H不是各边中点即可判断C项;画出符合题意的菱形EFGH,但满足E,F,G,H不是各边中点即可判断D项,进而可得答案.【详解】解:A.当E,F,G,H是四边形ABCD各边中点时,连接AC、BD,如图,则由三角形的中位线定理可得:EH=12BD,EH∥BD;FG=12BD,FG∥BD,所以EH=FG,EH∥FG,所以四边形EFGH是平行四边形;当AC=BD时,∵EH=12BD,EF=12AC,∴EF=EH,故四边形EFGH为菱形,故A正确;B.当E,F,G,H是四边形ABCD各边中点,且AC⊥BD时,如上图,由三角形的中位线定理可得:EH∥BD,EF∥AC,所以EH⊥EF,故平行四边形EFGH为矩形,故B正确;C.如图所示,若EF∥HG,EF=HG,则四边形EFGH为平行四边形,此时E,F,G,H不是四边形ABCD各边中点,故C正确;D.如图所示,若EF=FG=GH=HE,则四边形EFGH为菱形,此时E,F,G,H不是四边形ABCD各边中点,故D错误;故选:D.变式2-4.(广东惠州市·九年级一模)已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第2012个图形中直角三角形的个数有()A .8048个B .4024个C .2012个D .1066个 【答案】B 【解析】:第1个图形,有4个直角三角形, 第2个图形,有4个直角三角形, 第3个图形,有8个直角三角形, 第4个图形,有8个直角三角形, …,依次类推,当n 为奇数时,三角形的个数是2(n+1),当n 为偶数时,三角形的个数是2n 个, 所以,第2012个图形中直角三角形的个数是2×2012=4024. 故选B .变式2-5.(南昌市模拟)如图,四边形ABCD 中,AC =m ,BD =n ,且AC ⊥BD ,顺次连接四边形ABCD 各边中点,得到四边形A 1B 1C 1D 1,再顺次连接四边形A 1B 1C 1D 1各边中点,得到四边形A 2B 2C 2D 2……,如此进行下去,得到四边形A 5B 5C 5D 5的周长是( )A .4m n+ B .52mn C .5m n+ D .2n mn 【答案】A 【提示】根据三角形中位线定理、矩形的判定定理得到四边形A 1B 1C 1D 1是矩形,根据菱形的判定定理得到四边形A 2B 2C 2D 2是平行四边形,得到四边形A 5B 5C 5D 5为矩形,计算即可. 【详解】解:点A 1,D 1分别是AB 、AD 的中点,∴A 1D 1∥BD ,A 1D 1=12BD =12n , 同理:B 1C 1∥BD ,B 1C 1=12BD =12n ,∴A 1D 1∥B 1C 1,A 1D 1=B 1C 1, ∴四边形A 1B 1C 1D 1是平行四边形, ∵AC ⊥BD ,AC ∥A 1B 1,BD ∥A 1D 1, ∴A 1B 1⊥A 1D 1,∴四边形A 1B 1C 1D 1是矩形,其周长为2×(12m +12n )=m +n , 同理,四边形A 2B 2C 2D 2是平行四边形, ∵A 2B 2=12A 1C 1,B 2C 2=12A 1C 1, ∴A 2B 2=B 2C 2,∴四边形A 2B 2C 2D 2是菱形, 同理,A 3B 3C 3D 3为矩形,周长为2m n+, ∴矩形A 5B 5C 5D 5的周长为4m n+, 故选:A .考查题型三 利用平行四边形(特殊)的对称性求阴影面积典例3.(山东济南市一模)如图,EF 过矩形ABCD 对角线的交点O ,且分别交AB 、CD 于E 、F ,矩形ABCD 内的一个动点P 落在阴影部分的概率是( )A .B .C .D .【答案】B 【解析】试题提示:矩形的对角线将矩形分割成面积相等的四部分,如图,因为△DOF 和△EOB 是全等三角形,将△DOF 切割到△EOB 与△AOE 合并成△AOB ,刚好占了该矩形面积的,所以P 落在阴影部分的概率是.考点:矩形的性质和事件概率变式3-1.下面各图中,所有大正方形边长是4cm,所有小正方形边长是3cm.下面各图中阴影部分面积最大的是( )A.B.C.D.【答案】B【提示】大正方形的边长为4,小正方形的边长为3,根据:三角形的面积=底×高÷2,平行四边形的面积=底×高,分别求出四个选项中阴影部分的面积,然后进行比较即可.【详解】解:大正方形的边长为4,小正方形的边长为3,则:A、阴影部分的面积为:3×4=12;B、阴影部分的面积为:4×(3+4)÷2=14;C、阴影部分的面积为:3×(3+4)÷2=10.5;D、阴影部分的面积为:4×4÷2+3×3÷2=12.5;B图形的阴影面积最大.故选:B.变式3-2.(天津市一模)正方形ABCD的边长为1cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是( )cm2.A.B.C.D.【答案】B【解析】试题提示:阴影部分的面积可转化为两个三角形面积之和,根据角平分线定理,可知阴影部分两个三角形的高相等,正方形的边长已知,故只需将三角形的高求出即可,根据△DON∽△DEC可将△ODC的高求出,进而可将阴影部分两个三角形的高求出.连接AC,过点O作MN∥BC交AB于点M,交DC于点N,PQ∥CD交AD于点P,交BC于点Q∵AC为∠BAD的角平分线,∴OM=OP,OQ=ON;设OM=OP=h1,ON=OQ=h2,∵ON∥BC∴,即,解得∴OM=OP故选B.变式3-3.(襄樊市一模)如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积为()A.0.7B.0.9C.2√2−2D.√22【答案】C【解析】试题提示:如图,求出AE、BE的长度,证明△CFB1∽△BAB1,列出比例式求出CF的长度,运用三角形的面积公式即可解决问题.试题解析:如图:∵∠B=45°,AE⊥BC∴∠BAE=∠B=45°∴AE=BE由勾股定理得:BE2+AE2=22解得:BE=√2由题意得:△ABE≌△AB1E∴∠BAB1=2∠BAE=90°,BE=B1E=√2∴BB1=2√2,B1C=2√2-2∵四边形ABCD为菱形,∴∠FCB1=∠B=45°,∠CFB1=∠BAB1=90°,∴∠CB1F=45°,CF=B1F∵CF∥AB∴△CFB1∽△BAB1,∴CFAB =B1CBB1,解得:CF=2-√2∴△AEB1、△CFB1的面积分别为:12×√2×√2=1,12×(2−√2)2=3−2√2.∴△AB1E与四边形AECD重叠部分的面积=1−(3−2√2)=2√2−2.故选C.考查题型四平行四边形(特殊)动点问题典例4.(江苏南通市·中考真题)如图①,E为矩形ABCD的边AD上一点,点P从点B出发沿折线B﹣E ﹣D运动到点D停止,点Q从点B出发沿BC运动到点C停止,它们的运动速度都是1cm/s.现P,Q两点同时出发,设运动时间为x(s),△BPQ的面积为y(cm2),若y与x的对应关系如图②所示,则矩形ABCD的面积是()A.96cm2B.84cm2C.72cm2D.56cm2【答案】C【提示】过点E作EH⊥BC,由三角形面积公式求出EH=AB=6,由图2可知当x=14时,点P与点D重合,则AD=12,可得出答案.【详解】解:从函数的图象和运动的过程可以得出:当点P运动到点E时,x=10,y=30,过点E作EH⊥BC,由三角形面积公式得:y=111030 22BQ EH EH•=⨯⨯=,解得EH=AB=6,∴BH=AE=8,由图2可知当x=14时,点P与点D重合,∴ED=4,∴BC=AD=12,∴矩形的面积为12×6=72.故选:C.变式4-1.(贵州铜仁市·中考真题)如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B 开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是()A.B.C.D.【答案】D【提示】分别求出0≤x≤4、4<x<7时函数表达式,即可求解.【详解】解:由题意当0≤x≤4时,y=12×AD×AB=12×3×4=6,当4<x<7时,y=12×PD×AD=12×(7﹣x)×4=14﹣2x.故选:D.变式4-2.(江西赣州市模拟)如图,菱形ABCD的边长是4厘米,∠B=60°,动点P以1厘米/秒的速度自A点出发沿AB方向运动至B点停止,动点Q以2厘米/秒的速度自B点出发沿折线BCD运动至D点停止.若点P、Q同时出发运动了t秒,记△BPQ的面积为S厘米2,下面图象中能表示S与t之间的函数关系的是()A .B .C .D .【答案】D 【提示】应根据0≤t <2和2≤t <4两种情况进行讨论.把t 当作已知数值,就可以求出S ,从而得到函数的解析式,进一步即可求解. 【详解】当0≤t <2时,S=12(4﹣t )=2t ;当2≤t <4时,S=12×4×2×(4﹣t )= 只有选项D 的图形符合, 故选D .变式4-3.(邵阳市模拟)如图,正方形ABCD 边长为4,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 上的点,且AE =BF =CG =DH .设A 、E 两点间的距离为x ,四边形EFGH 的面积为y ,则y 与x 的函数图象可能是( )A .B .C .D .【答案】A【提示】本题考查了动点的函数图象,先判定图中的四个小直角三角形全等,再用大正方形的面积减去四个直角三角形的面积,得函数y 的表达式,结合选项的图象可得答案. 【详解】解:∵正方形ABCD 边长为4,AE =BF =CG =DH ∴AH =BE =CF =DG ,∠A =∠B =∠C =∠D ∴△AEH ≌△BFE ≌△CGF ≌△DHG ∴y =4×4﹣12x (4﹣x )×4 =16﹣8x+2x 2 =2(x ﹣2)2+8∴y 是x 的二次函数,函数的顶点坐标为(2,8),开口向上,从4个选项来看,开口向上的只有A 和B ,C 和D 图象开口向下,不符合题意; 但是B 的顶点在x 轴上,故B 不符合题意,只有A 符合题意. 故选:A .考查题型五 求四边形中线段最值问题典例5.(西藏中考真题)如图,在矩形ABCD 中,63AB AD =,=,动点P 满足13PAB ABCD S S ∆矩形=,则点P 到A B 、两点距离之和PA PB +的最小值为( )A .B .C . D【答案】A 【提示】先由13PAB ABCD S S ∆矩形=,得出动点P 在与AB 平行且与AB 的距离是2的直线l 上,作A 关于直线l 的对称点E ,连接AE BE ,,则BE 的长就是所求的最短距离.然后在直角三角形ABE 中,由勾股定理求得BE 的值,即可得到PA PB +的最小值. 【详解】设ABP ∆中AB 边上的高是h .13PAB ABCD S S ∆矩形=,1123AB h AB AD ∴⋅=⋅, 223h AD ∴==, ∴动点P 在与AB 平行且与AB 的距离是2的直线l 上,如图,作A 关于直线l 的对称点E ,连接AE BE ,,则BE 的长就是所求的最短距离, 在Rt ABE ∆中,6224AB AE +=,==,BE ∴==,即PA PB +的最小值为 故选:A .变式5-1.(浙江杭州市模拟)如图,在平行四边形ABCD 中,∠C=120°,AD=2AB=4,点H 、G 分别是边CD 、BC 上的动点.连接AH 、HG ,点E 为AH 的中点,点F 为GH 的中点,连接EF ,则EF 的最大值与最小值的差为( )A .1B 1C .2D .2【答案】C 【解析】如图,取AD 的中点M ,连接CM 、AG 、AC ,作AN ⊥BC 于N .∵四边形ABCD 是平行四边形,∠BCD=120°, ∴∠D=180°-∠BCD=60°,AB=CD=2, ∵AM=DM=DC=2, ∴△CDM 是等边三角形,∴∠DMC=∠MCD=60°,AM=MC , ∴∠MAC=∠MCA=30°, ∴∠ACD=90°,∴,在Rt △ACN 中,∵,∠ACN=∠DAC=30°,∴AN=12 ∵AE=EH ,GF=FH , ∴EF=12AG , 易知AG 的最大值为AC 的长,最小值为AN 的长,∴AG 的最大值为∴EF 2,∴EF 变式5-2.(洛阳模拟)如图,在△ABC 中,AB =3,AC =4,BC =5,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,M 为EF 中点,则AM 的最小值为 ( )A .65B .52C .53D .54【提示】先根据矩形的判定得出四边形AEPF 是矩形,再根据矩形的性质得出EF ,AP 互相平分且相等,再根据垂线段最短可以得出当⊥AP BC 时,AP 的值最小,即AM 的值最小,根据面积关系建立等式求解即可. 【详解】解:∵3AB =,4AC =,5BC =, ∴90EAF ∠=︒, ∵PE AB ⊥,PF AC ⊥, ∴四边形AEPF 是矩形, ∴EF ,AP 互相平分,且EF AP =,又∵M 为EF 与AP 的交点, ∴当AP 的值时,AM 的值就最小,而当⊥AP BC 时,AP 有最小值,即此时AM 有最小值, ∵1122AP BC AB AC =, ∴AP BC AB AC =,∵3AB =,4AC =,5BC =, ∴534AP =⨯, ∴125AP =, ∴1625AM AP ==. 故选:A .变式5-3.(辽宁铁岭市模拟)如图,在矩形ABCD 中,AB=9,BC=12,点E 是BC 中点,点F 是边CD 上的任意一点,当△AEF 的周长最小时,则DF 的长为( )A .4B .6C .8D .9【答案】B作点E关于直线CD的对称点E′,连接AE′交CD于点FAE的长度是固定的,要△AEF的周长最小,只要AF+EF最小即可,又根据三角形两边之和大于第三边可知,对CD上任意点F′,总有AF′+E′F′>AE′,所以点F是使得AF+EF最小的点.∵在矩形ABCD中,AB=9,BC=12,点E是BC中点,∴BE=CE=CE′=6,∵AB⊥BC,CD⊥BC,∴△CE′F∽△BE′A,即CE′·AB=CF·BE′,即6×9=CF·(12+6),解得CF=3,∴DF=CD-CF=9-3=6故选B。
(人教版)2023年九年级中考数学第一轮复习:四边形综合问题

(人教版)2023年九年级中考数学第一轮复习:四边形综合问题一、选择题(本大题共10小题,每小题4分,满分40分)1. (2020•菏泽)如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是( )A.互相平分B.相等C.互相垂直D.互相垂直平分2. (2020·广西河池·中考真题)如图,在▱ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )A.5B.6C.4D.53. (2020秋•海曙区月考)如图,已知Rt△ABC中,∠BAC=90°,∠C=30°,AB=6,M为边BC 上的一个动点,ME⊥AB,MF⊥AC,则EF的最小值为( )A.6B.6C.3D.34. (2020·广东广州·中考真题)如图,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为( )A.485B.325C.245D.1255. (2021绍兴)如图,菱形ABCD中,∠B=60°,点P从点B出发,沿折线BC-CD方向移动,移动到点D停止.在△ABP形状的变化过程中,依次出现的特殊三角形是( )第17题图A.直角三角形→等边三角形→等腰三角形→直角三角形B.直角三角形→等腰三角形→直角三角形→等边三角形C.直角三角形→等边三角形→直角三角形→等腰三角形D.等腰三角形→等边三角形→直角三角形→等腰三角形6. (2020•绥化)如图,在Rt△ABC中,CD为斜边AB的中线,过点D作DE⊥AC于点E,延长DE 至点F,使EF=DE,连接AF,CF,点G在线段CF上,连接EG,且∠CDE+∠EGC=180°,FG=2,GC=3.下列结论:①DEBC;②四边形DBCF 是平行四边形;③EF =EG;④BC =2.其中正确结论的个数是( )A.1个B.2个C.3个D.4个7. (2021•路北区二模)求证:直角三角形斜边上中线等于斜边的一半.已知:如图,在△ABC 中,∠ABC =90°,点O 是AC 的中点.求证:AC OB 21= 证明:延长BO 到D,使OD =OB,连接AD 、CD,中间的证明过程排乱了:①∵∠ABC =90°;②∵OD =OB,OA =OC;③∴四边形ABCD 是平行四边形;④∴四边形ABCD 是矩形.∴AC =BD,∴AC BD OB 2121==则中间证明过程正确的顺序是( ) A.①④②③ B.①③②④ C.②④①③ D.②③①④8. (2020•龙华区二模)如图,已知四边形ABCD 是边长为4的正方形,E 为CD 上一点,且DF=1,F 为射线BC 上一动点,过点E 作EG ⊥AF 于点P,交直线AB 于点G.则下列结论中:①AF=EG;②若∠BAF=∠PCF,则PC=PE;③当∠CPF=45o 时,BF=1;④PC 的最小值为-2.其中正确的有( )A.1个B.2个C.3个D.4个9. (2020•庆云县一模)如图,Rt △ABE 中,∠B=90o ,AB=BE,将△ABE 绕点A 逆时针旋转45o ,得到△AHD,过D 作DC ⊥BE 交BE 的延长线于点C,连接BH 并延长交DC 于点F,连接DE 交BF 于点O .下列结论:①DE 平分∠HDC;②DO=OE;③H 是BF 的中点;④BC-CF=2CE;⑤CD=HF,其中正确的有( )A.5个B.4个C.3个D.2个10. (2020•盐田区二模)如图,在正方形ABCD中,点M是AB上一动点,点E是CM的中点,AE 绕点E顺时针旋转90o得到EF,连接DE,DF.给出结论:①DE=EF;②∠CDF=45o;③=;④若正方形的边长为2,则点M在射线AB上运动时,CF有最小值2.其中结论正确的是( )A.①②③B.①②④C.①③④D.②③④二、填空题(本大共8小题,每小题5分,满分40分)11. (2020·内蒙古赤峰中考)一个n边形的内角和是它外角和的4倍,则n=______.12. (2020·山东烟台中考)若一个正多边形的每一个外角都是40°,则这个正多边形的内角和等于 .13. (2020•海门市一模)如图,正方形ABCD的边长为6,点M在CB延长线上,BM=2,作∠MAN=45o 交DC延长线于点N,则MN的长为________.14. (2020•娄星区一模)如图,正方形ABCD的对角线相交于点O,过点O任意作一条直线,分别交AD、BC于点E、F,若正方形的对角线长为2,则图中阴影部分的面积是__________.15. (2020·河南中考真题)如图,在边长为22ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD点G,H分别是EC,FD的中点,连接GH,则GH的长度为__________.16. (2020•温州模拟)如图,四边形ABCD,CEFG均为菱形,A F∠=∠,连结BE,EG,EG//BC,EB ⊥BC,若sin∠EGD=,菱形ABCD的周长为12,则菱形CEFG的周长为__________.17. (2020•成都模拟)如图,在矩形ABCD中,AB=9,AD=6,点O为对角线AC的中点,点E在DC 的延长线上且CE=1.5,连接OE,过点O作OF⊥OE交CB延长线于点F,连接FE并延长交AC的延长线于点G,则=______.18. (2022·北京·中国人民大学附属中学朝阳学校一模)如图1,将矩形ABCD和正方形EFGH 分别沿对角线AC和EG剪开,拼成如图2所示的平行四边形PQMN,中间空白部分的四边形KRST 是正方形.如果正方形EFGH和正方形KRST的面积分别是16和1,则矩形ABCD的面积为_______.三、解答题(本大题共6道小题,每小题6-12分)19. (6分)(2020·四川中考真题)如图,四边形ABCD为矩形,G是对角线BD的中点.连接GC 并延长至F,使CF=GC,以DC,CF为邻边作菱形DCFE,连接CE.(1)判断四边形CEDG的形状,并证明你的结论.(2)连接DF,若BC=,求DF的长.20. (6分)(2020•上虞区模拟)如图,矩形ABCD的四个顶点在正△EFG的边上,已知正△EFG 的边长为2,记矩形ABCD的面积为S,边长AB为x.求:(1)S关于x的函数表达式和自变量x的取值范围;(2)当S=时,x的值.21. (8分)(2020·北京中考真题)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.(1)求证:四边形OEFG是矩形;(2)若AD=10,EF=4,求OE和BG的长.22. (10分)(2020·四川内江中考)如图,正方形ABCD中,P是对角线AC上的一个动点(不与A、C重合),连结BP,将BP绕点B顺时针旋转90o到BQ,连结QP交BC于点E,QP延长线与边AD交于点F.(1)连结CQ,求证:AP=CQ;(2)若AP=AC,求CE:BC的值;(3)求证:PF=EQ.23. (12分)(2021•广州)如图,在菱形ABCD中,∠DAB=60°,AB=2,点E为边AB上一个动点,延长BA到点F,使AF=AE,且CF、DE相交于点G.(1)当点E运动到AB中点时,证明:四边形DFEC是平行四边形;(2)当CG=2时,求AE的长;(3)当点E从点A开始向右运动到点B时,求点G运动路径的长度.24. (12分)(2020·黑龙江齐齐哈尔·中考真题)综合与实践在线上教学中,教师和学生都学习到了新知识,掌握了许多新技能.例如教材八年级下册的数学活动﹣﹣折纸,就引起了许多同学的兴趣.在经历图形变换的过程中,进一步发展了同学们的空间观念,积累了数学活动经验.实践发现:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;再一次折叠纸片,使点A落在EF上的点N处,并使折痕经过点B,得到折痕BM,把纸片展平,连接AN,如图①.(1)折痕BM (填“是”或“不是”)线段AN的垂直平分线;请判断图中△ABN是什么特殊三角形?答: ;进一步计算出∠MNE=;(2)继续折叠纸片,使点A落在BC边上的点H处,并使折痕经过点B,得到折痕BG,把纸片展平,如图②,则∠GBN=;拓展延伸:(3)如图③,折叠矩形纸片ABCD,使点A落在BC边上的点A'处,并且折痕交BC边于点T,交AD 边于点S,把纸片展平,连接AA'交ST于点O,连接AT.求证:四边形SATA'是菱形.解决问题:(4)如图④,矩形纸片ABCD中,AB=10,AD=26,折叠纸片,使点A落在BC边上的点A'处,并且折痕交AB边于点T,交AD边于点S,把纸片展平.同学们小组讨论后,得出线段AT的长度有4,5,7,9.请写出以上4个数值中你认为正确的数值.。
中考数学第一轮复习四边形专项练习

中考数学第一轮复习四边形专项练习一、单选题1.如图,在▱ABCD中,对角线AC,BD相交于点O,若AC⊥AB,AC=6,BD=8,则AB的长为()A.10B.2√7C.5D.√72.如图,在直角坐标系xOy中,菱形ABCD的周长为16,点M是边AB的中点,⊥BCD=60°,则点M的坐标为()A.(- √3,-2)B.(- √3,-1)C.(-1,- √3)D.(- √3,2)3.如图网格中每个小正方形的边长为1,若把阴影部分剪拼成一个正方形,那么新正方形的边长是()A.√5B.√6C.√7D.√84.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若⊥CEF的周长为18,则OF的长为()A.3.2B.3.5C.3.6D.3.75.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是()A.4.8B.5C.6D.7.26.一个多边形的内角和等于1080°,这个多边形的边数为()A.6B.7C.8D.97.如图1,四边形ABCD是菱形,对角线AC,BD相交于点O,P,Q两点同时从点O 出发,以厘米/秒的速度在菱形的对角线及边上运动.P,Q的运动路线:点P为O−A−D−O,点Q为O−C−B−O.设运动的时间为x秒,P,Q间的距离为y厘米,y与x的函数关系的图象大致如图2所示,则菱形ABCD的面积为()图1 图2A.2√3cm2B.2cm2C.√3cm2D.√2cm28.如图,▱ABCD中,E,F分别是AB,CD的中点,则图中有()个平行四边形.A.7个B.8个C.9个D.10个9.顺次连接菱形四边中点得到的四边形是()A.矩形B.菱形C.正方形D.等腰梯形10.如图,在矩形ABCD中,AB=4,BC=8,点E为CD中点,P、Q为BC边上两个动点,且PQ=2,当四边形APQE周长最小时,BP的长为()A.2B.3C.4D.511.如图,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时,那么下列结论成立的是().A.线段EF的长逐渐增大B.线段EF的长逐渐减少C.线段EF的长不变D.线段EF的长不能确定12.已知等边ΔABC中,在射线BA上有一点D,连接CD,以CD为边向上作等边ΔCDE,连接BE和AE,下列结论:①AE=BD;②AE与AB的所夹锐角为60°;③当D在线段AB或BA延长线上时,总有∠BED−∠AED=2∠BDC;④∠BCD=90°时,CE2+AD2=AC2+DE2,正确的结论序号有()A.①②B.①②③C.①②④D.①②③④二、填空题13.若一个正多边形的外角与其相邻的内角之比为1:5,则该正多边形的内角和的度数为.14.一个n边形的内角和是1080°,那么n=.15.如图,在⊥ABC中,AB=AC,延长CB至点E,点D在AC边上,以CE,CD为边作▱DCEF.若⊥F=70°,则⊥A的度数为度.16.如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5 √5cm,且tan⊥EFC= 34,那么矩形ABCD的周长为cm.17.用正多边形镶嵌,设在一个顶点周围有m个正方形,n个正八边形,则m+n=.18.如图,对折矩形纸片ABCD,使AD与BC重合得到折痕EF,将纸片展平,再一次折叠,使点A落到EF上的点G处,并使折痕经过点B,交EF于点H,交AD于点M.已知AB=2,则线段HG的长度为.三、综合题19.如图,在矩形ABCD中,点O为对角线AC的中点,点E是CD上一点,连接EO并延长交AB于点F,连接AE、CF.(1)求证:ΔCOE≅ΔAOF;(2)当∠DEA=2∠CAB时,试判断四边形AECF的形状,并说明理由.20.如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H.(1)求证:HE=HG;(2)如图2,当BE=AB时,过点A作AP⊥DE于点P,连接BP,求PQ与PB的数量关系,并说明理由.21.如图,以BC为底的等腰△ABC的三个顶点都在⊙O上,过点A作AD//BC交BO的反向延长线于点D.(1)求证:AD是⊙O的切线;(2)若四边形ADBC是平行四边形,且BC=12,求⊙O的半径.22.已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,﹣3),B(4,0),反比例函数图象经过点C,直线AC交双曲线另一支于点E,连接DE,CD,设反比例函数解析式为y1= k x,直线AC解析式为y2=ax+b.(1)求反比例函数解析式;(2)当y1<y2时,求x的取值范围;(3)求⊥CDE的面积.23.已知:如图所示,在△ABC中,D是AC的中点,E是线段BC的延长线上一点,过点A作AF平行BE,交线段ED的延长线于点F,连接AE、CF .(1)求证:AF=CE;(2)若AF=CF=4,∠AFD=30°,求EF的长.24.在Rt△ABC中,∠ACB=90°点D是边AB上的一个动点,连接CD.作AE∥DC,CE∥AB,连接ED.(1)如图1,当CD⊥AB时,求证:AC=ED;(2)如图2,当D是AB的中点时,①四边形ADCE的形状是;请说明理由.②若AB=5,ED=4,则四边形ADCE的面积为.答案解析部分1.【答案】D2.【答案】B3.【答案】B4.【答案】B5.【答案】A6.【答案】C7.【答案】A8.【答案】B9.【答案】A10.【答案】C11.【答案】C12.【答案】C13.【答案】1800°14.【答案】815.【答案】4016.【答案】3617.【答案】318.【答案】2√3319.【答案】(1)证明:∵四边形ABCD是矩形∴AB//CD,∠D=90°∴∠OCE=∠OAF,∠OEC=∠OFA ∵点O是对角线AC的中点∴OC=OA在△COE和△AOF中,{∠OCE=∠OAF ∠OEC=∠OFA OC=OA∴△COE≅△AOF(AAS);(2)解:四边形AECF是菱形,理由如下:由(1)已证:△COE≅△AOF∴OE=OF,CE=AF又∵AB//CD,即CE//AF∴四边形AECF是平行四边形∵AB//CD∴∠DEA=∠BAE=∠CAB+∠CAE∵∠DEA=2∠CAB∴∠CAE=∠CAB,即OA是∠EAF的角平分线∴OA⊥EF(等腰三角形的三线合一)∴平行四边形AECF是菱形∵点E是CD上一点,∠D=90°∴∠DEA≠90°,即∠CEA≠90°∴菱形AECF不是正方形综上,四边形AECF是菱形.20.【答案】(1)证明:连接AG,并延长AG交DC的延长线于M,连接EM,∵G为BC的中点,∴BG=CG,∵四边形ABCD是矩形,∴⊥ABG=⊥DCB=90°,∴⊥ABG=⊥MCG=90°,在⊥ABG和⊥MCG中,{∠ABG=∠MCGBG=CG∠AGB=∠MGC,∴⊥ABG⊥⊥MCG(ASA),∴GA=GM,∵F为AE的中点,∴FA=FE,∴FG是⊥AEM的中位线,∴FG⊥EM,∴⊥HGE=⊥MEC,在⊥DCE和⊥MCE中,{CD=CM∠DCE=∠MCECE=CE,∴⊥DEC⊥⊥MEC(SAS),∴⊥DEC=⊥MEC,∵⊥HGE=⊥MEC,∴⊥HEG=⊥HGE,∴HE=HG(2)答:PQ =√2PB理由:过点B作BQ⊥BP交DE于Q,则⊥QBP=90°,∵AP⊥DE,四边形ABCD是矩形,∴⊥APE=⊥ABE=90°,∵⊥APO+⊥AOP+⊥BAP=180°,⊥EOB+⊥ABE+⊥BEP=180°,⊥AOP=⊥EOB,∴⊥BEQ=⊥BAP,∵⊥QBP=⊥ABE=90°,∴⊥EBQ=⊥ABP=90°﹣⊥ABQ,在⊥ABP和⊥EBQ中,{∠BAP=∠BEQAB=EB∠ABP=∠EBQ,∴⊥BEQ⊥⊥BAP(ASA),∴BQ=BP,PA=QE,∴⊥PBQ是等腰直角三角形,∴PQ =√2PB.21.【答案】(1)证明:如图,连接OA,∵ΔABC是以BC为底的等腰三角形;∴AB=AC,∴BC⊥OA,∵AD//BC,∴AD⊥OA,∵OA是⊙O的半径,∴AD是⊙O的切线(2)解:如图,设OA与BC交于E,∵四边形ADBC是平行四边形,∴AC//OD,∴∠C=∠CBO,∵AB=AC,∴∠ABC=∠C,∴∠ABC=∠CBO,∵OA⊥BC,∴BA=BO,∵AO=BO,∴ΔABO是等边三角形,∵BC=12,∴BE=12BC=6,,∴OB=BEsin60°=4√3∴⊙O的半径为4√322.【答案】(1)解:∵A(0,﹣3),B(4,0),∴AB= √32+42 =5=BC ,∴C (4,5),∵反比例函数y 1= k x图象经过点C , ∴k=4×5=20,∴反比例函数解析式为y 1= 20x(2)解:把A (0,﹣3),C (4,5)代入y 2=ax+b 得, {b =−34a +b =5 ,解得 {a =2b =−3直线AC 解析式为y 2=2x ﹣3,解 {y =2x −3y =20x 得 {x 1=4y 1=5 , {x 2=−52y 2=−8, ∴E (﹣ 52,﹣8) 当y 1<y 2时,x >4或﹣ 52<x <0 (3)解:S ⊥CDE =S ⊥ADE +S ⊥ADC = 12 ×× 5×52+ 12 ×5×4= 654 23.【答案】(1)证明: ∵D 点为 AC 的中点, ∴AD =CD ,∵AF//BE ,∴∠FAD =∠ECD ,在 △ADF 和 △CDE 中,{∠FAD =∠ECD ∠ADF =∠CDE AD =CD,∴△ADF ≌△CDE(AAS) ,∴AF =CE(2)解: ∵AF//BE ,AF =CE , ∴四边形 AFCE 为平行四边形, ∵AF =CF =4 ,∴四边形 AFCE 为菱形,∴AD ⊥EF ,EF =2FD ,∵∠AFD=30°,∴AD=12AF=2,∴FD=√AF2−AD2=√42−22=2√3,∴EF=2FD=4√3 24.【答案】(1)证明:∵AE//DC,CE//AB,∴四边形AECD是平行四边形,又∵CD⊥AB,⊥⊥ADC=90°,⊥四边形AECD是矩形,⊥AC=ED;(2)菱形;6。
多边形与平行四边形-中考数学第一轮总复习课件(全国通用)

中考数学第一轮总复习典例精讲考点聚集查漏补缺拓展提升第五单元 四边形专题5.1 多边形与平行四边形知识点多边形01平行四边形02拓展训练03【例1-1】如图所示的六边形花环是用六个全等的直角三角形拼成的,则∠ABC=____º.AC B30 1.n边形的内角和___________,外角和_____.2.n边形的对角线__________.考点聚焦(n-2)·180º360ºn(n-3)/2知识点一典例精讲多边形1.将一个矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和不可能是( ) A.360º B.540º C.720º D.900º2.若正多边形的一个外角是60º,则该正多边形的内角和为______.3.一个多边形的内角和是外角和的2倍,则这个多边形的边数为____,有____条对角线.4.用一条宽相等的足够长的纸条,打一个结,如图(1),然后轻轻拉紧,压平就可以得到如图(2)的正五边形ABCDE,其中∠BAC=____度D 720º 6 9 365.如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115º,则∠BAE的度数为______.6.如图,在五边形ABCDE中,∠A+∠B+∠E=300º,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是______.7.如图,∠A+∠B+∠C+∠D=_____º.8.如图,A,B,C,D,为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18º,则这个正多边形的边数为____.125º60º 26810知识点多边形01平行四边形02拓展训练03【例2-1】如图,在□ABCD中,点E,F分别在BC,AD上,AC与EF相交于点O,且AO=CO.(1)求证:△AOF≌△COE;(2)连接AE,CF,判断四边形AECF的形状,并说明理由.A DCBOEF考点聚焦证明四边形ABCD是平行四边形的方法(五种)边:①两组对边分别平行 ②两组对边分别相等 ③一组对边平行且相等角:④两组对角分别相等;对角线:⑤对角线互相平分.【例2-2】如图,□ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( ) A.15 B.18C.21D.24A ADCB1E O 考点聚焦平行四边形的性质(1)边:对边相等,对边平行;(2)角:对角相等;(3)对角线:对角线互相平分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学一轮复习之四边形●课堂导入大侦探福尔摩斯来平行四边形先生家作客. 见一群四边形孩子在玩耍,福尔摩斯问:“这些孩子都是你家的吗?”平行四边形先生说:“我们家哪有这么多孩子呀!都说您是神探,您能找出哪些是我们平行四边形家族的成员吗?”福尔摩斯答道:“那我试试吧!不过我有个要求,他们必须说说各自的特征”“当然可以”平行四边形先生爽快地答道.四边形1说:“我的两组对边分别平行. ”福尔摩斯判断说:“这个是. ”四边形2说:“我的两组对边分别相等. ”福尔摩斯判断说:“这个是. ”四边形3说:“我有一组对边平行且相等. ”福尔摩斯判断说:“这个是. ”四边形4说:“我的两组对边角分别相等. ”福尔摩斯判断说:“这个是. ”四边形5说:“我的对角线互相平分. ”福尔摩斯判断说:“这个是. ”四边形6说:“我有一组对边平行,另一组对边相等. ”福尔摩斯判断说:“这个不是. ”"真是名副其实的神探. ”平行四边形先生称赞道:“神探的判断完全正确,咱们回屋再叙. ”一边说一边走,二位老友径直向客厅迈去.同学们,你们还记得平行四边形有哪些性质吗?如何判定一个四边形是否为平行四边形呢?我们本节就要复习它,让我们一起来看看吧!●知识详解1-平行四边形的定义与性质平行四边形的定义:两组对边分别平行的四边形叫做平行四边形(如图) . 平行四边形ABCD 记作“ ABCD ”,读作“平行四边形ABCD ” .要点诠释:(1)平行四边形的基本元素:边、角、对角线; (2)相邻的两边为邻边,有四对;(3)相对的边为对边,有两对:AB 与CD ,AD 与CD ; (4)相邻的两角为邻角,有四对;(5)相对的角为对角,有两对:∠A 与∠C ,∠B 与∠D ; (6)对角线有两条:AC 、BD ,交点为点O .平行四边形的表示:一般按照一定的方向依次表示各顶点,如图,不能写作 ACBD ,应该写作 ABCD ,或者 ADCB .平行四边形的性质:平行四边形的对边相等,对角相等,对角线互相平分 . 平行四边形要素 性质数学语言边两组对边分别平行∵ ABCD ,∴AB ∥CD ,AD ∥BCADCBADBCO两组对边分别相等∵ ABCD,∴AB=CD,AD=BC角两组对角分别相等∵ ABCD,∴∠A=∠C,∠B=∠D对角线对角线互相平分∵ ABCD,∴OA=OC,OB=OD对称性中心对称图形,对称中心是两条对角线的交点重要的全等三角形△AOB≌△COD△AOD≌△COB△ABC≌△CDA△BCD≌△DAB需要证明平行四边形的面积:A DB CH典例精讲1【例题1】在 ABCD中,若∠BAD与∠CDA的平分线交于点E,则△AED 的形状是()A.锐角三角形B.直角三角形C.钝角三角形D.不能确定【练习1-1】如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.若∠EAF=56°,则∠B=____.【例题2】如图,在 ABCD中,AC=4 cm. 若△ACD的周长为13cm,则 ABCD的周长是()A. 26cmB. 24cmC. 20cmD. 18cm【练习2-1】如图,在 ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC 交BC边于点E,则BE等于cm.知识详解2-平行四边形的判定判定定理1:两组对边分别平行的四边形是平行四边形.判定定理2:两组对边分别相等的四边形是平行四边形. 判定定理3:一组对边平行且相等的四边形是平行四边形. 判定定理4:对角线互相平分的四边形是平行四边形.要点诠释:(1)这些判定方法是学习本章的基础,必须牢固掌握,当几种方法都能判定同一个平行四边形时,应选择较简单的方法.(2)这些判定方法既可作为判定平行四边形的依据,也可作为“画平行四边形”的依据.典例精讲2【例题1】四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是()A. OA=OC,AD∥BCB. ∠ABC=∠ADC,AD∥BCC. AB=DC,AD=BCD. ∠ABD=∠ADB,∠BAO=∠DCO【练习1-1】四边形ABCD的对角线AC与BD相交于点O,下列四组条件中,一定能判定四边形ABCD为平行四边形的是()A. AD∥BCB. OA=OC,OB=ODC. AD∥BC,AB=DCD. AC⊥BD【例题2】如图,已知 ABCD中,(1)若DE=BF,求证:四边形AFCE是平行四边形;(2)若AE、CF分别是∠DAB,∠BCD的平分线,求证:四边形AFCE 是平行四边形;【练习2-1】在 ABCD中,BE=DF. 求证:四边形AECF是平行四边形.知识详解3-矩形的性质与判定矩形的定义:有一个角是直角的平行四边形叫做矩形 .矩形的性质:(1)矩形具有平行四边形的所有性质,如对边平行且相等、对角相等、对角线互相平分等; (2)四个角都是直角; (3)对角线相等 .矩形要素性质数学语言ADCBADC BO直角三角形性质:直角三角形斜边上的中线等于斜边的一半. 矩形的判定:矩形的判定定理1:有一个角是直角的平行四边形是矩形.矩形的判定定理2:三个角是直角的四边形是矩形.矩形的判定定理3:对角线相等的平行四边形是矩形.四边形三个角是直角∵∠A =∠B =∠C =90°,∴四边ABCD 是矩形平行四边形一个角是直角∵ ABCD ,且∠A =90°∴ ABCD 是矩形对角线相等∵ ABCD ,且AC =BD , ∴ ABCD 是矩形典例精讲3【例题1】如图,在矩形ABCD 中,AB =8,BC =16,将矩形ABCD 沿EF 折叠,使点C 与点A 重合,则折痕EF 的长为 ( ) A.6B.12C.2√5D.4√5ADCBA DCB ADCB【练习1-1】如图,平面直角坐标系中有一个长方形ABCO ,C 点在x 轴上,A点在y轴上,B点坐标(8,4),将长方形沿EF折叠,使点B落到原点O处,点C落到点D处,则OF的长度是.【例题2】如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点D为斜边BC上的一个动点,过D分别作DM⊥AB于点M,作DN⊥AC于点N,连接MN,则线段MN的最小值为_______.B DMNCA【练习2-1】如图,矩形ABCD的顶点A,B,C分别落在∠MON的边OM,ON上,若OA=OC,要求只用无刻度的直尺作∠MON的平分线.小明的作法如下:连接AC,BD交于点E,作射线OE,则射线OE平分∠MON.有以下几条几何性质:①矩形的四个角都是直角,②矩形的对角线互相平分,③等腰三角形的“三线合一”.小明的作法依据是()A.①②B.①③C.②③D.①②③【例题3】如图,在平行四边形ABCD中,M、N是BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件是()A.B.MB=MO C.BD⊥AC D.∠AMB=∠CND【练习3-1】如图,顺次连接四边形ABCD各边的中点得到四边形EFGH,要使四边形EFGH为矩形,应添加的条件是()A.AB∥DC B.AC=BD C.AC⊥BD D.AB=CD知识详解4-菱形的性质与判定菱形的定义:有一组邻边相等的平行四边形叫做菱形.菱形的性质:A DCBA DCBO(1)菱形具有平行四边形的所有性质,如对边平行且相等、对角相等、对角线互相平分等;(2)四个边都相等;(3)对角线互相垂直.菱形的判定:(1)菱形的判定定理1:有一组邻边相等的平行四边形是菱形. (2)菱形的判定定理2:四个边都相等的四边形是菱形.(3)菱形的判定定理3:对角线互相垂直的平行四边形是菱形.已知需要证明图形语言数学语言四边形四个边都相等∵AB=BC=CD=DA,∴四边ABCD是菱形平行四边形一组邻边相等∵ ABCD,且AB=BC,∴ ABCD是菱形对角线垂直∵ ABCD,且AC⊥BD,∴ ABCD是菱形ADCBA DCBA DCB菱形的面积: (1) (2)典例精讲4【例题1】下列结论中,菱形具有而矩形不一定具有的是( ) A .内角和为360° B .对角线互相平分 C .对角线相等 D .对角线互相垂直【练习1-1】如图,点E 、F 分别是菱形ABCD 的边BC 、CD 上的点,且∠EAF =∠D =60°,∠FAD =45°,则∠CFE 的度数为( )A .30°B .45°C .60°D .75°ADBCH【例题2】点P是边长为1的菱形ABCD对角线AC上的一个动点,点M、N分别是AB,BC边上的中点,则MP+PN的最小值是()A.B.1C.D.2【练习2-1】如图,菱形ABCD的两个顶点B、D在反比例函数的图像上,对角线AC与BD的交点恰好是坐标原点O,已知点A(1,1),∠ABC=60°,则k的值是()A.-5 B.-4C.-3 D.-2【例题3】如图,四边形ABCD是菱形,对角线AC = 8 cm,DB = 6 cm,DH⊥AB于点H,则DH的长为()A.5 B.10C.D.【练习3-1】如图,在平面直角坐标系中,菱形OABC面积为12,点B在y轴上,点C在反比例函数的图像上,则k的值是_________.知识详解5-正方形的性质与判定正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形 .正方形的性质:(1)正方形具有平行四边形的所有性质,如对边平行且相等、对角相等、对角线互相平分等;(2)正方形具有矩形的所有性质,如对角线相等,四个角都是直角; (3)正方形具有菱形的所有性质,如对角线垂直 ,四个边都相等 .ADCB矩形菱形 正方形平行四边形正方形的判定:(1)正方形的判定定理1:有一组邻边相等的矩形是正方形 . (2)正方形的判定定理2:有一个角是直角的菱形是正方形 .已知需要证明图形语言数学语言矩形一组邻边相等∵矩形ABCD ,且AB =BC ,∴矩形ABCD 是正方形菱形一个角是直角∵菱形ABCD ,且∠A =90°,∴菱形ABCD 是正方形典例精讲5【例题1】如图,正方形ABCD 中,点P 在AC 上,PE ⊥AB ,PF ⊥BC ,垂足分别为E 、F ,若EF =3,则PD 的长为( )ADCBADCBA.1.5 B.2C.2.5 D.3【练习1-1】如图,在正方形ABCD的外侧,作等边△ABE,则∠BED为()A.15°B.35°C.45°D.55°【例题2】如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是.【练习2-1】如图,将边长为1的正方形ABCD绕点C按顺时针方向旋转到正方形FECG的位置,使得点D落在对角线CF上,EF与AD相交于点H,则HD=.(结果保留根号)知识详解●知识详解6-三角形中位线三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.中点四边形:顺次连接四边形各边中点所得的四边形,我们称之为中点四边形. 中点四边形形状的判定依据主要是三角形的中位线定理. 常见结论如下:●典例精讲6【例题1】如图,在任意四边形ABCD中,M、N、P、Q分别是AB、BC、CD、DA上的点,对于四边形MNPQ的形状,下面结论错误的是()A.当M,N,P,Q是各边中点,四边MNPQ一定为平行四边形B.当M,N,P,Q是各边中点,且∠ABC=90°时,四边形MNPQ为正方形C.当M,N,P,Q是各边中点,且AC=BD时,四边形MNPQ为菱形D.当M,N,P,Q是各边中点,且AC⊥BD时,四边形MNPQ为矩形【练习1-1】顺次连接一个四边形的各边中点,得到了一个正方形,则这个四边形可能是()A.平行四边形B.菱形C.矩形D.正方形【例题2】如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,点D为AB的中点,连接DF并延长,交AC于点E. 若AB = 8,BC = 14,则线段EF的长为___________.【练习2-1】如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC 绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF=____________.。
