数学模型第四版课后习题4—1答案
数学建模试题(带答案)四

数学建模部分课后习题解答1.在稳定的椅子问题中,如设椅子的四脚连线呈长方形,结论如何? 解:模型假设(1) 椅子四条腿一样长,椅脚与地面接触处视为一点,四脚的连线呈长方形 (2) 地面高度是连续变化的,沿任何方向都不会出现间断(没有像台阶那样的情况),即从数学角度来看,地面是连续曲面。
这个假设相当于给出了椅子能放稳的必要条件(3) 椅子在任何位置至少有三只脚同时着地。
为了保证这一点,要求对于椅脚的间距和椅腿的长度而言,地面是相对平坦的。
因为在地面上椅脚间距和椅腿长度的尺寸大小相当的范围内,如果出现深沟或凸峰(即使是连续变化的),此时三只脚是无法同时着地的。
模型建立在上述假设下,解决问题的关键在于选择合适的变量,把椅子四只脚同时着地表示出来。
首先,引入合适的变量来表示椅子位置的挪动。
生活经验告诉我们,要把椅子通过挪动放稳,通常有拖动或转动椅子两种办法,也就是数学上所说的平移与旋转变换。
然而,平移椅子后问题的条件没有发生本质变化,所以用平移的办法是不能解决问题的。
于是可尝试将椅子就地旋转,并试图在旋转过程中找到一种椅子能放稳的情形。
注意到椅脚连线呈长方形,长方形是中心对称图形,绕它的对称中心旋转180度后,椅子仍在原地。
把长方形绕它的对称中心旋转,这可以表示椅子位置的改变。
于是,旋转角度θ这一变量就表示了椅子的位置。
为此,在平面上建立直角坐标系来解决问题。
设椅脚连线为长方形ABCD,以对角线AC 所在的直线为x 轴,对称中心O 为原点,建立平面直角坐标系。
椅子绕O 点沿逆时针方向旋转角度θ后,长方形ABCD 转至A1B1C1D1的位置,这样就可以用旋转角)0(πθθ≤≤表示出椅子绕点O 旋转θ后的位置。
其次,把椅脚是否着地用数学形式表示出来。
当椅脚与地面的竖直距离为零时,椅脚就着地了,而当这个距离大于零时,椅脚不着地。
由于椅子在不同的位置是θ的函数,因此,椅脚与地面的竖直距离也是θ的函数。
由于椅子有四只脚,因而椅脚与地面的竖直距离有四个,它们都是θ的函数,而由假设(3)可知,椅子在任何位置至少有三只脚同时着地,即这四个函数对于任意的θ,其函数值至少有三个同时为0。
数学建模书本郑洲顺课后习题答案

数学建模书本郑洲顺课后习题答案第一章 课后习题6.利用1.5节药物中毒施救模型确定对于孩子及成人服用氨茶碱能引起严重中毒和致命的最小剂量。
解:假设病人服用氨茶碱的总剂量为a ,由书中已建立的模型和假设得出肠胃中的药量为:)()0(mg M x =由于肠胃中药物向血液系统的转移率与药量)(t x 成正比,比例系数0>λ,得到微分方程M x x dtdx=-=)0(,λ (1) 原模型已假设0=t 时血液中药量无药物,则0)0(=y ,)(t y 的增长速度为x λ。
由于治疗而减少的速度与)(t y 本身成正比,比例系数0>μ,所以得到方程:0)0(,=-=y y x dtdyμλ (2) 方程(1)可转换为:t Me t x λ-=)( 带入方程(2)可得:)()(t t e e M t y λμμλλ----=将01386=λ和1155.0=μ带入以上两方程,得:t Me t x 1386.0)(-=)(6)(13866.01155.0---=e e M t y t针对孩子求解,得:严重中毒时间及服用最小剂量:h t 876.7=,mg M 87.494=; 致命中毒时间及服用最小剂量:h t 876.7=,mg M 8.4694= 针对成人求解:严重中毒时间及服用最小剂量:h t 876.7=,mg M 83.945= 致命时间及服用最小剂量:h t 876.7=,mg M 74.1987= 课后习题7.对于1.5节的模型,如果采用的是体外血液透析的办法,求解药物中毒施救模型的血液用药量的变化并作图。
解:已知血液透析法是自身排除率的6倍,所以639.06==μut e t x λ-=1100)(,x 为胃肠道中的药量,1386.0=λ )(6600)(t t e e t y λμ---=1386.0,639.0,5.236)2(,1100,2,====≥-=-λλλu z e x t uz x dtdzt 解得:()2,274.112275693.01386.0≥+=--t e e t z t t 用matlab 画图:图中绿色线条代表采用体外血液透析血液中药物浓度的变化情况。
数据模型与决策习题与参考答案

《数据模型与决策》复习题及参考答案第一章绪言一、填空题1.运筹学的主要研究对象是各种有组织系统的管理问题,经营活动。
2.运筹学的核心是运用数学方法研究各种系统的优化途径及方案,为决策者提供科学决策的依据。
3.模型是一件实际事物或现实情况的代表或抽象。
4、通常对问题中变量值的限制称为约束条件,它可以表示成一个等式或不等式的集合。
5.运筹学研究和解决问题的基础是最优化技术,并强调系统整体优化功能。
运筹学研究和解决问题的效果具有连续性。
6.运筹学用系统的观点研究功能之间的关系。
7.运筹学研究和解决问题的优势是应用各学科交叉的方法,具有典型综合应用特性。
8.运筹学的发展趋势是进一步依赖于_计算机的应用和发展。
9.运筹学解决问题时首先要观察待决策问题所处的环境。
10.用运筹学分析与解决问题,是一个科学决策的过程。
11.运筹学的主要目的在于求得一个合理运用人力、物力和财力的最佳方案。
12.运筹学中所使用的模型是数学模型。
用运筹学解决问题的核心是建立数学模型,并对模型求解。
13用运筹学解决问题时,要分析,定议待决策的问题。
14.运筹学的系统特征之一是用系统的观点研究功能关系。
15.数学模型中,"s·t"表示约束。
16.建立数学模型时,需要回答的问题有性能的客观量度,可控制因素,不可控因素。
17.运筹学的主要研究对象是各种有组织系统的管理问题及经营活动。
二、单选题1.建立数学模型时,考虑可以由决策者控制的因素是〔 AA.销售数量B.销售价格C.顾客的需求D.竞争价格2.我们可以通过〔 C来验证模型最优解。
A.观察B.应用C.实验D.调查3.建立运筹学模型的过程不包括〔 A 阶段。
A.观察环境B.数据分析C.模型设计D.模型实施4.建立模型的一个基本理由是去揭晓那些重要的或有关的〔 BA数量 B变量 C 约束条件 D 目标函数5.模型中要求变量取值〔 DA可正 B可负 C非正 D非负6.运筹学研究和解决问题的效果具有〔 AA 连续性B 整体性C 阶段性D 再生性7.运筹学运用数学方法分析与解决问题,以达到系统的最优目标。
(完整版)数学模型(第四版)课后详细答案
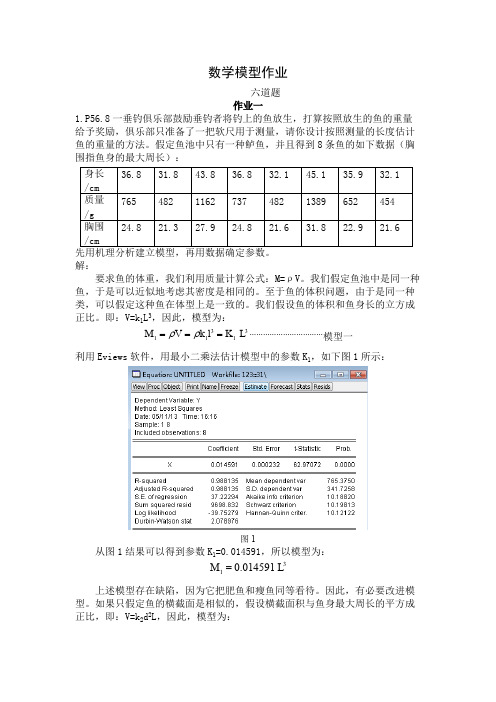
数学模型作业六道题作业一1.P56.8一垂钓俱乐部鼓励垂钓者将钓上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计鱼的重量的方法。
假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长):先用机理分析建立模型,再用数据确定参数。
解:要求鱼的体重,我们利用质量计算公式:M=ρV。
我们假定鱼池中是同一种鱼,于是可以近似地考虑其密度是相同的。
至于鱼的体积问题,由于是同一种类,可以假定这种鱼在体型上是一致的。
我们假设鱼的体积和鱼身长的立方成正比。
即:V=k 1L 3,因此,模型为:……………………………模型一33111M V k l K L ρρ===利用Eviews 软件,用最小二乘法估计模型中的参数K 1,如下图1所示:图1从图1结果可以得到参数K 1=0.014591,所以模型为:31M 0.014591 L =上述模型存在缺陷,因为它把肥鱼和瘦鱼同等看待。
因此,有必要改进模型。
如果只假定鱼的横截面是相似的,假设横截面积与鱼身最大周长的平方成正比,即:V=k 2d 2L ,因此,模型为:身长/cm 36.831.843.836.832.145.135.932.1质量/g 76548211627374821389652454胸围/cm24.821.327.924.821.631.822.921.6t h i ng sin………………………………模型二22222M V k d K d L L ρρ===利用Eviews 软件,用最小二乘法估计模型中的参数K 2,如下图2所示:图2从图2可以得到参数K 2=0. 032248,所以模型为:22M 0.032248d L=将实际数据与模型结果比较如表1所示:表1实际数据M 76548211627374821389652454模型一M 1727.165469.2141226.061727.165482.6291338.502675.108482.619模型二M 2729.877465.2481099.465729.877482.9601470.719607.106483.9602.P131.2 一家出版社准备在某市建立两个销售代理点,向7个区的大学生售书,每个区的大学生数量(单位:千人)已经表示在图上。
数学建模与数学实验课后习题答案

P594•学校共1002名学生,237人住在A 宿舍,333人住在B 宿舍,432 人住在C 宿舍。
学生要组织一个10人的委员会,使用Q 值法分配各 宿舍的委员数。
解:设P 表示人数,N 表示要分配的总席位数。
i 表示各个宿舍(分别取 A,B,C ), p i 表 示i 宿舍现有住宿人数, n i 表示i 宿舍分配到的委员席位。
首先,我们先按比例分配委员席位。
23710 A 宿舍为:n A ==2.365 1002 333"0 B 宿舍为:n B =3.323 1002 432X0 C 宿舍为:n C =4.3111002现已分完9人,剩1人用Q 值法分配。
经比较可得,最后一席位应分给 A 宿舍。
所以,总的席位分配应为: A 宿舍3个席位,B 宿舍3个席位,C 宿舍4个席位。
QA23722 3= 9361.5 Q B33323 4 = 9240.7 Q C4322 4 5=9331.2商人们怎样安全过河傻麴删舫紬削< I 11山名畝臥蹄峨颂禮训鋤嫌邂 韻靖甘讹岸讎鞍輯毗匍趾曲展 縣確牡GH 錚俩軸飙奸比臥鋪謎 smm 彌鯉械即第紘麵觎岸締熾 x^M 曲颁M 删牘HX …佛讪卜过樹蘇 卜允棘髒合 岡仇卅毘冋如;冋冋1卯;砰=口 於广歎煙船上觸人敦% V O J U;xMmm朗“…他1曲策D 咿川| thPl,2卜允隸策集合 刼為和啊母紳轉 多步贱 就匚叫=1入“山使曲并按 腿翻律由汩3』和騒側),模型求解 -穷举法〜编程上机 ■图解法S={(x ?jOI x=o, j-0,1,2,3;X =3? J =0,1,2,3; X =»*=1,2}J规格化方法,易于推广考虑4名商人各带一随从的情况状态$=(xy¥)~ 16个格点 允许状态〜U )个。
点 , 允许决策〜移动1或2格; k 奇)左下移;&偶,右上移. 右,…,必I 给出安全渡河方案评注和思考[廿rfn片,rfl12 3xmm賤縣臓由上题可求:4个商人,4个随从安全过河的方案。
数学模型第四版课后规范标准答案姜启源版

.
再由初始条件,得
又由
其解为
(1)
即乙方取胜时的剩余兵力数为
又令
注意到 .
(2) 若甲方在战斗开始后有后备部队以不变的速率 增援.则
相轨线为
此相轨线比书图11中的轨线上移了 乙方取胜的条件为
《数学模型》作业解答
第六章(2008年11月20日)
1.在6.1节捕鱼模型中,如果渔场鱼量的自然增长仍服从Logistic规律,而单位时间捕捞量为常数h.
S取最大值.
由 解得
此时 =20 =350(元)
2.某厂拟用集装箱托运甲乙两种货物,每箱的体积、重量以及可获利润如下表:
货物
体积
(立方米/箱)
重量
(百斤/箱)
利润
(百元/箱)
甲
5
2
20
乙
4
5
10
已知这两种货物托运所受限制是体积不超过24立方米,重量不超过13百斤.试问这两种货物各托运多少箱,使得所获利润最大,并求出最大利润.
A
B
C
3 2 2
3 3 3
4 5 5
4 4 3
5 5 5
6 6 7
总计
10 10 10
15 15 15
2.试用微积分方法,建立录像带记数器读数n与转过时间的数学模型.
解:设录像带记数器读数为n时,录像带转过时间为t.其模型的假设见课本.
考虑 到 时间内录像带缠绕在右轮盘上的长度,可得 两边积分,得
《数学模型》作业解答
故应改变订货策略.改变后的订货策略(周期)为T = ,能节约费用约53.33元.
《数学模型》作业解答
第四章(2008年10月28日)
《数学建模》课后习题及答案

第一部分课后习题1.学校共1000名学生,235人住在A宿舍,333人住在B宿舍,432人住在C宿舍。
学生们要组织一个10人的委员会,试用下列办法分配各宿舍的委员数:(1)按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者。
(2)2.1节中的Q值方法。
(3)d’Hondt方法:将A,B,C各宿舍的人数用正整数n=1,2,3,…相除,其商数如下表:将所得商数从大到小取前10个(10为席位数),在数字下标以横线,表中A,B,C行有横线的数分别为2,3,5,这就是3个宿舍分配的席位。
你能解释这种方法的道理吗。
如果委员会从10人增至15人,用以上3种方法再分配名额。
将3种方法两次分配的结果列表比较。
(4)你能提出其他的方法吗。
用你的方法分配上面的名额。
2.在超市购物时你注意到大包装商品比小包装商品便宜这种现象了吗。
比如洁银牙膏50g装的每支1.50元,120g装的3.00元,二者单位重量的价格比是1.2:1。
试用比例方法构造模型解释这个现象。
(1)分析商品价格C与商品重量w的关系。
价格由生产成本、包装成本和其他成本等决定,这些成本中有的与重量w成正比,有的与表面积成正比,还有与w无关的因素。
(2)给出单位重量价格c与w的关系,画出它的简图,说明w越大c越小,但是随着w 的增加c减少的程度变小。
解释实际意义是什么。
3.一垂钓俱乐部鼓励垂钓者将调上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计鱼的重量的方法。
假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长):先用机理分析建立模型,再用数据确定参数4.用宽w的布条缠绕直径d的圆形管道,要求布条不重叠,问布条与管道轴线的夹角 应多大(如图)。
若知道管道长度,需用多长布条(可考虑两端的影响)。
如果管道是其他形状呢。
5.用已知尺寸的矩形板材加工半径一定的圆盘,给出几种简便、有效的排列方法,使加工出尽可能多的圆盘。
数学模型第四版课后习题4—1答案
证券问题数学建模问题:某银行经理计划用一笔资金进行有价证劵的投资,可供购进的证劵以及其信用等级,到期年限,收益如表所示。
按照规定,市政证劵的收益可以免税,其他证劵的收益需按50%的税率纳税。
除外还有以下限制:(1)政府及代办机构的证劵总共至少要购进400万元。
(2)所购证劵的平均信用等级不超过(信用等级数字越小,信用程度越高);(3)所购证劵的平均到期年限步超过5年。
证劵名称证劵种类信用等级到期年限到期税前收益%A市政29B代办机构215C政府14D政府13E市政52(2)如果能够以%的利率借到不超过100万元资金,该经理该如何操作?(3)在1000万元资金情况下,若证劵A的税前收益增加为%。
投资应否改变?若证劵C的税前收益减少为%,投资应否改变?问题分析:这个投资方案的目标是使获取的税后收益最大化,要做好决策应是用多少钱购买多少不同的证劵。
此决策共受到四个条件的限制,资金总额必购证劵,信用等级,到期年限。
按照题目将决策变量,目标函数和约束条件用数学符号及式子表示出来得到如下模型。
基本模型:决策变量:设用x1万元购买A证劵,用x2万元购买B证劵,用x3万元购买C证劵,用x4万元购买D证劵,用x5万元购买E证劵。
目标函数:设总到期税后收益为Z万元,则由给出收益率可算出Z= x1+ x2+ x3+ x4+ x5约束条件:1.资金总额:所用投资金额不超过1000万元。
即x1+ x2+ x3+ x4+x5102.必购证劵政府及代办机构的证劵总共至少购进400万元即x2+ x3+ x443.信用等级:所购证劵的平均信用等级都不超过,即4.到期年限:所购证劵的平均到期年限步超过5年,即5.非负约束x1 x2x3x4x5为输入方便,将(3)(4)化简可得到该问题的基本模型Max Z= x1+ x2+ x3+ x4+ x5(1)x 1 +x2+ x3+ x4+x510(2)x 2+ x3+ x44(3)6x1+ 6x2-4x3-4x4+36x510(4)4x1+10 x2- x3-2x4-3x510(5)x 1x2x3x4 x5模型求解:用LINGO软件求解输入:model:max= *x1+* x2+* x3+* x4+* x5;[money] x1+ x2+ x3+ x4+x510;[must] x2+ x3+ x44;[credit] 6*x1+ 6*x2-4*x3-4*x4+36*x50;[time] 4*x1+10*x2-x3-2*x4-3*x50 ;end得到如下输出:Global optimal solution found.Objective value:Infeasibilities:Total solver iterations: 5Variable Value Reduced CostX1X2X3X4X5Row Slack or Surplus Dual Price1MONEYMUSTCREDITTIMERanges in which the basis is unchanged:Objective Coefficient RangesCurrent Allowable Allowable Variable Coefficient Increase Decrease X1X2 INFINITYX3X4 INFINITYX5Righthand Side RangesRow Current Allowable Allowable RHS Increase Decrease MONEY INFINITYMUST INFINITYCREDITTIME最优解为x1=,x2=0,x3=,x4=,x5=0;最优值为Z=;即证劵A,C,E分别投资百万元,百万元,百万元,最大税后收益为百万元。
笔记-数学模型(第四版) 姜启源等编

dx kx 当 t 0 得微分方程: dt x(0) x0
解微分方程
dx kdt x 1 x dx kdt ln( x) kt c1 x ce kt , c x0 x x0 e kt
dm dm 由死亡率的定义可得: dr ( r , t ), (r , t )dr m m
解得
( r ,t ) dr m( ) ln(m) | (r , t )dr , e m( )
t 时刻年龄为 的人的存活时间之和为: h( ) 所以时刻 t 年龄为 的人的期望寿命为:
P174 习题 4 1.设 x(t ), y (t ) 分别为 t 时刻甲乙双方的兵力,满足下列微分方程
x ay , (1) y bx, (2) x ( 0) x 0 , y ( 0) y 0 a 4, x 0 y 0 则当乙方取胜时,乙方的剩余兵力是多少?战斗时间 b 是多少? (2) 若甲方在战斗开始后,有后备兵力以不变的速率 r 增援,试重新建立模 型, 讨论如何判断双方的胜负
0
( r , t ) dr
0
d
解:
设 t 时刻年龄为 的人的数目随时间变化的规律为: m m( r ), r 0
dm dm 由死亡率的定义可得: dr ( r , t ), (r , t )dr m m
解得
( r ,t ) dr m( ) ln(m) | (r , t )dr , e 0 0 m(0)
2.试推导 logistic 人口增长模型.即设时刻 t 的人口为 x(t ) ,单位时间内人口的 增量与 x(1
数据模型与决策习题与参考答案

《数据模型与决策》复习题及参考答案第一章绪言一、填空题1.运筹学的主要研究对象是各种有组织系统的管理问题,经营活动。
2.运筹学的核心是运用数学方法研究各种系统的优化途径及方案,为决策者提供科学决策的依据。
3.模型是一件实际事物或现实情况的代表或抽象。
4、通常对问题中变量值的限制称为约束条件,它可以表示成一个等式或不等式的集合。
5.运筹学研究和解决问题的基础是最优化技术,并强调系统整体优化功能。
运筹学研究和解决问题的效果具有连续性。
6.运筹学用系统的观点研究功能之间的关系。
7.运筹学研究和解决问题的优势是应用各学科交叉的方法,具有典型综合应用特性。
8.运筹学的发展趋势是进一步依赖于_计算机的应用和发展。
9.运筹学解决问题时首先要观察待决策问题所处的环境。
10.用运筹学分析与解决问题,是一个科学决策的过程。
11.运筹学的主要目的在于求得一个合理运用人力、物力和财力的最佳方案。
12.运筹学中所使用的模型是数学模型。
用运筹学解决问题的核心是建立数学模型,并对模型求解。
13用运筹学解决问题时,要分析,定议待决策的问题。
14.运筹学的系统特征之一是用系统的观点研究功能关系。
15.数学模型中,"s·t"表示约束。
16.建立数学模型时,需要回答的问题有性能的客观量度,可控制因素,不可控因素。
17.运筹学的主要研究对象是各种有组织系统的管理问题及经营活动。
二、单选题1.建立数学模型时,考虑可以由决策者控制的因素是〔 AA.销售数量B.销售价格C.顾客的需求D.竞争价格2.我们可以通过〔 C来验证模型最优解。
A.观察B.应用C.实验D.调查3.建立运筹学模型的过程不包括〔 A 阶段。
A.观察环境B.数据分析C.模型设计D.模型实施4.建立模型的一个基本理由是去揭晓那些重要的或有关的〔 BA数量 B变量 C 约束条件 D 目标函数5.模型中要求变量取值〔 DA可正 B可负 C非正 D非负6.运筹学研究和解决问题的效果具有〔 AA 连续性B 整体性C 阶段性D 再生性7.运筹学运用数学方法分析与解决问题,以达到系统的最优目标。
高等数学教材四答案完整版

高等数学教材四答案完整版第一章:极限与连续1.1 极限的概念与性质1.1.1 数列极限的定义与性质对于数列$a_n$,当$n$趋向于无穷时,如果存在实数$a$,使得对于任意给定的正数$\varepsilon$,总存在正整数$N$,使得当$n>N$时,$|a_n-a|<\varepsilon$成立,那么我们称$a$为数列$a_n$的极限,记作$\lim_{n\to\infty} a_n=a$。
1.1.2 函数极限的定义与性质对于函数$f(x)$,当$x$趋向于$c$时,如果存在实数$L$,使得对于任意给定的正数$\varepsilon$,总存在正数$\delta$,使得当$0<|x-c|<\delta$时,$|f(x)-L|<\varepsilon$成立,那么我们称$L$为函数$f(x)$的极限,记作$\lim_{x\to c}f(x)=L$。
1.2 基本极限公式与极限计算1.2.1 三角函数极限1) $\lim_{x\to 0}\frac{\sin x}{x}=1$2) $\lim_{x\to 0}\frac{1-\cos x}{x}=0$3) $\lim_{x\to 0}\frac{\tan x}{x}=1$4) $\lim_{x\to 0}\frac{a^x-1}{x}=\ln a$,其中$a>0$1.2.2 自然对数的底$\lim_{x\to \infty}(1+\frac{1}{x})^x=e$1.2.3 无穷小与无穷大1) 当$x$趋向于$0$时,$x^n$与$x$同阶无穷小。
2) 当$x$趋向于无穷时,$a^x$与$x^n$同阶无穷大($a>1$,$n$为正整数)。
3) 当$x$趋向于无穷时,$a^x$与$b^x$同阶无穷大($a>1,b>1$)。
第二章:一元函数微分学2.1 导数的概念与性质2.1.1 导数的定义导数是描述函数变化率的概念。
(完整版)数学建模复习内容带习题答案

考试内容分布:1、线性规划2题,有1题需编程;2、非线性规划2题,有1题需编程;3、微分方程1题,需编程;4、差分方程2题,纯计算,不需编程;5、插值2题,拟合1题,纯计算,不需编程;;6、综合1题(4分),纯计算,不需编程。
一、列出下面线性规划问题的求解模型,并给出matlab计算环境下的程序1.某车间有甲、已两台机床,可用于加工三种工件,假定这两台车床的可用台时数分别为800和900,三种工件的数量分别为400,600和500,且已知用两种不同车床加工单位数量不同工件所需的台时数和加工费用如下表。
问怎样分配车床的加工任务,才能即满足加工工件的要求,又使加工费用最低。
(答案见课本P35, 例1)2.有两个煤厂A,B,每月进煤分别不少于60t、100t,它们负责供应三个居民区的用煤任务,这三个居民区每月需用煤分别为45t, 75t, 40t。
A厂离这三个居民区分别为10km, 5km, 6km,B厂离这三个居民区分别为4km, 8km, 15km,问这两煤厂如何分配供煤,才能使总运输量最小?(1)问题分析设A煤场向这三个居民区供煤分别为x1,x2,x3;B煤场向这三个居民区供煤分别为x4,x5,x6,则min f=10*x1+5*x2+6*x3+4*x4+8*x5+15*x6,再根据题目约束条件来进行解题。
(2) 模型的求解>> f=[10 5 6 4 8 15];>> A=[-1 -1 -1 0 0 00 0 0 -1 -1 -1-1 0 0 -1 0 00 -1 0 0 -1 00 0 -1 0 0 -1];>> b=[-60;-100;-45;-75;-40];>> Aeq=[];>> beq=[];>> vlb=zeros(6,1);>> vub=[];>> [x,fval]=linprog(f,A,b,Aeq,beq,vlb,vub)Optimization terminated.(3)结果分析x =0.0000 20.0000 40.0000 45.0000 55.0000 0.0000fval = 960.0000即A 煤场分别向三个居民区供煤0t,20t,40t ;B 煤场分别向三个居民区供煤45t,55t,0t 可在满足条件下使得总运输量最小。
大学数学第四册详细答案汇总

第四章 样本及其分布练习4.1 简单随机样本一、填空题(略) 二、解:)1061051039492(51++++=x =100, 412=S [(92–100)2+(94–100)2+(103–100)2+(105–100)2+(106–100)2]=42.6三、解:利用y i =100(x i –80),得变换后样本数据:–2, 4, 2, 4, 3, 3, 4, -3, 5, 3, 2, 0, 2这时,有131=x [(–2+4+2+4+3+3+4–3+5+3+2+2)1001+80×13]=80.02 1212=S [(42+4+0+4+1+1+4+25+9+1+0+4+0)/10000]=5.75×10-4四、解:∵ E (X i )=p ,D (X i )=p (1-p ),)(11)(11122212∑∑==--=--=ni i i n i X n X n X X n S , ∴p p n n X E n X n E X E i n i n i i =⋅===∑∑==1)(1)1()(11;)1(1)1(1)(1)1()(2121p p n p np n X D n X n D X D i n i n i i -=-⋅===∑∑==;)]()([1)(1)(11)(222212X E X E n n X E n n X E n S E in i --=---=∑= =)]()([1]}))(()([)]([)({122X D X D n n X E X D X E X D n n --=+-+- =)1()()(11)](1)([1p p X D X D nn n n X D n X D n n -==-⋅-=--。
五、解:∵ E (X i )=λ, D (X i )=λ, )(111222∑=--=ni i X n X n S ,∴ λλ=⋅==∑=n n X E n X E i n i 1)(1)(1;n n nX D n X D i n i λλ=⋅==∑=2121)(1)(;)]()([1)(1)(11)(222212X E X E n n X E n n X E n S E in i --=---=∑= =λλλ=-⋅-=--)(1)]()([1nn n X D X D n n 。
数学建模习题及答案

5.设圆盘半径为单位1,矩形板材长a,宽b;可以精确加工,即圆盘之间及圆盘与板材之间均可相切。
若 ,则 , 是平衡点; 的平衡点为 . 的平衡点为 ,其中 ,此时的差分方程变为
.
由 可得平衡点 .
在平衡点 处,由于 ,因此, 不稳定.
在在平衡点 处,因 ,所以
(i) 当 时,平衡点 不稳定;
(ii) 当 时,平衡点 不稳定.
第
1.判断下列数学模型是否为线性规划模型。(a,b,c为常数,x,y为变量)
(4)你能提出其他的方法吗。用你的方法分配上面的名额。
2.在超市购物时你注意到大包装商品比小包装商品便宜这种现象了吗。比如洁银牙膏50g装的每支1.50元,120g装的3.00元,二者单位重量的价格比是1.2:1。试用比例方法构造模型解释这个现象。
(1)分析商品价格C与商品重量w的关系。价格由生产成本、包装成本和其他成本等决定,这些成本中有的与重量w成正比,有的与表面积成正比,还有与w无关的因素。
(2)单位重量价格 ,其简图如下:
显然c是w的减函数,说明大包装比小包装的商品便宜,;曲线是下凸的,说明单价的减少值随着包装的变大是逐渐降低的,不要追求太大包装的商品。
3.对于同一种鱼不妨认为其整体形状是相似的,密度也大体上相同,所以重量w与身长 的立方成正比,即 , 为比例系数。
常钓得较肥的鱼的垂钓者不一定认可上述模型,因为它对肥鱼和瘦鱼同等看待。如果只假定鱼的横截面积是相似的,则横截面积与鱼身最大周长的平方成正比,于是 , 为比例系数。
蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答(第4章 线性模型与矩阵代数)【圣才出

4 30
CB 也有定义:
CB
7 6
2 2
2 3
3 3
7 6
0 0
2 8 3 8
20
21
16 24
BC=CB 不成立。
3.在例 9 给出的矩阵的基础上,判断 BA 是否有定义?若有,计算其积。在此例中,我们 是否有 AB=BA?
4 / 27
圣才电子书
1 4
1 2
5.在例 7 中,如果我们将数量和价格写成列向量而非行向量,Q·P 有定义吗?我们能否将 总采购成本表示为 Q·P?或 Q′·P?或 Q·P′? 答:Q·P 有定义。两个元素个数相同的向量的内积是对应元素的积的和,两个行向量、两个 列向量、一个行向量和一个列向量、一个列向量和一个行向量的内积均有定义。所以能将采 购成本表示为 Q·P 或 Q′·P 或 Q·P′。
1 / 27
圣才电子书 十万种考研考证电子书、题库视频学习平台
Qd1 Qs1 Qd1
Qs1
0
a1P1 a2 P2 a0
b1P1 b2 P2 b0
Qd 2 Qs2
0
Qd 2
1P1 2 P2 0
Qs2 1P1 2 P2 0
则系数矩阵为
1 1 0 0 0 0
Qd-Qs=0
Qd+bP=a
Qs-dP=-c
1 1 0
0
1 0
b
a
如果系数矩阵为 0 1 d ,则常数向量为 c 。
2.变量按下列顺序排列:Qd1,Qs1,Qd2,Qs2,P1,P2。按(4.1)方式改写方程组(3.12)。 写出系数矩阵、变量向量和常数向量。 解:将方程组(3.12)改写为:
,常数向量为
数学模型(第四版)课后详细答案

数学模型作业六道题 作业一1. P56.8 —垂钓俱乐部鼓励垂钓者将钓上的鱼放生,打算按照放生的鱼的重量 给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计 鱼的重量的方法。
假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长):先用机理分析建立模型,再用数据确定参数 解:要求鱼的体重,我们利用质量计算公式: M=p V 。
我们假定鱼池中是同一种 鱼,于是可以近似地考虑其密度是相同的。
至于鱼的体积问题,由于是同一种 类,可以假定这种鱼在体型上是一致的。
我们假设鱼的体积和鱼身长的立方成 正比。
即:V=k i L 3,因此,模型为:利用Eviews 软件,用最小二乘法估计模型中的参数 K i ,如下图1所示:□ Equition: UNKTLED Workfile; 123::31\*1 諭][Pror][口bject] [Print][Mame|[Frea«]旦tinatdForecast]甌:Dependent Variable: Y Method: I east SquaresDate-05/11/13 Trne;16;16Samplv; 1 8Included ob5e[v<itcins;8Coefficient Std Errort-StatisticProb.X0.014591 0.0C0232 62.9T 072 O.QOOOR-squanedAd listed R-squared S-E. of rearession Sum squared residLog IlkfilihODd DurtJin-Wats^n stat0.988135 0.988135 37r 22294 9698.B32 -39.75279 2.076976Mean dependert var S.D. dependentvar Akaike info criteionSchwarz criterion Hannan-Quinn triter765.3750 341.7258 10.18820 101S313 10.12122图1从图1结果可以得到参数K=0.014591,所以模型为:上述模型存在缺陷,因为它把肥鱼和瘦鱼同等看待。
中国人民大学出版社(第四版)高等数学一第1章课后习题详解

中国⼈民⼤学出版社(第四版)⾼等数学⼀第1章课后习题详解第⼀章函数、极限与连续内容概要课后习题全解习题1-1★1.求下列函数的定义域:思路:常见的表达式有① a log □,(□0>)② /N □, (□0≠)③(0)≥④ arcsin[]1,1-∈)等解:(1)[)(]1,00,11100101122-∈≤≤-≠≥-≠?--=x x x x x x x y ;(2)31121121arcsin≤≤-?≤-≤-?-=x x x y ;(3)()()3,00,030031arctan 3?∞-∈??≠≤≠≥-?+-=x x x x x x x y ;(4)()()3,11,1,,1310301lg 3?-∞-∈-<<-<--x x or x x x x x y x;(5)()()4,22,11601110)16(log 221?∈-<-≠-(1)2lg )(x x f =与x x g lg 2)(=;(2)12+=x y 与12+=y x知识点:函数相等的条件;思路:函数的两个要素是f (作⽤法则)及定义域D (作⽤范围),当两个函数作⽤法则f 相同(化简后代数表达式相同)且定义域相同时,两函数相同;解:(1)2lg )(x x f =的定义域D={}R x x x ∈≠,0,x x g lg )(=的定义域{},0R x x x D ∈>=,虽然作⽤法则相同x x lg 2lg 2=,但显然两者定义域不同,故不是同⼀函数;12+=x y ,以x 为⾃变量,显然定义域为实数R ;12+=y x ,以x 为⾃变量,显然定义域也为实数R ;两者作⽤法则相同“2□1+”与⾃变量⽤何记号表⽰⽆关,故两者为同⼀函数;★ 3.设≥<=3,03,sin )(ππ?x x x x ,求)2()4()4()6(--?ππ?π,,,,并做出函数)(x y ?=的图形思路:注意⾃变量的不同范围;解:216sin)6(==ππ?,224sin 4==??ππ?,224sin 4=-=? -ππ?()02=-?;如图:★ 4.试证下列各函数在指定区间内的单调性:(1)xxy (2)x x y ln 2+=,()+∞,0 知识点:单调性定义。
2021-11第4版姜启源数学模型复习总结(1)

2021-11第4版姜启源数学模型复习总结(1) 第四版姜启源数学模型复习总结第1章:了解模型的概念与分类,熟练掌握数学模型的定义,数学模型的重要应用,建模的重要例子-指数模型,Logist模型。
建模的一般方法及其在建模中的应用。
建模的一般步骤(每步的主要内容与问题)。
建模的全过程(框图)4个环节的含义。
模型的特点(技艺性)。
模型分类(表现特征),建模中的能力培养。
数学建模实例的建模思想及其步骤§1 数学模型的概念:模型:模型是为了一定目的,对客观事物的一部分信息进行简缩、抽象、提炼出来的原型的替代物。
模型的分类:具体模型(或物质模型,实的),包括直观模型,物理模型。
抽象模型(或理想模型,虚的),包括思维模型,符号模型,数学模型。
数学模型:对于一个现实对象,为了一个特定目的,根据其内在规律,作出必要的简化假设,运用适当的数学工具,得到的一个数学结构。
1-1-1 模型是为了特定的目的,将原型的()而得到的原型替代物。
1-1-2数学模型可以描述为:对于一个现实对象,()。
1-1-3 关于数学模型的如下论述中正确的是() A。
数学模型是以现实世界的特定问题为研究对象。
B。
数学模型只是对实际问题的近似表示,其中包含一些简化假设。
C。
数学模型表示是某一特定问题的内在规律的数学表示,是以方程和函数关系表示的数学结构。
D。
数学模型是现实问题的真实的描述,不能做任何假设和简化。
1-1-4 关于数学建模的如下论述中正确的是() A。
数学模型和数学建模是完全相同的概念。
B。
数学建模是一个全过程,包括表述、求解、解释和验证四个环节。
C。
数学建模全过程涉及两个世界是现实世界和虚拟世界,涉及的“双向翻译”是同声翻译和文献翻译。
D.数学建模过程是一个从理论-实践-再理论-再实践不断改进的过程。
§2 建模的重要意义(1)数学以空前的广度和深度向一切领域渗透在一般工程技术领域数学建模仍然大有用武之地;在高新技术领域数学建模几乎是必不可少的工具了; 数学进入一些新领域,为数学建模开辟了许多处女地. 数学建模的具体应用:分析与设计,预测与决策,优化与控制,规划与管理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
问题:
某银行经理计划用一笔资金进行有价证劵的投资,可供购进的证劵以及其信用等级,到期年限,收益如表所示。按照规定,市政证劵的收益可以免税,其他证劵的收益需按50%的税率纳税。除外还有以下限制:
(1)政府及代办机构的证劵总共至少要购进400万元。
(2)所购证劵的平均信用等级不超过1.4(信用等级数字越小,信用程度越高);
Infeasibilities: 0.000000
Total solver iterations: 5
Variable ValueReduced Cost
X12.400000 0.000000
X20.0000000.3181818E-02
X38.100000 0.000000
X40.0000000.6363636E-03
(3)所购证劵的平均到期年限步超过5年。
A
市政
2
9
4.3
B
代办机构
2
15
5.4
C
政府
1
4
5.0
D
政府
1
3
4.4
E
市政
5
2
4.5
(1)若该经理有1000万元资金,应如何投资?
(2)如果能够以2.75%的利率借到不超过100万元资金,该经理该如何操作?
(3)在1000万元资金情况下,若证劵A的税前收益增加为4.5%。投资应否改变?若证劵C的税前收益减少为4.8%,投资应否改变?
CREDIT 0.0105.7143 20.00000
TIME 0.010.00000 12.00000
最优解为x1=2.182,x2=0,x3=7.364,x4=0.454,x5=0;最优值为Z=0.298;
即证劵A,C,E分别投资2.182百万元,7.364百万元,0.454百万元,最大税后收益为0.298百万元。
即x2+ x3+ x4 4
3.信用等级:所购证劵的平均信用等级都不超过1.4,即
4.到期年限:所购证劵的平均到期年限步超过5年,即
5.非负约束x1 x2 x3 x4 x5
为输入方便,将(3)(4)化简可得到该问题的基本模型
Max Z=0.043 x1+0.054 x2+0.025 x3+0.022 x4+0.045 x5(1)
X40.0000000.6363636E-03
X50.4545455 0.000000
RowSlack or SurplusDual Price
10.2983636 1.000000
MONEY0.0000000.2983636E-01
MUST3.3636360.000000
CREDIT0.0000000.6181818E-03
目标函数:设总到期税后收益为Z万元,则由给出收益率可算出
Z=0.043 x1+0.054 x2+0.025 x3+0.022 x4+0.045 x5
约束条件:1.资金总额:所用投资金额不超过1000万元。
即x1+ x2+ x3+ x4+x5 10
2.必购证劵政府及代办机构的证劵总共至少购进400万元
X10.4300000E-010.3500000E-02 0.1300000E-01
X2 0.2700000E-010.3018182E-01 INFINITY
X3 0.2500000E-010.1733333E-01 0.5600000E-03
X4 0.2200000E-010.6363636E-03 INFINITY
X5 0.4500000E-010.5200000E-01 0.1400000E-01
Righthand Side Ranges
Row Current Allowable Allowable
RHSIncrease Decrease
MONEY 10.00000 INFINITY 4.567901
MUST4.000000 3.363636 INFINITY
X50.5000000 0.000000
RowSlack or Surplus Dual Price
[money]x1+ x2+ x3+ x4+x5 10;
[must]x2+ x3+ x4 4;
[credit]6*x1+ 6*x2-4*x3-4*x4+36*x5 0;
[time]4*x1+10*x2-x3-2*x4-3*x5 0 ;
end
得到如下输出:
Global optimal solution found.
TIME0.0000000.2363636E-02
Ranges in which the basis is unchanged:
Objective Coefficient Ranges
Current Allowable Allowable
Variable Coefficient Increase Decrease
x1+x2+ x3+ x4+x5 10(2)
x2+ x3+ x4 4(3)
6x1+ 6x2-4x3-4x4+36x5 10(4)
4x1+10 x2- x3-2x4-3x5 10(5)
x1 x2 x3 x4 x5
模型求解:用LINGO软件求解
输入:
model:
max=0.043 *x1+0.027* x2+0.025* x3+0.022* x4+0.045* x5;
Objective value: 0.2983636
Infeasibilities: 0.000000
Total solver iterations:5
Variable ValueReduced Cost
X12.181818 0.000000
X20.0000000.3181818E-02
X37.363636 0.000000
结果分析:
(1)由于输出结果中的影子价格可知资金每增加100万元,多获收益0.0298百万元。收差率为2.98%大于2.75%所以应进行投资,在上面约束条件的(2)右端约束改为小于11,lingo求解结果如下:
Global optimal solution found.
Objective value: 0.3282000
问题分析:这个投资方案的目标是使获取的税后收益最大化,要做好决策应是用多少钱购买多少不同的证劵。此决策共受到四个条件的限制,资金总额必购证劵,信用等级,到期年限。按照题目将决策变量,目标函数和约束条件用数学符号及式子表示出来得到如下模型。
基本模型:
决策变量:设用x1万元购买A证劵,用x2万元购买B证劵,用x3万元购买C证劵,用x4万元购买D证劵,用x5万元购买E证劵。
