初中数学知识总结大全 第十四章 尺规作图 (编辑:靳军强)
最新北师大版数学(七年级下册)章知识点总结及尺规作图

最新北师⼤版数学(七年级下册)章知识点总结及尺规作图北师⼤版《数学》(七年级下册)知识点总结第⼀章整式的运算⼀、单项式、单项式的次数:只含有数字与字母的积的代数式叫做单项式。
单独的⼀个数或⼀个字母也是单项式。
⼀个单项式中,所有字母的指数的和叫做这个单项式的次数。
⼆、多项式1、多项式、多项式的次数、项⼏个单项式的和叫做多项式。
其中每个单项式叫做这个多项式的项。
多项式中不含字母的项叫做常数项。
多项式中次数最⾼的项的次数,叫做这个多项式的次数。
三、整式:单项式和多项式统称为整式。
四、整式的加减法:整式加减法的⼀般步骤:(1)去括号;(2)合并同类项。
五、幂的运算性质:(1)同底数幂的乘法:a m ﹒a n =a m+n (同底,幂乘,指加)逆⽤: a m+n =a m ﹒a n (指加,幂乘,同底)(2)同底数幂的除法:a m ÷a n =a m-n (a ≠0)。
(同底,幂除,指减)逆⽤:a m-n = a m ÷a n (a ≠0)(指减,幂除,同底)(3)幂的乘⽅:(a m )n =a mn (底数不变,指数相乘)逆⽤:a mn =(a m )n(4)积的乘⽅:(ab )n =a n b n 推⼴:逆⽤, a n b n =(ab )n (当ab=1或-1时常逆⽤)(5)零指数幂:a 0=1(注意考底数范围a ≠0)。
(6)负指数幂:11()(0)pppa aa a-==≠(底倒,指反)六、整式的乘除法:1、单项式乘以单项式:法则:单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余的字母连同它的指数不变,作为积的因式。
2、单项式乘以多项式:m(a+b+c)=ma+mb+mc 。
法则:单项式与多项式相乘,就是根据分配律⽤单项式去乘多项式的每⼀项,再把所得的积相加。
3、多项式乘以多项式:(m+n)(a+b)=ma+mb+na+nb 。
多项式与多项式相乘,先⽤⼀个多项式的每⼀项乘另⼀个多项式的每⼀项,再把所得的积相加。
尺规作图篇(解析版)--中考数学必考考点总结+题型专训

专题13尺规作图知识回顾1.尺规作图是指用没有刻度的直尺和圆规作图.只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.2.基本要求它使用的直尺和圆规带有想像性质,跟现实中的并非完全相同.①直尺必须没有刻度,无限长,且只能使用直尺的固定一侧.只可以用它来将两个点连在一起,不可以在上画刻度.②圆规可以开至无限宽,但上面亦不能有刻度.它只可以拉开成你之前构造过的长度3.基本作图有:(1)作一条线段等于已知线段.(2)作一个角等于已知角.(3)作已知线段的垂直平分线.具体步骤:①以线段两个端点为圆心,大于线段长度的一半为半径画圆弧,两圆弧在线段的两侧别分交于M、N。
如图①②连接MN,过MN的直线即为线段的垂直平分线。
如图②(4)作已知角的角平分线.具体步骤:①以角的顶点O为圆心,一定长度为半径画圆弧,圆弧与角的两边分别交于两点M、N。
如图①。
②分别以点M与点N为圆心,大于MN长度的一半为半径画圆弧,两圆弧交于点P。
如图②。
即为角的平分线。
③连接OP,OP4.复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作。
5.设计作图:应用与设计作图主要把简单作图放入实际问题中.首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图。
专题练习1.尺规作图(保留作图痕迹,不要求写出作法):如图,已知线段m,n.求作△ABC,使∠A=90°,AB=m,BC=n.【分析】先在直线l上取点A,过A点作AD⊥l,再在直线l上截取AB=m,然后以B点为圆心,n为半径画弧交AD于C,则△ABC满足条件.【解答】解:如图,△ABC为所作.2.如图,在△ABC中,AB=AC,BD是△ABC的角平分线.(1)作∠ACB的角平分线,交AB于点E(尺规作图,不写作法,保留作图痕迹);(2)求证:AD=AE.【分析】(1)按照角平分线的作图步骤作图即可.(2)证明△ACE≌△ABD,即可得出AD=AE.【解答】(1)解:如图所示.(2)证明:∵AB=AC,∴∠ABC=∠ACB,∵BD是∠ABC的角平分线,CE是∠ABC的角平分线,∴∠ABD=∠ACE,∵AB=AC,∠A=∠A,∴△ACE≌△ABD(ASA),∴AD=AE.3.如图,已知线段AC和线段a.(1)用直尺和圆规按下列要求作图.(请保留作图痕迹,并标明相应的字母,不写作法)①作线段AC的垂直平分线l,交线段AC于点O;②以线段AC为对角线,作矩形ABCD,使得AB=a,并且点B在线段AC的上方.(2)当AC=4,a=21ABCD的面积.【分析】(1)①按照线段垂直平分线的作图步骤作图即可.②以点O为圆心,OA的长为半径画弧,再以点A为圆心,线段a的长为半径画弧,两弧在线段AC上方交于点B,同理,以点O为圆心,OC的长为半径画弧,再以点C为圆心,线段a的长为半径画弧,两弧在线段AC下方交于点D,连接AD,CD,AB,BC,即可得矩形ABCD.(2)利用勾股定理求出BC,再利用矩形的面积公式求解即可.【解答】解:(1)①如图,直线l即为所求.②如图,矩形ABCD即为所求.(2)∵四边形ABCD为矩形,∴∠ABC=90°,∵a=2,∴AB=CD=2,∴BC=AD===,∴矩形ABCD的面积为AB•BC=2×=.4.如图,四边形ABCD中,AB∥DC,AB=BC,AD⊥DC于点D.(1)用尺规作∠ABC的角平分线,交CD于点E;(不写作法,保留作图痕迹)(2)连接AE.求证:四边形ABCE是菱形.【分析】(1)根据角平分线的作图步骤作图即可.(2)由角平分线的定义和平行四边形的判定定理,可得四边形ABCE为平行四边形,再结合AB=BC,可证得四边形ABCE为菱形.【解答】(1)解:如图所示.(2)证明:∵BE是∠ABC的角平分线,∴∠ABE=∠CBE,∵AB∥CD,∴∠ABE=∠BEC,∴∠CBE=∠BEC,∴BC=EC,∵AB=BC,∴AB=EC,∴四边形ABCE为平行四边形,∵AB=BC,∴四边形ABCE为菱形.5.如图,在4×4的方格纸中,点A,B在格点上.请按要求画出格点线段(线段的端点在格点上),并写出结论.(1)在图1中画一条线段垂直AB.(2)在图2中画一条线段平分AB.【分析】(1)利用数形结合的思想作出图形即可;(2【解答】解:(1)如图1中,线段EF即为所求(答案不唯一);(2)如图2中,线段EF即为所求(答案不唯一).6.“水城河畔,樱花绽放,凉都宫中,书画成风”的风景,引来市民和游客争相“打卡”留念.已知水城河与南环路之间的某路段平行宽度为200米,为避免交通拥堵,请在水城河与南环路之间设计一条停车带,使得每个停车位到水城河与到凉都宫点F的距离相等.(1)利用尺规作出凉都宫到水城河的距离(保留作图痕迹,不写作法);(2)在图中格点处标出三个符合条件的停车位P1,P2,P3;(3)建立平面直角坐标系,设M(0,2),N(2,0),停车位P(x,y),请写出y与x之间的关系式,在图中画出停车带,并判断点P(4,﹣4)是否在停车带上.【分析】(1)利用过直线外一点作垂线的方法作图即可;(2)根据停车位到水城河与到凉都宫点F的距离相等,可得点P1,P2,P3;(3)根据停车位P(x,y)到点F(0,﹣1)和直线y=1的距离相等,得1﹣y=,从而解决问题.【解答】解:(1)如图,线段FA的长即为所求;(2)如图,点P1,P2,P3即为所求;(3)∵停车位P(x,y)到点F(0,﹣1)和直线y=1的距离相等,∴1﹣y=,化简得y=﹣,当x=4时,y=﹣4,∴点P(4,﹣4)在停车带上.7.图①、图②、图③均是5×5的正方形网格,每个小正方形的边长均为1,其顶点称为格点,△ABC 的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.(1)网格中△ABC的形状是;(2)在图①中确定一点D,连结DB、DC,使△DBC与△ABC全等;(3)在图②中△ABC的边BC上确定一点E,连结AE,使△ABE∽△CBA;(4)在图③中△ABC的边AB上确定一点P,在边BC上确定一点Q,连结PQ,使△PBQ∽△ABC,且相似比为1:2.【分析】(1)利用勾股定理的逆定理证明即可;(2(3)根据相似三角形的判定作出图形即可;(4)作出AB,BC的中点P,Q即可.【解答】解:(1)∵AC==,AB==2,BC=5,∴AC2+AB2=BC2,∴∠BAC=90°,∴△ABC是直角三角形;故答案为:直角三角形;(2)如图①中,点D,点D′,点D″即为所求;(3)如图②中,点E即为所求;(4)如图③,点P,点Q即为所求.8.如图,⊙O是△ABC的外接圆,∠ABC=45°.(1)请用尺规作出⊙O的切线AD(保留作图痕迹,不写作法);(2)在(1)的条件下,若AB与切线AD所夹的锐角为75°,⊙O的半径为2,求BC的长.【分析】(1)过点A作AD⊥AO即可;(2)连接OB,OC.证明∠=75°,利用三角形内角和定理求出∠CAB,推出∠BOC=120°,求出CH可得结论.【解答】解:(1)如图,切线AD即为所求;(2)过点O作OH⊥BC于H,连接OB,OC.∵AD是切线,∴OA⊥AD,∴∠OAD =90°,∵∠DAB =75°,∴∠OAB =15°,∵OA =OB ,∴∠OAB =∠OBA =15°,∴∠BOA =150°,∴∠BCA =∠AOB =75°,∵∠ABC =45°,∴∠BAC =180°﹣45°﹣75°=60°,∴∠BOC =2∠BAC =120°,∵OB =OC =2,∴∠BCO =∠CBO =30°,∵OH ⊥BC ,∴CH =BH =OC •cos30°=,∴BC =2.9.如图,在△ABC 中,AD 是△ABC 的角平分线,分别以点A ,D 为圆心,大于21AD 的长为半径作弧,两弧交于点M ,N ,作直线MN AB ,AD ,AC 于点E ,O ,F ,连接DE ,DF .(1)由作图可知,直线MN 是线段AD 的.(2)求证:四边形AEDF 是菱形.【分析】(1)根据作法得到MN 是线段AD 的垂直平分线;(2)根据垂直平分线的性质则AF =DF ,AE =DE ,进而得出DF ∥AB ,同理DE ∥AF ,于是可判断四边形AEDF 是平行四边形,加上FA =FD ,则可判断四边形AEDF 为菱形.【解答】(1)解:根据作法可知:MN 是线段AD 的垂直平分线;故答案为:垂直平分线;(2)证明:∵MN 是AD 的垂直平分线,∴AF=DF,AE=DE,∴∠FAD=∠FDA,∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠FDA=∠BAD,∴DF∥AB,同理DE∥AF,∴四边形AEDF是平行四边形,∵FA=FD,∴四边形AEDF为菱形.10.如图,已知Rt△ABC中,∠ACB=90°,AB=8,BC=5.(1)作BC的垂直平分线,分别交AB、BC于点D、H;(2)在(1)的条件下,连接CD,求△BCD的周长.【分析】(1)利用基本作图,作BC的垂直平分线即可;(2)根据线段垂直平分线的性质得到DC=DB,则利用等角的余角相等得到∠A=∠DCA,则DC=DA,然后利用等线段代换得到△BCD的周长=AB+BC.【解答】解:(1)如图,DH为所作;(2)∵DH垂直平分BC,∴DC=DB,∴∠B=∠DCB,∵∠B+∠A=90°,∠DCB+∠DCA=90°,∴∠A=∠DCA,∴DC=DA,∴△BCD的周长=DC+DB+BC=DA+DB+BC=AB+BC=8+5=13.11.已知:△ABC.(1)尺规作图:用直尺和圆规作出△ABC内切圆的圆心O.(只保留作图痕迹,不写作法和证明)(2)如果△ABC的周长为14cm,内切圆的半径为1.3cm,求△ABC的面积.【分析】(1)作∠ABC,∠ACB的角平分线交于点O,点O即为所求;(2)△ABC的面积=(a+b+c)•r计算即可.【解答】解:(1)如图,点O即为所求;(2)由题意,△ABC的面积=×14×1.3=9.1(cm2).12.已知四边形ABCD为矩形,点E是边AD的中点,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.(1)在图1中作出矩形ABCD的对称轴m,使m∥AB;(2)在图2中作出矩形ABCD的对称轴n,使n∥AD.【分析】(1)如图1中,连接,BD交于点O,作直线OE即可;(2)如图2中,同法作出点O,连接BE交AC于点T,连接DT,延长TD交AB于点R,作直线OR即可.【解答】解:(1)如图1中,直线m即为所求;(2)如图2中,直线n即为所求;13.如图,在10×10的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中△ABC为格点三角形.请按要求作图,不需证明.(1)在图1中,作出与△ABC全等的所有格点三角形,要求所作格点三角形与△ABC有一条公共边,且不与△ABC重叠;(2)在图2中,作出以BC为对角线的所有格点菱形.【分析】(1)根据全等三角形的判定画出图形即可;(2)根据菱形的定义画出图形即可.【解答】解:(1)如图1中,△ABD1,△ABD2,△ACD3,△ACD4,△CBD5即为所求;(2)如图2中,菱形ABDC,菱形BECF即为所求.14.【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?【初步尝试】如图1,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分;【问题联想】如图2,已知线段MN,请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP;【问题再解】如图3,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧,使扇形的面积被这条圆弧平分.(友情提醒:以上作图均不写作法,但需保留作图痕迹)【分析】【初步尝试】如图1,作∠AOB的角平分线OP即可;【问题联想】如图2,作线段MN的垂直平分线RT,垂足为R,在射线RT上截取RP=RM,连接MP,NP,三角形MNP即为所求;【问题再解】方法一:构造等腰直角三角形OBE,作BC⊥OE,以O为圆心,OC为半径画弧交OB于点D,交OA于点F,弧DF即为所求.方法二:作OB的中垂线交OB于点C,然后以C为圆心,CB 长为半径画弧交OB中垂线于点D,再以O为圆心,OD长为半径画弧分别交OA、OB于点E、F.则弧EF即为所求.【解答】解:【初步尝试】如图1,直线OP即为所求;【问题联想】如图2,三角形MNP即为所求;【问题再解】如图3中,即为所求.15.如图,在6×6的方格纸中,点A,B,C均在格点上,试按要求画出相应格点图形.(1)如图1,作一条线段,使它是AB向右平移一格后的图形;(2)如图2,作一个轴对称图形,使AB和AC是它的两条边;(3)如图3,作一个与△ABC相似的三角形,相似比不等于1.【分析】(1)把点B、A向右作平移1个单位得到CD;(2)作A点关于BC的对称点D即可;(3)延长CB到D使CD=2CB,延长CA到E点使CE=2CA,则△EDC满足条件.【解答】解:(1)如图1,CD为所作;(2)如图2,(3)如图3,△EDC为所作.。
八年级数学上册知识点总结第十四章

八年级数学上册知识点总结第十四章让努力学习八年级数学知识成为一种习惯。
要有最遥远的梦想和最朴素的生活,即使明天天寒地冻,路远马亡。
无论明日,有多落魄,至少今天,没有蹉跎。
以下是店铺为大家整理的八年级数学上册知识点总结,希望你们喜欢。
八年级数学上册知识点总结:第十四章一次函数1.画函数图象的一般步骤:一、列表(一次函数只用列出两个点即可,其他函数一般需要列出5个以上的点,所列点是自变量与其对应的函数值),二、描点(在直角坐标系中,以自变量的值为横坐标,相应函数的值为纵坐标,描出表格中的个点,一般画一次函数只用两点),三、连线(依次用平滑曲线连接各点).2.根据题意写出函数解析式:关键找到函数与自变量之间的等量关系,列出等式,既函数解析式.3.若两个变量x,y间的关系式可以表示成y=kx+b(k≠0)的形式,则称y是x的一次函数(x为自变量,y为因变量).特别地,当b=0时,称y是x的正比例函数.4.正比列函数一般式:y=kx(k≠0),其图象是经过原点(0,0)的一条直线.5.正比列函数y=kx(k≠0)的图象是一条经过原点的直线,当k>0时,直线y=kx经过第一、三象限,y随x的增大而增大,当k<0时,直线y=kx 经过第二、四象限,y随x的增大而减小,在一次函数y=kx+b中: 当k>0时,y随x的增大而增大; 当k<0时,y随x的增大而减小.6.已知两点坐标求函数解析式(待定系数法求函数解析式):把两点带入函数一般式列出方程组求出待定系数把待定系数值再带入函数一般式,得到函数解析式7.会从函数图象上找到一元一次方程的解(既与x轴的交点坐标横坐标值),一元一次不等式的解集,二元一次方程组的解(既两函数直线交点坐标值)八年级数学上册知识点总结(一)整式的乘法※(1). 单项式乘法法则:单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,连同它的指数作为积的一个因式.单项式乘法法则在运用时要注意以下几点:①积的系数等于各因式系数积,先确定符号,再计算绝对值.这时容易出现的错误的是,将系数相乘与指数相加混淆;②相同字母相乘,运用同底数的乘法法则;③只在一个单项式里含有的字母,要连同它的指数作为积的一个因式;④单项式乘法法则对于三个以上的单项式相乘同样适用;⑤单项式乘以单项式,结果仍是一个单项式.※(2).单项式与多项式相乘单项式乘以多项式,是通过乘法对加法的分配律,把它转化为单项式乘以单项式,即单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.单项式与多项式相乘时要注意以下几点:①单项式与多项式相乘,积是一个多项式,其项数与多项式的项数相同;②运算时要注意积的符号,多项式的每一项都包括它前面的符号;③在混合运算时,要注意运算顺序.※(3).多项式与多项式相乘多项式与多项式相乘,先用一个多项式中的每一项乘以另一个多项式的每一项,再把所得的积相加.多项式与多项式相乘时要注意以下几点:①多项式与多项式相乘要防止漏项,检查的方法是:在没有合并同类项之前,积的项数应等于原两个多项式项数的积;②多项式相乘的结果应注意合并同类项;③对含有同一个字母的一次项系数是1的两个一次二项式相乘,其二次项系数为1,一次项系数等于两个因式中常数项的和,常数项是两个因式中常数项的积.八年级数学上册知识点总结(二)平方差公式¤1.平方差公式:两数和与这两数差的积,等于它们的平方差,※即 .¤其结构特征是:①公式左边是两个二项式相乘,两个二项式中第一项相同,第二项互为相反数;②公式右边是两项的平方差,即相同项的平方与相反项的平方之差.完全平方公式¤1. 完全平方公式:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍,¤即 ;¤口决:首平方,尾平方,2倍乘积在中央;¤2.结构特征:①公式左边是二项式的完全平方;②公式右边共有三项,是二项式中二项的平方和,再加上或减去这两项乘积的2倍.¤3.在运用完全平方公式时,要注意公式右边中间项的符号,以及避免出现这样的错误.添括号法则:添正不变号,添负各项变号,去括号法则同样。
尺规作图知识梳理

尺柜作图知识梳理尺规作图是指用无刻度的直尺和圆规作图.尺规作图是起源于古希腊的数学课题.只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.尺规作图使用的直尺和圆规带有想像性质,跟现实中的并非完全相同:1、直尺必须没有刻度,无限长,且只能使用直尺的固定一侧.只可以用它来将两个点连在一起,不可以在上画刻度;2、圆规可以开至无限宽,但上面亦不能有刻度.它只可以拉开成之前构造过的长度.1,每次的操作只能是公认允许的五项根本操作(称为五项作图公法)之"o2,每次操作之前,操作者为决定是否操作和进行哪种操作可以进行的逻辑判断,也只能是几何学中公认允许的几种.基于作图公法〞的定义如下:成认以下五项前提,有限次运用以下五项公法而完成的作图方法,就是合法的尺规作图:五项前提是:(1)允许在平面上、直线上、圆弧线上已确定的范围内任意选定一点(所谓确定范围:依下面四条的规那么).(2)可以判断同一直线上不同点的位置次序.(3)可以判断同一圆弧线上不同点的位置次序.(4)可以判断平面上一点在直线的哪一侧.(5)可以判断平面上一点在圆的内部还是外部.五项公法是:(1)根据两个已经确定的点作出经过这两个点的直线.(2)以一个已经确定的点为圆心,以两个已经确定的点之间的距离为半径作圆.(3)确定两个已经做出的相交直线的交点.(4)确定已经做出的相交的圆和直线的交点.(5)确定已经做出的相交的两个圆的交点.也有些资料上给出的五项公法的后两条中的交点'改为公共点〞.这两种表达差异在于后者多包括了切点〞.但是,由于确定切点即使不算根本操作,也是可以用其它根本操作组合实现的.所以,两种表达的定义并无本质不同.中国古代规〞就是圆规,是用来画圆的工具,在我国古代甲骨文中就有规〞这个字. 矩〞就像木工使用的角尺, 由长短两尺相交成直角而成,两者间用木杠连接以使其牢固,其中短尺叫勾,长尺叫股.矩的使用是我国古代的一个创造,山东历城武梁祠石室造像中就有伏羲氏手执矩,女蜗氏手执规〞之图形.矩不仅可以画直线、直角,加上刻度可以测量,还可以代替圆规.甲骨文中也有矩字,这可追溯到大禹治水〔公元前2000年〕前.?史记?卷二记载大禹治水时左准绳,右规矩〞赵爽注?周髀算经?中有禹治洪水,……望山川之形,定高低之势,……乃勾股之所由生也.意即禹治洪水,要先测量地势的上下,就必定要用勾股的道理.这也说明矩起源于很远的中国古代.春秋时代也有不少著作涉及规矩的论述,?墨子?卷七中说轮匠〔制造车子的工匠〕执其规矩,以度天下之方圆.〞?孟子?卷四中说离娄〔传说中目力非常强的人〕之明,公输子〔即鲁班,传说木匠的祖师〕之巧,不以规矩,不能成方圆.可见,在春秋战国时期,规矩已被广泛地用于作图、制作器具了.由于我国古代的矩上已有刻度,因此使用范围较广,具有较大的实用性.古希腊古代希腊人较重视规、矩在数学中练习思维和智力的作用,而无视规矩的实用价值.因此,在作图中对规、矩的使用方法加以很多限制,提出了尺规作图问题.所谓尺规作图,就是只有限次地使用没有刻度的直尺和圆规进行作图.古希腊的安那萨哥拉斯首先提出作图要有尺寸限制.他因政治上的纠葛,被关进监狱,并被判处死刑.在监狱里,他思考改圆成方以及其他有关问题, 用来打发令人苦恼的无所事事的生活 .他不可能有标准的作图工具,只能用一根绳子画圆,用随便找来的破木棍作直尺,当然这些尺子上不可能有刻度.另外,对他来说,时间是不多了,因此他很自然地想到要有限次地使用尺规解决问题.后来以理论形式具体明确这个规定的是欧几里德的?几何原本?.格•W尚甲由于?几何原本?的巨大影响,希腊人所崇尚的尺规作图也一直被遵守并流传下来.近代西方由于对尺规作图的限制,使得一些貌似简单的几何作图问题无法解决.最著名的是被称为几何三大问题的三个古希腊古典作图难题:立方倍积问题、三等分任意角问题和化圆为方问题.当时很多有名的希腊数学家,都曾着力于研究这三大问题,虽然借助于其他工具或曲线,这三大难题都可以解决,但由于尺规作图的限制,却一直未能如愿以偿.以后两千年来,无数数学家为之绞尽脑汁,都以失败而告终.直到1637年笛卡尔创立了解析几何,关于尺规作图的可能性问题才有了准那么 .到了1837年万芝尔首先证实立方倍积问题和三等分任意角问题都属于尺规作图不可能问题.1882年林德曼证实了兀是超越数,化圆为方问题不可能用尺规作图解决,这才结束了历时两千年的数学难题公案.几何三大问题如果不限制作图工具,便很容易解决.从历史上看,好些数学结果是为解决三大问题而得出的副产品,特别是开创了对圆锥曲线的研究,发现了一批著名的曲线,等等 .不仅如此,三大问题还和近代的方程论、群论等数学分支发生了关系.1 .尺规作图著名问题尺规作图不能问题就是不可能用尺规作图完成的作图问题.其中最著名的是被称为几何三大问题的古典难题:■倍立方问题:作一个立方体,使它的体积是立方体的体积的两倍;■化圆为方问题:作一个正方形,使它的面积等于圆的面积.■三等分角:作一个角,将其分为三个相等的局部.以上三个问题在2400年前的古希腊已提出这些问题,但在欧几里得几何学的限制下,以上三个问题都不可能解决的.直至1837年,法国数学家万芝尔才首先证实“三等分角〞和“倍立方〞为尺规作图不能问题.而后在1882年德国数学家林德曼证实兀是超越数后,“化圆为方〞也被证实为尺规作图不能问题.还有另外两个著名问题:■〔乍正多边形只使用直尺和圆规,作正七边形一一这个看上去非常只使用直尺和圆规,作正五边形.只使用直尺和圆规,作正六边形.简单的题目,曾经使许多著名数学家都束手无策,由于正七边形是不能由尺规作出的.只使用直尺和圆规,作正九边形,此图也不能作出来,由于单用直尺和圆规,是缺乏以把一个角分成三等份的.问题的解决:高斯,大学二年级时得出正十七边形的尺规作图法,并给出了可用尺规作图的正多边形的条件:尺规作图正多边形的边数目必须是2的非负整数次方和不同的费马素数的积,解决了两千年来悬而未决的难题.■四等分圆周只准许使用圆规,将一个圆心的圆周4等分.这个问题传言是拿破仑波拿巴出的,向全法国数学家的挑战.尺规作图知识拓展在建筑工程图中,任何图形都可以分解为一些根本图形元素,如点、线、矩形、圆等.任何复杂几何图形都是有最根本的尺规作图为根底,掌握最基本的尺规作图的技能和技巧也是一切图学的根底.能独立完成线段等分、圆周等分、四心法椭圆、和圆弧连接等根本作图.2.1.1尺规作图根本方法尺规作图中可用的根本方法,也称为作图公法,任何尺规作图的步骤均可分解为以下五种方法:1、通过两个点可作一直线.2、圆心和半径可作一个圆.3、假设两直线相交,可求其交点.4、假设直线和一圆相交,可求其交点.5、假设两圆相交,可求其交点.2.2.2八种根本作图1、作一条线段等于线段2、作一个鱼等于角3、作线段的垂直平分线4、作角的角平分线5、过一点作直线的垂线6、三边作三角形7、两角、一边作三角形8、一角、两边作三角形(1)任意等分线段以最根本的尺规作图为根底等分线段.【例2.1-1]等分线段常采用辅助线法,图的作图方法.2.1-1为三等分线段ABC(c)连工耳艮分别由点八1 愧战早杼%与战交用等分点I, 2tb)过点』作位■-宜物& 触―勾।图2.1-1等分线段(2)等分两平行线间的距离以最根本的尺规作图为根底三等分平行线间的距离【例2.1-2 ] 绘制图2.1-2 , 开始一张新图.tc位置裁尺和用刷上的0点券在CD鳗上.龄动rue,更亢尺上的]出落在/!脚上.取等分立M NCb)出A N点分别作比期段必,门」前平行城图2.1-2等分两平行线间的距离(c)调理里面,加谭留拨,即得所求的:等分疝f灯UU上何的和甫拘平打线(3)等分圆周工程中在不考虑精度的前提下,还有一些近似作图的方法. 【例2.1-3 ]外接圆作圆内接正五边形.作图过程如图2.1-3所示【例2.1-4 ]外接圆作圆内接正七边形.作图过程如图2.1-4所示iI 二十、图 2.1-4方法2: 方法3:(略) 图2.1-3作正五边形【例2.1-5】外接圆作圆内接正九边形.作图过程如图2.1-5所示图 2.1-5敬再奔等好点.法精备等分点以K 点为阳心同阳半褥画孤交削 于上百,过A 作半程酬的承拨交 OHJ Q,胭即为七边席的边隹.以八点内圈心.炖为半径而狐交 圃用丁日、G.队以上为起分戒次画菰即可以用匕 等分回冏.(4)圆弧连接在零件上,经常会遇到由一外表(平面或曲面)光滑地过渡到另一外表的情况,这种过渡称为面面相切,而反映到投影图上,一般为线段(曲线与直线、曲线与曲线)相切.在制图中将这种相切称为连接,常见的连接形式有:一圆弧与直线连接、圆弧与圆弧连接,如图2.1-5所示.从图形可以看出,圆弧连接的实质是几何要素间相切的关系.圆弧连接的实质:就是要使连接圆弧与相邻线段相切,以到达光滑连接的目的.圆弧连接的根本原理(轨迹法)为保证连接光滑,必须准确地求出连接弧的圆心和切点的位置.圆弧连接的作图方法.由图2.1-5可知,圆弧连接的作图步骤一般为:(1)求连接圆弧的圆心;(2)找出连接点即切点的位置;(3)在两连接点之间作出连接圆弧.各种圆弧连接的作图方法举例如下;【例2.1-4 ]用半径为作图步骤:R的圆弧连接两直线AB和CD如图2.1-6所示.图2.1-5 扳手的连接图&知以挂接贝华如为间距. 分别柞两百线的平疗黑交于.点. 2汹口点作,在线的重线. 圣足E. F点即为切点,以 .为国心,口力半径,过艮即为所求.M直域8、逢接弧半径图2.1-6圆弧连接两直线也可以看作是用圆弧连接锐角的两边,当用圆弧连接钝角的两边或用圆弧连接直角的两边时,作法如下列图所示.【例2.1-5 ]用半径为R的圆弧连接直线AB和圆弧〔半径R1〕,如图2-7所示作图步骤:〔略〕「5匕如fOMfi,卡科有营的璘8.崖椎鼻gw?力阿距叶纯食糊的¥ir■与口Q为■心,史io,.即为祈求法耀式的・心,F如畦足,以.为■心,R为幸依比耳F点作■»所求.图2.1-9 圆弧连接直线和圆弧〔连接弧与圆内切〕〔5圆孤连接钟例的两边⑹圆弧连接直苑的两边图2.1-7圆弧连接两直线【例2.1-6 ]用圆弧连接直线和圆弧的方法和步骤如图2.1-8和2.1-9所示.圆弧与圆弧外切连接的方法和步骤如图2.1-10所示.俗以府力何和.快苴线的平行竣后以口力圆心, 启+马力半it所作的弧史于O H 0即为所求连接遍留心. 〔邙或8L交圆于F点.过口作O垂直比那么.F为垂足+以口为阙心,/?为半桂,过& F柞弧.印为所求.as网.,d. T•铳分别内图2.1-10圆弧连接圆弧和圆弧连接«a分别以白' 口划网心.慰知即用为半柱件芥空千点口,.即为市辖飒回心.姐选整ocv 8r4两国的财峨.立国心-启力骨捶,自因用知那交于E,F点,切点E、F柞・,即内斯聿.尻F点即角0点.图2.1-8圆弧连接直线和圆弧〔连接弧与圆外切〕作图实例5、过一点作直线的垂线7、两角、一边作三角形6、三边作三角形8、一角、两边作三角形姓名过三点作圆【】不共线的A、B、C三点【求作】过该三点之圆过三点作【作法】① 连接AB,连接AC;②分别作出线段AB、AC的中点D、E;③过D作AB的垂线,过E作AC的垂线,两垂线相交于O;④以O为圆心OA长为半径作圆, 即为求作之圆.作顶点分别在三平行线上的正三角形【】平行直线L1、L2、L3o【求作】正ABC ,使三个顶点分别落在三条平行线上.【作法一】① L1上任取一点D为顶点,作正三角形ADBE ,使B、E落在L2三顶点在三平行上〔图中虚线为正三角形简易作法〕;② 作过D、E直线交L3于C;③以B线的正三角形作为圆心BC为半径作弧交L1于A,连接A、B、C成MBC【作法二】① L2上任取一点B作三平行线公垂线交L1于E, L3于D;②作线段EB的垂直平分线L4 ;③过D作直线DG使/ EDG = 30° ,并交L4于G;④过B、G作直线交L1于A;⑤以B 为圆心BA为半径作弧交L3于C,连接A、B、C成MBC.注:可将第⑤步改为,过G作AB的垂线交L3于点C.这样G,B,D,C四点显然共圆.于是可证得/ B CG=/EDG = 30°.这样可以很快证得公BC为等边三角形.。
(完整版)初中最基本的尺规作图总结

尺规作图一、理解“尺规作图”的含义1.在几何中,我们把只限定用直尺(无刻度)和圆规来画图的方法,称为尺规作图.其中直尺只能用来作直线、线段、射线或延长线段;圆规用来作圆和圆弧.由此可知,尺规作图与一般的画图不同,一般画图可以动用一切画图工具,包括三角尺、量角器等,在操作过程中可以度量,但尺规作图在操作过程中是不允许度量成分的.2.基本作图:(1)用尺规作一条线段等于已知线段;(2)用尺规作一个角等于已知角. 利用这两个基本作图,可以作两条线段或两个角的和或差.二、熟练掌握尺规作图题的规范语言1.用直尺作图的几何语言:①过点×、点×作直线××;或作直线××;或作射线××;②连结两点××;或连结××;③延长××到点×;或延长(反向延长)××到点×,使××=××;或延长××交××于点×;2.用圆规作图的几何语言:①在××上截取××=××;②以点×为圆心,××的长为半径作圆(或弧);③以点×为圆心,××的长为半径作弧,交××于点×;④分别以点×、点×为圆心,以××、××的长为半径作弧,两弧相交于点×、×. 三、了解尺规作图题的一般步骤尺规作图题的步骤:1.已知:当作图是文字语言叙述时,要学会根据文字语言用数学语言写出题目中的条件;2.求作:能根据题目写出要求作出的图形及此图形应满足的条件;3.作法:能根据作图的过程写出每一步的操作过程.当不要求写作法时,一般要保留作图痕迹.对于较复杂的作图,可先画出草图,使它同所要作的图大致相同,然后借助草图寻找作法.在目前,我们只要能够写出已知,求作,作法三步(另外还有第四步证明)就可以了,而且在许多中考作图题中,又往往只要求保留作图痕迹,不需要写出作法,可见在解作图题时,保留作图痕迹很重要.尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。
初中尺规作图详细讲解(含图)

初中数学尺规作图讲解初等平面几何研究的对象,仅限于直线、圆以及由它们(或一部分)所组成的图形,因此作图的工具,习惯上使用没有刻度的直尺和圆规两种。
限用直尺和圆规来完成的作图方法,叫做尺规作图法.最简单的尺规作图有如下三条:⑴经过两已知点可以画一条直线;⑵已知圆心和半径可以作一圆;⑶两已知直线;一已知直线和一已知圆;或两已知圆,如果相交,可以求出交点;以上三条,叫做作图公法。
用直尺可以画出第一条公法所说的直线;用圆规可以作出第二条公法所说的圆;用直尺和圆规可以求得第三条公法所说的交点。
一个作图题,不管多么复杂,如果能反复应用上述三条作图公法,经过有限的次数,作出适合条件的图形,这样的作图题就叫做尺规作图可能问题;否则,就称为尺规作图不能问题.历史上,最著名的尺规作图不能问题是:⑴三等分角问题:三等分一个任意角;⑵倍立方问题:作一个立方体,使它的体积是已知立方体的体积的两倍;⑶化圆为方问题:作一个正方形,使它的面积等于已知圆的面积。
这三个问题后被称为“几何作图三大问题”。
直至1837年,万芝尔(Pierre Laurent Wantzel)首先证明三等分角问题和立方倍积问题属尺规作图不能问题;1882年,德国数学家林德曼(Ferdinand Lindemann)证明π是一个超越数(即π是一个不满足任何整系数代数方程的实数),由此即可推得根号π(即当圆半径1r=时所求正方形的边长)不可能用尺规作出,从而也就证明了化圆为方问题是一个尺规作图不能问题.若干著名的尺规作图已知是不可能的,而当中很多不可能证明是利用了由19世纪出现的伽罗华理论.尽管如此,仍有很多业余爱好者尝试这些不可能的题目,当中以化圆为方及三等分任意角最受注意。
数学家Underwood Dudley曾把一些宣告解决了这些不可能问题的错误作法结集成书。
还有另外两个著名问题:⑴正多边形作法·只使用直尺和圆规,作正五边形。
·只使用直尺和圆规,作正六边形.·只使用直尺和圆规,作正七边形—-这个看上去非常简单的题目,曾经使许多著名数学家都束手无策,因为正七边形是不能由尺规作出的.·只使用直尺和圆规,作正九边形,此图也不能作出来,因为单用直尺和圆规,是不足以把一个角分成三等份的.·问题的解决:高斯,大学二年级时得出正十七边形的尺规作图法,并给出了可用尺规作图的正多边形的条件:尺规作图正多边形的边数目必须是2的非负整数次方和不同的费马素数的积,解决了两千年来悬而未决的难题。
初中尺规作图详细讲解(含图)

初中数学尺规作图讲解初等平面几何研究的对象,仅限于直线、圆以及由它们(或一部分)所组成的图形,因此作图的工具,习惯上使用没有刻度的直尺和圆规两种.限用直尺和圆规来完成的作图方法,叫做尺规作图法. 最简单的尺规作图有如下三条:⑴ 经过两已知点可以画一条直线;⑵ 已知圆心和半径可以作一圆;⑶ 两已知直线;一已知直线和一已知圆;或两已知圆,如果相交,可以求出交点;以上三条,叫做作图公法. 用直尺可以画出第一条公法所说的直线;用圆规可以作出第二条公法所说的圆;用直尺和圆规可以求得第三条公法所说的交点. 一个作图题,不管多么复杂,如果能反复应用上述三条作图公法,经过有限的次数,作出适合条件的图形,这样的作图题就叫做尺规作图可能问题;否则,就称为尺规作图不能问题.历史上,最著名的尺规作图不能问题是:⑴ 三等分角问题:三等分一个任意角;⑵ 倍立方问题:作一个立方体,使它的体积是已知立方体的体积的两倍;⑶ 化圆为方问题:作一个正方形,使它的面积等于已知圆的面积.这三个问题后被称为“几何作图三大问题”. 直至1837 年,万芝尔(Pierre Laurent Wantzel )首先证明三等分角问题和立方倍积问题属尺规作图不能问题;1882 年,德国数学家林德曼(Ferdinand Lindemann )证明π是一个超越数(即π是一个不满足任何整系数代数方程的实数),由此即可推得根号π(即当圆半径r 1时所求正方形的边长)不可能用尺规作出,从而也就证明了化圆为方问题是一个尺规作图不能问题.若干著名的尺规作图已知是不可能的,而当中很多不可能证明是利用了由19 世纪出现的伽罗华理论. 尽管如此,仍有很多业余爱好者尝试这些不可能的题目,当中以化圆为方及三等分任意角最受注意. 数学家Underwood Dudley 曾把一些宣告解决了这些不可能问题的错误作法结集成书.还有另外两个著名问题:⑴ 正多边形作法·只使用直尺和圆规,作正五边形. ·只使用直尺和圆规,作正六边形. ·只使用直尺和圆规,作正七边形——这个看上去非常简单的题目,曾经使许多著名数学家都束手无策,因为正七边形是不能由尺规作出的.·只使用直尺和圆规,作正九边形,此图也不能作出来,因为单用直尺和圆规,是不足以把一个角分成三等份的.·问题的解决:高斯,大学二年级时得出正十七边形的尺规作图法,并给出了可用尺规作图的正多边形的条件:尺规作图正多边形的边数目必须是 2 的非负整数次方和不同的费马素数的积,解决了两千年来悬而未决的难题.⑵ 四等分圆周只准许使用圆规,将一个已知圆心的圆周 4 等分.这个问题传言是拿破仑·波拿巴出的,向全法国数学家的挑战.尺规作图的相关延伸:用生锈圆规(即半径固定的圆规)作图1. 只用直尺及生锈圆规作正五边形2. 生锈圆规作图,已知两点A、B ,找出一点C使得AB BC CA.3. 已知两点A、B ,只用半径固定的圆规,求作C使C是线段AB的中点.4. 尺规作图,是古希腊人按“尽可能简单”这个思想出发的,能更简洁的表达吗?顺着这思路就有了更简洁的表达. 10世纪时,有数学家提出用直尺和半径固定的圆规作图. 1672年,有人证明:如果把“作直线”解释为“作出直线上的 2 点”,那么凡是尺规能作的,单用圆规也能作出!从已知点作出新点的几种情况:两弧交点、直线与弧交点、两直线交点 ,在已有一个圆的情况下,那么凡是尺规能作的,单用直尺也能作出! . 五种基本作图: 初中数学的五种基本尺规作图为:1.做一线段等于已知线段2.做一角等于已知角3. 做一角的角平分线4.过一点做一已知线段的垂线5.做一线段的中垂线 下面介绍几种常见的尺规作图方法: ⑴ 轨迹交点法: 解作图题的一种常见方法 . 解作图题常归结到确定某一个点的位置 . 如果这两个点的位置是由两个条件确定的,先放弃其中一个条件,那么这个点的位置就不确定而形成一个轨迹;若改 变放弃另一个条件,这个点就在另一条轨迹上,故此点便是两个轨迹的交点 交点来解作图题的方法称为轨迹交点法,或称交轨法、轨迹交截法、轨迹法例 1】 电信部门要修建一座电视信号发射塔,如下图,按照设计要求,发射塔到两个城镇 相等,到两条高速公路 m 、 n 的距离也必须相等,发射塔 P 应修建在什么位置?分析】 这是一道实际应用题,关键是转化成数学问题,根据题意知道,点 P 应满足两个条件,一是在线段 AB的垂直平分线上;二是在两条公路夹角的平分线上,所以点 P 应是它们的交点 .解析】 ⑴ 作两条公路夹角的平分线 OD 或 OE ;⑵ 作线段 AB 的垂直平分线 FG ;则射线 OD , OE 与直线 FG 的交点 C 1 , C 2 就是发射塔的位置 .例 2】 在平面直角坐标系中,点 A 的坐标是 (4 , 0) , O 是坐标原点,在直线 y x 3上求一点 P ,使 AOP是等腰三角形,这样的 P 点有几个?解析】 首先要清楚点 P 需满足两个条件,一是点 P 在 y x 3上;二是 AOP 必须是等腰三角形 .其次,寻找P 点要分情况讨论,也就是当 OA OP 时,以 O 点为圆心, OA 为半径画圆,与直线有两个点 P 1、 P 2; 当 OA AP 时,以 A 点为圆心, OA 为半径画圆,与直线无交点;当 PO PA 时,作 OA 的垂直平分线,. 这个利用轨迹的A 、B 的距离必须C2G与直线有一交点 P 3,所以总计这样的 P 点有 3个.分析】 设⊙M 是符合条件的圆,即其半径为 r ,并与 ⊙O 及⊙O '外切,显然,点 M 是由两个轨迹确定的,即M 点既在以 O 为圆心以 R r 为半径的圆上, 又在以 O'为圆心以 R' r 为半径的圆上, 因此所求圆的圆 心的位置可确定 . 若⊙O 与⊙O'相距为 b ,当 2r b 时,该题无解,当 2r b 有唯一解;当 2r b 时, 有两解 .解析】 以当⊙O 与 ⊙O '相距为 b ,2r b 时为例:⑴ 作线段 OA R r , O' B R' r .⑵ 分别以 O , O '为圆心,以 R r , R' r 为半径作圆,两圆交于 M 1,M 2 两点. ⑶ 连接 OM 1 , OM 2 ,分别交以 R 为半径的 ⊙O 于 D 、C 两点. ⑷ 分别以 M 1,M 2 为圆心,以 r 为半径作圆 . ∴⊙M 1,⊙M 2 即为所求 .思考】若将例 3 改为: “设⊙O 与⊙O '相离,半径分别为 R 与 R' ,求作半径为 r (r R)的圆,使其与 ⊙O 内切,与 ⊙O'外切. ”又该怎么作图?⑵ 代数作图法: 解作图题时,往往首先归纳为求出某一线段长,而这线段长的表达式能用代数方法求出,然 后根据线段长的表达式设计作图步骤 . 用这种方法作图称为代数作图法 .【例 4】 只用圆规,不许用直尺,四等分圆周(已知圆心).【分析】 设半径为 1. 可算出其内接正方形边长为 2 ,也就是说用这个长度去等分圆周 .我们的任务就是做出这 个长度 . 六等分圆周时会出现一个 3的长度 .设法构造斜边为 3 ,一直角边为 1的直角三角形, 2 的 长度自然就出来了 .【解析】 具 体做法:⑴ 随便画一个圆 . 设半径为 1.⑵ 先六等分圆周 . 这时隔了一个等分点的两个等分点距离为例 3】 设⊙O 与 ⊙O '相离,半径分别为 R 与 R',求作半径为 r 的圆,使其与 ⊙O 及⊙O'外切 .rMDO' O R'RrCMAB⑶ 以这个距离为半径, 分别以两个相对的等分点为圆心, 同向作弧, 交于一点 .( “两个相对的等分点其实就是直径的两端点啦! 两弧交点与 “两个相对的等分点 ”形成的是一个底为 2,腰为 3 的等腰三 角形. 可算出顶点距圆心距离就是 2 .) ⑷ 以 2 的长度等分圆周就可以啦!例 5】 求作一正方形,使其面积等于已知 ABC 的面积 .分析】 设 ABC 的底边长为 a ,高为 h ,关键是在于求出正方形的边长 x ,使得 x 2 1 ah ,所以 x 是 1a 与h 的22 比例中项 .解析】 已知:在 ABC 中,底边长为 a ,这个底边上的高为 h ,求作:正方形 DEFG ,使得: S 正方形 DEFG S ABC作法:⑴ 作线段 MD 1 a ;2⑵ 在 MD 的延长线上取一点 N ,使得 DN h ;⑶ 取 MN 中点 O ,以 O 为圆心, OM 为半径作 ⊙O ; ⑷ 过 D 作 DE MN ,交⊙O 于 E , ⑸ 以 DE 为一边作正方形 DEFG . 正方形 DEFG 即为所求 .分析】 先利用代数方法求出点 M 与圆心 O 的距离 d ,再以 O 为圆心, d 为半径作圆,此圆与直线 l 的交点即 为所求 .解析】 ⑴ 作Rt OAB ,使得: A 90 ,OA r , AB a .例 6】 在已知直线 l 上求作一点 M ,使得过 M 作已知半径为 r 的 ⊙O 的切线,其切线长为a.a⑵ 以O 为圆心,OB 为半径作圆若此圆与直线l相交,此时有两个交点M1,M2.M1,M2 即为所求.若此圆与直线l相切,此时只有一个交点M.M即为所求.若此圆与直线l 相离,此时无交点.即不存在这样的M 点使得过M 作已知半径为r 的⊙O的切线,其切线长为 a.⑶ 旋转法作图:有些作图题,需要将某些几何元素或图形绕某一定点旋转适当角度,以使已知图形与所求图形发生联系,从而发现作图途径.例7】已知:直线a、b、c,且a∥b∥c.求作:正ABC ,使得A、 B 、C三点分别在直线a、b、c上.ab分析】假设ABC是正三角形,且顶点 A 、 B 、C三点分别在直线a、b、c上.作AD b于D,将ABD绕A点逆时针旋转60 后,置于ACD'的位置,此时点D' 的位置可以确定.从而点C也可以确定. 再作BAC 60 , B 点又可以确定,故符合条件的正三角形可以作出.解析】作法:⑴ 在直线a上取一点A,过A作AD b于点 D ;⑵ 以AD 为一边作正三角形ADD ' ;⑶ 过D'作D'C AD ' ,交直线 c 于C;⑷ 以A为圆心,AC为半径作弧,交b于B(使B与D'在AC异侧).⑸ 连接AB 、AC 、BC 得ABC .ABC 即为所求.例8】已知:如图,P 为AOB 角平分线OM 上一点.求作:PCD ,使得P 90 ,PC PD,且C在OA上,D在OB上.解析】 ⑴ 过 P 作 PE OB 于 E .⑵ 过 P 作直线 l ∥OB ;⑶ 在直线 l 上取一点 M ,使得 PM PE (或 PM ' PE );⑷ 过M (或M')作MC l (或 M'C l ),交OA 于C (或C')点;⑸ 连接PC (或PC' ),过 P 作PD PC (或PD' PC')交OB 于D (或 D')点. 连接 PD,CD (或 PD',C'D').则 PCD (或 PC'D')即为所求 .⑷ 位似法作图: 利用位似变换作图,要作出满足某些条件的图形,可以先放弃一两个条件,作出与其位似的 图形,然后利用位似变换,将这个与其位似得图形放大或缩小,以满足全部条件,从而作出 满足全部的条件 .【例 9】 已知:一锐角 ABC .求作:一正方形 DEFG ,使得 D 、 E 在BC 边上, F 在AC 边上, G 在AB 边上.分析】 先放弃一个顶点 F 在 AC 边上的条件, 作出与正方形 DEFG 位似的正方形 D 'E 'F ' G' ,然后利用位似变换将正方形 D'E'F 'G '放大(或缩小)得到满足全部条件的正方形DEFG .解析】 作 法:⑴ 在 AB 边上任取一点 G',过 G'作G'D' BC 于 D'⑵ 以G'D '为一边作正方形 D'E'F'G',且使 E'在 BD '的延长线上 . ⑶ 作直线 BF'交 AC 于 F .⑷ 过F 分别作 FG ∥F'G'交 AB 于G ;作 FE ∥F'E'交BC 于E . ⑸ 过G 作GD ∥G'D'交 BC 于 D . 则四边形 DEFG 即为所求 .A⑸ 面积割补法作图:对于等积变形的作图题,通常在给定图形或某一确定图形上割下一个三角形,再借助平行线补上一个等底等高的另一个三角形,使面积不变,从而完成所作图形.【例10】如图,过ABC的底边BC上一定点,P ,求作一直线l ,使其平分ABC的面积.分析】因为中线AM 平分ABC的面积,所以首先作中线AM ,假设PQ平分ABC的面积,在AMC 中先割去AMP ,再补上ANP .只要NM ∥ AP ,则AMP 和AMP就同底等高,此时它们的面积就相等了. 所以PN 就平分了ABC的面积.解析】作法:⑴ 取BC中点M ,连接AM ,AP;⑵ 过M 作MN∥AP交AB于N;⑶ 过P、N 作直线l . 直线l 即为所求.例11】如图:五边形ABCDE 可以看成是由一个直角梯形和一个矩形构成⑴ 请你作一条直线l ,使直线l 平分五边形ABCDE 的面积;⑵ 这样的直线有多少条?请你用语言描述出这样的直线.解析】⑴ 取梯形AFDE 的中位线MN 的中点O ,再取矩形BCDF 对角线的交点O ' ,则经过点O,O'的直线l 即为所求;⑵ 这样的直线有无数条. 设⑴中的直线l 交AE于Q,交BC于R,过线段RQ中点P ,且与线段AE、BC均有交点的直线均可平分五边形ABCDE的面积.例12】(07江苏连云港)如图1,点C将线段AB分成两部分,如果AC BC,那么称点C 为线段AB的黄金分AB AC割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l 将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2 ,如果S1 S2,那么称直线S S1 l 为该图形的黄金分割线.⑴ 研究小组猜想:在△ABC 中,若点 D 为AB边上的黄金分割点(如图 2 ),则直线CD是△ABC 的黄金分割线.你认为对吗?为什么?⑵ 请你说明:三角形的中线是否也是该三角形的黄金分割线?⑶ 研究小组在进一步探究中发现: 过点 C 任作一条直线交 AB 于点 E ,再过点 D 作直线 DF ∥CE ,交AC 于点F ,连接EF (如图3),则直线 EF 也是△ABC 的黄金分割线.请你说明理由.⑷ 如图 4 ,点 E 是 ABCD 的边 AB 的黄金分割点, 过点 E 作 EF ∥ AD ,交 DC 于点 F ,显然直线EF 是 ABCD 的黄金分割线.请你画一条 ABCD 的黄金分割线, 使它不经过 ABCD 各边黄金分割 点.解析】 ⑴ 直线 CD 是△ABC 的黄金分割线.理由如下:设 △ ABC 的边 AB 上的高为 h .1112 BD h , S △ABC 2AB h ,S △ ADC ADS △BDC BDS△ ABCABS △ ADC AD又∵点 D 为边 AB 的黄金分割点,∴AD BDS △ ADC S △ BDC . AB ADS△ ABC S △ ADC∴直线 CD 是 △ ABC 的黄金分割线.⑵ ∵ 三角形的中线将三角形分成面积相等的两部分, 此时 S 1 S 2 1S ,即 S1 S2 ,2 S S 1 ∴三角形的中线不可能是该三角形的黄金分割线.⑶ ∵ DF ∥ CE ,∴ △DEC 和 △FCE 的公共边 CE 上的高也相等,设直线 EF 与CD 交于点 G ,∴ S △ DGE S △ FGC . ∴ S △ ADCS四边形 AFGDS △ FGCS四边形 AFGDS△ DGES△ AEF ,∴直线 EF 也是 △ ABC 的黄金分割线. ⑷ 画法不惟一,现提供两种画法;A C B图 11 S△ADC2 AD h ,S△ BDCS△ DECS△FCE又∵S△ ADC S △ BDC S△ AEFS四边形BEFCS△ ABC,∴S△ ADCS△ ABCS△ AEF图2图3图4S△ BDCS四边形 BEFC .答案图 1) 答案图 2)画法一:如答图1,取EF中点G ,再过点G作一直线分别交AB,DC于M,N点,则直线MN 就是ABCD 的黄金分割线.画法二:如答图2,在DF上取一点N,连接EN ,再过点 F 作FM∥NE交AB于点M,连接MN ,则直线MN 就是ABCD 的黄金分割线.。
(完整)初中数学总复习尺规作图

尺规作图尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图五种基本作图:1、作一条线段等于已知线段;2、作一个角等于已知角;3、作已知线段的垂直平分线;4、作已知角的角平分线;5、过一点作已知直线的垂线;题目一:作一条线段等于已知线段。
已知:如图,线段 a . 求作:线段AB,使AB = a . 作法:①作射线AP ;②在射线AP 上截取AB=a . 则线段AB 就是所求作的图形。
题目二:作已知线段的中点。
已知:如图,线段MN. 求作:点O ,使MO=NO (即O 是MN 的中点)作法:①分别以M、N 为圆心,大于1/2MN 的相同线段为半径画弧,两弧相交于P,Q ;②连接PQ 交MN 于O .则点O 就是所求作的MN的中点。
(试问:PQ 与MN有何关系?)题目三:作已知角的角平分线。
已知:如图,∠AOB ,求作:射线OP, 使∠ AOP =∠ BOP (即OP 平分∠ AOB )作法:①以O 为圆心,任意长度为半径画弧,分别交OA ,OB 于M,N;②分别以M 、N为圆心,大于1/2MN 的相同线段为半径画弧,两弧交∠ AOB 内于P;③作射线OP。
则射线OP 就是∠AOB 的角平分线。
题目四:作一个角等于已知角。
(请自己写出“已知”“求作”并作出图形,不写作法)题目五:已知三边作三角形。
已知:如图,线段a,b,c.求作:△ ABC ,使AB = c ,AC = b ,BC = a. 作法:① 作线段AB = c ;② 以 A 为圆心 b 为半径作弧,以 B 为圆心a 为半径作弧与前弧相交于C;③连接AC ,BC 。
则△ABC 就是所求作的三角形。
题目六:已知两边及夹角作三角形。
已知:如图,线段m ,n, ∠ . 求作:△ABC,使∠A= ∠ ,AB=m ,AC=n. 作法:① 作∠ A= ∠ ;② 在AB 上截取AB=m ,AC=n ;③连接BC 。
则△ABC 就是所求作的三角形。
题目七:已知两角及夹边作三角形已知:如图,∠ ,∠ ,线段m .求作:△ABC,使∠A= ∠,∠ B= ∠,AB=m.作法:① 作线段AB=m ;② 在AB 的同旁作∠ A= ∠ ,作∠ B=∠∠A 与∠B 的另一边相交于C则△ABC 就是所求作的图形(三角形)一、尺规基本作图归纳1、作一条线段等于已知线段;2、作一个角等于已知角;3、作角的平分线;4、作线段的中垂线;5、已知三边 ,两边和其夹角或两角和其夹边作三角形 ;6、已知底边和底边上的高作等腰三角形;7、过直线上一点作直线的垂线;8、过直线外一点作直线的垂线 .例题:1、如图 ,有一破残的轮片 ,现要制作一个与原轮片同样大小的圆形零件 ,请你根据所学的有关知识 ,设计一种方案 ,确定这个圆形零件的半径 .2、 如图:107国道OA 和320国道 OB 在某市相交于点 O,在∠AOB 的内部有工厂 C 和D,现要修建一个货站 P,使P 到OA 、 OB 的距离相等且 PC=PD, 用尺规作出货站 P 的位置 (不写作法 ,保留作图痕迹 ,写出结论 )3、要求到三条公路的距离相等,问满足要求的加油站地址有几种情况?A公路两两个加油站,6、过直线外一点 A 作圆 O的切线4、过点 C 作一条线平行于 AB ;5、过不在同一直线上的三点 A 、 B 、C 作圆 O ;二、几何画图 :1、只利用一把有刻度的直尺 ,用度量的方法 ,按下列要求画图 : 1)画等腰三角形 ABC 的对称轴 : 2)画∠ AOB 的对称轴2、有一个未知圆心的圆形工件 .现只允许用一块三角板(注:不允许用三角板上的刻度)画出该工件表面上的一条直径并定出圆心 .要求在图上保留画图痕迹,写出画法 .3、某校有一个正方形的花坛,现要将它分成形状和面积都相同的四块种上不同颜色的花卉,请你帮助设计至少三种不同的 方案,分别画在下面正方形图形上(用尺规作图或画图均可,但要尽可能准确些、美观些) .4、某村一块若干亩土地的图形是Δ ABC ,现决定把这块土地平均分给四位 “花农”种植,请你帮他们分一分,提供至少两种 分法。
2025年中考数学考点分类专题归纳之尺规作图

2025年中考数学考点分类专题归纳尺规作图1、定义(1)尺规作图是指用没有刻度的直尺和圆规作图.只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.(2)基本要求它使用的直尺和圆规带有想像性质,跟现实中的并非完全相同.直尺必须没有刻度,无限长,且只能使用直尺的固定一侧.只可以用它来将两个点连在一起,不可以在上画刻度.圆规可以开至无限宽,但上面亦不能有刻度.它只可以拉开成你之前构造过的长度.2、基本作图有:(1)作一条线段等于已知线段.(2)作一个角等于已知角.(3)作已知线段的垂直平分线.(4)作已知角的角平分线.(5)过一点作已知直线的垂线.3、复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.4、应用与设计作图主要把简单作图放入实际问题中.首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.1.(2024•鄂尔多斯)如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于CD为半径作弧,两弧交于点M,N;②作直线MN,且MN恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是()A.∠ABC=60°B.S△ABE=2S△ADEC.若AB=4,则BE D.sin∠CBE2.(2024•河南)如图,已知▱AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为()A.(1,2)B.(,2)C.(3,2)D.(2,2)3.(2024•郴州)如图,∠AOB=60°,以点O为圆心,以任意长为半径作弧交OA,OB于C,D两点;分别以C,D为圆心,以大于CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上截取线段OM=6,则M点到OB的距离为()A.6 B.2 C.3 D.4.(2024•宜昌)尺规作图:经过已知直线外一点作这条直线的垂线,下列作图中正确的是()A.B.C.D.5.(2024•襄阳)如图,在△ABC中,分别以点A和点C为圆心,大于AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为()A.16cm B.19cm C.22cm D.25cm6.(2024•潍坊)如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:(1)作线段AB,分别以A,B为圆心,以AB长为半径作弧,两弧的交点为C;(2)以C为圆心,仍以AB长为半径作弧交AC的延长线于点D;(3)连接BD,BC.下列说法不正确的是()A.∠CBD=30°B.S△BDC AB2C.点C是△ABD的外心D.sin2A+cos2D=17.(2024•台州)如图,在▱ABCD中,AB=2,BC=3.以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是()A.B.1 C.D.8.(2024•巴中)如图,在Rt△ABC中,∠C=90°,按下列步骤作图:①以点B为圆心,适当长为半径画弧,与AB,BC分别交于点D,E;②分别以D,E为圆心,大于DE的长为半径画弧,两弧交于点P;③作射线BP交AC于点F;④过点F作FG⊥AB于点G.下列结论正确的是()A.CF=FG B.AF=AG C.AF=CF D.AG=FG9.(2024•昆明)如图,点A在双曲线y═(x>0)上,过点A作AB⊥x轴,垂足为点B,分别以点O和点A为圆心,大于OA的长为半径作弧,两弧相交于D,E两点,作直线DE交x轴于点C,交y轴于点F (0,2),连接AC.若AC=1,则k的值为()A.2 B.C.D.10.(2024•安顺)已知△ABC(AC<BC),用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是()A.B.C.D.11.(2024•湖州)尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;③连结OG.问:OG的长是多少?大臣给出的正确答案应是()A.r B.(1)r C.(1)r D.r12.(2024•益阳)如图,在△ABC中,AB=5,AC=4,BC=3.按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AC于点M,N;②分别以M,N为圆心,以大于MN的长为半径作弧,两弧相交于点E;③作射线AE;④以同样的方法作射线BF.AE交BF于点O,连接OC,则OC=_______.13.(2024•抚顺)如图,▱ABCD中,AB=7,BC=3,连接AC,分别以点A和点C为圆心,大于AC的长为半径作弧,两弧相交于点M,N,作直线MN,交CD于点E,连接AE,则△AED的周长是____.14.(2024•葫芦岛)如图,OP平分∠MON,A是边OM上一点,以点A为圆心、大于点A到ON的距离为半径作弧,交ON于点B、C,再分别以点B、C为圆心,大于BC的长为半径作弧,两弧交于点D、作直线AD分别交OP、ON于点E、F.若∠MON=60°,EF=1,则OA=_______.15.(2024•山西)如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,以大于CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为_______.16.(2024•东营)如图,在Rt△ABC中,∠B=90°,以顶点C为圆心,适当长为半径画弧,分别交AC,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线CP交AB于点D.若BD=3,AC=10,则△ACD的面积是____.17.(2024•淮安)如图,在Rt△ABC中,∠C=90°,AC=3,BC=5,分别以点A、B为圆心,大于AB的长为半径画弧,两弧交点分别为点P、Q,过P、Q两点作直线交BC于点D,则CD的长是__.18.(2024•南京)如图,在△ABC中,用直尺和圆规作AB、AC的垂直平分线,分别交AB、AC于点D、E,连接DE.若BC=10cm,则DE=___cm.19.(2024•赤峰)如图,D是△ABC中BC边上一点,∠C=∠DAC.(1)尺规作图:作∠ADB的平分线,交AB于点E(保留作图痕迹,不写作法);(2)在(1)的条件下,求证:DE∥AC.20.(2024•攀枝花)已知△ABC中,∠A=90°.(1)请在图1中作出BC边上的中线(保留作图痕迹,不写作法);(2)如图2,设BC边上的中线为AD,求证:BC=2AD.21.(2024•牡丹江)在四边形ABCD中,∠B=∠C=90°,AB=3,BC=4,CD=1.以AD为腰作等腰△ADE,使∠ADE=90°,过点E作EF⊥DC交直线CD于点F.请画出图形,并直接写出AF的长.22.(2024•贵港)尺规作图(只保留作图痕迹,不要求写出作法).如图,已知∠α和线段a,求作△ABC,使∠A=∠α,∠C=90°,AB=a.23.(2024•北京)下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.已知:直线l及直线l外一点P.求作:直线PQ,使得PQ∥l.作法:如图,①在直线l上取一点A,作射线PA,以点A为圆心,AP长为半径画弧,交PA的延长线于点B;②在直线l上取一点C(不与点A重合),作射线BC,以点C为圆心,CB长为半径画弧,交BC的延长线于点Q;③作直线PQ.所以直线PQ就是所求作的直线.根据小东设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明.证明:∵AB=____,CB=____,∴PQ∥l(__________)(填推理的依据).24.(2024•孝感)如图,△ABC中,AB=AC,小聪同学利用直尺和圆规完成了如下操作:①作∠BAC的平分线AM交BC于点D;②作边AB的垂直平分线EF,EF与AM相交于点P;③连接PB,PC.请你观察图形解答下列问题:(1)线段PA,PB,PC之间的数量关系是__________;(2)若∠ABC=70°,求∠BPC的度数.25.(2024•陇南)如图,在△ABC中,∠ABC=90°.(1)作∠ACB的平分线交AB边于点O,再以点O为圆心,OB的长为半径作⊙O;(要求:不写做法,保留作图痕迹)(2)判断(1)中AC与⊙O的位置关系,直接写出结果.26.(2024•青岛)已知:如图,∠ABC,射线BC上一点D.求作:等腰△PBD,使线段BD为等腰△PBD的底边,点P在∠ABC内部,且点P到∠ABC两边的距离相等.27.(2024•广安)下面有4张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长都是1,请在方格纸中分别画出符合要求的图形,所画图形各顶点必须与方格纸中小正方形的顶点重合,具体要求如下:(1)画一个直角边长为4,面积为6的直角三角形.(2)画一个底边长为4,面积为8的等腰三角形.(3)画一个面积为5的等腰直角三角形.(4)画一个一边长为2,面积为6的等腰三角形.28.(2024•河南)如图,反比例函数y(x>0)的图象过格点(网格线的交点)P.(1)求反比例函数的解析式;(2)在图中用直尺和2B铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:①四个顶点均在格点上,且其中两个顶点分别是点O,点P;②矩形的面积等于k的值.29.(2024•湖北)图①、图②都是由边长为1的小菱形构成的网格,每个小菱形的顶点称为格点.点O,M,N,A,B均在格点上,请仅用无刻度直尺在网格中完成下列画图.(1)在图①中,画出∠MON的平分线OP;(2)在图②中,画一个Rt△ABC,使点C在格点上.30.(2024•宁波)在5×3的方格纸中,△ABC的三个顶点都在格点上.(1)在图1中画出线段BD,使BD∥AC,其中D是格点;(2)在图2中画出线段BE,使BE⊥AC,其中E是格点.31.(2024•济宁)在一次数学活动课中,某数学小组探究求环形花坛(如图所示)面积的方法,现有以下工具;①卷尺;②直棒EF;③T型尺(CD所在的直线垂直平分线段AB).(1)在图1中,请你画出用T形尺找大圆圆心的示意图(保留画图痕迹,不写画法);(2)如图2,小华说:“我只用一根直棒和一个卷尺就可以求出环形花坛的面积,具体做法如下:将直棒放置到与小圆相切,用卷尺量出此时直棒与大圆两交点M,N之间的距离,就可求出环形花坛的面积.”如果测得MN=10m,请你求出这个环形花坛的面积.32.(2024•金华)如图,在6×6的网格中,每个小正方形的边长为1,点A在格点(小正方形的顶点)上.试在各网格中画出顶点在格点上,面积为6,且符合相应条件的图形.。
(完整)尺规作图专题详尽归纳,推荐文档

(完整)尺规作图专题详尽归纳,推荐⽂档考点名称:尺规作图【学习⽬标】1.了解什么是尺规作图.2.学会⽤尺规作图法完成下列五种基本作图:(1)画⼀条线段等于已知线段;(2)画⼀个⾓等于已知⾓;(3)画线段的垂直平分线;(4)过已知点画已知直线的垂线;(5)画⾓平分线.3.了解五种基本作图的理由.4.学会使⽤精练、准确的作图语⾔叙述画图过程.5.学会利⽤基本作图画三⾓形等较简单的图形.6.通过画图认识图形的本质,体会图形的内在美.【基础知识精讲】1.尺规作图:①定义:限定只⽤直尺和圆规来完成的画图,称为尺规作图.注意:这⾥所指的直尺是没有刻度的直尺,由于免去了度量,因此,⽤尺规作图法画出的图形的精确度更⾼,它在⼯程绘图等领域应⽤⽐较⼴泛.②步骤:(1)根据给出的条件和求作的图形,写出已知和求作部分;(2)分析作图的⽅法和过程;(3)⽤直尺和圆规进⾏作图; (4)写出作法步骤,即作法。
(根据题⽬要求来定是否需要写出作法)2.尺规作图中的最基本、最常⽤的作图称为基本作图.任何尺规作图的步骤均可分解为以下五种.3.基本作图共有五种:(1)画⼀条线段等于已知线段.如图24-4-1,已知线段DE.求作:⼀条线段等于已知线段.作法:①先画射线AB.②然后⽤圆规在射线AB上截取AC=MN.线段AC就是所要作的线段.(2)作⼀个⾓等于已知⾓.如图24-4-2,已知∠AOB.求作:∠A′O′B′,使∠A′O′B′=∠AOB.作法:①作射线O′A′;②以点O为圆⼼,以任意长为半径作弧,交OA于C,交OB于D.③以点O′为圆⼼,以OC长为半径作弧,交O′A′于C′.④以点C′为圆⼼,以CD为半径作弧,交前弧于D′.⑤经过点D′作射线O′B′,∠A′O′B′就是所求的⾓.(3)作线段的垂直平分线.如图24-4-3,已知线段AB.求作:线段AB的垂直平分线.作法:①分别以点A和点B为圆⼼,⼤于的长为半径作弧,两弧相交于点C和D.②作直线CD.直线CD就是线段AB的垂直平分线.注意:直线CD与线段AB的交点,就是AB的中点.(4)经过⼀点作已知直线的垂线.a.经过已知直线上的⼀点作这条直线的垂线,如图24-4-4.已知:直线AB和AB上⼀点C,求作:AB的垂线,使它经过点C.作法:作平⾓ACB的平分线CF.直线CF就是所求的垂线,如图24-4-4.b.经过已知直线外⼀点作这条直线的垂线.如图24-4-5,已知:直线AB和AB外⼀点C.求作:AB的垂线,使它经过点C.作法:①任意取⼀点K,使K和C在AB的两旁.②以C为圆⼼,CK长为半径作弧,交AB于点D和E.③分别以D和E为圆⼼,⼤于的长为半径作弧,两弧交于点F.④作直线CF.直线CF就是所求的垂线.注意:经过已知直线上的⼀点,作这条直线的垂线转化成画线段垂直平分线的⽅法解决.(5)平分已知⾓.如图24-4-6,已知∠AOB.求作:射线OC,使∠AOC=∠BOC.作法:①在OA和OB上,分别截取OD、OE.②分别以D、E为圆⼼,⼤于的长为半径作弧,在∠AOB内,两弧交于点C.③作射线OC.OC就是所求的射线.注意:以上五种基本作图是尺规作图的基础,⼀些复杂的尺规作图,都是由基本作图组成的,同学扪要⾼度重视,努⼒把这部分内容学习好.通过这⼀节的学习,同学们要掌握下列作图语⾔:(1)过点×和点×画射线××,或画射线××.(2)在射线××上截取××=××.(3)以点×为圆⼼,××为半径画弧.(4)以点×为圆⼼,××为半径画弧,交××于点×.(5)分别以点×,点×为圆⼼,以××,××为半径作弧,两弧相交于点×.(6)在射线××上依次截取××=××=××.(7)在∠×××的外部或内部画∠×××=∠×××.注意:学过基本作图后,在作较复杂图时,属于基本作图的地⽅,不必重复作图的详细过程,只⽤⼀句话概括叙述就可以了.如:(1)画线段××=××.(2)画∠×××=∠×××.(3)画××平分∠×××,或画∠×××的⾓平分线.(4)过点×画××⊥××,垂⾜为点×.(5)作线段××的垂直平分线××,等等.但要注意保留全部的作图痕迹,包括基本作图的操作程序,不能因为作法的叙述省略⽽作图就不按程序操作,只有保留作图痕迹,才能反映出作图的操作是否合理.【经典例题精讲】例1已知两边及其夹⾓,求作三⾓形.如图24-4-7,已知:∠α,线段a、b,求作:△ABC,使∠A=∠α,AB=a,AC=b.作法:①作∠MAN=∠α.②在射线AM、AN上分别作线段AB=a,AC=b.③连结BC.如图24-4-8,△ABC即为所求作的三⾓形.注意:⼀般⼏何作图题,应有下⾯⼏个步骤:已知、求作、作法,⽐较复杂的作图题,在作图之前可根据需要作⼀些分析.例2如图24-4-9,已知底边a,底边上的⾼h,求作等腰三⾓形.已知线段a、h.求作:△ABC,使AB=AC,且BC=a,⾼AD=h.分析:可先作出底边BC,根据等腰三⾓形的三线合⼀的性质,可再作出BC的垂直平分线,从⽽作出BC边上的⾼AD,分别连结AB和AC,即可作出等腰△ABC来.作法:(1)作线段BC=a.(2)作线段BC的垂直平分线MN,MN与BC交于点D.(3)在MN上截取DA,使DA=h.(4)连结AB、AC.如图24-4-10,△ABC即为所求的等腰三⾓形.例3已知三⾓形的⼀边及这边上的中线和⾼,作三⾓形.如图24-4-11,已知线段a,m,h(m>h).求作:△ABC使它的⼀边等于a,这边上的中线和⾼分别等于m和h(m>h).分析:如图24-4-12,假定△ABC已作出,其中BC=a,中线AD=m,⾼AE=h,在△AED中AD=m,AE=h,∠AED=90°,因此这个Rt△AED可以作出来(△AED为奠基三⾓形).当Rt△AED作出后,由的关系可作出点B和点C,于是△ABC即可得到.作法:(1)作△AED,使∠AED=90°,AE=h,AD=m.(2)延长ED到B,使.(3)在DE或BE的延长线上取.(4)连结AB、AC.则△ABC即为所求作的三⾓形.注意:因为三⾓形中,⼀边上的⾼不能⼤于这边上的中线,所以如果h>m,作图题⽆解;若m=h,则作出的图形为等腰三⾓形.例4如图24-4-13,已知线段a.求作:菱形ABCD,使其半周长为a,两邻⾓之⽐为1∶2.分析:因为菱形四边相等,“半周长为a”就是菱形边长为,为此⾸先要将线段a等分,⼜因为菱形对边平⾏,则同旁内⾓互补,由“邻⾓之⽐为1∶2”可知,菱形较⼩内⾓为60°,则菱形较短对⾓线将菱形分成两个全等的等边三⾓形.所以作图时只要作出两个有公共边的等边三⾓形,则得到的四边形即为所求的菱形ABCD.作法:(1)作线段a的垂直平分线,等分线段a.(2)作线段AC,使.(3)分别以A、C为圆⼼,为半径,在AC的两侧画弧,两弧分别交于B,D.(4)分别连结AB、BC、CD、DA得到四边形ABCD,则四边形ABCD为所求作的菱形(如图24-4-14).注意:这种通过先画三⾓形,然后再画出全部图形的⽅法即为“三⾓形奠基法”.例5如图24-4-15,已知∠AOB和C、D两点.求作⼀点P,使PC=PD,且使点P到∠AOB的两边OA、OB的距离相等.分析:要使PC=PD,则点P在CD的垂直平分线上,要使点P到∠AOB的两边距离相等,则P应在∠AOB的⾓平分线上,那么满⾜题设的P点就是垂直平分线与⾓平分线的交点了.作法:(1)连结CD.(2)作线段CD的中垂线l.(3)作∠AOB的⾓平分线OM,交l于点P,P点为所求.注意:这类定点问题应需确定两线,两直线的交点即为定点,当然这两直线应分别满⾜题⽬的不同要求.【中考考点】例6 (2000·安徽省)如图24-4-16,直线表⽰三条相互交叉的公路,现要建⼀个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A.⼀处 B.⼆处C.三处 D.四处分析:到直线距离相等的点在相交所构成的⾓的平分线上,可利⽤作⾓平分线的⽅法找到这些点.解:分别作相交所构成的⾓平分线,共可作出六条,三条⾓平分线相交的交点共有四个.答案:D.注意:本题应⽤了⾓平分线的性质,在具体作图时,不可只作出位于中⼼位置的⼀处,⽽要全⾯考虑其他满⾜条件的点.例7 (2002·陕西省)如图24-4-17,△ABC是⼀块直⾓三⾓形余料,∠C=90°,⼯⼈师傅要把它加⼯成—个正⽅形零件,使C为正⽅形的—个顶点,其他三个顶点分别在AB、BC、AC边上.(1)试协助⼯⼈师傅⽤尺规画出裁割线(不写作法,保留作图痕迹);(2)⼯⼈师傅测得AC=80 cm,BC=120cm,请帮助⼯⼈师傅算出按(1)题所画裁割线加⼯成的正⽅形零件的边长.解:(1)作∠ACB的平分线与AB的交点E即为正⽅形—顶点,作CE线段的中垂线HK 与AC、BC的交点F、D即为所作正⽅形另两个顶点,如图24-4-17.(2)设这个正⽅形零件的边长为x cm,∵DE∥AC,∴,∴.∴x=48.答:这个正⽅形零件的边长为48cm.注意:本题是⼏何作图和⼏何计算相结合题⽬,要求读者对基本作图务必掌握,同时对作出图形的性质要清楚.例8 (2002·⼭西省)如图24-4-18①,有⼀破残的轮⽚(不⼩于半个轮),现要制作⼀个与原轮⽚同样⼤⼩的圆形零件,请你根据所学的有关知识,设计两种⽅案,确定这个圆形零件的半径.分析:欲确定这个圆形零件的半径,可以借助三⾓板,T形尺或尺规作图均可,图②中是这个零件的半径,图③中OB是这个零件半径.解:如图24-4-18②③所⽰.【常见错误分析】例9如图24-4-19,已知线段a、b、h.求作△ABC,使BC=a,AC=b,BC边上的⾼AD=h.并回答问题,你作出的三⾓形唯⼀吗?从中你可以得到什么结论呢?错解:(1)作法:①作Rt△ADC,使AD=h,AC=b.②在直线CD上截取CB=a.如图24-4-20,则△ABC就是所求作的三⾓形.(2)作出的三⾓形唯⼀.(3)得出结论:有两边及⼀边上的⾼对应相等的两三⾓形全等.误区分析:本题错解在于忽略了三⾓形的⾼可能在三⾓形内部也可能在三⾓形的外部.正解:如图24-4-21,作法:①作Rt△ADC,使AD=h,AC=b.②在直线CD上截取CB=a(在点C的两侧).则△ABC,△AB′C都是所求作三⾓形.(2)作出的三⾓形不唯⼀.(3)得出结论有两边及—边上的⾼对应相等的两三⾓形不⼀定全等.注意:与三⾓形的⾼有关的题⽬应慎之⼜慎.【学习⽅法指导】学习基本作图,主要是运⽤观察法,通过具体的操作,了解各种基本作图的步骤,掌握作图语⾔.【规律总结】画复杂的图形时,如⼀时找不到作法,—般是先画出⼀个符合所设条件的草图,再根据这个草图进⾏分析,逐步寻找画图步骤.有时,也可以根据已知条件和基本作图,先作局部三⾓形,再以此为基础,根据有关条件画出其余部分,从⽽完成全图,这种⽅法称为三⾓形奠基法.拓展: 1.利⽤基本作图作三⾓形:(1)已知三边作三⾓形; (2)已知两边及其夹⾓作三⾓形; (3)已知两⾓及其夹边作三⾓形; (4)已知底边及底边上的⾼作等腰三⾓形;(5)已知⼀直⾓边和斜边作直⾓三⾓形.2.与圆有关的尺规作图:(1)过不在同⼀直线上的三点作圆(即三⾓形的外接圆). (2)作三⾓形的内切圆.(3)作圆的内接正⽅形和正六边形.附件:尺规作图简史:“规”就是圆规,是⽤来画圆的⼯具,在我国古代甲⾻⽂中就有“规”这个字.“矩”就像现在⽊⼯使⽤的⾓尺,由长短两尺相交成直⾓⽽成,两者间⽤⽊杠连接以使其牢固,其中短尺叫勾,长尺叫股.矩的使⽤是我国古代的⼀个发明,⼭东历城武梁祠⽯室造像中就有“伏羲⽒⼿执矩,⼥娲⽒⼿执规”之图形.矩不仅可以画直线、直⾓,加上刻度可以测量,还可以代替圆规.甲⾻⽂中也有矩字,这可追溯到⼤禹治⽔(公元前2000年)前.《史记》卷⼆记载⼤禹治⽔时“左准绳,右规矩”.赵爽注《周髀算经》中有“禹治洪⽔,……望⼭川之形,定⾼下之势,……乃勾股之所由⽣也.”意即禹治洪⽔,要先测量地势的⾼低,就必定要⽤勾股的道理.这也说明矩起源于很远的中国古代.春秋时代也有不少著作涉及规矩的论述,《墨⼦》卷七中说“轮匠(制造车⼦的⼯匠)执其规矩,以度天下之⽅圆.”《孟⼦》卷四中说“离娄(传说中⽬⼒⾮常强的⼈)之明,公输⼦(即鲁班,传说⽊匠的祖师)之巧,不以规矩,不能成⽅圆.”可见,在春秋战国时期,规矩已被⼴泛地⽤于作图、制作器具了.由于我国古代的矩上已有刻度,因此使⽤范围较⼴,具有较⼤的实⽤性.古代希腊⼈较重视规、矩在数学中训练思维和智⼒的作⽤,⽽忽视规矩的实⽤价值.因此,在作图中对规、矩的使⽤⽅法加以很多限制,提出了尺规作图问题.所谓尺规作图,就是只有限次地使⽤没有刻度的直尺和圆规进⾏作图.古希腊的安那萨哥拉斯⾸先提出作图要有尺⼨限制.他因政治上的纠葛,被关进监狱,并被判处死刑.在监狱⾥,他思考改圆成⽅以及其他有关问题,⽤来打发令⼈苦恼的⽆所事事的⽣活.他不可能有规范的作图⼯具,只能⽤⼀根绳⼦画圆,⽤随便找来的破⽊棍作直尺,当然这些尺⼦上不可能有刻度.另外,对他来说,时间是不多了,因此他很⾃然地想到要有限次地使⽤尺规解决问题.后来以理论形式具体明确这个规定的是欧⼏⾥德的《⼏何原本》.由于《⼏何原本》的巨⼤影响,希腊⼈所崇尚的尺规作图也⼀直被遵守并流传下来.由于对尺规作图的限制,使得⼀些貌似简单的⼏何作图问题⽆法解决.最著名的是被称为⼏何三⼤问题的三个古希腊古典作图难题:⽴⽅倍积问题、三等分任意⾓问题和化圆为⽅问题.当时很多有名的希腊数学家,都曾着⼒于研究这三⼤问题,虽然借助于其他⼯具或曲线,这三⼤难题都可以解决,但由于尺规作图的限制,却⼀直未能如愿以偿.以后两千年来,⽆数数学家为之绞尽脑汁,都以失败⽽告终.直到1637年笛卡尔创⽴了解析⼏何,关于尺规作图的可能性问题才有了准则.到了1837年万芝尔⾸先证明⽴⽅倍积问题和三等分任意⾓问题都属于尺规作图不可能问题.1882年林德曼证明了π是⽆理数,化圆为⽅问题不可能⽤尺规作图解决,这才结束了历时两千年的数学难题公案.。
初一数学尺规作图(可编辑修改word版)

POQ的线段长【知识回顾】七年级数学期末复习资料(七)尺规作图1、尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。
最基本,最常用的尺规作 图,通常称基本作图。
一些复杂的尺规作图都是由基本作图组成的。
2、五种基本作图:1、作一条线段等于已知线段;2、作一个角等于已知角;3、作已知线段的垂直平分线;4、作已知角的角平分线;5、过一点作已知直线的垂线;(1)题目一:作一条线段等于已知线段。
已知:如图,线段 a .a求作:线段 AB ,使 AB = a . 作法:(1) 作射线 AP ;A(2) 在射线 AP 上截取 AB=a . 则线段 AB 就是所求作的图形。
(2) 题目二:作已知线段的中点。
已知:如图,线段 MN.求作:点 O ,使 MO=NO (即 O 是 MN 的中点). 作法:(1)分别以 M 、N 为圆心,大于MN的相同线段为半径画弧, 两弧相交于 P ,Q ; (2)连接 PQ 交 MN 于 O .则点 O 就是所求作的MN的中点。
(3) 题目三:作已知角的角平分线。
已知:如图,∠AOB,求作:射线 OP, 使∠AOP=∠BOP(即 OP 平分∠AOB)。
作法:(1) 以 O 为圆心,任意长度为半径画弧,分别交 OA ,OB 于 M ,N ;(2) 分别以 M 、N为圆心,大于为半径画弧,两弧交∠AOB 内于P; (3) 作射线 OP 。
则射线 OP 就是∠AOB 的角平分线。
BPA MPON B(4) 题目四:作一个角等于已知角。
已知:如图,∠AOB。
求作:∠A’O’B’,使 A’O’B’=∠AOB①①①作法: (1) 作射线 O’A’; (2) 以 O 为圆心,任意长度为半径画弧,交 OA 于 M ,交 OB 于 N ;(3) 以 O’为圆心,以 OM 的长为半径画弧,交 O’A’于 M ’; (4) 以 M’为圆心,以 MN 的长为半径画弧,交前弧于 N ’; (5) 连接 O’N’并延长到 B ’。
中考数学知识点复习:尺规作图全面版

如何利用尺规作图解决最值问题?
最值问题的求解
最值问题是一类求解最优解的问题,可以利用尺规作图来解决。例如,在几何、代数等领域中,经常需要使用尺规作 图来求解最值问题。
作图方法
利用尺规作图求解最值问题,需要先了解问题的具体内容,然后根据问题内容进行尺规作图。在作图过程中,需要注 意图形绘制的准确性和规范性,以保证求解的准确性。
03
多边形的尺规作图
作已知线段的垂线
01
总结词:通过一个已知点,作 已知线段的垂线,是尺规作图
的基础。
02
详细描述
03
04
1. 分别以线段的两个端点为 圆心,以大于线段的一半为半 径画圆弧,得到两个交点。
2. 连接两个交点,得到的直 线即为已知线段的垂线。
已知二线段平行的垂线段的中垂线
总结词:找到一个已知的平行线段的中垂线,是尺规作 图的进阶技能。
1. 以平行线段的一个端点为圆心,以适当长度为半径画 圆弧,与平行线段相交于两点。
详细描述
2. 连接这两个交点得到的直线即为已知平行线段的中垂 线。
作已知直线的平行线
01
总结词:通过一个已知点,作已知直线的平行线,是尺规作图的基本 技能之一。
02
详细描述
03
1. 以已知点为圆心,以适当长度为半径画圆弧,与直线相交于两点。
04
2. 连接这两个交点得到的直线即为已知直线的平行线。
作已知二线段的中垂线
01 总结词:通过两个已知点,作已知二线段 的中垂线,是尺规作图的高级技能。
02
详细描述
Hale Waihona Puke 031. 以两个已知点为圆心,以适当长度为半 径画圆弧,得到两个交点。
04
初中尺规作图详细讲解含图

初中数学尺规作图讲解初等平面几何研究的对象,仅限于直线、圆以及由它们(或一部分)所组成的图形,因此作图的工具,习惯上使用没有刻度的直尺和圆规两种.限用直尺和圆规来完成的作图方法,叫做尺规作图法.最简单的尺规作图有如下三条:⑴经过两已知点可以画一条直线;⑵已知圆心和半径可以作一圆;⑶两已知直线;一已知直线和一已知圆;或两已知圆,如果相交,可以求出交点;以上三条,叫做作图公法.用直尺可以画出第一条公法所说的直线;用圆规可以作出第二条公法所说的圆;用直尺和圆规可以求得第三条公法所说的交点.一个作图题,不管多么复杂,如果能反复应用上述三条作图公法,经过有限的次数,作出适合条件的图形,这样的作图题就叫做尺规作图可能问题;否则,就称为尺规作图不能问题.历史上,最着名的尺规作图不能问题是:⑴三等分角问题:三等分一个任意角;⑵倍立方问题:作一个立方体,使它的体积是已知立方体的体积的两倍;⑶化圆为方问题:作一个正方形,使它的面积等于已知圆的面积.这三个问题后被称为“几何作图三大问题”.直至1837年,万芝尔(Pierre Laurent Wantzel)首先证明三等分角问题和立方倍积问题属尺规作图不能问题;1882年,德国数学家林德曼(Ferdinand Lindemann)证明π是一个超越数(即π是一个不满足任何整系数代数方程的实数),由此即可推得根r=时所求正方形的边长)不可能用尺规作出,从而也就证明了化圆为方问题是一个尺号π(即当圆半径1规作图不能问题.若干着名的尺规作图已知是不可能的,而当中很多不可能证明是利用了由19世纪出现的伽罗华理论.尽管如此,仍有很多业余爱好者尝试这些不可能的题目,当中以化圆为方及三等分任意角最受注意.数学家Underwood Dudley曾把一些宣告解决了这些不可能问题的错误作法结集成书.还有另外两个着名问题:⑴正多边形作法·只使用直尺和圆规,作正五边形.·只使用直尺和圆规,作正六边形.·只使用直尺和圆规,作正七边形——这个看上去非常简单的题目,曾经使许多着名数学家都束手无策,因为正七边形是不能由尺规作出的.·只使用直尺和圆规,作正九边形,此图也不能作出来,因为单用直尺和圆规,是不足以把一个角分成三等份的.·问题的解决:高斯,大学二年级时得出正十七边形的尺规作图法,并给出了可用尺规作图的正多边形的条件:尺规作图正多边形的边数目必须是2的非负整数次方和不同的费马素数的积,解决了两千年来悬而未决的难题.⑵四等分圆周只准许使用圆规,将一个已知圆心的圆周4等分.这个问题传言是拿破仑·波拿巴出的,向全法国数学家的挑战.尺规作图的相关延伸:用生锈圆规(即半径固定的圆规)作图1.只用直尺及生锈圆规作正五边形==.2.生锈圆规作图,已知两点A、B,找出一点C使得AB BC CA3.已知两点A、B,只用半径固定的圆规,求作C使C是线段AB的中点.4.尺规作图,是古希腊人按“尽可能简单”这个思想出发的,能更简洁的表达吗?顺着这思路就有了更简洁的表达.10世纪时,有数学家提出用直尺和半径固定的圆规作图. 1672年,有人证明:如果把“作直线”解释为“作出直线上的2点”,那么凡是尺规能作的,单用圆规也能作出!从已知点作出新点的几种情况:两弧交点、直线与弧交点、两直线交点 ,在已有一个圆的情况下,那么凡是尺规能作的,单用直尺也能作出!.五种基本作图:初中数学的五种基本尺规作图为:1.做一线段等于已知线段 2.做一角等于已知角 3.做一角的角平分线4.过一点做一已知线段的垂线5.做一线段的中垂线下面介绍几种常见的尺规作图方法:⑴ 轨迹交点法:解作图题的一种常见方法.解作图题常归结到确定某一个点的位置.如果这两个点的位置是由两个条件确定的,先放弃其中一个条件,那么这个点的位置就不确定而形成一个轨迹;若改变放弃另一个条件,这个点就在另一条轨迹上,故此点便是两个轨迹的交点.这个利用轨迹的交点来解作图题的方法称为轨迹交点法,或称交轨法、轨迹交截法、轨迹法.【例1】 电信部门要修建一座电视信号发射塔,如下图,按照设计要求,发射塔到两个城镇A 、B 的距离必须相等,到两条高速公路m 、n 的距离也必须相等,发射塔P 应修建在什么位置?【分析】 这是一道实际应用题,关键是转化成数学问题,根据题意知道,点P 应满足两个条件,一是在线段AB 的垂直平分线上;二是在两条公路夹角的平分线上,所以点P 应是它们的交点.【解析】 ⑴ 作两条公路夹角的平分线OD 或OE ;⑵ 作线段AB 的垂直平分线FG ;则射线OD ,OE 与直线FG 的交点1C ,2C 就是发射塔的位置.【例2】 在平面直角坐标系中,点A 的坐标是(4,0),O 是坐标原点,在直线3y x =+上求一点P ,使AOP ∆是等腰三角形,这样的P 点有几个?【解析】 首先要清楚点P 需满足两个条件,一是点P 在3y x =+上;二是AOP ∆必须是等腰三角形.其次,寻找P 点要分情况讨论,也就是当OA OP =时,以O 点为圆心,OA 为半径画圆,与直线有两个点1P 、2P ;当OA AP =时,以A 点为圆心,OA 为半径画圆,与直线无交点;当PO PA =时,作OA 的垂直平分线,与直线有一交点3P ,所以总计这样的P 点有3个.【例3】 设O ⊙与'O ⊙相离,半径分别为R 与'R ,求作半径为r 的圆,使其与O ⊙及'O ⊙外切.【分析】 设M ⊙是符合条件的圆,即其半径为r ,并与O ⊙及'O ⊙外切,显然,点M 是由两个轨迹确定的,即M 点既在以O 为圆心以R r +为半径的圆上,又在以'O 为圆心以'R r +为半径的圆上,因此所求圆的圆心的位置可确定.若O ⊙与'O ⊙相距为b ,当2r b <时,该题无解,当2r b =有唯一解;当2r b >时,有两解.【解析】 以当O ⊙与'O ⊙相距为b ,2r b >时为例:⑴ 作线段OA R r =+,''O B R r =+.⑵ 分别以O ,'O 为圆心,以R r +,'R r +为半径作圆,两圆交于12,M M 两点.⑶ 连接1OM ,2OM ,分别交以R 为半径的O ⊙于D 、C 两点.⑷ 分别以12M M ,为圆心,以r 为半径作圆.∴12,M M ⊙⊙即为所求.【思考】若将例3改为:“设O ⊙与'O ⊙相离,半径分别为R 与'R ,求作半径为r ()r R >的圆,使其与O ⊙ 内切,与'O ⊙外切.”又该怎么作图?⑵ 代数作图法:解作图题时,往往首先归纳为求出某一线段长,而这线段长的表达式能用代数方法求出,然后根据线段长的表达式设计作图步骤.用这种方法作图称为代数作图法.【例4】 只用圆规,不许用直尺,四等分圆周(已知圆心).【分析】 设半径为1.,也就是说用这个长度去等分圆周.我们的任务就是做出这个长度..设法构造斜边为1的的长度自然就出来了.【解析】 具体做法:⑴ 随便画一个圆.设半径为1.⑵ 先六等分圆周.⑶ 以这个距离为半径,分别以两个相对的等分点为圆心,同向作弧,交于一点.(“两个相对的等分点”其实就是直径的两端点啦!两弧交点与“两个相对的等分点”形成的是一个底为2.)⑷【例5】 求作一正方形,使其面积等于已知ABC ∆的面积.【分析】 设ABC ∆的底边长为a ,高为h ,关键是在于求出正方形的边长x ,使得212x ah =,所以x 是12a 与h 的比例中项.【解析】 已知:在ABC ∆中,底边长为a ,这个底边上的高为h ,求作:正方形DEFG ,使得:ABC DEFG S S ∆=正方形作法:⑴ 作线段12MD a =; ⑵ 在MD 的延长线上取一点N ,使得DN h =;⑶ 取MN 中点O ,以O 为圆心,OM 为半径作O ⊙;⑷ 过D 作DE MN ⊥,交O ⊙于E ,⑸ 以DE 为一边作正方形DEFG .正方形DEFG 即为所求.【例6】 在已知直线l 上求作一点M ,使得过M 作已知半径为r 的O ⊙的切线,其切线长为a .【分析】 先利用代数方法求出点M 与圆心O 的距离d ,再以O 为圆心,d 为半径作圆,此圆与直线l的交点即为所求.【解析】 ⑴ 作Rt OAB ∆,使得:90A ∠=︒,OA r =,AB a =.⑵ 以O 为圆心,OB 为半径作圆.若此圆与直线l 相交,此时有两个交点1M ,2M .1M ,2M 即为所求.若此圆与直线l 相切,此时只有一个交点M .M 即为所求.若此圆与直线l 相离,此时无交点.即不存在这样的M 点使得过M 作已知半径为r 的O ⊙的切线,其切线长为a .⑶ 旋转法作图:有些作图题,需要将某些几何元素或图形绕某一定点旋转适当角度,以使已知图形与所求图形发生联系,从而发现作图途径.【例7】 已知:直线a 、b 、c ,且a b c ∥∥.求作:正ABC ∆,使得A 、B 、C 三点分别在直线a 、b 、c 上.【分析】 假设ABC ∆是正三角形,且顶点A 、B 、C 三点分别在直线a 、b 、c 上.作AD b ⊥于D ,将ABD ∆绕A 点逆时针旋转60︒后,置于'ACD ∆的位置,此时点'D 的位置可以确定.从而点C 也可以确定.再作60BAC ∠=︒,B 点又可以确定,故符合条件的正三角形可以作出.【解析】 作法:⑴ 在直线a 上取一点A ,过A 作AD b ⊥于点D ;⑵ 以AD 为一边作正三角形'ADD ;⑶ 过'D 作''D C AD ⊥,交直线c 于C ;⑷ 以A 为圆心,AC 为半径作弧,交b 于B (使B 与'D 在AC 异侧).⑸ 连接AB 、AC 、BC 得ABC ∆.ABC ∆即为所求.【例8】 已知:如图,P 为AOB ∠角平分线OM 上一点.求作:PCD ∆,使得90P ∠=︒,PC PD =,且C 在OA 上,D 在OB 上.【解析】 ⑴ 过P 作PE OB ⊥于E .⑵ 过P 作直线l OB ∥;⑶ 在直线l 上取一点M ,使得PM PE =(或'PM PE =);⑷ 过M (或'M )作MC l ⊥(或'M C l ⊥),交OA 于C (或'C )点;⑸ 连接PC (或'PC ),过P 作PD PC ⊥(或''PD PC ⊥)交OB 于D (或'D )点. 连接,PD CD (或',''PD C D ).则PCD ∆(或''PC D ∆)即为所求.⑷ 位似法作图:利用位似变换作图,要作出满足某些条件的图形,可以先放弃一两个条件,作出与其位似的图形,然后利用位似变换,将这个与其位似得图形放大或缩小,以满足全部条件,从而作出满足全部的条件.【例9】 已知:一锐角ABC ∆.求作:一正方形DEFG ,使得D 、E 在BC 边上,F 在AC 边上,G 在AB 边上.【分析】 先放弃一个顶点F 在AC 边上的条件,作出与正方形DEFG 位似的正方形''''D E F G ,然后利用位似变换将正方形''''D E F G 放大(或缩小)得到满足全部条件的正方形DEFG .【解析】 作法:⑴ 在AB 边上任取一点'G ,过'G 作''G D BC ⊥于'D⑵ 以''G D 为一边作正方形''''D E F G ,且使'E 在'BD 的延长线上.⑶ 作直线'BF 交AC 于F .⑷ 过F 分别作''FG F G ∥交AB 于G ;作''FE F E ∥交BC 于E .⑸ 过G 作''GD G D ∥交BC 于D .则四边形DEFG 即为所求.⑸ 面积割补法作图:对于等积变形的作图题,通常在给定图形或某一确定图形上割下一个三角形,再借助平行线补上一个等底等高的另一个三角形,使面积不变,从而完成所作图形.【例10】 如图,过ABC ∆的底边BC 上一定点,P ,求作一直线l ,使其平分ABC ∆的面积.【分析】 因为中线AM 平分ABC ∆的面积,所以首先作中线AM ,假设PQ 平分ABC ∆的面积,在AMC ∆中先割去AMP ∆,再补上ANP ∆.只要NM AP ∥,则AMP ∆和AMP ∆就同底等高,此时它们的面积就相等了.所以PN 就平分了ABC ∆的面积.【解析】 作法:⑴ 取BC 中点M ,连接,AM AP ;⑵ 过M 作MN AP ∥交AB 于N ;⑶ 过P 、N 作直线l .直线l 即为所求.【例11】 如图:五边形ABCDE 可以看成是由一个直角梯形和一个矩形构成.⑴ 请你作一条直线l ,使直线l 平分五边形ABCDE 的面积;⑵ 这样的直线有多少条?请你用语言描述出这样的直线.【解析】 ⑴ 取梯形AFDE 的中位线MN 的中点O ,再取矩形BCDF 对角线的交点'O ,则经过点O ,'O 的直线l 即为所求;⑵ 这样的直线有无数条.设⑴中的直线l 交AE 于Q ,交BC 于R ,过线段RQ 中点P ,且与线段AE 、BC 均有交点的直线均可平分五边形ABCDE 的面积.【例12】 (07江苏连云港)如图1,点C 将线段AB 分成两部分,如果AC BC AB AC=,那么称点C 为线段AB 的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l 将一个面积为S 的图形分成两部分,这两部分的面积分别为1S ,2S ,如果121S S S S =,那么称直线l 为该图形的黄金分割线. ⑴ 研究小组猜想:在ABC △中,若点D 为AB 边上的黄金分割点(如图2),则直线CD 是ABC △的黄金分割线.你认为对吗?为什么?⑵ 请你说明:三角形的中线是否也是该三角形的黄金分割线?⑶ 研究小组在进一步探究中发现:过点C 任作一条直线交AB 于点E ,再过点D 作直线DF CE ∥,交AC 于点F ,连接EF (如图3),则直线EF 也是ABC △的黄金分割线.请你说明理由.⑷ 如图4,点E 是ABCD 的边AB 的黄金分割点,过点E 作EF AD ∥,交DC 于点F ,显然直线EF 是ABCD 的黄金分割线.请你画一条ABCD 的黄金分割线,使它不经过ABCD 各边黄金分割点. 【解析】 ⑴ 直线CD 是ABC △的黄金分割线.理由如下: 设ABC △的边AB 上的高为h . 12ADC S AD h=△,12BDC S BD h =△,12ABC S AB h =△, ∴ADC ABC S AD S AB =△△,BDC ADC S BD S AD=△△. 又∵点D 为边AB 的黄金分割点,∴AD BD AB AD =.∴ADC BDC ABC ADC S S S S =△△△△.∴直线CD 是ABC △的黄金分割线.⑵ ∵三角形的中线将三角形分成面积相等的两部分,此时1212S S S ==,即121S S S S ≠, ∴三角形的中线不可能是该三角形的黄金分割线.⑶ ∵DF CE ∥,∴DEC △和FCE △的公共边CE 上的高也相等,∴DEC FCE S S =△△.A CB 图1 ADB 图2C AD B 图3 C FE 图4设直线EF 与CD 交于点G ,∴DGE FGC S S =△△. ∴ADC FGC AFGD S S S =+△△四边形DGE AEF AFGD S S S =+=△△四边形,BDC BEFC S S =△四边形. 又∵ADC BDC ABC ADC S S S S =△△△△,∴BEFC AEF ABC AEF S S S S =四边形△△△. ∴直线EF 也是ABC △的黄金分割线.⑷ 画法不惟一,现提供两种画法; 画法一:如答图1,取EF 中点G ,再过点G 作一直线分别交AB ,DC 于M ,N 点,则直线MN 就是ABCD 的黄金分割线.画法二:如答图2,在DF 上取一点N ,连接EN ,再过点F 作FM NE ∥交AB 于点M ,连接MN ,则直线MN 就是ABCD 的黄金分割线.E M (答案图1)E M (答案图2)。
2024年中考数学一轮复习考点精析与真题精讲—尺规作图

2024年中考数学一轮复习考点精析与真题精讲—尺规作图→➊考点精析←一、尺规作图1.尺规作图的定义:在几何里,把限定用没有刻度的直尺和圆规来画图称为尺规作图.2.五种基本作图1)作一条线段等于已知线段;2)作一个角等于已知角;3)作一个角的平分线;4)作一条线段的垂直平分线;5)过一点作已知直线的垂线.3.根据基本作图作三角形1)已知三角形的三边,求作三角形;2)已知三角形的两边及其夹角,求作三角形;3)已知三角形的两角及其夹边,求作三角形;4)已知三角形的两角及其中一角的对边,求作三角形;5)已知直角三角形一直角边和斜边,求作直角三角形.4.与圆有关的尺规作图1)过不在同一直线上的三点作圆(即三角形的外接圆);2)作三角形的内切圆.5.有关中心对称或轴对称的作图以及设计图案是中考常见类型.6.作图题的一般步骤(1)已知;(2)求作;(3)分析;(4)作法;(5)证明;(6)讨论.其中步骤(3)(4)(5)(6)一般不作要求,但作图中一定要保留作图痕迹.二、尺规作图的方法1.尺规作图的关键1)先分析题目,读懂题意,判断题目要求作什么;2)读懂题意后,再运用几种基本作图方法解决问题.2.根据已知条件作等腰三角形或直角三角形求作三角形的关键是确定三角形的三个顶点,作图依据是三角形全等的判定,常借助基本作图来完成,如作直角三角形就先作一个直角.尺规作图是指用没有刻度的直尺和圆规作图。
尺规作图可以作出许多基本图形,如线段、角、等腰三角形、矩形、正方形、正五边形、正六边形等。
一、平行线的尺规作法:已知直线a和直线外一点A,过点A作已知直线的平行线b。
1.用直尺以点A为圆心,适当长为半径画弧,交直线a于点C和点D。
2.分别以点C、D为圆心,大于二分之一CD的长为半径画弧,两弧相交于点E。
3.连接AE,并延长AE交直线b于点B。
4.直线AB就是所求作的平行线。
已知直线a和直线外一点A,过点A作已知直线的平行线b。
尺规作图总结
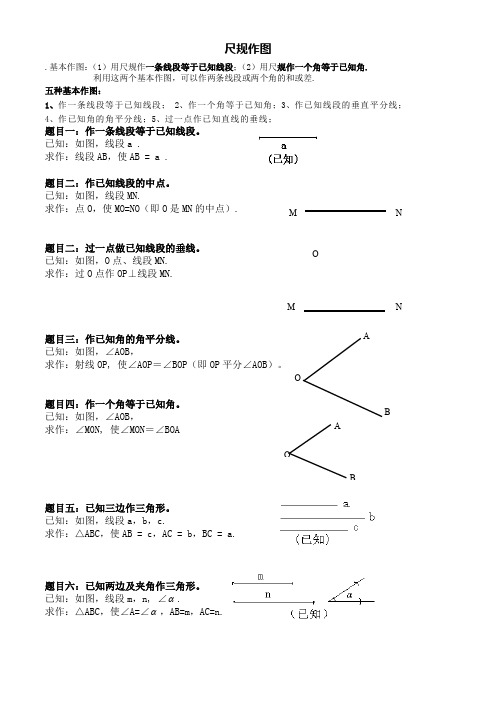
尺规作图.基本作图:(1)用尺规作一条线段等于已知线段;(2)用尺规作一个角等于已知角.利用这两个基本作图,可以作两条线段或两个角的和或差. 五种基本作图:1、作一条线段等于已知线段;2、作一个角等于已知角;3、作已知线段的垂直平分线;4、作已知角的角平分线;5、过一点作已知直线的垂线;题目一:作一条线段等于已知线段。
已知:如图,线段a .求作:线段AB ,使AB = a .题目二:作已知线段的中点。
已知:如图,线段MN.求作:点O ,使MO=NO (即O 是MN 的中点).题目二:过一点做已知线段的垂线。
已知:如图,O 点、线段MN.求作:过O 点作OP ⊥线段MN.题目三:作已知角的角平分线。
已知:如图,∠AOB ,求作:射线OP, 使∠AOP =∠BOP (即OP 平分∠AOB )。
题目四:作一个角等于已知角。
已知:如图,∠AOB ,求作:∠M0N, 使∠MON =∠BOA题目五:已知三边作三角形。
已知:如图,线段a ,b ,c.求作:△ABC ,使AB = c ,AC = b ,BC = a.题目六:已知两边及夹角作三角形。
已知:如图,线段m ,n, ∠α.求作:△ABC,使∠A=∠α,AB=m ,AC=n.M N O A B O A BM N O题目七:已知两角及夹边作三角形。
已知:如图,∠α,∠β,线段m .求作:△ABC,使∠A=∠α,∠B=∠β,AB=m.题目八:已知一个三角形,作一个点到各个顶点距离相等已知:如图,△ABC求作:一个点到三个顶点的距离相等题目九:已知一个三角形,做一个点到三边的距离相等已知:如图,△ABC求作:一个点到三条边的距离相等。
初中尺规作图典型例题归纳1、如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.(1)用尺规作图方法,作∠ADC的平分线DN;(保留作图痕迹,不写作法和证明)2、如图,△ABC是等腰三角形,AB=AC。
知识清单24 尺规作图-2020年中考数学知识清单大全25讲(附例释)

知识清单24:尺规作图1. 尺规作图2. 五种基本尺规作图3. 尺规作图的转化4. 尺规作图依据1.尺规作图在几何里,把限定用无刻度的直尺和圆规来画图,称作尺规作图.2.五种基本尺规作图(1)作一条线段等于已知线段; (2)作一个角等于已知角; (3)作已知角的角平分线 (4)经过一点作一直直线的垂线; (5)作线段的垂直平分线.3.尺规作图的转化——复杂尺规作图(1)作线段之间的和差倍数关系; (2)作角度之间的和差倍数关系;(3)运用基本作图确定满足条件的特殊位置的点; (4)作平行线:过直线外一点作已知直线的平行线; (5)作三角形中线/高线:作一个角等于已知角;(6)作三角形:利用全等判定条件作与已知三角形全等的全等三角形; (7)作等腰/等边三角形:以已知线段为边作等腰或等边三角形; (8)作切线:过圆上/外一点作已知圆的切线;(9)作外接圆/内切圆:作已知三角形的外接圆和内切圆; (10)利用中心对称性作一套直线将已知图形面积/周长均分为两份.4.尺规作图的作图依据通常尺规作图的依据为常见的公理、定理以及基本图形的性质及其 判定定理等.(3)一块方角形钢板如图所示,请你根据中心对称的性质用一条直线将它分为面积相等的两部分(不写作法,保留痕迹,在图中直接名师点睛:(1)已知:∠α,直线l 及l 上两点A ,B .求作:Rt∠ABC ,使点C 在直线l 的上方,且∠ABC=90°,∠BAC=∠α.答案:(2)下面是小明设计的“作三角形一边上的高”的尺规作图过程.如图,已知钝角△ABC ,依下列步骤用尺规作图,并保留作图痕迹.步骤1:以C 为圆心,CA 为半径画弧①;步骤2:以B 为圆心,BA 为半径画弧②,交弧①于点D ; 步骤3:连接AD ,交BC 延长线于点H ,则AH 即为所求. 作图依据:_____.答案:与线段两个端点距离相等的点在这条线段的垂直平分线上;两点确定一条直线.画出).你还有其他的分割方法吗?(4)如图,△ABC的顶点是方格纸中的三个格点,请按要求完成下列作图:①仅用无刻度直尺,且不能用直尺中的直角;②保留作图痕迹﹒(1)在图1中画出AC边上的点D,使得CD=2AD;(2)在图2中画出△ABC的重心G(5)如图,有3条公路a、b、c两两相交,现在要修建加气站,使得加气站到3条公路的距离都相等.(1)满足条件的加气站共有____处.(2)请你找出加气站P的位置,要求:①找出一个加气站P的位置即可;②尺规作图,保留作图痕迹,不写作法.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十四章尺规作图一、理解“尺规作图”的含义1.在几何中,我们把只限定用直尺(无刻度)和圆规来画图的方法,称为尺规作图.其中直尺只能用来作直线、线段、射线或延长线段;圆规用来作圆和圆弧.由此可知,尺规作图与一般的画图不同,一般画图可以动用一切画图工具,包括三角尺、量角器等,在操作过程中可以度量,但尺规作图在操作过程中是不允许度量成分的.2.基本作图:(1)用尺规作一条线段等于已知线段;(2)用尺规作一个角等于已知角. 利用这两个基本作图,可以作两条线段或两个角的和或差.二、熟练掌握尺规作图题的规范语言1.用直尺作图的几何语言:①过点×、点×作直线××;或作直线××;或作射线××;②连结两点××;或连结××;③延长××到点×;或延长(反向延长)××到点×,使××=××;或延长××交××于点×;2.用圆规作图的几何语言:①在××上截取××=××;②以点×为圆心,××的长为半径作圆(或弧);③以点×为圆心,××的长为半径作弧,交××于点×;④分别以点×、点×为圆心,以××、××的长为半径作弧,两弧相交于点×、×.三、了解尺规作图题的一般步骤尺规作图题的步骤:1.已知:当作图是文字语言叙述时,要学会根据文字语言用数学语言写出题目中的条件;2.求作:能根据题目写出要求作出的图形及此图形应满足的条件;3.作法:能根据作图的过程写出每一步的操作过程.当不要求写作法时,一般要保留作图痕迹.对于较复杂的作图,可先画出草图,使它同所要作的图大致相同,然后借助草图寻找作法.在目前,我们只要能够写出已知,求作,作法三步(另外还有第四步证明)就可以了,而且在许多中考作图题中,又往往只要求保留作图痕迹,不需要写出作法,可见在解作图题时,保留作图痕迹很重要.四、基本作图最基本,最常用的尺规作图,通常称基本作图。
一些复杂的尺规作图都是由基本作图组成的。
五种基本作图:1、作一条线段等于已知线段;2、作一个角等于已知角;3、作已知线段的垂直平分线;4、作已知角的角平分线;5、过一点作已知直线的垂线;1.作一条线段等于已知线段。
已知:如图,线段a .求作:线段AB ,使AB = a . 作法:(1) 作射线AP ;(2) 在射线AP 上截取AB=a . 则线段AB 就是所求作的图形。
2.作已知线段的中点。
已知:如图,线段MN.求作:点O ,使MO=NO (即O 是MN 的中点). 作法:(1)分别以M 、N 为圆心,大于的相同线段为半径画弧, 两弧相交于P ,Q ; (2)连接PQ 交MN 于O .则点O 就是所求作的MN的中点。
(试问:PQ 与MN有何关系?)3. 作已知角的角平分线。
已知:如图,∠AOB ,求作:射线OP, 使∠AOP =∠BOP (即OP 平分∠AOB )。
作法:(1)以O 为圆心,任意长度为半径画弧,分别交OA ,OB 于M ,N ;(2)分别以M 、N为圆心,大于的相同线段为半径画弧,两弧交∠AOB 内于P; (3) 作射线OP 。
则射线OP 就是∠AOB 的角平分线。
4. 作一个角等于已知角。
(请自己写出“已知”“求作”并作出图形,不写作法)五、典型题型1. 已知线段a 、b ,画一条线段,使其等于b a 2+.分析 所要画的线段等于b a 2+,实质上就是b b a ++.画法:1.画线段a AB =.2.在AB 的延长线上截取b BC 2=.线段AC 就是所画的线段.说明1.尺规作图要保留画图痕迹,画图时画出的所有点和线不可随意擦去.2.其它作图都可以通过画基本作图来完成,写画法时,只需用一句话来概括叙述基本作图.2.如下图,已知线段a 和b ,求作一条线段AD 使它的长度等于2a -b .错解 如图(1), (1)作射线AM ;(2)在射线AM 上截取AB =BC =a ,CD =b ,则线段AD 即为所求.错解分析 主要是作图语言不严密,当在射线上两次截取时,要写清是否顺次,而在求线段差时,要交待截取的方向.图(1) 图(2)正解 如图(2), (1)作射线AM ;(2)在射线AM 上,顺次截取AB =BC =a ; (3)在线段CA 上截取CD =b ,则线段AD 就是所求作的线段.3. 求作一个角等于已知角∠MON (如图1).图(1) 图(2)错解 如图(2),(1)作射线11M O ;(2)在图(1),以O 为圆心作弧,交OM 于点A ,交ON 于点B ; (3)以1O 为圆心作弧,交11M O 于C ;(4)以C 为圆心作弧,交于点D ;(5)作射线D O 1.则∠D CO 1即为所求的角.错解分析 作图过程中出现了不准确的作图语言,在作出一条弧时,应表达为:以某点为圆心,以其长为半径作弧.正解 如图(2), (1)作射线11M O ;(2)在图(1)上,以O 为圆心,任意长为半径作弧,交OM 于点A ,交ON 于点B ;(3)以1O 为圆心,OA 的长为半径作弧,交11M O 于点C ;(4)以C 为圆心,以AB 的长为半径作弧,交前弧于点D ;(5)过点D 作射线D O 1. 则∠D CO 1就是所要求作的角.4. 如下图,已知∠α及线段a ,求作等腰三角形,使它的底角为α,底边为a .分析 先假设等腰三角形已经作好,根据等腰三角形的性质,知两底角∠B =∠C =∠α,底边BC =a ,故可以先作∠B =∠α,或先作底边BC =a .作法 如下图(1)∠MBN =∠α;(2)在射线BM 上截取BC =a ;(3)以C 为顶点作∠PCB =∠α,射线CP 交BN 于点A .△ABC 就是所要求作的等腰三角形.说明 画复杂的图形时,如一时找不到作法,一般是先画出一个符合条件的草图,再根据这个草图进行分析,逐步寻找画图步骤.5. 如图(1),已知直线AB 及直线AB 外一点C ,过点C 作CD ∥AB (写出作法,画出图形).分析 根据两直线平行的性质,同位角相等或内错角相等,故作一个角∠ECD =∠EFB 即可. 作法 如图(2).图(1) 图(2) (1)过点C 作直线EF ,交AB 于点F ;(2)以点F 为圆心,以任意长为半径作弧,交FB 于点P ,交EF 于点Q ; (3)以点C 为圆心,以FP 为半径作弧,交CE 于M 点; (4)以点M 为圆心,以PQ 为半径作弧,交前弧于点D ; (5)过点D 作直线CD ,CD 就是所求的直线.说明 作图题都应给出证明,但按照教科书的要求,一般不用写出,但要知道作图的原由.6. 如下图,△ABC 中,a =5cm ,b =3cm ,c =3.5cm ,∠B =︒36,∠C =︒44,请你从中选择适当的数据,画出与△ABC 全等的三角形(把你能画的三角形全部画出来,不写画法但要在所画的三角形中标出用到的数据).分析本题实质上是利用原题中的5个数据,列出所有与△ABC全等的各种情况,依据是SSS、SAS、AAS、ASA.解与△ABC全等的三角形如下图所示.7. 正在修建的中山北路有一形状如下图所示的三角形空地需要绿化.拟从点A出发,将△ABC分成面积相等的三个三角形,以便种上三种不同的花草,请你帮助规划出图案(保留作图痕迹,不写作法).(2003年,桂林)分析这是尺规作图在生活中的具体应用.要把△ABC分成面积相等的三个三角形,且都是从A点出发,说明这三个三角形的高是相等的,因而只需这三个三角形的底边也相等,所以只要作出BC边的三等分点即可.作法如下图,找三等分点的依据是平行线等分线段定理.8.已知∠AOB,求作∠AOB的平分线OC.错解如图(1)作法(1)以O为圆心,任意长为半径作弧,分别交OA、OB于D、E两点;(2)分别以D 、E 为圆心,以大于21DE 的长为半径作弧,两弧相交于C 点; (3)连结OC ,则OC 就是∠AOB 的平分线.错解分析 对角平分线的概念理解不够准确而致误.作法(3)中连结OC ,则OC 是一条线段,而角平分线应是一条射线.图(1) 图(2)正解 如图(2)(1)以点O 为圆心,任意长为半径作弧,分别交OA 、OB 于D 、E 两点; (2)分别以D 、E 为圆心,以大于21DE 的长为半径作弧,两弧交于C 点; (3)作射线OC ,则OC 为∠AOB 的平分线.9. 如图(1)所示,已知线段a 、b 、h (h <b ).求作△ABC ,使BC =a ,AB =b , BC 边上的高AD =h .图(1)错解 如图(2), (1)作线段BC =a ;(2)作线段BA =b ,使AD ⊥BC 且AD =h . 则△ABC 就是所求作的三角形.错解分析 ①不能先作BC ;②第2步不能同时满足几个条件,完全凭感觉毫无根据;③未考虑到本题有两种情况.对于这种作图题往往都是按照由里到外的顺序依次作图,如本题先作高AD ,再作AB ,最后确定BC .图(2) 图(3)正解 如图(3).(1)作直线PQ ,在直线PQ 上任取一点D ,作DM ⊥PQ ; (2)在DM 上截取线段DA =h ;(3)以A 为圆心,以b 为半径画弧交射线DP 于B ;(4)以B 为圆心,以a 为半径画弧,分别交射线BP 和射线BQ 于1C 和2C ;(5)连结1AC 、2AC ,则△1ABC (或△2ABC )都是所求作的三角形.10. 如下图,已知线段a ,b ,求作Rt △ABC ,使∠ACB =90°,BC =a ,AC =b (用直尺和圆规作图,保留作图痕迹).分析 本题解答的关键在于作出∠ACB =90°,然后确定A 、B 两点的位置,作出△ABC .作法 如下图(1)作直线MN :(2)在MN 上任取一点C ,过点C 作CE ⊥MN ; (3)在CE 上截取CA =b ,在CM 上截取CB =a ; (4)连结AB ,△ABC 就是所求作的直角三角形.说明 利用基本作图画出所求作的几何图形的关键是要先分析清楚作图的顺序.若把握不好作图顺序,要先画出假设图形.11. 如下图,已知钝角△ABC ,∠B 是钝角.求作:(1)BC 边上的高;(2)BC 边上的中线(写出作法,画出图形). 分析 (1)作BC 边上的高,就是过已知点A 作BC 边所在直线的垂线;(2)作BC 边上的中线,要先确定出BC 边的中点,即作出BC 边的垂直平分线. 作法 如下图(1)①在直线CB 外取一点P ,使A 、P 在直线CB 的两旁; ②以点A 为圆心,AP 为半径画弧,交直线CB 于G 、H 两点; ③分别以G 、H 为圆心,以大于21GH 的长为半径画弧,两弧交于E 点; ④作射线AE ,交直线CB 于D 点,则线段AD 就是所要求作的△ABC 中BC 边上的高. (2)①分别以B 、C 为圆心,以大于21BC 的长为半径画弧,两弧分别交于M 、N 两点; ②作直线MN ,交BC 于点F ;③连结AF,则线段AF就是所要求作的△ABC中边BC上的中线.说明在已知三角形中求作一边上的高线、中线、角平分线时,首先要把握好高线、中线、角平分钱是三条线段;其次,高线、中线的一个端点必须是三角形中这边所对的顶点,而关键是找出另一个端点.12. 如图(1)所示,在图中作出点C,使得C是∠MON平分线上的点,且AC=OC.图(1)图(2)分析由题意知,点C不仅要在∠MON的平分线上,且点C到O、A两点的距离要相等,所以点C应是∠MON的平分线与线段OA的垂直平分线的交点.作法如图(2)所示(1)作∠MON的平分线OP;(2)作线段OA的垂直平分线EF,交OP于点C,则点C就是所要求作的点.说明(1)根据题意弄清要求作的点的特征是到各直线距离相等,还是到各端点距离相等.(2)两条直线交于一点.13. 如下图,已知线段a、b、∠α、∠β.求作梯形ABCD,使AD=a,BC=b,AD∥BC,∠B=∠α;∠C=∠β.分析假定梯形已经作出,作AE∥DC交BC于E,则AE将梯形分割为两部分,一部分是△ABE,另一部分是AECD.在△ABE中,已知∠B=∠α,∠AEB=∠β,BE=b-a,所以,可以首先把它作出来,而后作出AECD.作法如下图.(1)作线段BC=b;(2)在BC上截取BE=b-a;(3)分别以B、E为顶点,在BE同侧作∠EBA=∠α,∠AEB=∠β,BA、EA交于A;(4)以EA、EC为邻边作AECD.四边形ABCD就是所求作的梯形.说明基本作图是作出较简单图形的基础,三角形是最简单的多边形,它是许多复杂图形的基础.因此,要作一个复杂的图形,常常先作一个比较容易作出的三角形,然后以此为基础,再作出所求作的图形.六、小结1. 尺规作图是指用没有刻度的直尺和圆规作图。
