初二数学压轴几何题
初二数学压轴几何证明题(含答案)
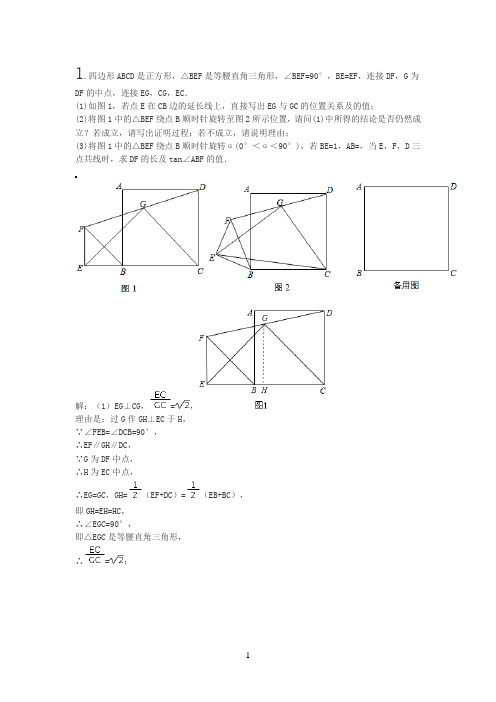
1.四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF,连接DF,G为DF的中点,连接EG,CG,EC.(1)如图1,若点E在CB边的延长线上,直接写出EG与GC的位置关系及的值;(2)将图1中的△BEF绕点B顺时针旋转至图2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)将图1中的△BEF绕点B顺时针旋转α(0°<α<90°),若BE=1,AB=,当E,F,D三点共线时,求DF的长及tan∠ABF的值.解:(1)EG⊥CG,=,理由是:过G作GH⊥EC于H,∵∠FEB=∠DCB=90°,∴EF∥GH∥DC,∵G为DF中点,∴H为EC中点,∴EG=GC,GH=(EF+DC)=(EB+BC),即GH=EH=HC,∴∠EGC=90°,即△EGC是等腰直角三角形,∴=;(2)解:结论还成立,理由是:如图2,延长EG到H,使EG=GH,连接CH、EC,过E作BC的垂线EM,延长CD,∵在△EFG和△HDG中∴△EFG≌△HDG(SAS),∴DH=EF=BE,∠FEG=∠DHG,∴EF∥DH,∴∠1=∠2=90°-∠3=∠4,∴∠EBC=180°-∠4=180°-∠1=∠HDC,在△EBC和△HDC中∴△EBC≌△HDC.∴CE=CH,∠BCE=∠DCH,∴∠ECH=∠DCH+∠ECD=∠BCE+∠ECD=∠BCD=90°,∴△ECH是等腰直角三角形,∵G为EH的中点,∴EG⊥GC,=,即(1)中的结论仍然成立;(3)解:连接BD,∵AB=,正方形ABCD,∴BD=2,∴cos∠DBE==,∴∠DBE=60°,∴∠ABE=∠DBE-∠ABD=15°,∴∠ABF=45°-15°=30°,∴tan∠ABF=,∴DE=BE=,∴DF=DE-EF=-1.解析:(1)过G作GH⊥EC于H,推出EF∥GH∥DC,求出H为EC中点,根据梯形的中位线求出EG=GC,GH=(EF+DC)=(EB+BC),推出GH=EH=BC,根据直角三角形的判定推出△EGC是等腰直角三角形即可;(2)延长EG到H,使EG=GH,连接CH、EC,过E作BC的垂线EM,延长CD,证△EFG≌△HDG,推出DH=EF=BE,∠FEG=∠DHG,求出∠EBC=∠HDC,证出△EBC≌△HDC,推出CE=CH,∠BCE=∠DCH,求出△ECH是等腰直角三角形,即可得出答案;(3)连接BD,求出cos∠DBE==,推出∠DBE=60°,求出∠ABF=30°,解直角三角形求出即可.2.已知正方形ABCD和等腰直角三角形BEF,BE=EF,∠BEF=90°,按图1放置,使点E在BC 上,取DF的中点G,连接EG,CG.(1)延长EG交DC于H,试说明:DH=BE.(2)将图1中△BEF绕B点逆时针旋转45°,连接DF,取DF中点G(如图2),莎莎同学发现:EG=CG且EG⊥CG.在设法证明时他发现:若连接BD,则D,E,B三点共线.你能写出结论“EG=CG且EG⊥CG”的完整理由吗?请写出来.(3)将图1中△BEF绕B点转动任意角度α(0<α<90°),再连接DF,取DF的中点G(如图3),第2问中的结论是否成立?若成立,试说明你的结论;若不成立,也请说明理由.(1)证明:∵∠BEF=90°,∴EF∥DH,∴∠EFG=∠GDH,而∠EGF=∠DGH,GF=GD,∴△GEF≌△GHD,∴EF=DH,而BE=EF,∴DH=BE;(2)连接DB,如图,∵△BEF为等腰直角三角形,∴∠EBF=45°,而四边形ABCD为正方形,∴∠DBC=45°,∴D,E,B三点共线.而∠BEF=90°,∴△FED为直角三角形,而G为DF的中点,∴EG=GD=GC,∴∠EGC=2∠EDC=90°,∴EG=CG且EG⊥CG;(3)第2问中的结论成立.理由如下:连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,如图,∵G为DF的中点,O为BD的中点,M为BF的中点,∴OG∥BF,GM∥OB,∴四边形OGMB为平行四边形,∴OG=BM,GM=OB,而EM=BM,OC=OB,∴EM=OG,MG=OC,∵∠DOG=∠GMF,而∠DOC=∠EMF=90°,∴∠EMG=∠GOC,∴△MEG≌△OGC,∴EG=CG,∠EGM=∠OCG,又∵∠MGF=∠BDF,∠FGC=∠GDC+∠GCD,∴∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°,∴EG=CG且EG⊥CG.解析:(1)由∠BEF=90°,得到EF∥DH,而GF=GD,易证得△GEF≌△GHD,得EF=DH,而BE=EF,即可得到结论.(2)连接DB,如图2,由△BEF为等腰直角三角形,得∠EBF=45°,而四边形ABCD为正方形,得∠DBC=45°,得到D,E,B三点共线,而G为DF的中点,根据直角三角形斜边上的中线等于斜边的一半得到EG=GD=GC,于是∠EGC=2∠EDC=90°,即得到结论.(3)连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,由G为DF的中点,O为BD的中点,M为BF的中点,根据三角形中位线的性质得OG∥BF,GM∥OB,得到OG=BM,GM=OB,而EM=BM,OC=OB,得到EM=OG,MG=OC,又∠DOG=∠GMF,而∠DOC=∠EMF=90°,得∠EMG=∠GOC,则△MEG≌△OGC,得到EG=CG,∠EGM=∠OCG,而∠MGF=∠BDF,∠FGC=∠GDC+∠GCD,所以有∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°.3.已知正方形ABCD和等腰Rt△BEF,BE=EF,∠BEF=90°,按图①放置,使点F在BC上,取DF的中点G,连接EG、CG.(1)探索EG、CG的数量关系和位置关系并证明;(2)将图①中△BEF绕B点顺时针旋转45°,再连接DF,取DF中点G(如图②),问(1)中的结论是否仍然成立.证明你的结论;(3)将图①中△BEF绕B点转动任意角度(旋转角在0°到90°之间),再连接DF,取DF的中点G(如图③),问(1)中的结论是否仍然成立,证明你的结论.解:(1)EG=CG且EG⊥CG.证明如下:如图①,连接BD.∵正方形ABCD和等腰Rt△BEF,∴∠EBF=∠DBC=45°.∴B、E、D三点共线.∵∠DEF=90°,G为DF的中点,∠DCB=90°,∴EG=DG=GF=CG.∴∠EGF=2∠EDG,∠CGF=2∠CDG.∴∠EGF+∠CGF=2∠EDC=90°,即∠EGC=90°,∴EG⊥CG.(2)仍然成立,证明如下:如图②,延长EG交CD于点H.∵BE⊥EF,∴EF∥CD,∴∠1=∠2.又∵∠3=∠4,FG=DG,∴△FEG≌△DHG,∴EF=DH,EG=GH.∵△BEF为等腰直角三角形,∴BE=EF,∴BE=DH.∵CD=BC,∴CE=CH.∴△ECH为等腰直角三角形.又∵EG=GH,∴EG=CG且EG⊥CG.(3)仍然成立.证明如下:如图③,延长CG至H,使GH=CG,连接HF交BC于M,连接EH、EC.∵GF=GD,∠HGF=∠CGD,HG=CG,∴△HFG≌△CDG,∴HF=CD,∠GHF=∠GCD,∴HF∥CD.∵正方形ABCD,∴HF=BC,HF⊥BC.∵△BEF是等腰直角三角形,∴BE=EF,∠EBC=∠HFE,∴△BEC≌△FEH,∴HE=EC,∠BEC=∠FEH,∴∠BEF=∠HEC=90°,∴△ECH为等腰直角三角形.又∵CG=GH,∴EG=CG且EG⊥CG.解析:(1)首先证明B、E、D三点共线,根据直角三角形斜边上的中线等于斜边的一半,即可证明EG=DG=GF=CG,得到∠EGF=2∠EDG,∠CGF=2∠CDG,从而证得∠EGC=90°;(2)首先证明△FEG≌△DHG,然后证明△ECH为等腰直角三角形.可以证得:EG=CG且EG ⊥CG.(3)首先证明:△BEC ≌△FEH ,即可证得:△ECH 为等腰直角三角形,从而得到:EG=CG 且EG ⊥CG .已知,正方形ABCD 中,△BEF 为等腰直角三角形,且BF 为底,取DF 的中点G ,连接EG 、CG .(1)如图1,若△BEF 的底边BF 在BC 上,猜想EG 和CG 的数量关系为______;(2)如图2,若△BEF 的直角边BE 在BC 上,则(1)中的结论是否还成立?请说明理由;(3)如图3,若△BEF 的直角边BE 在∠DBC 内,则(1)中的结论是否还成立?说明理由.解:(1)GC=EG ,(1分)理由如下:∵△BEF 为等腰直角三角形, ∴∠DEF=90°,又G 为斜边DF 的中点, ∴EG=DF , ∵ABCD 为正方形, ∴∠BCD=90°,又G 为斜边DF 的中点,∴CG= DF , ∴GC=EG ;(2)成立.如图,延长EG 交CD 于M ,∵∠BEF=∠FEC=∠BCD=90°,∴EF ∥CD ,∴∠EFG=∠MDG ,又∠EGF=∠DGM ,DG=FG ,∴△GEF ≌△GMD ,∴EG=MG ,即G 为EM 的中点.∴CG 为直角△ECM 的斜边上的中线,∴CG=GE= EM ;(3)成立.取BF 的中点H ,连接EH ,GH ,取BD 的中点O ,连接OG ,OC .∵CB=CD ,∠DCB=90°,∴CO= BD1 2 1 21212.∵DG=GF,∴GH∥BD,且GH= BD,OG∥BF,且OG= BF,∴CO=GH.为等腰直角三角形.∵△BEF∴EH= BF∴EH=OG.∵四边形OBHG为平行四边形,∴∠BOG=∠BHG.∵∠BOC=∠BHE=90°.∴∠GOC=∠EHG.∴△GOC≌△EHG.∴EG=GC.此题考查了正方形的性质,以及全等三角形的判定与性质.要求学生掌握直角三角形斜边上的中线等于斜边的一半,以及三角形的中位线与第三边平行且等于第三边的一半.掌握这些性质,熟练运用全等知识是解本题的关键.解析:(1)EG=CG,理由为:根据三角形BEF为等腰直角三角形,得到∠DEF为直角,又G为DF中点,根据在直角三角形中,斜边上的中线等于斜边的一半,得到EG为DF的一半,同理在直角三角形DCF中,得到CG也等于DF的一半,利用等量代换得证;(2)成立.理由为:延长EG交CD于M,如图所示,根据“ASA”得到三角形EFG与三角形GDM 全等,由全等三角形的对应边相等得到EG与MG相等,即G为EM中点,根据直角三角形斜边上的中线等于斜边的一半得到EG与CG相等都等于斜边EM的一半,得证;(3)成立.理由为:取BF的中点H,连接EH,GH,取BD的中点O,连接OG,OC,如图所示,1212因为直角三角形DCB中,O为斜边BD的中点,根据斜边上的中线等于斜边的一半得到OC等于BD 的一半,由HG为三角形DBF的中位线,根据三角形的中位线平行于第三边且等于第三边的一半,得到GH等于BD一半,OG等于BF的一半,又根据直角三角形斜边上的中线等于斜边的一半得到EH等于BF的一半,根据等量代换得到OG与EH相等,再根据OBHG为平行四边形,根据平行四边形的性质得到对边相等,对角相等,进而得到∠GOC与∠EHG相等,利用“SAS”得到△GOC与△EHG全等,利用全等三角形的对应边相等即可得证.。
初二数学压轴几何题
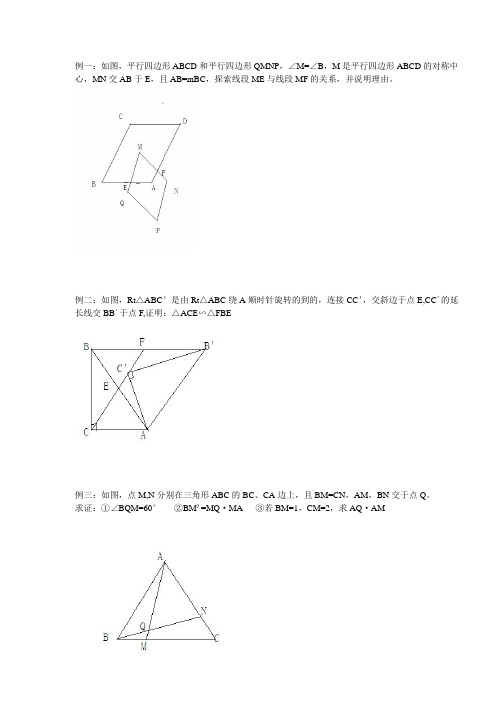
例一:如图,平行四边形ABCD和平行四边形QMNP,∠M=∠B,M是平行四边形ABCD的对称中心,MN交AB于E,且AB=mBC,探索线段ME与线段MF的关系,并说明理由。
例二:如图,Rt△ABC'是由Rt△ABC绕A顺时针旋转的到的,连接CC',交斜边于点E,CC´的延长线交BB´于点F,证明:△ACE∽△FBE例三:如图,点M,N分别在三角形ABC的BC、CA边上,且BM=CN,AM,BN交于点Q。
求证:①∠BQM=60°②BM²=MQ·MA ③若BM=1,CM=2,求AQ·AM例四:如图(1),点M,N分别是边长为4的正方形ABCD边AB、AD的中点,连接CN,DM。
①判断CN,DM的关系,并说明理由。
②设CN、DM的交点为H,连接BH,如图(2),求证:△BCH是等腰三角形;③设△ADM沿DM翻折后得到△A'DM,延长MA'交DC的延长线于点E,如图(3),求A'E例五:如图,矩形ABCD中,E是AD中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD 内部,小明将BG延长交DC于点F,认为GF=DF,你同意吗?请说明理由。
(2)保持(1)中的条件不变,若DC=2DF,求AD/AB的值(3)保持(1)中的条件不变,若DC=n·DF,求AD/AB的值例六:如图①,将边长为4的正方形纸片ABCD沿EF折叠(点E,F分别在边AB,CD上),使点B 落在AD边上的点M处,点C落在点N处,MN与CD交于点P,连接EP。
(1)如图②,若M为AD边的中点①②△AEM的周长=_cm③④求证:EP=AE=DP⑤⑥求△DMP三边的比值⑦(2)随着落点M在AD边上取遍所有的位置(点M不与A,D重合)。
△PDM的周长是否发生变化?请说明理由。
例七:如图所示,在△ABC中,D、E分别是AB、AC上的点,DE∥BC,如图①,然后将△ADE绕A点顺时针旋转一定角度,得到图②,然后将BD、CE分别延长至M、N,使DM=1/2BD,EN=1/2CE,得到图③,请解答下列问题:(1)(2)若AB=AC,请探究下列数量关系:①在图②中,BD与CE的数量关系是____;②在图③中,猜想AM与AN的数量关系、∠MAN和∠BAC的数量关系,并证明你的猜想;(3)(4)若AB=k·AC(k>1),按上述操作方法,得到图④,请继续探究:AM与AN的数量关系、∠MAN与∠BAC的数量关系,直接写出你的猜想,不必证明。
八年级数学期末几何压轴题

26.(本题满分10分)已知:在矩形ABCD 中,AB =10,BC =12,四边形EFGH 的三个顶点E 、F 、H 分别在矩形ABCD 边AB 、BC 、DA 上,AE =2.(1)如图①,当四边形EFGH 为正方形时,求△GFC 的面积;(5分)(2)如图②,当四边形EFGH 为菱形,且BF = a 时,求△GFC 的面积(用含a 的代数式表示);(5分)D(第26题图1)FD CA BE (第26题图2)FH G26.解:(1)如图①,过点G 作GM BC ⊥于M . …………………………………………(1分)在正方形EFGH 中,90,HEF EH EF ∠==. …………………………………………………………(1分)90.90,.AEH BEF AEH AHE AHE BEF ∴∠+∠=∠+∠=∴∠=∠又∵90A B ∠=∠=,∴⊿AH E ≌⊿BEF …………………………………………………………(1分)同理可证:⊿MFG ≌⊿BEF . …………………………………………………………(1分) ∴GM=BF=AE =2.∴FC=BC-BF =10. …………………………………………………………(1分) (2)如图②,过点G作GM BC ⊥于M .连接HF . …………………………………………(1分)//,.//,.AD BC AHF MFH EH FG EHF GFH ∴∠=∠∴∠=∠.AHE MFG ∴∠=∠ …………………………………………………(1分)又90,,A GMF EH GF ∠=∠==∴⊿AHE ≌⊿MFG . ………………………………………………………(1分)∴GM=AE =2. ……………………………………………………………(1分)11(12)12.22GFCSFC GM a a ∴=⋅=-=- …………………………………………(1分)3(1)求点A 和点B 的坐标;(2)过点A 作AC ⊥y 轴于点C ,过点B 作直线l ∥y 轴.动点P 从点O 出发,以每秒1个单位长的速度,沿O ﹣C ﹣A 的路线向点A 运动;同时直线l 从点B 出发,以相同速度向左平移,在平移过程中,直线l 交x 轴于点R ,交线段BA 或线段AO 于点Q .当点P 到达点A 时,点P 和直线l 都停止运动.在运动过程中,设动点P 运动的时间为t 秒)0( t .①当t 为何值时,以A 、P 、R 为顶点的三角形的面积为8?②是否存在以A 、P 、Q 为顶点的三角形是QA=QP 的等腰三角形?若存在,求t 的值;若不存在,请说明理由.3∴y =-x +7,0=x +7,∴x =7,∴B 点坐标为:(7,0),----------------------------1分 ∵y =-x +7=x 34,解得x =3,∴y =4,∴A 点坐标为:(3,4);-------------------1分 (2)①当0<t <4时,PO =t ,PC =4-t ,BR =t ,OR =7-t ,--------------1分 过点A 作AM ⊥x 轴于点M∵当以A 、P 、R 为顶点的三角形的面积为8,∴S 梯形ACOB -S △ACP -S △POR -S △ARB =8, ∴21(AC +BO )×CO -21AC ×CP -21PO ×RO -21AM ×BR =8, ∴(AC +BO )×CO -AC ×CP -PO ×RO -AM ×BR =16,∴(3+7)×4-3×(4-t )-t ×(7-t )-4t =16,∴t 2-8t +12=0. -----------------1分 解得t 1=2,t 2=6(舍去). --------------------------------------------------------------------1分 当4≤t ≤7时,S △APR =21AP ×OC =2(7-t )=8,t=3(舍去);--------------1分 ∴当t =2时,以A 、P 、R 为顶点的三角形的面积为8; ②存在.当0<t ≤4时,直线l 与AB 相交于Q ,∵一次函数y =-x +7与x 轴交于B (7,0)点,与y 轴交于N (0,7)点,∴NO =OB ,∴∠OBN =∠ONB =45°.∵直线l ∥y 轴,∴RQ =RB=t ,AM=BM=4∴QB=t 2,AQ=t 224-----------------1分 ∵RB =OP =QR =t ,∴PQ//OR,PQ=OR=7-t --------------------------------------1分 ∵以A 、P 、Q 为顶点的三角形是等腰三角形,且QP =QA ,∴7-t=t 224-,t=1-32(舍去)--------------------------------------------1分 当4<t ≤7时,直线l 与O A 相交于Q ,若QP =QA ,则t -4+2(t -4)=3,解得t =5;---------------------------------------1分 ∴当t =5,存在以A 、P 、Q 为顶点的三角形是PQ =AQ 的等腰三角形.已知边长为1的正方形ABCD 中, P 是对角线AC 上的一个动点(与点A 、C 不重合), 过点P 作 PE ⊥PB ,PE 交射线DC 于点E ,过点E 作EF ⊥AC ,垂足为点F . (1)当点E 落在线段CD 上时(如图10),① 求证:PB=PE ;② 在点P 的运动过程中,PF 的长度是否发生变化?若不变,试求出这个不变的值, 若变化,试说明理由;(2)当点E 落在线段DC 的延长线上时,在备用图上画出符合要求的大致图形,并判断上述(1)中的结论是否仍然成立(只需写出结论,不需要证明);(3)在点P 的运动过程中,⊿PEC 能否为等腰三角形?如果能,试求出AP 的长,如果不能,试说明理由.D CAE P 。
期末考试勾股定理与几何翻折压轴题专项训练—2023-2024学年八年级数学下学期(人教版)(解析版)

期末考试勾股定理与几何翻折压轴题专项训练【例题精讲】例1.(三角形翻折问题)如图,在Rt ABC △中,9086ABC AB BC ∠=︒==,,,分别在AB AC ,边上取点E F ,,将AEF △沿直线EF 翻折得到A EF '△,使得点A 的对应点A '恰好落在CB 延长线上,当60EA B '∠=︒时,AE 的长为 ,当A F AC '⊥时,AF 的长为 .【答案】 32− 407【分析】由折叠的性质可得AE A E '=,先求出30A EB '∠=︒,从而可得1122A B A E AE ''==,再由勾股定理可得BE AE =,最后由AE BE AB +=,进行计算即可;令A F '交AB 于G ,连接CG ,由折叠的性质可得:A EA F '∠=∠,AFE A FE '∠=∠,AEF A EF '∠=∠,AF A F '=,由A F AC '⊥得出90A FA A FC ''∠=∠=︒,45AFE A FE '∠=∠=︒,证明()ASA A FC AFG '≌得到CF FG =,设CF FG x ==,则10AF x =−,AG ,根据1122ACG S AC FG AG BC =⋅=⋅建立方程,解方程即可得出CF 的长,即可求解.【详解】解:由折叠的性质可得:AE A E '=,90ABC ∠=︒,18090A BE ABC '∴∠=︒−∠=︒,60EA B '∠=︒,9030A EB EA B ''∴∠=︒−∠=︒,1122A B A E AE ''∴==,BE AE∴==,AE BE AB+=,8AE AE∴=,32AE∴=−如图,令A F'交AB于G,连接CG,A F AC'⊥,90A FA A FC''∴∠=∠=︒,由折叠的性质可得:A EA F'∠=∠,AFE A FE'∠=∠,AEF A EF'∠=∠,AF A F'=,90AFE A FE'∠+∠=︒,45AFE A FE'∴∠=∠=︒,设A EA Fα'∠=∠=,则45FEB AFEα∠=∠=+︒,180135AEF FEB A EFα'∴∠=︒−∠=︒−=∠,()13545902A EB A EF BEFααα''∴∠=∠−∠=︒−−︒+=︒−,902EA B A EBα''∴∠=︒−∠=,FA C EA B EA F Aα'''∴∠=∠−∠==∠,在A FC'和AFG中,CA F AA F AFA FC AFG∠=∠⎧⎪=⎨⎪∠=∠''⎩',()ASAA FC AFG'∴≌,CF FG∴=,在Rt ABC△中,9086ABC AB BC∠=︒==,,,10AC∴,设CF FG x==,则10AF x=−,AG∴==1122ACGS AC FG AG BC=⋅=⋅,106x∴⋅=,整理得:271809000x x+−=,即29014400749x⎛⎫+=⎪⎝⎭,9012077x∴+=±,解得:307x=或30x=−(不符合题意,舍去),307CF∴=,30401077AF AC CF∴=−=−=,故答案为:32−407.【点睛】本题考查了折叠的性质、全等三角形的判定与性质、勾股定理、三角形的面积公式、等腰直角三角形的判定与性质、三角形外角的定义及性质、三角形内角和定理等知识,熟练掌握以上知识点,添加适当的辅助线是解此题的关键.例2.(坐标系中折叠问题)如图,在平面直角坐标系中,长方形ABCO的边OC OA、分别在x轴、y轴上,6AB=,点E在边BC上,将长方形ABCO沿AE折叠,若点B的对应点F 恰好是边OC的三等分点,则点E的坐标是.【答案】⎛−⎝⎭或(−【分析】本题主要考查了勾股定理与折叠问题,坐标与图形,由折叠的性质可得6AF AB==,BE EF=,90AFE B∠=∠=︒,再分当点F靠近点C时,24CF OF==,,当点F靠近点O 时,则42CF OF==,,两种情况利用勾股定理先求出OA的长,进而得到BC的长,设出CE 的长,进而得到EF的长,在Rt EFC△中,由勾股定理建立方程求解即可.【详解】解:在长方形ABCO 中,6CO AB ==,90BCO B AOC ∠=∠=∠=︒, 由折叠的性质可得6AF AB ==,BE EF =,90AFE B ∠=∠=︒,F 恰好是边OC 的三等分点,∴当点F 靠近点C 时,24CF OF ==,,在Rt AFO V中,OA =,∴BC OA ==设CE x =,则BE EF x ==,在Rt EFC △中,由勾股定理得到222EF CF CE =+,∴()2222xx =+,解得x =,∴点E的坐标是⎛− ⎝⎭; 当点F 靠近点O 时,则42CF OF ==,,在Rt AFO V中,OA ==∴BC OA ==设CE x =,则BE EF x ==,在Rt EFC △中,由勾股定理得到222CF CE =+,∴()2224x x =+,解得x =∴点E的坐标是(−;综上所述,点E的坐标是⎛− ⎝⎭或(−,故答案为:⎛− ⎝⎭或(−.例3.(四边形折叠问题)如图,已知矩形ABCD ,4AB =,5BC =,点P 是射线BC 上的动点,连接AP ,AQP △是由ABP 沿AP 翻折所得到的图形.(1)当点Q 落在边AD 上时,QC = ;(2)当直线PQ 经过点D 时,求BP 的长;(3)如图2,点M 是DC 的中点,连接MP 、MQ .①MQ 的最小值为 ;②当PMQ 是以PM 为腰的等腰三角形时,请直接写出BP 的长.【答案】(2)2BP =或8BP =(3) 2.9BP =或4BP =或10BP =【分析】(1)根据折叠的性质和勾股定理进行求解即可;(2)分点P 在线段BC 上,点P 在线段BC 的延长线上,两种情况,进行讨论求解;(3)①连接AM ,勾股定理求出AM 的长,折叠求出AQ 的长,根据MQ AM AQ ≥−,求出最小值即可;②分PM MQ =和PM PQ =两种情况,再分点P 在线段BC 上,点P 在线段BC 的延长线上,进行讨论求解即可.【详解】(1)解:当点Q 落在边AD 上时,如图所示,∵矩形ABCD ,4AB =,5BC =,∴4,5CD AB AD BC ====,90BAD B BCD ADC ∠=∠=∠=∠=︒,∵翻折,∴4,90AQ AB AQP B ==∠=∠=︒,∴1DQ AD AQ =−=,在Rt CDQ △中,CQ ==(2)当直线PQ 经过点D 时,分两种情况:当点P 在线段BC 上时,如图:∵翻折,∴4AQ AB ==,90AQP B ∠=∠=︒,BP PQ =,∴90AQD ∠=︒,∴3DQ ==,设BP PQ x ==,则:5PC BC BP x =−=−,3DP DQ PQ x =+=+,在Rt PCD △中,222DP CP CD=+,即:()()222345x x +=+−,∴2x =;∴2BP =;②当P 在线段BC 的延长线上时:∵翻折,∴4,90AQ AB Q B ==∠=∠=︒,BP PQ =,∴3DQ ==,设BP PQ x ==,则:5PC BP BC x =−=−,3DP PQ DQ x =−=−,在Rt PCD △中,222DP CP CD =+,即:()()222345x x −=+−,∴8x =;∴8BP =;综上:2BP =或8BP =;(3)①连接AM ,∵M 是CD 的中点, ∴122DM CM CD ===,∴AM =∵翻折,∴4AQ AB ==,∵MQ AM AQ ≥−,∴当,,A Q M 三点共线时,MQ 的值最小,即:4MQ AM AQ =−=4;②当PM PQ =时,如图:∵翻折,∴BP PQ PM ==,设BP x =,则:,5PM x CP BC BP x ==−=−,在Rt PCM 中,222PM CM PC =+,即:()22225x x =+−,解得: 2.9x =,即: 2.9BP =;当PM QM =,点P 在线段BC 上时,如图:∵,QM PM DM CM ==,90D C ∠=∠=︒,∴()HL MDQ MCP ≌,∴CP DQ =,点Q 在AD 上,由(1)知:1DQ =,∴1CP DQ ==,∴4BP BC CP =−=;当点P 在BC 的延长线上时:如图:此时点M 在AP 上,连接BM ,∵翻折,∴BM MQ PM ==,∵MC BP ⊥,∴210BP BC ==;综上: 2.9BP =或4BP =或10BP =.质,综合性强,难度大,属于压轴题.利用数形结合和分类讨论的思想进行求解,是解题的关键.【模拟训练】1.如图,在长方形ABCD 中,点E 是AD 的中点,将ABE 沿BE 翻折得到FBE ,EF 交BC 于点H ,延长BF DC 、相交于点G ,若8DG =,10BC =,则DC = .【答案】258【分析】本题考查了全等三角形的判定与性质,折叠的性质,勾股定理,连接EG ,根据点E 是AD 的中点得DE AE EF ==,根据四边形ABCD 是长方形得90D A ∠=∠=︒,根据将ABE 沿BE 翻折得到FBE 得90BFE D A ∠=∠=∠=︒,利用HL 证明Rt Rt EFG EDG △≌△,得8FG DG ==,设DC x =,则8CG DG DC x =−=−,8BG BF FG AB FG DC FG x =+=+=+=+,在Rt BCG V △中,根据勾股定理得,222CG BC BG +=,进行计算即可得.【详解】解:如图所示,连接EG ,∵点E 是AD 的中点,∴DE AE EF ==,∵四边形ABCD 是长方形,∴90D A ∠=∠=︒,∵将ABE 沿BE 翻折得到FBE ,∴90BFE D A ∠=∠=∠=︒在Rt EFG △和Rt EDG △中,EF ED EG EG =⎧⎨=⎩,∴()Rt Rt HL EFG EDG V V ≌,∴8FG DG ==,设DC x =,则8CG DG DC x =−=−,8BG BF FG AB FG DC FG x =+=+=+=+,在Rt BCG 中,根据勾股定理得,222CG BC BG +=,∴222(8)10(8)x x −+=+,解得258x =,故答案为:258.2.如图,在Rt ABC △中,90ACB ∠=︒,254AB =,154=AC ,点D 是AB 边上的一个动点,连接CD ,将BCD △沿CD 折叠,得到CDE ,当DE 与ABC 的直角边垂直时,AD 的长是 .【答案】154或54【分析】本题考查了勾股定理,平行四边形的判定和性质,折叠的性质,全等三角形的判定和性质,分DE BC ⊥和DE AB ⊥两种情况进行求解即可得到答案,根据题意,正确画出图形是解题的关键.【详解】解:如图,当DE BC ⊥时,延长ED 交BC 于点F ,CE 与AB 相交于点M ,∵EF BC ⊥,∴90EFC EFB ∠=∠=︒,∴90E ECF ∠+∠=︒,由折叠得,B E ∠=∠,CE CB =,MCD FCD ∠=∠,∴90B ECF ∠+∠=︒,∴90CMB ∠=︒,即C M A B ⊥,∵90ACB ∠=︒,254AB =,154=AC ,∴5BC ==, ∵1122ABC S AC BC AB CM ==△,∴11512552424CM ⨯⨯=⨯⨯,解得3CM =,∴4BM =,∵90CFD CMD FCD MCD CD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ∴()AAS CFD CMD ≌,∴3CF CM ==,DF DM =,∴532BF BC CF =−=−=,设DF DM x ==,则4BD x =−,在Rt BFD 中,222DF BF BD +=,∴()22224x x +=−, 解得32x =, ∴35422BD =−=, ∴25515424AD AB BD =−=−=;当DE AB ⊥时,如图,设DE 与AC 相交于点M ,由折叠可得,BCD ECD ∠=∠,DE DB =,ED BD =,5EC BC ==,∵DE AB ⊥,90ACB ∠=︒,∴DE BC ∥,∴EDC BCD ∠=∠,∴EDC ECD ∠=∠,∴5ED EC ==,∴5BD ED ==, ∴255544AD AB BD =−=−=;综上,AD 的长是154或54, 故答案为:154或54.3.如图,等边三角形ABC 中,16AB BD AC =⊥,于点D ,点E F 、分别是BC DC 、上的动点,沿EF 所在直线折叠CEF △,使点C 落在BD 上的点C '处,当BEC '△是直角三角形时,BE 的值为 .【答案】24−或323【分析】本题考查了翻折变换,等边三角形的性质,折叠的性质,熟练运用折叠的性质是本题的关键.由等边三角形的性质可得30DBC ∠=︒,分9090BEC BC E ''∠=︒∠=︒,两种情况讨论,由直角三角形的性质即可求解.【详解】解:ABC 是等边三角形,BD AC ⊥,30,DBC ∴∠=︒ 由折叠的性质可得:,CE C E '=若90,BEC ∠'=︒且30,C BE ∠'=︒,2,BE E B E C C ∴='''=16,BE CE BC +==16,CE +=8,E E C C ∴'==24BE ∴=−若90,30,E C B E C B ∠'=︒='∠︒2,,BE E B C E C ∴'''=16,BE CE BC +==16,3CE E C =='∴ 32.3BE ∴=故答案为∶ 24−323.4.如图,在ABC 中,120ACB ∠=︒,8AC =,4BC =,将边BC 沿CE 翻折,使点B 落在AB 上的点D 处,再将边AC 沿CF 翻折,使点A 落在CD 的延长线上的点A '处,两条折痕与斜边AB 分别交于点E 、F ,则线段FA '的长为 .【答案】【分析】本题考查了折叠的性质,勾股定理,直角三角形的性质,添加恰当辅助线构造直角三角形是本题的关键.过点A 作AH BC ⊥交BC 的延长线于H ,由直角三角形的性质可求142HC AC ==,AH =AB 的长,由面积法可求CE 的长,由折叠的性质可求90BEC DEC ∠=∠=︒,BCE DCE ∠=∠,ACF DCF ∠=∠,然后再求解即可.【详解】解:如图,过点A 作AH BC ⊥,交BC 的延长线于H ,120ACB ∠=︒,ACB H HAC ∠=∠+∠,30HAC ∴∠=︒,142HC AC ∴==,AH ==,448BH ∴=+=,AB ∴1122ACB S BC AH AB CE =⨯⨯=⨯⨯,4CE ∴=,CE ∴,将边BC 沿CE 翻折,使点B 落在AB 上的点D 处,再将边AC 沿CF 翻折,90BEC DEC ∴∠=∠=︒,BCE DCE ∠=∠,ACF DCF ∠=∠,1602ECF ACB ∴∠=∠=︒,30CFE ∴∠=︒,EF ∴,在Rt BCE中,BE ===,AF AB EF BE ∴=−−==FA AF '∴==故答案为:5.如图,点D 是ABC 的边AB 的中点,将BCD △沿直线CD 翻折能与ECD 重合,若4AB =,2CD =,1AE =,则点C 到直线AB 的距离为 .【答案】【分析】连接BE ,延长CD 交BE 于点G ,作CH AB ⊥于点H ,如图所示,由折叠的性质及中点性质可得AEB △为直角三角形,且G 为BE 中点,从而CG BE ⊥,由勾股定理可得BE的长,再根据2ABC BDC S S =△△,即11222AB CH CD BG ⋅=⨯⋅,从而可求得CH 的长.【详解】解:连接BE ,延长CD 交BE 于点G ,作CH AB ⊥于点H ,如图所示,由折叠的性质可得:BD ED =,CB CE =,∴CG 为BE 的中垂线, ∴12BG BE =,∵点D 是AB 的中点,4AB =,2CD =,1AE =, ∴122BD AD AB ===,CBD CAD S S =,AD DE =,∴DBE DEB ∠=∠,DEA DAE ∠=∠,∵180EDA DEA DAE ∠+∠+∠=︒,即22180DEB DEA ∠+∠=︒,∴90DEB DEA ∠+∠=︒,即90BEA ∠=︒,∴BE∴12BG BE ==, ∵2ABC BDCS S =△△, ∴11222AB CH CD BG ⋅=⨯⋅,∴422CH =⨯,∴CH ,∴点C 到直线AB 的距离为.故答案为:.【点睛】本题考查翻折变换,线段中垂线的判定,等腰三角形的性质,点到直线的距离,直角三角形的判定,勾股定理,利用面积相等求相应线段的长,解题的关键是得出CG 为BE 的中垂线,2ABC BDC S S =△△.6.如图,在ABC 中,90,A AB AC ∠=︒==D 为AC 边上一动点,将C ∠沿过点D 的直线折叠,使点C 的对应点C '落在射线CA 上,连接BC ',当Rt ABC '△的某一直角边等于斜边BC '长度的一半时,CD 的长度为 .【答案】 或 【分析】由翻折得,12CD CC '=,分三种情况:①当点C '在边AC 上,且12AC BC ''=(即2BC AC ''=)时;②当点C '在CA 的延长线上,且12AC BC ''=(即2BC AC ''=)时;③当点C '在CA 的延长线上,且12AB BC '=(即2BC AB '==时,分别根据勾股定理求出AC '的长,再求出CC '的长即可 【详解】解:由翻折得,12CD CC '=,分三种情况:①当点C '在边AC 上,且12AC BC ''=(即2BC AC ''=)时,90,A AB AC ∠=︒==∴由勾股定理得,222BC AC AB ''−=,即222(2)AC AC ''−=,AC '∴=CC '∴CD ∴;②当点C '在CA 的延长线上,且12AC BC ''=(即2BC AC ''=)时,同理得AC 'CC '∴CD ∴;③当点C '在CA 的延长线上,且12AB BC '=(即2BC AB '==由勾股定理得,222AC BC AB ''=−,即22218AC '=−=,AC '∴=CC '∴CD ∴=,0>,CD AB ∴>,此时点D 不在边AC 上,不符合题意,舍去,综上,当Rt ABC '△的某一直角边等于斜边BC '长度的一半时,CD 的长度为或.故答案为:或.【点睛】本题主要考查图形的翻折变换(折叠问题),勾股定理,等腰直角三角形的性质等知识,灵活运用折叠的性质及勾股定理是解答本题的关键,同时要注意分类思想的运用.7.如图,在ABC 中,90ACB ∠=︒,3AC =,4BC =,P 为斜边AB 上的一动点(不包含A ,B 两端点),以CP 为对称轴将ACP △翻折得到A CP ',连结BA '.当A P AB '⊥时,BA '的长为 .【答案】【分析】当A P AB '⊥时,过点C 作CD AB ⊥于D ,可知125CD =,95AD =,得出PDC △为等腰直角三角形,得到PD CD =,求出PA '和BP 的长,利用勾股定理即可求出BA '的长.【详解】过点C 作CD AB ⊥于D ,在Rt ADC 中,90ACB ∠=︒,3AC =,4BC =,∴5AB = ∵1122AC BC AB CD ⨯=⨯,125CD ∴=,在Rt ADC 中,3AC =∴95AD ==,当A P AB '⊥时,如图由折叠性质可知12∠=∠,PA PA '=,又1290A PA '∠=∠+∠=︒145∠=∠2=︒∴,又2390∠+∠=︒,345∴∠=︒,23∴∠=∠,125PD CD ∴==,又PA PD AD =+,12921555PA ∴=+=,又PA PA '=,215PA '∴=,又BP AB PA =−,214555BP ∴=−=,在Rt BPA '△中,90BPA ∠='︒,222BP PA BA ∴='+,2224214575525BA ⎛⎫⎛⎫'∴=+= ⎪ ⎪⎝⎭⎝⎭,BA '∴=,故答案为:.【点睛】本题考查了勾股定理的应用,折叠问题,熟练掌握勾股定理是解题的关键.8.如图,在ABC 中,90ACB ∠=︒,AC BC =,D 为AB 上一点,连接DC ,将BDC 沿DC 翻折,得到EDC △,连接AE ,若AE CE =,4BC =,则D 到CE 的距离是 .【答案】2【分析】本题考查等腰直角三角形中的折叠问题,涉及等边三角形判定与性质,勾股定理应用、面积法等知识.设BE 交CD 于G ,过E 作EF BC ⊥交BC 延长线于F ,根据将BDC 沿DC 翻折,得到EDC △,AC BC =,AE CE =,可得ACE △是等边三角形,即知60ACE ∠=︒,而90ACB ∠=︒,故150BCE ∠=︒,30ECF ∠=︒,可得75BCD ECD ∠=∠=︒,122EF CE ==,CF =BE =15CBE ∠=︒,可得90BGC ∠=︒,即CG BE ⊥,从而12BG BE GE ===,由勾股定理得CG ,在Rt BDG △中,DG ,即得CD DG CG =+,由面积法可得D 到CE 的距离是2. 【详解】解:设BE 交CD 于G ,过E 作EF BC ⊥交BC 延长线于F ,如图:将BDC 沿DC 翻折,得到EDC △,4BC CE ∴==,BCD ECD ∠=∠,AC BC =,AE CE =,AC BC CE AE ∴===,ACE ∴是等边三角形,60ACE ∴∠=︒,90ACB ∠=︒,150BCE ∴∠=︒,30ECF ∠=︒,75BCD ECD ∴∠=∠=︒,122EF CE ==,CF =在Rt BEF △中,BE ==BCE 中,BC CE =,150BCE ∠=︒,15CBE ∴∠=︒,18090BGC BGC BCD ∴∠=︒−∠−∠=︒,即CG BE ⊥,12BG BE GE ∴==,CG ∴===,45ABC ∠=︒,15CBE ∠=︒,30DBG ∴∠=︒,在Rt BDG△中,DG =,CD DG CG ∴=+=,设D 到CE 的距离是h ,2DCE S CE h DC GE ∆=⋅=⋅,324DC GE h CE ⋅∴===,故答案为:2.9.在生活中、折纸是一种大家喜欢的活动、在数学中,我们可以通过折纸进行探究,探寻数学奥秘.【纸片规格】三角形纸片ABC ,120ACB ∠=︒,CA CB =,点D是底边AB 上一点.【换作探究】(1)如图1,若6AC =,AD =CD ,求CD 的长度;(2)如图2,若6AC =,连接CD ,将ACD 沿CD 所在直线翻折得到ECD ,点A 的对应点为点.E 若DE 所在的直线与ABC 的一边垂直,求AD 的长;(3)如图3,将ACD 沿CD 所在直线翻折得到ECD ,边CE 与边AB 交于点F ,且DE BC ∥,再将DFE △沿DF 所在直线翻折得到DFG ,点E 的对应点为点G ,DG 与CE 、BC 分别交于H ,K ,若1KH =,请直接写出AC 边的长.【答案】(1)(2)3或(3)3【分析】(1)作CE AB ⊥于E ,求得30A B ==︒∠∠,从而得出132CE AC ==,AE AC =进而得出DE AE AD =−=(2)当DE AB ⊥时,连接AE ,作CG AB ⊥于G ,依次得出45DAE DEA ∠=∠=︒,304575CAE CAD DAE ∠=∠+∠=︒+︒=︒,75CEA CAE ∠=∠=︒,30ACE ∠=︒,15ACD DCE ∠=∠=︒,45CDG CAB DAC ∠=∠+∠=︒,从而DG CG =,进一步得出结果;当ED AC ⊥时,设ED 交AC 于点W CE ,交AB 于V ,可推出90AVC ∠=︒,60ACE ∠=︒,从而30ACD DCE ∠=∠=︒,进一步得出结果;当DE BC ⊥时,可推出180ACB BCE ∠+∠=︒,从而90ACD DCE ∠=∠=︒,进一步得出结果;(3)可推出CKH 和CDH △及CHK 是直角三角形,且30HCK ∠=︒,30HDF ∠=︒,45DCH ∠=︒,进一步得出结果.【详解】(1)解:如图1,作CE AB ⊥于E ,90AEC ∴∠=︒,CA CB =,120ACB ∠=︒,30A B ∴∠=∠=︒,132CE AC ∴==,AE =,DE AE AD ∴=−==CD ∴=;(2)解:如图2,当DE AB ⊥时,连接AE ,作CG AB ⊥于G ,由翻折得:AD DE =,CAD CED =∠∠,AC CE =,45DAE DEA ∠∠∴==︒,304575CAE CAD DAE ∴∠=∠+∠=︒+︒=︒,75CEA CAE ∴∠=∠=︒,30ACE ∴∠=︒,15ACD DCE ∴∠=∠=︒,45CDG CAB DAC ∴∠=∠+∠=︒,DG CG ∴=,由(1)知:3CG =,AG =3AD AG DG ∴=−=;如图3,当ED AC ⊥时,设ED 交AC 于点W CE ,交AB 于V ,90E ACE ∴∠+∠=︒,E A ∠=∠,90A ACE ∴∠+∠=︒,90AVC ∴∠=︒,60ACE∴∠=︒,30ACD DCE∴∠=∠=︒,ACD A∴∠=∠,AD CD∴=,3CV =,CD∴=,AD CD∴==如图4,当DE BC⊥时,30E A∠=∠=︒,60BCE∴∠=︒,180ACB BCE∴∠+∠=︒,90ACD DCE∴∠=∠=︒,AD∴=,综上所述:3AD=或(3)解:如图5,∵DE BC ∥,30B C ∠=∠=︒,30BCF E ∴∠=∠=︒,30EDF B ∠=∠=︒,120ACB ∠=︒,90ACE ∴∠=︒,1452ECD ACD ACE ∴∠=∠=∠=︒,将DFE △沿DF 所在直线翻折得到DFG ,30GDF EDF ∴∠=∠=︒,60EDG ∴∠=︒,90CHK EHD ∴∠=∠=︒,DH CH ∴=1FH ∴==,1CF CH FH ∴=+,3AC ∴==.【点睛】本题考查了等腰三角形的判定和性质,直角三角形的性质等知识,解决问题的关键是正确分类,画出图形.10.如图,在ABC 中,90BAC ∠=︒,AB AC =,点D 为线段BC 延长线上一点,以AD 为腰作等腰直角DAF △,使90DAF ∠=︒,连接CF .(1)请判断CF 与BC 的位置关系,并说明理由;(2)若8BC =,4CD BC =,求线段AD 的长;(3)如图2,在(2)的条件下,将DAF △沿线段DF 翻折,使点A 与点E 重合,连接CE ,求线段CE 的长.【答案】(1)CF BC ⊥,理由见解析(2)(3)【分析】(1)证明()SAS ABD ACF △≌△,则ADB AFC ∠=∠,如图1,记AD CF 、的交点为O ,根据180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠,AOF COD ∠=∠,可得90FAO DCO ∠=∠=︒,进而可得CF BC ⊥;(2)如图2,过A 作AH BC ⊥于H ,则142BH CH AH BC ====,6DH =,由勾股定理得,AD =(3)由翻折的性质可知,DE AD =,45EDF ADF ∠=∠=︒,90ADE ∠=︒,如图3,过A 作AM BC ⊥于M ,过E 作EN BC ⊥于N ,证明()AAS ADM DEN ≌,则46DN AM EN DM ====,,6CN =,由勾股定理得,CE =计算求解即可.【详解】(1)解:CF BC ⊥,理由如下:∵等腰直角DAF △,90DAF ∠=︒,∴AD AF =,又∵90BAC ∠=︒,∴BAC CAD DAF CAD ∠+∠=∠+∠,即BAD CAF ∠=∠,∵AB AC =,BAD CAF ∠=∠,AD AF =,∴()SAS ABD ACF △≌△,∴ADB AFC ∠=∠,如图1,记AD CF 、的交点为O ,∵180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠,AOF COD ∠=∠,∴90FAO DCO ∠=∠=︒,∴CF BC ⊥;(2)解:∵8BC =,4CD BC =,∴2CD =,如图2,过A 作AH BC ⊥于H ,∵ABC 是等腰直角三角形, ∴142BH CH AH BC ====,∴6DH =,由勾股定理得,AD =∴线段AD 的长为(3)解:由翻折的性质可知,DE AD =,45EDF ADF ∠=∠=︒,∴90ADE ∠=︒,如图3,过A 作AM BC ⊥于M ,过E 作EN BC ⊥于N ,∴90AMD DNE ∠=︒=∠,同理(2)可知,4AM =,6MD =,∵90ADM EDN EDN DEN ∠+∠=︒=∠+∠,∴ADM DEN ∠=∠,∵90AMD DNE ∠=︒=∠,ADM DEN ∠=∠,AD DE =,∴()AAS ADM DEN ≌,∴46DN AM EN DM ====,,∴6CN =,由勾股定理得,CE =,∴线段CE 的长为【点睛】本题考查了全等三角形的判定与性质,三角形内角和定理,勾股定理,折叠的性质,等腰三角形的性质.熟练掌握全等三角形的判定与性质,折叠的性质是解题的关键.11.如图1,在Rt ABC △中,90C ∠=︒,5AC =,12BC =,点D 为BC 边上一动点,将ACD 沿直线AD 折叠,得到AFD △,请解决下列问题.(1)AB =______;当点F 恰好落在斜边AB 上时,CD =______;(2)连接CF ,当CBF V 是以CF 为底边的等腰三角形时,请在图2中画出相应的图形,并求出此时点F 到直线AC 的距离;(3)如图3,E 为边BC 上一点,且4,连接EF ,当DEF 为直角三角形时,CD = .(请写出所有满足条件的CD 长)【答案】(1)13,103(2)画图见解析,600169(3)52或或5或10【分析】(1)根据勾股定理可得AB 的长,再利用等积法求出CD 即可;(2)过点F 作FG AC ^,交CA 的延长线于G ,首先由等积法求出CH 的长,再根据勾股定理求出AH 的长,再次利用等积法可得FG 的长;(3)分90DEF ∠=︒或90EDF ∠=︒或90EFD ∠=︒分别画出图形,从而解决问题.【详解】(1)解:在Rt ABC △中,由勾股定理得,13AB ,当点F 落在AB 上时,由折叠知,CD DF =, ∴111222AC CD AB DF AC BC ⋅+⋅=⋅,51360CD CD ∴+=,103CD ∴=,故答案为:13,103;(2)过点F 作FG AC ^,交CA 的延长线于G ,BC BF =,AC AF =,AB ∴垂直平分CF , 由等积法得6013AC BC CH AB ⋅==,在Rt ACH 中,由勾股定理得,2513AH ===, 1122ACF S AC FG CF AH =⋅=⋅△,6025260013135169CF AH FG AC ⨯⨯⋅∴===;(3)当90DEF ∠=︒时,当点D 在CE 上时,作FH AC ⊥于H ,则4HF CE ==,5AF AC ==,3AH ∴=,2CH EF AC AH ∴==−=,设CD x =,则4DE x =−,在Rt EDF 中,由勾股定理得,222(4)2x x =−+, 解得52x =,52CD ∴=, 当点D 在EB 上时,同理可得538CH AC AH =+=+=,设CD DF x ==,则4DE x =−,在Rt EDF 中,由勾股定理得,222(4)8x x −+=,解得10x =,10CD ∴=,当90DFE ∠=︒时,由勾股定理得AE设CD DF x ==,则520x +=,x ∴,CD ∴=;当90FDE ∠=︒时,则45ADC ADF ∠=∠=︒,5CD AC ∴==,综上:52CD =或或5或10,故答案为:52或或5或10.【点睛】本题是三角形综合题,主要考查了翻折的性质,直角三角形的性质,勾股定理,等腰直角三角形的判定与性质等知识,利用等积法求垂线段的长是解题的关键.。
初二数学几何压轴题选编

初二数学几何压轴题选编在三角形ABC中,角ABC为45度,CD垂直于AB,BE 垂直于AC,垂足分别为D和E,BC的中点为F。
BE与DF、DC分别交于点G、H,连接AG。
1)证明:BH=AC;2)若AB=BC,则证明:AG=BG。
将两个全等的直角三角形ABC和DBE按图①所示方式摆放,其中∠ACB=∠DEB=90度,∠A=∠D=30度,点E落在AB上,DE所在直线交AC所在直线于点F。
1)证明:AF+EF=DE;2)若将图①中的△DBE绕点B按顺时针方向旋转角度α,且0度小于α小于60度,其它条件不变,如图②,请直接写出你在(1)中猜想的结论是否仍然成立;3)若将图①中的△DBE绕点B按顺时针方向旋转角度β,且60度小于β小于180度,其它条件不变,如图③。
你认为(1)中猜想的结论还成立吗?若成立,请写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由。
已知:如图,点E在△XXX的边AC上,且∠XXX∠ABC。
1)证明:∠ABE=∠C;2)若∠BAE的平分线AF交BE于F,FD平行于BC交AC于D,设AB=6,AC=10,求DC的长;3)若BE平分∠ABC,AF平分∠BAC,且FD平行于BC交AC于点D,连接FC,则△DFC是什么三角形?为什么?如图①,在△ABC中,∠BAC为90度,AB=AC,∠ABC为45度。
MN是经过点A的直线,BD垂直于MN于D,CE垂直于MN于E。
1)证明:BD=AE;2)若将MN绕点A旋转,使MN与BC相交于点G(如图②),其他条件不变,则证明:BD=AE;3)在(2)的情况下,若CE的延长线过AB的中点F(如图③),连接GF,则证明:∠1=∠2.如图①,已知:△ABC中,∠BAC为90度,AB=AC,直线m经过点A,BD垂直于m于D,CE垂直于m于E。
1)证明:DE=BD+CE;2)拓展:如图②,将(1)中的条件改为:△ABC中,AB=AC,D、A、E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,点D、A、E都在直线m上,且BD垂直于m于D,CE垂直于m于E。
初二几何压轴题训练

1. BE ,CF 是△ABC 的高,且BP=AC ,CQ=AB ,试确定AP 与AQ 的数量关系和位置关系2.如图2所示,△ABC 是等腰直角三角形,∠ACB =90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E ,交AD 于点F ,求证:∠ADC =∠BDE .3.两个全等的含30,60角的三角板ADE 和三角板ABC ,如下图放置,,,E A C 三点在一条直线上,连结BD ,取BD 的中点M ,连结,ME MC .试判断EMC 的形状,并说明理由.MED CBA4.:如图,△ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F ,H 是BC 边的中点,连结DH 与BE 相交于点G 。
(1) BF =AC (2) CE =12BF (3)CE 与BC 的大小关系如何。
BAC E FQPD ABC D EF 图25. :△ABC 为等边三角形,M 是BC 延长线上一点,直角三角尺的一条直角边经过点A ,且60º角的顶点E 在BC 上滑动,〔点E 不与点B 、C 重合〕,斜边与∠ACM 的平分线CF 交于点F〔1〕如图〔1〕当点E 在BC 边得中点位置时○1猜测AE 与EF 满足的数量关系是 . ○2连结点E 与AB边得中点N,猜测BE和CF满足的数量关系是 . ○3请证明你的上述猜测; 〔2〕如图〔2〕当点E在BC边得任意位置时,AE和EF 有怎样的数量关系,并说明你的理由?6.如图,△BAD 和△BCE 均为等腰直角三角形,∠BAD=∠BCE=90°,点M 为DE 的中点,过点E 与AD 平行的直线交射线AM 于点N . 〔1〕当A ,B ,C 三点在同一直线上时〔如图1〕,求证:M 为AN 的中点;〔2〕将图1中的△BCE 绕点B 旋转,当A ,B ,E 三点在同一直线上时〔如图2〕,求证:△ACN 为等腰直角三角形;〔3〕将图1中△BCE 绕点B 旋转到图3位置时,〔2〕中的结论是否仍成立?假设成立,试证明之,假设不成立,请说明理由.图(1)NF AE图(2)FA。
初二几何压轴题专项练习题

初二几何压轴题专项练习题【初二几何压轴题专项练习题】题目一:线段比例定理已知线段AB上一点C,AC∶BC=3∶2,若AB=35cm,求AC和BC的长度。
解析:根据线段比例定理,可以得到:AC/BC = 3/2AB = AC + BC首先,我们可以设AC的长度为3x,BC的长度为2x。
根据AB的长度为35cm得到:3x + 2x = 35化简方程,得到:5x = 35x = 7代入x值,求得AC和BC的长度:AC = 3x = 3 * 7 = 21cmBC = 2x = 2 * 7 = 14cm因此,AC的长度为21cm,BC的长度为14cm。
题目二:相似三角形已知三角形ABC和三角形DEF相似,AB=10cm,BC=8cm,EF=12cm,求DF的长度。
解析:由于三角形ABC和三角形DEF相似,可以得到:AB/DE = BC/EF代入已知的数值,得到:10/DE = 8/12化简方程,得到:10 * 12 = 8 * DEDE = 120/8DE = 15因此,DF的长度为15cm。
题目三:直角三角形已知直角三角形ABC,∠B=90°,BC=7cm,AC=24cm,求AB的长度。
解析:根据勾股定理,可以得到:AB² + BC² = AC²代入已知的数值,得到:AB² + 7² = 24²化简方程,得到:AB² + 49 = 576AB² = 527AB ≈ 22.98因此,AB的长度约为22.98cm。
题目四:平行线与角平分线已知直线l₁和l₂平行,以及∠A和∠B被直线l₁切分,∠A和∠B 互为相对角,若∠A的度数为60°,求∠B的度数。
解析:由于直线l₁和l₂平行,∠A和∠B互为相对角,∠A的度数为60°,则可得到:∠A = ∠B因此,∠B的度数也为60°。
题目五:垂直平分线已知直线l与线段AB垂直且平分线段AB,若AB的长度为16cm,求直线l与AB的交点C的坐标。
八年级下几何压轴题

初二几何压轴题汇编12(1)(2)1.已知正方形.若一个等边三角形的三个顶点均在正方形的内部或边上,则称这个等边三角形为正方形的内等边三角形.正方形的边长为,点在边上.当点为边的中点时,求作:正方形的内等边(尺规作图,不写作法,保留作图痕迹).若是正方形的内等边三角形,连接,,则线段长的最小值是 ,线段长的取值范围是 .和都是正方形的内等边三角形,当边的长最大时,画出和,点,,按逆时针方向排序,连接.找出图中与线段相等的所有线段,并给予证明.(1)(2)2.如图①,已知正方形的边长为,点是边上的一个动点,点关于直线的对称点是点,连接、、、,设.的最小值是 ,此时的值是 .如图②,若的延长线交边于点,并且.12(3)求证:点是的中点.求的值.若点是射线上的一个动点,请直接写出当为等腰三角形时的值.(1)(2)(3)3.如图,在正方形中,,是边上一动点(不与点重合),点与点关于所在的直线对称,连接,,延长到点,使得,连接,.当时,依题意补全图.在()的条件下,求线段的长.当点在边上运动时,能使为等腰三角形,请直接写出此时与的数量关系 .4.12(1)(2)在正方形中,点在对角线上(与点、不重合),连接,过点作与边(或延长线)交于点,作交射线于点.如图:依题意补全图.判断与的数量关系为 ,并证明你的结论.若正方形的边长为,当时,请直接写出的长为 .12(1)(2)5.如图,正方形中,是对角线,点在射线上运动(与点、不重合),连接,过点作线段的平行线交直线于点,过点作直线的垂线,垂足为点,连接.如图,当点在线段上时.依题意补全图.判断与的数量关系并加以证明.如图,若点在线段的延长线上时,且,正方形的边长为,求的长.(1)(2)(3)6.如图,正方形中,为上一动点,过点作交边于点.求证:.用等式表示、、之间的数量关系,并证明.点从点出发,沿方向移动,若移动的路径长为,则的中点移动的路径长为 (直接写出答案).(1)7.在菱形中,,点是射线上一动点,以为边向右侧作等边,点的位置随着点的位置变化而变化.如图,当点在菱形内部或边上时,连接,与的数量关系是 ,与的位置关系是 .(2)(3)BDACPE当点在菱形外部时,()中的结论是否还成立?若成立,请予以证明.若不成立,请说明理由(选择图,图中的一种情况予以证明或说理).BDACP EBDAPEC如图,当点在线段的延长线上时,连接,若,,求四边形的面积.BDAPEC(1)(2)8.如图,在矩形中,,,是的中点,点是线段上一动点,连接并延长交直线于点,过作,交射线于点,连接,点是线段的中点.连接图中的,,求证:.如图,当点与重合时,求的长.(3)当点从点运动到点时,求点经过的路径长.(1)12(2)12(3)9.四边形是边长为的正方形,点是边上一动点(包含端点、不包含),点是正方形外角的平分线上一点,且满足.当点与点重合时,直接写出线段与线段的数量关系.如图,当点是边的中点时.补全图形.请证明①中的结论仍然成立.取线段的中点,连接、、.求证:.直接写出线段长度的取值范围.1(1)10.在正方形中,连接,为射线上的一个动点(与点不重合),连接,的垂直平分线交线段于点,连接,.提出问题:当点运动时,的度数,与的数量关系是否发生改变?探究问题:首先考察点的两个特殊位置.当点与点重合时,如图所示, ,用等式表示线段与之间的数量关系: .2(2)(3)当时,如图所示,①中的结论是否发生变化?直接写出你的结论: .(填“变化”或“不变化”)然后考察点的一般位置:依题意补全图,,通过观察、测量,发现:()中①的结论在一般情况 .(填“成立”或“不成立”)证明猜想:若()中①的结论在一般情况下成立,请从图和图中任选一个进行证明;若不成立,请说明理由.(1)(2)(3)11.在学习了正方形后,数学小组的同学对正方形进行了探究,发现:如图,在正方形中,点为边上任意一点(点不与、重合),点在线段上,过点的直线,分别交、于点、.此时,有结论,请进行证明.如图,当点为中点时,其他条件不变,连接正方形的对角线,与交于点,连接,此时有结论:,请利用图做出证明.如图,当点为直线上的动点时,如果中的其他条件不变,直线分别交直线、于点、,请你直接写出线段与之间的数量关系、线段与之间的数量关系.(1)(2)12.把一个含角的直角三角板和一个正方形摆放在一起,使三角板的直角顶点和正方形的顶点重合,连接,点,分别为,的中点,连接,.如图,点,分别在正方形的边,上,请判断,的数量关系和位置关系,直接写出结论.如图,点,分别在正方形的边,的延长线上,其他条件不变,那么你在()中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.(1)(2)(3)13.在矩形中,,,点是边上一点,过点作,交射线于点,交射线于点.如图,若,则 .当以、、为顶点的三角形是等边三角形时,依题意在图中补全图形,并求的长.过点作交射线于点,请探究:当为何值时,以、、、为顶点的四边形是平行四边形.(1)(2)(3)14.在正方形中,点是射线上一点,点是正方形外角平分线上一点,且,连接,.如图,当是线段的中点时,直接写出与的数量关系.当点不是线段的中点,其它条件不变时,请你在图中补全图形,判断中的结论是否成立,并证明你的结论.若正方形的边长为,当点,,在一条直线上时,求的面积.(直接写出结果即可)(1)(2)15.已知:如图,正方形中,是边上的一点,连结,作于,交正方形的外角的平分线于,易证:.当点在的延长线上时,其他条件不变,请在图中补全图形,猜想与的数量关系,并证明你的结论.当点在边上时,其他条件不变,连结,交边于点.12用等式表示线段、和之间的数量关系,并证明.若正方形的边长为,,求的长.123(1)(2)16.如图,在正方形中,点是边所在直线上一动点(不与点、重合),过点作,交射线于点,连接.如图,当点在线段上时,.按要求补全图形. (用含的式子表示).判断线段,,之间的数量关系,并证明.当点在直线上时,直接写出线段,,之间的数量关系,不需证明.(1)(2)17.如图,是正方形的对角线,点为线段上一个动点(点不与点,重合),连接,点在射线上,且.提出问题:当运动时,的度数,线段,之间的数量关系是否发生变化?探究问题:首先考察点的一个特殊位置:若,如图所示,,观察线段,之间的数量关系.然后考察点的一般位置:若,依题意补全图,通过观察、测量,发现:12在一般情况下 (用含的式子表示)此时,线段,之间的数量关系是 ,并证明.12(1)(2)18.如图,四边形是平行四边形,,是直线上的两点,点关于的对称点为,连接交于点.若,如图.依题意补全图形.判断与的数量关系是 .如图,当时,,的延长线相交于点,取的中点,连接.用等式表示线段与的数量关系,并证明.19.如图,在正方形中,是边上的一动点,点在边的延长线上,且,连接、、,平分交于点.(1)(2)(3)根据题意补全图形.求证:.过点作于点,用等式表示线段,与之间的数量关系,并证明.(1)12(2)(3)20.已知:在正方形中,点在对角线上运动(不与,重合)连接,过点作于交直线于点,作于交直线于点.当点在对角线上运动到图位置时,则与的数量关系是 .当点运动到图所示位置时.依据题意补全图形.上述结论还成立吗?若成立,请证明.若不成立,请说明理由.若正方形边长为,,直接写出长.(1)21.已知:如图,正方形,点是直线上一个动点,连接交直线于点,过点作于点,连接.如图,12(2)直接写出的度数.用等式表示线段、和之间的数量关系,并证明.当点运动到图和图所示的位置时,请选择其中一种情况补全图形,并直接写出线段、和之间的数量关系.(1)(2)22.已知,如图,正方形中,点是对角线上的一个动点.如图,连接,,直接写出与的数量关系.如图,点为边的中点,当点运动到线段上时,连接,,相交于点.123请你根据题意在图中补全图形.猜想与的位置关系,并证明.如果正方形的边长为,直接写出的长.12(1)(2)23.在正方形中,点是直线上一点,连接,将线段绕点顺时针旋转,得到线段,连接.如图,若点在线段的延长线上.过点作于,与对角线交于点.请根据题意补全图形.求证:.若点在射线上,直接写出,,三条线段的数量关系为 .12(1)(2)24.已知正方形中,点是边(或的延长线)上任意一点,平分,交射线于点.如图,若点在线段上.依题意补全图.用等式表示线段,,之间的数量关系,并证明.如图,若点在线段的延长线上,请直接写出线段,,之间的数量关系.(1)(2)(3)25.如图,在正方形中,为边上的一动点(不与点、重合),连接,点关于直线的对称点为,连接,.依题意补全图形.求的大小.过点作于,用等式表示线段、和的数量关系,并证明.12(1)12(2)26.正方形中,点是直线上的一个动点,连接,将线段绕点顺时针旋转得到线段,连接.如图,若点在线段上.直接写出的度数为 .求证:.如图,若点在的延长线上,,.依题意补全图.直接写出线段的长度为 .(1)12(2)27.已知:正方形的边长为,点在上,射线交直线于点,作于点.如图,当点在边上时,猜想与的数量关系并证明.若点在直线上.依题意,在备用图中补全图形.请直接写出与的数量关系 .12(1)(2)(3)28.如图,在正方形中,点在边上,点在正方形外部,且满足,.连接,,取的中点,连接,,交于点.回答下列问题:依题意补全图形.求证:.请探究线段,,所满足的等量关系,并证明你的结论.设,若点沿着线段从点运动到点,则在该运动过程中,线段所扫过的面积为 (直接写出答案).29.已知,点在正方形的边上(不与点,重合),是对角线,延长到点,使,过点作的垂线,垂足为,连接,.(1)12(2)根据题意补全图形,并证明.回答问题:用等式表示线段与的数量关系,并证明.用等式表示线段,,之间的数量关系(直接写出即可).12(1)(2)(3)30.某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在中,,,点为直线上一动点(点不与,重合),以为边在右侧作正方形,连接.观察猜想.如图,当点在线段上时.与的位置关系为: .,,之间的数量关系为: .(将结论直接写在横线上)数学思考.如图,当点在线段的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.拓展延伸.如图,当点在线段的延长线上时,延长交于点,连接,若已知,,请求出的长.(1)212(2)31.已知:四边形是正方形,点在边上,点在边上,且.如图,判断与有怎样的位置关系?写出你的结果,并加以证明.1如图,对角线与交于点.,分别与,交于点,点.求证:.连接,若,,求的长.(1)(2)32.在正方形和正方形中,顶点、、在同一直线上,是的中点.如图,若,,求的长.如图,连接,.试判断与的关系,并证明.(1)12(2)33.正方形中,点是直线上的一个动点(不与点,重合),作射线,过点作于点,连接.如图,当点在上时,如果,那么的度数是 .如图,当点在延长线上时.依题意补全图.用等式表示线段,和之间的数量关系,并证明.(1)34.已知如图,正方形,为等腰直角三角形,其中,,连接,,,点是的中点,连接.用等式表示线段与的数量关系是 .12(2)若将绕顶点旋转,使得点恰好在线段上,并且点在线段的上方,点仍是的中点,连接,.在图中依据题意补全图形.求证:.(1)(2)35.在正方形中,对角线、交于点,动点在线段上(不含点),,交于点,过点作,垂足为,交于点.当点与点重合时(如图),求证:≌.试猜想线段,的数量关系,并证明你的猜想.(1)36.如图,正方形中,为上一动点,过点作交边于点.求证:.(2)(3)用等式表示、、之间的数量关系,并证明.点从点出发,沿方向移动,若移动的路径长为,则的中点移动的路径长为 (直接写出答案).12(1)(2)37.四边形是正方形,是对角线,是平面内一点,且.过点作,且.连接,.是的中点,作射线交于点.如图,若点,分别在,边上.求证:..如图,若点在四边形内,点在直线的上方.求与的和的度数.(1)(2)(3)38.已知,正方形,是延长线上一点,连接,,作中边上的高,连接.依题意补全图形.求证:.猜想,,之间的数量关系,并说明理由.(1)(2)39.如图,在正方形中,点为的中点,为线段上任意一点,将线段绕点逆时针旋转,得到线段.请按要求补全图形:连接,过点作,交对角线于点,连接.判断与的数量关系并加以证明.(1)12(2)40.在正方形中,是边上一动点(不与点,重合),点关于射线的对称点为点,连接,连接并延长交于点.求出的度数.过点作于点,点作交延长线于点,连接.补全图形.用等式表示线段与的数量关系,并证明.。
人教版八年级数学上册期末专题复习:几何压轴题强化训练试题(含答案)

人教版八年级数学上册期末专题复习:几何压轴题强化训练试题1、如图,AB>AC,∠BAC的平分线与BC边的中垂线GD相交于点D,过点D作DE⊥AB于点E,DF⊥AC于点F,求证:BE=CF.2、如图,△ABC中,∠ACB=90°,AC=BC,将△ABC绕点C逆时针旋转角α.(0°<α<90°)得到△A1B1C1,连接BB1.设CB1交AB于D,A1B1分别交AB、AC于E、F.(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以说明(△ABC与△A1B1C1全等除外);(2)当△BB1D是等腰三角形时,求α.3、如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连结DE.(1)求证:点E到DA,DC的距离相等;(2)求∠DEB的度数.4、在△ABC中,∠ACB=90°,AC=BC,直线,MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.(1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE;(2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD﹣BE;(3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系?请你直接写出这个数量关系,不要证明.5、概念学习:规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.理解概念(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,请写出图中两对“等角三角形”.概念应用(2)如图2,在△ABC中,CD为角平分线,∠A=40°,∠B=60°.求证:CD为△ABC的等角分割线.(3)在△ABC中,∠A=42°,CD是△ABC的等角分割线,直接写出∠ACB的度数.6、如图,∠ABC=∠BAD=90°,点E,F分别是AC,BC的中点。
人教版八年级数学上册期末专题复习:几何压轴题强化训练试题(含答案)

人教版八年级数学上册期末专题复习:几何压轴题强化训练试题1、如图,AB>AC,∠BAC的平分线与BC边的中垂线GD相交于点D,过点D作DE⊥AB于点E,DF⊥AC于点F,求证:BE=CF.2、如图,△ABC中,∠ACB=90°,AC=BC,将△ABC绕点C逆时针旋转角α.(0°<α<90°)得到△A1B1C1,连接BB1.设CB1交AB于D,A1B1分别交AB、AC于E、F.(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以说明(△ABC与△A1B1C1全等除外);(2)当△BB1D是等腰三角形时,求α.3、如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连结DE.(1)求证:点E到DA,DC的距离相等;(2)求∠DEB的度数.4、在△ABC中,∠ACB=90°,AC=BC,直线,MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.(1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE;(2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD﹣BE;(3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系?请你直接写出这个数量关系,不要证明.5、概念学习:规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.理解概念(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,请写出图中两对“等角三角形”.概念应用(2)如图2,在△ABC中,CD为角平分线,∠A=40°,∠B=60°.求证:CD为△ABC的等角分割线.(3)在△ABC中,∠A=42°,CD是△ABC的等角分割线,直接写出∠ACB的度数.6、如图,∠ABC=∠BAD=90°,点E,F分别是AC,BC的中点。
初二数学全等三角形压轴几何题(讲义及答案)含答案

初二数学全等三角形压轴几何题(讲义及答案)含答案一、全等三角形旋转模型1.问题背景:如图1,在四边形ABCD 中,90BAD ∠=︒,90BCD ∠=︒,BA BC =,120ABC ∠=︒,60MBN ∠=︒,MBN ∠绕B 点旋转,它的两边分别交AD 、DC 于E 、F .探究图中线段AE ,CF ,EF 之间的数量关系.小李同学探究此问题的方法是:延长FC 到G ,使CG AE =,连接BG ,先证明BCG BAE △≌△,再证明BFC BFE △≌△,可得出结论,他的结论就是_______________;探究延伸1:如图2,在四边形ABCD 中,90BAD ∠=︒,90BCD ∠=︒,BA BC =,2ABC MBN ∠=∠,MBN ∠绕B 点旋转,它的两边分别交AD 、DC 于E 、F .上述结论是否仍然成立?请直接写出结论(直接写出“成立”或者“不成立”),不要说明理由. 探究延伸2:如图3,在四边形ABCD 中,BA BC =,180BAD BCD ∠+∠=︒,2ABC MBN ∠=∠,MBN ∠绕B 点旋转,它的两边分别交AD 、DC 于E 、F .上述结论是否仍然成立?并说明理由.实际应用:如图4,在某次军事演习中,舰艇甲在指挥中心(O 处)北偏西30的A 处舰艇乙在指挥中心南偏东70︒的B 处,并且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以75海里/小时的速度前进,同时舰艇乙沿北偏东50︒的方向以100海里/小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E 、F 处,且指挥中心观测两舰艇视线之间的夹角为70︒,试求此时两舰艇之间的距离.答案:E解析:EF=AE+CF .探究延伸1:结论EF=AE+CF 成立.探究延伸2:结论EF=AE+CF 仍然成立.实际应用:210海里.【分析】延长FC 到G ,使CG AE =,连接BG ,先证明BCG BAE △≌△,可得BG=BE ,∠CBG=∠ABE ,再证明BGF BEF ≌,可得GF=EF ,即可解题;探究延伸1:延长FC 到G ,使CG AE =,连接BG ,先证明BCG BAE △≌△,可得BG=BE ,∠CBG=∠ABE ,再证明BGF BEF ≌,可得GF=EF ,即可解题;探究延伸2:延长FC 到G ,使CG AE =,连接BG ,先证明BCG BAE △≌△,可得BG=BE ,∠CBG=∠ABE ,再证明BGF BEF ≌,可得GF=EF ,即可解题;实际应用:连接EF ,延长AE ,BF 相交于点C ,然后与探究延伸2同理可得EF=AE+CF ,将AE 和CF 的长代入即可.【详解】解:EF=AE+CF理由:延长FC 到G ,使CG AE =,连接BG ,在△BCG 和△BAE 中,90BC BA BCG BAE CG AE =⎧⎪∠=∠=︒⎨⎪=⎩,∴BCG BAE △≌△(SAS ),∴BG=BE ,∠CBG=∠ABE ,∵∠ABC=120°,∠MBN=60°,∴∠ABE+∠CBF=60°,∴∠CBG+∠CBF=60°,即∠GBF=60°,在△BGF 和△BEF 中,BG BE GBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩,∴△BGF ≌△BEF (SAS ),∴GF=EF ,∵GF=CG+CF=AE+CF ,∴EF=AE+CF .探究延伸1:结论EF=AE+CF 成立.理由:延长FC 到G ,使CG AE =,连接BG ,在△BCG 和△BAE 中,90BC BA BCG BAE CG AE =⎧⎪∠=∠=︒⎨⎪=⎩,∴BCG BAE △≌△(SAS ),∴BG=BE ,∠CBG=∠ABE ,∵∠ABC=2∠MBN ,∴∠ABE+∠CBF=12∠ABC , ∴∠CBG+∠CBF=12∠ABC , 即∠GBF=12∠ABC , 在△BGF 和△BEF 中,BG BE GBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩,∴△BGF ≌△BEF (SAS ),∴GF=EF ,∵GF=CG+CF=AE+CF ,∴EF=AE+CF .探究延伸2:结论EF=AE+CF 仍然成立.理由:延长FC 到G ,使CG AE =,连接BG ,∵180BAD BCD ∠+∠=︒,∠BCG+∠BCD=180°,∴∠BCG=∠BAD在△BCG 和△BAE 中,BC BA BCG BAE CG AE =⎧⎪∠=∠⎨⎪=⎩,∴BCG BAE △≌△(SAS ),∴BG=BE ,∠CBG=∠ABE ,∵∠ABC=2∠MBN ,∴∠ABE+∠CBF=12∠ABC , ∴∠CBG+∠CBF=12∠ABC , 即∠GBF=12∠ABC , 在△BGF 和△BEF 中,BG BE GBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩,∴△BGF ≌△BEF (SAS ),∴GF=EF ,∵GF=CG+CF=AE+CF ,∴EF=AE+CF .实际应用:连接EF ,延长AE ,BF 相交于点C ,∵∠AOB=30°+90°+(90°-70°)=140°,∠EOF=70°,∴∠EOF=12∠AOB ∵OA=OB ,∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°,∴符合探索延伸中的条件∴结论EF= AE+CF 仍然成立即EF=75×1.2+100×1.2=210(海里)答:此时两舰艇之间的距离为210海里.【点睛】本题考查了全等三角形的判定与性质.作辅助线构造全等三角形是解题的关键. 2.一位同学拿了两块45︒三角尺MNK ∆,ACB ∆做了一个探究活动:将MNK ∆的直角顶点M 放在ACB ∆的斜边AB 的中点处,设4AC BC ==.(1)如图1所示,两三角尺的重叠部分为ACM ∆,则重叠部分的面积为______,周长为______.(2)将如图1所示中的MNK ∆绕顶点M 逆时针旋转45︒,得到如图2所示,此时重叠部分的面积为______,周长为______.(3)如果将MNK ∆绕M 旋转到不同于如图1所示和如图2所示的图形,如图3所示,请你猜想此时重叠部分的面积为______.(4)在如图3所示情况下,若1AD =,求出重叠部分图形的周长.答案:A解析:(1)4,4+;(2)4,8;(3)4;(4)4+【分析】()1根据4AC BC ==,90ACB ∠=,得出AB 的值,再根据M 是AB 的中点,得出AM MC =,求出重叠部分的面积,再根据AM ,MC ,AC 的值即可求出周长;()2易得重叠部分是正方形,边长为12AC ,面积为214AC ,周长为2.AC ()3过点M 分别作AC 、BC 的垂线MH 、ME ,垂足为H 、.E 求得Rt MHD ≌Rt MEG ,则阴影部分的面积等于正方形CEMH 的面积. ()4先过点M 作ME BC ⊥于点E ,MH AC ⊥于点H ,根据DMH EMH ∠∠=,MH ME =,得出Rt DHM ≌Rt EMG ,从而得出HD GE =,CE AD =,最后根据AD 和DF 的值,算出DM =.【详解】解:()14AC BC ==,90ACB ∠=,AB ∴== M 是AB 的中点,AM ∴=45ACM ∠=,AM MC ∴=,∴重叠部分的面积是42=, ∴周长为:44AM MC AC ++==+故答案为4,4+;()2重叠部分是正方形,∴边长为1422⨯=,面积为14444⨯⨯=, 周长为248⨯=.故答案为4,8.()3过点M 分别作AC 、BC 的垂线MH 、ME ,垂足为H 、E , M 是ABC 斜边AB 的中点,4AC BC ==, 12MH BC ∴=, 12ME AC =, MH ME ∴=,又90NMK HME ∠∠==,90NMH HMK ∠∠∴+=,90EMG HMK ∠∠+=, HMD EMG ∠∠∴=,在MHD 和MEG 中,HMD GME MH MEDHM MEG ∠=∠⎧⎪=⎨⎪∠=∠⎩, MHD ∴≌()MEG ASA ,∴阴影部分的面积等于正方形CEMH 的面积, 正方形CEMH 的面积是1144422ME MH ⋅=⨯⨯⨯=; ∴阴影部分的面积是4;故答案为4.()4如图所示, 过点M 作ME BC ⊥于点E ,MH AC ⊥于点H ,∴四边形MECH 是矩形,MH CE ∴=,45A ∠=,45AMH ∠∴=,AH MH ∴=,AH CE ∴=,在Rt DHM 和Rt GEM 中,DMH EMG MH MEDHM GEM ∠=∠⎧⎪=⎨⎪∠=∠⎩, Rt DHM ∴≌.Rt GEMGE DH ∴=,AH DH CE GE ∴-=-,CG AD ∴=,1AD =,1.DH ∴= 145DM ∴=+= .∴四边形DMGC 的周长为:CE CD DM ME +++2AD CD DM =++425=+.【点睛】此题考查了等腰直角三角形,利用等腰直角三角形的性质,等腰直角三角形的面积公式,正方形的面积公式,全等三角形的判定和性质求解.3.如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是 ,位置关系是 ;(2)探究证明:把△ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由;(3)拓展延伸:把△ADE 绕点A 在平面内自由旋转,若AD =4,AB =10,请直接写出△PMN 面积的最大值.解析:(1)PM =PN ,PM ⊥PN ;(2)△PMN 是等腰直角三角形.理由见解析;(3)S △PMN 最大=492. 【分析】(1)由已知易得BD CE =,利用三角形的中位线得出12PM CE =,12PN BD =,即可得出数量关系,再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠,最后用互余即可得出位置关系;(2)先判断出ABD ACE ∆≅∆,得出BD CE =,同(1)的方法得出12PM BD =,12PN BD =,即可得出PM PN =,同(1)的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠,即可得出结论;(3)方法1:先判断出MN 最大时,PMN ∆的面积最大,进而求出AN ,AM ,即可得出MN 最大AM AN =+,最后用面积公式即可得出结论.方法2:先判断出BD 最大时,PMN ∆的面积最大,而BD 最大是14AB AD +=,即可得出结论.【详解】解:(1)点P ,N 是BC ,CD 的中点,//PN BD ∴,12PN BD =, 点P ,M 是CD ,DE 的中点, //PM CE ∴,12PM CE =, AB AC =,AD AE =,BD CE ∴=,PM PN ∴=,//PN BD ,DPN ADC ∴∠=∠,//PM CE ,DPM DCA ∴∠=∠,90BAC ∠=︒,90ADC ACD ∴∠+∠=︒,90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒,PM PN ∴⊥,故答案为:PM PN =,PM PN ⊥;(2)PMN ∆是等腰直角三角形.由旋转知,BAD CAE ∠=∠,AB AC =,AD AE =,()ABD ACE SAS ∴∆≅∆,ABD ACE ∴∠=∠,BD CE =, 利用三角形的中位线得,12PN BD =,12PM CE =, PM PN ∴=,PMN ∴∆是等腰三角形,同(1)的方法得,//PM CE ,DPM DCE ∴∠=∠,同(1)的方法得,//PN BD ,PNC DBC ∴∠=∠,DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠,MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠,90BAC ∠=︒,90ACB ABC ∴∠+∠=︒,90MPN ∴∠=︒,PMN ∴∆是等腰直角三角形;(3)方法1:如图2,同(2)的方法得,PMN ∆是等腰直角三角形,MN ∴最大时,PMN ∆的面积最大,//DE BC ∴且DE 在顶点A 上面,MN ∴最大AM AN =+,连接AM ,AN ,在ADE ∆中,4AD AE ==,90DAE ∠=︒,22AM ∴=在Rt ABC ∆中,10AB AC ==,52AN =22522MN ∴=最大,222111149(72)22242PMN S PM MN ∆∴==⨯=⨯=最大. 方法2:由(2)知,PMN ∆是等腰直角三角形,12PM PN BD ==, PM ∴最大时,PMN ∆面积最大,∴点D 在BA 的延长线上,14BD AB AD ∴=+=,7PM ∴=,2211497222PMN S PM ∆∴==⨯=最大. 【点睛】此题属于几何变换综合题,主要考查了三角形的中位线定理,等腰直角三角形的判定和性质,全等三角形的判断和性质,直角三角形的性质的综合运用;解(1)的关键是判断出12PM CE =,12PN BD =,解(2)的关键是判断出ABD ACE ∆≅∆,解(3)的关键是判断出MN 最大时,PMN ∆的面积最大.4.如图,△ABC 中,O 是△ABC 内一点,AO 平分∠BAC ,连OB ,OC .(1)如图1,若∠ACB =2∠ABC ,BO 平分∠ABC ,AC =5,OC =3,则AB = ; (2)如图2,若∠CBO +∠ACO =∠BAC =60°,求证:BO 平分∠ABC ;(3)如图3,在(2)的条件下,若BC =3B 绕点O 逆时针旋转60°得点D ,直接写出CD 的最小值为 .答案:A解析:(1)8;(2)见解析;(3)33【分析】(1)先补充证明角平分线的性质定理:如图,△ABC 中,AD 是角平分线,则:BD DC=AB AC .如图1中,延长CO 交AB 于E ,由OA 平分∠EAC ,推出AE AC =OE OC,推出AE EO =AC OC =53,设AE =5k ,OE =3k ,利用相似三角形的性质构建方程求出k 即可解决问题. (2)如图2中,过点O 作EF ⊥OA 交AB 于E ,交AC 于F ,作CG ∥EF 交AB 于G ,连接OG .证明△AGO ≌△ACO (SAS ),推出OG =OC ,推出∠OGC =∠OCG ,证明O ,G ,B ,C 四点共圆,可得结论.(3)如图3中,以BC 为边向上作等边△BCH ,连接OH ,作HM ⊥BC 于M .证明△HBO ≌△CBD (SAS ),推出OH =CD ,由(2)可知∠BOC =120°,推出当点O 落在HM 上时,OH 的值最小.【详解】解:(1)先补充证明角平分线的性质定理:如图,△ABC 中,AD 是角平分线,则:BD DC =AB AC. 理由:过C 作CE ∥DA ,交BA 的延长线于E ,∵CE∥DA,∴∠1=∠E,∠2=∠3,∠1=∠2,∴∠E=∠3,∴AE=AC,∵BDDC =BAAE,∴BDDC =ABAC.如图1中,延长CO交AB于E,∵OA平分∠EAC,∴AEAC=OEOC,∴AEEO =ACOC=53,设AE=5k,OE=3k,∵OB平分∠ABC,∴OC平分∠ACB,∵∠ACB=2∠ABC,∴∠BCE=12∠ACB=∠EBC,∴EB=EC=3k+3,∵∠ACE=∠ABC,∠CAE=∠BAC,∴△ACE∽△ABC,∴ACAB =AEAC,∴5533k k =55k,解得k=58或﹣1(舍弃),∴AB=8k+3=8.故答案为:8.(2)如图2中,过点O作EF⊥OA交AB于E,交AC于F,作CG∥EF交AB于G,连接OG.∵AO平分∠AEF,∴∠OAE=∠OAF,∵AO=AO,∠AOE=∠AOF=90°,∴△AOE≌△AOF(ASA),∴AE=AF,∵∠EAF=60°,∴△AEF是等边三角形,∴∠AEF=∠AFE=60°=∠FOC+∠FCO,∵∠OBC+∠FCO=60°,∴∠FOC=∠OBC,∵EF∥CG,∴∠AGC=∠AEF=60°,∠ACG=∠AFE=60°,∴∠AGC=∠ACG,∴AG=AC,∵∠GAO=∠CAO,AO=AO,∴△AGO≌△ACO(SAS),∴OG=OC,∴∠OGC=∠OCG,∵∠FOC=∠OCG,∴∠OBC=∠OGC,∴O,G,B,C四点共圆,∴∠ABO=∠OCG,∴∠ABO=∠OBC,∴OB平分ABC.(3)如图3中,以BC为边向上作等边△BCH,连接OH,作HM⊥BC于M.∵△OBD,△BCH都是等边三角形,∴∠HBC=∠OBD=60°,BH=BC,BO=BD,∴∠HBO=∠CBD,∴△HBO≌△CBD(SAS),∴OH=CD,由(2)可知∠BOC=120°,∴当点O落在HM上时,OH的值最小,此时OH=HM﹣OM=3﹣3,∴CD的最小值为3﹣3.故答案为:3﹣3.【点睛】本题主要考查角平分线、三角形相似的判定和性质、三角形全等的判定和性质、等边三角形等相关知识点,解题关键在于作出辅助线构造相应图形.5.已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.(1)如图1,当点D在线段BC上时,请直接写出线段BD与CF的数量关系:;(2)如图2,当点D在线段BC的延长线上时,其它条件不变,若AC=2,CD=1,则CF= ;(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系:;②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.答案:B解析:(1)BD=CF;(2)221;(3)①CD=CF+BC,②等腰三角形,见解析【分析】(1)△ABC 是等腰直角三角形,利用SAS 即可证明△BAD ≌△CAF ;(2)同(1)相同,利用SAS 即可证得△BAD ≌△CAF ,从而证得BD=CF ,即可得到CF=CD+BC ,然后求出答案;(3)中的①与(1)相同,可证明BD=CF ,又点D 、B 、C 共线,故:CD=BC+CF ; ②由(1)猜想并证明BD ⊥CF ,从而可知△FCD 为直角三角形,再由正方形的对角线的性质判定△AOC 三边的特点,再进一步判定其形状. 【详解】解:(1)证明:∵∠BAC=90°,AB=AC , ∴∠ABC=∠ACB=45°, ∵四边形ADEF 是正方形, ∴AD=AF ,∠DAF=90°,∵∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°, ∴∠BAD=∠CAF , 在△BAD 和△CAF 中,AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩, ∴△BAD ≌△CAF (SAS ), ∴BD=CF ,(2)与(1)同理,证△BAD ≌△CAF ; ∴BD=CF , ∴CF=BC+CD , ∵AC=AB=2,CD=1,∴BC ==∴CF=1;(3)①BC 、CD 与CF 的关系:CD=BC+CF理由:与(1)同法可证△BAD ≌△CAF ,从而可得: BD=CF , 即:CD=BC+CF②△AOC 是等腰三角形理由:与(1)同法可证△BAD ≌△CAF ,可得:∠DBA=∠FCA , 又∵∠BAC=90°,AB=AC , ∴∠ABC=∠ACB=45°, 则∠ABD=180°-45°=135°, ∴∠ABD=∠FCA=135° ∴∠DCF=135°-45°=90° ∴△FCD 为直角三角形.又∵四边形ADEF是正方形,对角线AE与DF相交于点O,∴OC=12DF,∴OC=OA∴△AOC是等腰三角形.【点睛】本题考查了等腰三角形、正方形的性质及全等三角形的判定与性质等知识点,一般情况下,要证明两条线段相等,就得证明这两条线段所在的两个三角形全等,关键是掌握图形特点挖掘题目所隐含的条件.6.综合与探究问题情境在Rt△ABC中,∠BAC=90°,AB=AC,点D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°至AE,连接DE,CE.探究发现(1)如图1,BD=CE,BD⊥CE,请证明;探究猜想;(2)如图2,当BD=2DC时,猜想AD与BC之间的数量关系,并说明理由;探究拓广(3)当点D在BC的延长线上时,探究并直接写出线段BD,DC,AD之间的数量关系.答案:B解析:(1)证明见解析;(2)10AD BC=,理由见解析;(3)2222BD CD AD+=.【分析】(1)根据题意计算得∠BAD=∠CAE;再根据旋转的性质,通过证明△BAD≌△CAE,从而完成求解;(2)结合(1)的结论,通过△BAD≌△CAE,得CE;通过勾股定理,得2DE=;再通过勾股定理计算,记得得到答案;(3)过点A作AM BC⊥交BC于点M;根据等腰三角形三线合一的性质,得BM CM=,再根据直角三角形斜边中线的性质,得12AM BM CM BC===;根据勾股定理的性质,通过计算,即可得到线段BD,DC,AD之间的数量关系.【详解】(1)由题意得,∠BAC =∠DAE =90° ∵∠BAD +∠CAD =∠CAE +∠CAD ∴∠BAD =∠CAE∵线段AD 绕点A 逆时针旋转90°至AE ∴AD=AE 又∵AB=AC , ∴△BAD ≌△CAE ∴BD=CE ,∠B =∠ACE =45° ∴∠ECD =90°,BD ⊥CE . (2)由(1)得:△BAD ≌△CAE ∴BD=CE ,∠B =∠ACE =45° ∵13CD BC =,BD =2DC ,即23BD BC =, ∴23BD CE BC ==, ∵AD=AE ∴222DE AD AE AD =+=∴∠B =∠ACB =45° ∴∠BCE =∠ACB+∠ACE =90°∴CD 2+CE 2=DE 2,即22212()()233BC BC AD +=, ∴106AD BC =; (3)如图,过点A 作AM BC ⊥交BC 于点M∵∠BAC =90°,AB =AC ∴12BM CM BC ==∴12AM BM CM BC ===∴()1122AM BC BD CD ==-,()1122DM CM CD BC CD BD CD =+=+=+ ∵222AM DM AD +=∴()()2221122BD CD BD CD AD ⎡⎤⎡⎤-++=⎢⎥⎢⎥⎣⎦⎣⎦∴2222BD CD AD +=. 【点睛】本题考查了旋转、等腰直角三角形、勾股定理、直角三角形斜边中线的知识;解题的关键是熟练掌握旋转、等腰三角形三线合一、勾股定理、直角三角形斜边中线的性质,从而完成求解.7.如图1所示,在Rt ABC △中90BAC ∠=︒,AB AC =,2BC =,以BC 所在直线为x 轴,边BC 的垂直平分线为y 轴建立平面直角坐标系,将ABC 绕P 点0,1顺时针旋转.(1)填空:当点B 旋转到y 轴正半轴时,则旋转后点A 坐标为______;(2)如图2所示,若边AB 与y 轴交点为E ,边AC 与直线1y x =-的交点为F ,求证:AEF 的周长为定值;(3)在(2)的条件下,求AEF 内切圆半径的最大值.解析:(1)2,21;(2)见解析;(3)324【分析】(1)作出图形,'''A B C 是ABC 绕 P 点0,1顺时针旋转,点B 旋转到y 轴正半轴时得到的图形,连接 BP ,CP ,根据2BC =,y 轴垂直平分BC , AB AC =,()0,1P -可证得四边形ABPC 是正方形,则有 '''2BP B PAB A B ,'0'21B B PPO,可得点 A 坐标;(2)作BPQ CPF ∠=∠,交AB 延长线于Q 点,根据四边形ABPC 是正方形,得到90QBP FCP ∠=∠=︒,BP CP =,可证BPQ CPF ASA ≌△△,得BQ CF =,QP FP =,利用ASA 再可证得QPE FPE ≌△△,得QE FE =则AEF 的周长22AB AC =+=(3)设EF m =,AE n =,Rt AEF 的内切圆半径为r ,由(2)可得22AF m n =--则2AE AF EF r +-=222n m n m+---=2m =-,当m 最小时,r 最大.得到22222n m nm 整理得:2224220nm n m,关于n的一元二次方程有解,即22244220m m化简得24280m m +-≥,利用二次函数图像可得422m ≥-或422m ≤--(不合题意,舍去)可得m 的最小值为422-,即r 的最大值为2422324,则有AEF 内切圆半径的最大值为324-.【详解】解:(1)如图示,'''A B C 是ABC 绕 P 点0,1顺时针旋转,点B 旋转到y 轴正半轴时得到的图形,连接 BP ,CP ,∵2BC =,y 轴垂直平分BC ∴1BO CO ==又∵Rt ABC △中,AB AC = ∴1AO =,2AB AC ==∵()0,1P - ∴1PO =∴AO BO CO PO === ∴四边形ABPC 是正方形 ∴'''2BP B P AB A B∴'0'21B B PPO∴点A 坐标为2,21(2)如图2所示,作BPQ CPF ∠=∠,交AB 延长线于Q 点 ∵四边形ABPC 是正方形∴90QBP FCP ∠=∠=︒, BP CP = ∴BPQ CPF ASA ≌△△∴ BQ CF =,QP FP =∵点F 在直线1y x =-∴45FPE ∠=︒∴ 45BPE FPC ∠+∠=︒ ∴45BPE BPQ ∠+∠=︒∴45QPE FPE ∠=∠=︒ ∵EP EP =∴QPE FPE ASA ≌△△∴ QE FE =∴AEF 的周长AE EF AF AE QE AF =++=++ AE BE BQ AF AE BE FC AF =+++=+++22AB AC =+=(3)设EF m =,AE n =,Rt AEF 的内切圆半径为 r , 由(2)可得22AF m n =-则2AE AF EFr +-=22n m n m+---=2m =∴当m 最小时,r 最大.∵在Rt AEF 中,222AE AF EF +=∴22222n m nm 整理得: 2224220nm nm ∵关于n 的一元二次方程有解∴22244220m m∴24280m m +-≥利用二次函数图像可得422m ≥-422m ≤--(不合题意,舍去) ∴m 的最小值为422-r 2422324即AEF 内切圆半径的最大值为324. 【点睛】本题主要考查了一次函数的综合应用以及根的判别式、全等三角形的判定与性质、旋转、三角形内切圆等知识,能熟练应用相关性质是解题关键. 8.问题解决一节数学课上,老师提出了这样一个问题:如图①,点P 是等边ABC 内的一点,6PA =,8PB = ,10PC =.你能求出APB ∠的度数和等边ABC 的面积吗?小明通过观察、分析、思考,形成了如下思路:如图①将BPC △绕点B 逆时针旋转60°,得到BPA △,连接PP ',可得BPP '是等边三角形,根据勾股定理逆定理可得AP P '是直角三角形,从而使问题得到解决. (1)结合小明的思路完成填空:PP '=_____________,APP '∠=_______________,APB ∠=_____________ ,ABCS= ______________.(2)类比探究Ⅰ如图②,若点P 是正方形ABCD 内一点,1PA = ,2PB =,3PC =,求APB ∠的度数和正方形的面积.Ⅱ如图③,若点P 是正方形ABCD 外一点,3PA = ,1PB =, 11PC =,求APB ∠的度数和正方形的面积.答案:B解析:(1)8,90˚,150˚,25336;(2)Ⅰ135APB ∠=︒, 722ABCD S =+正方形;Ⅱ45APB ∠=︒, 1032ABCD S =-正方形【分析】(1)根据小明的思路,然后利用等腰三角形和直角三角形性质计算即可;(2)Ⅰ将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,求出∠APB 的度数;先利用旋转求出∠PBP'=90°,BP'=BP=2,AP'=CP=3,利用勾股定理求出PP',进而判断出△APP'是直角三角形,得出∠APP'=90°,即可得出结论;过B 作BE ⊥AP 于点E ,然后利用勾股定理求出AB 的长度即可求出正方形面积;Ⅱ将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,求出∠APB 的度数;先利用旋转求出∠PBP'=90°,BP'=BP=2,AP'=CP=3,利用勾股定理求出PP',进而判断出△APP'是直角三角形,得出∠APP'=90°,即可得出结论;过B 作BF ⊥AP 于点F ,然后利用勾股定理求出AB 的长度即可求出正方形面积; 【详解】解:(1)由题易有P BP '∆是等边三角形,AP P '∆是直角三角形 ∴PP '=BP=8,90?APP '=∠,60?P PB '=∠,∴APB ∠=APP '∠+=P PB '∠150˚, 如图1,过B 作BD ⊥AP 于点D∵APB ∠=150°∴30?BPD =∠在Rt △BPD 中,30?BPD =∠,BP=8∴BD=4,PD=43 ∴AD=6+43∴AB 2=AD 2+BD 2=100+483∴ABC S =234AB =25336+ (2)Ⅰ.如图2,将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,∴△ABP'≌△CBP ,∴∠PBP'=90°,BP'=BP=2,AP'=CP=3,在Rt △PBP'中,BP=BP'=2,∴∠BPP'=45°,根据勾股定理得,PP'=2BP=22,∵AP=1,∴AP 2+PP'2=1+8=9,∵AP'2=32=9,∴AP 2+PP'2=AP'2,∴△APP'是直角三角形,且∠APP'=90°,∴∠APB=∠APP'+∠BPP'=90°+45°=135°;过B 作BE ⊥AP 于点E ,∵∠APB=135°∴∠BPE=45°∴△BPE 是等腰直角三角形∴BE=BP=22BP =2 ∴AE=1+2∴AB 2=AE 2+BE 2=7+22 ∴2722ABCD S AB ==+正方形Ⅱ.如图3,将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,∴△ABP'≌△CBP ,∴∠PBP'=90°,BP'=BP=1,AP'=CP=11,在Rt △PBP'中,BP=BP'=1,∴∠BPP'=45°,根据勾股定理得,PP'=2BP=2,∵AP=3,∴AP 2+PP'2=9+2=11,∵AP'2=(11)2=11,∴AP 2+PP'2=AP'2,∴△APP'是直角三角形,且∠APP'=90°,∴∠APB=∠APP'-∠BPP'=90°-45°=45°.过B 作BF ⊥AP 于点F∵∠APB=45°∴△BPF 为等腰直角三角形∴PF=BF=22BP =22 ∴2 ∴AB 2=AF 2+BF 2=1032-∴21032ABCD S AB ==-正方形【点睛】此题是四边形综合题,主要考查了正方形的性质,旋转的性质,直角三角形的性质和判定,勾股定理,正确作出辅助线是解本题的关键.9.如图1,在△ABC 和△ADE 中,∠DAE=∠BAC ,AD=AE ,AB=AC .(1)求证:△ABD ≌△ACE ;(2)如图2,在△ABC 和△ADE 中,∠DAE=∠BAC ,AD=AE ,AB=AC ,∠ADB=90°,点E 在△ABC 内,延长DE 交BC 于点F ,求证:点F 是BC 中点;(3)△ABC 为等腰三角形,∠BAC=120°,AB=AC ,点P 为△ABC 所在平面内一点,∠APB=120°,AP=2,BP=4,请直接写出 CP 的长.答案:D解析:(1)证明见详解;(2)证明见详解;(3)2713【分析】(1)因为∠DAE=∠BAC ,可以得到∠DAB=∠EAC ,因为AD=AE ,AB=AC ,即可得到△ABD ≌△ACE ;(2)连接CE ,延长EF 至点H ,取CF=CH ,连接CH ,由(1)可得△ABD ≌△ACE ,所以∠AEC=90°和CE=BD ,可以推出∠BDF=∠CEF ,再证明△DBF ≌△ECH ,所以BF=CH ,等量代换即可得到BF=FC ,即可解决;(3)点P 在△ABC 内部,将△ABP 逆时针旋转120°,得到ACP ∆',连接PP '和PC ,可以得到△PP C '是直角三角形,利用勾股定理即可求出PC 的值;当点P 在△ABC 外部,将△APB 绕点A 逆时针旋转120︒得到PDC ∆,连接PP '和PC ,过点P 作PD ⊥'CP 于点D ,连接PD 可以得到△PP D ',△PP D '是直角三角形和,利用勾股定理即可求出'DP 及PC 的值.【详解】解:(1)证明:∵∠DAE=∠BAC∴∠DAB=∠EAC∵AD=AE ,AB=AC∴△ABD ≌△ACE(2)证明:连接CE ,延长EF 至点H ,取CF=CH ,连接CH ,如图所示:∵△ADB≌△AEC∴BD=EC,∠ADB=∠AEC=90°∵AD=AE∴∠ADE=∠AED∵∠ADE+∠EDB=∠AED+∠CEH=90°∴∠EDB=∠CEH∵CF=CH∴∠CFH=∠CHF∴∠DFB=∠H∵CE=BD∴△DBF≌△ECH∴BF=CH∴BF=CF∴点F是BC的中点∆',连接(3)当点P在△ABC内部,如图所示,将△ABP逆时针旋转120°,得到ACPPP'和PC∆'∵将△ABP旋转120°得到ACP∴∠PAP'=120°,AP='AP=2,BP=CP'=4∴PP'3∵∠AP C'=120°,∠AP P'=30°,∴∠PP C'=90°,∴()2223427+=.当点P在△ABC外部,如图所示,将△APB 绕点A 逆时针旋转120︒到△'AP C ,过点P 作PD ⊥'CP 于点D ,连接PD , ∵将△ABP 旋转120°得到ACP ∆'∴∠PAP '=120°,AP='AP =2,BP=CP '=4,∴PP '=23, ∵∠AP C '=120°,∠AP P '=30°,∴∠PP C '=150°,∴∠PP D '=30°,在Rt 'PDP 中,1'32PD PP ==, 22''3DP PP PD ∴=-=,''347DC DP P C ∴=+=+=,()222237213PC PD DC ∴=+=+= . 综上所述,27213PC =或【点睛】本题主要考查了全等三角形以及旋转,合理的作出辅助线以及熟练旋转的性质是解决本题的关键.10.如图,直线y =﹣x +c 与x 轴交于点B (3,0),与y 轴交于点C ,过点B ,C 的抛物线y =﹣x 2+bx +c 与x 轴的另一个交点为A .(1)求抛物线的解析式和点A 的坐标;(2)P 是直线BC 上方抛物线上一动点,PA 交BC 于 D .设t =PD AD,请求出t 的最大值和此时点P 的坐标;(3)M 是x 轴上一动点,连接MC ,将MC 绕点M 逆时针旋转90°得线段ME ,若点E 恰好落在抛物线上,请直接写出此时点M 的坐标. 答案:A解析:(1)y=﹣x2+2x+3,A(﹣1,0);(2)t的最大值为916,此时P (32,154);(3)M(9332-,0)或(9332+,0).【分析】(1)利用待定系数法解决问题即可;(2)连接AC,PC,PB,过点A作AE⊥BC于E,过等P作PF⊥BC于F.设P(m,﹣m2+2m+3).利用相似三角形的性质构建二次函数解决问题即可;(3)过点E作EH⊥x轴于H.设M(m,0),利用全等三角形的性质求出点E的坐标(用m表示),再利用待定系数法解决问题即可.【详解】解:(1)∵直线y=﹣x+c与x轴交于点B(3,0),与y轴交于点C,∴0=﹣3+c,解得c=3,∴C(0,3),∵抛物线经过B,C,∴9303b cc-++=⎧⎨=⎩,解得23bc=⎧⎨=⎩,∴抛物线的解析式为y=﹣x2+2x+3,令y=0,得到﹣x2+2x+3=0,解得x=﹣1或3,∴A(﹣1,0);(2)如图,连接AC,PC,PB,过点A作AE⊥BC于E,过点P作PF⊥BC于F.设P(m,﹣m2+2m+3).∵AE∥PF,∴△PFD∽△AED,∴PDAD =PFAE,∵S△PBC=12•BC•PF,S△ACB=12•BC•AE,∴PDAD =PBCABCSS∆∆,∵S △ABC =12•AB •OC =12×4×3=6, ∴t =PD AD =6PBC S ∆=211133(23)332226m m m ⨯⨯+⨯⨯-++-⨯⨯=﹣14m 2+34m =﹣14(m ﹣32)2+916, ∵﹣14<0, ∴m =32时,t 有最大值,最大值为916,此时P (32,154); (3)如图,过点E 作EH ⊥x 轴于H ,∵∠COM =∠EHM =∠CME =90°,∴∠EMH +∠CMH =90°,∠EMH +∠MEH =90°,∴∠MEH =∠CMO ,∵MC =ME ,∴△COM ≌△MHE (AAS ),∴OC =MH =3,OM =EH ,设M (m ,0),则E (m ﹣3,﹣m ),把E (m ﹣3,﹣m )代入y =﹣x 2+2x +3,可得﹣(m ﹣3)2+2(m ﹣3)+3=﹣m , 整理得,m 2﹣9m +12=0,解得m 933-933+, ∴M 933-,0933+0). 【点睛】本题考查的是二次函数综合题,涉及全等三角形的性质和判定,相似三角形的性质和判定,解题的关键是利用数形结合的思想,在二次函数图象上构造全等三角形或相似三角形,利用几何的性质进行点坐标的求解.11.综合与实践实践操作:①如图1,ABC ∆是等边三角形,D 为BC 边上一个动点,将ACD ∆绕点A 逆时针旋转60︒得到AEF ∆,连接CE .②如图2,在ABC ∆中,AD BC ⊥于点D ,将ABD ∆绕点A 逆时针旋转90︒得到AEF ∆,延长FE 与BC 交于点G .③如图3,将图2中得到AEF ∆沿AE 再一次折叠得到AME ∆,连接MB .问题解决:(1)小明在探索图1时发现四边形ABCE 是菱形.小明是这样想的:请根据小明的探索直接写出图1中线段CD ,CF ,AC 之间的数量关系为 : (2)猜想图2中四边形ADGF 的形状,并说明理由;问题再探:(3)在图3中,若AD=6,BD=2,则MB 的长为 .答案:C解析:(1)CD+CF=AC ;(2)四边形ADGF 为正方形;理由见解析;(3)13【分析】(1)先证明C 、F 、E 在同一直线上,再证明△BAD ≌△CAF (SAS ),则∠ADB=∠AFC ,BD=CF ,可得AC=CF+CD ;(2)先根据∠ADC=∠DAF=∠F=90°,证明得四边形ADGF 是矩形,由邻边相等可得四边形ADGF 是正方形;(3)证明△BAM ≌△EAD (SAS ),根据BM=DE 及勾股定理可得结论.【详解】解:(1)如图:由旋转得:∠DAF=60°=∠BAC,AD=AF,∴∠BAD=∠CAF,∵△ABC是等边三角形,∴AB=AC,∴△BAD≌△CAF(SAS),∴∠ADB=∠AFC,BD=CF,∵∠ADC+∠ADB=∠AFC+∠AFE=180°,∴C、F、E在同一直线上,∴AC=BC=BD+CD=CF+CD,+=;故答案为:CD CF AC(2)四边形ADGF是正方形,理由如下:如图:∵Rt△ABD绕点A逆时针旋转90°得到△AEF,∴AF=AD,∠DAF=90°,∵AD⊥BC,∴∠ADC=∠DAF=∠F=90°,∴四边形ADGF是矩形,∵AF=AD,∴四边形ADGF是正方形;(3)如图3,连接DE,∵四边形ADGF是正方形,DG=FG=AD=AF=6,∵△ABD绕点A逆时针旋转90°,得到△AEF,∴∠BAD=∠EAF,BD=EF=2,∴EG=FG-EF=6-2=4,∵将△AFE沿AE折叠得到△AME,∴∠MAE=∠FAE,AF=AM,∴∠BAD=∠EAM,∴∠BAD+∠DAM=∠EAM+∠DAM,即∠BAM=∠DAE,∵AF=AD,∴AM=AD,在△BAM和△EAD中,∵AM ADBAM DAEAB AE=⎧⎪∠=∠⎨⎪=⎩,∴△BAM≌△EAD(SAS),∴BM=DE=22EG DG+=2246213+=.故答案为:213.【点睛】本题属于四边形综合题,主要考查了旋转的性质、全等三角形的判定与性质、等边三角形的判定与性质、正方形的性质以及勾股定理的综合应用,解决问题的关键是熟练掌握等边三角形和全等三角形的性质,依据图形的性质进行计算求解.12.如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.(1)求证:△ACE≌△BCD;(2)求证:BF⊥AE;(3)请判断∠CFE与∠CAB的大小关系并说明理由.答案:C解析:(1)见解析;(2)见解析;(3)∠CFE=∠CAB,见解析【分析】(1)根据垂直的定义得到∠ACB =∠DCE =90°,由角的和差得到∠BCD =∠ACE ,即可得到结论;(2)根据全等三角形的性质得到∠CBD =∠CAE ,根据对顶角的性质得到∠BGC =∠AGE ,由三角形的内角和即可得到结论;(3)过C 作CH ⊥AE 于H ,CI ⊥BF 于I ,根据全等三角形的性质得到AE =BD ,S △ACE =S △BCD ,根据三角形的面积公式得到CH =CI ,于是得到CF 平分∠BFH ,推出△ABC 是等腰直角三角形,即可得到结论.【详解】(1)证明:∵BC ⊥CA ,DC ⊥CE ,∴∠ACB =∠DCE =90°,∴∠BCD =∠ACE ,在△BCD 与△ACE 中,BC CA ACD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△BCD ;(2)∵△BCD ≌△ACE ,∴∠CBD =∠CAE ,∵∠BGC =∠AGE ,∴∠AFB =∠ACB =90°,∴BF ⊥AE ;(3)∠CFE =∠CAB ,过C 作CH ⊥AE 于H ,CI ⊥BF 于I ,∵△BCD ≌△ACE ,∴ACE BCD AE BD,S S ∆∆==,∴CH =CI ,∴CF 平分∠BFH ,∵BF ⊥AE ,∴∠BFH =90°,∠CFE =45°,∵BC ⊥CA ,BC =CA ,∴△ABC 是等腰直角三角形,∴∠CAB =45°,∴∠CFE =∠CAB .【点睛】角的和差、对顶角的性质这些知识点在证明全等和垂直过程中经常会遇到,需要掌握。
初二数学压轴几何证明题(含答案)

1.四边形是正方形,△是等腰直角三角形,∠90°,,连接,G 为的中点,连接,,.(1)如图1,若点E在边的延长线上,直接写出与的位置关系及的值;(2)将图1中的△绕点B顺时针旋转至图2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)将图1中的△绕点B顺时针旋转α(0°<α<90°),若1,,当E,F,D三点共线时,求的长及∠的值.解:(1)⊥,=,理由是:过G作⊥于H,∵∠∠90°,∴∥∥,∵G为中点,∴H为中点,∴,()=(),即,∴∠90°,即△是等腰直角三角形,∴=;(2)解:结论还成立,理由是:如图2,延长到H,使,连接、,过E作的垂线,延长,∵在△和△中∴△≌△(),∴,∠∠,∴∥,∴∠1=∠2=90°-∠3=∠4,∴∠180°-∠4=180°-∠1=∠,在△和△中∴△≌△.∴,∠∠,∴∠∠∠∠∠∠90°,∴△是等腰直角三角形,∵G为的中点,∴⊥,=,即(1)中的结论仍然成立;(3)解:连接,∵,正方形,∴2,∴∠,∴∠60°,∴∠∠∠15°,∴∠45°-15°=30°,∴∠,∴,∴1.解析:(1)过G作⊥于H,推出∥∥,求出H为中点,根据梯形的中位线求出,()=(),推出,根据直角三角形的判定推出△是等腰直角三角形即可;(2)延长到H,使,连接、,过E作的垂线,延长,证△≌△,推出,∠∠,求出∠∠,证出△≌△,推出,∠∠,求出△是等腰直角三角形,即可得出答案;(3)连接,求出∠,推出∠60°,求出∠30°,解直角三角形求出即可.2.已知正方形和等腰直角三角形,,∠90°,按图1放置,使点E在上,取的中点G,连接,.(1)延长交于H,试说明:.(2)将图1中△绕B点逆时针旋转45°,连接,取中点G(如图2),莎莎同学发现:且⊥.在设法证明时他发现:若连接,则D,E,B三点共线.你能写出结论“且⊥”的完整理由吗?请写出来.(3)将图1中△绕B点转动任意角度α(0<α<90°),再连接,取的中点G(如图3),第2问中的结论是否成立?若成立,试说明你的结论;若不成立,也请说明理由.(1)证明:∵∠90°,∴∥,∴∠∠,而∠∠,,∴△≌△,∴,而,∴;(2)连接,如图,∵△为等腰直角三角形,∴∠45°,而四边形为正方形,∴∠45°,∴D,E,B三点共线.而∠90°,∴△为直角三角形,而G为的中点,∴,∴∠2∠90°,∴且⊥;(3)第2问中的结论成立.理由如下:连接、相交于点O,取的中点M,连接、、,如图,∵G为的中点,O为的中点,M为的中点,∴∥,∥,∴四边形为平行四边形,∴,,而,,∴,,∵∠∠,而∠∠90°,∴∠∠,∴△≌△,∴,∠∠,又∵∠∠,∠∠∠,∴∠∠∠∠∠∠∠∠45°+45°=90°,∴且⊥.解析:(1)由∠90°,得到∥,而,易证得△≌△,得,而,即可得到结论.(2)连接,如图2,由△为等腰直角三角形,得∠45°,而四边形为正方形,得∠45°,得到D,E,B三点共线,而G为的中点,根据直角三角形斜边上的中线等于斜边的一半得到,于是∠2∠90°,即得到结论.(3)连接、相交于点O,取的中点M,连接、、,由G为的中点,O为的中点,M为的中点,根据三角形中位线的性质得∥,∥,得到,,而,,得到,,又∠∠,而∠∠90°,得∠∠,则△≌△,得到,∠∠,而∠∠,∠∠∠,所以有∠∠∠∠∠∠∠∠45°+45°=90°.3.已知正方形和等腰△,,∠90°,按图①放置,使点F在上,取的中点G,连接、.(1)探索、的数量关系和位置关系并证明;(2)将图①中△绕B点顺时针旋转45°,再连接,取中点G(如图②),问(1)中的结论是否仍然成立.证明你的结论;(3)将图①中△绕B点转动任意角度(旋转角在0°到90°之间),再连接,取的中点G(如图③),问(1)中的结论是否仍然成立,证明你的结论.解:(1)且⊥.证明如下:如图①,连接.∵正方形和等腰△,∴∠∠45°.∴B、E、D三点共线.∵∠90°,G为的中点,∠90°,∴.∴∠2∠,∠2∠.∴∠∠2∠90°,即∠90°,∴⊥.(2)仍然成立,证明如下:如图②,延长交于点H.∵⊥,∴∥,∴∠1=∠2.又∵∠3=∠4,,∴△≌△,∴,.∵△为等腰直角三角形,∴,∴.∵,∴.∴△为等腰直角三角形.又∵,∴且⊥.(3)仍然成立.证明如下:如图③,延长至H,使,连接交于M,连接、.∵,∠∠,,∴△≌△,∴,∠∠,∴∥.∵正方形,∴,⊥.∵△是等腰直角三角形,∴,∠∠,∴△≌△,∴,∠∠,∴∠∠90°,∴△为等腰直角三角形.又∵,∴且⊥.解析:(1)首先证明B、E、D三点共线,根据直角三角形斜边上的中线等于斜边的一半,即可证明,得到∠2∠,∠2∠,从而证得∠90°;(2)首先证明△≌△,然后证明△为等腰直角三角形.可以证得:且⊥.(3)首先证明:△≌△,即可证得:△为等腰直角三角形,从而得到:且⊥.已知,正方形中,△为等腰直角三角形,且为底,取的中点G,连接、.(1)如图1,若△的底边在上,猜想和的数量关系为;(2)如图2,若△的直角边在上,则(1)中的结论是否还成立?请说明理由;(3)如图3,若△的直角边在∠内,则(1)中的结论是否还成立?说明理由.解:(1),(1分)理由如下: ∵△为等腰直角三角形,∴∠90°,又G 为斜边的中点, ∴ , ∵为正方形, ∴∠90°,又G 为斜边的中点,∴ ,∴;(2)成立.如图,延长交于M ,∵∠∠∠90°,∴∥,∴∠∠,又∠∠,,1212∴,即G 为的中点.∴为直角△的斜边上的中线,∴ ;(3)成立.取的中点H ,连接,,取的中点O ,连接,.∵,∠90°,∴. ∵,∴∥,且 ,∥,且 , ∴.∵△为等腰直角三角形.∴∴.∵四边形为平行四边形,∴∠∠.∵∠∠90°.∴∠∠.121 212 1 2∴.此题考查了正方形的性质,以及全等三角形的判定与性质.要求学生掌握直角三角形斜边上的中线等于斜边的一半,以及三角形的中位线与第三边平行且等于第三边的一半.掌握这些性质,熟练运用全等知识是解本题的关键.解析:(1),理由为:根据三角形为等腰直角三角形,得到∠为直角,又G为中点,根据在直角三角形中,斜边上的中线等于斜边的一半,得到为的一半,同理在直角三角形中,得到也等于的一半,利用等量代换得证;(2)成立.理由为:延长交于M,如图所示,根据“”得到三角形与三角形全等,由全等三角形的对应边相等得到与相等,即G为中点,根据直角三角形斜边上的中线等于斜边的一半得到与相等都等于斜边的一半,得证;(3)成立.理由为:取的中点H,连接,,取的中点O,连接,,如图所示,因为直角三角形中,O为斜边的中点,根据斜边上的中线等于斜边的一半得到等于的一半,由为三角形的中位线,根据三角形的中位线平行于第三边且等于第三边的一半,得到等于一半,等于的一半,又根据直角三角形斜边上的中线等于斜边的一半得到等于的一半,根据等量代换得到与相等,再根据为平行四边形,根据平行四边形的性质得到对边相等,对角相等,进而得到∠与∠相等,利用“”得到△与△全等,利用全等三角形的对应边相等即可得证.。
八下各章压轴题

八年级下册数学几何压轴题一、四边形1.如图,已知菱形ABCD中,∠ABC=60°,AB=8,过线段BD上的一个动点P(不与B、D重合)分别向直线AB、AD作垂线,垂足分别为E、F.(1)BD的长是;(2)连接PC,当PE+PF+PC 取得最小值时,此时PB的长是;2.如图,在等边三角形ABC中,BC=6cm. 射线AG//BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;(2)填空:①当t为 s时,四边形ACFE是菱形;②当t为何值时,EF⊥BC,并加以说明;3.如图,在矩形纸片ABCD中,AB=33,BC=6,沿EF折叠后,点C落在AB边上的点P处,点D落在点Q处,AD与PQ相交于点H,∠BPE=30°;⑴求BE、QF的长;⑵求四边形PEFH的面积;4.如图,在矩形ABCD中,AB=3cm,∠DBC=30°,动点P以2cm/s的速度,从点B出发,沿B→D 的方向,向点D运动;动点Q以3cm/s的速度,从点D出发,沿D→C→B的方向,向点B移动.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.(1)求△PQD的面积S(cm2)与运动时间t(s)之间的函数关系式,并写出自变量t的取值范围.(2)在运动过程中,是否存在这样的t,使得△PQD为直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.5 如图1,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为边,在△OAB外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.(1)求证:四边形ABCE是平行四边形;(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.6 如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为t.(1)求CD的长;(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;(3)当点P 在AB、CD上运动时,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.7.如图,已知矩形ABCD ,AD=4,CD=10,P 是AB 上一动点,M 、N 、E 分别是PD 、PC 、CD 的中点. (1)求证:四边形PMEN 是平行四边形;(2)请直接写出当AP 为何值时,四边形PMEN 是菱形;(3)四边形PMEN 有可能是矩形吗?若有可能,求出AP 的长;若不可能,请说明理由.8..问题解决:如图1,将正方形纸片ABCD 折叠,使点B 落在CD 边上一点E (不与点C ,D 重合),压平后得到折痕MN.当21=CD CE 时,求BNAM的值.类比归纳:在图1中,若31=CD CE ,则BN AM 的值等于 ;若41=CD CE ,则BN AM 的值等于 ;若n CD CE 1= (n 为整数),则BNAM的值等于 (用含n 的式子表示)联系拓广:如图2,将矩形纸片ABCD 折叠,使点B 落在CD 边上一点E (不与点C ,D 重合),压平后得到折痕MN ,设m BC AB 1= (m >1),n 1=CD CE ,则BNAM 的值等于 ;(用含m ,n 的式子表示)11.已知正方形ABCD 。
八上有关几何综合压轴题训练题(1)
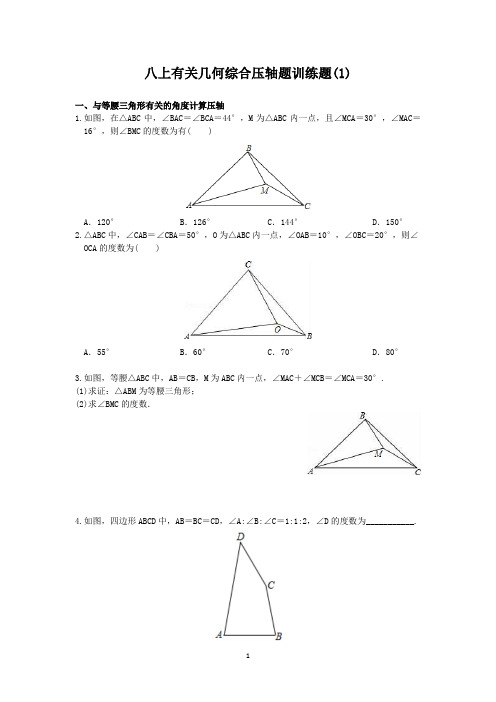
八上有关几何综合压轴题训练题(1)一、与等腰三角形有关的角度计算压轴1.如图,在△ABC中,∠BAC=∠BCA=44°,M为△ABC内一点,且∠MCA=30°,∠MAC=16°,则∠BMC的度数为有( )A.120°B.126°C.144°D.150°2.△ABC中,∠CAB=∠CBA=50°,O为△ABC内一点,∠OAB=10°,∠OBC=20°,则∠OCA的度数为( )A.55°B.60°C.70°D.80°3.如图,等腰△ABC中,AB=CB,M为ABC内一点,∠MAC+∠MCB=∠MCA=30°.(1)求证:△ABM为等腰三角形;(2)求∠BMC的度数.4.如图,四边形ABCD中,AB=BC=CD,∠A:∠B:∠C=1:1:2,∠D的度数为___________.5.如图,在等腰Rt△ABC中,AB=AC,过A作直线交BC于G,BG<GC,BD⊥AG于D,CE⊥AD于E,F为BC边中点,则下列结论中:①∠BAD=∠ACE;②BD=CE-ED;③FE=FD;④EF⊥DF.其中正确结论的个数为( )A.1个B.2个C.3个D.4个6.等腰△ABC和等腰△ADE中,AB=AC,AD=DE,∠BAC=∠ADE=α,点D在BC上,连CE.(1)如图1,α=90°时,求∠DCE的度数;(2)选用图2或图3其中的一个,求证:AB∥CE.图1 图2 图3二、与等腰直角三角形有关的全等压轴1.如图,∠C=90°,AC=BC,点C在第一象限内.若A(5,0),B(-2,4),C(m,n),则(m+n)(m-n)的值是__________.2.已知:等腰Rt△ABC,M为射线BC上一动点,AM=AN,AM⊥AN,连接BN与AC交于P点,其中BMBC=n.(1)如图1,若n=1时,则BPPN=___________;BMPC=__________(直接写出你的答案);(2)如图2,若n=12时,则BPPN=___________;APPC=__________;并证明你的结论.(3)如图3,若M点运动到C的下方时,且BN与AC交于P点,其他条件不变,当n=______时,APPC=13(直接写出你的答案).图1 图2 图33.如图,直线AB 交x 轴于点A(a ,0),交y 轴于点B(0,b),且a 、b 满足|a +b|+(a -5)2=0. (1)点A 的坐标为 ,点B 的坐标为 ;(2)如图,若点C 的坐标为(-3,-2),且BE ⊥AC 于点E ,OD ⊥OC 交BE 延长线于D ,试求点D 的坐标;(3)如图,M 、N 分别为OA 、OB 边上的点,OM =ON ,OP ⊥AN 交AB 于点P ,过点P 作PG ⊥BM 交AN 的延长线于点G ,请写出线段AG 、OP 与PG 之间的数列关系并证明你的结论.4.等腰Rt △ACB ,∠ACB =90°,AC =BC ,点A 、C 分别在x 轴,y 轴的正半轴上. (1)如图1,求证:∠BCO =∠CAO. (2)如图2,若OA =5,OC =2,求B 点的坐标。
初二下期末几何压轴题及解析

初二下期末几何压轴题及解析初二下期末几何及解析1、已知四边形ABCD,以边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G。
1) 当四边形ABCD为正方形时,EB和FD的数量关系是什么?2) 当四边形ABCD为矩形时,EB和FD具有什么数量关系?请证明。
3) 四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数。
解答:1) EB=FD。
2) EB=FD。
证明:因为△AFB为等边三角形,所以AF=AB,∠FAB=60°;因为△ADE为等边三角形,所以AD=AE,∠EAD=60°,所以∠FAB+∠BAD=∠EAD+∠BAD,即∠FAD=∠BAE。
因此,△FAD≌△BAE,从而EB=FD。
3) ∠EGD不发生变化,因为在任何情况下,∠EGD都等于60°。
2、已知:在□ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF。
1) 求证:△ABE≌△FCE;2) 若AF=AD,求证:四边形ABFC是矩形。
解答:1) 如图1.在△ABE和△XXX中,∠1=∠2,∠3=∠4,BE=CE,因此△ABE≌△XXX。
2) 因为△ABE≌△FCE,所以AB=FC。
又因为AB∥FC,所以四边形ABFC是平行四边形。
由于四边形ABCD是平行四边形,所以AD=BC。
又因为AF=AD,所以AF=BC,从而四边形ABFC是矩形。
3、已知△ABC是一张等腰直角三角形纸板,∠B=90°,AB=BC=1.1) 要在这张纸板上剪出一个正方形,使这个正方形的四个顶点都在△XXX的边上。
XXX设计出了一种剪法,如图1所示。
请你再设计出一种不同于图1的剪法,并在图2中画出来。
2) 请在图3和图4中画出两个不同于图1和图2的剪法。
解答:1) 另一种剪法如图2所示,将△XXX沿着AC折叠,使点C与点B重合,然后将纸张沿着BD剪去一部分,即可得到正方形。
初二几何专题-直击期末考点期末复习压轴题篇

专题一:线段和差1.(海淀2012.1)24. 已知在□ABCD 中,AE ⊥BC 于E ,DF 平分∠ADC 交线段AE 于F . (1)如图1,若AE =AD ,∠ADC =60︒, 请直接写出线段CD 与AF +BE 之间所满足的等量关系;(2)如图2, 若AE =AD ,你在(1)中得到的结论是否仍然成立, 若成立,对你的结论 加以证明, 若不成立, 请说明理由;(3)如图3, 若AE : AD =a : b ,试探究线段CD 、AF 、BE 之间所满足的等量关系, 请直接写出你的结论.解: (1)线段CD 与AF +BE 之间所满足的等量关系为:.(2) 图1图2 (3)线段CD 、AF 、BE 之间所满足的等量关系为:.图3DAFCEB AB EC DFB EC DA F2.(西城北区2012.1)24.已知:如图,正方形ABCD 的边长为a ,BM ,DN 分别平分正方形的两个外角,且满足45MAN ∠=︒,连结MC ,NC ,MN .(1)填空:与△ABM 相似的三角形是△ ,BM DN ⋅= ;(用含a 的代数式表示) (2)求MCN ∠的度数;(3)猜想线段BM ,DN 和MN 之间的等量关系并证明你的结论.3.(西城南区2012.1)24.已知:⊙O 是△ABC 的外接圆,点M 为⊙O 上一点.(1)如图,若△ABC 为等边三角形,BM =1,CM =2, 求AM 的长;(1) 若△ABC 为等腰直角三角形,∠BAC =90︒,BM a =,CM b =(其中b a >),直接写出AM 的长(用含有a ,b 的代数式表示).θA A 'C BB '30︒B 'A 'CB A 专题二:与旋转有关的几何问题1.(石景山2012.1)23.如图1,在△ABC 中,∠ACB =90°,AC =3,BC =4,将△ABC 绕顶点C 顺时针旋转30°,得到△A ′B ′C .联结A ′A 、B ′B ,设△ACA ′和△BCB ′的面积分别为S △ACA ′ 和S △BC B′. (1)直接写出S △ACA ′ ︰S △BC B′ 的值 ;(2)如图2,当旋转角为θ(0°<θ<180°)时,S △ACA ′ 与S △BC B′ 的比值是否发生变化,若不变请证明;若改变,写出变化后的比值(可用含θ的代数式表示).图1 图22.(东城南区2011.1)23.在Rt △ABC 中,AB =AC ,∠BAC =90°,O 为BC 的中点.(1)写出点O 到△ABC 的三个顶点A 、B 、C 的距离的大小关系(不要求证明);(2)如果点M 、N 分别在线段AB 、AC 上移动,在移动中保持AN =BM ,请判断△OMN 的形状,并证明你的结论.A B COM NE F D C B AE F D C B A E F CBA3.(平谷2011.1)25. △ABC 中,∠BAC =90°,AB=AC ,点D 是BC 的中点,把一个三角板的直角顶点放在点D 处,将三角板绕点D 旋转且使两条直角边分别交AB 、AC 于E 、F . (1)如图1,观察旋转过程,猜想线段AF 与BE 的数量关系并证明你的结论;(2)如图2,若连接EF ,试探索线段BE 、EF 、FC 之间的数量关系,直接写出你的结论(不需证明); (3)如图3,若将“AB=AC ,点D 是BC 的中点”改为:“∠B =30°,AD ⊥BC 于点D ”,其余条件不变,探索(1)中结论是否成立?若不成立,请探索关于AF 、BE 的比值.解:4.(朝阳2010.1)如图,AB 为⊙O 直径,点C 在⊙O 上,且 AC =BC =2,将一块等腰三角形的直角顶点放在圆心O 处之后,将此三角形绕点O 旋转,三角形的两直角边分别交射线AC 、CB 于D 、E 两点。
八年级数学下册专题11一次函数几何压轴训练(原卷版)

专题11 一次函数几何压轴训练1.(2023秋•东阳市期末)如图,在平面直角坐标系中,直线分别交x轴,y轴于点B,A,直线OC⊥AB,垂足为点C,D为线段OA上一点(不与端点重合),过点D 作直线l∥x轴,交直线AB于点E,交直线OC点F.(1)求线段OC的长;(2)当DE=EF时,求点D的坐标;(3)若直线l过点C,点M为线段OC上一点,N为直线l上的点,已知OM=CN,连结AN,AM,求线段AN+AM的最小值.2.(2023秋•和平县期末)如图1,在平面直角坐标系xOy中,点O是坐标原点,直线AB:y=kx+与直线AC:y=﹣2x+b交于点A,两直线与x轴分别交于点B(﹣3,0)和C (2,0).(1)求直线AB和AC的表达式.(2)点P是y轴上一点,当P A+PC最小时,求点P的坐标.(3)如图2,点D为线段BC上一动点,将△ABD沿直线AD翻折得到△ADE,线段AE 交x轴于点F,若△DEF为直角三角形,求点D坐标.3.(2023秋•槐荫区期末)如图,直线和直线l2与x轴分别相交于A,B两点,且两直线相交于点C,直线l2与y轴相交于点D(0,﹣4),OA=2OB.(1)求出直线l2的函数表达式;(2)E是x轴上一点,若S△ABC=2S△BCE,求点E的坐标;(3)若F是直线l1上方且位于y轴上一点,∠ACF=2∠CAO,判断△BCF的形状并说明理由.4.(2023秋•巴中期末)如图,在平面直角坐标系中,直线y=﹣x+3与x轴、y轴分别交于点A、B,直线BC与x轴负半轴交于点C,且CO=2AO.(1)求线段AC的长;(2)动点P从点C出发沿射线CA以每秒1个单位的速度运动,连接BP,设点P的运动时间为t(秒),△BPO的面积为S,求S与t的函数关系式,并直接写出自变量t的取值范围;(3)在(2)的条件下,在线段BC上是否存在点D,连接DP,使得△BDP是以BP为直角边的等腰直角三角形,若存在,请求出t的值,若不存在,请说明理由.5.(2023秋•金牛区期末)如图1,在平面直角坐标系中,直线y=2x+b与x轴、y轴分别交于点A、点B,S△AOB=4,点C(3,m)是直线AB上一点,在直线AB左侧过点C的直线交y轴于点D,交x轴于点E.(1)求m和b的值;(2)当∠ACD=45°时,求直线CD的解析式;(3)如图2,在(2)的条件下,过C作CM⊥x轴,在直线AC上一点P,直线CD上一点Q,直线CM上一点H,当四边形AHQP为菱形时,求P点的坐标.6.(2023秋•咸阳期末)如图,已知一次函数y=kx+b(k、b为常数,且k≠0)的图象与x 轴交于点A(﹣6,0),与y轴交于点B(0,8).(1)求该一次函数的表达式;(2)点C为点B上方y轴上的点,在该一次函数的图象上是否存在点P,使得以点P、B、C为顶点的三角形与△OAB全等?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.7.(2023秋•历城区期末)如图1,直线AB:y=﹣x+b分别与x,y轴交于A(3,0),B两点,点A沿x轴向右平移3个单位得到点D.(1)分别求直线AB和BD的函数表达式.(2)在线段BD上是否存在点E,使△ABE的面积为,若存在,求出点E坐标;若不存在,说明理由.(3)如图2,P为x轴上A点右侧的一动点,以P为直角顶点,BP为腰在第一象限内作等腰直角△BPQ,连接QA并延长交y轴于点K.当点P运动时,点K的位置是否发生变化?如果不变请求出它的坐标;如果变化,请说明理由.8.(2023秋•江门期末)如图所示,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a,b满足+(a﹣4)2=0.(1)a=,b=;(2)如图1,若点C的坐标为(﹣1,0),且AH⊥BC于点H,AH交OB于点P,试求点P的坐标;(3)如图2,若点D为AB的中点,点M为y轴正半轴上一动点,连接MD,过点D作DN⊥DM交x轴于点N,当点M在y轴正半轴上运动的过程中,式子S△BDM﹣S△ADN的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求出该式子的值.9.(2023秋•简阳市期末)如图,在平面直角坐标系xOy中,一次函数y=﹣x+8分别与x 轴、y轴交于A、B两点,过点B作BC⊥AB交x轴于点C.(1)求点C的坐标;(2)点D为直线AB上一点,且∠DCA=∠DAC,求直线CD的解析式;(3)若点Q是x轴上一点,连接BQ,将△ABQ沿着BQ所在直线折叠,当点A落在y 轴上时,求点Q的坐标.10.(2023秋•天桥区期末)如图1,已知函数y=x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.(1)请写出点A坐标,点B坐标,直线BC的函数解析式;(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q.①若△PQB的面积为,求点Q的坐标;②点M在线段AC上,连接BM,如图2,若∠BMP=∠BAC,直接写出P的坐标.11.(2023秋•万州区期末)如图1,在平面直角坐标系中,一次函数y=2x+4的图象与x轴,y轴分别交于A、B两点,点C是OB的中点.(1)求直线AC的解析式;(2)如图2,若点M是直线AC上的一动点,当S△ABM=2S△AOC时,求点M的坐标;(3)将直线AB向右平移3个单位长度得到直线l,若点E为平移后直线l上的一点,在平面直角坐标系中是否存在点F,使以点A、C、E、F为顶点,AE为边的四边形为菱形,若存在,请直接写出所有满足条件的点F的坐标;若不存在,请说明理由.12.(2023秋•盐都区期末)如图,直线AB:y=x+b分别与x、y轴交于A,B两点,点A的坐标为(−4,0),过点B的直线交x轴正半轴于点C,且OB:OC=4:3.(1)求直线BC的函数表达式;(2)在x轴上方是否存在点D,使以点A,B,D为顶点的三角形与△ABC全等.若存在,画出△ABD,并求出点D的坐标,若不存在,请说明理由;(3)点P是y轴上的一点,连接CP,将△BCP沿直线CP翻折,当点B的对应点B′恰好落在x轴上时,请直接写出此时直线CP的函数表达式.13.(2023春•阳江期末)如图,在平面直角坐标系中,直线l1:y=﹣x+5与y轴交于点A,直线l2与x轴、y轴分别交于点B(﹣4,0)和点C,且与直线l1交于点D(2,m).(1)求直线l2的解析式;(2)若点E为线段BC上一个动点,过点E作EF⊥x轴,垂足为F,且与直线l1交于点G,当EG=6时,求点G的坐标;(3)若在平面上存在点H,使得以点A,C,D,H为顶点的四边形是平行四边形,请直接写出点H的坐标.14.(2023春•潮阳区期末)如图,直线y=x﹣3交x轴于A,交y轴于B,(1)求A,B的坐标和AB的长(直接写出答案);(2)点C是y轴上一点,若AC=BC,求点C的坐标;(3)点D是x轴上一点,∠BAO=2∠DBO,求点D的坐标.15.(2023春•武穴市期末)如图,在平面直角坐标系xOy中,直线l1:y=x+2与x轴交于点A,直线l2:y=3x﹣6与x轴交于点D,与l1相交于点C.(1)求点D的坐标;(2)在y轴上一点E,若S△ACE=S△ACD,求点E的坐标;(3)直线l1上一点P(1,3),平面内一点F,若以A、P、F为顶点的三角形与△APD 全等,求点F的坐标.16.(2023春•淅川县期末)如图,已知直线y=kx+b经过A(6,0)、B(0,3)两点.(1)求直线y=kx+b的解析式;(2)若C是线段OA上一点,将线段CB绕点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上.①求点C和点D的坐标;②若点P在y轴上,Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点Q坐标,否则说明理由.17.(2023春•拜泉县期末)综合与探究.如图,平面直角坐标系中,矩形OABC的两条邻边分别在x轴、y轴上,对角线,点B的坐标为B(2a,a).(1)A,C.(2)把矩形OABC沿直线DE对折使点C落在点A处,直线DE与OC、AC、AB的交点分别为D,F,E,求直线DE的解析式(问题(1)中的结论可直接使用).(3)若点M在y轴上,则在平面直角坐标系中的x轴及x轴的下方,是否存在这样的点N,使得以A、D、N、M为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.18.(2023春•唐县期末)(1)基本图形的认识:如图1,在四边形ABCD中,∠B=∠C=90°,点E是边BC上一点,AB=EC,BE=CD,连结AE、DE,求证:△AED是等腰直角三角形.(2)基本图形的构造:如图2,在平面直角坐标系中,A(2,0),B(0,3),连结AB,过点A在第一象限内作AB的垂线,并在垂线截取AC=AB,求点C的坐标;(3)基本图形的应用:如图3,一次函数y=﹣2x+2的图象与y轴交于点A,与x轴交于点B,直线AC交x轴于点D,且∠CAB=45°,求点D的坐标.19.(2023春•新罗区期末)数形结合作为一种数学思想方法,数形结合包括两个方面:第一种情形是“以数解形”,而第二种情形是“以形助数”.例如:在我们学习数轴的时候,数轴上任意两点,A表示的数为a,B表示的数为b,则A,B两点的距离可用式子|a﹣b|表示.研一研:如图,在平面直角坐标系中,直线AB分别与x轴正半轴、y轴正半轴交于点A(a,0)、点B(0,b),且a、b满足(a﹣6)2+|b﹣4|=0.(1)直接写出以下点的坐标:A(,0),B(0,).(2)若点P、点Q分别是y轴正半轴(不与B点重合)、x轴负半轴上的动点,过Q作QC∥AB,连接PQ.已知∠BAO=34°,请探索∠BPQ与∠PQC之间的数量关系,并说明理由.(3)已知点D(3,2)是线段AB的中点,若点H为y轴上一点,且,求S△AHD=S△AOB,求点H的坐标.20.(2023春•红安县期末)如图,在平面直角坐标系中,直线l1:y=kx+8分别交x轴,y 轴于点A,B,点A(8,0).直线l2:经过线段AB的中点Q,分别交x轴,y 轴于点C,D.(1)请直接写出k的值;(2)请求出直线l2的解析式;(3)点P(t,0)为x轴上一动点,过点P作PE∥y轴交l1,l2于点E,F;①当EF=2EP时,求t的值.②连接BC,当∠OBC=∠ABF时,求t的值.21.(2023春•樊城区期末)如图,在平面直角坐标系中,一次函数y1=ax+b的图象与x轴,y轴交于A,B;与直线y2=kx交于P(2,1),且PO=P A.(1)求点A的坐标;(2)求函数y1,y2的解析式;(3)点D为直线y1=ax+b上一动点,其横坐标为t(t<2),DF⊥x轴于点F,交y2=kx于点E,且DF=2EF,求点D的坐标;(4)在(3)的条件下,如果点D在第一象限内,过点P的直线y=mx+n将四边形OBDE 分为两部分,两部分的面积分别设为S1,S2.若≤2,直接写出m的取值范围.22.(2023春•松北区期末)如图,直线y=x+10交x轴于点A,交y轴于点B,直线y=kx+b 过点A,交y轴于点C,且C为线段OB的中点.(i)求k、b的值;(2)点P为线段AC延长线上一点,连接PB,设点P的横坐标为t,△P AB的面积为S,求S与t的函数关系式;(3)在(2)的条件下,点D在线段AO的延长线上,连接CD、PD,且,点E在AD上,且∠DPE=45°,过点C作CF∥PE,交x轴于点F,若AF=DE,求P点的坐标.23.(2023春•碑林区校级期末)如图,在平面直角坐标系中,直线y=﹣2x+b与x轴,y轴分别交于A、B两点.直线交线段AB于点C(1,m),且S△AOB=2S△BOC.(1)求b的值;(2)若点D是y轴上一点,点E为平面上一点,是否存在以点A,B,D,E为顶点的四边形是矩形?若存在,请求出点E的坐标,若不存在请说明理由.24.(2023春•台江区期末)已知直线与x轴交于点A,与y轴交于点B,P为直线AB上的一个动点,过点P分别作PF⊥x轴于点F,PE⊥y轴于点E,如图所示.(1)若点P为线段AB的中点,求OP的长;(2)若四边形PEOF为正方形时,求点P的坐标;(3)点P在AB上运动过程中,EF的长是否有最小值,若有,求出这个最小值;若没有,请说明理由.25.(2023春•舞阳县期末)如图,在平面直角坐标系中,直线y=﹣x+6与x轴、y轴分别交于点D、C,直线AB与y轴交于点B(0,﹣3),与直线CD交于点A(m,3).(1)求直线AB的解析式;(2)点E是射线CD上一动点,过点E作EF∥y轴,交直线AB于点F.若以O、C、E、F为顶点的四边形是平行四边形,请求出点E的坐标;(3)设P是射线CD上一点,在平面内是否存在点Q,使以B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.26.(2023秋•新都区期末)如图所示,直线l1:y=x﹣1与y轴交于点A,直线l2:y=﹣2x ﹣4与x轴交于点B,直线l1与l2交于点C.(1)求点A,C的坐标;(2)点P在直线l1上运动,求出满足条件S△PBC=S△ABC且异于点A的点P的坐标;(3)点D(2,0)为x轴上一定点,当点Q在直线l1上运动时,请直接写出|DQ﹣BQ|的最大值.27.(2023秋•金华期末)如图,在平面直角坐标系中,直线l1:y=kx+1交y轴于点A,交x轴于点B(4,0),过点E(2,0)的直线l2平行于y轴,交直线l1于点D,点P是直线l2上一动点(异于点D),连接P A、PB.(1)直线l1的表达式为,点D的坐标为;(2)设P(2,m),当点P在点D的下方时,求△ABP的面积S的表达式(用含m的代数式表示);(3)当△ABP的面积为3时,则以点B为直角顶点作等腰直角△BPC,请直接写出点C 的坐标.28.(2023秋•新都区校级期末)如图,已知直线y=x﹣2分别与x轴,y轴交于A,B两点,直线OG:y=kx(k<0)交AB于点D.(1)求A,B两点的坐标;(2)如图1,点E是线段OB的中点,连接AE,点F是射线OG上一点,当OG⊥AE,且OF=AE时,在x轴上找一点P,当PE+PD的值最小时,求出△APE的面积;(3)如图2,若k=﹣2,过B点BC∥OG,交x轴于点C,此时在x轴上是否存在点M,使∠OBM+∠OBC=45°,若存在,求出点M的坐标;若不存在,请说明理由.29.(2023春•巴中期末)如图,在平面直角坐标系中,直线y=2x+10与x轴交于点A,与y轴交于点B,过点B的另一直线交x轴正半轴于点C,且△ABC面积为60.(1)求点C的坐标及直线BC的表达式;(2)若M为线段BC上一点,直线AM把△ABC的面积分成两部分,这两部分的面积之比为1:2,求M的坐标;(3)当△ABM的面积为20时,点E为直线AM上一动点,在x轴上是否存在点D,使以点D、E、B、C为顶点的四边形为平行四边形?若存在,直接写出点D的坐标;若不存在,请说明理由.30.(2023春•湘潭县期末)如图,长方形OABC,是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=6,在AB上取一点M使得△CBM沿CM翻折后,点B落在x轴上,记作B′点.(1)求B'点的坐标;(2)求折痕CM所在直线的表达式;(3)求折痕CM上是否存在一点P,使PO+PB'最小?若存在,请求出最小值,若不存在,请说出理由.。
初二数学平行四边形压轴:几何证明题

初二数学平行四边形压轴:几何证明题1.在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,顺次连接EF 、FG 、GH 、HE .(1)请判断四边形EFGH 的形状,并给予证明; (2)试探究当满足什么条件时,使四边形EFGH 是菱形,并说明理由。
2.如图,在直角三角形ABC 中,∠ACB=90°,AC=BC=10,将△ABC 绕点B 沿顺时针方向旋转90°得到△A 1BC 1.(1)线段A 1C 1的长度是 ,∠CBA 1的度数是 .(2)连接CC 1,求证:四边形CBA 1C 1是平行四边形.3. 如图,矩形ABCD 中,点P 是线段AD 上一动点,O 为BD 的中点, PO 的延长线交BC 于Q.(1)求证:OP=OQ ;(2)若AD=8厘米,AB=6厘米,P 从点A 出发,以1厘米/秒的速度向D 运动(不与D 重合).设点P 运动时间为t 秒,请用t 表示PD 的长;并求t 为何值时,四边形PBQD 是菱形.4.已知:如图,在□ABCD 中,AE 是BC 边上的高,将△ABE 沿BC 方向平移,使点E 与点C 重合,得△GFC. ⑴求证:BE =DG ;⑵若∠B =60︒,当AB 与BC 满足什么数量关系时,四边形ABFG 是菱形?证明你的结论.5. 如图,在四边形ABCD 中,AD ∥BC ,E 为CD 的中点,连结AE 、BE ,BE ⊥AE ,延长AE 交BC 的延长线于点F .求证:(1)FC =AD ; (2)AB =BC +AD .6.如图,在△ABC 中,AB=AC ,D 是BC 的中点,连结AD ,在AD 的延长线上取一点E ,连结BE ,CE.(1)求证:△ABE ≌△ACE(2)当AE 与AD 满足什么数量关系时,四边形ABEC 是菱形?并说明理由.A B E F C G D H B A 1 C 1A C AD G CB F E A QCD P B OA BE D C A D EF C B7.如图,在平行四边形ABCD 中,点E 是边AD 的中点,BE 的延长线与CD 的延长线交于点F.(1)求证:△ABE ≌△DFE(2)连结BD 、AF ,判断四边形ABDF 的形状,并说明理由.8. 如图,已知点D 在△ABC 的BC 边上,DE ∥AC 交AB 于E ,DF ∥AB 交AC 于F .(1)求证:AE =DF ;(2)若AD 平分∠BAC ,试判断四边形AEDF 的形状,并说明理由.9. 如图,在平行四边形中,点E F ,是对角线BD 上两点,且BF DE =.(1)写出图中每一对你认为全等的三角形;(2)选择(1)中的任意一对全等三角形进行证明.10.在梯形ABCD 中,AD ∥BC,AB=DC ,过点D 作DE ⊥BC ,垂足为点E ,并延长DE 至点F ,使EF=DE.连接BF 、CF 、AC.(1)求证:四边形ABFC 是平行四边形;(2)若CE BE DE ⋅=2,求证:四边形ABFC 是矩形.11.如图,△ABC 中,AB=AC ,AD 、AE 分别是∠BAC 和∠BAC 的外角平分线,BE ⊥AE. (1)求证:DA ⊥AE(2)试判断AB 与DE 是否相等?并说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例一:如图,平行四边形ABCD和平行四边形QMNP,∠M=∠B,M是平行四边形ABCD的对称中心,MN交AB于E,且AB=mBC,探索线段ME与线段MF的关系,并说明理由。
例二:如图,Rt△ABC'是由Rt△ABC绕A顺时针旋转的到的,连接CC',交斜边于点E,CC´的延长线交BB´于点F,证明:△ACE∽△FBE
例三:如图,点M,N分别在三角形ABC的BC、CA边上,且BM=CN,AM,BN交于点Q。
求证:①∠BQM=60°②BM²=MQ·MA ③若BM=1,CM=2,求AQ·AM
例四:如图(1),点M,N分别是边长为4的正方形ABCD边AB、AD的中点,连接CN,DM。
①判断CN,DM的关系,并说明理由。
②设CN、DM的交点为H,连接BH,如图(2),求证:△BCH是等腰三角形;
③设△ADM沿DM翻折后得到△A'DM,延长MA'交DC的延长线于点E,如图(3),求A'E
例五:如图,矩形ABCD中,E是AD中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD 内部,小明将BG延长交DC于点F,认为GF=DF,你同意吗?请说明理由。
(2)保持(1)中的条件不变,若DC=2DF,求AD/AB的值
(3)保持(1)中的条件不变,若DC=n·DF,求AD/AB的值
例六:如图①,将边长为4的正方形纸片ABCD沿EF折叠(点E,F分别在边AB,CD上),使点B 落在AD边上的点M处,点C落在点N处,MN与CD交于点P,连接EP。
(1)如图②,若M为AD边的中点
①△AEM的周长=_cm
②求证:EP=AE=DP
③求△DMP三边的比值
④(2)随着落点M在AD边上取遍所有的位置(点M不与A,D重合)。
△PDM的周长是否发生
变化?请说明理由。
例七:如图所示,在△ABC中,D、E分别是AB、AC上的点,DE∥BC,如图①,然后将△ADE绕A点顺时针旋转一定角度,得到图②,然后将BD、CE分别延长至M、N,使DM=1/2BD,EN=1/2CE,得到图③,请解答下列问题:
(1)若AB=AC,请探究下列数量关系:
①在图②中,BD与CE的数量关系是____;
②在图③中,猜想AM与AN的数量关系、∠MAN和∠BAC的数量关系,并证明你的猜想;(2)若AB=k·AC(k>1),按上述操作方法,得到图④,请继续探究:AM与AN的数量关系、∠MAN与∠BAC的数量关系,直接写出你的猜想,不必证明。
