MATLAB预测1回归分析
用MATLAB求解回归分析
估
F值、与F对应的概率p
计
相关系数 r2 越接近 1，说明回归方程越显著；
.
（
缺
省显
时著
为性
0
水 平
05
）
F > F1-α（k，n-k-1）时拒绝 H0，F 越大，说明回归方程越显著；
与 F 对应的概率 p 时拒绝 H0，回归模型成立.
3、画出残差及其置信区间： rcoplot（r，rint）
例1 解：1、输入数据：
stats = 0.9702 40.6656
0.0005
1、回归：
非线性回 归
是事先用m-文件定 义的非线性函数
（1）确定回归系数的命令： [beta，r，J]=nlinfit（x，y，’model’, beta0）
估计出的 回归系数
残差 Jacobian矩阵
输入数据x、y分别为 n m矩阵和n维列向 量，对一元非线性回 归，x为n维列向量。
r2=0.9282, F=180.9531, p=0.0000
p<0.05, 可知回归模型 y=-16.073+0.7194x 成立.
3、残差分析，作残差图： rcoplot(r,rint)
从残差图可以看出，除第二个数据外，其余数据的残
差离零点均较近，且残差的置信区间均包含零点，这说明 回归模型 y=-16.073+0.7194x能较好的符合原始数据，而第 二个数据可视为异常点.
2、预测和预测误差估计：
（1）Y=polyval（p，x）求polyfit所得的回归多项式在 x处 的预测值Y； （2）[Y，DELTA]=polyconf（p，x，S，alpha）求 polyfit所得的回归多项式在x处的预测值Y及预测值的 显著性为 1-alpha的置信区间Y DELTA；alpha缺省时为0.5
使用Matlab技术进行回归分析的基本步骤
使用Matlab技术进行回归分析的基本步骤回归分析是统计学中一种用于研究变量间关系的方法，可以用来预测和解释变量之间的相关性。
在实际应用中，使用计算工具进行回归分析可以提高分析效率和准确性。
本文将介绍使用Matlab技术进行回归分析的基本步骤，并探讨其中的一些关键概念和技巧。
一、数据准备在进行回归分析之前，首先需要收集和整理相关的数据。
这些数据通常包括自变量和因变量。
自变量是用来解释或预测因变量的变量，而因变量是需要解释或预测的变量。
在Matlab中，可以将数据保存为数据矩阵，其中每一列代表一个变量。
二、模型建立在回归分析中，需要建立一个数学模型来描述自变量和因变量之间的关系。
最简单的线性回归模型可以表示为：Y = βX + ε，其中Y是因变量，X是自变量，β是回归系数，ε是误差项。
在Matlab中，可以使用regress函数来进行线性回归分析。
三、模型拟合模型拟合是回归分析的核心步骤，它的目标是找到最佳的回归系数，使得预测值与实际观测值之间的差异最小。
在Matlab中，可以使用OLS（Ordinary Least Squares）方法来进行最小二乘法回归分析。
该方法通过最小化残差平方和来估计回归系数。
四、模型诊断模型诊断是回归分析中非常重要的一步，它可以帮助我们评估模型的合理性和有效性。
在Matlab中，可以使用多种诊断方法来检验回归模型是否满足统计假设，例如残差分析、方差分析和假设检验等。
这些诊断方法可以帮助我们检测模型是否存在多重共线性、异方差性和离群值等问题。
五、模型应用完成模型拟合和诊断之后，我们可以使用回归模型进行一些实际应用。
例如，可以使用模型进行因变量的预测，或者对自变量的影响进行解释和分析。
在Matlab中，可以使用该模型计算新的观测值和预测值，并进行相关性分析。
六、模型改进回归分析并不是一次性的过程，我们经常需要不断改进模型以提高预测的准确性和解释的可靠性。
在Matlab中，可以使用变量选择算法和模型改进技术来优化回归模型。
利用Matlab进行线性回归分析
利用Matlab进行线性回归分析回归分析是处理两个及两个以上变量间线性依存关系的统计方法;可以通过软件Matlab实现;1.利用Matlab软件实现在Matlab中,可以直接调用命令实现回归分析,1b,bint,r,rint,stats=regressy,x,其中b是回归方程中的参数估计值,bint是b的置信区间,r和rint分别表示残差及残差对应的置信区间;stats 包含三个数字,分别是相关系数,F统计量及对应的概率p值;2recplotr,rint作残差分析图;3rstoolx,y一种交互式方式的句柄命令;以下通过具体的例子来说明;例现有多个样本的因变量和自变量的数据,下面我们利用Matlab,通过回归分析建立两者之间的回归方程;% 一元回归分析x=1097 1284 1502 1394 1303 1555 1917 2051 2111 2286 2311 2003 2435 2625 2948 3, 55 3372;%自变量序列数据y=698 872 988 807 738 1025 1316 1539 1561 1765 1762 1960 1902 2013 2446 2736 2825;%因变量序列数据X=onessizex',x',pauseb,bint,r,rint,stats=regressy',X,,pause%调用一元回归分析函数rcoplotr,rint%画出在置信度区间下误差分布;% 多元回归分析% 输入各种自变量数据x1= 8 3 3 8 9 4 5 6 5 8 6 4 7';x2=31 55 67 50 38 71 30 56 42 73 60 44 50 39 55 7040 50 62 59'; x3=10 8 12 7 8 12 12 5 8 5 11 12 6 10 10 6 11 11 9 9';x4=8 6 9 16 15 17 8 10 4 16 7 12 6 4 4 14 6 8 13 11';%输入因变量数据y= 160 155 195';X=onessizex1,x1,x2,x3,x4;b,bint,r,rint,stats=regressy,X%回归分析Q=r'rsigma=Q/18rcoplotr,rint;%逐步回归X1=x1,x2,x3,x4;stepwiseX1,y,1,2,3%逐步回归% X2=onessizex1,x2,x3;% X3=onessizex1,x1,x2,x3;% X4=onessizex1,x2,x3,x4;% b1,b1int,r1,r1int,stats1=regressy,X2% b2,b2int,r2,r2int,stats2=regressy,X3;% b3,b3int,r3,r3int,stats3=regressy,X4;。
MATLAB回归分析
MATLAB回归分析回归分析是统计学中常用的一种方法，用于建立一个依赖于自变量（独立变量）的因变量（依赖变量）的关系模型。
在MATLAB环境下，回归分析可以实现简单线性回归、多元线性回归以及非线性回归等。
简单线性回归是一种最简单的回归分析方法，它假设自变量和因变量之间存在线性关系。
在MATLAB中，可以通过`polyfit`函数进行简单线性回归分析。
该函数可以拟合一元数据点集和一维多项式，返回回归系数和截距。
例如：```matlabx=[1,2,3,4,5];y=[2,3,4,5,6];p = polyfit(x, y, 1);slope = p(1);intercept = p(2);```上述代码中，`x`是自变量的数据点，`y`是因变量的数据点。
函数`polyfit`的第三个参数指定了回归的阶数，这里是1，即一次线性回归。
返回的`p(1)`和`p(2)`分别是回归系数和截距。
返回的`p`可以通过`polyval`函数进行预测。
例如：```matlabx_new = 6;y_pred = polyval(p, x_new);```多元线性回归是在有多个自变量的情况下进行的回归分析。
在MATLAB中，可以使用`fitlm`函数进行多元线性回归分析。
例如：```matlabx1=[1,2,3,4,5];x2=[2,4,6,8,10];y=[2,5,7,8,10];X=[x1',x2'];model = fitlm(X, y);coefficients = model.Coefficients.Estimate;```上述代码中，`x1`和`x2`是两个自变量的数据点，`y`是因变量的数据点。
通过将两个自变量放在`X`矩阵中，可以利用`fitlm`函数进行多元线性回归分析。
返回值`model`是回归模型对象，可以通过`model.Coefficients.Estimate`获得回归系数。
回归预测 matlab
回归预测 matlab回归预测是指利用已知的数据建立一个数学模型，然后使用该模型对未知数据进行预测。
在Matlab中，可以使用各种统计和机器学习工具来进行回归预测分析。
下面我将从多个角度来介绍在Matlab中进行回归预测的方法。
首先，Matlab中可以使用经典的线性回归模型来进行预测。
线性回归是一种常见的统计方法，可以用来建立自变量和因变量之间的线性关系。
在Matlab中，可以使用`fitlm`函数来拟合线性回归模型，并使用该模型来进行预测。
该函数可以处理单变量和多变量的线性回归分析，同时还可以考虑到误差项的自相关性和异方差性。
其次，Matlab还提供了支持向量机（SVM）和人工神经网络（ANN）等机器学习方法来进行回归预测分析。
使用`fitrsvm`函数可以构建支持向量机回归模型，而使用`fitrnet`函数可以构建人工神经网络回归模型。
这些方法在处理非线性关系和高维数据时表现出色，可以更准确地进行预测。
此外，在Matlab中还可以使用交叉验证等技术来评估回归模型的性能。
通过交叉验证可以更准确地评估模型的泛化能力，避免过拟合和欠拟合问题。
Matlab提供了`crossval`函数和`kfoldLoss`函数等用于交叉验证的工具，可以帮助用户选择最佳的回归模型。
最后，Matlab还提供了丰富的可视化工具，可以帮助用户对回归预测结果进行直观的分析和展示。
用户可以使用`plot`函数和`scatter`函数等绘图函数来展示观测数据和预测结果，从而更直观地了解模型的拟合情况和预测效果。
综上所述，Matlab提供了多种方法和工具来进行回归预测分析，用户可以根据自己的数据和需求选择合适的方法进行建模和预测。
通过合理选择模型和参数，并结合交叉验证和可视化分析，可以更准确地进行回归预测，并得到可靠的结果。
第三讲 MATLAB预测(1)回归分析
ˆ 489.2946 s t 2 65.8896 t 9.1329
方法二
化为多元线性回归：
t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
3
1
模型：记血压为 y ，年龄为 x1 ，体重指数为 x2 ，吸烟习惯为 x3 ， 用Matlab将 y 与 x2 的数据做散点图，看出大致也呈线性关系，建立 模型： y 0 1 x1 2 x2 3 x3 由数据估计系数 0，2，3，4 ，也可看做曲面拟合（其实为 超平面）
T=[ones(14,1) t‘ (t.^2)'];
[b,bint,r,rint,stats]=regress(s',T); b,stats
得回归模型为 ：
ˆ 9.1329 65.8896 s t 489.2946 t2
预测及作图
Y=polyconf(p,t,S) plot(t,s,'k+',t,Y,'r')
（二）多元二项式回归
命令：rstool（x，y，’model’, alpha）
nm矩阵
n维列向量
显著性水平
（缺省时为0.05）
由下列 4 个模型中选择 1 个（用字符串输入，缺省时为线性模型）： linear（线性）： y 0 1 x1 m xm purequadratic（纯二次）： interaction（交叉）： y
其中 x=（x1，x2，„，xn） ，y=（y1，y2 ，„，yn） ； m m-1 p=（a1，a2，„，am+1）是多项式 y=a1x +a2x +„+amx+am+1 的系数；S 是一个矩阵，用来估计预测误差.
Matlab技术回归分析方法
Matlab技术回归分析方法简介：回归分析是一种常用的数据分析方法，用于建立变量之间的关系模型。
Matlab是一种功能强大的数值计算软件，提供了丰富的函数和工具包，用于实现回归分析。
本文将介绍几种常见的Matlab技术回归分析方法，并探讨其应用场景和优缺点。
一、线性回归分析：线性回归分析是回归分析的经典方法之一，用于研究变量之间的线性关系。
在Matlab中，可以使用`fitlm`函数来实现线性回归分析。
该函数通过最小二乘法拟合出最优的线性模型，并提供了各种统计指标和图形展示功能。
线性回归分析的应用场景广泛，例如预测销售额、研究市场需求等。
然而，线性回归假设自变量和因变量之间存在线性关系，当数据呈现非线性关系时，线性回归会失效。
为了解决非线性关系的问题，Matlab提供了多种非线性回归分析方法，如多项式回归、指数回归等。
二、多项式回归分析：多项式回归分析是一种常见的非线性回归方法，用于建立多项式模型来描述变量之间的关系。
在Matlab中，可以使用`fitlm`函数中的`polyfit`选项来实现多项式回归分析。
多项式回归在处理非线性关系时具有很好的灵活性。
通过选择不同的多项式次数，可以适应不同程度的非线性关系。
然而，多项式回归容易过拟合，导致模型过于复杂，对新数据的拟合效果不佳。
为了解决过拟合问题，Matlab提供了正则化技术，如岭回归和Lasso回归，可以有效控制模型复杂度。
三、岭回归分析：岭回归是一种正则化技术，通过添加L2正则项来控制模型的复杂度。
在Matlab中，可以使用`fitlm`函数的`Regularization`选项来实现岭回归分析。
岭回归通过限制系数的大小，减少模型的方差，并改善模型的拟合效果。
然而，岭回归不能自动选择最优的正则化参数，需要通过交叉验证等方法进行调优。
四、Lasso回归分析：Lasso回归是另一种常用的正则化技术，通过添加L1正则项来控制模型的复杂度。
在Matlab中，可以使用`fitlm`函数的`Regularization`选项来实现Lasso回归分析。
Matlab回归分析：详解+实例
姚明女儿的身高
问 建立父母身高和女儿身高的模型 题 姚明2.26米，叶莉1.90米，预测姚明女儿身高
女孩身高y(cm) 156 172 162 158 164 166 160 155 174 165
父母平均身高 x(cm)
158.5
170.5
166
163.5
166
168.5 165.5
自变量X：用来解释Y的变量，通常有多个。
Y：薪资收入 X:学历、年龄、性别...
注意：（1）自变量可以是定量数据，也可以是定
性数据，它不决定回归模型的类型，决定回归模型 类型的是因变量；
（2）确定自变量的方法可以头脑风暴，但同时也 要看数据的可获得性，有时候可能头脑风暴想的很 好，但是没办法获取这个指标的数据也是不行的， 所以自变量的选取往往看一个数据的可获取性。
1 n
(x0 x)2 Lxx
小结
1.回归分析的任务 研究变量之间的相关关系
2.线性回归的步骤
(1) 推测回归函数; (3) 估计未知参数; (5) 预测.
(2) 建立回归模型; (4) 进行假设检验;
MATLAB中回归分析的实现
多元线性回归
1.确定回归系数的点估计值,用命令:
b=regress(Y,X)
女孩身高y(cm) 156 172 162 158 164 166 160 155 174 165
父母平均身高 x(cm)
158.5
170.5
166
163.5
166
168.5 165.5
159
180.5
169
基本模型
y 0 1x
y ~女孩身高
0, 1 ~回归系数
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
回 归 系 数 的 区 间
置
残
信
差
区
间
用于检验回归模型的统计量， 有三个数值：R2、F值、与F对应
0.05
（ 缺 省显 时著 为性
水 平 ）
估
的概率p、以及残差的方差的估
计
计值
R2 越接近 1，说明回归方程越显著；
F F1 (k, n k 1) 时，F 越大，说明回归方程越显著；
与 F 对应的概率 p 时回归模型成立，否则，则说明回归方程中 有多余的自变量，可以将这些多余的自变量从回归方程中剔除
y 0 1x1 2 x2 3x3 由数据估计系数 0，2，3，4 ，也可看做曲面拟合（其实为超平
面）
4
第三讲 MATLAB预测方法（1）回归分析
多元线性回归
y 0 1x1 ... p x p
1、确定回归系数的点估计值：
b=regress( Y, X )
b
ˆ 0 ˆ1
... ˆ p
8 124 42 19.7 0 18 114 18 18.8 0 28 130 29 22.0 1
9 158 67 27.2 1 19 116 20 22.6 0 29 125 25 25.3 0
10 154 56 19.3 0 20 124 19 21.5 0 30 175 69 27.4 1
3
模型：记血压为 y，年龄为 ，x1 体重指数为 ，x吸2 烟习惯为 ，用x3 Matlab将 与y 的x2数据做散点图，看出大致也呈线性关系，建立模型：
表2
序号
血压
年龄
体重 指数
吸烟 习惯
序号
血压
年龄
体重 指数
吸烟 习惯
序号
血压
年龄
体重 指数
吸烟 习惯
1 144 39 24.2 0 11 162 64 28.0 1 21 136 36 25.0 0
2 215 47 31.1 1 12 150 56 25.8 0 22 142 50 26.2 1
3 138 45 22.6 0 13 140 59 27.3 0 23 120 39 23.5 0
Y1
Y
Y2
...
Yn
1 x11 x12 ... x1p
X 1
x21
x22
...
x2
p
... ... ... ... ...
1
xn1
xn2
...
xnp
对一元线性回归，取 p=1 即可
2、求回归系数的点估计和区间估计、并检验回归模型： [b, bint,r,rint,stats]=regress(Y,X,alpha)
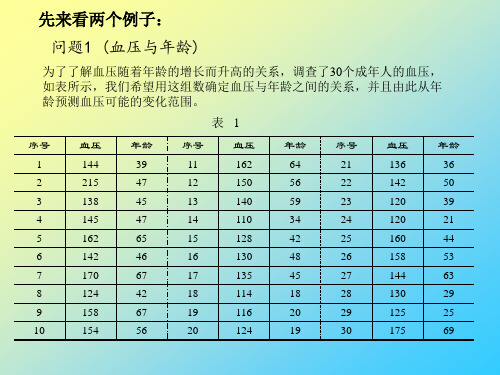
先来看两个例子：
问题1 (血压与年龄)
为了了解血压随着年龄的增长而升高的关系，调查了30个成年人的血压， 如表所示，我们希望用这组数确定血压与年龄之间的关系，并且由此从年 龄预测血压可能的变化范围。
序号 1 2 3 4 5 6 7 8 9 10
血压 144 215 138 145 162 142 170 124 158 154
4 145 47 24.0 1 14 110 34 20.1 0 24 120 21 20.3 0
5 162 65 25.9 1 15 128 42 21.7 0 25 160 44 27.1 1
6 142 46 25.1 0 16 130 48 22.2 1 26 158 53 28.6 1
7 170 67 29.5 1 17 135 45 27.4 0 27 144 63 28.3 0
回归系数
0 1
R2=0.4540
回归系数估计值
回归系数置信区间
98.4084
[74.7484, 118.0683]
0.9732
[0.5601 1.3864]
F=23.2834 p<0.001 s2=273.7137
从以下几点可以看出模型是有效的：参数的置信区间不含0点；p 小于显著性水平；用Matlab可以求出F1-α(1,n-2)=4.1960，显然小于F值。
血压 136 142 120 120 160 158 144 130 125 175
年龄 36 50 39 21 44 53 63 29 25 69
模型：记血压为y，年龄为x，可以做出如上图所示的散点图，从图形上直观 的可以看出，y与x大致呈线性关系，即有：
y 0 1x 需要由数据确定系数 0 , 的1 估计值 ˆ0 ,。ˆ1
9
剔除第二个点后得到的结果：
回归系数
0 1
R2=0.7123
但是由于β1的置信区间过长，R2较小，说明模型的精度不高！
8
残差图如图所示：
图中第二个点的残差置信区间中不包含0点，由于残差服从均值为0的正态分布， 因此可以认为这个点为异常数据，偏离数据整体的变化范围，应该剔除，重新 进行回归分析！！ 残差与残差区间杠杆图，最好在0点线附近比较均匀的分布，而不呈现一定的规律 性，如果是这样，就说明回归分析做得比较理想。
b, bint, s,
%输出回归系数及其置信区间
和统计量
rcoplot(r,rint)
%残差及其置信区间作图
输出结果为：
b=
bint =
98.4084 78.7484 118.0683
0.9732
0.5601 1.3864
s= 0.4540 23.2834 0.0000 273.7137
7
结果整理为下表：
3、画出残差及其置信区间：
rcoplot（r，rint） 6
问题1的求解：
y=[……];
%已知的因变量数组
x=[……];
%已知的自变量数组
n=……;
%已知的数据容量
X=[ones(n,1),x’];
%1与自变量组成的输入矩阵
[b,bint,r,rint,s]=regress(y’,X);
%回归分析程序(显著性水平为0.05)
此函数为一元Байду номын сангаас性函数！！
2
问题2 (血压与年龄，体重指数，吸烟习惯)
世界卫生组织颁布的“体重指数”的定义是体重(kg)除以身高(m)的平方，下 表给出了30个人的体重指数等数据，其中，0表示不吸烟，1表示吸烟，怎么考虑 吸烟这个因素，此因素对于血压升高有影响吗，并对体重指数为25,50岁的吸烟者 的血压做出预测。
年龄 39 47 45 47 65 46 67 42 67 56
表1
序号
血压
11
162
12
150
13
140
14
110
15
128
16
130
17
135
18
114
19
116
20
124
年龄 64 56 59 34 42 48 45 18 20 19
序号 21 22 23 24 25 26 27 28 29 30