第3章部分习题与解答
第3章习题及部分解答

3.5设有一个SPJ数据库,包括S,P,J,SPJ四个关系模式:S(SNO,SNAME,STATUS,CITY); P(PNO,PNAME,COLOR,WEIGHT); J(JNO,JNAME,CITY);SPJ(SNO,PNO,JNO,QTY);1、供应商表S由供应商代码(SNO)、供应商姓名(SNAME)、供应商状态(STATUS)、供应商所在城市(CITY)组成;2、零件表P由零件代码(PNO)、零件名(PNAME)、颜色(COLOR)、重量(WEIGHT)组成;3、工程项目表J由工程项目代码(JNO)、工程项目名(JNAME)、工程项目所在城市(CITY)组成;4、供应情况表SPJ由供应商代码(SNO)、零件代码(PNO)、工程项目代码(JNO)、供应数量(QTY)组成,表示某供应商供应某种零件给某工程项目的数量为QTY。
试用关系代数语言完成如下查询:1)找出所有供应商的姓名和所在城市;2)找出所有零件的名称、颜色、重量;3)找出使用供应商S1所供应零件的工程号码;4)找出工程项目J2使用的各种零件的名称及其数量;5)找出上海厂商供应的所有零件号码;6)找出使用上海产的零件的工程号码;7)找出没有使用天津产的零件的工程号码;8)把全部红色零件的颜色改成蓝色;9)由S5供给J4的零件P6改为由S3供应,请作必要的修改;10)从供应商关系中删除S2的记录,并从供应情况关系中删除相应的记录;11)求供应工程J1零件的供应商号码SNO;12)求供应工程J1零件P1的供应商号码SNO;13)求供应工程J1零件为红色的供应商号SNO;14)求没有使用天津供应商生产的红色零件的工程号JNO;15)求S1提供的零件名PNAME;16)求给工程J1和J2提供零件的供应商号码SNO;解:1)找出所有供应商的姓名和所在城市;Select SNAME,CITY From S2)找出所有零件的名称、颜色、重量;Select PNAME,COLOR,WEIGHT From P3)找出使用供应商S1所供应零件的工程号码;Select JNO From SPJ Where SNO= ‘S1’4)找出工程项目J2使用的各种零件的名称及其数量;Select PNAME,QTY From SPJ,PWhere SPJ.PNO=P.PNO And JNO=‘J2’5)找出上海厂商供应的所有零件号码;Select PNO From S,SPJWhere SPJ.SNO=S.SNO And CITY=‘上海’6)找出使用上海产的零件的工程号码;Select JNAME From J,SPJ,S Where J.JNO=SPJ.JNOAnd S.SNO=SPJ.SNO And S.CITY=‘上海’7)找出没有使用天津产的零件的工程号码;Select JNO From SPJ Where SNONOT IN(Select SNO From S Where CITY= ‘天津’)8)把全部红色零件的颜色改成蓝色;Updat P SET COLOR=‘蓝’ Where COLOR=‘红’9)由S5供给J4的零件P6改为由S3供应,请作必要的修改;Updat SPJ SET SNO=‘S3’Where SNO=‘S5’ And JNO=‘J4’ And PNO=‘P6’10)从供应商关系中删除S2的记录,并从供应情况关系中删除相应的记录;Delete From S Where SNO=‘S2’Delete From SPJ Where SNO=‘S2’11)求供应工程J1零件的供应商号码SNO;Select SNO From SPJ Where JNO=‘J1’12)求供应工程J1零件P1的供应商号码SNO;Select SNO From SPJ Where JNO=‘J1’ And PNO=‘P1’13)求供应工程J1零件为红色的供应商号SNO;Select SNO From P,SPJWhere P.PNO=SPJ.PNO And JNO=‘J1’ And COLOR=‘红’14)求没有使用天津供应商生产的红色零件的工程号JNO; Select JNO From SPJ Where JNO NOT IN(Select JNO From S,SPJ,P Where S.SNO=SPJ.SNOAnd P.PNO=SPJ.PNO And COLOR=‘红’ And CITY=‘天津’)15)求S1提供的零件名PNAME;Select PNAME From SPJ,PWhere P.PNO=SPJ.PNO And SNO=‘S1’16)求同时给工程J1和J2提供零件的供应商号码SNO;Select SNO From SPJ Where JNO=‘J1’And SNO IN(Select SNO From SPJ Where JNO=‘J2’)或Select SNO From SPJ Where JNO=‘J1’INTERSECT Select SNO From SPJ Where JNO=‘J1’3.6 什么是基本表?什么是视图?两者的区别和联系是什么?3.11 请为三建工程建立一个供应情况的视图,包括供应商代码SNO、零件代码PNO、供应数量QTY。
第3章 习题解答

第三章 习题解答(部分)[1]求以下序列)(n x 的频谱()j X e ω,其中0a >。
(2)()an e u n - (5)0sin()()an e n u n ω-解:对题中所给的)(n x 先进行z 变换,再求其频谱。
(2)由于111)]([)(----==ze n u e Z z X a an ,所以ωωωj a ez j e e z X e X j --=-==11)()(。
(5)由于aa a ane z e z e z n u n eZ z X 2201010cos 21sin )]()sin([)(-------+-==ωωω,所以ωωj e z j z X e X ==)()(aj a j a j e e e e e e 2200c o s 21s i n ------+-=ωωωωω [2] 设()j X e ω和()j Y e ω分别是()x n 和()y n 的傅里叶变换,试求下面序列的傅里叶变换。
(7)(2)x n (8)(),()20n x n g n n ⎧⎪=⎨⎪⎩=偶,=奇解:(7)2)()2()]2([ωωn jn n jn en x en x n x DTFT -∞∞-∞=-∑∑==为偶数 2)]()1()([21ωn j nn e n x n x -∞-∞=-+=∑)(21)(21)(21)(212222⎪⎭⎫⎝⎛+∞-∞=⎪⎭⎫⎝⎛+-∞-∞=-+=+=∑∑πωωπωωj j n n j n n j e X e X e n x e n x(8))()'()2/()]([2''2ωωωj n n j n jn e X en x en x n g DTFT ===∑∑∞-∞=-∞-为偶数[3]求出下面序列的傅里叶变换(1))5(2)(-δ=n n x (4))3()2()(--+=n u n u n x解:由DFT 定义有:(1)ωωωδ52)5(2)(j n jn j e en e X -∞-∞=-=-=∑(4)ωωωωωωj j j n jn n jn j ee e een u n u e X ---=-∞-∞=---==--+=∑∑1)]3()2([)(3222⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=--=------ωωωωωωωωωωωω21sin 25sin 11222225252525j j j j j j j j j j e e e e e e e e e e [5]已知001,()0,j X e ωωωωωπ⎧≤⎪=⎨<≤⎪⎩,求()j X e ω的傅里叶逆变换()x n 。
大学物理第3章 刚体力学习题解答

第3章 刚体力学习题解答3.13 某发动机飞轮在时间间隔t 内的角位移为):,:(43s t rad ct bt at θθ-+=。
求t 时刻的角速度和角加速度。
解:23212643ct bt ct bt a d d -==-+==ωθβω3.14桑塔纳汽车时速为166km/h ,车轮滚动半径为0.26m ,发动机转速与驱动轮转速比为0.909, 问发动机转速为每分多少转?解:设车轮半径为R=0.26m ,发动机转速为n 1, 驱动轮转速为n 2, 汽车速度为v=166km/h 。
显然,汽车前进的速度就是驱动轮边缘的线速度,909.0/2212Rn Rn v ππ==,所以:min/1054.1/1024.93426.014.3210166909.02909.013rev h rev n R v ⨯=⨯===⨯⨯⨯⨯π3.15 如题3-15图所示,质量为m 的空心圆柱体,质量均匀分布,其内外半径为r 1和r 2,求对通过其中心轴的转动惯量。
解:设圆柱体长为h ,则半径为r ,厚为dr 的薄圆筒的质量dm 为:2..dm h r dr ρπ=对其轴线的转动惯量dI z 为232..z dI r dm h r dr ρπ==212222112..()2r z r I h r r dr m r r ρπ==-⎰ 3.17 如题3-17图所示,一半圆形细杆,半径为,质量为,求对过细杆二端轴的转动惯量。
解:如图所示,圆形细杆对过O 轴且垂直于圆形细杆所在平面的轴的转动惯量为mR 2,根据垂直轴定理z x y I I I =+和问题的对称性知:圆形细杆对过轴的转动惯量为12mR 2,由转动惯量的可加性可求得:半圆形细杆对过细杆二端轴的转动惯量为:214AA I mR '=3.18 在质量为M ,半径为R 的匀质圆盘上挖出半径为r 的两个圆孔,圆孔中心在半径R 的中点,求剩余部分对过大圆盘中心且与盘面垂直的轴线的转动惯量。
人工智能教程习题及答案第3章习题参考解答

第三章确定性推理方法习题参考解答3.1 练习题3.1 什么是命题?请写出3个真值为T 及真值为F 的命题。
3.2 什么是谓词?什么是谓词个体及个体域?函数与谓词的区别是什么?3.3 谓词逻辑和命题逻辑的关系如何?有何异同?3.4 什么是谓词的项?什么是谓词的阶?请写出谓词的一般形式。
3.5 什么是谓词公式?什么是谓词公式的解释?设D= {1,2} ,试给出谓词公式( x)( y)(P(x,y) Q(x,y))的所有解释,并且对每一种解释指出该谓词公式的真值。
3.6对下列谓词公式分别指出哪些是约束变元?哪些是自由变元?并指出各量词的辖域。
(1)( x)(P(x, y) ( y)(Q(x, y) R(x, y)))(2)( z)( y)(P(z, y) Q(z, x)) R(u, v)(3)( x)(~ P( x, f (x )) ( z)(Q(x,z) ~ R(x,z)))(4)( z)(( y)(( t)(P(z, t) Q(y, t)) R(z, y))(5)( z)( y)(P(z, y) ( z)(( y)(P(z, y) Q(z, y) ( z)Q(z, y))))什么是谓词公式的永真性、永假性、可满足性、等价性及永真蕴含?3.7什么是置换?什么是合一?什么是最一般的合一?3.8判断以下公式对是否可合一;若可合一,则求出最一般的合一:3.9(1)P(a,b) ,P(x, y)(2)P(f(z),b) ,P(y, x)(3)P(f(x), y) ,P(y, f(a))(4)P(f(y), y,x) ,P(x, f(a), f(b))(5)P(x, y) ,P(y, x)什么是范式?请写出前束型范式与SKOLEM 范式的形式。
3.10什么是子句?什么是子句集?请写出求谓词公式子句集的步骤。
3.113.12谓词公式与它的子句集等值吗?在什么情况下它们才会等价?3.13 把下列谓词公式分别化为相应的子句集:(1)( z)( y)(P(z, y) Q(z, y))(2)( x)( y)(P(x, y) Q(x, y))(3)( x)( y)(P(x, y) (Q(x, y) R(x, y)))(4)( x)( y)( z)(P(x, y) Q(x, y) R(x, z))(5)( x)( y)( z)( u)( v)( w)(P(x, y,z,u,v,w) (Q(x, y, z,u, v, w) ~R(x, z, w)))3.14 判断下列子句集中哪些是不可满足的:(1)S {~ P Q,~ Q,P,~ P}(2)S {P Q,~ P Q,P ~ Q,~ P ~ Q}(3)S {P(y) Q(y), ~ P(f(x)) R(a)}(4)S {~ P(x) Q(x), ~ P(y) R(y), P(a),S(a),~ S(z) ~ R(z)}(5)S {~ P(x) ~ Q(y) ~ L(x, y), P(a), ~ R(z) L(a, z), R(b), Q(b)}(6)S {~ P(x) Q(f(x), a), ~ P(h(y)) Q(f(h(y)), a) ~ P(z)}(7)S {P(x) Q(x) R(x),~ P(y) R(y),~Q(a),~ R(b)}(8)S {P(x) Q(x),~ Q(y) R(y), ~ P(z) Q(z),~ R(u)}3.15 为什么要引入Herbrand 理论?什么是H 域?如何求子句集的H 域?3.16 什么是原子集?如何求子句集的原子集?3.17 什么是H 域解释?如何用域D 上的一个解释I 构造H 域上的解释I *呢?3.18 假设子句集S={P(z) ∨Q(z),R(f(t))} ,S 中不出现个体常量符号。
电磁场与电磁波(第4版)第3章部分习题参考解答
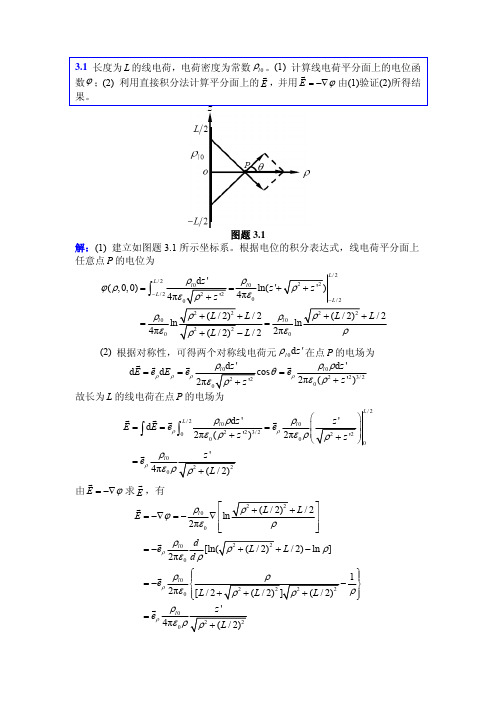
3 ∞ ρ R0 ρ R02 ρ R02 2ε r + 1 ρ 2 ρr dr + ∫ dr = + = ( ) R0 R R 0 0 3ε ε 6ε rε 0 3ε 0 2ε r 3ε 0 3ε 0 r 2 r 0 3.6 电场中有一半径为 a 、介电常数为 ε 的介质球,已知球内、外的电位函数分
ρ ≥ a 时, E = −∇ϕ = −eρ
G
G ∂ ∂ρ
3.4 已知 y > 0 的空间中没有电荷,试判断下列函数中哪些是可能的电位解? (1) e− y cosh x ;(2) e− y cos x ;(3) e− 2 sin x cos x ;(4) sin x sin y sin z 。 解:在电荷体密度 ρ = 0 的空间,电位函数应满足拉普拉斯方程 ∇ 2ϕ = 0 。
(2) 根据对称性,可得两个对称线电荷元 ρ l 0 dz ′ 在点 P 的电场为 G G ρl 0dz ' ρ l 0 ρ dz ' G G dE = eρ dEρ = eρ cos θ = eρ 2πε 0 ( ρ 2 + z '2 )3/ 2 2πε 0 ρ 2 + z '2 故长为 L 的线电荷在点 P 的电场为
G ρ = −eρ l 0 2πε 0 G = eρ
ρl 0 4πε 0 ρ
⎧ ρ 1⎫ ⎪ ⎪ − ⎬ ⎨ 2 2 2 2 ρ⎪ ⎪[ L / 2 + ρ + ( L / 2) ] ρ + ( L / 2) ⎩ ⎭ z'
ρ 2 + ( L / 2) 2
3.2 点电荷 q1 = q 位于 P 1 ( − a, 0, 0) ,另一点电荷 q2 = −2q 位于 P 2 ( a, 0, 0) ,求空间的 零电位面。 解:两个点电荷 + q 和 −2q 在空间产生的电位 ⎤ q 1 ⎡ 2q ϕ ( x, y , z ) = − ⎢ ⎥ 2 2 2 2 2 2 4 πε 0 ⎢ ( ) ( ) ⎥ x a y z x a y z + + + − + + ⎣ ⎦ 1 2 − =0 令 ϕ ( x, y, z ) = 0 ,则有 2 2 2 2 ( x + a) + y + z ( x − a) + y 2 + z 2
数字电子技术基础第三版课后习题解答与第章

【题3-2】 解:),=(A田B) C=A⑥B+C}、=AB+(AB)C=AB+(AB+AB)C=AB+ABC+ABC=AB+BC+AC)=A B CY,=AB+(A B)C=AB+BC+AC两个电路功能相同,均为全加器。
14
(2) CDAB 00 01 11o0[ X0111 1 1 X10 1 1
A₃B₃…A₀B₀ 91A₃B₃…A₀B₀A<B.A>R低位 A=B74LS85Fg FxBF,A>B
A₂B₇…A₄B₄A=B74LS85FAn FxnF
【题3-9】 解:连线图如图3-26所示。
图3 - 26
27
【题3-10】 解:A=A₃A₂A₁A₀ 8421BCD 码 B=B₃B₂B₁B₀ 余3 BCD 码C=C₃C₂C₁C₀ 2421BCD 码 D=D₃D₂D₁D₀ 余 3 循环码(1)卡诺图如图3 - 27所示。B₃=A₃+A₂A₁+A₂A₀=A₂A₂A₁A₂A₀
2
A
B
A
Y'
2
0
0
0
1
0
0
1
1
0
0
1
0
0
0
1
1
1
0
1
)
3-2 解:(1)X=AB;Y=AB+AB=AB+AB;Z=AB。真值表如表3-10所示。表3-10
(2)实现1 位数值比较功能。
3
Y₀=X,④X 。 Y₀=Y₁X₀=X₂X₇X。若令 X₂=B₂ 、X₁=B₁ 、λ₀=B, 则当 K=1 时电路可正确地实现3位二进制码到3位循环码的转换,即有 Y₂=G₂ 、Y,=G₁ 、Y₀=G₀ 。 若 令X₂=G₂ 、X,=G₁、X₀=G₀, 则当 K=0 时,通过比较可明显看出,只要去掉一个反相器便可实现3位循环码到3位二进制码的转换,即有 Y₂=B₂ 、Y₁=B₁ 、Y₀=B₀。
第三章练习试题和参考解答
第三章练习题及参考解答3、1 第三章得“引子”中分析了,经济增长、公共服务、市场价格、交通状况、社会环境、政策因素,都会影响中国汽车拥有量。
为了研究一些主要因素与家用汽车拥有量得数量关系,选择“百户拥有家用汽车量”、“人均地区生产总值”、“城镇人口比重”、“交通工具消费价格指数”等变量,2011年全国各省市区得有关数据如下:资料来源:中国统计年鉴2012、中国统计出版社1)建立百户拥有家用汽车量计量经济模型,估计参数并对模型加以检验,检验结论得依据就是什么。
2)分析模型参数估计结果得经济意义,您如何解读模型估计检验得结果?3) 您认为模型还可以如何改进?【练习题3、1参考解答】:1)建立线性回归模型:回归结果如下:由F统计量为17、87881, P值为0、000001,可判断模型整体上显著, “人均地区生产总值”、“城镇人口比重”、“交通工具消费价格指数”等变量联合起来对百户拥有家用汽车量有显著影响。
解释变量参数得t统计量得绝对值均大于临界值,或P值均明显小于,表明在其她变量不变得情况下,“人均地区生产总值”、“城镇人口比重”、“交通工具消费价格指数”分别对百户拥有家用汽车量都有显著影响。
2)X2得参数估计值为5、9911,表明随着经济得增长,人均地区生产总值每增加1万元,平均说来百户拥有家用汽车量将增加近6辆。
由于城镇公共交通得大力发展,有减少家用汽车得必要性,X3得参数估计值为0、5231,表明随着城镇化得推进,“城镇人口比重”每增加1%,平均说来百户拥有家用汽车量将减少0、5231辆。
汽车价格与使用费用得提高将抑制家用汽车得使用, X4得参数估计值为2、2677,表明随着家用汽车使用成本得提高, “交通工具消费价格指数”每增加1个百分点,平均说来百户拥有家用汽车量将减少2、2677辆。
3)模型得可决系数为0、6652,说明模型中解释变量变解释了百户拥有家用汽车量变动得66、52%,还有33、48%未被解释。
数据与计算机通信答案(第3章)

而对于数字彩色电视机,相当不错了。如果不提高数据率,还可以通过降低分辨率或刷新速 率,来换取色彩数的提高,但这也不实用的方法。
已知视频带宽 B=5MHz,所以有 5=P/105,则每行的像素数 P=5x105=525。 然而,通常 CCIR-M/NTSC 制式每行只约有 450 像素,带宽 B=P/105=450/105=4.3MHz (实 际技术指标 4.2Hz) 。 带宽由 4.2MHz 增加到 5MHz 时,水平分辨率约增加 75 像素,增幅 16.7%。 (2)计算垂直分辨率的增幅 由于信号最高频率 fH=5MHz,即最短的信号周期 1/fH=0.2υs。 又因为每个最短周期包含 2 个像素,则有 225 周期/行。那么,每行扫描时间为 0.2υs×225=45υs。加上水平回扫 11υs,每行往返扫描时间为 56υs ,即 56x10-6 s, 假定每屏 V 行,每秒扫描 30 场(帧、屏),则每秒扫描行数为 30V。 因此对于画面刷新,有 30V×56x10-6 = 1s,V = 595 行/屏。目前 NSTL 制式每行只有 525 行。垂直分辨率增加了 70 行,增幅 13.3%。
cos 2 t = cos t cos t = 1 (cos 2t + cos 0) = 1 (cos 2t + 1)
2
2
所以, f (t) = (10 cos t)2 = 100 cos 2 t = 50 + 50 cos 2t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章习题
4 .针对上题中建立的四个表试用SQL语言完成第2章习题5中的查询。
答案:
(1)求供应工程J1零件的供应商号码SNO;
SELECT SNO FROM SPJ WHERE JNO=‘J1’;
(2)求供应工程J1零件P1的供应商号码SNO;
SELECT SNO FROM SPJ WHERE JNO=‘J1’AND PNO=‘P1’;
(3)求供应工程J1零件为红色的供应商号码SNO;
SELECT SNO /*这是嵌套查询*/ FROM SPJ WHERE JNO=‘J1’AND PNO IN /*找出红色的零件的零件号码PNO */ (SELECT PNO FROM P /*从P表中找*/ WHERE COLOR=‘红’);
或SELECT SNO FROM SPJ,P /*这是两表连接查询*/ WHERE JNO=‘J1’/*这是复合条件连接查询*/ AND SPJ.PNO=P.PNO AND COLOR=‘红’;
(4)求没有使用天津供应商生产的红色零件的工程号JNO;
*解析:第一种解法是使用多重嵌套查询,第二种方法的子查询是一个多表连接。
注意:从J表入手,以包含那些尚未使用任何零件的工程号。
SELECT JNO FROM J
WHERE NOT EXISTS
(SELECT * FROM SPJ
WHERE SPJ.JNO=J.JNO AND SNO IN /*天津供应商的SNO*/
(SELECT SNO FROM S
WHERE CITY=‘天津’) AND PNO IN /*红色零件的PNO*/
(SELECT PNO FROM P WHERE COLOR=‘红’));
或SELECT JNO FROM J
WHERE NOT EXISTS
(SELECT * FROM SPJ, S, P
WHERE SPJ.JNO=J.JNO AND SPJ.SNO=S.SNO AND
SPJ.PNO=P.PNO AND S.CITY=‘天津’AND P. COLOR=‘红’);
//注:本例中父查询和子查询均引用了Student表,可以像自身连接那样用别名将父查询中的Student表与子查询中的Student表区分开://
(5)求至少用了供应商S1所供应的全部零件的工程号JNO (类似于P113例44)。
解析:它所表达的语义为:不存在这样的零件y,供应商S1供应了y,而工程x 没有选用y。
用SQL语言表示如下:
SELECT DISTINCT JNO FROM SPJ SPJZ WHERE NOT EXISTS
(SELECT * FROM SPJ SPJX
WHERE SNO='S1' AND NOT EXISTS
(SELECT * FROM SPJ SPJY
WHERE SPJY.PNO=SPJX.PNO
AND SPJY.JNO=SPJZ.JNO AND SPJY.SNO=’S1’));
5 .针对习题3中的四个表试用SQL语言完成以下各项操作:
(1) 找出所有供应商的姓名和所在城市。
(2) 找出所有零件的名称、颜色、重量。
(3) 找出使用供应商S1所供应零件的工程号码。
(4) 找出工程项目J2使用的各种零件的名称及其数量。
(5) 找出上海厂商供应的所有零件号码。
(6) 找出使用上海产的零件的工程名称。
(7) 找出没有使用天津产的零件的工程号码。
(8) 把全部红色零件的颜色改成蓝色。
(9) 由S5供给J4的零件P6改为由S3供应,请作必要的修改。
(填空题)
(10) 从供应商关系中删除S2的记录,并从供应情况关系中删除相应的记录。
(11) 请将(S2,J6,P4,200) 插入供应情况关系。
答案:
(1) 找出所有供应商的姓名和所在城市。
SELECT SNAME, CITY FROM S;
(2) 找出所有零件的名称、颜色、重量。
SELECT PNAME, COLOR, WEIGHT FROM P;
(3) 找出使用供应商S1所供应零件的工程号码。
SELECT JNO FROM SPJ WHERE SNO=‘S1’;
(4) 找出工程项目J2使用的各种零件的名称及其数量。
SELECT P.PNAME, SPJ.QTY FROM P, SPJ
WHERE P.PNO=SPJ.PNO AND SPJ.JNO='J2';
(5) 找出上海厂商供应的所有零件号码。
SELECT DISTINCT PNO FROM SPJ WHERE SNO IN
(SELECT SNO FROM S WHERE CITY='上海');
(6) 找出使用上海产的零件的工程名称。
SELECT JNAME FROM J, SPJ, S
WHERE J. JNO=SPJ. JNO AND SPJ. SNO=S.SNO AND S.CITY='上海';
或SELECT JNAME FROM J WHERE JNO IN
(SELECT JNO FROM SPJ, S
WHERE SPJ. SNO=S.SNO AND S.CITY='上海');
(7) 找出没有使用天津产的零件的工程号码。
SELECT JNO FROM J WHERE NOT EXISTS
(SELECT * FROM SPJ WHERE SPJ.JNO=J.JNO AND SNO IN
(SELECT SNO FROM S WHERE CITY=‘天津’));
或SELECT JNO FROM J WHERE NOT EXISTS
(SELECT * FROM SPJ, S
WHERE SPJ.JNO=J.JNO AND SPJ.SNO=S.SNO
AND S.CITY=‘天津’);
(8) 把全部红色零件的颜色改成蓝色。
UPDATE P SET COLOR='蓝' WHERE COLOR='红' ;
(9) 由S5供给J4的零件P6改为由S3供应,请作必要的修改。
UPDATE SPJ SET SNO='S3' WHERE SNO='S5' AND JNO='J4' AND PNO='P6';
(10) 从供应商关系中删除S2的记录,并从供应情况关系中删除相应的记录。
DELETE FROM SPJ WHERE SNO='S2';
DELETE FROM S WHERE SNO='S2';
解析:注意删除顺序,应该先从SPJ表中删除供应商S2所供应零件的记录,然后从S表中删除S2。
(11) 请将(S2,J6,P4,200) 插入供应情况关系。
INSERT INTO SPJ(SNO, JNO, PNO, QTY) V ALUES (S2,J6,P4,200); /*插入的属性值与指明列要对应*/
或INSERT INTO SPJ V ALUES (S2,P4,J6,200); /*插入的记录在每个属性列上有值,并且属性列要和表定义中的次序对应*/
设有一个SPJ数据库,包括S、P、J、SPJ四个关系:
供应商S(SNO、SNAME、STA TUS、CITY)
零件P(PNO,PNAME、COLOR、WEIGHT)
工程项目J(JNO,JNAME,CITY)
供应情况SPJ(SNO,PNO,JNO,QTY)
试用SQL语言完成以下查询:
(1)求供应工程J1零件为红色的供应商号码SNO。
(3分)
(2)求没有使用天津供应商生产的红色零件的工程号JNO 。
(3分) (3)求至少用了供应商S1所供应的全部零件的工程号JNO。
(4分)。
