三角形旋转全等常见模型
全等三角形旋转模型知识点总结附解析

全等三角形旋转模型知识点总结附解析一、全等三角形旋转模型1.(课题研究)旋转图形中对应线段所在直线的夹角(小于等于90°的角)与旋转角的关系.(问题初探)线段AB 绕点O 顺时针旋转得到线段CD ,其中点A 与点C 对应,点B 与点D 对应,旋转角的度数为α,且0°<α<180°.(1)如图①,当α=60°时,线段AB 、CD 所在直线夹角(锐角)为 ;(2)如图②,当90°<α<180°时,直线AB 与直线CD 所夹锐角与旋转角α存在怎样的数量关系?请说明理由;(形成结论)旋转图形中,当旋转角小于平角时,对应线段所在直线的夹角与旋转角 .(运用拓广)运用所形成的结论解决问题:(3)如图③,四边形ABCD 中,∠ABC =60°,∠ADC =30°,AB =BC ,CD =3,BD =19,求AD 的长.解析:(1)60°;(2)互补,理由见解析;【形成结论】相等或互补;(310【分析】(1)由旋转的性质可得AB CD =,OA OC =,BO DO =,可证()AOB COD SSS ,可得B D ∠=∠,由三角形内角和定理可求解;(2)由旋转的性质可得AB CD =,OA OC =,BO DO =,可证()AOBCOD SSS ,可得B D ∠=∠,由平角的定义和四边形内角和定理可求解; 【形成结论】由(1)(2)可知对应线段所在直线的所夹锐角角与旋转角:相等或互补;【运用拓广】(3)将BCD ∆绕点B 顺时针旋转60︒,得到BAF ∆,连接FD ,由旋转的性质可得BF BD =,3AF CD ==,由三角形内角和定理可求90FAD ∠=︒,由勾股定理可求解.【详解】解:(1)如图1,延长DC 交AB 于F ,交BO 于E ,α=︒,60∴∠=︒,60BOD线段AB绕点O顺时针旋转得线段CD,=,AB CD=,BO DO∴=,OA OCAOB COD SSS,()B D∴∠=∠,∠=∠,OED BEF,B DBFE EOD,60故答案为:60︒;(2)直线AB与直线CD所夹锐角角与旋转角α互补,理由如下:如图2,延长AB,DC交于点E,线段AB绕点O顺时针旋转得线段CD,=,=,BO DO∴=,OA OCAB CDAOB COD SSS,()ABO D,ABO EBO,180D EBO,180360EBO E D BOD,E BOD,180∴直线AB与直线CD所夹锐角角与旋转角α互补.形成结论由(1)(2)(3)可知:旋转图形中,当旋转角小于平角时,对应线段所在直线的所夹锐角角与旋转角:相等或互补.故答案为:相等或互补.运用拓广(3)如图3,将BCD ∆绕点B 顺时针旋转60︒,得到BAF ∆,连接FD ,延长FA ,DC 交于点E ,∴旋转角60ABC ∠=︒,BCD BAF ,60AED ABC ∴∠=∠=︒,3AF CD ==,BD BF =,30ADC ∠=︒,90FAD AED ADC ,又60FBD ABC ,BF BD =, BFD ∴∆是等边三角形,BF BD DF ,∴在Rt DAF 中,2219910ADDF AF . 【点睛】本题是几何变换综合题,考查了旋转的性质,全等三角形的判定和性质,等边三角形的判定和性质等知识,添加辅助线构造全等三角形是本题的关键.2.发现规律:(1)如图①,ABC 与ADE 都是等边三角形,直线,BD CE 交于点F .直线BD ,AC 交于点H .求BFC ∠的度数(2)已知:ABC 与ADE 的位置如图②所示,直线,BD CE 交于点F .直线BD ,AC 交于点H .若ABC ADE α∠=∠=,ACB AED β∠=∠=,求BFC ∠的度数 应用结论:(3)如图③,在平面直角坐标系中,点O 的坐标为(0,0),点M 的坐标为(3,0),N 为y 轴上一动点,连接MN .将线段MN 绕点M 逆时针旋转60得到线段MK ,连接NK ,OK ,求线段OK 长度的最小值答案:A解析:(1)BFC ∠的度数为60︒;(2)BFC ∠的度数为180αβ︒--;(3)线段OK 长度的最小值为32 【分析】(1)通过证明BAD CAE ≅△△可得ABD ACE ∠=∠,再由三角形内角和定理进行求解即可;(2)通过证明ABC ADE 可得BAC DAE ∠=∠,AB AC AD AE=,可证ABD ACE ,可得ABD ACE ∠=∠,由外角性质可得BFC BAC ∠=∠,再有三角形内角和定理进行求解即可;(3)由旋转的性质可得MNK △是等边三角形,可得MK MN NK ==,60NMK NKM KNM ∠=∠=∠=︒,如图③将MOK 绕点M 顺时针旋转60︒,得到MQN △,连接OQ ,可得60OMQ ∠=︒,OK =NQ ,MO =MQ ,则当NQ 为最小值时,OK 有最小值,由垂线段最短可得当QN y ⊥轴时,NQ 有最小值,由直角三角形的性质即可求解.【详解】 (1)∵ABC 与ADE 是等边三角形∴AB=AC ,AD=AE ,60BAC DAE ABC ACB ∠=∠=∠=∠=︒∴BAD CAE ∠=∠∴()BAD CAE SAS ≅ ∴ABD ACE ∠=∠∵60ABD DBC ABC ∠+∠=∠=︒∴60ACE DBC ∠+∠=︒∴18060BFC DBC ACE ACB ∠=︒-∠-∠-∠=︒;(2)∵ABC ADE α∠=∠=,ACB AED β∠=∠=∴ABC ADE∴BAC DAE ∠=∠,AB AC AD AE= ∴BAD CAE ∠=∠,AB AD AC AE = ∴ABD ACE ∴ABD ACE ∠=∠ ∵BHC ABD BAC BFC ACE ∠=∠+∠=∠+∠ ∴BFC BAC ∠=∠ ∵180BAC ABC ACB ∠+∠+∠=︒ ∴180BFC αβ∠++=︒∴180BFC αβ∠=︒--;(3)∵将线段MN 绕点M 逆时针旋转60︒得到线段MK∴MN MK =,60NMK ∠=︒∴MNK △是等边三角形∴MK MN NK ==,60NMK NKM KNM ∠=∠=∠=︒如下图,将MOK 绕点M 顺时针旋转60︒,得到MQN △,连接OQ∴MOK MQN ≅,60OMQ ∠=︒∴OK =NQ ,MO =MQ∴MOQ △是等边三角形∴60QOM ∠=︒∴30NOQ ∠=︒∵OK =NQ∴当NQ 为最小值时,OK 有最小值,由垂线段最短可得当QN y ⊥轴时,NQ 有最小值 ∵点M 的坐标为(3,0)∴3OM OQ ==∵QN y ⊥轴,30NOQ ∠=︒∴1322NQ OQ == ∴线段OK 长度的最小值为32. 【点睛】本题属于几何变换综合题,考查了等边三角形的判定和性质,全等三角形的判定和性质,相似三角形的判定和性质,旋转的性质,三角形内角和定理等知识,灵活运用这些性质进行推理是解决本题的关键.3.如图1,在等腰Rt △ABC 中,∠ABC =90°,AB =BC =6,过点B 作BD ⊥AC 交AC 于点D ,点E 、F 分别是线段AB 、BC 上两点,且BE =BF ,连接AF 交BD 于点Q ,过点E 作EH ⊥AF 交AF 于点P ,交AC 于点H .(1)若BF =4,求△ADQ 的面积;(2)求证:CH =2BQ ;(3)如图2,BE =3,连接EF ,将△EBF 绕点B 在平面内任意旋转,取EF 的中点M ,连接AM ,CM ,将线段AM 绕点A 逆时针旋转90°得线段AN ,连接MN 、CN ,过点N 作NR ⊥AC 交AC 于点R .当线段NR 的长最小时,直接写出△CMN 的周长.答案:A解析:(1)1.8;(2)证明见解析;(3)3263351022+. 【分析】(1)利用等腰直角三角形的性质求出1322BD AD CD AC ====积相等和勾股定理分别求出AQ 和QD ,最后利用三角形面积公式即可求解;(2)如图,先作辅助线构造()AEH CFG ASA ∆∆≌,得到AH CG =,再通过转化得到2AH DQ =,最后利用AC ,得到一个相等关系,即()2AH HC BQ QD +=+,利用等式性质即可得到所求;(3)如图,通过做辅助线构造全等三角形确定出当HN ⊥AC ,且N 点位于H 、R 之间时,此时NR 的长最小,接着利用勾股定理和等腰直角三角形的性质,分别求出CM 、MN 、CN 的长,相加即可.【详解】解:6AB BC ==,°90ABC =∠,AC ==∴又∵AC BD ⊥∴BD 平分AC ,且BD 是∠ABC 的角平分线∴12BD AD CD AC ====Q 点到BA 和BC 边的距离相等; ∵4BF =, ∴6342ABQBFQ S S ∆∆==, ∴32AQ FQ =,∵AF ===∴35AQ AF ==∴5QD ===,∴1 1.825ADQ S ∆=⨯⨯=, ∴△ADQ 的面积为1.8.(2)如图,作CG ⊥AC ,垂足为C ,交AF 的延长线于点G ,∴°90ACG =∠∵°45ACB CAB ==∠∠,∴°45GCB CAB ==∠∠,∵EH ⊥AF ,∴°90EAP AEP +=∠∠,又∵°90EAP AFB +=∠∠∴AEP AFB =∠∠,∴AEP CFG =∠∠∵BE BF =,BA BC =∴AE CF =,在AEH ∆和CFG ∆中,AEH CFG AE CFEAH FCG ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()AEH CFG ASA ∆∆≌∴AH CG =;∵BD ⊥AC ,CG ⊥AC ,∴BD ∥CG ,∵D 点是AC 的中点,且BD ∥CG ,∴DQ 是ACG ∆的中位线, ∴12DQ CG =, ∴2DQ CG AH ==; ∵AC =2BD ,∴()2AH HC BQ QD +=+,∵2AH DQ =,∴CH =2BQ .(3)如图①,作AH ⊥AB ,且AH =AB ,∴∠NAH +∠HAM =∠HAM +∠BAM =90°,∴∠BAM =∠NAH ,∵AB =AH ,AM =AN ,∴()ABM AHN SAS ∆∆≌, ∴HN =BM ,∵BE =BF =3,∠EBF =90°, ∴232EF BE ==∴由M 点是EF 的中点,可得1322BM EF == ∴322NH =, ∴N 点在以H 点为圆心,322为半径的圆上,如图②,当HN ⊥AC ,且N 点位于H 、R 之间时,此时NR 的长最小,为NR HR HN HR =-=-∵∠BAC =45°,∴∠HAC =45°,∴∠AHN =45°,HR =AR ,∵222HR AR AH +=,∴HR AR ===,∴22NR HR =-=, ∵AC == ∴CR AC AR =-=∴CN AN === ∵∠MAN =90°,AM =AN ,∴MN ==∴∠ABM =45°,∴∠EBM =45°,∴F 点在BA 上,E 点在CB 延长线上,如图,作MP ⊥EC ,垂足为P ,∴1322BP MP EB ===, ∴315622PC PB BC =+=+=,∴2MC ==∴MC MN CN ++=∴△CMN+.【点睛】本题综合考查了等腰直角三角形的性质、全等三角形的判定与性质、旋转的性质、勾股定理、圆等知识,要求学生熟练掌握相关概念并能灵活应用它们,本题的综合性较强,难点在于作辅助线构造全等三角形以及线段之间的关系转化等,考查了学生综合分析和推理论证以及计算的能力,本题属于压轴题,蕴含了数形结合和转化的思想方法等. 4.如图,已知ABC 和ADE 均为等腰三角形,AC =BC ,DE =AE ,将这两个三角形放置在一起.(1)问题发现:如图①,当60ACB AED ∠∠︒==时,点B 、D 、E 在同一直线上,连接CE ,则CEB ∠= °,线段BD 、CE 之间的数量关系是 ;(2)拓展探究:如图②,当90ACB AED ∠∠︒==时,点B 、D 、E 在同一直线上,连接CE ,请判断CEB ∠的度数及线段BD 、CE 之间的数量关系,并说明理由;(3)解决问题:如图③,90ACB AED ∠∠︒==,25AC =,AE =2,连接CE 、BD ,在AED 绕点A 旋转的过程中,当DE BD ⊥时,请直接写出EC 的长.答案:C解析:(1)60BD CE ,=;(2)452CEB BD CE ∠︒=,=,理由见解析;(3)CE 的长为2或2【分析】(1)证明ACE ABD ≌,得出CE =BD ,AEC ADB ∠=∠,即可得出结论; (2)证明ACE ABD ∽,得出AEC ADB ∠=∠,BD =,即可得出结论; (3)先判断出BD =,再求出AB =:①当点E 在点D 上方时,先判断出四边形APDE 是矩形,求出AP =DP =AE =2,再根据勾股定理求出,BP =6,得出BD =4;②当点E 在点D 下方时,同①的方法得,AP =DP =AE =1,BP =6,进而得出BD =BP +DP =8,即可得出结论.【详解】解:(1)ABC 为等腰三角形,60AC BC ACB ∠︒=,=,∴ABC 是等边三角形,同理可得ADE 是等边三角形6018012060BAD DAC DAC CAE BAD CAE AD AE AB ACEAC DAB ACE ABD SAS BD CEAEC ADB ADE AEC AED CEBCEB ∠+∠=∠+∠=︒∴∠=∠=⎧⎪=⎨⎪∠∠⎩∴∴=∠=∠=︒-∠=︒∠=∠+∠∴∠=︒=≌()故答案为:60CEB BD CE ∠=︒=;.(2)45CEB BD ∠︒=,,理由如下:在等腰三角形ABC 中,AC =BC ,90ACB ∠︒=,45AB CAB ∴∠︒,= ,同理,45AD ADE DAE ∠∠︒,==, ∴AE AC AD AB =,DAE CAB ∠∠=, EAC DAB ∴∠∠=,ACE ABD ∴∽ ,∴BD AD CE AE==∴AEC ADB BD ∠∠=,,点B 、D 、E 在同一条直线上:180135ADB ADE ∴∠︒-∠︒==135AEC ∴∠︒=45CEB AEC AED ∴∠∠-∠︒==;(3)由(2)知,ACE ABD ∽, 2BD CE ∴=, 在Rt ABC 中,25AC =,2210AB AC ∴== ,①当点E 在点D 上方时,如图③,过点A 作AP BD ⊥交BD 的延长线于P ,DE BD ⊥,PDE AED APD ∴∠∠∠==,∴四边形APDE 是矩形,AE DE = ,∴矩形APDE 是正方形,2AP DP AE ∴===,在Rt APB △中,根据勾股定理得,226BP AB AP -==,4BD BP AP ∴-==,1222CE BD ∴==; ②当点E 在点D 下方时,如图④同①的方法得,AP =DP =AE =2,BP =6,∴BD =BP +DP =8,122CE BD ∴==4, 综上CE 的长为22或42.【点睛】本题是几何变换的综合题,主要考查了旋转的性质,全等三角形的判定和定理,相似三角形的判定和性质,勾股定理,等边三角形的性质,判断出三角形ACE 和三角形ABD 相似是关键.5.如图,ABD △和ACE △都是等边三角形.(1)连接CD 、BE 交于点P ,求∠BPD ;(2)连接PA ,判断线段PA 、PB 、PD 之间的数量关系并证明;(3)如图,等腰ABC 中AB =AC ,∠BAC =α(0<α<90),在ABC 内有一点M ,连接MA 、MB 、MC .当MA +MB +MC 最小时,∠ABM = (用含α的式子表示)答案:D解析:(1)60BPD ∠=︒(2)PD PB PA =+,证明见详解(3)1602α︒-【分析】(1)证明()DAC BAE SAS ≅,得ADC ABE ∠=∠,就可以证明60BPD DAB ∠=∠=︒;(2)在DP 上截取PF=PB ,连接BF ,证明()DBF ABP SAS ≅,得DF PA =,即可证明PD PB PA =+;(3)分别以AB 和AC 为边,向两边作等边三角形ABD 和等边三角形ACE ,连接BE 和CD ,交于点M ,连接AM ,此时MA MB MC ++最小,然后利用等腰三角形ADC ,求出ADC ∠的度数,即可得到ABM ∠的度数.【详解】解:(1)∵ABD △和ACE △是等边三角形,∴AD AB =,AC AE =,60DAB CAE ∠=∠=︒,∵DAB BAC CAE BAC ∠+∠=∠+∠,∴DAC BAE ∠=∠,在DAC △和BAE △中,AD AB DAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩,∴()DAC BAE SAS ≅,∴ADC ABE ∠=∠,∵ADC DAB ABE BPD ∠+∠=∠+∠,∴60BPD DAB ∠=∠=︒;(2)如图,在DP 上截取PF=PB ,连接BF ,∵60BPD ∠=︒,PF PB =,∴PFB △是等边三角形,∴BF BP =,60FBP ∠=︒,∴DBA FBP ∠=∠,∵DBA FBA FBP FBA ∠-∠=∠-∠,∴DBF ABP ∠=∠,在DBF 和ABP △中,DB AB DBF ABP BF BP =⎧⎪∠=∠⎨⎪=⎩,∴()DBF ABP SAS ≅,∴DF PA =,∵PD PF FD =+,∴PD PB PA =+;(3)如图,分别以AB 和AC 为边,作等边三角形ABD 和等边三角形ACE ,连接BE 和CD ,交于点M ,连接AM ,此时MA MB MC ++最小,由(2)中的结论可得MD MA MB =+,则当D 、M 、C 三点共线时MA MB MC ++最小,即CD 的长,由(1)得ADC ABM ∠=∠,∵AD AB AC ==,60DAC α∠=︒+,∴()1806016022ADC αα︒-︒+∠==︒-, ∴1602ABM α∠=︒-,故答案是:1602α︒-.【点睛】本题考查全等三角形的性质和判定,等边三角形的性质,解题的关键是做辅助线构造全等三角形来进行证明求解.6.探究:(1)如图①,在△ABC中,∠ACB=90°,CD⊥AB于点D,若∠B=28°,则∠ACD的度数是.拓展:(2)如图②,∠MCN=90°,射线CP在∠MCN的内部,点A、B分别存CM、CN 上,分别过点A、B作AD⊥CP、BE⊥CP于点D、E,若AC=CB,则AD、DE、BE三者间的数量关系为.请说明理由;应用:(3)如图③,点A、B分别在∠MCN的边CM、CN上,射线CP在∠MCN的内部,点D、E在射线CP上,连结AD、BE、AE,且使∠MCN=∠ADP=∠BEP.当AC=BC 时,△≌△;此时如果CD=2DE,且S△CBE=6,则△ACE的面积是.答案:D解析:(1)28°(2)DE=AD﹣BE;理由见解析(3)ACD;CBE;9【分析】(1)利用直角三角形的两锐角互余,即可得出结论;(2)利用同角的余角相等判断出∠CAD=∠BCE,进而判断出△ACD≌△CBE,即可得出结论;(3)利用等式的性质判断出∠ADC=∠CEB,进而判断出△ACD≌△CBE,得出S△ACD=S△CBE,再求出S△ADE=3,即可得出结论.【详解】解:探究:∵CD⊥AB,∴∠CDB=90°,∵∠B=28°,∴∠BCD=90°﹣∠B=68°,∵∠ACB=90°,∴∠ACD=90°﹣∠BCD=28°,故答案为:28°;拓展:(2)∵∠MCN=90°,∴∠ACD+∠BCE=90°,∵AD⊥CP,BE⊥CP,∴∠ADC =∠BEC =90°,∴∠ACD+∠CAD =90°,∴∠CAD =∠BCE ,在△ACD 和△CBE 中,ADC CEB CAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△CBE (AAS ),∴CD =BE ,AD =CE ,∴DE =CE ﹣CD =AD ﹣BE ,故答案为:DE =AD ﹣BE ;应用:(3)∵∠MCN =∠ACD+∠BCD ,∠MCN =∠ADP ,∴∠ADP =∠ACD+∠BCD ,∵∠ADP =∠ACD+∠CAD ,∴∠CAD =∠BCE ,∵∠ADP =∠BEP ,∴∠ADC =∠CEB ,在△ACD 和△CBE 中,ADC CEB CAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△CBE (AAS ),∴S △ACD =S △CBE ,∵S △CBE =6,∴S △ACD =6,∵CD =2DE ,∴S △ACD =2S △ADE ,∴S △ADE =12S △ACD =3, ∴S △ACE =S △ACD +S △ADE =9,故答案为:ACD ,CBE ,9.【点睛】此题是三角形综合题,主要考查了直角三角形的性质,同角的余角相等,等式的性质,全等三角形的判定和性质,判断出△ACD ≌△CBE 是解本题的关键.7.问题解决一节数学课上,老师提出了这样一个问题:如图①,点P 是等边ABC 内的一点,6PA =,8PB = ,10PC =.你能求出APB ∠的度数和等边ABC 的面积吗? 小明通过观察、分析、思考,形成了如下思路:如图①将BPC △绕点B 逆时针旋转60°,得到BPA △,连接PP ',可得BPP '是等边三角形,根据勾股定理逆定理可得AP P '是直角三角形,从而使问题得到解决.(1)结合小明的思路完成填空:PP '=_____________,APP '∠=_______________,APB ∠=_____________ ,ABC S = ______________.(2)类比探究 Ⅰ如图②,若点P 是正方形ABCD 内一点,1PA = ,2PB =,3PC =,求APB ∠的度数和正方形的面积.Ⅱ如图③,若点P 是正方形ABCD 外一点,3PA = ,1PB =, 11PC =,求APB ∠的度数和正方形的面积.答案:B解析:(1)8,90˚,150˚,25336;(2)Ⅰ135APB ∠=︒,722ABCD S =+正方形;Ⅱ45APB ∠=︒, 1032ABCD S =-正方形【分析】(1)根据小明的思路,然后利用等腰三角形和直角三角形性质计算即可;(2)Ⅰ将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,求出∠APB 的度数;先利用旋转求出∠PBP'=90°,BP'=BP=2,AP'=CP=3,利用勾股定理求出PP',进而判断出△APP'是直角三角形,得出∠APP'=90°,即可得出结论;过B 作BE ⊥AP 于点E ,然后利用勾股定理求出AB 的长度即可求出正方形面积;Ⅱ将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,求出∠APB 的度数;先利用旋转求出∠PBP'=90°,BP'=BP=2,AP'=CP=3,利用勾股定理求出PP',进而判断出△APP'是直角三角形,得出∠APP'=90°,即可得出结论;过B 作BF ⊥AP 于点F ,然后利用勾股定理求出AB 的长度即可求出正方形面积;【详解】解:(1)由题易有P BP '∆是等边三角形,AP P '∆是直角三角形∴PP '=BP=8,90?APP '=∠,60?P PB '=∠,∴APB ∠=APP '∠+=P PB '∠150˚,如图1,过B 作BD ⊥AP 于点D∵APB ∠=150°∴30?BPD =∠在Rt △BPD 中,30?BPD =∠,BP=8∴BD=4,PD=43 ∴AD=6+43∴AB 2=AD 2+BD 2=100+483∴ABC S =234AB =25336+ (2)Ⅰ.如图2,将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,∴△ABP'≌△CBP ,∴∠PBP'=90°,BP'=BP=2,AP'=CP=3,在Rt △PBP'中,BP=BP'=2,∴∠BPP'=45°,根据勾股定理得,PP'=2BP=22,∵AP=1,∴AP 2+PP'2=1+8=9,∵AP'2=32=9,∴AP 2+PP'2=AP'2,∴△APP'是直角三角形,且∠APP'=90°,∴∠APB=∠APP'+∠BPP'=90°+45°=135°;过B 作BE ⊥AP 于点E ,∵∠APB=135°∴∠BPE=45°∴△BPE 是等腰直角三角形∴BE=BP=22BP =2 ∴AE=1+2∴AB 2=AE 2+BE 2=7+22 ∴2722ABCD S AB ==+正方形Ⅱ.如图3,将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,∴△ABP'≌△CBP ,∴∠PBP'=90°,BP'=BP=1,AP'=CP=11,在Rt △PBP'中,BP=BP'=1,∴∠BPP'=45°,根据勾股定理得,PP'=2BP=2,∵AP=3,∴AP 2+PP'2=9+2=11,∵AP'2=(11)2=11,∴AP 2+PP'2=AP'2,∴△APP'是直角三角形,且∠APP'=90°,∴∠APB=∠APP'-∠BPP'=90°-45°=45°.过B 作BF ⊥AP 于点F∵∠APB=45°∴△BPF 为等腰直角三角形∴PF=BF=22BP =22 ∴2 ∴AB 2=AF 2+BF 2=1032-∴21032ABCD S AB ==-正方形【点睛】此题是四边形综合题,主要考查了正方形的性质,旋转的性质,直角三角形的性质和判定,勾股定理,正确作出辅助线是解本题的关键.8.在等腰Rt ABC △中,AB AC =、90BAC ∠=︒.(1)如图1,D ,E 是等腰Rt ABC △斜边BC 上两动点,且45DAE ∠=︒,将ABE △绕点A 逆时针旋转90后,得到AFC △,连接DF .①求证:AED AFD ≌.②当3BE =,9CE =时,求DE 的长.(2)如图2,点D 是等腰Rt ABC △斜边BC 所在直线上的一动点,连接AD ,以点A 为直角顶点作等腰Rt ADE △(E 点在直线BC 的上方),当3BD =,9BC =时,求DE 的长.答案:D解析:(1)①证明见解析;②5;(2)35或317【分析】(1)①证明∠DAE=∠DAF=45°即可利用SAS 证明全等;②由①中全等可得DE=DF ,再在Rt △FDC 中利用勾股定理计算即可;(2)连接BE ,根据共顶点等腰直角三角形证明全等,再利用勾股定理计算即可。
模型构建专题:全等三角形中的常见八种模型(8类热点题型讲练)(解析版)--初中数学北师大版7年级下册

第05讲模型构建专题:全等三角形中的常见八种模型(8类热点题型讲练)目录【模型一平移型模型】 (1)【模型二轴对称型模型】 (3)【模型三四边形中构造全等三角形解题】 (5)【模型四一线三等角模型】 (9)【模型五三垂直模型】 (13)【模型六旋转型模型】 (18)【模型七倍长中线模型】 (24)【模型八截长补短模型】 (30)【模型一平移型模型】例题:(2023上·福建福州·八年级统考期末)如图,点B,E,C,F在同一直线上,A D∠=∠,AB DE∥,=.BE CF求证:AB DE=.【答案】证明见解析【分析】本题考查了三角形全等的性质与判定的应用以及两直线平行的判定定理,解此题的关键是推出△△,注意全等三角形的对应边相等;根据AB DE≌ABC DEF∠=∠,又根据∠A=∠D,BE=CF∥可知B DEF可以判定ABC DEF ≌△△,即可求证AB DE =.【详解】解:∵AB DE ∥,∴B DEF ∠=∠,∵BE CF =,∴BC EF =,∴在ABC 和DEF 中,A DB DEF BCEF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ABC DEF ≌△△,∴AB DE =.【变式训练】1.(2023秋·浙江·八年级专题练习)如图,在ACD 和CEB 中,点A 、B 、C 在一条直线上,D E AD EC AD EC ∠=∠=,∥,.求证:ACD CBE ≌.【答案】见解析【分析】根据平行线的性质得出A ECB ∠=∠,再根据全等三角形的判定定理ASA 证明ACD CBE ≌.【详解】AD EC ∥ ,A ECB ∴∠=∠,在ACD 和CEB 中,A ECB AD ECDE ∠=∠⎧⎪=⎨⎪∠=∠⎩,(ASA)ACD CBE ∴△≌△.【点睛】本题考查了全等三角形的判定定理和平行线的性质,能熟记全等三角形的判定定理是解此题的关键.2.(2024上·新疆和田·八年级统考期末)如图,点A 、D 、C 、F 在同一条直线上,AD CF =,AB DE =,BC EF =.(1)求证:ABC DEF ≌△△;(2)若65A ∠=︒,82B ∠=︒,求F ∠的度数.【答案】(1)见解析(2)33︒【分析】本题考查了全等三角形的性质与判定,三角形内角和定理的应用,掌握全等三角形的性质与判定是解题的关键.(1)先证明AC DF =,然后根据SSS 证明ABC DEF ≌△△即可;(2)根据全等三角形的性质得出F ACB ∠=∠,进而根据三角形内角和定理即可求解.【详解】(1)证明:AC AD DC =+∵,DF DC CF =+,且AD CF =,AC DF =∴,在ABC 和DEF 中,AB DE BC EF AC DF =⎧⎪=⎨⎪=⎩,(SSS)ABC DEF ∴△≌△,(2)解:由(1)可知,ABC DEF ≌△△,F ACB ∠=∠∴,65A ∠=︒ ,82B ∠=︒,180()180(6582)33ACB A B ∴∠=︒-∠+∠=︒-︒+︒=︒,33F ACB ∴∠=∠=︒.【模型二轴对称型模型】例题:(2024上·云南昆明·八年级统考期末)线段AC 、BD 相交于点E ,D A ∠=∠,DE AE =,求证:C B ∠=∠.【答案】证明见解析.【分析】本题考查了全等三角形的判定和性质,根据ASA 可证ABE ≌DCE △,根据全等三角形的性质即可得证.【详解】证明: 在DEC 和AEB △中D A DE AE DEA AEB ∠=∠⎧⎪=⎨⎪∠=∠⎩()ASA DEC AEB ∴△≌△,ABE ∴ ≌()ASA DCE ,C B∴∠=∠【变式训练】1.(2023·湖南益阳·统考一模)如图,点D 在AB 上,点E 在AC 上,AB AC =,BD CE =.求证:ACD ABE ≌.【答案】见解析【分析】根据AB AC =,BD CE =推出AD AE =,即可根据SAS 进行求证.【详解】证明:,,,AB AC BD CE AD AB BD AE AC CE ===-=- ,AD AE ∴=.在ABE 和ACD 中,AD AE A A AC AB =⎧⎪∠=∠⎨⎪=⎩,()SAS ACD ABE ∴ ≌.【点睛】本题主要考查了三角形全等的判定,解题的关键是熟练掌握证明三角形全等的方法有SSS,SAS,AAS,ASA,HL .2.(2024上·山西阳泉·八年级统考期末)如图1是小宁制作的燕子风筝,燕子风筝的骨架图如图2所示,AB AE =,AC AD =,BAD EAC ∠=∠,40C ∠=︒,求D ∠的度数.【答案】40︒【分析】本题考查了全等三角形的判定与性质,先证明BAC EAD ∠=∠,再证明BAC EAD ≌,即可得到40D C ∠=∠=︒.【详解】解:∵BAD EAC ∠=∠,BAD DAC EAC DAC ∴∠+∠=∠+∠,即BAC EAD ∠=∠.在BAC 与EAD 中,,,,AB AE BAC EAD AC AD =⎧⎪∠=∠⎨⎪=⎩()SAS BAC EAD ∴V V ≌.C D ∴∠=∠.∵40C ∠=︒,40C D =∠=︒∴∠.【模型三四边形中构造全等三角形解题】例题:如图,在四边形ABCD 中,CB AB ⊥于点B ,CD AD ⊥于点D ,点E ,F 分别在AB ,AD 上,AE AF =,CE CF =.(1)若8AE =,6CD =,求四边形AECF 的面积;(2)猜想∠DAB ,∠ECF ,∠DFC 三者之间的数量关系,并证明你的猜想.AE ⎧⎪∴∠DFC+∠BEC=∠FCA+∠FAC+∠ECA+∠EAC=∠DAB+∠ECF.∴∠DAB+∠ECF=2∠DFC【点睛】本题考查了三角形全等的性质与判定,三角形的外角的性质,掌握三角形全等的性质与判定是解题的关键.【变式训练】1.在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.(1)试说明:DE=DF:(2)在图中,若G在AB上且∠EDG=60°,试猜想CE,EG,BG之间的数量关系并证明所归纳结论.(3)若题中条件“∠CAB=60°,∠CDB=120°改为∠CAB=α,∠CDB=180°﹣α,G在AB上,∠EDG满足什么条件时,(2)中结论仍然成立?猜想CE 、EG 、BG 之间的数量关系为:证明:在ABD ∆和ACD ∆中,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩,ΔΔ()ABD ACD SSS ∴≅,【模型四一线三等角模型】【答案】探究:见解析;应用:61.已知CD 是经过BCA ∠顶点C 的一条直线,CA CB =.E 、F 分别是直线CD 上两点,且BEC CFA α∠=∠=∠.(1)若直线CD 经过BCA ∠的内部,且E 、F 在射线CD 上,请解决下面问题:①如图1,若90BCA ∠=︒,90α∠=︒,求证:BE CF =;②如图2,若180BCA α∠+∠=︒,探索三条线段EF BE AF ,,的数量关系,并证明你的结论;(2)如图3,若直线CD 经过BCA ∠的外部,BCA α∠=∠,题(1)②中的结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确的结论再给予证明.【答案】(1)①见解析;②EF BE AF =-,见解析(2)不成立,EF BE AF =+,见解析【分析】(1)①利用垂直及互余的关系得到ACF CBE ∠=∠,证明BCE ≌CAF V 即可;②利用三等角模型及互补证明ACF CBE ∠=∠,得到BCE ≌CAF V 即可;(2)利用互补的性质得到EBC ACF ∠=∠,证明BCE ≌CAF V 即可.【详解】(1)①证明:∵90EE CD AF CD ACB ⊥⊥∠=︒,,,∴90BEC AFC ∠=∠=︒,∴9090BCE ACF CBE BCE ∠+∠=︒∠+∠=︒,,∴ACF CBE ∠=∠,在BCE 和CAF V 中,EBC FCA BEC CFA BC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴BCE ≌CAF V ()AAS ,∴BE CF =;②解:EF BE AF =-.证明:∵180BEC CFA ACB αα∠=∠=∠∠+∠=︒,,∴180180CBE BCE ACF ACB BCE BCE αα∠=︒-∠-∠∠=∠-∠=︒-∠-∠,,∴ACF CBE ∠=∠,在BCE 和CAF V 中,EBC FCA BEC CFA BC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴BCE ≌CAF V ()AAS ,∴BE CF CE AF ==,,∴EF CF CE BE AF =-=-;(2)解:EF BE AF =+.理由:∵BEC CFA BCA αα∠=∠=∠∠=∠,,又∵180180EBC BCE BEC BCE ACF ACB ∠=∠=∠=︒∠+∠+∠=︒,,∴EBC BCE BCE ACF ∠+∠=∠+∠,∴EBC ACF ∠=∠,在BCE 和CAF V 中,EBC FCA BEC CFA BC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴BCE ≌CAF V ()AAS ,∴AF CE BE CF ==,,∵EF CE CF =+,∴EF BE AF =+.【点睛】本题主要考查三角形全等的判定及性质,能够熟练运用三等角模型快速证明三角形全等是解题关键.2.(2024上·湖南株洲·八年级校联考期末)(1)如图①,已知∶ABC 中,90,BAC AB AC ∠=︒=,直线m 经过点,A BD m ⊥于,D CE m ⊥于E ,求证∶ABD CAE △△≌;(2)拓展∶如图②,将(1)中的条件改为∶ABC 中,,AB AC D A E =、、三点都在直线m 上,并且BDA AEC BAC α∠=∠=∠=,α为任意锐角或钝角,请问结论DE BD CE =+是否成立?如成立,请证明;若不成立,请说明理由;(3)应用∶如图③,在ABC 中,BAC ∠是钝角,,AB AC BAD CAE =∠>∠,BDA AEC BAC ∠=∠=∠,直线m 与BC 的延长线交于点F ,若2,BC CF ABC = 的面积是12,求ABD △与CEF △的面积之和.【答案】(1)见解析;(2)成立,理由见解析;(3)6【分析】(1)先证明90BDA AEC BAC ∠=∠=∠=︒,DBA CAE ∠=∠,然后根据AAS 即可证明ABD CAE ≌ ;(2)先证明DBA CAE ∠=∠,再证明()AAS ABD CAE ≌,再利用全等三角形的性质可得结论;(3)同(2)可证()AAS ABD CAE ≌,得出ABD CEA S S = ,再由不同底等高的两个三角形的面积之比等于底的比,得出ACF S △即可得出结果.【详解】解:(1)∵90BDA AEC BAC ∠=∠=∠=︒,∴90BAD CAE ∠+∠=︒,且90DBA BAD ∠+∠=︒,∴DBA CAE ∠=∠,在ABD △和CAE V 中,【模型五三垂直模型】例题:(2023上·辽宁大连·八年级统考期中)通过对下面数学模型的研究学习,解决下列问题:(1)如图1,点A 在直线l 上,90,BAD AB AD ∠=︒=,过点B 作BC l ⊥于点C ,过点D 作DE l ⊥交于点E .得1D ∠=∠.又90BCA AED ∠=∠=︒,可以推理得到()ABC DAE AAS ≌.进而得到结论:AC =_____,BC =_____.我们把这个数学模型称为“K 字”模型或“一线三直角”模型;(2)如图2,∠90,,,BAD MAN AB AD AM AN BM l ∠=∠=︒==⊥于点C ,DE l ⊥于点E ,ND 与直线l 交于点P ,求证:NP DP =.【答案】(1)DE ,AE(2)见解析【分析】本题考查一线三直角全等问题,(1)由90CBA AED BAD ∠∠∠===︒,得12290D ∠∠∠∠+=+=︒,则1D ∠∠=,而AB DA =,即可证明ABC DAE ≌,得AC DE =,BC AE =,于是得到问题的答案;(2)作NF l ⊥于点F ,因为BM l ⊥于点C ,DE l ⊥于点E ,所以90ACM NFA NFP DEP ∠∠∠∠====︒,由(1)得AC DE =,因为90MAN ∠=︒,所以90CAM FAN FNA FAN ∠∠∠∠+=+=︒,则CAM FNA ∠∠=,而AM NA =,即可证明CAM FNA ≌,得AC NF =,所以NF DE =,再证明PFN PED ≌,则NP DP =.【详解】(1))解:BC l ⊥于点C ,DE l ⊥于点E ,∴90CBA AED ∠∠==︒,∵90BAD ∠=︒,∴12890D ∠∠∠∠+=+=︒,∴1D ∠∠=,在ABC 和DAE 中,1D BCA AED AB DA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴AAS ABC DAE ≌(),∴AC DE =,BC AE =,故答案为:DE ,AE .(2)证明:如图2,作NF l ⊥于点F ,∵BM l ⊥于点C ,DE l ⊥于点E ,∴90ACM NFA NFP DEP ∠∠∠∠====︒,由1AC DE=()得,同理(1)得AC NF =,∴NF DE =,在PFN 和PED 中,MFP DEF FPN EPD MF DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴AAS PFN PED ≌(),∴NP DP =.【变式训练】1.在△ABC 中,∠BAC =90°,AC=AB ,直线MN 经过点A ,且CD ⊥MN 于D ,BE ⊥MN 于E .(1)当直线MN 绕点A 旋转到图1的位置时,EAB DAC ∠+∠=度;(2)求证:DE=CD +BE ;(3)当直线MN 绕点A 旋转到图2的位置时,试问DE 、CD 、BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.【答案】(1)90°(2)见解析(3)CD=BE +DE ,证明见解析【解析】【分析】(1)由∠BAC =90°可直接得到EAB DAC ∠+∠=90°;(2)由CD ⊥MN ,BE ⊥MN ,得∠ADC =∠BEA =∠BAC =90°,根据等角的余角相等得到∠DCA =∠EAB ,根据AAS 可证△DCA ≌△EAB ,所以AD =CE ,DC =BE ,即可得到DE =EA +AD =DC +BE .(3)同(2)易证△DCA ≌△EAB ,得到AD =CE ,DC =BE ,由图可知AE =AD +DE ,所以CD =BE +DE .(1)∵∠BAC =90°∴∠EAB +∠DAC =180°-∠BAC =180°-90°=90°故答案为:90°.(2)证明:∵CD ⊥MN 于D ,BE ⊥MN 于E∴∠ADC =∠BEA =∠BAC =90°∵∠DAC +∠DCA =90°且∠DAC +∠EAB =90°∴∠DCA =∠EAB∵在△DCA 和△EAB 中90ADC BEA DCA EAB AC AB ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△DCA ≌△EAB (AAS )∴AD =BE 且EA =DC由图可知:DE =EA +AD =DC +BE .(3)∵CD ⊥MN 于D ,BE ⊥MN 于E∴∠ADC =∠BEA =∠BAC =90°∵∠DAC +∠DCA =90°且∠DAC +∠EAB =90°∴∠DCA =∠EAB∵在△DCA 和△EAB 中90ADC BEA DCA EAB AC AB ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△DCA ≌△EAB (AAS )∴AD =BE 且AE =CD由图可知:AE =AD +DE∴CD =BE +DE .【点睛】本题考查了旋转的性质:旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角,也考查了三角形全等的判定与性质.2.(2024上·吉林辽源·九年级统考期末)如图,在ABC 中,90ACB ∠=︒,AC BC =,直线MN 经过点C ,且AD MN ⊥于D ,BE MN ⊥于E .(1)当直线MN 绕点C 旋转到①的位置时,求证:①ADC CEB △△≌;②DE AD BE =+;(2)当直线MN 绕点C 旋转到②的位置时,求证:DE AD BE =-;(3)当直线MN 绕点C 旋转到③的位置时,试问DE 、AD 、BE 具有怎样的数量关系?请直接写出这个等量关系,不需要证明.【答案】(1)①见解析;②见解析(2)见解析(3)DE BE AD =-(或AD BE DE =-,BE AD DE =+).【分析】本题考查了几何变换综合题,需要掌握全等三角形的性质和判定,垂线的定义等知识点的应用,解此题的关键是推出证明ADC △和CEB 全等的三个条件.题型较好.(1)①已知已有两直角相等和AC BC =,再由同角的余角相等证明DAC BCE =∠∠即可证明()AAS ADC BEC ≌;②由全等三角形的对应边相等得到AD CE =,BE CD =,从而得证;(2)根据垂直定义求出BEC ACB ADC ∠=∠=∠,根据等式性质求出ACD CBE ∠=,根据AAS 证出ADC △和CEB 全等,再由全等三角形的对应边相等得到AD CE =,BE CD =,从而得证;(3)同样由三角形全等寻找边的关系,根据位置寻找和差的关系.【详解】(1)①证明:∵90ACB ∠=︒,90ADC ∠=︒,90BEC ∠=︒∴90ACD DAC ∠+∠=︒,90ACD BCE ∠+∠=︒,∴DAC BCE =∠∠,在ADC △与BEC 中,90ADC BEC DAC BCE AC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴()AAS ADC BEC ≌;②由①知,ADC BEC △△≌,∴AD CE =,BE CD =,∵DE CE CD =+,∴DE AD BE =+;(2)证明:∵AD MN ⊥于D ,BE MN ⊥于E ,∴90ADC BEC ACB ∠=∠=∠=︒,∴90CAD ACD ∠+∠=︒,90ACD BCE ∠+∠=︒,∴CAD BCE ∠=∠,在ADC △与BEC 中,90ADC BEC DAC BCE AC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴()AAS ADC CEB ≌.∴AD CE =,BE CD =,∴DE CE CD AD BE =-=-.(3)解:同(2)理可证()AAS ADC CEB ≌.∴AD CE =,BE CD =,∵CE CD DE=-∴AD BE DE =-,即DE BE AD =-;当MN 旋转到图3的位置时,AD 、DE 、BE 所满足的等量关系是DE BE AD =-(或AD BE DE =-,BE AD DE =+).【模型六旋转型模型】例题:如图,AB AC =,AE AD =,CAB EAD α∠=∠=.(1)求证:AEC ADB ≅△△1.如图,在△ABC中,AB=BC,∠ABC=120°,点D在边AC上,且线段BD绕着点B按逆时针方向旋转120°能与BE重合,点F是ED与AB的交点.(1)求证:AE=CD;(2)若∠DBC=45°,求∠BFE的度数.【答案】(1)AB⊥BE,AB=BD+BE;(2)图2中BE=AB+BD,图∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,∵CA=CB,CD=CE,∴△ACD≌△BCE(SAS),∴AD=BE,∠CBE=∠A,∵CA=CB,∠ACB=90°,∴∠A=∠CBA=45°,∴∠CBE=∠A=45°,∴ABE=90°,∴AB⊥BE,∵AB=AD+BD,AD=BE,∴AB=BD+BE,故答案为AB⊥BE,AB=BD+BE.(2)①如图2中,结论:BE=AB+BD.理由:∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,∵CA=CB,CD=CE,∴△ACD≌△BCE(SAS),∴AD=BE,∵AD=AB+BD,AD=BE,∴BE=AB+BD.②如图3中,结论:BD=AB+BE.理由:∵∠ACB =∠DCE =∴∠ACD =∠BCE ,【模型七倍长中线模型】例题:(2023秋·山东滨州·八年级统考期末)如图,BD 是ABC 的中线,10AB =,6BC =,求中线BD 的取值范围.【答案】28BD <<【分析】延长BD 到E ,使DE BD =,证明两边之和大于2BE BD =,两边之差小于2BE BD =,证明三角形全等,得到线段相等,等量代换得28BD <<.【详解】解:如图,延长BD 至E ,使DE BD =,连接CE ,∵D 为AC 中点,∴AD DC =,在ABD △和CED △中,BD DE ADB CDE AD CD =⎧⎪∠=∠⎨⎪=⎩∴()SAS ABD CED ≌△△,∴10EC AB ==,在BCE 中,CE BC BE CE BC -<<+,即106106BE -<<+,∴416BE <<,∴4216BD <<,∴28BD <<.【点睛】本题考查了全等三角形的判定和性质,三角形三边之间的关系,解题的关键是作辅助线,构造全等三角形.【变式训练】1.如图,在ABC 中,AD 是BC 边上的中线.延长AD 到点E ,使DE AD =,连接BE .(1)求证:ACD EBD △△≌;(2)AC 与BE 的数量关系是:____________,位置关系是:____________;(3)若90BAC ∠=︒,猜想AD 与BC 的数量关系,并加以证明.【答案】(1)见解析(2)AC BE =,AC BE∥(3)2AD BC =,证明见解析【分析】(1)根据三角形全等的判定定理SAS ,即可证得;(2)由ACD EBD △△≌,可得AC BE =,C EBC ∠=∠,据此即可解答;(3)根据三角形全等的判定定理SAS ,可证得BAC ABE ≌,据此即可解答.【详解】(1)证明:AD 是BC 边上的中线,BD CD ∴=,在ACD △与EBD △中AD ED ADC EDB BD CD =⎧⎪∠=∠⎨⎪=⎩,()SAS ACD EBD ∴ ≌;(2)解:ACD EBD ≌,AC BE ∴=,C EBC ∠=∠,∴∥AC BE ,故答案为:AC BE =,AC BE ∥;(3)解:2AD BC=证明:ACD EBD ≌,AC BE ∴=,C EBC ∠=∠,∴∥AC BE ,90BAC ∠=︒90BAC ABE ∴∠=∠=︒在BAC △和ABE △中,90AB BA BAC ABE AC BE =⎧⎪∠=∠=︒⎨⎪=⎩()SAS BAC ABE ∴ ≌,2BC AE AD ∴==.【点睛】本题考查了全等三角形的判定与性质,平行线的判定与性质,熟练掌握和运用全等三角形的判定与性质是解决本题的关键.2.(2023上·江苏南通·八年级统考期中)课外兴趣小组活动时,老师提出了如下问题:如图1,ABC 中,若6AB =,4AC =,求BC 边上的中线AD 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD 到E ,使DE AD =,连接BE .请根据小明的方法思考:(1)由已知和作图能得到ADC EDB V V ≌,得到BE AD =,在ABE 中求得2AD 的取值范围,从而求得取值范围是.方法总结:上述方法我们称为“倍长中线法”.“倍长中线法”多用于构造全等三角形和证明边之间的关系.(2)如图2,AD 是ABC 的中线,AB AE =,AC AF =,180BAE CAF ∠+∠=︒,试判断线段关系,并加以证明;(3)如图3,在ABC 中,D ,E 在边BC 上,且BD CE =.求证:AB AC AD AE +>+【答案】(1)15AD <<CD BD ADC EDB AD ED =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ADC EDB ≌,∴4BE AC ==,∵在ABE 中,AB BE AE AB BE -<<+,即64264AD -<<+,∴15AD <<.故答案为:15AD <<(2)2EF AD =,理由:如图,延长AD 到M ,使得DM AD =,连接BM ,∴2AM AD DM AD =+=,∵AD 是ABC 的中线,∴BD CD =,在BDM 和CDA 中BD CD BDM CDA DM DA =⎧⎪∠=∠⎨⎪=⎩∴()SAS BDM CDA ≌,∴BM AC =,∵AC AF =,∴BM AF =,∵BDM CAD ≌,∴∠=∠MBD ACD ,∴BM AC ∥,∴180ABM BAC ︒∠+∠=,∵180BAE CAF ∠+∠=︒,∴()360360180180BAC FAE BAE CAF ∠+∠=︒-∠+∠=︒-︒=︒,∴ABM FAE ∠=∠,在ABM 和EAF △中AB AE ABM EAF BM AF =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABM EAF ≌,∴AM EF =,∵2AM AD =,∴2EF AD =;(3)取BC 的中点为M ,连接AM 并延长至N ,使AM MN =,连接BN 、DN ,∵点M 是BC 的中点,∴CM BM =,在ACM △和NBM 中,CM BM AMC NMB AM NM =⎧⎪∠=∠⎨⎪=⎩∴()SAS ACM NBM ≌,∴AC NB=∵BD CE =,∴BM BD CM CE -=-,即=DM EM ,在AEM △和NDM 中,EM DM AME NMD AM NM =⎧⎪∠=∠⎨⎪=⎩∴()SAS AEM NDM ≌,∴AE ND =,延长AD 交BN 于F ,+>,则AB BF AD DF+>+,且FN DF DN+++>++,∴AB BF FN DF AD DF DN+>+,∴AB BN AD DN+>+.即AB AC AD AE【模型八截长补短模型】【点睛】本题是四边形综合题,考查了全等三角形的判定及性质的运用,等边三角形的性质的运用,解答时证明三角形全等是关键.【变式训练】(1)求证:CD BC DE =+;(2)若75B ∠=︒,求E ∠的度数.【答案】(1)见解析(2)105︒∵CA 平分BCD ∠,∴BCA FCA ∠=∠.在BCA V 和FCA △中,⎧⎪∠⎨⎪⎩【答案】(1)①见解析;②14x <<;(2)见解析【分析】(1)①根据三角形的中线得出BD CD =,再由对顶角相等得出②先由ABD ECD ≌,得出5CE =,再由ED AD =,得出可求出答案;(2)先根据SAS 判断出DEF DEH △≌△,得出EH EF =,BD CD ∴=,在ADB 和ECD 中,BD CD ADB CDE AD DE =⎧⎪∠=∠⎨⎪=⎩,()SAS ABD ECD ∴△≌△;②解:由①知,ABD ECD ≌,CE AB ∴=,5AB = ,5CE ∴=,ED AD = ,AD x =,22AE AD x ∴==,在ACE △中,3AC =,根据三角形的三边关系得,53253x -<<+,14x ∴<<,故答案为:14x <<;(2)证明:如图2,延长FD ,截取DH DF =,连接BH ,EH ,DH DF = ,DE DF ⊥,即90EDF EDH ∠=∠=︒,DE DE =,∴()SAS DEF DEH ≌,EH EF ∴=,AD 是中线,BD CD ∴=,DH DF = ,BDH CDF ∠=∠,∴()SAS BDH CDF ≌,CF BH ∴=,∵BE BH EH +>,BE CF EF ∴+>.【点睛】此题是三角形综合题,主要考查了三角形中线的定义,全等三角形的判定和性质,三角形的三边【答案】(1)正确;(2)成立,见解析;(3)正确,见解析【分析】本题考查了三角形全等的判定与性质,正确做辅助线构造全等三角形是解题关键.(1)延长FD 到点G ,使DG BE =,连接AG ,先证明ADG ABE △△≌AEF AGF △△≌,可得EF GF =,进而得出EF BE DF =+,即可解题;(2)证明方法同(1):延长FD 到点G ,使DG BE =,连接AG ,先证明再证明AEF AGF △△≌,可得EF GF =,进而得出EF BE DF =+即可解题;∵90B ADF ∠=∠=︒,∴ADG ADF ∠=∠=∠在ABE 和ADG △中,DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABE ADG ≌,∴AE AG =,BAE DAG ∠=∠,∵120BAD ∠=︒,60EAF ∠=︒,∴2BAD EAF ∠∠=,∴GAF DAG DAF BAE DAF BAD EAF EAF ∠=∠+∠=∠+∠=∠-∠=∠,在AEF △和AGF 中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴()SAS AEF AGF ≌,∴EF GF =,∵GF DG DF BE DF =+=+,∴EF BE DF =+,故答案为:正确;(2)解:上题中的结论依然成立;如图2,延长FD 到点G ,使DG BE =,连接AG ,∵110ADF ∠=︒,70B ∠=︒,∴18011070ADG B ∠=︒-︒=︒=∠,在ABE 和ADG △中,DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABE ADG ≌,∴AE AG =,BAE DAG ∠=∠,∵180B ADF ∠+∠=︒,∴ADG B ∠=∠,在ABE 和ADG △中,DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABE ADG ≌,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴()AEF AGF SAS ≌,∴EF GF =,∵GF DG DF BE DF =+=+,∴EF BE DF =+.。
中考数学常见的几种旋转模型

旋转常见模型一、遇60°旋转60°,构造等边三角形1、点P 是等边△ABC 内一点,且PC =3,PB =4,PA =5。
求∠BPC 的度数。
2、如图6-2,P 是等边ABC ∆外一点,若345PA PB PC ===,,,求APB ∠的度数。
图6-23、(2018年广州市节选)如图,在四边形 ABCD 中,∠B = 60︒ ,∠D = 30︒ ,AB = BC .(1)∠A +∠C = ° (2)连接 BD ,探究 AD , BD , CD 三者之间的数量关系,并说明理由.二、遇90°旋转90°,构造等腰直角三角形1、如图,在正方形ABCD内部有一点P,PA=5,PB=2,PC=1,求∠BPC的度数。
2、在△ABC中,∠BAC=90°,AB=AC,P是△ABC内一点,PA=2,PB=1,PC=3,求∠APB的度数.三、遇等腰旋转顶角,构造旋转全等FED CBA GABCDEABCDEF1、在ABC △中,AB AC =,BAC α∠=(060α︒<<︒),将线段BC 绕点B 逆时针旋转60°得到线段BD .(1)如图1,直接写出ABD ∠的大小(用含α的式子表示);(2)如图2,15060BCE ABE ∠=︒∠=︒,,判断ABE △的形状并加以证明; (3)在(2)的条件下,连结DE ,若45DEC ∠=︒,求α的值.四、半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
秘籍:角含半角要旋转:构造两次全等FED CBAG FED CBA1、如图,在正方形ABCD 中,E 、F 分别在BC 、CD 上,且∠EAF=45°连接EF . 求证:EF=BE+DF .(2016·徐州)如图,正方形的边长为2,点,分别在边,上,若EBF ∠=︒,则∆的周长等于.A BC D E F2、如图,在正方形ABCD 中,E 、F 分别在BC 、CD 上,且∠EAF=45°连接AD ,与AE 、AF 分别交于M 、N , 求证:MN 2=BM 2+DM 23、如图,在正方形ABCD 的边长为2,点E ,点F 分别在边AD,CD 上,若∠EBF=45°,则△EDF 的周长等于 。
初中数学全等三角形旋转模型知识归纳总结含答案

初中数学全等三角形旋转模型知识归纳总结含答案一、全等三角形旋转模型1.如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是 ,位置关系是 ;(2)探究证明:把△ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由;(3)拓展延伸:把△ADE 绕点A 在平面内自由旋转,若AD =4,AB =10,请直接写出△PMN 面积的最大值.解析:(1)PM =PN ,PM ⊥PN ;(2)△PMN 是等腰直角三角形.理由见解析;(3)S △PMN 最大=492. 【分析】(1)由已知易得BD CE =,利用三角形的中位线得出12PM CE =,12PN BD =,即可得出数量关系,再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠,最后用互余即可得出位置关系;(2)先判断出ABD ACE ∆≅∆,得出BD CE =,同(1)的方法得出12PM BD =,12PN BD =,即可得出PM PN =,同(1)的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠,即可得出结论;(3)方法1:先判断出MN 最大时,PMN ∆的面积最大,进而求出AN ,AM ,即可得出MN 最大AM AN =+,最后用面积公式即可得出结论.方法2:先判断出BD 最大时,PMN ∆的面积最大,而BD 最大是14AB AD +=,即可得出结论.【详解】解:(1)点P ,N 是BC ,CD 的中点,//PN BD ∴,12PN BD =, 点P ,M 是CD ,DE 的中点, //PM CE ∴,12PM CE =,AB AC =,AD AE =,BD CE ∴=,PM PN ∴=,//PN BD ,DPN ADC ∴∠=∠,//PM CE ,DPM DCA ∴∠=∠,90BAC ∠=︒,90ADC ACD ∴∠+∠=︒,90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒,PM PN ∴⊥,故答案为:PM PN =,PM PN ⊥;(2)PMN ∆是等腰直角三角形.由旋转知,BAD CAE ∠=∠,AB AC =,AD AE =,()ABD ACE SAS ∴∆≅∆,ABD ACE ∴∠=∠,BD CE =, 利用三角形的中位线得,12PN BD =,12PM CE =, PM PN ∴=,PMN ∴∆是等腰三角形,同(1)的方法得,//PM CE ,DPM DCE ∴∠=∠,同(1)的方法得,//PN BD ,PNC DBC ∴∠=∠,DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠,MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠,90BAC ∠=︒,90ACB ABC ∴∠+∠=︒,90MPN ∴∠=︒,PMN ∴∆是等腰直角三角形;(3)方法1:如图2,同(2)的方法得,PMN ∆是等腰直角三角形,MN ∴最大时,PMN ∆的面积最大,//DE BC ∴且DE 在顶点A 上面,MN ∴最大AM AN =+,连接AM ,AN ,在ADE ∆中,4AD AE ==,90DAE ∠=︒,22AM ∴=在Rt ABC ∆中,10AB AC ==,52AN =22522MN ∴=最大,222111149(72)22242PMN S PM MN ∆∴==⨯=⨯=最大. 方法2:由(2)知,PMN ∆是等腰直角三角形,12PM PN BD ==, PM ∴最大时,PMN ∆面积最大,∴点D 在BA 的延长线上,14BD AB AD ∴=+=,7PM ∴=,2211497222PMN S PM ∆∴==⨯=最大. 【点睛】此题属于几何变换综合题,主要考查了三角形的中位线定理,等腰直角三角形的判定和性质,全等三角形的判断和性质,直角三角形的性质的综合运用;解(1)的关键是判断出12PM CE =,12PN BD =,解(2)的关键是判断出ABD ACE ∆≅∆,解(3)的关键是判断出MN 最大时,PMN ∆的面积最大.2.问题提出:(1)如图1,在ABC 中,AB AC BC =≠,点D 和点A 在直线BC 的同侧,BD BC =,90BAC ∠=︒,30DBC ∠=︒,连接AD ,将ABD △绕点A 逆时针旋转90︒得到ACD ',连接BD '(如图2),可求出ADB ∠的度数为______.问题探究:(2)如图3,在(1)的条件下,若BAC α∠=,DBC β∠=,且120αβ+=︒,DBC ABC ∠<∠ ,①求ADB ∠的度数.②过点A 作直线AE BD ⊥,交直线BD 于点E ,7,2BC AD ==.请求出线段BE 的长.答案:A解析:(1)30°;(2)①30︒;②73-【分析】(1)由旋转的性质,得△ABD ≌ACD '∆,则ADB AD C '∠=∠,然后证明BCD '∆是等边三角形,即可得到30ADB AD C '∠=∠=︒;(2)①将ABD △绕点A 逆时针旋转,使点B 与点C 重合,得到'ACD △,连接'BD .与(1)同理证明D BC '∆为等边三角形,然后利用全等三角形的判定和性质,即可得到答案;②由解直角三角形求出3DE =【详解】解:(1)根据题意,∵AB AC BC =≠,90BAC ∠=︒,∴ABC ∆是等腰直角三角形,∴45ABC ACB ∠=∠=︒,∵30DBC ∠=︒,∴15ABD ∠=︒,由旋转的性质,则△ABD ≌ACD '∆,∴ADB AD C '∠=∠,15ABD ACD '∠=∠=︒,BC CD '=,∴60BCD '∠=︒,∴BCD '∆是等边三角形,∴60BD C '∠=︒,BD CD ''=∵AB AC =,AD AD ''=,∴ABD '∆≌ACD '∆,∴30AD B AD C ''∠=∠=︒,∴30ADB AD C '∠=∠=︒;(2)①DBC ABC ∠<∠,60120α︒︒∴<<.如图1,将ABD △绕点A 逆时针旋转,使点B 与点C 重合,得到'ACD △,连接'BD .AB AC =,ABC ACB ∴∠=∠,BAC α∠=, ()111809022ABC αα︒︒∴∠=-=-, 1902ABD ABC DBC αβ︒∴∠=∠-∠=--, 119090180()22D CB ACD ACB αβααβ''︒︒︒∴∠=∠+∠=--+-=-+. 120,αβ︒+=60D CB '︒∴∠=.,BD BC BD CD '==,,BC CD '∴=D BC '∴为等边三角形,D B D C ''∴=,AD B AD C ''∴≌,AD B AD C ''∴∠=∠,1302AD B BD C ''︒∴∠=∠=, 30ADB ︒∴∠=.②如图2,由①知,30ADB ︒∠=,在Rt ADE △中,30,2ADB AD ︒∠==, 3DE ∴=.BCD '是等边三角形,7BD BC '∴==,7BD BD '∴==,73BE BD DE ∴=-=-.【点睛】本题考查了解直角三角形,旋转的性质,全等三角形的判定和性质,等边三角形的判定和性质,等腰直角三角形的性质,以及三角形的内角和定理,解题的关键是熟练掌握所学的知识,正确利用旋转模型进行解题.3.如图,点B ,C ,D 在同一条直线上,△BCF 和△ACD 都是等腰直角三角形,连接AB ,DF ,延长DF 交AB 于点E .(1)如图1,若AD =BD ,DE 是∠ADB 的平分线,BC =1,求CD 的长度;(2)如图2,连接CE ,求证:DE =2CE +AE ;(3)如图3,改变△BCF 的大小,始终保持点在线段AC 上(点F 与点A ,C 不重合).将ED 绕点E 顺时针旋转90°得到EP ,取AD 的中点O ,连接OP .当AC =2时,直接写出OP 长度的最大值.解析:(1)21CD =;(2)证明见解析;(3)22+【分析】 (1)根据等腰直角三角形的性质,求出1FC BC ==,再判断出FA FB =,即可得出结论;(2)先判断出ABC DFC ≅△△,得出BAC CDF ∠=∠,进而判断出ACE DCH ≅△△,得出AE DH =,CE CH =,即可得出结论;(3)先判断出2OE OQ ==,再判断出OED QEP ≅△△,进而求出2PQ OD ==得出结论.【详解】(1)解:BCF 和ACD △都是等腰直角三角形,AC CD ∴=,1FC BC ==,2FB =,AD BD =,DE 是ABD ∆的平分线,DE ∴垂直平分AB ,2FA FB ∴==,21AC FA FC ∴=+=,21CD ∴=;(2)证明:如图2,过点C 作CH CE ⊥交ED 于点H ,BCF 和ACD △都是等腰直角三角形,AC DC ∴=,FC BC =,90ACB DCF ∠=∠=︒;()ABC DFC SAS ∴≅△△,BAC CDF ∴∠=∠,90ECH ∠=︒,90ACE ACH ∴∠+∠=︒,90ACD ∠=︒,90DCH ACH ∴∠+∠=︒,ACE DCH ∴∠=∠.在ACE 和DCH 中,BAC CDF AC DCACE DCH ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()ACE DCH ASA ∴≅△△,AE DH ∴=,CE CH =,2EH CE ∴=.2DE EH DH CE AE =+=+;(3)OP 的最大值是22+解:如图3,连接OE ,将OE 绕点E 顺时针旋转90︒得到EQ ,连接OQ ,PQ ,则2OQ OE =.由(2)知,90AED ABC CDF ABC BAC ∠=∠+∠=∠+∠=︒,在Rt AED △中,点O 是斜边AD 的中点,122222OE OD AD AC ∴===== 2222OQ OE ∴===,在OED 和QEP △中,OE QE OED QEP DE PE =⎧⎪∠=∠⎨⎪=⎩,()OED QEP SAS ∴≅△△,2PQ OD ∴==22OP OQ PQ +=+O 、P 、Q 三点共线时,取“=”号,OP ∴的最大值是22+【点睛】此题是几何变换综合题,主要等腰直角三角形的性质,全等三角形的判定和性质,构造出全等三角形是解本题的关键.4.如图1所示,在Rt ABC △中90BAC ∠=︒,AB AC =,2BC =,以BC 所在直线为x 轴,边BC 的垂直平分线为y 轴建立平面直角坐标系,将ABC 绕P 点0,1顺时针旋转.(1)填空:当点B 旋转到y 轴正半轴时,则旋转后点A 坐标为______;(2)如图2所示,若边AB 与y 轴交点为E ,边AC 与直线1y x =-的交点为F ,求证:AEF 的周长为定值;(3)在(2)的条件下,求AEF 内切圆半径的最大值.解析:(1)2,21;(2)见解析;(3)324【分析】 (1)作出图形,'''A B C 是ABC 绕 P 点0,1顺时针旋转,点B 旋转到y 轴正半轴时得到的图形,连接 BP ,CP ,根据2BC =,y 轴垂直平分BC , AB AC =,()0,1P -可证得四边形ABPC 是正方形,则有 '''2BP B PAB A B ,'0'21B B P PO ,可得点 A 坐标; (2)作BPQ CPF ∠=∠,交AB 延长线于Q 点,根据四边形ABPC 是正方形,得到90QBP FCP ∠=∠=︒,BP CP =,可证BPQ CPF ASA ≌△△,得BQ CF =,QP FP =,利用ASA 再可证得QPE FPE ≌△△,得QE FE =则AEF 的周长22AB AC =+=(3)设EF m =,AE n =,Rt AEF 的内切圆半径为r ,由(2)可得22AF m n =-则2AE AF EF r +-=222n m n m +--=2m =,当m 最小时,r 最大.得到22222n m n m 整理得:2224220nm n m ,关于n 的一元二次方程有解,即22244220m m 化简得24280m m +-≥,利用二次函数图像可得422m ≥-422m ≤--(不合题意,舍去)可得m 的最小值为42-r 2422324,则有AEF 内切圆半径的最大值为324.【详解】解:(1)如图示,'''A B C 是ABC 绕 P 点0,1顺时针旋转,点B 旋转到y 轴正半轴时得到的图形,连接 BP ,CP ,∵2BC =,y 轴垂直平分BC∴1BO CO ==又∵Rt ABC △中,AB AC =∴1AO =,2AB AC ==∵()0,1P -∴1PO =∴AO BO CO PO ===∴四边形ABPC 是正方形 ∴'''2BPB P AB A B ∴'0'21B B P PO ∴点A 坐标为2,21(2)如图2所示,作BPQ CPF ∠=∠,交AB 延长线于Q 点 ∵四边形ABPC 是正方形∴90QBP FCP ∠=∠=︒, BP CP = ∴BPQ CPF ASA ≌△△∴ BQ CF =,QP FP = ∵点F 在直线1y x =-∴45FPE ∠=︒∴ 45BPE FPC ∠+∠=︒ ∴45BPE BPQ ∠+∠=︒∴45QPE FPE ∠=∠=︒ ∵EP EP =∴QPE FPE ASA ≌△△∴ QE FE = ∴AEF 的周长AE EF AF AE QE AF =++=++ AE BE BQ AF AE BE FC AF =+++=+++22AB AC =+=(3)设EF m =,AE n =,Rt AEF 的内切圆半径为 r ,由(2)可得22AF m n =--则2AE AF EF r +-= 222n m n m +---= 2m =-∴当m 最小时,r 最大.∵在Rt AEF 中,222AE AF EF +=∴22222n m n m 整理得: 2224220n m nm ∵关于n 的一元二次方程有解∴22244220m m∴24280m m +-≥ 利用二次函数图像可得422m ≥-或422m ≤--(不合题意,舍去)∴m 的最小值为422-∴r 的最大值为2422324即AEF 内切圆半径的最大值为324-.【点睛】本题主要考查了一次函数的综合应用以及根的判别式、全等三角形的判定与性质、旋转、三角形内切圆等知识,能熟练应用相关性质是解题关键.5.如图1,在△ABC 和△ADE 中,∠DAE=∠BAC ,AD=AE ,AB=AC .(1)求证:△ABD ≌△ACE ;(2)如图2,在△ABC 和△ADE 中,∠DAE=∠BAC ,AD=AE ,AB=AC ,∠ADB=90°,点E 在△ABC 内,延长DE 交BC 于点F ,求证:点F 是BC 中点;(3)△ABC 为等腰三角形,∠BAC=120°,AB=AC ,点P 为△ABC 所在平面内一点,∠APB=120°,AP=2,BP=4,请直接写出 CP 的长.答案:D解析:(1)证明见详解;(2)证明见详解;(3)27或213.【分析】(1)因为∠DAE=∠BAC ,可以得到∠DAB=∠EAC ,因为AD=AE ,AB=AC ,即可得到△ABD ≌△ACE ;(2)连接CE ,延长EF 至点H ,取CF=CH ,连接CH ,由(1)可得△ABD ≌△ACE ,所以∠AEC=90°和CE=BD ,可以推出∠BDF=∠CEF ,再证明△DBF ≌△ECH ,所以BF=CH ,等量代换即可得到BF=FC ,即可解决;(3)点P 在△ABC 内部,将△ABP 逆时针旋转120°,得到ACP ∆',连接PP '和PC ,可以得到△PP C '是直角三角形,利用勾股定理即可求出PC 的值;当点P 在△ABC 外部,将△APB 绕点A 逆时针旋转120︒得到PDC ∆,连接PP '和PC ,过点P 作PD ⊥'CP 于点D ,连接PD 可以得到△PP D ',△PP D '是直角三角形和,利用勾股定理即可求出'DP 及PC 的值.【详解】解:(1)证明:∵∠DAE=∠BAC∴∠DAB=∠EAC∵AD=AE ,AB=AC∴△ABD ≌△ACE(2)证明:连接CE ,延长EF 至点H ,取CF=CH ,连接CH ,如图所示:∵△ADB ≌△AEC∴BD=EC ,∠ADB=∠AEC=90°∵AD=AE∴∠ADE=∠AED∵∠ADE+∠EDB=∠AED+∠CEH=90°∴∠EDB=∠CEH∵CF=CH∴∠CFH=∠CHF∴∠DFB=∠H∵CE=BD∴△DBF ≌△ECH∴BF=CH∴BF=CF∴点F 是BC 的中点(3)当点P 在△ABC 内部,如图所示,将△ABP 逆时针旋转120°,得到ACP ∆',连接PP '和PC∵将△ABP 旋转120°得到ACP ∆'∴∠PAP '=120°,AP='AP =2,BP=CP '=4∴PP '=23,∵∠AP C '=120°,∠AP P '=30°,∴∠PP C '=90°,∴PC=()2223427+=.当点P 在△ABC 外部,如图所示,将△APB 绕点A 逆时针旋转120︒到△'AP C ,过点P 作PD ⊥'CP 于点D ,连接PD , ∵将△ABP 旋转120°得到ACP ∆'∴∠PAP '=120°,AP='AP =2,BP=CP '=4,∴PP '3∵∠AP C '=120°,∠AP P '=30°,∴∠PP C '=150°,∴∠PP D '=30°,在Rt 'PDP 中,1'32PD PP ==, 22''3DP PP PD ∴=-=,''347DC DP P C ∴=+=+=,()222237213PC PD DC ∴=+=+=. 综上所述,27213PC =或【点睛】本题主要考查了全等三角形以及旋转,合理的作出辅助线以及熟练旋转的性质是解决本题的关键.6.如图,直线y=﹣x+c与x轴交于点B(3,0),与y轴交于点C,过点B,C的抛物线y=﹣x2+bx+c与x轴的另一个交点为A.(1)求抛物线的解析式和点A的坐标;(2)P是直线BC上方抛物线上一动点,PA交BC于D.设t=PDAD,请求出t的最大值和此时点P的坐标;(3)M是x轴上一动点,连接MC,将MC绕点M逆时针旋转90°得线段ME,若点E恰好落在抛物线上,请直接写出此时点M的坐标.答案:A解析:(1)y=﹣x2+2x+3,A(﹣1,0);(2)t的最大值为916,此时P(32,154);(3)M 933-,0933+0).【分析】(1)利用待定系数法解决问题即可;(2)连接AC,PC,PB,过点A作AE⊥BC于E,过等P作PF⊥BC于F.设P(m,﹣m2+2m+3).利用相似三角形的性质构建二次函数解决问题即可;(3)过点E作EH⊥x轴于H.设M(m,0),利用全等三角形的性质求出点E的坐标(用m表示),再利用待定系数法解决问题即可.【详解】解:(1)∵直线y=﹣x+c与x轴交于点B(3,0),与y轴交于点C,∴0=﹣3+c,解得c=3,∴C(0,3),∵抛物线经过B,C,∴9303b cc-++=⎧⎨=⎩,解得23bc=⎧⎨=⎩,∴抛物线的解析式为y=﹣x2+2x+3,令y=0,得到﹣x2+2x+3=0,解得x=﹣1或3,∴A(﹣1,0);(2)如图,连接AC,PC,PB,过点A作AE⊥BC于E,过点P作PF⊥BC于F.设P(m,﹣m2+2m+3).∵AE∥PF,∴△PFD∽△AED,∴PDAD =PFAE,∵S△PBC=12•BC•PF,S△ACB=12•BC•AE,∴PDAD =PBCABCSS∆∆,∵S△ABC=12•AB•OC=12×4×3=6,∴t=PDAD =6PBCS∆=211133(23)332226m m m⨯⨯+⨯⨯-++-⨯⨯=﹣14m2+34m=﹣14(m﹣32)2+916,∵﹣14<0,∴m=32时,t有最大值,最大值为916,此时P(32,154);(3)如图,过点E作EH⊥x轴于H,∵∠COM =∠EHM =∠CME =90°,∴∠EMH +∠CMH =90°,∠EMH +∠MEH =90°,∴∠MEH =∠CMO ,∵MC =ME ,∴△COM ≌△MHE (AAS ),∴OC =MH =3,OM =EH ,设M (m ,0),则E (m ﹣3,﹣m ),把E (m ﹣3,﹣m )代入y =﹣x 2+2x +3,可得﹣(m ﹣3)2+2(m ﹣3)+3=﹣m , 整理得,m 2﹣9m +12=0,解得m =9332-或9332+, ∴M (9332-,0)或(9332+,0). 【点睛】本题考查的是二次函数综合题,涉及全等三角形的性质和判定,相似三角形的性质和判定,解题的关键是利用数形结合的思想,在二次函数图象上构造全等三角形或相似三角形,利用几何的性质进行点坐标的求解.7.如图,BC ⊥CA ,BC =CA ,DC ⊥CE ,DC =CE ,直线BD 与AE 交于点F ,交AC 于点G ,连接CF .(1)求证:△ACE ≌△BCD ;(2)求证:BF ⊥AE ;(3)请判断∠CFE 与∠CAB 的大小关系并说明理由.答案:C解析:(1)见解析;(2)见解析;(3)∠CFE =∠CAB ,见解析【分析】(1)根据垂直的定义得到∠ACB =∠DCE =90°,由角的和差得到∠BCD =∠ACE ,即可得到结论;(2)根据全等三角形的性质得到∠CBD =∠CAE ,根据对顶角的性质得到∠BGC =∠AGE ,由三角形的内角和即可得到结论;(3)过C 作CH ⊥AE 于H ,CI ⊥BF 于I ,根据全等三角形的性质得到AE =BD ,S △ACE =S △BCD ,根据三角形的面积公式得到CH =CI ,于是得到CF 平分∠BFH ,推出△ABC 是等腰直角三角形,即可得到结论.【详解】(1)证明:∵BC ⊥CA ,DC ⊥CE ,∴∠ACB =∠DCE =90°,∴∠BCD =∠ACE ,在△BCD 与△ACE 中,BC CA ACD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△BCD ;(2)∵△BCD ≌△ACE ,∴∠CBD =∠CAE ,∵∠BGC =∠AGE ,∴∠AFB =∠ACB =90°,∴BF ⊥AE ;(3)∠CFE =∠CAB ,过C 作CH ⊥AE 于H ,CI ⊥BF 于I ,∵△BCD ≌△ACE ,∴ACE BCD AE BD,S S ∆∆==,∴CH =CI ,∴CF 平分∠BFH ,∵BF ⊥AE ,∴∠BFH =90°,∠CFE =45°,∵BC ⊥CA ,BC =CA ,∴△ABC 是等腰直角三角形,∴∠CAB =45°,∴∠CFE =∠CAB .【点睛】角的和差、对顶角的性质这些知识点在证明全等和垂直过程中经常会遇到,需要掌握。
专题 全等三角形六种基本模型(学生版)

专题全等三角形六种基本模型通用的解题思路:模型一:一线三等角模型一线三等角指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
或叫“K字模型”。
三直角相似可以看着是“一线三等角”中当角为直角时的特例,三直角型相似通常是以矩形或者正方形形为背景,或者在一条直线上有一个顶点在该直线上移动或者旋转的直角,几种常见的基本图形如下:当题目的条件中只有一个或者两个直角时,就要考虑通过添加辅助线构造完整的三直角型相似,这往往是很多压轴题的突破口,进而将三角型的条件进行转化。
一般类型:基本类型:同侧“一线三等角”异侧“一线三等角”模型二:手拉手模型--旋转型全等一、等边三角形手拉手-出全等二、等腰直角三角形手拉手-出全等两个共直角顶点的等腰直角三角形,绕点C旋转过程中(B、C、D不共线)始终有:①△BCD≌△ACE;②BD⊥AE(位置关系)且BD=AE(数量关系);③FC平分∠BFE;题型三:倍长中线模型构造全等三角形倍长中线是指加倍延长中线,使所延长部分与中线相等,往往需要连接相应的顶点,则对应角对应边都对应相等。
常用于构造全等三角形。
中线倍长法多用于构造全等三角形和证明边之间的关系(通常用“SAS”证明) (注:一般都是原题已经有中线时用)。
三角形一边的中线(与中点有关的线段),或中点,通常考虑倍长中线或类中线,构造全等三角形.把该中线延长一倍,证明三角形全等,从而运用全等三角形的有关知识来解决问题的方法.主要思路:倍长中线(线段)造全等在△ABC中AD是BC边中线延长AD到E,使DE=AD,连接BE作CF⊥AD于F,作BE⊥AD的延长线于E连接BE延长MD到N,使DN=MD,连接CD题型四:平行线+线段中点构造全等模型题型五:等腰三角形中的半角模型过等腰三角形顶点两条射线,使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型。
解题思路一般是将半角两边的三角形通过旋转到一边合并成新的三角形,从而进行等量代换,然后证明与半角形成的三角形全等,再通过全等的性质得到线段之间的数量关系。
全等模型-手拉手模型--常见几何模型归纳(学生版)

全等模型-手拉手模型全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(手拉手(旋转)模型)进行梳理及对应试题分析,方便掌握。
模型1.手拉手模型(三角形)【模型解读】将两个三角形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等。
公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
对应操作:左手拉左手(即连结BD),右手拉右手(即连结CE),得△ABD≅△ACE。
【常见模型及证法】(等边)(等腰直角)(等腰)1(2022·北京东城·九年级期末)如图,在等边三角形ABC中,点P为△ABC内一点,连接AP,BP,CP,将线段AP绕点A顺时针旋转60°得到AP ,连接PP ,BP .(1)用等式表示BP 与CP的数量关系,并证明;(2)当∠BPC=120°时, ①直接写出∠P BP的度数为;②若M为BC的中点,连接PM,请用等式表示PM与AP的数量关系,并证明.2(2022·黑龙江·中考真题)△ABC和△ADE都是等边三角形.(1)将△ADE绕点A旋转到图①的位置时,连接BD,CE并延长相交于点P(点P与点A重合),有PA+ PB=PC(或PA+PC=PB)成立;请证明.(2)将△ADE绕点A旋转到图②的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?并加以证明;(3)将△ADE绕点A 旋转到图③的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?直接写出结论,不需要证明.3(2023·黑龙江哈尔滨·九年级校考期中)如图,在△ABC中,∠C=90°,AC=BC,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则∠C′BA的度数为()A.15°B.20°C.30°D.45°4(2022·青海·中考真题)两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)问题发现:如图1,若△ABC和△ADE是顶角相等的等腰三角形,BC,DE分别是底边.求证:BD= CE;(2)解决问题:如图2,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系并说明理由.图1 图25(2022秋·江苏·八年级期中)点D为△ABC外一点,∠ACB=90°,AC=BC.(1)如图1,∠DCE=90°,CD=CE,求证:∠ADC=∠BEC;(2)如图2,若∠CDB=45°,AE∥BD,CE⊥CD,求证:AE=BD;模型2.手拉手模型(正多边形型)【模型解读】将两个多边形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个多边形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等。
中考数学全等三角形旋转模型知识归纳总结及解析

中考数学全等三角形旋转模型知识归纳总结及解析一、全等三角形旋转模型1.已知OP平分∠AOB,∠DCE的顶点C在射线OP上,射线CD交射线OA于点F,射线CE交射线OB于点G.(1)如图1,若CD⊥OA,CE⊥OB,请直接写出线段CF与CG的数量关系;(2)如图2,若∠AOB=120º,∠DCE=∠AOC,试判断线段CF与CG的数量关系,并说明理由.答案:C解析:(1)CF=CG;(2)CF=CG,见解析【分析】(1)结论CF=CG,由角平分线性质定理即可判断.(2)结论:CF=CG,作CM⊥OA于M,CN⊥OB于N,证明△CMF≌△CNG,利用全等三角形的性质即可解决问题.【详解】解:(1)结论:CF=CG;证明:∵OP平分∠AOB,CF⊥OA,CG⊥OB,∴CF=CG(角平分线上的点到角两边的距离相等);(2)CF=CG.理由如下:如图,过点C作CM⊥OA,CN⊥OB,∵OP平分∠AOB,CM⊥OA,CN⊥OB,∠AOB=120º,∴CM=CN(角平分线上的点到角两边的距离相等),∴∠AOC=∠BOC=60º(角平分线的性质),∵∠DCE=∠AOC,∴∠AOC=∠BOC=∠DCE=60º,∴∠MCO=90º-60º =30º,∠NCO=90º-60º =30º,∴∠MCN=30º+30º=60º,∴∠MCN=∠DCE ,∵∠MCF=∠MCN-∠DCN ,∠NCG=∠DCE-∠DCN ,∴∠MCF=∠NCG ,在△MCF 和△NCG 中,CMF CNG CM CNMCF NCG ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MCF ≌△NCG (ASA ),∴CF=CG (全等三角形对应边相等);【点睛】本题考查三角形综合题、角平分线的性质、全等三角形的判定和性质,解题的关键是掌握角平分线的性质的应用,熟练证明三角形全等 .2.(1)如图1,在OAB 和OCD 中,OA=OB ,OC=OD ,∠AOB=∠COD=40°,连接AC ,BD 交于点M .求:①AC BD 的值; ②∠AMB 的度数.(2)如图2,在OAB 和OCD 中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC 交BD 的延长线于点M .请判断AC BD的值及∠AMB 的度数,并说明理由; (3)在(2)的条件下,将OCD 点O 在平面内旋转,AC ,BD 所在直线交于点M ,若OD=2,OB=23,请直接写出当点C 与点M 重合时AC 的长.答案:A解析:(1)①1,②40°;(2)AC BD3∠AMB=90°,见解析;(3)33【分析】(1)①根据已知条件证明△COA ≌△DOB ,即可证明AC=BD ;②根据△COA ≌△DOB 可得∠CAO=∠DBO ,根据已知条件可得∠OAB+∠ABO=140°,然后在△AMB 中,根据等角的转换即可得到答案;(2)根据已知条件证明△AOC ∽△BOD ,可得∠CAO=∠DBO ,进而可得∠MAB=∠OAB+∠DBO ,最后可得∠AMB=180°-(∠OAB+∠ABM+∠DBO )=90°;(3)分两种情况讨论,根据题(2),同理可得OAC OBD △△,90AMB ∠=︒,3AC BD=,设BD=x ,则3AC x = 用x 表示出AM 、BM 的长,在Rt AMB 中,根据勾股定理222AM BM AB +=列出方程,求解即可. 【详解】 解:(1)①如图1,∵∠AOB=∠COD=40°,∴∠COA=∠DOB ,∵OC=OD ,OA=OB ,∴△COA ≌△DOB (SAS ),∴AC=BD ,∴AC BD=1, ②∵△COA ≌△DOB ,∴∠CAO=∠DBO ,∵∠AOB=40°,∴∠OAB+∠ABO=140°,在△AMB 中,∠AMB=180°﹣(∠CAO+∠OAB+∠ABD )=180°﹣(∠DBO+∠OAB+∠ABD )=180°﹣140°=40°,(2)如图2,AC BD3∠AMB=90°,理由是:在Rt △COD 中,∠DCO=30°,∠DOC=90°, ∴3tan 303OD OC =︒=, 同理得:3tan 303OB OA =︒=, ∴OD OB OC OA=, ∵∠AOB=∠COD=90°,∴∠AOC=∠BOD ,∴△AOC ∽△BOD ,∴AC OC BD OD==3,∠CAO=∠DBO , 在△AMB 中,∠AMB=180°﹣(∠MAB+∠ABM )=180°﹣(∠OAB+∠ABM+∠DBO )=90°;(3)AC 的长为23或43.①如图,点C 与点M 重合,同理可得:OAC OBD △△,90AMB ∴∠=︒,3AC BD =设BD=x ,则3AC x =,在Rt ODC 中,30OCD ∠=︒,OD=2,4CD ∴=,在Rt AOB 中,30OAB ∠=︒,OB=23,43AB ∴=,在Rt AMB 中,222AM BM AB +=, 即222(3)(4)(43)x x ++=,解得:x=2或-4(舍), AC=323x =;②如图,点C 与点M 重合,同理可得:90AMB ∠=︒,3AC BD =设BD=x ,则3x ,在Rt COD 中, 90OCD ∠=︒,OD=2,4CD ∴=,4BC x =-, 在Rt AOB 中,30OAB ∠=︒,3OB = 243AB OB ∴==,在Rt AMB 中,222AM BM AB +=,即222(3)(4)(43)x x +-=,解得:x=4或-2(舍),343x =综上所述,AC 的长为2343【点睛】本题主要考查三角形的综合运用,涉及全等三角形与相似三角形的性质和判定、勾股定理、解一元一次方程、图形旋转证明、特殊角的三角函数值等知识点,难度较大,第(1)题证明△COA ≌△DOB 是关键,第(2)题证明△AOC ∽△BOD 是关键,第(3)题要特别注意分情况讨论.3.如图1,在等腰Rt △ABC 中,∠ABC =90°,AB =BC =6,过点B 作BD ⊥AC 交AC 于点D ,点E 、F 分别是线段AB 、BC 上两点,且BE =BF ,连接AF 交BD 于点Q ,过点E 作EH ⊥AF 交AF 于点P ,交AC 于点H .(1)若BF =4,求△ADQ 的面积;(2)求证:CH =2BQ ;(3)如图2,BE =3,连接EF ,将△EBF 绕点B 在平面内任意旋转,取EF 的中点M ,连接AM ,CM ,将线段AM 绕点A 逆时针旋转90°得线段AN ,连接MN 、CN ,过点N 作NR ⊥AC 交AC 于点R .当线段NR 的长最小时,直接写出△CMN 的周长.答案:A解析:(1)1.8;(2)证明见解析;(3)3263351022+. 【分析】(1)利用等腰直角三角形的性质求出1322BD AD CD AC ====积相等和勾股定理分别求出AQ 和QD ,最后利用三角形面积公式即可求解;(2)如图,先作辅助线构造()AEH CFG ASA ∆∆≌,得到AH CG =,再通过转化得到2AH DQ =,最后利用AC ,得到一个相等关系,即()2AH HC BQ QD +=+,利用等式性质即可得到所求;(3)如图,通过做辅助线构造全等三角形确定出当HN ⊥AC ,且N 点位于H 、R 之间时,此时NR 的长最小,接着利用勾股定理和等腰直角三角形的性质,分别求出CM 、MN 、CN 的长,相加即可.【详解】解:6AB BC ==,°90ABC =∠,262AC ==∴又∵AC BD ⊥∴BD 平分AC ,且BD 是∠ABC 的角平分线 ∴1322BD AD CD AC ====Q 点到BA 和BC 边的距离相等; ∵4BF =, ∴6342ABQBFQ S S ∆∆==,∴32AQ FQ =,∵AF ===∴355AQ AF ==,∴5QD ===,∴1 1.825ADQ S ∆=⨯⨯=, ∴△ADQ 的面积为1.8.(2)如图,作CG ⊥AC ,垂足为C ,交AF 的延长线于点G ,∴°90ACG =∠∵°45ACB CAB ==∠∠,∴°45GCB CAB ==∠∠,∵EH ⊥AF ,∴°90EAP AEP +=∠∠,又∵°90EAP AFB +=∠∠∴AEP AFB =∠∠,∴AEP CFG =∠∠∵BE BF =,BA BC =∴AE CF =,在AEH ∆和CFG ∆中,AEH CFG AE CFEAH FCG ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()AEH CFG ASA ∆∆≌∴AH CG =;∵BD ⊥AC ,CG ⊥AC ,∴BD ∥CG ,∵D 点是AC 的中点,且BD ∥CG ,∴DQ 是ACG ∆的中位线,∴12DQ CG =, ∴2DQ CG AH ==; ∵AC =2BD ,∴()2AH HC BQ QD +=+,∵2AH DQ =,∴CH =2BQ .(3)如图①,作AH ⊥AB ,且AH =AB ,∴∠NAH +∠HAM =∠HAM +∠BAM =90°,∴∠BAM =∠NAH ,∵AB =AH ,AM =AN ,∴()ABM AHN SAS ∆∆≌,∴HN =BM ,∵BE =BF =3,∠EBF =90°, ∴232EF BE ==∴由M 点是EF 的中点,可得1322BM EF == ∴32NH =, ∴N 点在以H 点为圆心,322为半径的圆上, 如图②,当HN ⊥AC ,且N 点位于H 、R 之间时,此时NR 的长最小, 为32NR HR HN HR =-=-∵∠BAC =45°,∴∠HAC =45°,∴∠AHN =45°,HR =AR ,∵222HR AR AH +=, ∴322HR AR ===, ∴323222NR HR =-=, ∵262AC AB ==∴32CR AC AR =-=, ∴()22333221022CN AN ⎛⎫==+= ⎪⎝⎭, ∵∠MAN =90°,AM =AN ,∴235MN AN ==,∴∠ABM =45°,∴∠EBM =45°,∴F 点在BA 上,E 点在CB 延长线上,如图,作MP ⊥EC ,垂足为P ,∴1322BP MP EB ===, ∴315622PC PB BC =+=+=, ∴223262MC MP PC =+=, ∴3263351022MC MN CN ++=++, ∴△CMN 的周长为3263351022++.【点睛】本题综合考查了等腰直角三角形的性质、全等三角形的判定与性质、旋转的性质、勾股定理、圆等知识,要求学生熟练掌握相关概念并能灵活应用它们,本题的综合性较强,难点在于作辅助线构造全等三角形以及线段之间的关系转化等,考查了学生综合分析和推理论证以及计算的能力,本题属于压轴题,蕴含了数形结合和转化的思想方法等.4.在平面直角坐标系中,点A 在y 轴正半轴上,点B 在x 轴负半轴上,BP 平分∠ABO .(1)如图1,点T在BA延长线上,若AP平分∠TAO,求∠P的度数;(2)如图2,点C为x轴正半轴上一点,∠ABC=2∠ACB,且P在AC的垂直平分线上.①求证:AP//BC;②D是AB上一点,E是x轴正半轴上一点,连接AE交DP于H.当∠DHE与∠ABE满足什么数量关系时,DP=AE.给出结论并说明理由.答案:D解析:(1)45°;(2)①见解析;②∠DHE+∠ABE=180°,理由见解析【分析】(1)由三角形的外角性质和角平分线的性质可得∠AOB=2∠P=90°,可求解;(2)①过点P作PE⊥AB交BA延长线于E,过点P作PF⊥BC于F,连接PC,由角平分线的性质可得PE=PF,由垂直平分线的性质可得PA=PC,由“HL”可证Rt△APE≌Rt△CPF,可得∠EPA=∠CPF,由四边形内角和定理可得∠EBF+∠EPF=180°,由角的数量关系可证∠ACB=∠PAC,由平行线的判定可证AP∥BC;②如图3,在OE上截取ON=OB,连接AN,通过证明△ADP≌△NEA,可得DP=AE.【详解】解:(1)∵BP平分∠ABO,AP平分∠TAO,∴∠PBT=12∠ABO,∠TAP=12∠TAO,∵∠TAO=∠ABO+∠AOB,∠TAP=∠P+∠ABP,∴∠AOB=2∠P=90°,∴∠P=45°;(2)①如图2,过点P作PE⊥AB交BA延长线于E,过点P作PF⊥BC于F,连接PC,又∵PB平分∠ABC,∴PE=PF,∵P 在AC 的垂直平分线上, ∴PA =PC , ∴∠PAC =∠PCA , 在Rt △APE 和Rt △CPF 中,AP PCPE PF =⎧⎨=⎩, ∴Rt △APE ≌Rt △CPF (HL ), ∴∠EPA =∠CPF , ∴∠EPF =∠APC ,在四边形BEPF 中,∠EBF+∠BEP+∠EPF+∠PFB =180°, ∴∠EBF+∠EPF =180°, ∴∠ABC+∠APC =180°, ∵∠APC+∠PAC+∠PCA =180°, ∴∠ABC =∠PAC+∠PCA =2∠PAC , ∵∠ABC =2∠ACB , ∴∠ACB =∠PAC , ∴AP ∥BC ;②当∠DHE+∠ABE =180°时,DP =AE ,理由如下:如图3,在OE 上截取ON =OB ,连接AN ,∵OB =ON ,AO ⊥BE , ∴AB =AN , ∴∠ABN =∠ANB , ∵AP ∥BE ,BP 平分∠ABE ,∴∠APB =∠PBE =∠ABP ,∠ABN+∠BAP =180°, ∴AP =AB , ∴AP =AN ,∵∠ANB+∠ANE =180°, ∴∠BAP =∠ANE ,∵∠DHE+∠ABE =180°,∠DHE+∠ABE+∠BDH+∠BEH =360°, ∴∠BDH+∠BEH =180°, ∵∠ADP+∠BDP =180°,∴∠ADP =∠AEN , 在△ADP 和△NEA 中,DAP ANE ADP AEN AP AN ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ADP ≌△NEA (AAS ), ∴DP =AE . 【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,角平分线的性质,线段垂直平分线的性质,四边形内角和定理等知识,添加恰当辅助线构造全等三角形是本题的关键. 5.如图,直线y =﹣x +c 与x 轴交于点B (3,0),与y 轴交于点C ,过点B ,C 的抛物线y =﹣x 2+bx +c 与x 轴的另一个交点为A .(1)求抛物线的解析式和点A 的坐标;(2)P 是直线BC 上方抛物线上一动点,PA 交BC 于 D .设t =PDAD,请求出t 的最大值和此时点P 的坐标;(3)M 是x 轴上一动点,连接MC ,将MC 绕点M 逆时针旋转90°得线段ME ,若点E 恰好落在抛物线上,请直接写出此时点M 的坐标.答案:A解析:(1)y =﹣x 2+2x +3,A (﹣1,0);(2)t 的最大值为916,此时P (32,154);(3)M 933-,0933+0). 【分析】(1)利用待定系数法解决问题即可;(2)连接AC ,PC ,PB ,过点A 作AE ⊥BC 于E ,过等P 作PF ⊥BC 于F .设P (m ,﹣m 2+2m +3).利用相似三角形的性质构建二次函数解决问题即可;(3)过点E 作EH ⊥x 轴于H .设M (m ,0),利用全等三角形的性质求出点E 的坐标(用m 表示),再利用待定系数法解决问题即可. 【详解】解:(1)∵直线y =﹣x +c 与x 轴交于点B (3,0),与y 轴交于点C , ∴0=﹣3+c ,解得c =3,∴C(0,3),∵抛物线经过B,C,∴9303b cc-++=⎧⎨=⎩,解得23bc=⎧⎨=⎩,∴抛物线的解析式为y=﹣x2+2x+3,令y=0,得到﹣x2+2x+3=0,解得x=﹣1或3,∴A(﹣1,0);(2)如图,连接AC,PC,PB,过点A作AE⊥BC于E,过点P作PF⊥BC于F.设P(m,﹣m2+2m+3).∵AE∥PF,∴△PFD∽△AED,∴PDAD =PFAE,∵S△PBC=12•BC•PF,S△ACB=12•BC•AE,∴PDAD =PBCABCSS∆∆,∵S△ABC=12•AB•OC=12×4×3=6,∴t=PDAD =6PBCS∆=211133(23)332226m m m⨯⨯+⨯⨯-++-⨯⨯=﹣14m2+34m=﹣14(m﹣32)2+916,∵﹣14<0,∴m=32时,t有最大值,最大值为916,此时P(32,154);(3)如图,过点E作EH⊥x轴于H,∵∠COM =∠EHM =∠CME =90°,∴∠EMH +∠CMH =90°,∠EMH +∠MEH =90°, ∴∠MEH =∠CMO , ∵MC =ME ,∴△COM ≌△MHE (AAS ),∴OC =MH =3,OM =EH ,设M (m ,0),则E (m ﹣3,﹣m ),把E (m ﹣3,﹣m )代入y =﹣x 2+2x +3,可得﹣(m ﹣3)2+2(m ﹣3)+3=﹣m , 整理得,m 2﹣9m +12=0, 解得m =9332-或9332+, ∴M (9332-,0)或(9332+,0). 【点睛】本题考查的是二次函数综合题,涉及全等三角形的性质和判定,相似三角形的性质和判定,解题的关键是利用数形结合的思想,在二次函数图象上构造全等三角形或相似三角形,利用几何的性质进行点坐标的求解.6.问题:如图(1),点M 、N 分别在正方形ABCD 的边BC 、CD 上,∠MAN =45°,试判断 BM 、MN 、ND 之间的数量关系. (1)研究发现如图1,小聪把△ADN 绕点A 顺时针旋转90°至△ABG ,从而发现BM 、MN 、DN 之间的数量关系为 (直接写出结果,不用证明) (2)类比引申如图2,在(1)的条件下,AM 、AN 分别交正方形ABCD 的对角线BD 于点E 、F .已知EF=5,DF=4.求BE的长.(3)拓展提升如图3,在(2)的条件下,AM、AN分别交正方形ABCD的两个外角平分线于Q、P,连接PQ.请直接写出以BQ、PQ、DP为边构成的三角形的面积.答案:B解析:(1)BM+DN=MN,理由见解析;(2)BE=3;(3)以BQ、PQ、DP为边构成的三角形的面积为36.【分析】(1)结论是:BM+DN=MN,如图1,利用三角形AND旋转90º得三角形ABG,∠DAN=∠BAG,可证∠GAM=∠GAB+∠BAM=∠MAN,利用SAS证△AMN≌△AMG即可;(2)如图2,按同样方法△AFD顺时针旋转90º,使AD与AB重合,得△ABF′,连结EF′,△BEF′是直角三角形,用勾股定理求EF′=5,再证△AEF≌△AEF即可;(3)如图3,由(2)可得BD=12,可求正方形边长,构建△P′AQ,P′B=DP,将△ADP顺时针转90º,AD与AB重合,得△BQP′,连OP′,可证△BQP′是直角三角形,可证PQ=P′Q,再证△ABQ∽△PDA,将△P′BQ面积=12BQ•BP′=12BQ•DP=12AD•AB可求.【详解】(1)如图1,BM+DN=MN,理由如下:∵四边形ABCD是正方形,∴AB=AD,∠D=∠ABC=∠BAD=90°,小聪把△ADN绕点A顺时针旋转90°至△ABG,由旋转可得:BG=DN,AN=AG,∠1=∠2,∠ABG=∠D=90°,∴∠ABG+∠ABM=90°+90°=180°,因此,点G,B,M在同一条直线上,∵∠MAN=45°,∴∠2+∠3=∠BAD﹣∠MAN=90°﹣45°=45°,∵∠1=∠2,∴∠1+∠3=45°,∴∠GAM=∠MAN,∵AM=AM,∴△AMN≌△AMG(SAS),∴MN=GM,∵GM =BM +BG =BM +DN , ∴BM +DN =MN ; 故答案为:BM +DN =MN ;(2)如图2,把△ADF 绕点A 顺时针旋转90°至△ABF ',连接EF ',∴AF ′ =AF ,∠DAF =∠BAF ',∠ABF ′ =∠ADF =45°,BF ′ =DF =4, ∵∠ABE =45°,∴∠EBF ′ =45°+45°=90°, ∵AE =AE ,同理得△EAF ≌△EAF '(SAS ), ∴EF '=EF =5,在Rt △EBF '中,由勾股定理得:BE =()()2222EF +BF =5-4=3''=3;(3)由(2)知:BE =3,EF =5,DF =4, ∴BD =3+4+5=12,由勾股定理得:AB 2+AD 2=BD 2, ∵AB =AD , ∴AB 2=72,如图3,把△ADP 绕点A 顺时针旋转90°至△ABP ',连接BP ′,则∠ABP′=∠ADP ,PD =P ′B ,AP =AP ′,∵AM 、AN 分别交正方形ABCD 的两个外角平分线于Q 、P , ∴∠ADP =∠ABQ =135°, ∴∠DAP +∠APD =45°, ∵∠DAP +∠BAQ =45°, ∴∠BAQ =∠APD ,∴△ADP ∽△QBA ,∴AD PD=BQ AB, ∴BQ •PD =AD •AB =72, ∵∠ABP '=∠ABQ =135°, ∴∠QBP '=360°﹣135°﹣135°=90°, ∴S △BP 'Q =12BQ•BP′=12BQ•DP =12×72=36, ∵AP =AP ',∠PAQ =∠P 'AQ ,AQ =AQ , ∴△QAP ≌△QAP '(SAS ), ∴PQ =P 'Q ,∴以BQ 、PQ 、DP 为边构成的三角形的面积为36. 【点睛】本题是感知,探究,创新新题型,主要考查了学生对正方形的性质,旋转变换,勾股定理及全等三角形与相似三角形的判定方法的综合运用.关键是灵活掌握所学知识,同时会从感知中学到方法,结合下一图形,找到解决问题的方法,以及突破口,在创新中,注意把给出的问题进行转化,利用转化思想来解决.7.如图,在四边形ABCD 中,AB AC =,AD 是对角线,60BAC ∠=︒,4B C ADB BAC ∠+∠+∠=∠,(1)求ADC ∠的度数;(2)若AD BD CD =+,求证:AD 平分BDC ∠;(3)在(2)的条件下,E 、F 分别在AC 、AB 上,连接BE 、CF ,交于点P ,使得BPC BDC ∠=∠,若7BD EF ==,15AD =,求EFP ∆的面积答案:A解析:(1)=60∠︒ADC ;(2)证明见详解;(3)4003129. 【分析】(1)先由四边形内角和得到++300B C BDC ∠∠∠=︒,再由4B C ADB BAC ∠+∠+∠=∠可得答案;(2)把ABD △绕点A 逆时针旋转60︒得到ACE △,由(1)及题意易得D 、C 、E 三点共线,从而得到ADE 是等边三角形,由等边三角形的性质及旋转的性质易得60ADB E ∠=∠=︒,故得证;(3)过点B 、点F 分别作BG ⊥CD ,FH ⊥AC ,分别交CD 的延长线于点G 、AC 于点H ,连接BC ,由(2)及题意易得DC=8,由BPC BDC ∠=∠易得EBC FCA ∠=∠,进而得到AFC CEB △≌△,设AF=CE=x ,根据勾股定理得到AF 、CE 、BC 的长,最后根据BFE BPC 、的面积比等于FP 与PC 的比,进而求解即可. 【详解】(1)解:=60BAC ∠︒,∴++36060300B C BDC ∠∠∠=︒-︒=︒, 又BDC ADB ADC ∠=∠+∠,4B C ADB BAC ∠+∠+∠=∠,∴30024060ADC ∠=︒-︒=︒; (2)证明:把ABD △绕点A 逆时针旋转60︒得到ACE △,由(1)得:∴AD=AE ,BD=CE ,=ADC=60DAE ∠∠︒AD BD CD =+,DE=DC+CE ,∴D 、C 、E 三点共线,∴ADE 是等边三角形,∴60ADB E ∠=∠=︒, ∴60ADB ADC ∠=∠=︒,∴AD 平分BDC ∠; (3)解:过点B 、点F 分别作BG ⊥CD ,FH ⊥AC ,分别交CD 的延长线于点G 、AC 于点H ,连接BC ,由题意及(2)可得:ABC 是等边三角形,120BDC ∠=︒,∴AB=AC=BC ,60BDG ∠=︒,7BD EF ==,15AD =,∴72DG =,BG =,DC=AD-BD=8, ∴723822GC GD DC =+=+=,在Rt BGC △中,13BC ===, 又=120BPC BDC ∠=∠︒,∴18012060PBC PCB ∠+∠=︒-︒=︒,60ECP PCB ∠+∠=︒,∴=ECP EBC ∠∠,=60,FAC BCA AC BC ∠∠=︒=,∴AFC CEB △≌△,∴CE=AF ,设13,131322CE AF x AE x AH x FH x EH x ==∴=-==∴=-,,,,∴在Rt FHE 中,222FH EH EF +=即22231372x ⎛⎫+-= ⎪⎝⎭⎝⎭,解得125,8x x ==,①当CE=AF=5时,则AE=8,∴11132224BECAFCSSAC FH ==⋅=⨯⨯=16944ABEABCBECSSS =-=-=∴BFE ABEAFESSS=-==设BFPEFPBPCEPCSa Sb Sc Sd ====,,,,则有:a cb d FP PC ==∶∶∶,,BFE BFPFEP BEC BPCEPC S SSSSS=+=+,∴BFEBECSSFP PC =∶∶,∴6465BFE BECSS FP PC =∶∶,又1152224FECSCE FH =⋅=⨯⨯=,∴64641291294129EFP FECSS ==⨯=; ②当CE=AF=8时,AE=5,则有:∴111322BEAAFCSSAC FH ==⋅=⨯=,1694CBEABCBECSSS =-==∴65325310344BFEABEAFESSS=-=-=由①可得:25325=3=4104BFEBECSS FP PC =∶∶∶26, 又1184316322FECSCE FH =⋅=⨯⨯= ∴25254003163129129129EFPFECSS ==⨯=; 综上所述:4003129EFPS =. 【点睛】本题主要考查三角形与四边形的综合问题,主要是利用全等三角形、等边三角形、三角形面积比的转换及勾股定理,熟练掌握各个知识点是解题的关键,尤其是第三问的面积转换问题是本题的难点. 8.如图,抛物线y =24x 2+2x ﹣62交x 轴于A 、B 两点(点A 在点B 的左侧),交y 轴于C 点,D 点是该抛物线的顶点,连接AC 、AD 、CD . (1)求△ACD 的面积;(2)如图,点P 是线段AD 下方的抛物线上的一点,过P 作PE ∥y 轴分别交AC 于点E ,交AD 于点F ,过P 作PG ⊥AD 于点G ,求EF+52FG 的最大值,以及此时P 点的坐标; (3)如图,在对称轴左侧抛物线上有一动点M ,在y 轴上有一动点N ,是否存在以BN 为直角边的等腰Rt △BMN ?若存在,求出点M 的横坐标,若不存在,请说明理由.答案:A解析:(1)24;(2)最大值为22,点P (﹣2,﹣1522);(3)存在,点M 的2262﹣6. 【分析】(1)先求出抛物线与坐标轴的交点坐标和顶点坐标,再用待定系数法求得AC 的解析式,进而求出点N 、D 的坐标,再根据三角形的面积公式求出结果;(2)证明EF+52FG 即为EP 的长度,即可求解; (3)分∠BNM 为直角、∠MBN 为直角,利用三角形全等即可求解. 【详解】 解:(1)令x =0,得202062624y =⨯+⨯-=-, ∴C (0,﹣62),令y =0,得2226204y x x =+-=, 解得162x =-,222x =,∴A (62-,0),点B (22,0),设直线AC 的解析式为:y =kx+b (k ≠0),则62062k b b ⎧-+=⎪⎨=-⎪⎩, ∴162k b =-⎧⎪⎨=-⎪⎩, ∴直线AC 的解析式为:62y x =--,∵()2222262228244y x x x =+-=+-,∴D (22-,82-),过D 作DM ⊥x 轴于点M ,交AC 于点N ,如图,令22x =-,(226242y =---=-N (22-,42-∴42DN =∴1142622422ACD S DN AO =⋅=⨯=; (2)如图,过点D 作x 轴的平行线交FP 的延长线于点H ,由点A 、D 的坐标得,直线AD 的表达式为:2122y x =--∴tan ∠FDH =2,则sin ∠FDH 2555=, ∵∠HDF+∠HFD =90°,∠FPG+∠PFG =90°,∴∠FDH =∠FPG ,在Rt △PGF 中,PF =FG sin G FP ∠= FG sin FDH ∠255=5FG , 则5FG =EF+PF =EP , 设点P (x ,22224x x +-E (x ,62x -- 则5FG =EF+PF =EP =222262262344x x x x x ⎛--+-=-- ⎝, ∵2<0,故EP 有最大值,此时x =﹣2b a =﹣292 当x =32-2215226242y x x =+-=-, 故点P (32-1522-); (3)存在,理由: 设点M 的坐标为(m ,n ),则222624n m m =+-,点N (0,s ), ①当∠MNB 为直角时,如图,过点N 作x 轴的平行线交过点B 与y 轴的平行线于点H ,交过点M 与y 轴的平行线于点G ,∵∠MNG+∠BNH =90°,∠MNG+∠GMN =90°,∴∠GMN =∠BNH ,∵∠NGM =∠BHN =90°,MN =BN ,∴△NGM ≌△BHN (AAS ),∴GN =BH ,MG =NH , 即22n s -=且m s -=-,联立并解得:226m =-±(舍去正值),故226m =--,则点M (226--,226-); ②当∠NBM 为直角时,如图,过点B 作y 轴的平行线交过点N 与x 轴的平行线于点G ,交过点M 与x 轴的平行线于点H ,同理可证:△MHB ≌△BGN (AAS ), 则BH =NG ,即22n =- 当22n =-时,2222224m m +-=-2226m = 故2226m =M (2226,22-);综上,点M 的横坐标为226-2226.【点睛】本题考查二次函数的综合题,涉及三角形面积的求解,用胡不归原理求最值,等腰直角三角形的存在性问题,解题的关键是需要掌握这些特定题型的特定解法,熟练运用数形结合的思想去解决问题.9.如图,抛物线y =﹣x 2+bx+c 与x 轴交于A ,B 两点,其中A (3,0),B (﹣1,0),与y 轴交于点C ,抛物线的对称轴交x 轴于点D ,直线y =kx+b 1经过点A ,C ,连接CD . (1)求抛物线和直线AC 的解析式:(2)若抛物线上存在一点P ,使△ACP 的面积是△ACD 面积的2倍,求点P 的坐标; (3)在抛物线的对称轴上是否存在一点Q ,使线段AQ 绕Q 点顺时针旋转90°得到线段QA 1,且A 1好落在抛物线上?若存在,求出点Q 的坐标;若不存在,请说明理由.答案:A解析:(1)2y x 2x 3=-++;3y x =-+ ;(2)(﹣1,0)或(4,﹣5);(3)存在;(1,2)和(1,﹣3)【分析】(1)将点A ,B 坐标代入抛物线解析式中,求出b ,c 得出抛物线的解析式,进而求出点C 的坐标,再将点A ,C 坐标代入直线AC 的解析式中,即可得出结论;(2)利用抛物线的对称性得出BD =AD ,进而判断出△ABC 的面积和△ACP 的面积相等,即可得出结论;(3)分点Q 在x 轴上方和在x 轴下方,构造全等三角形即可得出结论.【详解】解:(1)把A (3,0),B (﹣1,0)代入y =﹣x 2+bc+c 中,得93010b c b c -++=⎧⎨--+=⎩, ∴23b c =⎧⎨=⎩, ∴抛物线的解析式为y =﹣x 2+2x+3,当x =0时,y =3,∴点C 的坐标是(0,3),把A (3,0)和C (0,3)代入y =kx+b 1中,得11303k b b +=⎧⎨=⎩, ∴113k b =-⎧⎨=⎩∴直线AC的解析式为y=﹣x+3;(2)如图,连接BC,∵点D是抛物线与x轴的交点,∴AD=BD,∴S△ABC=2S△ACD,∵S△ACP=2S△ACD,∴S△ACP=S△ABC,此时,点P与点B重合,即:P(﹣1,0),过B点作PB∥AC交抛物线于点P,则直线BP的解析式为y=﹣x﹣1①,∵抛物线的解析式为y=﹣x2+2x+3②,联立①②解得,1xy=-⎧⎨=⎩或45xy=⎧⎨=-⎩,∴P(4,﹣5),∴即点P的坐标为(﹣1,0)或(4,﹣5);(3)如图,①当点Q在x轴上方时,设AC与对称轴交点为Q',由(1)知,直线AC的解析式为y=﹣x+3,当x=1时,y=2,∴Q'坐标为(1,2),∵Q'D=AD=BD=2,∴∠Q'AB=∠Q'BA=45°,∴∠AQ'B=90°,∴点Q'为所求,②当点Q在x轴下方时,设点Q(1,m),过点A1'作A1'E⊥DQ于E,∴∠A1'EQ=∠QDA=90°,∴∠DAQ+∠AQD=90°,由旋转知,AQ=A1'Q,∠AQA1'=90°,∴∠AQD+∠A1'QE=90°,∴∠DAQ=∠A1'QE,∴△ADQ ≌△QEA 1'(AAS ),∴AD =QE =2,DQ =A 1'E =﹣m ,∴点A 1'的坐标为(﹣m+1,m ﹣2),代入y =﹣x 2+2x+3中,解得,m =﹣3或m =2(舍),∴Q 的坐标为(1,﹣3),∴点Q 的坐标为(1,2)和(1,﹣3).【点睛】本题考查的是二次函数的综合题,涉及解析式的求解,与三角形面积有关的问题,三角形“k”字型全等,解题的关键是利用数形结合的思想,设点坐标并结合几何图形的性质列式求解.10.回答下列问题:(1)(发现)如图1,点A 为线段BC 外一动点,且4BC =,2AB =.填空:线段AC 的最大值为 .图1(2)(应用)点A 为线段BC 外一动点,且3BC =,2AB =,如图2所示,分别以AB ,AC 为边,作等腰直角ABD △和等腰直角ACE ,连接CD ,BE .图2①证明:BE DC =.②求线段BE 的最大值.(3)(拓展)如图3,在平面直角坐标系中,直线l ;4y x =+与坐标轴交于点A 、B 两点,点C 为线段AB 外一动点,且2CB =,以AC 为边作等边ACD △,连接BD ,求线段BD 长的最大值并直接写出此时点C 的横坐标.图3答案:A解析:(1)6(2)①证明见解析. ②322+(3)42226-26+ 【分析】(1)根据点A 位于CB 的延长线上时,线段AC 的长取得最大值,即可得到结论;(2) ①由“SAS” 可证△DAC ≌△BAE ,可得BE=DC ;②由于线段长BE 的最大值=线段DC 的最大值,根据(1)中的结论即可得到结果,(3)以BC 为边作等边三角形BCE ,可以证明△ACE ≌△DCB(SAS) ,从而得到BD=AE ,BE=BC ,由AE≤AB+BE ,当且仅当A 、B 、E 三点共线时,AE 取得最大值,即BD 取得最大值,当BD 取得最大值时,①当C 在直线AB 的上方时,过C 作CH ⊥y 轴于H ,作BC 的垂直平分线交BH 于N ,求出CH 的长度,即可求出点C 的横坐标,②当C 在直线AB 的下方时,按同①的方法也可以求出点C 的横坐标.【详解】(1)当A 在选段BC 的延长线上时, max 6AC AB BC =+=.(2)①∵等腰直角AEC 与等腰直角三角形ABD ,∴AD AB =,AE AC =,90DAB EAC ∠=∠=︒,∴DAB BAC EAC BAC ∠+∠=∠+∠,∴DAC EAB ∠=∠,在DAC △和BAE 中,DA BA DAC BAE AB AE =⎧⎪∠=∠⎨⎪=⎩,∴()SAS DAC BAE ≌△△, ∴BE CD =.②由①可知,BE DC =,∵线段BE 的最大值即线段DC 的最大值. 在等腰直角ABD △中,222BD AB ==,∵CD BC BD ≤+,∴当点D 在CB 的延长线上时, CD 取得最大值为322+.∴线段BE 的最大值为322+.(3)如图,以BC 为边作等边三角形BCE ,则BC CE =,60BCE ∠=︒.∵60ACD ∠=︒,∴ACD ECD BCE ECD ∠-∠=∠-∠, ∴ACE DCB ∠=∠.在ACE 与DCB 中,AC DC ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ACE DCB ≌△△, ∴BD AE =.对于一次函数4y x =+,令0x =,则4y =, ∴()0,4B ,令0y =,则4x =-,∴()4,0A -.∴224442AB =+=又∵2BE BC ==,∴AE AB BE ≤+,∴当且仅当A 、B 、E 三点共线时, AE 取得最大值,即BD 取得最大值为422+;当BD 取得最大值时,①当C 在直线AB 的上方时过C 作CH y ⊥轴于H ,∵45ABO HBE ∠=∠=︒,60CBE ∠=︒, ∴15CBH CBE HBE ∠=∠-∠=︒, 作BC 的垂直平分线交BH 于N ,∴CN BN =,15NCB NBC ∠=∠=︒, ∴30CNB ∠=︒,在Rt CHN △中,设CH x =.则3HN x =, 2CN x =,∴2BN x =,∴)32BH HN BN x =+=, 在Rt BHC △中,22222HC BH BC +==, ∴)222322x x ⎡⎤+=⎣⎦, 整理得(227434x x ++=, 223x =,)12312x =,)22312x =-(舍), ∴62CH -=∴点C 的横坐标为262-. ②当C 在直线AB 的下方时,过C 作CL ⊥y 轴于L ,∵∠ABO=45°,∠CBE=60°,∴∠CBL=180°-∠CBE−∠ABO=75°,∴∠BCL=15°,作BC 的垂直平分线交BL 于M ,∴CM=BM ,∠MCB=∠MBC=15°,∴∠LMB=30°,在Rt △CLB 中,设BL=y .则3,BM=2y , ∴CM=2y ,∴3+2)y ,在Rt △BLC 中,BL 2+CL 2=BC 2=22,∴)222322y y ⎡⎤+=⎣⎦, 整理得(227434y y ++=, 223y = )1231y =,)2231y =(舍去), 622BL =∴CL=)32BL 26+所以点C 的横坐标为:262+ 综合以上可得点C 的横坐标为:262-或 262+ 【点睛】 本题是三角形综合题,考查了全等三角形的判.定和性质,等腰直角三角形的性质,最大值问题,旋转的性质正确的作出辅助线构造全等三角形是解题的关键.11.如图,在等边三角形ABC 中,点D 是射线CB 上一动点,连接DA ,将线段DA 绕点D 逆时针旋转60°得到线段DE ,过点E 作EF ∥BC 交直线AB 于点F ,连接CF .(1)如图1,若点D 为线段BC 的中点,则四边形EDCF 是 ;(2)如图2,若点D 为线段CB 延长线上任意一点,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;(3)若点D 为射线CB 上任意一点,当∠DAB =15°,△ABC 的边长为2时,请直接写出线段BD 的长.答案:A解析:(1)平行四边形;(2)成立,见解析;(3)423-或31-.【分析】(1)证明△ADB ≌△DEO (AAS )和四边形EOBF 为平行四边形,进而求解;(2)证明△OED ≌△DAC (SAS ),则∠EOD =∠ACD =60°=∠ABC ,故OE ∥AB ,进而求解;(3)分点D 在线段BC 上、点D (D ′)在BC 的延长线上两种情况,利用勾股定理和等腰直角三角形的性质分别求解即可.【详解】解:(1)过点E 作DE 的垂线交CB 的延长线于点O ,设BA 交ED 于点R ,∵点D为线段BC的中点,则AD⊥BC且∠BAD=30°,∵∠ADE=60°,∴∠EDB=∠ADB﹣ADE=90°﹣60°=30°,∵EF∥BC,∴∠EFD=∠ABC=60°,∠FED=∠EDO=30°,∴∠ERF=90°,∴DE⊥AB,∵AD=ED,∠BAD=∠EDO=30°,∠ADB=∠DEO=90°,∴△ADB≌△DEO(AAS),∴OE=BD=12BC=12AB,则OB=OD﹣BD=AB﹣12AB=12AB,∴OB=BD=CD,∵OE⊥DE,DE⊥AB,∴OE∥AB,∵EF∥BC,∴四边形EOBF为平行四边形,∴EF=OB=CD,而EF∥CD,∴四边形EFCD为平行四边形,故答案为:平行四边形;(2)如图2,在CD的延长线上截取DO=AC,连接OE,设∠ADC的度数为α,∵∠EDO=180°﹣∠EDA﹣∠ADC=180°﹣60°﹣α=120°﹣α,∠DAC=180°﹣∠ACD﹣∠ADC=120°﹣α=∠EDO,而AC=OD,DE=AD,∴△OED≌△DAC(SAS),∴∠EOD=∠ACD=60°=∠ABC,∴OE∥AB,而EF∥BC,∴四边形EFCD为平行四边形;(3)①当点D在线段BC时,过点A 作AH ⊥BC ,则∠BAH =30°,而∠DAB =15°,BH =12BC =1, 即BD 是∠BAH 的角平分线,过点D 作DG ⊥AB 于点G ,设DH =x ,则DG =DH =x ,BD =BH ﹣DH =1﹣x ,在△BDG 中,∠BDG =30°,则BG =12BD =12x - 由勾股定理得:()21x -=212x -⎛⎫ ⎪⎝⎭+2x ,解得:x =233-, ∴BD =1﹣x =423-,②当点D (D ′)在BC 的延长线上时,∵∠BAD ′=15°,∴∠D ′AH =30°+15°=45°,则D ′H =AH =2213-=,∴BD ′=D ′H ﹣BH =31-;综上,BD 的长度为423-或31-.【点评】本题是四边形综合题,主要考查了平行四边形性质、三角形全等、等边三角形性质等知识点,综合性强,难度较大.12.如图,△ABC 中,O 是△ABC 内一点,AO 平分∠BAC ,连OB ,OC .(1)如图1,若∠ACB =2∠ABC ,BO 平分∠ABC ,AC =5,OC =3,则AB = ; (2)如图2,若∠CBO +∠ACO =∠BAC =60°,求证:BO 平分∠ABC ;(3)如图3,在(2)的条件下,若BC =3B 绕点O 逆时针旋转60°得点D ,直接写出CD 的最小值为 .答案:A解析:(1)8;(2)见解析;(3)33【分析】(1)先补充证明角平分线的性质定理:如图,△ABC中,AD是角平分线,则:BD DC=AB AC .如图1中,延长CO交AB于E,由OA平分∠EAC,推出AEAC=OEOC,推出AEEO=AC OC =53,设AE=5k,OE=3k,利用相似三角形的性质构建方程求出k即可解决问题.(2)如图2中,过点O作EF⊥OA交AB于E,交AC于F,作CG∥EF交AB于G,连接OG.证明△AGO≌△ACO(SAS),推出OG=OC,推出∠OGC=∠OCG,证明O,G,B,C 四点共圆,可得结论.(3)如图3中,以BC为边向上作等边△BCH,连接OH,作HM⊥BC于M.证明△HBO≌△CBD(SAS),推出OH=CD,由(2)可知∠BOC=120°,推出当点O落在HM 上时,OH的值最小.【详解】解:(1)先补充证明角平分线的性质定理:如图,△ABC中,AD是角平分线,则:BD DC=AB AC.理由:过C作CE∥DA,交BA的延长线于E,∵CE∥DA,∴∠1=∠E,∠2=∠3,∠1=∠2,∴∠E=∠3,∴AE=AC,∵BDDC =BAAE,∴BDDC =ABAC.如图1中,延长CO交AB于E,∵OA平分∠EAC,∴AEAC=OEOC,∴AEEO =ACOC=53,设AE=5k,OE=3k,∵OB平分∠ABC,∴OC平分∠ACB,∵∠ACB=2∠ABC,∴∠BCE=12∠ACB=∠EBC,∴EB=EC=3k+3,∵∠ACE=∠ABC,∠CAE=∠BAC,∴△ACE∽△ABC,∴ACAB =AEAC,∴5533k k =55k,解得k=58或﹣1(舍弃),∴AB=8k+3=8.故答案为:8.(2)如图2中,过点O作EF⊥OA交AB于E,交AC于F,作CG∥EF交AB于G,连接OG.∵AO平分∠AEF,∴∠OAE=∠OAF,∵AO=AO,∠AOE=∠AOF=90°,∴△AOE≌△AOF(ASA),∴AE=AF,∵∠EAF=60°,∴△AEF是等边三角形,∴∠AEF=∠AFE=60°=∠FOC+∠FCO,∵∠OBC+∠FCO=60°,∴∠FOC=∠OBC,∵EF∥CG,∴∠AGC=∠AEF=60°,∠ACG=∠AFE=60°,∴∠AGC=∠ACG,∴AG=AC,∵∠GAO=∠CAO,AO=AO,∴△AGO≌△ACO(SAS),∴OG=OC,∴∠OGC=∠OCG,∵∠FOC=∠OCG,∴∠OBC=∠OGC,∴O,G,B,C四点共圆,∴∠ABO=∠OCG,∴∠ABO=∠OBC,∴OB平分ABC.(3)如图3中,以BC为边向上作等边△BCH,连接OH,作HM⊥BC于M.∵△OBD,△BCH都是等边三角形,∴∠HBC=∠OBD=60°,BH=BC,BO=BD,∴∠HBO=∠CBD,∴△HBO≌△CBD(SAS),∴OH=CD,由(2)可知∠BOC=120°,∴当点O落在HM上时,OH的值最小,此时OH=HM﹣OM=33∴CD的最小值为33.故答案为:33【点睛】本题主要考查角平分线、三角形相似的判定和性质、三角形全等的判定和性质、等边三角形等相关知识点,解题关键在于作出辅助线构造相应图形.13.如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是 ,位置关系是 ;(2)探究证明:把△ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由;(3)拓展延伸:把△ADE 绕点A 在平面内自由旋转,若AD =4,AB =10,请直接写出△PMN 面积的最大值.解析:(1)PM =PN ,PM ⊥PN ;(2)△PMN 是等腰直角三角形.理由见解析;(3)S △PMN 最大=492. 【分析】(1)由已知易得BD CE =,利用三角形的中位线得出12PM CE =,12PN BD =,即可得出数量关系,再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠,最后用互余即可得出位置关系;(2)先判断出ABD ACE ∆≅∆,得出BD CE =,同(1)的方法得出12PM BD =,12PN BD =,即可得出PM PN =,同(1)的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠,即可得出结论;(3)方法1:先判断出MN 最大时,PMN ∆的面积最大,进而求出AN ,AM ,即可得出MN 最大AM AN =+,最后用面积公式即可得出结论.方法2:先判断出BD 最大时,PMN ∆的面积最大,而BD 最大是14AB AD +=,即可得出结论.【详解】解:(1)点P ,N 是BC ,CD 的中点,//PN BD ∴,12PN BD =, 点P ,M 是CD ,DE 的中点, //PM CE ∴,12PM CE =,AB AC =,AD AE =,BD CE ∴=,PM PN ∴=,//PN BD ,DPN ADC ∴∠=∠,//PM CE ,DPM DCA ∴∠=∠,90BAC ∠=︒,90ADC ACD ∴∠+∠=︒,90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒,PM PN ∴⊥,故答案为:PM PN =,PM PN ⊥;(2)PMN ∆是等腰直角三角形.由旋转知,BAD CAE ∠=∠,AB AC =,AD AE =,()ABD ACE SAS ∴∆≅∆,ABD ACE ∴∠=∠,BD CE =, 利用三角形的中位线得,12PN BD =,12PM CE =, PM PN ∴=,PMN ∴∆是等腰三角形,同(1)的方法得,//PM CE ,DPM DCE ∴∠=∠,同(1)的方法得,//PN BD ,PNC DBC ∴∠=∠,DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠,MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠,90BAC ∠=︒,90ACB ABC ∴∠+∠=︒,90MPN ∴∠=︒,PMN ∴∆是等腰直角三角形;(3)方法1:如图2,同(2)的方法得,PMN ∆是等腰直角三角形,MN ∴最大时,PMN ∆的面积最大,//DE BC ∴且DE 在顶点A 上面,MN ∴最大AM AN =+,连接AM ,AN ,在ADE ∆中,4AD AE ==,90DAE ∠=︒,22AM ∴=在Rt ABC ∆中,10AB AC ==,52AN =22522MN ∴=最大,222111149(72)22242PMN S PM MN ∆∴==⨯=⨯=最大. 方法2:由(2)知,PMN ∆是等腰直角三角形,12PM PN BD ==, PM ∴最大时,PMN ∆面积最大,∴点D 在BA 的延长线上,14BD AB AD ∴=+=,7PM ∴=,2211497222PMN S PM ∆∴==⨯=最大. 【点睛】此题属于几何变换综合题,主要考查了三角形的中位线定理,等腰直角三角形的判定和性质,全等三角形的判断和性质,直角三角形的性质的综合运用;解(1)的关键是判断出12PM CE =,12PN BD =,解(2)的关键是判断出ABD ACE ∆≅∆,解(3)的关键是判断出MN 最大时,PMN ∆的面积最大.14.如图所示,ABC ∆中,1AB BC ==,90ABC ∠=︒,把一块含30角的直角三角板DEF 的直角顶点D 放在AC 的中点上(直角三角板的短直角边为DF ,长直角边为DE ),将三角板DEF 绕D 点按逆时针方向旋转.。
旋转中的三种全等模型(手拉手、半角、对角互补模型)—2023-2024学年九年级数学上册(解析版)
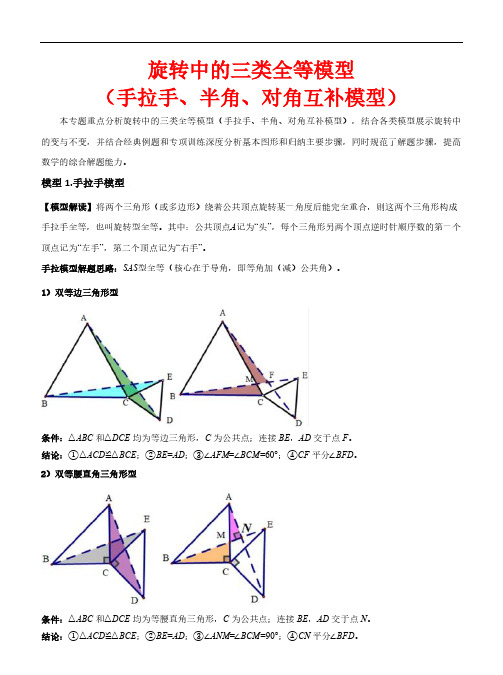
旋转中的三类全等模型(手拉手、半角、对角互补模型)本专题重点分析旋转中的三类全等模型(手拉手、半角、对角互补模型),结合各类模型展示旋转中的变与不变,并结合经典例题和专项训练深度分析基本图形和归纳主要步骤,同时规范了解题步骤,提高数学的综合解题能力。
模型1.手拉手模型【模型解读】将两个三角形(或多边形)绕着公共顶点旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等。
其中:公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
手拉模型解题思路:SAS型全等(核心在于导角,即等角加(减)公共角)。
1)双等边三角形型条件:△ABC和△DCE均为等边三角形,C为公共点;连接BE,AD交于点F。
结论:①△ACD≌△BCE;②BE=AD;③∠AFM=∠BCM=60°;④CF平分∠BFD。
2)双等腰直角三角形型条件:△ABC和△DCE均为等腰直角三角形,C为公共点;连接BE,AD交于点N。
结论:①△ACD≌△BCE;②BE=AD;③∠ANM=∠BCM=90°;④CN平分∠BFD。
3)双等腰三角形型条件:△ABC和△DCE均为等腰三角形,C为公共点;连接BE,AD交于点F。
结论:①△ACD≌△BCE;②BE=AD;③∠ACM=∠BFM;④CF平分∠BFD。
4)双正方形形型条件:△ABCFD和△CEFG都是正方形,C为公共点;连接BG,ED交于点N。
结论:①△△BCG≌△DCE;②BG=DE;③∠BCM=∠DNM=90°;④CN平分∠BNE。
【答案】(1)40;(2)60;(3)【分析】(1)证明△COD是等边三角形,得到∠ODC=60°,即可得到答案;∠=∠ADC-∠ODC求出答案;(3)由△BOC≌△ADC,推出∠ADC=∠BOC=150°,AD=OB=8,根据(2)利用ODA△COD 是等边三角形,得到∠ODC=60°,OD=4OC =,证得△AOD 是直角三角形,利用勾股定理求出.【详解】(1)解:∵CO=CD ,∠OCD=60°,∴△COD 是等边三角形;∴∠ODC=60°,∵∠ADC=∠BOC=100α=︒,∴ODA ∠=∠ADC -∠ODC=40°,故答案为:40;(2)∵∠ADC=∠BOC=120α=︒,∴ODA ∠=∠ADC -∠ODC=60°,故答案为:60;(3)解:当150α=︒,即∠BOC=150°,∴△AOD 是直角三角形.∵△BOC ≌△ADC ,∴∠ADC=∠BOC=150°,AD=OB=8,又∵△COD 是等边三角形,∴∠ODC=60°,OD=4OC =,∴∠ADO=90°,即△AOD 是直角三角形,∴OA =故答案为:【点睛】本题以“空间与图形”中的核心知识(如等边三角形的性质、全等三角形的性质与证明、直角三角形的判定、多边形内角和等)为载体,内容由浅入深,层层递进.试题中几何演绎推理的难度适宜,蕴含着丰富的思想方法(如运动变化、数形结合、分类讨论、方程思想等),能较好地考查学生的推理、探究及解决问题的能力. 备用图【答案】(1)△BEF 是等边三角形(2)证明见解析(3)131−【分析】(1)根据旋转即可证明△BEF 是等边三角形;(2)由△EBF 是等边三角形,可得FB=EB ,再证明∠FBA=∠EBC ,又因为AB=BC ,所以可证明△FBA ≌△EBC ,进而可得AF=CE ;(3)当点D ,E ,F 在同一直线上时,过B 作BM ⊥EF 于M ,再在Rt △BMD 中利用勾股定理列方程求解即可.(1)∵将线段EB 绕点E 顺时针旋转60°得到线段EF ,∴EB=EF ,60FEB =︒∠∴△BEF 是等边三角形(2)∵等边△ABC 和△BEF ∴BF=BE ,AB=BC ,60EBF ABC ∠=∠=︒∴EBF ABE ABC ABE ∠+∠=∠+∠即∠FBA=∠EBC∴△FBA ≌△EBC (SAS )∴AF=CE(3)图形如图所示:过B 作BM ⊥EF 于M ,∵△BEF 是等边三角形∴2BE EM =,BM =∵点D 是AB 的中点,∴142BD AB == 在Rt △BMD 中,222BM DM BD +=∵DE=2∴222)(2)4EM ++=解得EM 或EM =(舍去)∴21BE EM == 【点睛】本题考查了旋转的性质,全等三角形的判定和性质,勾股定理的运用,旋转的性质,等边三角形的判定和性质,解一元二次方程,利用手拉手模型构造全等三角形是解题的关键.例3.(2022·吉林·九年级期末)如图①,在ABC 中,90C ∠=︒,AC BC ==点D ,E 分别在边AC ,BC 上,且CD CE =AD BE =,AD BE ⊥成立.(1)将CDE △绕点C 逆时针旋转90︒时,在图②中补充图形,并直接写出BE 的长度;(2)当CDE △绕点C 逆时针旋转一周的过程中,AD 与BE 的数量关系和位置关系是否仍然成立?若成立,请你利用图③证明,若不成立请说明理由;(3)将CDE △绕点C 逆时针旋转一周的过程中,当A ,D ,E 三点在同一条直线上时,请直接写出AD 的长度.【答案】(1)补充图形见解析;BE =(2)AD BE =,AD BE ⊥仍然成立,证明见解析;(3)1AD或1=AD .【分析】(1)根据旋转作图的方法作图,再根据勾股定理求出BE 的长即可;(2)根据SAS 证明E ACD BC ≅∆∆得AD=BE ,∠1=∠2,再根据∠1+∠3+∠4=90°得∠2∠3+∠4=90°,从而可得出结论;(3)分两种情况,运用勾股定理求解即可.【详解】解:(1)如图所示,根据题意得,点D 在BC 上,∴BCE ∆是直角三角形,且由勾股定理得,BE ==(2)AD BE =,AD BE ⊥仍然成立. 证明:延长AD 交BE 于点H ,∵90ACB DCE ∠=∠=︒,ACD ACB BCD ∠=∠−∠,BCE DCE BCD ∠=∠−∠,∴ACD BCE ∠=∠,又∵CD CE =,AC BC =,∴ACD BCE ≅△△,∴AD BE =,12∠=∠,在Rt ABC 中,13490∠+∠+∠=︒,∴23490∠+∠+∠=︒,∴90AHB ∠=︒,∴AD BE ⊥.(3)①当点D 在AC 上方时,如图1所示,同(2)可得ACD BCE ≅△△∴AD=BE 同理可证BE AE ⊥在Rt △CDE 中,CD CE =2=在Rt △ACB 中,AC BC =AB ==设AD=BE=x ,在Rt △ABE 中,222BE AE AB +=∴222(2)x x ++=解得,1x ∴ 1AD =②当点D 在AC 下方时,如图2所示,同(2)可得ACD BCE ≅△△∴AD=BE 同理可证BE AE ⊥在Rt △CDE 中,CD CE =2=在Rt △ACB 中,AC BC =AB ==设AD=BE=x ,在Rt △ABE 中,222BE AE AB +=∴222(2)x x +−=解得,x = ∴ 1AD .所以,AD 1【点睛】本题考查了旋转的性质,全等三角形的判定与性质,勾股定理等知识,熟练解答本题的关键.例4.(2022·黑龙江·虎林市九年级期末)已知Rt △ABC 中,AC =BC ,∠ACB =90°,F 为AB 边的中点,且DF =EF ,∠DFE =90°,D 是BC 上一个动点.如图1,当D 与C 重合时,易证:CD 2+DB 2=2DF 2;(1)当D 不与C 、B ,CD 、DB 、DF 有怎样的数量关系,请直接写出你的猜想,不需证明.(2)当D 在BC 的延长线上时,如图3,CD 、DB 、DF 有怎样的数量关系,请写出你的猜想,并加以证明.【答案】(1)CD2+DB2=2DF2 ;(2)CD2+DB2=2DF2,证明见解析【分析】(1)由已知得222DE DF =,连接CF ,BE ,证明CDF BEF ∆≅∆得CD=BE ,再证明BDE ∆为直角三角形,由勾股定理可得结论;(2)连接CF ,BE ,证明CDF BEF ∆≅∆得CD=BE ,再证明BDE ∆为直角三角形,由勾股定理可得结论.【详解】解:(1)CD2+DB2=2DF2证明:∵DF=EF ,∠DFE =90°,∴222DF EF DE += ∴222DE DF =连接CF ,BE ,如图∵△ABC 是等腰直角三角形,F 为斜边AB 的中点∴CF BF =, CF AB ⊥,即90CFB ∠=︒ ∴45FCB FBC ∠=∠=︒,90CFD DFB ∠+∠=︒又90DFB EFB ∠+∠=︒ ∴CFD EFB ∠=∠在CFD ∆和BFE ∆中CF BF CFD BFE DF EF =⎧⎪∠=∠⎨⎪=⎩ ∴CFD ∆≅BFE ∆∴CD BE =,45EBF FCB ∠=∠=︒ ∴454590DBF EBF ∠+∠=︒+︒=︒ ∴222DB BE DE +=∵CD BE =,222DE DF =∴CD2+DB2=2DF2 ;(2)CD2+DB2=2DF2 证明:连接BE∵CF=BF ,DF=EF 又∵∠DFC+∠CFE=∠EFB+∠CFB=90°∴∠DFC=∠EFB ∴△DFC ≌△EFB ∴CD=BE ,∠DCF=∠EBF=135°∵∠EBD=∠EBF -∠FBD=135°-45°=90° 在Rt △DBE 中,BE2+DB2=DE2∵ DE2=2DF2 ∴ CD2+DB2=2DF2【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、证明三角形全等是解决问题的关键,学会添加常用辅助线,构造全等三角形解决问题.例5.(2022·山西大同·九年级期中)综合与实践:已知ABC 是等腰三角形,AB AC =.(1)特殊情形:如图1,当DE ∥BC 时,DB ______EC .(填“>”“<”或“=”);(2)发现结论:若将图1中的ADE 绕点A 顺时针旋转α(0180α︒<<︒)到图2所示的位置,则(1)中的结论还成立吗?请说明理由.(3)拓展运用:某学习小组在解答问题:“如图3,点P 是等腰直角三角形ABC 内一点,90BAC ∠=︒,且1BP =,2AP =,3CP =,求BPA ∠的度数”时,小明发现可以利用旋转的知识,将BAP △绕点A 顺时针旋转90°得到CAE V ,连接PE ,构造新图形解决问题.请你根据小明的发现直接写出BPA ∠的度数.【答案】(1)=;(2)成立,理由见解析;(3)∠BPA=135°.【分析】(1)由DE ∥BC ,得到∠ADE=∠B ,∠AED=∠C ,结合AB=AC ,得到DB=EC ;(2)由旋转得到的结论判断出△DAB ≌△EAC ,得到DB=CE ;(3)由旋转构造出△APB ≌△AEC ,再用勾股定理计算出PE ,然后用勾股定理逆定理判断出△PEC 是直角三角形,在简单计算即可.【详解】解:(1)∵DE ∥BC ,∴∠ADE=∠B ,∠AED=∠C ,∵AB=AC ,∴∠B=∠C ,∴∠ADE=∠AED AD=AE ,∴DB=EC ,故答案为:=;(2)成立.证明:由①易知AD=AE ,∴由旋转性质可知∠DAB=∠EAC ,在△DAB 和△EAC 中AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩,∴△DAB ≌△EAC (SAS ),∴DB=CE ;(3)如图,将△APB 绕点A 旋转90°得△AEC ,连接PE ,∴△APB ≌△AEC ,∴AE=AP=2,EC=BP=1,∠PAE=90°,∴∠AEP=∠APE=45°,在Rt △PAE 中,由勾股定理可得,在△PEC 中,PE2=(2=8,CE2=12=1,PC2=32=9,∵PE2+CE2=PA2,∴△PEC 是直角三角形,∴∠PEC=90°,∴∠AEC=135°,又∵△APB ≌△AEC ,∴∠BPA=∠CEA=135°.【点睛】本题主要考查了旋转的性质,平行线的性质,全等三角形的性质和判定,勾股定理及其逆定理,解本题的关键是构造全等三角形,也是本题的难点.【答案】(1)见解析;(2)48;(3)15︒【分析】(1)通过边角边判定三角形全等;(2)连接,BD GE ,设,BG DE 交于点O ,,DE CG 交于点M ,先证明DE BG ⊥,由勾股定理可得2222DG BE DB GE +=+;(3)作CK GE ⊥于点K ,则122CK GE ==,且1452GCK GCE ∠=∠=︒,由含30度角的直角三角形的性质求解.【详解】(1)四边形ABCE 与CEFG 为正方形,CG CE =,90BCG DCE ∠=∠=︒,90BCG α=∠︒+,90DCE α∠=︒+,BCG DCE ∴∠=∠,在BCG 和DCE △中,BC DC BCG DCECG CE =⎧⎪∠=∠⎨⎪=⎩BCG DCE ∴≌ (SAS), (2)连接,BD GE ,设,BG DE 交于点O ,,DE CG 交于点M ,90BCG α=∠︒+,90DCE α∠=︒+,BCG DCE ∴∠=∠, 在△BCG 和DCE △中,BC DC BCG DCE CG CE =⎧⎪∠=∠⎨⎪=⎩()SAS BCG DCE ∴△≌,BGC DEC ∠=∠,GMO EMC ∠=∠,18090GOM GMO BGC EMC DEC GCE ∴∠=︒−∠−∠=︒−∠−∠=∠=︒DE BG ∴⊥,由勾股定理得222DG DO GO =+,222BE OB OE =+,22222222DG BE DO GO OB OE DB GE ∴+=+++=+,4,AB CG ==,BD ∴==4GE ==,2222(448DG BE ++∴==,(3)作CK GE ⊥于点K ,如图,△CEG 为等腰直角三角形,122CK GE ==,且1452GCK GCE ∠=∠=︒,在Rt CDK 中,12CK CD =,30CDK ∴∠=︒,903060DCK ∴∠=︒−︒=︒, 604515DCG DCK GCK =∠−∠=︒−︒=︒∠.∴15α=︒.【点睛】本题考查四边形与三角形的综合问题,解题关键是熟练掌握正方形与直角三角形的性质,通过添加辅助线求解.模型2.半角模型【模型解读】半角模型概念:过多边形一个顶点作两条射线,使这两条射线夹角等于该顶角一半思想方法:通过旋转构造全等三角形,实现线段的转化1)正方形半角模型条件:四边形ABCD是正方形,∠ECF=45°;结论:①△BCE≌△DCG;②△CEF≌△CGF;③EF=BE+DF;④∆AEF的周长=2AB;⑤CE、CF分别平分∠BEF和∠EFD。
全等三角形旋转模型知识归纳总结附解析

全等三角形旋转模型知识归纳总结附解析一、全等三角形旋转模型1.(课题研究)旋转图形中对应线段所在直线的夹角(小于等于90°的角)与旋转角的关系.(问题初探)线段AB 绕点O 顺时针旋转得到线段CD ,其中点A 与点C 对应,点B 与点D 对应,旋转角的度数为α,且0°<α<180°.(1)如图①,当α=60°时,线段AB 、CD 所在直线夹角(锐角)为 ;(2)如图②,当90°<α<180°时,直线AB 与直线CD 所夹锐角与旋转角α存在怎样的数量关系?请说明理由;(形成结论)旋转图形中,当旋转角小于平角时,对应线段所在直线的夹角与旋转角 .(运用拓广)运用所形成的结论解决问题:(3)如图③,四边形ABCD 中,∠ABC =60°,∠ADC =30°,AB =BC ,CD =3,BD =19,求AD 的长.解析:(1)60°;(2)互补,理由见解析;【形成结论】相等或互补;(310【分析】(1)由旋转的性质可得AB CD =,OA OC =,BO DO =,可证()AOB COD SSS ,可得B D ∠=∠,由三角形内角和定理可求解;(2)由旋转的性质可得AB CD =,OA OC =,BO DO =,可证()AOBCOD SSS ,可得B D ∠=∠,由平角的定义和四边形内角和定理可求解; 【形成结论】由(1)(2)可知对应线段所在直线的所夹锐角角与旋转角:相等或互补;【运用拓广】(3)将BCD ∆绕点B 顺时针旋转60︒,得到BAF ∆,连接FD ,由旋转的性质可得BF BD =,3AF CD ==,由三角形内角和定理可求90FAD ∠=︒,由勾股定理可求解.【详解】解:(1)如图1,延长DC 交AB 于F ,交BO 于E ,α=︒,60∴∠=︒,60BOD线段AB绕点O顺时针旋转得线段CD,=,AB CD=,BO DO∴=,OA OCAOB COD SSS,()B D∴∠=∠,∠=∠,OED BEF,B DBFE EOD,60故答案为:60︒;(2)直线AB与直线CD所夹锐角角与旋转角α互补,理由如下:如图2,延长AB,DC交于点E,线段AB绕点O顺时针旋转得线段CD,=,=,BO DO∴=,OA OCAB CDAOB COD SSS,()ABO D,ABO EBO,180D EBO,180360EBO E D BOD,E BOD,180∴直线AB与直线CD所夹锐角角与旋转角α互补.形成结论由(1)(2)(3)可知:旋转图形中,当旋转角小于平角时,对应线段所在直线的所夹锐角角与旋转角:相等或互补.故答案为:相等或互补.运用拓广(3)如图3,将BCD ∆绕点B 顺时针旋转60︒,得到BAF ∆,连接FD ,延长FA ,DC 交于点E ,∴旋转角60ABC ∠=︒,BCD BAF ,60AED ABC ∴∠=∠=︒,3AF CD ==,BD BF =,30ADC ∠=︒,90FAD AED ADC ,又60FBD ABC ,BF BD =, BFD ∴∆是等边三角形,BF BD DF ,∴在Rt DAF 中,2219910ADDF AF . 【点睛】本题是几何变换综合题,考查了旋转的性质,全等三角形的判定和性质,等边三角形的判定和性质等知识,添加辅助线构造全等三角形是本题的关键.2.问题背景如图(1),在四边形ABCD 中,∠B+∠D =180°,AB =AD ,∠BAD =α,以点A 为顶点作一个角,角的两边分别交BC ,CD 于点E ,F ,且∠EAF 12=α,连接EF ,试探究:线段BE ,DF ,EF 之间的数量关系.(1)特殊情景在上述条件下,小明增加条件“当∠BAD =∠B =∠D =90°时”如图(2),小明很快写出了:BE ,DF ,EF 之间的数量关系为______.(2)类比猜想类比特殊情景,小明猜想:在如图(1)的条件下线段BE ,DF ,EF 之间的数量关系是否仍然成立?若成立,请你帮助小明完成证明;若不成立,请说明理由.(3)解决问题如图(3),在△ABC中,∠BAC=90°,AB=AC=4,点D,E均在边BC上,且∠DAE=45°,若BD2=,请直接写出DE的长.答案:B解析:(1)BE+DF=EF;(2)成立;(3)DE523 =【分析】(1)将△ABE绕点A逆时针旋转90°,得到△ADG,由旋转的性质可得AE=AG,BE=DG,∠BAE=∠DAG,根据∠EAF=12∠BAD可得∠BAE+∠DAF=45°,即可得出∠∠EAF=∠FAG,利用SAS可证明△AFE≌△AFG,可得EF=FG,进而可得EF=BE+FD;(2)将△ABE 绕点A逆时针旋转α得到△ADH,由旋转的性质可得∠ABE=∠ADH,∠BAE=∠DAH,AE=AH,BE=DH,根据∠BAD=α,∠EAF12=α可得∠BAE+∠FAD12=α,进而可证明∠FAH=∠EAF,利用SAS可证明△AEF≌△AHF,可得EF=FH=BE+FD;(3)将△AEC绕点A顺时针旋转90°,得到△AE′B,连接DE′,由旋转的性质可得BE′=EC,AE′=AE,∠C=∠ABE′,∠EAC=∠E′AB,根据等腰直角三角形的性质可得∠ABC=∠ACB=45°,BC=42,即可求出∠E′BD=90°,利用SAS可证明△AEF≌△AHF,可得DE=DE′,利用勾股定理求出DE的长即可的答案.【详解】(1)BE+DF=EF,如图1,将△ABE绕点A逆时针旋转90°,得到△ADG,∵∠ADC=∠B=∠ADG=90°,∴∠FDG=180°,即点F,D,G共线.由旋转可得AE=AG,BE=DG,∠BAE=∠DAG.∵∠BAE+∠DAF=∠BAD﹣∠EAF=90°﹣12∠BAD=90°-45°=45°,∴∠DAG+∠DAF=45°,即∠FAG=45°,∴∠EAF=∠FAG,∴△AFE≌△AFG(SAS),∴EF=FG.又∵FG=DG+DF=BE+DF,∴BE+DF=EF,故答案为BE+DF=EF.(2)成立.如图2,将△ABE绕点A逆时针旋转α得到△ADH,可得∠ABE=∠ADH,∠BAE=∠DAH,AE=AH,BE=DH.∵∠B+∠ADC=180°,∴∠ADH+∠ADC=180°,∴点C,D,H在同一直线上.∵∠BAD=α,∠EAF12=α,∴∠BAE+∠FAD12=α,∴∠DAH+∠FAD12=α,∴∠FAH=∠EAF,又∵AF=AF,∴△AEF≌△AHF(SAS),∴EF=FH=DF+DH=DF+BE;(3)DE523 =,如图3,将△AEC绕点A顺时针旋转90°,得到△AE′B,连接DE′.可得BE′=EC,AE′=AE,∠C=∠ABE′,∠EAC=∠E′AB,在Rt△ABC中,∵AB=AC=4,∠BAC=90°,∴∠ABC=∠ACB=45°,BC=2,∴2,∴∠ABC+∠ABE′=90°,即∠E′BD=90°,∴E′B 2+BD 2=E′D 2.易证△AE′D ≌△AED ,∴DE =DE′,∴DE 2=BD 2+EC 2,即DE 222(2)(32)DE =+-,解得523DE =. 【点睛】本题考查旋转的性质、全等三角形的判定与性质、勾股定理,旋转后不改变图形的大小和形状,并且对应点到旋转中心的距离相等,对应点与旋转中心的连线的夹角等于旋转角,熟练掌握旋转的性质及全等三角形的判定定理是解题关键.3.一位同学拿了两块45︒三角尺MNK ∆,ACB ∆做了一个探究活动:将MNK ∆的直角顶点M 放在ACB ∆的斜边AB 的中点处,设4AC BC ==.(1)如图1所示,两三角尺的重叠部分为ACM ∆,则重叠部分的面积为______,周长为______.(2)将如图1所示中的MNK ∆绕顶点M 逆时针旋转45︒,得到如图2所示,此时重叠部分的面积为______,周长为______.(3)如果将MNK ∆绕M 旋转到不同于如图1所示和如图2所示的图形,如图3所示,请你猜想此时重叠部分的面积为______.(4)在如图3所示情况下,若1AD =,求出重叠部分图形的周长.答案:A解析:(1)4,442+;(2)4,8;(3)4;(4)425+【分析】()1根据4AC BC ==,90ACB ∠=,得出AB 的值,再根据M 是AB 的中点,得出AM MC =,求出重叠部分的面积,再根据AM ,MC ,AC 的值即可求出周长;()2易得重叠部分是正方形,边长为12AC ,面积为214AC ,周长为2.AC ()3过点M 分别作AC 、BC 的垂线MH 、ME ,垂足为H 、.E 求得RtMHD ≌Rt MEG ,则阴影部分的面积等于正方形CEMH 的面积. ()4先过点M 作ME BC ⊥于点E ,MH AC ⊥于点H ,根据DMH EMH ∠∠=,MH ME =,得出Rt DHM ≌Rt EMG ,从而得出HD GE =,CE AD =,最后根据AD 和DF的值,算出DM =. 【详解】解:()14AC BC ==,90ACB ∠=,AB ∴== M 是AB 的中点,AM ∴=45ACM ∠=,AM MC ∴=,∴4=, ∴周长为:44AM MC AC ++==+故答案为4,4+;()2重叠部分是正方形,∴边长为1422⨯=,面积为14444⨯⨯=, 周长为248⨯=.故答案为4,8.()3过点M 分别作AC 、BC 的垂线MH 、ME ,垂足为H 、E , M 是ABC 斜边AB 的中点,4AC BC ==,12MH BC ∴=, 12ME AC =, MH ME ∴=,又90NMK HME ∠∠==,90NMH HMK ∠∠∴+=,90EMG HMK ∠∠+=,HMD EMG ∠∠∴=,在MHD 和MEG 中,HMD GME MH MEDHM MEG ∠=∠⎧⎪=⎨⎪∠=∠⎩, MHD ∴≌()MEG ASA ,∴阴影部分的面积等于正方形CEMH 的面积, 正方形CEMH 的面积是1144422ME MH ⋅=⨯⨯⨯=; ∴阴影部分的面积是4;故答案为4.()4如图所示, 过点M 作ME BC ⊥于点E ,MH AC ⊥于点H ,∴四边形MECH 是矩形,MH CE ∴=,45A ∠=,45AMH ∠∴=,AH MH ∴=,AH CE ∴=,在Rt DHM 和Rt GEM 中,DMH EMG MH MEDHM GEM ∠=∠⎧⎪=⎨⎪∠=∠⎩, Rt DHM ∴≌.Rt GEMGE DH ∴=,AH DH CE GE ∴-=-,CG AD ∴=,1AD =,1.DH ∴=145DM ∴=+=.∴四边形DMGC 的周长为:CE CD DM ME +++2AD CD DM =++425=+【点睛】此题考查了等腰直角三角形,利用等腰直角三角形的性质,等腰直角三角形的面积公式,正方形的面积公式,全等三角形的判定和性质求解.4.如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是 ,位置关系是 ;(2)探究证明:把△ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由;(3)拓展延伸:把△ADE 绕点A 在平面内自由旋转,若AD =4,AB =10,请直接写出△PMN 面积的最大值.解析:(1)PM =PN ,PM ⊥PN ;(2)△PMN 是等腰直角三角形.理由见解析;(3)S △PMN 最大=492. 【分析】(1)由已知易得BD CE =,利用三角形的中位线得出12PM CE =,12PN BD =,即可得出数量关系,再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠,最后用互余即可得出位置关系;(2)先判断出ABD ACE ∆≅∆,得出BD CE =,同(1)的方法得出12PM BD =,12PN BD =,即可得出PM PN =,同(1)的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠,即可得出结论;(3)方法1:先判断出MN 最大时,PMN ∆的面积最大,进而求出AN ,AM ,即可得出MN 最大AM AN =+,最后用面积公式即可得出结论.方法2:先判断出BD 最大时,PMN ∆的面积最大,而BD 最大是14AB AD +=,即可得出结论.【详解】解:(1)点P ,N 是BC ,CD 的中点,//PN BD ∴,12PN BD =, 点P ,M 是CD ,DE 的中点, //PM CE ∴,12PM CE =, AB AC =,AD AE =,BD CE ∴=,PM PN ∴=,//PN BD ,DPN ADC ∴∠=∠,//PM CE ,DPM DCA ∴∠=∠,90BAC ∠=︒,90ADC ACD ∴∠+∠=︒,90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒, PM PN ∴⊥,故答案为:PM PN =,PM PN ⊥;(2)PMN ∆是等腰直角三角形.由旋转知,BAD CAE ∠=∠,AB AC =,AD AE =,()ABD ACE SAS ∴∆≅∆,ABD ACE ∴∠=∠,BD CE =, 利用三角形的中位线得,12PN BD =,12PM CE =, PM PN ∴=,PMN ∴∆是等腰三角形,同(1)的方法得,//PM CE ,DPM DCE ∴∠=∠,同(1)的方法得,//PN BD ,PNC DBC ∴∠=∠,DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠,MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠ BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠,90BAC ∠=︒,90ACB ABC ∴∠+∠=︒,90MPN ∴∠=︒,PMN ∴∆是等腰直角三角形;(3)方法1:如图2,同(2)的方法得,PMN ∆是等腰直角三角形,MN ∴最大时,PMN ∆的面积最大,//DE BC ∴且DE 在顶点A 上面,MN ∴最大AM AN =+,连接AM ,AN ,在ADE ∆中,4AD AE ==,90DAE ∠=︒, 22AM ∴=, 在Rt ABC ∆中,10AB AC ==,52AN =,225272MN ∴=+=最大,222111149(72)22242PMN S PM MN ∆∴==⨯=⨯=最大. 方法2:由(2)知,PMN ∆是等腰直角三角形,12PM PN BD ==, PM ∴最大时,PMN ∆面积最大,∴点D 在BA 的延长线上,14BD AB AD ∴=+=,7PM ∴=,2211497222PMN S PM ∆∴==⨯=最大. 【点睛】此题属于几何变换综合题,主要考查了三角形的中位线定理,等腰直角三角形的判定和性质,全等三角形的判断和性质,直角三角形的性质的综合运用;解(1)的关键是判断出12PM CE =,12PN BD =,解(2)的关键是判断出ABD ACE ∆≅∆,解(3)的关键是判断出MN 最大时,PMN ∆的面积最大.5.如图,在ABC 中,,AB AC BAC α=∠=,过A 作AD BC ⊥于点D ,点E 为直线AD 上一动点,把线段CE 绕点E 顺时针旋转α,得到线段EF ,连接FC 、FB ,直线AD 与BF 相交于点G .(1)(发现)如图1,当60α=︒时,填空:①AE BF的值为___________; ②AGB ∠的度数为___________;(2)(探究)如图2,当120α=︒时,请写出AE BF的值及AGB ∠的度数,并就图2的情形给出证明;(3)(应用)如图3,当90α=︒时,若15AB ACE =∠=︒,请直接写出DFG 的面积.答案:G解析:(1)1;60°;(2)3AE BF =,∠G =30°,理由见解析;(3) 【分析】(1)①根据已知条件可以证明三角形ABC 和三角形EFC 都是等边三角形,然后根据等边三角形的性质证明△AEC ≌△BFC ,即BF =AE 从而得出答案;②根据①中的证明∠ABG =90°,∠BAG =30°,从而计算出∠AGB 的度数;(2)根据题目已知条件可以计算出BC =,同理可以证得CF =,再证ECA FCB ∠=∠即△ACE ∽△BCF ,从而得到比值和角的度数;(3)根据第(2)问的计算结论分E 在AD 上和E 在DA 的延长线上分类讨论求解即可.【详解】解:(1)①∵AB =AC ,CE =EF ,∠BAC =∠FEC =60°∴△ABC 和△EFC 都是等边三角形∴∠ACB =∠ECF =60°,AC =CB ,CE =CF∴∠ACE =∠BCF∴△ACE ≌△BCF∴A E =BF ,即1AE BF= ②∵△ACE ≌△BCF∴∠EAC =∠CBF 由①可知△ABC 是等边三角形∴AD 平分∠BAC ,BD ⊥AD∴∠CAE =∠CBF =30°∴∠AGB =∠180°-∠CBF -∠BDG =60°(2)AE BF = ∵AB =AC ,∠BAC =120°,AD ⊥BC∴∠ABD =30°=∠ACB∴22BD AB AC CD === ∴BC =同理∵∠FEC =120°,EF =EC ∴CF =∴BC CF AC CE=,∠ACB =∠ECF =30° ∴△ACE ∽△BCF∴∠CAE =∠CBF∴AE AC BF BC ==∵AD ⊥BC ,∠BAC =120°,∴∠CAE =∠CBF =60°又∵∠BDG =90°∴∠G =30°(3)第一种情况,如图所示,当E 在AD 上时 ∵AB AC ==∠BAC =90°,AD ⊥BC ∴sin 4562BC AD BD CD AB =====∠DAC =45° ∵∠ACE =15° ∴∠CED =∠CAD +∠ACE =60° ∴2tan 60DC DE ==∴AE AD DE =-=BC CF AC CE==,∠ACB =∠ECF =45° 又∵AD ⊥BC ,∠BAC =90°,∴∠CAE =∠CBF =45°∴△ACE ∽△BCF∴BF BC AE AC==∴2BF == ∵∠ADC =∠BDG∴∠G =∠ACB =45°∴BG ==∴2FG BG BF =-=过点D 作DM ⊥BG 交BG 于M ,∵∠G =∠ACB =45°,∠BDG =90°∴=DG BD CD ==∴DM DG == ∴132DFG S FG DM ==△第二种情况:当E 在DA 的延长线上时过点D 作DM ⊥BG 交BG 于M , 同上可证2BF BC AE AC ==,6BG BD ==,3DM = ∵∠ACE =15°,∠DAC =45°∴∠DEC =30° ∵AD ⊥CD ,6CD =∴32tan 30DC DE == ∴=6DG BD CD ==326AE DE AD =-=-∴2623FB AE ==-∴6FG BF BG =+=1332DFG S FG DM ==△ 故答案为:3或33.【点睛】本题主要考查了相似三角形的性质与判定,旋转的性质,三角函数等知识点,解题的关键在于能够熟练的掌握相关知识点.6.如图,点B ,C ,D 在同一条直线上,△BCF 和△ACD 都是等腰直角三角形,连接AB ,DF ,延长DF 交AB 于点E .(1)如图1,若AD =BD ,DE 是∠ADB 的平分线,BC =1,求CD 的长度;(2)如图2,连接CE ,求证:DE =2CE +AE ;(3)如图3,改变△BCF 的大小,始终保持点在线段AC 上(点F 与点A ,C 不重合).将ED 绕点E 顺时针旋转90°得到EP ,取AD 的中点O ,连接OP .当AC =2时,直接写出OP 长度的最大值.解析:(1)21CD =;(2)证明见解析;(3)22+【分析】 (1)根据等腰直角三角形的性质,求出1FC BC ==,再判断出FA FB =,即可得出结论;(2)先判断出ABC DFC ≅△△,得出BAC CDF ∠=∠,进而判断出ACE DCH ≅△△,得出AE DH =,CE CH =,即可得出结论;(3)先判断出2OE OQ ==,再判断出OED QEP ≅△△,进而求出2PQ OD ==得出结论.【详解】(1)解:BCF 和ACD △都是等腰直角三角形,AC CD ∴=,1FC BC ==,2FB =,AD BD =,DE 是ABD ∆的平分线,DE ∴垂直平分AB ,2FA FB ∴==,21AC FA FC ∴=+=,21CD ∴=;(2)证明:如图2,过点C 作CH CE ⊥交ED 于点H ,BCF 和ACD △都是等腰直角三角形,AC DC ∴=,FC BC =,90ACB DCF ∠=∠=︒;()ABC DFC SAS ∴≅△△,BAC CDF ∴∠=∠,90ECH ∠=︒,90ACE ACH ∴∠+∠=︒,90ACD ∠=︒,90DCH ACH ∴∠+∠=︒,ACE DCH ∴∠=∠.在ACE 和DCH 中,BAC CDF AC DCACE DCH ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()ACE DCH ASA ∴≅△△,AE DH ∴=,CE CH =,2EH CE ∴=.2DE EH DH CE AE =+=+;(3)OP 的最大值是22+解:如图3,连接OE ,将OE 绕点E 顺时针旋转90︒得到EQ ,连接OQ ,PQ ,则2OQ OE =.由(2)知,90AED ABC CDF ABC BAC ∠=∠+∠=∠+∠=︒,在Rt AED △中,点O 是斜边AD 的中点,122222OE OD AD AC ∴===== 2222OQ OE ∴===,在OED 和QEP △中,OE QE OED QEP DE PE =⎧⎪∠=∠⎨⎪=⎩,()OED QEP SAS ∴≅△△,2PQ OD ∴==22OP OQ PQ +=+O 、P 、Q 三点共线时,取“=”号,OP ∴的最大值是22+【点睛】此题是几何变换综合题,主要等腰直角三角形的性质,全等三角形的判定和性质,构造出全等三角形是解本题的关键.7.如图.四边形ABCD 、BEFG 均为正方形.(1)如图1,连接AG 、CE ,请直接写出.....AG 和CE 的数量和位置关系(不必证明).(2)将正方形BEFG 绕点B 顺时针旋转β角(0180β︒︒<<),如图2,直线AG 、CE 相交于点M .①AG 和CE 是否仍然满足(1)中的结论?如果是,请说明理由:如果不是,请举出反例:②连结MB ,求证:MB 平分AME ∠.(3)在(2)的条件下,过点A 作AN MB ⊥交MB 的延长线于点N ,请直接写出.....线段CM 与BN 的数量关系.答案:A解析:(1)AG=EC ,AG ⊥EC ;(2)①满足,理由见解析;②见解析;(3)2.【分析】(1)由正方形BEFG 与正方形ABCD ,利用正方形的性质得到两对边相等,一对直角相等,利用SAS 得出三角形ABG 与三角形CBE 全等,利用全等三角形的对应边相等,对应角相等得到CE=AG ,∠BCE=∠BAG ,再利用同角的余角相等即可得证;(2)①利用SAS 得出△ABG ≌△CEB 即可解决问题;②过B 作BP ⊥EC ,BH ⊥AM ,由全等三角形的面积相等得到两三角形面积相等,而AG=EC ,可得出BP=BH ,利用到角两边距离相等的点在角的平分线上得到BM 为角平分线;(3)在AN 上截取NQ=NB ,可得出三角形BNQ 为等腰直角三角形,利用等腰直角三角形的性质得到2BN ,接下来证明BQ=CM ,即要证明三角形ABQ 与三角形BCM 全等,利用同角的余角相等得到一对角相等,再由三角形ANM 为等腰直角三角形得到NA=NM ,利用等式的性质得到AQ=BM ,利用SAS 可得出全等,根据全等三角形的对应边相等即可得证.【详解】解:(1)AG=EC ,AG ⊥EC ,理由为:∵正方形BEFG ,正方形ABCD ,∴GB=BE ,∠ABG=90°,AB=BC ,∠ABC=90°,在△ABG 和△BEC 中,BG BE ABC EBC BA BC =⎧⎪∠=∠⎨⎪=⎩,∴△ABG ≌△BEC (SAS ),∴CE=AG ,∠BCE=∠BAG ,延长CE 交AG 于点M ,∴∠BEC=∠AEM ,∴∠ABC=∠AME=90°,∴AG=EC ,AG ⊥EC ;(2)①满足,理由是:如图2中,设AM 交BC 于O .∵∠EBG=∠ABC=90°,∴∠ABG=∠EBC ,在△ABG 和△CEB 中,AB BC ABG CBE BG EB =⎧⎪∠=∠⎨⎪=⎩,∴△ABG ≌△CEB (SAS ),∴AG=EC ,∠BAG=∠BCE ,∵∠BAG+∠AOB=90°,∠AOB=∠COM ,∴∠BCE+∠COM=90°,∴∠OMC=90°,∴AG ⊥EC .②过B 作BP ⊥EC ,BH ⊥AM ,∵△ABG ≌△CEB ,∴S △ABG =S △EBC ,AG=EC , ∴12EC•BP=12AG•BH , ∴BP=BH ,∴MB 平分∠AME ;(3)CM=2BN ,理由为:在NA 上截取NQ=NB ,连接BQ ,∴△BNQ 为等腰直角三角形,即BQ=2BN ,∵∠AMN=45°,∠N=90°,∴△AMN 为等腰直角三角形,即AN=MN ,∴MN-BN=AN-NQ ,即AQ=BM ,∵∠MBC+∠ABN=90°,∠BAN+∠ABN=90°,∴∠MBC=∠BAN ,在△ABQ 和△BCM 中,AQ BM BAN MBC AB BC =⎧⎪∠=∠⎨⎪=⎩,∴△ABQ ≌△BCM (SAS ),∴CM=BQ ,则CM=2BN .【点睛】此题考查了正方形,全等三角形的判定与性质,等腰直角三角形的判定与性质,角平分线的判定,熟练掌握正方形的性质是解本题的关键.8.问题解决一节数学课上,老师提出了这样一个问题:如图①,点P 是等边ABC 内的一点,6PA =,8PB = ,10PC =.你能求出APB ∠的度数和等边ABC 的面积吗? 小明通过观察、分析、思考,形成了如下思路:如图①将BPC △绕点B 逆时针旋转60°,得到BPA △,连接PP ',可得BPP '是等边三角形,根据勾股定理逆定理可得AP P '是直角三角形,从而使问题得到解决.(1)结合小明的思路完成填空:PP '=_____________,APP '∠=_______________,APB ∠=_____________ ,ABCS= ______________.(2)类比探究Ⅰ如图②,若点P 是正方形ABCD 内一点,1PA = ,2PB =,3PC =,求APB ∠的度数和正方形的面积.Ⅱ如图③,若点P 是正方形ABCD 外一点,3PA = ,1PB =, 11PC =,求APB ∠的度数和正方形的面积.答案:B解析:(1)8,90˚,150˚,25336;(2)Ⅰ135APB ∠=︒, 722ABCD S =+正方形;Ⅱ45APB ∠=︒, 1032ABCD S =-正方形【分析】(1)根据小明的思路,然后利用等腰三角形和直角三角形性质计算即可;(2)Ⅰ将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,求出∠APB 的度数;先利用旋转求出∠PBP'=90°,BP'=BP=2,AP'=CP=3,利用勾股定理求出PP',进而判断出△APP'是直角三角形,得出∠APP'=90°,即可得出结论;过B 作BE ⊥AP 于点E ,然后利用勾股定理求出AB 的长度即可求出正方形面积;Ⅱ将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,求出∠APB 的度数;先利用旋转求出∠PBP'=90°,BP'=BP=2,AP'=CP=3,利用勾股定理求出PP',进而判断出△APP'是直角三角形,得出∠APP'=90°,即可得出结论;过B 作BF ⊥AP 于点F ,然后利用勾股定理求出AB 的长度即可求出正方形面积; 【详解】解:(1)由题易有P BP '∆是等边三角形,AP P '∆是直角三角形 ∴PP '=BP=8,90?APP '=∠,60?P PB '=∠,∴APB ∠=APP '∠+=P PB '∠150˚, 如图1,过B 作BD ⊥AP 于点D∵APB ∠=150° ∴30?BPD =∠在Rt △BPD 中,30?BPD =∠,BP=8 ∴BD=4,PD=43 ∴AD=6+43∴AB 2=AD 2+BD 2=100+483 ∴ABCS=234AB =25336+ (2)Ⅰ.如图2,将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′, ∴△ABP'≌△CBP ,∴∠PBP'=90°,BP'=BP=2,AP'=CP=3, 在Rt △PBP'中,BP=BP'=2,∴∠BPP'=45°,根据勾股定理得,PP'=2BP=22, ∵AP=1,∴AP 2+PP'2=1+8=9, ∵AP'2=32=9, ∴AP 2+PP'2=AP'2,∴△APP'是直角三角形,且∠APP'=90°, ∴∠APB=∠APP'+∠BPP'=90°+45°=135°;过B 作BE ⊥AP 于点E , ∵∠APB=135°∴∠BPE=45°∴△BPE 是等腰直角三角形 ∴BE=BP=22BP =2 ∴AE=1+2∴AB 2=AE 2+BE 2=7+22 ∴2722ABCD S AB ==+正方形Ⅱ.如图3,将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′, ∴△ABP'≌△CBP ,∴∠PBP'=90°,BP'=BP=1,AP'=CP=11, 在Rt △PBP'中,BP=BP'=1,∴∠BPP'=45°,根据勾股定理得,PP'=2BP=2, ∵AP=3,∴AP 2+PP'2=9+2=11, ∵AP'2=(11)2=11, ∴AP 2+PP'2=AP'2,∴△APP'是直角三角形,且∠APP'=90°, ∴∠APB=∠APP'-∠BPP'=90°-45°=45°.过B 作BF ⊥AP 于点F ∵∠APB=45°∴△BPF 为等腰直角三角形 ∴PF=BF=22BP =22 ∴2 ∴AB 2=AF 2+BF 2=1032-∴21032ABCD S AB ==-正方形【点睛】此题是四边形综合题,主要考查了正方形的性质,旋转的性质,直角三角形的性质和判定,勾股定理,正确作出辅助线是解本题的关键.9.问题:如图(1),点M、N分别在正方形ABCD的边BC、CD上,∠MAN=45°,试判断BM、MN、ND之间的数量关系.(1)研究发现如图1,小聪把△ADN绕点A顺时针旋转90°至△ABG,从而发现BM、MN、DN之间的数量关系为(直接写出结果,不用证明)(2)类比引申如图2,在(1)的条件下,AM、AN分别交正方形ABCD的对角线BD于点E、F.已知EF =5,DF=4.求BE的长.(3)拓展提升如图3,在(2)的条件下,AM、AN分别交正方形ABCD的两个外角平分线于Q、P,连接PQ.请直接写出以BQ、PQ、DP为边构成的三角形的面积.答案:B解析:(1)BM+DN=MN,理由见解析;(2)BE=3;(3)以BQ、PQ、DP为边构成的三角形的面积为36.【分析】(1)结论是:BM+DN=MN,如图1,利用三角形AND旋转90º得三角形ABG,∠DAN=∠BAG,可证∠GAM=∠GAB+∠BAM=∠MAN,利用SAS证△AMN≌△AMG即可;(2)如图2,按同样方法△AFD顺时针旋转90º,使AD与AB重合,得△ABF′,连结EF′,△BEF′是直角三角形,用勾股定理求EF′=5,再证△AEF≌△AEF即可;(3)如图3,由(2)可得BD=12,可求正方形边长,构建△P′AQ,P′B=DP,将△ADP顺时针转90º,AD与AB重合,得△BQP′,连OP′,可证△BQP′是直角三角形,可证PQ=P′Q,再证△ABQ∽△PDA,将△P′BQ面积=12BQ•BP′=12BQ•DP=12AD•AB可求.【详解】(1)如图1,BM+DN=MN,理由如下:∵四边形ABCD 是正方形,∴AB =AD ,∠D =∠ABC =∠BAD =90°, 小聪把△ADN 绕点A 顺时针旋转90°至△ABG ,由旋转可得:BG =DN ,AN =AG ,∠1=∠2,∠ABG =∠D =90°, ∴∠ABG +∠ABM =90°+90°=180°, 因此,点G ,B ,M 在同一条直线上, ∵∠MAN =45°,∴∠2+∠3=∠BAD ﹣∠MAN =90°﹣45°=45°, ∵∠1=∠2, ∴∠1+∠3=45°, ∴∠GAM =∠MAN , ∵AM =AM ,∴△AMN ≌△AMG (SAS ), ∴MN =GM ,∵GM =BM +BG =BM +DN , ∴BM +DN =MN ; 故答案为:BM +DN =MN ;(2)如图2,把△ADF 绕点A 顺时针旋转90°至△ABF ',连接EF ',∴AF ′ =AF ,∠DAF =∠BAF ',∠ABF ′ =∠ADF =45°,BF ′ =DF =4, ∵∠ABE =45°,∴∠EBF ′ =45°+45°=90°, ∵AE =AE ,同理得△EAF ≌△EAF '(SAS ), ∴EF '=EF =5,在Rt △EBF '中,由勾股定理得:BE ()()2222EF +BF 5-4=3''=3;(3)由(2)知:BE =3,EF =5,DF =4, ∴BD =3+4+5=12,由勾股定理得:AB 2+AD 2=BD 2, ∵AB =AD , ∴AB 2=72,如图3,把△ADP 绕点A 顺时针旋转90°至△ABP ',连接BP ′,则∠ABP′=∠ADP ,PD =P ′B ,AP =AP ′,∵AM 、AN 分别交正方形ABCD 的两个外角平分线于Q 、P , ∴∠ADP =∠ABQ =135°, ∴∠DAP +∠APD =45°, ∵∠DAP +∠BAQ =45°, ∴∠BAQ =∠APD , ∴△ADP ∽△QBA , ∴AD PD=BQ AB, ∴BQ •PD =AD •AB =72, ∵∠ABP '=∠ABQ =135°, ∴∠QBP '=360°﹣135°﹣135°=90°, ∴S △BP 'Q =12BQ•BP′=12BQ•DP =12×72=36, ∵AP =AP ',∠PAQ =∠P 'AQ ,AQ =AQ , ∴△QAP ≌△QAP '(SAS ), ∴PQ =P 'Q ,∴以BQ 、PQ 、DP 为边构成的三角形的面积为36. 【点睛】本题是感知,探究,创新新题型,主要考查了学生对正方形的性质,旋转变换,勾股定理及全等三角形与相似三角形的判定方法的综合运用.关键是灵活掌握所学知识,同时会从感知中学到方法,结合下一图形,找到解决问题的方法,以及突破口,在创新中,注意把给出的问题进行转化,利用转化思想来解决.10.如图,在四边形ABCD 中,AB AC =,AD 是对角线,60BAC ∠=︒,4B C ADB BAC ∠+∠+∠=∠,(1)求ADC ∠的度数;(2)若AD BD CD =+,求证:AD 平分BDC ∠;(3)在(2)的条件下,E 、F 分别在AC 、AB 上,连接BE 、CF ,交于点P ,使得BPC BDC ∠=∠,若7BD EF ==,15AD =,求EFP ∆的面积答案:A解析:(1)=60∠︒ADC ;(2)证明见详解;(3)4003129. 【分析】(1)先由四边形内角和得到++300B C BDC ∠∠∠=︒,再由4B C ADB BAC ∠+∠+∠=∠可得答案;(2)把ABD △绕点A 逆时针旋转60︒得到ACE △,由(1)及题意易得D 、C 、E 三点共线,从而得到ADE 是等边三角形,由等边三角形的性质及旋转的性质易得60ADB E ∠=∠=︒,故得证;(3)过点B 、点F 分别作BG ⊥CD ,FH ⊥AC ,分别交CD 的延长线于点G 、AC 于点H ,连接BC ,由(2)及题意易得DC=8,由BPC BDC ∠=∠易得EBC FCA ∠=∠,进而得到AFC CEB △≌△,设AF=CE=x ,根据勾股定理得到AF 、CE 、BC 的长,最后根据BFE BPC 、的面积比等于FP 与PC 的比,进而求解即可. 【详解】(1)解:=60BAC ∠︒,∴++36060300B C BDC ∠∠∠=︒-︒=︒, 又BDC ADB ADC ∠=∠+∠,4B C ADB BAC ∠+∠+∠=∠,∴30024060ADC ∠=︒-︒=︒; (2)证明:把ABD △绕点A 逆时针旋转60︒得到ACE △,由(1)得:∴AD=AE ,BD=CE ,=ADC=60DAE ∠∠︒AD BD CD =+,DE=DC+CE ,∴D 、C 、E 三点共线,∴ADE 是等边三角形,∴60ADB E ∠=∠=︒, ∴60ADB ADC ∠=∠=︒,∴AD 平分BDC ∠; (3)解:过点B 、点F 分别作BG ⊥CD ,FH ⊥AC ,分别交CD 的延长线于点G 、AC 于点H ,连接BC ,由题意及(2)可得:ABC 是等边三角形,120BDC ∠=︒,∴AB=AC=BC ,60BDG ∠=︒,7BD EF ==,15AD =,∴72DG =,32BG =,DC=AD-BD=8, ∴723822GC GD DC =+=+=, 在Rt BGC △中,222273231322BC BG GC ⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭, 又=120BPC BDC ∠=∠︒,∴18012060PBC PCB ∠+∠=︒-︒=︒,60ECP PCB ∠+∠=︒,∴=ECP EBC ∠∠,=60,FAC BCA AC BC ∠∠=︒=,∴AFC CEB △≌△,∴CE=AF ,设133,1313222CE AF x AE x AH x FH x EH x ==∴=-==∴=-,,,,∴在Rt FHE 中,222FH EH EF +=即22231372x ⎛⎫+-= ⎪⎝⎭⎝⎭,解得125,8x x ==,①当CE=AF=5时,则AE=8,∴111322BECAFCSSAC FH ==⋅=⨯=16944ABEABCBECSSS =-=-=∴BFE ABEAFESSS=-==设BFPEFPBPCEPCSa Sb Sc Sd ====,,,,则有:a cb d FP PC ==∶∶∶,,BFE BFPFEP BEC BPCEPC S SSSSS=+=+,∴BFEBECSSFP PC =∶∶,∴6465BFE BECSS FP PC =∶∶,又1152224FECSCE FH =⋅=⨯⨯=,∴64641291294129EFP FECSS ==⨯=; ②当CE=AF=8时,AE=5,则有:∴111322BEAAFCSSAC FH ==⋅=⨯=,1694CBEABCBECSSS =-==∴654BFEABEAFESSS=-=-=由①可得:25=4104BFEBECSS FP PC =∶∶∶,又11822FECSCE FH =⋅=⨯⨯=∴2525129129EFPFECSS ==⨯=综上所述:129EFPS =. 【点睛】本题主要考查三角形与四边形的综合问题,主要是利用全等三角形、等边三角形、三角形面积比的转换及勾股定理,熟练掌握各个知识点是解题的关键,尤其是第三问的面积转换问题是本题的难点.11.探究:如图①和②,在四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.(1)如图①,若∠B、∠ADC都是直角,把ABE△绕点A逆时针旋转90°至△ADG,使AB与AD重合,则能得EF=BE+DF,请写出推理过程;(2)如图②,若∠B、∠D都不是直角,则当∠B与∠D满足数量关系时,仍有EF=BE+DF;(3)拓展:如图③,在ABC中,∠BAC=90°,AB=AC=22,点D、E均在边BC上,且∠DAE=45°.若BD=1,求DE的长.答案:B解析:(1)见解析;(2)∠B+∠D=180°;(3)5 3【分析】(1)根据已知条件证明△EAF≌△GAF,进而得到EF=FG,即可得到答案;(2)先作辅助线,把△ABE绕A点旋转到△ADG,使AB和AD重合,根据(1),要使EF=BE+DF,需证明△EAF≌△GAF,因此需证明F、D、G在一条直线上,即180ADG ADF∠+∠=︒,即180B D∠+∠=︒;(3)先作辅助线,把△AEC绕A点旋转到△AFB,使AB和AC重合,连接DF,根据已知条件证明△FAD≌△EAD,设DE=x,则DF=x,BF=CE=3﹣x,然后再Rt BDF中根据勾股定理即可求出x的值,即DE的长.【详解】(1)解:如图,∵把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,∴AE=AG,∠BAE=∠DAG,BE=DG,∵∠BAD=90°,∠EAF=45°,∴∠BAE+∠DAF=45°, ∴∠DAG+∠DAF=45°, 即∠EAF=∠GAF=45°, 在△EAF 和△GAF 中AF AF EAF GAF AE AG =⎧⎪∠=∠⎨⎪=⎩∴△EAF ≌△GAF (SAS ), ∴EF=GF , ∵BE=DG , ∴EF=GF=BE+DF ; (2)解:∠B+∠D=180°, 理由是:如图,把△ABE 绕A 点旋转到△ADG ,使AB 和AD 重合, 则AE=AG ,∠B=∠ADG ,∠BAE=∠DAG , ∵∠B+∠ADC=180°, ∴∠ADC+∠ADG=180°, ∴F 、D 、G 在一条直线上, 和(1)类似,∠EAF=∠GAF=45°, 在△EAF 和△GAF 中AF AF EAF GAF AE AG =⎧⎪∠=∠⎨⎪=⎩∴△EAF ≌△GAF (SAS ), ∴EF=GF , ∵BE=DG , ∴EF=GF=BE+DF ; 故答案为:∠B+∠D=180°;(3)解:∵△ABC 中,2∠BAC=90°, ∴∠ABC=∠C=45°,由勾股定理得:22AB AC +,如图,把△AEC 绕A 点旋转到△AFB ,使AB 和AC 重合,连接DF . 则AF=AE ,∠FBA=∠C=45°,∠BAF=∠CAE , ∵∠DAE=45°,∴∠FAD=∠FAB+∠BAD=∠CAE+∠BAD=∠BAC ﹣∠DAE=90°﹣45°=45°, ∴∠FAD=∠DAE=45°, 在△FAD 和△EAD 中AD AD FAD EAD AF AE =⎧⎪∠=∠⎨⎪=⎩∴△FAD ≌△EAD , ∴DF=DE , 设DE=x ,则DF=x , ∵BD=1,∴BF=CE=4﹣1﹣x=3﹣x , ∵∠FBA=45°,∠ABC=45°, ∴∠FBD=90°,由勾股定理得:222DF BF BD =+,22(3)1x x =-+,解得:x=53, 即DE=53. 【点睛】本题综合考查三角形的性质和判定、正方形的性质应用、全等三角形的性质和判定、勾股定理等知识,解题关键在于正确做出辅助线得出全等三角形.12.如图,抛物线y =﹣x 2+bx+c 与x 轴交于A ,B 两点,其中A (3,0),B (﹣1,0),与y 轴交于点C ,抛物线的对称轴交x 轴于点D ,直线y =kx+b 1经过点A ,C ,连接CD . (1)求抛物线和直线AC 的解析式:(2)若抛物线上存在一点P ,使△ACP 的面积是△ACD 面积的2倍,求点P 的坐标; (3)在抛物线的对称轴上是否存在一点Q ,使线段AQ 绕Q 点顺时针旋转90°得到线段QA 1,且A 1好落在抛物线上?若存在,求出点Q 的坐标;若不存在,请说明理由.答案:A解析:(1)2y x 2x 3=-++;3y x =-+ ;(2)(﹣1,0)或(4,﹣5);(3)存在;(1,2)和(1,﹣3) 【分析】(1)将点A ,B 坐标代入抛物线解析式中,求出b ,c 得出抛物线的解析式,进而求出点C 的坐标,再将点A ,C 坐标代入直线AC 的解析式中,即可得出结论;(2)利用抛物线的对称性得出BD =AD ,进而判断出△ABC 的面积和△ACP 的面积相等,即可得出结论;(3)分点Q 在x 轴上方和在x 轴下方,构造全等三角形即可得出结论. 【详解】解:(1)把A (3,0),B (﹣1,0)代入y =﹣x 2+bc+c 中,得93010b c b c -++=⎧⎨--+=⎩,∴23b c =⎧⎨=⎩, ∴抛物线的解析式为y =﹣x 2+2x+3, 当x =0时,y =3, ∴点C 的坐标是(0,3),把A (3,0)和C (0,3)代入y =kx+b 1中,得11303k b b +=⎧⎨=⎩,∴113k b =-⎧⎨=⎩∴直线AC 的解析式为y =﹣x+3; (2)如图,连接BC , ∵点D 是抛物线与x 轴的交点, ∴AD =BD , ∴S △ABC =2S △ACD , ∵S △ACP =2S △ACD ,∴S △ACP =S △ABC ,此时,点P 与点B 重合, 即:P (﹣1,0),过B 点作PB ∥AC 交抛物线于点P ,则直线BP 的解析式为y =﹣x ﹣1①,∵抛物线的解析式为y=﹣x2+2x+3②,联立①②解得,1xy=-⎧⎨=⎩或45xy=⎧⎨=-⎩,∴P(4,﹣5),∴即点P的坐标为(﹣1,0)或(4,﹣5);(3)如图,①当点Q在x轴上方时,设AC与对称轴交点为Q',由(1)知,直线AC的解析式为y=﹣x+3,当x=1时,y=2,∴Q'坐标为(1,2),∵Q'D=AD=BD=2,∴∠Q'AB=∠Q'BA=45°,∴∠AQ'B=90°,∴点Q'为所求,②当点Q在x轴下方时,设点Q(1,m),过点A1'作A1'E⊥DQ于E,∴∠A1'EQ=∠QDA=90°,∴∠DAQ+∠AQD=90°,由旋转知,AQ=A1'Q,∠AQA1'=90°,∴∠AQD+∠A1'QE=90°,∴∠DAQ=∠A1'QE,∴△ADQ≌△QEA1'(AAS),∴AD=QE=2,DQ=A1'E=﹣m,∴点A1'的坐标为(﹣m+1,m﹣2),代入y=﹣x2+2x+3中,解得,m=﹣3或m=2(舍),∴Q的坐标为(1,﹣3),∴点Q的坐标为(1,2)和(1,﹣3).【点睛】本题考查的是二次函数的综合题,涉及解析式的求解,与三角形面积有关的问题,三角形“k”字型全等,解题的关键是利用数形结合的思想,设点坐标并结合几何图形的性质列式求解.13.如图1,ABC ∆中,CA CB =,ACB α∠=,D 为ABC ∆内一点,将CAD ∆绕点C 按逆时针方向旋转角α得到CBE ∆,点,AD 的对应点分别为点,BE ,且,,A D E 三点在同一直线上.(1)填空:CDE ∠=______(用含α的代数式表示);(2)如图2,若60α=︒,请补全图形,再过点C 作CF AE ⊥于点F ,然后探究线段CF ,AE ,BE 之间的数量关系,并证明你的结论;(3)如图3,若90α=︒,52AC =ABEC 面积的最大值______. 解析:(1)1802α-;(2)33AE BE =+;证明见解析;(3)21)2. 【分析】(1)由旋转的性质可得CD CE =,DCE α∠=,即可求解;(2)由旋转的性质可得AD BE =,CD CE =,60DCE ∠=︒,可证CDE ∆是等边三角形,由等边三角形的性质可得33DF EF CF ==,即可求解; (3)如图3中,过点C 作CF BE ⊥交BE 的延长线于F ,设AE 交BC 于J .证明90ACJ BEJ,推出点E 在以AB 为直径的圆上运动,即图中BC 上运动,当CEEB 时,四边形ABEC 的面积最大,此时EC EB =,分别求出ABC ∆,BCE ∆的面积即可解决问题.【详解】解:(1)如图1中,将CAD ∆绕点C 按逆时针方向旋转角α得到CBE ∆ACD BCE ∴∆≅∆,DCE α∠= CD CE ∴=1802CDE α︒-∴∠=. 故答案为:1802α︒-. (2)233AE BE CF =+理由如下:如图2中,将CAD ∆绕点C 按逆时针方向旋转角60︒得到CBE ∆ACD BCE ∴∆≅∆AD BE ∴=,CD CE =,60DCE ∠=︒ CDE ∴∆是等边三角形,且CF DE ⊥33DF EF ∴==AE AD DF EF =++23AE BE ∴=+. (3)如图3中,过点C 作CWBE 交BE 的延长线于W ,设AE 交BC 于J .。
全等三角形的九大经典模型(解析版)
全等三角形的九大经典模型【题型1平移模型】【题型2轴对称模型】【题型3旋转模型】【题型4一线三等角模型】【题型5倍长中线模型】【题型6截长补短模型】【题型7手拉手模型】【题型8角平分线模型】【题型9半角全等模型】【知识点1平移模型】【模型解读】把△ABC沿着某一条直线l平行移动,所得到△DEF与△ABC称为平移型全等三角形,图①,图②是常见的平移型全等三角线.【常见模型】【题型1平移模型】1(2023春·陕西咸阳·八年级统考期末)如图,将△ABC沿BC方向平移得到△DEF,使点B的对应点E恰好落在边BC的中点上,点C的对应点F在BC的延长线上,连接AD,AC、DE交于点O.下列结论一定正确的是()A.∠B=∠FB.AC⊥DEC.BC=DFD.AC、DE互相平分【答案】D【分析】根据平移的性质得到∠B=∠DEF,BE=CF=CE=AD,AD∥BC,DF=AC,由于只有当∠BAC=90°时,AC⊥DE;只有当BC=2AC时,DF=AC=BE,则可对A、B、C选项的进行判断;AC交DE于O点,如图,证明△AOD≌△COE得到OD=OE,OA=OC,则可对D选项进行判断.【详解】解:∵△ABC沿BC方向平移得到△DEF,使点B的对应点E恰好落在边BC的中点上,∴∠B=∠DEF,BE=CF=CE=AD,AD∥BC,DF=AC,只有当∠BAC=90°时,AC⊥DE;只有当BC=2AC时,DF=AC=BE,所以A、B、C选项的结论不一定正确;∵AD∥BC,∴∠OAD=∠OCE,∠ODA=∠OEC,而AD=CE,∴△AOD≌△COE(ASA),∴OD=OE,OA=OC即AC、DE互相平分,所以D选项的结论正确.故选:D.【点睛】本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行(或共线)且相等.1.(2023·浙江·八年级假期作业)如图,△ABC的边AC与△CDE的边CE在一条直线上,且点C为AE的中点,AB=CD,BC=DE.(1)求证:△ABC≌△CDE;(2)将△ABC沿射线AC方向平移得到△A B C ,边B C 与边CD的交点为F,连接EF,若EF将CDE 分为面积相等的两部分,且AB=4,则CF=【答案】(1)见解析(2)2【分析】(1)首先由点C为AE的中点得出AC=CE,再根据SSS证明△ABC≌△CDE即可;(2)根据平移的性质得A B =CD=AB=4,再由EF将CDE分为面积相等的两部分得CF=DF=12CD =2【解析】(1)证明:∵点C为AE的中点,∴AC=CE在△ABC和△CDE中,AB=CD BC=DE AC=CE∴△ABC≌△CDE(2)解:将△ABC沿射线AC方向平移得到ΔA B C ,且AB=4,∴A B =CD =AB =4,∵边B C 与边CD 的交点为F ,连接EF ,EF 将CDE 分为面积相等的两部分,如图∴CF =DF =12CD =2,故答案为:2【点睛】本题主要考查了全等三角形的判定以及平移的性质,根据SSS 证明△ABC ≌△CDE 是解答本题的关键.2.(2023春·重庆·八年级校考期中)如图,将△ABC 沿射线BC 方向平移得到△DCE ,连接BD 交AC于点F .(1)求证:△AFB ≌△CFD ;(2)若AB =9,BC =7,求BF 的取值范围.【答案】(1)见解析(2)1<BF <8【分析】(1)根据∠A =∠FCD ,∠AFC =∠CFD ,即可证明;(2)在△BCD 中,利用三边关系求出BD 的取值范围即可解决问题.(1)证明:∵AB ∥CD ,∴∠A =∠FCD ,在△AFB 和△CFD 中,∠A =∠FCD ∠AFB =∠CFD AB =CD∴△AFB ≌△CFD .(2)【解析】解:∵△AFB ≌△CFD ,∴BF =FD ,在△BCD 中,BC =7,CD =9,∴2<BD <16,∴2<2BF <16,∴1<BF <8.【点睛】本题考查平移变换、全等三角形的判定和性质、三角形的三边关系等知识,解题的关键是正确寻找三角形全等的条件解决问题,属于中考常考题型.3.(2023春·八年级课时练习)已知△ABC ,AB =AC ,∠ABC =∠ACB ,将△ABC 沿BC 方向平移得到△DEF .如图,连接BD 、AF ,则BD AF (填“>”“<”或“=”),并证明.【答案】【答案】BD =AF ,证明见解析【分析】由△ABC 沿BC 方向平移得到△DEF ,得到AC =DF ,∠DFB =∠ACB =∠ABF ,即可证明;【解析】【详解】解:BD =AF .证明:由△ABC 沿BC 方向平移得到△DEF ,AB =AC ,得AC =DF =AB ,,∠DFB =∠ACB =∠ABF .在△ABF 和△DFB 中,{AB =DF∠ABF =∠DFB BF =FB,∴△ABF ≌△DFB (SAS ),∴BD =AF .故答案是=.【点睛】本题主要考查了全等三角形的判定和性质,准确分析证明是解题的关键.【知识点2轴对称模型】【模型解读】将原图形沿着某一条直线折叠后,直线两边的部分能够完全重合,这两个三角形称之为轴对称型全等三角形,此类图形中要注意期隐含条件,即公共边或公共角相等.【常见模型】【题型2轴对称模型】1(2023春·河北邯郸·八年级校考期末)如图,在长方形ABCD 中,点M 为CD 中点,将△MBC 沿BM 翻折至△MBE ,若∠AME =α,∠ABE =β,则α与β之间的数量关系为()A.α+3β=180°B.β-α=20°C.α+β=80°D.3β-2α=90°【答案】D【分析】直接利用平行线的性质结合翻折变换的性质得出△ADM≌△BCM(SAS),进而利用直角三角形的性质得出答案.【详解】∵M为CD中点,∴DM=CM,在△ADM和△BCM中∵AD=BC ∠D=∠C DM=CM ,∴△ADM≌△BCM(SAS),∴∠AMD=∠BMC,AM=BM∴∠MAB=∠MBA∵将点C绕着BM翻折到点E处,∴∠EBM=∠CBM,∠BME=∠BMC=∠AMD ∴∠DME=∠AMB∴∠EBM=∠CBM=12(90°-β)∴∠MBA=12(90°-β)+β=12(90°+β)∴∠MAB=∠MBA=12(90°+β)∴∠DME=∠AMB=180°-∠MAB-∠MBA=90°-β∵长方形ABCD中,∴CD∥AB∴∠DMA=∠MAB=12(90°+β)∴∠DME+∠AME=∠ABE+∠MBE∵∠AME=α,∠ABE=β,∴90°-β+α=β+12(90°-β)∴3β-2α=90°故选D.【点睛】本题考查的知识点是平行线的性质,解题关键是利用全等三角形对应角相等即可求解.1.(2023·全国·八年级专题练习)如图,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=12∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.【答案】DE +BF =EF ,见解析【解析】试题分析:通过延长CF ,将DE 和BF 放在一起,便于寻找等量关系,通过两次三角形全等证明,得出结论.猜想:DE +BF =EF .证明:延长CF ,作∠4=∠1,如图:∵将Rt △ABC 沿斜边翻折得到△ADC ,点E ,F 分别为DC ,BC 边上的点,且∠EAF =∠DAB ,∴∠1+∠2=∠3+∠5,∠2+∠3=∠1+∠5,∵∠4=∠1,∴∠2+∠3=∠4+∠5,∴∠GAF =∠FAE ,在△AGB 和△AED 中,∠4=∠1AB =AD ∠ABG =∠ADE,∴△AGB ≌△AED (ASA ),∴AG =AE ,BG =DE ,在△AGF 和△AEF 中,AG =AE ∠GAF =∠EAF AF =AF,∴△AGF ≌△AEF (SAS ),∴GF =EF ,∴DE +BF =EF .2.(2023春·山东青岛·八年级统考期中)如图,在Rt ΔABC 中,∠C =90°,将ΔABC 沿AB 向下翻折后,再绕点A 按顺时针旋转α度(α<∠ABC ).得到Rt ΔADE ,其中斜边AE 交BC 于点F ,直角边DE 分别AB 、BC 于点G ,H1 请根据题意用实线补全图形;(不得用铅笔作图).2 求证:ΔAFB ≅ΔAGE【答案】(1)作图见详解;(2)证明见详解.【分析】(1)根据题意画出图形,注意折叠与旋转中的对应关系;(2)由题意易得△ABC ≌△AED ,即可得AB =AE ,∠ABC =∠E ,然后利用ASA 的判定方法,即可证得△AFB ≌△AGE .【解析】解:(1)画图,如下图;证明:由题意得:△ABC ≌△AED .∴AB =AE ,∠ABC =∠E .在△AFB 和△AGE 中,∠ABC =∠EAB =AE∠α=∠α∴△AFB ≌△AGE (ASA ).【点睛】本题考查折叠与旋转的性质以及全等三角形的判定与性质,注意掌握数形结合思想的应用以及注意折叠与旋转中的对应关系.3.(2023春·山西临汾·八年级统考期末)阅读材料,并回答下列问题如图1,以AB 为轴,把△ABC 翻折180°,可以变换到△ABD 的位置;如图2,把△ABC 沿射线AC 平移,可以变换到△DEF 的位置.像这样,其中的一个三角形是另一个三角形经翻折、平移等方法变换成的,这种只改变位置,不改变形状大小的图形变换,叫三角形的全等变换.班里学习小组针对三角形的全等变换进行了探究和讨论(1)请你写出一种全等变换的方法(除翻折、平移外),.(2)如图2,前进小组把△ABC 沿射线AC 平移到△DEF ,若平移的距离为2,且AC =5,则DC =.(3)如图3,圆梦小组展开了探索活动,把△ABC 纸片沿DE 折叠,使点A 落在四边形BCDE 内部点A ′的位置,且得出一个结论:2∠A ′=∠1+∠2.请你对这个结论给出证明.(4)如图4,奋进小组则提出,如果把△ABC 纸片沿DE 折叠,使点A 落在四边形BCDE 外部点A ′的位置,此时∠A ′与∠1、∠2之间结论还成立吗?若成立,请给出证明,若不成立,写出正确结论并证明.【答案】(1)旋转;(2)3;(3)见解析;(4)不成立,正确结论:∠2-∠1=2∠A ',见解析【分析】(1)由题意根据三种全等变换翻折、平移、旋转的定义进行判断即可;(2)根据平移的距离的定义可知AD=2,则DC=AC-AD进行求解即可;(3)根据轴对称及三角形内角和定理进行分析即可得出结论;(4)由题意根据轴对称及三角形内角和定理,进行分析即可得出结论.【解析】解:(1)除翻折、平移外全等变换的方法还有旋转;故答案为:旋转.(2)∵AD=2,AC=5,∴DC=AC-AD=5-2=3;故答案为:3.(3)∵把△ADE沿DE翻折,得到△A'DE,∴△ADE≌△A'DE,∴∠ADE=∠A'DE,∠AED=∠A'ED,在△DEA'中,∠A'=180°-(∠A'DE+∠A'ED);由平角定义知,∠2=180°-∠A'DA=180°-2∠A'DE,∠1=180°-∠A'EA=180°-2∠A'ED,∴∠1+∠2=180°-2∠A'DE+180°-2∠A'ED=2(180°-∠A'ED-∠A'DE),∴2∠A′=∠1+∠2.(4)∠2-∠1=2∠A',理由如下:∵把△ADE沿DE翻折,得到△A'DE,∴△ADE≌△A'DE,∴∠ADE=∠A'DE,∠AED=∠A'ED,在△DEA'中,∠A'=180°-(∠A'DE+∠A'ED),由平角定义知,∠2=180°-∠A'DA=180°-2∠A'DE,∠1=2∠A'ED-180°,∴∠2-∠1=(180°-2∠A'DE)-(2∠A'ED-180°)=180°-(∠A'DE+∠A'ED),∴∠2-∠1=2∠A'.【点睛】本题是三角形综合题,综合考查平移的性质,折叠的性质,三角形内角和定理,全等三角形的性质等知识,灵活运用这些性质进行推理是解答本题的关键.【知识点3旋转模型】【模型解读】将三角形绕着公共顶点旋转一定角度后,两个三角形能够完全重合,则称这两个三角形为旋转型三角形,识别旋转型三角形时,涉及对顶角相等、等角加(减)公共角的条件.【常见模型】【题型3旋转模型】1(2023春·全国·八年级期末)(1)问题引入:如图1,点F是正方形ABCD边CD上一点,连接AF,将△ADF绕点A顺时针旋转90°与△ABG重合(D与B重合,F与G重合,此时点G,B,C在一条直线上),∠GAF的平分线交BC于点E,连接EF,判断线段EF与GE之间有怎样的数量关系,并说明理由.(2)知识迁移:如图2,在四边形ABCD中,∠ADC+∠B=180°,AB=AD,E,F分别是边BC,CD延长线上的点,连接AE,AF,且∠BAD=2∠EAF,试写出线段BE,EF,DF之间的数量关系,并说明理由.(3)实践创新:如图3,在四边形ABCD中,∠ABC=90°,AC平分∠DAB,点E在AB上,连接DE,CE,且∠DAB=∠DCE=60°,若DE=a,AD=b,AE=c,求BE的长.(用含a,b,c的式子表示)【答案】(1)EF=GE,理由见详解;(2)BE-DF=EF,理由见详解;(3)BE=a+b-c2,理由见详解【分析】(1)根据SAS直接可证△GAE≌△FAE即得GE=EF;(2)在BE上取BG=DF,连接AG,由∠ADC+∠B=180°,∠ADF+∠ADC=180°,得∠B=∠ADF,从而SAS证△ABG≌△ADF,再通过SAS证△GAE≌△FAE,得GE=EF,从而解决问题;(3)作CF⊥AD,交AD的延长线于F,取FG=BE,连接CG,由(2)同理可两次全等证明出DE=GD即可.【详解】解:(1)EF=GE,理由如下:∵△ADF绕点A顺时针旋转90°与△ABG重合,∴AG=AF,∵AE平分∠GAF,∴∠GAE=∠FAE,在△GAE和△FAE中,AG=AF∠GAE=∠FAE AE=AE,∴△GAE≌△FAE(SAS),∴GE=EF;(2)BE-DF=EF,理由如下:如图2,在BE上取BG=DF,连接AG,∵∠ADC+∠B=180°,∠ADF+∠ADC=180°,∴∠B=∠ADF,在△ABG和△ADF中,BG=DF∠B=∠ADF AB=AD,∴△ABG≌△ADF(SAS),∴∠BAG=∠FAD,AG=AF,∵∠BAD=2∠EAF,∴∠GAF=2∠EAF,∴∠GAE=∠EAF,在△GAE和△FAE中,AG=AF∠GAE=∠FAE AE=AE,∴△GAE≌△FAE(SAS),∴GE=EF,∴BE-DF=EF;(3)如图,作CF⊥AD,交AD的延长线于F,取FG=BE,连接CG,∵AC平分∠BAD,CF⊥AF,CB⊥AB,∴CF=CB,∠EBC=∠GFC,∵BE=GF,∴△CBE≌△CFG(SAS),∴∠BCE=∠FCG,CG=CE,∵∠DAB=60°,∴∠FCB=120°,∵∠DCE=60°,∴∠DCF+∠BCE=60°,∴∠DCG=60°,又∵CG=CE,∴△ECD≌△GCD(SAS),∴GD=DE,∵Rt△ACF≌Rt△ACB(HL),∴AF=AB,∴b+a-BE=c+BE,∴BE=a+b-c2.【点睛】本题主要考查了全等的判定与性质,结合问题引入,构造出全等三角形是解题的关键.1.(2023春·八年级课时练习)如图,等边△ABC中,∠AOB=115°,∠BOC=125°,则以线段OA,OB,OC为边构成的三角形的各角的度数分别为.【答案】55°,60°,65°.【分析】通过旋转△AOB至△CDB,可得△BOD是等边三角形,将OA,OB,OC放在一个三角形中,进而求出各角大小。
(完整版)初中数学九大几何模型

初中数学九大几何模型一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OABCDE图 2OABC DEOABCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90°将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OB CO ACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
全等三角形八大基本模型

全等三角形八大基本模型摘要:一、全等三角形的概念和性质二、全等三角形的判定方法三、八大基本模型概述1.手拉手模型2.一线三垂直模型3.一线三等角模型4.等腰三角形中边边角模型5.背对背模型6.半角旋转模型7.角分线模型8.正方形手拉手模型四、八大基本模型的应用举例五、总结与展望正文:全等三角形是初中数学中的一个重要内容,掌握全等三角形的性质和判定方法对于解决几何问题具有重要意义。
全等三角形的判定方法主要包括SSS、SAS、ASA、AAS 和HL 五种,其中SSS 和HL 是全等三角形的常见判定方法。
在实际应用中,全等三角形八大基本模型可以帮助我们更好地理解和解决几何问题。
这八大基本模型分别是:1.手拉手模型:这种模型是通过两个全等三角形的对应边相互牵手而形成的。
比如,若ABC 和DEF 是两个全等三角形,那么我们可以通过AB 与DE、BC 与EF、AC 与DF 的相互牵手形成一个新的全等三角形ABC。
2.一线三垂直模型:这种模型是通过一条直线与三个垂直的线段组成的。
比如,若AB 是直线,BC、CD 和DE 是垂直于AB 的线段,那么三角形ABC 和三角形DEB 是全等的。
3.一线三等角模型:这种模型是通过一条直线与三个相等的角组成的。
比如,若AB 是直线,∠ABC、∠BCD 和∠CDA 是相等的角,那么三角形ABC 和三角形CDA 是全等的。
4.等腰三角形中边边角模型:这种模型是通过对等腰三角形的一腰和一底边以及一个顶角进行操作而形成的。
比如,若AB=AC 是等腰三角形的腰,BC 是底边,∠ABC 是顶角,那么三角形ABC 和三角形ACB 是全等的。
5.背对背模型:这种模型是通过两个全等三角形的对应边背靠背而形成的。
比如,若ABC 和DEF 是两个全等三角形,那么我们可以通过AB 与DF、BC 与DE、AC 与EF 的相互背靠背形成一个新的全等三角形ABC。
6.半角旋转模型:这种模型是通过将一个全等三角形绕其一边的一半旋转而形成的。
三角形全等之手拉手模型、倍长中线、截长补短法、旋转、寻找三角形全等方法归纳总结

一、手拉手模型要点一:手拉手模型特点:由两个等顶角的等腰三角形所组成,并且顶角的 顶点为公共顶点结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180° (3)OA 平分∠BOC 变形:例1.如图在直线ABC 的同一侧作两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60 (4)DFB AGB ∆≅∆ (5)CFB EGB ∆≅∆ (6)BH 平分AHC ∠ (7)AC GF //变式精练1:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,BH 平分AHC ∠例2:如图,两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H问:(1)CDE ADG ∆≅∆是否成立 (2)AG 是否与CE 相等(3)AG 与CE 之间的夹角为多少度 (4)HD 是否平分AHE ∠例3:如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H 问:(1)CDE ADG ∆≅∆是否成立 (2)AG 是否与CE 相等(3)AG 与CE 之间的夹角为多少度 (4)HD 是否平分AHE ∠例4:两个等腰三角形ABD ∆与BCE ∆,其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ,问:(1)DBC ABE ∆≅∆是否成立 (2)AE 是否与CD 相等(3)AE 与CD 之间的夹角为多少度 (4)HB 是否平分AHC ∠二、倍长与中点有关的线段倍长中线类☞考点说明:凡是出现中线或类似中线的线段,都可以考虑倍长中线,倍长中线的目的是可以旋转等长度的线段,从而达到将条件进行转化的目的。
专题 五大常考的全等模型

专题四
五大常考的全等模型
(1)证明:∵AD⊥BC, ∴∠ADB=∠ADC=90°. ∵∠ABC=45°, ∴∠BAD=45°. ∴∠ABC=∠BAD, ∴AD=BD. 在△BDE和△ADC中,
BD=AD
∠EDB=∠CDA
DE=DC
∴△BDE≌△ADC(SAS). ∴BE=AC;
专题四
五大常考的全等模型
AF,EF,且∠EAF=45°,求证:BE+DF=EF. 【思维教练】延长CD到点G,使DG=BE,将BE,DF转化在一条直线上,再 证EF=GF即可.
例4题图
专题四
五大常考的全等模型
证明:如解图,延长CD到点G,使
DG=BE, 在正方形ABCD中,AB=AD,
∠B=∠ADC=90°, ∴∠ADG=∠B. 在△ABE和△ADG中, AB AD B ADG , BE DG ∴△ABE≌△ADG(SAS). ∴AG=AE,∠DAG=∠BAE.
五大常考的全等模型
针对训练
7. 在等边△ABC中,∠BDC=120°,BD=CD,∠EDF=60°点D和点E分别 在边AB和AC上,连接EF,试猜想∠EFD和∠DFE应满足的数量关系,并写 出推理过程.
专题四
五大常考的全等模型
综合训练
1. 如图①,△ABD,△ACE都是等边三角形,
(1)求证:△ABE≌△ADC;
例6题解图
专题四
五大常考的全等模型
基本模型
图示
等边三角 形含半角 (∠BDC=120°)
等腰直角三 角形含半角
专题四
五大常考的全等模型
图示
正方形含半角
模型总结
当一个角包含着这个角的半角,常将半角两边的三角形通过 旋转到一边合并形成新的三角形,从而进行等量代换,然后 证明与半角形成的三角形全等.
三角形旋转全等常见模型

1•绕点型(手拉手模型)(1 )自旋转:自旋转构造放方法:①遇60°旋60°,构造等边三角形;②遇90°旋90°,构造等腰直角三角形;③遇等腰旋转顶角,构造旋转全等;④遇中点180°,构造中心对称。
(2)共旋转(典型的手拉手模型)例1、在直线ABC的同一侧作两个等边三角形4ABD和aBCE,连接AE与CD,证明:(1)A ABE^A DBC(2)) AE=DC(3)AE与DC的夹角为60。
(4)A AGB^A DFB(5)A EGB^A CFB(6)BH 平分N AHC(7)GFllAC变式练习1、如果两个等边三角形4ABD和aBCE,连接AE与CD,证明:(1) A ABE^A DBC(2 ) AE=DC(3)AE与DC的夹角为60。
(4)AE与DC的交点设为H,BH平分N AHC变式练习2、如果两个等边三角形MBD和aBCE,连接AE与CD,证明:⑴MBE空4DBC(2)AE=DC(3)AE与DC的夹角为60。
(4)AE与DC的交点设为H,BH平分N AHC(1)如图1,点C是线段AB上一点,分别以AC, BC为边在AB的同侧作等边MCM和4BN,连接AN,BM .分别取BM , AN的中点E,F,连接CE,CF,EF .观察并猜想^CEF的形状,并说明理由.(2)若将(1)中的“以AC, BC为边作等边MCM和482 改为“以AC, BC为腰在AB的同侧作等腰4ACM和4BN,〃如图2,其他条件不变,那么(1)中的结论还成立吗?若成立,加以证明;若不成立,请说明理由.例4、例题讲解:1.已知^ABC为等边三角形,点D为直线BC上的一动点(点D不与B,C重合),以AD为边作菱形ADEF(按A,D,E,F逆时针排列),使NDAF=60°,连接CF.⑴如图1,当点D在边BC上时,求证:①BD=CF ,②AC=CF+CD.(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;(3)如图3,当点D在边BC的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系。
全等三角形八大基本模型

全等三角形八大基本模型
【原创实用版】
目录
1.全等三角形的定义与性质
2.全等三角形的八大基本模型
1.手拉手模型
2.一线三垂直模型
3.一线三等角模型
4.等腰三角形中边边角模型
5.背对背模型
6.半角旋转模型
7.角分线模型
8.正方形手拉手模型
正文
全等三角形是指两个三角形的对应边和对应角分别相等的三角形。
全等三角形的判定方法有很多,其中最常用的是 SSS(边 - 边-边)、SAS (边 - 角-边)、ASA(角 - 边-角)、AAS(角 - 角-边)和 HL(斜边 - 直角边)五种方法。
除此之外,全等三角形还有八大基本模型,分别为:
1.手拉手模型:两个三角形的两边分别平行,且其中一边的夹角等于另一边的夹角,则这两个三角形全等。
2.一线三垂直模型:两个三角形的一边和另外两个角的平分线垂直,则这两个三角形全等。
3.一线三等角模型:两个三角形的一边和另外两个角分别相等,则这两个三角形全等。
4.等腰三角形中边边角模型:两个等腰三角形的底边和腰分别相等,且底边上的高也相等,则这两个三角形全等。
5.背对背模型:两个三角形的一对相对角分别相等,另一对相对角也分别相等,则这两个三角形全等。
6.半角旋转模型:一个三角形绕着一边旋转 180 度后与另一个三角形重合,则这两个三角形全等。
7.角分线模型:两个三角形的一对相对角的角平分线重合,则这两个三角形全等。
8.正方形手拉手模型:两个正方形的一对相邻边分别平行且相等,则这两个正方形全等。
全等三角形八大基本模型

全等三角形八大基本模型摘要:1.全等三角形的定义与性质2.全等三角形的八大基本模型1.手拉手模型2.一线三垂直模型3.一线三等角模型4.等腰三角形中边边角模型5.背对背模型6.半角旋转模型7.角分线模型8.正方形手拉手模型正文:全等三角形是指两个三角形的对应边和对应角分别相等的三角形。
在解决全等三角形问题时,我们需要了解全等三角形的定义和性质,同时掌握一些常用的模型。
本文将介绍全等三角形的八大基本模型,希望能帮助大家更好地理解和解决全等三角形问题。
1.手拉手模型:两个三角形通过一个公共边,并且这个公共边的两个相邻角分别相等。
2.一线三垂直模型:两个三角形有一个公共边,并且这个公共边的两个相邻角分别相等,同时还有另一条公共边上的一个角与另一个角的补角相等。
3.一线三等角模型:两个三角形有一个公共边,并且这个公共边上的三个角分别相等。
4.等腰三角形中边边角模型:两个等腰三角形,其中一个等腰三角形的底边与另一个等腰三角形的腰相等,同时这两个等腰三角形的底角分别相等。
5.背对背模型:两个三角形分别有一个角和另一个角的补角相等,且这两个三角形的另一条边分别相等。
6.半角旋转模型:两个三角形有一个公共边,并且这个公共边的两个相邻角中有一个角是另一个角的一半。
7.角分线模型:两个三角形有一个公共边,并且这个公共边上的一个角平分另一个角。
8.正方形手拉手模型:两个正方形,其中一个正方形的边与另一个正方形的对角线相等。
在解决全等三角形问题时,我们可以根据题目所给的条件,结合全等三角形的性质和八大基本模型,通过适当的变换和推理,证明两个三角形全等。
全等三角形 六大模型

全等三角形六大模型学生版【题型1 平移模型】【模型解读】把△ABC沿着某一条直线l平行移动,所得到△DEF与△ABC称为平移型全等三角形,图①,图②是常见的平移型全等三角线.【常见模型】【例1】(2020秋•襄城区期末)如图,点B、E、C、F四点在一条直线上,∠A=∠D,AB∥DE,老师说:再添加一个条件就可以使△ABC≌△DEF.下面是课堂上三个同学的发言,甲说:添加AB=DE;乙说:添加AC∥DF;丙说:添加BE=CF.(1)甲、乙、丙三个同学说法正确的是;(2)请你从正确的说法中选择一种,给出你的证明.【变式1-1】(2020秋•苏州期末)如图,AD,BF相交于点O,AB∥DF,AB=DF,点E与点C在BF上,且BE=CF.(1)求证:△ABC≌△DFE;(2)求证:点O为BF的中点.【变式1-2】(2020秋•富顺县校级月考)如图1,A,B,C,D在同一直线上,AB=CD,DE∥AF,且DE =AF,求证:△AFC≌△DEB.如果将BD沿着AD边的方向平行移动,如图2,3时,其余条件不变,结论是否成立?如果成立,请予以证明;如果不成立,请说明理由.【变式1-3】(2021春•雁塔区校级期中)如图①点A、B、C、D在同一直线上,AB=CD,作CE⊥AD,BF ⊥AD,且AE=DF.(1)证明:EF平分线段BC;(2)若△BFD沿AD方向平移得到图②时,其他条件不变,(1)中的结论是否仍成立?请说明理由.【题型2 轴对称模型】【模型解读】将原图形沿着某一条直线折叠后,直线两边的部分能够完全重合,这两个三角形称之为轴对称型全等三角形,此类图形中要注意期隐含条件,即公共边或公共角相等.【常见模型】【例2】(2020秋•杭州校级月考)如图,在△ABC和△BAD中,AC与BD相交于点E,已知AD=BC,另外只能从下面给出的三个条件①∠DAB=∠CBA,②∠D=∠C③∠DBA=∠CAB选择其中的一个用来证明在△ABC和△BAD全等,这个条件是.(填写编号),并证明△ABC≌△BAD.【变式2-1】如图,AB=AC,BE⊥AC于E,CD⊥AB于D,BE、CD交于点O,求证:OB=OC.【变式2-2】(2020秋•海珠区校级期中)如图,PB⊥AB,PC⊥AC,PB=PC,D是AP上一点.求证:∠BDP=∠CDP.【变式2-3】如图,AB=AC,D、E分别是AB、AC的中点,AM⊥CD于M,AN⊥BE干N.求证:AM=AN.【题型3 旋转模型】【模型解读】将三角形绕着公共顶点旋转一定角度后,两个三角形能够完全重合,则称这两个三角形为旋转型三角形,识别旋转型三角形时,涉及对顶角相等、等角加(减)公共角的条件.【常见模型】【例3】(2020秋•渝水区校级期中)如图,AB=AC,AD=AE,∠BAC=∠DAE.求证:∠ABD=∠ACE.【变式3-1】(2020秋•怀宁县期末)如图,已知:AD=AB,AE=AC,AD⊥AB,AE⊥AC.猜想线段CD与BE之间的数量关系与位置关系,并证明你的猜想.【变式3-2】(2020秋•合江县月考)已知△ABC和△ADE均为等腰三角形,且∠BAC=∠DAE,AB=AC,AD=AE.(1)如图1,点E在BC上,求证:BC=BD+BE;(2)如图2,点E在CB的延长线上,求证:BC=BD﹣BE.【变式3-3】(2021春•浦东新区期末)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE =90°.(1)当点D在AC上时,如图①,线段BD,CE有怎样的数量关系和位置关系?请证明你的猜想;(2)将图①中的△ADE绕点A顺时针旋转α(0°<α<90°),如图②,线段BD,CE有怎样的数量关系和位置关系?请说明理由.【题型4 一线三等角模型】【模型解读】基本图形如下:此类图形通常告诉BD⊥DE,AB⊥AC,CE⊥DE,那么一定有∠B=∠CAE.【常见模型】【例4】(2020秋•覃塘区期中)已知:D,A,E三点都在直线m上,在直线m的同一侧作△ABC,使AB =AC,连接BD,CE.(1)如图①,若∠BAC=90°,BD⊥m,CE⊥m,求证:△ABD≌△ACE;(2)如图②,若∠BDA=∠AEC=∠BAC,请判断BD,CE,DE三条线段之间的数量关系,并说明理由.【变式4-1】(2020春•香坊区期末)如图,在△ABC中,点D是边BC上一点,CD=AB,点E在边AC上,且AD=DE,∠BAD=∠CDE.(1)如图1,求证:BD=CE;(2)如图2,若DE平分∠ADC,在不添加辅助线的情况下,请直接写出图中所有与∠ADE相等的角(∠ADE除外).【变式4-2】(2020春•历下区期中)CD是经过∠BCA定点C的一条直线,CA=CB,E、F分别是直线CD 上两点,且∠BEC=∠CF A=∠β.(1)若直线CD经过∠BCA内部,且E、F在射线CD上,①若∠BCA=90°,∠β=90°,例如图1,则BE CF,EF|BE﹣AF|.(填“>”,“<”,“=”);②若0°<∠BCA<180°,且∠β+∠BCA=180°,例如图2,①中的两个结论还成立吗?并说明理由;(2)如图3,若直线CD经过∠BCA外部,且∠β=∠BCA,请直接写出线段EF、BE、AF的数量关系(不需要证明).【变式4-3】(2020秋•余杭区月考)如图①,点B、C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.应用:如图②,在△ABC中,AB=AC,AB>BC,点D在边BC上,且CD=2BD,点E,F在线段AD 上.∠1=∠2=∠BAC,若△ABC的面积为15,求△ABE与△CDF的面积之和.【题型5 倍长中线模型】【模型解读】中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.【常见模型】【例5】(2020秋•津南区校级期中)已知:在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF.【变式5-1】(2020春•大庆期末)如图.AB=AE,AB⊥AE,AD=AC.AD⊥AC,点M为BC的中点,求证:DE=2AM.【变式5-2】(2020秋•西城区校级期中)如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.求证:BF=CG.【变式5-3】(2020秋•安陆市期中)八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧.【探究与发现】(1)如图1,AD是△ABC的中线,延长AD至点E,使ED=AD,连接BE,写出图中全等的两个三角形【理解与应用】(2)填空:如图2,EP是△DEF的中线,若EF=5,DE=3,设EP=x,则x的取值范围是.(3)已知:如图3,AD是△ABC的中线,∠BAC=∠ACB,点Q在BC的延长线上,QC=BC,求证:AQ=2AD.【题型6 截长补短模型】【模型解读】截长补短的方法适用于求证线段的和差倍分关系.截长,指在长线段中截取一段等于已知线段;补短,指将短线段延长,延长部分等于已知线段.该类题目中常出现等腰三角形、角平分线等关键词句,可以采用截长补短法构造全等三角形来完成证明过程【例6】(2020秋•涪城区校级月考)如图,AB∥CD,E为AD上一点,且BE、CE分别平分∠ABC,∠BCD.求证:AE=DE.【变式6-1】(2020秋•蕲春县期中)如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,若E在AD上.求证:(1)BE⊥CE;(2)BC=AB+CD.【变式6-2】(2020秋•新抚区校级月考)如图所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:DA平分∠CDE.【变式6-3】(2020秋•北流市期中)已知△ABC中,BD,CE分别平分∠ABC和∠ACB,BD、CE交于点O.(1)直接写出∠BOC与∠A的数量关系;(2)若∠A=60°,利用(1)的关系,求出∠BOC的度数;(3)利用(2)的结果,试判断BE,CD,BC的数量关系,并证明.全等三角形六大模型教师版【题型1 平移模型】【例1】(2020秋•襄城区期末)如图,点B、E、C、F四点在一条直线上,∠A=∠D,AB∥DE,老师说:再添加一个条件就可以使△ABC≌△DEF.下面是课堂上三个同学的发言,甲说:添加AB=DE;乙说:添加AC∥DF;丙说:添加BE=CF.(1)甲、乙、丙三个同学说法正确的是;(2)请你从正确的说法中选择一种,给出你的证明.【解题思路】(1)根据平行线的性质,由AB∥DE可得∠B=∠DEC,再加上条件∠A=∠D,只需要添加一个能得出边相等的条件即可证明两个三角形全等,添加AC∥DF不能证明△ABC≌△DEF;(2)添加AB=DE,然后再利用ASA判定△ABC≌△DEF即可.【解答过程】解:(1)说法正确的是:甲、丙,故答案为:甲、丙;(2)证明:∵AB∥DE,∴∠B=∠DEC,在△ABC 和△DEF 中 {∠A =∠DAB =DE ∠B =∠DEF, ∴△ABC ≌△DEF (ASA ).【变式1-1】(2020秋•苏州期末)如图,AD ,BF 相交于点O ,AB ∥DF ,AB =DF ,点E 与点C 在BF 上,且BE =CF .(1)求证:△ABC ≌△DFE ; (2)求证:点O 为BF 的中点.【变式1-2】(2020秋•富顺县校级月考)如图1,A ,B ,C ,D 在同一直线上,AB =CD ,DE ∥AF ,且DE =AF ,求证:△AFC ≌△DEB .如果将BD 沿着AD 边的方向平行移动,如图2,3时,其余条件不变,结论是否成立?如果成立,请予以证明;如果不成立,请说明理由.【变式1-3】(2021春•雁塔区校级期中)如图①点A 、B 、C 、D 在同一直线上,AB =CD ,作CE ⊥AD ,BF ⊥AD ,且AE =DF .(1)证明:EF 平分线段BC ;(2)若△BFD 沿AD 方向平移得到图②时,其他条件不变,(1)中的结论是否仍成立?请说明理由.【题型2 轴对称模型】【例2】(2020秋•杭州校级月考)如图,在△ABC 和△BAD 中,AC 与BD 相交于点E ,已知AD =BC ,另外只能从下面给出的三个条件①∠DAB =∠CBA ,②∠D =∠C ③∠DBA =∠CAB 选择其中的一个用来证明在△ABC 和△BAD 全等,这个条件是 .(填写编号),并证明△ABC ≌△BAD .【解题思路】选择条件①,根据全等三角形的判定定理SAS 进行证明即可. 【解答过程】解:这个条件是:①,证明如下: 在△ABD 与△BAC 中, {BC =AD∠CBA =∠DAB BA =AB, ∴△ABC ≌△BAD (SAS ).【变式2-1】如图,AB =AC ,BE ⊥AC 于E ,CD ⊥AB 于D ,BE 、CD 交于点O ,求证:OB =OC .【变式2-2】(2020秋•海珠区校级期中)如图,PB ⊥AB ,PC ⊥AC ,PB =PC ,D 是AP 上一点.求证:∠BDP =∠CDP .【变式2-3】如图,AB=AC,D、E分别是AB、AC的中点,AM⊥CD于M,AN⊥BE干N.求证:AM=AN.【题型3 旋转模型】【例3】(2020秋•渝水区校级期中)如图,AB=AC,AD=AE,∠BAC=∠DAE.求证:∠ABD=∠ACE.【解题思路】根据等式的性质得出∠BAD =∠CAE ,利用SAS 证明△ABD 与△ACE 全等,进而解答即可. 【解答过程】证明:∵∠BAC =∠DAE , ∴∠BAC ﹣∠CAD =∠DAE ﹣∠CAD , ∴∠BAD =∠CAE , 在△ABD 与△ACE 中, {AB =AC∠BAD =∠CAE AD =AE, ∴△ABD ≌△ACE (SAS ), ∴∠ABD =∠ACE .【变式3-1】(2020秋•怀宁县期末)如图,已知:AD =AB ,AE =AC ,AD ⊥AB ,AE ⊥AC .猜想线段CD 与BE 之间的数量关系与位置关系,并证明你的猜想.【变式3-2】(2020秋•合江县月考)已知△ABC 和△ADE 均为等腰三角形,且∠BAC =∠DAE ,AB =AC ,AD =AE .(1)如图1,点E 在BC 上,求证:BC =BD +BE ;(2)如图2,点E 在CB 的延长线上,求证:BC =BD ﹣BE .【变式3-3】(2021春•浦东新区期末)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE =90°.(1)当点D在AC上时,如图①,线段BD,CE有怎样的数量关系和位置关系?请证明你的猜想;(2)将图①中的△ADE绕点A顺时针旋转α(0°<α<90°),如图②,线段BD,CE有怎样的数量关系和位置关系?请说明理由.【题型4 一线三等角模型】【例4】(2020秋•覃塘区期中)已知:D,A,E三点都在直线m上,在直线m的同一侧作△ABC,使AB =AC,连接BD,CE.(1)如图①,若∠BAC=90°,BD⊥m,CE⊥m,求证:△ABD≌△ACE;(2)如图②,若∠BDA=∠AEC=∠BAC,请判断BD,CE,DE三条线段之间的数量关系,并说明理由.【解题思路】(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA;(2)由∠BDA=∠AEC=∠BAC,就可以求出∠BAD=∠ACE,进而由ASA就可以得出△BAD≌△ACE,就可以得出BD =AE ,DA =CE ,即可得出结论.【解答过程】解:(1)证明:如图①,∵D ,A ,E 三点都在直线m 上,∠BAC =90°, ∴∠BAD +∠CAE =90°, ∵BD ⊥m ,CE ⊥m , ∴∠ADB =∠CEA =90°, ∴∠BAD +∠ABD =90°, ∴∠ABD =∠CAE , 在△ABD 和△ACE 中, {∠ADB =∠AEC ∠ABD =∠CAE AB =AC, ∴△ABD ≌△ACE (AAS ); (2)DE =BD +CE .理由是:如图②,∵∠BDA =∠AEC =∠BAC , ∴由三角形内角和及平角性质,得:∠BAD +∠ABD =∠BAD +∠CAE =∠CAE +∠ACE , ∴∠ABD =∠CAE ,∠BAD =∠ACE , 在△ABD 和△ACE 中, {∠ABD =∠CAE AB =AC ∠BAD =∠ACE, ∴△ABD ≌△ACE (ASA ), ∴BD =AE ,AD =CE , ∴DE =AD +AE =BD +CE .【变式4-1】(2020春•香坊区期末)如图,在△ABC 中,点D 是边BC 上一点,CD =AB ,点E 在边AC 上,且AD =DE ,∠BAD =∠CDE . (1)如图1,求证:BD =CE ;(2)如图2,若DE 平分∠ADC ,在不添加辅助线的情况下,请直接写出图中所有与∠ADE 相等的角(∠ADE 除外).【变式4-2】(2020春•历下区期中)CD是经过∠BCA定点C的一条直线,CA=CB,E、F分别是直线CD 上两点,且∠BEC=∠CF A=∠β.(1)若直线CD经过∠BCA内部,且E、F在射线CD上,①若∠BCA=90°,∠β=90°,例如图1,则BE CF,EF|BE﹣AF|.(填“>”,“<”,“=”);②若0°<∠BCA<180°,且∠β+∠BCA=180°,例如图2,①中的两个结论还成立吗?并说明理由;(2)如图3,若直线CD经过∠BCA外部,且∠β=∠BCA,请直接写出线段EF、BE、AF的数量关系(不需要证明).【变式4-3】(2020秋•余杭区月考)如图①,点B、C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.应用:如图②,在△ABC中,AB=AC,AB>BC,点D在边BC上,且CD=2BD,点E,F在线段AD 上.∠1=∠2=∠BAC,若△ABC的面积为15,求△ABE与△CDF的面积之和.【题型5 倍长中线模型】【例5】(2020秋•津南区校级期中)已知:在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE =AC ,延长BE 交AC 于F ,求证:AF =EF .【解题思路】根据点D 是BC 的中点,延长AD 到点G ,得到△ADC ≌△GDB ,利用全等三角形的对应角相等,对应边相等进行等量代换,得到△AEF 中的两个角相等,然后用等角对等边证明AE 等于EF . 【解答过程】证明:如图,延长AD 到点G ,使得AD =DG ,连接BG . ∵AD 是BC 边上的中线(已知), ∴DC =DB ,在△ADC 和△GDB 中, {AD =DG∠ADC =∠GDB(对顶角相等)DC =DB∴△ADC ≌△GDB (SAS ), ∴∠CAD =∠G ,BG =AC 又∵BE =AC , ∴BE =BG ,∴∠BED=∠G,∵∠BED=∠AEF,∴∠AEF=∠CAD,即:∠AEF=∠F AE,∴AF=EF.【变式5-1】(2020春•大庆期末)如图.AB=AE,AB⊥AE,AD=AC.AD⊥AC,点M为BC的中点,求证:DE=2AM.【变式5-2】(2020秋•西城区校级期中)如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.求证:BF=CG.【变式5-3】(2020秋•安陆市期中)八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧.【探究与发现】(1)如图1,AD是△ABC的中线,延长AD至点E,使ED=AD,连接BE,写出图中全等的两个三角形【理解与应用】(2)填空:如图2,EP是△DEF的中线,若EF=5,DE=3,设EP=x,则x的取值范围是.(3)已知:如图3,AD是△ABC的中线,∠BAC=∠ACB,点Q在BC的延长线上,QC=BC,求证:AQ=2AD.【题型6 截长补短模型】【例6】(2020秋•涪城区校级月考)如图,AB∥CD,E为AD上一点,且BE、CE分别平分∠ABC,∠BCD.求证:AE=DE.【解题思路】作BE的延长线交CD的延长线于F,结合条件可证明△FCE≌△BCE,得出EF=BE,BC =FC,进一步可得出△AEB≌△DEF,可得出结论.【解答过程】证明:如图,延长BE交CD的延长线于F,∵CE是∠BCD的平分线,∴∠BCE=∠FCE,∵AB∥CD,∴∠F =∠FBA ,∵BE 是∠ABC 的平分线,∴∠ABF =∠FBC ,∴∠FBC =∠F .在△FCE 和△BCE 中{∠F =∠FBC ∠FCE =∠BCE CE =CE,∴△FCE ≌△BCE (AAS ),∴EF =BE ,BC =FC ,在△AEB 和△DEF 中,{∠AEB =∠DEF BE =EF ∠FBA =∠F,∴△AEB ≌△DEF (ASA ),∴AE =ED .【变式6-1】(2020秋•蕲春县期中)如图,AB ∥CD ,BE 平分∠ABC ,CE 平分∠BCD ,若E 在AD 上.求证:(1)BE ⊥CE ;(2)BC =AB +CD .【变式6-2】(2020秋•新抚区校级月考)如图所示,在五边形ABCDE 中,AB =AE ,BC +DE =CD ,∠ABC +∠AED =180°,求证:DA 平分∠CDE .【变式6-3】(2020秋•北流市期中)已知△ABC中,BD,CE分别平分∠ABC和∠ACB,BD、CE交于点O.(1)直接写出∠BOC与∠A的数量关系;(2)若∠A=60°,利用(1)的关系,求出∠BOC的度数;(3)利用(2)的结果,试判断BE,CD,BC的数量关系,并证明.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1绕点型(手拉手模型)
遇60°旋60°,造等边二角形
遇900旋900,造等腰直角 遇等腰
旋顶角,造旋转全等 遇中点旋
1800,造中心对称
(2)共旋转(典型的手拉手模型)
例1、在直线ABC 的同一侧作两个等边三角形△
(1)
△ ABE^A DBC (2)
AE=DC (3)
AE 与DC 的夹角为60。
(4)
△ AGB2A DFB (5)
△ EGB2A CFB (6)
BH 平分/ AHC (7) GF// AC
变式练习1、如果两个等边三角形△ ABD 和△ BCE 连接AE 与CD 证明:
(1)
△ ABE^A DBC (2)
AE=DC (3) AE 与DC 的夹角为60。
(4) AE 与DC 的交点设为H,BH 平分/ AHC
(1自旋转:自旋转构造方法 ABD 和△ BCE 连接 AE 与CD 证明: B
变式练习2、如果两个等边三角形厶ABD和厶BCE连接AE与CD,证明:
D
(1)△ABE^A DBC
(2) AE=DC
(3) AE与DC的夹角为60。
(4)AE与DC的交点设为H,BH平分/ AHC
(1)如图1,点C是线段AB上一点,分别以AC, BC为边在AB的同侧作等边△ ACM和厶
CBN,连接AN , BM .分别取BM , AN的中点E, F,连接CE, CF, EF.观察并猜想△ CEF的
形状,并说明理由.
(2)若将(1 )中的“以AC, BC为边作等边△ ACM和厶CBN'改为“以AC , BC为腰在AB的同
侧作等腰△ ACM
和厶CBN,”如图2,其他条件不变,那么(1)中的结论还成立吗?若成立,加以证明;若不成
立,请说明理由.
例4、例题讲解:
1.已知△ ABC为等边三角形,点D为直线BC上的一动点(点D不与B,C重合),以AD为边作菱形ADEF(按A,D,E,F 逆时针排列),使/ DAF=60 ° ,连接CF.
(1) 如图1,当点D在边BC上时,求证:① BD=CF 宓AC=CF+CD.
(2) 如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
⑶如图3,当点D在边BC的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系。
2、半角模型
说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,
成对称全等。
B E
C G B E C
例1、如图,正方形ABCD勺边长为AB,AD上各存在一点P、0,若厶APQ的周长为2,求PCQ的度数。
例2、在正方形ABCD中,若M、N分别在边BC、CD上移动,且满足MN=BM +DN ,求证:①/ MAN=45「②
△ CMN的周长=2AB :③AM、AN分别平分/ BMN和/ DNM。
例3、在正方形ABCD中,已知/ MAN=45 °,若M N分别在边CB DC的延长线上移动:①试探究线段MN BM、DN之间的数量关系;②求证: AB=AH.
例4、在四边形ABCD中, / B+Z D=180°AB=AD若E、F分别在边BGCD且上,满足EF=BE+DF求证:EAF - BAD 。
2
4、已如:如图1在甜扣曲匸中「生匸=* . AB = AC「点D、左分别为线段肚上两动点,若上口4£= 4于・探究线段
妙、DE、比三祭线段之间的数塑艾粟.
<1胡的思跆是:把厶狂匸疣点眉厕勺钉艇转◎,得到關E d连结FD「
使I可题得到解决•淸侬参考小盟的电路探究并解决下列问题:
⑴猜想阳、陽、区三圣线段之间存在B嫩量关系式「并对你的猜想舒证明;
⑵当动点E在线段E匚上,动点D运动在线段6延长牡时F如图2 ,其它条件不变(⑴中探究的结论是否发生改变?请说
明你的猜想并给予证明•。
